Đề học sinh giỏi Toán 7 năm 2022 – 2023 phòng GD&ĐT Việt Trì – Phú Thọ

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI LỚP 7 VIỆT TRÌ
CẤP THÀNH PHỐ, NĂM HỌC 2022- 2023 Môn: Toán ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút (không kể thời gian giao đề) (Đề có: 03 trang)
Thí sinh làm bài (cả phần trắc nghiệm khách quan và phần tự luận) trên tờ giấy thi
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (8,0 điểm)
Câu 1. Giá trị biểu thức  3 3   3 − 2  − + − +  bằng 5 4   4 5      A. 2. − B. 2. C. 1. − D. 13. 15
Câu 2. Giá trị biểu thức  3 − 3  20  4 − 2  20 + : + +     : bằng  7 5  21  7 5  21 A. 2. − B. 0. C. 1. − D. 1.
Câu 3. Giá trị x trong tỉ lệ thức 3 21 = bằng x −1 16
A. 16 . B. 23. C. 23 − . D. 16 − . 7 7 7 7 Câu 4. Bộ số ( ;
x y; z) thỏa mãn x y z
= = và x − y + z = 36 là 5 6 7
A. (30;36;42). B. (30; 36 − ;42). C. (30;36; 42 − ). D. ( 30 − ;36;42).
Câu 5. Cho tỉ lệ thức a c
= với a,b,c,d ≠ 0 thì b d A. 3a 2d =
. B. 3b 3d = . C. 5a b = . D. a d = . 2c 3b a c 5d c 2b 2c Câu 6. Cho 2 2 2
x + y + z = 0. Giá trị biểu thức 2
A = x (x − ) 2 + y (x − ) 2 1 1 + z (x − ) 1 −1 bằng A. 2.
− B. 1. C. 0. D. 1. −
Câu 7. Cho hai đa thức f (x) 2
= 3x + x − 4 và 2 g(x) = 3
− x − x + 3 thì f (x) + g (x) là A. 2 6
− x − 2x − 7. B. 1. C. 2x +1. D. 1. −
Câu 8. Rút gọn biểu thức A = (2x + 3)(4 − 6x) −(6 −3x)(4x + 2) ta được
A. A = 0. B. A = 28 −
.x C. A = 28 .x D. 2 A = 24x − 28 . x
Câu 9. Xác suất khi gieo một con xúc xắc sáu mặt để được mặt hơn 4 chấm bằng
A. 2. B. 1 ⋅ C. 1 ⋅ D. 1 ⋅ 2 3 6
Câu 10. Cho tam giác ABC có  =  
A 80 , B = 70 . Đường phân giác AD và CE cắt nhau tại I
(D ∈ BC, E ∈ AB) .  DIE bằng
A. 125 . B. 115 . C. 65 . D. 55 . Trang 1/3 Câu 11. Cho A ∆ BC = M
∆ NP biết AB + AC =15cm và MN − MP = 7c .
m Khi đó MN bằng A. 13c .
m B. 12c .
m C. 11c .
m D. 4c . m Câu 12. Cho DE ∆ F , P
∆ QR có DE = PQ . Điều kiện để DE ∆ F = P ∆ QR là A. =  =  DF ; QR D . P B. =  =  DF P ; R D . P C.  =   =  E ; R D . P D. =  =  EF ; QR E . P Câu 13. Cho A
∆ BC có  =  
B 60 ,C = 50 . Kẻ tia phân giác BD (D∈ AC). Khẳng định nào sau đây đúng?
A. AD > A .
B B. AB > B .
D C. BD > BC. D. BD > A . B Câu 14. Cho A
∆ BC có AB < AC. Kẻ BD vuông góc với AC tại D , kẻ CE vuông góc với AB tại E .
Kết luận nào sau đây là đúng? A.  >  DBC EC .
B B.  <  DBC EC . B C.  =  DBC EC .
B D.  ≤  DBC EC . B Câu 15. Cho x − 6 D =
. Tổng các giá trị nguyên của x để D có giá trị nguyên bằng x + 3 A. 18. − B. 24. − C. 12. D. 14. −
Câu 16. Anh đọc quyển sách trong hai ngày. Ngày thứ nhất Anh đọc được 1 quyển sách. Ngày thứ hai 7
Anh đọc được 7 số trang sách còn lại của quyển sách đó. Hỏi sau hai ngày Anh đọc được bao nhiêu 12 phần quyển sách?
A. 61⋅ B. 1 ⋅ C. 9 ⋅ D. 11 ⋅ 84 2 14 14
II. PHẦN TỰ LUẬN (12,0 điểm)
Câu 1. (3,0 điểm)
x + 23 x + 22 x + 21 x + 20 a) Tìm x biết + − − = 0. 2021 2022 2023 2024 12 5 6 2 10 3 5 2
b) Thực hiện phép tính: 2 .3 − 4 .9 5 .7 − 25 .49 − . 2 6 4 5 3 9 3 (2 .3) + 8 .3 (125.7) + 5 .14
c) Tìm tất cả các cặp số nguyên ( ; x y) thỏa mãn: 2
2xy + 6x − y − 3x = 7. Câu 2. (4,0 điểm)
a) Cho a,b,c,d ≠ 0, 3 3 3
b + c − d ≠ 0;b + c ≠ d thỏa mãn 2 2
b = ac, c = bd. Chứng minh rằng: 3 3 3 3
a + b − c
 a + b − c  = ⋅ 3 3 3 b c d   b c d  + − + − 
b) Cho a,b,c,d ≠ 0;a − b + c = 0;c = 5d.
Tính giá trị của biểu thức:
1 a 1 b 1 c  a−b A 4 = − − + −     .  b  c  a  d  c) Cho đa thức 3 2
f (x) = ax + bx + 8x − 6. Tìm a, b để f (x) chia cho x − 2 dư 14 và f (x) chia cho x +1 dư 16. − Trang 2/3
Câu 3. (4,0 điểm) Cho tam giác ABC nhọn, đường cao BE,CF (E ∈ AC, F ∈ AB). Gọi M là trung điểm
của BC. Trên tia đối của tia MF lấy điểm D sao cho MF = . MD
a) Chứng minh CD = BF và CD / /BF.
b) Lấy điểm P bất kì nằm giữa B và F , trên tia đối của tia MP lấy điểm Q sao cho MP = . MQ
Chứng minh D,Q,C thẳng hàng.
c) Trên tia đối của tia EF lấy điểm K , trên tia đối của tia FE lấy điểm I sao cho EK = FI. Chứng
minh tam giác MIK cân.
Câu 4. (1,0 điểm) Xét các số thực a,b,c thỏa mãn 1
− ≤ a,b,c ≤ 2; a + b + c = 0. Tìm giá trị lớn nhất của biểu thức 2 2 2
P = a + b + c .
………… HẾT …………
Họ và tên thí sinh: ...............................................................Số báo danh: ............................................ Trang 3/3
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI LỚP 7 VIỆT TRÌ
CẤP THÀNH PHỐ, NĂM HỌC 2022- 2023 Môn: Toán HƯỚNG DẪN CHẤM
Thời gian làm bài: 150 phút (không kể thời gian giao đề) (HDC có: 06 trang)
I.PHẦN TRẮC NGHIỆM (8,0 điểm) Câu 1 2 3 4 5 6 7 8 ĐA C B B A B D D B Câu 9 10 11 12 13 14 15 16 ĐA C A C B B A A C II. PHẦN TỰ LUẬN Câu 1. (3,0 điểm) + + + +
a) Tìm x biết x 23 x 22 x 21 x 20 + − − = 0. 2021 2022 2023 2024 12 5 6 2 10 3 5 2
b) Thực hiện phép tính: 2 .3 − 4 .9 5 .7 − 25 .49 − . 2 6 4 5 3 9 3 (2 .3) + 8 .3 (125.7) + 5 .14
c) Tìm tất cả các cặp số nguyên ( ; x y) thỏa mãn : 2
2xy + 6x − y − 3x = 7. Phần Nội dung Điểm a) + + + +
Tìm x biết x 23 x 22 x 21 x 20 + − − = 0. 1, 0 2021 2022 2023 2024 + + + +
x 23 x 22 x 21 x 20 + − − = 0. 2021 2022 2023 2024 0,25
=> x + 23   x + 22   x + 21   x + 20 1 1 1 1 + + + − + − + =         0  2021   2022   2023   2024  x + x + x + x + => 2044 2044 2044 2044 + − − = 0 0,25 2021 2022 2023 2024 =>(x ) 1 1 1 1 2044  + + − − =   0 0.25  2021 2022 2023 2024 
=> x + 2044 = 0 (vì 1 1 1 1 + − − ≠ 0 ) 2021 2022 2023 2024 0,25 => x = 2044 − 12 5 6 2 10 3 5 2 b)
Thực hiện phép tính: 2 .3 − 4 .9 5 .7 − 25 .49 − . 1,0 2 6 4 5 3 9 3 (2 .3) + 8 .3 (125.7) + 5 .14 12 5 6 2 10 3 5 2 Ta có : 2 .3 − 4 .9 5 .7 − 25 .49 − 2 6 4 5 3 9 3 (2 .3) + 8 .3 (125.7) + 5 .14 0,25 12 5 12 4 10 3 10 4 − − = 2 .3 2 .3 5 .7 5 .7 − 12 6 12 5 9 3 9 3 3 2 .3 + 2 .3 5 .7 + 5 .7 .2 12 4 2 .3 (3− ) 10 3 1 5 .7 (1− 7) = − 0,5 12 5 2 .3 (3+ ) 9 3 1 5 .7 (1+8) Trang 1/3 1 5.( 6 − ) 21 7 = − = = ⋅ 0,25 6 9 6 2 c)
Giải phương trình nghiệm nguyên 2
2xy + 6x − y − 3x = 7. 1,0 2
2xy + 6x − y − 3x = 7 ⇒ (2x − )
1 y + 3x(2x − ) 1 = 7 0,25 ⇒ (2x − ) 1 ( y + 3x) = 7
Vì x, y∈ nên 2x −1, y + 3x ∈ = = − − Mà 7 1.7 ( ) 1 .( 7) nên ta có bảng 0,25 2x-1 1 7 -1 -7 y+3x 7 1 -7 -1 x 1 4 0 -3 0,25 y 4 -11 -7 8 (tm) (tm ) (tm) (tm) Vậy (x; y) = ( { 1;4);(4; 1 − ) 1 ;(0; 7 − );( 3 − ;8)}. 0,25 Câu 2. (4,0 điểm)
a) Cho a,b,c,d ≠ 0, 3 3 3
b + c − d ≠ 0;b + c ≠ d thỏa mãn 2 2
b = ac, c = bd. Chứng minh rằng: 3 3 3 3
a + b − c
 a + b − c  = ⋅ 3 3 3 b c d   b c d  + − + − 
b) Cho a,b,c,d ≠ 0;a −b + c = 0;c = 5d.
Tính giá trị của biểu thức:
1 a 1 b 1 c  a −b A 4 = − − + −     .  b  c  a  d  c) Cho 3 2
f (x) = ax + bx + 8x − 6. Tìm a, b để f (x) chia cho x − 2 dư 14 và f (x) chia cho x +1 dư 16. − Phần Nội dung Điểm
Cho a,b,c,d khác 0, 3 3 3
b + c − d ≠ 0;b + c ≠ d thỏa mãn a) 3 3 3 3 1,5 2 2 b + −  + −
= ac, c = bd. Chứng minh rằng: a b c a b c  = ⋅ 3 3 3 b c d   b c d  + − + − 
Ta có 2 = ⇒ a = b b ac ; 2 = ⇒ b = c c bd . 0,25 b c c d 3 3 3 Do đó a b c a b c = = ⇒ = = 0,25 b c d 3 3 3 b c d 3 3 3 Đặt a b c a b c = = = k 3 ⇒ = = = k 0,25 b c d 3 3 3 b c d
Áp dụng tính chất dãy tỉ số bằng nhau ta có 3 3 3 3 3 3 a b c a + b − c 3 = = = = k ( ) 1 0,25 3 3 3 3 3 3 b c d b + c − d
Mặt khác, theo tính chất dãy tỉ số bằng nhau ta có a b c a + b − c 3  a + b − c = = = = k  3 ⇒ =   k (2) 0,25 b c d b + c − d  b + c − d  Trang 2/3 3 3 3 3 Từ ( )
1 và (2) ta có a + b − c
 a + b − c  = (đpcm). 0,25 3 3 3 b c d   b c d  + − + − 
Cho a,b,c,d ≠ 0;a −b + c = 0;c = 5d. Tính giá trị của biểu b) 1,5 thức:
1 a 1 b 1 c  a −b A 4 = − − + −     .  b  c  a  d  Ta có
1 a 1 b1 c  a−b A  4 = − − + −   b  c  a  d   0,25
 b − a  c − b  a + c  a − b    4 = −  b c a d      
Mà a −b + c = 0 ⇒ b − a = c 0,25
Tương tự, ta có c − b = − ; a a + c = ;
b a − b = −c 0,25
  −   − Ta có A c a b c =    4 −  0,25 b c a d       −  − abc 5d  4 = − 0,25 abc d    = (− ) 1 .( 9 − ) = 9 0,25 c) Cho 3 2
f (x) = ax + bx + 8x − 6. Tìm a, b để f (x) chia cho 1,0
x − 2 dư 14 và f (x) chia cho x +1 dư 16. − Vì 3 2
f (x) = ax + bx + 8x − 6 chia cho x − 2 dư 14 nên f (x)
có dạng: f (x) = (x − 2) g (x) +8
Ta có f (2) = (2 − 2) g (2) +14 0,25 3 2 ⇒ .2 a + .2 b + 8.2 − 6 =14
⇒ 8a + 4b = 4 ( ) 1 Vì 3 2
f (x) = ax + bx + 8x − 6 chia cho x +1 dư 16 − nên f (x)
có dạng: f (x) = (x + ) 1 h(x) −16 Ta có f ( 1) − = ( 1 − + ) 1 h(− ) 1 −16 0,25
⇒ a (− )3 + b (− )2 . 1 . 1 + 8.(− ) 1 − 6 = 1 − 6 ⇒ −a + b = 2
− ⇒ b = a − 2 (2) Thay (2) vào ( ) 1 ta có
8a + 4(a − 2) = 4 0,25 ⇒12a −8 = 4 ⇒ a =1
Thay a =1 vào (2) ta có b =1− 2 = 1 − 0,25 Vậy a =1; b = 1 − .
Câu 3. (4,0 điểm) Cho tam giác ABC nhọn, đường cao BE,CF (E ∈ AC, F ∈ AB). Gọi M là trung
điểm của BC. Trên tia đối của tia MF lấy điểm D sao cho MF = . MD
a) Chứng minh CD = BF và CD / /BF. Trang 3/3
b) Lấy điểm P bất kì nằm giữa B và F , trên tia đối của tia MP lấy điểm Q sao cho MP = . MQ
Chứng minh D,Q,C thẳng hàng.
c) Trên tia đối của tia EF lấy điểm K , trên tia đối của tia FE lấy điểm I sao cho EK = FI.
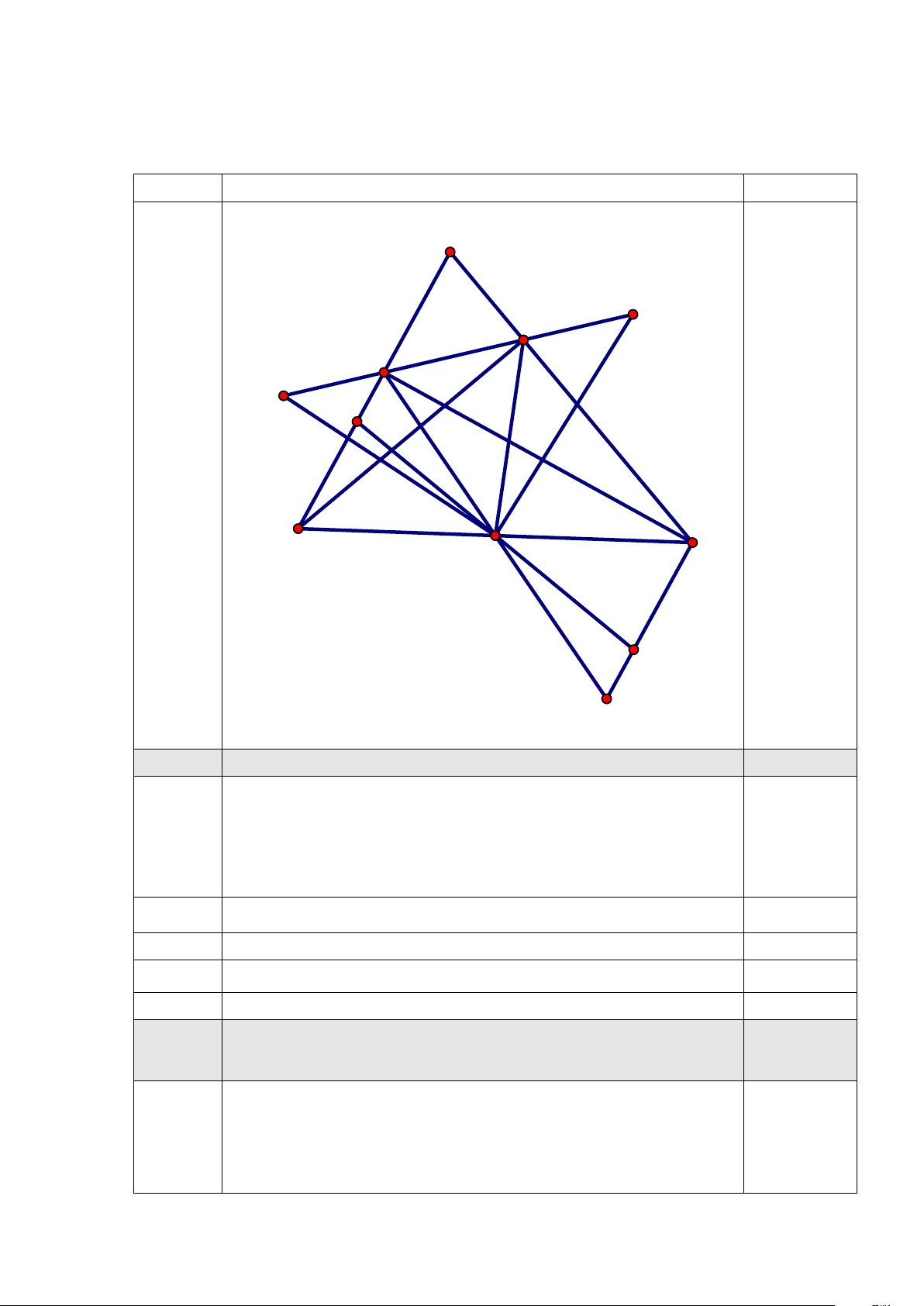
Chứng minh tam giác MIK cân. Phần Nội dung Điểm Hình vẽ A K E F I P B M C Q D a)
Chứng minh CD = BF và CD / /BF. 2,0 Xét B ∆ MF và C ∆ MD
Có: BM = CM ( Vì M là trung điểm của BC )  0,75 = 
BMF CMD (Hai góc đối đỉnh)
MF = MD(gt) ⇒ B ∆ MF = C
∆ MD(c − g − c) 0,25 ⇒ CD = BF 0,25 Và  = 
MBF MCD mà chúng ở vị trí so le trong 0,5 ⇒ CD / /BF 0,25 b)
Lấy điểm P bất kì nằm giữa B và F trên tia đối của tia MP lấy 1,0
điểm Q sao cho MP = .
MQ Chứng minh D,Q,C thẳng hàng. Xét B ∆ MP và C ∆ MQ
Có: MB = MC (Vì M là trung điểm của BC ) 0,5  = 
BMP CMQ ( hai góc đối đỉnh) Trang 4/3
MP = MQ(gt) ⇒ B ∆ MP = C
∆ MQ(c − g − c) 0,25 ⇒  = 
MBP MCQ mà chúng ở vị trí so le trong ⇒ BP / /CQ 0,25
Mà CD / /BF theo tiên đề ơclit⇒ C,Q, D thẳng hàng c)
Trên tia đối của tia EF lấy điểm K , trên tia đối của tia FE lấy 1,0
điểm I sao cho EK = FI. Chứng minh tam giác MIK cân. Xét B ∆ FC và DC ∆ F
Có: BF = CD ( theo a)) 0,25  = 
BFC DCF = 90 ( Vì BF / /CD và BF ⊥ CF ) CF cạnh chung ⇒ B ∆ FC = D
∆ CF (c − g − c) ⇒ BC = DF 0,25
Mà DF = 2FM (Vì M là trung điểm FD ) 1 ⇒ FM = BC (1) 2 Chứng minh tương tự: 1
ME = BC (2). Từ (1) và (2) 2 0,25
⇒ MF = ME ⇒ MF ∆ E cân tại M ⇒  =  ⇒  =  MFE MEF MFI MEK (kề bù) Xét MF ∆ I và ME ∆ K
Có: MF = ME (chứng minh trên)  = 
MFI MEK (chứng minh trên) 0,25
FI = EK (gt) ⇒ MF ∆ I = ME ∆
K (c − g − c) ⇒ MI = MK ⇒ MIK ∆ cân tại M
Câu 4. (1,0 điểm) Xét các số thực a,b,c thỏa mãn 1
− ≤ a,b,c ≤ 2; a + b + c = 0. Tìm giá trị lớn nhất của biểu thức 2 2 2
P = a + b + c . Phần Nội dung Điểm a +1 ≥ 0 Vì 1
− ≤ a,b,c ≤ 2 ⇒  a − 2 ≤ 0 0,25
⇒ (a + )(a − ) 2 2 1
2 ≤ 0 ⇒ a − 2a + a − 2 ≤ 0 ⇒ a ≤ a + 2 0,25 Chứng minh tương tự: 2 b  ≤ b + 2 2 2 2 
⇒ a + b + c ≤ a + b + c + 6 = 6 0,25 2
c ≤ c + 2 Trang 5/3
Dấu đẳng thức sảy ra khi:( ; a ; b c) = ( 1; − 1; − 2) và các hoán vị 0,25
Vậy Max P = 6 ⇔ (a; ; b c) = ( 1; − 1; − 2) và các hoán vị Trang 6/3
Document Outline

• TOÁN 7 (1)
• HDC TOÁN 7