PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI VĂN HÓA CẤP HUYỆN SƠN ĐỘNG NĂM HỌC 2023-2024 MÔN: TOÁN LỚP 7 ĐỀ CHÍNH THỨC Ngày thi: 29/01/2024
(Đề thi có 03 trang)
Thời gian làm bài 120 phút, không kể thời gian giao đề
PHẦN I. TRẮC NGHIỆM (6,0 điểm)
Câu 1. Cho hình chữ nhật ABCD có chu vi 36c ,
m tỉ số độ dài hai cạnh AB : BC = 5 : 4 . Diện tích
hình chữ nhật ABCD là A. 2 320cm . B. 2 180cm . C. 2 80cm . D. 2 40cm . Câu 2. x 5
Cho hai số x ; y biết = và x + y = 72. Vậy 2x − 3y bằng y 7 A. 30. B. 40 . C. 44 − . D. 66 − . −
Câu 3. Giá trị của biểu thức 0 1 1 2 A = ( 2024) − + − − là 4 3 5 7 23 7 − 43 A. . B. . C. . D. . 10 30 10 30
Câu 4. Cho bảng thống kê về mức độ ảnh hưởng (đơn vị %) của các yếu tố đến chiều cao của trẻ: Yếu tố Vận Di Dinh Giấc ngủ và môi động truyền dưỡng trường Yếu tố khác
Mức độ ảnh hưởng (%) 20 23 32 16 9
Ngoài yếu tố di truyền, ba yếu tố ảnh hưởng nhiều nhất đến chiều cao chiếm tổng số bao nhiêu phần trăm? A. 65% . B. 75% . C. 68% . D. 67% . Câu 5. Cho đa thức 5 4 5 2 4 ( A x) = 2
− x + 3x + 2x + x − 2x − 2024 − 3x . Bậc của đa thức ( A x) là: A. 5. B. 4. C. 3. D. 2.
Câu 6. Nếu x = 5(x ≥ 0) thì 2 x bằng A. 5. B. 25 . C. 125. D. 625.
Câu 7. Cho biết 50 người thợ may xong một lượng quần áo trong 12 ngày. Hỏi 30 người thợ may hết
lượng quần áo đó trong bao nhiêu ngày? (Giả sử năng suất làm việc của mỗi người thợ là như nhau). A. 20 ngày. B. 10 ngày. C. 15 ngày. D. 25 ngày. Câu 8. Đa thức 1 (
A x) = x + 6 có nghiệm là 2 A. 12. B. 3. C. 12. − D. 3. −
Câu 9. Cho tam giác ABC có    ; A ;
B C lần lượt tỉ lệ với 3;2;1. Số đo các góc    ,
A B,C lần lượt A. 0 0 0 30 ;90 ;60 . B. 0 0 0 30 ;60 ;90 . C. 0 0 0 90 ;30 ;60 . D. 0 0 0 90 ;60 ;30 . + + Câu 10. 2x 3y 4 Cho x y z ; y z =
= . Giá trị biểu thức A = là 3 4 5 6
3x + 4y + 2z 173 186 173 − 186 − A. . B. . C. . D. . 186 173 186 173
Câu 11. Giá trị của x để biểu thức 2
P = (x − 2) − 5. đạt giá trị nhỏ nhất là A. 1. B. 2. C. 2. − D. 5. −
Câu 12. Kim tự tháp Kheops là công trình kiến trúc nổi tiếng thế giới. Để xây dựng được công trình này,
người ta phải sử dụng tới hơn 2,5 triệu mét khối đá, với diện tích đáy lên tới 2 52198,16m . (Theo khoahoc.tv)
Biết rằng đáy của kim tự tháp Kheops có dạng một hình vuông. Độ dài cạnh đáy của kim tự tháp này là
(Làm tròn kết quả với độ chính xác 0,05) A. 228,5 . m B. 228,47 . m C. 228,4 . m D. 228,46 . m Câu 13.
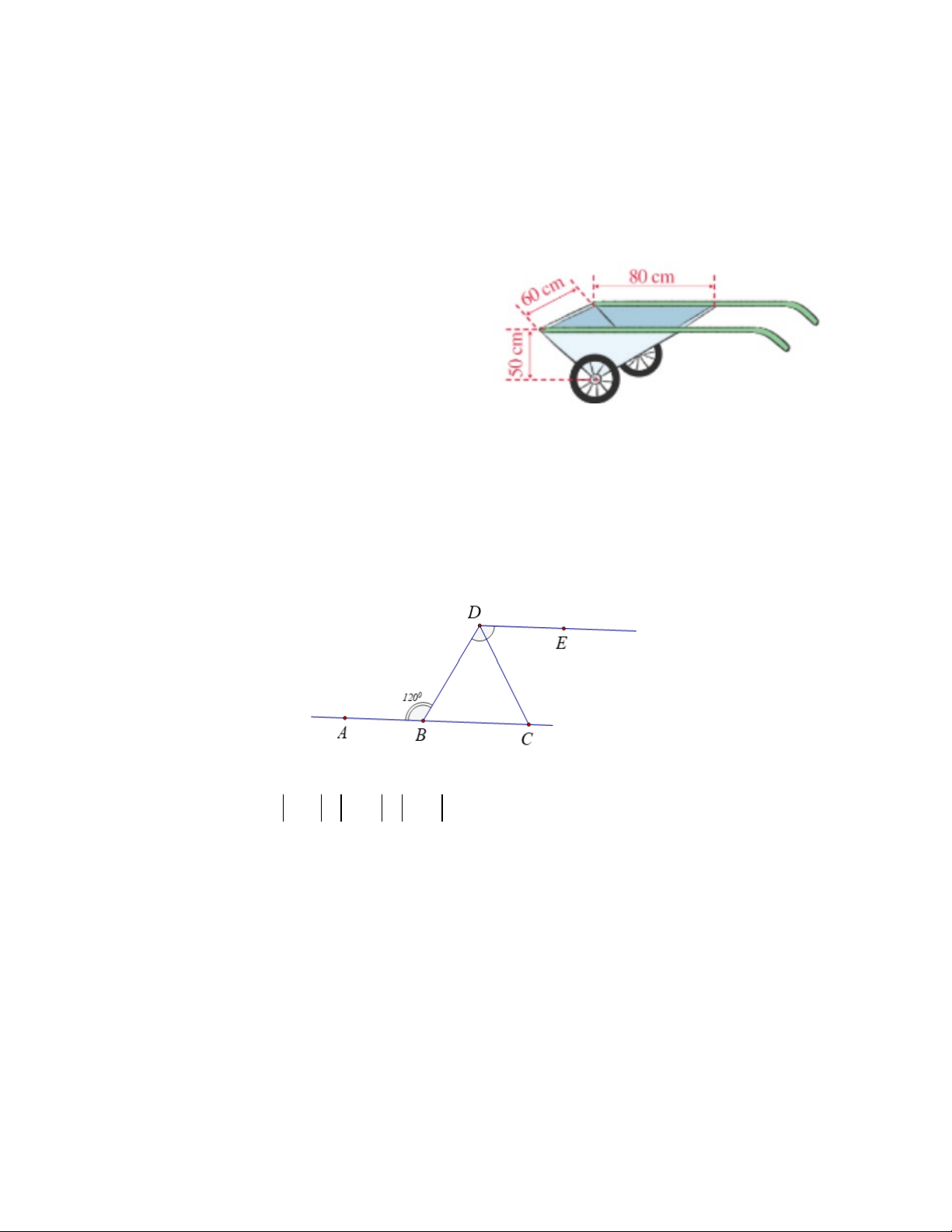
Hình bên mô tả xe chở hai bánh mà thùng chứa
của nó có dạng hình lăng trụ đứng tam giác với
các kích thước cho trên hình. Tính thể tích thùng
chứa của xe chở hai bánh đó? A. 3 2,4m . B. 3 0,24m . C. 3 0,12m . D. 3 1,2m .
Câu 14. Số các giá trị của x để x − ( 2 x + )( 2 ( 4)
16 x −16)(x +1) = 0 là A. 3. B. 4. C. 5. D. 6.
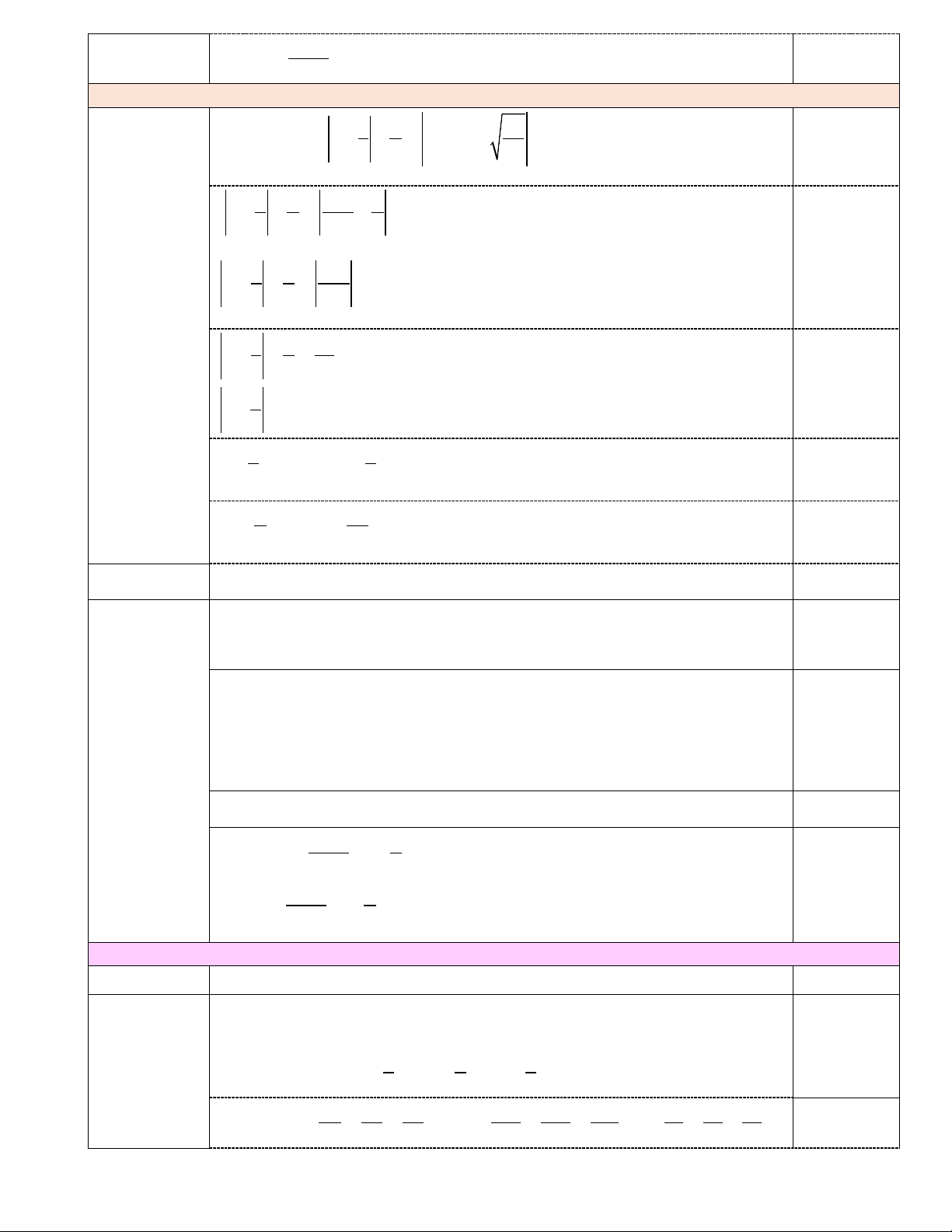
Câu 15. Cho hình vẽ dưới đây, Biết  0
AB/ DE; ABD = 120 và ba điểm ,
A B,C thẳng hàng. DC là tia phân giác của  BDE , số đo  CDB là A. 0 120 . B. 0 80 . C. 0 60 . D. 0 40 .
Câu 16. Cho x thỏa mãn x +1 + x + 2 + x + 3 = 9x . Giá trị biểu thức 2024x − 2023 là A. 1. − B. 1. C. 2023. D. 2024. Câu 17. Cho A ∆ BC = M
∆ NP, biết AB = 7c ; m AC = 9c ; m NP = 5c .
m Độ dài cạnh MP là A. 9c . m B. 7c . m C. 5cm. D. 12cm.
Câu 18. Cho x, y là các số thỏa mãn 2024
(x − 3) + | 2x + 3y − 9 |= 0. Tổng các giá trị x, y là A. 4. B. 2. − C. 3. − D. 3.
Câu 19. Cho đa thức: 2
f (x) = x − 3x + a giá trị của a để đa thức f (x) chia hết cho đa thức x − 2 là A. 2. − B. 2. C. 10. D. 10. − Câu 20. Cho A
∆ BC vuông tại A có  0
C = 40 , trên cạnh BC lấy điểm D sao cho AB = DB . Tia phân
giác của B cắt cạnh AC tại E. Số đo góc  AED là A. 0 120 . B. 0 65 . C. 0 100 . D. 0 130 .
PHẦN II. TỰ LUẬN (14,0 điểm)
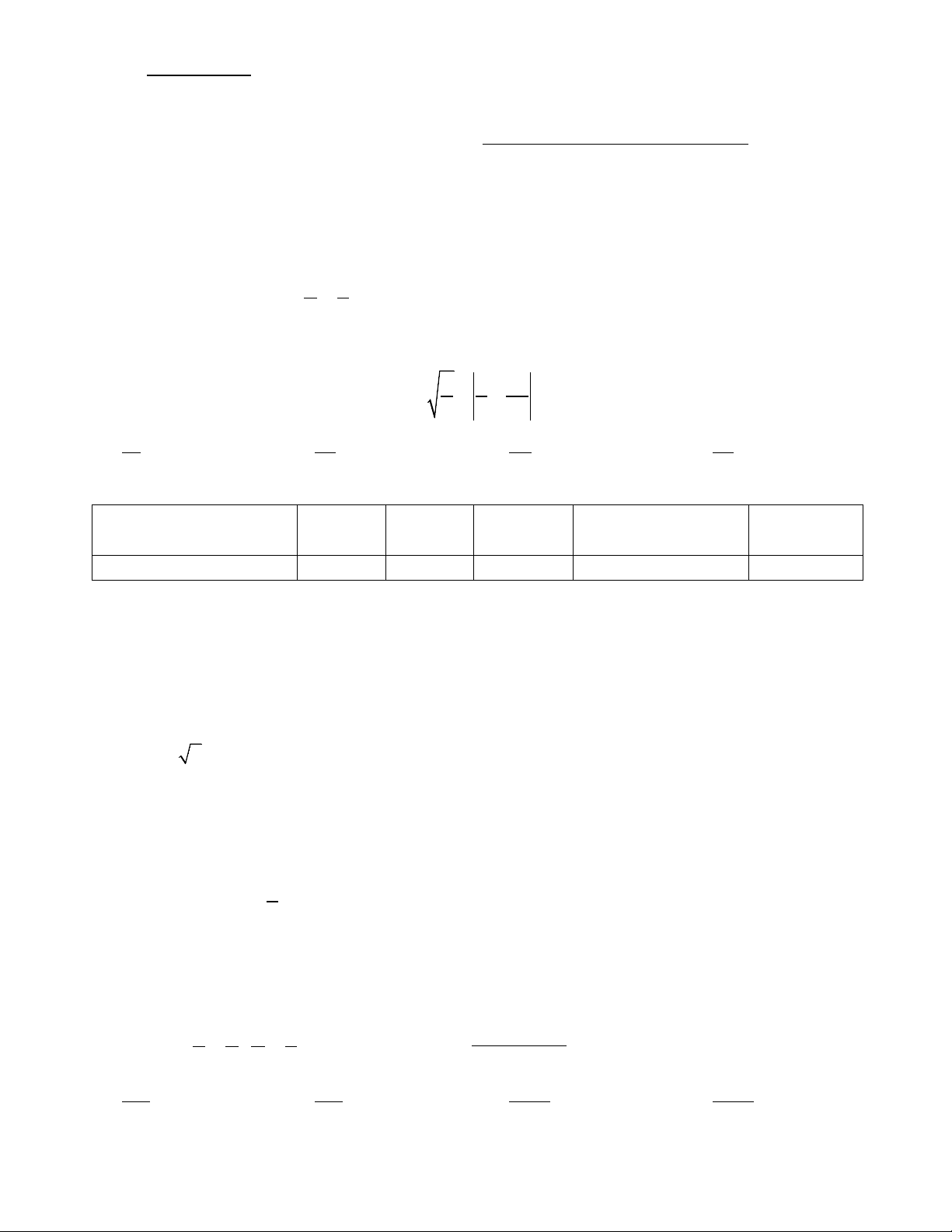
Bài 1. (5,0 điểm)  2 2 5  0,4 − + −1,25 +  1 
1) Tính giá trị biểu thức: 9 11 3 2023 M =  +  :  7 7 1 7  2024  1,4 − + 2 −1,75 +   9 11 3 5 
2) Tìm x biết: 1 4 4 x − + = ( 3, − 2) + 3 5 25 3) Cho đa thức ( ) 2
f x = ax + bx + c . Biết f (0) = 0, f ( ) 1 = 2024 và f (− )
1 = 2023. Tính a,b,c ?
Bài 2. (4,0 điểm)
1) Ba khối 6,7,8 của một trường THCS A trên địa bàn huyện Sơn Động có tổng số 294 học sinh.
Nếu 1 số học sinh khối 6 ; 1 số học sinh khối 7 và 1 số học sinh khối 8 tham gia dự thi học 3 4 5
sinh giỏi cấp huyện đợt 2, năm học 2023 − 2024 thì số học sinh còn lại của ba khối bằng nhau.
Tính số học sinh mỗi khối của trường THCS A?
2) Tìm cặp số ( ;x y) nguyên thỏa mãn 3xy + 2x + 3y = 5 .
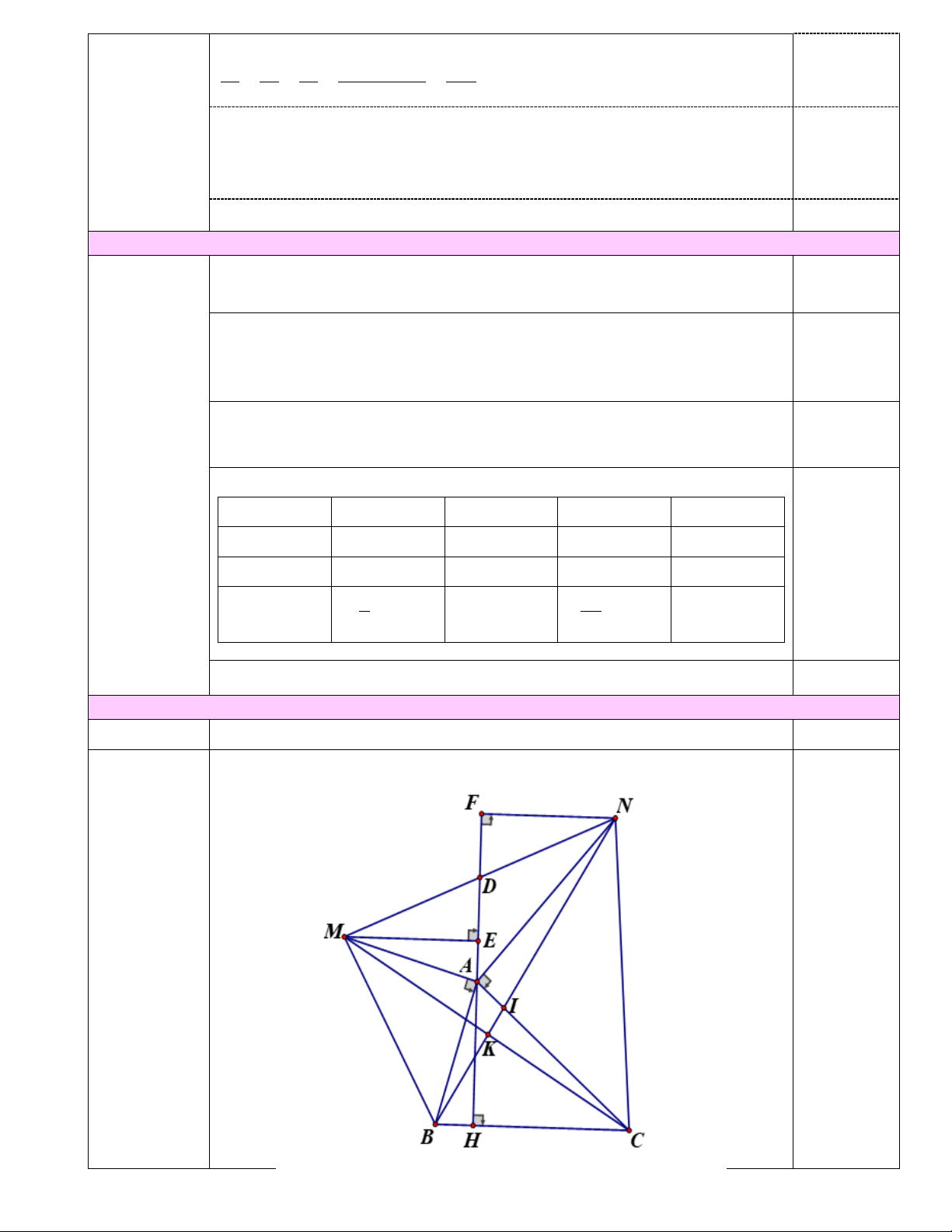
Bài 3. (4,0 điểm) Cho A
∆ BC nhọn. Vẽ ra ngoài tam giác A
∆ BC các tam giác vuông cân tại A là A ∆ BM ; A ∆ CN.
a) Chứng minh rằng: A ∆ MC = A ∆ BN .
b) Chứng minh BN ⊥ CM .
c) Kẻ AH ⊥ BC (H ∈ BC). Chứng minh AH đi qua trung điểm của MN . − + Bài 4 | x 2022 | 2023
. (1.0 điểm) Tìm giá trị nhỏ nhất của biểu thức A = | x − 2022 | 2024 +
--------------- Hết ----------------
Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh: .................................................................Số báo danh:..................................
Giám thị 1 (Họ tên và ký)..............................................................................................................
Giám thị 2 (Họ tên và ký)..............................................................................................................
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM THI HỌC SINH GIỎI HUYỆN SƠN ĐỘNG
VĂN HÓA CẤP HUYỆN NGÀY THI 12/04/2023
ĐÁP ÁN CHÍNH THỨC MÔN: TOÁN LỚP 7
Bản hướng dẫn chấm có 05 trang
A- TRẮC NGHIỆM (6 điểm) Mỗi câu học sinh chọn đúng đáp án được 0,3 điểm CÂU ĐÁP ÁN CÂU ĐÁP ÁN 1 C 11 B 2 D 12 A 3 B 13 C 4 C 14 A 5 D 15 C 6 D 16 B 7 A 17 A 8 C 18 A 9 D 19 B 10 B 20 D
B- TỰ LUẬN (14 điểm) Bài Hướng dẫn giải Điểm Bài 1 (5.0 điểm)  2 2 5  0,4 − + −1,25 +  1 
Tính giá trị biểu thức: 9 11 3 2023 A =  +  :  7 7 1 7  2024  1,4 − + 2 −1,75 +   9 11 3 5   2 2 2 5 5 5  − + − +   5 9 11 3 4 5 2023 A =  +  : 0,5  7 7 7 7 7 7  2024  − + − +   5 9 11 3 4 5  1   1 1 1   1 1 1   2 − + 5 − +      (2,0 điểm)   5 9 11  3 4 5   2023 A = + :  0,5  1 1 1   1 1 1  2024 7 − + 7 − +       5 9 11  3 4 5   2 5  2023 A = +   : 0,25  7 7  2024 2023 A = 1: 2024 0,5 2024 A = 2023 Vậy 2024 A = 0,25 2023 Tìm x biết: 1 4 4 x − + = ( 3, − 2) + 3 5 25 1 4 16 2 x − − + = + 3 5 5 5 0,25 1 4 14 x − − + = 3 5 5 2 (1,5 điểm) 1 4 14 x − + = 3 5 5 0,5 1 x − = 2 3 1 x − = 2 hoặc 1 x − = 2 − 3 3 0,5 7 x = hoặc 5 x − = 3 3 0,5 KL:… 0,25 Cho đa thức ( ) 2
f x = ax + bx + c . Biết f (0) = 0, f ( ) 1 = 2024 và f (− )
1 = 2023 Tính a,b,c a) Tính được f (0) = c = 0
f (1) = a + b + c = 2024 0,5 3 f ( 1
− ) = a − b + c = 2023 (1,5 điểm)
Tính được : a + b = 2024 và a − b = 2023 0,5 Suy ra: 4047 1 a = ; b = 2 2 0,5 Vậy 4047 1 a = ;b = ;c = 0 2 2 Bài 2 (4,0 điểm)
Gọi số học sinh của ba khối 6, 7, 8 của trường THCS A lần lượt là x, y, z (học sinh) *
(x, y, z∈ N ; x, y, z < 294 0,5 1 (2,0 điểm) Theo bài ra ta có: 1 1 1
x − x = y − y = z − z (*) và x + y + z = 294 3 4 5 Từ (*) ta có: 2x 3y 4z = = Do đó: 12x 12y 12z = = Hay x y z = = 0,5 3 4 5 18 16 15 18 16 15
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được: x y z x + y + z 294 = = = = = 6 . 0,5 18 16 15 18 +16 +15 49 x = 18.6 = 108 (TM)
Suy ra: y = 16.6 = 96 (TM) 0,25 z =15.6 = 90  (TM)
Vậy tổng số học sinh của ba khối 6, 7, 8 lần lượt là 108, 96 và 90 học sinh. 0,25 Tìm cặp số ( ;
x y) nguyên thỏa mãn 3xy + 2x + 3y = 5 .
3xy + 2x + 3y = 5
x(3y + 2) + (3y + 2) = 7 0,5
(3y + 2)(x +1) = 7
Vì x, y nguyên Nên (3y + 2); (x +1) cũng nhận giá trị nguyên
Do đó: (3y + 2)(x +1) ∈Ư(7)={1; 7;-1;-7} 0,5 2 (2,0 điểm) Ta có bảng giá trị x+1 1 -1 7 -7 3y+2 7 -7 1 -1 0,75 x 0 -2 (TM) 6 -8 (TM) 5 1 − y (Loại) 3 − (TM) (Loại) -1(TM) 3 3 Vậy ( ; x y) ∈{( 2; − − 3);( 8 − ; 1 − )} 0,25 Bài 3 (4.0 điểm)
- Vẽ hình và viết GT – KL đúng a (1,5 điểm) a) Xét A ∆ MC và A ∆ BN có:
AM = AB ( A
∆ MB vuông cân tại A ) 0,5
AC = AN ( A
∆ CN vuông cân tại A )  =  0 = +  MAB NAC ( 90 BAC) 0,5 Vậy A ∆ MC = A ∆ BN ( . c g.c) 0,5
a) Gọi I là giao điểm của BN và AC, K là giao điểm của BN và MC Trong K ∆ IC có  0 = −  + 
IKC 180 (KIC KCI) 0,5 Trong A ∆ IN có  0 = −  + 
IAN 180 (AIN ANI) b (1,5 điểm) Mà :  =  ANI KCI vì ( A ∆ MC = A ∆ BN ) 0,5  = 
AIN KIC (đối đỉnh) ⇒  =  0
IKC NAI = 90 . Vậy MC ⊥ BN 0,5
Kẻ ME ⊥ AH tại E, NF ⊥ AH tại F . Gọi D là giao điểm của MN và AH Ta có:  +  0 =  BAH MAE ( 0 90 MAB = 90 ) Lại có:  +  0
MAE AME = 90 nên  =  AME BAH Xét MA ∆
E vuông tại E và A
∆ BH vuông tại H ta có:  =  AME BAH 0,5 MA = AB ⇒ M ∆ AE = A
∆ BH (cạnh huyền góc nhọn) c ⇒ = (1,0 điểm) ME AH
Chứng minh tương tự ta có A ∆ FN = C ∆ HA ⇒ FN = AH Xét ME ∆
D vuông tại E và N
∆ FD vuông tại F
ME = NF (= AH )  = 
EMD FND ( cùng phụ với  MDE và  FDN mà  =  MDE FDN ) 0,5 ⇒ M ∆ ED = N ∆ FD ⇒ BD = ND Bài 4 (1 điểm) Ta có | x − 2022 | 2023 + 1 A 1 − = = + | x − 2022 | 2024 + x − 2022 + 2024 0,25 (1,0 điểm)
Với mọi giá trị của x ta có: x − 2022 ≥ 0
⇒ x − 2022 + 2024 ≥ 2024 > 0 1 1 ⇒ ≤ x − 2022 + 2024 2024 1 − 1 − ⇒ ≥ x − 2022 + 2024 2024 0,5 1 − 1 1 1 − ⇒ + ≥ + x − 2022 + 2024 2024 Hay 2023 A ≥
dấu bằng xảy ra khi x − 2022 = 0 ⇒ x = 2022 2024 0,25 Tổng (14 điểm)
Lưu ý khi chấm bài:
+ Trên đây chỉ là sơ lược các bước giải, lời giải của học sinh cần lập luận chặt chẽ, hợp logic. Nếu
học sinh trình bày cách làm khác mà đúng thì cho điểm các phần theo thang điểm tương ứng.
+ Với bài 3 nếu học sinh vẽ hình sai hoặc không vẽ hình thì không chấm..