Đề học sinh năng khiếu Toán 6 năm 2024 – 2025 phòng GD&ĐT Kim Thành – Hải Dương

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH NĂNG KHIẾU HUYỆN KIM THÀNH MÔN: TOÁN 6 NĂM HỌC 2024-2025
Thời gian làm bài: 120 phút
(Không tính thời gian phát đề)
(Đề khảo sát gồm có 05 câu, 01 trang) Câu 1 (2,0 điểm)
1) Tính giá trị của các biểu thức sau:
a) A= 38.66 − 56.38 + 62.65 − 55.62 b) B = −{ 3 3 2 3 −  − + ( 2 1500 5 .2 11. 7 5.2 8. 11 −  ) 121 }
2) Tính giá trị của các biểu thức sau: a) 9 9 9 9 A =1+ + + + ...+ 45 105 189 29997 1 1 1 4 4 4 1+ + + 4 + + − b) B = 3 9 27 7 49 343 : 2 2 2 1 1 1 2 + + + 1+ + − 3 9 27 7 49 343 Câu 2 (2,0 điểm) 1) Tìm x, biết: x+2 x x a) 3 + 3 −15 =1200 − 5.3 b)  1 1   1 1  7 x + −  :2 + − =  4 3 6 4      46
2) Tìm số học sinh của một trường A. Biết rằng số học sinh của trường đó nếu xếp thành
17 hàng thì dư 8 em, xếp thành 25 hàng thì dư 16 em và số học sinh nhỏ hơn 800. Câu 3 (2,0 điểm)
1) Một số tự nhiên chia cho 4 dư 1 và chia cho 15 dư 12. Tìm số dư khi chia số đó cho 30.
2) Cho a,b,c,d là các số nguyên dương thỏa mãn: 2 2 2 2 a + 3b =11c +185d
Chứng minh: a + 3b +11c + d là hợp số. Câu 4 (3,0 điểm)
1) Cho đoạn thẳng AB = 5 cm, lấy điểm M bất kì thuộc đoạn thẳng AB. Trên tia đối của
tia AB lấy điểm N sao cho AN = AM.
a) Tính độ dài đoạn thẳng BN khi MB = 2 cm.
b) Hãy xác định vị trí của điểm M trên đoạn thẳng AB để BN có độ dài lớn nhất. Khi
đó độ dài của đoạn thẳng BN là bao nhiêu.
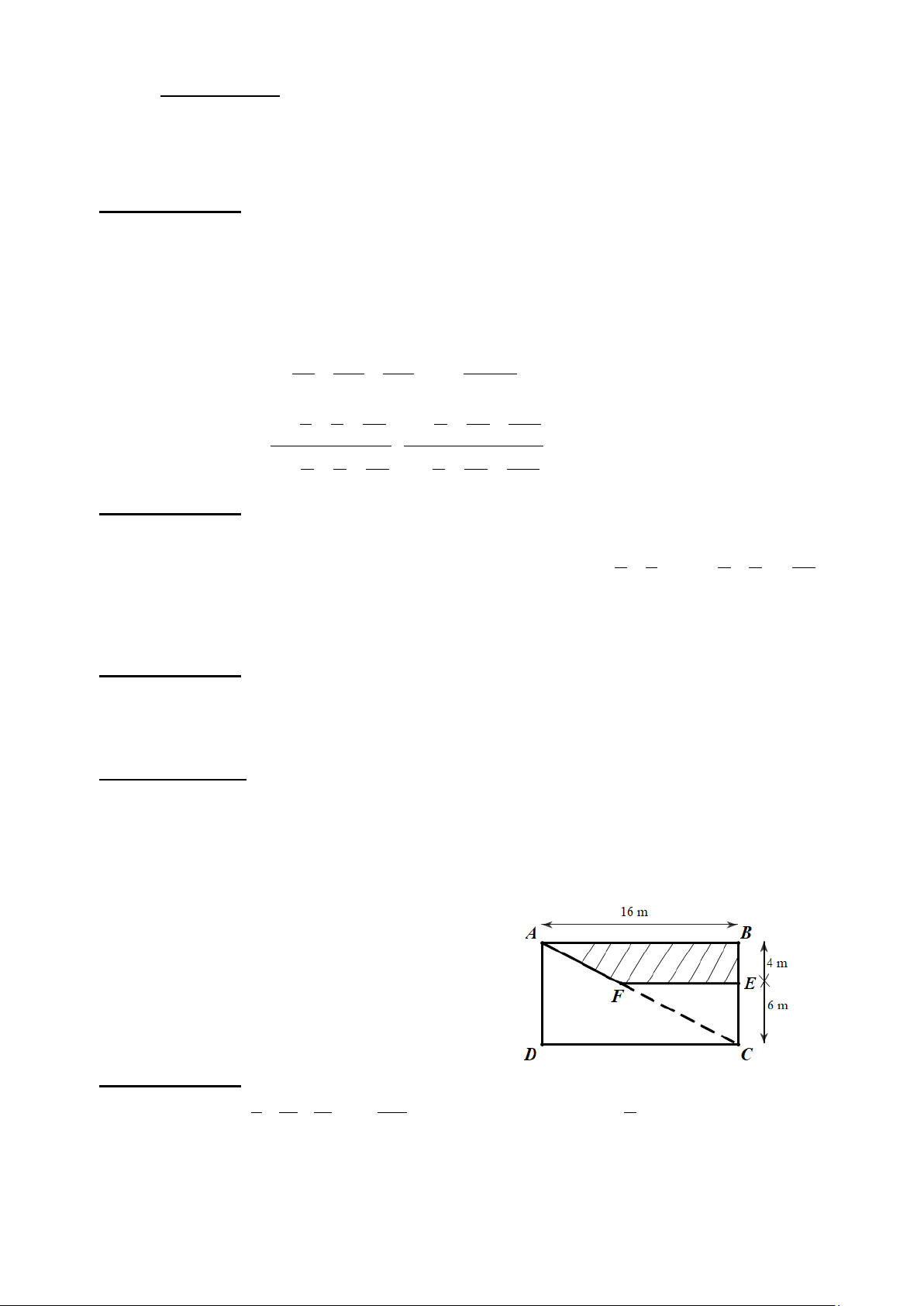
2) Cho mảnh đất hình chữ nhật có các
kích thước như hình vẽ. Người ta làm một
bể cá hình thang ABEF. Toàn bộ diện
tích đất còn lại dùng làm vườn trồng rau. Tính diện tích bể cá. Câu 5 (1,0 điểm) Cho số 5 8 11 302 M = + + +...+ . Chứng minh rằng: 1 M < 3 2 3 100 3 3 3 3 2
–––––––– Hết ––––––––
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM HUYỆN KIM THÀNH
ĐỀ KHẢO SÁT HỌC SINH NĂNG KHIẾU MÔN: TOÁN 6 NĂM HỌC 2024-2025
(Hướng dẫn chấm gồm có 03 trang) Câu Phần Đáp án Điểm
= 38.66 −56.38+ 62.65−55.62 = 38.(66 −56) + 62.(65−55) 1.a = 38.10 + 62.10 0,25 = 10.(38 + 62) = 10.100 =1000 0,25 C = −{ 3 3 2 3 −  − + ( 2 1500 5 .2 11. 7 5.2 8. 11 −  ) 121 } 0,25
1.b =1500−{125.8−11.49−5.8+8.(121− ) 121 }   
= 1500 −{1000 −11.[49 − 40 +8.0]} =1500 −{1000 − } 11.9 = 599 0,25 9 9 9 9 A =1+ + + + ...+ 45 105 189 29997 3 3 3 3 3 3 3 =1+ + + + ...+ =1+ + + ...+ 0,25 15 35 63 9999 3.5 5.7 99.101  1 1 1 1 3  ...  = + ⋅ + + + 3 5 . 5 7 . 99 101 .    2.a  2 2 2 2A 2 3  = + + + ...+  3.5 5.7 99.101    1 1  98 300 2A = 2 + 3 − = 2 + =   0,25  3 101 101 101 150 A = 101 1 1 1 4 4 4 1+ + + 4 + + − 3 9 27 7 49 343 1 B = : 2 2 2 1 1 1 2 điểm 2 + + + 1+ + − 3 9 27 7 49 343  1 1 1   1 1 1 0,25 1. 1  4.1  + + + + + −   3 9 27   7 49 343  2.b B = :   1 1 1   1 1 1 2. 1  1.1  + + + + + −  3 9 27 7 49 343      B = 1 1 : 4 = 2 8 0,25 Vậy B = 1 8 3x + 1 + – 15 = 1200 – 5. 1.a + + 5. = 1200 + 15 0,25 = 1215 . 15 = 1215 0,25 = 4. Vậy x = 4. 2  1 1   1 1  7 2 điểm x + − :2 + − =  4 3 6 4      46 0,25  1  23 7 x − : =   12  12 46 1 7 23 x − = ⋅ 1.b 12 46 12 1 7 x − = 12 24 0,25 7 1 x = + 24 12 3 x = . Vậy 3 x = 8 8
Gọi số học sinh trường A là x (học sinh) ( *
x ∈ N , x < 800 ) Theo bài ra, ta có:
x chia 17 dư 8 suy ra x + 9 chia hết cho 17 0,25
x chia 25 dư 16 suy ra x + 9 chia hết cho 25
Suy ra x + 9 thuộc BC(17, 25) 2
Tính được BCNN(17, 25) = 425 0,25
Suy ra: x + 9∈ B(425) = (0; 425; 850,...) 0,25 x ∈(416; 841; ...)
Mà x nhỏ hơn 800 nên x = 416
Vậy số Học sinh trường A là 416 học sinh 0,25
Gọi số đó là a (a ∈ N). Vì a chia cho 4 dư 1, chia cho 15 dư 12
Do đó (a + 3)4; (a + 3) 1  5 0,25
mà (4, 15) = 1 nên (a + 3)4.15 1 0,25 Suy ra a + 3 = 60k (k∈N)
a = 60k - 3 = 60k – 30 + 27 = 30(2k - 1) + 27 (k∈N) 0,25 Vậy a chia cho 30 dư 27. 0,25 Ta có: 2 2 2 2 2 2 2 2
a + 3b =11c +185d ⇒ a + 3b −11c −185d = 0 0,25 3 Ta có: 2 2 2 2
(a + 3b −11c −185d ) − (a + 3b +11c + d) 2 2 2 2 2 2 điểm
= (a − a) + (3b − 3b) − (11c +11c) − (d + d) −184d 0,25 2 2
= a(a −1) + 3b(b −1) −11c(c +1) − d(d +1) −184d 2
Do a, b, c, d là các số nguyên dương nên ta có: 2
a(a −1)2; 3b(b −1)2;c(c +1)2;d(d +1)2;184d 2 0,25
Suy ra: a + 3b +11c + d2 mà a + 3b +11c + d > 2
Vậy a + 3b +11c + d là hợp số. 0,25 4 N A M B 0.25 3 điểm
Vì điểm M nằm giữa hai điểm A và B nên:
1.a AM + MB = AB 0.25
Hay AM = AB − MB = 5 − 2 = 3 (cm)
Do đó: AN = AM = 3 (cm) 0.25
Vì điểm N nằm giữa hai điểm A và B nên: 0.25
BN = AN + AB = 3 + 5 = 8 (cm)
Để BN có độ dài lớn nhất thì AM có độ dài lớn nhất. 0,25
Khi đó điểm M trùng với điểm B. 0,25
Suy ra AM = AN = 5 (cm) 0,25
Suy ra BN = AB + AN = 5+ 5 =10 (cm) 0,25
Diện tích tam giác ABF là 1 1 S = AB.EB = . . = m ABF 16 4 32( 2 ) 0,25 2 2
1.b Diện tích tam giác ABC là 1 1 S = AB.BC = . . = m ABC 16 10 80( 2 ) 0,25 2 2
Diện tích tam giác BFC là S = S − S = − = m BFC ABC ABF ( 2 80 32 48 ) 2S . 0,25 BCF 2 48 ⇒ EF = = = 9,6(m) BC 10 Diện tích bể cá là
BE ( AB + EF ) 4(16 + 9,6) S = = = , m 0,25 ABEF 51 2( 2 ) 2 2 5 8 11 296 299 302 M = + + + ...+ + + 2 3 98 99 100 3 3 3 3 3 3 8 11 14 299 302 0,25 3M = 5 + + + + ...+ + 2 3 98 99 3 3 3 3 3 3M – M =  8 11 14 299 302   5 8 11 296 299 302 5 ...   ...  = + + + + + + − + + + + + +  2 3 98 99 2 3 98 99 100 3 3 3 3 3 3 3 3 3 3 3     
 8 5  11 8  14 11
 299 296   302 299  302 2M = 5+ − + − + − + 0,25    ...+ − + − −    2 2 3 3  98 98   99 99  100
 3 3   3 3   3 3   3 3   3 3  3 1 1 1 1 302 5 2M = 5+1+ + +....+ + − 2 97 98 100 3 3 3 3 3 1 điểm Đặt B = 1 1 1 1 + + ....+ + 2 97 98 3 3 3 3
Suy ra: 3B – B = 2B = 1 - 1 suy ra B = 1  1 1  − 98 3 98 2 3    Thay B vào 2M ta được: 0,25 2M 1  1  302 1 1 302 = 5 +1+ 1− − =  6 + − −  98 100 98 100 2  3  3 2 2.3 3 Suy ra: M = 1 1 302 3+ − − 98 100 4 4.3 2.3 Suy ra: M < 1 1 1 3+ < 3+ = 3 (đpcm) 4 2 2 0,25
Xem thêm: ĐỀ THI HSG TOÁN 6
https://thcs.toanmath.com/de-thi-hsg-toan-6
Document Outline

• Toán 6_CHÍNH THỨC
• HSG 6