








Preview text:
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1: 2x dx bằng x 1 + x + 2 2 A. 1 2x + C . B. + C .
C. 2x ln 2 + C . D. + C . x +1 ln 2 Lời giải Chọn D x 2x Ta có 2 dx = + C . ln 2 Câu 2:
Nghiệm của phương trình log 2x −3 = 2 là 3 ( ) 9 11 A. x = . B. x = 5. C. x = 6 . D. x = . 2 2 Lời giải Chọn C 3 2x − 3 0 x
Ta có log 2x − 3 = 2 2 x = 6 3 ( ) 2x − 3 = 9 x = 6
Vậy tập nghiệm của bất phương trình S = 6 . Câu 3:
Cho cấp số nhân (u có u = 2 và u = 4
− . Công bội của cấp số nhân bằng n ) 2 3 A. 2 − . B. 6 − . C. 6 . D. 2 . Lời giải Chọn A u −
Công bội của cấp số nhân là 4 3 q = = = 2 − . u 2 2 2 Câu 4:
Cho a là số thực dương và biểu thức 3 P = a
a . Khẳng định nào sau đây đúng? 1 7 5 A. 3 P = a . B. 6 P = a . C. 6 P = a . D. 5 P = a . Lời giải Chọn B 2 1 7 Ta có 3 2 6
P = a .a = a . Câu 5:
Cho hình nón có bán kính đáy r = 3 và độ dài đường sinh l = 9 . Diện tích xung quanh của hình nón đã cho bằng A. 9 . B. 27 . C. 3 . D. 12 . Lời giải Chọn B
Diện tích xung quanh S = rl = 27 . xq Câu 6:
Số cách chọn 5 học sinh từ 35 học sinh của một lớp là A. 5!. B. 5 35 . C. 5 C . D. 5 A . 35 35 Lời giải Chọn B Số cách chọn là 5 C . 35 1 Câu 7: Giá trị của 5 dx bằng 0 A. 5 . B. 10 . C. 15 . D. 20 . Lời giải Chọn B 4 Ta có 4 5 = 5 = 10 dx x . 2 2 Câu 8:
Khối đa diện đều loại 4; 3 là
A. Khối tứ diện đều.
B. Khối bát diện đều.
C. Khối hộp chữ nhật.
D. Khối lập phương. Lời giải Chọn D Câu 9:
Tìm đạo hàm của hàm số = x y . x − A. 1 ' = x y x ln . B. ' = x y ln .
C. y ' = ln . D. 1 ' − = x y x . Lời giải Chọn D
Áp dụng ( x )' = x a
a .ln a (a 0,a ) 1 .
Câu 10: Tập xác định của hàm số y = ( x − 2) là A. \ 2 . B. . C. ( ;2 − ). D. (2;+) . Lời giải Chọn D . Vì
nên hàm số y = ( x −
2) xác định khi x − 2 0 x 2 .
Vậy tập xác định của hàm số đã cho là (2;+) . 2x −1
Câu 11: Tiệm cận đứng của đồ thị hàm số y = x − là đường thẳng có phương trình 3 1 A. x = . B. x = 3. C. x = 3 − . D. x = 2 . 2 Lời giải Chọn B . 2x −1
Vì lim y = − nên đồ thị hàm số y = − x 3 → x −
có tiệm cận đứng là đường thẳng có phương 3 trình x = 3.
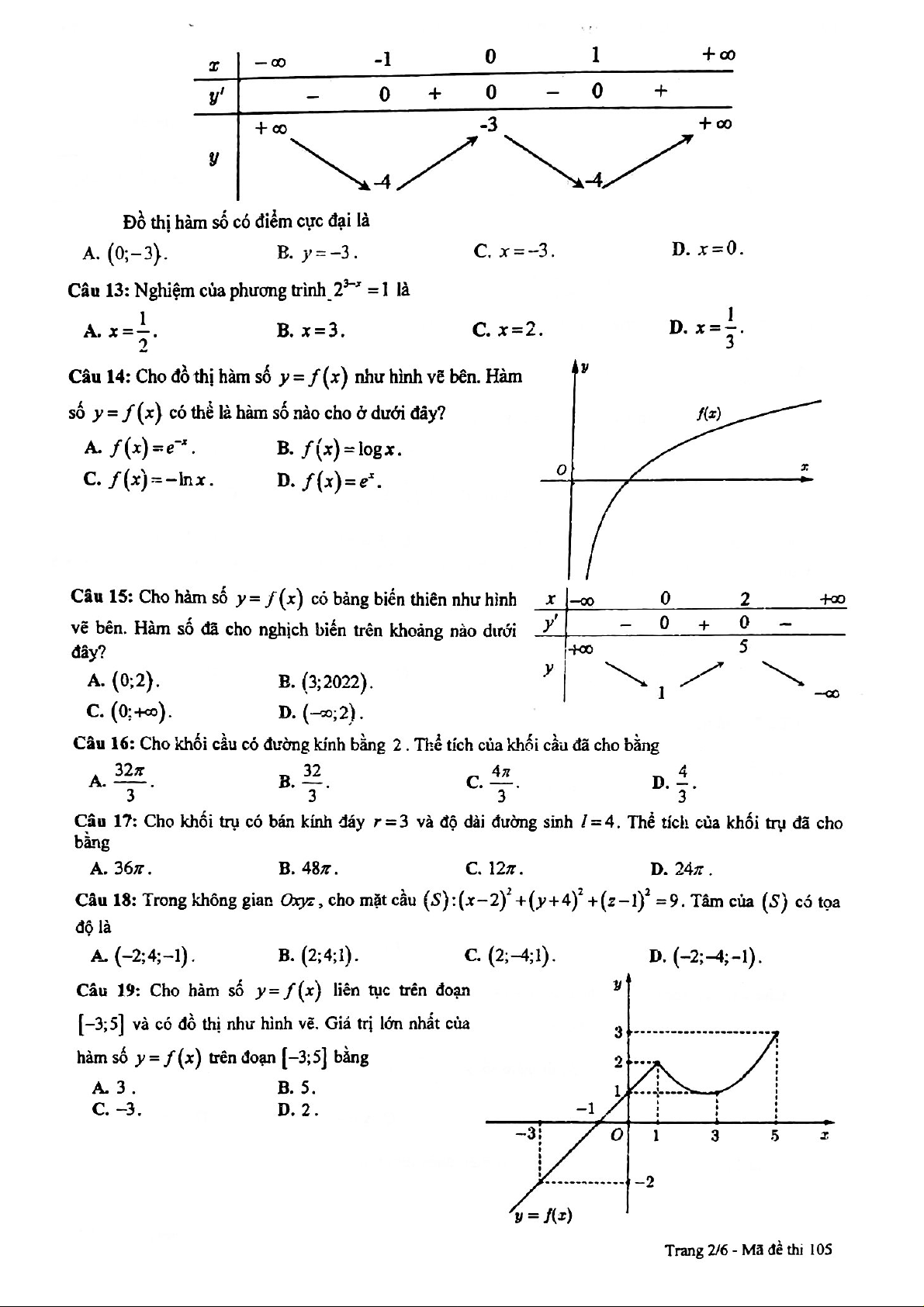
Câu 12: Cho hàm số y = f ( x) có bảng biến thiên như sau: x − 1 − 0 1 + y − 0 + 0 − 0 + y + 3 − + 4 − 4 −
Đồ thị hàm số có điểm cực đại là A. (0; ) 3 − . B. y = 3 − . C. x = 3 − . D. x = 0 . Lời giải Chọn A .
Dựa vào bảng biến thiên, ta thấy y đổi dấu từ + sang − khi qua x = 0 nên đồ thị hàm số
đã cho có điểm cực đại là (0; ) 3 − .
Câu 13: Nghiệm của phương trình 3 2 −x = 1 là. 1 1 A. x = .
B. x = 3.
C. x = 2 . D. x = . 2 3 Lời giải Chọn B Ta có 3
2 −x = 1 3 − x = 0 x = 3 .
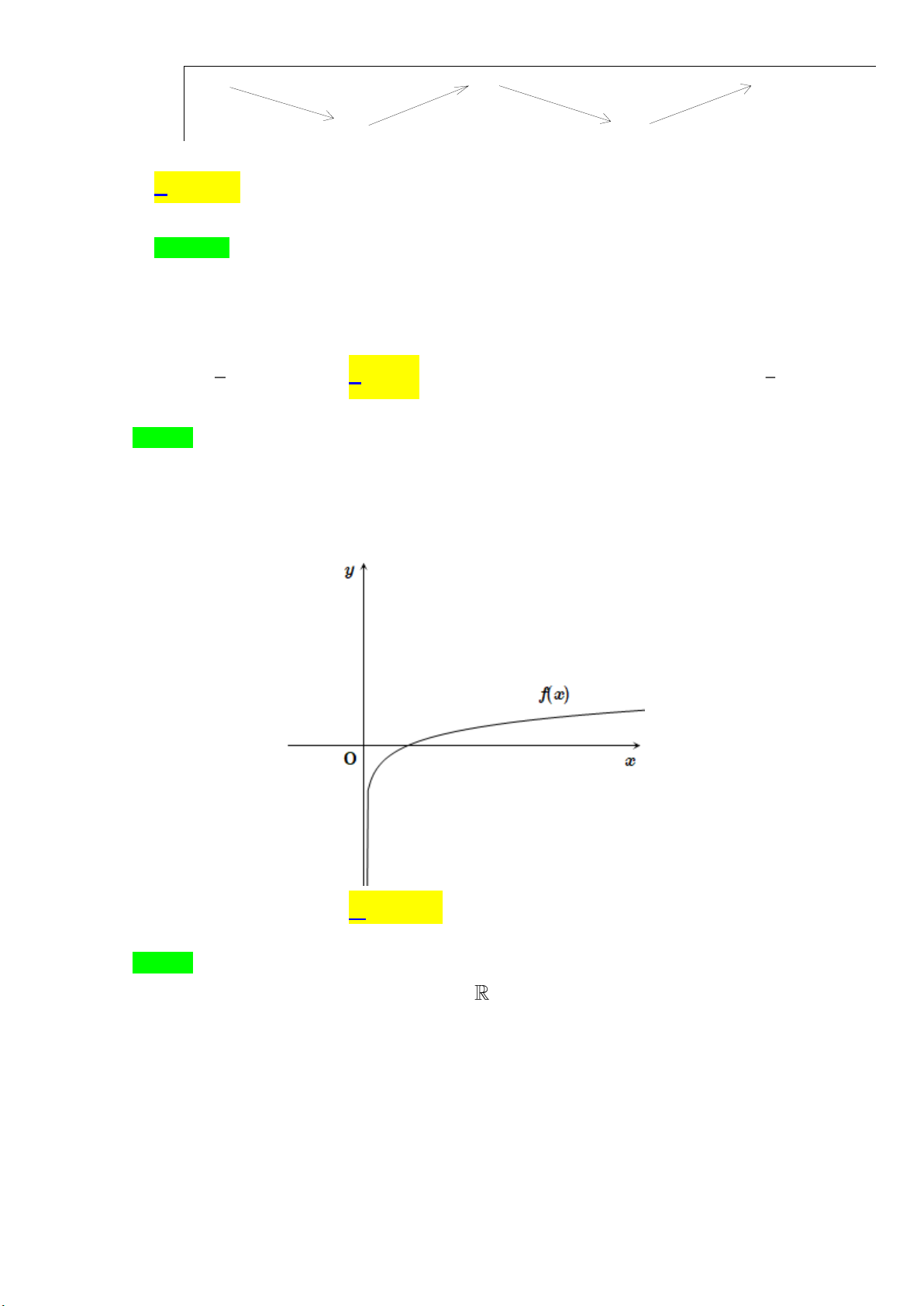
Câu 14: Cho đồ thị hàm số y = f ( x) như hình vẽ bên. Hàm số y = f ( x) có thể là hàm số nào dưới đây? x A. y e− = .
B. y = log x .
C. y = − ln x . D. x y = e . Lời giải Chọn B
Nhận xét hàm số y = f ( x) có miền giá trị là nên ta loại phương án , A D
Mặt khác quan sát đò thị hàm số y = f ( x) f ( x) 0 nên y = log x .
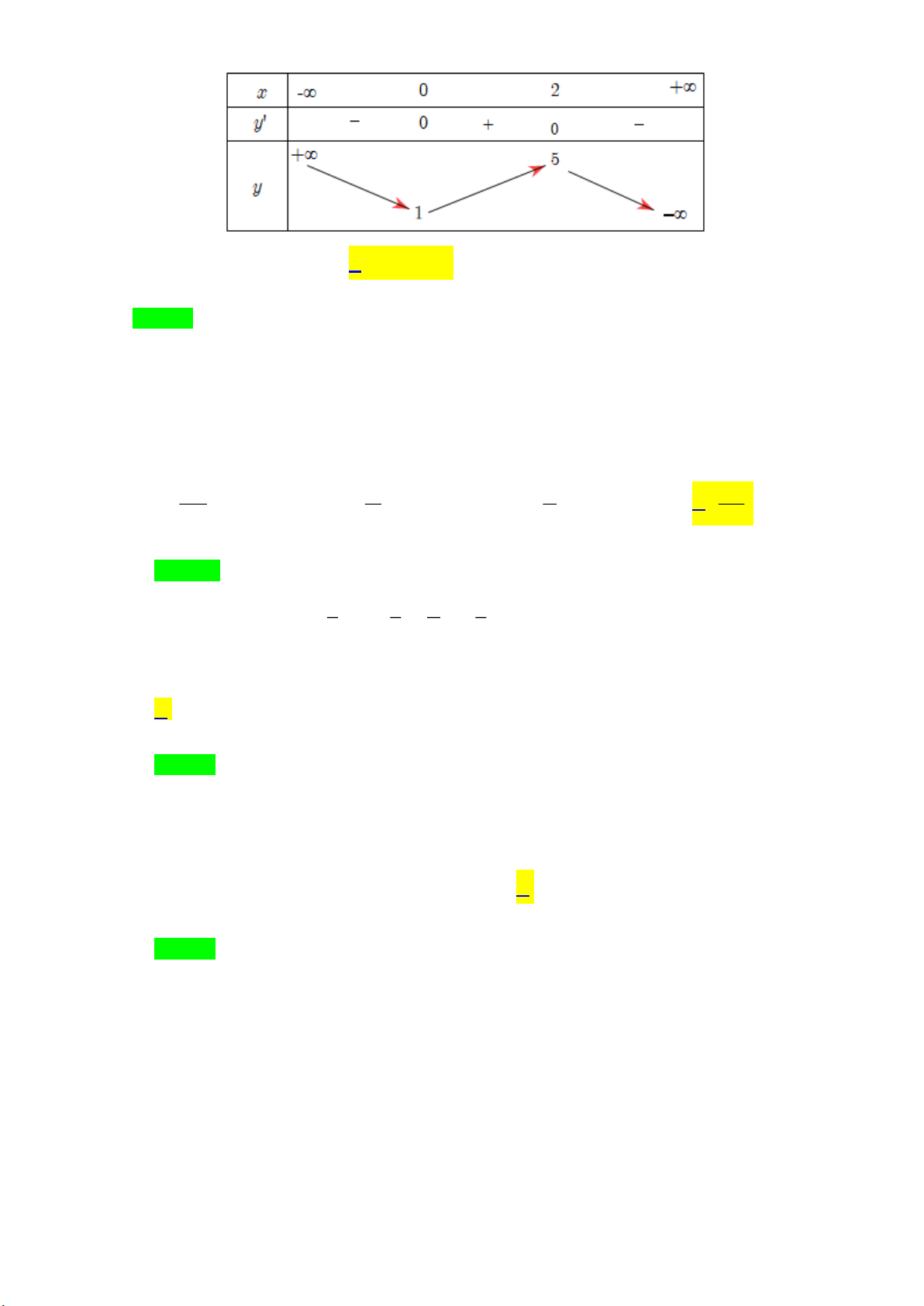
Câu 15: Cho hàm số y = f ( x) có bảng biến thiên như hình vẽ bên. Hàm số đã cho nghịch biến trong khoảng nào dưới đây A. (0;2) . B. (3;2022) .
C. (0; + ) . D. (−; 2) . Lời giải Chọn B
Quan sát bảng biến thiên hàm số y = f ( x) nghịch biến trong các khoảng (−;0) và (2;+).
Mặt khác (3;2022) (2;+ ) . Do đó hàm số y = f ( x) nghịch biến (3;2022) .
Câu 16: Cho khối cầu có đường kính bằng 2 . Thể tích khối cầu đã cho bằng 32 32 4 4 A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn D 3 4 4 d 4 Thể tích khối cầu: 3 V = R = = 3 3 2 3
Câu 17: Cho khối trụ có bán kính đáy r = 3 và độ dài đường sinh l = 4 . Thể tích của khối trụ đã cho bằng A. 36 . B. 48 . C. 12 . D. 24 . Lời giải Chọn A Thể tích khối trụ: 2
V = r h = 36 2 2 2
Câu 18: Trong không gian Oxyz , cho mặt cầu (S ) : ( x − 2) + ( y + 4) + ( z − ) 1
= 9 . Tâm của (S ) có tọa độ là A. ( 2 − ;4;− ) 1 . B. (2;4; ) 1 . C. (2; 4 − ; ) 1 . D. ( 2 − ; 4 − ;− ) 1 . Lời giải Chọn C
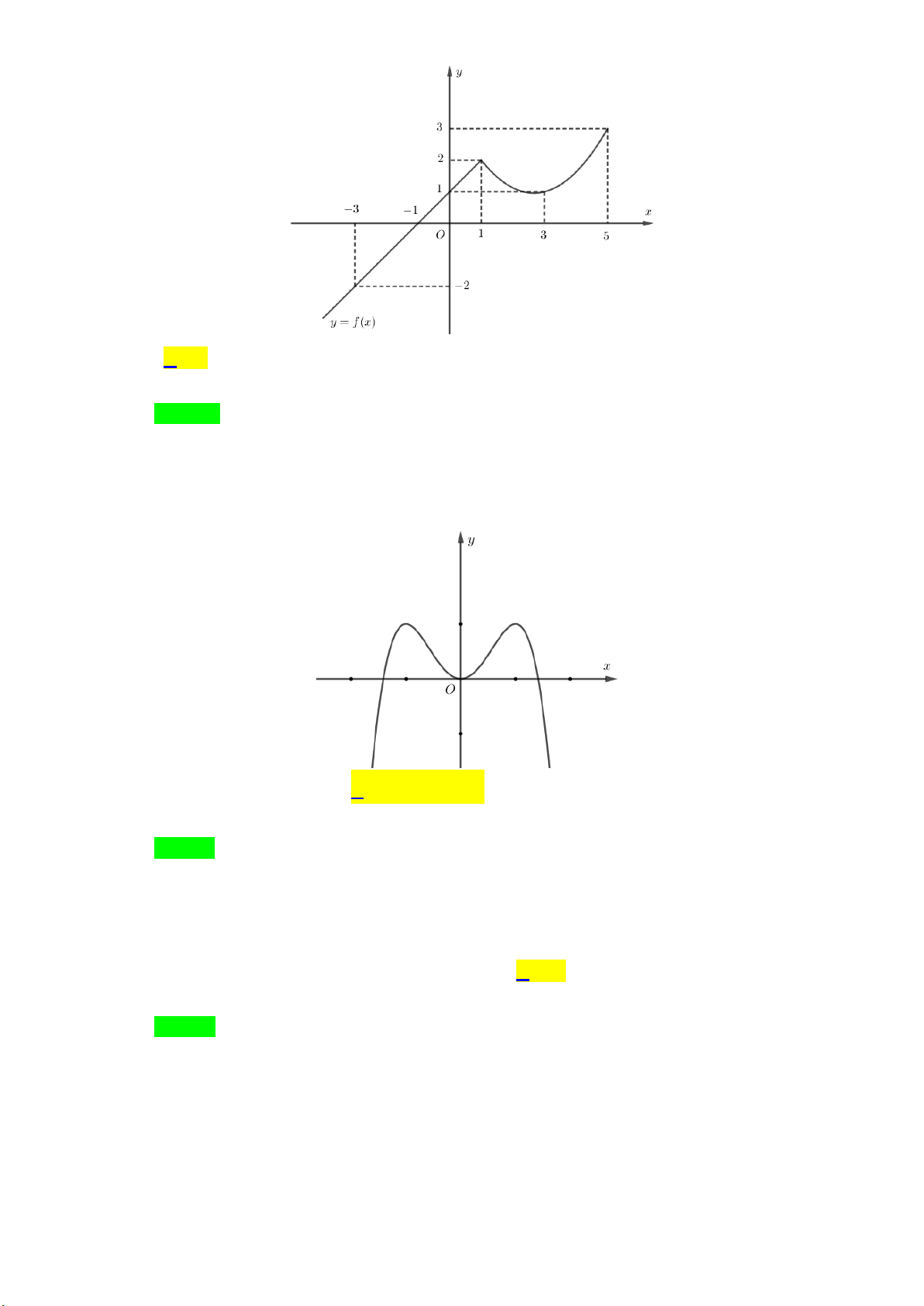
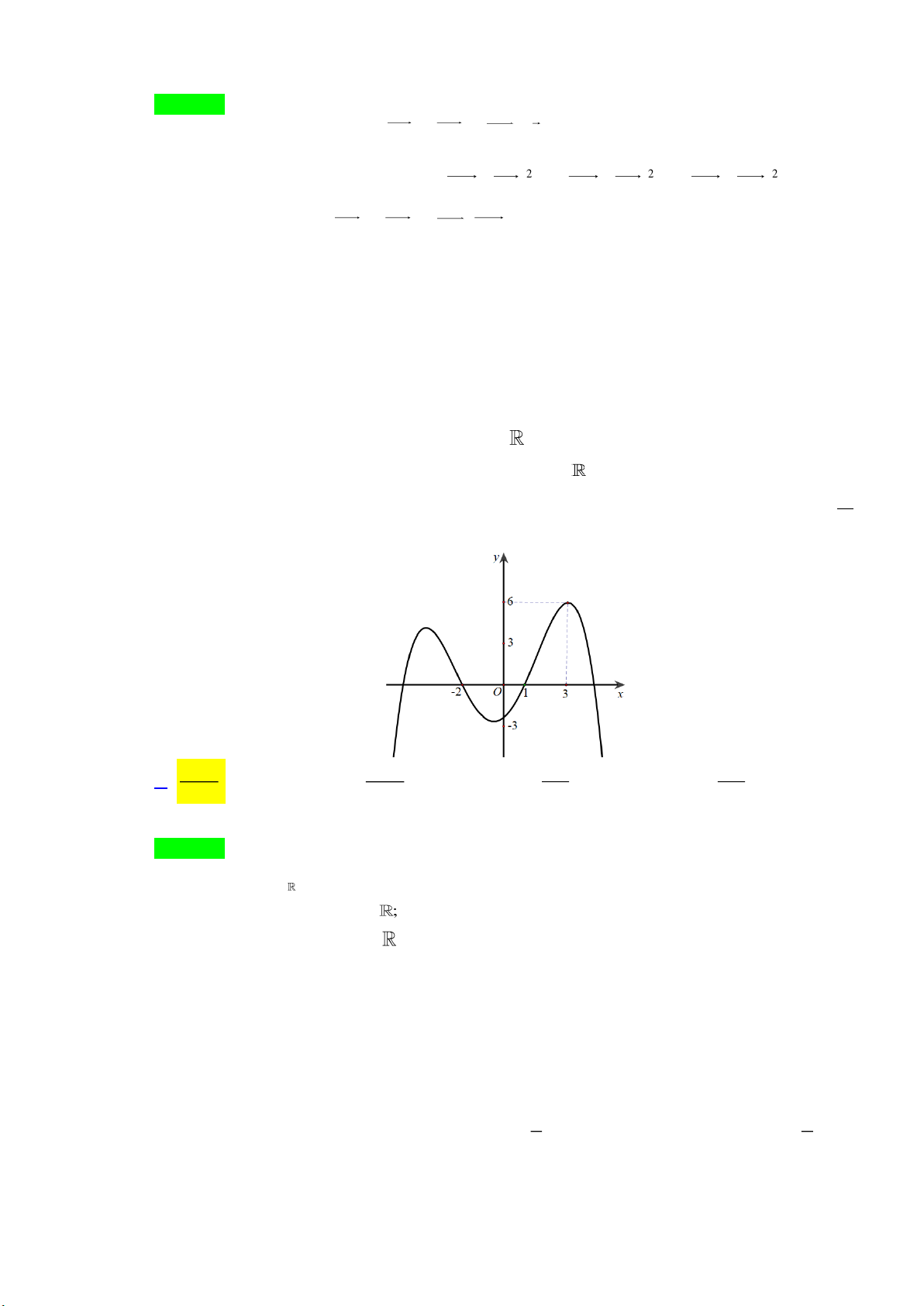
Câu 19: Cho hàm số y = f ( x) liên tục trên đoạn 3 − ;
5 và có đồ thị như hình vẽ. Giá trị lớn nhất
của hàm số y = f (x) trên đoạn 3 − ; 5 bằng A. 3. B. 5. C. 3. − D. 2. Lời giải Chọn A
Từ đồ thị hàm số ta thấy giá trị lớn nhất của hàm số y = f (x) trên đoạn 3 − ; 5 bằng 3 đạt được tại x = 5.
Câu 20: Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên 3 2 4 2 2 4 2
A. y = x + 2x − x −1. B. y = −x + 2x .
C. y = −x + 2 .
x D. y = x − 2x . Lời giải Chọn B
Đồ thị hàm số trên là đồ thị hàm bậc bốn trùng phương nên loại đáp án A và C .
Vì lim y = − nên chọn đáp án B . x→
Câu 21: Thể tích khối lập phương có cạnh bằng 3 là A. 36 . B. 9 . C. 27 . D. 81. Lời giải Chọn C
Thể tích khối lập phương có cạnh bằng 3 là 3 V = 3 = 27 . Chọn đáp án C.
Câu 22: Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y = x − 2, trục Ox và các đường thẳng x = 1
, x = 2 được tính bằng công thức nào sau đây? 2 2 2 2 2 A. ( 2 x − 2) dx . B. ( 2 x − 2)dx . C. ( 2 x − 2)dx . D. 2 x − 2 dx . 1 1 1 1 Lời giải Chọn D
Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y = x − 2, trục Ox và các đường thẳng x = 1 2 , x = 2 là: 2 x − 2 dx 1
Câu 23: Trong không gian Oxyz , cho hai điểm A(1;1;− )
1 và B(2;3;2) . Vectơ BA có tọa độ là A. ( 1 − ;−2;− ) 3 . B. (3;4; ) 1 . C. (1;2; ) 3 . D. ( 3 − ;− 4;− ) 1 . Lời giải Chọn A
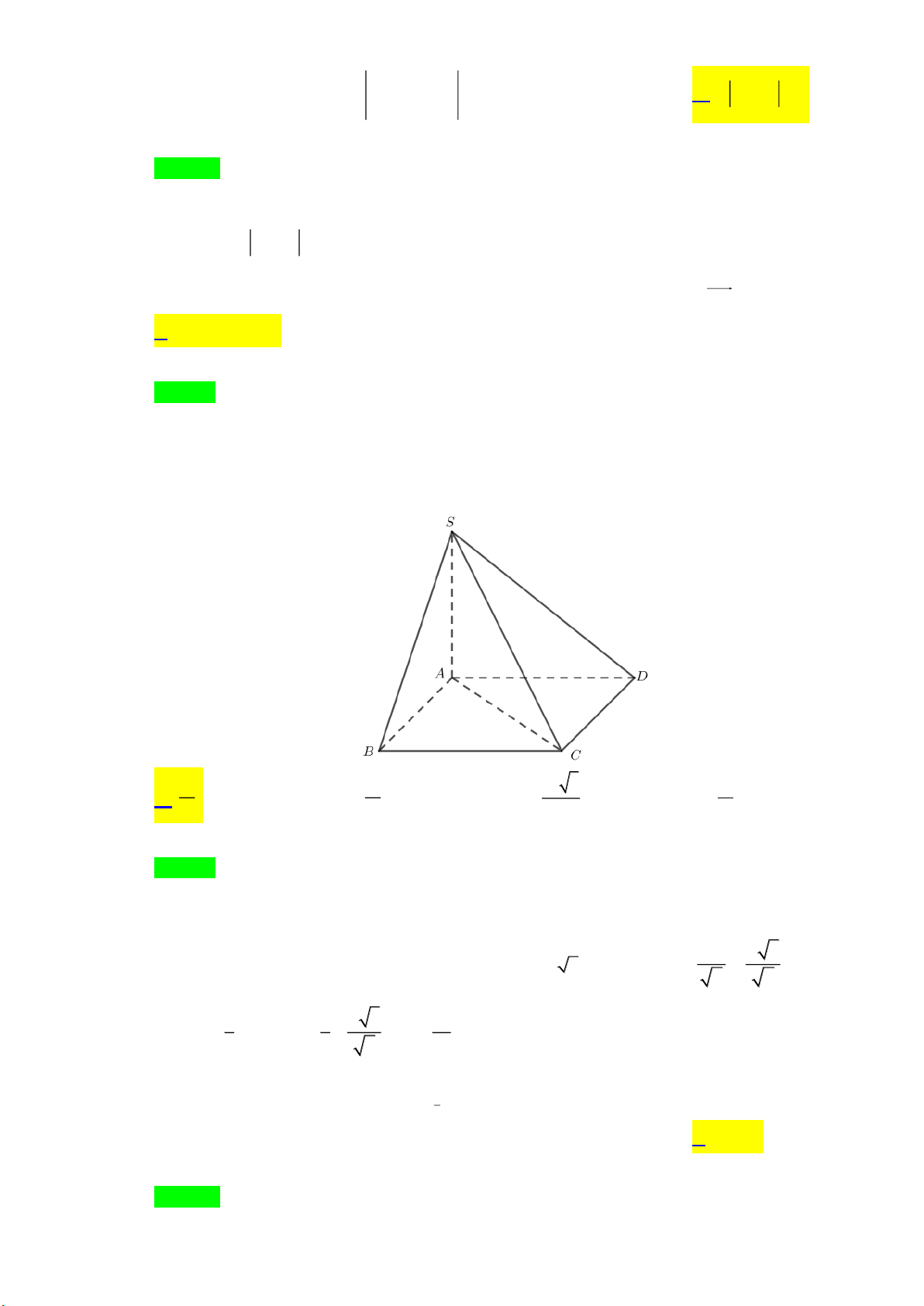
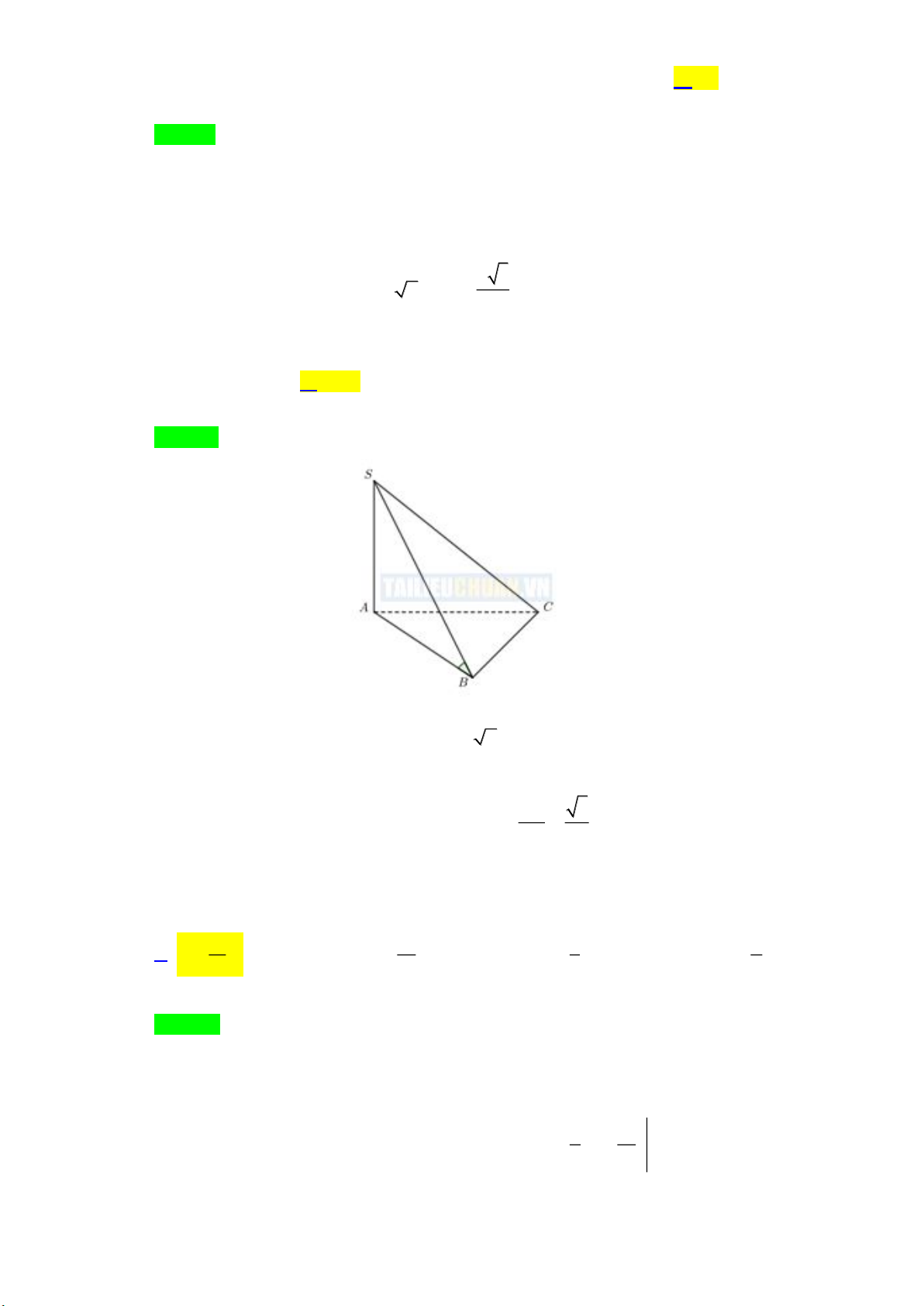
Câu 24: Cho khối chóp S.ABCD có đáy ABCD là hình vuông, SA ⊥ ( ABCD) và SA = a , góc giữa
đường thẳng SC và mặt phẳng ( ABCD) bằng 30o (tham khảo hình vẽ). Thể tích khối chóp S.ABCD bằng 3 a 3 a 3 a 3 3 a A. . B. . C. . D. . 2 4 6 6 Lời giải Chọn A
SA ⊥ ( ABCD) ( ,( )) = = 30O SC ABCD SCA . AC a 3
Xét tam giác vuông SAC , ta có: = .cot 30o AC SA
= a 3 . Suy ra: AB = = . 2 2 2 3 1 1 a 3 a V = S . A S = . .a = . S.ABCD 3 ABCD 3 2 2
Câu 25: Tập nghiệm của bất phương trình log x −1 0 là 1 ( ) 2 A. (1;2) . B. 2;+ ) . C. ( ;2 − . D. (1; 2 . Lời giải Chọn D. x −1 0 x 1 Ta có log ( x − ) 0 1 0 x 1;2 . 1 1 ( x −1 x 2 2 2
Câu 26: Cho khối lăng trụ đứng có chiều cao bằng 3 và đáy là tam giác đều có độ dài cạnh bằng 2 .
Tính thể tích khối lăng trụ đã cho A. 3 . B. 3 3 . C. 3 . D. 6 . Lời giải Chọn B. 2 2 3
Diện tích đáy bằng B = = 3 . 4
Thể tích của khối lăng trụ là V . B h 3 3 .
Câu 27: Cho hàm số y = f ( x) có đồ thị hàm số y = f ( x) như hình bên. Hàm số đồng biến trên khoảng nào dưới đây? A. ( 1 − ; ) 3 . B. (0;2) . C. (1;+ ) . D. ( 1 − ;0) . Lời giải Chọn D.
Từ đồ thị suy ra f ( x) 0 x ( ; a b) ( ;
c + ) với a 1 − ;b(0; ) 1 ;c (1;2)
Do đó hàm số đồng biến trên khoảng ( 1 − ;0) .
Câu 28: Trong không gian Oxyz , cho ba điểm A
1;2; 3 ,B 1;0;2 ,C x; ; y 2 thẳng hàng. Khi đó tổng x
y bằng bao nhiêu? 11 11 A. x y 17 . B. x y . C. x y 1 . D. x y . 5 5 Lời giải Chọn C AB 2; 2; 5 , AC x 1;y 2;1 , A , B C thẳng hàng AB cùng phương AC 3 1 2 1 x x y 5 x y 1 . 2 2 5 8 y 5
Câu 29: Trong không gian Oxyz , mặt cầu tâm I 1;2; 3 và đi qua điểm A 1;1;2 có phương trình là 2 2 2 2 2 2 A. x 1 y 2 z 2 2 . B. x 1 y 2 z 3 2 . 2 2 2 2 2 2 C. x 1 y 2 z 3 2 . D. x 1 y 2 z 2 2 Lời giải Chọn C 2 2 2 R IA 1 1 1 2 2 3 2 2 2 2
Phương trình mặt cầu cần tìm là x 1 y 2 z 3 2 . 2 f x x sin x 1 F x f x Câu 30: Cho hàm số , biết
là một nguyên hàm của hàm số và F 0 1 F x . Khi đó bằng 3 x A. F x cosx 2 . B. 3 F x x cosx x 2 . 3 3 x 3 x C. F x cosx x . D. F x cosx x 2 . 3 3 Lời giải Chọn D 3 3 x x 2 f x dx x sinx 1 dx cosx x C F x cosx x C . 3 3 3 x F 0 1 C 2 . Vậy F x cosx x 2 . 3 Câu 31: Với 2
a, b là hai số thực dương tùy ý, biểu thức log 2022a b bằng 2022 ( ) 1 A. + + . B. 2022 + log a + log b . 1 2log a log b 2022 2022 2022 2022 2 1 C. 2022 + 2log a + log b . D. 1+ log a + log b . 2022 2022 2022 2022 2 Lời giải Chọn A. Ta có: log ( 2 2022a b) 2 = log 2022 + log a + log b =1+ 2log a + log b . 2022 2022 2022 2022 2022 2022
Câu 32: Một hộp chứa 5 bi xanh và 10 bi đỏ, lấy ngẫu nhiên 3 bi. Xác suất để lấy được đúng một bi xanh là 3 2 45 200 A. . B. . C. . D. . 4 3 91 273 Lời giải Chọn C. Ta có: n() 3 = C = 455. 15
Gọi A: ” 3 bi lấy ra có đúng 1 bi màu xanh”. n( A) 2 1 = C .C = 225. 10 5 p ( A) n ( A) 225 45 = = = n () . 455 91
Câu 33: Giá trị nhỏ nhất của hàm số f ( x) 4 2
= x − 24x − 4 trên đoạn 0;1 9 bằng A. 144 − . B. 150 − . C. 148 − . D. 149 − . Lời giải Chọn C.
Tập xác định: D = . x = 0(0;19) 3
y ' = 4x − 48x = 0 x = 12 (0;19) . x = − 12 (0;19) y (0) = 4 − ; y ( 12) = 1
− 48; y (19) =121653. Vậy min y = 148 − tại x = 12. 0;19
Câu 34: Cắt một hình trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có
cạnh bằng 3a , tính diện tích toàn phần của hình trụ đã cho. 2 9 a 2 27 a 2 13 a A. . B. 2 9 a . C. . D. . 2 2 6 Lời giải Chọn C
Theo giả thiết, hình trụ có bán kính 3a r =
, chiều cao bằng độ dài đường sinh: h = l = 3a . 2
Vậy nên diện tích toàn phần của hình trụ là a a a = + = + = tp S r (l r ) 2 3 3 27 2 2 3a . 2 2 2 5 2
f ( x)dx = 10 2 − 4 f (x) d x Câu 35: Cho 2 . Khi đó 5 bằng A. 46 . B. 32 . C. 42 . D. 34 . Lời giải Chọn D 2 2 2 5 5 Có 2 − 4 f (x) d
x = 2dx − 4 f
(x)dx = 4 f (x)dx − 2 dx = 34 . 5 5 5 2 2
Câu 36: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và SA vuông góc với mặt a 3
phẳng đáy. Biết rằng AC = a 2 , SA =
. Tính góc giữa hai mặt phẳng (SBC ) và 3 (ABC). A. 0 90 . B. 0 30 . C. 0 60 . D. 0 45 . Lời giải Chọn B
Tam giác ABC vuông cân tại B mà AC = a 2 nên AB = AC = a .
Ta có (SBC) ( ABC) = BC và BC ⊥ (SAB) nên góc giữa hai mặt phẳng (SBC ) và ( ABC) là SA 3 0
góc SBA. Trong tam giác vuông SBA có tan SBA = = SBA = 30 . AB 3
Câu 37: Cho hình phẳng (H ) giới hạn bởi đồ thị hàm số 2
y = 3x − x và trục hoành. Tính thể tích V
của vật thể tròn xoay sinh ra khi cho (H ) quay quanh trục Ox . 81 81 9 9 A. V = . B. V = . C. V = . D. V = . 10 10 2 2 Lời giải Chọn A. x = 0
Phương trình hoành độ giao điểm: 2
3x − x = 0 . x = 3 3 3 3 5 3 x
V = (3x − x )2 2 dx = ( 2 3 4
9x − 6x + x ) dx 3 4
= 3x − x + 2 5 0 0 0 5 3 3 81 3 4 = 3.3 − .3 + = . 2 5 10
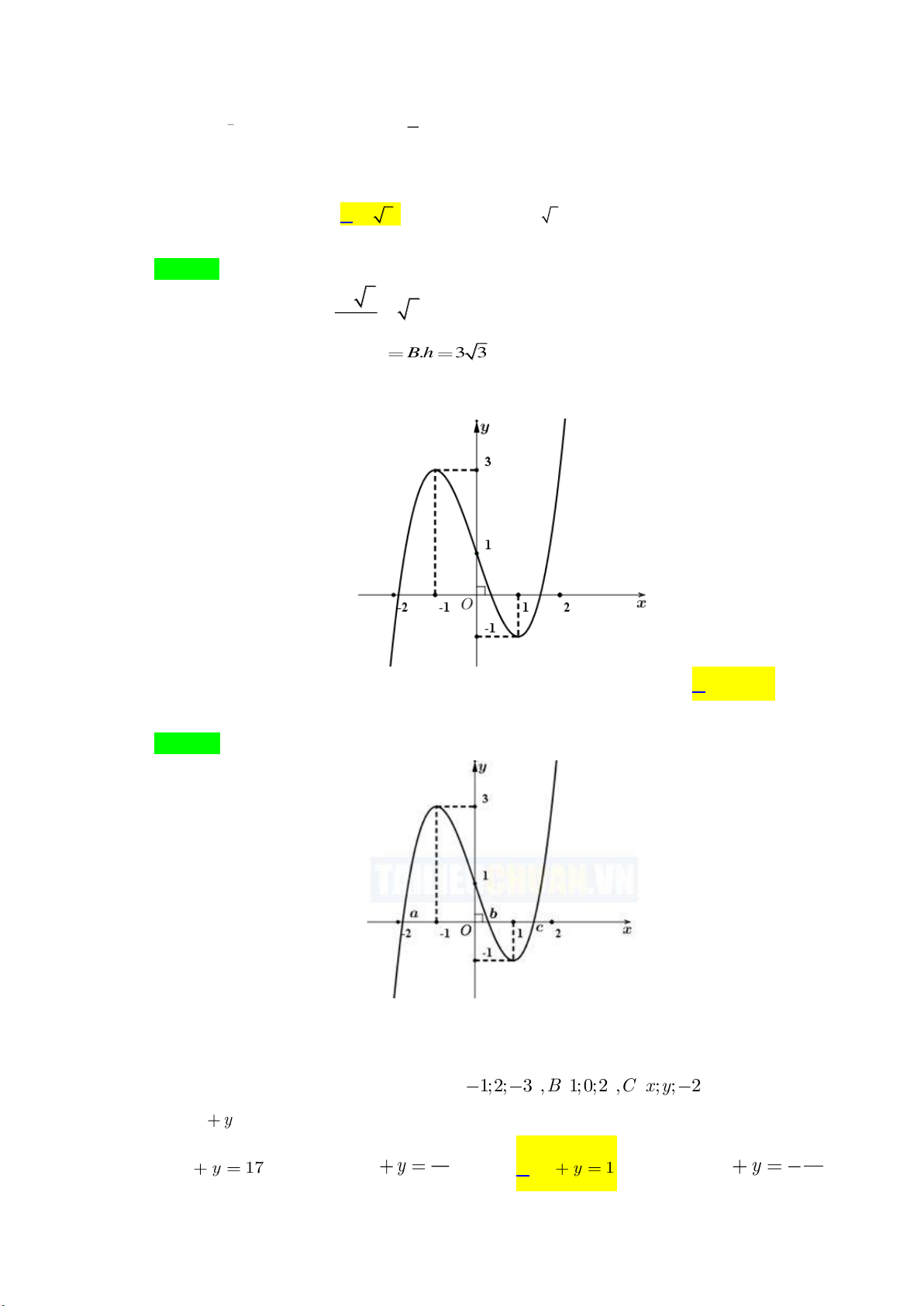
Câu 38: Cho hàm số bậc bốn y = f ( x) có đồ thị hàm số y = f ( x) như hình vẽ bên. Hàm số g ( x) = f ( 2 x − ) 4 2 4.
4 + x − 8x có bao nhiêu điểm cực tiểu? A. 4. B. 7. C. 3. D. 5. Lời giải Chọn C.
Ta có: g( x) = x f ( 2 x − ) 3 8 . 4 + 4x −16x ; x = 0
g(x) = 0 x f ( 2x − ) 2 4 2 . 4 + x − 4 = 0 . 2 f .
( 4x −4) = −( 4x −4) (2) 2 t = 2 − x − 4 = 2 − x = 2 t − Đặ 2 t 4
t = x − 4 , khi đó (2) f (t ) =
t = 0 x − 4 = 0 x = 2 . 2 t = 4 2 x − 4 = 4 x = 2 2 Bảng xét dấu
Vậy hàm số có 3 điểm cực tiểu.
Câu 39: Trong không gian Oxyz , cho bốn điểm A(2;3;5), B( 1 − ;3;2),C( 2
− ;1;3), D(5;7;4). Điểm M ( ; a ;
b c) di động trên mặt phẳng (Oxy) . Khi biểu thức 2 2 2 4
T = 4MA + 5MB − 6MC + MD
đạt giá trị nhỏ nhất thì tổng a + b + c bằng A. 11. B. 11 − . C. 12 . D. 9 . Lời giải Chọn C.
Ta thấy D là điểm thỏa mãn 4DA + 5DB − 6DC = 0 . Khi đó:
T = MA + MB − MC + MD = (MD + DA)2 + (MD + DB)2 − (MD + DC)2 2 2 2 4 4 4 5 6 4 5 6 + MD 2 4
= MD + MD + ( DA+ DB − DC) 2 2 2 3 2 4 5 6
MD + 4DA + 5DB − 6DC . 2 4 2 2 2
= 3MD + MD + 4DA + 5DB − 6DC .
Đặt x = MD 0 và hằng số 2 2 2
4DA + 5DB − 6DC = m . Khi đó: 4 2
T = x + 3x + m đồng biến trên khoảng (0;+) .
Suy ra T đạt giá trị nhỏ nhất khi MD nhỏ nhất, và MD nhỏ nhất khi M là hình chiếu vuông
góc của D trên mặt phẳng (Oxy) . Suy ra M (5;7;0) .
Vậy a + b + c = 12. Câu 40: Cho hàm số
y = f (x) liên tục trên
và có đồ thị như hình vẽ. Đặt 2
T =103. f (a + a +1) + 234. f (af ( ) b + bf ( )
a ) với a,b . Gọi m là số cặp số ( ; a b) mà tại đó biể M
u thức T đạt giá trị lớn nhất, gọi giá trị lớn nhất của T là M . Giá trị biểu thức m bằng 1011 1011 337 674 A. . B. . C. . D. . 4 8 2 3 Lời giải Chọn A.
Từ đồ thị ta có: max f (x) = f (3) = 6 . Suy ra: 2
f (a + a +1) 6 a
; dấu “=” xảy ra khi 2
a + a +1 = 3 a =1; a = 2 − . f (af ( )
b + bf (a)) 6, , a b
, dấu “=” xảy ra khi af (b) + bf (a) = 3 .
af (b) + bf (a) = 3
Do đó, T 103.6 + 234.6 = 2022, dấu “=” xảy ra khi a =1 . a = 2 −
Với a = 1 thì 1. f ( )
b + bf (1) = 3 f (b) = 3. Dựa vào đồ thị suy ra f (b) = 3 có 4 nghiệm b phân biệt. 3 3 Với a = 2 − thì 2
− . f (b) + bf ( 2
− ) = 3 f (b) = − . Dựa vào đồ thị suy ra f (b) = − có 4 2 2
nghiệm b phân biệt.
Do đó có 8 cặp (a;b) thỏa mãn T = 2022. max M 2022 1011 Vậy = = . m 8 4
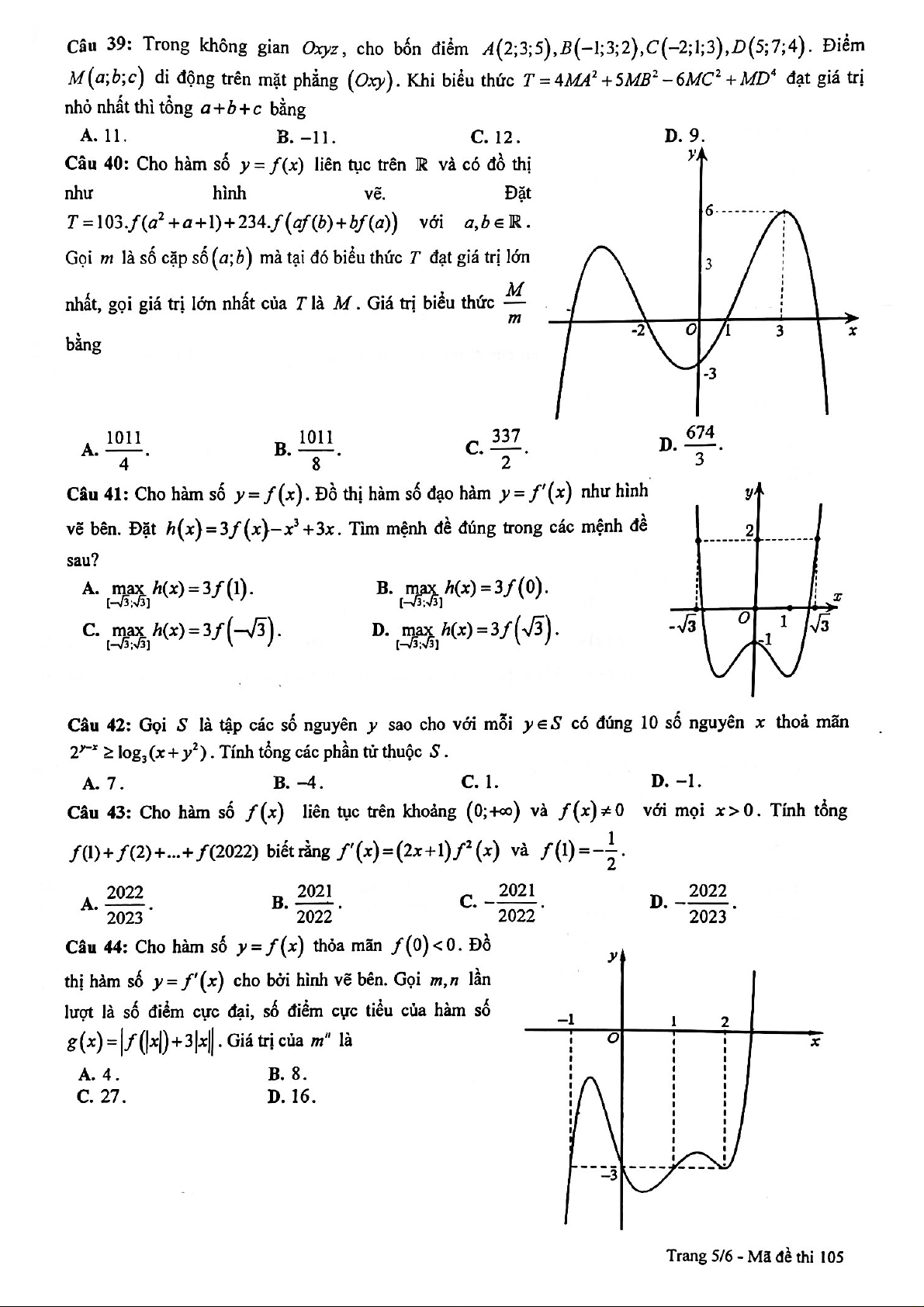
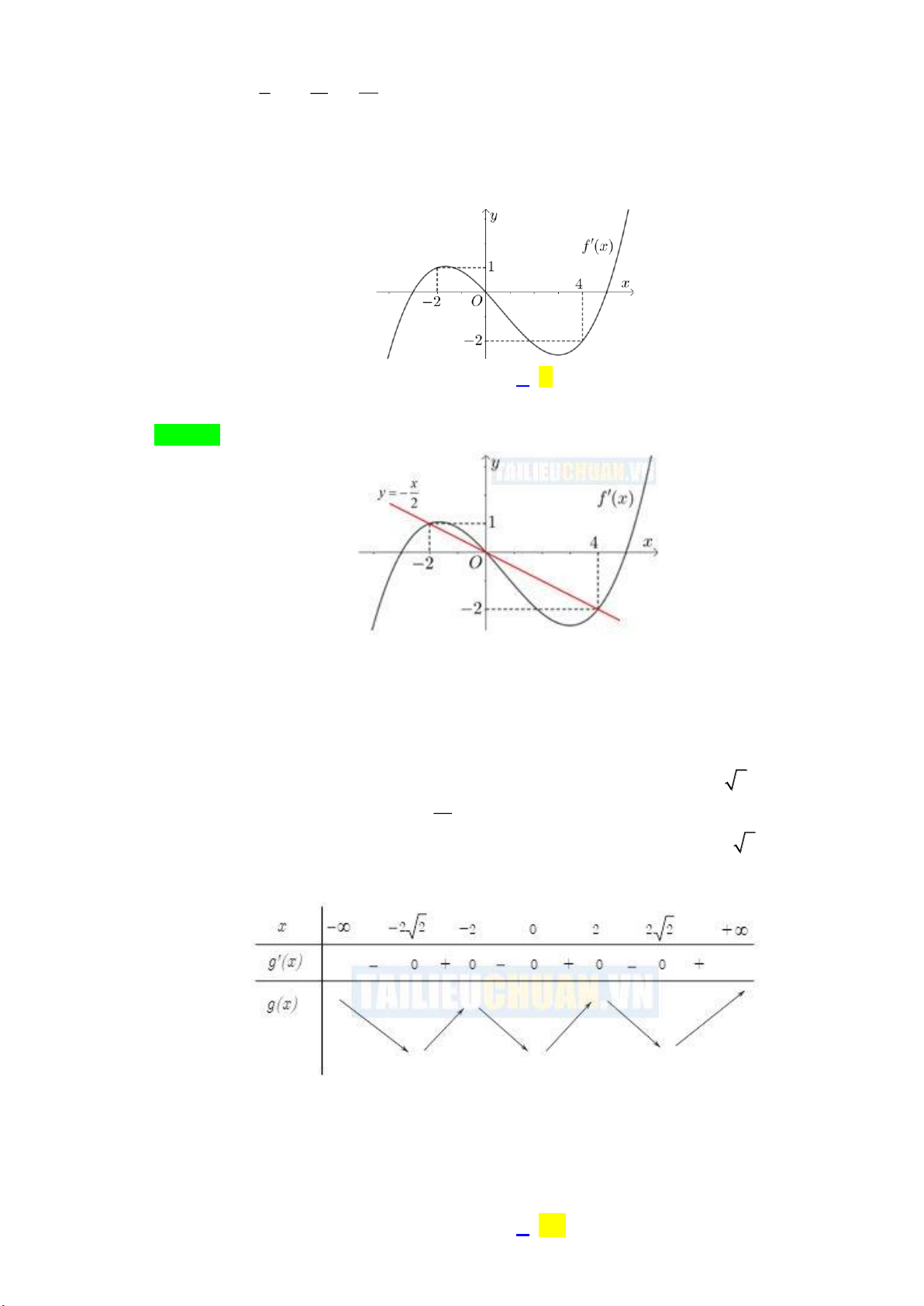
Câu 41: Cho hàm số y = f ( x) . Đồ thị hàm số đạo hàm y = f ( x) như hình vẽ bên.
Đặt h(x) = f (x) 3 3
− x +3x . Tìm mệnh đề đúng trong các mệnh đề sau?
A. max h ( x) = 3 f ( ) 1 .
B. max h( x) = 3 f (0) . − 3; 3 − 3; 3
C. max h ( x) = 3 f (− 3) .
D. max h ( x) = 3 f ( 3) . − 3; 3 − 3; 3 Lời giải Chọn C. x = 0
Ta có: h( x) = f ( x) 2 3
−3x +3; h(x) = 0 f (x) 2
= x −1 x = 3 . x = − 3
Dựa vào đồ thị suy ra f ( x) 2 x −1, x
− 3; 3 h '(x) 0, x − 3; 3 .
Suy ra hàm số h ( x) đồng biến trên − 3; 3 .
Vậy max h ( x) = h(− 3) = 3 f (− 3) . − 3; 3
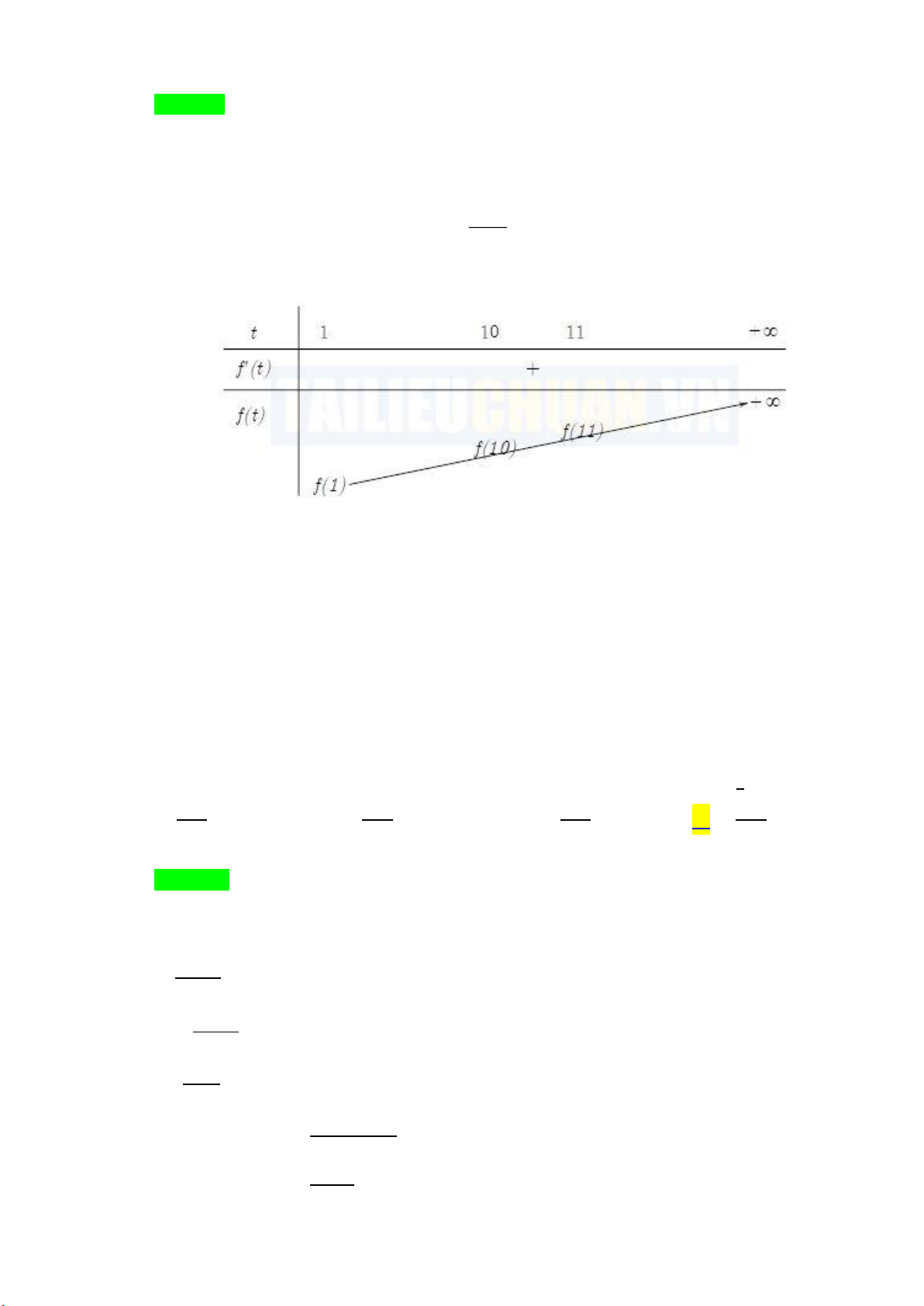
Câu 42: Gọi S là tập hợp các số nguyên y sao cho với mỗi y S có đúng 10 số nguyên x thỏa mãn 2y−x log ( 2 x + y
. Tính tổng số phần tử thuộc S . 3 ) A. 7 . B. 4 − . C. 1. D. 1 − . Lời giải Chọn D. Điều kiện: 2
x + y 0. Với mỗi số nguyên y , ta đặt 2 2
t = x + y x = t − y . 2 + −
Bất phương trình 2y−x log ( 2 x + y 2y y t 2 log t log 2y y t t + − − 0. 3 ) 3 3 Đặt ( ) 2
= log − 2y+y −t f t t , t 0 ; ( ) 2 1 =
+ 2y+y −t f t .ln 2 0, t 0. 3 t.ln 3
Suy ra f (t ) đồng biến trên (0;+) . Ta có bảng xét dấu sau:
Bất phương trình 2y−x log ( 2 x + y
có đúng 10 nghiệm nguyên x . 3 ) 2 log 2y y t t + − −
0 có đúng 10 nghiệm nguyên t 0. 3 2 y + y 10 2 2 log 10 − 2 − 0 y + y 10
2 − log 10 y + y −10−log log 10 0 2 ( 3 ) 3 3 2 y + y 11 2 2 log 11− 2 − 0 y + y 11 2 − log 11
y + y −11− log log 11 0 2 ( 3 ) 3 3
Từ hệ bất phương trình trên ta có 2 số nguyên y = −4 ; y = 3 . Vậy đáp án chọn D.
Câu 43: Cho hàm số 𝑓(𝑥) liên tục trên khoảng (0; +∞) và 𝑓(𝑥) ≠ 0 với mọi 𝑥 > 0. Tính tổng 1
𝑓(1) + 𝑓(2) + ⋯ + 𝑓(2022) biết rằng 𝑓′(𝑥) = (2𝑥 + 1)𝑓2(𝑥) và 𝑓(1) = − . 2 2022 2021 2021 2022 A. . B. .. C. − . D. − .. 2023 2022 2022 2023 Lời giải Chọn D . Ta có :
𝑓′(𝑥) = (2𝑥 + 1)𝑓2(𝑥) 𝑓′(𝑥) ⇒ = 2𝑥 + 1 𝑓2(𝑥) 𝑓′(𝑥) ⇒ ∫
𝑑𝑥 = ∫(2𝑥 + 1) 𝑑𝑥 𝑓2(𝑥) −1 ⇒ = 𝑥2 + 𝑥 + 𝐶 𝑓(𝑥) 1 ⇒ 𝑓(𝑥) = − 𝑥2 + 𝑥 + 𝐶 1 ⇒ 𝑓(1) = − 2 + 𝐶 1
Mà 𝑓(1) = − ⇒ 𝐶 = 0 2 1 1 1 1 ⇒ 𝑓(𝑥) = − = − = − + 𝑥2 + 𝑥 𝑥(𝑥 + 1) 𝑥 𝑥 + 1 1 1 1 1 1 1 2022
⇒ 𝑓(1) + ⋯ + 𝑓(2022) = −1 + − + − ⋯ − + = −1 + = − 2 2 3 2022 2023 2023 2023
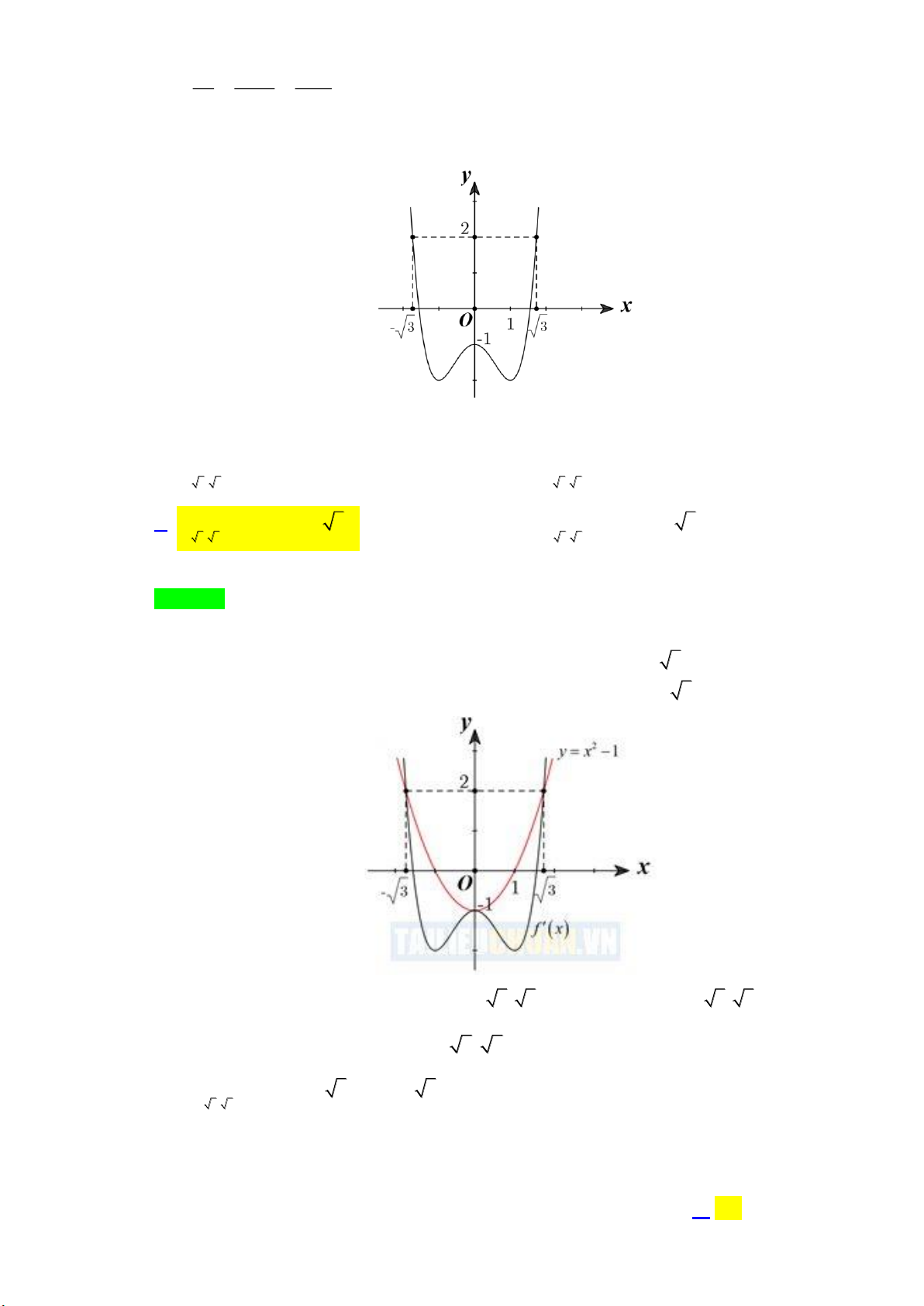
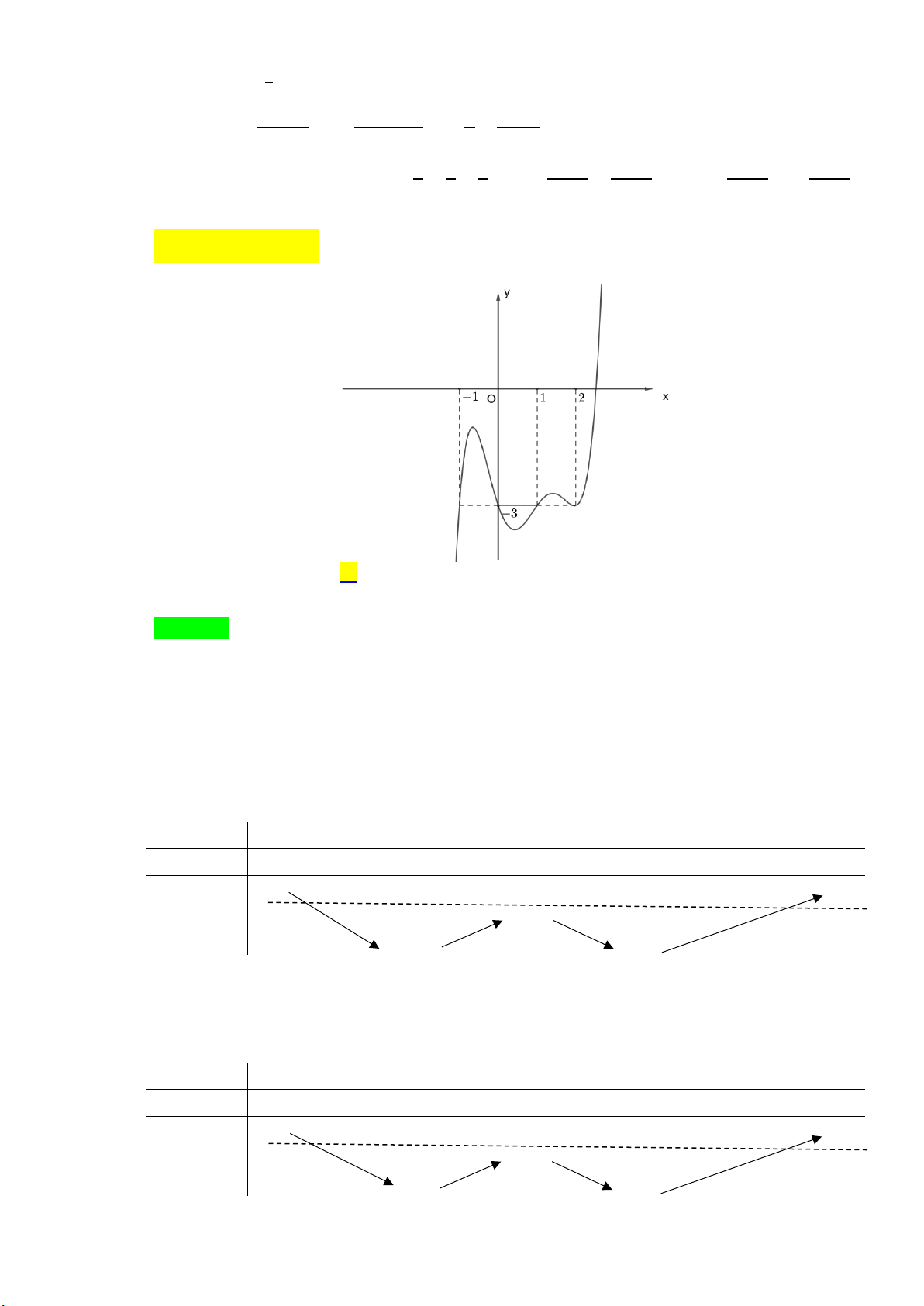
Câu 44: Cho hàm số 𝑦 = 𝑓(𝑥) thỏa mãn 𝑓(𝑥) < 0. Đồ thị hàm số 𝑦 = 𝑓′(𝑥) cho bởi hình vẽ bên.
Biết lim f (x) = + . Gọi 𝑚, 𝑛 lần lượt là số điểm cực đại, số điểm cực tiểu của hàm số x→
𝑔(𝑥) = |𝑓(|𝑥|) + 3|𝑥||. Giá trị của 𝑚𝑛 là: A. 4. B. 8. C. 27. D. 16. Lời giải Chọn B .
Xét ℎ(𝑥) = 𝑓(𝑥) + 3𝑥
ℎ′(𝑥) = 𝑓′(𝑥) + 3 = 0 ⇔ 𝑓′(𝑥) = −3 𝑥 = −1
[ 𝑥 = 0 (do nghiệm 𝑥 = 2 tiếp xúc nên không là cực trị) 𝑥 = 1
ℎ(𝑥) có 3 cực trị: 2 cực tiểu tại {−1; 1} và 1 cực đại tại 0.
Ta có bảng biến thiên của ℎ(𝑥): x −∞ −1 0 1 2 +∞ ℎ′(𝑥) − 0 + 0 − 0 + 0 + +∞ +∞ ℎ(𝑥) ℎ(0) ℎ(−1) ℎ(1)
Do ℎ(0) = 𝑓(0) + 3 × 0 = 𝑓(0) < 0 nên ℎ(0) = 0 có 2 nghiệm duy nhất (1 nghiệm âm, 1 nghiệm dương)
Lấy đối xứng qua trục Oy, ta có bảng biến thiên đồ thị hàm ℎ(|𝑥|) = 𝑓(|𝑥|) + 3|𝑥| như sau: x −∞ −1 0 1 2 +∞ ℎ′(𝑥) − 0 + 0 − 0 + 0 + +∞ +∞ ℎ(𝑥) ℎ(0) ℎ(1) ℎ(1) 2 cực tiểu tại − 1; 1
Hàm ℎ(|𝑥|) 3 cực trị gồm: { 1 cực đại tại 0
Lấy đối xứng qua trục Ox, ta có bảng biến thiên hàm 𝑔(𝑥) = |ℎ(|𝑥|)| = |𝑓(|𝑥|) + 3|𝑥|| như sau: x −∞ −1 0 1 2 +∞ ℎ′(𝑥) − 0 − 0 + 0 + + 0 + + h( ) 1 h( ) 1 h ( x) h(0) .
Hàm h ( x ) ó 5 cực trị.
Vậy m = 2; n = 3 nên n 3 m = 2 = 8.
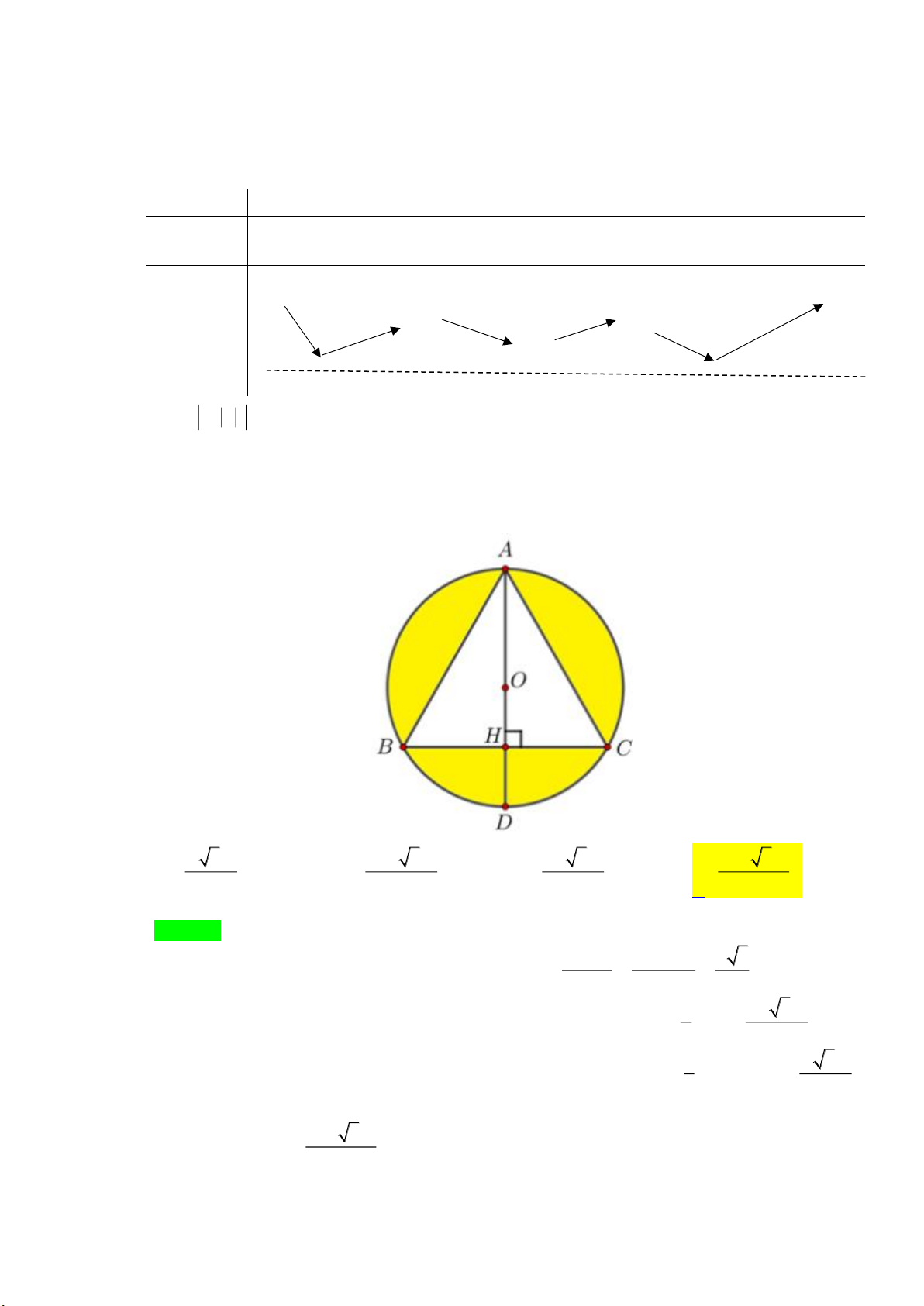
Câu 45: Cho tam giác ABC đều cạnh a nội tiếp đường tròn tâm O , AD là đường kính của đường
tròn tâm O . Thể tích của khối nón xoay được tạo thành khi cho phần tô đậm quay quanh
đường thẳng AD bằng 3 3a 3 20 3a 3 4 3a 3 23 3a A. 24 . B. 217 . C. 27 . D. 216 . Lời giải Chọn D. Bán kính đườ BC a a 3
ng tròn ngoại tiếp tam giác ABC là R = = = 0 2sin A 2sin 60 3 3 Khi quay quanh đườ 4 4 3a
ng thẳng AD thì thể tích hình cầu tạo thành : 3 V = R = 1 3 27 3 Khi quay quanh đườ 1 3a
ng thẳng AD thì thể tích khối nón tạo thành : 2
V = .BH .AH = 2 3 24
Thể tích của khối nón xoay được tạo thành khi cho phần tô đậm quay quanh đường thẳng 3 23 3a
AD bằng: V −V = . 1 2 216 2 cos x − 6
Câu 46: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn 1 − 0;1
0 để hàm số y = 3cos x − m
nghịch biến trên khoảng 0; 3 B. 15 . B. 17 . C. 16 . D. 18 . Lời giải Chọn D. Đặ 1
t t = cos x , với x 0; t ;1 3 2
Do y = cos x nghịch biến trên 0;
nên yêu cầu bài toán trở thành tìm m để hàm số 3 − 1
y = f (t ) 2t 6 = ;1 . 3t − đồng biến trên m 2 − Khi đó m
y = f (t ) 2t 6 = D = 3t −
là hàm số có tập xác định \ m 3 1
Vậy hàm số đồng biến trên khoảng ;1 khi và chỉ khi 2 − + f (t) 2m 18 1 = ( t − m + m 3t − m) 0, ;1 2 2 18 0 9 2 3 3 . m ;3 m ;3 m 1 ;1 2 2 3 2
Vì m nguyên và m thuộc đoạn 1 − 0;1
0 nên ta có 18 giá trị nguyên của m .
Câu 47: Cho hàm số f ( x) có đạo hàm liên tục trên , thỏa mãn 2 f ( x) + xf '( x) = 3x +10, x 4 ln (2 + f (x)) và f ( ) 1 = 6 Biết
dx = a ln 5 + b ln 6 + c ln 2 + 3
với a, b, c là các số 2 ( ) f x − 6 f x + 9 1 − ( ) ( )
hữu tỉ. Giá trị của biểu thức T = a + b + c thuộc khoảng nào sau đây? A. (1; 2) . B. (2;3). C. (0 ) ;1 . D. ( 1 − ;0) . Lời giải Chọn C
2 f ( x) + xf '( x) = 3x +10 2xf ( x) 2 + x f '(x) 2 = 3x +10x (x f (x))' 2 2 = 3x +10x 2 x f (x) 3 2
= x + 5x + C Vì f ( )
1 = 6 C = 0 f ( x) = x + 5 (thỏa mãn giả thiết) 4 ln (2 + x + 5) I = − ( dx x + 2)2 1 u = ( + x+ ) 1 1 ln 2 5 du = . dx + + + Đặ 2 x 5 2 x 5 t 1 dv = − + ( = + = x + ) dx 1 x 1 2 v 1 2 x + 2 x + 2 x +1 + I = ( + x+ ) 4 4 x 1 1 ln 2 5 − . dx x + 2 1 − x + 2 + + + 1 − 2 x 5 (2 x 5 ) 4 4 5 x + 5 − 2 1 5 x + 5 − 2 − = − dx = − ( x+ ) 3 5 t 2 ln 5 . ln 5 . 5 dx = ln 5 − dt 2 6 x + 2 + + − − 2 x 5 6 x 2 6 t 3 1 1 − 2 5 1 3 2 t − 3 3 5 1 1 2 = ln 5 − ln t − 3 + ln = ln 5 − ln 6 + ln ( 3 + 2). 6 2 2 2 3 t + 3 2 6 2 3 5 a = 6 1 2 b = −
a + b + c = . 2 3 1 c = 3 − Câu 48: Cho hàm số x x 3 f ( ) x = 2 − 2
+ 2022x . Biết rằng tồn tại số thực m sao cho bất phương trình
(4x − +37 )+ ( − −37).2x f mx m f x m
)0 nghiệm đúng với mọi x . Hỏi m thuộc khoảng nào dưới đây? A. (30;50) . B. (10;30) . C. (50;70) . D. ( 1 − 0;10). Lời giải Chọn A Xét hàm số x −x 3 f ( ) x = 2 − 2
+ 2022x có tập xác định D = . Ta có
Với mọi x D −x D và f (−x) −x x 3
= 2 − 2 − 2022x = − f (x) . Suy ra f (x) là hàm lẻ. −
Mặt khác f ( x) x x 2
= 2 ln 2 + 2 ln 2 + 6066x 0, x
. Suy ra hàm số f (x) là hàm đồng biến trên .
Bất phương trình đã cho tương đương
f (4x − mx + 37m) − f ( x − m − 37).2x )
f (4x − mx +37m) f (−(x − m−37).2x )
4x − mx + 37m −(x − m −37).2x
4x − mx + 37m −(x − m −37).2x
(2x − m)(x + 2x −37) 0. Xét phương trình 2x x +
− 37 = 0 . Nhận xét phương trình có một nghiệm x = 5. Xét hàm số ( ) = +2x g x x
−37, có ( ) =1+ 2x g x ln 2 0, x
suy ra x = 5 là nghiệm đơn duy nhất.
Suy ra g ( x) đổi dấu từ âm sang dương khi qua nghiệm x = 5.
Ta cũng có hàm số hàm số ( ) = 2x h x
− m đồng biến trên nên từ giả thiết bất phương trình (2x − )( +2x m x
− 37) 0 nghiệm đúng với mọi x ta có ( ) = 2x h x
− m đổi dấu từ âm
sang dương khi x qua điểm x = 5. Do đó h(5) = 0 hay m = 32. 0
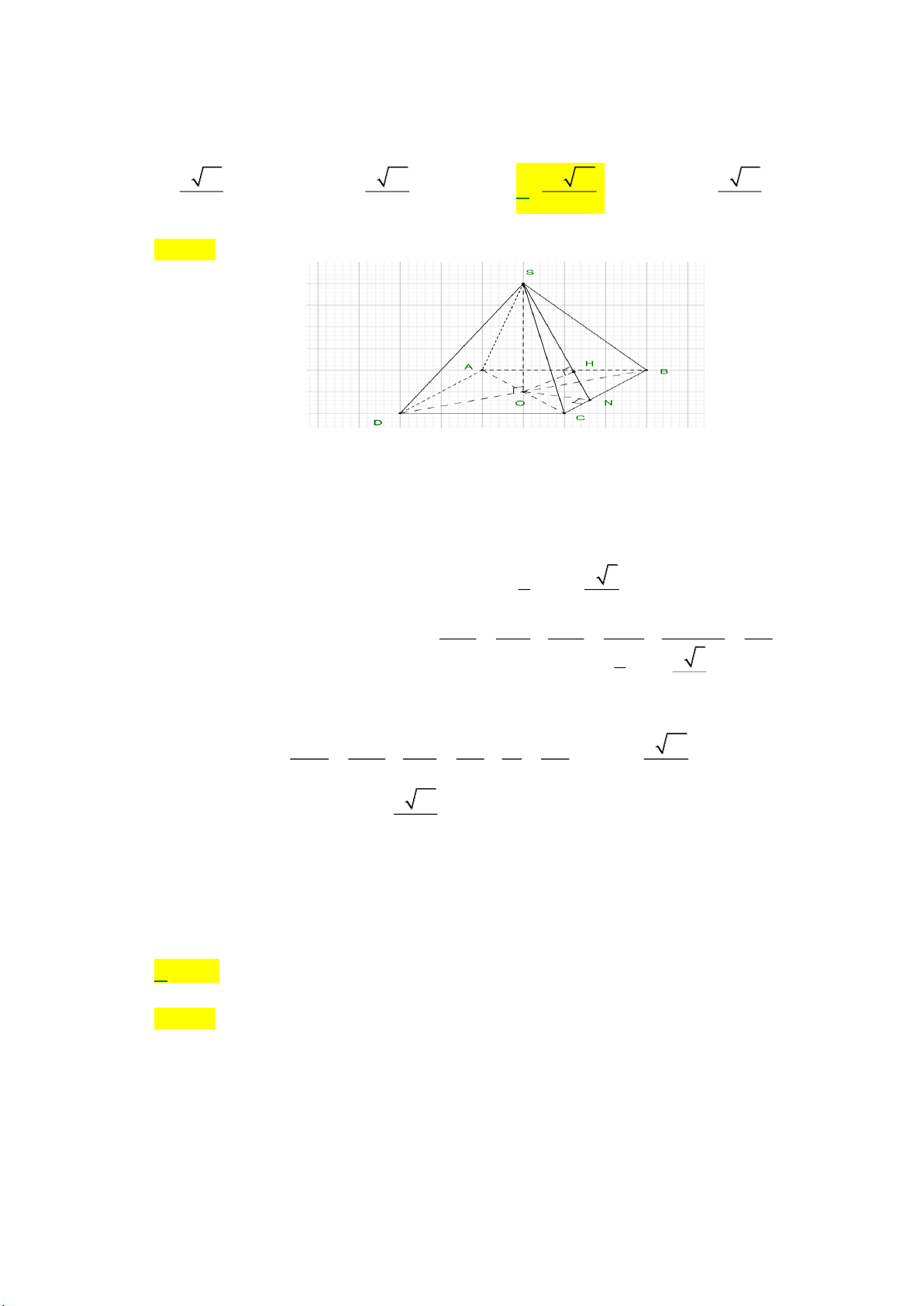
Câu 49: Cho hình chóp S ABCD có đáy S.ABCD là hình thoi tâm O , cạnh a , góc BAD = 60 ,
đường thẳng SO vuông góc với = ( ABCD) và SO
a . Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng a 21 a 57 2a 57 a 21 A. . B. . C. . D. . 7 19 19 14 Lời giải Chọn C
Gọi N , H lần lượt là hình chiếu của O lên BC, SN .
Ta có AC = 2OC d ( ,
A (SBC)) = 2d ( ,
O (SBC)) = 2OH ( ) 1 . O H ⊥ SN Vì ⊥ OH ⊥ BC
(BC ⊥ON BC ⊥ SO (SO ⊥(ABCD)) BC
(ABCD)) OH (SBC) , , , , a a 3 Do góc BAD 60 =
nên tam giác BAD đều OB = , OA = = OC . 2 2 1 1 1 1 1 16
Tam giác OBC vuông tại O nên ta có = + = + = . 2 2 2 2 2 2 ON OB OC a 3 a 3 a 2 2
Tam giác SON vuông tại O nên ta có 1 1 1 16 1 19 a 57 = + = + = OH = 2 . 2 2 2 2 2 2 ( ) OH ON OS 3a a 3a 19
Từ (1) và (2) d ( A (SBC)) 2 57 , = . 19
Câu 50: Cho khối chóp S.ABCD với đáy ABCD là hình bình hành, có thể tích bằng 3
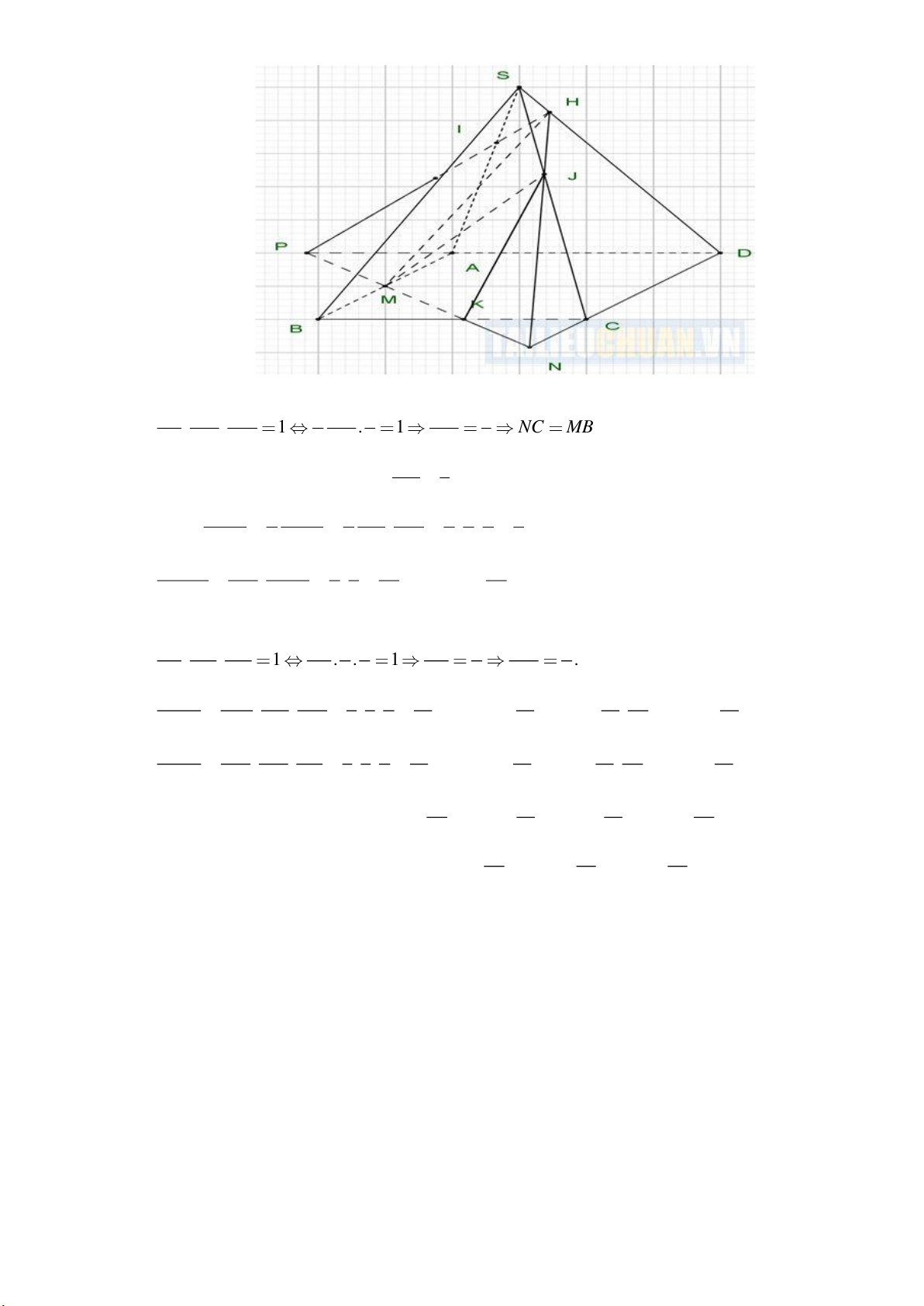
84a . Gọi M là
trung điểm của AB ; J thuộc cạnh SC sao cho JC = 2JS; H thuộc cạnh SD sao cho
HD = 6HS . Mặt phẳng (MHJ ) chia khối chóp thành 2 phần. Thể tích khối đa diện của phần
chứa đỉnh S bằng A. 3 17a . B. 3 19a . C. 3 24a . D. 3 21a . Lời giải Chọn A
Ta có 3 điểm N, H, J thẳng hang. Theo định lý Menelaus ta có JS NC HD 1 NC 6 NC 1 . . 1 . 1 NC MB . JC ND HS 2 ND 1 ND 3 PA 1
K là trung điểm của BC = . PD 3 S 1 S 1 DP DN 1 3 3 9 Ta có D NP D NP = = . = . . = . S 2 S 2 DA DC 2 2 2 8 ABCD DCA V HD S 6 9 27 27 HPND = . D NP = . = V = V HPND S. V SD S 7 8 28 28 ABCD S.ABCD ABCD
Ta có 3 điểm S, I, A thẳng hàng. Áp dụng định lý Menelaus cho tam giác PHD ta có PI HS DA PI 1 2 PI 7 PI 7 . . 1 . . 1 . IH SD AP IH 7 1 IH 2 PH 9 V PM PA PI 1 1 7 7 7 7 27 1 PMAI = . . = . . = V = .V = . V = V . PMAI PNDH S.ABCD S. V PN PD PH 3 3 9 81 81 81 28 12 ABCD PNDH V NK NC NJ 1 1 7 7 7 7 27 1 NKCJ = . . = . . = V = V = . V = V . NKCJ NPDH S .ABCD S . V NP ND NS 3 3 9 81 81 81 28 12 ABCD NPDH 27 1 1 67
Thể tích của phần không chứa S là V − V − V = V . S . ABCD S . ABCD S . ABCD S . 28 12 12 84 ABCD 67 17 17
Thể tích của phần chứa đỉnh S là 3 3 V − V = V = .8a = 17a . S . ABCD S . ABCD S . 84 84 ABCD 84
_______________ HẾT _______________
Document Outline
- de-khao-sat-chat-luong-toan-12-dot-1-nam-2021-2022-so-gddt-thanh-hoa
- 28. Đề thi thử tốt nghiệp THPT năm 2021-2022 môn Toán - Sở Thanh Hóa lần 1 (File word có lời giải)-LigMgku6z-1648397573




