Đề khảo sát chất lượng Toán 12 lần 1 năm 2023 – 2024 trường THPT chuyên Thái Bình

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề khảo sát chất lượng môn Toán 12 lần 1 năm học 2023 – 2024 trường THPT chuyên Thái Bình, tỉnh Thái Bình

38 19 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

27 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
Trang 1/6 - Mã đề 123
SỞ GIÁO DỤC & ĐÀO TẠO THÁI BÌNH
TRƯỜNG THPT CHUYÊN THÁI BÌNH
ĐỀ KHẢO SÁT CHẤT LƯỢNG LỚP 12, LẦN THỨ 1
Môn: TOÁN
NĂM HỌC 2023 - 2024
ĐỀ CHÍNH THỨC
Thời gian: 90 phút (Không kể thời gian phát đề)
(Đề gồm 6 trang, 50 câu trắc nghiệm)
Họ và tên thí sinh:.............................................................................. SBD:.....................
Mã đề thi
123
Câu 1. Cho cấp số cộng
( )
n
u
có
2
3u =
và
3
6u =
. Công sai của cấp số cộng đó bằng
A.
. B.
1
2
. C. 3. D. 2.
Câu 2. Số tập con có hai phần tử của tập hợp gồm 10 phần tử là
A.
2
10
A
. B.
10
2
. C.
2
10
. D.
2
10
C
.
Câu 3. Kết luận nào sau đây về tính đơn điệu của hàm số
1
21
x
y
x
+
=
+
là kết luận đúng?
A. Hàm số đồng biến trên
1
\
2

−


.
B. Hàm số nghịch biến trên
1
\
2

−


.
C. Hàm số đồng biến trên các khoảng
1
;
2

−∞ −


và
1
;
2

− +∞


.
D. Hàm số nghịch biến trên các khoảng
1
;
2

−∞ −


và
1
;
2

− +∞


.
Câu 4. Cho hàm số
()
y fx=
có bảng biến thiên như sau:
Tổng số đường tiệm cận ngang và đường tiệm cận đứng của đồ thị hàm số đã cho là
A.
0
. B.
2
. C.
3
. D.
1
.
Câu 5. Chọn ngẫu nhiên đồng thời hai số từ tập hợp 17 số nguyên dương đầu tiên. Xác suất để chọn được hai
số lẻ bằng
A.
9
34
. B.
9
17
. C.
7
34
. D.
8
17
.
Câu 6. Cho khối chóp có đáy là hình vuông cạnh
a
và chiều cao bằng
4a
. Thể tích khối chóp đã cho bằng
A.
3
16a
. B.
3
4a
C.
3
4
3
a
. D.
3
16
3
a
.
Câu 7. Cho hàm số
( )
y fx=
có bảng biến thiên như sau:
Đồ thị hàm số
( )
( )
1
1
gx
fx
=
+
có tất cả bao nhiêu đường tiệm cận (đường tiệm cận đứng và đường tiệm
cận ngang)?
A.
2
. B.
0
. C.
1
. D.
3
.
Trang 2/6 - Mã đề 123
Câu 8. Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
B
,
2
AC SA a= =
và
( )
SA ABC⊥
. Khoảng
cách từ
A
đến mặt phẳng
( )
SBC
bằng
A.
23
3
a
. B.
2a
. C.
3a
. D.
a
.
Câu 9. Cho hình chóp
.
S ABC
có
SA
vuông góc với mặt đáy, tam giác
ABC
đều,
3
SA AB= =
. Góc giữa
SC
và mặt phẳng
(
)
ABC
bằng
A.
90°
. B.
30°
. C.
45°
. D.
60°
.
Câu 10. Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây.
Hàm số đó là hàm số nào?
A.
3
31
yx x=−−
. B.
42
1yx x=++
.
C.
21
1
x
y
x
−
=
−
. D.
1
1
x
y
x
+
=
−
.
Câu 11. Cho hàm số
( )
y fx=
liên tục trên
và có đạo hàm
( ) ( )( ) ( )
2
' 12 1fx x x x=+− −
. Điểm cực đại
của hàm số đã cho là
A.
1x = −
. B.
2x = −
. C.
1x =
. D.
2x =
.
Câu 12. Cho hàm số
(
)
y fx=
có bảng biến thiên như sau:
Số các giá trị nguyên của tham số
m
để phương trình
( )
fx m=
có 2 nghiệm phân biệt là
A.
4
. B.
2
. C.
3
. D.
1
.
Câu 13. Cho khối lăng trụ
.ABC A B C
′′′
có đáy
ABC
là tam giác đều cạnh bằng
1
. Biết thể tích khối lăng trụ
.ABC A B C
′′′
bằng
1
. Khoảng cách giữa hai mặt phẳng
( )
ABC
và
( )
ABC
′′′
bằng
A.
43
3
. B.
3
4
. C.
3
. D.
.
Câu 14. Cho hình lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy bằng
a
và cạnh bên bằng
2a
. Thể tích của
lăng trụ
.ABC A B C
′′′
bằng.
A.
3
3
6
a
B.
3
3
3
a
C.
3
3
2
a
D.
3
3
4
a
Câu 15. Cho hàm số
42
y ax bx c
=++
có đồ thị như hình vẽ bên. Mệnh
đề nào sau đây là đúng?
A.
0, 0ac><
.
B.
0, 0ac<>
.
C.
0, 0ac<<
.
D.
0, 0ac>>
.
Trang 3/6 - Mã đề 123
Câu 16. Cho hàm số
(
)
y fx=
có bảng biến thiên như sau:
Số nghiệm thực của phương trình
( )
2 30fx+=
là
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 17. Hàm số
42
21yx x=+−
có bao nhiêu điểm cực trị ?
A.
0
. B.
3
. C.
1
. D.
2
.
Câu 18. Cho khối chóp
.
S ABC
. Gọi
', ', 'ABC
lần lượt là trung điểm
,,SA SB SC
. Tỉ số thể tích
.'''
.
SABC
S ABC
V
V
bằng
bao nhiêu?
A.
1
16
. B.
1
6
. C.
3
8
. D.
.
Câu 19. Cho hàm số
( ) ( )
32
3 34yxmxmx=+− +− +
. Có bao nhiêu giá trị nguyên của tham số m để hàm số
đã cho đồng biến trên
( )
;−∞ +∞
?
A.
4
. B.
6
. C.
5
. D.
3
.
Câu 20. Hình chóp tứ giác có bao nhiêu mặt?
A.
6
. B.
7
. C.
4
. D.
5
.
Câu 21. Giá trị lớn nhất của hàm số
( )
y fx=
trên đoạn
[ ]
;ab
bằng
3
. Giá trị nhỏ nhất của hàm số
( )
() 5 2gx f x= −
trên đoạn
[ ]
;ab
bằng bao nhiêu?
A.
1
. B.
2
. C.
1−
. D.
3−
.
Câu 22. Cho hàm số
( )
y fx=
có bảng biến thiên như hình vẽ sau:
Giá trị cực tiểu của hàm số đã cho là
A.
0
. B.
4−
. C.
2
−
. D.
1
.
Câu 23. Cho hình lập phương
.ABCD A B C D
′′′′
có cạnh bằng
2a
. Khoảng cách giữa hai đường thẳng
AB
′
và
AD
′′
bằng
A.
2
2
a
. B.
3a
. C.
3
3
a
. D.
2a
.
Câu 24. Cho khối chóp ngũ giác
.S ABCDE
. Khi ta chia khối chóp này bằng hai mặt phẳng
( )
SAC
và
( )
SCE
thì sẽ được
A. 3 khối tứ diện. B. 4 khối chóp tam giác.
C. Hai khối chóp tam giác. D. 3 khối chóp tứ giác.
Câu 25. Đường tiệm cận đứng của đồ thị hàm số
21
1
x
y
x
−
=
−
là đường thẳng có phương trình là
A.
2x =
. B.
1x = −
. C.
1
2
x =
. D.
1x =
.
Câu 26. Có bao nhiêu cách xếp
4
người ngồi vào dãy
5
ghế xếp theo hàng ngang (mỗi ghế không ngồi quá
một người) ?
A.
120
. B.
20
. C.
9
. D.
10
.
Trang 4/6 - Mã đề 123
Câu 27. Cho hàm số
()y fx
=
xác định trên
và có bảng biến thiên như hình vẽ sau.
Hàm số đã cho đồng biến trên khoảng nào?
A.
( )
;1−∞ −
. B.
( )
2; 4−
. C.
( )
2; +∞
. D.
( )
1; 2−
.
Câu 28. Hàm số
( )
32
34
fx x x=−+
có đồ thị
( )
C
. Viết phương trình tiếp tuyến với
( )
C
tại điểm
A
nằm
trên
( )
C
có hoành độ
1
A
x =
.
A.
35
yx=−+
. B.
35yx
= −
. C.
53yx= −
. D.
53yx=−+
.
Câu 29. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông tâm
O
,
()SA ABCD⊥
. Gọi
I
là trung điểm
SC
. Khoảng cách từ
I
đến mặt phẳng
()ABCD
bằng độ dài đoạn thẳng nào sau?
A.
IB
. B.
IC
. C.
ID
. D.
IO
.
Câu 30. Hàm số nào liệt kê dưới đây có đồ thị như hình vẽ bên?
A.
42
32
yx x
=+−
.
B.
32
32yx x=−+ −
.
C.
32
32yx x=+−
.
D.
2
1
x
y
x
−
=
+
.
Câu 31. Điểm nào dưới đây thuộc đồ thị hàm số
32
3yx x= −
?
A.
( )
1; 4M −−
. B.
( )
1; 2M −−
. C.
( )
1; 2M −
. D.
( )
1; 4M −
.
Câu 32. Cho hàm số
( )
y fx=
có bảng biến thiên như sau:
Khẳng định nào sau đây đúng?
A.
[ ]
( )
3;2
max 2fx
−
=
. B.
[ ]
( )
3;2
max 2fx
−
= −
. C.
[ ]
( )
3;2
max 1
fx
−
=
. D.
[ ]
(
)
3;2
max 3fx
−
=
.
Câu 33. Cho hình lập phương
.' ' ' 'ABCD A B C D
. Tính góc giữa hai đường thẳng
''BD
và
'AA
.
A.
60°
. B.
45°
. C.
90°
. D.
30°
.
Câu 34. Một khối lập phương có thể tích bằng
8
. Độ dài cạnh của khối lập phương đó là
A.
512
. B.
22
. C.
8
. D.
2
.
Câu 35. Cho một cấp số nhân có số hạng đầu bằng công bội và số hạng thứ ba lớn hơn công bội 6 đơn vị. Số
hạng thứ hai của cấp số nhân này là
A.
2
. B.
6
. C.
4
. D.
1
.
Trang 5/6 - Mã đề 123
Câu 36. Cho hàm số
()y fx
=
là hàm đa thức bậc ba có đồ thị
như hình vẽ bên. Giá trị của
(1) (0)
ff
−
bằng
A.
4
−
. B.
2−
.
C.
6−
. D.
2
.
Câu 37. Cho khối lăng trụ
.' ' 'ABC A B C
có thể tích bằng
12
. Thể tích khối chóp
'.A ABC
bằng
A.
6
. B.
4
. C.
3
. D.
12
.
Câu 38. Hàm số nào sau đây nghịch biến trên
?
A.
32
3 35
yx x x=−+ − +
. B.
( )
2
1yx=−+
.
C.
1
1
x
y
x
+
=
−
. D.
2
1yx=−−
.
Câu 39. Giá trị nhỏ nhất của hàm số
42
43yx x=−+ −
trên đoạn
[ ]
1;3−
bằng
A.
1
. B.
48−
. C.
0
. D.
50−
.
Câu 40.
Cho hàm số đa thức bậc bốn
( )
y fx=
có đồ thị như hình vẽ bên
Số điểm cực đại của hàm số
( ) ( )
2
gx f x=


là
A.
5
. B.
2
.
C.
4
. D.
3
.
Câu 41. Cho khối chóp
.
S ABC
có
17SA SB SC a= = =
,
3, 5AB a BC a= =
và
7CA a=
. Thể tích của khối
chóp
.S ABC
bằng
A.
3
52
4
a
. B.
3
15 2
4
a
. C.
3
5 17
4
a
. D.
3
15 17
4
a
.
Câu 42. Có bao nhiêu giá trị nguyên của tham số
(
]
;2023m∈ −∞
sao cho hàm số
32
( 2) 9yx m x m= + + +−
nghịch biến trên khoảng
( )
0;1
?
A.
2019
. B.
2023
. C.
2020
. D.
2022
.
Câu 43. Cho hàm số
( )
32
3 5.fx x x=−+
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
( )
( )
21f fx m−=
có 3 nghiệm phân biệt?
A. 3. B. 486. C. 484. D. 485.
Câu 44. Cho hàm số
( )
( )
32 2
3 3 22fx x x m m xm=− + −+ +
(với
m
là tham số) có giá trị lớn nhất trên
[ ]
1;1−
bằng
2
, khi đó tổng các giá trị của tham số
m
là
A.
2
3
. B.
5
3
. C. 0. D.
7
3
.
Trang 6/6 - Mã đề 123
Câu 45. Cho hàm số
(
)
y fx=
có đạo hàm
( ) ( )( )
2
2
94fx xx x
′
= −−
. Khi đó hàm số
( )
2
()gx f x=
nghịch
biến trên khoảng nào?
A.
( )
3; 0−
. B.
( )
2; 2−
. C.
( )
;3−∞ −
. D.
( )
3; +∞
.
Câu 46. Cho hình lập phương
.ABCD A B C D
′′′′
có
,,M NO
lần lượt là trung điểm của
,,AB A D BD
′′ ′
(tham khảo hình
bên). Biết khối lập phương
.ABCD A B C D
′′′′
có thể tích là
3
a
. Thể tích của khối tứ diện
ODMN
là
A.
3
16
a
. B.
3
3
8
a
.
C.
3
3
16
a
. D.
3
6
a
.
Câu 47. Có bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
[ ]
2;3−
để hàm
số
32
3
(2 3) 2
2
yx m x m= − − ++
có cực đại và cực tiểu đồng thời hoành độ điểm cực tiểu nhỏ hơn 2 ?
A. 4. B. 6. C. 5. D. 3.
Câu 48. Tìm tất cả các giá trị của tham số
m
để đồ thị hàm số
( ) ( )
322 2
2 21 1y x mx m x m m=− + −+ −
cắt
trục hoành tại 3 điểm phân biệt có hoành độ dương.
A.
1m <
. B.
23
3
m >
. C.
23
1
3
m<<
. D.
23
1
3
m≤<
.
Câu 49.
Cho hàm số
( )
y fx=
xác định trên
và có đồ thị
( )
fx
′
như hình
bên. Giá trị nhỏ nhất của hàm số
( ) (
)
2 21gx f x x= −+
trên
1
;1
2

−


bằng
A.
( )
1f
. B.
( )
12f −+
.
C.
( )
01f −
. D.
( )
21f
−
.
Câu 50. Có bao nhiêu giá trị nguyên của tham số
m
sao cho đồ thị của hàm số
42
22y x mx=−+
có ba điểm
cực trị
,,ABC
thỏa mãn diện tích tam giác
ABC
nhỏ hơn
2023
?
A.
21
. B.
15
. C.
2023
. D.
44
.
------------- HẾT -------------
ĐÁP ÁN CÁC MÃ ĐỀ
MÔN TOÁN - LỚP 12
NĂM HỌC 2023 - 2024
------------------------
Mã đề [123]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
C
D
D
C
A
C
D
A
C
D
A
C
A
C
C
D
C
D
A
D
C
B
D
A
D
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
A
D
A
D
C
A
D
C
D
C
B
B
A
B
B
A
C
D
B
C
A
C
C
D
A
Mã đề [234]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
D
C
B
B
C
C
C
A
D
D
B
C
B
C
A
B
D
A
A
A
A
D
C
B
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
A
A
C
B
C
A
C
B
B
D
B
D
C
D
D
B
B
C
B
B
D
D
A
C
C
Mã đề [345]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
B
A
A
B
C
D
B
D
C
A
D
C
A
B
B
D
B
B
C
C
B
D
A
D
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
B
A
A
D
D
B
A
A
B
B
C
B
D
B
B
B
D
B
D
A
A
D
C
A
D
Mã đề [456]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
D
B
C
A
B
C
A
A
A
A
D
B
B
A
C
A
D
B
A
D
C
C
A
D
D
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
A
D
B
B
B
D
B
A
A
D
B
D
B
C
D
B
B
A
D
A
C
D
B
A
A
HƯỚNG DẪN GIẢI
Câu 1. Cho cấp số cộng
( )
n
u
có
2
3u =
và
3
6u
=
. Công sai của cấp số cộng đó bằng
A.
1
3
. B.
1
2
. C. 3. D. 2.
Lời giải
Chọn C
Ta có công sai:
32
633du u= − =−=
.
Câu 2. Số tập con có hai phần tử của tập hợp gồm 10 phần tử là
A.
2
10
A
. B.
10
2
. C.
2
10
. D.
2
10
C
.
Lời giải
Chọn D
Số tập con có hai phần tử của tập hợp gồm 10 phần tử là tổ hợp chập 2 của 10:
2
10
C
Câu 3. Kết luận nào sau đây về tính đơn điệu của hàm số
1
21
x
y
x
+
=
+
là kết luận đúng?
A. Hàm số đồng biến trên
1
\
2

−


.
B. Hàm số nghịch biến trên
1
\
2

−


.
C. Hàm số đồng biến trên các khoảng
1
;
2

−∞ −


và
1
;
2

− +∞


.
D. Hàm số nghịch biến trên các khoảng
1
;
2

−∞ −


và
1
;
2

− +∞


.
Lời giải
Chọn D
Tập xác định:
2
\
1−



.
Ta có
(
)
2
1
'0
21
y
x
−
= <
+
,
2
\
1
x
−

∀∈


.
Câu 4. Cho hàm số
()y fx=
có bảng biến thiên như sau:
Tổng số đường tiệm cận ngang và đường tiệm cận đứng của đồ thị hàm số đã cho là
A.
0
. B.
2
. C.
3
. D.
1
.
Lời giải
Chọn C
( )
lim 2
x
fx
→+∞
=
ta được tiệm cận ngang
2y =
( )
lim 5
x
fx
→−∞
=
ta được tiệm cận ngang
5y
=
( )
( )
1
lim
x
fx
+
→−
= +∞
ta được tiệm cận đứng
1x = −
Câu 5. Chọn ngẫu nhiên đồng thời hai số từ tập hợp 17 số nguyên dương đầu tiên. Xác suất để chọn được
hai số lẻ bằng
A.
9
34
. B.
9
17
. C.
7
34
. D.
8
17
.
Lời giải
Chọn A
Số phần tử của không gian mẫu
(
)
2
17
136nCΩ= =
.
Gọi A là biến cố: “chọn được 2 số lẻ”.
Vậy
( )
2
9
36nA C= =
Vậy xác suất cần tìm là:
( )
36 9
.
136 34
PA= =
Câu 6. Cho khối chóp có đáy là hình vuông cạnh
a
và chiều cao bằng
4a
. Thể tích khối chóp đã cho bằng
A.
3
16a
. B.
3
4a
. C.
3
4
3
a
. D.
3
16
3
a
.
Lời giải
Chọn C
Áp dụng công thức
1
3
V Bh=
.
Suy ra
23
14
.4
33
V aa a
= =
.
Câu 7. Cho hàm số
( )
y fx=
có bảng biến thiên như sau
Đồ thị hàm số
( )
( )
1
1
gx
fx
=
+
có tất cả bao nhiêu đường tiệm cận( đường tiệm cận đứng và đường
tiệm cận ngang)?
A.
2
. B.
0
. C.
1
. D.
3
.
Lời giải
Chọn D
Ta có
( )
( )
1
lim lim 0
1
xx
gx
fx
→+∞ →+∞
= =
+
và
( )
( )
1
lim lim 0
1
xx
gx
fx
→−∞ →−∞
= =
+
suy ra TCN
0y =
.
Lại có
( ) ( )
10 1fx fx+= ⇔ =−
có 2 nghiệm phân biệt suy ra có 2 đường tiệm cận đứng.
Vậy đồ thị hàm số
( )
( )
1
1
gx
fx
=
+
có tất cả 3 đường tiệm cận.
Câu 8. Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
B
,
2AC SA a
= =
và
( )
SA ABC⊥
. Khoảng
cách từ
A
đến mặt phẳng
( )
SBC
bằng
A.
23
3
a
. B.
2a
. C.
2a−
. D.
a
.
Lời giải
Chọn A
Ta có
(
)
( )
(
)
,
BC AB
BC SA do SA ABC BC ABC
⊥
⊥⊥ ⊂
( )
BC SAB⇒⊥
Gọi
H
là hình chiếu của
A
lên cạnh
SB
.
Suy ra
( ) ( )
( )
,
AH SB
AH BC do BC SAB AH SAB
⊥
⊥ ⊥⊂
( )
AH SCD⇒⊥
Vậy
AH
là khoảng cách từ điểm
A
đến mặt phẳng
( )
SBC
Xét tam giác
SAB
vuông tại
A
có
AH
là đường cao
22 2
1 11
AH SA AB
⇒=+
Mà
22222 2
2AC AB BC AB AB AB=+=+=
2
2
22
AC a
AB a
⇒= ==
2222
1 11 3
424AH a a a
⇒ =+=
23
3
a
AH⇒=
Vậy khoảng cách từ
A
tới mặt phẳng
( )
SBC
bằng
23
3
a
.
H
C
B
A
S
Câu 9. Cho hình chóp
.S ABC
có
SA
vuông góc với mặt đáy, tam giác
ABC
đều,
3SA AB= =
. Góc
giữa
SC
và mặt phẳng
( )
ABC
bằng
A.
90°
. B.
30°
. C.
45
°
. D.
60
°
.
Lời giải
Chọn C
Ta có
( )
SA ABC⊥
⇒
AC
là hình chiếu của
SC
lên mặt phẳng
( )
ABC
.
Suy ra
( )
( )
( )
,,SC ABC SC AC SCA= =
Ta lại có tam giác
ABC
đều
⇒
3
AC AB SA= = =
⇒
SAC∆
vuông cân tại
A
⇒
45SCA = °
Vậy góc giữa
SC
và mặt phẳng
(
)
ABC
bằng
45°
.
Câu 10. Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
A.
3
31yx x=−−
. B.
42
1yx x=++
. C.
21
1
x
y
x
−
=
−
. D.
1
1
x
y
x
+
=
−
.
Lời giải
Chọn D
Đồ thị là của hàm số phân thức
⇒
loại
A
và
B
.
Từ đồ thị ta có đường tiệm cận ngang
1y =
và đường tiệm cận đứng
1x =
⇒
loại
C
.
Vậy đồ thị trên là của hàm số
1
1
x
y
x
+
=
−
.
Câu 11. Cho hàm số
( )
y fx=
liên tục trên
và có đạo hàm
( ) ( )(
) ( )
2
1 2 1.fx x x x
′
=+− −
Điểm cực đại
của hàm số đã cho là
A.
1x = −
. B.
2x = −
. C.
1x =
. D.
2x =
.
C
B
A
S
6
4
2
2
4
5
Lời giải
Chọn A
Ta có:
( ) ( )( ) ( )
2
12 1fx x x x
′
=+− −
, suy ra
( ) ( )
2
10
1
0 2 0 2.
1
10
x
x
fx x x
x
x
+=
= −
′
=⇔ − =⇔=
=
−=
Bảng biến thiên:
Từ bảng biến thiên, suy ra điểm cực đại của hàm số đã cho là
1.x = −
Câu 12. Cho hàm số
( )
y fx=
có bảng biến thiên như sau:
Số các giá trị nguyên của tham số
m
để phương trình
( )
fx m=
có
2
nghiệm phân biệt là
A.
4
. B.
2
. C.
3
. D.
1
.
Lời giải
Chọn C
Để phương trình
( )
fx m=
có hai nghiệm phân biệt khi và chỉ khi đường thẳng
ym=
cắt đồ thị
hàm số
( )
y fx=
tại hai giao điểm.
Từ bảng biến thiên, suy ra:
{ }
3
0;1; 3 .
11
m
m
m
m
∈
=
→ ∈
−< ≤
Câu 13. Cho khối lăng trụ
.ABC A B C
′′′
có đáy
ABC
là tam giác đều cạnh bằng
1
. Biết thể tích khối lăng
trụ
.ABC A B C
′′′
bằng
1.
Khoảng cách giữa hai mặt phẳng
( )
ABC
và
( )
ABC
′′′
bằng
A.
43
3
. B.
3
4
. C.
3
. D.
1
3
.
Lời giải
Chọn A
Vì
ABC∆
đều cạnh
1
nên
2
13 3
.
44
ABC
S
∆
= =
Ta có:
( ) ( )
( )
,.d ABC A B C h
′′′
=
Ta có:
.
.
1 43
.
3
3
4
ABC A B C
ABC A B C ABC
ABC
V
V S hh
S
′′′
′′′
∆
∆
= ⋅⇒= = =
Câu 14. Cho lăng trụ tam giác đều
.ABC A B C
′′′
có cạnh đáy bằng
a
và cạnh bên bằng
2.a
Thể tích của
lăng trụ
.ABC A B C
′′′
bằng
A.
3
3
6
a
. B.
3
3
3
a
. C.
3
3
2
a
. D.
3
3
4
a
.
Lời giải
Chọn C
Vì
.ABC A B C
′′′
là lăng trụ tam giác đều có cạnh đáy bằng
a
và cạnh bên bằng
2a
nên lăng trụ đã
cho có:
2
3
.
4
2
ABC
a
S
h AA a
∆
=
′
= =
Vậy thể tích của lăng trụ
.
ABC A B C
′′′
bằng
23
.
33
2.
42
ABC A B C ABC
aa
V Sh a
′′′
∆
= ⋅= ⋅ =
Câu 15. Cho hàm số
42
y ax bx c
=++
có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng?
A.
0, 0ac
><
. B.
0, 0ac<>
. C.
0, 0ac<<
. D.
0, 0ac>>
.
Lời giải
Chọn A
Dựa vào đồ thị hàm số đã cho ta có:
Khoảng ngoài cùng đồ thị hàm số đi xuống nên hàm số nghịch biến, suy ra:
0.a
<
Đồ thị hàm số giao với
Oy
tại điểm
( )
0;c
, từ đồ thị suy ra
0.c <
Câu 16. Cho hàm số
( )
y fx=
có bảng biến thiên như sau:
Số nghiệm thực của phương trình
( )
2 30fx+=
là
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn D
Ta có phương trình
( ) ( )
3
2 30
2
fx fx+=⇔ =−
.
Số nghiệm của phương trình
( )
2 30fx+=
là số giao điểm
( )
y fx=
và đường thẳng
3
2
y
= −
.
Vậy phương trình
( )
2 30fx+=
có 4 nghiệm phân biệt.
Câu 17. Hàm số
42
21
yx x
=+−
có bao nhiêu điểm cực trị ?
A.
0
. B.
3
. C.
1
. D.
2
.
Lời giải
Chọn C
Ta hàm số dạng
42
y ax bx c=++
có
. 20ab
= >
. Vậy hàm số có 1 điểm cực trị.
Câu 18. Cho khối chóp
.S ABC
. Gọi
', ', 'ABC
lần lượt là trung điểm
,,SA SB SC
. Tỉ số thể tích
.
.
S ABC
S ABC
V
V
′′′
bằng bao nhiêu?
A.
1
16
. B.
1
6
. C.
3
8
. D.
1
8
.
Lời giải
Chọn D
Ta có
.
.
1
..
8
S ABC
S ABC
V
SA SB SC
V SA SB SC
′′′
′′′
= =
.
Câu 19. Cho hàm số
( ) ( )
32
3 34yxmxmx=+− +− +
. Có bao nhiêu giá trị nguyên của tham số
m
để hàm
số đã cho đồng biến trên
( )
;−∞ +∞
?
A.
4
. B.
6
. C.
5
. D.
3
.
Lời giải
Chọn A
Ta có
( )
2
3 2 3 30y x m xm x
′
= + − + −≥∀∈
Hay
( ) ( )
2
3 3 3 0 0 33 3 6mm m m
′
∆= − − − ≤ ⇔ ≤ − ≤ ⇔ ≤ ≤
.
Do
m
nguyên nên có 4 giá trị
m
thỏa mãn.
Câu 20. Hình chóp tứ giác có bao nhiêu mặt?
A.
6
. B.
7
. C.
4
. D.
5
.
Lời giải
Chọn D
Hình chóp tứ giác có 5 mặt.
Câu 21. Giá trị lớn nhất của hàm số
( )
y fx=
trên
[
]
;ab
bằng 3. Giá trị nhỏ nhất của hàm số
(
) (
)
52
gx f x= −
trên đoạn
[ ]
;ab
bằng bao nhiêu?
A.
1
. B.
2
. C.
1−
. D.
3−
.
Lời giải
Chọn C
Ta có:
( )
( )
52
gx f x
= −
.
Suy ra
( )
gx
đạt GTNN khi
( )
fx
đạt GTLN
[ ]
( )
[ ]
(
)
;
;
min 5 2 max 5 2.3 1
ab
ab
gx f x
⇒ =− =−=−
.
Câu 22. Cho hàm số
( )
y fx=
có bảng biến thiên như hình vẽ sau:
Giá trị cực tiểu của hàm số đã cho là
A.
0
. B.
4
−
. C.
2−
. D.
1
.
Lời giải
Chọn B
Quan sát BBT của hàm số
( )
y fx=
suy ra giá trị cực tiểu của
( )
fx
là
4−
.
Câu 23. Cho hình lập phương
.' ' ' 'ABCD A B C D
có cạnh bằng
2a
. Khoảng cách giữa hai đường thẳng
'AB
và
''AD
bằng
A.
2
2
a
. B.
3a
. C.
3
3
a
. D.
2a
.
Lời giải
Chọn D
Do
''' '
ABC D
là hình bình hành nên
' '/ / ' '
AD BC
Gọi
O
là tâm hình vuông
''A B BA
. Khi đó:
( ) (
)
(
)
( )
( )
' ', ' ' ', ' ' ', ' ' ' 2d A D AB d A D AB C D d A AB C D A O a= = = =
.
Câu 24. Cho khối chóp ngũ giác
.S ABCDE
. Khi ta chia khối chóp này bằng hai mặt phẳng
( )
SAC
và
( )
SCE
thì sẽ được
A.
3
khối tứ diện. B.
4
khối chóp tam giác.
C.
2
khối chóp tam giác. D.
3
khối chóp tứ giác.
Lời giải
Chọn A
Khi chia khối chóp ngũ giác
.S ABCDE
bằng hai mặt phẳng
( )
SAC
và
( )
SCE
ta thu được ba khối
tứ diện:
,,SACE SABC SCDE
.
Câu 25. Đường tiệm cận đứng của đồ thị hàm số
21
1
x
y
x
−
=
−
là đường thẳng có phương trình là
A.
2
x =
. B.
1x = −
. C.
1
2
x =
. D.
1x =
.
Lời giải
Chọn D
Hàm số
21
1
x
y
x
−
=
−
có tiệm cận đứng là
1x =
.
Câu 26. Có bao nhiêu cách xếp 4 người ngồi vào dãy 5 ghế xếp theo hàng ngang(mỗi ghế không ngồi quá
một người)?
A. 120. B. 20. C. 9. D. 10.
Lời giải
Chọn A
Số cách xếp 4 người ngồi vào dãy 5 ghế xếp theo hàng ngang(mỗi ghế không ngồi quá một người)
là:
4
5
120A =
.
Câu 27. Cho hàm số
( )
y fx=
xác định trên
và có bảng biến thiên như hình vẽ sau
Hàm số đã cho đồng biến trên khoảng nào?
A.
( )
;1−∞ −
. B.
( )
2;4
−
. C.
(
)
2;
+∞
. D.
( )
1;2−
.
Lời giải
Chọn D
Câu 28. Hàm số
32
34fx x x

có đồ thị
(
)
C
. Viết phương trình tiếp tuyến với
( )
C
tại điểm
A
nằm
trên
C
có hoành độ
1
A
x =
.
A.
35yx=−+
. B.
35yx= −
. C.
53
yx= −
. D.
53yx=−+
.
Lời giải
Chọn A
1
A
x =
2
A
y⇒=
( )
1;2A⇒
.
2
36fx x x

.
Phương trình tiếp tuyến với
( )
C
tại điểm
A
là:

A AA
y fx xx y

35yx 
.
Câu 29. Cho hình chóp
.S ABCD
có đáy
ABCD
la hình vuông tâm
( )
,.O SA ABCD⊥
Gọi
I
là trung điểm
.SC
Khoảng cách từ
I
đến mặt phẳng
( )
ABCD
bằng độ dài đoạn thẳng nào ?
A.
IB
. B.
IC
. C.
ID
. D.
IO
.
Lời giải
Chọn D
Xét tam giác
SAC
có
,
IO
lần lượt là trung điểm các cạnh
;SC AC
IO⇒
là đường trung bình
SAC∆
.
IO
⇒
//
SA
.
Mà
(
)
SA ABCD⊥
nên
(
)
IO ABCD⊥
tại
.O
Do đó khoảng cách từ
I
đến mặt phẳng
( )
ABCD
.IO=
Câu 30. Hàm số nào liệt kê dưới đây có đồ thị như hình vẽ bên ?
A.
42
22yx x=+−
. B.
32
32yx x=−+ −
. C.
32
32yx x
=+−
. D.
2
1
x
y
x
−
=
+
.
Lời giải
Chọn C
Đồ thị hàm số trong hình vẽ là của hàm số bậc 3 với hệ số
0a >
.
Câu 31. Điểm nào dưới đây thuộc đồ thị hàm số
32
3yx x= −
?
A.
(
)
1; 4M −−
. B.
(
)
1; 2M −−
. C.
( )
1; 2M −
. D.
( )
1; 4M −
.
Lời giải
Chọn A
Xét điểm
( )
1; 4M −−
, thay
1; 4xy
=−=−
vào đồ thị hàm số
32
3yx x= −
ta được:
( ) ( )
32
4 1 31 4 4−=− − − ⇔−=−
(luôn đúng).
Vậy điểm
( )
1; 4M −−
thuộc đồ thị hàm số
32
3yx x= −
.
Câu 32. Cho hàm số
( )
y fx=
có bảng biến thiên như sau:
Khẳng định nào sau đây đúng?
A.
[ ]
( )
3;2
max 2fx
−
=
. B.
[ ]
( )
3;2
max 2fx
−
= −
. C.
[ ]
(
)
3;2
max 1fx
−
=
. D.
[ ]
(
)
3;2
max 3fx
−
=
.
Lời giải
Chọn D
Từ BBT,
[ ]
( )
( )
3;2
max 3 1fx f
−
= = −
.
Câu 33. Cho hình lập phương
.ABCD A B C D
′′′′
. Tính góc giữa hai đường thẳng
BD
′′
và
AA
′
.
A.
0
60
. B.
0
45
. C.
0
90
. D.
0
30
.
Lời giải
Chọn C
Ta có
(
)
( )
, 90
AA ABCD AA BD AA BD
′ ′′′′ ′ ′′ ′ ′′
⊥ ⇒⊥ ⇒ =°
.
Câu 34. Một khối lập phương có thể tích bằng
8
. Độ dài cạnh của khối lập phương đó là
A.
512
. B.
22
. C.
8
. D.
2
.
Lời giải
Chọn D
Giả sử, độ dài cạnh hình lập phương là
x
.
Ta có
3
82xx=⇔=
.
Câu 35. Cho một cấp số nhân có số hạng đầu bằng công bội và số hạng thứ ba lớn hơn công bội
6
đơn vị.
Số hạng thứ hai của cấp số nhân này là
A.
2
. B.
6
. C.
4
. D.
1
.
Lời giải
Chọn C
Giả sử cấp số nhân cần tìm có số hạng đầu
1
u
, công bội
q
.
Ta có
1
uq
=
.
Ta có
23
31
6 6 60 2u q uq q q q q−=⇔ −=⇔ −−=⇔=
.
Ta có
21
. 2.2 4u uq= = =
.
Câu 36. Cho hàm số
( )
y fx=
là hàm đa thức bậc ba có đồ thị như hình vẽ bên. Giá trị của
( ) ( )
10ff−
bằng
A.
4−
. B.
2−
. C.
6−
. D.
2
.
Lời giải
Chọn B
( ) ( ) ( )
1 0422ff− =−−− =−
.
Câu 37. Cho khối lăng trụ
.’’’ABC A B C
có thể tích bằng
12
. Thể tích khối chóp
’A ABC
bằng
A.
6
.
B.
4
.
C.
3
.
D.
12
.
Lời giải
Chọn B
'. . ' ' '
1
4
3
A ABC ABC A B C
VV
= =
.
Câu 38. Hàm số nào sau đây nghịch biến trên
R
A.
32
3 35yx x x=−+ − +
.
B.
( )
2
1yx=−+
.
C.
1
1
x
y
x
+
=
−
.
D.
2
1yx=−−
.
Lời giải
Chọn A
32 2
3 3 5 ' 3 6 30 1yx x x y x x x
=− + − +⇒ =− + −=⇒ =
là nghiệm kép
Nên
'0
yx≤ ∀∈
Câu 39. Giá trị nhỏ nhất của hàm số
42
43yx x=−+ −
trên đoạn
[ ]
1; 3−
bằng
A.
1
.
B.
48−
.
C.
0
.
D.
50−
.
Lời giải
Chọn B
Xét
[ ]
1; 3−
( )
42 3
0
4 3 '4 80 2
2
x
yx x y x x x
xL
=
=− + −⇒ =− + =⇒ =
= −
( )
10y −=
( )
3 48y = −
( )
21y =
Câu 40. Cho hàm số đa thức bậc bốn
( )
y fx=
có đồ thị như hình vẽ bên dưới. Số điểm cực đại của hàm
số
( ) ( )
2
gx f x=

là
A. 5. B. 2. C. 4. D. 3.
Lời giải
Chọn B
Xét
( ) ( ) ( )
( )
( )
0
2. 0
0
fx
xa xb
gx fxf x
xc xd xe
fx
=
=∨=
′′
= =⇔⇔
=∨= ∨=
′
=
với các số
1a cbd e<− < < < <
.
Ta có bảng xét dấu như sau
Như vậy,
( )
gx
′
đổi dấu từ “dương” sang “âm” 2 lần.
Vậy hàm số
( ) ( )
2
gx f x=

có 2 điểm cực đại.
Câu 41. Cho khối chóp
.S ABC
có
17SA SB SC a= = =
,
3AB a=
,
5BC a=
và
7CA a=
. Thể tích khối
chóp
.S ABC
bằng
A.
3
52
4
a
. B.
3
15 2
4
a
. C.
3
5 17
4
a
. D.
3
15 17
4
a
.
Lời giải
Chọn A
Vì khối chóp
.S ABC
có
SA SB SC= =
nên hình chiếu của
S
lên
( )
ABC
trùng với
O
là tâm đường
tròn ngoại tiếp tam giác
ABC
.
(
)( )( )
2
15 3
4
ABC
a
S p p AB p AC p BC
∆
= − − −=
.
Mặt khác
.. .. 73
4 43
ABC
ABC
AB AC BC AB AC BC a
S OA
OA S
∆
∆
= ⇒= =
.
SOA∆
vuông tại
O
có
22
6
3
a
SO SA OA= −=
.
Vậy
3
.
1 52
..
34
S ABC ABC
a
V S SO
∆
= =
.
Câu 42. Có bao nhiêu giá trị nguyên của tham số
(
]
;2023m ∈ −∞
thỏa hàm số
( )
32
29yx m x m= + + +−
nghịch biến trên khoảng
(
)
0;1
?
A. 2019. B. 2023. C. 2020. D. 2022.
Lời giải
Chọn C
Xét hàm số
( ) ( )
32
29fx x m x m= + + +−
có đạo hàm
( )
2
32fx x m
′
= ++
.
Trường hợp 1.
( ) ( )
( )
( )
( )
2
2
2
0, 0;1
3 2 0, 0;1
3 2, 0;1
10
34
12 0
fx x
xm x
mx x
f
m
mm
′
≤ ∀∈
+ + ≤ ∀∈
≤− − ∀ ∈

⇔⇔

≥
−≤ ≤
− ++ ≥
(*)
Xét hàm số
( )
2
32gx x=−−
có
( )
60 0gx x x
′
=− =⇔=
.
Dựa vào bảng biến thiên, điều kiện (*) tương đương
5
34
m
m
≤−
−≤ ≤
(vô lí).
Trường hợp 2.
A
C
B
O
S
(
)
( )
( )
(
)
( )
2
2
2
3 2, 0;1
0, 0;1
3 2 0, 0;1
3
10
12 0
4
mx x
fx x
xm x
m
f
mm
m
≥− − ∀ ∈
′
≥ ∀∈
+ + ≥ ∀∈

⇔⇔
≤−

≤
− ++ ≤
≥
(**)
Dựa vào bảng biến thiên ở trên, điều kiện (**) tương đương
2
4
3
4
m
m
m
m
≥−
⇔≥
≤−
≥
.
Vì
m
nguyên và
(
]
;2023m ∈ −∞
nên
{
}
4;5;6;...;2023
m ∈
.
Vậy có tất cả 2020 giá trị nguyên
m
thỏa mãn.
Câu 43. Cho hàm số
( )
32
3 5.fx x x=−+
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
( )
( )
21f fx m−=
có 3 nghiệm phân biệt?
A. 3. B. 486. C. 484. D. 485.
Lời giải
Chọn D
Ta có:
( )
(
)
2
36 0fx x x fx
′′
= −→ =⇔
0
2
x
x
=
=
và
( ) ( ) ( ) ( )
0 5, 2 1, 1 3, 9 491f fff= = = =
.
Đặt
( ) ( )
21 2u fx u f x
′′
= −→ =
. Cho
( )
0
00
2
x
u fx
x
=
′′
=⇒=⇔
=
.
Sử dụng phương pháp ghép trục, ta có BBT
Điều kiện phương trình có 3 nghiệm phân biệt thì
5 491m
<<
.
Kết hợp với
{ }
6;7;.......;490mm∈⇒∈ →
có 485 giá trị.
Câu 44. Cho hàm số
( )
( )
32 2
3 3 22fx x x m m x m=− + −+ +
(với
m
là tham số) có giá trị lớn nhất trên
[ ]
1;1−
bằng
2
, khi đó tổng các giá trị của tham số
m
là
A.
2
3
. B.
5
3
. C. 0. D.
7
3
.
Lời giải
Chọn B
Xét hàm số
( )
fx
trên đoạn
[ ]
1;1−
.
Ta có:
( )
( )
22
3 63 2 2fx x x m m
′
= −+ − +
( )
2
9 1 0,
f
mm
′
′
→∆ =− − ≤ ∀
.
Từ đó suy ra
( )
( )
22
3 6 3 2 2 0,fx x x m m x
′
= − + − + ≥∀
.
Vậy
[ ]
( ) ( )
1;1
max 1fx f
−
=
22
12
5
235 3520
3
mm mm mm⇔= − ⇔ − −=→ + =
.
Câu 45. Cho hàm số
( )
y fx=
có đạo hàm
( ) ( )( )
2
2
94fx xx x
′
= −−
. Khi đó hàm số
(
)
2
()
gx f x=
nghịch
biến trên khoảng nào?
A.
( )
3; 0−
. B.
( )
2; 2
−
. C.
( )
;3−∞ −
. D.
( )
3; +∞
.
Lời giải
Chọn C
( )
0( )
09
4( )
xk
fx x
xk
=
′
=⇔=
=
Ta có:
( )
2
() 2.g x xf x
′′
=
. Cho
( )
2
0
0
93
x
gx
xx
=
′
= ⇒
=⇔=±
.
Bảng xét dấu
( )
gx
′
Câu 46. Cho hình lập phương
′′′ ′
⋅
ABCD A B C D
có
,,M NO
lần lượt là trung điểm của
,,
′′ ′
AB A D BD
(tham
khảo hình bên).
Biết khối lập phương
′′′ ′
⋅ABCD A B C D
có thể tích là
3
a
. Thể tích của khối tứ diện
ODMN
là
A.
3
16
a
. B.
3
3
8
a
. C.
3
3
16
a
. D.
3
6
a
.
Lời giải
Chọn A
Gọi
K
là trung điểm của
.BC
Ta có
( )
( )
'
1 11 1
, ..
2 26 6
∆∆
= = = =
ODMN B DMN KDMN KMD KMD
V V V d N KMD S a S
22 2
111 3
.. . .
22222228
∆ ∆∆ ∆
=−−−=−−− =
KMD CKD ADM BMK
a a aa
S aS S S a a a a
Do đó
23
13
..
6816
= =
ODMN
aa
Va
Câu 47. Có bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
[ 2; 3]−
để hàm số
32
3
(2 3) 2
2
= − − ++
yx m x m
có cực đại và cực tiểu đồng thời hoành độ điểm cực tiểu nhỏ hơn 2 ?
A. 4. B. 6. C. 5. D. 3.
Lời giải
Chọn C
Ta có
( )
2
3 3(2 3) 3 2 3
′
= − − = − +⇒
y x m x xx m
0
0.
23
=
′
= ⇔
= −
x
y
xm
Để hàm số có cực đại, cực tiểu khi
3
2 30 .
2
−≠⇔ ≠mm
+ Trường hợp 1:
3
2 30
2
−<⇔ <
mm
. Khi đó dấu của
′
y
Do
[ 2; 3]
0, 1, 1, 2.
3
2
∈−
∈ ⇒= = =− =−
<
m
m m mm m
m
+ Trường hợp 2:
3
2 30
2
2 32 5
2
>
−>
⇔

−<
<
m
m
m
m
. Khi đó dấu của
′
y
Do
[ 2; 3]
2.
35
22
∈−
∈ ⇒=
<<
m
mm
m
Vậy có 5 giá trị nguyên của
m
thỏa mãn yêu cầu bài toán.
Câu 48. Tìm tất cả các giá trị của tham số
m
để đồ thị hàm số
( ) ( )
322 2
2 21 1=− + −+ −y x mx m x m m
cắt
trục hoành tại 3 điểm phân biệt có hoành độ dương.
A.
1<m
. B.
23
3
>
m
. C.
23
1
3
<<m
. D.
23
1
3
≤<m
.
Lời giải
Chọn C
Phương trình hoành độ giao điểm
( ) ( )
( )
322 2
2 2 1 1 01.− + −+ − =x mx m x m m
( )
( )
22
22
10 .
10
=
⇔ − −+ −=⇔
− + −=
xm
xmx mm
x mx m
Đặt
(
)
22
1.
=−+−h x x mx m
Để đồ thị hàm số
(
) ( )
322 2
2 21 1=− + −+ −
y x mx m x m m
cắt trục hoành tại 3 điểm phân biệt có
hoành độ dương điều kiện là (1) có 3 nghiệm phâm biệt có hoành độ dương
( )
2
2
2
2
0, 0
0
0
0
3 40
22 2
1.
10
33 3
0
2
1
10
10
1
> ∆>
>
>
≠
− +>

⇔ ⇔− << ⇔<<

−≠
>


>
−>
−>

<−
h
m
m
m
hm
m
mm
m
m
m
m
m
m
Câu 49. Cho hàm số
( )
y fx=
xác định trên
và có đồ thị
( )
fx
′
như hình bên. Giá trị nhỏ nhất của hàm
số
( ) ( )
2 21gx f x x= −+
trên
1
;1
2

−


bằng
A.
( )
1f
. B.
12f 
. C.
01f
. D.
21f
.
Lời giải
Chọn D
Ta có
2 2 22 2 1gx fx fx


.
Với mọi
1
;1
2
x





, ta có
2 1; 2x

suy ra
21fx
.
Do đó
0gx
, với mọi
1
;1
2
x





.
Vậy
1
;1
2
min 1 2 1gx g f





.
Câu 50. Có bao nhiêu giá trị nguyên của tham số
m
sao cho đồ thị của hàm số
42
22y x mx
=−+
có ba điểm
cực trị
,,
ABC
thỏa mãn diện tích tam giác
ABC
nhỏ hơn
2023
?
A.
21
. B.
15
. C.
2023
. D.
44
.
Lời giải
Chọn A
Ta có
( )
32
44 4y x mx x x m
′
=−= −
.
2
02
0
2
xy
y
x m ym
= ⇒=
′
= ⇔
=± ⇒=− +
( )
0m >
.
Khi đó
( )
( )
(
)
22
0;2, ;2,;2A B mm C mm− −+ −+
.
Diện tích tam giác
ABC
là
2
1
2
B CA B
S x xy y mm= − −=
.
Suy ra
2
2023 21,08mm m< ⇔<
.
Vậy có
21
giá trị nguyên của tham số
m
thỏa yêu cầu bài toán.
HẾT
| 1/27
| | Tải xuống

Có thể bạn quan tâm:

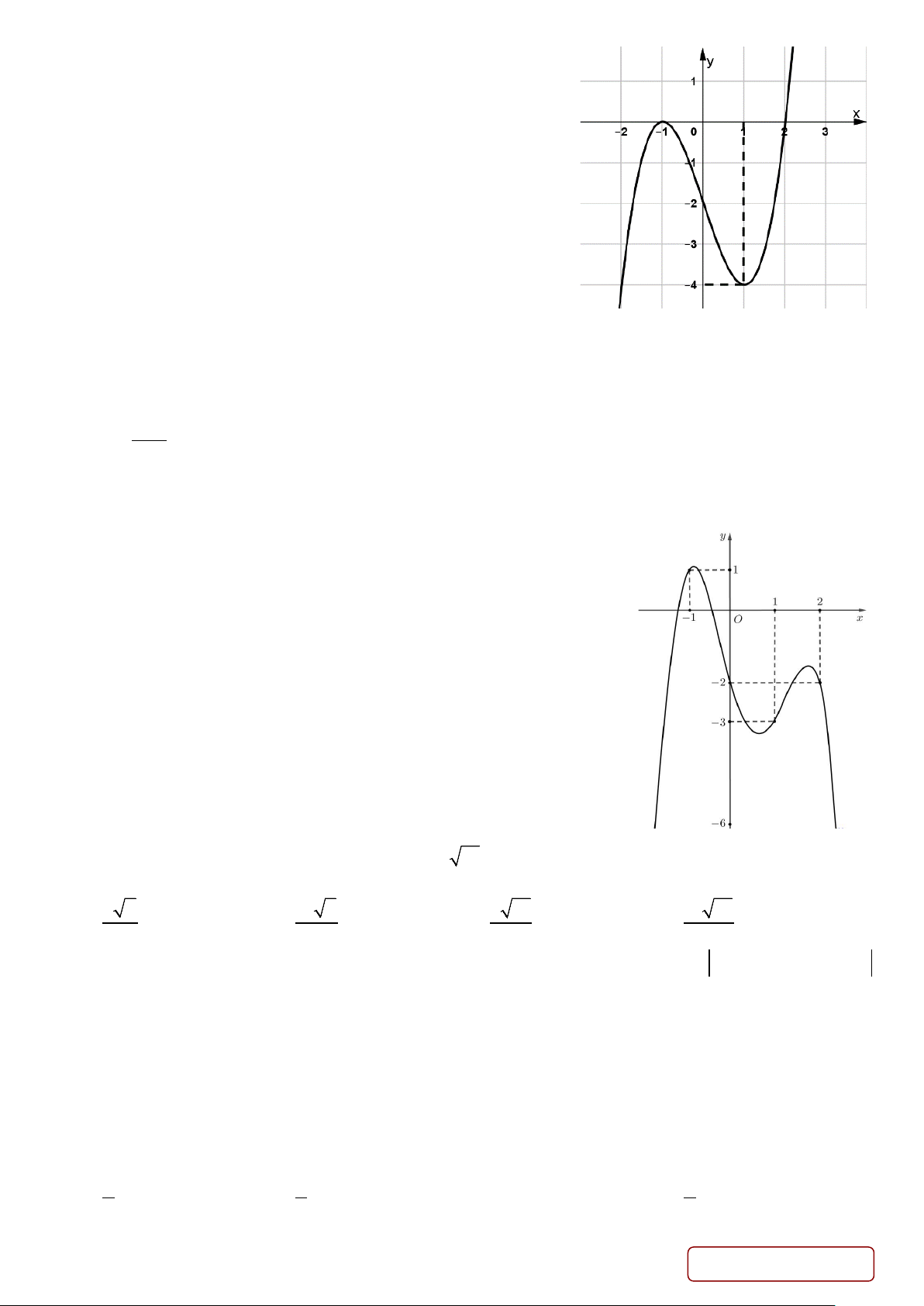
Preview text:

SỞ GIÁO DỤC & ĐÀO TẠO THÁI BÌNH ĐỀ KHẢO SÁT CHẤT LƯỢNG LỚP 12, LẦN THỨ 1
TRƯỜNG THPT CHUYÊN THÁI BÌNH Môn: TOÁN
NĂM HỌC 2023 - 2024 ĐỀ CHÍNH THỨC
Thời gian: 90 phút (Không kể thời gian phát đề)
(Đề gồm 6 trang, 50 câu trắc nghiệm) Mã đề thi
Họ và tên thí sinh:.............................................................................. SBD:..................... 123
Câu 1. Cho cấp số cộng (u có u = 3 và u = 6 . Công sai của cấp số cộng đó bằng n ) 2 3 A. 1 . B. 1 . C. 3. D. 2. 3 2
Câu 2. Số tập con có hai phần tử của tập hợp gồm 10 phần tử là A. 2 A . B. 10 2 . C. 2 10 . D. 2 C . 10 10
Câu 3. Kết luận nào sau đây về tính đơn điệu của hàm số x +1 y =
là kết luận đúng? 2x +1
A. Hàm số đồng biến trên  1  \  − . 2  
B. Hàm số nghịch biến trên  1  \  − . 2  
C. Hàm số đồng biến trên các khoảng  1 ;  −∞ −    và 1 −  ;+∞ . 2      2 
D. Hàm số nghịch biến trên các khoảng  1 ;  −∞ −    và 1 −  ;+∞ . 2      2 
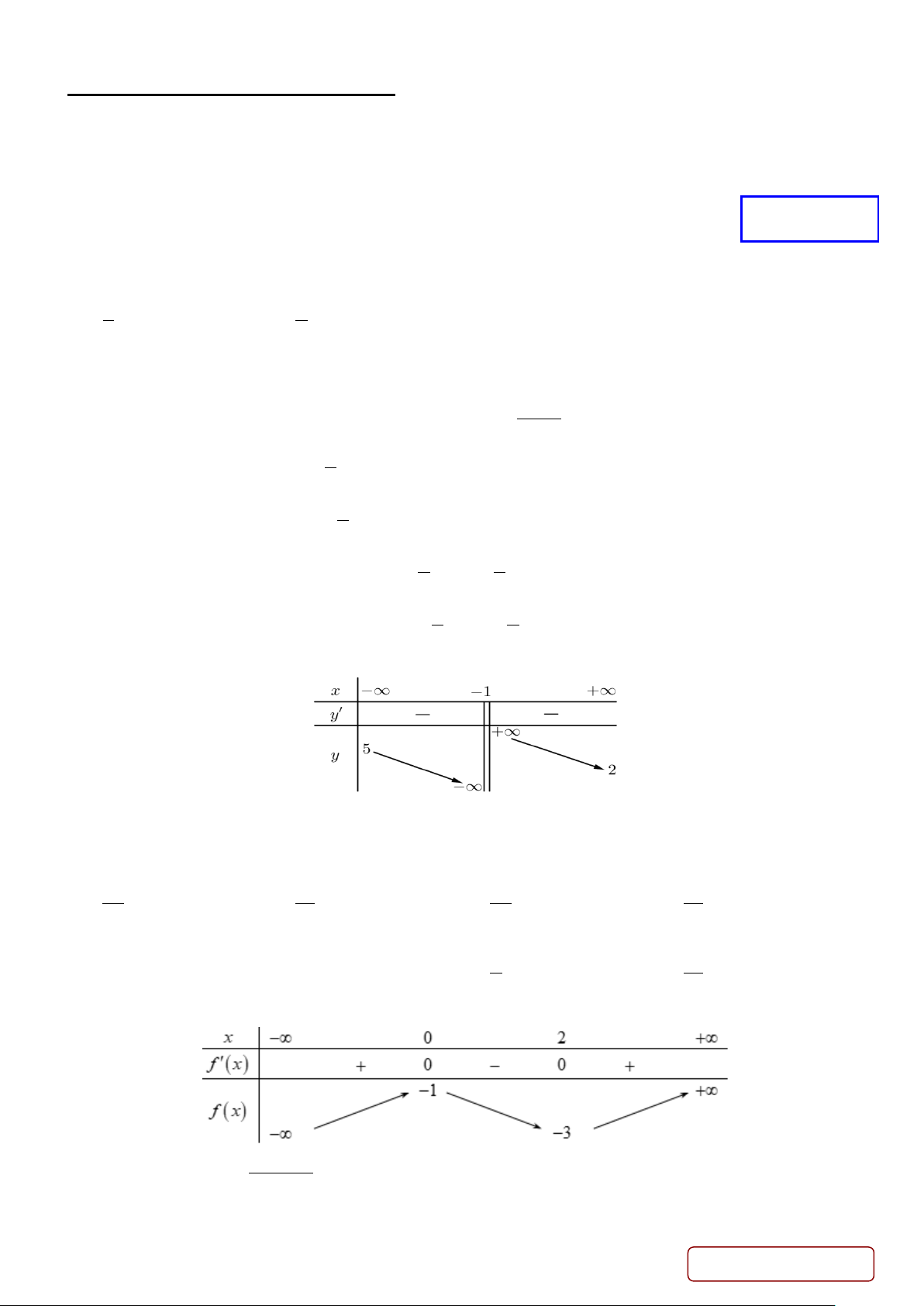
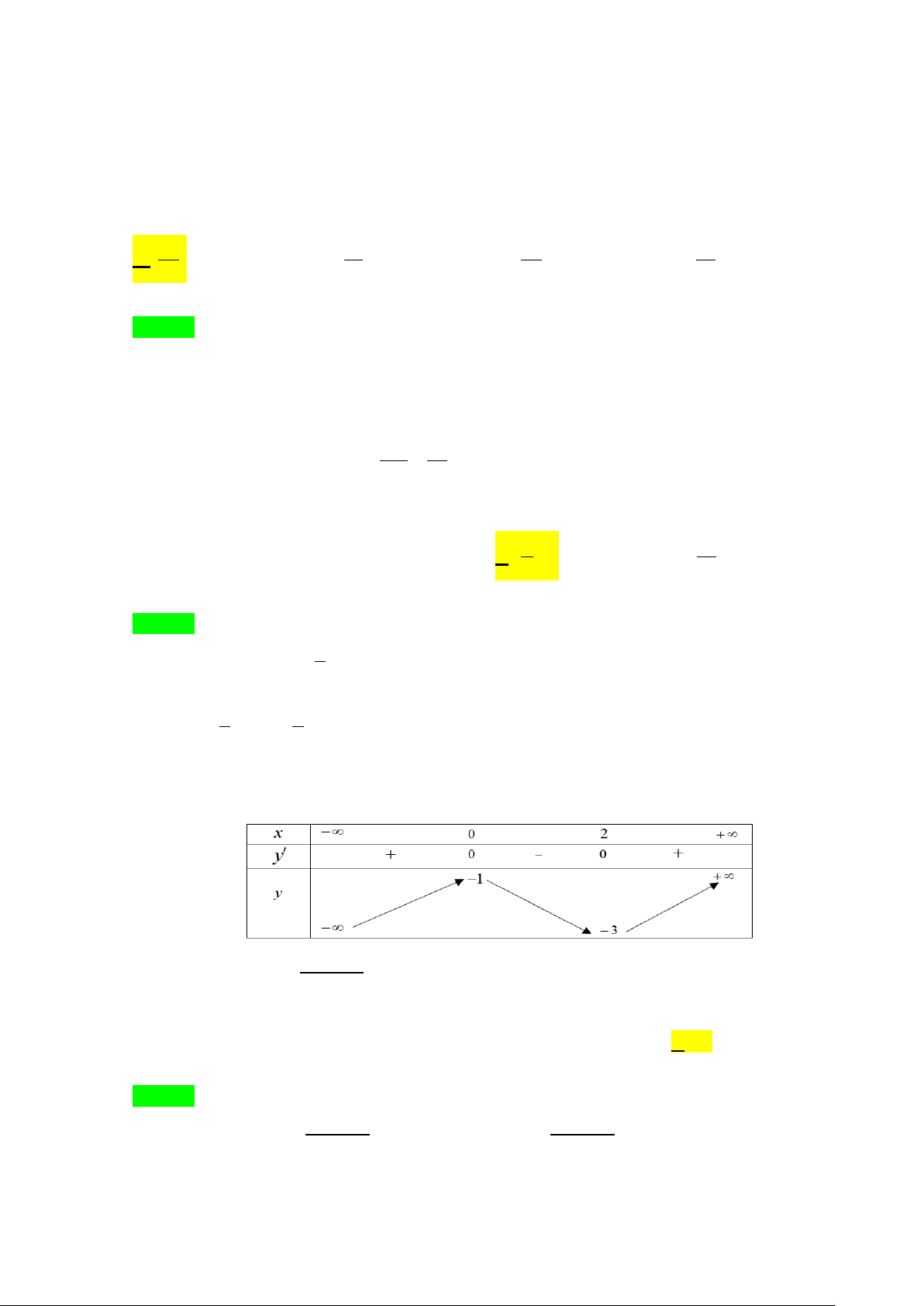
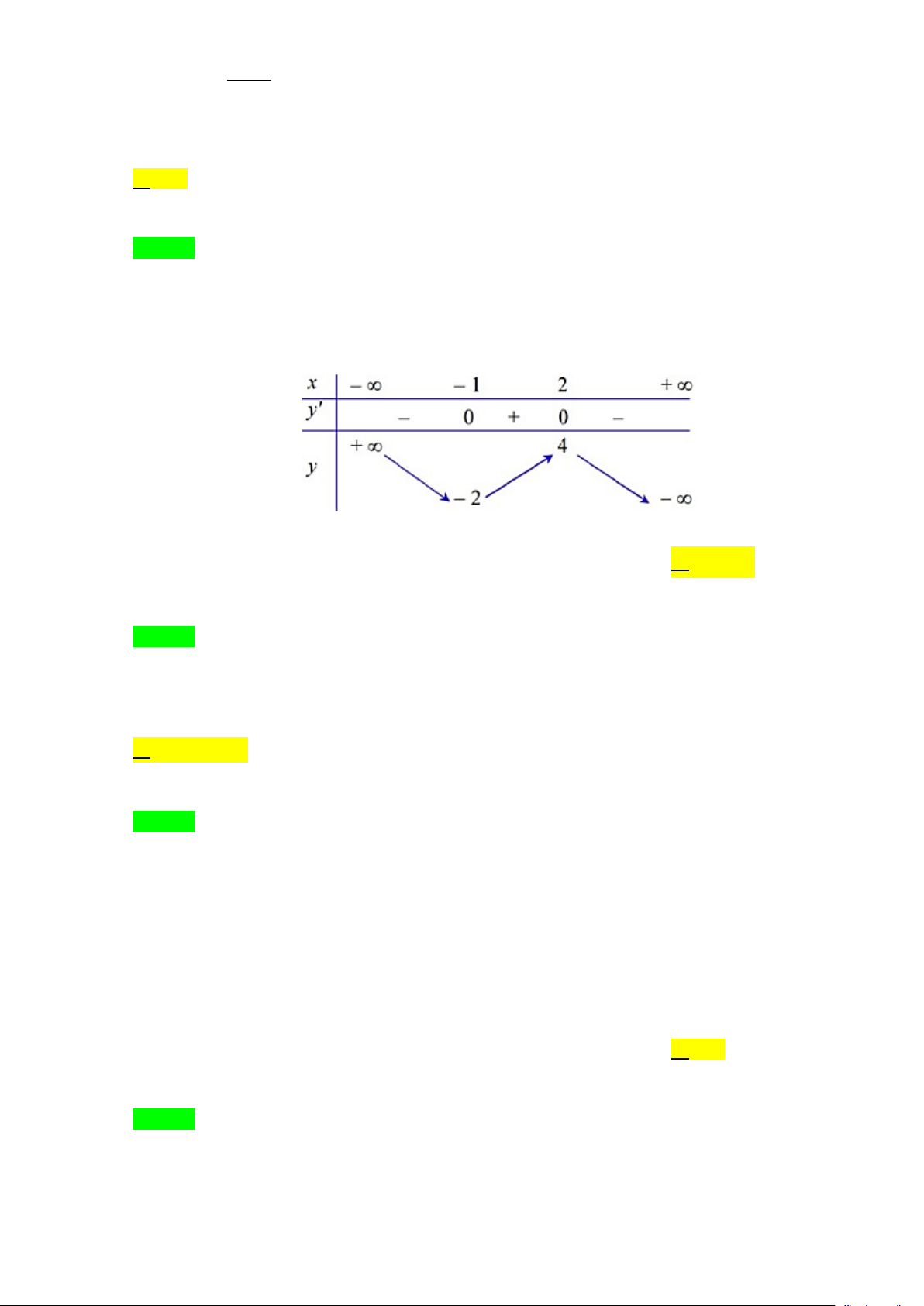
Câu 4. Cho hàm số y = f (x) có bảng biến thiên như sau:
Tổng số đường tiệm cận ngang và đường tiệm cận đứng của đồ thị hàm số đã cho là A. 0 .
B. 2 . C. 3. D. 1.
Câu 5. Chọn ngẫu nhiên đồng thời hai số từ tập hợp 17 số nguyên dương đầu tiên. Xác suất để chọn được hai số lẻ bằng A. 9 . B. 9 . C. 7 . D. 8 . 34 17 34 17
Câu 6. Cho khối chóp có đáy là hình vuông cạnh a và chiều cao bằng 4a . Thể tích khối chóp đã cho bằng A. 3 16a . B. 3 4a C. 4 3 a . D. 16 3 a . 3 3
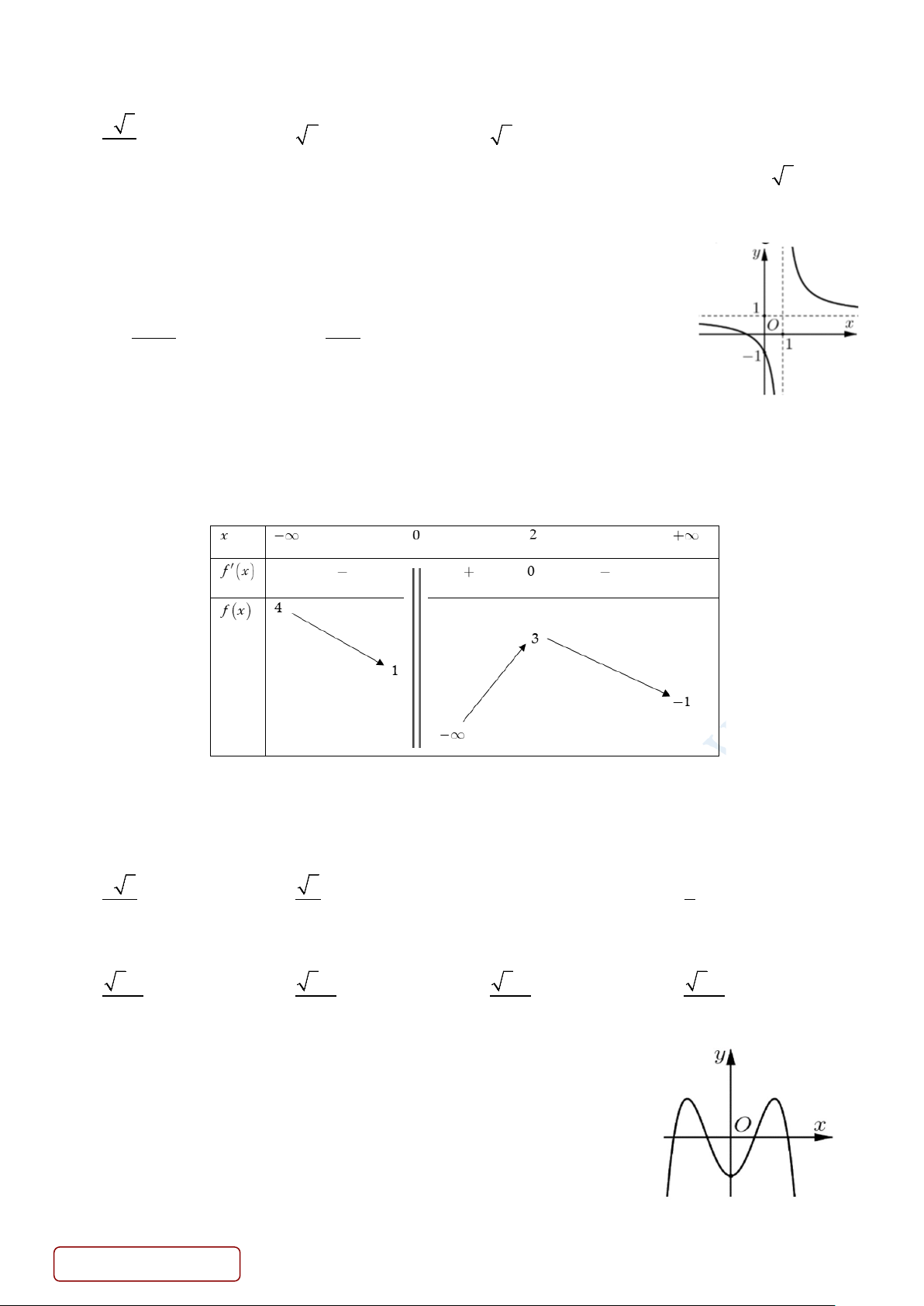
Câu 7. Cho hàm số y = f (x) có bảng biến thiên như sau:
Đồ thị hàm số g (x) 1 =
có tất cả bao nhiêu đường tiệm cận (đường tiệm cận đứng và đường tiệm f (x) +1 cận ngang)? A. 2 .
B. 0 . C. 1. D. 3. Trang 1/6 - Mã đề 123
Câu 8. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B , AC = SA = 2a và SA ⊥ ( ABC) . Khoảng
cách từ A đến mặt phẳng (SBC) bằng
A. 2 3 a . B. 2a . C. 3a . D. a . 3
Câu 9. Cho hình chóp S.ABC có SA vuông góc với mặt đáy, tam giác ABC đều, SA = AB = 3 . Góc giữa
SC và mặt phẳng ( ABC) bằng A. 90° . B. 30° . C. 45°. D. 60°.
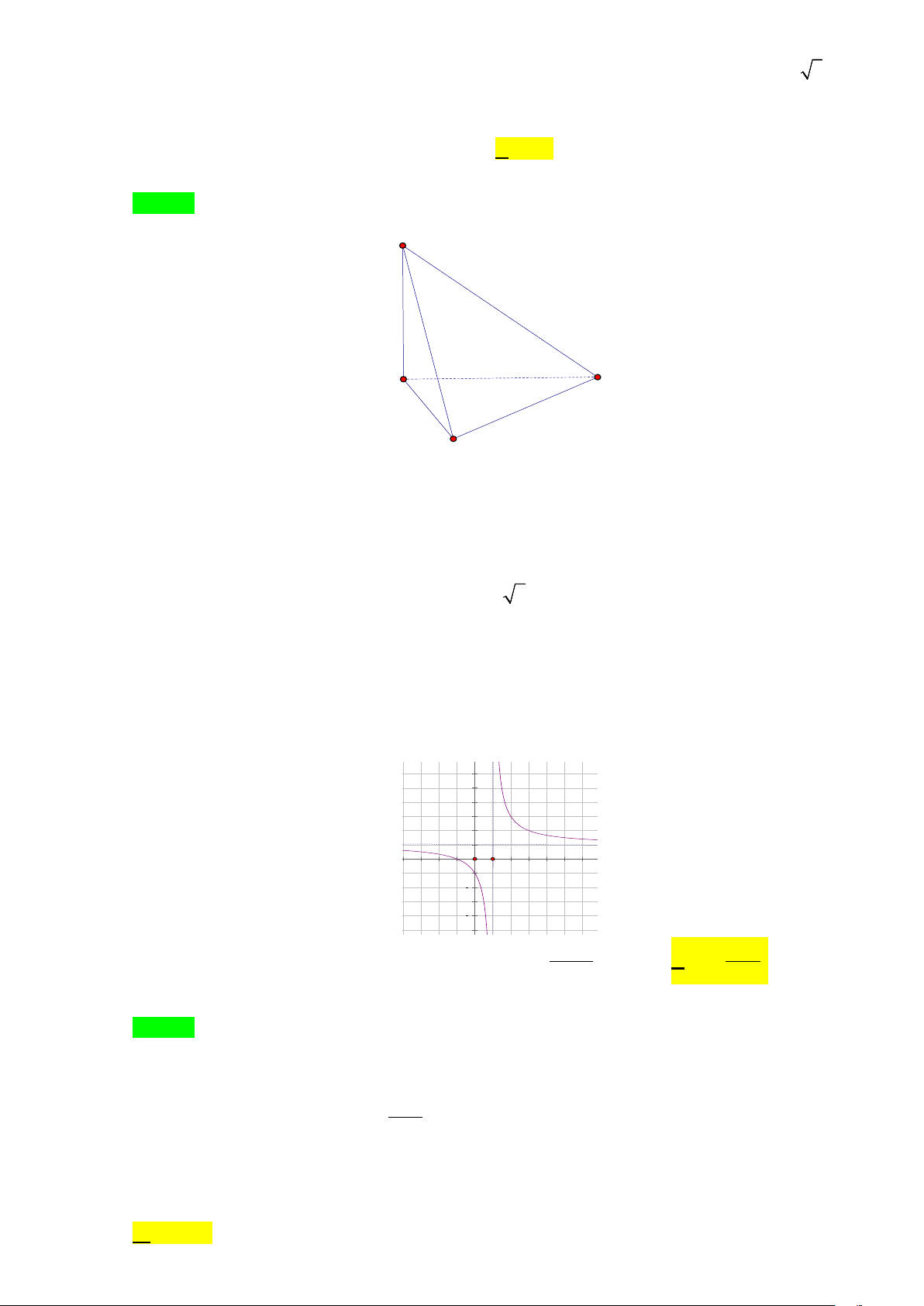
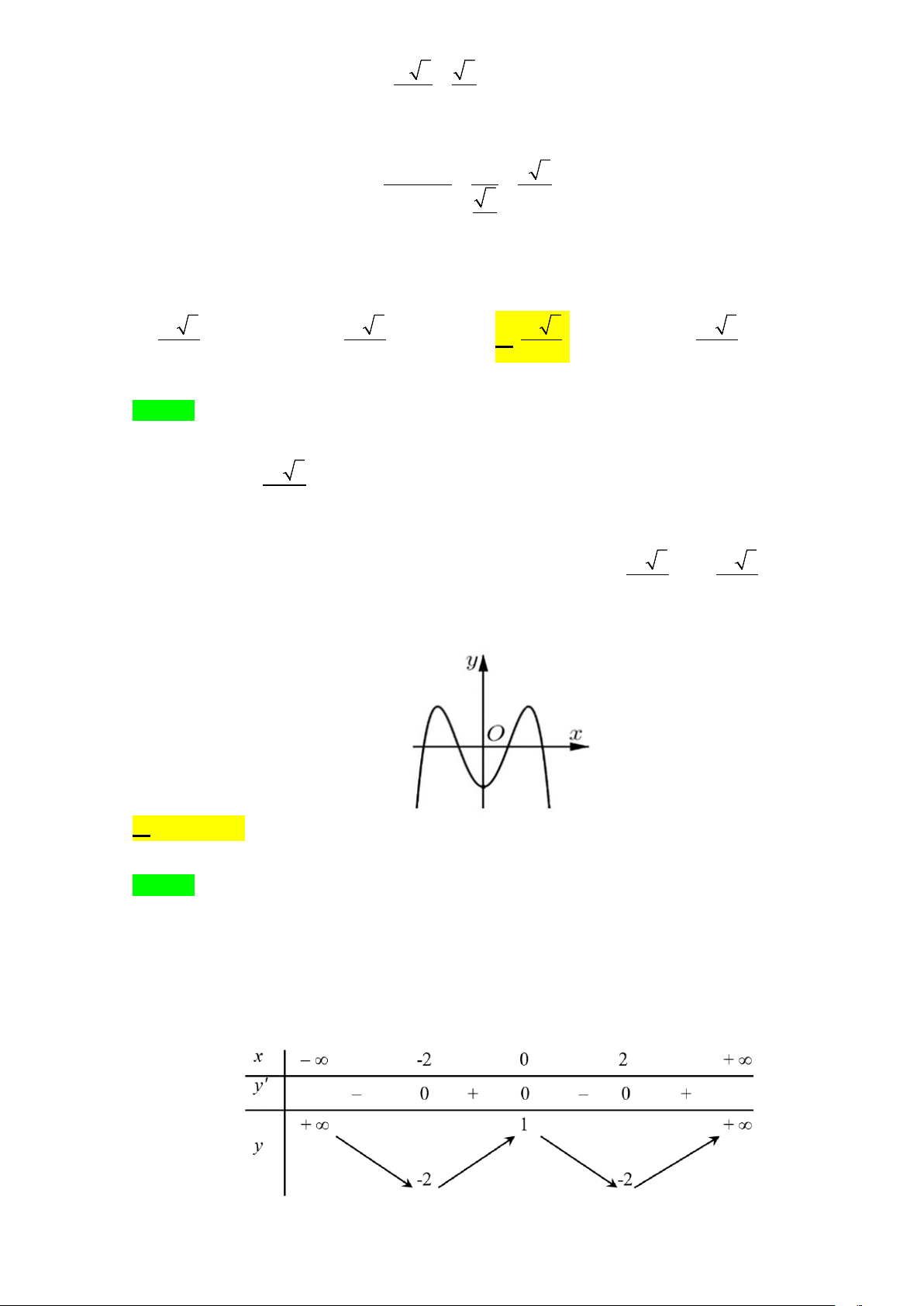
Câu 10. Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây.
Hàm số đó là hàm số nào? A. 3
y = x − 3x −1. B. 4 2
y = x + x +1. C. 2x −1 y + = . D. x 1 y = . x −1 x −1
Câu 11. Cho hàm số y = f (x) liên tục trên  và có đạo hàm f (x) = (x + )(x − )2 ' 1 2 (x − ) 1 . Điểm cực đại
của hàm số đã cho là A. x = 1 − . B. x = 2 − . C. x =1. D. x = 2 .
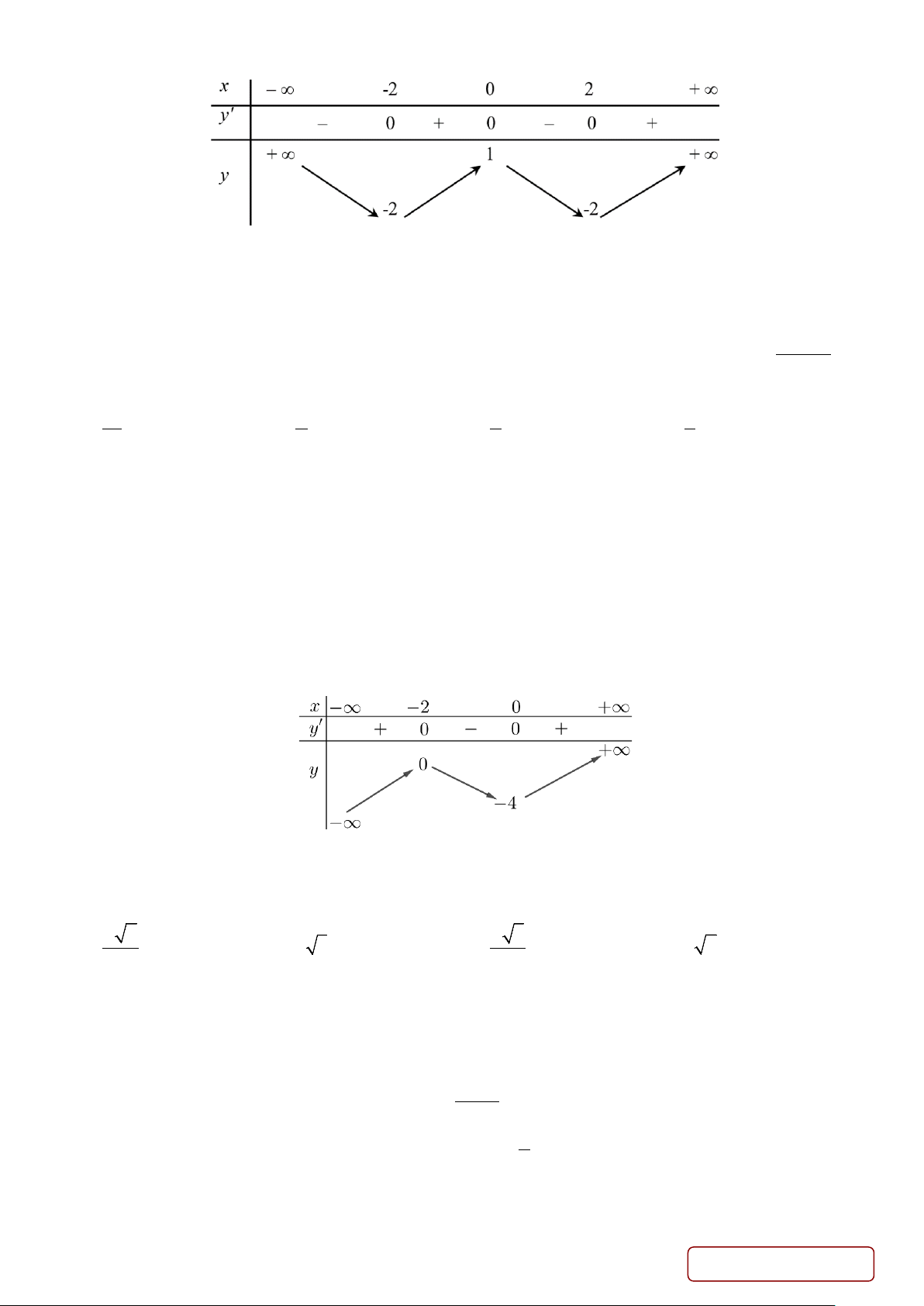
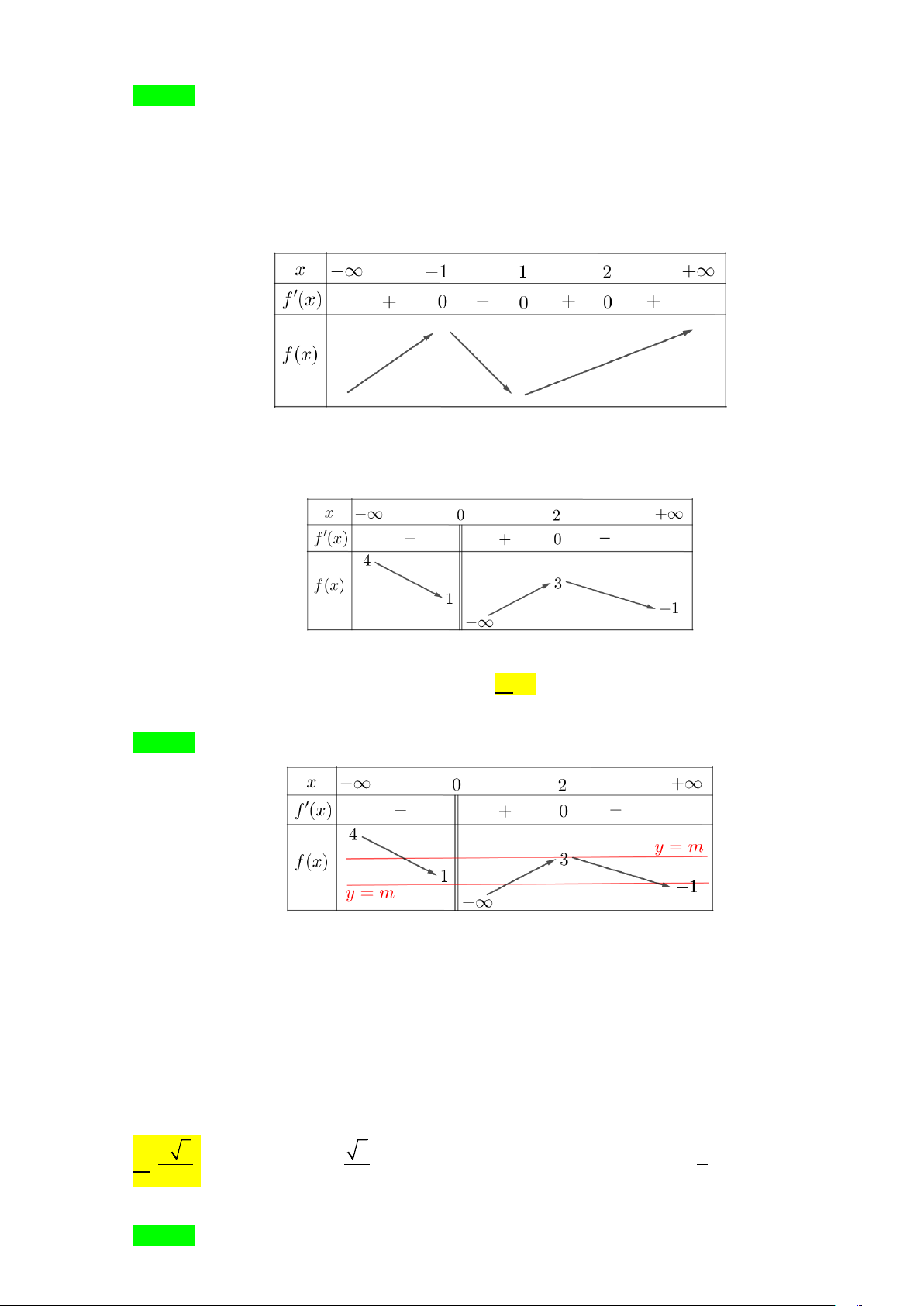
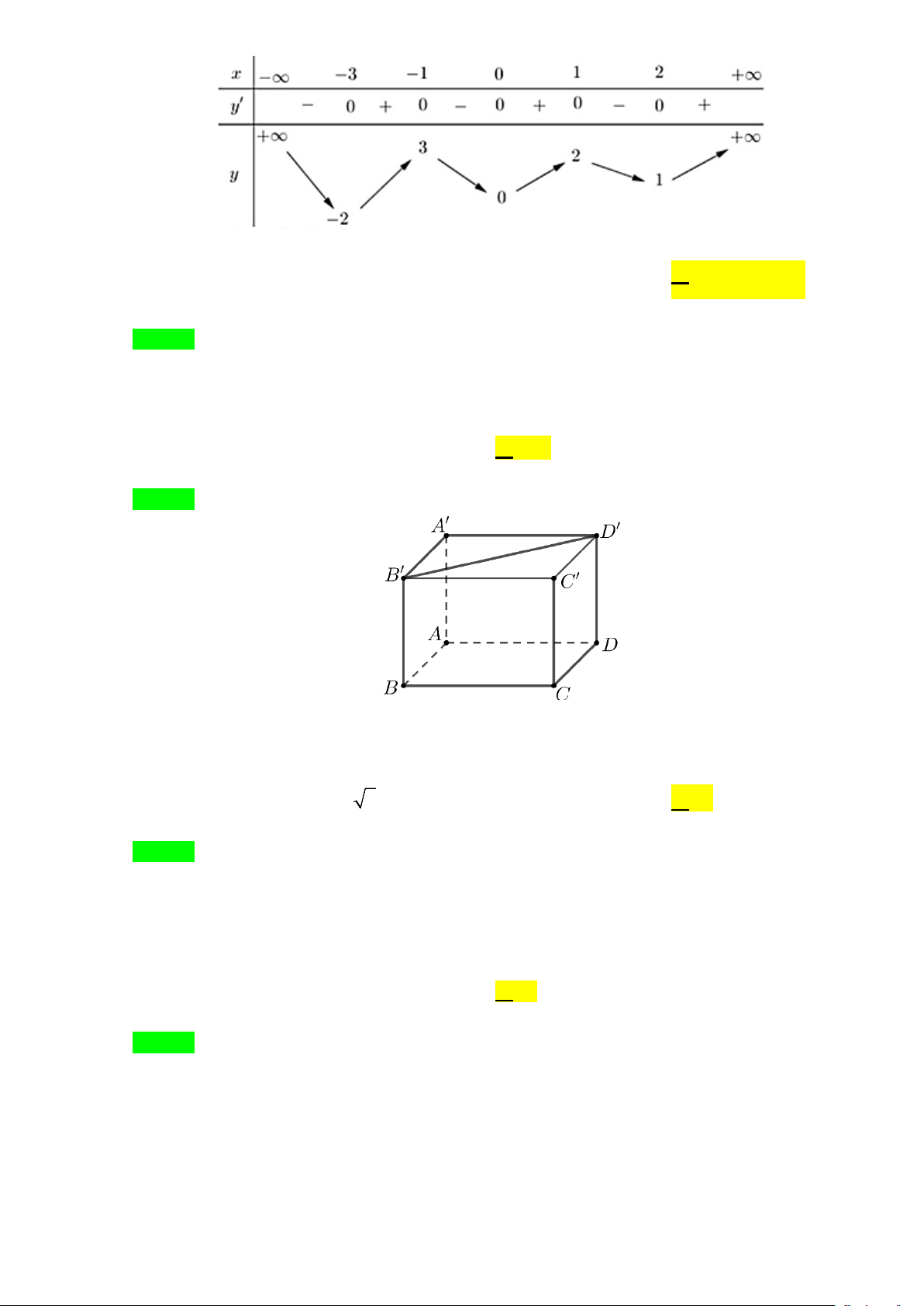
Câu 12. Cho hàm số y = f (x) có bảng biến thiên như sau:
Số các giá trị nguyên của tham số m để phương trình f (x) = m có 2 nghiệm phân biệt là A. 4 .
B. 2 . C. 3. D. 1.
Câu 13. Cho khối lăng trụ ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh bằng 1. Biết thể tích khối lăng trụ
ABC.A′B C
′ ′ bằng 1. Khoảng cách giữa hai mặt phẳng ( ABC) và ( A′B C ′ ′) bằng A. 4 3 . B. 3 . C. 3. D. 1 . 3 4 3
Câu 14. Cho hình lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng a và cạnh bên bằng 2a . Thể tích của
lăng trụ ABC.A′B C ′ ′ bằng. 3 3 3 3 A. 3a B. 3a C. 3a D. 3a 6 3 2 4 Câu 15. Cho hàm số 4 2
y = ax + bx + c có đồ thị như hình vẽ bên. Mệnh
đề nào sau đây là đúng?
A. a > 0,c < 0.
B. a < 0,c > 0.
C. a < 0,c < 0 .
D. a > 0,c > 0. Trang 2/6 - Mã đề 123
Câu 16. Cho hàm số y = f (x) có bảng biến thiên như sau:
Số nghiệm thực của phương trình 2 f (x) + 3 = 0 là A. 1.
B. 2 . C. 3. D. 4 . Câu 17. Hàm số 4 2
y = x + 2x −1 có bao nhiêu điểm cực trị ? A. 0 . B. 3. C. 1. D. 2 .
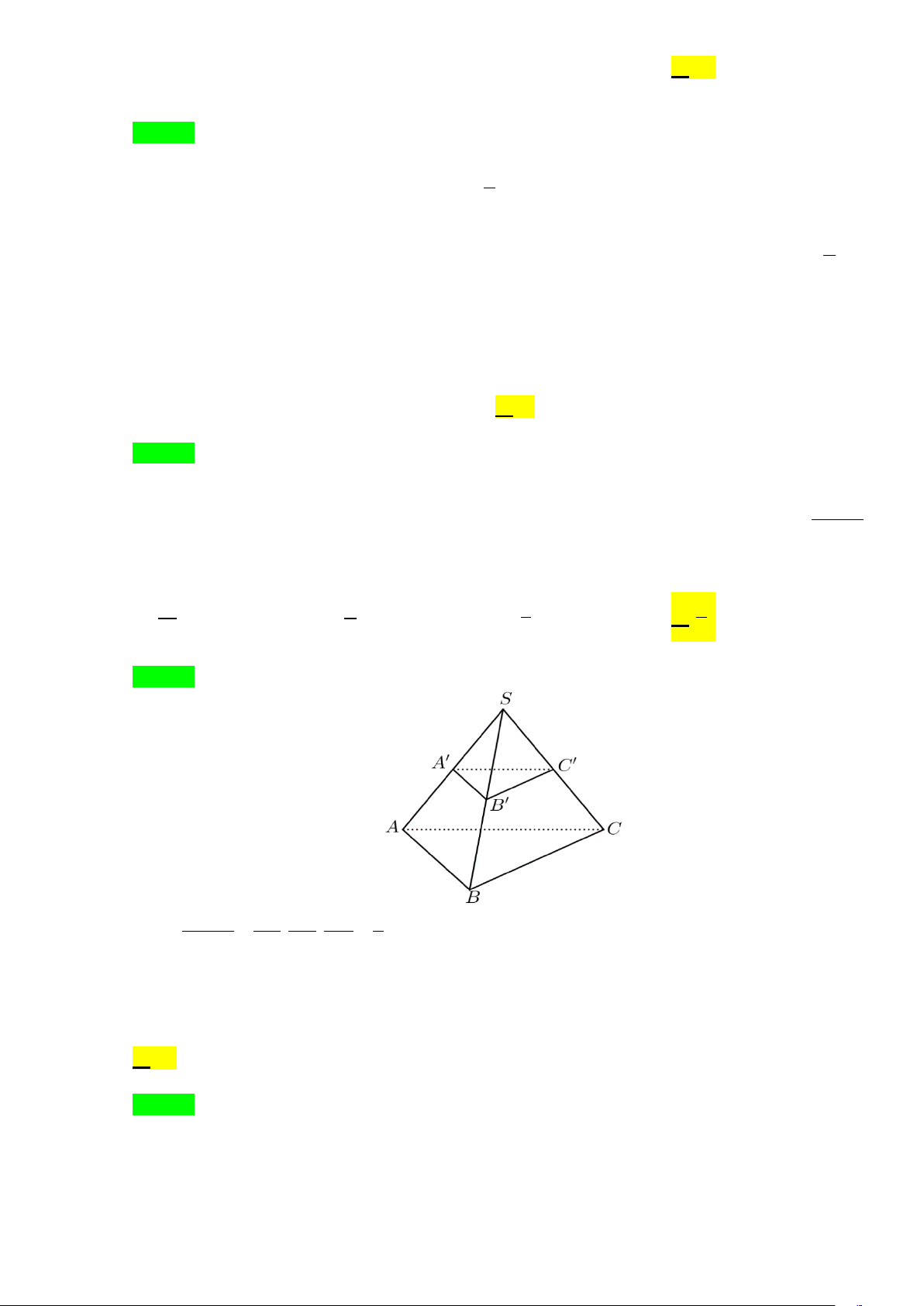
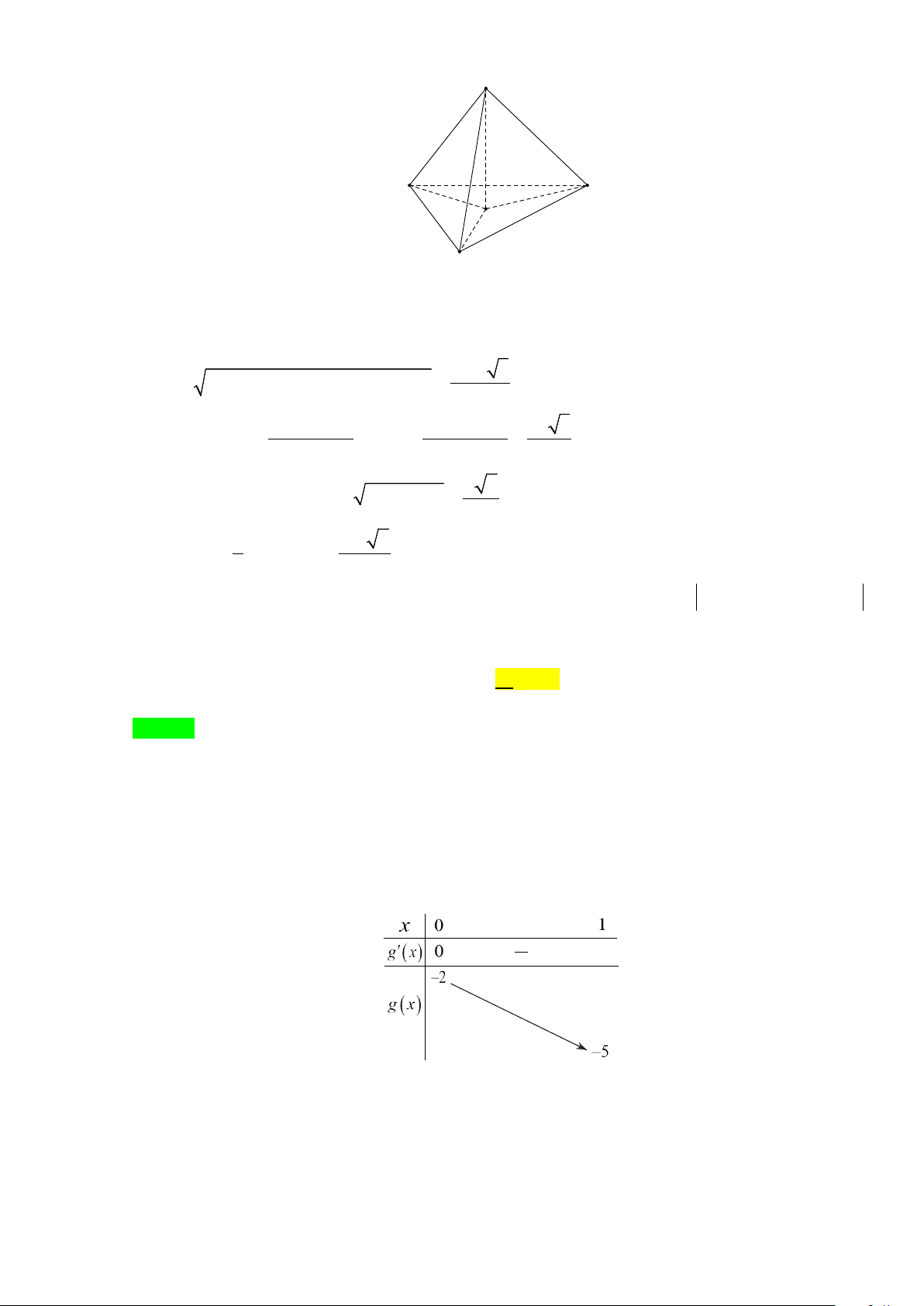
Câu 18. Cho khối chóp S.ABC . Gọi A', B ',C ' lần lượt là trung điểm ,
SA SB, SC . Tỉ số thể tích VS.A'B'C' bằng VS.ABC bao nhiêu? A. 1 . B. 1 . C. 3 . D. 1 . 16 6 8 8 Câu 19. Cho hàm số 3
y = x + (m − ) 2
3 x + (m −3) x + 4 . Có bao nhiêu giá trị nguyên của tham số m để hàm số
đã cho đồng biến trên ( ; −∞ +∞) ? A. 4 . B. 6 . C. 5. D. 3.
Câu 20. Hình chóp tứ giác có bao nhiêu mặt? A. 6 . B. 7 . C. 4 . D. 5.
Câu 21. Giá trị lớn nhất của hàm số y = f (x) trên đoạn [a;b] bằng 3. Giá trị nhỏ nhất của hàm số
g(x) = 5 − 2 f (x) trên đoạn [a;b] bằng bao nhiêu? A. 1. B. 2 . C. 1 − . D. 3 − .
Câu 22. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ sau:
Giá trị cực tiểu của hàm số đã cho là A. 0 . B. − 4 . C. 2 − . D. 1.
Câu 23. Cho hình lập phương ABC . D A′B C ′ D
′ ′ có cạnh bằng 2a . Khoảng cách giữa hai đường thẳng AB′ và
A′D′ bằng
A. a 2 . B. a 3 . C. a 3 . D. a 2 . 2 3
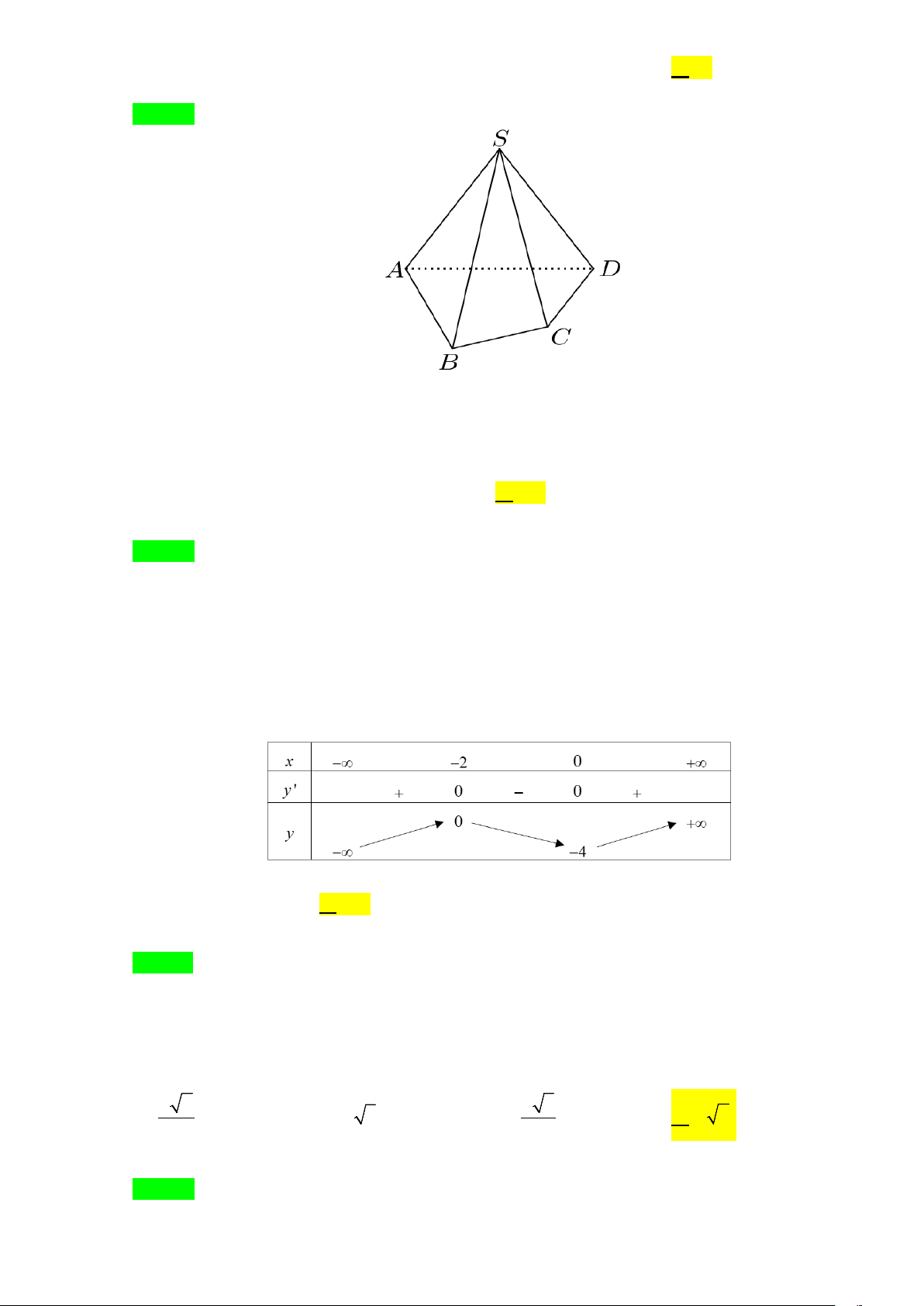
Câu 24. Cho khối chóp ngũ giác S.ABCDE . Khi ta chia khối chóp này bằng hai mặt phẳng (SAC) và
(SCE) thì sẽ được
A. 3 khối tứ diện.
B. 4 khối chóp tam giác.
C. Hai khối chóp tam giác.
D. 3 khối chóp tứ giác.
Câu 25. Đường tiệm cận đứng của đồ thị hàm số 2x −1 y =
là đường thẳng có phương trình là x −1
A. x = 2 . B. x = 1 − . C. 1 x = . D. x =1. 2
Câu 26. Có bao nhiêu cách xếp 4 người ngồi vào dãy 5 ghế xếp theo hàng ngang (mỗi ghế không ngồi quá một người) ? A. 120. B. 20 . C. 9. D. 10. Trang 3/6 - Mã đề 123
Câu 27. Cho hàm số y = f (x) xác định trên  và có bảng biến thiên như hình vẽ sau.
Hàm số đã cho đồng biến trên khoảng nào? A. ( ; −∞ − ) 1 . B. ( 2; − 4) .
C. (2;+∞) . D. ( 1; − 2) .
Câu 28. Hàm số f (x) 3 2
= x − 3x + 4 có đồ thị (C). Viết phương trình tiếp tuyến với (C) tại điểm A nằm
trên (C) có hoành độ x = . A 1 A. y = 3 − x + 5.
B. y = 3x − 5.
C. y = 5x − 3. D. y = 5 − x + 3.
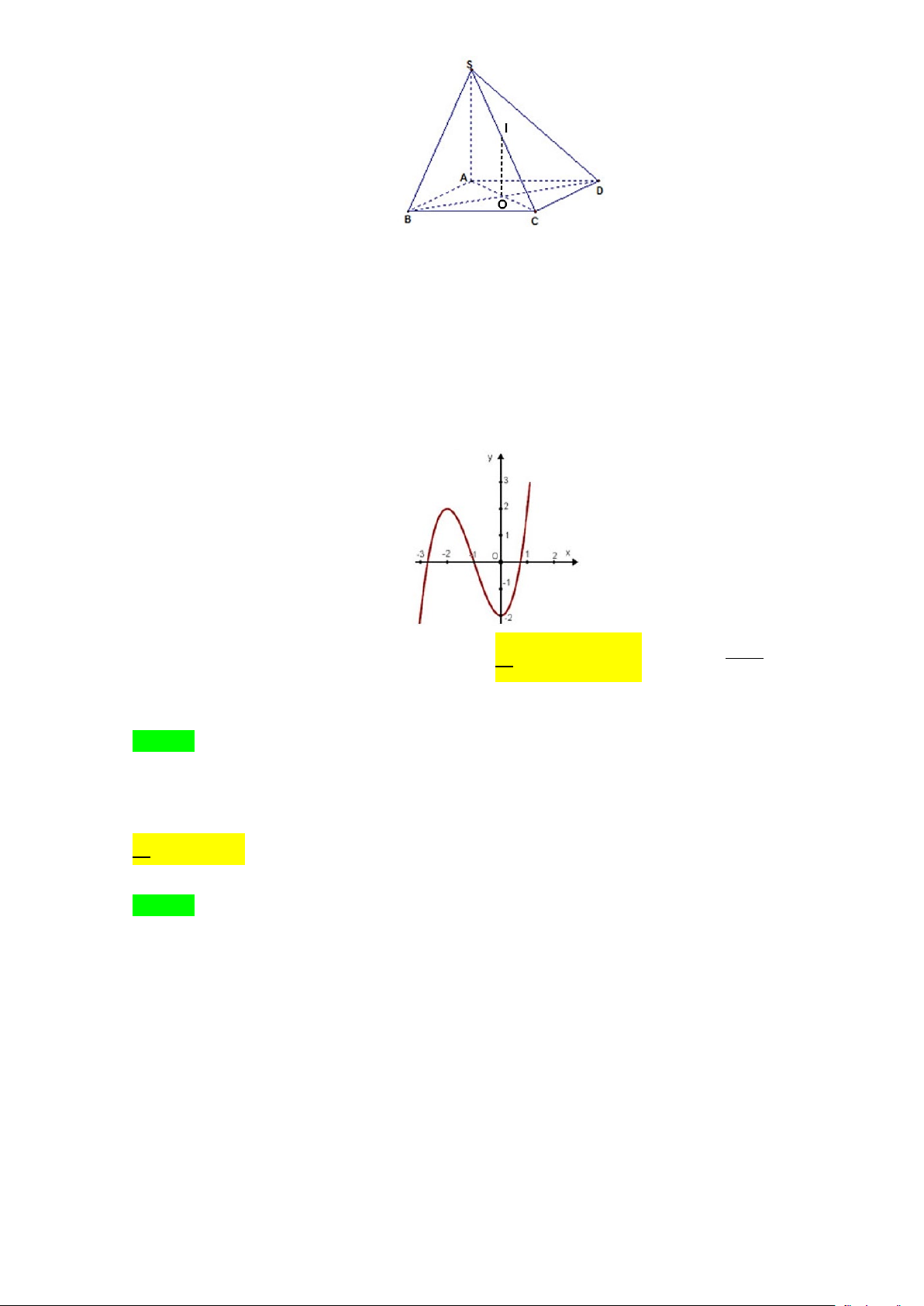
Câu 29. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , SA ⊥ (ABCD) . Gọi I là trung điểm
SC . Khoảng cách từ I đến mặt phẳng (ABCD) bằng độ dài đoạn thẳng nào sau? A. IB . B. IC . C. ID . D. IO .
Câu 30. Hàm số nào liệt kê dưới đây có đồ thị như hình vẽ bên? A. 4 2
y = x + 3x − 2 . B. 3 2
y = −x + 3x − 2. C. 3 2
y = x + 3x − 2. D. x − 2 y = . x +1
Câu 31. Điểm nào dưới đây thuộc đồ thị hàm số 3 2
y = x − 3x ? A. M ( 1; − 4 − ) . B. M ( 1; − 2 − ) . C. M ( 1; − 2) . D. M (1; 4 − ) .
Câu 32. Cho hàm số y = f (x) có bảng biến thiên như sau:
Khẳng định nào sau đây đúng?
A. max f (x) = 2 .
B. max f (x) = 2 − .
C. max f (x) =1.
D. max f (x) = 3. [ 3 − ;2] [ 3 − ;2] [ 3 − ;2] [ 3 − ;2]
Câu 33. Cho hình lập phương ABC .
D A'B 'C 'D ' . Tính góc giữa hai đường thẳng B 'D ' và A' A . A. 60°. B. 45°. C. 90° . D. 30° .
Câu 34. Một khối lập phương có thể tích bằng 8 . Độ dài cạnh của khối lập phương đó là A. 512. B. 2 2 . C. 8 . D. 2 .
Câu 35. Cho một cấp số nhân có số hạng đầu bằng công bội và số hạng thứ ba lớn hơn công bội 6 đơn vị. Số
hạng thứ hai của cấp số nhân này là A. 2 . B. 6 . C. 4 . D. 1. Trang 4/6 - Mã đề 123
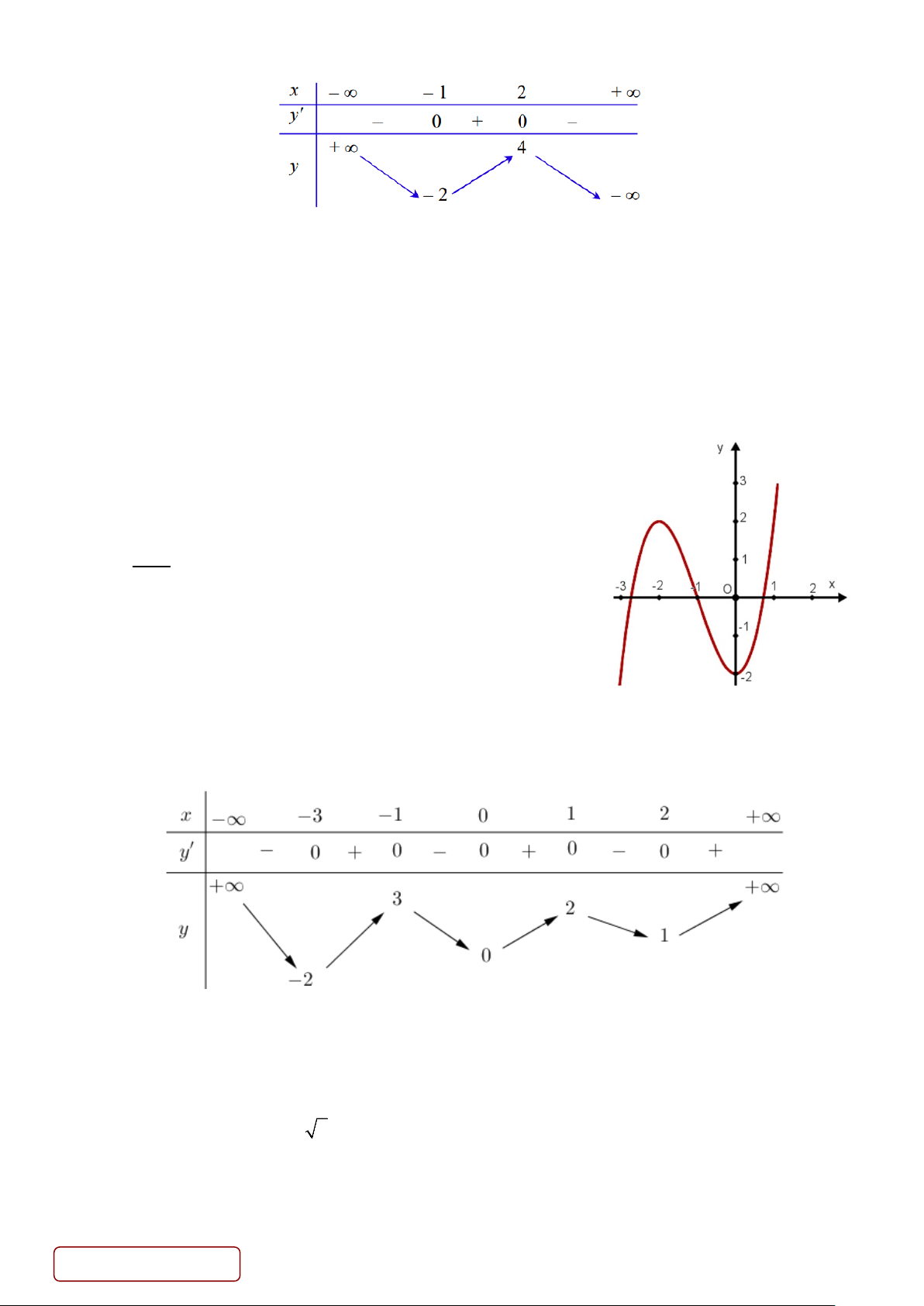
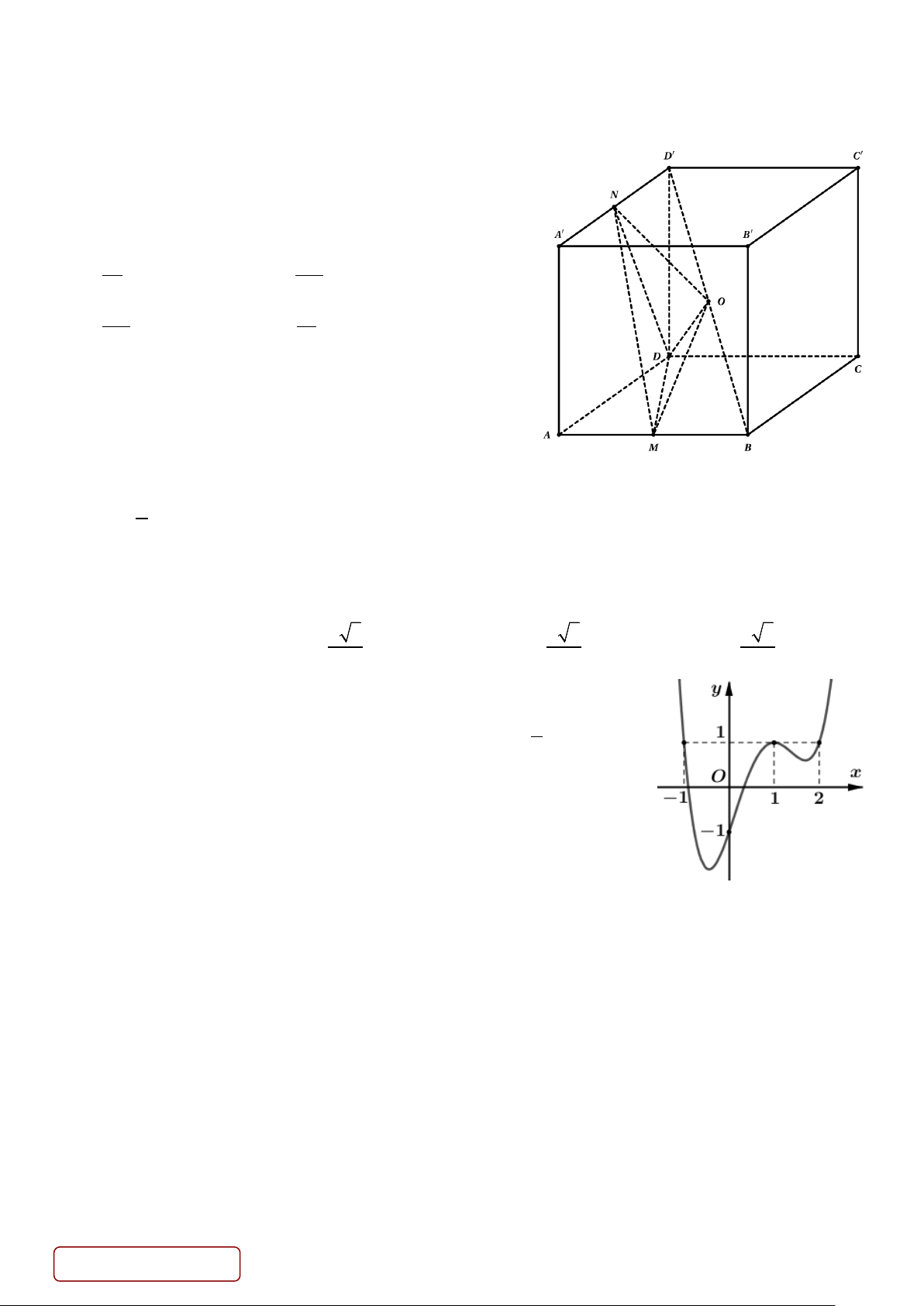
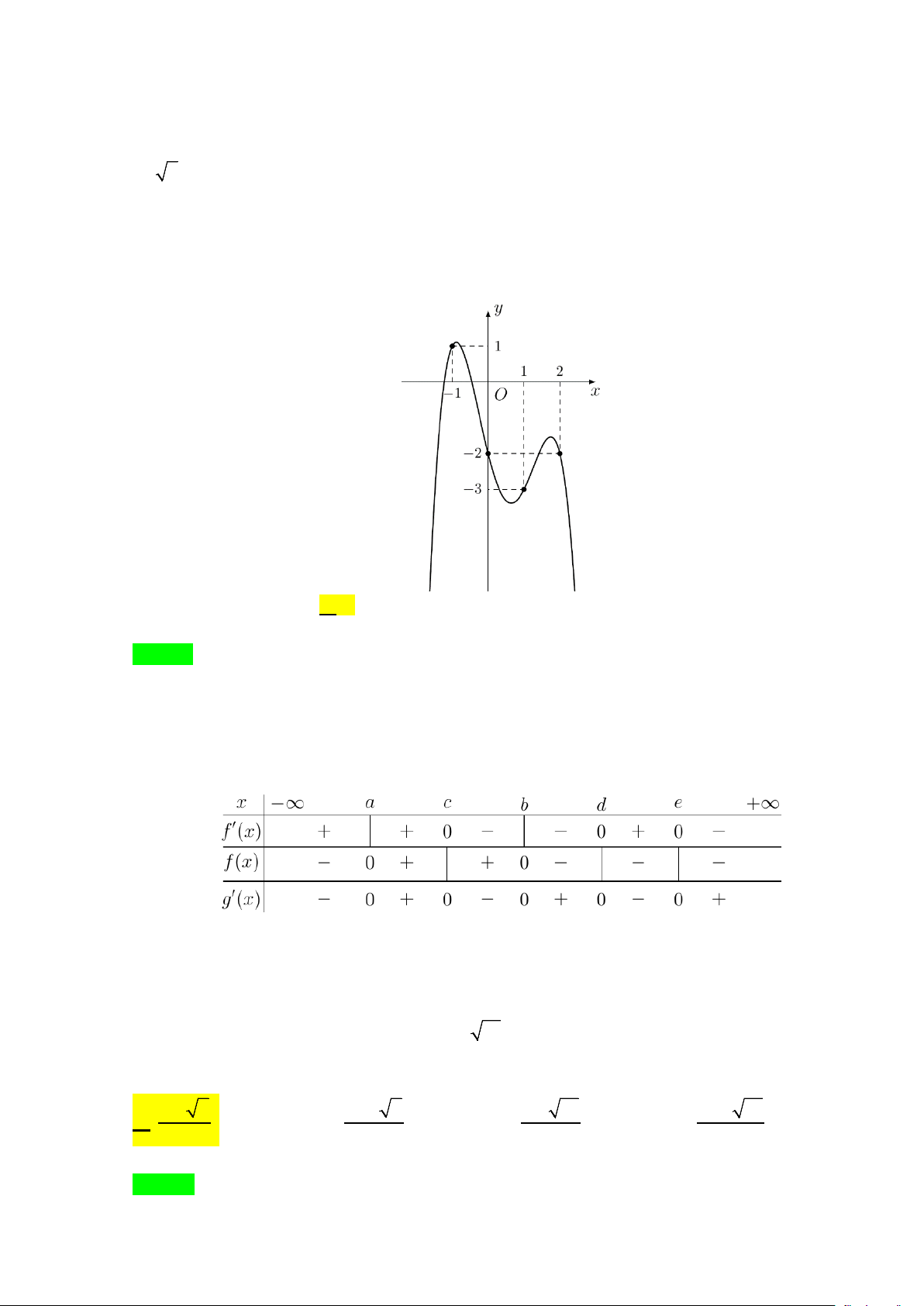
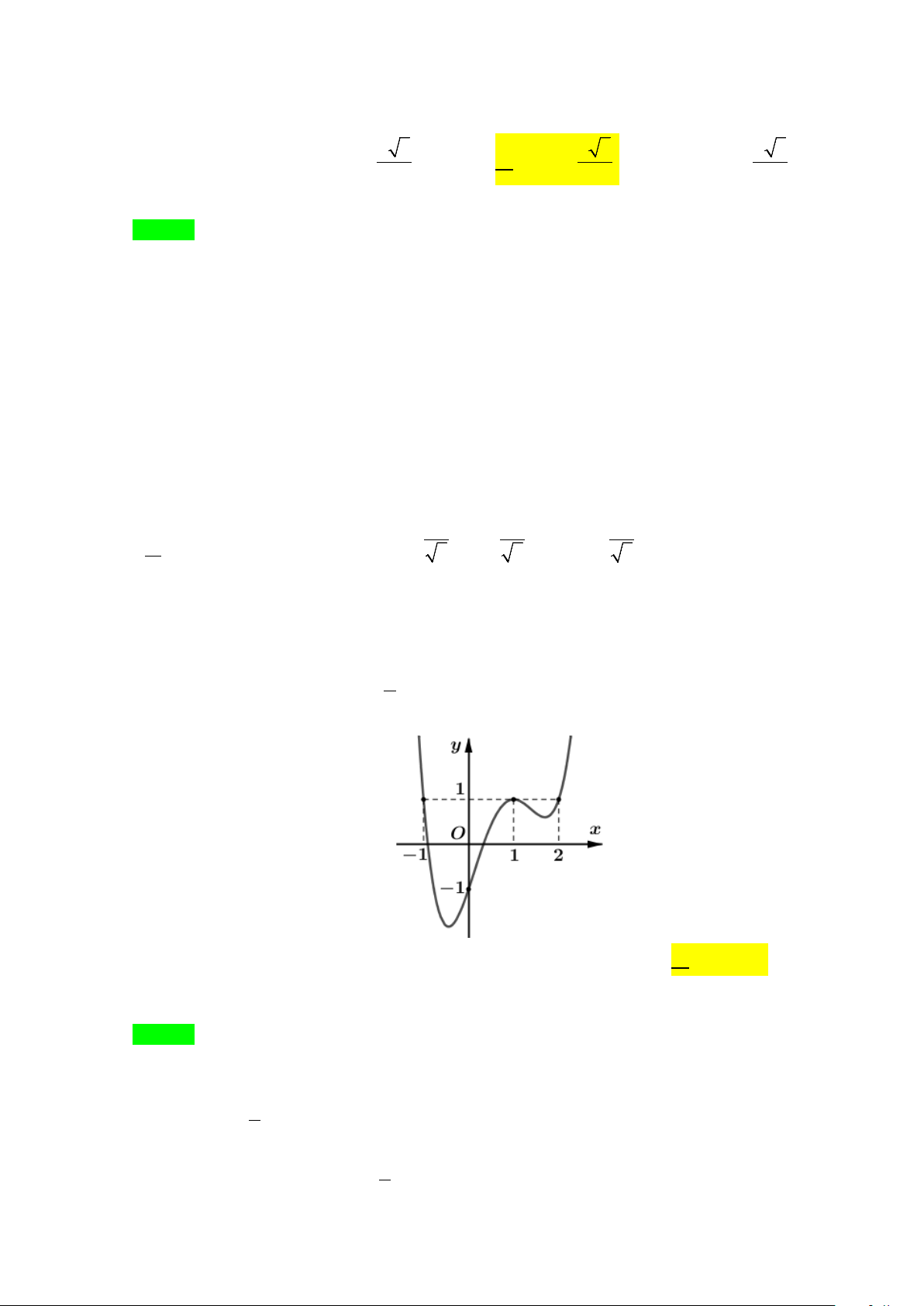
Câu 36. Cho hàm số y = f (x) là hàm đa thức bậc ba có đồ thị
như hình vẽ bên. Giá trị của f (1)− f (0) bằng A. 4 − . B. 2 − . C. 6 − . D. 2 .
Câu 37. Cho khối lăng trụ ABC.A'B 'C ' có thể tích bằng 12. Thể tích khối chóp A'.ABC bằng A. 6 . B. 4 . C. 3. D. 12.
Câu 38. Hàm số nào sau đây nghịch biến trên  ? A. 3 2
y = −x + 3x − 3x + 5.
B. y = −(x + )2 1 . C. x +1 y = . D. 2
y = −x −1. x −1
Câu 39. Giá trị nhỏ nhất của hàm số 4 2
y = −x + 4x − 3 trên đoạn [ 1; − ]3 bằng A. 1. B. 48 − . C. 0 . D. 50 − .
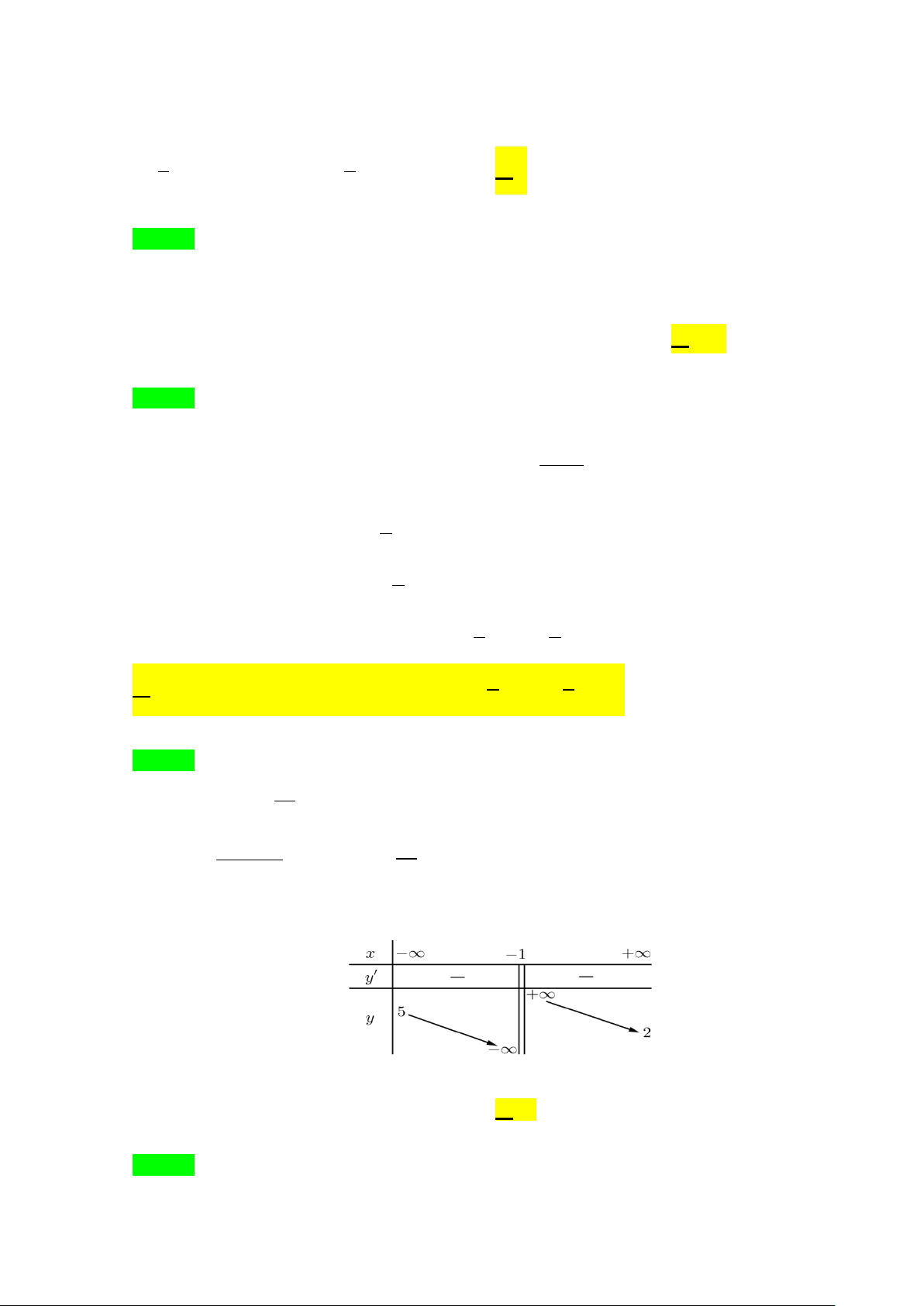
Câu 40. Cho hàm số đa thức bậc bốn y = f (x) có đồ thị như hình vẽ bên
Số điểm cực đại của hàm số ( ) =  ( ) 2 g x f x    là A. 5. B. 2 . C. 4 . D. 3.
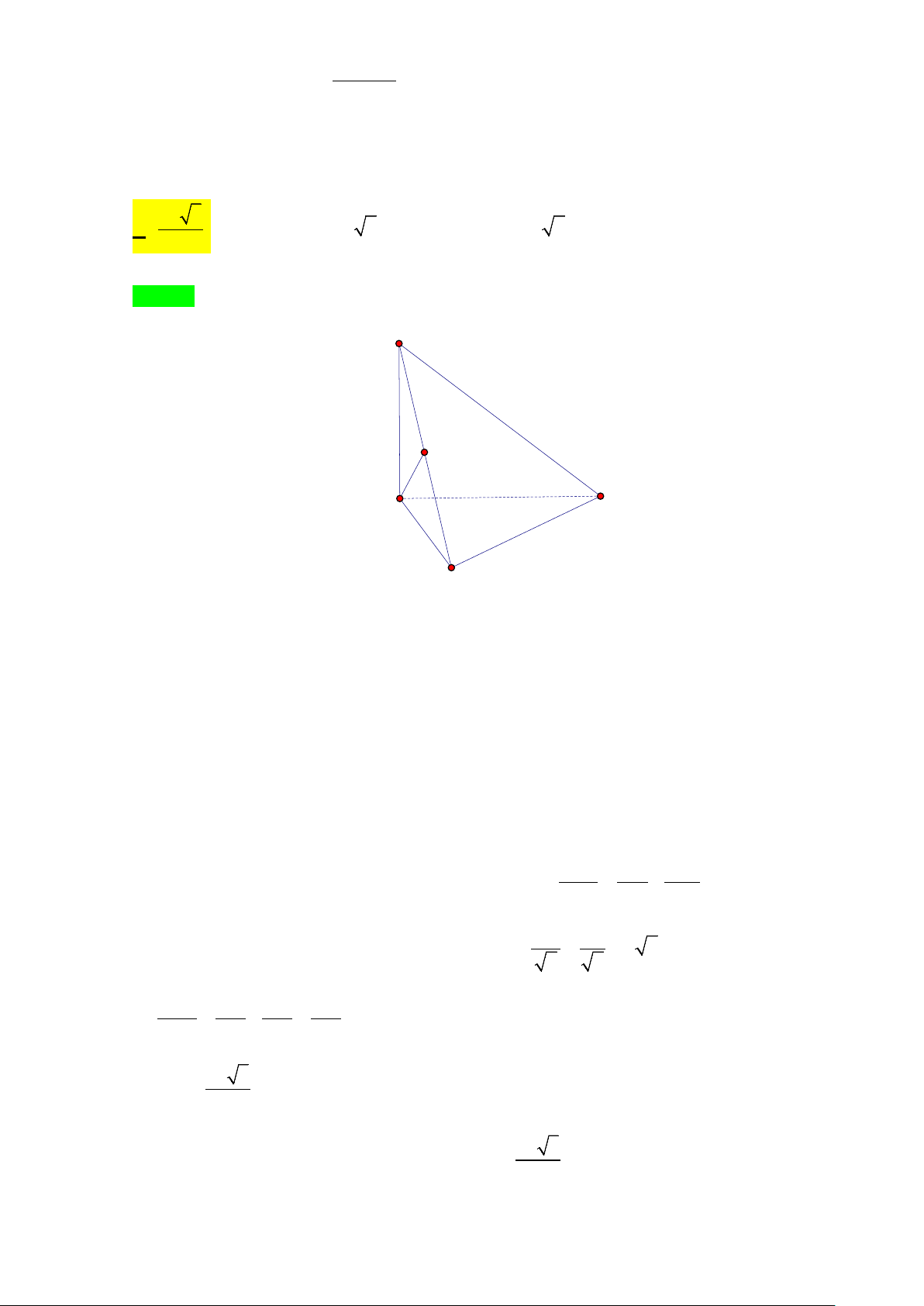
Câu 41. Cho khối chóp S.ABC có SA = SB = SC = 17a , AB = 3a, BC = 5a và CA = 7a . Thể tích của khối
chóp S.ABC bằng A. 5 2 3 a . B. 15 2 3 a . C. 5 17 3 a . D. 15 17 3 a . 4 4 4 4
Câu 42. Có bao nhiêu giá trị nguyên của tham số m∈( ; −∞ ] 2023 sao cho hàm số 3 2
y = x + (m + 2)x + 9 − m
nghịch biến trên khoảng (0; ) 1 ? A. 2019 . B. 2023. C. 2020 . D. 2022 .
Câu 43. Cho hàm số f (x) 3 2
= x − 3x + 5. Có bao nhiêu giá trị nguyên của tham số m để phương trình
f (2 f (x) − )
1 = m có 3 nghiệm phân biệt? A. 3. B. 486. C. 484. D. 485.
Câu 44. Cho hàm số f (x) 3 2 = x − x + ( 2 3
3 m − 2m + 2) x + m 1; − 1
(với m là tham số) có giá trị lớn nhất trên [ ]
bằng 2 , khi đó tổng các giá trị của tham số m là A. 2 . B. 5 . C. 0. D. 7 . 3 3 3 Trang 5/6 - Mã đề 123
Câu 45. Cho hàm số y = f (x) có đạo hàm f ′(x) 2
= x (x − 9)(x − 4)2 . Khi đó hàm số g x = f ( 2 ( ) x ) nghịch
biến trên khoảng nào? A. ( 3 − ;0) . B. ( 2; − 2) . C. ( ; −∞ 3 − ) . D. (3;+∞) .
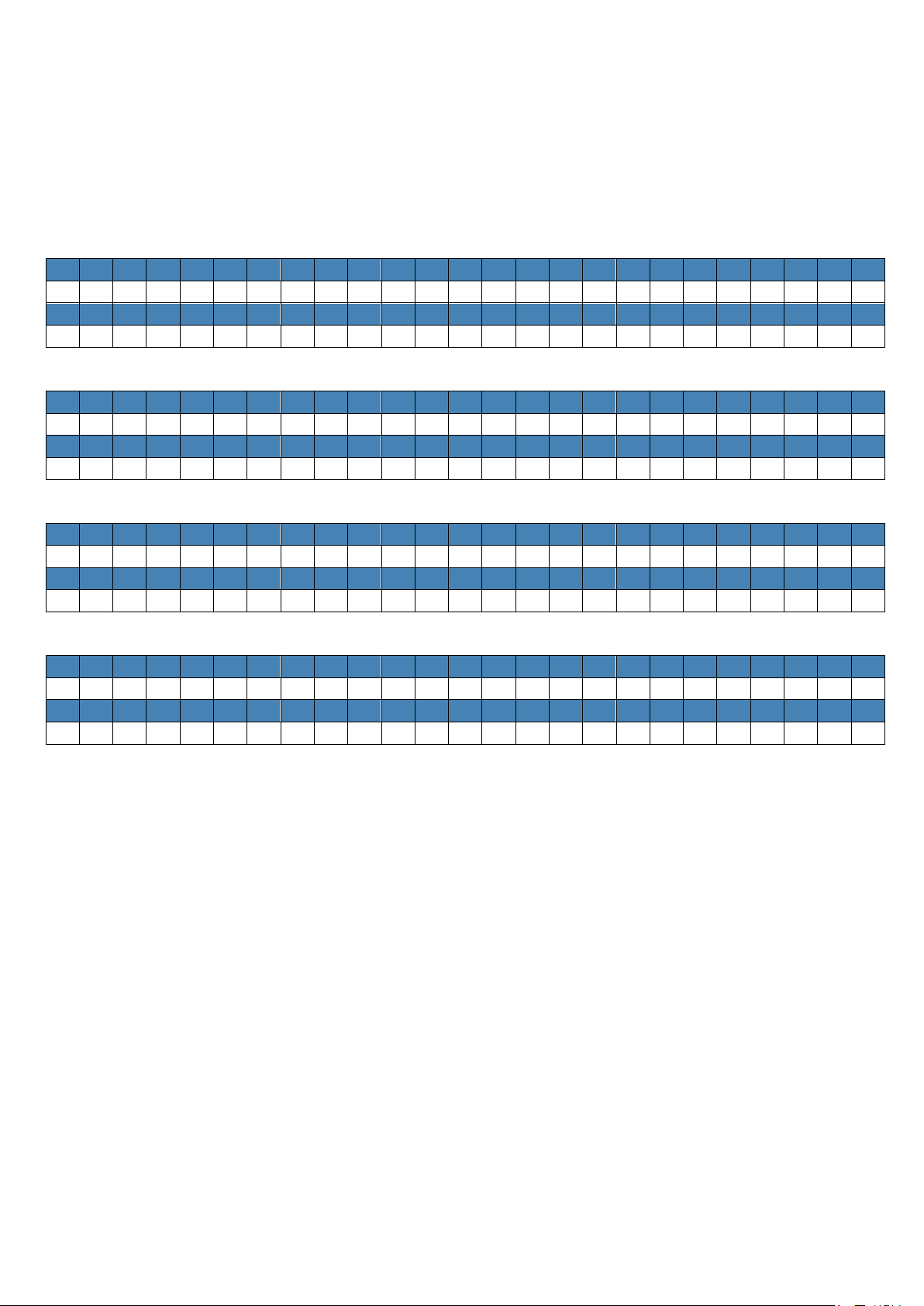
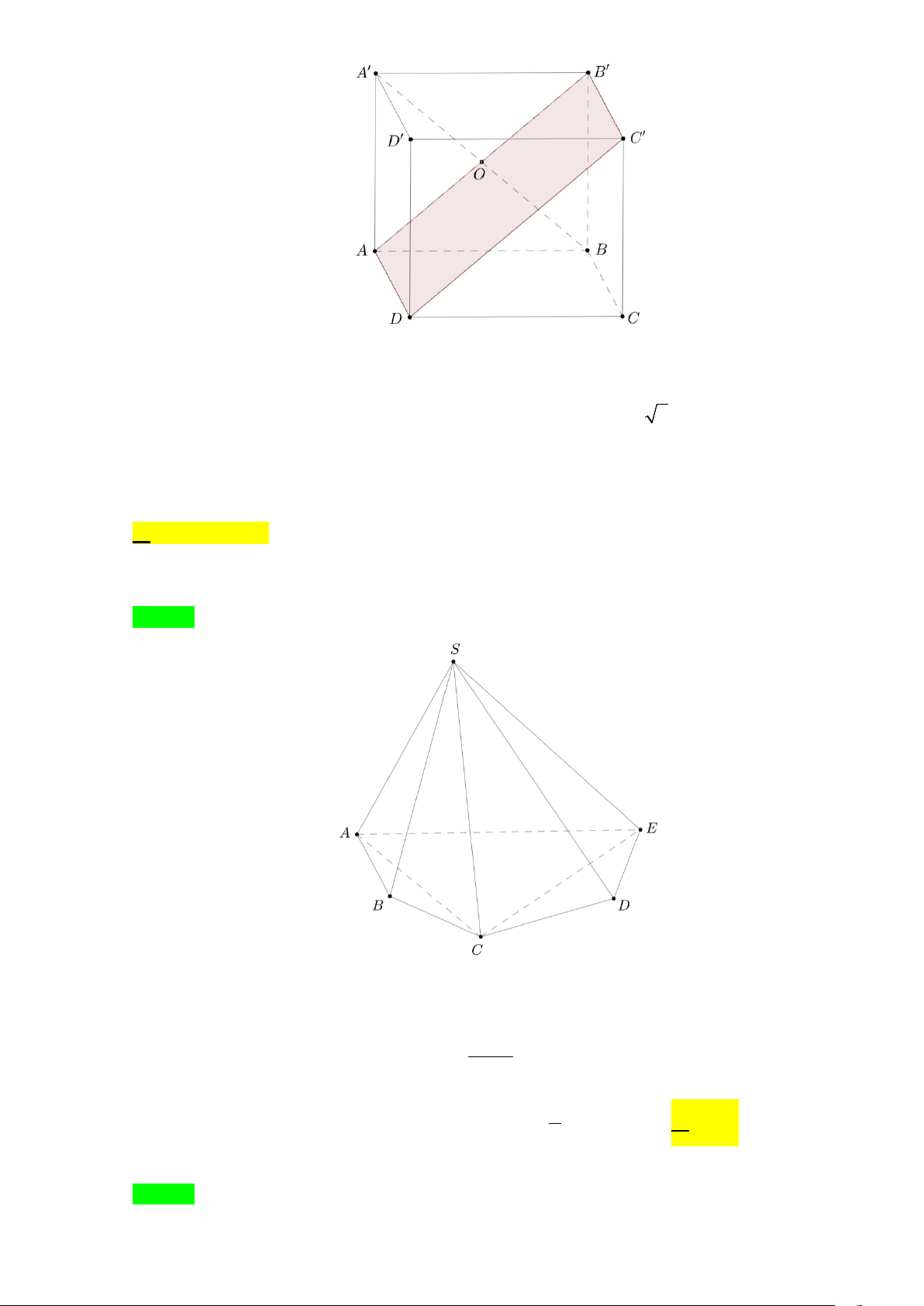
Câu 46. Cho hình lập phương ABC . D A′B C ′ D
′ ′ có M , N,O
lần lượt là trung điểm của AB, A′D ,′ BD′ (tham khảo hình
bên). Biết khối lập phương ABC . D A′B C ′ D ′ ′ có thể tích là 3
a . Thể tích của khối tứ diện ODMN là 3 3 A. a . B. 3a . 16 8 3 3 C. 3a . D. a . 16 6
Câu 47. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ 2; − ]3 để hàm số 3 3 2
y = x − (2m − 3)x + m + 2 có cực đại và cực tiểu đồng thời hoành độ điểm cực tiểu nhỏ hơn 2 ? 2 A. 4. B. 6. C. 5. D. 3.
Câu 48. Tìm tất cả các giá trị của tham số m để đồ thị hàm số 3 2
y = x − mx + ( 2
m − ) x + m( 2 2 2 1 1− m ) cắt
trục hoành tại 3 điểm phân biệt có hoành độ dương.
A. m <1. B. 2 3 m > . C. 2 3 1< m < . D. 2 3 1≤ m < . 3 3 3
Câu 49. Cho hàm số y = f (x) xác định trên  và có đồ thị f ′(x) như hình
bên. Giá trị nhỏ nhất của hàm số g (x) = f (2x) − 2x +1 trên  1 ;1 −  bằng 2    A. f ( ) 1 . B. f (− ) 1 + 2 .
C. f (0) −1.
D. f (2) −1.
Câu 50. Có bao nhiêu giá trị nguyên của tham số m sao cho đồ thị của hàm số 4 2
y = x − 2mx + 2 có ba điểm cực trị ,
A B,C thỏa mãn diện tích tam giác ABC nhỏ hơn 2023? A. 21. B. 15. C. 2023. D. 44 .
------------- HẾT ------------- Trang 6/6 - Mã đề 123
ĐÁP ÁN CÁC MÃ ĐỀ MÔN TOÁN - LỚP 12 NĂM HỌC 2023 - 2024
------------------------ Mã đề [123]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C D D C A C D A C D A C A C C D C D A D C B D A D
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
A D A D C A D C D C B B A B B A C D B C A C C D A Mã đề [234]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A D C B B C C C A D D B C B C A B D A A A A D C B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
A A C B C A C B B D B D C D D B B C B B D D A C C Mã đề [345]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A B A A B C D B D C A D C A B B D B B C C B D A D
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
B A A D D B A A B B C B D B B B D B D A A D C A D Mã đề [456]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
D B C A B C A A A A D B B A C A D B A D C C A D D
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
A D B B B D B A A D B D B C D B B A D A C D B A A HƯỚNG DẪN GIẢI
Câu 1. Cho cấp số cộng (u có u = 3 và u = 6 . Công sai của cấp số cộng đó bằng n ) 2 3 A. 1 . B. 1 . C. 3. D. 2. 3 2 Lời giải Chọn C
Ta có công sai: d = u − u = 6 − 3 = 3. 3 2
Câu 2. Số tập con có hai phần tử của tập hợp gồm 10 phần tử là A. 2 A . B. 10 2 . C. 2 10 . D. 2 C . 10 10 Lời giải Chọn D
Số tập con có hai phần tử của tập hợp gồm 10 phần tử là tổ hợp chập 2 của 10: 2 C 10
Câu 3. Kết luận nào sau đây về tính đơn điệu của hàm số x +1 y =
là kết luận đúng? 2x +1
A. Hàm số đồng biến trên  1  \  − . 2  
B. Hàm số nghịch biến trên  1  \  − . 2  
C. Hàm số đồng biến trên các khoảng  1 ;  −∞ −    và 1 −  ;+∞ . 2      2 
D. Hàm số nghịch biến trên các khoảng  1 ;  −∞ −    và 1 −  ;+∞ . 2      2  Lời giải Chọn D Tập xác định: \  1 −   . 2    Ta có 1 y ' −   = < 0, ∀ ∈ \ 1 x − . (   2x + )2 1  2 
Câu 4. Cho hàm số y = f (x) có bảng biến thiên như sau:
Tổng số đường tiệm cận ngang và đường tiệm cận đứng của đồ thị hàm số đã cho là A. 0 . B. 2 . C. 3. D. 1. Lời giải Chọn C
lim f (x) = 2 ta được tiệm cận ngang y = 2 x→+∞
lim f (x) = 5 ta được tiệm cận ngang y = 5 x→−∞
lim f (x) = +∞ ta được tiệm cận đứng x = 1 − x ( ) 1 + → −
Câu 5. Chọn ngẫu nhiên đồng thời hai số từ tập hợp 17 số nguyên dương đầu tiên. Xác suất để chọn được hai số lẻ bằng A. 9 . B. 9 . C. 7 . D. 8 . 34 17 34 17 Lời giải Chọn A
Số phần tử của không gian mẫu n(Ω) 2 = C =136 . 17
Gọi A là biến cố: “chọn được 2 số lẻ”. Vậy n( A) 2 = C = 36 9
Vậy xác suất cần tìm là: P( A) 36 9 = = . 136 34
Câu 6. Cho khối chóp có đáy là hình vuông cạnh a và chiều cao bằng 4a . Thể tích khối chóp đã cho bằng A. 4 16 3 16a . B. 3 4a . C. 3 a . D. 3 a . 3 3 Lời giải Chọn C Áp dụng công thức 1 V = Bh . 3 Suy ra 1 2 4 3
V = a .4a = a . 3 3
Câu 7. Cho hàm số y = f (x) có bảng biến thiên như sau
Đồ thị hàm số g (x) 1 =
có tất cả bao nhiêu đường tiệm cận( đường tiệm cận đứng và đường f (x) +1 tiệm cận ngang)? A. 2 . B. 0 . C. 1. D. 3. Lời giải Chọn D Ta có g (x) 1 lim = lim = và g (x) 1 lim = lim = 0 suy ra TCN y = 0. x→+∞
x→+∞ f ( x) 0 +1 x→−∞
x→−∞ f ( x) +1
Lại có f (x) +1 = 0 ⇔ f (x) = 1
− có 2 nghiệm phân biệt suy ra có 2 đường tiệm cận đứng.
Vậy đồ thị hàm số g (x) 1 =
có tất cả 3 đường tiệm cận. f (x) +1
Câu 8. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B , AC = SA = 2a và SA ⊥ ( ABC) . Khoảng
cách từ A đến mặt phẳng (SBC) bằng A. 2a 3 . B. a 2 .
C. −a 2 . D. a . 3 Lời giải Chọn A S H A C B BC ⊥ AB Ta có 
⇒ BC ⊥ (SAB) BC ⊥ SA
(do SA ⊥ (ABC),BC ⊂  ( ABC))
Gọi H là hình chiếu của A lên cạnh SB . AH ⊥ SB Suy ra 
⇒ AH ⊥ (SCD) AH ⊥ BC
(do BC ⊥ (SAB), AH ⊂  (SAB))
Vậy AH là khoảng cách từ điểm A đến mặt phẳng (SBC)
Xét tam giác SAB vuông tại A có AH là đường cao 1 1 1 ⇒ = + 2 2 2 AH SA AB Mà 2 2 2 2 2 2 AC 2 AC a
= AB + BC = AB + AB = 2AB ⇒ AB = = = a 2 2 2 1 1 1 3 ⇒ = + = 2 2 2 2 AH 4a 2a 4a 2a 3 ⇒ AH = 3
Vậy khoảng cách từ A tới mặt phẳng (SBC) bằng 2a 3 . 3
Câu 9. Cho hình chóp S.ABC có SA vuông góc với mặt đáy, tam giác ABC đều, SA = AB = 3 . Góc
giữa SC và mặt phẳng ( ABC) bằng A. 90° . B. 30° . C. 45°. D. 60°. Lời giải Chọn C S A C B
Ta có SA ⊥ ( ABC) ⇒ AC là hình chiếu của SC lên mặt phẳng ( ABC).
Suy ra (SC ( ABC))  = (SC AC)  =  , , SCA
Ta lại có tam giác ABC đều ⇒ AC = AB = SA = 3 ⇒ S
∆ AC vuông cân tại A ⇒  SCA = 45°
Vậy góc giữa SC và mặt phẳng ( ABC) bằng 45°.
Câu 10. Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? 6 4 2 5 2 4 A. 3
y = x − 3x −1. B. 4 2
y = x + x +1. C. 2x −1 y + = . D. x 1 y = . x −1 x −1 Lời giải Chọn D
Đồ thị là của hàm số phân thức ⇒ loại A và B .
Từ đồ thị ta có đường tiệm cận ngang y =1 và đường tiệm cận đứng x =1 ⇒ loại C .
Vậy đồ thị trên là của hàm số x +1 y = . x −1
Câu 11. Cho hàm số y = f (x) liên tục trên  và có đạo hàm f ′(x) = (x + )(x − )2 1 2 (x − ) 1 . Điểm cực đại
của hàm số đã cho là A. x = 1 − . B. x = 2 − . C. x =1. D. x = 2 . Lời giải Chọn A x +1 = 0 x = 1 − 
Ta có: f ′(x) = (x + )(x − )2 1 2 (x − )
1 , suy ra f (x) 0 ( x 2)2 0  ′ = ⇔ − = ⇔ x = 2 .  x −1= 0 x =1  Bảng biến thiên:
Từ bảng biến thiên, suy ra điểm cực đại của hàm số đã cho là x = 1. −
Câu 12. Cho hàm số y = f (x) có bảng biến thiên như sau:
Số các giá trị nguyên của tham số m để phương trình f (x) = m có 2 nghiệm phân biệt là A. 4 . B. 2 . C. 3. D. 1. Lời giải Chọn C
Để phương trình f (x) = m có hai nghiệm phân biệt khi và chỉ khi đường thẳng y = m cắt đồ thị
hàm số y = f (x) tại hai giao điểm. m = 3
Từ bảng biến thiên, suy ra: m∈  → m∈  {0;1; } 3 .  1 − < m ≤1
Câu 13. Cho khối lăng trụ ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh bằng 1. Biết thể tích khối lăng
trụ ABC.A′B C
′ ′ bằng 1. Khoảng cách giữa hai mặt phẳng ( ABC) và ( A′B C ′ ′) bằng A. 4 3 . B. 3 . C. 3. D. 1 . 3 4 3 Lời giải Chọn A 2 Vì A
∆ BC đều cạnh 1 nên 1 3 3 S = = ABC ∆ . 4 4
Ta có: d (( ABC),( A′B C ′ ′)) = .h Ta có:
VABC A′BC′′ 1 4 3 . V = ⋅ ⇒ = = = ′ ′ ′ S∆ h h ABC A B C ABC . . S ABC ∆ 3 3 4
Câu 14. Cho lăng trụ tam giác đều ABC.A′B C
′ ′ có cạnh đáy bằng a và cạnh bên bằng 2 . a Thể tích của
lăng trụ ABC.A′B C ′ ′ bằng 3 3 3 3 A. a 3 . B. a 3 . C. a 3 . D. a 3 . 6 3 2 4 Lời giải Chọn C
Vì ABC.A′B C
′ ′ là lăng trụ tam giác đều có cạnh đáy bằng a và cạnh bên bằng 2a nên lăng trụ đã 2  a 3 cho có: S = ABC ∆  4 .
h = AA′ = 2a 2 3
Vậy thể tích của lăng trụ ABC.A′B C ′ ′ bằng a 3 a 3 V = ⋅ = ⋅ = ′ ′ ′ S∆ h a ABC A B C ABC 2 . . 4 2 Câu 15. Cho hàm số 4 2
y = ax + bx + c có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng?
A. a > 0,c < 0.
B. a < 0,c > 0.
C. a < 0,c < 0 .
D. a > 0,c > 0. Lời giải Chọn A
Dựa vào đồ thị hàm số đã cho ta có:
Khoảng ngoài cùng đồ thị hàm số đi xuống nên hàm số nghịch biến, suy ra: a < 0.
Đồ thị hàm số giao với Oy tại điểm (0;c), từ đồ thị suy ra c < 0.
Câu 16. Cho hàm số y = f (x) có bảng biến thiên như sau:
Số nghiệm thực của phương trình 2 f (x) + 3 = 0 là A. 1. B. 2 . C. 3. D. 4 . Lời giải Chọn D
Ta có phương trình f (x) + = ⇔ f (x) 3 2 3 0 = − . 2 3
Số nghiệm của phương trình 2 f (x) + 3 = 0 là số giao điểm y = f (x) và đường thẳng y = − . 2
Vậy phương trình 2 f (x) + 3 = 0 có 4 nghiệm phân biệt. Câu 17. Hàm số 4 2
y = x + 2x −1 có bao nhiêu điểm cực trị ? A. 0 . B. 3. C. 1. D. 2 . Lời giải Chọn C Ta hàm số dạng 4 2
y = ax + bx + c có .
a b = 2 > 0 . Vậy hàm số có 1 điểm cực trị. Câu 18. V
Cho khối chóp S.ABC . Gọi A', B ',C ' lần lượt là trung điểm ,
SA SB, SC . Tỉ số thể tích S.A′B C′′ VS.ABC bằng bao nhiêu? A. 1 1 . B. 1 . C. 3 . D. . 16 6 8 8 Lời giải Chọn D V ′ ′ ′ ′ ′ ′ SA SB SC S A B C 1 Ta có . = . . = . V SA SB SC S ABC 8 . Câu 19. Cho hàm số 3
y = x + (m − ) 2
3 x + (m −3) x + 4 . Có bao nhiêu giá trị nguyên của tham số m để hàm
số đã cho đồng biến trên ( ; −∞ +∞) ? A. 4 . B. 6 . C. 5. D. 3. Lời giải Chọn A Ta có 2
y′ = 3x + 2(m −3) x + m −3 ≥ 0 x ∀ ∈  Hay ∆′ = (m − )2
3 − 3(m −3) ≤ 0 ⇔ 0 ≤ m −3 ≤ 3 ⇔ 3 ≤ m ≤ 6 .
Do m nguyên nên có 4 giá trị m thỏa mãn.
Câu 20. Hình chóp tứ giác có bao nhiêu mặt? A. 6 . B. 7 . C. 4 . D. 5. Lời giải Chọn D
Hình chóp tứ giác có 5 mặt.
Câu 21. Giá trị lớn nhất của hàm số y = f (x) trên [ ;
a b] bằng 3. Giá trị nhỏ nhất của hàm số
g (x) = 5− 2 f (x) trên đoạn [ ;
a b] bằng bao nhiêu? A. 1. B. 2 . C. 1 − . D. 3 − . Lời giải Chọn C
Ta có: g (x) = 5 − 2 f (x) .
Suy ra g (x) đạt GTNN khi f (x) đạt GTLN
⇒ min g (x) = 5 − 2max f (x) = 5 − 2.3 = 1 − . [a;b] [a;b]
Câu 22. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ sau:
Giá trị cực tiểu của hàm số đã cho là A. 0 . B. 4 − . C. 2 − . D. 1. Lời giải Chọn B
Quan sát BBT của hàm số y = f (x) suy ra giá trị cực tiểu của f (x) là 4 − .
Câu 23. Cho hình lập phương ABC .
D A'B 'C 'D ' có cạnh bằng 2a . Khoảng cách giữa hai đường thẳng AB '
và A'D ' bằng A. a 2 . B. a 3 . C. a 3 . D. a 2 . 2 3 Lời giải Chọn D
Do A'B 'C 'D ' là hình bình hành nên A'D '/ /B 'C '
Gọi O là tâm hình vuông A'B 'BA . Khi đó:
d ( A'D ', AB ') = d ( A'D',( AB'C 'D)) = d ( A',( AB'C 'D)) = A'O = a 2 .
Câu 24. Cho khối chóp ngũ giác S.ABCDE . Khi ta chia khối chóp này bằng hai mặt phẳng (SAC) và
(SCE) thì sẽ được
A. 3 khối tứ diện.
B. 4 khối chóp tam giác.
C. 2 khối chóp tam giác.
D. 3 khối chóp tứ giác. Lời giải Chọn A
Khi chia khối chóp ngũ giác S.ABCDE bằng hai mặt phẳng (SAC) và (SCE) ta thu được ba khối
tứ diện: SACE, SABC, SCDE .
Câu 25. Đường tiệm cận đứng của đồ thị hàm số 2x −1 y =
là đường thẳng có phương trình là x −1
A. x = 2 . B. x = 1 − . C. 1 x = . D. x =1. 2 Lời giải Chọn D Hàm số 2x −1 y =
có tiệm cận đứng là x =1. x −1
Câu 26. Có bao nhiêu cách xếp 4 người ngồi vào dãy 5 ghế xếp theo hàng ngang(mỗi ghế không ngồi quá một người)? A. 120. B. 20. C. 9. D. 10. Lời giải Chọn A
Số cách xếp 4 người ngồi vào dãy 5 ghế xếp theo hàng ngang(mỗi ghế không ngồi quá một người) là: 4 A =120 . 5
Câu 27. Cho hàm số y = f (x) xác định trên  và có bảng biến thiên như hình vẽ sau
Hàm số đã cho đồng biến trên khoảng nào? A. (−∞;− ) 1 . B. ( 2; − 4) . C. (2;+ ∞) . D. ( 1; − 2) . Lời giải Chọn D
Câu 28. Hàm số f x 3 2
x 3x  4 có đồ thị (C). Viết phương trình tiếp tuyến với (C) tại điểm A nằm
trên C có hoành độ x = . A 1 A. y = 3 − x + 5.
B. y = 3x − 5.
C. y = 5x −3. D. y = 5 − x + 3. Lời giải Chọn A
x = ⇒ y = ⇒ A(1;2) . A 2 A 1 f x 2  3x 6x .
Phương trình tiếp tuyến với (C) tại điểm A là: y f x xx y . A  A
A y  3x  5
Câu 29. Cho hình chóp S.ABCD có đáy ABCD la hình vuông tâm O, SA ⊥ ( ABCD). Gọi I là trung điểm
SC. Khoảng cách từ I đến mặt phẳng ( ABCD) bằng độ dài đoạn thẳng nào ? A. IB . B. IC . C. ID . D. IO . Lời giải Chọn D
Xét tam giác SAC có I,O lần lượt là trung điểm các cạnh SC; AC
⇒ IO là đường trung bình S ∆ AC . ⇒ IO // SA.
Mà SA ⊥ ( ABCD) nên IO ⊥ ( ABCD) tại . O
Do đó khoảng cách từ I đến mặt phẳng ( ABCD) = . IO
Câu 30. Hàm số nào liệt kê dưới đây có đồ thị như hình vẽ bên ? − A. x 2 4 2
y = x + 2x − 2 . B. 3 2
y = −x + 3x − 2. C. 3 2
y = x + 3x − 2. D. y = . x +1 Lời giải Chọn C
Đồ thị hàm số trong hình vẽ là của hàm số bậc 3 với hệ số a > 0 .
Câu 31. Điểm nào dưới đây thuộc đồ thị hàm số 3 2
y = x − 3x ? A. M ( 1; − 4 − ) . B. M ( 1; − 2 − ) . C. M ( 1; − 2) . D. M (1; 4 − ). Lời giải Chọn A Xét điểm M ( 1; − 4 − ) , thay x = 1; − y = 4
− vào đồ thị hàm số 3 2
y = x − 3x ta được: − = (− )3 − (− )2 4 1 3 1 ⇔ 4 − = 4 − (luôn đúng). Vậy điểm M ( 1; − 4
− ) thuộc đồ thị hàm số 3 2
y = x − 3x .
Câu 32. Cho hàm số y = f (x) có bảng biến thiên như sau:
Khẳng định nào sau đây đúng?
A. max f (x) = 2 .
B. max f (x) = 2 − .
C. max f (x) =1.
D. max f (x) = 3. [ 3 − ;2] [ 3 − ;2] [ 3 − ;2] [ 3 − ;2] Lời giải Chọn D
Từ BBT, max f (x) = 3 = f (− ) 1 . [ 3 − ;2]
Câu 33. Cho hình lập phương ABC . D A′B C ′ D
′ ′ . Tính góc giữa hai đường thẳng B D
′ ′ và A′A . A. 0 60 . B. 0 45 . C. 0 90 . D. 0 30 . Lời giải Chọn C
Ta có AA′ ⊥ ( A′B C ′ D ′ ′) ⇒ ′ ⊥ ′ ′ ⇒  AA B D
(AA,′BD′′)=90°.
Câu 34. Một khối lập phương có thể tích bằng 8 . Độ dài cạnh của khối lập phương đó là A. 512. B. 2 2 . C. 8 . D. 2 . Lời giải Chọn D
Giả sử, độ dài cạnh hình lập phương là x . Ta có 3
x = 8 ⇔ x = 2 .
Câu 35. Cho một cấp số nhân có số hạng đầu bằng công bội và số hạng thứ ba lớn hơn công bội 6 đơn vị.
Số hạng thứ hai của cấp số nhân này là A. 2 . B. 6 . C. 4 . D. 1. Lời giải Chọn C
Giả sử cấp số nhân cần tìm có số hạng đầu u , công bội 1 q . Ta có u = q . 1 Ta có 2 3
u − q = 6 ⇔ u q − q = 6 ⇔ q − q − 6 = 0 ⇔ q = 2 . 3 1
Ta có u = u .q = 2.2 = 4 . 2 1
Câu 36. Cho hàm số y = f (x) là hàm đa thức bậc ba có đồ thị như hình vẽ bên. Giá trị của f ( ) 1 − f (0) bằng A. 4 − . B. 2 − . C. 6 − . D. 2 . Lời giải Chọn B f ( ) 1 − f (0) = 4 − − ( 2 − ) = 2 − .
Câu 37. Cho khối lăng trụ ABC. ’ A ’
B C’ có thể tích bằng 12. Thể tích khối chóp ’ A ABC bằng A. 6 . B. 4 . C. 3. D. 12. Lời giải Chọn B 1 V = V = . A ABC ABC A B C 4 '. . ' ' ' 3
Câu 38. Hàm số nào sau đây nghịch biến trên R A. 3 2
y = −x + 3x − 3x + 5 .
B. y = −(x + )2 1 . + C. x 1 y = y = −x − x −1 . D. 2 1. Lời giải Chọn A 3 2 2
y = −x + 3x − 3x + 5 ⇒ y ' = 3
− x + 6x − 3 = 0 ⇒ x = 1 là nghiệm kép Nên y ' ≤ 0 x ∀ ∈ 
Câu 39. Giá trị nhỏ nhất của hàm số 4 2
y = −x + 4x − 3 trên đoạn [ 1; − ] 3 bằng A. 1. B. 48 − . C. 0 . D. 50 − . Lời giải Chọn B Xét [ 1; − ] 3 x = 0  4 2 3
y = −x + 4x − 3 ⇒ y ' = 4
− x + 8x = 0 ⇒ x = 2 x = − 2  (L) y(− ) 1 = 0 y(3) = 48 − y ( 2) =1
Câu 40. Cho hàm số đa thức bậc bốn y = f (x) có đồ thị như hình vẽ bên dưới. Số điểm cực đại của hàm số ( ) =  ( ) 2 g x f x    là A. 5. B. 2. C. 4. D. 3. Lời giải Chọn B f (x) = 0
x = a ∨ x = b
Xét g′(x) = 2 f (x). f ′(x) = 0 ⇔  ⇔  f ′  ( x) = 0 
x = c ∨ x = d ∨ x = e
với các số a < 1
− < c < b < d < e .
Ta có bảng xét dấu như sau
Như vậy, g′(x) đổi dấu từ “dương” sang “âm” 2 lần.
Vậy hàm số ( ) =  ( ) 2 g x f x  
 có 2 điểm cực đại.
Câu 41. Cho khối chóp S.ABC có SA = SB = SC = a 17 , AB = 3a , BC = 5a và CA = 7a . Thể tích khối
chóp S.ABC bằng 3 3 3 3
A. 5a 2 .
B. 15a 2 .
C. 5a 17 . D. 15a 17 . 4 4 4 4 Lời giải Chọn A S A C O B
Vì khối chóp S.ABC có SA = SB = SC nên hình chiếu của S lên ( ABC) trùng với O là tâm đường
tròn ngoại tiếp tam giác ABC . 2 a S = − − − = . ∆ p p AB p AC p BC ABC ( )( )( ) 15 3 4 Mặt khác A . B AC.BC A .
B AC.BC 7a 3 S = ⇒ = = . ∆ OA ABC 4OA 4S ABC ∆ 3 S
∆ OA vuông tại O có 2 2 a 6
SO = SA − OA = . 3 3 Vậy 1 5a 2 V = S = . ∆ SO S ABC . ABC. . 3 4
Câu 42. Có bao nhiêu giá trị nguyên của tham số m∈( ; −∞ ] 2023 thỏa hàm số 3
y = x + (m + ) 2 2 x + 9 − m
nghịch biến trên khoảng (0; ) 1 ? A. 2019. B. 2023. C. 2020. D. 2022. Lời giải Chọn C
Xét hàm số f (x) 3 = x + (m + ) 2
2 x + 9 − m có đạo hàm f ′(x) 2 = 3x + m + 2 . Trường hợp 1.
 f ′(x) ≤ 0, x ∀ ∈(0; ) 2 1 3
 x + m + 2 ≤ 0, x ∀ ∈(0; ) 2 1 m ≤ 3 − x − 2, x ∀ ∈(0; ) 1  ⇔  ⇔  (*)  f  ( ) 2 1 ≥ 0
−m + m +12 ≥ 0  3 − ≤ m ≤ 4
Xét hàm số g (x) 2 = 3
− x − 2 có g′(x) = 6
− x = 0 ⇔ x = 0 . m ≤ 5 −
Dựa vào bảng biến thiên, điều kiện (*) tương đương  (vô lí).  3 − ≤ m ≤ 4 Trường hợp 2. 2  ′  ( )
m ≥ − x − x ∀ ∈ f x ≥ 0, x ∀ ∈(0; ) 3 2, 0;1 2 1 3
 x + m + 2 ≥ 0, x ∀ ∈(0; ) ( ) 1   ⇔  ⇔  ≤ − (**)  f  ( ) m 3 2 1 ≤ 0
−m + m +12 ≤ 0  m ≥ 4 m ≥ 2 −
Dựa vào bảng biến thiên ở trên, điều kiện (**) tương đương m ≤ 3 − ⇔ m ≥ 4 .  m ≥ 4
Vì m nguyên và m∈( ; −∞ ]
2023 nên m∈{4;5;6;...; } 2023 .
Vậy có tất cả 2020 giá trị nguyên m thỏa mãn.
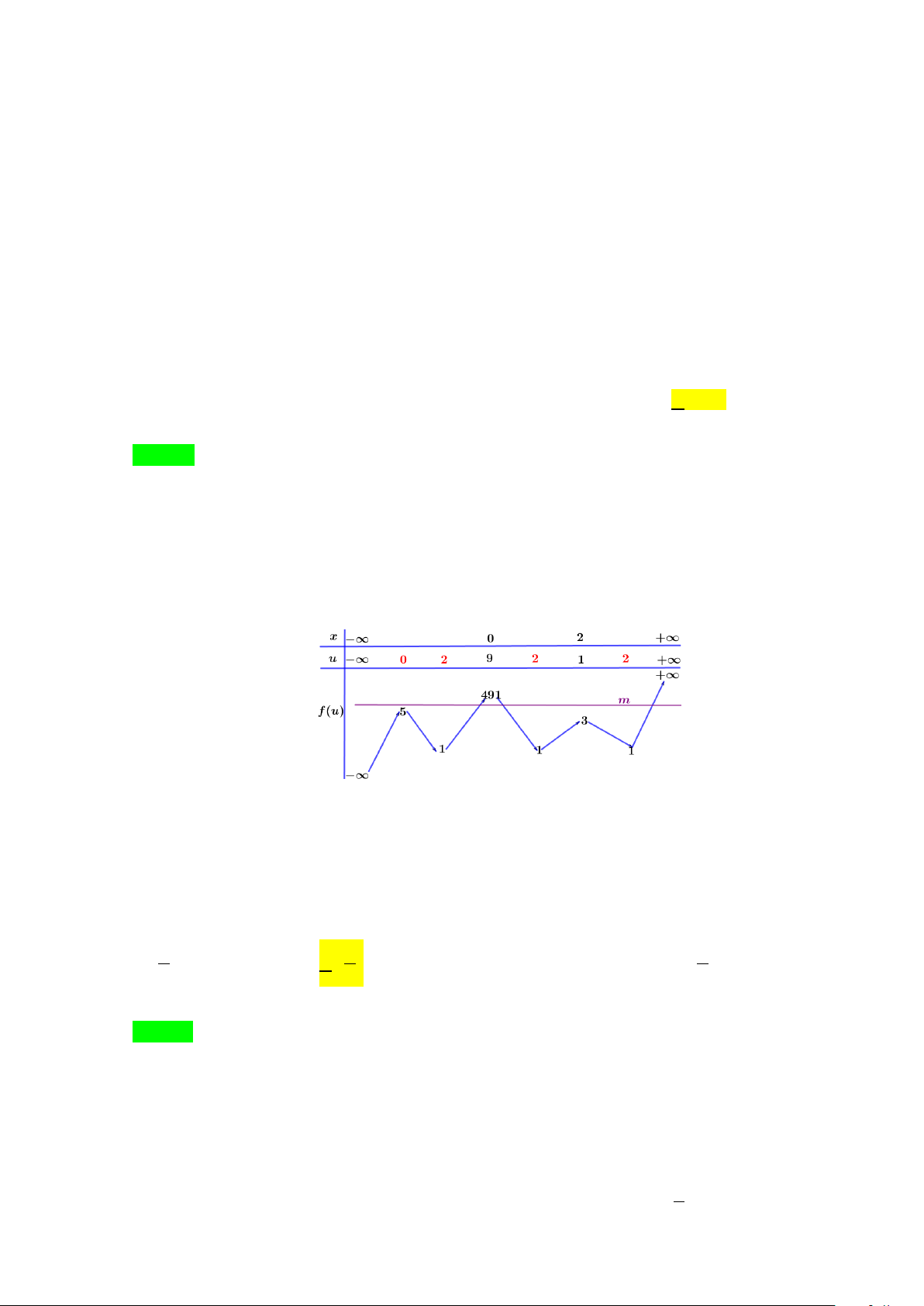
Câu 43. Cho hàm số f (x) 3 2
= x − 3x + 5. Có bao nhiêu giá trị nguyên của tham số m để phương trình
f (2 f (x) − )
1 = m có 3 nghiệm phân biệt? A. 3. B. 486. C. 484. D. 485. Lời giải Chọn Dx = 0 Ta có: f ′(x) 2
= 3x − 6x → f ′(x) = 0 ⇔ 
và f (0) = 5, f (2) =1, f ( ) 1 = 3, f (9) = 491. x = 2 x =
Đặt u = 2 f (x) −1→ u′ = 2 f ′(x). Cho u′ = ⇒ f ′(x) 0 0 = 0 ⇔  . x = 2
Sử dụng phương pháp ghép trục, ta có BBT
Điều kiện phương trình có 3 nghiệm phân biệt thì 5 < m < 491.
Kết hợp với m∈ ⇒m∈{6;7;.......; } 490 → có 485 giá trị.
Câu 44. Cho hàm số f (x) 3 2 = x − x + ( 2 3
3 m − 2m + 2) x + m (với m là tham số) có giá trị lớn nhất trên [ 1; − ]
1 bằng 2 , khi đó tổng các giá trị của tham số m là A. 2 . B. 5 . C. 0. D. 7 . 3 3 3 Lời giải Chọn B
Xét hàm số f (x) trên đoạn [ 1; − ] 1 . Ta có: f ′(x) 2 = x − x + ( 2 3 6
3 m − 2m + 2) → ∆′ = − − ≤ ∀ ′ m m . f ( )2 9 1 0,
Từ đó suy ra f ′(x) 2 = x − x + ( 2 3
6 3 m − 2m + 2) ≥ 0, x ∀ .
Vậy max f (x) = f ( ) 1 2 2 5
⇔ 2 = 3m − 5m ⇔ 3m − 5m − 2 = 0 → m + m = . [ 1 − ; ] 1 1 2 3
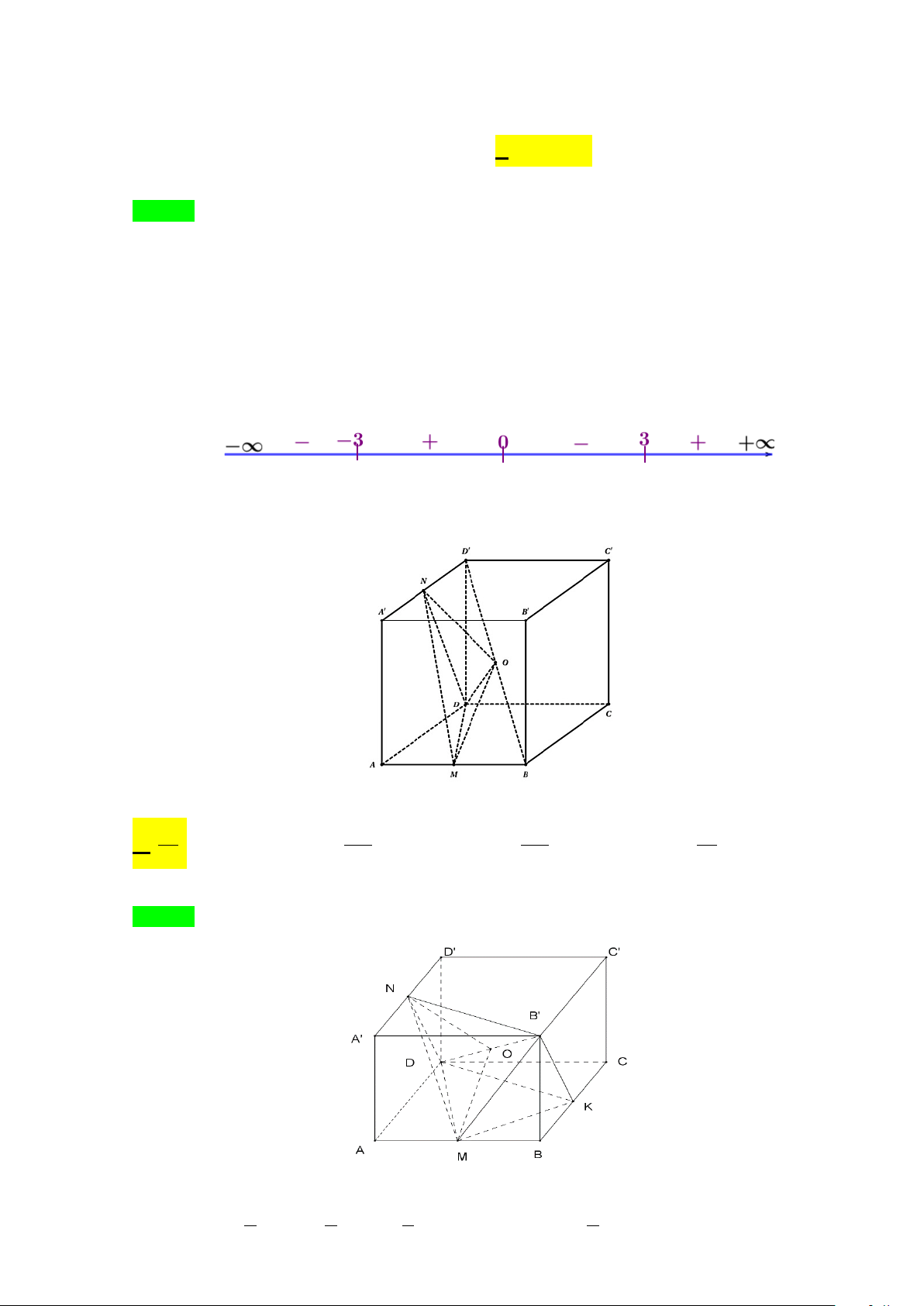
Câu 45. Cho hàm số y = f (x) có đạo hàm f ′(x) 2
= x (x − 9)(x − 4)2 . Khi đó hàm số g x = f ( 2 ( ) x ) nghịch
biến trên khoảng nào? A. ( 3 − ;0). B. ( 2; − 2) . C. ( ; −∞ 3 − ) . D. (3;+∞) . Lời giải Chọn C x = 0(k) f (x) 0  ′ = ⇔ x = 9  x =  4(k) x = 0
Ta có: g′ x = x f ′( 2 ( ) 2 .
x ) . Cho g′(x) = 0 ⇒ . 2
x = 9 ⇔ x = 3 ±
Bảng xét dấu g′(x)
Câu 46. Cho hình lập phương ′ ′ ′ ′
ABCD ⋅ A B C D có M , N,O lần lượt là trung điểm của , ′ ′, ′ AB A D BD (tham khảo hình bên). Biết khối lập phương ′ ′ ′ ′
ABCD ⋅ A B C D có thể tích là 3
a . Thể tích của khối tứ diện ODMN là 3 3 3 3 A. a . B. 3a . C. 3a . D. a . 16 8 16 6 Lời giải Chọn A
Gọi K là trung điểm của BC. Ta có 1 1 1 1 V = V = V = d N, KMD S = a S ODMN B DMN KDMN ∆KMD . ∆KMD. ' ( ( )) 2 2 6 6 2 2
1 a 1 a 1 a a 3 2 S = a − S − S − S
= a − a − a − = a ∆KMD ∆CKD ∆ADM ∆BMK . . . . 2 2 2 2 2 2 2 8 2 3 Do đó 1 3 = . a = a V a ODMN . 6 8 16
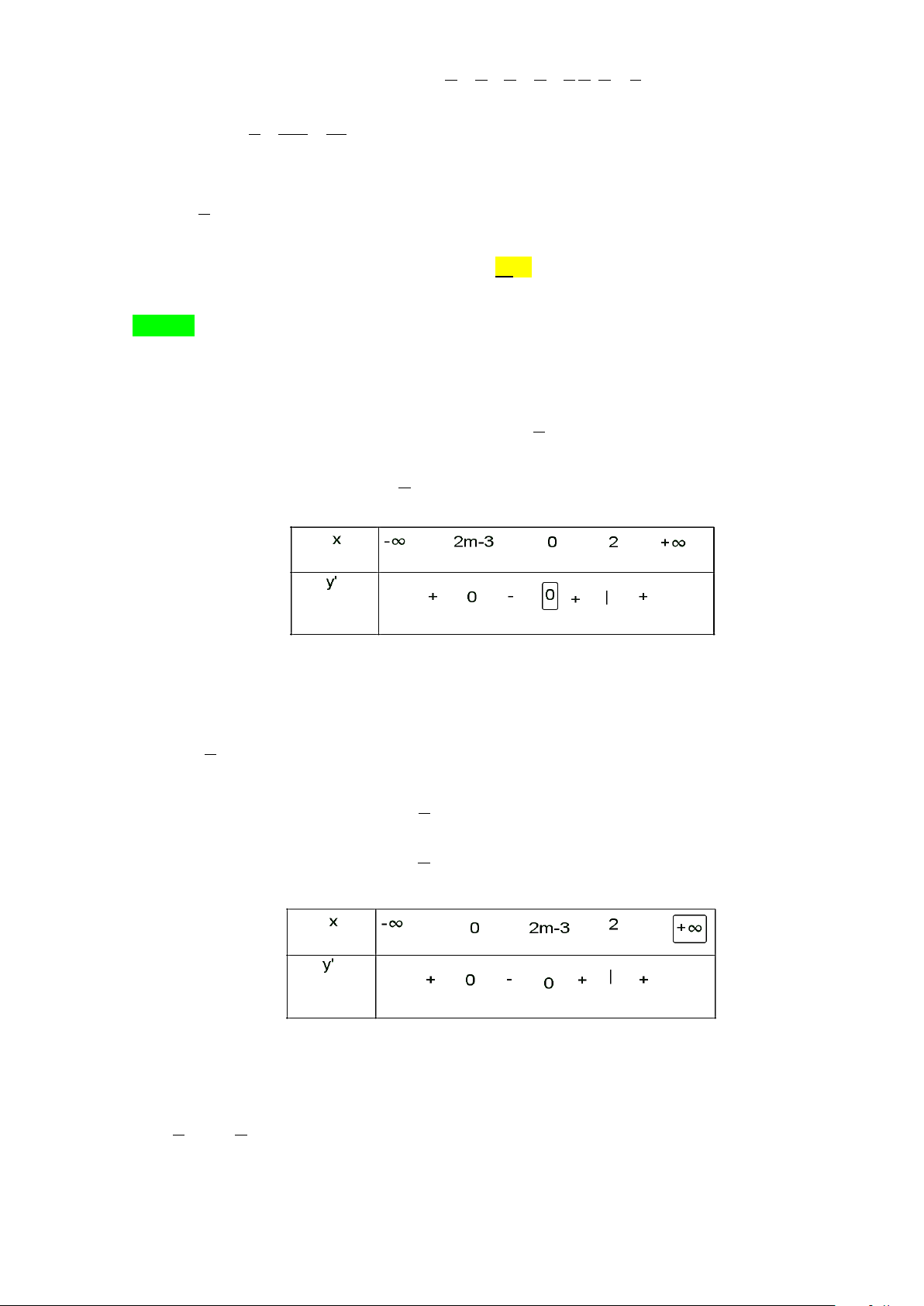
Câu 47. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ 2; − 3] để hàm số 3 3 2
y = x − (2m − 3)x + m + 2 có cực đại và cực tiểu đồng thời hoành độ điểm cực tiểu nhỏ hơn 2 ? 2 A. 4. B. 6. C. 5. D. 3. Lời giải Chọn C x = 0 Ta có 2
y′ = 3x − 3(2m − 3)x = 3x(x − 2m + 3) ⇒ y′ = 0 ⇔  . x = 2m − 3
Để hàm số có cực đại, cực tiểu khi 3
2m − 3 ≠ 0 ⇔ m ≠ . 2 + Trường hợp 1: 3
2m − 3 < 0 ⇔ m < . Khi đó dấu của y′ 2  m∈[ 2; − 3] Do m∈
⇒ m = 0,m =1,m = 1, − m = 2 − .  3 m <  2  3 2m − 3 > 0 m >  + Trường hợp 2:  2  ⇔
. Khi đó dấu của y′ 2m 3 2  − < 5 m <  2  m∈[ 2; − 3] Do m∈ ⇒ m = 2. 3 5  < m < 2 2
Vậy có 5 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Câu 48. Tìm tất cả các giá trị của tham số m để đồ thị hàm số 3 2
y = x − mx + ( 2
m − ) x + m( 2 2 2 1 1− m ) cắt
trục hoành tại 3 điểm phân biệt có hoành độ dương.
A. m <1. B. 2 3 m > . C. 2 3 1< m < . D. 2 3 1≤ m < . 3 3 3 Lời giải Chọn C Phương trình hoành độ giao điểm 3 2 x − mx + ( 2
m − ) x + m( 2 2 2 1 1− m ) = 0( ) 1 . x m ⇔ (x − m)(  = 2 2
x − m + m − ) 1 = 0 ⇔  . 2 2
x − mx + m −1 = 0 Đặt h(x) 2 2
= x − mx + m −1. Để đồ thị hàm số 3 2
y = x − mx + ( 2
m − ) x + m( 2 2 2 1
1− m ) cắt trục hoành tại 3 điểm phân biệt có
hoành độ dương điều kiện là (1) có 3 nghiệm phâm biệt có hoành độ dương  m > 0, ∆ > h 0 m 0  >  mh(m) >  0 ≠ 0  2   3 − m + 4 > 0  2 2 2  ⇔ m  ⇔ − < m < ⇔ 1< m < . 2 >  0 m −  1 ≠ 0  3 3 3 2   2 m −1 > 0 m >1 2 m −1> 0  m < 1 −
Câu 49. Cho hàm số y = f (x) xác định trên  và có đồ thị f ′(x) như hình bên. Giá trị nhỏ nhất của hàm
số g (x) = f (2x) − 2x +1 trên  1 ;1 −  bằng 2    A. f ( ) 1 . B. f   1  2 .
C. f 01.
D. f 21. Lời giải Chọn D
Ta có gx 2 f 2x2  2 f 2x  1 .   Với mọi 1
x   ;1 , ta có 2x 1;2 suy ra f 2x1.  2     
Do đó gx 0, với mọi 1 x   ;1 .  2   
Vậy min gx g  1  f 21.  1   ;1  2   
Câu 50. Có bao nhiêu giá trị nguyên của tham số m sao cho đồ thị của hàm số 4 2
y = x − 2mx + 2 có ba điểm cực trị ,
A B,C thỏa mãn diện tích tam giác ABC nhỏ hơn 2023? A. 21. B. 15. C. 2023. D. 44 . Lời giải Chọn A Ta có 3
y′ = x − mx = x( 2 4 4 4 x − m) . x = 0 ⇒ y = 2 y′ = 0 ⇔  (m > 0) . 2
x = ± m ⇒ y = −m + 2 Khi đó A( ) B( 2
− m −m + ) C ( 2 0;2 , ; 2 , m;−m + 2).
Diện tích tam giác ABC là 1 2
S = x − x y − y = m m . 2 B C A B Suy ra 2
m m < 2023 ⇔ m < 21,08 .
Vậy có 21 giá trị nguyên của tham số m thỏa yêu cầu bài toán.  HẾT
Document Outline

  • de-khao-sat-chat-luong-toan-12-lan-1-nam-2023-2024-truong-thpt-chuyen-thai-binh
    • Made 123
    • ĐÁP ÁN TOÁN 12
  • 08. Đề thi thử TN THPT môn Toán năm 2024 - THPT CHUYÊN THÁI BÌNH - Lần 1