-
Thông tin
-
Quiz
Đề khảo sát chất lượng Toán 12 lần 3 năm 2019 – 2020 sở GD&ĐT Hà Nội
Giới thiệu đến với quý thầy, cô giáo và các em học sinh đề khảo sát chất lượng Toán 12 lần 3 năm 2019 – 2020 sở GD&ĐT Hà Nội gồm 50 câu hỏi và bài toán dạng trắc nghiệm
Chủ đề: Đề thi THPTQG môn Toán năm 2023 1.2 K tài liệu
Môn: Toán 1.9 K tài liệu
Thông tin:
Tác giả:
Preview text:
Kỳ khảo sát chất lượng THPT 2019 - 2020 lần 3 - Môn Toán Ó•
¬¸·æ ÅïîðïòéèçìïÃóÅðððïíÃ
Í ½—« ¸ ·æ ëð Ý—« ¸ · ï ݸ± ¸˜³ ã ø ÷ ½‰ ¬¸ ²¸ ¸²¸ ª ¾² ¼ ·ò
ؘ³ • ½¸± ²¹¸ ½¸ ¾· ² ¬®² µ¸± ²¹ ²˜± ¼ · —§á ø å ï÷ ò î å ï ò î î ßò Þò ø ïå ð÷ ò ï å î ò í î Ýò Üò î ݸ± µ¸ · ²‰² ½‰ ¼˜·
²¹ ·²¸ ¾ ²¹ î ô ¹‰½ ¹· ¿
²¹ ·²¸ ª˜ ™§ ¾ ²¹ êð± ò ̸ ¬Ž½¸ ½ ¿
µ¸ · ²‰² • ½¸± ´˜ í P í í ò í íò í ßò Þò í í ò î ò í í í Ýò Üò ݸ± °¸ ½ ã í
î ò Í °¸ ½ ´·² ¸ ° ½ ¿ °¸ ½ ¦ ´˜ í (( ã í î ò (( ã î õ í ò ßò Þò (( ã í õ î ò (( ã í õ î ò Ýò Üò ì
Ì®±²¹ µ¸‡²¹ ¹·¿² ô ½¸± ¸¿· · ³ øïå
ïå î÷ ô øíå ïå ð÷ ò ̱
¬®«²¹ · ³ Ó ½ ¿ ± ² ¬¸ ²¹ ßÞ ´˜ øîå îå î÷ ò øìå ðå î÷ ò ßò Þò øïå ïå ï÷ ò øîå ðå ï÷ ò Ýò Üò ë
Ì®±²¹ µ¸‡²¹ ¹·¿²
ô ½¸± ³ ¬ °¸ ²¹ ³ ¬ °¸ ²¹ ø ÷ æ î
õ í ã ðò Ê»½¬ °¸™° ¬«§ ² ½ ¿
³ ¬ °¸ ²¹ ø ÷ ½‰ ¬± ´˜ ã øîå ïå ð÷ ò ã øîå ïå í÷ ò ßò Þò ã øîå ïå í÷ ò ã øîå ïå ð÷ ò Ýò Üò ê ؘ³ ã î
ï ½‰ ¾¿± ²¸·« · ³ ½ ½ ¬® á õï ðò íò ßò Þò ïò îò Ýò Üò P
̸ ¬Ž½¸ ½ ¿ µ¸ · ½ « ²¹± · ¬· ° µ¸ · ´ ° °¸ ²¹ ½‰ ¼˜· ½ ²¸ ¾ ²¹ í ´˜æ é í íò í ò í ßò Þò ì í ò ç í ò í î Ýò Üò è ؘ³ ²˜± ¼ · —§ ½‰ ¬¸ ²¸ ¸²¸ ª ¬®² ã í õ í ïò ã í í ïò ßò Þò ã í í õ ïò ã ì õ î î õ ïò Ýò Üò
Ø ²¹«§² ¸˜³ ½ ¿ ¸˜³ ø ÷ ã ´˜ ç î î õï õ ò õ ò î ßò Þò ï õ ò î õï õ ò î õï Ýò Üò ïð
Ì®±²¹ µ¸‡²¹ ¹·¿²
ô ½¸± · ³ ø ïå îå í÷ ò Ó ¬ ½ « ø ÷ ½‰ ¬—³ × ª˜ ¬· ° ¨„½ ª · ³ ¬ °¸ ²¹ ø ÷ ½‰ °¸ ²¹ ¬®²¸ ´˜ ø õ ï÷î õ ø î÷î õ ø í÷î ã çò ø õ ï÷î õ ø î÷î õ ø í÷î ã ïò ßò Þò ø õ ï÷î õ ø î÷î õ ø í÷î ã ïìò ø õ ï÷î õ ø î÷î õ ø í÷î ã ìò Ýò Üò ؘ³ ã î ½‰ ± ¸˜³ ´˜ ïï P ã î ´² ò ã î ´² îò ßò Þò P ã îò î ïò îõï ã ò õ î ï Ýò Üò í î ïî ݸ± ¸˜³ ã í
õ îò Õ¸ ²¹ ²¸ ²˜± ¿« —§ ´˜ „²¹á ؘ³ ¬ ½ ½ · ¬ · ã 𠪘 ¬ ½ ½ ؘ³ ¬ ½ ½ · ¬ · ã î ª˜ ¬ ½ ½ ¬· « ¬ · ã îò ¬· « ¬ · ã ðò ßò Þò ؘ³ ¬ ½ ½ · ¬ · ã î ª˜ ¬ ½ ½ ؘ³ ¬ ½ ½ ¬· « ¬ · ã î ª˜ ¬ ½ ½ ¬· « ¬ · ã ðò · ¬ · ã ðò Ýò Üò Ê · ¬¸ ½ ¼ ²¹ ½¸± ¬® ½ô °¸ ²¹ ¬®²¸ ´±¹
î ã î´±¹ ½‰ ¬ ° ²¹¸· ³ ´˜ ïí í í ¥ £ ò î ò ßò Þò ¥ å £ ò î å î ò Ýò Üò ïì îô ï î ݸ± ¸˜³ ø ÷ ã ò ÌŽ½¸ °¸—² ø ÷ ¼ ¾ ²¹ î ô ä ï ð ë ò ë ò î í ßò Þò íò ïð ò í Ýò Üò í î ïë ݸ± ¸˜³ ã õ í ç õ ïò Ù · ô ´ ² ´
¬ ´˜ ¹·™ ¬® ´ ² ²¸ ¬ ª˜ ¹·™ ¬® ²¸ ²¸ ¬
½ ¿ ¸˜³ ¬®² ± ² Åðå ìÃò Õ¸· ‰ õ î ¾ ²¹ á êçò éçò ßò Þò îðò ééò Ýò Üò î é î ã î ïê
݉ ¾¿± ²¸·« ¹·™ ¬® ²¹«§² —³ ½ ¿ °¸ ²¹ ¬®²¸ ½‰ ²¹¸· ³ á îò ïò ßò Þò íò ìò Ýò Üò ¬¸ ¸˜³ ²˜± ¼
· —§ ²¸ ² ¸¿· ¬® ½ ¬ ¿ ô ´˜³ ¬· ³ ½ ² á ïé ã ´±¹ ò ï î ã î ò ßò Þò ã î ò ã îò Ýò Üò ïè
Ì®±²¹ µ¸‡²¹ ¹·¿² ô ½¸± · ³ øïå
ïå î÷ ª˜ ¸¿· ³ ¬ °¸ ²¹ ø ÷ æ î õ õ ï ã ðô ø ÷ æ
õ î õ õ í ã ðò Ó ¬ °¸ ²¹ ø ÷ · ¯«¿ · ³ ß ª˜ ª«‡²¹ ¹‰½ ª · ½ ¸¿· ³ ¬ °¸ ²¹ ø ÷ ô ø ÷ ½‰ °¸ ²¹ ¬®²¸ ´˜ õ ì ã ðò õ õ î ã ðò ßò Þò ã ðò õ õ î ã ðò Ýò Üò ïç
Ó ¬ µ¸ · ¬® ½‰ ¬¸· ¬ ¼· ² ¯«¿ ¬® ½ ´˜ ³ ¬ ¸²¸ ª«‡²¹ò Þ· ¬ ¼· ² ¬Ž½¸ ¨«²¹ ¯«¿²¸ ½ ¿ µ¸ · ¬® ¾ ²¹
ïê ò ̸ ¬Ž½¸ ½ ¿ µ¸ · ¬® ¾ ²¹ îì ò íî ò ßò Þò ïê ò è ò Ýò Üò îð ݸ± ¸²¸ ´ ²¹ ¬® ²¹ ò
½‰ ™§ ´˜ ¬¿³ ¹·™½ « ½ ²¸ ô ¬ ± ª · ³ ¬ °¸ ²¹
™§ ¹‰½ êð ò ̸ ¬Ž½¸ µ¸ · ´ ²¹ ¬® ò ¾ ²¹ í í ò í í ò è ì ßò Þò í í í ò ò î ì Ýò Üò îï
Ì®±²¹ µ¸‡²¹ ¹·¿² ô ³ ¬ °¸ ²¹ ø ÷ æ î î õ ï ã ð ½ ¬ ³ ¬ ½ « ø ÷ æ î õ î õ î õ î ì î í ã 𠬸»± ³ ¬
²¹ ¬®ˆ² ½‰ ¾™² µŽ²¸ ¾ ²¹ ëê ò î ïì ò í í ßò Þò P ëò îò Ýò Üò Ì®² ³ ¬ °¸ ²¹ ¬ ¿ ô ¬¸ ¸˜³ ²˜± ¼ · —§ · ¨ ²¹ ª · ¬¸ ¸˜³ ã ë ¯«¿ îî ²¹ ¬¸ ²¹ ã á ã ë ò ã ëò ßò Þò ã ´±¹ ò ë ã ë ò Ýò Üò îí ݸ± ¸˜³ ã ø ÷ ¨™½ ²¸ ¬®²
¥ð£ ½‰ ¾ ²¹ ¾· ² ¬¸·² ²¸ ¸²¸ ª ò î Í ²¹¸· ³ ½ ¿ °¸ ²¹ ¬®²¸ ø ÷ õ ø ÷ ã ð ´˜ êò ìò ßò Þò ëò íò Ýò Üò îì
Ì®±²¹ µ¸‡²¹ ¹·¿² ô ½‰ ¾¿± ²¸·« ²¹ ¬¸ ²¹
ª«‡²¹ ¹‰½ ª · ³ ¬ °¸ ²¹ ø ÷ æ õ î õ í ã ð ï õî ª˜ ±²¹ ±²¹ ª · ²¹ ¬¸ ²¹ æ ã ã á î ï ì îò ðò ßò Þò ʇ ò ïò Ýò Üò Ê · ¸¿· ¬¸ ½ ô
¾ ¬ µ ¬¸ ¿ ³•² â ïô
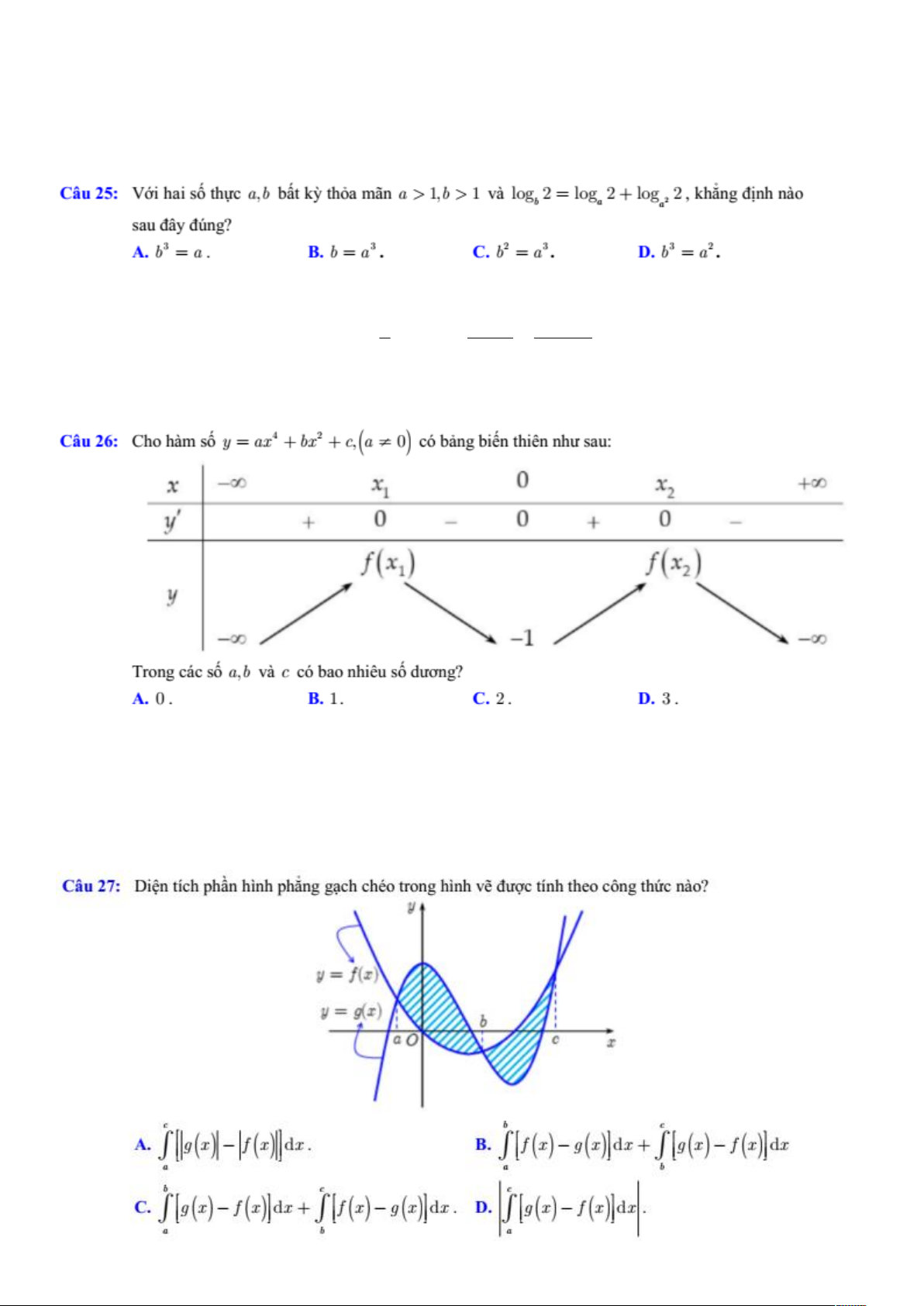
â ï ª˜ ´±¹ î ã ´±¹ î õ ´±¹ î îô µ¸ ²¹ ²¸ ²˜± îë ¿« —§ „²¹ á í ã ò ã íò ßò Þò î ã íò í ã îò Ýò Üò ì î îê ݸ± ¸˜³ ã õ õ ô ø
ð÷ ½‰ ¾ ²¹ ¾· ² ¬¸·² ²¸ ¿«æ
Ì®±²¹ ½™½ ô ª˜ ½‰ ¾¿± ²¸·« ¼ ²¹á ðò ïò ßò Þò îò íò Ýò Üò
Ü· ² ¬Ž½¸ °¸ ² ¸²¸ °¸ ²¹ ¹ ½¸ ½¸’± ¬®±²¹ ¸²¸ ª
½ ¬Ž²¸ ¬¸»± ½‡²¹ ¬¸ ½ ²˜±á îé Ť ø ÷¤ ¤ ø ÷¤Ã ¼ Å ø ÷ ø ÷à ¼ õ Å ø ÷ ø ÷à ¼ ßò Þò Å ø ÷ ø ÷à ¼ õ Å ø ÷ ø ÷à ¼ ò Å ø ÷ ø ÷à ¼ ò Ýò Üò îè
Ì®±²¹ µ¸‡²¹ ¹·¿²
ô ½¸± ³ ¬ °¸ ²¹ ø ÷ æ õ õ ï ã 𠪘 ²¹ ¬¸ ²¹ æ ï ã ã õî È’¬ ´˜
²¹ ¬¸ ²¹ ±²¹ ±²¹ ª · ³ ¬ °¸ ²¹ ø ÷ ô
²¹ ¬¸ · ª«‡²¹ ¹‰½ î ï ï ª ·
²¹ ¬¸ ²¹ ¼ò Ê»½¬ ²˜± ¿« —§ ´˜ ª»½¬ ½¸ °¸ ²¹ ½ ¿ ²¹ ¬¸ ²¹ á ã øïå ïå ð÷ ò ã øðå ïå ï÷ ò ßò Þò ã ø ïå ïå î÷ ò ã øïå îå ï÷ ò Ýò Üò îç
Ì®±²¹ ³ ¬ °¸ ²¹ ¬±
ô ¬ ° ¸ ° ½™½ · ³ ¾· « ¼· ² ½¸± ½™½ °¸ ½ ¦ ¬¸± ³•² · « µ· ² ¤
í õ î ¤ ã ¤ï õ î ¤ ´˜
²¹ ¬¸ ²¹ ª«‡²¹ ¹‰½ ª · ¬® ½ ò ²¹ ¬®ˆ² ¬—³ øíå î÷ ô ¾™² µŽ²¸ ã ëò ßò Þò ²¹ ¬®ˆ² ¬—³ øíå î÷ ô ¾™² µŽ²¸
²¹ ¬¸ ²¹ ª«‡²¹ ¹‰½ ª · ¬® ½ ò P ã ëò Üò Ýò
Ì ³ ¬ ¸ ° ½¸ ¿ ï𠬸 ™²¸ ¬ ï
² ïðò Í ½™½¸ ´ § ®¿ ¸¿· ¬¸ ½‰ ¹¸· ¬®² ¬¸ « ´˜ íð ²¹«§² ¬ ¾ ²¹ ìò ïðò ßò Þò ïîò êò Ýò Üò íï
È’¬ ¸¿· °¸ ½ ïô î ¬« ò 虬 ¾· « ²˜± ¿« —§ ¿·á (((((( ( (( (( ( (( (( ( (( ï î ã ïò îò
¤ ï î¤ ã ¤ ï¤ ò ¤ î¤ ò ßò Þò (((((((((((((( ( (( ( (( (( ( ((
¤ ï õ î¤ ã ¤ ï¤ õ ¤ î¤ ò ï õ î ã ï õ îò Ýò Üò íî î õï Ì ²¹ ²¹ ¬· ³ ½ ² ½ ¿ ¬¸ ¸˜³ ã ´˜ ï îò ïò ßò Þò ðò íò Ýò Üò ì î íí Í ¹·¿± · ³ ½ ¿ ¬¸ ¸˜³ ã ë
õ ì ª · ¬® ½ ¸±˜²¸ ´˜ ìò îò ßò Þò ïò íò Ýò Üò íì ݸ± ¸²¸ ½¸‰° « ò ½‰ ã ô
ã î ò ݱ·² ½ ¿ ¹‰½ ¹· ¿ ³ ¬ ¾² ª˜ ³ ¬ ™§ ¾ ²¹ ë í ïë ê ßò Þò í ë ò í ë Ýò Üò ݸ± ½ ° ½ ²¹ ø
÷ ½‰ ë ã îå é ã è ¬¸ ê ¾ ²¹ íë í êò ßò Þò ëò ìò Ýò Üò íê
ݸ± ¸²¸ °¸ ²¹ øÿ÷
½ ¹· · ¸ ² ¾ · ½™½ ²¹
ã ïô ã ô þ ã 𠪘 ã ´² ò ̸ ¬Ž½¸ øÊ÷
½ ¿ µ¸ · ¬®ˆ² ¨±¿§ ¬ ± ¬¸˜²¸ µ¸· ¯«¿§ øÿ÷ ¨«²¹ ¯«¿²¸ ¬® ½ ýü
½ ¬Ž²¸ ¬¸»± ½‡²¹ ¬¸ ½ ã ´² ¼ ò ã ¤´² ¤ ¼ ò ï ï ßò Þò ã ´²î ¼ ò ã ´²î ¼ ò ï ï Ýò Üò íé Ó ²¸ ²˜± ¼ · —§ ¿·á ø ÷ ã ø ÷ õ ª · ³ · ¸˜³ Å ø ÷ ø ÷à ã ø ÷ ø ÷
ø ÷ ½‰ ± ¸˜³ ¬®² ò
ª · ³ · ¸˜³ ø ÷ô ø ÷ ´·² ¬ ½ ¬®² ò ßò Þò Å ø ÷ õ ø ÷à ã ø ÷ õ ø ÷ î ø ÷ ã ø ø ÷ ÷î ª · ³ · ¸˜³
ª · ³ · ¸˜³ ø ÷ô ø ÷ ´·² ¬ ½ ¬®² ò ø ÷ ´·² ¬ ½ ¬®² ò Ýò Üò íè
Ì®±²¹ µ¸‡²¹ ¹·¿²
ô ½¸± ½™½ · ³ øîå ðå ð÷ ô øðå
îå ð÷ ò ݉ ¾¿± ²¸·« · ³ Ó ¬¸« ½ ¬® ½
Ѧ ¿± ½¸± ¬¿³ ¹·™½ ÓßÞ ½—² ¬ · Óá ðò ïò ßò Þò îò ʇ ò Ýò Üò P íç ݸ± ´ ²¹ ¬® ò ½‰ ™§
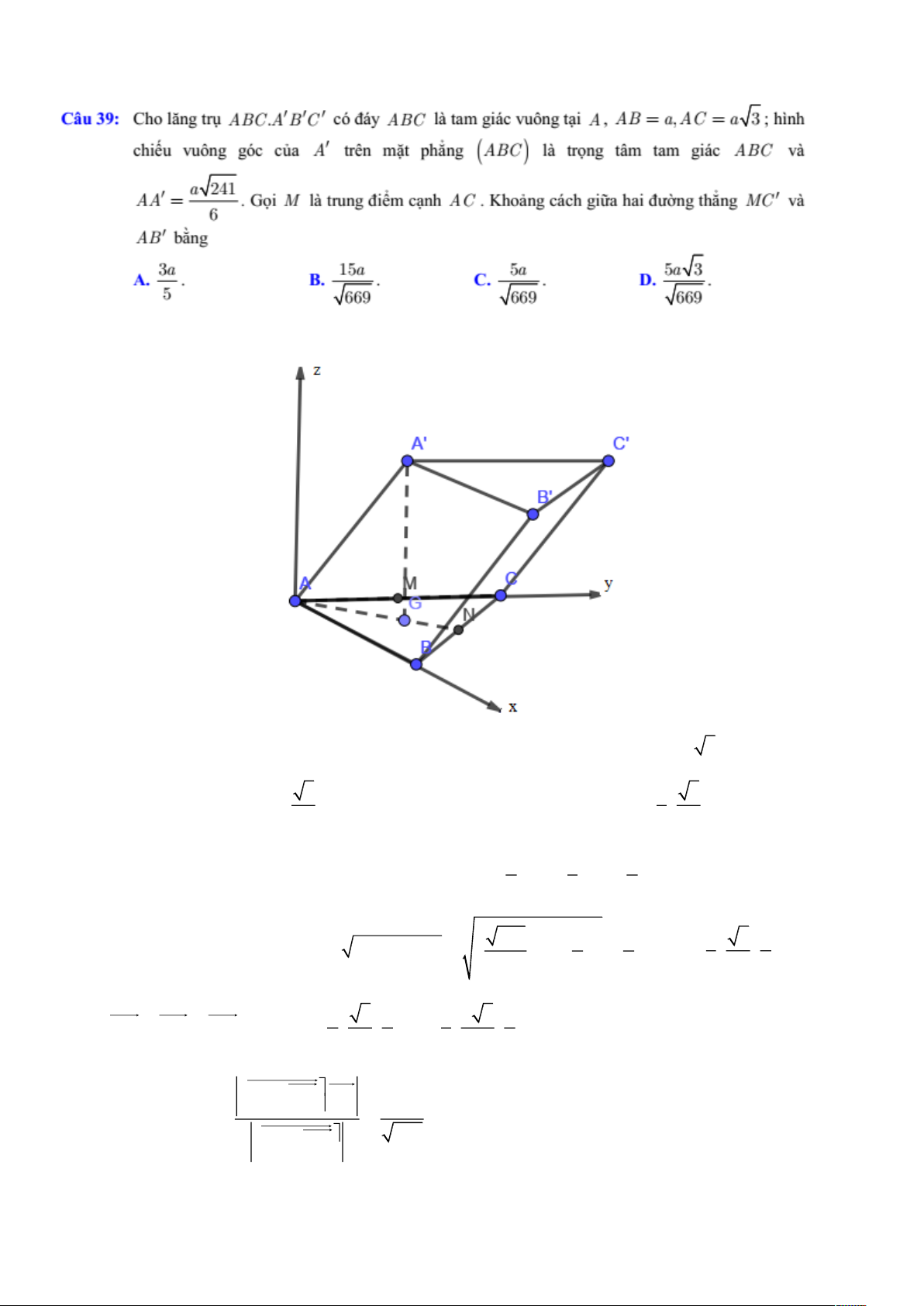
´˜ ¬¿³ ¹·™½ ª«‡²¹ ¬ · ßô ã ô ã íå ¸²¸ îìï
½¸· « ª«‡²¹ ¹‰½ ½ ¿ ¬®² ³ ¬ °¸ ²¹ ø
÷ ´˜ ¬® ²¹ ¬—³ ¬¿³ ¹·™½ ª˜ ã ò ê
Ù · Ó ´˜ ¬®«²¹ · ³ ½ ²¸ ßÝò Õ¸± ²¹ ½™½¸ ¹· ¿ ¸¿· ²¹ ¬¸ ²¹ ª˜ ¾ ²¹ í ò ïë ò ë êêç ßò Þò ë ò ë í êêç ò êêç Ýò Üò Ø¿·
· ¬¸ ²¹¿²¹ ¬˜· ²¸¿«ô ½ƒ²¹ ¬¸· « ª · ²¸¿«
¬®¿²¸ ½¸ ½ ª‡ ½¸ò Ò¹ · ¬¸ ²¹ ½« ½ ´˜ ìð ²¹ · « ¬·² ¬¸ ²¹ ½ ê ª™²
«ò Ø ¬ ¾« · ™²¹ô ²¹
· × • ¬¸ ²¹ ë ª™²ô ½ˆ² ²¹ · ×× ½¸ ³ ·
¬¸ ²¹ í ª™²ò Þ« · ½¸· « ¸¿· ²¹ · ¬· ° ¬ ½ ¬¸· «ò È™½ « ¬ ²¹ · × ª‡ ½¸ ¾ ²¹ ë ò ï ò è î ßò Þò í ò é ò ì è Ýò Üò ݸ± ¸˜³ ã
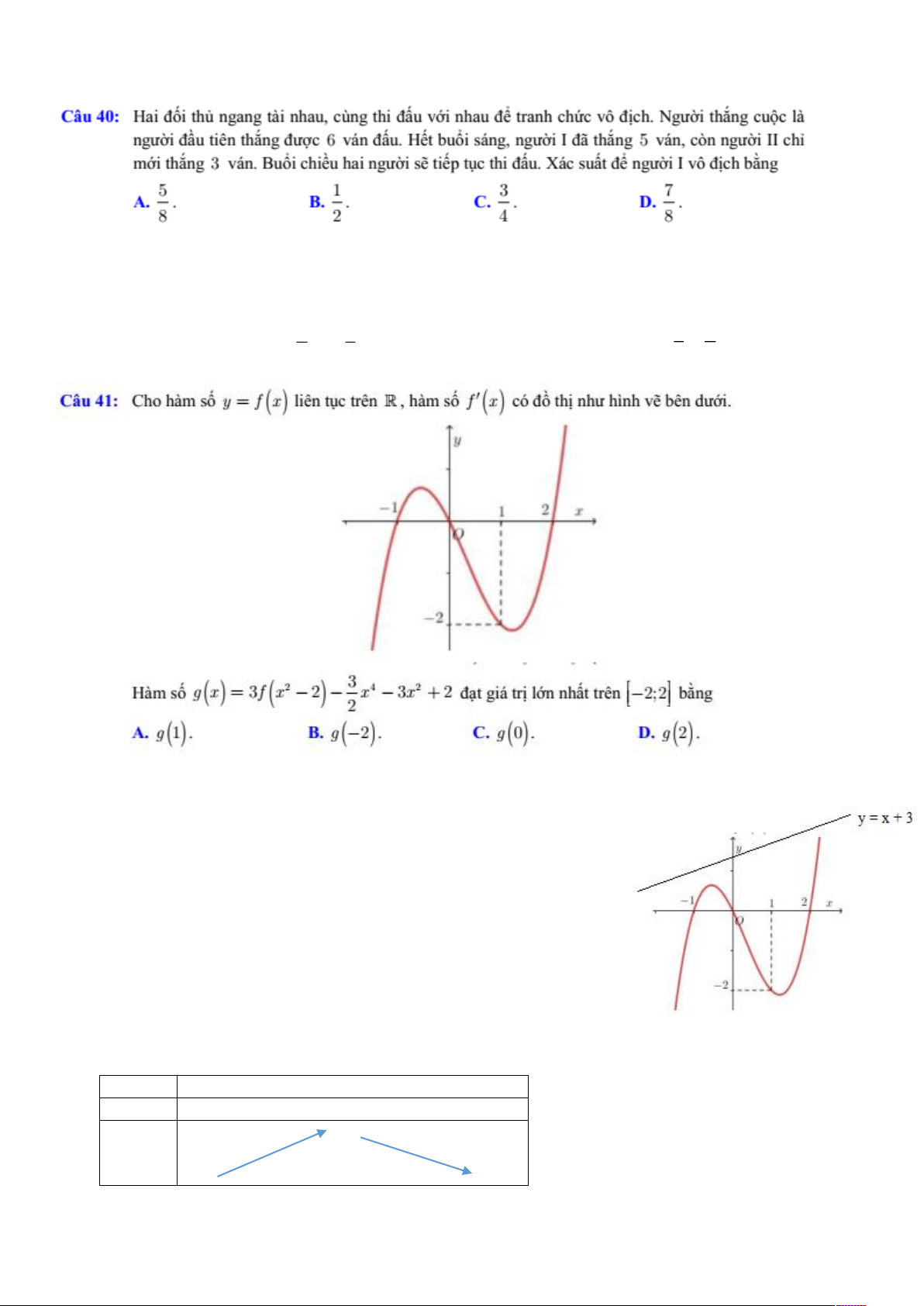
ø ÷ ´·² ¬ ½ ¬®² Îô ¸˜³
ø ÷ ½‰ ¬¸ ²¸ ¸²¸ ª ¾² ¼ · ìï ؘ³ ø ÷ ã í î î í ì í î õ î
¬ ¹·™ ¬® ´ ² ²¸ ¬ ¬®² ¾ ²¹ î Å îå îà øï÷ ò ø î÷ ò ßò Þò øð÷ ò øî÷ ò Ýò Üò
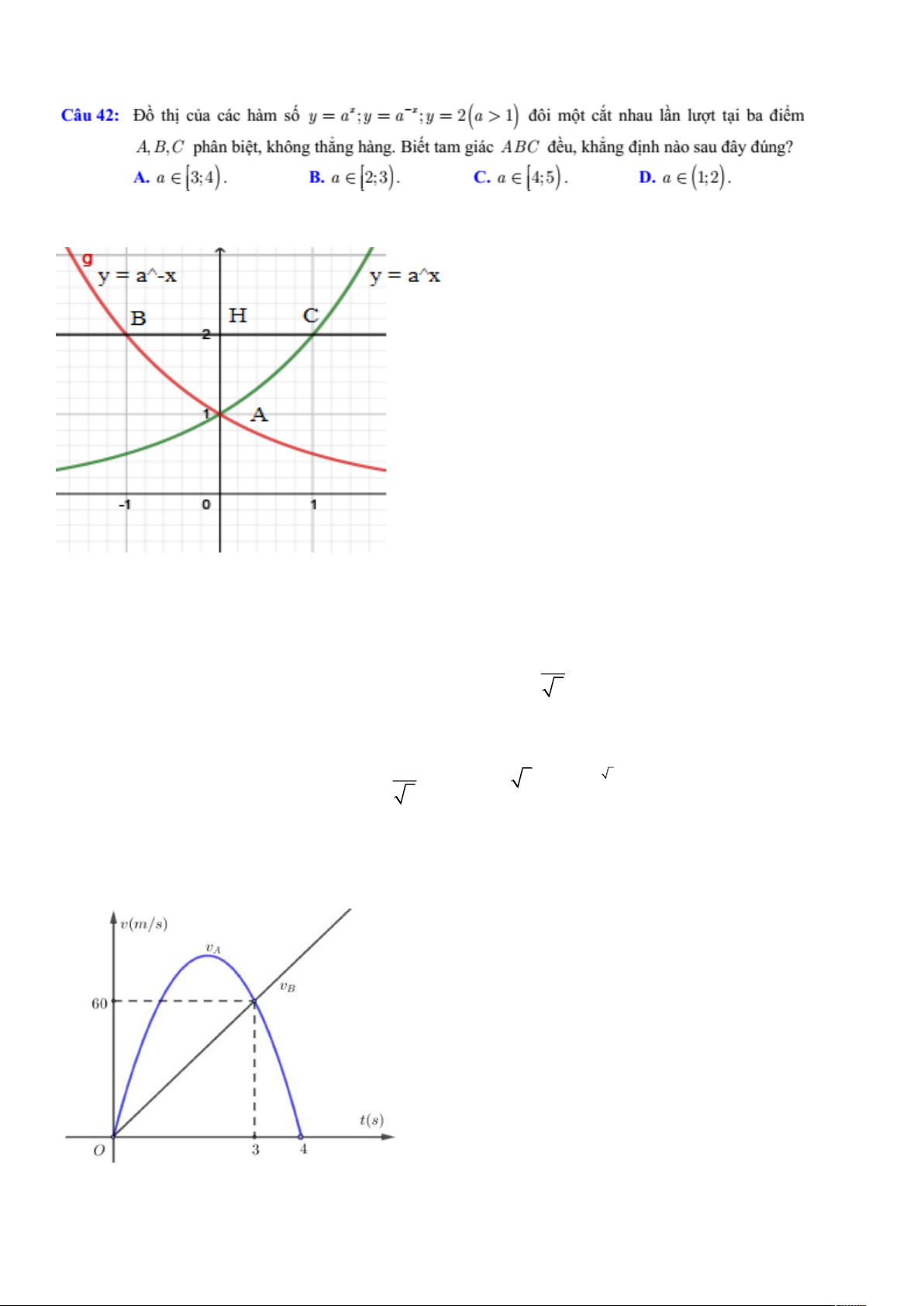
¬¸ ½ ¿ ½™½ ¸˜³ ã å ã
å ã î ø â ï÷ ‡· ³ ¬ ½ ¬ ²¸¿« ´ ² ´ ¬ ¬ · ¾¿ · ³ ìî ô ô
°¸—² ¾· ¬ô µ¸‡²¹ ¬¸ ²¹ ¸˜²¹ò Þ· ¬ ¬¿³ ¹·™½
«ô µ¸ ²¹ ²¸ ²˜± ¿« —§ „²¹á Åíå ì÷ ò Åîå í÷ ò ßò Þò Åìå ë÷ ò øïå î÷ ò Ýò Üò ìí ݸ±
¬¸ ¾· « ¬¸ ª ² ¬ ½ ½ ¿ ¸¿· ½¸ ¬ · ³ ª˜
¨« ¬ °¸™¬ ½ƒ²¹ ³ ¬ ´„½ô ¾² ½ ²¸ ²¸¿« ª˜ ¬®² ½ƒ²¹ ³ ¬ ½±² ²¹ò Þ· ¬
¬¸ ¾· « ¼· ² ª ² ¬ ½ ½ ¿ ½¸ ¬ · ³ ´˜ ³ ¬ ²¹ п®¿¾±´ô
¬¸ ¾· « ¼· ² ª ² ¬ ½ ½ ¿ ½¸ ¬ · ³ ´˜ ³ ¬
²¹ ¬¸ ²¹ ²¸ ¸²¸ ª ¿«ò Ø · ¿« µ¸· ·
½ í ¹·—§ô µ¸± ²¹ ½™½¸ ¹· ¿ ¸¿· ½¸ ¬ · ³ ´˜ ¾¿± ²¸·« ³’¬á ïîð ò êð ò ßò Þò îéð ò çð ò Ýò Üò î ø ÷ ìì
ݸ± µ¸ · ¬® ½‰ ¬¸· ¬ ¼· ² ¯«¿ ¬® ½
´˜ ³ ¬ ¸²¸ ª«‡²¹ ½ ²¸ ¾ ²¹ ò Ó ¬ °¸ ²¹ ¯«¿ ¬®«²¹ · ³ ½ ¿
ª˜ ¬ ± ª · ³ ¬ °¸ ²¹ ½¸ ¿ ™§ ¹‰½ íð± ò Ü· ² ¬Ž½¸ ½ ¿ ¬¸· ¬ ¼· ² ¼± ø ÷ ½ ¬ µ¸ ·
¬® ¹ ² ²˜± ¿« —§ ²¸ ¬á íô éò íô ëò ßò Þò íô êò íô èò Ýò Üò ìë
݉ ¾¿± ²¸·« ¹·™ ¬® ²¹«§² ½ ¿ ¬¸¿³ ¸˜³ ã ø ï÷î ì î îðîð
î õ í ½‰ „²¹ ³ ¬ ½ ½ ¬® á îðîðò îðïçò ßò Þò îðîïò îðîî Ýò Üò î ´² î îõîõ í î í ìê ´² î õî
݉ ¾¿± ²¸·« ¹·™ ¬® ²¹«§² ½ ¿ ¬¸¿³ °¸ ²¹ ¬®²¸ ã ´²ø îõî÷ ´² î õîõø í í ÷î
½‰ „²¹ í ²¹¸· ³ °¸—² ¾· ¬ á ïò îò ßò Þò íò ʇ ò Ýò Üò ݸ± ¸˜³ ã
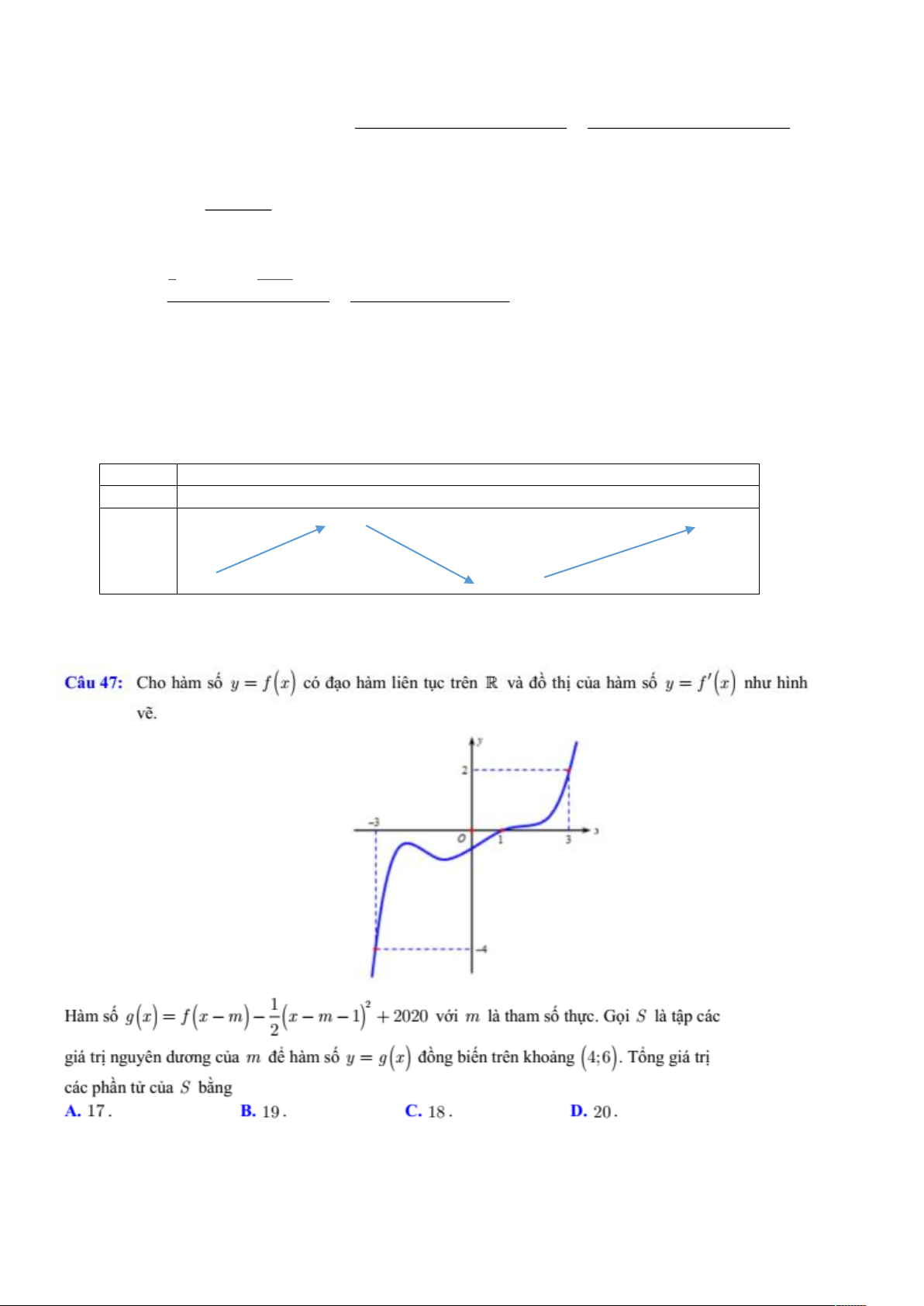
ø ÷ ½‰ ± ¸˜³ ´·² ¬ ½ ¬®² ª˜ ¬¸ ½ ¿ ¸˜³ ã ø ÷ ²¸ ¸²¸ ª ò ìé ؘ³ ø ÷ ã ø ÷ ï ø
ï÷î õ îðîð ª · ´˜ ¬¸¿³ ¬¸ ½ò Ù · ´˜ ¬ ° ½™½ î ¹·™ ¬® ²¹«§² ¼ ²¹ ½ ¿ ¸˜³ ã ø ÷
²¹ ¾· ² ¬®² µ¸± ²¹ øìå ê÷òÌ ²¹ ¹·™ ¬® ½™½ °¸ ² ¬ ½ ¿ ¾ ²¹ ïéò ïçò ßò Þò ïèò îðò Ýò Üò ìè ݸ± ¸²¸ ½¸‰° ò
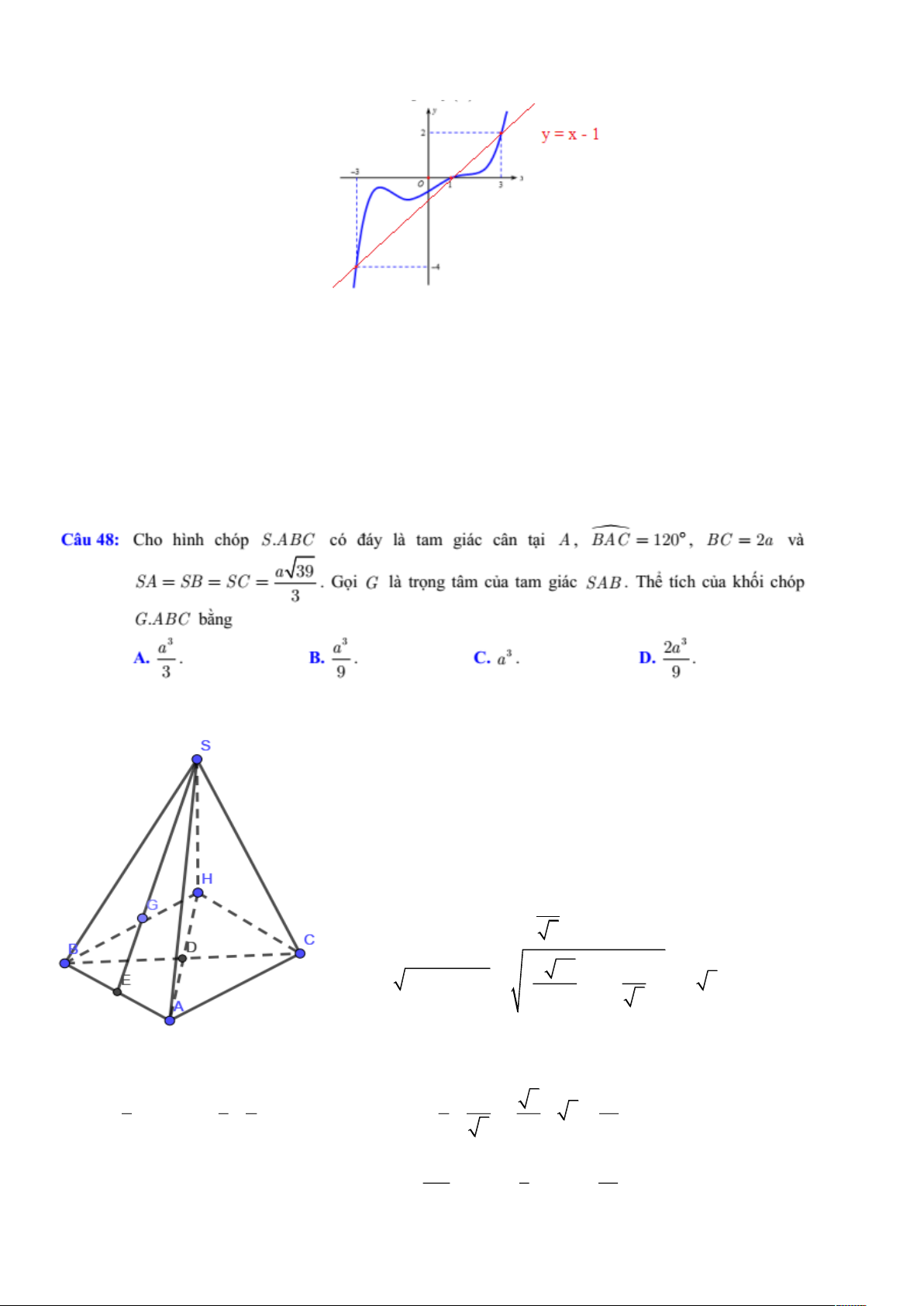
½‰ ™§ ´˜ ¬¿³ ¹·™½ ½—² ¬ · ô ã ïîð ô ã î ª˜ ã ã ã
íç ò Ù · ´˜ ¬® ²¹ ¬—³ ½ ¿ ¬¿³ ¹·™½
ò ̸ ¬Ž½¸ ½ ¿ µ¸ · ½¸‰° í ò ¾ ²¹ í í ò ò í ç ßò Þò íò î í ò ç Ýò Üò í ìç
݉ ¾¿± ²¸·« ¹·™ ¬® ²¹«§² ½ ¿ ¬¸¿³ ¬¸ ¸˜³ ã ïí õ ½ ¬ ¬® ½ ¸±˜²¸ ¬ · ¾¿ · ³ « ½‰ ¸±˜²¸ ²¹«§²á ïò îò ßò Þò íò ðò Ýò Üò ݸ± ¸˜³ ã
ø ÷ ½‰ ± ¸˜³ ´·² ¬ ½ ¬®² Åðå ïÃô ¬¸ ¿ ³•² Å ø ÷Ãî ã ìò î î õ ï ø ÷ ª · ëð ï
³ · ¬¸« ½ ± ² Åðå ïà ª˜ øï÷ ã îò Ù·™ ¬® ã ø ÷ ò ¼ ¾ ²¹ ð í ò ë ò ì í ßò Þò ïï ò ì ì í Ýò Üò
Thầy Quỳnh Toán - ĐT: 0989.853.628
https://www.facebook.com/vu.x.quynh
HƯỚNG DẪN CHI TIẾT ĐỀ KHẢO SÁT CHẤT LƯỢNG SỞ HÀ NỘI 2020 - LẦN 3 BẢNG ĐÁP ÁN: 1. D 2. A 3. C 4. D 5. A 6. A 7. D 8. C 9. A 10. D 11. C 12. D 13. C 14. D 15. A 16. A 17. D 18. A 19. C 20. B 21. C 22. C 23. C 24. B 25. D 26. B 27. C 28. B 29. C 30. D 31. D 32. D 33. A 34. A 35. C 36. C 37. D 38. D 39. B 40. D 41. C 42. A 43. D 44. C 45. C 46. C 47. B 48. B 49. B 50. A
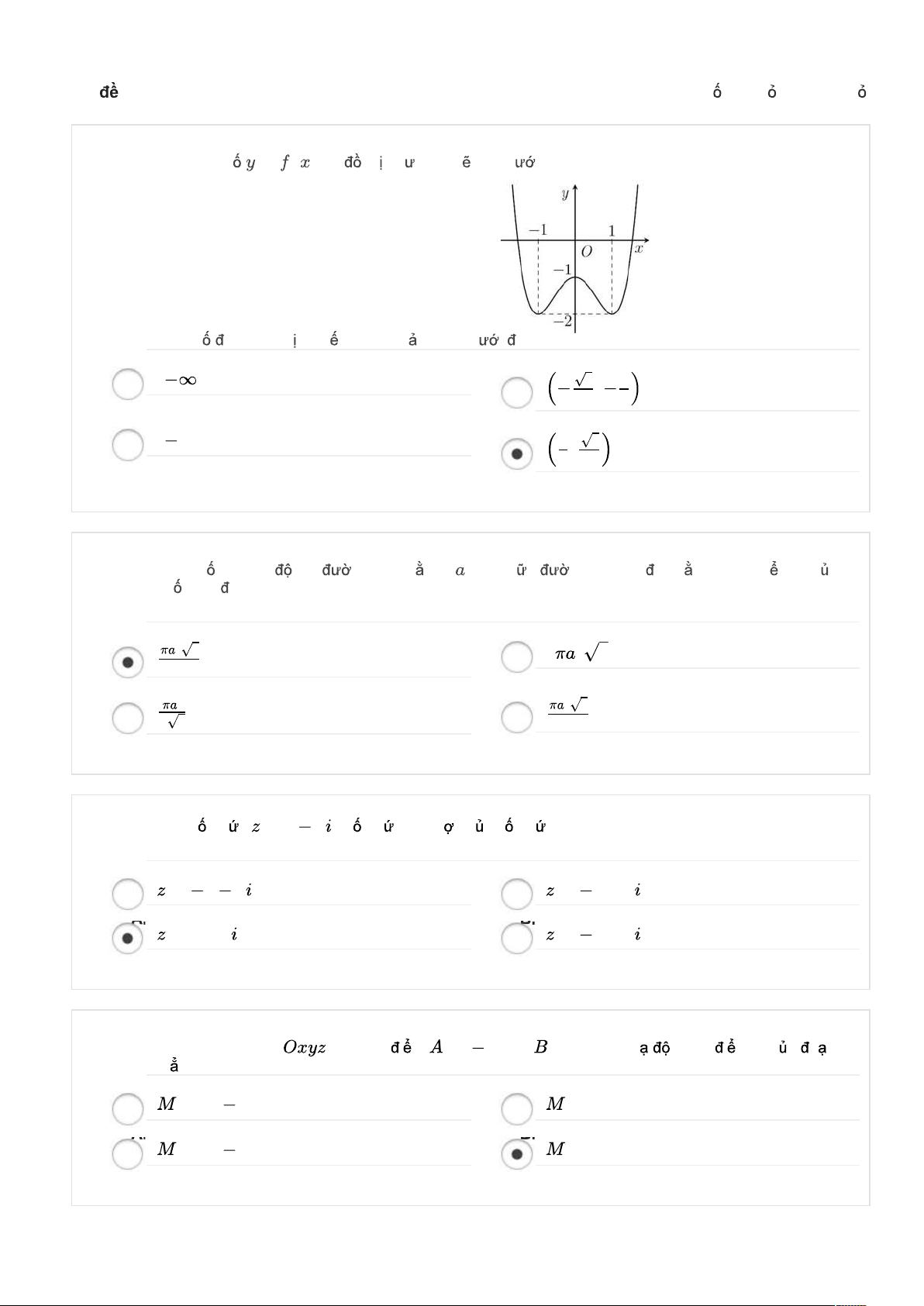
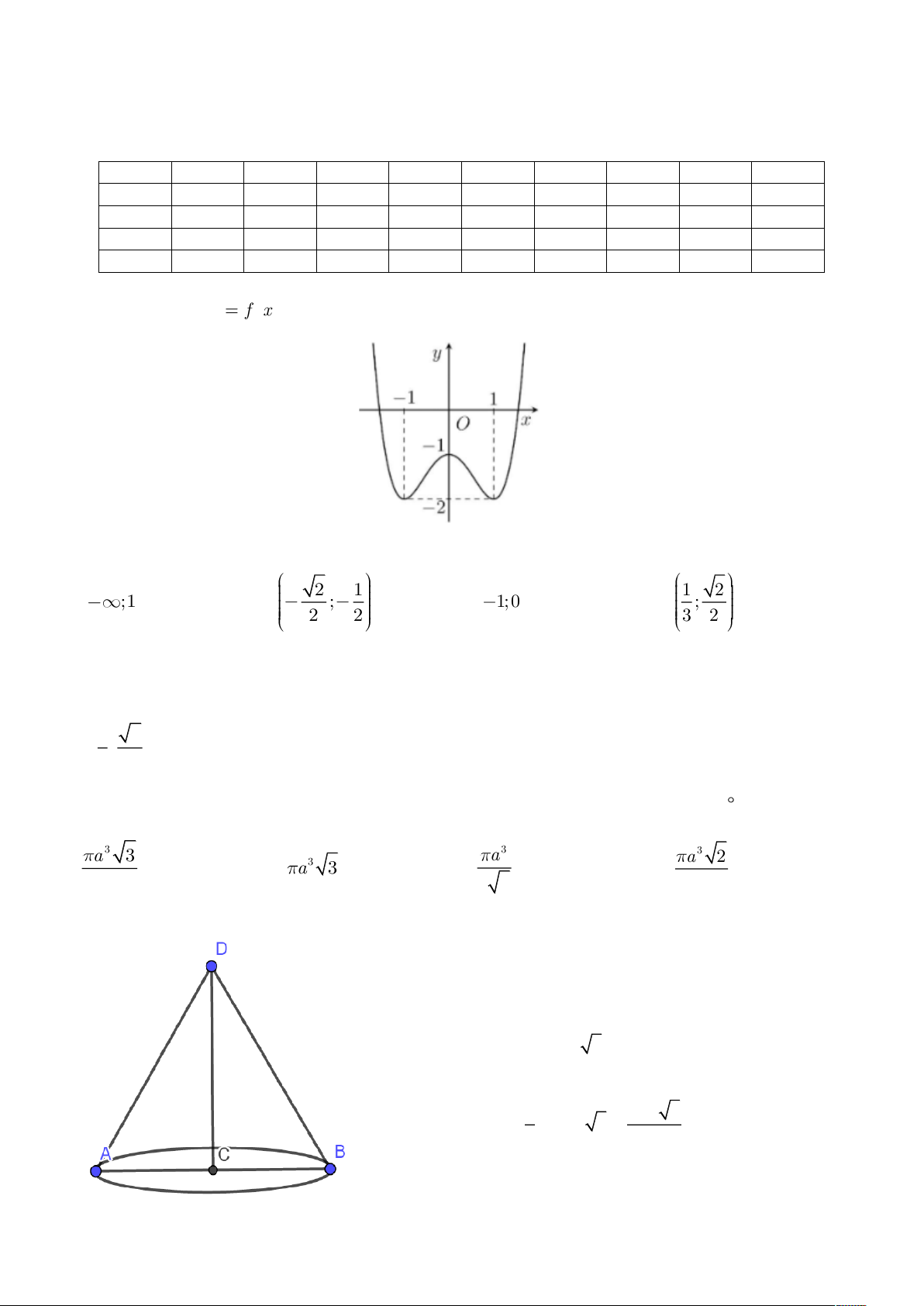
Câu 1: Cho hàm số y
f x có đồ thị như hình vẽ bên dưới.
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? 2 1 1 2 A. ;1 . B. ; . C. 1; 0 . D. ; . 2 2 3 2 Đáp án D.
Từ đồ thị suy ra hàm số nghịch biến trên các khoảng ; 1 và 0 ;1 . 1 2 Mà ; 0 ;1
suy ra hàm số nghịch biến trên 0 ;1 . 3 2
Câu 2: Cho khối nón có độ dài đường sinh bằng 2a , góc giữa đường sinh và đáy bằng 60 . Thể tích của khối nón đã cho là 3 a 3 3 a 3 a 2 A. . B. 3 3 a 3 . C. . D. . 3 3 3 3 Đáp án A.
Ta có: BD 2a và góc 60o DBC suy ra đường
cao DC a 3 và bán kính đáy BC a .
Vậy thể tích của khối nón là 3 1 a 3 2 V .a .a 3 3 3
Thầy Quỳnh Toán - ĐT: 0989.853.628
https://www.facebook.com/vu.x.quynh Đáp án C. Đáp án D Đáp án A. Đáp án A 3 Ta có: y '
do đó hàm số không có điểm cực trị. x 0, x 1 2 1 Đáp án D
Hình lập phương có độ dài đường chéo chính là A'C 3.a 3 3a 1 3a
Suy ra bán kính mặt cầu là R IA ' A 'C . 2 2
Thể tích khối cầu ngoại tiếp khối lập phương là 3 3 4 3a 9 a V 3 2 2
Thầy Quỳnh Toán - ĐT: 0989.853.628
https://www.facebook.com/vu.x.quynh Đáp án C.
Đồ thị hàm bậc ba có hệ số a > 0 và đi qua điểm (1;-1) suy ra đáp án C. Đáp án A
Dùng bảng nguyên hàm cơ bản Đáp án D.
Ta có: mặt phẳng (Oxz) có phương trình là y = 0 mà mặt cầu (S) tiếp xúc mp (Oxz) 2
Do đó bán kính mặt cầu (S) là R d I;(Oxz) 2 . 2 1 Vậy chọn đáp án D. Đáp án C
Áp dụng công thức x 1 ' x
Thầy Quỳnh Toán - ĐT: 0989.853.628
https://www.facebook.com/vu.x.quynh Đáp án D x 0 Ta có: 2
y ' 3x 6x y ' 0 x 2
Do hệ số a 1 0 nên x 0 và x 2 CĐ CT Đáp án C Ta có: 2 2 2 2 2
log x 2log a log x log a x a x a 3 3 3 3 Đáp án D 2 1 2 1 2 10 Ta có: 2
f (x)dx
f (x)dx
f (x)dx 2xdx x dx 3 0 0 1 0 1 Đáp án A x 1 Ta có: 2
y ' 3x 6x 9 y ' 0 . x 3
Mà y(0) 1; y(1) 4
; y(4) 77 suy ra M 77;m 4
M 2m 69 Đáp án A 2 Ta có: 2 x 2 x 1 x 2x 1 7 7
. Do đó phương trình đã cho có nghiệm khi và chỉ khi
Thầy Quỳnh Toán - ĐT: 0989.853.628
https://www.facebook.com/vu.x.quynh m 1 1 2 7 m log 7 2
,8 . Mà m là số nguyên âm nên m { 2 ; 1
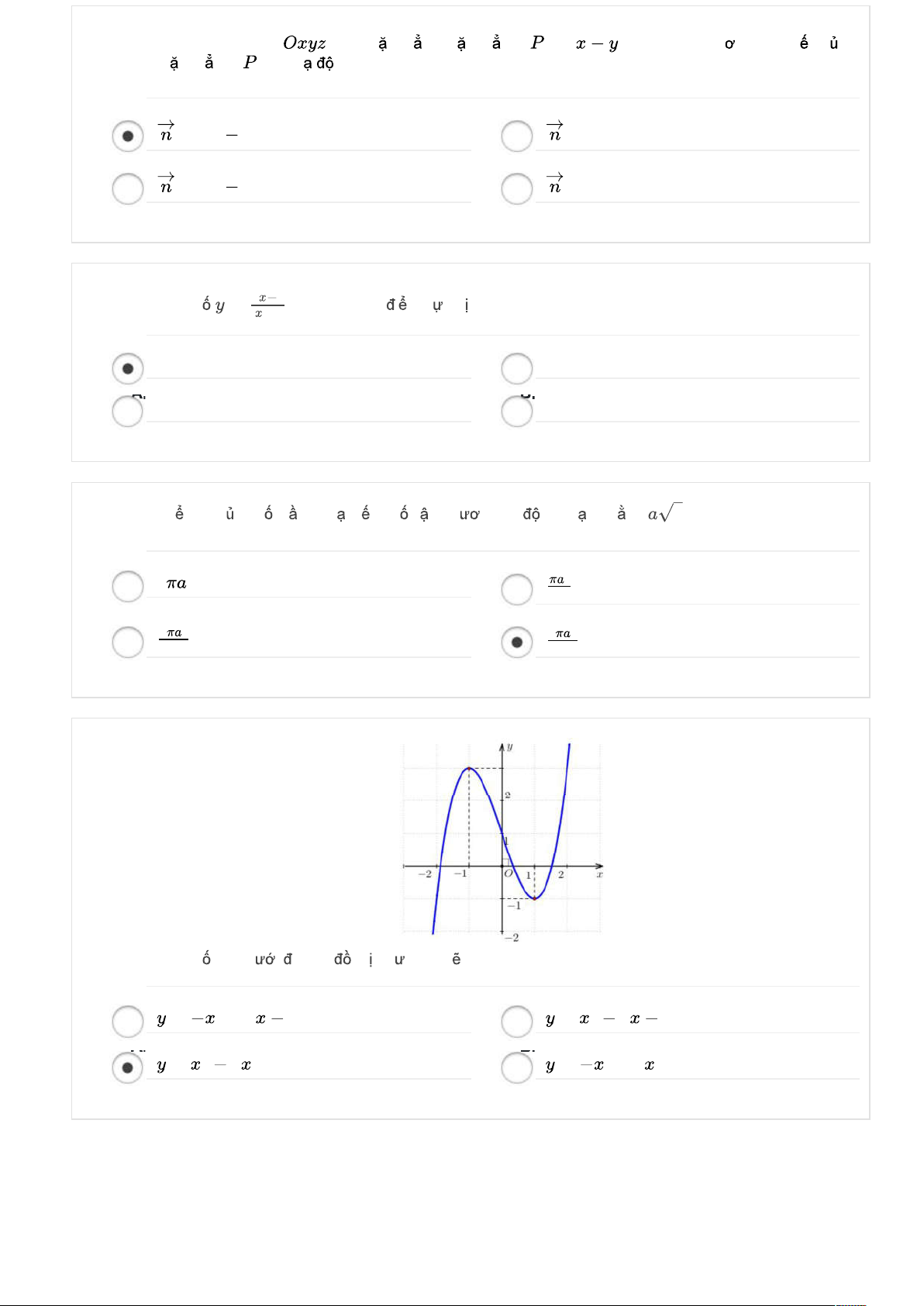
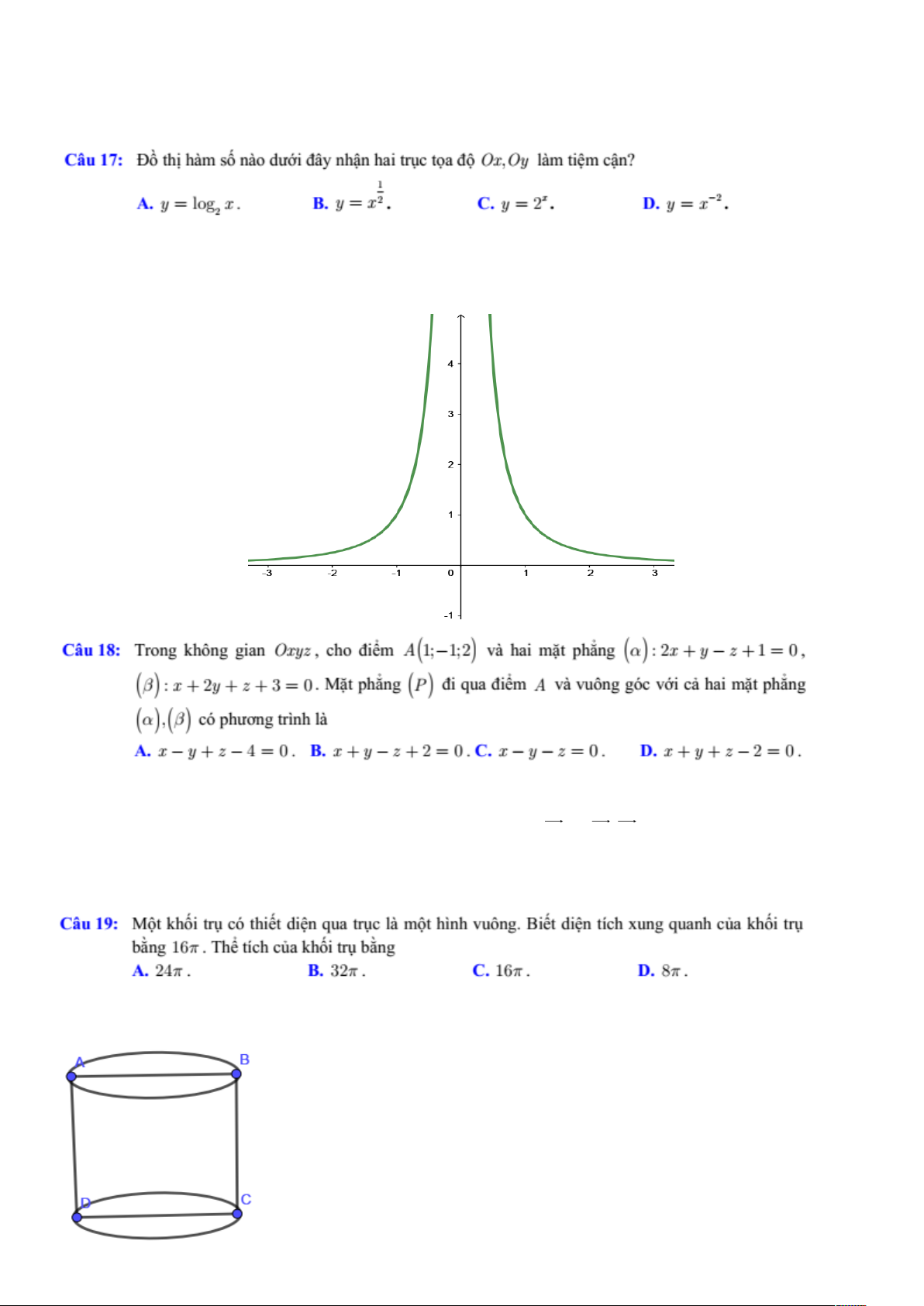
}. Vậy có 2 giá trị thỏa mãn. 2 Đáp án D Đồ thị hàm số 2 y x
như hình dưới. Nhận hai trục tọa độ Ox và Oy làm tiệm cận. Đáp án A.
Do mặt phẳng (P) vuông góc với cả hai mặt phẳng ; nên n n ; n 3; 3;3 31; 1; 1 P Điểm ( A 1; 1
;2) (P) suy ra (P) :1(x 1) 1(y 1) 1(z 2) 0 hay (P) : x y z 4 0 Đáp án C
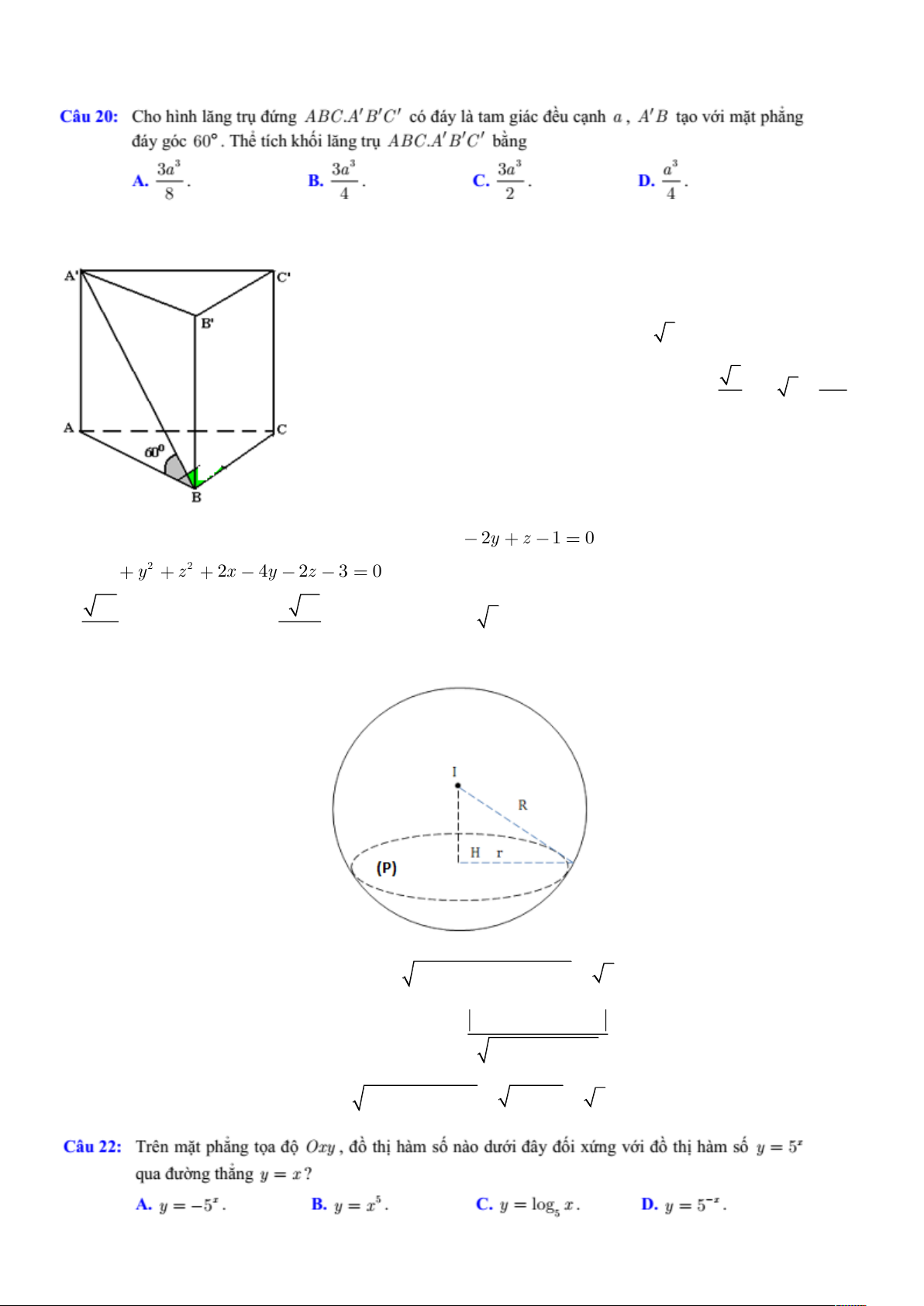
Thiết diện qua trục là hình vuông ABCD do đó h 2r (1) Ta có: S
2 rh 16 rh 8 (2) xq
Từ (1) và (2) suy ra h 4; r 2 .
Vậy thể tích khối trụ là : 2 2
V r h .2 .4 16
Thầy Quỳnh Toán - ĐT: 0989.853.628
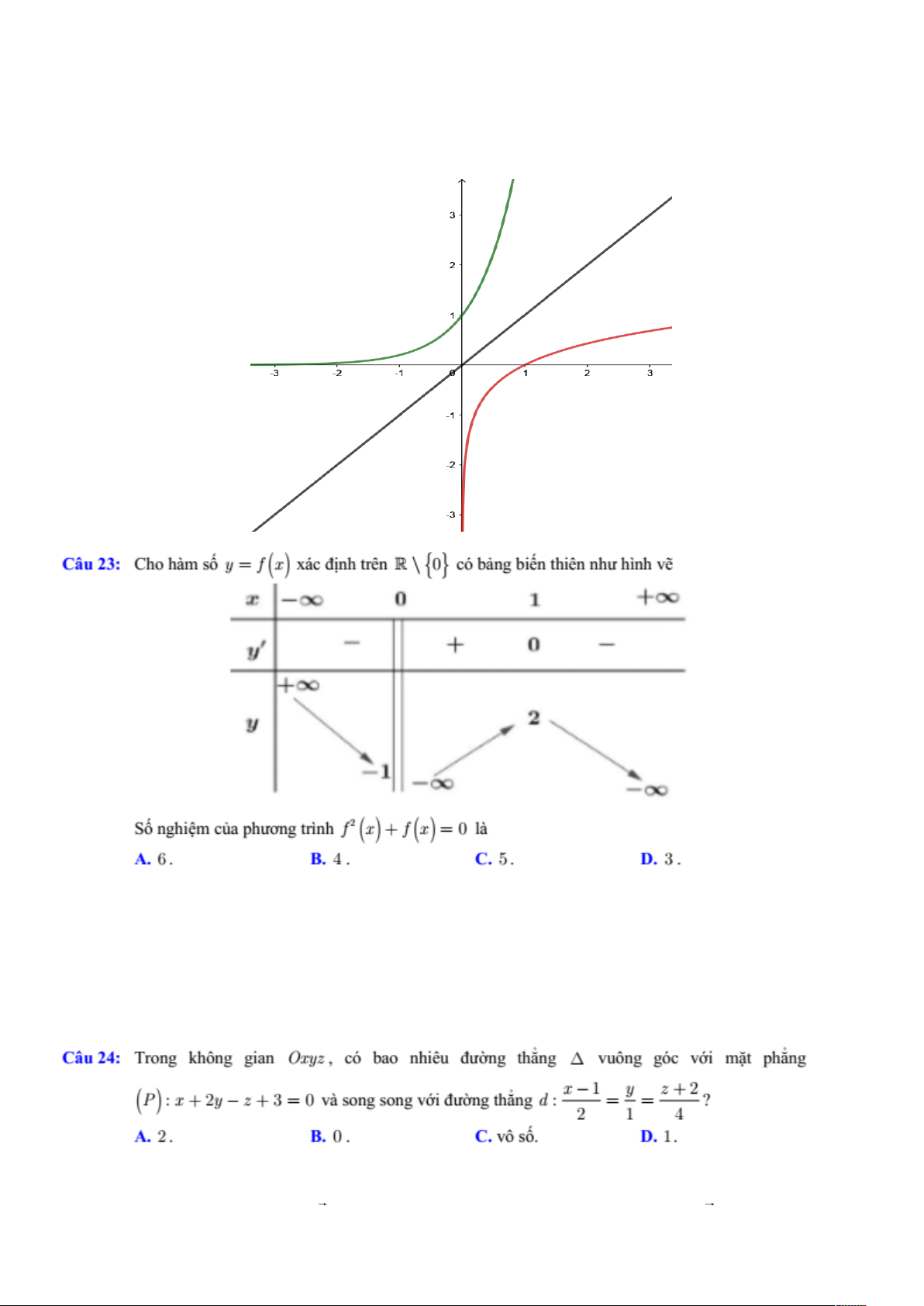
https://www.facebook.com/vu.x.quynh Đáp án B Ta có: góc ' 60O A BA suy ra ' .tan 60o AA AB a 3 . 3 3 3a
Thể tích khối lăng trụ là : 2 V a .a 3 4 4
Câu 21: Trong không gian Oxyz , mặt phẳng P : 2x 2y z 1 0 cắt mặt cầu 2 2 2 S : x y z 2x 4y 2z 3
0 theo một đường tròn có bán kính bằng 56 2 14 A. . B. . C. 5 . D. 2 . 3 3 Đáp án C
Mặt cầu (S) có tâm I(-1;2;1) và bán kính 2 2 2 R ( 1 ) 2 1 ( 3 ) 9 3 . 2.( 1 ) 2.2 11
Khoảng cách từ tâm I tới mặt phẳng (P) là: d (I; (P)) 2 2 2 2 2 ( 2) 1
Đường tròn giao tuyến có bán kính 2 2 2 2 r
R d (I; (P)) 3 2 5
Thầy Quỳnh Toán - ĐT: 0989.853.628
https://www.facebook.com/vu.x.quynh Đáp án C Đồ thị hàm số 5x y
và y log x đối xứng với nhau qua đường thẳng y x 5 Đáp án C
f (x) 0,(1) Ta có: 2
f (x) f (x) 0 f (x) 1 ,(2)
Từ Bảng biến thiên của hàm số y f (x) suy ra phương trình (1) có 3 nghiệm và phương trình (2) có 2
nghiệm và không nghiệm nào trùng nhau. Vậy phương trình đã cho có tất cả 5 nghiệm. Đáp án B
Ta có: vecto pháp tuyến của (P) là ( n 1; 2; 1
) vuông góc với vecto chỉ phương của d là a(2;1;4) .
Thầy Quỳnh Toán - ĐT: 0989.853.628
https://www.facebook.com/vu.x.quynh Mà ( A 1;0; 2
) d nhưng không thuộc (P) do đó d / /(P) .
Do đó không có đường thẳng nào vuông góc với (P) và song song với d. Đáp án D 3 1 3
Ta có: log 2 log 2 log 2 log 2 log 2 2 b a b 2 a a log b 2 log a 2 2 2 3 2 3
2log a 3log b log a log b a b 2 2 2 2 Đáp án B
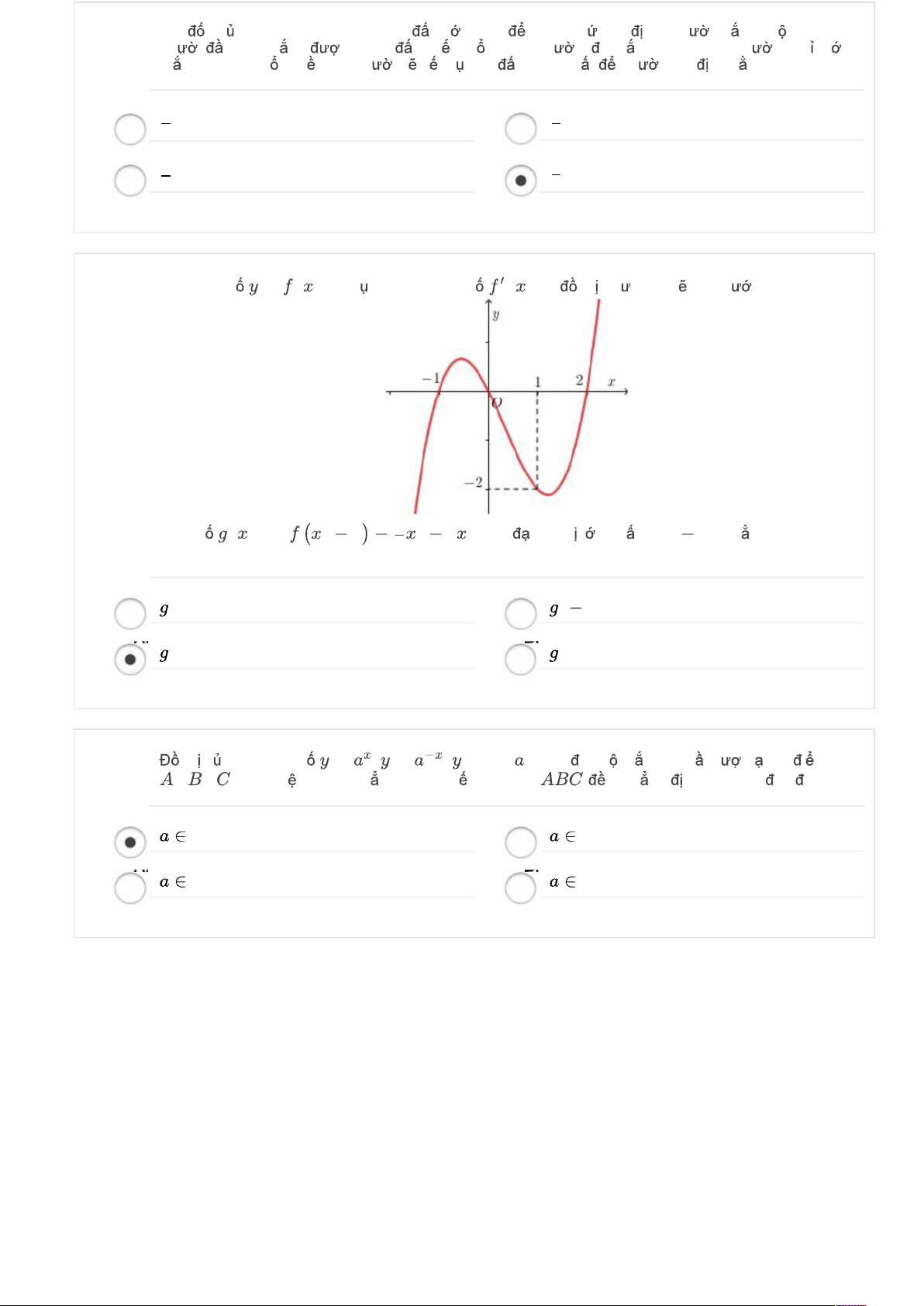
Đồ thị hàm số đi qua điểm (0;-1) suy ra c = -1.
Đồ thị hàm trùng phương có 3 cực trị khi và chỉ khi . a b 0 . Do đó trong 3 số ; a ;
b c có đúng 1 số dương.
Thầy Quỳnh Toán - ĐT: 0989.853.628
https://www.facebook.com/vu.x.quynh Đáp án C
g(x) f (x), x ( ; a b) Từ đồ thị suy ra
f (x) g(x), x ( ; b c)
Do đó diện tích phần gạch chéo trong hình là : c b c b c
f (x) g(x) dx
f (x) g(x) dx
f (x) g(x) dx
g(x) f (x)dx f (x) g(x)dx a a b a b Đáp án B / /(P) a n Ta có : P
a n ;a (0;3;3) 3(0;1;1) P d d a a d
Do đó vécto chỉ phương của đường thẳng là : u (0;1;1) Đáp án C
Đặt z x yi trong đó ; x y R .
Từ giả thiết ta có: x yi 3 2i 1 2i (x 3) ( y 2)i 5
x 2 y 2
x 2 y 2 3 2 5 3 2 5
Vậy tập hợp điểm biểu diễn là đường tròn tâm I(3;-2) bán kính R 5 . Đáp án D
Trong các số từ 1 tới 10 có 4 số nguyên tố là 2; 3; 5; 7.
Số cách lấy 2 thẻ có ghi trên thẻ đều là số nguyên tố là 2 C 6 cách. 4
Thầy Quỳnh Toán - ĐT: 0989.853.628
https://www.facebook.com/vu.x.quynh Đáp án D
Các phát biểu A, B, C đều là tính chất của số phức. Đáp án D 2 x 1 2 x 1 Ta có: 1 lim và 1 lim
nên đồ thị có hai tiệm cận ngang là y = 1 và y = -1. x x 1 x x 1 2 x 1 lim
nên đồ thị có tiệm cận đứng x = 1. x 1 x 1 Đáp án A x 1 x 1
Phương trình hoành độ giao điểm là x 5x 4 0 x 1 x 4 2 4 2 2 2 0 2 x 4 x 2 Đáp án A
Gọi N là trung điểm BC, G là trọng tâm tam giác ABC.
Khi đó BC AN và BC SG suy ra góc giữa 2 mp (SBC) và (ABC) là góc SNA. 1 1 a 3 a 3
Xét tam giác vuông SGN có: GN AN . . 3 3 2 6
Xét tam giác vuông SNB có: 2 a a 15 2 2 2 SN SB BN (2a) . 2 2
Thầy Quỳnh Toán - ĐT: 0989.853.628
https://www.facebook.com/vu.x.quynh a 3 Do đó: GN 5 6 cos SNA SN a 15 15 2 Đáp án C u u 2 8 Ta có: 5 7 u 5 6 2 2 Đáp án C
Áp dụng công thức tính thể tích khối tròn xoay.
Câu 37: Mệnh đề nào dưới đây sai? A. f x dx f x
C với mọi hàm f x có đạo hàm trên . B. f x g x dx f x dx
g x dx với mọi hàm f x ,g x liên tục trên . C. f x g x dx f x dx
g x dx với mọi hàm f x ,g x liên tục trên . 2 D. 2 f x dx
f x dx với mọi hàm f x liên tục trên . Đáp án D.
Các mệnh đề A, B, C đều là tính chất của nguyên hàm. Đáp án D.
Gọi M 0;0; a Oz khi đó 2 MA MB 4 a luôn đúng.
Do đó mọi điểm M thuộc trục Oz đều thỏa mãn.
Thầy Quỳnh Toán - ĐT: 0989.853.628
https://www.facebook.com/vu.x.quynh Đáp án B
Gắn hệ trục Oxyz như hình vẽ A trùng O. Đặt a 1 . Khi đó ( A 0;0;0), (
B 1;0;0),C(0; 3;0) M là trung điể 3 1 3 m AC nên M 0; ; 0
và G là trọng tâm tam giác ABC nên G ; ; 0 . 2 3 3 2 1 2
Ta có: tam giác ABC vuông tại A nên BC = 2 suy ra AG AN BC . 3 3 3 2 2
Xét tam giác vuông AA’G có: 241 2 5 1 3 5 2 2 A'G AA' AG nên A ' ; ; 6 3 2 3 3 2 4 3 5 1 4 3 5
Ta có: AA ' BB ' CC ' suy ra B ' ; ; ,C ' ; ; 3 3 2 3 3 2
MC '; AB ' MA Khi đó: 15
d (MC ', AB ')
. Do đó chọn đáp án B. 669 MC '; AB '
Thầy Quỳnh Toán - ĐT: 0989.853.628
https://www.facebook.com/vu.x.quynh Đáp án D
Giả sử người thứ II vô địch. Khi đó người II cần thắng liên tiếp 3 ván buổi chiều. 3 1 1 1 7
Xác suất để điều này xảy ra là
. Do đó xác suất để người I vô địch là 1 . 2 8 8 8 Đáp án C
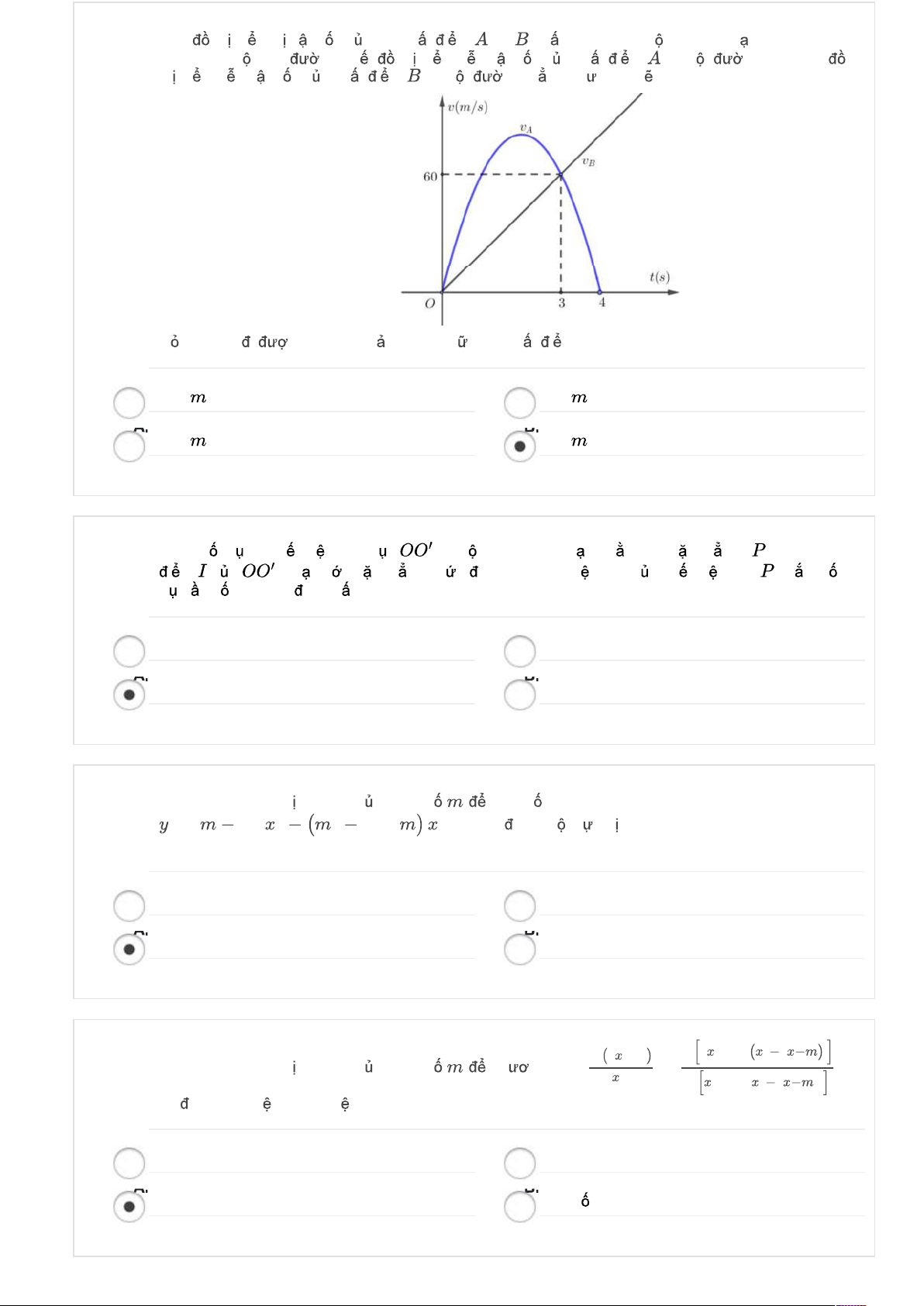
Ta có: g x xf 2 x 3
x x x f 2 x 2 '( ) 6 ' 2 6 6 6 ' 2 x 1 x 0
Do đó: g '(x) 0 2 2
f '(x 2) x 2 3
Từ đồ thị hàm số y f '(x) và y = x + 3 suy ra 2 2
f '(x 2) x 1 0, x 2 ;2 Bảng biến thiên : x -2 0 +2 g’ + 0 - g g(0) g(-2) g(2)
Vậy giá trị lớn nhất trên đoạn [ 2 ;2] là g(0).
Thầy Quỳnh Toán - ĐT: 0989.853.628
https://www.facebook.com/vu.x.quynh Đáp án A Do đồ thị hai hàm số x ; x y a y a
đối xứng với nhau qua trục Oy nên AB = AC.
Tam giác ABC đều nên góc 0
CAH 30 và H nằm trên đường thẳng y = 2 nên H(0;2). 1
Xét tam giác vuông AHC có AH = 1 suy ra 0
CH AH . tan 30 . 3
Mặt khác C là giao điểm của hai đồ thị x
y a ; y 2 nên hoành độ C thỏa mãn 1 x
a 2 x log 2 . Từ đó suy ra 3 log 2
log a 3 a 2 3;4 a 2 a 3
Câu 43: Cho đồ thị biểu thị vận tốc của hai chất điểm A và B xuất phát cùng một lúc, bên cạnh nhau và
trên cùng một con đường. Biết đồ thị biểu diễn vận tốc của chất điểm A là một đường parabol, đồ thị biểu
diễn vận tốc của chất điểm B là một đường thẳng như hình vẽ sau.
Hỏi sau khi đi được 3 giây, khoảng cách giữa hai chất điểm là bao nhiêu mét?
A. 120m . B. 60 m .
C. 270m .
D. 90 m . Đáp án D
Thầy Quỳnh Toán - ĐT: 0989.853.628
https://www.facebook.com/vu.x.quynh
Từ đồ thị hàm vận tốc ta thấy đồ thị của v là đường thẳng đi qua gốc O và điểm (3;60) suy ra : v 20t B B
Đồ thị của v là parabol đi qua gốc O và các điểm (4;0) , (3;60) suy ra: 2 v 2
0t 80t; . A A
Khi đó sau 3 giây quãng đường mỗi chất điểm đi được là: 3 3 3 3 2
S v dt ( 2
0t 80t)dt 180m
và S v dt 20tdt 90m A A B B 0 0 0 0
Do đó sau 3 giây khoảng cách giữa 2 chất điểm là: 180 – 90 = 90 m Đáp án C
Ta có: thiết diện qua trục là hình vuông suy ra r 1
Thiết diện của (P) và khối trụ là một hình elip có hình chiếu (vuông
góc) xuống đáy là đường tròn đáy. 2 Do đó diệ .r 2
n tích thiết diện là: S 3,6 0 cos 30 3
(Công thức tính diện tích hình chiếu lớp 11) Đáp án C TH1: m = 1 khi đó 2
f (x) 2019x 3 có đúng 1 cực trị (cực tiểu) => thỏa mãn
TH2: m 1 khi đó hàm số có đúng 1 cực trị khi m 2 2 2
1 . (m 2020m) 0 m 2020m 0 0 m 2020 m {0; 2;3; 4;...; 2020}
Vậy có tất cả 2021 giá trị m thỏa mãn. Đáp án C
Nhận thấy phương trình đã cho luôn có nghiệm x = 0.
Thầy Quỳnh Toán - ĐT: 0989.853.628
https://www.facebook.com/vu.x.quynh 2 2
Phương trình đã cho tương đương ln(2x 2) ln(x 2) với: (*)
ln 2x 2 x 3x m2 lnx 2 x 3x m2 2 3 2 3 ln t
Xét hàm số: f (t) t a . ln t trong đó 2; 0 a 1 1 ln(t a) ln(t)
(t a) ln(t a) t ln t Ta có: '( ) t t a f t
0 với mọi t 2;a 0 . 2 2 (ln(t a))
t.(t a)(ln(t a))
Do đó hàm số f (t) đồng biến suy ra (*) xảy ra khi 3
x 3x m 0 có đúng 2 nghiệm khác 0. Xét hàm số : 3 2
f (x) x 3x f '(x) 3x 3 nên f '(x) 0 x 1 Bảng biến thiên: x - 1 1 + y’ + 0 - 0 + y 2 + - -2
Để phương trình có 2 nghiệm khác 0 thì có 3 giá trị của m thỏa mãn là : m = 2; m = -2 và m = 0. Đáp án B
Thầy Quỳnh Toán - ĐT: 0989.853.628
https://www.facebook.com/vu.x.quynh
Ta có: g '(x) f '(x )
m (x m 1) 0, x
(4;6) f '(x )
m (x m 1), x (4;6) (*) 3 t 1 3
x m 1
m 3 x m 1
Từ đồ thị ta thấy f '(t) t 1 . Do đó (*) t 3 x m 3 x m 3
m 3 4 6 m 1 5 m 7
Để bất phương trình (*) đúng với mọi x (4;6) thì 4 m 3 1 m
Do m là số nguyên dương nên các giá trị m thỏa mãn là tập: S {1;5;6;7} suy ra tổng giá trị bằng 19. Đáp án B.
Do SA SB SC nên hình chiếu vuông góc của S xuống (ABC) là
H (tâm đường tròn ngoại tiếp tam giác ABC). Suy ra HA HB HC
. Xét tứ giác ABHC có H nằm trên trung trực BC nên góc 0 HAB 60
Do đó: tam giác ABH là tam giác đều nên AH = AB Xét tam giác ABC có : 2 2 2 0
BC AB AC 2A . B A . C cos120 2a 2 2
4a 3AB AB . Từ đó suy ra 3 2 2 a 39 2a 2 2 SH SA AH a 3 3 3
Thể tích khối chóp S.ABC là : 2 3 1 1 1 1 2a 3 a 0 V S .SH . A . B AC.sin120 .SH . . .a 3 S . ABC 3 ABC 3 2 6 3 2 3 3 GE 1 a
Ta có G là trọng tâm tam giác SAB nên V .V .V G. ABC S . ABC S . SE 3 ABC 9
Thầy Quỳnh Toán - ĐT: 0989.853.628
https://www.facebook.com/vu.x.quynh Đáp án B
Ta có phương trình hoành độ giao điểm : 3 3
x 13x m 0 x 13x m (*) 13 x 3 Xét hàm số : 3 2
y x 13x y ' 3
x 13 ; y ' 0 13 x 3 Bảng biến thiên: x 13 13 - + 3 3 y’ - 0 + 0 - y 26 39 + 3 26 39 - 3
Phương trình (*) có 3 nghiệm nguyên thì điề 26 39 26 39 u kiện cần là m . 3 3
Khi đó phương trình có 1 nghiệ 13 13 m nằm trong khoảng ; . 3 3
Do nghiệm này là số nguyên nên ta có bảng sau: x -2 -1 0 1 2 m -18 -12 0 12 18
Kiểm tra trực tiếp được 2 giá trị m = 12 và m = -12 thỏa mãn. Đáp án A. 1 1 Ta có: 2 f x f x 2 [ '( )] 4 ( ) 4 2x 1 2
[ f '(x)] 4 f (x)dx 4 2 2x 1dx 0 0
Thầy Quỳnh Toán - ĐT: 0989.853.628
https://www.facebook.com/vu.x.quynh 1 1 1 1 20 1 20 2
[ f '(x)] dx 4 f (x)dx 2
[ f '(x)] dx 4 . x f (x)
xf '(x)dx 3 0 3 0 0 0 0 1 1 20 1 1 2 4
[ f '(x)] dx 4
2 xf '(x)dx 2
[ f '(x)] dx 4 xf '(x)dx 0 3 3 0 0 0 0 1 1 1 1 2 2
[ f '(x)] dx 4 xf '(x)dx 4x dx 0 2
[ f '(x) 2x] dx 0 f '(x) 2x 0 0 0 0 1 1 3 Do 2
f (1) 2 f (x) x 1 x f (x)dx x 2 x 1 dx 4 0 0
-------------------- HẾT --------------------
Document Outline
- deHN.pdf
- HƯỚNG-DẪN-CHI-TIẾT-ĐỀ-SỞ-HÀ-NỘI-2020-LẦN-3.pdf