Đề khảo sát chất lượng Toán 12 năm 2021 sở GD&ĐT thành phố Cần Thơ

Giới thiệu đến với quý thầy, cô giáo và các em học sinh đề khảo sát chất lượng Toán 12 năm 2021 sở GD&ĐT thành phố Cần Thơ mã đề 106 gồm 06 trang với 50 câu trắc nghiệm.

Chủ đề:

Đề thi THPTQG môn Toán năm 2023 1.2 K tài liệu

Môn:

Toán 1.8 K tài liệu

Thông tin:
102 trang 10 tháng trước
Tác giả:
T
Thanh Hoa
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Đề khảo sát chất lượng Toán 12 năm 2021 sở GD&ĐT thành phố Cần Thơ

Giới thiệu đến với quý thầy, cô giáo và các em học sinh đề khảo sát chất lượng Toán 12 năm 2021 sở GD&ĐT thành phố Cần Thơ mã đề 106 gồm 06 trang với 50 câu trắc nghiệm.

27 14 lượt tải Tải xuống

Chủ đề: Đề thi THPTQG môn Toán năm 2023 1.2 K tài liệu

Môn: Toán 1.8 K tài liệu

Thông tin:

102 trang 10 tháng trước

Tác giả:

Profile Thanh Hoa
101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124
1 A B A D D B A A A B A D B C B C A B A C D C A A
2 B D B D A A B C A A D A D D B C B A D A B A A A
3 A B C D D A D C C D D D B A C A B A A D C B B A
4 C A B D B B A D A A C B C B C D A D A C C D B B
5 C B A C C A A D B B B A A A A A C A C C C B B D
6 B C C D D C C C B B C B D D A C B B C A C B C D
7 C C A C A B B D A A B A C C C A B D C A A A A A
8 C B C A A B C B A A A C A D A D C A D C A B B A
9 C A C B D C D A B C C A D A C A A B A A B D B A
10 A A B A B B C A A D D B D A A B C C D C C A D B
11 C D D A A C D D C D D A A C A D B B B A D D C A
12 C B B A C C B D B B B D A D B C A B C B A C A C
13 D B B B C C B D C B B A C C A B C A B D D D D D
14 B A A A C B A C C A B D A B C A C D C A B D A D
15 C B B B D A D D B B B C D B B C B D C A D B D C
16 A D A B C C D C C A A D C C D A B A B C A B B C
17 B D A B C B B C A A A B D A B B B C A A B D C C
18 A D C C B A A C C D A C D C B B A A D C C B D D
19 B D B A A C D A C A B B C A D B A D A D B A D C
20 C A A B A C A A C D C A A D A B A B C D D A D A
21 B A D A C A B A A C A A B D D C C D C D D A A C
22 A A C D D C B A C B B B B C A C D B A D A D D A
23 A D D A A A D A B B A C B A C B D C B A B A B D
24 B A C D D A A A C D D B C A B C D B A C C D B C
25 C D C D A C A D C D B B A D D D C D B D A D B C
26 D A A B D B C C B B D A D A D A B B A B D D C D
MÃ ĐỀ
Câu
KHẢO SÁT CHẤT LƯỢNG HỌC SINH LỚP 12 NĂM 2021 - MÔN TOÁN
ĐÁP ÁN
27 A D A D B B B D C D A A D A A A C B B B A A A A
28 A C A D C C B C B D C B B C B A C B A C B C C A
29 C B A A C A B A D D D D C A B A A A D D C C B A
30 A D C B A D B B D A B D A C A D B D B D B B A D
31 B A B A B C A A A D D B D D C B B A C C B D C C
32 B D D A B D A D C A A B B A D B C C A A B B C D
33 D B B C A A A C A A D D A C C C B B A B A A B A
34 D B C B B B C C B D B A A D B C B D C A D D C B
35 C D B B D C C A B B B C A A C B A A C A C B D D
36 A A C A D D C B A B D D C D B C B D B C D A A C
37 A C C A B B C C C B B B A D B A C D A A C B C B
38 C B A B C A D C C A B D B D C A C A C A A C A C
39 A A B D C B A D A D B D C C D A C D B D D A D A
40 A B B D B C C A B C A B B C D C A B C B D A D D
41 D B B B B A C D B C D A C A C A A D C D B D A C
42 C A A B B D D D A B A D D C C C D A B C B D C D
43 B B D D B C D C A C D D A C D B D D C C A A D A
44 B A C C D A B A D D D D D D B A A A A C D A D C
45 B B C A D B A B B B A A B D A C A A B D C D C B
46 A C A B B A D B B A D A C D D C C B A D C B A D
47 B A A B A B C A D D A B B B A B A D B A A B B C
48 B D B D A D B C D A D A B A D B C A B C A B A C
49 C D B A C B D D B A A B B C D B B C B D A B C D
50 B D C D A A C D A B A D C B A B A B B D B A B D
GIẢI CHI TIẾT
ĐỀ THI THỬ MÔN TOÁN LỚP 12 SỞ CẦN THƠ
NĂM HỌC 2020-2021
BẢNG ĐÁP ÁN
1.A 2.B 3.A 4.C 5.C 6.B 7.C 8.C 9.C 10.A
11.C
12.C
13.D
14.B
15.C
16.A
17.B
18.A
19.B
20.C
21.B 22.A 23.A 24.B 25.C 26.D 27.A 28.A 29.C 30.A
31.B 32.B 33.D 34.D 35.C 36.A 37.A 38.C 39.A 40.A
41.D
42.C
43.B
44.B
45.B
46.A
47.B
48.B
49.C
50.B
Câu 1. Nghiệm của phương trình
1
5 125
x
là
A.
x
B.
3.
x
C.
x
D.
0
sin .
xdx
Lời giải:
1 1 3
5 125 5 5 2.
x x
x
Chọn đáp án A
Câu 2. Với
a
là số thực dương tùy ý,
3
log 3
a
bằng
A.
3
3log .
B.
3
1 log .
a
C.
3
1 log .
a
D.
3
3 log .
a
Lời giải:
3 3 3 3
log 3 log 3 log 1 log .
a a a
Chọn đáp án B
Câu 3. Hàm số
2021
2
4 3y x x
có tập xác định là
A.
\ 3; 1 .
B.
; 3 1; .
 
C.
.
D.
3; 1 .
Lời giải:
Hàm số
2021
2
4 3y x x
có nghĩa khi
2
1
4 3 0
3
x
x x
x
Vậy tập xác định của hàm số là
\ 3; 1 .
Chọn đáp án A
Câu 4. Cho hàm số
( )
f x
có bảng biến thiên như sau:
Hàm số
( )
f x
nghịch biến trên khoảng nào dưới đây?
A.
1;3 .
B.
1;3 .
C.
1;1 .
D.
3;1 .
Lời giải:
Dựa vào bảng biến thiên ta thấy hàm số
( )
f x
nghịch biến trên
1;1 .
Chọn đáp án C
Câu 5. Số các chỉnh hợp chập
k
của
n
phần tử
, , 1
n k N k n
là
A.
.
n
k
A
B.
.
k
n
C
C.
.
k
n
A
D.
.
k
P
Lời giải:
Số các chỉnh hợp chập
k
của
n
phần tử
, ,1
n k N k n
là
.
k
n
A
Chọn đáp án C
Câu 6. Cho hình trụ có chiều cao bằng 2 và bán kính đáy bằng 3. Thể tích của khối trụ đã cho bằng
A.
6 .
B.
18 .
C.
15 .
D.
9 .
Lời giải:
Thể tích của khối trụ:
2 2
.3 .2 18 .
V Bh r h
Chọn đáp án B
Câu 7. Số phức liên hợp của số phức
5 7
i
là
A.
5 7 .
i
B.
5 7 .
i
C.
5 7 .
i
D.
5 7 .
i
Lời giải:
Ta có: số phức
5 7 5 7 .
z i z i
Chọn đáp án C
Câu 8. Tập nghiệm của bất phương trình
3
log 1
x
là
A.
0;1 .
B.
;3 .
 C.
0;3 .
D.
;1 .

Lời giải:
Điều kiện:
0.
x
Ta có:
3
log 1 3.
x x
Kết hợp điều kiện ta có tập nghiệm của phương trình đã cho là
0;3 .
Chọn đáp án C
Câu 9. Thể tích khối lăng trụ có chiều cao bằng
4
và diện tích đáy bằng
3 3
là
A.
6 3.
B.
4 3.
C.
12 3.
D.
8 3.
Lời giải:
Ta có công thức tính thể tích khối lăng trụ:
. 4.3 3 12 3.
V B h V
Chọn đáp án C
Câu 10. Trong không gian
Oxyz
, phương trình đường thẳng đi qua hai điểm
(3; 1;2)
A
và
B(4;1;0)
là
A.
3 1 2
1 2 2
x y z
.
B.
1 2 2
3 1 2
x y z
.
C.
1 2 2
1 1 2
x y z
. D.
3 1 2
1 2 2
x y z
.
Lời giải:
Đường thẳng AB đi qua điểm
(3; 1;2)
A
và có vecto chỉ phương
(1;2; 2)
AB
có dạng
3 1 2
1 2 2
x y z
.
Chọn đáp án A
Câu 11. Cho hàm số
( )
y f x
có bảng biến thiên như sau
Hàm số đã cho đạt cực tiểu tại
A.
5.
x
B.
1.
x
C.
3.
x
D.
2.
x
Lời giải:
Chọn đáp án C
Câu 12. Nếu hàm số
( )
F x
là một nguyên hàm của hàm số
( )
f x
thì
A.
'( ) ( ).
f x F x
B.
( ) ( ).
F x f x
C.
'( ) ( ).
F x f x
D.
'( ) '( ).
F x f x
Lời giải:
Định nghĩa nguyên hàm của hàm số.
Chọn đáp án C
Câu 13. Cho cấp số nhân
n
u
có
3
6
u
và
4
12.
u
Công bội của cấp số nhân đã cho bằng
A.
6.
B.
6.
C.
1
.
2
D.
2.
Lời giải:
Ta có công bội
4
3
12
2.
6
u
q
u
Chọn đáp án D
Câu 14. Tiệm cận ngang của đồ thị hàm số
4 3
4 5
x
y
x
là đường thẳng
A.
1.
y
B.
3
.
4
y
C.
1.
y
D.
5
.
4
y
Lời giải:
4 3 3 4 3 3
lim lim ; lim lim .
4 5 4 4 5 4
x x x x
x x
y y
x x
   
Vậy
3
4
y
là TCN của đồ thị hàm số đã cho.
Chọn đáp án B
Câu 15. Trong mặt phẳng
,
Oxy
số phức
,z a bi a b
có điểm biểu diễn
M
như sau:
Giá trị của
,
a b
lần lượt là
A.
2
và
3.
B.
3
và
2.
C.
3
và
2.
D.
2
và
3.
Lời giải:
Ta có
3; 2 3, 2
M a b
Chọn đáp án A
Câu 16. Đồ thị của nào dưới đây có dạng như đường cong như hình bên dưới?
A.
4 2
4 2 .
x x
B.
4 2
4 2 .
x x
C.
4 2
4 2 .
x x
D.
3 2
4 2 .
x x
Lời giải:
Nhìn vào đồ thị ta thấy đây là dạng đồ thị của hàm số bậc bốn có hệ số
0
a
Hàm số có 3 cực trị nên a, b khác dấu.
Chọn đáp án A
Câu 17. Trong không gian
Oxyz
, phương trình mặt cầu có tâm
(2;0;1)
I
và bán kính
2
R
là
A.
2
2 2
( 2) 1 2.
x y z
B.
2
2 2
( 2) 1 4.
x y z
C.
2
2 2
( 2) 1 2.
x y z
D.
2
2 2
( 2) 1 4.
x y z
Lời giải:
Áp dụng công thức
2
2 2 2
( ) ( ) .
x a y b z c R
Ta có
2
2 2
( 2) 1 4.
x y z
Chọn đáp án B
Câu 18. Trong không gian
Oxyz
, phương trình mặt phẳng đi qua
(1; 2;2)
A
và có vectơ pháp tuyến
3; 1; 2
n
là
A.
3 2 1 0.
x y z
B.
2 2 1 0.
x y z
C.
3 2 1 0.
x y z
D.
2 2 1 0.
x y z
Lời giải:
Áp dụng công thức
0 0 0
( ) ( ) 0
a x x b y y c z z
ta có
3 1 2 2 2 0 3 2 1 0.
x y z x y z
Chọn đáp án A
Câu 19. Thể tích của khối chóp có diện tích đáy bằng
B
và chiều cao bằng
h
là
A.
.
Bh
B.
1
.
3
Bh
C.
1
.
6
Bh
D.
1
.
2
Bh
Lời giải:
Công thức
1
.
3
V Bh
Chọn đáp án B
Câu 20. Nếu
2
1
3
f x dx
và
5
2
1
f x dx
thì
5
1
f x dx
bằng
A.
4.
B.
2.
C.
2.
D.
3.
Lời giải:
Ta có
5 2 5
1 1 2
3 1 2.
f x dx f x dx f x dx
Chọn đáp án C
Câu 21. Số nghiệm nguyên của bất phương trình
3 3
log 16 log 9 .
x x
A. 0. B. 1. C. 2. D. 3.
Lời giải:
Với điều kiện:
16 0 16
0
9 0 0
x x
x
x x
Ta có:
3 3
log 16 log 9 .
x x
16 9 .
8 16.
2
x x
x
x
So với đk ta được 1 nghiệm nguyên
x
1
.
Chọn đáp án B
Câu 22. Gọi
1 2
,
z z
là 2 nghiệm của phương trình
2
2 4 0.
z z
Tính
1 2
1 1
.
z z
A. 1. B.
1
.
2
C. 2. D.
2
.
2
Lời giải:
Phương trình
2
2 4 0.
z z
Có nghiệm
1 2
1 3 , 1 3 .
z i z i
Nên
1 2
1 1
z z
Chọn đáp án A
Câu 23. Số giao điểm của đồ thị hàm số
2
( 1) 2
y x x x
với trục hoành là
A. 3. B. 1. C. 0. D. 2.
Lời giải:
Số giao điểm của đồ thị và trục hoành là số nghiệm của phương trình
2
( 1) 2 0
x x x
Ta có:
2
1
( 1) 2 0 0
2
x
x x x x
x
Chọn đáp án A
Câu 24. Cho hàm số
3 2
( )
f x ax bx cx d
có đồ thị như sau:
Số nghiệm của phương trình
( )[ ( ) 1] 0
f x f x
là
A. 4. B. 5. C. 2. D. 1.
Lời giải:
( ) 1 (1)
( )[ ( ) 1] 0
( ) 0 (2)
f x
f x f x
f x
Nghiệm của phương trình (1) là giao điểm của đồ thị và đường thẳng
( ) 1
y f x
, nên số
nghiệm là 2.
Nghiệm của phương trình (2) là giao điểm của đồ thị và trục hoành, nên số nghiệm là 3.
Chọn đáp án B
Câu 25. Cho hàm số
f x liên tục trên đoạn
1;2 thỏa mãn
2
1
6.f x dx
Giá trị của
1
0
3 1f x dx
bằng
A. 18.
B. 1. C. 2. D. 3.
Lời giải:
Đặt
3 1 3 .t x dt dx
0 1
1 2
x t
x t
1 2
0 1
1
3 1 2.
3
f x dx f t dt
Chọn đáp án C
Câu 26. Cho hình nón có bán kính đáy bằng 5 và góc ở đỉnh bằng
60 .
Diện tích xung quanh của hình
nón đã cho bằng
A. 55 .
B. 100 .
C. 75 .
D. 50 .
Lời giải:
Do góc ở đỉnh bằng60
nên
30 .OSA
Lại có
5
sin sin30 10.
OA
OSA SA
SA SA
Vậy
50 .
xq
S Rl
Chọn đáp án D
Câu 27. Gọi
,M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
18 6f x x x trên
đoạn
3;5 .
Giá trị của M m bằng
A. 47 12 6.
B.
141
.
8
C. 39 12 6. D.
77
.
8
Lời giải:
Ta có:
3 2
18 6 ( ) 3 18f x x x f x x
Cho
6 [ 3;5]
( ) 0
6 [ 3;5]
x
f x
x
Tính ( 3) 33; (5) 41; ( 6) 6 12 6; ( 6) 6 12 6 f f f f
Vậy
[ 3;5]
[ 3;5]
Max ( ) 41; Min ( ) 6 12 6
M f x m f x
41 6 12 6 47 12 6.
M m
Chọn đáp án A
Câu 28. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
,
a
SA
vuông góc với mặt phẳng
ABCD
và
3 .
SA a
Gọi
là góc giữa hai mặt phẳng
SBC
và
.
ABCD
Giá trị
tan
bằng
A.
3.
B.
3
.
3
C.
6
.
2
D.
3
.
2
Lời giải:
Ta có:
,
BC SB AB
SBC ABCD
3
tan 3
SA a
AB a
Chọn đáp án A
Câu 29. Cho và
b
là hai số thực dương thỏa mãn
2 2
64
a b
. Giá trị của
2 2
2log 2log
a b
bằng
A.
8.
B.
32.
C.
6.
D.
4.
Lời giải:
Ta có:
2 2
2 2 2 2 2
2log 2log 2log log log 64 6.
a b ab a b
Chọn đáp án C
Câu 30. Cho hình trụ có bán kính đáy
3
r
và độ dài đường sinh
5
l
. Diện tích toàn phần của hình
trụ đã cho bằng
A.
48 .
B.
30 .
C.
15 .
D.
33 .
Lời giải:
Ta có:
2 2
2 2 2 .3.5 2. .3 48 .
tp
S rl r
Chọn đáp án A
Câu 31. Cho hình nón
N
có bán kính đáy bằng
3
và chiều cao bằng
4.
Thể tích khối nón
N
bằng
A.
6 .
B.
12 .
C.
15 .
D.
36 .
Lời giải:
Thể tích khối nón
N
là
2 2
1 1
.3 .4 12 .
3 3
V r h
Chọn đáp án B
Câu 32. Cho hai số phức
4 3
z i
và
w 1 .
i
Môđun của số phức
.
z w
bằng
A.
4 2.
B.
5 2.
C.
5.
D.
3 2.
Lời giải:
a
Ta có
. 4 3 1 1 7 5 2.
z w i i i
Chọn đáp án B
Câu 33. Trong không gian
Oxyz
, cho hai điểm
1;2; 3
A
và
2; 1;1
B
. Tọa độ trung điểm của đoạn
thẳng
AB
là
A.
3;1; 2
. B.
1 3
; ;2
2 2
. C.
1 3
; ; 2
2 2
. D.
3 1
; ; 1
2 2
.
Lời giải:
Tọa độ trung điểm của đoạn thẳng
AB
là
; ;
2 2 2
A B A B A B
x x y y z z
I
hay
3 1
; ; 1
2 2
I
.
Chọn đáp án D
Câu 34. Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi đồ thị hàm số
sin
y x
,
trục hoành và các đường thẳng
0,x x
quanh trục
Ox
bằng
A.
.
4
B.
.
2
C.
2
.
4
D.
2
.
2
Lời giải:
2
2
0
sin d
2
V x x
.
Chọn đáp án D
Câu 35. Cho hàm số
( )
f x
có
2 2
'( ) ( 3) 2 3
f x x x x x
. Số điểm cực đại của hàm số
( )
f x
là
A.
4.
B.
2.
C.
1.
D.
3.
Lời giải:
3
0
'( ) 0 . 3 1 0 3
1
x
f x x x x x
x
Bảng xét dấu
Dựa vào bảng xét dấu
'( )
f x
suy ra
( )
f x
có 1 cực đại.
Chọn đáp án C
Câu 36. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
6
a
, mặt bên
SAB
là tam giác đều
nằm trong mặt phẳng vuông góc với đáy. Mặt cầu ngoại tiếp hình chóp
.
S ABC
có diện tích
bằng
A.
2
60 .
a
B.
2
15 .
a
C.
2
75 .
a
D.
2
80 .
a
Lời giải:
Áp dụng công thức:
2
2 2
4
C D B
GT
R R R
+
2
2 3
3
D
R CH a
+
2
2 3
3
B
R SH a
+
6
GT AB a
Khi đó:
2
2 2
15 .
4
C D B
GT
R R R a
Diện tích mặt cầu:
2 2
4 60
mc
S R a
Chọn đáp án A
Câu 37. Một tổ có
12
học sinh gồm
4
nam trong đó có Vinh và
8
nữ trong đó có Hoa. Chia tổ thành 3
nhóm, mỗi nhóm gồm
4
học sinh và phải có ít nhất một học sinh nam. Xác suất để Vinh và
Hoa cùng một nhóm là
A.
7
.
32
B.
1
.
8
C.
3
.
32
D.
5
.
16
Lời giải:
Ta có:
1 3 1 3
4 8 3 5
C . C .1 6720
n C C
?
n A
TH1: nhóm 1: Vinh,Hoa và 1 bạn nam cùng 1 bạn nữ khác:
1 1
3 7
.
C C
nhóm 2: 1 nam và 3 nữ:
1 3
2 6
.
C C
, nhóm còn lại có 1 cách chọn
Vậy trường hợp 1 có
1 1 1 3
3 7 2 6
. . . 840
C C C C
cách chọn.
TH2: nhóm 1: Vinh,Hoa và 2 bạn nữ khác:
2
7
C
nhóm 2: 2 nam và 2 nữ:
2 2
3 5
.
C C
, nhóm còn lại có 1 cách chọn
Vậy trường hợp 1 có
2 2 2
7 3 5
. . .1 630
C C C
cách chọn.
1470
n A
1470 7
6720 32
P A
Chọn đáp án A
Câu 38. Biết
3
2
2
2
2 14
ln2 ln3 , , , .
1
x x
dx a b c a b c
x
Giá trị của
2
a b c
bằng
A.
494.
B.
484.
C.
474.
D.
464.
Lời giải:
Ta có:
2
2 2
3 3
2
3
2
2
2 2
2
2 14 14 2 6 8
2 2 .
1 1 1 1
2 14 6 8
2 2 6ln 1 8ln 1
1 1 1
22ln 2 8ln3 2
22, 8, 2
474.
x x x
x x x x
x x
dx dx x x x
x x x
a b c
a b c
Chọn đáp án C
Câu 39. Trong không gian
,
Oxyz
cho hai đường thẳng
1
1 1
1
: 4
3
x t
d y t
z t
và
2
2 2
2
1 2
: 3 .
4
x t
d y t
z t
Đường
thẳng vuông góc với mặt phẳng
( ),
Oxz
cắt hai đường thẳng
1
d
và
2
d
có phương trình là
A.
1
3
7
.
3
10
3
x
y t
z
B.
1
7
7
1 .
3
10
3
x t
y t
z t
C.
3
7
25
1 .
7
18
7
x t
y t
z t
D.
3
7
25
.
7
18
7
x
y t
z
Lời giải:
- Gọi
d
là đường thẳng vuông góc với mặt phẳng
( ),
Oxz
cắt hai đường thẳng
1
d
và
2
d
lần lượt
tại
, .
M N
- Vì
1
M d
nên
1 1 1 1
( ; 4 ;3 ),t .
M t t t
- Vì
2
N d
nên
2 2 2 2
(1 2 ; 3 ;4 ), .
N t t t t
- Vì
,
M d N d
nên
d
có VTCP là
1 2 1 2 1 2
(1 2 ;1 ;1 )
MN t t t t t t
- Vì
d
vuông góc với mặt phẳng
( )
Oxz
nên
(0;1;0)
j
cũng là một VTCP của
d
1
1 2
1 2
1 2
2
1
1 2 0
3
0: 1 2
2
1 0
3
t
t t
k MN kj t t k k
t t
t
- Với
2
2
3
t
thì
1 7 10
; ;
3 3 3
N
- Vậy đường thẳng
d
đi qua điểm
1 7 10
; ;
3 3 3
N
và có một VTCP là
(0;1;0)
j
nên có
phương trình tham số là
1
3
7
.
3
10
3
x
y t
z
Chọn đáp án A
Câu 40. Có bao nhiêu số nguyên dương
m
sao cho hàm số
3 2
1 2
y x x m x
đồng biến trên
1; ?

A.
6.
B.
5.
C.
8.
D.
7.
Lời giải:
2
' 3 2 1 0, 1;y x x m x

2
3 2 1 , 1;x x m x

Xét hàm số
2
1
3 2 1 ' 6 2 0
3
y x x g x x x
Do đó
6.
m
Chọn đáp án A
Câu 41. Cho số phức
,z x yi x y
thỏa mãn
2 3 4
z i z i
và
2 3 2 1 1
z i y y i
là số thuần ảo. Giá trị của
11 11
x y
bằng
A.
16.
B.
28.
C.
16.
D.
28.
Lời giải:
Ta có:
2 2 2 2
2 3 4
2 1 3 4
5 3 10
z i z i
x y x y
x y
2 3 2 1 1
x yi i y y i
là số thuần ảo
2 3 2 1 0
2 1
x y y
x y
Giải hệ pt
13
5 3 10
11
2 1 15
11
x
x y
x y
y
Vậy
11 11 28
x y
Chọn đáp án D
Câu 42. Cho hàm số
3 2
, , ,y ax bx cx d a b c d
có đồ thị như sau
Có bao nhiêu số dương trong các số
, , , ?
a b c d
A.
4.
B.
2.
C.
1.
D.
3.
Lời giải:
Dựa vào đồ thị, ta có:
0
a
.
Đồ thị cắt trục tung tại điểm có tung độ dương,
0.
d
Hàm số đạt cực trị tại
1 2
,
x x
nên
1 2
,
x x
là nghiệm của phương trình
2
3 2 0 ( ' 0)
ax bx c y
1 2
1 2
1 2
0
, 0
. 0
2
0
0 0
3
.
0 0
0
3
x x
x x
x x
b
a b
a
c a c
a
Trong các số
, , ,
a b c d
có một giá trị dương.
Chọn đáp án C
Câu 43. Số nghiệm nguyên của bất phương trình
2
2
2
log 4 43log 4 16 75 0
x x
là
A.
2047.
B.
2048.
C.
2049.
D.
2052.
Lời giải:
2
2
2
2
2 2
2
1
11
4
1
4
log 4 43log 4 16 75 0
4
4log 4 43log 4 11 0
4
1
log 4 11
4
4
2 4 2
4 2 2052. 5;6;7;...;2052
x x
x
x x
x
x
x
x
x x
Vậy số nghiệm nguyên của phương trình là 2048.
Chọn đáp án B
Câu 44. Trong không gian
Oxyz
, cho hai điểm
1;1; 1
A
,
7; 2;2
B và đường thẳng
1 3
: 2 2
2 2
x t
y t
z t
. Gọi
P
là mặt phẳng chứa đường thẳng
, khoảng cách từ
A
đến
P
gấp
đôi khoảng cách từ
B
đến
P
và
A
,
B
nằm khác phía với
P
. Biết rằng phương trình
P
có dạng
28 0
ax by cz
. Giá trị của
a b c
bằng
A.
26
.
B.
26
. C.
34
. D.
34
.
Lời giải:
Gọi
,
H K
lần lượt là hình chiếu của
,
A B
lên mặt phẳng
P
và
I
là giao điểm của
AB
và
P
. Khi đó
AHI
đồng dạng với
BKI
nên
2 2 0 5; 1;1
IA AH
IA IB I
IB BK
Khi đó
P
chứa
và
I
nên có phương trình là
:8 15 3 28 0
P x y z
.
Do đó:
26
a b c
.
Chọn đáp án B
Câu 45. Bạn An được gia đình gởi vào số tiền tiết kiệm
200
triệu đồng với lãi suất
0,5%
một tháng theo
thể thức lãi kép. Nếu mỗi tháng an rút ra một số tiền như nhau vào ngày ngân hàng trả lãi thì
hàng tháng An rút ra số tiền gần nhất với số nào sau đây để đúng sau 4 năm vừa hết số tiền
trong sổ tiết kiệm?
A.
4687000
đồng.
B.
4697000
đồng. C.
4690000
đồng. D.
4700000
đồng.
Lời giải:
Áp dụng công thức
48
48
200. 1 0,5% .0,5%
(1 )
4,697
1 1 1 0,5% 1
n
n
N r r
A
r
triệu đồng
Chọn đáp án B
Câu 46. Xét hai số phức
1 2
,
z z
thỏa mãn
1 2
1 1, 1 2
z i z i
và
1 2
2 2 3
z z i . Giá trị lớn
nhất của
1 2
3 2 1 5
z z i
bằng
A.
6 37.
B.
5 23.
C.
6 11.
D.
6 13.
Lời giải:
Gọi
,
M N
lần lượt là điểm biểu diễn cho số phức
1 2
,
z z
Từ
1
1 1
z i
ta có
1
MA
với
1; 1
A
Từ
2
1 2
z i
ta có
2
NB
với
1;1
B
Xét
1 2 1 2
2 2 3 1 1 3
z z i z i z i
2 2
3 2 . 3 . 1
MA NB MA NB MA NB MA NB

1 2 1 2 1 2
3 2 1 5 3 1 2 1 6 3 1 2 1 6 6
z z i z i z i i z i z i i P
Với
1 2
3 1 2 1 3 2
P z i z i MA NB
Xét
2 2 2 2 2
3 2 9 4 12 . 9.1 4.2 12.1 37
P MA NB MA NB MA NB
37
P
Vậy giá trị lớn nhất cần tìm là
6 37
Chọn đáp án A
Câu 47. Cho phương trình
2
log (2 ) 4
x
x m m
với
m
là tham số thực. Có bao nhiêu giá trị nguyên
của tham số
( 27;27)
m
sao cho phương trình trên có nghiệm?
A.
10.
B.
26.
C.
1.
D.
53.
Lời giải:
Ta có:
2 0
m
x m x
2
2 2
log (2 ) 4 log (2 ) 2 2 2 (1)
x x
x m m x m x m x
( ) 2 ( ) 2 .ln2 1 0.
t t
f t t f t
Suy ra
( )
f t
đồng biến trên
2
2
(1) log (2 ) 2 2 2 2 4
x x
x m x x m m x
Đặt
( ) 2 4 ( ) 2 4 .ln4
x x
g x x g x
4
1
( ) 0 4 log (ln2)
ln2
x
g x x
Do
( 27;27)
m
nên phương trình có nghiệm khi
27 0.91
m
. Vậy có 26 giá trị nguyên
m
thỏa yêu cầu bài toán.
Chọn đáp án B
Câu 48. Cho hàm số
3 2
f x x bx cx d
có đồ thị là đường cong trong hình bên dưới.
Số nghiệm của phương trình
4 1
f f x f x
là
A.
7
.
B.
4
. C.
3
. D.
2
.
Lời giải:
Đặt
t f x
, Khi đó phương trình đã cho trở thành:
4 1
f t t
2
4 2 1
1
f t t t
t
2
2 3 *
1
f t t t
t
Vẽ thêm đồ thị hàm số
2
2 3y t t trên hệ trục trên
Dựa vào sự tương giao 2 đồ thị ta có:
1
2
2
1
2 3 1
2
t t l
f t t t t
t t
Dựa vào đồ thị ta có
1f x có 3 nghiệm,
2
2f x t có 1 nghiệm
Chọn đáp án B
Câu 49. Cho hai số thực dương
,x y
thỏa mãn
1
2 2
3
log 2 1 9 1 .
y
x y x y
Giá trị nhỏ nhất
của biểu thức
2
2P x y
bằng
A. 5 6 3. B.
11
.
2
C. 4 6 2. D.
27
.
5
Lời giải:
Ta có:
1
2 2 2 2
3 3
log 2 1 9 1 1 log 2 1 9 1
y
x y x y y x y x y
2 2 2 2
3 3 3 3
9 9
log 2 log 1 log 2 2 log 1 2
1 1
x y x x x y
y y
2 2
3 3 3
9 1
log 2 2 log log 9
1 1
x x
y y
2 2
3 3
9 9
log 2 2 log 1
1 1
x x
y y
Đặt
2
2, 0
9
, 0
1
u x u
v v
y
Phương trình
1 trở thành
3 3
log logu u v v
Xét hàm số
3
log , 0f t t t t
1
1 0, 0
ln3
f t t
t
Suy ra hàm số
f t đồng biến trên
0;
Mà
f u f v
nên
2 2
9 9
2 2.
1 1
u v x x
y y
Do đó:
2
9
2 2 2, 0
1
P x y y y
y
2
9
2
1
P
y
,
2
3 2 3 2
1 1
9
2 2
0 1
2
3 2 3 2
1 1
2 2
y y N
P y
y y L
Bảng biến thiên
Vậy giá trị nhỏ nhất của P bằng 4 6 2.
Chọn đáp án C
Câu 50. Cho hình chóp .S ABCD có đáy ABCD là hình bình hành. Gọi ,M N lần lượt thuộc các đoạn
thẳng
,AB AD
(
,M N
không trùng với A ) sao cho
AB
x
AM
và
AD
y
AN
thỏa mãn
2 4x y
và
.
.
S AMN
S ABCD
V
V
đạt giá trị nhỏ nhất. Giá trị của
2 2
.
.
S ABD
S AMN
V
x y
V
bằng
A. 9.
B. 7. C. 5. D. 6.
Lời giải:
Ta có:
.
1
; .
3
S AMN AMN
V d S ABCD S
.
1
; .
3
S ABCD ABCD
V d S ABCD S
Mà:
1
. .sin
2
AMN
S AM AN A
1
2 2. . .sin
2
ABCD ABD
S S AB AD A
1
.
2
AMN
ABCD
S
AM AN
S AB AD
.
.
1 1 1 1 1 1 1
. . . .
4
2 2 2 4
2
S AMN
S ABCD
V
AM AN
x x
V AB AD x y x x
Vì:
2
.
.
4 1
4 4
2 4
S AMN
S ABCD
Vx x
x x
V
Khi đó:
.
.
min
1
4 2 1
4
S AMN
S ABCD
V
x x x y
V
Vậy:
2 2 2 2
.
.
2 1 2 7
S ABD
S AMN
V
x y
V
Chọn đáp án B
GIẢI CHI TIẾT
ĐỀ THI THỬ MÔN TOÁN LỚP 12 SỞ CẦN THƠ
NĂM HỌC 2020-2021
BẢNG ĐÁP ÁN
1.B 2.D 3.B 4.A 5.B 6.C 7.C 8.B 9.A 10.A
11.D
12.B
13.B
14.A
15.B
16.D
17.D
18.D
19.D
20.A
21.A 22.A 23.D 24.A 25.D 26.A 27.D 28.C 29.B 30.D
31.A 32.D 33.B 34.B 35.D 36.A 37.C 38.B 39.A 40.B
41.B
42.A
43.B
44.A
45.B
46.C
47.A
48.D
49.D
50.D
Câu 1. Trong không gian
,
Oxyz
tọa độ một vectơ chỉ phương của đường thẳng
28 5 21
:
2 1 2
x z y
d
là
A.
2;1;2 .
B.
2; 1;2 .
C.
28;5;21 .
D.
1; 1;1 .
Lời giải:
Từ
28 5 21 28 21 5
: :
2 1 2 2 2 1
x z y x y z
d d
Do đó một véctơ chỉ phương của
d
là
2;2; 1
u
Không có đáp án đúng
* Đề nghị sửa lại:
Câu 1. Trong không gian
,
Oxyz
tọa độ một vectơ chỉ phương của đường thẳng
28 5 21
:
2 1 2
x y z
d
là
A.
2;1;2 .
B.
2; 1;2 .
C.
28;5;21 .
D.
1; 1;1 .
Lời giải:
Một vectơ chỉ phương của
d
là
2; 1;2
u
Chọn đáp án B
Câu 2. Cho cấp số nhân
,
n
u
biết
1
2
u
và công bội
3.
q
Số hạng
2
u
bằng
A.
18.
B.
6.
C.
1.
D.
6.
Lời giải:
Áp dụng công thức:
1
1 2 1
2.3 6
n
n
u u q u u q
Chọn đáp án D
Câu 3. Điểm cực đại của đồ thị hàm số
3
3 2019
y x x
là
A.
1;2017 .
B.
1;2021 .
C.
0;2019 .
D.
3;2037 .
Lời giải:
2
3 3
y x
1
0
1
x
y
x
Dựa vào bảng biến thiên ta có điểm cực đại của đồ thị hàm số là
1;2021 .
Chọn đáp án B
Câu 4. Phần ảo của số phức
2020 2021
i
là
A.
2021.
B.
2021.
C.
2020.
D.
2020.
Lời giải:
Phần ảo của số phức
2020 2021
i
là
2021.
Chọn đáp án A
Câu 5. Họ các nguyên hàm của hàm số
2
4
( ) 3 5
f x x
x
là
A.
3
ln .
x x C
B.
3
4ln 5 .
x x x C
C.
3
4ln 5 .
x x x C
D.
3
ln 5 .
x x x C
Lời giải:
Họ các nguyên hàm của hàm số
2
4
( ) 3 5
f x x
x
là
3
4ln 5 .
x x x C
Chọn đáp án B
Câu 6. Diện tích xung quanh của hình trụ có bán kính đáy
2
r
và độ dài đường sinh
2 5
l bằng
A.
6 5 .
B.
4 5 .
C.
8 5 .
D.
2 5 .
Lời giải:
Diện tích xung quanh của hình trụ:
2 2 .2.2 5 8 5 .
xq
S rl
Chọn đáp án C
Câu 7. Thể tích khối lăng trụ có diện tích đáy
2
4
a
và có chiều cao
2
a
bằng
A.
3
8
.
3
a
B.
3
6 .
a
C.
3
8 .
a
D.
3
4
.
3
a
Lời giải:
Ta có công thức tính thể tích khối lăng trụ:
2 3
. 4 .2 8 .
V B h a a a
Chọn đáp án C
Câu 8. Thể tích của khối cầu có bán kính
2
a
bằng
A.
3
8
.
3
a
B.
3
32
.
3
a
C.
3
16
.
3
a
D.
3
4
.
3
a
Lời giải:
Ta có công thức tính thể tích khối cầu là:
3
3 3
4 4 32
2 .
3 3 3
V R a a
Chọn đáp án B
Câu 9. Cho hàm số
y f x có bảng biến thiên như sau:
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là
A. 2. B. 3. C. 4. D. 1.
Lời giải:
Ta có:
1 1
lim , lim 1
x x
f x f x x
 
 
là tiệm cận đứng.
lim 3 3
x
f x y

là tiệm cận ngang.
Vậy tổng số tiệm cận là
2.
Chọn đáp án A
Câu 10. Cho hàm số
3 2
( ) ,( , , ; 0)f x ax bx cx d a b c a
có đồ thị như sau:
Hàm số đã cho nghịch biến trong khoảng nào dưới đây?
A.
1; .
B.
1;1 .
C.
;0 .
D.
0;1 .
Lời giải:
Dựa vào đồ thị, hàm số nghịch biến trên khoảng
1; .
Chọn đáp án A
Câu 11. Cho hình chóp .S ABCD có đáy là hình vuông cạnh bằng
2
a
, SA vuông góc với mặt phẳng
( )ABCD
và
3 .SA a
Thể tích khối chóp
.S ABCD
bằng
A.
3
3
2
a
B.
3
3
4
a
C.
3
2
a
D.
3
4
a
Lời giải:
2 3
1 1
. . .3
3 3 4 4
a a
V S h a
Chọn đáp án D
Câu 12. Diện tích xung quanh của hình nón có độ dài đường sinh
l
và bán kính
r
bằng
A.
2
rl
B.
rl
C.
2
1
3
r h
D.
2
r h
Lời giải:
Công thức diện tích xung quanh hình nón:
xq
S rl
Chọn đáp án B
Câu 13. Tập nghiệm của bất phương trình
2
4 5
3 9
x x
là
A.
1;5 .
B.
1;3 .
C.
1;5 .
D.
1;3 .
Lời giải:
2 2
4 5 4 5 2 2 2
3 9 3 3 4 5 2 4 3 0 1 3.
x x x x
x x x x x
Chọn đáp án B
Câu 14. Hàm số
f x
liên tục trên
.
Mệnh đề nào sau đây đúng?
A.
3 2 3
1 1 2
.
f x dx f x dx f x dx
B.
3 3 3
1 1 2
.
f x dx f x dx f x dx
C.
2 2 3
1 1 2
.
f x dx f x dx f x dx
D.
3 3 2
2 1 1
.
f x dx f x dx f x dx
Lời giải:
Áp dụng tính chất:
; .
b c b
a a c
f x dx f x dx f x dx a c b
Chọn đáp án A
Câu 15. Trong không gian
,
Oxyz
tọa độ tâm của mặt cầu
2 2 2
: 2 2 6 0
S x y z x y
là
A.
1; 1;3 .
B.
1; 1;0 .
C.
2;2;0 .
D.
2;2; 6 .
Lời giải:
Ta có
1, 1, 0
a b c
Chọn đáp án B
Câu 16. Giá trị của
4
0,2
3
1 1
32 8
bằng
A.
6.
B.
9
.
16
C.
33
.
2
D.
18.
Lời giải:
4
0,2
4 4
3
3.
0,2 5.0,2
3 3
1 1
32 8 2 2 18
32 8
Chọn đáp án D
Câu 17. Trên mặt phẳng
Oxy
, điểm nào trong hình vẽ bên dưới là điểm biểu diễn của số phức
2
z i
?
A.
.
Q
B.
.
M
C.
.
N
D.
.
P
Lời giải:
2 2;1 .
z i P
Chọn đáp án D
Câu 18. Nghiệm của phương trình
2
log ( 10) 3
x
là
A.
19.
x
B.
16.
x
C.
15.
x
D.
18.
x
Lời giải:
Điều kiện
10 0 10
x x
3
10 2 18( ).
x x n
Chọn đáp án D
Câu 19. Số cách sắp xếp 5 quyển sách Toán khác nhau và 3 quyển sách Ngữ văn khác nhau thành một
hàng trên kệ sách là
A.
5 3
8 8
.
A A
B.
5!3!.
C.
5 3
8 8
.
C C
D.
8!.
Lời giải:
Vì mỗi cách sắp xếp thỏa YCBT là một hoán vị của 8 phần tử nên số cách sắp xếp là 8!.
Chọn đáp án D
Câu 20. Tập xác định của hàm số
2021
y x
là
A.
2021; .

B.
;2021 .
 C.
\ 2021 .
D.
2021; .

Lời giải:
ĐK:
2021 0 2021
x x
Vậy TXĐ là
2021; .

Chọn đáp án A
Câu 21. Cho hàm số
f x
có đạo hàm liên tục trên đoạn
0;2
thỏa
2
0
2 12, 8.
f xf x
Giá trị
2
0
f x
bằng
A. 16. B. -32. C. 32. D. -16.
Lời giải:
Đặt
. .
' . .
u x du dx
dv f x dx v f x
Nên
2
0
'
xf x dx
=
2 2
2
0
0 0
2 2 0 0 8.
xf x f x f f f x
Suy ra
2
0
2.12 8 16.
f x dx
Chọn đáp án A
Câu 22. Cho
,
x y
là 2 số thực thỏa mãn
2 2 3 2 .
x y xi x y x i
Giá trị của
16
xy
bằng
A. 11. B.
1
.
4
C.
11
.
4
D.
11
.
6
Lời giải:
Ta có
1
2 3. 3
4
2 2. 3 2 11
4
x
x y x x y
x y x x y
y
Vậy giá trị của
16 11.
xy
Chọn đáp án A
Câu 23. Cho hình trụ có bán kính đáy bằng
2 2
và thiết diện qua trục là một hình vuông. Thể tích của
khối trụ đã cho bằng
A.
6 2.
B.
16 2.
C.
8 2.
D.
32 2.
Lời giải:
Do thiết diện qua trục là hình vuông nên
4
2
h
Thể tích của khối trụ là
2
2 2 . 4 2 32 2V
Chọn đáp án D
Câu 24. Giá trị nhỏ nhất của hàm số
2
16
y x
x
trên đoạn
[1;4]
bằng
A. 12. B. 17. C. 20. D. 4.
Lời giải:
Ta có:
'
2
16
( ) 2f x x
x
;
3
'
2 2
16 2 16
( ) 0 2 0 0 2
x
f x x x
x x
2
16
(1) (1) 17
1
f
2
16
(2) (2) 12
2
f Vậy
min
12.f
2
16
(4) (4) 20
4
f
Chọn đáp án A
Câu 25. Với
2
log 3,a giá trị của
2
2
log 9 log 6 bằng
A. 5 1.a B. 5 2.a C. 5 .a D. 5 1.a
Lời giải:
Ta có
1
2
2
2 2 2 2
2
2
log 9 log 6 log 3 log 2.3 4log 3 1 log 3 5 1.a
Chọn đáp án D
Câu 26. Cho hàm số
4 2
, , , , 0f x ax bx c a b c a có đồ thị như sau:
Số nghiệm thực của phương trình
2ln6 0f x
là
A.
4.
B.
3.
C.
2.
D.
0.
Lời giải:
Ta có:
2ln 6 0 2ln6 1
f x f x
Số nghiệm phương trình (1) chính là số giao điểm của 2 đồ thị hàm số
y f x
và
2ln6
y
Dựa vào đồ thị ta thấy có 4 giao điểm.
Vậy phương trình
2ln6 0
f x
có 4 nghiệm phân biệt.
Chọn đáp án A
Câu 27. Cho hàm số
4 2
( , , ; 0)
y ax bx c a b c a
có bảng biến thiên như sau:
Bảng biến thiên đã cho là của hàm số nào dưới đây?
A.
4 2
18 1.
y x x
B.
4 2
1 9
1.
4 2
y x x
C.
4 2
1 9
4 2
.
y x x
D.
4 2
1 9
1
4 2
.
y x x
Lời giải:
Hàm số
4 2
( , , ; 0)
y ax bx c a b c a
có 3 cực trị và hệ số
0
a
nên loại đáp án
,
B C
.
Ta có:
77 77
( 3) ; (3) ; (0) 1
4 4
y y y
nên chọn đáp án
D
Chọn đáp án D
Câu 28. Cho hàm số
2
( , , )
ax
y a b c
bx c
có đồ thị như sau:
Khẳng định nào dưới đây đúng?
A.
0 .
b a c
B.
0
.
b a c
C.
0
.
a b c
D.
0
.
b c a
Lời giải:
Cho
2
0 1 2
x y c
c
TCĐ
1 2
c
x b c
b
;
TCN 2 2 4
a
y a b
b
.0a b c
Chọn đáp án C
Câu 29. Trong không gian Oxyz , cho hai mặt phẳng ( ): 2 2021 0x y z
và
( ): 3 4 5 2021 0x y z
. Góc giữa hai mặt phẳng
( )
và mặt phẳng
( )
bằng
A.
0
150 .
B.
0
30 .
C.
0
120 .
D.
0
60 .
Lời giải:
Ta có:
2 2 2
(2; 1; 1) 2 ( 1) ( 1) 6.n n
2 2 2
( 3;4;5) ( 3) 4 5 2 5.n n
. 2.( 3) ( 1).4 ( 1).5 15.n n

Gọi
là góc giữa hai mặt phẳng
( )
và mặt phẳng
( )
, ta có:
0
.
15
3
cos
2
6.2 5
.
30
n n
n n
Chọn đáp án B
Câu 30. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông và
SA
vuông góc với mặt phẳng
( )ABCD
(tham khảo hình vẽ).
Góc giữa hai mặt phẳng ( )SCD và mặt phẳng ( )ABCD là
A.
.SDC B.
.SCD C.
.DSA D.
.SDA
Lời giải:
Ta có:
( ),( ) ,SCD ABCD SD AD SDA
Chọn đáp án D
Câu 31. Trong không gian ,Oxyz cho hình hộp .ABCD A B C D
có (1;0;1), (2;1;2), (1; 1;1)A B D và
(1;1; 1).A
Tọa độ AC
là
A. (1;1; 1).
B. (1;1;1). C. (0;1; 2). D. (0; 1;0).
Lời giải:
Ta có
(0;1; 2), (1;1;1)AA AB
Giả sử
( , , )
C x y z
suy ra
( 1; 1; 1)
DC x y z
Ta có
1 1 2
1 1 0 (2;0;2)
1 1 2
x x
AB DC y y C
z z
Gọi
( , , )
C x y z
suy ra
( 2; ; 2)
CC x y z
Ta có
2 0 2
1 ' 1 (2;1;0)
2 2 0
x x
AA CC y y C
z z

Vậy
(1;1; 1)
AC
Chọn đáp án A
Câu 32. Cho số phức
z
thỏa mãn
2
(3 ) 2 (1 2 ) .
i z i i i
Môđun của số phức
z
bằng
A.
5.
B.
5.
C.
2.
D.
2.
Lời giải:
Ta có
2
2 (1 2 )
1 2
3
i i i
z i z
i
Chọn đáp án D
Câu 33. Số giao điểm của hai đồ thị hàm số
4 2
2 1
y x x
và
3
y x x
là
A.
3
. B.
4
. C.
2
. D.
1
.
Lời giải:
Phương trình hoành độ giao điểm
4 2 3
2 1
x x x x
4 3 2
2 1 0
x x x x
1
1
1 5
2
1 5
2
x
x
x
x
.
Phương trình hoành độ giao điểm có 4 nghiệm nên số giao điểm của đồ thị hai hàm số đã cho là 4.
Chọn đáp án B
Câu 34. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số
3 2
2 1
y x x
và
2
1
y x
là
A.
189
.
4
B.
27
.
4
C.
6
D.
3
.
4
Lời giải:
Phương trình hoành độ giao điểm
3 2 2
2 1 1
x x x
3 2
0
3 0
3
x
x x
x
.
Diện tích hình phẳng cần tìm là
3
3 2
0
27
3 d
4
S x x x
.
Chọn đáp án B
Câu 35. Gọi
1 2
,
z z
là hai nghiệm phức của phương trình
2
6 73 0.
z z
Giá trị của biểu thức
2 2
1 2 1 2
.
z z z z
bằng
A.
213.
B.
110.
C.
37.
D.
183.
Lời giải:
2
2 2
1 2 1 2 1 2 1 2 1 2
2
z z z z z z z z z z
2
6 2.73 73 183.
Chọn đáp án D
Câu 36. Biết
2
2
1
ln2 ln3 ln5 , ,
2 3 1
dx
a b c a b c
x x
. Giá trị
a b c
bằng
A.
4.
B.
0.
C.
6.
D.
2.
Lời giải:
Cách 1.
2 2
2
1 1
1 1
.
1
2 3 1 1
2
dx
dx
x x x
x
2
1
1
2
ln ln10 ln9 ln 2 2ln3 ln5
1
x
x
1, 2, 1 4.
a b c a b c
Cách 2. Đặt
2
2
1
2 3 1
dx
I
x x
. Khi đó:
2
ln2 ln3 ln5 ln 2 .3 .5
10
2 .3 .5 2.3 .5
9
1, 2, 1 4.
a b c
a b c I
a b c I I
e
a b c a b c
Chọn đáp án A
Câu 37. Trong không gian
,
Oxyz
cho đường thẳng
1 2
:
1 1 1
x y z
d
và mặt phẳng
:2 2 1 0.
P x y z
Đường thẳng
nằm trong
,
P
cắt và vuông góc với
d
có phương
trình là
A.
2 1 3
.
3 4 1
x y z
B.
1 1 1
.
3 4 1
x y z
C.
5 3 4
.
3 4 1
x y z
D.
2 1 3
.
3 4 1
x y z
Lời giải:
Ta có:
1
: 2; 1; 2
p
P VTPT n n
1 t; ;2
d A A t t
thế điểm
A
vào
:2 1 2 2 1 0
P t t t
1 2; 1;3
t A
2
: 1; 1;1
d VTPT n
1 2
: ; 3;4;1
VTCP u n n
Loại câu D.
Vậy thế
2; 1;3
A
vào câu C thỏa.
Chọn đáp án C
Câu 38. Cho hàm số bậc bốn
y f x
và có đồ thị
'
f x
như sau:
Số điểm cực trị của hàm số
2
1
g x f x
là
A.
1.
B.
3.
C.
2.
D.
4.
Lời giải:
Ta có:
2
2
2 0 0
0
0
' 2 ' 1 0 3
' 1 0 3
3
3
x x
x
x
g x xf x x
f x x
x
x
Chọn đáp án B
Câu 39. Trong không gian
,
Oxyz
cho mặt cầu
2 2 2
( ) :( 1) ( 1) ( 2) 4
S x y z
và điểm
A(1;1; 1).
Ba mặt phẳng đi qua
A
và đôi một vuông góc với nhau, cắt mặt cầu
( )
S
theo ba giao tuyến là
các đường tròn
1 2
( ),( )
C C
và
3
( ).
C
Tổng diện tích của ba hình tròn
1 2
( ),( )
C C
và
3
( )
C
bằng
A.
11 .
B.
9 .
C.
12 .
D.
8 .
Lời giải:
+ Mặt cầu
( )
S
có tâm
(1;1; 2)
I
và bán kính
2.
R
+ Vì
1 2
IA R
nên điểm
nằm bên trong mặt cầu
( ).
S
+ Gọi
( )
P
là mặt phẳng đi qua
A
và vuông góc với
2 2
1
3
IA r R IA
+ Gọi
2 3
( ),( )
P P
là mặt phẳng chứa
IA
và
2 3 2 3
( ) ( ) 2
P P r r
Vậy
2
2 3 2 2 2
1 2 3 1 2 3
. 3 .2 .2 11 .
S S S r r r
Chọn đáp án A
Câu 40. Ông An gửi
200000000
đồng vào một ngân hàng với lãi suất ban đầu là
6,8%
năm và tiền lãi
hằng năm được nhập vốn. Cứ sau 1 năm lãi suất tăng thêm
0,2%.
Sau 5 năm ông An thu được
tổng số tiền ( làm tròn đến hàng nghìn) là
A.
283135000
đồng. B.
283137000
đồng. C.
283140000
đồng. D.
283 130000
đồng.
Lời giải:
Gọi
n
S
là số tiền ông An nhận sau
n
năm,
là số tiền ban đầu,
r
là lãi suất
1
1
S A r
2 1
(1 0.2)
S S r
Suy ra
5 1
(1 ) 1 0.2% 1 0.4% 1 0.6% (1 0.8%) 283137000
S S r r r r r
Chọn đáp án B
Câu 41. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
, 2
BC a AB a
và
3 .
SA a
Biết
rằng mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng
(ABCD). Khoảng cách từ điểm D đến mặt phẳng (SAC) bằng
A.
2 82
.
41
a
B.
4 82
.
41
a
C.
82
.
41
a
D.
82
.
82
a
Lời giải:
Gọi I, K, M, lần lượt là trung điểm AB, CD, DK
O, N lần lượt là giao điểm của AC và BD, IM và AC
IH là đường cao của ΔSIN vuông tại I
Khi đó: IN là đường cao của ΔAIO vuông tại I và ΔSIA vuông tại I nên ta có
2 2
2 2 2 2 2 2 2 2 2
2
1 1 1 1 1 1 1 1 1 41
8
3
2
IH IN SI IA IO SA AI a a
a aa
2 82
41
a
IH
Mà
1 1
, , ,
2 2
IH d I SAC d B SAC d D SAC
4 82
, 2
41
a
d D SAC IH
Chọn đáp án B
Câu 42. Cho hình thang ABCD vuông tại A và D,
, 2 .
AD CD a AB a
Quay hình thang ABCD
quanh cạnh AB được một khối tròn xoay có thể tích là
A.
3
4
.
3
a
B.
3
5
.
3
a
C.
3
.
3
a
D.
3
.
a
Lời giải:
Quay hình thang ABCD quanh cạnh AB được một khối tròn xoay gồm hai khối là khối trụ và
khối nón có cùng bán kính đáy là
.
a
Gọi
V
là thể tích của khối tròn xoay. Ta có:
1 2
V V V
1
V
là thể tích khối trụ,
2 2 3
1
. . . .
V r h a a a
2
V
là thể tích khối nón,
2 2 3
2
1 1 1
. . . .
3 3 3
V r h a a a
3 3 3
1 4
3 3
V a a a
Chọn đáp án A
Câu 43. Xếp ngẫu nhiên 6 bạn nam và 5 bạn nữ ngồi vào 11 cái ghế được bố trí thành một hàng ngang.
Xác suất để 5 bạn nữ ngồi cạnh nhau là
A.
1
.
7920
B.
1
.
66
C.
1
.
231
D.
1
.
462
Lời giải:
Số phần tử của không gian mẫu là:
11!.
n
Gọi B là biến cố “5 bạn nữ ngồi cạnh nhau”
Khi đó:
7!5!.
n B
Vậy xác suất cần tìm là
7!.5! 1
.
11! 66
P B
Chọn đáp án B
Câu 44. Số các giá trị nguyên của tham số thực
m
sao cho hàm số
2025
mx
y
x m
đồng biến trên
khoảng
2;2
là
A.
86
.
B.
88
. C.
89
. D.
84
.
Lời giải:
2025
mx
y
x m
. Tập xác định:
\
D m
.
2
2
2025
m
y
x m
.
Hàm số đồng biến trên khoảng
2;2
khi
0, 2;2
y x
2
45 45
2025 0
2 45
2
2
45 2
2
2
m
m
m
m
m
m
m
m
Vậy
2,3,...,44 44, 43,..., 2
m
. Có 86 giá trị
m
.
Chọn đáp án A
Câu 45. Có 4 học sinh nam và 8 học sinh nữ, trong các bạn nữ có An và Bình. Xếp những học sinh này
thành một hàng ngang. Xác suất để mỗi bạn nam đều đứng giữa hai bạn nữ đồng thời An và
Bình luôn đứng cạnh nhau bằng
A.
1
.
264
B.
1
.
132
C.
1
.
396
D.
2
.
33
Lời giải:
Số phần tử của không gian mẫu
12!
n
Gọi
A
là biến cố: “mỗi bạn nam đều đứng giữa hai bạn nữ đồng thời An và Bình luôn đứng
cạnh nhau”
- Xem bạn An và Bình là 1 bạn nữ.
- Xếp 7 bạn nữ theo hàng ngang có
7!
cách
- Giữa các bạn nữ có 6 chỗ trống, xếp 4 nam vào 6 chỗ trống đó có
4
6
A
cách
- Hoán vị An và Bình với nhau có
2!
cách
4
6
7!. .2!
n A A
1
.
132
n A
P A
n
Chọn đáp án B
Câu 46. Cho hình chóp tứ giác đều
.
S ABCD
có tất cả các cạnh bằng
a
và
O
là tâm của hình vuông
ABCD
. Gọi mặt phẳng
P
là mặt phẳng qua
S
, song song với đường thẳng
BD
, cắt đoạn
OC
và khoảng cá ch từ
A
đến mặt phẳng
P
bằng
3 10
10
a
. Biết rằng
P
chia khối chóp
thành hai khối đa diện, trong đó khối đa diện chứa điểm
có thể tích
1
V
và khối đa diện còn
lại có thể tích
2
V
. Giá trị của
2
1
V
V
bằng
A.
2
.
7
B.
1
.
8
C.
1
.
7
D.
3
.
8
Lời giải:
Ta có
2
2 2 2
2
4 2
a a
SO SB OB a .
Đặt
OF x
Ta có
2 2
2 2
,
3 10 2 .
. .
10 2
,
d A P
AF a a SO OF
x x
OF SO OF
d O P
Chọn đáp án C
Câu 47. Có bao nhiêu số nguyên
( ; )
x y
thỏa mãn
2 2020
x
và
2 2021
y
sao cho
log 6log 5?
x y
y x
A.
54.
B.
11.
C.
43.
D.
52.
Lời giải:
2
3
log 2
6
log 6log 5 log 5 0
log 3log
x
x y x
xx
y
y x
y x y
yy
y x
Ta có
2
2
3
3
2 2021 2 2021 44,95
2 2021
2 2021
2 2021 12,64
x x
y
x
x
Chọn đáp án A
Câu 48. Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
sao cho đồ thị hàm số
3
3 2
y x x
cắt đường thẳng
2
: 1
d y m x
tại 3 điểm phân biệt có hoành độ
1 2 3
, ,
x x x
thỏa mãn
3 3 3
1 2 3
2057
x x x
. Số phần tử của tập
S
là
A.
19
.
B.
36
. C.
18
. D.
37
.
Lời giải:
Ta có phương trình hoành độ giao điểm của đồ thị hàm số và đường thẳng
d
3 2
3 2 1
x x m x
2 2
1 2 2 0
x x x m
3
2 2
1
2 2 0 *
x
x x m
Từ đó ta có:
1 2
2
1 2
2
2
x x
x x m
Theo đề bài:
3 3 3
1 2 3
2057
x x x
3
1 2 1 2 1 2
3 2056
x x x x x x
2
6 2 2048
m
2
1024
2
3
m
2
1024 1018
2
3 3
m
1018 1018
3 3
m
Vì
m
nên
18; 17;...;17;18
m
Vậy có 37 giá trị nguyên
m
cần tìm
Chọn đáp án D
Câu 49. Cho số phức
z
thỏa mãn
1 1
3 4
z
i
i
sao cho
3 8
z i
đạt giá trị lớn nhất tại
1 1 1
z x y i
và đạt giá trị nhỏ nhất tại
2 2 2
.
z x y i
Giá trị của
1 2 1 2
.
x x y y
bằng
A.
44.
B.
55.
C.
25.
D.
46.
Lời giải:
Gọi
M
là điểm biểu diễn số phức
z
và
3;8
A là điểm biểu diễn số phức
3 8
w i
.
Ta có
1 1 1 7 3 4
3 4
z
i z i i
i
1 7 5
z i
Suy ra tập hợp các điểm biểu diễn số phức
z
là đường tròn
C
tâm
1;7
I
, bán kính
5.
R
Phương trình đường tròn
C
là
2 2
1 7 25
x y
Phương trình đường thẳng
1 2
:
7
x t
IA
y t
Gọi
1 2
,
M M
lần lượt là giao điểm của đường thẳng
IA
và đường tròn
.
C
Ta có
3 8
z i MA
. Dựa vào hình vẽ ta thấy
min 2 max 1
,
AM AM AM AM
Xét phương trình
2 2
2
1 2 1 7 7 25 5 5
t t t t
- Với
2 1
5 1 2 5;7 5 1 2 5 7 5
t M z i
- Với
2 1
5 1 2 5;7 5 1 2 5 7 5
t M z i
Vậy
1 2 1 2
. 1 2 5 1 2 5 7 5 7 5 46.
x x y y
Chọn đáp án D
Câu 50. Cho
,
x y
là các số thực dương thỏa mãn
2 3
1
2 .
1
x y xy
xy
xy
Giá trị nhỏ nhất của biểu thức
2 2
2 5
x y
bằng
A.
3 2 5.
B.
3 2 5.
C.
3 5.
D.
3 5.
Lời giải:
Ta có:
2 3
1
2 1
x y xy
xy
x y
Điều kiện:
, 0 , 0
.
1 0 1
x y x y
xy xy
2 3
2 2
2
1
1 log 2 log
1
2 3 log
x y xy
xy
x y
xy
x y xy
x y
2
2 1
2 2 log
xy
x y xy
x y
2 2
2 1 log 2 1 logx y xy xy x y
2 2
log 2 1 log 2 1x y x y xy xy
(*)
Xét hàm:
2
log 0f t t t t
Vì:
1
' 1 0
ln 2
f t f t
t
đồng biến trên
0; .
Từ (*), ta được:
2 1 2 2f x y f xy x y xy
Với: 2 2x y xy
Áp dụng Bất đẳng thức Cauchy ta được: 2 2 2 2 1 0x y xy xy xy xy xy
1 5 3 5
0 0 .
2 2
xy xy
Ta có:
2 2 2
2 2
2 5 2 2 5 2 2 2 2 5 4 10 4 2 5.P x y x y xy xy xy xy xy
Đặt:
3 5
0
2
t xy t
Khi đó:
2
4 10 4 2 5g t t t
5
' 8 10, ' 0
4
g t t g t t (loại).
Bảng biến thiên:
Chọn đáp án D
GIẢI CHI TIẾT
ĐỀ THI THỬ MÔN TOÁN LỚP 12 SỞ CẦN THƠ
NĂM HỌC 2020-2021
BẢNG ĐÁP ÁN
1.D 2.A 3.D 4.B 5.C 6.D 7.A 8.A 9.D 10.B
11.A
12.C
13.C
14.C
15.D
16.C
17.C
18.B
19.A
20.A
21.C 22.D 23.A 24.D 25.A 26.D 27.B 28.C 29.C 30.A
31.B 32.B 33.A 34.B 35.D 36.D 37.B 38.C 39.C 40.B
41.B
42.B
43.B
44.D
45.D
46.B
47.A
48.A
49.C
50.A
Câu 1. Họ nguyên hàm của hàm số
3
x
f x e
là
A.
3 1
.
3 1
x
e
C
x
B.
3
3 .
x
e C
C.
3
.
x
e C
D.
3
.
3
x
e
C
Lời giải:
Áp dụng công thức
1
ax b ax b
e dx e C
a
suy ra
3 3
1
3
x x
e dx e C
Chọn đáp án D
Câu 2. Bất phương trình
1 1
2 4
x
có tập nghiệm là
A.
;2 .
 B.
;2 .
 C.
2; .

D.
2; .

Lời giải:
2
1 1 1 1
2 4 2 2
x x
x
Chọn đáp án A
Câu 3. Đường cong hình bên dưới là đồ thị hàm số nào sau đây?
A.
4 2
2 .
y x x
B.
4
2 .
y x x
C.
3 2
2 .
y x x
D.
4 2
2 .
y x x
Lời giải:
Nhìn dạng đồ thị là hàm bậc bốn trùng phương với hệ số
0
a
và có 3 điểm cực trị là
1;0;1
Chọn đáp án D
Câu 4. Cho
1
0
( ) 3
f x dx
và
3
1
( ) 2
f x dx
. Giá trị của
3
0
( )
f x dx
bằng
A.
5.
B.
1.
C.
5.
D.
1.
Lời giải:
Ta có:
3 1 3
0 0 1
( ) ( ) ( ) 3 2 1.
f x dx f x dx f x dx
Chọn đáp án B
Câu 5. Số phức
1 2
z i
có phần thực và phần ảo lần lượt là
A.
2
và
1.
B.
1
và
2.
C.
1
và
2.
D.
2
và
1.
Lời giải:
Số phức
1 2
z i
có phần thực là 1 và phần ảo là
2.
Chọn đáp án C
Câu 6. Cho lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông tại
,
B
2 ,
AB a
,
BC a
2 3 .
AA a
Thể tích của khối lăng trụ
.
ABC A B C
bằng
A.
3
4 3 .
a
B.
3
2 3
.
3
a
C.
3
4 3
.
3
a
D.
3
2 3 .
a
Lời giải:
Thể tích lăng trụ là
.
V B h
Ta có
2 3
.
. .2 3 2 3 .
ABC A B C ABC
V S AA a a a
Chọn đáp án D
Câu 7. Tập xác định của hàm số
ln 2
y x
là
A.
2; .

B.
; 2 .

C.
2; .

D.
; 2 .

Lời giải:
Ta có điều kiện:
2 0 2.
x x
Vậy tập xác định của hàm số
ln 2
y x
là
2; .

Chọn đáp án A
Câu 8. Trong không gian
,
Oxyz
tọa độ một vectơ pháp tuyến của mặt phẳng
: 2 3 0
x y z
là
A.
1; 1;2 .
B.
1; 1; 2 .
C.
1;0;2 .
D.
0;1;2 .
Lời giải:
Ta có:
: 2 3 0
x y z
Ta đã biết ptmp
: 0
Ax By Cz D
với
; ;
n A B C
là vectơ pháp tuyến.
Áp dụng ta có
1; 1;2
n
là một vectơ pháp tuyến của ptmp đã cho.
Chọn đáp án A
Câu 9. Với
a
là số thực dương tùy ý,
2
log 8
a
bằng
A.
2
8log .
a
B.
2
8 log .
a
C.
2
log 8.
a
D.
2
3 log .
a
Lời giải:
Áp dụng công thức:
log log log , 0
a a a
bc b c a b
Ta có:
2 2 2 2
log 8 log 8 log 3 log .
a a a
Chọn đáp án D
Câu 10. Cho hàm số
( )
y f x
có bảng biến thiên như sau:
Mệnh đề nào dưới đây đúng?
A. Hàm số không có cực trị.
B. Hàm số đạt cực đại tại
0.
x
C. Hàm số đạt cực đại tại
5.
x
D. Hàm số đại cực tiểu tại
1.
x
Lời giải:
Dựa vào BBT, hàm số đạt cực đại tại điểm
0
x
, hàm số đạt cực tiểu tại điểm
x
Chọn đáp án B
Câu 11. Cho cấp số cộng
( )
n
u
có
1
1
u
và
2
3
u
. Giá trị của
3
u
bằng
A.
5.
B.
9.
C.
4.
D.
6.
Lời giải:
Công sai
2 1
2
d u u
3 2
3 2 5
u u d
Chọn đáp án A
Câu 12. Cho hình trụ có bán kính
3
r
và chiều cao
5
h
. Thể tích của khối trụ đã cho bằng
A.
36 .
B.
45.
C.
45 .
D.
15 .
Lời giải:
. 9.5 45
V S h
Chọn đáp án C
Câu 13. Cho hàm số
y f x
có bảng biến thiên như sau:
Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên
1
;1 .
3
B. Hàm số nghịch biến trên
1;3 .
C. Hàm số nghịch biến trên
3; .

D. Hàm số đồng biến trên
1; .

Lời giải:
Dựa vào bảng biến thiên, hàm số nghịch biến trên
3; .

Chọn đáp án C
Câu 14. Trong mặt phẳng
,
Oxy
điểm
M
trong hình vẽ là điểm biểu diễn số phức nào dưới đây
A.
4 3 .
i
B.
3 4 .
i
C.
3 4 .
i
D.
3 4 .
i
Lời giải:
Ta có
3
x
và
4
y
. Vậy số phức cần tìm là
3 4 .
i
Chọn đáp án C
Câu 15. Số cách chọn ra 3 học sinh từ một nhóm có 5 học sinh là
A.
3
5 .
B.
5!.
C.
3
5
.
A
D.
3
5
.
C
Lời giải:
Số cách chọn là
3
5
.
C
Chọn đáp án D
Câu 16. Cho hình nón
N
có bán kính đáy bằng
2
và chiều cao bằng
12.
Thể tích của khối nón
N
bằng
A.
48 .
B.
24 .
C.
16 .
D.
9 .
Lời giải:
Thể tích của khối nón
N
là
2 2
1 1
.2 .12 16
3 3
V r h
Chọn đáp án C
Câu 17. Nghiệm của phương trình
4
log (3 2) 2
x
là
A.
10
.
3
x
B.
7
.
2
x
C.
6.
x
D.
3.
Lời giải:
Điều kiện
2
3 2 0 .
3
x x
2
3 2 4 6( ).
x x n
Chọn đáp án C
Câu 18. Trong không gian
Ox ,
yz
điểm nào sau đây thuộc đường thẳng
1 4
: ?
2 1 2
x y z
d
A.
(2; 1;2).
M
B.
(1; 4;0).
M
C.
(1; 4; 2).
M
D.
( 2;1; 1).
M
Lời giải:
Phương trình đường thẳng có dạng
0 0 0
1 2 3
x x y y z z
u u u
nên ta có điểm
(1; 4;0)
M
thuộc
.
d
Chọn đáp án B
Câu 19. Với
a
là số thực dương tùy ý,
5
a
bằng
A.
5
2
.
a
B.
1
5
.
a
C.
2
5
.
a
D.
1
10
.
a
Lời giải:
Ta có công thức
m
n m
n
a a
5
5
2
a a
Chọn đáp án A
Câu 20. Cho hình chóp
.
S ABC
có đáy là tam giác đều cạnh
2 ,
a SA
vuông góc với mặt phẳng đáy và
3.
SA a
Thể tích khối chóp
.
S ABC
bằng
A.
3
.
a
B.
3
.
4
a
C.
3
3
.
4
a
D.
3
3 .
a
Lời giải:
Diện tích đáy
2
2
2 3
3
4
a
B a
Chiều cao
3.
h SA a
Thể tích
2 3
1 1
3. 3 .
3 3
V Bh a a a
Chọn đáp án A
Câu 21. Diện tích hình phẳng giới hạn bởi đồ thị của hàm số
ln ,
y x
trục Ox và đường thẳng
3
x e
bằng
A.
3
3 1.
e
B.
3
4 1.
e
C.
3
2 1.
e
D.
3
2 1.
e
Lời giải:
Phương trình hoành độ giao điểm:
0
ln 0 1.
x x e
Nên diện tích hình phẳng
3 3
3
3 3 3 3
1
1 1
ln ln ln 1 2 1
e e
e
S xdx x x xdx e e e e
Chọn đáp án C
Câu 22. Nếu đặt
5
x
t
thì bất phương trình
2 2
5 3.5 2021 0
x x
trở thành
A.
2
3 2021 0.
t t
B.
2
6 2021 0.
t t
C.
2
9 2021 0.
t t
D.
2
75 2021 0.
t t
Lời giải:
Ta có:
2 2
5 3.5 2021 0
x x
2 2
5 3.5 .5 2021 0
x x
Đặt
5
x
t
ta được:
2
75 2021 0.
t t
Chọn đáp án D
Câu 23. Gọi
1
và
2
z
là hai nghiệm phức của phương trình
2
2 3 3 0
z z
. Giá trị của
2 2
1 2
z z
bằng
A.
9
.
4
B.
9.
C.
4.
D.
9
.
4
Lời giải:
Ta có :
1
2
2
3 21
4 4
2 3 3 0
3 21
4 4
z i
z z
z i
; Vậy
2 2
1 2
9
4
z z
Chọn đáp án A
Câu 24. Cho hàm số
( )
y f x
có đạo hàm là
' 2 3
( ) ( 1) ( 2)
f x x x x
. Khẳng định nào sau đây sai?
A. Hàm số có hai điểm cực trị. B. Hàm số đạt cực tiểu tại
0
x
.
C. Hàm số đạt cực đại tại
2
x
. D. Hàm số đạt cực đại tại
1
x
.
Lời giải:
Ta có :
' 2 3
2
0
0( ) 0 ( 1) ( )
1
2
f x
x
x x
x
x x
Chọn đáp án D
Câu 25. Trong không gian Oxyz, phương trình mặt phẳng đi qua điểm
1;2;3
A và vuông góc với đường
thẳng
1 1 2
:
2 1 3
x y z
d
là
A.
2 3 9 0.
x y z
B.
2 3 9 0.
x y z
C.
2 3 9 0.
x y z
D.
2 3 9 0.
x y z
Lời giải:
Mặt phẳng đi qua A vuông góc với đường thẳng d nên vectơ chỉ phương
2; 1;3
d
u
cũng là
một vectơ pháp tuyến của mặt phẳng.
Vậy phương trình mặt phẳng
2 1 2 3 3 0 2 3 9 0.
x y z x y z
Chọn đáp án A
Câu 26. Cho hàm số
y f x
xác định trên
và hàm số
'
y f x
có bảng xét dấu như sau:
Số điểm cực trị của hàm số
2
3
y f x x
là
A.
7.
B.
2.
C.
3.
D.
5.
Lời giải:
2
3
y f x x
' ' 2
'
' 2
2 3 3
3
2
0
3 0
y x f x x
x
y
f x x
Dựa vào bảng biến thiên ta thấy
2
' 2 2
2
1 2.
3 2
3 13 3 13
3 0 3 1 .
2 2
3 3
3 21 3 21
.
2 2
x x
x x
f x x x x k x x
x x
x x
Mà
3 13 3 13
,
2 2
x x
là nghiệm kép còn các nghiệm còn lại là nghiệm đơn nên hàm
số
2
3
y f x x
có 5 cực trị.
Chọn đáp án D
Câu 27. Cho hàm số
2
y f x ax bx c
có đồ thị như sau:
Số nghiệm của phương trình
–1 0
f x
là
A.
3.
B.
2.
C.
0.
D.
1.
Lời giải:
Ta có :
1
–1 0f x f x
Đường thẳng
1
y
cắt đồ thị tại
2
điểm phân biệt, suy ra số nghiệm của phương trình
–1 0
f x
là
2.
Chọn đáp án B
Câu 28. Giá trị lớn nhất của hàm số
2
x
f x x e
trên đoạn
1;1
là
A.
0.
B.
1
.
e
C.
.
e
D.
2 .
e
Lời giải:
Ta có:
2 2
( ) 2
x x x
f x x e f x xe x e
Cho
2
( ) 0 2 0
x x
f x xe x e
2
0 1;1
0
2 1;1
2 0
x
x
e
x
x x
Tính
1
( 1) ; (0) 0; (1)
f f f e
e
Vậy
[ 1;1]
Max ( )
f x e
Chọn đáp án C
Câu 29. Trong không gian
,
Oxyz
cho mặt cầu
2 2 2
( ):( 2) ( 4) ( 1) 9.
S x y z
Tâm
I
và bán kính
R
của
( )
S
là
A.
(2; 4;1)
I
và
9.
R
B.
( 2;4; 1)
I
và
9.
R
C.
(2; 4;1)
I
và
3.
R
D.
( 2;4; 1)
I
và
3.
R
Lời giải:
Áp dụng lý thuyết : Phương trình mặt cầu dạng
2 2 2 2
( ) ( ) ( )
x a y b z c R
thì tâm
( ; ; )
I a b c
và bán kính
R
.
Ta có : Tâm
(2; 4;1)
I
và bán kính
9 3.
R
Chọn đáp án C
Câu 30. Số giao điểm của đồ thị hai hàm số
4 2
4 2
y x x
và
2
1
y x
là
A.
2.
B.
3.
C.
1.
D.
4.
Lời giải:
Phương trình hoành độ giao điểm:
2
4 2 2 4 2
2
3 21 3 21
2 2
4 2 1 3 3 0
3 21
0 ( )
2
x x
x x x x x
x VN
Vậy phương trình có 2 nghiệm nên có 2 giao điểm
Chọn đáp án A
Câu 31. Cho hình chóp .
S ABC
có tam giác
ABC
vuông tại
B
có
3 , ,
AB a BC a SA
vuông góc
với mặt phẳng
( )
ABC
và
2 .
SA a
Góc giữa đường thẳng
SC
và mặt phẳng
( )
ABC
bằng
A.
90 .
B.
45 .
C.
30 .
D.
60 .
Lời giải:
Ta có
AC
là hình chiếu của
SC
lên
( )
ABC
Suy ra góc giữa đường thẳng
SC
và mặt phẳng
( )
ABC
bằng
SCA
Ta có
2
2 2 2
3 2
AC AB BC a a a SA
SAC
là tam giác vuông cân
Vậy
45
SCA
.
Chọn đáp án B
Câu 32. Trong không gian
,
Oxyz
phương trình đường thẳng đi qua điểm
(1;2;0)
A
và vuông góc với
mặt phẳng
( ) :2 3 5 0
P x y z
là
A.
1 2
2 .
3
x t
y t
z t
B.
3 2
3 .
3 3
x t
y t
z t
C.
1 2
2 .
3
x t
y t
z t
D.
3 2
3 .
3 3
x t
y t
z t
Lời giải:
Gọi
d
là đường thẳng cần tìm.
d
có vectơ chỉ phương là
(2;1; 3)
u
Phương trình đường thẳng
d
đi qua điểm
(1;2;0)
A
là
3 2
3 .
3 3
x t
y t
z t
Chọn đáp án B
Câu 33. Nếu đặt
u x
và
2
1
d d
sin
v x
x
thì
3
2
6
d
sin
x
x
x
bằng
A.
3
3
6
6
cot cot d
x x x x
. B.
3
3
6
6
cot cot d
x x x x
.
C.
3
3
6
6
cot cot d
x x x x
. D.
3
3
6
6
cot cot d
x x x x
.
Lời giải:
Ta có
2
d d
1
cot
d d
sin
u x
u x
v x
v x
x
Áp dụng công thức tích phân từng phần, ta được
3
3
6
6
cot cot d
I x x x x
Chọn đáp án A
Câu 34. Tiệm cận đứng của đồ thị hàm số
1
2 4
x
y
x
là đường thẳng
A.
1.
x
B.
2.
x
C.
2.
x
D.
1
.
2
x
Lời giải:
Tiệm cận đứng của đồ thị hàm số
1
2 4
x
y
x
là đường thẳng
2
x
.
Chọn đáp án B
Câu 35. Cho hai số phức
1
2
z i
và
2
1 3
z i
. Phần thực của số phức
1 2
z z
bằng
A.
4.
B.
2.
C.
1.
D.
3.
Lời giải:
1 2
3 4
z z i
Phần thực:
3.
a
Chọn đáp án D
Câu 36. Cho hình chóp
.
S ABC
có tam giác
ABC
vuông cân tại B,
,
BA BC a SA
vuông góc với mặt
phẳng đáy và góc giữa mặt phẳng
SBC
với mặt phẳng
ABC
bằng
0
60
. Gọi
I
là tâm của
đường tròn ngoại tiếp tam giác
SBC
. Khoảng cách giữa hai đường thẳng
AI
và
BC
bằng
A.
6
.
2
a
B.
3
.
4
a
C.
2
.
3
a
D.
3
.
2
a
Lời giải:
0
( ),( ) 60
SBC ABC SBA
0
.tan 60 3
SA a a
3
.
1 3
.
3 6
S ABC ABC
a
V S SA
Tam giác
SBC
vuông tại B nên I là trung điểm của SC.
Gọi J là trung điểm của SB. Khi đó:
//IJ BC//(AIJ) d , ,( )
( ,( )) ( ,( ))
BC BC AI d BC AIJ
d B AIJ d S AIJ
Có:
3
.
. .
.
1 1 3
. .
4 4 24
S AIJ
S AIJ S ABC
S ABC
V a
V V
V
Tam giác AIJ vuông tại J có:
2
; .
2 4
AIJ
a a
AJ a IJ S
3 3
.
3 1 3
. . ,( )
24 3 24
3
,( ) .
2
S AIJ AIJ
a a
V S d S AIJ
d S AIJ a
Chọn đáp án D
Câu 37. Cho hình nón có chiều cao
20
h
và bán kính đáy
25.
r
Mặt phẳng
P
đi qua đỉnh của
hình nón và cách tâm của mặt đáy một khoảng bằng
12.
Thiết diện của hình nón cắt bởi mặt
phẳng
P
có diện tích bằng
A.
200.
B.
500.
C.
400.
D.
300.
Lời giải:
Thiết diện cần tìm là tam giác
,
SAB
ta có:
1
.
2
SAB
S SI AB
2 2
2 2 2 2 2
1 1 1 1 1
15 25
12 20
OI SI SO OI
OI OH SO
2 2
2 2. 40
AB AI AO IO
Vậy
1
. 500
2
SAB
S SI AB
Chọn đáp án B
Câu 38. Trong không gian
,
Oxyz
cho bốn điểm
0;2 ;1 , 3; 1;1 , 2;4;2
A a a B a C và
2; ; 3 .
D a a
Gọi
S
là tập hợp tất cả giá trị của
a
sao cho bốn điểm
, , ,
A B C D
đồng
phẳng. Tập hợp
S
là tập con của tập hợp nào sau đây?
A.
3;6 .
B.
5;8 .
C.
6;2 .
D.
7; 2 .
Lời giải:
Ta có:
, , ,
A B C D
đồng phẳng khi:
; . 0
AB AC AD
2 2
2 2
2
3; 3; ; 2;2 ;1
; 4 3; 6 3; 7
2; 2; 4
; . 0 8 6 2 12 6 4 28 0
2 10
2 8 12 0
2 10
AB a a a AC a a
AB AC a a a a a
AD
AB AC AD a a a a a
a
a a
a
Chọn đáp án C
Câu 39. Cho hàm số
3 2 2
1
( 1) (3 2 ) 1,
3
y x m x m m x
với
m
là tham số thực. Gọi
[ ; ]
a b
là tập hợp
tất cả các giá trị của
m
để hàm số đã cho đồng biến trên khoảng
(4; ).

Giá trị của biểu thức
3
a b
bằng
A.
2.
B.
3.
C.
2.
D.
3.
Lời giải:
Tập xác định:
.
D
2 2
2( 1) 3 2
y x m x m m
2 2
0 2( 1) 3 2 0
3 2
x m
y x m x m m
x m
TH1:
1
3 2
2
m m m
Hàm số đã cho đồng biến trên mỗi khoảng
( ; )
m

và
(3 2; )
m

Do đó, để hàm số đã cho đồng biến trên khoảng
(4; )

thì
2
3 2 4
3
m m
1 2
2 3
m
thỏa đề bài (1)
TH2:
1
3 2
2
m m m
Hàm số đã cho đồng biến trên
nên đồng biến trên khoảng
(4; ).

1
2
m
thỏa đề bài (2)
TH3:
1
3 2
2
m m m
Hàm số đã cho đồng biến trên mỗi khoảng
( ;3 2)
m

và
( ; )
m

Do đó, để hàm số đã cho đồng biến trên khoảng
(4; )

thì
4 4
m m
1
4
2
m
thỏa đề bài (3)
Từ (1), (2) và (3)
2 2 2
4 4; 4, 3 2.
3 3 3
m m a b a b
Chọn đáp án C
Câu 40. Anh Tâm vay ngân hàng 50 triệu đồng mỗi tháng trả góp cho ngân hang 3 triệu đồng và phải
chịu lãi suất chưa trả là
0,7% /
tháng. Hỏi sau ít nhất bao nhiêu tháng thì anh Tâm trả hết tiền
nợ ngân hàng?
A.
20
tháng. B.
18
tháng. C.
17
tháng. D.
19
tháng.
Lời giải:
Gọi
A
là số tiền phải trả hàng tháng,
N
là số tiền ban đầu,
r
là lãi suất,
n
là số tháng
Sau 1 tháng thì số tiền người đó còn nợ lại là
(1 )
N r A
Sau 2 tháng, số tiền còn nợ là
2 2
1 1 . 1 1 1
A
N r A N r A r A N r r
r
Sau
n
tháng số tiền nợ là
1 (1 ) 1
n
n
A
N r r
r
Để trả hết nợ, thì sau
n
tháng số tiền nợ phải bằng
1
0 log 17,784
r
A
n
Nr A
tháng
Chọn đáp án B
Câu 41. Cho hàm số
, ,0 và
bx c
y a
x a
a b c
có đồ thị như sau:
Khẳng định nào sau đây là đúng?
A.
0, 0, 0.
a b c
B.
0, 0, 0.
a b c
C.
0, 0, 0.
a b c
D.
0, 0, 0.
a b c
Lời giải:
Dựa vào đồ thị ta thấy:
TCĐ:
0
x a a
TCN:
0
y b b
Giao với Ox tại
;0 0 0
c c
c
b b
Chọn đáp án B
Câu 42. Cho hình trụ có thiết diện qua trục là hình vuông cạnh bằng
2 .
Mặt phẳng
( )
P
song song với
trục và cách trục một khoảng bằng
.
2
a
Diện tích thiết diện của hình trụ cắt bởi mặt phẳng
( )
P
là
A.
2
.
a
B.
2
2 3 .
a
C.
2
.
a
D.
2
4 .
a
Lời giải:
Theo đề, hình trụ có chiều cao bằng
2 ,
a
bán kính đáy là
.
a
( ',( )) .
2
a
OI d OO P
Thiết diện của hình trụ cắt bởi mặt phẳng
( )
P
là hình chữ nhật
.
ABCD
Chiều dài
2 .
AD a
Tính chiều rộng
:
AB
2 2
2
2
2 2
2 3.
2
AB IA OA OI
a
a a
.
Diện tích hình chữ nhật
2
2 . 3 2 3 .
ABCD a a a
Chọn đáp án B
Câu 43. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng
đáy và
7
SA a
. Khoảng cách giữa hai đường thẳng
BD
và
SC
bằng
A.
14
.
3
a
B.
14
.
6
a
C.
14 .
a
D.
14
.
12
a
Lời giải:
Gọi
.
O AC BD
Trong
SAC
, kẻ
.
OH SC H SC
Ta có:
, .
,
OH SC
d BD SC OH
OH BD BD SAC OH SAC
2 , 3 .
AC a SC a
. 14
.
6
SA SC SAOC
SAC OHC OH a
OH OC SC
Chọn đáp án B
Câu 44. Cho hàm số
f x
có đạo hàm liên tục trên đoạn
1;2
, thỏa mãn
1
1
2
f
và
2
3 2
2 , 1;2
f x xf x x x f x x
. Giá trị của
2
1
xf x dx
bằng
A.
ln3
.
B.
3
ln
2
. C.
4
ln
3
. D.
3
ln
4
.
Lời giải:
O
B
C
A
D
S
H
Ta có:
2
3 2
2
1
2 2 1 2 1
xf x
f x xf x x x f x x x
xf x
xf x
2
1
x x C
xf x
. Từ
1
1
2
f suy ra 0C . Hay
2
1
xf x
x x
Khi đó:
2 2 2
2
1 1 1
1 1 1 3
d d d ln
1 4
xf x x x x
x x x x
Chọn đáp án D
Câu 45. Cho mặt cầu
S
tâm O và các điểm , ,A B C nằm trên mặt cầu
S
sao cho
3, 4, 5AB AC BC
và khoảng cách từ
O
đến mặt phẳng
ABC bằng
1.
Thể tích của khối
cầu
S
bằng
A.
39 39
.
6
B.
20 5
.
3
C.
4 17
.
3
D.
29 29
.
6
Lời giải:
Tam giác ABC vuông tại .A Gọi D là trung điểm cạnh huyền .BC
2 2
5 29
, 1, .
2 2
DC OD R OC OD DC
Thể tích khối cầu:
3
4 29 29 29
.
3 2 6
V
Chọn đáp án D
Câu 46. Tất cả các giá trị thực của tham số m sao cho phương trình
1
4 .2 3 2 0
x x
m m
có hai
nghiệm phân biệt là
A.
2;3 .m
B.
3
1; .
2
m
C.
;2 .m
D.
3;2 .m
Lời giải:
Đặt
2 , 0
x
t t
Ta có PT
2
2 3 2 0
t mt m
(1)
Phương trình có 2 nghiệm phân biệt thì PT (1) có 2 nghiệm dương phân biệt
2
3
1
0 2 3 0
3 3
0 3 2 0 1
2 2
0 2 0
0
m
m
m m
P m m m
S m
m
Chọn đáp án B
Câu 47. Cho các số thực
,
x y
thỏa mãn
1, 1
x y
và
3
log ,
x
xy m
với
m
là tham số thực. Giá trị
của
m
sao cho
2
log 16log
x y
P y x
đạt giá trị nhỏ nhất thuộc khoảng nào sau đây?
A.
(0;2).
B.
(2;3).
C.
( 2;0).
D.
(3;4).
Lời giải:
3
log log 3 log 3 1
x x x
xy m xy m y m
Ta có
log 0
x
y
2 2 2
2
3
16 8 8
log 16log log log
log log log
8 8
3. log . . 12
log log
x y x x
x x x
x
x x
P y x y y
y y y
y
y y
P
đạt GTNN khi
2 3
8
log log 8 log 2 3 1 2 1
log
x x x
x
y y y m m
y
Chọn đáp án A
Câu 48. Cho hàm số bậc ba
y f x
có đồ thị như sau:
Số nghiệm của phương trình
2
2 2
1 2 1 3 0
f x f x
là
A.
4
.
B.
5
. C.
2
. D.
3
.
Lời giải:
Đặt
2
1
t x
, điều kiện
1
t
phương trình đã cho trở thành
2
1
2 3 0
3
f t
f t f t
f t
Xét
1
f t
. Dựa vào đồ thị ta có
1
1
2
t l
f t
t
Suy ra
2
1 2 1
x x
Xét
3
f t
. Dựa vào đồ thị ta có
1
0
3
2
t l
f t
t t
Từ đó:
2
1
1 2
x t
suy ra có 2 nghiệm
1
1
x t
Vậy phương trình đã cho có 4 nghiệm
Chọn đáp án A
Câu 49. Cho số phức
z
thỏa mãn điều kiện
1 2
z z i
là số thực. Giá trị nhỏ nhất của
z
bằng
A.
4 5
.
5
B.
5
.
5
C.
2 5
.
5
D.
3 5
.
5
Lời giải:
Gọi
,
z x yi x y z x yi
Ta có
2 2
1 2 1 2 2 2 2
z z i x yi x y i x x y y x y i
là số thực
Suy ra
2 2 0.
x y
Do đó, tập hợp các điểm biểu diễn số phức
z
là đường thẳng
: 2 2 0
d x y
.
Vậy
min
2 2
2
2 5
, .
5
2 1
z d O d
Câu 50. Cho hình lăng trụ
. ' ' ',
ABC A B C
gọi
,
M N
lần lượt là trung điểm của
'
BB
và
'.
CC
Mặt phẳng
'
A MN
chia khối lăng trụ đã cho thành hai khối đa diện. Gọi
1
V
là thể tích của khối đa diện
chứa đỉnh
B
và
2
V
là thể tích khối đa diện còn lại. Tỉ số
1
2
V
V
bằng
A.
2.
B.
3.
C.
5
.
2
D.
13
.
3
Lời giải:
Ta có:
2 '. ' ' '. ' ' ' ' '. ' ' '.
1 1 2 1
. .
2 2 3 3
A B C MN A B C CB A B C ABC A B C ABC
V V V V V
Khi đó:
1 ' ' '.
2
3
A B C ABC
V V
Vậy:
1
2
2.
V
V
Chọn đáp án A
GIẢI CHI TIẾT
ĐỀ THI THỬ MÔN TOÁN LỚP 12 SỞ CẦN THƠ
NĂM HỌC 2020-2021
BẢNG ĐÁP ÁN
1.B 2.A 3.A 4.B 5.A 6.C 7.B 8.B 9.C 10.B
11.C
12.C
13.C
14.B
15.A
16.C
17.B
18.A
19.C
20.C
21.A 22.C 23.A 24.A 25.C 26.B 27.B 28.C 29.A 30.D
31.C 32.D 33.A 34.B 35.C 36.D 37.B 38.A 39.B 40.C
41.A
42.D
43.C
44.A
45.B
46.A
47.B
48.D
49.B
50.A
Câu 1. Cho
F x
là một nguyên hàm của hàm số
f x
trên đoạn
; .
a b
Khẳng định nào sau đây
đúng?
A.
.
b
a
f x dx f a f b
B.
.
b
a
f x dx F b F a
C.
.
b
a
f x dx F a F b
D.
.
b
a
f x dx f b f a
Lời giải:
Áp dụng định nghĩa nguyên hàm
Chọn đáp án B
Câu 2. Một hình nón có độ dài đường sinh
3
l
và bán kính đáy
2.
r
Diện tích xung quanh của hình
nón đã cho bằng
A.
6 .
B.
12 .
C.
5 .
D.
8 .
Lời giải:
.2.3 6 .
xq
S rl
Chọn đáp án A
Câu 3. Với
a
là số thực dương tùy ý,
5
2
log
a
bằng
A.
2
5log .
a
B.
2
5 log .
a
C.
2
1
log .
5
a
D.
2
1
log .
5
a
Lời giải:
5
2 2
log 5log
a a
Chọn đáp án A
Câu 4. Thể tích của khối lăng trụ có diện tích đáy bằng 4 và chiều cao bằng 3 là
A.
36.
B.
12.
C.
6.
D.
4.
Lời giải:
. 4.3 12.
V B h
Chọn đáp án B
Câu 5. Tập xác định của hàm số
log 1
y x
là
A.
;1 . B.
0; . C.
1; . D.
;0 .
Lời giải:
ĐKXĐ của hàm số
log 1y x là 1 0 1.x x
Chọn đáp án A
Câu 6. Có bao nhiêu cách chọn một học sinh từ một nhóm gồm 6 học sinh nam và 5 học sinh nữ?
A.
6.
B.
30.
C.
11.
D.
5.
Lời giải:
Tổng số học sinh là: 6 5 11.
Số cách chọn một học sinh từ 11 học sinh là
1
11
11.C
Chọn đáp án C
Câu 7. Diện tích của mặt cầu có bán kính bằng
4
là
A. 16 .
B. 64 .
C.
256
.
3
D.
16
.
3
Lời giải:
Ta có công thức tính diện tích là:
2 2
4 4 4 64 .S R
Chọn đáp án B
Câu 8. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên dưới?
A.
3 2
3 1.y x x
B.
3 2
3 1.y x x
C.
4 2
2 1.y x x
D.
4 2
2 1.y x x
Lời giải:
Dựa vào đồ thị hàm số đã cho loại phương án C, D.
Ta thấy
x 
thì
y
nên loại A.
Chọn đáp án B
Câu 9. Cho số phức
3 4 .z i
Môđun của z bằng
A. 1. B. 7. C. 5. D. 7.
Lời giải:
Ta có số phức
2 2
z a bi z a b
Áp dụng công thức ta có
2
2
3 4 5.z
Chọn đáp án C
Câu 10. Cho hai hàm số
( ), ( )
f x g x
liên tục trên
và
k
là một số thực khác
0.
Khẳng định nào sau
đây sai?
A.
( ) ( ) .
kf x dx k f x dx
B.
( ) ( ) ( ) ( ) .
f x g x dx f x dx f x dx
C.
( ) ( ) ( ) ( ) .
f x g x dx f x dx f x dx
D.
( ) ( ) ( ) ( ) .
f x g x dx f x dx f x dx
Lời giải:
Theo tính chất của nguyên hàm.
Chọn đáp án B
Câu 11. Tập nghiệm của bất phương trình
log(2 3) log5
x
là
A.
8; .

B.
5; .

C.
4; .

D.
;3 .

Lời giải:
Điều kiện
3
2
x
log(2 3) log5
2 3 5
4
x
x
x
Chọn đáp án C
Câu 12. Trong không gian
Oxyz
, mặt cầu tâm
( 1;0;2)
I
, bán kính
3
R
có phương trình là
A.
2
2 2
1 ( 2) 3.
x y z
B.
2
2 2
1 ( 2) 9.
x y z
C.
2
2 2
1 ( 2) 9.
x y z
D.
2
2 2
1 ( 2) 3.
x y z
Lời giải:
Mặt cầu tâm
( 1;0;2)
I
, bán kính
3
R
có phương trình là
2
2 2
1 ( 2) 9.
x y z
Chọn đáp án C
Câu 13. Nghiệm của phương trình
2
2 8
x
là
A.
2.
B.
1.
C.
3
.
2
D.
1
.
2
Lời giải:
2 2 3
3
2 8 2 2 2 3 .
2
x x
x x
Chọn đáp án C
Câu 14. Thể tích của khối chóp có diện tích đáy
B
và chiều cao
h
là
A.
.
Bh
B.
1
.
3
Bh
C.
3 .
Bh
D.
1
.
2
Bh
Lời giải:
Thể tích của khối chóp
1
.
3
V Bh
Chọn đáp án B
Câu 15. Tiệm cận đứng của đồ thị hàm số
2 3
2
x
y
x
là đường thẳng
A.
2.
x
B.
3
.
2
x
C.
x
D.
3
.
2
x
Lời giải:
2
lim 2
x
y x

là TCĐ
Chọn đáp án A
Câu 16. Cho hai số phức
1
2 3
z i
và
2.
3 .
z i
Số phức
1 2
z z
bằng
A.
5 2 .
i
B.
5 4 .
i
C.
5 2 .
i
D.
5 4 .
i
Lời giải:
Ta có:
1 2
2 3 3 5 2
z z i i i
Chọn đáp án C
Câu 17. Cho hàm số
( )
y f x
có đồ thị như sau:
Điểm cực tiểu của hàm số đã cho là
A.
x
B.
1.
x
C.
1.
x
D.
2.
x
Lời giải:
Dựa vào đồ thị ta có điểm cực tiểu của hàm số là
1.
x
Chọn đáp án B
Câu 18. Cho cấp số cộng
( )
n
u
có
1
1
u
và
3
7.
u
Số hạng
2
u
bằng
A.
4.
B.
8.
C.
6.
D.
10.
Lời giải:
Ta có
1 3
2
1 7
4.
2 2
u u
u
Chọn đáp án A
Câu 19. Cho hàm số
f x
có đồ thị như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
2; .

B.
;0 .
 C.
0;2 .
D.
2;2 .
Lời giải:
Dựa vào đồ thị ta thấy hàm số đã cho nghịch biến trên khoảng
0;2 .
Chọn đáp án C
Câu 20. Trong không gian
,
Oxyz
khoảng cách từ điểm
1;2; 1
M
đến mặt phẳng
:2 2 13 0
P x y z
bằng
A.
11
.
3
B.
15.
C.
5.
D.
3.
Lời giải:
Ta có
2 2 2
2 1 2 2 1 13
, 5
2 ( 1) 2
d M P
Chọn đáp án C
Câu 21. Trong không gian
O
xyz
, cho hình bình hành
ABCD
với
1;0;2 , 2;1; 3 , 1; 1;0 .
A B C
Tọa độ điểm
D
là
A.
2; 2;5 .
B.
0;2; 1 .
C.
2;2;5 .
D.
2;2; 5 .
Lời giải:
Gọi
; ;
D x y z
là điểm cần tìm. Ta có
3;1; 5 .
AB
1 ; 1 :
DC x y z
ABCD
là hình bình hành
.
AB DC

3 1 2
1 1 2.
5 5
x x
y y
z z
Chọn đáp án A
Câu 22. Cho tam giác
ABC
vuông tại
A
có
13
BC
và
12
AB
. Khi quay tam giác
ABC
xung
quanh cạnh
AB
ta được khối tròn xoay có thể tích bằng
A.
60 .
B.
300
C.
100 .
. D.
325 .
Lời giải:
Khối tròn xoay thu được là khối nón có
12, 13
h l
Suy ra
169 144 25 5.
r
Thể tích
2
1
3
V r h
=
100 .
Chọn đáp án C
Câu 23. Cho hàm số
( )
y f x
có bảng biến thiên như sau:
Phương trình
3 ( ) 4 0
f x
có bao nhiêu nghiệm?
A. 3. B. 1. C. 2. D. 6.
Lời giải:
4
3 ( ) 4 0 ( )
3
f x f x
; số nghiệm của phương trình là giao điểm của đồ thị và đường
thẳng
4
( )
3
f x
;
4
0 4
3
. Nên phương trình
3 ( ) 4 0
f x
có 3 nghiệm.
Chọn đáp án A
Câu 24. Cho hàm số
4 2
1
( ) ,( , )
4
f x x bx c b c
có đồ thị như sau:
Khẳng định nào sau đây đúng?
A.
0; 0
b c
. B.
0; 0
b c
. C.
0; 0
b c
. D.
0; 0
b c
.
Lời giải:
Ta có đồ thị cắt trục
Oy
tại điểm có tung độ dương nên
0
c
. Mặt khác
3
'( ) 2
f x x bx
3
2
0
'( ) 0 2 0
2 0
x
f x x bx
x b
; đồ thị có 3 cực trị nên
0
b
.
Chọn đáp án A
Câu 25. Với x là số thực dương tùy ý,
1
3
6
.x x
bằng
A.
2
9
x
. B.
1
8
x
. C.
1
2
x
. D.
2
x
.
Lời giải:
Ta có
1 1 1 1 1 1
3
6 6 3 6 3
2
. . .x x x x x x
Chọn đáp án C
Câu 26. Cho hình chóp .S ABC có đáy ABC là tam giác vuông tại B , ,BC 2,SAAB a a vuông
góc với mặt phẳng
ABC
và .SA a Góc giữa đường thẳng SC và mặt phẳng
ABC
bằng
A.
45 .
B.
30 .
C.
60 .
D.
90 .
Lời giải:
Tam giác ABC vuông tại B , ,BC 2 3.AB a a AC a
Góc giữa đường thẳng SC và mặt phẳng
ABC là
.SCA
Tam giác SCA vuông tại A
Suy ra
3
tan 30 .
3
SA
SCA SCA
AC
Chọn đáp án B
Câu 27. Tập nghiệm của bất phương trình
2
6
7 49
x
là
A. [ .6; 6]
B. [ 2;2]. C. ( ;2].
D. [2; ).
Lời giải:
Ta có:
2 2
6 6 2
2
7 49 7 7
4 0
2 2
x x
x
x
Chọn đáp án B
Câu 28. Cho hình phẳng giới hạn bởi đồ thị hàm số
2
( ) 2f x x x và trục hoành. Thể tích khối tròn
xoay được sinh ra khi quay hình phẳng đã cho quanh trục hoành bằng
A.
4
.
3
B.
15
.
16
C.
16
.
15
D.
3
.
4
Lời giải:
Ta có:
2
2 0 0; 2.
x x x x
2
2
2
0
16
2
15
V x x dx
Chọn đáp án C
Câu 29. Khẳng định nào sau đây đúng?
A.
1
1 1
ln d ln d .
e e
e
x x x x x
B.
1
1 1
ln d ln d .
e e
e
x x x x x x
C.
1
1 1
1
ln d ln d .
e e
e
x x x x x
x
D.
2
1
1 1
ln d ln d .
e e
e
x x x x x x
Lời giải:
Áp dụng công thức tích phân từng phần :
d d .
b b
b
a
a a
u v uv v u
Ta có:
1
ln d
e
I x x
Đặt
1
ln d d
d d
u x u x
x
v x v x
Vậy
1
1 1
ln d ln d .
e e
e
I x x x x x
Chọn đáp án A
Câu 30. Gọi
,
M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
2
( ) 2 3 4
3
x
f x x x
trên đoạn
[ 4;0]
. Giá trị của
m M
bằng
A.
4
.
3
B.
4
.
3
C.
4.
D.
28
.
3
Lời giải:
Ta có:
3
2 2
( ) 2 3 4 '( ) 4 3
3
x
f x x x f x x x
Cho
3 [ 4;0]
'( ) 0
1 [ 4;0]
x
f x
x
Tính
16 16
( 4) , ( 3) 4, ( 1) , (0) 4
3 3
f f f f
Vậy
[ 4;0]
[ 4;0]
16
Max ( ) 4, Min ( )
3
M f x m f x
16 28
( 4) .
3 3
m M
Chọn đáp án D
Câu 31. Số giao điểm của đồ thị các hàm số
3
( ) 2 1
f x x x
và
( ) 1
g x x
là
A.
3.
B.
2.
C.
1.
D.
0.
Lời giải:
Phương trình hoành độ giao điểm của hai đồ thị là
3 3
2 1 1 0 0 1
x x x x x x y
Đồ thi hai hàm số cắt nhau tại một điểm.
Chọn đáp án C
Câu 32. Số phức liên hợp của
14 2
1
i
z
i
là
A.
16 12 .
z i
B.
6 8 .
z i
C.
16 12 .
z i
D.
6 8 .
z i
Lời giải:
Ta có
14 2
6 8 6 8
1
i
z i z i
i
Chọn đáp án D
Câu 33. Gọi
1
,
2
z
là hai nghiệm phức của phương trình
2
2 10 0
z z
. Giá trị của
2 2
1 2
z z
bằng
A.
16.
B.
16.
C.
2.
D.
2.
Lời giải:
Phương trình
2
2 10 0
z z
có hai nghiệm phức
1
1 3
z i
và
2
1 3
z i
.
2 2
2 2
1 2
1 3 1 3 8 6 8 6 16
z z i i i i
.
Chọn đáp án A
Câu 34. Trong không gian
Oxyz
, cho ba điểm
2;0;0
A ,
0; 3;0
B ,
0;0;1
C . Phương trình mặt
phẳng
ABC
là
A.
2 0
x y z
. B.
3 2 6 6 0
x y z
.
C.
6 0
x y z
. D.
3 2 6 6 0
x y z
.
Lời giải:
Phương trình mặt phẳng
ABC
có dạng:
1
2 3 1
x y z
3 2 6 6 0
x y z
.
Chọn đáp án B
Câu 35. Trong mặt phẳng
Oxy
, điểm biểu diễn số phức
3
1
i
z
i
có tọa độ là
A.
4; 2 .
B.
2;0 .
C.
2; 1 .
D.
2;4 .
Lời giải:
3
2 .
1
i
z i
i
Suy ra điểm biểu diễn số phức
z
là
2; 1 .
Chọn đáp án C
Câu 36. Cho hình nón đỉnh
S
có đáy là đường tròn tâm
O
và bán kính
R
. Trên đường tròn
O
lấy hai
điểm
,
A B
sao cho tam giác
OAB
vuông. Biết diện tích tam giác
SAB
bằng
2
2
R
. Thể tích
khối nón đã cho bằng
A.
3
14
.
3
R
B.
3
14
.
12
R
C.
3
14
.
2
R
D.
3
14
.
6
R
Lời giải:
2
2 .
2
R
AB R OH
2 2
1
2 . 2 2 .
2
SAB
S R SH AB R SH R
2 2
14
.
2
R
SO SH OH
Thể tích khối nón:
3
2
1 14 14
. .
3 2 6
n
R R
V R
Chọn đáp án D
Câu 37. Cho hàm số
2
2
3 1 khi 1
.
khi 1
2
x x
f x
x
x x
Giá trị của
2
1
0
ln 1
1
e
f x
dx
x
bằng
A.
17
.
3
B.
17
.
6
C.
14
.
3
D.
7
.
3
Lời giải:
Ta có:
2 2
1 1
2 3 1 1 2
x x
lim x x lim x f
Vậy hàm số liên tục tại
1
x
và có đạo hàm tại
1.
x
2
1
0
2
2 1 2
2 2
0 0 1
ln 1
1
1
ln 1
1
0 0; 1 2
17
3 1 2
6
e
f x
I dx
x
t x dt dx
x
x t x e t
I f t dt t dt t t dt
Chọn đáp án B
Câu 38. Cho hàm số bậc bốn
y f x
và có đồ thị
'
f x
như sau:
Số điểm cực trị của hàm số
2
2
g x f x x
là
A.
5.
B.
3.
C.
6.
D.
4.
Lời giải:
Ta có:
2
2
2 2 0 1
1
1( )
0
' 2 2 ' 2 0
0
' 2 0
2
2
1 2
1 2
1 2
1 2
x x
x
x kep
x
g x x f x x
x
f x x x
x
x
x
x
x

Chọn đáp án A
Câu 39. Trong không gian
,
Oxyz
cho điểm
(3;1; 2)
A
và đường thẳng
1 2
: .
1 2 1
x y z
d
Phương
trình tham số của đường thẳng đi qua điểm
,
A
cắt và vuông góc với đường thẳng
d
là
A.
1 2
2 .
0
x t
y t
z
B.
3 2
1 .
2
x t
y t
z
C.
2 3
1 .
3 2
x t
y t
z t
D.
3 3
1 .
2 2
x t
y t
z t
Lời giải:
- Đường thẳng
d
có VTCP là
(1;2; 1).
d
u
- Gọi
là đường thẳng đi qua điểm
,
A
cắt và vuông góc với đường thẳng
d
tại
.
B
- Vì
B d
nên
( 1 ; 2 2 ; ), .
B t t t t
- Vì
,
A d B d
nên
d
có VTCP là
( 4 ; 3 2 ;2 )
u AB t t t
- Vì
d
nên
. 0 1( 4 ) 2( 3 2 ) 1(2 ) 0 t 2
d
u u t t t
( 2;1;0) (2; 1;0).
u
Vậy
3 2
: 1 .
2
x t
y t
z
Chọn đáp án B
Câu 40. Trong không gian
,
Oxyz
đường thẳng đi qua điểm
1;2;2
M , song song với mặt phẳng
: 3 0
P x y z
đồng thời cắt đường thẳng
1 2 3
:
1 1 1
x y z
d
có phương trình là
A.
1
2 .
2
x t
y t
z
B.
1
2 .
2
x t
y
z t
C.
1
2 .
2
x t
y t
z
D.
1
2 .
2
x t
y t
z t
Lời giải:
Gọi
N
là giao điểm cùa đường thẳng
d
và đường thẳng cần tìm
1 ;2 ;3
N t t t
Khi đó
; ;1
MN t t t
là vectơ chỉ phương của đường thẳng cần tìm
Do đường thẳng song song với mặt phẳng
. 0 1 0 1.
P
P MN n t t t t

Vậy
1; 1;0
MN
Chọn đáp án C
Câu 41. Cho hình trụ có bán kính đáy bằng
3 2 .
a
Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng
song song với trụ và cách trục một khoảng bằng
3
a
thì thiết diện thu được là một hình vuông.
Thể tích của khối trụ đã cho bằng
A.
3
108 .
a
B.
3
216 .
a
C.
3
150 .
a
D.
3
54 .
a
Lời giải:
Ta có
2
2
3 2 3 3
2
h
a a a
6
h a
Vậy
2
3
3 2 .6 108
V a a a
Chọn đáp án A
Câu 42. Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
3 4
mx m
y
x m
nghịch biến trên
khoảng
2; ?

A.
2.
B.
4.
C.
5.
D.
3.
Lời giải:
ĐKXĐ:
.
x m
Ta có:
2
2
3 4
'
( )
m m
y
x m
Hàm số
3 4
mx m
y
x m
nghịch biến trên khoảng
2;

khi
' 0, (2, )
(2, )
y x
m

2
3 4 0
1 2
2
0;1;2
m m
m
m
m
Có 3 giá trị nguyên của
m
để hàm số đã cho thỏa ycbt.
Chọn đáp án D
Câu 43. Cho hình lăng trụ
.
ABC A B C
có đáy là tam giác vuông cân tại
, 3
A AB AC a
và
2 .
AA a
Hình chiếu vuông góc của
B
lên mặt đáy là điểm
H
thuộc cạnh
BC
sao cho
2
HC HB
.
Khoảng cách từ điểm
B
đến mặt phẳng
B AC
bằng
A.
2 3
.
3
a
B.
3 3
.
2
a
C.
3 .
a
D.
.
2
a
Lời giải:
Ta có:
,
3
, , .
2
,
d B B AC
CB
d B B AC d H B AC
CH
d H B AC
Trong
ABC
, kẻ
.
HE AC E AC
Ta có
HE AC
AC EHB B AC EHB
B H AC
Trong
B EH
, kẻ
.
HK B E K B E
A
B
C
B'
A'
C'
H
E
K
Khi đó
3 3
, , .
2 2
HK B E
B AC EHB HK B AC
B AC EHB B E
d B B AC d H B AC HK
Ta có
1
2 .
3
BH BC a
2
2
3
EH AB a
.
2 2
6
B E EH B H a
.
. 2 3
. . .
3
EH HB
KH B E EH HB KH a
B E
3 3
, , 3
2 2
d B B AC d H B AC HK a
.
Chọn đáp án C
Câu 44. Chọn ngẫu nhiên ba số khác nhau từ 17 số nguyên dương đầu tiên. Xác suất để chọn được ba số
có tổng là một số chia hết cho ba bằng
A.
23
68
.
B.
27
34
. C.
9
34
. D.
9
17
.
Lời giải:
Xét phép thử: “Chọn ba số khác nhau từ 17 số nguyên dương đầu tiên”.
Khi đó:
3
17
680
n C .
Biến cố A: “chọn được ba số có tổng là một số chia hết cho 3”.
Ta chọn 3 số khác nhau
, ,
a b c
từ 17 số nguyên dương đầu tiên sao cho
a b c
chia hết cho
3. Xét 4 trường hợp sau:
* Trường hợp 1: Cả
, ,
a b c
đều chia hết cho 3, suy ra
, , 3, 6, 9, 12, 15
a b c . Số cách chọn
trong trường hợp này là
3
5
10
C
cách.
* Trường hợp 2: Cả
, ,
a b c
chia cho 3 đều dư 1, suy ra
, , 1, 4, 7, 10, 13, 16
a b c . Số cách
chọn trong trường hợp này là
3
6
20
C
cách.
* Trường hợp 3: Cả ba số
, ,
a b c
chia cho 3 đều dư 2, suy ra
, , 2, 5, 8, 11, 14, 17
a b c . Số
cách chọn trong trường hợp này là
3
6
20
C
cách.
* Trường hợp 4: Trong ba số
, ,
a b c
có 1 số chia hết cho 3, 1 số chia cho 3 dư 1 và 1 số chia
cho 3 dư 2. Số cách chọn trong trường hợp này là
5.6.6 180
cách.
230
n A
23
68
n A
p A
n
Chọn đáp án A
Câu 45. Anh Nam mua một chiếc ô tô trị giá 700 triệu đồng với hình thức trả góp. Anh Nam trả trước
500 triệu đồng và phải chịu lãi suất
0,75%
/tháng đối với số tiền còn nợ. Mỗi tháng, anh Nam
trả một số tiền không đổi vào đúng ngày tính lãi. Hỏi số tiền không đổi mà anh Nam phải trả
mỗi tháng là bao nhiêu, biết rằng sau đúng ba năm thì anh Nam trả hết nợ (làm tròn đến hàng
nghìn)?
A.
5900000
đồng.
B.
6360000
đồng. C.
9137000
đồng. D.
6500000
đồng.
Lời giải:
Áp dụng công thức
36
36
200. 1 0,75% .0,75%
(1 )
6,36
1 1 1 0,75% 1
n
n
N r r
A
r
triệu đồng
Chọn đáp án B
Câu 46. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật với
, 2
AB a AD a
,
SA
vuông góc
với mặt phẳng đáy,
SB
tạo với mặt phẳng đáy một góc
60
. Trên
SA
lấy điểm
M
sao cho
3
3
a
AM . Mặt phẳng
BMC
cắt cạnh
SD
tại
N
. Tỉ số thể tích giữa khối chóp
.
S BCNM
và
.
S ABCD
bằng
A.
5
.
9
B.
4
.
9
C.
5
.
7
D.
4
.
7
Lời giải:
Vì
, / / ,
/ /
BC MBC
AD SAD
MBC SAD MN MN AD N MN SD
BC AD
M MBC SAD
Ta có
, 60
SB ABCD SBA
Xét tam giác vuông
SAB
ta có
tan60 . 3
SA AB a
Và
3 2 3
3
3 3
a a
SM SA AM a
Cách 1:
.
. . . .
.
2 2 4 4 4 1 2
. . . (1)
3 3 9 9 9 2 9
S MNC
S MNC S ADC S ABCD S ABCD
S ADC
V SM SN
V V V V
V SA SO
.
. . . .
.
2 2 2 1 1
. (2)
3 3 3 2 3
S MBC
S MBC S ABC S ABCD S ABCD
S ABC
V
SM
V V V V
V SA
Từ (1) và (2) ta có
. .
. . .
. . .
2 1
5
9 3
9
S ABCD S ABCD
S BCNM S MNC S MBC
S ABCD S ABCD S ABCD
V V
V V V
V V V
.
Cách 2: Áp dụng công thức tính nhanh (chỉ đúng khi đáy là hình bình hành)
.
.
3 3
1 1
1 1
5
2 2
3 3
9
4. . .1.1 4. . .1.1
2 2
S BCNM
S ABCD
SA SD
V
SM SN
SA SD
V
SM SN
.
Chọn đáp án A
Câu 47. Cho các số thực dương
,
x y
thỏa mãn
3 3
2
log 8 2 1.
x
x x y y
y
Giá trị nhỏ nhất của biểu
thức
2
P x y
bằng
A.
1
.
8
B.
1
.
16
C.
1
.
4
D.
1
.
4
Lời giải:
Ta có:
3 3
2
log 8 2 1
x
x x y y
y
3 3
2 2
log (2 ) 2 log (2 ) (1)
x x x y y y
3 2
2
1
( ) log ( ) 3 1 0 ( 1).
ln 2
f t t t t f t t t
t
Suy ra
( )
f t
đồng biến trên
.
(1) 2
x y
2 2
1
4 min
16
P x y y y P
khi
1
8
y
Chọn đáp án B
Câu 48. Có bao nhiêu số nguyên
y
sao cho tồn tại số thực
x
thỏa mãn
2 2 2
4 3
log 3 .log 3 7
y y
x x x x y y
?
A.
8
.
B.
10
. C.
11
. D.
9
.
Lời giải:
Đặt
2
4
2
3
log 3
log 3
y
y
u x x
v x x
2
2
4 3
3 3
u y
v y
x x
x x
4 .3 3
u v y
3
log 4
y v u
3
log 4
v y u
Theo đề bài:
2 2
3
7 log 7
uv y y u y u u y y
2 2
3
.log 4 7 0 *
u uy y y
Điều kiện tồn tại
,
x y
là
*
có nghiệm
u
hay
2 2 2
3 3 3
4 7 log 4 0 1 4log 4 28 .4log 4 0
y y y y y
3
3
28log 4
0 8.7
1 4log 4
y
Vì
y
nên
0;1;...;7;8
y
Vậy có 9 giá trị nguyên của
y
thỏa yêu cầu bài toán
Chọn đáp án D
Câu 49. Cho số phức
1
thỏa mãn
1
3 1
z i
và số phức
2
2
1
z m m i
với
.
m
Giá trị nhỏ
nhất của
1 2
z z
bằng
A.
5 1.
B.
5 1.
C.
1.
D.
2.
Lời giải:
Gọi
1 1
;
M x y
là điểm biểu diễn số phức
1
. Ta có
1 1
3 1 3 1
z i z i
Suy ra tập hợp cấc điểm biểu diễn số phức
1
nằm trên đường tròn
C
có tâm
3;1
I , bán
kính
1.
R
Gọi
2 2
;
N x y
là điểm biểu diễn số phức
2
z
. Suy ra
2
; 1
N m m
Ta có
1
MN IN R IN
.
Suy ra
1 2 min min
min
z z MN IN R
Ta có
2
2
2 4 2
3 1 1 6 9
IN m m m m m
Xét hàm số
4 2
6 9, .
f m m m m m
3
4 2 6, 0 1
f m m m f m m
Bảng biến thiên
Suy ra
min 5
f m
Vậy
1 2 min min
min
5 1.
z z MN IN R
Chọn đáp án B
Câu 50. Cho hàm số
4 3 2
1
f x ax bx cx dx
có bảng biến thiên
'
f x
như sau:
Tất cả các giá trị của tham số
m
sao cho phương trình
3
1
4
m
f x
có nghiệm thuộc khoảng
; 1

là
A.
12.
m
B.
3.
m
C.
3
.
4
m
D.
1.
m
Lời giải:
Ta có:
4 3 2 3 2
1 ' 4 3 2
f x ax bx cx dx f x ax bx cx d
Vì
' 0
f x
có
3 2 3 3 2 3
; ; ;
3 9 3 9
A B
là hai điểm cực trị nên điểm uốn
0;0
O
0
d
Ta lại có:
0
3
" 0
4 2 0
3
b
f
a c
Vì:
3 2 3 4 3 2 3 2 3
'
3 9 9 3 9
f a c
Khi đó ta có hệ phương trình:
1
4 2 0
4
4 3 2 3 2 3
1
9 3 9
2
a c
a
a c
c
3 4 2
1 1
' ; 1
4 2
f x x x f x x x
Xét:
3 3 2
1 ' ' 1 . 3
g x f x g x f x x
2
3
3
3
3
0
0
1 0
' 0 1
1 1
2
1 1
x
x
x
g x x
x
x
x
(loại)
Bảng biến thiên:
Vậy: phương trình có nghiệm khi 3 12.
4
m
m
Chọn đáp án A
| 1/102

Tài liệu khác của Toán

Preview text:

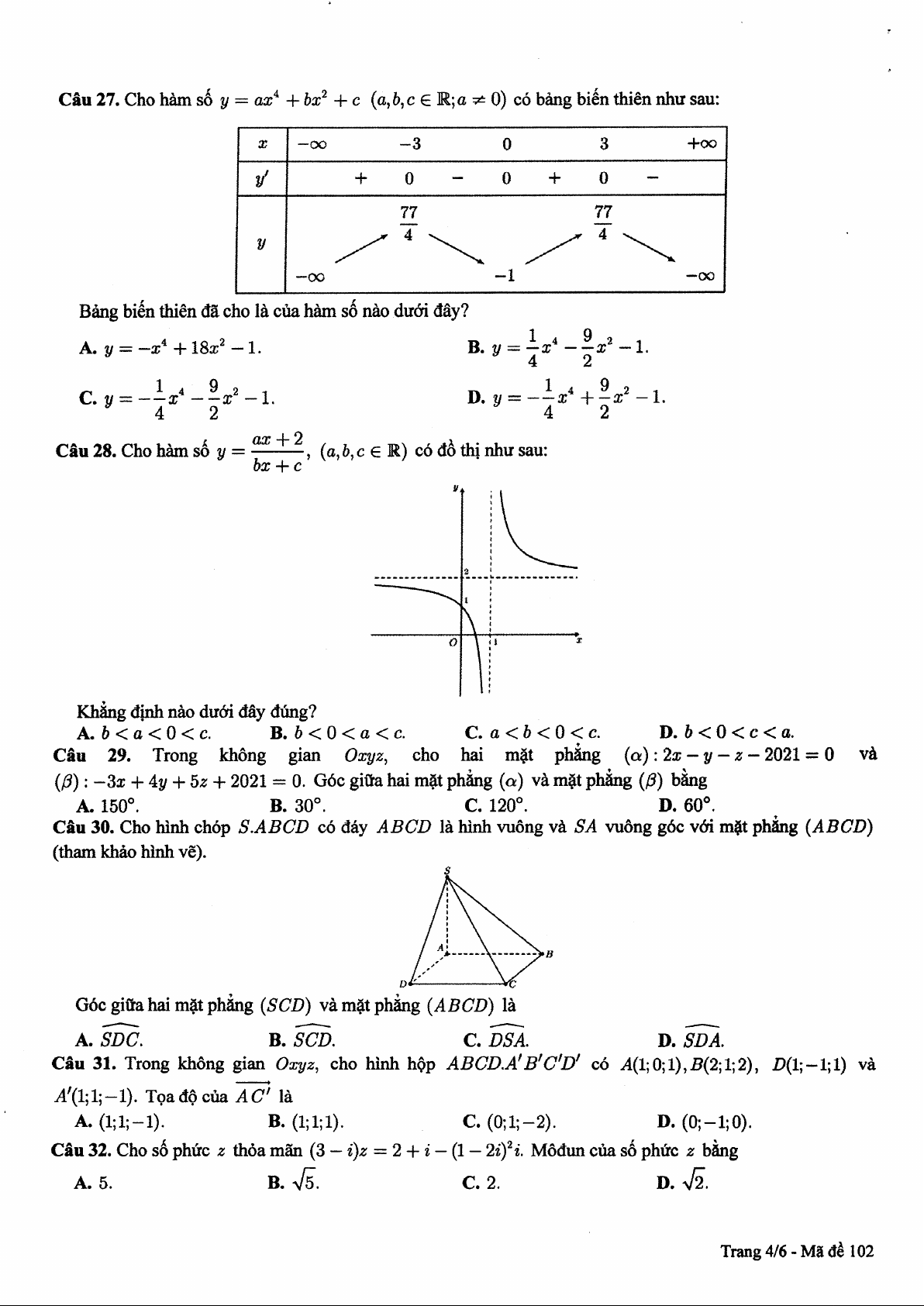
KHẢO SÁT CHẤT LƯỢNG HỌC SINH LỚP 12 NĂM 2021 - MÔN TOÁN ĐÁP ÁN MÃ ĐỀ
Câu 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 1 A B A D D B A A A B A D B C B C A B A C D C A A 2 B D B D A A B C A A D A D D B C B A D A B A A A 3 A B C D D A D C C D D D B A C A B A A D C B B A 4 C A B D B B A D A A C B C B C D A D A C C D B B 5 C B A C C A A D B B B A A A A A C A C C C B B D 6 B C C D D C C C B B C B D D A C B B C A C B C D 7 C C A C A B B D A A B A C C C A B D C A A A A A 8 C B C A A B C B A A A C A D A D C A D C A B B A 9 C A C B D C D A B C C A D A C A A B A A B D B A 10 A A B A B B C A A D D B D A A B C C D C C A D B 11 C D D A A C D D C D D A A C A D B B B A D D C A 12 C B B A C C B D B B B D A D B C A B C B A C A C 13 D B B B C C B D C B B A C C A B C A B D D D D D 14 B A A A C B A C C A B D A B C A C D C A B D A D 15 C B B B D A D D B B B C D B B C B D C A D B D C 16 A D A B C C D C C A A D C C D A B A B C A B B C 17 B D A B C B B C A A A B D A B B B C A A B D C C 18 A D C C B A A C C D A C D C B B A A D C C B D D 19 B D B A A C D A C A B B C A D B A D A D B A D C 20 C A A B A C A A C D C A A D A B A B C D D A D A 21 B A D A C A B A A C A A B D D C C D C D D A A C 22 A A C D D C B A C B B B B C A C D B A D A D D A 23 A D D A A A D A B B A C B A C B D C B A B A B D 24 B A C D D A A A C D D B C A B C D B A C C D B C 25 C D C D A C A D C D B B A D D D C D B D A D B C 26 D A A B D B C C B B D A D A D A B B A B D D C D 27 A D A D B B B D C D A A D A A A C B B B A A A A 28 A C A D C C B C B D C B B C B A C B A C B C C A 29 C B A A C A B A D D D D C A B A A A D D C C B A 30 A D C B A D B B D A B D A C A D B D B D B B A D 31 B A B A B C A A A D D B D D C B B A C C B D C C 32 B D D A B D A D C A A B B A D B C C A A B B C D 33 D B B C A A A C A A D D A C C C B B A B A A B A 34 D B C B B B C C B D B A A D B C B D C A D D C B 35 C D B B D C C A B B B C A A C B A A C A C B D D 36 A A C A D D C B A B D D C D B C B D B C D A A C 37 A C C A B B C C C B B B A D B A C D A A C B C B 38 C B A B C A D C C A B D B D C A C A C A A C A C 39 A A B D C B A D A D B D C C D A C D B D D A D A 40 A B B D B C C A B C A B B C D C A B C B D A D D 41 D B B B B A C D B C D A C A C A A D C D B D A C 42 C A A B B D D D A B A D D C C C D A B C B D C D 43 B B D D B C D C A C D D A C D B D D C C A A D A 44 B A C C D A B A D D D D D D B A A A A C D A D C 45 B B C A D B A B B B A A B D A C A A B D C D C B 46 A C A B B A D B B A D A C D D C C B A D C B A D 47 B A A B A B C A D D A B B B A B A D B A A B B C 48 B D B D A D B C D A D A B A D B C A B C A B A C 49 C D B A C B D D B A A B B C D B B C B D A B C D 50 B D C D A A C D A B A D C B A B A B B D B A B D GIẢI CHI TIẾT
ĐỀ THI THỬ MÔN TOÁN LỚP 12 SỞ CẦN THƠ NĂM HỌC 2020-2021 BẢNG ĐÁP ÁN 1.A 2.B 3.A 4.C 5.C 6.B 7.C 8.C 9.C 10.A 11.C 12.C 13.D 14.B 15.C 16.A 17.B 18.A 19.B 20.C 21.B 22.A 23.A 24.B 25.C 26.D 27.A 28.A 29.C 30.A 31.B 32.B 33.D 34.D 35.C 36.A 37.A 38.C 39.A 40.A 41.D 42.C 43.B 44.B 45.B 46.A 47.B 48.B 49.C 50.B Câu 1.
Nghiệm của phương trình x 1 5   125 là
A. x  2.
B. x  3.
C. x  4. D.  sin xdx.  0 Lời giải: x 1  x 1  3 5  125  5  5  x  2. Chọn đáp án A Câu 2.
Với a là số thực dương tùy ý, log 3a bằng 3   A. 3log . a B. 1 log . a C. 1 log . a D. 3  log . a 3 3 3 3 Lời giải:
log 3a  log 3  log a  1 log . a 3   3 3 3 Chọn đáp án B Câu 3.
Hàm số y   x x   2021 2 4 3 có tập xác định là A.  \  3  ;   1 . B.  ;  3
   1;. C. .  D. 3;  1 . Lời giải:  x  1
Hàm số y   x x   2021 2 4 3 có nghĩa khi 2
x  4x  3  0   x  3 
Vậy tập xác định của hàm số là  \ 3;  1 . Chọn đáp án A Câu 4.
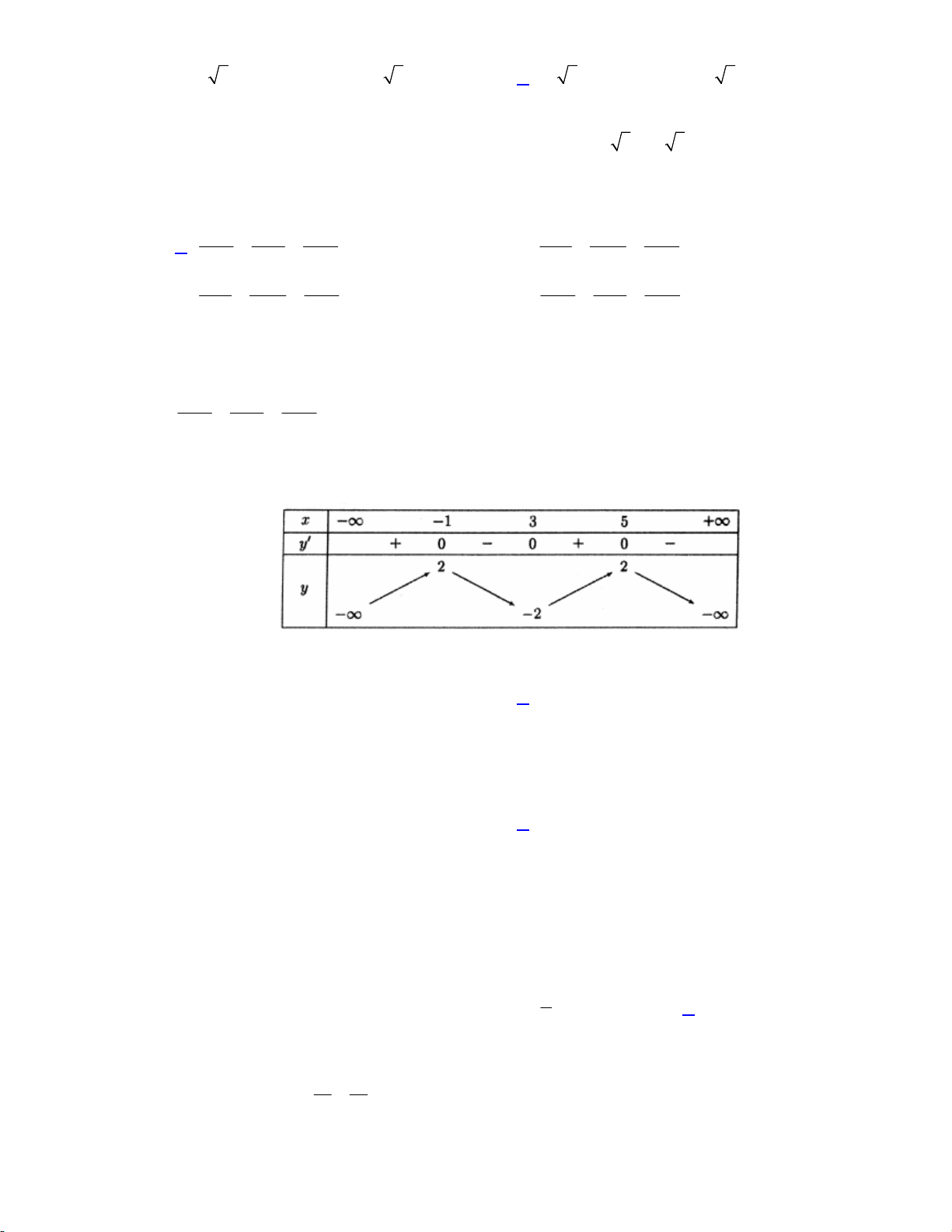
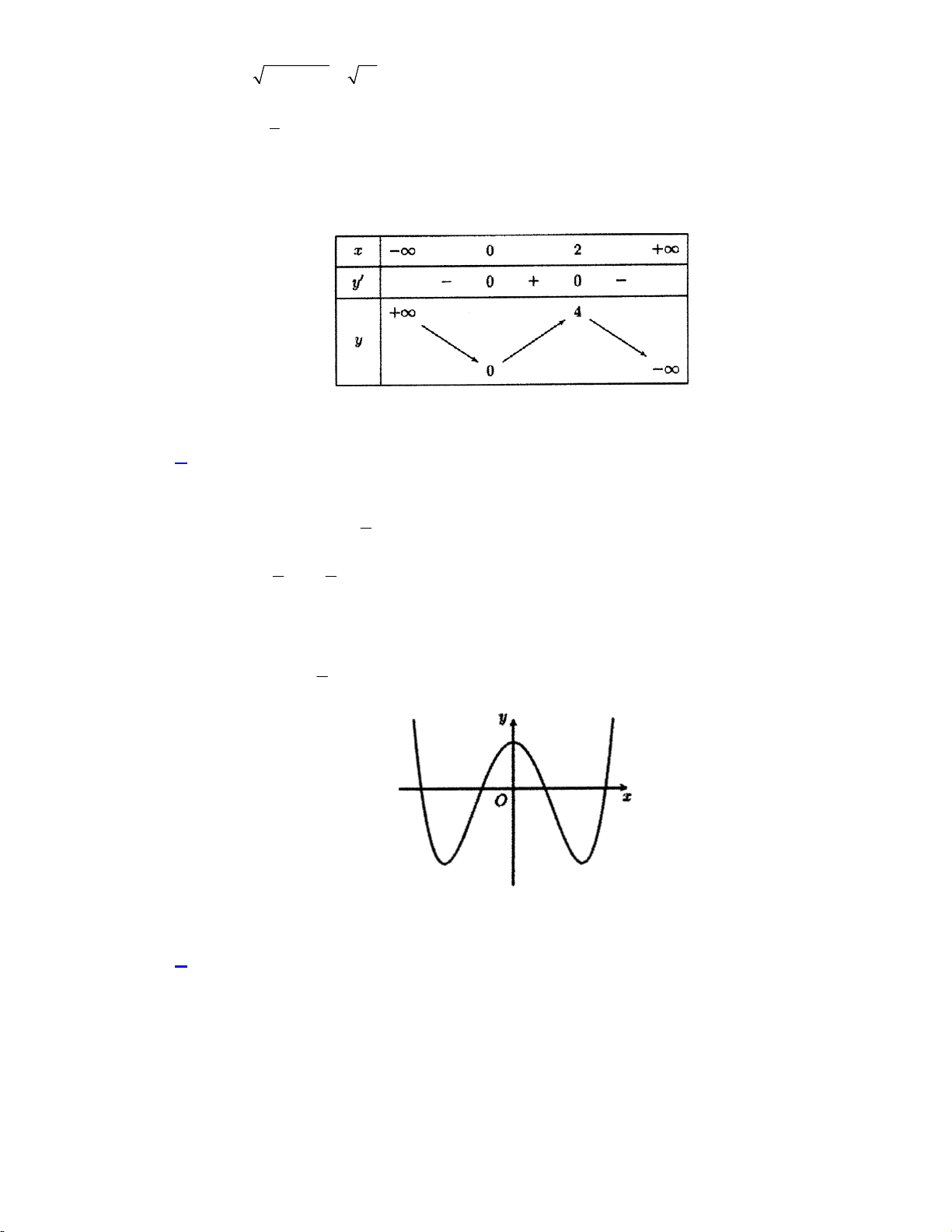
Cho hàm số f (x) có bảng biến thiên như sau:
Hàm số f (x) nghịch biến trên khoảng nào dưới đây? A. 1;3.
B. 1;3. C. 1;  1 . D. 3;  1 . Lời giải:
Dựa vào bảng biến thiên ta thấy hàm số f (x) nghịch biến trên 1;  1 . Chọn đáp án C Câu 5.
Số các chỉnh hợp chập k của n phần tử n, k N, 1  k n là A. n A . B. k C . C. k A . D. P . k n n k Lời giải:
Số các chỉnh hợp chập k của n phần tử  ,
n k N ,1  k n là k A . n Chọn đáp án C Câu 6.
Cho hình trụ có chiều cao bằng 2 và bán kính đáy bằng 3. Thể tích của khối trụ đã cho bằng A. 6.
B. 18.
C. 15.
D. 9. Lời giải:
Thể tích của khối trụ: 2 2
V Bh  r h .3 .2  18. Chọn đáp án B Câu 7.
Số phức liên hợp của số phức 5  7i là A. 5  7 . i B. 5  7 . i C. 5  7 . i D. 5  7 . i Lời giải:
Ta có: số phức z  5  7i z  5  7 . i Chọn đáp án C Câu 8.
Tập nghiệm của bất phương trình log x  1 là 3 A. 0;  1 . B.  ;   3 . C. 0;  3 . D.  ;   1 . Lời giải:
Điều kiện: x  0.
Ta có: log x  1  x  3. 3
Kết hợp điều kiện ta có tập nghiệm của phương trình đã cho là 0;  3 . Chọn đáp án C Câu 9.
Thể tích khối lăng trụ có chiều cao bằng 4 và diện tích đáy bằng 3 3 là A. 6 3. B. 4 3. C. 12 3. D. 8 3. Lời giải:
Ta có công thức tính thể tích khối lăng trụ: V  .
B h V  4.3 3  12 3. Chọn đáp án C
Câu 10. Trong không gian Oxyz , phương trình đường thẳng đi qua hai điểm ( A 3; 1  ; 2) và B(4;1; 0) là x  3 y 1 z  2 x 1 y  2 z  2 A.   . B.   . 1 2 2  3 1  2  x 1 y  2 z  2 x  3 y 1 z  2 C.   . D.   . 1 1  2 1 2 2  Lời giải: 
Đường thẳng AB đi qua điểm ( A 3; 1
 ; 2) và có vecto chỉ phương AB  (1; 2; 2) có dạng x  3 y 1 z  2   . 1 2 2  Chọn đáp án A
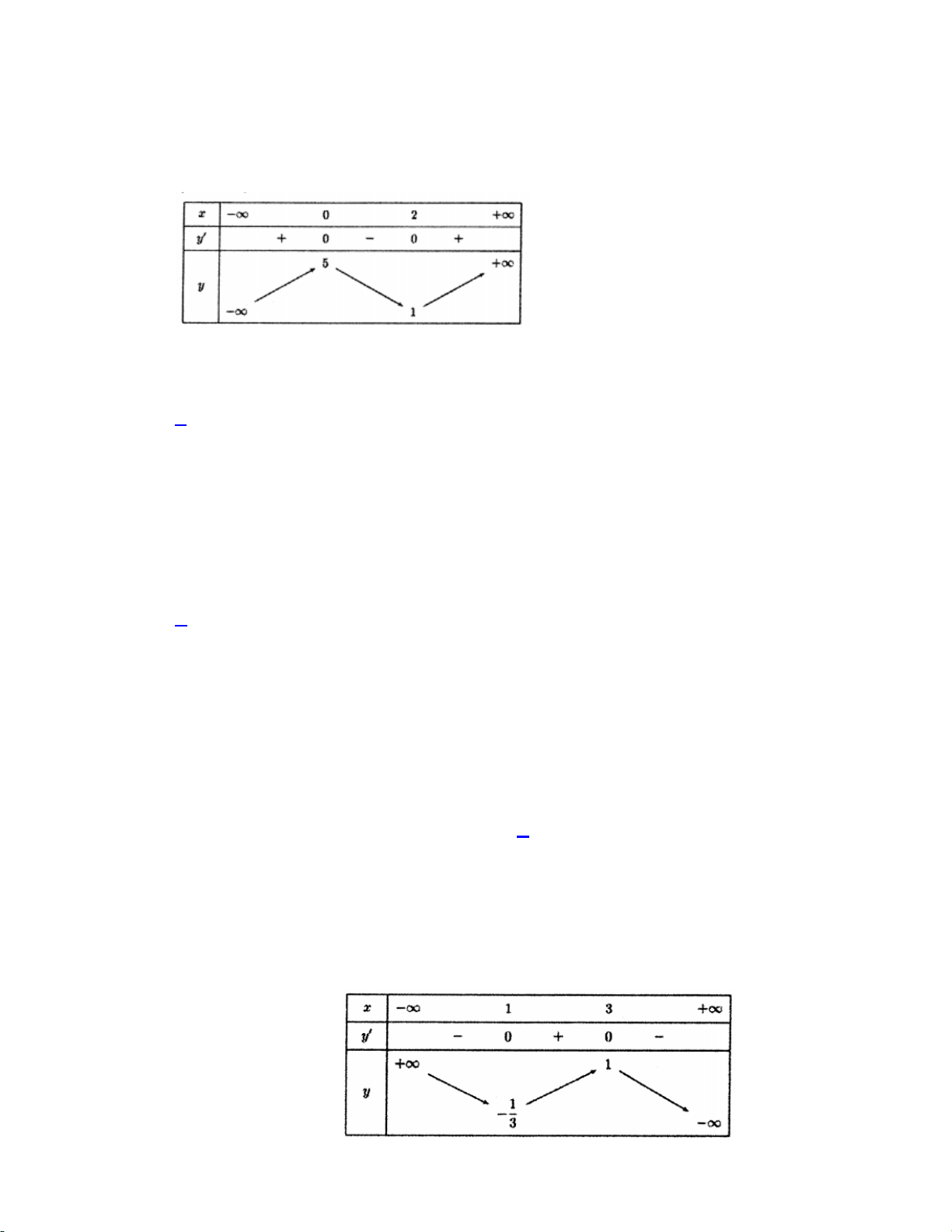
Câu 11. Cho hàm số y f ( x) có bảng biến thiên như sau
Hàm số đã cho đạt cực tiểu tại
A. x  5. B. x  1. 
C. x  3. D. x  2.  Lời giải: Chọn đáp án C
Câu 12. Nếu hàm số F (x) là một nguyên hàm của hàm số f (x) thì
A. f '(x)  F (x).
B. F (x)  f (x).
C. F '(x)  f (x).
D. F '(x)  f '(x). Lời giải:
Định nghĩa nguyên hàm của hàm số. Chọn đáp án C
Câu 13. Cho cấp số nhân u có u  6 và u  12. Công bội của cấp số nhân đã cho bằng n  3 4 1 A. 6  . B. 6. C. . D. 2. 2 Lời giải: u 12 Ta có công bội 4 q    2. u 6 3 Chọn đáp án D 4  3x
Câu 14. Tiệm cận ngang của đồ thị hàm số y  là đường thẳng 4x  5 3 5 
A. y  1.
B. y   .
C. y  1. D. y  . 4 4 Lời giải: 4  3x 3  4  3x 3  lim y  lim  ; lim y  lim  . x
x 4x  5 4 x
x 4x  5 4 3 Vậy y  
là TCN của đồ thị hàm số đã cho. 4 Chọn đáp án B
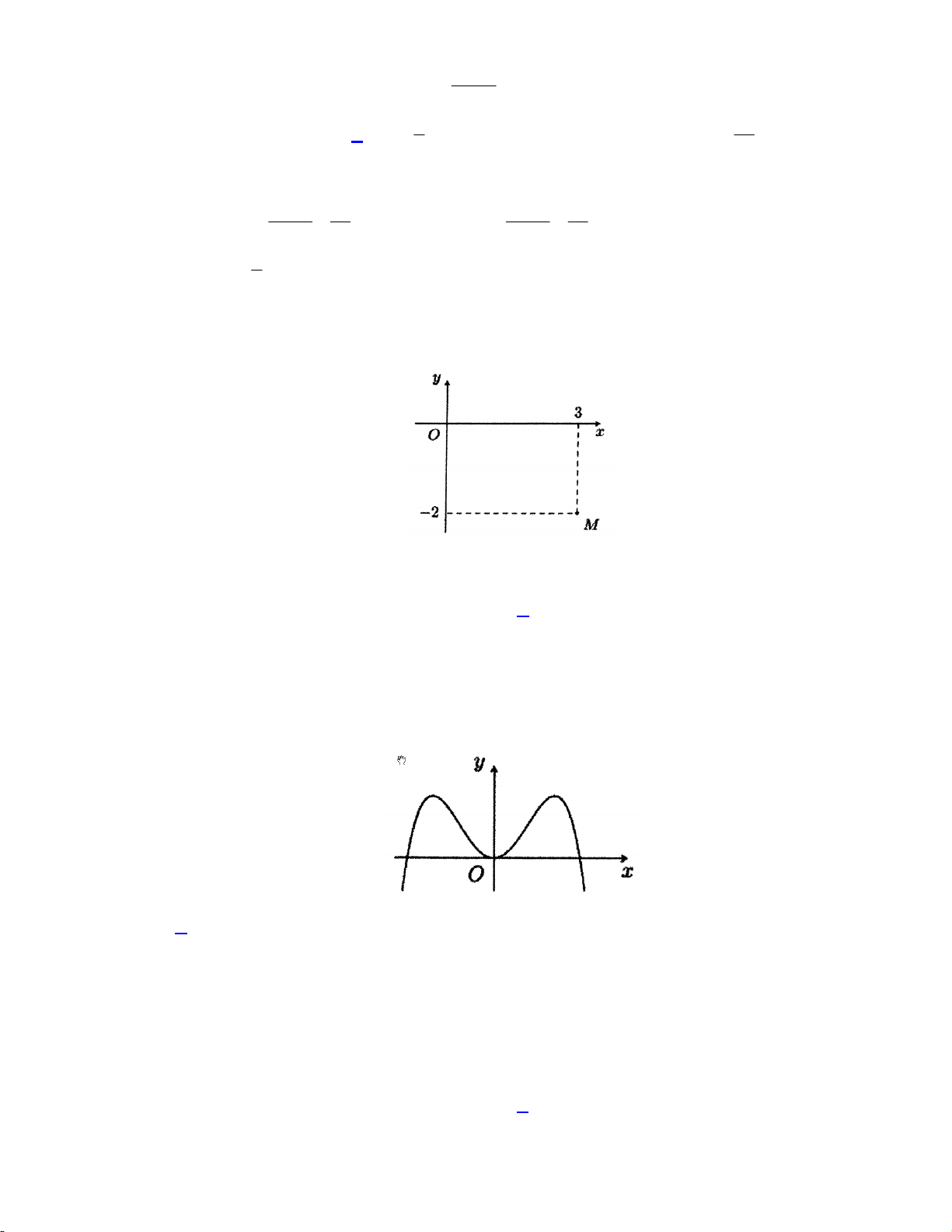
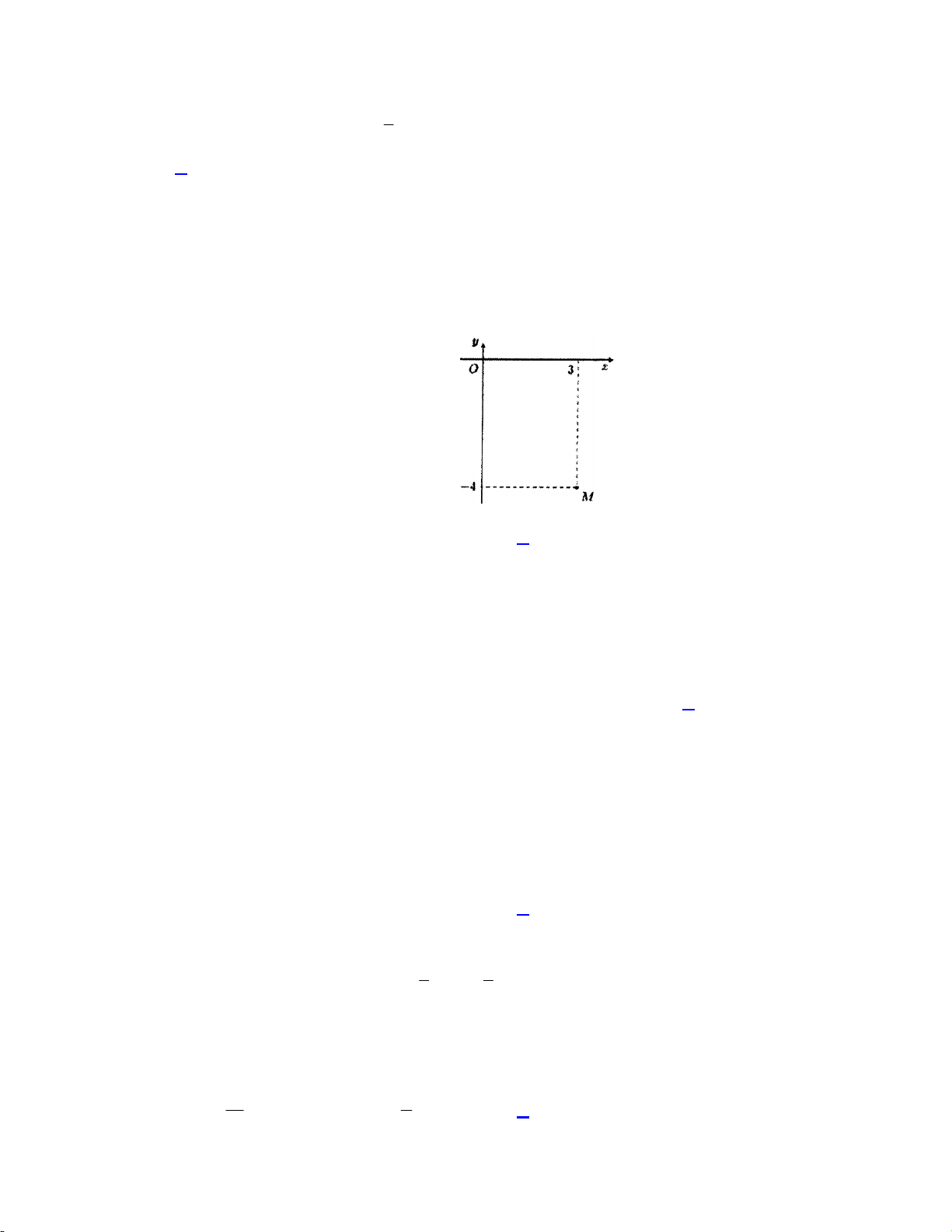
Câu 15. Trong mặt phẳng Oxy, số phức z a bia,b   có điểm biểu diễn M như sau:
Giá trị của a, b lần lượt là A. 2  và 3. B. 3 và 2. C. 3 và 2  . D. 2  và 3  . Lời giải:
Ta có M 3;2  a  3,b  2 Chọn đáp án A
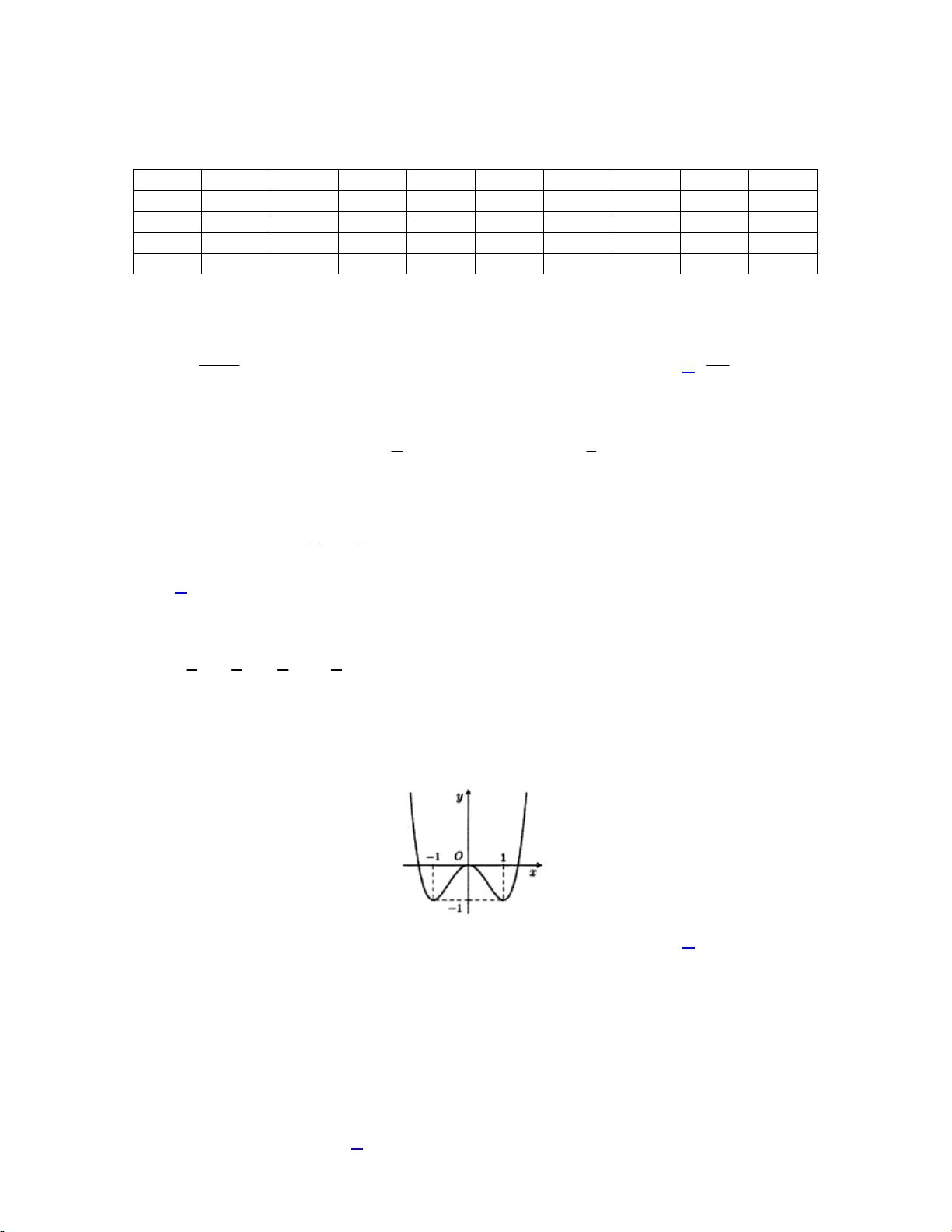
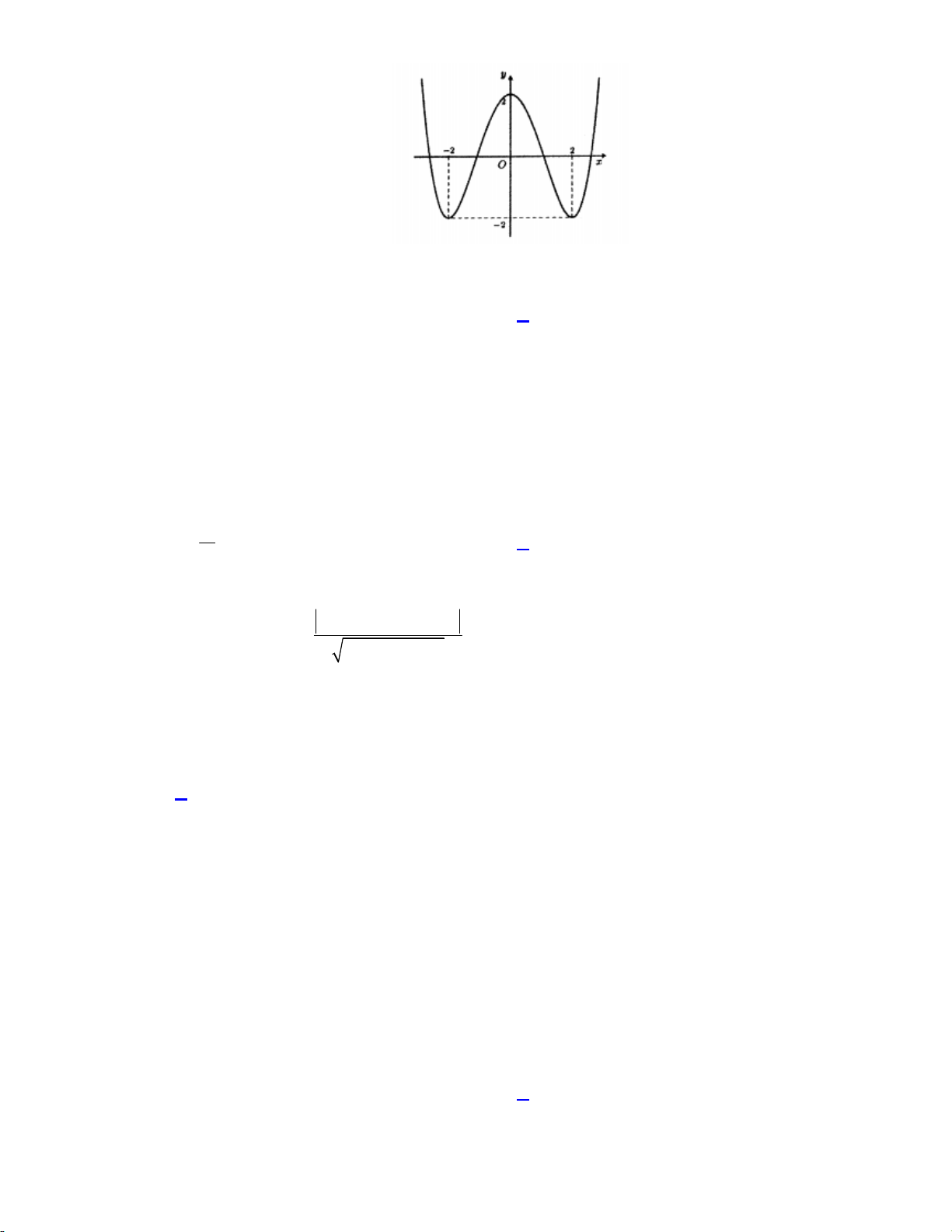
Câu 16. Đồ thị của nào dưới đây có dạng như đường cong như hình bên dưới? A. 4 2
4x  2x . B. 4 2
4x  2x . C. 4 2
4x  2x . D. 3 2 4x  2x . Lời giải:
Nhìn vào đồ thị ta thấy đây là dạng đồ thị của hàm số bậc bốn có hệ số a  0
Hàm số có 3 cực trị nên a, b khác dấu. Chọn đáp án A
Câu 17. Trong không gian Oxyz , phương trình mặt cầu có tâm I (2; 0;1) và bán kính R  2 là A. x
y   z  2 2 2 ( 2) 1  2. B. x
y   z  2 2 2 ( 2) 1  4. C. x
y   z  2 2 2 ( 2) 1  2. D. x
y   z  2 2 2 ( 2) 1  4. Lời giải:
Áp dụng công thức x ay b
  z c2 2 2 2 ( ) ( )  R . Ta có x
y   z  2 2 2 ( 2) 1  4. Chọn đáp án B
Câu 18. Trong không gian Oxyz , phương trình mặt phẳng đi qua (
A 1; 2; 2) và có vectơ pháp tuyến 
n  3; 1; 2 là
A. 3x y  2z 1  0.
B. x  2 y  2z 1  0.
C. 3x y  2z 1  0.
D. x  2 y  2z 1  0. Lời giải:
Áp dụng công thức a(x x )  b( y y )  c z z  0 ta có 0 0  0  3 x  
1   y  2  2 z  2  0  3x y  2z 1  0. Chọn đáp án A
Câu 19. Thể tích của khối chóp có diện tích đáy bằng B và chiều cao bằng h là 1 1 1 A. B . h B. . Bh C. . Bh D. . Bh 3 6 2 Lời giải: 1 Công thức V  . Bh 3 Chọn đáp án B 2 5 5 Câu 20. Nếu
f xdx  3  và
f xdx  1  thì
f xdx  bằng 1 2 1 A. 4. B. 2  . C. 2. D. 3  . Lời giải: 5 2 5 Ta có
f xdx f xdx f xdx  3    1  2.    1 1 2 Chọn đáp án C
Câu 21. Số nghiệm nguyên của bất phương trình log 16  x  log 9 . x 3   3 A. 0. B. 1. C. 2. D. 3. Lời giải: x 16  0 x  16 Với điều kiện:     x  0 9x  0 x  0  
Ta có: log 16  x  log 9 . x 3   3  16  x  9 . x  8x  16.  x  2
So với đk ta được 1 nghiệm nguyên x  1. Chọn đáp án B 1 1
Câu 22. Gọi z , z là 2 nghiệm của phương trình 2
z  2z  4  0.Tính  . 1 2 z z 1 2 1 2 A. 1. B. . C. 2. D. . 2 2 Lời giải: Phương trình 2
z  2z  4  0. Có nghiệm z  1 3i, z  1  3 . i 1 2 1 1 Nên   1. z z 1 2 Chọn đáp án A
Câu 23. Số giao điểm của đồ thị hàm số y x   2 (
1) x  2x với trục hoành là A. 3. B. 1. C. 0. D. 2. Lời giải:
Số giao điểm của đồ thị và trục hoành là số nghiệm của phương trình x   2 (
1) x  2x  0 x  1 
Ta có: (x 1)  2
x  2x  0  x  0  x  2  Chọn đáp án A
Câu 24. Cho hàm số 3 2
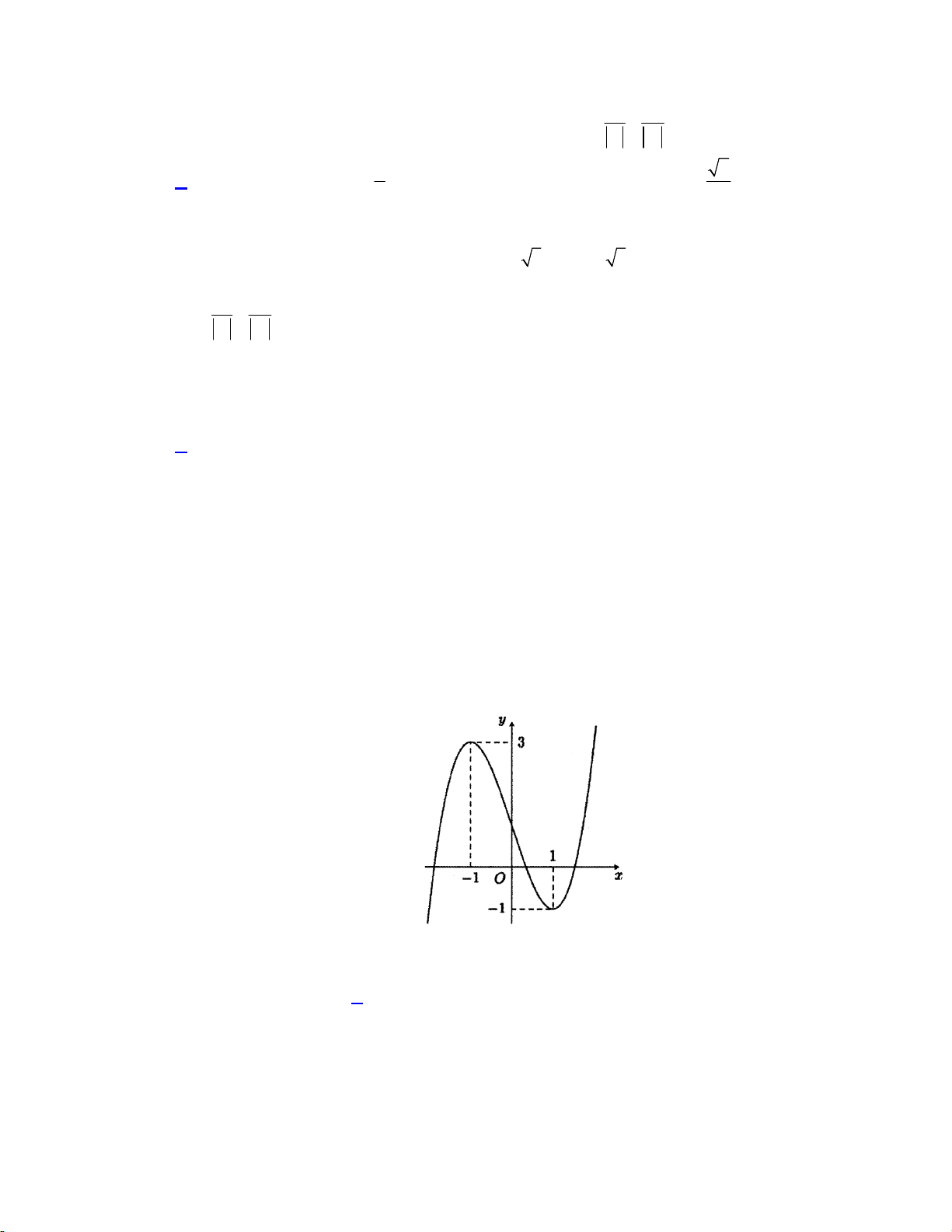
f (x)  ax bx cx d có đồ thị như sau:
Số nghiệm của phương trình f (x)[ f ( x) 1]  0 là A. 4. B. 5. C. 2. D. 1. Lời giải:
f ( x)  1 (1)
f (x)[ f (x) 1]  0   f ( x)  0 (2) 
Nghiệm của phương trình (1) là giao điểm của đồ thị và đường thẳng y f (x)  1, nên số nghiệm là 2.
Nghiệm của phương trình (2) là giao điểm của đồ thị và trục hoành, nên số nghiệm là 3. Chọn đáp án B 2 1
Câu 25. Cho hàm số f x liên tục trên đoạn 1;2 thỏa mãn
f xdx  6. 
Giá trị của f 3x   1 dx  1 0 bằng A. 18. B. 1. C. 2. D. 3. Lời giải:
Đặt t  3x 1  dt  3d . x
x  0  t  1
x  1  t  2 1 2 1 f 3x   1 dx
f t dt  2.   3 0 1 Chọn đáp án C
Câu 26. Cho hình nón có bán kính đáy bằng 5 và góc ở đỉnh bằng 60 . Diện tích xung quanh của hình nón đã cho bằng
A. 55.
B. 100.
C. 75.
D. 50. Lời giải: OA  5
Do góc ở đỉnh bằng 60 nên OSA  30 .
 Lại có sin OSA   sin 30   SA  10. SA SA Vậy S
 Rl  50. xq Chọn đáp án D
Câu 27. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x 3
x 18x  6 trên đoạn  3
 ;5. Giá trị của M m bằng 141 77 A. 47 12 6. B. . C. 39 12 6. D. . 8 8 Lời giải:
Ta có: f x 3 2
x 18x  6  f (x)  3x 18
x  6 [  3;5] Cho f (  x)  0  
x   6 [  3;5] 
Tính f (3)  33; f (5)  41; f ( 6)  6 12 6; f ( 6 )  6  12 6
Vậy M  Max f (x)  41; m  Min f (x)  6 12 6 [ 3  ;5] [ 3  ;5]
M m  41 6 12 6  47 12 6. Chọn đáp án A
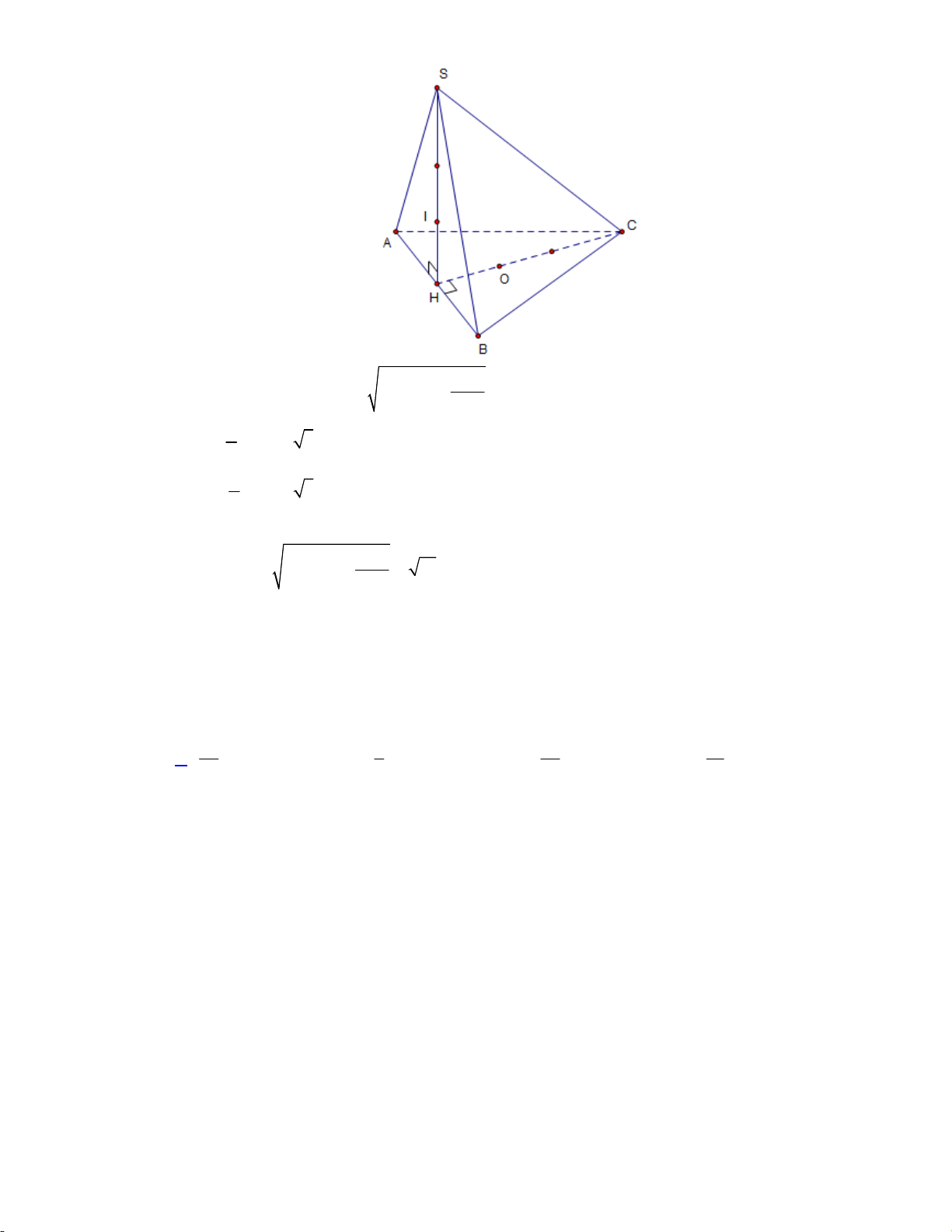
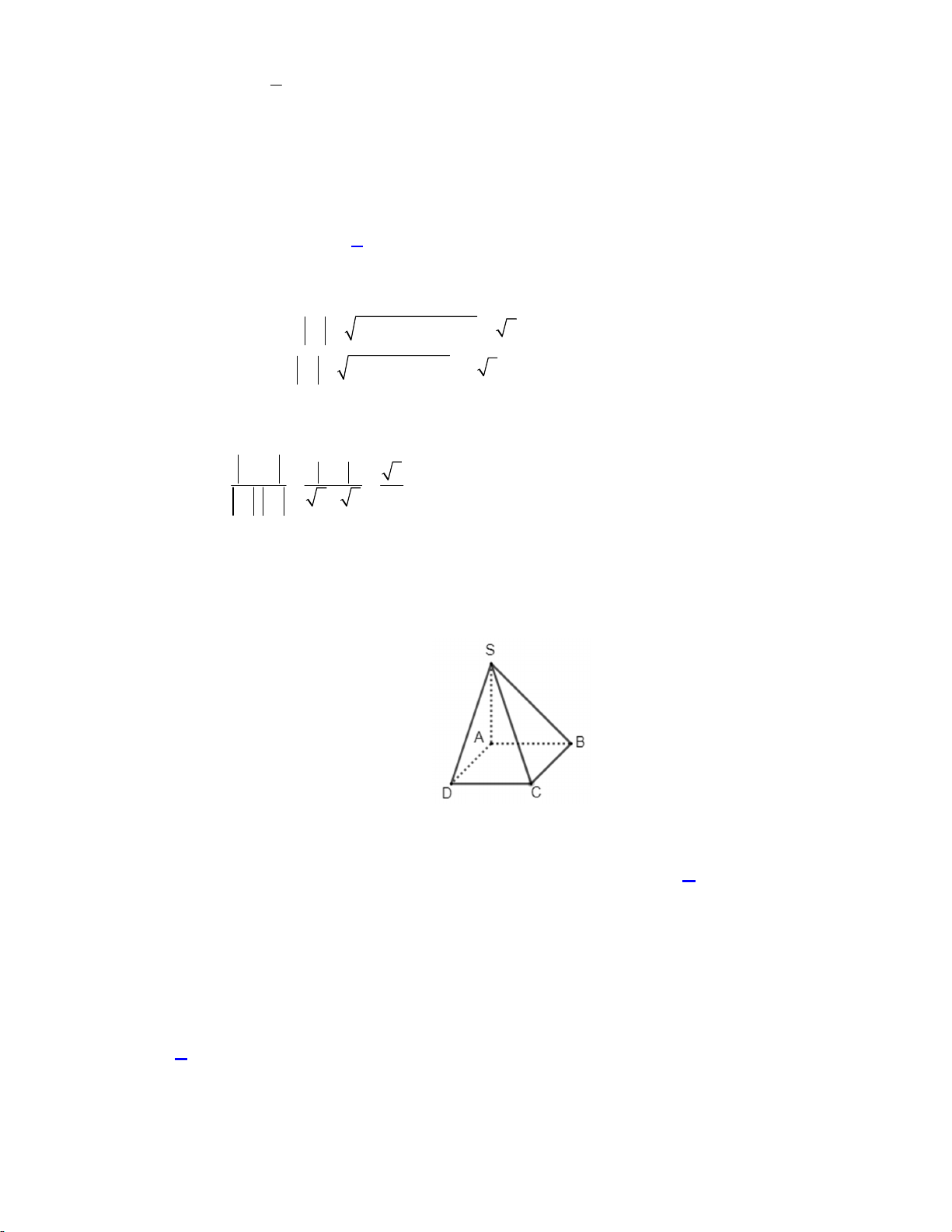
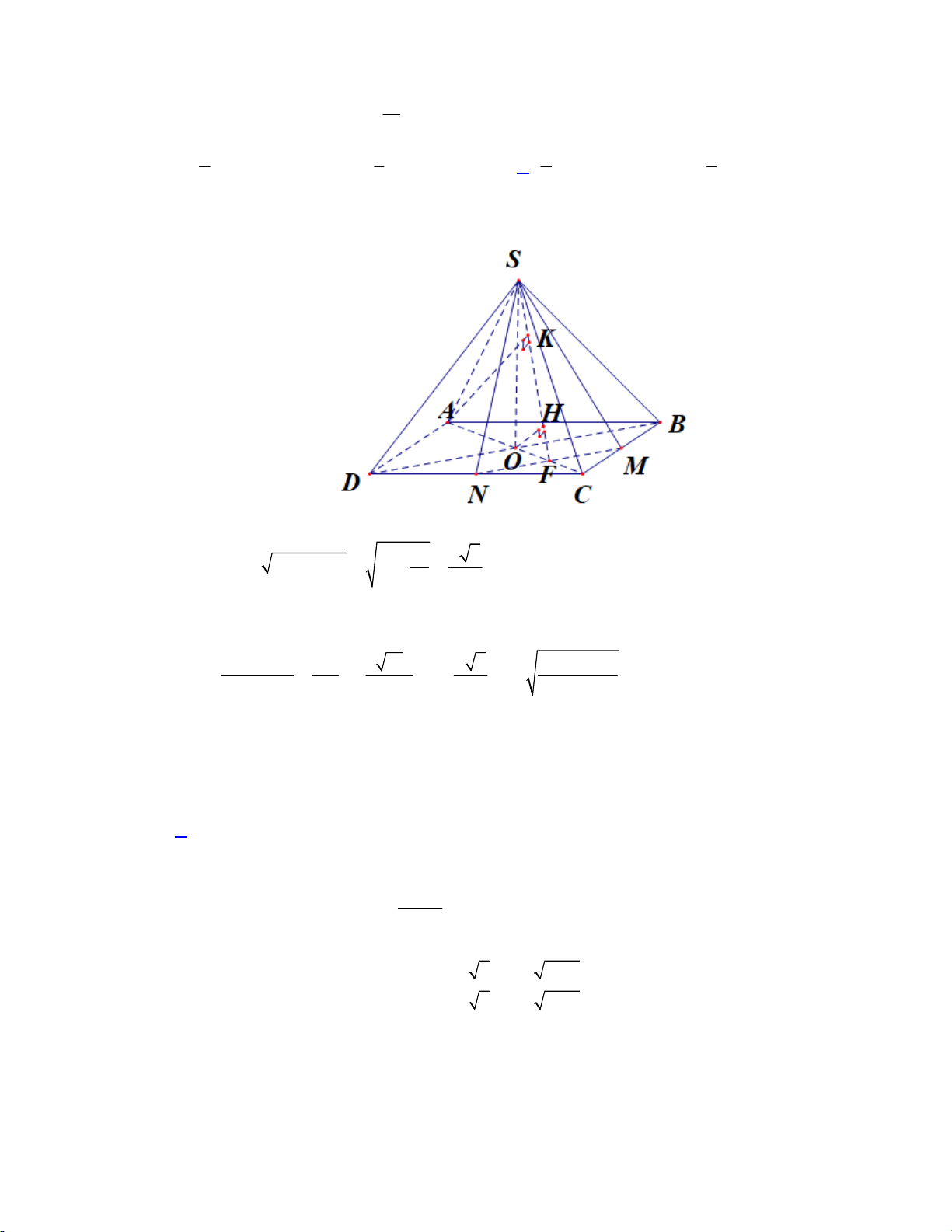
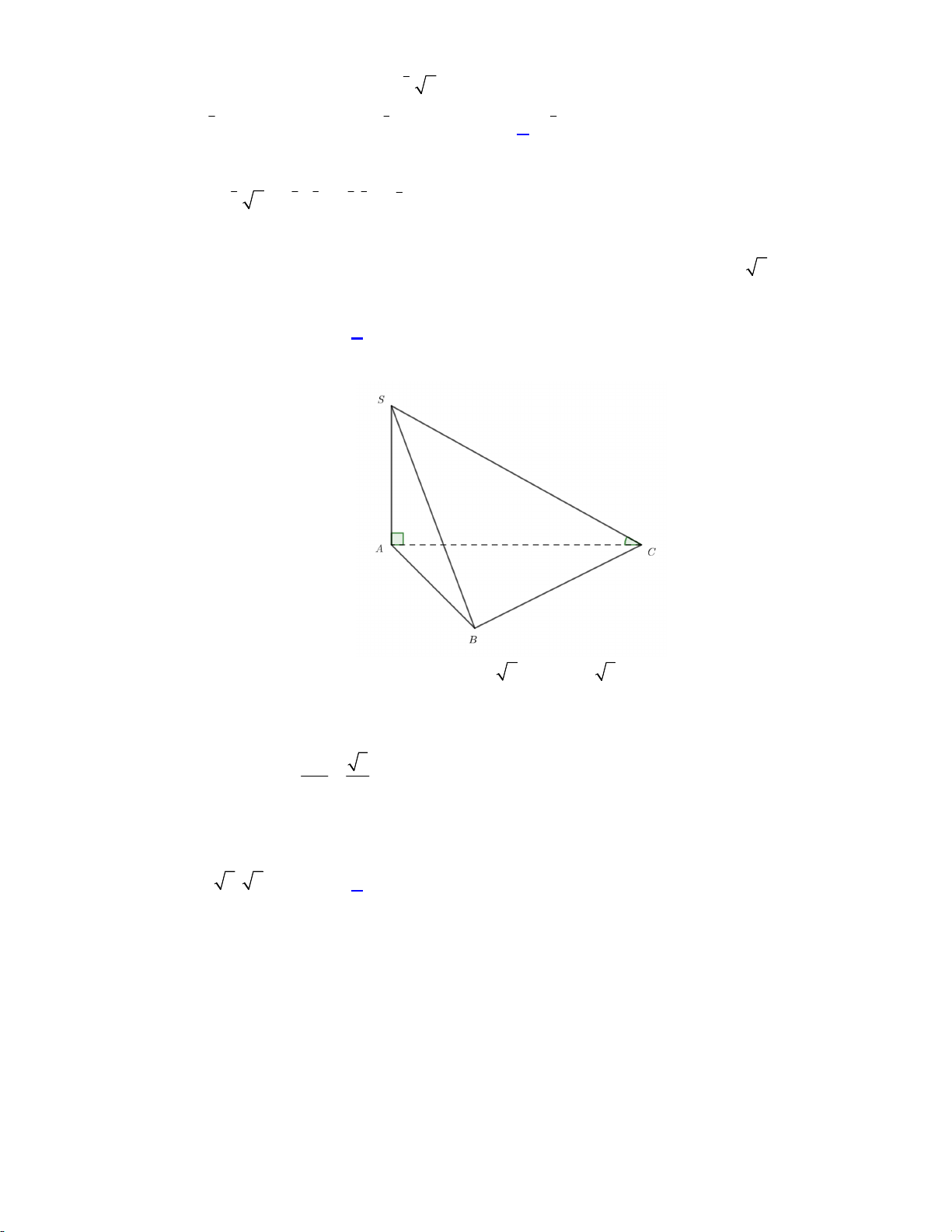
Câu 28. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng
ABCD và SA  3 .
a Gọi là góc giữa hai mặt phẳng SBC  và  ABCD. Giá trị tan bằng 3 6 3 A. 3. B. . C. . D. . 3 2 2 Lời giải:
Ta có: SBC    ABCD  BC   SB, ABSA 3a  tan    3 AB a Chọn đáp án A
Câu 29. Cho a và b là hai số thực dương thỏa mãn 2 2
a b  64 . Giá trị của 2 log a  2 log b bằng 2 2 A. 8. B. 32. C. 6. D. 4. Lời giải: Ta có: 2 2
2 log a  2 log b  2 log ab  log a b  log 64  6. 2 2 2 2 2 Chọn đáp án C
Câu 30. Cho hình trụ có bán kính đáy r  3 và độ dài đường sinh l  5 . Diện tích toàn phần của hình trụ đã cho bằng
A. 48.
B. 30.
C. 15.
D. 33. Lời giải: Ta có: 2 2
S  2 rl  2 r  2.3.5  2..3  48. tp Chọn đáp án A
Câu 31. Cho hình nón  N  có bán kính đáy bằng 3 và chiều cao bằng 4. Thể tích khối nón  N  bằng A. 6.
B. 12.
C. 15. D. 36. Lời giải: 1 1
Thể tích khối nón  N  là 2 2
V  r h .3 .4  12. 3 3 Chọn đáp án B
Câu 32. Cho hai số phức z  4  3i và w  1 .
i Môđun của số phức . z w bằng A. 4 2. B. 5 2. C. 5. D. 3 2. Lời giải: Ta có .
z w  4  3i1 i  1 7i  5 2. Chọn đáp án B
Câu 33. Trong không gian Oxyz , cho hai điểm A1;2; 3 và B2; 1; 
1 . Tọa độ trung điểm của đoạn thẳng AB là  1 3   1 3   3 1 
A. 3;1; 2 . B. ; ; 2   . C.  ; ; 2   . D. ; ;1   .  2 2   2 2   2 2  Lời giải: x x y y z z   3 1 
Tọa độ trung điểm của đoạn thẳng AB là A B I ; A B ; A B   hay I ; ;1   .  2 2 2   2 2  Chọn đáp án D
Câu 34. Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi đồ thị hàm số y  sin x ,
trục hoành và các đường thẳng x  0, x   quanh trục Ox bằng   2  2  A. . B. . C. . D. . 4 2 4 2 Lời giải:  2  2
V   sin xdx   . 2 0 Chọn đáp án D
Câu 35. Cho hàm số f (x) có 2 f x x x   2 '( ) ( 3)
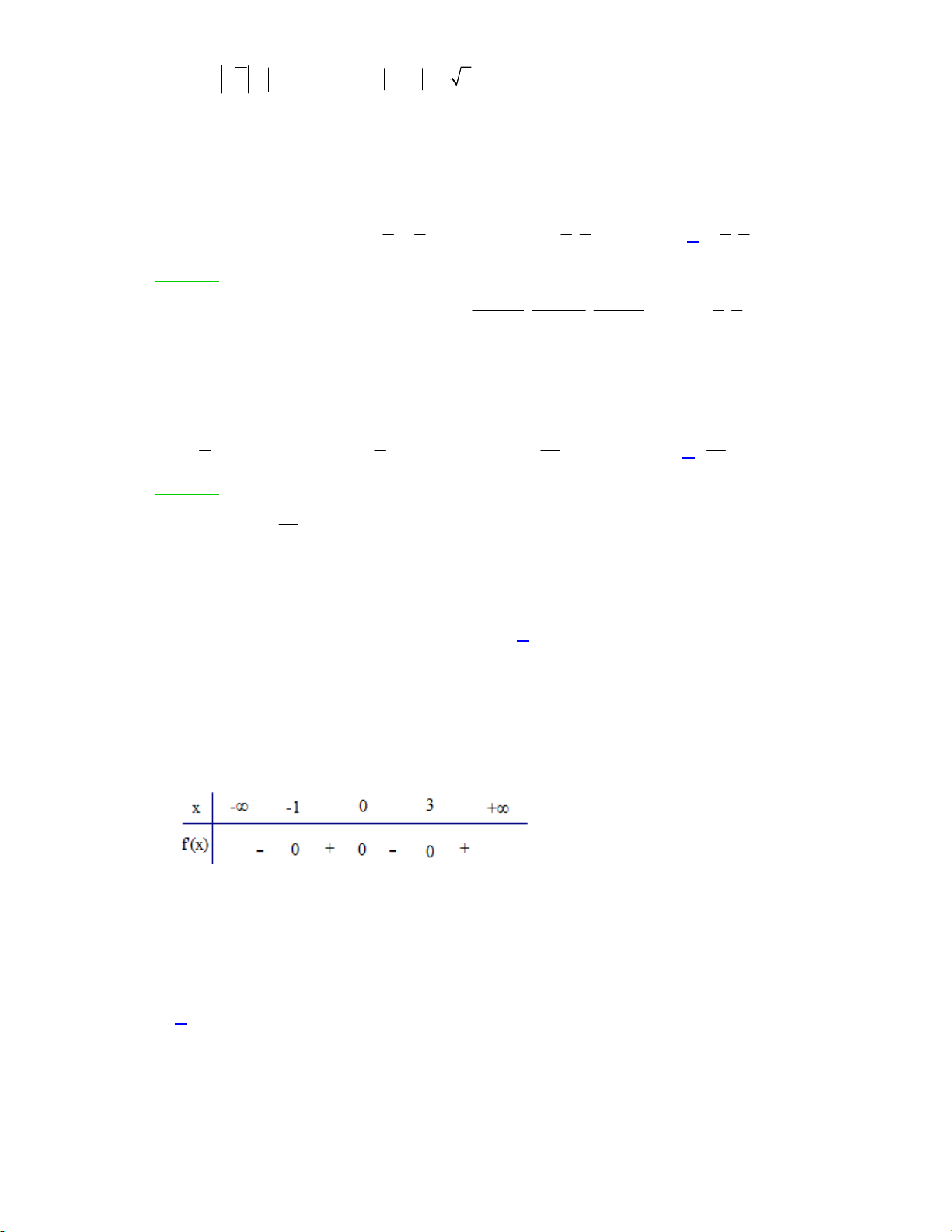
x  2x  3 . Số điểm cực đại của hàm số f (x) là A. 4. B. 2. C. 1. D. 3. Lời giải: x  0 
f '(x)  0  .
x x  33  x   1  0  x  3  x  1  Bảng xét dấu
Dựa vào bảng xét dấu f '(x) suy ra f (x) có 1 cực đại. Chọn đáp án C
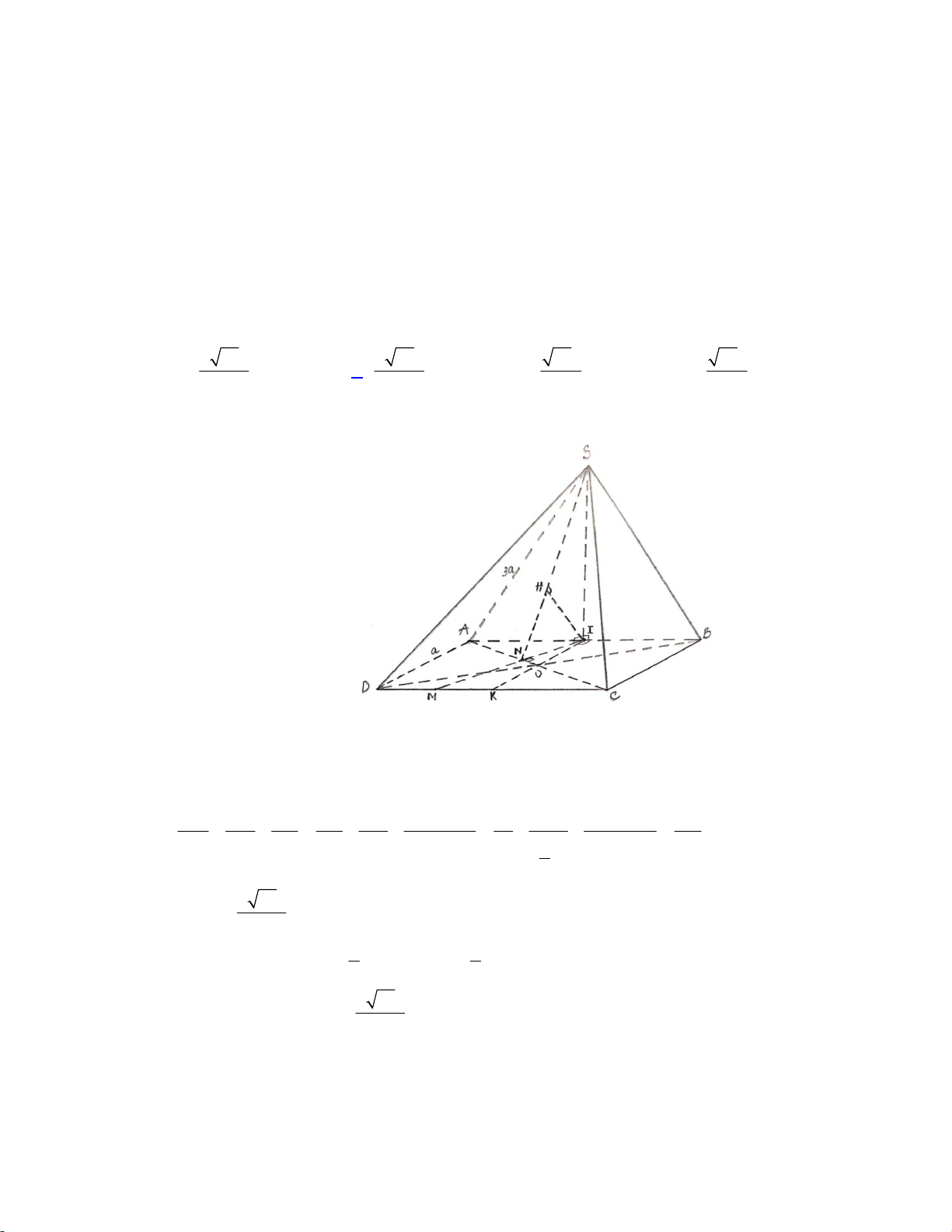
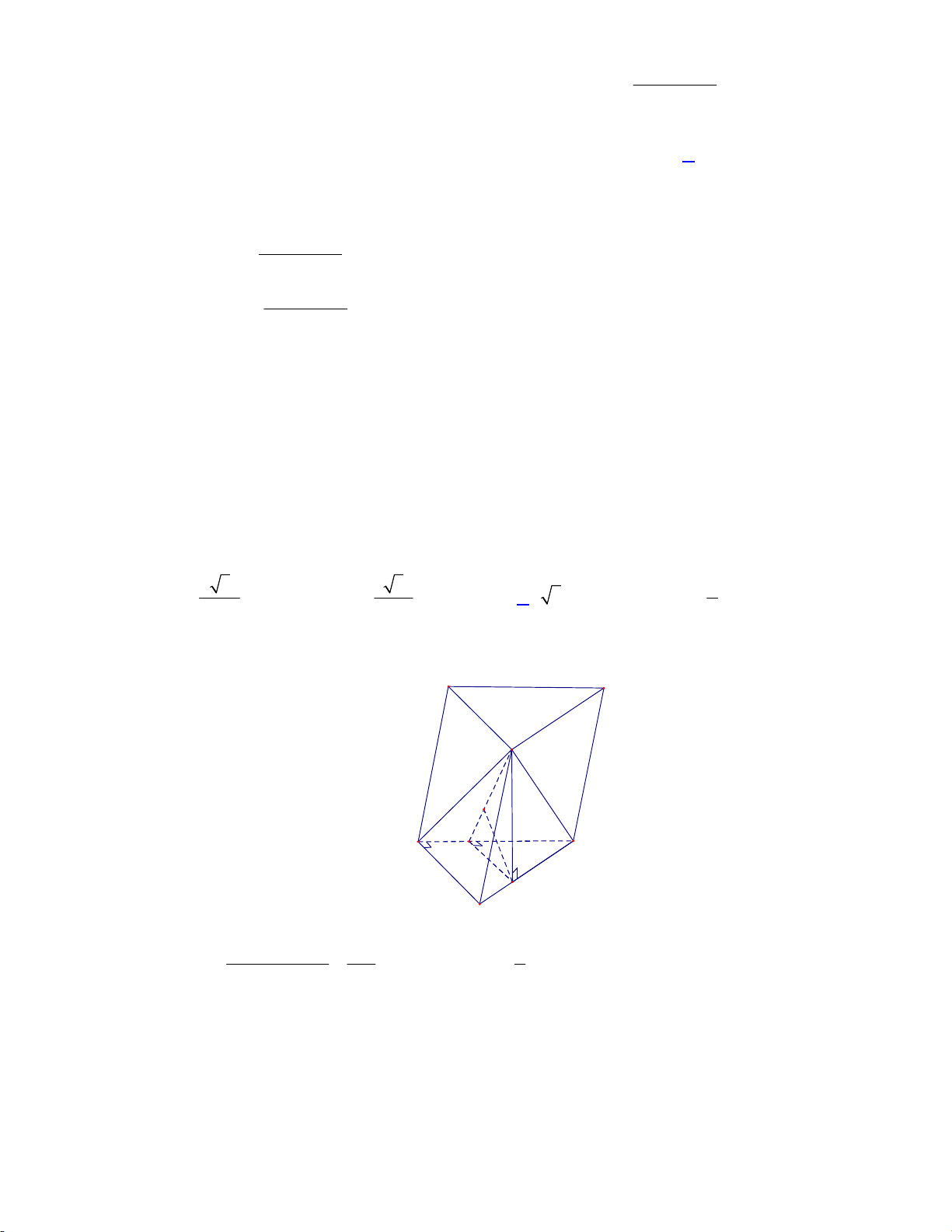
Câu 36. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 6a , mặt bên SAB là tam giác đều
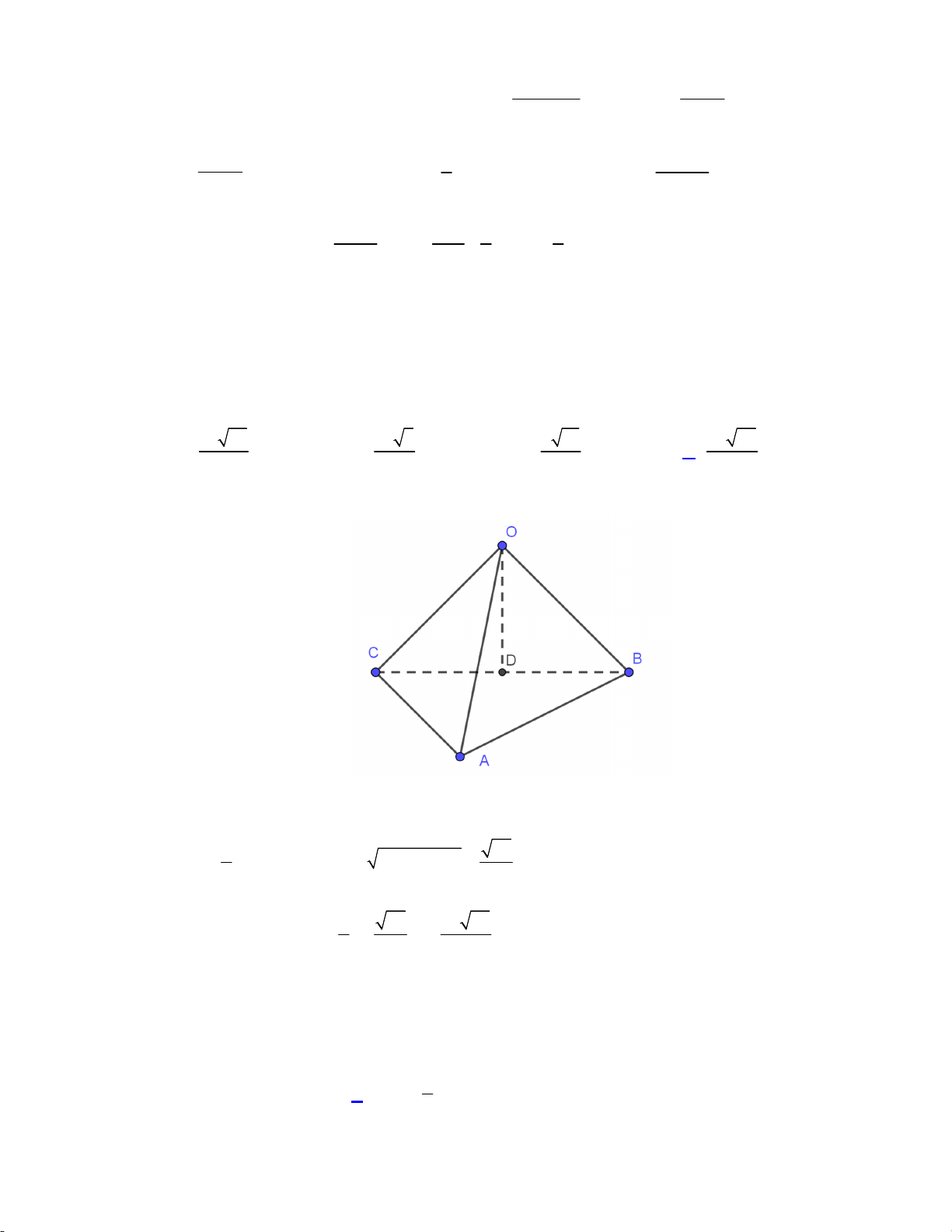
nằm trong mặt phẳng vuông góc với đáy. Mặt cầu ngoại tiếp hình chóp S.ABC có diện tích bằng A. 2 60 a . B. 2 15 a . C. 2 75 a . D. 2 80 a . Lời giải: 2 GT
Áp dụng công thức: 2 2 R R R C D B 4 2 + R CH  2 3a D 3 2 + R SH  2 3a B 3
+ GT AB  6a 2 GT Khi đó: 2 2 R R R   15 . a C D B 4 Diện tích mặt cầu: 2 2 S
 4 R  60 a mc Chọn đáp án A
Câu 37. Một tổ có 12 học sinh gồm 4 nam trong đó có Vinh và 8 nữ trong đó có Hoa. Chia tổ thành 3
nhóm, mỗi nhóm gồm 4 học sinh và phải có ít nhất một học sinh nam. Xác suất để Vinh và Hoa cùng một nhóm là 7 1 3 5 A. . B. . C. . D. . 32 8 32 16 Lời giải: Ta có: n  1 3 1 3
C C .C C .1  6720 4 8 3 5
n A  ?
TH1: nhóm 1: Vinh,Hoa và 1 bạn nam cùng 1 bạn nữ khác: 1 1 C .C 3 7 nhóm 2: 1 nam và 3 nữ: 1 3
C .C , nhóm còn lại có 1 cách chọn 2 6 Vậy trường hợp 1 có 1 1 1 3
C .C .C .C  840 cách chọn. 3 7 2 6
TH2: nhóm 1: Vinh,Hoa và 2 bạn nữ khác: 2 C 7 nhóm 2: 2 nam và 2 nữ: 2 2
C .C , nhóm còn lại có 1 cách chọn 3 5 Vậy trường hợp 1 có 2 2 2
C .C .C .1  630 cách chọn. 7 3 5
n A  1470 1470 7
P A   6720 32 Chọn đáp án A 3 2 2x 14x Câu 38. Biết
dx a ln 2  b ln 3  c, a, , b c  .   Giá trị của 2
a b c bằng 2   x 1 2 A. 494. B. 484. C. 474. D. 464. Lời giải: Ta có: 2 2x 14x 14x  2 6 8  2    2    . 2 2 x 1 x 1 x 1 x  1 3 2 3 2x 14x  6 8   dx  2   dx       2
x  6 ln x 1  8 ln x 1  3 2 2 x 1  x 1 x 1  2 2  22 ln 2  8 ln 3  2
a  22,b  8,c  2  2
a b c  474. Chọn đáp án C x tx  1 2t 1 2  
Câu 39. Trong không gian Oxyz, cho hai đường thẳng d : y  4  t và d :  y  3  t . Đường 1 1 2 2 z  3 t   z  4  t 1  2
thẳng vuông góc với mặt phẳng (Oxz), cắt hai đường thẳng d và d có phương trình là 1 2  1  1  3  3 x    x   t x t x  3  7  7  7      7  7  25  25
A. y    t .
B. y  1 t .
C. y  1 t . D. y    t . 3  3  7  7   10  10  18  18 z   z tz tz    3  3  7  7 Lời giải:
- Gọi d là đường thẳng vuông góc với mặt phẳng (Oxz), cắt hai đường thẳng d và d lần lượt 1 2 tại M , N.
- Vì M d nên M (t ; 4  t ;3  t ), t  .  1 1 1 1 1
- Vì N d nên N (1 2t ; 3
  t ; 4  t ), t  . 2 2 2 2 2 
- Vì M d , N d nên d có VTCP là MN  (1 t  2t ;1 t t ;1 t t ) 1 2 1 2 1 2 
- Vì d vuông góc với mặt phẳng (Oxz) nên j  (0;1;0) cũng là một VTCP của d  1 t   1 1
  t  2t  0  1 2 3    
 k  0 : MN kj  1
  t t k  k  2 1 2 1  t t 0     2  1 2 t   2  3 2  1 7 10  - Với t  thì N  ;  ; 2   3  3 3 3   1 7 10  
- Vậy đường thẳng d đi qua điểm N  ;  ; 
 và có một VTCP là j  (0;1;0) nên có  3 3 3   1 x    3   7
phương trình tham số là  y    t . 3   10 z     3 Chọn đáp án A
Câu 40. Có bao nhiêu số nguyên dương m sao cho hàm số 3 2
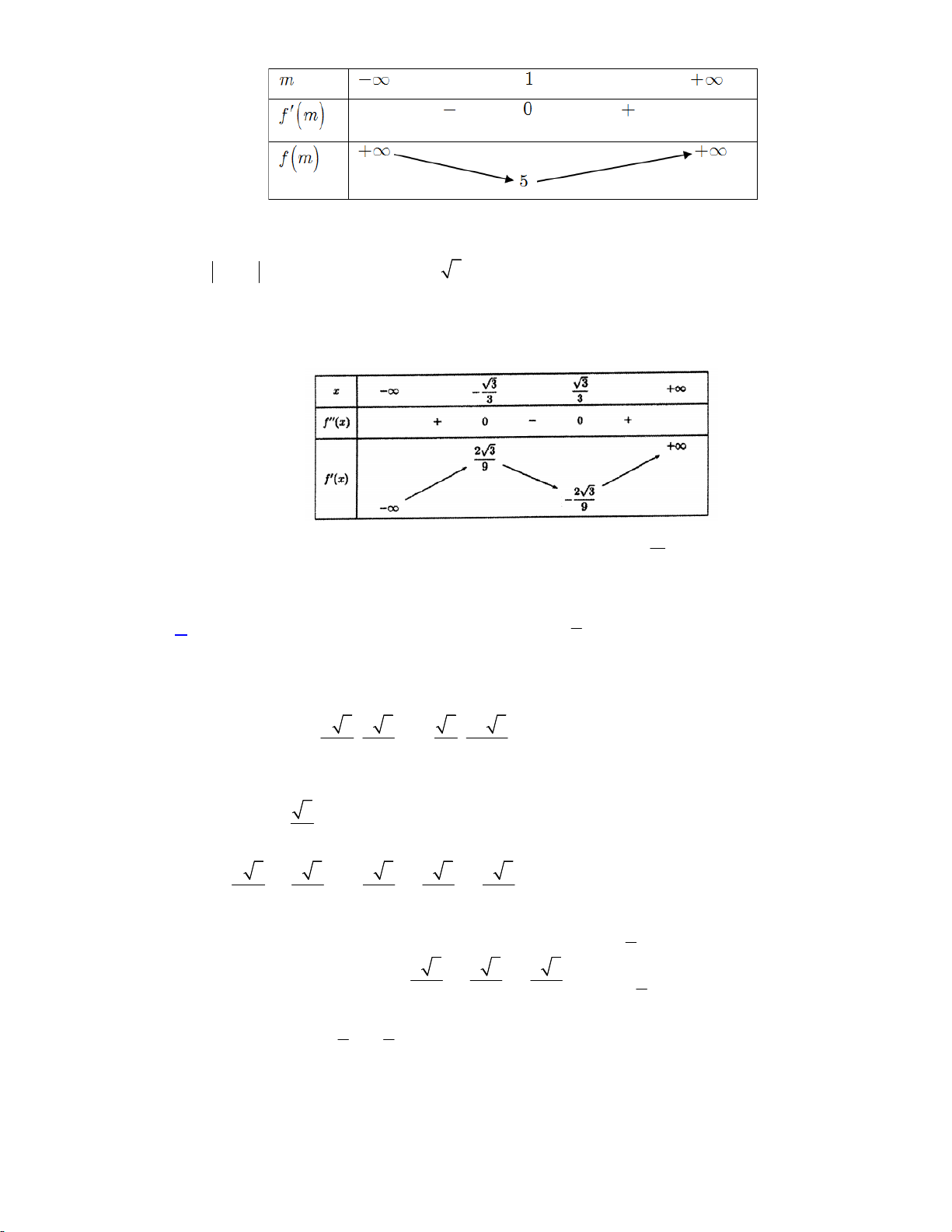
y x x  1 mx  2 đồng biến trên 1; ? A. 6. B. 5. C. 8. D. 7. Lời giải: 2
y '  3x  2x  1 m  0, x   1; 2
 3x  2x 1  , m x   1; 1 Xét hàm số 2
y  3x  2x 1 g ' x  6x  2  0  x   3 Do đó m  6. Chọn đáp án A Câu 41. Cho số phức
z x yi x, y   thỏa mãn
z  2  i z  3  4i và
z 2  3i  2 y 1  y  
1 i là số thuần ảo. Giá trị của 11x 11y bằng A. 16. B. 28. C. 16. D. 28. Lời giải: Ta có:
z  2  i z  3  4i
  x  22   y  2 1
  x  32   y  42
 5x  3 y  10
 x yi2  3i  2y 1  y  
1 i là số thuần ảo
 2x  3y  2 y 1  0
 2x y  1  Giải hệ pt  13 x   5
x  3y  10   11   
2x y  1 15   y     11
Vậy 11x 11y  28 Chọn đáp án D Câu 42. Cho hàm số 3 2
y ax bx cx d a, ,
b c, d   có đồ thị như sau
Có bao nhiêu số dương trong các số a, , b c, d ? A. 4. B. 2. C. 1. D. 3. Lời giải:
Dựa vào đồ thị, ta có: a  0 .
Đồ thị cắt trục tung tại điểm có tung độ dương, d  0.
Hàm số đạt cực trị tại x , x nên x , x là nghiệm của phương trình 2
3ax  2bx c  0 ( y '  0) 1 2 1 2 x x  0 1 2 x , x  0  1 2 x .x  0  1 2  2b  0  
a  0  b  0 3a     . c
a  0  c  0   0   3a Trong các số a, ,
b c, d có một giá trị dương. Chọn đáp án C
Câu 43. Số nghiệm nguyên của bất phương trình 2 log
x  4  43log 4x 16  75  0 là 2   2 A. 2047. B. 2048. C. 2049. D. 2052. Lời giải: 2 log
x  4  43log 4x 16  75  0 2   2 x  4    2 4 log x  4  43log x  4 11  0   2   2   x  4    1   log x  4  11  2    4 x  4   1   11 4 2  x  4  2  1  4  4  2
x  2052.  x 5;6;7;...;205  2
Vậy số nghiệm nguyên của phương trình là 2048. Chọn đáp án B
Câu 44. Trong không gian Oxyz , cho hai điểm A1;1;  
1 , B 7; 2;2 và đường thẳng
x  1 3t
 :  y  2  2t . Gọi  P là mặt phẳng chứa đường thẳng  , khoảng cách từ A đến  P gấp
z  2  2t
đôi khoảng cách từ B đến  P và A , B nằm khác phía với  P . Biết rằng phương trình  P
có dạng ax by cz  28  0 . Giá trị của a b c bằng A. 2  6 . B. 26 . C. 34 . D. 34 . Lời giải:
Gọi H , K lần lượt là hình chiếu của ,
A B lên mặt phẳng  P và I là giao điểm của AB và
P . Khi đó   AHI đồng dạng với   BKI nên IA AH    
 2  IA  2IB  0  I 5;1;  1 IB BK
Khi đó  P chứa  và I nên có phương trình là  P :8x 15y  3z  28  0 .
Do đó: a b c  26 . Chọn đáp án B
Câu 45. Bạn An được gia đình gởi vào số tiền tiết kiệm 200 triệu đồng với lãi suất 0, 5% một tháng theo
thể thức lãi kép. Nếu mỗi tháng an rút ra một số tiền như nhau vào ngày ngân hàng trả lãi thì
hàng tháng An rút ra số tiền gần nhất với số nào sau đây để đúng sau 4 năm vừa hết số tiền trong sổ tiết kiệm?
A. 4687000 đồng.
B. 4697000 đồng.
C. 4690000 đồng.
D. 4700000 đồng. Lời giải: Áp dụng công thức
N (1 r)n r 200.1 0,5%48 .0,5% A  
 4, 697 triệu đồng n 1  r  1 1 0,5%48 1 Chọn đáp án B
Câu 46. Xét hai số phức z , z thỏa mãn z 1 i  1, z 1 i  2 và z z  2  2i  3 . Giá trị lớn 1 2 1 2 1 2
nhất của 3z  2z 1 5i bằng 1 2 A. 6  37. B. 5  23. C. 6  11. D. 6  13. Lời giải:
Gọi M , N lần lượt là điểm biểu diễn cho số phức z , z 1 2
Từ z 1 i  1 ta có MA  1 với A1;  1 1
Từ z 1 i  2 ta có NB  2 với B 1;  1 2
Xét z z  2  2i  3  z 1 i z  1 i  3 1 2  1   2        2 2
MA NB  3  MA NB  2M .
A NB  3  M . A NB  1
3z  2z 1 5i  3 z 1 i  2 z 1 i  6i  3 z 1  i  2 z 1 i  6i P  6 1 2  1   2   1   2   
Với P  3 z 1 i  2 z 1 i  3MA  2NB 1   2      Xét 2 2 2 2 2
P  3MA  2NB  9MA  4NB 12M .
A NB  9.1  4.2 12.1  37  P  37
Vậy giá trị lớn nhất cần tìm là 6  37 Chọn đáp án A
Câu 47. Cho phương trình log (2  )  4x x m
m với m là tham số thực. Có bao nhiêu giá trị nguyên 2
của tham số m  (27; 27) sao cho phương trình trên có nghiệm? A. 10. B. 26. C. 1. D. 53. Lời giải: m
Ta có: 2x m  0  x  2 x 2 log (2  )  4   log (2  )  2   2 x x m m x m x m  2x (1) 2 2 ( )  2t   (  )  2t f t t f t
.ln 2 1  0. Suy ra f (t) đồng biến trên  2 (1)  log (2  )  2  2   2 x   2  4x x m x x m m x 2
Đặt ( )  2  4x  (  )  2  4 . x g x x g x ln 4 x 1 g (  x)  0  4 
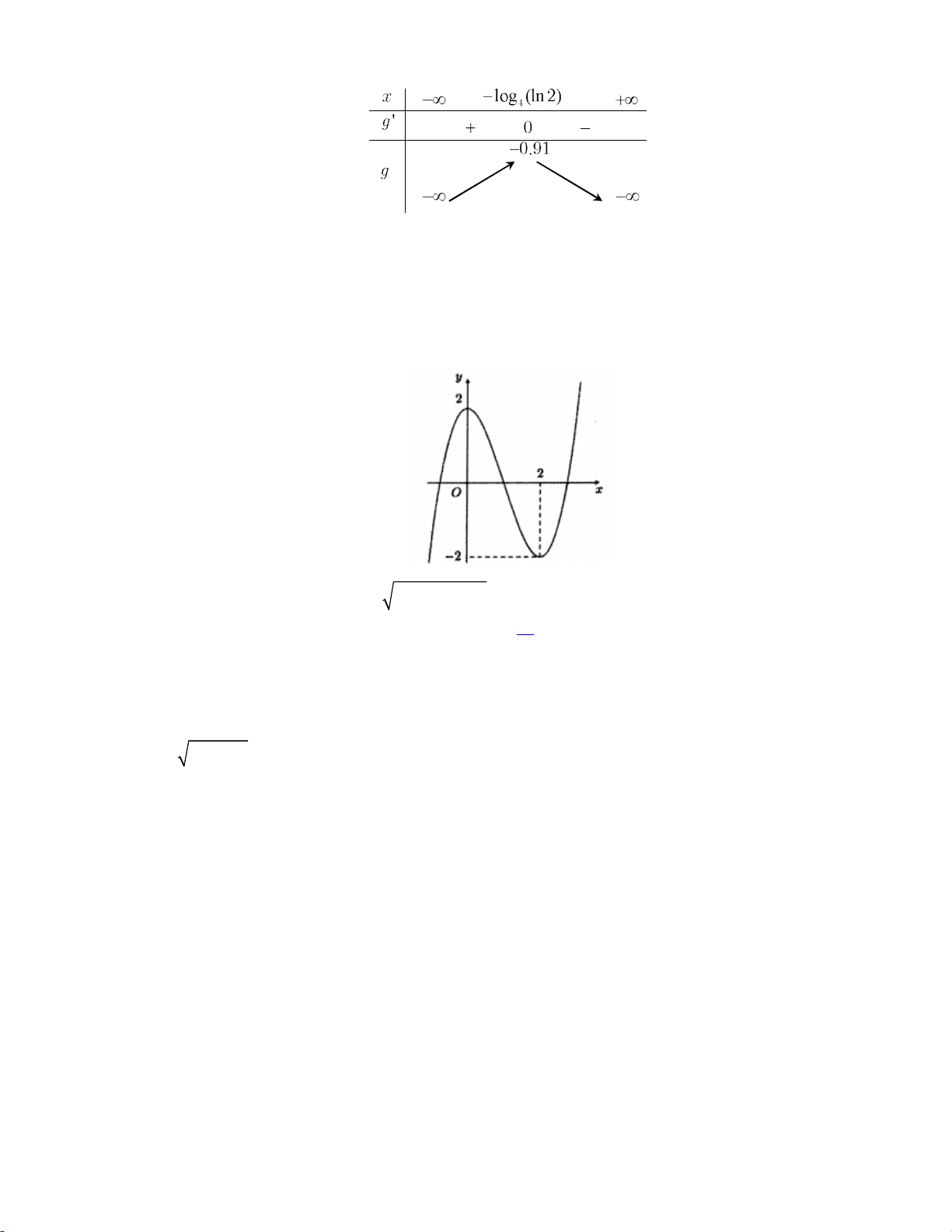
x   log (ln 2) 4 ln 2
Do m  (27; 27) nên phương trình có nghiệm khi 27  m  0.91 . Vậy có 26 giá trị nguyên
m thỏa yêu cầu bài toán. Chọn đáp án B Câu 48. Cho hàm số   3 2
f x x bx cx d có đồ thị là đường cong trong hình bên dưới.
Số nghiệm của phương trình
f f x  4  f x 1   là A. 7 . B. 4 . C. 3 . D. 2 . Lời giải:
Đặt t f x , Khi đó phương trình đã cho trở thành:   f t  2
 4  t  2t 1
f t  4  t 1   t   1     f t  2
t  2t  3*   t   1  
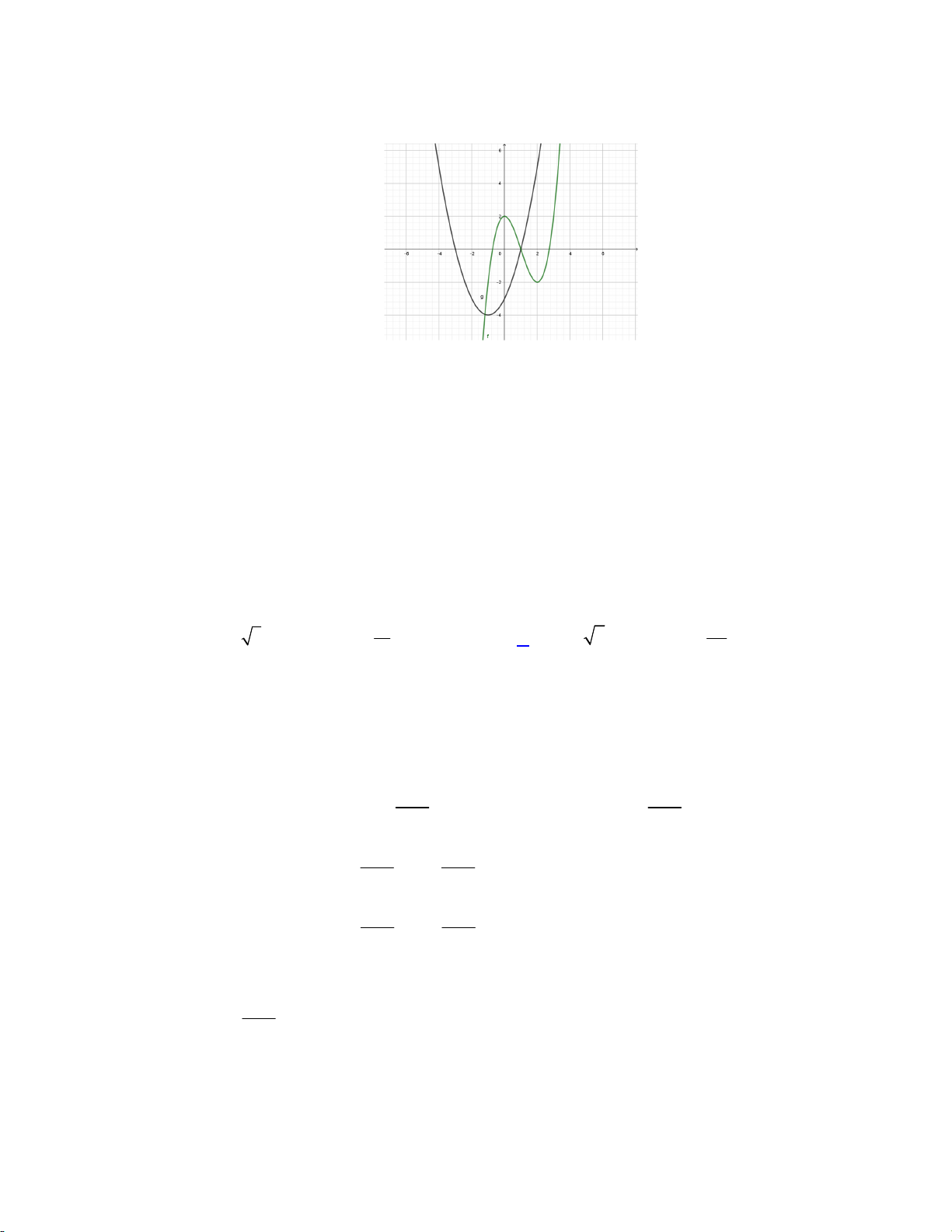
Vẽ thêm đồ thị hàm số 2
y t  2t  3 trên hệ trục trên
Dựa vào sự tương giao 2 đồ thị ta có: t t  1  l 1    f t  2
t  2t  3  t  1  t t  2  2
Dựa vào đồ thị ta có f x  1 có 3 nghiệm, f x  t  2 có 1 nghiệm 2 Chọn đáp án B y 1 
Câu 49. Cho hai số thực dương x, y thỏa mãn log  2
x  2 y   2 1   9  x
y 1 . Giá trị nhỏ nhất 3     của biểu thức 2
P x  2 y bằng 11 27 A. 5   6 3. B. . C. 4   6 2. D. . 2 5 Lời giải: Ta có: y log  x  2 1 2  y   2 1 
 9  x y   1   y   1 log  2
x  2 y   2 1   9  x y 1 3 3        log  9 9 2
x  2  log  y   2 1   x  log  2 x  2 2  x  2   log y  1  2 3 3 3 3   y 1 y 1  log  9 1 2 x  2 2  x  2   log  log 9 3 3 3 y 1 y 1  log  9 9 2 x  2 2  x  2   log 1 3 3   y 1 y 1 2 u
  x  2,u  0  Đặt  9 v  ,v  0  y 1 
Phương trình 1 trở thành log u u  log v v 3 3
Xét hàm số f t   log t t,t  0 3 1 f t  1  0, t   0 t ln 3
Suy ra hàm số f t  đồng biến trên 0;   9 9
Mà f u  f v nên 2 2
u v x  2   x   2. y 1 y 1 9 Do đó: 2
P x  2 y
 2 y  2, y  0 y 1  3 2  3 2 y 1  y  1    N  9 2 9 2 2 P  
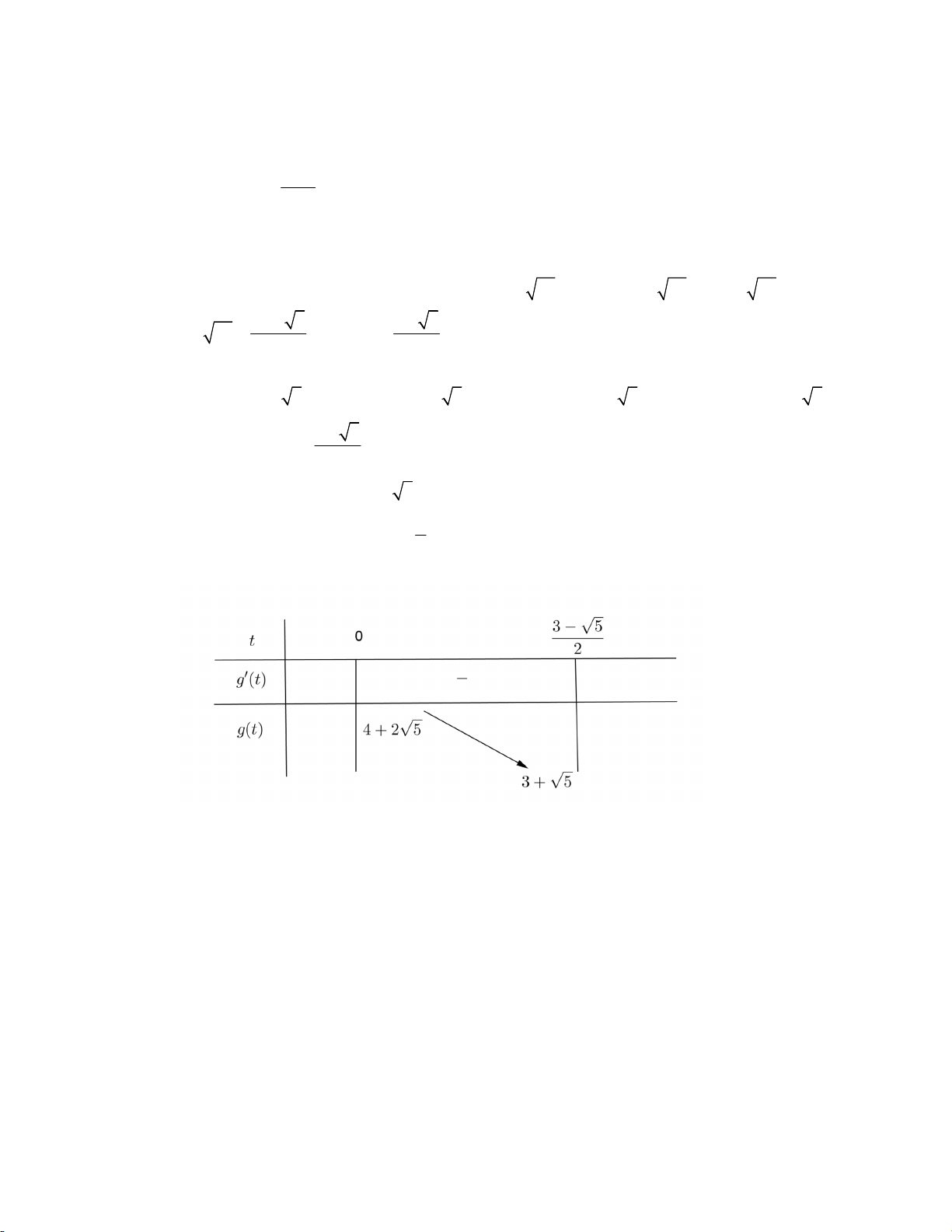
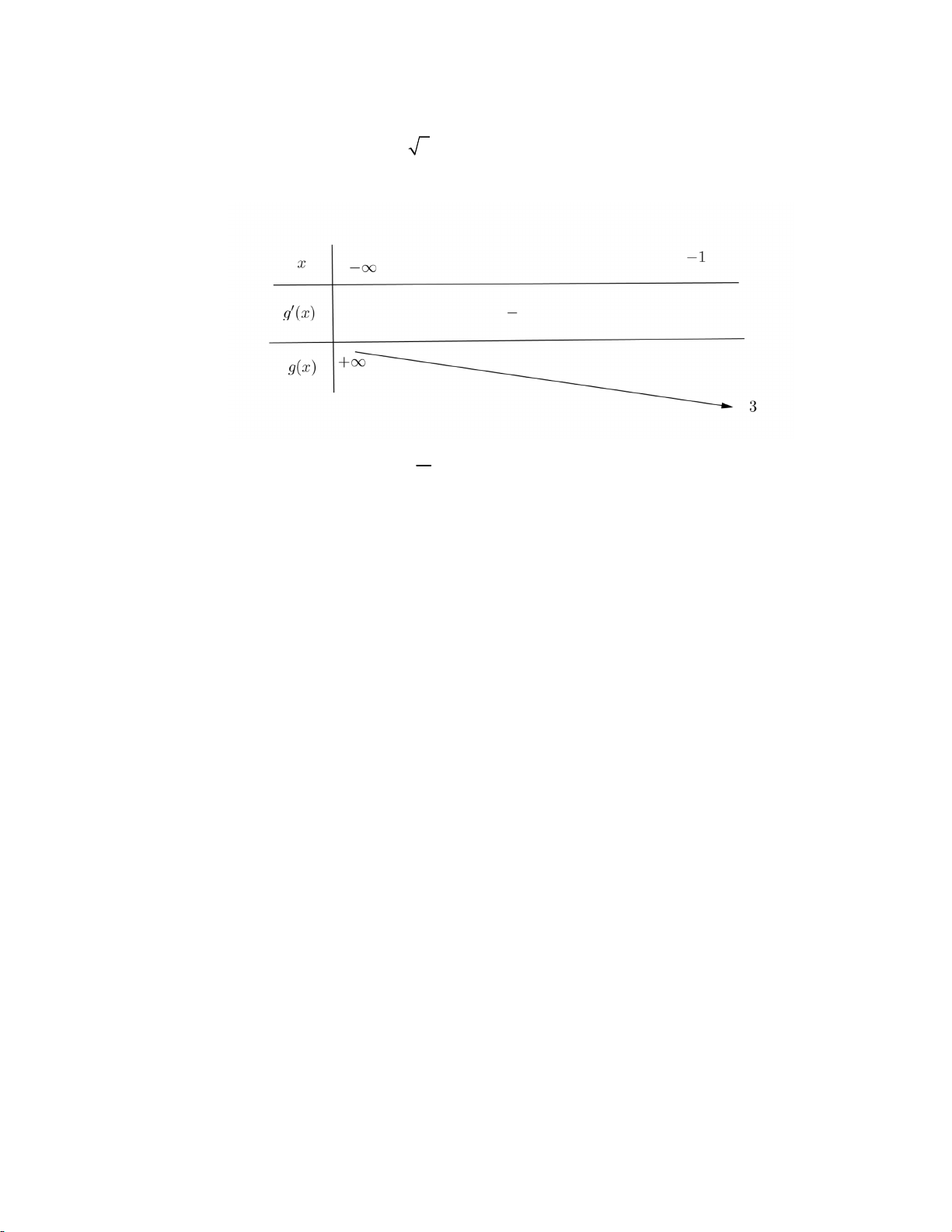
 2 , P  0   y   1       y  2 1 2  3 2  3 2  y 1    y   1  L  2  2 Bảng biến thiên
Vậy giá trị nhỏ nhất của P bằng 4   6 2. Chọn đáp án C
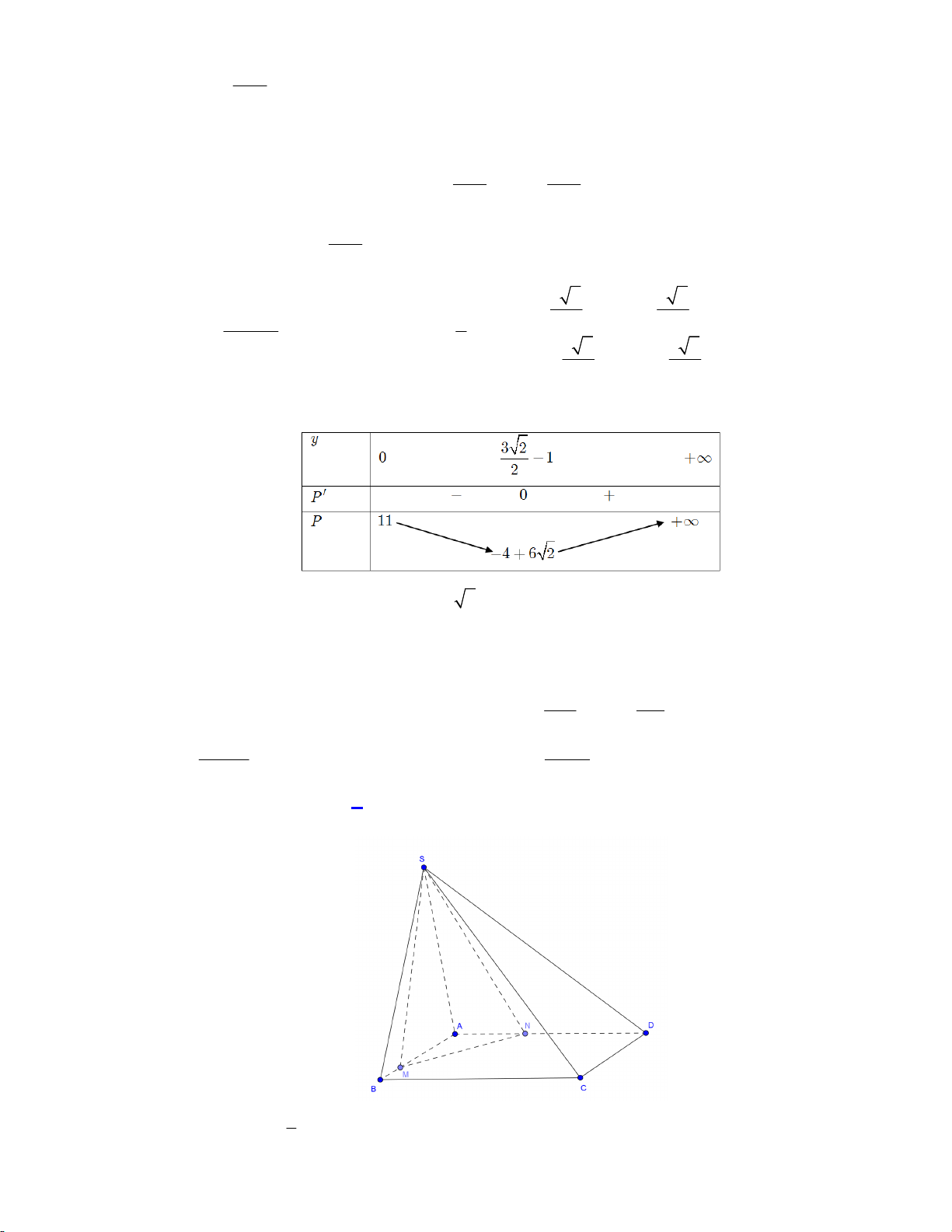
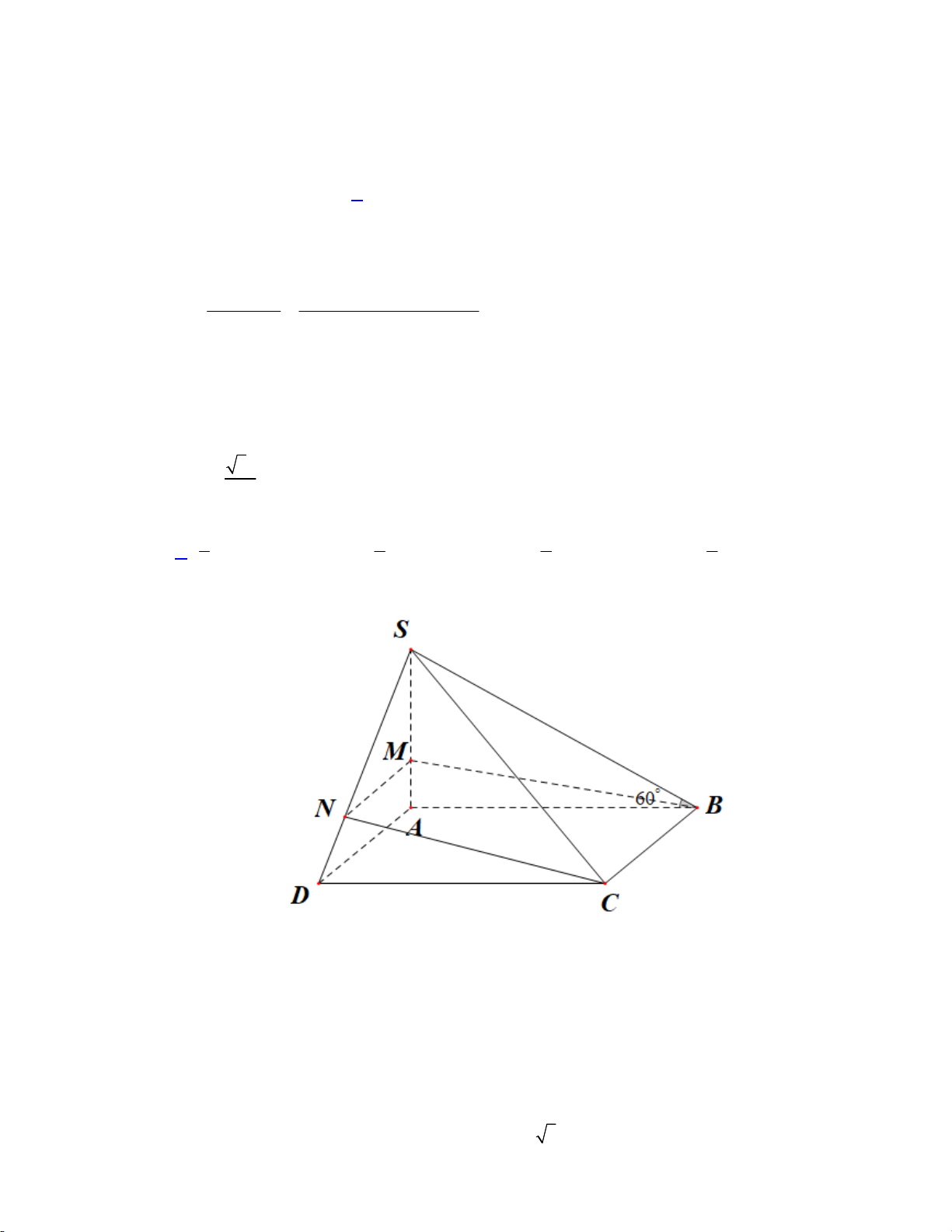
Câu 50. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt thuộc các đoạn AB AD
thẳng AB, AD ( M , N không trùng với A ) sao cho  x và
y thỏa mãn x  2 y  4 AM AN V V
và S.AMN đạt giá trị nhỏ nhất. Giá trị của 2 2 S . ABD x y  bằng V V S . ABCD S .AMN A. 9. B. 7. C. 5. D. 6. Lời giải: 1 Ta có: V
d S; ABCD .S S .AMN    3 AMN 1 V
d S; ABCD .S S. ABCD    3 ABCD 1 Mà: S
AM .AN.sin A AMN 2 1 S  2S  2. . AB A . D sin A ABCD ABD 2 S 1 AM AN AMN   . S 2 AB AD ABCD V 1 AM AN 1 1 1 1 1 1 S.AMN   .  . .  .  V 2 AB AD 2 x y 2 x 4  x x 4  x S. ABCD     2 2
x  4  x V 1
Vì: x 4  xS.   4 AMN      2  V 4 S. ABCDV  1 Khi đó: S.AMN
x  4  x x  2  y  1   V 4
S.ABCD min V Vậy: 2 2 S . ABD 2 2 x y   2 1  2  7 VS.AMN Chọn đáp án B GIẢI CHI TIẾT
ĐỀ THI THỬ MÔN TOÁN LỚP 12 SỞ CẦN THƠ NĂM HỌC 2020-2021 BẢNG ĐÁP ÁN 1.B 2.D 3.B 4.A 5.B 6.C 7.C 8.B 9.A 10.A 11.D 12.B 13.B 14.A 15.B 16.D 17.D 18.D 19.D 20.A 21.A 22.A 23.D 24.A 25.D 26.A 27.D 28.C 29.B 30.D 31.A 32.D 33.B 34.B 35.D 36.A 37.C 38.B 39.A 40.B 41.B 42.A 43.B 44.A 45.B 46.C 47.A 48.D 49.D 50.D Câu 1. Trong không gian
Oxyz, tọa độ một vectơ chỉ phương của đường thẳng x  28 z  5 y  21 d :   là 2 1  2
A. 2;1; 2. B. 2; 1  ; 2. C. 28;5;2  1 . D. 1; 1;  1 . Lời giải: x  28 z  5 y  21 x  28 y  21 z  5 Từ d :    d :   2 1  2 2 2 1 
Do đó một véctơ chỉ phương của d là u  2; 2;   1
Không có đáp án đúng
* Đề nghị sửa lại:
Câu 1. Trong không gian Oxyz, tọa độ một vectơ chỉ phương của đường thẳng x  28 y  5 z  21 d :   là 2 1 2
A. 2;1; 2. B. 2; 1  ; 2. C. 28;5;2  1 . D. 1; 1;  1 . Lời giải:
Một vectơ chỉ phương của d là u  2;1;2 Chọn đáp án B Câu 2.
Cho cấp số nhân u , biết u  2
 và công bội q  3. Số hạng u bằng n 1 2 A. 1  8. B. 6. C. 1. D. 6  . Lời giải: Áp dụng công thức: n 1 u u q  
u u q  2.3  6 n 1 2 1 Chọn đáp án D Câu 3.
Điểm cực đại của đồ thị hàm số 3
y x  3x  2019 là
A. 1; 2017. B.  1  ; 202  1 .
C. 0;2019.
D. 3; 2037. Lời giải: 2
y  3x  3  x  1  y  0   x  1 
Dựa vào bảng biến thiên ta có điểm cực đại của đồ thị hàm số là  1  ; 202  1 . Chọn đáp án B Câu 4.
Phần ảo của số phức 2020  2021i là A. 2021. B. 2021. C. 2020. D. 2020. Lời giải:
Phần ảo của số phức 2020  2021i là 2021. Chọn đáp án A 4 Câu 5.
Họ các nguyên hàm của hàm số 2
f (x)  3x   5 là x A. 3
x  ln x C. B. 3
x  4 ln x  5x C. C. 3
x  4 ln x  5x C. D. 3
x  ln x  5x C. Lời giải: 4
Họ các nguyên hàm của hàm số 2
f (x)  3x   5 là 3
x  4 ln x  5x C. x Chọn đáp án B Câu 6.
Diện tích xung quanh của hình trụ có bán kính đáy r  2 và độ dài đường sinh l  2 5 bằng
A. 6 5 .
B. 4 5 .
C. 8 5 .
D. 2 5 . Lời giải:
Diện tích xung quanh của hình trụ: S
 2 rl  2.2.2 5  8 5 . xq Chọn đáp án C Câu 7.
Thể tích khối lăng trụ có diện tích đáy 2
4a và có chiều cao 2a bằng 3 8a 3 4a A. . B. 3 6a . C. 3 8a . D. . 3 3 Lời giải:
Ta có công thức tính thể tích khối lăng trụ: 2 3 V  .
B h  4a .2a  8a . Chọn đáp án C Câu 8.
Thể tích của khối cầu có bán kính 2a bằng 8 32 16 4 A. 3  a . B. 3  a . C. 3  a . D. 3  a . 3 3 3 3 Lời giải: 4 4 32
Ta có công thức tính thể tích khối cầu là: V  R 2a3 3 3   a . 3 3 3 Chọn đáp án B Câu 9.
Cho hàm số y f x có bảng biến thiên như sau:
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là A. 2. B. 3. C. 4. D. 1. Lời giải:
Ta có: lim f x  , lim f x    x  1  là tiệm cận đứng. x 1 x 1  
lim f x  3  y  3 là tiệm cận ngang. x
Vậy tổng số tiệm cận là 2. Chọn đáp án A Câu 10. Cho hàm số 3 2
f ( x)  ax bx cx d , (a, , b c  ;
a  0) có đồ thị như sau:
Hàm số đã cho nghịch biến trong khoảng nào dưới đây? A. 1;. B. 1;  1 . C.  ;  0. D. 0;  1 . Lời giải:
Dựa vào đồ thị, hàm số nghịch biến trên khoảng 1;. Chọn đáp án A a
Câu 11. Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng
, SA vuông góc với mặt phẳng 2
( ABCD) và SA  3 .
a Thể tích khối chóp S.ABCD bằng 3 3a 3 3a 3 a 3 a A. B. C. D. 2 4 2 4 Lời giải: 2 3 1 1 a a V S.h  . .3a  3 3 4 4 Chọn đáp án D
Câu 12. Diện tích xung quanh của hình nón có độ dài đường sinh l và bán kính r bằng 1 A. 2 rl B.  rl C. 2  r h D. 2  r h 3 Lời giải:
Công thức diện tích xung quanh hình nón: S rl xq Chọn đáp án B 2
Câu 13. Tập nghiệm của bất phương trình x 4x5 3  9 là A. 1;5. B. 1;  3 . C. 1;5. D. 1;3. Lời giải: 2 2 x 4 x5 x 4 x5 2 2 2 3  9  3
 3  x  4x  5  2  x  4x  3  0  1  x  3. Chọn đáp án B
Câu 14. Hàm số f x liên tục trên .
 Mệnh đề nào sau đây đúng? 3 2 3 3 3 3 A.
f xdx f xdx f xd . x    B.
f xdx f xdx f xd . x    1 1 2 1 1 2 2 2 3 3 3 2 C.
f xdx f xdx f xd . x    D.
f xdx f xdx f xd . x    1 1 2 2 1 1 Lời giải: b c b Áp dụng tính chất:
f xdx f xdx f xd ;
x a c b.    a a c Chọn đáp án A
Câu 15. Trong không gian Oxyz, tọa độ tâm của mặt cầu S  2 2 2
: x y z  2x  2 y  6  0 là A. 1;1;3.
B. 1;1;0.
C. 2;2;0.
D. 2;2;6. Lời giải:
Ta có a  1, b  1  , c  0 Chọn đáp án B 4 0,2  3  1   1 
Câu 16. Giá trị của      bằng  32   8  9 33 A. 6. B. . C. . D. 18. 16 2 Lời giải: 4 0  ,2  4 4 3 3.  1   1  0,2 5.0,2 3 3   32  8  2  2  18      32   8  Chọn đáp án D
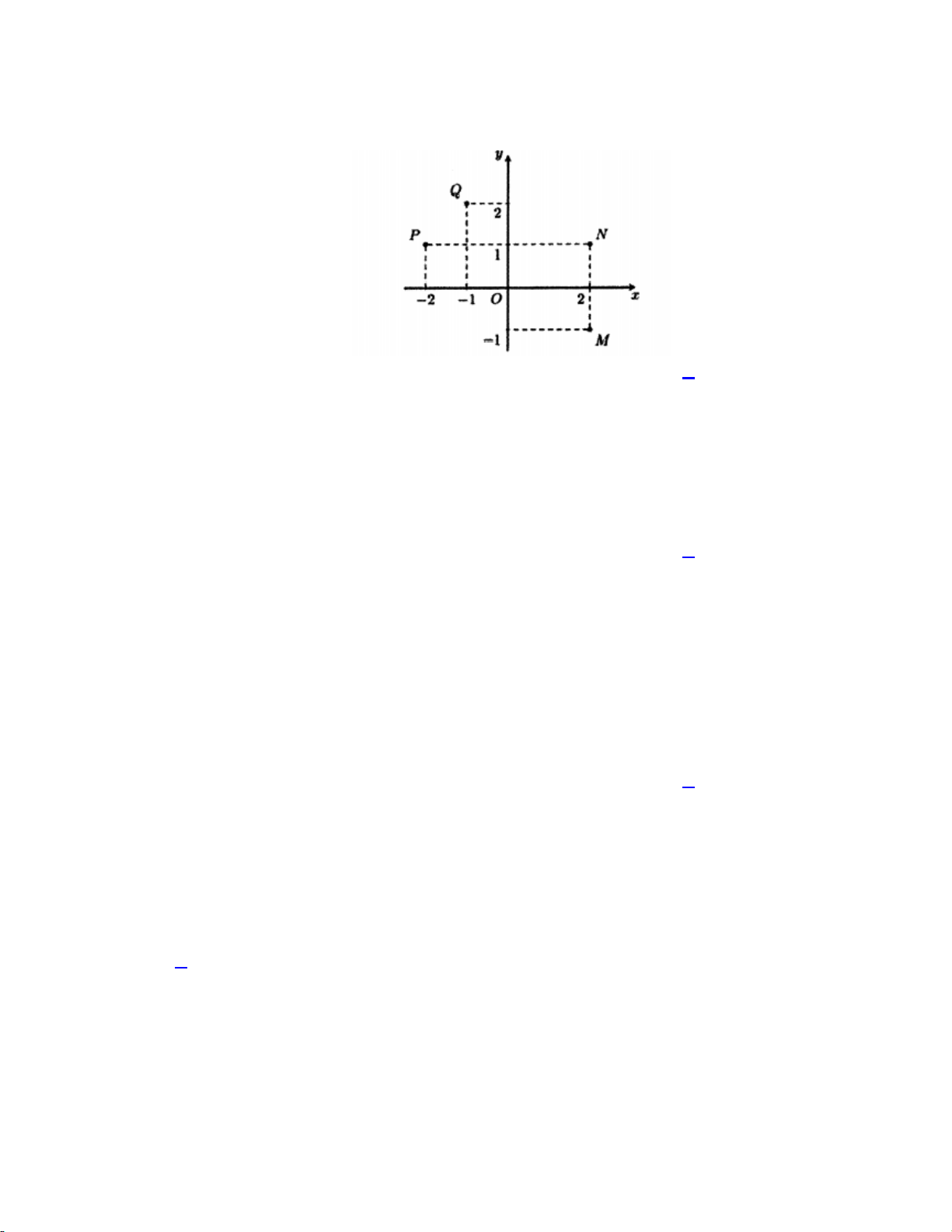
Câu 17. Trên mặt phẳng Oxy , điểm nào trong hình vẽ bên dưới là điểm biểu diễn của số phức
z  2  i ? A. . Q B. M . C. N. D. . P Lời giải:
z  2  i P  2  ;  1 . Chọn đáp án D
Câu 18. Nghiệm của phương trình log (x 10)  3 là 2 A. x  19. B. x  16. C. x  15. D. x  18. Lời giải:
Điều kiện x 10  0  x  10 3
x 10  2  x  18(n). Chọn đáp án D
Câu 19. Số cách sắp xếp 5 quyển sách Toán khác nhau và 3 quyển sách Ngữ văn khác nhau thành một hàng trên kệ sách là A. 5 3 A A . B. 5!3!. C. 5 3 C C . D. 8!. 8 8 8 8 Lời giải:
Vì mỗi cách sắp xếp thỏa YCBT là một hoán vị của 8 phần tử nên số cách sắp xếp là 8!. Chọn đáp án D
Câu 20. Tập xác định của hàm số y   x  202  1 là
A. 2021; . B.  ;  202  1 . C.  \ 202  1 .
D. 2021;. Lời giải:
ĐK: x  2021  0  x  2021
Vậy TXĐ là 2021; . Chọn đáp án A 2
Câu 21. Cho hàm số f x có đạo hàm liên tục trên đoạn 0;2 thỏa f 2  12, xf  x  8.  Giá trị 0 2 f x  bằng 0 A. 16. B. -32. C. 32. D. -16. Lời giải: u   . x  du d . x  Đặt    dv f '   xd . x v f    x.  2 2 2 2
Nên xf ' xdx
= xf x  f x  2 f 2  0 f 0  f x  8.   0 0 0 0 2 Suy ra
f xdx  2.12  8  16.  0 Chọn đáp án A
Câu 22. Cho x, y là 2 số thực thỏa mãn 2x y  2xi   x  3   y x  2 .
i Giá trị của 16xy bằng 1 11 11 A. 11. B.  . C.  . D. . 4 4 6 Lời giải:  1 x  
2x y x  3.
x y  3   4 Ta có     
2x y x  2. 3x y  2 11    y     4
Vậy giá trị của 16xy  11. Chọn đáp án A
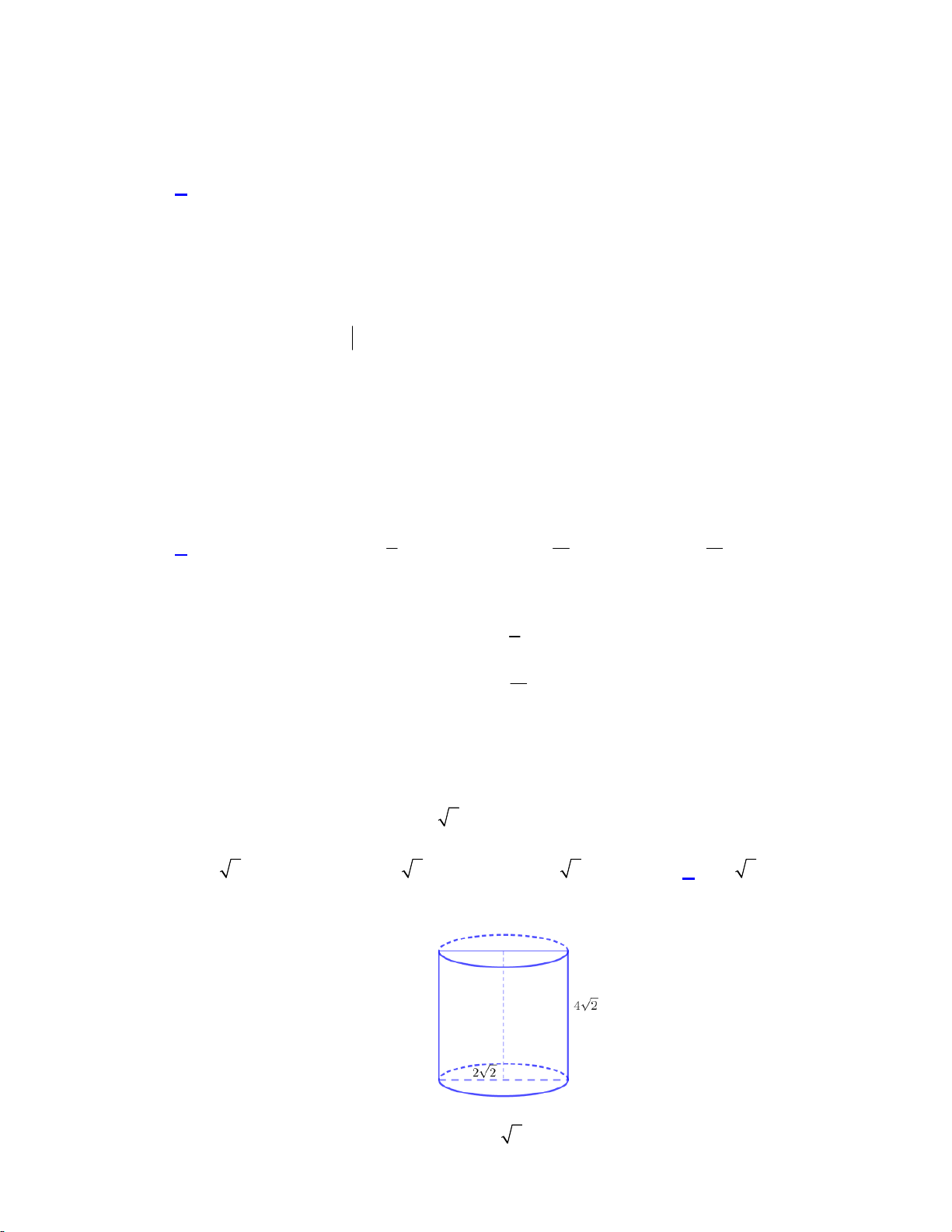
Câu 23. Cho hình trụ có bán kính đáy bằng 2 2 và thiết diện qua trục là một hình vuông. Thể tích của khối trụ đã cho bằng
A. 62.
B. 162.
C. 82.
D. 322. Lời giải:
Do thiết diện qua trục là hình vuông nên h  4 2 2
Thể tích của khối trụ là V 2 2 .4 2   32 2 Chọn đáp án D 16
Câu 24. Giá trị nhỏ nhất của hàm số 2 y x
trên đoạn [1; 4] bằng x A. 12. B. 17. C. 20. D. 4  . Lời giải: 16 3 16 2x 16 Ta có: '
f (x)  2x ; '
f (x)  0  2x   0 
 0  x  2 2 x 2 2 x x 16 2 f (1)  (1)   17 1 16 2 f (2)  (2)   12 Vậy f  12. 2 min 16 2 f (4)  (4)   20 4 Chọn đáp án A
Câu 25. Với a  log 3, giá trị của log 9  log 6 bằng 2 2 2 A. 5a 1. B. 5a  2. C. 5 . a
D. 5a 1. Lời giải: Ta có 2 log 9  log 6  log 3  log
2.3  4 log 3 1 log 3  5a 1. 1 2 2   2 2 2 2 2 Chọn đáp án D
Câu 26. Cho hàm số f x 4 2
ax bx c,a,b,c  , a  0 có đồ thị như sau:
Số nghiệm thực của phương trình f x  2 ln 6  0 là A. 4. B. 3. C. 2. D. 0. Lời giải:
Ta có: f x  2ln 6  0  f x  2  ln 6   1
Số nghiệm phương trình (1) chính là số giao điểm của 2 đồ thị hàm số y f x và y  2  ln 6
Dựa vào đồ thị ta thấy có 4 giao điểm.
Vậy phương trình f x  2 ln 6  0 có 4 nghiệm phân biệt. Chọn đáp án A Câu 27. Cho hàm số 4 2
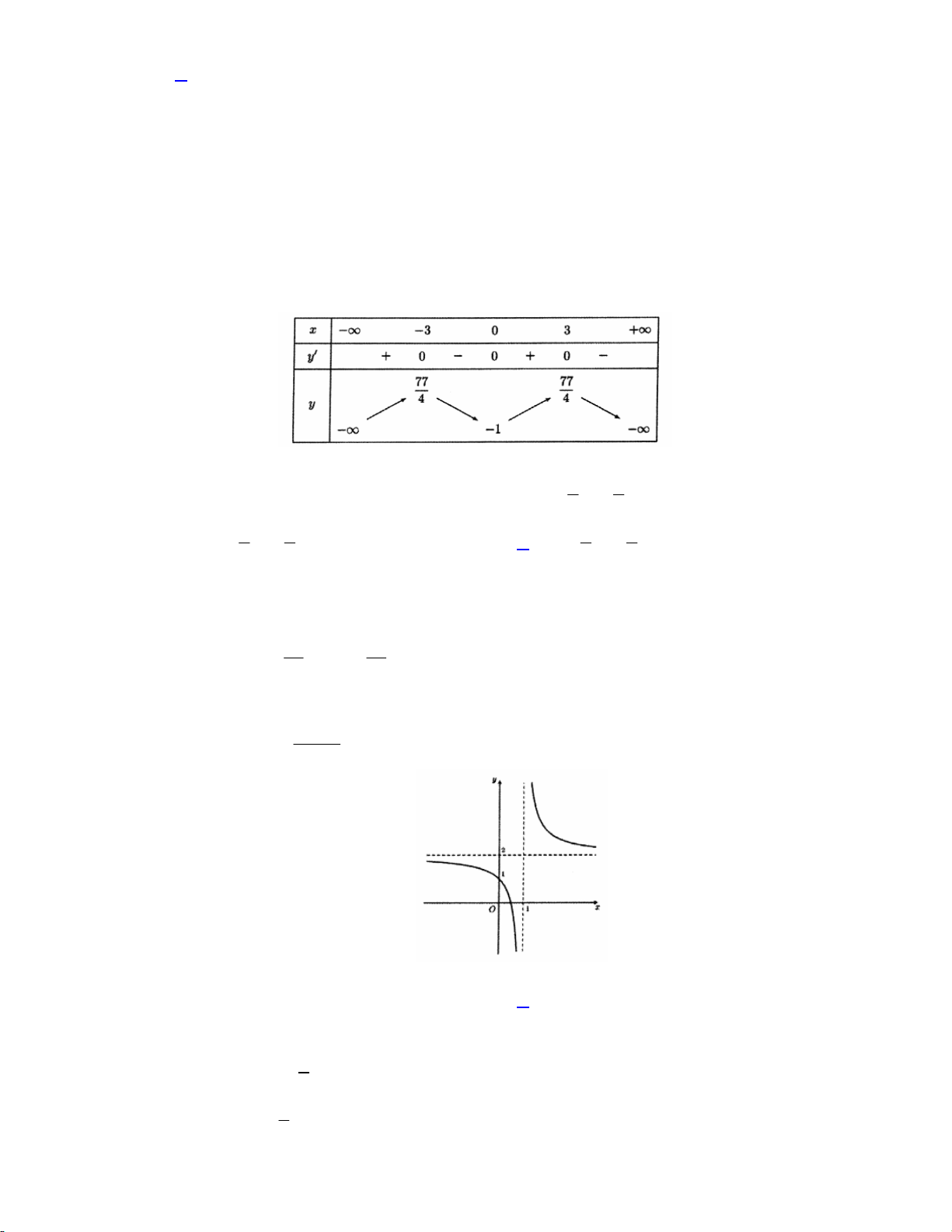
y ax bx c (a, , b c  ;
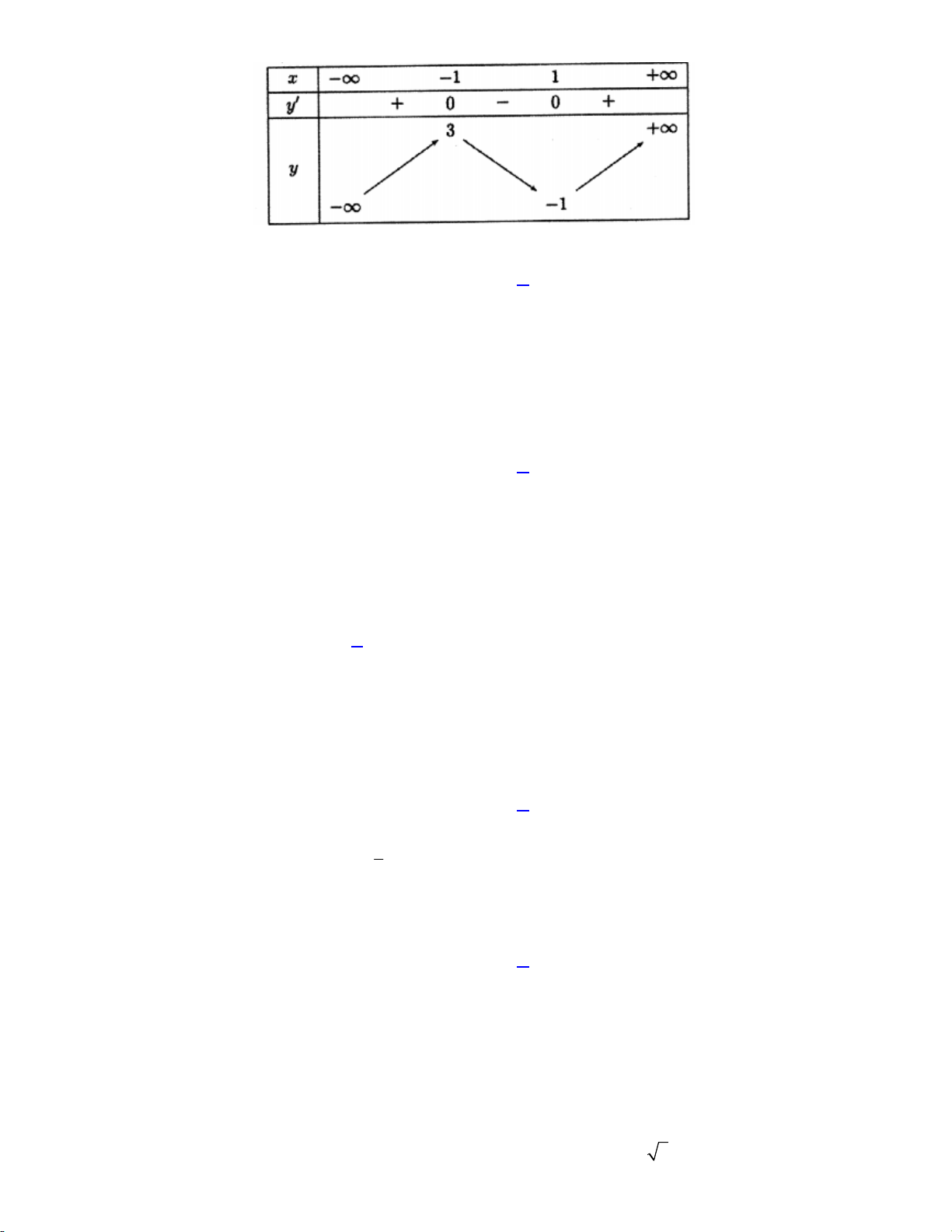
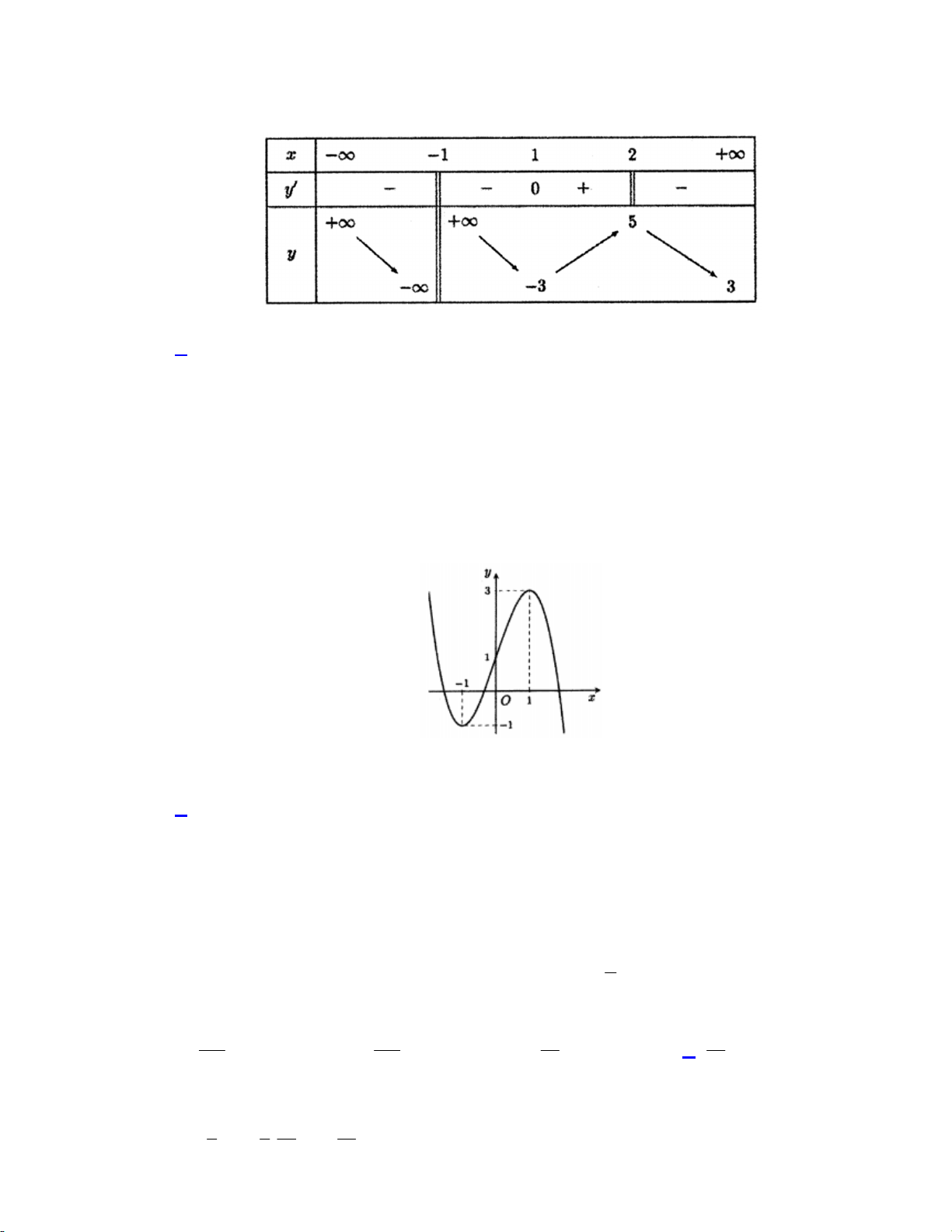
a  0) có bảng biến thiên như sau:
Bảng biến thiên đã cho là của hàm số nào dưới đây? 1 9 A. 4 2
y  x 18x 1. B. 4 2 y x x 1. 4 2 1 9 1 9 C. 4 2 y   x x 1. D. 4 2 y   x x 1. 4 2 4 2 Lời giải: Hàm số 4 2
y ax bx c (a,b, c  ;
a  0) có 3 cực trị và hệ số a  0 nên loại đáp án B,C . 77 77 Ta có: y(3)  ; y(3) 
; y(0)  1 nên chọn đáp án D 4 4 Chọn đáp án D ax  2
Câu 28. Cho hàm số y  (a, ,
b c  ) có đồ thị như sau: bx c
Khẳng định nào dưới đây đúng?
A. b a  0  . c
B. b  0  a  . c
C. a b  0  . c
D. b  0  c  . a Lời giải: 2
Cho x  0  y   1  c  2 c c TCĐ x  1  
b  c  2 ; b a TCN y  2 
a  2b  4 b
a b  0  . c Chọn đáp án C Câu 29. Trong không gian Oxyz , cho hai mặt phẳng
() : 2x y z  2021  0 và
() :  3x  4 y  5z  2021  0 . Góc giữa hai mặt phẳng () và mặt phẳng () bằng A. 0 150 . B. 0 30 . C. 0 120 . D. 0 60 . Lời giải: Ta có:   2 2 2 n  (2; 1; 1  )  n  2  (1)  ( 1  )  6.   2 2 2 n  ( 3  ; 4;5)  n  ( 3  )  4  5  2 5.  
n .n  2.(3)  (1).4  (1).5  15.
Gọi là góc giữa hai mặt phẳng () và mặt phẳng () , ta có:   n .n 15 3
cos     n . n 6.2 5 2 0   30 Chọn đáp án B
Câu 30. Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc với mặt phẳng
( ABCD) (tham khảo hình vẽ).
Góc giữa hai mặt phẳng (SCD) và mặt phẳng ( ABCD) là     A. SDC. B. SCD. C. DS . A D. SD . A Lời giải: Ta có:  SCD
ABCD    SD AD  ( ), ( ) ,  SDA Chọn đáp án D
Câu 31. Trong không gian Oxyz, cho hình hộp ABC . D AB CD   có (
A 1; 0;1), B(2;1; 2), D(1; 1  ;1) và  A (
 1;1; 1). Tọa độ AC là
A. (1;1; 1). B. (1;1;1).
C. (0;1; 2). D. (0; 1;0). Lời giải:  
Ta có AA  (0;1; 2), AB  (1;1;1) 
Giả sử C(x, y, z) suy ra DC  (x 1; y 1; z 1) x 1  1 x  2    
Ta có AB DC   y 1  1   y  0  C(2;0; 2) z 1 1    z  2    Gọi C (
x , y , z )
 suy ra CC  (x  2; y ; z  2) x  2  0 x  2    
Ta có AA  CC   y  1
  y '  1  C (  2;1;0) z  2  2   z  0   
Vậy AC  (1;1; 1) Chọn đáp án A
Câu 32. Cho số phức z thỏa mãn 2
(3  i)z  2  i  (1 2i) .
i Môđun của số phức z bằng A. 5. B. 5. C. 2. D. 2. Lời giải: 2
2  i  (1  2i) i Ta có z   1
  i z  2 3  i Chọn đáp án D
Câu 33. Số giao điểm của hai đồ thị hàm số 4 2
y  x  2x 1 và 3
y  x x là A. 3 . B. 4 . C. 2 . D. 1. Lời giải:
Phương trình hoành độ giao điểm 4 2 3
x  2x 1  x x x  1  x  1   4 3 2
 x x  2x x 1  0 1 5  x  . 2   1  5  x   2
Phương trình hoành độ giao điểm có 4 nghiệm nên số giao điểm của đồ thị hai hàm số đã cho là 4. Chọn đáp án B
Câu 34. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số 3 2
y x  2x 1 và 2
y x  1 là 189 27 3 A. . B. . C. 6 D. . 4 4 4 Lời giải: x  0
Phương trình hoành độ giao điểm 3 2 2
x  2x 1  x  1 3 2
x  3x  0   . x  3  3 27
Diện tích hình phẳng cần tìm là 3 2 S
x  3x dx   . 4 0 Chọn đáp án B
Câu 35. Gọi z , z là hai nghiệm phức của phương trình 2
z  6z  73  0. Giá trị của biểu thức 1 2 2 2
z z z . z bằng 1 2 1 2 A. 2  13. B. 1  10. C. 37. D. 1  83. Lời giải:
z z z z   z z 2 2 2
 2z z z z 1 2 1 2 1 2 1 2 1 2 2  6  2.73  73  1  83. Chọn đáp án D 2 dx Câu 36. Biết
a ln 2  b ln 3  c ln 5 a, , b c  
 . Giá trị a b c bằng 2   2x  3x 1 1 A. 4. B. 0. C. 6. D. 2. Lời giải: 2   1 2 2 x dx  1 1  Cách 1.   .dx  2  ln
 ln10  ln 9  ln 2  2 ln 3  ln 5 2    2x  3x 1 1 x 1 x 1 1 1  x    2  1
a  1, b  2, c  1  a b c  4. 2 dx Cách 2. Đặt I  . Khi đó: 2 2x  3x 1 1
a ln 2  b ln 3  c ln 5  I  ln 2 .a3 .b5c   I a b c I 10 2  2 .3 .5  e   2.3 .5 9
a  1,b  2
 , c  1  a b c  4. Chọn đáp án A x 1 y z  2
Câu 37. Trong không gian Oxyz, cho đường thẳng d :   và mặt phẳng 1 1 1
P : 2x y  2z 1  0. Đường thẳng  nằm trong P, cắt và vuông góc với d có phương trình là x  2 y 1 z  3 x 1 y  1 z 1 A.   . B.   . 3 4 1 3 4 1 x  5 y  3 z  4 x  2 y 1 z  3 C.   . D.   . 3 4 1 3 4 1 Lời giải: Ta có:  
   P  VTPT :
n n  2; 1; 2 1 p  
  d A A  1 t; t
 ; 2  t  thế điểm A vào P : 21 t   t  22  t 1  0
t  1  A2; 1;3 
  d VTPT :
n  1; 1;1 2     
VTCP  : u  n ; n   3; 4;1  Loại câu D. 1 2    
Vậy thế A2;1;3 vào câu C thỏa. Chọn đáp án C
Câu 38. Cho hàm số bậc bốn y f x và có đồ thị f ' x như sau:
Số điểm cực trị của hàm số g x  f  2 x   1 là A. 1. B. 3. C. 2. D. 4. Lời giải: Ta có: 
2x  0  x  0   x  0  x  0  
g ' x  2xf ' 2 x   1  0    x   3   f ' 2 x   1  0  x   3    x  3    x  3   Chọn đáp án B
Câu 39. Trong không gian Oxyz, cho mặt cầu 2 2 2
(S ) : (x 1)  ( y 1)  (z  2)  4 và điểm A(1;1; 1).
Ba mặt phẳng đi qua A và đôi một vuông góc với nhau, cắt mặt cầu (S ) theo ba giao tuyến là
các đường tròn (C ), (C ) và (C ). Tổng diện tích của ba hình tròn (C ), (C ) và (C ) bằng 1 2 3 1 2 3
A. 11.
B. 9.
C. 12. D. 8. Lời giải:
+ Mặt cầu (S) có tâm I (1;1; 2) và bán kính R  2.
+ Vì IA  1  2  R nên điểm A nằm bên trong mặt cầu (S ).
+ Gọi (P ) là mặt phẳng đi qua A và vuông góc với 2 2 IA r R IA  3 1 1
+ Gọi (P ), (P ) là mặt phẳng chứa IA và (P )  (P )  r r  2 2 3 2 3 2 3
Vậy S S S  r  r  r . 32 2 3 2 2 2
.2  .2  11. 1 2 3 1 2 3 Chọn đáp án A
Câu 40. Ông An gửi 200 000 000 đồng vào một ngân hàng với lãi suất ban đầu là 6,8% năm và tiền lãi
hằng năm được nhập vốn. Cứ sau 1 năm lãi suất tăng thêm 0, 2%.Sau 5 năm ông An thu được
tổng số tiền ( làm tròn đến hàng nghìn) là A. 283135 000 đồng.
B. 283137 000 đồng. C. 283140 000 đồng. D. 283 130 000 đồng. Lời giải:
Gọi S là số tiền ông An nhận sau n năm, A là số tiền ban đầu, r là lãi suất n
S A 1 r 1  
S S (1 r  0.2) 2 1
Suy ra S S (1  r) 1 r  0.2% 1  r  0.4% 1 r  0.6% (1 r  0.8%)  283137 000 5 1     Chọn đáp án B
Câu 41. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, BC a, AB  2a và SA  3 . a Biết
rằng mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng
(ABCD). Khoảng cách từ điểm D đến mặt phẳng (SAC) bằng 2 82a 4 82a 82a 82a A. . B. . C. . D. . 41 41 41 82 Lời giải:
Gọi I, K, M, lần lượt là trung điểm AB, CD, DK
O, N lần lượt là giao điểm của AC và BD, IM và AC
IH là đường cao của ΔSIN vuông tại I
Khi đó: IN là đường cao của ΔAIO vuông tại I và ΔSIA vuông tại I nên ta có 1 1 1 1 1 1 1 1 1 41          2 2 2 2 2 2 2 2 2 IH IN SI IA IO SA AI aa  3a2 2 2  a 8a    2  2 82aIH  41 1 1
Mà IH d I ,SAC   d B, SAC   d D, SAC  2 2   a
d D SAC  4 82 ,  2IH  41 Chọn đáp án B
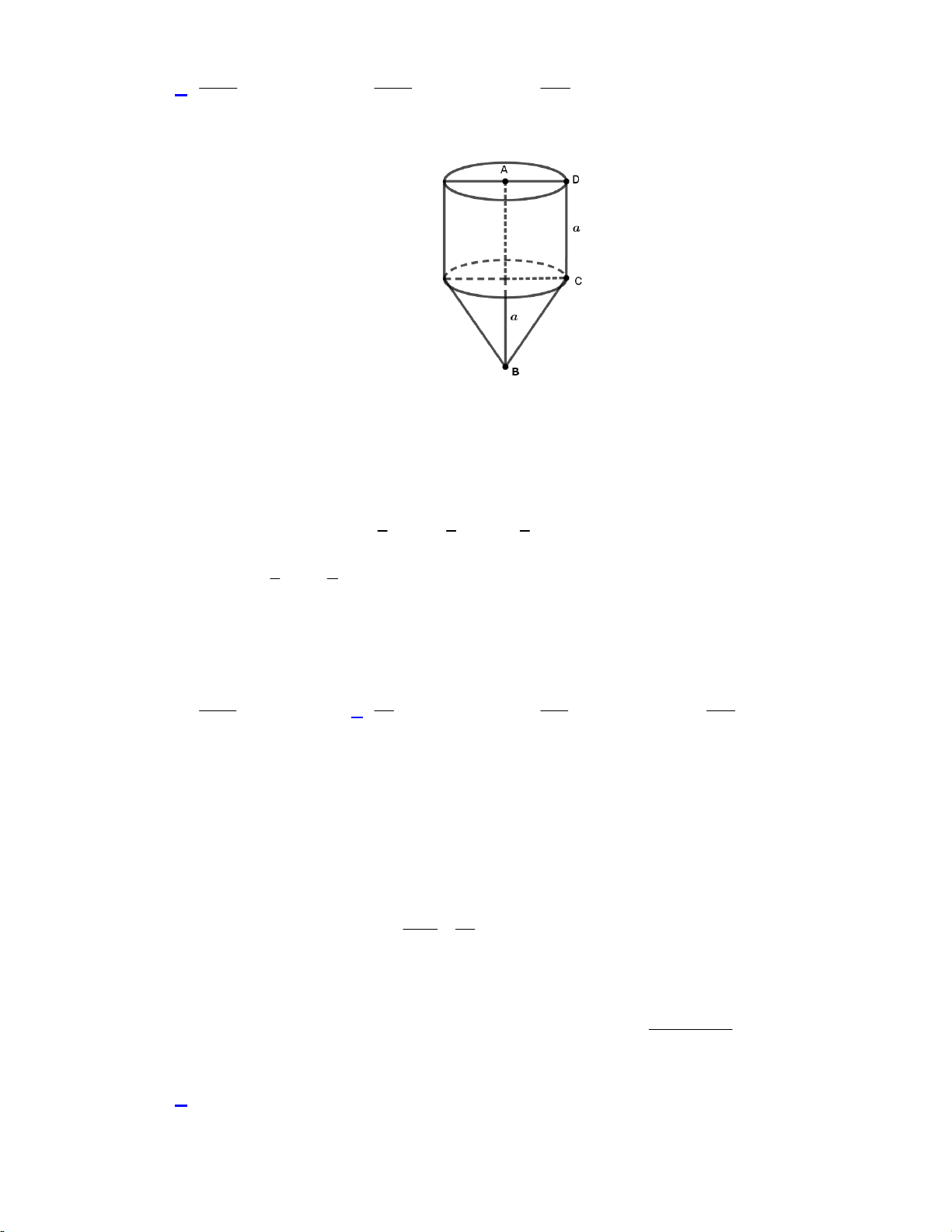
Câu 42. Cho hình thang ABCD vuông tại A và D, AD CD a, AB  2 .
a Quay hình thang ABCD
quanh cạnh AB được một khối tròn xoay có thể tích là 3 4 a 3 5 a 3  a A. . B. . C. . D. 3  a . 3 3 3 Lời giải:
Quay hình thang ABCD quanh cạnh AB được một khối tròn xoay gồm hai khối là khối trụ và
khối nón có cùng bán kính đáy là . a
Gọi V là thể tích của khối tròn xoay. Ta có: V V V 1 2
V là thể tích khối trụ, 2 2 3
V  r .h .a .a .a 1 1 1 1 1
V là thể tích khối nón, 2 2 3 V
 r .h .a .a .a 2 2 3 3 3 1 4 3 3 3
V  a  a  a 3 3 Chọn đáp án A
Câu 43. Xếp ngẫu nhiên 6 bạn nam và 5 bạn nữ ngồi vào 11 cái ghế được bố trí thành một hàng ngang.
Xác suất để 5 bạn nữ ngồi cạnh nhau là 1 1 1 1 A. . B. . C. . D. . 7920 66 231 462 Lời giải:
Số phần tử của không gian mẫu là: n   11!.
Gọi B là biến cố “5 bạn nữ ngồi cạnh nhau”
Khi đó: n B  7!5!. 7!.5! 1
Vậy xác suất cần tìm là P B   . 11! 66 Chọn đáp án B mx  2025
Câu 44. Số các giá trị nguyên của tham số thực m sao cho hàm số y  đồng biến trên x m khoảng 2;2 là A. 86 . B. 88 . C. 89 . D. 84 . Lời giải: mx  2025 y
. Tập xác định: D   \   m . x m 2 m  2025 y  .  x m2
Hàm số đồng biến trên khoảng 2;2 khi y  0, x  2; 2 2 m  2025  0  4  5  m  45   2  m  45  m  2  m  2   45  m  2    m  2 m  2  
Vậy m 2,3,..., 4  4  4  4,  43,...,  
2 . Có 86 giá trị m . Chọn đáp án A
Câu 45. Có 4 học sinh nam và 8 học sinh nữ, trong các bạn nữ có An và Bình. Xếp những học sinh này
thành một hàng ngang. Xác suất để mỗi bạn nam đều đứng giữa hai bạn nữ đồng thời An và
Bình luôn đứng cạnh nhau bằng 1 1 1 2 A. . B. . C. . D. . 264 132 396 33 Lời giải:
Số phần tử của không gian mẫu n   12!
Gọi A là biến cố: “mỗi bạn nam đều đứng giữa hai bạn nữ đồng thời An và Bình luôn đứng cạnh nhau”
- Xem bạn An và Bình là 1 bạn nữ.
- Xếp 7 bạn nữ theo hàng ngang có 7! cách
- Giữa các bạn nữ có 6 chỗ trống, xếp 4 nam vào 6 chỗ trống đó có 4 A cách 6
- Hoán vị An và Bình với nhau có 2!cách n A 4  7!.A .2! 6 n A 1 P A   . n  132 Chọn đáp án B
Câu 46. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a và O là tâm của hình vuông
ABCD . Gọi mặt phẳng  P là mặt phẳng qua S , song song với đường thẳng BD , cắt đoạn 3 10a
OC và khoảng cá ch từ A đến mặt phẳng  P bằng
. Biết rằng  P chia khối chóp 10
thành hai khối đa diện, trong đó khối đa diện chứa điểm A có thể tích V và khối đa diện còn 1 V
lại có thể tích V . Giá trị của 2 bằng 2 V1 2 1 1 3 A. . B. . C. . D. . 7 8 7 8 Lời giải: 2 a a 2 Ta có 2 2 2 SO
SB OB a   . 4 2
Đặt OF x d  , A P 2 2 AF 3 10aa 2  SO .OF Ta có   .x    x .
d O, P 2 2 OF 10  2  SO OF   Chọn đáp án C
Câu 47. Có bao nhiêu số nguyên ( ;
x y) thỏa mãn 2  x  2020 và 2  y  2021 sao cho
log y  6 log x  5? x y A. 54. B. 11. C. 43. D. 52. Lời giải: 2 6 log y  2  y x
log y  6 log x  5  log y   5  0 x   x y x   3 log y log y  3 xx y x  2 2  x  2021
 2  x  2021  44,95
Ta có 2  y  2021     2 3 3 2  x  2021 
 2  x  2021  12, 64  Chọn đáp án A
Câu 48. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho đồ thị hàm số 3
y x  3x  2 cắt đường thẳng 2
d : y m x  
1 tại 3 điểm phân biệt có hoành độ x , x , x thỏa mãn 1 2 3 3 3 3
x x x  2057 . Số phần tử của tập S là 1 2 3 A. 19 . B. 36 . C. 18 . D. 37 . Lời giải:
Ta có phương trình hoành độ giao điểm của đồ thị hàm số và đường thẳng d 3 2
x  3x  2  m x   1   x   2 2
1 x  2x  2  m   0 x  1 3   2 2
x  2x  2  m  0  *  x x  2 Từ đó ta có: 1 2  2
x x  m  2  1 2 3 Theo đề bài: 3 3 3
x x x  2057   x x  3x x x x  2056 1 2  1 2  1 2  1 2 3 1024    2
6 m  2  2048 2  m  2  3 1024 1018 1018 1018 2  m   2     m  3 3 3 3
Vì m   nên m 18; 1  7;...;17;1  8
Vậy có 37 giá trị nguyên m cần tìm Chọn đáp án D z
Câu 49. Cho số phức z thỏa mãn
 1 i  1 sao cho z  3  8i đạt giá trị lớn nhất tại z x y i 3  4i 1 1 1
và đạt giá trị nhỏ nhất tại z x y .
i Giá trị của x x y .y bằng 2 2 2 1 2 1 2 A. 44. B. 55. C. 25. D. 46. Lời giải:
Gọi M là điểm biểu diễn số phức z và A3;8 là điểm biểu diễn số phức w  3  8i . z Ta có
1 i  1  z 1 7i  3  4i z  1 7i  5 3  4i
Suy ra tập hợp các điểm biểu diễn số phức z là đường tròn C tâm I 1;7 , bán kính R  5. 2 2
Phương trình đường tròn C  là  x   1
  y  7  25 x  1 2t
Phương trình đường thẳng IA :  y  7  t
Gọi M , M lần lượt là giao điểm của đường thẳng IA và đường tròn C . 1 2
Ta có z  3  8i  MA . Dựa vào hình vẽ ta thấy AMAM , AMAM min 2 max 1 2 2
Xét phương trình   t      t   2 1 2 1 7 7
 25  t  5  t   5
- Với t  5  M 1 2 5;7  5  z  1 2 5  7  5 i 2   1  
- Với t   5  M 1 2 5; 7  5  z  1 2 5  7  5 i 2   1  
Vậy x x y .y  1 2 5  1 2 5  7  5 7  5  46. 1 2 1 2        Chọn đáp án D     xy x y xy 1
Câu 50. Cho x, y là các số thực dương thỏa mãn 2 3 2 
. Giá trị nhỏ nhất của biểu thức 1 xy 2 2
x y  2 5 bằng A. 3  2 5. B. 3  2 5. C. 3  5. D. 3  5. Lời giải: Ta có:     xy x y xy 1 2 3 2    1 x yx, y  0 x, y  0 Điều kiện:    . 1 xy  0 xy  1       xy x y xy 1   2 3 1  log 2  log 2 2 x y 1 xy
x y  2xy  3  log2 x y 2 1 xy
x y  2xy  2  log 2 x y
  x y  2 xy  
1  log 2 1  xy   log x y 2     2  
  x y  log x y  2 1 xy  log 2 1 xy  2     2     (*)
Xét hàm: f t   t  log t t  0 2   1
Vì: f 't   1
 0  f t  đồng biến trên 0;  . t ln 2
Từ (*), ta được: f x y   f 21 xy  x y  2  2xy  
Với: x y  2  2xy
Áp dụng Bất đẳng thức Cauchy ta được: x y  2 xy  2  2xy  2 xy xy xy 1  0 1 5 3  5 0  xy   0  xy  . 2 2 Ta có:
P x y
  x y2  xy
   xy2  xy    xy 2 2 2 2 5 2 2 5 2 2 2 2 5 4 10xy  4  2 5.  3  5 
Đặt: t xy  0  t    2   
Khi đó: g t  2
 4t 10t  4  2 5 5
g 't   8t 10, g 't   0  t  (loại). 4 Bảng biến thiên: Chọn đáp án D GIẢI CHI TIẾT
ĐỀ THI THỬ MÔN TOÁN LỚP 12 SỞ CẦN THƠ NĂM HỌC 2020-2021 BẢNG ĐÁP ÁN 1.D 2.A 3.D 4.B 5.C 6.D 7.A 8.A 9.D 10.B 11.A 12.C 13.C 14.C 15.D 16.C 17.C 18.B 19.A 20.A 21.C 22.D 23.A 24.D 25.A 26.D 27.B 28.C 29.C 30.A 31.B 32.B 33.A 34.B 35.D 36.D 37.B 38.C 39.C 40.B 41.B 42.B 43.B 44.D 45.D 46.B 47.A 48.A 49.C 50.A Câu 1.
Họ nguyên hàm của hàm số   3x f x e là 3 x 1 e  3 x e A. C. x x B. 3
3e C. C. 3 eC. D. C. 3x 1 3 Lời giải: x 1 axb 1 Áp dụng công thức axb e dx eC  suy ra 3 3 x e dx eCa 3 Chọn đáp án D x  1  1 Câu 2. Bất phương trình    có tập nghiệm là  2  4 A.  ;  2. B.  ;  2.
C. 2;.
D. 2; . Lời giải: x x 2  1  1  1   1      x  2.        2  4  2   2  Chọn đáp án A Câu 3.
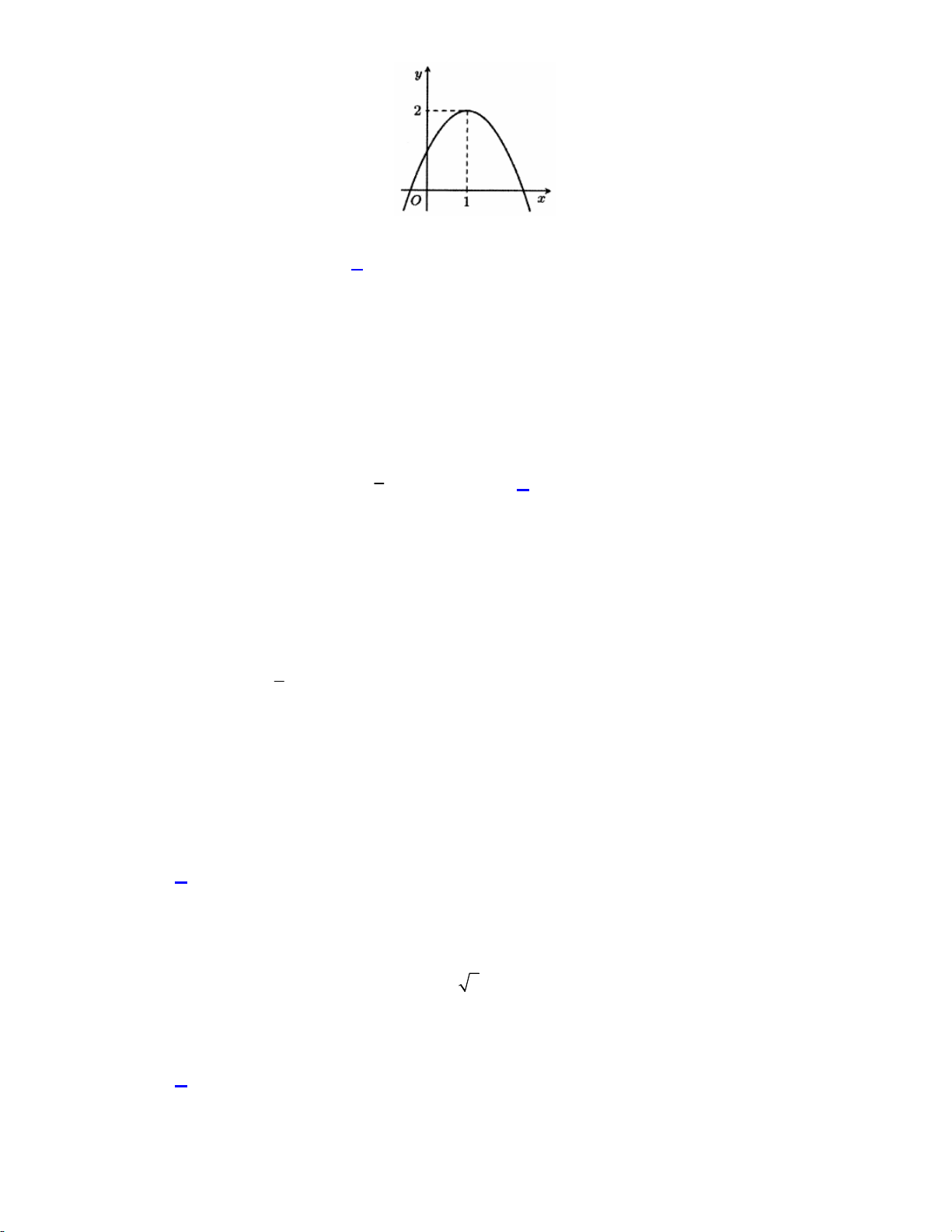
Đường cong hình bên dưới là đồ thị hàm số nào sau đây? A. 4 2
y  x  2x . B. 4 y x  2 . x C. 3 2
y x  2x . D. 4 2
y x  2x . Lời giải:
Nhìn dạng đồ thị là hàm bậc bốn trùng phương với hệ số a  0 và có 3 điểm cực trị là 1;0;1 Chọn đáp án D 1 3 3 Câu 4. Cho
f (x)dx  3  và
f (x)dx  2 
. Giá trị của f (x)dx  bằng 0 1 0 A. 5. B. 1. C. 5  . D. 1  . Lời giải: 3 1 3 Ta có:
f (x)dx
f (x)dx
f (x)dx  3  2  1.    0 0 1 Chọn đáp án B Câu 5.
Số phức z  1 2i có phần thực và phần ảo lần lượt là A. 2 và 1  . B. 1 và 2. C. 1 và 2. D. 2 và 1. Lời giải:
Số phức z  1 2i có phần thực là 1 và phần ảo là 2  . Chọn đáp án C Câu 6.
Cho lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác vuông tại B, AB  2a, BC a, AA  2 3 .
a Thể tích của khối lăng trụ AB . C A BC   bằng 3 2 3a 3 4 3a A. 3 4 3a . B. . C. . D. 3 2 3a . 3 3 Lời giải:
Thể tích lăng trụ là V  . B h Ta có 2 3 VS
.AA  a .2 3a  2 3a . ABC.A BC   ABC Chọn đáp án D Câu 7.
Tập xác định của hàm số y  ln  x  2 là A. 2;. B.  ;  2. C. 2;. D.  ;  2. Lời giải:
Ta có điều kiện: x  2  0  x  2.
Vậy tập xác định của hàm số y  ln  x  2 là 2;. Chọn đáp án A Câu 8.
Trong không gian Oxyz, tọa độ một vectơ pháp tuyến của mặt phẳng  : x y  2z  3  0 là A. 1;1;2. B. 1;1; 2. C. 1;0;2. D. 0;1;2. Lời giải:
Ta có:  : x y  2z  3  0 
Ta đã biết ptmp  : Ax By Cz D  0 với n   ; A ;
B C  là vectơ pháp tuyến. 
Áp dụng ta có n  1;1; 2 là một vectơ pháp tuyến của ptmp đã cho. Chọn đáp án A Câu 9.
Với a là số thực dương tùy ý, log 8a bằng 2   A. 8 log . a B. 8  log . a C. a  log 8. D. 3  log . a 2 2 2 2 Lời giải:
Áp dụng công thức: log bc  log b  log c a,b  0 a a a  Ta có: log
8a  log 8  log a  3  log . a 2   2 2 2 Chọn đáp án D
Câu 10. Cho hàm số y f (x) có bảng biến thiên như sau:
Mệnh đề nào dưới đây đúng?
A. Hàm số không có cực trị.
B. Hàm số đạt cực đại tại x  0.
C. Hàm số đạt cực đại tại x  5.
D. Hàm số đại cực tiểu tại x  1. Lời giải:
Dựa vào BBT, hàm số đạt cực đại tại điểm x  0 , hàm số đạt cực tiểu tại điểm x  2. Chọn đáp án B
Câu 11. Cho cấp số cộng (u ) có u  1 và u  3 . Giá trị của u bằng n 1 2 3 A. 5. B. 9. C. 4. D. 6. Lời giải:
Công sai d u u  2 2 1
u u d  3  2  5 3 2 Chọn đáp án A
Câu 12. Cho hình trụ có bán kính r  3 và chiều cao h  5 . Thể tích của khối trụ đã cho bằng
A. 36. B. 45.
C. 45.
D. 15. Lời giải:
V S.h 9.5  45 Chọn đáp án C
Câu 13. Cho hàm số y f x có bảng biến thiên như sau:
Khẳng định nào sau đây đúng?  1 
A. Hàm số đồng biến trên  ;1 .  
B. Hàm số nghịch biến trên 1;3.  3 
C. Hàm số nghịch biến trên 3; .
D. Hàm số đồng biến trên 1;. Lời giải:
Dựa vào bảng biến thiên, hàm số nghịch biến trên 3;. Chọn đáp án C
Câu 14. Trong mặt phẳng Oxy, điểm M trong hình vẽ là điểm biểu diễn số phức nào dưới đây A. 4  3 . i B. 3  4 . i C. 3  4 . i D. 3  4 . i Lời giải:
Ta có x  3 và y  4 . Vậy số phức cần tìm là 3  4 . i Chọn đáp án C
Câu 15. Số cách chọn ra 3 học sinh từ một nhóm có 5 học sinh là A. 3 5 . B. 5!. C. 3 A . C . 5 D. 35 Lời giải: Số cách chọn là 3 C . 5 Chọn đáp án D
Câu 16. Cho hình nón  N  có bán kính đáy bằng 2 và chiều cao bằng 12. Thể tích của khối nón  N  bằng
A. 48.
B. 24.
C. 16. D. 9. Lời giải: 1 1
Thể tích của khối nón  N  là 2 2
V  r h
.2 .12  16 3 3 Chọn đáp án C
Câu 17. Nghiệm của phương trình log (3x  2)  2 là 4 10 7 A. x  . B. x  . C. x  6. D. 3. 3 2 Lời giải: 2
Điều kiện 3x  2  0  x  . 3 2
3x  2  4  x  6(n). Chọn đáp án C x 1 y  4 z
Câu 18. Trong không gian Oxyz, điểm nào sau đây thuộc đường thẳng d :   ? 2 1 2 A. M (2; 1  ; 2). B. M (1; 4  ;0).
C. M (1; 4; 2). D. M (2;1; 1  ). Lời giải: x x y y z z
Phương trình đường thẳng có dạng 0 0 0  
nên ta có điểm M (1; 4  ; 0) thuộc u u u 1 2 3 d. Chọn đáp án B
Câu 19. Với a là số thực dương tùy ý, 5 a bằng 5 1 2 1 A. 2 a . B. 5 a . C. 5 a . D. 10 a . Lời giải: m 5 Ta có công thức n m n aa  5 2 a a Chọn đáp án A
Câu 20. Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a, SA vuông góc với mặt phẳng đáy và
SA a 3. Thể tích khối chóp S.ABC bằng 3 a 3 3a A. 3 a . B. . C. . D. 3 3a . 4 4 Lời giải: 2a2 3 Diện tích đáy 2 B   a 3 4
Chiều cao h SA a 3. 1 1 Thể tích 2 3 V Bh a 3.a 3  a . 3 3 Chọn đáp án A
Câu 21. Diện tích hình phẳng giới hạn bởi đồ thị của hàm số y  ln x, trục Ox và đường thẳng 3 x e bằng A. 3 3e 1. B. 3 4e 1. C. 3 2e 1. D. 3 2e 1. Lời giải:
Phương trình hoành độ giao điểm: 0
ln x  0  x e  1. 3 3 e e 3 e
Nên diện tích hình phẳng 3 3 3 3
S  ln xdx x ln x
xdx e ln e e 1  2e 1  1  1 1 Chọn đáp án C Câu 22. Nếu đặt 5x t
thì bất phương trình 2x x2 5  3.5  2021  0 trở thành A. 2
t  3t  2021  0. B. 2
t  6t  2021  0. C. 2
t  9t  2021  0. D. 2
t  75t  2021  0. Lời giải: Ta có: 2x x2 5  3.5  2021  0  2x x 2 5  3.5 .5  2021  0 Đặt 5x t  ta được: 2
t  75t  2021  0. Chọn đáp án D
Câu 23. Gọi z và z là hai nghiệm phức của phương trình 2
2z  3z  3  0 . Giá trị của 2 2
z z bằng 1 2 1 2 9 9 A.  . B. 9. C. 4. D. . 4 4 Lời giải:  3 21 z    i 1 4 4 9 Ta có : 2
2z  3z  3  0   ; Vậy 2 2 z z    1 2 3 21 4 z    i 2  4 4 Chọn đáp án A
Câu 24. Cho hàm số y f (x) có đạo hàm là ' 2 3
f (x)  x(x 1) (x  2) . Khẳng định nào sau đây sai?
A. Hàm số có hai điểm cực trị.
B. Hàm số đạt cực tiểu tại x  0 .
C. Hàm số đạt cực đại tại x  2  .
D. Hàm số đạt cực đại tại x  1 . Lời giải: x  0  Ta có : ' 2 3
f ( x)  0  x(x 1) (x  2)  0  x  1   x  2   Chọn đáp án D
Câu 25. Trong không gian Oxyz, phương trình mặt phẳng đi qua điểm A1;2;3 và vuông góc với đường x 1 y  1 z  2 thẳng d :   là 2 1  3
A. 2x y  3z  9  0. B. 2x y  3z  9  0. C. x  2 y  3z  9  0. D. x  2 y  3z  9  0. Lời giải:
Mặt phẳng đi qua A vuông góc với đường thẳng d nên vectơ chỉ phương ud  2;1;3 cũng là
một vectơ pháp tuyến của mặt phẳng.
Vậy phương trình mặt phẳng 2  x  
1   y  2  3 z  3  0  2x y  3z  9  0. Chọn đáp án A
Câu 26. Cho hàm số y f x xác định trên  và hàm số y f ' x có bảng xét dấu như sau:
Số điểm cực trị của hàm số y f  2 x  3x là A. 7. B. 2. C. 3. D. 5. Lời giải: y f  2 x  3x '
y  2x  3 ' f  2 x  3x  3 x   '  y  0  2  '  f  2
x  3x  0 
Dựa vào bảng biến thiên ta thấy  x  1   x  2. 2
x  3x  2     3  13 3   13 ' f  2 x  3x 2
 0  x  3x  1 
k   x   x  .  2 2  2 x 3x 3      3  21 3   21 x   x  .  2 2 3  13 3  13 Mà x  , x
là nghiệm kép còn các nghiệm còn lại là nghiệm đơn nên hàm 2 2
số y f  2
x  3x có 5 cực trị. Chọn đáp án D Câu 27. Cho hàm số    2 y
f x ax bx c có đồ thị như sau:
Số nghiệm của phương trình f x –1  0 là A. 3. B. 2. C. 0. D. 1. Lời giải:
Ta có : f x –1  0  f x  1
Đường thẳng y  1 cắt đồ thị tại 2 điểm phân biệt, suy ra số nghiệm của phương trình
f x –1  0 là 2. Chọn đáp án B
Câu 28. Giá trị lớn nhất của hàm số   2 x
f x x e trên đoạn  1  ;  1 là 1 A. 0. B. . C. . e D. 2 . e e Lời giải: Ta có:   2 x x 2   (  )  2 x f x x e f x xe x e Cho x 2 (  )  0  2 x f x
xe x e  0 xe  0
x  0 1;  1     2 x  2x  0 x  2      1  ;  1  1 Tính f (1) 
; f (0)  0; f (1)  e e
Vậy Max f (x)  e [ 1  ;1] Chọn đáp án C
Câu 29. Trong không gian Oxyz, cho mặt cầu 2 2 2
(S ) : (x  2)  ( y  4)  (z 1)  9. Tâm I và bán kính
R của (S) là A. I (2; 4
 ;1) và R  9. B. I (2;4; 1) và R  9. C. I (2; 4
 ;1) và R  3. D. I ( 2
 ; 4; 1) và R  3. Lời giải:
Áp dụng lý thuyết : Phương trình mặt cầu dạng 2 2 2 2
(x a)  ( y b)  ( z c)  R thì tâm I (a; ;
b c) và bán kính R . Ta có : Tâm I (2; 4
 ;1) và bán kính R  9  3. Chọn đáp án C
Câu 30. Số giao điểm của đồ thị hai hàm số 4 2
y x  4x  2 và 2
y  1 x là A. 2. B. 3. C. 1. D. 4. Lời giải:
Phương trình hoành độ giao điểm:  3  21 3  21 2 x   x   4 2 2 4 2  2 2
x  4x  2  1  x x  3x  3  0   3  21 2 x   0 (VN )  2
Vậy phương trình có 2 nghiệm nên có 2 giao điểm Chọn đáp án A
Câu 31. Cho hình chóp S.ABC có tam giác ABC vuông tại B có AB  3a, BC a, SA vuông góc
với mặt phẳng ( ABC) và SA  2 .
a Góc giữa đường thẳng SC và mặt phẳng ( ABC) bằng A. 90 .  B. 45 .  C. 30 .  D. 60 .  Lời giải:
Ta có AC là hình chiếu của SC lên ( ABC)
Suy ra góc giữa đường thẳng SC và mặt phẳng ( ABC) bằng  SCA Ta có AC
AB BC  a 2 2 2 2 3
a  2a SA SA
C là tam giác vuông cân Vậy  SCA  45 . Chọn đáp án B
Câu 32. Trong không gian Oxyz, phương trình đường thẳng đi qua điểm (
A 1; 2;0) và vuông góc với
mặt phẳng (P) : 2x y  3z  5  0 là x  1 2t
x  3  2tx  1 2t
x  3  2t    
A. y  2  t .
B. y  3  t .
C. y  2  t .
D. y  3  t . z  3  t    
z  3  3tz  3tz  3  3tLời giải:
Gọi d là đường thẳng cần tìm. 
d có vectơ chỉ phương là u  (2;1; 3  )
x  3  2t
Phương trình đường thẳng d đi qua điểm (
A 1; 2;0) là  y  3  t .
z  3  3tChọn đáp án B  1 3 x
Câu 33. Nếu đặt u x và dv  dx thì dx 2  bằng sin x 2 sin x  6    3  3 A. 3
x cot x  cot d x x 3
x cot x  cot d x x   . B.   . 6  6  6 6    3  3 C. 3
x cot x  cot xdx 3
x cot x  cot d x x   . D.   . 6  6  6 6 Lời giải: u x   du  dx Ta có  1   dv  dx v   cot x  2   sin x   3
Áp dụng công thức tích phân từng phần, ta được 3
I  x cot x  cot d x x   6  6 Chọn đáp án A x 1
Câu 34. Tiệm cận đứng của đồ thị hàm số y  là đường thẳng 2x  4 1
A. x  1.
B. x  2.
C. x  2. D. x  . 2 Lời giải: x 1
Tiệm cận đứng của đồ thị hàm số y
là đường thẳng x  2 . 2x  4 Chọn đáp án B
Câu 35. Cho hai số phức z  2  i và z  1 3i . Phần thực của số phức z z bằng 1 2 1 2 A. 4. B. 2  . C. 1. D. 3. Lời giải:
z z  3  4i  Phần thực: a  3. 1 2 Chọn đáp án D
Câu 36. Cho hình chóp S.ABC có tam giác ABC vuông cân tại B, BA BC a, SA vuông góc với mặt
phẳng đáy và góc giữa mặt phẳng SBC  với mặt phẳng  ABC bằng 0
60 . Gọi I là tâm của
đường tròn ngoại tiếp tam giác SBC . Khoảng cách giữa hai đường thẳng AI và BC bằng 6a 3a 2a 3a A. . B. . C. . D. . 2 4 3 2 Lời giải:   SBC ABC   0 ( ), ( )  SBA  60 0 SA  .
a tan 60  a 3 3 1 a 3 VS .SA S .ABC 3 ABC 6
Tam giác SBC vuông tại B nên I là trung điểm của SC.
BC //IJ  BC//(AIJ)  d  BC, AI   d BC, ( AIJ )
Gọi J là trung điểm của SB. Khi đó:
d (B, ( AIJ ))  d (S, ( AIJ )) 3 V 1 1 a 3 Có: S.AIJ   V  .V  . S .AIJ S . V 4 4 ABC 24 S . ABC
Tam giác AIJ vuông tại J có: 2 a a AJ  ; a IJ   S  . 2 AIJ 4 3 3 a 3 1 a 3 V   .S
.d S, ( AIJ )  S .AIJ AIJ   24 3 24 3
d S, ( AIJ )  . a 2 Chọn đáp án D
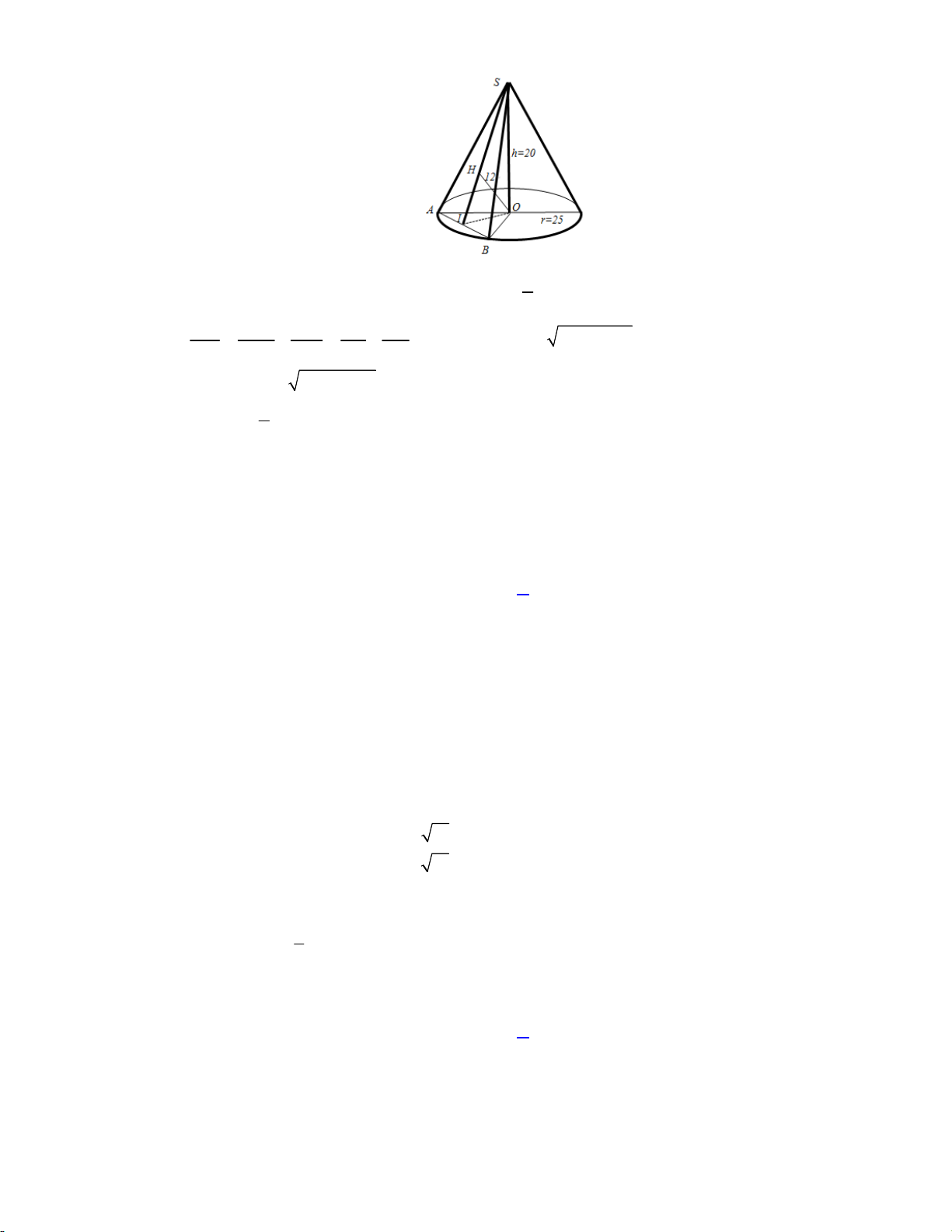
Câu 37. Cho hình nón có chiều cao h  20 và bán kính đáy r  25. Mặt phẳng  P đi qua đỉnh của
hình nón và cách tâm của mặt đáy một khoảng bằng 12. Thiết diện của hình nón cắt bởi mặt
phẳng  P có diện tích bằng A. 200. B. 500. C. 400. D. 300. Lời giải: 1
Thiết diện cần tìm là tam giác SAB, ta có: SSI.AB SAB 2 1 1 1 1 1 2 2     
OI  15  SI
SO OI  25 2 2 2 2 2 OI OH SO 12 20 2 2
AB  2 AI  2. AO IO  40 1 Vậy SSI.AB  500 SAB 2 Chọn đáp án B
Câu 38. Trong không gian Oxyz, cho bốn điểm A0;2  a;1 a, B a  3;1; 
1 ,C 2; 4;2 và D  2  ;  ;
a a  3. Gọi S là tập hợp tất cả giá trị của a sao cho bốn điểm ,
A B, C, D đồng
phẳng. Tập hợp S là tập con của tập hợp nào sau đây? A. 3;6. B. 5;8. C. 6; 2. D. 7;2. Lời giải:
   Ta có: ,
A B, C, D đồng phẳng khi:  AB; AC .AD  0    
AB  a  3;a  3; a; AC  2;2  ;1 a a   
  AB; AC    2 2
4a  3; a  6a  3; a  7a    
AD  2;2;4
   2 2
  AB; AC  .AD  0  8a  6  2a 12a  6  4a  28a  0   a  2  10 2
 2a  8a  12  0   a  2  10  Chọn đáp án C 1 Câu 39. Cho hàm số 3 2 2 y
x  (m  1) x  (3m  2m)x  1, với m là tham số thực. Gọi [ ; a b] là tập hợp 3
tất cả các giá trị của m để hàm số đã cho đồng biến trên khoảng (4; ). Giá trị của biểu thức
a  3b bằng A. 2. B. 3. C. 2  . D. 3  . Lời giải:
Tập xác định: D  .  2 2
y  x  2(m 1)x  3m  2m x  m 2 2
y  0  x  2(m  1)x  3m  2m  0   x  3m  2  1
TH1:m  3m  2  m   2
 Hàm số đã cho đồng biến trên mỗi khoảng ( ;
 m) và (3m  2; ) 2
Do đó, để hàm số đã cho đồng biến trên khoảng (4; ) thì 3m  2  4  m  3 1 2    m  thỏa đề bài (1) 2 3 1
TH2:m  3m  2  m   2
 Hàm số đã cho đồng biến trên  nên đồng biến trên khoảng (4; ). 1  m   thỏa đề bài (2) 2 1
TH3: m  3m  2  m   2
 Hàm số đã cho đồng biến trên mỗi khoảng ( ;
 3m  2) và ( ; m )
Do đó, để hàm số đã cho đồng biến trên khoảng (4; ) thì m  4  m  4  1  4  m   thỏa đề bài (3) 2 2  2  2 Từ (1), (2) và (3)  4   m   m  4;
a  4,b
a  3b  2. 3  3    3 Chọn đáp án C
Câu 40. Anh Tâm vay ngân hàng 50 triệu đồng mỗi tháng trả góp cho ngân hang 3 triệu đồng và phải
chịu lãi suất chưa trả là 0, 7% / tháng. Hỏi sau ít nhất bao nhiêu tháng thì anh Tâm trả hết tiền nợ ngân hàng? A. 20 tháng. B. 18 tháng. C. 17 tháng. D. 19 tháng. Lời giải:
Gọi A là số tiền phải trả hàng tháng, N là số tiền ban đầu, r là lãi suất, n là số tháng
Sau 1 tháng thì số tiền người đó còn nợ lại là N (1 r)  A 2 A 2
Sau 2 tháng, số tiền còn nợ là N 1 r   A   N 1 r  A.r A N 1 r   1 r    1 r n A
Sau n tháng số tiền nợ là N 1 r  
(1 r)n 1 r    A
Để trả hết nợ, thì sau n tháng số tiền nợ phải bằng 0  n  log  17, 784 tháng 1r Nr A Chọn đáp án B bx c
Câu 41. Cho hàm số y
a  0 và a, ,
b c    có đồ thị như sau: x a
Khẳng định nào sau đây là đúng?
A. a  0,b  0, c  0.
B. a  0,b  0, c  0.
C. a  0, b  0, c  0.
D. a  0, b  0, c  0. Lời giải:
Dựa vào đồ thị ta thấy:
TCĐ: x a a  0
TCN: y b b  0  cc Giao với Ox tại ; 0   0  c  0    bb Chọn đáp án B
Câu 42. Cho hình trụ có thiết diện qua trục là hình vuông cạnh bằng 2 .
a Mặt phẳng (P) song song với a
trục và cách trục một khoảng bằng
. Diện tích thiết diện của hình trụ cắt bởi mặt phẳng (P) 2 là A. 2  a . B. 2 2 3a . C. 2 a . D. 2 4a . Lời giải:
Theo đề, hình trụ có chiều cao bằng 2a, bán kính đáy là . a a
OI d (OO ', (P))  . 2
Thiết diện của hình trụ cắt bởi mặt phẳng (P) là hình chữ nhật ABC . D Chiều dài AD  2 . a
Tính chiều rộng AB : 2 2
AB  2IA  2 OA OI 2 .  a 2   2 a   a 3.    2 
Diện tích hình chữ nhật 2 ABCD  2 .
a a 3  2 3a . Chọn đáp án B
Câu 43. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với mặt phẳng
đáy và SA  7a . Khoảng cách giữa hai đường thẳng BD và SC bằng 14a 14a 14a A. . B. . C. 14 . a D. . 3 6 12 Lời giải: S A D H O B C
Gọi O AC B . D
Trong SAC  , kẻ OH SC H SC . OH SC  Ta có: 
d BD, SC   OH.
OH BD BD  SAC ,OH   SAC   AC  2a, SC  3 . a SA SC S . A OC 14
SAC  OHC    OH   . a OH OC SC 6 Chọn đáp án B 1
Câu 44. Cho hàm số f x có đạo hàm liên tục trên đoạn 1;2 , thỏa mãn f   1   và 2 2
f x  xf  x   x x   f x 2 3 2 2  , x  1;2  
. Giá trị của xf xdx  bằng 1 3 4 3 A. ln 3 . B. ln . C. ln . D. ln . 2 3 4 Lời giải:   2 xf x  1  3 2   
Ta có: f x  xf  x  2x x   f x    2x 1     2x 1     2  xf  x  xf x      1 2 1 1 
 x x C . Từ f   1  
suy ra C  0 . Hay xf x  xf x 2 2  x x 2 2 2 1  1 1  3
Khi đó: xf xdx  dx   dx  ln   2  x x   x 1 x     4 1 1 1 Chọn đáp án D
Câu 45. Cho mặt cầu S  tâm O và các điểm ,
A B, C nằm trên mặt cầu S  sao cho
AB  3, AC  4, BC  5 và khoảng cách từ O đến mặt phẳng  ABC  bằng 1. Thể tích của khối cầu S  bằng 39 39 20 5 4 17 29 29 A. . B. . C. . D. . 6 3 3 6 Lời giải:
Tam giác ABC vuông tại .
A Gọi D là trung điểm cạnh huyền BC. 5 29 2 2 DC
, OD  1, R OC OD DC  . 2 2 3 4  29  29 29
Thể tích khối cầu: V    . 3  2  6   Chọn đáp án D
Câu 46. Tất cả các giá trị thực của tham số m sao cho phương trình x x 1 4 . m 2  
 32m  0 có hai nghiệm phân biệt là  3  
A. m 2;  3 .   B. m 1  ; .  m   ; 2 . m  3;2 .  D.   2 C.   Lời giải: Đặt  2x t ,t  0 Ta có PT 2
t 2mt 32m  0 (1)
Phương trình có 2 nghiệm phân biệt thì PT (1) có 2 nghiệm dương phân biệt m 3  m1 2       0
m  2m3  0        3 3     P  0  3   2m  0  m    1 m     2 2    S  0 2m  0    m   0  Chọn đáp án B
Câu 47. Cho các số thực x, y thỏa mãn x  1, y  1 và 3 log
xy   m, với m là tham số thực. Giá trị x của m sao cho 2
P  log y 16 log x đạt giá trị nhỏ nhất thuộc khoảng nào sau đây? x y A. (0; 2). B. (2;3). C. (2;0). D. (3; 4). Lời giải: 3 log
xy   m  log xy  3m  log y  3m 1 x x x Ta có log y  0 x 16 8 8 2 2 2
P  log y 16 log x  log y   log y   x y x log x y log y log y x x x 8 8 2  3.3 log y. .  12 x log y log y x x 8 P đạt GTNN khi 2 3 log y
 log y  8  log y  2  3m 1  2  m  1 x log x x y x Chọn đáp án A
Câu 48. Cho hàm số bậc ba y f x có đồ thị như sau: 2
Số nghiệm của phương trình  f  2
x    f  2 1 2 x   1  3  0 là   A. 4 . B. 5 . C. 2 . D. 3 . Lời giải: Đặt 2
t x 1, điều kiện t  1 phương trình đã cho trở thành  f t  1  2  
f t   2 f t   3  0    
f t   3 
t  1l
Xét f t   1
 . Dựa vào đồ thị ta có f t   1   t  2  Suy ra 2
x 1  2  x  1 
t  0 l
Xét f t   3 . Dựa vào đồ thị ta có f t   3   t t  2  1 Từ đó: 2
x 1  t  2 suy ra có 2 nghiệm x   t 1 1 1
Vậy phương trình đã cho có 4 nghiệm Chọn đáp án A
Câu 49. Cho số phức z thỏa mãn điều kiện  z  
1 z  2i là số thực. Giá trị nhỏ nhất của z bằng 4 5 5 2 5 3 5 A. . B. . C. . D. . 5 5 5 5 Lời giải:
Gọi z x yi x, y    z x yi
Ta có  z  z i  x   yix    yi 2 2 1 2 1 2
x x y  2 y  2x y  2i là số thực
Suy ra 2x y  2  0.
Do đó, tập hợp các điểm biểu diễn số phức z là đường thẳng d : 2x y  2  0 . 2 2 5 Vậy z
d O, d    . min 2 2 5 2 1
Câu 50. Cho hình lăng trụ ABC.A ' B 'C ', gọi M , N lần lượt là trung điểm của BB ' và CC '. Mặt phẳng
A'MN  chia khối lăng trụ đã cho thành hai khối đa diện. Gọi V là thể tích của khối đa diện 1 V
chứa đỉnh B và V là thể tích khối đa diện còn lại. Tỉ số 1 bằng 2 V2 5 13 A. 2. B. 3. C. . D. . 2 3 Lời giải: 1 1 2 1 Ta có: V VV  . .VV 2
A '.B 'C ' MN
A'.B 'C 'CB
A' B 'C '. ABC
A ' B 'C '. 2 2 3 3 ABC 2 Khi đó: V V 1 ' ' '. 3 A B C ABC V Vậy: 1  2. V2 Chọn đáp án A GIẢI CHI TIẾT
ĐỀ THI THỬ MÔN TOÁN LỚP 12 SỞ CẦN THƠ NĂM HỌC 2020-2021 BẢNG ĐÁP ÁN 1.B 2.A 3.A 4.B 5.A 6.C 7.B 8.B 9.C 10.B 11.C 12.C 13.C 14.B 15.A 16.C 17.B 18.A 19.C 20.C 21.A 22.C 23.A 24.A 25.C 26.B 27.B 28.C 29.A 30.D 31.C 32.D 33.A 34.B 35.C 36.D 37.B 38.A 39.B 40.C 41.A 42.D 43.C 44.A 45.B 46.A 47.B 48.D 49.B 50.A Câu 1.
Cho F x là một nguyên hàm của hàm số f x trên đoạn a;b. Khẳng định nào sau đây đúng? b b A.
f xdx f a  f b.  B.
f xdx F
 b  F a .  a a b b C.
f xdx F
 a  F b.  D.
f xdx f b  f a.  a a Lời giải:
Áp dụng định nghĩa nguyên hàm Chọn đáp án B Câu 2.
Một hình nón có độ dài đường sinh l  3 và bán kính đáy r  2. Diện tích xung quanh của hình nón đã cho bằng A. 6.
B. 12.
C. 5.
D. 8. Lời giải: S
 rl .2.3  6. xq Chọn đáp án A Câu 3.
Với a là số thực dương tùy ý, 5 log a bằng 2 1 1 A. 5 log . a B. 5  log . a C. log . a D.  log . a 2 2 2 5 2 5 Lời giải: 5
log a  5 log a 2 2 Chọn đáp án A Câu 4.
Thể tích của khối lăng trụ có diện tích đáy bằng 4 và chiều cao bằng 3 là A. 36. B. 12. C. 6. D. 4. Lời giải: V  . B h  4.3  12. Chọn đáp án B Câu 5.
Tập xác định của hàm số y  log 1 x là A.  ;   1 .
B. 0; .
C. 1;. D.  ;  0. Lời giải:
ĐKXĐ của hàm số y  log 1 x là 1 x  0  x  1. Chọn đáp án A Câu 6.
Có bao nhiêu cách chọn một học sinh từ một nhóm gồm 6 học sinh nam và 5 học sinh nữ? A. 6. B. 30. C. 11. D. 5. Lời giải:
Tổng số học sinh là: 6  5  11.
Số cách chọn một học sinh từ 11 học sinh là 1 C  11. 11 Chọn đáp án C Câu 7.
Diện tích của mặt cầu có bán kính bằng 4 là 256 16 A. 16. B. 64. C. . D. . 3 3 Lời giải:
Ta có công thức tính diện tích là: 2 2
S  4 R  44  64. Chọn đáp án B Câu 8.
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên dưới? A. 3 2
y x  3x 1. B. 3 2
y  x  3x 1. C. 4 2
y x  2x  1. D. 4 2
y  x  2x  1. Lời giải:
Dựa vào đồ thị hàm số đã cho loại phương án C, D.
Ta thấy x   thì y   nên loại A. Chọn đáp án B Câu 9.
Cho số phức z  3  4 .
i Môđun của z bằng A. 1. B. 7. C. 5. D. 7. Lời giải: Ta có số phức 2 2
z a bi z a b
Áp dụng công thức ta có z    2 2 3 4  5. Chọn đáp án C
Câu 10. Cho hai hàm số f ( x), g (x) liên tục trên  và k là một số thực khác 0. Khẳng định nào sau đây sai?
A. kf (x)dx k f (x)d . x  
B. f (x)g(x)dx f (x)dx f (x)d . x   
C. f (x)  g(x)dx f (x)dx f (x)d . x   
D. f (x)  g(x)dx f (x)dx f (x)d . x    Lời giải:
Theo tính chất của nguyên hàm. Chọn đáp án B
Câu 11. Tập nghiệm của bất phương trình log(2x  3)  log 5 là A. 8; . B. 5; . C. 4; . D. ;3. Lời giải: 3 Điều kiện x  2 log(2x  3)  log 5  2x  3  5  x  4 Chọn đáp án C
Câu 12. Trong không gian Oxyz , mặt cầu tâm I (1; 0; 2) , bán kính R  3 có phương trình là
A. x  2 2 2 1
y  (z  2)  3.
B. x  2 2 2 1
y  (z  2)  9.
C. x  2 2 2 1
y  (z  2)  9.
D. x  2 2 2 1
y  (z  2)  3. Lời giải:
Mặt cầu tâm I (1; 0; 2) , bán kính R  3 có phương trình là  x  2 2 2
1  y  (z  2)  9. Chọn đáp án C
Câu 13. Nghiệm của phương trình 2 2 x  8 là 3 1 A. 2. B. 1. C. . D. . 2 2 Lời giải: x x 3 2 2 3 2  8  2
 2  2x  3  x  . 2 Chọn đáp án C
Câu 14. Thể tích của khối chóp có diện tích đáy B và chiều cao h là 1 1 A. B . h B. B . h C. 3B . h D. B . h 3 2 Lời giải: 1
Thể tích của khối chóp V B . h 3 Chọn đáp án B 2x  3
Câu 15. Tiệm cận đứng của đồ thị hàm số y  là đường thẳng x  2 3 3 A. x  2. 
B. x   .
C. x  2. D. x  . 2 2 Lời giải:
lim y    x  2 là TCĐ x2 Chọn đáp án A
Câu 16. Cho hai số phức z  2
  3i và z  3  i. Số phức z z bằng 1 2. 1 2 A. 5  2 . i B. 5  4 . i C. 5  2 . i D. 5  4 . i Lời giải:
Ta có: z z  2
  3i  3  i  5  2i 1 2 Chọn đáp án C
Câu 17. Cho hàm số y f (x) có đồ thị như sau:
Điểm cực tiểu của hàm số đã cho là A. x  2. B. x  1. C. x  1  . D. x  2  . Lời giải:
Dựa vào đồ thị ta có điểm cực tiểu của hàm số là x  1. Chọn đáp án B
Câu 18. Cho cấp số cộng (u ) có u  1 và u  7. Số hạng u bằng n 1 3 2 A. 4. B. 8. C. 6. D. 10. Lời giải: u u 1  7 Ta có 1 3 u    4. 2 2 2 Chọn đáp án A
Câu 19. Cho hàm số f x có đồ thị như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. 2;. B.  ;  0. C. 0;2.
D. 2;2. Lời giải:
Dựa vào đồ thị ta thấy hàm số đã cho nghịch biến trên khoảng 0;2. Chọn đáp án C
Câu 20. Trong không gian
Oxyz, khoảng cách từ điểm M 1; 2;  1 đến mặt phẳng
P : 2x y  2z 13  0 bằng 11 A. . B. 15. C. 5. D. 3. 3 Lời giải:
2 1 2  2   1 13
Ta có d M , P   5 2 2 2 2  ( 1  )  2 Chọn đáp án C
Câu 21. Trong không gian Oxyz , cho hình bình hành ABCD với A 1
 ;0; 2, B 2;1;3, C 1; 1  ;0.
Tọa độ điểm D là A.  2  ; 2  ;5. B. 0; 2;  1 . C. 2;2;5. D. 2;2;5. Lời giải:  
Gọi D x; y; z là điểm cần tìm. Ta có AB  3;1; 5
 . DC  1 x; 1 y : z   3   1 xx  2   
ABCD là hình bình hành  AB DC.  1
  1 y   y  2  .  5 z     z  5   Chọn đáp án A
Câu 22. Cho tam giác ABC vuông tại A có BC  13 và AB  12 . Khi quay tam giác ABC xung
quanh cạnh AB ta được khối tròn xoay có thể tích bằng A. 60. B. 300 C. 100.. D. 325. Lời giải:
Khối tròn xoay thu được là khối nón có h  12, l  13
Suy ra r  169 144  25  5. 1 Thể tích 2 V
 r h = 100. 3 Chọn đáp án C
Câu 23. Cho hàm số y f (x) có bảng biến thiên như sau:
Phương trình 3 f (x)  4  0 có bao nhiêu nghiệm? A. 3. B. 1. C. 2. D. 6. Lời giải: 4
3 f (x)  4  0  f (x) 
; số nghiệm của phương trình là giao điểm của đồ thị và đường 3 4 4
thẳng f ( x)  ; 0 
 4 . Nên phương trình 3 f (x)  4  0 có 3 nghiệm. 3 3 Chọn đáp án A 1 Câu 24. Cho hàm số 4 2 f (x) 
x bx c, ( ,
b c  ) có đồ thị như sau: 4
Khẳng định nào sau đây đúng?
A. b  0;c  0 .
B. b  0;c  0 .
C. b  0; c  0 .
D. b  0;c  0 . Lời giải:
Ta có đồ thị cắt trục Oy tại điểm có tung độ dương nên c  0 . Mặt khác 3
f '(x)  x  2bx x  0 3
f '(x)  0  x  2bx  0  
; đồ thị có 3 cực trị nên b  0 . 2 x  2b  0  Chọn đáp án A 1
Câu 25. Với x là số thực dương tùy ý, 6 3 x . x bằng 2 1 1 A. 9 x . B. 8 x . C. 2 x . D. 2 x . Lời giải: 1 1 1 1 1 1  Ta có 6 3 6 3 6 3 2
x . x x .x xx . Chọn đáp án C
Câu 26. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AB a, BC  a 2,SA vuông
góc với mặt phẳng  ABC và SA  .
a Góc giữa đường thẳng SC và mặt phẳng  ABC bằng A. 45 .  B. 30 .  C. 60 .  D. 90 . Lời giải:
Tam giác ABC vuông tại B , AB a, BC  a 2  AC a 3.
Góc giữa đường thẳng SC và mặt phẳng  ABC  là SC . A
Tam giác SCA vuông tại A SA 3 Suy ra   tan SCA    SCA  30 .  AC 3 Chọn đáp án B 2
Câu 27. Tập nghiệm của bất phương trình 6 7 x  49 là A. [ 6; 6 . ] B. [2; 2]. C. (  ; 2]. D. [2;  ). Lời giải: Ta có: 2 2 6 x 6x 2 7  49  7  7 2  x  4  0  2   x  2 Chọn đáp án B
Câu 28. Cho hình phẳng giới hạn bởi đồ thị hàm số 2
f (x)  x  2x và trục hoành. Thể tích khối tròn
xoay được sinh ra khi quay hình phẳng đã cho quanh trục hoành bằng 4 15 16 3 A. . B. . C. . D. . 3 16 15 4 Lời giải: Ta có: 2
x  2x  0  x  0; x  2. 2
V x  2x2 16 2 dx   15 0 Chọn đáp án C
Câu 29. Khẳng định nào sau đây đúng? e e e e e e
A. ln x dx x ln x  d . x  
B. ln x dx x ln x x d . x   1 1 1 1 1 1 e e e e e 1 e
C. ln x dx x ln x  d . x   D. 2
ln x dx x ln x x d . x   1 x 1 1 1 1 1 Lời giải: b b b
Áp dụng công thức tích phân từng phần : u dv uv v d . uaa a e
Ta có: I  ln x dx  1 Đặt 1
u  ln x  du  dx x
dv  dx v x e e e
Vậy I  ln x dx x ln x  d . x   1 1 1 Chọn đáp án A 3 x
Câu 30. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2 f (x) 
 2x  3x  4 3
trên đoạn [  4; 0] . Giá trị của m M bằng 4 4 28 A. . B.  . C. 4  . D.  . 3 3 3 Lời giải: 3 x Ta có: 2 2 f (x) 
 2x  3x  4  f '(x)  x  4x  3 3
x  3[  4; 0]
Cho f '(x)  0  
x  1[  4; 0]  16 16 Tính f (4) 
, f (3)  4, f (1)  , f (0)  4 3 3 16
Vậy M  Max f (x)  4
 , m  Min f (x)  [4;0] [ 4  ;0] 3 16 2  8 m M   (4)  . 3 3 Chọn đáp án D
Câu 31. Số giao điểm của đồ thị các hàm số 3
f (x)  x  2x 1 và g( x)  x 1 là A. 3. B. 2. C. 1. D. 0. Lời giải:
Phương trình hoành độ giao điểm của hai đồ thị là 3 3
x  2x 1  x 1  x x  0  x  0  y  1 
Đồ thi hai hàm số cắt nhau tại một điểm. Chọn đáp án C 14  2i
Câu 32. Số phức liên hợp của z  là 1 i
A. z  16 12 . i
B. z  6  8 . i
C. z  16 12 . i
D. z  6  8 . i Lời giải: 14  2i Ta có z
 6  8i z  6  8i 1 i Chọn đáp án D
Câu 33. Gọi z , z là hai nghiệm phức của phương trình 2
z  2z  10  0 . Giá trị của 2 2 z z bằng 1 2 1 2 A. 1  6. B. 16. C. 2. D. 2. Lời giải: Phương trình 2
z  2z  10  0 có hai nghiệm phức z  1 3i và z  1 3i . 1 2 z z
 1 3i2  1 3i2 2 2
 8  6i  8  6i  1  6 . 1 2 Chọn đáp án A
Câu 34. Trong không gian Oxyz , cho ba điểm A2;0;0 , B0; 3;0 , C 0;0;  1 . Phương trình mặt phẳng  ABC là
A. x y z  2  0 .
B. 3x  2 y  6z  6  0 .
C. x y z  6  0 .
D. 3x  2 y  6z  6  0 . Lời giải: x y z
Phương trình mặt phẳng  ABC có dạng:  
 1  3x  2 y  6z  6  0 . 2 3 1 Chọn đáp án B i  3
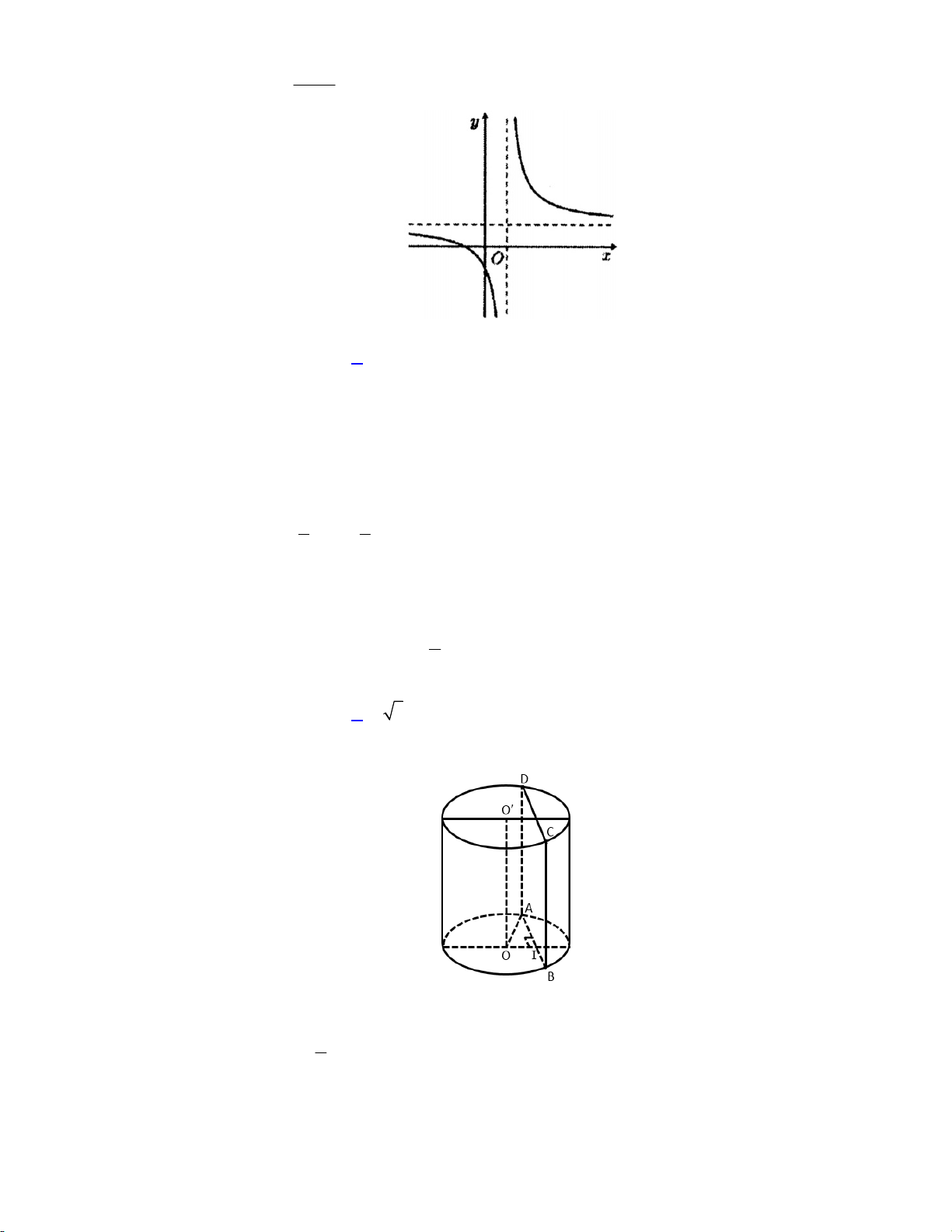
Câu 35. Trong mặt phẳng Oxy , điểm biểu diễn số phức z có tọa độ là 1 i A. 4; 2  . B. 2;0. C. 2;   1 .
D. 2;4. Lời giải: i  3 z   2  . i 1 i
Suy ra điểm biểu diễn số phức z là 2;   1 . Chọn đáp án C
Câu 36. Cho hình nón đỉnh S có đáy là đường tròn tâm O và bán kính R . Trên đường tròn O lấy hai điểm ,
A B sao cho tam giác OAB vuông. Biết diện tích tam giác SAB bằng 2 2R . Thể tích khối nón đã cho bằng 3 14R 3 14R 3 14R 3 14R A. . B. . C. . D. . 3 12 2 6 Lời giải: R 2
AB R 2  OH  . 2 1 2 2 S  2R SH .AB
2R SH  2 . R SAB 2 R 14 2 2 SO SH OH  . 2 Thể tích khối nón: 3 1 R 14 14R 2 V  R .  . n 3 2 6 Chọn đáp án D 2 2 3  e 1   x 1 khi x  1
f ln  x   1   
Câu 37. Cho hàm số f x   . Giá trị của dx  bằng 2
x x  2 khi x  1  x 1 0 17 17 14 7 A. . B. . C. . D. . 3 6 3 3 Lời giải: Ta có:  lim         2 x x 2 lim  2 3x  1 f   1 2 x 1  x 1 
Vậy hàm số liên tục tại x  1 và có đạo hàm tại x  1. 2 e 1 
f ln  x   1    I dxx 1 0 1
t  ln  x   1  dt dx x 1 2
x  0  t  0; x e 1  t  2 2 1 2 17  I
f t dt    2 3t   1 dt    2
t t  2dt  6 0 0 1 Chọn đáp án B
Câu 38. Cho hàm số bậc bốn y f x và có đồ thị f ' x như sau:
Số điểm cực trị của hàm số g x  f  2 x  2x là A. 5. B. 3. C. 6. D. 4. Lời giải: Ta có: 
2x  2  0  x  1         x  1  x  1(kep)   x  0 
g ' x  2x  2 f ' 2
x  2x  0   x     f ' 0 2
x  2x  0    x  2  x  2      x  1 2 x  1 2    x  1 2   x  1 2   Chọn đáp án A x  1 y  2 z
Câu 39. Trong không gian Oxyz, cho điểm (
A 3;1; 2) và đường thẳng d :   . Phương 1 2 1
trình tham số của đường thẳng đi qua điểm ,
A cắt và vuông góc với đường thẳng d là x  1   2t
x  3  2t
x  2  3t
x  3  3t     A. y  2   t .
B. y  1 t .
C. y  1 t .
D. y  1 t . z  0     z  2 
z  3  2t
z  2  2tLời giải:
- Đường thẳng d có VTCP là u  (1; 2; 1). d
- Gọi  là đường thẳng đi qua điểm ,
A cắt và vuông góc với đường thẳng d tại . B
- Vì B d nên B( 1   t; 2
  2t; t), t  .   
- Vì A d, B d nên d có VTCP là u AB  ( 4   t; 3
  2t; 2  t)   
- Vì d   nên u .u  0  1( 4
  t)  2(3  2t) 1(2  t)  0  t  2 d
x  3  2t    u  ( 2
 ;1;0)  (2; 1;0). Vậy  :  y  1 t .  z  2   Chọn đáp án B
Câu 40. Trong không gian Oxyz, đường thẳng đi qua điểm M 1;2; 2 , song song với mặt phẳng     x 1 y 2 z 3
P : x y z  3  0 đồng thời cắt đường thẳng d :   có phương trình là 1 1 1 x  1 tx  1 tx  1 tx  1 t    
A. y  2  t . B. y  2 .
C. y  2  t .
D. y  2  t . z  2     z  2  tz  2  z  2  tLời giải:
Gọi N là giao điểm cùa đường thẳng d và đường thẳng cần tìm  N 1 t; 2  t;3  t 
Khi đó MN t;t;1 t  là vectơ chỉ phương của đường thẳng cần tìm  
Do đường thẳng song song với mặt phẳng  P  MN.n  0  t t 1 t  0  t  1. P 
Vậy MN 1; 1; 0 Chọn đáp án C
Câu 41. Cho hình trụ có bán kính đáy bằng 3 2 .
a Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng
song song với trụ và cách trục một khoảng bằng 3a thì thiết diện thu được là một hình vuông.
Thể tích của khối trụ đã cho bằng A. 3 108 a . B. 3 216 a . C. 3 150 a . D. 3 54 a . Lời giải: Ta có
h   a2  a2 3 2 3  3a 2  h  6a
Vậy V a2 3 3 2
.6a  108 a Chọn đáp án A mx  3m  4
Câu 42. Có bao nhiêu giá trị nguyên của tham số m để hàm số y  nghịch biến trên x m khoảng 2; ? A. 2. B. 4. C. 5. D. 3. Lời giải: ĐKXĐ: x  . m 2 m  3m  4 Ta có: y '  2 (x m) mx  3m  4  y '  0, x   (2, ) Hàm số y
nghịch biến trên khoảng 2;  khi  x m m  (2, )  2
m  3m  4  0   1   m  2 m  2  m 0;1;  2
Có 3 giá trị nguyên của m để hàm số đã cho thỏa ycbt. Chọn đáp án D
Câu 43. Cho hình lăng trụ AB . C A BC
  có đáy là tam giác vuông cân tại ,
A AB AC  3a và AA  2 . a
Hình chiếu vuông góc của B lên mặt đáy là điểm H thuộc cạnh BC sao cho HC  2HB .
Khoảng cách từ điểm B đến mặt phẳng  B AC  bằng 2 3a 3 3a a A. . B. . C. 3 . a D. . 3 2 2 Lời giải: A' C' B' K A C E H B
d B, B AC  CB 3 Ta có: 
d B,  B A
C   d H ,B AC .
d H , B AC  CH 2
Trong  ABC , kẻ HE AC E AC. HE AC Ta có 
AC   EHB   B A
C    EHB B H   AC  Trong  B E
H  , kẻ HK B E
  K B E  . HK B E
B AC  EHB
HK   B AC  Khi đó   B A
C    EHB  B E    d  3 3 B,  B A
C   d H ,B A
C   HK. 2 2 1 2 Ta có BH BC  2 . a EH AB  2a . 2 2 B E
  EH B H   6a . 3 3 EH .HB 2 3 KH .B E
  EH .HB  KH   . a B E  3  d  3 3 B,  B A
C   d H , B A
C   HK  3a . 2 2 Chọn đáp án C
Câu 44. Chọn ngẫu nhiên ba số khác nhau từ 17 số nguyên dương đầu tiên. Xác suất để chọn được ba số
có tổng là một số chia hết cho ba bằng 23 27 9 9 A. . B. . C. . D. . 68 34 34 17 Lời giải:
Xét phép thử: “Chọn ba số khác nhau từ 17 số nguyên dương đầu tiên”. Khi đó: n  3  C  680 . 17
Biến cố A: “chọn được ba số có tổng là một số chia hết cho 3”.
Ta chọn 3 số khác nhau a, ,
b c từ 17 số nguyên dương đầu tiên sao cho a b c chia hết cho
3. Xét 4 trường hợp sau:
* Trường hợp 1: Cả a, ,
b c đều chia hết cho 3, suy ra a, b, c 3, 6, 9, 12, 1  5 . Số cách chọn
trong trường hợp này là 3 C  10 cách. 5
* Trường hợp 2: Cả a, ,
b c chia cho 3 đều dư 1, suy ra a, b, c 1, 4, 7, 10, 13, 1  6 . Số cách
chọn trong trường hợp này là 3 C  20 cách. 6
* Trường hợp 3: Cả ba số a, b, c chia cho 3 đều dư 2, suy ra a, b, c 2, 5, 8, 11, 14, 1  7 . Số
cách chọn trong trường hợp này là 3 C  20 cách. 6
* Trường hợp 4: Trong ba số a, ,
b c có 1 số chia hết cho 3, 1 số chia cho 3 dư 1 và 1 số chia
cho 3 dư 2. Số cách chọn trong trường hợp này là 5.6.6  180 cách. n A 23
n A  230  p A   n  68 Chọn đáp án A
Câu 45. Anh Nam mua một chiếc ô tô trị giá 700 triệu đồng với hình thức trả góp. Anh Nam trả trước
500 triệu đồng và phải chịu lãi suất 0, 75% /tháng đối với số tiền còn nợ. Mỗi tháng, anh Nam
trả một số tiền không đổi vào đúng ngày tính lãi. Hỏi số tiền không đổi mà anh Nam phải trả
mỗi tháng là bao nhiêu, biết rằng sau đúng ba năm thì anh Nam trả hết nợ (làm tròn đến hàng nghìn)?
A. 5900000 đồng.
B. 6360000 đồng.
C. 9137000 đồng.
D. 6500000 đồng. Lời giải: Áp dụng công thức
N (1 r)n r
200.1 0, 75%36 .0, 75% A  
 6, 36 triệu đồng n 1 r  1 1 0,75%36 1 Chọn đáp án B
Câu 46. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB a, AD  2a , SA vuông góc
với mặt phẳng đáy, SB tạo với mặt phẳng đáy một góc 60 . Trên SA lấy điểm M sao cho 3a AM
. Mặt phẳng  BMC  cắt cạnh SD tại N . Tỉ số thể tích giữa khối chóp S.BCNM 3
và S.ABCD bằng 5 4 5 4 A. . B. . C. . D. . 9 9 7 7 Lời giải:
BC  MBC   AD   SAD Vì 
 MBC   SAD  MN, MN / / AD, N MN SD BC / / AD
M MBCSAD 
Ta có SB ABCD   ,  SBA  60 Xét tam giác vuông 
SAB ta có SA  tan 60 .AB a 3 a 3 2a 3
Và SM SA AM a 3   3 3 Cách 1: V SM SN 2 2 4 4 4 1 2 S.MNC  .  .   VV  . VV (1) S.MNC S.ADC S. ABCD S. V SA SO 3 3 9 9 9 2 9 ABCD S .ADC V SM 2 2 2 1 1 S.MBC    VV  . VV (2) S .MBC S .ABC S. ABCD S . V SA 3 3 3 2 3 ABCD S. ABC Từ (1) và (2) ta có 2 1 VV S .ABCD S . ABCD V VV 5 S.BCNM S .MNC S .MBC 9 3    . V V V 9 S. ABCD S .ABCD S .ABCD
Cách 2: Áp dụng công thức tính nhanh (chỉ đúng khi đáy là hình bình hành) SA SD 3 3  1 1  11 V 5 S.BCNM SM SN 2 2    . V SA SD 3 3 9 S.ABCD 4. . .1.1 4. . .1.1 SM SN 2 2 Chọn đáp án A x
Câu 47. Cho các số thực dương x, y thỏa mãn 3 3 x x  log
 8 y  2 y 1. Giá trị nhỏ nhất của biểu 2 y thức 2
P x y bằng 1 1 1 1 A. . B.  . C.  . D. . 8 16 4 4 Lời giải: x Ta có: 3 3 x x  log
 8 y  2 y 1  3 3
x x  log x  (2 y)  2 y  log (2 y) (1) 2 y 2 2 1 3 2
f (t)  t t  log t f (
t)  3t 1  0 ( t
  1). Suy ra f (t) đồng biến trên .  2 t ln 2
(1)  x  2 y 1 1 2 2
P x y  4 y y  min P   khi y  16 8 Chọn đáp án B Câu 48. Có bao nhiêu số nguyên y sao cho tồn tại số thực x thỏa mãn
log  2  3y  .log  2  3y x x xx 2  y  7 y ? 4 3 A. 8. B. 10. C. 11 . D. 9. Lời giải: u   log u 2 y
 2x 3y x 4
 4  x 3  x Đặt u v y     4 .3  3 v  log  2
x  3y x v 2 3  
x  3y x 3   
y v u log 4  v y u log 4 3 3 Theo đề bài: 2
uv y  7 y u y u log u 2  y  7 y 3 2 2
u .log 4  uy y  7 y  0 * 3  
Điều kiện tồn tại x, y là * có nghiệm u hay 2   y  4  2 y  7 y  2
log 4  0  y 1 4 log 4  28y.4 log 4  0 3  3  3 28 log 4 3  0  y    8.7 1 4 log 4 3
Vì y   nên y 0;1;...;7;  8
Vậy có 9 giá trị nguyên của y thỏa yêu cầu bài toán Chọn đáp án D
Câu 49. Cho số phức z thỏa mãn z  3  i  1 và số phức z m   2
m  1 i với m  .  Giá trị nhỏ 2  1 1
nhất của z z bằng 1 2 A. 5  1. B. 5 1. C. 1. D. 2. Lời giải:
Gọi M x ; y là điểm biểu diễn số phức z . Ta có z  3  i  1  z  3  i  1 1 1   1 1  1
Suy ra tập hợp cấc điểm biểu diễn số phức z nằm trên đường tròn C có tâm I 3;  1 , bán 1 kính R  1.
Gọi N x ; y là điểm biểu diễn số phức z . Suy ra N  2 ; m m   1 2 2  2
Ta có MN IN R IN 1. Suy ra z zMNINR 1 2 min min min
Ta có IN  m    m   2 2 2 4 2 3 1 1 
m m  6m  9
Xét hàm số f m 4 2
m m  6m  9, m  .  f  m 3
 4m  2m  6, f m  0  m  1 Bảng biến thiên
Suy ra min f m  5  Vậy z zMNINR  5 1. 1 2 min min min Chọn đáp án B
Câu 50. Cho hàm số f x 4 3 2
ax bx cx dx 1 có bảng biến thiên f ' x như sau: m
Tất cả các giá trị của tham số m sao cho phương trình f  3 1 x  
có nghiệm thuộc khoảng 4  ;    1 là 3
A. m  12.
B. m  3. C. m  .
D. m  1. 4 Lời giải:
Ta có: f x 4 3 2
ax bx cx dx   f x 3 2 1 '
 4ax  3bx  2cx d   3 2 3   3 2  3 
Vì f ' x  0 có A ; ; B  ;
 là hai điểm cực trị nên điểm uốn O 0; 0  3 9   3 9       d  0  3  b   0
Ta lại có: f "    0    3  4a  2c  0      3  2 3 4 3 2 3 2 3 Vì: f '     a c   3  9 9 3 9    1
4a  2c  0 a     4
Khi đó ta có hệ phương trình:  4 3 2 3 2 3    a c  1   9 3 9 c      2 1 1 f ' x 3  x  ; x f x 4 2  x x 1 4 2
Xét: g x  f  3
x   g x  f  3  x   2 1 ' ' 1 . 3x  2 x  0   x  0 3 1 x  0  
g ' x  0   x  1 (loại)  3  1 x  1   3 x  2 3  1   x  1   Bảng biến thiên: m
Vậy: phương trình có nghiệm khi  3  m  12. 4 Chọn đáp án A
Document Outline

  • de-khao-sat-chat-luong-toan-12-nam-2021-so-gddt-thanh-pho-can-tho
    • 101
    • 102
    • 105
    • 106
    • pôppo
  • MA-101-GIAI-CHI-TIET
  • MA-102-GIAI-CHI-TIET
  • MA-105-GIAI-CHI-TIET
  • MA-106-GIAI-CHI-TIET