



Preview text:
UBND HUYỆN NINH GIANG
ĐỀ KHẢO SÁT NĂNG LỰC HỌC SINH GIỎI
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
NĂM HỌC: 2023 - 2024 Môn: TOÁN 7
Ngày khảo sát: 27/01/2024
Thời gian làm bài: 150 phút (Đề gồm 01 trang) Câu 1. (2.0 điểm) 13 13
a) Tính giá trị của biểu thức : 3 .10+3 .6 12 4 3 .2
b) Rút gọn biểu thức: A= 1 1 1 1 1 1 1 ...1 − − − − 2 3 4 100
c) Chứng minh rằng 8 10 12 10 10
4 .3 + 5.2 .3 − 6 .16 chia hết cho 17 Câu 2. (2.0 điểm) 1. Tìm x biết: a) 1 1 2 x 3 x + − − = 4x − 1 3 2 ( x − )3 2 1 b) 27 = 3 2x −1
2. Tìm x, y thỏa mãn: x −
y + ( y − )2024 2023 1 = 0 Câu 3. (2.0 điểm) a) Tìm x,y nguyên biết 2
25 − y = 8(x −15)2
b) Chứng minh rằng với mọi số nguyên dương a, b thì ab( 2 a − )( 2 1 b + 2) chia hết cho 9. Câu 4. (3.0 điểm)
1. Cho tam giác ABC nhọn. Kẻ AH vuông góc với BC tại H. Trên nửa mặt
phẳng bờ AB không chứa điểm C lấy điểm E sao cho tam giác ABE vuông cân
tại B. Kẻ EM vuông góc với đường thẳng BC tại M. a) Chứng minh BH = EM
b) Trên tia đối của tia AH lấy điểm F sao cho AF = BC. Chứng minh BF vuông góc với CE.
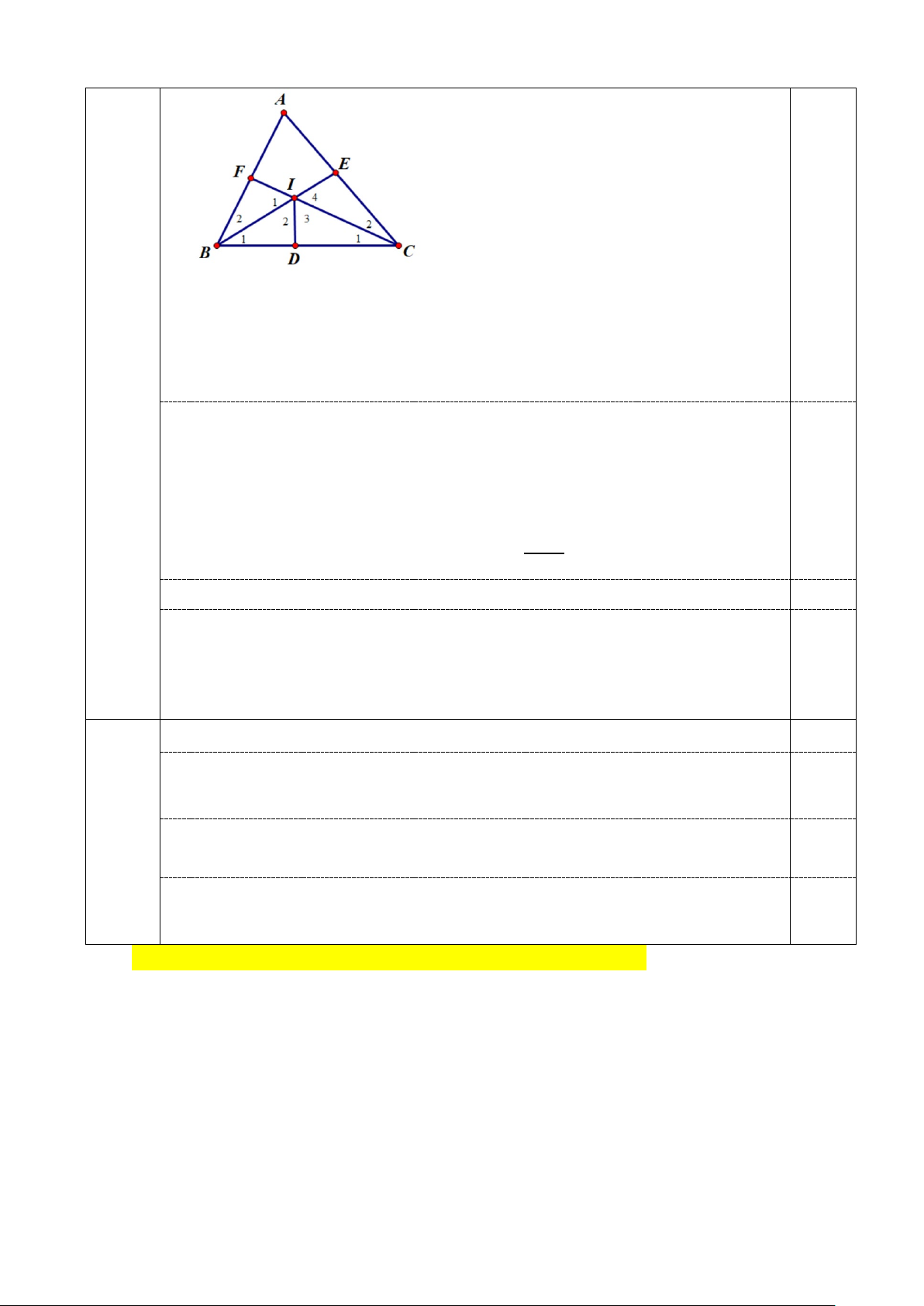
2. Cho tam giác ABC có góc BAC = 60o. Tia phân giác của góc ABC cắt AC tại
E, tia phân giác của góc ACB cắt AB tại F. BE cắt CF tại I. Chứng minh IE = IF
Câu 5. (1 điểm) Tìm số tự nhiên a nhỏ nhất sao cho a +1 chia hết cho 2 ; a chia
hết cho tích của hai số nguyên tố liên tiếp và tích 2023a là số chính phương.
……… Hết………
*Lưu ý: Học sinh không được sử dụng máy tính cầm tay
Họ và tên thí sinh: ……………………………. Số BD…………
Giám thị………………………………………………………….. UBND HUYỆN NINH GIANG
KHẢO SÁT NĂNG LỰC HỌC SINH GIỎI
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO Môn Toán lớp 7 Đợt I Năm học 2023-2024
Ngày 27 tháng 01 năm 2024
( Thời gian làm bài 150 phút ) HƯỚNG DẪN CHẤM Câu Đáp án Điểm 13 13 13 3 .10 + 3 .6 3 . 10 + 6 a) ( ) = 12 4 12 4 3 .2 3 .2 0,25 13 4 3 .2 = = 0,25 Câu 1 3 12 4 3 .2 (2 b) 1 1 1 1 A 1 1 1 ...1 = − − − − điểm) 2 3 4 100 1 2 3 4 99 = . . . ..... 2 3 4 5 100 0,5 1.2.3.....99 1 = = 2.3.4....100 100 0,25 8 10 12 10 10 4 .3 + 5.2 .3 − 6 .16 c) = (2 )8 .3 + 5.2 .3 −(2.3)10 2 10 12 10 4 .2 0,25 16 10 12 10 14 10 = 2 .3 + 5.2 .3 − 2 .3 0,25 12 = ( 4 2 2 . 2 + 5 − 2 ) 12 = 2 .17 17 0,25 a) 1 1 2 x 3 x + − − = 4x − 1 3 2 2 3
2x + − + 3x = 4x −1 0,25 3 2 2 3 5x − 4x = 1 − − + Câu 2 3 2 0,25 (2 1 x − = điểm) 6 b) ( x − )3 2 1 27 = 3 2x −1 ( x − )4 2 1 = 81 0,25 2x −1 = 3 ⇒ 2x −1 = 3 − 0,25 x = 2 ⇒ x = 1 −
Học sinh thiếu 1 trường hợp trừ 0,25đ 2) x −
y + ( y − )2024 2023 1 = 0
x − 2023y ≥ 0 x ∀ , y Vì ( 0,25 y − )2024 1 ≥ 0 y ∀ ⇒ x −
y + ( y − )2024 2023 1 ≥ 0 x ∀ , y
x − 2023y = 0 0,25 Dấu bằng xảy ra khi ( y − )2024 1 = 0 0,25
x − 2023y = 0 x = 2023 ⇒ ⇒ y 1 0 − = y =1 0,25
Học sinh không lập luận mà chỉ xét bằng 0 thì trừ 0,25đ
a) − y = (x − )2 2 25 8 15 0,25 Vì − y ≤ y ∀ ⇒ (x − )2 2 25 25 8 15 ≤ 25 2 ⇒ (x − )2 25 15 ≤ . Vì (x − )2
15 là scp ⇒ (x −15) ∈{0, } 1 8 0,25 Câu 3 TH1: ( y = x −15)2 5 2
= 0 ⇒ 25 − y = 0 ⇒ y = 5 − ( 0,25 x − )2
15 = 0 ⇒ x −15 = 0 ⇒ x =15 TH2:(x − )2 2 2
15 =1⇒ 25 − y = 8 ⇒ y =17 (Loại vì 17 ko là scp) 0,25
Vậy (x, y)∈ ( { 15,5);(15,−5)}
Không kết luận hoặc kết luận không theo cặp số trừ 0,25đ
b) Chứng minh rằng với mọi số nguyên dương a, b thì ab( 2 a − )( 2
1 b + 2) chia hết cho 9
Nếu a chia hết cho 3 thì a( 2a − )1 chia hết cho 3 0,25
Nếu a không chia hết cho 3 thì 2
a chia 3 dưa 1 nên a( 2 a − ) 1 chia hết 0,25 cho 3.
Vậy a( 2a − )1 luôn chia hết cho 3 với mọi a
Chứng minh tương tự b( 2b + 2) luôn chia hết cho 3 với mọi b 0,25 Suy ra ab( 2 a − )( 2
1 b + 2) chia hết cho 3.3 hay 0,25 ab( 2 a − )( 2
1 b + 2) chia hết cho 9 Câu 4 0,25 I Vẽ hình đúng + BAH ABH = 90° a) + ABH EBM = 90° 0,25 ⇒ = BAH EBM Xét ∆ AHB ∆ BME có Có = AHB BME = 90° 0,25
AB = BE (tam giác AB vuông cân tại B = BAH EBM
=> ∆ AHB = ∆ BME (ch-gn)
=> BH = ME (2 cạnh tương ứng) 0,25
*Học sinh viết nhầm trường hợp bằng nhau trừ 0,25đ + Có EBC EBM =180° + BA F BAH =180° 0,25 Mà = ⇒ = BAH EBM EBC BA F Xét E ∆ BC và B ∆ AF có BE = BA(cmt) 0,25 = EBC BA F AF = BC ⇒ E ∆ BC = B ∆ AF ( . c g.c) ⇒ = A FB BCE mà + A FB HBF = 90° 0,25 ⇒ + BCE HBF = 90° B ∆ IC có +
BCE HBF = 90° ⇒ B ∆ IC vuông tại I 0,25
Suy ra BF vuông góc với CE. 2)
Vẽ ID là tia phân giác góc BIC với D thuộc BC
Xét tam giác ABC có + = ° − ABC ACB 180 A =120°
Mà BE, CF là tia phân giác góc ABC và góc ACB 0,25 + = ° ⇒ + 2B 2C 120
B C = 60° 1 1 1 1 Xét tam giác BIC có = ° − +
BIC 180 (B C =120° 1 1 ) Lại có I và
I là 2 góc kề bù với BIC 1 4 = = ° − I I 180 BIC = 60° 0,25 1 4 Vì ID là tia phân giác BIC nên = BIC I I = = 60° 2 3 2 Chứng minh được B ∆ FI = B ∆ DI (g. . c g) => IF = ID 0,25
Chứng minh tương tự CD ∆ I = CE ∆
I (g. .cg) => IE = ID IE = IF (đpcm) 0,25
*Học sinh có thể chỉ chứng minh một cặp tam giác bằng nhau, cặp
còn lại ghi chứng minh tương tự vẫn cho điểm tối đa Vì (a + )
1 2 ⇒ a là số lẻ, a khác 0. 0,25
2023a là số chính phương nên 2 = ( *
2023a k k ∈ N ). 2 2 2 ⇒
a = k ⇒ a = t ( * 7.17 .
7 t ∈ N ) ⇒ a7. 0,25
Câu 5 Mà a nhỏ nhất, a khác 0 và a chia hết cho tích của hai số nguyên tố
liên tiếp nên t = 5. 0,25 Khi đó 2 a = 7.5 =175. 0,25
Vậy a =175 là số cần tìm.
Lưu ý: Học sinh làm cách khác đúng vẫn cho điểm tối đa




