30 trang 33 lượt tải

Đề khảo sát lần 1 Toán 12 năm 2020 – 2021 trường Lê Quý Đôn – Hải Phòng

66

Đề khảo sát chất lượng lần 1 môn Toán lớp 12 năm học 2020 – 2021 trường THPT Lê Quý Đôn – Hải Phòng có đáp án và lời giải chi tiết.

Chủ đề: Đề thi THPTQG môn Toán năm 2023 1.2 K tài liệu

Môn: Toán 2.2 K tài liệu

Tác giả:

Profile

Thanh Hoa

1 năm trước
Danh sách Quiz
/30
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 1
ĐỀ BÀI
Câu 1: Cho
0;2;...;98A
là tập hợp gồm các số tự nhiên chẵn nhỏ hơn
100
. Số tập con có hai phần
tử của
A
là
A.
2
49
C
. B.
2
50
C
. C.
2
49
A
. D.
2
98
C
.
Câu 2: Cho cấp số nhân
n
u
với
1
1u
và công bội
2q
. Tìm
.
A.
15
. B.
128
. C.
13
. D.
64
.
Câu 3: Cho hàm số
4 2
2 3y x x
. Khẳng định nào sau đây đúng?
A. Hàm số có ba điểm cực trị. B. Hàm số chỉ có đúng hai điểm cực trị.
C. Hàm số không có cực trị. D. Hàm số chỉ có một điểm cực trị.
Câu 4: Hàm số
1
2
3
4y x
có tập xác định là:
A.
2;2
B.
2;2
C.
; 2 2; 
D.
Câu 5: Tìm giá trị nhỏ nhất của hàm số
9
y x
x
trên đoạn
2;4
.
A.
2;4
25
min
4
y
B.
2;4
13
min
2
y
C.
2;4
6
min
y
D.
2;4
6
min
y
Câu 6: Cho hàm số
y f x
liên tục trên
\ 1
. Có bảng biến thiên như hình vẽ. Tổng số đường
tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số
y f x
bằng:
A.
4
B.
2
C.
3
D.
1
Câu 7: Cho khối lăng trụ đứng có cạnh bên bằng
5
, đáy là hình vuông có cạnh bằng
4
. Thể tích của
khối lăng trụ đã cho bằng
A.
100
. B.
80
. C.
20
. D.
64
.
Câu 8: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ sau
A.
3 2
3y x x
. B.
4 2
3y x x
. C.
3 2
3y x x
. D.
4 2
3y x x
.
Câu 9: Trong không gian
Oxyz
, cho hai điểm
2; 4;3A
,
2;2;7B
. Trung điểm của
AB
có tọa độ là
A.
1;3;2
. B.
4; 2;10
. C.
2; 1;5
. D.
2; 6; 4
.
Câu 10: Thể tích
V
của khối trụ có bán kính và chiều cao đều bằng
5a
là
A.
3
75 a
. B.
3
125 a
. C.
3
25 a
. D.
3
50 a
.
ĐỀ THI KHẢO SÁT CHẤT LƯỢNG LẦN 1
NĂM HỌC 2020 - 2021
Môn: TOÁN - Lớp: 12
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
_________________________
SỞ GD&ĐT HẢI PHÒNG
TRƯỜNG THPT LÊ QUÝ ĐÔN
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 2
Câu 11: Trong các khẳng định sau, khẳng định nào sai?
A.
cf x dx c f x dx c
. B.
f x g x dx f x dx g x dx
.
C.
f x dx f x
.D.
f x dx f x C
.
Câu 12: Cho
, , 0a b c
,
1a
,
1b
. Trong các khẳng định sau, khẳng định nào sai?
A.
log .log log
a b a
b c c
. B.
log log log
a a a
b c b c
.
C.
log log log
a a a
bc b c
. D.
1
log
log
a
b
b
a
.
Câu 13: Gọi
, ,l h r
lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình nón. Diện tích
xung quanh
xq
S
của hình nón là:
A.
2
1
3
xq
S r h
. B.
xq
S rh
. C.
xq
S rl
. D.
2
xq
S rl
.
Câu 14: Có bao nhiêu loại khối đa diện đều?
A.
5
. B.
2
. C.
3
. D. vô số.
Câu 15: Cho hàm số
y f x
có bảng biến thiên như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
;2
. B.
1;1
. C.
2;
. D.
; 1
.
Câu 16: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông tại
C
,
3AB a
,
2BC a
.
Góc giữa
BC
và mặt phẳng
ABC
bằng
60
. Tính thể tích khối lăng trụ đó.
A.
3
2 15a
. B.
3
2 15
3
a
. C.
3
15a
. D.
3
15
3
a
.
Câu 17: Cho hàm số
3 2
6 7 5y x x x
có đồ thị là
C
. Số tiếp tuyến của
C
song song với đường
thẳng
2 9 0x y
là
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 18: Một người gửi tiền vào ngân hàng với lãi suất không thay đổi là
8%
/năm. Biết rằng nếu không
rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu (người
ta gọi là lãi suất kép). Người đó định gửi tiền trong vòng
3
năm, sau đó rút tiền ra để mua một
căn hộ chung cư trị giá
500
triệu đồng. Hỏi số tiền ít nhất người đó phải gửi vào ngân hàng để
có đủ tiền mua căn hộ chung cư (kết quả làm tròn đến hàng triệu) là bao nhiêu?
A.
396
triệu đồng. B.
397
triệu đồng. C.
395
triệu đồng. D.
394
triệu đồng.
Câu 19: Biết một nguyên hàm của hàm số
1
1
1 3
f x
x
là hàm số
F x
thỏa mãn
2
1
3
F
Khi đó
F x
là hàm số nào sau đây?
A.
2
4 1 3
3
F x x
. B.
2
1 3 3
3
F x x x
.
C.
2
1 3 1
3
F x x x
. D.
2
1 3 3
3
F x x x
.
Câu 20: Cắt hình nón bởi một mặt phẳng đi qua trục ta được thiết diện là một tam giác vuông cân có
cạnh huyền bằng
6a
. Tính thể tích
V
của khối nón đó.
A.
3
6
3
a
V
. B.
3
6
4
a
V
. C.
3
6
2
a
V
D.
3
6
6
a
V
.
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 3
Câu 21: Tìm tất cả các giá trị của tham số
m
để hàm số
3 2 2 2
2 3 1
1
3
y x m m x m x
đạt cực
tiểu tại
2x
.
A.
3
1
m
m
. B.
3m
.
C.
1m
. D.
3
1
m
m
.
Câu 22: Cho
1
dx
3
F x
x x
. Kết quả nào sau đây đúng ?
A.
2 3
ln
3
x
F x C
x
. B.
2
ln
3 3
x
F x C
x
.
C.
1
ln
3 3
x
F x C
x
. D.
1
ln
3 3
x
F x C
x
.
Câu 23: Hàm số
cos2 2siny x x
có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn
0;
2
lần lượt là
1 2
;y y
. Khi đó tích
1 2
.y y
có giá trị bằng
A.
9
4
. B.
3
2
. C.
3
2
. D.
3
.
Câu 24: Cho hàm số
ax b
y
x c
+
=
+
với
, ,a b c Î ¡
có đồ thị như hình vẽ bên.
Giá trị của
2 3a b c+ +
bằng
A.
2
. B.
0
. C.
6
. D.
8
.
Câu 25: Cho hàm số
y f x
liên tục trên
và có bảng biến thiên như sau
Phương trình
2 3 0f x
có bao nhiêu nghiệm phân biệt?
A.
4
. B.
3
. C.
0
. D.
2
.
Câu 26: Cho hình chóp tam giác đều
.S ABC
có cạnh đáy bằng
a
và cạnh bên hợp với đáy một góc
0
60
.
Tính thể tích
V
của khối chóp
.S ABC
.
A.
3
3
a
. B.
3
3
24
a
. C.
3
3
12
a
. D.
3
6
a
.
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 4
Câu 27: Thể tích khối cầu ngoại tiếp hình hộp chữ nhật
.ABCD A B C D
với
1, 2, 2AB BC AA
bằng:
A.
27
. B.
9
2
. C.
36
. D.
9
.
Câu 28: Phương trình
2
2 2
log 1 6log 1 2 0x x
có tổng các nghiệm là
A.
4
. B.
3
. C.
6
. D.
18
.
Câu 29: Cho hàm số
3 2
1
( ) 3 2 5.
3
f x x mx m x
Tập hợp các giá trị của tham số
m
để hàm số
nghịch biến trên
là
; .a b
Khi đó
2a b
bằng:
A.
5
. B.
1
. C.
6
. D.
3
.
Câu 30: Cho
, ,a b c
là các số thực dương và khác 1. Hình vẽ đưới đây là đồ thi của hàm số
log , log , log .
a b c
y x y x y x
Khẳng định này sau đây là đúng?
A.
c a b
. B.
b c a
. C.
b a c
. D.
a b c
.
Câu 31: Số nghiệm nguyên dương nhỏ hơn
10
của bất phương trình
1 2 1
2
3 2 12 0
x
x x
là
A.
8
. B.
. C.
7
. D.
9
.
Câu 32: Khối bát diện đều có bao nhiêu mặt đối xứng?
A.
4
. B.
6
. C.
9
. D.
8
.
Câu 33: Trong không gian với hệ toạ độ
Oxyz
, cho ba điểm
1;1;1 , 5; 1;2 , 3;2; 4A B C
. Tìm toạ
độ điểm
M
thoả mãn
2 0MA MB MC
A.
3 9
4; ;
2 2
M
. B.
3 9
4; ;
2 2
M
. C.
3 9
4; ;
2 2
M
. D.
3 9
4; ;
2 2
M
.
Câu 34: Ông A dự định sử dụng hết
2
6,7m
kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật
không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có
thể tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)
A.
3
1,57m
. B.
3
1,11m
. C.
3
1,23m
. D.
3
2,48m
.
Câu 35: Một cây kem ốc quế gồm hai phần, phần em có dạng hình cầu, phần ốc quế có dạng hình nón,
giải sử hình cầu và hình nón có bán kính bằng nhau, biết rằng nếu kem tan chảy hết sẽ làm đầy
phần ốc quế. Biết thể tích kem sau khi tan chảy bằng
75%
thể tích kem đóng băng ban đầu, gọi
h
,
r
lần lượt là chiều cao và bán kính của phần ốc quế. Tỉnh tỉ số
h
r
.
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 5
A.
3
h
r
. B.
2
h
r
. C.
4
3
h
r
. D.
16
3
h
r
.
Câu 36: Gọi
S
là tập hợp các giá trị của tham số
m
để đồ thị hàm số
3 2 2 2
3 3 1 3 1y x x m x m
có điểm cực đại và cực tiểu cùng với gốc tọa độ tạo thành
tam giác vuông tại
O
. Tích tất cả các giá trị của tập
S
bằng
A.
1
. B.
3
2
. C.
3
2
. D.
1
.
Câu 37: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi cạnh
a
;
0
60ABC
và
SB a
. Hình
chiếu vuông góc của điểm
S
lên mặt phẳng
ABC
trùng với trọng tâm tam giác
ABC
. Gọi
là góc giữa đường thẳng
SB
và mặt phẳng
SCD
. Tính
sin
.
A.
3
sin
2
. B.
1
sin
4
. C.
1
sin
2
. D.
2
sin
2
.
Câu 38: Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ dưới đây
Tập hợp tất cả các giá trị thực của tham số
m
để phương trình
2
4f x m
có nghiệm
thuộc nữa khoảng
2; 3
là
A.
1; 2f
. B.
1;3
. C.
1;3
. D.
1; 2f
.
Câu 39: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật với
2 2AD AB a
. Cạnh bên
2SA a
và vuông góc với mặt phẳng đáy. Gọi
M
,
N
lần lượt là trung điểm của
SB
và
SD
.
Tính khoảng cách từ
S
đến mặt phẳng
AMN
.
A.
5a
. B.
2a
. C.
3
2
a
. D.
6
3
a
.
Câu 40: Cho hàm số
y f x
có đồ thị như hình vẽ bên dưới.
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 6
Gọi
S
là tập tất cả các giá trị nguyên dương của tham số
m
để hàm số
2020y f x m
có
5
điểm cực trị. Tổng tất cả các giá trị của các phần tử của tập
S
bằng
A.
9
. B.
7
. C.
12
. D.
18
.
Câu 41: Tính tổng
S
tất cả các nghiệm của phương trình
1
5 3
ln 5 5.3 30 10 0.
6 2
x x
x x
x
x
A.
3S
. B.
1S
. C.
2S
. D.
1S
.
Câu 42: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Tam giác
SAB
đều và nằm
trong mặt phẳng vuông góc với đáy, bán kính mặt cầu ngoại tiếp khối chóp là:
A.
21
.
6
a
B.
11
.
4
a
C.
2
.
3
a
D.
7
.
3
a
Câu 43: Cho phương trình
2
3
3
1
log 2 1 log 4 2 0
4
x m x m
, có bao nhiêu giá trị nguyên của tham
số
m
để phương trình trên có nghiệm thuộc đoạn
1
;3
3
?
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 44: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với đáy, côsin góc hợp
bởi
SD
và mặt phẳng đáy
ABCD
bằng
1
3
. Gọi
E
;
F
lần lượt là hình chiếu của
A
lên
SB
;
SD
. Mặt phẳng
AEF
chia khối chóp thành hai phần. Tính thể tích phần khối chóp
không chứa đỉnh
S
:
A.
3
2
9
a
V
. B.
3
2
4
a
V
. C.
3
2 2
9
a
V
. D.
3
2
6
a
V
.
Câu 45: Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ bên.
Số nghiệm thực của phương trình
3
4
3
3
f x x
là
A.
7
. B.
4
. C.
3
. D.
8
.
Câu 46: Cho hàm số
f x
. Hàm số
'y f x
có đồ thị như hình bên.
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 7
Số điểm cực trị của hàm số
2
1
2ln
2
g x f x x
.
A.
3
. B.
6
. C.
4
. D.
5
.
Câu 47: Cho
,x y
là những số thực dương không đổi. Xét hình chóp
.S ABC
có
,SA x BC y
và các
cạnh còn lại đều bằng 1. Khi thể tích khối chóp
.S ABC
đạt giá trị lớn nhất thì tích
.x y
bằng
A.
1
3
. B.
4
3
. C.
4 3
3
. D.
2 3
.
Câu 48: Cho lăng trụ tam giác đều
. ' ' 'ABC A B C
. Trên tia đối của tia
' 'B A
lấy điểm
M
sao cho
1
' ' '
2
B M B A
. Gọi
,N P
lần lượt là trung điểm của
' ', 'A C BB
. Mặt phẳng
( )MNP
chia khối
trụ
. ' ' 'ABC A B C
thành hai khối đa diện, trong đó khối đa diện có chứa đỉnh
'A
có thể tích
1
V
và
khối đa diện chứa đỉnh
'C
có thể tích
2
V
. Tỉ số
1
2
V
V
bằng
A.
95
144
. B.
97
59
. C.
49
144
. D.
49
95
.
Câu 49: Có 18 bạn thi Toán và KHTN bằng Tiếng Anh được khen thưởng gồm 9 nam và 9 nữ, tất cả
các học sinh nam có chiều cao khác nhau, học sinh nữ có chiều cao khác nhau. Thầy Chinh xếp
ngẫu nhiên các bạn thành một hàng ngang để chụp ảnh kỉ niệm sao cho tính từ trái sang phải
các học sinh nam có chiều cao giảm dần và các học sinh nữ có chiều cao tăng dần. Xác suất để
các bạn nam và các bạn nữ đứng xen kẽ theo cách trên là
A.
1
24310
. B.
1
48620
. C.
1
2002
. D.
14
2002
.
Câu 50: Có bao nhiêu giá trị nguyên dương của tham số
m
nhỏ hơn 2021 để phương trình
2
log 2 2
x
m m x
có nghiệm thực?
A.
2018
. B.
2019
. C.
2021
. D.
2020
.
BẢNG ĐÁP ÁN
1.B
2.D
3.A
4.A
5.D
6.C
7.B
8.C
9.C
10.B
11.A
12.B
13.C
14.A
15.D
16.A
17.D
18.B
19.D
20.B
21.B
22.C
23.C
24.B
25.A
26.C
27.B
28.A
29.D
30.B
31.D
32.C
33.C
34.A
35
36.A
37.D
38.B
39.D
40.C
41.B
42.A
43.C
44.C
45.D
46.A
47.B
48.D
49.A
50.D
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 8
ĐÁP ÁN CHI TIẾT
Câu 1: Cho
0;2;...;98A
là tập hợp gồm các số tự nhiên chẵn nhỏ hơn
100
. Số tập con có hai phần
tử của
A
là
A.
2
49
C
. B.
2
50
C
. C.
2
49
A
. D.
2
98
C
.
Lời giải
Chọn B
Số phần tử của
A
là:
98 0
1 50
2
.
Số tập con có hai phần tử của
A
là
2
50
C
.
Câu 2: Cho cấp số nhân
n
u
với
1
1u
và công bội
2q
. Tìm
.
A.
15
. B.
128
. C.
13
. D.
64
.
Lời giải
Chọn D
Ta có:
6 6
7 1
. 1.2 64u u q
.
Câu 3: Cho hàm số
4 2
2 3y x x
. Khẳng định nào sau đây đúng?
A. Hàm số có ba điểm cực trị. B. Hàm số chỉ có đúng hai điểm cực trị.
C. Hàm số không có cực trị. D. Hàm số chỉ có một điểm cực trị.
Lời giải
Chọn A
Ta thấy hàm số đã cho là hàm trùng phương
4 2
0y ax bx c a
với
0ab
nên
đây là trường hợp hàm số có ba điểm cực trị.
Câu 4: Hàm số
1
2
3
4y x
có tập xác định là:
A.
2;2
B.
2;2
C.
; 2 2; 
D.
Lời giải
Chọn A
Hàm số
1
2
3
4y x
có số mũ
1
3
không nguyên.
Do đó hàm số xác định
2
4 0 2 2 x x
.
Câu 5: Tìm giá trị nhỏ nhất của hàm số
9
y x
x
trên đoạn
2;4
.
A.
2;4
25
min
4
y
B.
2;4
13
min
2
y
C.
2;4
6
min
y
D.
2;4
6
min
y
Lời giải
Chọn D
TXĐ:
\ 0D
. Suy ra hàm số
9
y x
x
liên tục trên
2;4
.
Ta có:
2
9 9
' 1 y x y
x x
2
3
9
' 0 1 0
3
x
y
x
x
Vì
3 2;4
. Ta có:
13 25
2 ; 3 6; 4
2 4
y y y
Do đó:
2;4
3 6
min
 y
y
.
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 9
Câu 6: Cho hàm số
y f x
liên tục trên
\ 1
. Có bảng biến thiên như hình vẽ. Tổng số đường
tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số
y f x
bằng:
A.
4
B.
2
C.
3
D.
1
Lời giải
Chọn C
Từ BBT ta có:
lim 1
lim 1
x
x
y
y
®-¥
®+¥
ì
ï
=
ï
ï
Þ
í
ï
= -
ï
ï
î
ĐTHS có tiệm cận ngang
1, 1.y y= = -
1
lim
x
y
-
®
= +
ĐTHS có tiệm cận đứng
1.x =
Câu 7: Cho khối lăng trụ đứng có cạnh bên bằng
5
, đáy là hình vuông có cạnh bằng
4
. Thể tích của
khối lăng trụ đã cho bằng
A.
100
. B.
80
. C.
20
. D.
64
.
Lời giải
Chọn B
Diện tích đáy
2
4 16B
.
Thể tích của khối lăng trụ đã cho là
16.5 80V Bh
.
Câu 8: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ sau
A.
3 2
3y x x
. B.
4 2
3y x x
. C.
3 2
3y x x
. D.
4 2
3y x x
.
Lời giải
Chọn C
Từ đồ thị ta suy ra hàm số cần tìm là hàm số bậc ba có hệ số
0a
nên ta chọn C.
Câu 9: Trong không gian
Oxyz
, cho hai điểm
2; 4;3A
,
2;2;7B
. Trung điểm của
AB
có tọa độ là
A.
1;3;2
. B.
4; 2;10
. C.
2; 1;5
. D.
2; 6; 4
.
Lời giải
Chọn C
Gọi
I
là trung điểm
AB
.
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 10
Ta có
2
2
1
2
5
2
A B
I
A B
I
A B
I
x x
x
y y
y
z z
z
.
Vậy
2; 1;5I
.
Câu 10: Thể tích
V
của khối trụ có bán kính và chiều cao đều bằng
5a
là
A.
3
75 a
. B.
3
125 a
. C.
3
25 a
. D.
3
50 a
.
Lời giải
Chọn B
Thể tích khối trụ là
2
3
5 .5 125V a a a
.
Câu 11: Trong các khẳng định sau, khẳng định nào sai?
A.
cf x dx c f x dx c
. B.
f x g x dx f x dx g x dx
.
C.
f x dx f x
.D.
f x dx f x C
.
Lời giải
Chọn A
Ta có
\ 0cf x dx c f x dx c
nên chọn A.
Câu 12: Cho
, , 0a b c
,
1a
,
1b
. Trong các khẳng định sau, khẳng định nào sai?
A.
log .log log
a b a
b c c
. B.
log log log
a a a
b c b c
.
C.
log log log
a a a
bc b c
. D.
1
log
log
a
b
b
a
.
Lời giải
Chọn B
Câu 13: Gọi
, ,l h r
lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình nón. Diện tích
xung quanh
xq
S
của hình nón là:
A.
2
1
3
xq
S r h
. B.
xq
S rh
. C.
xq
S rl
. D.
2
xq
S rl
.
Lời giải
Chọn C
Câu 14: Có bao nhiêu loại khối đa diện đều?
A.
5
. B.
2
. C.
3
. D. vô số.
Lời giải
Chọn A
Có 5 loại khối đa diện đều:
3;3
- Tứ diện đều;
4;3
- Khối lập phương;
3;4
- Khối bát diện
đều;
5;3
- Khối 12 mặt đều và
3;5
- Khối 20 mặt đều.
Câu 15: Cho hàm số
y f x
có bảng biến thiên như sau
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 11
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
;2
. B.
1;1
. C.
2;
. D.
; 1
.
Lời giải
Chọn D
Dựa vào bảng biến thiên, ta thấy hàm số đồng biến trên các khoảng
; 1
và
1;
.
Câu 16: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông tại
C
,
3AB a
,
2BC a
.
Góc giữa
BC
và mặt phẳng
ABC
bằng
60
. Tính thể tích khối lăng trụ đó.
A.
3
2 15a
. B.
3
2 15
3
a
. C.
3
15a
. D.
3
15
3
a
.
Lời giải
Chọn A
Tam giác
ABC
vuông tại
C
nên diện tích
2 2 2 2 2
1 1 1
9 4 2 5
2 2 2
ABC
S CA CB AB BC BC a a a a
.
Góc giữa
BC
và
ABC
là góc
60C BC
.
Tam giác
CC B
vuông tại
C
nên
tan tan 2 tan 60 2 3
CC
C BC CC BC C BC a a
BC
.
Thể tích khối lăng trụ
2 3
5 2 3 2 15
ABC
V S CC a a a
.
Câu 17: Cho hàm số
3 2
6 7 5y x x x
có đồ thị là
C
. Số tiếp tuyến của
C
song song với đường
thẳng
2 9 0x y
là
A.
2
. B.
3
. C.
0
. D.
1
.
Lời giải
Chọn D
Đạo hàm
2
3 12 7y x x
.
Viết lại phương trình đường thẳng
: 2 9y x
.
Tiếp tuyến song song với đường thẳng khi hệ số góc tiếp tuyến
2 2
1
3 12 7 2 3 12 9 0
3
x
x x x x
x
.
Với
0
1x
,
0
7y
, phương trình tiếp tuyến
2 1 7 2 9y x y x
(trùng với
).
Với
0
3x
,
0
1y
, phương trình tiếp tuyến
2 3 1 2 5y x y x
(thỏa mãn).
Vậy có
1
tiếp tuyến song song với đường thẳng đã cho.
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 12
Câu 18: Một người gửi tiền vào ngân hàng với lãi suất không thay đổi là
8%
/năm. Biết rằng nếu không
rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu (người
ta gọi là lãi suất kép). Người đó định gửi tiền trong vòng
3
năm, sau đó rút tiền ra để mua một
căn hộ chung cư trị giá
500
triệu đồng. Hỏi số tiền ít nhất người đó phải gửi vào ngân hàng để
có đủ tiền mua căn hộ chung cư (kết quả làm tròn đến hàng triệu) là bao nhiêu?
A.
396
triệu đồng. B.
397
triệu đồng. C.
395
triệu đồng. D.
394
triệu đồng.
Lời giải
Chọn B
Gọi
A
là số tiền gửi ban đầu.
Theo công thức lãi suất kép, số tiền người đó nhận được sau
3
năm là
3
1T A r
.
Theo đề bài, ta cần có
3
3
500
500 1 500 397
1 8%
T A r A
triệu đồng.
Vậy người đó phải gửi ít nhất
397
triệu đồng.
Câu 19: Biết một nguyên hàm của hàm số
1
1
1 3
f x
x
là hàm số
F x
thỏa mãn
2
1
3
F
Khi đó
F x
là hàm số nào sau đây?
A.
2
4 1 3
3
F x x
.B.
2
1 3 3
3
F x x x
.
C.
2
1 3 1
3
F x x x
. D.
2
1 3 3
3
F x x x
.
Lời giải
Chọn D
Ta có
F x
1
1 d
1 3
x
x
2
1 3
3
x x C
.
Theo giả thiết, ta có
2
1 3
3
F C
.
Vậy
2
1 3 3
3
F x x x
.
Câu 20: Cắt hình nón bởi một mặt phẳng đi qua trục ta được thiết diện là một tam giác vuông cân có
cạnh huyền bằng
6a
. Tính thể tích
V
của khối nón đó.
A.
3
6
3
a
V
. B.
3
6
4
a
V
. C.
3
6
2
a
V
D.
3
6
6
a
V
.
Lời giải
Chọn B
Theo bài ra ta có
6
2
a
AH
.
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 13
Lại có
SAB
vuông cân tại
S
nên
2
AB
SH
6
2
a
AH
.
Thể tích khối nón là
2
1
. .
3
V SH AH
2
1 6 6
. .
3 2 2
a a
3
6
4
a
.
Câu 21: Tìm tất cả các giá trị của tham số
m
để hàm số
3 2 2 2
2 3 1
1
3
y x m m x m x
đạt cực
tiểu tại
2x
.
A.
3
1
m
m
. B.
3m
.
C.
1m
. D.
3
1
m
m
.
Lời giải
Chọn B
Xét
3 2 2 2
2 3 1
1
3
y x m m x m x
.
Tập xác định
D
.
Ta có:
2 2 2
3 122y x m m x m
.
Hàm số đạt cực tiểu tại
2x
nên
2 0y
.
Ta có
2 2 2
1 44 0 32 04 3 mm m m m
1
3
m
m
.
2
22 2y x m m
.
2
22 2y m m

.
2
1
2
0
2 0 2 0
m
y m m
m
Để hàm số hàm số đạt cực tiểu tại
2x
thì
3m
thỏa mãn.
Câu 22: Cho
1
dx
3
F x
x x
. Kết quả nào sau đây đúng ?
A.
2 3
ln
3
x
F x C
x
. B.
2
ln
3 3
x
F x C
x
.
C.
1
ln
3 3
x
F x C
x
. D.
1
ln
3 3
x
F x C
x
.
Lời giải
Chọn C.
Ta có
1 1 1 1
dx dx
3 3 3
F x
x x x x
1
ln
3 3
x
C
x
.
Câu 23: Hàm số
cos2 2siny x x
có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn
0;
2
lần lượt là
1 2
;y y
. Khi đó tích
1 2
.y y
có giá trị bằng
A.
9
4
. B.
3
2
. C.
3
2
. D.
3
.
Lời giải
Chọn C.
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 14
Xét hàm số
cos2 2siny x x
trên
0;
2
.
Ta có
2sin 2 2cos 4sin .cos 2cos 2cos 2sin 1y x x x x x x x
.
Giải
2
cos 0
0 2
1
6
sin
2
5
2
6
x k
x
y x k k
x
x k
.
Xét trên đoạn
0;
2
,
0y
có các nghiệm
;
6 2
x x
.
Ta có
3
0 1; 1;
2 6 2
y y y
.
Suy ra
1
0;
2
3
max
2
y y
,
2
0;
2
min 1y y
.
Vậy
1 2
3
.
2
y y
.
Câu 24: Cho hàm số
ax b
y
x c
+
=
+
với
, ,a b c Î ¡
có đồ thị như hình vẽ bên.
Giá trị của
2 3a b c+ +
bằng
A.
2
. B.
0
. C.
6
. D.
8
.
Lời giải
Chọn B.
Tiệm cận đứng của đồ thị hàm số:
x c= -
suy ra
1c- =
1cÛ = -
.
Tiệm cận ngang của đồ thị hàm số:
y a=
suy ra
1a = -
.
Đồ thị cắt trục
Oy
tại điểm
0;
b
c
÷
ç
÷
ç
÷
ç
nên
2
b
c
= -
mà
1c = -
suy ra
2b =
.
Vậy,
2 3 0.a b c+ + =
Câu 25: Cho hàm số
y f x
liên tục trên
và có bảng biến thiên như sau
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 15
Phương trình
2 3 0f x
có bao nhiêu nghiệm phân biệt?
A.
4
. B.
3
. C.
0
. D.
2
.
Lời giải
Chọn A.
Ta có:
3
2 3 0 .
2
f x f x
Ứng với bảng biến thiên ta thấy đường thẳng
3
2
y
cắt
đồ thị hàm số
f x
tại
4
điểm nên
2 3 0f x
có
4
nghiệm phân biệt.
Câu 26: Cho hình chóp tam giác đều
.S ABC
có cạnh đáy bằng
a
và cạnh bên hợp với đáy một góc
0
60
.
Tính thể tích
V
của khối chóp
.S ABC
.
A.
3
3
a
. B.
3
3
24
a
. C.
3
3
12
a
. D.
3
6
a
.
Lời giải
Chọn C.
S
A
B
C
H
M
60
Gọi
H
là hình chiếu vuông góc của
S
lên
( )ABC
, khi đó
.
1
. . .
3
S ABC ABC
V SH S
Xét tam giác
SHA
vuông tại
A
có:
0
2 2 3 3
.
3 3 2 3
.
3
tan . tan60 .
3
a a
AH AM
a
SH SAH AH a
Khi đó
2 3
.
1 1 3 3
. . . . .
3 3 4 12
S ABC ABC
a a
V SH S a
Câu 27: Thể tích khối cầu ngoại tiếp hình hộp chữ nhật
.ABCD A B C D
với
1, 2, 2AB BC AA
bằng:
A.
27
. B.
9
2
. C.
36
. D.
9
.
Lời giải
Chọn B.
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 16
A
B
C
D
B
A
C
D
Gọi
R
là bán kính khối cầu ngoại tếp
.ABCD A B C D
. Khi đó:
R=
2 2 2 2 2 2
3
1 2 2 3 4 4 27 9
. . .
2 2 2 2 3 3 8 2
AC AB AD AA
V R
Câu 28: Phương trình
2
2 2
log 1 6log 1 2 0x x
có tổng các nghiệm là
A.
4
. B.
3
. C.
6
. D.
18
.
Lời giải
Chọn A
Điều kiện:
1.x
Ta có:
2
2 2
2
2 2
2
2
log 1 6log 1 2 0
log 1 3log 1 2 0
log 1 1
1
.
3
log 1 2
x x
x x
x
x
x
x
So với điều kiện thấy thỏa mãn.
Vậy tổng các nghiệm là:
1 3 4.
Câu 29: Cho hàm số
3 2
1
( ) 3 2 5.
3
f x x mx m x
Tập hợp các giá trị của tham số
m
để hàm số
nghịch biến trên
là
; .a b
Khi đó
2a b
bằng:
A.
5
. B.
1
. C.
6
. D.
3
.
Lời giải
Chọn A
Ta có:
2
( ) 2 3 2.f x x mx m
Hàm số nghịch biến trên
2
( ) 0, 3 2 0 2 1.f x x m m m
Suy ra:
2, 1 2 2 2 1 3.a b a b
Câu 30: Cho
, ,a b c
là các số thực dương và khác 1. Hình vẽ đưới đây là đồ thi của hàm số
log , log , log .
a b c
y x y x y x
Khẳng định này sau đây là đúng?
A.
c a b
. B.
b c a
. C.
b a c
. D.
a b c
.
Lời giải
Chọn A
Dựa vào đồ thị ta với thấy với
0
1x
thì:
0 0
0 0
0 0
1 1
log log 0 0 log log 0 1.
log log
c a x x
x x
x x a c a c
c a
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 17
Mặt khác:
0
0
log 0 log 0 1.
b x
x b b
Từ đây suy ra:
.b c a
Câu 31: Số nghiệm nguyên dương nhỏ hơn
10
của bất phương trình
1 2 1
2
3 2 12 0
x
x x
là
A.
8
. B.
. C.
7
. D.
9
.
Lời giải
Chọn D
Ta biến đổi bất phương trình
2
1 2 1
2 2
2
3 12 3 12
3 2 12 0 3.3 2.4 12 0 3. 2 0 3. 2 0
4 4
4 4
3 3
3. 2 0 1
2 2
x
x
x x
x
x
x x x x
x x
x x
Đặt
3
2
x
t
, điều kiện
0t
.
Bất phương trình
1
trở thành:
2
2
3 2 0 1
3
t t t
.
Kết hợp với điều kiện ta được
0 1t
. Suy ra
3
0 1 0.
2
x
x
Do đó nghiệm nguyên dương nhỏ hơn
10
của bất phương trình là tập
1;2;3;...;8;9 .
Vậy số nghiệm nguyên dương nhỏ hơn
10
của bất phương trình là 9.
Câu 32: Khối bát diện đều có bao nhiêu mặt đối xứng?
A.
4
. B.
6
. C.
9
. D.
8
.
Lời giải
Chọn C
Khối bát diện đều có
9
mặt phẳng đối xứng bao gồm:
Loại 1. Mặt phẳng đối xứng đi qua 4 đỉnh đồng phẳng của khối bát
diện đều (có 3 mặt).
Loại 2. Mặt phẳng đối xứng đi qua 2 đỉnh đối diện và trung điểm 2
cạnh đối diện không chứa 2 đỉnh đó (có 6 mặt).
Câu 33: Trong không gian với hệ toạ độ
Oxyz
, cho ba điểm
1;1;1 , 5; 1;2 , 3;2; 4A B C
. Tìm toạ
độ điểm
M
thoả mãn
2 0MA MB MC
A.
3 9
4; ;
2 2
M
. B.
3 9
4; ;
2 2
M
. C.
3 9
4; ;
2 2
M
. D.
3 9
4; ;
2 2
M
.
Lời giải
Chọn C
Gọi
; ;M a b c
.
Ta có:
1 ;1 ;1MA a b c
,
5 ; 1 ;2MB a b c
,
3 ;2 ; 4MC a b c
.
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 18
2 0MA MB MC
1 2 5 3 0
1 2 1 2 0
1 2 2 4 0
a a a
b b b
c c c
4
3
2
9
2
a
b
c
3 9
4; ;
2 2
M
.
Câu 34: Ông A dự định sử dụng hết
2
6,7m
kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật
không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có
thể tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)
A.
3
1,57m
. B.
3
1,11m
. C.
3
1,23m
. D.
3
2,48m
.
Lời giải
Chọn A
Gọi chiều rộng, chiều dài và chiều cao của bể cá lần lượ là :
;2 ; , 0x x y x y
Tổng diện tích tất cả các mặt của bể cá (trừ nắp trên) là:
2
2 6S x xy
2
2 6 6,7x xy
2
6,7 2
6
x
y
x
.
Thể tích cái bể là:
2
1
.2 . 6.7 2
3
V x x y x x
.
Xét hàm số
3
6,7 2f x x x
với
0x
, ta có:
2
6,7 6f x x
,
6,7
0
6
f x x
.
BBT
Vậy thể tích bể cá lớn nhất là
3
13,4 6,7
. 1,57
9 6
V m
.
Câu 35: Một cây kem ốc quế gồm hai phần, phần em có dạng hình cầu, phần ốc quế có dạng hình nón,
giải sử hình cầu và hình nón có bán kính bằng nhau, biết rằng nếu kem tan chảy hết sẽ làm đầy
phần ốc quế. Biết thể tích kem sau khi tan chảy bằng
75%
thể tích kem đóng băng ban đầu, gọi
h
,
r
lần lượt là chiều cao và bán kính của phần ốc quế. Tỉnh tỉ số
h
r
.
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 19
A.
3
h
r
. B.
2
h
r
. C.
4
3
h
r
. D.
16
3
h
r
.
Lời giải
Chọn A
Thể tích khối cầu (phần kèm) khi chưa tan chảy bằng
2
4
3
C
V r
.
Thể tích khối nón bằng
2
1
3
N
V r h
.
Theo đề bài ra ta có
75%.
N C
V V
2 3
1 3 4
.
3 4 3
r h r
3
h
r
.
Câu 36: Gọi
S
là tập hợp các giá trị của tham số
m
để đồ thị hàm số
3 2 2 2
3 3 1 3 1y x x m x m
có điểm cực đại và cực tiểu cùng với gốc tọa độ tạo thành
tam giác vuông tại
O
. Tích tất cả các giá trị của tập
S
bằng
A.
1
. B.
3
2
. C.
3
2
. D.
1
.
Lời giải
Chọn A
Ta có
2 2
3 6 3 3 0y x x m
2 2
2 1 0x x m
1
Để hàm số có hai điểm cực đại và cực tiểu thì
1
phải có hai nghiệm phân biệt, nên
2
0m
suy ra
0m
.
Dễ thấy
1
có hai nghiệm
1
1x m
và
2
1x m
nên
3
1 ; 2 2A m m
và
3
1 ; 2 2B m m
là hai điểm cực trị của đồ thị hàm số
Tam giác
OAB
vuông ở
O
. 0OAOB
3 3
1 1 2 2 2 2 0m m m m
2 6
1 4 1 0m m
2 4
1 4 4 5 0m m m
2
1m
1m
.
Do đó tích các giá trị thỏa mãn của
m
bằng
1
.
Câu 37: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi cạnh
a
;
0
60ABC
và
SB a
. Hình
chiếu vuông góc của điểm
S
lên mặt phẳng
ABC
trùng với trọng tâm tam giác
ABC
. Gọi
là góc giữa đường thẳng
SB
và mặt phẳng
SCD
. Tính
sin
.
A.
3
sin
2
. B.
1
sin
4
. C.
1
sin
2
. D.
2
sin
2
.
Lời giải
Chọn D
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 20
Vì
60
AB AC a
ABC
ABC
là tam giác đều cạnh
a
.
Gọi
G
là trọng tâm của tam giác
ABC
SG ABCD
.
Gọi
E
là hình chiếu của
B
trên
SCD
nên
SE
là hình chiếu của
SB
trên mặt phẳng
SCD
Góc giữa
SB
và mặt phẳng
SCD
là góc giữa hai đường thẳng
SB
,
SE
và bằng
BSE
BSE
.
Ta có
,BE d B SCD
.
BG SCD D
,
3
2
,
d B SCD
BG
GC
d G SCD
3
, ,
2
d B CD d G SCD
Kẻ
GH SC
tại
1H
.
Ta có:
CD CG
CD SCG
CD SG
2 .CD HG
Từ
1
và
2
suy ra
GH SCD
,d G SCD GH
.
2 3
.
3 2
3
a a
CG
.
Xét tam giác
SBG
vuông tại
G
có
2
2 2 2
6
3 3
a a
SG SB AG a
.
Xét tam giác
SCG
vuông tại
G
ta có
2 2 2 2 2
1 1 1 9 3
6HG GS GC a a
2
9
2a
2
3
a
HG
3 2
2 2
a
BE HG
.Xét tam giác
SEB
vuông tại
E
ta có
2
2
2
sin
2
a
BE
SB a
.
Câu 38: Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ dưới đây
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 21
Tập hợp tất cả các giá trị thực của tham số
m
để phương trình
2
4f x m
có nghiệm
thuộc nữa khoảng
2; 3
là
A.
1; 2f
. B.
1;3
. C.
1;3
. D.
1; 2f
.
Lời giải
Chọn B
Đặt
2
2
2
4
2 4
x
t x t
x
;
' 0 0t x
Với
2 ; 3x
ta có bảng biến thiên của hàm số
2
4t x
.
Với
2; 3 1;2x t
Từ đồ thị ta có:
1;2 1;3t f t
Vây để phương trình
2
4f x m
có nghiệm thì
1;3m
.
Câu 39: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật với
2 2AD AB a
. Cạnh bên
2SA a
và vuông góc với mặt phẳng đáy. Gọi
M
,
N
lần lượt là trung điểm của
SB
và
SD
.
Tính khoảng cách từ
S
đến mặt phẳng
AMN
.
A.
5a
. B.
2a
. C.
3
2
a
. D.
6
3
a
.
Lời giải
Chọn D
Ta có:
3
. .
1 1 1 2
. . 2 . .2
2 6 6 3
S ABD S ABCD
V V AS AB AD a a a a
.
.
.
1 1 1
. . 1. .
2 2 4
S AMN
S ABD
V
SA SM SN
V SA SB SD
3 3
. .
1 1 2 1
.
4 4 3 6
S AMN S ABD
V V a a
.
Mặt khác:
2 2 2 2
1 1 1 5
4
2 2 2 2
a
AM SB AB AS a a
.
2 2 2 2
1 1 1
4 4 2
2 2 2
AN SD AD AS a a a
.
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 22
2 2 2 2
1 1 1 5
4
2 2 2 2
a
MN BD AB AD a a
.
Suy ra:
2
6
4
AMN
a
S
.
Vậy
3
.
2
3
1 4 6
; .
2 3
6
S AMN
AMN
V
a
d S AMN a
S
a
.
Câu 40: Cho hàm số
y f x
có đồ thị như hình vẽ bên dưới.
Gọi
S
là tập tất cả các giá trị nguyên dương của tham số
m
để hàm số
2020y f x m
có
5
điểm cực trị. Tổng tất cả các giá trị của các phần tử của tập
S
bằng
A.
9
. B.
7
. C.
12
. D.
18
.
Lời giải
Chọn C
Ta có:
2020y f x m
.
Từ đồ thị hàm số
y f x
Hàm số
y f x
có
3
điểm cực trị
Hàm số
2020f x m
cũng luôn có
3
điểm cực trị
Do đó, yêu cầu bài toán
số giao điểm của đồ thị hàm số
2020f x m
với trục hoành là
2
.
Tương đương với phương trình
2020f x m
*
có hai nghiệm đơn phân biệt.
Từ đồ thị hàm số
y f x
ta tịnh tiến sang phải
2020
đơn vị được đồ thị hàm số
2020y f x
.
Khi đó phương trình
*
có hai nghiệm đơn phân biệt khi
2
6 3
m
m
2
3 6
m
m
3;4;5S
.
Vậy tổng giá trị các phần tử của
S
là:
3 4 5 12
.
Câu 41: Tính tổng
S
tất cả các nghiệm của phương trình
1
5 3
ln 5 5.3 30 10 0.
6 2
x x
x x
x
x
A.
3S
. B.
1S
. C.
2S
. D.
1S
.
Lời giải
Chọn B.
Ta có:
1
5 3
ln 5 5.3 30 10 0
6 2
x x
x x
x
x
ln 5 3 5 5 3 ln 6 2 5 6 2 .
x x x x
x x
Khi đó phương trình có dạng
5 3 6 2 ,
x x
f f x
với
ln 5 , 0;f t t t t 
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 23
1
' 5 0, 0;f t t f t
t

đồng biến trên
0;
nên từ phương trình
5 3 6 2 5 3 6 2 5 3 6 2 0.
x x x x x x
f f x x g x x
2 2
' 5 ln 5 3 ln3 6 '' 5 ln 5 3 ln 3 0,
x x x x
g x g x x
Do
'' 0,g x x
phương trình
' 0g x
có nhiều nhất là một nghiệm, từ đó phương trình
0g x
có nhiều nhất là hai nghiệm. Ta thấy
1 2
0; 1x x
là hai nghiệm của phương trình
0g x
.
Vậy phương trình có hai nghiệm là
1 2 1 2
0; 1 1.x x S x x
Câu 42: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Tam giác
SAB
đều và nằm
trong mặt phẳng vuông góc với đáy, bán kính mặt cầu ngoại tiếp khối chóp là:
A.
21
.
6
a
B.
11
.
4
a
C.
2
.
3
a
D.
7
.
3
a
Lời giải
Chọn A.
Để thuận lợi trong việc tính toán ta có thể giả sử cạnh hình vuông đáy
1.a
Gọi
H
là trung điểm
AB
. Ta có tam giác
SAB
đều và nằm trong mặt phẳng vuông góc với
đáy
3
, .
2
SH ABCD SH
Chọn hệ tọa độ
Oxyz
như hình vẽ
3 1 1 1 1
0;0; , 0; ;0 , 0; ;0 , 1; ;0 1; ;0 .
2 2 2 2 2
S A B C D
Gọi phương trình mặt cầu có dạng
2 2 2
: 2 ' 2 ' 2 ' ' 0.T x y z a x b y c z d
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 24
Do các điểm
3
1
3 ' ' 0
'
4
2
1
' 0
' ' 0
4
, , ,
3
1
'
' ' 0
6
4
1
5
'
2 ' ' ' 0
4
4
c d
a
b
b d
S A B C T
c
b d
d
a b d
2 2 2
21
' ' ' ' .
6
R a b c d
Vậy bán kính mặt cầu ngoại tiếp khối chóp là
21
.
6
a
R
Cách khác: ta có thể áp dụng công thức giải nhanh
2
2 2
1 2
.
2
AB
R R R
Trong đó là
1
R
bán kính đường tròn ngoại tiếp đáy
1
2
2 2
AC a
ABCD R
và
2
R
là bán
kính đường tròn ngoại tiếp mặt bên
2
2 2 3 3
. .
3 3 2 3
a a
SAB R SH
2
2 2
1 2
21
.
2 6
AB a
R R R
Câu 43: Cho phương trình
2
3
3
1
log 2 1 log 4 2 0
4
x m x m
, có bao nhiêu giá trị nguyên của tham
số
m
để phương trình trên có nghiệm thuộc đoạn
1
;3
3
?
A.
1
. B.
4
. C.
2
. D.
3
.
Lời giải
Chọn C
ĐKXĐ:
0x
.
Ta có:
2
3
3
1
log 2 1 log 4 2 0
4
x m x m
2
2 3
log 2 1 log 4 2 0x m x m
3
3
log 2 1
log 2
x m
x
2 1
3
9
m
x
x
Do đó yêu cầu bài toán
2 1
1
3 3
3
m
1 2 1 1m
0 1m
.
Vậy có
2
giá trị nguyên của
m
thoả mãn yêu cầu bài toán.
Câu 44: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với đáy, côsin góc hợp
bởi
SD
và mặt phẳng đáy
ABCD
bằng
1
3
. Gọi
E
;
F
lần lượt là hình chiếu của
A
lên
SB
;
SD
. Mặt phẳng
AEF
chia khối chóp thành hai phần. Tính thể tích phần khối chóp
không chứa đỉnh
S
:
A.
3
2
9
a
V
. B.
3
2
4
a
V
. C.
3
2 2
9
a
V
. D.
3
2
6
a
V
.
Lời giải
Chọn C
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 25
Dễ thấy
SAB SAD
AE AF
SE SF
SA SB
/ /EF BD
Do
SA ABCD
nên
AD
là hình chiếu của
SD
lên mặt phẳng
ABCD
1
cos ; cos
3
AD
SD ABCD SDA
SD
3 3SD AD a
2
2 2 2
3 2SA SD AD a a a AC
Tam giác
SAC
vuông cân tại
A
Trong
ABCD
: gọi
O AC BD
Trong
SBD
: gọi
I SO EF
Trong
SAC
: gọi
M SC AI
Lại có:
SA BC
AB BC
BC SAB
BC AE
Mà
AE SB
AE SBC
AE SC
1
SA CD
AD CD
CD SAD
CD AF
Mà
AF SD
AF SCD
AF SC
2
Từ
1
và
2
SC AEF
SC AM
M
là trung điểm
SC
I
là trọng tâm tam
giác
SAC
2
3
SE SF
SA SB
2 3
3
a
SE SF
Ta có:
1
. .
3
SAEM
SABC
V
SA SE SM
V SA SB SC
.
1 1
3 6
SAEM SABC S ABCD
V V V
1
. .
3
SAMF
SACD
V
SA SM SF
V SA SC SD
.
1 1
3 6
SAMF SACD S ABCD
V V V
. .
1
3
S AEMF SAEM SAMF S ABCD
V V V V
3
. . .
2 2 1 2 3
. .
3 3 3 9
S ABCD S AEMF S ABCD ABCD
a
V V V V SA S
.
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 26
Câu 45: Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ bên.
Số nghiệm thực của phương trình
3
4
3
3
f x x
là
A.
7
. B.
4
. C.
3
. D.
8
.
Lời giải
Chọn D
Dựa vào đồ thị trên, ta có:
3
3
3
3
3
3 ; 2 1
3 2;0 2
4
3
3
3 0;2 3
3 2; 4
x x a
x x b
f x x
x x c
x x d


Xét hàm số
3
3y x x
có bảng biến thiên:
Dựa vào bảng biến thiên trên, mỗi phương trình
2 , 3
có 3 nghiệm phân biệt và
1 , 4
có
1 nghiệm.
Vậy tổng số nghiệm của phương trình
3
4
3
3
f x x
là 8.
Câu 46: Cho hàm số
f x
. Hàm số
'y f x
có đồ thị như hình bên.
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 27
Số điểm cực trị của hàm số
2
1
2ln
2
g x f x x
.
A.
3
. B.
6
. C.
4
. D.
5
.
Lời giải
Chọn A
Hàm số
2
1
2ln
2
g x f x x
có tập xác định
0;D
.
2
1 2
' 2 . '
2
g x x f x
x
.
Với
0;x
, ta xét
' 0g x
2
2
1 1
' *
2
f x
x
Đặt
2
1
2
t x
, (với
1
0
2
x t
, khi đó
*
trở thành:
2
'
2 1
f t
t
Dựa vào đồ thị trên, ta có:
0 0,5
2
'
1,5
2 1
t
f t
t
t
Khi đó:
2
2
0
2
1 1
1
0
2
2 2
1 3
2
2 2
x
x
x
x
x
.
Bảng xét dấu của
'g x
:
Vậy hàm số
g x
có 3 điểm cực trị.
Câu 47: Cho
,x y
là những số thực dương không đổi. Xét hình chóp
.S ABC
có
,SA x BC y
và các
cạnh còn lại đều bằng 1. Khi thể tích khối chóp
.S ABC
đạt giá trị lớn nhất thì tích
.x y
bằng
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 28
A.
1
3
. B.
4
3
. C.
4 3
3
. D.
2 3
.
Lời giải
Chọn B
Ta có: do
AB AC SB SC
nên các tam giác
SBC
và
ABC
cân tại
,S A
. Gọi
,M N
lần
lượt là trung điểm
,BC SA
thì
( )
BC SM
BC SAM
BC AM
. Từ đây ta hạ
,SH AM H AM
Mà
( ( ))SH BC BC ASM
nên
( )SH ABC
Suy ra
2
1
4
y
AM
nên
2
1
. . 1
2 2 4
ABC
y y
S AM BC
Mặt khác vì
SM AM
nên
SAM
cân tại
M
2 2
2 2
1
4 4
y x
MN AM AN
Mà ta có:
2 2
2 2
2
2
1
. 4
4
. .
4
1
4
x y
x
MN SA x y
MN SA SH AM SH x
y
AM y
Suy ra, ta có được
2 2 2 2
2 2 2
2 2
.
2
2 2 2 2
(4 )
1 1 4
. . . 1 4
3 3 4 2 4 12 12
1 4 2 3
12 3 27
S ABC ABC
x y x y
x y y y xy
V SH S x x y
y
x y x y
Vậy
. max
2 3
27
S ABC
V
khi và chỉ khi
2
2 2 2
2 2 4
4 2
3
3 3
x y x x y xy
Câu 48: Cho lăng trụ tam giác đều
. ' ' 'ABC A B C
. Trên tia đối của tia
' 'B A
lấy điểm
M
sao cho
1
' ' '
2
B M B A
. Gọi
,N P
lần lượt là trung điểm của
' ', 'A C BB
. Mặt phẳng
( )MNP
chia khối
trụ
. ' ' 'ABC A B C
thành hai khối đa diện, trong đó khối đa diện có chứa đỉnh
'A
có thể tích
1
V
và
khối đa diện chứa đỉnh
'C
có thể tích
2
V
. Tỉ số
1
2
V
V
bằng
A.
95
144
. B.
97
59
. C.
49
144
. D.
49
95
.
Lời giải
Chọn D
Ta gọi:
, ', ;K MP AB S MP AA L NS AC
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 29
Khi đó thiết diện cần tìm chính là ngũ giác
NJPKL
chia hình lăng trụ
. ' ' 'ABC A B C
thành 2
phần như hình vẽ. Cho
J
là trung điểm
BF
mà ta có:
/ / '
'
'
NF B M
B J JF
NF B M
Tương tự ta lại có thêm được:
MJ JN
nên từ đó suy ra
'B NFM
là hình bình hành
Mặt khác:
' 1
'
/ /
' 3
AK KB
MP B P
SA BP B P
SA BP
MS A S
Ta có:
. '
. ' . '
. '
' 1 1 1 1 1
. . . .
' 3 2 3 18 18
M PJB
M PJB M SNA
M SNA
V MP MJ MB
V V
V MS MN MA
Mặt khác: ta có
3
.
. . '
. '
1 1 1 1
. .
' 3 ' 3 27 27
S ALK
S ALK S A NM
S A NM
SL SA V SK SA SL
V V
SN SA V SM SA SN
Khi đó:
1 . ' . ' . . ' . '
1 1 49
1
18 27 54
S MNA M PJB S ALK M SNA M SNA
V V V V V V
Ta lại có:
. ' . ' . ' ' ' . ' ' ' 2 . ' ' ' 1 . ' ' '
49 49 3 49 95
.
54 54 8 144 144
S A NM M SNA ABC A B C ABC A B C ABC A B C ABC A B C
V V V V V V V V
Vậy:
1
2
49
95
V
V
Câu 49: Có 18 bạn thi Toán và KHTN bằng Tiếng Anh được khen thưởng gồm 9 nam và 9 nữ, tất cả
các học sinh nam có chiều cao khác nhau, học sinh nữ có chiều cao khác nhau. Thầy Chinh xếp
ngẫu nhiên các bạn thành một hàng ngang để chụp ảnh kỉ niệm sao cho tính từ trái sang phải
các học sinh nam có chiều cao giảm dần và các học sinh nữ có chiều cao tăng dần. Xác suất để
các bạn nam và các bạn nữ đứng xen kẽ theo cách trên là
A.
1
24310
. B.
1
48620
. C.
1
2002
. D.
14
2002
.
Lời giải
Chọn A
Cần tất cả 18 vị trị cho 18 học sinh.
Bước 1: Chọn vị trí cho 9 học sinh, có
9
18
C
cách chọn. Sau đó ta xếp 9 học sinh nam vào 9 vị trí
đã chọn sao cho chiều cao giảm dần từ trái sang phải, chỉ có 1 cách xếp như vậy.
NHÓM TOÁN VD–VDC NĂM HỌC 2020 – 2021
https:/www.facebook.com/groups/toanvd. Trang 30
Bước 2: Xếp 9 nữ vào 9 vị trí còn lại sao cho chiều cao tăng dần từ trái sang phải, chỉ có một
cách xếp như vậy.
Vậy
9
18
48620C
.
Gọi A là biến cố: “Thầy giáo xếp các bạn nam và các bạn nữ đứng xen kẽ nhau ”.
Theo cách xếp trên giả sử thầy giáo xếp các bạn nam trước(tính từ trái sang phải các
học sinh nam có chiều cao giảm dần) có 1 cách xếp.
Để xếp các bạn nữ xen kẽ theo cách trên(các học sinh nữ có chiều cao tăng dần) vào
các vị trí có 2 cách.
Theo quy tắc nhân có 2 cách để xếp các bạn học sinh thỏa mãn đề bài.
Do đó
2
A
.
Vậy
2 1
48620 24310
P A
.
Câu 50: Có bao nhiêu giá trị nguyên dương của tham số
m
nhỏ hơn 2021 để phương trình
2
log 2 2
x
m m x
có nghiệm thực?
A.
2018
. B.
2019
. C.
2021
. D.
2020
.
Lời giải
Chọn D
Ta có phương trình:
2
log 2 2
x
m m x
(1)
Đặt:
2
x
t m
( 0)t
thì phương trình (1) trở thành
2
log 2 4 4
x x
m t x m t t m
Mà
2
x
t m
nên suy ra
4 2 4 2
x x x x
m m m m
4 2 2 2
x x x x
m m
Từ đây ta xét hàm đặc trưng
2
( )y f t t t
,
0t
có
'( ) 2 1 0, 0f t t t
( ) [0; ) (2 ) 2 2 2 4 2
x x x x x x
f t trên f f m m m 
Xét hàm
( ) 4 2
x x
y g x
có
'( ) 4 .2ln(2) 2 ln(2) 0 1
x x
g x x
Ta có bảng biến thiên của hàm
( )g x
như sau:
Từ đó để phương trình trên có 2 nghiệm thực thì
1
( 1)
4
m g m
Mà m nguyên dương và nhỏ hơn
2021
nên suy ra
[1;2020]m
Vậy có tất cả 2020 giá trị nguyên
m
thỏa mãn yêu cầu đề bài

Tài liệu khác của Toán

Preview text:

NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021
SỞ GD&ĐT HẢI PHÒNG
ĐỀ THI KHẢO SÁT CHẤT LƯỢNG LẦN 1
TRƯỜNG THPT LÊ QUÝ ĐÔN NĂM HỌC 2020 - 2021 Môn: TOÁN - Lớp: 12
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
_________________________ ĐỀ BÀI
Câu 1: Cho A  0;2;. .;9 
8 là tập hợp gồm các số tự nhiên chẵn nhỏ hơn 100 . Số tập con có hai phần tử của A là A. 24 C 9 . B. 25 C 0. C. 24 A 9. D. 29 C 8.
Câu 2: Cho cấp số nhân un  với 1
u 1và công bội q  2 . Tìm u7 . A. 15. B. 128 . C. 13. D. 64 . Câu 3: Cho hàm số 4 2
y x  2x  3. Khẳng định nào sau đây đúng?
A. Hàm số có ba điểm cực trị.
B. Hàm số chỉ có đúng hai điểm cực trị.
C. Hàm số không có cực trị.
D. Hàm số chỉ có một điểm cực trị.
Câu 4: Hàm số y    x 1 2 3 4 có tập xác định là: A. 2;2 B.  2  ;2 C.  ;  2  2; D.
Câu 5: Tìm giá trị nhỏ nhất của hàm số 9
y x  trên đoạn 2;4 . x A. 25 13 min  y B. min  y C. min  6  y D. min  y 6 2;4 4 2;4 2 2;4 2;4
Câu 6: Cho hàm số y f x liên tục trên  \ 
1 . Có bảng biến thiên như hình vẽ. Tổng số đường
tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số y f x bằng: A. 4 B. 2 C. 3 D. 1
Câu 7: Cho khối lăng trụ đứng có cạnh bên bằng 5 , đáy là hình vuông có cạnh bằng 4 . Thể tích của
khối lăng trụ đã cho bằng A. 100. B. 80 . C. 20 . D. 64 .
Câu 8: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ sau A. 3 2
y  x  3x . B. 4 2
y x  3x . C. 3 2
y x  3x . D. 4 2
y  x  3x .
Câu 9: Trong không gian Oxyz , cho hai điểm A2;4;3 , B 2;2;7 . Trung điểm của AB có tọa độ là A. 1;3;2 . B. 4;2;10 . C. 2;1;5 . D. 2; 6; 4 .
Câu 10: Thể tích V của khối trụ có bán kính và chiều cao đều bằng 5a là A. 3 75a . B. 3 125a . C. 3 25a . D. 3 50a .
https:/www.facebook.com/groups/toanvd.Trang 1 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021
Câu 11: Trong các khẳng định sau, khẳng định nào sai?
A. cf xdx c f xdxc    . B. f
  x gxdx f
 xdx g  xdx . C. f
  x  dx f
x .D. f
 xdx f xC .
Câu 12: Cho a,b,c  0 , a  1, b 1. Trong các khẳng định sau, khẳng định nào sai? A. log b c c log b c b c . a loga log a .logb loga . B.   a 1 C. log bc b c log b a   loga loga . D. a . log a b
Câu 13: Gọi l,h,r lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình nón. Diện tích
xung quanh S của hình nón là: xq A. 1 2 S  r h .
B. S  rh .
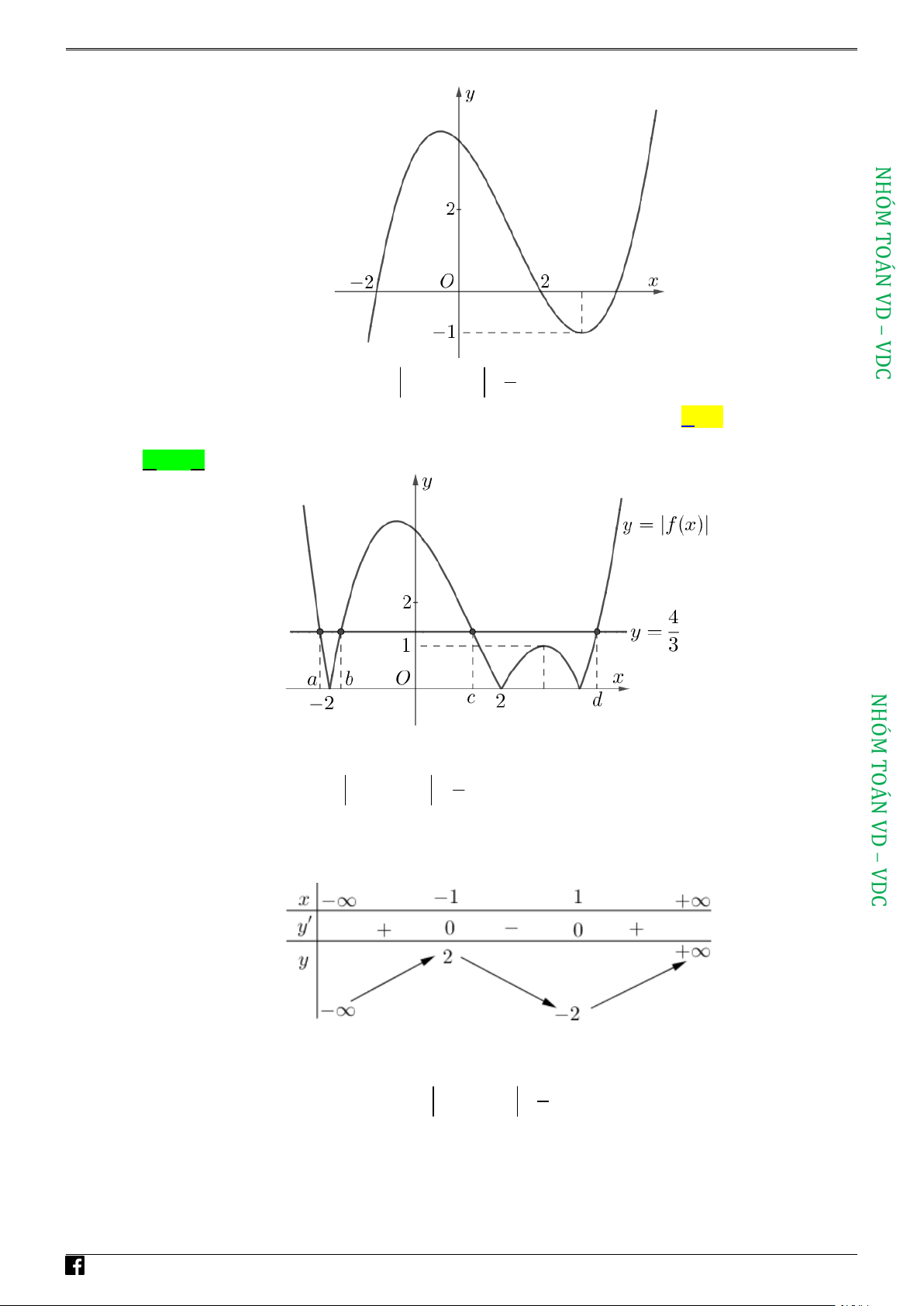
C. S  rl .
D. S  rl . xq 2 xq 3 xq xq
Câu 14: Có bao nhiêu loại khối đa diện đều? A. 5. B. 2 . C. 3. D. vô số.
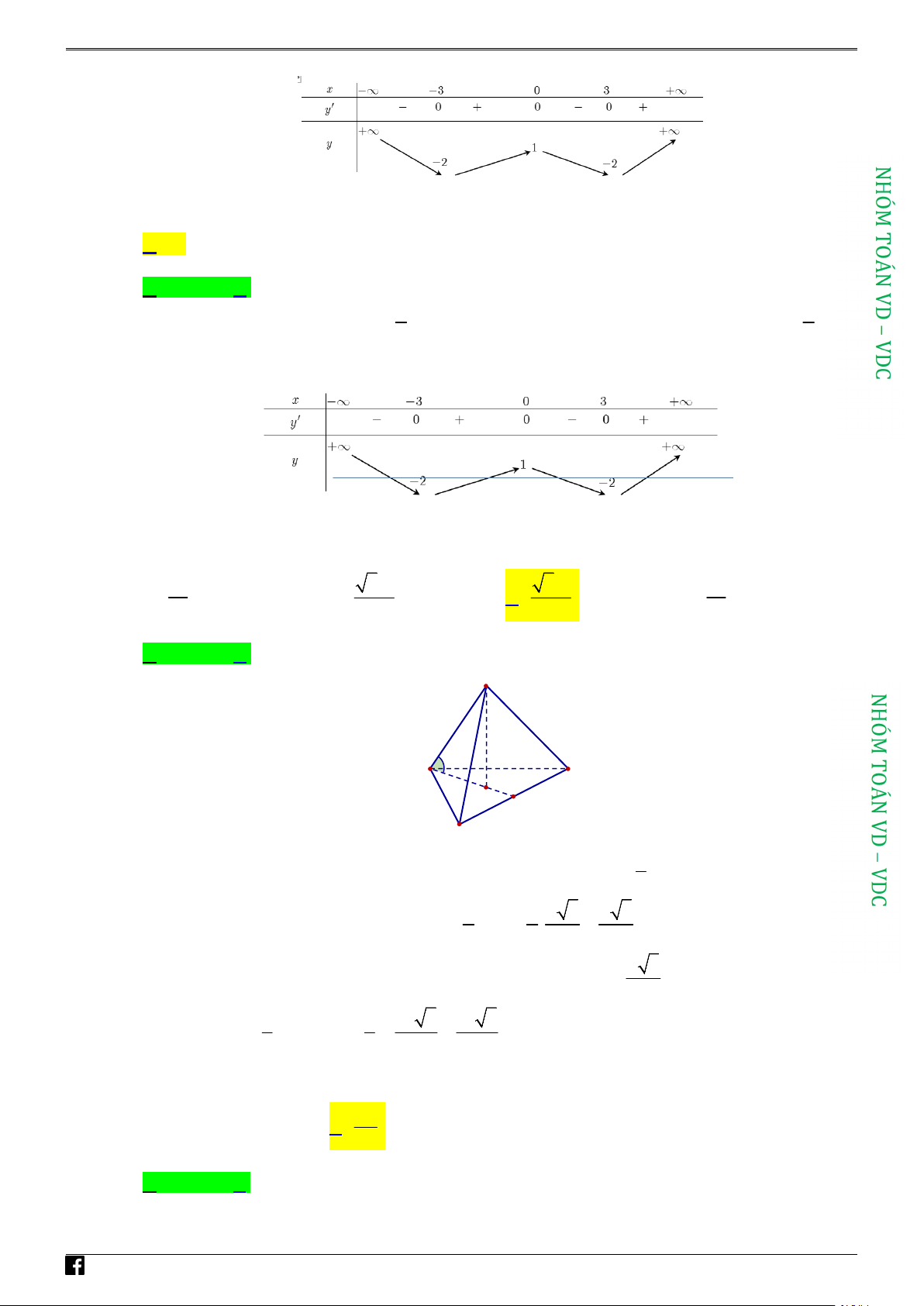
Câu 15: Cho hàm số y f x có bảng biến thiên như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. ;2 . B. 1;  1 . C. 2;  . D. ;  1 .
Câu 16: Cho hình lăng trụ đứng ABC.A BC
  có đáy ABC là tam giác vuông tại C , AB  3a, BC  2a .
Góc giữa BC và mặt phẳng  ABC bằng 60. Tính thể tích khối lăng trụ đó. 3 3 A. 3 2a 15 . B. 2a 15 . C. 3 a 15 . D. a 15 . 3 3 Câu 17: Cho hàm số 3 2
y x  6x  7x  5 có đồ thị là C . Số tiếp tuyến của C song song với đường
thẳng 2x y  9  0 là A. 2 . B. 3 . C. 0 . D. 1.
Câu 18: Một người gửi tiền vào ngân hàng với lãi suất không thay đổi là 8% /năm. Biết rằng nếu không
rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu (người
ta gọi là lãi suất kép). Người đó định gửi tiền trong vòng 3 năm, sau đó rút tiền ra để mua một
căn hộ chung cư trị giá 500 triệu đồng. Hỏi số tiền ít nhất người đó phải gửi vào ngân hàng để
có đủ tiền mua căn hộ chung cư (kết quả làm tròn đến hàng triệu) là bao nhiêu? A. 396 triệu đồng. B. 397 triệu đồng. C. 395 triệu đồng. D. 394 triệu đồng.
Câu 19: Biết một nguyên hàm của hàm số f x 1 
1 là hàm số F x thỏa mãn F   2 1  13x 3
Khi đó F x là hàm số nào sau đây?
A. F x 2  4  13x .
B. F x 2  x  13x 3. 3 3
C. F x 2  x  13x 1.
D. F x 2  x  13x 3 . 3 3
Câu 20: Cắt hình nón bởi một mặt phẳng đi qua trục ta được thiết diện là một tam giác vuông cân có
cạnh huyền bằng a 6 . Tính thể tích V của khối nón đó. 3 3 3 3 A.a 6    V  . B. a 6 V  . C. a 6 V D. a 6 V  . 3 4 2 6
https:/www.facebook.com/groups/toanvd.Trang 2 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021
Câu 21: Tìm tất cả các giá trị của tham số m để hàm số 1 3
y x   2
m m   2 x   2 2 3m   1 x đạt cực 3 tiểu tại x  2  . m  3 A. . B. m  3 . m  1 m  3
C. m 1. D. .m  1
Câu 22: Cho F x 1  
. Kết quả nào sau đây đúng ? xx   dx 3 A.F x 2 x 3  ln  C . B.   2  ln x F xC . 3 x 3 x  3 C.   1  ln x F xC . D.   1   ln x F xC . 3 x  3 3 x  3 Câu 23: Hàm số  
y  cos 2x  2sin x có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn 0;   lần lượt là 2   
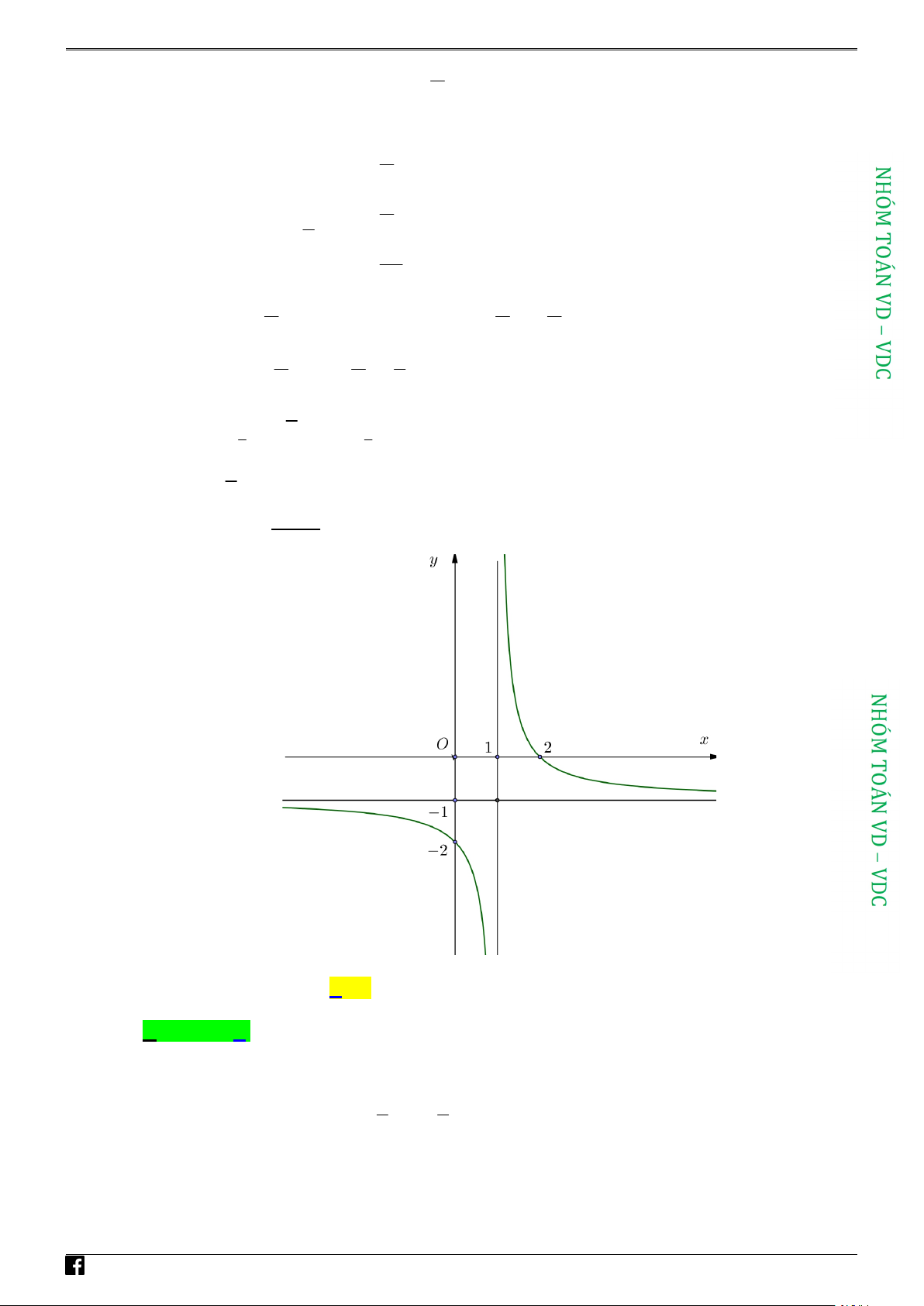
y ; y . Khi đó tích y .y có giá trị bằng 1 2 1 2 A. 9  . B. 3  . C. 3 . D. 3 . 4 2 2 Câu 24: Cho hàm số ax +b y =
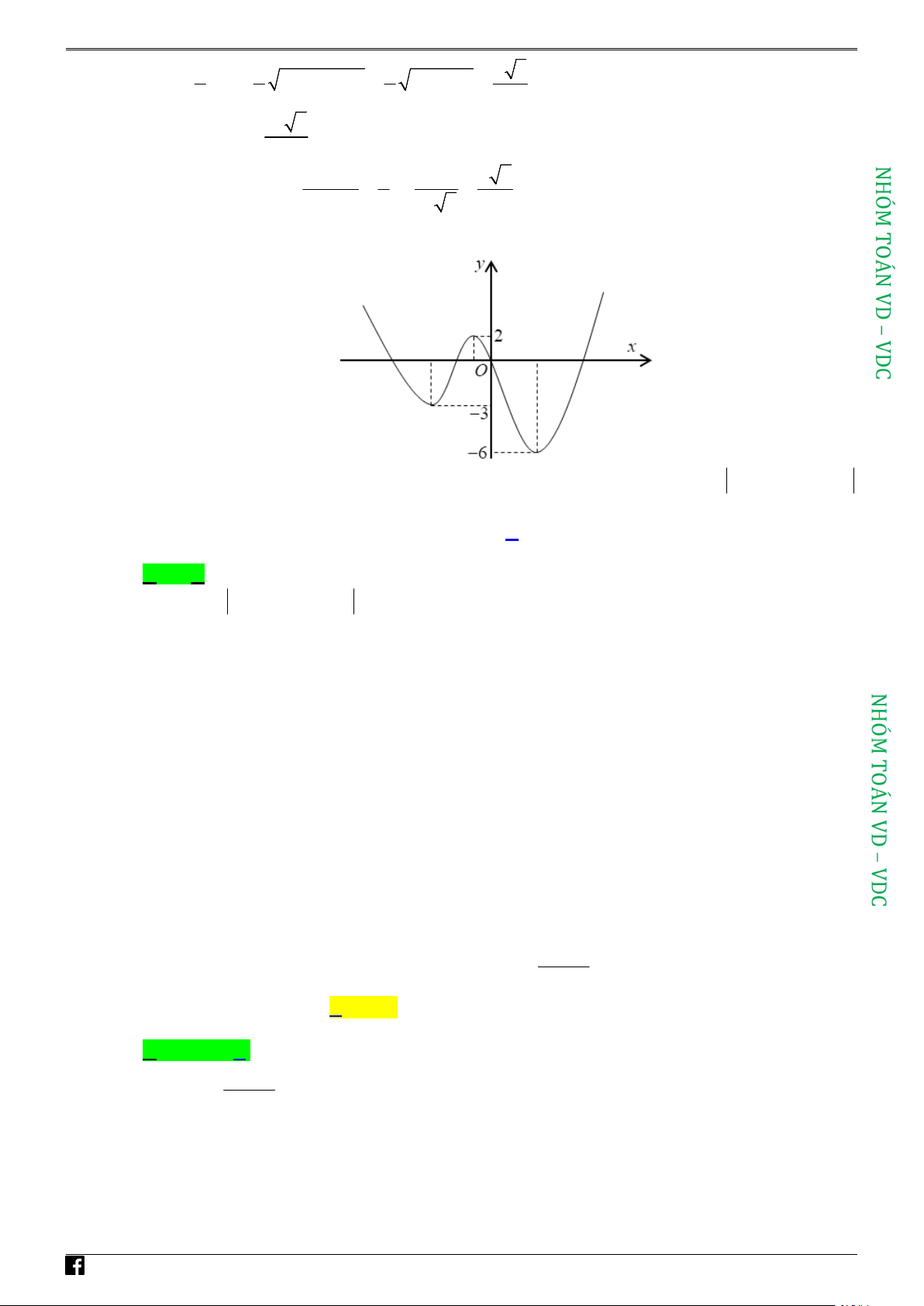
với a,b,c Î ¡ có đồ thị như hình vẽ bên. x +c
Giá trị của a + 2b +3c bằng A. 2 . B. 0 . C. 6 . D. 8 .
Câu 25: Cho hàm số y f x liên tục trên  và có bảng biến thiên như sau
Phương trình 2 f x 3  0 có bao nhiêu nghiệm phân biệt? A. 4 . B. 3 . C. 0 . D. 2 .
Câu 26: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên hợp với đáy một góc 0 60 .
Tính thể tích V của khối chóp S.ABC . 3 3 3 3 A. a . B. 3a . C. 3a . D. a . 3 24 12 6
https:/www.facebook.com/groups/toanvd.Trang 3 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021
Câu 27: Thể tích khối cầu ngoại tiếp hình hộp chữ nhật ABCD.A BCD
  với AB 1,BC  2, AA  2 bằng: A.  27 . B. 9 . C. 36 . D. 9 . 2
Câu 28: Phương trình 2
log2 x 1 6log2 x 1  2  0 có tổng các nghiệm là A. 4 . B. 3 . C. 6 . D. 18. Câu 29: Cho hàm số 1 3 2
f (x)   x mx  3m  2x 5. Tập hợp các giá trị của tham số m để hàm số 3
nghịch biến trên  là a;b. Khi đó 2a b bằng: A. 5. B. 1. C. 6 . D. 3  .
Câu 30: Cho a, b, c là các số thực dương và khác 1. Hình vẽ đưới đây là đồ thi của hàm số
y  loga x, y  logb x, y  logc .x Khẳng định này sau đây là đúng?
A. c a b .
B. b c a .
C. b a c .
D. a b c . x
Câu 31: Số nghiệm nguyên dương nhỏ hơn 10 của bất phương trình x 1  2x 1  2 3  2 12  0 là A. 8. B. 10 . C. 7 . D. 9.
Câu 32: Khối bát diện đều có bao nhiêu mặt đối xứng? A. 4 . B. 6 . C. 9. D. 8.
Câu 33: Trong không gian với hệ toạ độ Oxyz , cho ba điểm A1;1;  1 , B5; 1  ;2,C 3;2; 4   . Tìm toạ 
  
độ điểm M thoả mãn MA 2MB MC  0 A. 3 9 M  4; ;        . B. 3 9 M  4; ; . C. 3 9 M  4;  ; . D. 3 9 M  4;  ; . 2 2        2 2   2 2   2 2 
Câu 34: Ông A dự định sử dụng hết 2
6,7m kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật
không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có
thể tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm) A. 3 1,57m . B. 3 1,11m . C. 3 1,23m . D. 3 2,48m .
Câu 35: Một cây kem ốc quế gồm hai phần, phần em có dạng hình cầu, phần ốc quế có dạng hình nón,
giải sử hình cầu và hình nón có bán kính bằng nhau, biết rằng nếu kem tan chảy hết sẽ làm đầy
phần ốc quế. Biết thể tích kem sau khi tan chảy bằng 75% thể tích kem đóng băng ban đầu, gọi
h , r lần lượt là chiều cao và bán kính của phần ốc quế. Tỉnh tỉ số h . r
https:/www.facebook.com/groups/toanvd.Trang 4 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021 A. h  3. B. h  2 . C. h 4  . D. h 16  . r r r 3 r 3 Câu 36: Gọi S
là tập hợp các giá trị của tham số m để đồ thị hàm số 3 2
y  x x   2 m   2 3 3
1 x  3m 1 có điểm cực đại và cực tiểu cùng với gốc tọa độ tạo thành
tam giác vuông tại O . Tích tất cả các giá trị của tập S bằng A. 1. B. 3  . C. 3 . D. 1. 2 2
Câu 37: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a ;  0
ABC  60 và SB a . Hình
chiếu vuông góc của điểm S lên mặt phẳng  ABC trùng với trọng tâm tam giác ABC . Gọi 
là góc giữa đường thẳng SB và mặt phẳng SCD . Tính sin . A. 3 sin  . B. 1 sin  . C. 1 sin  . D. 2 sin  . 2 4 2 2
Câu 38: Cho hàm số y f x liên tục trên  và có đồ thị như hình vẽ dưới đây
Tập hợp tất cả các giá trị thực của tham số m để phương trình f  2
4  x   m có nghiệm
thuộc nữa khoảng  2; 3   là
A. 1; f  2 . B. 1;3. C. 1;3 . D. 1; f   2 .
Câu 39: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AD  2AB  2a . Cạnh bên
SA  2a và vuông góc với mặt phẳng đáy. Gọi M , N lần lượt là trung điểm của SB và SD .
Tính khoảng cách từ S đến mặt phẳng  AMN . 3a a 6 A. a 5 . B. 2a . C. . D. . 2 3
Câu 40: Cho hàm số y f x có đồ thị như hình vẽ bên dưới.
https:/www.facebook.com/groups/toanvd.Trang 5 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021
Gọi S là tập tất cả các giá trị nguyên dương của tham số m để hàm số y f x  2020 m
có 5 điểm cực trị. Tổng tất cả các giá trị của các phần tử của tập S bằng A. 9. B. 7 . C. 12. D. 18. x x   
Câu 41: Tính tổng S tất cả các nghiệm của phương trình 5 3 x 1 ln 
 5  5.3x 30 x 10  0.  6x  2  A. S  3. B. S 1. C. S  2 . D. S  1.
Câu 42: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Tam giác SAB đều và nằm
trong mặt phẳng vuông góc với đáy, bán kính mặt cầu ngoại tiếp khối chóp là: A. a 21 . B. a 11 . C. 2a . D. a 7 . 6 4 3 3
Câu 43: Cho phương trình 1 2
log x  2m 1log x  4m  2  0 , có bao nhiêu giá trị nguyên của tham 3 3 4
số m để phương trình trên có nghiệm thuộc đoạn 1 ;3  ? 3    A. 1. B. 4 . C. 2 . D. 3.
Câu 44: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với đáy, côsin góc hợp
bởi SD và mặt phẳng đáy  ABCD bằng 1 . Gọi E ; F lần lượt là hình chiếu của A lên 3
SB ; SD . Mặt phẳng  AEF chia khối chóp thành hai phần. Tính thể tích phần khối chóp
không chứa đỉnh S : 3 3 3 3 A. 2a V  . B. 2a V  . C. 2 2a V  . D. 2a V  . 9 4 9 6
Câu 45: Cho hàm số bậc ba y f x có đồ thị như hình vẽ bên.
Số nghiệm thực của phương trình f  3 x x 4 3  là 3 A. 7 . B. 4 . C. 3 . D. 8 .
Câu 46: Cho hàm số f x . Hàm số y f ' x có đồ thị như hình bên.
https:/www.facebook.com/groups/toanvd.Trang 6 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021
Số điểm cực trị của hàm số g x  2 1 f x       2ln x .  2  A. 3 . B. 6 . C. 4 . D. 5 .
Câu 47: Cho x, y là những số thực dương không đổi. Xét hình chóp S.ABC có SA x,BC y và các
cạnh còn lại đều bằng 1. Khi thể tích khối chóp S.ABC đạt giá trị lớn nhất thì tích .xy bằng 4 4 3 A. 1 . B. . C. . D. 2 3 . 3 3 3
Câu 48: Cho lăng trụ tam giác đều ABC.A'B'C ' . Trên tia đối của tia B' A' lấy điểm M sao cho 1
B'M B' A' . Gọi N,P lần lượt là trung điểm của A'C ',BB' . Mặt phẳng (MNP) chia khối 2
trụ ABC.A'B'C ' thành hai khối đa diện, trong đó khối đa diện có chứa đỉnh A' có thể tích V và 1
khối đa diện chứa đỉnh C 'có thể tích V . Tỉ số V1 bằng 2 V2 97 49 49 A. 95 . B. . C. . D. . 144 59 144 95
Câu 49: Có 18 bạn thi Toán và KHTN bằng Tiếng Anh được khen thưởng gồm 9 nam và 9 nữ, tất cả
các học sinh nam có chiều cao khác nhau, học sinh nữ có chiều cao khác nhau. Thầy Chinh xếp
ngẫu nhiên các bạn thành một hàng ngang để chụp ảnh kỉ niệm sao cho tính từ trái sang phải
các học sinh nam có chiều cao giảm dần và các học sinh nữ có chiều cao tăng dần. Xác suất để
các bạn nam và các bạn nữ đứng xen kẽ theo cách trên là 1 1 A. 1 . B. . C. . D. 14 . 24310 48620 2002 2002
Câu 50: Có bao nhiêu giá trị nguyên dương của tham số m nhỏ hơn 2021 để phương trình log   2x m m
 2x có nghiệm thực? 2   A. 2018 . B. 2019 . C. 2021. D. 2020 . BẢNG ĐÁP ÁN 1.B 2.D 3.A 4.A 5.D 6.C 7.B 8.C 9.C 10.B 11.A 12.B 13.C 14.A 15.D 16.A 17.D 18.B 19.D 20.B 21.B 22.C 23.C 24.B 25.A 26.C 27.B 28.A 29.D 30.B 31.D 32.C 33.C 34.A 35 36.A 37.D 38.B 39.D 40.C 41.B 42.A 43.C 44.C 45.D 46.A 47.B 48.D 49.A 50.D
https:/www.facebook.com/groups/toanvd.Trang 7 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021 ĐÁP ÁN CHI TIẾT
Câu 1: Cho A  0;2;. .;9 
8 là tập hợp gồm các số tự nhiên chẵn nhỏ hơn 100. Số tập con có hai phần tử của A là A. 24 C 9 . B. 25 C 0. C. 24 A 9. D. 29 C 8. Lời giải Chọn B
Số phần tử của A là: 98  0 1  50. 2
Số tập con có hai phần tử của A là 25 C 0.
Câu 2: Cho cấp số nhân un  với 1
u 1và công bội q  2 . Tìm u7 . A. 15. B. 128 . C. 13. D. 64 . Lời giải Chọn D Ta có: 6 6 u7  1
u .q  1.2  64 . Câu 3: Cho hàm số 4 2
y x  2x  3. Khẳng định nào sau đây đúng?
A. Hàm số có ba điểm cực trị.
B. Hàm số chỉ có đúng hai điểm cực trị.
C. Hàm số không có cực trị.
D. Hàm số chỉ có một điểm cực trị. Lời giải Chọn A
Ta thấy hàm số đã cho là hàm trùng phương 4 2
y ax bx c a  0 với ab  0 nên
đây là trường hợp hàm số có ba điểm cực trị.
Câu 4: Hàm số y    x 1 2 3 4 có tập xác định là: A. 2;2 B.  2  ;2 C.  ;  2  2; D. Lời giải Chọn A
Hàm số y    x 1 2 3 4 có số mũ 1   không nguyên. 3 Do đó hàm số xác định 2
 4  x  0  2  x  2 .
Câu 5: Tìm giá trị nhỏ nhất của hàm số 9
y x  trên đoạn 2;4 . x A. 25 13 min  y B. min  y C. min  6  y D. min  y 6 2;4 4 2;4 2 2;4 2;4 Lời giải Chọn D
TXĐ: D   \  0 . Suy ra hàm số 9
y x  liên tục trên 2;4 . x Ta có: 9 9
y x   y '  1 2 x x 9 x  3 y '  0  1  0  2 x  x  3 Vì 3 13 25
2;4. Ta có: y 2  ; y 3  6; y 4  2 4 Do đó: min  y y 3  6 . 2;4
https:/www.facebook.com/groups/toanvd.Trang 8 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021
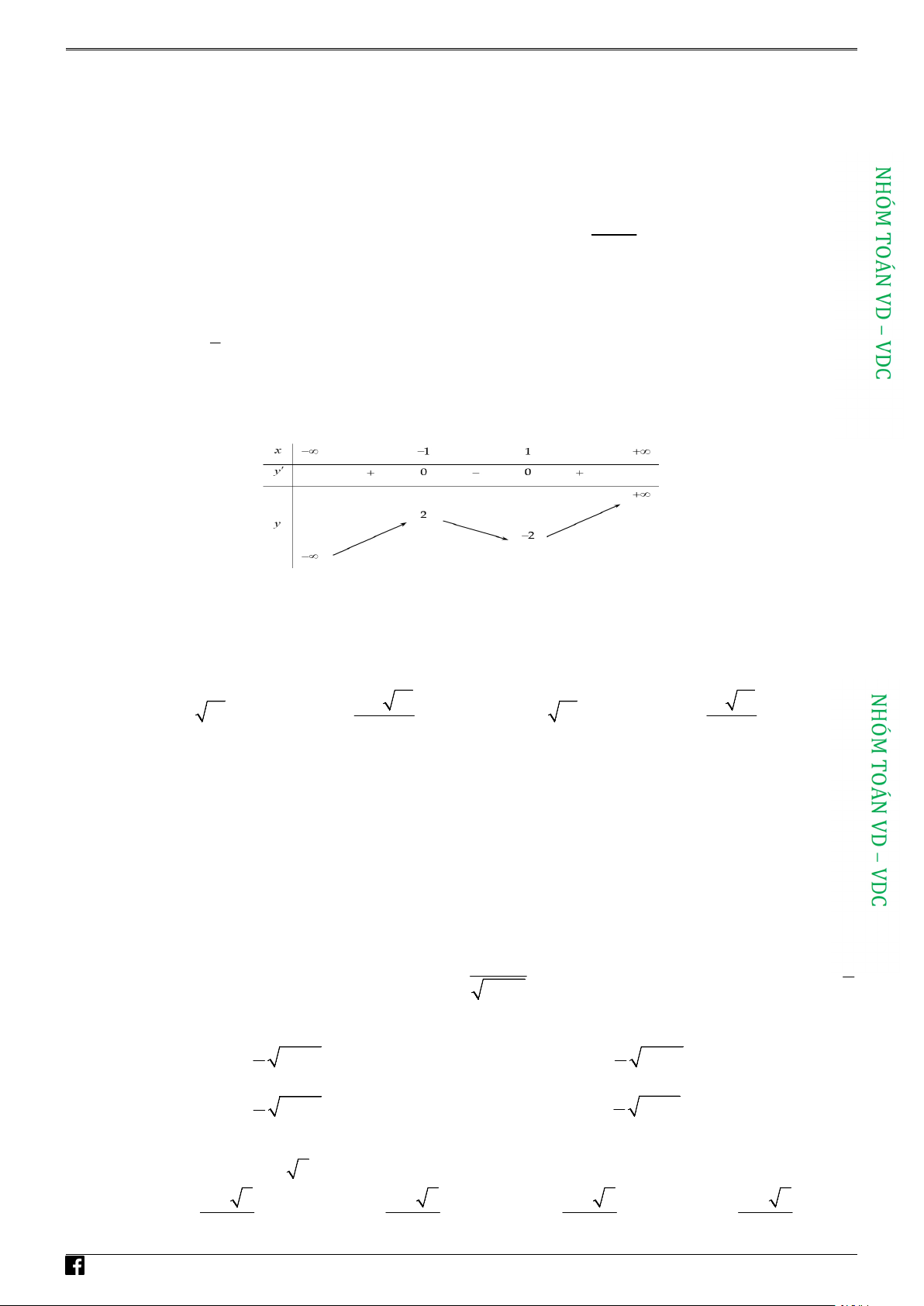
Câu 6: Cho hàm số y f x liên tục trên  \ 
1 . Có bảng biến thiên như hình vẽ. Tổng số đường
tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số y f x bằng: A. 4 B. 2 C. 3 D. 1 Lời giải Chọn C Từ BBT ta có: l ìï imy = 1 ïïx®-¥ í
Þ ĐTHS có tiệm cận ngang y = 1, y = -1. l ï im y = 1 - ïïîx®+¥ lim y = +
ĐTHS có tiệm cận đứng x = 1. x 1- ®
Câu 7: Cho khối lăng trụ đứng có cạnh bên bằng 5 , đáy là hình vuông có cạnh bằng 4 . Thể tích của
khối lăng trụ đã cho bằng A. 100. B. 80 . C. 20 . D. 64 . Lời giải Chọn B Diện tích đáy 2 B  4 16 .
Thể tích của khối lăng trụ đã cho là V Bh  16.5  80 .
Câu 8: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ sau A. 3 2
y  x  3x . B. 4 2
y x  3x . C. 3 2
y x  3x . D. 4 2
y  x  3x . Lời giải Chọn C
Từ đồ thị ta suy ra hàm số cần tìm là hàm số bậc ba có hệ số a  0 nên ta chọn C.
Câu 9: Trong không gian Oxyz , cho hai điểm A2;4;3 , B 2;2;7 . Trung điểm của AB có tọa độ là A. 1;3;2 . B. 4;2;10 . C. 2;1;5 . D. 2; 6; 4 . Lời giải Chọn C
Gọi I là trung điểm AB .
https:/www.facebook.com/groups/toanvd.Trang 9 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021x x A B x    I 2 2  Ta có  y y A By    . I 1 2   z z A B z    I 5  2
Vậy I 2;1;5 .
Câu 10: Thể tích V của khối trụ có bán kính và chiều cao đều bằng 5a là A. 3 75a . B. 3 125a . C. 3 25a . D. 3 50a . Lời giải Chọn B
Thể tích khối trụ là V    a2 3 5
.5a  125a .
Câu 11: Trong các khẳng định sau, khẳng định nào sai?
A. cf xdx c f xdxc    . B. f
  x gxdx f
 xdx g  xdx . C. f
  x  dx f
x .D. f
 xdx f xC . Lời giải Chọn A Ta có cf
 xdx c f
 xdxc \  0  nên chọn A.
Câu 12: Cho a,b,c  0 , a  1, b 1. Trong các khẳng định sau, khẳng định nào sai? A. log b c c log b c b c . a loga log a .logb loga . B.   a 1 C. log bc b c log b a   loga loga . D. a . log a b Lời giải Chọn B
Câu 13: Gọi l,h,r lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình nón. Diện tích
xung quanh S của hình nón là: xq A. 1 2 S  r h .
B. S  rh .
C. S  rl .
D. S  rl . xq 2 xq 3 xq xq Lời giải Chọn C
Câu 14: Có bao nhiêu loại khối đa diện đều? A. 5. B. 2 . C. 3. D. vô số. Lời giải Chọn A
Có 5 loại khối đa diện đều: 3; 
3 - Tứ diện đều; 4; 
3 - Khối lập phương; 3;  4 - Khối bát diện đều; 5; 
3 - Khối 12 mặt đều và 3;  5 - Khối 20 mặt đều.
Câu 15: Cho hàm số y f x có bảng biến thiên như sau
https:/www.facebook.com/groups/toanvd.Trang 10 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. ;2 . B. 1;  1 . C. 2;  . D. ;  1 . Lời giải Chọn D
Dựa vào bảng biến thiên, ta thấy hàm số đồng biến trên các khoảng ;  1 và 1; .
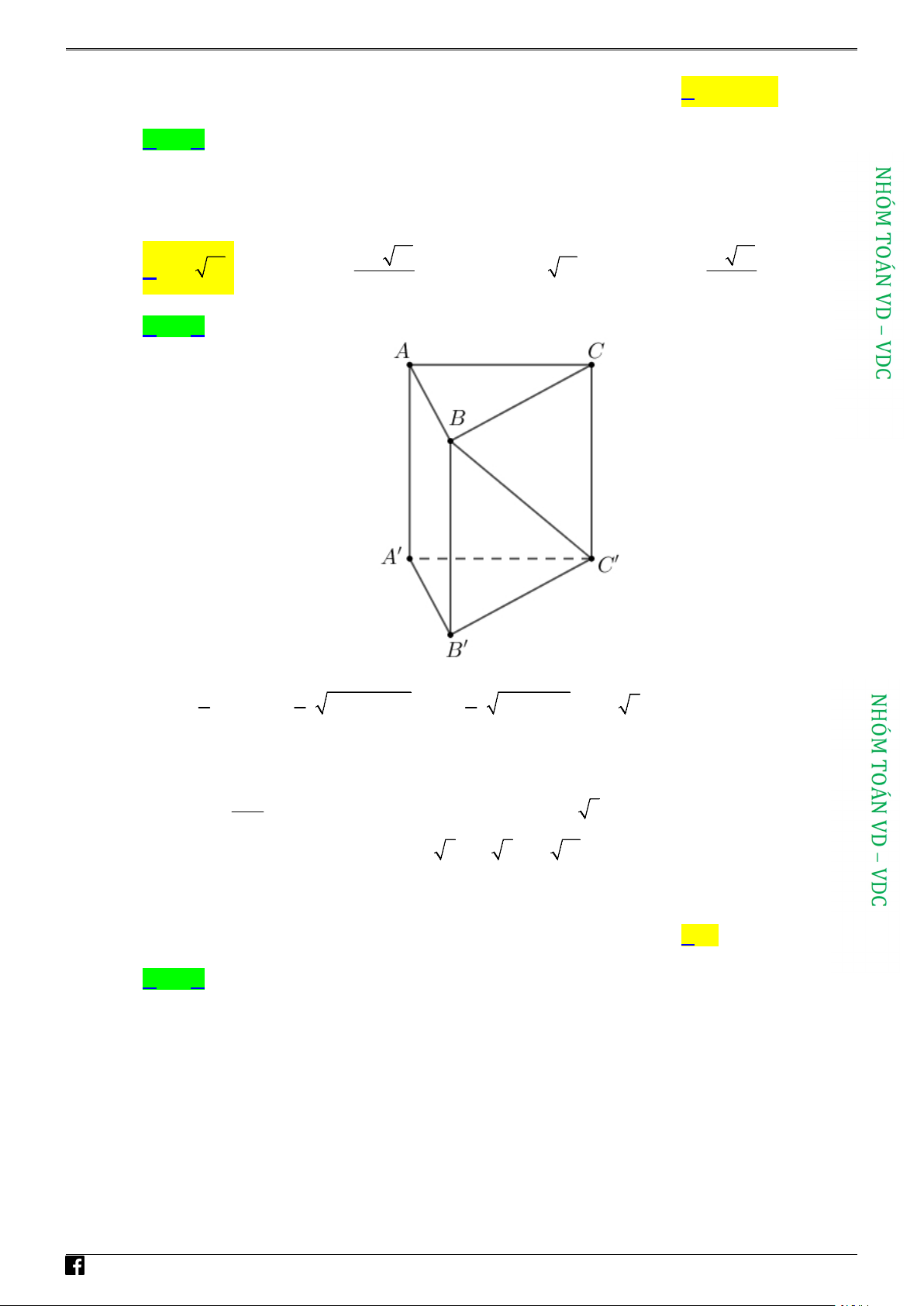
Câu 16: Cho hình lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác vuông tại C , AB  3a, BC  2a .
Góc giữa BC và mặt phẳng  ABC bằng 60. Tính thể tích khối lăng trụ đó. 3 3 A. 3 2a 15 . B. 2a 15 . C. 3 a 15 . D. a 15 . 3 3 Lời giải Chọn A
Tam giác ABC vuông tại C nên diện tích 1 1 2 2 1 2 2 2 S
 CACB   AB BC BC   a a a a . ABC 9 4 2 5 2 2 2
Góc giữa BC và  ABC là góc  C BC  60 . Tam giác CC B  vuông tại C nên  CC        tan C BC CC BC tan C B
C  2a tan 60  2a 3 . BC Thể tích khối lăng trụ 2 3 V SCC  a a a . ABC 5 2 3 2 15 Câu 17: Cho hàm số 3 2
y x  6x  7x  5 có đồ thị là C . Số tiếp tuyến của C song song với đường
thẳng 2x y  9  0 là A. 2 . B. 3 . C. 0 . D. 1. Lời giải Chọn D Đạo hàm 2
y  3x 12x  7 .
Viết lại phương trình đường thẳng  : y  2x  9 .
Tiếp tuyến song song với đường thẳng khi hệ số góc tiếp tuyến x  1 2 2
3x 12x  7  2
  3x 12x  9  0   . x  3
Với x 1, y  7 , phương trình tiếp tuyến y  2  x   1  7  y  2
x  9 (trùng với  ). 0 0
Với x  3, y  1, phương trình tiếp tuyến y  2
 x 3 1 y  2
x  5 (thỏa mãn). 0 0
Vậy có 1 tiếp tuyến song song với đường thẳng đã cho.
https:/www.facebook.com/groups/toanvd.Trang 11 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021
Câu 18: Một người gửi tiền vào ngân hàng với lãi suất không thay đổi là 8% /năm. Biết rằng nếu không
rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu (người
ta gọi là lãi suất kép). Người đó định gửi tiền trong vòng 3 năm, sau đó rút tiền ra để mua một
căn hộ chung cư trị giá 500 triệu đồng. Hỏi số tiền ít nhất người đó phải gửi vào ngân hàng để
có đủ tiền mua căn hộ chung cư (kết quả làm tròn đến hàng triệu) là bao nhiêu? A. 396 triệu đồng. B. 397 triệu đồng. C. 395 triệu đồng. D. 394 triệu đồng. Lời giải Chọn B
Gọi A là số tiền gửi ban đầu.
Theo công thức lãi suất kép, số tiền người đó nhận được sau 3 năm là T A  r3 1 .
Theo đề bài, ta cần có T
A  r3 500 500 1  500  A   397 triệu đồng. 18%3
Vậy người đó phải gửi ít nhất 397 triệu đồng.
Câu 19: Biết một nguyên hàm của hàm số f x 1 
1 là hàm số F x thỏa mãn F   2 1  13x 3
Khi đó F x là hàm số nào sau đây?
A. F x 2  4 
13x .B. F x 2  x  13x 3. 3 3
C. F x 2  x  13x 1.
D. F x 2  x  13x 3 . 3 3 Lời giải Chọn D
Ta có F x  1 1    2   dx x  1 3x C .  1 3x  3
Theo giả thiết, ta có F   2 1   C  3. 3 Vậy F x 2  x  13x 3 . 3
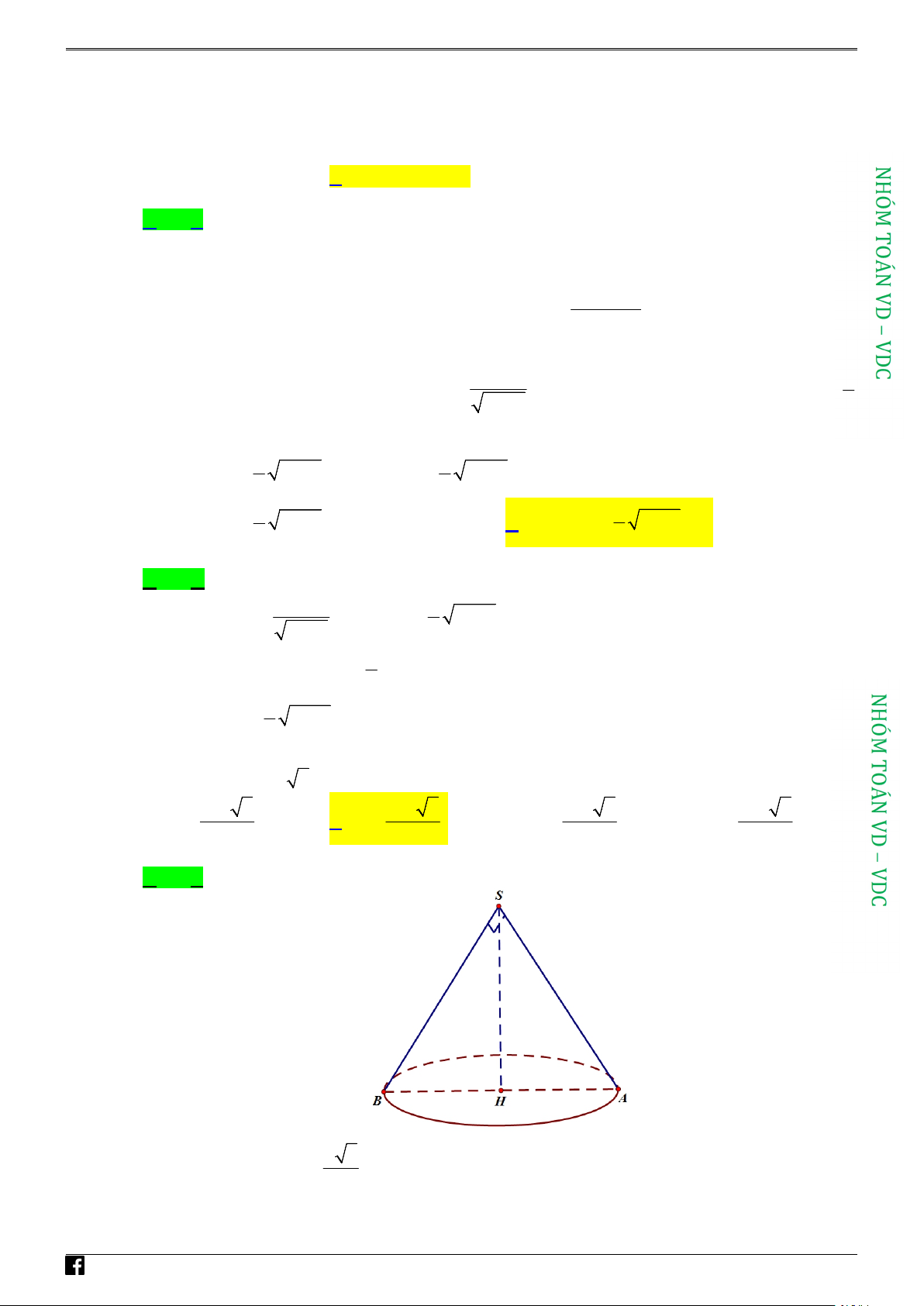
Câu 20: Cắt hình nón bởi một mặt phẳng đi qua trục ta được thiết diện là một tam giác vuông cân có
cạnh huyền bằng a 6 . Tính thể tích V của khối nón đó. 3 3 3 3 A.a 6    V  . B. a 6 V  . C. a 6 V D. a 6 V  . 3 4 2 6 Lời giải Chọn B Theo bài ra ta có a 6 AH  . 2
https:/www.facebook.com/groups/toanvd.Trang 12 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021 Lại có S
AB vuông cân tại S nên AB SH a 6  AH  . 2 22   Thể tích khối nón là 1 2 
V SH..AH 1 a 6 a 6  .. 6 3  a . 3 3 2  2    4
Câu 21: Tìm tất cả các giá trị của tham số m để hàm số 1 3
y x   2
m m   2 x   2 2 3m   1 x đạt cực 3 tiểu tại x  2  . m  3 A. . B. m  3 . m  1 m  3
C. m 1. D. .m  1 Lời giải Chọn B Xét 1 3
y x   2
m m   2 x   2 2 3m   1 x . 3
Tập xác định D   . Ta có: 2
y  x  2 2
m m  2 x  2 3m   1 .
Hàm số đạt cực tiểu tại x  2
 nên y2  0 . m 1 Ta có 4  4 2 m m  2 2 2
 3m 1 0  m  4m  3  0   . m  3
y  2x   2
2 m m  2 . y 2 2  2m  2m .   m y 2 1 2
 0  2m  2m  0  m  0
Để hàm số hàm số đạt cực tiểu tại x  2
 thì m  3 thỏa mãn.
Câu 22: Cho F x 1  
. Kết quả nào sau đây đúng ? xx   dx 3 A.F x 2 x 3  ln  C . B.   2  ln x F xC . 3 x 3 x  3 C.   1  ln x F xC . D.   1   ln x F xC . 3 x  3 3 x  3 Lời giải Chọn C. Ta có F x 1 1  1 1      x   C . xx  1 ln   dx  dx 3 3  x x  3  3 x  3 Câu 23: Hàm số  
y  cos 2x  2sin x có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn 0;   lần lượt là 2   
y ; y . Khi đó tích y .y có giá trị bằng 1 2 1 2 A. 9  . B. 3  . C. 3 . D. 3 . 4 2 2 Lời giải Chọn C.
https:/www.facebook.com/groups/toanvd.Trang 13 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021  
Xét hàm số y  cos 2x  2sin x trên 0;   . 2   
Ta có y  2sin 2x  2cos x  4sin .
x cos x  2cos x  2cos x 2sin x 1  .   x   k  2 cos x  0  Giải  y  0   1 
x   k2 k   . sin x   6  2  5 x   k 2  6   Xét trên đoạn   0;  
, y  0 có các nghiệm x  ; x  . 2    6 2      Ta có y    3 0 1; y   1; y   . 2  6      2 Suy ra 3
y  max y  , y  min y 1. 1   2   0;  2   0; 2     2   Vậy 3 y .y  . 1 2 2 Câu 24: Cho hàm số ax +b y =
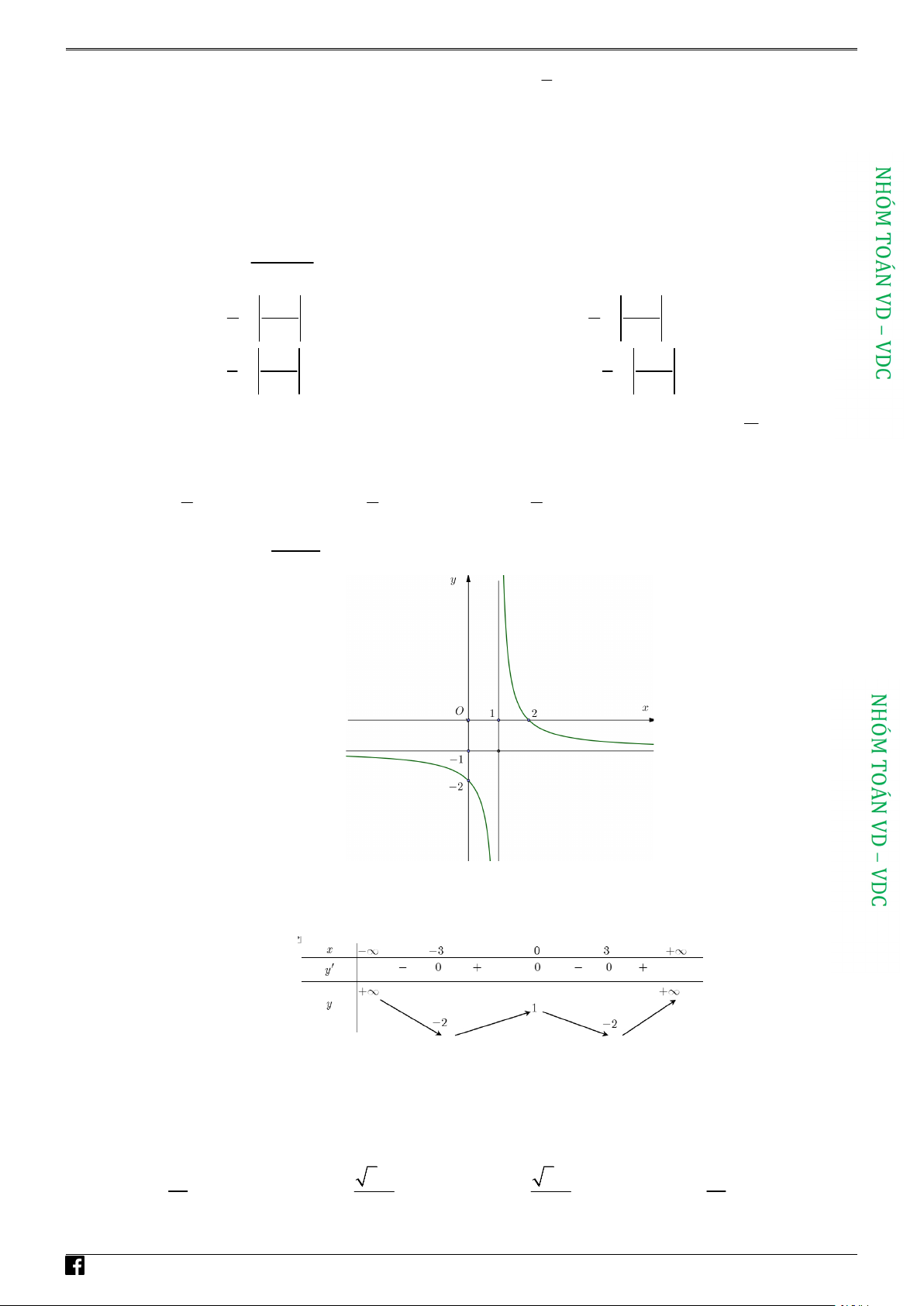
với a,b,c Î ¡ có đồ thị như hình vẽ bên. x +c
Giá trị của a + 2b +3c bằng A. 2 . B. 0 . C. 6 . D. 8 . Lời giải Chọn B.
Tiệm cận đứng của đồ thị hàm số: x = c - suy ra c - =1 Û c = -1.
Tiệm cận ngang của đồ thị hàm số: y = a suy ra a = -1.
Đồ thị cắt trục Oy tại điểm ç b ç0; b÷÷ ç
nên = -2 mà c = -1 suy ra b = 2. c÷ c
Vậy, a + 2b +3c = 0.
Câu 25: Cho hàm số y f x liên tục trên  và có bảng biến thiên như sau
https:/www.facebook.com/groups/toanvd.Trang 14 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021
Phương trình 2 f x 3  0 có bao nhiêu nghiệm phân biệt? A. 4 . B. 3 . C. 0 . D. 2 . Lời giải Chọn A.
Ta có: f x    f x 3 2 3 0
  . Ứng với bảng biến thiên ta thấy đường thẳng 3 y   cắt 2 2
đồ thị hàm số f x tại 4 điểm nên 2 f x 3  0 có 4 nghiệm phân biệt.
Câu 26: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên hợp với đáy một góc 0 60 .
Tính thể tích V của khối chóp S.ABC . 3 3 3 3 A. a . B. 3a . C. 3a . D. a . 3 24 12 6 Lời giải Chọn C. S 60 A C H M B
Gọi H là hình chiếu vuông góc của S lên (ABC) , khi đó 1 VSH S S ABC . . ABC. . 3  2 2 a 3 a 3
AH AM  . 
Xét tam giác SHA vuông tại A có:  3 3 2 3  .    0 a 3
SH tan SAH.AH  tan 60 .  a  3 2 3 Khi đó 1 1 a 3 a 3 VSH S    a S ABC . . ABC . . . . 3 3 4 12
Câu 27: Thể tích khối cầu ngoại tiếp hình hộp chữ nhật ABCD.A BCD
  với AB 1,BC  2, AA  2 bằng: A.  27 . B. 9 . C. 36 . D. 9 . 2 Lời giải Chọn B.
https:/www.facebook.com/groups/toanvd.Trang 15 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021 A D B C ADBC
Gọi R là bán kính khối cầu ngoại tếp ABCD.A BCD   . Khi đó: 2 2 2 2 2 2     R= AC AB AD AA 1  2  2 3 4 3 4 27 9  
  V  .R  .  . 2 2 2 2 3 3 8 2
Câu 28: Phương trình 2
log2 x 1 6log2 x 1  2  0 có tổng các nghiệm là A. 4 . B. 3 . C. 6 . D. 18. Lời giải Chọn A
Điều kiện: x  1. Ta có: 2
log2 x 1 6log2 x 1  2  0 2
 log2 x 1 3log2 x 1 2  0
log2 x 1 1 x  1     . log  2  x 1  2 x  3
So với điều kiện thấy thỏa mãn.
Vậy tổng các nghiệm là: 1 3  4. Câu 29: Cho hàm số 1 3 2
f (x)   x mx  3m  2x 5. Tập hợp các giá trị của tham số m để hàm số 3
nghịch biến trên  là a;b. Khi đó 2a b bằng: A. 5. B. 1. C. 6 . D. 3  . Lời giải Chọn A Ta có: 2
f (x)  x  2mx  3m  2.
Hàm số nghịch biến trên 2
  f (x)  0, x    m  3m  2  0  2  m  1.
Suy ra: a  2, b  1 2a b  2 2 1 3.
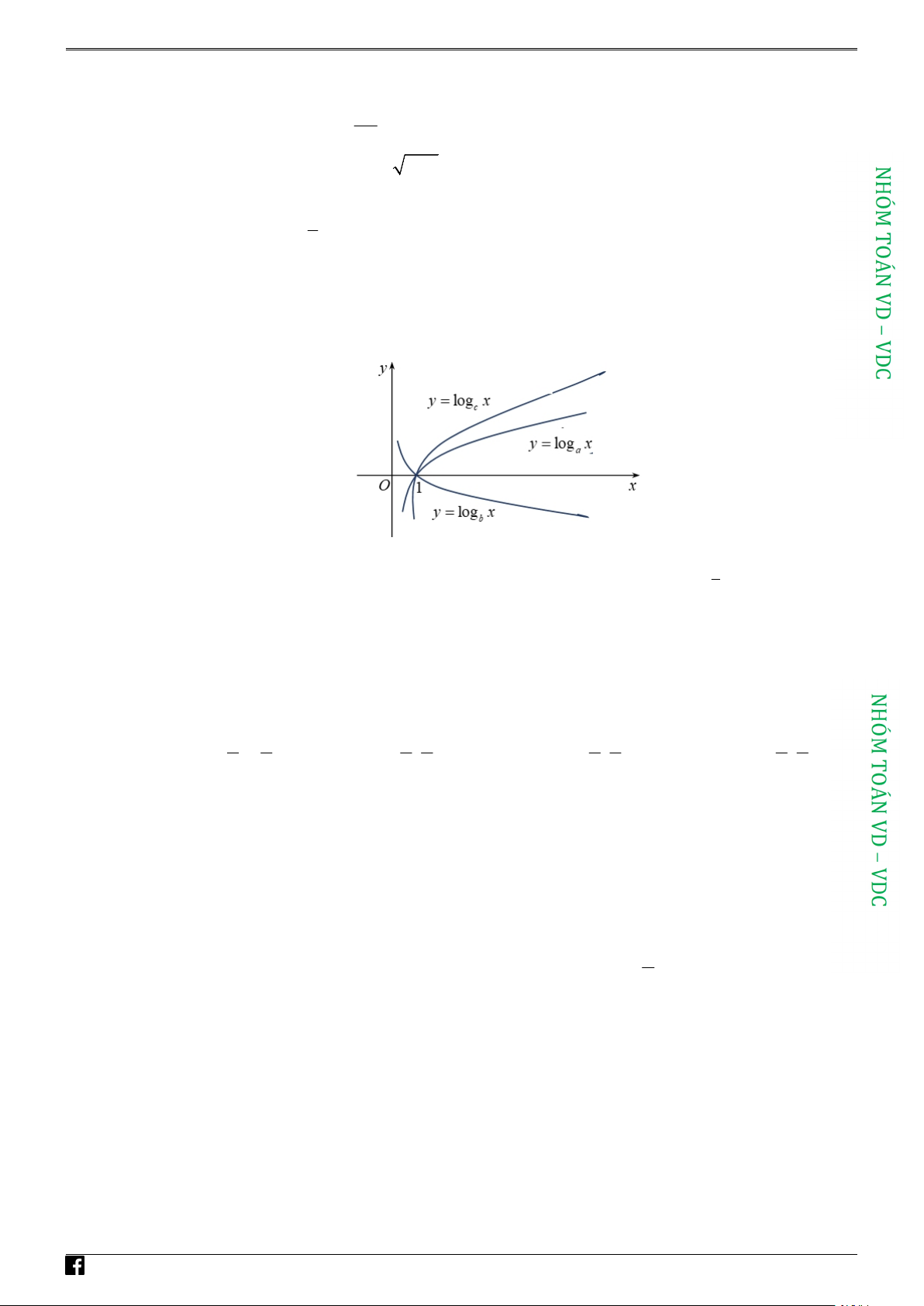
Câu 30: Cho a, b, c là các số thực dương và khác 1. Hình vẽ đưới đây là đồ thi của hàm số
y  loga x, y  logb x, y  logc .x Khẳng định này sau đây là đúng?
A. c a b .
B. b c a .
C. b a c .
D. a b c . Lời giải Chọn A
Dựa vào đồ thị ta với thấy với 0 x 1 thì: 1 1 logc 0 x  loga 0 x  0  
 0  logx a  logx c  0  a c 1. 0 0 logx c log a 0 0 x
https:/www.facebook.com/groups/toanvd.Trang 16 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021 Mặt khác: logb 0
x  0  logx b  0  b 1. 0
Từ đây suy ra: b c a. x
Câu 31: Số nghiệm nguyên dương nhỏ hơn 10 của bất phương trình x 1  2x 1  2 3  2 12  0 là A. 8. B. 10 . C. 7 . D. 9. Lời giải Chọn D
Ta biến đổi bất phương trình x x x x x 2 x x 1  2x 1      2 x x 2 3 12 3 12 3  2
12  0  3.3  2.4 12  0  3.  2   0  3.    2    0 4x 4x 4  4      2x x  3   3   3.      2  0   1  2   2      x   Đặt 3 t  
, điều kiện t  0. 2      Bất phương trình   1 trở thành: 2 2
3t t  2  0    t 1 . 3 x  
Kết hợp với điều kiện ta được 0  t 1. Suy ra 3 0     1  x  0.  2   
Do đó nghiệm nguyên dương nhỏ hơn 10 của bất phương trình là tập 1;2;3;. .;8;  9 .
Vậy số nghiệm nguyên dương nhỏ hơn 10 của bất phương trình là 9.
Câu 32: Khối bát diện đều có bao nhiêu mặt đối xứng? A. 4 . B. 6 . C. 9. D. 8. Lời giải Chọn C
Khối bát diện đều có 9 mặt phẳng đối xứng bao gồm:
Loại 1. Mặt phẳng đối xứng đi qua 4 đỉnh đồng phẳng của khối bát diện đều (có 3 mặt).
Loại 2. Mặt phẳng đối xứng đi qua 2 đỉnh đối diện và trung điểm 2
cạnh đối diện không chứa 2 đỉnh đó (có 6 mặt).
Câu 33: Trong không gian với hệ toạ độ Oxyz , cho ba điểm A1;1;  1 , B5; 1  ;2,C 3;2; 4   . Tìm toạ 
  
độ điểm M thoả mãn MA 2MB MC  0 A. 3 9 M  4; ;        . B. 3 9 M  4; ; . C. 3 9 M  4;  ; . D. 3 9 M  4;  ; . 2 2        2 2   2 2   2 2  Lời giải Chọn C Gọi M  ; a ; b c .   
Ta có: MA  1 a;1b;1 c  , MB  5 a;1b;2  c  , MC  3 a;2 b;4 c .
https:/www.facebook.com/groups/toanvd.Trang 17 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021  1
  a  2 5  a 3 a  0 a  4 
    
MA 2MB MC  0  3  1 3 9 
  b  2 1 b  2  b  0  b
    M  4;  ; . 2 2 2    1  c2   2  c  4   c  0  9 c   2
Câu 34: Ông A dự định sử dụng hết 2
6,7m kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật
không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có
thể tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm) A. 3 1,57m . B. 3 1,11m . C. 3 1,23m . D. 3 2,48m . Lời giải Chọn A
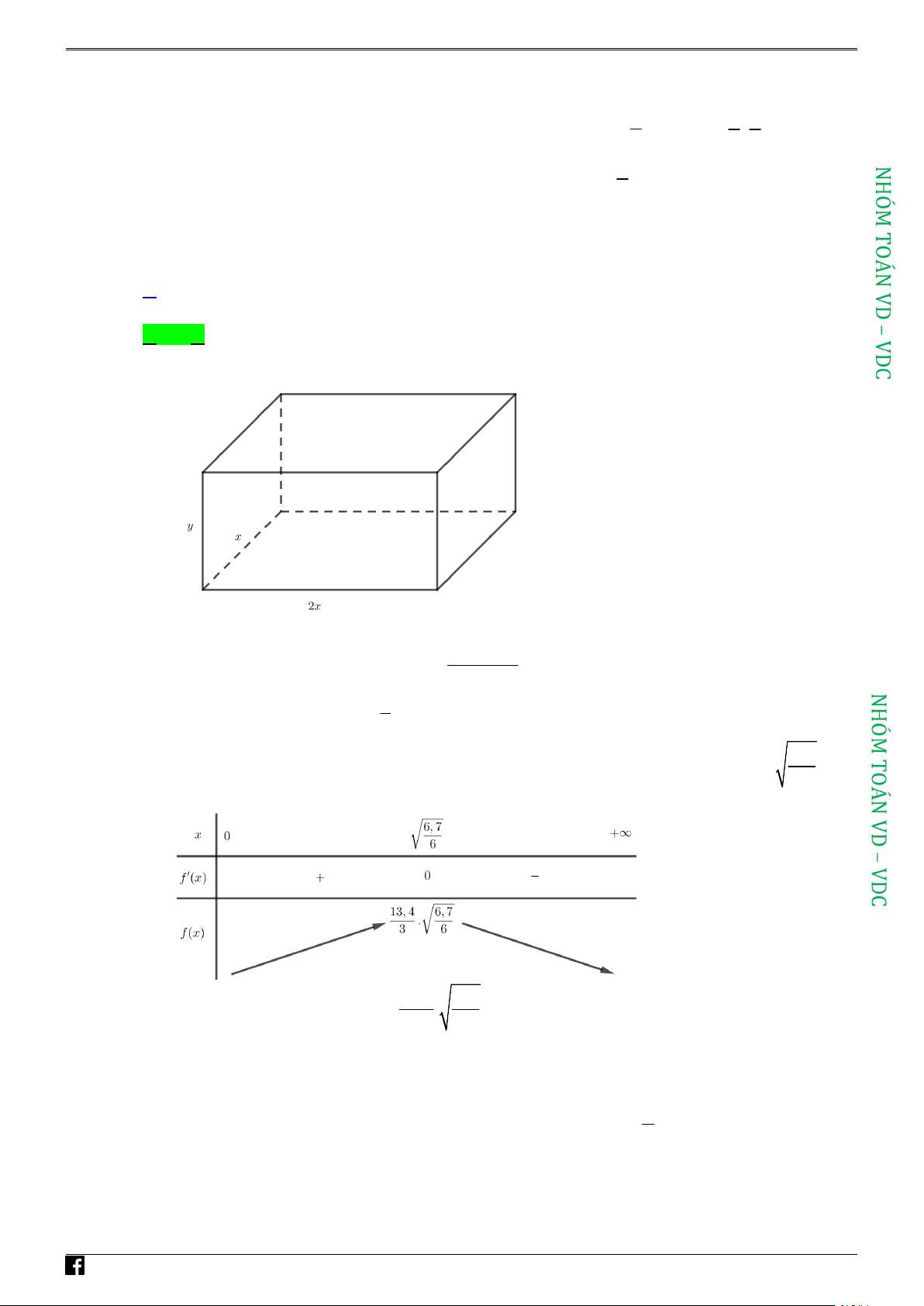
Gọi chiều rộng, chiều dài và chiều cao của bể cá lần lượ là : ; x 2 ; x y , x y  0
Tổng diện tích tất cả các mặt của bể cá (trừ nắp trên) là: 2 2  S 6,7 2  2x  6xy 2
 2x  6xy  6,7 xy  . 6x Thể tích cái bể là: 1 V  . x 2 . x y   2
6.7  2x x . 3
Xét hàm số f x 3
 6,7x  2x với x  0 , ta có: f x 2
 6,7  6x , f x 6,7  0  x  . 6 BBT
Vậy thể tích bể cá lớn nhất là 13,4 6,7 3 V  .  1,57m . 9 6
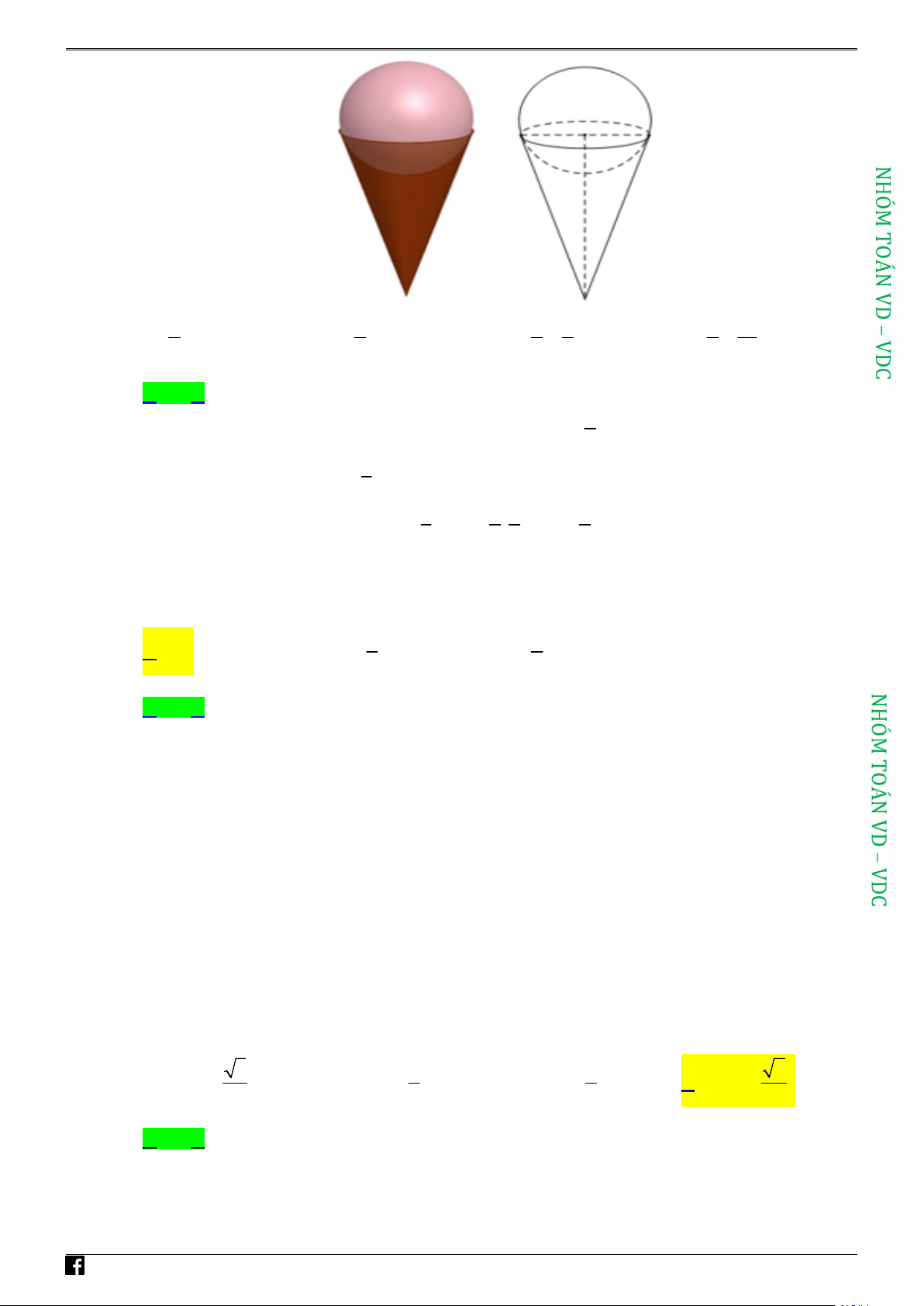
Câu 35: Một cây kem ốc quế gồm hai phần, phần em có dạng hình cầu, phần ốc quế có dạng hình nón,
giải sử hình cầu và hình nón có bán kính bằng nhau, biết rằng nếu kem tan chảy hết sẽ làm đầy
phần ốc quế. Biết thể tích kem sau khi tan chảy bằng 75% thể tích kem đóng băng ban đầu, gọi
h , r lần lượt là chiều cao và bán kính của phần ốc quế. Tỉnh tỉ số h . r
https:/www.facebook.com/groups/toanvd.Trang 18 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021 A. h  3. B. h  2 . C. h 4  . D. h 16  . r r r 3 r 3 Lời giải Chọn A
Thể tích khối cầu (phần kèm) khi chưa tan chảy bằng 4 2 V   r . C 3 Thể tích khối nón bằng 1 2 V  r h . N 3
Theo đề bài ra ta có V V 1 2 3 4 3
  r h  .  r h   3 . N 75%. C 3 4 3 r Câu 36: Gọi S
là tập hợp các giá trị của tham số m để đồ thị hàm số 3 2
y  x x   2 m   2 3 3
1 x  3m 1 có điểm cực đại và cực tiểu cùng với gốc tọa độ tạo thành
tam giác vuông tại O . Tích tất cả các giá trị của tập S bằng A. 1. B. 3  . C. 3 . D. 1. 2 2 Lời giải Chọn A Ta có 2 2 y  3
x  6x  3m 3  0 2 2
 x  2x m 1 0   1
Để hàm số có hai điểm cực đại và cực tiểu thì  
1 phải có hai nghiệm phân biệt, nên 2 
  m  0 suy ra m  0 . Dễ thấy   1
có hai nghiệm x 1 m và x 1 m nên A 3 1 ; m 2   2m  và 1 2 B 3 1 ; m 2
  2m  là hai điểm cực trị của đồ thị hàm số  
Tam giác OAB vuông ở O O .
AOB  0    m  m  3   m  3 1 1 2 2 2  2m  0 2   m   6 1
4 1 m   0   2  m  4 1
4m  4m  5  0 2
m 1  m  1  .
Do đó tích các giá trị thỏa mãn của m bằng 1.
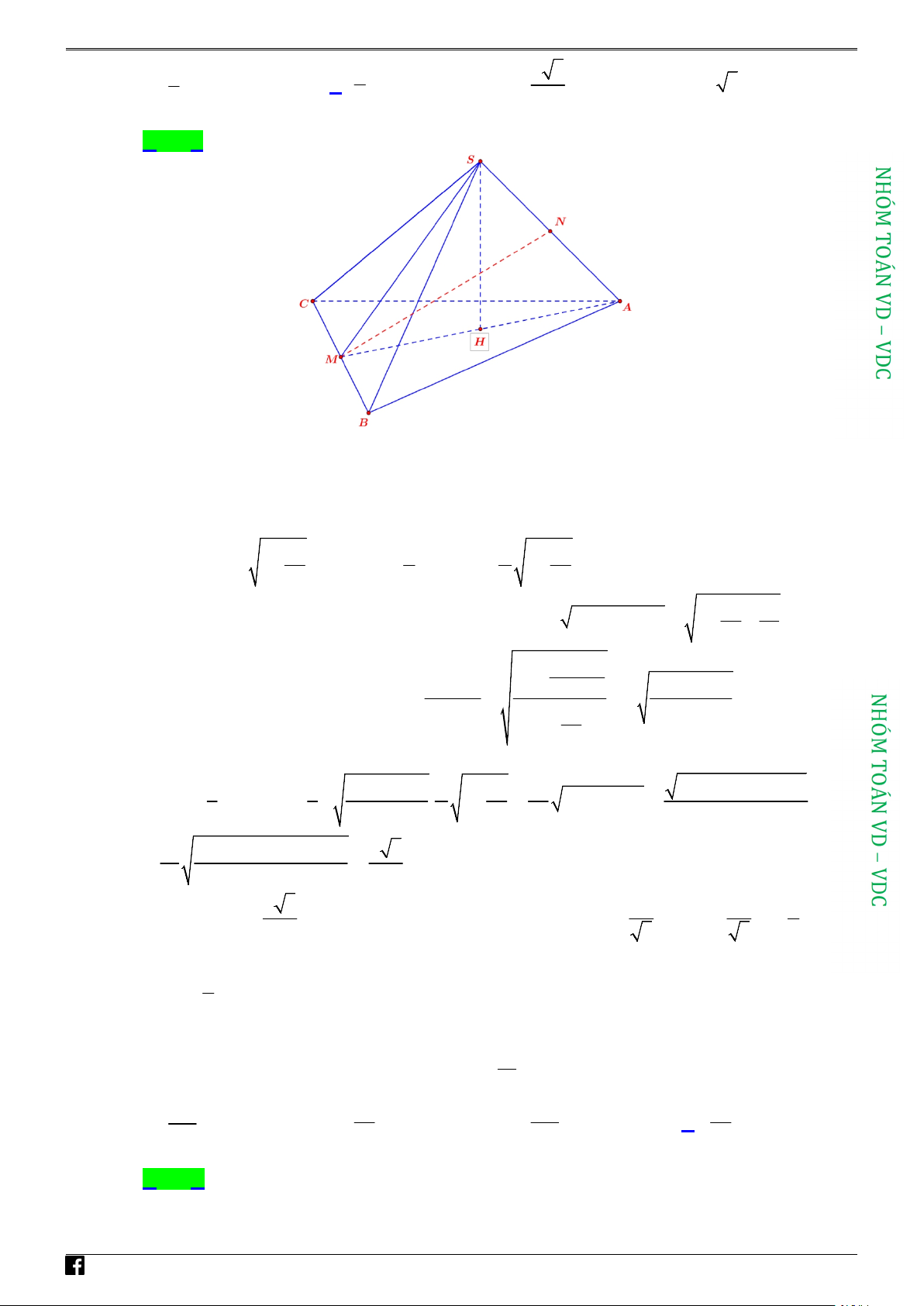
Câu 37: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a ;  0
ABC  60 và SB a . Hình
chiếu vuông góc của điểm S lên mặt phẳng  ABC trùng với trọng tâm tam giác ABC . Gọi 
là góc giữa đường thẳng SB và mặt phẳng SCD . Tính sin . A. 3 sin  . B. 1 sin  . C. 1 sin  . D. 2 sin  . 2 4 2 2 Lời giải Chọn D
https:/www.facebook.com/groups/toanvd.Trang 19 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021
AB AC a Vì 
 ABC là tam giác đều cạnh a . ABC  60
Gọi G là trọng tâm của tam giác ABC SG   ABCD.
Gọi E là hình chiếu của B trên SCD nên SE là hình chiếu của SB trên mặt phẳng SCD
 Góc giữa SB và mặt phẳng SCD là góc giữa hai đường thẳng SB , SE và bằng  BSE   BSE   .
Ta có BE d B,SCD.
d B,SCD BG 3
 SCD   D BG 3   
d B,CD  d G,SCD 
d G,SCD GC 2 2
Kẻ GH SC tại H   1 . CD CG Ta có: 
CD  SCG  CD HG 2. CD SG Từ  
1 và 2 suy ra GH  SCD  d G,SCD  GH . 2 a 3 . a CG   . 3 2 3 2
Xét tam giác SBG vuông tại G có 2 2 2 a a 6
SG SB AG a   . 3 3 Xét tam giác SCG vuông tại G ta có 1 1 1 9 3     9  a 2  HG  3 a 2
BE HG  .Xét tam giác SEB 2 2 2 2 2 HG GS GC 6a a 2 2a 3 2 2 a 2 vuông tại E ta có BE 2 2 sin    . SB a 2
Câu 38: Cho hàm số y f x liên tục trên  và có đồ thị như hình vẽ dưới đây
https:/www.facebook.com/groups/toanvd.Trang 20 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021
Tập hợp tất cả các giá trị thực của tham số m để phương trình f  2
4  x   m có nghiệm
thuộc nữa khoảng  2; 3   là
A. 1; f  2 . B. 1;3. C. 1;3 . D. 1; f   2 . Lời giải Chọn B Đặt 2 2  4 x t
x t 
; t '  0  x  0 2 2 4  x
Với x   2 ; 3 
 ta có bảng biến thiên của hàm số 2 t  4  x . Với x   2; 3  t1;2
Từ đồ thị ta có: t 1;2 f t  1;3
Vây để phương trình f  2
4  x   m có nghiệm thì m1; 3.
Câu 39: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AD  2AB  2a . Cạnh bên
SA  2a và vuông góc với mặt phẳng đáy. Gọi M , N lần lượt là trung điểm của SB và SD .
Tính khoảng cách từ S đến mặt phẳng  AMN . 3a a 6 A. a 5 . B. 2a . C. . D. . 2 3 Lời giải Chọn D Ta có: 1 1 1 2 3 VVAS AB AD a a a a . S ABD S ABCD . . 2 . .2 . . 2 6 6 3 V SA SM SN 1 1 2 1 S AMN 1 1 1 .  . .  1. .  3 3  VVa a . S AMN S ABD . V SA SB SD . . 4 4 3 6 S ABD 2 2 4 . Mặt khác: 1 1 2 2 1 2 2 a 5 AM SB AB AS a  4a  . 2 2 2 2 1 1 2 2 1 2 2 AN SD AD AS
4a  4a a 2 . 2 2 2
https:/www.facebook.com/groups/toanvd.Trang 21 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021 1 1 2 2 1 2 2 a 5 MN BD AB AD a  4a  . 2 2 2 2 2 Suy ra: a 6 S  . AMN 4
Vậy d S; AMN  3V a S AMN 1 4 6 . 3   a .  . 2 SAMN 2 a 6 3
Câu 40: Cho hàm số y f x có đồ thị như hình vẽ bên dưới.
Gọi S là tập tất cả các giá trị nguyên dương của tham số m để hàm số y f x  2020 m
có 5 điểm cực trị. Tổng tất cả các giá trị của các phần tử của tập S bằng A. 9. B. 7 . C. 12. D. 18. Lời giải Chọn C
Ta có: y f x  2020 m .
Từ đồ thị hàm số y f x  Hàm số y f x có 3 điểm cực trị
 Hàm số f x  2020  m cũng luôn có 3 điểm cực trị
Do đó, yêu cầu bài toán  số giao điểm của đồ thị hàm số f x  2020  m với trục hoành là 2 .
Tương đương với phương trình f x  2020  m * có hai nghiệm đơn phân biệt.
Từ đồ thị hàm số y f x ta tịnh tiến sang phải 2020 đơn vị được đồ thị hàm số
y f x  2020.
Khi đó phương trình * có hai nghiệm đơn phân biệt khi m  2 m  2     S  3;4;  5 .
6  m  3 3  m  6
Vậy tổng giá trị các phần tử của S là: 3 4  5 12 . x x   
Câu 41: Tính tổng S tất cả các nghiệm của phương trình 5 3 x 1 ln 
 5  5.3x 30 x 10  0.  6x  2  A. S  3. B. S 1. C. S  2 . D. S  1. Lời giải Chọn B. x x    Ta có: 5 3 x 1 ln 
 5  5.3x 30 x 10  0  6x  2 
 ln 5x  3x  55x  3x  ln 6 x 2  5 6 x 2 .
Khi đó phương trình có dạng 5x 3x f
  f 6x 2, với f t  lnt 5t,t0;
https:/www.facebook.com/groups/toanvd.Trang 22 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021f t 1 '   5  0, t
 0;  f t đồng biến trên 0; nên từ phương trình t
5x 3x   6 25x 3x  6 2    5x 3x f f x x g x  6x  2  0.    x x       x   2 x g x g x   2 ' 5 ln 5 3 ln 3 6 ' 5 ln 5 3 ln 3  0,x
Do g ' x  0, x
  phương trình g 'x  0 có nhiều nhất là một nghiệm, từ đó phương trình
g x  0 có nhiều nhất là hai nghiệm. Ta thấy x  0; x 1 là hai nghiệm của phương trình 1 2
g x  0 .
Vậy phương trình có hai nghiệm là x  0; x 1 S x x 1. 1 2 1 2
Câu 42: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Tam giác SAB đều và nằm
trong mặt phẳng vuông góc với đáy, bán kính mặt cầu ngoại tiếp khối chóp là: A. a 21 . B. a 11 . C. 2a . D. a 7 . 6 4 3 3 Lời giải Chọn A.
Để thuận lợi trong việc tính toán ta có thể giả sử cạnh hình vuông đáy a 1.
Gọi H là trung điểm AB . Ta có tam giác SAB đều và nằm trong mặt phẳng vuông góc với
đáy SH  ABCD  3 ,SH  . 2
Chọn hệ tọa độ Oxyz như hình vẽ  3   1   1   1   1 S 0;0; , A   0;
;0 ,B 0; ;0,C 1  ; ;0 D 1  ; ;0     . 2    2   2   2   2 
Gọi phương trình mặt cầu có dạng T  2 2 2
: x y z  2a ' x  2b ' y  2c ' z d '  0.
https:/www.facebook.com/groups/toanvd.Trang 23 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021
3  3c' d ' 0  1  a ' 4    2 1 
  b' d '  0 b '  0 
Do các điểm S A B C T  4 , , ,       3 1  c '
b ' d '  0  6 4    1 5 d '
 2a ' b' d '  0     4 4 2 2 2 21
R a '  b '  c '  d ' 
. Vậy bán kính mặt cầu ngoại tiếp khối chóp là a 21 R  . 6 6 2
Cách khác: ta có thể áp dụng công thức giải nhanh 2 2 AB R R R        . 1 2  2 
Trong đó là R bán kính đường tròn ngoại tiếp đáy AC a 2 ABCD R   và R là bán 1 1 2 2 2
kính đường tròn ngoại tiếp mặt bên 2 2 a 3 a 3
SAB R SH  .  . 2 3 3 2 3 2 2 2 AB a 21 R R R          . 1 2  2  6
Câu 43: Cho phương trình 1 2
log x  2m 1log x  4m  2  0 , có bao nhiêu giá trị nguyên của tham 3 3 4
số m để phương trình trên có nghiệm thuộc đoạn 1 ;3  ? 3    A. 1. B. 4 . C. 2 . D. 3. Lời giải Chọn C ĐKXĐ: x  0 . Ta có: 1 2
log x  2m 1log x  4m  2  0  2
log x  2m 1 log x  4m  2  0 2   3 3 4 3
log x  2m 1 2m 1 x 3     3   log x    2 3 x  9
Do đó yêu cầu bài toán  1 2m 1 3    3  1
  2m 11  0  m 1. 3
Vậy có 2 giá trị nguyên của m thoả mãn yêu cầu bài toán.
Câu 44: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với đáy, côsin góc hợp
bởi SD và mặt phẳng đáy  ABCD bằng 1 . Gọi E ; F lần lượt là hình chiếu của A lên 3
SB ; SD . Mặt phẳng  AEF chia khối chóp thành hai phần. Tính thể tích phần khối chóp
không chứa đỉnh S : 3 3 3 3 A. 2a V  . B. 2a V  . C. 2 2a V  . D. 2a V  . 9 4 9 6 Lời giải Chọn C
https:/www.facebook.com/groups/toanvd.Trang 24 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021 Dễ thấy SAB S
AD AE AF SE SF   EF / /BD SA SB
Do SA   ABCD nên AD là hình chiếu của SD lên mặt phẳng  ABCD 
SD ABCD    AD 1 cos ; cos SDA  
SD AD 3  a 3 SD 3
SA SD AD  a 2 2 2 2
3  a a 2  AC  Tam giác SAC vuông cân tại A
Trong  ABCD : gọi O AC BD
Trong SBD: gọi I SO EF
Trong SAC: gọi M SC AISA BC Lại có: 
BC  SAB  BC AEAB BC
Mà AE SB AE  SBC  AE SC   1 SA CD
CD  SAD  CD AFAD CD
Mà AF SD AF  SCD  AF SC 2 Từ  
1 và 2  SC   AEF   SC AM M là trung điểm SC I là trọng tâm tam
giác SAC SE SF 2    2 3a SE SF SA SB 3 3 Ta có: V SA SE SM 1 1 SAEM 1  . .   VVV V SA SB SC SAEM SABC S . 3 6 ABCD SABC 3 V SA SM SF 1 1 SAMF 1  . .   VVV V SA SC SD SAMF SACD S . 3 6 ABCD SACD 3  1 VVVV S.AEMF SAEM SAMF S. 3 ABCD 3 2 2 1 2 3  a V VVVSA S  . S ABCD S AEMF S ABCD . . . . . 3 3 3 ABCD 9
https:/www.facebook.com/groups/toanvd.Trang 25 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021
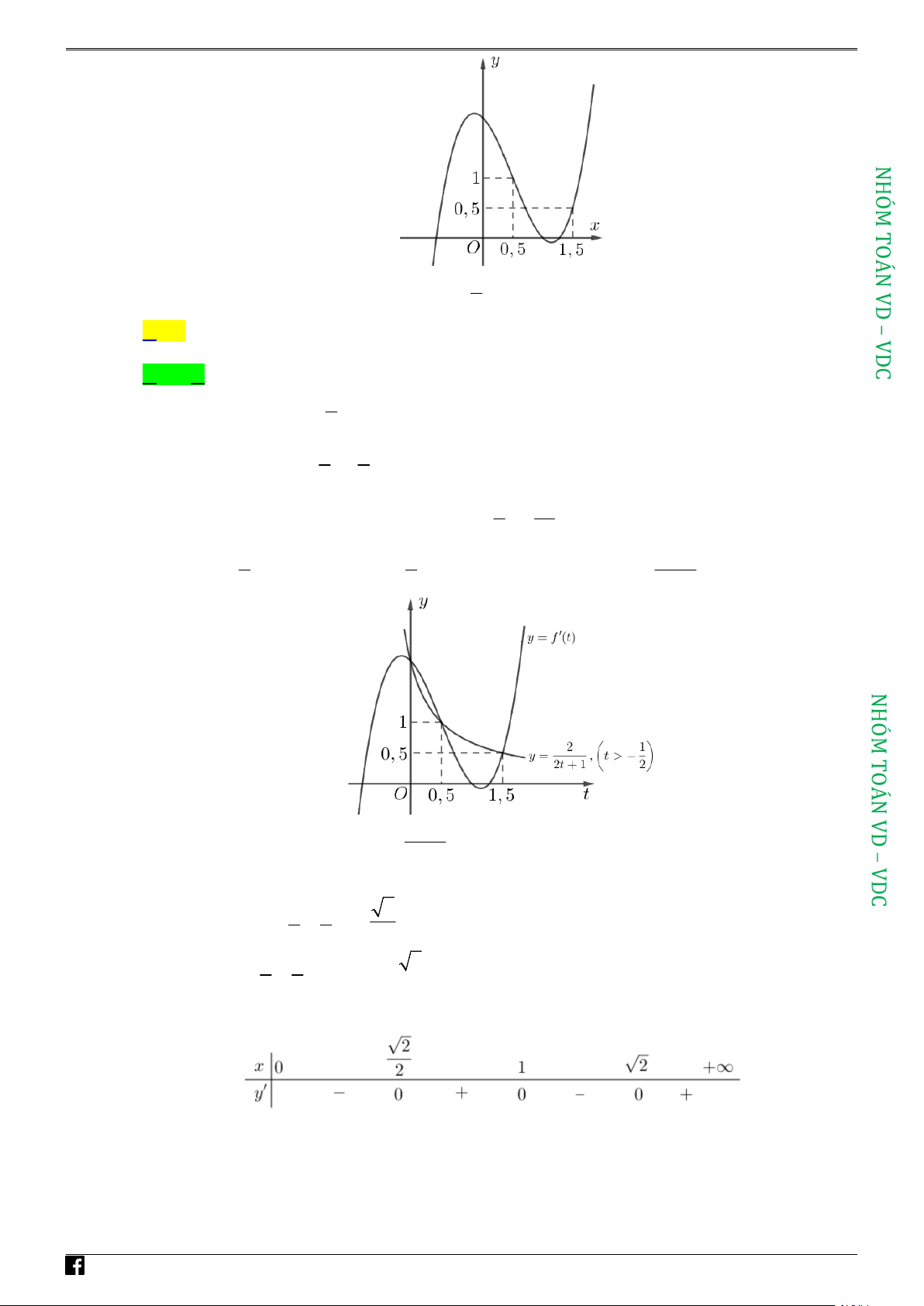
Câu 45: Cho hàm số bậc ba y f x có đồ thị như hình vẽ bên.
Số nghiệm thực của phương trình f  3 x x 4 3  là 3 A. 7 . B. 4 . C. 3 . D. 8 . Lời giải Chọn D 3
x  3x a   ;  2 1  3 4
x  3x b  2;0 2
Dựa vào đồ thị trên, ta có: f  3
x  3x    3 3
x  3x c   0;2 3  3
x  3x d  2;   4 Xét hàm số 3
y x  3x có bảng biến thiên:
Dựa vào bảng biến thiên trên, mỗi phương trình 2, 3 có 3 nghiệm phân biệt và 1, 4 có 1 nghiệm.
Vậy tổng số nghiệm của phương trình f  3 x x 4 3  là 8. 3
Câu 46: Cho hàm số f x . Hàm số y f ' x có đồ thị như hình bên.
https:/www.facebook.com/groups/toanvd.Trang 26 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021
Số điểm cực trị của hàm số g x  2 1 f x       2ln x .  2  A. 3 . B. 6 . C. 4 . D. 5 . Lời giải Chọn A
Hàm số g x  2 1 f x     
 2ln x có tập xác định D  0; .  2   g x  2 1  2 '  2 . x f ' x    . 2    x Với  1  1
x  0; , ta xét g ' x  0 2  f ' x       * 2  2  x Đặt 2 1
t x  , (với 1
x  0  t   , khi đó * trở thành: f t 2 '  2 2 2t 1   t
Dựa vào đồ thị trên, ta có: f 't 2 0 0,5   2t 1  t  1,5 x  0  1 1   2 2  0  x     x  1 Khi đó:   2 2  2  .     2 1 3 x  2  x     2 2
Bảng xét dấu của g 'x :
Vậy hàm số g x có 3 điểm cực trị.
Câu 47: Cho x, y là những số thực dương không đổi. Xét hình chóp S.ABC có SA x,BC y và các
cạnh còn lại đều bằng 1. Khi thể tích khối chóp S.ABC đạt giá trị lớn nhất thì tích .xy bằng
https:/www.facebook.com/groups/toanvd.Trang 27 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021 4 4 3 A. 1 . B. . C. . D. 2 3 . 3 3 3 Lời giải Chọn B
 Ta có: do AB AC SB SC nên các tam giác SBC và ABC cân tại S, A . Gọi M , N lần BC SM
lượt là trung điểm BC,SA thì 
BC  (SAM ) . Từ đây ta hạ SH AM,H AMBCAM
Mà SH BC(BC  (ASM )) nên SH (ABC) 2 2 Suy ra 1 y AM 1   nên y y S     AM BC ABC . . 1 4 2 2 4 2 2
Mặt khác vì SM AM nên SAM cân tại M 2 2     1 y x MN AM AN   4 4 2 2 1 x yx 2 2 Mà ta có: MN.SA 4 4 .  .  x y
MN SA SH AM SH    x 2 2 AM y 4 1  y  4 Suy ra, ta có được 2 2 2 2 2 2 2 1 1 4  x y y y xy   2 2 x y (4 x y ) VSH S        x x y S ABC . ABC . . 1 4 . 2 3 3 4  y 2 4 12 12 2 2 2 2
1 x y  4  x y 2 3   12 3 27 2 Vậy 2 3 V  khi và chỉ khi 2 2 2 2 2 4 x y 4 2x x y xy            S.ABC max 27 3  3    3
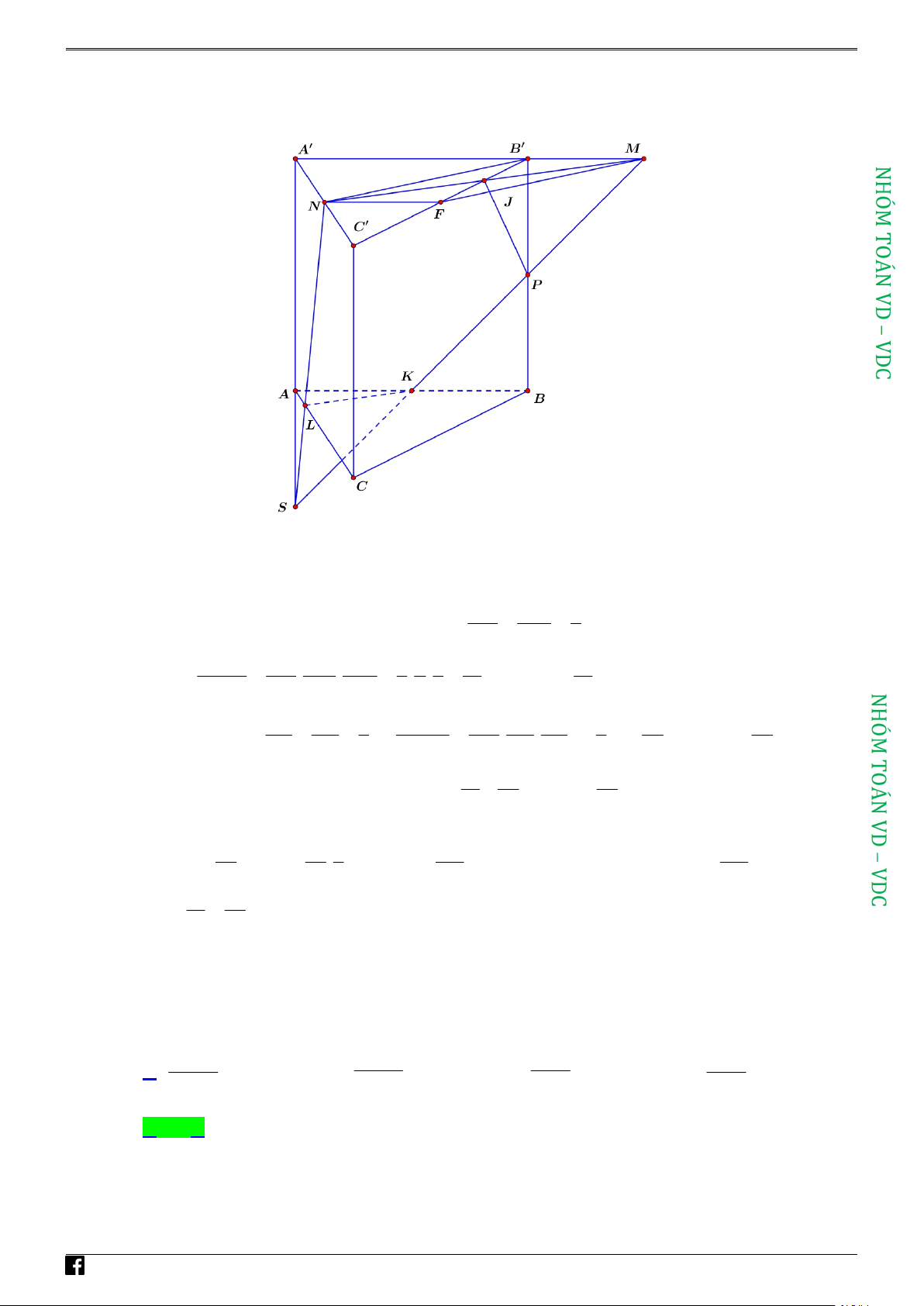
Câu 48: Cho lăng trụ tam giác đều ABC.A'B'C ' . Trên tia đối của tia B' A' lấy điểm M sao cho 1
B'M B' A' . Gọi N,P lần lượt là trung điểm của A'C ',BB' . Mặt phẳng (MNP) chia khối 2
trụ ABC.A'B'C ' thành hai khối đa diện, trong đó khối đa diện có chứa đỉnh A' có thể tích V và 1
khối đa diện chứa đỉnh C 'có thể tích V . Tỉ số V1 bằng 2 V2 97 49 49 A. 95 . B. . C. . D. . 144 59 144 95 Lời giải Chọn D
 Ta gọi: K MP AB,S MP AA',L NS AC;
https:/www.facebook.com/groups/toanvd.Trang 28 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021
Khi đó thiết diện cần tìm chính là ngũ giác NJPKL chia hình lăng trụ ABC.A'B'C ' thành 2
NF / /B 'M
phần như hình vẽ. Cho J là trung điểm BF mà ta có: 
B'J JF
NF B 'M
Tương tự ta lại có thêm được: MJ JN nên từ đó suy ra B'NFM là hình bình hành AK KB Mặt khác: MP B 'P 1 
SA BP B 'P   SA / /BP MS A'S 3 Ta có: V MP MJ MB M PJB ' 1 1 1 1 1 . '  . .  . .   VV M .PJB ' M .SNA' V MS MN MA M SNA ' 3 2 3 18 18 . ' 3 Mặt khác: ta có SL SA 1 V SK SA SL S ALK 1  1 1 .     . .    V    V S.ALK S.A' SN SA' 3 V SM SA SN A NM ' 3  27 27 NM S. ' Khi đó:  1 1  49 V VVV    V    V S MNA M PJB S ALK 1 1 . ' . ' . M .SNA' M .SNA'  18 27  54 Ta lại có: 49 49 3 49 95 VVVVV VV V S A NM M SNA . . ' . '
ABC.A' B 'C '
ABC.A' B 'C ' 2
ABC.A' B 'C ' 1
ABC.A' B 'C ' 54 54 8 144 144 Vậy: V 49 1  V 95 2
Câu 49: Có 18 bạn thi Toán và KHTN bằng Tiếng Anh được khen thưởng gồm 9 nam và 9 nữ, tất cả
các học sinh nam có chiều cao khác nhau, học sinh nữ có chiều cao khác nhau. Thầy Chinh xếp
ngẫu nhiên các bạn thành một hàng ngang để chụp ảnh kỉ niệm sao cho tính từ trái sang phải
các học sinh nam có chiều cao giảm dần và các học sinh nữ có chiều cao tăng dần. Xác suất để
các bạn nam và các bạn nữ đứng xen kẽ theo cách trên là 1 1 A. 1 . B. . C. . D. 14 . 24310 48620 2002 2002 Lời giải
Chọn ACầntất cả18vị trị cho18họcsinh.
Bước 1: Chọn vị trí cho 9 học sinh, có 9
C cách chọn. Sau đó ta xếp 9 học sinh nam vào 9 vị trí 18
đã chọn sao cho chiều cao giảm dần từ trái sang phải, chỉ có 1 cách xếp như vậy.
https:/www.facebook.com/groups/toanvd.Trang 29 NHÓM TOÁN VD–VDC
NĂM HỌC 2020 – 2021
Bước 2: Xếp 9 nữ vào 9 vị trí còn lại sao cho chiều cao tăng dần từ trái sang phải, chỉ có một cách xếp như vậy. Vậy   9 C  48620 . 18
Gọi A là biến cố: “Thầy giáo xếp các bạn nam và các bạn nữ đứng xen kẽ nhau ”.
Theo cách xếp trên giả sử thầy giáo xếp các bạn nam trước(tính từ trái sang phải các
học sinh nam có chiều cao giảm dần) có 1 cách xếp.
Để xếp các bạn nữ xen kẽ theo cách trên(các học sinh nữ có chiều cao tăng dần) vào các vị trí có 2 cách.
Theo quy tắc nhân có 2 cách để xếp các bạn học sinh thỏa mãn đề bài. Do đó   . A 2 Vậy PA 2 1   . 48620 24310
Câu 50: Có bao nhiêu giá trị nguyên dương của tham số m nhỏ hơn 2021 để phương trình log   2x m m
 2x có nghiệm thực? 2   A. 2018 . B. 2019 . C. 2021. D. 2020 . Lời giải Chọn D
 Ta có phương trình: log   2x m m  2x (1) 2   Đặt:  2x t
m (t  0) thì phương trình (1) trở thành  log
  2    4x   4x m t x m t tm 2   Mà  2x t
m nên suy ra 4x   2x   4x  2x m mm m
 4x  2x  2x   2x mm
Từ đây ta xét hàm đặc trưng 2
y f (t)  t t , t
  0 có f '(t)  2t 1  0, t   0  ( ) 
[0;)  (2x)   2x   2x  2x    4x  2x f t trên f f m m m
Xét hàm  ( )  4x  2x y g x
có '( )  4 .x2ln(2)  2x g x ln(2)  0  x  1 
Ta có bảng biến thiên của hàm g(x) như sau:
Từ đó để phương trình trên có 2 nghiệm thực thì 1
m g(1)  m  4
Mà m nguyên dương và nhỏ hơn 2021nên suy ra m [1;2020]
Vậy có tất cả 2020 giá trị nguyên m thỏa mãn yêu cầu đề bài
https:/www.facebook.com/groups/toanvd.Trang 30

Tài liệu liên quan: