







Preview text:
SỞ GD&ĐT VĨNH PHÚC
ĐỀ KIỂM TRA KHẢO SÁT
TRƯỜNG THPT QUANG HÀ
ÔN THI TỐT NGHIỆP THPT 2021, LẦN 1 Môn Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Mã đề thi: 121
Họ, tên thí sinh:..................................................................... Số báo danh: .............................
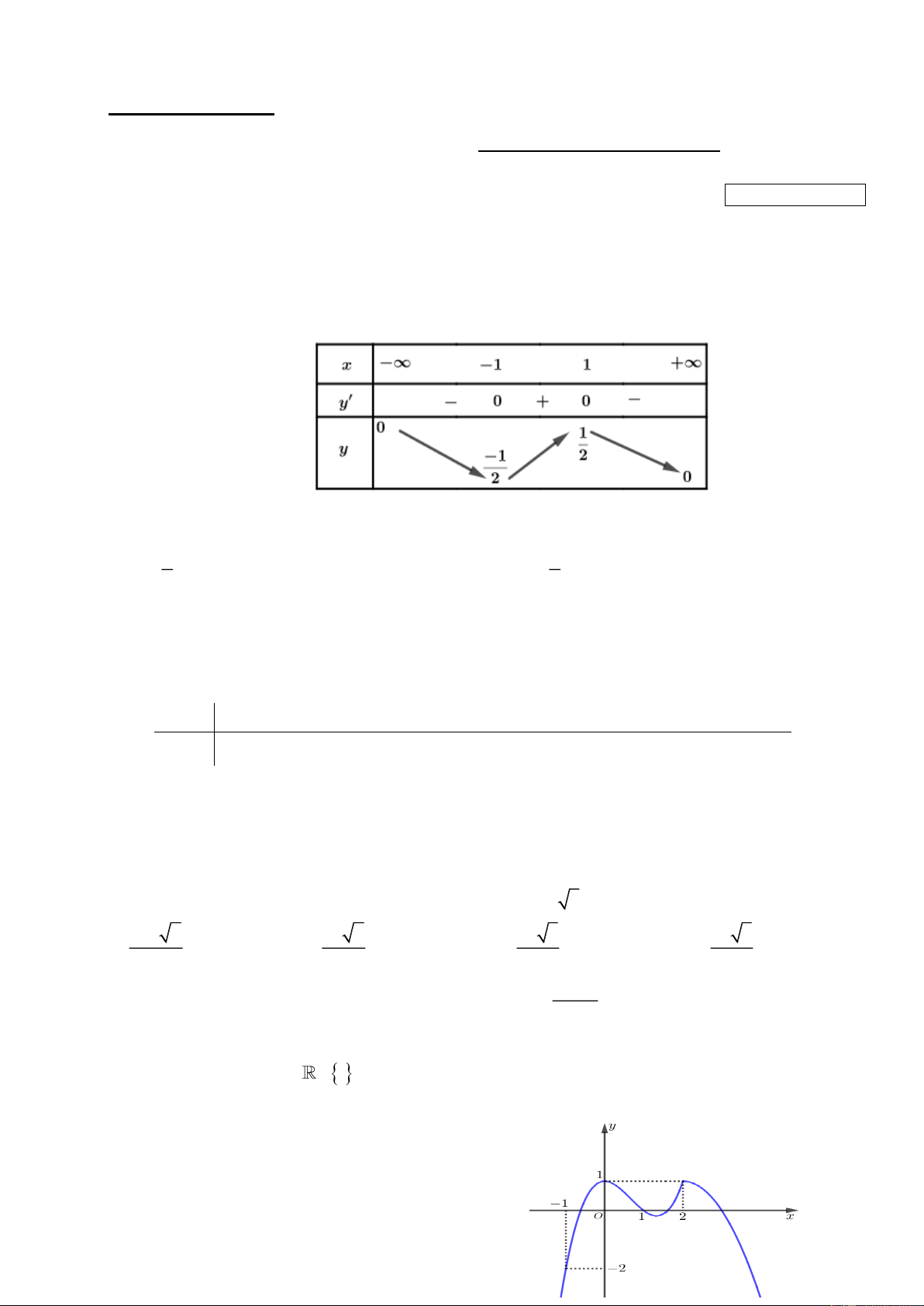
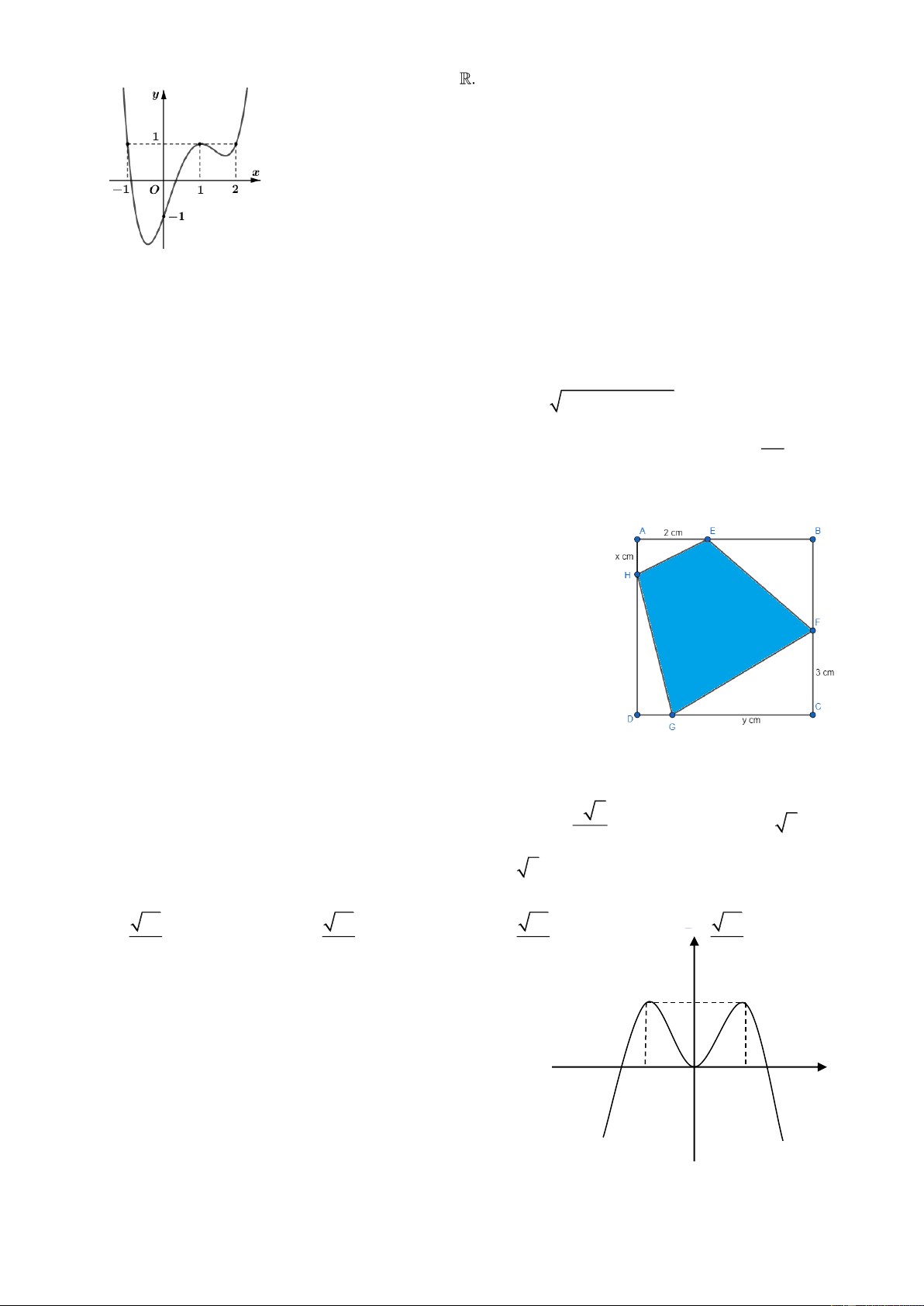
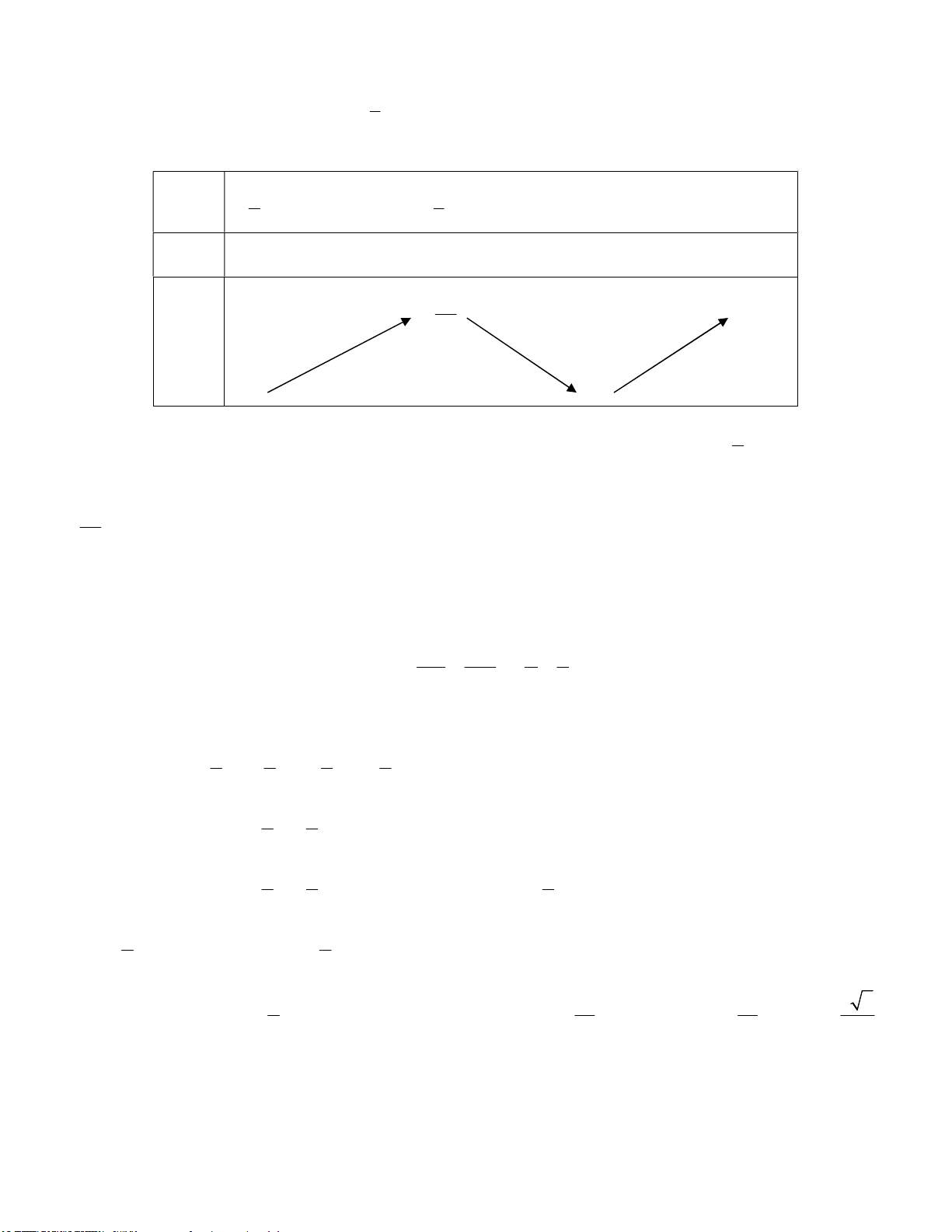
Câu 1: Cho hàm số y f x có bảng biến thiên như sau
Biết giá trị lớn nhất và giá trị nhỏ nhất của hàm số lần lượt là M , m . Giá trị biểu thức 2 2
P M m bằng 1 1 A. P . B. 1. C. P . D. 2 . 2 4
Câu 2: Cho cấp số nhân u có u n
1 = 2, và công bội q = 2. Tính u3. A. u 8 B. u 4 C. u 18 D. u 6 3 3 3 3
Câu 3: Cho hàm số y f x có bảng xét dấu như sau: x 2 0 y ' 0 + 0
Hàm số y f x đồng biến trên khoảng nào dưới đây? A. 2 ;0 B. 0; C. ; 2 D. 3 ; 1
Câu 4: Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a và hai mặt bên (SAB), (SAC) cùng
vuông góc với đáy. Tính thể tích khối chóp S.ABC biết SC a 3. 3 2a 6 3 a 6 3 a 3 3 a 3 A. . B. . C. . D. . 9 12 4 2 x
Câu 5: Kết luận nào sau đây về tính đơn điệu của hàm số 2 1 y là đúng? x 1
A. Hàm số nghịch biến trên R \ 1
B. Hàm số đồng biến trên \ 1
C. Hàm số nghịch biến trên ;1 và 1;
D. Hàm số đồng biến trên ;1 và 1;
Câu 6: Cho hàm số f ' x như hình vẽ.
Trang 1/8 - Mã đề thi 121
Hàm số g x f x 6 x 2 4 2
x x đạt cực tiểu tại bao nhiêu điểm? 3 A. 3 . B. 2 . C. 0 . D. 1.
Câu 7: Biết rằng đồ thị hàm số (m 2n 3)x 5 y
nhận hai trục tọa độ làm hai đường tiệm cận. x m n Tính tổng 2 2 S m n 2 . A. S 0 B. S 2 C. S 1 D. S 1
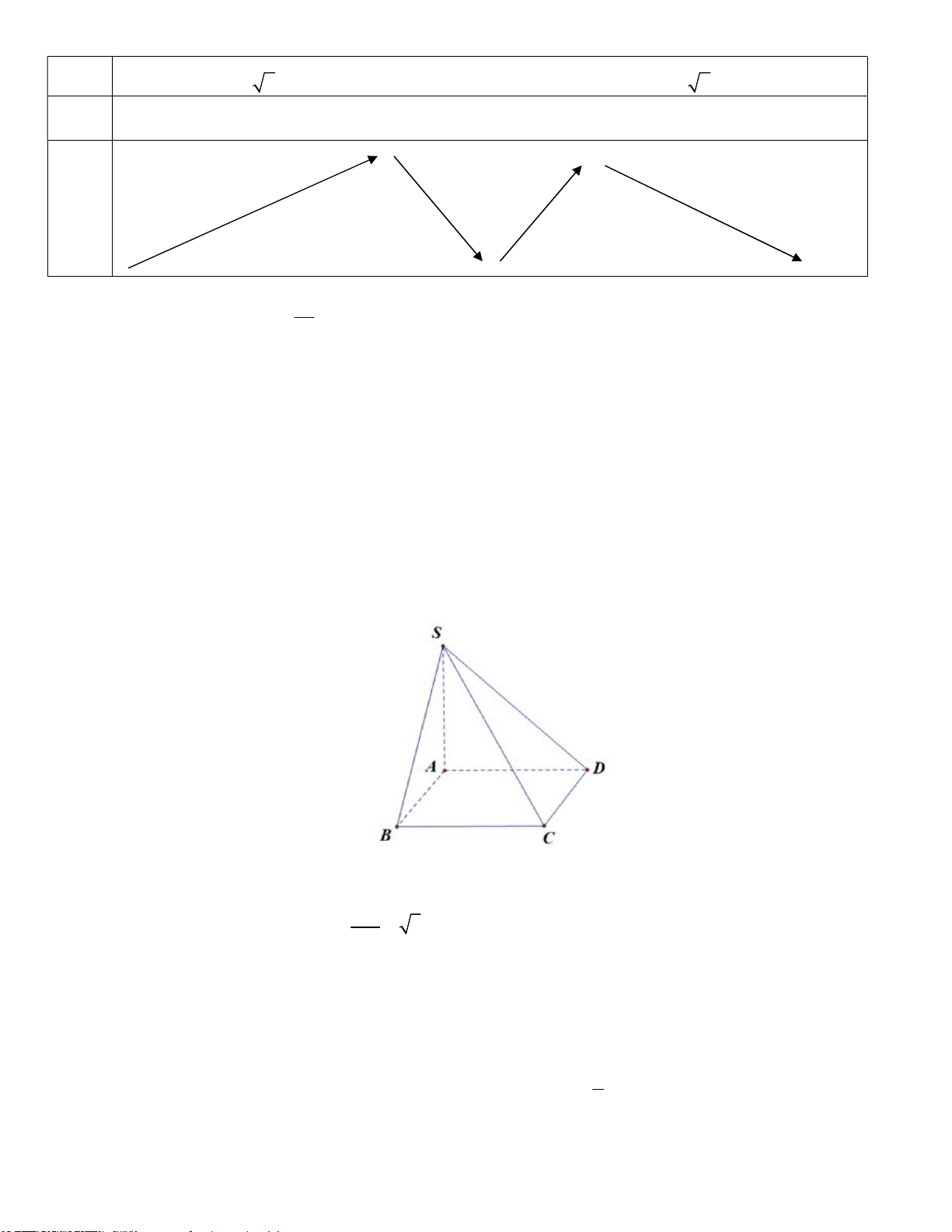
Câu 8: Cho hình chóp .
S ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy và
SA a 3 . Góc giữa đường thẳng SD và mặt phẳng ABCD bằng 3 A. 30 . B. 60 . C. arcsin . D. 45. 5
Câu 9: Giá trị lớn nhất của hàm số f x 3 2
x 8x 16x 9 trên đoạn 1; 3 là 13
A. max f x 5 .
B. max f x 6 .
C. max f x .
D. max f x 0 . 1; 3 1; 3 1; 3 27 1; 3
Câu 10: Số đỉnh của hình mười hai mặt đều là: A. Mười sáu B. Mười hai C. Ba mươi D. Hai mươi
Câu 11: Cho hình chóp có 20 cạnh. Tính số mặt của hình chóp đó. A. 12 B. 10 C. 11 D. 20
Câu 12: Đường cong sau đây là đồ thị hàm số nào? A. 3 y x 3x 2 B. 3 y x 3x 2 C. 3 y x 3x 2 D. 3 y x 3x 2 7 2
Câu 13: Tìm hệ số h của số hạng chứa 5 x trong khai triển 2 x ? x A. h = 84 B. h = 560 C. h = 672 D. h = 280
Câu 14: Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số 2 x mx m y
trên 1; 2 bằng 2. Số phần tử của S là x 1 A. 1. B. 4. C. 3. D. 2. x
Câu 15: Đồ thị hàm số 1 y
có đường tiệm cận ngang là đường thẳng nào dưới đây? 4x 1 1 1 A. x 1 B. y 1 C. y D. x 4 4 m
Câu 16: Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số 3 2 y
x 2mx 3m 5 x 3 đồng biến trên . A. 6 . B. 2 . C. 5 . D. 4 .
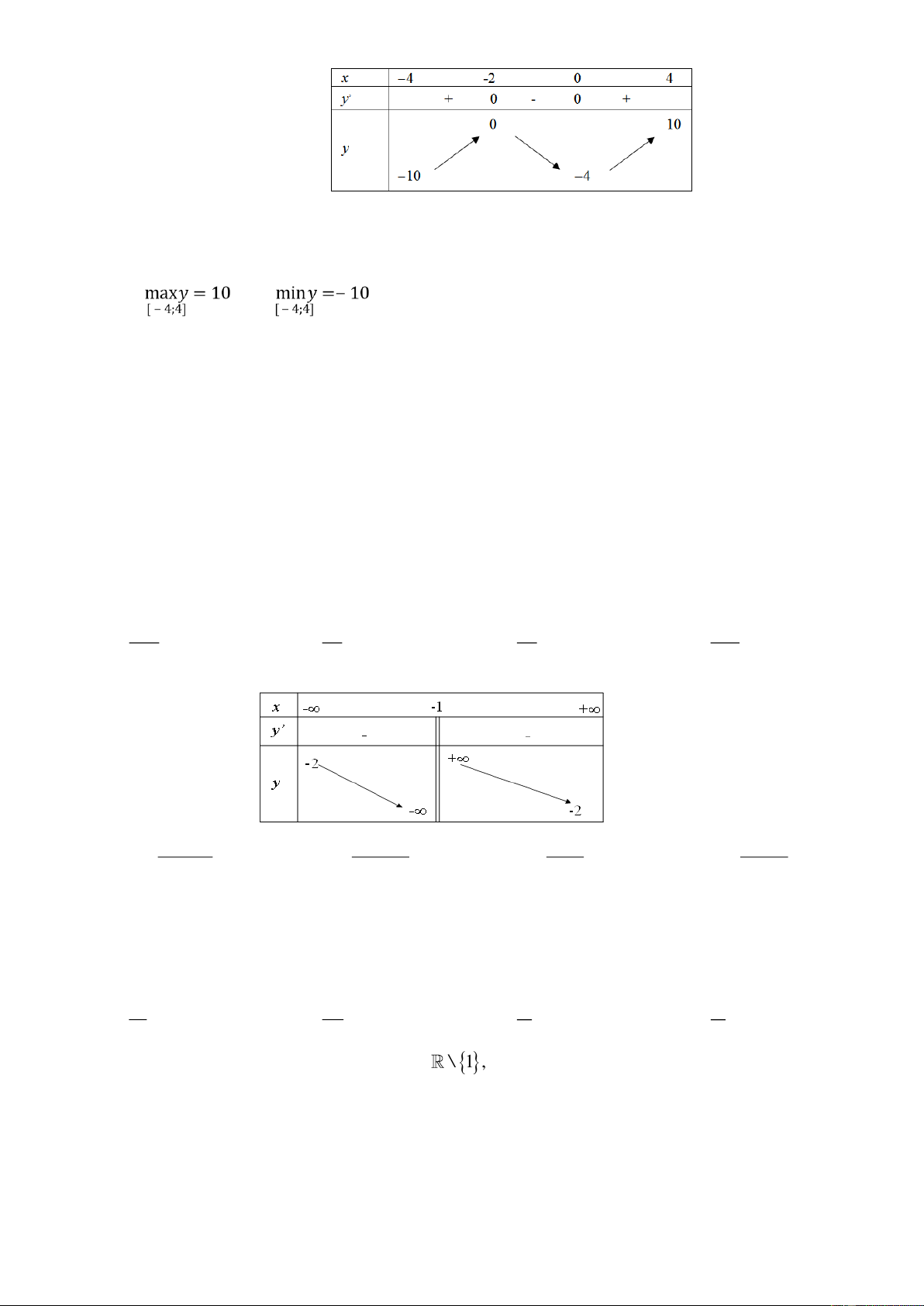
Câu 17: Cho hàm số y f (x) liên tục trên đoạn [-4; 4] và có bảng biến thiên trên đoạn [-4; 4] như sau
Trang 2/8 - Mã đề thi 121
Phát biểu nào sau đây đúng?
A. Hàm số không có GTLN, GTNN trên (4; 4) . B. min y 4 và max y 10 . ( 4 ;4) ( 4 ;4) C. và .
D. max y 0 và min y 4 . ( 4 ;4) ( 4 ;4)
Câu 18: Cho K là một khoảng hoặc nữa khoảng hoặc một đoạn. Hàm số y f x liên tục và xác
định trên K . Mệnh đề nào không đúng?
A. Nếu hàm số y f x đồng biến trên K thì f x 0,x K .
B. Nếu f x 0,x K thì hàm số y f x đồng biến trên K .
C. Nếu hàm số y f x là hàm số hằng trên K thì f x 0,x K .
D. Nếu f x 0,x K thì hàm số y f x không đổi trên K .
Câu 19: Cho hai dãy ghế dối diện nhau, mỗi dãy có 5 ghế. Xếp ngẫu nhiên 10 học sinh, gồm 5 nam, 5
nữ ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Tính xác suất để mỗi học sinh
nam đều ngồi đối diện với một học sinh nữ. 1 8 1 1 A. B. C. D. 252 63 63 945
Câu 20: Bảng biến thiên trong hình vẽ là của hàm số 2x 3 2x 4 2 x x 4 A. y . B. y . C. y D. y . x 1 x 1 x 1 2x 2
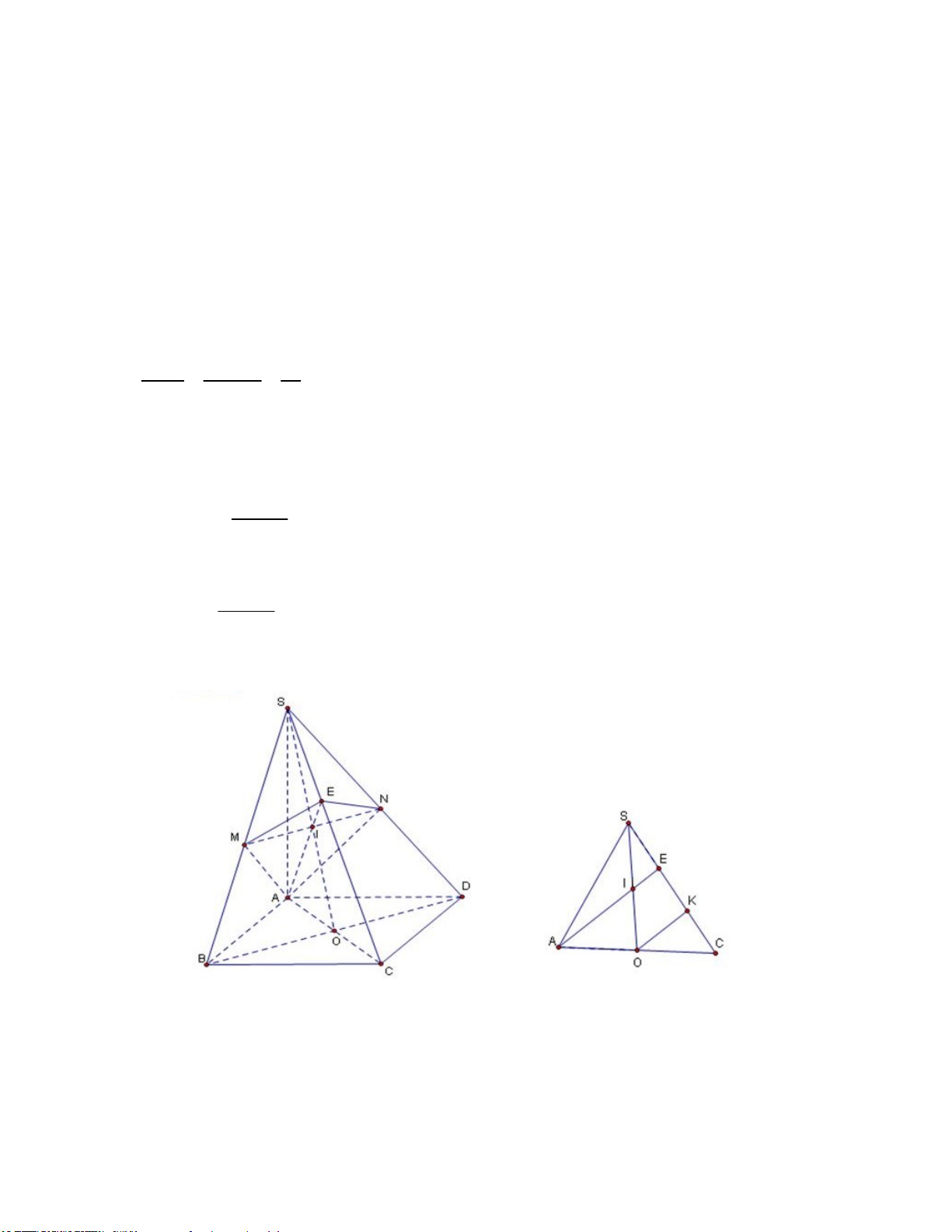
Câu 21: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích V. Gọi E là điểm trên
cạnh SC sao cho EC 2ES. Gọi là mặt phẳng chứa đường thẳng AE và song song với đường
thẳng BD, cắt hai cạnh SB, SD lần lượt tại hai điểm M, N. Tính theo V thể tích khối chóp S.AMEN. V V V V A. B. C. D. 12 27 9 6
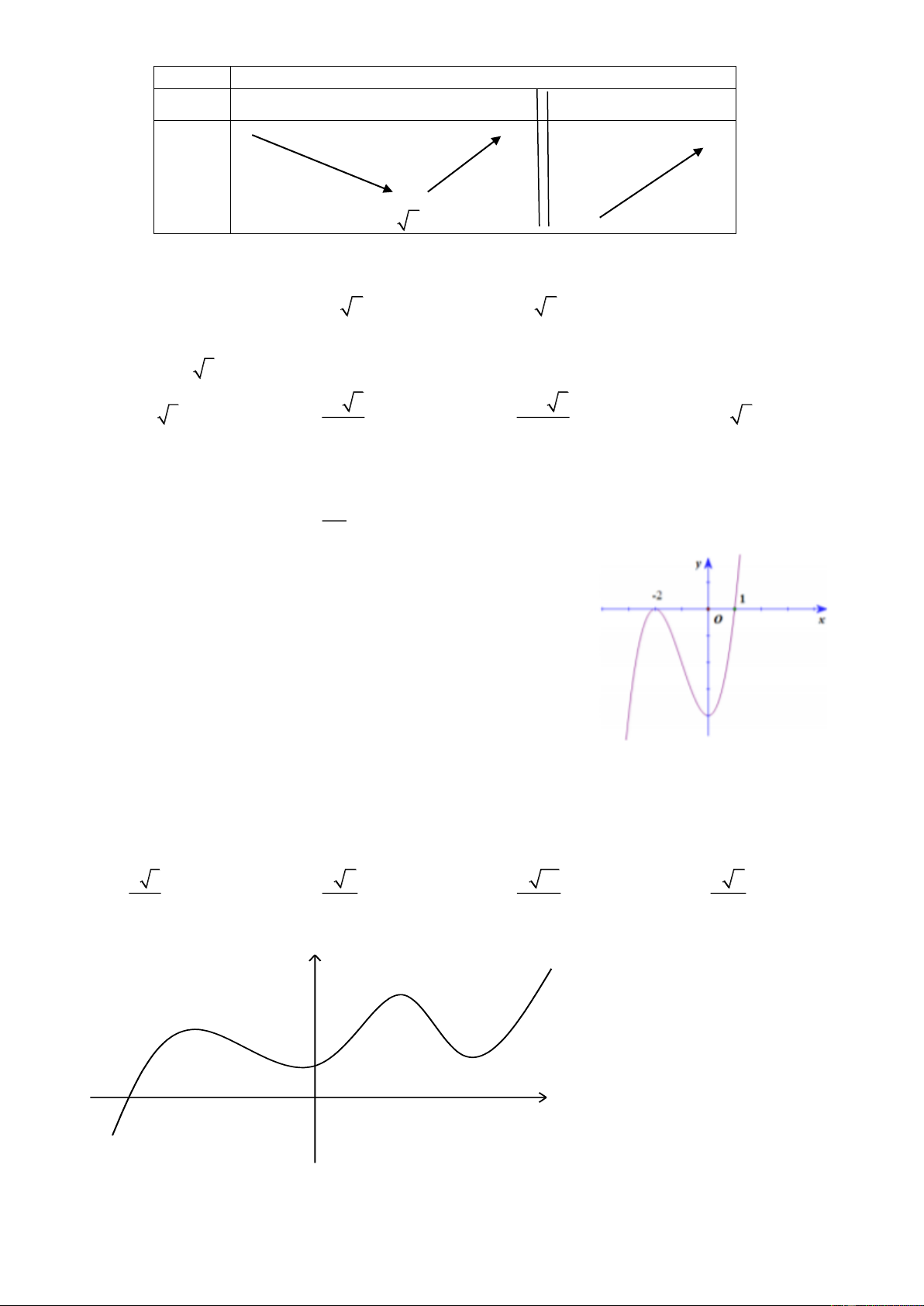
Câu 22: Cho hàm số y f x xác định trên \
1 , liên tục trên mỗi khoảng và có bảng biến thiên như hình vẽ.
Trang 3/8 - Mã đề thi 121 x -1 1 +
f ' x 0 + + f x 1 + -1 2 -
Tìm tập hợp tất cả các giá trị thực của tham số m sao cho phương trình f x m có ba nghiệm thực phân biệt A. (-1;1]. B. 2;1. C. 2;1. D. (-1;1).
Câu 23: Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB = a, AD = 2a, SA vuông góc với mặt
đáy và SA a 3. Thể tích khối chóp S.ABCD bằng: 3 a 3 3 2a 3 A. 2 3 a 3 . B. . C. . D. 3 a 3. 3 3
Câu 24: Cho tập A có 20 phần tử. Hỏi tập A có bao nhiêu tập hợp con khác rỗng mà có số phần tử chẵn 20 2 A. 20 2 B. 1 C. 20 2 1 D. 19 2 2
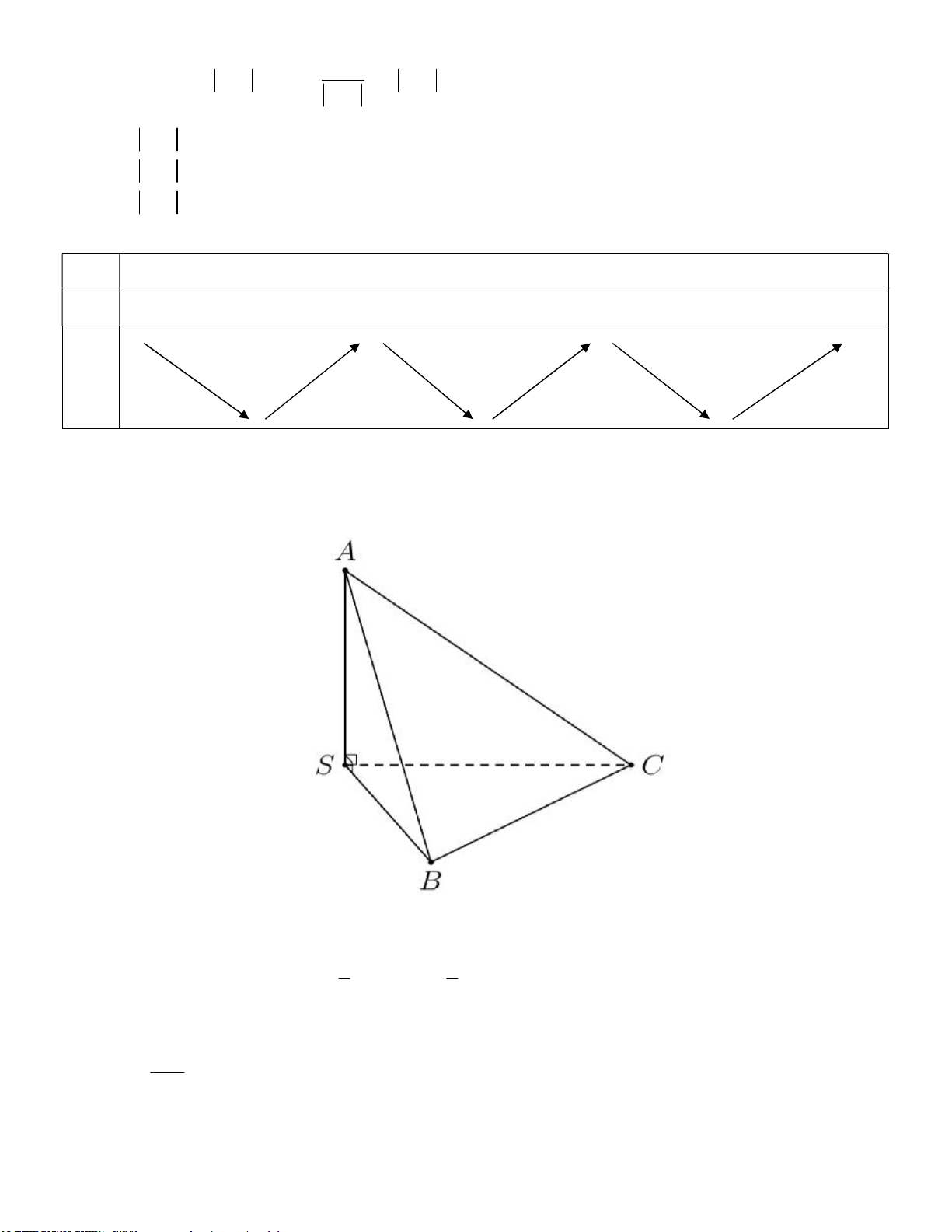
Câu 25: Cho hàm số y f x có đồ thị như hình vẽ sau. Tìm
số nghiệm thực phân biệt của phương trình f x 1. A. 0. B. 2. C. 1. D. 3.
Câu 26: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA ABC , góc giữa đường
thẳng SB và mặt phẳng ABC bằng 60. Khoảng cách giữa hai đường thẳng AC và SB bằng a 3 a 2 a 15 a 7 A. . B. . C. . D. . 7 2 5 7
Câu 27: Cho hàm số y f (x) có đạo hàm và liên tục trên R, có đồ thị như hình vẽ: y 0 x
Số điểm cực trị của hàm số đã cho là A. 3 B. 1 C. 4 D. 0
Trang 4/8 - Mã đề thi 121
Câu 28: Gọi M x ;
M yM là một điểm thuộc C 3 2 : y x 3x
2, biết tiếp tuyến của (C) tại M cắt
(C) tại điểm N x ; N N
y (khác M) sao cho 2 2 P 5xM N
x đạt GTNN. Tính OM. 5 10 7 10 10 10 10 A. OM . B. OM . C. OM . D. OM . 27 27 27 27 Câu 29: Hàm số 3 2
y x 3x 4 đồng biến trên khoảng nào? A. ; 0 B. 1; 2 C. 2; D. 0; 2 2x 1 Câu 30: Tìm lim . x x 1 A. 3 B. 1 C. -1 D. 2
Câu 31: Cho khối chóp có thể tích V, diện tích đáy là B và chiều cao h. Tìm khẳng định đúng? 1 A. V . Bh B. V Bh.
C. V B . h
D. V 3B . h 3
Câu 32: Cho hàm số y f x liên tục trên R và có bảng biến thiên x 1 0 1 y ' 0 + 0 0 + 2 y 1 1
Khẳng định nào dưới đây sai? A. f
1 là một giá trị cực tiểu của hàm số
B. x 0 là điểm cực đại của hàm số 0
C. x 1 là điểm cực tiểu của hàm số
D. M 0;2 là điểm cực tiểu của đồ thị hàm số 0
Câu 33: Tính thể tích của khối tứ diện đều có cạnh bằng 2. 4 2 2 2 A. . B. 2. C. . D. 2 3. 3 3
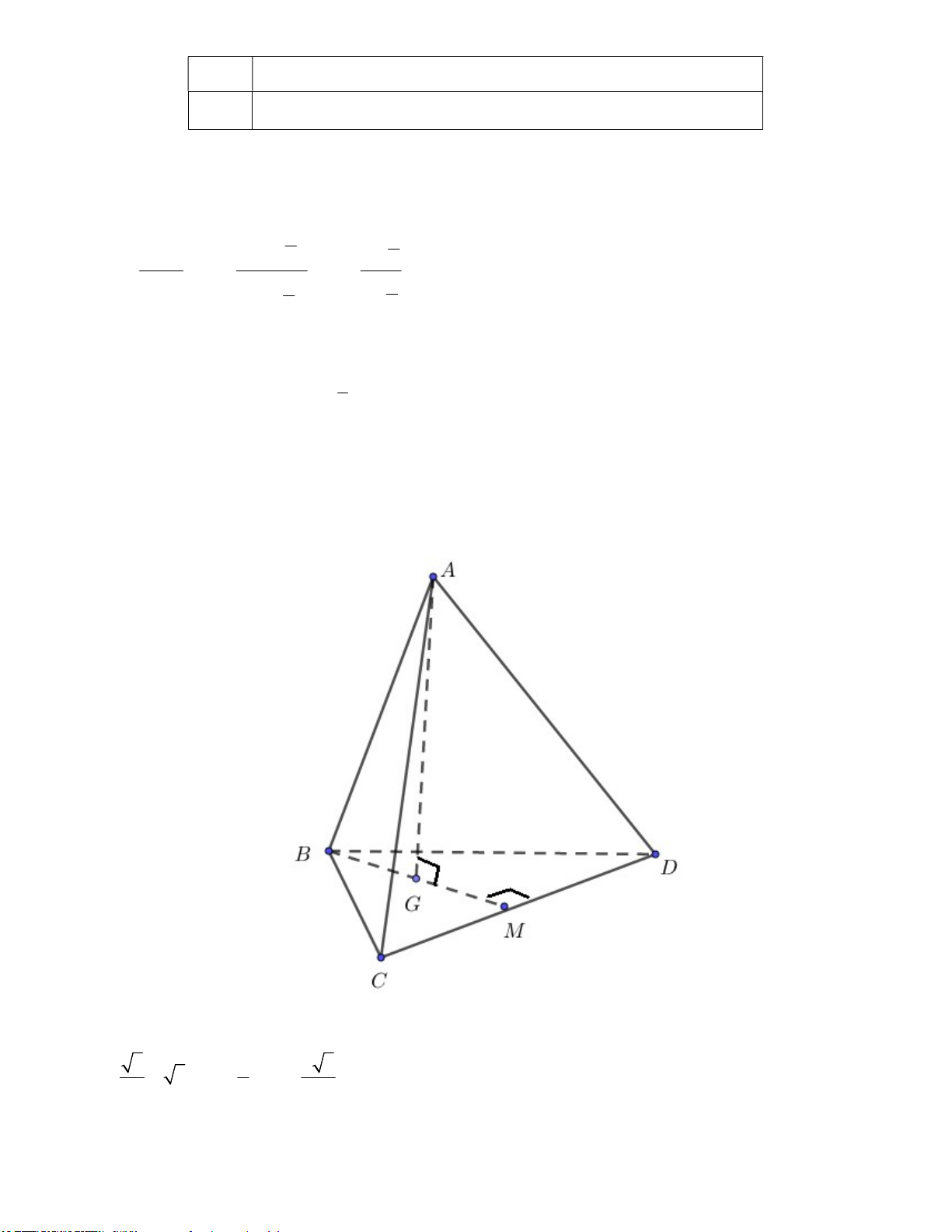
Câu 34: Cho tứ diện đều
có cạnh bằng a. Gọi
lần lượt là trọng tâm của các tam giác
và là điểm đối xứng với qua Mặt phẳng ) chia khối tứ diện thành hai
khối đa diện, trong đó khối đa diện chứa đỉnh có thể tích là . Tính . 3 3 2a 3 9 2a 3 a 2 3 3 2a A. V . B. V . C. V . D. V . 320 320 96 80
Câu 35: Cho k N, n N. Trong các công thức về số các chỉnh hợp và số các tổ hợp sau, công thức nào là công thức đúng? n k ! A. k k k 1 C
C C (với 1 k n ). B. A
(với 0 k n ). n 1 n n n
k !(n k)! n k ! C. k k 1 C
C (với 0 k n 1). D. C
(với 0 k n ). n 1 n n (n k)!
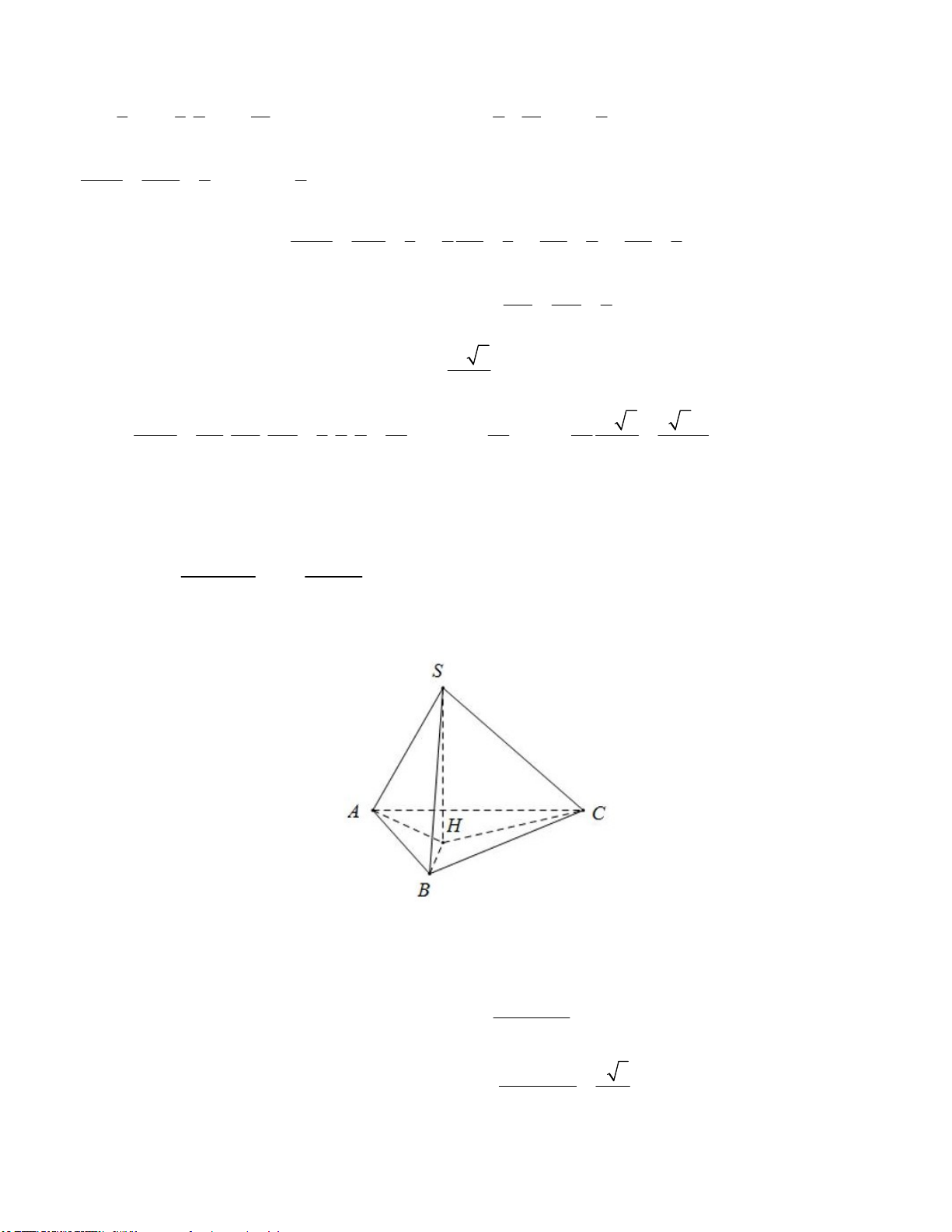
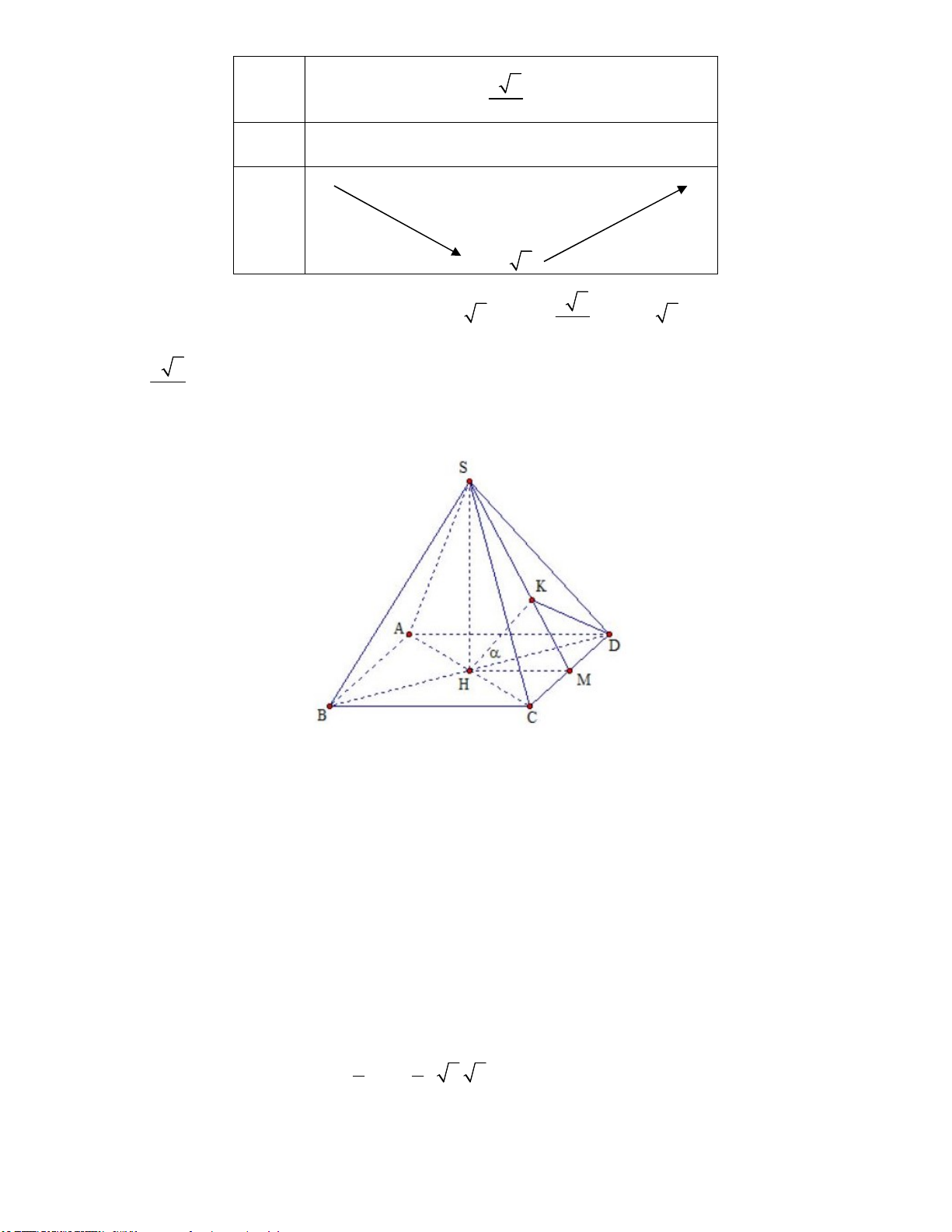
Câu 36: Cho hình chóp S.ABC có mặt đáy là tam giác đều cạnh bằng 2 và hình chiếu của S lên mặt
phẳng (ABC) là điểm H nằm trong tam giác ABC sao cho 0 0
AHB 150 , BHC 120 , 0 CHA 90 . Biết
tổng diện tích mặt cầu ngoại tiếp các hình chóp S.HAB, S.HBC, S.HCA là 124 . Tính thể tích khối 3 chóp S.ABC.
Trang 5/8 - Mã đề thi 121 9 4 A. B. C. 3 4a D. 4 2 3
Câu 37: Cho hàm số f x xác định và liên tục trên . Đồ thị hàm số f x như hình vẽ dưới đây.
Xét hàm số g x f x 1 3 3 3 2
x x x 2019 . Trong các mệnh đề sau: 3 4 2
(I) g 0 g 1
(II) min g x g 1 3 ; 1
(III) Hàm số g x nghịch biến trên 3 ; 1
(IV) max g x maxg 3 ; g 1 3 ; 1 3 ; 1
Số mệnh đề đúng là? A. 2. B. 1. C. 3. D. 4.
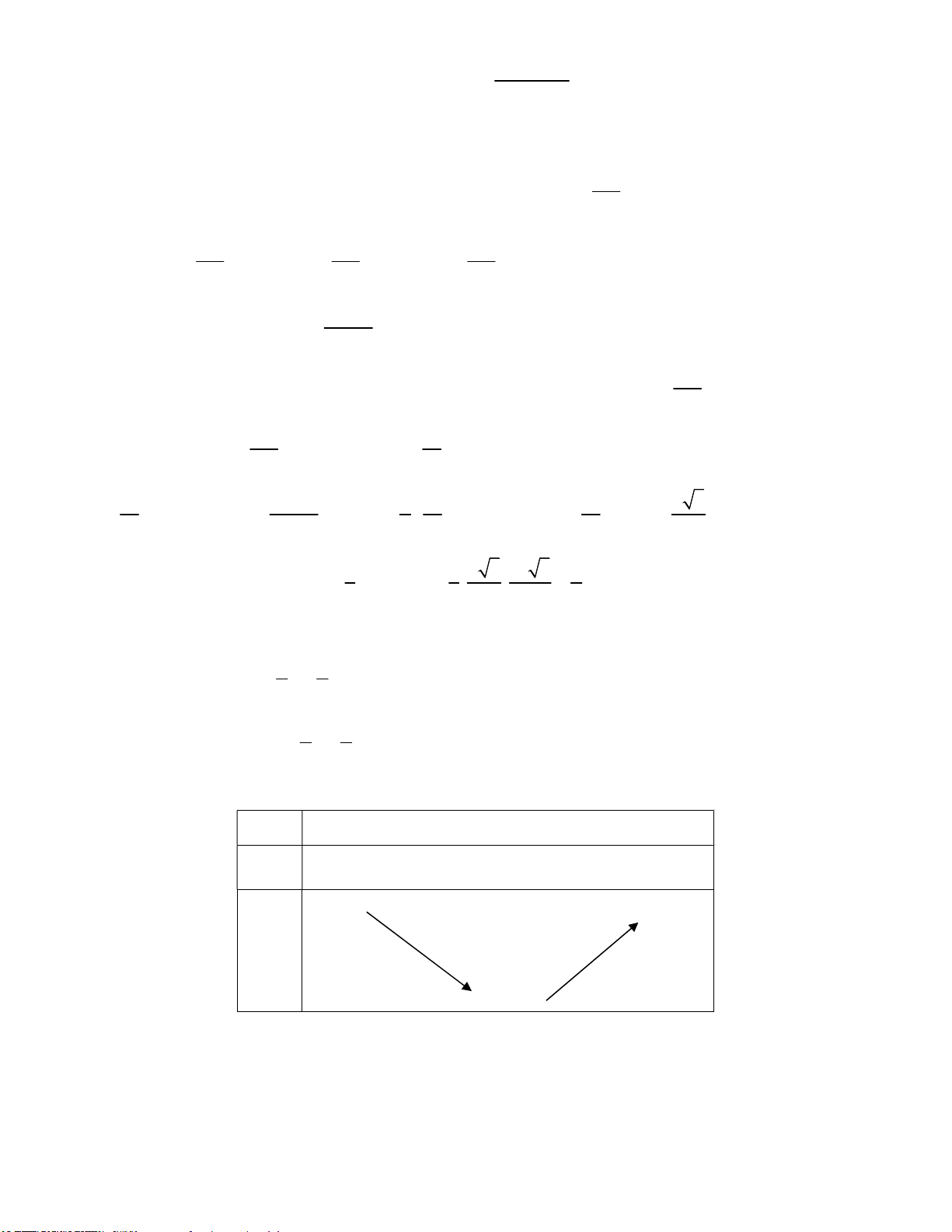
Câu 38: Cho hình chóp SABCD có đáy ABCD là hình bình hành. Hai điểm M, N lần lượt thuộc các
đoạn thẳng AB và AD (M và N không trùng với A) sao cho AB AD 2
4.Kí hiệu V ,V lần lượt là AM AN 1
thể tích của các khối chóp SABCD và SMBCDN. Tìm giá trị lớn nhất của tỉ số V1 V 2 1 3 17 A. B. C. D. 3 6 4 14
Câu 39: Cho hàm số 𝑦 = 𝑓(𝑥). Đồ thị hàm số 𝑦 = 𝑓′(𝑥) như hình bên dưới
Hàm số 𝑔(𝑥) = 𝑓(|3−𝑥|) đồng biến trên khoảng nào trong các khoảng sau ? A. (4;7). B. (−1;2). C. 2;3). D. (−∞;−1)
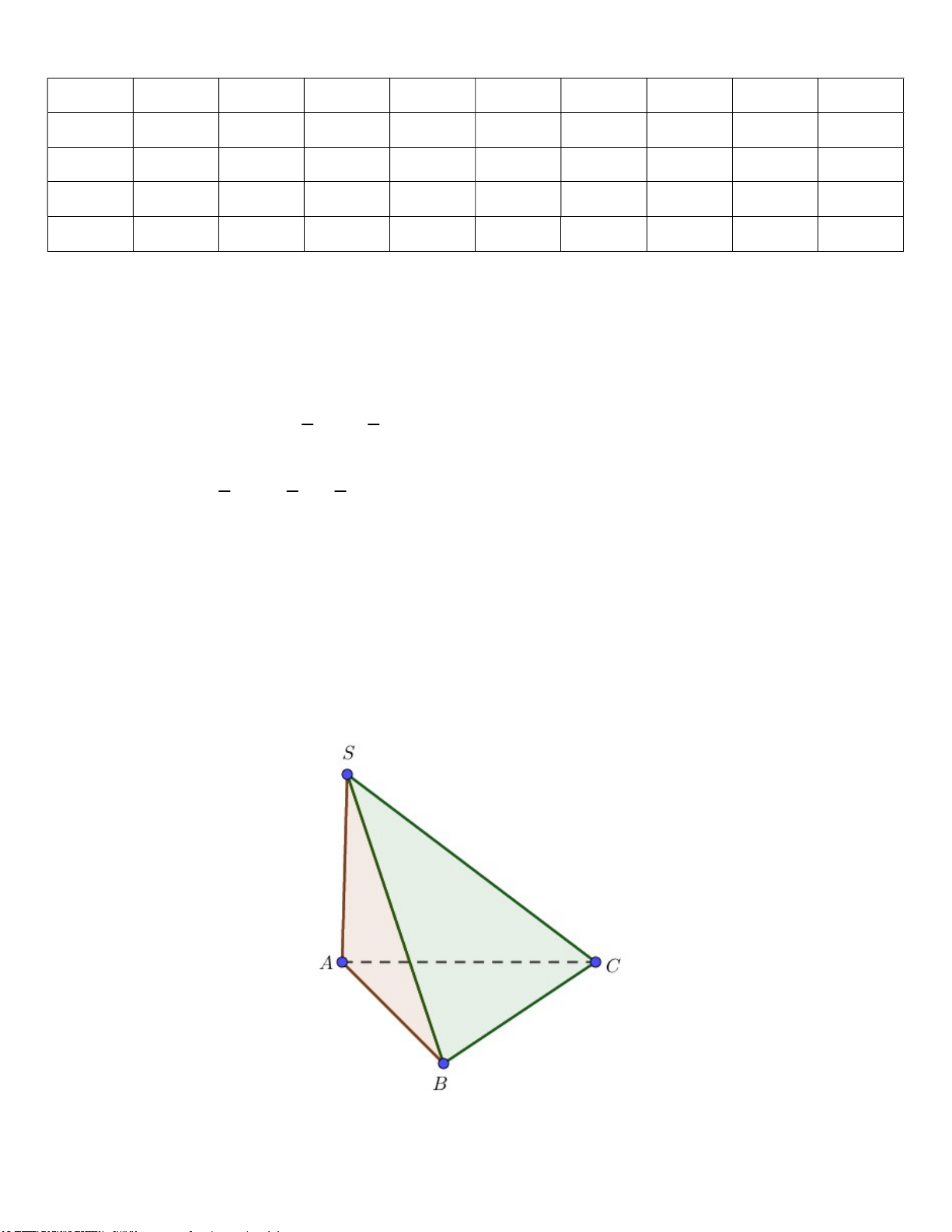
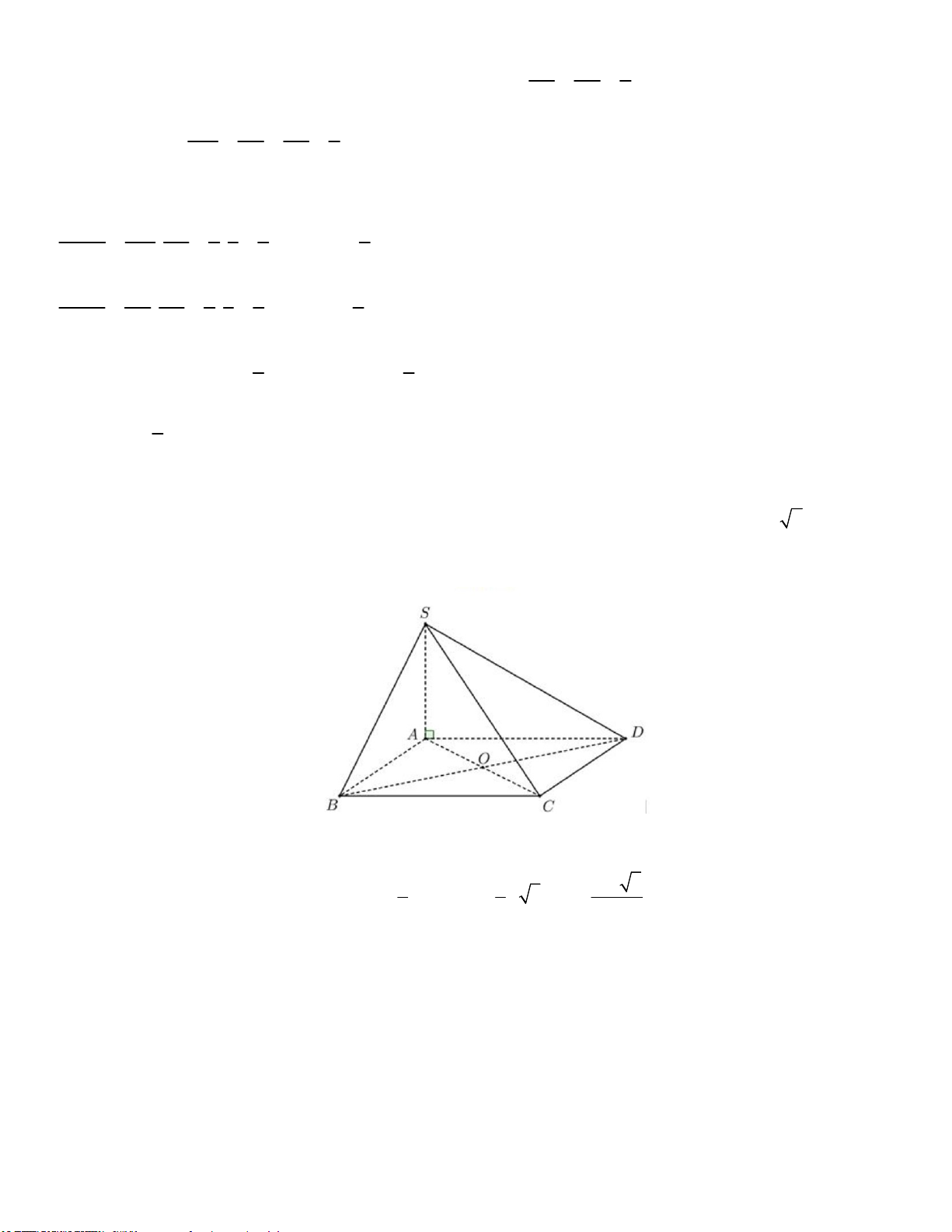
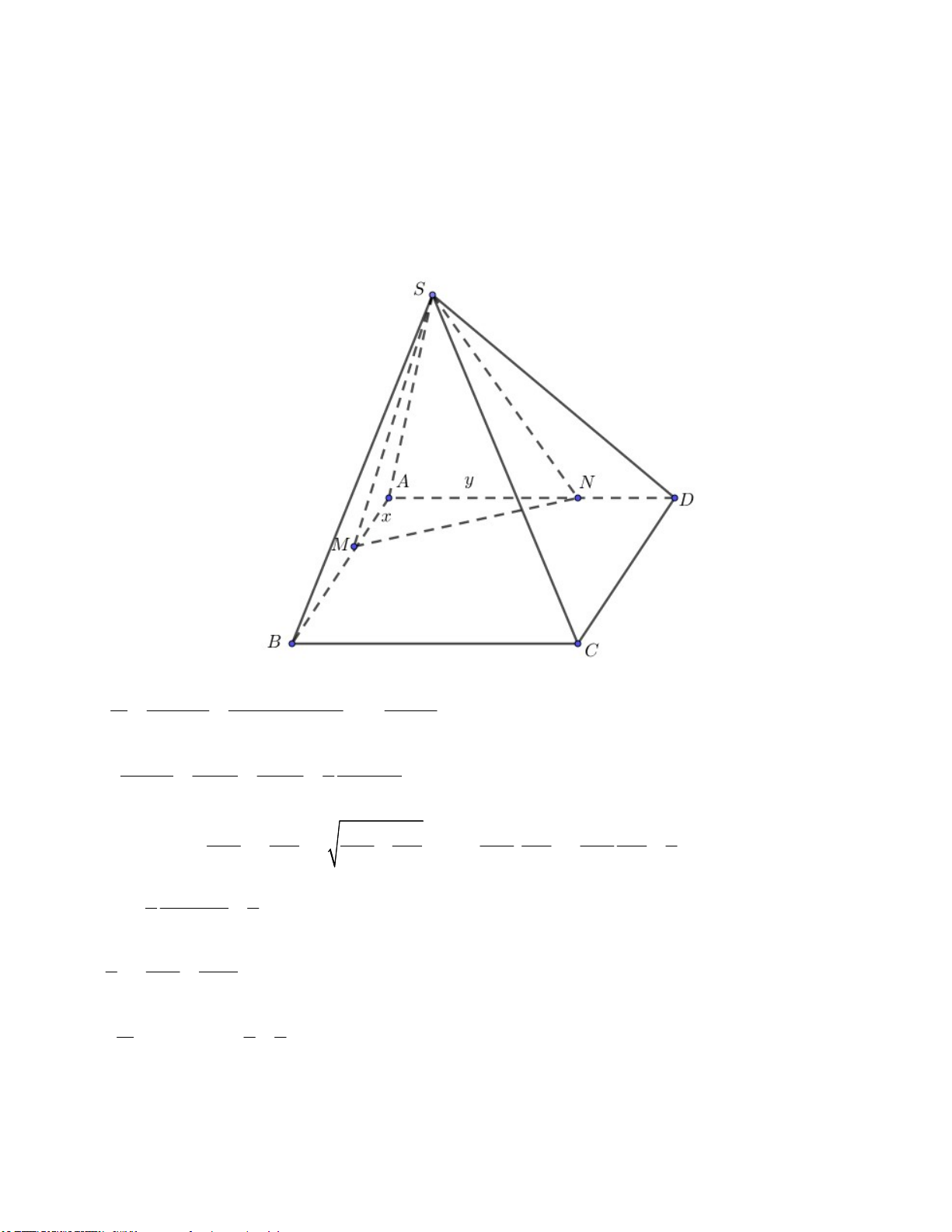
Câu 40: Cho tứ diện SABC có các cạnh ,
SA SB, SC đôi một vuông góc với nhau. Biết
SA 3a, SB 4a, SC 5a Tính theo a thể tích V của khối tứ diện SABC 3 5a A. 3 V 20a B. 3 V 10a C. V . D. 3 V 5a 2
Câu 41: Đồ thị của hàm số nào sau đây có tiệm cận? x 1 A. 2 y x B. y 2x C. y D. y 0 x
Trang 6/8 - Mã đề thi 121
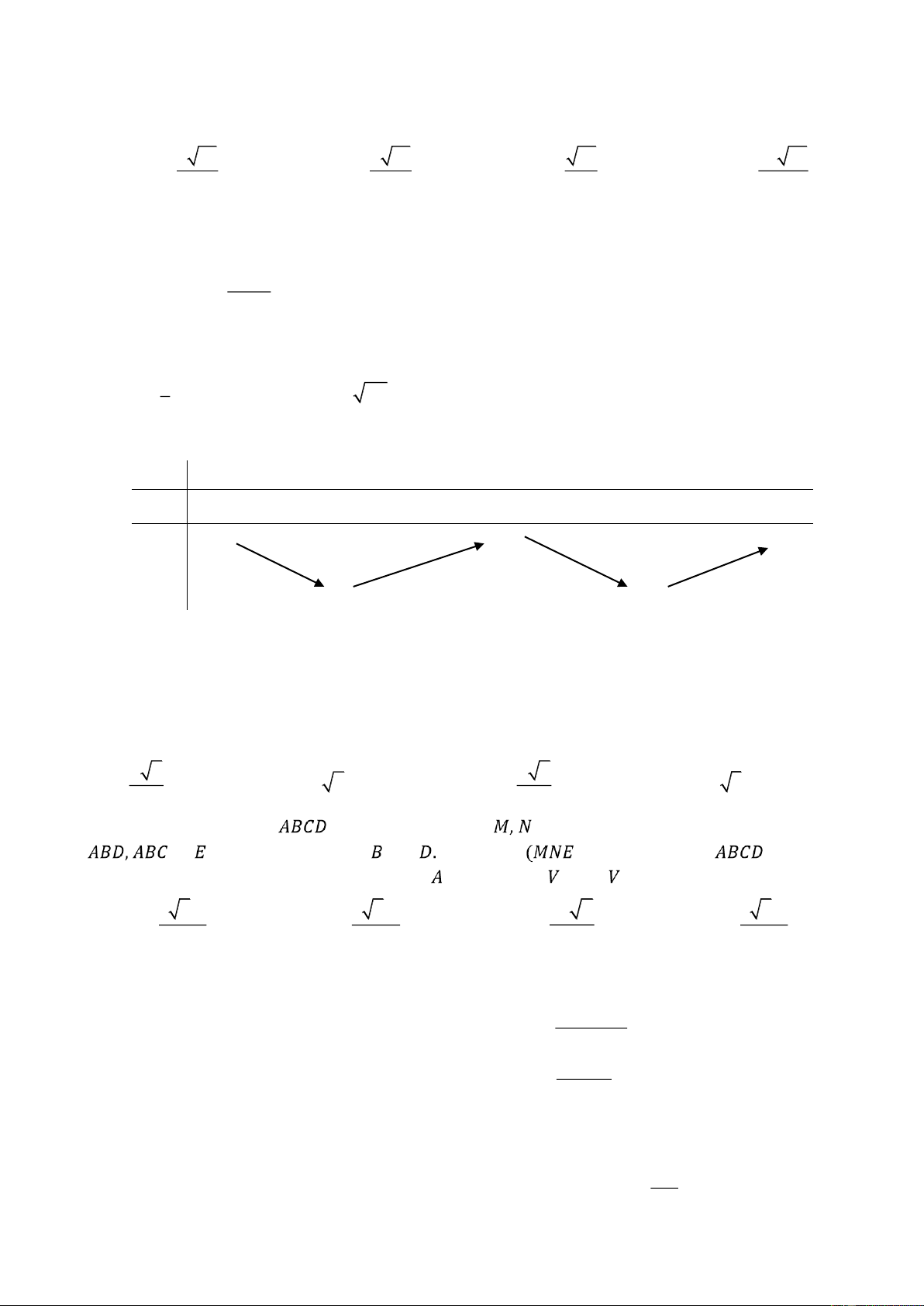
Câu 42: Cho hàm số 𝑦 = 𝑓(𝑥) có đạo hàm liên tục trên . Đồ thị hàm số 𝑦 = 𝑓′(𝑥) như hình bên dưới
Đặt 𝑔(𝑥) = 𝑓(𝑥) − 𝑥, khẳng định nào sau đây là đúng ?
A. 𝑔(−1) > 𝑔(1) > 𝑔(2).
B. 𝑔(−1) < 𝑔(1) < 𝑔(2).
C. 𝑔(2) < 𝑔(−1) < 𝑔(1).
D. 𝑔(1) < 𝑔(−1) < 𝑔(2).
Câu 43: Viết phương trình tiếp tuyến với đồ thị C 3 2
: y x 3x tại điểm M(1;-2) A. y 3 x 1 B. y 3 x 1
C. y 3x 5 D. y 2.
Câu 44: Cho phương trình: 3 x x 3 x m 3 3 2 sin 2 sin 3 2 cos
2 cos x m 2 2 cos x cos x m .
Có bao nhiêu giá trị nguyên của tham số m để phương trình trên có đúng 1 nghiệm 2 x 0; ? 3 A. 4. B. 3 C. 2 D. 1
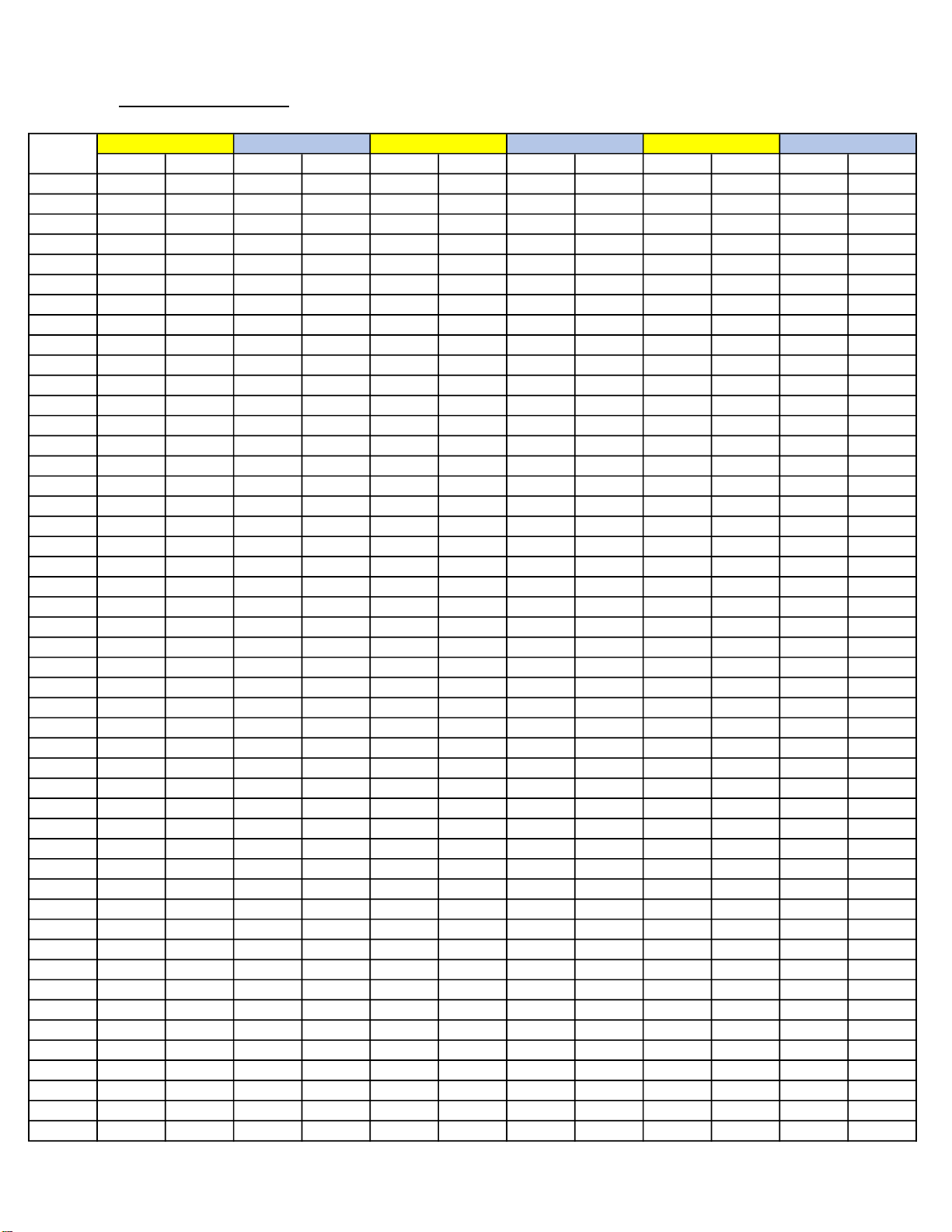
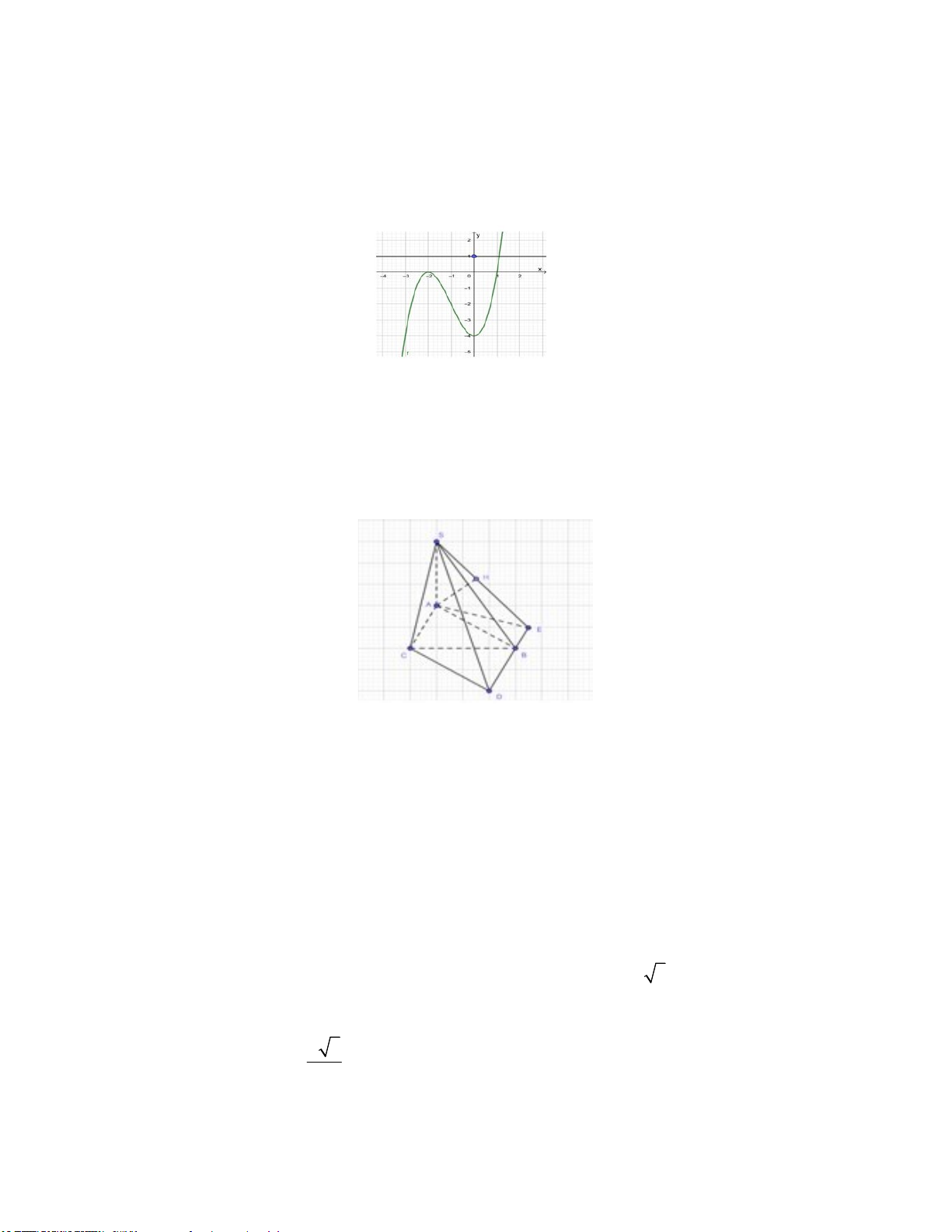
Câu 45: Cho một tấm nhôm hình vuông cạnh 6cm. Người ta
muốn cắt một hình thang như hình vẽ. Trong đó
AE 2(cm), AH x(cm), CF 3(cm), CG y(cm) . Tìm tổng
x y để diện tích hình thang EFGH đạt giá trị nhỏ nhất. 7 2 A. x y 7 B. x y 5 C. x y D. x y 4 2 2
Câu 46: Cho hình chóp đều S.ABCD có cạnh đáy bằng a 2 , cạnh bên bằng 2a. Gọi là góc tạo bởi
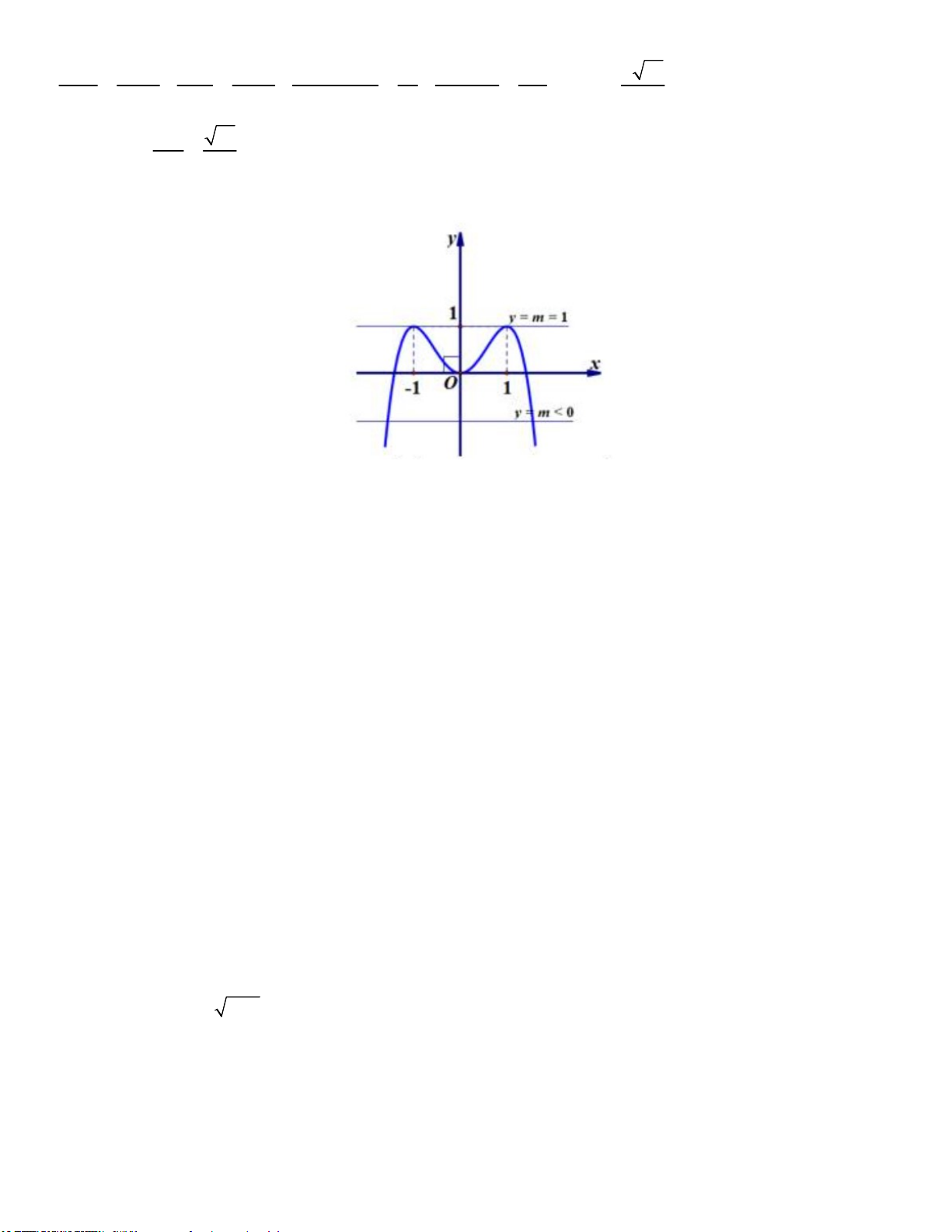
hai mặt phẳng (SAC) và (SCD). Tính cos 21 21 21 21 A. B. C. D. 2 14 3 y 7 Câu 47: Cho hàm số 4 2
y x 2x có đồ thị như hình 1
bên. Tìm tất cả các giá trị thực của tham số m để phương trình 4 2
x 2x m có hai nghiệm phân biệt. -1 O 1 x
A. m 1 hoặc m 0.
B. 0 m 1. C. m 1. D. m 0.
Câu 48: Có bao nhiêu giá trị nguyên của m để hàm số 3 2
y (m 2)x 3x mx 6 có 2 cực trị:
Trang 7/8 - Mã đề thi 121 A. 1 B. 4 C. Vô số D. 2 1 x 1
Câu 49: Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y có hai 2
x 1 m x 2m tiệm cận đứng? A. 2. B. 3. C. 1. D. 0.
Câu 50: Cho khối đa diện đều giới hạn bởi hình đa diện (H), khẳng định nào sau đây là sai?
A. Các mặt của (H) là những đa giác đều có cùng số cạnh.
B. Mỗi cạnh của một đa giác của (H) là cạnh chung của nhiều hơn hai đa giác.
C. Khối da diện đều (H) là một khối đa diện lồi.
D. Mỗi đỉnh của (H) là đỉnh chung của cùng một số cạnh.
----------------------------------------------- ----------- HẾT ----------
(Thí sinh không được sử dụng tài liệu)
Trang 8/8 - Mã đề thi 121 TRƯỜNG THPT QUANG HÀ Phụ lục 3
ĐÁP ÁN TRẮC NGHIỆM KHẢO SÁT TỐT NGHIỆP THPT 2021, LẦN 1, MÔN TOÁN Mã đề 121 Mã đề 220 Mã đề 321 Mã đề 420 Mã đề 521 Mã đề 620 Stt Câu ĐA Câu ĐA Câu ĐA Câu ĐA Câu ĐA Câu ĐA 1 1 A 1 C 1 A 1 A 1 A 1 C 2 2 A 2 C 2 C 2 C 2 A 2 B 3 3 A 3 C 3 B 3 B 3 C 3 A 4 4 B 4 D 4 C 4 A 4 B 4 D 5 5 C 5 C 5 B 5 B 5 C 5 B 6 6 D 6 B 6 C 6 A 6 B 6 A 7 7 A 7 D 7 A 7 A 7 A 7 D 8 8 B 8 A 8 B 8 B 8 B 8 A 9 9 C 9 A 9 D 9 A 9 C 9 B 10 10 D 10 A 10 D 10 D 10 B 10 C 11 11 C 11 D 11 D 11 A 11 D 11 C 12 12 C 12 A 12 C 12 B 12 D 12 B 13 13 D 13 C 13 C 13 B 13 D 13 B 14 14 D 14 B 14 B 14 C 14 C 14 B 15 15 C 15 C 15 C 15 D 15 B 15 C 16 16 A 16 A 16 B 16 C 16 B 16 C 17 17 C 17 B 17 A 17 D 17 D 17 C 18 18 B 18 B 18 D 18 A 18 D 18 D 19 19 B 19 D 19 B 19 B 19 B 19 A 20 20 A 20 C 20 B 20 C 20 A 20 C 21 21 D 21 B 21 D 21 C 21 D 21 B 22 22 B 22 C 22 D 22 C 22 C 22 A 23 23 C 23 C 23 B 23 D 23 D 23 B 24 24 B 24 B 24 D 24 B 24 D 24 D 25 25 C 25 D 25 B 25 A 25 A 25 C 26 26 C 26 A 26 C 26 A 26 C 26 B 27 27 C 27 D 27 D 27 A 27 C 27 D 28 28 D 28 A 28 D 28 A 28 C 28 B 29 29 D 29 B 29 A 29 C 29 B 29 B 30 30 D 30 A 30 D 30 D 30 A 30 A 31 31 A 31 B 31 A 31 C 31 C 31 C 32 32 D 32 A 32 B 32 A 32 C 32 D 33 33 C 33 D 33 C 33 B 33 B 33 D 34 34 B 34 D 34 A 34 B 34 B 34 D 35 35 A 35 D 35 A 35 C 35 A 35 A 36 36 B 36 B 36 A 36 D 36 A 36 B 37 37 D 37 A 37 C 37 D 37 C 37 A 38 38 C 38 A 38 B 38 D 38 D 38 B 39 39 B 39 B 39 A 39 B 39 B 39 D 40 40 B 40 B 40 A 40 C 40 C 40 A 41 41 C 41 A 41 D 41 B 41 C 41 A 42 42 A 42 C 42 C 42 D 42 A 42 C 43 43 A 43 B 43 A 43 A 43 A 43 C 44 44 A 44 A 44 C 44 B 44 D 44 A 45 45 C 45 C 45 D 45 C 45 D 45 D 46 46 D 46 D 46 B 46 D 46 A 46 B 47 47 A 47 B 47 A 47 C 47 C 47 D 48 48 D 48 D 48 B 48 D 48 B 48 C 49 49 B 49 C 49 C 49 A 49 A 49 D 50 50 B 50 D 50 B 50 D 50 D 50 A ĐÁP ÁN 1-A 2-A 3-A 4-B 5-C 6-D 7-A 8-B 9-C 10-D 11-C 12-B 13-D 14-D 15-C 16-A 17-C 18-B 19-C 20-A 21-D 22-B 23-C 24-B 25-C 26-C 27-C 28-D 29-B 30-D 31-A 32-D 33-C 34-A 35-A 36-B 37-D 38-C 39-B 40-B 41-C 42-A 43-A 44-A 45-C 46-D 47-A 48-D 49-A 50-B
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1: Chọn A. 1 1
Từ bảng biến thiên, ta thấy M , m . 2 2 2 2 Vậy 2 2 1 1 1 P M m . 2 2 2 Câu 2: Chọn A. Ta có: 2 2 u u .q 2.2 8. 3 1 Câu 3: Chọn A.
f ' x 0 với x 2;0 nên hàm số đồng biến trên khoảng 2;0. Câu 4: Chọn B. 11 2 a 3
ABC là tam giác đều cạnh a nên S . ABC 4
Hai mặt bên SAB,SAC cùng vuông góc với mặt đáy nên SA ABC.
Trong tam giác vuông SAC ta có: 2 2 2 2
SA SC AC 3a a a 2. 2 3 1 1 a 3 a 6
Thể tích của khối chóp S.ABC là V S .SA . .a 2 3 ABC 3 4 12 Câu 5: Chọn C.
Tập xác định D \ 1 . 3 Ta có y ' 0 với mọi x .
D Suy ra, hàm số nghịch biến trên ; 1 và 1;. x 2 1 Câu 6: Chọn D. Ta có g x xf 2 x 5 3 ' 2 ' 2x 4x 2 . x 2x 0 g ' x 0 f ' . 2 x 4 2 x 2x 1 0 1 t 0 Đặt 2
t x t 0, khi đó 2 t 1 1 có nghiệm x 0, x 1 , x 2. t 2 f t 2 2 '
t 2t 1 0 t 1 0 x 1 1 x 1. t x f 't 0 1 2 t 2t 1 . t 1 x 1 Bảng biến thiên 12 x
2 1 0 1 2
g ' x + 0 + 0 0 + 0 0 g x x
Suy ra, hàm số g x f x 6 2 4 2
x x đạt cực tiểu tại một điểm. 3 Câu 7: Chọn A.
Đồ thị hàm số có đường tiệm cận ngang là trục Ox m 2n 3 0 .
Đồ thị hàm số có đường tiệm cận đứng là trục Oy m n 0. Suy ra ,
m n là nghiệm của hệ phương trình: m 2n 3 0 m 1 S 0. m n 0 n 1 Câu 8: Chọn B.
Có SD, ABCD SD, AD SD . A SA
Xét SAD vuông tại A có: 0 SDA SDA SD ABCD 0 tan 3 60 , 60 . AD Câu 9: Chọn C.
Hàm số liên tục trên đoạn [1;3]. x 41; 3 + Ta có: f ' x 2 3x 16x 16; f ' x 2 0 3x 16x 16 0 4 x 1; 3 3 13 13 + f f 4 13 1 0; 3 6; f . Vậy max f x . 3 27 1; 3 27 Câu 10: Chọn D.
Hình mười hai mặt đều có 20 đỉnh. Câu 11: Chọn C.
Giả sử hình chóp có đáy là đa giác n cạnh n 3 nên có n cạnh bên.
Tổng số cạnh của hình chóp là 2n 20 n 10. Khi đó hình chóp có 10 mặt bên và 1 mặt đáy. Vậy hình chóp có 11 mặt. Câu 12: Chọn B.
Đồ thị hình vẽ là đồ thị hàm số bậc ba có hệ số a 0, đồ thị hàm số đi qua điểm 0;2 nên chỉ có hàm số 3
y x 3x 2 thỏa mãn điều kiện trên. Câu 13: Chọn D.
Số hạng thứ k 1 trong khai triển là: k k k T C x k k k C x k 7 2 2 143 2 . . 1 7 7 x Vì số hạng có chứa 5
x nên: 14 3k 5 k 3.
Vậy hệ số cần tìm là 3 3 h C .2 280. 7 Câu 14: Chọn D. 2 x mx m Đặt y h x x 1 2 2 x mx m x 2 x 2x Xét hàm số f x m, ta có: f ' x 0,x 1;2 . 2 x 1 x 1 x 1
Suy ra hàm số f x đồng biến trên đoạn 1;2. 1 4 min f x f 1 ,
m max f x f 2 . m 1;2 2 1;2 3 1 1 4 4 2
Nếu m 0 m thì max h x m , suy ra: m 2 m (thỏa mãn). 2 2 1;2 3 3 3 3 m l 4 4 1 1
Nếu m 0 m thì max h x m , suy ra: 2 m 1 . 3 3 1;2 2 2 5 m 2 14 1 4 4 1 1 1 4 1 11
Nếu m 0 m m thì: m m 2, suy ra: 2 3 3 2 2 2 3 2 6 4 2 m 2 m 4 3 3 m 2 (không thỏa mãn). 3 4 10 m 2 m 3 3 5 2
Vậy có hai giá trị m thỏa mãn: m và m . 2 3 Câu 15: Chọn C. 1 1 1
Ta có: lim y ; lim y đường thẳng y là đường tiệm cận ngang của đồ thị hàm số. x 4 x 4 4 Câu 16: Chọn A. Tập xác định: D .
*) Nếu m 0 ta có y 5 .
x Đồ thị hàm số luôn đồng biến trên . *) Nếu m 0. Ta có: 2
y ' mx 4mx 3m 5.
Hàm số đồng biến trên y ' 0,x . 2
mx 4mx 3m 5 0,x . 2 ' 0
4m m3m 5 0 . a 0 m 0 2 m 5m 0 m 0 0 m 5 0 m 5 m 0
Kết hợp với điều kiện ta có: 0 m 5.
Vậy 0 m 5, m m0;1;2;3;4; 5 . Câu 17: Chọn C.
Dựa vào đồ thị ta có max y 10 khi x 4 và min y 10 khi x 4 . 4;4 4 ;4
Tuy nhiên hàm số không có GTLN, GTNN trên 4;4. Câu 18: Chọn B.
Phát biểu đúng là “nếu f ' x 0,x K và f ' x 0 chỉ tại một số hữu hạn điểm thì hàm số y f x đồng biến trên K ". 15 Câu 19: Chọn C.
Số phần tử của không gian mẫu là n 10!
Gọi A là biến cố “xếp 5 nam và 5 nữ ngồi đối diện nhau”
Đánh số cặp ghế đối diện nhau là C ,C ,C ,C ,C 1 2 3 4 5
Xếp 5 bạn nam vào 5 cặp ghế có 5! cách.
Xếp 5 bạn nữ vào 5 cặp ghế có 5! cách.
Ở mỗi cặp ghế, ta có 2 cách xếp một cặp nam, nữ ngồi đối diện.
Số phần tử của A là n A 5 5!.5!.2 460800. n A P A 460800 8 n . 10! 63 Câu 20: Chọn A.
Do đồ thị hàm số có tiệm cận ngang y 2 nên loại đáp án C và D. 5 Xét đáp án A có y '
0,x D, tiệm cận ngang là đường thẳng y 2, tiệm cận đứng là đường x 2 1 thẳng x 1 nên chọn. 2 Xét đáp án B có y ' 0,x D nên loại. x 2 1 Câu 21: Chọn D.
Gọi O là tâm của hình bình hành ABCD.
Trong SAC. Gọi I SO AE.
Từ I, kẻ đường thẳng song song với đường thẳng BD cắt hai cạnh SB, SD lần lượt tại M , N.
Gọi K là trung điểm EC SE EK KC. 16 SI SE 1
Do OK là đường trung bình của tam giác CAE OK / /IE . SO SK 2 SM SN SI 1 Do MN / /BD SB SD SO 2 Ta có: V V V . S.AMBN S.AMB S. ABN V SM SE 1 1 1 1 S.AME . . V V . S.AME S. V SB SC 2 3 6 6 ABC S.ABC V SN SE 1 1 1 1 S.ANE . . V V . S.ANE S . V SD SC 2 3 6 6 ACD S.ADC 1 1 V V V V V V . S .AMBN S.AMB S .ABN S.ABC S.ACD S. 6 6 ABCD 1 V V. S.AMBN 6 Câu 22: Chọn B.
Dựa vào bảng biến thiên ta thấy phương trình f x m có ba nghiệm thực phân biệt khi m 2; 1 . Câu 23: Chọn C.
Diện tích của hình chữ nhật ABCD là 2 S A . B AD . a 2a 2a . ABCD 3 1 1 2a 3
Thể tích của khối chóp S.ABCD là 2 V S . A S a 3.2a (đvtt). S .ABCD 3 ABCD 3 3 Câu 24: Chọn B.
Số tập hợp con khác rỗng của tập hợp A mà có k phần tử là k C k ,0 k 20 . 20
Khi đó tổng số tập hợp con khác rỗng mà có số phần tử chẵn là 2 4 20 S C C ... C . 20 20 20 Xét 1 x20 0 1 2 2 20 20
C C x C x ... C x . 20 20 20 20 Cho x 1, ta được 20 0 1 2 20
2 C C C ... C 1 20 20 20 20 17 Cho x 1 , ta được 0 1 2 20
0 C C C ... C 2 . 20 20 20 20
Công vế theo vế (1) và (2), ta được 20 2 2 0 2 4 20
C C C ... C 2S 20 19 1 2 S 2 1. 20 20 20 20 Câu 25: Chọn C.
Từ đồ thị hàm số dễ thấy đường thẳng y 1 cắt đồ thị hàm số y f x tại đúng 1 điểm nên phương trình
f x 1 có đúng 1 nghiệm. Vậy mệnh đề C đúng. Câu 26: Chọn C.
Trong mp ABC kẻ hình bình hành ABDC, AE BD; trong mp SAE kẻ AH SE. Theo giả thiết: SA ABC
SA BD BD SAE AE BD
BD AH mà AH SE nên AH SBD.
Ta lại có BD / / AC AC / / SBD d AC, SB d AC,SBD d , A ABD AH .
Mặt khác: Vì SA ABC nên SA ABC 0 0 , SBA 60 , SA A . B tan 60 a 3.
Vì ABDC là hình bình hành nên 0 ABD 0 180
BAC 120 do đó điểm E nằm ngoài đoạn thẳng BD và góc 0 0 3 60 sin 60 a ABE AE AB . 2 Tam giác SAE vuông có: 18 2 1 1 1 1 1 5 3a a 15 2 AH AH . 2 2 2 AH SA AE a 32 2 2 a 3a 5 5 3 2 a 15
Vậy khoảng cách giữa 2 đường thẳng AC và SB là . 5 Câu 27: Chọn C.
Dựa vào đồ thị của hàm số ta thấy hàm số có 4 điểm cực trị
Vậy đáp án đúng là đáp án C. Câu 28: Chọn D. Hàm số 3 2 y x 3x 2 TXĐ: D Ta có: 2
y ' 3x 6x Tiếp tuyến của C tại M x ; y có phương trình là: M M y 2 x x x x x x M M M 3 2 3 6 3 2 M M
Tiếp tuyến của C tại M cắt C tại điểm N x ; y (khác M ) nên x ; x là nghiệm của phương trình: N N M N 3 2 x x 2 x x x x x x M M M 3 2 3 2 3 6 3 2 M M 3 3 x x x x x x x x M 2 2 M 2 3 3 6 M M M 0 x x x x
2 x 2x 3 0 M M M x 2x 3 M M khác N x 2
x 3 3x 3 x 1 x 2 x 3 M M M M N M 2
Khi đó: P x x x x x x x với x M N M M M M M 2 2 2 2 2 5 5 2 3 9 12 9 3 2 5 5 M
Dấu “=” xảy ra x 2 2 3
2 0 3x 2 0 3x 2 x (thỏa mãn) M M M M 3 2 2 2 26 2 26 10 10 Với x y OM M M 3 27 3 27 27 10 10 Vậy OM . 27 Câu 29: Chọn B. x 0 Ta có 2 y ' 3 x 6x 0 x 2 19 x 0 2 y ' 0 + 0
Vậy hàm số đồng biến trên khoảng 1;2. Câu 30: Chọn D. 1 1 x 2 2 2x 1 x Ta có lim lim lim x 2. x x 1 x 1 x 1 x 1 1 x x Câu 31: Chọn A. 1
Thể tích của khối chóp đã cho là V B . h 3 Câu 32: Chọn D.
M 0;2 là điểm cực đại của đồ thị hàm số. Câu 33: Chọn C.
Gọi G là trọng tâm tam giác BCD, M là trung điểm của CD ta có: 3 2 2 3 BM 2 3; BG BM 2 3 3 20 2 3 2 6 2 2 2 2
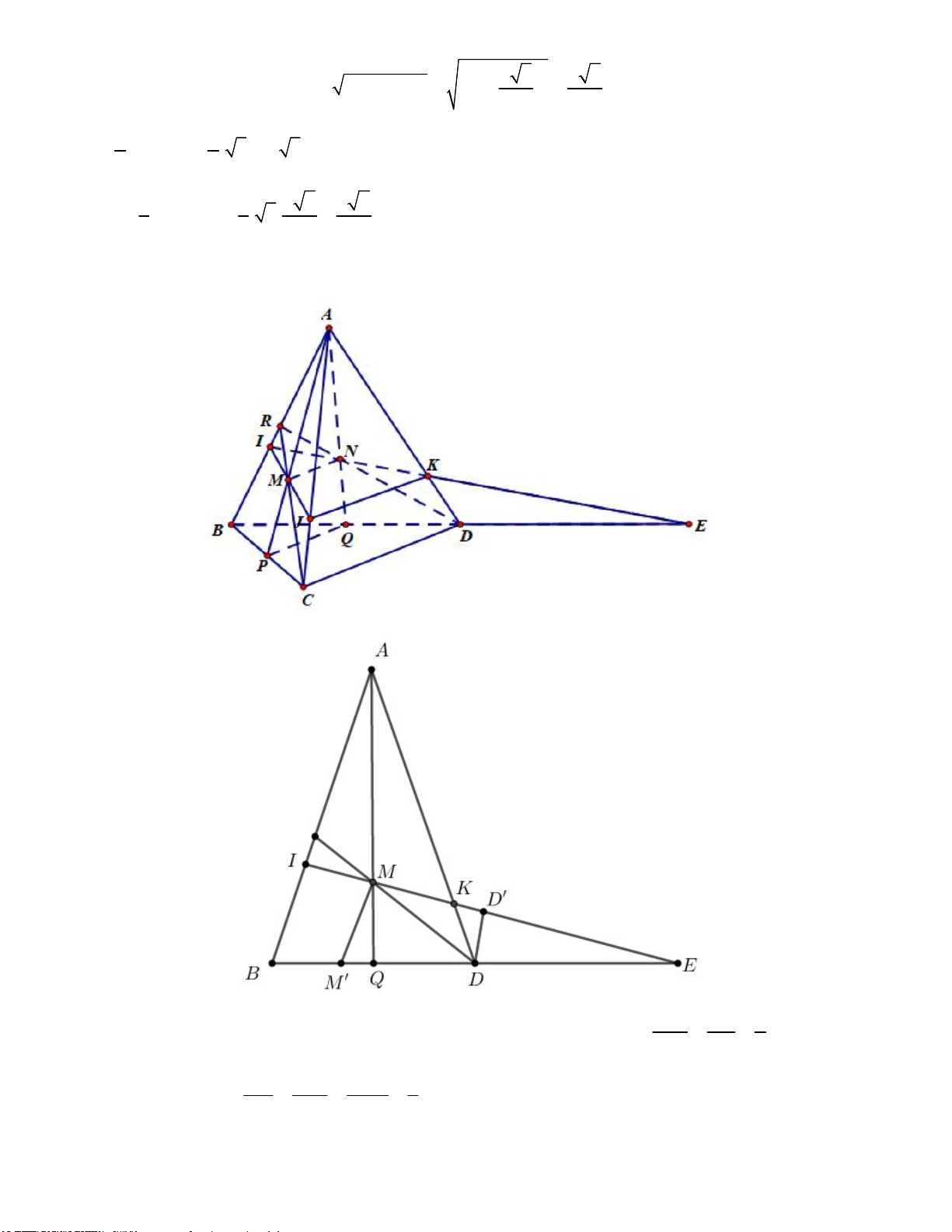
AG (BCD) AG BG SG AB BG 2 ( ) . 3 3 1 1 S BM .CD . 3.2 3 BCD 2 2 1 1 2 6 2 2 V A . G S . 3. ABCD 3 BCD 3 3 3 Câu 34: Chọn A. DD ' ED 2
Xét mặt phẳng chứa tam giác ABD . Gọi D ' trên IE sao cho DD '/ / AQ ta có: MQ EQ 3 KD DD ' DD ' 1 Mà KDD ' KAM KA AM 2MQ 3 21
Gọi M ' trên BD sao cho MM '/ / A . B Ta có: 1 1 1 1 3 1 5 M 'Q BQ . BE
BE EM ' 3EQ QM ' BE BE 3 3 4 12 4 12 6 MM ' EM ' 5 5 MM ' IB IB EB 6 6 MM ' QM 1 5 IB 1 IB 2 AI 3
Xét mặt tam giác ABQ . Ta có AB QA 3 6 AB 3 AB 5 AB 5 AJ AK Vì MN PQ CD MN ACD 3 / / / / / / MN / /JK / /CD AC AD 4 3 a 2
Vì ABCD là tứ diện đều có cạnh bằng a V ABCD 12 3 3 V AI AJ AK 3 3 3 27 27 27 a 2 9 2a Ta lại có: AIJK . . . . V V V AB AC AD 5 4 4 80 AIJK 80 ABCD 80 12 320 ABCD Câu 35: Chọn A.
Trong các công thức về số các chỉnh hợp và số các tổ hợp công thức đúng là k k k 1 C
C C (với 1 k n). n 1 n n n n k ! k ! Công thức k k 1 A C C C là các công thức sai. n k ! n k , ! n n k , n 1 ! n Câu 36: Chọn B.
Gọi R , R , R lần lượt là bán kính đường tròn ngoại tiếp các tam giác HAB, HBC, HAC 1 2 3
Áp dụng định lý sin vào các HAB, HBC, HAC ta có: AB AB 2R sin AHB R 2. 1 1 2sin AHB BC 2 3 BC 2R sin BHC R . 2 2 2sin BHC 3 22 AC AC 2R sin CHA R 1. 3 1 2sin CHA
Gọi r , r , r lần lượt là bán kính mặt cầu ngoại tiếp các tứ diện S.HAB, S.HBC, S.HAC. 1 2 3 2 SH
Nhận xét: Trong hình chóp S.HAB với SH HAB ta có 2 2 r R . 1 1 2 2 2 2 SH SH SH Khi đó 2 2 2 2 2 2 r R ; r R ; r R . 1 1 2 2 3 3 2 2 2 2 3. Suy ra 2 2 2 2 2 2 SH r r r R R R . 1 2 3 1 2 3 4 124
Do tổng diện tích các mặt cầu ngoại tiếp các hình chóp S.HAB, S.HBC, S.HCA là 3 124 31 Ta có: 4 2 2 2 r r r 2 2 2 r r r . 1 2 3 1 2 3 3 3 2 31 3.SH 4 31 16 4 3 Khi đó: 2 2 2 2 2 2 2 R R R SH R R R SH . 1 2 3 1 2 3 3 4 3 3 3 3 2 1 1 4 3 2 3 4
Vậy thể tích khối chóp S.ABC là V .S .SH . . (đvtt). 3 ABC 3 3 4 3 Câu 37: Chọn D.
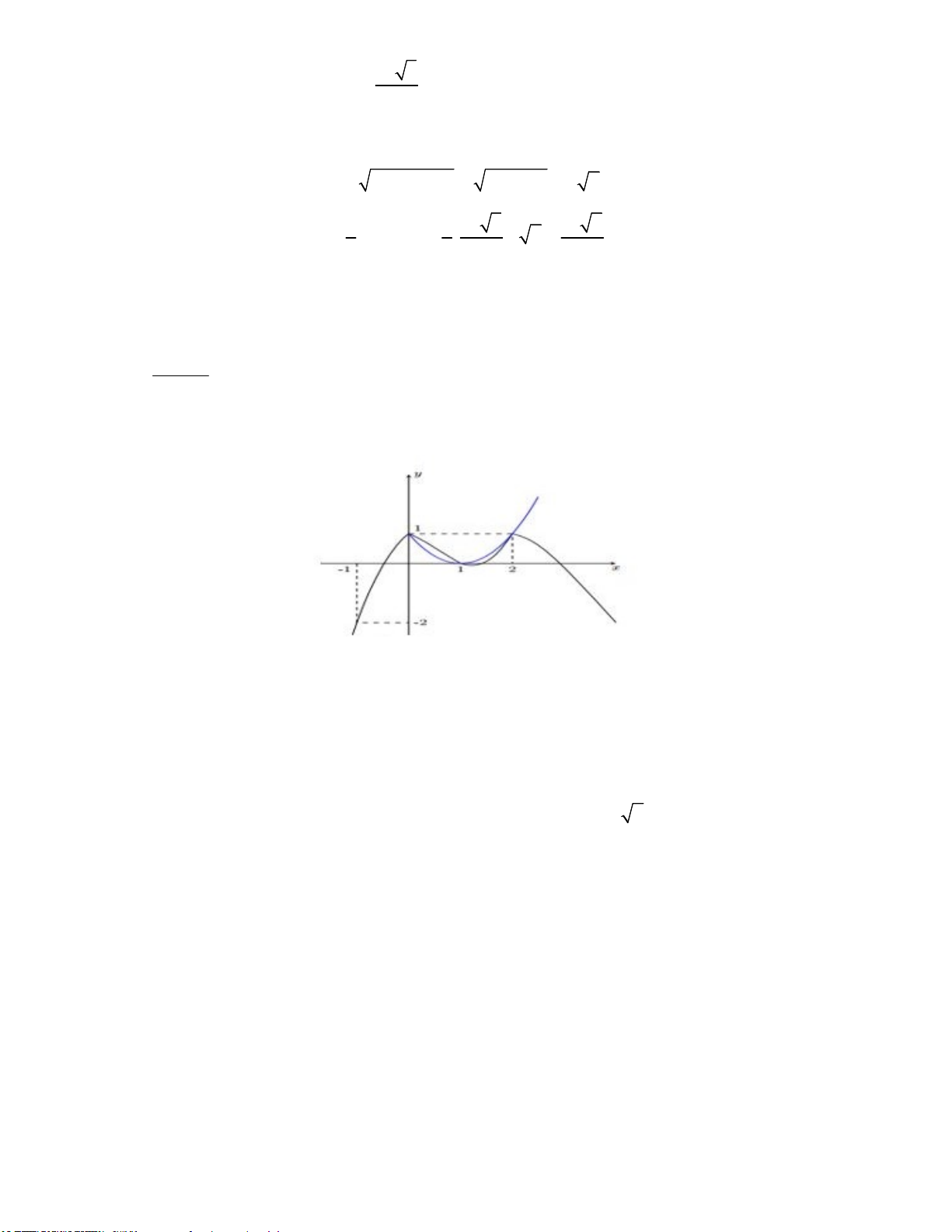
Ta có: g x f x 2 3 3 ' ' x x f ' x h x. 2 2
Ta vẽ đồ thị hàm số h x 2 3 3
x x và y f 'x trên cùng một hệ trục: 2 2
Đồ thị hàm số y h x có đỉnh I 1;2 và đi qua các điểm 3;3,1; 1 . x 3 1 1 g ' x 0 0 + 0
g x g 3 g 1 g 1
Từ bảng biến thiên suy ra
I g 0 g 1 . Đúng. 23
II min g x g 1. Đúng. 3; 1
III Hàm số g x nghịch biến trên 3; 1. Đúng.
IV max g x maxg 3;g 1. Đúng. 3 ; 1 3; 1
Vậy cả bốn mệnh đề đều đúng. Câu 38: Chọn C. V V V V V Ta có: 1 S.MBCDN S.ABCD S.AMN S. 1 AMN 1 k V V V V S.ABCD S.ABCD S.ABCD V S S 1 AM .AN Với S.AMN AMN k AMN V S 2S 2 A . B AD S.ABCD ABCD ABD AB AD AB AD AB AD AM AN 1 Mặt khác ta có: 4 2 2 .2 2 . . AM AN AM AN AM AN AB AD 2 1 AM .AM 1 Suy ra: k . 2 A . B AD 4 1 AB 2AD AM 2AM k 2
N D, M là trung điểm của A . B min 4 AM AN AD AN V 1 3 Suy ra: 1 1 k 1 . min V 4 4 Câu 39: Chọn B. 24 x 3
Ta có y g x f x 3 y ' . f ' x 3 . x 3 x 3 1 L x 2 x 4 y ' 0 x 3 1
(Hàm số không có đạo hàm tại x 3). x 1 x 7 x 3 4 BBT x 1 2 3 4 7 y '
0 + 0 | | + 0 0 + y
Vậy hàm số đồng biến trên khoảng 1;2. Câu 40: Chọn B. Vì S ,
A SB, SC đôi một vuông góc nên AS SBC và SBC vuông tại S. 1 1
Nên thể tích khối chóp SABC là 3 V .S . A S . B SC .3 . a 4 . a 5a 10a . 6 6 Câu 41: Chọn C. 1 Hàm số x y
có tập xác định D ; 0 0;. x Ta có: 25
lim y 1; lim y 1. Suy ra đồ thị hàm số có tiệm cận ngang là y 1. x x lim y ; lim y .
Suy ra đồ thị hàm số có tiệm cận đứng là x 0. x 0 x 0 1
Vậy đồ thị của hàm số x y có tiệm cận. x Câu 42: Chọn A.
Hàm số g x f x x có tập xác định D , có đạo hàm g ' x f ' x 1.
Ta có: g ' x 0 f ' x 1. 1
Nhận xét số nghiệm của phương trình
1 chính là số giao điểm của đồ thị hàm số y f ' x và đường thẳng y 1. Ta có đồ thị như sau: x 1 Khi đó g ' x 0 x 1 . x 2
Với x 1 là nghiệm kép, x 1; x 2 là nghiệm đơn. Ta có bảng biến thiên: x 1 1 2 g ' x + 0 0 0 + g x g 1 g 1 g 2 26 Suy ra g 1 g 1 g 2. Câu 43: Chọn A. Ta có 2 y ' 3x 6x
Hệ số góc của tiếp tuyến với đồ thị hàm số tại M là k y ' 1 3
Phương trình tiếp tuyến với đồ thị C 3 2
: y x 3x tại điểm M 1;2 là y y ' 1 x 1 2 3 x 1. Câu 44: Chọn A. 2 x x 3 x m 3 3 2 sin 2sin 3 2cos
2 cos x m 2 2cos x cos x m 3 2 x x x 3 x m 3 3 sin 2sin 1 cos 2 2cos
2cos x m 2 2cos x m 3 2 x x x 3 x m 3 3 sin 2sin sin 2 2cos
2cos x m 2 2cos x m Đặt 3 2 3
u 2cos m 2 u 2cos x m 2 Phương trình trở thành: 3 2 x x x 2 u 2 sin 2sin sin 2 2 u u 2 3 2 3 2
sin x 2sin x sin x 2 u u 2u 2 1
Xét hàm đặc trưng: f t 3 2 t t 2t 2 f t 2 '
3t 2t 2 0,t f t là hàm đồng biến Phương trình
1 f sin x f u u sin x Với u sin x ta có 3 3 2
2cos x m 2 sin x 2cos x m 2 sin x 3 2
m 2cos x cos x 1
Đặt X cos x phương trình trở thành 3 2 m 2X X 12 3 1 Với x 0; X ;1 . 2 2 1 2 Ứng với mỗi X ;1
thì có duy nhất một giá trị của x 0;
do đó phương trình ban đầu có đúng một 2 3 2 1 nghiệm x 0;
thì phương trình (2) có duy nhất một nghiệm thuộc X ;1 3 2 Xét hàm g X 3 2 2X X 1 27 X 0 g ' X 2 6X 2X ; g ' X 0 1 X 3 Bảng biến thiên X 1 1 0 1 2 3 g ' X + 0 0 + g X 80 0 27 3 3 1
Từ bảng biến thiên ta có phương trình (2) có duy nhất một nghiệm thuộc X ;1 khi và chỉ khi 2 m 3 80 m 0 27
Mà m nguyên nên m 3;2;1;
0 do vậy có 4 giá trị nguyên của m thỏa mãn bài toán. Câu 45: Chọn C. CG CF y 3
Hai tam giác AHE và CFG đồng dạng suy ra: xy 6. AE AH 2 x Ta có: S S S S S S EFGH ABCD AHE BEF CFG DGH 1 1 1 1
36 .2x .4.3 .3.y .6 x.6 y 2 2 2 2 3 1
36 x 6 .y .36 6x y xy 2 2 3 1 3
36 x 6 .y .36 6 x y 6 9 2x y 2 2 2 6 9 Với y , ta có: S 9 2x . x EFGH x 9 9 3 2 Xét hàm số f x 9
9 2x , trên khoảng 0;6 ta có: f ' x 2 , f ' x 0 2 0 x . x 2 x 2 x 2 Ta có bảng biến thiên: 28 x 3 2 0 6 2 f ' x 0 + f x 9 6 2 3 2
Từ bảng biến thiên suy ra: min min f x khi x y 2 2. S 9 6 2 EFGH 0;6 2 7 2 Vậy x y . 2 Câu 46: Chọn D.
Gọi H là hình chiếu của S trên mặt phẳng ABCD. Hình chóp S.ABCD đều nên H là tâm hình vuông
ABCD,SAC ABCD AC và SH ABCD SAC ABCD.
Ta có: HD AC HD SAC . 1 CD HM
Gọi M là trung điểm của CD, suy ra:
CD SHM mà CD SCD. CD SH SCD SHM
nên từ H kẻ đường thẳng vuông góc với SM tại K, suy ra HK SCD2
SCD SHM SM Từ
1 và 2 suy ra: SAC ,SCD HD, HK KH . D 1 1
Tam giác KHD vuông tại K có HD BD a 2. 2 . a 2 2 29 1 1 1 1 1 2 1 7 a 21 HK . 2 2 2 2 2 2 2 2 2 2 HK HM SH HM SD HD a 4a a 3a 7 HK 21 Vậy cos . HD 7 Câu 47: Chọn A. Số nghiệm của 4 2
x 2x m là số điểm chung giữa đường thẳng y m và đồ thị hàm số đã vẽ. m 1
Phương trình đã cho có hai nghiệm . m 0 Câu 48: Chọn D. Tập xác định D . Nếu m 2 thì 2
y 3x 2x 6 là hàm số bậc hai nên không thể có hai điểm cực trị.
Xét m 2 lúc đó y m 3 2
2 x 3x mx 6 là hàm số bậc ba, hàm số có hai điểm cực trị y ' 0 có hai nghiệm phân biệt. Ta có y m 2 ' 3 2 x 6x ,
m phương trình y ' 0 có hai nghiệm phân biệt ' 0 mm 2 9 3
2 0 m 2m 3 0 3 m 1.
Vậy tập các giá trị m để hàm số có hai điểm cực trị là m 3; 1 \
2 . Do đó có tất cả là 2 số nguyên để hàm số y m 3 2
2 x 3x mx 6 có hai điểm cực trị là m 1 và m 0. Câu 49: Chọn A. ĐK: x 1 và 2
x 1 m x 2m 0
Xét phương trình 1 x 1 0 vô nghiệm. Xét phương trình 2
x 1 m x 2m 0*. Để đồ thị hàm số có hai TCĐ thì phương trình có 2 nghiệm phân
biệt thỏa mãn ĐK x 1. 30 m
0 1 m2 5 2 6 2
8m 0 m 10m 1 0 . m 5 2 6
Khi đó gọi hai nghiệm của phương trình là x x ta có: 1 2 af 1 0 m 2 0 m 2 x x 1 2 m 4 1 2 S 1 2 m 2 m 4 2 m
Kết hợp điều kiện ta có: m 2;5 2 6
m 2; 1; 0. Thử lại: x 4 Với 2 m 2
x 3x 4 0 TXD : D 4; x 1 1 x 1
Khi đó hàm số có dạng y
có 1 tiệm cận đứng x 4 Loại. 2 x 3x 4 x 1 3 Với 2 m 1
x 2x 2 0 TXD : D 1 ;1 3 1 3; x 1 3 1 x 1
Khi đó hàm số có dạng y
có 2 tiệm cận đứng x 1 3 TM . 2 x 2x 2 x 1 Khi 2 m 0 x x 0 TXD : D 1; 1 0; x 0 1 x 1
Khi đó hàm số có dạng y
có 2 tiệm cận đứng x 0; x 1 TM . 2 x x Vậy m 1 ; 0 . Câu 50: Chọn B. 31
Document Outline
- de-khao-sat-thi-thpt-2021-lan-1-mon-toan-truong-thpt-quang-ha-vinh-phuc
- TOÁN_121
- quang ha
- ccc