Đề khảo sát Toán 12 lần 2 năm 2019 – 2020 trường Thạch Thành 3 – Thanh Hóa

Đề khảo sát Toán 12 lần 2 năm 2019 – 2020 trường Thạch Thành 3 – Thanh Hóa mã đề 001, đề gồm có 06 trang với 50 câu trắc nghiệm

20 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

28 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
MÃ ĐỀ 001 - Trang 1/7
Câu 1. Cho hàm số
y f x
có bảng biến thiên như hình dưới đây. Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực đại tại
1
x
. B. Hàm số đạt cực tiểu tại
0
x
.
C. Hàm số đạt cực tiểu tại
x
. D. Hàm số đạt cực đại tại
0
x
.
Câu 2. Hình vẽ sau đây là đồ thị của hàm số nào ?
A.
3
3 1
y x x
B.
4 2
2 1
y x x
C.
2020
x
y
D.
2020
log 2020
y x
Câu 3. Trong các hàm số sau, hàm số nào nghịch biến trên
0;

?
A.
2
3
log
y x
. B.
2020
log
y x
. C.
log
y x
. D.
ln
y x
.
Câu 4. Cho hàm số
( )
y f x
liên tục trên đoạn
1;3
và có đồ
thị như hình vẽ. Gọi
,
M m
lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của hàm số
( )
y f x
trên đoạn
1;3
. Ta có giá trị
của
2
M m
là :
A.
2 1
M m
B.
2 2
M m
C.
2 3
M m
D.
2 4
M m
Câu 5. Hàm số
y f x
có đồ thị như hình vẽ .
Số nghiệm của phương trình:
2 1 0
f x
là:
A.
4
. B.
1
. C.
2
. D.
3
.
SỞ GD&ĐT THANH HÓA
TRƯỜNG THPT THẠCH THÀNH 3
ĐỀ THI KHẢO SÁT CHẤT LƯỢNG LỚP 12 - LẦN 2
NĂM HỌC 2019-2020
MÔN : TOÁN Thời gian : 90 phút
( Đề gồm có 7 trang )
TỔ TOÁN - TIN
Mã đề thi 001
MÃ ĐỀ 001 - Trang 2/7
Câu 6. Hàm số
log
a
y x
có đồ thị như hình vẽ . Khẳng định
nào sau đây là đúng?
A.
0 1
a
. B.
1
a
.
C.
0
a
. D.
0
a
.
Câu 7. Cho số thực
a
thỏa mãn
0 1
a
. Mệnh đề nào sau đây sai ?
A.
log . log log
a a a
x y x y
, 0, 0
x y
B.
log log log
a a a
x
x y
y
, 0, 0
x y
C.
log .log .lo g 1
a b c
b c a
với
0 , 1
b c
D.
2
log 2log
a a
x x
,
x R
Câu 8. Đường tiệm cận ngang của đồ thị hàm số
2 2020
5
x
y
x
là :
A.
5
y
. B.
1010
y
. C.
404
y
. D.
2
y
.
Câu 9. Cho hàm số
1
2
x
y
. Khẳng định nào sau đây là sai?
A. Hàm số nghịch biến trên
R
. B. Đồ thị hàm số nhận
Oy
làm tiệm cận đứng
C. Đồ thị hàm số luôn nằm trên
Ox
D. Đồ thị hàm số nhận
Ox
làm tiệm cận ngang.
Câu 10. Đạo hàm của hàm số
3
log 1, 0
x
y e x x
là:
A.
1
'
ln 3
x
y e
x
. B.
1
1
'
x
y xe
x
. C.
1
1
'
ln 3
x
y xe
x
. D.
1
'
x
y e
x
.
Câu 11 . Hàm số
y f x
có đồ thị như hình vẽ .
Hàm số
y f x
đồng biến trên khoảng nào dướ
i đây ?
A.
1;1
. B.
0;2
.
C.
2; 1
. D.
2;1
.
Câu 12. Tính tích phân
1
2
0
1
x
I x e dx
A.
2 1
I e
B.
1
I e
C.
2 1
I e
D.
1
I e
Câu 13. Một nguyên hàm
F x
của hàm số
2
x
f x
là :
A.
2 2020
x
F x
. B.
2
2020
ln 2
x
F x . C.
2
2020
ln 2
x
F x x
. D.
2 ln 2
x
F x
.
Câu 14. Trong các hàm số sau,hàm số nào là hàm số lũy thừa ?
A.
2020
x
y
. B.
3
2
y x
. C.
1
4
y x
. D.
x
y e
.
Câu 15. Cho
1
0
2
f x dx
và
6
1
5
f x dx
,
khi đó
6
0
f x dx
bằng ?
A.
7
. B.
3
. C.
6
. D.
10
.
MÃ ĐỀ 001 - Trang 3/7
Câu 16. Đường cong trong hình bên là đồ thị của
hàm số nào dưới đây ?
A.
4 2
4 1
y x x
B.
4 2
4 1
y x x
C.
4 2
4 1
y x x
D.
4 2
1
y x x
Câu 17. Cho biểu thức
3
2 3
4
P x x x
với
0
x
. Mệnh đề nào dưới đây đúng ?
A.
13
24
P x
B.
23
12
P x
C.
12
23
P x
D.
23
24
P x
Câu 18. Cho
a
là số thực dương tùy ý,
ln 9 ln 7
a a
bằng ?
A.
ln 9
ln 7
a
a
. B.
9
ln
7
. C.
ln 2
a
. D.
ln9
ln7
.
Câu 19. Diện tích mặt cầu bán kính
R
bằng ?
A.
2
4
R
. B.
4
R
. C.
2
R
. D.
2
2
R
.
Câu 20. Khối nón tròn xoay bán kính đáy
R
, đường
sinh
l
, chiều cao
h
,
có thể tích
V
bằng ?
A.
V Rl
. B.
2
V R h
.
C.
2
1
3
V R h
D.
2
V R l
.
Câu 21. Khối lập phương là khối đa diện đều loại ?
A.
3;4
. B.
3;3
. C.
3;5
. D.
4;3
.
Câu 22. Khối bát diện đều có số mặt phẳng đối xứng ?
A.
3
. B.
4
. C.
5
. D.
6
.
Câu 23. Mặt trụ tròn xoay bán kính đáy
R
, chiều cao
h
,
có
diện tích xung quanh
xq
S
bằng ?
A.
xq
S Rh
. B.
2
2
xq
S Rh R
C.
2
2
xq
S R
D. 2
xq
S Rh
.
Câu 24. Khối hai mươi mặt đều có số đỉnh là ?
A.
20
. B.
12
.
C.
30
. D.
8
.
MÃ ĐỀ 001 - Trang 4/7
Câu 25. Nghiệm của phương trình
2 1
2 32
x
bằng ?
A.
2
x
. B.
3
x
. C.
3
2
x
. D.
5
2
x
.
Câu 26. Cho phương trình
3
log 1 1
x
. Mệnh đề nào sau đây đúng ?
A.
1;3
x
. B.
0;2
x
. C.
3;4
x
. D.
3;5
x
.
Câu 27. Nguyên hàm
F x
của hàm số
3
1
f x x x
là :
A.
4 2
4 2
x x
F x x
B.
4 2
4 2
x x
F x x C
. C.
2
3 1
F x x
. D.
4 2
1
F x x x C
.
Câu 28. Khối mười hai mặt đều có số cạnh là ?
A.
20
. B.
12
.
C.
30
. D.
8
.
Câu 29. Thể tích của khối trụ có bán kính đáy
R a
và chiều cao
2
h a
bằng :
A.
3
2
a
B.
3
4
a
. C.
3
2
3
a
. D.
3
2
a
.
Câu 30. Để làm một sản phẩm lịch Canh Tý 2020 để bàn như hình vẽ cần dùng
2
50
cm
giấy cho
mỗi mặt ( ứng với một tháng trong năm). Biết đơn giá giấy trên thị trường là
200.000
đồng
2
/
m
. Hỏi
chi phí giấy cần dùng để làm một sản phẩm lịch trên bằng :
A.
12.000
đồng B.
20.000
đồng . C.
6.000.000
đồng . D.
200.000
đồng .
Câu 31. Tính độ dài đoạn thẳng
AB
trong hình vẽ :
A.
3 3
AB
. B.
13
AB
.
C.
26
AB
. D.
2 2
AB
.
MÃ ĐỀ 001 -
Trang 5/7
Câu 32. Gọi
S
là tập hợp tất cả các nghiệm nguyên của bất phương trình
1
2
log 2 2x
. Tổng
các phần tử của
S
bằng ?
A.
2
. B.
2
. C.
0
. D.
3
Câu 33. Thể tích của khối lập phương cạnh
5cm
bằng ?
A.
3
20cm
. B.
3
125cm
. C.
3
25cm
. D.
3
30cm
Câu 34. Tích phân
2
2
0
4
ln3 ln 2
3 2
x
I dx a b
x x
. Khi đó
2
b a
bằng ?
A.
2
1b a
B.
2
1b a
C.
2
0b a
D.
2
4b a
Câu 35. Hình lăng trụ tam giác
.A'B'C'ABC
có đáy là tam
giác đều cạnh
a
,
AA ' 6a
. Hình chiếu vuông góc
H
của
A
trên mặt phẳng
' ' 'A B C
trùng với trọng tâm của
tam giác
' ' 'A B C
. Côsin của góc giữa cạnh bên và mặt đáy
bằng ?
A.
2
3
. B.
2
6
.
C.
3
6
. D.
15
15
.
Câu 36. Tổng các nghiệm của phương trình
3
2 8
log log 3 2x x
bằng ?
A.
3
. B.
2
. C.
4
. D.
0
.
Câu 37. Bất phương trình
4 3
3. 5. 2 0
9 2
x x
có tập nghiệm
;S a b
.
Khi đó, giá trị của
2 2
a b
bằng ?
A.
13
9
. B.
5
3
. C.
13
4
. D.
1
.
Câu 38. E.coli là vi khuẩn đường ruột gây tiêu chảy, đau bụng dữ dội. Cứ sau
20
phút thì số lượng vi
khuẩn E.coli lại tăng gấp đôi. Ban đầu chỉ có
40
vi khuẩn E.coli trong đường ruột. Hỏi sau bao lâu,
số lượng vi khuẩn E.coli là
671088640
con ?
A.
48
giờ. B.
24
giờ. C.
8
giờ. D.
12
giờ.
Câu 39. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang
vuông tại
A
và
B
,
AB AD a
,
2BC a
. Cạnh bên
SB
vuông
góc với đáy và
7SB a
,
M
là trung điểm của
BC
. Tính
khoảng cách
d
giữa hai đường thẳng
AM
và
SC
?
A.
14
3
a
d
. B.
3 14
2
a
d
.
C.
14
6
a
d
. D.
3 7
7
a
d
.
Câu 40. Số giá trị nguyên dương của
m
để bất phương trình
2
2 2 2 0
x x
m
có tập nghiệm
chứa không quá
6
số nguyên ?
A.
62
. B.
33
. C.
32
. D.
31
.
MÃ ĐỀ 001 - Trang 6/7
Câu 41. Cho giới hạn
4 2
0
f x ax bx c a
có đồ thị là đường cong như hình vẽ.
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
3 2 2
2002 3 4 2020
x x x
g x
f x
là ?
A.
3
. B.
5
. C.
4
. D.
2
Câu 42. Nhân dịp đi du Xuân Canh Tý, ba bạn Trang, Hoàng, Tân rủ nhau rút quẻ xem vận mệnh.
Khi đó trong hộp chỉ còn các quẻ có số thứ tự từ
5
đến
15
(luôn có ít nhất ba quẻ cùng ghi một số).
Mỗi bạn rút ngẫu nhiên một quẻ và yêu cầu bạn Linh tính xác suất để tổng các số ghi trên ba quẻ là
một số chia hết cho
3
. Kết quả đúng là ?
A.
112
1331
. B.
60
1331
. C.
203
1331
. D.
443
1331
.
Câu 43. Bà chủ khách sạn trên đèo Mã Pì Lèng muốn
trang trí một góc nhỏ trên ban công sân thượng cho đẹp
nên quyết định thuê nhân công xây một bức tường gạch
với xi măng (như hình vẽ), biết hàng dưới cùng có
500
viên, mỗi hàng tiếp theo đều có ít hơn hàng trước
1
viên
và hàng trên cùng có
1
viên . Hỏi số gạch cần dùng để
hoàn thành bức tường trên là bao nhiêu viên ?
A.
25250
. B.
125250
. C.
12550
. D.
250500
.
Câu 44. Cho tứ diện
ABCD
có
2
CD a
,
ABC
là tam giác đều cạnh
a
,
ACD
vuông tại
A
. Mặt
phẳng
BCD
vuông góc với mặt phẳng
ABD
.
Thể tích khối cầu ngoại tiếp tứ diện
ABCD
bằng ?
A.
3
4
3
a
. B.
3
3
2
a
.
C.
3
6
a
. D.
3
4
a
.
Câu 45. Cho phương trình
5
5 log
x
m x m
, với
m
là tham số. Số giá trị nguyên của
2020; 2020
m
để phương trình đã cho có nghiệm là ?
A.
9
. B.
2021
. C.
2020
. D.
2019
.
Câu 46. Gọi
S
là tập hợp tất cả các nghiệm thuộc đoạn
0;13
của phương trình
3 2
2 cos cos cos 2 0
x x x
. Tổng các phần tử của
S
bằng ?
A.
380
3
. B.
400
3
. C.
420
3
. D.
120
MÃ ĐỀ 001 - Trang 7/7
Câu 47. Tìm tất cả các giá trị của tham số
m
để đường thẳng đi qua cực đai, cực tiểu của đồ thị hàm số
3
3 2
y x mx
cắt đường tròn
C
tâm
1;1
I , bán kính bằng
1
tại hai điểm phân biệt
,
A B
sao cho
diện tích tam giác
IAB
đạt giá trị lớn nhất ?
A.
2 3
3
m
. B.
1 3
2
m
. C.
2 3
2
m
. D.
2 5
2
m
.
Câu 48. Cho hàm số
y f x
có đạo hàm liên tục trên
1;4
thỏa mãn
1 26
f
và
3 2
. ' 8 5
f x x f x x x
. Tính giá trị của
4
f
?
A.
400
. B.
2020
. C.
404
. D.
2022
.
Câu 49. Cho hình chữ nhật
ABCD
tâm
I
, biết
AB a
,
2
AD a
. Gọi
J
là trung điểm của
BC
, đường thẳng qua
I
và vuông góc với
AC
cắt
CD
tại điểm
K
. Thể tích
V
của khối tròn xoay tạo thành khi cho tứ giác
CKIJ
quay
xung quanh trục
CK
bằng ?
A.
3
5
6
a
. B.
3
7
6
a
.
C.
3
5
2
a
. D.
3
14
3
a
.
Câu 50. Cho hình chóp .
S ABCD
có đáy
ABCD
là hình bình hành. Gọi
E
là điểm đối xứng với
C
qua
B
và
F
là điểm thỏa mãn :
2.
SF BF
. Mặt phẳng
DEF
chia khối chóp .
S ABCD
thành
2
khối đa
diện, trong đó khối đa diện chứa đỉnh
S
có thể tích
1
V
, khối đa diện còn lại có thể tích
2
V
( tham khảo
hình vẽ). Tính tỉ số
2
V
V
?
A.
3
5
. B.
1
5
. C.
7
5
. D.
12
7
.
---------- HẾT ----------
LỜI GIẢI CHI TIẾT
Câu 1. Cho hàm số
( )
y fx=
có bảng biến thiên như hình dưới đây. Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực đại tại
1x =
. B. Hàm số đạt cực tiểu tại
0x =
.
C. Hàm số đạt cực tiểu tại
3x = −
. D. Hàm số đạt cực đại tại
0x =
.
Lời giải
Chọn D
Dựa vào bảng biến thiên ta có hàm số đạt cực đại tại
0x =
.
Câu 2. Hình vẽ sau đây là đồ thị của hàm số nào?
A.
3
31
yx x=−+
B.
42
21yx x=−+
. C.
2020
x
y =
. D.
( )
2020
log 2020yx= +
.
Lời giải
Chọn C
Do đồ thị hàm số luôn đồng biến trên
nên loại các phương án A, B.
Mà đồ thị luôn nằm phía trên trục
Ox
nên loại phương án D.
Câu 3. Trong các hàm số sau, hàm số nào nghịch biến trên
( )
0; +∞
?
A.
2
3
logyx=
. B.
2020
log
yx=
. C.
logyx
π
=
. D.
lnyx=
.
Lời giải
Chọn A
Xét hàm số
2
3
logyx=
có
2
3
a = ⇒
01a< <⇒
hàm số nghịch biến trên
( )
0;+∞
.
Xét hàm số
2020
logyx
=
có
2020 1a = >⇒
hàm số đồng biến trên
(
)
0;+∞
.
Xét hàm số
logyx=
π
có
1a
π
= >⇒
hàm số đồng biến trên
( )
0;+∞
.
Xét hàm số
lnyx=
có
e > 1
a = ⇒
hàm số đồng biến trên
( )
0;+∞
.
Câu 4. Cho hàm số
fx
liên tục trên
[ ]
1; 3−
và có đồ thị như hình vẽ bên. Gọi
,Mm
lần lượt là giá
trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
y fx=
trên
[ ]
1; 3−
. Ta có giá trị của
2Mm+
là:
A.
21Mm+=
. B.
22Mm+=
.
C.
23Mm+=
. D.
24Mm+=
.
Lời giải
ChọnB
Quan sát đồ thị ta thấy hàm số
( )
y fx=
đạt giá trị nhỏ nhất trên
[ ]
1; 3−
là
1−
tại điểm
1
x = −
và đạt giá trị lớn nhất trên
[ ]
1; 3
−
là
4
tại điểm
3x =
. Do đó
1, 4mM=−=
.
Giá trị
( )
2 4 2. 1 2Mm+ =+ −=
.
Câu 5. Hàm số
( )
=y fx
có đồ thị như hình vẽ. Số nghiệm của phương trình
( )
2 10−=fx
là
A. 4. B. 1. C. 2. D. 3.
Lời giải
Chọn A
Ta có:
( ) ( )
1
2 10
2
−= ⇔ =fx fx
;
Số nghiệm của phương trình
( )
1
2
=fx
chính là số giao điểm của đồ thị hàm số
( )
=
y fx
và
đường thẳng
1
2
=y
.
Đường thẳng
1
2
=y
cắt đồ thị hàm số
( )
=y fx
tại 4 điểm phân biệt.
Vậy phương trình
( )
2 10−=fx
có 4 nghiệm phân biệt.
Câu 6. Cho hàm số
( )
log
a
y fx x= =
. Tìm tất cả các giá trị thực của
a
để hàm số
( )
fx
đồng biến
trên
( )
0; +∞
.
A.
01
<<a
. B.
1>a
. C.
0≠a
. D.
0>a
.
Lời giải
Chọn B
Dựa vào đồ thị ta có hàm số
log
=
a
yx
là hàm đồng biến trên
( )
0; +∞
1⇒>a
.
Câu 7. Cho số thực
a
thỏa mãn
01a
<≠
. Mệnh đề nào sau đây là sai?
A.
( )
log . log log
a aa
xy x y= +
,
0
x∀>
,
0y >
. B.
log log log
a aa
x
xy
y

= −


,
0x∀>
,
0y >
.
C.
log .log .log 1
abc
bca=
, với
0 b<
,
1c ≠
. D.
2
log 2log
aa
xx=
,
x∀∈
.
Lời giải
Chọn C
Ta có
log .log .log 1
abc
bca
=
có chứa
a
,
b
,
c
là cơ số của lôgarit nên điều kiện là
a
,
b
,
c
là
các số dương khác 1.
Câu 8. Đường tiệm cận ngang của đồ thị hàm số
2 2020
5
x
y
x
−
=
+
là:
A.
5y = −
. B.
1010y
=
. C.
404y = −
. D.
2y =
.
Lời giải
Chọn D
Ta có
2 2020
lim 2
5
x
x
x
→+∞
−
=
+
và
2 2020
lim 2
5
x
x
x
→−∞
−
=
+
nên đồ thị hàm số có tiệm cận ngang là đường
thẳng
2y =
.
Câu 9. Cho hàm số
1
2
x
y

=


. Khẳng định nào sau đây là sai?
A. Hàm số nghịch biến trên
. B. Đồ thị hàm số nhận
Oy
làm tiệm cận đứng.
C. Đồ thị hàm số luôn nằm trên
Ox
D. Đồ thị hàm số nhận
Ox
làm tiệm cận ngang
Lời giải
Chọn B
Đồ thị của hàm số mũ không nhận
Oy
làm tiệm cận đứng.
Câu 10. Đạo hàm của hàm số
( )
3
log 1, 0
x
ye x x=− +>
là:
A.
1
ln 3
x
ye
x
′
= −
. B.
1
1
x
y xe
x
−
′
= −
. C.
1
1
ln 3
x
y xe
x
−
′
= −
. D.
1
x
ye
x
′
= −
.
Lời giải
Chọn A
Ta có
( )
3
1
log 1 .
ln 3
xx
ye x e
x
′
′
= − +=−
Câu 11. Hàm số
(
)
y fx=
có đồ thị như hình vẽ. Hàm số
(
)
y fx=
đồng biến trên khoảng nào dưới
đây ?
A.
( )
1;1−
. B.
( )
0; 2
. C.
( )
2; 1−−
. D.
( )
2;1−
.
Lời giải
Chọn C
Dựa vào đồ thị ta có hàm số
( )
y fx
=
đồng biến trên
( )
2; 1−−
và
( )
1;+∞
.
Câu 12. Tính tích phân
( )
1
2
0
1d
x
I x ex= +
∫
A.
21Ie= +
. B.
1Ie
= +
. C.
21
Ie= −
. D.
1Ie= −
.
Lời giải
Chọn C
( )
1
2
0
1d
x
I x ex= +
∫
Đặt
( )
2
1
ux= +
suy ra
( )
d 2 1dux x= +
d ed
x
vx=
, chọn
e
x
v =
Do đó
( ) ( )
1
1
2
0
0
1e 2 1 d
xx
I x x ex=+ −+
∫
( )
1
412eI= −−
.
( )
1
Tính
( )
1
1
0
1d
x
I x ex= +
∫
Đặt
1ux= +
suy ra
ddux=
d ed
x
vx
=
, chọn
e
x
v =
Do đó
( )
1
1
1
0
0
1e d
xx
I x ex=+−
∫
( )
1
0
1e
xx
xe

=+−

( ) (
)
2 11ee e= −−−=
.
( )
2
Từ
( )
1
và
( )
2
ta được
21Ie= −
.
Câu 13. Một nguyên hàm
( )
Fx
của hàm số
( )
2
x
fx
=
là:
A.
( )
2 2020
x
Fx= +
. B.
( )
2
2020
ln 2
x
Fx= +
.
C.
( )
2
2020
ln 2
x
Fx x= +
. D.
( )
2 ln 2
x
Fx=
.
Lời giải
Chọn B
Ta có
2
2
ln 2
x
x
dx C= +
∫
. Cho
2020C =
ta được một nguyên hàm của hàm số
( )
2
x
fx=
là
( )
2
2020
ln 2
x
Fx= +
.
Câu 14. Trong các hàm số sau, hàm số nào là hàm số lũy thừa?
A.
2020
x
y =
. B.
3
2
yx=
. C.
1
4
yx=
. D.
x
ye
=
.
Lời giải
Chọn C
Ta có theo định nghĩa hàm số lũy thừa là hàm số có dạng
;yx
α
α
= ∈
.
Câu 15. Cho
( )
1
0
d2fx x=
∫
và
( )
6
1
d5
fx x=
∫
. Khi đó
( )
6
0
dfx x
∫
bằng?
A. 7. B.
3−
. C.
6
. D.
10
.
Lời giải
Chọn A
( )
( ) ( )
6 16
0 01
d d d 257fx x fx x fx x= + =+=
∫∫∫
.
Câu 16. Đường cong trong hình bên dưới là đồ thị của hàm số nào sau đây?
A.
42
41yx x
. B.
42
41yx x
.
C.
42
41yx x
. D.
42
1yx x

.
Lời giải
Chọn C
Đây là đồ thị một hàm số bậc bốn trùng phương có dạng:
42
0y ax bx c a
.
Mà
lim
x
y


chứng tỏ
0a
. Do đó ta loại phương án B.
Đồ thị cắt trục tung tại điểm có tung độ
1y
nên
1c
. Do đó ta loại phương án A.
Đồ thị hàm số có 3 điểm cực trị nên
,ab
trái dấu. Vậy ta chọn phương án C.
Câu 17. Cho biểu thức
3
23
4
P xx x
với
0
x
. Mệnh đề nào sau đây là đúng?
A.
13
24
Px
. B.
23
12
Px
. C.
12
23
Px
. D.
23
24
Px
.
Lời giải
Chọn D
Với
0x
, ta có:
3 11 11 23 23
33
3
23 2
4
4 4 12 12 24
..
P xx x xxx xx xx x x 
.
Câu 18. Cho
a
là số thực dương tùy ý,
ln 9 ln 7aa
bằng?
A.
ln 9
ln 7
a
a
. B.
ln
7
. C.
ln 2a
. D.
ln 9
ln 7
.
Lời giải
Chọn B
Với
a
là số dương, ta có:
ln 9 ln 7aa
9
ln
7
a
a
9
ln
7
.
Câu 19. Diện tích mặt cầu bán kính
R
bằng?
A.
2
4
R
. B.
4 R
. C.
2
R
. D.
2
2 R
.
Lời giải
Chọn A
Diện tích mặt cầu bán kính
R
bằng:
2
4SR
.
Câu 20. Cho khối nón tròn xoay bán kính đáy
R
, đường sinh
l
, đường cao
h
có thể tích
V
bằng bao
nhiêu?
A.
V Rl
. B.
2
V Rh
. C.
2
1
3
V Rh
. D.
2
V Rl
.
Lời giải
Chọn C
Với khối nón tròn xoay bán kính đáy
R
, đường sinh
l
, đường cao
h
có thể tích
2
1
3
V Rh
.
Câu 21. Khối lập phương là khối đa diện đều loại?
A.
3; 4
. B.
3; 3
. C.
3; 5
. D.
4;3
.
Lời giải
Chọn D
Khối đa diện đều loại
;pq
là khối đa diện lồi có
- Mỗi mặt là một đa giác đều có
p
cạnh.
- Mỗi đỉnh là đỉnh chung của đúng
q
mặt.
Do đó khối lập phương là khối đa diện đều loại
4;3
.
Câu 22. Khối bát diện đều có số mặt phẳng đối xứng?
A.
3
. B.
4
. C.
9
. D.
6
.
Lời giải
Chọn C
Các mặt phẳng đối xứng của bát diện đều
+ Xem
ABCD
là mặt phẳng đáy và hai đỉnh
E
,
F
ta có ba mặt phẳng đối xứng sau
ABCD
EMFN
EPFQ
+ Tương tự, xem
AECF
là mặt phẳng đáy và hai đỉnh
B
,
D
ta cũng có ba mặt phẳng đối
xứng và xem
BEDF
là mặt phẳng đáy và hai đỉnh
A
,
C
ta cũng có ba mặt phẳng đối xứng.
Vậy có tất cả
9
mặt phẳng đối xứng.
Câu 23. Mặt trụ tròn xoay bán kính đáy
R
, chiều cao
h
, có diện tích xung quanh
xq
S
bằng
A.
.
xq
S Rh
B.
2
2.
xq
S Rh R
C.
2
2.
xq
SR
D.
2.
xq
S Rh
Lời giải
Chọn D
Diện tích xung quanh hình trụ bằng chu vi đường tròn đáy nhân với chiều cao:
2.
xq
S Rh
Câu 24. Khối hai mươi mặt đều có số đỉnh là
A.
20
. B.
12
. C.
30
. D.
8
.
Lời giải
Chọn B
Câu 25. Nghiệm của phương trình
21
2 32
x
bằng
A.
2x
. B.
3x
. C.
3
2
x
. D.
5
2
x
.
Lời giải
Chọn A
Ta có
21
2 32
x
21 5
22
x

2 15
x 
2
x
.
Câu 26. Cho phương trình
( )
3
log 1 1x −=
. Mệnh đề nào sau đây đúng?
A.
( )
1; 3x ∈
. B.
( )
0; 2x ∈
. C.
( )
2; 4x ∈
. D.
(
)
3; 5
x
∈
.
Lời giải
Chọn D
Ta có phương trình:
(
)
3
log 1 1x −=
10
13
x
x
−>
⇔
−=
1
4
x
x
>
⇔
=
4x
⇔=
. Vậy
( )
3; 5x
∈
.
Câu 27. Họ nguyên hàm của hàm số
( )
3
1fx x x= −+
là
A.
(
)
42
42
xx
Fx x=−+
. B.
( )
42
42
xx
Fx x C= − ++
.
C.
(
)
2
31Fx x= −
. D.
( )
42
1Fx x x C= − ++
.
Lời giải
Chọn B
Họ nguyên hàm của hàm số
( )
3
1fx x x= −+
là
( )
42
42
xx
Fx x C= − ++
.
Câu 28. Khối mười hai mặt đều có số cạnh là
A.
20
. B.
12
. C.
30
. D.
8
.
Lời giải
Chọn C
Khối mười hai mặt đều là khối đa diện đều loại
{ }
5; 3
. Do đó có số mặt là
12
, số đỉnh là
20
và
số cạnh là
20 12 2 30+ −=
.
Câu 29. Thể tích của khối trụ có bán kính đáy
Ra=
và chiều cao
2ha=
bằng:
A.
3
2a
. B.
3
4 a
π
. C.
3
2
3
a
π
. D.
3
2
a
π
.
Lời giải
Chọn D
Thể tích khối trụ là:
23
.2 2V Bh a a a
ππ
= = =
.
Câu 30. Để làm làm một sản phẩm lịch Canh Tý 2020 như hình vẽ cần dùng
2
50 cm
giấy cho mỗi mặt
(ứng cho mỗi tháng trong năm). Biết đơn giá giấy trên thị trường là
200.000
đồng/
2
m
. Hỏi chi
phí giấy cần dùng để làm một sản phẩm lịch trên bằng bao nhiêu?
A.
12.000
đồng. B.
20.000
đồng. C.
6.000.000
đồng. D.
200.000
đồng.
Lời giải
Chọn A
Số tiền cần dùng để làm sản phẩm lịch Canh Tý 2020 trên là:
50
.200000.12 12000
10000
T = =
đồng.
Câu 31. Tính độ dài đoạn thẳng AB trong hình vẽ
A.
33AB
=
. B.
13AB =
. C.
26AB =
. D.
22AB =
.
Lời giải
Chọn C
Từ hình vẽ ta thấy
A
và
B
chính là hai giao điểm của đồ thị hàm số
1
2
x
y
x
−
=
−
với đường thẳng
2yx= +
.
Ta có hoành độ hai điểm
A
và
B
là nghiệm của phương trình:
1
2
2
x
x
x
−
= +
−
, ĐK:
2x ≠
2
14
xx⇔ −= −
2
30xx⇔ −−=
1 13 5 13
;
22
A

−−
⇒



,
1 13 5 13
;
22
B

++



( )
13; 13AB⇒=

26AB
⇒=
.
Vậy độ dài đoạn thẳng
AB
bằng
26
.
Câu 32. Gọi
S
là tập hợp tất cả các nghiệm nguyên của bất phương trình
( )
1
2
log 2 2x + ≥−
. Tổng các
phần tử của
S
bằng
A.
2
−
. B.
2
. C.
0
. D.
3
.
Lời giải
Chọn B
( )
1
2
log 2 2x + ≥−
0 24x⇔<+≤
22x
⇔− < ≤
mà
x ∈
nên
{ }
1; 0; 1; 2x ∈−
.
Do đó, tập hợp tất cả các nghiệm nguyên của bất phương trình đã cho là:
{ }
1; 0; 1; 2S = −
.
Vậy tổng các phần tử của
S
bằng 2.
Câu 33. Thể tích của khối lập phương cạnh
5cm
bằng
A.
3
20cm
. B.
3
125cm
. C.
3
25
cm
. D.
3
30cm
.
Lời giải
Chọn B
Thể tích của khối lập phương là:
33
5 125V cm= =
.
Câu 34. Tích phân
2
2
0
4
d ln 3 ln 2
32
x
I xa b
xx
+
= = +
++
∫
. Khi đó
2
ba−
bằng
A.
2
1ba−=
. B.
2
1ba−=−
. C.
2
0ba−=
. D.
2
4ba−=−
.
Lời giải
Chọn A
Ta có:
( )
( )
22
2
00
44
dd
32 1 2
xx
xx
xx x x
++
=
++ + +
∫∫
2
0
32
d
12
x
xx

= −

++

∫
(
)
2
0
3ln 1 2ln 2 |
3ln 3 2ln 4 ( 2ln 2)
3ln 3 2ln 2
xx= +− +
= − −−
= −
3
2
a
b
=
⇒
= −
. Do đó:
2
1ba−=
.
Câu 35. Hình lăng trụ tam giác
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
,
6AA a
′
=
. Hình chiếu
vuông góc
H
của
A
lên mặt phẳng
( )
ABC
′′′
trùng với trọng tâm của tam giác
ABC
′′′
. Côsin
của góc giữa cạnh bên và mặt đáy bằng bao nhiêu?
A.
2
3
. B.
2
6
. C.
3
6
. D.
15
15
.
Lời giải
Chọn B
Do
H
là hình chiếu vuông góc của
A
lên mặt phẳng
( )
ABC
′′′
nên góc tạo bởi cạnh bên và
mặt đáy là
AA H
′
.
Ta có
H
là trọng tâm tam giác đều
ABC
′′′
cạnh
a
nên
23 3
32 3
AH a a
′
= =
.
Vậy nên
3
2
3
cos
6
6
a
AH
AA H
AA
a
′
′
= = =
′
.
Câu 36. Tổng các nghiệm của phương trình
( )
3
28
log log 3 2
xx+ −=
bằng bao nhiêu?
A.
3
. B.
2
. C.
4
. D.
0
.
Lời giải
Chọn C
Điều kiện
0
3
30
x
x
x
>
⇔>
−>
.
( ) ( )
3
33
28 2
2
log log 3 2 log log 3 2xx x x+ −=⇔ + −=
( )
22
log log 3 2xx⇔ + −=
( ) (
)
2
log 32 34xx xx⇔ −=⇔ −=
2
1
3 40
4
x
xx
x
= −
⇔ − −=⇔
=
. Kết hợp điều kiện thì nghiệm
phương trình là
4x =
, nên tổng các nghiệm của phương trình là
4
.
Câu 37. Bất phương trình
43
3. 5. 2 0
92
−
 
− +≤
 
 
xx
có tập nghiệm
[ ]
;=S ab
. Khi đó giá trị của
22
+ab
bằng
A.
13
9
. B.
5
3
. C.
13
4
. D.
1
.
Lời giải
Chọn D
42
3. 5. 2 0
93
 
⇔ − +≤
 
 
xx
BPT
2
22
3. 5. 2 0
33
 
⇔ − +≤
 
 
xx
22
1
33

⇔≤ ≤


x
0
22 2
33 3
 
⇔≤ ≤
 
 
x
2
01
3
0 1.
<=<
⇔ ≤≤
a
x
Câu 38. Ecoli là vi khuẩn đường ruột gây tiêu chảy, đau bụng dữ dội. Cứ sau
20
phút thì số lượng vi
khuẩn Ecoli lại tăng gấp đôi. Ban đầu chỉ có
40
vi khuẩn Ecoli trong đường ruột. Hỏi sau bao
lâu số lượng vi khuẩn Ecoli là 671088640?
A.
48
giờ. B.
24
giờ. C.
8
giờ. D.
12
giờ.
Lời giải
Chọn C
Cứ sau
20
(phút) thì số lượng vi khuẩn Ecoli lại tăng gấp đôi và ban đầu chỉ có
40
vi khuẩn
Ecoli trong đường ruột nên
- Sau
20
phút thì số lượng vi khuẩn Ecoli là:
1
80 40.2 .
=
- Sau
20.2
phút thì số lượng vi khuẩn Ecoli là:
2
160 40.2 .=
- Sau
20.3
phút thì số lượng vi khuẩn Ecoli là:
3
320 40.2 .=
……
- Sau
20.n
phút thì số lượng vi khuẩn Ecoli là:
40.2 .
n
S =
Theo giả thiết ta có phương trình:
40.2 671088540
n
=
24n
⇔=
20.24 480⇒= =t
(phút) hay
8
(giờ).
Câu 39. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
B
,
AB AD a= =
,
2BC a=
. Cạnh bên
SB
vuông góc với đáy và
7SB a=
,
M
là trung điểm của
BC
. Tính
khoảng cách
d
giữa hai đường thẳng
AM
và
SC
.
A.
14
3
a
d =
. B.
3 14
2
a
d =
. C.
14
6
a
d =
. D.
37
7
a
d =
.
Lời giải
Chọn C
Theo giả thiết
AMCD
là hình bình hành (
// ,
= =AD CM AD CM a
). Khi đó,
( )
( )
//
⊂
⊄
AM CD
CD SCD
AM SCD
( )
//⇒ AM SCD
( )
(
)
( )
,,
⇒=d AM SC d M SCD
.
Ta có
(
)
( )
(
)
(
)
,
2
,
d B SCD
BC
MC
d M SCD
= =
(
)
(
)
( )
( )
,
,
2
d B SCD
d M SCD⇒=
.
Vì
ABCD
là hình thang vuông tại
A
và
B
,
AB AD a= =
,
2BC a=
nên
2BD DC a= =
.
Do đó
BD
vuông góc với
DC
. Trong tam giác
SBD
vuông tại
B
kẻ đường cao
BH
.
Suy ra
( )
(
)
,
d B SCD BH=
.
Ta có
22 2
1 11
BH SB BD
= +
( ) ( )
22
11
72aa
= +
2
9
14a
=
2
2
14
9
a
BH⇒=
14
3
a
BH
⇒=
( )
( )
14
,
6
a
d M SCD⇒=
. Vậy
14
6
a
d =
.
Câu 40. Số giá trị nguyên dương của
m
để bất phương trình
( )
(
)
2
2 22 0
xx
m
+
− −<
có tập nghiệm
chứa không quá 6 số nguyên là:
A.
62
. B.
33
. C.
32
. D.
31
.
Lời giải
Chọn C
Ta có: bất phương trình
( )
( )
2
2 22 0
xx
m
+
− −<
2
2
2 20
20
2 20
20
x
x
x
x
m
m
+
+
−>
−<
⇔
−<
−>
2
2
22
2
22
2
x
x
x
x
m
m
+
+
>
<
⇔
<
>
2
2
1
2
2
log
1
2
2
log
x
xm
x
xm
+>
<
⇔
+<
>
( )
2
2
3
2
log
3
*
2
log
>−
<
⇔
<−
>
x
xm
x
xm
2
3
log
2
⇔− < <xm
.
(Vì
1≥m
2
log 0⇒≥m
nên (*) vô nghiệm).
Bất phương trình đã cho có tập nghiệm chứa không quá 6 số nguyên
2
log 5⇔≤m
5
2⇔≤m
32⇔≤m
Mà
m
nguyên dương nên
{ }
1;2;3;....32m ∈
.
Vậy có 32 giá trị của
m
thỏa mãn yêu cầu bài toán.
Câu 41. Cho hàm số
( ) ( )
42
0=++ ≠f x ax bx c a
có đồ thị là đường cong như hình vẽ
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
( )
( )
( )
32 2
2002 3 4 2020+− +
=
xx x
gx
fx
là
A.
3
B.
5
C.
4
D.
2
Lời giải
Chọn C
Dựa vào đồ thị ta có
( ) ( ) (
)
22
11=+−f x ax x
mà đồ thị hàm số
(
)
fx
qua
( )
0;1M
1⇒=a
.
Vậy
( ) ( ) ( )
22
11=+−fx x x
.
Khi đó:
( )
( )
( ) ( )
32 2
22
2002 3 4 2020
11
+− +
=
+−
xx x
gx
xx
( )
( )( )
( ) ( )
2
2
22
2002 1 2 2020
11
−+ +
⇒=
+−
xx x
gx
xx
.
Tập xác định:
{ }
\1= ±D
.
-
( )
(
)
( ) ( )
2
2
2
2002 2 2020
lim lim
11
→−∞ →−∞
++
=
+−
xx
xx
gx
xx
2
2
2
2 2020
2002 1 1
lim
11
11
→−∞

−++


=

+−


x
xx
xx
2002= −
.
Suy ra đường thẳng
2002= −y
là một tiệm cận ngang của đồ thị hàm số
(
)
gx
.
-
( )
( )
( ) ( )
2
2
2
2002 2 2020
lim lim
11
→+∞ →+∞
++
=
+−
xx
xx
gx
xx
2
2
2
2 2020
2002 1 1
lim
11
11
→+∞

++


=

+−


x
xx
xx
2002=
.
Suy ra đường thẳng
2002=y
là một tiệm cận ngang của đồ thị hàm số
( )
gx
.
-
( )
( )
( ) ( )
2
2
2
11
2002 2 2020
lim lim
11
→− →−
++
=
+−
xx
xx
gx
xx
= −∞
Vì
( )
( )
( )
( )
2
2
1
2
1
2
2002 2 2020
lim 1001 2021 0
1
lim 1 0
1 10
→−
→−
++
=−<
−
+=
→− ⇒ + >
x
x
xx
x
x
xx
Suy ra đường thẳng
1= −
x
là một tiệm cận đứng của đồ thị hàm số
( )
gx
.
-
( )
(
)
(
) (
)
2
2
2
11
2002 2 2020
lim lim
11
xx
xx
gx
xx
++
→→
++
=
+−
= +∞
(vì
(
)
(
)
( )
2
2
2
1
1
2002 2 2020
9009
lim 2021 0
2
1
lim 1 0
1 10
x
x
xx
x
x
xx
+
+
→
→
+
++
= >
+
−=
→ ⇒ −>
)
Suy ra đường thẳng
1=x
là một tiệm cận đứng của đồ thị hàm số
( )
gx
.
Vậy tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
( )
gx
là
4
.
Câu 42. Nhân dịp đi du Xuân Canh Tý, ba bạn Trang, Hoàng, Tân rủ nhau rút quẻ xem vận mệnh.
Khi đó trong hộp chỉ có các quẻ có số thứ tự
5
đến
15
(luôn có ít nhất ba quẻ ghi cùng một số).
Mỗi bạn rút ngẫu nhiên một quẻ và yêu cầu bạn Linh tính xác suất để tổng các số ghi trên ba
quẻ là một số chia hết cho
3
. Kết quả đúng là?
A.
112
1331
. B.
60
1331
. C.
203
1331
. D.
443
1331
.
Lời giải
Chọn D
Số phần tử của không gian mẫu:
(
)
3
11 1331n Ω= =
. Ta chia các số đã cho thành ba nhóm.
Nhóm I: Chia
3
dư
0
có các số:
6; 9; 12; 15
.
Nhóm II: Chia
3
dư
1
có các số:
7; 10; 13
.
Nhóm III: Chia
3
dư
2
có các số:
5; 8; 11; 14
.
Gọi
A
là biến cố: “tổng các số ghi trên ba quẻ là một số chia hết cho
3
”. Ta có:
TH1: rút
3
số cùng thuộc một nhóm có
333
434++
cách.
TH2: rút
3
số từ ba nhóm (mỗi số thuộc một nhóm) có
4.3.4.3!
cách.
Vậy xác suất cần tìm:
( )
333
4 3 4 4.3.4.3! 443
.
1331 1331
PA
+++
= =
Câu 43. Bà chủ khách sạn trên đèo Mã Pi Lèng muốn trang trí một góc nhỏ trên ban công sân thượng
cho đẹp nên quyết định thuê nhân công xây một bức tường gạch với xi măng (như hình vẽ),
biết hàng dưới cùng có
500
viên, mỗi hàng tiếp theo đều có ít hơn hàng trước
1
viên và hàng
trên cùng có một viên. Hỏi số gạch cần dùng để hoàn thành bức tường trên là bao nhiêu viên?
A.
25250
. B.
125250
. C.
12550
. D.
250500
.
Lời giải
Chọn B
Theo bài ra ta có số viên gạch từ hàng dưới cùng đến hàng trên cùng lập thành một cấp số cộng
với số hạng đầu
1
500
u =
, công sai
1d = −
nên công thức số hạng tổng quát là:
( )(
)
500 1 1
n
un= +−−
Hay
501
n
un
= −
. Vì hàng trên cùng một viên nên giải phương trình
501 1n−=
500n
⇔=
.
Vậy có tất cả
500
hàng gạch và hàng trên cùng là
500
1u =
.
Do đó số gạch cần dùng để hoàn thành bức tường là:
500
500 499 498 ... 1S
= + + ++
( )
500 500 1
2
+
=
125250=
.
Câu 44. Cho tứ diện
ABCD
có
2=CD a
,
ABC
là tam giác đều cạnh
a
,
ACD
vuông tại
A
. Mặt
phẳng
( )
BCD
vuông góc với mặt phẳng
( )
ABD
. Thể tích khối cầu ngoại tiếp tứ diện
ABCD
bằng?
A.
3
4
3
a
. B.
3
3
2
a
.
C.
3
6
a
. D.
3
4 a
.
Lời giải
Chọn A
Gọi
M
,
N
,
K
lần lượt là trung điểm của
AD
,
CD
,
BD
ACD
vuông tại
A
22
= −=AD CD AC a
ABD
cân tại
A
AK BD
⊥
.
Mặt khác
( ) (
)
ABD BCD⊥
( )
AK BCD⊥
( )
1AK CD
⊥
.
ACD
cân tại
A
( )
2AN CD⊥
.
Từ
( )
1
và
( )
2
CD KN⊥
Mà
//BC KN
(tính chất đường trung bình)
CD BC⊥
Suy ra
K
là tâm đường tròn ngoại tiếp
BCD
.
Đường trung trực của
AD
trong mặt phẳng
( )
ABD
cắt
AK
tại
I
I
là tâm mặt cầu ngoại
tiếp tứ diện
ABCD
.
22
3BD CD BC a= +=
,
2
2 22
3
42
aa
AK AD KD a= − =−=
.
( )
.AKD AMI g g
AI AM
AD AK
=
..
2
2
AM AD a a
R AI a
a
AK
= = = =
.
Thể tích khối cầu ngoại tiếp tứ diện
ABCD
:
3
3
44
33
a
VR= =
.
Câu 45. Cho phương trình
( )
5
5 log
x
m xm+= −
, với
m
là tham số. Số giá trị nguyên của
( )
2020;2020m
∈−
để phương trình đã cho có nghiệm là?
A.
9
. B.
2021
. C.
2020
. D.
2019
.
Lời giải
Chọn D
Điều kiện của phương trình:
xm>
.
Ta có
( )
5
5 log
x
m xm+= −
5
5
x
m
xm
+
⇔=−
5
5
x
m
mx
+
⇔ +=
.
Đặt
5
x
mt+=
( )
1
, phương trình trên trở thành
5
t
mx+=
( )
2
.
Trừ tương ứng vế với vế của
( )
1
cho
( )
2
, ta được:
55
xt
tx
−=−
55
xt
xt⇔ += +
.
Đặt
( )
5
x
fx x= +
( )
5 .ln 5 1 0
x
fx
′
⇒ = +>
x∀
, vậy
( )
fx
là hàm đơn điệu trên tập xác định.
Từ đây suy ra
55
xt
xt+= +
( ) ( )
fx ft⇔=
xt⇔=
, thế vào phương trình
( )
1
, ta được:
5
x
mx+=
5
x
xm
⇔− =
.
Xét hàm
( )
5
x
gx x
= −
có
( )
1 5 .ln 5
x
gx
′
= −
( )
0gx
′
⇒=
1 5 .ln 5 0
x
⇔− =
5
1
log
ln 5
x

⇔=


.
Ta có bảng biến thiên của hàm
( )
gx
như sau:
x
−∞
5
1
log
ln 5



+∞
( )
gx
′
+
0
−
( )
gx
−∞
5
11
log
ln 5 ln 5

−


−∞
Vậy phương trình
( )
gx m=
có nghiệm
5
11
log
ln 5 ln 5
m

⇔≤ −


0,92≈−
.
Lại có
(
)
2020;2020m
∈−
và
m ∈
, từ đây suy ra
m ∈
và
2019 1m− ≤ ≤−
.
Vậy có
2019
giá trị nguyên của
m
thỏa mãn yêu cầu bài toán.
Câu 46. Gọi
S
là tập hợp tất cả các nghiệm thuộc đoạn
[ ]
0;13
π
của phương trình
32
2 cos cos cos 2 0xxx
++ =
. Tổng các phần tử của
S
bằng:
A.
380
3
π
. B.
400
3
π
. C.
420
3
π
. D.
120
π
.
Lời giải
Chọn B
32
2 cos cos cos 2 0xxx++ =
32
2 cos 3cos 1 0xx⇔ + −=
( ) ( )
2
cos 1 2cos 1 0xx⇔ + −=
cos 1 0
2 cos 1 0
x
x
+=
⇔
−=
cos 1
1
cos
2
x
x
= −
⇔
=
+) Với
( ) ( )
cos 1 2 1
x xk k
π
=−⇔ = + ∈
.
Hơn nữa, ta lấy
[ ]
0;13
x
π
∈
nên có:
( )
21xk
π
= +
, với
,0 6
kk∈ ≤≤
.
+) Với
( )
2
1
3
cos cos cos ,
23
2
3
xm
x x ml
xl
π
π
π
π
π
= +
=⇔= ⇔ ∈
=−+
.
Tương tự, do lấy
[
]
0;13x
π
∈
nên ta có:
2
3
xm
π
π
= +
, với
,0 6mm∈ ≤≤
và
2
3
xl
π
π
=−+
, với
,1 6ll∈ ≤≤
.
Do đó,
( )
{ }
2 1 | ,0 6 2 | ,0 6 2 | ,1 6
33
S k k k mm m ll l
ππ
ππ π

= + ∈≤≤∪+ ∈≤≤∪−+ ∈≤≤



Vậy, tổng các phần tử của
S
là:
( )
66 6
00 1
21 2 2
33
km l
Tk m l
ππ
ππ π
= = =

= + + + + −+


∑∑ ∑
(
)
6 6 66 6
0 0 01 1
21 2 2
33
k m ml l
k ml
ππ
πππ
= = = = =

= ++ + + − +


∑ ∑ ∑∑ ∑
( ) ( ) ( )
7 1 13 7 0 12 6 2 12
76
23 2 3 2
ππ
ππ π
++ +

= + + +− +


400
3
π
=
.
Câu 47. Tìm tất cả các giá trị của tham số
m
để đường thẳng đi qua điểm cực đại và cực tiểu của đồ thị
hàm số
3
32
y x mx
cắt đường tròn
C
tâm
1; 1I
, bán kính bằng
1
tại hai điểm phân
biệt
A
,
B
sao cho diện tích tam giác
IAB
đạt giá trị lớn nhất?
A.
23
3
m
. B.
13
2
m
. C.
23
2
m
. D.
25
2
m
.
Lời giải
Chọn C
2
33yxm

.
Hàm số có hai điểm cực trị khi
0m
1
.
Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
3
32y x mx
có phương trình
22y mx
2 20mx y 
.
Diện tích tam giác
IAB
là
1
. . .sin
2
IAB
S IA IB AIB
1
.1.1.sin
2
AIB
11
sin
22
AIB
.
Dấu
""
xảy ra khi
90AIB 
tức là
IAB
vuông tại
I
.
Khi đó
2
,
2
d I AB
2
2
22
2
2
21
II
mx y
m


.
2
2 2 1 2. 4 1mm 
23
2
23
2
m
m
2
.
Từ
1
và
2
ta được
23
2
m
.
Câu 48. Cho hàm số
(
)
y fx=
có đạo hàm liên tục trên
[ ]
1; 4
thỏa mãn
( )
1 26f =
và
( ) ( )
32
. 85f x xf x x x
′
= −−
. Tính giá trị của
( )
4f
?
A.
400
. B.
2020
. C.
404
. D.
2022
.
Lời giải
Chọn C
Trên
[ ]
1; 4
, ta có
( ) ( )
( ) ( )
32
2
.
. 8 5 85
xf x f x
f x xf x x x x
x
′
−
′
= −−⇔ =+
.
Lấy nguyên hàm hai vế ta được
( )
2
45
fx
x xC
x
= ++
hay
( )
32
45f x x x Cx=++
(với
C
là
hằng số).
Vì
( )
1 26f =
nên
17C =
. Do đó
(
)
32
4 5 17fx x x x=++
.
Vậy
( )
4 404f =
.
Câu 49. Cho hình chữ nhật
ABCD
có tâm
I
, biết
AB a=
,
2AD a=
.
Gọi
J
là trung điểm
BC
, đường thẳng đi qua
I
và vuông góc
với
AC
cắt
CD
tại điểm
K
.Thể tích
V
của khối tròn xoay tạo
thành khi cho tứ giác
CKIJ
quay xung quanh trục
CK
bằng
A.
3
5
6
a
π
B.
3
7
6
a
π
.
C.
3
5
2
a
π
. D.
3
14
3
a
π
.
Lời giải
Chọn B
Gọi
,HE
lần lượt là điểm đối xứng của
,IJ
qua
CD
.
Gọi
F
là hình chiếu vuông góc của
I
lên
BC
.
Khi cho tứ giác
CKIJ
quay xung quanh trục
CK
tạo thành hai khối tròn xoay.
+) Khối I là khối nón đỉnh là
K
đáy là đường tròn đường kính
IH
và có tâm là
F
có thể tích là
1
V
.
Ta có
ACD KCI
∆∆
(g.g).
.5
2
AC CD AC IC a
CK
KC CI DC
⇒ =⇒= =
.
2
KF a
⇒=
.
(
)
( )
3
22
1
1 12
. .2
333
a
V IF KF a a
π
ππ
⇒= = =
.
+) Khối II là khối trụ có đáy một là hình tròn đường kính
IH
và có tâm là
F
, đáy hai là hình
tròn đường kính
JE
và có tâm là
C
có thể tích là
2
V
.
(
)
3
2
2
2
22
aa
V IF CF a
π
ππ
⇒= = =
.
Vậy
33 3
12
27
326
aa a
VVV
ππ π
=+= + =
.
Câu 50. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành. Gọi
E
là điểm đối xứng với
C
qua
B
và
F
là điểm thỏa mãn:
2.SF BF= −
 
. Mặt phẳng
( )
DEF
chia khối chóp
.S ABCD
thành 2 khối đa diện, trong đó khối đa diện chứa đỉnh
S
có thể tích
1
V
, khối đa
diện còn lại có thể tích
2
V
(tham khảo hình vẽ). Tính tỉ số
1
2
V
V
?
A.
3
5
. B.
1
5
. C.
7
5
. D.
12
7
.
Lời giải
Chọn C
Gọi
G
là giao điểm của
ED
và
AB
,
H
là giao điểm của
EF
và
SC
.
Vì
B
là trung điểm của
EC
và
2.SF BF= −
 
nên
F
là trọng tâm
SEC
∆
suy ra
H
là trung
điểm của
SC
, từ đó suy ra
..
1
2
A HCD A SCD
VV=
.
1
4
S ABCD
V=
.
Ta có
2EC AD=
và
/ / ADEC
do đó
..
2
E HCD A HCD
VV=
.
1
2
S ABCD
V
=
.
.
.H
..
E FBG
E CD
V
EB EG EF
V EC ED EH
=
112
..
223
=
1
6
=
. .H
1
6
E FBG E CD
VV⇒=
.
1
12
S ABCD
V=
.
2 . .F
E HCD E BG
VV V= −
..
11
2 12
S ABCD S ABCD
VV= −
.
5
12
S ABCD
V=
.
1. . .
57
12 12
S ABCD S ABCD S ABCD
VV V V=−=
Vậy
1
2
7
.
5
V
V
=
------------------------- HẾT -------------------------
| 1/28
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD&ĐT THANH HÓA
ĐỀ THI KHẢO SÁT CHẤT LƯỢNG LỚP 12 - LẦN 2
TRƯỜNG THPT THẠCH THÀNH 3 NĂM HỌC 2019-2020
MÔN : TOÁN Thời gian : 90 phút ( Đề gồm có 7 trang ) Mã đề thi 001 TỔ TOÁN - TIN
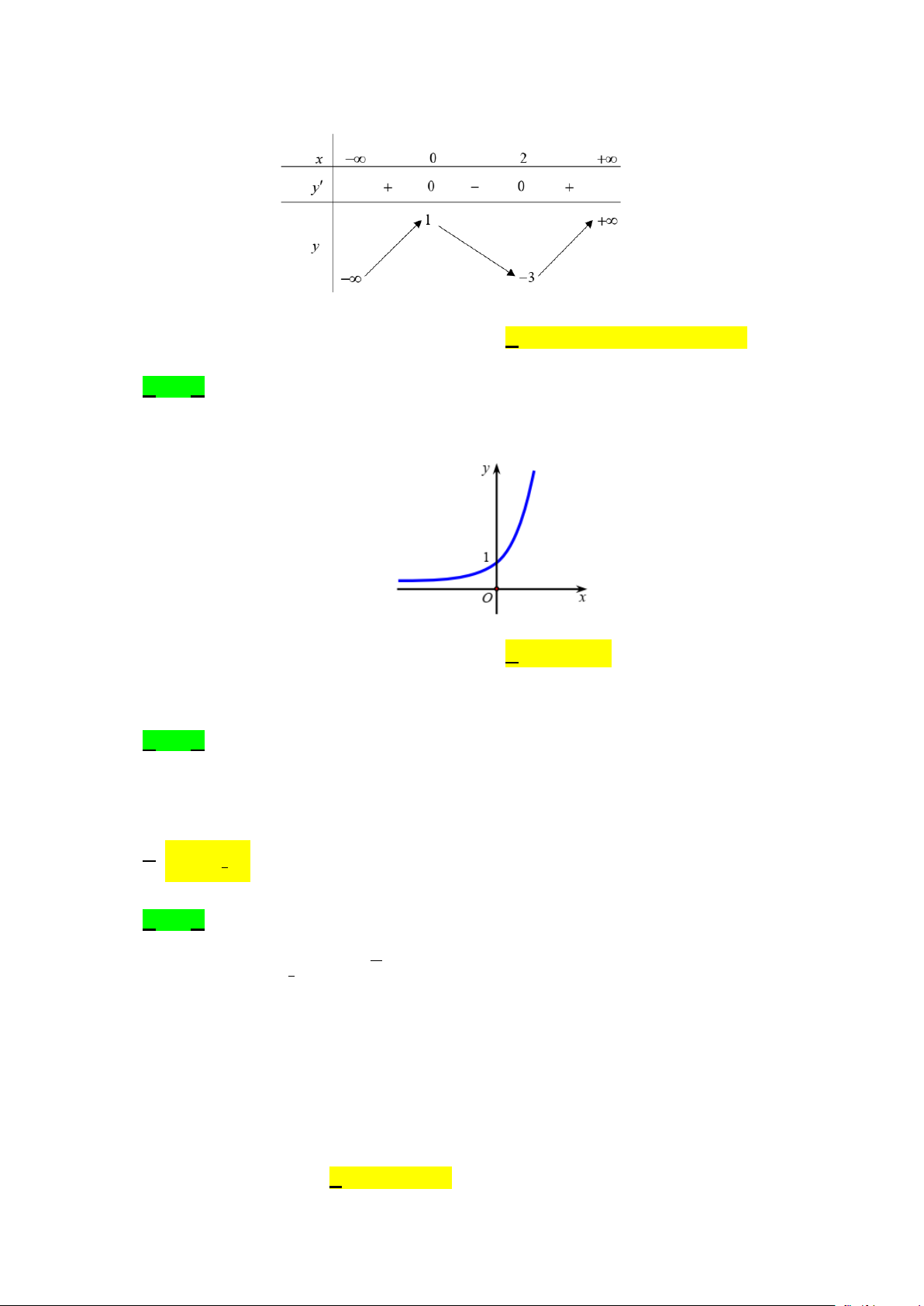
Câu 1. Cho hàm số y f  
x có bảng biến thiên như hình dưới đây. Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực đại tại x 1.
B. Hàm số đạt cực tiểu tại x  0 .
C. Hàm số đạt cực tiểu tại x  3  .
D. Hàm số đạt cực đại tại x  0 .
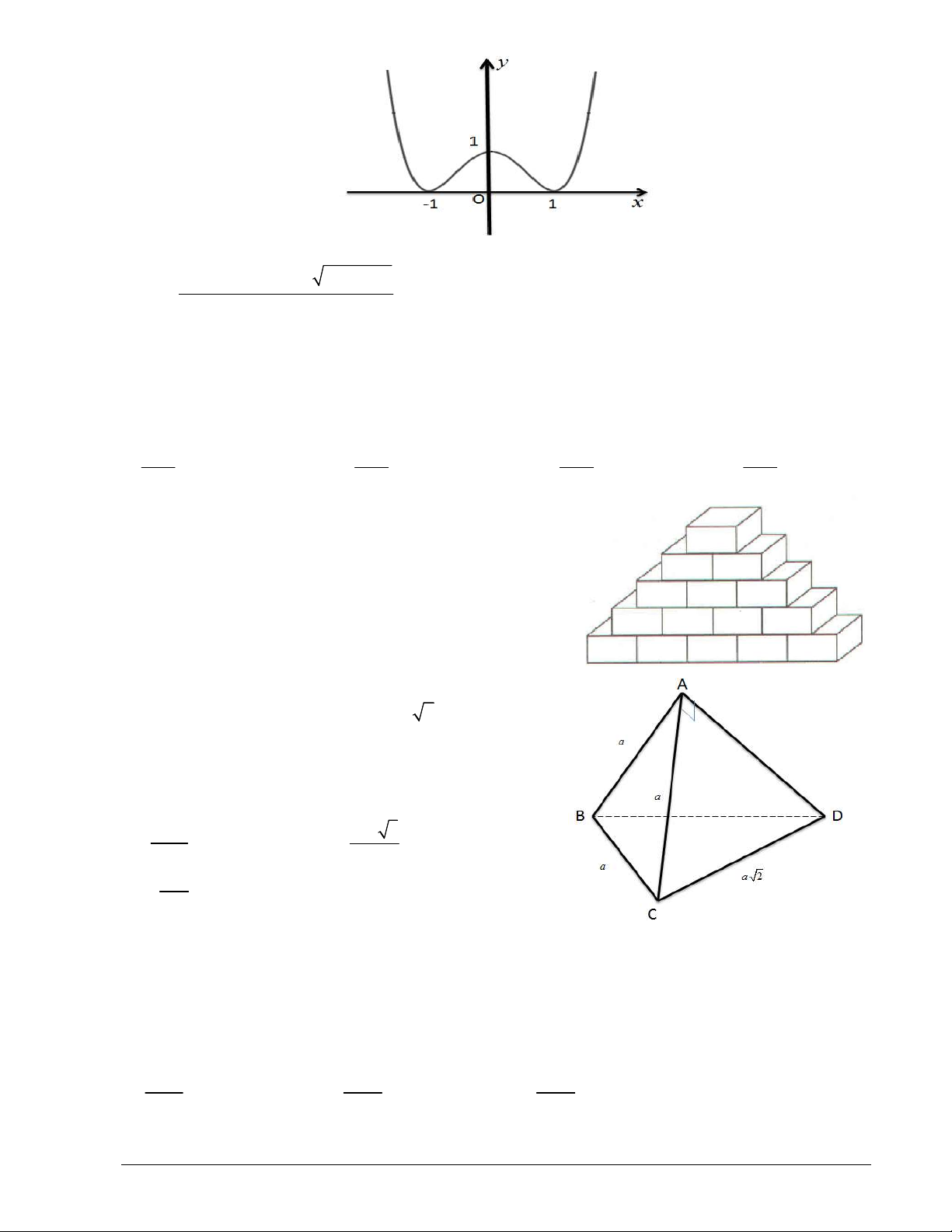
Câu 2. Hình vẽ sau đây là đồ thị của hàm số nào ? A. 3 y  x  3x 1 B. 4 2 y  x  2x 1 C. 2020x y  D. y  log x  2020 2020  
Câu 3. Trong các hàm số sau, hàm số nào nghịch biến trên 0; ? A. y  log x . B. y  log x . C. y  log x . D. y  ln x . 2 2020  3
Câu 4. Cho hàm số y  f (x) liên tục trên đoạn  1  ;  3 và có đồ
thị như hình vẽ. Gọi M , m lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của hàm số y  f (x) trên đoạn 1;  3 . Ta có giá trị của M  2m là :
A. M  2m 1 B. M  2m  2
C. M  2m  3 D. M  2m  4
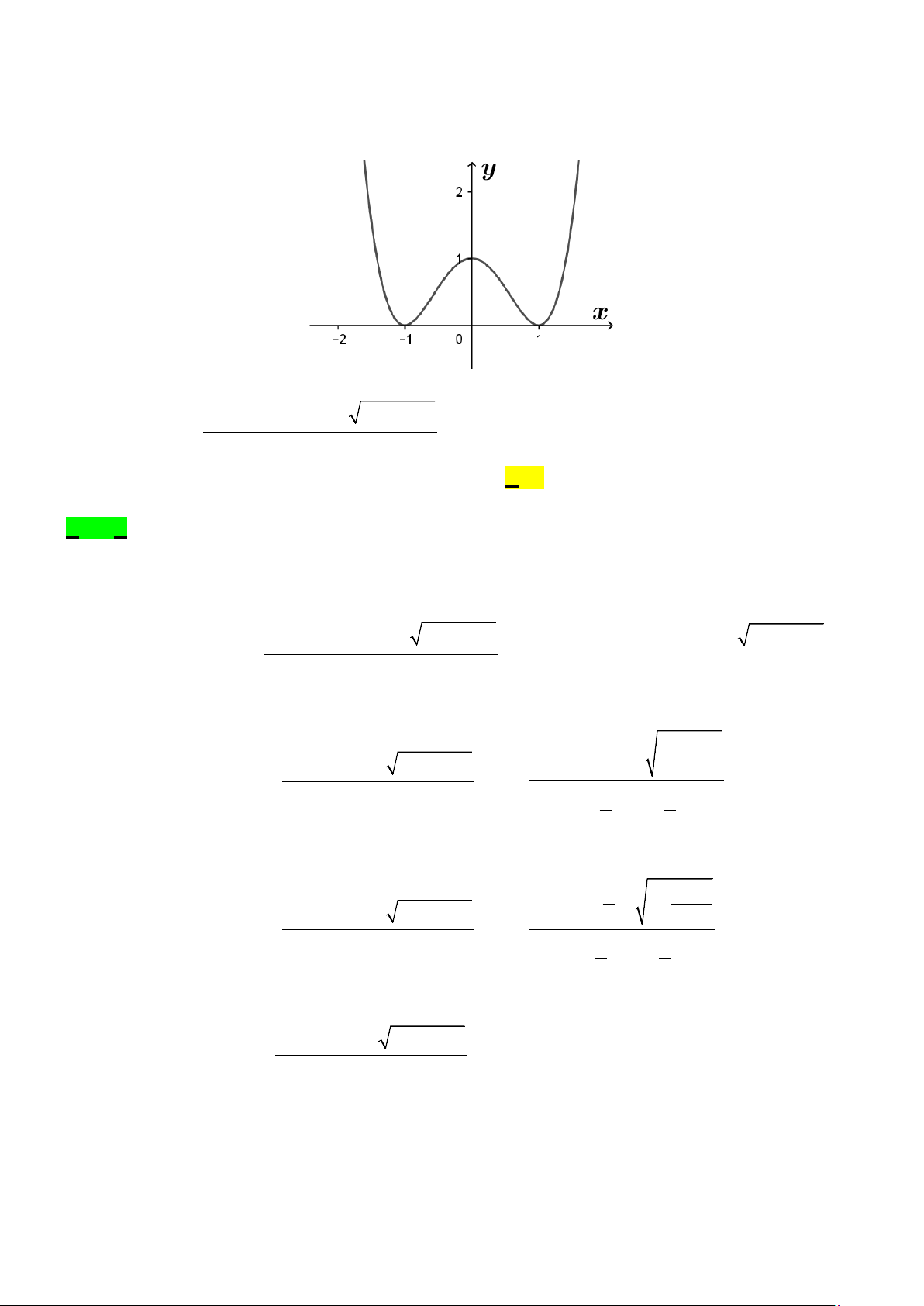
Câu 5. Hàm số y  f  x có đồ thị như hình vẽ .
Số nghiệm của phương trình: 2 f  x 1  0 là: A. 4 . B. 1. C. 2 . D. 3 . MÃ ĐỀ 001 - Trang 1/7
Câu 6. Hàm số y  log x có đồ thị như hình vẽ . Khẳng định a nào sau đây là đúng? A. 0  a 1. B. a  1. C. a  0 . D. a  0 .
Câu 7. Cho số thực a thỏa mãn 0  a 1 . Mệnh đề nào sau đây sai ?  x  A. log  . x y  log x  log y , x   0, y  0  x  y , x   0, y  0 a a a B. log log log a   a a  y  C. log b.log c.log a  1  b c  x  x   a b c với 0 , 1 D. 2 log 2log a a , x R 2x  2020
Câu 8. Đường tiệm cận ngang của đồ thị hàm số y  là : x  5 A. y  5 .
B. y  1010 . C. y  404 . D. y  2 .  1 x 
Câu 9. Cho hàm số y    . Khẳng định nào sau đây là sai?  2 
A. Hàm số nghịch biến trên R . B. Đồ thị hàm số nhận Oy làm tiệm cận đứng
C. Đồ thị hàm số luôn nằm trên Ox D. Đồ thị hàm số nhận Ox làm tiệm cận ngang.
Câu 10. Đạo hàm của hàm số x
y  e  log x 1, x  0 là: 3   A.  1 x  1 x 1 y '  e  . B. 1 ' x y  xe  . C. 1 y '  xe  . D. 1 ' x y  e  . x ln 3 x x ln 3 x
Câu 11 . Hàm số y  f  x có đồ thị như hình vẽ .
Hàm số y  f  x đồng biến trên khoảng nào dưới đây ? A. 1;  1 . B. 0;2 . C. 2;  1 . D.  2  ;  1 . 1
Câu 12. Tính tích phân     2 1 x I x e dx 0
A. I  2e 1 B. I  e 1 C. I  2e 1 D. I  e 1
Câu 13. Một nguyên hàm F x của hàm số   2x f x  là : x x A.   2x F x   2020 . B. F x 2   2020 . C. F x 2   2020x . D.   2x F x  ln 2 . ln 2 ln 2
Câu 14. Trong các hàm số sau,hàm số nào là hàm số lũy thừa ? 1 A. 2020x y  . B. 3 2 y  x . C. 4 y  x . D. x y  e . 1 6 6 Câu 15. Cho f  xdx  2 và f
 xdx  5, khi đó f xdx  bằng ? 0 1 0 A. 7 . B. 3  . C. 6 . D. 10 . MÃ ĐỀ 001 - Trang 2/7
Câu 16. Đường cong trong hình bên là đồ thị của
hàm số nào dưới đây ? A. 4 2 y  x  4x 1 B. 4 2 y  x  4x 1 C. 4 2 y  x  4x 1 D. 4 2 y  x  x 1 Câu 17. Cho biểu thức 3 2 4 3 P  x x x
với x  0 . Mệnh đề nào dưới đây đúng ? 13 23 12 23 A. 24 P  x 23 B. 12 P  x C. P  x D. 24 P  x
Câu 18. Cho a là số thực dương tùy ý, ln9a  ln7a bằng ? ln 9a 9 ln 9 A. . B. ln . C. ln 2a . D. . ln 7a 7 ln 7
Câu 19. Diện tích mặt cầu bán kính R bằng ? A. 2 4 R . B. 4 R . C. 2  R . D. 2 2 R .
Câu 20. Khối nón tròn xoay bán kính đáy R , đường
sinh l , chiều cao h , có thể tích V bằng ? A. V   Rl . B. 2 V   R h . C. 1 2 V   R h D. 2 V   R l . 3
Câu 21. Khối lập phương là khối đa diện đều loại ? A. 3;  4 . B.3;  3 . C. 3;  5 . D. 4;  3 .
Câu 22. Khối bát diện đều có số mặt phẳng đối xứng ? A. 3 . B. 4 . C. 5 . D. 6 .
Câu 23. Mặt trụ tròn xoay bán kính đáy R , chiều cao h , có
diện tích xung quanh S bằng ? xq A. S   Rh . B. 2 S  2 Rh   R xq xq     C. 2 S 2 R D. S 2 Rh . xq xq
Câu 24. Khối hai mươi mặt đều có số đỉnh là ? A. 20 . B.12 . C. 30. D. 8 . MÃ ĐỀ 001 - Trang 3/7
Câu 25. Nghiệm của phương trình 2x 1 2   32 bằng ? A. x  2 . B. x  3 . C. 3 x  . D. 5 x  . 2 2
Câu 26. Cho phương trình log x 1 1 3 
 . Mệnh đề nào sau đây đúng ?
A. x 1;3 . B. x 0;2 . C. x3;4 . D. x 3;5 .
Câu 27. Nguyên hàm F x của hàm số f x 3  x  x 1 là : 4 2 x x 4 2 x x A. F x  
 x B. F x    xC. C. F x 2  3x 1 . D. F x 4 2  x  x 1C . 4 2 4 2
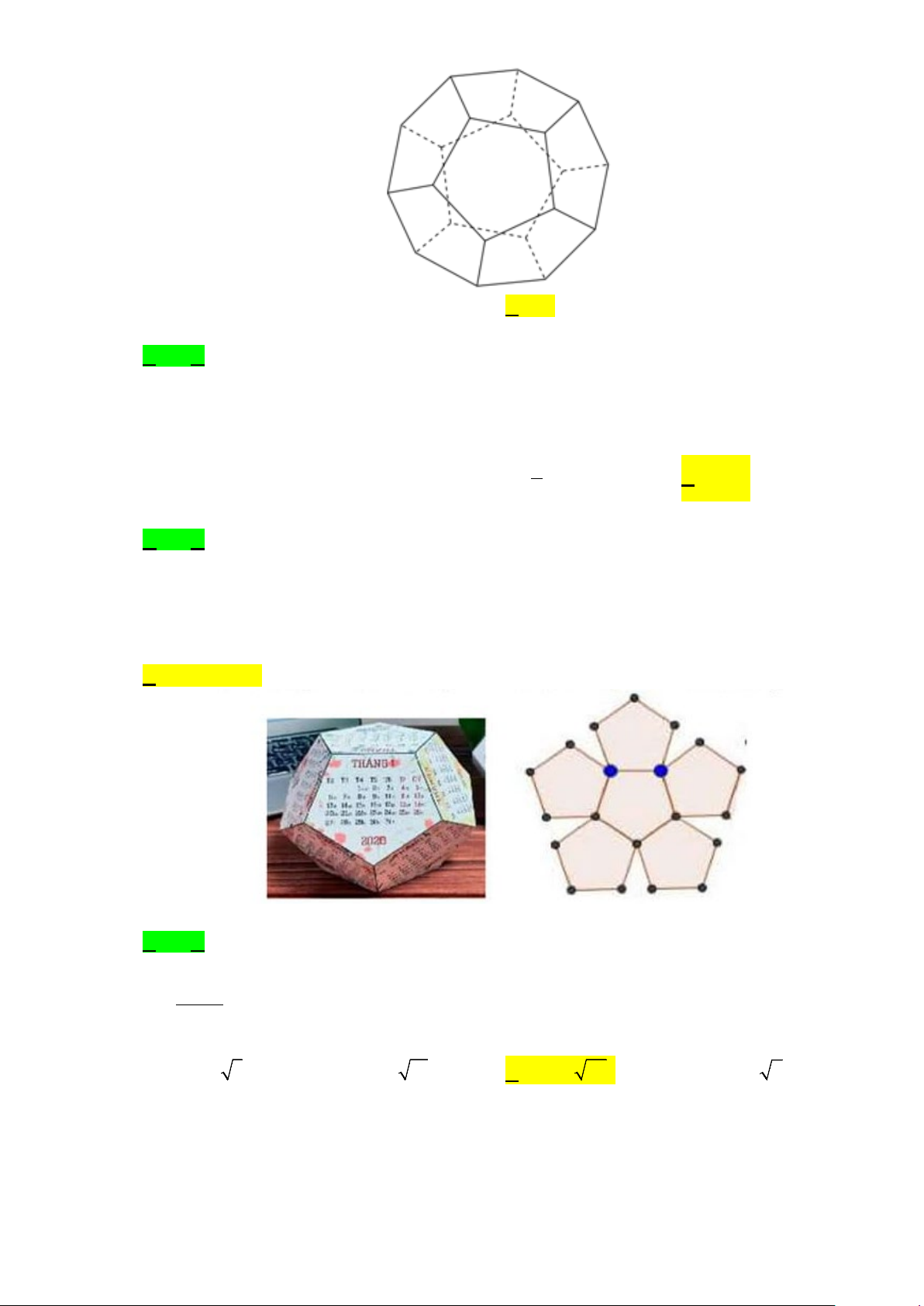
Câu 28. Khối mười hai mặt đều có số cạnh là ? A. 20 . B.12 . C. 30. D. 8 .
Câu 29. Thể tích của khối trụ có bán kính đáy R  a và chiều cao h  2a bằng : A. 3 2 2a B. 3 4 a . C. 3  a . D. 3 2 a . 3
Câu 30. Để làm một sản phẩm lịch Canh Tý 2020 để bàn như hình vẽ cần dùng 2 50cm giấy cho
mỗi mặt ( ứng với một tháng trong năm). Biết đơn giá giấy trên thị trường là 200.000 đồng 2 /m . Hỏi
chi phí giấy cần dùng để làm một sản phẩm lịch trên bằng :
A. 12.000 đồng B. 20.000 đồng . C. 6.000.000 đồng . D. 200.000 đồng .
Câu 31. Tính độ dài đoạn thẳng AB trong hình vẽ :
A. AB  3 3 . B. AB  13 .
C. AB  26 . D. AB  2 2 . MÃ ĐỀ 001 - Trang 4/7
Câu 32. Gọi S là tập hợp tất cả các nghiệm nguyên của bất phương trình log x  2  2 . Tổng 1   2
các phần tử của S bằng ? A. 2 . B. 2 . C. 0 . D. 3
Câu 33. Thể tích của khối lập phương cạnh 5cm bằng ? A. 3 20cm . B. 3 125cm . C. 3 25cm . D. 3 30cm 2 x  4 Câu 34. Tích phân I  dx  a ln 3  b ln 2  . Khi đó 2 b  a bằng ? 2 x  3x  2 0 A. 2 b  a  1 B. 2 b  a  1 C. 2 b  a  0 D. 2 b  a  4
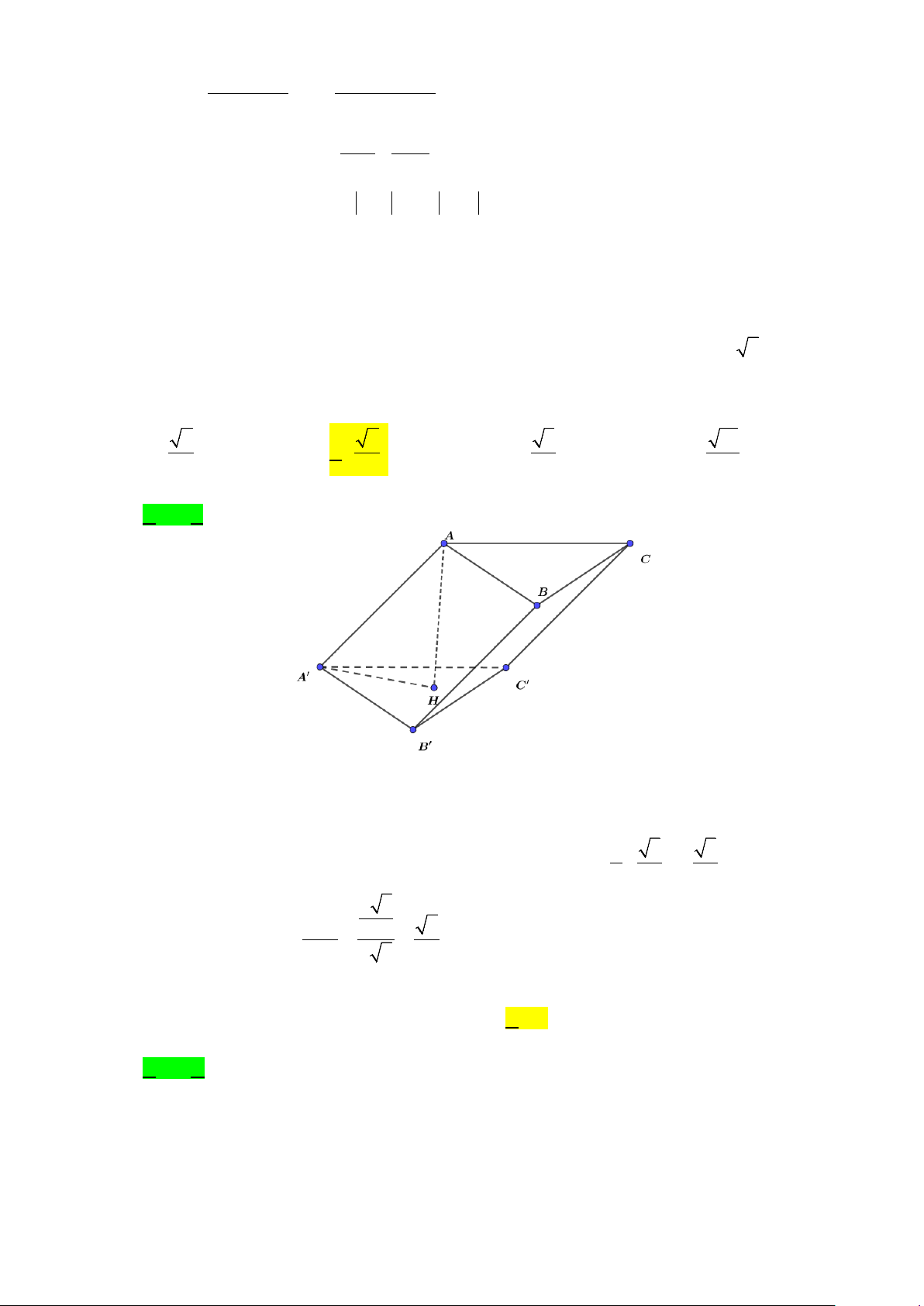
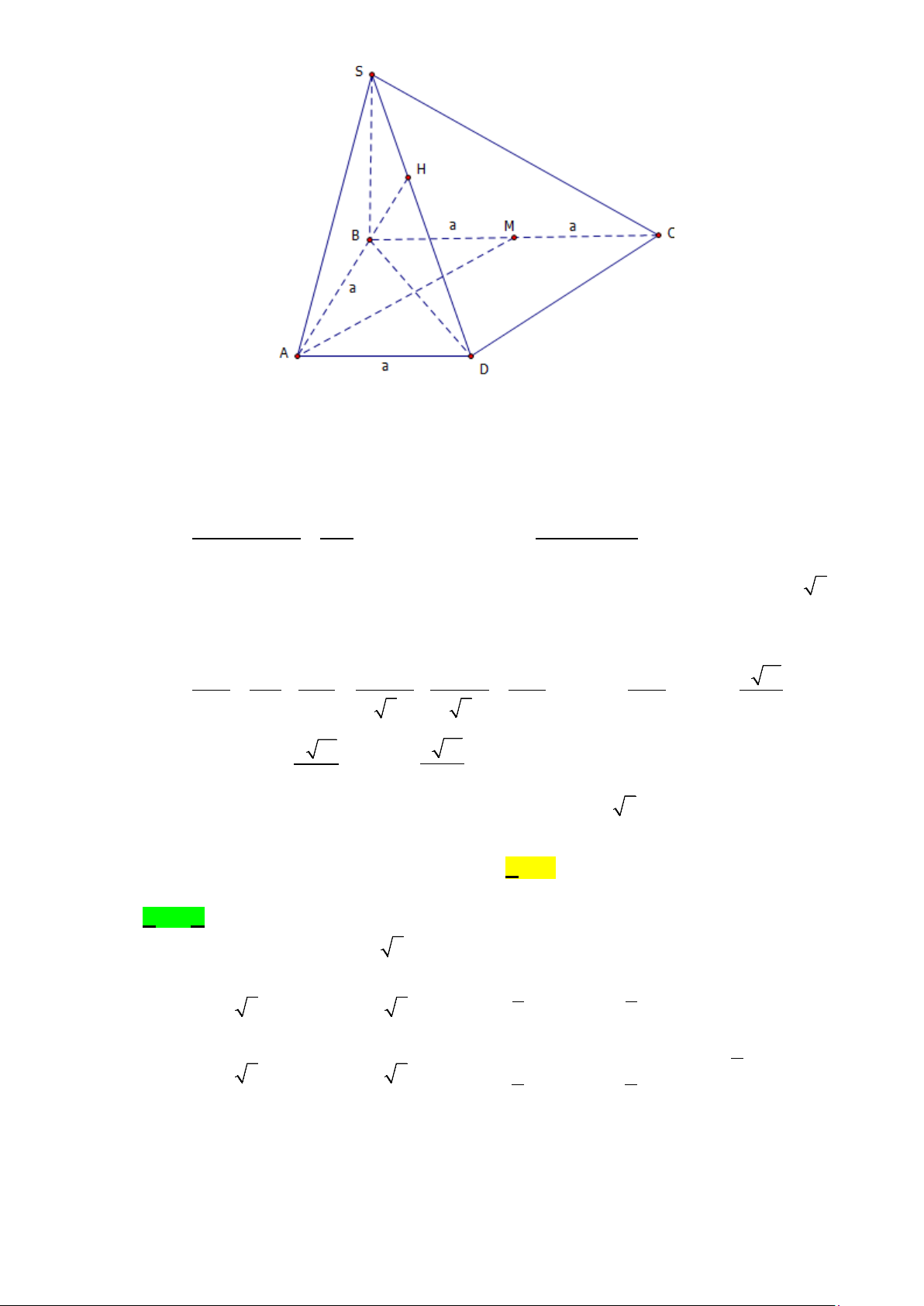
Câu 35. Hình lăng trụ tam giác ABC.A'B'C' có đáy là tam
giác đều cạnh a , AA '  a 6 . Hình chiếu vuông góc H
của A trên mặt phẳng  A' B 'C ' trùng với trọng tâm của
tam giác A' B 'C ' . Côsin của góc giữa cạnh bên và mặt đáy bằng ? A. 2 . B. 2 . 3 6 C. 3 . D. 15 . 6 15
Câu 36. Tổng các nghiệm của phương trình log x  log  x  3 3  2 2 8 bằng ? A. 3 . B. 2 . C. 4 . D. 0 .  4 x   3 x 
Câu 37. Bất phương trình 3.  5.  2  0    
có tập nghiệm S   ; a b .  9   2  Khi đó, giá trị của 2 2 a  b bằng ? 13 5 13 A. . B. . C. . D. 1 . 9 3 4
Câu 38. E.coli là vi khuẩn đường ruột gây tiêu chảy, đau bụng dữ dội. Cứ sau 20 phút thì số lượng vi
khuẩn E.coli lại tăng gấp đôi. Ban đầu chỉ có 40 vi khuẩn E.coli trong đường ruột. Hỏi sau bao lâu,
số lượng vi khuẩn E.coli là 671088640 con ? A. 48 giờ. B. 24 giờ. C. 8 giờ. D. 12 giờ.
Câu 39. Cho hình chóp S.ABCD có đáy ABCD là hình thang
vuông tại A và B , AB  AD  a, BC  2a . Cạnh bên SB vuông
góc với đáy và SB  a 7 , M là trung điểm của BC . Tính
khoảng cách d giữa hai đường thẳng AM và SC ? A. a 14 a d  . B. 3 14 d  . 3 2 C. a 14 a d  . D. 3 7 d  . 6 7
Câu 40. Số giá trị nguyên dương của m để bất phương trình  x2 2
 2 2x  m  0 có tập nghiệm
chứa không quá 6 số nguyên ? A. 62 . B. 33 . C. 32. D. 31 . MÃ ĐỀ 001 - Trang 5/7
Câu 41. Cho giới hạn f x 4 2
 ax  bx  c a  0 có đồ thị là đường cong như hình vẽ. Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số 2002 3 2 x  3x  4 2  g  x x 2020  là ? f  x A. 3 . B. 5 . C. 4 . D. 2
Câu 42. Nhân dịp đi du Xuân Canh Tý, ba bạn Trang, Hoàng, Tân rủ nhau rút quẻ xem vận mệnh.
Khi đó trong hộp chỉ còn các quẻ có số thứ tự từ 5 đến 15 (luôn có ít nhất ba quẻ cùng ghi một số).
Mỗi bạn rút ngẫu nhiên một quẻ và yêu cầu bạn Linh tính xác suất để tổng các số ghi trên ba quẻ là
một số chia hết cho 3 . Kết quả đúng là ? 112 60 203 443 A. . B. . C. . D. . 1331 1331 1331 1331
Câu 43. Bà chủ khách sạn trên đèo Mã Pì Lèng muốn
trang trí một góc nhỏ trên ban công sân thượng cho đẹp
nên quyết định thuê nhân công xây một bức tường gạch
với xi măng (như hình vẽ), biết hàng dưới cùng có 500
viên, mỗi hàng tiếp theo đều có ít hơn hàng trước 1 viên
và hàng trên cùng có 1 viên . Hỏi số gạch cần dùng để
hoàn thành bức tường trên là bao nhiêu viên ?
A. 25250 . B.125250 . C.12550 . D. 250500 .
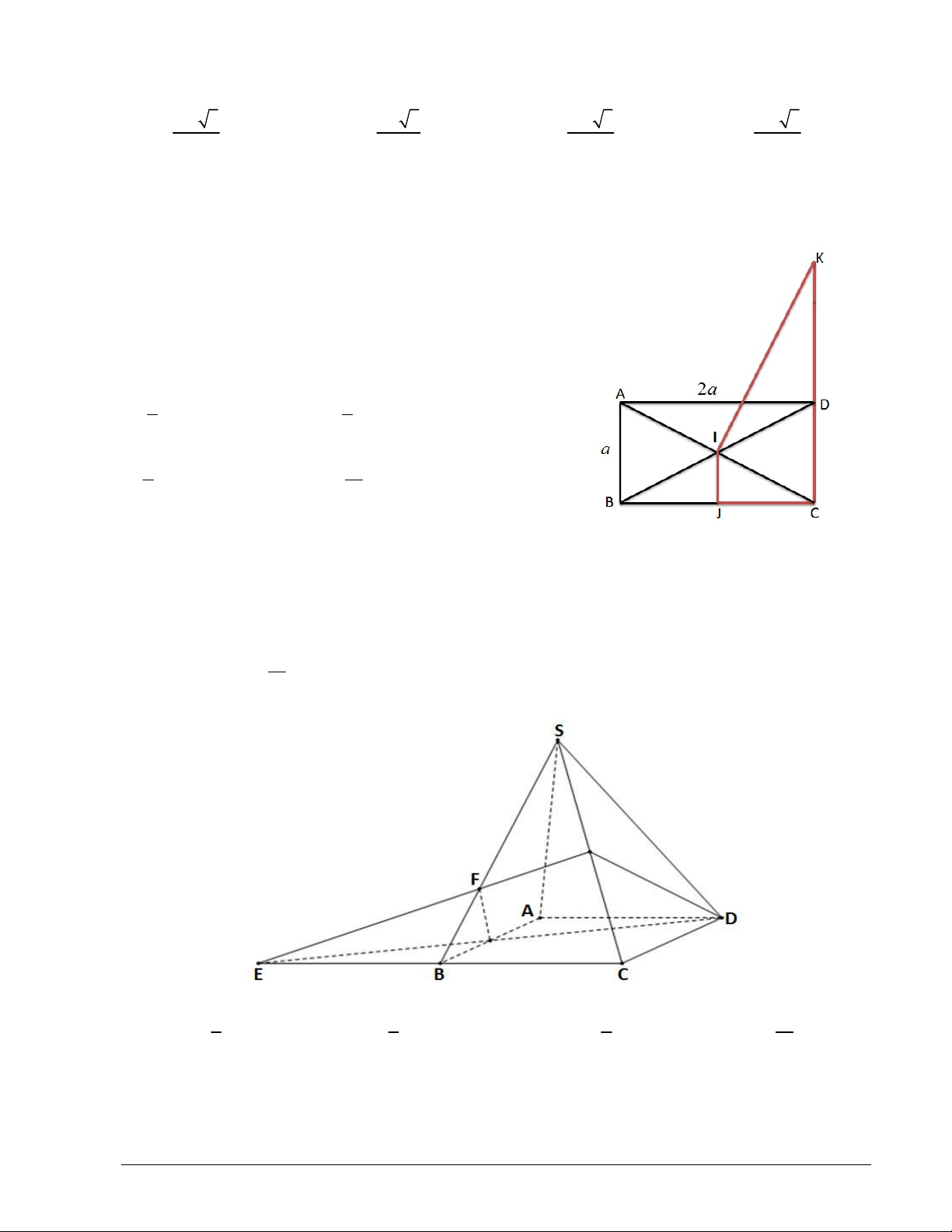
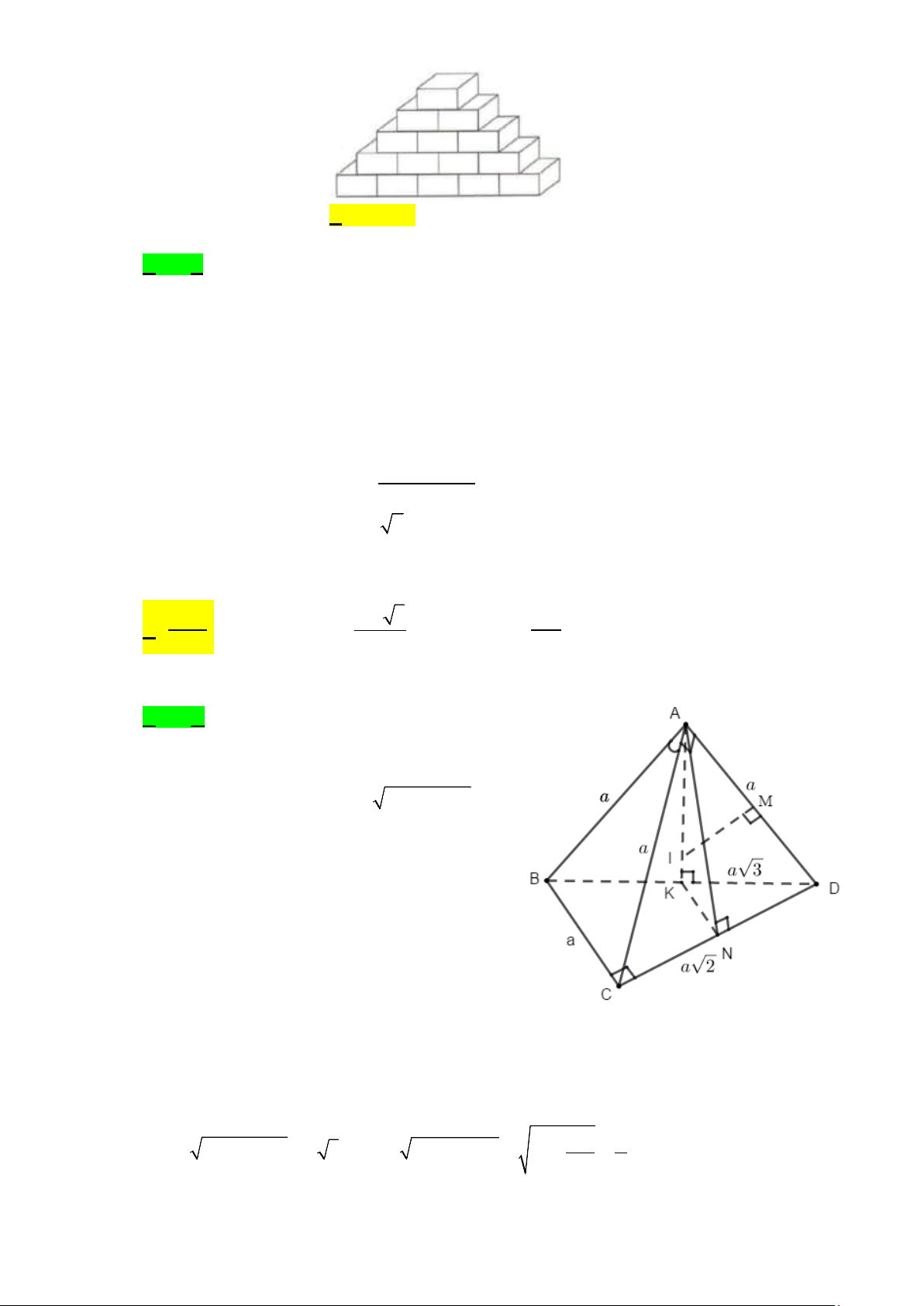
Câu 44. Cho tứ diện ABCD có CD  a 2 , A  BC
là tam giác đều cạnh a , A  CD vuông tại A . Mặt
phẳng BCD vuông góc với mặt phẳng  ABD .
Thể tích khối cầu ngoại tiếp tứ diện ABCD bằng ? 3 4 a 3  a 3 A. . B. . 3 2 3  a C. . D. 3 4 a . 6
Câu 45. Cho phương trình 5x  m  log x  m , với m là tham số. Số giá trị nguyên của 5   m  2
 020; 2020 để phương trình đã cho có nghiệm là ?
A. 9 . B. 2021 . C. 2020 . D. 2019 .
Câu 46. Gọi S là tập hợp tất cả các nghiệm thuộc đoạn 0;13  của phương trình 3 2
2 cos x  cos x  cos 2x  0 . Tổng các phần tử của S bằng ? 380 400 420 A. . B. . C. . D.120 3 3 3 MÃ ĐỀ 001 - Trang 6/7
Câu 47. Tìm tất cả các giá trị của tham số m để đường thẳng đi qua cực đai, cực tiểu của đồ thị hàm số 3
y  x 3mx  2 cắt đường tròn C  tâm I 1; 
1 , bán kính bằng 1 tại hai điểm phân biệt , A B sao cho
diện tích tam giác IAB đạt giá trị lớn nhất ? 2  3 1 3 2  3 2  5 A. m  . B. m  . C. m  . D. m  . 3 2 2 2
Câu 48. Cho hàm số y  f  x có đạo hàm liên tục trên 1;4 thỏa mãn f   1  26 và f  x  x f x 3 2 . '
8x  5x . Tính giá trị của f 4 ? A. 400 . B. 2020 . C. 404 . D. 2022 .
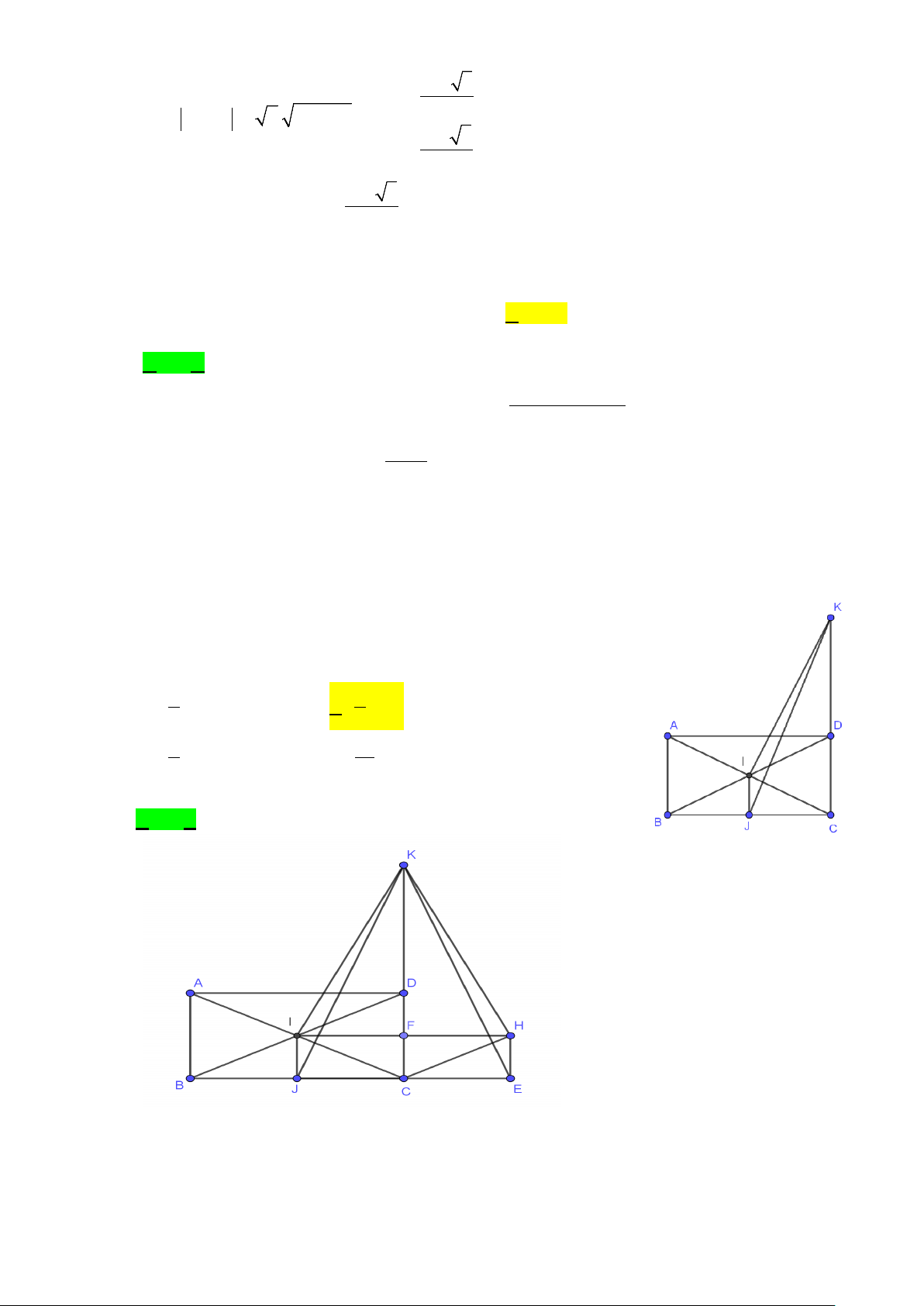
Câu 49. Cho hình chữ nhật ABCD tâm I , biết AB  a ,
AD  2a . Gọi J là trung điểm của BC , đường thẳng qua
I và vuông góc với AC cắt CD tại điểm K . Thể tích V
của khối tròn xoay tạo thành khi cho tứ giác CKIJ quay xung quanh trục CK bằng ? 5 7 A. 3 a . B. 3  a . 6 6 5 14 C. 3  a . D. 3  a . 2 3
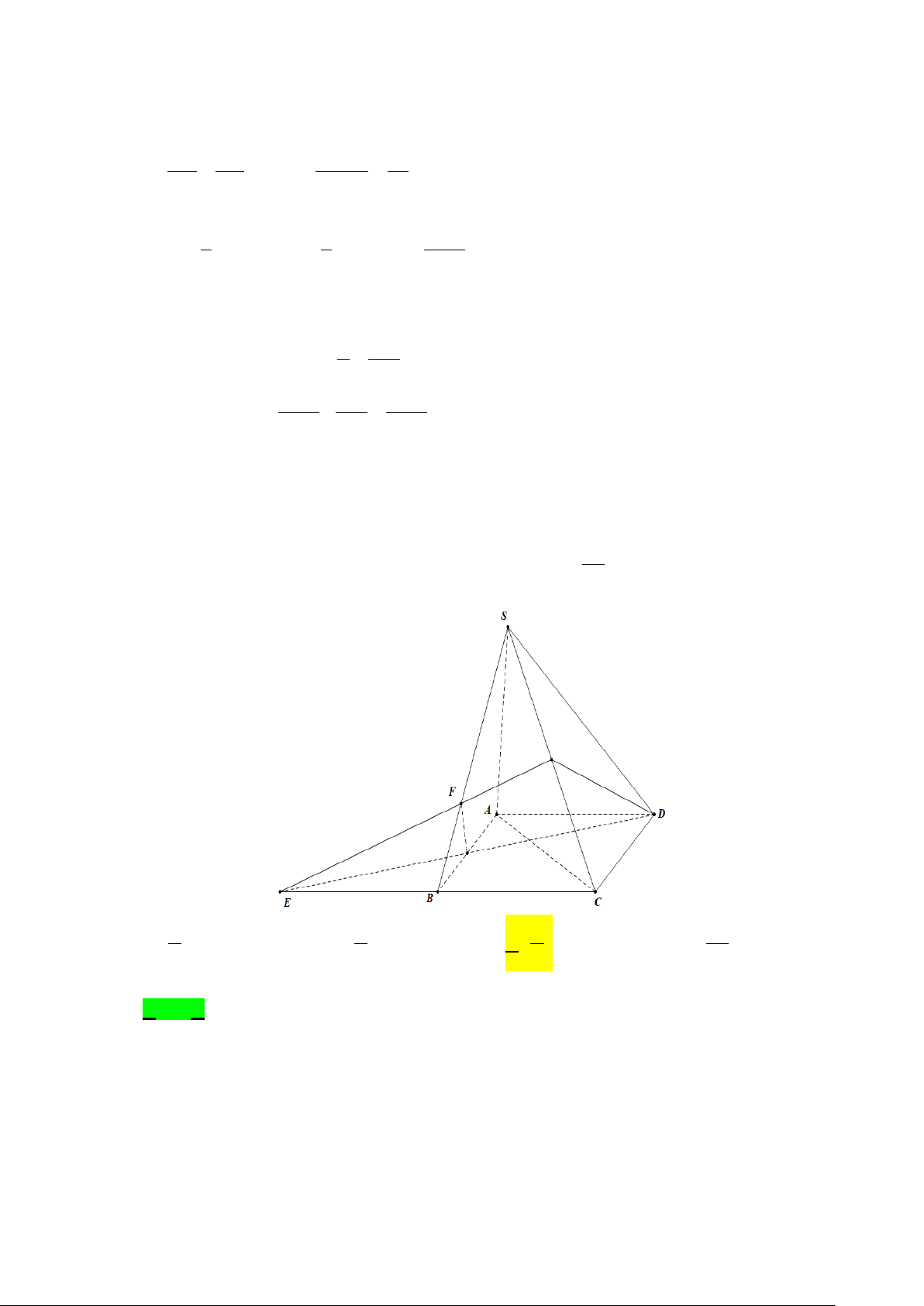
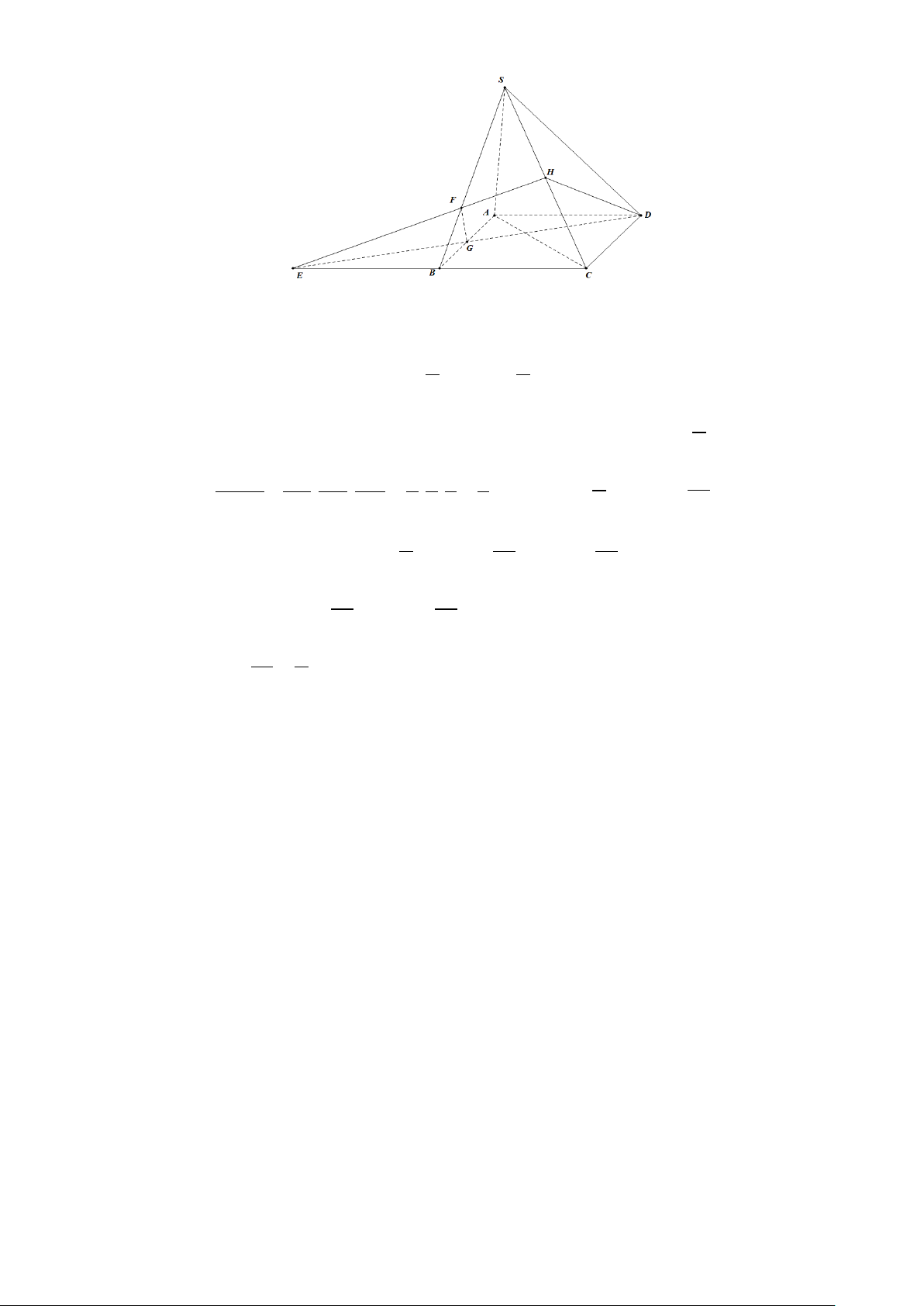
Câu 50. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi E là điểm đối xứng với C qua  
B và F là điểm thỏa mãn : SF  2
 .BF . Mặt phẳng DEF chia khối chóp S.ABCD thành 2 khối đa
diện, trong đó khối đa diện chứa đỉnh S có thể tích V , khối đa diện còn lại có thể tích V ( tham khảo 1 2 V
hình vẽ). Tính tỉ số 1 ? V2 3 1 7 12 A. . B. . C. . D. . 5 5 5 7 ---------- HẾT ---------- MÃ ĐỀ 001 - Trang 7/7
LỜI GIẢI CHI TIẾT
Câu 1. Cho hàm số y = f (x) có bảng biến thiên như hình dưới đây. Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực đại tại x =1.
B. Hàm số đạt cực tiểu tại x = 0 .
C. Hàm số đạt cực tiểu tại x = 3 − .
D. Hàm số đạt cực đại tại x = 0 . Lời giải Chọn D
Dựa vào bảng biến thiên ta có hàm số đạt cực đại tại x = 0 .
Câu 2. Hình vẽ sau đây là đồ thị của hàm số nào? A. 3
y = x − 3x +1 B. 4 2
y = x − 2x +1. C. 2020x y = . D. y = log x + 2020 . 2020 ( ) Lời giải Chọn C
Do đồ thị hàm số luôn đồng biến trên  nên loại các phương án A, B.
Mà đồ thị luôn nằm phía trên trục Ox nên loại phương án D.
Câu 3. Trong các hàm số sau, hàm số nào nghịch biến trên (0;+∞)?
A. y = log x . B. y = log x .
C. y = log .
D. y = ln x . π x 2 2020 3 Lời giải Chọn A 2
Xét hàm số y = log x có a = ⇒ 0 < a <1⇒ hàm số nghịch biến trên (0;+ ∞). 2 3 3 Xét hàm số y = log
x có a = 2020 >1⇒ hàm số đồng biến trên (0;+ ∞) . 2020
Xét hàm số y = log có a = π >1⇒ hàm số đồng biến trên (0;+ ∞). π x
Xét hàm số y = ln x có a = e> 1⇒ hàm số đồng biến trên (0;+ ∞).
Câu 4. Cho hàm số f x liên tục trên [ 1; − ]
3 và có đồ thị như hình vẽ bên. Gọi M ,m lần lượt là giá
trị lớn nhất và giá trị nhỏ nhất của hàm số y = f (x) trên [ 1; − ]
3 . Ta có giá trị của M + 2m là:
A. M + 2m =1.
B. M + 2m = 2 .
C. M + 2m = 3 .
D. M + 2m = 4 . Lời giải ChọnB
Quan sát đồ thị ta thấy hàm số y = f (x) đạt giá trị nhỏ nhất trên [ 1; − ] 3 là 1 − tại điểm x = 1 −
và đạt giá trị lớn nhất trên [ 1; − ]
3 là 4 tại điểm x = 3 . Do đó m = 1, − M = 4 .
Giá trị M + 2m = 4 + 2.(− ) 1 = 2 .
Câu 5. Hàm số y = f (x) có đồ thị như hình vẽ. Số nghiệm của phương trình 2 f (x) −1= 0 là A. 4. B. 1. C. 2. D. 3. Lời giải Chọn A
Ta có: f (x) − = ⇔ f (x) 1 2 1 0 = ; 2
Số nghiệm của phương trình f (x) 1
= chính là số giao điểm của đồ thị hàm số y = f (x) và 2 đường thẳng 1 y = . 2 Đường thẳng 1
y = cắt đồ thị hàm số y = f (x) tại 4 điểm phân biệt. 2
Vậy phương trình 2 f (x) −1 = 0 có 4 nghiệm phân biệt.
Câu 6. Cho hàm số y = f (x) = log x . Tìm tất cả các giá trị thực của a để hàm số f (x) đồng biến a trên (0;+ ∞).
A. 0 < a <1. B. a >1. C. a ≠ 0 . D. a > 0 . Lời giải Chọn B
Dựa vào đồ thị ta có hàm số y = log x là hàm đồng biến trên (0;+ ∞) ⇒ a >1. a
Câu 7. Cho số thực a thỏa mãn 0 < a ≠1. Mệnh đề nào sau đây là sai?  x A. log x y = x + y = x −   y a ( . ) loga loga , x
∀ > 0 , y > 0. B. loga loga loga , x ∀ > 0 , y > 0.  y C. log b c a = < x = x
a .logb .logc
1, với 0 b , c ≠1. D. 2 loga 2loga , x ∀ ∈  . Lời giải Chọn C Ta có log b c a =
a .logb .logc
1 có chứa a , b , c là cơ số của lôgarit nên điều kiện là a , b , c là các số dương khác 1.
Câu 8. Đường tiệm cận ngang của đồ thị hàm số 2x − 2020 y = là: x + 5 A. y = 5 − . B. y =1010. C. y = 404 − . D. y = 2 . Lời giải Chọn D Ta có 2x − 2020 lim − = 2 và 2x 2020 lim
= 2 nên đồ thị hàm số có tiệm cận ngang là đường x→+∞ x + 5 x→−∞ x + 5 thẳng y = 2 . x Câu 9. Cho hàm số 1 y   = 
. Khẳng định nào sau đây là sai? 2   
A. Hàm số nghịch biến trên  .
B. Đồ thị hàm số nhận Oy làm tiệm cận đứng.
C. Đồ thị hàm số luôn nằm trên Ox
D. Đồ thị hàm số nhận Ox làm tiệm cận ngang Lời giải Chọn B
Đồ thị của hàm số mũ không nhận Oy làm tiệm cận đứng.
Câu 10. Đạo hàm của hàm số x
y = e − log x +1, x > 0 là: 3 ( ) A. x 1 y′ = e − . B. x 1 − 1 y′ = xe − . C. x 1 − 1 y′ = xe − . D. x 1 y′ = e − . x ln 3 x x ln 3 x Lời giải Chọn A
Ta có y′ = ( x ′ x 1
e − log x +1 = e − . 3 ) x ln 3
Câu 11. Hàm số y = f (x) có đồ thị như hình vẽ. Hàm số y = f (x) đồng biến trên khoảng nào dưới đây ? A. ( 1; − ) 1 . B. (0;2) . C. ( 2; − − ) 1 . D. ( 2; − ) 1 . Lời giải Chọn C
Dựa vào đồ thị ta có hàm số y = f (x) đồng biến trên ( 2; − − ) 1 và (1;+ ∞) . 1
Câu 12. Tính tích phân = ( + ∫ )2 1 x I x e dx 0
A. I = 2e +1.
B. I = e +1.
C. I = 2e −1.
D. I = e −1. Lời giải Chọn C 1 = ( + ∫ )2 1 x I x e dx 0
Đặt u = (x + )2
1 suy ra du = 2(x + ) 1 dx d = ex v dx , chọn ex v = 1 1 Do đó = ( + )2 1 ex − 2 ( + ∫ )1 x I x x
e dx = (4e − ) 1 − 2 1I. ( ) 1 0 0 1 Tính x 1 I = (x + ∫ )1e dx 0
Đặt u = x +1 suy ra du = dx d = ex v dx , chọn ex v = 1 1 Do đó x x =  + −  1 I = (x + )
1 e − ∫e dx ( ) 1 1 ex x x e
= 2e − e − 1−1 = e. (2) 0   ( ) ( ) 0 0 Từ ( )
1 và (2) ta được I = 2e −1.
Câu 13. Một nguyên hàm F (x)của hàm số ( ) 2x f x = là: x A. ( ) 2x F x = + 2020 .
B. F (x) 2 = + 2020. ln 2 x
C. F (x) 2 = + 2020x . D. ( ) 2x F x = ln 2 . ln 2 Lời giải Chọn B x Ta có x 2 2 dx = + C ∫
. Cho C = 2020 ta được một nguyên hàm của hàm số ( ) 2x f x = là ln 2 x F (x) 2 = + 2020. ln 2
Câu 14. Trong các hàm số sau, hàm số nào là hàm số lũy thừa? 1 A. 2020x y = . B. 3 2 y = x . C. 4 y = x . D. x y = e . Lời giải Chọn C
Ta có theo định nghĩa hàm số lũy thừa là hàm số có dạng y = xα ;α ∈ . 1 6 6 Câu 15. Cho f
∫ (x)dx = 2 và f
∫ (x)dx = 5. Khi đó f (x)dx ∫ bằng? 0 1 0 A. 7. B. 3 − . C. 6 . D. 10. Lời giải Chọn A 6 1 6 f
∫ (x)dx = f
∫ (x)dx+ f
∫ (x)dx = 2+5 = 7. 0 0 1
Câu 16. Đường cong trong hình bên dưới là đồ thị của hàm số nào sau đây? A. 4 2
y x 4x 1. B. 4 2
y  x  4x 1. C. 4 2
y x 4x 1. D. 4 2
y x x 1. Lời giải Chọn C
Đây là đồ thị một hàm số bậc bốn trùng phương có dạng: 4 2
y ax bx c a  0.
Mà lim y   chứng tỏ a  0 . Do đó ta loại phương án B. x
Đồ thị cắt trục tung tại điểm có tung độ y 1 nên c 1. Do đó ta loại phương án A.
Đồ thị hàm số có 3 điểm cực trị nên a, b trái dấu. Vậy ta chọn phương án C.
Câu 17. Cho biểu thức 3 2 4 3
P x x x với x  0 . Mệnh đề nào sau đây là đúng? 13 23 12 23 A. 24 P x . B. 12 P x . C. 23 P x . D. 24 P x . Lời giải Chọn D 3 11 11 23 23
Với x  0 , ta có: 3 3 3 2 4 3 2 4 4 12 12 24
P x x x x x .x x x
.xx x x .
Câu 18. Cho a là số thực dương tùy ý, ln9aln7a bằng? ln9aA. . B. ln  . C. ln2a. D. ln 9 . ln7a 7 ln 7 Lời giải Chọn B
Với a là số dương, ta có: ln9a 9 9
ln7a  ln a  ln . 7a 7
Câu 19. Diện tích mặt cầu bán kính R bằng? A. 2 4R . B. 4R . C. 2 R . D. 2 2R . Lời giải Chọn A
Diện tích mặt cầu bán kính R bằng: 2 S  4R .
Câu 20. Cho khối nón tròn xoay bán kính đáy R , đường sinh l , đường cao h có thể tích V bằng bao nhiêu? A. V 1  Rl . B. 2 V R h . C. 2 V R h . D. 2 V R l . 3 Lời giải Chọn C
Với khối nón tròn xoay bán kính đáy R , đường sinh l , đường cao h có thể tích 1 2
V R h . 3
Câu 21. Khối lập phương là khối đa diện đều loại? A. 3;  4 . B. 3;  3 . C. 3;  5 . D. 4;  3 . Lời giải Chọn D
Khối đa diện đều loại  ;
p q là khối đa diện lồi có
- Mỗi mặt là một đa giác đều có p cạnh.
- Mỗi đỉnh là đỉnh chung của đúng q mặt.
Do đó khối lập phương là khối đa diện đều loại 4;  3 .
Câu 22. Khối bát diện đều có số mặt phẳng đối xứng? A. 3. B. 4 . C. 9. D. 6 . Lời giải Chọn C
Các mặt phẳng đối xứng của bát diện đều
+ Xem ABCD là mặt phẳng đáy và hai đỉnh E , F ta có ba mặt phẳng đối xứng sau ABCD EMFN EPFQ
+ Tương tự, xem AECF là mặt phẳng đáy và hai đỉnh B , D ta cũng có ba mặt phẳng đối
xứng và xem BEDF là mặt phẳng đáy và hai đỉnh A , C ta cũng có ba mặt phẳng đối xứng.
Vậy có tất cả 9 mặt phẳng đối xứng.
Câu 23. Mặt trụ tròn xoay bán kính đáy R , chiều cao h , có diện tích xung quanh S bằng xq
A. S Rh
S Rh R S R S Rh xq . B. 2 xq 2 . C. 2 xq 2 . D. xq 2 . Lời giải Chọn D
Diện tích xung quanh hình trụ bằng chu vi đường tròn đáy nhân với chiều cao: S Rh xq 2 .
Câu 24. Khối hai mươi mặt đều có số đỉnh là A. 20 . B. 12. C. 30. D. 8 . Lời giải Chọn B
Câu 25. Nghiệm của phương trình 2x 1 2   32 bằng A. x  2 . B. x  3. C. 3 x  . D. 5 x  . 2 2 Lời giải Chọn A Ta có 2x 1 2   32 2x 1  5  2
 2  2x 1 5  x  2.
Câu 26. Cho phương trình log x −1 =1. Mệnh đề nào sau đây đúng? 3 ( ) A. x∈(1;3) . B. x∈(0;2) . C. x∈(2;4) . D. x∈(3;5) . Lời giải Chọn D
Ta có phương trình: log x −1 =1 3 ( ) x −1 > 0 x > 1 ⇔  ⇔ 
⇔ x = 4. Vậy x∈(3;5) . x −1 = 3 x = 4
Câu 27. Họ nguyên hàm của hàm số f (x) 3
= x − x +1 là 4 2 4 2 A. ( ) x x F x = − + x . B. ( ) x x F x = −
+ x + C . 4 2 4 2 C. F (x) 2 = 3x −1. D. F (x) 4 2
= x − x +1+ C . Lời giải Chọn B 4 2
Họ nguyên hàm của hàm số f (x) 3
= x − x +1 là ( ) x x F x = − + x + C . 4 2
Câu 28. Khối mười hai mặt đều có số cạnh là A. 20 . B. 12. C. 30. D. 8 . Lời giải Chọn C
Khối mười hai mặt đều là khối đa diện đều loại {5; }
3 . Do đó có số mặt là 12, số đỉnh là 20 và
số cạnh là 20 +12 − 2 = 30 .
Câu 29. Thể tích của khối trụ có bán kính đáy R = a và chiều cao h = 2a bằng: A. 3 2a . B. 3 4π a . C. 2 3 π a . D. 3 2π a . 3 Lời giải Chọn D
Thể tích khối trụ là: 2 3
V = Bh = π a .2a = 2π a .
Câu 30. Để làm làm một sản phẩm lịch Canh Tý 2020 như hình vẽ cần dùng 2
50 cm giấy cho mỗi mặt
(ứng cho mỗi tháng trong năm). Biết đơn giá giấy trên thị trường là 200.000 đồng/ 2 m . Hỏi chi
phí giấy cần dùng để làm một sản phẩm lịch trên bằng bao nhiêu?
A. 12.000 đồng.
B. 20.000 đồng.
C. 6.000.000 đồng. D. 200.000 đồng. Lời giải Chọn A
Số tiền cần dùng để làm sản phẩm lịch Canh Tý 2020 trên là: 50 T = .200000.12 =12000 đồng. 10000
Câu 31. Tính độ dài đoạn thẳng AB trong hình vẽ A. AB = 3 3 . B. AB = 13 . C. AB = 26 . D. AB = 2 2 . Lời giải Chọn C −
Từ hình vẽ ta thấy A và B chính là hai giao điểm của đồ thị hàm số x 1 y = với đường thẳng x − 2 y = x + 2 . −
Ta có hoành độ hai điểm A và B là nghiệm của phương trình: x 1 = x + 2, ĐK: x ≠ 2 x − 2 2
⇔ x −1 = x − 4 2
⇔ x − x − 3 = 0 1− 13 5− 13   + +  ⇒ A 1 13 5 13  ; , B ; 2 2         2 2   
⇒ AB = ( 13; 13) ⇒ AB = 26 .
Vậy độ dài đoạn thẳng AB bằng 26 .
Câu 32. Gọi S là tập hợp tất cả các nghiệm nguyên của bất phương trình log x + 2 ≥ 2 − 1 ( ) . Tổng các 2
phần tử của S bằng A. 2 − . B. 2 . C. 0 . D. 3. Lời giải Chọn B log x + 2 ≥ 2
− ⇔ 0 < x + 2 ≤ 4 ⇔ 2 − < x ≤ 2 x∈ 1; − 0;1;2 1 ( ) mà x ∈ nên { }. 2
Do đó, tập hợp tất cả các nghiệm nguyên của bất phương trình đã cho là: S = { 1; − 0;1; } 2 .
Vậy tổng các phần tử của S bằng 2.
Câu 33. Thể tích của khối lập phương cạnh 5cm bằng A. 3 20cm . B. 3 125cm . C. 3 25cm . D. 3 30cm . Lời giải Chọn B
Thể tích của khối lập phương là: 3 3 V = 5 =125cm . 2 Câu 34. Tích phân x + 4 I =
dx = a ln 3+ bln 2 ∫ . Khi đó 2
b − a bằng 2 x + 3x + 2 0 A. 2
b − a =1. B. 2 b − a = 1 − . C. 2 b − a = 0. D. 2 b − a = 4 − . Lời giải Chọn A 2 2 Ta có: x + 4 x + 4 dx = dx ∫ 2x ∫ + 3x + 2 x +1 x + 2 0 0 ( )( ) 2  3 2 d = − ∫  x x +1 x + 2 0 
= (3ln x +1 − 2ln x + 2 ) 2|0 = 3ln 3− 2ln 4 − ( 2 − ln 2) = 3ln 3− 2ln 2 a = 3 ⇒ . Do đó: 2 b − a =1. b   = 2 −
Câu 35. Hình lăng trụ tam giác ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a , AA′ = a 6 . Hình chiếu
vuông góc H của A lên mặt phẳng ( A′B C
′ ′) trùng với trọng tâm của tam giác A′B C ′ ′ . Côsin
của góc giữa cạnh bên và mặt đáy bằng bao nhiêu? A. 2 . B. 2 . C. 3 . D. 15 . 3 6 6 15 Lời giải Chọn B
Do H là hình chiếu vuông góc của A lên mặt phẳng ( A′B C
′ ′) nên góc tạo bởi cạnh bên và mặt đáy là  AA′H .
Ta có H là trọng tâm tam giác đều A′B C ′ ′ cạnh a nên 2 3 3 A′H = a = a . 3 2 3 a 3 ′ Vậy nên  A H 3 2 cos AA′H = = = . AA′ a 6 6
Câu 36. Tổng các nghiệm của phương trình log x + log (x −3)3 = 2 2 8 bằng bao nhiêu? A. 3. B. 2 . C. 4 . D. 0 . Lời giải Chọn C x > 0 Điều kiện  ⇔ x > 3. x − 3 > 0
log x + log x − 3 = 2 ⇔ log x + log x − 3 = 2 ⇔ log x + log x − 3 = 2 2 2 ( ) 2 8 ( )3 3 3 2 ( ) 2 x = 1 −
⇔ log x x − 3 = 2 ⇔ x x − 3 = 4 2
⇔ x − 3x − 4 = 0 ⇔
. Kết hợp điều kiện thì nghiệm 2 ( ) ( )  x = 4
phương trình là x = 4 , nên tổng các nghiệm của phương trình là 4 . x − x
Câu 37. Bất phương trình  4   3 3. 5.  − + 2 ≤    
0 có tập nghiệm S = [ ;
a b]. Khi đó giá trị của 2 2 a + b  9   2  bằng A. 13 . B. 5 . C. 13 . D. 1. 9 3 4 Lời giải Chọn D  4 x  2 x 2x x x BPT 3. 5.  ⇔ − + 2 ≤  2   2  2  2      0 ⇔ 3. − 5. + 2 ≤     0 ⇔ ≤ ≤   1  9   3   3   3  3  3  2 x 0 2  2   2  0<a= 1 < 3 ⇔ ≤ ≤
⇔ 0 ≤ x ≤1. 3  3   3    
Câu 38. Ecoli là vi khuẩn đường ruột gây tiêu chảy, đau bụng dữ dội. Cứ sau 20 phút thì số lượng vi
khuẩn Ecoli lại tăng gấp đôi. Ban đầu chỉ có 40 vi khuẩn Ecoli trong đường ruột. Hỏi sau bao
lâu số lượng vi khuẩn Ecoli là 671088640? A. 48 giờ. B. 24 giờ. C. 8 giờ. D. 12giờ. Lời giải Chọn C
Cứ sau 20 (phút) thì số lượng vi khuẩn Ecoli lại tăng gấp đôi và ban đầu chỉ có 40 vi khuẩn
Ecoli trong đường ruột nên
- Sau 20 phút thì số lượng vi khuẩn Ecoli là: 1 80 = 40.2 .
- Sau 20.2 phút thì số lượng vi khuẩn Ecoli là: 2 160 = 40.2 .
- Sau 20.3 phút thì số lượng vi khuẩn Ecoli là: 3 320 = 40.2 . ……
- Sau 20.n phút thì số lượng vi khuẩn Ecoli là: 40.2 .n S =
Theo giả thiết ta có phương trình:
40.2n = 671088540 ⇔ n = 24 ⇒ t = 20.24 = 480(phút) hay 8 (giờ).
Câu 39. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B , AB = AD = a ,
BC = 2a . Cạnh bên SB vuông góc với đáy và SB = a 7 , M là trung điểm của BC . Tính
khoảng cách d giữa hai đường thẳng AM và SC . A. a 14 d = . B. 3a 14 d = . C. a 14 d = . D. 3a 7 d = . 3 2 6 7 Lời giải Chọn C
Theo giả thiết AMCD là hình bình hành ( AD // CM , AD = CM = a ). Khi đó, AM // CD
CD ⊂ (SCD) ⇒ AM // (SCD) ⇒ d ( AM , SC ) = d (M ,(SCD)) . AM ⊄  (SCD)
d (B,(SCD))
d (B, SCD ) Ta có BC =
= ⇒ d (M ,(SCD)) ( ) = .
d (M (SCD)) 2 , MC 2
Vì ABCD là hình thang vuông tại A và B , AB = AD = a , BC = 2a nên BD = DC = a 2 .
Do đó BD vuông góc với DC . Trong tam giác SBD vuông tại B kẻ đường cao BH .
Suy ra d (B,(SCD)) = BH . 2 Ta có 1 1 1 1 1 a = + = + 9 = 2 14 ⇒ BH = a 14 ⇒ BH = 2 2 2 BH SB BD (a 7)2 (a 2)2 2 14a 9 3 a
⇒ d (M (SCD)) a 14 , = . Vậy 14 d = . 6 6
Câu 40. Số giá trị nguyên dương của m để bất phương trình ( x+2
2 − 2)(2x − m) < 0 có tập nghiệm
chứa không quá 6 số nguyên là: A. 62 . B. 33. C. 32. D. 31. Lời giải Chọn C
Ta có: bất phương trình ( x+2
2 − 2)(2x − m) < 0  1  3 x+2 2 − 2 > 0 x+2 2 > 2 x + 2 > x > −    2   2 
2x − m < 0
2x < m
x < log m   x <  log m ⇔ 2 2 3  ⇔  ⇔  ⇔ 
⇔ − < x < log m . x+2  2 2 − 2 < 0 x+2  2 < 2  1   3 2 x + 2 < x < −    2  2 (*)
2x − m > 0
2x > m x >   log mx >  log m 2 2
(Vì m ≥1 ⇒ log m ≥ 0 nên (*) vô nghiệm). 2
Bất phương trình đã cho có tập nghiệm chứa không quá 6 số nguyên ⇔ log m ≤ 5 5
⇔ m ≤ 2 ⇔ m ≤ 32 2
Mà m nguyên dương nên m∈{1;2;3; } ....32 .
Vậy có 32 giá trị của m thỏa mãn yêu cầu bài toán. f x =
Câu 41. Cho hàm số ( ) 4 2
ax + bx + c (a ≠ 0) có đồ thị là đường cong như hình vẽ
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số 2002( 3 2 x + 3x − 4) 2 g (x) x + 2020 = là f (x) A. 3 B. 5 C. 4 D. 2 Lời giải Chọn C
Dựa vào đồ thị ta có f (x) = a(x + )2 (x − )2 1
1 mà đồ thị hàm số f (x) qua M (0 ) ;1 ⇒ a =1.
Vậy f (x) = (x + )2 (x − )2 1 1 . 2002( 3 2 x + 3x − 4) 2 x + 2020 2 2
2002 x −1 x + 2 x + 2020
Khi đó: g (x) = ⇒ g (x) ( )( ) = . (x + )2 1 (x − )2 1 (x + )2 1 (x − )2 1
Tập xác định: D =  \{± } 1 . 2  2  2020 2 2 2002 − + + x 20021  1 + 2 x + 2020 2 - lim g (x) ( ) = lim lim  x  = x = 2002 − . x→−∞ x→−∞ (x + )2 1 (x − ) 1 2 x→−∞  1   1 1 1  + −      x   x
Suy ra đường thẳng y = 2002 −
là một tiệm cận ngang của đồ thị hàm số g (x) . 2  2  2020 2 2 2002 + + x 20021  1 + 2 x + 2020 2 - lim g (x) ( ) = lim lim  x  = x = 2002 . x→+∞ x→+∞ (x + )2 1 (x − ) 1 2 x→+∞  1   1 1 1  + −      x   x
Suy ra đường thẳng y = 2002 là một tiệm cận ngang của đồ thị hàm số g (x) . 2 2 2002 x + 2 x + 2020 - lim g (x) ( ) = lim = −∞ x→− x→− (x + )2 1 1 1 (x − ) 1  2002(x + 2)2 2 x + 2020 lim = 1001 − 2021 < 0 x→ 1 −  (x − )1  Vì lim (x + )2 1 = 0 x→ 1 −  x → 1 − ⇒ (x + )2 1 > 0  
Suy ra đường thẳng x = 1
− là một tiệm cận đứng của đồ thị hàm số g ( x) . 2 2 2002 x + 2 x + 2020 - lim g (x) ( ) = lim = +∞ x + x + → → (x + )2 1 1 1 (x − ) 1  2002(x + 2)2 2 x + 2020 9009 lim = 2021 > 0 x + →  (x + )2 1 1 2  (vì lim (x − ) 1 = 0 ) x 1+ → 
x →1+ ⇒ x −1 > 0  
Suy ra đường thẳng x =1 là một tiệm cận đứng của đồ thị hàm số g (x) .
Vậy tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số g (x) là 4 .
Câu 42. Nhân dịp đi du Xuân Canh Tý, ba bạn Trang, Hoàng, Tân rủ nhau rút quẻ xem vận mệnh.
Khi đó trong hộp chỉ có các quẻ có số thứ tự 5 đến 15 (luôn có ít nhất ba quẻ ghi cùng một số).
Mỗi bạn rút ngẫu nhiên một quẻ và yêu cầu bạn Linh tính xác suất để tổng các số ghi trên ba
quẻ là một số chia hết cho 3. Kết quả đúng là? A. 112 . B. 60 . C. 203 . D. 443 . 1331 1331 1331 1331 Lời giải Chọn D
Số phần tử của không gian mẫu: n(Ω) 3
=11 =1331. Ta chia các số đã cho thành ba nhóm.
Nhóm I: Chia 3 dư 0 có các số: 6; 9; 12; 15.
Nhóm II: Chia 3 dư 1 có các số: 7; 10; 13 .
Nhóm III: Chia 3 dư 2 có các số: 5; 8; 11; 14 .
Gọi A là biến cố: “tổng các số ghi trên ba quẻ là một số chia hết cho 3”. Ta có:
TH1: rút 3 số cùng thuộc một nhóm có 3 3 3 4 + 3 + 4 cách.
TH2: rút 3 số từ ba nhóm (mỗi số thuộc một nhóm) có 4.3.4.3! cách. 3 3 3
Vậy xác suất cần tìm: P( A) 4 + 3 + 4 + 4.3.4.3! 443 = = . 1331 1331
Câu 43. Bà chủ khách sạn trên đèo Mã Pi Lèng muốn trang trí một góc nhỏ trên ban công sân thượng
cho đẹp nên quyết định thuê nhân công xây một bức tường gạch với xi măng (như hình vẽ),
biết hàng dưới cùng có 500 viên, mỗi hàng tiếp theo đều có ít hơn hàng trước1 viên và hàng
trên cùng có một viên. Hỏi số gạch cần dùng để hoàn thành bức tường trên là bao nhiêu viên? A. 25250 . B. 125250. C. 12550. D. 250500 . Lời giải Chọn B
Theo bài ra ta có số viên gạch từ hàng dưới cùng đến hàng trên cùng lập thành một cấp số cộng
với số hạng đầu u = 500 , công sai d = 1
− nên công thức số hạng tổng quát là: 1 u = + n − − n 500 ( )1( )1 Hay u =
− n . Vì hàng trên cùng một viên nên giải phương trình 501− n =1 ⇔ n = 500 . n 501
Vậy có tất cả 500 hàng gạch và hàng trên cùng là u =1. 500
Do đó số gạch cần dùng để hoàn thành bức tường là: 500(500 + ) 1
S = 500 + 499 + 498 +...+1 = =125250 . 500 2
Câu 44. Cho tứ diện ABCD có CD = a 2 , A
BC là tam giác đều cạnh a , A
CD vuông tại A . Mặt
phẳng (BCD) vuông góc với mặt phẳng ( ABD). Thể tích khối cầu ngoại tiếp tứ diện ABCD bằng? 3 3 3 A. 4 a  . B. a  3 . C. a  . D. 3 4 a  . 3 2 6 Lời giải Chọn A
Gọi M , N , K lần lượt là trung điểm của AD , CD , BD A
CD vuông tại A 2 2
AD = CD − AC = a A
BD cân tại A AK ⊥ BD .
Mặt khác ( ABD) ⊥ (BCD)  AK ⊥ (BCD)
AK ⊥ CD ( ) 1 . A
CD cân tại A AN ⊥ CD (2) . Từ ( )
1 và (2)  CD ⊥ KN
Mà BC // KN (tính chất đường trung bình)  CD ⊥ BC
Suy ra K là tâm đường tròn ngoại tiếp BCD .
Đường trung trực của AD trong mặt phẳng ( ABD) cắt AK tại I I là tâm mặt cầu ngoại
tiếp tứ diện ABCD . 2 2 2
BD = CD + BC = a 3 , 2 2 2 3a a
AK = AD − KD = a − = . 4 2 A AM.AD . a aKD A
MI (g.g) AI AM  =  R = AI = = = a . AD AK AK 2 a2 3
Thể tích khối cầu ngoại tiếp tứ diện 4 4 a ABCD : 3 V = R =   . 3 3
Câu 45. Cho phương trình 5x + m = log x − m , với 5 ( )
m là tham số. Số giá trị nguyên của m∈( 2020 −
;2020) để phương trình đã cho có nghiệm là? A. 9. B. 2021. C. 2020 . D. 2019 . Lời giải Chọn D
Điều kiện của phương trình: x > m .
Ta có 5x + m = log x − m 5 ⇔ 5 x+m = − 5 ⇔ 5 x+m + = . 5 ( ) x m m x
Đặt 5x + m = t ( )
1 , phương trình trên trở thành 5t + m = x (2) .
Trừ tương ứng vế với vế của ( )
1 cho(2) , ta được: 5x −5t = t − x ⇔ 5x + = 5t x + t . Đặt ( ) = 5x f x
+ x ⇒ ′( ) = 5x f x .ln 5 +1 > 0 x
∀ , vậy f (x) là hàm đơn điệu trên tập xác định.
Từ đây suy ra 5x + = 5t x
+ t ⇔ f (x) = f (t) ⇔ x = t , thế vào phương trình ( ) 1 , ta được:
5x + m = x ⇔ − 5x x = m . Xét hàm ( ) = −5x g x x có ′( ) =1−5x g x
.ln 5 ⇒ g′(x) = 0 1 5x ⇔ − .ln 5 = 0  1 x log  ⇔ = . 5  ln5   
Ta có bảng biến thiên của hàm g (x) như sau: x  1  −∞ log 5  ln5  +∞   g′(x) + 0 −  1  1 − g (x) log5  ln5   ln 5 −∞ −∞
Vậy phương trình g (x) = m có nghiệm  1  1 ⇔ m ≤ log − ≈ 0, − 92 . 5  ln5    ln 5 Lại có m∈( 2020 −
;2020) và m∈ , từ đây suy ra m∈ và 2019 − ≤ m ≤ 1 − .
Vậy có 2019 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Câu 46. Gọi S là tập hợp tất cả các nghiệm thuộc đoạn [0;13π ] của phương trình 3 2
2cos x + cos x + cos 2x = 0 . Tổng các phần tử của S bằng: A. 380π . B. 400π . C. 420π . D. 120π . 3 3 3 Lời giải Chọn B 3 2
2cos x + cos x + cos 2x = 0 3 2
⇔ 2cos x + 3cos x −1 = 0 ⇔ ( x + )2 cos 1 (2cos x − ) 1 = 0 cos x +1 = 0 ⇔  2cos x −1 = 0 cos x = 1 −  ⇔ 1 cos x =  2 +) Với cos x = 1
− ⇔ x = (2k + ) 1 π (k ∈) .
Hơn nữa, ta lấy x∈[0;13π ] nên có: x = (2k + )
1 π , với k ∈, 0 ≤ k ≤ 6 .  π x = + m2π  +) Với 1 π 3
cos x = ⇔ cos x = cos ⇔  ( , m l ∈). 2 3  π x = − + l2π  3
Tương tự, do lấy x∈[0;13π ] nên ta có: π
x = + m2π , với m∈, 0 ≤ m ≤ 6 3 và π
x = − + l2π , với l ∈,1≤ l ≤ 6. 3 Do đó, π   π S
({2k )1π | k , 0 k } 6 
m2π | m , 0 m 6 
l2π | l ,1 l 6 = + ∈ ≤ ≤ ∪ + ∈ ≤ ≤ ∪ − + ∈ ≤ ≤ 3 3     
Vậy, tổng các phần tử của S là: 6  π   π T ∑(2k ) 6 6 1 π ∑ 2mπ ∑ 2lπ  = + + + + − +     k= 0 m = 0  3  l =1  3  6 ∑( π  π π 2k ) 6 6 6 6 1 ∑ π ∑ 2m  = + + + + ∑ − +π   ∑2l k= 0 m = 0 3 m = 0 l =1  3  l =1 7(1+13) 7π 7(0 +12)  6π  6(2 +12) = π + +π + − +π 2 3 2  3    2 400π = . 3
Câu 47. Tìm tất cả các giá trị của tham số m để đường thẳng đi qua điểm cực đại và cực tiểu của đồ thị hàm số 3
y x 3mx  2 cắt đường tròn C tâm I 1; 
1 , bán kính bằng 1 tại hai điểm phân
biệt A , B sao cho diện tích tam giác IAB đạt giá trị lớn nhất? A. 2 3 m   . B. 1 3 m   . C. 2 3 m   . D. 2 5 m   . 3 2 2 2 Lời giải Chọn C 2
y  3x 3m .
Hàm số có hai điểm cực trị khi m  0   1 .
Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số 3
y x 3mx  2 có phương trình
y  2mx  2  2mx y 2  0 .
Diện tích tam giác IAB là 1  S 1 1 1    .1.1.sin AIB   sin AIB  .  IA IB AIB IAB . . .sin 2 2 2 2 Dấu " " xảy ra khi 
AIB  90 tức là IA
B vuông tại I . 2mx y I I 2
Khi đó d I AB 2 , 2    . 2  m2 2 2 2 1  2 3 m   2
 2 2m1  2. 4m 1 2   2.  2 3 m   2 Từ   1 và 2 ta được 2 3 m   . 2
Câu 48. Cho hàm số y = f (x) có đạo hàm liên tục trên [1; 4] thỏa mãn f ( ) 1 = 26 và
f (x) = x f ′(x) 3 2 .
− 8x − 5x . Tính giá trị của f (4) ? A. 400 . B. 2020 . C. 404 . D. 2022 . Lời giải Chọn C .
x f ′ x − f x
Trên [1; 4], ta có f (x) = .x f ′(x) 3 2 ( ) ( )
− 8x − 5x ⇔ = 8x + 5 . 2 x f (x)
Lấy nguyên hàm hai vế ta được 2
= 4x + 5x + C hay f (x) 3 2
= 4x + 5x + Cx (với C là x hằng số). Vì f ( )
1 = 26 nên C = 17 . Do đó f (x) 3 2
= 4x + 5x +17x . Vậy f (4) = 404 .
Câu 49. Cho hình chữ nhật ABCD có tâm I , biết AB = a , AD = 2a .
Gọi J là trung điểm BC , đường thẳng đi qua I và vuông góc
với AC cắt CD tại điểm K .Thể tích V của khối tròn xoay tạo
thành khi cho tứ giác CKIJ quay xung quanh trục CK bằng A. 5 3 π a B. 7 3 π a . 6 6 C. 5 3 π a . D. 14 3 π a . 2 3 Lời giải Chọn B
Gọi H, E lần lượt là điểm đối xứng của I, J qua CD .
Gọi F là hình chiếu vuông góc của I lên BC .
Khi cho tứ giác CKIJ quay xung quanh trục CK tạo thành hai khối tròn xoay.
+) Khối I là khối nón đỉnh là K đáy là đường tròn đường kính IH và có tâm là F có thể tích là V . 1 Ta có A ∆ CD KCI ∆ (g.g). AC CD AC.IC 5a ⇒ = ⇒ CK = = . KC CI DC 2 ⇒ KF = 2a . 3 1 ⇒ = ( )2 1 = π ( )2 2π π . .2 a V IF KF a a = . 1 3 3 3
+) Khối II là khối trụ có đáy một là hình tròn đường kính IH và có tâm là F , đáy hai là hình
tròn đường kính JE và có tâm là C có thể tích là V . 2 3 ⇒ = π ( )2 2 a π a V IF CF = π a = . 2 2 2 3 3 3 Vậy 2π a π a 7π a
V = V +V = + = . 1 2 3 2 6
Câu 50. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi E là điểm đối xứng với C  
qua B và F là điểm thỏa mãn: SF = 2.
− BF . Mặt phẳng (DEF ) chia khối chóp
S.ABCD thành 2 khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V1, khối đa V
diện còn lại có thể tích V2 (tham khảo hình vẽ). Tính tỉ số 1 ? V2 3 1 7 12 A. . B. . C. . D. . 5 5 5 7 Lời giải Chọn C
Gọi G là giao điểm của ED và AB , H là giao điểm của EF và SC .  
Vì B là trung điểm của EC và SF = 2.
− BF nên F là trọng tâm S
∆ EC suy ra H là trung 1 1
điểm của SC , từ đó suy ra V = V = V . A HCD . . 2 A SCD . 4 S ABCD 1
Ta có EC = 2AD và EC / / AD do đó V = V = V E HCD 2 . . A HCD . . 2 S ABCD V EB EG EF 1 1 2 1 1 1 E.FBG = . . = . . = ⇒ V = V = V . V EC ED EH 2 2 3 6 E.FBG E.HCD . E.HCD 6 12 S ABCD 1 1 5 V =V −V = V − V = V 2 E.HCD E.F BG S.ABCD S. . 2 12 ABCD . 12 S ABCD 5 7 V =V − V = V 1 S.ABCD S.ABCD S. 12 12 ABCD V 7 Vậy 1 = . V 5 2
------------------------- HẾT -------------------------
Document Outline

  • de-khao-sat-toan-12-lan-2-nam-2019-2020-truong-thach-thanh-3-thanh-hoa
  • Tổ-12-đợt-22-THI-THỬ-LẦN-2-THẠCH-THÀNH-3-THANH-HOÁ-1920