Đề khảo sát Toán 12 năm 2022 – 2023 cụm chuyên môn số 6 – Đắk Lắk

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề khảo sát chất lượng môn Toán 12 năm học 2022 – 2023 cụm chuyên môn số 6, tỉnh Đắk Lắk

36 18 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

15 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
1/6-Mãđề601
SỞGIÁODỤCVÀĐÀOTẠOTỈNHĐẮKLẮK
CỤM CHUYÊN MÔN SỐ 6
ĐỀCHÍNHTHỨC
(Đề thi có 06 trang)
ĐỀ KHẢO SÁT CHẤT LƯỢNG LỚP 12
NĂM HỌC 2022 - 2023
Bài thi: TOÁN
Thời gian làm bài : 90 phút(không kể thời gian phát đề)
Họvàtênhọcsinh:.....................................................Sốbáodanh:...................
Câu 1. Chohàmsố
x
exxf 2
.Khẳngđịnhnàodướiđâyđúng?
A.
.
ln
2
C
x
e
dxxf
x
B.
.
2
Cexdxxf
x
C.
.2
Cedxxf
x
D.
.
2
Cexdxxf
x
Câu 2. Trongkhônggian
Oxyz
,đườngthẳng
1 2
: 2 2
3 3
x t
d y t
z t
điquađiểmnàodướiđây?
A.
1;2;3
. B.
. C.
1;2; 3
. D.
2; 2; 3
.
Câu 3. Chohàmsố
y f x
cóbảngbiếnthiênnhưhìnhvẽ:
Sốđiểmcựctrịcủahàmsốđãchobằng
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 4. Phầnthựccủasốphức
iz 64
là
A.
.4
B. 4. C.
.6
D. 6.
Câu 5. ChotậphợpAcó7phầntử.Sốtậpcongồm3phầntửcủatậphợpAlà
A.
3
7
.A
B.
7
3 .
C.
3
7
.C
D.
3
7 .
Câu 6. Nếu
2
3
1
dxxf
thì
dxxf
3
1
4
bằng
A. 8. B. 10. C. 24. D.
2
.
Câu 7. Nếu
5
3
0
dxxf
và
2
1
0
dxxf
thì
dxxf
3
1
bằng
A.
3
. B. 3. C. 10. D. 7.
Câu 8. Chohàmsốbậcba
( )y f x
cóđồthịnhưhìnhvẽ:
Mã đề 601
2/6-Mãđề601
Hàmsốđãchođạtcựctiểutạiđiểm
A.
1.
x
B.
2.
x
C.
2.
x
D.
3.
x
Câu 9. Trongkhônggian
Oxyz
,chomặtcầu
2 2 2
: 1 3 2 25
S x y z
.Tâm
I
và
bánkính
R
củamặtcầu
S
là:
A.
1;3;2 , 25
I R
. B.
1; 3; 2 , 5
I R
.
C.
1;3;2 , 5
I R
. D.
1; 3; 2 , 25
I R
.
Câu 10. Trênmặtphẳngtọađộ,điểmbiểudiễnsốphức
iz 32
cótọađộlà
A.
.3;2
M
B.
.2;3M
C.
.3;2
M
D.
.3;2M
Câu 11. Chohìnhlăngtrụđứng
. ' ' 'ABC A B C
cóđáy
ABC
làtamgiácvuôngcântại
A
với
4AC a
vàmặtbên
' 'AA B B
làhìnhvuông.Thểtíchcủakhốilăngtrụ
. ' ' 'ABC A B C
bằng
A.
3
.
8
a
B.
3
64 .a
C.
3
.
4
a
D.
3
32 .a
Câu 12. Chohàmsố
y f x
cóbảngbiếnthiênnhưhìnhvẽ:
Hàmsốđãchonghịchbiếntrênkhoảngnàodướiđây?
A.
;2

. B.
1;

. C.
1;3
. D.
;1
.
Câu 13. Nghiệmcủaphươngtrình
2 1
2 8
x
là
A.
5
.
2
x
B.
3.
x
C.
2.
x
D.
3
.
2
x
Câu 14. Trongkhônggian
Oxyz
,chođiểm
2; 1;3
M
vàmặtphẳng
:3 2 1 0
P x y z
.
Phươngtrìnhmặtphẳngđiqua
M
vàsongsongvới
P
là
A.
3 2 11 0x y z
. B.
2 3 14 0x y z
.
C.
3 2 11 0x y z
. D.
2 3 14 0x y z
.
3/6-Mãđề601
Câu 15. Trongkhônggianvớihệtọađộ
Oxyz
,gọi
làgócgiữahaimặtphẳng
: 3 2 1 0
P x y z
vàmặtphẳng
Oxy
.Khẳngđịnhnàosauđâyđúng?
A.
o
45
. B.
o
30
. C.
o
60
. D.
o
90
.
Câu 16. Trongkhônggian
Oxyz
,chomặtphẳng
P
:
2 3 0x y z
.Vectơnàodướiđây
làmộtvectơpháptuyếncủamặtphẳng
P
?
A.
1
2;1; 1
n
. B.
3
1; 1;3
n
. C.
4
2; 1;3
n
. D.
2
2;1;3
n
.
Câu 17. Chokhốichópcódiệntíchđáy
2
2B a
vàchiềucao
9h a
.Thểtíchcủakhốichóp
đãchobằng
A.
3
9a
. B.
3
6a
. C.
3
3a
. D.
3
18a
.
Câu 18. ChohìnhchópS.ABCcó SAvuônggócvới mặt phẳng
,ABC
2 ,SA a
tamgiác
ABCvuôngtạiB,
3AB a
và
BC a
.GócgiữađườngthẳngSCvàmặtphẳng
ABC
bằng
A.
90 .
B.
30 .
C.
45 .
D.
60 .
Câu 19. Tậpnghiệmbấtphươngtrình
2
3
2 16
x x
là
A.
4;

. B.
; 1 4;

. C.
1;4
. D.
; 1
.
Câu 20. Tậpxácđịnhcủahàmsố
ln 2
y x
là
A.
.
D
B.
;2 .
D 
C.
2; .
D

D.
\ 2 .
D
Câu 21. Đồthịcủahàmsốnàodướiđâycódạngnhưđườngcongtronghìnhvẽ?
A.
4 2
2 3.
y x x
B.
3
3 .y x x
C.
4 2
2 3.
y x x
D.
3
3 3y x x
.
Câu 22. Mộthìnhtrụcóbánkínhđáybằnga,chuvithiếtdiệnquatrụcbằng10a.Chiềucao
củakhốitrụđãchobằng
A.
3a
.
B.
a
. C.
4a
. D.
9a
.
Câu 23. Cho
CxFxdxsin
.Khẳngđịnhnàodướiđâyđúng?
A.
.sin' xxF
B.
.sin' xxF
C.
.cos' xxF
D.
.cos' xxF
Câu 24. Thểtíchcủakhốinóncóchiềucaohvàbánkínhrlà
A.
2
4
3
r h
. B.
2
2
r h
. C.
2
r h
. D.
2
1
3
r h
.
4/6-Mãđề601
Câu 25. Hìnhlăngtrụ
. ' ' 'ABC A B C
cóđáyABClàtamgiácvuôngtại
, , 2A AB a AC a
.Hình
chiếuvuônggóccủa
'A
lênmặtphẳng
ABC
làđiểmIthuộccạnhBC. Khoảngcáchtừ Atới
mặtphẳng
'
A BC
bằng
A.
2
5
a
B.
3
2
a
C.
2 5
5
a
D.
5
5
a
Câu 26. Đồthịhàmsố
4
2 2
x
y
x
cắttrụctungtạiđiểmcótungđộbằng
A.
1
.
2
B.
1.
C.
2.
D.
4.
Câu 27. Tiệmcậnđứngcủađồthịhàmsố
2 1
1
x
y
x
làđườngthẳngcóphươngtrình
A.
1.
y
B.
1.
x
C.
2.
y
D.
2.
x
Câu 28. Diệntíchhìnhphẳnggiớihạnbởiđồthịcủahàmsố
5
xy
,trụchoànhvàhai
đườngthẳng
1x
,
1x
bằng
A.
.
2
3
B.
.
3
1
C. 7. D. 5.
Câu 29. Giátrịnhỏnhấtcủahàmsố
3 2
3y x x
trênđoạn
1;5
bằng
A.
50
. B.
4
. C.
45
. D.
2
.
Câu 30. Có
30
chiếcthẻđượcđánhsốthứtựtừ1đến30.Chọnngẫunhiênmộtchiếcthẻ.
Tínhxácsuấtđểchiếcthẻđượcchọnmangsốchiahếtcho3.
A.
2
3
. B.
3
10
. C.
1
3
. D.
1
2
.
Câu 31. Với
a
làsốthựcdươngbấtkỳ,
ln 2023 ln 2022a a
bằng
A.
2023
.
2022
B.
2023
ln .
2022
C.
ln 2023
.
ln 2022
D.
ln .a
Câu 32. Chohaisốphức
iz
3
1
và
iz 52
2
.Khiđómôđuncủasốphức
21
zzz
bằng
A.
.17
B.
.172
C.
.39
D.
.10
Câu 33. Chocấpsốcộng
n
u
cósốhạngđầu
1
2
u
,côngsai
5
d
.Giátrịcủa
4
u
bằng
A.
250
. B.
1 2
. C.
22
. D.
17
.
Câu 34. Trongkhônggian
Oxyz
,khoảngcáchtừđiểm
1;2;3
M
đếnmặtphẳng
( ): 2 2 5 0
P x y z
bằng:
A.
, 2.
d M P
B.
, 4.
d M P
C.
, 1.
d M P
D.
, 3.
d M P
Câu 35. Hàmsố
3 2
1 1 5
6
3 2 6
y x x x
đồngbiếntrênkhoảng
A.
3; .
B.
; 3 .

C.
2; 3 .
D.
2; .
5/6-Mãđề601
Câu 36. Tậpnghiệmcủabấtphươngtrình
3
log 2 2
x
là
A.
;11
S 
. B.
2;11
S
. C.
2;8
S
. D.
;8
S 
.
Câu 37. Liênhợpcủasốphức
iz 21
là
A.
.21 iz
B.
.2 iz
C.
.21 iz
D.
.21 iz
Câu 38. Nếu
5
1
0
dxxf
và
4
1
0
dxxg
thì
dxxgxf
1
0
bằng
A. 54. B. 20. C. 9. D. 1.
Câu 39. Chohìnhchóp
.
S ABC
cóđáy
ABC
làtamgiácđềucạnh
a
.Hìnhchiếuvuônggóc
của
S
trênđáylàđiểm
H
trêncạnh
AC
saocho
2
3
AH AC
;mặtphẳng
SBC
tạovớiđáy
mộtgóc
60
o
.Thểtíchkhốichóp
.
S ABC
là?
A.
3
3
48
a
B.
3
3
36
a
C.
3
3
24
a
D.
3
3
12
a
Câu 40. Trongtậphợp sốphức,xétphương trình
3 2
2 1 3 0
z m z mz m
(
m
làthamsố
thực).Cóbaonhiêugiátrịcủa
m
đểphươngtrìnhđócóbanghiệmphânbiệt
1 2 3
, ,z z z
thỏa
mãn
1 2 3
3
z z z
?
A.
0.
B.
2
. C.
3
. D.
1
.
Câu 41. Chohìnhnónđỉnh
S
,đườngcaoSO,
A
và
B
làhaiđiểmthuộcđườngtrònđáysao
chokhoảngcáchtừ
O
đến
SAB
bằng
3
3
a
và
0 0
30 , 60
SAO SAB
.Độdàiđườngsinhcủa
hìnhnóntheo
a
bằng
A.
3a
. B.
5a
. C.
2a
. D.
2 3a
.
Câu 42. Chohàmsố
y f x
cóđạohàm
2 5
2
' 2 1 2 6
f x x x x m x m
vớimọi
x
.Sốgiátrịnguyêndươngcủathamsố
m
đểhàmsốđãchocóđúngmộtđiểmcựctrịlà
A.
4
. B.
6
. C.
5
. D.
7
.
Câu 43. Chohàmsố
f x
liêntụctrên
.Gọi
F x
và
G x
làhainguyênhàmcủa
f x
thỏamãn
2 3 3 9 2 1 1
F G F G
.Khiđó
2
2
0
3 2
x f x dx
bằng
A.
3
. B.
25
6
. C.
43
6
. D.
7
6
.
Câu 44. Trongkhônggian
Oxyz
,chođiểm
1;2; 3
A
,mặtphẳng
:3 1 0
P x y z
vàmặt
phẳng
: 3 3 0
Q x y z
Gọi
làđườngthẳngđiqua
A
,cắtvàvuônggócvớigiaotuyến
của
P
và
Q
.Sincủagóctạobởiđườngthẳng
vàmặtphẳng
P
bằng:
A.
55
55
. B.
3 55
11
. C.
0
. D.
7 55
55
.
6/6-Mãđề601
Câu 45. Tìm số nghiệm nguyên của bất phương trình
2 2
2 4 9 5 1
2023 2023 1 8 0
x x x x
x x
A.
8
. B.
5
. C.
6.
D.
7
.
Câu 46. Có baonhiêu sốnguyêndương x saochotồntại sốthựcy lớnhơn 1thỏa mãn
2
2 3
2 1 log log
y x
xy x y y
x
A.
2
. B. Vôsố C.
3
. D.
1
.
Câu 47. Xétcácsốphức
z
thỏamãnđiềukiện
2 3
1 1
3 2
i
z
i
.Gọi
,m M
lầnlượtlàgiátrị
nhỏnhấtvàgiátrịlớnnhấtcủabiểuthức
.P z
Tính
2023 3 2 .S M m
A.
2021
S
B.
2019
S
C.
2017
S
D.
2023
S
Câu 48. Trongkhônggian
Oxyz
,chohaiđiểm
1;4;3
A
,
5;0;3
B
.Mộthìnhtrụ
T
nộitiếp
trongmặtcầuđườngkính
AB
đồngthờinhận
AB
làmtrụccủahìnhtrụ.Gọi
M
và
N
lần
lượtlàtâmcácđườngtrònđáycủa
T
(
M
nằmgiữa
A
,
N
).Khithiếtdiệnquatrụccủa
T
códiệntíchlớnnhấtthìmặtphẳngchứađườngtrònđáytâm
M
của
T
códạng
0
ax by cz d
.Giátrịcủa
b d
bằng
A.
4 2
. B.
2 2 2
. C.
2 2
. D.
2 2
.
Câu 49. Có bao nhiêu giá trị nguyên của tham số
a
thuộc đoạn
10;10
để hàm
số
3 2 2
3 1 3 2 3
y x a x a a x a a
đồngbiếntrênkhoảng
0;1
A.
2
. B.
21
. C.
8
. D.
10
.
Câu 50. Cho hàm số
( )y f x
có đạo hàm liên tục trên
và thỏa mãn
23
) 6( ) ( 4 ,f xx xf x x x
. Diện tích hình phẳng giới hạn bởi các đường
( )y f x
và
( )y f x
bằng
A.
7
12
. B.
1
2
. C.
45
4
. D.
71
6
.
------ HẾT ------
SỞ GIÁO DỤC VÀ ĐÀO TẠO TỈNH ĐẮK LẮK
CỤM CHUYÊN MÔN SỐ 6
ĐỀ CHÍNH THỨC
ĐÁP ÁN ĐỀ KHẢO SÁT CHẤT LƯỢNG LỚP 12
NĂM HỌC 2022 - 2023
Bài thi: TOÁN
Câu hỏi
601
602
603
604
605
606
607
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
624
1 B A B
B
A B A B D C C D C D C C B A D A B D A D
2 C
C
B
C
D D B C B B A A D A C D A B C C C D B A
3 C
A
D
C
A D A B C A B A A B B C A C D C C C B A
4 B
B
B
D
C D A D C D D D B A A B A C A C C D D A
5 C
C
D
D
B B D A A A B A B B A A C A B B C C B C
6 B
A
B
B
A B D B A B B D B A B D D B C C B C D C
7 B
A
C
D
A D C A B C B B B D B D A B C B B C A C
8 D
C
C
A
C D C C D B C C C D B C A D D D B A D C
9 C
C
A
A
D C B C D C A B A D C A B A A A D B D D
10 D
D
B
C B D A D A C D A A B A A C D A B C A B C
11 D
A
B
A
D D A D D D A B D C C A B C C D B A B C
12 C
B
D
B
B A A B A B B B D D B D B A A A B B B D
13 C
D
D
C
D C C C B A C C B C B C A C D C B B A A
14 A
B
D
B
D D B D B B B A B C A D A D A A D A B A
15 A
B
C
D
D D C B B A C C A C D C A B A C A A A C
16 A
D
B
D
D B C C D B C B D A B C A D B C D C C B
17 B
A
A
B
B B A C B C D C D D A C C B A B A C D B
18 C
B
B
C
C A B C D D D C B C C B C D C D A D C B
19 C
C
C
A
A D A B A D C B C C C B A C D D B C B C
20 B
D
A
D
C A A C D C A D C D D A B D C B B A D C
21 C
A
D
C
A D D D B C D D B D D B D B A C A A D D
22 A
D
C
D
D C D A D A A C C B B A A D D D D D A B
23 B
C
C
A
B B A B C C B B C D B A B A B A C B C B
24 D
B
C
C
D C C C A C D C D B A B A C B C A C B B
25 C
C
B
C
A B B A A B A D C C A C A D B C C A B D
26 C
C
A
C
B B A D A D A B A B A D B D A D D D B C
27 B
B
D
B
C D B D D C C D C A B B B C D D B D D B
28 B
A
A
D
B C A D A A A C A B C B A D A B C D D B
29 B
D
D
B
D A C A D C A B B A B D A B D A D C A B
30 C
D
C
A
A A D D D C D C D D B D D C D C C D B C
31 B
A
D
A
D A D C D B C A C B C C D A C C B C D A
32 A
A
D
C
B A B C C B D A D C D A D B A D B A C C
33 D C
C
B
B A A A C A B C D A B B B B B A D A D D
34 A
A
A
D
C A B D A A B D D B D D D A D B D C D A
35 A
A
B
B
C A A A D D C B B D D B B C B A A B B D
36 B
B
A
C
B A C D B D D B B B D D C C D D B C A C
37 D
A
D
D
B A B C D C A A C D B C B B D A B B A D
38 D
B
B
A
A B D D D C C A B D D D C B D C C D C A
39 A
C D
B A D D A A C B C A A D B B D C A D D B B
40 D
B B
D D A C C C A A B D B A B A A C D A D A B
41 C
A D
D D C C B D A B A A A D B A B A A B C A D
42 D
D A
B D B B C D A A D B B D C A A A A C A A A
43 B
C A
D D C D C A A A D A B D A A B A A A B D D
44 D
C C
B D A D C D D C A D B A A D B A D A C B A
45 C
A C
C B C D A B A C A A B D D A C C C C C B B
46 A
D B
C D B B A C A D D B B B B D C B B A C A D
47 C
D A
B B A C D D B B A B D C A B D D C D B C A
48 D
A C
B D A C B B A D D B B D D A D B D C D A B
49 D
B D
C C A B D A B C D C B D D B C A A A A A B
50 D
C D
C D C A D D D B B C A A C B C C B A A C A
ĐÁP ÁN CHI TIẾT
Câu 39: Cho hình chóp
S.ABC
có đáy
ABC
là tam giác đều cạnh
a
. Hình chiếu vuông góc của
S
trên đáy là điểm
H
trên cạnh
AC
sao cho
2
3
AH
AC
; m
ặt phẳng
SBC
tạo v
ới đáy một góc
60
o
. T
hể tích khối chóp
.S A
BC
là?
A.
3
3
12
a
B.
3
3
48
a
C.
3
3
36
a
D.
3
3
24
a
Lời giải:
Gọi
M
là trung đ
iểm của
BC
.
1
:
3
CN
CH
N CM
CM CA
//H
N AM
. Mà
ABC
đều nê
n
AM BC HN BC BC SHN
.
Nên
; ; 60
o
SB
C ABC SN HN SNH
.
Do
ABC
đều nên
3 1
3
2 3 6
a a
AM HN AM
.
SHN
vuông
tại
H
có
3
.sin .sin 60
6 4
o
a a
SH HN SNH
.
2 3
.
1 1
3 3
. . .
3 3 4 4 48
S ABC AB
C
a a
a
V SH S
.
Câu
40: Trong tập hợp số phức, xét phương trình
3 2
2 1
3 0z m z mz m
(
m
là tham số thực).
Có bao nhiêu giá trị của
m
để phươn
g trình đó có ba nghiệm phân biệt
1 2 3
, ,z z z
thỏa
mãn
1 2
3
3z z
z
?
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
3 2
2 1
3 0 (1)z m z mz m
2
1 2
0z z mz m
2
1
2 0
(2)
z
z mz m
Đặt
3
1z
, g
ọi
1 2
,z z
là hai n
ghiệm của phương trình
(2)
.
Phươn
g trình
(2
)
có
2
' m m
và :
1 2
1
2
2z z
m
z z m
*) TH1: Nếu
1m
ta c
ó
' 0
và phư
ơng trình
2
có hai
nghiệm thực phân biệt dương
khác 1. Khi đó
1 2
3
3z z
z
1 2
1 3
2 1 3 1z z m m
(loại).
*) TH2: Nếu
0m
ta có
' 0
và ph
ương trình
2
có ha
i nghiệm thực phân biệt là:
2 2
1 1 2 2
( 0); (
0)z m m m z z m m m z
Khi đó
1 2
3
3z z z
2 2 2
1 3
2 2m m m m m m m m
2
1 5
2
1 0
1 5
2
m
m m
m
. Vì
0
m
nên
1 5
2
m
.
*) TH3: Nếu
0 1
m
ta có
' 0
, khi đó phương trình
2
có hai nghiệm phức :
2 2
1 2
. ; .z m m m i z m m m i
Vậy
1 2 3
3
z z z
2 2 2 2
1 3
m m m m m m
1 1
m m
(loại).
Vậy chỉ có một giá trị
1 5
2
m
thỏa mãn yêu cầu đề bài.
Câu 41: Cho hình nón đỉnh
S
, đường cao SO,
A
và
B
là hai điểm thuộc đường tròn đáy sao cho
khoảng cách từ
O
đến
SAB
bằng
3
3
a
và
0 0
30 , 60
SAO SAB
. Độ dài đường sinh của hình nón
theo
a
bằng
A.
2a
. B.
3a
. C.
2 3a
. D.
5a
.
Lời giải:
Gọi
K
là trung điểm của
AB
ta có
OK AB
vì tam giác
OAB
cân tại
O
Mà
SO AB
nên
AB SOK
SOK SAB
mà
SOK SAB SK
nên từ
O
dựng
OH SK
thì
,
OH SAB OH d O SAB
Xét tam giác
SAO
ta có:
sin
2
SO SA
SAO SO
SA
Xét tam giác
SAB
ta có:
3
sin
2
SK SA
SAB SK
SA
Xét tam giác
SOK
ta có:
2 2 2 2 2 2
1 1 1 1 1
OH OK OS SK SO SO
2 2 2
2 2 2
1 1 1 4 2
3
4 4 4
SA SA SA
OH SA SA
2SA a
K
H
B
A
O
S
Câu 42: Cho hàm số
y f x
có đạo hàm
2 5
2
' 2 1 2 6
f x x x x m x m
với mọi
x
. Số giá trị nguyên dương của tham số
m
để hàm số đã cho có đúng một điểm cực trị là
A.
7
. B.
5
. C.
6
. D.
4
.
Lời giải:
Ta có:
' 0
f x
2
2
1
2 6 0 1
x
x
x m x m
.
Yêu cầu bài toán thỏa mãn khi và chỉ khi
1
1
2
0
4 9
0
13
1 2 6 .1 0
m
m
m m
. Vậy có 7 số nguyên dương thỏa mãn
Câu 43: Cho hàm số
f x
liên tục trên
. Gọi
F x
và
G x
là hai nguyên hàm của
f x
thỏa
mãn
2 3 3 9 2 1 1
F G F G
. Khi đó
2
2
0
3 2
x f x dx
bằng
A.
25
6
. B.
7
6
. C.
43
6
. D.
3
.
Lời giải
Ta có
2 2 2
2
0 0 0
8
3 2 d 3 2 d
3
I x dx f x x f x x
.
Đặt
3 2 2t x dt dx
.
Khi đó
2 1 3
0 3 1
1 1 1
3 2 d d d 3 1
2 2 2
f x x f t t f x x F F
.
Mặt khác
3
1
d 3 1 3 1
f x x F F G G
.
2 3 3 9 2 1 1 2 3 1 3 1 9
F G F G F F G G
3 3 1 9 3 1 3
F F F F
.
Suy ra
2
0
8 8 1 8 3 25
3 2 d 3 1
3 3 2 3 2 6
I f x x F F
.
Câu 44: Trong không gian
Oxyz
, cho điểm
1;2; 3
A
, mặt phẳng
:3 1 0
P x y z
và mặt
phẳng
: 3 3 0
Q x y z
Gọi
là đường thẳng đi qua
A
, cắt và vuông góc với giao tuyến
của
P
và
Q
. Sin của góc tạo bởi đường thẳng
và mặt phẳng
P
bằng:
A.
7 55
55
. B.
55
55
. C.
0
. D.
3 55
11
.
Lời giải
+) Ta có:
3;1; 1
P
n

,
1;3;1
Q
n
và
0;1;0
M P Q
.
Gọi
d
là giao tuyến của hai mặt phẳng
P
và
Q
d
qua
0;1;0
M
và có VTCP
; 1; 1;2
P Q
u n n
: 1
2
x t
d y t
z t
.
+) Gọi
B d
;1 ;2B d B b b b
1; 1;2 3
AB b b b

.
Ta có:
. 0 1. 1 1 2 2 3 0
d AB u b b b

1
b
.
2;0;1
u AB
.
.
sin ;
.
P
P
u n
P
u n
2.3 1.1
7 55
55
5. 11
.
Câu 45: Tìm số nghiệm nguyên của bất phương trình
2 2
2 4 9 5 1
2023 2023 1 8 0
x x x x
x x
A.
7
. B.
5
. C.
6.
D.
8
.
Lời giải:
Đặt
2 2 2
2 4 9, 5 1 9 8 1 8
a x x b x x a b x x x x
Khi đó:
2023 2023
a b
a b
Xét hàm số:
2023 ' 2023 .ln 2023 1 0
x x
f x x f x x
Hàm số đơn điệu tăng
f a f b a b
2 2
2 4 9 5 1 1 8 0
x x x x x x
Nên bất phương trình có 6 nghiệm nguyên.
Câu 46: Có bao nhiêu số nguyên dương x sao cho tồn tại số thực y lớn hơn 1 thỏa mãn
2
2 3
2 1 log log
y x
xy x y y
x
A.
3
. B.
1
. C. Vô số D.
2
.
Lời giải:
Ta có:
2
2 3
2 1 log log
y x
xy x y y
x
2 2
2 2
2 3 2 3
2 3 log log 2 3
1
y x y
xy x y y xy y x x
xy y
Dễ thấy hàm số
2
2 3
1
y
f y
y
nghịch biến trên
1;
. Nên ta có bảng biến thiên:
Để tồn tại số thực số thực y lớn hơn 1 thì
5
0
2
x
. Vậy có 2 số nguyên dương thỏa mãn.
Câu 47: Xét các số phức
z
thỏa mãn điều kiện
2 3
1 1
3 2
i
z
i
. Gọi
, m M
lần lượt là giá trị nhỏ
nhất và giá trị lớn nhất của biểu thức
.P z
Tính
2023 3 2 .S M m
A.
2021S
B.
2017S
C.
2019S
D.
2023S
Lời giải
Ta có
2 3
3 2
i
i
i
nên
2 3
1 1 1 1
3 2
i
z iz
i
1
. 1 1i z z i
i
.
Suy ra tập hợp các số phức
z
là đường tròn tâm
0; 1I
, bán kính
1R
.
Khi đó
min
max
1 1 0
0
2017.
2
1 1 2
P OI R
m
S
M
P OI R
 
Câu 48: Trong không gian , cho hai điểm
1;4;3A
,
5;0;3B
. Một hình trụ nội tiếp
trong mặt cầu đường kính
AB
đồng thời nhận
AB
làm trục của hình trụ. Gọi
M
và
N
lần lượt là
tâm các đường tròn đáy của
T
(
M
nằm giữa
A
,
N
). Khi thiết diện qua trục của
T
có diện tích
lớn nhất thì mặt phẳng chứa đường tròn đáy tâm
M
của
T
có dạng
0ax by cz d
. Giá trị
của bằng
A.
2 2
. B.
2 2 2
. C.
2 2
. D. .
Lời giải
Oxyz
T
b d
4 2
Ta có:
4; 4;0AB
.
Mặt cầu đường kính
AB
có tâm
3;2;3I
và bán kính
2 2
2
AB
R
.
Gọi là bán kính của hình trụ
0 2 2x
. Diện tích thiết diện là
2 2 2
. 2 .2 8 2. 8
TD
S GH GE x x x x
.
Do đó
16
TD
S
. Vậy
max
16
TD
S
khi
2 2
8 2.x x x
Khi đó
2
2 2 2
2 2 2 2IM IH MH
,
2 2IA
nên
2 3 2;2 2;3IA IM M
.
Phương trình mặt phẳng chứa đường tròn đáy tâm
M
của
T
và có véctơ pháp tuyến
1
1; 1;0
4
n AB
là:
( 3 2) 2 2 0 2 2 1 0x y x y
Ta có
1; 2 2 1b d
. Do đó
2 2b d
.
Câu 49: Có bao nhiêu giá trị nguyên của tham số
a
thuộc đoạn
10;10
để hàm số
3 2 2
3 1 3 2 3y x a x a a x a a
đồng biến trên khoảng
0;1
A.
21
. B.
10
. C.
8
. D.
2
.
Lời giải:
Đặt
2
3 2 2
3 1 3 2 3 3f x x a x a a x a a x a a x
.
Ta có:
0
3
x a
f x
x a
2
' 0 3 6 1 3 2 0
2
x a
f x x a x a a
x a
x
K
hi đó:
2
.
'
'
f x f x
y f x f x y
f x
T
a có bảng xét dấu:
Dựa vào bảng xét dấu ta thấy yêu cầu bài toán thỏa mãn khi và chỉ khi:
0
1
0
2 1
3
3 0
a
a
a
a
a
.
Vậy có 10 số nguyên a thỏa mãn yêu cầu bài toán.
Câu 50: Cho hàm số
(
)y f x
có
đạo hàm liên tục trên
và
thỏa mãn
23
) 6( ) ( 4 ,f xx xf x x x
.
Diện tích hình phẳng giới hạn bởi các đường
(
)y f x
và
(
)y f x
bằng
A.
7
12
. B.
4
5
4
. C.
1
2
. D.
7
1
6
.
Lời giải
Ta có
x
:
23
( ) . ( 6) 4f x x f x x x
23
6( ) ( ) . ( ) 4x f x x f x x x
23
[ . ( )] 4 6x f x x x
4 3
. ( ) 2x f x x Cx
Với
0
0x C
.
D
o đó:
23
( 2)f xx x
2
4( ) 3f x xx
.
Phươ
ng trình hoành độ giao điểm của
(
)y f x
và
(
)y f x
l
à nghiệm của phương trình:
3
22 3 2
0
3
1
4
2 4 5 4 0
x
x xx x xx x x
x
.
Suy ra, diện tích phẳng giới hạn bởi các đường cong
(
)y f x
và
(
)y f x
là:
0
4
( ) ( ) dS f x f x x
1
4
3 2 3 2
0 1
7
45 71
5 4 d 5 4 d
12 4 6
x x x x x x x x
.
--------------- TOANMATH.com ---------------
| 1/15
| | Tải xuống

Có thể bạn quan tâm:

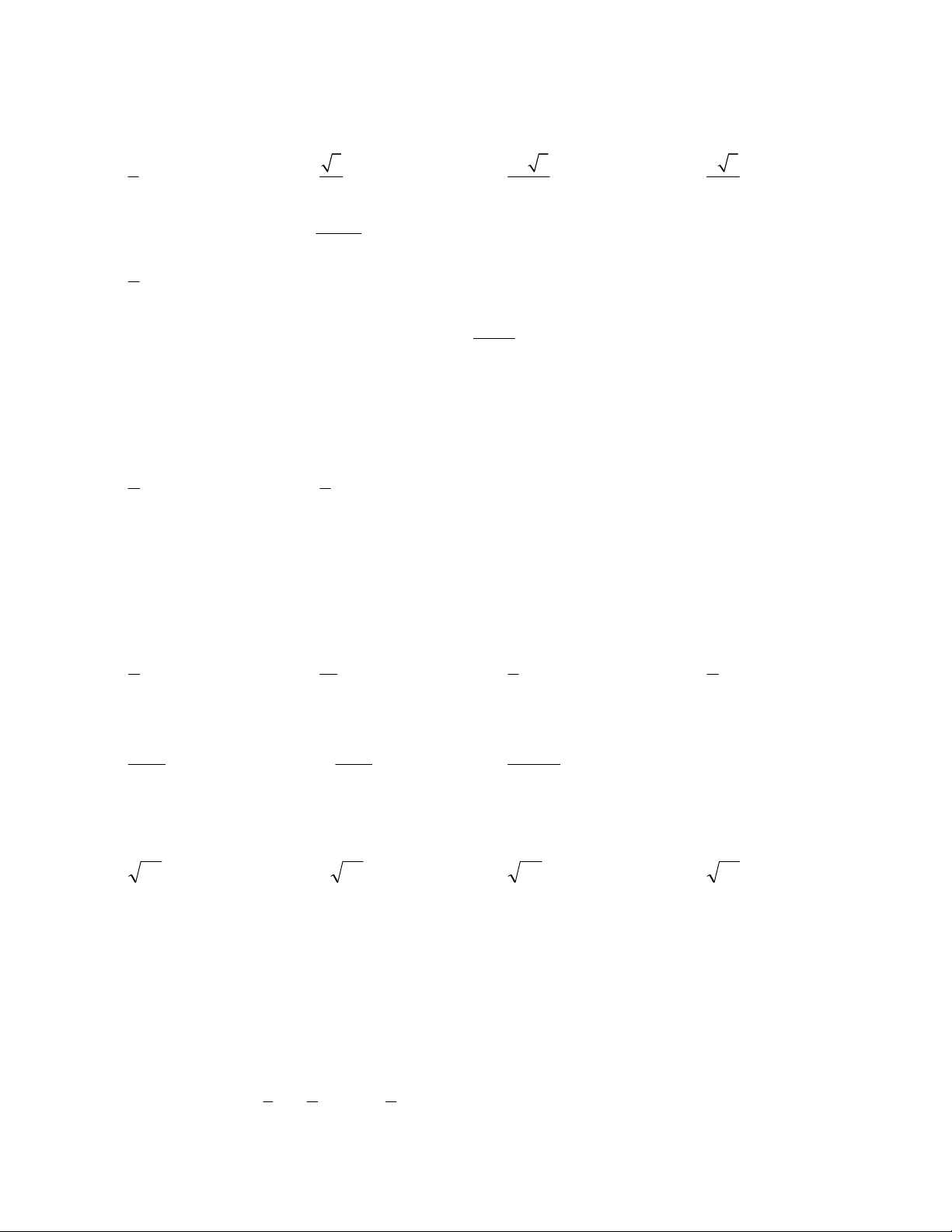
Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO TỈNH ĐẮK LẮK
ĐỀ KHẢO SÁT CHẤT LƯỢNG LỚP 12
CỤM CHUYÊN MÔN SỐ 6 NĂM HỌC 2022 - 2023 Bài thi: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài : 90 phút (không kể thời gian phát đề)
(Đề thi có 06 trang)
Họ và tên học sinh :..................................................... Số báo danh : ................... Mã đề 601
Câu 1. Cho hàm số f xx
 2x e . Khẳng định nào dưới đây đúng? e x
A. f xdx  2  C. 2 x  
B. f xdx x e C.   ln x
C. f xdx  2  ex C.  
D. f x 2
dx x ex C.  
x  1  2t
Câu 2. Trong không gian Oxyz , đường thẳng d : y  2  2t đi qua điểm nào dưới đây? z  3   3t
A. 1;2;3 .
B. 2;2;3 . C. 1;2; 3   . D. 2; 2  ; 3   .
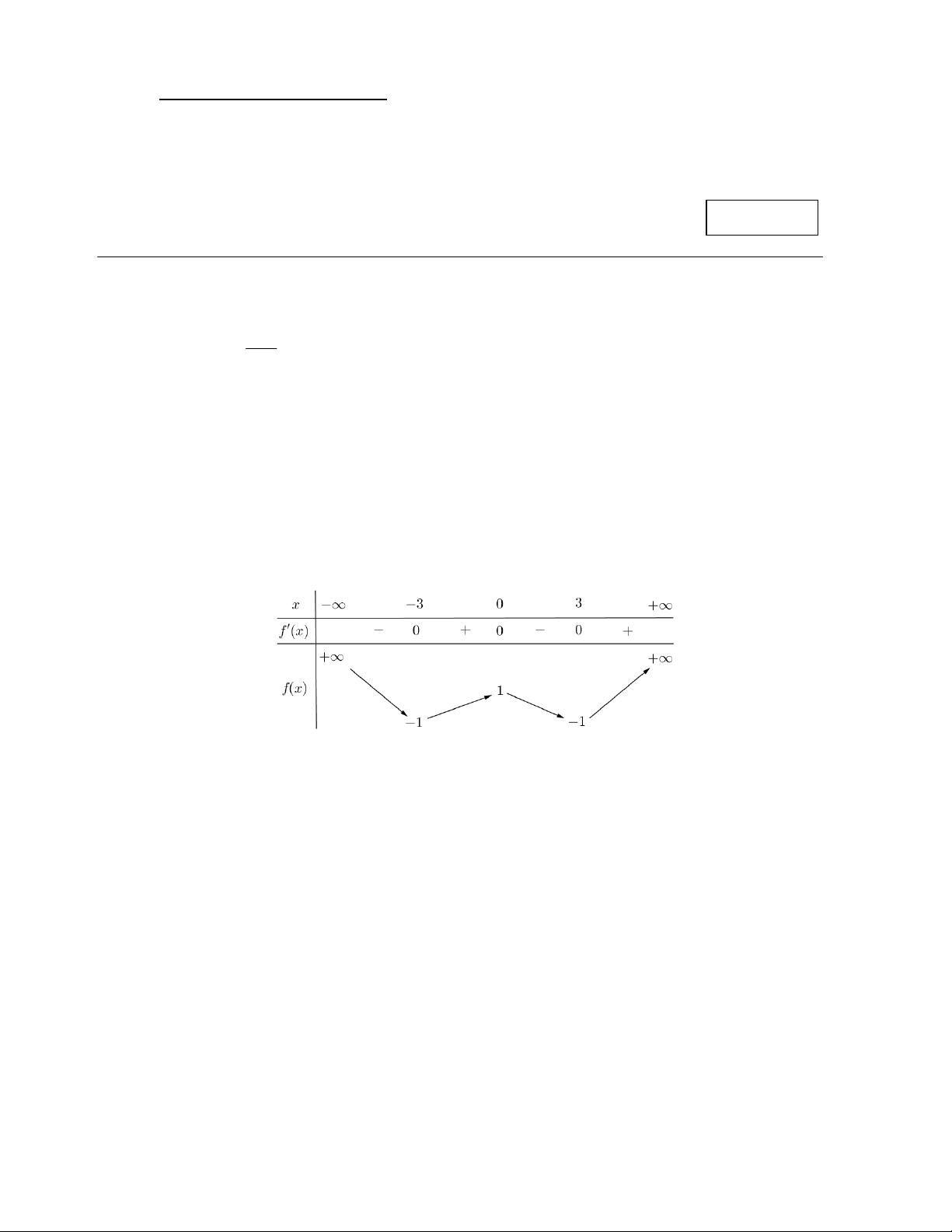
Câu 3. Cho hàm số y f x có bảng biến thiên như hình vẽ:
Số điểm cực trị của hàm số đã cho bằng A. 1. B. 2 . C. 3 . D. 0 .
Câu 4. Phần thực của số phức z  4  i 6 là A.  4. B. 4. C.  6. D. 6.
Câu 5. Cho tập hợp A có 7 phần tử. Số tập con gồm 3 phần tử của tập hợp A là A. 3 A . B. 7 3 . C. 3 C . D. 3 7 . 7 7 3 3
Câu 6. Nếu f x  2  dx
thì  f x 4dx   bằng 1 1 A. 8. B. 10. C. 24. D.  2. 3 1 3
Câu 7. Nếu f x  5  dx và f x  2  dx
thì f xdx  bằng 0 0 1 A.  3. B. 3. C. 10. D. 7.
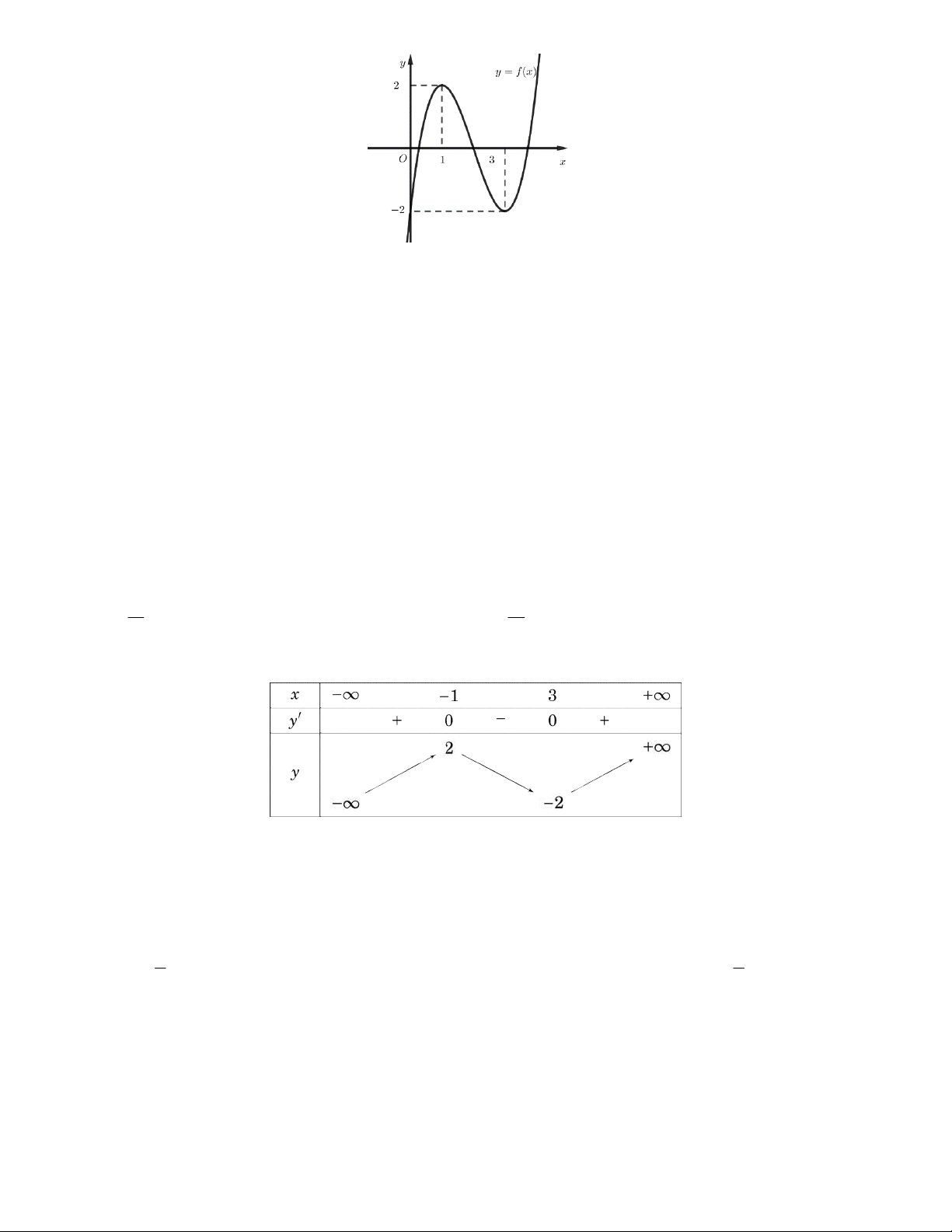
Câu 8. Cho hàm số bậc ba y f (x) có đồ thị như hình vẽ: 1/6 - Mã đề 601
Hàm số đã cho đạt cực tiểu tại điểm
A. x  1. B. x  2. 
C. x  2. D. x  3. 2 2 2
Câu 9. Trong không gian Oxyz , cho mặt cầu S  :  x  
1   y  3   z  2  25. Tâm I và
bán kính R của mặt cầu S  là: A. I  1
 ;3; 2, R  25 . B. I 1; 3  ; 2  , R  5 . C. I  1
 ;3; 2, R  5 . D. I 1; 3  ; 2  , R  25 .
Câu 10. Trên mặt phẳng tọa độ , điểm biểu diễn số phức z  2  i 3 có tọa độ là A. M  3 ; 2 . B. M  ; 3 2. C. M  ; 2 3  . D. M  3 ; 2 .
Câu 11. Cho hình lăng trụ đứng ABC.A' B'C ' có đáy ABC là tam giác vuông cân tại A với
AC  4a và mặt bên AA' B' B là hình vuông. Thể tích của khối lăng trụ ABC.A' B'C ' bằng 3 a 3 a A. . B. 3 64a . C. . D. 3 32a . 8 4
Câu 12. Cho hàm số y f x có bảng biến thiên như hình vẽ:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A.  ;  2 .
B. 1; . C. 1;3 . D.  ;   1 .
Câu 13. Nghiệm của phương trình 2x 1 2   8 là 5 3
A. x  .
B. x  3.
C. x  2. D. x  . 2 2
Câu 14. Trong không gian Oxyz , cho điểm M 2; 1
 ;3 và mặt phẳng  P : 3x  2 y z 1  0 .
Phương trình mặt phẳng đi qua M và song song với  P là
A. 3x  2 y z 11  0 .
B. 2x y  3z 14  0 .
C. 3x  2 y z 11  0 .
D. 2x y  3z 14  0 . 2/6 - Mã đề 601
Câu 15. Trong không gian với hệ tọa độ Oxyz , gọi  là góc giữa hai mặt phẳng
P : x  3y  2z 1  0 và mặt phẳng Oxy . Khẳng định nào sau đây đúng? A. o   45 . B. o   30 . C. o   60 . D. o   90 .
Câu 16. Trong không gian Oxyz , cho mặt phẳng  P : 2x y z  3  0 . Vectơ nào dưới đây
là một vectơ pháp tuyến của mặt phẳng  P ?     A. 1 n  2;1;  1 .
B. n3  1;1;3 .
C. n4  2;1;3 .
D. n2  2;1;3 .
Câu 17. Cho khối chóp có diện tích đáy 2
B  2a và chiều cao h  9a . Thể tích của khối chóp đã cho bằng A. 3 9a . B. 3 6a . C. 3 3a . D. 3 18a .
Câu 18. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng  ABC , SA  2a, tam giác
ABC vuông tại B, AB a 3 và BC a . Góc giữa đường thẳng SC và mặt phẳng  ABC  bằng A. 90. B. 30 .  C. 45. D. 60. 2
Câu 19. Tập nghiệm bất phương trình x 3 2 x 16là
A. 4; . B.  ;   
1  4; . C.  1  ; 4 . D.  ;    1 .
Câu 20. Tập xác định của hàm số y  ln 2  x là A. D  .  B. D   ;  2.
C. D  2;.
D. D   \  2 .
Câu 21. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ? A. 4 2
y  x  2x  3. B. 3
y  x  3 . x C. 4 2
y x  2x  3. D. 3
y x  3x  3.
Câu 22. Một hình trụ có bán kính đáy bằng a, chu vi thiết diện qua trục bằng 10a. Chiều cao
của khối trụ đã cho bằng
A. 3a . B. a . C. 4a . D. 9a .
Câu 23. Cho sin xdx F x 
C . Khẳng định nào dưới đây đúng?
A. F 'x  sin . x
B. F 'x  sin . x
C. F 'x  cos . x
D. F 'x  cos . x
Câu 24. Thể tích của khối nón có chiều cao h và bán kính r là 4 1 A. 2 rh . B. 2 2 rh . C. 2 rh . D. 2 rh . 3 3 3/6 - Mã đề 601
Câu 25. Hình lăng trụ ABC.A' B 'C ' có đáy ABC là tam giác vuông tại ,
A AB a, AC  2a . Hình
chiếu vuông góc của A' lên mặt phẳng  ABC  là điểm I thuộc cạnh BC. Khoảng cách từ A tới
mặt phẳng  A' BC  bằng 2 3 2a 5 a 5 A. a B. a C. D. 5 2 5 5 x  4
Câu 26. Đồ thị hàm số y
cắt trục tung tại điểm có tung độ bằng 2x  2 1 A. . B. 1  . C. 2  . D. 4. 2 2x 1
Câu 27. Tiệm cận đứng của đồ thị hàm số y
là đường thẳng có phương trình x 1
A. y  1. B. x  1. 
C. y  2. D. x  2.
Câu 28. Diện tích hình phẳng giới hạn bởi đồ thị của hàm số 5
y x , trục hoành và hai
đường thẳng x  1, x  1 bằng 3 1 A. . B. . C. 7. D. 5. 2 3
Câu 29. Giá trị nhỏ nhất của hàm số 3 2
y x  3x trên đoạn 1;5 bằng A. 50 . B. 4 . C. 45 . D. 2 .
Câu 30. Có 30 chiếc thẻ được đánh số thứ tự từ 1 đến 30. Chọn ngẫu nhiên một chiếc thẻ.
Tính xác suất để chiếc thẻ được chọn mang số chia hết cho 3. 2 3 1 1 A. . B. . C. . D. . 3 10 3 2
Câu 31. Với a là số thực dương bất kỳ, ln 2023a  ln2022a bằng 2023 2023 ln 2023 A. . B. ln . C. . D. ln . a 2022 2022 ln 2022
Câu 32. Cho hai số phức z  3  i và z  2   i
5 . Khi đó mô đun của số phức z z z 1 2 1 2 bằng A. 17. B. 2 17. C. . 39 D. 10.
Câu 33. Cho cấp số cộng u có số hạng đầu u  2 , công sai d  5 . Giá trị của u bằng n  1 4 A. 250 . B. 1 2 . C. 22 . D. 17 .
Câu 34. Trong không gian Oxyz , khoảng cách từ điểm M 1;2;3 đến mặt phẳng
(P) : x  2 y  2z  5  0 bằng:
A. d M ,P  2.
B. d M ,P  4.
C. d M ,P  1.
D. d M ,P  3. 1 1 5 Câu 35. Hàm số 3 2 y x x  6x
đồng biến trên khoảng 3 2 6
A. 3;  . B.  ;  3. C.  2  ; 3. D.  2  ;  . 4/6 - Mã đề 601
Câu 36. Tập nghiệm của bất phương trình log x  2  2 là 3  
A. S   ;1   1 . B. S  2  ;11 .
C. S  2;  8 .
D. S   ;   8 .
Câu 37. Liên hợp của số phức z  1   i 2 là
A. z  1  2 . i B. z  2  . i
C. z  1  2 . i D. z  1   2 . i 1 1 1
Câu 38. Nếu f x  5  dx và gx  4  dx
thì  f xgxdx   bằng 0 0 0 A. 54. B. 20. C. 9. D. 1.
Câu 39. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a . Hình chiếu vuông góc 2
của S trên đáy là điểm H trên cạnh AC sao cho AH
AC ; mặt phẳng SBC  tạo với đáy 3
một góc 60o . Thể tích khối chóp S.ABC là? 3 a 3 3 a 3 3 a 3 3 a 3 A. B. C. D. 48 36 24 12
Câu 40. Trong tập hợp số phức, xét phương trình 3
z   m   2 2
1 z  3mz m  0 ( m là tham số
thực). Có bao nhiêu giá trị của m để phương trình đó có ba nghiệm phân biệt 1 z , z2, 3 z thỏa mãn ? 1
z z2  z3  3 A. 0. B. 2 . C. 3 . D. 1.
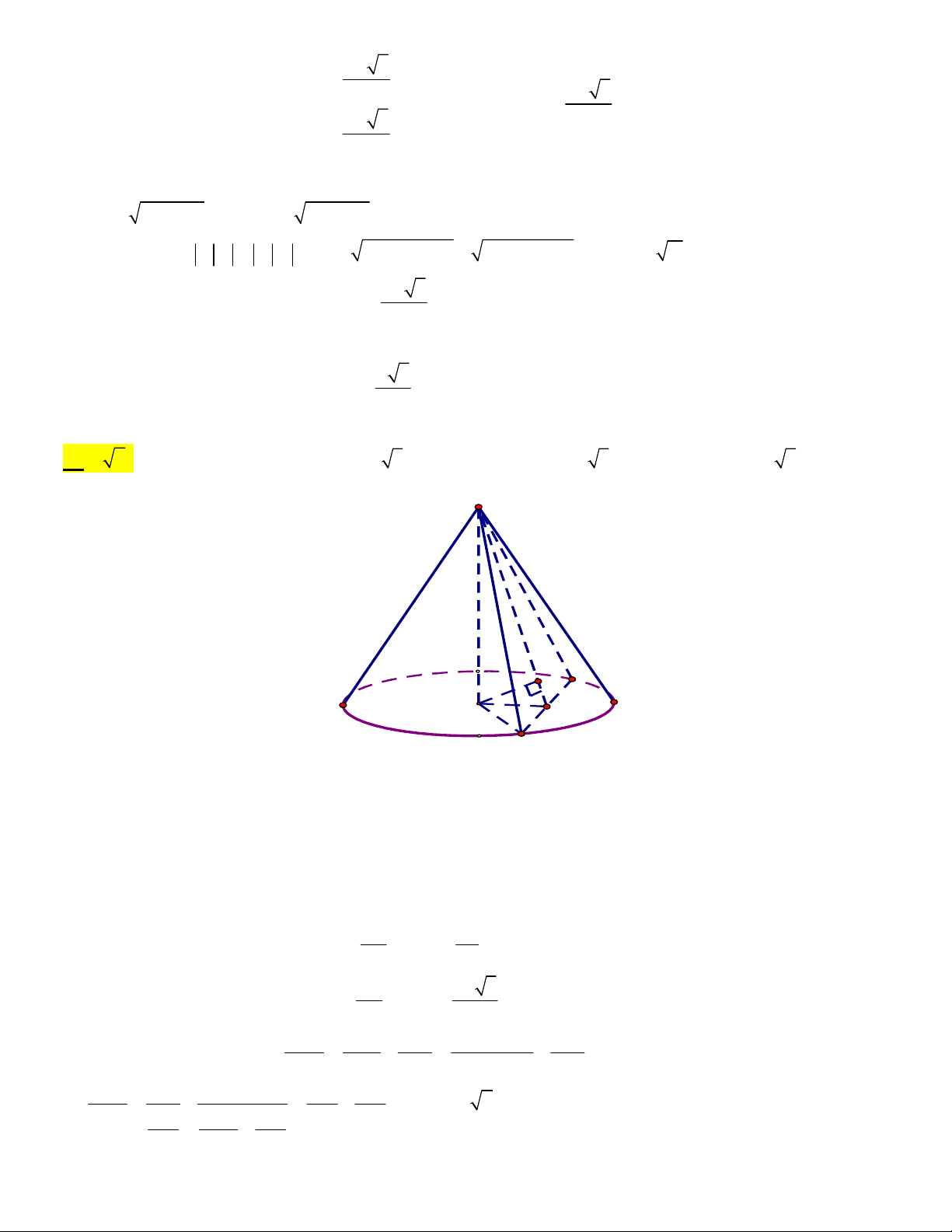
Câu 41. Cho hình nón đỉnh S , đường cao SO, A và B là hai điểm thuộc đường tròn đáy sao a 3
cho khoảng cách từ O đến SAB bằng và  0  0
SAO  30 , SAB  60 . Độ dài đường sinh của 3
hình nón theo a bằng
A. a 3 . B. a 5 . C. a 2 . D. 2a 3 . Câu 42. Cho hàm số 2 5
y f x có đạo hàm f x   x    x    2 ' 2 1
x  2 m  6 x m với mọi
x   . Số giá trị nguyên dương của tham số m để hàm số đã cho có đúng một điểm cực trị là A. 4 . B. 6 . C. 5 . D. 7 .
Câu 43. Cho hàm số f x liên tục trên  . Gọi F x và G x là hai nguyên hàm của f x 2
thỏa mãn 2F 3  G 3  9  2F   1  G   1 . Khi đó  2
x f 3  2xdx bằng 0 25 43 7 A. 3 . B. . C. . D. . 6 6 6
Câu 44. Trong không gian Oxyz , cho điểm A1;2; 3
  , mặt phẳng  P : 3x y z 1  0 và mặt
phẳng Q : x  3y z  3  0 Gọi  là đường thẳng đi qua A , cắt và vuông góc với giao tuyến
của P và Q . Sin của góc tạo bởi đường thẳng  và mặt phẳng P bằng: 55 3  55 7 55 A. . B. . C. 0 . D. . 55 11 55 5/6 - Mã đề 601 Câu 45. Tìm số nghiệm nguyên của bất phương trình 2 2 2 x 4 x9 x 5 x 1 2023 2023     x  
1 8  x  0 A. 8 . B. 5. C. 6. D. 7 .
Câu 46. Có bao nhiêu số nguyên dương x sao cho tồn tại số thực y lớn hơn 1 thỏa mãn  2 y x  3 2
xy x  2 y   1 log y  log x A. 2 . B. Vô số C. 3 . D. 1.  2  3i
Câu 47. Xét các số phức z thỏa mãn điều kiện z 1  1 . Gọi ,
m M lần lượt là giá trị 3  2i
nhỏ nhất và giá trị lớn nhất của biểu thức P z . Tính S  2023 3M  2 . m
A. S  2021
B. S  2019
C. S  2017 D. S  2023
Câu 48. Trong không gian Oxyz , cho hai điểm A1;4;  3 , B5;0; 
3 . Một hình trụ T  nội tiếp
trong mặt cầu đường kính AB đồng thời nhận AB làm trục của hình trụ. Gọi M và N lần
lượt là tâm các đường tròn đáy của T  ( M nằm giữa A , N ). Khi thiết diện qua trục của T
có diện tích lớn nhất thì mặt phẳng chứa đường tròn đáy tâm M của T  có dạng
ax by cz d  0 . Giá trị của b d bằng A. 4  2 . B. 2  2 2 . C. 2 2 . D. 2 2 .
Câu 49. Có bao nhiêu giá trị nguyên của tham số a thuộc đoạn  10  ;10 để hàm số 3
y  x  a   2
x a a   2 3 1 3
2 x a a  3 đồng biến trên khoảng 0  ;1 A. 2 . B. 21. C. 8. D. 10.
Câu 50. Cho hàm số y f (x) có đạo hàm liên tục trên  và thỏa mãn 3 2
f (x)  xf (
x)  4x  6x , x
   . Diện tích hình phẳng giới hạn bởi các đường y f ( x) và y f (  x) bằng 7 1 45 71 A. . B. . C. . D. . 12 2 4 6
------ HẾT ------ 6/6 - Mã đề 601 Câu h 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 ỏ i 601 B A C B C C B A A A C C D D C D B B C B C C B S 602 C D A D C B A D B B D B A D C C A A C B A C A Ở GIÁ 6 C C D A C B A B C D D D B B A C C B D B D B B 03 O C D 604 Ụ A D C D A C B D D B C B A C Ụ A A D B D D C C B M C C Đ VÀ 605 Ề B D A C A C B D D D D B D B D C A A B C A D A H CHÍ UYÊ Đ 606 ÀO B C D A D A B B D D C A D D C D D B B D D D B N H T N T 6 MÔ Ạ A D D A A B A C C B C A A A B C C D D A A B A 07 H O T Ứ N S C 608 Ỉ B A D C B C C C B D C B D D C C A B A D B C B NH Ố 6 609 Đ C D B D A D B D B B B A D A D D B A A C C B D Ắ K 610 L C A C C D D C B A B A B D C C B C B A D A B C Ắ K 611 B A D A C D D C C B C B A D A C B B B D B A C 612 B C D D B C C B C A C B B A B C B D A D A A D 613 C C B C C B D D A B B D D A A C B B B B A D C 614 D B D D C C D A C C C D C B D D D A B A B A D ĐÁP 615 B B D D C C A B D A B B C A C B B B A A B C C ÁN 616 Đ A A B A B B C C C D C D A A A C D D A B C D C Ề NĂM K 617 B A D B A C C A A A A B B C B A A D C A A A B H Ả Bài t H O 618 A D B D C D B D B D C A C D A D B B A C C B A Ọ SÁT hi: T C 20 6 B D A C D C A B A A D A C A A D C C B A D C D 19 CH OÁN 22 620 Ấ A D C B D D B C C A C A D B A D B C B C C C A - T LƯ 20 23 621 C D A B B A A D A D B B B C D B B B C C C C B Ợ NG 622 B D A A C D C C A A B B A A B A C C C D C D D L Ớ 623 C A D D B C D C A B A B B B D D A D B D B B A P 12 624 B B D C C B B B C A A D C C D C C C C A A A D 50 49 48 47 46 45 44 43 42 41 40 39 38 37 36 3 34 33 32 31 30 29 28 27 26 25 24 5 D D D D C A C D B D C D A D D B A A A B C B B B C C D C B A D D A C C D A B C B A B A A C A A D D A B C C B D D C A B C C A A D B D B D A B A C D D C D A D A B C C C B B C C B D B D D B A D C B D B C A A B D B C C C D C D B D B D D D D D A A B B C C B B D A D B C B A D C A A A B C A C B C A D B A A A A A A A A A C D B B C A B C C B D D D B C C D D B C A B A B D D C A B A B C D D B D A A C C C B C A D C D A D A C C D A D D D A C D A B D C B D A D D C A D D B D A C C D D D A D A A A D B A B A A D A A A A C C C D D A A B B C C A C D B C B C D B D C C A A B A B C A D C B B D C D A A C A A D B D D A D A A D D A B C A A B B D C A A C B C D B D C C C B B B A D A B A D A B C B B D D D C D B A C A C D A B B D B B B B B A B A D D B D B A C B D A B A B C B A D D C B D A D D D A D D B D D D B D C B B C B A A A C D D A B D A A C B B B D C D B D B A C D D B B D C B B B A B D A D A A A A B C B C B D B D D D A A B B A A C C D D C C B B A B A D B B C C A B B A C B D C D D C C A B D B C A A A A C C D D D B D B A C D D A D A B B B A D C B C D A A A D A C A D A B A D C C A B D D C C A A C D A C A A C B A D C B B A D D B B C D C B D C A A A D B C C C B A C D D D B C B C A A C D C D D D A C C A A C A B B D A A A B C A A B D D C D B A D D B B B A B B A D B A D A D B B A D C D A D C A C B B B C D B ĐÁP ÁN CHI TIẾT
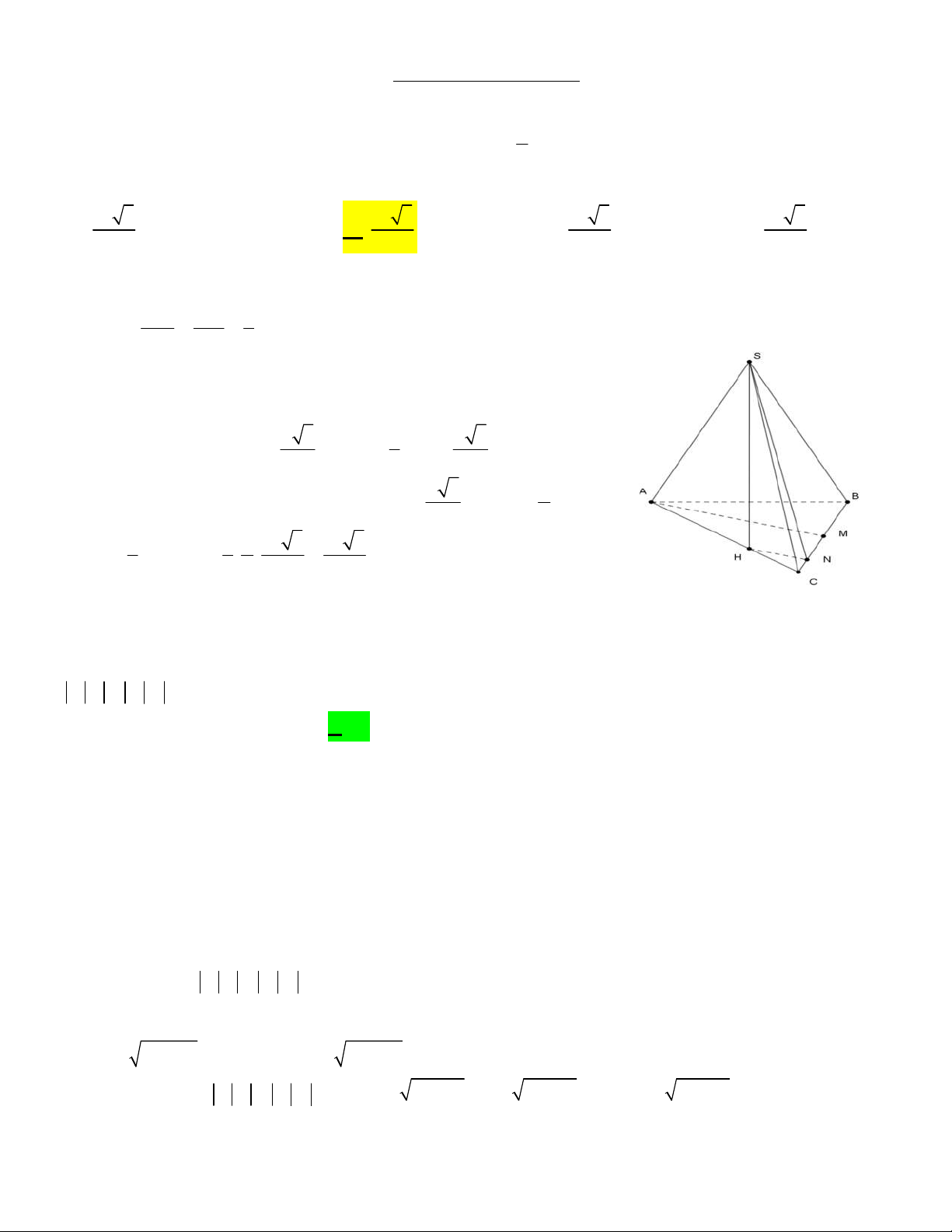
Câu 39: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a . Hình chiếu vuông góc của 2
S trên đáy là điểm H trên cạnh AC sao cho AH
AC ; mặt phẳng SBC  tạo với đáy một góc 3
60o . Thể tích khối chóp S.ABC là? 3 a 3 3 a 3 3 a 3 3 a 3 A. B. C. D. 12 48 36 24 Lời giải:
Gọi M là trung điểm của BC . CN CH 1 N CM :  
HN //AM . Mà CM CA 3 AB
C đều nên AM BC HN BC BC  SHN  . Nên        ;  ;   60o SBC ABC SN HN SNH . a 3 1 a 3 Do AB
C đều nên AM   HN AM  . 2 3 6 a a SH
N vuông tại H có  3
SH HN.sin SNH  .sin 60o  . 6 4 2 3 1 1 a a 3 a 3 VSH.S  . .  . S . ABC 3 ABC 3 4 4 48
Câu 40: Trong tập hợp số phức, xét phương trình 3
z   m   2 2
1 z  3mz m  0 ( m là tham số thực).
Có bao nhiêu giá trị của m để phương trình đó có ba nghiệm phân biệt 1
z , z2, z thỏa mãn 3 ? 1 z z2  3 z  3 A. 0 . B. 1. C. 2 . D. 3 . Lời giải z  1 3 2
z   m   2 2
1 z  3mz m  0 (1)   z  
1  z  2mz m  0   2
z  2mz m  0 (2) 
Đặt z 1, gọi z , z là hai nghiệm của phương trình (2) . 3 1 2
z z  2m
Phương trình (2) có 2
 '  m m và : 1 2 z z m  1 2
*) TH1: Nếu m  1 ta có  '  0 và phương trình 2 có hai nghiệm thực phân biệt dương khác 1. Khi đó
z z 1  3  2m 1  3  m  1 (loại). 1 z z2  3 z  3 1 2
*) TH2: Nếu m  0 ta có  '  0 và phương trình 2 có hai nghiệm thực phân biệt là: 2 2
z m m m (z  0); z m m m (z  0) 1 1 2 2 Khi đó 2 2 2 1 z z2  3
z  3  m m m m m m 1  3  2 m m  2  1 5 m   1 5 2 2
m m 1  0  
. Vì m  0 nên m  .  1 5 2 m   2
*) TH3: Nếu 0  m  1 ta có  '  0 , khi đó phương trình 2 có hai nghiệm phức : 2 2
z m  m m.i ; z m  m m.i 1 2 Vậy 2 2 2 2
m  1  m  1 (loại). 1 z z2  3 z  3 
m m m m m m 1  3 1 5
Vậy chỉ có một giá trị m
thỏa mãn yêu cầu đề bài. 2
Câu 41: Cho hình nón đỉnh S , đường cao SO, A và B là hai điểm thuộc đường tròn đáy sao cho a 3
khoảng cách từ O đến SAB bằng và  0  0
SAO  30 , SAB  60 . Độ dài đường sinh của hình nón 3 theo a bằng A. a 2 . B. a 3 . C. 2a 3 . D. a 5 . Lời giải: S H B O K A
Gọi K là trung điểm của AB ta có OK AB vì tam giác OAB cân tại O
Mà SO AB nên AB  SOK   SOK   SAB mà  SOK   SAB  SK nên từ O dựng
OH SK thì OH  SAB  OH d O,SAB SO SA
Xét tam giác SAO ta có:  sin SAO   SO SA 2 SK SA
Xét tam giác SAB ta có:  3 sin SAB   SK SA 2 1 1 1 1 1
Xét tam giác SOK ta có:     2 2 2 2 2 2 OH OK OS SK SO SO 1 1 1 4 2       SA a 2 2 2 2 2 2 2 OH SA 3SA SA SA SA  4 4 4 Câu 42: Cho hàm số 2 5
y f x có đạo hàm f x   x    x    2 ' 2 1
x  2 m  6 x m với mọi
x   . Số giá trị nguyên dương của tham số m để hàm số đã cho có đúng một điểm cực trị là A. 7 . B. 5. C. 6 . D. 4 . Lời giải: x  2  
Ta có: f ' x  0  x  1  .  2
x  2m  6 x m  0   1 
Yêu cầu bài toán thỏa mãn khi và chỉ khi   0   1  4  m  9    0    
. Vậy có 7 số nguyên dương thỏa mãn 1 m 13   2  1  2 
m  6.1 m  0 
Câu 43: Cho hàm số f x liên tục trên  . Gọi F x và G x là hai nguyên hàm của f x thỏa 2
mãn 2F 3  G 3  9  2F   1  G   1 . Khi đó  2
x f 3  2xdx bằng 0 25 7 43 A. . B. . C. . D. 3 . 6 6 6
Lời giải 2 2 2 8 Ta có 2 I x dx
f 3  2x dx   f 3  2x dx    . 3 0 0 0
Đặt t  3  2x dt  2  dx . 2 1 3  1  1 1
Khi đó f 3  2x dx f t   dt
f x dx    
F 3  F     1  .  2  2 2 0 3 1 3
Mặt khác f x dx F 3  F  
1  G 3  G   1  . 1 
2F 3  G 3  9  2F   1  G  
1  2  F 3  F  
1   G 3  G   1   9
 3 F 3  F  
1   9  F 3  F   1  3 . 2 8 8 1 8 3 25
Suy ra I   f 3  2x dx   F 3  F   1      . 3 3 2 3 2 6 0
Câu 44: Trong không gian Oxyz , cho điểm A1;2; 3
  , mặt phẳng  P : 3x y z 1  0 và mặt
phẳng Q : x  3y z  3  0 Gọi  là đường thẳng đi qua A , cắt và vuông góc với giao tuyến
của P và Q . Sin của góc tạo bởi đường thẳng  và mặt phẳng P bằng: 7 55 55 3  55 A. . B. . C. 0 . D. . 55 55 11 Lời giải   +) Ta có: n   , n
và M 0;1;0 P Q . Q 1;3  ;1 P 3;1;  1    
Gọi d là giao tuyến của hai mặt phẳng P và Q    x t
d qua M 0;1;0 và có VTCP u  n ; n   1; 1
 ; 2  d :  y  1 t . P Q        z  2t  
+) Gọi B    d B d B ; b 1 ;
b 2b  AB  b 1; b 1; 2b  3 .  
Ta có:   d A .
B u  0  1.b   1  b  
1  2 2b  3  0  b  1  .  
u AB   .   2;0;  1   u .nP 2  .3 1.1 7 55 sin  ;   P        . u . n 5. 11 55   P 2 2
Câu 45: Tìm số nghiệm nguyên của bất phương trình 2 x 4 x9 x 5 x 1 2023 2023     x  
1 8  x  0 A. 7 . B. 5. C. 6. D. 8 . Lời giải: Đặt 2 2 2
a  2x  4x  9, b x  5x  1  a b x  9x  8   x   1  x  8
Khi đó: 2023a   2023b ab
Xét hàm số:    2023x   '   2023x f x x f x
.ln 2023  1  0 x
 Hàm số đơn điệu tăng
f a  f b  a b  2 2
2x  4x  9  x  5x  1   x   1  x  8  0
Nên bất phương trình có 6 nghiệm nguyên.
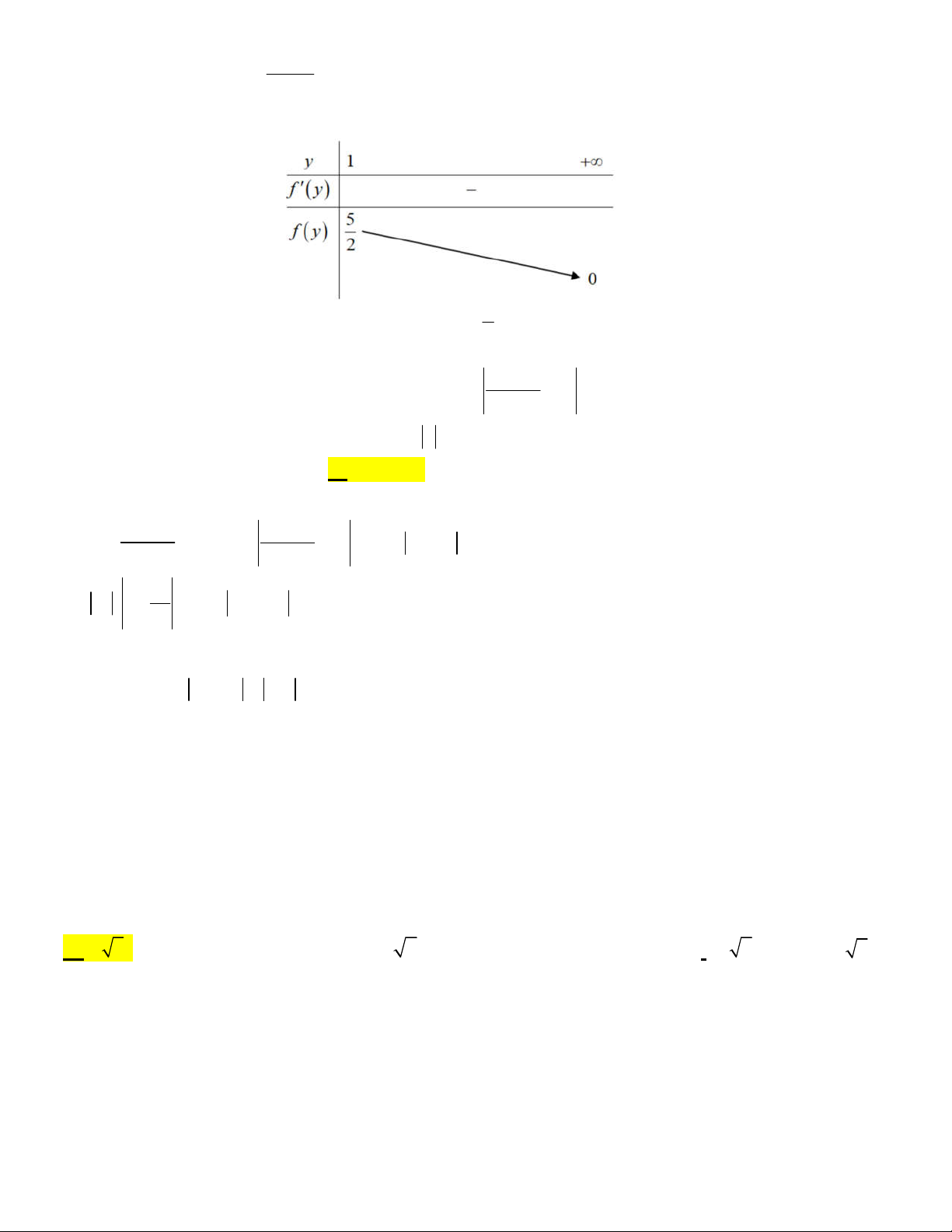
Câu 46: Có bao nhiêu số nguyên dương x sao cho tồn tại số thực y lớn hơn 1 thỏa mãn  2 y x  3 2
xy x  2 y   1 log y  log x A. 3 . B. 1. C. Vô số D. 2 . Lời giải: 2 y x  3 Ta có:  2
xy x  2 y   1 log y  log x 2 y x  3 2 y  3   2
xy x  2 y  3 2 log y  log
xy  2 y x  3  x  2 2 xy y  1 2 y  3
Dễ thấy hàm số f y 
nghịch biến trên 1; . Nên ta có bảng biến thiên: 2 y 1 5
Để tồn tại số thực số thực y lớn hơn 1 thì 0  x  . Vậy có 2 số nguyên dương thỏa mãn. 2  2  3i
Câu 47: Xét các số phức z thỏa mãn điều kiện z 1  1 . Gọi ,
m M lần lượt là giá trị nhỏ 3  2i
nhất và giá trị lớn nhất của biểu thức P z . Tính S  2023 3M  2 . m
A. S  2021
B. S  2017
C. S  2019 D. S  2023 Lời giải  2  3i  2  3i Ta có  i  nên
z 1  1   iz 1  1 3  2i 3  2i 1
  i . z
 1  z  i  1.  i
Suy ra tập hợp các số phức z là đường tròn tâm I 0; 
1 , bán kính R  1 . P
OI R  11  0  m  0 Khi đó min     
S  2017. P
OI R  11  2 M  2  max 
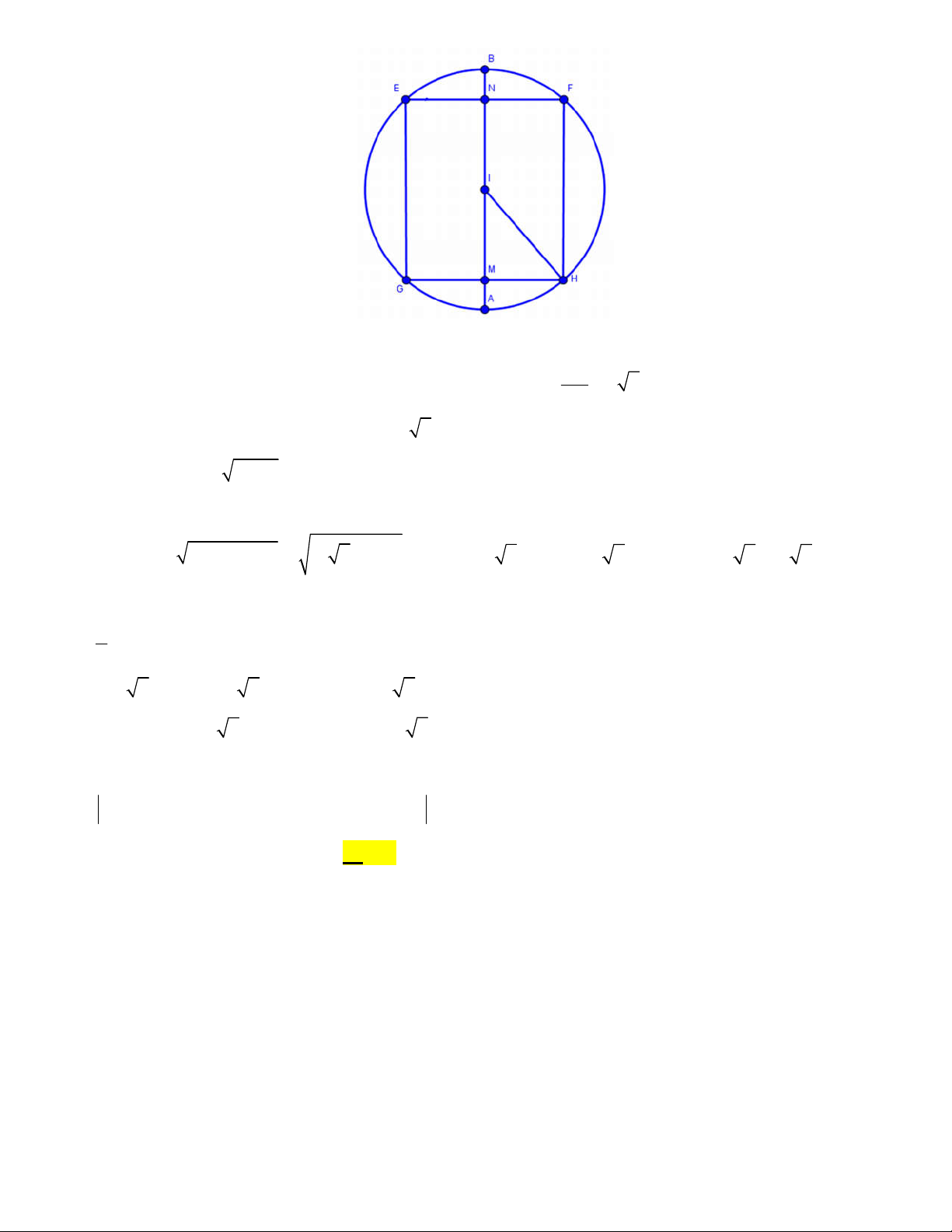
Câu 48: Trong không gian Oxyz , cho hai điểm A1;4;  3 , B5;0; 
3 . Một hình trụ T  nội tiếp
trong mặt cầu đường kính AB đồng thời nhận AB làm trục của hình trụ. Gọi M và N lần lượt là
tâm các đường tròn đáy của T  ( M nằm giữa A , N ). Khi thiết diện qua trục của T  có diện tích
lớn nhất thì mặt phẳng chứa đường tròn đáy tâm M của T  có dạng ax by cz d  0 . Giá trị
của b d bằng A. 2 2 . B. 2  2 2 . C. 2  2 . D. 4  2 . Lời giải  Ta có: AB 4; 4  ; 0 . AB
Mặt cầu đường kính AB có tâm I 3;2;  3 và bán kính R   2 2 . 2
Gọi x là bán kính của hình trụ 0  x  2 2 . Diện tích thiết diện là 2 SGH GE xx   2 2 . 2 .2 8 2. x  8  x . TD  Do đó S  16 . Vậy S  16 khi 2 2
x  8  x x  2. TD TD max  
Khi đó IM IH MH   2 2 2 2 2 2
 2  2 , IA  2 2 nên IA  2 IM M 3 2;2  2;3 .
Phương trình mặt phẳng chứa đường tròn đáy tâm M của T  và có véctơ pháp tuyến  1  n AB  1; 1  ;0 là: 4
(x  3  2)   y  2  2  0  x y  2 2 1  0 Ta có b  1
 ; d  2 2 1 . Do đó b d  2 2 .
Câu 49: Có bao nhiêu giá trị nguyên của tham số a thuộc đoạn  10  ;10 để hàm số 3
y  x  a   2
x a a   2 3 1 3
2 x a a  3 đồng biến trên khoảng 0;  1 A. 21. B. 10 . C. 8 . D. 2 . Lời giải:
Đặt f x  x  a   x a a   x a a     x a2 3 2 2 3 1 3 2 3
a  3  x .  x a
Ta có: f x  0   x a  3   x a f x 2 '
 0  3x  6 a  
1 x  3a a  2  0   x a  2 
f x . f ' x 2    
Khi đó: y f x 
f x  y '  f x Ta có bảng xét dấu:
Dựa vào bảng xét dấu ta thấy yêu cầu bài toán thỏa mãn khi và chỉ khi: a  0  1  a  0 a  2  1   
. Vậy có 10 số nguyên a thỏa mãn yêu cầu bài toán. a  3  a  3  0  Câu 50: Cho hàm số
y f ( x) có đạo hàm liên tục trên  và thỏa mãn 3 2
f (x)  xf (
x)  4x  6x , x
   . Diện tích hình phẳng giới hạn bởi các đường y f ( x) và y f (  x) bằng 7 45 1 71 A. . B. . C. . D. . 12 4 2 6 Lời giải Ta có x   : 3 2 f (x)  . x f (
x)  4x  6x 3 2
 (x)  f (x)  . x f (
x)  4x  6x 3 2  [ .
x f (x)]  4x  6x 4 3  .
x f (x)  x  2x C
Với x  0  C  0 . Do đó: 3 2
f (x)  x  2x 2  f (
x)  3x  4x .
Phương trình hoành độ giao điểm của y f (x) và y f (
x) là nghiệm của phương trình: x  0 3 2 2 3 2 
x  2x  3x  4x x  5x  4x  0  x  1 .  x  4 
Suy ra, diện tích phẳng giới hạn bởi các đường cong y f (x) và y f (  x) là: 4 1 4 7 45 71 S
f (x)  f (  x) dx    3 2
x  5x  4xdx   3 2
x  5x  4xdx      . 12 4 6 0 0 1
--------------- TOANMATH.com ---------------
Document Outline

  • de 601
  • Đáp án đề thi thử cụm 6
  • ĐÁP ÁN CHI TIẾT MÃ ĐỀ 601