Đề kiểm tra cuối học kỳ 2 Toán 7 năm 2020 – 2021 phòng GD&ĐT thành phố Bắc Ninh

UBND THÀNH PHỐ BẮC NINH
ĐỀ KIỂM TRA CUỐI HỌC KỲ II
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
NĂM HỌC: 2020 - 2021 Môn: Toán - Lớp 7 (Đề có 02 trang)
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
I. TRẮC NGHIỆM (3,0 điểm)
Chọn phương án trả lời đúng trong các câu sau:
Câu 1. Biểu thức đại số biểu thị bình phương của một tổng hai số a và b là A. 2 2
a − b . B. 2 2 a + b . C. ( − )2 a b . D. ( + )2 a b .
Câu 2. Điểm kiểm tra môn Toán của 20 bạn học sinh lớp 7 được ghi lại ở bảng sau Điểm số ( x) 5 6 7 8 9 10 Tần số 2 6 4 5 2 1
Điểm trung bình môn Toán của 20 bạn trên là
A. X = 7, 2 .
B. X = 7, 25 .
C. X = 7,1. D. X = 7,15.
Câu 3. Giá trị của biểu thức 3 2
x − 2x tại x = 2 − là A. 16 − . B.16 . C. 0 . D. 8 − . 7 − Câu 4. Đơn thức 5 2
x y có phần hệ số là 5 −7 A. 7 . B. 7 − . C. 5 2 x y . D. . 5
Câu 5. Biểu thức nào sau đây không là đơn thức? A. 2 4x y ( 2 − x). B. 2x . C. 2
2xy − x . D. 2021.
Câu 6. Bậc của đơn thức 3 5 2 − x y là A. 2 − . B. 3. C.8 . D. 3 5 x y .
Câu 7. Nghiệm của đa thức P( x) =15x − 3 là 1 − 1 A. . B. . C. 5 . D. 5 − . 5 5
Câu 8. Sắp xếp các hạng tử của đa thức P( x) 3 2 4
= 2x − 7x + x − 4 theo lũy thừa giảm dần của biến ta được A. P( x) 4 3 2
= x + 2x − 7x − 4. B. P(x) 2 3 4
= 7x + 2x + x − 4. C. P( x) 2 3 4 = 4
− − 7x + 2x + x . D. P(x) 4 3 2
= x − 2x − 7x − 4 .
Câu 9. Cho tam giác MNP cân tại M có 0
N = 50 . Số đo của góc M là A. 0 65 . B. 0 50 . C. 0 130 . D. 0 80 .
Câu 10. Cho tam giác DEF vuông tại D có DE = 5cm, EF = 13cm. Độ dài cạnh DF là A.12 cm. B. 5 cm. C.13 cm. D. 119 cm.
Câu 11. Cho tam giác MNP có NP = 1cm, MP = 7 cm. Độ dài cạnh MN là một số nguyên
(cm). Độ dài cạnh MN là A. 8 cm. B. 5 cm. C. 6 cm. D. 7 cm.
Câu 12. Cho tam giác ABC cân tại A có AB 5 cm, BC
6 cm vàAM là đường trung
tuyến. Độ dài đoạn AM là A. 3 cm. B. 61 cm. C. 11 cm. D. 4 cm.
II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm) −
1. Tính giá trị biểu thức: 3
4x − 3xy tại 1 x = ; y = 6 . 2  2 
2. Cho đơn thức A = ( 3 − xy) 2  x y 
 . Hãy thu gọn đơn thức và chỉ ra hệ số và  3 
phần biến của đơn thức A.
Bài 2. (1,5 điểm) Cho hai đa thức: f ( x) 5 3 5
= x + x − 4x − x + 3x + 7 và g (x) 2 3 2
= 3x − x + 8x − 3x −14.
1. Thu gọn và sắp xếp hai đa thức f ( x) và g ( x) theo luỹ thừa giảm dần của biến.
2. Tính f (x) + g (x) và tìm nghiệm của đa thức f (x) + g (x) .
Bài 3. (3,0 điểm)
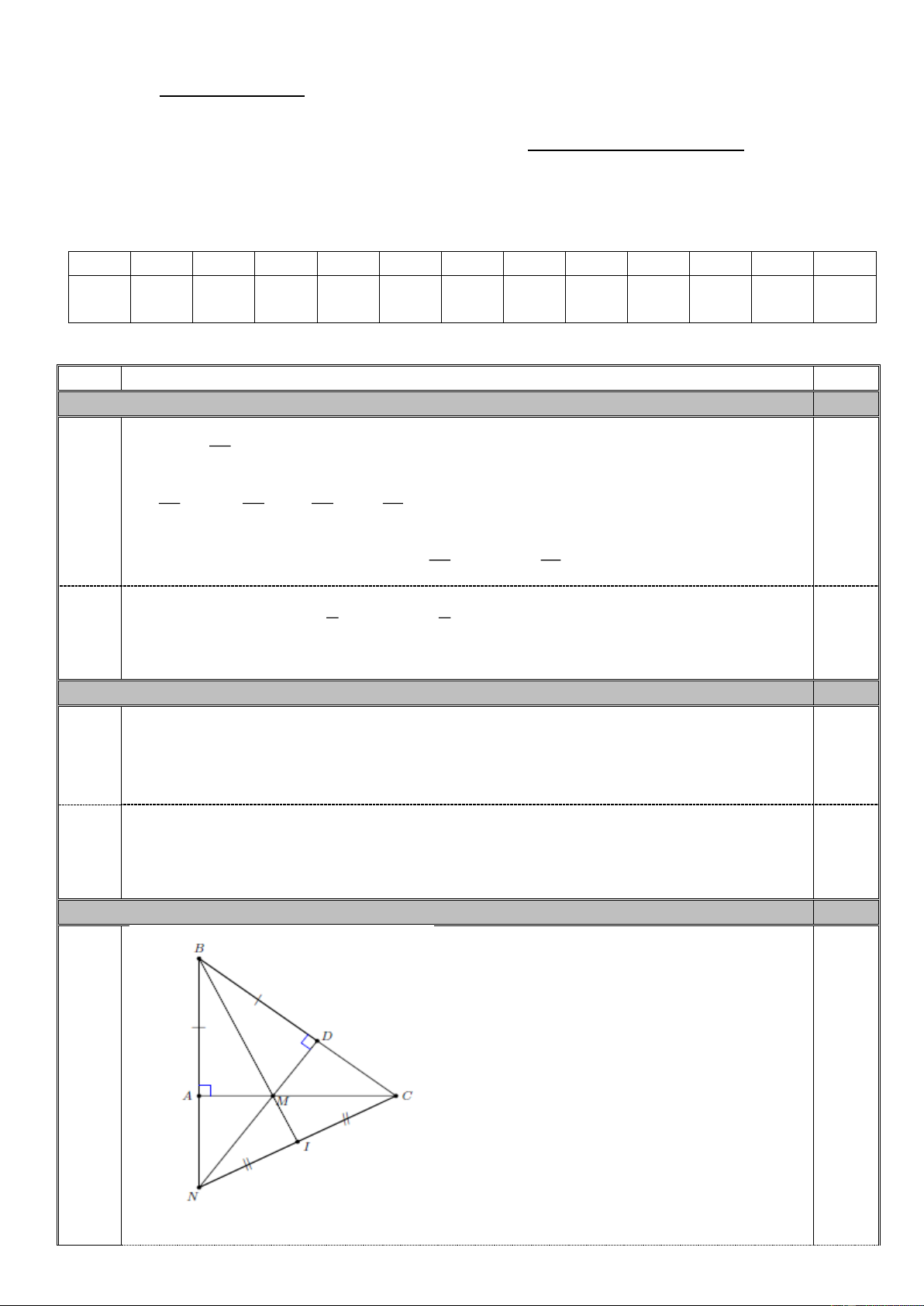
Cho tam giác ΑΒC vuông tại  , có AB = 3 cm, BC = 5 cm. Trên cạnh ΒC lấy
điểm D sao cho ΒD = 3 cm. Đường thẳng vuông góc với ΒC tại D cắt cạnh ΑC tại
 , cắt tia  tại  .
1.Tính AC và so sánh các góc của tam giác ΑΒC .
2. Chứng minh MΑ = MD và tam giác ΜΝC cân.
3. Gọi I là trung điểm của CN . Chứng minh ba điểm B ,  , I thẳng hàng.
Bài 4 (1, 0 điểm) a − b b − a
1. Tính giá trị của biểu thức 4 4 +
a − b = ; a  1 − ; b  1. 3a + 3 3b − với 3 3
2. Cho đa thức f ( x) 2
= ax + bx + c thỏa mãn f ( ) 3 = f (− ) 3 .
Chứng minh rằng f (x) = f (−x) . ====== Hết ====== UBND THÀNH PHỐ BẮC NINH HƯỚNG DẪN CHẤM
PHÒNG GIÁO DỤC & ĐÀO TẠO
ĐỀ KIỂM TRA CUỐI HỌC KỲ II NĂM HỌC: 2020-2021 Môn: Toán - Lớp 7
I. TRẮC NGHIỆM (3,0 điểm) Mỗi câu trả lời đúng 0,25 điểm Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp D C A D C C B A D A D D án
II. TỰ LUẬN (7,0 điểm) Bài Đáp án Điểm 1 1,5 1 − Thay x =
; y = 6 vào biểu thức ta được 2 3  1 −   1 −  1 − 17 1.1 4. − 3. .6 = + 9 =      2   2  2 2 −
Vậy giá trị của biểu thức trên tại 1 17 0,5 x = ; y = 6 là 2 2  2   2  +Thu gọn A = ( 3 − xy) 2  x y = 3 − .    ( 2 . x x )( . y y) 3 2 = 2 − x y 0,5 1.2  3   3  +Hệ số là 2 − ,phần biến 3 2 x y 0,5 2 1,5
Thu gọn và sắp xếp hai đa thức: f ( x) 5 3 5
= x + x − x − x + x + = ( 5 5 x − x ) 3
+ x + (− x + x) 3 4 3 7 4 3
+ 7 = x − x + 7 2.1 g ( x) 2 3 2 3
= x − x + x − x − = −x + ( 2 2 x − x ) 3 3 8 3 14 3 3
+ 8x −14 = −x + 8x −14 0,5
Tính: f ( x) + g ( x) 3 3
= (x − x + 7) + (−x + 8x −14) = 7x − 7 0,5 2.2
f ( x) + g ( x) = 0  7x − 7 = 0  x = 1
Vậy đa thức f (x) + g (x) có nghiệm là x =1. 0,5 3 3,0 0,25 Vẽ hình đúng, ghi GT, KL 3.1
Tính AC và so sánh các góc của tam giác ΑΒC . 1,0
+ Áp dụng định lí Pitago trong tam giác vuông ABC, ta có 0,5 2 2 2 2 2 2
BC = AB + AC  5 = 3 + AC  AC = 4 cm
+Xét tam giác ABC có BC  AC  AB      C (quan hệ giữa góc và cạnh 0,5
đối diện trong tam giác) 3.2
Chứng minh MΑ=MD và tam giác ΜΝC cân 1,0 +Xét A  BM và D  BM có 0 BAM = BDM = 90 BA=BD (gt) BM là cạnh chung  A  BM= D
 BM(cạnh huyền-cạnh góc vuông)
 MA=MD(hai cạnh tương ứng) 0,5 + Xét A  NM và D  CM có 0 NAM = CDM = 90 MA=MD (cmt)
AMN = DMC (hai góc đối đỉnh)  A  NM= D  CM (g-c-g)
 MN=MC(hai cạnh tương ứng)  Μ  ΝC cân tại Μ . 0,5 3.3
Gọi I là trung điểm của CN . Chứng minh ba điểm B , M , I thẳng hàng 0,75 + A  NM= D
 CM (cmt)  AN=DC mà BA=BD (gt)  BN=BC  B  NCcân tại B
Mà I là trung điểm của CN  BI là đường trung tuyến của B  NC
Khi đó, BI đồng thời là đường cao của B  NC hay BI ⊥ NC (1) 0,25 +Xét Μ
 ΝC cân tại Μ (cmt) có I là trung điểm của CN  MI là đường trung
tuyến đồng thời là đường cao của Μ  ΝC  MI ⊥ NC (2) 0,25
Từ (1) và (2) suy ra ba điểm B , M , I thẳng hàng 0,25 4.1 0,5
Với a − b = 3; a  1 − ; b  1 ta có 4a − b 4b − a
3a + a − b
3b + b − a
3a + a − b
3b − (a − b) + = + = + 0,25 3a + 3 3b − 3 3a + 3 3b − 3 3a + 3 3b − 3 3a + 3 3b − 3 = + = 0,25 2 3a + 3 3b − 3 4.2 0,5 + f ( ) 2 3 = a.3 + .
b 3 + c = 9a + 3b + c + f (− ) = (− )2 3 a. 3 + . b ( 3
− ) + c = 9a − 3b + c f ( ) 3 = f (− )
3  9a + 3b + c = 9a − 3b + c 0,25  b = 0 Với
b = 0, f ( x) 2
= ax + c và f (−x) = (−x)2 2 a + c = ax + c
nên suy ra f ( x) = f (−x) . 0,25
Ghi chú: Học sinh làm cách khác đúng vẫn cho điểm tối đa