


















Preview text:
NHÓM TOÁN STRONG TEAM-TỔ 25
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI ĐỊNH KÌ LẦN 1 NĂM 2019-2020
THPT CHUYÊN BẮC NINH MÔN: TOÁN
Thời gian làm bài: 90 phút
(không kể thời gian giao đề) Mã Đề: 103 Câu 1:
Dãy số nào sau đây có giới hạn bằng 0 ? n n n n 1 4 5 − 5 A. . B. . C. . D. . 3 e 3 3 Lời giải
Tác giải: Trần Tuấn huy; Fb: Trần Tuấn Huy Chọn A
Ta có: nếu q 1 thì lim n q = 0 . n Trong các đáp án chỉ 1 1 có 1 nên lim = 0 . 3 3 Câu 2:
Tính đạo hàm của hàm số y = ( 2 ln x + 1+ x ) . 1 x x 1 A. . B. . C. . D. . 2 x + 1+ x 2 x + 1+ x 2 1+ x 2 1+ x Lời giải
Tác giả: Nguyễn Diệu Linh; Fb: Dieulinh Nguyen Chọn D 2x + x + ( 2 x + 1+ x ) 1 1 2 2 1+ x 2 1+ x 1 Ta có: y = ( ( 2 ln x + 1+ x ) = = = = . 2 x + 1+ x 2 x + 1+ x 2 x + 1+ x 2 1+ x Câu 3:
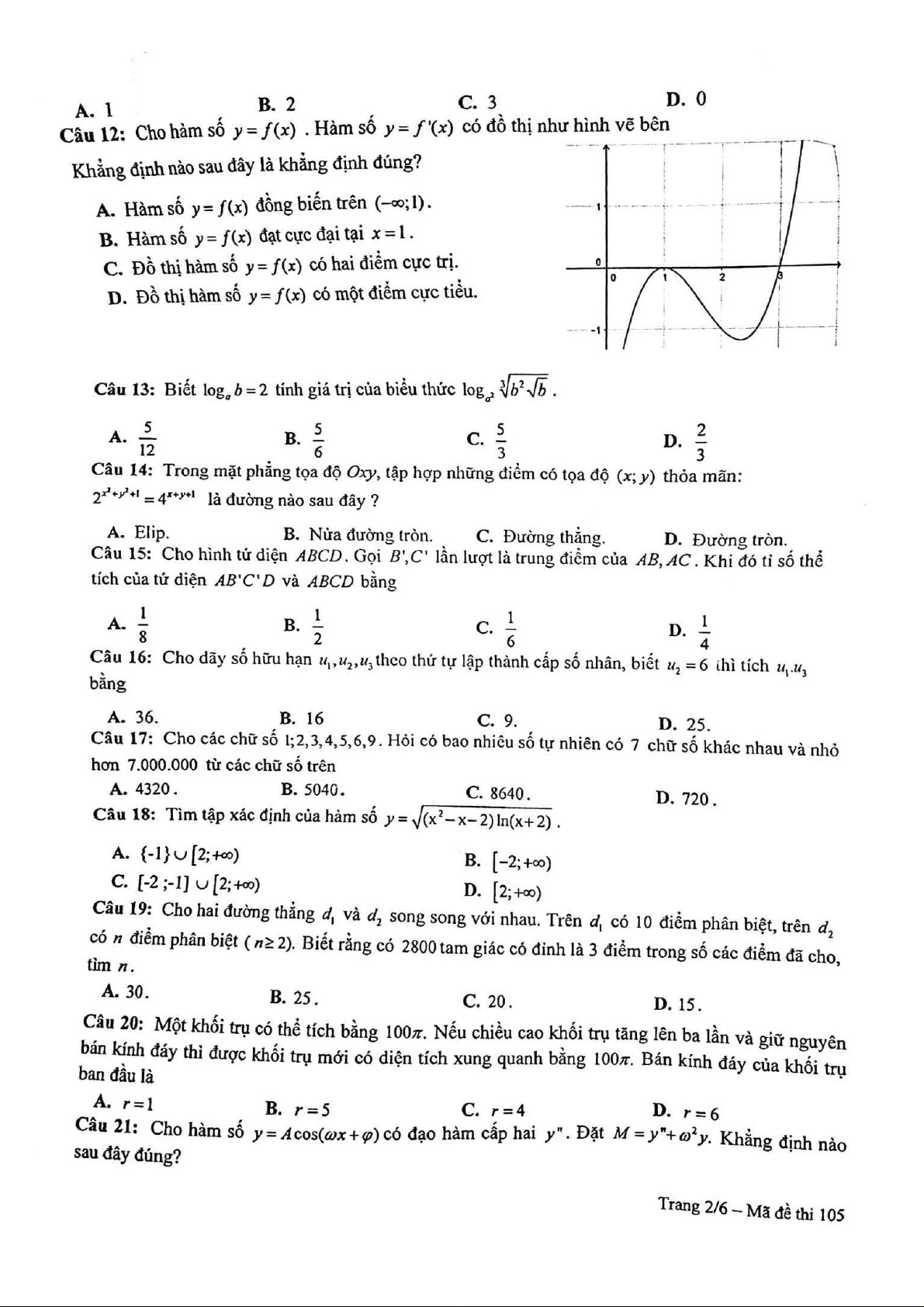
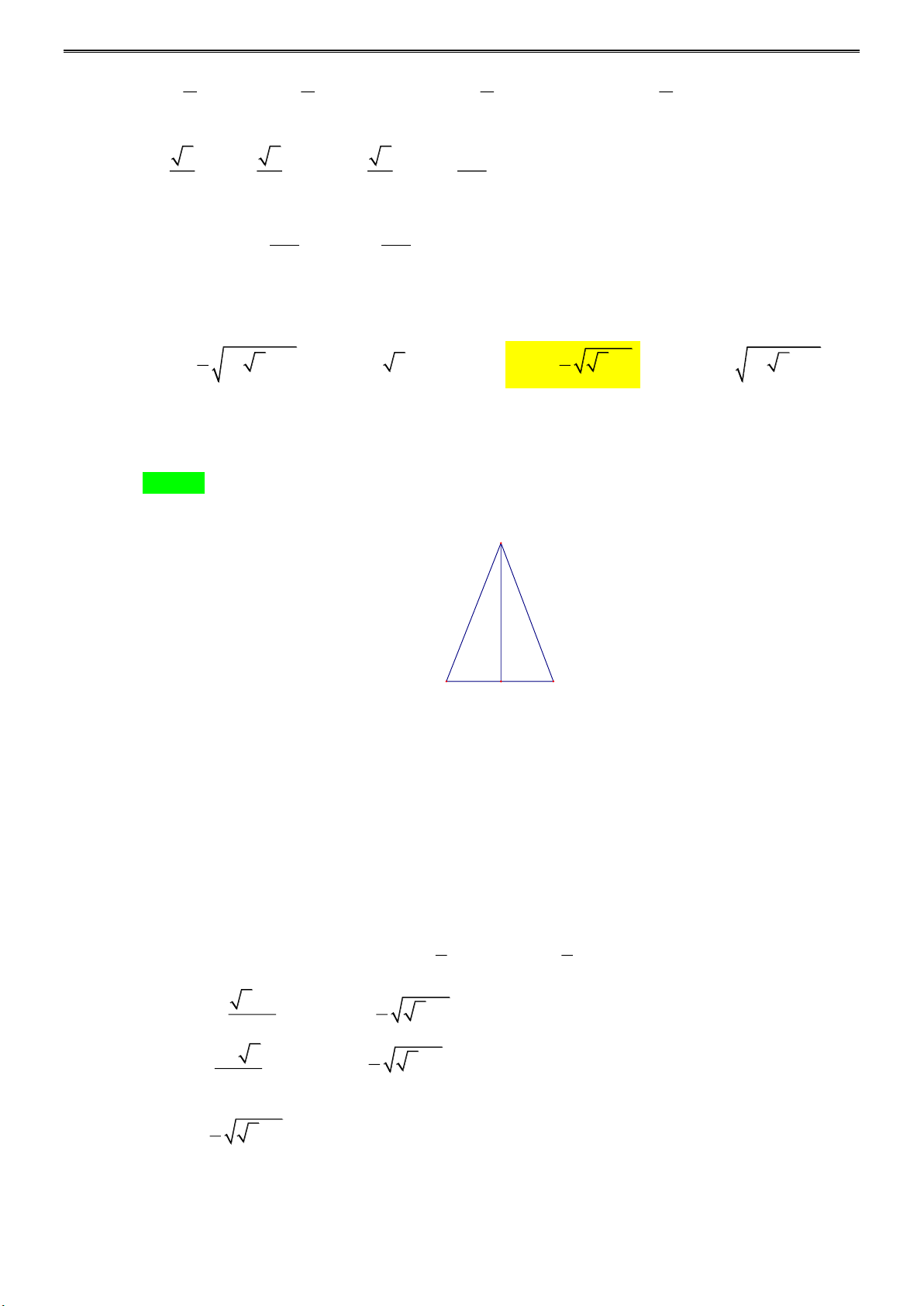
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, cạnh bên SA vuông góc mặt
đáy. Góc giữa đường thẳng AC và mp(SAB) là A. CSB . B. CAB . C. SAC . D. ACB Lời giải
Tác giả: Trần Thanh Sang; Fb: Thanh Sang Trần Chọn B
NHÓM TOÁN STRONG TEAM-TỔ 25
Vì CB ⊥ AB (do tam giác ABC vuông tại B ).
Và CB ⊥ SA (do SA ⊥ ( ABC) ).
Nên CB ⊥ (SAB)
Hình chiếu của C lên (SAB) là điểm B
Hình chiếu của AC lên (SAB) là AB
Vậy góc giữa đường thẳng AC và (SAB) là CAB . Câu 4:
Diện tích toàn phần của hình lập phương bằng 96 . Tính thể tích của khối lập phương. A. 48 . B. 81. C. 64 . D. 72 . Lời giải
Tác giả: Lưu Thị Minh Phượng; Fb: Jerry Kem Chọn C
Giả sử hình lập phương có độ dài cạnh là a . Diện tích toàn phần của hình lập phương: 2
S = 6a = 96 a = 4 . tp
Thể tích của khối lập phương là: 3 V = a = 64 . Câu 5:
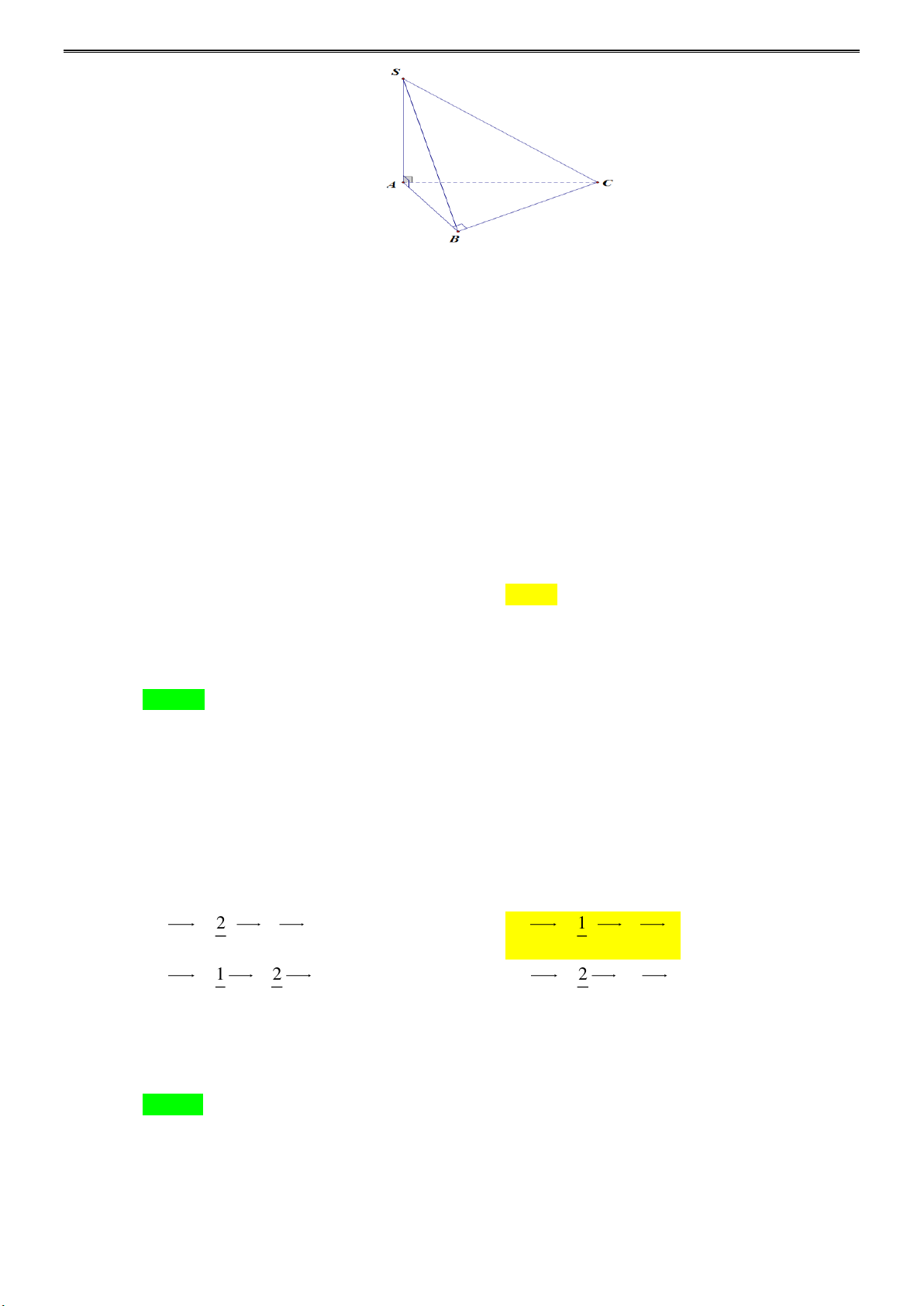
Cho tam giác ABC có M là trung điểm của BC , G là trọng tâm tam giác ABC . Khẳng định nào sau đây đúng? 2 1 A. AG = (AB + AC). B. AG = (AB + AC). 3 3 1 2 2 C. AG = AB + AC . D. AG = AB + 3AC . 3 2 3 Lời giải
Tác giả: Nguyễn Văn Đăng; Fb: nguyenvandang Chọn B A
NHÓM TOÁN STRONG TEAM-TỔ 25 1
Vì M là trung điểm của BC nên ta có AM = (AB + AC). ( )1 2 2
Mặt khác G là trọng tâm tam giác ABC nên AG = AM . (2) 3 2 1 1 Từ ( )
1 và (2) suy ra AG = . ( AB + AC) = ( AB + AC). 3 2 3
Vậy chọn đáp án B. Câu 6:
Cho dãy số hữu hạn u ;u ;u ;u ;u theo thứ tự lập thành một cấp số cộng, biết tổng của chúng 1 2 3 4 5
bằng 20. Tìm số hạng u . 3 A. 4. B. 5. C. 2. D. 3. Giải Chọn A
Ta có: u + u + u + u + u = 20 5u = 20 u = 4. 1 2 3 4 5 3 3
Tác giả: Trương Thúy; Fb: Thúy Trương. Câu 7:
Cho hàm số f (x) = 2x +1. Gọi S là tập nghiệm của phương trình f (x) = f (x). Số phần tử x -1 của S là A. 0. B. 1. C. 3. D. 2 . Lời giải
Tác giả & Fb: Nguyễn Trần Phong. Chọn B
Điều kiện: x ¹ 1. 3 − 6 Ta có y = = ( . x − ) y 2 1 (x − )3 1
NHÓM TOÁN STRONG TEAM-TỔ 25 Xét phương trình −
f ( x) = f ( x) x 1 3 6 x 1 = = − ( . x − ) x 1 2 1 (x − )3 1 ( x − )2 1 ( x + ) 1 = 0 x =1; x = 1 − Suy ra S = {-1}.
Vậy số phần tử của S là 1. Câu 8:
Hàm số nào sau đây không có cực trị A. 3 2
y = x + 3x . B. 3 y = x . C. 4 2
y = x − 3x + 2 . D. 3
y = x − x . Lời giải
Tác giả: Nguyễn Thị Hương; Fb: Nguyễn Hương Chọn B Xét phương án A: 3 2 2
y = x + 3x y = 3x + 6x . x = 0 Do y = 0
và y đổi dấu khi x qua hai nghiệm này nên hàm số có 2 điểm cực trị. x = 2 −
Do đó loại phương án A. Xét phương án B: 3 2
y = x y ' = 3x 0, x
nên hàm số không có cực trị. Chọn phương án B. Xét phương án C: 4 2 3
y = x − 3x + 2 y = 4x − 6x . x = 0 Do y = 0 6
và y đổi dấu khi x qua ba nghiệm này nên hàm số có 3 điểm cực trị. x = 2
Do đó loại phương án C. Xét phương án D: 3 2
y = x − x y ' = 3x −1. 3
Do y = 0 x =
, và y đổi dấu khi x qua hai nghiệm này nên hàm số có 2 điểm cực trị. 3
Do đó loại phương án D. Câu 9:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc mặt
đáy, SA = a 6 . Tính thể tích khối chóp S.ABCD . 3 a 6 3 a 6 3 a 6 A. . B. 3 a 6 . C. . D. . 4 3 4 Lời giải Chọn C
NHÓM TOÁN STRONG TEAM-TỔ 25
Vì ABCD là hình vuông cạnh a nên 2 S
= a . Ta có SA ⊥ ( ABCD), suy ra SA là đường ABCD 3 1 1 a 6 cao. Vậy 2 V = . SA S = a 6.a = . S . ABCD 3 ABCD 3 3 2x −1
Câu 10: Số đường tiệm cận của đồ thị hàm số y = là 2 x − 3x + 2 A. 3. B. 1. C. 0. D. 2. Lời giải Chọn A x =1( ) tm 2
x − 3x + 2 = 0 x = 2( ) tm
x = 1, x = 2 là TCĐ 2x −1 lim y = lim = 0 2 x→+
x→+ x − 3x + 2 2x −1 lim y = lim = 0 2 x→−
x→+ x − 3x + 2 y = 0 là TCN 2x −1
Vậy đồ thị hàm số y =
có ba đường tiệm cận. 2 x − 3x + 2 3 2
x − 5x + 6x
Câu 11: Số nghiệm của phương trình = 0 là log x − 2 3 ( ) A. 1. B. 2. C. 3. D. 0. Lời giải
Tác giả: Phạm Thị Minh Thư; Fb: Pham Minh Thu Chọn D x − 2 0 x 2 x 2
Điều kiện xác định: log x − 2 0 x − 2 1 x 3 3 ( ) 3 2
x − 5x + 6x 3
= 0 x − 5x + 6x = 0 log x − 2 3 ( ) x = 0 x = 0 x = 2 2
x − 5x + 6 = 0 x = 3
Kết hợp với điều kiện thì cả ba giá trị x = 0, x = 2, x = 3 đều không thỏa điều kiện bài toán.
Vậy phương trình vô nghiệm.
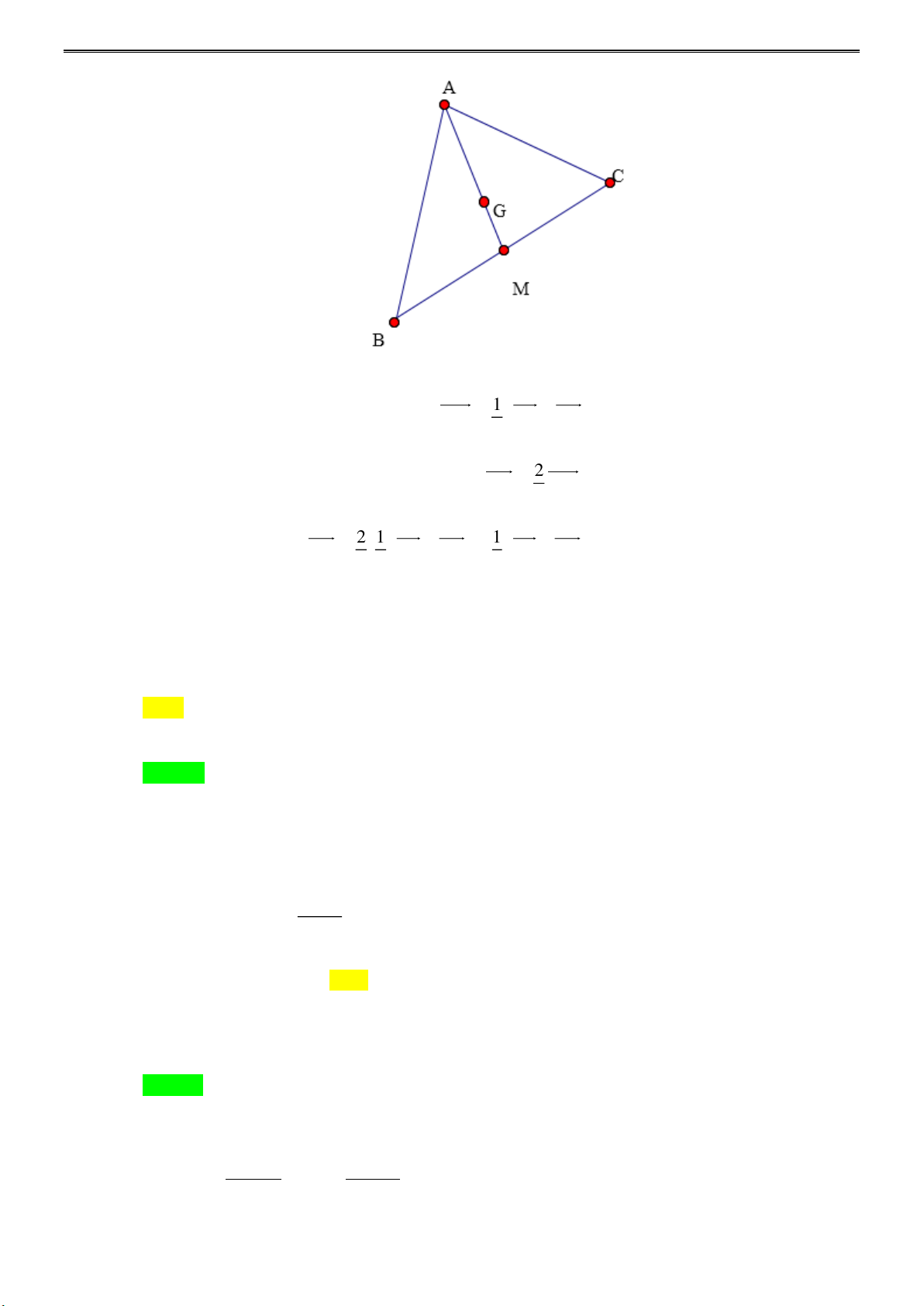
Câu 12: Cho hàm số y = f ( x) . Hàm số y = f ( x) có đồ thị như hình vẽ bên. Khẳng định nào sau đây là khẳng định đúng?
NHÓM TOÁN STRONG TEAM-TỔ 25
A. Hàm số y = f ( x) đồng biến trên ( ) ;1 − .
B. Hàm số y = f ( x) đạt cực đại tại x =1.
C. Đồ thi hàm số y = f ( x) có hai điểm cực trị.
D. Đồ thị hàm số y = f ( x) có 1 điểm cực tiểu. Lời giải
Tác giả: Phạm Hồng Giang; Fb: Pham Hong Giang Chọn D
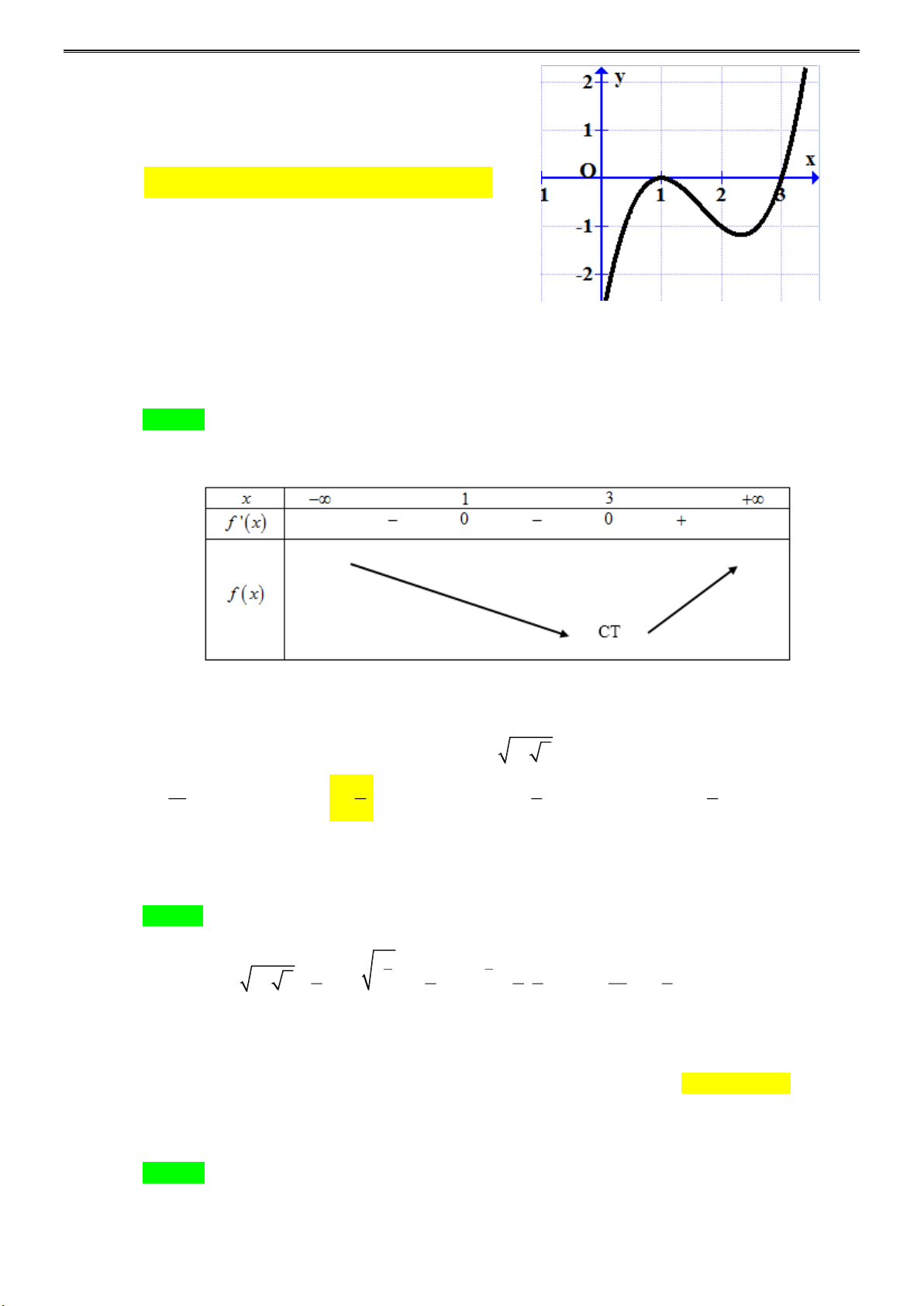
Dựa vào đồ thị hàm số y = f ( x) ta có bảng biến thiên của hàm số y = f ( x) sau:
Vậy đồ thị hàm số y = f ( x) có 1điểm cực tiểu. Câu 13: Biết log 2 3 2 a b =
, tính giá trị của biểu thức log 2 b b a 5 5 5 2 A. . B. . C. . D. . 12 6 3 3 Lời giải
Tác giả:Lê Thị Như Thủy; Fb: Nhuthuy Le Chọn B 5 5 3 1 1 1 5 5 5 Ta có: 3 2 2 log = 6 = = = = 2 b b loga b log b . log b .2 . a a a 2 2 2 6 12 6 2 2
Câu 14: Trong mặt phẳng tọa độ Oxy , tập hợp những điểm có tọa độ ( ;
x y) thỏa mãn: x +y 1 + x+ y 1 2 4 + =
là đường nào sau đây? A. Elip.
B. Nửa đường tròn. C. Đường thẳng. D. Đường tròn. Lời giải
Tác giả: Đinh Thị Ba; Fb: Ba đinh Chọn D Ta có:
NHÓM TOÁN STRONG TEAM-TỔ 25 2 2 2 2 x + y 1 + x+ y 1 + x + y 1 + 2 x+2 y+2 2 2 2 = 4 2 = 2
x + y +1 = 2x + 2y + 2
x + y − 2x − 2y −1 = 0 (x − )2 1 + ( y − )2 2 2 1 = 3
Vậy trong mặt phẳng tọa độ Oxy , tập hợp những điểm có tọa độ ( ; x y) thỏa mãn: 2 2 x + y 1 + x+ y 1 2 4 + =
là một đường tròn có tâm I (1; ) 1 , bán kính R = 3 .
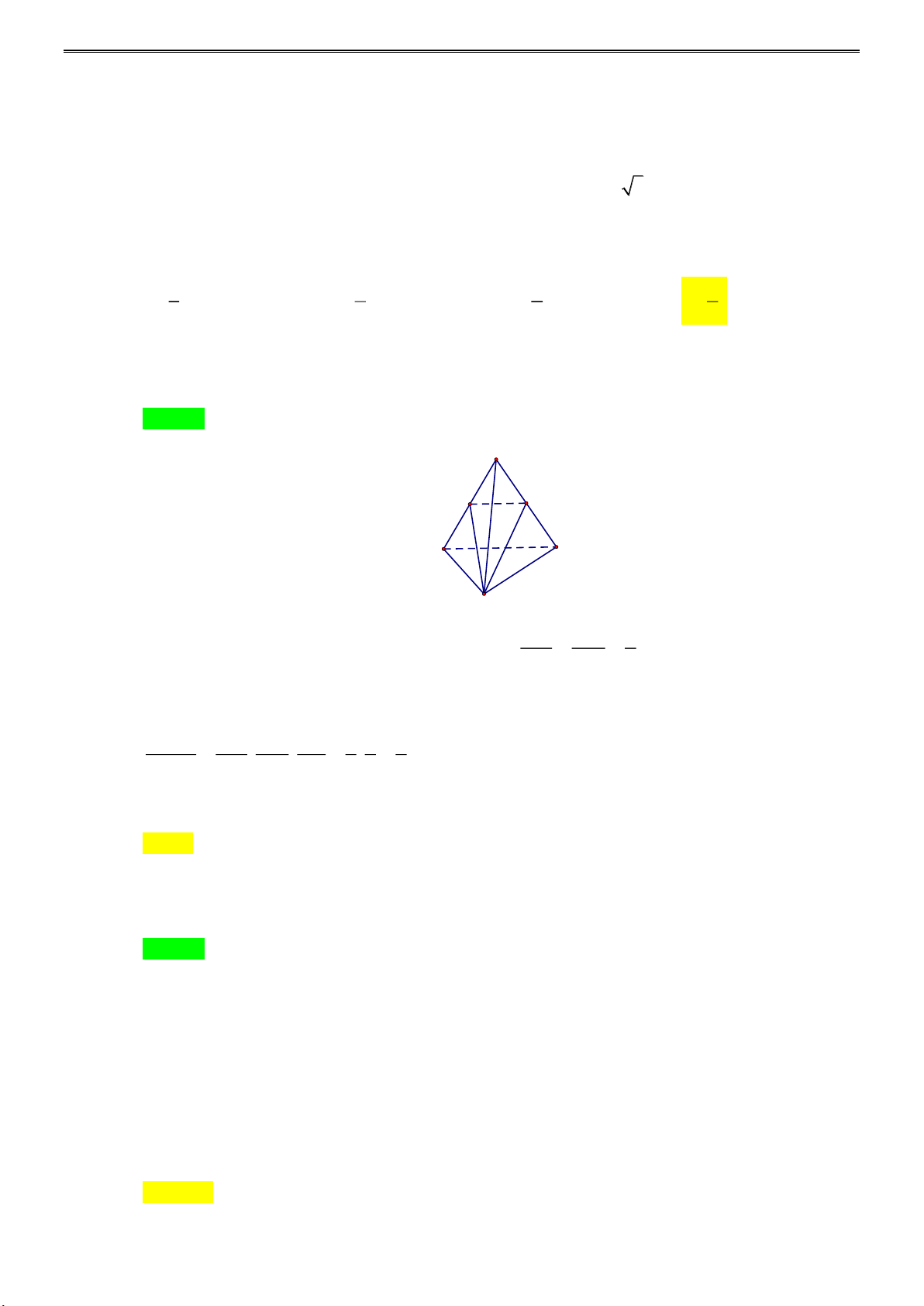
Câu 15: Cho hình tứ diện D
ABC . Gọi B ', C ' lần lượt là trung điểm của AB, AC . Khi đó tỉ số thể tích
của tứ diện AB'C 'D và D ABC bằng 1 1 1 1 A. . B. . C. . D. . 8 2 6 4 Lời giải
Tác giả: Trần Huy Tuyển; Fb:Trân TuyenHuy Chọn D A B' C' B C D AB ' AC ' 1
Vì B ', C ' lần lượt là trung điểm của AB, AC nên = = AB AC 2
Áp dụng công thức tỉ số thể tích có V
AB ' AC ' AD 1 1 1
AB 'C ' D = . . = . = . V AB AC AD 2 2 4 ABCD
Câu 16: Cho dãy số hữu hạn u , u , u theo thứ tự lập thành cấp số nhân, biết u = 6 thì tích u .u bằng 1 2 3 2 1 3 A. 36 . B. 16 . C. 9 . D. 25 . Lời giải
Tác giả: Nguyễn Thị Thanh; Fb: Thanhh Thanhh Chọn A
Giả sử u , u , u theo thứ tự lập thành cấp số nhân có công bội là q . 1 2 3 Khi đó, ta có: 2
u = u .q, u = u .q . 2 1 3 1
Vậy u .u = u .(u .q ) = (u .q)2 2 2 2 = u = 6 = 36 . 1 3 1 1 1 2
Câu 17: Cho các chữ số 1; 2;3; 4;5; 6;9 hỏi có bao nhiêu số tự nhiên có 7 chữ số khác nhau và nhỏ hơn
7000.000 từ các số trên? A. 4320 . B. 5040 . C. 8640 . D. 720 . Lời giải
Tác giả: Kim Oanh; Facebook: Kim Oanh
NHÓM TOÁN STRONG TEAM-TỔ 25 Chọn A
Gọi số có dạng a a a a a a a . 1 2 3 4 5 6 7
Vì số đã cho có 7 chữ số phân biệt và nhỏ hơn 7000.000 nên a 7 , vậy có 6 cách chọn a . 1 1
Các chữ số a ; a ; a ; a ; a ; a là hoán vị của 6 số còn lại. 2 3 4 5 6 7
Vậy có 6.6!= 4320 số thỏa mãn bài toán.
Câu 18: Tìm tập xác định của hàm số y = ( 2
x − x − 2)ln(x + 2) . A. − 1 2;+) . B. 2; − +). C. 2 − ;−
1 2;+) . D. 2; +) . Lời giải
Tác giả: Trần Hùng; Fb: Hung Tran Chọn A x + 2 0
Điều kiện xác định: ( 2 x − x − 2 )ln(x+2) 0 x −2 x −2 x 2 2
x − x − 2 0 x −1 x 2 x + 2 1 x −1 . x = 1 − 2
x − x − 2 0 x −2 x + 2 1 −1 x 2 x −1
Câu 19: Cho hai đường thẳng d và d song song với nhau. Trên d có 10 điểm phân biệt, trên d có 1 2 1 2
n điểm phân biệt (n 2) . Biết rằng có 2800 tam giác có đỉnh là 3 điểm trong số các điểm đã cho, tìm n . A. 30 . B. 25 . C. 20 . D. 15 . Lời giải
Tác giả: Nguyễn Thị Duyên; Fb: Nguyễn Duyên Chọn C
Một tam giác được tạo bởi ba điểm phân biệt nên ta xét:
TH1. Chọn 1 điểm thuộc d và 2 điểm thuộc d ¾ ¾ ® có 1 2
C .C tam giác. 1 2 10 n
TH2. Chọn 2 điểm thuộc d và 1 điểm thuộc d ¾ ¾ ® có 2 1
C .C tam giác. 1 2 10 n Như vậy, ta có 1 2 2 1
C .C + C .C = 2800 10 n 10 n
NHÓM TOÁN STRONG TEAM-TỔ 25 n! n! 10. ( + = − + = n − )
45. (n− ) 2800 5n(n )1 45n 2800 2! 2 ! 1! 1 ! n = 20 ( ) tm 2
5n + 40n − 2800 = 0 n = 2−8 (l) Vậy n = 20 .
Câu 20: Một khối trụ có thể tích 100 . Nếu chiều cao khối trụ tăng lên ba lần và giữ nguyên bán kính
đáy thì được khối trụ mới có diện tích xung quanh bằng 100 . Bán kính đáy khối trụ ban đầu là A. r = 1 . B. r = 5 . C. r = 4 . D. r = 6 . Lời giải
Tác giả: Trần Minh Lộc; Fb: Trần Lộc Chọn D
Khối trụ ban đầu có chiều cao là h và bánh kính đáy là r . Thể tích khối trụ ban đầu 2 V = r h Suy ra 2 2
r h =100 r h =100 (1) .
Khi tăng chiều cao lên ba lần và giữ nguyên bán kính đáy ta có diện tích xung quanh khối trụ mới là S
= 2 r(3h) = 6 rh =100 6rh =100 (2) xq 2 r h
Chia vế theo vế của (1) cho (2) ta có: = 1 Û r = 6 . 6rh
Câu 21: Cho hàm số y = A cos( x + ) có đạo hàm cấp hai y . Đặt 2
M = y + y . Khẳng định nào sau đây đúng? A. M = 1 − . B. M = 1 . C. 2
M = 2A cos(x + ) . D. M = 0 . Lời giải
Tác giả: Đặng Tấn Khoa; Fb: Đặng Tấn Khoa Chọn D
Ta có y = − A sin( x + ) , 2
y = −A cos(x +) . Khi đó 2 2
M = −A cos(x +) + Acos(x +) = 0 .
2x +1 − x + 5 khi x 4
Câu 22: Cho hàm số f (x) = x − 4
. Tìm tất cả các giá trị thực của tham số a để
a + 2 khi x = 4
hàm số liên tục tại x = 4 . 0 5 11 A. a = 3. B. a = . C. a = 2 . D. a = − . 2 6 Lời giải
Tác giả: Nguyễn Thị Thảo; Fb:Cỏ Vô Ưu Chọn D
NHÓM TOÁN STRONG TEAM-TỔ 25 2x +1 − x + 5 lim f (x) = lim x→4 x→4 x − 4
( 2x+1− x+5).( 2x+1+ x+5) = lim x→4
(x − 4).( 2x+1+ x+5) 1 1 = lim =
x→4 ( 2x +1 + x + 5) 6 1 11
Hàm số liên tục tại x = 4 f (4) = lim f (x) a + 2 = a = − . 0 x→4 6 6
Câu 23: Mệnh đề nào trong các mệnh đề dưới đây là đúng?
A. Đồ thị của hai hàm số y = log x và y = log x đối xứng qua trục tung. e 1 e
B. Đồ thị của hai hàm số x
y = e và y = ln x đối xứng nhau qua đường phân giác của góc phần tư thứ nhất.
C. Đồ thị của hai hàm số x
y = e và y = ln x đối xứng nhau qua đường phân giác của góc phần tư thứ hai. x 1
D. Đồ thị của hai hàm số x
y = e và y = đối xứng nhau qua trục hoành. e Lời giải
Tác giả: Ngô Gia Khánh; Fb:Khánh Ngô Gia Chọn B
Nhận xét: Với 0 a 1 đồ thị của hai hàm số x
y = a và y = log x đối xứng nhau qua đường a
phân giác của góc phần tư thứ nhất.
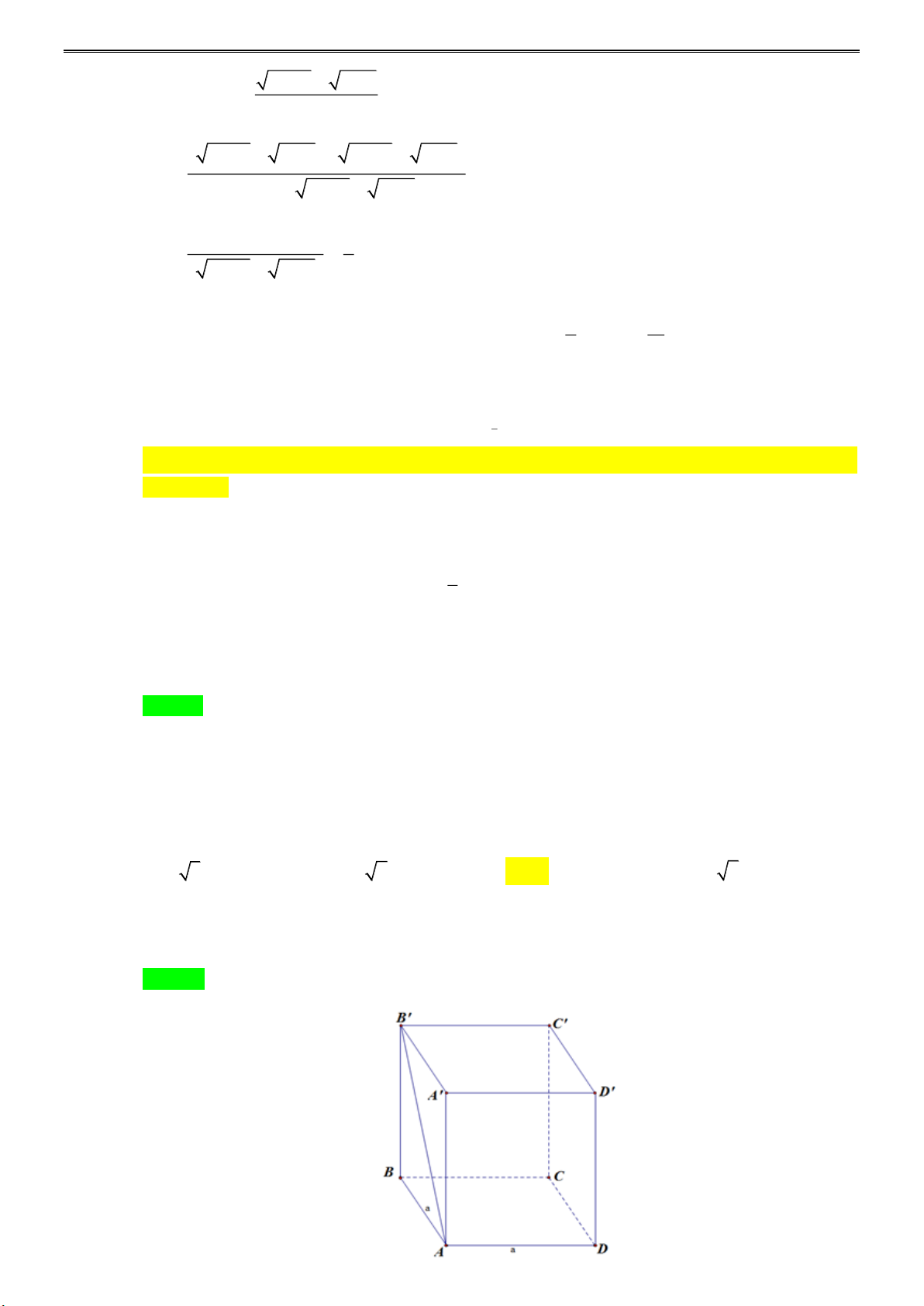
Câu 24: Cho hình lập phương ABC .
D A' B 'C ' D' có cạnh bằng a , khoảng cách giữa hai đường thẳng AB ' và C D bằng A. a 3 . B. a 2 . C. a . D. a 6 . Lời giải
Tác giả: Đinh Thị Mỹ; Fb:Mỹ Đinh Chọn C
NHÓM TOÁN STRONG TEAM-TỔ 25
Ta có: B'C ' ⊥ C ' D' ( vì A' B'C ' D' là hình vuông) (1)
B 'C ' ⊥ A' B ' Ta có:
B 'C ' ⊥ ( AA' B ' B)
B 'C ' ⊥ BB '
Mà AB ' ( AA' B' B) nên B'C ' ⊥ AB' (2)
Từ (1) và (2), suy ra B'C ' là đường vuông góc chung của AB ' và C ' D ' nên
d ( AB ',C ' D') = B 'C ' = a
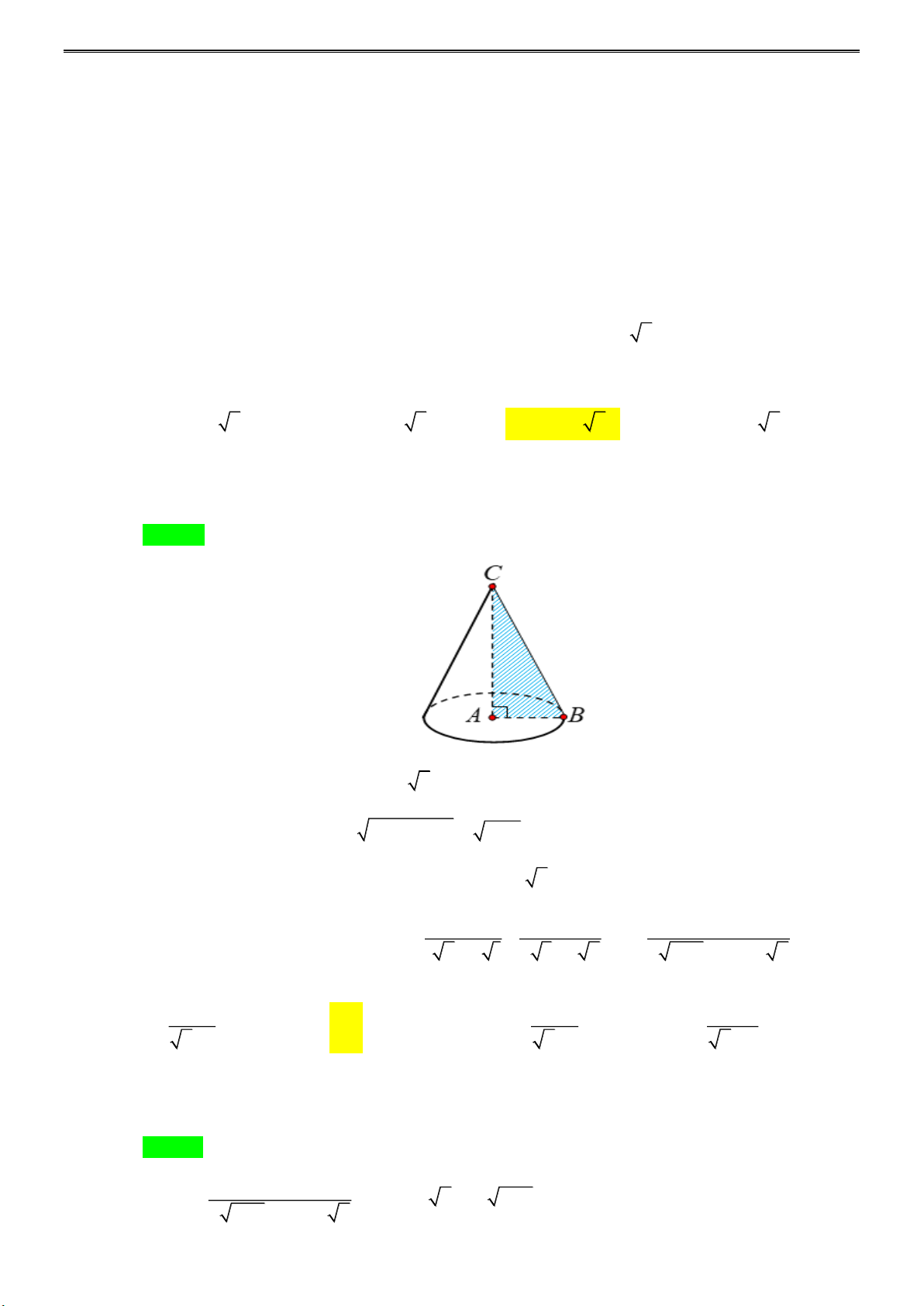
Câu 25: Trong không gian, cho tam giác ABC vuông tại A có AB = 7, AC = 3 . Quay đường gấp
khúc CBA xung quanh cạnh AC tạo thành hình nón tròn xoay. Tính diện tích xung quanh S xq của hình nón đó. A. S = 3 7 . B. S = 8 7 . C. S = 4 7 . D. S = 6 7 xq xq xq xq Lời giải
Tác giả: Trần Đình Xuyền; Fb: Trần Đình Xuyền Chọn C
Bán kính đáy hình nón là r = AB = 7 Độ dài đường sinh 2 2 l = BC =
AB + AC = 7 + 9 = 4
Diện tích xung quanh của hình nón là S = rl = 4 7 . xq 1 1 1
Câu 26: Với n là số nguyên dương, đặt S = + + ...+ . Khi đó n 1 2 + 2 1 2 3 + 3 2
n n +1 + (n +1) n lim S bằng n 1 1 1 A. . B. 1. C. . D. 2 −1 2 +1 2 + 2 Lời giải
Tác giả: Quỳnh Như Fb: Quỳnh Như Chọn B 1 Xét A =
. Đặt a = n,b = n +1 ( , a b 0) .
n n +1 + (n +1) n
NHÓM TOÁN STRONG TEAM-TỔ 25 1 1 A = = 2 2 a b + b a ab(a + b) Ta có 1 2 2
b − a = n +1− n = 1 (b − a)(b + a) = 1 b − a = a + b b − a 1 1 1 1 Nên A = = − = − ab a b n n +1
Từ chứng mình trên ta có 1 1 1 S = + +...+ n 1 2 + 2 1 2 3 + 3 2
n n +1 + (n +1) n 1 1 1 1 1 1 = − + − + ...+ − 1 2 2 3 n n +1 1 1 1 1 1 1 = − + − + ...+ − 1 2 2 3 n n +1 1 =1− n+1 1 1 lim S = lim 1− = lim1− lim =1. n n +1 n +1
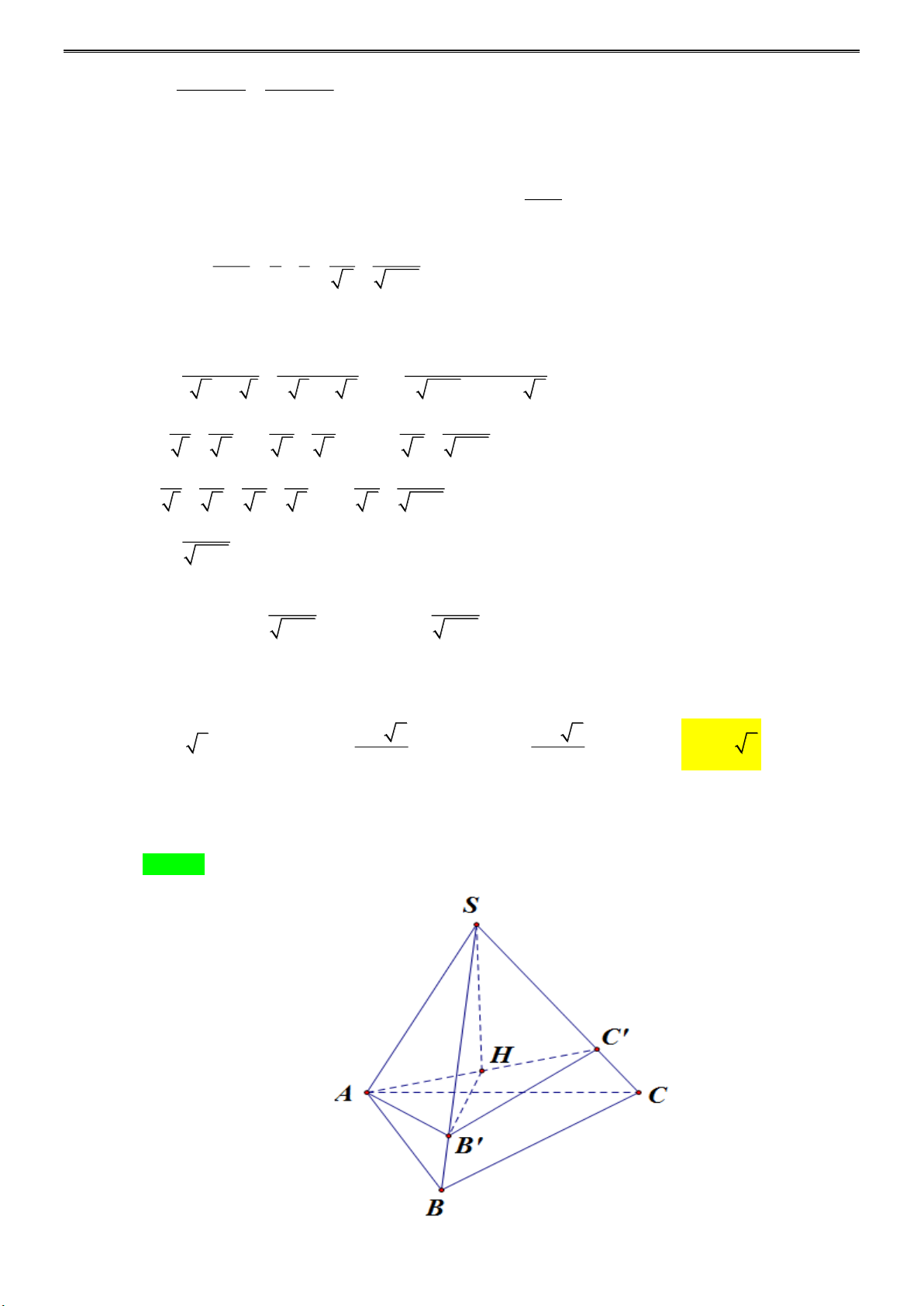
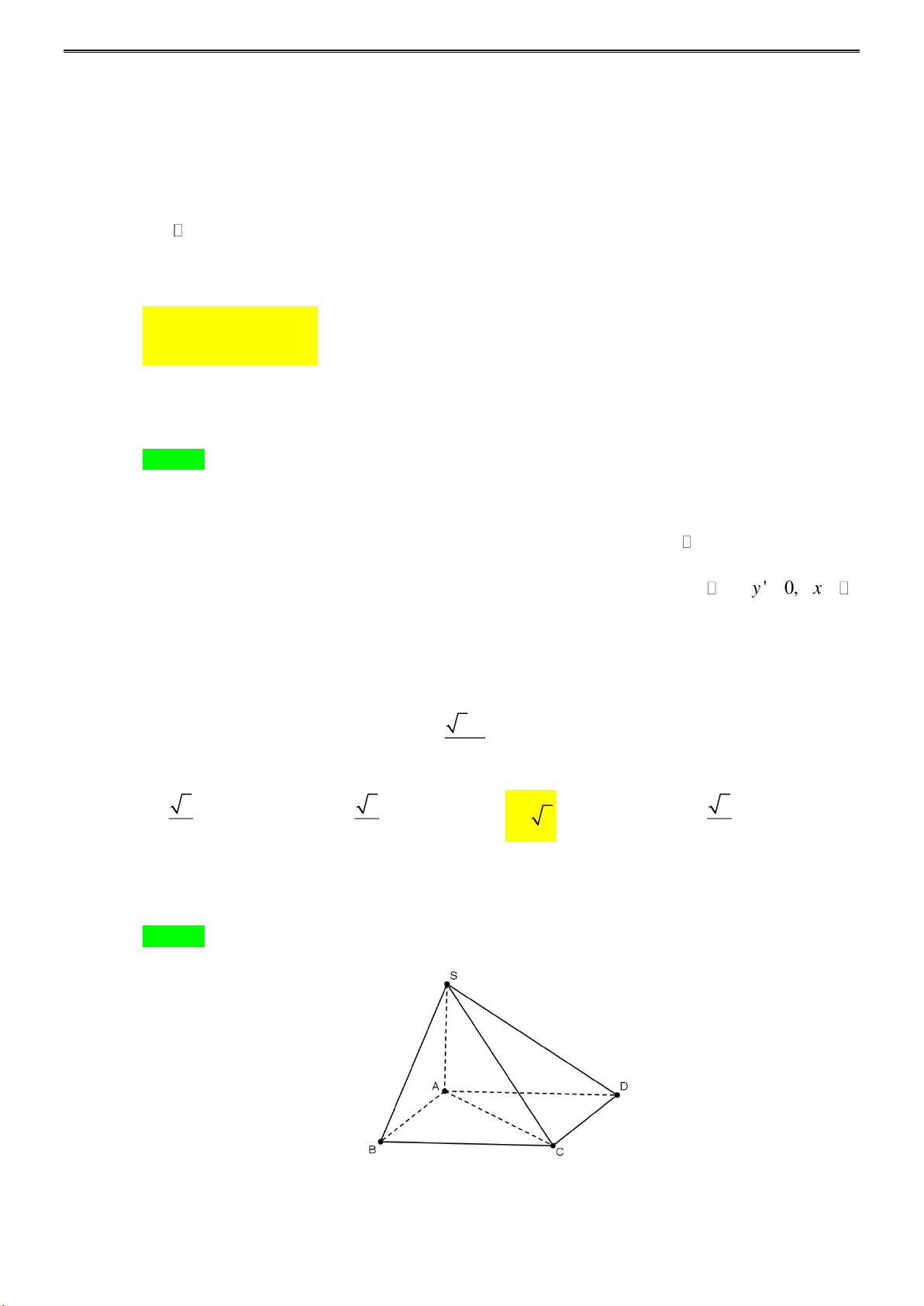
Câu 27: Hình chóp S.ABC có SA = 2a , SB = 3a , SC = 4a và ASB = BSC = 60 , ASC = 90 . Thể tích của khối chóp là 3 4a 2 3 2a 2 A. 3 a 2 . B. . C. . D. 3 2a 2 . 3 9 Lời giải
Tác giả: Phạm Thị Kiều Khanh; Fb: Kiều Khanh Phạm Thị Chọn D
Cách 1: Trên SB, SC lần lượt lấy B ,
C sao cho SB = SC = 2a.
NHÓM TOÁN STRONG TEAM-TỔ 25 SA = SC '
SAC vuông cân tại S AC = SA 2 = 2a 2 . ASC = 90 SA = SB ' SA
△ B đều AB = 2a (1). ASB = 60 SB = SC S △ B C đều B C = 2a (2). B S C = 60 (1) và (2) cho ta A
△ B'C cân tại B.
Gọi H là trung điểm của AC B H ⊥ AC . 2 AC 2 2 2 B H
= AB − AH = AB − = a 2 . 2 AH ⊥ SH
AH ⊥ (SHB ). AH ⊥ HB Ta có: 1 S = = = 2S V 2V 2. .AH.S . AB C ' AB H S . AB 'C S . AHB 3 SHB S = − − − =
p ( p SH )( p SB )( p HB ) 2 a . SHB
SH + SB + HB Với p = = (1+ 2)a . 2 3 1 2a 2 2 V = = 2. .a 2.a . S . AB C 3 3 V SB SC ' 2a 2a 1 S . AB C = . = . = 3 V = 2a 2 . V SB SC 3a 4a 3 S.ABC S . ABC Cách 2: . SA . SB SC 2 2 2 3 V =
1− cos 60 − cos 90 − cos 60 + 2 cos 60 cos 90 cos 60 = 2a 2 . 6
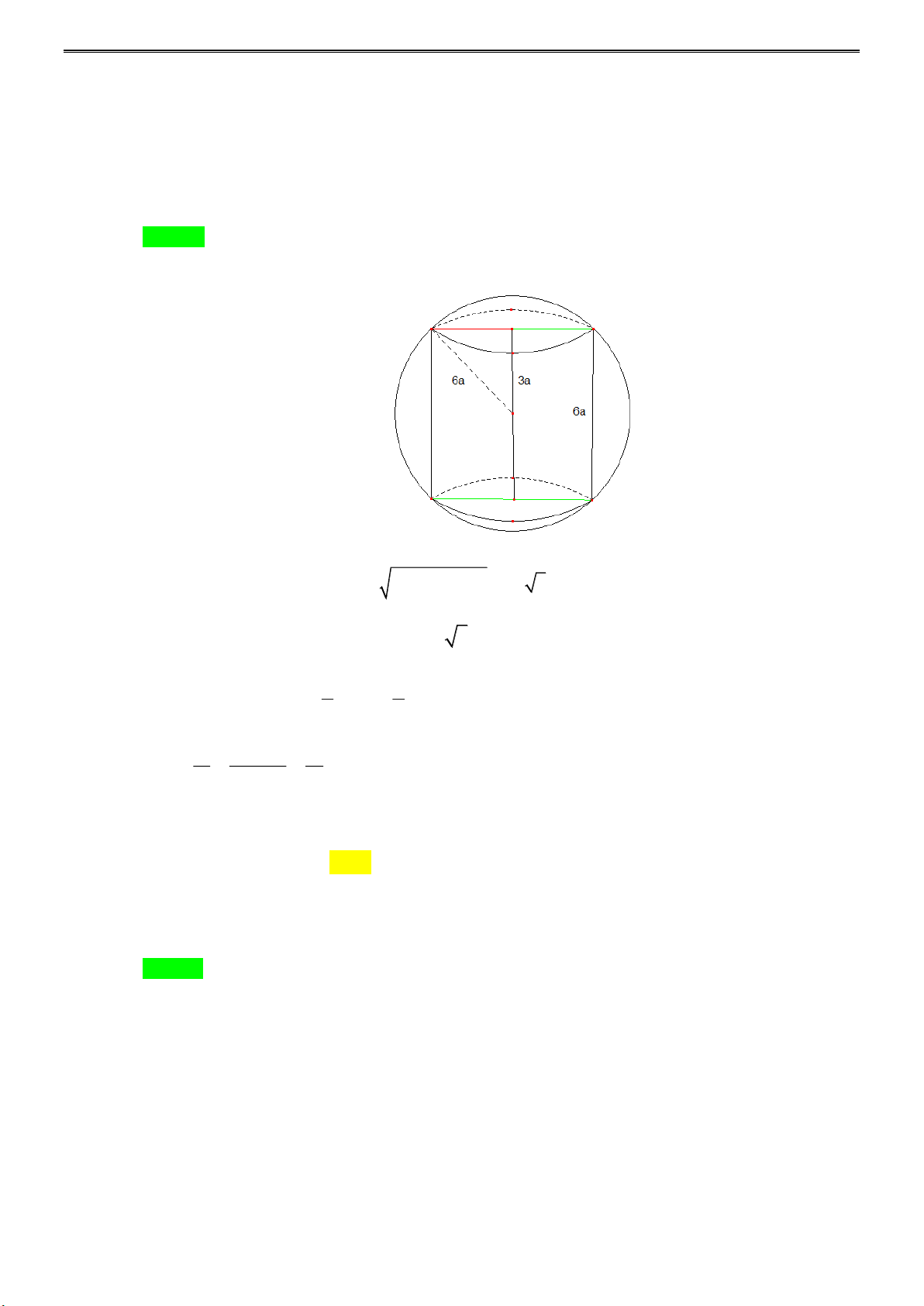
Câu 28: cho mặt cầu (S ) có bán kính bằng 6a, hình trụ ( H ) có chiều cao bằng 6a và chia hai đường
tròn đáy nằm trên (S ). gọi v là thể tích của khối trụ (H ),v là thể tích khối cầu (S ).tính tỉ số 1 2 v1 v2 v 9 v 3 v 1 A. 1 = . B. 1 = . C. v 2 1 = . D. 1 = . v 16 v 16 v 3 v 3 2 2 2 2
NHÓM TOÁN STRONG TEAM-TỔ 25 Lời giải
Tác giả: Hà Trường Giang; Fb: Trường Giang Chọn A
Bán kính mặt đáy hình trụ: r = (6a) − (3a)2 2 = 3a 3 1 2 2
Thể tích hình trụ v = . h .r = 6 .
a .(3a 3) =162. . a : 1 1 4 4 Thể tích hình cầu: 3 3 v = . .r = . .(6a) = 288. . a 2 2 3 3 v 162. . a 9 Tỉ số: 1 = = . v 288. . a 16 2
Câu 29: Tìm tổng các nghiệm của phương trình: log ( 3 x − x − 2) 3
+ x + 7x = log (x − ) 2 1 + 4x + 7 4 2 A. 17 . B. 2 . C. 9 . D. 11. Lời giải
Tác giả: Phạm Thành; Fb: Phạm Thành Chọn B x −1 0 Điều kiện: 3
x − x − 2 0 Ta có log ( 3 x − x − 2) 3
+ x + 7x = log (x − ) 2 1 + 4x + 7 4 2
log (x − x −2)+ 2x +14x = log (x − )2 3 3 2 1 + 8x +14 2 2 log ( 3
x − x − 2) + 2( 3
x − x − 2) = log ( 2
4x − 8x + 4) + 2( 2 4x − 8x + 4 1 2 2 )( )
NHÓM TOÁN STRONG TEAM-TỔ 25
Đặt hàm số f (t) = log t + 2t, t
0 có f (t) 1 = + 2 0, t 0 2 t ln 2
Vậy hàm số f (t ) đồng biến trên khoảng (0; +) Từ ( ) 1 có f ( 3
x − x − ) = f ( 2 x − x + ) 3 2 2 4 8
4 x − x − 2 = 4x − 8x + 4 3 2
x − 4x + 7x − 6 = 0 x = 2 (thỏa mãn điều kiện).
Ta có phương trình có 1 nghiệm x = 2
Vậy tổng các nghiệm của phương trình bằng 2
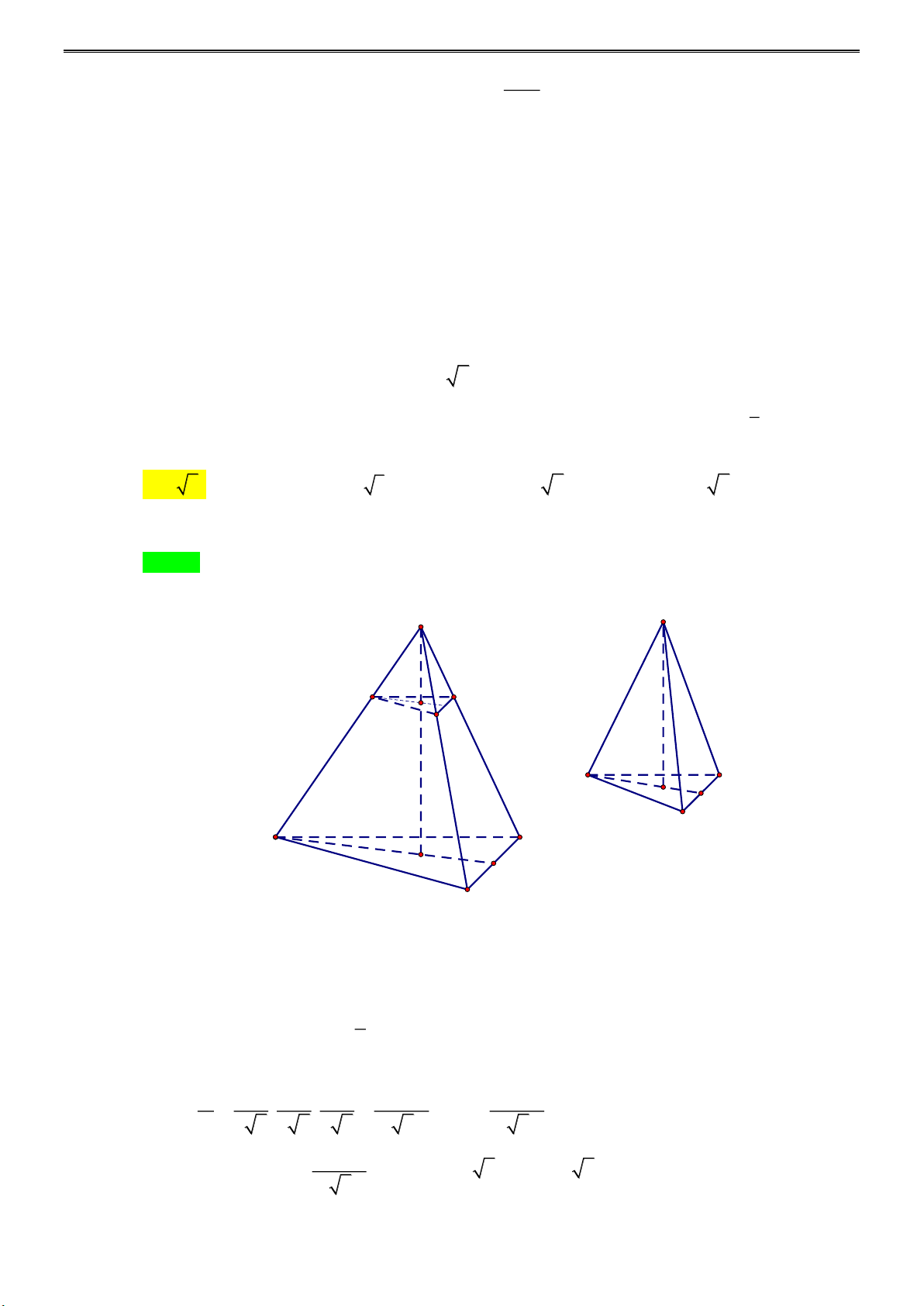
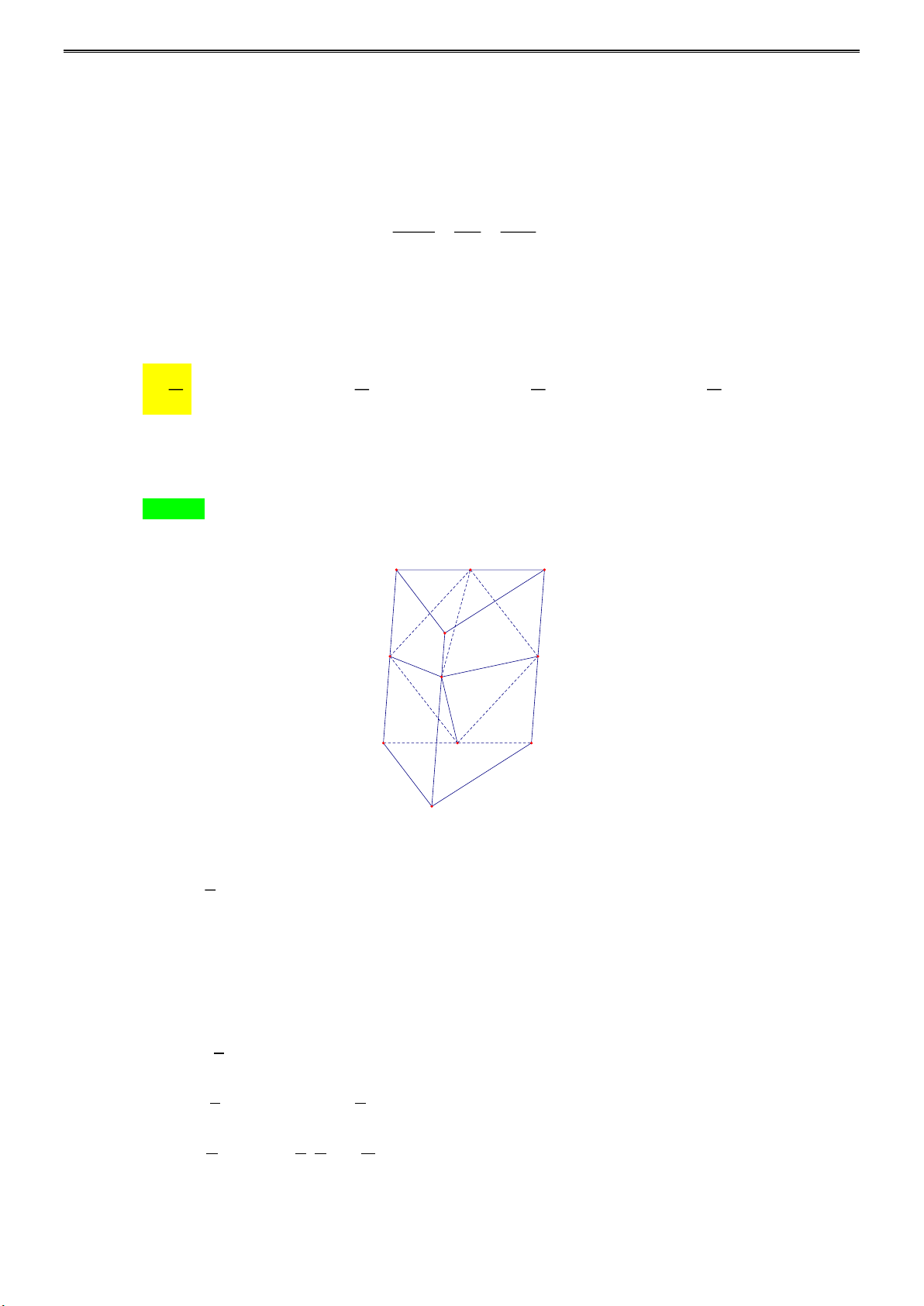
Câu 30: Cho tứ diện đều ABCD có cạnh bằng 6 2 . Ở bốn đỉnh của tứ diện người ta cắt đi các tứ diện đề 1
u bằng nhau có cạnh x . Biết khối đa diện còn lại sau khi cắt có thể tích bằng thể tích khối 2
tứ diện ABCD . Giá trị của x là A. 3 2 . B. 2 3 . C. 2 2 . D. 2 . Lời giải
Tác giả:Nguyễn Ngọc Hà; Fb:Hangocnguyen ChọnA Cách 1: A A' x x x G' B' D' x x C' x x B' x D' x G' M' C' B D G M C
4 góc cắt đi là các tứ diện bằng nhau nên 4 tứ diện này có cùng thể tích.
Gọi thể tích của một khối tứ diện cắt đi là V , thể tích khối tứ diện ABCD là V và thể tích 1
khối đa diện sau khi cắt bỏ góc là V . 2 1
Ta có: V = V − 4V mà V =
V V = 8V (1) 2 1 2 1 2
Xét khối tứ diện đều ở đỉnh A là AB C D
có các cạnh là x . 3 3 V x x x x x Ta có: 1 = . . = V = V (2) 1 3 3 V 6 2 6 2 6 2 (6 2) (6 2) 3 x Từ ( ) 1 và (2) 3 3 V =
8.V x = (3 2) x = 3 2 1 1 3 (6 2)
NHÓM TOÁN STRONG TEAM-TỔ 25 Cách 2.
4 góc cắt đi là các tứ diện bằng nhau nên 4 tứ diện này có cùng thể tích.
Gọi thể tích của một khối tứ diện cắt đi là V , thể tích khối tứ diện ABCD là V và thể tích khối 1
đa diện sau khi cắt bỏ góc là V . 2 1
Ta có: V = V − 4V mà V =
V V = 8V 2 1 2 1 2
Xét khối tứ diện đều ở đỉnh A là AB’C’D’ có các cạnh là x.
Gọi M’ là trung điểm của C’D’; G’ là tâm của tam giác B’C’D’ 1
AG ' ⊥ (B'C'D') V = AG '.S 1 1 3
Với S1 diện tích tam giác B’C’D’
Do tam giác B’C’D’ đề 2 2 x 3 x 3
u cạnh x B 'G ' = B ' M ' = . = 3 3 2 3
AG ' ⊥ (B'C ' D ') AG ' ⊥ B'G ' x 3 x 6 2 2 2 2 = − = − =
tam giác AB’G’ vuông tại G’ AG ' (AB ') (B 'G ') x ( ) 3 3 2 x 3 2 3 1 x 6 x 3 x 2
Diện tích tam giác B’C’D’ là S1 = V = . . 1 = 4 3 3 4 12 1
Gọi G là tâm tam giác BCD AG ⊥ (BCD) V = AG.S 1 ⊥ 3 và AG BG
Với S là diện tích tam giác BCD. Ta có: 2 2 6 2 3 BG = BM = = 2 6 2 2 2 2
AG = AB − BG = (6 2) − (2 6) = 4 3 3 3 2 2 (6 2) 3 1 S = =18 3 V = 4 3.18 3 = 72 4 3 3 x 2 3 72 = 8 x = 54 2 x = 3 2 12
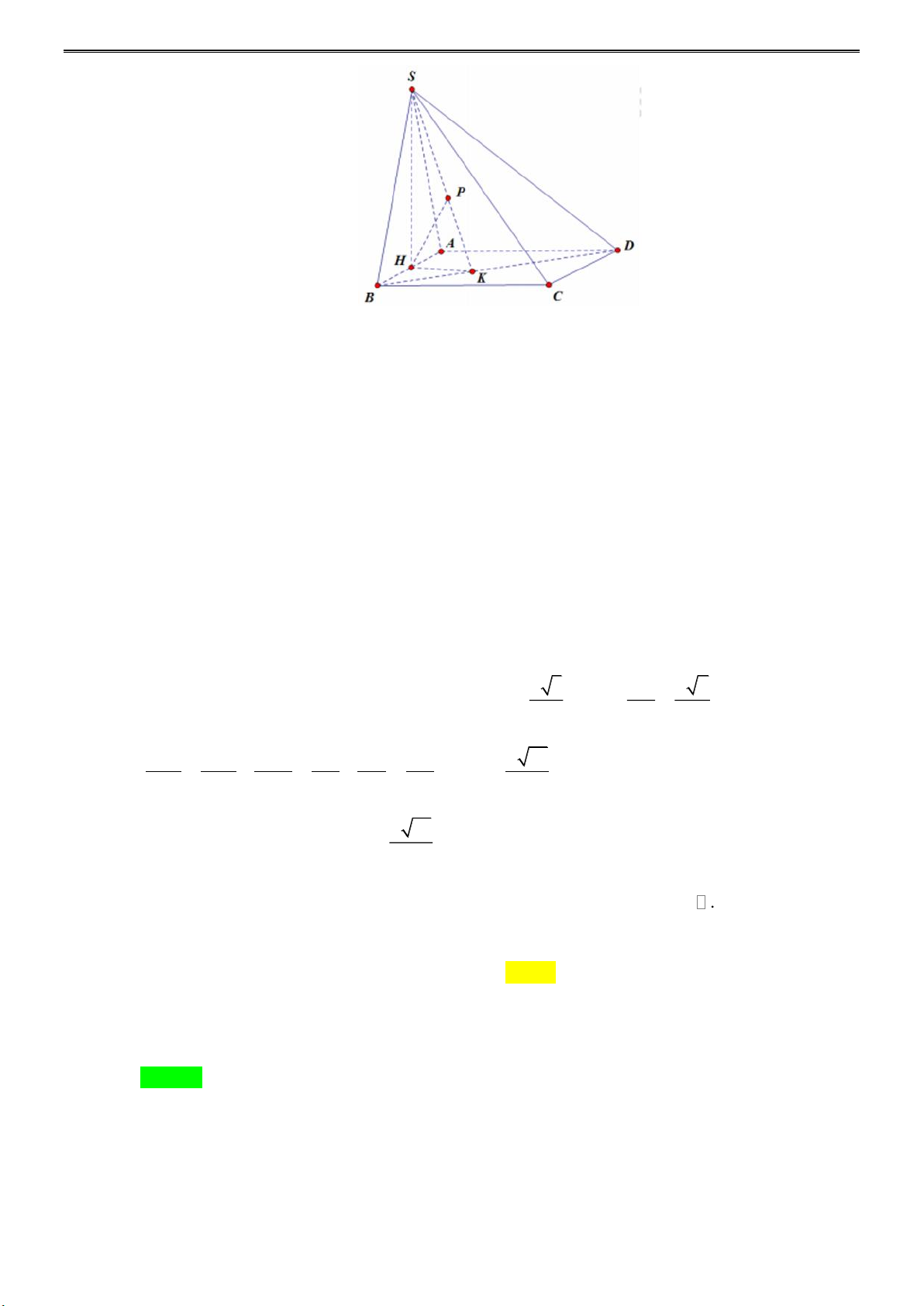
Câu 31: Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a , mặt bên SAB là tam giác đều và
nằm trong mặt phẳng vuông góc với đáy. Khoảng cách từ A đến mặt phẳng (SBD) bằng: a 2 a 21 a 21 a 21 A. . B. . C. . D. . 2 7 28 14 Lời giải
Tác giả: Phạm Thị Huyền; Fb: HuyenPham Chọn C
NHÓM TOÁN STRONG TEAM-TỔ 25 Ta có d ( ;
A (SBD)) = 2d (H;(SBD)) .
Từ H kẻ đường thẳng vuông góc với BD tại K , từ H kẻ HP ⊥ SK . BD ⊥ HK BD ⊥ SH
BD ⊥ (SHK ) BD ⊥ HP
SH HK = H ; SH , HK (SHK ) Ta có: HP ⊥ BD HP ⊥ SK
HP ⊥ (SBD) tại K d (H;(SBD)) = HP
BD SK = K; BD, SK (SBD) a 3 AC a 2
Tam giác SAB đều có SH là đường cao nên SH = ; HK = = 2 4 4 1 1 1 4 16 28 a 21 = + = + = HP = 2 2 2 2 2 2 HP SH HK 3a 2a 3a 14
d ( A (SBD)) = d ( H (SBD)) a 21 ; 2 ; = . 28 2
Câu 32: Cho hàm số f ( x) có đạo hàm f ( x) = ( x − ) ( 2 1
x − 2x) với mọi x . Có bao nhiêu số
nguyên m 100 để hàm số g ( x) = f ( 2
x − 8x + m) đồng biến trên khoảng (4;+) . A. 83 . B. 18 . C. 82 . D. 84 . Lời giải
Tác giả: Nguyenphamminhtri ; Fb:Tri Nguyen Chọn C
Do hàm f có đạo hàm trên R nên hàm g có đạo hàm và theo đề bài ta có đẳng thức sau:
g ( x) = ( x − ) f ( 2 ' 2 8
' x − 8x + m) 2
Hay g ( x) = ( x − )( 2
x − x + m − ) ( 2
x − x + m)( 2 ' 2 4 8 1 8
x − 8x + m − 2)
NHÓM TOÁN STRONG TEAM-TỔ 25
Khi đó để hàm g đồng biến trên khoảng (4;+) thì ta phải có
( 2x − x+m)( 2 8
x − 8x + m − 2) 0 x 4
Bất đẳng thức trên viết lại thành: ( x − x + m − )2 2 8 1 −1 0 (*)
Ta xét các trường hợp sau: - Với m 18 thì 2
x − 8x + m −1 1 với mọi x nên bất đẳng thức (*) hiển nhiên đúng. Vậy hàm
g đồng biên trên (4;+) với mọi m 18 .
- Với m = 17 g '( x) = 0 với mọi x (4;+) nên hàm g không phải hàm đồng biến trên (4;+)
- Với m 16 . Khi đó ta để ý rằng phương trình 2
x − 8x + m = 0 sẽ có một nghiệm là
x = 4 + 16 − m , phương trình 2
x − 8x + m − 2 = 0 sẽ có 1 nghiệm là x = 4 + 18 − m . 1 2
Dễ thấy rằng 4 x x với mọi số nguyên m m 16 , do đó ta có thể chọn được một số thực 1 2
x ' thỏa mãn 4 x x ' x . Theo định lý về dấu của tam thức bậc 2, ta có ( x )2 '
−8x '+ m 0 và 1 2 ( 2 2 x )2 '
−8x '+ m − 2 0 . Do đó ( x') −8x'+m)( x') −8x'+m−2) 0. Do đó hàm g không
đồng biến trên (4;+) .
Vậy để hàm g đồng biến trên (4;+) thì m 18 . Mà theo đề bài m là số nguyên và m 100 .
Do đó có 99 −18+1= 82 giá trị của m thỏa yêu cầu bài toán Cách 2 Chọn C x =1 2
Ta có f ( x) = ( x − ) 1 ( 2
x − 2x) = 0 x = 0 . x = 2 x − 0 2 + f ( x) + 0 − 0 +
Xét g( x) = ( x − ) f ( 2 2 8 .
x − 8x + m). Để hàm số g ( x) đồng biến trên khoảng (4;+) khi và
chỉ khi g( x) 0, x 4 .
( x − ) f ( 2 2 8 .
x − 8x + m) 0, x 4. f ( 2
x − 8x + m) 0, x 4. 2
x −8x + m 0, x (4;+) m 18. 2
x −8x + m 2, x (4;+)
Vậy 18 m 100. Do đó có (99 −18) +1 = 82 số nguyên m thỏa đề bài.
NHÓM TOÁN STRONG TEAM-TỔ 25
Câu 33: Cho số thực m nhỏ nhất để cho phương trình 2 2 1+ 1−x 1+ 1 9 + (1− )3 −x m
− 2m = 0 có nghiệm được a
viết dưới dạng m =
, ở đó a, b là hai số nguyên tố cùng nhau. Tính P = a + b . b A. P = 11 . B. P = 83. C. P = 17 . D. P = 75. Lời giải Chọn C Đặ 2 t 1 1 3 x t + − = ,vì x 1 − ; 1 t 3; 9 . 2 + Ta có phương trình t t 2
t + (1− m)t − 2m = 0 m = (*) t + 2 2 t + t Xét f (t) = t 3;9 t + 2 2
Có f '(t) = 1− 0 t
3;9 f (t) đồng biến trên đoạn 3;9 2 (t + 2) 12
(*) có nghiệm với m nhỏ nhất m = f (3) = . 5
Vậy P = a + b =12 + 5 =17 .
Câu 34: Gọi M là giá trị lớn nhất, m là giá trị nhỏ nhất của hàm số 20 20 y = sin
x + cos x +1. Khi đó tích
M.m bằng: 169 513 513 A. 2 . B. . C. . D. . 84 256 512 Lời giải
Tác giả: Lê Tiếp; Fb:Lê Tiếp Chọn C
Cách 1: Tập xác định của hàm số: D = R . 10 10 10 10 Ta có: 20 20 y = f x = x + cos x + = ( 2 x) + ( 2 ( ) sin 1 sin cos x) +1 = ( 2 x) + ( 2 sin 1− sin x) +1. Đặt 2 t = sin ,
x ta có f t = t + ( − t )10 10 ( ) 1 +1, t 0; 1 . f (t ) = t − ( −t)9 9 ' 10 10 1
f '(t ) = 0 10t −10(1− t )9 1 9
= 0 t =1− t t = 2 Ta có bảng biến thiên:
NHÓM TOÁN STRONG TEAM-TỔ 25 t 1 0 2 1
f (t ) - 0 - 0 + f (t ) 2 2 513 512
Từ bảng biến thiên ta có: 513 513 M = 2, m = M.m = 512 256 Cách 2: Đặt 20 20
y = f (x) = sin
x + cos x +1. Ta có: 19 19
f '(x) = 20sin xcosx − 20sin xcos x . 18 18
f '(x) = 20sin xcosx(sin x − cos x) 18 18
=10sin 2x(sin x − cos x). x = k sin 2x = 0 2 = f ( x) sin 2x 0 ' = 0 sin x = cosx x = + k , k Z . 18 18 sin x cos x 0 − = 4 sin x = −cosx
x = − + k 4
+) Với k = 2n , n Z ta có: f k = f (n ) =
(n )+ cos (n )+ = + ( )20 20 20 sin 1 0 1 +1 = 2. 2 20 2 513 f + k = f + 2n 20 20 = sin + 2n + cos + 2n +1 = 2 +1 = . 4 4 4 4 2 512 f −
+ k = f − + 2n 20 20 = sin
− + 2n + cos − + 2n +1 4 4 4 4 20 20 20 2 2 = 2 513 − + +1 = 2 +1 = . 2 2 2 512
+) Với k = 2n +1, n Z ta có: f k = f + n = + n + cos + n + = ( )20 20 20 sin 1 1 + 0 +1 = 2 . 2 2 2 2 f + k = f + + 2n 20 20 = sin
+ + 2n + cos + + 2n +1 4 4 4 4 20 20 20 2 2 2 513 = − + − +1 = 2 +1 = . 2 2 2 512
NHÓM TOÁN STRONG TEAM-TỔ 25 f −
+ k = f − + + 2n 20 20 = sin
− + + 2n + cos − + + 2n +1 4 4 4 4 20 20 20 2 2 2 513 = + − +1 = 2 +1 = . 2 2 2 512 513 513
Vậy: M = 2 , m = M .m = . 512 256
Câu 35: Cho tam giác ABC cân tại A , có cạnh đáy BC , đường cao AH , cạnh bên AB theo thứ tự lập
thành cấp số nhân công bội q . Tính giá trị của công bội q . 1 1 A. q = 2 ( 2 + ) 1 . B. q = 2 +1 . C. q = 2 +1 . D. q = 2 ( 2 + ) 1 . 2 2 Lời giải
Tác giả: Nguyễn Thị Phương; Fb: Phương Nguyễn Chọn C A B C H
Đặt BC = x(x 0) .
Vì cạnh đáy BC , đường cao AH , cạnh bên AB theo thứ tự lập thành cấp số nhân công bội q AH = . x q nên q 0 . 2 ( ) AB = . x q Theo Định lý Pytago có: 2 x 1 2 2 2 2 4 2 2 4 2
AB = AH + BH x .q = x .q +
q − q − = 0 2 4 2 +1 1 2 q = q = 2 +1 4 2 (q 0) − 1 1 2 2 = ( ) q = − 2 +1 ( L q L ) 2 4 1 Vậy q = 2 +1 . 2
NHÓM TOÁN STRONG TEAM-TỔ 25
Câu 36: Có bao nhiêu giá trị nguyên thuộc đoạn [ − 2019, 2019] của tham số m để trên đồ thị (C ) của m 1 hàm số 3 2 y =
x + mx + (2m − 3)x +10 có hai điểm nằm về hai phía của trục tung mà tiếp tuyến 3
của (C ) tại hai điểm đó cùng vuông góc với đường thẳng (d ) : x + 2 y + 2020 = 0 m A. 2022 . B. 2020 . C. 2019 . D. 2021 Lời giải
Tác giả:; Fb: Vuong Pham Chọn A 2 y ' = x + 2 x m + (2m − 3) Đườ 1
ng thẳng (d ) : x + 2 y + 2020 = 0 y = − x −1010 2 1
Hệ số góc (d ) : k = − 2
Tiếp tuyến vuông góc với (d ) nên hệ số góc của tiếp tuyến là 2 Yêu cầu bài toán 2 x + 2 x
m + (2m − 3) = 2 có hai nghiệm trái dấu 5 .
a c 0 2m − 5 0 m
mà m nguyên thuộc đoạn[ − 2019, 2019] 2
Nên m { -2019, -2018,...,2} do đó c
ó 2022 giá trị nguyên thỏa mãn.
Câu 37: Cho hình đa giác đều ( H ) có 24 đỉnh, chọn ngẫu nhiên 4 đỉnh của ( H ) . Tính xác suất để 4
đỉnh được chọn ra tạo thành một hình chữ nhật không phải hình vuông. 11 10 1 15 A. . B. . C. . D. . 46 1771 161 322 Lời giải
Tác giả: Bùi Chí Tính; Fb: Chí Tính Chọn B
Hình đa giác đều (H ) có 24 đỉnh nên có 12 đường chéo đi qua tâm đường tròn nội tiếp ngoại tiếp ( H ) .
Cứ 2 đường chéo đi qua tâm đường tròn ngoại tiếp ( H ) cho ta một hình chữ nhật. Số hình chữ nhật là 2
C = 66 (hình chữ nhật) 12
Trong 66 hình chữ nhật này có ta chọn hình chữ nhật có 2 đường chéo vuông góc. 0 360 0 90 Góc ở tâm là 0 =15 . Cần 0 90 tức là cần = 6 . 24 0 15
Vậy có 6 hình vuông trong 66 hình chữ nhật đó.
NHÓM TOÁN STRONG TEAM-TỔ 25
Số phần tử không gian mẫu: 4 C 24
Gọi A: “ 4 đỉnh được chọn ra tạo thành một hình chữ nhật không phải hình vuông”
n( A) = 66−6 = 60 n A 60 10
Xác suất của biến cố A : P ( A) ( ) = = = . n () 4 C 1771 24
Câu 38: Cho lăng trụ tam giác AB .
C A' B'C ' có thể tích V . Gọi M , N, P,Q lần lượt là trung điểm của
cạnh AB, BB ', B ' A', A' .
A . Thể tích khối chóp có đáy là tứ giác MNPQ và đỉnh là một điểm bất kì trên cạnh CC '. V V V V A. . B. . C. . D. . 3 4 8 2 Lời giải
Tác giả:Nguyễn Thị Hường; Fb: Nguyen Huong Chọn A A' P B' C' Q N E M A B C 1 S = S MNPQ ABB ' A' 2
Gọi E là một điểm trên cạnh CC '. Khi đó d ( ;
E ( ABB' A')) = d ( ;
C ( ABB' A')). 1 V = d E ABB A S EMNPQ ( ;( ' ')). 3 MNPQ 1
= d ( ( ABB A )) 1 C; ' ' . S ABB ' A' 3 2 1 1 2 = V .V = . V = . CABB ' A' 2 2 3 3
Câu 39: Gọi S là tập hợp tất cả các số tự nhiên gồm 4 chữ số đôi một khác nhau được lập từ các chữ số
1, 2, 3, 4, 5, 6, 7, 8, 9 và lấy ngẫu nhiên một số từ tập hợp S. Tìm xác suất để số được lấy chia
hết cho 11 và có tổng các chữ số của nó cũng chia hết cho 11.
NHÓM TOÁN STRONG TEAM-TỔ 25 8 1 1 1 A. . B. . C. . D. . 21 126 252 63 Lời giải
Tác giả:Nguyễn Phương; Fb:Nguyễn Phươngg Chọn D
Ta có không gian mẫu n() 4 = A . 9
Giả sử số cần lập là abcd . Theo giả thiết ta có
Vì abcd chia hết cho 11 nên ta có b + d − (a + c) 11 (1)
abcd có tổng các chữ số chia hết cho 11 => a + b + c + d 11 (2)
Từ (1) và (2) ta được a + c = b + d và cùng chia hết cho 11. Vì , a , b ,
c d 1;2;3;4;5;6;7;8;
9 4 a + b + c + d 36
a + b + c + d 11; 22; 3 3
Do a + c = b + d a + c = b + d = 11 ( , a c) và ( ,
b d ) là một trong các cặp số (2,9) , (3,8) , (4,7),(5,6). Có 2
C cách chọn 2 trong 4 cặp số trên, ứng với mỗi cách đó ta có: a có 4 cách chọn, b có 2 4
cách chọn, c và d mỗi chữ số có 1 cách chọn. Suy ra n( A) 2 = C .4.2 . 4 2 C .4.2 1
Từ đây suy ra P ( A) 4 = = . 4 A 63 9 x - 4
Câu 40: Cho hàm số y =
có đồ thị là (C )và đường thẳng d : y + 2x = m với m là tham số. Biết x + 1
rằng với mọi giá trị của m thì d luôn cắt (C ) tại hai điểm phân biệt A
và B . Tìm độ dài AB ngắn nhất. A. 3 2. B. 4 2. C. 6 2. D. 5 2. Lời giải
Tác giả:; Fb:Cuongkhtn Chọn D Phương trình x - 4 hoành độ giao điểm:
= - 2x + m (x ¹ - ) 1 x + 1 2 Û 2x + (3- ) m x - m- 4 = 0.
NHÓM TOÁN STRONG TEAM-TỔ 25
Ta có D > 0, " m Î ¡ nên d luôn cắt (C) tại hai điểm phân biệt.
Gọi x , x là hai nghiệm của * . 1 2 ( ) ìï m - 3 ï x + x 1 2 = ï Theo đị ï 2 nh lí Viet, ta có í . ï - m - 4 ïï x x 1 2 = ïïî 2
Giả sử A(x ;- 2x + m và B x ;- 2x + m là tọa độ giao điểm của d và C . 1 1 ) ( 2 2 ) ( ) Ta có 2 2 5 2 2 AB 5(x x 5 é x x 4x x ù ém 1 40ù = - = + - = + + ³ 50. 2 1 ) ( ê 1 2 ) 1 2 ú ( ê ) 4 ú ë û ë û Û AB ³ 5 2
Dấu ' = ' xảy ra Û m = - 1.
Câu 41: Cho a và b là hai số thực dương thỏa mãn 2 2
5a + 2b + 5 = 2a + 4b + 4ab . Xét các hệ thức sau: Hệ thức 1:
(a + ) + (b + ) = ( 2 2 ln 1 ln 1 ln a + b + ) 1 . Hệ thức 2:
( 2a + )+ (b+ ) = ( 2 ln 1 ln 1 ln b + ) 1 + ln (a + ) 1 .
Hệ thức 3: ln (a + b + 3ab − )
1 = 2ln (a + b) .
Hệ thức 4: ln (a + b + 2ab + 2) = 2ln (a + b).
Trong các hệ thức trên, có bao nhiêu hệ thức đúng? A. 1. B. 2 . C. 3 . D. 4 . Lời giải
Tác giả: Trần Quang Kiên; Fb: Kien Tranquang. Chọn B Ta có: 2 2
5a + 2b + 5 = 2a + 4b + 4ab ( 2 2
a − ab + b ) + ( 2
a − a + ) + ( 2 4 4 2 1
b − 4b + 4) = 0
( a − b)2 + (a − )2 + (b − )2 2 1 2 = 0 a =1 . b = 2
Thay a = 1, b = 2 lần lượt vào các hệ thức ta được:
Hệ thức 1: ln 2 + ln 3 = ln 6 . Đúng.
Hệ thức 2: ln 2 + ln 3 = ln 5 + ln 2 . Sai.
NHÓM TOÁN STRONG TEAM-TỔ 25
Hệ thức 3: ln 8 = 2ln 3. Sai.
Hệ thức 4: ln 9 = 2ln 3. Đúng.
Vậy có 2 hệ thức đúng. Câu 42: Cho hàm số 3 2
y = ax + bx + cx + d , với a, b, c là các hệ số. Tìm điều kiện để hàm số đồng biến trên
a = b = 0; c 0
a = b = c = 0 A. . B. . 2
b −3ac 0 2
a 0; b −3ac 0
a = b = 0; c 0
a = b = 0; c 0 C. . D. 2
a 0; b −3ac 0 2
a 0; b − 3ac 0 Lời giải
Tác giả: Nguyễn Văn Hùng; Fb:Nguyễn Văn Hùng Chọn C
Quan sát các đáp án, ta sẽ xét hai trường hợp là: a = b = 0 và a 0.
Nếu a = b = 0 thì y = cx + d là hàm bậc nhất →để y đồng biến trên khi c 0 .
Nếu a 0 , ta có 2
y ' = 3ax + 2bx + c . Để hàm số đồng biến trên y ' 0, x a 0 a 0 . Chọn đáp án C. 2 ' 0 b − 3ac 0
Câu 43: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với mặt 3 đáy. 3a
Thể tích khối chóp S.ABC bằng
. Gọi là góc giữa mp( SCD ) và mp( ABCD ) . 6
Khi đó tan bằng? 3 3 3 A. . B. . C. 3 . D. 4 3 2 Lời giải
Tác giả: Vũ Hương; Fb: Vũ Hương Chọn C
( ABCD ) ( SCD) = CD
Ta có: AD ⊥ CD SD ⊥ CD
NHÓM TOÁN STRONG TEAM-TỔ 25
Suy ra: (( SCD ), ( ABCD)) = (SD, AD) = SDA = 3 1 a 3 Mà V = S .SA = SA = a 3 S .ABC 3 ABC 6 a 3 Vậy tan = = 3 . a
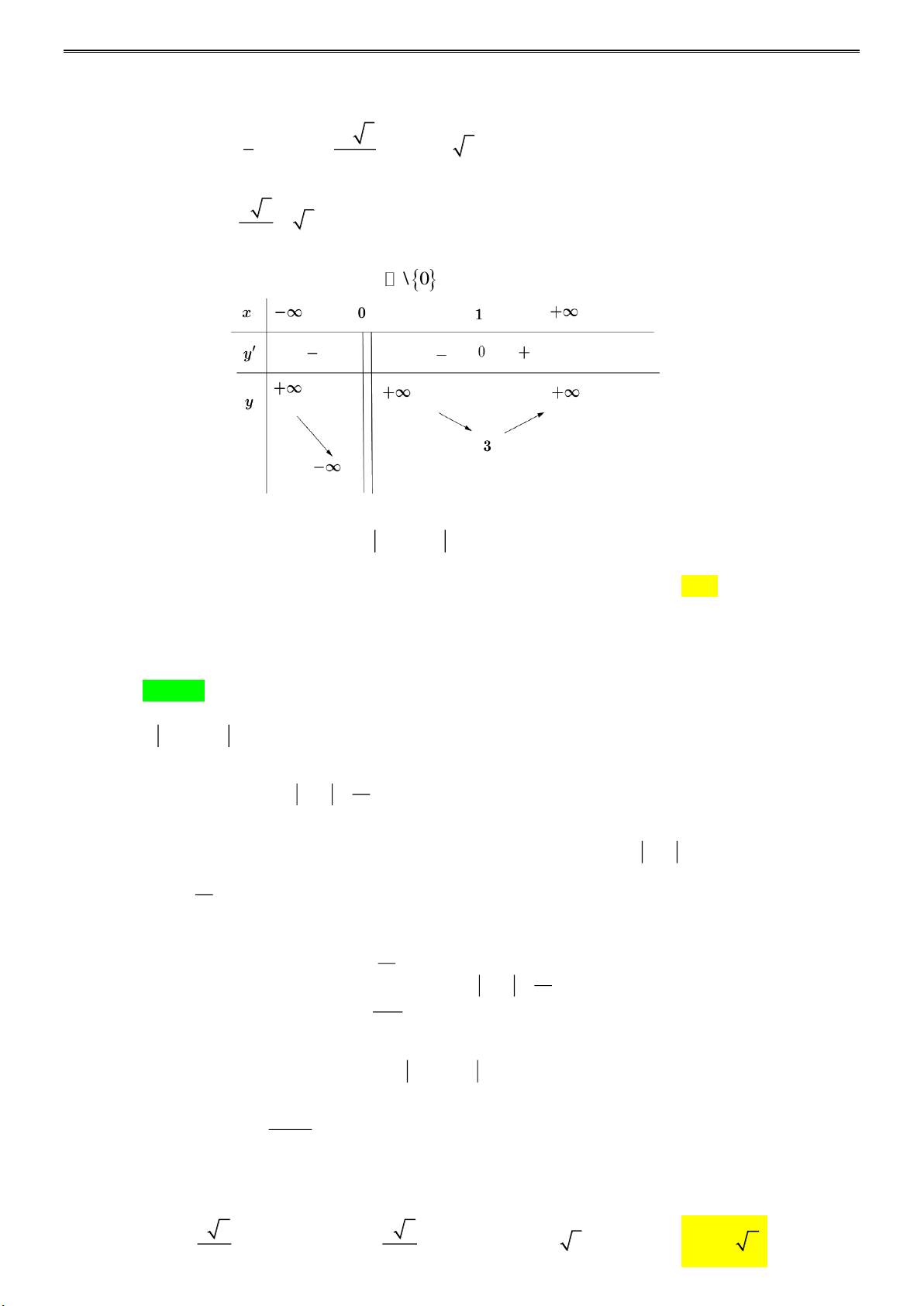
Câu 44: Cho hàm số f (x) xác đị nh trên \
0 v à có bảng biến thiên như hình vẽ
Số nghiệm của phương trình 4 f (3x −1) −13 = 0 là: A. 1. B. 3. C. 2. D. 4. Lời giải
Tác giả: Phạm Quang Linh, Fb: Linh Phạm Quang Chọn D
4 f (3x −1) −13 = 0 ( ) 1 Đặ 13
t 3x −1 = t ta có: f (t) = . 4
Số nghiệm phân biệt của ( )
1 bằng số giao điểm của đồ thị hàm số f (t) với đường thẳng 13 d : y = . 4 13 f (t) = → 3n o 13 Từ bảng biến thiên 4 f (t) = có 4 nghiệm. 13 − 4 f (t) = →1n 4 o
Vậy số nghiệm của phương trình 4 f (3x −1) −13 = 0 là 4. x +1
Câu 45: Cho hàm số y =
có đồ thị (C) . Gọi A( x ; y , B x ; y là hai điểm phân biệt thuộc (C) 1 1 ) ( 2 2) 2x +1
sao cho tiếp tuyến của (C) tại A và B song song với nhau. Độ dài nhỏ nhất của đoạn AB bằng 3 2 2 2 A. h = . B. h = . C. h = 3 . D. h = 2 . 4 3
NHÓM TOÁN STRONG TEAM-TỔ 25 Lời giải
Tác giả: Nguyễn Thị Liên; Fb: Nguyễn Thị Liên Chọn D 1 Tập xác định: D = \ − 2 1 Ta có y ' = − ( 2x + )2 1
Tiếp tuyến của (C) tại A và B song song với nhau nên k = k y '( x = y ' x A B 1 ) ( 2) 1 1 2x +1 = 2x +1
x = x A B loai 1 2 1 2 ( ) − = − + = − ( x x 1 2x +1 2x +1 2x +1 = 2 − x −1
2x +1 = − 2x +1 1 )2 ( 2 )2 1 2 2 ( 1 ) 1 2 Do x + x = 1
− nên không mất tính tổng quát giả sử x 0. 1 2 2 2 + + 2 x 1 x 1 Ta có: 2
AB = ( x − x ) 2 1 + − 2 1 2x +1 2x +1 2 1 2 = ( + ( x + x + x 1+ x ))2 1 1 2 1 + +
(do x + x = 1 − ) 2 2 2x +1 2x +1 1 2 2 2 = ( x + )2 1 2 1 +
2 (bất đẳng thức Cauchy). 2 (2x + )2 1 2 AB = 2 khi A(0; ) 1 , B( 1 − ;0).
Vậy độ dài nhỏ nhất của đoạn AB bằng 2 . 1 Câu 46: Cho hàm số f (x) = . Tính giá trị của biểu thức sau: 1 2 1 x + − 2 1009 2 2 2 Q = f sin + f sin ) + ... + f (sin 2020 2020 2020 1009 A. 1009. B. 504 . C. . D. 505 . 2 Lời giải
Tác giả: Phạm Hồng Quang; Fb:Quang Phạm ChọnC 1 1 x
Biến đổi: f (x) = = = . 1−2 x 1 x + + 1+ x Ta thấy
NHÓM TOÁN STRONG TEAM-TỔ 25 −
f ( x) + f ( x x x x x 1− x) 1 = + = + = + = 1 , x R x 1− x x x x + + + + + + x Vậy 1009 504 506 505 2 2 2 2 2 Q = f (sin ) + f (sin ) + ... + f (sin ) + f (sin ) + f (sin ) 2020 2020 2020 2020 2020 . 1009 2 = 504 + f (sin ) = . 4 2 3 x e −1 a
Câu 47: Cho giới hạn lim
= , với a,b nguyên tố cùng nhau. Tính giá trị của 2a +b x→0 x +1 −1 b A. 8 . B. 7 . C. 5 . D. 6 Lời giải
Tác giả: Trần Văn Huấn; Fb: Huấn Trần Chọn B x 3 e −1 x +1 +1 3 x ( ) e −1 Ta có lim = lim x→0 x→0 x +1 −1 x x 3 e −1 ( x +1 + )1 2 2 a = lim . = 1. = = x→0 x 3 3 3 b 3
Nên 2a + b = 7 .
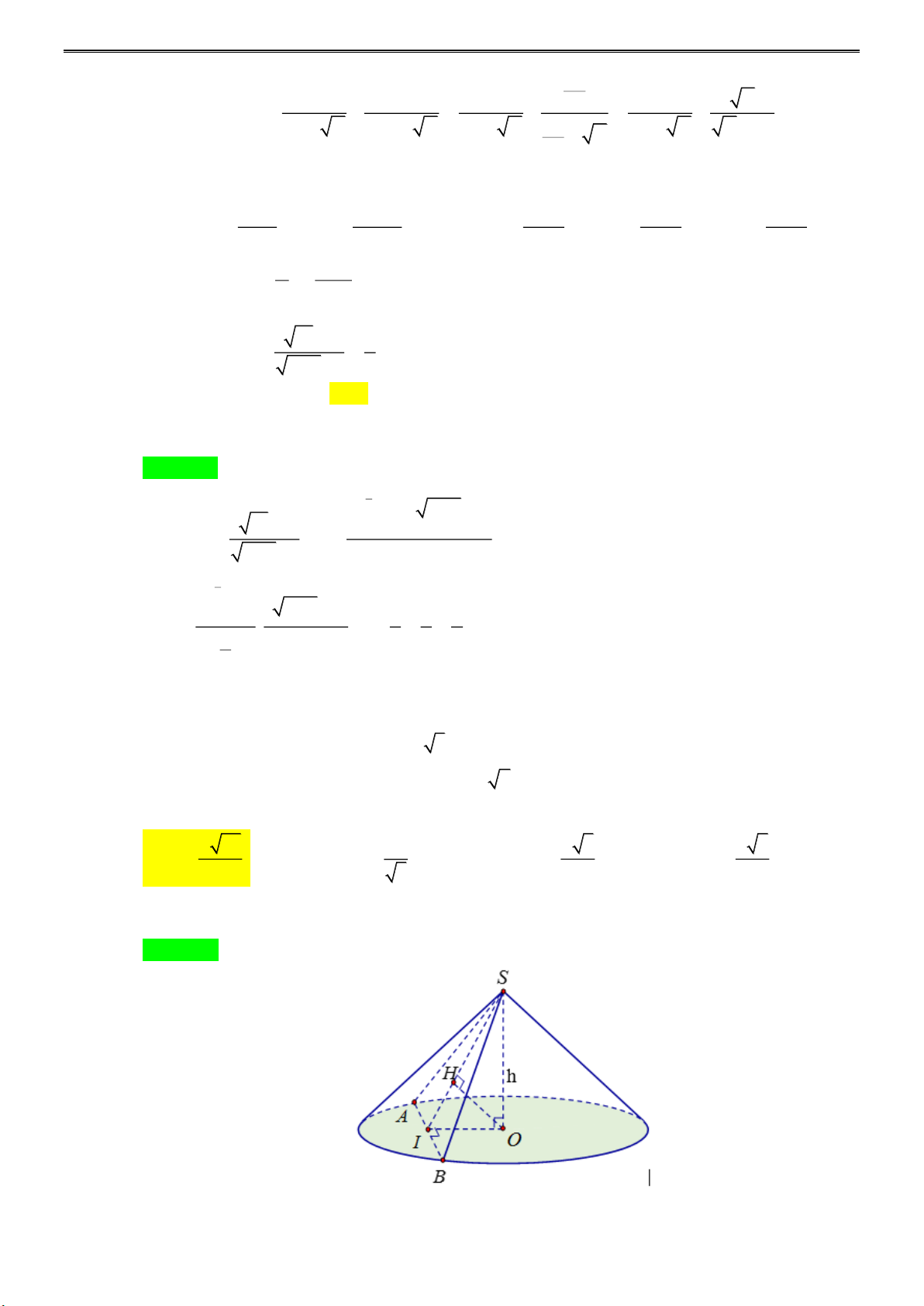
Câu 48: Cho một hình nón có chiều cao h = a 3 và bán kính đáy r = 2a . Mặt phẳng ( P) đi qua S cắt
đường tròn đáy tại A và B sao cho AB = 2a 2 . Tính khoảng cách d từ tâm của đường tròn đáy đến (P) . a 30 6a a 5 a 6 A. d = . B. d = . C. d = . D. d = . 5 5 30 5 Lời giải
Tác giả: Trịnh Thúy; Fb: Catus Smile Chọn A
Gọi I là trung điểm AB . Kẻ OH ⊥ SI vuông góc với SI tại H .
NHÓM TOÁN STRONG TEAM-TỔ 25 AB ⊥ OI
Ta có: AB ⊥ SO
AB ⊥ (SOI ) AB ⊥ OH .
OI SO = O O H ⊥ SI O
H ⊥ AB OH ⊥ (SAB) tại H .
SI AB = I Suy ra d ( ,
O (P)) = d ( ,
O (SAB)) = OH .
Tam giác SOI vuông tại O và OH là đường cao, nên ta có 1 1 1 = + 2 2 2 OH OS OI OS = h = a 3 2 2 2 2 OI
= r − AI = 4a − 2a = a 2 1 1 1 5 = + = . 2 2 2 2 OH 3a 2a 6a a 30 OH = . 5
Câu 49: Cho hai cấp số cộng (u ) : 4,7,10,13,16,... và (v
. Hỏi trong 100 số hạng đầu k ) :1, 6,11,16, 21,... n
của mỗi cấp số cộng có bao nhiêu số hạng chung? A. 30 . B. 10 . C. 20 . D. 40 . Lời giải
Tác giả: Nguyễn Thị Thơm; Fb:Thom Nguyen Chọn C u = 1+ 3 n n
. Do đó: u = v 1+ 3n =1+ 5 k − n = k − . n k ( ) 1 3 5( ) 1 (*)
v = 1+ 5 k − k ( ) 1 * , n k n 5 n = 5m Vì nên từ ( ) * * (m , l ) . (3,5) =1 k −1 3 k −1 = 3l
Khi đó (*) trở thành: 3.5m = 5.3l m = l . 1 n 100 1 m 20
Vì ta chỉ xét 100 số hạng đầu của mỗi cấp số cộng nên 1 k 100 0 l 33
mà m = l 1 m = l 20 Số giá trị m = l thỏa mãn là 20 Số giá trị ,
n k tương ứng là 20 .
Vậy trong 100 số hạng đầu của mỗi cấp số cộng có 20 số hạng chung.
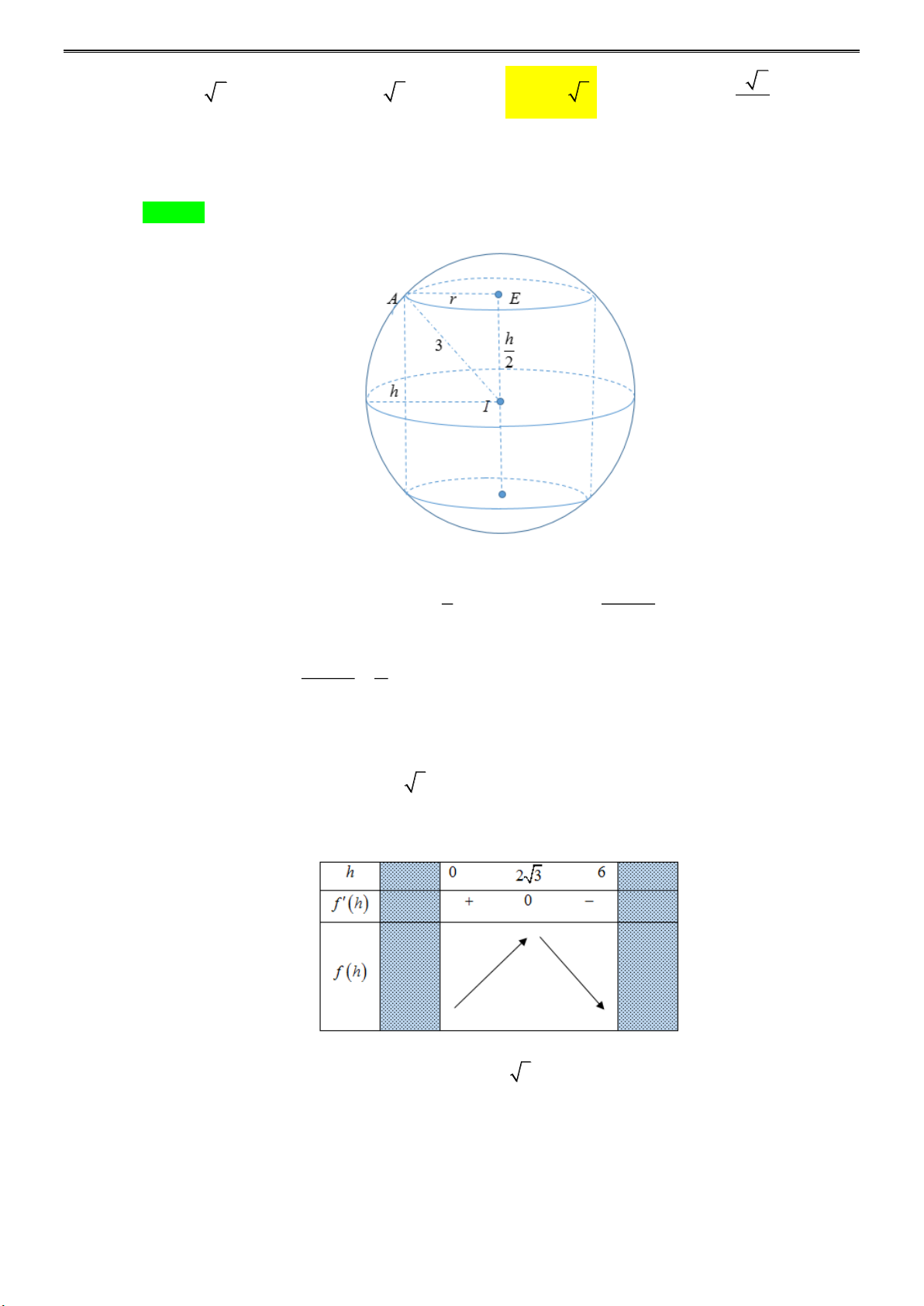
Câu 50: Cho khối cầu (S ) có tâm I , bán kính bằng R = 3. Một khối trụ thay đổi nội tiếp khối cầu có
chiều cao h và bán kính đáy r . Tính chiều cao h để thể tích khối trụ lớn nhất.
NHÓM TOÁN STRONG TEAM-TỔ 25 3 2 A. h = 3 2 . B. h = 3 . C. h = 2 3 . D. h = . 2 Lời giải
Tác giả: Mai Thanh Lâm; Fb: Mai Thanh Lâm Chọn C 2 2 h 36 − h
Ta có tam giác IEA vuông tại E , nên 2 2 2 + r = 3 r = , (0 h 6) 2 4 2 36 h mà 2 V . h r . h − = = = h − h tru ( 3 36 ) 4 4 Đặt 3
f (h) = 36h − h , khi đó 2 f ( ) h = 36 − 3h 2 f (
h) = 0 36 −3h = 0 h = 2 3 Bảng biến thiên
Từ bảng biến thiên ta thấy V lớn nhất khi h = 2 3 . tru
Document Outline
- de-kiem-tra-dinh-ki-lan-1-toan-12-nam-2019-2020-truong-chuyen-bac-ninh.pdf
- [STRONG TEAM TOÁN VD-VDC]-Giải chi tiết-DE-KIEM-TRA-CHUYEN-BAC-NINH-LAN-1-2020.pdf




