TRƯỜNG TRUNG HỌC CƠ SỞ
ĐỀ KIỂM TRA HỌC KÌ II MÔN TOÁN LỚP 8 CỬU LONG
Thời gian làm bài: 90 phút (không kể thời gian giao đề) Năm học: 2019 – 2020 Đ Ề C HÍNH THỨC Câu 1 (3,0 điểm) Giải phương trình: a) 3(x 14)  2(1 5x) b) 2 3 8   2 x  3 x  3 x  9 c) x  4  2x  3 Câu 2 (2,0 điểm)
Giải bất phương trình và biểu diễn tập nghiệm trên trục số:
a) 5x  2  4  3 4(x  2) x  3 2x 1 x  2 b)   1 3 4 4 Câu 3 (1,5 điểm)
Một miếng đất hình chữ nhật có chiều dài gấp 3 lần chiều rộng, nếu tăng chiều dài thêm 2m và
giảm chiều rộng 3m thì diện tích giảm 90m2. Tính diện tích của miếng đất ban đầu. Câu 4 (1,0 điểm)
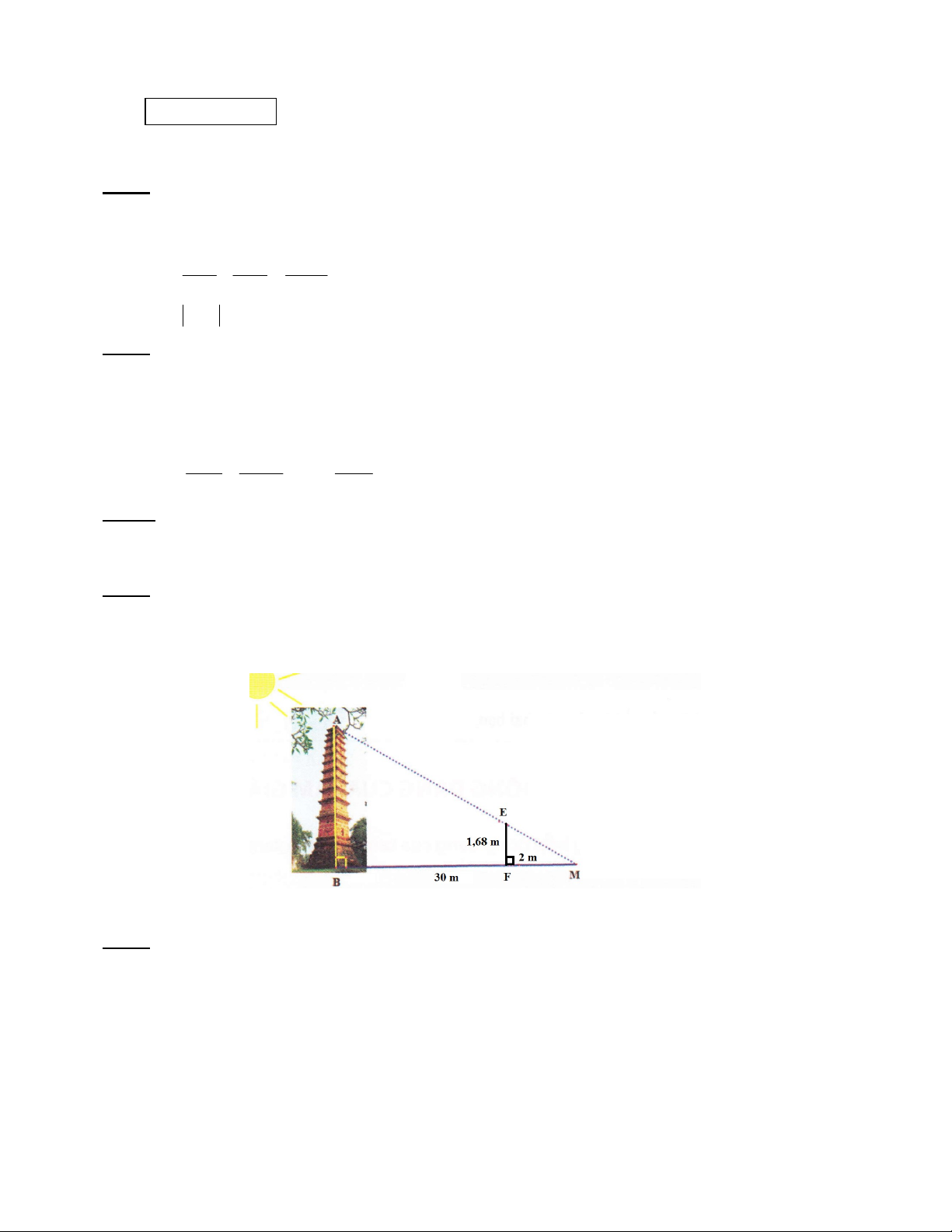
Bóng của một cái tháp trên mặt đất có độ dài 30 m. Cùng thời điểm đó, một cột sắt cao 1,68 m
cắm vuông góc với mặt đất có bóng dài 2 m. Tính chiều cao của tháp. Câu 5 (2,5 điểm)
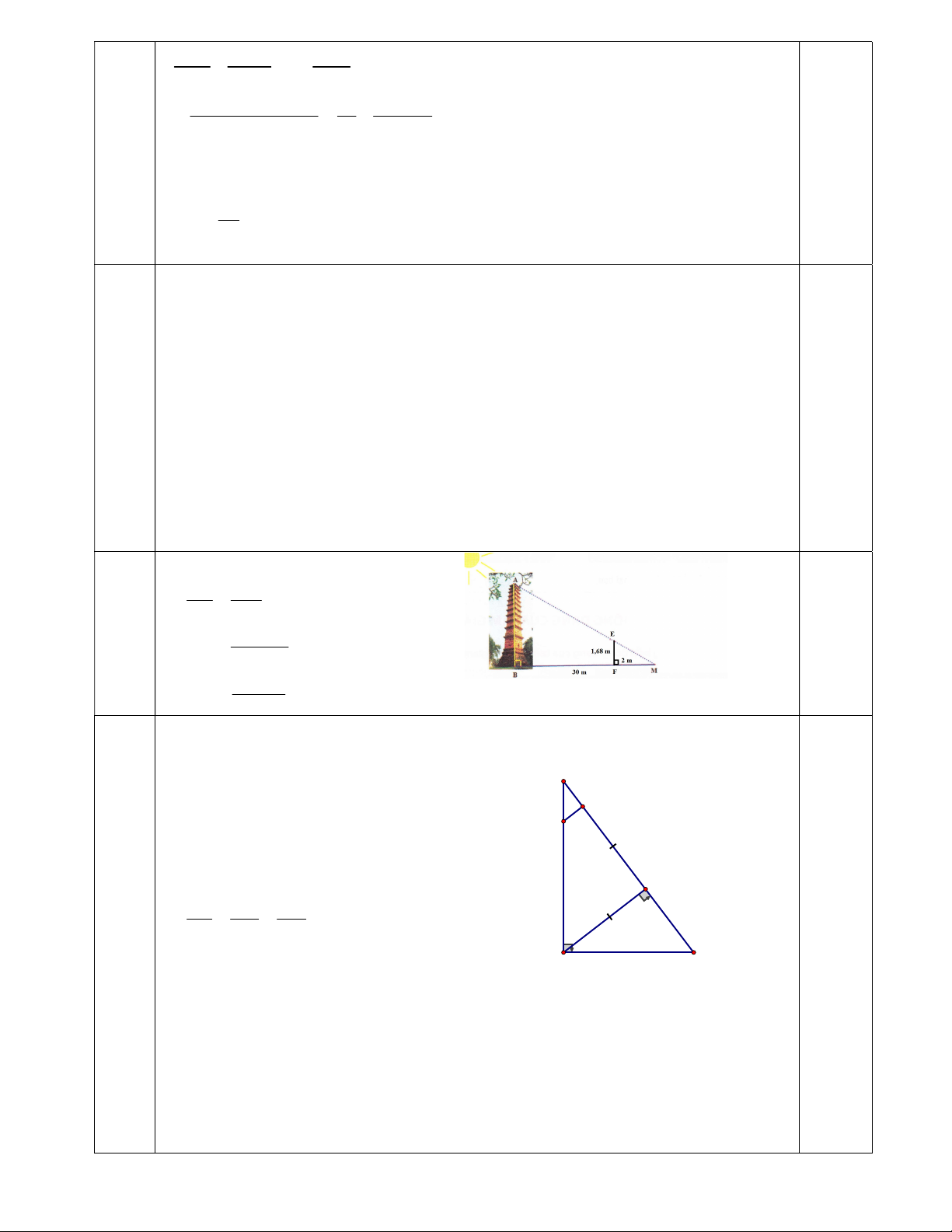
Cho ∆ABC vuông tại A (AB < AC), AH là đường cao.
a) Chứng minh ∆BAC đồng dạng ∆BHA và viết tỉ số đồng dạng. b) Chứng minh 2 AH  BH.HC .
c) Trên tia HC, xác định điểm D sao cho HA = HD. Từ D vẽ DE // AH (E thuộc AC). Chứng minh: CD.CB = CE.CA. ---- HẾT ----
HƯỚNG DẪN CHẤM KIỂM TRA HỌC KÌ II MÔN TOÁN LỚP 8 Câu Nội dung Điểm 3(x 14)  2(1 5x) 1a  3x  42  2 10x 0,25  3x 10x  2  42  13x  4  0 0,25 4  0  x  13 0,25  40 
Vậy tập nghiệm của phương trình là S     13  0,25 2 3 8   ĐKXĐ: x  3 2 x  3 x  3 x  9 2 3 8   2 x  3 x  3 x  9 2(x  3)  3(x  3) 8 1b   (x  3)(x  3) (x  3)(x  3) 0,25  5x  3  8  5x  11 0,25 11  x  (n) 5 0,25 1  1
Vậy tập nghiệm của phương trình: S     5  0,25 1c x  4  2x  3 (*)
TH1: x  4  0  x  4 (*)  x  4  2x  3 0,25  x  1(l) 0,25
TH2: x  4  0  x  4 (*)  4  x  2x  3 0,25 7  x  (n) 3 0,25 7
Vậy tập nghiệm của phương trình:  S    3
5 x  2  4  3 4(x  2) 2a
 5x 10  4  3  4x  8 0,5  x  17 0,25 Biểu diễn 0,25 x  3 2x 1 x  2    1 3 4 4
4(x  3)  3(x 1) 12 3(x  2) 0,25    12 12 12 2b  0,25
4x 12  3x  3  12  3x  6  4x  27 0,25 27  x  4 0,25 Biểu diễn
Gọi chiều rộng miếng đất ban đầu là x (m), x>0. 0,25
Chiều dài miếng đất ban đầu là 3x
Chiều rộng miếng đất lúc sau là x-3 0,25 3
Chiều dài miếng đất lúc sau là 3x+2 Ta có phương trình 2
3x  x-33x+2  90 0,25 2 2
 3x  3x  2x  9x  6  90  7x  84  x  12(n) 0,25
Vậy chiều rộng miếng đất ban đầu là 12m 0,25
Chiều dài miếng đất ban đầu là 36m
Diện tích miếng đất ban đầu là 12.36 = 432m2 0,25 A  BM  EFM (g  g) 0,25 BA BM 4   EF FM 0,25 EF.BM  BA  FM 0,25 1,68.30   25, 2(m) 0,25 2 a. C Xét A  BH và CBA D 5  A   0 H  90 E 0,25  0,25 B chung  A  BH  C  BA (g  g) H 0,25 AB BH AH 0,25    CB AB CA 0,25 (tỉ số đồng dạng) A B b. Xét A  BH và CAH 0,25 0,25 0,25 0,25  AHB   0 AHC ( 90 )  BAH   ACB ( A  BH  CB ) A  A  BH  C  AH (g  g) AH BH 0,25   CH AH 2  AH  BH.CH c. Ta có: ED // AH (gt) Nên  CDE   0
CHA  90 (2 góc đồng vị) 0,25 Xét ∆CDE và ∆CAB có  CDE   0 CAB  90 C là góc chung  CDE  C  AB (g  g) CD CE   CA CB  C . D CB  CE.CA