Đề kiểm tra khảo sát Toán 12 năm 2022 – 2023 sở GD&ĐT Hà Nội

Đề kiểm tra khảo sát Toán 12 năm 2022 – 2023 sở GD&ĐT Hà Nội mã đề 101 gồm 06 trang, hình thức trắc nghiệm với 50 câu

26 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

31 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
1/6 - Mã đề 101
UBND THÀNH PHỐ HÀ NỘI
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ CHÍNH THỨC
(Đề kiểm tra có 06 trang)
KỲ KIỂM TRA KHẢO SÁT HỌC SINH LỚP 12 THPT
NĂM HỌC 2022 - 2023
Đề kiểm tra môn: Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Họ, tên thí sinh:……………………………………………
Số báo danh
:……………………………………………….
Mã đề kiểm tra 101
Câu 1. Cho hàm số bậc bốn
y f x
có đồ thị như hình vẽ
Số nghiệm của phương trình
2 1 0
f x
là
A.
4.
B.
3.
C.
1.
D.
2.
Câu 2. Số cạnh của hình đa diện như hình vẽ dưới đây là
A.
B.
C.
16.
D.
8.
Câu 3. Trong không gian
,Oxyz
một vectơ pháp tuyến của mặt phẳng
: 2 4 2 0
x y z
có tọa độ là
A.
1; 2;4 .
B.
1;2;4 .
C.
1;2;4 .
D.
1;2; 4 .
Câu 4. Cho hàm số
y f x
liên tục trên đoạn
1;3
và có đồ thị như hình vẽ
Giá trị lớn nhất của hàm số đã cho trên đoạn
1;3
bằng
A.
3.
B.
1.
C.
4.
D.
2.
Câu 5. Diện tích xung quanh của hình nón có đường sinh
l
và bán kính đáy
r
bằng
A.
.rl
B.
.r l r
C.
2
.rl
D.
2 .rl
Câu 6. Bất phương trình
2
log 2 3 1
x
có tập nghiệm là khoảng
; .a b
Giá trị của
a b
bằng
A.
4.
B.
2.
C.
5.
D.
3.
2/6 - Mã đề 101
Câu 7. Trong không gian
,Oxyz
cho
2 2 3 .a i j k
Tọa độ của vectơ
a
là
A.
2; 2; 3 .
B.
2;2; 3 .
C.
2; 2;3 .
D.
2;2; 3 .
Câu 8. Cho hàm số
y f x
có bảng biến thiên
Giá trị cực đại của hàm số đã cho bằng
A.
3.
B.
2.
C.
2.
D.
3.
Câu 9. Trong các hàm số dưới đây, hàm số nào nghịch biến trên tập
?
A.
3
log .y x
B.
2
.
x
y
e
C.
.
3
x
y
D.
1
2
log .y x
Câu 10. Thể tích của khối trụ có bán kính đáy
r
và chiều cao
h
bằng
A.
2
.r h
B.
2 .rh
C.
.rh
D.
2
1
.
3
r h
Câu 11. Cho hàm số
y f x
có
1 .
f x x x
Hàm số đã cho có số điểm cực trị là
A.
1.
B.
0.
C.
3.
D.
2.
Câu 12. Số cách chọn
5
học sinh bất kì từ
12
học sinh bằng
A.
12
5 .
B.
5
12
.C
C.
5
12
.A
D.
5
12 .
Câu 13. Trong không gian
,Oxyz
mặt cầu tâm
1;4;2
I
và bán kính
2R
có phương trình là
A.
2 2 2
1 4 2 4.
x y z
B.
2 2 2
1 4 2 2.
x y z
C.
2 2 2
1 4 2 4.
x y z
D.
2 2 2
1 4 2 2.
x y z
Câu 14. Đường tiệm cận đứng của đồ thị hàm số
1
1
x
y
x
là
A.
1.
y
B.
1.
x
C.
1.
x
D.
1.
y
Câu 15. Hàm số nào dưới đây có đồ thị như hình vẽ ?
A.
2
2 1.
y x
B.
4 2
2 .y x x
C.
3 2
2 2.
y x x
D.
2 3
.
1
x
y
x
Câu 16. Cho hình phẳng
H
giới hạn bởi đồ thị hàm số
,y f x
trục
Ox
và các đường thẳng
,x a
.x b a b
Gọi
V
là thể tích khối tròn xoay thu được khi cho
H
quay quanh trục
.Ox
Khẳng
định nào sau đây đúng ?
A.
d .
b
a
V f x x
B.
d .
b
a
V f x x
C.
2
d .
b
a
V f x x
D.
2
d .
b
a
V f x x
3/6 - Mã đề 101
Câu 17. Nghiệm của phương trình
2 1
2 2
x x
là
A.
2.
x
B.
2.
x
C.
1.
x
D.
1.
x
Câu 18. Với mọi số thực
,
và số thực dương
a
khác
1,
khẳng định nào sau đây sai ?
A.
.
a a a
B.
.a a a
C.
.a a

D.
.
a
a
a
Câu 19. Cho hàm số
y f x
có bảng xét dấu
f x
Hàm số đã cho đồng biến trên khoảng nào sau đây ?
A.
0;2 .
B.
1;1 .
C.
1; .
D.
; 1 .
Câu 20. Tập nghiệm của phương trình
3 3
log 3 log 2 1
x x
là
A.
2 .
B.
0 .
C.
2 .
D.
.
Câu 21. Khẳng định nào sau đây sai ?
A.
.
x x
e dx e C
B.
2
.
2
x
xdx C
C.
1
ln .dx x C
x
D.
.dx x C
Câu 22. Với
,a b
là các số thực dương tùy ý,
2 3
log
a b
bằng
A.
6log( ).ab
B.
1
2log log .
3
a b
C.
1 1
log log .
2 3
a b
D.
2log 3log .a b
Câu 23. Cho hình chóp tứ giác
.
S ABCD
có đáy
ABCD
là hình vuông cạnh bằng
3,
a
6SA a
và
vuông góc mặt phẳng đáy. Thể tích khối chóp
.
S ABCD
bằng
A.
3
6
.
2
a
B.
3
6
.
3
a
C.
3
3.
a
D.
3
6.
a
Câu 24. Nếu
6
2
7
f x dx
và
6
2
2
g x dx
thì
6
2
f x g x dx
bằng
A.
5.
B.
5.
C.
9.
D.
9.
Câu 25. Cho
2
2
1
2 1 .I x x dx
Nếu đặt
2
1
u x
thì khẳng định nào sau đây đúng ?
A.
3
0
1
.
2
I udu
B.
2
1
.I udu
C.
3
0
.I udu
D.
3
0
2 .I udu
Câu 26. Với hàm số
f x
tùy ý, hàm số
F x
là một nguyên hàm của hàm số
.f x
Khẳng định nào sau
đây đúng ?
A.
.f x F x
B.
.F x f x
C.
.F x f x
D.
.F x f x
Câu 27. Cho cấp số nhân
n
u
với
1 6
5, 160.
u u
Công bội của cấp số nhân bằng
A.
31.
B.
2.
C.
32.
D.
3.
Câu 28. Trong không gian
,Oxyz
mặt cầu
2 2 2
: 8 4 2 4 0
S x y z x y z
có bán kính bằng
A.
5.
B.
25.
C.
2.
D.
5.
Câu 29. Cho hình phẳng
H
giới hạn bởi các đường
2
4
y x
và
0.
y
Thể tích khối tròn xoay được
sinh bởi hình
H
quay quanh trục
Ox
có giá trị bằng
A.
256
.
15
B.
512
.
15
C.
128
.
5
D.
512
.
15
4/6 - Mã đề 101
Câu 30. Cho hình lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
B
có
,AB a
2.
AA a
Góc giữa đường thẳng
A C
và mặt phẳng
AA B B
bằng
A.
60 .
o
B.
30 .
o
C.
90 .
o
D.
45 .
o
Câu 31. Cho
3
log 2
a
và
2
1
log .
2
b
Khi đó
2
3 2
log 3 log
a b
bằng
A.
4.
B.
0.
C.
3
.
2
D.
5
.
4
Câu 32. Trong không gian
,Oxyz
cho mặt phẳng
: 1 1 6 4 0
m x m y z
và
: 2 3 3 0.
x y z
Giá trị của tham số
m
để hai mặt phẳng song song bằng
A.
2.
B.
1.
C.
3.
D.
1.
Câu 33. Cho hàm số bậc bốn
.f x
Hàm số
y f x
có đồ thị như hình vẽ
Số điểm cực đại của hàm số
f x
là
A.
2.
B.
3.
C.
1.
D.
0.
Câu 34. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh bằng
,
2
a
3SA a
và
vuông
góc mặt phẳng đáy. Khoảng cách từ
A
đến mặt phẳng
( )SBD
bằng
A.
.
3a
B.
30
5
.
a
C.
.a
D.
.
3
2
a
Câu 35. Gọi
,M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
4
f x x
x
trên đoạn
1;3 .
Khi đó tích
M
và
m
bằng
A.
B.
25.
C.
6.
D.
20.
Câu 36. Cho các hàm số
f x
và
F x
liên tục trên
thỏa mãn
F x f x x
và
0 2, 1 6.
F F
Khi đó
1
0
df x x
bằng
A.
8.
B.
8.
C.
4.
D.
4.
Câu 37. Một hộp có
5
viên bi đen,
4
viên bi trắng. Lấy ngẫu nhiên
2
viên bi trong hộp. Xác suất để lấy
được
2
viên bi cùng màu bằng
A.
4
.
9
B.
1
.
9
C.
5
.
9
D.
1
.
4
Câu 38. Trong không gian
,Oxyz
cho
1;1; 1 ,
A
5;2;1 .
B
Phương trình mặt phẳng trung trực của đoạn
AB
là
A.
8 2 4 27 0.
x y z
B.
8 2 4 27 0.
x y z
C.
6 2 21 0.
x y
D.
4 2 3 0.
x y z
5/6 - Mã đề 101
Câu 39. Trong không gian
,Oxyz
cho tam giác
OAB
có
2;2; 1
A
và
0; 4;3 .
B
Độ dài đường phân giác
trong góc
AOB
bằng
A.
30
.
5
B.
30
.
4
C.
9
.
8
D.
15
.
8
Câu 40. Cho hàm số bậc bốn
y f x
có đồ thị như hình vẽ
Số giá trị nguyên dương của tham số
m
để hàm số
2
g x f x m
có
5
điểm cực trị là
A.
3.
B.
5.
C.
4.
D.
6.
Câu 41. Gọi
S
là tập tất cả các giá trị nguyên của tham số
m
để phương trình
2
4 2 0
x x
m
có đúng hai
nghiệm phân biệt. Tích các phần tử của
S
bằng
A.
6.
B.
12.
C.
6.
D.
0.
Câu 42. Cho hàm số bậc năm
.f x
Hàm số
y f x
có đồ thị như hình vẽ
Số điểm cực trị của hàm số
3 2
2
2 3
3
g x f x x x x
là
A.
0.
B.
1
. C.
3.
D.
2.
Câu 43. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông cân tại
,A
tam giác
SBA
vuông tại
B
và tam
giác
SBC
là tam giác đều cạnh
2 .a
Thể tích khối chóp
.
S ABC
bằng
A.
3
.
6
a
B.
3
3
.
3
a
C.
3
2
.
3
a
D.
3
.
3
a
Câu 44. Một xe bồn chở nước có bồn nước gồm hai nửa hình cầu đường kính
18
dm
và một hình trụ có
chiều cao
36
dm
(như hình vẽ). Thể tích của bồn đã cho bằng
A.
3
9216 dm .
B.
3
1024
dm .
9
C.
3
3888 dm .
D.
3
16
dm .
243
6/6 - Mã đề 101
Câu 45. Cho hàm số
y f x
có đạo hàm trên
0;

thoả mãn
1 1
f
và
1 .
x x x
e f e e
Khi đó
1
d
e
f x x
bằng
A.
2
1
.
2
e
B.
2
3 2
.
2
e
C.
2
1
.
2
e
D.
2
.
2
e
Câu 46. Trong không gian
,Oxyz
cho điểm
2;6;0
A
và mặt phẳng
:3 4 89 0.
x y
Đường thẳng
d
thay đổi nằm trên mặt phẳng
Oxy
và luôn đi qua điểm
.A
Gọi
H
là hình chiếu vuông góc của
4; 2;3
M
trên đường thẳng
.d
Khoảng cách nhỏ nhất từ
H
đến mặt phẳng
bằng
A.
B.
20.
C.
68
.
5
D.
93
.
5
Câu 47. Cho hàm số
3
3 .f x x x
Số hình vuông có bốn đỉnh nằm trên đồ thị hàm số
y f x
là
A.
2.
B.
4.
C.
3.
D.
1.
Câu 48. Số giá trị nguyên âm của tham số
m
để phương trình
4 2
5 1 5 2
x
x x
e m
có hai nghiệm phân
biệt là
A.
4.
B.
3.
C.
5.
D.
6.
Câu 49. Cho hai hàm số bậc bốn
,f x
g x
có đồ thị
y f x
và
y g x
như hình vẽ
Số giá trị thực của tham số
m
để phương trình
f x g x m
có một nghiệm duy nhất trên
1;3
là
A. Vô số. B.
0.
C.
2.
D.
1.
Câu 50. Có bao nhiêu cặp số nguyên dương
;x y
thỏa mãn điều kiện
2023
x
và
3
3
3 9 2 log 1 2
y
y x x
?
A.
3870.
B.
4046.
C.
2023.
D.
3780.
------ HẾT ------
1
UBND THÀNH PHỐ HÀ NỘI
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐÁP ÁN
KỲ KIỂM TRA KHẢO SÁT HỌC SINH LỚP 12 THPT
NĂM HỌC 2022 - 2023
Đề kiểm tra môn: Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Phần đáp án câu trắc nghiệm:
Tổng câu trắc nghiệm: 50.
101 102 103 104 105
1
A
D
B
D
D
2
A
D
D
C
C
3
D
B
D
D
C
4
C
A
C
B
A
5
A
B
B
D
A
6
A
A
D
D
D
7
B
D
D
A
C
8
C
B
A
A
D
9
B
A
C
B
D
10
A
A
A
C
B
11
D
C
A
C
A
12
B
D
D
A
D
13
A
D
C
B
B
14
C
C
A
C
B
15
D
A
D
C
A
16
C
D
B
A
C
17
C
C
B
B
C
18
B
A
D
D
A
19
B
C
C
B
D
20
D
D
A
B
C
21
C
B
B
A
A
22
D
B
C
C
B
23
D
C
A
D
B
24
A
A
C
B
C
25
C
C
C
A
D
26
C
B
B
A
B
27
B
B
A
C
B
28
D
C
B
D
A
29
B
A
B
A
C
30
B
D
B
D
C
31
A
D
B
B
C
32
C
A
A
C
D
33
A
B
C
D
B
2
34
D
A
A
A
D
35
D
C
C
A
B
36
D
B
B
B
C
37
A
C
C
C
C
38
B
A
C
D
D
39
B
C
C
B
C
40
C
B
D
A
B
41
A
A
D
A
A
42
A
A
C
D
D
43
C
D
B
A
D
44
C
C
B
B
B
45
C
C
D
B
B
46
A
B
B
B
B
47
A
A
C
D
A
48
C
C
A
B
A
49
D
C
C
D
C
50
D
D
B
B
D
106 107 108 109 110
1
D
B
B
A
D
2
D
D
D
B
C
3
C
A
B
A
C
4
C
A
D
D
A
5
B
C
B
D
B
6
D
C
C
A
D
7
B
B
D
B
A
8
B
A
D
C
A
9
C
C
A
D
D
10
C
B
A
B
B
11
A
C
C
D
C
12
D
A
B
D
B
13
A
B
B
C
D
14
D
B
D
C
C
15
A
D
C
D
C
16
A
A
B
B
D
17
B
D
A
D
D
18
B
D
A
A
C
19
D
A
B
C
C
20
A
C
C
C
A
21
C
A
A
B
B
22
D
B
D
A
B
23
A
C
A
B
A
3
24
C
D
A
B
D
25
C
B
C
A
A
26
A
C
D
A
B
27
C
D
B
C
B
28
B
D
C
C
A
29
B
C
C
D
A
30
B
C
B
B
C
31
C
A
C
C
C
32
C
C
D
A
B
33
B
D
C
B
A
34
D
A
A
C
A
35
C
B
D
C
A
36
A
C
B
C
C
37
B
C
A
A
C
38
B
D
D
A
D
39
B
A
C
D
D
40
A
A
B
D
D
41
D
A
A
C
C
42
C
D
A
B
A
43
B
A
A
B
B
44
A
B
D
C
B
45
D
C
C
A
B
46
B
A
D
A
B
47
C
C
A
D
D
48
D
B
D
B
A
49
C
B
C
D
A
50
A
D
A
D
C
111 112 113 114 115
1
A
B
C
C
D
2
B
B
D
D
A
3
C
A
D
C
C
4
C
C
A
C
C
5
B
A
C
D
D
6
B
B
B
D
A
7
D
C
D
C
B
8
A
A
B
B
A
9
D
B
B
A
B
10
B
D
D
D
B
11
C
C
D
D
D
12
D
C
A
A
C
13
C
A
A
B
B
4
14
B
D
D
C
D
15
A
D
C
C
D
16
B
A
B
A
C
17
C
C
B
B
C
18
D
A
D
A
D
19
C
C
A
A
B
20
D
D
C
C
D
21
C
B
B
B
A
22
A
D
B
A
C
23
B
A
A
A
A
24
D
D
A
D
A
25
D
D
C
C
C
26
A
C
C
B
B
27
A
B
A
B
A
28
B
B
B
B
D
29
B
C
C
D
C
30
A
C
C
B
B
31
A
A
A
C
A
32
B
B
B
C
C
33
D
C
B
B
A
34
A
A
A
D
B
35
A
A
C
C
C
36
C
C
B
D
B
37
A
D
B
B
D
38
D
C
B
B
D
39
D
C
D
B
D
40
B
A
C
A
D
41
C
D
A
C
C
42
A
B
B
A
A
43
C
B
A
D
D
44
C
D
C
C
A
45
A
B
D
A
C
46
C
D
D
C
C
47
C
D
C
B
B
48
C
C
B
C
B
49
B
B
D
B
B
50
B
A
D
D
D
116 117 118 119 120
1
D
B
C
B
C
2
C
C
B
B
C
3
C
C
A
C
A
5
4
D
A
A
A
B
5
A
B
B
C
C
6
B
A
D
B
A
7
A
A
C
C
A
8
B
B
C
B
D
9
D
C
D
D
C
10
B
B
B
C
A
11
C
D
A
B
C
12
B
D
B
A
B
13
A
B
C
D
D
14
A
B
B
A
A
15
D
D
C
B
A
16
C
D
D
D
B
17
A
B
D
C
D
18
B
A
B
A
B
19
C
C
B
A
B
20
C
C
A
B
D
21
B
A
C
D
A
22
D
A
D
D
C
23
C
C
D
A
D
24
B
C
A
A
C
25
D
D
A
C
B
26
D
D
C
C
D
27
A
B
B
A
B
28
A
A
D
B
C
29
C
A
A
D
D
30
B
D
B
D
A
31
C
C
B
B
C
32
B
A
A
C
C
33
D
D
B
B
C
34
D
A
B
A
B
35
B
B
D
A
B
36
D
B
D
D
D
37
D
C
B
A
B
38
C
D
C
B
A
39
A
B
A
B
C
40
A
D
C
B
C
41
B
C
A
C
A
42
D
A
A
A
D
43
D
D
C
C
C
44
B
D
B
B
D
45
D
C
C
A
B
6
46
B
C
D
A
C
47
B
D
D
B
B
48
D
A
C
B
D
49
B
D
D
C
A
50
B
A
D
B
D
121 122 123 124
1
C
A
A
D
2
B
A
A
A
3
A
D
B
C
4
A
C
B
D
5
D
C
A
A
6
D
D
C
A
7
B
B
D
D
8
A
C
B
B
9
B
D
B
B
10
C
B
C
D
11
C
C
C
A
12
D
B
A
A
13
B
A
A
C
14
A
C
D
C
15
C
B
D
B
16
D
B
A
A
17
B
C
B
C
18
B
A
B
C
19
C
D
D
D
20
A
A
A
A
21
D
A
C
B
22
A
C
C
B
23
D
B
B
D
24
A
B
D
D
25
D
A
C
C
26
B
A
C
B
27
A
D
D
C
28
A
A
D
B
29
C
D
B
C
30
C
A
C
B
31
C
D
B
D
32
C
C
D
A
33
C
B
A
C
34
C
A
C
A
35
B
C
C
B
7
36
B
B
A
A
37
D
D
A
D
38
D
B
B
D
39
A
C
D
B
40
A
C
B
B
41
C
A
D
C
42
A
D
D
C
43
C
B
D
D
44
B
C
C
B
45
A
C
B
D
46
A
C
A
A
47
D
B
A
D
48
A
B
A
D
49
A
C
B
B
50
B
A
B
A
BẢNG ĐÁP ÁN
1
2
3
4
5
6
7
8
9
1
0
1
1
1
2
1
3
1
4
1
5
1
6
1
7
1
8
1
9
2
0
2
1
2
2
2
3
2
4
2
5
A
A
D
C
A
A
B
C
B
A
D
B
A
C
D
C
C
B
B
D
C
D
D
A
C
2
6
2
7
2
8
2
9
3
0
3
1
3
2
3
3
3
4
3
5
3
6
3
7
3
8
3
9
4
0
4
1
4
2
4
3
4
4
4
5
4
6
4
7
4
8
4
9
5
0
C
B
D
B
B
A
C
A
D
D
D
A
B
B
C
A
A
C
C
C
A
A
C
D
D
Câu 1: Cho hàm số bậc bốn có đồ thị như hình vẽ.
y f x
Số nghiệm của phương trình là
2 1 0 f x
A. 4. B. 3. C. 1. D. 2.
Lời giải
Chọn A
Ta có: . Suy ra số nghiệm của phương trình đã cho bằng số giao
2 1 0 f x
1
2
f x
điểm của đồ thị hàm số và đường thẳng . Do vậy phương trình đã cho có 4
y f x
1
2
y
nghiệm.
Câu 2: Số cạnh của hình đa diện như hình vẽ dưới đây là
A. 12. B. 10. C. 16. D. 8.
Lời giải
Chọn A
Câu 3: Trong không gian , một vectơ pháp tuyến của mặt phẳng có tọa
Oxyz
: 2 4 2 0
x y z
độ là
A. . B. . C. . D. .
1; 2;4
1;2;4
1;2;4
1;2; 4
Lời giải
Chọn D
Câu 4: Cho hàm số liên tục trên đoạn và có đồ thị như hình vẽ.
y f x
1;3
Giá trị lớn nhất của hàm số đã cho trên đoạn bằng
1;3
A. . B. . C. . D. .
3
1
4
2
Lời giải
Chọn C
Trên đoạn thì hàm số có giá trị lớn nhất là
1;3
4.
Câu 5: Diện tích xung quanh của hình nón có đường sinh và bán kính đáy bằng.
l
r
A. . B. . C. . D. .
rl
r l r
2
rl
2 rl
Lời giải
Chọn A
Câu 6: Bất phương trình có tập nghiệm là khoảng Giá trị của bằng
2
log 2 3 1x
; .a b
a b
A. . B. . C. . D. .
4
2
5
3
Lời giải
Chọn A
Ta có .
2
5
2 3 2
2
log 2 3 1
2 3 0 3
2
x
x
x
x
x
Bất phương trình có tập nghiệm là khoảng
3 5
; .
2 2
Vậy .
3 5
4
2 2
a b
Câu 7: Trong không gian cho Tọa độ của vectơ là
,Oxyz
2 2 3 .a i j k= - + -
a
A. . B. . C. . D. .
( )
2; 2; 3- -
( )
2;2; 3- -
( )
2; 2; 3-
( )
2;2; 3-
Lời giải
Chọn B
Tọa độ của vectơ là .
a
( )
2;2; 3- -
Câu 8: Cho hàm số có bảng biến thiên
y f x
Giá trị cực đại của hàm số đã cho bằng
A. . B. . C. . D. .
3
2
2
3
Lời giải
Chọn C
Giá trị cực đại của hàm số đã cho bằng 2.
Câu 9: Trong các hàm số dưới đây, hàm số nào nghịch biến trên tập ?
A. . B. . C. . D. .
3
logy x
2
x
y
e
3
x
y
1
2
logy x
Lời giải
Chọn B
Phương án A và D là các hàm số logarit nên không đồng biến hoặc nghịch biến trên
log
a
y x
, vì có tập xác định .
0;D 
Phương án B và C là các hàm số mũ . Hàm số mũ đồng biến trên khi và nghịch
x
y a
1a
biến trên khi . Khi đó hàm số nghịch biến trên tập , vì .
0 1a
2
x
y
e
2
0,74 1a
e
Câu 10: Thể tích của khối trụ có bán kính đáy và chiều cao bằng
r
h
A. . B. . C. . D. .
2
r h
2 rh
rh
2
1
3
r h
Lời giải
Chọn A.
Thể tích của khối trụ có bán kính đáy và chiều cao bằng .
r
h
2
r h
Câu 11: Cho hàm số có . Hàm số đã cho có số điểm cực trị là
y f x
f x x x 1
A. . B. . C. . D. .
1
0
3
2
Lời giải
Chọn D
là hai nghiệm bội lẻ nên hàm số có hai điểm cưc trị.
x 0
f x x x 1 0
x 1
Câu 12: Số cách chọn 5 học sin bất kì từ 12 học sinh bằng
A. . B. . C. . D. .
12
5
5
12
C
5
12
A
5
12
Lời giải
Chọn A.
Câu 13: Trong không gian , mặt cầu tâm và bán kính có phương trình là
Oxyz
I 1;4;2
R 2
A. . B. .
2 2 2
x 1 y 4 z 2 4
2 2 2
x 1 y 4 z 2 2
C. . D. .
2 2 2
x 1 y 4 z 2 4
2 2 2
x 1 y 4 z 2 2
Lời giải
Chọn A
Câu 14: Đường tiệm cận đứng của dồ thị hàm số là
1
1
x
y
x
A. . B. . C. . D. .
1y
1x
1x
1y
Lời giải
Chọn C
Câu 15: Hàm số nào dưới đây có đồ thị như hình vẽ?
A. . B. . C. . D. .
2
2 1y x
4 2
2y x x
3 2
2 2y x x
2 3
1
x
y
x
Lời giải
Chọn D
Câu 16: Cho hình phẳng giới hạn bởi đồ thị hàm số , trục và các đường thẳng
H
y f x
Ox
. Gọi là thể tích khối tròn xoay thu được khi cho quay xung quanh
,x a x b a b
V
H
trục . Khẳng định nào sau đây đúng?
Ox
A. . B. . C. . D. .
d
b
a
V f x x
d
b
a
V f x x
2
d
b
a
V f x x
2
d
b
a
V f x x
Lời giải
Chọn C
Câu 17: Nghiệm của phương trình là
2 1
2 2
x x
A. . B. . C. . D. .
2x
2x
1x
1x
Lời giải
Chọn C
Ta có:
2 1
2 2 2 1 1.
x x
x x x
Câu 18: Với mọi số thực và số thực dương , khẳng định nào sau đây sai?
,
1a
A. . B. . C. . D. .
.a a a
.
.a a a
.
( )a a
a
a
a
Lời giải
Chọn B
Câu 19: Cho hàm số có bảng xét dấu
y f x
f x
Hàm số đã cho đồng biến trên khoảng nào sau đây?
A. . B. . C. . D. .
0;2
1;1
1;
; 1
Lời giải
Chọn B
Từ bảng xét dấu ta có với . Suy ra hàm số đã cho đồng biến trên
f x
0f x
1;1x
khoảng .
1;1
Câu 20: Tập nghiệm của phương trình là
3 3
log 3 log 2 1x x
A. . B. . C. . D. .
2
0
2
Lời giải
Chọn D
ĐK: .
3x
Với điều kiện trên, phương trình .
3 3
log 3 log 2 1 3 2 1 2x x x x x loai
Vậy phương trình đã cho vô nghiệm.
Câu 21: Khẳng định nào sau đây sai?
A. B. . C. . D. .
d .
x x
e x e C
2
d
2
x
x x C
1
d lnx x C
x
dx x C
Lời giải
Chọn C
Ta có:
1
d lnx x C
x
Câu 22: Với là các số thực dương tùy ý, bằng
,a b
2 3
log a b
A. . B. . C. . D. .
6log ab
1
2log log
3
a b
1 1
log log
2 3
a b
2log 3loga b
Lời giải
Chọn D
Ta có:
2 3 2 3
log log log 2log 3log .a b a b a b
Câu 23: Cho hình chóp tứ giác có đáy là hình vuông cạnh bằng và
.S ABCD
ABCD
3,a
6SA a=
vuông góc mặt phẳng đáy. Thể tích khối chóp bằng
SA
.S ABCD
A. . B. . C. . D. .
2
6
2
a
3
6
3
a
3
3a
3
6a
Lời giải
Chọn D
Thể tích
2
3
1
6 3 6.
3
V a a a
Câu 24: Nếu và thì bằng
6
2
d 7f x x
6
2
d 2g x x
6
2
df x g x x
A. . B. . C. . D. .
5
5
9
9
Lời giải
Chọn A.
Ta có:
6 6 6
2 2 2
d d d 7 2 5f x g x x f x x g x x
Câu 25: Cho . Nếu đặt thì khẳng định nào sau đây đúng?
2
2
1
2 1dI x x x
2
1u x
A. . B. . C. . D.
3
0
1
d
2
I u u
2
1
dI u u
3
0
dI u u
3
0
2 d .I u u
Lời giải
Chọn C
Đặt , ta có
2
1u x
1 0; 2 3x u x u
Ta có: .
3
2
0
1 d 2 d du x u x x I u u
Câu 26: Với hàm số tùy ý, hàm số là một nguyên hàm của hàm số . Khẳng định nào
f x
F x
f x
sau đây đúng.
A. . B. . C. . D. .
f x F x
F x f x
F x f x
F x f x
Lời giải
Chọn C
Theo khái niệm nguyên hàm ta có hàm số là một nguyên hàm của hàm số :
F x
f x
.
F x f x
Câu 27: Cho cấp số nhân với . Công bội của cấp số nhân bằng
u n
1
5;u
6
160u
A. . B. . C. . D. .
31
2
32
3
Lời giải
Chọn B
là cấp số nhân công bội nên ; .
u n
q
5 5 5
6 1
. 5. 160 32u u q q q
2q
Câu 28: Trong không gian , mặt cầu có bán kính bằng
Oxyz
2 2 2
: 8 4 2 4 0S x y z x y z
A. . B. . C. . D. .
5
25
2
5
Lời giải
Chọn D
, mặt cầu có tâm , bán kính mặt cầu
2 2 2
: 8 4 2 4 0S x y z x y z
4, 2, 1I
.
2 2
2
4 2 1 4 5R
Câu 29: Cho hình phẳng giới hạn bởi và . Thể tích khối tròn xoay được sinh ra bởi
H
2
4y x
0y
hình quay quanh trục có giá trị bằng
H
Ox
A. . B. . C. . D. .
256
15
512
15
128
5
256
15
Lời giải
Chọn B
Xét .
2
4 0 2; 2x x x
Thể tích khối tròn xoay được sinh ra bởi hình quay quanh trục có giá trị bằng
H
Ox
2
2
2
2
512
4
15
V x dx
Câu 30: Cho hình lăng trụ đứng có đáy là tam giác vuông cân tại , có ;
.ABC A B C
ABC
B
AB a
. Góc giữa và bằng
2AA a
A C
AA B B
A. . B. . C. . D. .
60
30
90
45
Lời giải
Chọn B
Theo bài là lăng trụ đứng nên , mà , do đó ,
.ABC A B C
BC BB
BC AB
BC ABB A
suy ra góc giữa và bằng góc .
A C
AA B B
BA C
Ta có ;
3A B a
Tam giác vuông có .
CBA
1
tan 30
3 3
BC a
BA C BA C
A B
a
Câu 31: Cho và Khi đó bằng
3
log 2a
2
1
log .
2
b
2
3 2
log 3 loga b
A. B. C. D.
4.
0.
3
.
2
5
.
4
Lời giải
Chọn A
.
2
3 2 3 2
log 3 log 1 log 2log 4a b a b
Câu 32: Trong không gian cho mặt phẳng và
,Oxyz
: 1 1 6 4 0m x m y z
Giá trị của tham số để hai mặt phẳng song song bằng
: 2 3 3 0.x y z
m
A. B. C. D.
2.
1.
3.
1.
Lời giải
Chọn C
Để hai mặt phẳng song song .
1 1 6 4
3
2 1 3 3
m m
m
Câu 33: Cho hàm số bậc bốn Hàm số có đồ thị như hình vẽ
.f x
y f x
Số điểm cực đại của hàm số là
f x
A. B. C. D.
2.
3.
1.
0.
Lời giải
Chọn A
.
0 ;
x a
f x x b a b c
x c
Từ đồ thị của hàm số ta có bảng biến thiên như sau
y f x
Vậy hàm số có 2 điểm cực đại.
f x
Câu 34: Cho hình chóp có đáy là hình vuông cạnh bằng và
.S ABCD
ABCD
,2a
3SA a
SA
vuông góc mặt phẳng đáy. Khoảng cách từ đến mặt phẳng bằng
A
( )SBD
A. B. C. D.
.3a
30
5
.
a
.a
.
3
2
a
Lời giải
Chọn D
Gọi là giao điểm của và , suy ra .
O
AC
BD
BD SAO
Từ , kẻ đường tại . Khi đó .
A
AH SO
H
,AH SBD d A SBD AH
Xét tam giác vuông tại, có là đường cao, , .
SAO
A
AH
3SA a
1
2
AO AC a
Suy ra
2 2
. 3
2
SA AO a
AH
SA AO
Câu 35: Gọi lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn
,M m
4
f x x
x
Khi đó tích và bằng
1;3 .
M
m
A. B. C. D.
15.
25.
6.
20.
Lời giải
Chọn D
Tập xác định: .
\ 0D
2
2
2 2
2 1; 3
4 4
' 1 ; 0 4 0
2 1; 3
x
x
y y x
x x
x
Ta có:
13
1 5; 2 4; 3 .
3
f f f
Vậy
1;3
1;3
max 5; min 4y y
1;3
1;3
max .min 20y y
Câu 36: Cho các hàm số và liên tục trên và thỏa mãn và
f x
F x
,F x f x x
. Khi đó bằng
0 2, 1 6F F
1
0
df x x
A. B. C. D.
8.
8.
4.
4.
Lời giải
Chọn D
Ta có
1
0
d 1 0 4F x f x f x x F F
Câu 37: Một hộp có 5 viên bi đen, 4 viên bi trắng. Lấy ngẫu nhiên 2 viên bi trong hộp. Xác suất để lấy
được 2 viên bi cùng màu bằng
A. B. C. D.
4
.
9
1
.
9
5
.
9
1
.
4
Lời giải
Chọn A
Số cách lấy ra 2 viên bi bất kì là: .
2
9
36C
Số cách lấy ra 2 viên bi cùng màu là: .
2 2
4 5
16C C
Xác suất để lấy được 2 viên bi cùng màu bằng
2 2
4 5
2
9
16 4
36 9
C C
C
Câu 38: Trong không gian Oxyz, cho . Phương trình mặt phẳng trung trực của đoạn
1;1; 1 , 5;2;1A B
AB là
A. B.
8 2 4 27 0.x y z
8 2 4 27 0.x y z
C. D.
6 2 21 0.x y
4 2 3 0.x y z
Lời giải
Chọn B
Ta có , trung điểm của AB là . Khi đó, mặt phẳng trung trực của đoạn
4;1;2AB
3
3; ;0
2
I
AB là:
3
: 4 3 1 2 0 0 :8 2 4 27 0
2
x y z x y z
Câu 39: Trong không gian cho tam giác có và Độ dài đường phân
,Oxyz
OAB
2;2; 1A
0; 4;3 .B
giác trong góc bằng
AOB
A. B. C. D.
30
.
5
30
.
4
9
.
8
15
.
8
Lời giải
Chọn B
Gọi là chân đường phân giác trong góc .
M
AOB
Ta có: , theo tính chất đường phân giác trong:
3, 5OA OB
3 3 3
5 8 8
MA OA MA MA OA
MA AB
MB OB AB MA MB OA OB
Nên:
3
5
2 0 2
8
4
3 1 5 1 1 30
2 4 2 ; ; .
8 4 4 4 2 4
1
3
1 3 1
2
8
M
M
M M
M
M
x
x
y y M OM
z
z
Câu 40: Cho hàm số bậc bốn có đồ thị như hình vẽ
y f x
Số giá trị nguyên dương của tham số
để hàm số
có điểm cực trị là
m
2
g x f x m
5
A. B. C. D.
3.
5.
4.
6.
Lời giải
Chọn C
Ta có:
2
2. .g x f x m g x f x f x m
Nên: . Mà có nghiệm nên để hàm số có
0
0
f x
g x
f x m
0f x
3
y g x
5
điểm cực trị thì phương trình: phải có nghiệm bội lẻ phân biệt.
*f x m
2
Dựa vào hình ảnh đồ thị hàm số thì phương trình (*) có nghiệm phân biệt khi:
2
2 2
.
6 4 4 6
m m
m m
Do nguyên dương nên: Có giá trị thỏa mãn.
m
1;2;4;5m
4
m
Câu 41: Gọi là tập tất cả các giá trị nguyên của tham số để phương trình có đúng
S
m
2
4 2 0
x x
m
hai nghiệm phân biệt. Tích các phần tử của bằng
S
A. . B. . C. . D. .
6
12
6
0
Lời giải
Chọn A
Đặt .
2 , 0
x
t t
Khi đó phương trình trở thành .
2
4 0t t m
1
Để thoả mãn thì phương trình có hai nghiệm dương phân biệt
1
Hay .
4 0
4 0
0
m
m
m
Do hay .
3; 2; 1m m
3; 2; 1S
Vậy tích các phần tử của là .
S
3 . 2 . 1 6
Câu 42: Cho hàm số bậc năm Hàm số có đồ thị như hình vẽ
.f x
y f x
Số điểm cực trị của hàm số là
3 2
2
2 3
3
g x f x x x x
A. . B. . C. . D. .
0
1
3
2
Lời giải
Chọn A
Ta có
2
2 4 3g x f x x x
Khi đó .
2
0 2 4 3 1g x f x x x
Ta thấy số nghiệm của là số giao điểm của và parabol (hình
1
y f x
2
2 4 3y x x
vẽ).
Từ đồ thị ta thấy có nghiệm bội chẵn. Vậy hàm số không có
1
3 2
2
2 3
3
g x f x x x x
cực trị.
Câu 43: Cho hình chóp có đáy là tam giác vuông cân tại tam giác vuông tại và
.S ABC
ABC
,A
SBA
B
tam giác là tam giác đều cạnh Thể tích khối chóp bằng
SBC
2 .a
.S ABC
A. B. C. D.
3
.
6
a
3
3
.
3
a
3
2
.
3
a
3
.
3
a
Lời giải
Chọn C
M
A
B
C
S
Gọi M là trung điểm BC, suy ra .
AM BC
Tam giác SBC đều có SM là trung tuyến nên SM cũng là đường cao, do đó .
SM BC
Ta có .
BC SM
BC SAM
BC AM
Suy ra .
. .
2
2 .
3
S ABC B SAM SAM
V V BM S
Ta có , , , ,
1
2
BM BC a
3
3
2
BC
SM a
1
2
AM BC a
2
2
BC
AB a
.
2 2
6SA AB SB a
Suy ra với .
2
2
2
SAM
a
S p p AM p SA p SM
2
AM SM SA
p
Vậy .
2 3
.
2 2 2
. .
3 2 3
S ABC
a a
V a
Câu 44: Một xe bồn chở nước có bồn nước gồm hai nửa hình cầu đường kính
18
và một hình trụ
dm
có chiều cao
36
(như hình vẽ). Thể tích của bồn đã cho bằng
dm
A. B. C. D.
3
9216 dm .
3
1024
dm .
9
3
3888 dm .
3
16
dm .
243
Lời giải
Chọn C
Bán kính nửa hình cầu là dm.
9
Thể tích phần khối trụ bằng .
2
.9 .36 2916
Thể tích phần khối cầu bằng .
3
4
.9 972
3
Vậy thể tích bồn đã cho bằng .
3
2916 972 3888 dm
Câu 45: Cho hàm số có đạo hàm trên thỏa mãn và . Khi đó
y f x
0;
1 1f
' 1
x x x
e f e e
bằng
1
e
f x dx
A. . B. . C. . D. .
2
1
2
e
2
3 2
2
e
2
1
2
e
2
2
e
Lời giải
Chọn C
Ta có: .
' 1 ' 1
x x x x x x
e f e e e f e dx e dx
.
'
x x x
t e f t dt x e C f t x e C
x x
f e x e C
Vì .
0 0
1 1 1 0f f e e C C
Đặt hay .
ln ln
x
u e x u f u u u
lnf x x x
.
2
2
1 1
1
1 1 1 1
1 1
ln ln .ln
2 2
e
e e e e
e e
e
f x dx x x dx xdx xdx x x x x
Câu 46: Cho Trong không gian cho điểm và mặt phẳng . Đường
Oxyz
2;6;0A
:3 4 89 0x y
thẳng thay đổi nằm trong mặt phẳng và luôn đi qua điểm . Gọi là hình chiếu
d
Oxy
A
H
vuông góc của trên đường thẳng . Khoảng cách nhỏ nhất từ đến mặt phẳng
4; 2;3M
d
H
bằng
A. . B. . C. . D. .
15
20
68
5
93
5
Lời giải
Chọn A.
Gọi là hình chiếu vuông góc của lên mặt phẳng .
K
M
4; 2;0Oxy K
Vì là hình chiêu vuông góc của lên đường thẳng .
H
M
d
Nên thuộc đường tròn có đường kính là đoạn và có tâm là trung điểm của
H
C
10AK
I
.
AK
1;2;0I
Mặt khác nên .
Oxy
1
d , d , d , 20 5 15
2
Min H I r I AK
.
1
Max d , d , d , 20 5 25
2
H I r I AK
Câu 47: Cho hàm số Số hình vuông có bốn đỉnh nằm trên đồ thị hàm số là
3
3 .f x x x
y f x
A. . B. . C. . D. .
2
4
3
1
Lời giải
Chọn A.
Ta có nên điểm uốn .
3 2
3 3 3 0 1f x x x f x x x
0;0O
Giả sử hình vuông tâm có bốn đỉnh nằm trên đồ thị, do là tâm đối xứng hình vuông
ABCD
I
I
nên là tâm đối xứng đồ thị.
Suy ra là điểm uốn nên .
I
I O
Ta có nên . Khi đó giao của đồ thị và
;90O
Q ABCD BCDA
;90O
Q f x F
f x
là đỉnh hình vuông.
F
Vẽ đồ thị hàm số và lên cùng một phẳng phẳng như hình vẽ.
f x
F
Dựa vào hình vẽ, ta có hai hình vuông thỏa yêu cầu bài toán.
Câu 48: Số giá trị nguyên âm của tham số để phương trình có hai nghiệm
m
4 2
e
5 1 5 2
x
x x
m
phân biệt là
A. . B. . C. . D. .
4
3
5
6
Lời giải
Chọn C
Phương trình .
4 2 4 2
e e
5 1 5 2 5 1 5 2
x x
x x x x
m m
Đặt . Tập xác định .
4 2
e
5 1 5 2
x
x x
f x
5
\ 0;log 2D
.
2 2
5 ln5 5 ln 5
4. 2. e 0,
5 1 5 2
x x
x
x x
f x x D
Lập bảng biến thiên
Dựa vào bảng biến thiên, ta thấy phương trình có hai nghiệm phân biệt khi và chỉ khi .
5m
Vậy có giá trị nguyên âm của tham số để phương trình có hai
5
m
4 2
e
5 1 5 2
x
x x
m
nghiệm phân biệt.
Câu 49: Cho hai hàm số bậc bốn có đồ thị và như hình vẽ
( ), ( )f x g x
( )y f x
( )y g x
Số giá trị thực của tham số để phương trình có một nghiệm duy nhất trên
m
( ) ( )f x g x m
là
[ 1;3]
A. . B. C. D.
5
0.
2.
1.
Lời giải
Chọn D
Dựa vào đồ thị ta có
3 2
( ) ( ) 1 1 3 ( ) ( ) 3 3f x g x a x x x f x g x dx a x x x dx
,
4 2
3
( ) ( ) 3
4 2
x x
f x g x a x x b
0a
Đặt
1
( ) ( ) 0 1 .
3
x
h x f x g x h x x
x
Ta có bảng biến thiên của
y h x
Để phương trình có nghiệm duy nhất trên thì chỉ có duy nhất
( ) ( )f x g x m
[ 1;3]
giá trị của
1
.m
Câu 50: Có bao nhiêu cặp số nguyên dương thỏa mãn điều kiện và
( ; )x y
2023x
3
3
3 9 2 log ( 1) 2?
y
y x x
A. B. C. D.
3870.
4046.
2023.
3780.
Lời giải
Chọn D
Đặt . Khi đó bất phương trình trở
3
log ( 1) 3 1
t
x t x
3
3
3 9 2 log ( 1) 2
y
y x x
thành
2 1
3.9 6 3 1 3 2 3 3(2 1) 3 3 (*)
y t y t
y t y t
Xét hàm đặc trưng trên
( ) 3 3
u
f u u
Ta có nên hàm số đồng biến trên
'( ) 3 ln3 3 0,
u
f u u
( )f u
Vậy BPT (*)
3
(2 1) ( ) 2 1 2 1 log ( 1)f y f t y t y x
Mà nguyên dương và nên
x
2023x
3
3
1 log 2024
2 1 log 2024 2,9
2
y y
Lại có nguyên dương nên
y
{1;2}.y
+) Với ta được . Kết hợp điều kiện nguyên dương
1y
3
3
3 log ( 1) 3 1 26x x x
x
và ta được . Vậy trường hợp này có cặp thỏa
2023x
{26; 27; 28;....; 2023}x
1998
( ; )x y
mãn
+) Với ta được . Kết hợp điều kiện nguyên
2y
5
3
5 log ( 1) 3 1 242x x x
x
dương và ta được . Vậy trường hợp này có cặp
2023x
{242; 243; 244;....; 2023}x
1782
thỏa mãn
( ; )x y
Vậy có cặp số nguyên dương thỏa mãn.
1998 1782 3780
( ; )x y
| 1/31
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

UBND THÀNH PHỐ HÀ NỘI
KỲ KIỂM TRA KHẢO SÁT HỌC SINH LỚP 12 THPT
SỞ GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2022 - 2023
Đề kiểm tra môn: Toán ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút, không kể thời gian phát đề
(Đề kiểm tra có 06 trang)
Họ, tên thí sinh:……………………………………………
Mã đề kiểm tra 101
Số báo danh:……………………………………………….
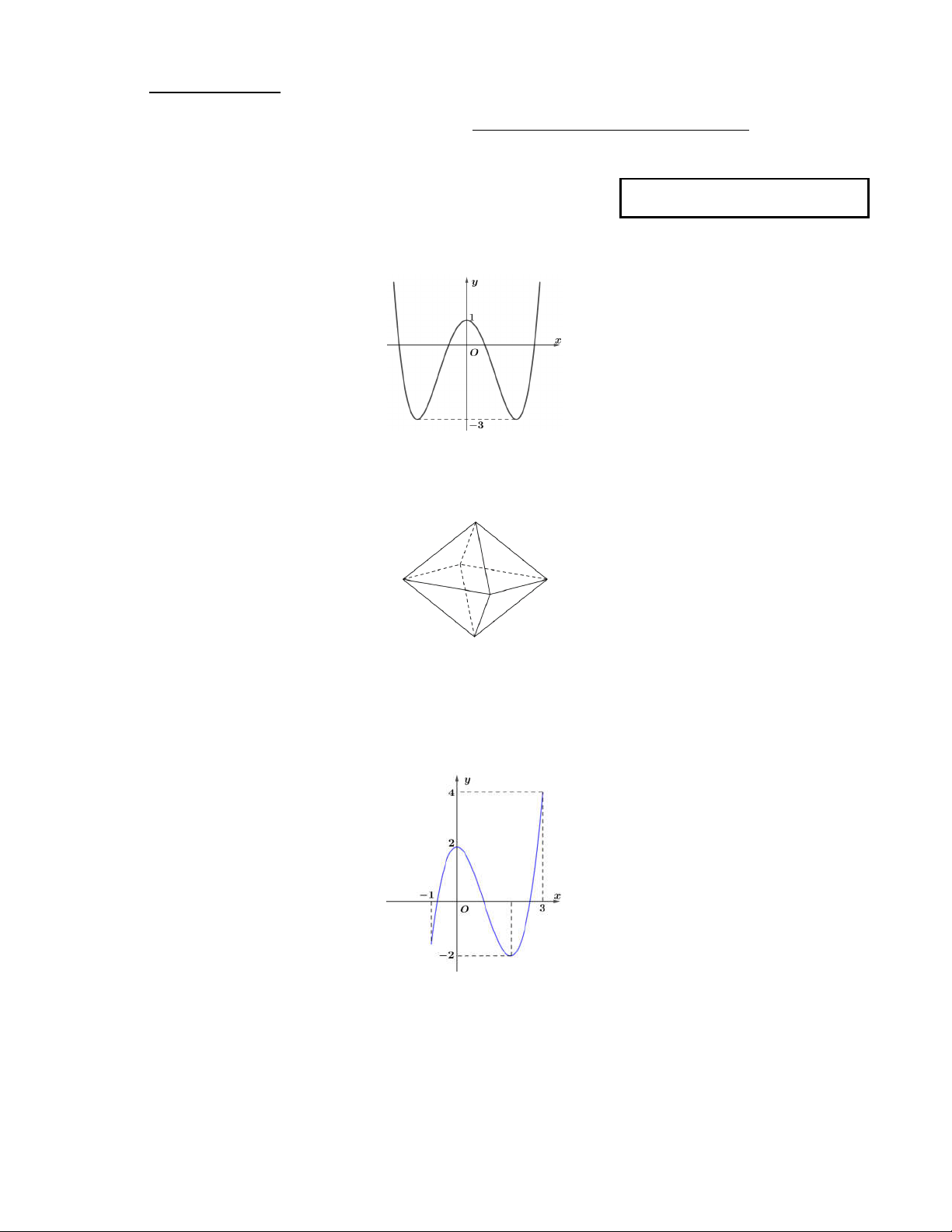
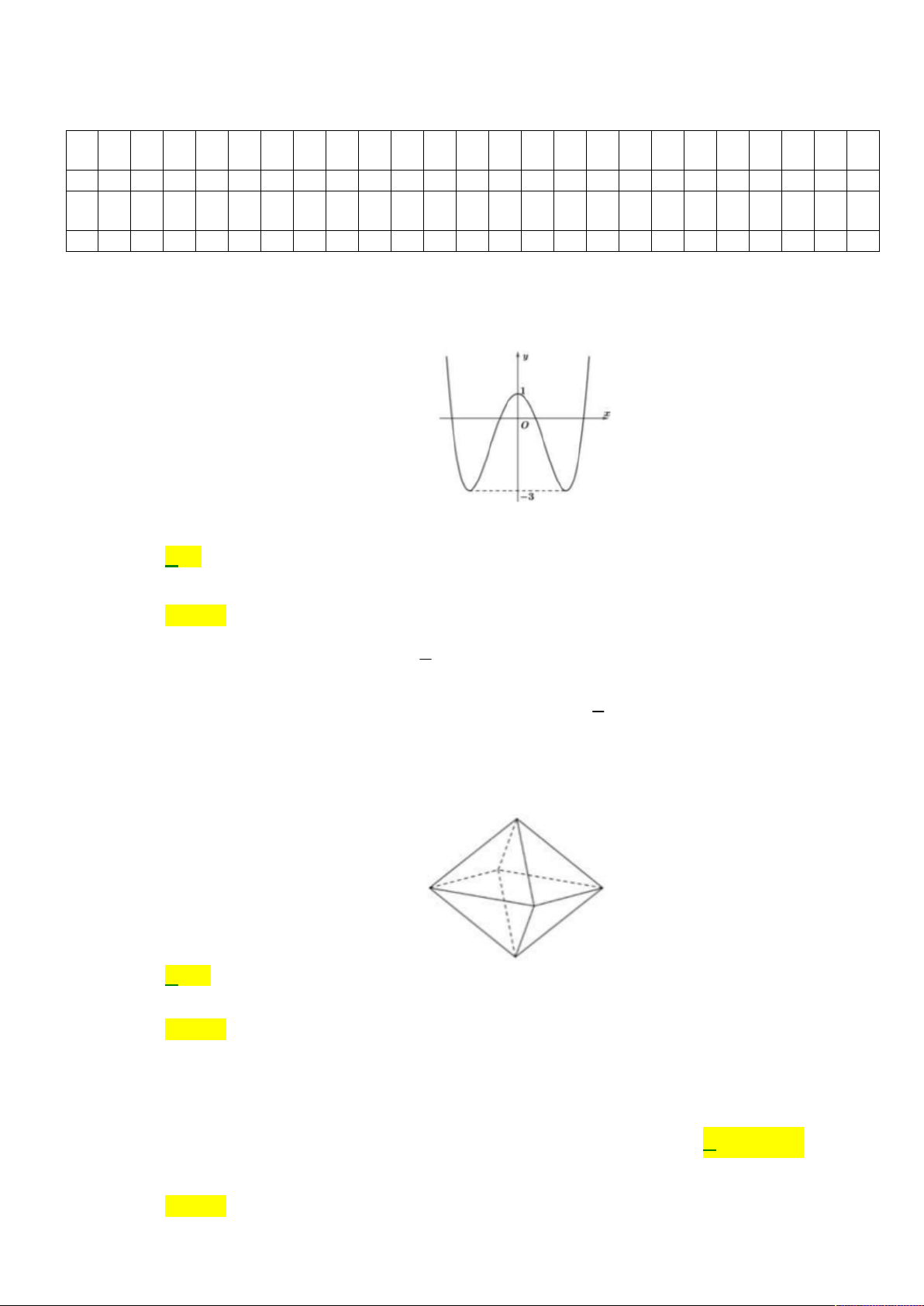
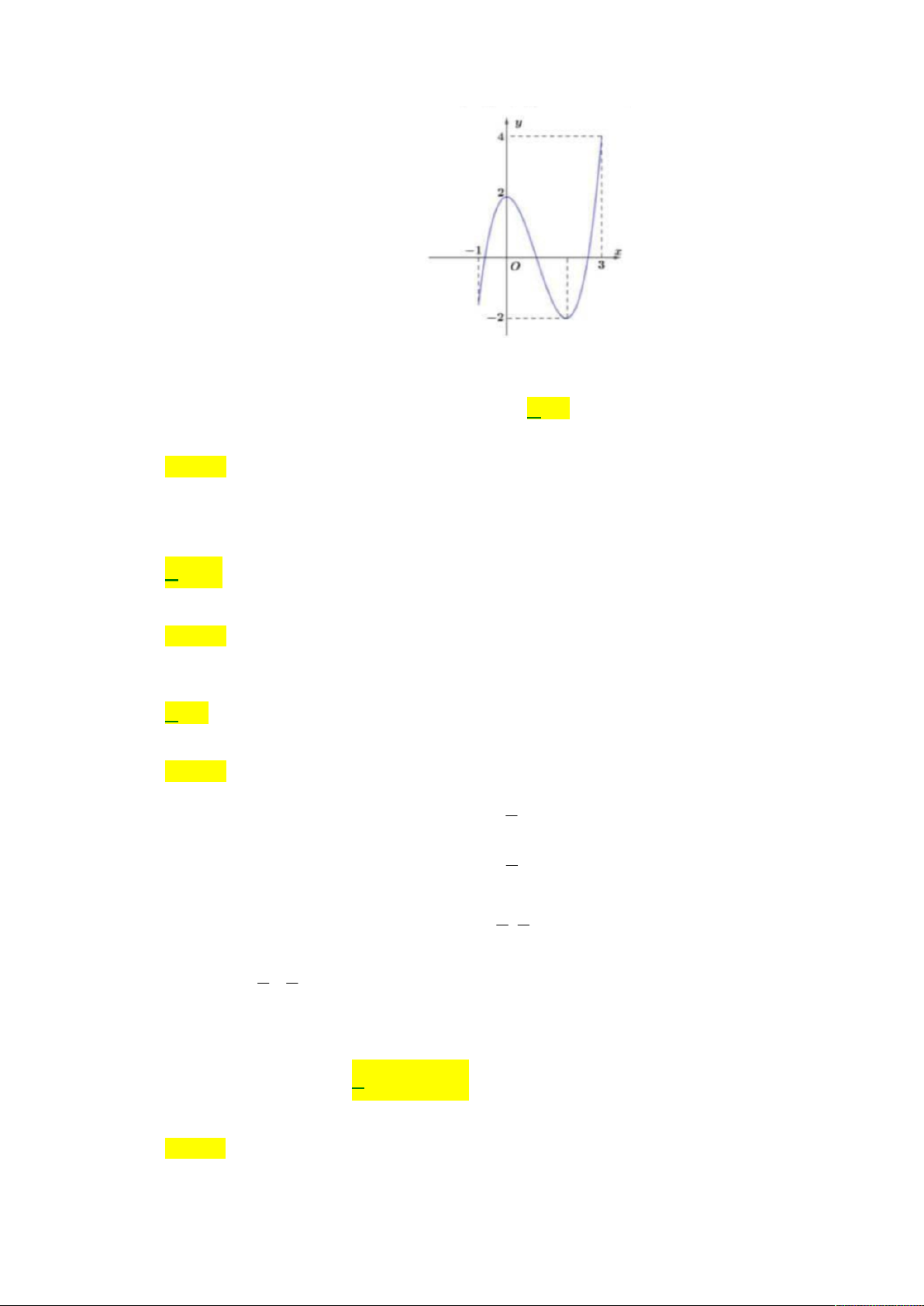
Câu 1. Cho hàm số bậc bốn y f x có đồ thị như hình vẽ
Số nghiệm của phương trình 2 f x 1  0 là A. 4. B. 3. C. 1. D. 2.
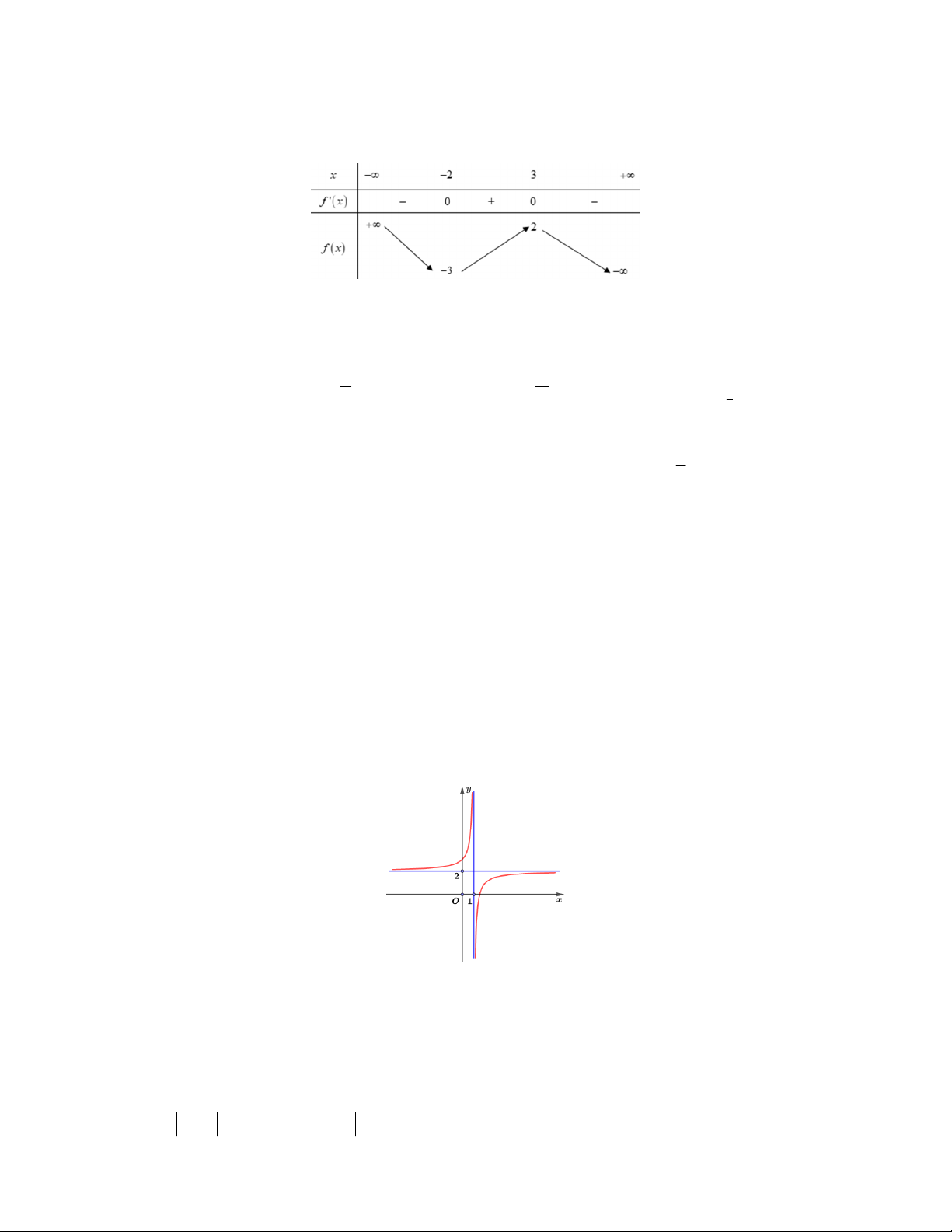
Câu 2. Số cạnh của hình đa diện như hình vẽ dưới đây là A. 12. B. 10. C. 16. D. 8.
Câu 3. Trong không gian Oxyz, một vectơ pháp tuyến của mặt phẳng   : x  2 y  4z  2  0 có tọa độ là A. 1; 2  ; 4.
B. 1;2; 4.
C. 1; 2; 4. D. 1; 2; 4  .
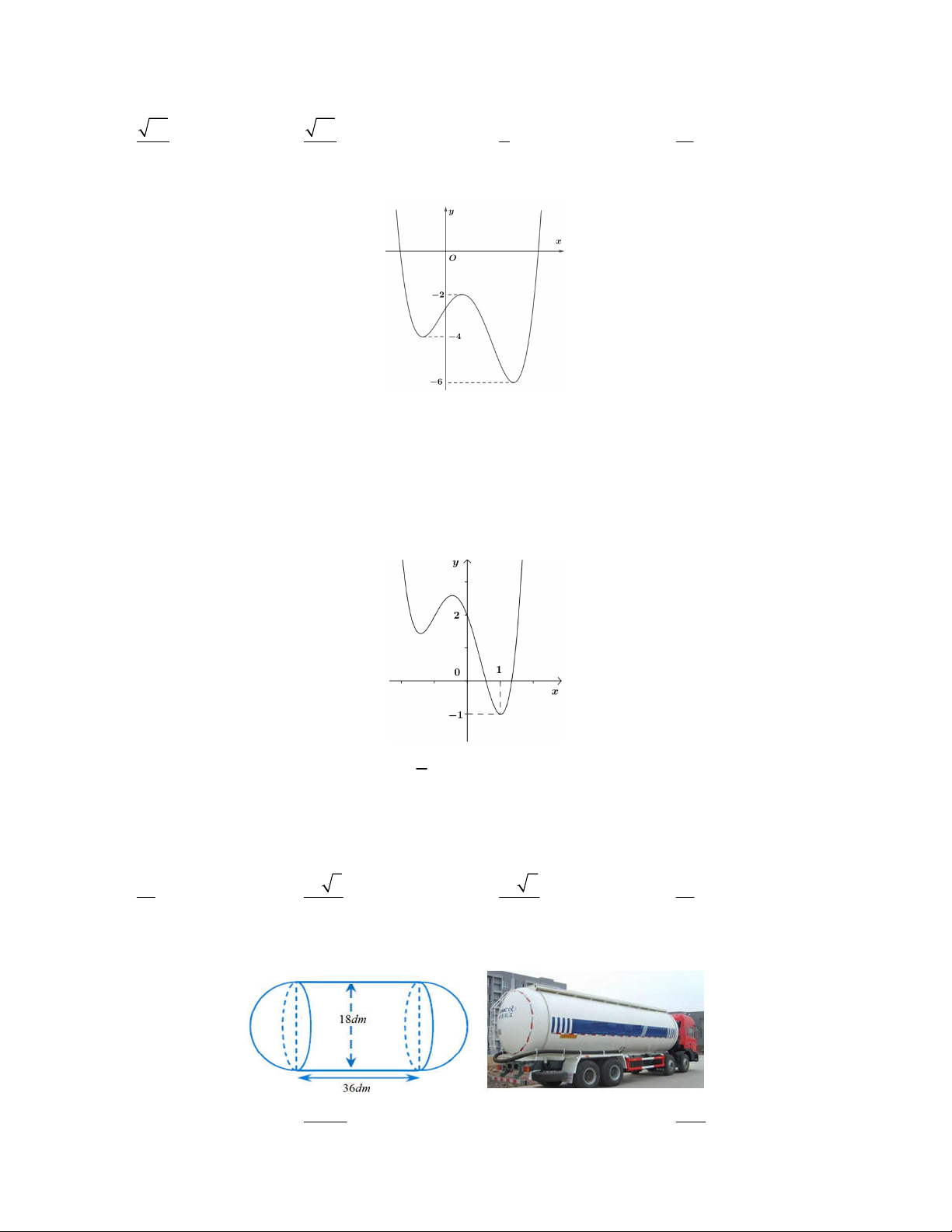
Câu 4. Cho hàm số y f x liên tục trên đoạn 1; 
3 và có đồ thị như hình vẽ
Giá trị lớn nhất của hàm số đã cho trên đoạn 1;  3 bằng A. 3. B. 1. C. 4. D. 2.
Câu 5. Diện tích xung quanh của hình nón có đường sinh l và bán kính đáy r bằng
A.rl.
B.r l r . C. 2  rl. D. 2 rl.
Câu 6. Bất phương trình log
2x  3  1 có tập nghiệm là khoảng  ;
a b. Giá trị của a b bằng 2   A. 4. B. 2. C. 5. D. 3. 1/6 - Mã đề 101     
Câu 7. Trong không gian Oxyz, cho a  2
i  2j  3k . Tọa độ của vectơ a là A. 2; 2;  3 . B.  2  ;2;  3 . C. 2; 2;  3 . D. 2;2;  3 .
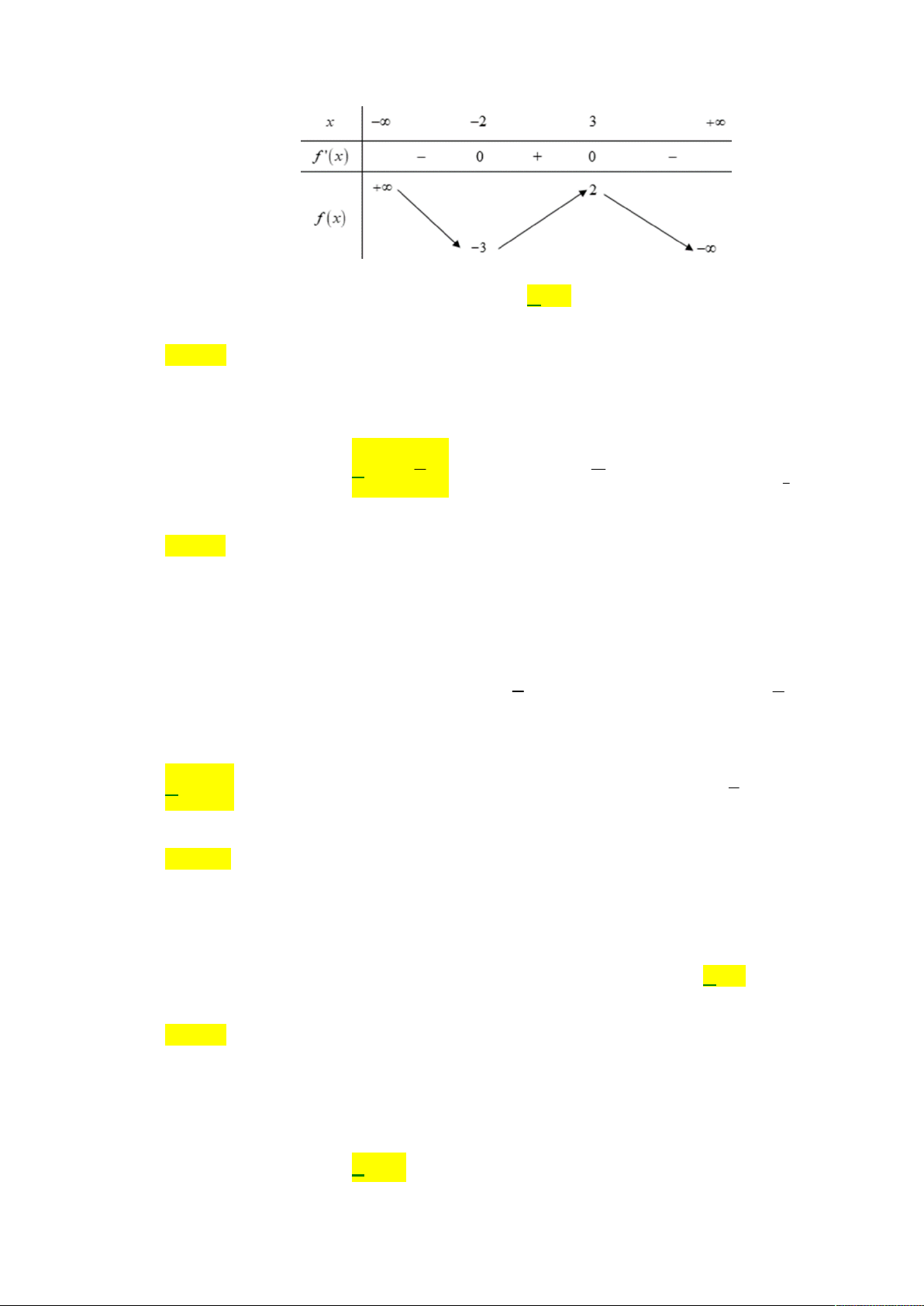
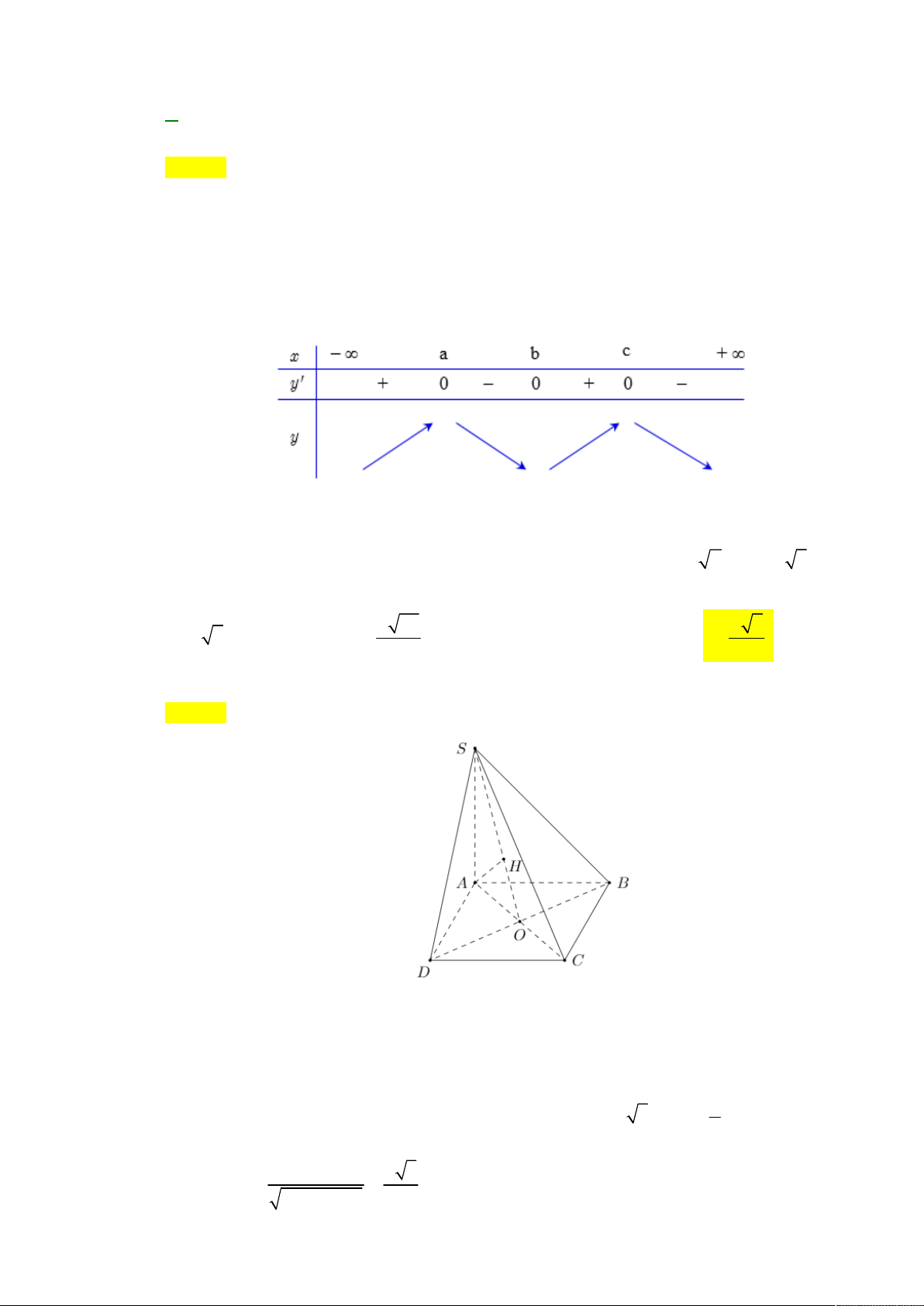
Câu 8. Cho hàm số y f x có bảng biến thiên
Giá trị cực đại của hàm số đã cho bằng A. 3. B. 2. C. 2. D. 3.
Câu 9. Trong các hàm số dưới đây, hàm số nào nghịch biến trên tập  ? x x  2     A. y  log . x B. y  . C. y  . D. y  log . x 3     1  e   3  2
Câu 10. Thể tích của khối trụ có bán kính đáy r và chiều cao h bằng 1 A. 2  r . h B. 2 . rh C.  . rh D. 2  r . h 3
Câu 11. Cho hàm số y f x có f  x  x x  
1 . Hàm số đã cho có số điểm cực trị là A. 1. B. 0. C. 3. D. 2.
Câu 12. Số cách chọn 5 học sinh bất kì từ 12 học sinh bằng A. 12 5 . B. 5 C . C. 5 A . D. 5 12 . 12 12
Câu 13. Trong không gian Oxyz, mặt cầu tâm I 1; 4; 2 và bán kính R  2 có phương trình là 2 2 2 2 2 2 A.x  
1   y  4   z  2  4. B.x  
1   y  4   z  2  2. 2 2 2 2 2 2 C.x  
1   y  4   z  2  4. D.x  
1   y  4   z  2  2. x 1
Câu 14. Đường tiệm cận đứng của đồ thị hàm số y  là x 1
A. y  1.
B. x  1.
C. x  1. D. y  1. 
Câu 15. Hàm số nào dưới đây có đồ thị như hình vẽ ? 2x  3 A. 2 y  2  x 1. B. 4 2
y x  2x . C. 3 2
y x  2x  2. D. y  . x 1
Câu 16. Cho hình phẳng H  giới hạn bởi đồ thị hàm số y f x, trục Ox và các đường thẳng
x a, x b a b. Gọi V là thể tích khối tròn xoay thu được khi cho H  quay quanh trục . Ox Khẳng
định nào sau đây đúng ? b b b b A. V f x d . x B. V   f x d . x C. 2 V   f x d . x D. 2 V f x d . xa a a a 2/6 - Mã đề 101
Câu 17. Nghiệm của phương trình 2x 1
2   2x là A. x  2. 
B. x  2.
C. x  1. D. x  1. 
Câu 18. Với mọi số thực  ,  và số thực dương a khác 1, khẳng định nào sau đây sai ?   a
A. aa  a  .
B. aaa  . C.a  a  . D.a  . a
Câu 19. Cho hàm số y f x có bảng xét dấu f  x
Hàm số đã cho đồng biến trên khoảng nào sau đây ? A. 0; 2. B. 1;  1 .
C. 1;  . D.  ;    1 .
Câu 20. Tập nghiệm của phương trình log x  3  log 2x 1 là 3   3   A.   2 . B.   0 . C.   2 . D. . 
Câu 21. Khẳng định nào sau đây sai ? 2 x 1 A. x x
e dx e C.  B. xdx   C.  C.
dx  ln x C. 
D. dx x C.  2 x Câu 22. Với ,
a b là các số thực dương tùy ý,  2 3
log a b  bằng 1 1 1
A. 6 log(ab).
B. 2 log a  log . b C. log a  log . b
D. 2 log a  3log . b 3 2 3
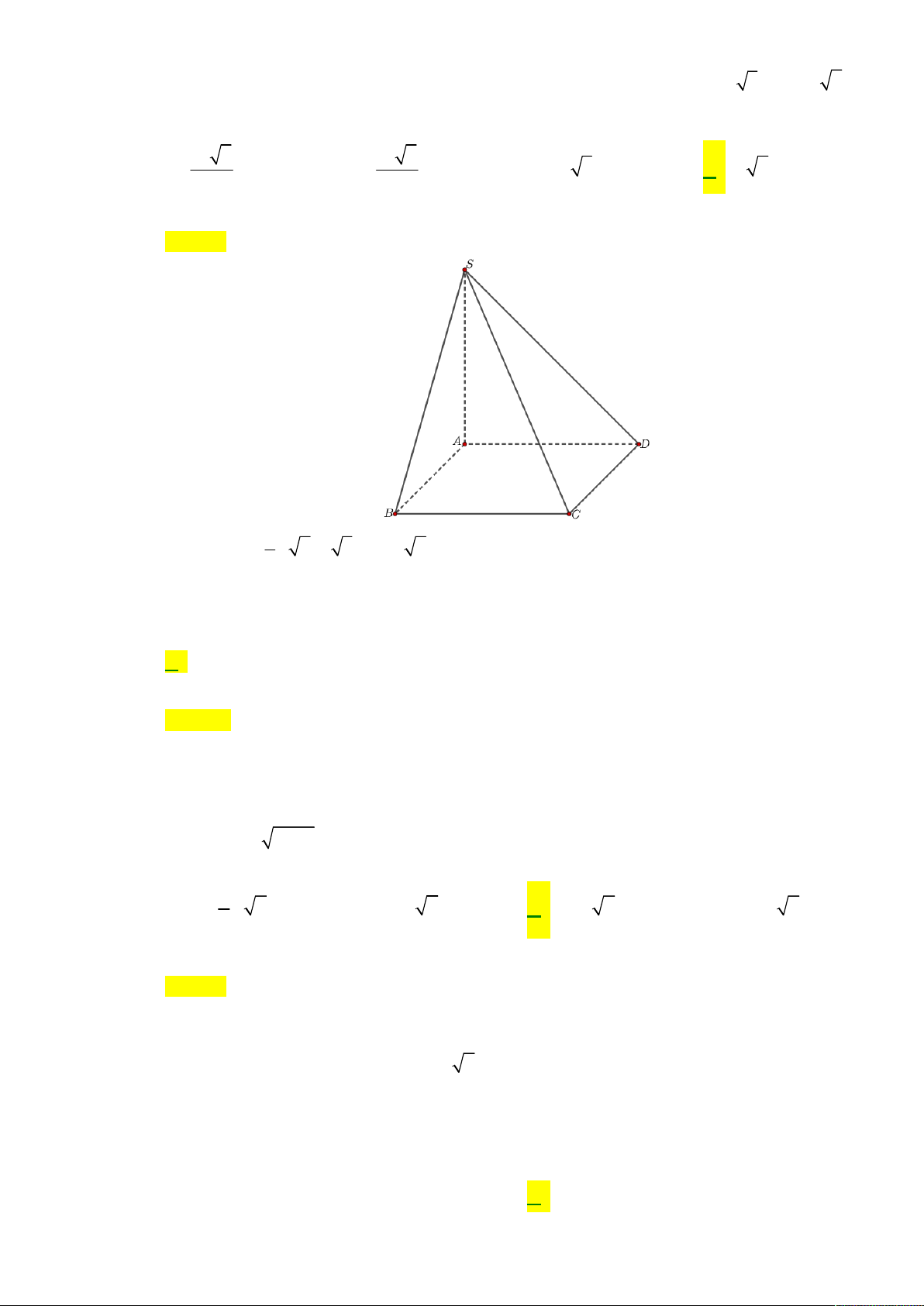
Câu 23. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng a 3, SA a 6 và SA
vuông góc mặt phẳng đáy. Thể tích khối chóp S.ABCD bằng 3 a 6 3 a 6 A. . B. . C. 3 a 3. D. 3 a 6. 2 3 6 6 6 Câu 24. Nếu
f xdx  7 
và g xdx  2 
thì  f x  g x dx    bằng 2 2 2 A. 5. B. 5. C. 9.  D. 9. 2 Câu 25. Cho 2
I  2x x 1 . dx  Nếu đặt 2
u x 1 thì khẳng định nào sau đây đúng ? 1 3 1 2 3 3 A. I u . du B. I u . du C. I u . du D. I  2 u . du  2 0 1 0 0
Câu 26. Với hàm số f x tùy ý, hàm số F x là một nguyên hàm của hàm số f x. Khẳng định nào sau đây đúng ?
A. f x  F x.
B. F x  f x.
C. F x  f x.
D. F x  f x.
Câu 27. Cho cấp số nhân u với u  5,u  160. Công bội của cấp số nhân bằng n  1 6 A. 31. B. 2. C. 32. D. 3.
Câu 28. Trong không gian Oxyz, mặt cầu  S  2 2 2
: x y z  8x  4 y  2z  4  0 có bán kính bằng A. 5. B. 25. C. 2. D. 5.
Câu 29. Cho hình phẳng  H  giới hạn bởi các đường 2
y x  4 và y  0. Thể tích khối tròn xoay được
sinh bởi hình  H  quay quanh trục Ox có giá trị bằng 256 512 128 512 A. . B. . C. . D. . 15 15 5 15 3/6 - Mã đề 101
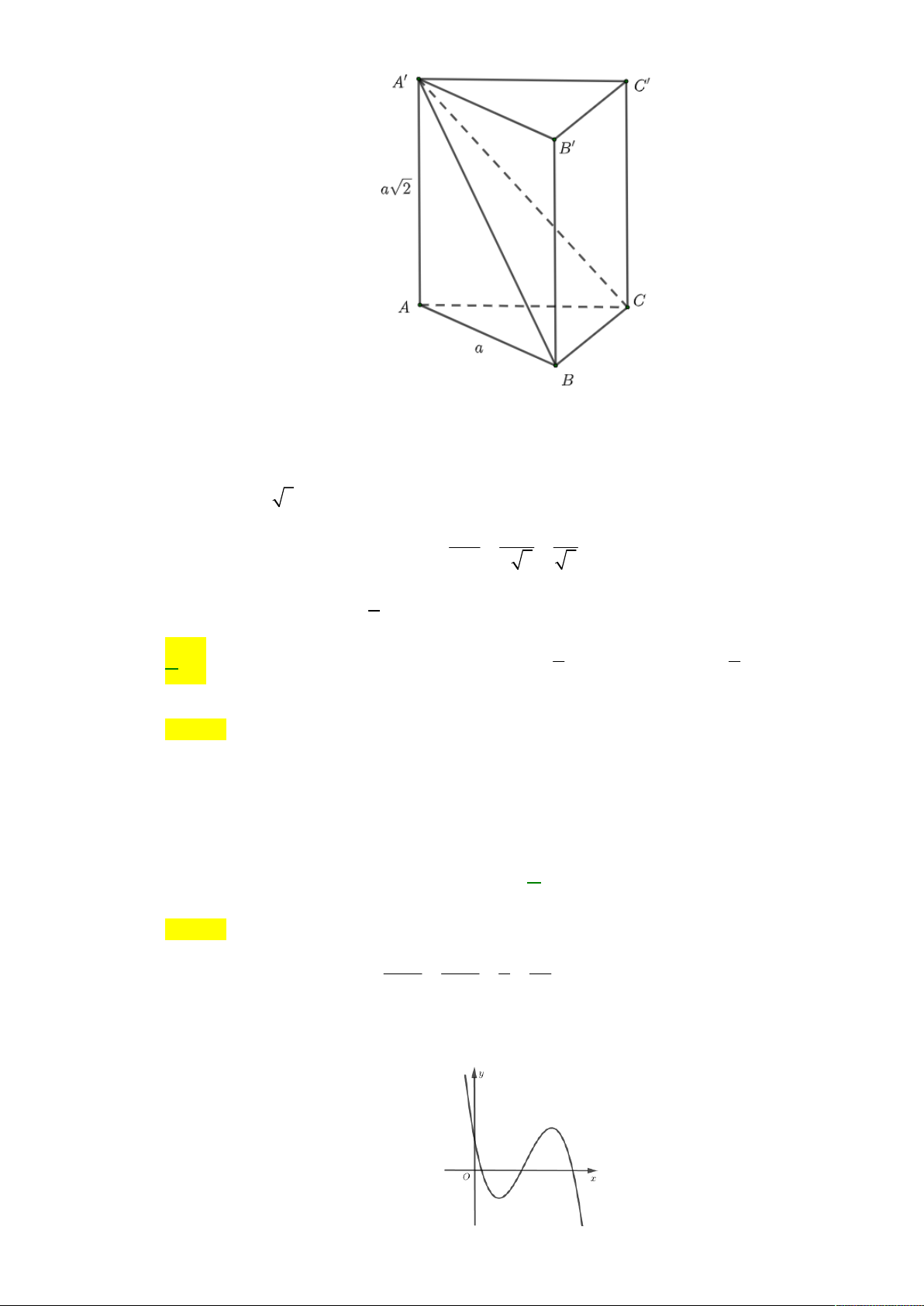
Câu 30. Cho hình lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác vuông cân tại B
có AB a, AA  a 2. Góc giữa đường thẳng AC và mặt phẳng  AAB B   bằng A. 60 . o B. 30 . o C. 90 . o D. 45 . o 1
Câu 31. Cho log a  2 và log b
. Khi đó log 3a  log b bằng 3   2 3 2 2 2 3 5 A. 4. B. 0. C. . D. . 2 4
Câu 32. Trong không gian
Oxyz, cho mặt phẳng
  : m  
1 x  m  
1 y  6z  4  0 và
  : 2x y  3z  3  0. Giá trị của tham số m để hai mặt phẳng song song bằng A. 2. B. 1. C. 3. D. 1.
Câu 33. Cho hàm số bậc bốn f x. Hàm số y f  x có đồ thị như hình vẽ
Số điểm cực đại của hàm số f x là A. 2. B. 3. C. 1. D. 0.
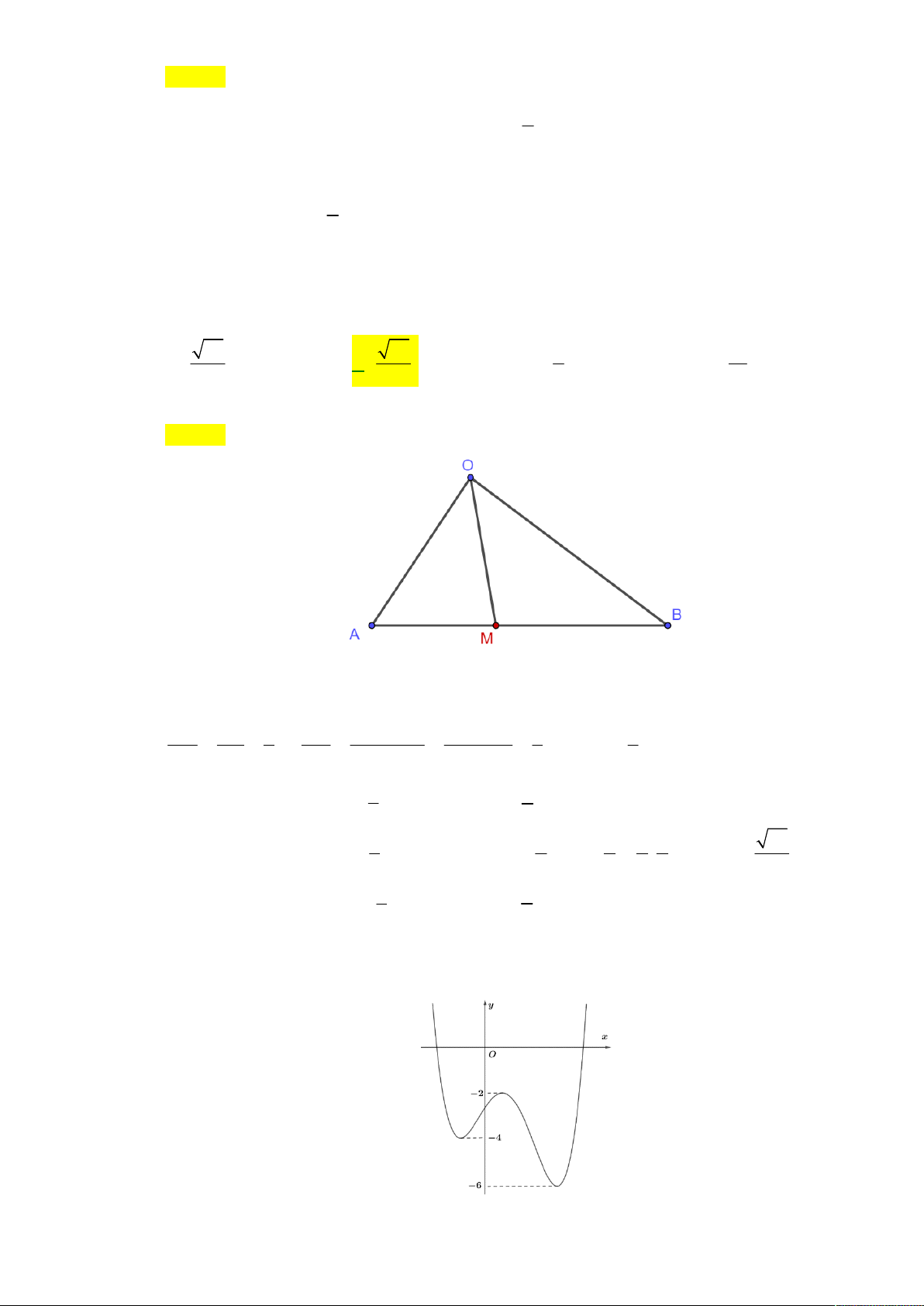
Câu 34. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a 2, SA a 3 và SA vuông
góc mặt phẳng đáy. Khoảng cách từ A đến mặt phẳng (SB ) D bằng a 30 a 3 A. a . 3 B. . C. . a D. . 5 2 4
Câu 35. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x  x  trên đoạn 1;  3 . x
Khi đó tích M và m bằng A. 15. B. 25. C. 6. D. 20.
Câu 36. Cho các hàm số f x và F x liên tục trên  thỏa mãn F x  f xx    và 1
F 0  2, F   1  6. Khi đó
f x dx  bằng 0 A. 8. B. 8. C. 4.  D. 4.
Câu 37. Một hộp có 5 viên bi đen, 4 viên bi trắng. Lấy ngẫu nhiên 2 viên bi trong hộp. Xác suất để lấy
được 2 viên bi cùng màu bằng 4 1 5 1 A. . B. . C. . D. . 9 9 9 4
Câu 38. Trong không gian Oxyz, cho A1;1;   1 , B 5; 2 
;1 . Phương trình mặt phẳng trung trực của đoạn AB là
A. 8x  2 y  4z  27  0.
B. 8x  2 y  4z  27  0.
C. 6x  2 y  21  0.
D. 4x y  2z  3  0. 4/6 - Mã đề 101
Câu 39. Trong không gian Oxyz, cho tam giác OAB có A2; 2;  
1 và B 0;4;3. Độ dài đường phân giác trong góc  AOB bằng 30 30 9 15 A. . B. . C. . D. . 5 4 8 8
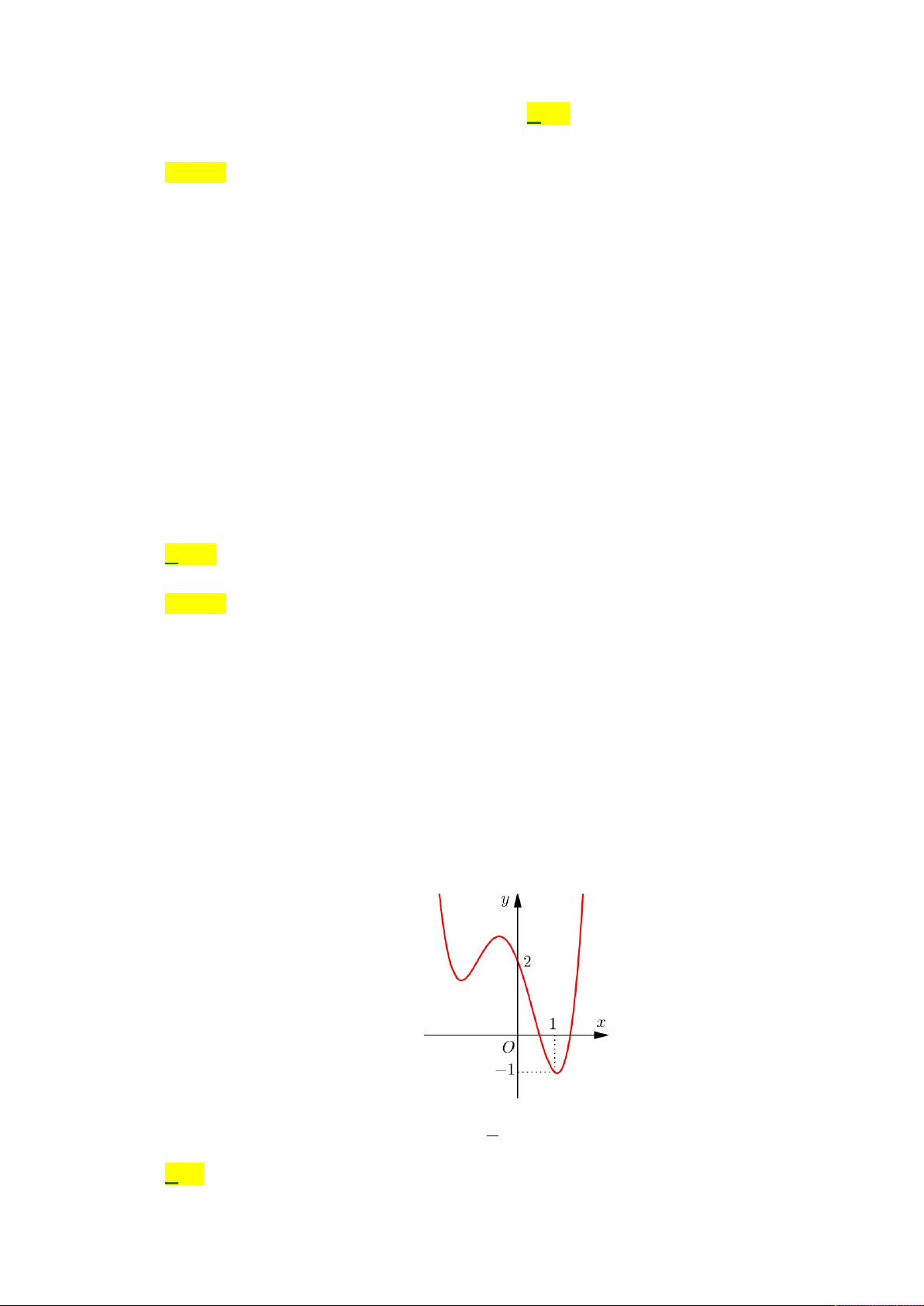
Câu 40. Cho hàm số bậc bốn y f x có đồ thị như hình vẽ
Số giá trị nguyên dương của tham số m để hàm số        2 g x f x m
có 5 điểm cực trị là A. 3. B. 5. C. 4. D. 6.
Câu 41. Gọi S là tập tất cả các giá trị nguyên của tham số m để phương trình x x2 4  2
m  0 có đúng hai
nghiệm phân biệt. Tích các phần tử của S bằng A. 6. B. 12. C. 6. D. 0.
Câu 42. Cho hàm số bậc năm f x. Hàm số y f  x có đồ thị như hình vẽ 2
Số điểm cực trị của hàm số g x  f x 3 2 
x  2x  3x là 3 A. 0. B. 1. C. 3. D. 2.
Câu 43. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại ,
A tam giác SBA vuông tại B và tam
giác SBC là tam giác đều cạnh 2 .
a Thể tích khối chóp S.ABC bằng 3 a 3 a 3 3 a 2 3 a A. . B. . C. . D. . 6 3 3 3
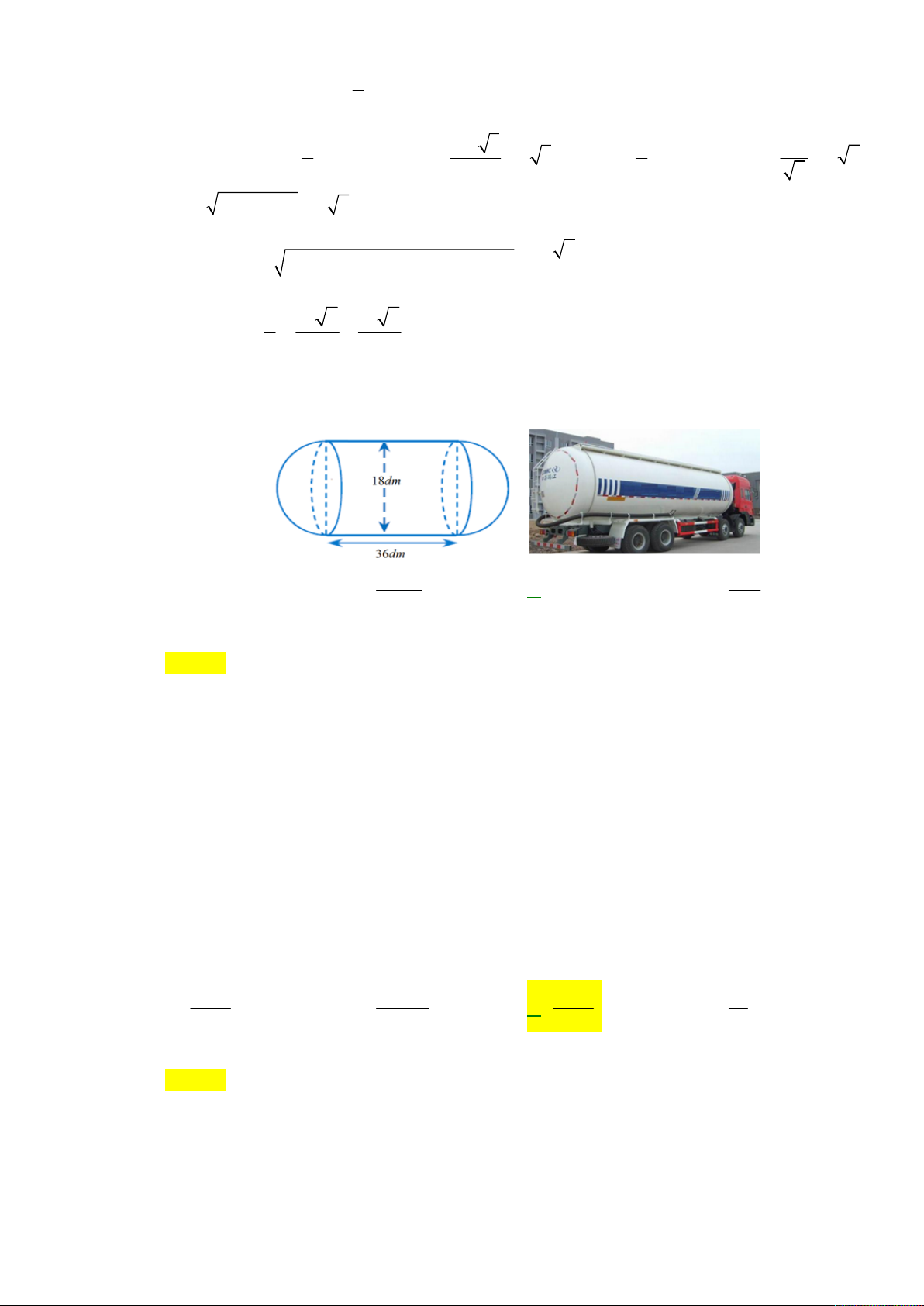
Câu 44. Một xe bồn chở nước có bồn nước gồm hai nửa hình cầu đường kính 18 dm và một hình trụ có
chiều cao 36 dm (như hình vẽ). Thể tích của bồn đã cho bằng 1024 16 A. 3 9216 dm . B. 3 dm . C. 3 3888 dm . D. 3 dm . 9 243 5/6 - Mã đề 101
Câu 45. Cho hàm số y f x có đạo hàm trên 0;  thoả mãn f  
1  1 và x  x   1 x e f ee . Khi đó e
f x dx  bằng 1 2 e 1 2 3e  2 2 e 1 2 e A. . B. . C. . D. . 2 2 2 2
Câu 46. Trong không gian Oxyz, cho điểm A 2
 ; 6; 0 và mặt phẳng   : 3x  4 y  89  0. Đường thẳng
d thay đổi nằm trên mặt phẳng Oxy và luôn đi qua điểm .
A Gọi H là hình chiếu vuông góc của
M 4; 2;3 trên đường thẳng d. Khoảng cách nhỏ nhất từ H đến mặt phẳng   bằng 68 93 A. 15. B. 20. C. . D. . 5 5
Câu 47. Cho hàm số f x 3  x  3 .
x Số hình vuông có bốn đỉnh nằm trên đồ thị hàm số y f x là A. 2. B. 4. C. 3. D. 1. x 4 2
Câu 48. Số giá trị nguyên âm của tham số m để phương trình e m   có hai nghiệm phân 5x 1 5x  2 biệt là A. 4. B. 3. C. 5. D. 6.
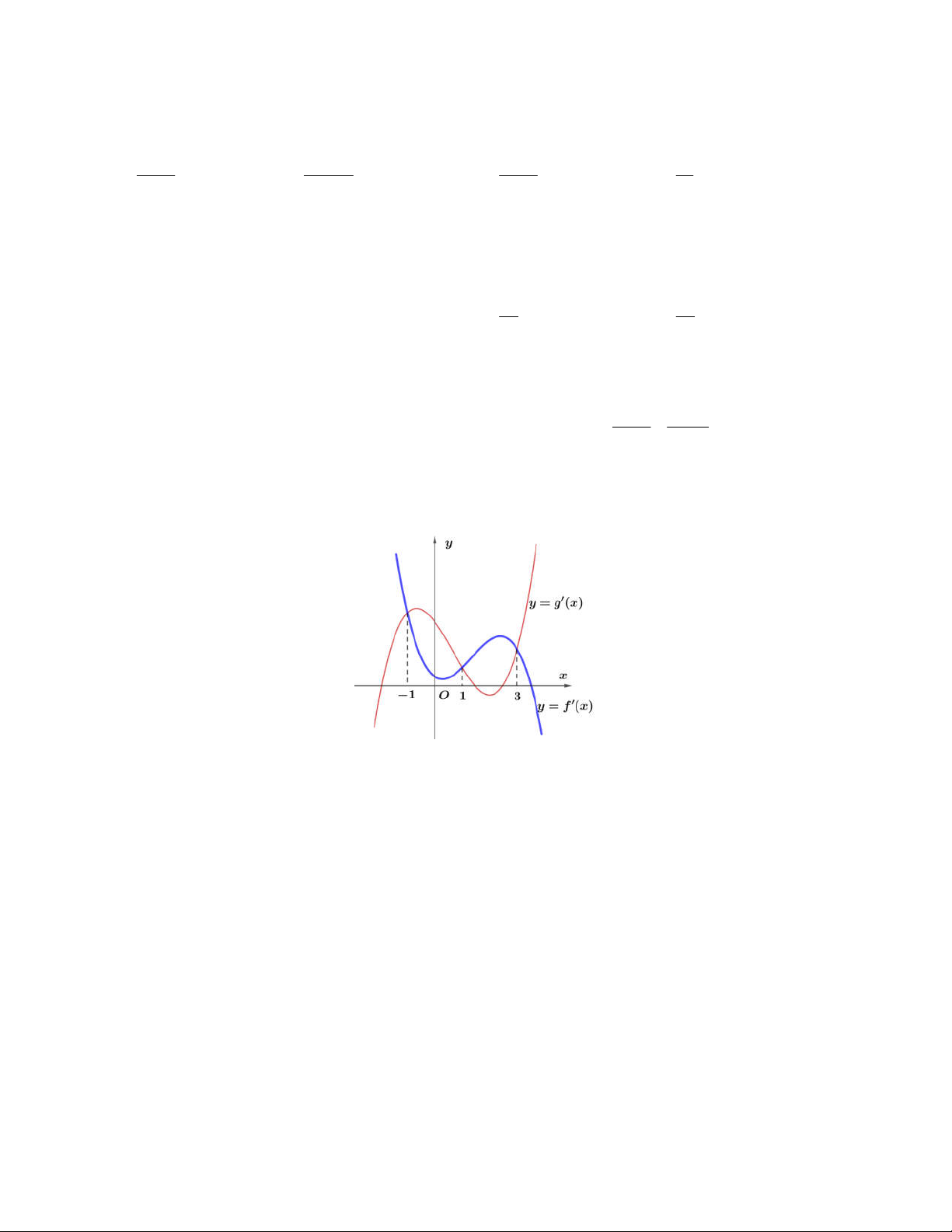
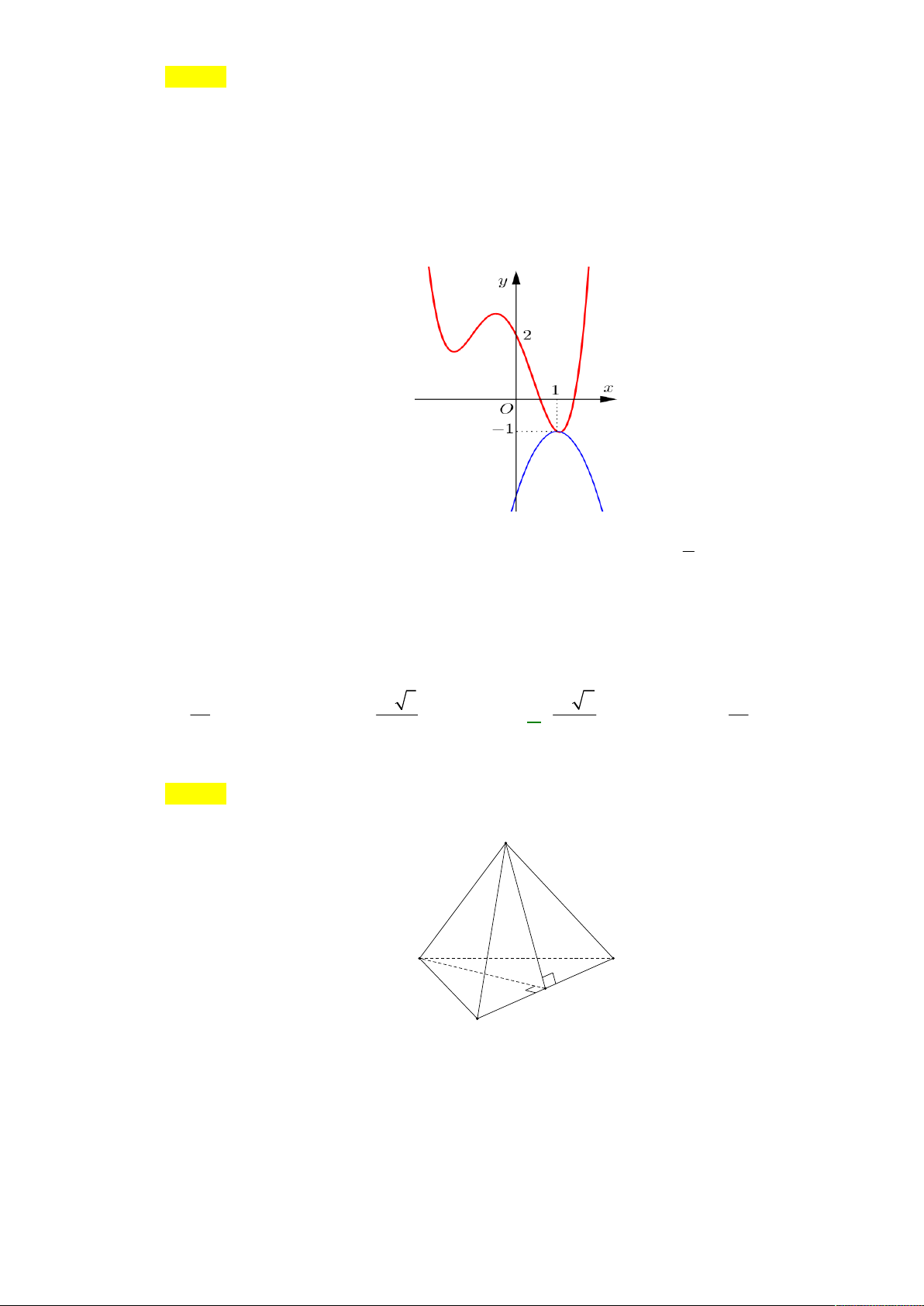
Câu 49. Cho hai hàm số bậc bốn f x, g x có đồ thị y f  x và y g x như hình vẽ
Số giá trị thực của tham số m để phương trình f x  g x  m có một nghiệm duy nhất trên 1;  3 là A. Vô số. B. 0. C. 2. D. 1.
Câu 50. Có bao nhiêu cặp số nguyên dương  x; y thỏa mãn điều kiện x  2023 và
39y  2y  x  log  x  3 1  2 ? 3 A. 3870. B. 4046. C. 2023. D. 3780.
------ HẾT ------ 6/6 - Mã đề 101 UBND THÀNH PHỐ HÀ NỘI
KỲ KIỂM TRA KHẢO SÁT HỌC SINH LỚP 12 THPT
SỞ GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2022 - 2023
Đề kiểm tra môn: Toán ĐÁP ÁN
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Phần đáp án câu trắc nghiệm:
Tổng câu trắc nghiệm: 50. 101 102 103 104 105 1 A D B D D 2 A D D C C 3 D B D D C 4 C A C B A 5 A B B D A 6 A A D D D 7 B D D A C 8 C B A A D 9 B A C B D 10 A A A C B 11 D C A C A 12 B D D A D 13 A D C B B 14 C C A C B 15 D A D C A 16 C D B A C 17 C C B B C 18 B A D D A 19 B C C B D 20 D D A B C 21 C B B A A 22 D B C C B 23 D C A D B 24 A A C B C 25 C C C A D 26 C B B A B 27 B B A C B 28 D C B D A 29 B A B A C 30 B D B D C 31 A D B B C 32 C A A C D 33 A B C D B 1 34 D A A A D 35 D C C A B 36 D B B B C 37 A C C C C 38 B A C D D 39 B C C B C 40 C B D A B 41 A A D A A 42 A A C D D 43 C D B A D 44 C C B B B 45 C C D B B 46 A B B B B 47 A A C D A 48 C C A B A 49 D C C D C 50 D D B B D 106 107 108 109 110 1 D B B A D 2 D D D B C 3 C A B A C 4 C A D D A 5 B C B D B 6 D C C A D 7 B B D B A 8 B A D C A 9 C C A D D 10 C B A B B 11 A C C D C 12 D A B D B 13 A B B C D 14 D B D C C 15 A D C D C 16 A A B B D 17 B D A D D 18 B D A A C 19 D A B C C 20 A C C C A 21 C A A B B 22 D B D A B 23 A C A B A 2 24 C D A B D 25 C B C A A 26 A C D A B 27 C D B C B 28 B D C C A 29 B C C D A 30 B C B B C 31 C A C C C 32 C C D A B 33 B D C B A 34 D A A C A 35 C B D C A 36 A C B C C 37 B C A A C 38 B D D A D 39 B A C D D 40 A A B D D 41 D A A C C 42 C D A B A 43 B A A B B 44 A B D C B 45 D C C A B 46 B A D A B 47 C C A D D 48 D B D B A 49 C B C D A 50 A D A D C 111 112 113 114 115 1 A B C C D 2 B B D D A 3 C A D C C 4 C C A C C 5 B A C D D 6 B B B D A 7 D C D C B 8 A A B B A 9 D B B A B 10 B D D D B 11 C C D D D 12 D C A A C 13 C A A B B 3 14 B D D C D 15 A D C C D 16 B A B A C 17 C C B B C 18 D A D A D 19 C C A A B 20 D D C C D 21 C B B B A 22 A D B A C 23 B A A A A 24 D D A D A 25 D D C C C 26 A C C B B 27 A B A B A 28 B B B B D 29 B C C D C 30 A C C B B 31 A A A C A 32 B B B C C 33 D C B B A 34 A A A D B 35 A A C C C 36 C C B D B 37 A D B B D 38 D C B B D 39 D C D B D 40 B A C A D 41 C D A C C 42 A B B A A 43 C B A D D 44 C D C C A 45 A B D A C 46 C D D C C 47 C D C B B 48 C C B C B 49 B B D B B 50 B A D D D 116 117 118 119 120 1 D B C B C 2 C C B B C 3 C C A C A 4 4 D A A A B 5 A B B C C 6 B A D B A 7 A A C C A 8 B B C B D 9 D C D D C 10 B B B C A 11 C D A B C 12 B D B A B 13 A B C D D 14 A B B A A 15 D D C B A 16 C D D D B 17 A B D C D 18 B A B A B 19 C C B A B 20 C C A B D 21 B A C D A 22 D A D D C 23 C C D A D 24 B C A A C 25 D D A C B 26 D D C C D 27 A B B A B 28 A A D B C 29 C A A D D 30 B D B D A 31 C C B B C 32 B A A C C 33 D D B B C 34 D A B A B 35 B B D A B 36 D B D D D 37 D C B A B 38 C D C B A 39 A B A B C 40 A D C B C 41 B C A C A 42 D A A A D 43 D D C C C 44 B D B B D 45 D C C A B 5 46 B C D A C 47 B D D B B 48 D A C B D 49 B D D C A 50 B A D B D 121 122 123 124 1 C A A D 2 B A A A 3 A D B C 4 A C B D 5 D C A A 6 D D C A 7 B B D D 8 A C B B 9 B D B B 10 C B C D 11 C C C A 12 D B A A 13 B A A C 14 A C D C 15 C B D B 16 D B A A 17 B C B C 18 B A B C 19 C D D D 20 A A A A 21 D A C B 22 A C C B 23 D B B D 24 A B D D 25 D A C C 26 B A C B 27 A D D C 28 A A D B 29 C D B C 30 C A C B 31 C D B D 32 C C D A 33 C B A C 34 C A C A 35 B C C B 6 36 B B A A 37 D D A D 38 D B B D 39 A C D B 40 A C B B 41 C A D C 42 A D D C 43 C B D D 44 B C C B 45 A C B D 46 A C A A 47 D B A D 48 A B A D 49 A C B B 50 B A B A 7 BẢNG ĐÁP ÁN 1 2 3 4 5 6 7 8 9 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 A A D C A A B C B A D B A C D C C B B D C D D A C 2 2 2 2 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 C B D B B A C A D D D A B B C A A C C C A A C D D Câu 1:
Cho hàm số bậc bốn y f x có đồ thị như hình vẽ.
Số nghiệm của phương trình 2 f x 1  0 là A. 4. B. 3. C. 1. D. 2. Lời giải Chọn A
Ta có: 2 f x 1  0  f x 1
  . Suy ra số nghiệm của phương trình đã cho bằng số giao 2 1
điểm của đồ thị hàm số y f x và đường thẳng y   . Do vậy phương trình đã cho có 4 2 nghiệm. Câu 2:
Số cạnh của hình đa diện như hình vẽ dưới đây là A. 12. B. 10. C. 16. D. 8. Lời giải Chọn A Câu 3:
Trong không gian Oxyz , một vectơ pháp tuyến của mặt phẳng  : x  2y 4z 2  0 có tọa độ là A. 1; 2;4 . B. 1;2;4 . C.  1  ;2;4. D. 1;2; 4 . Lời giải Chọn D Câu 4:
Cho hàm số y f x liên tục trên đoạn  1  ; 
3 và có đồ thị như hình vẽ.
Giá trị lớn nhất của hàm số đã cho trên đoạn  1  ;  3 bằng A. 3. B. 1. C. 4 . D. 2 . Lời giải Chọn C Trên đoạn  1  ; 
3 thì hàm số có giá trị lớn nhất là 4. Câu 5:
Diện tích xung quanh của hình nón có đường sinh l và bán kính đáy r bằng. A.  rl .
B.  r l r . C. 2  rl . D. 2 rl . Lời giải Chọn A Câu 6:
Bất phương trình log 2x  3  1 a;b. a b 2 
 có tập nghiệm là khoảng Giá trị của bằng A. 4 . B. 2 . C. 5 . D. 3 . Lời giải Chọn A  5  2  3  2 x x  Ta có 2
log 2x  3  1    2    . 2x  3  0 3 x   2  3 5 
Bất phương trình có tập nghiệm là khoảng ; .    2 2  3 5
Vậy a b    4 . 2 2     Câu 7:
Trong không gian Oxyz, cho a = -2i + 2j - 3k. Tọa độ của vectơ a là A. 2;- 2;- 3 . B. -2;2;- 3 . C. 2;- 2;3 . D. 2;2;- 3 . ( ) ( ) ( ) ( ) Lời giải Chọn B
Tọa độ của vectơ a là -2;2;- 3 . ( ) Câu 8:
Cho hàm số y f x có bảng biến thiên
Giá trị cực đại của hàm số đã cho bằng A. 3 . B. 2  . C. 2 . D. 3 . Lời giải Chọn C
Giá trị cực đại của hàm số đã cho bằng 2. Câu 9:
Trong các hàm số dưới đây, hàm số nào nghịch biến trên tập  ?   xA. y  2 x log x . B. y  . C. y  .
D. y  log x . 3      e   3  1 2 Lời giải Chọn B
Phương án A và D là các hàm số logarit y  log x nên không đồng biến hoặc nghịch biến trên a
 , vì có tập xác định D  0; .
Phương án B và C là các hàm số mũ x
y a . Hàm số mũ đồng biến trên  khi a 1 và nghịch  2 x
biến trên  khi 0  a 1. Khi đó hàm số y
nghịch biến trên tập  2
, vì a   0,74  1.    e e
Câu 10: Thể tích của khối trụ có bán kính đáy r và chiều cao h bằng 1 A. 2  r h . B. 2 rh . C.  rh . D. 2  r h . 3 Lời giải Chọn A.
Thể tích của khối trụ có bán kính đáy r và chiều cao h bằng 2  r h .
Câu 11: Cho hàm số y  f x có f x  x x  
1 . Hàm số đã cho có số điểm cực trị là A. 1. B. 0 . C. 3 . D. 2 . Lời giải Chọn D       x  0 f x x x 1  0 
là hai nghiệm bội lẻ nên hàm số có hai điểm cưc trị.  x  1
Câu 12: Số cách chọn 5 học sin bất kì từ 12 học sinh bằng A. 12 5 . B. 5 C . C. 5 A . D. 5 12 . 12 12 Lời giải Chọn A.
Câu 13: Trong không gian Oxyz , mặt cầu tâm I1;4;2 và bán kính R  2 có phương trình là
A.   2    2    2 x 1 y 4 z 2  4 .
B.   2    2    2 x 1 y 4 z 2  2 .
C.   2    2    2 x 1 y 4 z 2  4 .
D.   2    2    2 x 1 y 4 z 2  2 . Lời giải Chọn A x 1
Câu 14: Đường tiệm cận đứng của dồ thị hàm số y  là x 1
A. y  1.
B. x  1.
C. x  1 .
D. y  1. Lời giải Chọn C
Câu 15: Hàm số nào dưới đây có đồ thị như hình vẽ? x A. 2 y  2  x 1. B. 4 2
y x  2x . C. 3 2
y x  2x  2 3 2 . D. y  . x 1 Lời giải Chọn D
Câu 16: Cho hình phẳng H  giới hạn bởi đồ thị hàm số y f x , trục Ox và các đường thẳng
x a, x b a b . Gọi V là thể tích khối tròn xoay thu được khi cho H  quay xung quanh
trục Ox . Khẳng định nào sau đây đúng? b b b b A. V f  xdx .
B. V  f
 xdx . C. 2 V  f
 xdx . D. 2 V f  xdx . a a a a Lời giải Chọn C
Câu 17: Nghiệm của phương trình 2x 1 2   2x là A. x  2  . B. x  2 . C. x  1. D. x  1  . Lời giải Chọn C Ta có: 2x 1
2   2x  2x 1  x x  1.
Câu 18: Với mọi số thực , và số thực dương a  1, khẳng định nào sau đây sai?
A. a . a a. B. . a . a a   . C.   . (a ) a a . D. a. a Lời giải Chọn B
y f xf  xCâu 19: Cho hàm số có bảng xét dấu
Hàm số đã cho đồng biến trên khoảng nào sau đây? A. 0;2 . B.  1  ;  1 . C. 1;  . D.  ;    1 . Lời giải Chọn B
Từ bảng xét dấu f  x ta có f  x  0 với x   1  ; 
1 . Suy ra hàm số đã cho đồng biến trên khoảng  1  ;  1 .
Câu 20: Tập nghiệm của phương trình log x  3  log 2x 1 3   3   là A.   2  . B.   0 . C.   2 . D.  . Lời giải Chọn D ĐK: x  3 .
Với điều kiện trên, phương trình log x  3  log 2x 1  x  3  2x 1  x  2  loai 3   3    .
Vậy phương trình đã cho vô nghiệm.
Câu 21: Khẳng định nào sau đây sai? 2 x A. xd x
e x e C. B. d x x   C . C. x x C . D.   .   1 d ln  dx x C  2 x Lời giải Chọn C 1 Ta có:
dx  ln x Cx
Câu 22: Với a,b là các số thực dương tùy ý,  2 3 log a b  bằng 1
A. 6log ab . B. 2log a  1 1 log b .
C. log a  log b .
D. 2log a  3log b . 3 2 3 Lời giải Chọn D Ta có:  2 3 a b  2 3 log
 log a  log b  2log a  3log . b
Câu 23: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng a 3, SA = a 6 và
SA vuông góc mặt phẳng đáy. Thể tích khối chóp S.ABCD bằng 2 a 6 3 a 6 A. . B. . C. 3 a 3 . D. 3 a 6 . 2 3 Lời giải Chọn D 1
Thể tích V a 6 a 32 3  a 6. 3 6 6 6 Câu 24: Nếu f
 xdx  7 và g
 xdx  2  thì  f
 x gxdx bằng  2 2 2 A. 5 . B. 5  . C. 9  . D. 9 . Lời giải Chọn A. 6 6 6 Ta có:  f
 x gxdx f
 xdxg
 xdx  7 2    5 2 2 2 2 Câu 25: Cho 2
I  2x x 1dx . Nếu đặt u x  thì khẳng định nào sau đây đúng?  2 1 1 3 1 2 3 3 A. I udu . B. I udu . C. I udu . D.    I  2 ud . u  2 0 1 0 0 Lời giải Chọn C Đặt 2
u x 1, ta có x  1 u  0; x  2  u  3 3 Ta có: 2
u x 1 du  2 d x x I udu . 0
Câu 26: Với hàm số f x tùy ý, hàm số F x là một nguyên hàm của hàm số f x . Khẳng định nào sau đây đúng.
A. f  x  F x .
B. F x  f x .
C. F x  f x .
D. F x  f  x . Lời giải Chọn C
Theo khái niệm nguyên hàm ta có hàm số F x là một nguyên hàm của hàm số f x :
F x  f x.
Câu 27: Cho cấp số nhân u n với u  5; u 160 . Công bội của cấp số nhân bằng 1 6 A. 31. B. 2 . C. 32 . D. 3 . Lời giải Chọn B
u n là cấp số nhân công bội qnên 5 5 5
u u .q  5.q  160  q  32 ;  q  2 . 6 1
Câu 28: Trong không gian Oxyz , mặt cầu S  2 2 2
: x y z  8x  4y  2z  4  0 có bán kính bằng A. 5 . B. 25 . C. 2 . D. 5 . Lời giải Chọn DS 2 2 2
: x y z  8x  4y  2z  4  0 , mặt cầu có tâm I 4, 2  ,   1 , bán kính mặt cầu R
  2   2 2 4 2 1  4  5 .
Câu 29: Cho hình phẳng H  giới hạn bởi 2
y x  4 và y  0 . Thể tích khối tròn xoay được sinh ra bởi
hình H  quay quanh trục Ox có giá trị bằng 256 512 128 256 A. . B. . C. . D. . 15 15 5 15 Lời giải Chọn B Xét 2
x  4  0  x  2  ; x  2 .
Thể tích khối tròn xoay được sinh ra bởi hình H  quay quanh trục Ox có giá trị bằng 2
V x  42 512 2 dx   15 2 
Câu 30: Cho hình lăng trụ đứng ABC.AB C
 có đáy ABC là tam giác vuông cân tại B , có AB a ;
AA  a 2 . Góc giữa AC và  AAB B   bằng A. 60 . B. 30 . C. 90 . D. 45 . Lời giải Chọn B
Theo bài ABC.AB C
  là lăng trụ đứng nên BC BB , mà BC AB , do đó BC   ABB A   ,
suy ra góc giữa AC và  AAB B   bằng góc  BAC .
Ta có AB a 3 ; BC a 1
Tam giác vuông CBA có tan  BAC     
BAC  30 . AB a 3 3 1
Câu 31: Cho log a  2 và log b  . Khi đó log 3a  log b 3   2 bằng 3 2 2 2 3 5 A. 4. B. 0. C. . D. . 2 4 Lời giải Chọn A
log 3a  log b  1 log a  2log b  4 3   2 . 2 3 2
Câu 32: Trong không gian Oxyz, cho mặt phẳng  : m  
1 x  m  
1 y  6z  4  0 và
:2x y 3z 3  0. Giá trị của tham số m để hai mặt phẳng song song bằng A. 2. B. 1. C. 3. D. 1  . Lời giải Chọn C m 1 m 1 6 4 
Để hai mặt phẳng song song     m  3 . 2 1 3 3 
Câu 33: Cho hàm số bậc bốn f x. Hàm số y f  x có đồ thị như hình vẽ
Số điểm cực đại của hàm số f x là A. 2. B. 3. C. 1. D. 0. Lời giải Chọn Ax a f x 0  
  x b ; a b c .  x c
Từ đồ thị của hàm số y f  x ta có bảng biến thiên như sau
Vậy hàm số f x có 2 điểm cực đại.
Câu 34: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a 2, SA a 3 và SA
vuông góc mặt phẳng đáy. Khoảng cách từ A đến mặt phẳng (SBD) bằng a a 3 A. a 30 . 3 B. . C. . a D. . 5 2 Lời giải Chọn D
Gọi O là giao điểm của AC và BD , suy ra BD  SAO .
Từ A , kẻ đường AH SO tại H . Khi đó AH  SBD  d  ,
A SBD  AH .
Xét tam giác SAO vuông tại, A có AH là đường cao, SA  1
a 3 , AO AC a . 2 S . A AO a 3 Suy ra AH   2 2 SA AO 2
Câu 35: Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số   4
f x x  trên đoạn x
1; 3. Khi đó tích M và m bằng A. 15. B. 25. C. 6. D. 20. Lời giải Chọn D
Tập xác định: D   \  0 . 2 4 x  4 x  21;  3 2 y '  1 
; y  0  x  4  0   2 2 x xx  2    1; 3 Ta có: f    f    f   13 1 5; 2 4; 3  . 3
Vậy max y  5; min y  4  max . y min y  20 1; 3 1; 3 1; 3 1; 3
Câu 36: Cho các hàm số f x và F x liên tục trên  và thỏa mãn F x  f x, x    và 1
F 0  2, F   1  6 . Khi đó f
 xdxbằng 0 A. 8. B. 8  . C. 4  . D. 4. Lời giải Chọn D 1
Ta có F x  f x  f
 xdx F  1 F 0  4 0
Câu 37: Một hộp có 5 viên bi đen, 4 viên bi trắng. Lấy ngẫu nhiên 2 viên bi trong hộp. Xác suất để lấy
được 2 viên bi cùng màu bằng 4 1 5 1 A. . B. . C. . D. . 9 9 9 4 Lời giải Chọn A
Số cách lấy ra 2 viên bi bất kì là: 2 C  36 . 9
Số cách lấy ra 2 viên bi cùng màu là: 2 2 C C  16 . 4 5 2 2 C C 16 4
Xác suất để lấy được 2 viên bi cùng màu bằng 4 5   2 C 36 9 9
Câu 38: Trong không gian Oxyz, cho A1;1;  1 , B 5;2; 
1 . Phương trình mặt phẳng trung trực của đoạn AB là
A. 8x  2y  4z  27  0.
B. 8x  2y  4z  27  0.
C. 6x  2y  21 0.
D. 4x y  2z  3  0. Lời giải Chọn B   3 
Ta có AB  4;1;2 , trung điểm của AB là I 3; ;0 . Khi đó, mặt phẳng trung trực của đoạn    2  AB là:     x   3 : 4 3 1 y   2  
z 0  0  :8x  2y  4z  27  0  2 
Câu 39: Trong không gian Oxyz, cho tam giác OAB có A2;2;  1 và B 0; 4
 ;3. Độ dài đường phân giác trong góc  AOB bằng 30 30 9 15 A. . B. . C. . D. . 5 4 8 8 Lời giải Chọn B
Gọi M là chân đường phân giác trong góc  AOB .
Ta có: OA  3,OB  5 , theo tính chất đường phân giác trong: MA OA 3 MA MA OA 3  3      
  MA   AB MB OB 5 AB MA MB OA OB 8 8  3   x    x   M   5 2 0 2 8  M 4    3  1  5 1 1  30
Nên: 2  y    
 y    M   OM M  4 2 ; ; .   8 M 4    4 4 2  4  3  1   z    z   M 3  1 1  8  M  2
Câu 40: Cho hàm số bậc bốn y f x có đồ thị như hình vẽ
Số giá trị nguyên dương của tham số m để hàm số        2 g x f x m có 5 điểm cực trị là A. 3. B. 5. C. 4. D. 6. Lời giải Chọn C
Ta có: g x   f x  m2  g x  2. f  x. f x  m
f x  0
Nên: g x  0  
. Mà f  x  0 có 3 nghiệm nên để hàm số y g x có 5  f
  x  m
điểm cực trị thì phương trình: f x  m * phải có 2 nghiệm bội lẻ phân biệt.
Dựa vào hình ảnh đồ thị hàm số thì phương trình (*) có 2 nghiệm phân biệt khi: m  2  m  2  .   6 m 4       4  m  6
Do m nguyên dương nên: m 1;2;4; 
5  Có 4 giá trị m thỏa mãn.
Câu 41: Gọi S là tập tất cả các giá trị nguyên của tham số m để phương trình x x2 4  2  m  0 có đúng
hai nghiệm phân biệt. Tích các phần tử của S bằng A. 6  . B. 1  2 . C. 6 . D. 0 . Lời giải Chọn A Đặt  2x t ,t  0 .
Khi đó phương trình trở thành 2
t  4t m  0   1 .
Để thoả mãn thì phương trình  
1 có hai nghiệm dương phân biệt 4  m  0 Hay   4   m  0 . m  0
Do m    m 3  ; 2  ;  1 hay S   3  ; 2  ;  1 .
Vậy tích các phần tử của S là  3  . 2  .  1  6  .
Câu 42: Cho hàm số bậc năm f x. Hàm số y f  x có đồ thị như hình vẽ 2
Số điểm cực trị của hàm số g x  f x 3 2
x  2x  3x là 3 A. 0 . B. 1. C. 3 . D. 2 . Lời giải Chọn A
Ta có g x  f  x 2
 2x  4x  3
Khi đó g x   f  x 2 0  2
x  4x  3   1 .
Ta thấy số nghiệm của  
1 là số giao điểm của y f  x và parabol 2 y  2
x  4x  3 (hình vẽ). 2
Từ đồ thị ta thấy  
1 có nghiệm bội chẵn. Vậy hàm số g x  f x 3 2
x  2x  3x không có 3 cực trị.
Câu 43: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại ,
A tam giác SBA vuông tại B và
tam giác SBC là tam giác đều cạnh 2 .
a Thể tích khối chóp S.ABC bằng 3 a 3 a 3 3 a 2 3 a A. . B. . C. . D. . 6 3 3 3 Lời giải Chọn C S A C M B
Gọi M là trung điểm BC, suy ra AM BC .
Tam giác SBC đều có SM là trung tuyến nên SM cũng là đường cao, do đó SM BC . BC SM Ta có 
BC  SAM  . BC AM 2 Suy ra V  2VBM.S . S.ABC B.SAM 3 SAM 1 BC BC Ta có BM BC  3 a , SM   1 a 3 ,
AM BC a , AB   a 2 , 2 2 2 2 2 2
SA AB SB a 6 . 2 a 2
AM SM SA Suy ra S
p p AM p SA p SM p SAM     với . 2 2 2 3 2 a 2 a 2 Vậy V  . . a  . S.ABC 3 2 3
Câu 44: Một xe bồn chở nước có bồn nước gồm hai nửa hình cầu đường kính 18 dm và một hình trụ
có chiều cao 36 dm (như hình vẽ). Thể tích của bồn đã cho bằng 1024 16 A. 3 9216dm . B. 3 dm . C. 3 3888dm . D. 3 dm . 9 243 Lời giải Chọn C
Bán kính nửa hình cầu là 9 dm.
Thể tích phần khối trụ bằng 2
.9 .36  2916. 4
Thể tích phần khối cầu bằng 3
.9  972. 3
Vậy thể tích bồn đã cho bằng 3
2916 972 3888 dm .
Câu 45: Cho hàm số y f x có đạo hàm trên 0; thỏa mãn f  
1  1 và x ' x  1 x e f ee . Khi đó e f
 xdx bằng 1 2 e 1 2 3e  2 2 e 1 2 e A. . B. . C. . D. . 2 2 2 2 Lời giải Chọn C
Ta có: x ' x  1 x x   ' 
x  1 x e f e e e f e dxe dx . x  '
   x       x t e f t dt x e C
f t x e C   x x
f e x e C .
Vì f     f  0 e  0 1 1
e C  1 C  0 . Đặt x
u e x  ln u f u  ln u u hay f x  ln x x . e e e e e 2      e   f x dx ln x xe e 1 1 2
dx  ln xdx xdx  .
x ln x x x  .   1 1 2 2 1 1 1 1 1
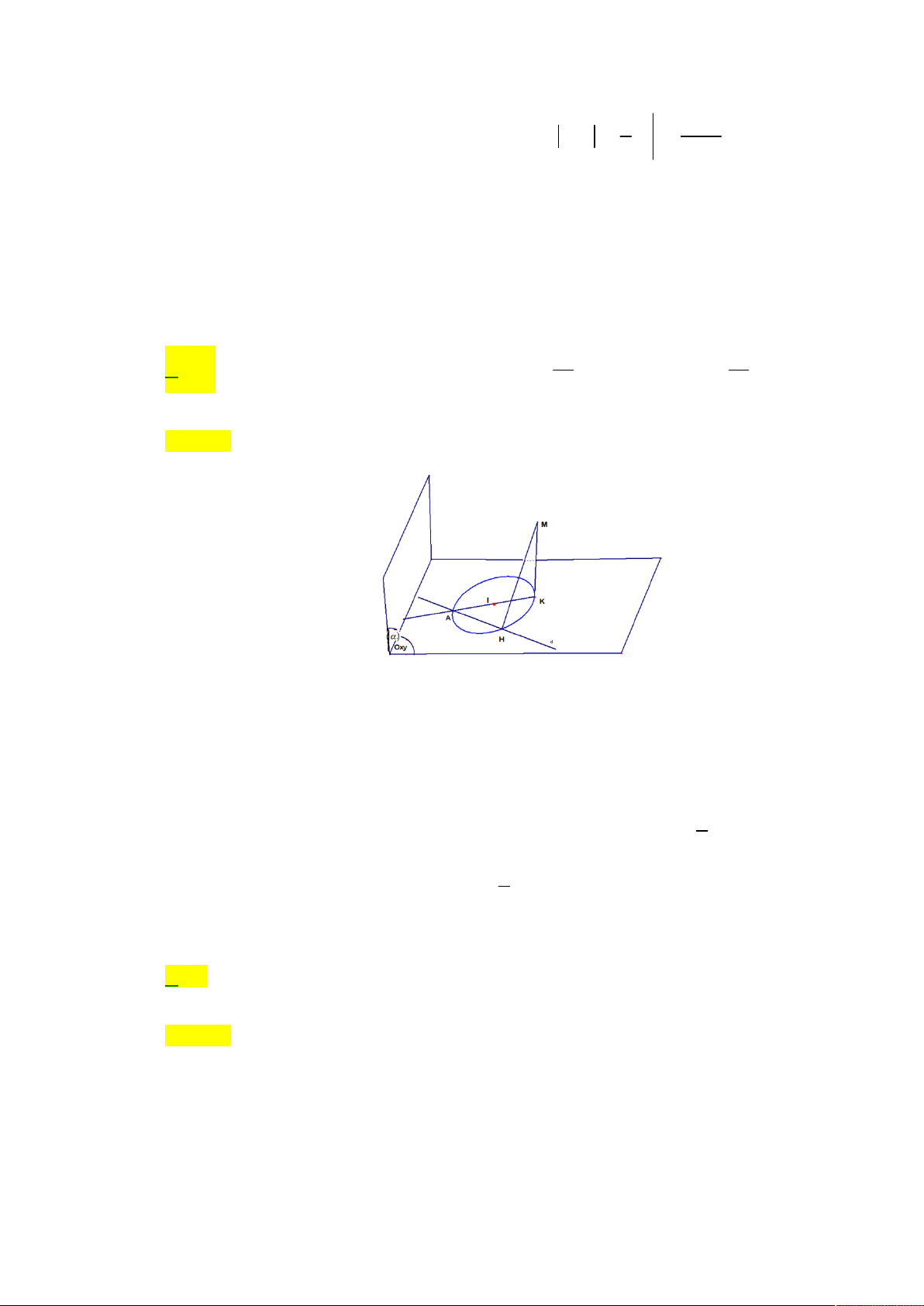
Câu 46: Cho Trong không gian Oxyz cho điểm A 2
 ;6;0 và mặt phẳng  :3x  4y 89  0. Đường
thẳng d thay đổi nằm trong mặt phẳng Oxy và luôn đi qua điểm A . Gọi H là hình chiếu
vuông góc của M 4; 2
 ;3 trên đường thẳng d . Khoảng cách nhỏ nhất từ H đến mặt phẳng bằng 93 A. 15 . B. 20 68 . C. . D. . 5 5 Lời giải Chọn A.
Gọi K là hình chiếu vuông góc của M lên mặt phẳng Oxy  K 4; 2  ;0 .
Vì H là hình chiêu vuông góc của M lên đường thẳng d .
Nên H thuộc đường tròn C có đường kính là đoạn AK 10 và có tâm I là trung điểm của
AK I 1;2;0 .
Mặt khác   Oxy nên Min H   I   r  I  1 d , d , d ,
AK  20  5  15 . 2
H   I  r  I  1 Max d , d , d ,
AK  20  5  25 . 2
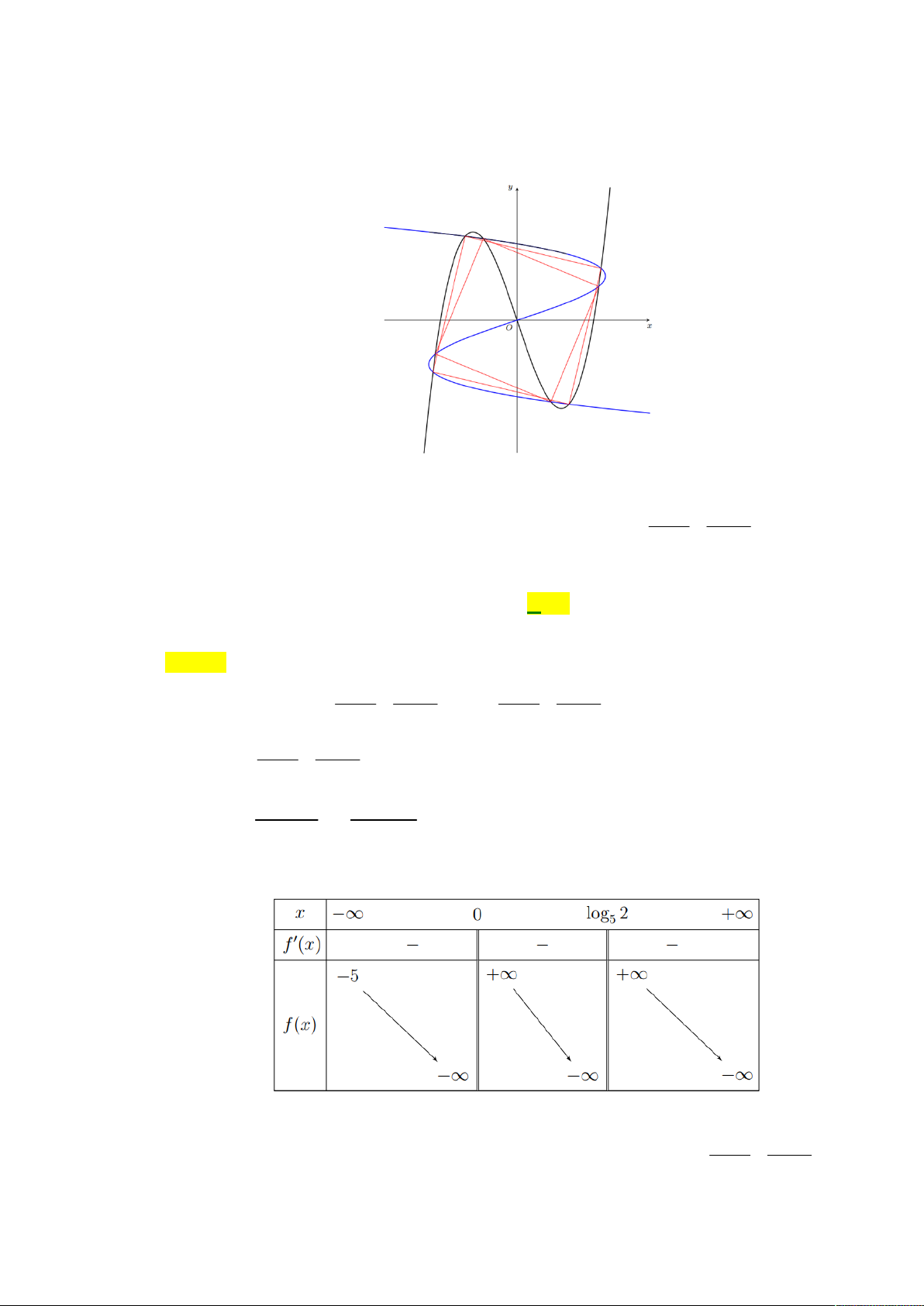
Câu 47: Cho hàm số f x 3  x  3 .
x Số hình vuông có bốn đỉnh nằm trên đồ thị hàm số y f x là A. 2 . B. 4 . C. 3 . D. 1. Lời giải Chọn A.
Ta có f x 3
x x f x 2 3
 3x  3  0  x  1
 nên điểm uốn O0;0.
Giả sử hình vuông ABCD tâm I có bốn đỉnh nằm trên đồ thị, do I là tâm đối xứng hình vuông
nên là tâm đối xứng đồ thị.
Suy ra I là điểm uốn nên I O . Ta có Q ABCD BCDA Q f x F f xO;90    O;90   nên
. Khi đó giao của đồ thị và    
F là đỉnh hình vuông.
Vẽ đồ thị hàm số f x và F lên cùng một phẳng phẳng như hình vẽ.
Dựa vào hình vẽ, ta có hai hình vuông thỏa yêu cầu bài toán. x 4 2
Câu 48: Số giá trị nguyên âm của tham số m để phương trình e  m   có hai nghiệm 5x 1 5x  2 phân biệt là A. 4 . B. 3 . C. 5 . D. 6 . Lời giải Chọn C x 4 2 4 2
Phương trình e  m    m    ex . 5x 1 5x  2 5x 1 5x  2
Đặt f x 4 2  
 ex . Tập xác định D   \0;log 2 5 . 5x 1 5x  2 x x f  x 5 ln 5 5 ln 5  4  .  2.  ex  0, x   D . 5x  2 1 5x 22 Lập bảng biến thiên
Dựa vào bảng biến thiên, ta thấy phương trình có hai nghiệm phân biệt khi và chỉ khi m  5  . x 4 2
Vậy có 5 giá trị nguyên âm của tham số m để phương trình e  m   có hai 5x 1 5x  2 nghiệm phân biệt.
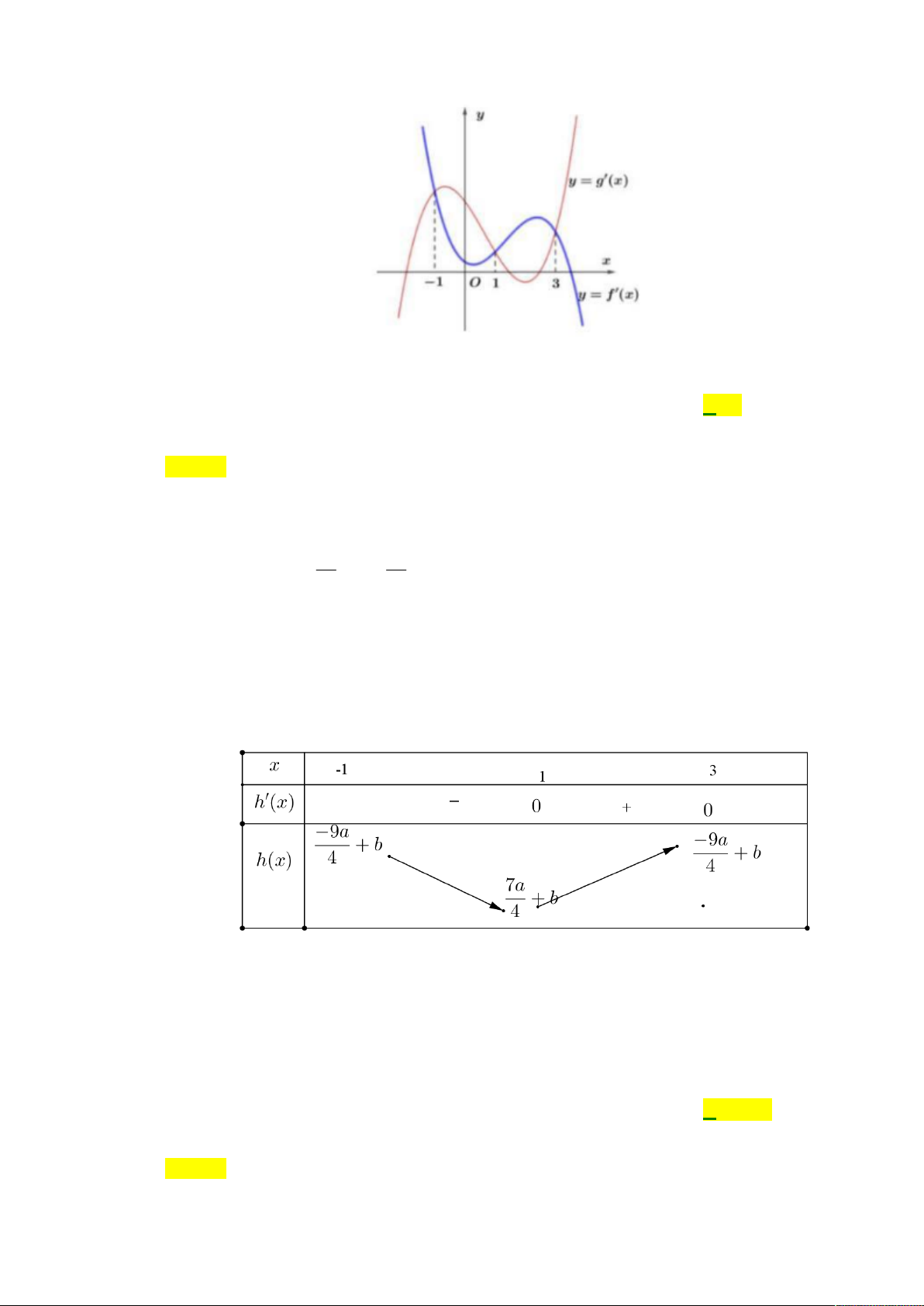
Câu 49: Cho hai hàm số bậc bốn f (x), g(x) có đồ thị y f
 (x) và y g  (x) như hình vẽ
Số giá trị thực của tham số m để phương trình f (x)  g(x)  m có một nghiệm duy nhất trên [ 1  ;3] là A. 5 . B. 0. C. 2. D. 1. Lời giải Chọn D
Dựa vào đồ thị ta có
f x gx a x   x   x     f x gx dx a 3 2 ( ) ( ) 1 1 3 ( ) ( )
x  3x x  3dx 4 2  x x  3
f (x)  g(x)  a   x   3x  b , a  0 4 2   x  1 
Đặt hx  f (x)  g(x)  h x  0    x 1 .  x  3 
Ta có bảng biến thiên của y hx
Để phương trình f (x)  g(x)  m có nghiệm duy nhất trên [ 1
 ;3] thì chỉ có duy nhất 1 giá trị của . m
Câu 50: Có bao nhiêu cặp số nguyên dương ( ;
x y) thỏa mãn điều kiện x  2023 và 39y  2y 3
x  log (x 1)  2? 3 A. 3870. B. 4046. C. 2023. D. 3780. Lời giải Chọn D
Đặt log ( 1)    3t x t x
1. Khi đó bất phương trình 39y  2y 3
x  log (x 1)  2 trở 3 3 thành y t 2 y 1 3.9 6 3 1 3 2 3         3(2 1)  3t y t y  3t (*)
Xét hàm đặc trưng ( )  3u f u  3u trên  Ta có '( )  3u f u ln 3  3  0, u
   nên hàm số f (u) đồng biến trên 
Vậy BPT (*)  f (2y 1)  f (t)  2y 1  t  2y 1  log (x 1) 3 1   log 2024
Mà x nguyên dương và x  2023 nên 3
2y 1  log 2024  y   2,9 3 2
Lại có y nguyên dương nên y {1; 2}.
+) Với y  1 ta được 3
3  log (x 1)  3  x 1  26  x . Kết hợp điều kiện x nguyên dương 3
và x  2023 ta được x {26; 27; 28;....; 2023}. Vậy trường hợp này có 1998 cặp ( ; x y) thỏa mãn
+) Với y  2 ta được 5
5  log (x 1)  3  x 1  242  x . Kết hợp điều kiện x nguyên 3
dương và x  2023 ta được x {242; 243; 244;....; 2023} . Vậy trường hợp này có 1782 cặp ( ; x y) thỏa mãn
Vậy có 1998 1782  3780 cặp số nguyên dương ( ; x y) thỏa mãn.
Document Outline

  • de-kiem-tra-khao-sat-toan-12-nam-2022-2023-so-gddt-ha-noi
    • de-kiem-tra-khao-sat-toan-12-nam-2022-2023-so-gddt-ha-noi
    • Phieu soi dap an Môn Toan So HaNoi nam 2022-2023
  • 58. ĐỀ THI THỬ TN THPT 2023 - MÔN TOÁN - SỞ GIÁO DỤC HÀ NỘI - Lần 1 (Bản word kèm giải).Image.Marked