Đề kiểm tra kiến thức Toán 12 năm 2022 – 2023 trường THPT chuyên KHTN – Hà Nội

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi kiểm tra kiến thức môn Toán 12 năm học 2022 – 2023 trường THPT chuyên KHTN, Đại học Khoa học Tự nhiên Hà Nội

16 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

22 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
TRƯỜNG
ĐẠI HỌC KHTN
TRƯỜNG THPT CHUYÊN KHTN
Câu 1: Hàm nào sau đây là một nguyên hàm của hàm số ?
1
2
x
y
A. . B. . C. . D. .
ln 2x
2ln x
1
ln
2
x
2
1
2
x
Câu 2: Cho hàm số có đạo hàm là . Số điểm cực trị của hàm số đã cho là
f x
2 3
1 2
f x x x x
A. . B. . C. . D. .
0
2
3
Câu 3: Tập nghiệm của bất phương trình
1
2
log 2 1 0x
A. . B. . C. . D. .
;1
1;
1
;1
2
1
;
2

Câu 4: Mô-đun của số phức bằng
3 4 1 2z i i
A. . B. . C. . D. .
25
25 5
5
5 5
Câu 5: Cho hàm số . Tính .
3 1f x x
1
0
dI f x f x x
A. . B. . C. . D. .
1I
3I
3
2
I
1
2
I
Câu 6: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là
2
2
4 3
x
y
x x
A. . B. . C. . D. .
0
1
2
3
Câu 7: Trong không gian với hệ tọa độ , cho hai véc-tơ , . Tích vô
Oxyz
1;2; 3u
2; 1; 2v
hướng của hai véc-tơ và bằng
u
v
A. . B. . C. . D. .
6
6
10
10
Câu 8: Tập xác định của hàm số là
2
log 4y x x
A. . B. . C. . D. .
0;4
0;2
2;2
2;0
Câu 9: Số nghiệm thực của phương trình là
2 2
2
4.3 3.2
x x
A. . B. . C. . D. .
0
1
2
3
Câu 10: Khẳng định nào sau đây đúng?
A. . B. .
1
2 .3 d 3.6
x x x
x C
1 1
2 .3 d 3.6
x x x
x C
C. . D. .
1
3.6
2 .3 d
ln 6
x
x x
x C
1
1
3.6
2 .3 d
1
x
x x
x C
x
Câu 11: Trong không gian với hệ trục tọa độ , cho mặt cầu . Tìm tất cả
Oxyz
2 2 2
( ) : 2 3S x y z x
các giá trị thực dương của tham số để mặt phẳng tiếp xúc với mặt cầu
m
2 2 0x y z m
( )S
A. . B. . C. . D. .
7m
5m
6m
19m
ĐỀ KIỂM TRA KIẾN THỨC LỚP 12 NĂM 2022 - 2023
MÔN TOÁN
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Câu 12: Cho số phức có phần ảo âm thoả mãn . Tính
z
(2 ) 2z z
3z i
A. . B. . C. . D. .
17
17
5
5
Câu 13: Cho hình chóp tứ giác đều có góc giữa cạnh bên với đáy một góc . Tính cosin của
.S ABCD
45
góc giữa mặt bên và đáy của hình chóp đã cho.
A. . B. . C. . D. .
1
3
1
2
1
2
1
3
Câu 14: Cho tập M gồm các số tự nhiên có ba chữ số đôi một khác nhau lấy từ tập . Chọn
0;1;2;3;4;5
ngẫu nhiên một số từ tập M. Tính xác xuất để số được chọn có chữ số hàng trăm nhỏ hơn chữ số
hàng chục.
A. . B. . C. . D. .
3
5
2
5
1
3
2
3
Câu 15: Biết . Tính .
4
2
d 8f x x
2
1
2 dI f x x
A. . B. . C. . D. .
2I
4I
6I
8I
Câu 16: Cho thỏa mãn . Tính .
0a
1
log
2
a
log 1000 a
A. . B. . C. . D. .
13
4
4
3
4
3
2
Câu 17: Cho hình chóp có đáy là hình vuông cạnh và vuông góc với đáy. Tính
.S ABCD
, 2a SA a
SA
theo khoảng cách từ đến mặt phẳng .
a
A
SBD
A. . B. . C. . D. .
4
9
a
9
4
a
2
3
a
3
2
a
Câu 18: Số giao điểm của đồ thị hàm số với đường thẳng là:
3
2 lny x x x
2y x
A. . B. . C. . D. .
0
2
3
Câu 19: Phần ảo của số phức là:
1 3
1
i
z
i
A. . B. . C. . D. .
4
4 i
2 i
2
Câu 20: Từ các chữ số lập được bao nhiêu số chẵn gồm ba chữ số đôi một khác nhau?
0,1,2,3, 4,5,6
A. . B. . C. . D. .
80
120
68
105
Câu 21: Hàm số nào dưới đây không có cực trị?
A. . B. . C. . D. .
3
1y x x
4 2
1y x x
3
1y x x
4 2
1y x x
Câu 22: Thể tích khối chóp có diện tích đáy và chiều cao là
2
a
2a
A. . B. . C. . D. .
3
a
3
2
3
a
3
2a
3
1
3
a
Câu 23: Cho hàm số . Tìm các giá trị thực của tham số để hàm số có đúng 1 cực
4 2
(2 1) 1y x m x
m
trị?
A. . B. . C. . D. .
1
2
m
1
2
m
1
2
m
1
2
m
Câu 24: Cho cấp số nhân có và công bội . Tính
( )
n
u
2
2u
2q
10
u
A. . B. . C. . D. .
2048
256
512
1024
Câu 25: Cho hàm số có đạo hàm là . Hàm số đã cho đồng biến trên
( )f x
' 2
( ) ( 1) ( 2)(3 )f x x x x
khoảng nào dưới đây?
A. . B. . C. . D. .
(2;3)
(1;2)
(1;3)
(3; )
Câu 26: Trong không gian với hệ toạ độ cho mặt cầu . Tâm của
Oxyz
2 2 2
( ) : 2 4 3 0S x y z x y
mặt cầu đã cho có toạ độ là:
A. . B. . C. . D. .
( 1,2,0)
(1, 2,0)
(2, 4,0)
( 2,4,0)
Câu 27: Cho khối chóp tam giác đều S.ABC có cạnh đáy AB=2a, cạnh bên . Thể tích khối chóp
2SA a
đã cho bằng:
A. . B. . C. . D. .
3
2a
3
2
3
a
3
2
6
a
3
2
2
a
Câu 28: Hình chiếu vuông góc của điểm M(1,-2,3) lên mặt phẳng (Oyz) có toạ độ là:
A. . B. . C. . D. .
( 1, 2,3)
(0, 2,3)
(0,2, 3)
(1,0,0)
Câu 29: Trong không gian với hệ tọa độ cho đường thẳng và mặt phẳng
Oxyz
1 2
:
2 1 3
x y z
d
. Tìm tọa độ giao điểm của d và (P).
( ): 2 8 0P x y z
A. (1,3,-3). B. (-3,1,-3). C. (-1,3,-3). D. (3,1,3).
Câu 30: Cho số thực a>0, a 1. Giá trị của biểu thức bằng:
log
a
a a
A. 6. B. 3. C. . D. .
3
2
3
4
Câu 31:
Trong không gian với hệ tọa độ cho đường thẳng . Viết phương trình
Oxyz
1 1
:
2 3 4
x y z
d
mặt phẳng qua và vuông góc với đường thẳng .
1;0; 2M
d
A. . B. .
1 0x y
2 3 4 10 0x y z
C. . D. .
2 3 4 10 0x y z
2 3 4 6 0x y z
Câu 32: Cho hàm số có đạo hàm là với là tham số thực. Tìm tất cả các
f x
1f x x x m
m
giá trị của để hàm số đồng biến trên .
m
; 
A. . B. . C. . D. .
1m
1m
1m
1m
Câu 33:
Tập nghiệm của bất phương trình là
2
3 3
x x
A. . B. . C. . D. .
;1
1;
0;
0;1
Câu 34:
Trong không gian với hệ tọa độ cho ba điểm , , . Phương
Oxyz
1;0;0A
0; 1;0B
0;0;1C
trình mặt phẳng là
ABC
A. . B. . C. . D. .
0x y z
1x y z
0x y z
1x y z
Câu 35: Trong mặt phẳng tọa độ, tập hợp các điểm biểu diễn các số phức thỏa mãn là
z
1z z i
đường thẳng có phương trình?
A. . B. . C. . D. .
y x
y x
1y x
1y x
Câu 36: Tìm tất cả các giá trị thực của tham số để đường thẳng cắt đồ thị hàm số
m
y m
2 2
4y x x
tại đúng điểm phân biệt.
4
A. . B. . C. . D. .
4m
4m
4m
2 4m
Câu 37: Cho khối nón có đường kính đáy bằng và chiều cao bằng . Thể tích của khối nón đã cho
4a
2a
bằng
A. . B. . C. . D. .
3
8
3
a
3
32
3
a
3
8 a
3
32 a
Câu 38: Khẳng định nào sau đây đúng?
A. . B. .
ln d ln 1x x x x
ln d ln 1x x x x C
C. . D. .
ln d ln 1x x x x C
ln d ln 1x x x x
Câu 39: Cho hàm số với là số thực. Tìm tất cả các giá trị của để tổng giá trị lớn nhất và
1
x m
y
x
m
m
giá trị nhỏ nhất của hàm số đã cho trên bằng
0;2
6.
A. B. C. D.
4.m
4.m
1.m
1.m
Câu 40: Số các số nguyên dương thỏa mãn là:
x
4 2023 1 2024 .2
x x
x x
A. B. C. D.
7.
9.
8.
10.
Câu 41: Diện tích hình phẳng giới hạn bởi các đồ thị hàm số và là
2
y x
2
2 y x
A. . B. . C. . D. 0.
8
3
4
3
2
3
Câu 42: Cho khối lăng trụ đứng có đáy là tam giác cân tại và , cạnh bên
.
ABC A B C
A
120
o
BAC
, góc giữa và mặt phẳng bằng . Thể tích khối lăng trụ đã cho bằng
AA
a
A B
ABC
60
A. . B. . C. . D. .
3
13
12
a
3
3
36
a
3
3
4
a
3
3
6
a
Câu 43: Tìm tất cả các giá trị thực của tham số m giá trị lớn nhất của hàm số là
3 2
3y x x m
2;3
trị nhỏ nhất?
A. . B. . C. . D. .
m 8
m 8
10m
10m
Câu 44: Trong không gian với hệ tọa độ cho mặt cầu và mạt
Oxyz
2 2 2
S : 2 2 2 1 0 x y z x y z
phẳng . Lấy điểm di động trên và điểm di động trên sao cho
P : 2 5 0x y z
A
S
B
S
cùng phương . Tìm giá trị lớn nhất của độ dài đoạn .
B A
2;1; 1a
AB
A. B. C. 2+ D. .
2 3 6
4 3 6
3 6
2
3 6
4
2
Câu 45: Cho số phức thỏa mãn . Tìm giá trị lớn nhất của .
z
2
z z z z z
2 3z i
A. . B. . C. . D. .
27 10 2
5 2
7 5 2
20 5 2
Câu 46: Cho hàm số xác định và có đạo hàm cấp hai trên thỏa mãn ,
f x
0;
0 0f
và . Tính .
0
lim 1
x
f x
x
2
2
'' ' 1 2 'f x f x x xf x
2f
A. . B. . C. . D. .
1 ln 3
2 ln3
2 ln 3
1 ln3
Câu 47: Gọi là tập hợp tất cả giá trị thực của tham số sao cho có đúng một số phức thỏa mãn
M
m
z
và là số thuần ảo. Tính tổng tất cả các phần tử của .
3 z m
4z z
M
A. . B. . C. . D. .
2
4
8
10
Câu 48: Cho hình nón có đỉnh có bán kính đáy bằng và góc ở đỉnh bằng . Thiết diện tạo bởi
S
a
120
một mặt phẳng đi qua đỉnh và hình nón là một tam giác có diện tích lớn nhất bằng:
S
A. B. C. D.
2
2
3
a
2
1
3
a
2
4
3
a
2
2
3
a
Câu 49: Cho hàm số xác định và có đạo hàm trên thỏa mãn và
f x
0;
4
1f
e
với mọi . Tính .
1 2 1
x
x f x xf x x e
0x
2
1
x
e f x dx
A. B. C. D.
4 ln 4.
5
2ln 2.
2
4 ln 4.
5
2ln 2.
2
Câu 50: Biết x, y là các số thực thỏa mãn với mọi số thực . Tìm giá trị lớn nhất
2
2 3 2 log
10
x y x a
a
0a
của biểu thức
3 4P x y
A. B. C. D.
10
13
25
8.
--------------- TOANMATH.com ---------------
BẢNG ĐÁP ÁN
1
2
3
4
5
6
7
8
9
1
0
1
1
1
2
1
3
1
4
1
5
1
6
1
7
1
8
1
9
2
0
2
1
2
2
2
3
2
4
2
5
C
C
C
D
C
C
B
A
C
C
A
C
D
B
B
A
C
B
D
C
C
B
B
C
A
2
6
2
7
2
8
2
9
3
0
3
1
3
2
3
3
3
4
3
5
3
6
3
7
3
8
3
9
4
0
4
1
4
2
4
3
4
4
4
5
4
6
4
7
4
8
4
9
5
0
B
B
B
D
C
C
C
D
D
A
B
A
C
B
D
A
A
C
B
B
B
C
A
D
A
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Hàm nào sau đây là một nguyên hàm của hàm số ?
1
2
x
y
A. . B. . C. . D. .
ln 2x
2ln x
1
ln
2
x
2
1
2
x
Lời giải
Chọn C
là một nguyên hàm của hàm số
1 1 1 1 1
ln ln
2 2 2 2
x x x C x
x x
d d
1
.
2
x
y
Câu 2: Cho hàm số có đạo hàm là . Số điểm cực trị của hàm số đã cho là
f x
2 3
1 2
f x x x x
A. . B. . C. . D. .
0
2
3
Lời giải
Chọn C
2 3
0
0 1 2 0 1
2.
x
f x x x x x
x
Trong các nghiệm của phương trình thì là các nghiệm bội lẻ nên chúng là
0
f x
0, 2 x x
cực trị của hàm số . Còn là nghiệm bội chẵn nên nó không phải là cực trị của hàm số
f x
1x
.
f x
Vậy hàm số đã cho có cực trị.
2
Câu 3: Tập nghiệm của bất phương trình
1
2
log 2 1 0x
A. . B. . C. . D. .
;1
1;
1
;1
2
1
;
2

Lời giải
Chọn C
Bất phương trình .
1
2
1
log 2 1 0 0 2 1 1 1
2
x x x
Vậy tập nghiệm .
1
;1
2
S
Câu 4: Mô-đun của số phức bằng
3 4 1 2z i i
A. . B. . C. . D. .
25
25 5
5
5 5
Lời giải
Chọn D
.
3 4 1 2 11 2z i i i
5 5z
Câu 5: Cho hàm số . Tính .
3 1f x x
1
0
dI f x f x x
A. . B. . C. . D. .
1I
3I
3
2
I
1
2
I
Lời giải
Chọn C
.
1
2
1 1
0 0
0
3.1 1 3.0 1 3
d d
2 2 2 2
f x
I f x f x x f x f x
Câu 6: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là
2
2
4 3
x
y
x x
A. . B. . C. . D. .
0
1
2
3
Lời giải
Chọn C
Hàm số xác định khi và chỉ khi
2
2
2 0
2
1
1
4 3 0
3
x
x
x
x
x
x x
x
Tập xác định
;2 \ 1D 
Ta có ,
2
2
lim 0
4 3
x
x
x x

2
1
2
lim
4 3
x
x
x x

Suy ra TCĐ: và TCN: .
1x
0y
Câu 7: Trong không gian với hệ tọa độ , cho hai véc-tơ , . Tích vô
Oxyz
1;2; 3u
2; 1; 2v
hướng của hai véc-tơ và bằng
u
v
A. . B. . C. . D. .
6
6
10
10
Lời giải
Chọn B
Ta có
. 1.2 2 1 3 2 6u v
Câu 8: Tập xác định của hàm số là
2
log 4y x x
A. . B. . C. . D. .
0;4
0;2
2;2
2;0
Lời giải
Chọn A
Hàm số xác định khi và chỉ khi
2
4 0 0 4x x x
Câu 9: Số nghiệm thực của phương trình là
2 2
2
4.3 3.2
x x
A. . B. . C. . D. .
0
1
2
3
Lời giải
Chọn C
Ta có
2 2 2 2 2 2
2 2 2 1 2 2 2 2 2
2 2
4.3 3.2 2 .3 3.2 3 2 2 2 1 log 3 1 2 log 3 0
x x x x x x
x x x
2
1
1 0
1
x
x
x
Vậy phương trình đã cho có hai nghiệm.
Câu 10: Khẳng định nào sau đây đúng?
A. . B. .
1
2 .3 d 3.6
x x x
x C
1 1
2 .3 d 3.6
x x x
x C
C. . D. .
1
3.6
2 .3 d
ln 6
x
x x
x C
1
1
3.6
2 .3 d
1
x
x x
x C
x
Lời giải
Chọn C
Ta có
1
3.6
2 .3 d 3 2 .3 d 3 6 d
ln 6
x
x x x x x
x x x C
Câu 11: Trong không gian với hệ trục tọa độ , cho mặt cầu . Tìm tất cả
Oxyz
2 2 2
( ) : 2 3S x y z x
các giá trị thực dương của tham số để mặt phẳng tiếp xúc với mặt cầu
m
2 2 0x y z m
( )S
A. . B. . C. . D. .
7m
5m
6m
19m
Lời giải
Chọn A
Ta có .
1;0;0
( ) :
2
I
S
R
Để tiếp xúc với thì .
( )P
( )S
5( )
1
; 2
7
3
m l
m
d I P R
m
Câu 12: Cho số phức có phần ảo âm thoả mãn . Tính
z
(2 ) 2z z
3z i
A. . B. . C. . D. .
17
17
5
5
Lời giải
Chọn C
Ta có :
2
2 2 0z z
. Vậy nghiệm phức có phần ảo âm của phương trình là
2
2 2 0z z
1
1
z i
z i
1z i
3 1 3 1 2 5z i i i i
Câu 13: Cho hình chóp tứ giác đều có góc giữa cạnh bên với đáy một góc . Tính cosin của
.S ABCD
45
góc giữa mặt bên và đáy của hình chóp đã cho.
A. . B. . C. . D. .
1
3
1
2
1
2
1
3
Lời giải
Chọn D
Gọi cạnh đáy bằng
2a BD a
- Góc giữa cạnh bên với đáy một góc là vuông cân
45 SBD
2
2 2
BD a
SO
- Gọi là trung điểm góc giữa mặt bên và đáy là
M
CD CD OM
SMO
2 2
1
cos
3
OM OM
SMO
SM
OM SO
Câu 14: Cho tập M gồm các số tự nhiên có ba chữ số đôi một khác nhau lấy từ tập . Chọn
0;1;2;3;4;5
ngẫu nhiên một số từ tập M. Tính xác xuất để số được chọn có chữ số hàng trăm nhỏ hơn chữ số
hàng chục.
A. . B. . C. . D. .
3
5
2
5
1
3
2
3
Lời giải
Chọn B
- Số tự nhiên có ba chữ số đôi một khác nhau lấy từ tập :
abc
0;1;2;3;4;5
2
4
Ω 5. 60A
- Gọi A là biến cố: “số được chọn có chữ số hàng trăm nhỏ hơn chữ số hàng chục”
+ Vì chữ số hàng trăm nhỏ hơn chữ số hàng chục và . Đồng thời cứ 1 bộ 2 chữ số thì có 1
0a
chữ số đứng trước bé hơn chữ số đứng sau. Suy ra số cách chọn ,
2
4
ab C
+ Cách chọn : 4
c
Số cách chọn
2
4
: .4 24
A
abc n C
24 2
60 5
A
P
Câu 15: Biết . Tính .
4
2
d 8f x x
2
1
2 dI f x x
A. . B. . C. . D. .
2I
4I
6I
8I
Lời giải
Chọn B
Ta có
2
1
2 dI f x x
Đặt suy ra
2 2t x dt dx
0 2
1 4
x t
x t
2 4 4
1 2 2
1 1
2 d dt= dx=4
2 2
I f x x f t f x
Câu 16: Cho thỏa mãn . Tính .
0a
1
log
2
a
log 1000 a
A. . B. . C. . D. .
13
4
4
3
4
3
2
Lời giải
Chọn A
Ta có .
1 1 1 13
log 1000 log1000 log 3 log 3 .
2 2 2 4
a a a
Câu 17: Cho hình chóp có đáy là hình vuông cạnh và vuông góc với đáy. Tính
.S ABCD
, 2a SA a
SA
theo khoảng cách từ đến mặt phẳng .
a
A
SBD
A. . B. . C. . D. .
4
9
a
9
4
a
2
3
a
3
2
a
Lời giải
Chọn C
Gọi là giao điểm của và .
O
AC
BD
Gọi là hình chiếu của lên .
H
SO
Ta có và nên .
BD AC
BD SA
BD SAC BD AH
Lại có và nên .
AH SO
AH BD
,AH SBD d A SBD AH
Trong tam giác có .
ABC
2 2 2 2
2
2
2
a
AC AB BC a a a AO
Trong tam giác có .
SAO
2 2
2 2 2 2
1 1 1 1 1 9 2
4 3
2
2
2
a
AH
AH AO SA a
a
a
Vậy .
2
,
3
a
d A SBD AH
Câu 18: Số giao điểm của đồ thị hàm số với đường thẳng là:
3
2 lny x x x
2y x
A. . B. . C. . D. .
0
2
3
Lời giải
Chọn B
Phương trình hoành độ giao điểm của đồ thị hàm số với đường thẳng
3
2 lny x x x
2y x
là .
3
22 lnx x x x
Điều kiện .
0x
Khi đó phương trình trở thành .
3
0ln 2x x x
Xét hàm số , với .
3
ln 2f x x x x
0x
Ta có . Do đó hàm số đồng biến trên
2
1
3 1 0, 0f x x x
x
3
ln 2f x x x x
khoảng .
0;
Khi đó phương trình có nhiều nhất là 1 nghiệm.
3
0ln 2x x x
Nhận thấy là nghiệm của phương trình.
1x
Vậy đồ thị hàm số với đường thẳng có 1 giao điểm.
3
2 lny x x x
2y x
Câu 19: Phần ảo của số phức là:
1 3
1
i
z
i
A. . B. . C. . D. .
4
4 i
2 i
2
Lời giải
Chọn D
Ta có .
2 2
1 3 1
1 3 2 4
1 2
1 1 1 2
i i
i i
z i
i
Vậy phần ảo của số phức là: .
1 3
1
i
z
i
2
Câu 20: Từ các chữ số lập được bao nhiêu số chẵn gồm ba chữ số đôi một khác nhau?
0,1,2,3, 4,5,6
A. . B. . C. . D. .
80
120
68
105
Lời giải
Chọn C
Số cần tìm có dạng: .
0abc a
TH1: , chọn số.
0c
2
5
: 20ab A
Suy ra lập được số thỏa mãn.
20
TH2: cách chọn
2;4;6 :3c
Chọn cách.
: 4a
Chọn cách.
: 4b
Suy ra có số.
4.4.3 48
Vậy có số.
20 48 68
Câu 21: Hàm số nào dưới đây không có cực trị?
A. . B. . C. . D. .
3
1y x x
4 2
1y x x
3
1y x x
4 2
1y x x
Lời giải
Chọn C
Xét hàm số có . Do đó hàm số không có cực
3
1y x x
' 2
3 1 0,y x x
3
1y x x
trị
Câu 22: Thể tích khối chóp có diện tích đáy và chiều cao là
2
a
2a
A. . B. . C. . D. .
3
a
3
2
3
a
3
2a
3
1
3
a
Lời giải
Chọn B
Thể tích khối chóp là : .
2 3
1 2
. .2
3 3
V a a a
Câu 23: Cho hàm số . Tìm các giá trị thực của tham số để hàm số có đúng 1 cực
4 2
(2 1) 1y x m x
m
trị?
A. . B. . C. . D. .
1
2
m
1
2
m
1
2
m
1
2
m
Lời giải
Chọn B
Hàm số có đúng 1 cực trị .
4 2
(2 1) 1y x m x
1
. 0 2 1 0
2
a b m m
Câu 24: Cho cấp số nhân có và công bội . Tính
( )
n
u
2
2u
2q
10
u
A. . B. . C. . D. .
2048
256
512
1024
Lời giải
Chọn C
Ta có: .
8 8
10 2
. 2.2 512u u q
Câu 25: Cho hàm số có đạo hàm là . Hàm số đã cho đồng biến trên
( )f x
' 2
( ) ( 1) ( 2)(3 )f x x x x
khoảng nào dưới đây?
A. . B. . C. . D. .
(2;3)
(1;2)
(1;3)
(3; )
Lời giải
Chọn A
' 2
(2;3) ( 2)(3 ) 0 ( ) ( 1) ( 2)(3 ) 0x x x f x x x x
Do đó hàm số đồng biến trên khoảng .
(2;3)
Câu 26: Trong không gian với hệ toạ độ cho mặt cầu . Tâm của
Oxyz
2 2 2
( ) : 2 4 3 0S x y z x y
mặt cầu đã cho có toạ độ là:
A. . B. . C. . D. .
( 1,2,0)
(1, 2,0)
(2, 4,0)
( 2,4,0)
Lời giải
Chọn B
Ta có tâm của mặt cầu có toạ độ là .
2 2 2
( ) : 2 4 3 0S x y z x y
(1, 2,0)
Câu 27: Cho khối chóp tam giác đều S.ABC có cạnh đáy AB=2a, cạnh bên . Thể tích khối chóp
2SA a
đã cho bằng:
A. . B. . C. . D. .
3
2a
3
2
3
a
3
2
6
a
3
2
2
a
Lời giải
Chọn B
Gọi H là trọng tâm của tam giác ABC và M là trung điểm của BC
Ta có
2 2 3
3
3 3
a
AM a AH AM
Mặt khác
2
2 2 2
2 3 6
( 2 )
3 3
a
SH SA AH a a
Vậy thể tích của khối chóp đã cho là: .
3
2
1 1 3 6 2
. . .(2 ) . .
3 3 4 3 3
ABC
a a
V S SH a
Câu 28: Hình chiếu vuông góc của điểm lên mặt phẳng có toạ độ là:
1, 2,3M
Oyz
A. . B. . C. . D. .
( 1, 2,3)
(0, 2,3)
(0,2, 3)
(1,0,0)
Lời giải
Chọn B
Hình chiếu vuông góc của điểm M(1,-2,3) lên mặt phẳng (Oyz) có toạ độ là:
(0, 2,3)
.
Câu 29: Trong không gian với hệ tọa độ cho đường thẳng và mặt phẳng
Oxyz
1 2
:
2 1 3
x y z
d
. Tìm tọa độ giao điểm của d và (P).
( ): 2 8 0P x y z
A. (1,3,-3). B. (-3,1,-3). C. (-1,3,-3). D. (3,1,3).
Lời giải
Chọn D
Gọi M(a,b,c) vì M thuộc (d) nên suy ra:
2 1
2
3
a t
b t
c t
Vì M thuộc (P) nên:
2 1 ( 2) 2.3 8 0 1t t t t
Vậy tọa độ giao điểm của d và (P) là (3,1,3).
Câu 30: Cho số thực a>0, a 1. Giá trị của biểu thức bằng:
log
a
a a
A. 6. B. 3. C. . D. .
3
2
3
4
Lời giải
Chọn C
1
2
3
4
1 3 3
log log . log
1
4 2
2
a
a
a
a a a a
Câu 31:
Trong không gian với hệ tọa độ cho đường thẳng . Viết phương trình
Oxyz
1 1
:
2 3 4
x y z
d
mặt phẳng qua và vuông góc với đường thẳng .
1;0; 2M
d
A. . B. .
1 0x y
2 3 4 10 0x y z
C. .D. .
2 3 4 10 0x y z
2 3 4 6 0x y z
Lời giải
Chọn C
Đường thẳng có vectơ chỉ phương .
d
2;3; 4
d
u
Theo đề bài, ta có mặt phẳng qua điểm và có vectơ pháp tuyến
P
1;0; 2M
.
2;3; 4
d
n u
Khi đó: .
: 2. 1 3. 0 4. 2 0 2 3 4 10 0P x y z x y z
Câu 32: Cho hàm số có đạo hàm là với là tham số thực. Tìm tất cả các
f x
1f x x x m
m
giá trị của để hàm số đồng biến trên .
m
; 
A. . B. . C. . D. .
1m
1m
1m
1m
Lời giải
Chọn C
Hàm số đồng biến trên khi
; 
0, 1 0,f x x x x m x
2
1 0,x m x m x
2
1 0
1 4 0
a
m m
2
2 1 0m m
.
2
1 0 1 0 1m m m
Câu 33:
Tập nghiệm của bất phương trình là
2
3 3
x x
A. . B. . C. . D. .
;1
1;
0;
0;1
Lời giải
Chọn D
Ta có: .
2
0 0
0
3 3
0 1
1
2 1
x x
x x
x
x
x
x x x
Do vậy, tập nghiệm của bất phương trình là: .
0;1S
Câu 34:
Trong không gian với hệ tọa độ cho ba điểm , , . Phương
Oxyz
1;0;0A
0; 1;0B
0;0;1C
trình mặt phẳng là
ABC
A. . B. . C. . D. .
0x y z
1x y z
0x y z
1x y z
Lời giải
Chọn D
Phương trình mặt phẳng có dạng: .
ABC
1 1
1 1 1
x y z
x y z
Câu 35: Trong mặt phẳng tọa độ, tập hợp các điểm biểu diễn các số phức thỏa mãn là
z
1z z i
đường thẳng có phương trình?
A. . B. . C. . D. .
y x
y x
1y x
1y x
Lời giải
Chọn A
Giả sử được biểu diễn bởi điểm .
,z x iy x y
;M x y
Khi đó .
2 2
2 2
1 1 1 0z z i x y x y x y y x
Câu 36: Tìm tất cả các giá trị thực của tham số để đường thẳng cắt đồ thị hàm số
m
y m
2 2
4y x x
tại đúng điểm phân biệt.
4
A. . B. . C. . D. .
4m
4m
4m
2 4m
Lời giải
Chọn B
Xét phương trình hoành độ giao điểm của đường thẳng và đồ thị hàm số :
y m
2 2
4y x x
2 2 4 2
4 4x x m x x m
Ta có đồ thị hàm số như sau
4 2
4y x x
Từ đồ thị suy ra để đường thẳng cắt đồ thị hàm số tại đúng điểm phân
y m
2 2
4y x x
4
biệt .
4m
Câu 37: Cho khối nón có đường kính đáy bằng và chiều cao bằng . Thể tích của khối nón đã cho
4a
2a
bằng
A. . B. . C. . D. .
3
8
3
a
3
32
3
a
3
8 a
3
32 a
Lời giải
Chọn A
Thể tích của khối nón đã cho là .
2
2
1 1
. . 2 .2
3 3
V r h a a
3
8
3
a
Câu 38: Khẳng định nào sau đây đúng?
A. . B. .
ln d ln 1x x x x
ln d ln 1x x x x C
C. . D. .
ln d ln 1x x x x C
ln d ln 1x x x x
Lời giải
Chọn C
Đặt
1
lnu x
du dx
x
dv dx
v x
.
ln d .ln d ln ln 1x x x x x x x x C x x C
Câu 39: Cho hàm số với là số thực. Tìm tất cả các giá trị của để tổng giá trị lớn nhất và
1
x m
y
x
m
m
giá trị nhỏ nhất của hàm số đã cho trên bằng
0;2
6.
A. B. C. D.
4.m
4.m
1.m
1.m
Lời giải
Chọn B
Tổng giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn bằng khi:
0;2
6
2
0 2 6 6 4.
3
m
y y m m
Câu 40: Số các số nguyên dương thỏa mãn là:
x
4 2023 1 2024 .2
x x
x x
A. B. C. D.
7.
9.
8.
10.
Lời giải
Chọn D
Ta có:
4 2023 1 2024 .2 4 2024.2 2023 2 2023 . 0
2 1 2 2023 2 2023 . 0
2 2023 2 1 0
x x x x x
x x x
x x
x x x
x
x
Do nguyên dương nên
x
2 1 2 1 0
x x
x x
Do đó bpt .
2 2023 1;2;....;10
x
x
Vậy có số nguyên dương thỏa mãn.
10
x
Câu 41: Diện tích hình phẳng giới hạn bởi các đồ thị hàm số và là
2
y x
2
2 y x
A. . B. . C. . D. 0.
8
3
4
3
2
3
Lời giải
Chọn A
Xét phươn trình .
2 2
2 x x
1 x
Vậy diện tích hình phẳng đã cho bằng .
1 1
2 2 2
1 1
8
2 d 2 2d
3
x x x x x
Câu 42: Cho khối lăng trụ đứng có đáy là tam giác cân tại và , cạnh bên
.
ABC A B C
A
120
o
BAC
, góc giữa và mặt phẳng bằng . Thể tích khối lăng trụ đã cho bằng
AA
a
A B
ABC
60
A. . B. . C. . D. .
3
13
12
a
3
3
36
a
3
3
4
a
3
3
6
a
Lời giải
Chọn A
.
AA ABC
, 60
o
AA ABC A BA
Xét tam giác vuông có: .
ABA
cot
3
a
AB AA ABA
Vậy .
3
.
1 3
. . . .sin120
2 12
o
ABC A B C ABC
a
V AA S AA AB AC
Câu 43: Tìm tất cả các giá trị thực của tham số m giá trị lớn nhất của hàm số là
3 2
3y x x m
2;3
trị nhỏ nhất?
A. . B. . C. . D. .
m 8
m 8
10m
10m
Lời giải
Chọn C
Xét hàm số liên tục trên đoạn .
3 2
3y f x x x m
2;3
+) ; .
2
3 6xf x x
0 0; 2 2;3f x x x
+) , , .
2 20f m
2 4f m
3 0f f m
Khi đó .
2;3
max max ; 20f x m m M
Ta có: .
2 20 20 20 10
20 20
M m
M m m m m M
M m m
Dấu xảy ra .
" "
20 10
10
20 0
m m
m
m m
Câu 44: Trong không gian với hệ tọa độ cho mặt cầu và mạt
Oxyz
2 2 2
S : 2 2 2 1 0 x y z x y z
phẳng . Lấy điểm di động trên và điểm di động trên sao cho
P : 2 5 0x y z
A
S
B
S
cùng phương . Tìm giá trị lớn nhất của độ dài đoạn .
B A
2;1; 1a
AB
A. B. C. 2+ D. .
2 3 6
4 3 6
3 6
2
3 6
4
2
Lời giải
Chọn B
+) có tâm , bán kính R = 2.
S
1;1;1I
+) có VTPT , đường thẳng có VTVP .
P
1;1;2n
AB
2;1; 1a
+) Ta có , suy ra góc giữa và bằng 30
0
.
1
sin ;
2
AB P
AB
P
+) Gọi là hình chiếu của . trên . Ta có . Do đó khi và chỉ
H
P
A
P
2.AB AH
AB max
khi
AH max
3 6
d I; P R 2
2
AH max
+) Vậy
4 3 6AB max
Câu 45: Cho số phức thỏa mãn . Tìm giá trị lớn nhất của .
z
2
z z z z z
2 3z i
A. . B. . C. . D. .
27 10 2
5 2
7 5 2
20 5 2
Lời giải
Chọn B
Đặt biểu diễn .
, ;z x yi x y M x y
z
Do
.
2
2 2 2
2 2
2 2
1 1 2
z z z z z z z z z z x y x y
x y
Từ đó suy ra: Tập hợp điểm biểu diễn là 4 phần của 4 đường tròn như hình vẽ:
M
z
Mà với biểu diễn số phức .
2 3 2 3T z i z i MA
2; 3A
2 3i
Ta có .
1 2 3 4
17; 5; 13; 5AI AI AI AI
Do đó
2
5 2MaxT AI R
Câu 46: Cho hàm số xác định và có đạo hàm cấp hai trên thỏa mãn ,
f x
0;
0 0f
và . Tính .
0
lim 1
x
f x
x
2
2
'' ' 1 2 'f x f x x xf x
2f
A. . B. . C. . D. .
1 ln3
2 ln3
2 ln 3
1 ln3
Lời giải
Chọn B
Do .
0 0
0
lim 1 lim 1 ' 0 1
0
x x
f x f x f
f
x x
Ta có: , (1)
2 2
2
'' ' 1 2 ' ' '' 1f x f x x xf x f x x f x
Đặt , nên (1) trở thành
' ' '' 1g x f x x g x f x
2
2
'
' 1.
g x
g x g x
g x
Lấy nguyên hàm hai vế, ta được
1 1 1
'x C g x f x x
g x x C x C
Cho . Do đó
1
0 ' 0 1x f C
C
2
1
1
' ln 1
1 2
x
f x x f x x C
x
Mặt khác . Suy ra . Vậy .
1
0 0 0f C
2
ln 1
2
x
f x x
2 2 ln3f
Câu 47: Gọi là tập hợp tất cả giá trị thực của tham số sao cho có đúng một số phức thỏa mãn
M
m
z
và là số thuần ảo. Tính tổng tất cả các phần tử của .
3 z m
4z z
M
A. . B. . C. . D. .
2
4
8
10
Lời giải
Chọn C
Đặt khi đó . Khi đó tập các số phức là đường tròn
z x yi
3 3 z m x m yi
z
có tâm và .
1
C
1
;0I m
1
3R
Ta có . Để là số thuần ảo khi và chỉ khi
2
2 2
4 4 4 4 z z z z x y x yi
4z z
. Khi đó tập hợp các số phức là đường tròn có tâm và .
2 2
4 0 x y x
z
2
C
2
2;0I
2
2R
Ta có độ dài đường nối tâm là .
1 2
2 I I m
Để có một số phức thỏa mãn .
z
1 2 1 2
1 2 1 2
7
2 5
3
2 1
3
1
m
I I R R
m
m
I I R R
m
m
m
Câu 48: Cho hình nón có đỉnh có bán kính đáy bằng và góc ở đỉnh bằng . Thiết diện tạo bởi
S
a
120
một mặt phẳng đi qua đỉnh và hình nón là một tam giác có diện tích lớn nhất bằng:
S
A. B. C. D.
2
2
3
a
2
1
3
a
2
4
3
a
2
2
3
a
Lời giải
Chọn A
Ta có
2
2
2 2 2
2
2 3
2 2 cos
2 2cos120 3
2 2cos
a
AB a
AB SA SB SA SB ASB SA
ASB
Ta có diện tích thiết diện là .
2 2 2 2
1 1 1 2
' sin
2 2 2 3
S l l SA a
Đẳng thức xảy ra khi hay .
sin 1
' ' 90
A SB
Câu 49: Cho hàm số xác định và có đạo hàm trên thỏa mãn và
f x
0;
4
1f
e
với mọi . Tính .
1 2 1
x
x f x xf x x e
0x
2
1
x
e f x dx
A. B. C. D.
4 ln 4.
5
2ln 2.
2
4 ln 4.
5
2ln 2.
2
Lời giải
Chọn D
Ta có
1 2 1
x
x f x xf x x e
1 2 1
x x
x e f x e xf x x
.
2 1
x
xe f x x
2 1
x
xe f x dx x dx
2x
xe f x x x C
Vì nên . Suy ra .
4
1f
e
1 2 2C ef
2
1
x
e f x x
x
Khi đó
2 2
2
2
1
1 1
2
1 2ln
2
x
x
e f x dx x dx x x
x
5
2ln 2.
2
Câu 50: Biết x, y là các số thực thỏa mãn với mọi số thực . Tìm giá trị lớn nhất
2
2 3 2 log
10
x y x a
a
0a
của biểu thức
3 4P x y
A. B. C. D.
10
13
25
8.
Lời giải
Chọn A
2
2 3 2 log 2 2 2
1 00 2 3 2 log log log 2 log 2 3
x y x a
a x y x a a a x a x y
Đặt ta được bất phương trình
logt a
2 2
02 2 3t xt x y
Để bất phương trình đúng với mọi số thực .
0a
Điều kiện là .
2
2 2 2
' 0 2 3 0 1 4x x y x y
2
2 2 2 2
3 4 3 1 4 3 4 1 25.4 10.P x y x y P x y P
Đẳng thức xảy ra khi .
1
0
x
y
| 1/22
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG ĐẠI HỌC KHTN
ĐỀ KIỂM TRA KIẾN THỨC LỚP 12 NĂM 2022 - 2023
TRƯỜNG THPT CHUYÊN KHTN MÔN TOÁN
Thời gian làm bài: 90 phút (không kể thời gian phát đề) 1 Câu 1:
Hàm nào sau đây là một nguyên hàm của hàm số y  ? 2x 1 1  A. ln 2x . B. 2ln x . C. ln x . D. . 2 2 2x Câu 2:
Cho hàm số f x có đạo hàm là f x  xx  2  x  3 1
2 . Số điểm cực trị của hàm số đã cho là A. 0 . B. 1. C. 2 . D. 3. Câu 3:
Tập nghiệm của bất phương trình log1 2x   1  0 2 A.   1   1  ;   1 . B. 1; . C. ;1 . D. ;  .      2   2  Câu 4:
Mô-đun của số phức z  3 4i1 2i bằng A. 25 . B. 25 5 . C. 5. D. 5 5 . 1 Câu 5:
Cho hàm số f x  3x 1 . Tính I f
 xf xdx . 0 A. I  1. B. I  3 3 . C. I  1 . D. I  . 2 2 2  x Câu 6:
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y  là 2 x  4x  3 A. 0 . B. 1. C. 2 . D. 3 .   Câu 7:
Trong không gian với hệ tọa độ Oxyz , cho hai véc-tơ u  1;2; 3   , v  2; 1  ; 2   . Tích vô  
hướng của hai véc-tơ u và v bằng A. 6  . B. 6 . C. 10 . D. 10  . Câu 8:
Tập xác định của hàm số y   2
log 4x x  là A. 0;4 . B. 0;2 . C.  2  ;2 . D.  2  ;0 . Câu 9:
Số nghiệm thực của phương trình 2 2 x 2 4.3 3.2 x  là A. 0 . B. 1. C. 2 . D. 3 .
Câu 10: Khẳng định nào sau đây đúng? A. x x 1 2 .3  d  3.6x xC . B. x xx x    C .  1 1 2 .3 d 3.6  x 1  x x 3.6x x x 3.6 C. 1 2 .3 dx   C . D. 1 2 .3 dx   C .   ln 6 x 1
Câu 11: Trong không gian với hệ trục tọa độ Oxyz , cho mặt cầu 2 2 2
(S) : x y z  2x  3 . Tìm tất cả
các giá trị thực dương của tham số m để mặt phẳng x  2y  2z m  0 tiếp xúc với mặt cầu (S) A. m  7 . B. m  5 . C. m  6 . D. m  19 .
Câu 12: Cho số phức z có phần ảo âm thoả mãn z(2  z)  2 . Tính z  3i A. 17 . B. 17 . C. 5 . D. 5 .
Câu 13: Cho hình chóp tứ giác đều S.ABCD có góc giữa cạnh bên với đáy một góc 45 . Tính cosin của
góc giữa mặt bên và đáy của hình chóp đã cho. 1 1 1 1 A. . B. . C. . D. . 3 2 2 3
Câu 14: Cho tập M gồm các số tự nhiên có ba chữ số đôi một khác nhau lấy từ tập 0;1;2;3;4;  5 . Chọn
ngẫu nhiên một số từ tập M. Tính xác xuất để số được chọn có chữ số hàng trăm nhỏ hơn chữ số hàng chục. 3 2 1 2 A. . B. . C. . D. . 5 5 3 3 4 2
Câu 15: Biết f
 xdx  8. Tính I f  2xdx . 2 1 A. I  2 . B. I  4 . C. I  6 . D. I  8 . 1
Câu 16: Cho a  0 thỏa mãn loga  . Tính log 1000 a  . 2 13 3 3 A. . B. 4 . C. . D. . 4 4 2
Câu 17: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA  2a và SA vuông góc với đáy. Tính
theo a khoảng cách từ A đến mặt phẳng SBD . 4 9 2 3 A. a . B. a . C. a . D. a . 9 4 3 2
Câu 18: Số giao điểm của đồ thị hàm số 3
y x  2x  lnx với đường thẳng y x  2 là: A. 0 . B. 1. C. 2 . D. 3 . 1 3i
Câu 19: Phần ảo của số phức z  là: 1 i A. 4  . B. 4  i . C. 2  i . D. 2  .
Câu 20: Từ các chữ số 0,1, 2,3, 4,5,6 lập được bao nhiêu số chẵn gồm ba chữ số đôi một khác nhau? A. 80 . B. 120 . C. 68 . D. 105 .
Câu 21: Hàm số nào dưới đây không có cực trị? A. 3
y x x 1. B. 4 2
y x x 1. C. 3
y x x 1. D. 4 2
y x x 1.
Câu 22: Thể tích khối chóp có diện tích đáy 2
a và chiều cao 2a là 2 1 A. 3 a . B. 3 a . C. 3 2a . D. 3 a . 3 3 Câu 23: Cho hàm số 4 2
y x  (2m 1)x 1. Tìm các giá trị thực của tham số m để hàm số có đúng 1 cực trị? 1 A. m  1 . B. m  1 . C. m  1 .
D. m . 2 2 2 2
Câu 24: Cho cấp số nhân (u ) có u  2 và công bội q  2 . Tính u n 2 10 A. 2048 . B. 256 . C. 512 . D. 1024 .
Câu 25: Cho hàm số f (x) có đạo hàm là ' 2
f (x)  (x 1) (x  2)(3  x) . Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. (2;3) . B. (1; 2) . C. (1;3) . D. (3; ) .
Câu 26: Trong không gian với hệ toạ độ Oxyz cho mặt cầu 2 2 2
(S) : x y z  2x  4y  3  0 . Tâm của
mặt cầu đã cho có toạ độ là: A. ( 1  , 2,0) . B. (1, 2  ,0) . C. (2, 4  ,0) . D. ( 2  , 4,0) .
Câu 27: Cho khối chóp tam giác đều S.ABC có cạnh đáy AB=2a, cạnh bên SA a 2 . Thể tích khối chóp đã cho bằng: 2 2 2 A. 3 2a . B. 3 a . C. 3 a . D. 3 a . 3 6 2
Câu 28: Hình chiếu vuông góc của điểm M(1,-2,3) lên mặt phẳng (Oyz) có toạ độ là: A. ( 1  , 2  ,3) . B. (0, 2  ,3) . C. (0, 2, 3  ) . D. (1,0,0) . x 1 y  2 z
Câu 29: Trong không gian với hệ tọa độ Oxyz cho đường thẳng d :   và mặt phẳng 2 1  3
(P) : x y  2z  8  0 . Tìm tọa độ giao điểm của d và (P). A. (1,3,-3). B. (-3,1,-3). C. (-1,3,-3). D. (3,1,3).
Câu 30: Cho số thực a>0, a  1. Giá trị của biểu thức log a a bằng: a 3 3 A. 6. B. 3. C. . D. . 2 4 x 1 y 1 z
Câu 31: Trong không gian với hệ tọa độ Oxyz cho đường thẳng d :   . Viết phương trình 2 3 4 
mặt phẳng qua M 1;0; 2
  và vuông góc với đường thẳng d .
A. x y 1  0 .
B. 2x  3y  4z 10  0 .
C. 2x  3y  4z 10  0 .
D. 2x  3y  4z  6  0 .
Câu 32: Cho hàm số f x có đạo hàm là f  x   x  
1  x m với m là tham số thực. Tìm tất cả các
giá trị của m để hàm số đồng biến trên  ;   . A. m  1. B. m  1. C. m  1. D. m  1. x 2  3   3  x
Câu 33: Tập nghiệm của bất phương trình  là         A.  ;   1 . B. 1; . C. 0; . D. 0;  1 .
Câu 34: Trong không gian với hệ tọa độ Oxyz cho ba điểm A1;0;0 , B 0; 1
 ;0, C 0;0;  1 . Phương
trình mặt phẳng  ABC là
A. x y z  0 .
B. x y z  1.
C. x y z  0 .
D. x y z 1.
Câu 35: Trong mặt phẳng tọa độ, tập hợp các điểm biểu diễn các số phức z thỏa mãn z 1  z i là
đường thẳng có phương trình?
A. y  x .
B. y x .
C. y x 1.
D. y  x 1.
Câu 36: Tìm tất cả các giá trị thực của tham số m để đường thẳng y m cắt đồ thị hàm số 2 2 y x x  4
tại đúng 4 điểm phân biệt. A. m  4 . B. m  4 . C. m  4 .
D. 2  m  4 .
Câu 37: Cho khối nón có đường kính đáy bằng 4a và chiều cao bằng 2a . Thể tích của khối nón đã cho bằng 8 32 A. 3  a . B. 3  a . C. 3 8 a . D. 3 32 a . 3 3
Câu 38: Khẳng định nào sau đây đúng? A. ln d
x x x ln x   1. B. ln d x x x
ln x  1C . C. ln d x x x
ln x  1C . D. ln d
x x x ln x   1. x m
Câu 39: Cho hàm số y
với m là số thực. Tìm tất cả các giá trị của m để tổng giá trị lớn nhất và x 1
giá trị nhỏ nhất của hàm số đã cho trên 0;2 bằng 6. A. m  4. B. m  4  . C. m  1. D. m  1  .
Câu 40: Số các số nguyên dương x thỏa mãn 4x  2023  
1    2024.2x x x là: A. 7. B. 9. C. 8. D. 10.
Câu 41: Diện tích hình phẳng giới hạn bởi các đồ thị hàm số 2 y x và 2
y  2  x là 8 4 2 A. . B. . C. . D. 0. 3 3 3
Câu 42: Cho khối lăng trụ đứng ABC. 
A BC có đáy là tam giác cân tại A và  120o BAC  , cạnh bên
AA  a, góc giữa 
A B và mặt phẳng  ABC bằng 60 . Thể tích khối lăng trụ đã cho bằng 13 3 3 3 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 12 36 4 6
Câu 43: Tìm tất cả các giá trị thực của tham số m giá trị lớn nhất của hàm số 3 2
y x  3x m  2  ;  3 là trị nhỏ nhất? A. m  8 . B. m  8  . C. m  10 . D. m  1  0 .
Câu 44: Trong không gian với hệ tọa độ Oxyz cho mặt cầu   2 2 2
S : x y z  2x  2y  2z 1  0 và mạt
phẳng P : x y  2z  5  0 . Lấy điểm A di động trên S và
điểm B di động trên S s ao cho   B A cùng phương a   2  ;1; 
1 . Tìm giá trị lớn nhất của độ dài đoạn AB . A. 2  3 6  B. 4  3 6  3 6 C. 2+  3 6 D. 4  . 2 2
Câu 45: Cho số phức z thỏa mãn 2
z z z z z . Tìm giá trị lớn nhất của z  2  3i . A. 27 10 2 . B. 5  2 . C. 7  5 2 . D. 20  5 2 .
Câu 46: Cho hàm số f x xác định và có đạo hàm cấp hai trên 0; thỏa mãn f 0  0, f x lim
 1 và f x   f   x 2 2 ' '
  x 1 2xf ' 
x . Tính f 2 . x0 x A. 1 ln 3. B. 2  ln 3 . C. 2  ln 3 . D. 1 ln 3.
Câu 47: Gọi M là tập hợp tất cả giá trị thực của tham số m sao cho có đúng một số phức z thỏa mãn
z m  3 và z z  4 là số thuần ảo. Tính tổng tất cả các phần tử của M . A. 2  . B. 4 . C. 8 . D. 10 .
Câu 48: Cho hình nón có đỉnh S có bán kính đáy bằng a và góc ở đỉnh bằng 120 . Thiết diện tạo bởi
một mặt phẳng đi qua đỉnh S và hình nón là một tam giác có diện tích lớn nhất bằng: 2 1 4 2 A. 2 a B. 2 a C. 2 a D. 2 a 3 3 3 3
Câu 49: Cho hàm số f x xác định và có đạo hàm trên 0; thỏa mãn f   4 1  và e 2    1
     2 1 x x f x xf x x e 
với mọi x  0 . Tính x e f  xdx . 1 A. 4  5 ln 4. B.  2ln 2. C. 4  5 ln 4. D.  2ln 2. 2 2
Câu 50: Biết x, y là các số thực thỏa mãn 2 2 3 2 log 10 x y x aa
với mọi số thực a  0 . Tìm giá trị lớn nhất
của biểu thức P  3x  4y A. 10 B. 13 C. 25 D. 8.
--------------- TOANMATH.com --------------- BẢNG ĐÁP ÁN 1 2 3 4 5 6 7 8 9 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5
C C C D C C B A C C A C D B B A C B D C C B B C A 2 2 2 2 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0
B B B D C C C D D A B A C B D A A C B B B C A D A
HƯỚNG DẪN GIẢI CHI TIẾT 1 Câu 1:
Hàm nào sau đây là một nguyên hàm của hàm số y  ? 2x 1 1  A. ln 2x . B. 2ln x . C. ln x . D. . 2 2 2x Lời giải Chọn C 1 1 1 1 1 1 x d  x
d  ln x C  ln x là một nguyên hàm của hàm số   y  . 2x 2 x 2 2 2x Câu 2:
Cho hàm số f x có đạo hàm là f x  xx  2 x  3 1
2 . Số điểm cực trị của hàm số đã cho là A. 0 . B. 1. C. 2 . D. 3. Lời giải Chọn Cx  0 f x 0 x x 2 1  x 23 0         x 1  x  2. 
Trong các nghiệm của phương trình f  x  0 thì x  0, x  2 là các nghiệm bội lẻ nên chúng là
cực trị của hàm số f x . Còn x  1 là nghiệm bội chẵn nên nó không phải là cực trị của hàm số f x .
Vậy hàm số đã cho có 2 cực trị. Câu 3:
Tập nghiệm của bất phương trình log1 2x   1  0 2 A.   1   1  ;   1 . B. 1;. C. ;1 . D. ;  .      2   2  Lời giải Chọn C 1
Bất phương trình log1 2x  
1  0  0  2x 1  1   x  1. 2 2 Vậy tập nghiệm  1  S  ;1 .    2  Câu 4:
Mô-đun của số phức z  3 4i1 2i bằng A. 25 . B. 25 5 . C. 5. D. 5 5 . Lời giải Chọn D
z  3  4i1 2i 11 2i z  5 5 . 1 Câu 5:
Cho hàm số f x  3x 1 . Tính I f
 xf xdx . 0 A. I  1. B. I  3 3 . C. I  1 . D. I  . 2 2 Lời giải Chọn C 1 1   I f
 xf xx f
 x  f x f x 1 2 3.1 1 3.0 1 3 d d     . 2 2 2 2 0 0 0 2  x Câu 6:
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y  là 2 x  4x  3 A. 0 . B. 1. C. 2 . D. 3 . Lời giải Chọn Cx  2 2  x  0  x  2
Hàm số xác định khi và chỉ khi   x 1   2
x  4x  3  0  x  1 x  3 
Tập xác định D   ;  2 \  1 2  x 2  x Ta có lim  0 , lim   2
x x  4x  3  2 x 1  x  4x  3
Suy ra TCĐ: x  1 và TCN: y  0 .   Câu 7:
Trong không gian với hệ tọa độ Oxyz , cho hai véc-tơ u  1;2; 3   , v  2; 1  ; 2   . Tích vô  
hướng của hai véc-tơ u và v bằng A. 6  . B. 6 . C. 10 . D. 1  0 . Lời giải Chọn B   Ta có .
u v  1.2  2  1  3 2    6 Câu 8:
Tập xác định của hàm số y   2
log 4x x  là A. 0;4 . B. 0;2 . C.  2  ;2 . D.  2  ;0 . Lời giải Chọn A
Hàm số xác định khi và chỉ khi 2
4x x  0  0  x  4 Câu 9:
Số nghiệm thực của phương trình 2 2 x 2 4.3 3.2 x  là A. 0 . B. 1. C. 2 . D. 3 . Lời giải Chọn C Ta có 2 2 2 2 2 2 x 2 x 2 x 2 x x 1  2 x 2 2 4.3  3.2  2 .3  3.2  3  2  2x  2   2 x   1 log 3   2
x 1 2  log 3  0 2  2  x 1 2
x 1  0  x  1
Vậy phương trình đã cho có hai nghiệm.
Câu 10: Khẳng định nào sau đây đúng? A. x x 1 2 .3  d  3.6x xC . B. x xx x    C .  1 1 2 .3 d 3.6  x 1  x x 3.6x x x 3.6 C. 1 2 .3 dx   C . D. 1 2 .3 dx   C .   ln 6 x 1 Lời giải Chọn C x xx x x 3.6x Ta có 1
2 .3 dx  3 2 .3 dx  3 6 dx   C    ln 6
Câu 11: Trong không gian với hệ trục tọa độ Oxyz , cho mặt cầu 2 2 2
(S) : x y z  2x  3 . Tìm tất cả
các giá trị thực dương của tham số m để mặt phẳng x  2y  2z m  0 tiếp xúc với mặt cầu (S) A. m  7 . B. m  5 . C. m  6 . D. m  19 . Lời giải Chọn A I  1  ;0;0 Ta có (S) :  . R  2 1   mm   l
Để (P) tiếp xúc với (S) thì d I;P 5( )  R   2  . 3  m  7
Câu 12: Cho số phức z có phần ảo âm thoả mãn z(2  z)  2 . Tính z  3i A. 17 . B. 17 . C. 5 . D. 5 . Lời giải Chọn C Ta có : 2
z  2z  2  0 z  1 i 2
z  2z  2  0 
. Vậy nghiệm phức có phần ảo âm của phương trình là  z  1 iz  1 i
z  3i  1 i  3i  1 2i  5
Câu 13: Cho hình chóp tứ giác đều S.ABCD có góc giữa cạnh bên với đáy một góc 45 . Tính cosin của
góc giữa mặt bên và đáy của hình chóp đã cho. 1 1 1 1 A. . B. . C. . D. . 3 2 2 3 Lời giải Chọn D
Gọi cạnh đáy bằng a BD a 2 BD a
- Góc giữa cạnh bên với đáy một góc 45   2
SBD là vuông cân  SO   2 2
- Gọi M là trung điểm CD CD OM  góc giữa mặt bên và đáy là  SMOOM OM 1 cos SMO    2 2 SM OM SO 3
Câu 14: Cho tập M gồm các số tự nhiên có ba chữ số đôi một khác nhau lấy từ tập 0;1;2;3;4;  5 . Chọn
ngẫu nhiên một số từ tập M. Tính xác xuất để số được chọn có chữ số hàng trăm nhỏ hơn chữ số hàng chục. 3 2 1 2 A. . B. . C. . D. . 5 5 3 3 Lời giải Chọn B
- Số tự nhiên có ba chữ số abc đôi một khác nhau lấy từ tập 0;1;2;3;4;  5 : 2 Ω  5.A  60 4
- Gọi A là biến cố: “số được chọn có chữ số hàng trăm nhỏ hơn chữ số hàng chục”
+ Vì chữ số hàng trăm nhỏ hơn chữ số hàng chục và a  0 . Đồng thời cứ 1 bộ 2 chữ số thì có 1
chữ số đứng trước bé hơn chữ số đứng sau. Suy ra số cách chọn 2 ab C , 4 + Cách chọn c : 4 Số cách chọn 2
abc : n C .4  24 A 4 24 2  P   A 60 5 4 2 f
 xdx 8 I f  2xdx Câu 15: Biết 2 . Tính 1 . A. I  2 . B. I  4 . C. I  6 . D. I  8 . Lời giải Chọn B 2 Ta có I f  2xdx 1
x  0  t  2
Đặt t  2x dt  2dx suy ra x 1t  4 2 4 4 I f   x 1 x f  t 1 2 d dt= f  xdx=4 2 2 1 2 2 1
Câu 16: Cho a  0 thỏa mãn loga  . Tính log 1000 a  . 2 13 3 3 A. . B. 4 . C. . D. . 4 4 2 Lời giải Chọn A Ta có  a  1 1 1 13 log 1000
 log1000  log a  3  loga  3  .  . 2 2 2 4
Câu 17: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA  2a và SA vuông góc với đáy. Tính
theo a khoảng cách từ A đến mặt phẳng SBD . 4 9 2 3 A. a . B. a . C. a . D. a . 9 4 3 2 Lời giải Chọn C
Gọi O là giao điểm của AC và BD .
Gọi H là hình chiếu của lên SO .
Ta có BD AC và BD SA nên BD  SAC  BD AH .
Lại có AH SO và AH BD nên AH  SBD  d  ,
A SBD  AH . a 2
Trong tam giác ABC có 2 2 2 2
AC AB BC a a a 2  AO  . 2 1 1 1 1 1 9 2a
Trong tam giác SAO có       AH  . 2 2 2 2 AH AO SAa 2  2a2 2 4a 3   2   a
Vậy d A SBD 2 ,  AH  . 3
Câu 18: Số giao điểm của đồ thị hàm số 3
y x  2x  lnx với đường thẳng y x  2 là: A. 0 . B. 1. C. 2 . D. 3 . Lời giải Chọn B
Phương trình hoành độ giao điểm của đồ thị hàm số 3
y x  2x  lnx với đường thẳng y x  2 là 3
x  2x  lnx x  2 .
Điều kiện x  0 .
Khi đó phương trình trở thành 3
x x  lnx  2  0 .
Xét hàm số f x 3
x x  lnx  2 , với x  0 . 1
Ta có f  x 2
 3x 1  0, x
  0 . Do đó hàm số f x 3
x x  lnx  2 đồng biến trên x khoảng 0; . Khi đó phương trình 3
x x  lnx  2  0 có nhiều nhất là 1 nghiệm.
Nhận thấy x  1 là nghiệm của phương trình. Vậy đồ thị hàm số 3
y x  2x  lnx với đường thẳng y x  2 có 1 giao điểm. 1 3i
Câu 19: Phần ảo của số phức z  là: 1 i A. 4  . B. 4  i . C. 2  i . D. 2  . Lời giải Chọn D 1 3i
13i1i 2   4i Ta có z     1   2i . 2 2 1 i 1 1 2 1 3i
Vậy phần ảo của số phức z  là: 2  . 1 i
Câu 20: Từ các chữ số 0,1, 2,3, 4,5,6 lập được bao nhiêu số chẵn gồm ba chữ số đôi một khác nhau? A. 80 . B. 120 . C. 68 . D. 105 . Lời giải Chọn C
Số cần tìm có dạng: abc a  0 . TH1: c  0 , chọn 2
ab : A  20 số. 5
Suy ra lập được 20 số thỏa mãn. TH2: c 2;4;  6 : 3 cách chọn Chọn a : 4 cách. Chọn b : 4 cách. Suy ra có 4.4.3  48 số.
Vậy có 20  48  68 số.
Câu 21: Hàm số nào dưới đây không có cực trị? A. 3
y x x 1. B. 4 2
y x x 1. C. 3
y x x 1. D. 4 2
y x x 1. Lời giải Chọn C Xét hàm số 3
y x x 1có ' 2
y  3x 1  0, x
   . Do đó hàm số 3
y x x 1không có cực trị
Câu 22: Thể tích khối chóp có diện tích đáy 2
a và chiều cao 2a là 2 1 A. 3 a . B. 3 a . C. 3 2a . D. 3 a . 3 3 Lời giải Chọn B 1 2
Thể tích khối chóp là : 2 3
V  .a .2a a . 3 3 Câu 23: Cho hàm số 4 2
y x  (2m 1)x 1. Tìm các giá trị thực của tham số m để hàm số có đúng 1 cực trị? 1 A. m  1 . B. m  1 . C. m  1 .
D. m . 2 2 2 2 Lời giải Chọn B Hàm số 4 2
y x  (2m 1)x  1
1 có đúng 1 cực trị  .
a b  0  2m 1  0  m  . 2
Câu 24: Cho cấp số nhân (u ) u  2 u n có 2
và công bội q  2 . Tính 10 A. 2048 . B. 256 . C. 512 . D. 1024 . Lời giải Chọn C Ta có: 8 8
u u .q  2.2  512 . 10 2
Câu 25: Cho hàm số f (x) có đạo hàm là ' 2
f (x)  (x 1) (x  2)(3  x) . Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. (2;3) . B. (1; 2) . C. (1;3) . D. (3; ) . Lời giải Chọn A ' 2 x
 (2;3)  (x  2)(3  x)  0  f (x)  (x 1) (x  2)(3  x)  0
Do đó hàm số đồng biến trên khoảng (2;3) .
Câu 26: Trong không gian với hệ toạ độ Oxyz cho mặt cầu 2 2 2
(S) : x y z  2x  4y  3  0 . Tâm của
mặt cầu đã cho có toạ độ là: A. ( 1  , 2,0) . B. (1, 2  ,0) . C. (2, 4  ,0) . D. ( 2  , 4,0) . Lời giải Chọn B Ta có tâm của mặt cầu 2 2 2
(S) : x y z  2x  4y  3  0 có toạ độ là (1, 2  ,0) .
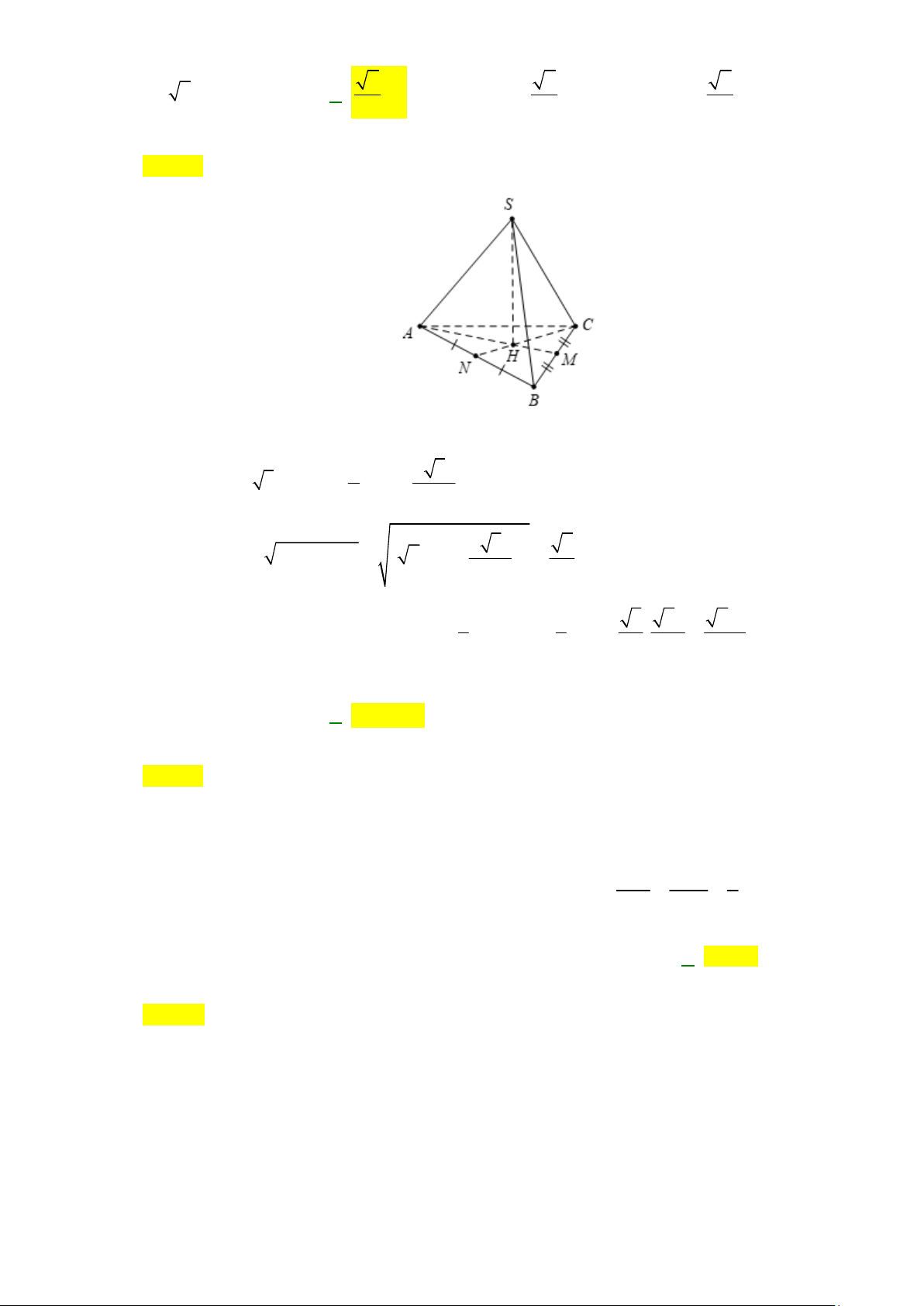
Câu 27: Cho khối chóp tam giác đều S.ABC có cạnh đáy AB=2a, cạnh bên SA a 2 . Thể tích khối chóp đã cho bằng: 2 2 2 A. 3 2a . B. 3 a . C. 3 a . D. 3 a . 3 6 2 Lời giải Chọn B
Gọi H là trọng tâm của tam giác ABC và M là trung điểm của BC 2 2 3a
Ta có AM a 3  AH AM  3 3 2  2 3a  6 Mặt khác 2 2 2
SH SA AH  ( 2a)     a  3  3   3 1 1 3 6a 2a
Vậy thể tích của khối chóp đã cho là: 2 V  .S .SH  .(2a) . .  . 3 ABC 3 4 3 3
Câu 28: Hình chiếu vuông góc của điểm M 1, 2
 ,3 lên mặt phẳng Oyz có toạ độ là: A. ( 1  , 2  ,3) . B. (0, 2  ,3) . C. (0, 2, 3  ) . D. (1,0,0) . Lời giải Chọn B
Hình chiếu vuông góc của điểm M(1,-2,3) lên mặt phẳng (Oyz) có toạ độ là: (0, 2  ,3) . x 1 y  2 z
Câu 29: Trong không gian với hệ tọa độ Oxyz cho đường thẳng d :   và mặt phẳng 2 1  3
(P) : x y  2z  8  0 . Tìm tọa độ giao điểm của d và (P). A. (1,3,-3). B. (-3,1,-3). C. (-1,3,-3). D. (3,1,3). Lời giải Chọn Da  2t 1 
Gọi M(a,b,c) vì M thuộc (d) nên suy ra: b   t   2 c  3t
Vì M thuộc (P) nên: 2t 1 ( t
  2)  2.3t  8  0  t  1
Vậy tọa độ giao điểm của d và (P) là (3,1,3).
Câu 30: Cho số thực a>0, a  1. Giá trị của biểu thức log a a bằng: a 3 3 A. 6. B. 3. C. . D. . 2 4 Lời giải Chọn C 3 1 3 3 4 log
a a  log a  . log a  1 a 1 a 2 a 4 2 2 x 1 y 1 z
Câu 31: Trong không gian với hệ tọa độ Oxyz cho đường thẳng d :   . Viết phương trình 2 3 4 
mặt phẳng qua M 1;0; 2
  và vuông góc với đường thẳng d .
A. x y 1  0 .
B. 2x  3y  4z 10  0 .
C. 2x  3y  4z 10  0 . D. 2x  3y  4z  6  0 . Lời giải Chọn C 
Đường thẳng d có vectơ chỉ phương u  2;3; 4  d  .
Theo đề bài, ta có mặt phẳng P qua điểm M 1;0; 2
  và có vectơ pháp tuyến  
n u  2;3; 4  d  .
Khi đó: P : 2. x  
1  3. y  0  4. z  2  0  2x  3y  4z 10  0 .
Câu 32: Cho hàm số f x có đạo hàm là f  x   x  
1  x m với m là tham số thực. Tìm tất cả các
giá trị của m để hàm số đồng biến trên  ;   . A. m  1. B. m  1. C. m  1. D. m  1. Lời giải Chọn C
Hàm số đồng biến trên  ;   khi
f  x  0, x
    x  
1  x m  0, x    2
x  m  
1 x m  0, x    a  1  0      m  2 1  4m  0 2
m  2m 1  0  m  2
1  0  m 1  0  m  1. x 2  3   3  x
Câu 33: Tập nghiệm của bất phương trình  là         A.  ;   1 . B. 1; . C. 0; . D. 0;  1 . Lời giải Chọn D x 2  3   3  x  x  0  x  0  x  0 Ta có:             0  x 1.   
 x  2  x  x 1 x 1
Do vậy, tập nghiệm của bất phương trình là: S  0;  1 .
Câu 34: Trong không gian với hệ tọa độ Oxyz cho ba điểm A1;0;0 , B 0; 1
 ;0, C 0;0;  1 . Phương
trình mặt phẳng  ABC là
A. x y z  0 .
B. x y z  1.
C. x y z  0 .
D. x y z 1. Lời giải Chọn D x y z
Phương trình mặt phẳng  ABC có dạng: 
  1  x y z  1. 1 1  1
Câu 35: Trong mặt phẳng tọa độ, tập hợp các điểm biểu diễn các số phức z thỏa mãn z 1  z i là
đường thẳng có phương trình?
A. y  x .
B. y x .
C. y x 1.
D. y  x 1. Lời giải Chọn A
Giả sử z x iy x, y   được biểu diễn bởi điểm M  ; x y .
Khi đó z   z i   x  2  y x   y  2 2 2 1 1
1  x y  0  y  x .
Câu 36: Tìm tất cả các giá trị thực của tham số m để đường thẳng y m cắt đồ thị hàm số 2 2 y x x  4
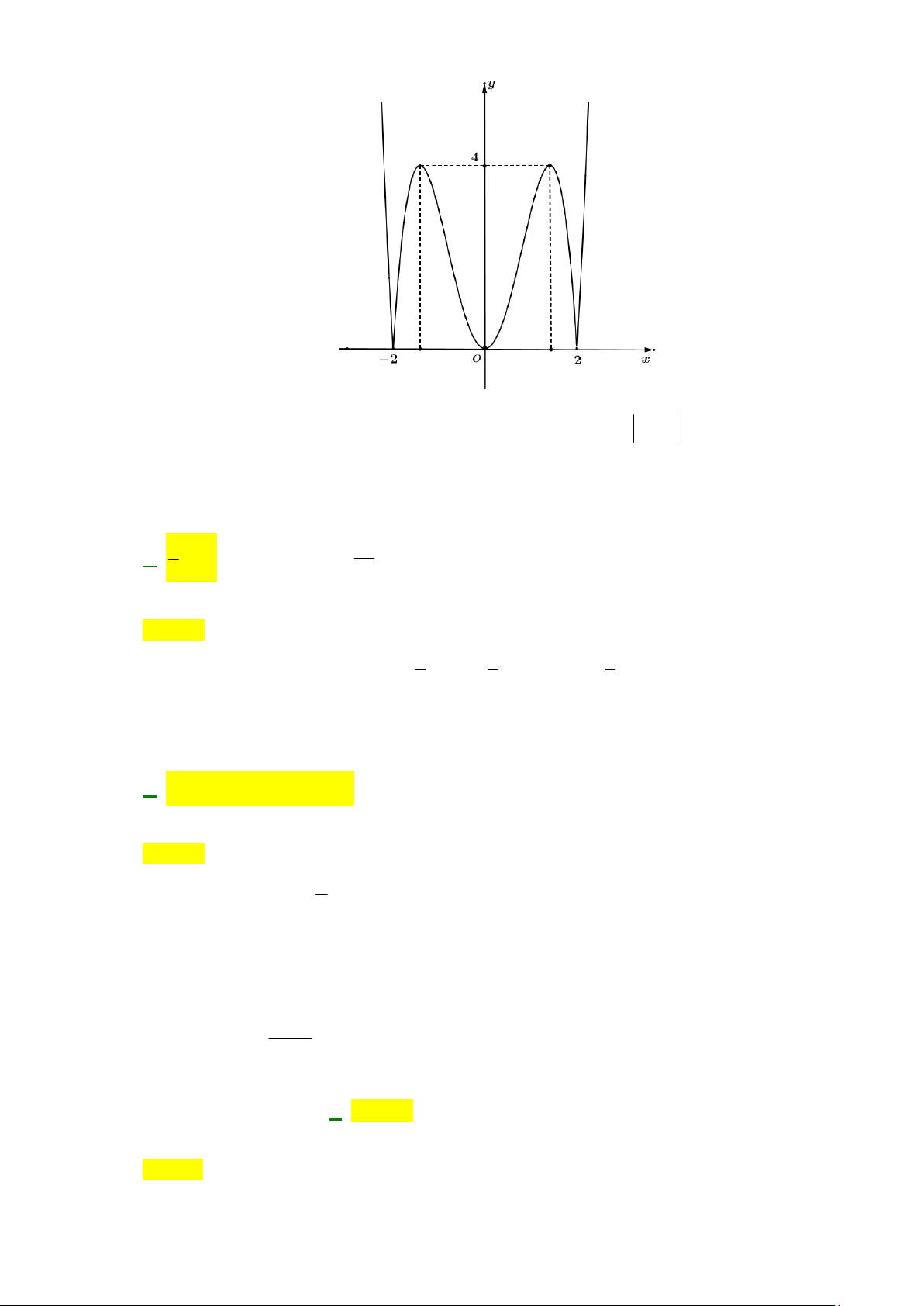
tại đúng 4 điểm phân biệt. A. m  4 . B. m  4 . C. m  4 .
D. 2  m  4 . Lời giải Chọn B
Xét phương trình hoành độ giao điểm của đường thẳng y m và đồ thị hàm số 2 2
y x x  4 : 2 2 4 2
x x  4  m x  4x m Ta có đồ thị hàm số 4 2
y x  4x như sau
Từ đồ thị suy ra để đường thẳng y m cắt đồ thị hàm số 2 2
y x x  4 tại đúng 4 điểm phân biệt  m  4 .
Câu 37: Cho khối nón có đường kính đáy bằng 4a và chiều cao bằng 2a . Thể tích của khối nón đã cho bằng 8 32 A. 3  a . B. 3  a . C. 3 8 a . D. 3 32 a . 3 3 Lời giải Chọn A 1 1 8
Thể tích của khối nón đã cho là V  r .h .2a2 2 .2a  3  a . 3 3 3
Câu 38: Khẳng định nào sau đây đúng? A. ln d
x x x ln x   1. B. ln d x x x
ln x  1C . C. ln d x x x
ln x  1C . D. ln d
x x x ln x   1. Lời giải Chọn C  1 u   ln xdu dx Đặt    xdv dx v x  ln d x x  .
x ln x  dx x ln x x C x  
ln x  1C . x m
Câu 39: Cho hàm số y
với m là số thực. Tìm tất cả các giá trị của m để tổng giá trị lớn nhất và x 1
giá trị nhỏ nhất của hàm số đã cho trên 0;2 bằng 6. A. m  4. B. m  4  . C. m  1. D. m  1  . Lời giải Chọn B
Tổng giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn 0;2 bằng 6 khi:     y  2 m y 0 2  6  m   6  m  4  . 3
Câu 40: Số các số nguyên dương x thỏa mãn 4x  2023  
1    2024.2x x x là: A. 7. B. 9. C. 8. D. 10. Lời giải Chọn D Ta có:
4x  2023 x  
1   x  2024.2x  4x  2024.2x  2023  2x  2023.x  0  2x  
1 2x  2023  2x  2023.x  0
 2x  20232x x   1  0
Do x nguyên dương nên 2x  1 2x xx 1  0
Do đó bpt  2x  2023  x 1;2;....;1  0 .
Vậy có 10 số nguyên dương x thỏa mãn.
Câu 41: Diện tích hình phẳng giới hạn bởi các đồ thị hàm số 2 y x và 2
y  2  x là 8 4 2 A. . B. . C. . D. 0. 3 3 3 Lời giải Chọn A Xét phươn trình 2 2
x  2  x x  1  . 1 1 8
Vậy diện tích hình phẳng đã cho bằng 2 x    2 2  x  2
dx  2x  2dx  .  3 1  1 
Câu 42: Cho khối lăng trụ đứng ABC. 
A BC có đáy là tam giác cân tại A và  120o BAC  , cạnh bên
AA  a, góc giữa 
A B và mặt phẳng  ABC bằng 60 . Thể tích khối lăng trụ đã cho bằng 13 3 3 3 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 12 36 4 6 Lời giải Chọn A A
A   ABC  ,        60o AA ABC A BA . a
Xét tam giác vuông ABA có: AB AAcot  ABA  . 3 3 1 o a 3 Vậy V         AA.S AA.A . B A . C sin120 . AB . C A B C ABC 2 12
Câu 43: Tìm tất cả các giá trị thực của tham số m giá trị lớn nhất của hàm số 3 2
y x  3x m  2  ;  3 là trị nhỏ nhất? A. m  8 . B. m  8  . C. m  10 . D. m  1  0 . Lời giải Chọn C
Xét hàm số y f x 3 2
x  3x m liên tục trên đoạn  2  ;  3 . +) f  x 2
 3x  6x ; f x  0  x  0; x  2 2  ;  3 . +) f  2
   m  20 , f 2  m  4 , f 3  f 0  m .
Khi đó max f x  max m ; m  20  M .  2  ;  3  M m Ta có: 
 2M m  20  m m  20  m  20  M  10 .
M m  20  20  m
 m  20  m 10 Dấu "  " xảy ra    m  10 .  m  20 m  0
Câu 44: Trong không gian với hệ tọa độ Oxyz cho mặt cầu   2 2 2
S : x y z  2x  2y  2z 1  0 và mạt
phẳng P : x y  2z  5  0 . Lấy điểm A di động trên S và
điểm B di động trên S s ao cho   B A cùng phương a   2  ;1; 
1 . Tìm giá trị lớn nhất của độ dài đoạn AB . A. 2  3 6  B. 4  3 6  3 6 C. 2+  3 6 D. 4  . 2 2 Lời giải Chọn B
+) S có tâm I 1;1;  1 , bán kính R = 2.  
+) P có VTPT n  1;1;2 , đường thẳng AB có VTVP a   2  ;1;  1 . +) Ta có
AB P 1 sin ;
 , suy ra góc giữa AB và P bằng 300. 2
+) Gọi H là hình chiếu của P . A trên P . Ta có AB  2.AH . Do đó AB max khi và chỉ khi AH max
AH max     3 6 d I; P  R  2   2
+) Vậy AB max  4  3 6
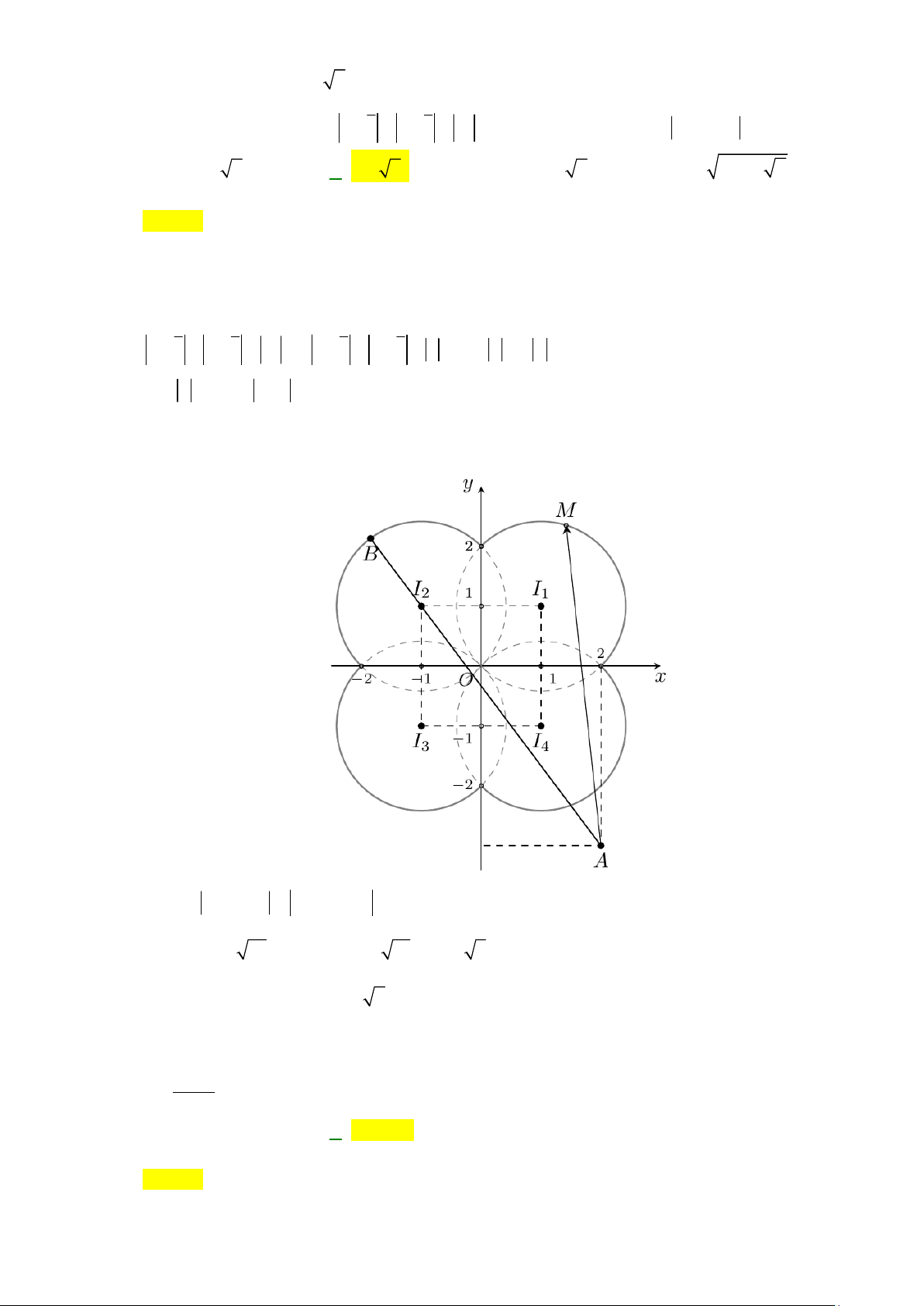
Câu 45: Cho số phức z thỏa mãn 2
z z z z z . Tìm giá trị lớn nhất của z  2  3i . A. 27 10 2 . B. 5  2 . C. 7  5 2 . D. 20  5 2 . Lời giải Chọn B
Đặt z x yi x, y    M  ;
x y biểu diễn z . Do 2 2 2 2
z z z z z z z z z z  2 x  2 y x y .   x  2
1   y 1 2  2
Từ đó suy ra: Tập hợp điểm M biểu diễn z là 4 phần của 4 đường tròn như hình vẽ:
MàT z  2  3i z  2  3i  MA với A2; 3
  biểu diễn số phức 2  3i .
Ta có AI  17; AI  5; AI  13; AI  5 . 1 2 3 4
Do đó MaxT AI R  5  2 2
Câu 46: Cho hàm số f x xác định và có đạo hàm cấp hai trên 0; thỏa mãn f 0  0, f x lim
 1 và f x   f   x 2 2 ' '
  x  1 2xf ' 
x . Tính f 2 . x0 x A. 1 ln 3. B. 2  ln 3 . C. 2  ln 3 . D. 1 ln 3. Lời giải Chọn B f x
f x  f 0 Do lim  1  lim
 1  f '0 1. x0 x0 x x  0
Ta có: f x   f   x 2
  x   xf
x   f   x 2 2 ' ' 1 2 ' '  x   
f ' x 1, (1) g ' x
Đặt g x  f ' x  x g ' x  f '  x 1, nên (1) trở thành 2
g x  g ' x     1  . 2 g x 1 1 1
Lấy nguyên hàm hai vế, ta được     xC gx 
f 'x  x g x x C x C 2 1 x
Cho x   f   1 0 ' 0   C  1
 . Do đó f 'x  x
f x 
 ln x 1  C C  1 x 1 2 2 x
Mặt khác f 0  0  C  0 . Suy ra f x 
 ln x 1 . Vậy f 2  2  ln 3 . 1 2
Câu 47: Gọi M là tập hợp tất cả giá trị thực của tham số m sao cho có đúng một số phức z thỏa mãn
z m  3 và z z  4 là số thuần ảo. Tính tổng tất cả các phần tử của M . A. 2  . B. 4 . C. 8 . D. 10 . Lời giải Chọn C
Đặt z x yi khi đó z m  3   x m  yi  3 . Khi đó tập các số phức z là đường tròn C I ; m 0 R  3 1   1  có tâm và . 1
Ta có z z   2
z z   2 2 4 4
x y  4x  4yi . Để z z  4 là số thuần ảo khi và chỉ khi 2 2
x y  4x  0 . Khi đó tập hợp các số phức z là đường tròn C I 2;0 R  2 2   2  có tâm và . 2
Ta có độ dài đường nối tâm là I I m  2 . 1 2  m  7  I I R R m 2 5       m  3 
Để có một số phức z thỏa mãn 1 2 1 2       .
I I R R m  2  1  m  3  1 2 1 2    m  1
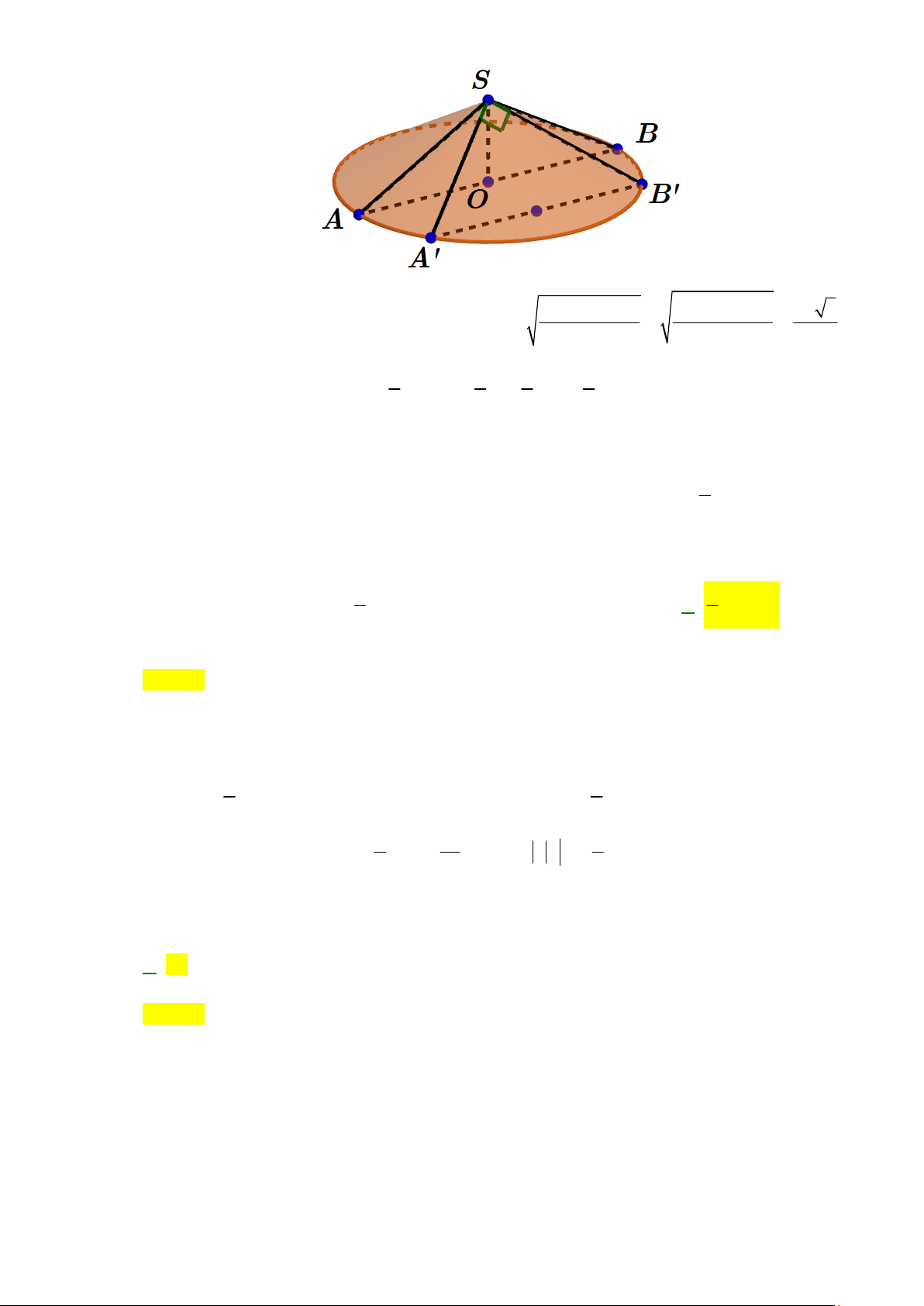
Câu 48: Cho hình nón có đỉnh S có bán kính đáy bằng a và góc ở đỉnh bằng 120 . Thiết diện tạo bởi
một mặt phẳng đi qua đỉnh S và hình nón là một tam giác có diện tích lớn nhất bằng: 2 1 4 2 A. 2 a B. 2 a C. 2 a D. 2 a 3 3 3 3 Lời giải Chọn A AB 2a 2a 3 2 2 2  2 2
Ta có AB SA SB  2S 2 A SB cos  ASB SA    2  2cos  ASB 2  2cos120 3 1 1 1 2
Ta có diện tích thiết diện là 2 2 2 2
S '  l sinl SA a . 2 2 2 3
Đẳng thức xảy ra khi sin 1 hay  
A' SB '  90 .
Câu 49: Cho hàm số f x xác định và có đạo hàm trên 0; thỏa mãn f   4 1  và e 2    1
      2   1 x x f x xf x x e 
với mọi x  0 . Tính x e f  xdx . 1 A. 4  5 ln 4. B.  2ln 2. C. 4  5 ln 4. D.  2ln 2. 2 2 Lời giải Chọn D Ta có    1
      2   1 x x f x xf x x e      1 x   x x
e f x e xf  x  2x 1 x
xe f x     2x 1 xxe f x  
dx  2x 1 dx xxe f x 2
x x C .          Vì f   4
1  nên C ef  
1  2  2 . Suy ra x e f x 2  x 1 . e x 2 2 2    xx 2 Khi đó e f  x 2 dx x 1 dx   5   
x  2ln x    2ln 2. 1  x   2 2 1 1 
Câu 50: Biết x, y là các số thực thỏa mãn 2 2 3 2 log 10 x y x aa
với mọi số thực a  0 . Tìm giá trị lớn nhất
của biểu thức P  3x  4y A. 10 B. 13 C. 25 D. 8. Lời giải Chọn A 2 2 x3 y 2 xlog a 2 0  a
 2x  3  y  2x  log a 2 2 1
log a  log a  2x log a  2x  3  y  0
Đặt t  log a ta được bất phương trình 2 2
t  2xt  2x  3  y  0
Để bất phương trình đúng với mọi số thực a  0 .
Điều kiện là    x x   y    x  2 2 2 2 ' 0 2 3 0 1  y  4 .
P x y   x    y P      x  2 2 2 2 2 3 4 3 1 4 3 4
1  y   25.4  P  10.     x  1
Đẳng thức xảy ra khi  . y  0