Đề KSCL học sinh giỏi Toán 7 năm 2024 – 2025 phòng GD&ĐT Vinh – Nghệ An

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
KỲ KHẢO SÁT CHẤT LƯỢNG HỌC SINH GIỎI THÀNH PHỐ VINH NĂM HỌC 2024 - 2025
ĐỀ THI CHÍNH THỨC
Môn thi: Toán lớp 7
(Đề thi gồm có 01 trang)
Thời gian: 120 phút (không kể thời gian giao đề)
Câu 1: (4,5 điểm)
1. Tính giá trị các biểu thức sau: 3 3 3 1 1 1     a) 4 11 13 2 3 4 A   5 5 5 5 5 5     4 11 13 4 6 8 1 1 1 1
b) B  1 (1 2)  (1 2  3)  (1 2  3  4)  ....  (1 2  3  ...  57) 2 3 4 57 25 24 a c  24 24 a  b   25 25 a  b 
2. Cho các số dương a, ,
b c, d thỏa mãn
 và c  d. Chứng minh:  b d 24 24 25 c  d  25 25 ( ) c  d 24
Câu 2: (4,0 điểm) x  y z  x y  z
a) Tìm x, y, z biết 3 2 2 4 4 3  
và x  y  z  18 4 3 2
b) Tìm tất cả các số tự nhiên x, y sao cho: 2x  2025  y  2024  y
c) Tìm các số a,b, c nguyên dương thỏa mãn 3 2  3  5  5b a a và 3 5c a  
Câu 3: (3,5 điểm) 1. Cho đa thức 4 2 2
f (x)  2025x  30(25k  20)x  k 100 (với k là số thực dương cho trước).
Biết đa thức f (x) có đúng ba nghiệm phân biệt a, ,
b c với a  b  c . Tính hiệu a  c .
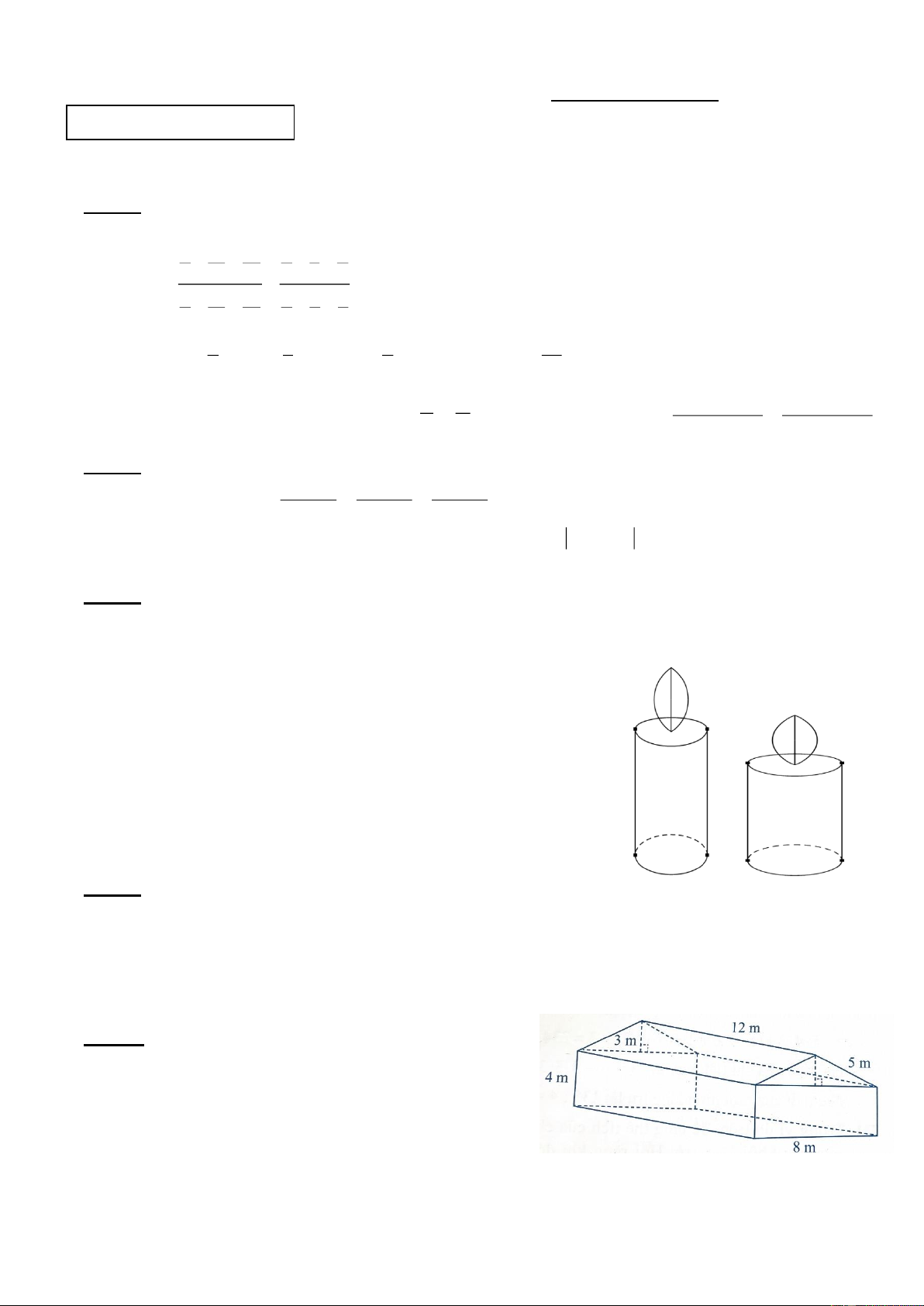
2. Hai ngọn nến hình trụ có chiều cao và đường kính khác
nhau được đặt thẳng đứng trên mặt bàn. Ngọn nến thứ nhất cháy
hết trong 6 giờ, ngọn nến thứ hai cháy hết trong 8 giờ. Hai
ngọn nến được thắp sáng cùng lúc, sau 3 giờ chúng có cùng
chiều cao. Giả sử tốc độ tiêu hao của hai cây nến khi cháy là không đổi.
a) Tìm tỉ lệ chiều cao lúc đầu của hai ngọn nến.
b) Biết tổng chiều cao lúc đầu của hai ngọn nến là 63cm .
Tính chiều cao lúc đầu của mỗi ngọn nến.
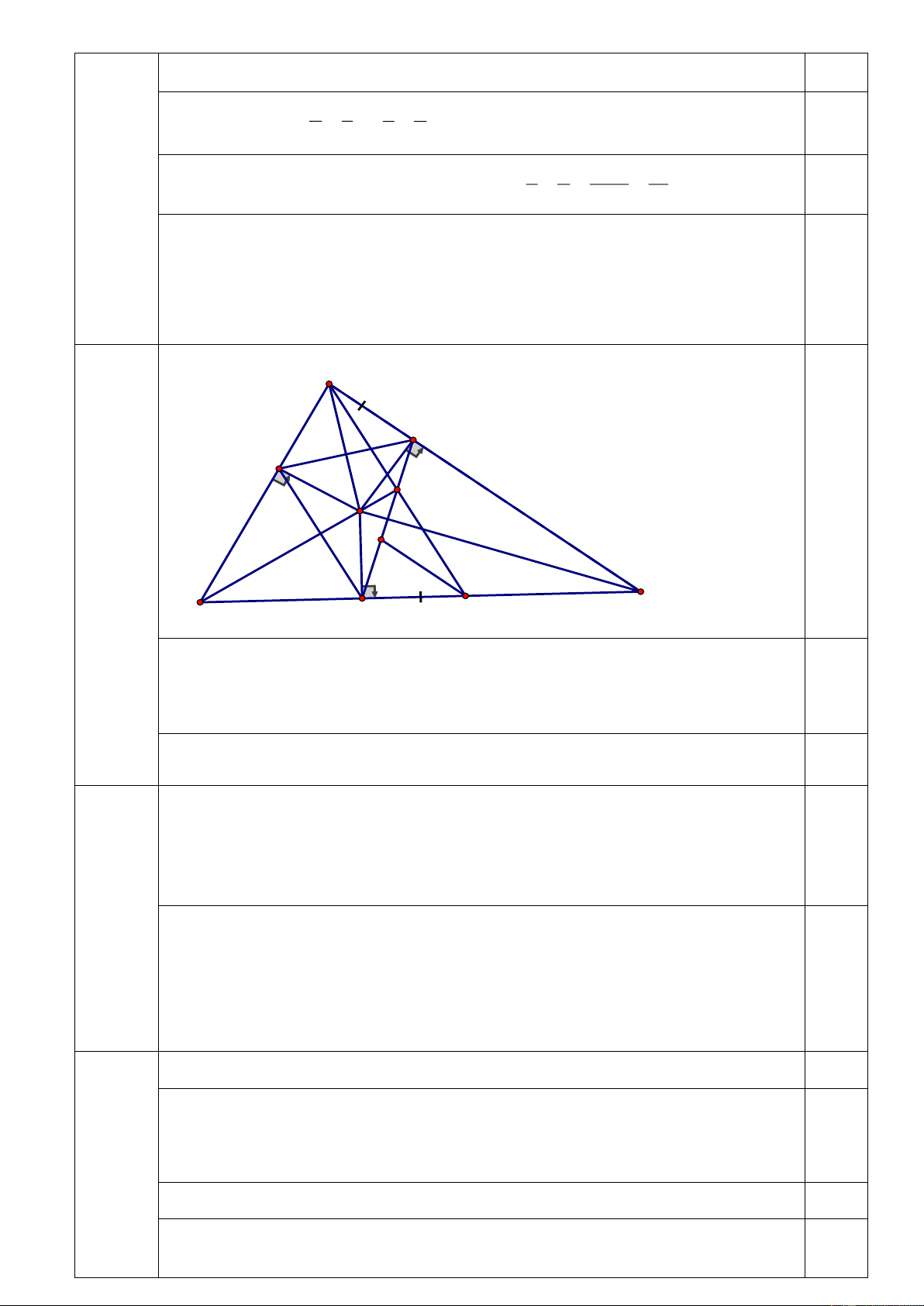
Câu 4: (6,0 điểm) Cho ABC 
có 3 góc nhọn, AB  AC  B . C
Các tia phân giác của góc Avà góc C cắt nhau tại O . Kẻ OF  BC ( F  BC ), OH  AC ( H  AC
). Lấy điểm I trên đoạn FC sao cho FI  AH. Gọi K là giao điểm của FH và AI. a) Chứng minh F  CH cân;
b) Qua I kẻ IG / / AC G  FH . Chứng minh: K là trung điểm của GH ; c) Chứng minh 3 điểm , B , O K thẳng hàng.
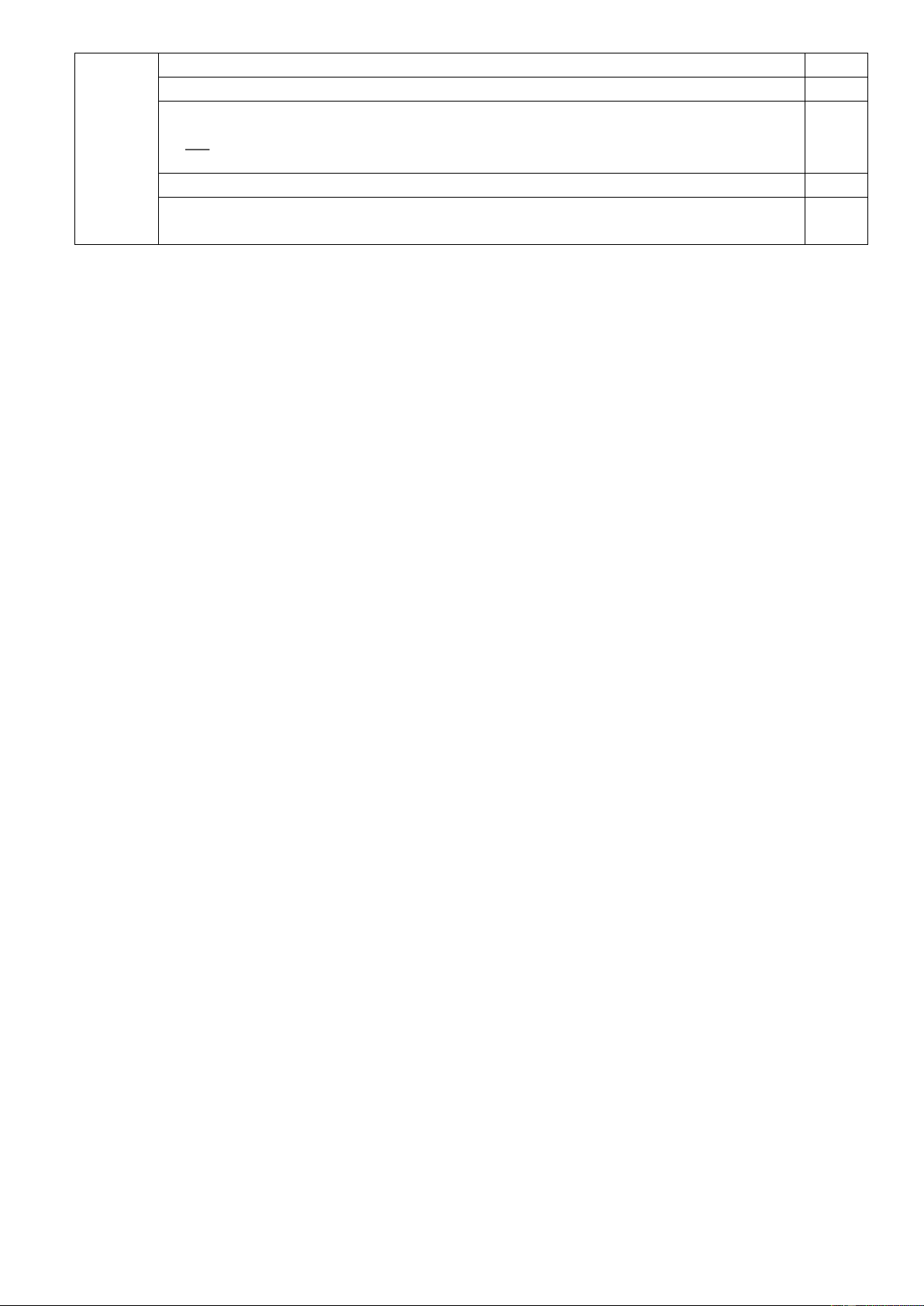
Câu 5: (2,0 điểm) Người ta làm một nhà kính trồng
cây thí nghiệm gồm 2 phần, phần dưới là một hình
hộp chữ nhật có kích thước 4m, 8m, 12m và phần trên
là một hình lăng trụ đứng có đáy tam giác cân với
cạnh bên 5m, chiều cao ứng với cạnh đáy dài 3m (hình
vẽ bên) được ghép hoàn toàn bằng kính cường lực.
Biết rằng mỗi mét vuông kính cường lực có giá 800 nghìn đồng. Tính chi phí mua kính cường lực
để ghép được ngôi nhà này (giả sử các chỗ ghép nối không đáng kể).
………………. Hết …………….
PHÒNG GIÁO DỤC VÀ ĐÀO
KỲ THI KHẢO SÁT CHẤT LƯỢNG HỌC SINH GIỎI
TẠO THÀNH PHỐ VINH NĂM HỌC 2024 - 2025
Hướng dẫn chấm môn Toán 7
(Hướng dẫn chấm gồm có 04 trang)
Lưu ý: Học sinh làm cách khác đúng vẫn cho điểm tối đa. Câu Đáp án Điểm 3 3 3 1 1 1       1 1 1 1 1 1 3        4 11 13  Ta có : 4 11 13 2 3 4 A   2 3 4   Câu 1a 5 5 5 5 5 5  1 1 1  5  1 1 1      5   .   (1,5 đ)     4 11 13 4 6 8
 4 11 13  2  2 3 4  1 3 2   1 0,5 5 5 1 B      1      1       1 1 1 2 1 2 3 1 2 3 4  ......  1 23....57 2 3 4 57
1  2.3  1  3.4  1  4.5   57.58  B  1   . ....... 57.         0,5 Câu 1b
2  2  3  2  4  2   2  (1,5 đ) 3 4 58 1 1   .....
 .2  3 4 ...... 58 0,5 2 2 2 2 1  57.60   .  855   0,5 2  2  a c a b
Vì a,b, c, d là các số dương và c  d   , mà nên b d c d 24 24 24 24 a b a  b    24 24 24 24 c d c  d 0,25 25 25 24 24 24  a   a  b        0,25 24 24 24  c   c  d  a b a 25 24 24 24.25   (1) Câu 1c 24.25 c  24 24 c  d 25 0,25 (1,5 đ) 25 25 25 25  Lại có a b  a b a b    25 25 25 25 c d c d c  d 0,25 24 24 24 25 25 25  25 25 a   a  b  25.24 a b a          (2) 25 25 25  c   c  d  25.24 c  25 25 c  d 24 0,25
a b 25 a b 24 24 24 25 25 Từ (1) và (2)   24 24 25 c  d  25 25 ( ) c  d 24 0,25   
Ta có : 3x 2y 2z 4x 4y 3z   4 3 2
4 3x  2 y 32z  4x
2 4 y  3z 
12x  8 y  6z 12x  8 y  6z Suy ra     0 Câu 2a 16 9 4 29 0,5 (1,5 đ) 3x  2y x y
 0  3x  2y    4 2 3 x y z      2z  4x x z 2 3 4 
 0  2z  4x    0,5  3 2 4
Áp dụng tính chất dãy tỉ số bằng nhau, ta có: x y z
x  y  z 18    
 2  x  4; y  6; z  8 0,5 2 3 4 2  3  4 9 Ta có: 2x  2025   2024   2x y y
1  y  2024  y  2024 0,25 2 ( A A  0)
Mà A  A   0(A  0) Câu 2b x  0,5 (1,5 đ)
 y  2024  y  2024 là số chẵn => 2
1 là số chẵn => 2x lẻ => x = 0
Do đó: y  2024  y  2024  2  y  2024 1 y  2025 0,5 Vậy: (x,y) là ( 0,25 0,2025) Do  b 3 2   5 
 3  5   3  5c a a a a
 5b  5c    5b 5c b c 0,25   3 2
a  a   a   2 3 5
3  a a  3  5 a  3 Mà 2
a a  3 a  3  5 a  3  a  3U (5)   1  ;  5 (1) Câu 2c 0,25  (1 đ) Do a   a  3  4 2
Từ (1) và (2)  a  3  5  a  2 0,25 3 2
 2  3.2  5  5b;25  5b  b  2
 2  3  5c  c 1
Vậy a  2;b  2;c  1 0,25
Ta thấy đa thức f (x) nếu có nghiệm x  a (a khác 0) thì x  a cũng là một nghiệm của 0,25
f (x) nên f (x) có 2m nghiệm
Mà đa thức f (x) có đúng ba nghiệm phân biệt nên một trong ba nghiệm sẽ Câu 3.1  0,25 (1,0 đ)
bằng 0. Thay x  0 vào đa thức đã cho ta được: 2
k 100 0 nên k 10 (vì k dương) Với k 10 ta có 4 2 2 2
f (x)  2025x  8100x  2025x .(x  4)  0 0,25
Từ đó f (x) sẽ có 3 nghiệm phân biệt là a  2
 ;b  0;c  2nên a c  4  0,25
Gọi chiều cao ban đầu ngọn nến thứ nhất là x cm
Chiều cao ban đầu ngọn nến thứ hai là y cm
Điều kiện: x  0, y  0 0,25 Mỗi x
giờ cây nến thứ nhất giảm cm 6  x x
Sau 3 giờ chiều cao cây nến thứ nhất còn: x  3.  cm 0,25 Câu 6 2 3.2.a (1,5 đ) Mỗi y
giờ cây nến thứ hai giảm cm 8  y y
Sau 3 giờ chiều cao cây nến thứ hai còn: 5 y  3.  cm 8 8 0,25 x 5 y x 5
Vì sau 3 giờ cháy, hai cây nến có cùng chiều cao nên ta có:    0,5 2 8 y 4 Vậy tỉ lệ chiều c x 5 0,25
ao ban đầu của hai ngọn nến là  y 4
Vì tổng chiều cao lúc đầu của hai ngọn nến là 63cm nên x  y  63 0,25 x 5 x y 0,25 Theo câu a ta có:    y 4 5 4 0,25 Câu x y x  y 63
Áp dụng tính chất dãy tỉ số bằng nhau ta có:     7 3.2.b 5 4 5  4 9 (1 đ)
Suy ra: x  5.7  35 (tm)
y  4.7  28 (tm)
Vậy chiều cao ban đầu của cây nến thứ nhất là 35cm ; chiều cao ban đầu cây nến thứ hai là 28cm . 0,25 A H E K O Câu 4a G (2 đ) C B F I Ta có 0
CHO  CFO  90 ( vì OH  AC,OF  BC) Xét C
 HO vuông và C
 FOvuông có: OC chung; HCO  FCO(CO là phân giác 1,0 C) Vậy C  HO  C
 FO(cạnh huyền – góc nhọn)
 CH  CF (hai cạnh tương ứng). Vậy F  CH cân tại C 1,0 Ta có F
 CH cân tại C (cmt)  CHF  CFH (1) Mà
CHF  FGI (đồng vị, IG / / AC) (2)
Từ (1) và (2)  CFH  FGI hay IFG  IGF => I  FG cân tại I 1,0
Câu 4b  FI  GI , mặt khác : FI  AH nên GI  AH( FI) (2 đ)
Ta lại có : IGK  AHK; HAK  GIK (so le trong , IG / / AC) Xét A  HK và I
 GK có: IGK  AHK(cmt);GI  AH (cmt); HAK  GIK(cmt)  A  HK  I
 GK(gcg)  HK  KG (hai cạnh tương ứng)
Vậy K là trung điểm của GH 1,0
Kẻ OE  AB tại E, Chứng minh được BO là tia phân giác của ABC (*) 0,5
Chứng minh được AB  BI Theo câu b A  HK  I
 GK(gcg)  AK  KI (hai cạnh tương ứng)
Câu 4c Chứng minh được: A  BK  I  BK( . c . c c) (2 đ) 0,5
 ABK  IBK Từ đó suy ra BK là tia phân giác của ABC ** 0,5
Từ (*) và (**) suy ra tia BK, BO trùng nhau Hay , B ,
O K là ba điểm thẳng hàng. 0,5
Diện tích xung quanh của phần hình hộp chữ nhật là: 4.2.(8 +12) = 160 (m2) 0,5
Tổng diện tích hai mái nhà là: 2.12.5 = 120 (m2) 0,25
Tổng diện tích hai đáy của phần hình lăng trụ đứng tam giác là: Câu 5 3.8  0,25 (2 đ) 2. 24 (m2) 2
Tổng diện tích kính cường lực cần phải sử dụng là: 160 +120 + 24 = 304 (m2) 0,5
Chi phí mua kính cường lực để ghép được ngôi nhà này là: 0,5
304. 800 = 243200 (nghìn đồng)