29 trang 16 lượt tải

Đề KSCL môn Toán học sinh lớp 12 năm 2020 – 2021 sở GD&ĐT Phú Thọ

31

Đề KSCL môn Toán học sinh lớp 12 năm 2020 – 2021 sở GD&ĐT Phú Thọ gồm 07 trang với 50 câu trắc nghiệm, đề thi có đáp án và lời giải chi tiết.

Chủ đề: Đề thi THPTQG môn Toán năm 2023 1.2 K tài liệu

Môn: Toán 2.2 K tài liệu

Tác giả:

Profile

Thanh Hoa

1 năm trước
Danh sách Quiz
/29
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
SỞ GIÁO DỤC VÀ ĐÀO TẠO
PHÚ THỌ
MÃ ĐỀ THI: 361
KHẢO SÁT CHẤT LƯỢNG HỌC SINH LỚP 12 THPT
NĂM HỌC 2020 – 2021
MÔN: TOÁN
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
Đề thi gồm có 05 trang
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh: . . . . . . . . . . . . .
Câu 1: Trong không gian
Oxyz
, mặt cầu tâm
2; 1;0
I
, bán kính
5
R
có phương trình là
A.
2 2 2
x y z x y
. B.
2 2 2
4 2 20 0
x y z x y
.
C.
2 2 2
2 25 0
x y z x y
. D.
2 2 2
4 2 25 0
x y z x y
.
Câu 2: Cho hàm số
y f x
có đồ thị như hình vẽ.
Điểm cực tiểu của hàm số đã cho là
A.
2
x
. B.
1
x
. C.
0
x
. D.
5
x
.
Câu 3: Có bao nhiêu cách chọn ra
2
cái bút từ một hộp đựng
10
chiếc bút?
A.
2
10
C
. B.
10
2
. C.
20
. D.
2
10
A
.
Câu 4: Cho hình lăng trụ có bán kính đáy
2
r
và diện tích xung quanh
36
xq
s
. Độ dài đường sinh
l
của hình trụ đã cho bằng
A.
9
. B.
6
. C.
12
. D.
18
.
Câu 5: Cho hàm số
y f x
có bảng biến thiên như sau
Số nghiệm của phương trình
2 5 0
f x
là
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
A. 1 B. 2 C. 4 D. 3
Câu 6: Đạo hàm của hàm số
5
logy x là
A.
1
y
x
B.
1
ln5
y
x
C.
ln5
x
y
D.
1
5ln
y
x
Câu 7: Cho hàm số
y f x
có bảng biến thiên như sau:
Đồ thị hàm số có đường tiệm cận ngang là
A.
1x
. B.
2x
. C.
1y
. D.
2y
.
Câu 8: Với
x
là số thực dương bất kỳ, biểu thức
3
P x
bằng
A.
2
3
x
. B.
5
6
x
. C.
1
6
x
. D.
3
2
x
.
Câu 9: Cho hàm số
y f x
có đồ thị như hình vẽ
Hàm số đã cho nghịch biến trên khoảng nào dưới đây ?
A.
1;
. B.
0;1
. C.
;0
. D.
1;1
.
Câu 10: Họ nguyên hàm của hàm số
1
1
f x
x
là
A.
ln 1x C
. B.
ln 1x C
. C.
2
1
x C
x
. D.
2
1
1
C
x
.
Câu 11: Cho khối chóp có diện tích đáy
3B
và thể tích
6V
. Chiều cao
h
của khối chóp đã cho bằng?
A. 18. B. 2. C. 4. D. 6.
Câu 12: Trong không gian
Oxyz
, cho hai vectơ
1;3; 2u
và
2;5; 1v
. Vectơ
u v
có tọa độ là
A.
1;8; 3
. B.
3;8; 3
. C.
3;8; 3
. D.
1; 8;3
.
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
Câu 13: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ?
A.
4 2
2 2.
y x x
B.
3 2
2 2.
y x x
C.
3 2
2 2.
y x x
D.
4 2
2 2.
y x x
Câu 14: Tập xác định của hàm số
3
log
y x
là
A.
3; .
B.
; .

C.
0; .
D.
0; .

Câu 15: Nghiệm của phương trình
2 1
2 32
x
là
A.
4
x
. B.
3
x
. C.
5
x
. D.
2
x
.
Câu 16: Trong không gian
Oxyz
cho hai điểm
1 1 1 3 3 5
A ; ; ,B ; ;
. Tọa độ trung điểm của đoạn thẳng
AB
là
A.
4; 2;4
. B.
1; 2;3
. C.
2; 1; 2
. D.
2; 4;6
.
Câu 17: Cho hàm số
y f x
có đạo hàm liên tục trên
1; 2 .
Biết
1 1, 2 4.
f f
Giá trị
2
1
d
f x x
bằng
A.
3
. B.
4
. C.
4
. D.
3
.
Câu 18: Cho khối cầu có bán kính
.
r a
Thể tích của khối cầu đã cho bằng
A.
3
4
a
. B.
3
2
3
a
. C.
3
a
. D.
3
4
3
a
.
Câu 19: Với
a
,
b
là các số thực dương bất kỳ khác 1, khi đó
log
b
a
bằng
A.
log .
a
b
B.
1
.
log
a
b
C.
log log .
a b
D.
log b.
a
Câu 20: Cho hình nón có bán kính đáy
4
r
và chiều cao
9
h
. Thể tích
V
của khối nón đã cho bằng
A.
126
. B.
36
. C.
48
. D.
108
.
Câu 21: Cho cấp số nhân
n
u
với
1
1
u
và công bội
3
q
. Giá trị của
3
u
là
A.
27
. B.
3
. C.
9
. D.
2
.
Câu 22: Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 2 2 4z 2 0
S x y z x y
. Tâm của
S
có
toạ độ là
A.
1; 1; 2
. B.
1;1; 2
. C.
1;1; 2
. D.
2; 2;4
.
Câu 23: Cho
4 4
0 0
d 1, d 1
f x x g x x
. Giá trị
4
0
2 d
f x g x x
bằng
A.
0
. B.
1
. C.
1
. D.
3
.
Câu 24: Cho hàm số
y f x
có bảng biến thiên như sau
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
; 2

. B.
2;0
. C.
0;

. D.
3;1
.
Câu 25: Họ nguyên hàm của hàm số
3sin
f x x
là
A.
3sin
x C
. B.
3cos
x C
. C.
3cos 2
x C
. D.
3cos
x C
.
Câu 26: Một mặt cầu có tâm
O
nằm trên mặt đáy của hình chóp tam giác đều .
S ABC
có tất cả các cạnh
bằng nhau. Các đỉnh
, ,
A B C
thuộc mặt cầu. Biết bán kính mặt cầu bằng
3
. Tổng độ dài
l
các
giao tuyến của mặt cầu với các mặt bên của hình chóp thỏa mãn điều kiện nào sau đây?
A.
3;2
l
. B.
3 3;6
l
. C.
13 2;12 3
l
. D.
1; 2
l
.
Câu 27: Cho
a
là số thực dương. Giả sử
F x
là một nguyên hàm của hàm số
2
2
e ln
x
f x ax
x
trên tập
\ 0
và thỏa mãn
1 5; 2 21
F F
. Khẳng định nào sau đây đúng ?
A.
3;a

. B.
0;1
a
. C.
1;2
a
. D.
2;3
a
.
Câu 28: Có bao nhiêu cặp số nguyên
;
x y
thỏa mãn
0 2021
y
và
3
3
3 3 6 9 log
x
x y y
?
A.
2021
. B.
7
. C.
9
. D.
2020
.
Câu 29: Cho hình trụ có thiết diện qua trục là hình vuông cạnh
4 .
a
Diện tích xung quanh của hình trụ đã
cho bằng
A.
2
16
a
. B.
2
4
a
. C.
2
64
a
. D.
2
8
a
.
Câu 30: Cho bất phương trình
2
2
1 1
2 2
1
1 log 2 4 5 log 4 4 0
2
m x m m
x
với m là tham số
thực. Tập hợp tất cả các giá trị của m để bất phương trình có nghiệm thuộc đoạn
5
;4
2
là?
A.
3;

. B.
7
;
3

. C.
7
3;
3
. D.
7
;
3

.
Câu 31: Giá trị lớn nhất của hàm số
2
3 5 e
x
f x x x
trên đoạn
1;2
bằng
A.
2
e
. B.
2
4
e
. C.
2
3
e
. D.
3
e
.
Câu 32: Cho hàm số
y f x
, biết
3
3 1
f x x x
có tất cả bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
5;5
sao cho hàm số
2 1 6
y f x m x
nghịch biến trên khoảng
2;3
?
A.
10
. B.
9
. C.
7
. D.
8
.
Câu 33: Biết
F x
là một nguyên hàm của hàm số
2 3
1 2
f x x x
. Khẳng định nào dưới đây đúng
?
A.
3
3
2
1 2
9
F x x
. B.
3
3
2
1 2
3
F x x
.
C.
3
3
1
1 2
2
F x x
D.
3
3
1
1 2
9
F x x
.
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
Câu 34: Cho hàm số
( )
y f x
có
3
2
2 3 2 3
f x x x x x
. Tập hợp tất cả các giá trị của tham
số
m
sao cho hàm số
2
6
y f x x m
có 3 điểm cực trị phân biệt là nửa khoảng
;
a b
. Giá
trị của
a b
bằng
A.
21
. B.
23
. C.
22
. D.
20
.
Câu 35: Cho hàm số
f x
có đạo hàm liên tục trên đoạn
0;3
thỏa mãn
3 4
f
,
3
2
0
1
d
27
f x x
và
3
3
0
333
d
4
x f x x
. Giá trị của
3
0
d
f x x
bằng
A.
3
2
x
. B.
153089
1215
x
. C.
25
2
x
. D.
150893
21
x
.
Câu 36: Có tất cả bao nhiêu giá trị nguyên của m thuộc đoạn
10;10
để hàm số
3 2 2
3 6 2 1
y x mx m x
đồng biến trên khoảng
2;

A.
21
. B.
18
. C.
20
. D.
19
.
Câu 37: Tổng tất cả số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
2
9
6 5
x
y
x x
bằng
A.
2
. B.
4
. C.
1
. D.
3
.
Câu 38: Tổng các giá trị nguyên của tham số m để phương trình
3
3
log 1 log 8
x mx
có hai
nghiệm phân biệt bằng
A.
11
. B.
22
. C.
3
. D.
18
.
Câu 39: Cho hàm số
f x
có đồ thị như hình vẽ.
Gọi
,
M m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3
sin 1
f x
trên đoạn
5
2 ;
2
. Giá trị của 2
M m
bằng
A.
5
. B.
11
. C.
13
. D.
7
.
Câu 40: Cho hình lăng trụ đứng .
ABC A B C
có đáy là tam giác đều cạnh bằng
a
(tham khảo hình vẽ)
x
y
2
-5
-3
-1
-1
O
1
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
Khoảng cách giữa hai đường thẳng
AA
và
BC
bằng
A.
a
. B.
3
3
a
. C.
2
a
. D.
3
2
a
.
Câu 41: Trong không gian
,
Oxyz
cho hai điểm
1;1;2
A
và
3; 2; 3
B
. Mặt cầu
S
có tâm
I
thuộc
trục
Ox
và đi qua hai điểm
,
A B
có bán kính bằng
A.
4
. B.
4 2
. C.
14
. D.
3
.
Câu 42: Cho khối hộp
.
ABCD A B C D
có đáy
ABCD
là hình chữ nhật
2 , 2
AB a AD a
. Điểm
A
cách đều các điểm
, , ,
A B C D
. Mặt bên
CDD C
tạo với mặt phẳng đáy một góc
45
(tham
khảo hình vẽ).
Thể tích khối hộp đã cho bằng
A.
3
2 6
a
. B.
3
2
a
. C.
3
2 2
a
. D.
3
2 2
3
a
.
Câu 43: Cho hai số thực
1, 1
a b
. Biết phương trình
2
1
. 1
x x
a b
có hai nghiệm phân biệt
1 2
,
x x
. Giá trị
nhỏ nhất của biểu thức
2
1 2
1 2
1 2
4
x x
S x x
x x
bằng
A.
3
3 4
. B.
4
. C.
3
4
. D.
3
3 2
.
Câu 44: Cho hình nón đỉnh
S
có đáy là đường tròn tâm
O
, thiết diện qua trục là tam giác đều. Mặt phẳng
P
đi qua
S
và cắt đường tròn đáy tại
,
A B
sao cho
120
AOB
. Biết rằng khoảng cách từ
O
đến
P
bằng
3 13
13
a
. Thể tích của khối nón đã cho bằng
A.
3
3
3
a
. B.
3
a
. C.
3
3
2
a
. D.
3
3
a
.
C
B
A'
C'
B'
A
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
Câu 45: Cho hàm số
4 2
f x ax bx c
có đồ thị như hình vẽ
Số nghiệm của phương trình
2 1 2 1 5 0
f x x
là
A.
2
. B.
3
. C.
5
. D.
4
.
Câu 46: Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
để hàm số
2 3 2
1 3 5 1
y m x m x x
có hai điểm cực trị
1 2
,
x x
sao cho
1 2
8
x x
. Tích các
phần tử của
S
bằng
A.
9
4
. B.
1
4
. C.
1
4
. D.
9
4
.
Câu 47: Trong không gian
Oxyz
, cho hình vuông
ABCD
có
3;0;8
B
và
5; 4;0
D
. Độ dài cạnh của
hình vuông đã cho bằng
A.
6 2
. B.
5 2
. C.
6
. D.
12
.
Câu 48: Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng đáy và
2
SA a
( tham khảo hình vẽ).
Góc giữa đường thẳng
SC
và mặt phẳng đáy bằng
A.
60
. B.
45
. C.
90
. D.
30
.
Câu 49: Một đội thanh niên tình nguyện của trường gồm
6
học sinh nam và
5
học sinh nữ. Chọn ngẫu
nhiên
4
học sinh để cùng với các giáo viên tham gia đo thân nhiệt cho học sinh khi đến trường.
Xác suất để chọn được
4
học sinh trong đó số học sinh nam bằng số học sinh nữ bằng:
A.
5
66
. B.
5
11
. C.
6
11
. D.
2
33
.
Câu 50: Tập nghiệm của bất phương trình
0,5 0,5
log 2 8 log 2 4
x x
là:
A.
1;
. B.
4; 1
.
C.
1;2
. D.
; 1 2;

.
------------------------- HẾT -------------------------
A
D
B
C
S
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
BẢNG ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
A
A
A
C
B
D
C
B
A
D
A
D
D
B
C
A
D
B
C
C
B
B
B
D
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
B
C
B
A
C
C
A
D
C
C
C
C
C
B
D
C
C
A
D
C
C
A
B
B
C
Câu 1: Trong không gian
Oxyz
, mặt cầu tâm
2; 1;0
I
, bán kính
5
R
có phương trình là
A.
2 2 2
x y z x y
. B.
2 2 2
4 2 20 0
x y z x y
.
C.
2 2 2
2 25 0
x y z x y
. D.
2 2 2
4 2 25 0
x y z x y
.
Lời giải
Chọn A
Mặt cầu tâm
2; 1;0
I
, bán kính
5
R
có phương trình là
2 2
2 2 2 2 2
2 1 5 4 2 20 0
x y z x y z x y
Câu 2: Cho hàm số
y f x
có đồ thị như hình vẽ.
Điểm cực tiểu của hàm số đã cho là
A.
2
x
. B.
1
x
. C.
0
x
. D.
5
x
.
Lời giải
Chọn A
Dựa vào đồ thị suy ra hàm số đạt cực tiểu tại
2
x
.
Câu 3: Có bao nhiêu cách chọn ra
2
cái bút từ một hộp đựng
10
chiếc bút?
A.
2
10
C
. B.
10
2
. C.
20
. D.
2
10
A
.
Lời giải
Chọn A
Số cách lấy ra ra
2
cái bút từ một hộp đựng
10
chiếc bút là một tổ hợp chập
2
của
10
phần tử
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
Có
2
10
C
cách.
Câu 4: Cho hình lăng trụ có bán kính đáy
2
r
và diện tích xung quanh
36
xq
s
. Độ dài đường sinh
l
của hình trụ đã cho bằng
A.
9
. B.
6
. C.
12
. D.
18
.
Lời giải
Chọn A
Ta có diện tích xung quanh của hình trụ là
36
2 9
2 2 .2
xq
xq
S
S rl l l l
r
Câu 5: Cho hàm số
y f x
có bảng biến thiên như sau
Số nghiệm của phương trình
2 5 0
f x
là
A. 1 B. 2 C. 4 D. 3
Lời giải
Chọn B
Phương trình đã cho đưa về
5
2
f x
.
Dựa vào bảng biến thiên ta thấy đồ thị đã cho cắt đường thẳng
5
2
y
tại 4 điểm phân biệt.
Từ đây ta thu được 4 nghiệm.
Câu 6: Đạo hàm của hàm số
5
log
y x
là
A.
1
y
x
B.
1
ln5
y
x
C.
ln5
x
y
D.
1
5ln
y
x
Lời giải
Chọn B
Ta có
5
1
log
ln5
y x y
x
.
Câu 7: Cho hàm số
y f x
có bảng biến thiên như sau:
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
Đồ thị hàm số có đường tiệm cận ngang là
A.
1x
. B.
2x
. C.
1y
. D.
2y
.
Lời giải
Chọn D
Ta có
lim lim 2
x x
y y
 
nên đường thẳng
2y
là tiệm cận ngang của đồ thị hàm số
.y f x
Câu 8: Với
x
là số thực dương bất kỳ, biểu thức
3
P x
bằng
A.
2
3
x
. B.
5
6
x
. C.
1
6
x
. D.
3
2
x
.
Lời giải
Chọn C
Với
x
là số thực dương bất kỳ, ta có:
1
1
1 1 1
1
3
.
3
3
2 3 6
2
P x x x x x
.
Câu 9: Cho hàm số
y f x
có đồ thị như hình vẽ
Hàm số đã cho nghịch biến trên khoảng nào dưới đây ?
A.
1;
. B.
0;1
. C.
;0
. D.
1;1
.
Lời giải
Chọn B
Nhìn vào đồ thị ta thấy trên khoảng
0;1
đồ thị đi xuống nên hàm số
y f x
nghịch biến trên
0;1
.
Câu 10: Họ nguyên hàm của hàm số
1
1
f x
x
là
A.
ln 1x C
. B.
ln 1x C
. C.
2
1
x C
x
. D.
2
1
1
C
x
.
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
Lời giải
Chọn A
Áp dụng hệ quả
1
ln
dx
ax b C
ax b a
ta được nguyên hàm của hàm số
1
1
f x
x
là
ln 1
F x x C
.
Câu 11: Cho khối chóp có diện tích đáy
3
B
và thể tích
6
V
. Chiều cao
h
của khối chóp đã cho bằng?
A. 18. B. 2. C. 4. D. 6.
Lời giải
Chọn D
Chiều cao
h
của khối chóp đã cho là
6
6
1 1
.3
3 3
V
h
B
.
Câu 12: Trong không gian
Oxyz
, cho hai vectơ
1;3; 2
u
và
2;5; 1
v
. Vectơ
u v
có tọa độ là
A.
1;8; 3
. B.
3;8; 3
. C.
3;8; 3
. D.
1; 8;3
.
Lời giải
Chọn A
1 2;3 5; 2 1 1;8; 3
u v
.
Câu 13: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ?
A.
4 2
2 2.
y x x
B.
3 2
2 2.
y x x
C.
3 2
2 2.
y x x
D.
4 2
2 2.
y x x
Lời giải
Chọn D
Đồ thị hàm số nhận
Oy
làm trục đối xứng nên loại đáp án B và C.
Ta có
lim
x
y
nên loại đáp án A.
Chọn đáp án D.
Câu 14: Tập xác định của hàm số
3
log
y x
là
A.
3; .
B.
; .

C.
0; .
D.
0; .

Lời giải
Chọn D
Điều kiện:
0 0;x x
.
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
Vậy tập xác định
0; .
D
Câu 15: Nghiệm của phương trình
2 1
2 32
x
là
A.
4
x
. B.
3
x
. C.
5
x
. D.
2
x
.
Lời giải
Chọn B
Ta có:
2 1 2 1 5
2 32 2 2 2 1 5 3
x x
x x
.
Câu 16: Trong không gian
Oxyz
cho hai điểm
1 1 1 3 3 5
A ; ; ,B ; ;
. Tọa độ trung điểm của đoạn thẳng
AB
là
A.
4; 2;4
. B.
1; 2;3
. C.
2; 1; 2
. D.
2; 4;6
.
Lời giải
Chọn C
Ta có:
I
là trung điểm đoạn thẳng
AB
2
2
1
2
2
2
A B
A B
A B
x x
x
x
y y
y y
z
z z
z
.
Câu 17: Cho hàm số
y f x
có đạo hàm liên tục trên
1;2 .
Biết
1 1, 2 4.
f f
Giá trị
2
1
d
f x x
bằng
A.
3
. B.
4
. C.
4
. D.
3
.
Lời giải
Chọn A
Câu 18: Cho khối cầu có bán kính
.
r a
Thể tích của khối cầu đã cho bằng
A.
3
4
a
. B.
3
2
3
a
. C.
3
a
. D.
3
4
3
a
.
Lời giải
Chọn D
Ta có thể tích khối cầu
3 3
4 4
.
3 3
V r a
Câu 19: Với
a
,
b
là các số thực dương bất kỳ khác 1, khi đó
log
b
a
bằng
A.
log .
a
b
B.
1
.
log
a
b
C.
log log .
a b
D.
log b.
a
Lời giải
Chọn B
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
Có
1
log .
log
b
a
a
b
Câu 20: Cho hình nón có bán kính đáy
4
r
và chiều cao
9
h
. Thể tích
V
của khối nón đã cho bằng
A.
126
. B.
36
. C.
48
. D.
108
.
Lời giải
Chọn C
Thể tích
V
của khối nón đã cho bằng
2 2
1 1
.9. .4 48 .
3 3
V h r
Câu 21: Cho cấp số nhân
n
u
với
1
1
u
và công bội
3
q
. Giá trị của
3
u
là
A.
27
. B.
3
. C.
9
. D.
2
.
Lời giải
Chọn C
Ta có:
2 2
3 1
. 1.3 9
u u q
.
Câu 22: Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 2 2 4z 2 0
S x y z x y
. Tâm của
S
có
toạ độ là
A.
1; 1;2
. B.
1;1; 2
. C.
1;1; 2
. D.
2; 2;4
.
Lời giải
Chọn B
Ta có:
2 2 2
2 2 2
2 2 4z 2 0
1 1 2 8
x y z x y
x y z
Khi đó Tâm của
S
có toạ độ là
1;1; 2
I
.
Câu 23: Cho
4 4
0 0
d 1, d 1
f x x g x x
. Giá trị
4
0
2 d
f x g x x
bằng
A.
0
. B.
1
. C.
1
. D.
3
.
Lời giải
Chọn B
Ta có
4 4 4
0 0 0
2 d d 2 d 1 2 1
f x g x x f x x g x x
.
Câu 24: Cho hàm số
y f x
có bảng biến thiên như sau
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
; 2

. B.
2;0
. C.
0;

. D.
3;1
.
Lời giải
Chọn B
Dựa vào bảng biến thiên ta có hàm số đã cho đồng biến trên khoảng
2;0
.
Câu 25: Họ nguyên hàm của hàm số
3sin
f x x
là
A.
3sin
x C
. B.
3cos
x C
. C.
3cos 2
x C
. D.
3cos
x C
.
Lời giải
Chọn D
3sin d 3cos
x x x C
Câu 26: Một mặt cầu có tâm
O
nằm trên mặt đáy của hình chóp tam giác đều .
S ABC
có tất cả các cạnh
bằng nhau. Các đỉnh
, ,
A B C
thuộc mặt cầu. Biết bán kính mặt cầu bằng
3
. Tổng độ dài
l
các
giao tuyến của mặt cầu với các mặt bên của hình chóp thỏa mãn điều kiện nào sau đây?
A.
3; 2
l
. B.
3 3;6
l
. C.
13 2;12 3
l
. D.
1; 2
l
.
Lời giải
Chọn A
Gọi
D
là trung điểm của
AB
, kẻ
OI SD I
là hình hình chiếu của
O
lên
SAB
. Suy ra
I
là tâm đường tròn giao tuyến của mặt cầu và
SAB
. Gọi
MN
là đoạn giao tuyến
3
l MN
.
Gọi
K
là trung điểm của
MB
, đặt
AB a
.
Ta có
3
OA OB OC
2
3 3
3
CD AB a
2 2
3 2
SO SC OC
.
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
Ta có
2 2 2
1 1 1
2
OI
OI OS OD
;
4
SI
;
1
2
DI
2 2
7
r R OI
Xét tam giác vuông
SIK
ta có
0
1
.sin 30 2
2
IK SI SI
Xét tam giác vuông
MIK
ta có
0
2
cosM M 40,89
7
IK
IK IK
IM
0
M 38,2
IN
Ta có độ dài cung
.38,2. 7
3. 3 5,29
180
l MN
.
Câu 27: Cho
a
là số thực dương. Giả sử
F x
là một nguyên hàm của hàm số
2
2
e ln
x
f x ax
x
trên tập
\ 0
và thỏa mãn
1 5; 2 21
F F
. Khẳng định nào sau đây đúng ?
A.
3;a

. B.
0;1
a
. C.
1;2
a
. D.
2;3
a
.
Lời giải
Chọn C
Xét
2 2
2 2 2
e ln d ln d e . d e . d
x x x x
F x ax x e ax x x I x
x x x
Xét
2
e .ln d
x
I ax x
Đặt
2
2
ln
d d
d e d
e
x
x
u ax
u x
x
v x
v
Khi đó:
2 2
2
e .ln d e ln e . d
x x x
I ax x ax x
x
Suy ra:
2
ln
x
F x e ax C
Vì :
2
2
.ln 5
1 5
.ln 5
. ln4 ln 21
.ln4 21
2 21
e a C
F
e a C
e a C
e a C
F
2 2
.ln 5 (1)
ln 21 2 .ln 2 (2)
e a C
e a C e
Lấy
(2) (1)
ta được:
2
2
16 2 ln 2
2
2
16 2 ln 2
ln 3,43
e
e e
e
a a e
e e
.
Suy ra:
3;a

.
Câu 28: Có bao nhiêu cặp số nguyên
;
x y
thỏa mãn
0 2021
y
và
3
3
3 3 6 9 log
x
x y y
?
A.
2021
. B.
7
. C.
9
. D.
2020
.
Lời giải
Chọn B
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
Ta có:
3
3
3 3 6 9 log
x
x y y
3
3 3 6 9 3log
x
x y y
3
3 3 9 6 3log
x
x y y
3
3 3 9 3 2 log
x
x y y
2
3 3
3 3 9 3 log 3 log
x
x y y
3
3 3 9 3log 9
x
x y y
Đặt:
3
log 9 9 3
t
t y y
Phương trình trở thành:
3 3 3 3
x t
x t x t
3
3
log 9 2 log
x y x y
Để
x
thì
3
log y
mà
0 2021
y
Suy ra:
0 1 2 3 4 5 6
3 ;3 ;3 ;3 ;3 ;3 ;3
y
Vậy: có 7 cặp số nguyên
;
x y
thỏa mãn YCBT.
Câu 29: Cho hình trụ có thiết diện qua trục là hình vuông cạnh
4 .
a
Diện tích xung quanh của hình trụ đã
cho bằng
A.
2
16
a
. B.
2
4
a
. C.
2
64
a
. D.
2
8
a
.
Lời giải
Chọn A
Gọi hình trụ như hình vẽ, thiết diện qua trục là hình vuông ABCD.
Ta có
4 , 2 .
2
AB
h AD a R a
2
2 16 .
xq
S Rh a
Câu 30: Cho bất phương trình
2
2
1 1
2 2
1
1 log 2 4 5 log 4 4 0
2
m x m m
x
với m là tham số
thực. Tập hợp tất cả các giá trị của m để bất phương trình có nghiệm thuộc đoạn
5
;4
2
là?
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
A.
3;

. B.
7
;
3

. C.
7
3;
3
. D.
7
;
3

.
Lời giải
Chọn C
Điều kiện
2.
x
2
2
1 1
2 2
1
1 log 2 4 5 log 4 4 0
2
m x m m
x
2
2 2
1 log 2 5 log 2 1 0
m x m x m
Đặt
2
log 2 ,
t x
do
5
;4 1;1 .
2
x t
Bất phương trình trở thành
2
1 5 1 0
m t m t m
2 2
1 5 1
m t t t t
2
2
5 1
.
1
t t
m
t t
Xét hàm số
2
2
5 1
1
t t
g t
t t
trên
1;1 ,
từ table ta có bảng giá trị của
( )
g t
như sau:
3;m

.
Câu 31: Giá trị lớn nhất của hàm số
2
3 5 e
x
f x x x
trên đoạn
1;2
bằng
A.
2
e
. B.
2
4
e
. C.
2
3
e
. D.
3
e
.
Lời giải
Chọn C
TXĐ:
D
Ta có
2
2 3 e 3 5 e
x x
f x x x x
2
2 e
x
x x
2
1 7
e
2 4
x
x
Vì
2
1 7
e 0
2 4
x
f x x
với mọi
x
Suy ra hàm số
f x
đồng biến trên
hay hàm số
f x
đồng biến trên
1;2
Do đó hàm số
f x
đạt giá trị lớn nhất trên đoạn
1;2
tại
2
x
Ta có
2
1;2
max 2 3e
f x f
.
Câu 32: Cho hàm số
y f x
, biết
3
3 1
f x x x
có tất cả bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
5;5
sao cho hàm số
2 1 6
y f x m x
nghịch biến trên khoảng
2;3
?
A.
10
. B.
9
. C.
7
. D.
8
.
Lời giải
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
Chọn A
Xét hàm số
2 1 6
y f x m x
trên khoảng
2;3
.
Ta có
3
2 1 2 3 2 1 1
y f x m x x m
3 2
6 9 4
y x x x m
.
Để hàm số
2 1 6
y f x m x
nghịch biến trên khoảng
2;3
0, 2;3
y x
3 2
6 9 4, 2;3
m x x x x
(1)
Xét hàm số
3 2
6 9 4
g x x x x
trên khoảng
2;3
.
Ta có
2
1 2;3
3 12 9; 0
3 2;3
x
g x x x g x
x
Từ BBT, bất PT (1)
2
m
.
Vì
5;5 5;2 ,
m m m m
có
8
giá trị.
Câu 33: Biết
F x
là một nguyên hàm của hàm số
2 3
1 2
f x x x
. Khẳng định nào dưới đây đúng
?
A.
3
3
2
1 2
9
F x x
. B.
3
3
2
1 2
3
F x x
.
C.
3
3
1
1 2
2
F x x D.
3
3
1
1 2
9
F x x
.
Lời giải
Chọn D
Ta có:
2 3
( ) 1 2
f x x x
2 3
d 1 2 d
F x f x x x x x
Đặt
3 2 3 2 2
1 2 1 2 2 6
3
tdt
t x t x tdt x dx x dx
Từ đó nguyên hàm trên trở thành:
3 3
2 3 2
1 1
( ) 1 2 .
3 3 3 9
t t
F x x x dx t dt C C
Vậy
3
3 3
3 3
1 1
( ) 1 2 1 2
9 9 9
t
F x C x C x
.
Câu 34: Cho hàm số
( )
y f x
có
3
2
2 3 2 3
f x x x x x
. Tập hợp tất cả các giá trị của tham
số
m
sao cho hàm số
2
6
y f x x m
có 3 điểm cực trị phân biệt là nửa khoảng
;
a b
. Giá
trị của
a b
bằng
A.
21
. B.
23
. C.
22
. D.
20
.
Lời giải
Chọn C
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
Ta có:
3 3
2
2 3 2 3 2 1 2 3
f x x x x x x x x x
2 3
1 2 3
x x x
1
0 2
3
x
f x x
x
với
2
x
là nghiệm bội chẵn nên suy ra
f x
có 2 điểm cực trị
Đặt
2 2
6 2 3 6
g x f x x m g x x f x x m
Để hàm số
g x
có 3 điểm cực trị thì
0
g x
phải có 3 nghiệm bội lẻ phân biệt
Cho
2
2
1
2
2
2
2
2
3
3
3
6 1
0 6 1
6 0
6 2
6 3
6 3
x
x
x
x x m
g x m x x g x
f x x m
x x m
m x x g x
x x m
Do
2
x
là nghiệm bội chẵn nên các nghiệm của phương trình
2
6 2
x x m
đều là nghiệm
bội chẵn của phương trình
0
g x
, vì thế nên ta không xét phương trình này
Từ đó, để
0
g x
phải có 3 nghiệm bội lẻ phân biệt thì phương trình (1) và (2) đều tạo với
nhau đúng 2 nghiệm, nên ta vẽ lần lượt hai hàm số
1
g x
và
2
g x
lên cùng 1 hệ trục tọa độ
Oxy
để từ đó đường thẳng
y m
chỉ cắt đúng 2 nghiệm từ 2 hai hàm này
Dựa vào đó ta kết luận
10;12
m
. Suy ra
10, 12
a b
Vậy
10 12 22
a b
Câu 35: Cho hàm số
f x
có đạo hàm liên tục trên đoạn
0;3
thỏa mãn
3 4
f
,
3
2
0
1
d
27
f x x
và
3
3
0
333
d
4
x f x x
. Giá trị của
3
0
d
f x x
bằng
A.
3
2
x
. B.
153089
1215
x
. C.
25
2
x
. D.
150893
21
x
.
Lời giải
Chọn C
Tính:
3
3
0
d
x f x x
. Đặt
4
3
d d
d d
4
u f x x
u f x
x
v x x
v
.
Ta có:
3
4
3 3
3 4
0 0
0
1
d . d
4 4
x f x
x f x x x f x x
3 3
4 4
0 0
81. 3 0. 0
1 1
. d 81 . d
4 4 4
f f
x f x x x f x x
.
Mà
3
4
0
333
d
4
x f x x
3 3
4 4
0 0
1 9
. d . d 9
4 4
x f x x x f x x
.
Ta có
3
2
0
1
d
27
f x x
(1).
3
3
9
8
0
0
d 2187
9
x
x x
2
3
4
0
1 1
d
243 27
x x
(2).
(1)
(2)
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
3 3
4 4
0 0
2 2
. d 9 . d
243 27
x f x x x f x x
(3).
Cộng hai vế (1) (2) và (3) suy ra
3 3 3
2
8 4
0 0 0
1 1 1 1 2
d d 2 . d 0
59049 243 27 27 27
f x x x x x f x x
.
3
2
4 8
2
0
1 1
2. d 0
243 243
f x x f x x x
2
3
4
0
1
d 0
243
f x x x
.
Do
2
4
1
0
243
f x x
2
3
4
0
1
d 0
243
f x x x
. Mà
2
3
4
0
1
d 0
243
f x x x
4
1
0
243
f x x
.
5
1215
x
f x C
. Mà
243 21
3 4 4
1215 5
f C C
.
Do đó
5
21
1215 5
x
f x
.
Vậy
3
3 1
5 6
0 0
0
21 21 25
d d
1215 5 7290 5 2
x x
f x x x x
.
Câu 36: Có tất cả bao nhiêu giá trị nguyên của m thuộc đoạn
10;10
để hàm số
3 2 2
3 6 2 1
y x mx m x
đồng biến trên khoảng
2;

A.
21
. B.
18
. C.
20
. D.
19
.
Lời giải
Chọn C
Ta có :
2 2
=3 6 6 2
y x mx m
Khi đó :
2
2
3 3.6 2
m m
2
9 4
m
TH1 : Nếu
0
2
2
m
m
. Khi đó ta có
3 0
a
nên
0
y
với mọi x
. Do đó hàm số
đã cho đồng biến trên
2;

. Kết hợp với giả thiết
; 10;10
m m
ta được
10; 9; 8;...; 2;2;3;...;10
m
. Vậy trường hợp này có 18 số nguyên thỏa mãn.
TH2: Nếu
0
2 2
m
. Khi đó
0
y
có hai nghiệm phân biệt
1
x
và
2
x
. Giả sử
1 2
x x
Ta có
1 2
0 ; ;y x x x
và
1 2
0 ;
y x x x
. Do đó để hàm số đã cho đồng
biến trên
2;

thì
2
2; ;x

.
Ta có :
1 2
2
x x
1 2
1 2
2
2
2 . 2 0
x x
x x
Xét
1 2
2
2
x x
2
m
.(1)
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
Xét
1 2
2 . 2 0
x x
1 2 1 2
2
2
. 2 4 0
2 2 4 4 0
2 0
0
(2)
2
x x x x
m m
m m
m
m
Kết hợp điều kiện
(1)
và
(2)
và giả thiết
; 10;10
m m
ta được
1;0
m
. Vậy trường
hợp này có 2 số nguyên thỏa mãn.
Vậy có 20 giá trị nguyên của m để hàm số đã cho đồng biến trên
2;

.
Câu 37: Tổng tất cả số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
2
9
6 5
x
y
x x
bằng
A.
2
. B.
4
. C.
1
. D.
3
.
Lời giải
Chọn C
Hàm số
2
2
9
6 5
x
y
x x
có tập xác định
3;3D
Hàm số không có tiệm cận ngang.
Trên tập
D
, xét phương trình:
2
1
6 5 0
5( )
x
x x
x L
, khi đó:
2
2
1
1
9
lim lim
6 5
x
x
x
y
x x

, nên
1
x
là tiệm cận đứng.
Vậy hàm số đã cho có 1 đường tiệm cận.
Câu 38: Tổng các giá trị nguyên của tham số m để phương trình
3
3
log 1 log 8
x mx
có hai
nghiệm phân biệt bằng
A.
11
. B.
22
. C.
3
. D.
18
.
Lời giải
Chọn C
2
2
2
3 3
1 0
1
1
1
8 0
9
2 (*)
2 9
1 8
log 1 log 8
x
x
x
x
PT mx
x m
x x mx
x mx
x
x mx
Phương trình đã cho có 2 nghiệm phân biệt khi phương trình (*) có hai nghiệm phân biệt.
Xét hàm số:
2
9 9
2 ' 1y x y
x x
. Ta có:
3
( ) 0
3( )
x
f x
x L
Bảng biến thiên:
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
Phương trình (*) có hai nghiệm phân biệt khi đường thẳng
y m
cắt đồ thị hàm số
9
2y x
x
trên khoảng
1;

tại 2 điểm phân biệt
4 8
m
.
Vậy có 3 giá trị
5;6;7
m
thỏa mãn yêu cầu bài toán.
Câu 39: Cho hàm số
f x
có đồ thị như hình vẽ.
Gọi
,
M m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3
sin 1
f x
trên đoạn
5
2 ;
2
. Giá trị của 2
M m
bằng
A.
5
. B.
11
. C.
13
. D.
7
.
Lời giải
Chọn B
Với
5
2 ; sin 0;1
2
x x
.
Đặt
3
sin 1 1;0
t x t .
Suy ra
1;0 1;0
max max 3
M f t f x
1;0 1;0
min min 5
m f t f x
Khi đó
2 2. 3 5 11
M m
.
Câu 40: Cho hình lăng trụ đứng
.
ABC A B C
có đáy là tam giác đều cạnh bằng
a
(tham khảo hình vẽ)
x
y
2
-5
-3
-1
-1
O
1
C
B
A'
C'
B'
A
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
Khoảng cách giữa hai đường thẳng
AA
và
BC
bằng
A.
a
. B.
3
3
a
. C.
2
a
. D.
3
2
a
.
Lời giải
Chọn D
Gọi
M
là trung điểm
B C
.
Có
A M B C
và
A M BB
A M BCC B
và
3
2
a
A M
.
Do
// //
AA BB AA BCC B
3
, , ,
2
a
d AA BC d AA BCC B d A BCC B A M
.
Câu 41: Trong không gian
,
Oxyz
cho hai điểm
1;1; 2
A
và
3; 2; 3
B
. Mặt cầu
S
có tâm
I
thuộc
trục
Ox
và đi qua hai điểm
,
A B
có bán kính bằng
A.
4
. B.
4 2
. C.
14
. D.
3
.
Lời giải
Chọn C
Giả sử mặt cầu
S
có tâm
;0;0
I m Ox
và bán kính
R
.
Ta có
,
A B S
nên
IA IB R
.
+)
IA IB
2 2
IA IB
2 2 2
2 2 2
1 1 2 3 2 3
m m
4 4;0;0
m I
.
+) Vậy
14
R IA
.
Câu 42: Cho khối hộp
.
ABCD A B C D
có đáy
ABCD
là hình chữ nhật
2 , 2
AB a AD a
. Điểm
A
cách đều các điểm
, , ,
A B C D
. Mặt bên
CDD C
tạo với mặt phẳng đáy một góc
45
(tham
khảo hình vẽ).
M
C
B
A'
C'
B'
A
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
Thể tích khối hộp đã cho bằng
A.
3
2 6
a
. B.
3
2
a
. C.
3
2 2
a
. D.
3
2 2
3
a
.
Lời giải
Chọn C
Gọi
O AC BD
, ta có
ABCD
là hình chữ nhật nên
O
là tâm đường tròn ngoại tiếp hình chữ
nhật
ABCD
.
Mặt khác
A
cách đều các điểm
, , ,
A B C D A O ABCD
.
Gọi
M
là trung điểm của
AB OM AB
, mà
AB A O AB A M
.
Ta có
/ / , , 45
ABB A CDD C ABB A ABCD CDD C ABCD
Lại có
, , 45
,
ABB A ABCD AB
OM ABCD OM AB ABB A ABCD A MO
A M ABB A A M AB
(vì
A OM
vuông tại
O
nên
A MO
là góc nhọn).
+) Ta có
2
. 2 2
ABCD
S AB AD a
.
+) Tam giác
A OM
vuông tại
O
, có
1
, 45
2
OM AD a A MO
A MO
vuông cân tại
O A O OM a
.
Vậy
3
.
. 2 2
ABCD A B C D ABCD
V S A O a
.
Câu 43: Cho hai số thực
1, 1
a b
. Biết phương trình
2
1
. 1
x x
a b
có hai nghiệm phân biệt
1 2
,
x x
. Giá trị
nhỏ nhất của biểu thức
2
1 2
1 2
1 2
4
x x
S x x
x x
bằng
A.
3
3 4
. B.
4
. C.
3
4
. D.
3
3 2
.
Lời giải
Chọn A
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
Ta có
2 2
1 1 2
. 1 log . log 1 log 1 0
x x x x
b b b
a b a b x a x
*
Điều kiện để phương trình đã cho có 2 nghiệm phân biệt
1 2
,
x x
là
2
log 4 0
b
a
.
Theo hệ thức Vi-et của phương trình
*
, ta có:
1 2
1 2
log
1
b
x x a
x x
.
Mặt khác,
2
2
1 2
1 2
1 2
4
4 log
log
a
a
x x
S x x b
x x b
. Đặt
log log 1 0
a a
t b
Khi đó
2 2
3
4 2 2
3 4
Cauchy
S t t
t t t
.
Suy ra
2
3
2
min 3 4S t
t
hay
3
2
3
log 2
a
b b a
.
Câu 44: Cho hình nón đỉnh
S
có đáy là đường tròn tâm
O
, thiết diện qua trục là tam giác đều. Mặt phẳng
P
đi qua
S
và cắt đường tròn đáy tại
,
A B
sao cho
120
AOB
. Biết rằng khoảng cách từ
O
đến
P
bằng
3 13
13
a
. Thể tích của khối nón đã cho bằng
A.
3
3
3
a
. B.
3
a
. C.
3
3
2
a
. D.
3
3
a
.
Lời giải
Chọn D
Ta có hình minh họa sau:
Gọi thiết diện qua trục
SO
của hình nón là
SBC
và
SAB
là thiết diện của mặt phẳng
P
cắt hình nón (xem hình vẽ).
Do
SBC
đều nên
3
2 3
2
BC
BC R SB SO R
.
Gọi
M
là trung điểm
AB
,
0 0
120 60 tan
2
OM R
AOB MOB MOB OM
OB
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
Dễ thấy,
OAB
cân tại
AB SAB
AB SO
O AB OM AB SOM SOM SAB
 
theo giao tuyến
SM
.
Trong
SOM
, kẻ
OH SM
tại
H OH SAB
tại
H
3 13
;
13
a
OH d O SAB
.
Xét
SOM
vuông tại
O
:
2 2
2 2 2 2
1 1 1 1 1 1
3
9
3
13 4
R a
a R
OH OS OM R
.
Vậy
2 3
. 3
3
V SO R a
.
Câu 45: Cho hàm số
4 2
f x ax bx c
có đồ thị như hình vẽ
Số nghiệm của phương trình
2 1 2 1 5 0
f x x
là
A.
2
. B.
3
. C.
5
. D.
4
.
Lời giải
Chọn C.
Từ đồ thị hàm số :
4 2
2 2
y x x
. Xét
0,54
5
1,3
2
x
f x
x
Phương trình :
5
2 1 2 1 5 0 1 2 1 (*)
2
f x x f x x
1 2 1 1,3 1
1 2 1 0,54 2
1 2 1 0,54 3
1 2 1 1,3 4
x x
x x
x x
x x
Xét hàm số :
1 2 1
g x x x
với
1
2
x
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
1
1
2 1
g x
x
1
0 1 0 2 1 1 1
2 1
g x x x
x
BBT :
Dựa vào bảng biến thiên, ta có:
+ Phương trình (1) vô nghiệm.
+ Phương trình (2) có đúng 2 nghiệm phân biệt.
+ Phương trình (3) có đúng 1 nghiệm phân biệt.
+ Phương trình (4) có đúng 1 nghiệm phân biệt.
Vậy phương trình đã cho có tất cả 4 nghiệm.
Câu 46: Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
để hàm số
2 3 2
1 3 5 1y m x m x x
có hai điểm cực trị
1 2
,x x
sao cho
1 2
8x x
. Tích các
phần tử của
S
bằng
A.
9
4
. B.
1
4
. C.
1
4
. D.
9
4
.
Lời giải
Chọn C.
Ta có:
2 2
3 1 6 5 1y m x m x
Nhận xét:
2
. 3 1 1 0,a c m m
nên phương trình
0y
luôn có 2 nghiệm
1 2
,x x
trái dấu.
Khi đó :
1 2 1 2
8x x x x
2
2
2
6 5
8
3 1
5 4 1
4 1 0
1 17
8
1 17
8
m
m
m m
m m
m
m
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
Vậy:
1 17 1 17 1
8 8 4
S
.
Câu 47: Trong không gian
Oxyz
, cho hình vuông
ABCD
có
3;0;8
B
và
5; 4;0
D
. Độ dài cạnh của
hình vuông đã cho bằng
A.
6 2
. B.
5 2
. C.
6
. D.
12
.
Lời giải
Chọn A
2 2 2
5 3 4 0 0 8 12
BD
.
Do
ABCD
là hình vuông nên
. 2 12 . 2 6 2
BD AB AB AB
.
Câu 48: Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng đáy và
2
SA a
( tham khảo hình vẽ).
Góc giữa đường thẳng
SC
và mặt phẳng đáy bằng
A.
60
. B.
45
. C.
90
. D.
30
.
Lời giải
Chọn B
SA ABCD
AC
là hình chiếu vuông góc của
SC
lên mặt phẳng
ABCD
.
Do đó:
, ,
SC ABCD SC AC SCA
.
SAC
vuông tại
A
:
2
tan 1 45
2
SA a
SCA SCA
AC
a
.
Câu 49: Một đội thanh niên tình nguyện của trường gồm
6
học sinh nam và
5
học sinh nữ. Chọn ngẫu
nhiên
4
học sinh để cùng với các giáo viên tham gia đo thân nhiệt cho học sinh khi đến trường.
Xác suất để chọn được
4
học sinh trong đó số học sinh nam bằng số học sinh nữ bằng:
A.
5
66
. B.
5
11
. C.
6
11
. D.
2
33
.
Lời giải
A
D
B
C
S
NHÓM TOÁN VD–VDC
NHÓM TOÁN VD
–
VDC
NHÓM TOÁN VD
–
VDC
Chọn B
Ta có:
4
11
C
Gọi
A
là biến cố: “Chọn được
4
học sinh trong đó số học sinh nam bằng số học sinh nữ”
Do số học sinh nam bằng số học sinh nữ nên trong
4
học sinh được chọn có
2
học sinh nam và
2
học sinh nữ
2 2
6 5
.
A
C C
Vậy xác suất để chọn được
4
học sinh trong đó số học sinh nam bằng số học sinh nữ là:
2 2
6 5
4
11
.
5
11
A
C C
P A
C
.
Câu 50: Tập nghiệm của bất phương trình
0,5 0,5
log 2 8 log 2 4
x x
là:
A.
1;
. B.
4; 1
. C.
1;2
. D.
; 1 2;

.
Lời giải
Chọn C
ĐKXĐ:
4 2
x
.
Do cơ số
0,5 0;1
nên bất phương trình đã cho
2 8 2 4
x x
1
x
.
Kết hợp với ĐKXĐ ta có tập nghiệm của bất phương trình đã cho là:
1;2
S
.
Từ gt
SA ABCD
Gọi
E
là trung điểm
AD
AB AE a
Do đó
ABCE
là hình vuông cạnh
a
2
SA AC a
.
Dễ thấy
/ /
CD SAE
; ; ; ;
d SB CD d CD SBE d C SBE d A SBE
Mà
SA
;
AB
;
AE
đôi một vuông góc.
2 2
2 2 2 2 2 2
1 1 1 1 1 1 1 5
2
;
2
SA AB AE a a a
d A SBE
a
10
; ;
5
a
d SB CD d A SBE
.
------------------------- HẾT -------------------------

Tài liệu khác của Toán

Preview text:

NHÓM TOÁN VD–VDC
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KHẢO SÁT CHẤT LƯỢNG HỌC SINH LỚP 12 THPT PHÚ THỌ NĂM HỌC 2020 – 2021 N MÃ ĐỀ THI: 361 MÔN: TOÁN H Ó
Thời gian làm bài: 90 phút (không kể thời gian giao đề) M TO Đề thi gồm có 05 trang ÁN
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh: . . . . . . . . . . . . . VD –
Câu 1: Trong không gian Oxyz , mặt cầu tâm I 2;1;0 , bán kính R  5 có phương trình là VD A. 2 2 2
x  y  z  4x  2y  20  0. B. 2 2 2
x  y  z  4x  2y  20  0. C C. 2 2 2
x  y  z  2x  y  25  0 . D. 2 2 2
x  y  z  4x  2y  25  0 .
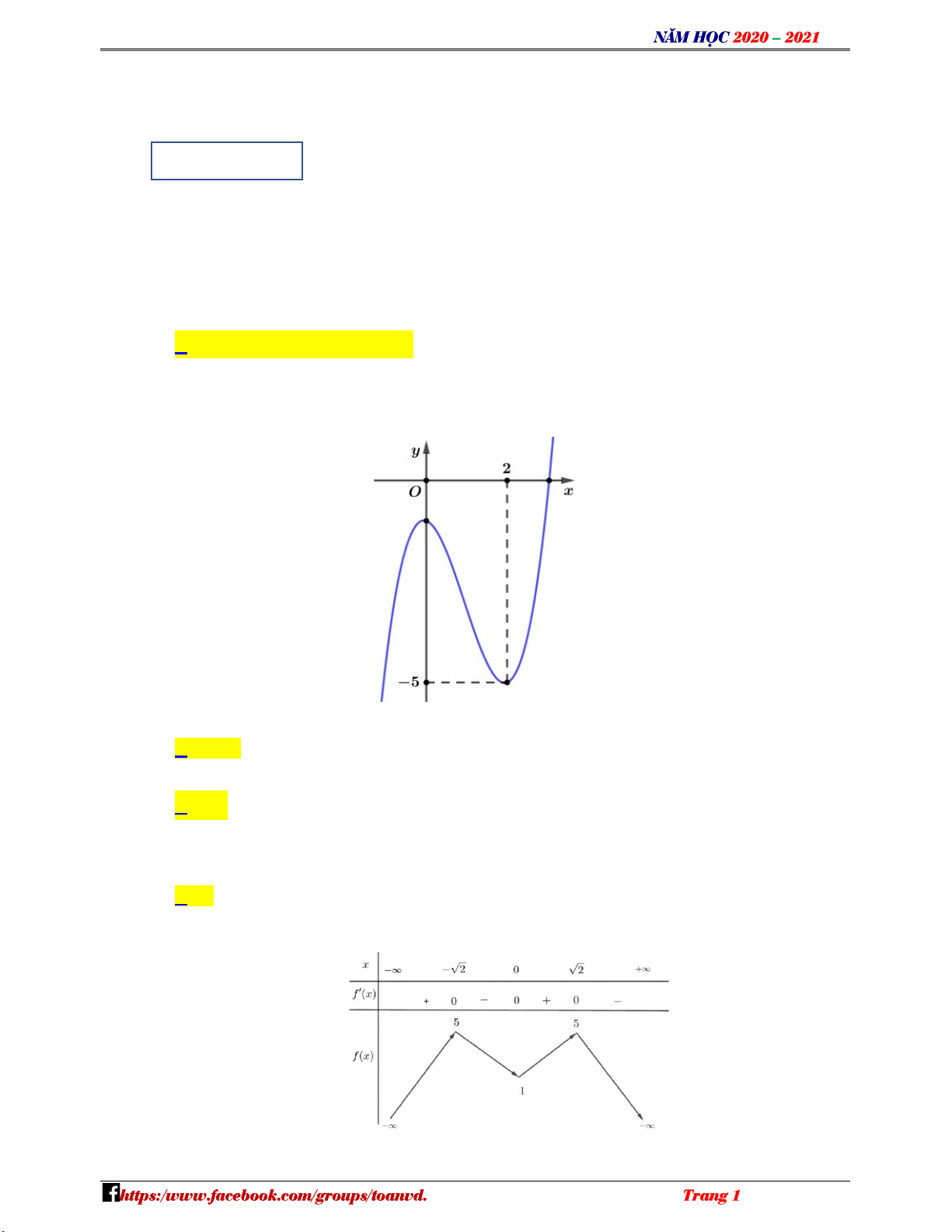
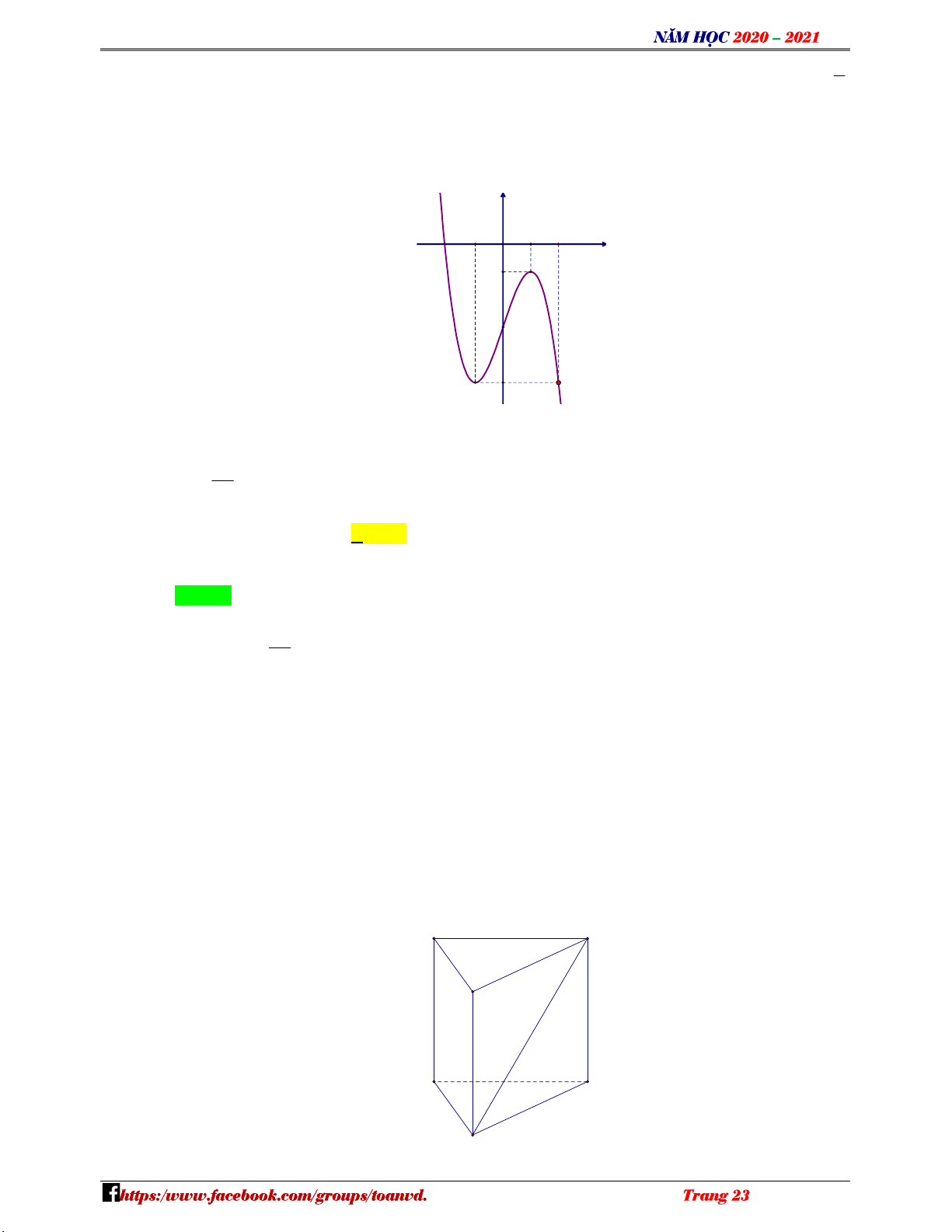
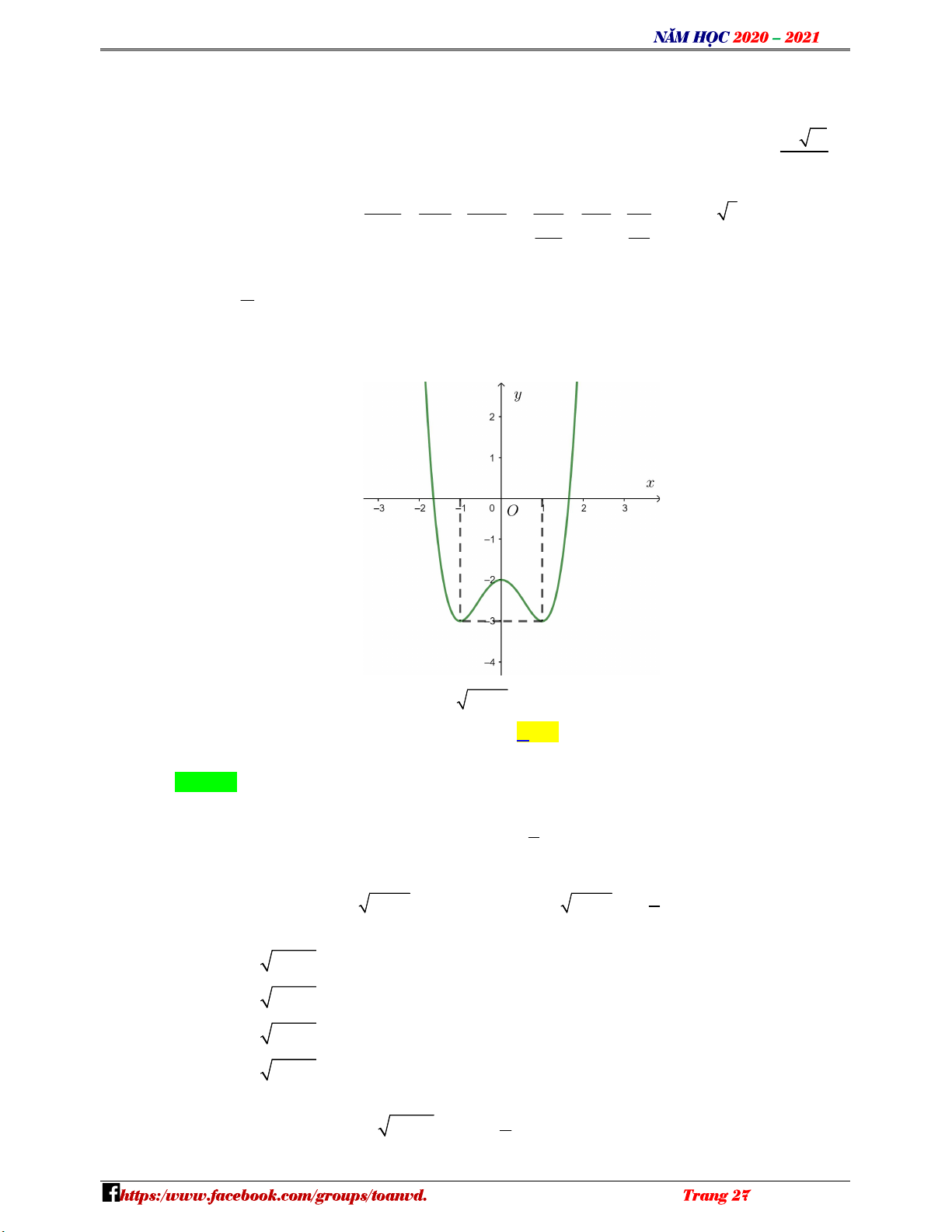
Câu 2: Cho hàm số y  f  x có đồ thị như hình vẽ. N H Ó M T
Điểm cực tiểu của hàm số đã cho là O Á A. x  2 . B. x  1 . C. x  0 . D. x  5 . N V
Câu 3: Có bao nhiêu cách chọn ra 2 cái bút từ một hộp đựng 10 chiếc bút? D A. 2 C . B. 10 2 . C. 20 . D. 2 A . – 10 10 VDC
Câu 4: Cho hình lăng trụ có bán kính đáy r  2 và diện tích xung quanh s  36 . Độ dài đường sinh xq
l của hình trụ đã cho bằng A. 9 . B. 6 . C. 12 . D. 18 .
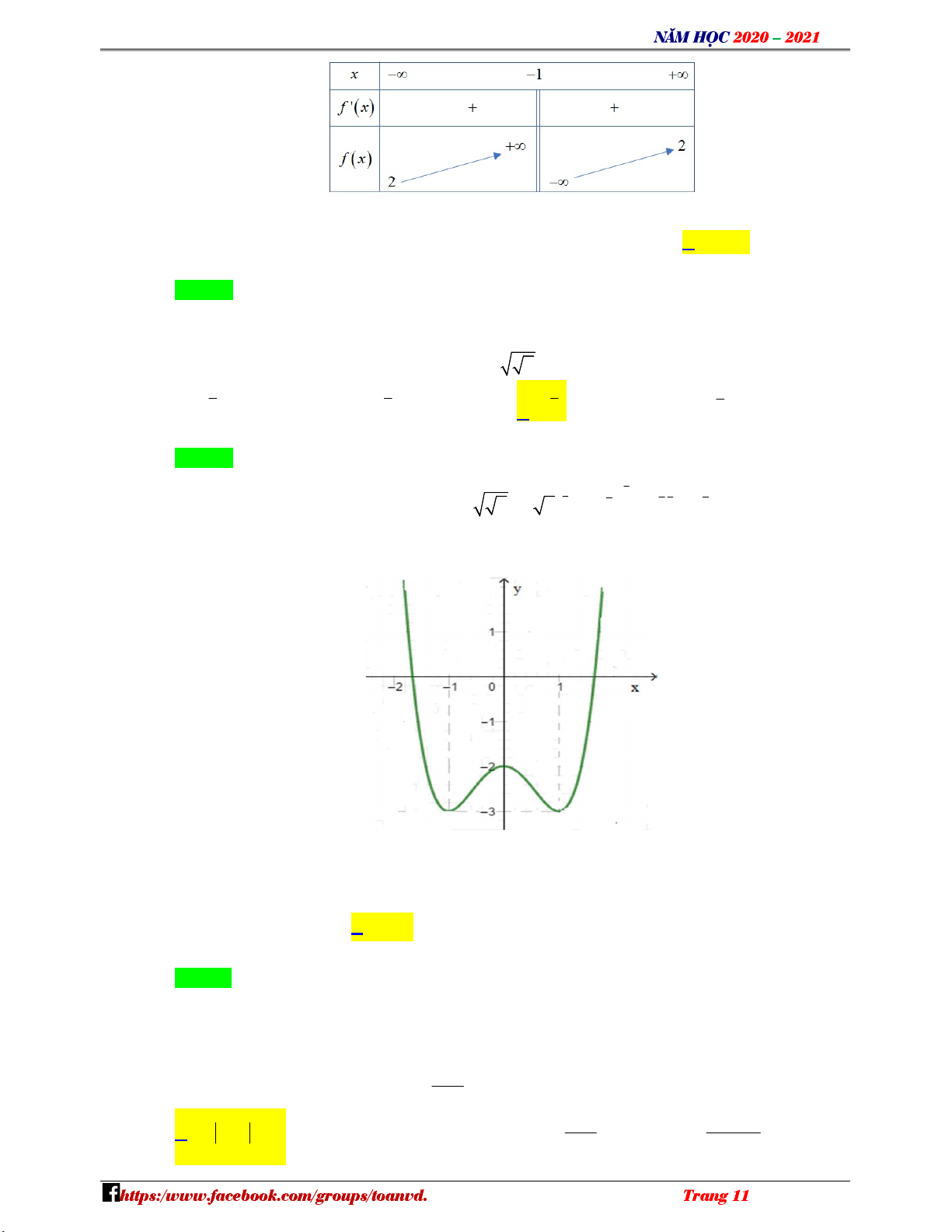
Câu 5: Cho hàm số y  f  x có bảng biến thiên như sau
Số nghiệm của phương trình 2 f  x  5  0 là  NHÓM TOÁN VD–VDC A. 1 B. 2 C. 4 D. 3
Câu 6: Đạo hàm của hàm số y  log x là 5 1 1 x 1 A. y  B. y  C. y  D. y  x x ln 5 ln 5 5ln x N H
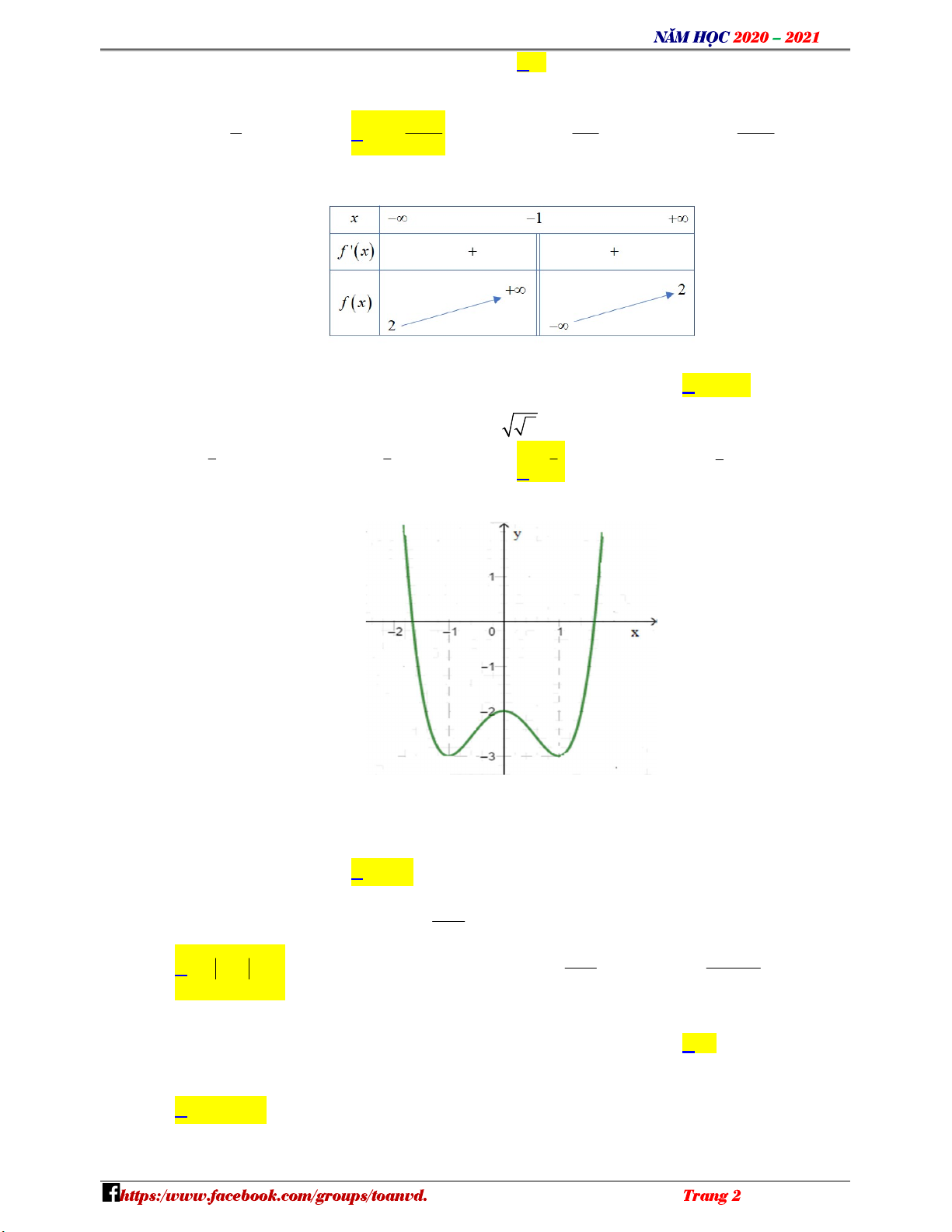
Câu 7: Cho hàm số y  f  x có bảng biến thiên như sau: Ó M TOÁN VD – VD C
Đồ thị hàm số có đường tiệm cận ngang là A. x  1  . B. x  2 . C. y  1  . D. y  2 .
Câu 8: Với x là số thực dương bất kỳ, biểu thức 3 P  x bằng 2 5 1 3 A. 3 x . B. 6 x . C. 6 x . D. 2 x . N H Ó M TOÁN VD
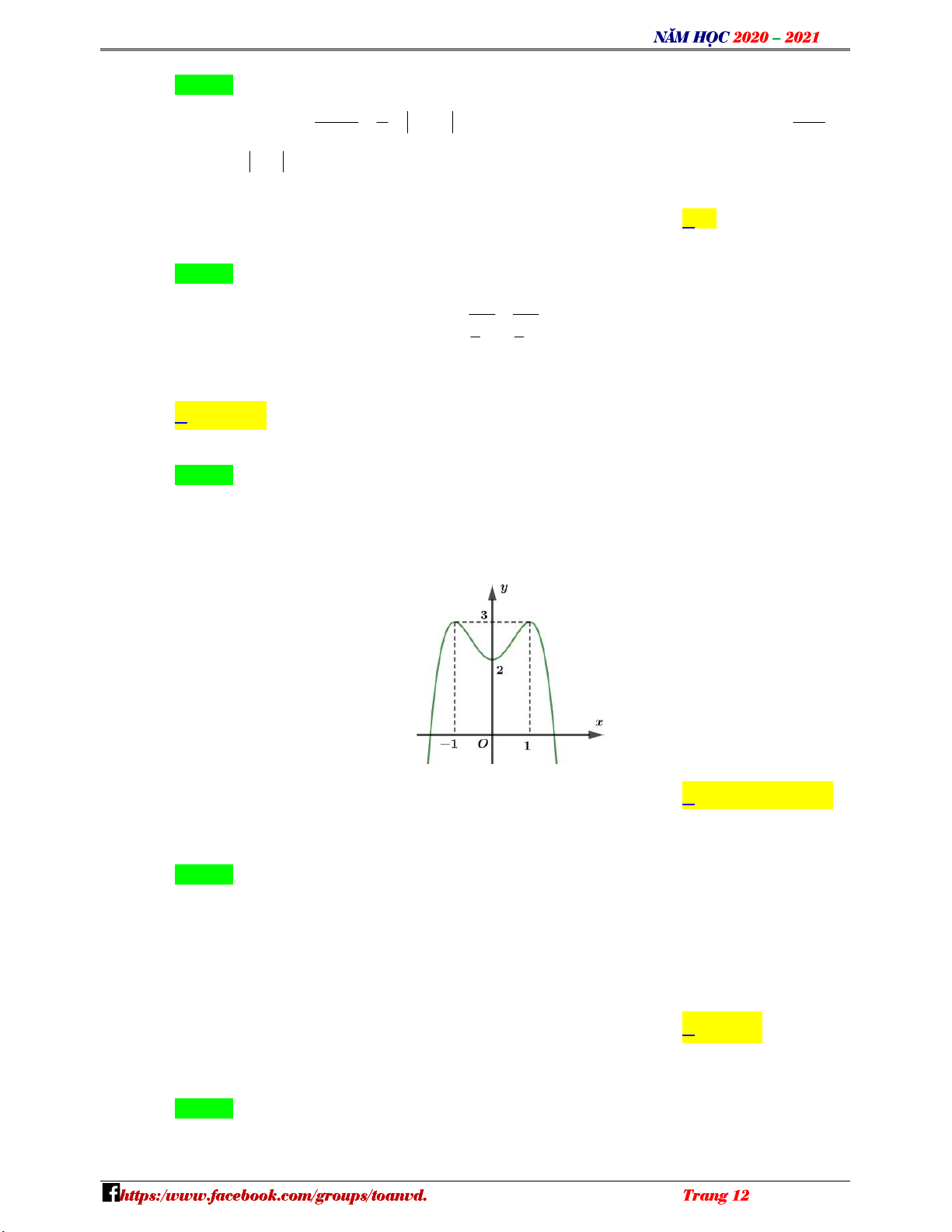
Câu 9: Cho hàm số y  f x có đồ thị như hình vẽ – V D
Hàm số đã cho nghịch biến trên khoảng nào dưới đây ? C A. 1;. B. 0;  1 . C.  ;  0. D.  1  ;  1 .
Câu 10: Họ nguyên hàm của hàm số f  x 1  là x 1 2 1 A. ln x 1  C . B. ln  x   1  C . C. x   C . D.  C . x 1 x  2 1
Câu 11: Cho khối chóp có diện tích đáy B  3 và thể tích V  6 . Chiều cao h của khối chóp đã cho bằng? A. 18. B. 2. C. 4. D. 6.    
Câu 12: Trong không gian Oxyz , cho hai vectơ u   1  ;3; 2
  và v  2;5; 
1 . Vectơ u  v có tọa độ là A. 1;8;3 . B.  3  ;8;3 . C. 3;8; 3   . D. 1;8;3 .  NHÓM TOÁN VD–VDC
Câu 13: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ? N H Ó M TOÁ A. 4 2 y  x  2x  2. B. 3 2 y  x  2x  2. C. 3 2 y  x  2x  2. D. 4 2 y  x  2x  2. N VD
Câu 14: Tập xác định của hàm số y  log x là 3 – A. 3;   . B. ;. C. 0;. D. 0;. VDC x
Câu 15: Nghiệm của phương trình 2 1 2  32 là A. x  4 . B. x  3 . C. x  5 . D. x  2 .
Câu 16: Trong không gian Oxyz cho hai điểm A1 1 ; ; 
1 ,B 3;3;5 . Tọa độ trung điểm của đoạn thẳng AB là A. 4;2;4 . B. 1; 2;3 . C. 2;1; 2 . D. 2;4;6 . 2
Câu 17: Cho hàm số y  f  x có đạo hàm liên tục trên 1; 2. Biết f  
1  1, f 2  4. Giá trị f   xdx 1 bằng A. 3 . B. 4 . C. 4 . D. 3  .
Câu 18: Cho khối cầu có bán kính r  .
a Thể tích của khối cầu đã cho bằng 2 4 N A. 3 4 a . B. 3 a . C. 3 a . D. 3  a . H 3 3 Ó M
Câu 19: Với a , b là các số thực dương bất kỳ khác 1, khi đó log a bằng b T 1 O A. log . b B. . C. log a  log . b D. log b. Á a log b a N a VD
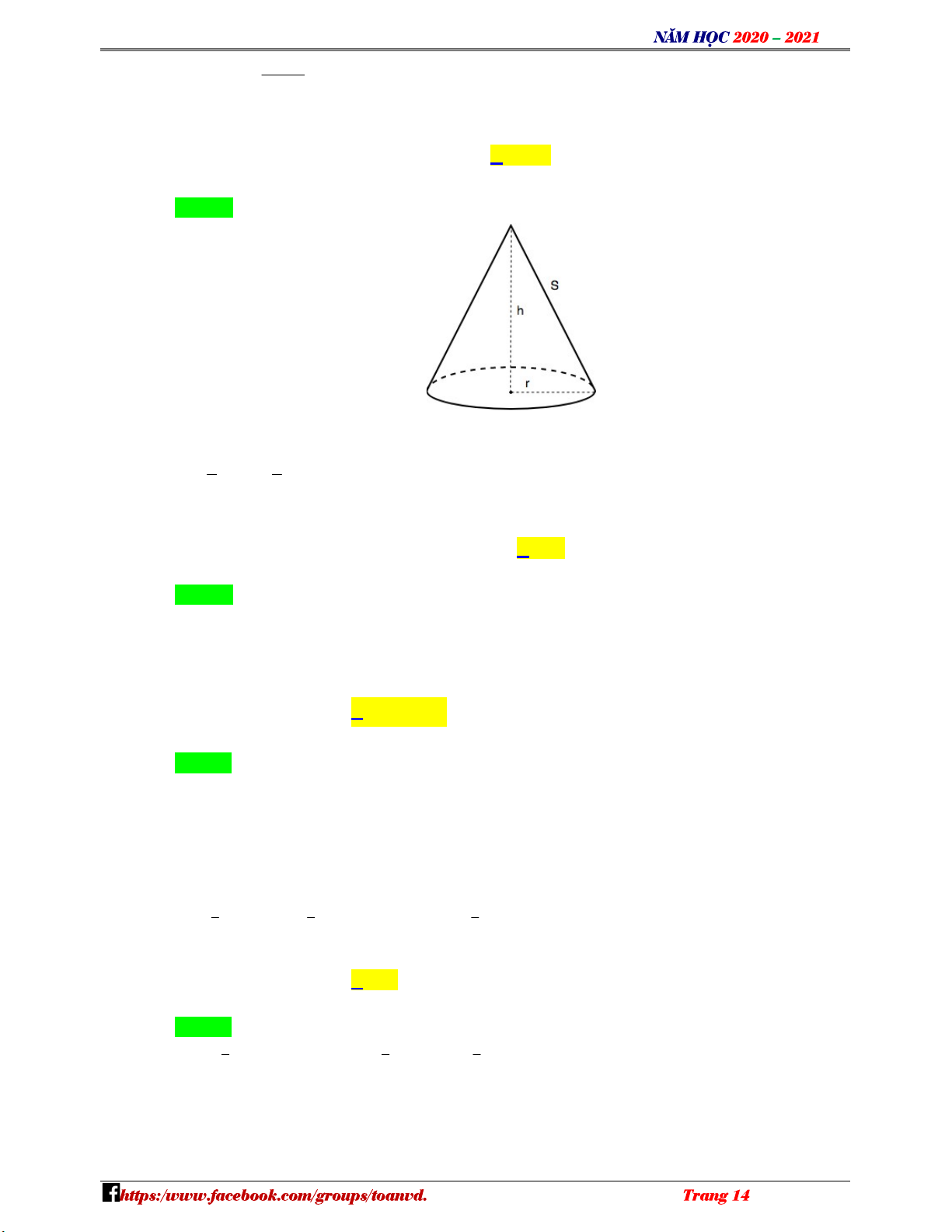
Câu 20: Cho hình nón có bán kính đáy r  4 và chiều cao h  9 . Thể tích V của khối nón đã cho bằng – A. 126 . B. 36 . C. 48 . D. 108 . VDC
Câu 21: Cho cấp số nhân u với u  1 và công bội q  3. Giá trị của u là n  1 3 A. 2  7. B. 3 . C. 9  . D. 2 .
Câu 22: Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x  y  z  2x  2 y  4z  2  0 . Tâm của S  có toạ độ là A. 1; 1;2 . B.  1  ;1; 2  . C. 1;1; 2   . D. 2; 2  ;4 .    4 4 4 f  xdx 1, g  xdx  1  f
  x 2gxdx  Câu 23: Cho 0 0 . Giá trị 0 bằng A. 0 . B. 1. C. 1. D. 3 .
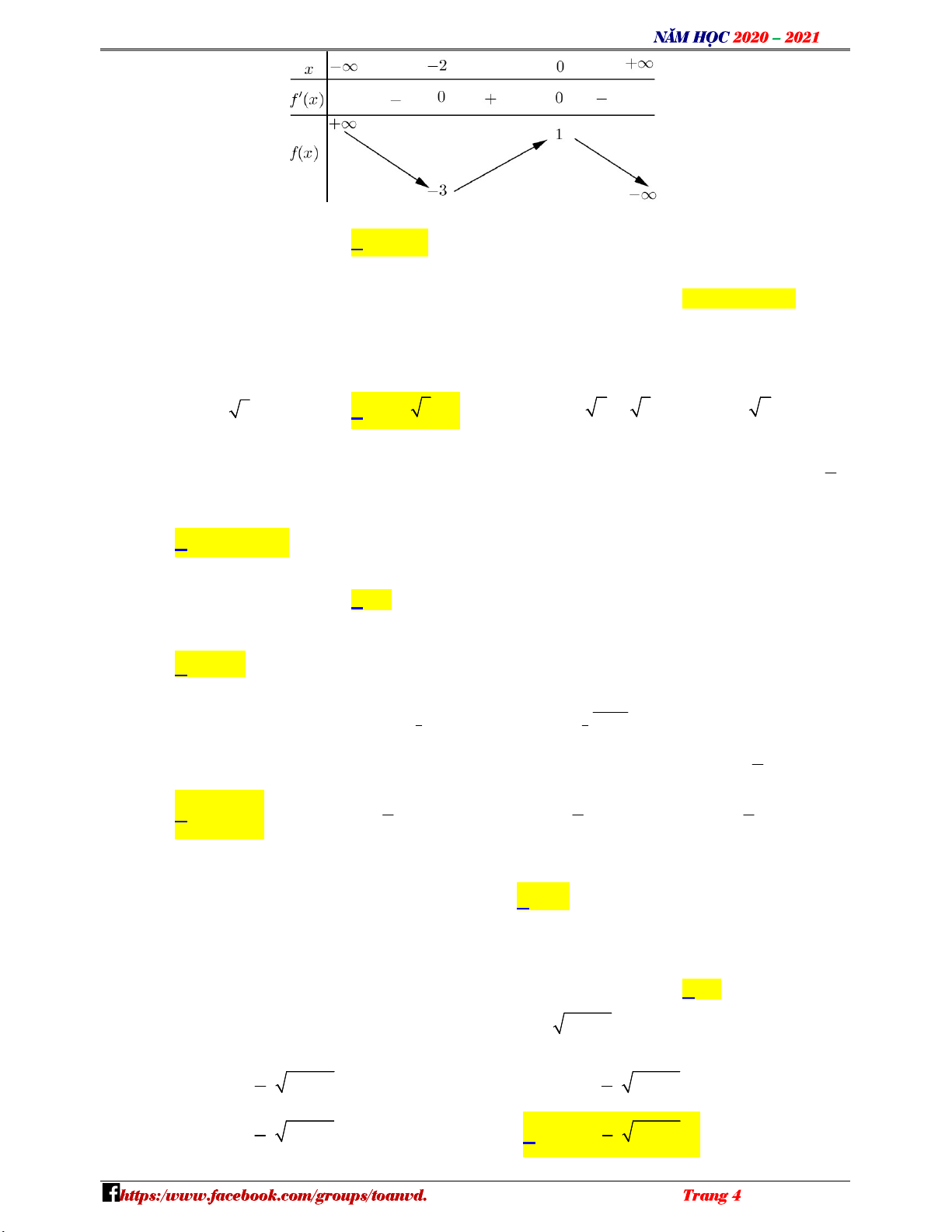
Câu 24: Cho hàm số y  f  x có bảng biến thiên như sau  NHÓM TOÁN VD–VDC N H Ó M
Hàm số đã cho đồng biến trên khoảng nào dưới đây? TO A.  ;  2 . B. 2;0 . C. 0;. D.  3  ;  1 . ÁN
Câu 25: Họ nguyên hàm của hàm số f x  3sin x là VD A. 3sin x  C . B. 3cos x  C . C. 3cos 2x  C . D. 3cos x  C . – V
Câu 26: Một mặt cầu có tâm O nằm trên mặt đáy của hình chóp tam giác đều S.ABC có tất cả các cạnh DC bằng nhau. Các đỉnh ,
A B,C thuộc mặt cầu. Biết bán kính mặt cầu bằng 3. Tổng độ dài l các
giao tuyến của mặt cầu với các mặt bên của hình chóp thỏa mãn điều kiện nào sau đây? A. l   3;2 . B. l 3 3;6 .
C. l 13 2;12 3 . D. l 1; 2. x  2
Câu 27: Cho a là số thực dương. Giả sử F  x là một nguyên hàm của hàm số f x  e ln 2 ax    x   trên tập  \  0 và thỏa mãn F  
1  5; F 2  21. Khẳng định nào sau đây đúng ? A. a  3; . B. a  0;  1 . C. a  1;2 . D. a 2;3 .
Câu 28: Có bao nhiêu cặp số nguyên  ;
x y thỏa mãn 0  y  2021 và x 3
3  3x  6  9y  log y ? 3 A. 2021 . B. 7 . C. 9 . D. 2020 .
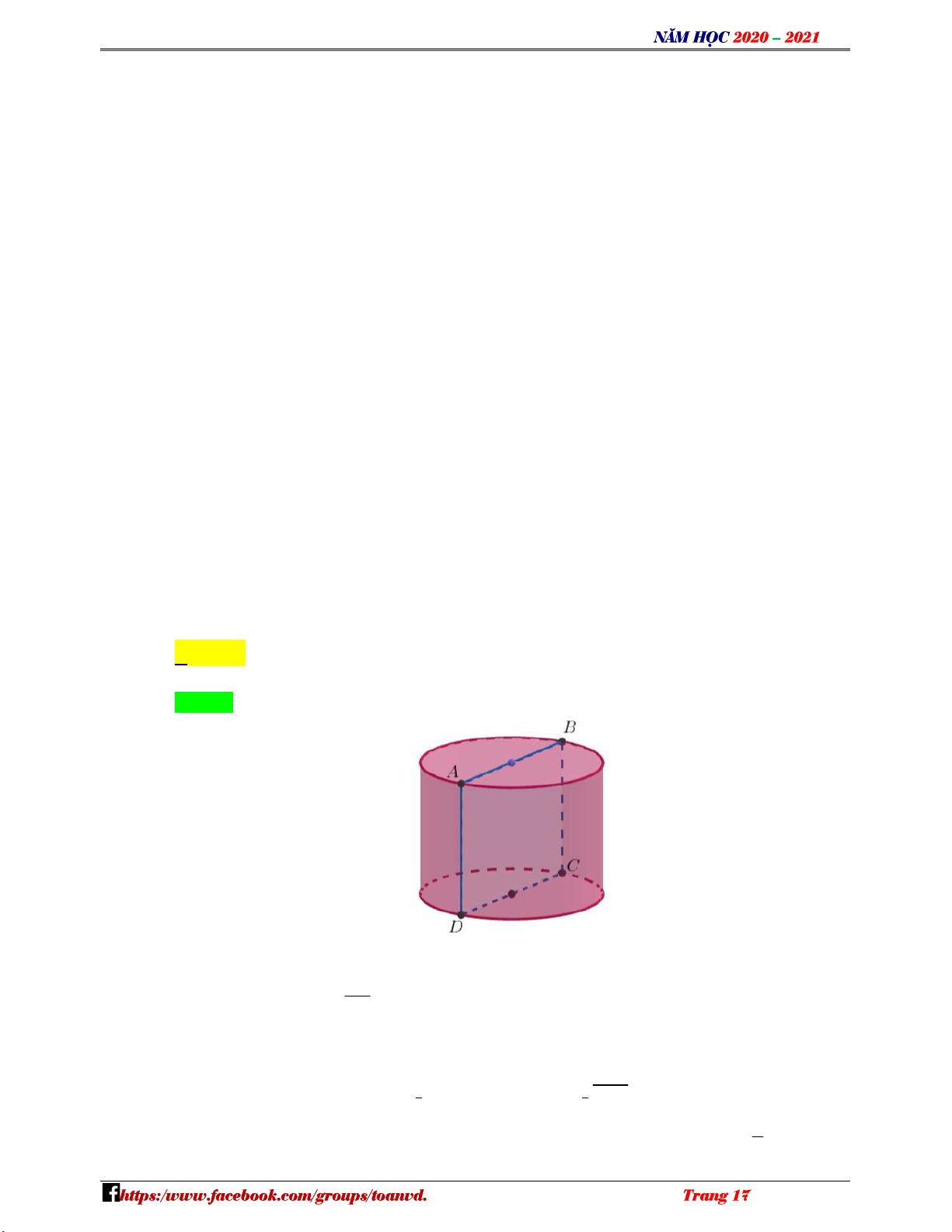
Câu 29: Cho hình trụ có thiết diện qua trục là hình vuông cạnh 4 .
a Diện tích xung quanh của hình trụ đã cho bằng N H A. 2 16a . B. 2 4 a . C. 2 64 a . D. 2 8 a . Ó M 2 1 2       
Câu 30: Cho bất phương trình m 1log x 2 4 m 5 log 4m 4 0 với m là tham số 1     1 T x  2 O 2 2 Á 5  N
thực. Tập hợp tất cả các giá trị của m để bất phương trình có nghiệm thuộc đoạn ; 4 là?   V 2  D  7   7   7  – A. 3; . B. ; . C. 3  ; . D.  ;  .       V  3   3   3  D C 2
Câu 31: Giá trị lớn nhất của hàm số      3  5ex f x x x
trên đoạn 1;2 bằng A. 2e . B. 2 4e . C. 2 3e . D. 3e .
Câu 32: Cho hàm số y  f  x , biết f  x 3
 x  3x 1 có tất cả bao nhiêu giá trị nguyên của tham số m
thuộc đoạn 5;5 sao cho hàm số y  f 2  x  1 m x  6 nghịch biến trên khoảng 2;3? A. 10 . B. 9 . C. 7 . D. 8 .
Câu 33: Biết F  x là một nguyên hàm của hàm số f  x 2 3
 x 1 2x . Khẳng định nào dưới đây đúng ? 2 2
A. F  x   1 2x 3 3 .
B. F  x   1 2x 3 3 . 9 3 1 1
C. F  x   1 2x 3 3
D. F  x   1 2x 3 3 . 2 9  NHÓM TOÁN VD–VDC
Câu 34: Cho hàm số y  f (x) có f  x   x  x  x  x  3 2 2 3 2
3 . Tập hợp tất cả các giá trị của tham
số m sao cho hàm số y  f  2
x  6x  m có 3 điểm cực trị phân biệt là nửa khoảng a;b . Giá trị của a  b bằng A. 21. B. 23. C. 22 . D. 20 . N 3 H 2 1 Ó
Câu 35: Cho hàm số f  x có đạo hàm liên tục trên đoạn 0; 
3 thỏa mãn f 3  4 ,  f   x dx   M 27 0 T 3 333 3 3 O và x f  xdx  
. Giá trị của f  xdx  bằng Á 4 N 0 0 V 3 153089 25 150893 D A. x  . B. x  . C. x  . D. x  . 2 1215 2 21 – VD
Câu 36: Có tất cả bao nhiêu giá trị nguyên của m thuộc đoạn 10;10 để hàm số C 3 2 y  x  mx   2 3
6 m  2 x 1 đồng biến trên khoảng 2; A. 21. B. 18 . C. 20 . D. 19. 2 9  x
Câu 37: Tổng tất cả số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y  bằng 2 x  6x  5 A. 2 . B. 4 . C. 1. D. 3 .
Câu 38: Tổng các giá trị nguyên của tham số m để phương trình log  x   1  log mx  8 có hai 3 3   nghiệm phân biệt bằng A. 11. B. 22 . C. 3 . D. 18.
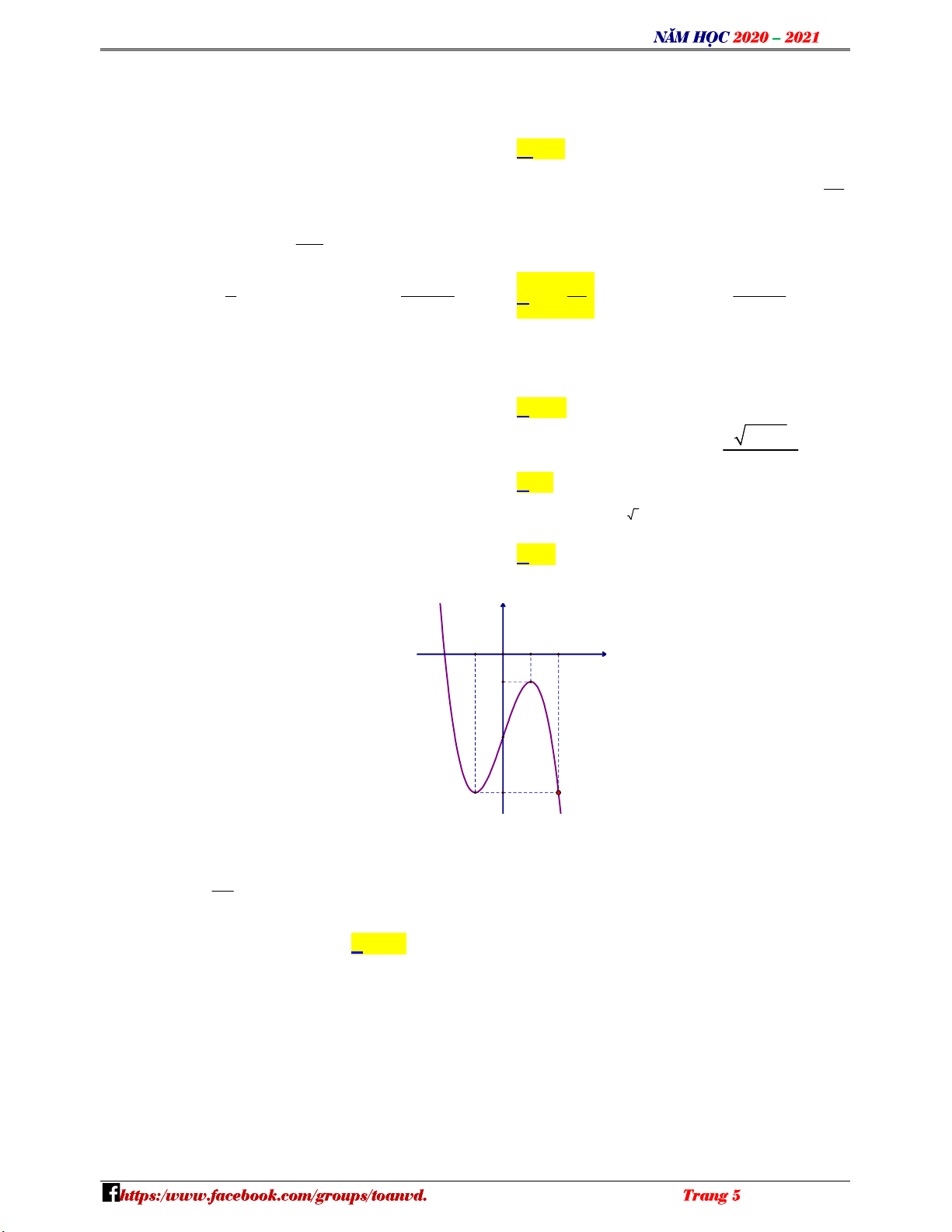
Câu 39: Cho hàm số f  x có đồ thị như hình vẽ. y -1 O 1 2 N x H Ó -1 M TO -3 ÁN VD -5 – VD
Gọi M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f  3 sin x   1 trên đoạn C  5  2 ; 
. Giá trị của 2M  m bằng 2    A. 5  . B. 1  1. C. 1  3. D. 7  .
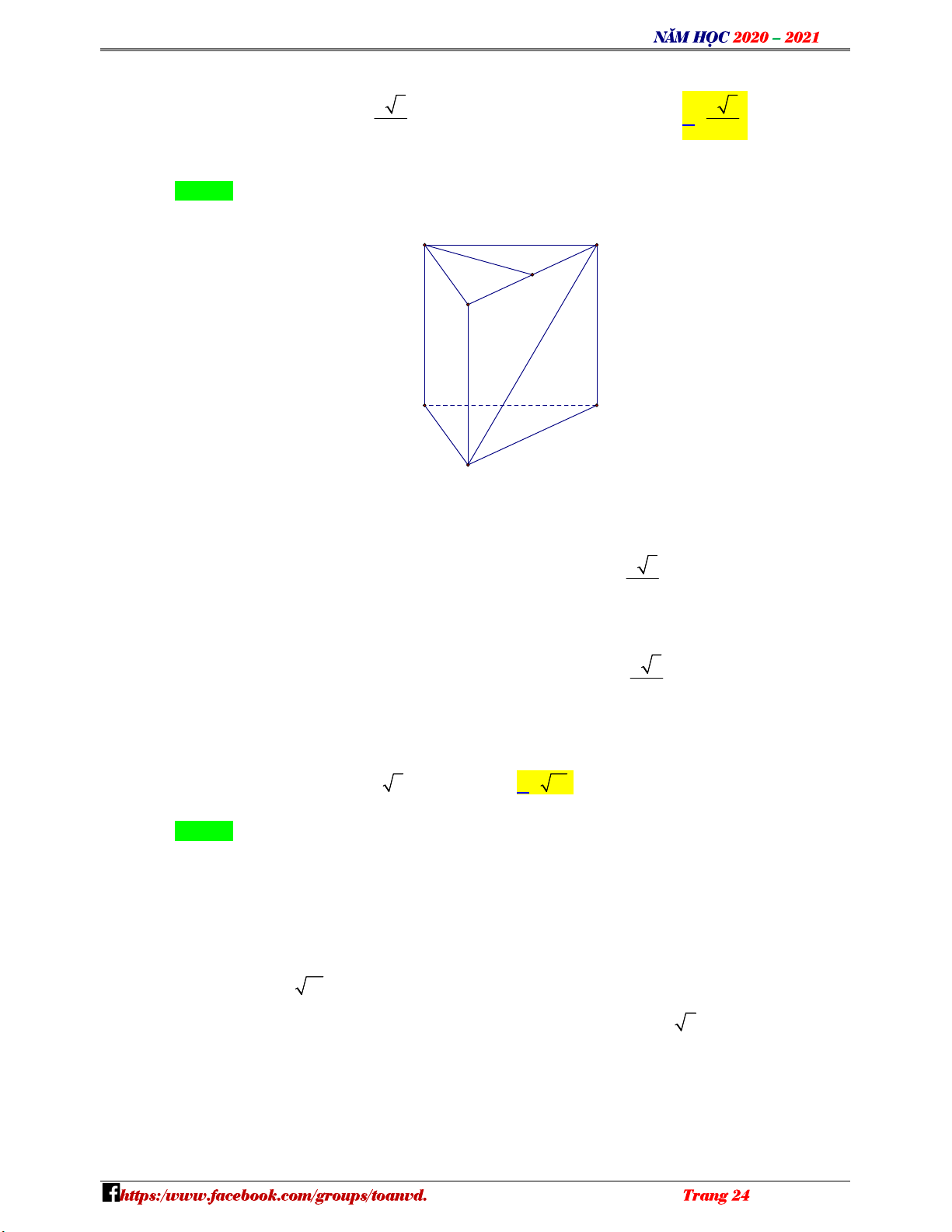
Câu 40: Cho hình lăng trụ đứng ABC.A B  C
  có đáy là tam giác đều cạnh bằng a (tham khảo hình vẽ)  NHÓM TOÁN VD–VDC A' C' B' N H Ó M A T C O ÁN V B D –
Khoảng cách giữa hai đường thẳng AA và BC bằng VDC a 3 a 3 A. a . B. . C. 2a . D. . 3 2
Câu 41: Trong không gian Oxyz, cho hai điểm A1;1;2 và B 3;2;3 . Mặt cầu S  có tâm I thuộc
trục Ox và đi qua hai điểm , A B có bán kính bằng A. 4 . B. 4 2 . C. 14 . D. 3 .
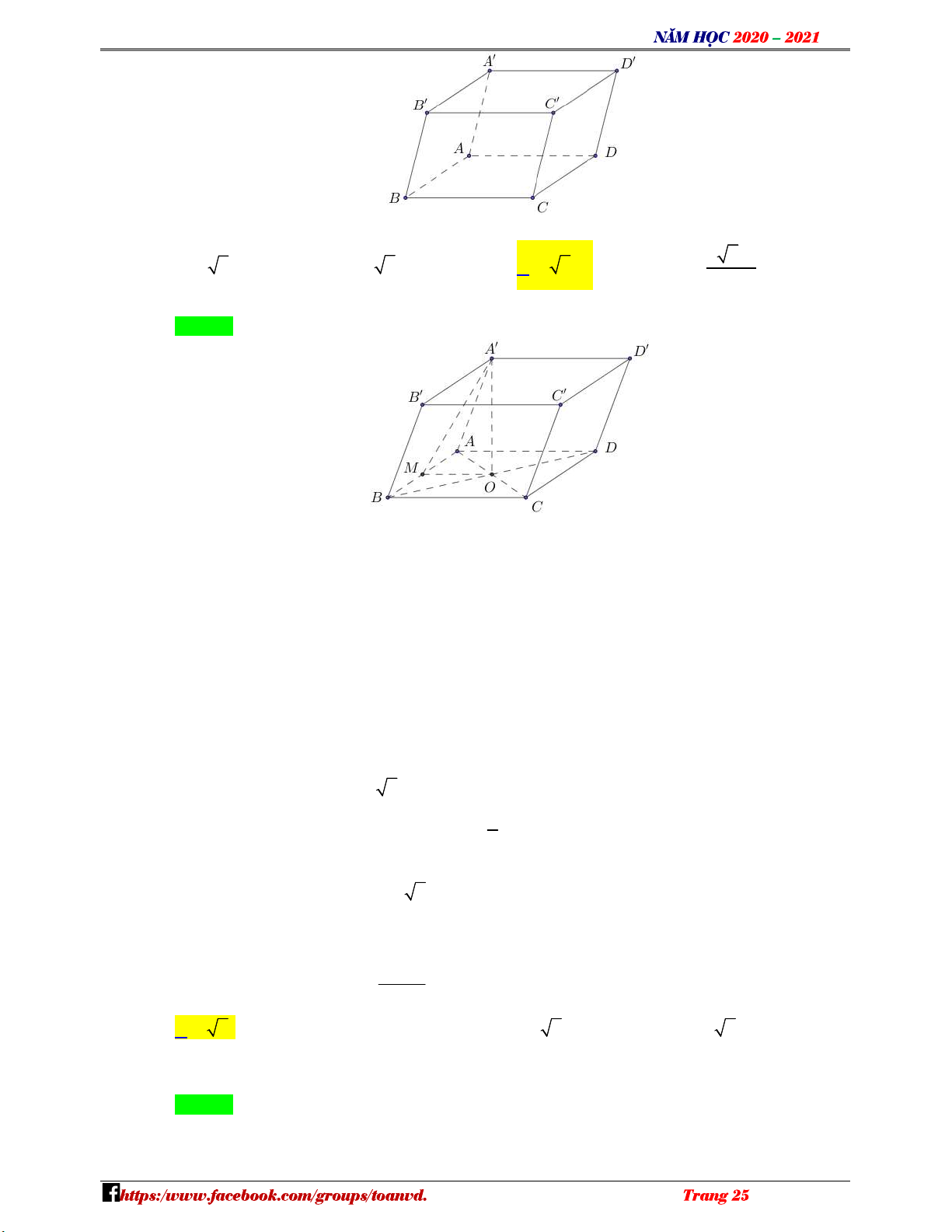
Câu 42: Cho khối hộp ABCD.A B  C  D
  có đáy ABCD là hình chữ nhật AB  2a, AD  2a . Điểm A cách đều các điểm , A , B C, D . Mặt bên CDD C
  tạo với mặt phẳng đáy một góc 45 (tham khảo hình vẽ). N H Ó M TO ÁN
Thể tích khối hộp đã cho bằng V 3 2 2a D A. 3 2 6a . B. 3 2a . C. 3 2 2a . D. . – 3 VD
Câu 43: Cho hai số thực a  1,b  1. Biết phương trình 2 x x 1
a .b   1 có hai nghiệm phân biệt x , x . Giá trị C 1 2 2  x x 
nhỏ nhất của biểu thức 1 2 S     4 x  x bằng 1 2  x  x  1 2  A. 3 3 4 . B. 4 . C. 3 4 . D. 3 3 2 .
Câu 44: Cho hình nón đỉnh S có đáy là đường tròn tâm O , thiết diện qua trục là tam giác đều. Mặt phẳng
P đi qua S và cắt đường tròn đáy tại , A B sao cho 
AOB  120 . Biết rằng khoảng cách từ O 3 13a đến P bằng
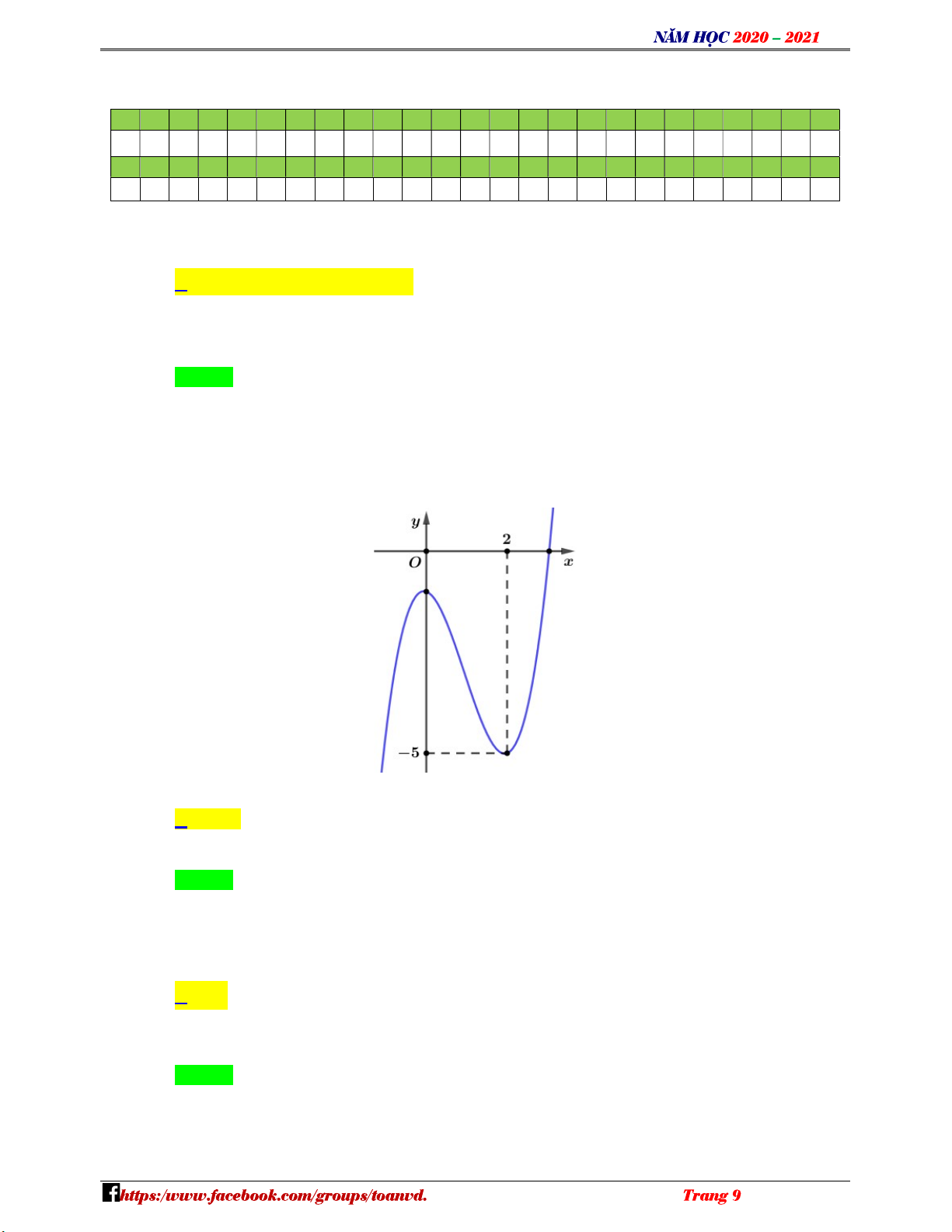
. Thể tích của khối nón đã cho bằng 13 3 3 a 3 3 a A. . B. 3 a . C. . D. 3 3 a . 3 2  NHÓM TOÁN VD–VDC Câu 45: Cho hàm số   4 2
f x  ax  bx  c có đồ thị như hình vẽ N H Ó M TOÁN VD – VDC
Số nghiệm của phương trình 2 f x 1 2x 1 5  0 là A. 2 . B. 3. C. 5 . D. 4 .
Câu 46: Gọi S là tập hợp tất cả các giá trị thực của tham số m để hàm số y   2 m   3 x  m   2 1 3
5 x  x 1 có hai điểm cực trị x , x sao cho x  x  8. Tích các 1 2 1 2 phần tử của S bằng 9 1 1 9 A. . B. . C.  . D.  . 4 4 4 4
Câu 47: Trong không gian Oxyz , cho hình vuông ABCD có B 3;0;8 và D 5;4;0 . Độ dài cạnh của hình vuông đã cho bằng A. 6 2 . B. 5 2 . C. 6 . D. 12. N H Ó
Câu 48: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với mặt phẳng đáy và M
SA  2a ( tham khảo hình vẽ). TO S ÁN VD – A D VDC B C
Góc giữa đường thẳng SC và mặt phẳng đáy bằng A. 60 . B. 45 . C. 90 . D. 30 .
Câu 49: Một đội thanh niên tình nguyện của trường gồm 6 học sinh nam và 5 học sinh nữ. Chọn ngẫu
nhiên 4 học sinh để cùng với các giáo viên tham gia đo thân nhiệt cho học sinh khi đến trường.
Xác suất để chọn được 4 học sinh trong đó số học sinh nam bằng số học sinh nữ bằng: 5 5 6 2 A. . B. . C. . D. . 66 11 11 33
Câu 50: Tập nghiệm của bất phương trình log 2x  8  log 2  x  4 là: 0,5   0,5   A.  1  ;  . B.  4  ;  1 . C.  1  ;2 . D. ;  1  2;  .
------------------------- HẾT -------------------------  NHÓM TOÁN VD–VDC
BẢNG ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A A A A C B D C B A D A D D B C A D B C C B B B D N
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 H Ó
B C B A C C A D C C C C C B D C C A D C C A B B C M TOÁ
Câu 1: Trong không gian Oxyz , mặt cầu tâm I 2;1;0 , bán kính R  5 có phương trình là N V A. 2 2 2
x  y  z  4x  2y  20  0. B. 2 2 2
x  y  z  4x  2y  20  0. D – C. 2 2 2
x  y  z  2x  y  25  0 . D. 2 2 2
x  y  z  4x  2y  25  0 . VD Lời giải C Chọn A Mặt cầu tâm I 2; 1;0 , bán kính R  5 có phương trình là
x  2   y  2 2 2 2 2 2 2
1  z  5  x  y  z  4x  2 y  20  0
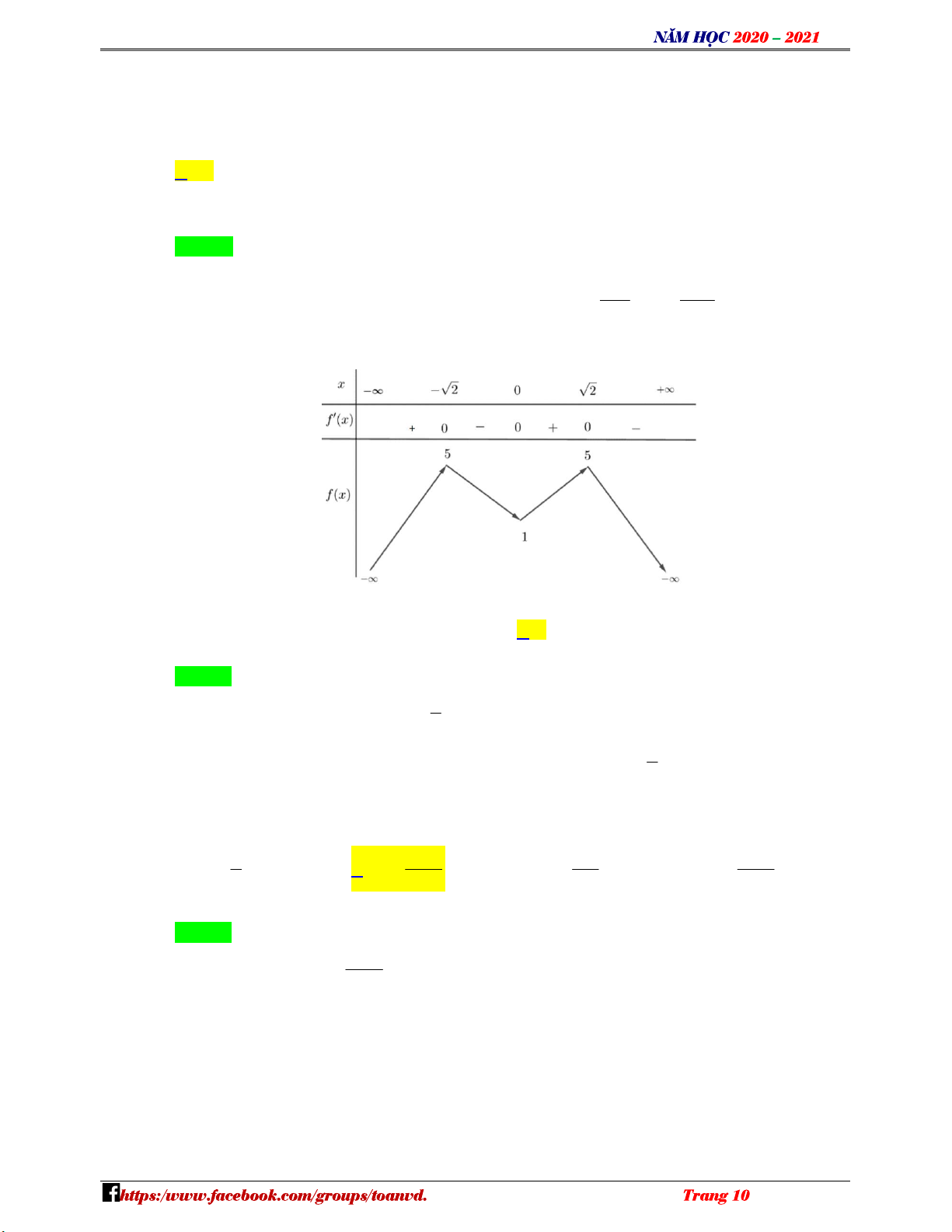
Câu 2: Cho hàm số y  f  x có đồ thị như hình vẽ. N H Ó M TOÁN VD
Điểm cực tiểu của hàm số đã cho là – A. x  2 . B. x  1 . C. x  0 . D. x  5 . VD Lời giải C Chọn A
Dựa vào đồ thị suy ra hàm số đạt cực tiểu tại x  2 .
Câu 3: Có bao nhiêu cách chọn ra 2 cái bút từ một hộp đựng 10 chiếc bút? A. 2 C . B. 10 2 . C. 20 . D. 2 A . 10 10 Lời giải Chọn A
Số cách lấy ra ra 2 cái bút từ một hộp đựng 10 chiếc bút là một tổ hợp chập 2 của 10 phần tử  NHÓM TOÁN VD–VDC Có 2 C cách. 10
Câu 4: Cho hình lăng trụ có bán kính đáy r  2 và diện tích xung quanh s  36 . Độ dài đường sinh xq
l của hình trụ đã cho bằng N H A. 9 . B. 6 . C. 12. D. 18. Ó M Lời giải TO Chọn A ÁN V S  xq 36 D
Ta có diện tích xung quanh của hình trụ là S  2 rl  l   l   l  9 xq – 2 r 2.2 VD y  f x C Câu 5: Cho hàm số
  có bảng biến thiên như sau
Số nghiệm của phương trình 2 f  x  5  0 là A. 1 B. 2 C. 4 D. 3 N Lời giải H Chọn B Ó M
Phương trình đã cho đưa về f  x 5  . T 2 O Á 5 N
Dựa vào bảng biến thiên ta thấy đồ thị đã cho cắt đường thẳng y  tại 4 điểm phân biệt. V 2 D
Từ đây ta thu được 4 nghiệm. – V
Câu 6: Đạo hàm của hàm số y  log x là D 5 C 1 1 x 1 A. y  B. y  C. y  D. y  x x ln 5 ln 5 5ln x Lời giải Chọn B 1
Ta có y  log x  y  . 5 x ln 5
Câu 7: Cho hàm số y  f  x có bảng biến thiên như sau:  NHÓM TOÁN VD–VDC N H Ó M
Đồ thị hàm số có đường tiệm cận ngang là TO A. x  1  . B. x  2 . C. y  1  . D. y  2 . ÁN Lời giải V Chọn D D –
Ta có lim y  lim y  2 nên đường thẳng y  2 là tiệm cận ngang của đồ thị hàm số y  f  x. x x VDC
Câu 8: Với x là số thực dương bất kỳ, biểu thức 3 P  x bằng 2 5 1 3 A. 3 x . B. 6 x . C. 6 x . D. 2 x . Lời giải Chọn C 1 1 1 1 1 1 3   .
Với x là số thực dương bất kỳ, ta có: 3 P  x   x 3 2 2 3 6   x   x  x .   N H Ó M TOÁN VD – VDC
Câu 9: Cho hàm số y  f  x có đồ thị như hình vẽ
Hàm số đã cho nghịch biến trên khoảng nào dưới đây ? A. 1;. B. 0;  1 . C.  ;  0. D.  1  ;  1 . Lời giải Chọn B
Nhìn vào đồ thị ta thấy trên khoảng 0; 
1 đồ thị đi xuống nên hàm số y  f  x nghịch biến trên 0; 1 .
Câu 10: Họ nguyên hàm của hàm số f  x 1  là x 1 2 1 A. ln x 1  C . B. ln  x   1  C . C. x   C . D.  C . x 1 x  2 1  NHÓM TOÁN VD–VDC Lời giải Chọn A dx 1 Áp dụng hệ quả  ln ax  b  C 
ta được nguyên hàm của hàm số f  x 1  là ax  b a x 1 N
F  x  ln x 1  C . H Ó
Câu 11: Cho khối chóp có diện tích đáy B  3 và thể tích V  6 . Chiều cao h của khối chóp đã cho bằng? M A. 18. B. 2. C. 4. D. 6. TO Lời giải ÁN Chọn D VD V 6 –
Chiều cao h của khối chóp đã cho là h    6. 1 1 V B .3 D 3 3 C    
Câu 12: Trong không gian Oxyz , cho hai vectơ u  1;3; 2
  và v  2;5; 
1 . Vectơ u  v có tọa độ là A. 1;8;3 . B.  3  ;8;3 . C. 3;8;3 . D. 1;8;3. Lời giải Chọn A  
u  v  1 2;3  5; 2    1  1;8;3 .
Câu 13: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ? N H Ó M TOÁN VD A. 4 2 y  x  2x  2. B. 3 2 y  x  2x  2. C. 3 2 y  x  2x  2. D. 4 2 y  x  2x  2. – VD Lời giải C Chọn D
Đồ thị hàm số nhận Oy làm trục đối xứng nên loại đáp án B và C.
Ta có lim y   nên loại đáp án A. x Chọn đáp án D.
Câu 14: Tập xác định của hàm số y  log x là 3 A. 3;   . B. ;. C. 0;. D. 0;. Lời giải Chọn D
Điều kiện: x  0  x 0; .  NHÓM TOÁN VD–VDC
Vậy tập xác định D  0;.
Câu 15: Nghiệm của phương trình 2x 1 2   32 là A. x  4 . B. x  3 . C. x  5 . D. x  2 . N Lời giải H Chọn B Ó M Ta có: 2x 1  2x 1  5 T 2  32  2
 2  2x 1  5  x  3. O ÁN
Câu 16: Trong không gian Oxyz cho hai điểm A1 1 ; ; 
1 ,B 3;3;5 . Tọa độ trung điểm của đoạn thẳng VD AB là – A. 4;2;4 . B. 1; 2;3 . C. 2;1; 2 . D. 2;4;6 . VDC Lời giải Chọn C Ta có:  x  x A B x   2  x  2  y  y 
I là trung điểm đoạn thẳng AB A B  y   y  1  . 2  z  2  z z   A B z   2 2
Câu 17: Cho hàm số y  f  x có đạo hàm liên tục trên 1;2. Biết f  
1  1, f 2  4. Giá trị f   xdx N 1 H bằng Ó A. 3 . B. 4  . C. 4 3  M . D. . T Lời giải O Á Chọn A N V
Câu 18: Cho khối cầu có bán kính r  .
a Thể tích của khối cầu đã cho bằng D 2 4 3 3 3 – A. 3 4 a . B.  a . C.  a . D.  a . V 3 3 D C Lời giải Chọn D 4 4
Ta có thể tích khối cầu 3 3 V   r   a . 3 3
Câu 19: Với a , b là các số thực dương bất kỳ khác 1, khi đó log a bằng b 1 A. log . b B. . C. log a  log . b D. log b. a log b a a Lời giải Chọn B  NHÓM TOÁN VD–VDC 1 Có log a  . b log b a
Câu 20: Cho hình nón có bán kính đáy r  4 và chiều cao h  9 . Thể tích V của khối nón đã cho bằng A. 126 . B. 36 . C. 48 . D. 108 . N H Lời giải Ó M Chọn C TOÁN VD – VDC
Thể tích V của khối nón đã cho bằng 1 1 2 2
V  h r  .9. .4  48 . 3 3
Câu 21: Cho cấp số nhân u với u  1
 và công bội q  3. Giá trị của u là n  1 3 A. 2  7. B. 3 . C. 9  . D. 2 . Lời giải Chọn C Ta có: 2 2
u  u .q  1.3  9 . 3 1 N
Câu 22: Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x  y  z  2x  2y  4z  2  0 . Tâm của S  có HÓ toạ độ là M A. 1; 1  ;2 . B. 1  ;1; 2  . C. 1;1; 2  . D. 2; 2  ;4 .         TO Lời giải ÁN Chọn B VD Ta có: 2 2 2 –
x  y  z  2x  2 y  4z  2  0 V 2 2 2 D   x   1   y   1   z  2  8 C
Khi đó Tâm của S  có toạ độ là I  1  ;1; 2   .    4 4 4 Câu 23: Cho f  xdx 1, g
 xdx  1. Giá trị  f
  x 2gxdx  bằng 0 0 0 A. 0 . B. 1. C. 1. D. 3 . Lời giải Chọn B    4 4 4 Ta có  f
  x 2gxdx  f   xdx  2 g
 xdx 12  1. 0 0 0
Câu 24: Cho hàm số y  f  x có bảng biến thiên như sau  NHÓM TOÁN VD–VDC N H Ó M
Hàm số đã cho đồng biến trên khoảng nào dưới đây? TO A.  ;  2 . B. 2;0 . C. 0;. D.  3  ;  1 . ÁN Lời giải VD Chọn B –
Dựa vào bảng biến thiên ta có hàm số đã cho đồng biến trên khoảng 2;0 . VDC
Câu 25: Họ nguyên hàm của hàm số f x  3sin x là A. 3sin x  C . B. 3cos x  C . C. 3cos 2x  C . D. 3cos x  C . Lời giải Chọn D 3sin d x x  3cos x  C 
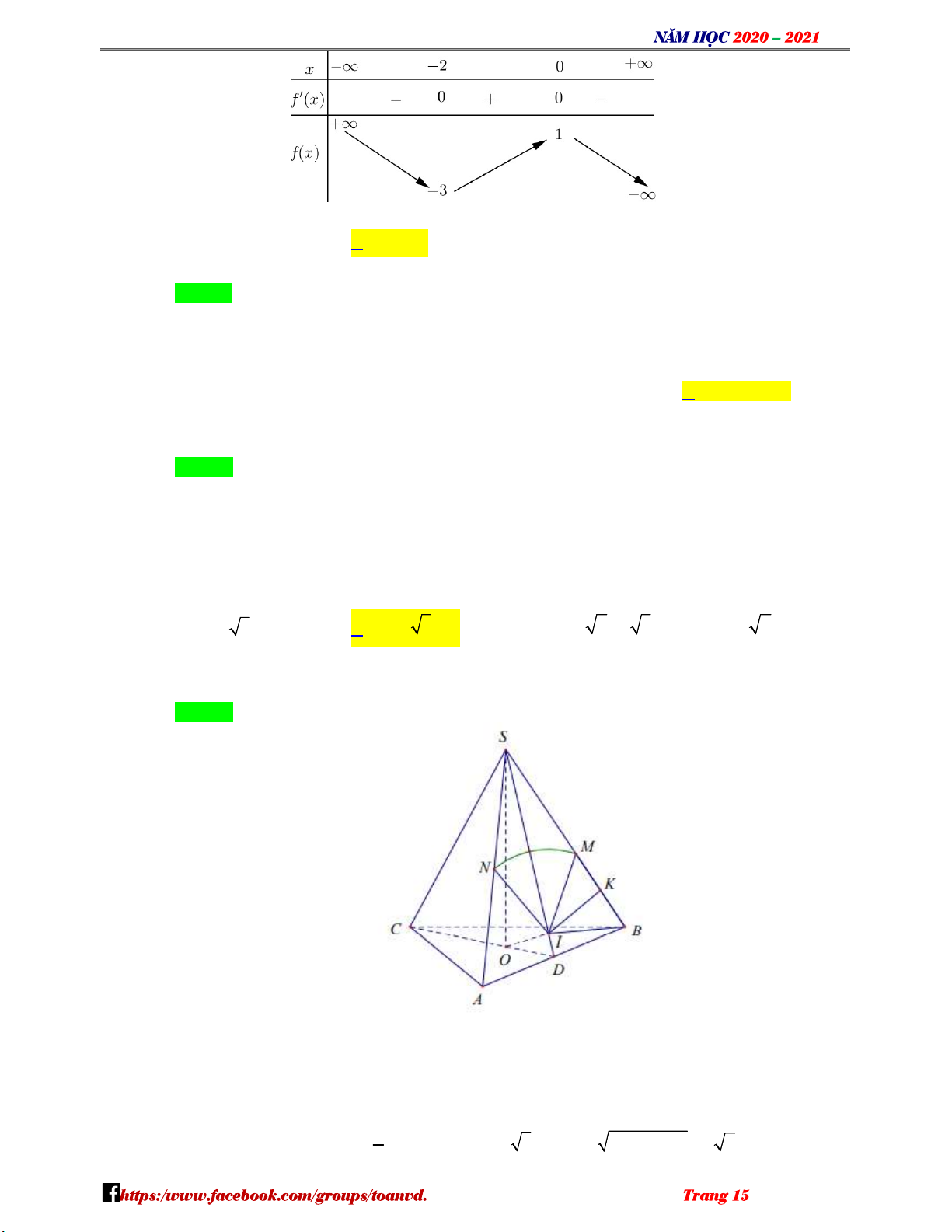
Câu 26: Một mặt cầu có tâm O nằm trên mặt đáy của hình chóp tam giác đều S.ABC có tất cả các cạnh bằng nhau. Các đỉnh , A ,
B C thuộc mặt cầu. Biết bán kính mặt cầu bằng 3. Tổng độ dài l các
giao tuyến của mặt cầu với các mặt bên của hình chóp thỏa mãn điều kiện nào sau đây? A. l   3;2 . B. l 3 3;6 .
C. l 13 2;12 3 . D. l 1; 2. N H Lời giải Ó M Chọn A TOÁN VD – VDC
Gọi D là trung điểm của AB , kẻ OI  SD  I là hình hình chiếu của O lên SAB . Suy ra
I là tâm đường tròn giao tuyến của mặt cầu và SAB . Gọi  MN là đoạn giao tuyến  l  3MN .
Gọi K là trung điểm của MB , đặt AB  a . Ta có OA  OB  OC  2 3  CD  AB  a  3 3 2 2
 SO  SC  OC  3 2 . 3  NHÓM TOÁN VD–VDC 1 1 1 1 Ta có  
 OI  2 ; SI  4; DI  2 2 2 OI OS OD 2 2 2  r  R  OI  7 1
Xét tam giác vuông SIK ta có 0 IK  SI.sin 30  SI  2 N 2 H IK 2 Ó
Xét tam giác vuông MIK ta có cos MIK     0 MIK  40,89   0 MIN  38, 2 M IM 7 T  O
Ta có độ dài cung l   .38, 2. 7 3.MN  3  5, 29 . Á 180 N V x  2 2 D
Câu 27: Cho a là số thực dương. Giả sử F  x là một nguyên hàm của hàm số f x  e lnax      x – V trên tập  \  0 và thỏa mãn F  
1  5; F 2  21. Khẳng định nào sau đây đúng ? D C A. a  3; . B. a  0;  1 . C. a  1;2 . D. a 2;3 . Lời giải Chọn C x  2 x x 2 x 2 Xét F x  e ln    2 ax   dx  e ln    2
ax dx  e . dx  I  e . dx    x x x Xét x I    2 e .ln ax dx  u    2 ax  2 ln du  dx Đặt    x dv  exdx v  ex N H x 2 x 2 x 2 Ó Khi đó: I  e .ln 
ax dx  e lnax  e . dx  M x TO Suy ra:   x F x  e  2 ln ax  C ÁN VD F    1  5  . e lna C  5  . e lna C  5  Vì :     –  2 2 F  2  21 e  .ln4a C  21 e  .
 ln4 lna C  21 VDC  . e ln a  C  5 (1)   2 2
e ln a  C  21 2e .ln 2 (2) 2 2 162e ln 2 16  2e ln 2
Lấy (2)  (1) ta được: 2 ln e e a   a  e  3,43 . 2 e  e
Suy ra: a  3; .
Câu 28: Có bao nhiêu cặp số nguyên  ;
x y thỏa mãn 0  y  2021 và x 3
3  3x  6  9y  log y ? 3 A. 2021 . B. 7 . C. 9 . D. 2020 . Lời giải Chọn B  NHÓM TOÁN VD–VDC Ta có: x 3
3  3x  6  9y  log y 3
 3x  3x  6  9 y  3log y 3
 3x  3x  9y  6  3log y N  3  H Ó x M
 3  3x  9y  32  log y 3  TO x 2
 3  3x  9y  3 log 3  log y Á  3 3  N V x D
 3  3x  9 y  3log 9y 3 – VD
Đặt:  log 9   9  3t t y y 3 C
Phương trình trở thành: 3x  3  3t x  3t  x  t
 x  log 9y  x  2  log y 3 3
Để x  thì log y  mà 0  y  2021 3 Suy ra: y  0 1 2 3 4 5 6 3 ;3 ;3 ;3 ;3 ;3 ;3 
Vậy: có 7 cặp số nguyên  ; x y thỏa mãn YCBT.
Câu 29: Cho hình trụ có thiết diện qua trục là hình vuông cạnh 4 .
a Diện tích xung quanh của hình trụ đã cho bằng N A. 2 16a . B. 2 4 a . C. 2 64 a . D. 2 8 a . H Ó Lời giải M Chọn A TOÁN VD – VDC
Gọi hình trụ như hình vẽ, thiết diện qua trục là hình vuông ABCD. AB Ta có h  AD  4a, R   2 . a 2 2 S  2 Rh  16 a . xq 1
Câu 30: Cho bất phương trình m   1 log x  22 2  4 m  5 log
 4m  4  0 với m là tham số 1   1 x2 2 2 5 
thực. Tập hợp tất cả các giá trị của m để bất phương trình có nghiệm thuộc đoạn ; 4  là? 2     NHÓM TOÁN VD–VDC  7   7   7  A. 3; . B. ;   . C. 3; . D.  ;    .  3   3     3  Lời giải Chọn C N Điều kiện x  2. H Ó m 1log x  22 1 2  4 m  5 log  4m  4  0 1   M 1 x  2 2 2 T 2 O  m  
1 log x  2  m  5 log x  2  m 1  0 2     2   ÁN 5  V
Đặt t  log x  2 , do x  ; 4  t  1  ;  1 . 2     D 2  –
Bất phương trình trở thành VD m   2
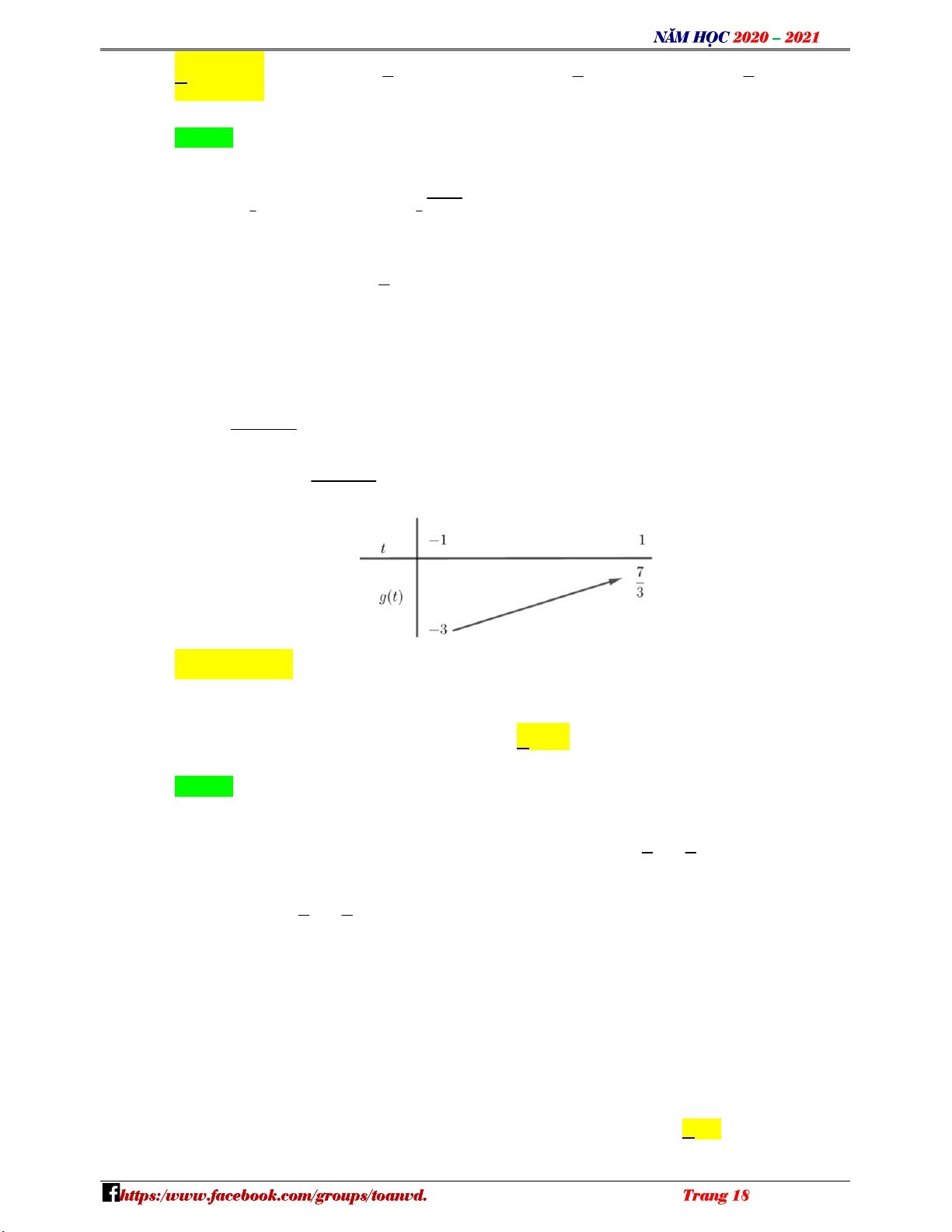
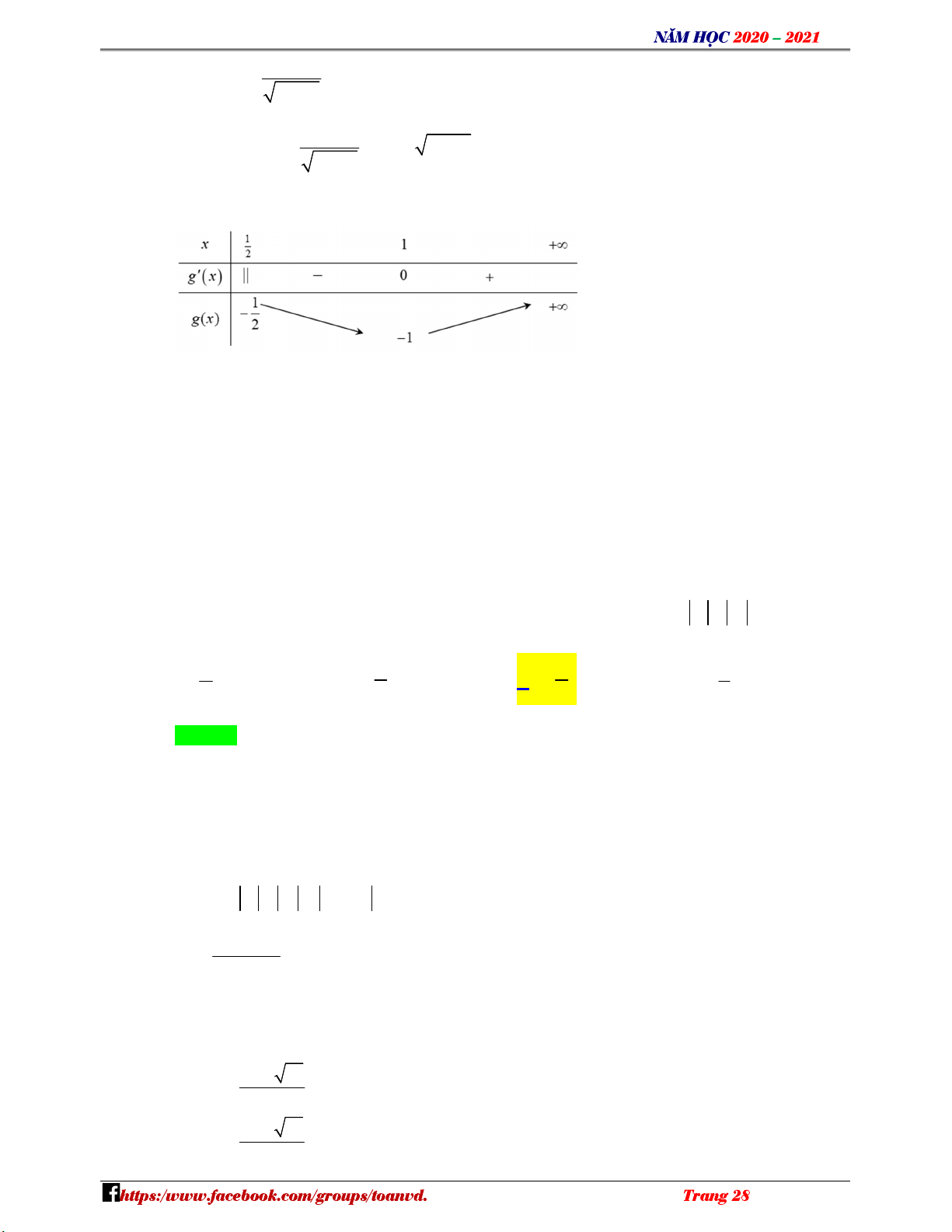
1 t  m  5t  m 1  0 C  m 2t t   2 1  t  5t 1 2 t  5t 1  m  . 2 t  t 1 2 t  5t 1 Xét hàm số g t  trên 1; 
1 , từ table ta có bảng giá trị của g(t) như sau: 2 t  t 1 N  m 3  ; . H   Ó M
Câu 31: Giá trị lớn nhất của hàm số     2 3  5ex f x x x
trên đoạn 1;2 bằng TO A. 2e . B. 2 4e . C. 2 3e . D. 3e . ÁN Lời giải VD Chọn C – TXĐ: D   V 2 D  1 7    x 2 x 2 x C
Ta có f  x  2x  3e  x  3x  5e     2ex x x   x      e  2  4   2  1 7    Vì          ex f x x  0 với mọi x  2  4  
Suy ra hàm số f  x đồng biến trên  hay hàm số f  x đồng biến trên 1;2
Do đó hàm số f  x đạt giá trị lớn nhất trên đoạn 1;2 tại x  2
Ta có max f  x  f 2 2  3e . 1;2
Câu 32: Cho hàm số y  f  x , biết f  x 3
 x  3x 1 có tất cả bao nhiêu giá trị nguyên của tham số m
thuộc đoạn 5;5 sao cho hàm số y  f 2  x  1 m x  6 nghịch biến trên khoảng 2;3? A. 10 . B. 9 . C. 7 . D. 8 . Lời giải  NHÓM TOÁN VD–VDC Chọn A
Xét hàm số y  f 2  x  1 m x  6 trên khoảng 2;3.
Ta có y   f   x   m    x3 2 1 2
 32  x 11 m 3 2
 y  x  6x  9x  4  m . N H
Để hàm số y  f 2  x  1 m x  6 nghịch biến trên khoảng 2;3 Ó      3 2         M y 0, x 2;3 m x 6x 9x 4, x 2;3 (1) T Xét hàm số g  x 3 2
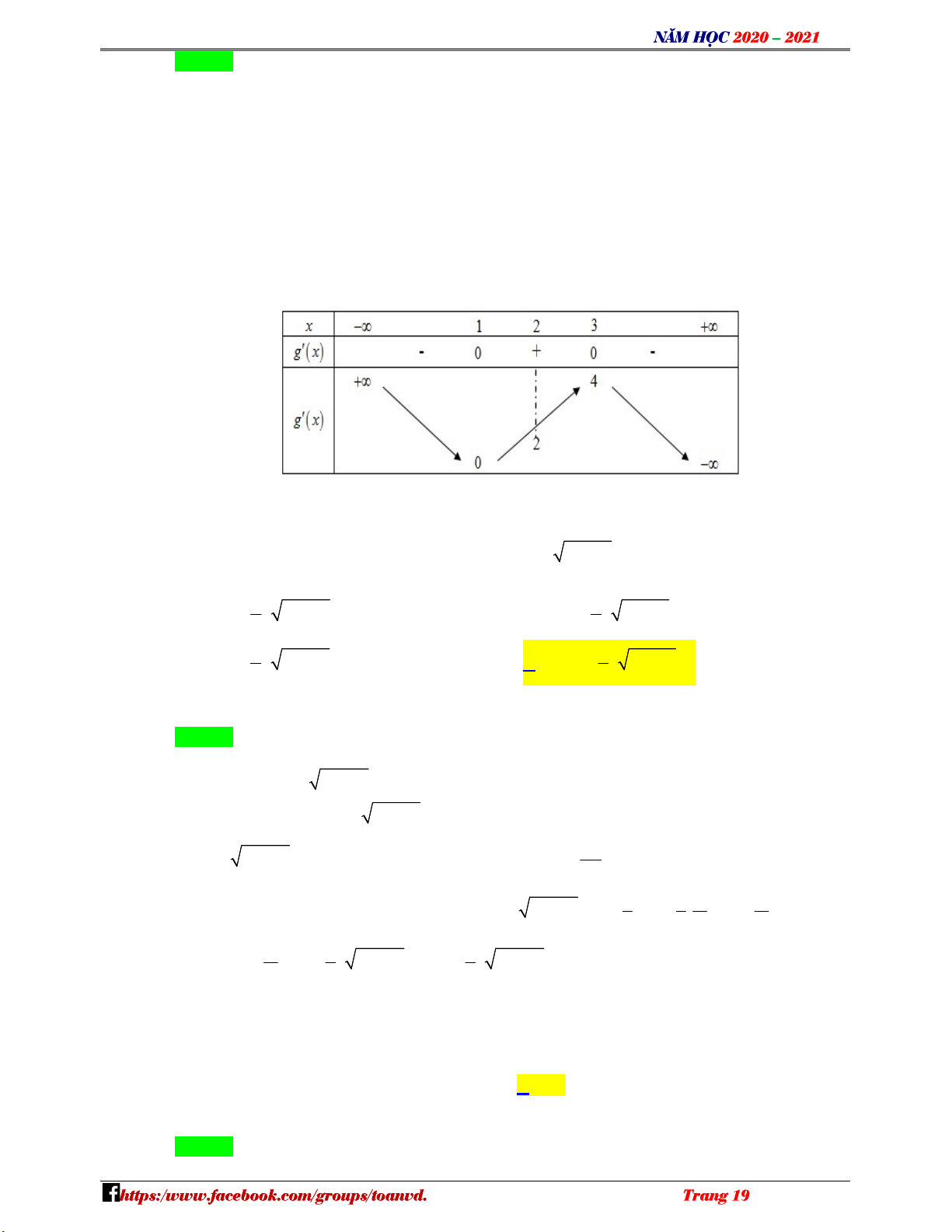
 x  6x  9x  4 trên khoảng 2;3. O Á x  12;3 N Ta có g x 2
 3x 12x  9; g x  0   V x  3  2;3 D – VDC
Từ BBT, bất PT (1)  m  2 .
Vì m 5;5 m 5; 2,m    m có 8 giá trị.
Câu 33: Biết F  x là một nguyên hàm của hàm số f  x 2 3
 x 1 2x . Khẳng định nào dưới đây đúng ? 2 2
A. F  x   1 2x 3 3 .
B. F  x   1 2x 3 3 . 9 3 N 1 1 C. F  x  1 2x D. F  x  1 2x . H  33  33 2 9 Ó M Lời giải TO Chọn D ÁN V  Ta có: 2 3 f (x)  x 1  2x D –  F x  f x x  x  x x      2 3 d 1 2 d  VD tdt C Đặt 3 2 3 2 2
t  1 2x  t  1 2x  2tdt  6x dx  x dx  3 3 3 1 1 t t
Từ đó nguyên hàm trên trở thành: 2 3 2  F(x)  x 1 2x dx  t dt  .  C   C   3 3 3 9 3 3 3 t 1 1 Vậy F (x)   C   3 1 2x   C   3 1 2x  . 9 9 9
Câu 34: Cho hàm số y  f (x) có f  x   x  x  x  x  3 2 2 3 2
3 . Tập hợp tất cả các giá trị của tham
số m sao cho hàm số y  f  2
x  6x  m có 3 điểm cực trị phân biệt là nửa khoảng a;b . Giá trị của a  b bằng A. 21. B. 23. C. 22 . D. 20 . Lời giải Chọn C  NHÓM TOÁN VD–VDC
 Ta có: f  x   x  x  x   x  3   x  x  x  x  3 2 2 3 2 3 2 1 2 3
 x   x  2  x  3 1 2 3 x  1  N
f  x  0  x  2 với x  2 là nghiệm bội chẵn nên suy ra f  x có 2 điểm cực trị H  Ó x  3  M 2 2  Đặt           T g  x f  x 6x m
g  x 2 x 3 f x 6x m O Á
Để hàm số g  x có 3 điểm cực trị thì g x  0 phải có 3 nghiệm bội lẻ phân biệt N V x  3 D   x  3 2 – x  3 x  6x  m  1   2 V Cho g x  0   
 m  x  6x 1  g x (1) 2      2 1 D f  x 6x m   0 x  6x  m  2  2 C 
m  x  6x  3  g x 2  2   x  6x  m  3 (2)
Do x  2 là nghiệm bội chẵn nên các nghiệm của phương trình 2
x  6x  m  2 đều là nghiệm
bội chẵn của phương trình g x  0 , vì thế nên ta không xét phương trình này
Từ đó, để g x  0 phải có 3 nghiệm bội lẻ phân biệt thì phương trình (1) và (2) đều tạo với
nhau đúng 2 nghiệm, nên ta vẽ lần lượt hai hàm số g x và g x lên cùng 1 hệ trục tọa độ 2   1  
Oxy để từ đó đường thẳng y  m chỉ cắt đúng 2 nghiệm từ 2 hai hàm này
Dựa vào đó ta kết luận m 10;12 . Suy ra a  10,b  12
Vậy a  b  10 12  22 3 2 1
Câu 35: Cho hàm số f  x có đạo hàm liên tục trên đoạn 0;3 thỏa mãn f 3  4 ,  f   x dx   27 0 N 3 333 3 H và 3 x f  xdx  . Giá trị của f  xdx bằng Ó 4 0 0 M 3 153089 25 150893 T A. x  . B. x  . C. x  . D. x  . O 2 1215 2 21 ÁN Lời giải VD Chọn C – d  u  f  x dx 3 V u   f x    3 D Tính: x f  xdx  . Đặt   4  . 3 x C     0 dv x dx v  4 3 3 4 3 x f x 1 Ta có: 3 x f  x   4 dx   x . f   xdx 4 4 0 0 0 81. f 3  0. f 0 3 3 1 1 4   x . f   x 4 dx  81 x . f   xdx . 4 4 4 0 0 3 333 3 3 1 9 Mà 4 x f  xdx   4   x . f x 4
dx   x . f  xdx  9    . 4 4 4 0 0 0 3 2 1 Ta có  f   x dx   (1). 27 0 3 3 9 x 3 2  1  1 8 x dx   2187  4  x dx    (2). 9  243  27 0 0 0  NHÓM TOÁN VD–VDC 3 3 2 2 4 x . f  x 4 dx  9   x . f  xdx     (3). 243 27 0 0
Cộng hai vế (1) (2) và (3) suy ra 3 3 3  f   x 2 1 1 1 1 2 8 4  dx  x dx  2 x . f     xdx     0. N 59049 243 27 27 27 H 0 0 0 Ó 3  3 2 2 1 1  1 M      f    x 4   2. x f   x 8  x dx  0  f   x 4  x dx  0 . 2   T  243 243   243  0 0 O 2 3 2 3 2 Á  1   1  1 4  4  N Do f  x 4  x  0  f   x x dx  0. Mà f   x x dx  0       V  243   243   243  0 0 D 1 –  f  x 4  x  0 . V 243 D 5 C   x f x    C . Mà f   243 21 3  4    C  4  C  . 1215 1215 5 5 x 21 Do đó f  x    . 1215 5 3 3 1 5 6  x 21  x 21  25 Vậy f  xdx    dx    x      . 1215 5 7290 5 2 0 0     0
Câu 36: Có tất cả bao nhiêu giá trị nguyên của m thuộc đoạn 10;10 để hàm số 3 2 y  x  mx   2 3
6 m  2 x 1 đồng biến trên khoảng 2; A. 21. B. 18 . C. 20 . D. 19. Lời giải Chọn C N Ta có : 2 2     H y =3x 6mx 6m 2 Ó M 2 2 2
Khi đó :   3m  3.6 m  2  9 4  m T     O ÁN m  2  V TH1 : Nếu  0  
. Khi đó ta có a  3  0 nên y  0 với mọi x   . Do đó hàm số D m  2 –
đã cho đồng biến trên 2; . Kết hợp với giả thiết m  ;m 10;10ta được VDC
m 10;9;8;...; 2; 2;3;...;1 
0 . Vậy trường hợp này có 18 số nguyên thỏa mãn.
TH2: Nếu   0  2  m  2 . Khi đó y  0 có hai nghiệm phân biệt x và x . Giả sử x  x 1 2 1 2
Ta có y  0  x  ; x  x ; và y  0  x   x ; x . Do đó để hàm số đã cho đồng 1 2  1   2 
biến trên 2; thì 2;   x ; . 2   x  x 1 2   2
Ta có : x  x  2   2 1 2   x  2 . x  2  0  1   2  x  x Xét 1 2  2  m  2 .(1) 2  NHÓM TOÁN VD–VDC
Xét  x  2 . x  2  0 1   2 
 x .x  2 x  x  4  0 1 2  1 2  2 2 m  2  4m  4  0 N 2 H  m  2m  0 Ó M m  0  (2)  T m  2 O ÁN
Kết hợp điều kiện (1) và (2) và giả thiết m  ;m 10;10 ta được m 1;  0 . Vậy trường VD
hợp này có 2 số nguyên thỏa mãn. – VD
Vậy có 20 giá trị nguyên của m để hàm số đã cho đồng biến trên 2; . C 2 9  x
Câu 37: Tổng tất cả số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y  bằng 2 x  6x  5 A. 2 . B. 4 . C. 1. D. 3 . Lời giải Chọn C 2 9  x Hàm số y 
có tập xác định D  3;3  Hàm số không có tiệm cận ngang. 2 x  6x  5 x  1
Trên tập D , xét phương trình: 2 x  6x  5  0   , khi đó: x  5(L) 2 9  x lim y  lim
  , nên x  1 là tiệm cận đứng.  2  x 1 x 1   x  6x  5 N
Vậy hàm số đã cho có 1 đường tiệm cận. H Ó
Câu 38: Tổng các giá trị nguyên của tham số m để phương trình log  x   1  log mx  8 có hai 3 3   M nghiệm phân biệt bằng T A. 11. B. 22 . C. 3 . D. 18. O Á Lời giải N Chọn C VD x 1 0 x  1 –  x  1   x  1  V PT  mx 8  0       9 D    x   2 2 1  mx  8 x  2x  9  mx x  2   m (*) 2  C log x 1  log mx  8  x  3   3  
Phương trình đã cho có 2 nghiệm phân biệt khi phương trình (*) có hai nghiệm phân biệt. 9 9 x  3
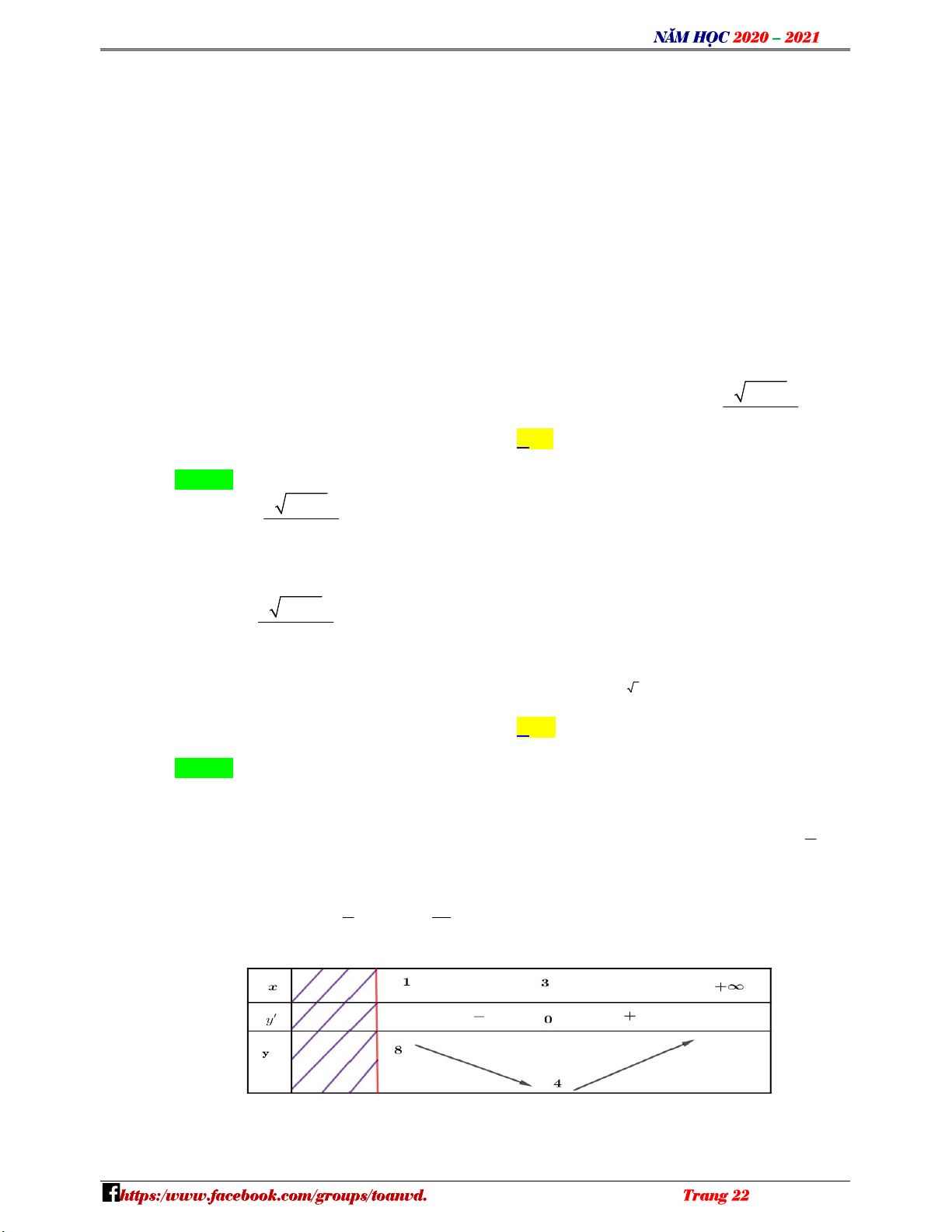
Xét hàm số: y  x  2   y ' 1 . Ta có: f (  x)  0  2 x x  x  3  (L) Bảng biến thiên:  NHÓM TOÁN VD–VDC 9
Phương trình (*) có hai nghiệm phân biệt khi đường thẳng y  m cắt đồ thị hàm số y  x  2  x
trên khoảng 1; tại 2 điểm phân biệt  4  m  8 .
Vậy có 3 giá trị m 5;6; 
7 thỏa mãn yêu cầu bài toán. N H
Câu 39: Cho hàm số f  x có đồ thị như hình vẽ. Ó y M TO -1 O 1 2 x ÁN -1 VD – -3 VDC -5
Gọi M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f  3 sin x   1 trên đoạn  5  2 ; 
. Giá trị của 2M  m bằng 2    A. 5  . B. 1  1. C. 1  3. D. 7  . Lời giải Chọn B  5  Với x  2 ;  sin x    0; 1. N  2  H Ó M Đặt 3 t  sin x 1 t  1  ;0. TOÁ
Suy ra M  max f t  max f  x  3  N  1  ;0  1  ;0 VD     – m min f t min f  x 5 1  ;0 1  ;0     VDC
Khi đó 2M  m  2.3   5    11.
Câu 40: Cho hình lăng trụ đứng ABC.A B  C
  có đáy là tam giác đều cạnh bằng a (tham khảo hình vẽ) A' C' B' A C B  NHÓM TOÁN VD–VDC
Khoảng cách giữa hai đường thẳng AA và BC bằng a 3 a 3 A. a . B. . C. 2a . D. . 3 2 Lời giải N H Ó Chọn D M TO A' C' ÁN V M D B' – VDC A C B Gọi M là trung điểm B C  . a 3 Có A M   B C   và A M   BB  A M   BCC B   và AM  . 2
Do AA//BB  AA// BCC B   N H
 d  AA BC  d  AA BCC B
   d  A BCC B   a 3 , , ,  AM  . Ó 2 M TO
Câu 41: Trong không gian Oxyz, cho hai điểm A1;1;2 và B 3;2; 3 . Mặt cầu S  có tâm I thuộc ÁN
trục Ox và đi qua hai điểm , A B có bán kính bằng V A. 4 . B. 4 2 . C. 14 . D. 3 . D – Lời giải V Chọn C D C
Giả sử mặt cầu S  có tâm I m;0;0Ox và bán kính R . Ta có ,
A B  S  nên IA  IB  R . +) IA  IB 2 2
 IA  IB    m2      m2    2 2 2 2 1 1 2 3 2 3
 m  4  I 4;0;0 . +) Vậy R  IA  14 .
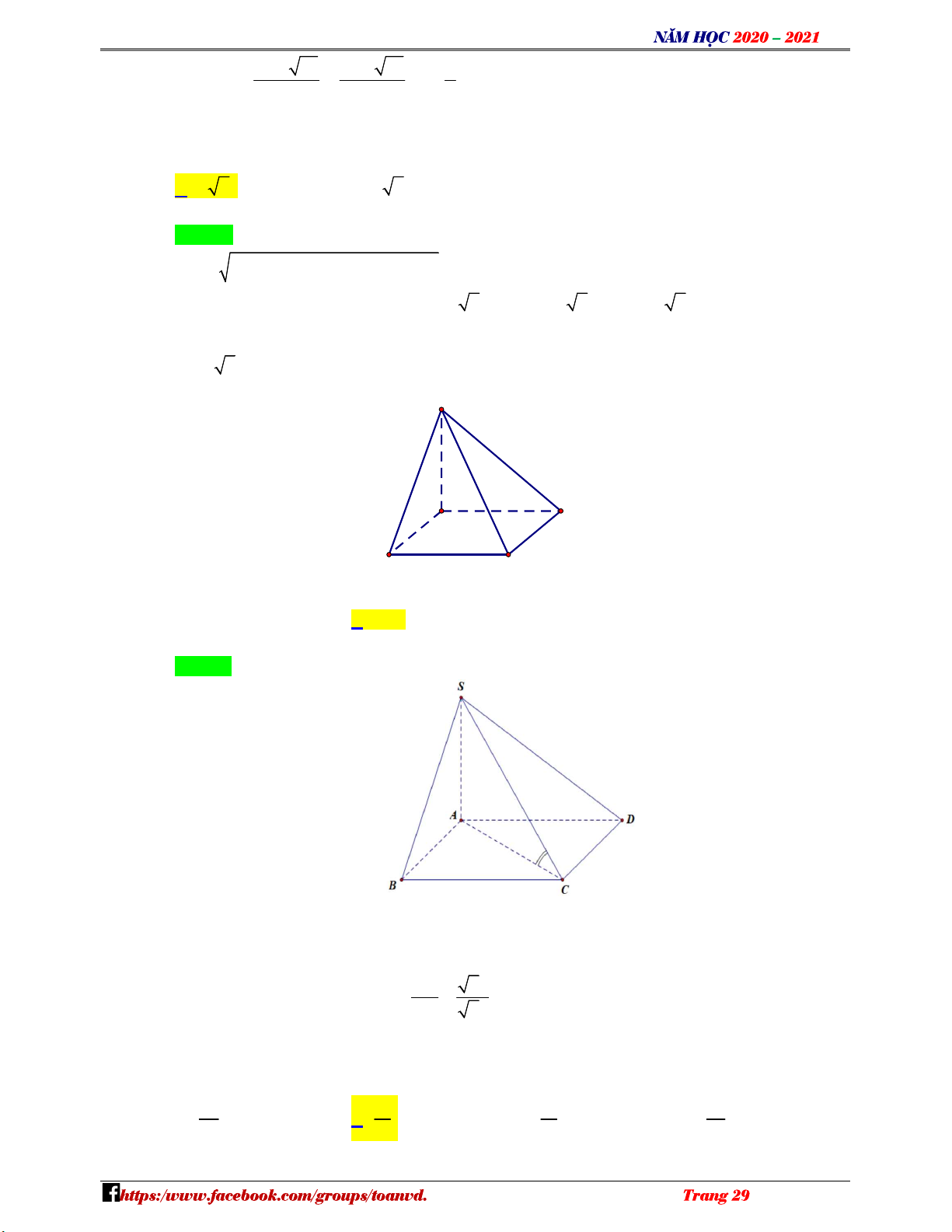
Câu 42: Cho khối hộp ABCD.AB C  D
  có đáy ABCD là hình chữ nhật AB  2a, AD  2a . Điểm A cách đều các điểm , A , B C, D . Mặt bên CDD C
  tạo với mặt phẳng đáy một góc 45 (tham khảo hình vẽ).  NHÓM TOÁN VD–VDC N H Ó M T
Thể tích khối hộp đã cho bằng O 3 Á 2 2a N A. 3 2 6a . B. 3 2a . C. 3 2 2a . D. . V 3 D Lời giải – Chọn C VDC
Gọi O  AC  BD , ta có ABCD là hình chữ nhật nên O là tâm đường tròn ngoại tiếp hình chữ nhật ABCD .
Mặt khác A cách đều các điểm ,
A B, C, D  AO   ABCD.
Gọi M là trung điểm của AB  OM  AB , mà AB  AO  AB  AM . Ta có  ABB A   / / CDD C     ABB A
 , ABCD  CDD C
 , ABCD  45 N H  ABB A
  ABCD  AB Ó  M
Lại có OM   ABCD,OM  AB   ABB A
 , ABCD  
AMO  45 (vì AOM  T AM    ABB A  , AM  AB O ÁN vuông tại O nên  AMO là góc nhọn). VD +) Ta có 2 S  AB.AD  2 2a . ABCD – 1 V
+) Tam giác AOM vuông tại O , có OM  AD  a,  A M  O  45 D 2 C
 AMO vuông cân tại O  AO  OM  a . Vậy 3 V        S .A O 2 2a . ABCD. A B C D ABCD
Câu 43: Cho hai số thực a  1,b  1. Biết phương trình 2 x x 1
a .b   1 có hai nghiệm phân biệt x , x . Giá trị 1 2 2  x x 
nhỏ nhất của biểu thức 1 2 S     4 x  x bằng 1 2  x  x  1 2  A. 3 3 4 . B. 4 . C. 3 4 . D. 3 3 2 . Lời giải Chọn A  NHÓM TOÁN VD–VDC Ta có 2 x x a b  a b      x  a x   * b  2 1 x x 1  2 . 1 log . log 1 b logb  1 0
Điều kiện để phương trình đã cho có 2 nghiệm phân biệt x , x là    a   . b 2 log 4 0 1 2 N H x  x   log a
Theo hệ thức Vi-et của phương trình * , ta có: 1 2 b . Ó   x x  1 M  1 2 TO 2  x x  2 4 Á Mặt khác, 1 2 S  
  4 x  x  log b 
. Đặt t  log b  log 1  0 N  1 2   a  x  x log b a a  1 2  a VD – 4 2 2 Cauchy V Khi đó 2 2 3 S  t   t    3 4 . D t t t C 2 Suy ra 3 2 min S  3 4  t  hay 3 3 2 log b  2  b  a . t a
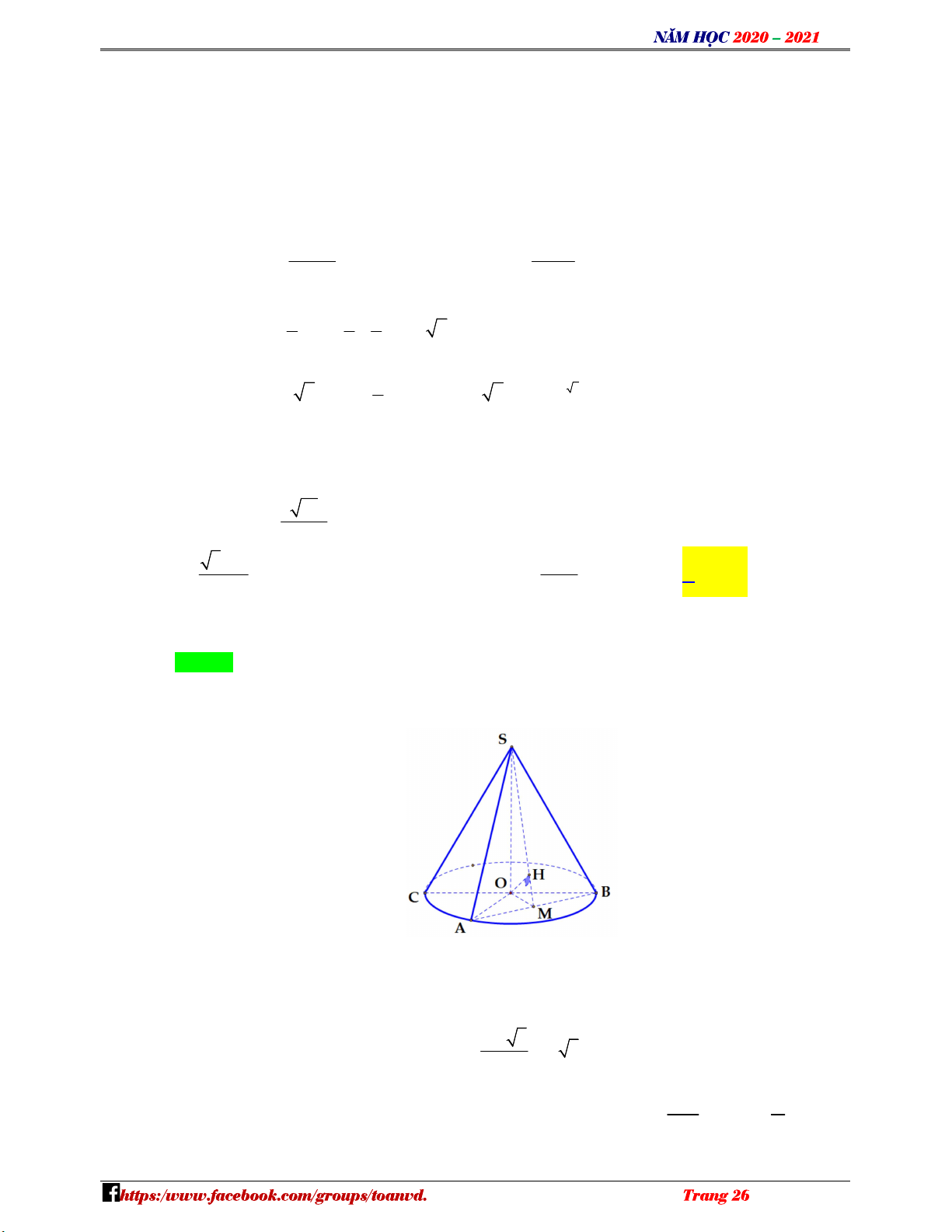
Câu 44: Cho hình nón đỉnh S có đáy là đường tròn tâm O , thiết diện qua trục là tam giác đều. Mặt phẳng
P đi qua S và cắt đường tròn đáy tại , A B sao cho 
AOB  120 . Biết rằng khoảng cách từ O 3 13a đến P bằng
. Thể tích của khối nón đã cho bằng 13 3 3 a 3 3 a A. . B. 3 a . C. . D. 3 3 a . 3 2 Lời giải N Chọn D H Ó M Ta có hình minh họa sau: TOÁN VD – VDC
Gọi thiết diện qua trục SO của hình nón là SBC và SAB là thiết diện của mặt phẳng P
cắt hình nón (xem hình vẽ). BC 3
Do SBC đều nên BC  2R  SB  SO   R 3 . 2 OM R
Gọi M là trung điểm AB ,  0 AOB    0 120 MOB  60  tan  MOB   OM  OB 2  NHÓM TOÁN VD–VDC
Dễ thấy, OAB cân tại ABSO
O  AB  OM  AB  SOM  ABSAB
SOM   SAB theo giao tuyến SM . a
Trong SOM  , kẻ OH  SM tại H  OH  SAB tại H  OH  d O SAB 3 13 ;  . N 13 H Ó M 1 1 1 1 1 1 Xét SOM vuông tại O :       R  a 3 . 2 2 2 2 2 2 T OH OS OM 9a 3R R O 13 4 ÁN V  D Vậy 2 3 V  S . O R  3 a . – 3 VDC Câu 45: Cho hàm số   4 2
f x  ax  bx  c có đồ thị như hình vẽ N H Ó M
Số nghiệm của phương trình 2 f x 1 2x 1 5  0 là TO A. 2 . B. 3. C. 5 . D. 4 . ÁN Lời giải V Chọn C. D – V 5 x   D Từ đồ thị hàm số : 4 2
y  x  2x  2 . Xét f x 0,54     C 2 x   1  ,3
Phương trình : f x   x      f x   x   5 2 1 2 1 5 0 1 2 1   (*) 2 x 1 2x 1  1  ,3   1  x 1 2x 1  0  ,54 2  
x 1 2x 1  0,54   3  x 1 2x 1 1,3  4 1
Xét hàm số : g  x  x 1 2x 1 với x  2  NHÓM TOÁN VD–VDC gx 1 1 2x 1 g x 1  0 1
 0  2x 1 1  x 1 N 2x 1 H Ó M BBT : TOÁN VD – VD C
Dựa vào bảng biến thiên, ta có:
+ Phương trình (1) vô nghiệm.
+ Phương trình (2) có đúng 2 nghiệm phân biệt.
+ Phương trình (3) có đúng 1 nghiệm phân biệt.
+ Phương trình (4) có đúng 1 nghiệm phân biệt.
Vậy phương trình đã cho có tất cả 4 nghiệm.
Câu 46: Gọi S là tập hợp tất cả các giá trị thực của tham số m để hàm số y   2 m   3 x  m   2 1 3
5 x  x 1 có hai điểm cực trị x , x sao cho x  x  8. Tích các 1 2 1 2 phần tử của S bằng N H 9 1 1 9 Ó A. . B. . C.  . D.  . M 4 4 4 4 Lời giải TO Chọn C. ÁN 2 2 V Ta có: y  3m   1 x  6m  5 x 1 D – 2 V Nhận xét: . a c  3m   1   1  0, m
   nên phương trình y  0 luôn có 2 nghiệm x , x D 1 2 C trái dấu.
Khi đó : x  x  x  x  8 1 2 1 2 6m 5    3 8 2 m   1  m 5  4 2 m   1 2  4m  m 1  0  1   17 m  8   1   17 m   8  NHÓM TOÁN VD–VDC
 1 17  1 17  1 Vậy: S       . 8 8 4   
Câu 47: Trong không gian Oxyz , cho hình vuông ABCD có B 3;0;8 và D 5;4;0 . Độ dài cạnh của N hình vuông đã cho bằng H Ó A. 6 2 . B. 5 2 . C. 6 . D. 12. M Lời giải TO Chọn A Á 2 2 2 N BD   5   3   4
  0  0 8 12 . VD Do ABCD BD  AB   AB  AB  . là hình vuông nên . 2 12 . 2 6 2 – V Câu 48: Cho hình chóp D
S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với mặt phẳng đáy và C
SA  2a ( tham khảo hình vẽ). S A D B C
Góc giữa đường thẳng SC và mặt phẳng đáy bằng A. 60 . B. 45 . C. 90 . D. 30 . Lời giải N H Chọn B Ó M TOÁN VD – VDC
SA   ABCD  AC là hình chiếu vuông góc của SC lên mặt phẳng  ABCD . Do đó: SC, ABCD  SC, AC    SCA .  SA 2a SAC vuông tại A : tan  SCA    1   SCA  45 . AC 2a
Câu 49: Một đội thanh niên tình nguyện của trường gồm 6 học sinh nam và 5 học sinh nữ. Chọn ngẫu
nhiên 4 học sinh để cùng với các giáo viên tham gia đo thân nhiệt cho học sinh khi đến trường.
Xác suất để chọn được 4 học sinh trong đó số học sinh nam bằng số học sinh nữ bằng: 5 5 6 2 A. . B. . C. . D. . 66 11 11 33 Lời giải  NHÓM TOÁN VD–VDC Chọn B Ta có: 4   C 11
Gọi A là biến cố: “Chọn được 4 học sinh trong đó số học sinh nam bằng số học sinh nữ” N
Do số học sinh nam bằng số học sinh nữ nên trong 4 học sinh được chọn có 2 học sinh nam và H 2 học sinh nữ Ó M  2 2   C .C A 6 5 TO
Vậy xác suất để chọn được 4 học sinh trong đó số học sinh nam bằng số học sinh nữ là: Á 2 2 N  P  A C C A . 5 6 5    . 4 V  C 11 11 D –
Câu 50: Tập nghiệm của bất phương trình log 2x  8  log 2x  4 là: 0,5   0,5   VD A.  1  ;  . B.  4  ;  1 . C.  1  ;2 . D. ;  1 2; . C Lời giải Chọn C ĐKXĐ: 4   x  2 . Do cơ số 0,50; 
1 nên bất phương trình đã cho  2x  8  2  x  4  x  1  .
Kết hợp với ĐKXĐ ta có tập nghiệm của bất phương trình đã cho là: S   1  ;2.
Từ gt  SA   ABCD
Gọi E là trung điểm AD  AB  AE  a
Do đó ABCE là hình vuông cạnh a  SA  AC  a 2 .
Dễ thấy CD / / SAE   d SB;CD  d CD;SBE  d C ;SBE  d  A;SBE
Mà SA ; AB ; AE đôi một vuông góc. N H 1 1 1 1 1 1 1 5 Ó         2 2 2 2 2 2 2 2 M     SA AB AE a a    2 ; 2 a d A SBE a TO a Á
 d SB CD  d  A SBE 10 ; ;  . N 5 VD
------------------------- HẾT ------------------------- – VD C 

Tài liệu liên quan: