Đề KSCL môn Toán thi ĐH 2019 trường THPT Hàm Rồng – Thanh Hóa lần 3

TRƯỜNG THPT HÀM RỒNG
ĐỀ KSCL CÁC MÔN THEO KHỐI THI ĐẠI HỌC Mã đề 061 MÔN: TOÁN LỚP 12
Thời gian làm bài: 90 phút
(50 câu trắc nghiệm) Ngày thi: 12/05/ 2019 .
Câu 1: Tính thể tích của khối lập phương ABC .
D A' B 'C ' D ' có cạnh bằng . a 3 a 3 a 3 a A. . B. . C. 3 a . D. . 2 3 6 2
Câu 2: Tích phân I  2x  
1 dx có giá trị bằng: 0 A. 1. B. 0 . C. 3 . D. 2 . x 1 y 1 z  2
Câu 3: Trong không gian với hệ tọa độ Oxyz , cho dường thẳng d:   điểm nào dưới 2 1  3
đây thuộc đường thẳng d?
A. M (2;1;3) .
B. P(1;1; 2) .
C. Q(1; 1; 2) .
D. N (2; 1;3) .
Câu 4: Hàm số nào dưới đây có đồ thị như hình vẽ sau? y 2 1 O -2 1 2 x -1 -1 A. 3 2
y  x  3x 1. B. 4 2
y  x  2x 1. C. 3 2
y  x  3x 1. D. 4 2
y  x  2x 1.
Câu 5: Trong không gian Oxyz, viết phương trình đường thẳng d qua M (3; 2; 5) và vuông góc với
mặt phẳng P : x  2y  5z 1  0. x  3  t x  3  t x  3  t x  3  t    
A. d : y  2  2t .
B. d : y  2  2t .
C. d : y  2  2t .
D. d : y  2  2t . z  5   5t     z  5   5t  z  5   5t  z  5   5t 
Câu 6: Thể tích của của tứ diện SABC vuông tại đỉnh S có các cạnh SA  a, SB  b, SC  c là: abc abc abc A. . B. abc . C. . D. . 6 2 3
Câu 7: Tính mô đun của số phức z  1 3i A. z  2 . B. z  3 .
C. z  1 3 . D. z  1.
Câu 8: Diện tích của mặt cầu bán kính 2a là: 2 4 a A. 2 16a . B. 2 16 a . C. 2 4 a . D. . 3
Câu 9: Trong không gian Oxyz , cho hai mặt phẳng P : x  2y  2z  3  0 ,Q : x  2y  2z 1  0 .
Khoảng cách giữa hai mặt phẳng đã cho là:
Trang 1/11 - Mã đề thi 061 4 4 2 A. . B. . C. 4 . D. . 9 3 3
Câu 10: Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng P : 2x  y 1  0 . Mặt phẳng P
có một vectơ pháp tuyến là:    
A. n  (2; 1;1) .
B. n  (2;1;0) .
C. n  (2; 1;1) .
D. n  (2;1;1) .
Câu 11: Với các số thực dương a , b bất kì. Mệnh đề nào dưới đây đúng? a a ln a
A. ln ab  ln a  ln b . B. ln  ln b  ln a . C. ln ab  ln .
a ln b . D. ln  . b b ln b
Câu 12: Tập nghiệm của bất phương trình log x  2 là: 1 3 1   1  1   1  A. ;    . B. 0;  . C. 0;   . D. ;    . 9  9     9   9 
Câu 13: Gọi l, h, r lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của một hình nón. Tính
diện tích xung quanh S của hình nón đó theo l, h, r. xq 1
A. S   rl . B. 2 S   r h .
C. S  2 rl .
D. S   rh . xq xq 3 xq xq
Câu 14: Trong không gian Oxyz, cho mặt cầu có phương trình 2 2 2
x  y  z  2x  4y  6z  9  0 . Tọa
độ tâm I và bán kính R của mặt cầu là: A. I  1  ;2; 3   và R  5 . B. I 1; 2  ;3 và R  5. C. I  1  ;2; 3   và R  5. D. I 1; 2
 ;3 và R  5 .
Câu 15: Hỏi hàm số 3 2
y  x  3x  2 nghịch biến trên khoảng nào? A.  ;0  . B. (2; ) . C. 0;2 . D.  .
Câu 16: Tính thể tích V của khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường
y  2x , y  0 và hai đường thẳng x  1 , x  2 quanh Ox . A. V  3 . B. V  1 . C. V   . D. V  3 .
Câu 17: Tập hợp các điểm biểu diễn số phức z là đường tròn 2 2
(x 1)  ( y  2)  9 . Tập hợp các điểm
biểu diễn số phức liên hợp z là đường tròn nào sau đây? A. 2 2
(x  2)  ( y 1)  9 . B. 2 2
(x 1)  ( y  2)  9 . C. 2 2
(x 1)  ( y  2)  9 . D. 2 2
(x 1)  ( y  2)  9 .
Câu 18: Trong không gian với hệ tọa độ Oxyz , cho ba điểm A1;0;0, B0; 2;
 0 và C 0;0;3.
Phương trình nào dưới đây là phương trình của mặt phẳng  ABC . x y z x y z x y z x y z A.    1. B.    1. C.    1. D.    1. 3 1 2 1 2 3 3 2 1 2 1 3
Câu 19: Hàm số nào sau đây là hàm số chẵn?
A. y  tan x .
B. y  sin x .
C. y  cos x .
D. y  cot x .
Câu 20: Đạo hàm của hàm số y   2
ln x  x   1 là:
Trang 2/11 - Mã đề thi 061 2x 1 1 1 2x 1 A. y '  . B. y '  . C. y '  . D. y '  . ln  2 x  x   1 2 x  x 1 ln  2 x  x   1 2 x  x 1
Câu 21: Điểm M biểu diễn số phức z  3  2i trong mặt phẳng tọa độ phức là:
A. M (3; 2) . B. M (2;3) .
C. M (3; 2) . D. M (3; 2)
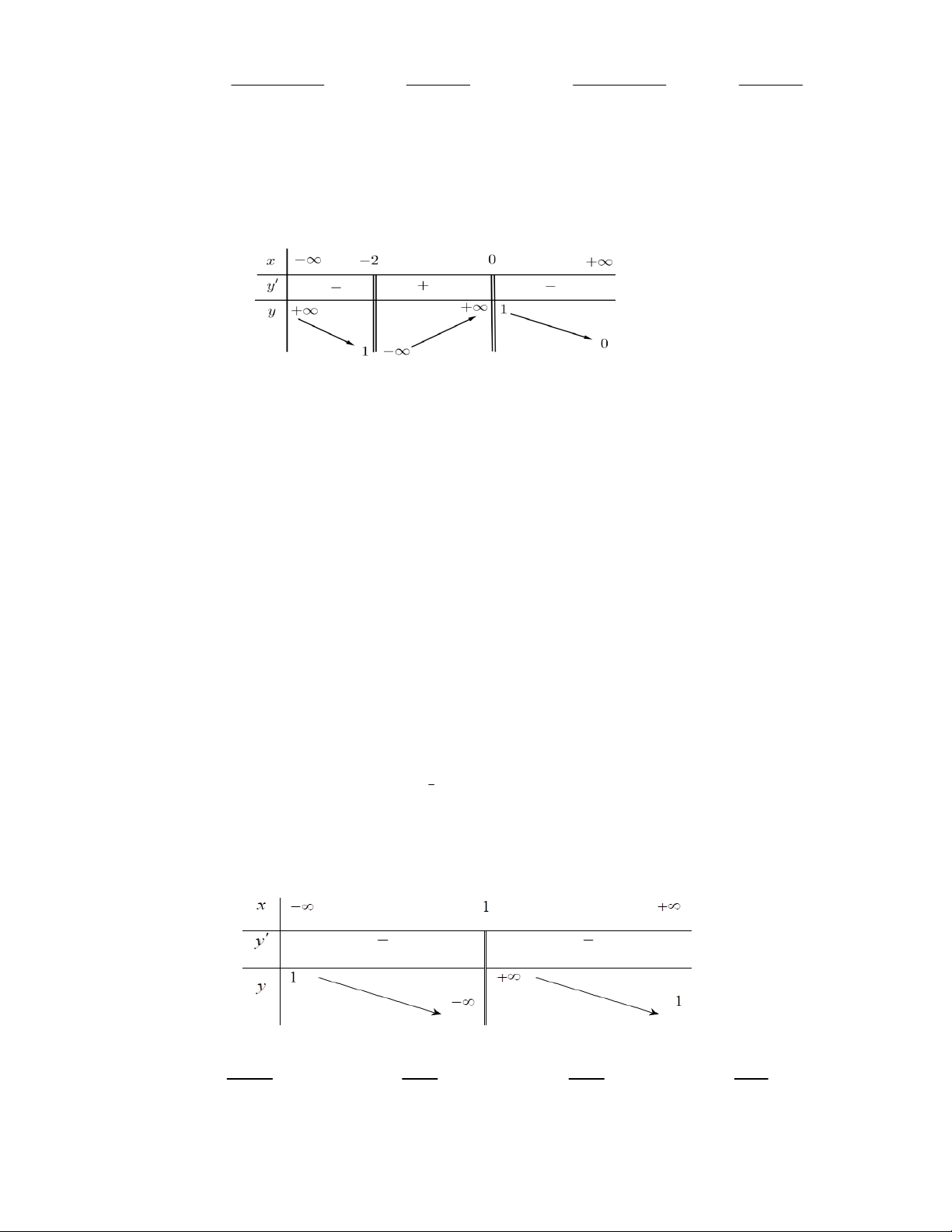
Câu 22: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y  f  x có bảng biến thiên như sau là: A. 2 . B. 0 . C. 1. D. 3 .
Câu 23: Sắp xếp năm bạn học sinh gồm 4 nam và 1 nữ thành một hàng dọc. Số cách sắp xếp sao cho
bạn nữ luôn luôn đứng ở đầu hàng là: A. 16 . B. 120 . C. 24 . D. 60 .
Câu 24: Cho cấp số cộng u có: u  42,u  26 . Công sai của cấp số cộng là: n  13 17 A. d  2 . B. d  4 . C. d  6  . D. d  4  . 10 6
Câu 25: Cho hàm số f  x liên tục trên đoạn 0;10 và f
 xdx  7 và f
 xdx  3. Tính 0 2 2 10 P  f
 xdx f  xdx . 0 6 A. P  7 . B. P  4 . C. P 10. D. P  4 . Câu 26: Hàm số 4 2
y  x  2mx 1 đạt cực tiểu tại x  0 khi: A. m  0 . B. m  0 . C. 1   m  0 . D. m  1  .
Câu 27: Tập xác định của hàm số y   x  15 1 là: A. 1;  . B.  . C. 1;  . D. 0; 
Câu 28: Bảng biến thiên dưới đây là bảng biến thiên của của hàm số nào sau đây? x  2 x  2 x  2 x  3 A. y  . B. y  . C. y  . D. y  . x 1 x 1 x 1 x 1
Câu 29: Tính thể tích khối lăng trụ đều ABC.A' B 'C ' có cạnh đáy và cạnh bên cùng bằng . a
Trang 3/11 - Mã đề thi 061 3 a 3 3 a 6 3 a 3 3 a 6 A. . B. . C. . D. . 12 4 4 12
Câu 30: Hình chóp tam giác đều S.ABC có cạnh đáy là a và mặt bên tạo với đáy một góc 0 45 . Tính
theo a thể tích khối chóp S.ABC . 3 a 3 a 3 a 3 a A. . B. . C. . D. . 4 8 12 24
Câu 31: Hàm số nào dưới đây không có cực trị? 2x 1 A. y  . B. 2
y  x  2x  3 . C. 4 y  x . D. 3
y  x  x . x 1 mx  4
Câu 32: Tìm tất cả các giá trị thực của tham số m sao cho hàm số y 
nghịch biến trên khoảng x  m   ;1  ? A. 2   m  1  . B. 2   m  1  . C. 2   m  2 . D. 2   m  2 .
Câu 33: Tìm tập nghiệm S của phương trình x 1 2   8
A. S    1 . B. S    4 . C. S    1 . D. S    2 .
Câu 34: Một người gửi ngân hàng 100 triệu đồng theo hình thức lãi kép với lãi suất 0,5% một tháng.
Sau ít nhất bao nhiêu tháng, người đó có nhiều hơn 125 triệu? A. 45 tháng. B. 47 tháng. C. 46 tháng. D. 44 tháng.
Câu 35: Cho số phức z  a  bi a,b,a  0 thỏa .
z z 12 z   z  z  1310i . Tính S  a  b . A. S  17  . B. S  7 . C. S 17 . D. S  5.
Câu 36: Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng  20
 19;2019 để bất phương trình x   2 3log
2 log m x  x  1 x 1 x  có nghiệm thực. A. 2020 . B. 2019 . C. 2017 . D. 2018 y
Câu 37: Cho hàm số y  f (x) có đạo hàm trên  . Đường 1 -1 o 1 2 x
cong trong hình vẽ bên là đồ thị của hàm số y  f (  x) , -1 ( y  f (
 x) liên tục trên  ). Xét hàm số -2 2
g(x)  f (x  2) . Mệnh đề nào dưới đây sai? -4
A. Hàm số g(x) đồng biến trên 2; .
B. Hàm số g(x) nghịch biến trên  1  ;0 .
C. Hàm số g(x) nghịch biến trên 0;2 .
D. Hàm số g(x) nghịch biến trên  ;  2   .
Câu 38: Cho hình phẳng H  giới hạn bởi các đường 2 y  x 1
và y  k,0  k  1. Tìm k để diện tích của hình phẳng
H  gấp hai lần diện tích hình phẳng được kẻ sọc trong hình vẽ bên.
Trang 4/11 - Mã đề thi 061 A. 3 k  2 1. B. 3 k  2 . C. 3 k  4 1. D. 3 k  4 . 100
Câu 39: Cho khai triển: 2  x100 100
 a  a x . . .  a x . Tính tổng: S  a  a  a . . .  a 0 `1 100 k 0 1 100 k 0 A. 100 3 . B. 1. C. 100 3 1 . D. 100 3 1 .
Câu 40: Cho hình chóp S.ABC có cạnh bên SA vuông góc với đáy, SA  BC  a và  o BAC  60 . Gọi
H và K lần lượt là hình chiếu vuông góc của A lên SB và SC . Tính thể tích khối cầu ngoại tiếp khối chóp . A BCKH 3 4 a 3 3 4 a 3 4 a 3 3  a 3 A. . B. . C. . D. . 27 9 9 27
Câu 41: Biết rằng phương trình: 2
log x  (m  2) log x  3m 1  0 có hai nghiệm phân biệt x ; x thỏa 3 3 1 2
mãn x x  27 . Khi đó tổng  x  x bằng: 1 2  1 2 34 1 A. . B. 6 . C. 12 . D. . 3 3
Câu 42: Cho hàm số f  x có đạo hàm liên tục trên đoạn 0;  1 thỏa mãn f   1  0 và 1 1 2 1      2       x f x x x f  x e 1 d 1 e dx 
. Tính f  xdx  4 0 0 0 e 1 2 e e A. . B. . C. . D. e  2. 2 4 2 x  3
Câu 43: Họ nguyên hàm của hàm số f (x)  là: 2 x  3x  2
A. 2ln x 1  ln x  2  C .
B.  ln x 1  2ln x  2  C .
C. ln x 1  2ln x  2  C .
D. 2ln x 1  ln x  2  C
Câu 44: Cho hình nón đỉnh S có độ dài đường sinh l  5 , bán S
kính đáy r  3. Gọi O là tâm đường tròn đáy hình
nón. M là điểm thay đổi trên đoạn SO  M
M  S, M  O . Mặt phẳng   qua M , vuông góc
với SO cắt hình nón theo đường tròn có bán kính R .
Xác định R để hình trụ có bán kính đáy R (xem hình) O có thể tích lớn nhất. 3 5 A. R  1 . B. R  2 . C. R  . D. R  . 2 2 x  3 y  2 z 1
Câu 45: Trong không gian với hệ tọa độ Oxyz , cho hai đường thẳng d :   , 1 1 1 2 x  2 y 1 z 1 d :  
và mặt phẳng P : x  3y  2z  5  0 . Đường thẳng vuông góc với 2 2 1 1
P, cắt cả d và d có phương trình là: 1 2 x y z  2 x  7 y  6 z  7 A.   . B.   . 1 3 2 1 3 2
Trang 5/11 - Mã đề thi 061 x  3 y  2 z 1 x  4 y  3 z 1 C.   . D.   . 1 3 2 1 3 2
Câu 46: Cho phương trình: 2
cos x  2(m 1) cos x  4m  0 . Giá trị m để phương trình có nghiệm là: 1 1 A. 1   m  0 . B. 1   m 1.
C. 0  m  1.
D.   m  . 2 2 1 1
Câu 47: Tìm tất cả các giá trị thực của tham số m để hàm số 3
f (x)  mx  m   2
1 x  (m 1)x 1 3 2
đồng biến trên khoảng 1;2 2 3 3 2 A. m   . B. m   . C. m   . D. m   . 7 7 7 7
Câu 48: Gọi S là tập hợp các số tự nhiên gồm 6 chữ số khác nhau được tạo từ tập hợp
M   0,1,2,3,4,5, 
6 . Chọn ngẫu nhiên một số từ S. Xác suất để số được chọn có dạng
a a a a a a thỏa mãn điều kiện a  a  a  a  a  a là: 1 2 3 4 5 6 1 6 2 5 3 4 11 1 4 2 A. . B. . C. . D. . 540 72 135 135
Câu 49: Cho khối tứ diện ABC .
D Trên các cạnh AB, AD lấy điểm M, N sao cho MB = 2MA; NA= 2ND;
Mặt phẳng qua MN và song song với AC chia khối tứ diện thành hai phần. Tính tỉ số thể tích
lớn hơn 1 giữa hai phần 6 4 9 5 A. . B. . C. . D. 5 5 4 4 y
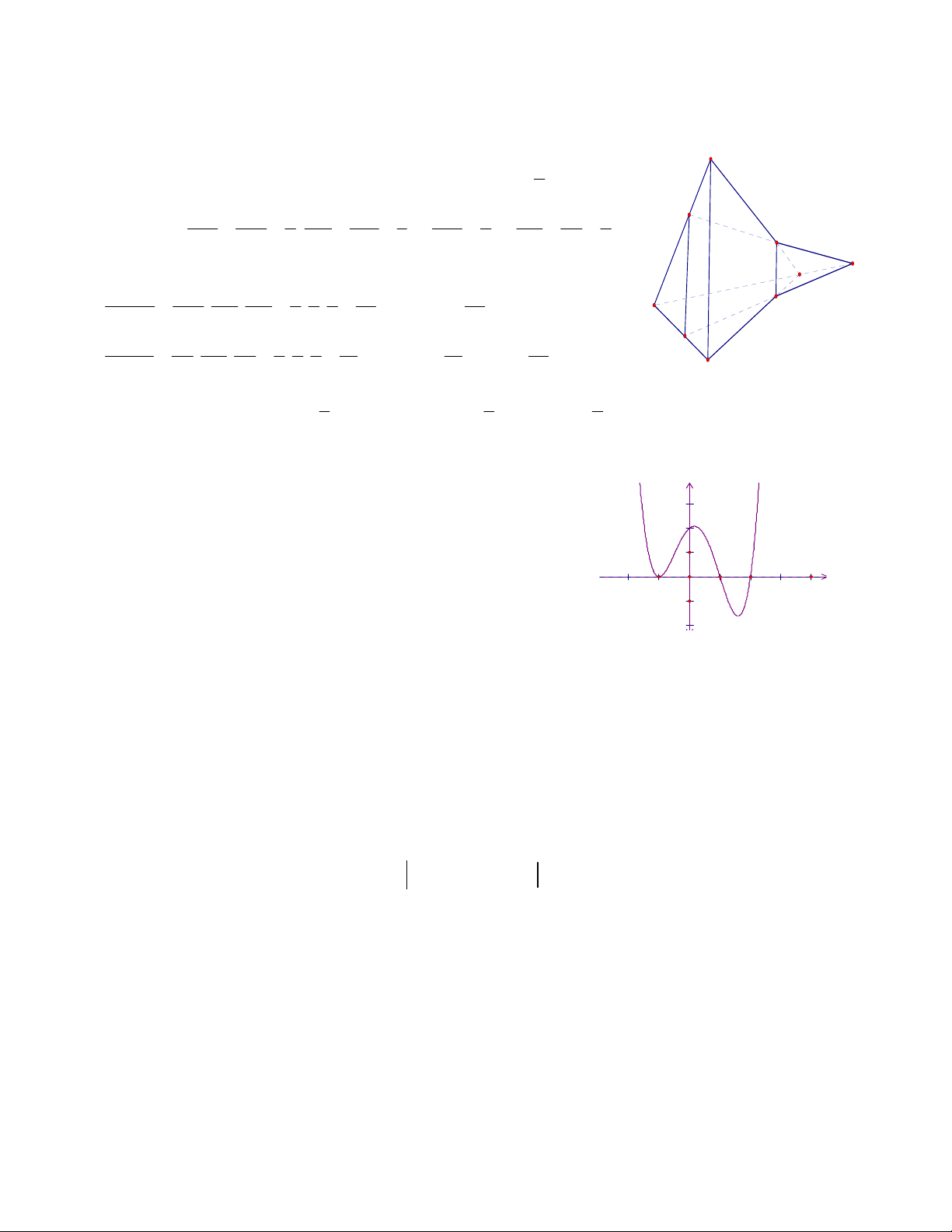
Câu 50: Cho hàm số y  f (x) liên tục trên  và có đồ thị như
hình vẽ. Hỏi hàm số y  f  f  x có bao nhiêu điểm 2 cực trị? 1 -1 o 1 2 x -1 -2 A. 13 . B. 12 . C. 8 . D. 10
----------- HẾT ----------
Trang 6/11 - Mã đề thi 061 1 C 26 B 2 D 27 A 3 C 28 C 4 B 29 C 5 A 30 D 6 A 31 A 7 A 32 A 8 B 33 D 9 B 34 A 10 B 35 B 11 A 36 C 12 C 37 B 13 A 38 C 14 D 39 B 15 C 40 A 16 A 41 C 17 B 42 D 18 B 43 D 19 C 44 B 20 D 45 D 21 D 46 D 22 D 47 B 23 C 48 C 24 D 49 D 25 B 50 A
Trang 7/11 - Mã đề thi 061
HƯỚNG DẪN GIẢI MỘT SỐ CÂU VẬN DỤNG VÀ VẬN DỤNG CAO.
CÂU 35. Cho số phức z  a  bi a,b,a  0 thỏa .
z z 12 z   z  z  1310i . Tính
S  a  b . Lời giải: .
z z 12 z   z  z  1310i 2 2 2 2
 a  b 12 a  b  2bi 1310i 2 2 2 2
a  b 12 a  b 13 2 2  
a  25 12 a  25  13    2b  10 b   5 2 2
 a  25 13; a  25  1  VN  a  12  a  12      
, vì a  0 S  a  b  7 . b   5  b   5  b   5 
CÂU 36. Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng  20  19;2019 để bất phương trình x   2 3log
2log m x  x  1 x 1 x  có nghiệm thực.     0  x  1 0 x 1  0  x  1  
Lời giải:      1 x . 2 m x  x  
1 x 1 x  0 m x   1 x  0 m   0   x 3  x   2 2 BPT log
log m x  x  1 x 1 x   x x   2
m x  x  1 x 1 x 
x x  1 x 1 x x 1 x  m    . Ta 2 x  x 1 x x  x  1 x  có  1 x 
 x  2 x  2 1 x     .  1 x   x 
Vì vậy m  x  1 x .Khảo sát hàm số f  x  x  1 x trên 0;  1 ta được
f  x  2 1,414 .
Vậy m có thể nhận được 2017 giá trị từ 2,3, 4,..., 2018.
CÂU. Cho hàm số y  f (x) có đạo hàm trên  . Đường cong trong y 1
hình vẽ bên là đồ thị của hàm số y  f (
 x) , ( y  f (x) liên tục trên -1 o 1 2 x  ). Xét hàm số 2
g(x)  f (x  2) . Mệnh đề nào dưới đây sai? -1 -2
Lời giải: Từ đồ thị ta có 2
f '(x)  (x 1) (x  2) . Do đó 2 2 2 2
g '(x)  2xf '(x  2)  2x(x 1)  3(x  4) -4
Xét dấu của g'(x) Ta có g'(x)  0, x  ( 1  ;0) .
CÂU. Cho hình phẳng H  giới hạn bởi các đường 2
y  x 1 và y  k, 0  k  1. Tìm k để diện
tích của hình phẳng H  gấp hai lần diện tích hình phẳng được kẻ sọc trong hình vẽ bên. Lời giải:
Do đồ thị nhận trục Oy làm trục đối xứng nên yêu cầu bài toán trở thành: k k  2 2  2
1 y  1 y  1 dy  1 ydy 
   1 y    1 y      1 y 1 3 3 3 3 3  3 0 k 0 k
   k 3   k 3     k 3 3 3 1 1 2 1
 1 k  4  k  4 1
Trang 8/11 - Mã đề thi 061
CÂU.Cho hình chóp S.ABC có cạnh bên SA vuông góc với đáy, SA  BC  a và  o BAC  60 .
Gọi H và K lần lượt là hình chiếu vuông góc của A lên SB và SC . Tính thể tích khối cầu ngoại tiếp khối chóp . A BCKH
Lời giải: Gọi I là tâm đường tròn ngoại tiếp A
 BC , kẻ đường kính AD S
Ta có SA   ABC  SA  B ;
D AB  BD  BD  SAB K
 (SBD)  SAB  AH  (SBD)  AH  HD . a
Tương tự AK  KD  H , K, B,C thuộc mặt cầu đường kính AD  2R H C A 60o BC
Áp dụng định lí sin trong A  BC ta có  2R I a sin A D B a 3  a 3 4 a 3 2R   R   V  o sin 60 3 27
CÂU. Biết rằng phương trình: 2
log x  (m  2) log x  3m 1  0 có hai nghiệm phân biệt x ; x 3 3 1 2
thỏa mãn x x  27 . Khi đó tổng  x  x bằng: 1 2  1 2
Lời giải: Điều kiện: x  0 . Đặt log    3t x t x
phương trình trở thành:: 3 2
t  (m  2)t  3m 1  0 (1)
Phương trình đã cho có hai nghiệm phân biệt  phương trình (1) có hai nghiệm t phân biệt 2 2
   0  (m  2)  4(3m 1)  0  m 8m  8  0
 m  (;4  2 2)  (4  2 2;) (*)
Với đ/k (*) Pt (1)có hai nghiệm t  t thì pt đã cho có 2 nghiệm x ; x với 1 2 1 2 t  2 1  3 ,  3t x x 1 t t2 x x  3
 27  t  t  3 Áp dụng Vi-ét với pt (1) ta 1 2 1 2 1 2
có: t  t  m  2  3  m  1(tm) 1 2 Với 2
m 1 (*)  t  3t  2  0  t 1;t  2  x  3; x  9  x  x  3 9 12 . 1 2 1 2 1 2 CÂU. Cho hàm số
f  x có đạo hàm liên tục trên 0;  1 thỏa mãn 1 1 2 1       2       x f x x x f  x e 1 d 1 e dx  và f  
1  0 . Tính f xdx  4 0 0 0 1 1 1 1 2  x x e 1
Lời giải:       2 d     1ex I f x x x
f  xdx  e
x f  xdx  e f  xdx  J  K    . 4 0 0 0 0 x x x 1
u  e f (x)
du  e f (x)  e f (x) dx 1 Đặt   x   
 K  e f (x) x  xe f (x) x
 xe f (x) dx   0 dv  dx v  x 0 1 1 1 1 Do   1  0 x    ( ) x  (  ) x    (  ) x f K xe f x dx xe f x dx J
xe f x dx  J  K   xe f (
 x)dx  I     0 0 0 0 . 1 2 1 2 e 1  x e 1 Ta có  f 
 x 2 dx  I  (1)  2 e x f    xdx  2  I   (2). Lại 4 2 0 0 1 2  x e 1 có : 2 2 x e dx  (3)  . 4 0
Trang 9/11 - Mã đề thi 061
CÂU. Cho hình nón đỉnh S có độ dài đường sinh l  5 , bán kính đáy r  3. Gọi O là tâm
đường tròn đáy hình nón. M là điểm thay đổi trên đoạn SO M  S, M  O . Mặt phẳng  
qua M , vuông góc với SO cắt hình nón theo đường tròn có bán kính R . Xác định R để hình
trụ có bán kính đáy R (xem hình) có thể tích lớn nhất.
Lời giải: Chiều cao của hình nón là 2 2
h  l  r  4 . S SM R Tta có:  4  SM  4
R  OM  4  R SO 3 3 3 P Q M 4 2
 V   R .OM 2     R . 4  R    3  B 2  A O 
R R   R 4 . . . 6 2  . 2 3
3R  R   f (R) . 3 3 16
Lập BBT của hàm số: V  f (R)  V   R  2 . max 3
CÂU. Tìm tất cả các giá trị thực của tham số m để hàm số 1 1 3
f (x)  mx  m   2
1 x  (m 1)x 1 đồng biến trên khoảng 1;2 3 2
Lời giải: Hs đồng biến x 1 trên 1;2 2
 f '(x)  mx  m  
1 x  m 1  0 x
 1;2  m  x   1;2 2   x  x 1 x 1
Xét hàm số f (x)  x  1;2; 2 x  x 1 2 x  2x 3 f (  x)   0, x
 [1;2]  max f (x)  f (2)  m   . 2 2 (x  x 1) [1;2] 7
CÂU. Gọi S là tập hợp các số tự nhiên gồm 6 chữ số khác nhau được tạo từ tập hợp
M   0,1,2,3,4,5, 
6 . Chọn ngẫu nhiên một số từ S. Tính xác suất P để số được chọn có dạng
a a a a a a thỏa mãn điều kiện a  a  a  a  a  a 1 2 3 4 5 6 1 6 2 5 3 4
Lời giải: Số các số có 6 chữ số khác nhau được tạo từ tập M là: 5
6A  n   4320 6  
Xét các số a a a a a a (a  M ) . Giả sử x  M \ a ,a ,a ,a ,a ,a . Đặt 1 2 3 4 5 6 1 2 3 4 5 6 i
k  a  a  a  a  a  a 1 6 2 5 3 4
Ta có: a  a  a  a  a  a  x  0 1 2  3  4  5  6  3k  x  21 x chia hết cho 3 1 6 2 5 3 4
1/ Trường hợp x  0  k  7;a 1,2,3,4,5,  6 i
- Có 6 cách chọn a , a , có 4 cách chọn a , a , có 2 cách chọn a , a Trường hợp này có 48 1 6 2 5 3 4 cách chọn
2/ Trường hợp x  3  k  6;a  0,1,2,4,5,  6 i
- Có 5 cách chọn a , a , có 4 cách chọn a , a , có 2 cách chọn a , a Trường hợp này có 40 1 6 2 5 3 4 cách chọn
2/ Trường hợp x  6  k  5;a  0,1,2,3,4, 
5 . Tương tự như k = 6. Ta có 40 cách chọn i 128 4
Gọi A là biến cố thỏa mãn bài toán, khi đó n( )
A  48  40  40  128  P( ) A   . 4320 135
Trang 10/11 - Mã đề thi 061
CÂU. Cho khối tứ diện ABC .
D Trên các cạnh AB, AD lấy điểm M, N sao cho MB = 2MA; NA=
2ND; Mặt phẳng qua MN và song song với AC chia khối tứ diện thành hai phần. Tính tỉ số thể
tích lớn hơn 1 giữa hai phần Lời giải: A      1  Từ gt: MB  2  M ; A NA  2
 ND Theo Mê nê la uýt  ID  IB 4 M MQ BM 2 NP DN 1 NP 1 IN IP 1 Theo Talet:   ;        AC BA 3 AC DA 3 MQ 2 IM IQ 2 N Ta có: D I B V .MQI BM BQ BI 2 2 4 16 16  . .  . .    B V . V (1) MQI ABCD B P B V . BA BC BD 3 3 3 27 27 ACD I V . ID IN IP 1 1 1 1 1 1 DNP  . .  . .     Q I V .DNP B V . V (2) MQI ABCD I V . IB IM IQ 4 2 2 16 16 27 BMQ C 5 5 5 Từ(1),(2)        B V .MQI I V .DNP VABCD B V MQ.DNP VABCD k 9 9 4
CÂU. Cho hàm số y  f (x) liên tục trên R và có đồ thị như hình vẽ. y
Hỏi hàm số y  f  f  x có bao nhiêu điểm cực trị? 2  f '(x)  0 1
Lời giải: y  f ( f (x))  y '  f '(x) f '( f (x))  0   -1 o 1 2 x
 f '( f (x))  0 -1
1/ f '(x)  0 có 3 nghiệm x  1;
 x  x (0;1), x  x (1;2) 1 2 -2
2/ f '( f (x))  0  f (x)  1
 ; f (x)  x (0;1), f (x)  x (1;2) 1 2
*/ f (x)  1 có 2 nghiệm; f (x)  x (0;1) có 4 nghiệm; f (x)  x (1;2) có 4 nghiệm 1 2
Phương trình y’ = 0 có 13 nghiệm phân biệt Do vậy hàm số y  f ( f (x)) có 13 điểm cực trị
Cộng vế với vế (1), (2) và (3) ta được 1
 f x x  x 2 e
dx  0     ex  0      ex f x x f x
x      ex f x x dx  o
    1 ex f x x  C; Ta có f  
1  0     1 ex f x x 1 1 1 1
   d  1 exd   1 ex 1 1  exd  1   ex f x x x x x x  e  2  f 
 xdx  e2 0 0 0 0 0 0
Trang 11/11 - Mã đề thi 061