Đề KSCL Toán 12 lần 1 năm 2019 – 2020 trường chuyên Lê Quý Đôn – BR VT

Giới thiệu đến quý thầy, cô giáo và các em học sinh khối 12 đề KSCL Toán 12 lần 1 năm học 2019 – 2020 trường THPT chuyên Lê Quý Đôn – Bà Rịa – Vũng Tàu, đề thi gồm có 06 trang với 50 câu trắc nghiệm.

21 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

31 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
STRONG TEAM TOÁN VD-VDC
TỔ 03
ĐỀ CHUYÊN LÊ QUÝ ĐÔN – BÀ
RỊA – VŨNG TÀU
Họ và tên: ....................................................... SBD: ......................................
Câu 1: Đồ thị trong hình vẽ sau đây là đồ thị của hàm số nào trong các hàm số bên dưới?
A.
4
31y x x= − +
. B.
4
3 1.y x x= − + +
C.
3
3 1.y x x= − +
D.
Câu 2: Phương trình
42
20x x m− + =
(
m
là tham số thực) có 4 nghiệm phân biệt khi và chỉ khi
A.
11m−
. B.
1 0.m−
C.
1.m
D.
0 1.m
Câu 3: Giá trị nhỏ nhất của hàm số
2
( ) 2 5 10 10f x x x x= + − +
trên đoạn
2;1−
là
A.
4 5 2−+
. B.
10
. C.
13+
. D.
3
.
Câu 4: Cho hình bát diện đều có cạnh bằng
a
. Khoảng cách giữa hai mặt phẳng song song của bát
diện này bằng
A.
3
3
a
. B.
2
2
a
. C.
6
3
a
. D.
2
a
.
Câu 5: Trong các hàm số sau, hàm số nào đạt cực tiểu tại
0x =
?
A.
43
y x x=−
. B.
32
y x x=+
. C.
32
y x x=-
. D.
43
y x x=+
.
Câu 6: Hàm số
32
y x x=+
nghịch biến trên khoảng
A.
( )
1;0−
. B.
2
0;
3



. C.
2
;0
3

−


. D.
( )
0;1
.
Câu 7: Cho lăng trụ
.ABC A B C
, biết rằng tứ diện
A ABC
là tứ diện đều cạnh a. Thể tích khối chóp
.ABCB C

bằng
A.
3
2
12
a
. B.
3
2
6
a
. C.
3
2
8
a
. D.
3
2
4
a
.
Câu 8: Cho hình chóp
S.ABC
có tam giác
ABC
vuông cân tại
A
,
SA
vuông góc với mặt phẳng
( )
ABC
. Biết rằng
2BC a=
,
5SB a=
. Thể tích khối chóp
S.ABC
bằng
A.
3
2
3
a
. B.
3
2
3
a
. C.
3
3
3
a
. D.
3
1
3
a
.
Câu 9: Cho hàm số
( )
y f x=
có đạo hàm trên và
( )
( )( )
( )
22
' 2 3 1 3 1f x x x x x= − − − −
x
.
Số điểm cực trị của hàm số
( )
y f x=
là
A.
2
. B.
3
. C. 4. D. 1.
Câu 10: Tiếp tuyến của đồ thị hàm số
31
1
x
y
x
+
=
+
tại điểm có hoành độ
1x =
tạo với hai trục tọa độ
một tam giác có diện tích bằng
A.
9
2
. B.
3
2
. C.
9
4
. D.
3
4
.
Câu 11: Cho hai số hữu tỉ
,mn
sao cho phương trình
3
33x x m n− = +
có ba nghiệm dương phân
biệt
,,abc
thỏa mãn
23abc+ + = +
. Biểu thức
64mn+
có giá trị là:
A.
1
B.
3
C.
13
4
D.
11
4
Câu 12: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông, tam giác
SBC
đều và tam giác
SAD
vuông. Góc taọ bởi hai mặt phẳng
( ) ( )
,SBC ABCD
là
A.
0
45 .
B.
0
30 .
C.
0
60 .
D.
0
15
.
Câu 13: Khối chóp tứ giác đều có độ dài cạnh đáy bằng
a
, mặt bên tạo với đáy một góc
0
60
thì thể
tích bằng:
A.
3
6
2
a
. B
3
6
6
a
. C.
3
3
2
a
. D.
3
3
6
a
Câu 14: Cho khối chóp
.S ABC
có thể tích
V
. Gọi
,,M N P
lần lượt là trọng tâm của các tam giác
,,SBC SCA SAB
. Thể tích của khối chóp
.S MNP
bằng
A.
4
27
V
. B.
8
27
V
. C.
2
27
V
. D.
1
27
V
.
Câu 15: Số cạnh của hình chóp tứ giác là
A.
8
. B.
9
. C.
10
. D.
12
.
Câu 16: Khoảng cách giữa hai điểm cực trị của đồ thị hàm số
32
31y x x= − −
là
A.
25
. B.
23
. C.
2
. D.
4
.
Câu 17: Tập hợp các giá trị thực của tham số
m
để hàm số
32
9 (3 )y x x m x m= − + − +
đồng biến trên
là
A.
( )
; 24− −
.
B.
(
; 24− −
. C.
( )
24;− +
. D.
)
24;− +
.
Câu 18: Cho hàm số
1
1
x
y
x
+
=
−
, mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên hai khoảng
( ) ( )
;1 ; 1;− +
.
B. Hàm số nghịch biến trên
( ) ( )
;1 1;− +
.
C. Hàm số đồng biến trên hai khoảng
( ) ( )
;1 ; 1;− +
.
D. Hàm số đồng biến trên
( ) ( )
;1 1;− +
.
Câu 19: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ. Phương trình
( )
f x m−=
( với
m
là tham số
thực) có nhiều nhất bao nhiêu nghiệm?
A.
8
. B.
2
. C.
4
. D.
6
.
Câu 20: Xét hai số thực dương thay đổi
x
,
y
sao cho
1xy
. Giá trị nhỏ nhất của biểu thức
55
2
1
xy
P x y
xy
+
= + +
−
đạt được khi
0
xx=
và
0
yy=
. Giá trị của biểu thức
0
0
1x
Q
y
+
=
là
A.
3
. B.
2
. C.
2
. D.
1
.
Câu 21: Điểm cực tiểu của hàm số
32
6 9 1y x x x= − + − +
là
A.
0x =
. B.
3x =
. C.
2x =
. D.
1x =
.
Câu 22: Cho hàm số
( )
y f x=
có bảng biến thiên như hình vẽ
Số điểm cực trị của hàm số
( )
y f x=
là
A.
5
. B.
3
. C.
4
. D.
2
.
Câu 23: Có bao nhiêu giá trị của tham số
m
để đồ thị hàm số
( ) ( )
32
1 2 2 2y x m x m x m= − + + − + −
có
điểm cực trị thuộc trục hoành?
A.
3
. B.
1
. C.
0
. D.
2
.
Câu 24: Có bao nhiêu giá trị thực của tham số
m
để đồ thị hàm số
( )
2
2
1
2 2 1
−
=
+ − + +
x
y
x m x m
có đúng
hai đường tiệm cận?
A.
1
. B.
3
. C.
2
. D.
4
.
Câu 25: Cho hàm số bậc ba
( )
y f x=
mà đồ thị hàm số có hai điểm cực trị là
( ) ( )
1;3 , 2;1AB
. Số điểm
cực trị của hàm số
( )
y f x=
là
A.
1
. B.
5
. C.
4
. D. 3.
Câu 26: Cho hình lập phương
.ABCD A BC D
có cạnh bằng
a
. Khoảng cách từ điểm
A
đến mặt
phẳng
( )
A BD
bằng
A.
2
2
a
. B.
3
3
a
. C.
2
a
. D.
2
3
a
.
Câu 27: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông tại
,AD
.
SA
vuông góc với mặt
phẳng
( )
ABCD
. Cho biết
AD CD a==
,
2AB a=
,hai mặt phẳng
( ) ( )
,SBC ABCD
tạo với
nhau góc
0
45
. Khoảng cách từ điểm
D
đến mặt phẳng
( )
SBC
bằng.
A.
2
a
. B.
3
2
a
. C.
2
2
a
. D.
a
.
Câu 28: Gọi
S
là tập các giá trị thực của tham số
m
để đồ thị hàm số
42
24y x mx m= − + +
có ba
điểm cực trị cách đều trục hoành. Tính tổng tất cả các phần tử của tập
S
là
A. 2. B. 6. C. 0. D. 4.
Câu 29: Cho hai hình vuông
ABCD
và
ABEF
có cạnh bằng
a
và nằm trên hai mặt mặt phẳng
vuông góc với nhau. Thể tích khối đa diện
EBCFAD
bằng
A.
3
2
3
a
. B.
3
3
a
. C.
3
2
a
. D.
3
a
.
Câu 30: Cho lăng trụ đứng
. ' ' 'ABC A B C
có tam giác
'A BC
là tam giác đều cạnh
a
và tam giác
ABC
vuông tại
A
. Thể tích khối lăng trụ
. ' ' 'ABC A B C
là
A.
3
2
4
a
. B.
3
2
12
a
C.
3
2
8
a
. D.
3
2
6
a
.
Câu 31:
Có bao nhiêu tiếp tuyến của đồ thị hàm số
32
2y x x=−
tạo với hai trục tọa độ một tam giác
cân?
A.
3
. B.
1
. C.
4
. D.
2
.
Câu 32: Cho lăng trụ có đáy là hình vuông cạnh
3a
và chiều cao là
b
. Thể tích khối lăng trụ đó
bằng
A.
2
ab
. B.
2
3ab
. C.
2
3ab
. D.
2
ab
.
Câu 33: Đường tiệm cận ngang của đồ thị hàm số
32
1
x
y
x
−
=
+
có phương trình là
A.
3y =−
. B.
2y =
. C.
2y =−
. D.
3y =
.
Câu 34: Hai đường tiệm cận của đồ thị hàm số
23
1
x
y
x
−
=
+
và hai trục tọa độ cắt nhau tạo thành hình
chữ nhật. Diện tích của hình chữ nhật đó là?
A.
2.S =
B.
4.S =
C.
1.S =
. D.
3.S =
.
Câu 35: Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3sin 1
sin 2
x
x
y
+
+
=
là
A.
11
6
. B.
0
. C.
2
3
−
. D.
3
2
−
Câu 36: Tập hợp các giá trị thực của tham số
m
để hàm số
2
2cos
cos
xm
y
xm
+
=
+
nghịch biến trên khoảng
( )
0;
là
A.
( )
0;2 .
B.
( )
2;+
. C.
)
1;0−
D.
)
1;2
.
Câu 37: Số điểm chung của hai đồ thị hàm số
32
2y x x=−
và
23yx=−
là
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 38: Tổng diện tích các mặt của tứ diện đều cạnh
a
là
A.
2
2a
. B.
2
3a
. C.
2
4a
. D.
2
23a
.
Câu 39: Trong các hàm số sau, hàm số nào đồng biến trên khoảng
( )
;− +
?
A.
2
21
x
y
x
−
=
+
. B.
3
31y x x= + +
. C.
2
1y x x= − +
. D.
42
21y x x= + +
.
Câu 40: Số điểm cực đại của hàm số
42
2 3 1y x x= − +
là
A.
0
. B.
2
. C.
3
. D.
1
.
Câu 41: Số đường tiệm cận đứng của đồ thị hàm số
2
3
1
32
x
y
xx
−
=
−+
là
A. 2. B. 0. C. 1. D. 3.
Câu 42: Cho khối chóp
.S ABC
có thể tích
3
3
3
Va=
, tam giác
SBC
là tam giác đều có cạnh bằng
a
.
Khi đó, khoảng cách từ điểm
A
đến mặt phẳng
( )
SBC
bằng
A.
43
3
a
. B.
4
3
a
. C.
4a
. D.
23a
.
Câu 43: Cho hàm số
( )
y f x=
có bảng biến thiên như hình vẽ
Hàm số
( )
2
y f x=
nghịch biến trên khoảng nào trong các khoảng dưới đây?
A.
( )
2;0−
. B.
( )
;2− −
. C.
( )
1; +
. D.
( )
0;1
.
Câu 44: Cho hàm số
( )
y f x=
liên tục trên có bảng biến thiên như sau:
Số nghiệm của phương trình
( )
0fx=
là
A.
2
. B.
5
. C.
3
. D.
4
.
Câu 45: Số điểm cực trị của hàm số
34
(3 1) ( 1)y x x= − +
A.
3
. B.
2
. C.
1
. D.
4
.
Câu 46: Cho hàm số
2
1
x
y
x
−
=
+
có đồ thị
( )
C
cắt hai trục tọa độ lần lượt tại
A
,
B
. Tiếp tuyến của
( )
C
tại hai điểm
A
,
B
tạo với nhau một góc
. Giá trị của
sin
bằng
A.
4
5
. B.
1
10
. C.
3
5
. D.
3
10
.
Câu 47: Cho hình lăng trụ có đáy là hình vuông cạnh
a
, thể tích khối lăng trụ bằng
3
a
và độ dài các
cạnh bên là
2a
. Góc tạo bởi cạnh bên và mặt phẳng đáy là:
A.
90
. B.
30
. C.
45
. D.
60
.
Câu 48: Cho khối chóp
SABCD
có thể tích
V
, đáy
ABCD
là hình bình hành,
M
là trung điểm của
SB
N
là điểm trên cạnh
SD
. Mặt phẳng
( )
AMN
cắt cạnh
SC
tại điểm
P
sao cho thể tích khối
chóp
SAMPN
bằng
4
V
. Tỉ số
SN
SD
bằng
A.
2
3
. B.
2
2
. C.
1
2
. D.
1
3
.
Câu 49: Gọi
là góc tạo bởi hai mặt bên của một tứ diện đều. Mệnh đề nào sau đây đúng?
A.
tan 2 2
=
. B.
tan 2
=
. C.
tan 2
=
. D.
tan 3
=
.
Câu 50: Tập hợp giá trị thực của tham số
m
để hàm số
42
( 2) 2y mx m x m= + − +
có điểm cực tiểu là
A.
(0;2]
. B.
( ;0]−
. C.
(0; )+
. D.
(0;2)
.
BẢNG ĐÁP ÁN
1.C
2.D
3.D
4.C
5.B
6.C
7.B
8.C
9.B
10.C
11.C
12.B
13.D
14.C
15.A
16.A
17.B
18.A
19.D
20.B
21.D
22.A
23.A
24.B
25.B
26.B
27.A
28.D
29.C
30.C
31.C
32.C
33.C
34.A
35.C
36.D
37.B
38.B
39.B
40.D
41.A
42.C
43.D
44.B
45.B
46.A
47.B
48.B
49.A
50.C
HƯỚNG DẪN GIẢI
Câu 1. Đồ thị trong hình vẽ sau đây là đồ thị của hàm số nào trong các hàm số bên dưới?
A.
4
31y x x= − +
. B.
4
3 1.y x x= − + +
C.
3
3 1.y x x= − +
D.
Lời giải
Chọn C
Đồ thị đi qua điểm
( )
1;3−
nên loại đáp án A, B và D. Chọn đáp án C.
Câu 2. Phương trình
42
20x x m− + =
(
m
là tham số thực) có 4 nghiệm phân biệt khi và chỉ khi
A.
11m−
. B.
1 0.m−
C.
1.m
D.
0 1.m
Lời giải
Chọn D
Cách 1. Đặt
2
0tx=
thì phương trình
42
20x x m− + =
(1) trở thành
2
20t t m− + =
(2).
Phương trình (1) có 4 nghiệm phân biệt khi và chỉ khi phương trình (2) có 2 nghiệm dương
phân biệt. Điều kiện là
4 4 0
1
2 0 0 1.
0
0
m
m
Sm
m
Pm
= −
=

=
Vậy phương trình (1) có 4 nghiệm phân biệt khi và chỉ khi
0 1.m
Cách 2. Ta có
4 2 4 2
2 0(1) 2 .x x m m x x− + = = − +
Hàm số
42
2y x x= − +
có
3
' 4 4 ,y x x= − +
' 0 0yx= =
hoặc
1.x =
Bảng biến thiên của hàm số này như sau
Phương trình (1) có 4 nghiệm phân biệt khi và chỉ khi đường thẳng
ym=
và đồ thị hàm số
42
2y x x= − +
có 4 giao điểm phân biệt. Từ bảng biến thiên của hàm số
42
2y x x= − +
suy ra
đường thẳng
ym=
và đồ thị hàm số
42
2y x x= − +
có 4 giao điểm phân biệt khi và chỉ khi
0 1.m
Vậy phương trình (1) có 4 nghiệm phân biệt khi và chỉ khi
0 1.m
Câu 3. Giá trị nhỏ nhất của hàm số
2
( ) 2 5 10 10f x x x x= + − +
trên đoạn
2;1−
là
A.
4 5 2−+
. B.
10
. C.
13+
. D.
3
.
x
'y
y
−
+
1−
0
1
0
0
0
0
−
−
+
+
1
1
−
−
Lời giải
Chọn D
Hàm số
()fx
xác định và liên tục trên đoạn
2;1−
.
2
22
5 5 2 5 10 10 5 5
'( ) 2
5 10 10 5 10 10
x x x x
fx
x x x x
− − + + −
= + =
− + − +
.
2 2 2
'( ) 0 2 5 10 10 5 5 4(5 10 10) 25 25 50f x x x x x x x x= − + = − − + = + −
2
1 2;1
5 10 15 0
3 2;1
x
xx
x
= − −
− − =
= −
Ta có
(1) 2 5f =+
;
( 2) 4 5 2f − = − +
;
( 1) 3f −=
.
Vậy
( )
2;1
min 3
x
fx
−
=
.
Câu 4. Cho hình bát diện đều có cạnh bằng
a
. Khoảng cách giữa hai mặt phẳng song song của bát
diện này bằng
A.
3
3
a
. B.
2
2
a
. C.
6
3
a
. D.
2
a
.
Lời giải
Chọn C
O
A
D
C
B
E
F
M
H
Xét bát diện đều tâm
O
như hình vẽ.
Ta có:
( ) ( )
//FDA EBC
nên
( ) ( )
( )
( )
( )
;;d FDA EBC d A EBC=
.
Vì
( )
AO EBC C=
nên
( )
( )
( )
( )
;
2
;
d A EBC
CA
CO
d O EBC
==
.
Gọi
,MH
lần lượt là hình chiếu vuông góc của
O
lên đường thẳng
,BC EM
. Ta chứng
minh được
( )
OH EBC⊥
tại
H
nên
( )
( )
;d O EBC OH=
.
Ta có:
2
a
OM =
,
2
2
a
OE OB==
(vì bát diện đều cạnh bằng
a
)
Xét tam giác vuông
EOM
có
OH
là đường cao nên
2 2 2
1 1 1
OH OE OM
=+
2 2 2
2 4 6
a a a
= + =
6
6
a
OH=
.
Do đó
( )
( )
6
;2
3
a
d A EBC OH==
.
Chú ý :
a) Có thể tính
( )
( )
;d O EBC d=
theo công thức
2 2 2 2
1 1 1 1
d OE OB OC
= + +
do
,,OE OB OC
đôi
một vuông góc.
b) Có thể tính
( ,( ))d A EBC
theo công thức
.
3
( ,( ))
E ABC
EBC
V
d A EBC
S
=
với
..
1
2
E ABC E ABCD
VV=
.
Câu 5. Trong các hàm số sau, hàm số nào đạt cực tiểu tại
0x =
?
A.
43
y x x=−
. B.
32
y x x=+
. C.
32
y x x=-
. D.
43
y x x=+
.
Lời giải
Chọn B
Hàm số
43
y x x=−
có đạo hàm
2
' (4 3)y x x=−
không đổi dấu khi đi qua
0x =
nên không
đạt cực trị tại
0x =
.
Hàm số
43
y x x=+
có đạo hàm
2
' (4 3)y x x=+
không đổi dấu khi đi qua
0x =
nên không
đạt cực trị tại
0x =
.
Hàm số
32
y x x=−
có đạo hàm
( )
32y x x
=−
đổi dấu từ dương sang âm khi đi qua
0x =
nên đạt cực đại tại
0x =
.
Hàm số
32
y x x=+
có đạo hàm
( )
32y x x
=+
đổi dấu từ âm sang dương khi đi qua
0x =
nên đạt cực tiểu tại
0x =
.
Vậy chọn đáp án B.
Câu 6. Hàm số
32
y x x=+
nghịch biến trên khoảng
A.
( )
1;0−
. B.
2
0;
3



. C.
2
;0
3

−


. D.
( )
0;1
.
Lời giải
Tác giả :Chu Quốc Hùng, FB: Chu Quốc Hùng Edu
Chọn C
Hàm số
32
y x x=+
có đạo hàm
2
' 3 2y x x=+
;
2
0
' 0 3 2 0
2
3
x
y x x
x
=
= + =
−
=
.
Bảng xét dấu đạo hàm
x
−
2
3
−
0
+
y
+
0
−
0
+
Từ bảng xét dấu ta suy ra hàm số nghịch biến trên
2
;0
3

−


.
Câu 7. Cho lăng trụ
.ABC A B C
, biết rằng tứ diện
A ABC
là tứ diện đều cạnh a. Thể tích khối chóp
.ABCB C

bằng
A.
3
2
12
a
. B.
3
2
6
a
. C.
3
2
8
a
. D.
3
2
4
a
.
Lời giải
Tác giả :Trần Thị Phượng Uyên, FB: UyenTran
Chọn B
Gọi
H
là trọng tâm tam giác
ABC
( )
A H ABC
⊥
.
Tính được
2
2 2 2
36
()
33
aa
A H AA AH a


= − = − =



.
A
A'
B
B'
C
C'
H
Ta có
1
.
3
A ABC ABC
V A H S
=
23
1 6 3 2
3 3 4 12
a a a
==
.
Vậy
3
. .A B C
22
.2
36
A BCB C ABC A ABC ABC A ABC
a
V V V A H S V
= − = = =
.
Câu 8. Cho hình chóp
S.ABC
có tam giác
ABC
vuông cân tại
A
,
SA
vuông góc với mặt phẳng
( )
ABC
. Biết rằng
2BC a=
,
5SB a=
. Thể tích khối chóp
S.ABC
bằng
A.
3
2
3
a
. B.
3
2
3
a
. C.
3
3
3
a
. D.
3
1
3
a
.
Lời giải
Tác giả: Trần Thị Thủy; Fb: Thủy Trần
Chọn C
Do tam giác
ABC
vuông cân tại
A
nên
2
22
22
BC a
BC AB AB a= Þ = = =
( )
2
22
2
1
22
ABC
a
S AB a
D
Þ = = =
.
Do
( )
SA ABC SA AB^ Þ ^
. Suy ra tam giác
SAB
vuông tại
A
.
2 2 2 2 2 2
5 2 3 3SA SB AB a a a SA a= - = - = Þ =
.
Thể tích khối chóp
S.ABC
là
3
13
33
S.ABC ABC
V S .SA a
D
==
(đvtt).
Câu 9. Cho hàm số
( )
y f x=
có đạo hàm trên và
( )
( )( )
( )
22
' 2 3 1 3 1f x x x x x= − − − −
x
.
Số điểm cực trị của hàm số
( )
y f x=
là
A.
2
. B.
3
. C. 4. D. 1.
Lời giải
Tác giả và giải: Nguyễn Văn Bình ; Fb: Nguyễn Văn Bình
Chọn B
( )
( )( )
( ) ( ) ( )( )( )
2
22
' 2 3 1 3 1 1 3 1 3 1f x x x x x x x x x= − − − − = + − − −
Ta thấy
( )
'fx
chỉ đổi dấu khi đi qua các nghiệm
1
; 1; 3
3
x x x= = =
. Do đó
( )
y f x=
có
3
điểm cực trị.
Câu 10. Tiếp tuyến của đồ thị hàm số
31
1
x
y
x
+
=
+
tại điểm có hoành độ
1x =
tạo với hai trục tọa độ
một tam giác có diện tích bằng
A.
9
2
. B.
3
2
. C.
9
4
. D.
3
4
.
Lời giải
Tác giả: Lê Xuân Sơn; Fb: Lê Xuân Sơn
Chọn C
Ta có:
( )
2
3 1 2
1
1
x
yy
x
x
+
= =
+
+
.
Ta có:
( )
( )
2
21
1
2
11
y
==
+
;
( )
12y =
Phương trình tiếp tuyến tại điểm có hoành độ
1x =
là:
( ) ( ) ( )
1 . 1 1y y x y
= − +
13
22
yx = +
.
Tiếp tuyến cắt trục hoành tại
( )
3;0A −
, cắt trục tung tại
3
0;
2
B



, tiếp tuyến tạo với hai trục
tọa độ tam giác
OAB
vuông tại
O
có
3OA =
,
3
2
OB =
.
Diện tích tam giác
OAB
là
1 1 3 9
. . .3.
2 2 2 4
S OAOB= = =
.
Câu 11. Cho hai số hữu tỉ
,mn
sao cho phương trình
3
33x x m n− = +
có ba nghiệm dương phân
biệt
,,abc
thỏa mãn
23abc+ + = +
. Biểu thức
64mn+
có giá trị là:
A.
1
B.
3
C.
13
4
D.
11
4
Lời giải
Tác giả: Trần Văn Trưởng; FB: Trần Văn Trưởng
Chọn C
x
y
y=k
-1
2
1
O
-a
-b
-c
c
b
a
1
Đặt
3k m n=+
, phương trình
( )
3
33
3
3
3 3 3 *
3
x x k
x x m n x x k
x x k
−=
− = + − =
− = −
Ta có đồ thị của hàm số
3
3y x x=−
và
3
3y x x=−
như hình vẽ.
Từ đồ thị ta thấy phương trình (*) có 3 nghiệm dương phân biệt
,,abc
khi và chỉ khi
02k
. (1)
Khi đó không mất tổng quát giả sử
abc
. Chú ý rằng hàm số
3
3y x x=−
là hàm chẵn
nên dựa vào đồ thị trên suy ra phương trình
3
3x x k−=
sẽ có 3 nghiệm phân biệt là
;;b a c−−
.
Theo định lý Viet của hàm bậc 3 thì
0b a c a b c− − + = + =
.
Theo đề bài
23
23
2
a b c c
+
+ + = + =
.
Vì
c
là nghiệm của phương trình (1) nên
3
2 3 2 3
3. 0
22
k

++
− − =



.
13
3
48
k = +
(thỏa mãn điều kiện (1)).
Từ đó ta có
31
;
84
mn==
nên
3 1 13
6 4 6. 4.
8 4 4
mn+ = + =
.
Câu 12. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông, tam giác
SBC
đều và tam giác
SAD
vuông. Góc taọ bởi hai mặt phẳng
( ) ( )
,SBC ABCD
là
A.
0
45 .
B.
0
30 .
C.
0
60 .
D.
0
15
.
Lời giải
Tác giả: Lê Thị Phương; Fb: Plus kính gửi
Chọn B
H
K
A
D
B
C
S
Ta có
( ) ( )
.SBC ABCD BC=
Gọi
,HK
lần lượt là trung điểm của
,.BC AD
Tam giác
SBC
đều nên
.SH BC⊥
Tứ giác
ABCD
là hình vuông nên
KH BC⊥
. Góc tạo
bởi hai mặt phẳng
( ) ( )
,SBC ABCD
là góc tạo bởi hai đường thẳng
,.SH KH
Gọi độ dài cạnh của hình vuông
ABCD
là
a
. Vì
,BC SH BC KH⊥⊥
nên
,BC SK⊥
suy ra
.AD SK⊥
Do đó tam giác
SAD
cân tại
.S
Hơn nữa, tam giác
SAD
vuông nên nó vuông cân
tại
S
. Suy ra
1
.
22
a
SK AD==
Tam giác
SHK
có
3
2
a
SH =
,
2
a
SK =
, nên áp dụng định côsin ta có
22
2
2 2 2
3
3
44
cos
2. . 2
3
2. .
2
aa
a
SH HK SK
SHK
SK SH
a
a
+−
+−
= = =
.
Suy ra
SHK =
0
30
. Vậy góc giữa hai mặt phẳng
( ) ( )
,SBC ABCD
bằng
0
30 .
Câu 13. Khối chóp tứ giác đều có độ dài cạnh đáy bằng
a
, mặt bên tạo với đáy một góc
0
60
thì thể
tích bằng:
A.
3
6
2
a
. B
3
6
6
a
. C.
3
3
2
a
. D.
3
3
6
a
Lời giải
Tác giả:ThanhLoan ; Fb: ThanhLoan
Chọn D
Gọi khối chóp tứ giác đều là
.S ABCD
,
O
là tâm của đáy
( )
SO ABCD⊥
.
Gọi
M
là trung điểm của
CD
( )
0
( ),( ) 60SCD ABCD SMO = =
SMO
vuông tại
O
0
3
.tan60
2
a
SO OM = =
23
.
1 1 3 3
. . . .
3 3 2 6
S ABCD ABCD
a
V SO S a a = = =
.
Câu 14. Cho khối chóp
.S ABC
có thể tích
V
. Gọi
,,M N P
lần lượt là trọng tâm của các tam giác
,,SBC SCA SAB
. Thể tích của khối chóp
.S MNP
bằng
A.
4
27
V
. B.
8
27
V
. C.
2
27
V
. D.
1
27
V
.
Lời giải
Tác giả: Nguyễn Thị Huệ ; Fb: Nguyễn Thị Huệ
Chọn C
Gọi
,,E D F
lần lượt là trung điểm của các cạnh
,,AB BC CA
. Vì
,,M N P
lần lượt là trọng
tâm của các tam giác
,,SBC SCA SAB
nên
,,M N P
lần lượt thuộc các đoạn
,,SD SF SE
và
2
3
SM SN SP
SD SF SE
= = =
.
Ta có
.
..
.
2 2 2 8 8
. . . . .
3 3 3 27 27
S MNP
S MNP S DFE
S DFE
V
SM SN SP
VV
V SD SF SE
= = = =
Vì
,,E D F
lần lượt là trung điểm của các cạnh
,,AB BC CA
nên
1
4
DEF ABC
SS

=
. Mặt khác
hai hình chóp
.S ABC
và
.S DEF
có cùng chiều cao nên
..
1
4
S DFE S ABC
VV=
.
Suy ra
. . . .
8 8 1 2 2
. . . .
27 27 4 27 27
S MNP S DFE S ABC S ABC
V V V V V= = = =
.
Câu 15. Số cạnh của hình chóp tứ giác là
A.
8
. B.
9
. C.
10
. D.
12
.
Lời giải
Tác giả:Huỳnh Hữu Hùng; Fb: Huuhung Huynh
Chọn A
Hình chóp tứ giác có 4 cạnh đáy và 4 cạnh bên nên có tất cả 8 cạnh.
Câu 16. Khoảng cách giữa hai điểm cực trị của đồ thị hàm số
32
31y x x= − −
là
A.
25
. B.
23
. C.
2
. D.
4
.
Lời giải
Tác giả:Huỳnh Hữu Hùng; Fb: Huuhung Huynh
Chọn A
Tập xác định
D =
2
36y x x
=−
;
0
0
2
x
y
x
=
=
=
;
(0) 1y =−
;
(2) 5y =−
.
y
đổi dấu qua các điểm
0x =
và
2x =
.
Do đó, hai điểm cực trị của đồ thị hàm số là
(0; 1)A −
và
(2; 5)B −
.
Khoảng cách giữa hai điểm cực trị của đồ thị hàm số là
22
(2 0) ( 5 1) 2 5.AB = − + − + =
Phamquynhanhbaby56@gmail.com
Câu 17. Tập hợp các giá trị thực của tham số
m
để hàm số
32
9 (3 )y x x m x m= − + − +
đồng biến trên
là
A.
( )
; 24− −
.
B.
(
; 24− −
. C.
( )
24;− +
. D.
)
24;− +
.
Lời giải
Tác giả: Nguyễn Thị Thỏa; Fb: Nguyễn Thị Thỏa
Chọn B
Ta có
2
3 18 3y x x m
= − + −
.
Hàm số đã cho đồng biến trên
0,yx
2
3 18 3 0, x x m x − + −
72 3 0m
= +
24m −
.
Vậy tập hợp các giá trị của tham số
m
thỏa mãn yêu cầu bài toán là
(
; 24− −
.
Câu 18. Cho hàm số
1
1
x
y
x
+
=
−
, mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên hai khoảng
( ) ( )
;1 ; 1;− +
.
B. Hàm số nghịch biến trên
( ) ( )
;1 1;− +
.
C. Hàm số đồng biến trên hai khoảng
( ) ( )
;1 ; 1;− +
.
D. Hàm số đồng biến trên
( ) ( )
;1 1;− +
.
Lời giải
Tác giả: Hà Minh Yên; Fb: Hà Minh Yên
Chọn A
Hàm số
1
1
x
y
x
+
=
−
có tập xác định
\1D =
.
( )
2
2
01
1
yx
x
−
=
−
,
.
Do đó hàm số nghịch biến trên hai khoảng
( ) ( )
;1 ; 1;− +
.
Câu 19. Cho hàm số
( )
y f x=
có đồ thị như hình vẽ. Phương trình
( )
f x m−=
( với
m
là tham số
thực) có nhiều nhất bao nhiêu nghiệm?
A.
8
. B.
2
. C.
4
. D.
6
.
Lời giải
Tác giả: Nguyễn Ngọc Diệp, FB: Nguyễn Ngọc Diệp
Chọn D
Nhận thấy hàm số
( )
y f x=−
là hàm số chẵn nên đồ thị của hàm số
( )
y f x=−
nhận trục
Oy
làm trục đối xứng.
Đồ thị hàm số
( )
y f x=−
gồm hai phần:
Phần 1: giữ nguyên phần đồ thị hàm số
( )
y f x=
với
0x
.
Phần 2: lấy đối xứng đồ thị phần 1 qua trục
Oy
.
Từ đó ta có đồ thị hàm số
( )
y f x=−
như sau:
Từ đồ thị hàm số
( )
y f x=−
ta thấy phương trình
( )
f x m−=
có tối đa 6 nghiệm.
Câu 20. Xét hai số thực dương thay đổi
x
,
y
sao cho
1xy
. Giá trị nhỏ nhất của biểu thức
55
2
1
xy
P x y
xy
+
= + +
−
đạt được khi
0
xx=
và
0
yy=
. Giá trị của biểu thức
0
0
1x
Q
y
+
=
là
A.
3
. B.
2
. C.
2
. D.
1
.
Lời giải
Tác giả: Phạm Văn Tuân (lời giải: Thầy Nguyễn Duy Hiếu); Fb: mr.vtuan.
Chọn B
Ta có:
( ) ( ) ( )
5 5 1 5 1
55
22
11
x y xy xy
xy
P x y x y
xy xy x y x y
+ − −
+
= + + = + + + −
− − + +
22
3 2 5 5
10
AM GM
x xy y xy
xy
−
+ + − +
+
+
22
2 2 5
10
x xy y
P
xy
− + +
+
+
22
2 2 2 2 5
12
x xy y x y
xy
− + − − +
=+
+
( ) ( ) ( )
( )
2 2 2
2 3 3 2 2 3
12 12
6
x y y x
P
xy
− + − + −
+
+
.
Dấu bằng xảy ra khi và chỉ khi
2 3 0
30
3
20
2
1
1
xy
x
x
y
y
x y xy
xy x y
−=
−=
=
−=

=
+−
=
−+
.
Do đó
0
0
1
2
x
Q
y
+
==
.
Câu 21. Điểm cực tiểu của hàm số
32
6 9 1y x x x= − + − +
là
A.
0x =
. B.
3x =
. C.
2x =
. D.
1x =
.
Lời giải
Tác giả: Trân Minh; Fb: Tran Minh
Chọn D
Ta có
2
3 12 9y x x
= − + −
2
0 3 12 9 0y x x
= − + − =
1; 3xx = =
.
Bảng biến thiên
Điểm cực tiểu của hàm số là
1x =
.
Câu 22. Cho hàm số
( )
y f x=
có bảng biến thiên như hình vẽ
Số điểm cực trị của hàm số
( )
y f x=
là
A.
5
. B.
3
. C.
4
. D.
2
.
Lời giải
Tác giả: Lê Thanh Hùng; Fb: Hung Le Thanh
Chọn A
Cách 1:
Ta có:
( )
( ) ( )
( ) ( )
,0
,
f x f x
y f x
f x f x
==
−
neáu
neáu < 0
Dựa vào bảng biến thiên của hàm số
( )
y f x=
, ta có bảng biến thiên của hàm số
( )
y f x=
như sau:
Do đó, số điểm cực trị của hàm số
( )
y f x=
là
5
.
Cách 2:
( )
y f x=
( ) ( )
( )
.f x f x
y
fx
=
Ta có:
( )
( )
( )
( )
11
22
33
1
0 1 1
1
x x x
f x x x x
x x x
= −
= = −
=
( )
4
5
1
0
1
x
fx
x
=−
=
=
.
Do
y
đổi dấu khi đi qua
5
nghiệm này nên hàm số
( )
y f x=
có 5 điểm cực trị.
Cách 3:
Đồ thị hàm số
( )
y f x=
cắt trục hoành tại
3
điểm phân biệt không trùng với
2
điểm cực trị,
nên số điểm cực trị của đồ thị hàm số
( )
y f x=
là
5
.
Câu 23. Có bao nhiêu giá trị của tham số
m
để đồ thị hàm số
( ) ( )
32
1 2 2 2y x m x m x m= − + + − + −
có
điểm cực trị thuộc trục hoành?
A.
3
. B.
1
. C.
0
. D.
2
.
Lời giải
Tác giả: Bùi Văn Khánh ; Fb:Khánh Bùi Văn
Chọn A
Phương trình hoành độ giao điểm của đồ thị hàm số đã cho với trục hoành là
( ) ( ) ( )
( )
3 2 2
1 2 2 2 0 1 2 2 0x m x m x m x x mx m− + + − + − = − − − + =
(1)
( )
2
1
2 2 0 2
x
x mx m
=
− − + =
Đồ thị hàm số có điểm cực trị thuộc trục hoành
Phương trình (1) có đúng hai nghiệm phân
biệt
(2) có nghiệm kép khác 1 hoặc (2) có hai nghiệm phân biệt trong đó có 1 nghiệm
bằng 1.
TH1: (2) có nghiệm kép khác 1
2
8 8 0
4 2 6
1
2
mm
m
m
= + − =
= −
TH2: (2) có hai nghiệm phân biệt trong đó có một nghiệm bằng 1
2
8 8 0
1
1
mm
m
m
+ −
=
=
Vậy có 3 giá trị của
m
để đồ thị hàm số có điểm cực trị thuộc trục hoành.
Câu 24. Có bao nhiêu giá trị thực của tham số
m
để đồ thị hàm số
( )
2
2
1
2 2 1
−
=
+ − + +
x
y
x m x m
có đúng
hai đường tiệm cận?
A.
1
. B.
3
. C.
2
. D.
4
.
Lời giải
Tác giả: Minh Tuấn ; Fb: Mác Lênin
Chọn B.
Ta thấy rằng đồ thị của hàm số đã cho có đường tiệm cận ngang
1=y
, do vậy đồ thị đó có
đúng 2 đường tiệm cận khi và chỉ khi đồ thị hàm số có đúng một đường tiệm cận đứng.
Đồ thị hàm số đã cho có đúng một đường tiệm cận đứng
phương trình
( ) ( )
2
2 2 1 0 *+ − + + =x m x m
có nghiệm kép hoặc có nghiệm
1=−x
hoặc
1=x
.
Trường hợp 1: Phương trình
( )
*
có nghiệm
1=x
4m = −
.
Trường hợp 2: Phương trình
( )
*
có nghiệm
1x =−
0m=
.
Trường hợp 3: Phương trình
( )
*
có nghiệm kép
( ) ( )
2
2
0
0 2 4 2 1 0 12 0
12
m
m m m m
m
=
= − − + = − =
=
Như vậy có 3 giá trị của
m
thỏa mãn yêu cầu bài toán.
Dongque84@gmail.com
Câu 25. Cho hàm số bậc ba
( )
y f x=
mà đồ thị hàm số có hai điểm cực trị là
( ) ( )
1;3 , 2;1AB
. Số
điểm cực trị của hàm số
( )
y f x=
là
A.
1
. B.
5
. C.
4
. D. 3.
Lời giải
Tác giả: Vũ Thị Thu Huyền; Fb: HuyenVu
Chọn B.
Hàm số
( )
( ) ( )
( )
y x f x f x y x− = − = =
x
nên
( )
y f x=
là hàm chẵn trên .
Do đó đồ thị hàm số
( )
y f x=
nhận
Oy
trục đối xứng.
Vì vậy đồ thị hàm số
( )
y f x=
có 5 điểm cực trị là
( ) ( )
1;3 , 2;1AB
,
( ) ( )
' 1;3 , ' 2;1AB−−
và
điểm có hoành độ
0x =
.
Câu 26. Cho hình lập phương
.ABCD A B C D
có cạnh bằng
a
. Khoảng cách từ điểm
A
đến mặt
phẳng
( )
A BD
bằng
A.
2
2
a
. B.
3
3
a
. C.
2
a
. D.
2
3
a
.
Lời giải
Tác giả:Nguyễn Thanh Mai; Fb: Nguyen Thanh Mai
Chọn B
Kẻ
AH A O
⊥
. Ta dễ dàng chứng minh được
( )
AH A BD
⊥
. Suy ra
( )
( )
,d A A BD AH
=
.
Ta có
2 2 2 2 2
1 1 1 1 3 3
3
a
AH
AH AB AD AA a
= + + = =
. Vậy
( )
( )
3
,
3
a
d A A BD
=
.
Linh19781978@gmail.com
Câu 27. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông tại
,AD
.
SA
vuông góc với mặt
phẳng
( )
ABCD
. Cho biết
AD CD a==
,
2AB a=
,hai mặt phẳng
( ) ( )
,SBC ABCD
tạo với
nhau góc
0
45
. Khoảng cách từ điểm
D
đến mặt phẳng
( )
SBC
bằng.
A.
2
a
. B.
3
2
a
. C.
2
2
a
. D.
a
.
Lời giải
Tác giả:Đặng Thị Phương Huyền; Fb: Phuong Huyen Dang
Chọn A
Do
ABCD
là hình thang vuông tại
,AD
và
AD CD a==
,
2AB a=
nên
AC
vuông góc với
CB
, lại có
CB SA⊥
( do
SA
vuông góc với mặt phẳng
( )
ABCD
. Do đó góc
SCA
bằng
0
45
và
( )
CB SAC⊥
.Suy ra tam giác
SAC
vuông cân tại
A
.
Gọi
E
là trung điểm cạnh
AB
. Ta có :
( )
( )
( )
( )
( )
( )
1
, , ,
2
d D SBC d E SBC d A SBC==
.
Gọi H là trung điểm SC . Do tam giác
SAC
vuông cân tại
A
nên
AH SC⊥
, mà
AH CB⊥
(do
( )
CB SAC⊥
). Suy ra
( )
AH SBC⊥
và
( )
( )
0
2
, .Sin 45 2.
2
d A SCD AH AC a a= = = =
.
Vậy :
( )
( )
( )
( )
1
,,
22
a
d D SBC d A SBC==
.
Câu 28 . Gọi
S
là tập các giá trị thực của tham số
m
để đồ thị hàm số
42
24y x mx m= − + +
có ba
điểm cực trị cách đều trục hoành. Tính tổng tất cả các phần tử của tập
S
là
A. 2. B. 6. C. 0. D. 4.
Lời giải
Tác giả:Minh Trang ; Fb: Minh Trang
Chọn D
Ta có
3
' 4 4y x mx=−
.
2
0
' 0 .
x
y
xm
=
=
=
Đồ thị hàm số
42
24y x mx m= − + +
có ba điểm cực trị
phương trình
'0y =
có ba nghiệm
phân biệt
0m
.
Ta có
( )
( ) ( )
22
0; 4 , ; 4 , ; 4A m B m m m C m m m+ − + + − − + +
là ba điểm cực trị của đồ thị
hàm số.
,,A B C
cách đều trục hoành
2
44
A B C
y y y m m m = = + = − + +
( )
( )
( )
2
2
0
44
4
2
44
4
mL
m m m
m
mL
m m m
m TM
=
+ = − + +
=
=−
+ = − −
=
.
Vậy
4m=
. Suy ra tổng tất cả các phần tử của tập
S
là 4.
Câu 29: Cho hai hình vuông
ABCD
và
ABEF
có cạnh bằng
a
và nằm trên hai mặt mặt phẳng
vuông góc với nhau. Thể tích khối đa diện
EBCFAD
bằng
A.
3
2
3
a
. B.
3
3
a
. C.
3
2
a
. D.
3
a
.
Lời giải
Tác giả: Trần Thị Thảo; Facebook: Trần Thảo
Chọn C
Dựng hình lập phương
ABCDEFMN
cạnh
a
.
3
11
22
EBCFAD ABCDFEMN
V V a==
. Chọn C.
Câu 30: Cho lăng trụ đứng
. ' ' 'ABC A B C
có tam giác
'A BC
là tam giác đều cạnh
a
và tam giác
ABC
vuông tại
A
. Thể tích khối lăng trụ
. ' ' 'ABC A B C
là
A.
3
2
4
a
. B.
3
2
12
a
C.
3
2
8
a
. D.
3
2
6
a
.
Lời giải
Tác giả: Trịnh Xuân Mạnh ; Fb:Trịnh Xuân Mạnh
Chọn C.
C'
A'
B
C
A
B'
Ta có
' ' ' 'BB A CC ADD=
nên
' ' ' 'A B A C=
. Từ đó
' ' 'A B CD
vuông cân.
Suy ra:
2
' ' ' ' ' '.sin .sin45
2
o
a
A B A C B C A B C a
= = = =
.
Xét
''BB AD
vuông tại
'B
theo định lí Pi–ta-go ta có
2
2 2 2
22
'
22
aa
BB A B B A a

= − = − =


.
Vậy
3
.
1 1 2 2 2 2
. . . . .
2 2 2 2 2 8
ABC A B C
a a a a
V S h A B A C AA
= = = =
.
Câu 31. Có bao nhiêu tiếp tuyến của đồ thị hàm số
32
2y x x=−
tạo với hai trục tọa độ một tam giác
cân?
A.
3
. B.
1
. C.
4
. D.
2
.
Lời giải
Tác giả: Tạ Tiến Thanh ; Fb: Thanh Ta
Chọn C
Ta có
3 2 2
2 ' 3 4y x x y x x= − = −
.
Gọi
( )
00
;M x y
là tọa độ tiếp điểm của tiếp tuyến với đồ thị hàm số. Vì tiếp tuyến tạo với hai
trục tọa độ một tam giác cân tại
O
(vuông cân) tương đương
0
'( ) 1yx =
.
0
2
0 0 0
0
27
3
( ) 1 3 4 1
27
3
x
y x x x
x
+
=
= − =
−
=
;
0
2
0 0 0
0
1
( ) 1 3 4 1
1
3
x
y x x x
x
=
= − − = −
=
.
Vậy có 4 tiếp tuyến thỏa mãn yêu cầu bài toán.
Câu 32. Cho lăng trụ có đáy là hình vuông cạnh
3a
và chiều cao là
b
. Thể tích khối lăng trụ đó
bằng
A.
2
ab
. B.
2
3ab
. C.
2
3ab
. D.
2
ab
.
Lời giải
Tác giả: Ngô Thị Thơ ; Fb: Ngô Thị Thơ
Chọn C
( )
2
2
. 3 3V b a a b==
.
Câu 33. Đường tiệm cận ngang của đồ thị hàm số
32
1
x
y
x
−
=
+
có phương trình là
A.
3y =−
. B.
2y =
. C.
2y =−
. D.
3y =
.
Lời giải
Tác giả: Ngô Thị Thơ ; Fb: Ngô Thị Thơ
Chọn C
lim 2
x
y
→+
=−
;
lim 2
x
y
→−
=−
, suy ra tiệm cận ngang của đồ thị hàm số là
2y =−
.
Câu 34: Hai đường tiệm cận của đồ thị hàm số
23
1
x
y
x
−
=
+
và hai trục tọa độ cắt nhau tạo thành hình
chữ nhật. Diện tích của hình chữ nhật đó là?
A.
2.S =
B.
4.S =
C.
1.S =
. D.
3.S =
.
Lời giải
Tác giả: Trịnh Xuân Mạnh ; Fb:Trịnh Xuân Mạnh.
Chọn A
Ta có các tiệm cận của đồ thị hàm số
23
1
x
y
x
−
=
+
là:
1; 2xy= − =
Gọi giao điểm của hai đường tiệm cận là
( )
1;2A −
, giao điểm của TCN với trục tung là
( )
0;2B
, giao điểm của TCĐ với trục hoành là
( )
1;0C −
. Ta có hình chữ nhật
ABOC
.
Lại có
2 2; 1 1
Bc
OB y OC x= = = = = − =
.
Vậy diện tích hình chữ nhật
AOBC
:
. 2.1 2
AOBC
S OBOC= = =
.
Câu 35. Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3sin 1
sin 2
x
x
y
+
+
=
là
A.
11
6
. B.
0
. C.
2
3
−
. D.
3
2
−
Lời giải
Tác giả: Tạ Tiến Thanh ; Fb: Thanh Ta
Chọn C
Đặt
sin ; 1;1t x t= −
, ta có
31
2
t
t
y
+
+
=
, khi đó
2
5
' 0 1;1
( 2)
yt
t
= −
+
.
Hàm số đồng biến trên
1;1−
, suy ra
[ 1;1]
[ 1;1]
3.1 1 4 3.( 1) 1
max ; min 2.
1 2 3 ( 1) 2
t
t
yy
−
−
+ − +
= = = = −
+ − +
Khi đó tổng giá trị lớn nhất và giá trị nhỏ nhất là
42
( 2) .
33
+ − = −
Câu 36 . Tập hợp các giá trị thực của tham số
m
để hàm số
2
2cos
cos
xm
y
xm
+
=
+
nghịch biến trên khoảng
( )
0;
là
A.
( )
0;2 .
B.
( )
2;+
. C.
)
1;0−
D.
)
1;2
.
Lời giải
Tác giả:Minh Trang ; Fb: Minh Trang
Chọn D
Ta có
( )
( )
( )
( )
( )
22
2
22
2sin . cos sin . 2cos 2 sin .
2cos
'
cos
cos cos
x x m x x m m m x
xm
yy
xm
x m x m
− + + + −
+
= = =
+
++
.
Hàm số
2
2cos
cos
xm
y
xm
+
=
+
nghịch biến trên khoảng
( ) ( )
0; ' 0 0;yx

và
( )
cos 0;x m x
−
. Mà
( ) ( )
sin 0, cos 1;1 0;x x x
−
.
Suy ra ycbt
2
20
1
1
mm
m
m
−
−
12m
.
Câu 37: Số điểm chung của hai đồ thị hàm số
32
2y x x=−
và
23yx=−
là
A.
2
. B.
3
. C.
0
. D.
1
.
Lời giải
Tác giả: Trần Thị Thảo; Facebook: Trần Thảo
Chọn B
Phương trình hoành độ giao điểm của hai đồ thị hàm số là:
3 2 3 2
1
1 13
2 2 3 2 2 3 0
2
1 13
2
x
x x x x x x x
x
=
+
− = − − − + = =
−
=
.
Vậy hai đồ thị hàm số có 3 điểm chung.
Câu 38: Tổng diện tích các mặt của tứ diện đều cạnh
a
là
A.
2
2a
. B.
2
3a
. C.
2
4a
. D.
2
23a
.
Lời giải
Tác giả: Mai Quỳnh Vân ; Fb: Vân Mai
Chọn B
Mỗi mặt của tứ diện đều cạnh
a
, là một tam giác đều cạnh bằng
a
nên diện tích mỗi mặt là:
2
1
13
. . .sin 60
24
a
S a a= =
.
Diện tích 4 mặt của tứ diện đều là:
2
2
1
3
4. 4. 3
4
a
S S a= = =
.
Câu 39: Trong các hàm số sau, hàm số nào đồng biến trên khoảng
( )
;− +
?
A.
2
21
x
y
x
−
=
+
. B.
3
31y x x= + +
. C.
2
1y x x= − +
. D.
42
21y x x= + +
.
Lời giải
Tác giả: Mai Quỳnh Vân ; Fb: Vân Mai
Chọn B
Loại A do tập xác định của hàm số là
\
2

−


.
Loại C do
1
0 2 1 0
2
y x x
= − = =
do đó
y
đổi dấu qua
1
2
x =
.
Loại D do
3
0 4 4 0 0y x x x
= + = =
do đó
y
đổi dấu qua
0x =
.
Xét B ta có
2
3 3 0y x x
= +
nên hàm số luôn đồng biến trên khoảng
( )
;− +
.
Do đó chọn phương án B.
Câu 40: Số điểm cực đại của hàm số
42
2 3 1y x x= − +
là
A.
0
. B.
2
. C.
3
. D.
1
.
Lời giải
Tác giả: Nguyễn Thị Xuyến; Fb: Nguyen Xuyen
Chọn D
Tập xác định
D =
.
Ta có:
3
' 8 6y x x=−
;
3
0
' 0 8 6 0
3
2
x
y x x
x
=
= − =
=
.
Bảng xét dấu y':
x
−
3
2
−
0
3
2
+
'y
- 0 + 0 - 0 +
Vậy hàm số đã cho có 1 điểm cực đại.
Câu 41: Số đường tiệm cận đứng của đồ thị hàm số
2
3
1
32
x
y
xx
−
=
−+
là
A. 2. B. 0. C. 1. D. 3.
Lời giải
Tác giả: Nguyễn Thị Xuyến; Fb: Nguyen Xuyen
Chọn A
Tập xác định:
\ 2; 1D =−
.
Ta có:
( ) ( ) ( )
( )( )
( )
( )
( )
( )
( )
2
3
22
2 2 2 2
1 1 1
1
lim lim lim lim
32
1 2 2
x x x x
x x x
x
y
xx
x x x x x
+ + + +
→ − → − → − → −
− + +
−
= = = = +
−+
− + − + −
.
( )( )
( )
( )
( )
( )
2
3
22
1 1 1 1
1 1 1
1
lim lim lim lim
32
1 2 2
x x x x
x x x
x
y
xx
x x x x x
+ + + +
→ → → →
− + +
−
= = = = +
−+
− + − + −
.
Các đường thẳng
2x =−
và
1x =
là các đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có 2 đường tiệm cận đứng.
Câu 42: Cho khối chóp
.S ABC
có thể tích
3
3
3
Va=
, tam giác
SBC
là tam giác đều có cạnh bằng
a
.
Khi đó, khoảng cách từ điểm
A
đến mặt phẳng
( )
SBC
bằng
A.
43
3
a
. B.
4
3
a
. C.
4a
. D.
23a
.
Lời giải
Tác giả: Trần Thanh Hà ; Fb: Hà Trần
Phản biện: Đồng Anh Tú; FB: Anh Tú
Chọn C
Ta có:
( )
( )
( )
( )
.
.
3
1
, . ,
3
S ABC
S ABC SBC
SBC
V
V d A SBC S d A SBC
S
= =
.
Có:
3
.
3
3
S ABC
Va=
.
Vì
SBC
là tam giác đều có cạnh bằng
a
nên
( )
2
3
4
SBC
a
S đvdt
=
.
Vậy: Khoảng cách từ điểm
A
đến mặt phẳng
( )
SBC
là:
( )
( )
3
2
3
3
3
,4
3
4
a
d A SBC a
a
==
.
Câu 43: Cho hàm số
( )
y f x=
có bảng biến thiên như hình vẽ
Hàm số
( )
2
y f x=
nghịch biến trên khoảng nào trong các khoảng dưới đây?
A.
( )
2;0−
. B.
( )
;2− −
. C.
( )
1; +
. D.
( )
0;1
.
Lời giải
Tác giả:Trần kim Nhung ; Fb: Nhung trần thị Kim
Chọn D
Quan sát bảng biến thiên của hàm số
( )
y f x=
ta thấy
( )
0fx
=
1
2
=
=
x
x
.
Với
( )
2
=y f x
ta có
( )
2
2.

=y x f x
.
Vậy
0y
=
( )
2
2
2
0
20
1
'0
2
=
=
=
=
=
x
x
x
fx
x
0
1
2
=
=
=
x
x
x
.
Từ bảng biến thiên của hàm số
( )
y f x=
ta thấy
( )
1
0
2

x
fx
x
.
Vậy
( )
2
2
2
11
1
02
2
2
−
−
x
x
f x x
x
x
Ta có bảng xét dấu:
Dựa vào bảng xét dấu ta chọn đáp án D.
Câu 44: Cho hàm số
( )
y f x=
liên tục trên có bảng biến thiên như sau:
Số nghiệm của phương trình
( )
0fx=
là
A.
2
. B.
5
. C.
3
. D.
4
.
Lời giải
Tác giả: Trần Quang Đạt; Fb: Quang Đạt
Chọn B
Số nghiệm của phương trình
( )
0fx=
là số giao điểm của đồ thị hàm số
( )
y f x=
với đường
thẳng
0y =
.
Dựa vào bảng biến thiên ta có: Phương trình
( )
0fx=
có 5 nghiệm phân biệt.
Câu 45: Số điểm cực trị của hàm số
34
(3 1) ( 1)y x x= − +
A.
3
. B.
2
. C.
1
. D.
4
.
Lời giải
Tác giả:Nguyễn Ngọc Hà ; Fb:Hangocnguyen
Chọn B
Tập các định
D =
Ta có :
2 4 3 3 2 3
' 9(3 1) ( 1) 4(3 1) ( 1) (3 1) ( 1) (21 5)y x x x x x x x= − + + − + = − + +
1
3
' 0 1
5
21
x
yx
x
=
= = −
−
=
Bảng biến thiên
Vậy hàm số có 2 cực trị.
Câu 46. Cho hàm số
2
1
x
y
x
−
=
+
có đồ thị
( )
C
cắt hai trục tọa độ lần lượt tại
A
,
B
. Tiếp tuyến của
( )
C
tại hai điểm
A
,
B
tạo với nhau một góc
. Giá trị của
sin
bằng
A.
4
5
. B.
1
10
. C.
3
5
. D.
3
10
.
Lời giải
Tác giả: Nguyễn Thị Hồng Hợp ; Fb: Nguyễn Thị Hồng Hợp
Chọn A
Giao điểm của đồ thị
( )
C
với hai trục tọa độ lần lượt là
( )
0; 2A −
,
( )
2;0B
.
Ta có
( )
2
3
1
=
+
y
x
.
Phương trình tiếp tuyến của đồ thị
( )
C
tại điểm
A
là:
( )
( )
2
3
32
1
AA
A
y x x y x
x
= − + = −
+
3 2 0xy − − =
.
Phương trình tiếp tuyến của đồ thị
( )
C
tại điểm
B
là:
( )
( )
2
3 1 2
33
1
BB
B
y x x y x
x
= − + = −
+
3 2 0xy − − =
.
Từ giả thiết suy ra
( ) ( )
( ) ( )
22
22
3.1 1 . 3
3
cos
5
3 1 . 1 3
+ − −
==
+ − + −
2
4
sin 1 cos
5

= − =
.
Câu 47. Cho hình lăng trụ có đáy là hình vuông cạnh
a
, thể tích khối lăng trụ bằng
3
a
và độ dài các
cạnh bên là
2a
. Góc tạo bởi cạnh bên và mặt phẳng đáy là:
A.
90
. B.
30
. C.
45
. D.
60
.
Lời giải
Tác giả: Nguyễn Thị Tnh ; Fb: Ngọc Tnh
Chọn B
Gọi
H
là hình chiếu vuông góc của
D
lên mặt phẳng đáy
( )
' ' ' 'A B C D
. Góc
DD H
chính
là góc giữa cạnh bên và mặt phẳng đáy.
Ta có
3
2
ABCD
Va
h DH a
Sa
= = = =
.
Xét tam giác vuông
DHD
ta có
1
sin
DD 2 2
' = = =
D
DH
H
a
D
a
30
=
o
DD H
.
Câu 48. Cho khối chóp
SABCD
có thể tích
V
, đáy
ABCD
là hình bình hành,
M
là trung điểm của
SB
N
là điểm trên cạnh
SD
. Mặt phẳng
( )
AMN
cắt cạnh
SC
tại điểm
P
sao cho thể tích khối
chóp
SAMPN
bằng
4
V
. Tỉ số
SN
SD
bằng
A.
2
3
. B.
2
2
. C.
1
2
. D.
1
3
.
Lời giải
Tác giả: Thân Thế Luân ; Fb: Luan Vu
Phản biện: Trần Hà
Chọn B
Bổ đề: Cho khối chóp
SABCD
có đáy
ABCD
là hình bình hành. Một mặt phẳng không qua S
cắt các cạnh SA, SB, SC, SD lần lượt tại A’, B’, C’, D’ .
Đặt
; ; ;
' ' ' '
SA SB SC SD
a b c d
SA SB SC SD
= = = =
. Khi đó ta có kết luận sau
1.
a c b d+ = +
2.
' ' ' '
4
SA B C D
SABCD
V
a b c d
V abcd
+ + +
=
Chứng minh
Gọi
=AC BD O
,
' ' ' '=A C B D I
S, I, O thẳng hàng (cùng nằm trên giao tuyến của
hai mặt phẳng (SAC) và (SBD)).
Chứng minh 1: Đặt
SO
x
SI
=
Ta có
( )
''
2
' 1 1
.1
SA I SA I
SAO SAC
SS
SA SI
S SA SO ax S ax


= = =
Và
( )
''
2
' 1 1
.2
SC I SC I
SCO SAC
SS
SC SI
S SC SO cx S cx


= = =
Suy ra
' ' 'C'
2 2 2
1 1 1 1
SA I SC I SA
SAC SAC SAC
S S S
S S ax cx S ax cx
+ = + = +
Hay
2 ' ' 1 1 2 1 1
.2
SA SC
a c x
SA SC ax cx ac ax cx
= + = + + =
Tương tự cũng có
2b d x+=
. Vậy
a c b d+ = +
.
Chứng minh 2: Ta có
' ' '
' ' ' 1
..
SA B C
SABC
V
SA SB SC
V SA SB SC abc
==
Và
' 'D'
' ' ' 1
..
SA C
SACD
V
SA SD SC
V SA SD SC acd
==
Mà
D
2
==
ABC
SABC SACD
V
VV
nên
' ' ' ' ' ' ' ' ' '
11
SA B C SA C D SA B C D
SABC SACD SABC
V V V
bd
V V V abc acd abcd
+
+ = = + =
Hay
( )
' ' ' '
2
44
SA B C D
SABCD
bd
V
a b c d
V abcd abcd
+
+ + +
==
Trở lại bài toán:
Đặt
;
SC SD
xy
SP SN
==
Áp dụng bổ đề trên ta có:
1 2 1x y x y+ = + = +
1 2 3 1
4 .2 8 4
AMNP
SABCD
V
x y x y
V xy xy
+ + + + +
= = =
Suy ra
( )
2
21
22
4 1 4
y
yy
yy
+
= = =
+
Vậy
2
2
SN
SD
=
.
Câu 49: Gọi
là góc tạo bởi hai mặt bên của một tứ diện đều. Mệnh đề nào sau đây đúng?
A.
tan 2 2
=
. B.
tan 2
=
. C.
tan 2
=
. D.
tan 3
=
.
Lời giải
Tác giả:Nguyễn Ngọc Hà ; Fb:Hangocnguyen
Chọn A
G
F
E
B
D
C
A
A
G
E
Xét tứ diện đều
ABCD
cạnh có độ dài
a
. Vì các mặt của tứ diện đều đều tạo với nhau những
góc bằng nhau nên ta đi tính góc tạo bởi hai mặt phẳng
()ACD
và
()BCD
Gọi
E
là trung điểm của
CD
.
Do các tam giác
ACD
và
BCD
là các tam giác đều nên
; (1)BE CD AE CD⊥⊥
mà
( ) ( ) (2)CD ABD BCD=
. Từ
(1)&(2)
AEB
=
(
AEB
là góc nhọn)
Gọi
G
là trọng tâm tam giác
( );B,G,EBCD AG BCD⊥
thẳng hàng ;
1
3
GE GB AEG
= =
Tam giác
BCD
đều cạnh
a
nên
3 1 3
2 3 6
aa
BE EG BE= = =
;
Tam giác
ACD
đều nên
3
2
a
AE =
.Do
( ) AG GE AGEAG BCD⊥ ⊥
là vuông tại
G
.
Xét tam giác vuông
AGE
có
22
22
3 3 6
2 6 3
a a a
AG AE GE
= − = − =
6
3
tan 2 2
3
6
a
AG
GE
a
= = =
.
Câu 50. Tập hợp giá trị thực của tham số
m
để hàm số
42
( 2) 2y mx m x m= + − +
có điểm cực tiểu là
A.
(0;2]
. B.
( ;0]−
. C.
(0; )+
. D.
(0;2)
.
Lời giải
Tác giả: Đồng Anh Tú; Fb: Anh tu
Chọn C
Ta có
32
' 4 2( 2) ' 2 (2 2)y mx m x y x mx m= + − = + −
nên
2
0
'0
2 2 (1)
x
y
mx m
=
=
=−
.
TH1:
0m
thì
2
2 2 0, mx m x+ −
nên ta có bảng xét dấu
'y
Ta có
0x =
là điểm cực đại, nên
0m
không thỏa mãn.
TH2:
2m
thì
2
2 2 0, mx m x+ −
nên ta có bảng xét dấu
'y
Ta có
0x =
là điểm cực tiểu, nên
2m
thỏa mãn.
TH3:
02m
, khi đó
2
22
(1)
22
mm
xx
mm
−−
= =
nên phương trình
'0y =
có 3 nghiệm
phân biệt nên hàm số
42
( 2) 2y mx m x m= + − +
có 3 cực trị và nó luôn có ít nhất một cực tiểu,
nên
02m
thỏa mãn.
Vậy ta có
(0; )m +
thì hàm số đã cho có điểm cực tiểu.
| 1/31
| | Tải xuống

Có thể bạn quan tâm:

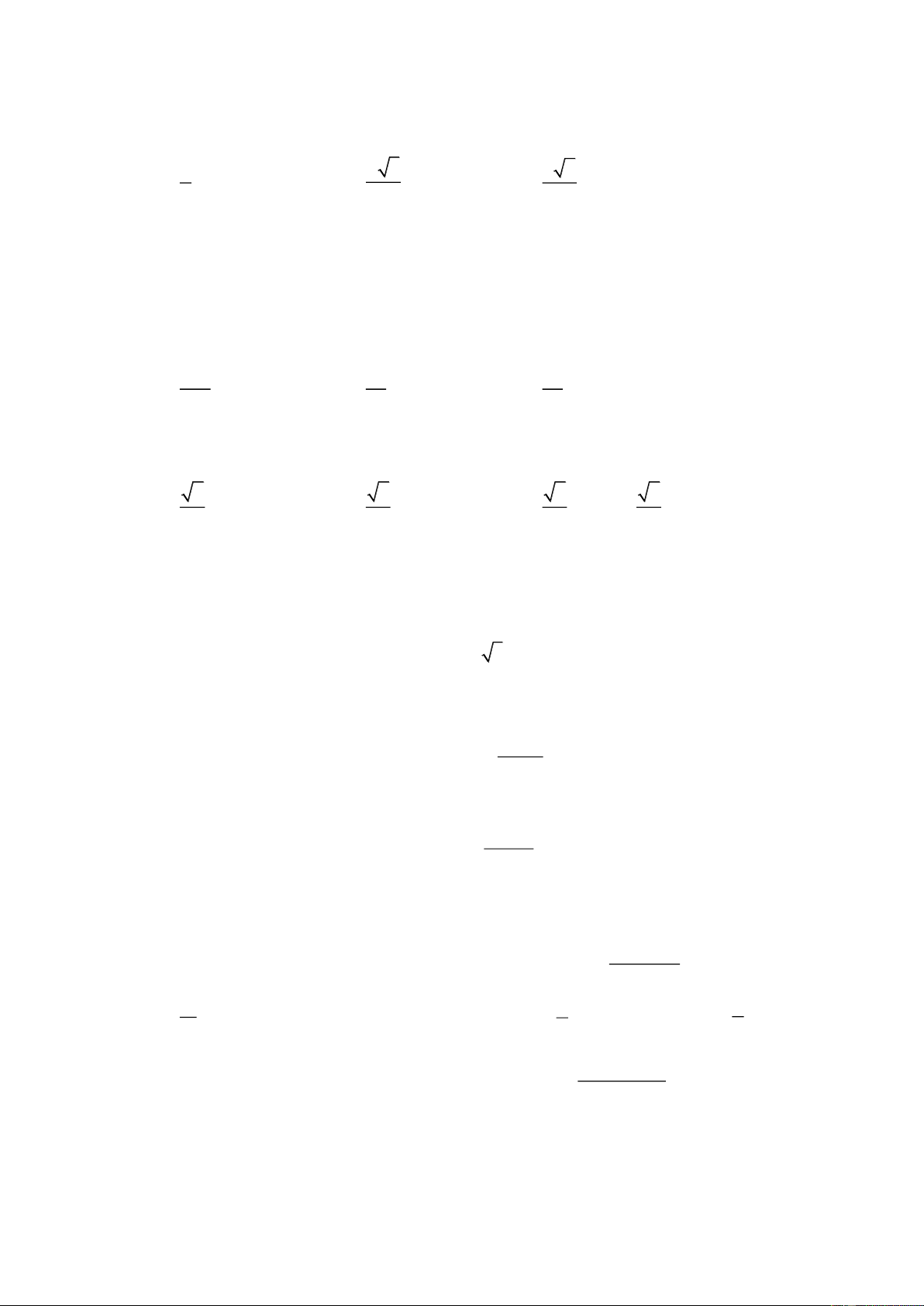
Preview text:

STRONG TEAM TOÁN VD-VDC
ĐỀ CHUYÊN LÊ QUÝ ĐÔN – BÀ TỔ 03 RỊA – VŨNG TÀU
Họ và tên: ....................................................... SBD: ...................................... Câu 1:
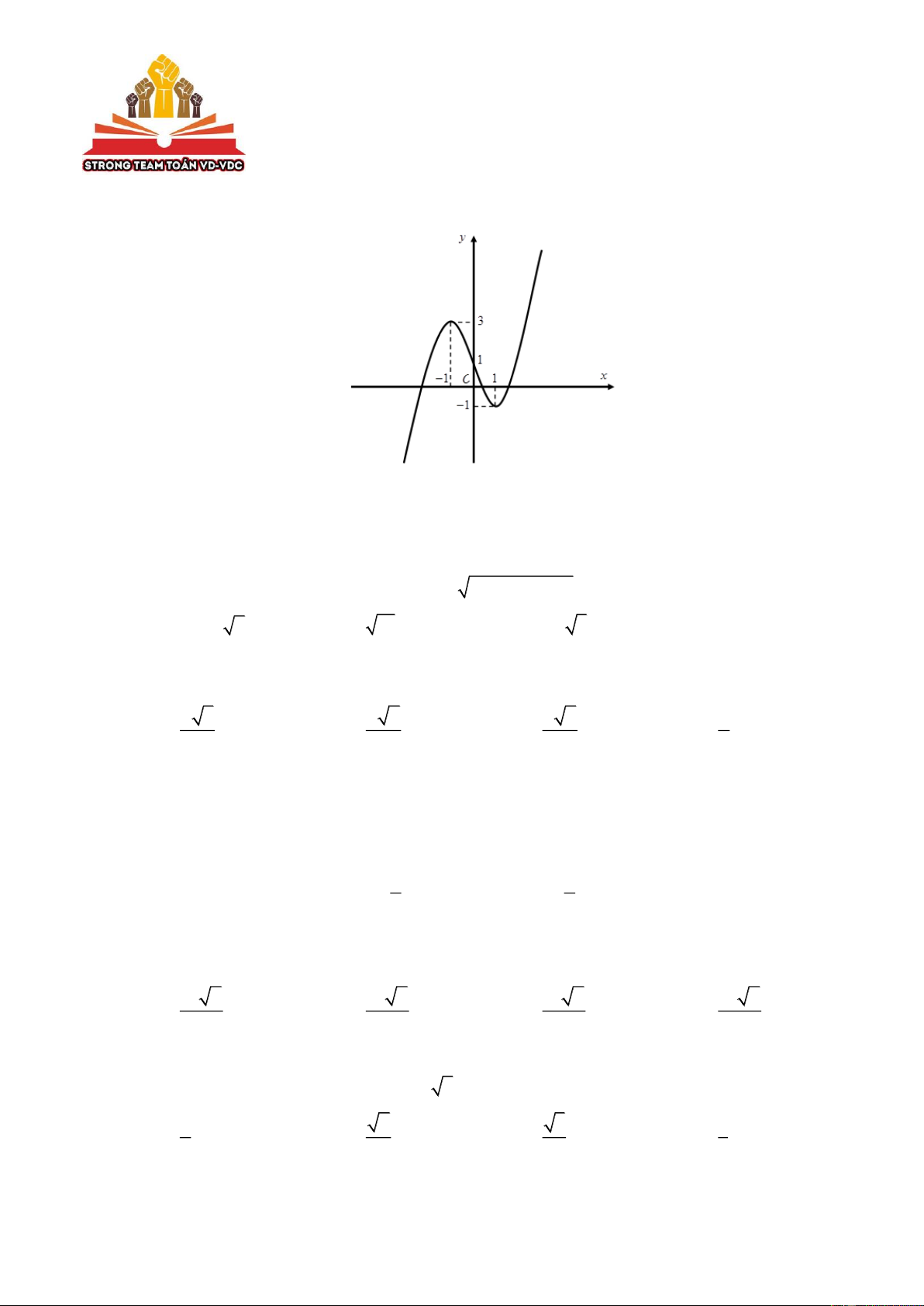
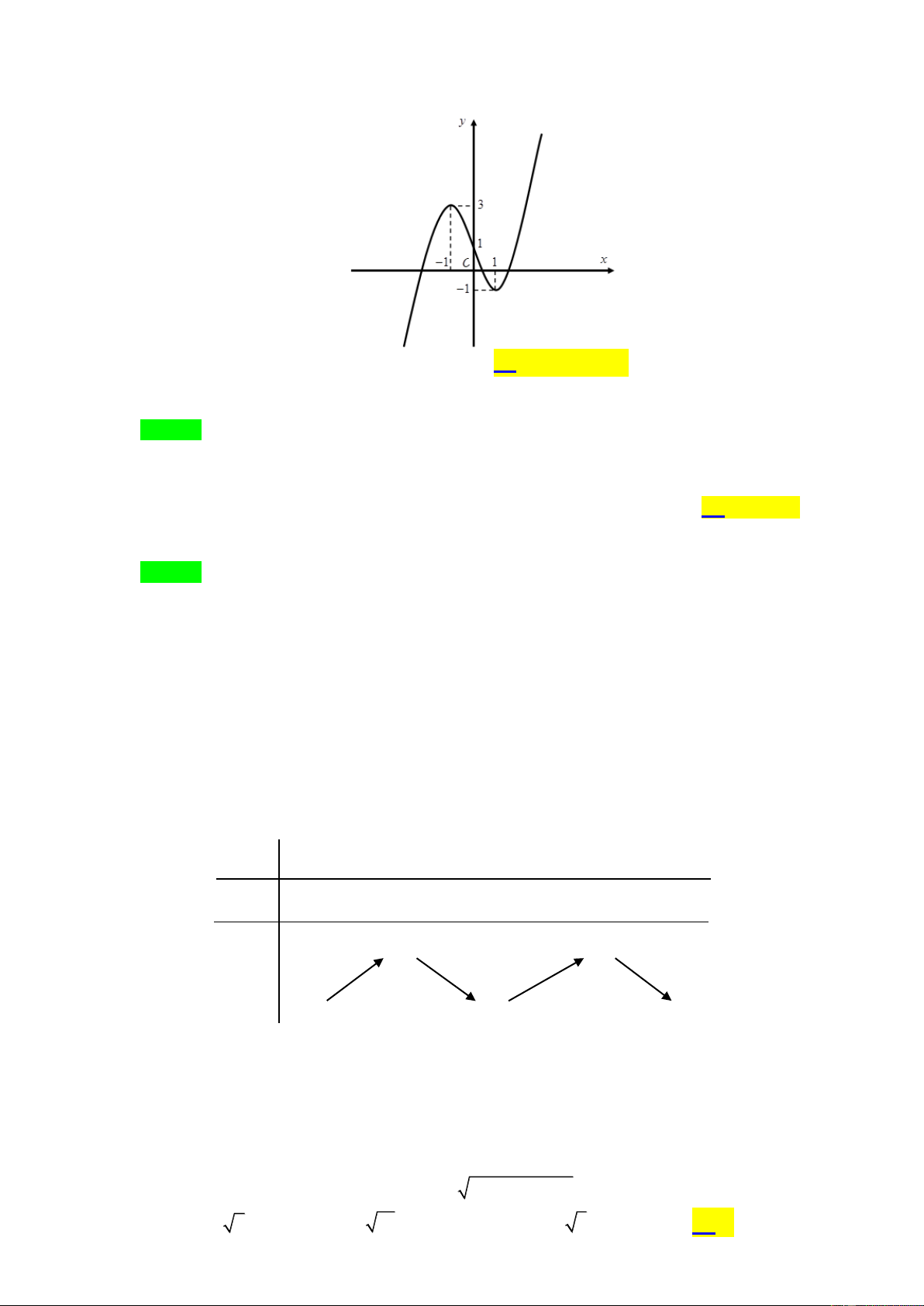
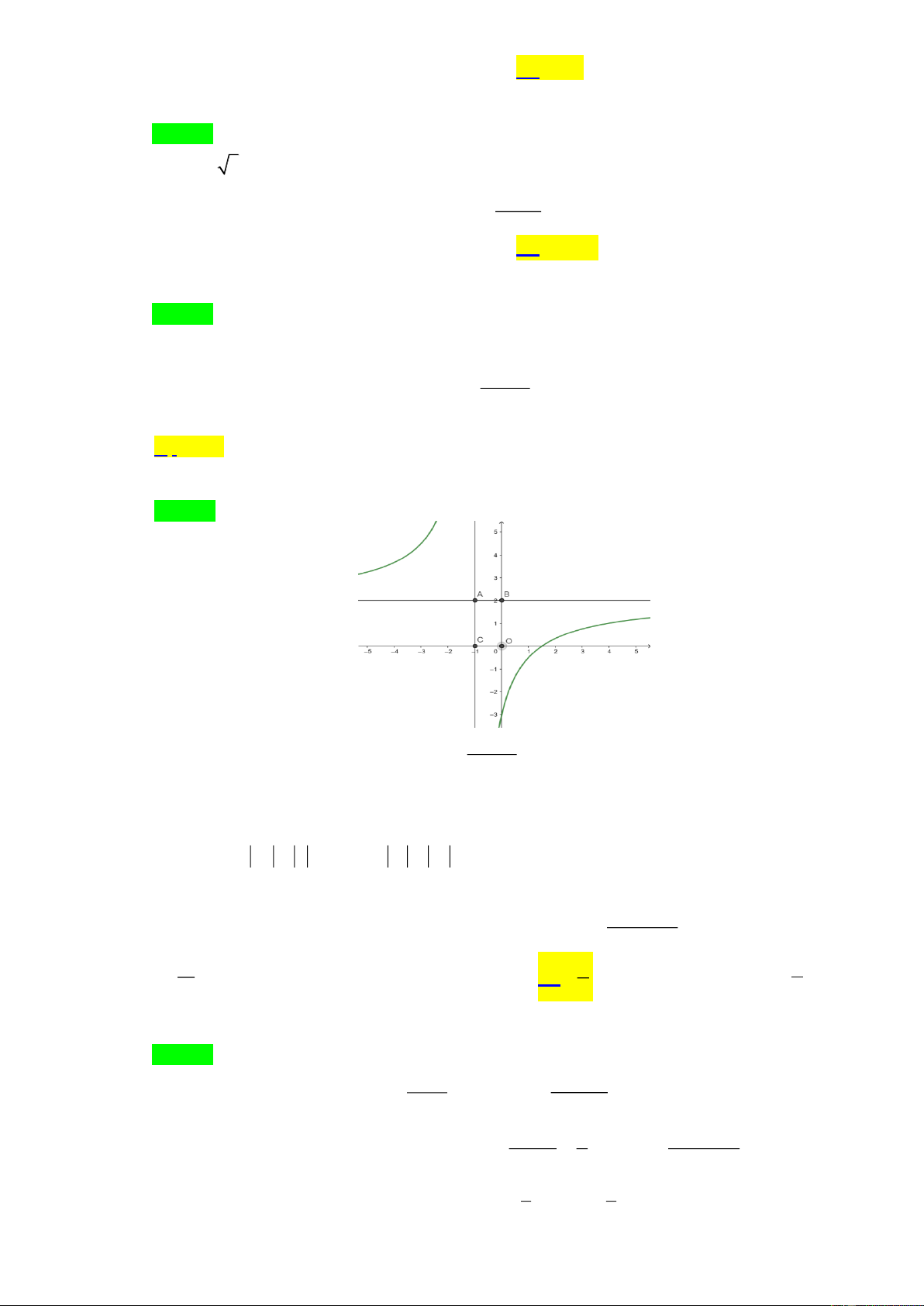
Đồ thị trong hình vẽ sau đây là đồ thị của hàm số nào trong các hàm số bên dưới? A. 4
y = x − 3x +1. B. 4
y = −x + 3x +1. C. 3
y = x − 3x +1. D. 3
y = −x + 3x +1. Câu 2: Phương trình 4 2
x − 2x + m = 0 ( m là tham số thực) có 4 nghiệm phân biệt khi và chỉ khi A. 1 −  m 1. B. 1 −  m  0. C. m  1.
D. 0  m 1. Câu 3:
Giá trị nhỏ nhất của hàm số 2
f (x) = 2x + 5x −10x +10 trên đoạn  2 − ;  1 là A. 4 − +5 2 . B. 10 . C. 1+ 3 . D. 3 . Câu 4:
Cho hình bát diện đều có cạnh bằng a . Khoảng cách giữa hai mặt phẳng song song của bát diện này bằng a 3 a 2 a 6 a A. . B. . C. . D. . 3 2 3 2 Câu 5:
Trong các hàm số sau, hàm số nào đạt cực tiểu tại x = 0 ? A. 4 3
y = x − x . B. 3 2
y = x + x . C. 3 2
y = x - x . D. 4 3
y = x + x . Câu 6: Hàm số 3 2
y = x + x nghịch biến trên khoảng  2   2  A. ( 1 − ;0) . B. 0;   . C. − ; 0   . D. (0; ) 1 .  3   3  Câu 7: Cho lăng trụ AB . C A BC
 , biết rằng tứ diện A A
BC là tứ diện đều cạnh a. Thể tích khối chóp . A BCB C   bằng 3 a 2 3 a 2 3 a 2 3 a 2 A. . B. . C. . D. . 12 6 8 4 Câu 8:
Cho hình chóp S.ABC có tam giác ABC vuông cân tại A , SA vuông góc với mặt phẳng
(ABC). Biết rằng BC = 2a , SB = a 5 . Thể tích khối chóp S.ABC bằng 2 2 3 1 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 3 3 3 3 Câu 9:
Cho hàm số y = f ( x) có đạo hàm trên
và f ( x) = ( 2 x − x − )( 2 ' 2 3 x − ) 1 (3x − ) 1 x   .
Số điểm cực trị của hàm số y = f ( x) là A. 2 . B. 3 . C. 4. D. 1. 3x + 1
Câu 10: Tiếp tuyến của đồ thị hàm số y =
tại điểm có hoành độ x = 1 tạo với hai trục tọa độ x + 1
một tam giác có diện tích bằng 9 3 9 3 A. . B. . C. . D. . 2 2 4 4
Câu 11: Cho hai số hữu tỉ m, n sao cho phương trình 3
x − 3x = m 3 + n có ba nghiệm dương phân
biệt a, b, c thỏa mãn a + b + c = 2 + 3 . Biểu thức 6m + 4n có giá trị là: 13 11 A. 1 B. 3 C. D. 4 4
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, tam giác SBC đều và tam giác SAD
vuông. Góc taọ bởi hai mặt phẳng (SBC),( ABCD) là A. 0 45 . B. 0 30 . C. 0 60 . D. 0 15 .
Câu 13: Khối chóp tứ giác đều có độ dài cạnh đáy bằng a , mặt bên tạo với đáy một góc 0 60 thì thể tích bằng: 6 6 3 3 A. 3 a . B 3 a . C. 3 a . D. 3 a 2 6 2 6
Câu 14: Cho khối chóp S.ABC có thể tích V . Gọi M , N , P lần lượt là trọng tâm của các tam giác SBC, SC ,
A SAB . Thể tích của khối chóp S.MNP bằng 4 8 2 1 A. V . B. V . C. V . D. V . 27 27 27 27
Câu 15: Số cạnh của hình chóp tứ giác là A. 8 . B. 9 . C. 10 . D. 12 .
Câu 16: Khoảng cách giữa hai điểm cực trị của đồ thị hàm số 3 2
y = x − 3x −1 là A. 2 5 . B. 2 3 . C. 2 . D. 4 .
Câu 17: Tập hợp các giá trị thực của tham số m để hàm số 3 2
y = x − 9x + (3 − )
m x + m đồng biến trên là A. (− ;  2 − 4). − − − + − + B. ( ; 24. C. ( 24; ). D.  24; ). x +1
Câu 18: Cho hàm số y =
, mệnh đề nào sau đây đúng? x −1
A. Hàm số nghịch biến trên hai khoảng (− ;  ) 1 ;(1;+) .
B. Hàm số nghịch biến trên (− ;  ) 1 (1;+) .
C. Hàm số đồng biến trên hai khoảng (− ;  ) 1 ;(1;+) .
D. Hàm số đồng biến trên (− ;  ) 1 (1;+) .
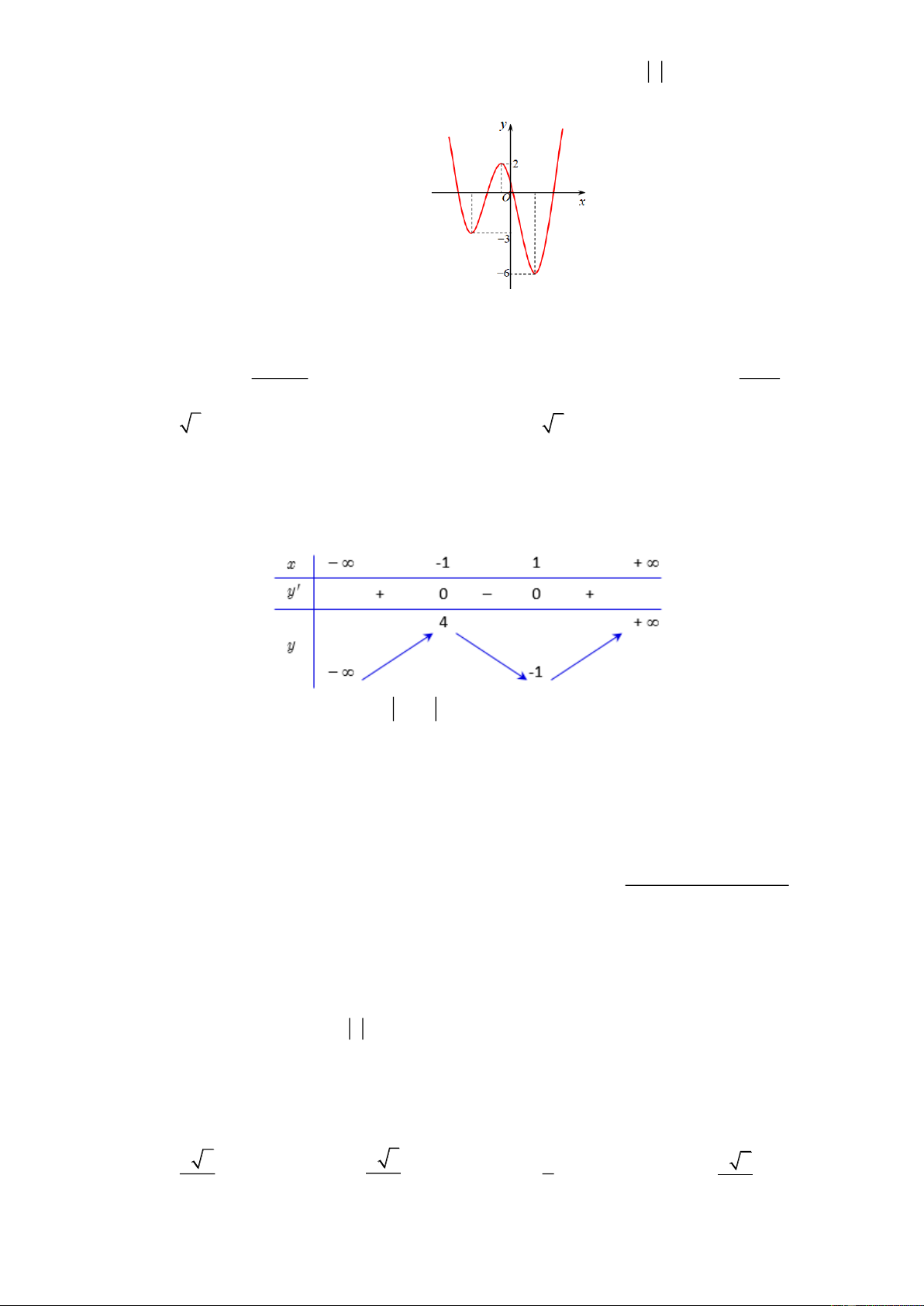
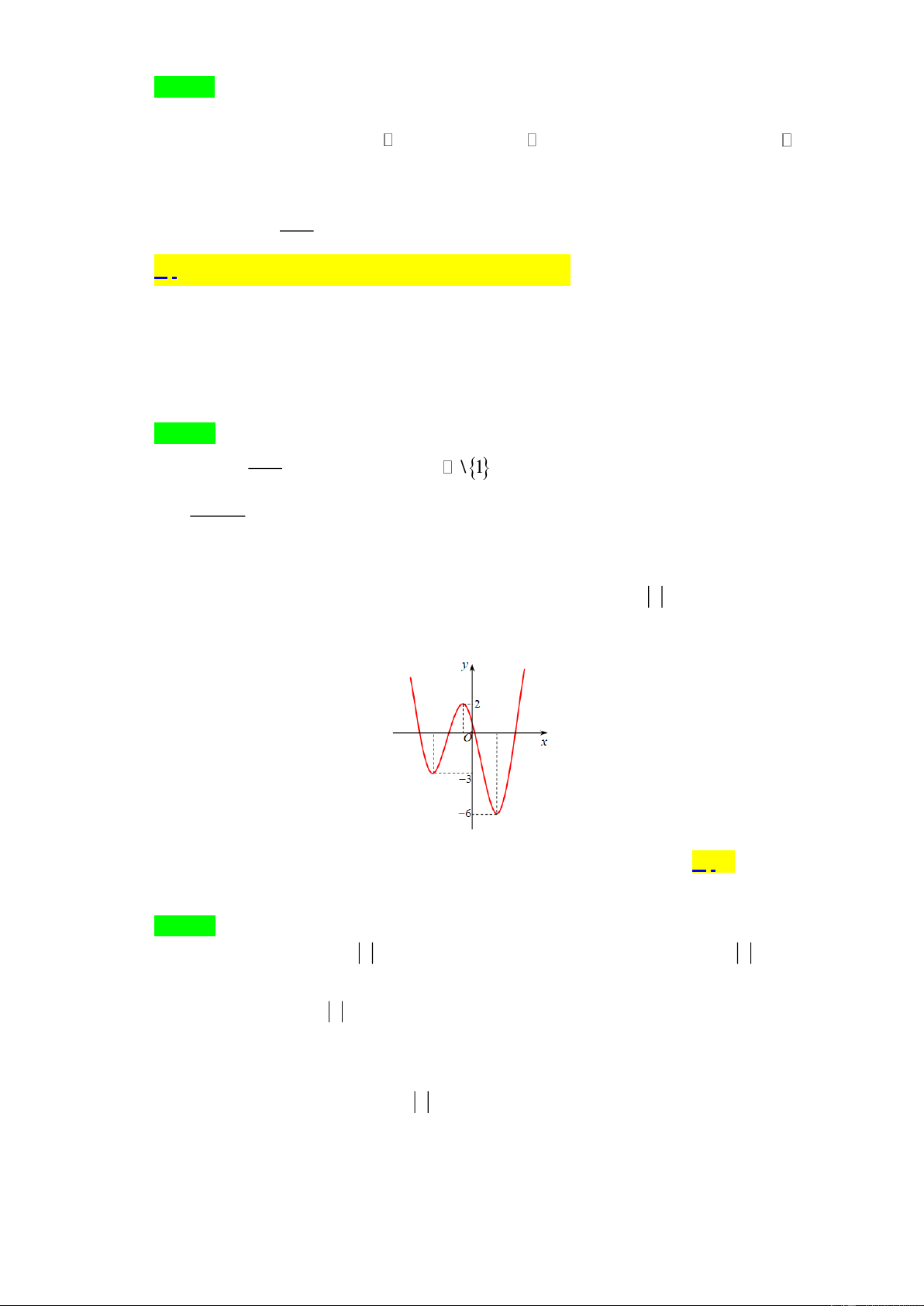
Câu 19: Cho hàm số y = f ( x) có đồ thị như hình vẽ. Phương trình f (− x ) = m ( với m là tham số
thực) có nhiều nhất bao nhiêu nghiệm? A. 8 . B. 2 . C. 4 . D. 6 .
Câu 20: Xét hai số thực dương thay đổi x , y sao cho xy  1. Giá trị nhỏ nhất của biểu thức 5x + 5 y x +1
P = x + 2 y +
đạt được khi x = x và y = y . Giá trị của biểu thức 0 Q = là 0 0 xy −1 y0 A. 3 . B. 2 . C. 2 . D. 1.
Câu 21: Điểm cực tiểu của hàm số 3 2
y = −x + 6x − 9x +1 là
A. x = 0 .
B. x = 3. C. x = 2 . D. x = 1.
Câu 22: Cho hàm số y = f ( x) có bảng biến thiên như hình vẽ
Số điểm cực trị của hàm số y = f ( x) là A. 5 . B. 3 . C. 4 . D. 2 .
Câu 23: Có bao nhiêu giá trị của tham số m để đồ thị hàm số 3
y = x − (m + ) 2
1 x + (2 − m) x + 2m − 2 có
điểm cực trị thuộc trục hoành? A. 3 . B. 1. C. 0 . D. 2 . 2 x −1
Câu 24: Có bao nhiêu giá trị thực của tham số m để đồ thị hàm số y = có đúng 2
x + (2 − m) x + 2m +1 hai đường tiệm cận? A. 1. B. 3 . C. 2 . D. 4 .
Câu 25: Cho hàm số bậc ba y = f ( x) mà đồ thị hàm số có hai điểm cực trị là A(1; ) 3 , B(2; ) 1 . Số điểm
cực trị của hàm số y = f ( x ) là A. 1. B. 5 . C. 4 . D. 3.
Câu 26: Cho hình lập phương ABC . D A BCD
  có cạnh bằng a . Khoảng cách từ điểm A đến mặt phẳng ( A BD) bằng a 2 a 3 a a 2 A. . B. . C. . D. . 2 3 2 3
Câu 27: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại ,
A D . SA vuông góc với mặt
phẳng ( ABCD) . Cho biết AD = CD = a , AB = 2a ,hai mặt phẳng (SBC),( ABCD) tạo với nhau góc 0
45 . Khoảng cách từ điểm D đến mặt phẳng (SBC) bằng. a a 3 a 2 A. . B. . C. . D. a . 2 2 2
Câu 28: Gọi S là tập các giá trị thực của tham số m để đồ thị hàm số 4 2
y = x − 2mx + m + 4 có ba
điểm cực trị cách đều trục hoành. Tính tổng tất cả các phần tử của tập S là A. 2. B. 6. C. 0. D. 4.
Câu 29: Cho hai hình vuông ABCD và ABEF có cạnh bằng a và nằm trên hai mặt mặt phẳng
vuông góc với nhau. Thể tích khối đa diện EBCFAD bằng 3 2a 3 a 3 a A. . B. . C. . D. 3 a . 3 3 2
Câu 30: Cho lăng trụ đứng AB .
C A' B'C ' có tam giác A' BC là tam giác đều cạnh a và tam giác
ABC vuông tại A . Thể tích khối lăng trụ AB .
C A' B'C ' là 2 2 2 2 A. 3 a . B. 3 a C. 3 a . D. 3 a . 4 12 8 6
y = x − x
Câu 31: Có bao nhiêu tiếp tuyến của đồ thị hàm số 3 2 2
tạo với hai trục tọa độ một tam giác cân? A. 3 . B. 1. C. 4 . D. 2 .
Câu 32: Cho lăng trụ có đáy là hình vuông cạnh a 3 và chiều cao là b . Thể tích khối lăng trụ đó bằng A. 2 ab . B. 2 3ab . C. 2 3a b . D. 2 a b . 3 − 2x
Câu 33: Đường tiệm cận ngang của đồ thị hàm số y = 1+ có phương trình là x A. y = −3 . B. y = 2 . C. y = −2 . D. y = 3 . 2x − 3
Câu 34: Hai đường tiệm cận của đồ thị hàm số y = x + và hai trục tọa độ cắt nhau tạo thành hình 1
chữ nhật. Diện tích của hình chữ nhật đó là? A. S = 2. B. S = 4. C. S =1.. D. S = 3. . 3sin x +1
Câu 35: Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = là sin x + 2 11 2 3 A. . B. 0 . C. − . D. − 6 3 2 2 2 cos x + m
Câu 36: Tập hợp các giá trị thực của tham số m để hàm số y =
nghịch biến trên khoảng cos x + m (0; ) là A. (0; 2). B. (2;+) . C.  1 − ;0) D. 1; 2) .
Câu 37: Số điểm chung của hai đồ thị hàm số 3 2
y = x − 2x và y = 2x − 3 là A. 2 . B. 3. C. 0 . D. 1 .
Câu 38: Tổng diện tích các mặt của tứ diện đều cạnh a là A. 2 2a . B. 2 a 3 . C. 2 4a . D. 2 2a 3 .
Câu 39: Trong các hàm số sau, hàm số nào đồng biến trên khoảng (− ;  +) ? x − 2 A. y =
y = x + x + . C. 2
y = x − x +1. D. 4 2
y = x + 2x +1. 2x + . B. 3 3 1 1
Câu 40: Số điểm cực đại của hàm số 4 2
y = 2x − 3x +1 là A. 0 . B. 2 . C. 3 . D. 1. 2 x −1
Câu 41: Số đường tiệm cận đứng của đồ thị hàm số y = là 3 x − 3x + 2 A. 2. B. 0. C. 1. D. 3. 3
Câu 42: Cho khối chóp S. ABC có thể tích 3 V =
a , tam giác SBC là tam giác đều có cạnh bằng a . 3
Khi đó, khoảng cách từ điểm A đến mặt phẳng (SBC)bằng 4a 3 4 A. . B. a . C. 4a . D. 2a 3 . 3 3
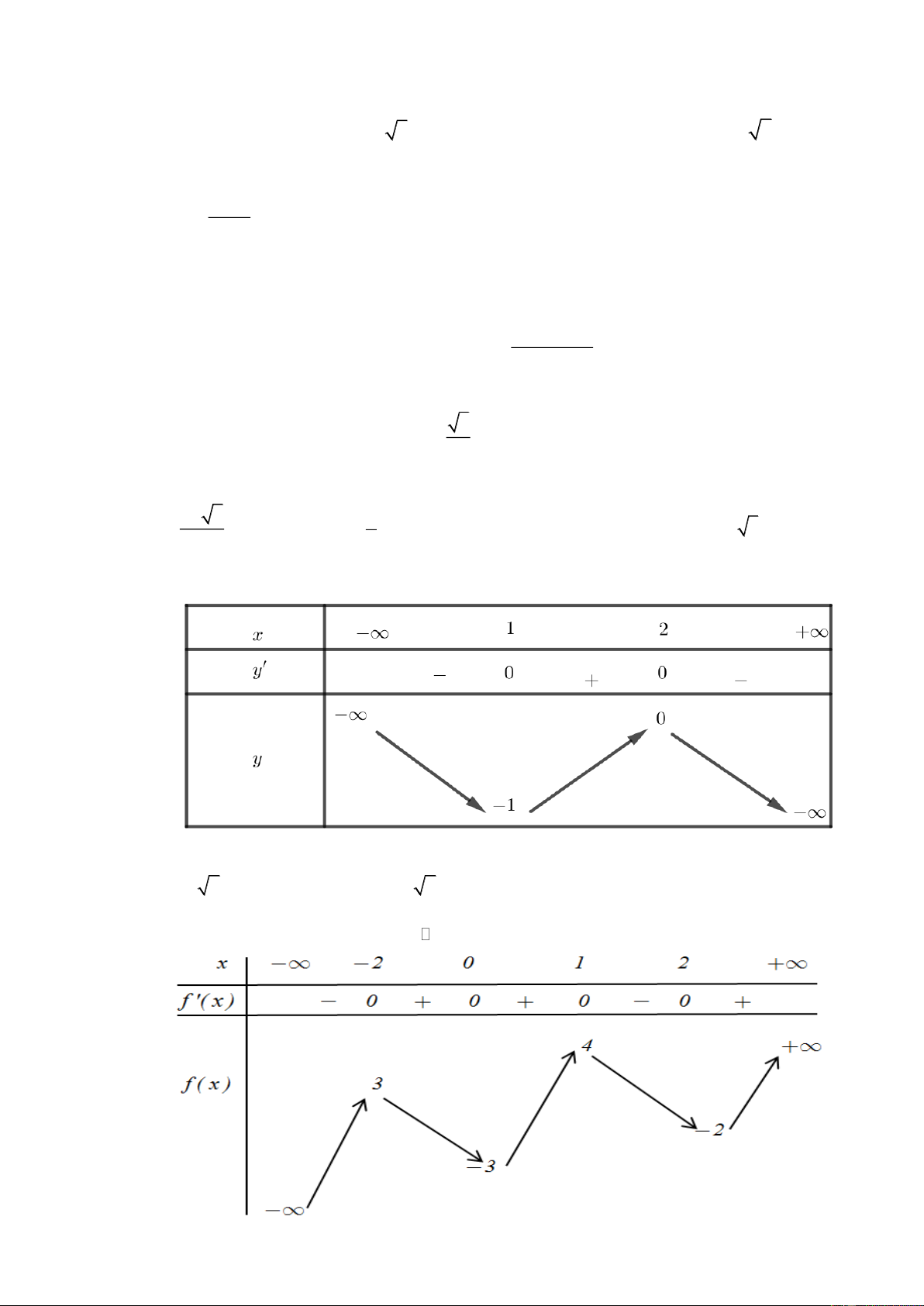
Câu 43: Cho hàm số y = f ( x) có bảng biến thiên như hình vẽ Hàm số = ( 2 y
f x ) nghịch biến trên khoảng nào trong các khoảng dưới đây? A. (− 2; ) 0 . B. (− ;  − 2). C. (1;+) . D. (0; ) 1 .
Câu 44: Cho hàm số y = f ( x) liên tục trên
có bảng biến thiên như sau:
Số nghiệm của phương trình f ( x) = 0 là A. 2 . B. 5 . C. 3 . D. 4 .
Câu 45: Số điểm cực trị của hàm số 3 4
y = (3x −1) (x +1) A. 3 . B. 2 . C. 1. D. 4 . x − 2
Câu 46: Cho hàm số y =
có đồ thị (C) cắt hai trục tọa độ lần lượt tại A , B . Tiếp tuyến của (C) x +1
tại hai điểm A , B tạo với nhau một góc  . Giá trị của sin  bằng 4 1 3 3 A. . B. . C. . D. . 5 10 5 10
Câu 47: Cho hình lăng trụ có đáy là hình vuông cạnh a , thể tích khối lăng trụ bằng 3 a và độ dài các
cạnh bên là 2a . Góc tạo bởi cạnh bên và mặt phẳng đáy là: A. 90 . B. 30 . C. 45. D. 60 .
Câu 48: Cho khối chóp SABCD có thể tích V , đáy ABCD là hình bình hành, M là trung điểm của SB
N là điểm trên cạnh SD . Mặt phẳng ( AMN ) cắt cạnh SC tại điểm P sao cho thể tích khối V SN chóp SAMPN bằng . Tỉ số bằng 4 SD 2 2 1 1 A. . B. . C. . D. . 3 2 2 3
Câu 49: Gọi  là góc tạo bởi hai mặt bên của một tứ diện đều. Mệnh đề nào sau đây đúng?
A. tan  = 2 2 . B. tan  = 2 .
C. tan  = 2 .
D. tan  = 3 .
Câu 50: Tập hợp giá trị thực của tham số m để hàm số 4 2
y = mx + (m − 2)x + 2m có điểm cực tiểu là A. (0; 2] . B. ( ; − 0] . C. (0; +) . D. (0; 2) . BẢNG ĐÁP ÁN 1.C 2.D 3.D 4.C 5.B 6.C 7.B 8.C 9.B 10.C 11.C 12.B 13.D 14.C 15.A 16.A 17.B 18.A 19.D 20.B 21.D 22.A 23.A 24.B 25.B 26.B 27.A 28.D 29.C 30.C 31.C 32.C 33.C 34.A 35.C 36.D 37.B 38.B 39.B 40.D 41.A 42.C 43.D 44.B 45.B 46.A 47.B 48.B 49.A 50.C HƯỚNG DẪN GIẢI
Câu 1. Đồ thị trong hình vẽ sau đây là đồ thị của hàm số nào trong các hàm số bên dưới? A. 4
y = x − 3x +1. B. 4
y = −x + 3x +1. C. 3
y = x − 3x +1. D. 3
y = −x + 3x +1. Lời giải
Chọn C
Đồ thị đi qua điểm ( 1 − ; )
3 nên loại đáp án A, B và D. Chọn đáp án C.
Câu 2. Phương trình 4 2
x − 2x + m = 0 ( m là tham số thực) có 4 nghiệm phân biệt khi và chỉ khi A. 1 −  m 1. B. 1 −  m  0. C. m  1.
D. 0  m 1. Lời giải
Chọn D Cách 1. Đặt 2
t = x  0 thì phương trình 4 2
x − 2x + m = 0 (1) trở thành 2
t − 2t + m = 0 (2).
Phương trình (1) có 4 nghiệm phân biệt khi và chỉ khi phương trình (2) có 2 nghiệm dương
phân biệt. Điều kiện là  = 4 − 4m  0  m 1 S = 2  0    0  m 1.  m  0 P = m  0 
Vậy phương trình (1) có 4 nghiệm phân biệt khi và chỉ khi 0  m 1. Cách 2. Ta có 4 2 4 2
x − 2x + m = 0(1)  m = −x + 2x . Hàm số 4 2
y = −x + 2x có 3 y ' = 4 − x + 4 , x
y ' = 0  x = 0 hoặc x = 1.
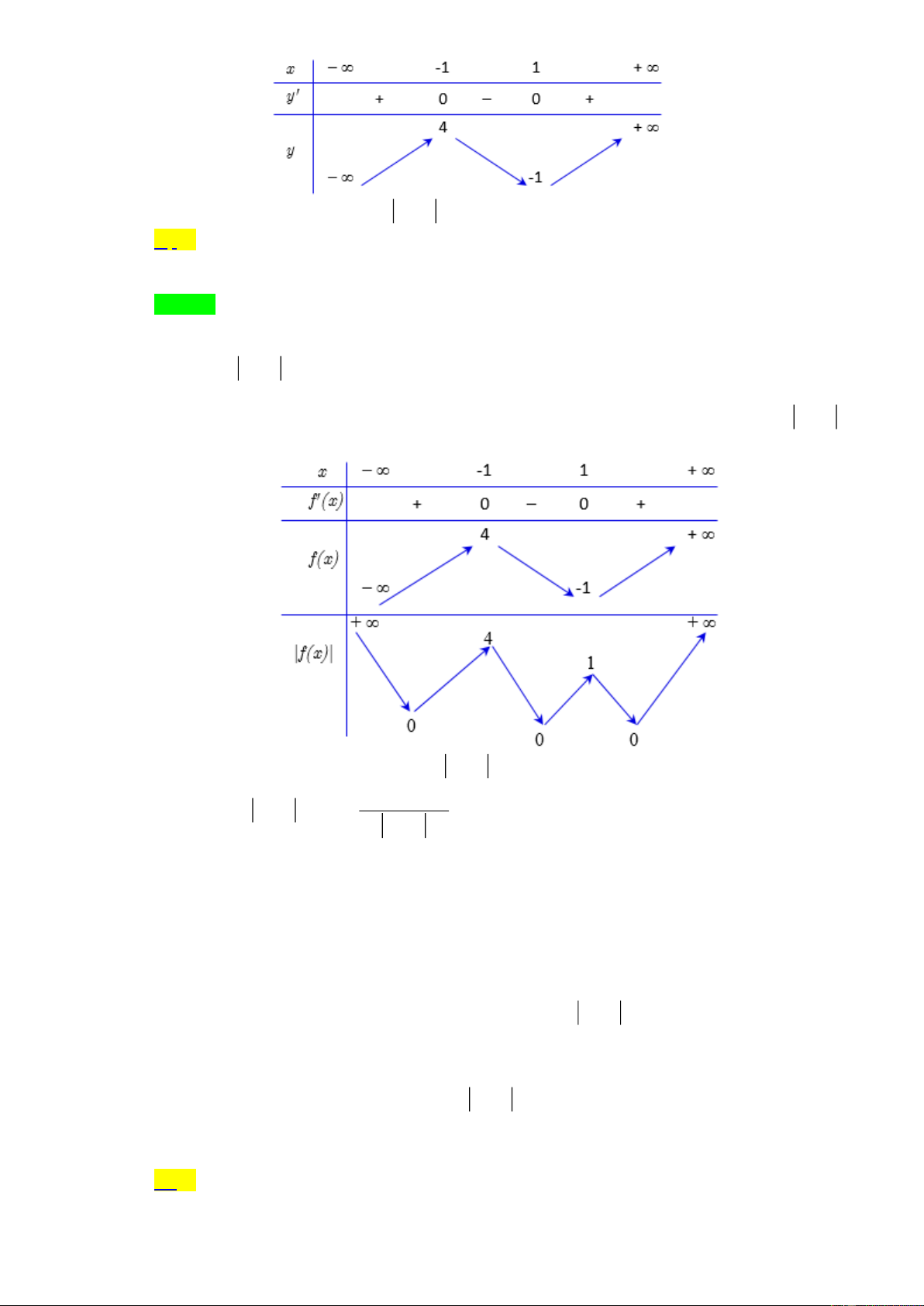
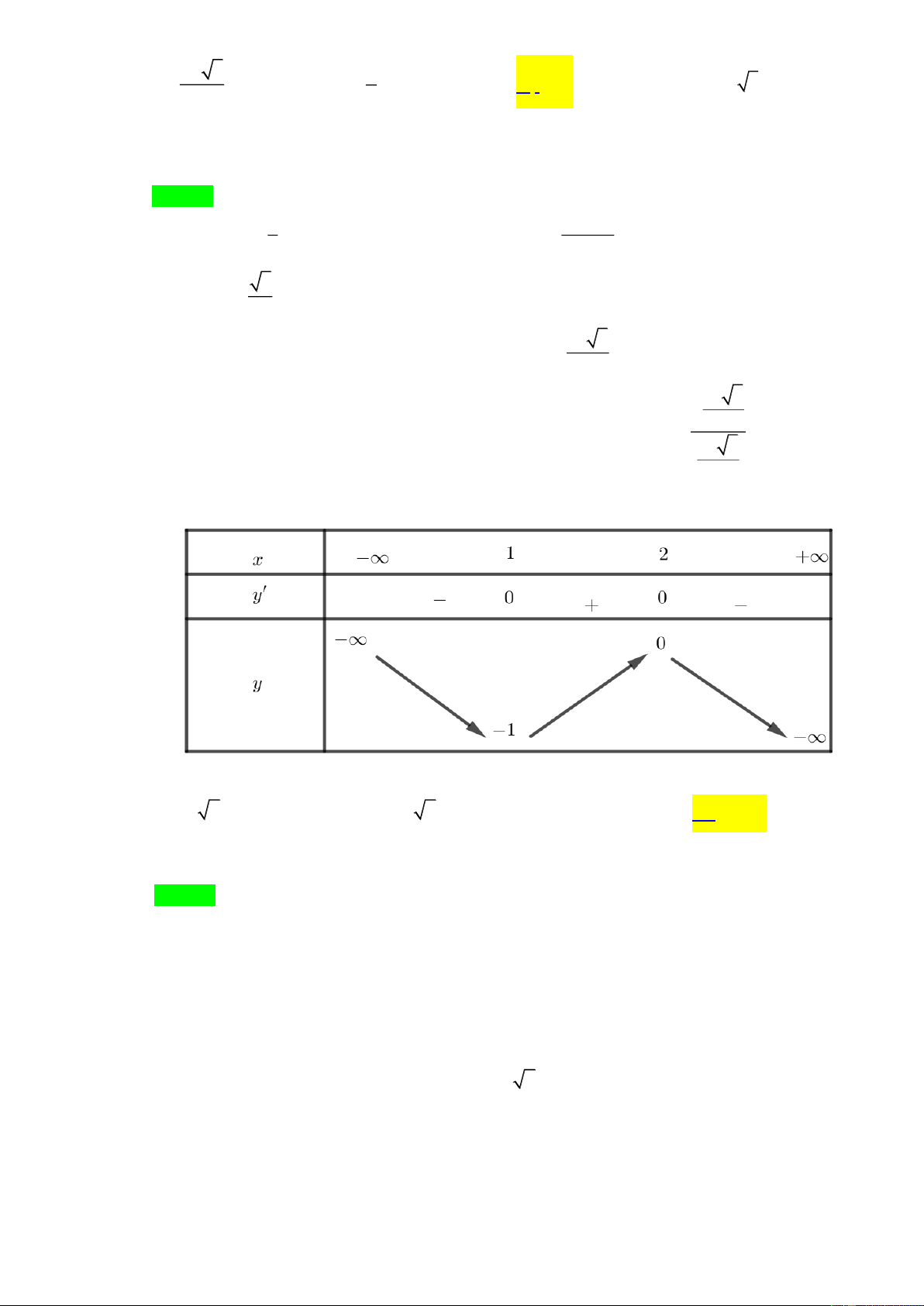
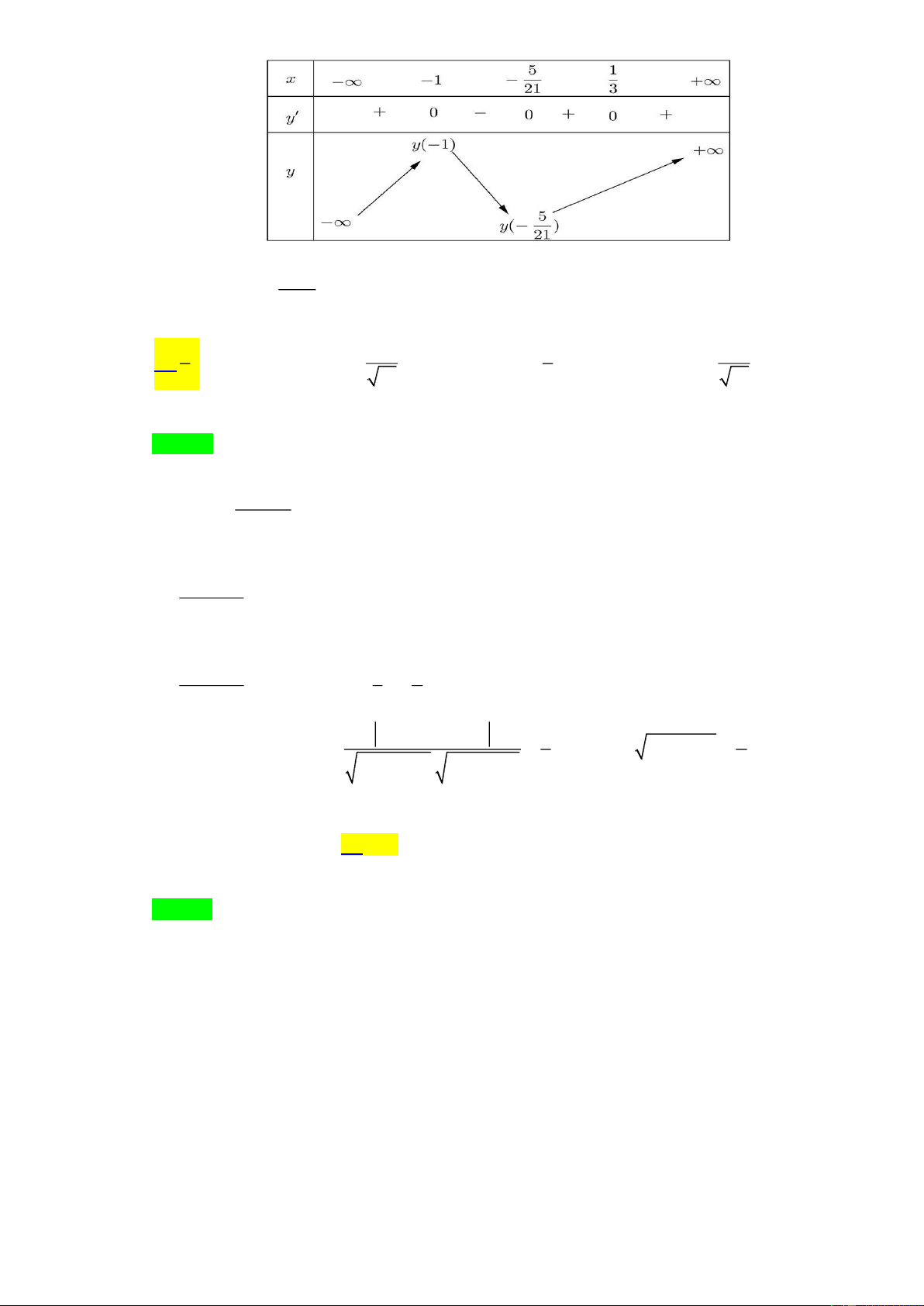
 Bảng biến thiên của hàm số này như sau x −  −1 0 1 + y ' + − 0 0 + 0 − 1 1 y −  0 − 
Phương trình (1) có 4 nghiệm phân biệt khi và chỉ khi đường thẳng y = m và đồ thị hàm số 4 2
y = −x + 2x có 4 giao điểm phân biệt. Từ bảng biến thiên của hàm số 4 2
y = −x + 2x suy ra
đường thẳng y = m và đồ thị hàm số 4 2
y = −x + 2x có 4 giao điểm phân biệt khi và chỉ khi
0  m 1. Vậy phương trình (1) có 4 nghiệm phân biệt khi và chỉ khi 0  m 1. Câu 3.
Giá trị nhỏ nhất của hàm số 2
f (x) = 2x + 5x −10x +10 trên đoạn  2 − ;  1 là A. 4 − +5 2 . B. 10 . C. 1+ 3 . D. 3 . Lời giải Chọn D
Hàm số f (x) xác định và liên tục trên đoạn  2 − ;  1 . 2 5x − 5
2 5x −10x +10 + 5x − 5 f '(x) = 2 + = . 2 2 5x −10x +10 5x −10x +10 2 2 2
f '(x) = 0  2 5x −10x +10 = 5 − 5x  4(5x −10x +10) = 25 + 25x − 50x x = 1 −  2 −  ;1 2
 5x −10x −15 = 0   x = 3   2 −  ;1
Ta có f (1) = 2 + 5 ; f ( 2)
− = −4 + 5 2 ; f ( 1 − ) = 3.
Vậy min f ( x) = 3 . x   2 − ;  1 Câu 4.
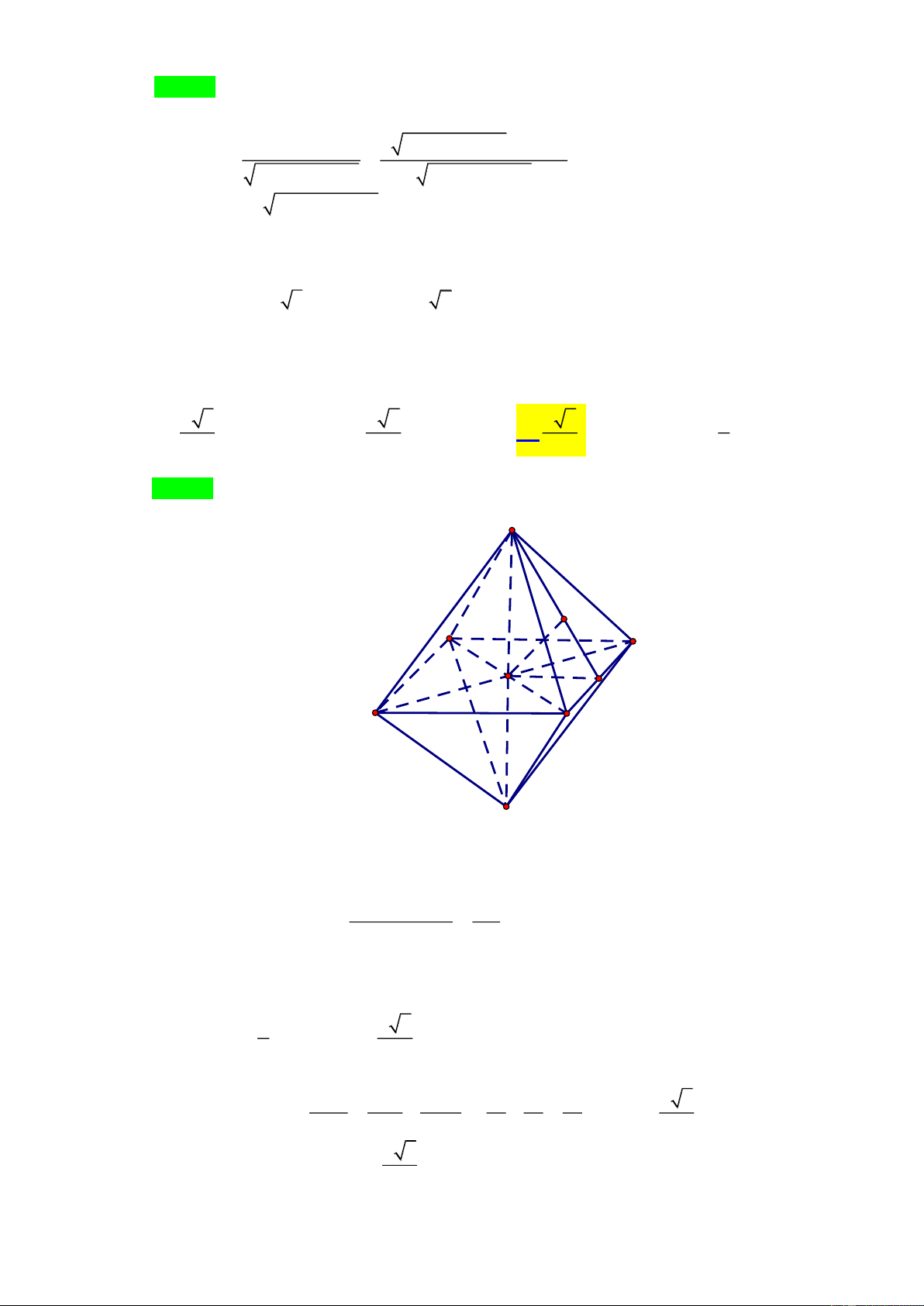
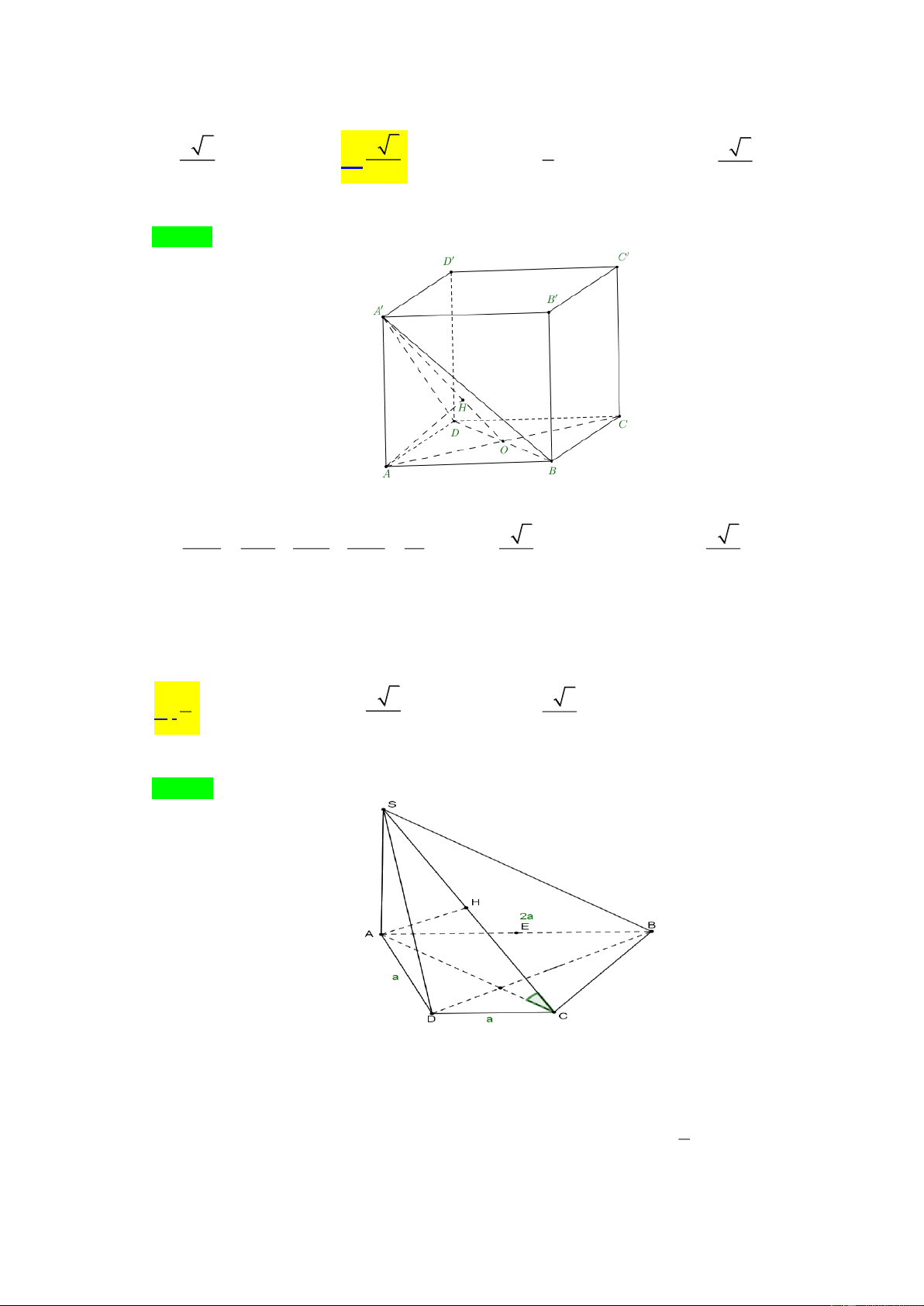
Cho hình bát diện đều có cạnh bằng a . Khoảng cách giữa hai mặt phẳng song song của bát diện này bằng a 3 a 2 a 6 a A. . B. . C. . D. . 3 2 3 2 Lời giải Chọn C E H A B O M D C F
Xét bát diện đều tâm O như hình vẽ.
Ta có: (FDA) // (EBC) nên d ((FDA);(EBC)) = d ( A;(EBC)) .
d ( A;( EBC )) CA
Vì AO (EBC) = C nên = = .
d (O ( EBC )) 2 ; CO
Gọi M , H lần lượt là hình chiếu vuông góc của O lên đường thẳng BC , EM . Ta chứng
minh được OH ⊥ (EBC) tại H nên d (O;(EBC)) = OH . a a 2 Ta có: OM = , OE = OB =
(vì bát diện đều cạnh bằng a ) 2 2
Xét tam giác vuông EOM có OH là đường cao nên 1 1 1 = + 2 4 6 a = + = 6  OH = . 2 2 2 OH OE OM 2 2 2 a a a 6
Do đó d ( A (EBC)) a 6 ; = 2OH = . 3 Chú ý : 1 1 1 1
a) Có thể tính d (O;(EBC)) = d theo công thức = + +
do OE, OB, OC đôi 2 2 2 2 d OE OB OC một vuông góc. 3V 1
b) Có thể tính d ( ,
A (EBC)) theo công thức . d ( , A (EBC)) E ABC = với V = V . S E. ABC E. 2 ABCD EBC
Câu 5. Trong các hàm số sau, hàm số nào đạt cực tiểu tại x = 0 ? A. 4 3
y = x − x . B. 3 2
y = x + x . C. 3 2
y = x - x . D. 4 3
y = x + x . Lời giải Chọn B Hàm số 4 3
y = x − x có đạo hàm 2
y ' = x (4x − 3) không đổi dấu khi đi qua x = 0 nên không
đạt cực trị tại x = 0 . Hàm số 4 3
y = x + x có đạo hàm 2
y ' = x (4x + 3) không đổi dấu khi đi qua x = 0 nên không
đạt cực trị tại x = 0 . Hàm số 3 2
y = x − x có đạo hàm y = x (3x − 2) đổi dấu từ dương sang âm khi đi qua x = 0
nên đạt cực đại tại x = 0 . Hàm số 3 2
y = x + x có đạo hàm y = x (3x + 2) đổi dấu từ âm sang dương khi đi qua x = 0
nên đạt cực tiểu tại x = 0 . Vậy chọn đáp án B. Câu 6. Hàm số 3 2
y = x + x nghịch biến trên khoảng  2   2  A. ( 1 − ;0) . B. 0;   . C. − ; 0   . D. (0; ) 1 .  3   3  Lời giải
Tác giả :Chu Quốc Hùng, FB: Chu Quốc Hùng Edu Chọn Cx = 0  Hàm số 3 2
y = x + x có đạo hàm 2
y ' = 3x + 2x ; 2
y ' = 0  3x + 2x = 0  −2  . x =  3 Bảng xét dấu đạo hàm −2 x − 0 + 3 y + 0 − 0 +  2 
Từ bảng xét dấu ta suy ra hàm số nghịch biến trên − ; 0   .  3  Câu 7. Cho lăng trụ AB . C A BC
 , biết rằng tứ diện A A
BC là tứ diện đều cạnh a. Thể tích khối chóp . A BCB C   bằng 3 a 2 3 a 2 3 a 2 3 a 2 A. . B. . C. . D. . 12 6 8 4 Lời giải
Tác giả :Trần Thị Phượng Uyên, FB: UyenTran Chọn B
Gọi H là trọng tâm tam giác ABC A H  ⊥ ( ABC). 2   Tính đượ a 3 a 6 c 2 2 2
AH = ( AA )
 − AH = a −   =   . 3 3   A' C' B' A C H B 1 2 3 1 a 6 a 3 a 2 Ta có V =  = =  A H .S . A ABC 3 ABC 3 3 4 12 3 2 a 2 Vậy V = − =  = =    V    V A H .S 2V . A .BCB C ABC.A B C A ABC  3 ABC A ABC 6
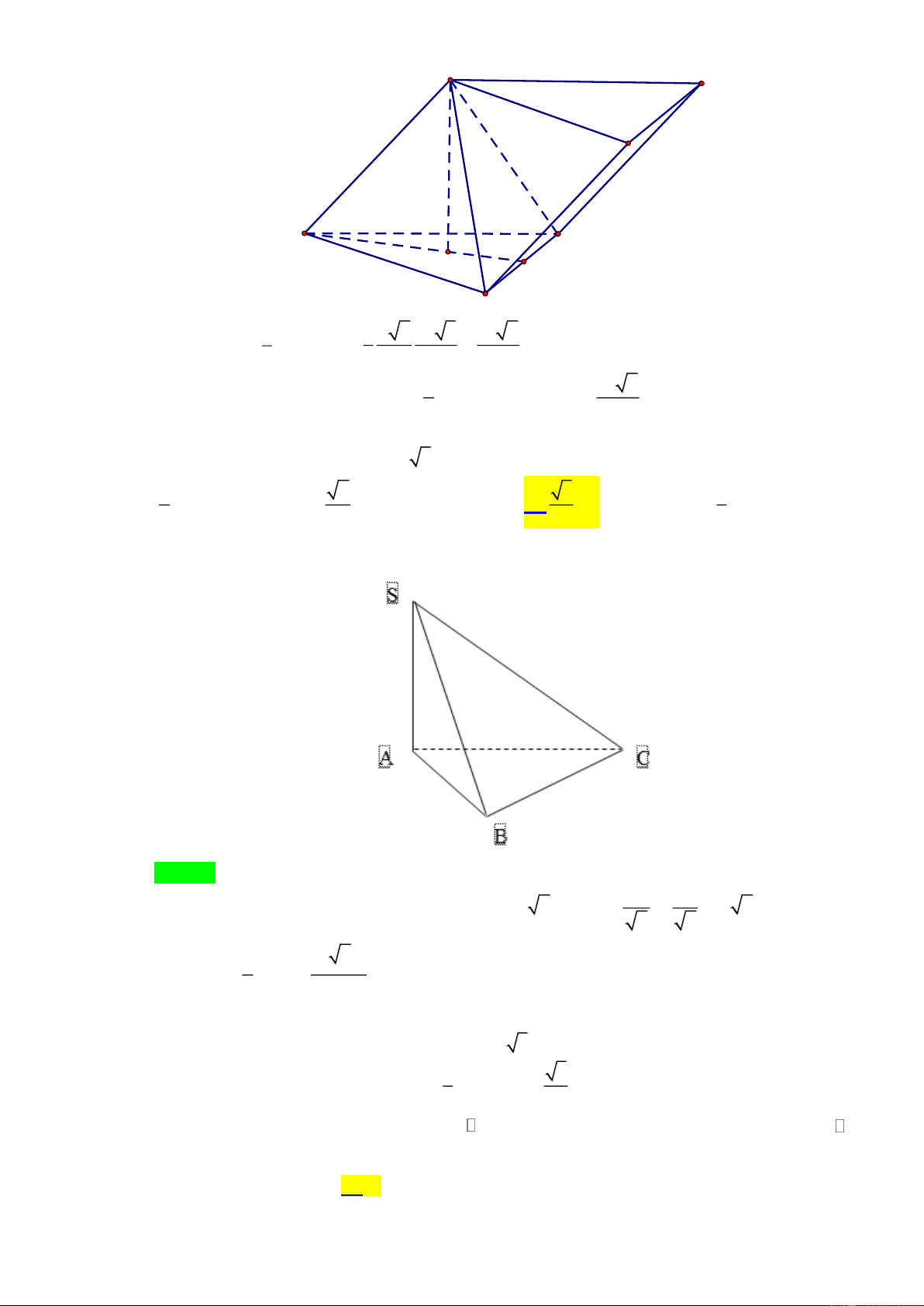
Câu 8. Cho hình chóp S.ABC có tam giác ABC vuông cân tại A , SA vuông góc với mặt phẳng
(ABC). Biết rằng BC = 2a , SB = a 5 . Thể tích khối chóp S.ABC bằng 2 2 3 1 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 3 3 3 3 Lời giải
Tác giả: Trần Thị Thủy; Fb: Thủy Trần Chọn C BC 2a
Do tam giác ABC vuông cân tại A nên BC = AB 2 Þ AB = = = a 2 2 2 (a 2 1 )2 2 2 Þ S = AB = = a . DABC 2 2
Do SA ^ (ABC)Þ SA ^ AB . Suy ra tam giác SAB vuông tại A . 2 2 2 2 2 2
SA = SB - AB = 5a - 2a = 3a Þ SA = a 3 . 1 3
Thể tích khối chóp S.ABC là 3 V = S .SA = a (đvtt). S .ABC 3 DABC 3
Câu 9. Cho hàm số y = f ( x) có đạo hàm trên
và f ( x) = ( 2 x − x − )( 2 ' 2 3 x − ) 1 (3x − ) 1 x   .
Số điểm cực trị của hàm số y = f ( x) là A. 2 . B. 3 . C. 4. D. 1. Lời giải
Tác giả và giải: Nguyễn Văn Bình ; Fb: Nguyễn Văn Bình Chọn B
f ( x) = (x − x − )(x − )( x − ) = (x + )2 2 2 ' 2 3 1 3 1
1 ( x − 3)( x − ) 1 (3x − ) 1 1
Ta thấy f '( x) chỉ đổi dấu khi đi qua các nghiệm x = ; x = 1; x = 3. Do đó y = f ( x) có 3 3 điểm cực trị. 3x + 1
Câu 10. Tiếp tuyến của đồ thị hàm số y =
tại điểm có hoành độ x = 1 tạo với hai trục tọa độ x + 1
một tam giác có diện tích bằng 9 3 9 3 A. . B. . C. . D. . 2 2 4 4 Lời giải
Tác giả: Lê Xuân Sơn; Fb: Lê Xuân Sơn Chọn C 3x + 1 2 Ta có: y =  y = . x + 1 (x + )2 1 2 1 Ta có: y( ) 1 = = = ( ; y ( ) 1 2 1 + )2 1 2
Phương trình tiếp tuyến tại điểm có hoành độ x =1 là: y = y( ) 1 .( x − ) 1 + y ( ) 1 1 3  y = x + . 2 2  3 
Tiếp tuyến cắt trục hoành tại A( 3
− ;0) , cắt trục tung tại B 0; 
 , tiếp tuyến tạo với hai trục  2  3
tọa độ tam giác OAB vuông tại O có OA = 3, OB = . 2 1 1 3 9
Diện tích tam giác OAB là S = . . OA OB = .3. = . 2 2 2 4
Câu 11. Cho hai số hữu tỉ m, n sao cho phương trình 3
x − 3x = m 3 + n có ba nghiệm dương phân
biệt a, b, c thỏa mãn a + b + c = 2 + 3 . Biểu thức 6m + 4n có giá trị là: 13 11 A. 1 B. 3 C. D. 4 4 Lời giải
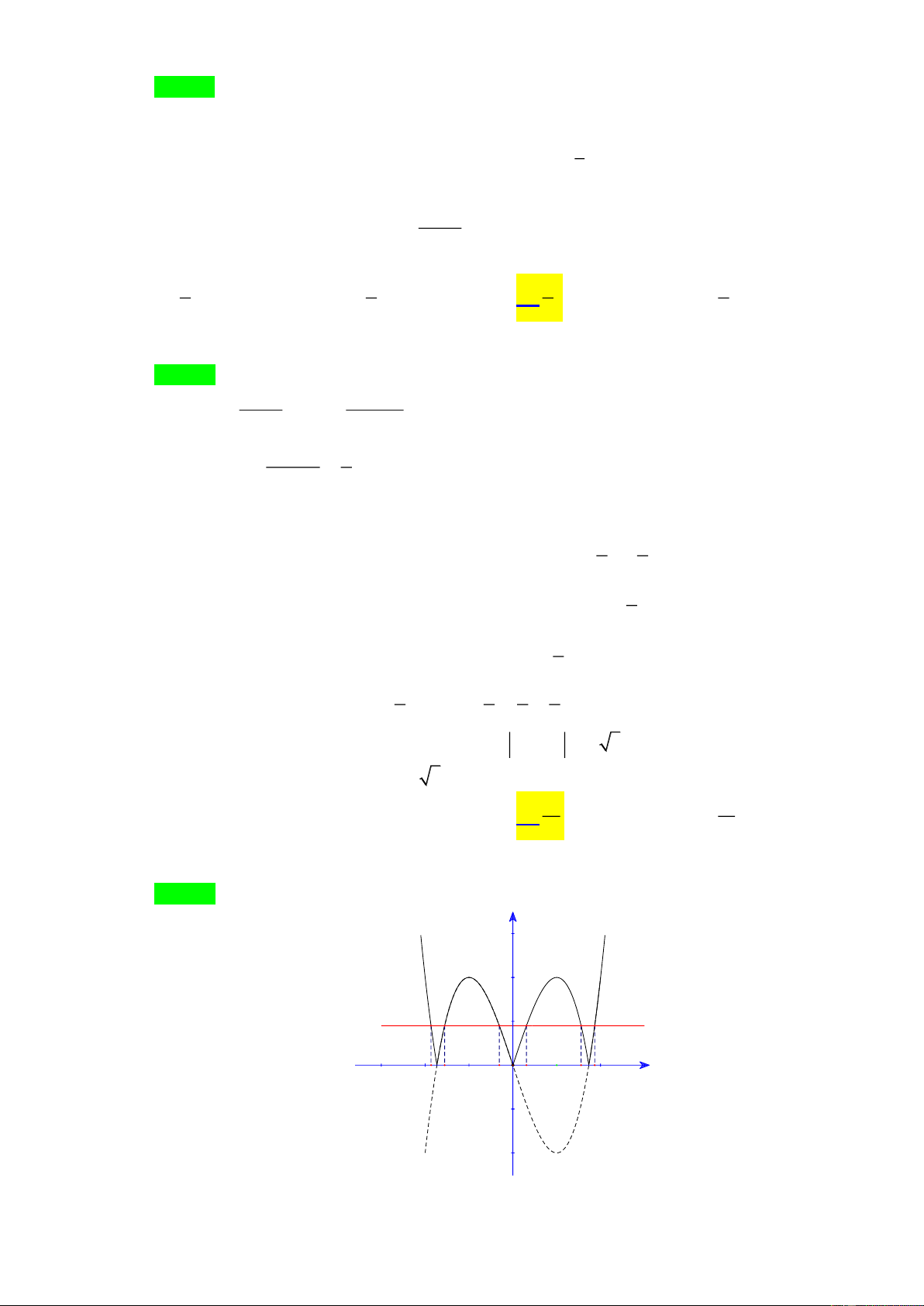
Tác giả: Trần Văn Trưởng; FB: Trần Văn Trưởng Chọn C y 2 1 y=k x -c -a -b -1 O a 1 b c 3
x − 3x = k
Đặt k = m 3 + n , phương trình 3 3
x − 3x = m 3 + n x − 3x = k (*)   3
x − 3x = −k
Ta có đồ thị của hàm số 3
y = x − 3x và 3
y = x − 3x như hình vẽ.
Từ đồ thị ta thấy phương trình (*) có 3 nghiệm dương phân biệt a, , b c khi và chỉ khi 0  k  2 . (1)
Khi đó không mất tổng quát giả sử a b c . Chú ý rằng hàm số 3
y = x − 3x là hàm chẵn
nên dựa vào đồ thị trên suy ra phương trình 3
x − 3x = k sẽ có 3 nghiệm phân biệt là − ;
b − a; c .
Theo định lý Viet của hàm bậc 3 thì b
− −a +c = 0  a +b = c . + Theo đề 2 3
bài a + b + c = 2 + 3  c = . 2 3  2 + 3  2 + 3
Vì c là nghiệm của phương trình (1) nên   − 3. − k = 0   . 2 2   1 3  k = + 3
(thỏa mãn điều kiện (1)). 4 8 3 1 13 Từ đó ta có 3 1 m = ; n =
nên 6m + 4n = 6. + 4. = . 8 4 8 4 4
Câu 12. Cho hình chóp S.ABCD có đáy ABCD là hình vuông, tam giác SBC đều và tam giác SAD
vuông. Góc taọ bởi hai mặt phẳng (SBC),( ABCD) là A. 0 45 . B. 0 30 . C. 0 60 . D. 0 15 . Lời giải
Tác giả: Lê Thị Phương; Fb: Plus kính gửi Chọn B S D A K B H C
Ta có (SBC) ( ABCD) = B .
C Gọi H , K lần lượt là trung điểm của BC, A . D
Tam giác SBC đều nên SH ⊥ B .
C Tứ giác ABCD là hình vuông nên KH ⊥ BC . Góc tạo
bởi hai mặt phẳng (SBC),( ABCD) là góc tạo bởi hai đường thẳng SH , KH.
Gọi độ dài cạnh của hình vuông ABCD là a . Vì BC ⊥ SH , BC ⊥ KH nên BC ⊥ SK , suy ra
AD ⊥ SK. Do đó tam giác SAD cân tại S. Hơn nữa, tam giác SAD vuông nên nó vuông cân 1 a
tại S . Suy ra SK = AD = . 2 2 a 3 a
Tam giác SHK có SH = , SK =
, nên áp dụng định côsin ta có 2 2 2 2 3a a 2 + − 2 2 2 a
SH + HK − SK 3 4 4 cos SHK = = = . 2.SK.SH a 3 2 2. . a 2 Suy ra SHK = 0
30 . Vậy góc giữa hai mặt phẳng (SBC),( ABCD) bằng 0 30 .
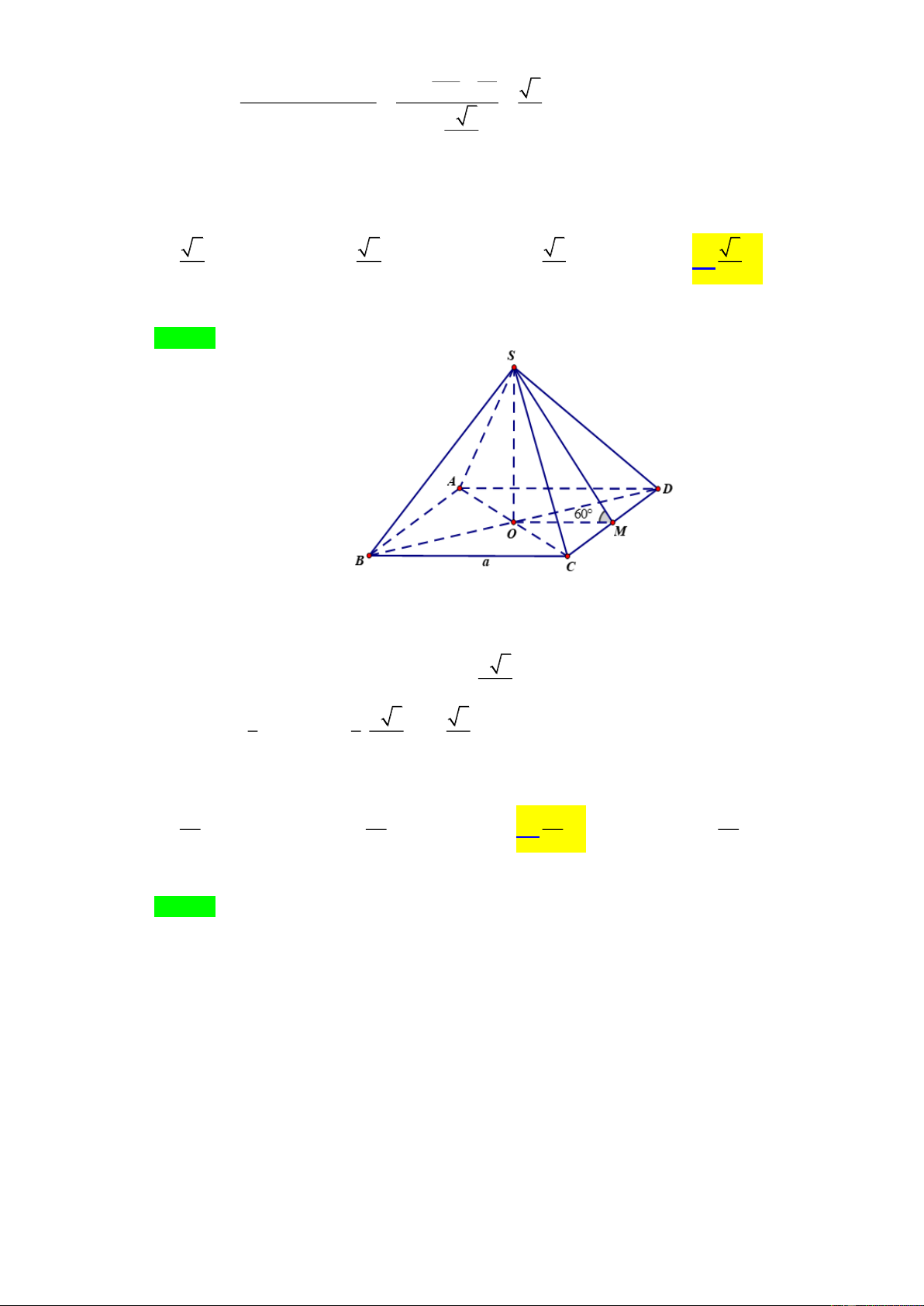
Câu 13. Khối chóp tứ giác đều có độ dài cạnh đáy bằng a , mặt bên tạo với đáy một góc 0 60 thì thể tích bằng: 6 6 3 3 A. 3 a . B 3 a . C. 3 a . D. 3 a 2 6 2 6 Lời giải
Tác giả:ThanhLoan ; Fb: ThanhLoan Chọn D
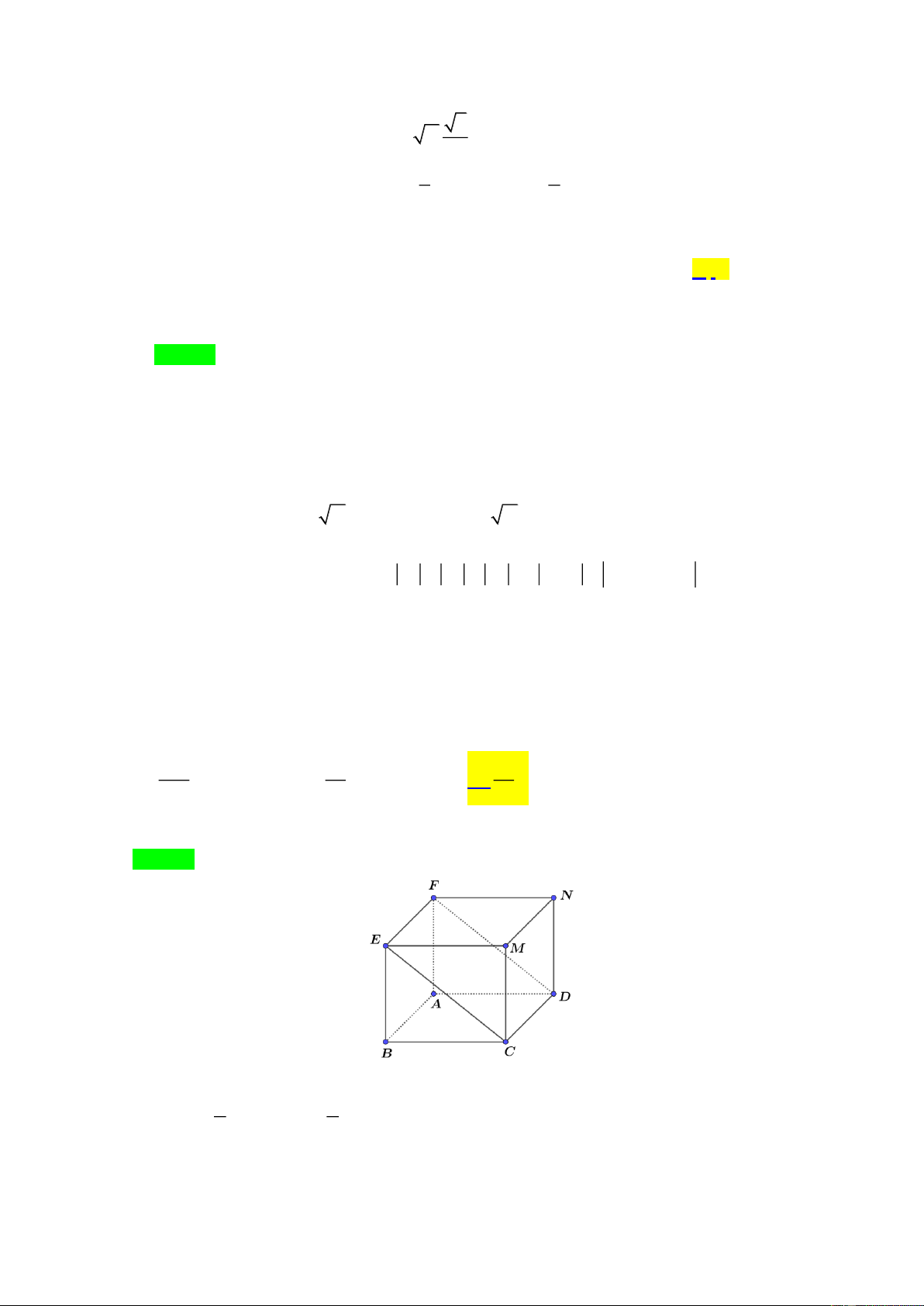
Gọi khối chóp tứ giác đều là S.ABCD , O là tâm của đáy  SO ⊥ ( ABCD) .
Gọi M là trung điểm của CD  ( SCD ABCD ) 0 ( ), ( ) = SMO = 60 a 3 S
MO vuông tại O 0
SO = OM .tan 60 = 2 1 1 a 3 3 2 3  V = . . SO S = . .a = a . S . ABCD 3 ABCD 3 2 6
Câu 14. Cho khối chóp S.ABC có thể tích V . Gọi M , N , P lần lượt là trọng tâm của các tam giác SBC, SC ,
A SAB . Thể tích của khối chóp S.MNP bằng 4 8 2 1 A. V . B. V . C. V . D. V . 27 27 27 27 Lời giải
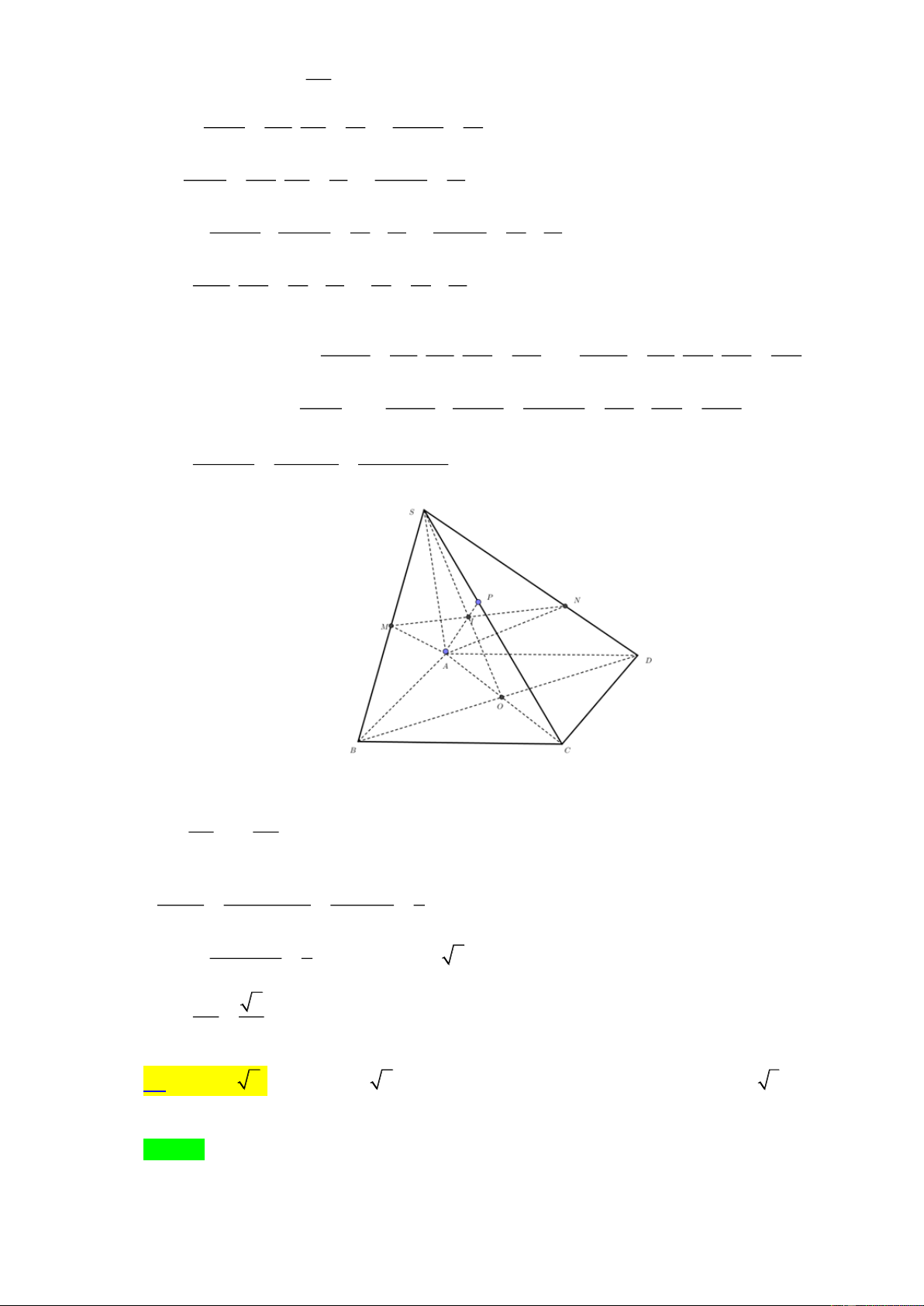
Tác giả: Nguyễn Thị Huệ ; Fb: Nguyễn Thị Huệ Chọn C
Gọi E, D, F lần lượt là trung điểm của các cạnh AB, BC,CA . Vì M , N , P lần lượt là trọng
tâm của các tam giác SBC, SC ,
A SAB nên M , N , P lần lượt thuộc các đoạn SD, SF , SE và SM SN SP 2 = = = . SD SF SE 3 V SM SN SP 2 2 2 8 8 Ta có S.MNP = . . = . . =  V = .V S .MNP S . V SD SF SE 3 3 3 27 27 DFE S .DFE 1
Vì E, D, F lần lượt là trung điểm của các cạnh AB, BC,CA nên S = S . Mặt khác DEF  4 ABC 1
hai hình chóp S.ABC và S.DEF có cùng chiều cao nên V = V . S .DFE S . 4 ABC 8 8 1 2 2 Suy ra V = .V = . .V = .V = V . S .MNP S .DFE S . ABC S . 27 27 4 27 ABC 27
Câu 15. Số cạnh của hình chóp tứ giác là A. 8 . B. 9 . C. 10 . D. 12 . Lời giải
Tác giả:Huỳnh Hữu Hùng; Fb: Huuhung Huynh Chọn A
Hình chóp tứ giác có 4 cạnh đáy và 4 cạnh bên nên có tất cả 8 cạnh.
Câu 16. Khoảng cách giữa hai điểm cực trị của đồ thị hàm số 3 2
y = x − 3x −1 là A. 2 5 . B. 2 3 . C. 2 . D. 4 . Lời giải
Tác giả:Huỳnh Hữu Hùng; Fb: Huuhung Huynh Chọn A
Tập xác định D = x = 0 2
y = 3x − 6x ; y = 0   ; y(0) = 1 − ; y(2) = 5 − . x = 2
y đổi dấu qua các điểm x = 0 và x = 2 .
Do đó, hai điểm cực trị của đồ thị hàm số là ( A 0; 1 − ) và B(2; 5 − ) .
Khoảng cách giữa hai điểm cực trị của đồ thị hàm số là 2 2 AB = (2 − 0) + ( 5 − +1) = 2 5.
Phamquynhanhbaby56@gmail.com
Câu 17. Tập hợp các giá trị thực của tham số m để hàm số 3 2
y = x − 9x + (3 − )
m x + m đồng biến trên là A. (− ;  2 − 4). − − − + − + B. ( ; 24. C. ( 24; ). D.  24; ). Lời giải
Tác giả: Nguyễn Thị Thỏa; Fb: Nguyễn Thị Thỏa Chọn B Ta có 2
y = 3x −18x + 3 − m .
Hàm số đã cho đồng biến trên
y  0, x   2
 3x −18x + 3− m  0, x    
 = 72+3m  0  m  24 − .
Vậy tập hợp các giá trị của tham số m thỏa mãn yêu cầu bài toán là (− ;  2 − 4. x +1
Câu 18. Cho hàm số y =
, mệnh đề nào sau đây đúng? x −1
A. Hàm số nghịch biến trên hai khoảng (− ;  ) 1 ;(1;+) .
B. Hàm số nghịch biến trên (− ;  ) 1 (1;+) .
C. Hàm số đồng biến trên hai khoảng (− ;  ) 1 ;(1;+) .
D. Hàm số đồng biến trên (− ;  ) 1 (1;+) . Lời giải
Tác giả: Hà Minh Yên; Fb: Hà Minh Yên Chọn A x +1 Hàm số y =
có tập xác định D = \   1 . x −1 −2 y =   ,  ( . x − ) 0 x 1 2 1
Do đó hàm số nghịch biến trên hai khoảng (− ;  ) 1 ;(1;+) .
Câu 19. Cho hàm số y = f ( x) có đồ thị như hình vẽ. Phương trình f (− x ) = m ( với m là tham số
thực) có nhiều nhất bao nhiêu nghiệm? A. 8 . B. 2 . C. 4 . D. 6 . Lời giải
Tác giả: Nguyễn Ngọc Diệp, FB: Nguyễn Ngọc Diệp Chọn D
Nhận thấy hàm số y = f (− x ) là hàm số chẵn nên đồ thị của hàm số y = f (− x ) nhận trục
Oy làm trục đối xứng.
Đồ thị hàm số y = f (− x ) gồm hai phần:
Phần 1: giữ nguyên phần đồ thị hàm số y = f ( x) với x  0 .
Phần 2: lấy đối xứng đồ thị phần 1 qua trục Oy .
Từ đó ta có đồ thị hàm số y = f (− x ) như sau:
Từ đồ thị hàm số y = f (− x ) ta thấy phương trình f (− x ) = m có tối đa 6 nghiệm.
Câu 20. Xét hai số thực dương thay đổi x , y sao cho xy  1. Giá trị nhỏ nhất của biểu thức 5x + 5 y x +1
P = x + 2 y +
đạt được khi x = x và y = y . Giá trị của biểu thức 0 Q = là 0 0 xy −1 y0 A. 3 . B. 2 . C. 2 . D. 1. Lời giải
Tác giả: Phạm Văn Tuân (lời giải: Thầy Nguyễn Duy Hiếu); Fb: mr.vtuan. Chọn B Ta có: 5x + 5y
5( x + y) 5( xy − ) 1 5( xy − ) 1
P = x + 2 y + = + + x + 2y − xy −1 xy −1 x + y x + y AM G − M 2 2
x + 3xy + 2 y − 5xy + 5  10 + x + y 2 2
x − 2xy + 2 y + 5 2 2
x − 2xy + 2 y − 2x − 2 y + 5 P  10 + =12 + x + y x + y
( x − y)2 + ( y − )2 + (x − )2 2 3 3 2 2 3 P  12 + (  . x + y) 12 6 2x − 3y = 0 x −3 = 0  x = 3
Dấu bằng xảy ra khi và chỉ khi  y − 2 = 0   .  y = 2 x + y xy −1  =
 xy −1 x + y + Do đó 0 x 1 Q = = 2 . 0 y
Câu 21. Điểm cực tiểu của hàm số 3 2
y = −x + 6x − 9x +1 là
A. x = 0 .
B. x = 3. C. x = 2 . D. x = 1. Lời giải
Tác giả: Trân Minh; Fb: Tran Minh Chọn D Ta có 2 y = 3 − x +12x −9 2 y = 0  3
− x +12x − 9 = 0  x = 1; x = 3 . Bảng biến thiên
Điểm cực tiểu của hàm số là x =1.
Câu 22. Cho hàm số y = f ( x) có bảng biến thiên như hình vẽ
Số điểm cực trị của hàm số y = f ( x) là A. 5 . B. 3 . C. 4 . D. 2 . Lời giải
Tác giả: Lê Thanh Hùng; Fb: Hung Le Thanh Chọn A Cách 1: f
 ( x), neáu f ( x)  0
Ta có: y = f ( x) =  − f
(x),neáu f (x) < 0
Dựa vào bảng biến thiên của hàm số y = f ( x) , ta có bảng biến thiên của hàm số y = f ( x) như sau:
Do đó, số điểm cực trị của hàm số y = f ( x) là 5 .
f ( x). f ( x)
Cách 2: y = f ( x)  y = f ( x) x = x x  1 − 1 ( 1 ) 
Ta có: f ( x) = 0  x = x 1 −  x 1 2 ( 2 ) x = x x 1  3 ( 3 )  = − f ( x) x 1 4 = 0   . x = 1  5
Do y đổi dấu khi đi qua 5 nghiệm này nên hàm số y = f ( x) có 5 điểm cực trị. Cách 3:
Đồ thị hàm số y = f (x) cắt trục hoành tại 3 điểm phân biệt không trùng với 2 điểm cực trị,
nên số điểm cực trị của đồ thị hàm số y = f ( x) là 5 .
Câu 23. Có bao nhiêu giá trị của tham số m để đồ thị hàm số 3
y = x − (m + ) 2
1 x + (2 − m) x + 2m − 2 có
điểm cực trị thuộc trục hoành? A. 3 . B. 1. C. 0 . D. 2 . Lời giải
Tác giả: Bùi Văn Khánh ; Fb:Khánh Bùi Văn Chọn A
Phương trình hoành độ giao điểm của đồ thị hàm số đã cho với trục hoành là 3 x − (m + ) 2
x + ( − m) x + m − =  ( x − )( 2 1 2 2 2 0
1 x − mx − 2m + 2) = 0 (1) x =1   2
x − mx − 2m + 2 = 0  (2)
Đồ thị hàm số có điểm cực trị thuộc trục hoành  Phương trình (1) có đúng hai nghiệm phân
biệt  (2) có nghiệm kép khác 1 hoặc (2) có hai nghiệm phân biệt trong đó có 1 nghiệm bằng 1. 2
 = m + 8m − 8 = 0 
TH1: (2) có nghiệm kép khác 1    m = −4  2 6 m 1  2
TH2: (2) có hai nghiệm phân biệt trong đó có một nghiệm bằng 1 2
m +8m −8  0    m =1 m =1 
Vậy có 3 giá trị của m để đồ thị hàm số có điểm cực trị thuộc trục hoành. 2 x −1
Câu 24. Có bao nhiêu giá trị thực của tham số m để đồ thị hàm số y = có đúng 2
x + (2 − m) x + 2m +1 hai đường tiệm cận? A. 1. B. 3 . C. 2 . D. 4 . Lời giải
Tác giả: Minh Tuấn ; Fb: Mác Lênin Chọn B.
Ta thấy rằng đồ thị của hàm số đã cho có đường tiệm cận ngang y = 1, do vậy đồ thị đó có
đúng 2 đường tiệm cận khi và chỉ khi đồ thị hàm số có đúng một đường tiệm cận đứng.
Đồ thị hàm số đã cho có đúng một đường tiệm cận đứng  phương trình 2
x + (2 − m) x + 2m +1 = 0( )
* có nghiệm kép hoặc có nghiệm x = 1 − hoặc x = 1.
Trường hợp 1: Phương trình ( )
* có nghiệm x = 1  m = 4 − .
Trường hợp 2: Phương trình ( ) * có nghiệm x = 1 −  m = 0 . Trường hợp 3: Phương trình ( ) * có nghiệm kép m =
  = 0  (2 − m)2 − 4(2m + ) 0 2
1 = 0  m −12m = 0   m =12
Như vậy có 3 giá trị của m thỏa mãn yêu cầu bài toán. Dongque84@gmail.com
Câu 25. Cho hàm số bậc ba y = f ( x) mà đồ thị hàm số có hai điểm cực trị là A(1; ) 3 , B(2; ) 1 . Số
điểm cực trị của hàm số y = f ( x ) là A. 1. B. 5 . C. 4 . D. 3. Lời giải
Tác giả: Vũ Thị Thu Huyền; Fb: HuyenVu Chọn B.
Hàm số y (−x) = f ( −x ) = f ( x ) = y ( x) x
  nên y = f ( x ) là hàm chẵn trên .
Do đó đồ thị hàm số y = f ( x ) nhậnOy trục đối xứng.
Vì vậy đồ thị hàm số y = f ( x ) có 5 điểm cực trị là A(1; ) 3 , B(2; ) 1 , A'( 1 − ; ) 3 , B'( 2 − ; ) 1 và
điểm có hoành độ x = 0 .
Câu 26. Cho hình lập phương ABC . D A BCD
  có cạnh bằng a . Khoảng cách từ điểm A đến mặt phẳng ( A BD) bằng a 2 a 3 a a 2 A. . B. . C. . D. . 2 3 2 3 Lời giải
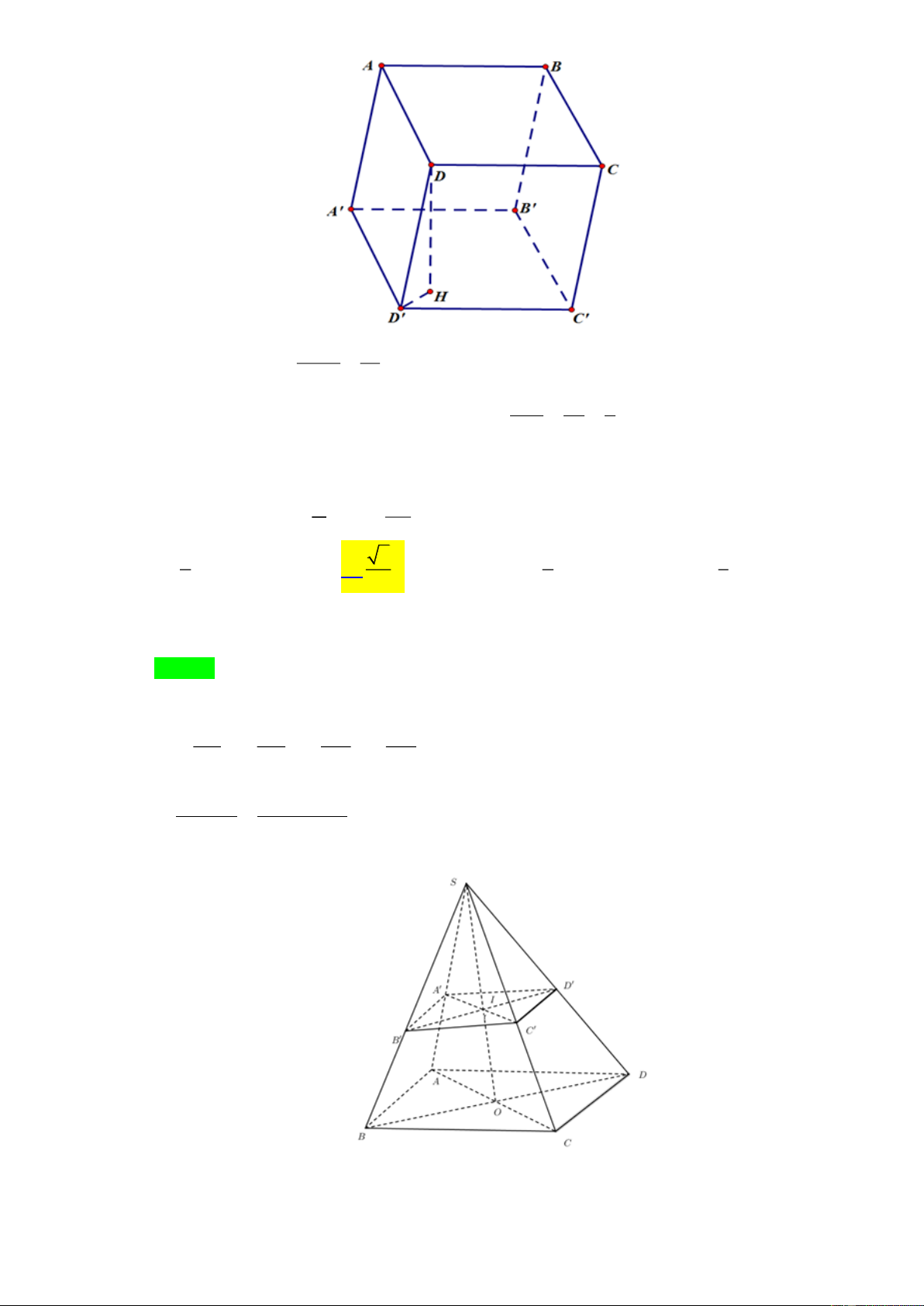
Tác giả:Nguyễn Thanh Mai; Fb: Nguyen Thanh Mai Chọn B Kẻ AH ⊥ A O
 . Ta dễ dàng chứng minh được AH ⊥ ( A B
D) . Suy ra d ( , A ( A BD)) = AH . 1 1 1 1 3 a 3 a Ta có = + + =  AH =
. Vậy d ( A ( ABD)) 3 , = . 2 2 2 2 2 AH AB AD AAa 3 3 Linh19781978@gmail.com
Câu 27. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại ,
A D . SA vuông góc với mặt
phẳng ( ABCD) . Cho biết AD = CD = a , AB = 2a ,hai mặt phẳng (SBC),( ABCD) tạo với nhau góc 0
45 . Khoảng cách từ điểm D đến mặt phẳng (SBC) bằng. a a 3 a 2 A. . B. . C. . D. a . 2 2 2 Lời giải
Tác giả:Đặng Thị Phương Huyền; Fb: Phuong Huyen Dang Chọn A
Do ABCD là hình thang vuông tại ,
A D và AD = CD = a , AB = 2a nên AC vuông góc với
CB , lại có CB ⊥ SA ( do SA vuông góc với mặt phẳng ( ABCD) . Do đó góc SCA bằng 0 45 và
CB ⊥ (SAC) .Suy ra tam giác SAC vuông cân tại A . 1
Gọi E là trung điểm cạnh AB . Ta có : d ( D,(SBC )) = d (E,(SBC )) = d ( , A (SBC )) . 2
Gọi H là trung điểm SC . Do tam giác SAC vuông cân tại A nên AH ⊥ SC , mà
AH ⊥ CB (do CB ⊥ (SAC) ). Suy ra AH ⊥ (SBC) và d ( , A (SCD)) 2 0
= AH = AC.Sin 45 = a 2. = a . 2 1 a
Vậy : d ( D,(SBC )) = d ( , A (SBC )) = . 2 2
Câu 28 . Gọi S là tập các giá trị thực của tham số m để đồ thị hàm số 4 2
y = x − 2mx + m + 4 có ba
điểm cực trị cách đều trục hoành. Tính tổng tất cả các phần tử của tập S là A. 2. B. 6. C. 0. D. 4. Lời giải
Tác giả:Minh Trang ; Fb: Minh Trang Chọn D Ta có 3
y ' = 4x − 4mx .  x = 0 y ' = 0  .  2 x = m Đồ thị hàm số 4 2
y = x − 2mx + m + 4 có ba điểm cực trị  phương trình y ' = 0 có ba nghiệm
phân biệt  m  0 .
Ta có A( m + ) B ( 2
m −m + m + ) C ( 2 0; 4 , ; 4 ,
− m;−m + m + 4) là ba điểm cực trị của đồ thị hàm số. ,
A B,C cách đều trục hoành 2
y = y = y m + 4 = −m + m + 4 A B Cm = 0 (L) 2
m + 4 = −m + m + 4      m = 2 −  (L)  m = 4. 2
m + 4 = m − m − 4   m = 4  (TM )
Vậy m = 4 . Suy ra tổng tất cả các phần tử của tập S là 4.
Câu 29: Cho hai hình vuông ABCD và ABEF có cạnh bằng a và nằm trên hai mặt mặt phẳng
vuông góc với nhau. Thể tích khối đa diện EBCFAD bằng 3 2a 3 a 3 a A. . B. . C. . D. 3 a . 3 3 2 Lời giải
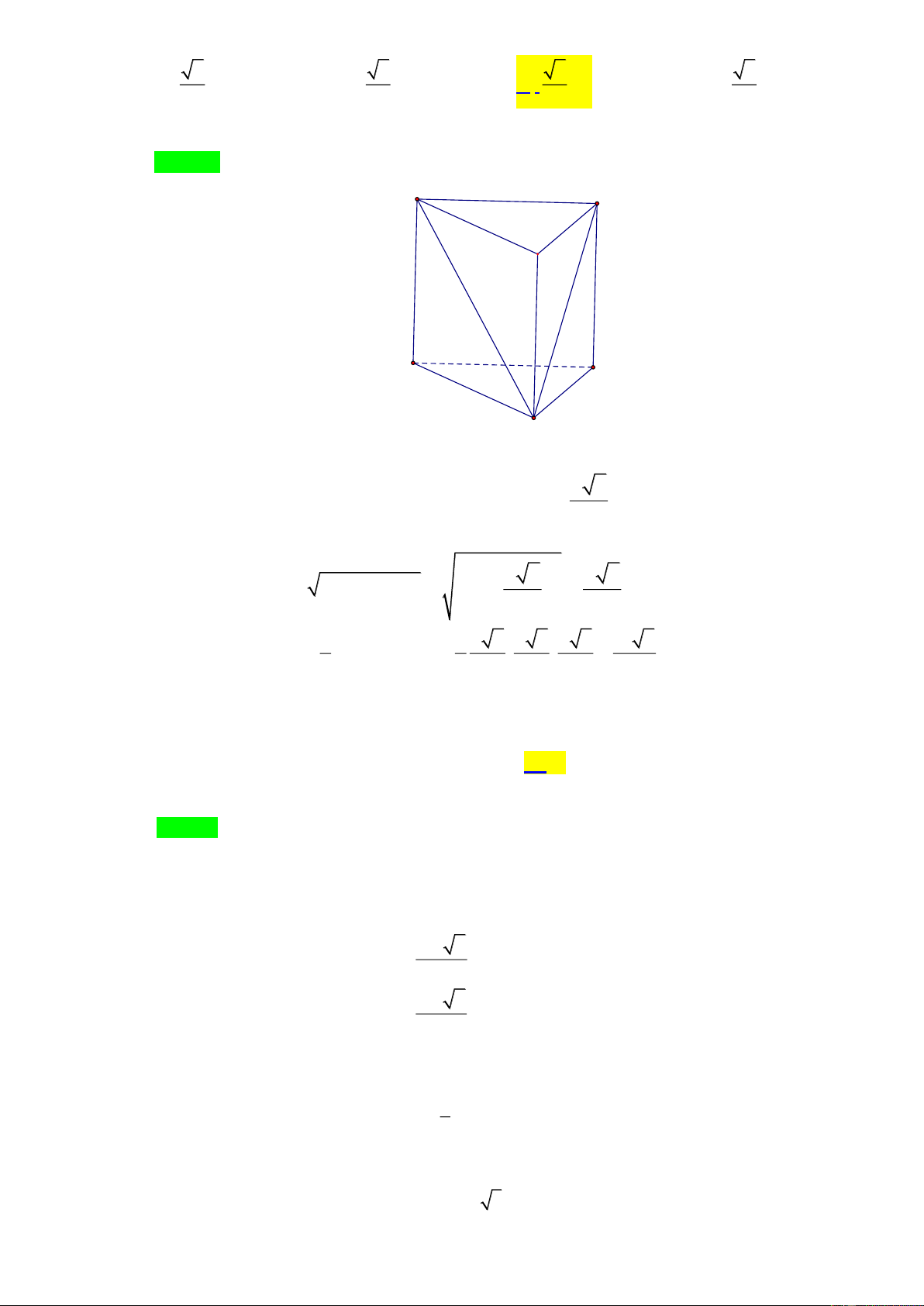
Tác giả: Trần Thị Thảo; Facebook: Trần Thảo Chọn C
Dựng hình lập phương ABCDEFMN cạnh a . 1 1 3 V = V = a EBCFAD . Chọn C. 2 ABCDFEMN 2
Câu 30: Cho lăng trụ đứng AB .
C A' B'C ' có tam giác A' BC là tam giác đều cạnh a và tam giác
ABC vuông tại A . Thể tích khối lăng trụ AB .
C A' B'C ' là 2 2 2 2 A. 3 a . B. 3 a C. 3 a . D. 3 a . 4 12 8 6 Lời giải
Tác giả: Trịnh Xuân Mạnh ; Fb:Trịnh Xuân Mạnh Chọn C. B C A B' C' A'
Ta có D BB' A' = D CC ' A' nên A' B' = A'C '. Từ đó D A' B'C ' vuông cân. a o 2
Suy ra: A' B ' = A'C ' = B 'C '.sin A BC   = . a sin 45 = . 2
Xét D BB' A' vuông tại B ' theo định lí Pi–ta-go ta có 2  a 2  a 2 2 2 2 BB ' =
AB − B A   = a −   = . 2 2   3 1
1 a 2 a 2 a 2 a 2 Vậy V = =      = =    S.h
A B .A C .AA . . . ABC. A B C 2 2 2 2 2 8
Câu 31. Có bao nhiêu tiếp tuyến của đồ thị hàm số 3 2
y = x − 2x tạo với hai trục tọa độ một tam giác cân? A. 3 . B. 1. C. 4 . D. 2 . Lời giải
Tác giả: Tạ Tiến Thanh ; Fb: Thanh Ta
Chọn C Ta có 3 2 2
y = x − 2x y ' = 3x − 4x .
Gọi M ( x ; y là tọa độ tiếp điểm của tiếp tuyến với đồ thị hàm số. Vì tiếp tuyến tạo với hai 0 0 )
trục tọa độ một tam giác cân tại O (vuông cân) tương đương y '(x ) = 1  0 .  2 + 7 x = 0 2 3 y (
x ) =1  3x − 4x =1   0 0 0  2 − 7 ; x = 0  3 x =1 0 2  y (  x ) = 1
−  3x − 4x = 1 −  0 0 0 1 x = . 0  3
Vậy có 4 tiếp tuyến thỏa mãn yêu cầu bài toán.
Câu 32. Cho lăng trụ có đáy là hình vuông cạnh a 3 và chiều cao là b . Thể tích khối lăng trụ đó bằng A. 2 ab . B. 2 3ab . C. 2 3a b . D. 2 a b . Lời giải
Tác giả: Ngô Thị Thơ ; Fb: Ngô Thị Thơ Chọn C V = b (a )2 2 . 3 = 3a b . 3 − 2x
Câu 33. Đường tiệm cận ngang của đồ thị hàm số y = 1+ có phương trình là x A. y = −3 . B. y = 2 . C. y = −2 . D. y = 3 . Lời giải
Tác giả: Ngô Thị Thơ ; Fb: Ngô Thị Thơ Chọn C lim y = 2 − ; lim y = 2
− , suy ra tiệm cận ngang của đồ thị hàm số là y = −2 . x→+ x→− 2x − 3
Câu 34: Hai đường tiệm cận của đồ thị hàm số y = x + và hai trục tọa độ cắt nhau tạo thành hình 1
chữ nhật. Diện tích của hình chữ nhật đó là? A. S = 2. B. S = 4. C. S =1. . D. S = 3. . Lời giải
Tác giả: Trịnh Xuân Mạnh ; Fb:Trịnh Xuân Mạnh. Chọn A 2x − 3
Ta có các tiệm cận của đồ thị hàm số y = x = − y = x + là: 1; 2 1
Gọi giao điểm của hai đường tiệm cận là A( 1
− ;2) , giao điểm của TCN với trục tung là
B(0;2) , giao điểm của TCĐ với trục hoành là C ( 1
− ;0) . Ta có hình chữ nhật ABOC.
Lại có OB = y = 2 = 2;OC = x = 1 − =1. B c
Vậy diện tích hình chữ nhật AOBC : S = O . B OC = 2.1 = 2 . AOBC 3sin x +1
Câu 35. Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = là sin x + 2 11 2 3 A. . B. 0 . C. − . D. − 6 3 2 Lời giải
Tác giả: Tạ Tiến Thanh ; Fb: Thanh Ta Chọn C 3t +1 5
Đặt t = sin x;t  1 − ;  1 , ta có y = , khi đó y ' =  0 t   1 − ;  1 t + 2 2 (t + . 2) 3.1+1 4 3.( 1 − ) +1
Hàm số đồng biến trên  1 − ;  1 , suy ra max y = = ; min y = = 2 − . t [  1 − ;1] + t [  1 − ;1] 1 2 3 ( 1 − ) + 2 Khi đó tổ 4 2
ng giá trị lớn nhất và giá trị nhỏ nhất là + ( 2 − ) = − . 3 3 2 2 cos x + m
Câu 36 . Tập hợp các giá trị thực của tham số m để hàm số y =
nghịch biến trên khoảng cos x + m (0; ) là A. (0; 2). B. (2;+) . C.  1 − ;0) D. 1; 2) . Lời giải
Tác giả:Minh Trang ; Fb: Minh Trang Chọn D + 2 − sin .
x (cos x + m) + sin . x ( 2 2cos x + m ) ( 2 2 m − 2m)sin . 2 cos x x m Ta có y =  y ' = = . cos x + m (cos x + m)2 (cos x + m)2 2 2 cos x + m Hàm số y =
nghịch biến trên khoảng (0; )  y '  0  x(0; ) và cos x + m
cos x  −mx (0; ). Mà sin x  0, cos x( 1 − ; ) 1  x (0; ) . 2
m − 2m  0 
Suy ra ycbt  m  −1 1 m  2.  m  1
Câu 37: Số điểm chung của hai đồ thị hàm số 3 2
y = x − 2x và y = 2x − 3 là A. 2 . B. 3 . C. 0 . D. 1 . Lời giải
Tác giả: Trần Thị Thảo; Facebook: Trần Thảo Chọn B
Phương trình hoành độ giao điểm của hai đồ thị hàm số là:  x = 1   1 + 13 3 2 3 2
x − 2x = 2x − 3  x − 2x − 2x + 3 = 0  x =  2 .   1 − 13 x =  2
Vậy hai đồ thị hàm số có 3 điểm chung.
Câu 38: Tổng diện tích các mặt của tứ diện đều cạnh a là A. 2 2a . B. 2 a 3 . C. 2 4a . D. 2 2a 3 . Lời giải
Tác giả: Mai Quỳnh Vân ; Fb: Vân Mai Chọn B
Mỗi mặt của tứ diện đều cạnh a , là một tam giác đều cạnh bằng a nên diện tích mỗi mặt là: 2 1 a 3 S = . . a . a sin 60 = . 1 2 4 2
Diện tích 4 mặt của tứ diện đều là: a 3 2 S = 4.S = 4. = a 3 . 1 4
Câu 39: Trong các hàm số sau, hàm số nào đồng biến trên khoảng (− ;  +) ? x − 2 A. y =
y = x + x + . C. 2
y = x − x +1 . D. 4 2
y = x + 2x +1 . 2x + . B. 3 3 1 1 Lời giải
Tác giả: Mai Quỳnh Vân ; Fb: Vân Mai Chọn B   
Loại A do tập xác định của hàm số là \ −   .  2 1 1
Loại C do y = 0  2x −1 = 0  x =
do đó y đổi dấu qua x = . 2 2 Loại D do 3
y = 0  4x + 4x = 0  x = 0 do đó y đổi dấu qua x = 0 . Xét B ta có 2
y = 3x + 3  0 x
  nên hàm số luôn đồng biến trên khoảng (− ;  +) .
Do đó chọn phương án B.
Câu 40: Số điểm cực đại của hàm số 4 2
y = 2x − 3x +1 là A. 0 . B. 2 . C. 3 . D. 1 . Lời giải
Tác giả: Nguyễn Thị Xuyến; Fb: Nguyen Xuyen Chọn D
Tập xác định D = . x = 0  Ta có: 3
y ' = 8x − 6x ; 3
y ' = 0  8x − 6x = 0   3  . x =  2 Bảng xét dấu y': 3 3 x − − 0 + 2 2 y ' - 0 + 0 - 0 +
Vậy hàm số đã cho có 1 điểm cực đại. 2 x −1
Câu 41: Số đường tiệm cận đứng của đồ thị hàm số y = là 3 x − 3x + 2 A. 2. B. 0. C. 1. D. 3. Lời giải
Tác giả: Nguyễn Thị Xuyến; Fb: Nguyen Xuyen Chọn A
Tập xác định: D = \  2 − ;  1 . 2 x −1 (x − ) 1 ( x + ) 1 (x + ) 1
Ta có: lim y = lim = lim = lim = + . + + + + x ( → − ) x ( → − ) 3 x − 3x + 2 x ( → − ) ( x − ) 1 ( 2 x + x − 2) x ( → − ) ( 2 2 2 2 2 x + x − 2) 2 x −1 (x − ) 1 ( x + ) 1 (x + ) 1 lim y = lim = lim = lim = + . + + 3 + + x→ x→ x − 3x + 2 x→ (x − ) 1 ( 2 x + x − 2) x→ ( 2 1 1 1 1 x + x − 2)
 Các đường thẳng x = 2
− và x = 1 là các đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có 2 đường tiệm cận đứng. 3
Câu 42: Cho khối chóp S. ABC có thể tích 3 V =
a , tam giác SBC là tam giác đều có cạnh bằng a . 3
Khi đó, khoảng cách từ điểm A đến mặt phẳng (SBC)bằng 4a 3 4 A. . B. a . C. 4a .
D. 2a 3 . 3 3 Lời giải
Tác giả: Trần Thanh Hà ; Fb: Hà Trần
Phản biện: Đồng Anh Tú; FB: Anh Tú Chọn C 1 3V Ta có: V = d A SBC Sd A SBC = . ABC ( ,( )). SBC ( ,( )) S . ABC S . 3 S SBC 3 Có: 3 V = a . S . ABC 3 2 a 3
Vì  SBC là tam giác đều có cạnh bằng a nên S = đvdt . SBC  ( ) 4 3 a 3 3
Vậy: Khoảng cách từ điểm A đến mặt phẳng (SBC) là: d ( A (SBC )) 3 , = = 4a . 2 a 3 4
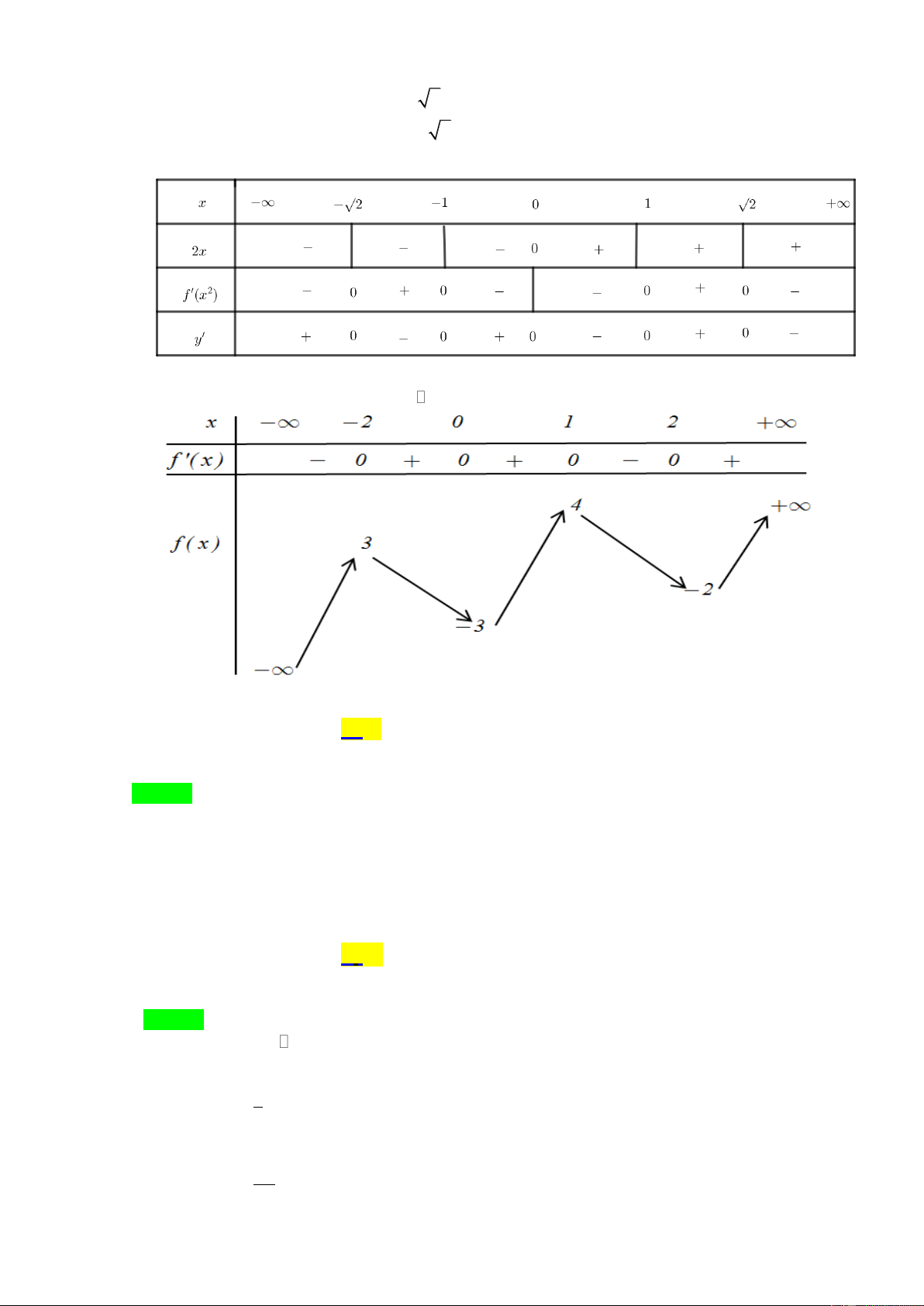
Câu 43: Cho hàm số y = f ( x) có bảng biến thiên như hình vẽ Hàm số = ( 2 y
f x ) nghịch biến trên khoảng nào trong các khoảng dưới đây? A. (− 2; ) 0 . B. (− ;  − 2) . C. (1;+) . D. (0; ) 1 . Lời giải
Tác giả:Trần kim Nhung ; Fb: Nhung trần thị Kim Chọn Dx =1
Quan sát bảng biến thiên của hàm số y = f ( x) ta thấy f ( x) = 0   . x = 2 Với y f ( 2 =
x ) ta có y = x f ( 2 2 . x ) . x = 0   x = 2x = 0 0   Vậy y = 0    x =   x = 1  . f '  (x ) 2 1 2 = 0 2   x = 2  x =  2 x
Từ bảng biến thiên của hàm số y = f ( x) ta thấy f ( x) 1  0   . x  2  1 −  x 1 x 1  Vậy f ( x ) 2 2  0    x  2  2 x  2 x  − 2  Ta có bảng xét dấu:
Dựa vào bảng xét dấu ta chọn đáp án D.
Câu 44: Cho hàm số y = f ( x) liên tục trên
có bảng biến thiên như sau:
Số nghiệm của phương trình f ( x) = 0 là A. 2 . B. 5 . C. 3 . D. 4 . Lời giải
Tác giả: Trần Quang Đạt; Fb: Quang Đạt Chọn B
Số nghiệm của phương trình f ( x) = 0 là số giao điểm của đồ thị hàm số y = f ( x) với đường thẳng y = 0 .
Dựa vào bảng biến thiên ta có: Phương trình f ( x) = 0 có 5 nghiệm phân biệt.
Câu 45: Số điểm cực trị của hàm số 3 4
y = (3x −1) (x +1) A. 3 . B. 2 . C. 1. D. 4 . Lời giải
Tác giả:Nguyễn Ngọc Hà ; Fb:Hangocnguyen Chọn B
Tập các định D = Ta có : 2 4 3 3 2 3
y ' = 9(3x −1) (x +1) + 4(3x −1) (x +1) = (3x −1) (x +1) (21x + 5)  1 x =  3 
y ' = 0  x = −1   −5 x =  21 Bảng biến thiên
Vậy hàm số có 2 cực trị. x − 2
Câu 46. Cho hàm số y =
có đồ thị (C) cắt hai trục tọa độ lần lượt tại A , B . Tiếp tuyến của (C) x +1
tại hai điểm A , B tạo với nhau một góc  . Giá trị của sin  bằng 4 1 3 3 A. . B. . C. . D. . 5 10 5 10 Lời giải
Tác giả: Nguyễn Thị Hồng Hợp ; Fb: Nguyễn Thị Hồng Hợp Chọn A
Giao điểm của đồ thị (C) với hai trục tọa độ lần lượt là A(0; 2 − ), B(2;0) . 3 Ta có y = ( . x + )2 1
Phương trình tiếp tuyến của đồ thị (C) tại điểm A là: 3 y =
x − x + y = 3x − 2  3x − y − 2 = 0 . 2 ( A ) (x + A ) A 1
Phương trình tiếp tuyến của đồ thị (C) tại điểm B là: 3 1 2 y =
x − x + y = x −  x − 3y − 2 = 0 . 2 ( B ) (x + B ) B 1 3 3 3.1+ (− ) 1 .( 3 − ) 3 4
Từ giả thiết suy ra cos = = 2  sin = 1− cos  = . + (− )2 + (− )2 2 2 5 3 1 . 1 3 5
Câu 47. Cho hình lăng trụ có đáy là hình vuông cạnh a , thể tích khối lăng trụ bằng 3 a và độ dài các
cạnh bên là 2a . Góc tạo bởi cạnh bên và mặt phẳng đáy là: A. 90 . B. 30 . C. 45. D. 60 . Lời giải
Tác giả: Nguyễn Thị Tỉnh ; Fb: Ngọc Tỉnh Chọn B
Gọi H là hình chiếu vuông góc của D lên mặt phẳng đáy ( A' B'C ' D') . Góc DD H  chính
là góc giữa cạnh bên và mặt phẳng đáy. 3 V a Ta có h = DH = = = a . 2 S a ABCD DH a 1
Xét tam giác vuông DHD ta có sin D D ' H = = =   = 30o DD H . DD 2a 2
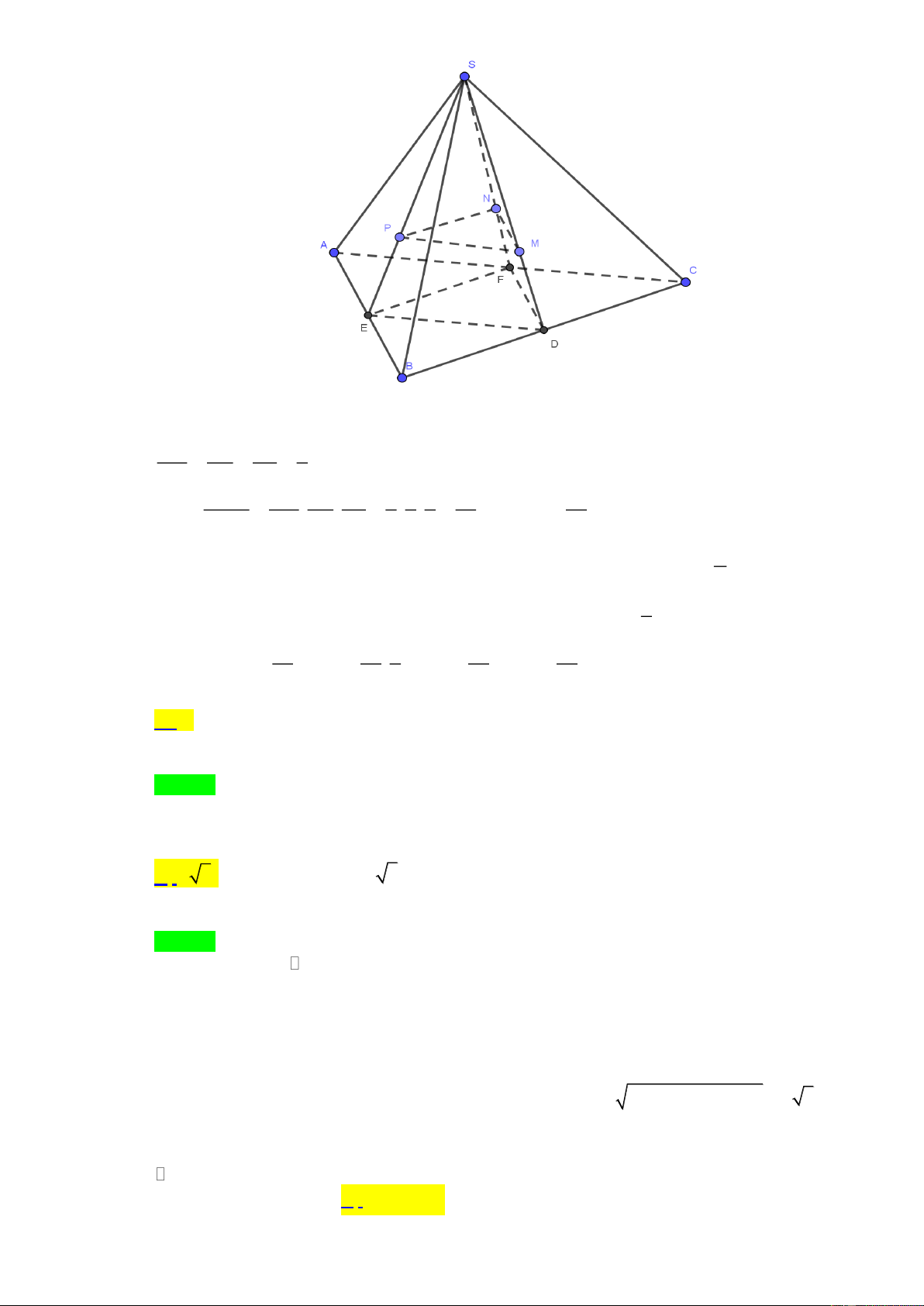
Câu 48. Cho khối chóp SABCD có thể tích V , đáy ABCD là hình bình hành, M là trung điểm của SB
N là điểm trên cạnh SD . Mặt phẳng ( AMN ) cắt cạnh SC tại điểm P sao cho thể tích khối V SN chóp SAMPN bằng . Tỉ số bằng 4 SD 2 2 1 1 A. . B. . C. . D. . 3 2 2 3 Lời giải
Tác giả: Thân Thế Luân ; Fb: Luan Vu
Phản biện: Trần Hà Chọn B
Bổ đề: Cho khối chóp SABCD có đáy ABCD là hình bình hành. Một mặt phẳng không qua S
cắt các cạnh SA, SB, SC, SD lần lượt tại A’, B’, C’, D’ . SA SB SC SD Đặt = ; a = ; b = ; c
= d . Khi đó ta có kết luận sau SA ' SB ' SC ' SD '
1. a + c = b + d V
a + b + c + d
2. SA'B'C'D' = V 4abcd SABCD Chứng minh
Gọi AC BD = O , A'C ' B' D' = I S, I, O thẳng hàng (cùng nằm trên giao tuyến của
hai mặt phẳng (SAC) và (SBD)). SO Chứng minh 1: Đặt = x SI S SA ' SI 1 2S 1 Ta có SA  'I SA  ' = . I =  = ( ) 1 S SA SO ax S ax SAO SAC S SC ' SI 1 2S 1 Và SC  ' I SC  ' = . I =  = (2) S SC SO cx S cx SCOSAC 2S 2S 1 1 2S 1 1 Suy ra SA  'I SC  ' I SA  'C' + = +  = + S S ax cx S ax cx SAC SACSAC 2SA' SC ' 1 1 2 1 1 Hay . = +  = +
a + c = 2x SA SC ax cx ac ax cx
Tương tự cũng có b + d = 2x . Vậy a + c = b + d . V
SA ' SB ' SC ' 1 V
SA' SD ' SC ' 1
Chứng minh 2: Ta có SA'B'C' = . . = Và SA'C'D' = . . = V SA SB SC abc V SA SD SC acd SABC SACD V V V V 1 1 b + d Mà D V = V
= ABC nên SA'B'C'
SA'C ' D '
SA' B 'C ' D ' + = = + = SABC SACD 2 V V V abc acd abcd SABC SACD SABC V 2 b + d
a + b + c + d
SA' B 'C ' D ' ( ) Hay = = V 4abcd 4abcd SABCD
Trở lại bài toán: Đặ SC SD t = ; x = y SP SN
Áp dụng bổ đề trên ta có: x +1 = y + 2  x = y +1 V x +1+ 2 + y x + y + 3 1 AMNP = = = V 4x .2 y 8xy 4 SABCD y + 2 1 Suy ra 2 =  =  = y ( y + ) y 2 y 2 4 1 4 SN 2 Vậy = . SD 2
Câu 49: Gọi  là góc tạo bởi hai mặt bên của một tứ diện đều. Mệnh đề nào sau đây đúng?
A. tan  = 2 2 . B. tan  = 2 .
C. tan  = 2 .
D. tan  = 3 . Lời giải
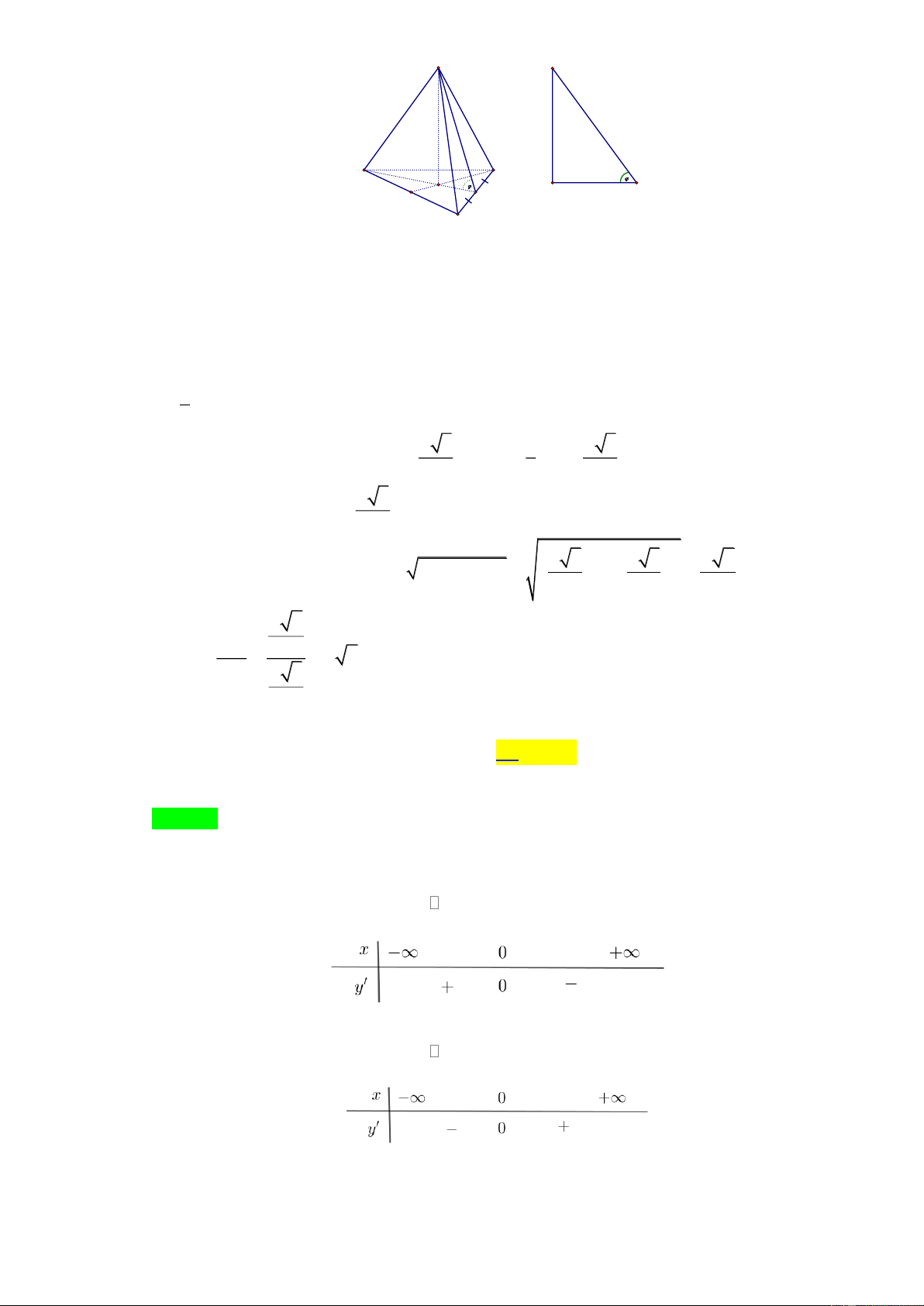
Tác giả:Nguyễn Ngọc Hà ; Fb:Hangocnguyen Chọn A A A B D G E G F E C
Xét tứ diện đều ABCD cạnh có độ dài a . Vì các mặt của tứ diện đều đều tạo với nhau những
góc bằng nhau nên ta đi tính góc tạo bởi hai mặt phẳng ( ACD) và (BCD)
Gọi E là trung điểm của CD .
Do các tam giác ACD và BCD là các tam giác đều nên BE ⊥ C ; D AE ⊥ CD (1)
mà CD = ( ABD)  (BCD) (2) . Từ (1) & (2)   = AEB ( AEB là góc nhọn)
Gọi G là trọng tâm tam giác BCD AG ⊥ (BCD); B, G, E thẳng hàng ; 1 GE =
GB   = AEG 3 a 3 1 a 3
Tam giác BCD đều cạnh a nên BE =  EG = BE = ; 2 3 6 a 3
Tam giác ACD đều nên AE =
.Do AG ⊥ (BCD)  AG ⊥ GE   AGE là vuông tại G . 2 2 2
a 3   a 3  a 6 Xét tam giác vuông AGE có 2 2 AG = AE − GE =   −   =     2 6 3     a 6 AG 3  tan = = = 2 2 . GE a 3 6
Câu 50. Tập hợp giá trị thực của tham số m để hàm số 4 2
y = mx + (m − 2)x + 2m có điểm cực tiểu là A. (0; 2] . B. ( ; − 0] . C. (0; +) . D. (0; 2) . Lời giải
Tác giả: Đồng Anh Tú; Fb: Anh tu Chọn C x = 0 Ta có 3 2
y ' = 4mx + 2(m − 2)x y ' = 2x(2mx + m − 2) nên y ' = 0   . 2
2mx = 2 − m (1) TH1: m  0 thì 2
2mx + m − 2  0, x
  nên ta có bảng xét dấu y '
Ta có x = 0 là điểm cực đại, nên m  0 không thỏa mãn. TH2: m  2 thì 2
2mx + m − 2  0, x
  nên ta có bảng xét dấu y '
Ta có x = 0 là điểm cực tiểu, nên m  2 thỏa mãn. 2 − m 2 − m
TH3: 0  m  2 , khi đó 2 (1)  x =  x = 
nên phương trình y ' = 0 có 3 nghiệm 2m 2m phân biệt nên hàm số 4 2
y = mx + (m − 2)x + 2m có 3 cực trị và nó luôn có ít nhất một cực tiểu,
nên 0  m  2 thỏa mãn.
Vậy ta có m  (0; +) thì hàm số đã cho có điểm cực tiểu.