Đề KSCL Toán 12 ôn thi THPTQG năm 2018 – 2019 trường chuyên Vĩnh Phúc lần 3

Giới thiệu đến thầy, cô và các em học sinh khối 12 nội dung đề KSCL Toán 12 ôn thi THPTQG năm 2018 – 2019 trường chuyên Vĩnh Phúc lần 3, đề thi gồm 50 câu trắc nghiệm khách quan

43 22 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

70 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
Trang 1/6 - Mã đề thi 345 - https://toanmath.com/
SỞ GIÁO DỤC VÀ ĐÀO TẠO VĨNH PHÚC
TRƯỜNG THPT CHUYÊN VĨNH PHÚC
(Đề thi có 6 trang)
ĐỀ KSCL CÁC MÔN THI THPT QUỐC GIA - LẦN 3
NĂM HỌC 2018-2019
MÔN TOÁN 12
Thời gian làm bài: 90 phút;
(Không kể thời gian giao đề)
Mã đề thi 345
Họ, tên thí sinh:..........................................................................
Số báo danh:...............................................................................
Câu 1: Trong không gian với hệ tọa độ
Oxyz
, cho
1;0;0
A
,
0;0;2
B
,
0; 3;0
C
. Tính bán kính
mặt cầu ngoại tiếp tứ diện
OABC
là
A.
14
4
. B.
14
. C.
14
3
. D.
14
2
.
Câu 2: Cho cấp số cộng
n
u
có
1
u
và công sai
4
d
. Hãy tính
99
u
.
A.
401
. B.
404
. C.
403
. D.
402
.
Câu 3: Tìm
a
để hàm số
2
1
khi 1
1
khi 1
x
x
f x
x
a x
liên tục tại điểm
0
1
x
.
A.
0
a
. B.
1
a
. C.
2
a
. D.
1
a
.
Câu 4: Cho hình chóp
.
S ABCD
có đáy là hình thang vuông tại
A
và
B
. Biết
SA ABCD
,
AB BC a
,
2AD a
,
2SA a
. Gọi
E
là trung điểm của
AD
. Tính bán kính mặt cầu đi qua
các điểm
S
,
A
,
B
,
C
,
E
.
A.
3
2
a
. B.
a
. C.
6
3
a
. D.
30
6
a
.
Câu 5: Gọi
0
x
là nghiệm dương nhỏ nhất của phương trình
2 2
3sin 2sin cos cos 0
x x x x
. Chọn
khẳng định đúng?
A.
0
;
2
x
. B.
0
3
;2
2
x
. C.
0
0;
2
x
. D.
0
3
;
2
x
.
Câu 6: Hàm số
4 3
2019
y x x x có bao nhiêu điểm cực trị?
A.
2
.
B.
3
.
C.
0
.
D.
1
.
Câu 7: Giá trị lớn nhất của hàm số
3
x
f x
x
trên đoạn
2;3
bằng
A.
2
. B.
1
2
. C.
3
. D.
2
.
Câu 8: Cho hàm số
y f x
xác định và liên tục trên
R
, có bảng biến thiên như sau:
Mệnh đề nào sau đây là đúng ?
A. Hàm số nghịch biến trên khoảng
. B. Hàm số đồng biến trên khoảng
; 2
.
C. Hàm số nghịch biến trên khoảng
1;
. D. Hàm số đồng biến trên khoảng
1;

.
Câu 9: Hàm số
3 2
3 1
y x x
có đồ thị nào trong các đồ thị dưới đây?
x

1
1
y
0
0
y

2
1
Trang 2/6 - Mã đề thi 345 - https://toanmath.com/
Hình
1
Hình
2
Hình
3
Hình
4
A. Hình
3
. B. Hình
1
. C. Hình
2
. D. Hình
4
.
Câu 10: Gọi
n
là số nguyên dương sao cho
2 3
3 3
3 3 3
1 1 1 1 190
...
log log log log log
n
x x x x x
đúng với
mọi
x
dương,
1
x
. Tìm giá trị của biểu thức
2 3
P n
.
A.
23
P
. B.
41P
. C.
43
P
. D.
32
P
.
Câu 11: Có bao nhiêu số hạng trong khai triển nhị thức
2018
2 3x
thành đa thức
A.
2019
. B.
2020
. C.
2018
. D.
2017
.
Câu 12: Cho khối lăng trụ
.
ABC A B C
có thể tích bằng
V
. Tính thể tích khối đa diện
ABCB C
.
A.
2
V
. B.
4
V
. C.
3
4
V
. D.
2
3
V
.
Câu 13: Một người gửi tiết kiệm số tiền
80000000
đồng với lãi suất là
6,9
%/ năm. Biết rằng tiền
lãi hàng năm được nhập vào tiền gốc, hỏi sau đúng
5
năm người đó có rút được cả gốc và lãi số tiền
gần với con số nào nhất sau đây?
A.
107 667 000
đồng.
B.
105 370 000
đồng.
C.
111 680 000
đồng.
D.
116 570 000
đồng.
Câu 14: Cho hàm số
y f x
xác định trên
có đồ thị của hàm số
y f x
như hình vẽ. Hỏi
hàm số
y f x
đồng biến trên khoảng nào dưới đây?
A.
0;1
.
B.
2;

.
C.
1;2
.
D.
0;1
và
2;

.
Câu 15: Cho tứ diện
ABCD
có hai mặt
ABC
và
ABD
là các tam giác đều. Tính góc giữa hai đường
thẳng
AB
và
CD
.
A.
30
. B.
60
. C.
90
. D.
120
.
Câu 16: Cho
6 8 7
2 3 2 d 3 2 3 2
x x x A x B x C
với , ,
A B C R
. Tính giá trị của biểu
thức
12 7A B
.
A.
23
252
. B.
241
252
. C.
52
9
. D.
7
9
.
Câu 17: Tập nghiệm của bất phương trình
2 1
2
1
1
1
x
a
(với
a
là tham số,
0
a
) là
A.
1
;
2

. B.
;0

. C.
1
;
2
. D.
0;
.
O
x
y
1
2
Trang 3/6 - Mã đề thi 345 - https://toanmath.com/
Câu 18: Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số đạt cực đại tại điểm nào trong các điểm sau đây?
A.
2.
x
B.
3.
x
C.
2.
x
D.
4.
x
Câu 19: Tìm tập nghiệm của phương trình
2
2
3 1
x x
.
A.
1;3
S
. B.
0; 2 .
S
C.
1; 3 .
S
D.
0;2
S
.
Câu 20: Trong không gian với hệ trục tọa độ
,Oxyz
cho
2 3a i j k
. Tìm tọa độ của vectơ
a
.
A.
2; 3; 1 .
B.
3;2; 1 .
C.
1;2; 3 .
D.
2; 1; 3 .
Câu 21: Hàm số nào dưới đây nghịch biến trên tập xác định của nó?
A.
3
log
y x
. B.
4
logy x
. C.
3
x
y
. D.
2
log 1
y x
.
Câu 22: Cho hình chóp
.
S ABC
có đáy là tam giác cân tại
A
,
AB AC a
,
120
BAC
. Tam giác
SAB
là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích
V
của khối chóp
.
S ABC
.
A.
3
V a
. B.
3
2
a
V . C.
3
2V a
. D.
3
8
a
V .
Câu 23: Có bao nhiêu giá trị nguyên của tham số
m
trên đoạn
2018;2018
để hàm số
2
ln 2 1
y x x m
có tập xác định là
.
A.
2018
. B.
1009
. C.
2019
. D.
2017
.
Câu 24: Cho hàm số
y f x
có đạo hàm trên
và đồ thị hàm số
y f x
trên
như hình
vẽ. Mệnh đề nào sau đây là đúng?
A. Hàm số
y f x
có 1 điểm cực tiểu và không có cực đại.
B. Hàm số
y f x
có 1 điểm cực đại và không có cực tiểu.
C. Hàm số
y f x
có 1 điểm cực đại và 2 điểm cực tiểu.
D. Hàm số
y f x
có 1 điểm cực đại và 1 điểm cực tiểu.
Câu 25: Cho hình trụ có thiết diện đi qua trục là một hình vuông có cạnh bằng
4a
. Diện tích xung
quanh của hình trụ là
A.
2
4
S a
. B.
2
8
S a
. C.
2
24
S a
. D.
2
16
S a
.
Câu 26: Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng?
A.
4
. B.
8
. C.
6
. D.
2.
Câu 27: Cho hàm số
y f x
xác định, liên tục trên
và có bảng biến thiên như sau
x

2
4
y
0
0
y

3
2
x

1
3
y
0
y
2
1
2
1
x
y
O
Trang 4/6 - Mã đề thi 345 - https://toanmath.com/
Khẳng định nào sau đây là đúng?
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị cực tiểu bằng 3.
C. Hàm số đạt cực đại tại
1x
và đạt cực tiểu tại
3
x
.
D. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng 1.
Câu 28: Tìm nguyên hàm của hàm số
2
1
3y x x
x
.
A.
3 2
3
ln
3 2
x x
x C
. B.
3 2
2
3 1
3 2
x x
C
x
.
C.
3 2
3
ln
3 2
x x
x C
. D.
3 2
3
ln
3 2
x x
x C
.
Câu 29: Cho hàm số
f x
liên tục trên đoạn
0;10
và
10
0
d 7
f x x
và
6
2
d 3
f x x
. Tính
2 10
0 6
d dP f x x f x x
.
A.
. B.
10
P
. C.
7
P
. D.
4P
.
Câu 30: Tìm tất cả các giá trị của tham số
m
để giá trị nhỏ nhất của hàm số
3 2
3
y x x m
trên
đoạn
1;1
bằng 0.
A.
6
m
.
B.
4
m
.
C.
0
m
.
D.
2
m
.
Câu 31: Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ. Hỏi đồ thị hàm số
y f x
có tất cả bao nhiêu điểm cực trị?
A.
9
B.
7
. C.
6
D.
8
Câu 32: Biết
F x
là nguyên hàm của hàm số
2
cosx x
f x
x
. Hỏi đồ thị của hàm số
y F x
có bao nhiêu điểm cực trị?
A.
1
. B. vô số điểm. C. 2. D. 0.
Câu 33: Có bao nhiêu số tự nhiên có 4 chữ số được viết từ các chữ số
1
,
2
,
3
,
4
,
5
,
6
,
7
,
8
,
9
sao
cho số đó chia hết cho
15
?
A.
432
B.
234
. C.
132
. D.
243
.
Câu 34: Cho hình trụ có đáy là hai đường tròn tâm
O
và
O
, bán kính đáy bằng chiều cao và bằng
2a
. Trên đường tròn đáy có tâm
O
lấy điểm
A
, trên đường tròn tâm
O
lấy điểm
B
. Đặt
là góc
giữa
AB
và đáy. Tính
tan
khi thể tích khối tứ diện
OO AB
đạt giá trị lớn nhất.
A.
1
tan
2
. B.
1
tan
2
. C.
tan 1
. D.
tan 2
.
Câu 35: Tìm số đường tiệm cận của đồ thị hàm số
1
4 3 1 3 5
x
y
x x
.
A.
1
.
B.
0
.
C.
2
.
D.
3
.
O
x
y
2
2
1
1
3
1
Trang 5/6 - Mã đề thi 345 - https://toanmath.com/
Câu 36: Cho hình chóp
.
S ABC
có đáy là
ABC
vuông cân ở
,B
2,
AC a
,SA ABC
.SA a
Gọi
G
là trọng tâm của
SBC
,
mp
đi qua
AG
và song song với
BC
chia khối chóp thành hai
phần. Gọi
V
là thể tích của khối đa diện không chứa đỉnh
S
. Tính
.V
A.
3
5
.
54
a
B.
3
4
.
9
a
C.
3
2
.
9
a
D.
3
4
.
27
a
Câu 37: Cho hình chóp
.
S ABC
có các cạnh
3
SA BC
;
4
SB AC
;
2 5
SC AB . Tính thể
tích khối chóp
.
S ABC
.
A.
390
12
. B.
390
6
. C.
390
8
. D.
390
4
.
Câu 38: Trong không gian
Oxyz
, lấy điểm
C
trên tia
Oz
sao cho
1
OC
. Trên hai tia
lần
lượt lấy hai điểm
,A B
thay đổi sao cho
OA OB OC
. Tìm giá trị nhỏ nhất của bán kính mặt cầu
ngoại tiếp tứ diện
.
O ABC
?
A.
6
.
4
B.
6.
C.
6
.
3
D.
6
.
2
Câu 39: Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
A
,
1cm
AB
,
3cm
AC . Tam
giác
SAB
,
SAC
lần lượt vuông tại
B
và
C
. Khối cầu ngoại tiếp hình chóp
.
S ABC
có thể tích
bằng
3
5 5
cm
6
. Tính khoảng cách từ
C
tới
SAB
A.
3
. B.
5
. C.
3
. D.
5
.
Câu 40: Cho hàm số
y f x
có đạo hàm liên tục trên đoạn
0;1
và thỏa mãn
0 0
f
. Biết
1
2
0
9
d
2
f x x
và
1
0
3
cos d
2 4
x
f x x
. Tích phân
1
0
df x x
bằng
A.
6
. B.
2
. C.
4
. D.
1
.
Câu 41: Tìm tất cả các giá trị thực của tham số
m
để phương trình
3 2 2
2 1 1 1
m m
e e x x x x
có nghiệm.
A.
1
ln 2;
2

. B.
1
0; ln 2
2
. C.
1
; ln 2
2

. D.
1
0;
e
.
Câu 42: Cho hàm số
y f x
có đạo hàm cấp hai trên
. Biết
0 3
f
,
2 2018
f
và bảng
xét dấu của
f x
như sau:
Hàm số
2017 2018y f x x
đạt giá trị nhỏ nhất tại điểm
0
x
thuộc khoảng nào sau đây?
A.
0;2
. B.
; 2017

. C.
2017;0
. D.
2017;

.
Câu 43: Có bao nhiêu giá trị nguyên của tham số
m
thuộc khoảng
2019;2019
để hàm số
3 2
sin 3cos sin 1y x x m x
đồng biến trên đoạn
0;
2
.
A.
2020
. B.
2019
. C.
2028
. D.
2018
.
Trang 6/6 - Mã đề thi 345 - https://toanmath.com/
Câu 44: Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn có dạng
abcd
,
trong đó
1 9
a b c d
.
A.
0,079
. B.
0,055
. C.
0,014
. D.
0,0495
.
Câu 45: Xét các số thực dương
x
,
y
thỏa mãn
2
1 1 1
2 2 2
log log log
x y x y
. Tìm giá trị nhỏ nhất
min
P
của biểu thức
3P x y
.
A.
min
17
2
P
. B.
min
8
P
. C.
min
9
P
. D.
min
25 2
4
P
.
Câu 46: Cho hàm số
f x
liên tục trên
thỏa mãn
2 3
f x f x
,
x
. Biết rằng
1
0
d 1f x x
. Tính tích phân
2
1
dI f x x
.
A.
3
I
. B.
5
I
. C.
2I
. D.
6
I
.
Câu 47: Tìm tập
S
tất cả các giá trị thực của tham số
m
để tồn tại duy nhất cặp số
;x y
thỏa mãn
2 2
2
2
log 4 4 6 1
x y
x y m
và
2 2
2 4 1 0
x y x y
.
A.
5;5
S
B.
7; 5; 1;1;5;7
S
.
C.
5; 1;1;5
S
D.
1;1
S
.
Câu 48: Có tất cả bao nhiêu giá trị nguyên của tham số
a
thuộc khoảng
0;2019
để
1
9 3 1
lim
5 9 2187
n n
n n a
?
A.
2018
. B.
2011
. C.
2012
. D.
2019
.
Câu 49: Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
SA ABC
, góc giữa đường
thẳng
SB
và mặt phẳng
ABC
bằng
60
. Tính khoảng cách giữa hai đường thẳng
AC
và
SB
.
A.
15
5
a
. B.
2
2
a
. C.
7
7
a
. D.
2a
.
Câu 50: Cho hàm số
y f x
có đạo hàm trên
và có đồ thị là đường cong trong hình vẽ dưới.
Đặt
g x f f x
. Tìm số nghiệm của phương trình
0
g x
.
A.
8
. B.
4
. C.
6
. D.
2
.
----------- HẾT ----------
O
1
2
3
4
4
3
2
1
1
2
1
2
3
x
y
5
6
7
Trang 1/7 - Mã đề thi 678
SỞ GIÁO DỤC VÀ ĐÀO TẠO VĨNH PHÚC
TRƯỜNG THPT CHUYÊN VĨNH PHÚC
(Đề thi có 6 trang)
ĐỀ KSCL CÁC MÔN THI THPT QUỐC GIA - LẦN 3
NĂM HỌC 2018-2019
MÔN TOÁN 12
Thời gian làm bài: 90 phút;
(Không kể thời gian giao đề)
Mã đề thi 678
Họ, tên thí sinh:..........................................................................
Số báo danh:...............................................................................
Câu 1: Cho hàm số
( )
y fx=
có bảng biến thiên như sau:
Hàm số đạt cực đại tại điểm nào trong các điểm sau đây?
A.
3.x =
B.
2.x
=
C.
2.x = −
D.
4.x =
Câu 2: Tập nghiệm của bất phương trình
21
2
1
1
1
x
a
+

>

+

(với
a
là tham số,
0a ≠
) là
A.
1
;
2

−∞ −


. B.
( )
0; +∞
. C.
( )
;0−∞
. D.
1
;
2

− +∞


.
Câu 3: Cho hình chóp
.S ABCD
có đáy là hình thang vuông tại
A
và
B
. Biết
( )
SA ABCD⊥
,
AB BC a= =
,
2AD a=
,
2SA a=
. Gọi
E
là trung điểm của
AD
. Tính bán kính mặt cầu đi qua
các điểm
S
,
A
,
B
,
C
,
E
.
A.
6
3
a
. B.
3
2
a
. C.
30
6
a
. D.
a
.
Câu 4: Tìm nguyên hàm của hàm số
2
1
3yx x
x
=−+
.
A.
32
3
ln
32
xx
xC−− +
. B.
32
3
ln
32
xx
xC−++
.
C.
32
2
31
32
xx
C
x
− ++
. D.
32
3
ln
32
xx
xC−+ +
.
Câu 5: Cho cấp số cộng
( )
n
u
có
và công sai
4d =
. Hãy tính
99
u
.
A.
404
. B.
402
. C.
401
. D.
403
.
Câu 6: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
0;10
và
( )
10
0
d7
fx x=
∫
và
(
)
6
2
d3fx x=
∫
. Tính
( ) ( )
2 10
06
ddP fx x fx x= +
∫∫
.
A.
4P
=
. B.
. C.
7P =
. D.
10P =
.
Câu 7: Cho hình chóp
.S ABC
có đáy là tam giác cân tại
A
,
AB AC a= =
,
120BAC = °
. Tam giác
SAB
là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích
V
của khối chóp
.S ABC
.
A.
3
8
a
V =
. B.
3
Va=
. C.
3
2
a
V =
. D.
3
2Va=
.
Câu 8: Cho hàm số
( )
y fx=
xác định và liên tục trên
R
, có bảng biến thiên như sau:
x
−∞
2
4
+∞
y
′
+
0
−
0
+
y
−∞
3
2−
+∞
Trang 2/7 - Mã đề thi 678
Mệnh đề nào sau đây là đúng ?
A. Hàm số đồng biến trên khoảng
( )
1;− +∞
. B. Hàm số đồng biến trên khoảng
( )
;2−∞ −
.
C. Hàm số nghịch biến trên khoảng
. D. Hàm số nghịch biến trên khoảng
.
Câu 9: Cho hàm số
( )
y fx=
có đạo hàm trên
và đồ thị hàm số
( )
y fx
′
=
trên
như hình vẽ.
Mệnh đề nào sau đây là đúng?
A. Hàm số
(
)
y fx=
có 1 điểm cực tiểu và không có cực đại.
B. Hàm số
(
)
y fx
=
có 1 điểm cực đại và không có cực tiểu.
C. Hàm số
( )
y fx=
có 1 điểm cực đại và 2 điểm cực tiểu.
D. Hàm số
( )
y fx=
có 1 điểm cực đại và 1 điểm cực tiểu.
Câu 10: Hàm số
43
2019yx x x= − −+
có bao nhiêu điểm cực trị?
A.
3
.
B.
0
.
C.
1
.
D.
2
.
Câu 11: Có bao nhiêu số hạng trong khai triển nhị thức
( )
2018
23x −
thành đa thức
A.
2018
. B.
2019
. C.
2017
. D.
2020
.
Câu 12: Một người gửi tiết kiệm số tiền
80000000
đồng với lãi suất là
6,9
%/ năm. Biết rằng tiền
lãi hàng năm được nhập vào tiền gốc, hỏi sau đúng
5
năm người đó có rút được cả gốc và lãi số tiền
gần với con số nào nhất sau đây?
A.
105 370 000
đồng.
B.
107 667 000
đồng.
C.
111 680 000
đồng.
D.
116 570 000
đồng.
Câu 13: Tìm
a
để hàm số
( )
2
1
khi 1
1
khi 1
x
x
fx
x
ax
−
≠
=
−
=
liên tục tại điểm
0
1
x =
.
A.
1a =
. B.
0a
=
. C.
2a =
. D.
1a = −
.
Câu 14: Hàm số
32
31yx x=−+ −
có đồ thị nào trong các đồ thị dưới đây?
Hình
1
Hình
2
Hình
3
Hình
4
A. Hình
3
. B. Hình
1
. C. Hình
4
. D. Hình
2
.
1
−
2
1
x
y
O
x
−∞
1
−
1
+∞
y
′
+
0
−
0
+
y
−∞
2
1−
+∞
Trang 3/7 - Mã đề thi 678
Câu 15: Hàm số nào dưới đây nghịch biến trên tập xác định của nó?
A.
3
logyx=
. B.
4
log
yx=
π
. C.
( )
2
log 1yx= +
. D.
3
x
y

=


π
.
Câu 16: Gọi
0
x
là nghiệm dương nhỏ nhất của phương trình
22
3sin 2sin cos cos 0x xx x+ −=
. Chọn
khẳng định đúng?
A.
0
;
2
x

∈


π
π
. B.
0
3
;
2
x

∈


π
π
. C.
0
0;
2
x

∈


π
. D.
0
3
;2
2
x

∈


π
π
.
Câu 17: Có bao nhiêu giá trị nguyên của tham số
m
trên đoạn
[ ]
2018; 2018−
để hàm số
(
)
2
ln 2 1
y x xm
= − −+
có tập xác định là
.
A.
2018
. B.
1009
. C.
2019
. D.
2017
.
Câu 18: Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng?
A.
6
. B.
4
. C.
2.
D.
8
.
Câu 19: Cho
(
) ( ) ( )
6 87
232d 32 32xx x Ax Bx C
− = −+ −+
∫
với
,,ABC R∈
. Tính giá trị của biểu
thức
12 7AB+
.
A.
241
252
. B.
52
9
. C.
23
252
. D.
7
9
.
Câu 20: Cho hình trụ có thiết diện đi qua trục là một hình vuông có cạnh bằng
4a
. Diện tích xung
quanh của hình trụ là
A.
2
24Sa
π
=
. B.
2
16Sa
π
=
. C.
2
8Sa
π
=
. D.
2
4
Sa
π
=
.
Câu 21: Cho tứ diện
ABCD
có hai mặt
ABC
và
ABD
là các tam giác đều. Tính góc giữa hai đường
thẳng
AB
và
CD
.
A.
90°
. B.
30°
. C.
120°
. D.
60°
.
Câu 22: Tìm tất cả các giá trị của tham số
m
để giá trị nhỏ nhất của hàm số
32
3
y x xm=−− +
trên
đoạn
[ ]
1;1−
bằng 0.
A.
2
m
=
.
B.
6m =
.
C.
0m
=
.
D.
4m
=
.
Câu 23: Giá trị lớn nhất của hàm số
(
)
3
x
fx
x
=
+
trên đoạn
[
]
2;3−
bằng
A.
1
2
. B.
2−
. C.
3
. D.
2
.
Câu 24: Cho hàm số
(
)
y fx=
xác định trên
có đồ thị của hàm số
( )
y fx
′
=
như hình vẽ. Hỏi
hàm số
( )
y fx=
đồng biến trên khoảng nào dưới đây?
A.
( )
0;1
và
( )
2; +∞
.
B.
( )
0;1
.
C.
(
)
2; +∞
.
D.
( )
1; 2
.
Câu 25: Trong không gian với hệ trục tọa độ
,Oxyz
cho
23a i jk=−+ −

. Tìm tọa độ của vectơ
a
.
A.
( )
3; 2; 1 .−−
B.
( )
1; 2; 3 .−−
C.
( )
2;3;1.−−
D.
( )
2;1;3.−−
Câu 26: Tìm tập nghiệm của phương trình
2
2
31
xx+
=
.
A.
{ }
1; 3 .S = −
B.
{ }
0; 2S =
. C.
{ }
0; 2 .S = −
D.
{ }
1; 3S = −
.
O
x
y
1
2
Trang 4/7 - Mã đề thi 678
Câu 27: Trong không gian với hệ tọa độ
Oxyz
, cho
( )
1;0;0A −
,
( )
0; 0; 2B
,
( )
0; 3; 0C −
. Tính bán
kính mặt cầu ngoại tiếp tứ diện
OABC
là
A.
14
3
. B.
14
4
. C.
14
2
. D.
14
.
Câu 28: Cho hàm số
( )
=
y fx
xác định, liên tục trên
và có bảng biến thiên như sau
Khẳng định nào sau đây là đúng?
A. Hàm số có giá trị cực tiểu bằng 3.
B. Hàm số đạt cực đại tại
1
=x
và đạt cực tiểu tại
3=x
.
C. Hàm số có đúng một cực trị.
D. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng 1.
Câu 29: Cho khối lăng trụ
.ABC A B C
′′′
có thể tích bằng
V
. Tính thể tích khối đa diện
ABCB C
′′
.
A.
4
V
. B.
2
V
. C.
3
4
V
. D.
2
3
V
.
Câu 30: Gọi
n
là số nguyên dương sao cho
23
33
33 3
1 1 1 1 190
...
log log log log log
n
x x x xx
+ + ++ =
đúng với
mọi
x
dương,
1x ≠
. Tìm giá trị của biểu thức
23Pn= +
.
A.
32=
P
. B.
23=P
. C.
43=P
. D.
41P =
.
Câu 31: Cho hình chóp
.S ABC
có các cạnh
3SA BC= =
;
4SB AC= =
;
25
SC AB= =
. Tính thể
tích khối chóp
.S ABC
.
A.
390
4
. B.
390
6
. C.
390
12
. D.
390
8
.
Câu 32: Trong không gian
Oxyz
, lấy điểm
C
trên tia
Oz
sao cho
1OC =
. Trên hai tia
lần
lượt lấy hai điểm
,AB
thay đổi sao cho
OA OB OC+=
. Tìm giá trị nhỏ nhất của bán kính mặt cầu
ngoại tiếp tứ diện
.O ABC
?
A.
6
.
2
B.
6.
C.
6
.
3
D.
6
.
4
Câu 33: Cho hàm số
y fx
có đạo hàm liên tục trên đoạn
[ ]
0;1
và thỏa mãn
( )
00f =
. Biết
( )
1
2
0
9
d
2
f xx=
∫
và
( )
1
0
3
cos d
24
x
fx x
ππ
′
=
∫
. Tích phân
( )
1
0
dfx x
∫
bằng
A.
2
π
. B.
1
π
. C.
6
π
. D.
4
π
.
Câu 34: Có bao nhiêu số tự nhiên có 4 chữ số được viết từ các chữ số
1
,
2
,
3
,
4
,
5
,
6
,
7
,
8
,
9
sao
cho số đó chia hết cho
15
?
A.
132
. B.
234
. C.
432
D.
243
.
Câu 35: Cho hàm số
( )
y fx=
có đạo hàm trên
và có đồ thị là đường cong trong hình vẽ dưới.
Đặt
( ) ( )
gx f f x
=


. Tìm số nghiệm của phương trình
( )
0gx
′
=
.
x
−∞
1
3
+∞
y
′
+
0
−
+
y
2
+∞
Trang 5/7 - Mã đề thi 678
A.
8
. B.
2
. C.
6
. D.
4
.
Câu 36: Cho hàm số
( )
y fx=
có đạo hàm cấp hai trên
. Biết
( )
03f
′
=
,
( )
2 2018f
′
= −
và bảng
xét dấu của
(
)
fx
′′
như sau:
Hàm số
(
)
2017 2018y fx x
=++
đạt giá trị nhỏ nhất tại điểm
0
x
thuộc khoảng nào sau đây?
A.
(
)
2017;0−
. B.
( )
0; 2
. C.
( )
; 2017
−∞ −
. D.
( )
2017;+∞
.
Câu 37: Cho hình trụ có đáy là hai đường tròn tâm
O
và
O
′
, bán kính đáy bằng chiều cao và bằng
2a
. Trên đường tròn đáy có tâm
O
lấy điểm
A
, trên đường tròn tâm
O
′
lấy điểm
B
. Đặt
α
là góc
giữa
AB
và đáy. Tính
tan α
khi thể tích khối tứ diện
OO AB
′
đạt giá trị lớn nhất.
A.
1
tan
2
α
=
. B.
1
tan
2
α
=
. C.
tan 1
α
=
. D.
tan 2
α
=
.
Câu 38: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
A
,
1cm
AB =
,
3cm
AC =
. Tam
giác
SAB
,
SAC
lần lượt vuông tại
B
và
C
. Khối cầu ngoại tiếp hình chóp
.S ABC
có thể tích
bằng
3
55
cm
6
π
. Tính khoảng cách từ
C
tới
(
)
SAB
A.
. B.
. C.
. D.
.
Câu 39: Tìm tập
S
tất cả các giá trị thực của tham số
m
để tồn tại duy nhất cặp số
( )
;xy
thỏa mãn
( )
22
2
2
log 4 4 6 1
xy
xy m
++
+ −+ ≥
và
22
2 4 10xy xy+ + − +=
.
A.
{ }
5; 1;1; 5S
=−−
B.
{
}
1;1S
= −
.
C.
{ }
5; 5S = −
D.
{ }
7; 5; 1;1; 5; 7S =−−−
.
Câu 40: Cho hình chóp
.S ABC
có đáy là
ABC∆
vuông cân ở
,B
2,AC a=
( )
,SA ABC⊥
.SA a=
Gọi
G
là trọng tâm của
SBC∆
,
( )
mp
α
đi qua
AG
và song song với
BC
chia khối chóp thành hai
phần. Gọi
V
là thể tích của khối đa diện không chứa đỉnh
S
. Tính
.V
A.
3
4
.
9
a
B.
3
4
.
27
a
C.
3
5
.
54
a
D.
3
2
.
9
a
Câu 41: Tìm tất cả các giá trị thực của tham số
m
để phương trình
(
)
(
)
3 22
2 1 11
+= +− + −
mm
ee x x x x
có nghiệm.
A.
1
0;



e
. B.
1
0; ln 2
2



. C.
1
; ln 2
2

−∞

. D.
1
ln 2;
2

+∞

.
O
1
2
3
4
4−
3−
2−
1−
1−
2−
1
2
3
x
y
5−
6−
7−
Trang 6/7 - Mã đề thi 678
Câu 42: Cho hàm số
( )
y fx=
liên tục trên
và có đồ thị như hình vẽ. Hỏi đồ thị hàm số
( )
y fx
=
có tất cả bao nhiêu điểm cực trị?
A.
8
B.
6
C.
9
D.
7
.
Câu 43: Có tất cả bao nhiêu giá trị nguyên của tham số
a
thuộc khoảng
( )
0;2019
để
1
93 1
lim
5 9 2187
nn
n na
+
+
+
≤
+
?
A.
2018
. B.
2012
. C.
2019
. D.
2011
.
Câu 44: Cho hàm số
(
)
fx
liên tục trên
thỏa mãn
( ) ( )
23f x fx=
,
x∀∈
. Biết rằng
(
)
1
0
d1fx x=
∫
. Tính tích phân
( )
2
1
d
I fx x=
∫
.
A.
2
I =
. B.
5I =
. C.
6I =
. D.
3I =
.
Câu 45: Tìm số đường tiệm cận của đồ thị hàm số
1
43 1 3 5
x
y
xx
−
=
+− −
.
A.
2
.
B.
3
.
C.
1
.
D.
0
.
Câu 46: Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn có dạng
abcd
,
trong đó
19
abcd
≤≤≤≤ ≤
.
A.
0,079
. B.
0,0495
. C.
0,055
. D.
0,014
.
Câu 47: Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
( )
SA ABC⊥
, góc giữa đường
thẳng
SB
và mặt phẳng
( )
ABC
bằng
60°
. Tính khoảng cách giữa hai đường thẳng
AC
và
SB
.
A.
2
2
a
. B.
2a
. C.
7
7
a
. D.
15
5
a
.
Câu 48: Có bao nhiêu giá trị nguyên của tham số
m
thuộc khoảng
( )
2019;2019−
để hàm số
32
sin 3cos sin 1y x xm x=− −−
đồng biến trên đoạn
0;
2
π



.
A.
2028
. B.
2020
. C.
2019
. D.
2018
.
Câu 49: Xét các số thực dương
x
,
y
thỏa mãn
( )
2
11 1
22 2
log log logx y xy+≤ +
. Tìm giá trị nhỏ nhất
min
P
của biểu thức
3Px y= +
.
A.
min
8P =
. B.
min
17
2
P
=
. C.
min
25 2
4
P =
. D.
min
9P =
.
Câu 50: Biết
( )
Fx
là nguyên hàm của hàm số
( )
2
cosxx
fx
x
−
=
. Hỏi đồ thị của hàm số
( )
y Fx=
có bao nhiêu điểm cực trị?
A.
1
. B. 2. C. vô số điểm. D. 0.
----------- HẾT ----------
O
x
y
2−
2
1
1−
3
1−
Trang 7/7 - Mã đề thi 678
BẢNG ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
B
A
D
D
D
A
A
B
A
C
B
C
C
B
B
C
A
B
D
B
A
D
A
C
B
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
C
C
B
D
D
A
D
C
D
A
C
B
A
B
C
C
D
B
B
A
C
D
C
D
A
ST
RONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang
1
Tổng biên tập: Thầy Nguyễn Việt Hải- Admin STRONG, Gv Chuyên Quang Trung, Bình Phước
Câu 1: Hàm số
3
2
3 1
y x x
có đồ thị nào trong các đồ thị dưới đây?
Hình
1
Hình
2
Hình
3
Hình
4
A. Hình
3
. B. Hình
4
. C. Hình
2
. D. Hình
1
.
Câu 2: Cho hình chóp
.
S
ABCD
có đáy là hình thang vuông tại
A
và
B
. Biết
SA ABCD
,
AB BC a
,
2AD a
,
2SA a
. Gọi
E
là trung điểm của
AD
. Tính bán kính mặt cầu đi qua các
điểm
S
,
A
,
B
,
C
,
E
.
A.
30
6
a
. B.
a
. C.
3
2
a
. D.
6
3
a
.
Câu 3: Gọi
0
x
là nghiệm dương nhỏ nhất của phương trình
2 2
3
sin 2sin cos cos 0
x
x x x
. Chọn
khẳng định đúng?
A.
0
3
;
2
x
. B.
0
;
2
x
. C.
0
0;
2
x
. D.
0
3
;2
2
x
.
Câu 4: Cho hàm số
y
f x
có bảng biến thiên như sau:
+
2
+
3
+
+
2
y
y'
x
4
0
0
Hàm số đạt cực đại tại điểm nào trong các điểm sau đây?
A.
2.
x
B.
2.
x
C.
3.
x
D.
4.
x
SỞ GD VÀ ĐÀ
O TẠO VĨNH PHÚC
THPT CHUYÊN VĨNH PHÚC
(Đề thi có 6 trang)
THI THỬ ĐẠI HỌC THPTQG
NĂM HỌC 2018 - 2019
MÔN: TOÁN
Thời gian: 90 phút
MÃ ĐỀ: 123
Bản quyền thuộc về tập thể thầy cô STRONG.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 2
Câu 5: Có bao nhiêu giá trị nguyên của tham số
m
trên đoạn
2018;2018
để hàm số
2
ln 2 1
y x x m
có tập xác định là
.
A.
2019
. B.
2017
. C.
2018
. D.
1009
.
Câu 6: Cho hình trụ có thiết diện đi qua trục là một hình vuông có cạnh bằng
4a
. Diện tích xung quanh
của hình trụ là
A.
2
8
S a
. B.
2
24
S a
. C.
2
16
S a
. D.
2
4
S a
.
Câu 7: Cho hàm số
y f x
có đạo hàm trên
và đồ thị hàm số
y f x
trên
như hình vẽ.
Mệnh đề nào sau đây là đúng?
A. Hàm số
y f x
có 1 điểm cực tiểu và không có cực đại.
B. Hàm số
y f x
có 1 điểm cực đại và 2 điểm cực tiểu.
C. Hàm số
y f x
có 1 điểm cực đại và không có cực tiểu.
D. Hàm số
y f x
có 1 điểm cực đại và 1 điểm cực tiểu.
Câu 8: Cho hàm số
y f x
xác định trên
có đồ thị của hàm số
y f x
như hình vẽ. Hỏi hàm số
y f x
đồng biến trên khoảng nào dưới đây?
A.
2;

.
B.
1;2
.
C.
0;1
.
D.
0;1
và
2;

.
Câu 9: Tìm
a
để hàm số
2
1
khi 1
1
khi 1
x
x
f x
x
a x
liên tục tại điểm
0
1
x
.
A.
1
a
. B.
0
a
. C.
2
a
. D.
1
a
.
Câu 10: Trong không gian với hệ trục tọa độ
,Oxyz
cho
2 3a i j k
. Tìm tọa độ của vectơ
a
.
A.
2; 1; 3 .
B.
3;2; 1 .
C.
2; 3; 1 .
D.
1;2; 3 .
Câu 11: Một người gửi tiết kiệm số tiền
80000000
đồng với lãi suất là
6,9
%/ năm. Biết rằng tiền lãi
hàng năm được nhập vào tiền gốc, hỏi sau đúng
5
năm người đó có rút được cả gốc và lãi số tiền gần với
con số nào nhất sau đây?
A.
105370000
đồng. B.
11680000
đồng. C.
107667000
đồng. D.
116570000
đồng.
O
x
y
1
2
1
2
1
x
y
O
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 3
Câu 12: Cho tứ diện
ABCD
có hai mặt
ABC
và
ABD
là các tam giác đều. Tính góc giữa hai đường
thẳng
AB
và
CD
.
A.
120
. B.
60
. C.
90
. D.
30
.
Câu 13: Cho hàm số
f x
liên tục trên đoạn
0;10
và
10
0
d 7
f x x
và
6
2
d 3
f x x
. Tính
2 10
0 6
d dP f x x f x x
.
A.
4P
. B.
10
P
. C.
7
P
. D.
.
Câu 14: Tìm tất cả các giá trị của tham số
m
để giá trị nhỏ nhất của hàm số
3 2
3
y x x m
trên đoạn
1;1
bằng 0.
A.
0
m
.
B.
6
m
.
C.
2
m
.
D.
4
m
.
Câu 15: Tìm tập nghiệm của phương trình
2
2
3 1
x x
.
A.
1; 3 .
S
B.
1;3
S
. C.
0;2
S
. D.
0; 2 .
S
Câu 16: Hàm số
4 3
2019
y x x x có bao nhiêu điểm cực trị?
A.
2
.
B.
3
.
C.
0
.
D.
1
.
Câu 17: Tìm nguyên hàm của hàm số
2
1
3y x x
x
.
A.
3 2
3
ln
3 2
x x
x C
. B.
3 2
3
ln
3 2
x x
x C
.
C.
3 2
3
ln
3 2
x x
x C
. D.
3 2
2
3 1
3 2
x x
C
x
.
Câu 18: Cho cấp số cộng
n
u
có
1
u
và công sai
4
d
. Hãy tính
99
u
.
A.
401
. B.
404
. C.
403
. D.
402
.
Câu 19: Cho hình chóp
.
S ABC
có đáy là tam giác cân tại
A
,
AB AC a
,
120
BAC
. Tam giác
SAB
là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích
V
của khối chóp
.
S ABC
.
A.
3
V a
. B.
3
8
a
V . C.
3
2
a
V . D.
3
2V a
.
Câu 20: Giá trị lớn nhất của hàm số
3
x
f x
x
trên đoạn
2;3
bằng
A.
3
. B.
2
. C.
1
2
. D.
2
.
Câu 21: Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng?
A.
2.
B.
4
. C.
6
. D.
8
.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 4
Câu 22: Gọi
n
là số nguyên dương sao cho
2 3
3 3
3 3 3
1 1 1 1 190
...
log log log log log
n
x x x x x
đúng với mọi
x
dương,
1
x
. Tìm giá trị của biểu thức
2 3
P n
.
A.
32
P
. B.
23
P
. C.
43
P
. D.
41P
.
Câu 23: Hàm số nào dưới đây nghịch biến trên tập xác định của nó?
A.
3
log
y x
. B.
2
log 1
y x
. C.
4
logy x
. D.
3
x
y
.
Câu 24: Tập nghiệm của bất phương trình
2 1
2
1
1
1
x
a
(với
a
là tham số,
0
a
) là
A.
;0

. B.
1
;
2

. C.
0;
. D.
1
;
2
.
Câu 25: Có bao nhiêu số hạng trong khai triển nhị thức
2018
2 3x
thành đa thức
A.
2018
. B.
2019
. C.
2020
. D.
2017
.
Câu 26: Cho hàm số
y f x
xác định, liên tục trên
và có bảng biến thiên như sau
Khẳng định nào sau đây là đúng?
A. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng 1.
B. Hàm số có đúng một cực trị.
C. Hàm số đạt cực đại tại
1x
và đạt cực tiểu tại
3
x
.
D. Hàm số có giá trị cực tiểu bằng 3.
Câu 27: Cho khối lăng trụ
.
ABC A B C
có thể tích bằng
V
. Tính thể tích khối đa diện
ABCB C
.
A.
2
3
V
. B.
4
V
. C.
2
V
. D.
3
4
V
.
Câu 28: Trong không gian với hệ tọa độ
Oxyz
, cho
1;0;0
A
,
0;0;2
B
,
0; 3;0
C
. Tính bán kính
mặt cầu ngoại tiếp tứ diện
OABC
là
A.
14
3
. B.
14
4
. C.
14
2
. D.
14
.
Câu 29: Cho hàm số
y f x
xác định và liên tục trên
R
, có bảng biến thiên như sau:
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 5
Mệnh đề nào sau đây là đúng ?
A. Hàm số đồng biến trên khoảng
; 2
. B. Hàm số nghịch biến trên khoảng
.
C. Hàm số nghịch biến trên khoảng
1;
. D. Hàm số đồng biến trên khoảng
1;

.
Câu 30: Cho
6 8 7
2 3 2 d 3 2 3 2
x x x A x B x C
với , ,
A B C R
. Tính giá trị của biểu thức
12 7A B
.
A.
23
252
. B.
241
252
. C.
52
9
. D.
7
9
.
Câu 31: Có bao nhiêu số tự nhiên có 4 chữ số được viết từ các chữ số
1
,
2
,
3
,
4
,
5
,
6
,
7
,
8
,
9
sao cho
số đó chia hết cho
15
?
A.
234
. B.
132
. C.
243
. D.
432
Câu 32: Có bao nhiêu giá trị nguyên của tham số
m
thuộc khoảng
2019;2019
để hàm số
3 2
sin 3cos sin 1y x x m x
đồng biến trên đoạn
0;
2
.
A.
2028
. B.
2018
. C.
2020
. D.
2019
.
Câu 33: Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ. Hỏi đồ thị hàm số
y f x
có tất cả bao nhiêu điểm cực trị?
A.
6
B.
8
C.
7
. D.
9
Câu 34: Cho hình chóp
.
S ABC
có các cạnh
3
SA BC
;
4
SB AC
;
2 5
SC AB . Tính thể tích
khối chóp
.
S ABC
.
A.
390
12
. B.
390
4
. C.
390
6
. D.
390
8
.
Câu 35: Cho hình chóp
.
S ABC
có đáy là
ABC
vuông cân ở
,B
2,
AC a
,SA ABC
.SA a
Gọi
G
là trọng tâm của
SBC
,
mp
đi qua
AG
và song song với
BC
chia khối chóp thành hai phần. Gọi
V
là thể tích của khối đa diện không chứa đỉnh
S
. Tính
.V
A.
3
5
.
54
a
B.
3
2
.
9
a
C.
3
4
.
27
a
D.
3
4
.
9
a
O
x
y
2
2
1
1
3
1
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 6
Câu 36: Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
SA ABC
, góc giữa đường
thẳng
SB
và mặt phẳng
ABC
bằng
60
. Tính khoảng cách giữa hai đường thẳng
AC
và
SB
.
A.
15
5
a
. B.
2
2
a
. C.
2a
. D.
7
7
a
.
Câu 37: Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
A
,
1cm
AB
,
3cm
AC . Tam giác
SAB
,
SAC
lần lượt vuông tại
B
và
C
. Khối cầu ngoại tiếp hình chóp
.
S ABC
có thể tích
bằng
3
5 5
cm
6
. Tính khoảng cách từ
C
tới
SAB
A.
5
. B.
5
. C.
3
. D.
3
.
Câu 38: Cho hàm số
f x
liên tục trên
thỏa mãn
2 3
f x f x
,
x
. Biết rằng
1
0
d 1f x x
.
Tính tích phân
2
1
dI f x x
.
A.
5
I
. B.
6
I
. C.
3
I
. D.
2I
.
Câu 39: Tìm số đường tiệm cận của đồ thị hàm số
1
4 3 1 3 5
x
y
x x
.
A.
3
.
B.
2
.
C.
1
.
D.
0
.
Câu 40: Trong không gian
Oxyz
, lấy điểm
C
trên tia
Oz
sao cho
1
OC
. Trên hai tia
lần lượt
lấy hai điểm
,A B
thay đổi sao cho
OA OB OC
. Tìm giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp
tứ diện
.
O ABC
?
A.
6
.
4
B.
6.
C.
6
.
3
D.
6
.
2
Câu 41: Cho hàm số
y f x
có đạo hàm cấp hai trên
. Biết
0 3
f
,
2 2018
f
và bảng xét
dấu của
f x
như sau:
Hàm số
2017 2018y f x x
đạt giá trị nhỏ nhất tại điểm
0
x
thuộc khoảng nào sau đây?
A.
; 2017

. B.
2017;

. C.
0;2
. D.
2017;0
.
Câu 42: Cho hàm số
y f x
có đạo hàm liên tục trên đoạn
0;1
và thỏa mãn
0 0
f
. Biết
1
2
0
9
d
2
f x x
và
1
0
3
cos d
2 4
x
f x x
. Tích phân
1
0
df x x
bằng
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 7
A.
2
. B.
4
. C.
1
. D.
6
.
Câu 43: Biết
F x
là nguyên hàm của hàm số
2
cosx x
f x
x
. Hỏi đồ thị của hàm số
y F x
có
bao nhiêu điểm cực trị?
A. vô số điểm. B. 0. C.
1
. D. 2.
Câu 44: Tìm tất cả các giá trị thực của tham số
m
để phương trình
3 2 2
2 1 1 1
m m
e e x x x x
có nghiệm.
A.
1
0; ln 2
2
. B.
1
; ln 2
2

. C.
1
0;
e
. D.
1
ln 2;
2

.
Câu 45: Tìm tập
S
tất cả các giá trị thực của tham số
m
để tồn tại duy nhất cặp số
;x y
thỏa mãn
2 2
2
2
log 4 4 6 1
x y
x y m
và
2 2
2 4 1 0
x y x y
.
A.
1;1
S
. B.
5; 1;1;5
S
C.
5;5
S
D.
7; 5; 1;1;5;7
S
.
Câu 46: Cho hình trụ có đáy là hai đường tròn tâm
O
và
O
, bán kính đáy bằng chiều cao và bằng
2a
.
Trên đường tròn đáy có tâm
O
lấy điểm
A
, trên đường tròn tâm
O
lấy điểm
B
. Đặt
là góc giữa
AB
và đáy. Tính
tan
khi thể tích khối tứ diện
OO AB
đạt giá trị lớn nhất.
A.
tan 2
. B.
1
tan
2
. C.
1
tan
2
. D.
tan 1
.
Câu 47: Xét các số thực dương
x
,
y
thỏa mãn
2
1 1 1
2 2 2
log log log
x y x y
. Tìm giá trị nhỏ nhất
min
P
của biểu thức
3P x y
.
A.
min
9
P
. B.
min
8
P
. C.
min
25 2
4
P
. D.
min
17
2
P
.
Câu 48: Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn có dạng
abcd
,
trong đó
1 9
a b c d
.
A.
0,014
. B.
0,0495
. C.
0,079
. D.
0,055
.
Câu 49: Có tất cả bao nhiêu giá trị nguyên của tham số
a
thuộc khoảng
0;2019
để
1
9 3 1
lim
5 9 2187
n n
n n a
?
A.
2011
. B.
2018
. C.
2019
. D.
2012
.
Câu 50: Cho hàm số
y f x
có đạo hàm trên
và có đồ thị là đường cong trong hình vẽ dưới. Đặt
g x f f x
. Tìm số nghiệm của phương trình
0
g x
.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 8
A.
2
. B.
8
. C.
4
. D.
6
.
-----------------------------------------------
----------- HẾT ----------
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 9
PHÂN TÍCH – GIẢI ĐỀ THI THỬ ĐẠI HỌC
THPTCHUYÊN VĨNH PHÚC LẦN 3 - NĂM 2018 – 2019
Câu 1. Hàm số
3 2
3 1
y x x
có đồ thị nào trong các đồ thị dưới đây?
x
y
x
y
Hình 2
Hình 1
2
-1
1
4
3
-1
2
O
1
-1
4
3
3
2-1
O
1
5
1
x
y
y
x
Hình 4Hình 3
2
3
-1
-3
-1
2
1
O
2
-2
1
-1
3
-1
2
O
1
1
A. Hình 3. B. Hình 1. C. Hình 2. D. Hình 4.
Lời giải.
Tác giả: Nguyễn Thị Nguyệt Cầm; Fb: Nguyet Cam Nguyen.
Chọn B.
Đồ thị hàm số đã cho cắt trục tung tại điểm có tung độ
1
.
Câu 2. Cho hình chóp
.
S ABCD
có đáy là hình thang vuông tại
A
và
B
. Biết
( )SA ABCD
,
AB BC a
,
2SA a
,
2AD a
. Gọi
E
là trung điểm của
AD
. Tính bán kính mặt cầu đi
qua các điểm
S
,
A
,
B
,
C
,
E
.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 10
A.
3
2
a
. B.
a
. C.
6
3
a
. D.
30
6
a
.
Lời giải.
Tác giả: Nguyễn Thị Nguyệt Cầm; Fb: Nguyet Cam Nguyen.
Chọn B.
Vì
90
SAC SBC SEC
nên mặt cầu đi qua các điểm
S
,
A
,
B
,
C
,
E
có đường kính
2 2
SC SA AC
2 2
2 2a a
2
4 2a a
. Do đó, mặt cầu có bán kính là
2
SC
R a
.
Câu 3. Gọi
0
x
là nghiệm dương nhỏ nhất của phương trình
2 2
3sin 2sin cos cos 0
x x x x
. Chọn
khẳng định đúng?
A.
0
3
;
2
x
. B.
0
;
2
x
. C.
0
0;
2
x
. D.
0
3
;2
2
x
.
Lời giải
Tác giả: Phạm Hoài Trung ; Fb: Phạm Hoài Trung
Chọn C
2 2
3sin 2sin cos cos 0
x x x x
2 2
3sin 3sin cos sin cos cos 0
x x x x x x
(3sin cos )(sin cos ) 0
x x x x
3sin cos 0
sin cos 0
x x
x x
3sin
1
cos
sin
1
cos
x
x
x
x
1
tan
3
tan 1
x
x
1
arctan
3
4
x k
x k
k
.
Do
0
x
là nghiệm dương nhỏ nhất của phương trình
2 2
3sin 2sin cos cos 0
x x x x
nên
E
S
A
D
B
C
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 11
0
1
arctan
3
x
.
Câu 4. Cho hàm số
y f x
có bảng biến thiên như sau:
+
2
+
3
+
+
2
y
y'
x
4
0
0
Hàm số đạt cực đại tại điểm nào trong các điểm sau đây?
A.
2
x
. B.
2
x
. C.
3
x
. D.
4
x
.
Lời giải
Tác giả: Phạm Hoài Trung ; Fb: Phạm Hoài Trung
Chọn B
Hàm số đạt cực đại tại điểm
2
x
.
Câu 5. Có bao nhiêu giá trị nguyên của tham số
m
trên
2018; 2018
để hàm số
2
ln 2 1
y x x m
có tập xác định là
?
A.
2019
. B.
2017
. C.
2018
. D.
1009
.
Lời giải.
Tác giả: Quỳnh Giao; Fb: QGiaoDo.
Chọn C.
Hàm số
2
ln 2 1
y x x m
có tập xác định là
khi và chỉ khi:
2
2 1 0 x x m x
' 0 1 1 0 0
m m
.
Kết hợp với điều kiện
m
nguyên thuộc
2018; 2018
ta có 2018 giá trị của
m
.
Câu 6. Cho hình trụ có thiết diện qua trục là hình vuông cạnh
4a
. Diện tích xung quanh của hình trụ là
A.
2
8
a
. B.
2
24
a
. C.
2
16
a
. . D.
2
4
a
.
Lờigiải.
Tác giả: Quỳnh Giao; Fb: QGiaoDo.
Chọn C.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 12
4a
O
O'
Thiết diện qua trục của hình trụ là hình vuông cạnh
4a
nên hình trụ có chiều cao
4h a
, bán
kính đáy
.
Vậy diện tích xung quanh của hình trụ là
2
2 16
S Rh a
.
Câu 7. Cho hàm số
y f x
có đạo hàm trên
và đồ thị hàm số
y f x
trên
như hình vẽ.
Mệnh đề nào sau đây là đúng?
x
y
2
1
-1
O
A. Hàm số
y f x
có 1 điểm cực tiểu và không có cực đại.
B. Hàm số
y f x
có 1 điểm cực đại và 2 điểm cực tiểu.
C. Hàm số
y f x
có 1 điểm cực đại và không có cực tiểu.
D. Hàm số
y f x
có 1 điểm cực đại và 1 điểm cực tiểu.
Lời giải.
Tác giả: Nguyễn Thị Thơm; Fb: Thơm nguyễn.
Chọn A.
Dựa vào hình vẽ ta thấy hàm số
y f x
đổi dấu một lần và đổi dấu từ âm sang dương nên
suy ra hàm số có một điểm cực tiểu và không có điểm cực đại.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 13
Câu 8. Cho hàm số
y f x
xác định trên
có đồ thị của hàm số
y f x
như hình vẽ. Hỏi hàm
số
y f x
đồng biến trên khoảng nào dưới đây?
x
y
21
O
A.
2;
. . B.
1;2
.
C.
0;1
. . D.
0;1
và
2;
.
Lời giải.
Tác giả: Nguyễn Thị Thơm; Fb: Thơm nguyễn.
Chọn A.
Ta có hàm số
y f x
đồng biến khi và chỉ khi
0
f x
.
Dựa vào đồ thị hàm số
'y f x
ta thấy
0 2
f x x
.
Vậy hàm số đồng biến trên
2;
.
Câu 9. Tìm
a
để hàm số
2
1
1
1
1
x
khi x
f x
x
a khi x
liên tục tại điểm
0
1
x
.
A.
1
a
. B.
0
a
. C.
2
a
. D.
1
a
.
Lời giải
Tác giả: Nguyễn Thị Thu Trang; Fb: Trang nguyễ
n
Chọn C
TXĐ:
0
1
D x D
.
Ta có :
1
f a
.
2
1 1 1
1 1
1
lim lim lim 1 2
1 1
x x x
x x
x
x
x x
.
Hàm số
f x
liên tục tại điểm
0
1
x
khi và chỉ khi
1
lim 1 2
x
f x f a
.
Câu 10. Trong không gian với hệ trục tọa độ
Oxyz
, cho
2 3a i j k
. Tìm tọa độ của
a
.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 14
A.
2; 1; 3
. B.
3;2; 1
. C.
2; 3; 1
. D.
1;2; 3
.
Lời giải
Tác giả: Nguyễn Thị Thu Trang; Fb: Trang nguyễ
n
Chọn D
Câu 11. Một người gửi tiết kiệm số tiền
80000000
đồng với lãi suất
6,9%
/ năm. Biết rằng tiền lãi
hàng năm được nhập vào tiền gốc, hỏi sau đúng 5 năm người đó rút được cả tiền gốc lẫn tiền lãi
gần với con số nào sau đây?
A.
105370000
đồng. B.
111680000
đồng. C.
107667000
đồng. D.
116570000
đồng.
Lời giải.
Tác giả: Văn Bùi Vũ; Fb: Van Tuan Vu.
Chọn B.
Gọi
0
P
là số tiền gửi ban đầu,
r
là lãi suất / năm.
Số tiền gốc và lãi sau năm thứ nhất:
1 0 0 0
. 1
P P P r P r
.
Số tiền gốc và lãi sau năm thứ hai:
2
2 1 1 0
. 1
P P P r P r
.
….
Số tiền gốc và lãi người đó rút ra được sau 5 năm là
5 5
5 0
. 1 80000000. 1 6,9% 111680799
P P r
(đồng).
Câu 12. Cho tứ diện
có hai mặt
ABC
và
ABD
là các tam giác đều. Tính góc giữa hai đường
thẳng
AB
và
CD
.
A.
120
. B.
60
. C.
90
. D.
30
.
Lời giải.
Tác giả: Văn Bùi Vũ; Fb: Van Tuan Vu.
Chọn C.
Cách 1.
E
B
C
D
A
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 15
Gọi
E
là trung điểm của
CD
. Ta có:
BCD
cân tại
B
, do đó
CD BE
.
ACD
cân tại
A
, do đó
CD AE
.
Suy ra
CD ABE
, mà
AB ABE
nên
CD AB
.
Vậy góc giữa hai đường thẳng
AB
và
CD
bằng
90
.
Cách 2.
Xét
.
AB CD AB AD AC
. .AB AD AB AC
cos cos 0
AB AD BAD AB AC BAC
.
( Vì
AB AD AC
,
60
BAD BAC
).
Vậy góc giữa hai đường thẳng
AB
và
CD
bằng
90
.
Câu 13. Cho hàm số
f x
liên tục trên đoạn
0;10
và
10
0
7
f x dx
;
6
2
3
f x dx
. Tính
2 10
0 6
P f x dx f x dx
.
A.
4P
. B.
10
P
. C.
7
P
. D.
.
Lời giải.
Tác giả: Lê Viết Thương; Fb: Lê Viết Thương.
Chọn A.
Ta có:
10 2 6 10
0 0 2 6
f x dx f x dx f x dx f x dx
.
7 3 4
P P
.
Câu 14. Tìm tất cả các giá trị của tham số
m
để giá trị nhỏ nhất của hàm số
3 2
3
y x x m
trên đoạn
1;1
bằng
0
.
A.
0
m
. B.
6
m
. C.
2
m
. D.
4
m
.
Lời giải.
Tác giả: Lê Viết Thương; Fb: Lê Viết Thương.
Chọn D.
3 2
3
y f x x x m
.
Ta có:
2
3 6y x x
.
0 1;1
0
2 1;1
x
y
x
.
1 2
f m
;
0
f m
;
1 4
f m
.
Ta thấy
4 min 1 ; 0 ; 1
m f f f
. Suy ra yêu cầu bài toán
4 0 4
m m
.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 16
Câu 15. Tìm tập nghiệm của phương trình
2
2
3 1
x x
.
A.
S 1; 3
. B.
1;3
S
C.
0;2
S
. D.
0; 2
S
.
Lời giải.
Tác giả: Nguyễn Phương; Fb: Nguyễn Phương.
Chọn D.
2
2 2
0
3 1 2 0
2
x x
x
x x
x
.
Vậy tập nghiệm của phương trình là
0; 2
S
.
Câu 16. Hàm số
4 3
2019
y x x x có bao nhiêu điểm cực trị?
A.
2
. B.
3
. C.
0
. . D.
1
.
Lời giải.
Tác giả: Nguyễn Phương; Fb: Nguyễn Phương.
Chọn D.
Ta có :
4 3
2019
y x x x .
3 2
4 3 1
y x x
.
0 1y x
.
Nhận xét:
1x
là nghiệm đơn của phương trình
0
y
, nên qua điểm
1x
,
y
đổi dấu.
Vậy hàm số
4 3
2019
y x x x có 1 điểm cực trị.
Câu 17. Tìm nguyên hàm của hàm số:
2
1
3y x x
x
.
A.
3 2
3
ln
3 2
x x
x C
. . B.
3 2
3
ln
3 2
x x
x C
.
C.
3 2
3
ln
3 2
x x
x C
. D.
3 2
2
3 1
3 2
x x
C
x
.
Lời giải.
Tác giả: Tống Thúy; Fb: Thuy Tong.
Chọn A.
Ta có:
2
1
3 dx x x
x
2
1
d 3 d dx x x x x
x
3 2
3
ln
3 2
x x
x C
.
Câu 18. Cho cấp số cộng
n
u
có
1
11
u
và công sai
4
d
. Hãy tính
99
u
.
A.
401
. B.
404
. C.
403
. D.
402
.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 17
Lời giải.
Tác giả: Tống Thúy; Fb: Thuy Tong.
Chọn C.
Ta có:
1
1
n
u u n d
,
1,
n n N
.
99 1
98.u u d
11 98.4 403
.
Vậy
99
403
u .
Câu 19. Cho hình chóp
.
S ABC
có đáy là tam giác cân tại
A
,
AB AC a
,
120
BAC
. Tam giác
SAB
là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích
V
của khối chóp
.
S ABC
.
A.
3
V a
. B.
3
8
a
V . C.
3
2
a
V . D.
3
2V a
Lời giải
Tác giả: Hoàng Thị Thúy; Fb: Thúy Hoàng
120°
a
a
H
S
B
C
A
Chọn B
Gọi
H
là trung điểm của
AB
SH AB
SH SAB
Ta có:
3
2
a
SH
,
2
1 3
. .sin
2 4
ABC
a
S AB AC BAC
Suy ra:
3
.
1
.S
3 8
S ABC ABC
a
V SH
Câu 20. Giá trị lớn nhất của hàm số
3
x
f x
x
trên đoạn
2;3
bằng
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 18
A. 3. B. 2 C.
1
2
. D.
2
.
Lời giải
Tác giả: Hoàng Thị Thúy; Fb: Thúy Hoàng
Chọn C
Ta có:
2
3
' 0
3
f x
x
,
2;3
x
Do đó hàm số
f x
đồng biến trên
2;3
Suy ra:
2;3
1
max 3
2
f x f
Câu 21. Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng?
A. 2. B. 4. C. 6. D. 8.
Lời giải.
Tác giả: Phạm Văn Tuấn; Fb: Phạm Tuấn.
Chọn B.
Hình chóp tứ giác đều có 4 mặt phẳng đối xứng.
S
A
B
C
D
D
C
B
A
S
S
A
B
C
D
S
A
B
C
D
MỞ RỘNG:
Mặt phẳng đối xứng của hình chóp tam giác đều (3 mặt phẳng)
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 19
B
C
D
A
A
D
C
B
A
D
C
B
Mặt phẳng đối xứng của tứ diện đều (6 mặt phẳng)
B
C
D
A
A
D
C
B
A
D
C
B
A
D
C
B
B
C
D
A
B
C
D
A
Câu 22. Gọi
n
là số nguyên dương sao cho
2 3
3 3
3 3 3
1 1 1 1 190
...
log log log log log
n
x x x x x
đúng với
mọi
x
dương,
1x
. Tìm giá trị của biểu thức
2 3P n
.
A.
32
P
. B.
23
P
. C.
43
P
. D.
41P
.
Lời giải.
Tác giả: Phạm Văn Tuấn; Fb: Phạm Tuấn.
Chọn D.
Ta có:
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 20
2 3
3 3
3 3 3
1 1 1 1 190
...
log log log log log
n
x x x x x
2 3
log 3 log 3 log 3 ... log 3 190.log 3
n
x x x x x
log 3 2.log 3 3.log 3 ... .log 3 190.log 3
x x x x x
n
1 2 3 ... log 3 190.log 3
x x
n
1
190
2
n n
19
20
n thoûa maõn
n loaïi
.
Vậy
P n2 3 41
.
Câu 23. Hàm số nào dưới đây nghịch biến trên tập xác định của nó?
A.
3
log
y x
. B.
2
log 1
y x
. C.
4
logy x
. D.
3
x
y
.
Lời giải
Tác giả: Phạm Hoài Tâm; Fb: Phạm Hoài Tâm
Chọn C
Xét hàm số
4
logy x
có tập xác định:
0;D

.
Nhận thấy cơ số
1
4
nên
4
logy x
nghịch biến trên tập xác định.
Câu 24. Tập nghiệm của bất phương trình
2 1
2
1
1
1
x
a
(với
a
là tham số,
0
a
) là:
A.
;0

. B.
1
;
2

. C.
0;
. D.
1
;
2
.
Lời giải
Tác giả: Phạm Hoài Tâm; Fb: Phạ
m Hoài Tâm
Chọn B
Ta có:
2 1 2 1 0
2 2 2
1 1 1
1
1 1 1
x x
a a a
1
.
Nhận thấy
2
1 1, 0
a a nên:
2
1
1
1
a
.
Khi đó bất phương trình
1
tương đương
1
2 1 0
2
x x
.
Vậy tập nghiệm của bất phương trình đã cho :
1
;
2
S

.
Câu 25. Có bao nhiêu số hạng trong khai triển nhị thức
2018
2 3x
thành đa thức.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 21
A.
2018
. B.
2019
. C.
2020
. D.
2017
.
Lời giải.
Tác giả: Nguyễn Việt Thảo; Fb: Việt Thảo.
Chọn B.
2018 2018 2017 2016 2 2018
0 1 2 2018
2018 2018 2018 2018
2 3 2 2 3 2 3 ... 3x C x C x C x C
.
Vậy khai triển trên có 2019 số hạng.
Câu 26. Cho hàm số
y f x
xác định, liên tục trên
và có bảng biến thiên như sau.
+
1
+
2
+
+
1
y
y'
x
3
0
Khẳng định nào sau đây là đúng?
A. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng 1. .
B. Hàm số có đúng một cực trị.
C. Hàm số đạt cực đại tại
1x
và đạt cực tiểu tại
3
x
.
D. Hàm số có giá trị cực tiểu bằng 3.
Lời giải.
Tác giả: Nguyễn Việt Thảo; Fb: Việt Thảo.
Chọn C.
Từ bảng biến thiên, ta dễ dàng thấy được A, B, D sai, C đúng.
Câu 27. Cho khối lăng trụ
.
ABC A B C
có thể tích bằng
V
. Tính thể tích khối đa diện
ABCC B
.
A.
2
3
V
. B.
4
V
. C.
2
V
. D.
3
4
V
.
Lời giải.
Tác giả: Vũ Nga; Fb: Nga Vu.
Chọn A.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 22
Gọi
S
,
h
lần lượt là diện tích đáy và chiều cao của khối lăng trụ
.
ABC A B C
.
Ta có:
.
1 1
.
3 3
A A B C
V S h V
.
2
3
ABCC B A A B C
V V V V
.
Câu 28. Trong không gian với hệ tọa độ
Oxyz
, cho
1;0;0
A
,
0;0;2
B
,
0; 3;0
C
. Tính bán kính
mặt cầu ngoại tiếp tứ diện
OABC
là
A.
14
3
. B.
14
4
. C.
14
2
. D.
14
.
Lời giải.
Tác giả: Vũ Nga; Fb: Nga Vu.
Chọn C.
Cách 1: Tìm tọa độ tâm mặt cầu suy ra bán kính.
Gọi
; ;I x y z
và
R
lần lượt là tâm và bán kính mặt cầu ngoại tiếp tứ diện
OABC
.
Ta có:
IO IA IB IC R
2 2
2 2
2 2
IO IA
IO IB
IO IC
2
2 2 2 2 2
2
2 2 2 2 2
2
2 2 2 2 2
1
2
3
x y z x y z
x y z x y z
x y z x y z
1
2
3
2
1
x
y
z
.
1 3
; ;1
2 2
I
14
2
R IO
.
Cách 2: Tìm phương trình mặt cầu suy ra bán kính.
Gọi phương trình mặt cầu
S
ngoại tiếp tứ diện
OABC
là:
2 2 2
2 2 2 0
x y z ax by cz d
.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 23
Do
S
đi qua bốn điểm
, , ,A B C O
nên ta có:
1 2 0
4 4 0
9 6 0
0
a d
c d
b d
d
1
2
3
2
1
0
a
b
c
d
.
bán kính của
S
là:
2 2 2
14
2
R a b c d
.
Cách 3: Sử dụng công thức tính bán kính mặt cầu ngoại tiếp của tứ diện vuông.
Do tứ diện
OABC
có ba cạnh
, ,OA OB OC
đôi một vuông góc nên bán kính mặt cầu ngoại tiếp
tứ diện
OABC
là
2 2 2
1
2
R OA OB OC
1 14
1 4 9
2 2
.
Câu 29. Cho hàm số
y f x
xác định và liên tục trên
, có bảng biến thiên như sau:
0
+
1
+
2
+
+
1
y
y'
x
1
0
Mệnh đề nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng
; 2
. B. Hàm số nghịch biến trên khoảng
;1

.
C. Hàm số nghịch biến trên khoảng
1;

. D. Hàm số đồng biến trên khoảng
1;

.
Lời giải.
Tác giả: Trần Thị Thơm; Fb: Tranthom.
Chọn A.
Dựa vào bảng biến thiên ta thấy
hàm số đồng biến trên mỗi khoảng
; 1
và
1;
. Suy
ra hàm số đồng biến trên khoảng
; 2
.
Câu 30. Cho
6
2 3 2 dx x x
8 7
3 2 3 2
A x B x C
với
, ,A B C
. Tính giá trị của biểu thức
12 7A B
.
A.
23
252
. B.
241
252
. C.
52
9
. D.
7
9
.
Lời giải.
Tác giả: Trần Thị Thơm; Fb: Tranthom.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 24
Chọn D.
Đặt
3 2
t x
d
d 3d d
3
t
t x x
.
Khi đó.
6
6
2 2
2 3 2 d d
3 3
t
x x x t t
8 7
7 6
2 2 2
2 d
9 9 8 7
t t
t t t C
.
8 7
1 4
3 2 3 2
36 63
x x C
.
Từ đó ta có
1
36
A
,
4
63
B
. Suy ra
7
12 7
9
A B
.
Câu 31 . Có bao nhiêu số tự nhiên có 4 chữ số được viết từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9 sao cho số
đó chia hết cho 15?
A. 234. B. 132. C. 243. D. 432.
Lời giải
Tác giả: Phạm Thị Thu Trang; Fb: Trang Phạ
m
Chọn C
Gọi số cần tìm là
N abcd
. Do
N
chia hết cho 15 nên
N
phải chia hết cho 3 và 5, vì vậy
d
có 1 cách chọn là bằng 5 và
a b c d
chia hết cho 3.
Do vai trò các chữ số
, ,a b c
như nhau, mỗi số
a
và
b
có 9 cách chọn nên ta xét các trường
hợp:
TH1:
a b d
chia hết cho 3, khi đó
3 3;6;9
c c
, suy ra có 3 cách chọn
c
.
TH2:
a b d
chia 3 dư 1, khi đó
c
chia 3 dư 2
2;5;8
c
, suy ra có 3 cách chọn
c
.
TH3:
a b d
chia 3 dư 2, khi đó
c
chia 3 dư 1
1;4;7
c
, suy ra có 3 cách chọn
c
.
Vậy trong mọi trường hợp đều có 3 cách chọn
c
nên có tất cả:
9.9.3.1 243
số thỏa mãn.
Câu 32. Có bao nhiêu giá trị nguyên của tham số
m
thuộc khoảng
2019;2019
để hàm số
3 2
sin 3cos sin 1y x x m x
đồng biến trên đoạn
0;
2
.
A.
2028
. B.
2018
. C.
2020
. D.
2019
.
Lời giải
Tác giả: Phạm Thanh My ; Fb: Thanh My Phạ
m
Chọn D
3 2
sin 3cos sin 1y x x m x
3 2
sin 3sin sin 4
y x x m x
.
2
' 3sin 6sin cosy x x m x
.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 25
Hàm số đồng biến trên đoạn
0;
2
khi và chỉ khi hàm số liên tục trên
0;
2
và hàm số đồng
biến trên
0;
2
π
' 0 0;
2
π
y x
2
3sin 6sin 0 0;
2
π
x x m x
2
3sin 6sin 0;
2
π
x x m x
1
.
Đặt
sin , 0; 0;1
2
π
t x x t
.
Xét hàm số
2
3 6f t t t
trên
0;1
ta có bảng biến thiên sau
Dựa vào bảng biến thiên ta có
1
xảy ra khi và chỉ khi
0
m
.
Suy ra có 2019 giá trị nguyên của
m
thuộc khoảng
2019;2019
thỏa mãn đề bài.
Câu 33 . Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ. Hỏi đồ thị hàm số
y f x
có tất cả bao nhiêu điểm cực trị?
A.
6
. B.
8
. C. 7. D. 9.
Lời giải
Tác giả: Lê Thị Phương L
iên ; Fb: Phuonglien Le
Chọn C
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 26
Gọi các nghiệm của phương trình
0
f x
lần lượt là
1 2 3
; ;x x x
trong đó
1 2 3
0 1 .x x x
khi 0
khi 0
f x f x
y
f x f x
2 3
2 3
3 2
3 2
, 0; ;
, ;
, ; ;0
, ;
f x x x x
f x x x x
f x x x x
f x x x x


.
2 3
2 3
3 2
3 2
, 0; ;
, ;
, ; ;0
, ;
f x x x x
f x x x x
y
f x x x x
f x x x x


0 1
y x
y
không xác định tại
2
3
0
x
x x
x x
Khi đó ta có bảng biến thiên của hàm số
y f x
như sau:
Nên hàm số có 7 cực trị.
Cách 2: (Admin Hue Tran)
Hàm số
y f x
có một cực trị dương là
1x
và phương trình
0
f x
có 2 nghiệm dương
nên hàm số
y f x
có 3 cực trị và phương trình
0
f x
có 4 nghiệm nên hàm số
y f x
có 7 cực trị.
Cách khác: Từ đồ thị của hàm số
y f x
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 27
Ta có đồ thị hàm số
y f x
là:
Và đồ thị hàm số
y f x
là:
Từ đồ thị suy ra hàm số
y f x
có 7 điểm cực trị.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 28
Câu 33.1 (ĐH Vinh L1 – 2019)
Cho hàm số
f x
có đồ thị hàm số
'y f x
được cho như hình vẽ bên. Hàm số
2
1
0
2
y f x x f
có nhiều nhất bao nhiêu điểm cực trị trong khoảng
?
Bài giải (Nguyễn Việt Hải)
Đặt
2
0
2
x
g x f x f
Ta có:
' '
g x f x x
,
2( )
' 0 0
2
x L
g x x
x
( Nhận xét:
2
x
là nghiệm bội lẻ,
0
x
có thể nghiệm bội lẻ hoặc nghiệm bội chẳn tuy nhiên không ảnh
hưởng đáp số bài toán)
Suy ra hàm số
y g x
có nhiều nhất 3 điểm cực trị trong khoảng
Câu 34. Cho hình chóp
.
S ABC
có các cạnh
3
SA BC
;
4
SB AC
;
2 5
SC AB . Tính thể
tích khối chóp
.
S ABC
.
A.
390
12
. B.
390
4
. C.
390
6
. D.
390
8
.
Lời giải.
Tác giả: Nguyễn Văn Nghĩa; Fb: Nghĩa Văn Nguyễn.
Chọn B.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 29
+ Dựng hình chóp
. ' ' 'S A B C
sao cho A là trung điểm
' 'B C
,
B
là trung điểm
' 'A C
,
C
là
trung điểm
' 'A B
.
+ Khi đó
' ' 4
SB AC BA BC
nên
' 'SA C
vuông tại
S
và
2
2 2
' ' 2. 64 (1)
SA SC SB
.
+ Tương tự
' 'SB C
,
' 'SA B
vuông tại
S
và
2 2
2 2
' ' 80 (2)
' ' 36 (3)
SA SB
SB SC
.
+ Từ
1 ; 2 ; 3
ta suy ra
' 10
SC ;
' 26
SB ;
' 54
SA .
+ Ta tính được
. ' ' '
1 1
'. . '. ' 390
3 2
S A B C
V SC SA SB
và
. . ' ' '
1 390
4 4
S ABC S A B C
V V
(đvtt).
Câu 35. Cho hình chóp
.
S ABC
có đáy là
ABC
vuông cân ở
,B
2,
AC a
SA ABC
,
.SA a
Gọi
G
là trọng tâm của
SBC
,
mp
đi qua
AG
và song song với
BC
chia khối chóp
thành hai phần. Gọi
V
là thể tích của khối đa diện không chứa đỉnh
S
. Tính
V
.
A.
3
5
54
a
. B.
3
2
9
a
. C.
3
4
27
a
. D.
3
4
9
a
.
Lời giải.
Tác giả: Nguyễn Thị Thanh Vân; Fb: Thanh Van.
Chọn A.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 30
Trong mặt phẳng
SBC
, qua
G
kẻ đường thẳng song song với
BC
cắt
,SB SC
lần lượt tại
,M N
. Suy ra
//
BC MAN
,
AG MAN
. Vì vậy
MAN
.
Ta có tam giác
ABC
vuông cân tại
B
,
2
AC a AB BC a
.
3
1 1
. . .
3 2 6
SABC
a
V SA AB BC .
Gọi
E
là trung điểm của
BC
. Ta có
2
//
3
SM SN SG
MN BC
SB SC SE
.
Khi đó:
2 2 4
. .
3 3 9
SAMN
SABC
V
SM SN
V SB SC
5
9
SABC
V
V
.
3 3
5 5 5
.
9 9 6 54
SABC
a a
V V .
Cách tính khác:
Gọi
H
là hình chiếu vuông góc của
A
trên
SB
. Ta chứng minh được
AH SBC
và
BMNC
là hình thang vuông tại
,B M
.
Khi đó
1 1
. . . .
3 2
ABMNC
V AH BM MN BC
3
1 2 1 2 2 5
. . . .
3 2 2 3 3 54
a a a a
a
.
Câu 36. Cho hình chóp
ABCS.
có đáy
ABC
là tam giác đều cạnh
a
,
ABCSA
, góc giữa đường
thẳng
SB
và mặt phẳng
ABC
bằng
o
60
. Tính khoảng cách giữa hai đường thẳng
AC
và
SB
.
A.
5
15a
. B.
2
2a
. C.
a2
. D.
7
7a
.
Lời giải
Tác giả: Nguyễn Bả
o Mai; Fb: Bao An
Chọn A
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 31
Vì
SB
có hình chiếu là
AB
trên
ABC
nên góc giữa
SB
và
ABC
là
o
60
SBA SBA .
SAB
vuông tại
A
nên
tan 3SA AB SBA a
.
Gọi
M
là trung điểm của
AC
. Vì
ABC
đều nên
3
,
2
a
BM AC BM
.
Từ
B
kẻ đường thẳng
1
d
song song với
AC
,
A
kẻ đường thẳng
2
d
song song với
BM
.
Gọi
1 2
D d d
. Vì
// //
AC BD AC SBD
, , ,
d AC SB d AC SBD d A SBD
.
Ta có
,
BD AD BD SA BD SAD
.
Gọi
H
là hình chiếu vuông góc của
A
trên
SD
, vì
AH SD
và
AH BD
nên
AH SBD
, suy ra
H
chính là hình chiếu của
A
trên
SAD
,
d A SBD AH
.
SAD
vuông tại
A
có đường cao
AH
nên
2 2 2 2 2 2
1 1 1 1 4 5
3 3 3AH SA AD a a a
15 15
,
5 5
a a
AH d AC SB
(đvđd).
NHẬN XÉT: (Nguyễn Việt Hải)
Cùng nhìn lại khoảng cách:
,
d A AH
với
AH
tại
H
Bài toán cơ bản: Cho
SH HAB
. Ta có
1 2
2 2
1 2
? . ?
,
? ?
H H
d H SAB
H H
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 32
Với
1
?
S
,
2
?
M
,
HM AB
tại
M
LƯU Ý: Nếu
HSAB
là tam diện vuông tại
H
. Tính
,
d H SAB
(không cần dùng
điểm
M
)
Ta có:
2 2 2
2
1 2 3
1 1 1 1
,
? ? ?
d H SAB
H H H
Trong đó
1 2 3
? ,? ,?
S A B
(Kỷ thuật trượt điểm quy về bài toán cơ bản)
1
1
?
, ,
?
A
d A d H
H
Trong đó
1
?
M
với
M AH
Trở lại bài toán 36. Học sinh sẽ không cần sử dụng điểm D và lời giải (có thể không cần
dùng hình vẽ) mất vài giây ra đáp số. Hơn nữa học sinh mức TB cũng dễ dàng thấy được
đáp số.
Ta có:
0
.tan 60 3SA AB a
Ta có:
, ,
d AC SB d AC SBx
với
/ /Bx AC
2 2
.
,
AS AN
d A SBx
AS AN
với
3
, ,
2
a
AN d A Bx d B AC
Suy ra:
15
,
5
a
d AC SB
(Lưu ý lời giải trên điểm N chỉ mượn tạm chứ không cần dùng đến)
Câu 37. Cho hình chóp
.
S ABC
có đáy là tam giác vuông tại
A
,
1cm
AB
,
3 cm
AC
. Tam giác
SAB
SAC
lần lượt vuông tại
B
và
C
. Khối cầu ngoại tiếp hình chóp
.
S ABC
có thể tích bằng
5 5
6
3
cm
. Tính khoảng cách từ
C
tới
SAB
.
A.
5
. B.
5
. C.
3
. D.
3
.
Lời giải
Tác giả : Nguyễn Thị Thu Hằng ; Fb: Nguyễn Thu Hằng.
Chọn D
Cách 1: Vì
90
SBA SCA
suy ra trung điểm
I
của cạnh
SA
là tâm mặt cầu ngoại tiếp hình
chóp
.
S ABC
với bán kính
2
SA
R
.
Thể tích khối cầu là
5 5
6
V
3
4 5 5
3 6
R
5
2
R
5
SA
.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 33
Gọi
O
là trung điểm
BC
, điểm
D
đối xứng với
A
qua
O
nên tứ giác
ABDC
là hình chữ
nhật.
Dễ thấy
CD SB
,
CD DB
CD SD
1
.
SC DB
,
CD DB
DB SD
2
.
Từ (1) (2)
SD ABDC
2 2
5 4 1
SD SA AD
.
Gọi
H
là chân đường vuông góc của
D
lên cạnh
SB
.
, ,
d C SAB d D SAB DH
.
Thật vậy
AB BD
;
AB SD
AB SDB
AB DH
;
DH SB
DH SAB
.
2 2 2
1 1 1
DH SD DB
2
1 1 1 4
1 3 3DH
3
2
DH
.
Vậy khoảng cách từ
C
đến mặt phẳng
SAB
là
3
.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 34
Cách 2: Vì
90
SBA SCA
suy ra trung điểm
I
của cạnh
SA
là tâm mặt cầu ngoại tiếp hình
chóp
.
S ABC
với bán kính
2
SA
R
.
Thể tích khối cầu là
5 5
6
V
3
4 5 5
3 6
R
5
2
R
5
SA
.
Gọi
O
là trung điểm
BC
, vì
BIC
cân nên
OI BC
;
2 2
1
2
OI IC OC
.
Mà
O
là tâm đường tròn ngoại tiếp
ABC
OI ABC
, 2 ,
d C SAB d O ABI
.
Gọi
N
là trung điểm
AB
nên
ON AB
,
OI AB
AB ONI
.
ABI ONI
theo giao tuyến
IN
.
Kẻ
OH IN
OH ABI
, 2 , 2
d C SAB d O ABI OH
.
2 2 2
1 1 1
OH ON OI
4 16
4
3 3
3
4
OH
.
Vậy khoảng cách từ
C
đến mặt phẳng
SAB
là
3
.
Câu 38. Cho hàm số
f x
liên tục trên
thỏa mãn
2 3
f x f x
,
x
. Biết rằng
1
0
d 1f x x
.
Tính tích phân
2
1
dI f x x
.
A.
5
I
. B.
6
I
. C.
3
I
. D.
2I
.
Lời giải.
Tác giả: Nguyễn Mạnh Dũng ; Fb: Mạnh Dũng.
Chọn A.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 35
Ta có:
1 1 1 1
0 0 0 0
1
3 3.1 3. d 3 d 2 d 2 d 2 ,
2
f x x f x x f x x f x x x
.
Đặt
2 d 2 dx t x t
, với
0 0x t
;
1 2x t
.
1 2 2
0 0 0
1 1 1
3 2 d 2 d d ,
2 2 2
f x x f t t f x x x
(do hàm số
f x
liên tục trên
).
2
0
d 6,f x x x
1 2
0 1
d d 6,f x x f x x x
.
2
1
1 d 6,f x x x
.
2
1
d 5,f x x x
.
Câu 38.1 Cho hàm số
f x
liên tục trên
thỏa mãn
f mx nf x p
,
x
0
m
. Biết rằng
1
0
d
f x x q
0
q
. Tính tích phân
1
d
m
I f x x
.
Lời giải.
Tác giả: Nguyễn Mạnh Dũng ; Fb: Mạnh Dũng.
Ta có:
.
n
n q
q
1
0
. d
n
f x x
q
1
0
d
n
f x x
q
1
0
d
f mx p
x
q
1 1
0 0
d d ,
f mx
p
x x x
q q
.
1
0
1
1
d
0
p
n f mx mx x
mq q
1
0
1
d ,
p
f mx mx x
mq q
.
1
0
d . ,
p
f mx mx n mq x
q
.
Đặt
d dmx t mx t
, với
0 0x t
;
1
x t m
.
1
0
d . ,
p
f mx mx n mq x
q
.
0 0
d d . ,
m m
p
f t t f x x n mq x
q
(do hàm số
f x
liên tục trên
).
1
0 1
d d . ,
m
p
f x x f x x n mq x
q
.
1
d . ,
m
p
q f x x n mq x
q
.
1
d .
m
p
f x x n mq q
q
,nmq mp q x
.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 36
1
d ,
m
f x x nmq mp q x

.
Câu 39. Tìm số đường tiệm cận của đồ thị hàm số
1
4 3 1 3 5
x
y
x x
.
A. 3. B. 2. C. 1. D. 0.
Lời giải.
Tác giả: Trần Mạnh Tường; Fb: Trần Tuệ Minh.
Chọn B.
Ta có:
4 3 1 3 5 0
x x
4 3 1 3 5x x
2
16 3 1 9 30 25
3 5
1
0
x x x
x
x
Tập xác định:
1
; \ 1
3
D

+ Ta có:
2
1 1 1
1 4 3 1 3 5
1 4 3 1 3 5
lim lim lim
9 1
4 3 1 3 5
9 1
x x x
x x x
x x x
x
x x
x

do đó đường thẳng
1x
là đường tiệm cận đứng của đồ thị hàm số.
+
2
1
1
1 1
lim lim
3
4 3 1 3 5 3 1 5
4 3
x x
x
x
x x
x x x
 
do đó đường thẳng
1
3
y
là đường
tiệm cận ngang của đồ thị hàm số.
Kết luận: Đồ thị hàm số có hai tiệm cận.
Câu 40. Trong không gian
Oxyz
, lấy điểm
C
trên tia
Oz
sao cho
1
OC
. Trên hai tia
lần lượt
lấy hai điểm
,A B
thay đổi sao cho
OA OB OC
. Tìm giá trị nhỏ nhất của bán kính mặt cầu
ngoại tiếp tứ diện
.
O ABC
?
A.
6
.
4
. B.
6.
. C.
6
.
3
. D.
6
.
2
.
Lời giải.
Tác giả: Lê Anh Đông; Fb: Le Anh Đong.
Chọn A.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 37
Bốn điểm
, , ,O A B C
tạo thành 1 tam diện vuông.
Bán kính mặt cầu ngoại tiếp tứ diện
.
O ABC
là
2 2 2
2
OA OB OC
R
.
Đặt
; , , 0.
OA a OB b a b
Ta có
1 1a b b a
.
Vậy
2 2 2
2
OA OB OC
R
2 2 2
1
2
a b
2
2 2
1 1
2
a a
2
1 3
2
2 4
6
2 4
a
.
Vậy
min
6
4
R
, tại
1
.
2
a b
.
Câu 41. Cho hàm số
y f x
có đạo hàm cấp hai trên
. Biết
0 3
f
,
2 2018
f
và bảng xét
dấu của
f x
như sau:
Hàm số
2017 2018y f x x
đạt giá trị nhỏ nhất tại điểm
0
x
thuộc khoảng nào sau đây?
A.
; 2017

. B.
2017;

. C.
0;2
. D.
2017;0
.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 38
Lời giải.
Tác giả: Giáp Văn Quân; Fb: quanbg. quan.
Chọn A.
Dựa vào bảng xét dấu của
f x
ta có bảng biến thiên của hàm sồ
f x
Đặt
2017
t x
.
Ta có
2017 2018 2018 2017.2018
y f x x f t t g t
.
2018
g t f t
.
Dựa vào bảng biến thiên của hàm số
f x
suy ra phương trình
g t
có một nghiệm đơn
;0

và một nghiệm kép
2
t
.
Ta có bảng biến thiên
g t
Hàm số
g t
đạt giá trị nhỏ nhất tại
0
;0
t

.
Suy ra hàm số
2017 2018y f x x
đạt giá trị nhỏ nhất tại
0
x
mà
0 0
2017 ;0 ; 2017
x x  
.
Câu 42. Cho hàm số
y f x
có đạo hàm liên tục trên đoạn
0;1
và thỏa mãn
0 0
f
. Biết
1
2
0
9
d
2
f x x
và
1
0
3
cos d
2 4
x
f x x
. Tích phân
1
0
df x x
bằng
A.
6
. B.
2
. C.
4
. D.
1
.
Lời giải
Chọn A
Ta có:
1
1 1
0
0 0
2 2 3
( )sin ( ).cos '( ).cos
2 2 2 2
f x xdx f x x f x xdx
1 1 1 1
2 2 2
0 0 0 0
( ( ) 3sin ) ( ) 6 ( )sin 9 sin 0
2 2 2
f x x dx f x dx f x xdx xdx
Từ đây ta suy ra
1 1
0 0
6
( ) 3sin d 3sin
2 2
f x x f x x xdx
.
PHÁT TRIỂN BÀI TOÁN CÂU 42
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 39
Câu 42.1. Cho hàm số
f x
có đạo hàm liên tục trên đoạn
0;1
thỏa mãn
1 0
f
,
1
2
0
d 7
f x x
và
1
2
0
1
d
3
x f x x
. Tích phân
1
0
df x x
bằng
A.
7
5
. B.
1
. C.
7
4
. D.
4
.
Lời giải
Chọn A.
Nhận xét
- Ý tưởng sáng tác bài toán giống câu 50 trong đề minh họa của BGD năm 2018. Vì thầy
Nguyễn Việt Hải phân tích quá hay nên tôi trích dẫn lại nguyên văn nhận xét và ý tưởng đó
Từ giả thiết:
1
2
0
1
d
3
x f x x
1
2
0
3 d 1
x f x x
.
Tính:
1
2
0
3 d
I x f x x
.
Đặt:
2 3
d d
d 3 d
u f x u f x x
v x x v x
.
Ta có:
1 1
1
2 3 3
0
0 0
3 d . d
I x f x x x f x x f x x
1
3
0
1. 1 0. 0 . d
f f x f x x
1
3
0
. d
x f x x
.
Mà:
1
2
0
3 d 1
x f x x
1
3
0
1 . d
x f x x
1
3
0
. d 1
x f x x
1
3
0
7 . d 7
x f x x
1 1
2
3
0 0
7 . d d
x f x x f x x
, (theo giả thiết:
1
2
0
d 7
f x x
).
1
2
3
0
7 . + d 0
x f x f x x
1
3
0
7 + d 0
f x x f x x
3
7 + 0
x f x
3
7
f x x
4
7
4
f x x C
.
Với
1 0
f
4
7
.1 0
4
C
7
4
C
.
Khi đó:
4
7 7
4 4
f x x
.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 40
Vậy:
1 1
4
0 0
7 7
d d
4 4
f x x x x
1
5
0
7
4 5
x
x
7
5
.
PHÂN TÍCH
1 1 1 1
3 3 3
2 1 3
0
0 0 0 0
1
( )d d ( ) | d ( ) . '( )d
3 3 3 3
x x x
x f x x f x f x f x x f x x
Từ đây, chúng ta quan sát giả thiết bài toán: Ta thấy xuất hiện
2
'( )f x
và
3
. '( )x f x
Nghĩ ngay đến hằng đẳng thức
2
3
'( )
f x ax
, như vậy số
?a
tương ứng với bài toán?
+
1
2
0
'( ) 7
f x dx
+
1
3
0
2 . '( ) 2ax f x dx a
+
1
2
2
3
0
7
a
ax dx
Do đó số a chọn tương ứng là
1
2
2
3
0
'( ) 7 2 0 7
7
a
f x ax dx a a
.
. Suy ra
4
3
7 7
'( ) 7 ( )
4 4
x
f x x f x .
Vậy đáp chọn: A
NHẬN XÉT:
Vì đây là trắc nghiệm chỉ cần ĐS đúng do đó ta sử dụng kỷ thuật đồng nhất suy ra đáp
số dễ dàng.
1
2
0
'( ) 7
f x dx
và
1
3
0
7 '( ) 7
x f x dx
. Vì trắc nghiệm nên đồng nhất hai biểu thức dưới dấu
tích phân. Suy ra
4
3
7 7
'( ) 7 ( )
4 4
x
f x x f x A
.
Hướng tiếp cận khác theo con đường BĐT.
+ Quan sát giả thiêt bài toán:
1
2
0
(1) 0, '( ) 7
f f x dx
và
1
2
0
1
( )
3
x f x dx
.
+ Ta nghĩ đến đánh giá bằng BĐT: Thật vậy sử dụng kiến thức dấu tam thức bậc hai. Chúng ta
có kết quả BĐT Cauchy – Schawz
2
2 2 2
2 . 0,
b b b b
a a a a
t f x dx t f x g x dx g x dx t f x g x dx t
.
Suy ra: BĐT Cauchy – Schawz
2
2 2
.
b b b
a a a
f x g x dx f x dx g x dx
Do đó ta có hướng giải bài toán trên:
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 41
1 1 1 1
3 3 3
2 1 3
0
0 0 0 0
1 1
( ) ( ) | ( ) . '( )
3 3 3 3 3
x x x
x f x dx f x d f x df x x f x dx
.
Ta suy ra:
2
1 1
2
2
3 3
0 0
1 1 1 1
' '
9 3 9 9
x f x dx x dx f x dx .
Tương đương
3
' .f x k x
Ý TƯỞNG SÁNG TẠO ĐỀ
Tạo hằng tích phân có dạng đẳng thức:
2
0
0
a
A B dx
Hoặc
2
0
0
a
A B C dx
…
Chọn a, A, B thích hợp tương ứng ta có bài toán.
2
2 2
0 0 0 0
0 2 .
a a a a
A B dx A dx A Bdx B dx
MỘT SỐ BÀI TOÁN TƯƠNG TỰ
Câu 42.2. Cho hàm số
f x
có đạo hàm liên tục trên đoạn
0;1
thỏa mãn
1 4
f
,
1
2
0
d 36
f x x
và
1
0
1
. d
5
x f x x
. Tích phân
1
0
df x x
bằng
A.
5
6
. B.
3
2
. C.
4
. D.
2
3
.
Lời giải
Chọn B.
Từ giả thiết:
1
0
1
. d
5
x f x x
1
0
5 . d 1
x f x x
.
Tính:
1
0
5 . d
I x f x x
.
Đặt:
2
d d
5
d 5 d
2
u f x x
u f x
v x x
v x
.
Ta có:
1
1 1
2 2
0
0 0
5 5
5 . d . . d
2 2
I x f x x x f x x f x x
1
2
0
5 5
. 1 . d
2 2
f x f x x
1
2
0
5
10 . d
2
x f x x
, (vì
1 4
f
)
Mà:
1
0
5 . d 1
I x f x x
1
2
0
5
1 10 . d
2
x f x x
1
2
0
18
. d
5
x f x x
1
2
0
10 . d 36
x f x x
1 1
2
2
0 0
10 . d d
x f x x f x x
, (theo giả thiết:
1
2
0
d 36
f x x
)
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 42
1
2
2
0
10 . d 0
x f x f x x
1
2
0
10 d 0
f x x f x x
2
10 0
x f x
2
10
f x x
3
10
3
x
f x C
Với
1 4
f
10.1
4
3
C
2
3
C
.
Khi đó:
3
10 2
3 3
x
f x .
Vậy:
1 1
3
0 0
10 2
d d
3 3
x
f x x x
1
4
0
5 2 3
6 3 2
x
x .
Câu 42.3 Cho hàm số
f x
có đạo hàm liên tục trên đoạn
0;2
thỏa mãn
2 3
f
,
2
2
0
d 4
f x x
và
2
2
0
1
d
3
x f x x
. Tích phân
2
0
d
f x x
bằng
A.
2
115
. B.
297
115
. C.
562
115
. D.
266
115
.
Lời giải
Chọn C.
Từ giả thiết:
2
2
0
1
d
3
x f x x
2
2
0
3 d 1
x f x x
.
Tính:
2
2
0
3 d
I x f x x
.
Đặt:
2 3
d d
d 3 d
u f x u f x x
v x x v x
.
Ta có:
2 2
2
2 3 3
0
0 0
3 d . . d
I x f x x x f x x f x x
2
3
0
24 . d
x f x x
, (vì
2 3
f
)
Mà:
2
2
0
3 d 1
I x f x x
2
3
0
1 24 . d
x f x x
2
3
0
. d 23
x f x x
2
3
0
4
. d 4
23
x f x x
2 2
2
3
0 0
4
. d d
23
x f x x f x x
, (theo giả thiết:
1
2
0
d 4
f x x
)
2
2
3
0
4
. d 0
23
x f x f x x
2
3
0
4
d 0
23
f x x f x x
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 43
3
4
0
23
x f x
3
4
23
f x x
4
1
23
f x x C
Với
2 3
f
16
3
23
C
53
23
C
.
Khi đó:
4
1 53
23 23
f x x
.
Vậy
2 2
4
0 0
1 53
d d
23 23
f x x x x
2
5
0
1 53 562
115 23 115
x x .
Câu 42.4. Cho hàm số
f x
có đạo hàm liên tục trên đoạn
0;1
thỏa mãn
1 4
f
,
1
2
0
d 5
f x x
và
1
0
1
. d
2
x f x x
. Tích phân
1
0
df x x
bằng
A.
15
19
. B.
17
4
. C.
17
18
. D.
15
4
.
Lời giải
Chọn D.
Tính:
1
0
. dI x f x x
. Đặt:
2
d d
1
d d
2
u f x x
u f x
v x x
v x
Ta có:
1
2 2
0
1
1 1
. d
0
2 2
I x f x x f x x
1
2
0
1
2 d
2
x f x x
, (vì
1 4
f
).
Mà:
1
0
1
. d
2
x f x x
1
2
0
1 1
2 d
2 2
x f x x
1
2
0
d 5
x f x x
, (theo giả thiết:
1
2
0
d 5
f x x
)
1 1
2
2
0 0
d d
x f x x f x x
1
2
2
0
d 0
x f x f x x
1
2
0
. d 0
f x x f x x
2
0
x f x
2
f x x
3
1
3
f x x C
.
Với
1 4
f
C
.
Khi đó:
3
1 11
3 3
f x x
.
Vậy
1 1
3 4
0 0
1
1 11 1 11 15
d d
0
3 3 12 3 4
f x x x x x x
.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 44
Câu 42.5. Cho hàm số
f x
có đạo hàm liên tục trên đoạn
0;2
thỏa mãn
2 6
f
,
2
2
0
d 7
f x x
và
2
0
17
. d
2
x f x x
. Tích phân
2
0
df x x
bằng
A.
8
. B.
6
. C.
7
. D.
5
.
Lời giải
Chọn A.
Tính:
2
0
. dI x f x x
.
Đặt:
2
d d
1
d d
2
u f x x
u f x
v x x
v x
Ta có:
2
2 2
0
2
1 1
. d
0
2 2
I x f x x f x x
2
2
0
1
12 d
2
x f x x
, (vì
2 6
f
).
Theo giả thiết:
2
0
17
. d
2
x f x x
2
2
0
17 1
12 d
2 2
x f x x
2
2
0
d 7
x f x x
2 2
2
2
0 0
d dx f x x f x x
2
2
2
0
d 0
x f x f x x
2
2
0
. d 0
f x x f x x
2
0
x f x
2
f x x
3
1
3
f x x C
.
Với
2 6
f
10
3
C
.
Khi đó:
3
1 10
3 3
f x x
.
Vậy
2 2
3 4
0 0
2
1 10 1 10
d d 8
0
3 3 12 3
f x x x x x x
.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 45
Câu 42.6. Cho hàm số
f x
có đạo hàm liên tục trên đoạn
0;3
thỏa mãn
3 6
f
,
3
2
0
d 2
f x x
và
3
2
0
154
. d
3
x f x x
. Tích phân
3
0
df x x
bằng
A.
53
5
. B.
117
20
. C.
153
5
. D.
13
5
.
Lời giải
Chọn B.
Tính
3
2
0
. dI x f x x
.
Đặt
3
2
d d
1
d d
3
u f x x
u f x
v x
v x x
.
Ta có
3
3 3
0
3
1 1
. d
0
3 3
I x f x x f x x
3
3
0
1
54 d
3
x f x x
, (vì
3 6
f
).
Theo giả thiết:
3
2
0
154
. d
3
x f x x
3
3
0
154 1
54 d
3 3
x f x x
3
3
0
d 8
x f x x
3 3
2
3
0 0
d 4 d
x f x x f x x
3
2
3
0
4 d 0
x f x f x x
3
3
0
4 d 0
f x x f x x
.
3
4 0
x f x
3
4
x
f x
4
16
x
f x C
.
Với
3 6
f
15
16
C
.
Khi đó:
4
15
16 16
x
f x .
Vậy
3 3
4 5
0 0
3
1 15 1 15 117
d d
0
16 16 80 16 20
f x x x x x x
.
Câu 42.7. Cho hàm số
f x
có đạo hàm liên tục trên đoạn
0;1
thỏa mãn
1 2
f
,
1
2
0
d 8
f x x
và
1
3
0
. d 10
x f x x
. Tích phân
1
0
df x x
bằng
A.
2
285
. B.
194
95
. C.
116
57
. D.
584
285
.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 46
Lời giải
Chọn C.
Tính:
1
3
0
. dI x f x x
.
Đặt:
4
3
d d
1
d d
4
u f x x
u f x
v x
v x x
.
Ta có:
1
4 4
0
1
1 1
. d
0
4 4
I x f x x f x x
1
4
0
1 1
d
2 4
x f x x
, (vì
1 2
f
).
Theo giả thiết:
1
3
0
. d 10
x f x x
1
4
0
d 38
x f x x
1
4
0
8. d 38.8
x f x x
1 1
2
4
0 0
8. d 38. d
x f x x f x x
1
2
4
0
8 38 d 0
x f x f x x
1
4
0
. 8 38 d 0
f x x f x x
4
8 38 0
x f x
4
4
19
f x x
5
4
95
f x x C
.
Với
1 2
f
194
95
C
.
Khi đó:
5
4 194
95 95
f x x
.
Vậy
1 1
5 6
0 0
1
4 194 2 194 116
d d
0
95 95 285 95 57
f x x x x x x
.
Câu 43. Biết
F x
là nguyên hàm của hàm số
2
cosx x
f x
x
. Hỏi đồ thị của hàm số
y F x
có
bao nhiêu điểm cực trị?
A. Vô số điểm. B. 0. C. 1. D. 2.
Lời giải
Tác giả: Võ Minh Chung; Fb: Võ Minh Chung
Chọn C.
Vì
F x
là nguyên hàm của hàm số
2
cosx x
f x
x
nên suy ra:
2
cos
( ) ( )
x x
F x f x
x
.
Ta có:
( ) 0
F x
2
cos
0
x x
x
cos 0
1;1 \ 0
x x
x
1
.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 47
Xét hàm số
( ) cosg x x x
trên
1;1
, ta có :
( ) 1 sin 0, 1;1
g x x x
. Suy ra hàm số
( )g x
đồng biến trên
1;1
. Vậy phương trình
( ) cos 0
g x x x
có nhiều nhất một nghiệm
trên
1;1
2
.
Mặt khác ta có: hàm số
( ) cosg x x x
liên tục trên
0;1
và
0 0 cos 0 1 0
g
,
(1) 1 cos 1 0
g
nên
0 . 1 0
g g
. Suy ra
0
0;1
x
sao cho
0
0
g x
3
.
Từ
1
,
2
,
3
suy ra: phương trình
( ) 0
F x
có nghiệm duy nhất
0
0
x
. Đồng thời vì
0
x
là nghiệm bội lẻ nên
( )F x
đổi qua
0
x x
.
Vậy đồ thị hàm số
y F x
có
1
điểm cực trị.
PHÂN TÍCH VÀ PHÁT TRIỂN CÂU 43: Cô Nguyễn Thị Bích Ngọc – Fb: Bích Ngọc.
PHÂN TÍCH: Bản chất bài toán là muốn khai thác định nghĩa nguyên hàm của một hàm số và
cách giải phương trình chứa hàm số hỗn hợp gồm đa thức và hàm số lượng giác. Phương trình
này sử dụng tính chất đơn điệu của hàm số dẫn đến số nghiệm tối đa là một, khi đó chỉ cần
nhẩm một nghiệm hoặc sử dụng định lí liên tục của hàm số suy ra phương trình có nghiệm duy
nhất.
Câu 43.1 Cho biết
2
9
ln
x
e
e
f x t tdt
, tìm điểm cực trị của hàm số đã cho
A.
2
x
B.
0
x
C.
1
x
D.
6
x
Lời giải
Chọn B
Gọi
G x
là một nguyên hàm của hàm số
9
lng x x x
. Theo định nghĩa:
2x
f x G e G e
9
2 2 4
' ' .e .2 ' 2. 2
x x x
f x G e G e e x
/
( ) 0 0
f x x
. Suy ra chọn đáp án B.
Câu 43.2 Cho hàm số
2
0
( ) sin .
x
G x tdt
Tính đạo hàm của hàm số
( ).G x
A.
( ) 2 sinG x x x
B.
( ) 2 cosG x x x
C.
( ) cosG x x
D.
( ) 2 sinG x x x
Lời giải
Chọn A
Gọi
F x
là một nguyên hàm của hàm số
sinf x x
. Theo định nghĩa:
2
0
G x F x F
2 2
' ' .2 ' 0 2 .sin 2 .sinG x F x x F x x x x
. Chọn A
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 48
Câu 43.3 Biết
F x
là nguyên hàm của hàm số
2
1
cos 1
2
f x x x
. Hỏi đồ thị của hàm số
y F x
có bao nhiêu điểm cực trị?
A. Vô số điểm. B.
0
. C.
1
. D.
2
.
Lời giải
Chọn D
Ta có
/ 2
1
( ) cos 1
2
F x f x x x
.
/
( ) sinx
f x x
;
//
( ) cos 1 0
f x x x R
.
Suy ra hàm số
/
( )f x
đồng biến trên
R
, từ đó dẫn đến phương trình
/
( ) 0
f x
có nhiều nhất
một nghiệm.
Mặt khác
/
(0) 0
f
suy ra
0
x
là nghiệm duy nhất của phương trình
/
( ) 0
f x
.
Do hàm số
/
( )f x
liên tục trên mỗi khoảng
;0 ; 0;
 
và vô nghiệm trên mỗi khoảng này
nên dấu của
/
( )f x
không đổi trên mỗi khoảng trên.
Mà
/ /
( 1) 0; (1) 0
f f
suy ra
/
( ) 0 ;0
f x x 
và
/
( ) 0 0;f x x

.
Vậy hàm số
( )f x
nghịch biến trên khoảng
;0

và đồng biến trên khoảng
0;

. Mà
(0) 0
f
nên phương trình
( ) 0
f x
có nghiệm duy nhất
0
x
hay phương trình
/
( ) 0
F x
có nghiệm duy nhất
0
x
.
Vậy đồ thị của hàm số
y F x
có duy nhất một điểm cực trị.
BÀI TOÁN TỔNG QUÁT: Cho hàm số
u x
v x
F x g t dt
. Tìm đạo hàm của hàm số
F x
.
CHỨNG MINH:
Gọi
G t
là nguyên hàm của hàm số
g t
. Theo định nghĩa tích phân, ta có:
( ) G
u x
v x
F x g t dt G u v
.
Suy ra:
( ) ( ) G
F x G u v
. ( ) . ( )u G u v G v
. ( ) '. ( )u g u v g v
.
Vậy, ta có công thức tổng quát:
. ( ) '. ( )
u x
v x
g t dt u g u v g v
.
Câu 44. Tìm tất cả các giá trị thực của tham số
m
để phương trình
3 2 2
2 1 1 1
m m
e e x x x x
có nghiệm.
A.
1
0; ln 2
2
. B.
1
; ln 2
2

. C.
1
0;
e
. D.
1
ln 2;
2

.
Lời giải
.
Tác giả: Trần Quốc Thép; Fb: Thép Trần Quốc.
Chọn B.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 49
Đặt
2
2 2 2 2
1
1 1 2 1 1
2
t
t x x t x x x x
.
Ta có
2
2
1 1
' , ' 0
2
1
x x
t t x
x
.
Vậy
1; 2
t
.
Phương trình trở thành
2
3 3 3
1
2 1
2
m m m m m
t
e e t e e t t e t
. (sử dụng hàm đặc
trưng).
Phương trình có nghiệm khi và chi khi
1
1 2 ln 2 ( ; ln 2]
2
m
e m m 
.
Câu 45. Tìm tập
S
tất cả các giá trị thực của tham số
m
để tồn tại duy nhất cặp số
;x y
thỏa mãn
2 2
2
2
log 4 4 6 1
x y
x y m
và
2 2
2 4 1 0
x y x y
.
A.
1;1
S
. B.
5; 1;1;5
S
.
C.
5;5
S
. D.
7; 5; 1;1;5;7
S
.
Lời giải.
Tác giả: Nguyễn Đình Hải; Fb: Nguyen Dinh Hai.
Chọn A.
Ta có
2 2
2
2
log 4 4 6 1
x y
x y m
2 2 2
4 4 6 2
x y m x y
2 2 2
4 4 8 0
x y x y m
2 2
2
2 2
x y m
là một hình tròn
1
C
tâm
2;2
I
,
bán kính
1
R m
với
0
m
hoặc là điểm
2;2
I
với
0
m
và
2 2
2 4 1 0
x y x y
2 2
1 2 4
x y
là một đường tròn
2
C
tâm
1;2
J
, bán kính
2
2
R
.
TH1: Với
0
m
ta có:
2
2;2
I C
suy ra
0
m
không thỏa mãn điều kiện bài toán.
TH2: Với
0
m
.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 50
Để hệ
2 2
2
2
2 2
log 4 4 6 1
2 4 1 0
x y
x y m
x y x y
tồn tại duy nhất cặp số
;x y
thì hình tròn
1
C
và
đường tròn
2
C
tiếp xúc ngoài với nhau
1 2
IJ R R
2 2
3 0 2
m
1
m
1
m
.
Câu 46. Cho hình trụ có đáy là hai đường tròn tâm
O
và
O
, bán kính đáy bằng chiều cao và bằng
2a
.
Trên đường tròn đáy có tâm
O
lấy điểm
A
, trên đường tròn tâm
O
lấy điểm
B
. Đặt
là góc
giữa
AB
và đáy. Tính
tan
khi thể tích khối tứ diện
OO AB
đạt giá trị lớn nhất.
A.
tan 2
. B.
1
tan
2
. C.
1
tan
2
. D.
tan 1
.
Lời giải
Tác giả: Nguyễn Việt Hải; Fb: Nguyễn Việt Hải
Chọn B
Cách 1:
α
H
D
B
A
O
O'
Gọi
D
là hình chiếu vuông góc của
B
lên mặt phẳng
O
.
Kẻ
AH OD
,
H OD
.
Ta có thể tích của khối chóp
OO AB
:
1
.
3
OO AB OO B
V AH S
2
2
.
3
a
AH
2
2
.
3
a
AO
3
4
3
a
.
max
OO AB
V H O
. Suy ra
2 2AD a
.
Suy ra:
tan tan
BAD
1
2
.
Cách 2: Tác giả: Võ Thị Ngọc Ánh; Fb: Võ Ánh
Nhận xét: Nên thêm giả thiết
AB
chéo với
'OO
để tứ diện
OO AB
tồn tại.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 51
C
α
D
B
A
O
O'
Gọi
D
là hình chiếu vuông góc của
B
lên mặt phẳng chứa đường tròn
O
.
Gọi
C
là hình chiếu vuông góc của
A
lên mặt phẳng chứa đường tròn
'O
.
Ta có
' .
O CB OAD
là một hình lăng trụ đứng.
Ta có thể tích của khối chóp
OO AB
:
3
' .
1 1 1 4
2 . .2 . .2 .2 .sin
3 3 2 3
OO AB O BC OAD OAD
a
V V a S a a a AOD
.
0
'
max
90 2 2
O ABCD
V AOD AD a
.
Suy ra:
tan tan
BAD
1
2
.
PHÂN TÍCH VÀ PHÁT TRIỂN CÂU 46: Tác giả: Võ Thị Ngọc Ánh; Fb: Võ Ánh
Câu 46.1. Cho hình trụ có đáy là hai đường tròn tâm
O
và
O
, bán kính đáy bằng chiều cao và bằng
2a
.
Trên đường tròn đáy có tâm
O
lấy điểm
A
,
D
sao cho
2 3AD a
; gọi
C
là hình chiếu
vuông góc của
D
lên mặt phẳng chứa đường tròn
'O
; trên đường tròn tâm
O
lấy điểm
B
(
AB
chéo với
CD
) . Đặt
là góc giữa
AB
và đáy. Tính
tan
khi thể tích khối tứ diện
CDAB
đạt giá trị lớn nhất.
A.
tan 3
. B.
1
tan
2
. C.
tan 1
. D.
3
tan
3
.
Lời giải
Tác giả: Võ Thị Ngọc Ánh; Fb: Võ Ánh
Chọn D
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 52
K
α
H
O
C
D
B
A
O'
Gọi
H
là hình chiếu vuông góc của
B
lên mặt phẳng chứa đường tròn
O
.
Gọi
K
là hình chiếu vuông góc của
A
lên mặt phẳng chứa đường tròn
'O
.
Ta có
.
HAD BKC
là một hình lăng trụ đứng.
Ta có thể tích của tứ diện
CDAB
là
.
1 1 1 1 1 1
.2 . .2 . . . ; .2 . .2 3. ;
3 3 3 2 3 2
ABCD HAD BKC HAD
V V a S a AD d H AD a a d H AD
.
max
max
;
ABCD
V d H AD
H
là điểm chính giữa cung lớn
AD
của đường tròn
O
(1).
Theo định lý sin ta có
2 3 3
2.2 sin
4 4 2
sin
AD AD a
a AHD
a a
AHD
nên
0
60
AHD .
Do đó (1) xảy ra khi
đều
2 3AH AD a
.
Suy ra:
2 3
tan tan
3
2 3
BH a
BAH
AH
a
.
Câu 46.2. Cho hình trụ có đáy là hai đường tròn tâm
O
và
O
, bán kính đáy bằng chiều cao và bằng
2a
.
Trên đường tròn đáy có tâm
O
lấy điểm
A
,
D
trên đường tròn tâm
O
lấy điểm
B
,
C
sao cho
//AB CD
và
AB
không cắt
'OO
. Tính
AD
để thể tích khối chóp
'.
O ABCD
đạt giá trị lớn
nhất.
A.
2 2AD a
. B.
4AD a
. C.
4 3
3
AD a
. D.
2AD a
.
Lời giải
Tác giả: Võ Thị Ngọc Ánh; Fb: Võ Ánh
Chọn A
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 53
O
1
O
C
D
B
A
O'
Kẻ đường thẳng qua
'O
song song với
AB
cắt mặt phẳng chứa đường tròn
( )O
tại
1
O
.
Lúc đó
1
. 'AO D BO C
là một hình lăng trụ chiều cao bằng
2a
.
Vì
AD BC
nên
'
BO C OAD
S S
Ta có thể tích của khối chóp
'.
O ABCD
:
1
3
' . ' '
1 2 2 2 1 8
.2 . .2 . .2 . .2 .2 .sin
3 3 3 3 2 3
O ABCD AO D BO C BO C OAD
a
V V a S a S a a a AOD
.
0
'
max
90 2 2
O ABCD
V AOD AD a
.
Câu 47. Xét các số thực dương
x
,
y
thỏa mãn
2
1 1 1
2 2 2
log log log
x y x y
. Tìm giá trị nhỏ nhất
min
P
của biểu thức
3P x y
.
A.
min
9
P
. B.
min
8
P
. C.
min
25 2
4
P
. D.
min
17
2
P
.
Lời giải.
Tác giả: Nguyễn Huỳnh Tấn Trung ; Fb: Nguyễn Huỳnh Tấn Trung.
Chọn A.
Ta có:
2
1 1 1
2 2 2
log log log
x y x y
2 2
1 1
2 2
log log
xy x y xy x y
2
2
1
1
1
y
x
x y y
y
y
( Vì
; 0
x y
).
Ta có:
2
1
3 3 4 1
1 1
y
P x y y y
y y
.
Xét hàm số:
1
4 1 ; 1
1
f y y y
y
.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 54
Đạo hàm:
/
2
1
4
1
f y
y
.
/
3
2
0
1
2
y n
f y
y l
.
Bảng biến thiên.
BÀI TOÁN TƯƠNG TỰ
Câu 47. 1 Cho
,x y
là các số thực dương thỏa mãn
2019 201 2
2
9 019
log log logx y
x y
. Gọi
min
T
là giá
trị nhỏ nhất của biểu thức
2
T x y
. Mệnh đề nào dưới đây đúng?
A.
min
7;8
T
. B.
min
6;7
T
. C.
min
5;6
T
. D.
min
8;9
T
.
Lời giải.
Tác giả: Nguyễn Huỳnh Tấn Trung ; Fb: Nguyễn Huỳnh Tấn Trung.
Chọn A.
Ta có:
2019 201 2
2
9 019
log log logx y
x y
2019 2019
2
log logxy
x y
2
xy x y
2
1
y x x
2
1
1
x
y
x
x
Ta có:
2
1
2 2 3 1
1 1
x
T x y x x
x x
.
Xét hàm số:
1
3 1 ; 1
1
f x x x
x
.
Đạo hàm:
/
2
1
3
1
f x
x
.
/
3
0 1 ( 1)
3
f x x do x
.
Bảng biến thiên.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 55
Do đó:
min
4 2 3
T
.
Câu 48. Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn có dạng
abcd
,
trong đó
1 9
a b c d
.
A.
0,014
. B.
0,0495
. C.
0,079
. D.
0,055
.
Lời giải
Tác giả: Nguyễn Trườ
ng Giang; Fb: Giang Nguyen
Chọn D
Chọn số tự nhiên có 4 chữ số bất kỳ có:
9.10.10.10 9000
n
(cách).
Gọi
A
là biến cố: “Số được chọn có dạng
abcd
, trong đó
1 9
a b c d
”. (*)
Cách 1: Dùng tổ hợp
Nhận xét rằng với 2 số tự nhiên bất kỳ ta có:
1m n m n
.
Do đó nếu đặt:
1
2
3
x a
y b
z c
t d
Từ giả thuyết
1 9
a b c d
ta suy ra:
1 12
x y z t
(**).
Với mỗi tập con gồm 4 phần tử đôi một khác nhau được lấy ra từ
1,2,...,12
ta đều có được duy
nhất một bộ số thoả mãn (**) và do đó tương ứng ta có duy nhất một bộ số
, , ,a b c d
thoả mãn
(*). Số cách chọn tập con thoả tính chất trên là tổ hợp chập 4 của 12 phần tử, do đó:
4
12
495
n A C
.
Vậy:
495
0,055
9000
n A
P A
n
.
Cách 2: Dùng tổ hợp lặp
Chọn số tự nhiên có 4 chữ số bất kỳ có:
9.10.10.10 9000
n
(cách).
Mỗi tập con có 4 phần tử được lấy từ tập
1,2,...,9
(trong đó mỗi phần tử có thể được chọn lặp
lại nhiều lần) ta xác định được một thứ tự không giảm duy nhất và theo thứ tự đó ta có được
một số tự nhiên có dạng
abcd
(trong đó
1 9
a b c d
). Số tập con thoả tính chất trên là
số tổ hợp lặp chập 4 của 9 phần tử.
Do đó theo công thức tổ hợp lặp ta có:
4
9 4 1
495
n A C
.
STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang 56
Vậy:
495
0,055
9000
n A
P A
n
.
Câu 49. Có tất cả bao nhiêu giá trị nguyên của tham số
a
thuộc khoảng
0;2019
để
1
9 3 1
lim
5 9 2187
n n
n n a
?
A.
2011
. B.
2018
. C.
2019
. D.
2012
.
Lời giải
Tác giả: Lê Hữu Đức; Fb: Le Huu Duc
ChọnD
Ta có:
1
1
1 3
9 3 1
3
lim lim
5 9 9
5
9
9
n
n n
n
n n a a
a
Suy ra
2
9
1 1 1 1
0 9 4782969 log 4782969 7
9 2187 9 2187
a
a a
a a
Kết hợp điều kiện của bài toán ta được
a
và
7 2019
a
nên có 2012 giá trị của
a
Câu 50. Cho hàm số
y f x
có đạo hàm trên
và có đồ thị là đường cong trong hình vẽ dưới. Đặt
g x f f x
. Tìm số nghiệm của phương trình
0
g x
.
.
A.
2
. B.
8
. C.
4
. D.
6
.
Lời giải.
Tác giả: Lương Văn Huy; Fb: Lương Văn Huy.
Chọn B.
Ta có:
0
0
0
f x
g x f x f f x
f f x
*
.
ST
RONG TEAM TOÁN VD-VDC ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam
Trang
57
Theo đồ thị hàm số suy ra.
1
0
0
x
f
x
x
a
, với
1
2 3
a
.
1
0 , 1
0
, 2
f x
f f x
f x a
.
Phương trình
1
:
0
f
x
có
3
nghiệm phân biệt khác nghiệm phương trình
*
.
Phương trình
2
:
1
f x a
có 3 nghiệm phân biệt khác nghiệm phương trình
1
và phương
trình
*
.
Vậy phương trình ban đầu có 8 nghiệm phân biệt.
| 1/70
| | Tải xuống

Có thể bạn quan tâm:

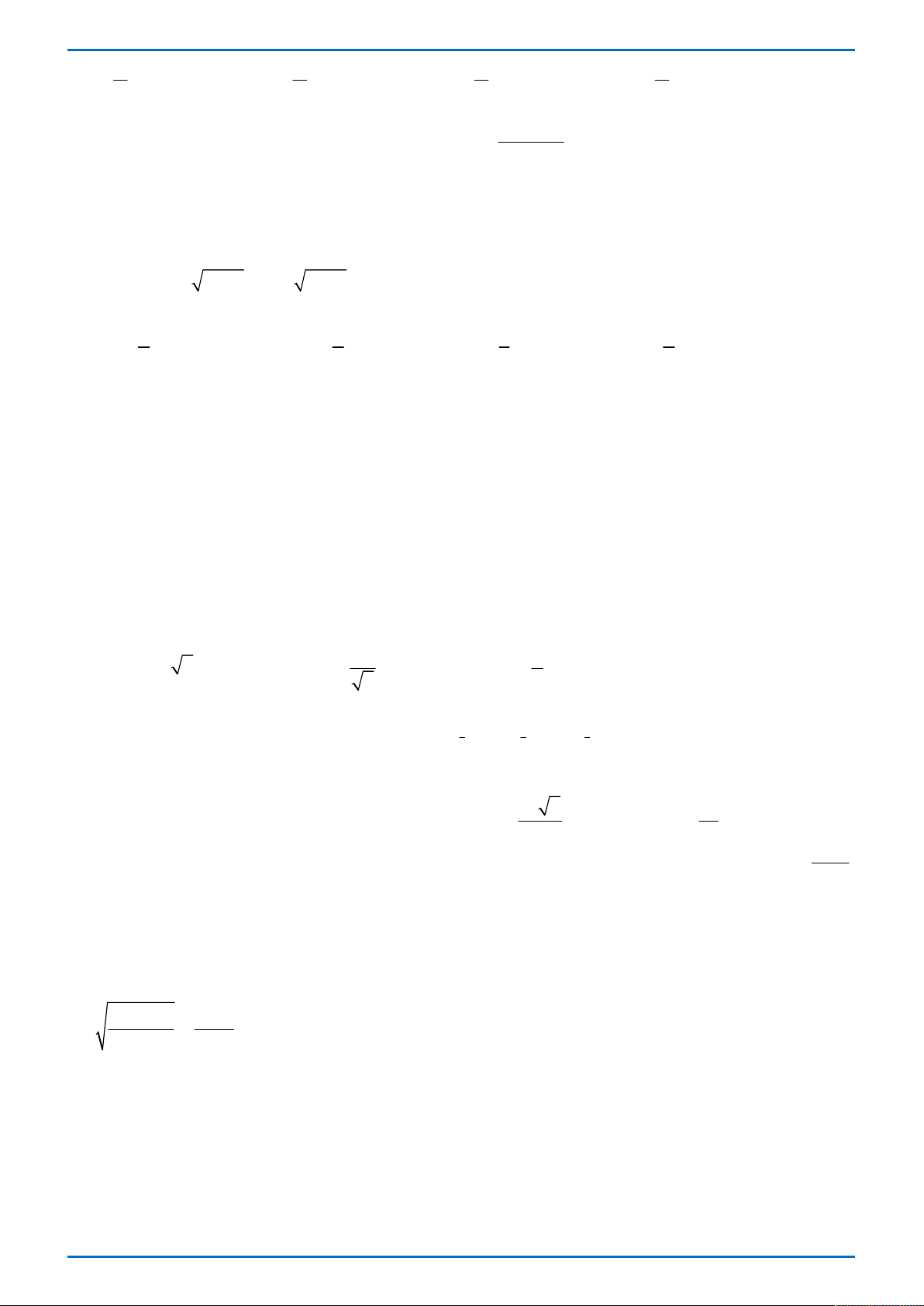
Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO VĨNH PHÚC
ĐỀ KSCL CÁC MÔN THI THPT QUỐC GIA - LẦN 3
TRƯỜNG THPT CHUYÊN VĨNH PHÚC NĂM HỌC 2018-2019
(Đề thi có 6 trang) MÔN TOÁN 12
Thời gian làm bài: 90 phút;
(Không kể thời gian giao đề) Mã đề thi 345
Họ, tên thí sinh:..........................................................................
Số báo danh:...............................................................................
Câu 1: Trong không gian với hệ tọa độ Oxyz , cho A 1
 ;0; 0 , B 0;0; 2 , C 0; 3  ; 0 . Tính bán kính
mặt cầu ngoại tiếp tứ diện OABC là 14 14 14 A. . B. 14 . C. . D. . 4 3 2
Câu 2: Cho cấp số cộng u có u  11 và công sai d  4 . Hãy tính u . n  1 99 A. 401. B. 404 . C. 403 . D. 402 . 2  x 1  khi x  1
Câu 3: Tìm a để hàm số f x   x 1
liên tục tại điểm x  1. 0 a khi x  1  A. a  0 . B. a  1  . C. a  2 . D. a  1 .
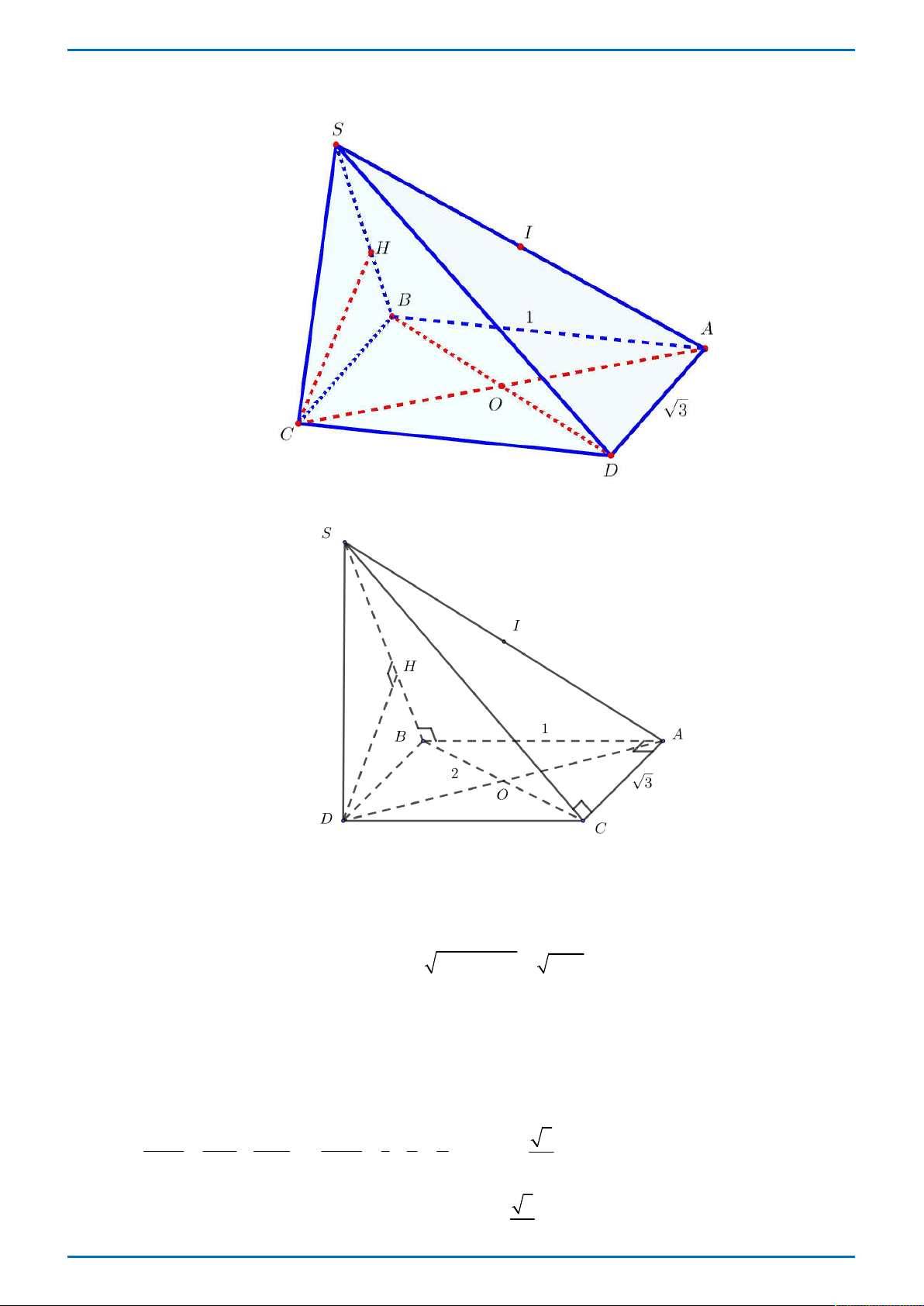
Câu 4: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B . Biết SA   ABCD ,
AB BC a , AD  2a , SA a 2 . Gọi E là trung điểm của AD . Tính bán kính mặt cầu đi qua
các điểm S , A , B , C , E . a 3 a 6 a 30 A. . B. a . C. . D. . 2 3 6
Câu 5: Gọi x là nghiệm dương nhỏ nhất của phương trình 2 2
3sin x  2sin x cos x  cos x  0 . Chọn 0 khẳng định đúng?     3      3  A. x  ; . B. x  ; 2 . C. x  0; . D. x   ; . 0   0   0   0    2   2   2   2  Câu 6: Hàm số 4 3
y x x x  2019 có bao nhiêu điểm cực trị? A. 2 . B. 3 . C. 0 . D. 1. x
Câu 7: Giá trị lớn nhất của hàm số f x  trên đoạn  2  ;  3 bằng x  3 1 A. 2 . B. . C. 3 . D. 2 . 2
Câu 8: Cho hàm số y f x xác định và liên tục trên R , có bảng biến thiên như sau: x  1 1  y  0  0  2  y  1
Mệnh đề nào sau đây là đúng ?
A. Hàm số nghịch biến trên khoảng  ;   1 .
B. Hàm số đồng biến trên khoảng  ;  2   .
C. Hàm số nghịch biến trên khoảng 1;  .
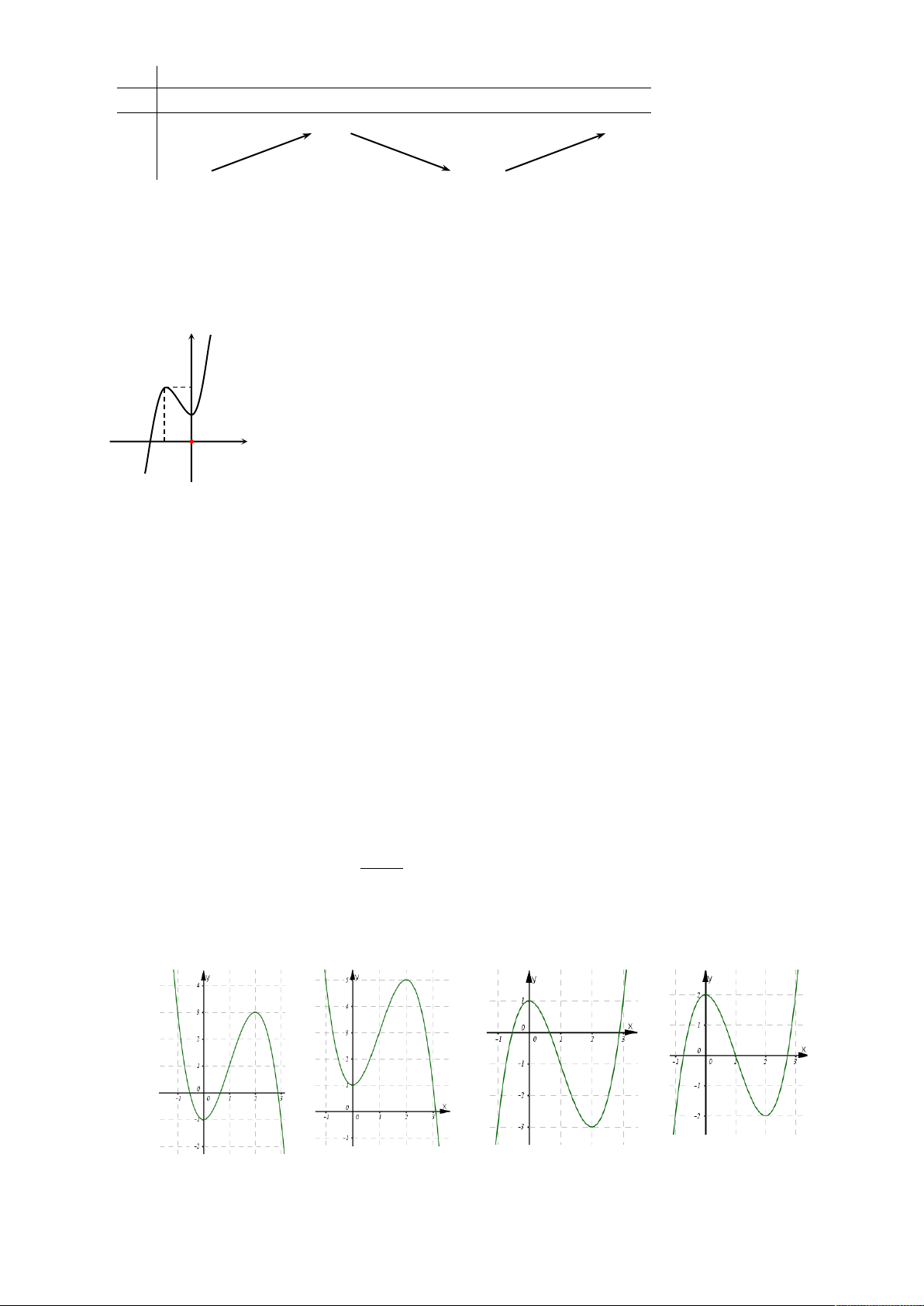
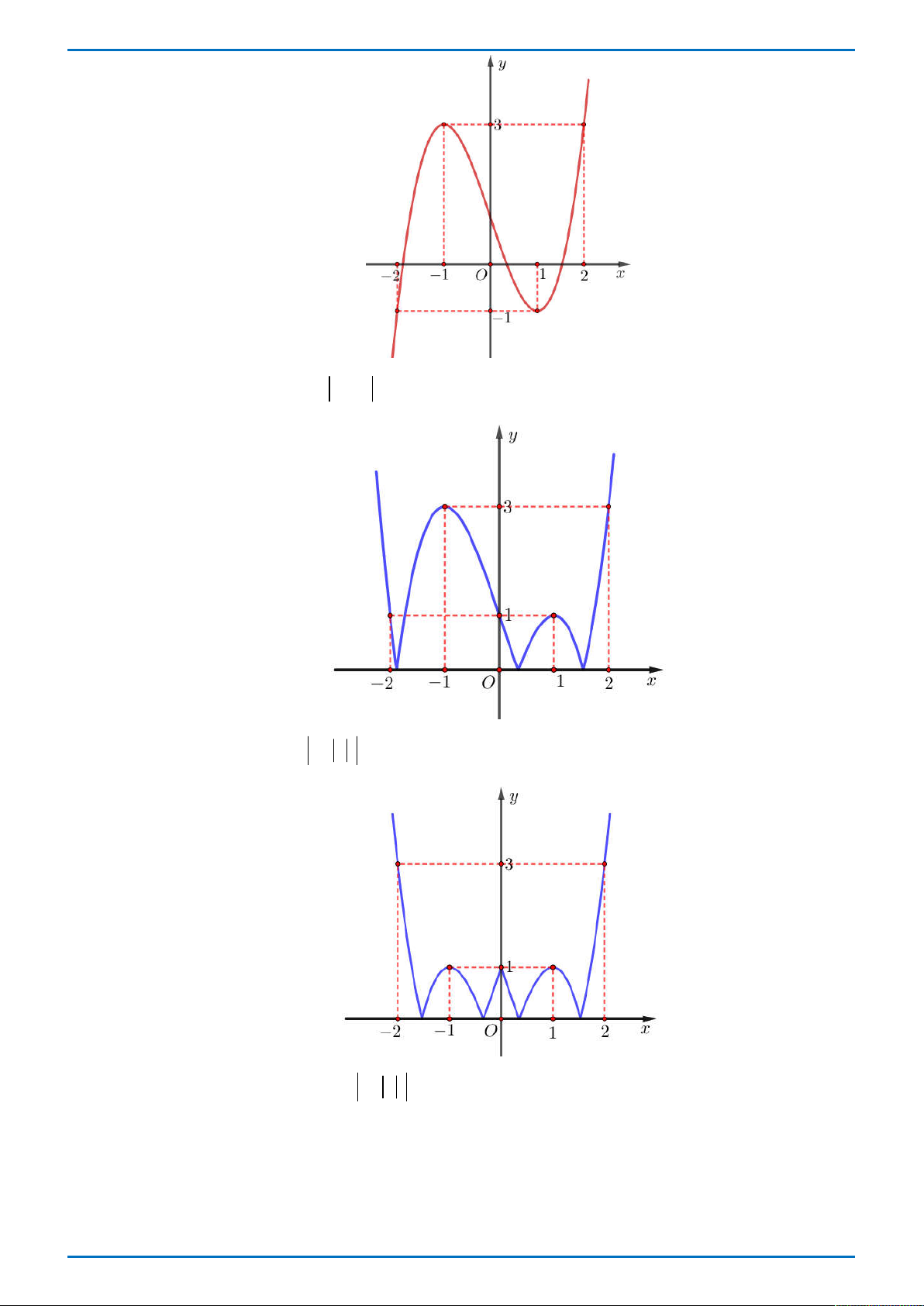
D. Hàm số đồng biến trên khoảng  1  ;  . Câu 9: Hàm số 3 2
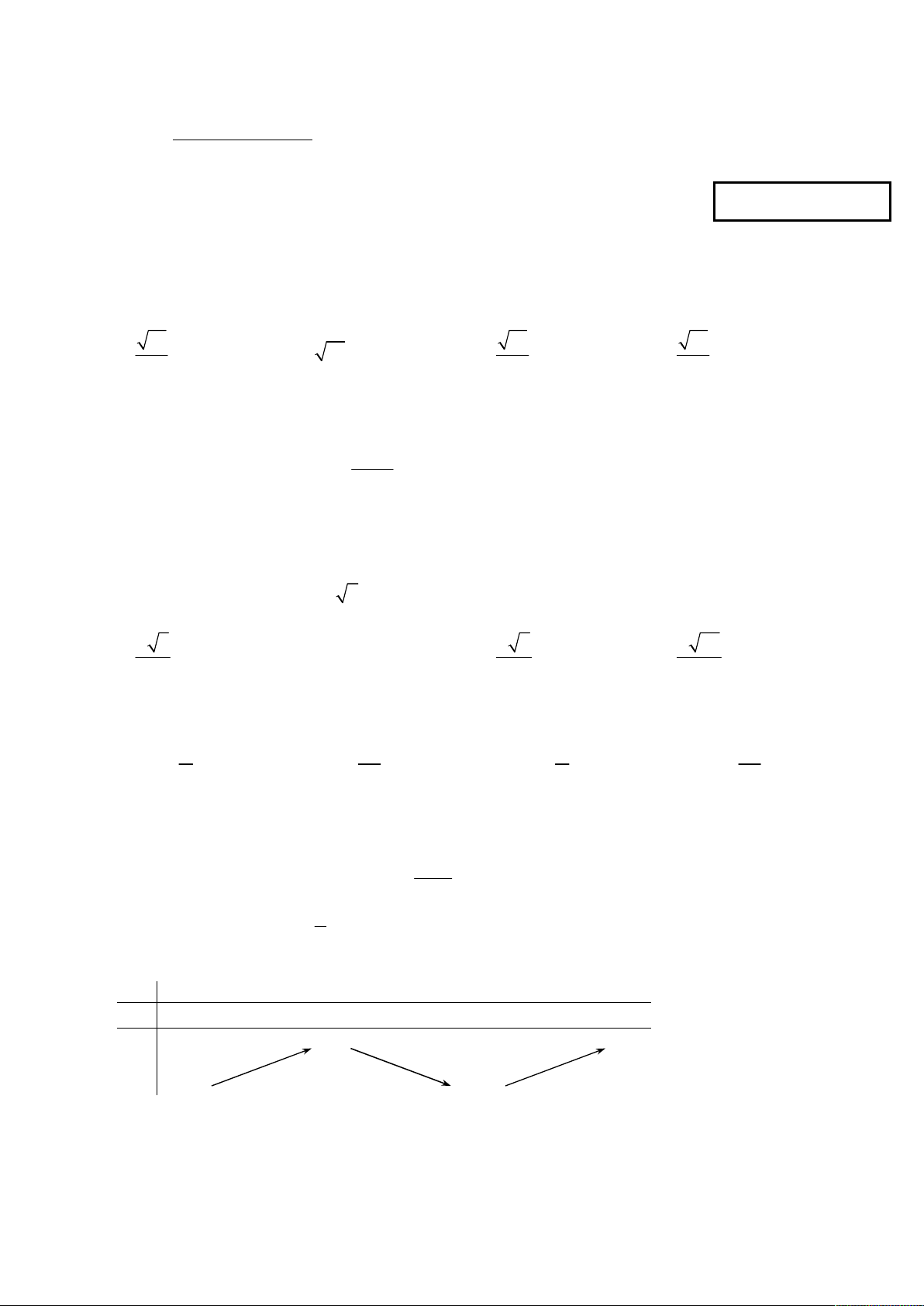
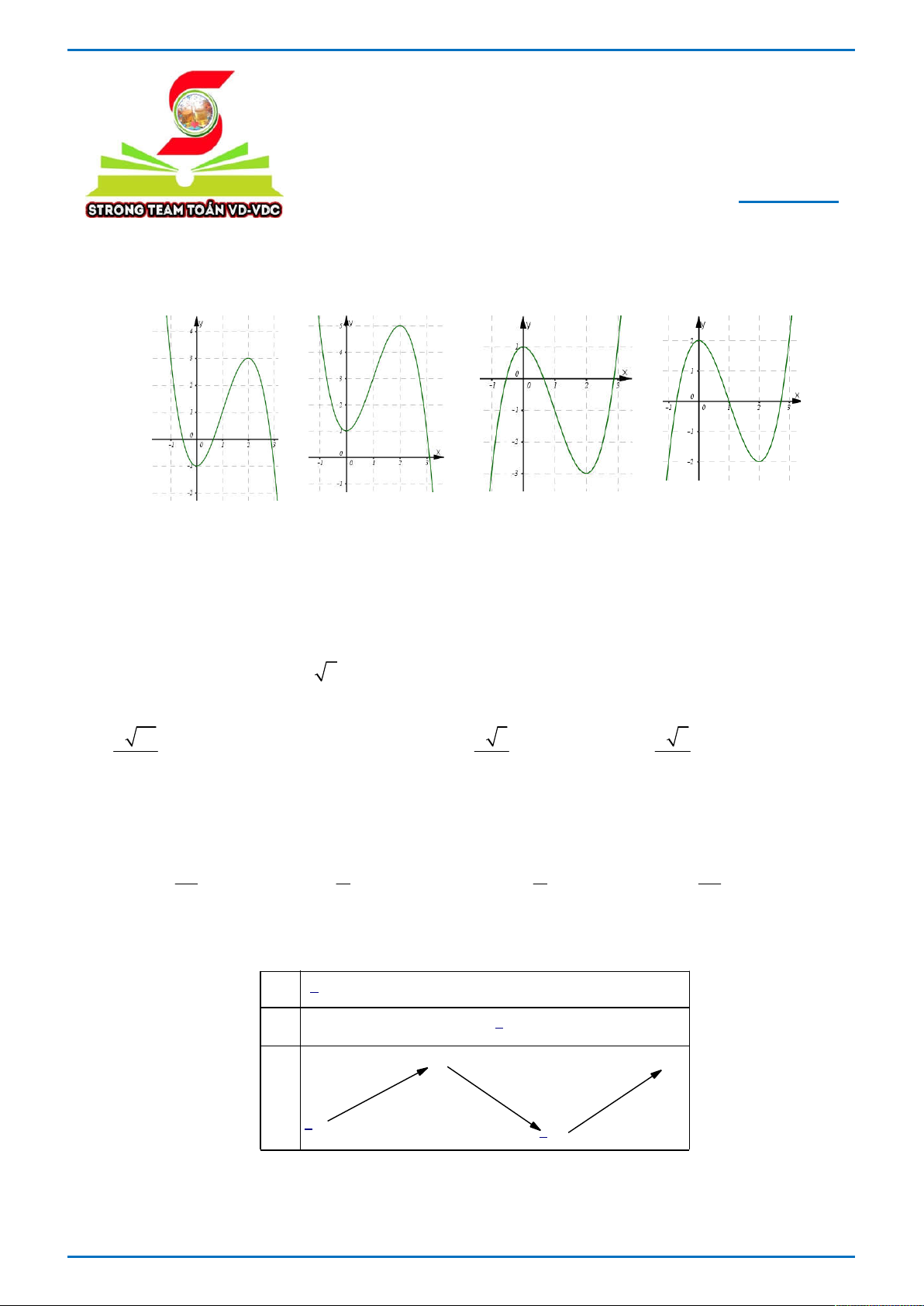
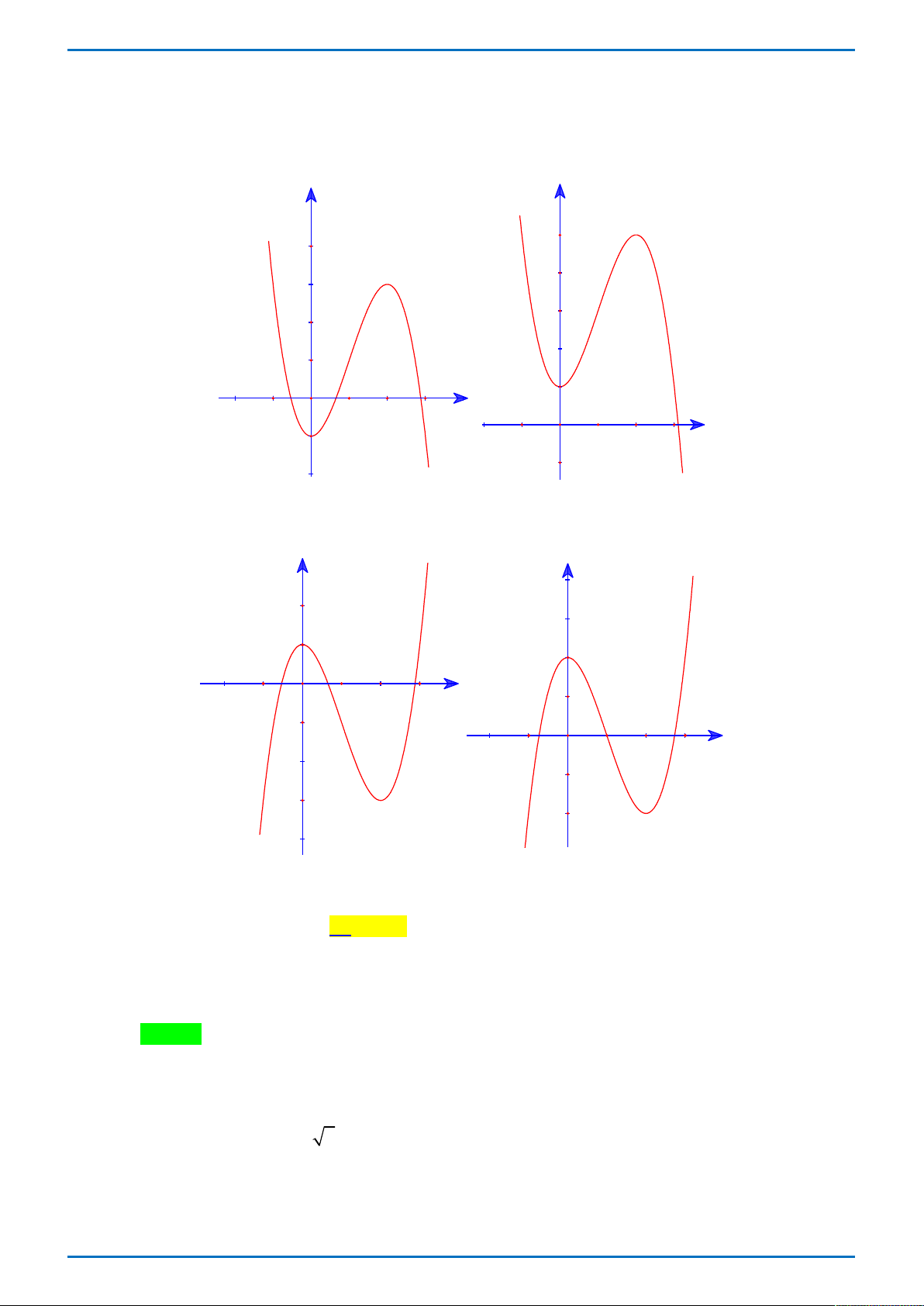
y  x  3x 1 có đồ thị nào trong các đồ thị dưới đây?
Trang 1/6 - Mã đề thi 345 - https://toanmath.com/ Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 3 . B. Hình 1 . C. Hình 2 . D. Hình 4 . 1 1 1 1 190
Câu 10: Gọi n là số nguyên dương sao cho    ...   đúng với log x log x log x log x x n log 2 3 3 3 3 3 3
mọi x dương, x  1 . Tìm giá trị của biểu thức P  2n  3 . A. P  23 . B. P  41 . C. P  43 . D. P  32 .
Câu 11: Có bao nhiêu số hạng trong khai triển nhị thức  x  2018 2 3 thành đa thức A. 2019 . B. 2020 . C. 2018 . D. 2017 .
Câu 12: Cho khối lăng trụ ABC.AB C
  có thể tích bằng V . Tính thể tích khối đa diện ABCB C   . V V 3V 2V A. . B. . C. . D. . 2 4 4 3
Câu 13: Một người gửi tiết kiệm số tiền 80 000 000 đồng với lãi suất là 6, 9 %/ năm. Biết rằng tiền
lãi hàng năm được nhập vào tiền gốc, hỏi sau đúng 5 năm người đó có rút được cả gốc và lãi số tiền
gần với con số nào nhất sau đây? 107 667 000 105 370 000 111 680 000 116 570 000 A. đồng. B. đồng. C. đồng. D. đồng.
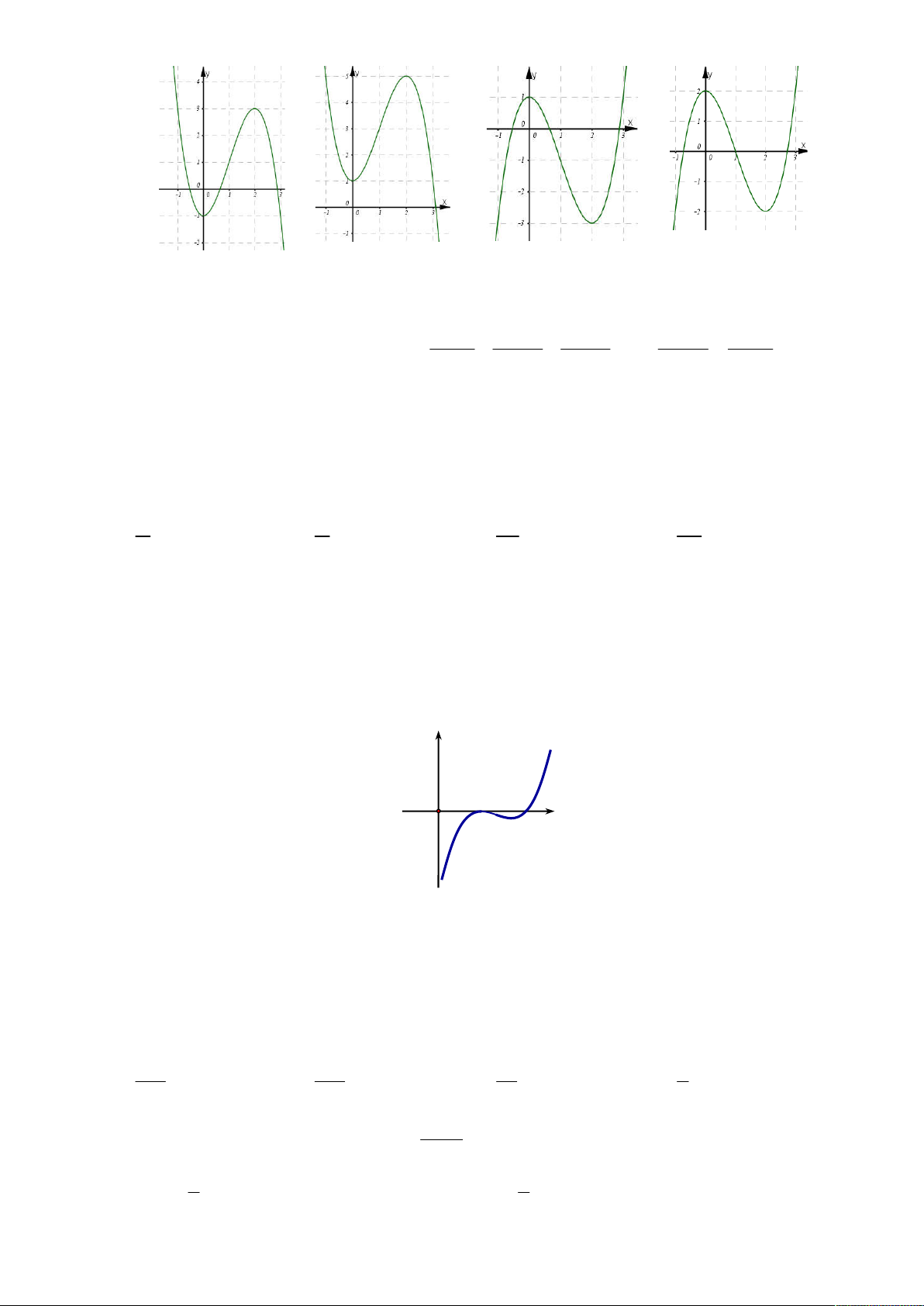
Câu 14: Cho hàm số y f x xác định trên  có đồ thị của hàm số y f  x như hình vẽ. Hỏi
hàm số y f x đồng biến trên khoảng nào dưới đây? y O 1 2 x 0;  1 . 2;  . 1; 2 . 0;  1 và 2;  . A. B. C. D.
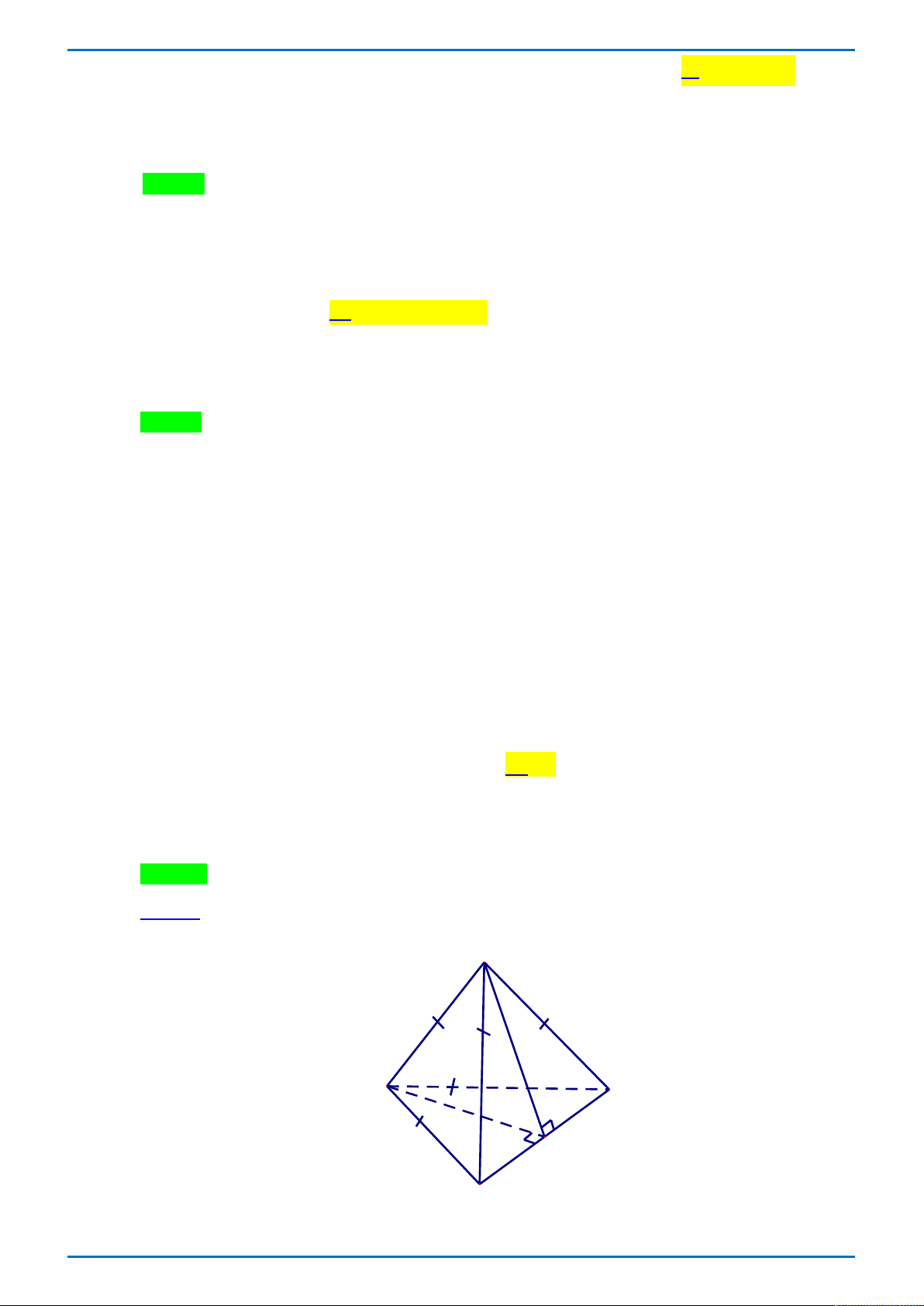
Câu 15: Cho tứ diện ABCD có hai mặt ABC và ABD là các tam giác đều. Tính góc giữa hai đường
thẳng AB và CD . A. 30 . B. 60 . C. 90 . D. 120 . 6 8 7 Câu 16: Cho
2x 3x  2 dx A3x  2  B 3x  2  C  với ,
A B,C R . Tính giá trị của biểu
thức 12A  7B . 23 241 52 7 A. . B. . C. . D. . 252 252 9 9 2 x 1   1 
Câu 17: Tập nghiệm của bất phương trình  1 
(với a là tham số, a  0 ) là 2   1 a   1   1  A. ;     . B.  ;  0 . C.  ;     . D. 0;   .  2   2 
Trang 2/6 - Mã đề thi 345 - https://toanmath.com/
Câu 18: Cho hàm số y f x có bảng biến thiên như sau: x  2 4  y  0  0  3  y  2
Hàm số đạt cực đại tại điểm nào trong các điểm sau đây? A. x  2  . B. x  3. C. x  2. D. x  4. 2
Câu 19: Tìm tập nghiệm của phương trình x 2 3 x  1. A. S   1  ;  3 . B. S  0;   2 . C. S  1;   3 . D. S  0;  2 .     
Câu 20: Trong không gian với hệ trục tọa độ Oxyz, cho a  i  2 j  3k . Tìm tọa độ của vectơ a . A. 2; 3  ;   1 . B.  3  ; 2;   1 . C.  1  ; 2; 3  . D. 2; 1  ; 3  .
Câu 21: Hàm số nào dưới đây nghịch biến trên tập xác định của nó? x    A. y  log x .
B. y  log x . C. y  . D. y  log x 1 . 2   3     3  4
Câu 22: Cho hình chóp S.ABC có đáy là tam giác cân tại A , AB AC a , 
BAC  120 . Tam giác
SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích V của khối chóp S.ABC . 3 a 3 a A. 3 V a . B. V  . C. 3 V  2a . D. V  . 2 8
Câu 23: Có bao nhiêu giá trị nguyên của tham số m trên đoạn  2
 018; 2018 để hàm số y   2
ln x  2x m  
1 có tập xác định là  . A. 2018 . B. 1009 . C. 2019 . D. 2017 .
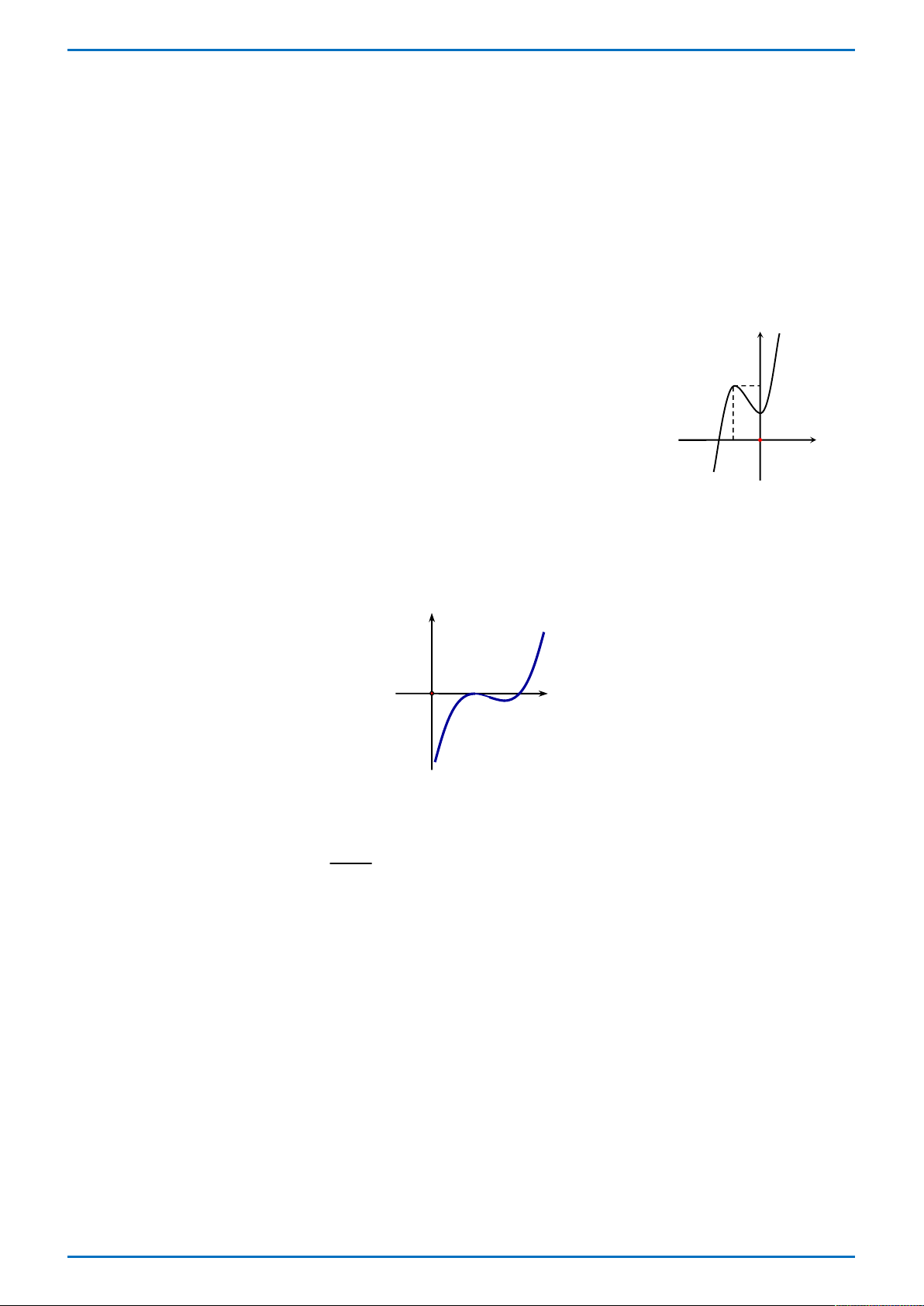
Câu 24: Cho hàm số y f x có đạo hàm trên  và đồ thị hàm số y f  x trên  như hình
vẽ. Mệnh đề nào sau đây là đúng? y
A. Hàm số y f x có 1 điểm cực tiểu và không có cực đại. 2
B. Hàm số y f x có 1 điểm cực đại và không có cực tiểu. 1 x
C. Hàm số y f x có 1 điểm cực đại và 2 điểm cực tiểu. 1 O
D. Hàm số y f x có 1 điểm cực đại và 1 điểm cực tiểu.
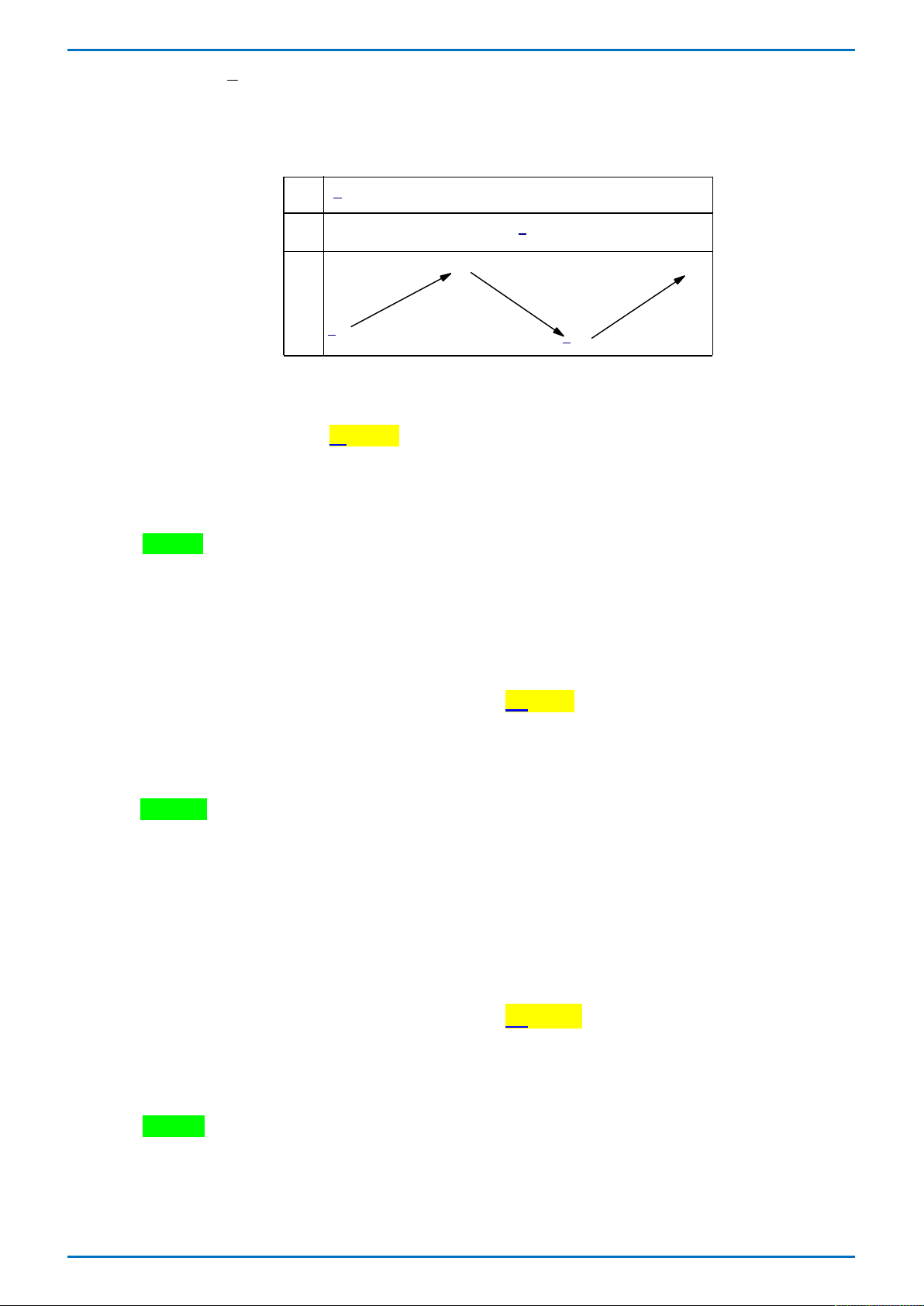
Câu 25: Cho hình trụ có thiết diện đi qua trục là một hình vuông có cạnh bằng 4a . Diện tích xung quanh của hình trụ là A. 2 S  4 a . B. 2 S  8 a . C. 2 S  24 a . D. 2 S  16 a .
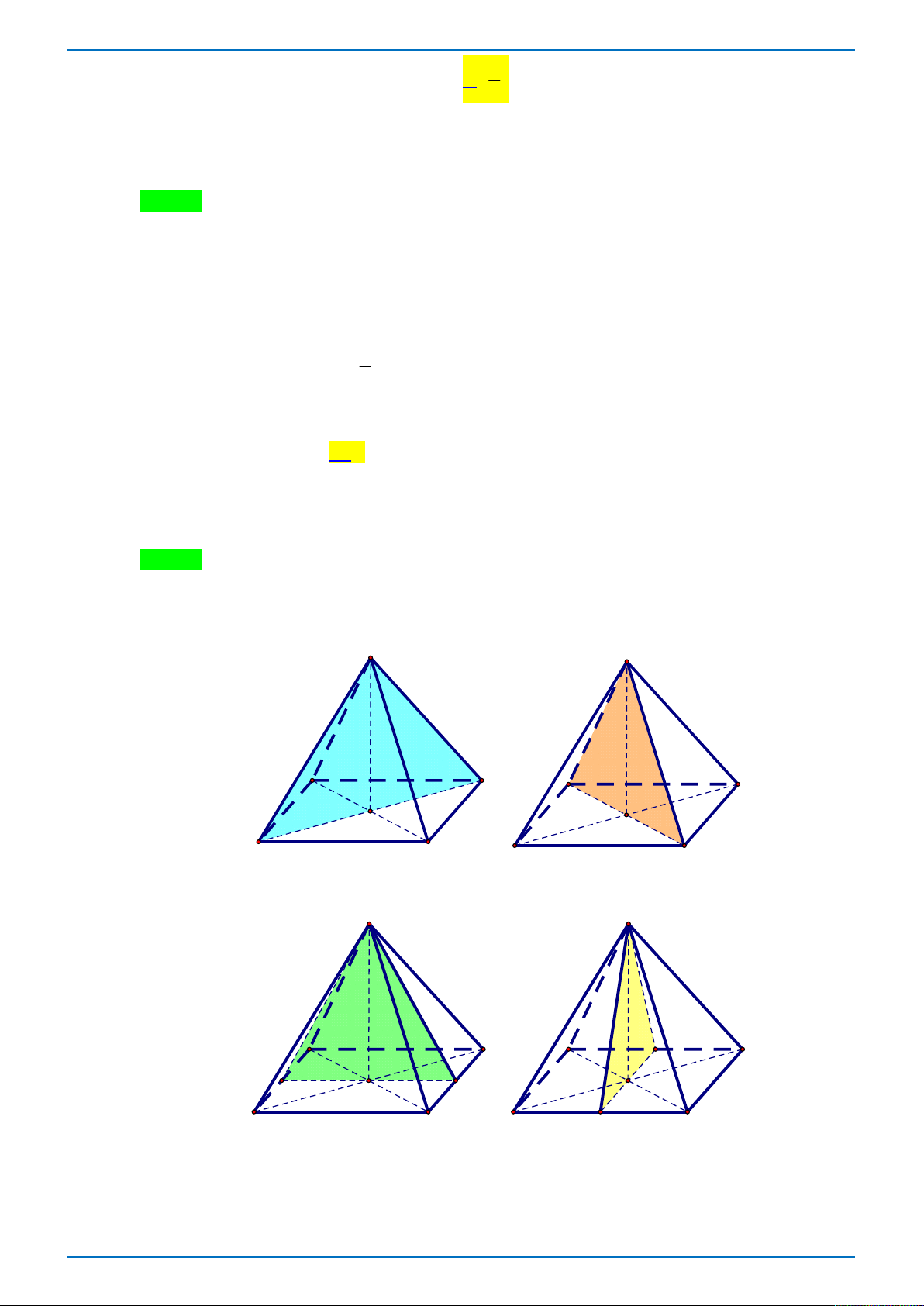
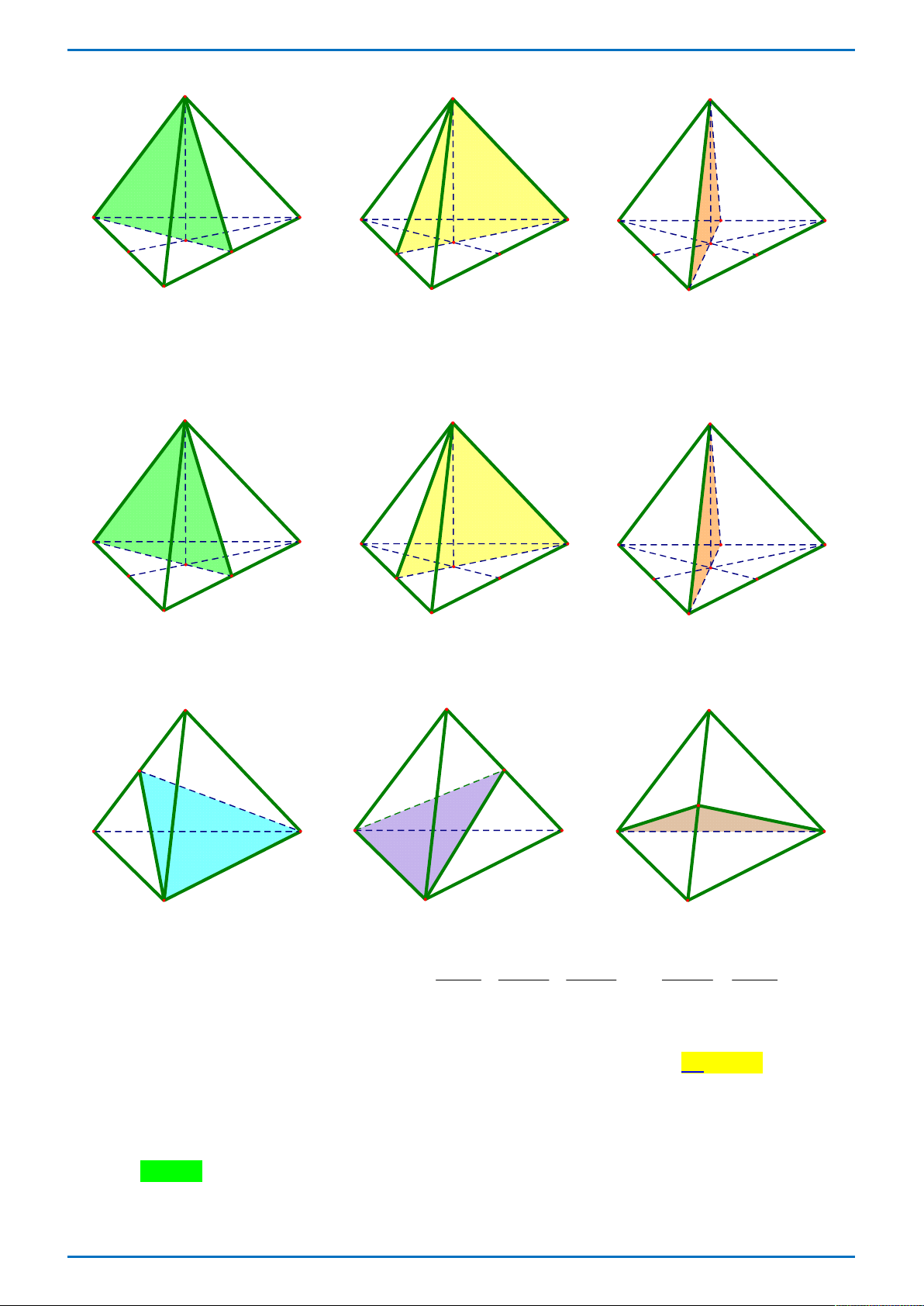
Câu 26: Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng? A. 4 . B. 8 . C. 6 . D. 2.
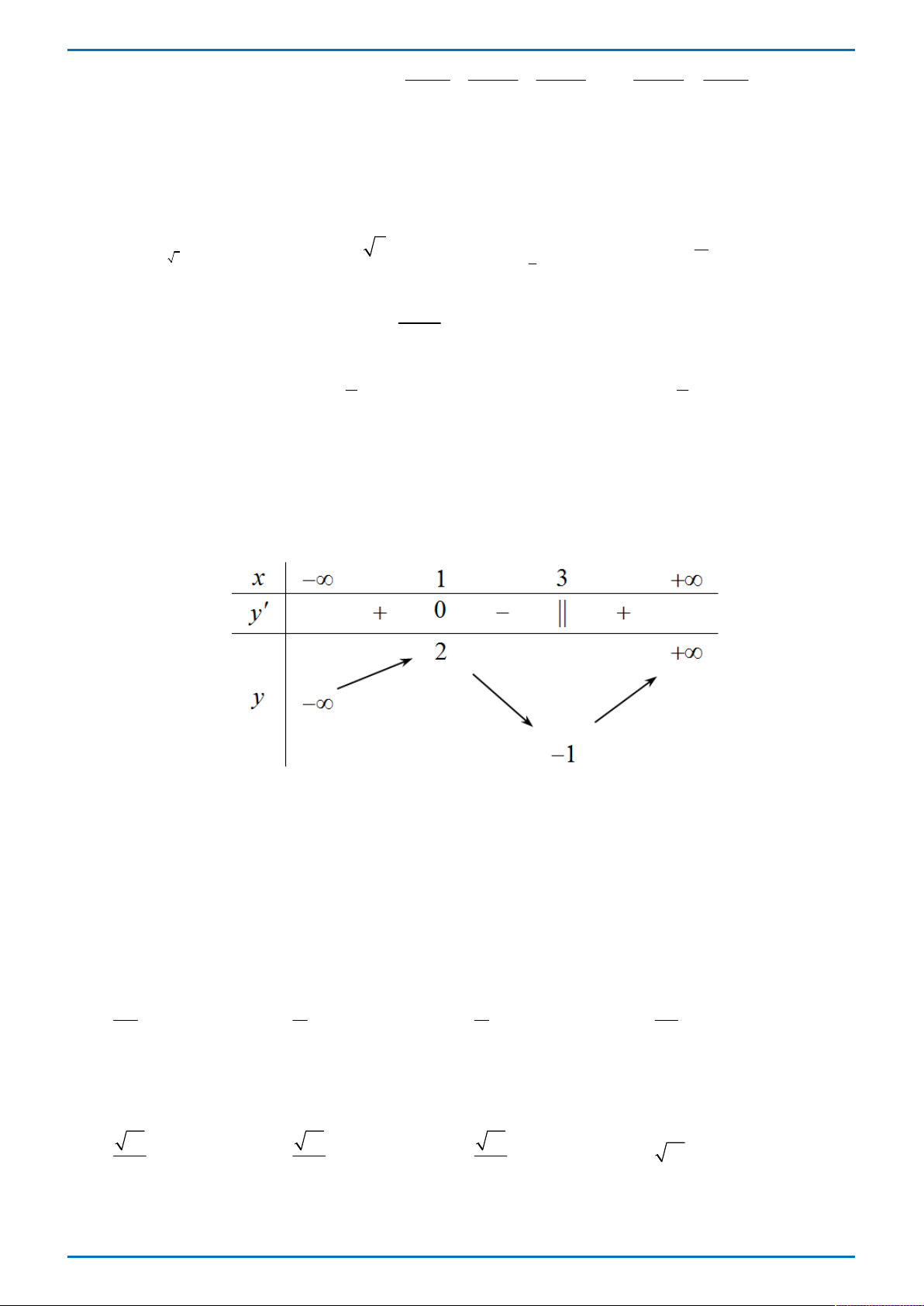
Câu 27: Cho hàm số y f x xác định, liên tục trên  và có bảng biến thiên như sau  x 1 3  y  0   2  y
Trang 3/6 - Mã đề thi 345 - https://toanmath.com/
Khẳng định nào sau đây là đúng?
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị cực tiểu bằng 3.
C. Hàm số đạt cực đại tại x  1 và đạt cực tiểu tại x  3 .
D. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng 1. 1
Câu 28: Tìm nguyên hàm của hàm số 2
y x  3x  . x 3 2 x 3x 3 2 x 3x 1 A. 
 ln x C . B.    C . 3 2 2 3 2 x 3 2 x 3x 3 2 x 3x C. 
 ln x C . D. 
 ln x C . 3 2 3 2 10 6
Câu 29: Cho hàm số f x liên tục trên đoạn 0;10 và
f x dx  7  và
f x dx  3  . Tính 0 2 2 10 P
f x dx f x dx   . 0 6 A. P  4  . B. P  10 . C. P  7 . D. P  4 .
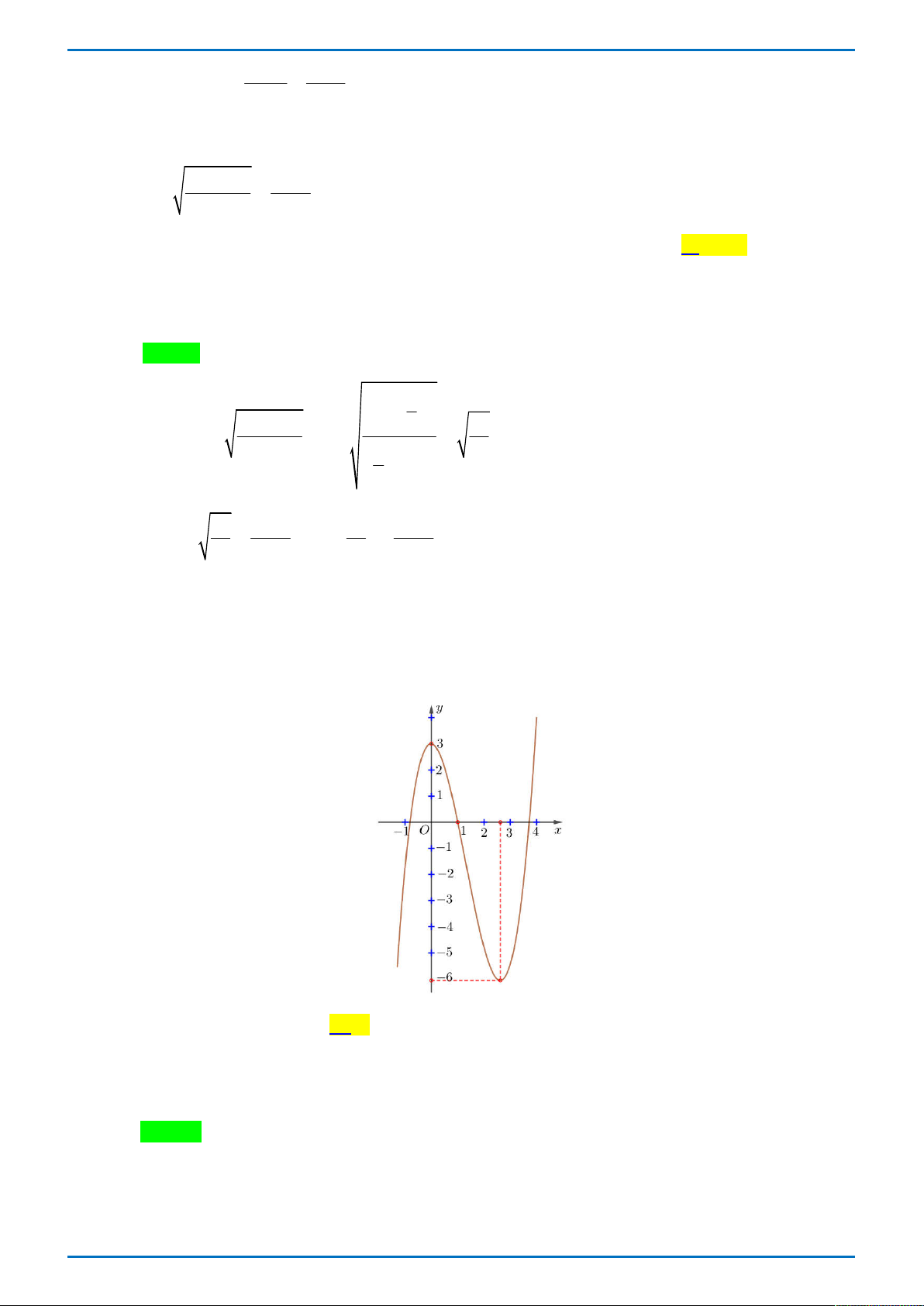
Câu 30: Tìm tất cả các giá trị của tham số m để giá trị nhỏ nhất của hàm số 3 2
y  x  3x m trên đoạn 1;  1 bằng 0. A. m  6 . B. m  4 . C. m  0 . D. m  2 .
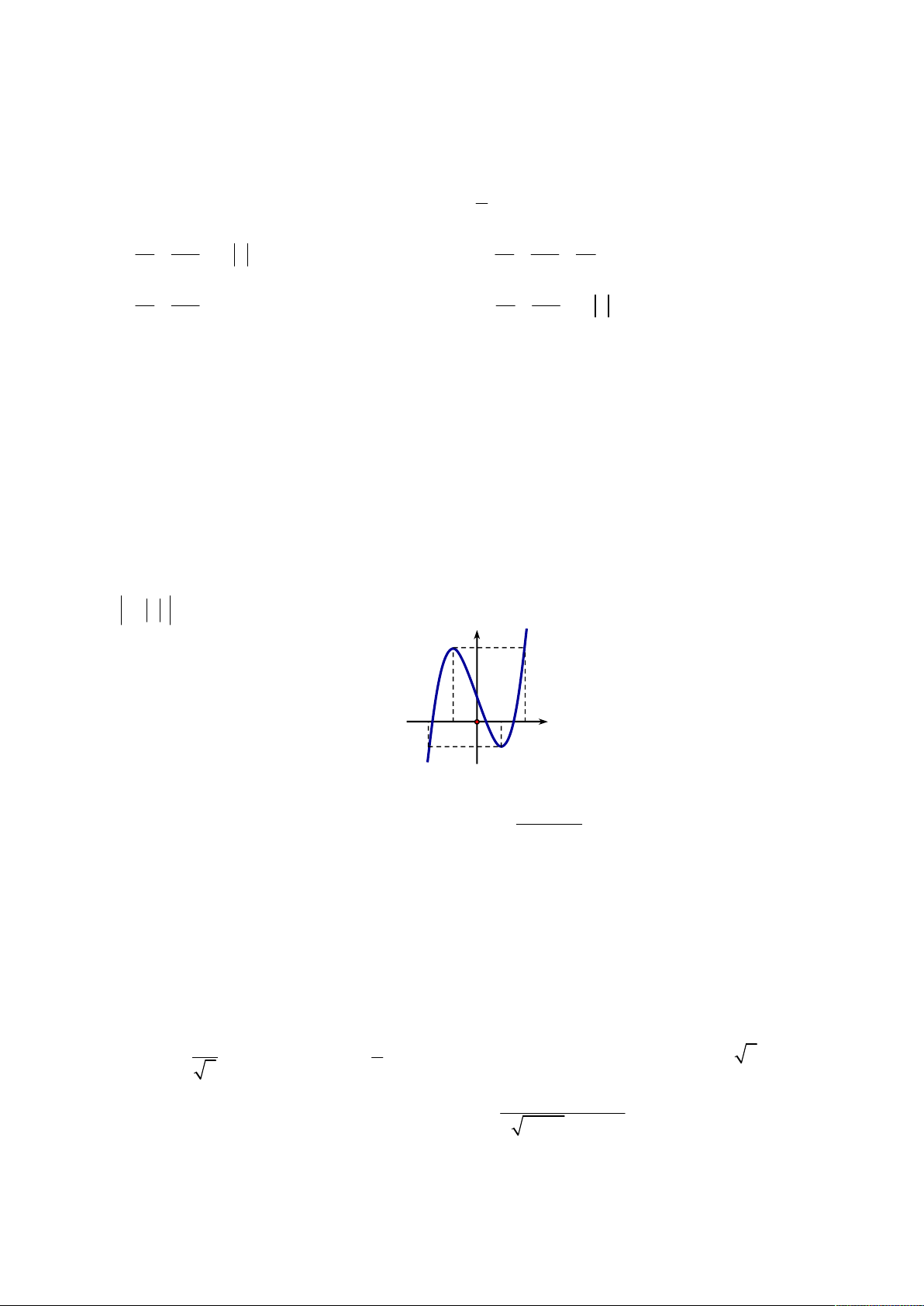
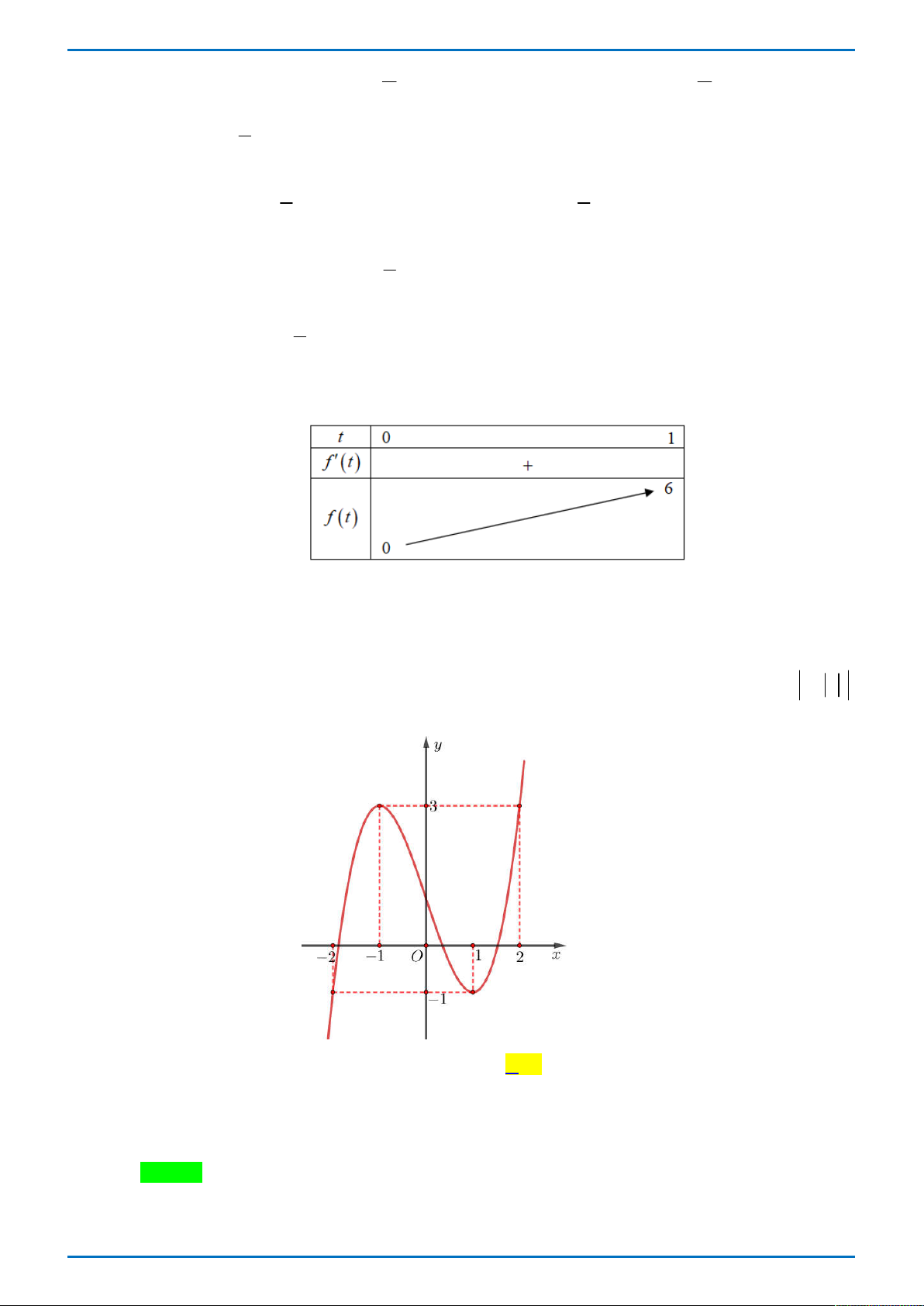
Câu 31: Cho hàm số y f x liên tục trên  và có đồ thị như hình vẽ. Hỏi đồ thị hàm số
y f x  có tất cả bao nhiêu điểm cực trị? y 3 2 1 1O 2 x 1 A. 9 B. 7 . C. 6 D. 8 x  cos x
Câu 32: Biết F x là nguyên hàm của hàm số f x 
. Hỏi đồ thị của hàm số y F x 2 x
có bao nhiêu điểm cực trị? A. 1. B. vô số điểm. C. 2. D. 0.
Câu 33: Có bao nhiêu số tự nhiên có 4 chữ số được viết từ các chữ số 1, 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 sao
cho số đó chia hết cho 15 ? A. 432 B. 234 . C. 132 . D. 243 .
Câu 34: Cho hình trụ có đáy là hai đường tròn tâm O và O , bán kính đáy bằng chiều cao và bằng
2a . Trên đường tròn đáy có tâm O lấy điểm A , trên đường tròn tâm O lấy điểm B . Đặt  là góc
giữa AB và đáy. Tính tan  khi thể tích khối tứ diện OO A
B đạt giá trị lớn nhất. 1 1 A. tan   . B. tan   . C. tan   1. D. tan   2 . 2 2 x 1
Câu 35: Tìm số đường tiệm cận của đồ thị hàm số y  .
4 3x 1  3x  5 A. 1. B. 0 . C. 2 . D. 3 .
Trang 4/6 - Mã đề thi 345 - https://toanmath.com/
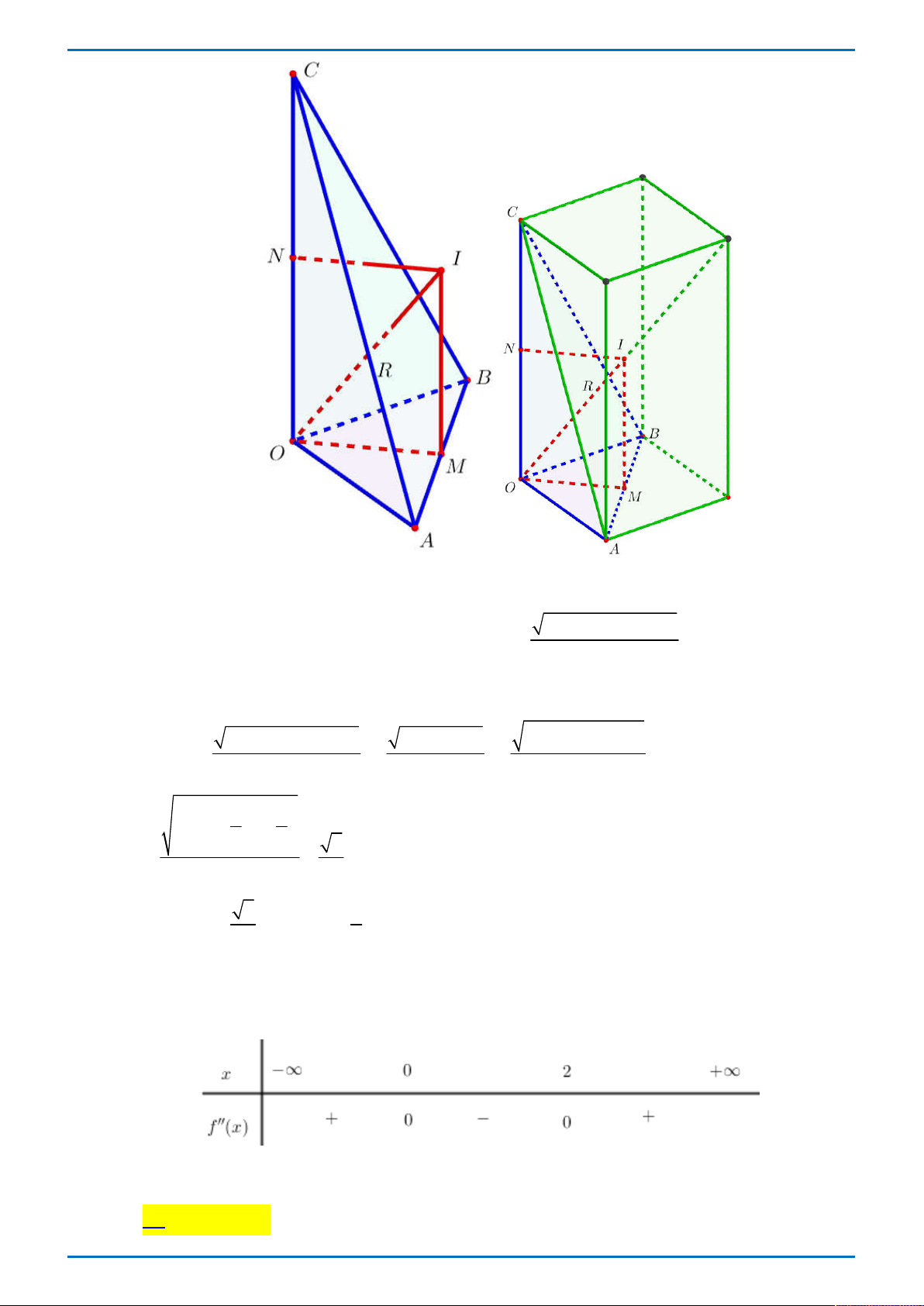
Câu 36: Cho hình chóp S.ABC có đáy là AB
C vuông cân ở B, AC a 2, SA   ABC, SA a.
Gọi G là trọng tâm của S
BC , mp   đi qua AG và song song với BC chia khối chóp thành hai
phần. Gọi V là thể tích của khối đa diện không chứa đỉnh S . Tính V . 3 5a 3 4a 3 2a 3 4a A. . B. . C. . D. . 54 9 9 27
Câu 37: Cho hình chóp S.ABC có các cạnh SA BC  3 ; SB AC  4 ; SC AB  2 5 . Tính thể
tích khối chóp S.ABC . 390 390 390 390 A. . B. . C. . D. . 12 6 8 4
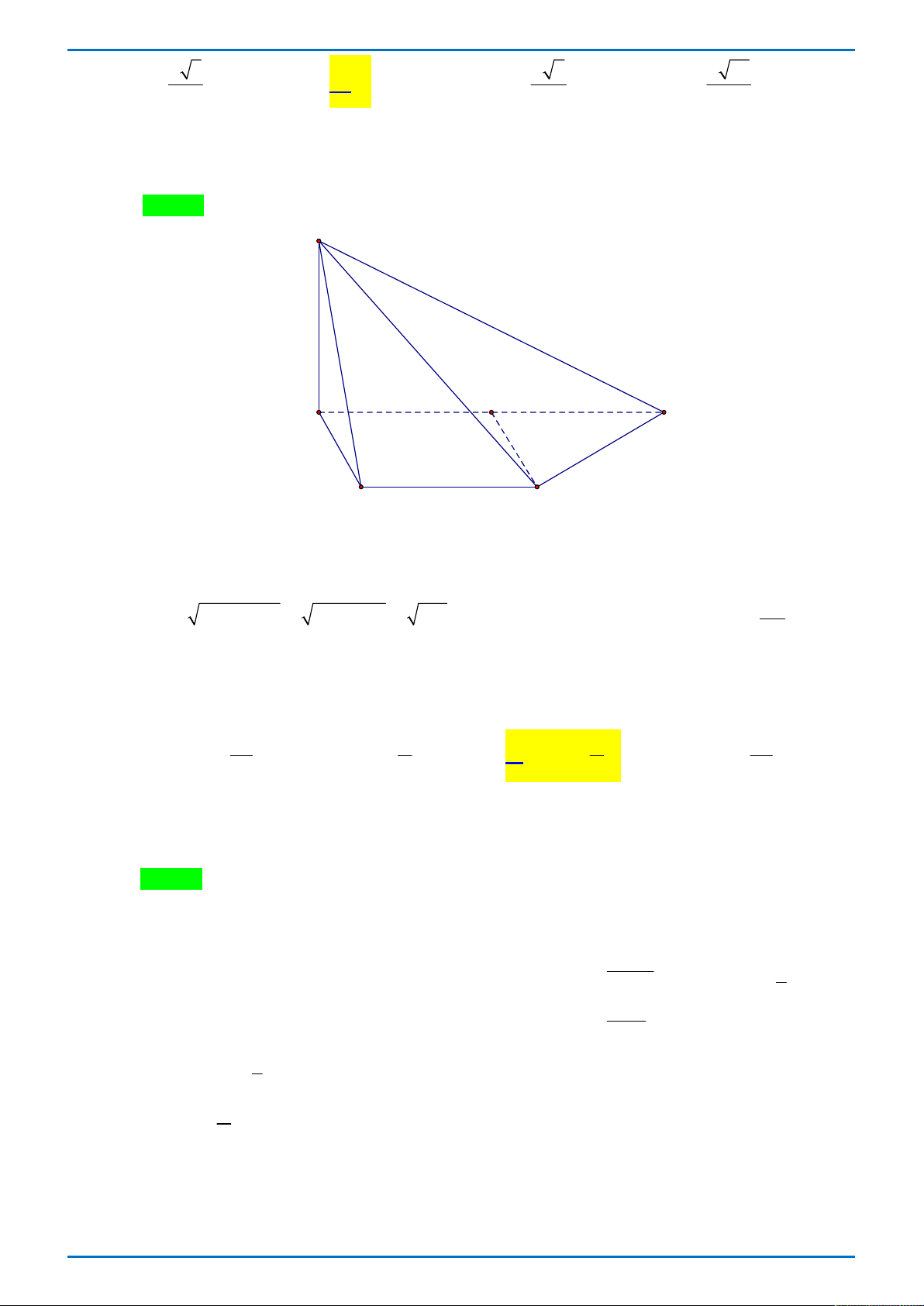
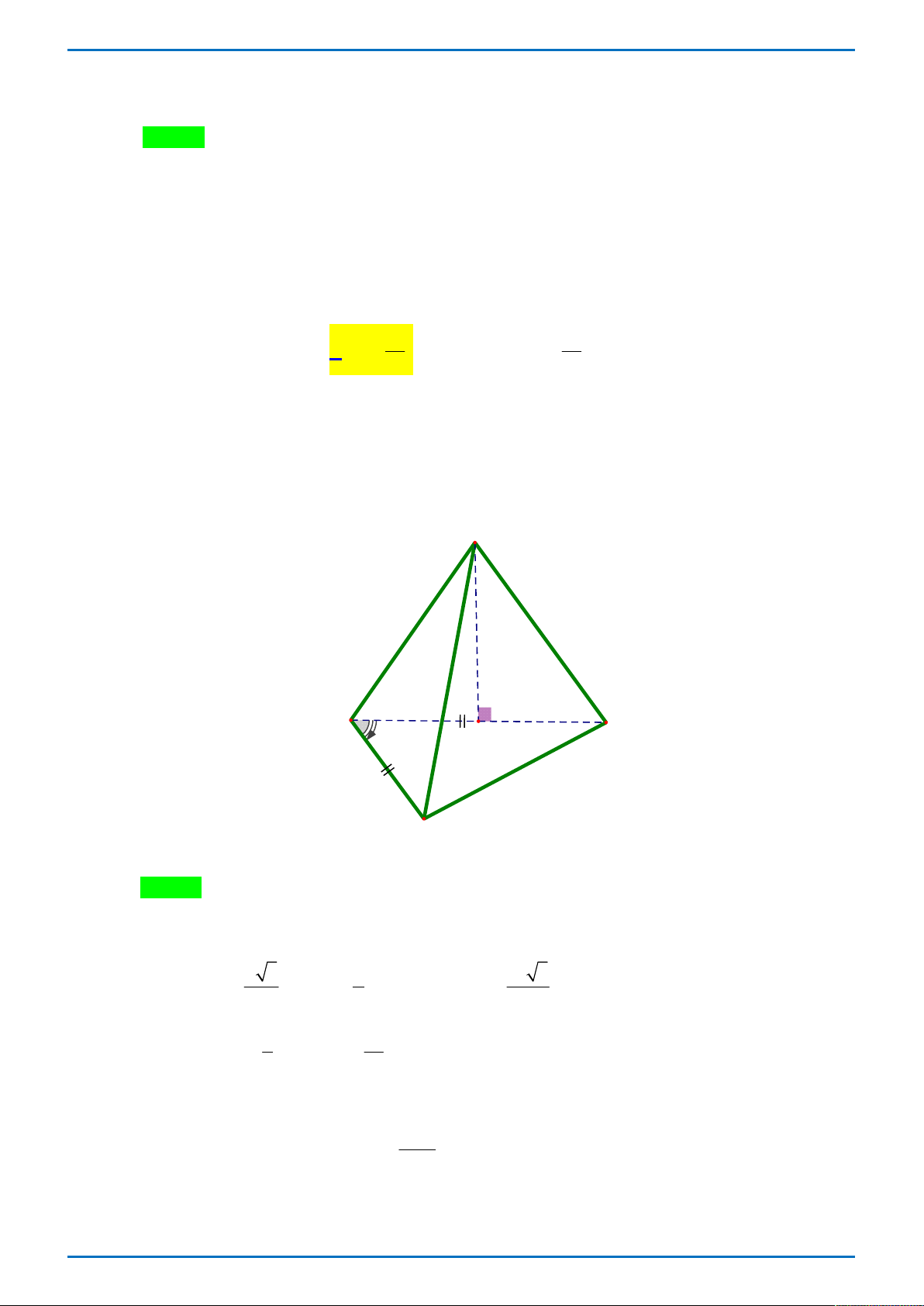
Câu 38: Trong không gian Oxyz , lấy điểm C trên tia Oz sao cho OC  1 . Trên hai tia Ox, Oy lần lượt lấy hai điểm ,
A B thay đổi sao cho OA OB OC . Tìm giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp tứ diện . O ABC ? 6 6 6 A. . B. 6. C. . D. . 4 3 2
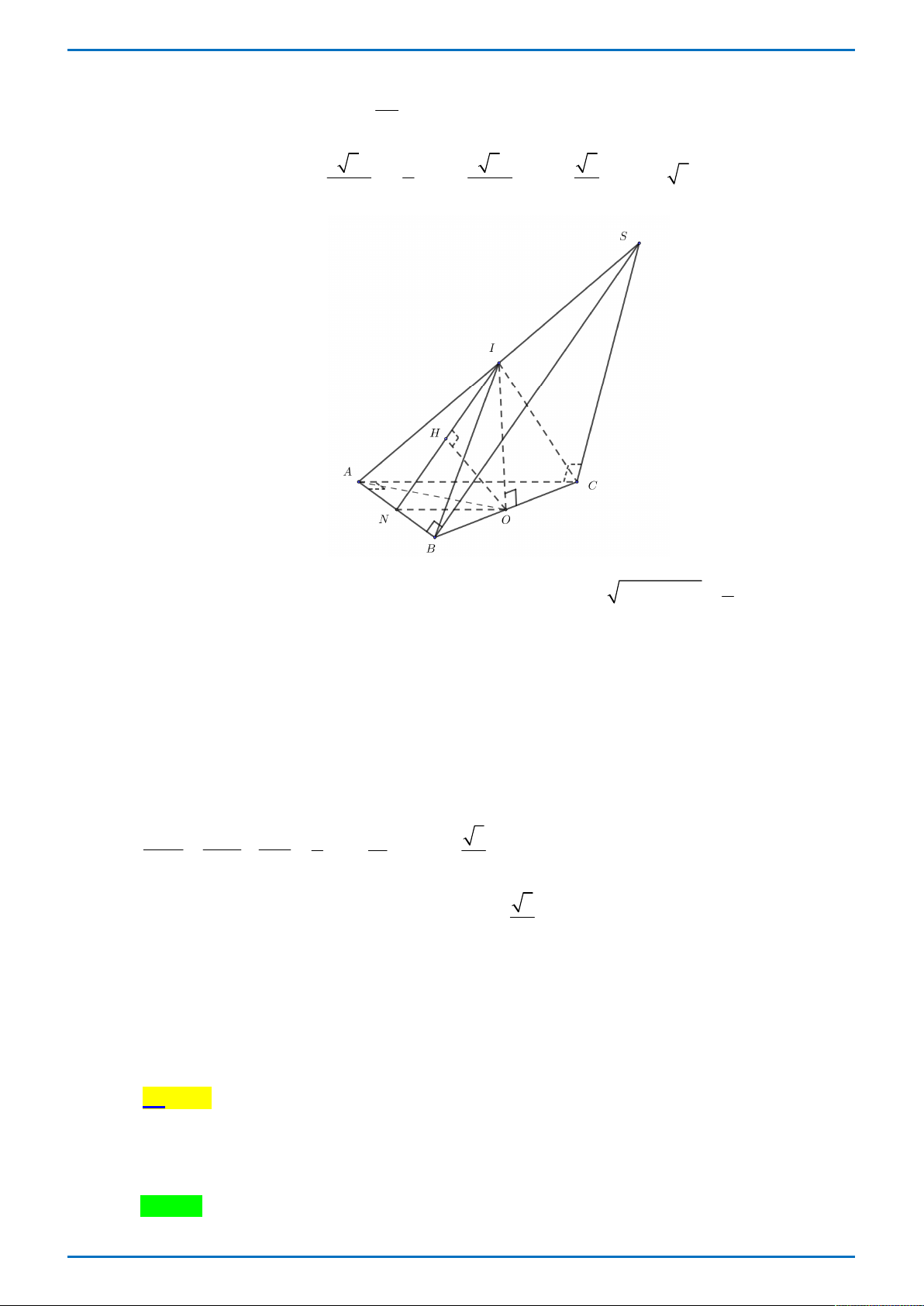
Câu 39: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , AB  1cm , AC  3cm . Tam
giác SAB , SAC lần lượt vuông tại B và C . Khối cầu ngoại tiếp hình chóp S.ABC có thể tích 5 5 bằng 3
cm . Tính khoảng cách từ C tới  SAB 6 3 5 3 5 A. cm . B. cm . C. cm . D. cm . 2 2 4 4
Câu 40: Cho hàm số y f x có đạo hàm liên tục trên đoạn 0 
;1 và thỏa mãn f 0  0 . Biết 1 9 1  x 3 1 2
f x dx   và
f  x cos dx   . Tích phân
f x dx  bằng 2 2 4 0 0 0 6 2 4 1 A. . B. . C. . D. .     Câu 41: Tìm tất cả các giá trị thực của tham số
m để phương trình 3m m e e   2 x   x  2 2 1
1 x 1 x  có nghiệm.  1   1   1   1  A. ln 2;    . B. 0; ln 2   . C. ;  ln 2   . D. 0;   .  2   2   2   e
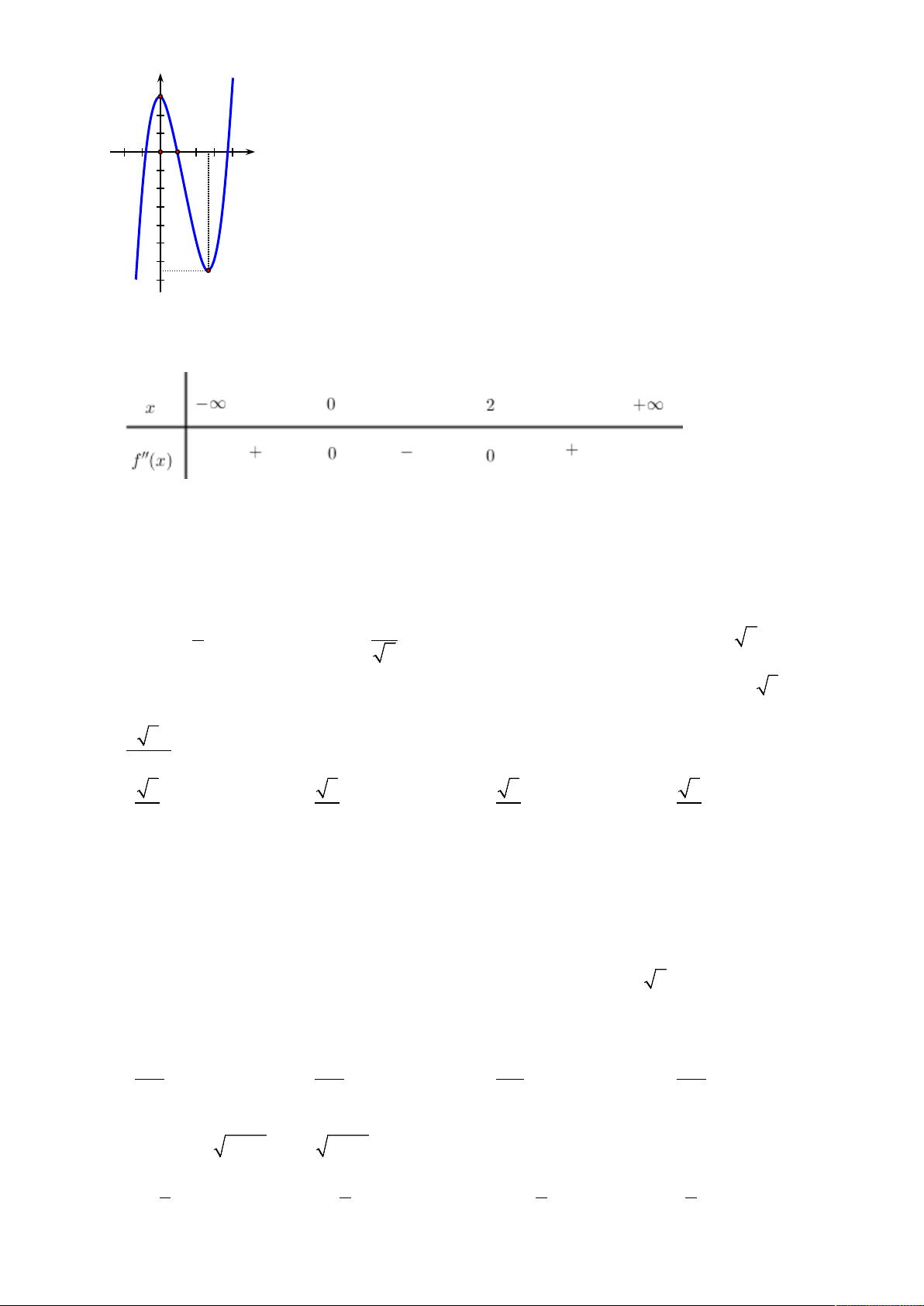
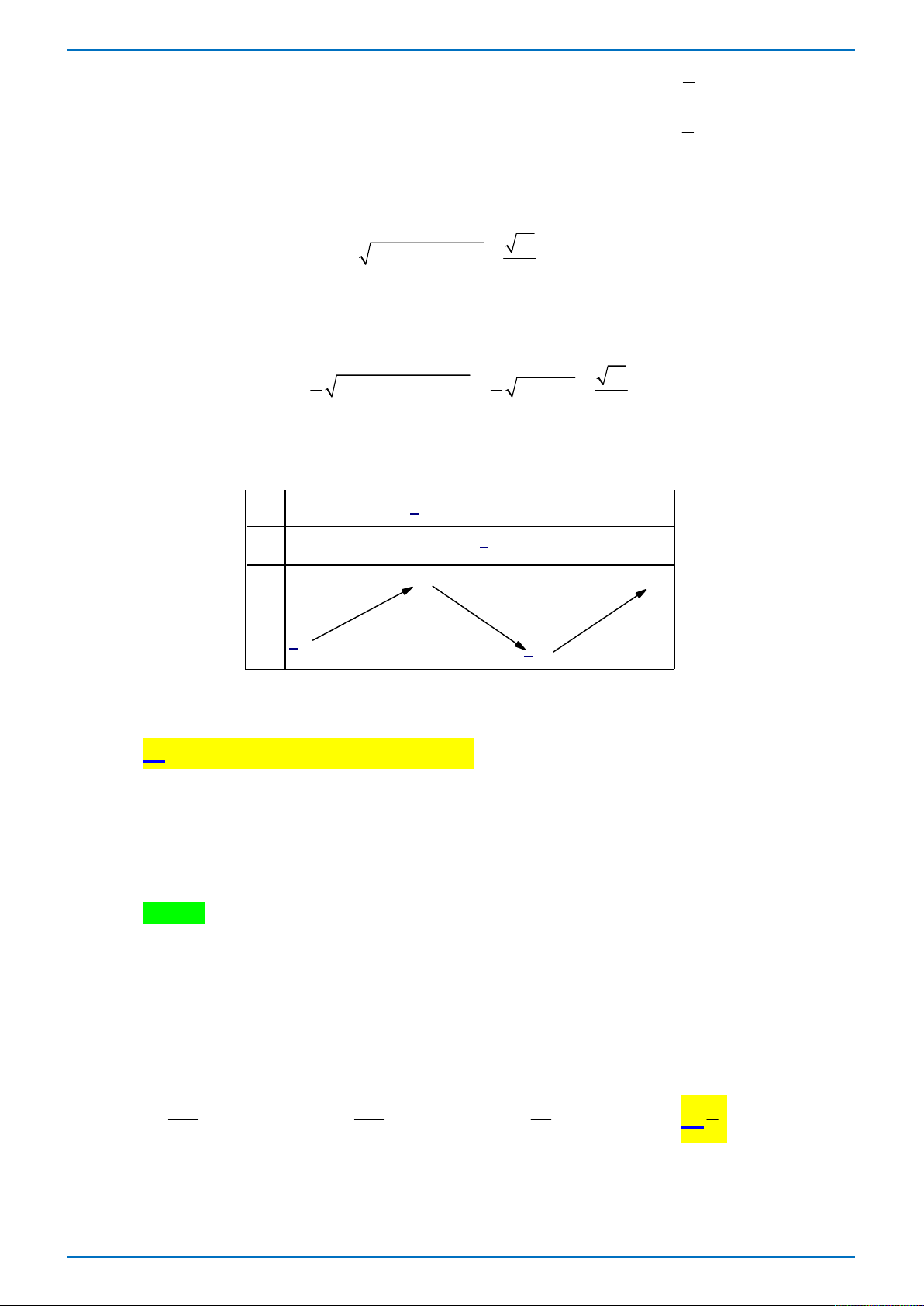
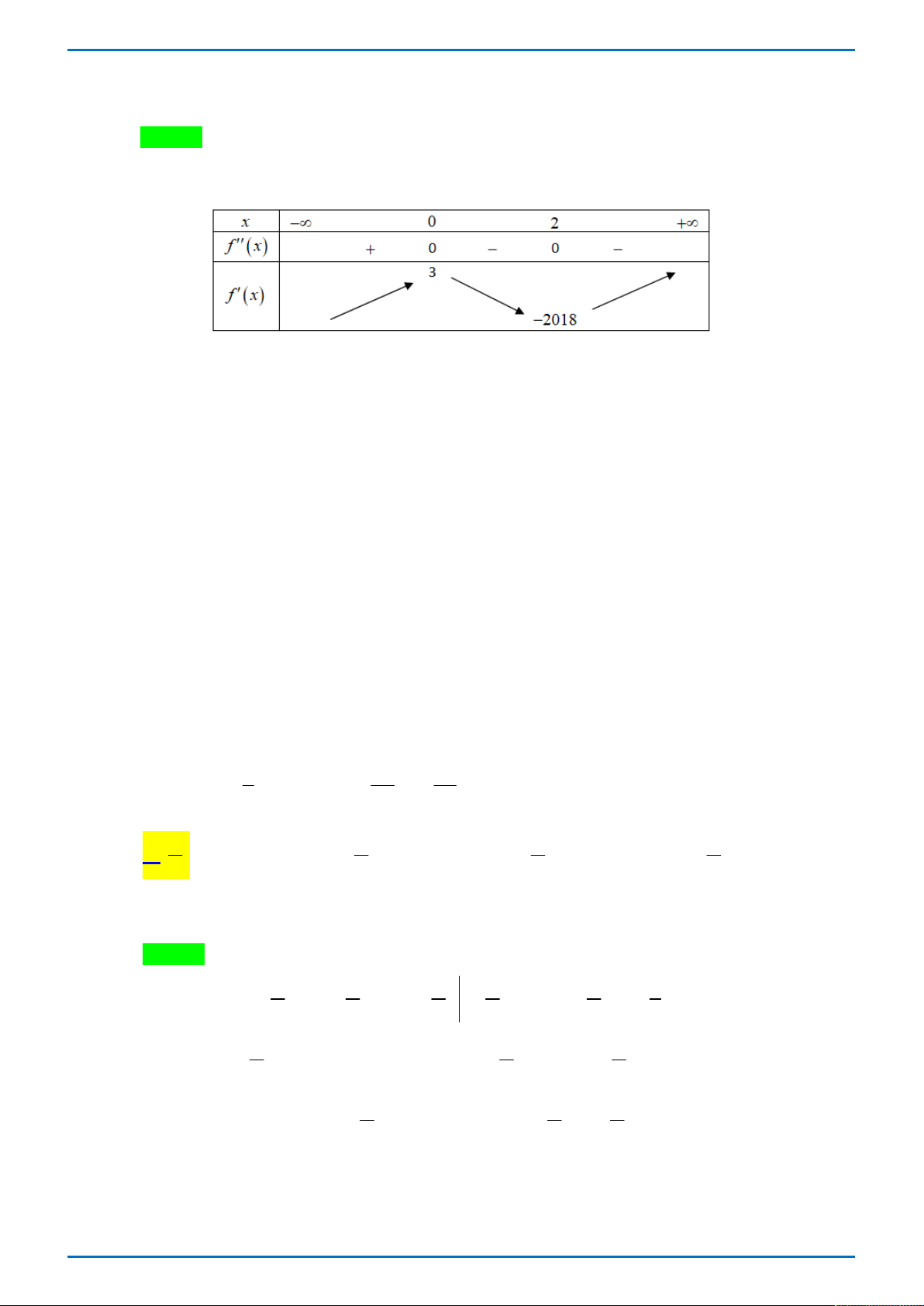
Câu 42: Cho hàm số y f x có đạo hàm cấp hai trên  . Biết f 0  3 , f 2  2  018 và bảng
xét dấu của f  x như sau:
Hàm số y f x  2017  2018x đạt giá trị nhỏ nhất tại điểm x thuộc khoảng nào sau đây? 0 A. 0; 2 . B.  ;   2017 . C.  2  017;0 . D. 2017;  .
Câu 43: Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng  2
 019;2019 để hàm số   3 2 
y  sin x  3cos x m sin x 1 đồng biến trên đoạn 0;  . 2    A. 2020 . B. 2019 . C. 2028 . D. 2018 .
Trang 5/6 - Mã đề thi 345 - https://toanmath.com/
Câu 44: Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn có dạng abcd ,
trong đó 1  a b c d  9 . A. 0, 079 . B. 0, 055 . C. 0, 014 . D. 0, 0495 .
Câu 45: Xét các số thực dương x , y thỏa mãn log x  log y  log  2 x y
. Tìm giá trị nhỏ nhất 1 1 1  2 2 2
P của biểu thức P x  3y . min 17 25 2 A. P  . B. P  8 . C. P  9 . D. P  . min 2 min min min 4
Câu 46: Cho hàm số f x liên tục trên  thỏa mãn f 2x  3 f x , x    . Biết rằng 1 2
f x dx  1 
. Tính tích phân I
f x dx  . 0 1 A. I  3 . B. I  5 . C. I  2 . D. I  6 .
Câu 47: Tìm tập S tất cả các giá trị thực của tham số m để tồn tại duy nhất cặp số  ; x y thỏa mãn 2 log
4x  4 y  6  m  1 và 2 2
x y  2x  4 y  1  0 . 2 2 x y 2   A. S   5  ;  5 B. S   7  ; 5  ; 1  ;1;5;  7 . C. S   5  ; 1  ;1;  5 D. S   1   ;1 .
Câu 48: Có tất cả bao nhiêu giá trị nguyên của tham số a thuộc khoảng 0; 2019 để n n 1 9  3  1 lim  ?
5n  9na 2187 A. 2018 . B. 2011 . C. 2012 . D. 2019 .
Câu 49: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA   ABC  , góc giữa đường
thẳng SB và mặt phẳng  ABC bằng 60 . Tính khoảng cách giữa hai đường thẳng AC và SB . a 15 a 2 a 7 A. . B. . C. . D. 2a . 5 2 7
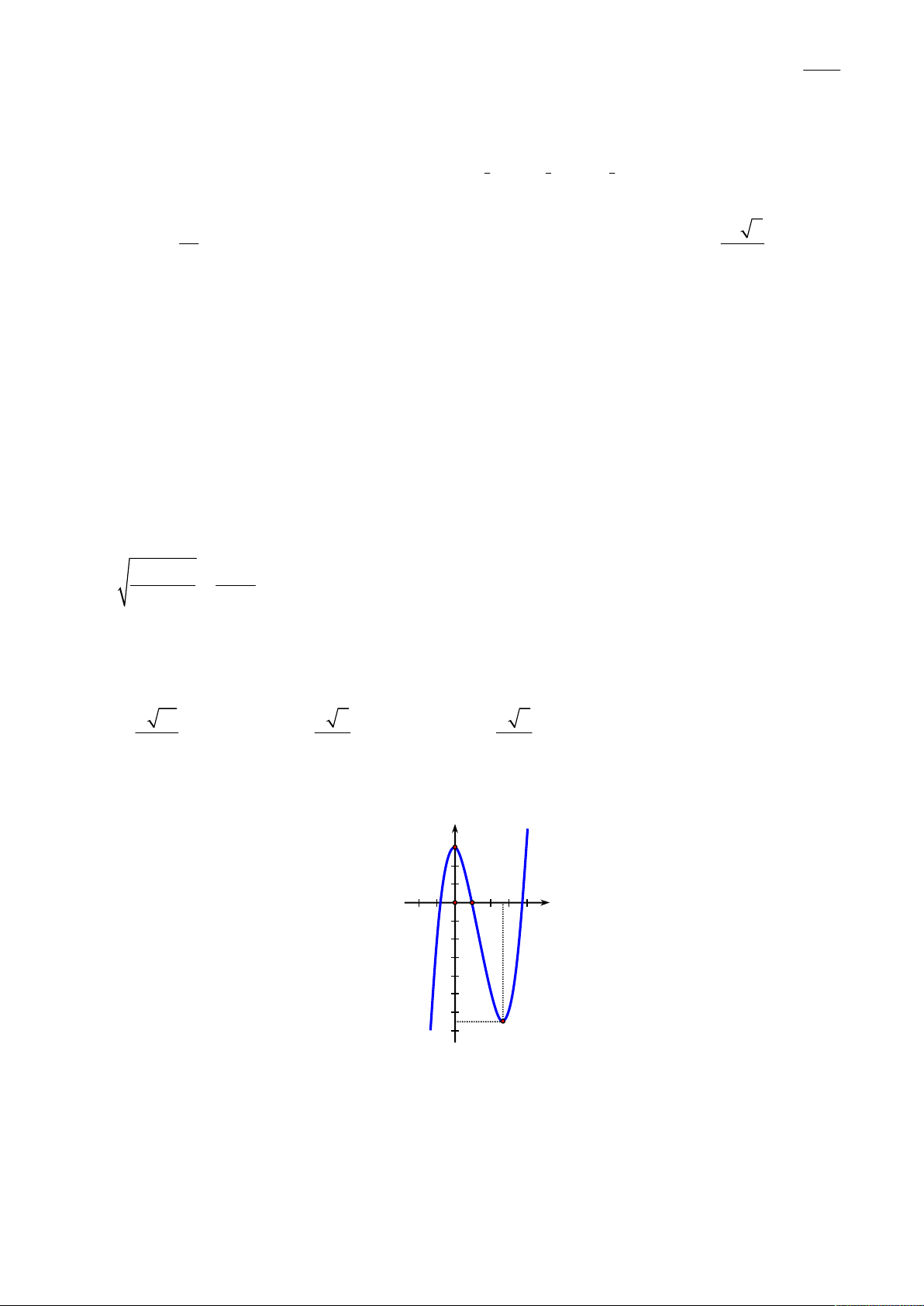
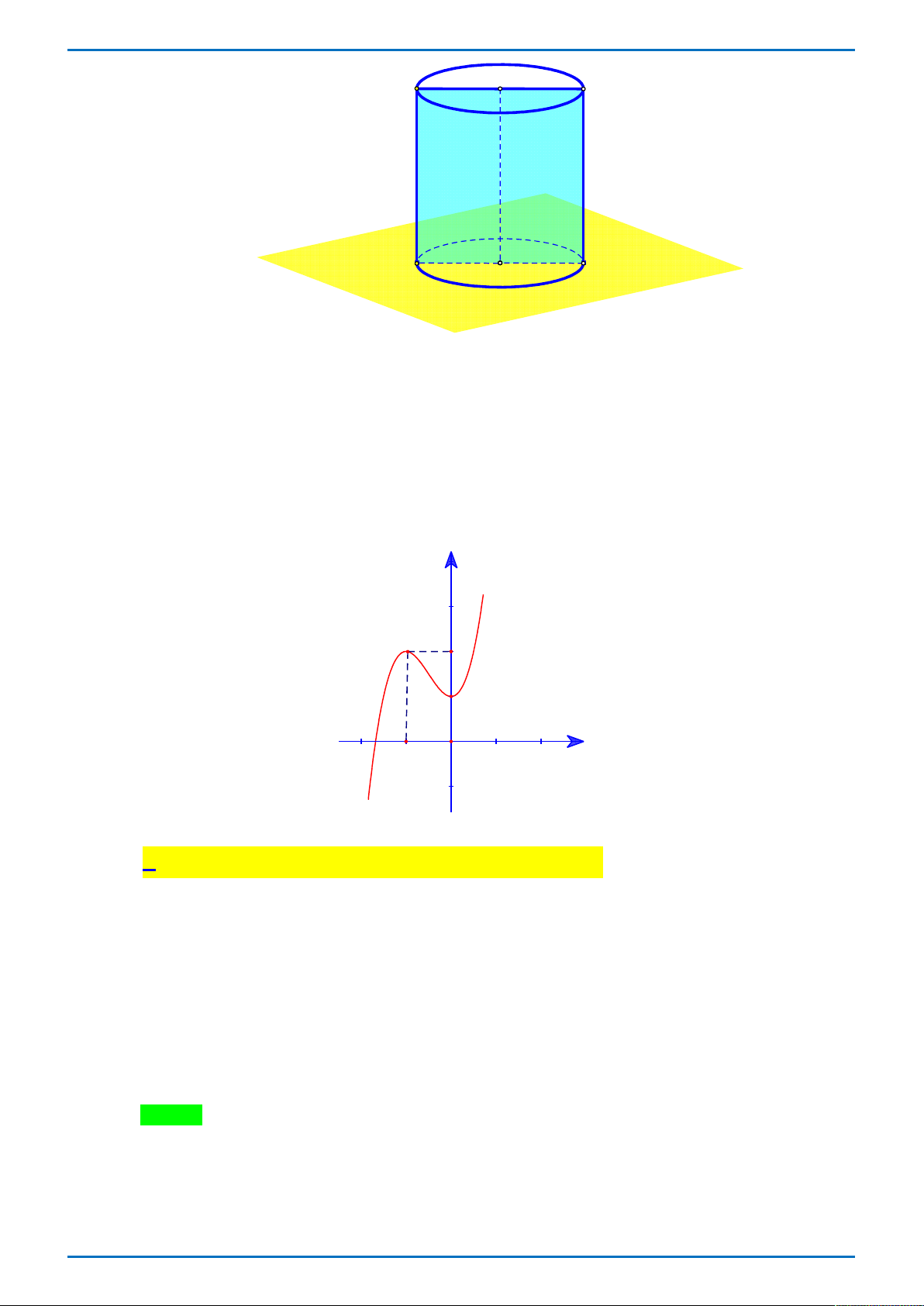
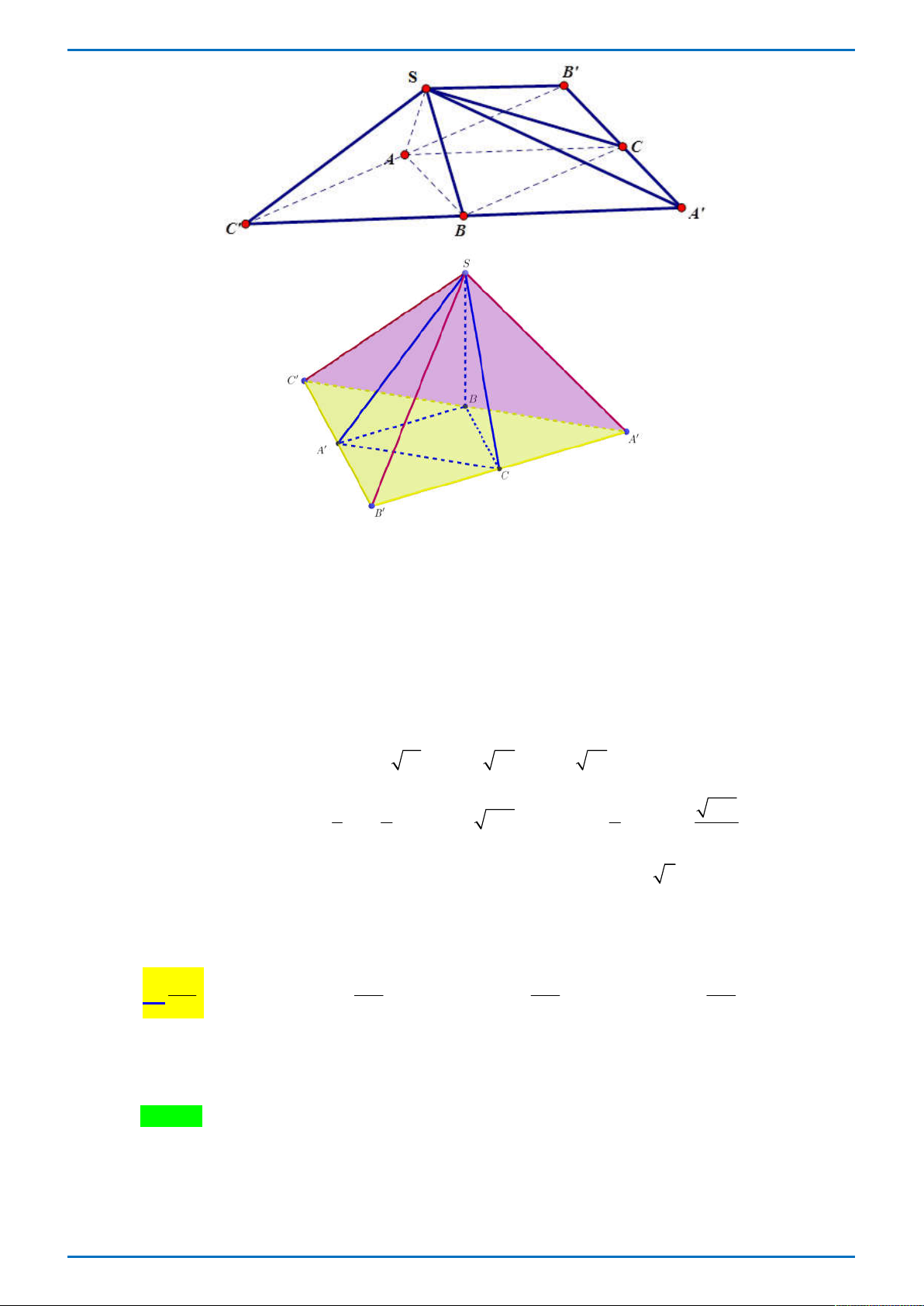
Câu 50: Cho hàm số y f x có đạo hàm trên và có đồ thị là đường cong trong hình vẽ dưới.
Đặt g x  f f x 
 . Tìm số nghiệm của phương trình g x  0 . y 3 2 1 1 2 3 4 2  1 O x 1  2  3  4  5  6  7  A. 8 . B. 4 . C. 6 . D. 2 . ----------- HẾT ----------
Trang 6/6 - Mã đề thi 345 - https://toanmath.com/
SỞ GIÁO DỤC VÀ ĐÀO TẠO VĨNH PHÚC
ĐỀ KSCL CÁC MÔN THI THPT QUỐC GIA - LẦN 3
TRƯỜNG THPT CHUYÊN VĨNH PHÚC NĂM HỌC 2018-2019
(Đề thi có 6 trang) MÔN TOÁN 12
Thời gian làm bài: 90 phút;
(Không kể thời gian giao đề) Mã đề thi 678
Họ, tên thí sinh:..........................................................................
Số báo danh:...............................................................................
Câu 1: Cho hàm số y = f (x) có bảng biến thiên như sau: x −∞ 2 4 +∞ y′ + 0 − 0 + 3 +∞ y −∞ 2 −
Hàm số đạt cực đại tại điểm nào trong các điểm sau đây? A. x = 3. B. x = 2. C. x = 2. − D. x = 4. 2x 1 +
Câu 2: Tập nghiệm của bất phương trình  1  >  
1 (với a là tham số, a ≠ 0 ) là 2 1+ a A.  1 ;  −∞ −    . B. (0;+ ∞). C. ( ;0 −∞ ). D. 1 −  ;+ ∞ . 2      2 
Câu 3: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B . Biết SA ⊥ ( ABCD),
AB = BC = a , AD = 2a , SA = a 2 . Gọi E là trung điểm của AD . Tính bán kính mặt cầu đi qua
các điểm S , A , B , C , E . A. a 6 . B. a 3 . C. a 30 . D. a . 3 2 6
Câu 4: Tìm nguyên hàm của hàm số 2 1
y = x − 3x + . x 3 2 3 2 A. x 3x − − ln x + C . B. x 3x − + ln x + C . 3 2 3 2 3 2 3 2 C. x 3x 1 − + + C . D. x 3x − + ln x + C . 2 3 2 x 3 2
Câu 5: Cho cấp số cộng (u có
u =11 và công sai d = 4 . Hãy tính u . n ) 1 99 A. 404 . B. 402 . C. 401. D. 403. 10 6
Câu 6: Cho hàm số f (x) liên tục trên đoạn [0;10] và f
∫ (x)dx = 7 và f
∫ (x)dx = 3. Tính 0 2 2 10 P = f
∫ (x)dx+ f ∫ (x)dx. 0 6 A. P = 4 . B. P = 4 − . C. P = 7 . D. P =10.
Câu 7: Cho hình chóp S.ABC có đáy là tam giác cân tại A , AB = AC = a ,  BAC =120° . Tam giác
SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích V của khối chóp S.ABC . 3 3 A. a V = . B. 3 V a = a . C. V = . D. 3 V = 2a . 8 2
Câu 8: Cho hàm số y = f (x) xác định và liên tục trên R , có bảng biến thiên như sau:
Trang 1/7 - Mã đề thi 678 x −∞ 1 − 1 +∞ y′ + 0 − 0 + 2 +∞ y −∞ 1 −
Mệnh đề nào sau đây là đúng ?
A. Hàm số đồng biến trên khoảng ( 1; − +∞) .
B. Hàm số đồng biến trên khoảng ( ; −∞ 2 − ) .
C. Hàm số nghịch biến trên khoảng (1;+∞). D. Hàm số nghịch biến trên khoảng ( ) ;1 −∞ .
Câu 9: Cho hàm số y = f (x) có đạo hàm trên  và đồ thị hàm số y = f ′(x) trên  như hình vẽ.
Mệnh đề nào sau đây là đúng? y 2 1 x 1 − O
A. Hàm số y = f (x) có 1 điểm cực tiểu và không có cực đại.
B. Hàm số y = f (x) có 1 điểm cực đại và không có cực tiểu.
C. Hàm số y = f (x) có 1 điểm cực đại và 2 điểm cực tiểu.
D. Hàm số y = f (x) có 1 điểm cực đại và 1 điểm cực tiểu. Câu 10: Hàm số 4 3
y = x − x − x + 2019 có bao nhiêu điểm cực trị? A. 3. B. 0 . C. 1. D. 2 .
Câu 11: Có bao nhiêu số hạng trong khai triển nhị thức ( x − )2018 2 3 thành đa thức A. 2018 . B. 2019 . C. 2017 . D. 2020 .
Câu 12: Một người gửi tiết kiệm số tiền 80000000 đồng với lãi suất là 6,9%/ năm. Biết rằng tiền
lãi hàng năm được nhập vào tiền gốc, hỏi sau đúng 5 năm người đó có rút được cả gốc và lãi số tiền
gần với con số nào nhất sau đây?
A. 105 370 000 đồng. B. 107 667 000 đồng. C. 111 680 000 đồng. D. 116 570 000 đồng. 2  x −1
Câu 13: Tìm a để hàm số  ≠ f (x) khi x 1 =  x −1
liên tục tại điểm x =1. 0 a khi x =1 A. a = 1. B. a = 0. C. a = 2. D. a = −1. Câu 14: Hàm số 3 2
y = −x + 3x −1 có đồ thị nào trong các đồ thị dưới đây? Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 3. B. Hình 1. C. Hình 4 . D. Hình 2 .
Trang 2/7 - Mã đề thi 678
Câu 15: Hàm số nào dưới đây nghịch biến trên tập xác định của nó? x A. y π = log x . B. y = log . C. y = log
x +1 . D. y   = . 2 ( ) π x 3   3  4 
Câu 16: Gọi 0x là nghiệm dương nhỏ nhất của phương trình 2 2
3sin x + 2sin xcos x − cos x = 0 . Chọn khẳng định đúng? A. π π π π x  3   3   ;  ∈ π . B. x  ∈π; . C. x  ∈0; . D. x  ∈ ;2π . 0 2       0  2  0  2  0  2 
Câu 17: Có bao nhiêu giá trị nguyên của tham số m trên đoạn [ 2018 − ;2018] để hàm số y = ( 2
ln x − 2x − m + )
1 có tập xác định là  . A. 2018 . B. 1009. C. 2019 . D. 2017 .
Câu 18: Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng? A. 6 . B. 4 . C. 2. D. 8 . Câu 19: Cho x
∫ ( x − )6 x = A( x − )8 + B( x − )7 2 3 2 d 3 2 3 2 + C với ,
A B,C ∈ R . Tính giá trị của biểu
thức 12A + 7B . A. 241 . B. 52 . C. 23 . D. 7 . 252 9 252 9
Câu 20: Cho hình trụ có thiết diện đi qua trục là một hình vuông có cạnh bằng 4a . Diện tích xung quanh của hình trụ là A. 2 S = 24π a . B. 2 S =16π a . C. 2 S = 8π a . D. 2 S = 4π a .
Câu 21: Cho tứ diện ABCD có hai mặt ABC và ABD là các tam giác đều. Tính góc giữa hai đường
thẳng AB và CD . A. 90° . B. 30°. C. 120°. D. 60°.
Câu 22: Tìm tất cả các giá trị của tham số m để giá trị nhỏ nhất của hàm số 3 2
y = −x − 3x + m trên đoạn [ 1; − ] 1 bằng 0. A. m = 2 . B. m = 6. C. m = 0. D. m = 4 .
Câu 23: Giá trị lớn nhất của hàm số ( ) x f x = trên đoạn [ 2; − ]3 bằng x + 3 A. 1 . B. 2 − . C. 3. D. 2 . 2
Câu 24: Cho hàm số y = f (x) xác định trên  có đồ thị của hàm số y = f ′(x) như hình vẽ. Hỏi
hàm số y = f (x) đồng biến trên khoảng nào dưới đây? y O 1 2 x A. (0; )
1 và (2;+∞) . B. (0; )1. C. (2;+∞) . D. (1;2) .     
Câu 25: Trong không gian với hệ trục tọa độ Oxyz, cho a = i
− + 2 j − 3k . Tìm tọa độ của vectơ a . A. ( 3 − ;2;− ) 1 . B. ( 1; − 2; 3 − ). C. (2; 3 − ;− ) 1 . D. (2; 1 − ; 3 − ).
Câu 26: Tìm tập nghiệm của phương trình 2x+2 3 x = 1. A. S = {1;− } 3 . B. S = {0; } 2 . C. S = {0;− } 2 . D. S = { 1; − } 3 .
Trang 3/7 - Mã đề thi 678
Câu 27: Trong không gian với hệ tọa độ Oxyz , cho A( 1
− ;0;0), B(0;0;2) , C (0; 3 − ;0). Tính bán
kính mặt cầu ngoại tiếp tứ diện OABC là A. 14 . B. 14 . C. 14 . D. 14 . 3 4 2
Câu 28: Cho hàm số y = f (x) xác định, liên tục trên  và có bảng biến thiên như sau x −∞ 1 3 +∞ y′ + 0 − + 2 +∞ y Khẳ
ng định nào sau đây là đúng?
A. Hàm số có giá trị cực tiểu bằng 3.
B. Hàm số đạt cực đại tại x =1 và đạt cực tiểu tại x = 3.
C. Hàm số có đúng một cực trị.
D. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng 1.
Câu 29: Cho khối lăng trụ ABC.A′B C
′ ′ có thể tích bằng V . Tính thể tích khối đa diện ABCB C ′ ′ . A. V . B. V . C. 3V . D. 2V . 4 2 4 3
Câu 30: Gọi n là số nguyên dương sao cho 1 1 1 1 190 + + + ... + = đúng với
log x log x log x log x x n log 2 3 3 3 3 3 3
mọi x dương, x ≠ 1. Tìm giá trị của biểu thức P = 2n + 3. A. P = 32. B. P = 23. C. P = 43. D. P = 41.
Câu 31: Cho hình chóp S.ABC có các cạnh SA = BC = 3; SB = AC = 4 ; SC = AB = 2 5 . Tính thể
tích khối chóp S.ABC . A. 390 . B. 390 . C. 390 . D. 390 . 4 6 12 8
Câu 32: Trong không gian Oxyz , lấy điểm C trên tia Oz sao cho OC =1. Trên hai tia Ox,Oy lần lượt lấy hai điểm ,
A B thay đổi sao cho OA + OB = OC . Tìm giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp tứ diện . O ABC ? A. 6 . B. 6. C. 6 . D. 6 . 2 3 4
Câu 33: Cho hàm số y f x có đạo hàm liên tục trên đoạn [0; ]
1 và thỏa mãn f (0) = 0. Biết 1 1 1 2 π π f (x) 9 dx = ∫ và f ′ ∫ (x) x 3 cos dx = . Tích phân f
∫ (x)dx bằng 2 2 4 0 0 0 A. 2 . B. 1 . C. 6 . D. 4 . π π π π
Câu 34: Có bao nhiêu số tự nhiên có 4 chữ số được viết từ các chữ số 1, 2 , 3, 4 , 5, 6 , 7 , 8 , 9 sao
cho số đó chia hết cho 15? A. 132. B. 234 . C. 432 D. 243.
Câu 35: Cho hàm số y = f (x) có đạo hàm trên và có đồ thị là đường cong trong hình vẽ dưới.
Đặt g (x) = f f (x) 
 . Tìm số nghiệm của phương trình g′( x) = 0 .
Trang 4/7 - Mã đề thi 678 y 3 2 1 1 2 3 4 2 − 1 − O x 1 − 2 − 3 − 4 − 5 − 6 − 7 − A. 8 . B. 2 . C. 6 . D. 4 .
Câu 36: Cho hàm số y = f (x) có đạo hàm cấp hai trên  . Biết f ′(0) = 3 , f ′(2) = 2018 − và bảng
xét dấu của f ′′(x) như sau:
Hàm số y = f (x + 2017) + 2018x đạt giá trị nhỏ nhất tại điểm x thuộc khoảng nào sau đây? 0 A. ( 2017 − ;0) . B. (0;2) . C. ( ; −∞ − 2017). D. (2017;+∞) .
Câu 37: Cho hình trụ có đáy là hai đường tròn tâm O và O′ , bán kính đáy bằng chiều cao và bằng
2a . Trên đường tròn đáy có tâm O lấy điểm A , trên đường tròn tâm O′ lấy điểm B . Đặt α là góc
giữa AB và đáy. Tính tan α khi thể tích khối tứ diện OO A
′ B đạt giá trị lớn nhất. A. 1 tanα = . B. 1 tanα = . C. tanα =1. D. tanα = 2 . 2 2
Câu 38: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , AB =1cm , AC = 3cm . Tam
giác SAB , SAC lần lượt vuông tại B và C . Khối cầu ngoại tiếp hình chóp S.ABC có thể tích bằng 5 5π 3
cm . Tính khoảng cách từ C tới (SAB) 6 A. 3 cm . B. 5 cm . C. 3 cm . D. 5 cm . 2 4 4 2
Câu 39: Tìm tập S tất cả các giá trị thực của tham số m để tồn tại duy nhất cặp số ( ; x y) thỏa mãn 2 log
4x + 4y − 6 + m ≥ 1 và 2 2
x + y + 2x − 4y +1 = 0 . 2 2 x + y +2 ( )
A. S = {−5;−1;1; } 5 B. S = {−1; } 1 . C. S = {−5; } 5
D. S = {−7;−5;−1;1;5; } 7 .
Câu 40: Cho hình chóp S.ABC có đáy là ABC ∆
vuông cân ở B, AC = a 2, SA ⊥ ( ABC), SA = a.
Gọi G là trọng tâm của SB
∆ C , mp(α ) đi qua AG và song song với BC chia khối chóp thành hai
phần. Gọi V là thể tích của khối đa diện không chứa đỉnh S . Tính V. 3 3 3 3 A. 4a . B. 4a . C. 5a . D. 2a . 9 27 54 9
Câu 41: Tìm tất cả các giá trị thực của tham số m để phương trình 3m + m e e = ( 2 x + − x )( 2 2 1
1+ x 1− x ) có nghiệm. A.  1 0;          . B. 1 0; ln 2 . C. 1 ; −∞  ln 2 . D. 1 ln 2;+∞   .  e   2  2    2 
Trang 5/7 - Mã đề thi 678
Câu 42: Cho hàm số y = f (x) liên tục trên  và có đồ thị như hình vẽ. Hỏi đồ thị hàm số
y = f ( x ) có tất cả bao nhiêu điểm cực trị? y 3 2 − 1 1 − O 2 x 1 − A. 8 B. 6 C. 9 D. 7 .
Câu 43: Có tất cả bao nhiêu giá trị nguyên của tham số a thuộc khoảng (0;2019) để n n 1 9 + 3 + 1 lim ≤ 5n + 9n+a 2187 ? A. 2018. B. 2012 . C. 2019 . D. 2011.
Câu 44: Cho hàm số f (x) liên tục trên  thỏa mãn f (2x) = 3 f (x) , x ∀ ∈  . Biết rằng 1 2 f
∫ (x)dx =1. Tính tích phân I = f ∫ (x)dx . 0 1 A. I = 2 . B. I = 5 . C. I = 6 . D. I = 3 .
Câu 45: Tìm số đường tiệm cận của đồ thị hàm số x −1 y = .
4 3x +1 − 3x − 5 A. 2 . B. 3. C. 1. D. 0 .
Câu 46: Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn có dạng abcd ,
trong đó 1≤ a ≤ b ≤ c ≤ d ≤ 9 . A. 0,079 . B. 0,0495. C. 0,055. D. 0,014 .
Câu 47: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA ⊥ ( ABC) , góc giữa đường
thẳng SB và mặt phẳng ( ABC) bằng 60°. Tính khoảng cách giữa hai đường thẳng AC và SB . A. a 2 . B. 2a . C. a 7 . D. a 15 . 2 7 5
Câu 48: Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (−2019;2019) để hàm số 3 2  π
y = sin x − 3cos x − msin x −1 đồng biến trên đoạn 0;   . 2    A. 2028. B. 2020 . C. 2019 . D. 2018.
Câu 49: Xét các số thực dương x , y thỏa mãn log x + log y ≤ log ( 2
x + y . Tìm giá trị nhỏ nhất 1 1 1 ) 2 2 2
P của biểu thức P = x + 3y . min A. P = 8. B. 17 P = . C. 25 2 P = . D. P = 9 . min min 2 min 4 min Câu 50: Biết −
F (x) là nguyên hàm của hàm số ( ) x cos x f x =
. Hỏi đồ thị của hàm số y = F (x) 2 x
có bao nhiêu điểm cực trị? A. 1. B. 2. C. vô số điểm. D. 0. ----------- HẾT ----------
Trang 6/7 - Mã đề thi 678 BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
B A D D D A A B A C B C C B B C A B D B A D A C B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
C C B D D A D C D A C B A B C C D B B A C D C D A
Trang 7/7 - Mã đề thi 678 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
SỞ GD VÀ ĐÀO TẠO VĨNH PHÚC THI THỬ ĐẠI HỌC THPTQG THPT CHUYÊN VĨNH PHÚC NĂM HỌC 2018 - 2019 MÔN: TOÁN
(Đề thi có 6 trang) Thời gian: 90 phút MÃ ĐỀ: 123
Bản quyền thuộc về tập thể thầy cô STRONG.
Tổng biên tập: Thầy Nguyễn Việt Hải- Admin STRONG, Gv Chuyên Quang Trung, Bình Phước Câu 1: Hàm số 3 2
y  x  3x 1 có đồ thị nào trong các đồ thị dưới đây? Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 3 . B. Hình 4 . C. Hình 2 . D. Hình 1 .
Câu 2: Cho hình chóp S.ABCD có đáy là hình thang vuông tại
A và B . Biết SA   ABCD ,
AB BC a , AD  2a , SA a 2 . Gọi E là trung điểm của AD . Tính bán kính mặt cầu đi qua các
điểm S , A , B , C , E . a 30 a 3 a 6 A. . B. a . C. . D. . 6 2 3
Câu 3: Gọi x là nghiệm dương nhỏ nhất của phương trình 2 2
3sin x  2sin x cos x  cos x  0 . Chọn 0 khẳng định đúng?  3         3  A. x   ; . B. x  ; . C. x  0; . D. x  ; 2 . 0   0   0   0    2   2   2   2 
Câu 4: Cho hàm số y f x có bảng biến thiên như sau: x  2 4 +  y' + 0 0 + +  3 y  2
Hàm số đạt cực đại tại điểm nào trong các điểm sau đây? A. x  2.  B. x  2. C. x  3. D. x  4.
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 1 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
Câu 5: Có bao nhiêu giá trị nguyên của tham số m trên đoạn 2018;  2018 để hàm số y   2
ln x  2x m  
1 có tập xác định là  . A. 2019 . B. 2017 . C. 2018 . D. 1009 .
Câu 6: Cho hình trụ có thiết diện đi qua trục là một hình vuông có cạnh bằng 4a . Diện tích xung quanh của hình trụ là A. 2 S  8 a . B. 2 S  24 a . C. 2 S  16 a . D. 2 S  4 a .
Câu 7: Cho hàm số y f x có đạo hàm trên  và đồ thị hàm số y f  x trên  như hình vẽ.
Mệnh đề nào sau đây là đúng? y
A. Hàm số y f x có 1 điểm cực tiểu và không có cực đại. 2
B. Hàm số y f x có 1 điểm cực đại và 2 điểm cực tiểu. 1 x 1 O
C. Hàm số y f x có 1 điểm cực đại và không có cực tiểu.
D. Hàm số y f x có 1 điểm cực đại và 1 điểm cực tiểu.
Câu 8: Cho hàm số y f x xác định trên  có đồ thị của hàm số y f  x như hình vẽ. Hỏi hàm số
y f x đồng biến trên khoảng nào dưới đây? y O 1 2 x 2; . 1;2 . 0  ;1 . 0  ;1 và 2;  . A. B. C. D. 2  x 1  khi x  1
Câu 9: Tìm a để hàm số f x   x 1
liên tục tại điểm x  1. 0 a khi x  1  A. a  1 . B. a  0 . C. a  2 . D. a  1  .     
Câu 10: Trong không gian với hệ trục tọa độ Oxyz, cho a  i  2 j  3k . Tìm tọa độ của vectơ a . A. 2; 1  ; 3  . B. 3; 2;   1 . C. 2; 3  ;   1 . D. 1; 2; 3  .
Câu 11: Một người gửi tiết kiệm số tiền 80000000 đồng với lãi suất là 6, 9 %/ năm. Biết rằng tiền lãi
hàng năm được nhập vào tiền gốc, hỏi sau đúng 5 năm người đó có rút được cả gốc và lãi số tiền gần với
con số nào nhất sau đây? A. 105370000 đồng. B. 11680000 đồng. C. 107667000 đồng. D. 116570000 đồng.
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 2 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
Câu 12: Cho tứ diện ABCD có hai mặt ABC và ABD là các tam giác đều. Tính góc giữa hai đường
thẳng AB và CD . A. 120 . B. 60 . C. 90 . D. 30 . 10 6
Câu 13: Cho hàm số f x liên tục trên đoạn 0;10 và
f x dx  7  và
f x dx  3  . Tính 0 2 2 10 P
f x dx f x dx   . 0 6 A. P  4 . B. P  10 . C. P  7 . D. P  4  .
Câu 14: Tìm tất cả các giá trị của tham số m để giá trị nhỏ nhất của hàm số 3 2
y  x  3x m trên đoạn 1;  1 bằng 0. A. m  0 . B. m  6 . C. m  2 . D. m  4 . 2
Câu 15: Tìm tập nghiệm của phương trình x 2 3 x  1. A. S  1;   3 . B. S  1;  3 . C. S  0;  2 . D. S  0;   2 . Câu 16: Hàm số 4 3
y x x x  2019 có bao nhiêu điểm cực trị? A. 2 . B. 3 . C. 0 . D. 1. 1
Câu 17: Tìm nguyên hàm của hàm số 2
y x  3x  . x 3 2 x 3x 3 2 x 3x A. 
 ln x C . B. 
 ln x C . 3 2 3 2 3 2 x 3x 3 2 x 3x 1 C. 
 ln x C . D.    C . 3 2 2 3 2 x
Câu 18: Cho cấp số cộng u có u  11 và công sai d  4 . Hãy tính u . n  1 99 A. 401 . B. 404 . C. 403 . D. 402 .
Câu 19: Cho hình chóp S.ABC có đáy là tam giác cân tại A , AB AC a , 
BAC  120 . Tam giác
SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích V của khối chóp S.ABC . 3 a 3 a A. 3 V a . B. V  . C. V  . D. 3 V  2a . 8 2 x
Câu 20: Giá trị lớn nhất của hàm số f x  trên đoạn  2  ;  3 bằng x  3 1 A. 3 . B. 2 . C. . D. 2 . 2
Câu 21: Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng? A. 2. B. 4 . C. 6 . D. 8 .
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 3 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 1 1 1 1 190
Câu 22: Gọi n là số nguyên dương sao cho    ...   đúng với mọi log x log x log x log x x n log 2 3 3 3 3 3 3
x dương, x  1 . Tìm giá trị của biểu thức P  2n  3 . A. P  32 . B. P  23. C. P  43. D. P  41.
Câu 23: Hàm số nào dưới đây nghịch biến trên tập xác định của nó? x    A. y  log x . B. y  log
x 1 . C. y  log x . D. y  . 2   3     3  4 2 x 1   1 
Câu 24: Tập nghiệm của bất phương trình  1 
(với a là tham số, a  0 ) là 2   1 a   1   1  A.  ;  0 . B. ;     . C. 0;   . D.  ;     .  2   2 
Câu 25: Có bao nhiêu số hạng trong khai triển nhị thức  x  2018 2 3 thành đa thức A. 2018 . B. 2019 . C. 2020 . D. 2017 .
Câu 26: Cho hàm số y f x xác định, liên tục trên  và có bảng biến thiên như sau
Khẳng định nào sau đây là đúng?
A. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng 1.
B. Hàm số có đúng một cực trị.
C. Hàm số đạt cực đại tại x  1 và đạt cực tiểu tại x  3 .
D. Hàm số có giá trị cực tiểu bằng 3.
Câu 27: Cho khối lăng trụ ABC.AB C
  có thể tích bằng V . Tính thể tích khối đa diện ABCB C   . 2V V V 3V A. . B. . C. . D. . 3 4 2 4
Câu 28: Trong không gian với hệ tọa độ Oxyz , cho A 1
 ; 0; 0 , B 0;0; 2 , C 0; 3;0 . Tính bán kính
mặt cầu ngoại tiếp tứ diện OABC là 14 14 14 A. . B. . C. . D. 14 . 3 4 2
Câu 29: Cho hàm số y f x xác định và liên tục trên R , có bảng biến thiên như sau:
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 4 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
Mệnh đề nào sau đây là đúng ?
A. Hàm số đồng biến trên khoảng  ;  2 .
B. Hàm số nghịch biến trên khoảng  ;   1 .
C. Hàm số nghịch biến trên khoảng 1;  .
D. Hàm số đồng biến trên khoảng  1  ;  . 6 8 7
Câu 30: Cho 2x 3x  2 dx A3x  2  B 3x  2  C  với ,
A B,C R . Tính giá trị của biểu thức 12 A  7B . 23 241 52 7 A. . B. . C. . D. . 252 252 9 9
Câu 31: Có bao nhiêu số tự nhiên có 4 chữ số được viết từ các chữ số 1, 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 sao cho số đó chia hết cho 15 ? A. 234 . B. 132 . C. 243 . D. 432
Câu 32: Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng  2019  ; 2019 để hàm số   3 2 
y  sin x  3cos x m sin x 1 đồng biến trên đoạn 0;  . 2    A. 2028 . B. 2018 . C. 2020 . D. 2019 .
Câu 33: Cho hàm số y f x liên tục trên  và có đồ thị như hình vẽ. Hỏi đồ thị hàm số y f x
có tất cả bao nhiêu điểm cực trị? y 3 2 1 1O 2 x 1 A. 6 B. 8 C. 7 . D. 9
Câu 34: Cho hình chóp S.ABC có các cạnh SA BC  3 ; SB AC  4 ; SC AB  2 5 . Tính thể tích
khối chóp S.ABC . 390 390 390 390 A. . B. . C. . D. . 12 4 6 8
Câu 35: Cho hình chóp S.ABC có đáy là ABC vuông cân ở B, AC a 2, SA   ABC , SA  . a Gọi
G là trọng tâm của SBC , mp   đi qua AG và song song với BC chia khối chóp thành hai phần. Gọi
V là thể tích của khối đa diện không chứa đỉnh S . Tính V . 3 5a 3 2a 3 4a 3 4a A. . B. . C. . D. . 54 9 27 9
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 5 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
Câu 36: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA   ABC  , góc giữa đường
thẳng SB và mặt phẳng  ABC  bằng 60 . Tính khoảng cách giữa hai đường thẳng AC và SB . a 15 a 2 a 7 A. . B. . C. 2a . D. . 5 2 7
Câu 37: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , AB  1cm , AC  3cm . Tam giác
SAB , SAC lần lượt vuông tại B và C . Khối cầu ngoại tiếp hình chóp S.ABC có thể tích 5 5 bằng 3
cm . Tính khoảng cách từ C tới SAB 6 5 5 3 3 A. cm . B. cm . C. cm . D. cm . 2 4 4 2 1
Câu 38: Cho hàm số f x liên tục trên  thỏa mãn f 2x  3 f x , x    . Biết rằng
f x dx  1  . 0 2 Tính tích phân I
f x dx  . 1 A. I  5 . B. I  6 . C. I  3 . D. I  2 . x 1
Câu 39: Tìm số đường tiệm cận của đồ thị hàm số y  .
4 3x 1  3x  5 A. 3 . B. 2 . C. 1. D. 0 .
Câu 40: Trong không gian Oxyz , lấy điểm C trên tia Oz sao cho OC  1 . Trên hai tia Ox, Oy lần lượt lấy hai điểm ,
A B thay đổi sao cho OA OB OC . Tìm giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp tứ diện . O ABC ? 6 6 6 A. . B. 6. C. . D. . 4 3 2
Câu 41: Cho hàm số y f x có đạo hàm cấp hai trên  . Biết f 0  3 , f 2  2018  và bảng xét
dấu của f  x như sau:
Hàm số y f x  2017  2018x đạt giá trị nhỏ nhất tại điểm x thuộc khoảng nào sau đây? 0 A.  ;   2017 . B. 2017;  . C. 0; 2 . D. 2017;0 .
Câu 42: Cho hàm số y f x có đạo hàm liên tục trên đoạn 0 
;1 và thỏa mãn f 0  0 . Biết 1 9 1  x 3 1 2
f x dx   và
f  x cos dx   . Tích phân
f x dx  bằng 2 2 4 0 0 0
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 6 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 2 4 1 6 A. . B. . C. . D. .     x  cos x
Câu 43: Biết F x là nguyên hàm của hàm số f x 
. Hỏi đồ thị của hàm số y F x có 2 x
bao nhiêu điểm cực trị? A. vô số điểm. B. 0. C. 1. D. 2. Câu 44: Tìm tất cả các giá trị thực của tham số m để phương trình 3m m e e   2 x   x  2 2 1
1 x 1 x  có nghiệm.  1   1   1   1  A. 0; ln 2   . B. ;  ln 2   . C. 0;   . D. ln 2;    .  2   2   e   2 
Câu 45: Tìm tập S tất cả các giá trị thực của tham số m để tồn tại duy nhất cặp số  ; x y  thỏa mãn 2 log
4x  4 y  6  m  1 và 2 2
x y  2x  4 y  1  0 . 2 2 x y 2   A. S  1;  1 .
B. S  5;1;1;  5 C. S  5;  5
D. S  7;5; 1  ;1;5;  7 .
Câu 46: Cho hình trụ có đáy là hai đường tròn tâm O và O , bán kính đáy bằng chiều cao và bằng 2a .
Trên đường tròn đáy có tâm O lấy điểm A , trên đường tròn tâm O lấy điểm B . Đặt  là góc giữa AB
và đáy. Tính tan  khi thể tích khối tứ diện OO AB
đạt giá trị lớn nhất. 1 1 A. tan  2 . B. tan   . C. tan   . D. tan  1. 2 2
Câu 47: Xét các số thực dương x , y thỏa mãn log x  log y  log  2 x y
. Tìm giá trị nhỏ nhất P 1 1 1  min 2 2 2
của biểu thức P x  3y . 25 2 17 A. P  9 . B. P  8 . C. P  . D. P  . min min min 4 min 2
Câu 48: Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn có dạng abcd ,
trong đó 1  a b c d  9 . A. 0, 014 . B. 0, 0495 . C. 0, 079 . D. 0, 055 . 0;2019
Câu 49: Có tất cả bao nhiêu giá trị nguyên của tham số a thuộc khoảng để n n 1 9  3  1 lim 
5n  9na 2187 ? A. 2011 . B. 2018 . C. 2019 . D. 2012 .
Câu 50: Cho hàm số y f x có đạo hàm trên và có đồ thị là đường cong trong hình vẽ dưới. Đặt
g x  f f x 
 . Tìm số nghiệm của phương trình g x  0 .
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 7 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 A. 2 . B. 8 . C. 4 . D. 6 .
----------------------------------------------- ----------- HẾT ----------
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 8 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
PHÂN TÍCH – GIẢI ĐỀ THI THỬ ĐẠI HỌC
THPTCHUYÊN VĨNH PHÚC LẦN 3 - NĂM 2018 – 2019 Câu 1. Hàm số 3 2
y  x  3x 1 có đồ thị nào trong các đồ thị dưới đây? y y 5 4 4 2 3 1 O 1 -1 1 2 3 x O -1 -1 1 2 3 x -1 Hình 1 Hình 2 y y 2 1 2 O -1 1 2 3 x 1 -1 O -1 1 2 3 x -1 -3 -2 Hình 3 Hình 4 A. Hình 3. B. Hình 1. C. Hình 2. D. Hình 4. Lời giải.
Tác giả: Nguyễn Thị Nguyệt Cầm; Fb: Nguyet Cam Nguyen. Chọn B.
Đồ thị hàm số đã cho cắt trục tung tại điểm có tung độ 1. Câu 2.
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B . Biết SA  ( ABCD) ,
AB BC a , SA a 2 , AD  2a . Gọi E là trung điểm của AD . Tính bán kính mặt cầu đi
qua các điểm S , A , B , C , E .
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 9 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 a 3 a 6 a 30 A. . B. a . C. . D. . 2 3 6 Lời giải.
Tác giả: Nguyễn Thị Nguyệt Cầm; Fb: Nguyet Cam Nguyen. Chọn B. S E A D B C Vì    SAC SBC SEC 90   
nên mặt cầu đi qua các điểm S , A , B , C , E có đường kính SC 2 2 SC SA AC 2 2  2a  2a 2
 4a  2a . Do đó, mặt cầu có bán kính là R   a . 2 Câu 3.
Gọi x là nghiệm dương nhỏ nhất của phương trình 2 2
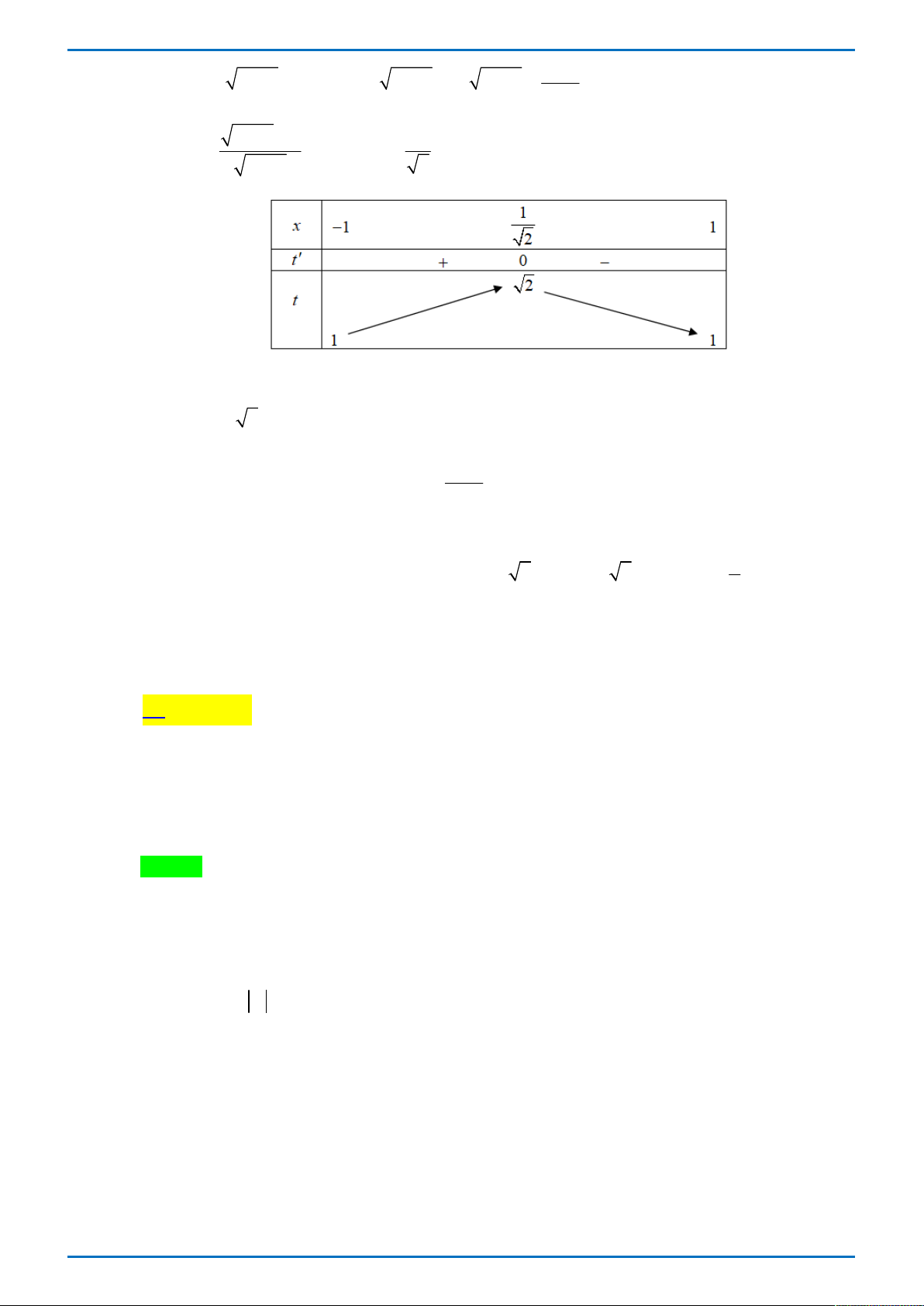
3sin x  2sin x cos x  cos x  0 . Chọn 0 khẳng định đúng?  3         3  A. x   ; . B. x  ; . C. x  0; . D. x  ; 2 . 0   0   0   0    2   2   2   2  Lời giải
Tác giả: Phạm Hoài Trung ; Fb: Phạm Hoài Trung Chọn C 2 2
3sin x  2sin x cos x  cos x  0 2 2
 3sin x  3sin x cos x  sin x cos x  cos x  0  3sin x 1  1
3sin x  cos x  0  cos x tan x
 (3sin x  cos x)(sin x  cos x)  0       3
sin x  cos x  0  sin x    1 tan x  1     cos x  1 x  arctan  k  3   k  . 
x    k  4
Do x là nghiệm dương nhỏ nhất của phương trình 2 2
3sin x  2sin x cos x  cos x  0 nên 0
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 10 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 1 x  arctan . 0 3 Câu 4.
Cho hàm số y f x có bảng biến thiên như sau: x  2 4 +  y' + 0 0 + +  3 y  2
Hàm số đạt cực đại tại điểm nào trong các điểm sau đây? A. x  2  . B. x  2 . C. x  3 . D. x  4 . Lời giải
Tác giả: Phạm Hoài Trung ; Fb: Phạm Hoài Trung Chọn B
Hàm số đạt cực đại tại điểm x  2 . Câu 5.
Có bao nhiêu giá trị nguyên của tham số m trên  2018  ; 2018 để hàm số y   2
ln x  2x m  
1 có tập xác định là  ? A. 2019 . B. 2017 . C. 2018 . D. 1009 . Lời giải.
Tác giả: Quỳnh Giao; Fb: QGiaoDo. Chọn C. Hàm số y   2
ln x  2x m  
1 có tập xác định là  khi và chỉ khi: 2
x  2x m 1  0 x
     '  0  1 m 1  0  m  0 .
Kết hợp với điều kiện m nguyên thuộc  2018 
; 2018 ta có 2018 giá trị của m . Câu 6.
Cho hình trụ có thiết diện qua trục là hình vuông cạnh 4a . Diện tích xung quanh của hình trụ là A. 2 8 a . B. 2 24 a . C. 2 16 a . . D. 2 4 a . Lờigiải.
Tác giả: Quỳnh Giao; Fb: QGiaoDo. Chọn C.
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 11 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 O' 4a O
Thiết diện qua trục của hình trụ là hình vuông cạnh 4a nên hình trụ có chiều cao h  4a , bán
kính đáy R  2a .
Vậy diện tích xung quanh của hình trụ là 2
S  2 Rh  16 a . Câu 7.
Cho hàm số y f x có đạo hàm trên  và đồ thị hàm số y f  x trên  như hình vẽ.
Mệnh đề nào sau đây là đúng? y 2 1 O -1 x
A. Hàm số y f x có 1 điểm cực tiểu và không có cực đại.
B. Hàm số y f x có 1 điểm cực đại và 2 điểm cực tiểu.
C. Hàm số y f x có 1 điểm cực đại và không có cực tiểu.
D. Hàm số y f x có 1 điểm cực đại và 1 điểm cực tiểu. Lời giải.
Tác giả: Nguyễn Thị Thơm; Fb: Thơm nguyễn. Chọn A.
Dựa vào hình vẽ ta thấy hàm số y f  x đổi dấu một lần và đổi dấu từ âm sang dương nên
suy ra hàm số có một điểm cực tiểu và không có điểm cực đại.
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 12 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 Câu 8.
Cho hàm số y f x xác định trên  có đồ thị của hàm số y f  x như hình vẽ. Hỏi hàm
số y f x đồng biến trên khoảng nào dưới đây? y O 1 2 x A. 2;   . . B. 1; 2 . C. 0  ;1 . . D. 0  ;1 và 2;   . Lời giải.
Tác giả: Nguyễn Thị Thơm; Fb: Thơm nguyễn. Chọn A.
Ta có hàm số y f x đồng biến khi và chỉ khi f  x  0 .
Dựa vào đồ thị hàm số y f ' x ta thấy f  x  0  x  2 .
Vậy hàm số đồng biến trên 2;   . 2  x 1  khi x  1 Câu 9.
Tìm a để hàm số f x   x 1
liên tục tại điểm x  1. 0 a khi x  1  A. a  1. B. a  0 . C. a  2 . D. a  1 . Lời giải
Tác giả: Nguyễn Thị Thu Trang; Fb: Trang nguyễn Chọn C
TXĐ: D    x  1 D . 0 Ta có : f   1  a . 2 x 1  x   1  x   1 lim  lim  lim  x   1  2 . x 1  x 1  x 1 x 1 x 1 
Hàm số f x liên tục tại điểm x  1 khi và chỉ khi lim f x  f   1  a  2 . 0 x 1      
Câu 10. Trong không gian với hệ trục tọa độ Oxyz , cho a  i  2 j  3k . Tìm tọa độ của a .
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 13 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 A. 2; 1;  3 . B. 3; 2;   1 . C. 2;  3;   1 . D. 1; 2;  3 . Lời giải
Tác giả: Nguyễn Thị Thu Trang; Fb: Trang nguyễn Chọn D
Câu 11. Một người gửi tiết kiệm số tiền 80 000 000 đồng với lãi suất 6, 9% / năm. Biết rằng tiền lãi
hàng năm được nhập vào tiền gốc, hỏi sau đúng 5 năm người đó rút được cả tiền gốc lẫn tiền lãi
gần với con số nào sau đây? A. 105370 000 đồng.
B. 111680 000 đồng. C. 107 667 000 đồng. D. 116570 000 đồng. Lời giải.
Tác giả: Văn Bùi Vũ; Fb: Van Tuan Vu. Chọn B.
Gọi P là số tiền gửi ban đầu, r là lãi suất / năm. 0
Số tiền gốc và lãi sau năm thứ nhất: P P P .r P 1 r . 1 0 0 0  
Số tiền gốc và lãi sau năm thứ hai: P P P.r P 1 r 2 . 2 1 1 0 ….
Số tiền gốc và lãi người đó rút ra được sau 5 năm là
P P .1 r 5  80 000 000.1 6,9%5  111680 799 (đồng). 5 0
Câu 12. Cho tứ diện ABCD có hai mặt ABC và ABD là các tam giác đều. Tính góc giữa hai đường
thẳng AB và CD . A. 120 . B. 60 . C. 90 . D. 30 . Lời giải.
Tác giả: Văn Bùi Vũ; Fb: Van Tuan Vu. Chọn C. Cách 1. A B D E C
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 14 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
Gọi E là trung điểm của CD . Ta có: BCD
cân tại B , do đó CD BE . ACD
cân tại A , do đó CD AE .
Suy ra CD   ABE, mà AB   ABE nên CD AB .
Vậy góc giữa hai đường thẳng AB và CD bằng 90 . Cách 2.
    
        Xét .
AB CD AB AD AC  . AB AD  . AB AC  
AB AD cos BAD AB AC cos BAC  0 .
( Vì AB AD AC ,   BAD BAC 60   ).
Vậy góc giữa hai đường thẳng AB và CD bằng 90 . 10 6
Câu 13. Cho hàm số f x liên tục trên đoạn 0;10 và
f xdx  7  ;
f xdx  3  . Tính 0 2 2 10 P
f xdx f xdx   . 0 6 A. P  4 . B. P  10 . C. P  7 . D. P  4 . Lời giải.
Tác giả: Lê Viết Thương; Fb: Lê Viết Thương. Chọn A. 10 2 6 10 Ta có:
f xdx f xdx f xdx f xdx     . 0 0 2 6
 7  P  3  P  4 .
Câu 14. Tìm tất cả các giá trị của tham số m để giá trị nhỏ nhất của hàm số 3 2
y  x  3x m trên đoạn  1   ;1 bằng 0 . A. m  0 . B. m  6 . C. m  2 . D. m  4 . Lời giải.
Tác giả: Lê Viết Thương; Fb: Lê Viết Thương. Chọn D.
y f x 3 2
 x  3x m . Ta có: 2
y  3x  6x .
x  0 1  ;1 y  0   .
x  2 1  ;1  f  
1  m  2 ; f 0  m ; f   1  m  4 .
Ta thấy m  4  min f  
1 ; f 0; f  
1  . Suy ra yêu cầu bài toán  m  4  0  m  4 .
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 15 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 2
Câu 15. Tìm tập nghiệm của phương trình x 2 3 x  1 . A. S  1;   3 . B. S   1  ;  3 C. S  0;  2 . D. S  0;   2 . Lời giải.
Tác giả: Nguyễn Phương; Fb: Nguyễn Phương. Chọn D. 2  x  0 x 2 x 2 3
 1  x  2x  0   . x  2 
Vậy tập nghiệm của phương trình là S  0;   2 . Câu 16. Hàm số 4 3
y x x x  2019 có bao nhiêu điểm cực trị? A. 2 . B. 3 . C. 0 . . D. 1. Lời giải.
Tác giả: Nguyễn Phương; Fb: Nguyễn Phương. Chọn D. Ta có : 4 3
y x x x  2019 . 3 2
y  4x  3x 1.
y  0  x  1.
Nhận xét: x  1 là nghiệm đơn của phương trình y  0 , nên qua điểm x  1 , y đổi dấu. Vậy hàm số 4 3
y x x x  2019 có 1 điểm cực trị. 1
Câu 17. Tìm nguyên hàm của hàm số: 2
y x  3x  . x 3 2 x 3x 3 2 x 3x A. 
 ln x C . . B. 
 ln x C . 3 2 3 2 3 2 x 3x 3 2 x 3x 1 C. 
 ln x C . D.    C . 3 2 2 3 2 x Lời giải.
Tác giả: Tống Thúy; Fb: Thuy Tong. Chọn A.  1  1 3 2 x 3x Ta có: 2 x  3x  dx  2    x dx  3 d x x  dx     
 ln x C .  x x 3 2
Câu 18. Cho cấp số cộng u có u  11 và công sai d  4 . Hãy tính u . n  1 99 A. 401 . B. 404 . C. 403 . D. 402 .
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 16 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 Lời giải.
Tác giả: Tống Thúy; Fb: Thuy Tong. Chọn C.
Ta có: u u n 1 d , n  1, n N  . n 1  
u u  98.d  11 98.4  403 . 99 1 Vậy u  403 . 99 
Câu 19. Cho hình chóp S.ABC có đáy là tam giác cân tại A , AB AC a , BAC 120  . Tam giác SAB
là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích V của khối chóp S.ABC . 3 a 3 a A. 3 V a . B. V  . C. V  . D. 3 V  2a 8 2 Lời giải
Tác giả: Hoàng Thị Thúy; Fb: Thúy Hoàng S a A B 120° H a C Chọn B
Gọi H là trung điểm của AB SH AB SH  SABa 3 a Ta có: SH  ,  2 1 3 S  .
AB AC.sin BAC  2 ABC 2 4 3 1 a Suy ra: VSH .S  S . ABC 3 ABC 8 x
Câu 20. Giá trị lớn nhất của hàm số f x  trên đoạn 2;  3 bằng x  3
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 17 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 1 A. 3. B. 2 C. . D. 2 . 2 Lời giải
Tác giả: Hoàng Thị Thúy; Fb: Thúy Hoàng Chọn C 3
Ta có: f ' x   0 , x   2  ;  3  x  32
Do đó hàm số f x đồng biến trên  2  ;  3 1
Suy ra: max f x  f 3   2  ;  3 2
Câu 21. Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng? A. 2. B. 4. C. 6. D. 8. Lời giải.
Tác giả: Phạm Văn Tuấn; Fb: Phạm Tuấn. Chọn B.
Hình chóp tứ giác đều có 4 mặt phẳng đối xứng. S S A A D D B C B C S S A A D D B C B C MỞ RỘNG:
 Mặt phẳng đối xứng của hình chóp tam giác đều (3 mặt phẳng)
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 18 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 A A A B D B D B D C C C
 Mặt phẳng đối xứng của tứ diện đều (6 mặt phẳng) A A A B D B D B D C C C A A A B D B D B D C C C 1 1 1 1 190
Câu 22. Gọi n là số nguyên dương sao cho    ...   đúng với log x log x log x log x x n log 2 3 3 3 3 3 3
mọi x dương, x  1. Tìm giá trị của biểu thức P  2n  3 . A. P  32 . B. P  23. C. P  43. D. P  41 . Lời giải.
Tác giả: Phạm Văn Tuấn; Fb: Phạm Tuấn. Chọn D. Ta có:
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 19 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 1 1 1 1 190    ...   log x log x log x log x x n log 2 3 3 3 3 3 3   2  3 log 3 log 3
log 3  ...  log 3n  190.log 3 x x x x x
 log 3  2.log 3  3. log 3  ...  . n log 3  190.log 3 x x x x x nn   1
n  19 thoûa maõn
 1 2  3  ...  n log 3  190.log 3   190   . x x 2
n  20 loaïi 
Vậy P  2n  3  41 .
Câu 23. Hàm số nào dưới đây nghịch biến trên tập xác định của nó? x    A. y  log x . B. y  log
x 1 . C. y  log x . D. y  . 2   3     3  4 Lời giải
Tác giả: Phạm Hoài Tâm; Fb: Phạm Hoài Tâm Chọn C
Xét hàm số y  log x có tập xác định: D  0;  .  4  Nhận thấy cơ số
 1 nên y  log x nghịch biến trên tập xác định. 4  4 2 x 1   1 
Câu 24. Tập nghiệm của bất phương trình  1 
(với a là tham số, a  0 ) là: 2   1 a   1   1  A.  ;  0 . B. ;     . C. 0;   . D.  ;     .  2   2  Lời giải
Tác giả: Phạm Hoài Tâm; Fb: Phạm Hoài Tâm Chọn B 2 x 1  2 x 1  0  1   1   1  Ta có:  1      1 . 2   2   2   1 a   1 a   1 a  1 Nhận thấy 2
1 a  1,a  0 nên:  1 . 2 1 a 1
Khi đó bất phương trình  
1 tương đương 2x 1  0  x   . 2  1 
Vậy tập nghiệm của bất phương trình đã cho : S  ;     .  2 
Câu 25. Có bao nhiêu số hạng trong khai triển nhị thức  x  2018 2 3 thành đa thức.
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 20 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 A. 2018 . B. 2019 . C. 2020 . D. 2017 . Lời giải.
Tác giả: Nguyễn Việt Thảo; Fb: Việt Thảo. Chọn B.
2x  32018  C
2x2018  C
2x2017 3  C
2x2016 32  ... C 32018 0 1 2 2018 . 2018 2018 2018 2018
Vậy khai triển trên có 2019 số hạng.
Câu 26. Cho hàm số y f x xác định, liên tục trên  và có bảng biến thiên như sau. x  1 3 +  y' + 0 + +  2 y  1
Khẳng định nào sau đây là đúng?
A. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng 1. .
B. Hàm số có đúng một cực trị.
C. Hàm số đạt cực đại tại x  1 và đạt cực tiểu tại x  3 .
D. Hàm số có giá trị cực tiểu bằng 3. Lời giải.
Tác giả: Nguyễn Việt Thảo; Fb: Việt Thảo. Chọn C.
Từ bảng biến thiên, ta dễ dàng thấy được A, B, D sai, C đúng.
Câu 27. Cho khối lăng trụ ABC.AB C
  có thể tích bằng V . Tính thể tích khối đa diện ABCC B   . 2V V V 3V A. . B. . C. . D. . 3 4 2 4 Lời giải.
Tác giả: Vũ Nga; Fb: Nga Vu. Chọn A.
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 21 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
Gọi S , h lần lượt là diện tích đáy và chiều cao của khối lăng trụ ABC.AB C   . 1 1 2 Ta có: V
S.h V VV VV . . A AB C   3 3 ABCC B   . A AB C   3
Câu 28. Trong không gian với hệ tọa độ Oxyz , cho A1;0;0 , B 0;0; 2 , C 0; 3;0 . Tính bán kính
mặt cầu ngoại tiếp tứ diện OABC là 14 14 14 A. . B. . C. . D. 14 . 3 4 2 Lời giải.
Tác giả: Vũ Nga; Fb: Nga Vu. Chọn C.
Cách 1: Tìm tọa độ tâm mặt cầu suy ra bán kính.
Gọi I x ; y ; z và R lần lượt là tâm và bán kính mặt cầu ngoại tiếp tứ diện OABC .  1 x   2  2 2 2 2 2 2 2 IO IA
x y z   x   1  y z 2     2  3
Ta có: IO IA IB IC R 2 2  2 2 2 2 2
IO IB  x y z x y   z  2   y   .  2 2 2   IO IC 2 2 2 2 2 2 
x y z x  
y  3  z  z  1    1 3  14 I  ;  ;1 
  R IO  .  2 2  2
Cách 2: Tìm phương trình mặt cầu suy ra bán kính.
Gọi phương trình mặt cầu S  ngoại tiếp tứ diện OABC là: 2 2 2
x y z  2ax  2by  2cz d  0 .
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 22 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019  1 a   1
  2a d  0  2  
4  4c d  0  3
Do S  đi qua bốn điểm ,
A B, C, O nên ta có:   b    .
9  6b d  0  2  d  0 c  1  d  0  14
 bán kính của S  là: 2 2 2 R
a b c d  . 2
Cách 3: Sử dụng công thức tính bán kính mặt cầu ngoại tiếp của tứ diện vuông.
Do tứ diện OABC có ba cạnh ,
OA OB, OC đôi một vuông góc nên bán kính mặt cầu ngoại tiếp 1 1 14 tứ diện OABC là 2 2 2 R
OA OB OC  1 4  9  . 2 2 2
Câu 29. Cho hàm số y f x xác định và liên tục trên  , có bảng biến thiên như sau: x  1 1 +  y' + 0 0 + +  2 y  1
Mệnh đề nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng ; 2   .
B. Hàm số nghịch biến trên khoảng   ;1 .
C. Hàm số nghịch biến trên khoảng 1;  .
D. Hàm số đồng biến trên khoảng  1;   . Lời giải.
Tác giả: Trần Thị Thơm; Fb: Tranthom. Chọn A.
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên mỗi khoảng ;  1 và 1;    . Suy
ra hàm số đồng biến trên khoảng ;  2 . 8 7 Câu 30. Cho x x  6 2 3 2 dx  
A3x  2  B 3x  2  C với ,
A B, C   . Tính giá trị của biểu thức 12 A  7B . 23 241 52 7 A. . B. . C. . D. . 252 252 9 9 Lời giải.
Tác giả: Trần Thị Thơm; Fb: Tranthom.
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 23 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 Chọn D. dt
Đặt t  3x  2  dt  3dx  dx  . 3 Khi đó. 2 t  2 8 7 2 2  t 2t
2x 3x  26 6 dx t dt     7 6
t  2t dt    C   3 3 9 9 8 7   . 1 4  3x  28 
3x  27  C . 36 63 1 4 7 Từ đó ta có A  , B
. Suy ra 12 A  7B  . 36 63 9
Câu 31 . Có bao nhiêu số tự nhiên có 4 chữ số được viết từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9 sao cho số đó chia hết cho 15? A. 234. B. 132. C. 243. D. 432. Lời giải
Tác giả: Phạm Thị Thu Trang; Fb: Trang Phạm Chọn C
Gọi số cần tìm là N abcd . Do N chia hết cho 15 nên N phải chia hết cho 3 và 5, vì vậy d
có 1 cách chọn là bằng 5 và a b c d chia hết cho 3.
Do vai trò các chữ số a, b, c như nhau, mỗi số a và b có 9 cách chọn nên ta xét các trường hợp:
TH1: a b d chia hết cho 3, khi đó c  3  c 3;6; 
9 , suy ra có 3 cách chọn c .
TH2: a b d chia 3 dư 1, khi đó c chia 3 dư 2  c 2;5; 
8 , suy ra có 3 cách chọn c .
TH3: a b d chia 3 dư 2, khi đó c chia 3 dư 1  c 1; 4; 
7 , suy ra có 3 cách chọn c .
Vậy trong mọi trường hợp đều có 3 cách chọn c nên có tất cả: 9.9.3.1  243 số thỏa mãn.
Câu 32. Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng  2019  ; 2019 để hàm số   3 2 
y  sin x  3cos x m sin x 1 đồng biến trên đoạn 0;  . 2    A. 2028 . B. 2018 . C. 2020 . D. 2019 . Lời giải
Tác giả: Phạm Thanh My ; Fb: Thanh My Phạm Chọn D 3 2
y  sin x  3cos x m sin x 1 3 2
y  sin x  3sin x m sin x  4 . y   2 '
3sin x  6 sin x mcos x .
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 24 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019      
Hàm số đồng biến trên đoạn 0; 
khi và chỉ khi hàm số liên tục trên 0; và hàm số đồng 2       2   π  biến trên 0;    2   π   π   y '  0 x   0;   2
 3sin x  6sin x m  0 x   0;    2   2   π 2 
 3sin x  6sin x m x   0;     1 .  2   π
Đặt t  sin x, x  0;  t    0  ;1 .  2 
Xét hàm số f t  2
 3t  6t trên 0 
;1 ta có bảng biến thiên sau
Dựa vào bảng biến thiên ta có  
1 xảy ra khi và chỉ khi m  0 .
Suy ra có 2019 giá trị nguyên của m thuộc khoảng  2019 
; 2019 thỏa mãn đề bài.
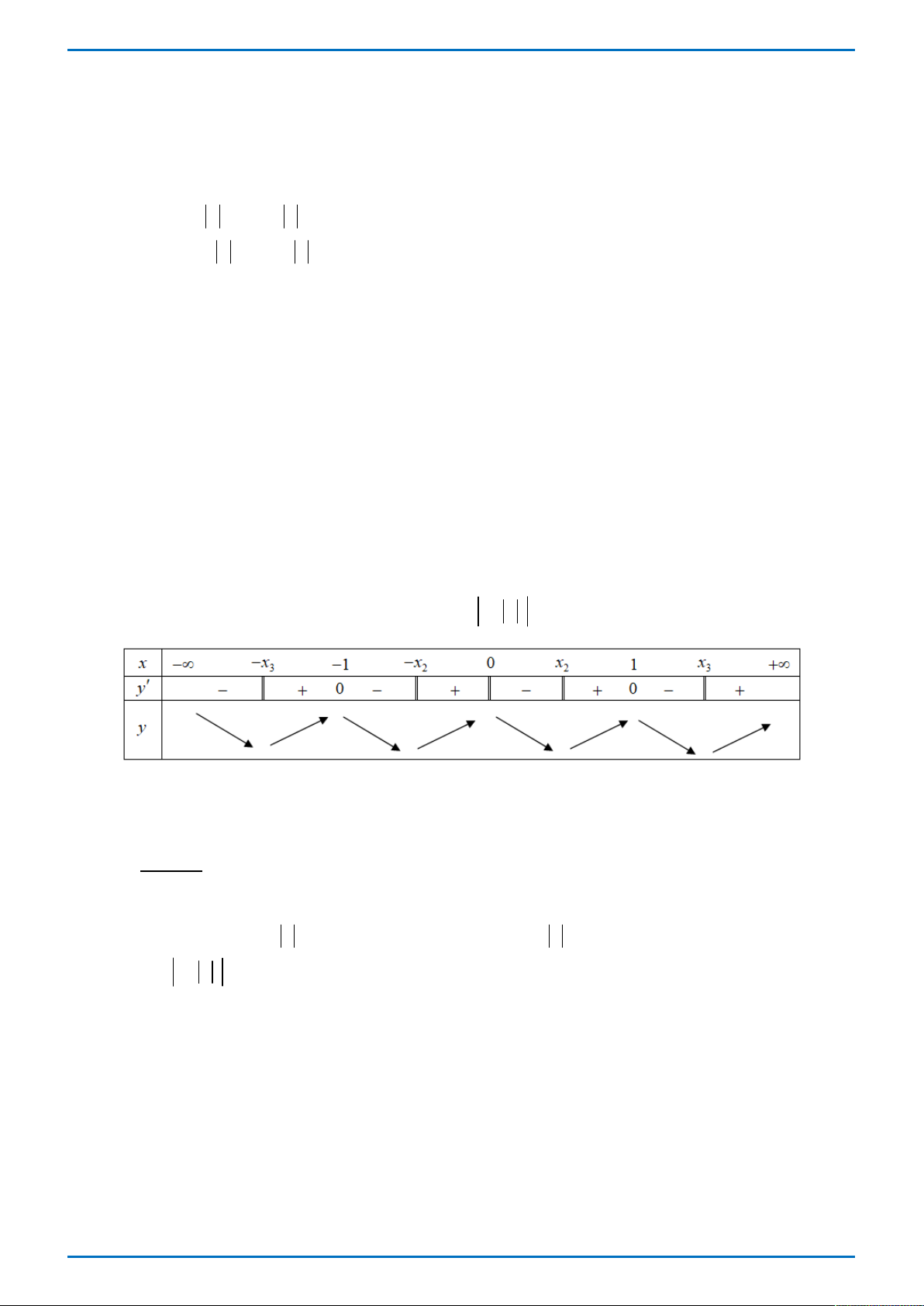
Câu 33 . Cho hàm số y f x liên tục trên  và có đồ thị như hình vẽ. Hỏi đồ thị hàm số y f x
có tất cả bao nhiêu điểm cực trị? A. 6 . B. 8 . C. 7. D. 9. Lời giải
Tác giả: Lê Thị Phương Liên ; Fb: Phuonglien Le Chọn C
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 25 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
Gọi các nghiệm của phương trình f x  0 lần lượt là x ; x ; x trong đó x  0  x  1  x . 1 2 3 1 2 3
f x, x
  0; x x ;  2   3    f
  x  khi f x   0
f x, x     x ; x 2 3  y     .  f
x  khi f x   0 f
 x , x    ;
 x  x ; 0 3   2  
 f x, x
  x ; x 3 2  
f  x, x
  0; x x ;  2   3 
 f x, x     x ; x 2 3  y    f   x, x    ;
 x  x ; 0 3   2 
f x, x
  x ; x 3 2  
y  0  x  1 x  0 
y không xác định tại x  x 2  x  x  3
Khi đó ta có bảng biến thiên của hàm số y f x  như sau:
Nên hàm số có 7 cực trị. Cách 2: (Admin Hue Tran)
Hàm số y f x có một cực trị dương là x  1 và phương trình f x  0 có 2 nghiệm dương
nên hàm số y f x  có 3 cực trị và phương trình f x   0 có 4 nghiệm nên hàm số
y f x  có 7 cực trị.
Cách khác: Từ đồ thị của hàm số y f x
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 26 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
Ta có đồ thị hàm số y f x là:
Và đồ thị hàm số y f x  là:
Từ đồ thị suy ra hàm số y f x  có 7 điểm cực trị.
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 27 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
Câu 33.1 (ĐH Vinh L1 – 2019)
Cho hàm số f x có đồ thị hàm số y f ' x được cho như hình vẽ bên. Hàm số 1
y f x 2 
x f 0 có nhiều nhất bao nhiêu điểm cực trị trong khoảng  2  ;3 ? 2
Bài giải (Nguyễn Việt Hải) 2 x
Đặt g x  f x   f 0 2 x  2(L) 
Ta có: g ' x  f ' x  x , g ' x  0  x  0  x  2 
( Nhận xét: x  2 là nghiệm bội lẻ, x  0 có thể nghiệm bội lẻ hoặc nghiệm bội chẳn tuy nhiên không ảnh
hưởng đáp số bài toán)
Suy ra hàm số y g x có nhiều nhất 3 điểm cực trị trong khoảng  2  ;3
Câu 34. Cho hình chóp S.ABC có các cạnh SA BC  3 ; SB AC  4 ; SC AB  2 5 . Tính thể
tích khối chóp S.ABC . 390 390 390 390 A. . B. . C. . D. . 12 4 6 8 Lời giải.
Tác giả: Nguyễn Văn Nghĩa; Fb: Nghĩa Văn Nguyễn. Chọn B.
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 28 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
+ Dựng hình chóp S.A ' B 'C ' sao cho A là trung điểm B 'C ' , B là trung điểm A'C ' , C là
trung điểm A' B ' .
+ Khi đó SB AC BA'  BC '  4 nên SA
'C ' vuông tại S và SA SC   SB2 2 2 ' ' 2.  64 (1) . 2 2 
SA '  SB '  80 (2) + Tương tự SB  'C ' , SA
' B ' vuông tại S và  . 2 2
SB '  SC '  36 (3)  + Từ  
1 ;2;3 ta suy ra SC '  10 ; SB '  26 ; SA'  54 . 1 1 1 390 + Ta tính được V
SC '. .SA'.SB '  390 và VV  (đvtt).
S . A' B 'C ' 3 2 S . ABC
S . A' B 'C ' 4 4
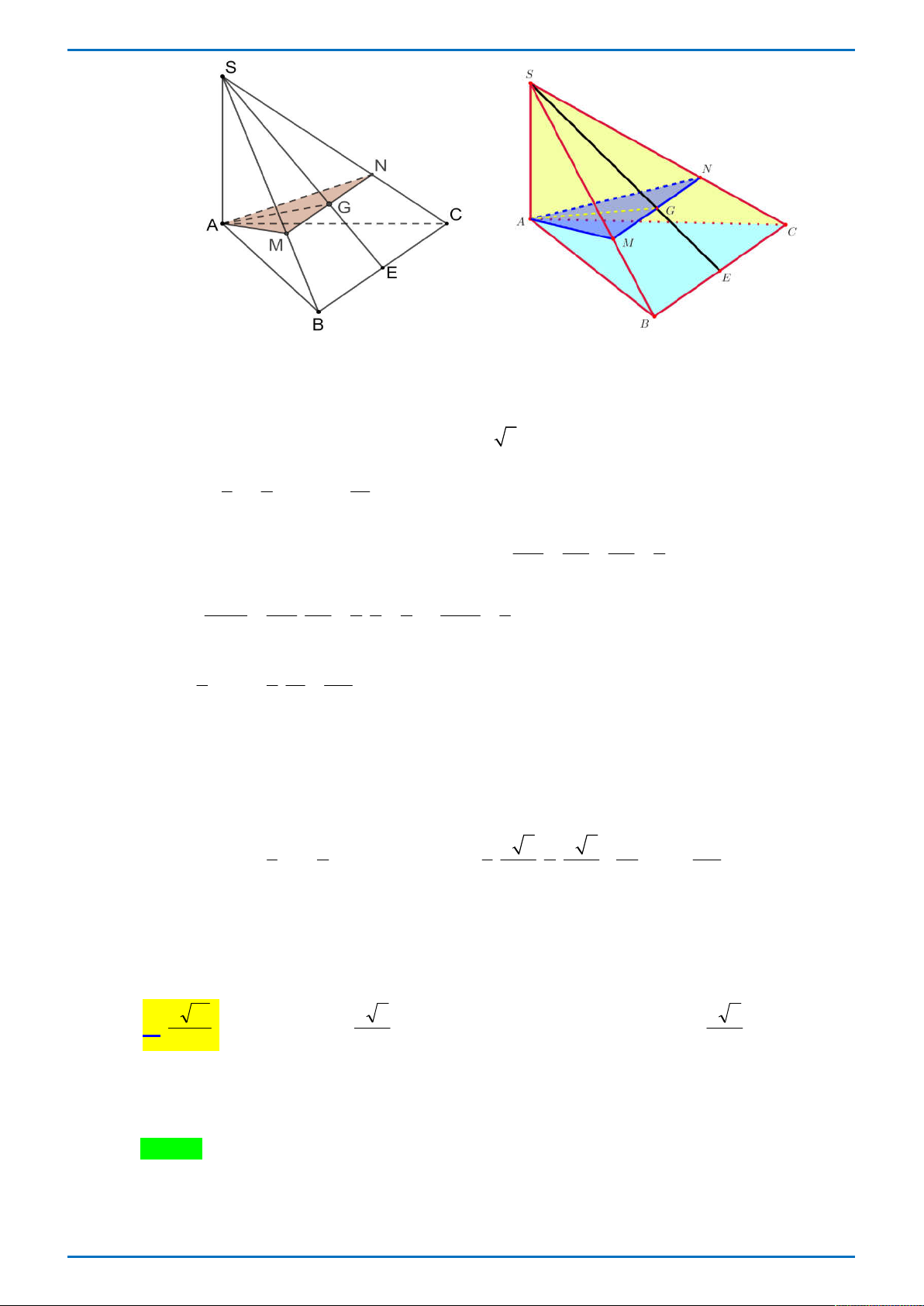
Câu 35. Cho hình chóp S.ABC có đáy là ABC vuông cân ở B, AC a 2, SA   ABC  , SA  . a
Gọi G là trọng tâm của SBC , mp   đi qua AG và song song với BC chia khối chóp
thành hai phần. Gọi V là thể tích của khối đa diện không chứa đỉnh S . Tính V . 3 5a 3 2a 3 4a 3 4a A. . B. . C. . D. . 54 9 27 9 Lời giải.
Tác giả: Nguyễn Thị Thanh Vân; Fb: Thanh Van. Chọn A.
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 29 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
Trong mặt phẳng SBC  , qua G kẻ đường thẳng song song với BC cắt SB, SC lần lượt tại
M , N . Suy ra BC // MAN  , AG  MAN  . Vì vậy MAN     .
Ta có tam giác ABC vuông cân tại B , AC a 2  AB BC a . 3 1 1 aV  . SA . . AB BC  . SABC 3 2 6 SM SN SG 2
Gọi E là trung điểm của BC . Ta có MN //BC     . SB SC SE 3 V SM SN 2 2 4 V 5 Khi đó: SAMN  .  .    . V SB SC 3 3 9 V 9 SABC SABC 3 3 5 5 a 5aV V  .  . 9 SABC 9 6 54 Cách tính khác:
Gọi H là hình chiếu vuông góc của A trên SB . Ta chứng minh được AH  SBC  và
BMNC là hình thang vuông tại B, M . 1 1 3
1 a 2 1 a 2  2a  5a Khi đó V
 .AH. .BM . MN BC  . . . .  a  . ABMNC     3 2 3 2 2 3  3  54
Câu 36. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA  ABC , góc giữa đường
thẳng SB và mặt phẳng ABC bằng o
60 . Tính khoảng cách giữa hai đường thẳng AC và SB . a 15 a 2 a 7 A. . B. . C. 2a . D. . 5 2 7 Lời giải
Tác giả: Nguyễn Bảo Mai; Fb: Bao An Chọn A
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 30 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
Vì SB có hình chiếu là AB trên  ABC  nên góc giữa SB và ABC là   o
SBA SBA  60 .  SAB
vuông tại A nên SA AB tan SBA a 3 . a 3
Gọi M là trung điểm của AC . Vì AB
C đều nên BM AC, BM  . 2
Từ B kẻ đường thẳng d song song với AC , A kẻ đường thẳng d song song với BM . 1 2
Gọi D d d . Vì AC //BD AC // SBD  d AC, SB  d AC,SBD  d  ,
A SBD . 1 2
Ta có BD AD, BD SA BD  SAD .
Gọi H là hình chiếu vuông góc của A trên SD , vì AH SD và AH BD nên
AH  SBD , suy ra H chính là hình chiếu của A trên SAD  d  ,
A SBD  AH . 1 1 1 1 4 5 SAD
vuông tại A có đường cao AH nên      2 2 2 2 2 2 AH SA AD 3a 3a 3a a 15 a 15  AH
d AC, SB  (đvđd). 5 5
NHẬN XÉT: (Nguyễn Việt Hải)
Cùng nhìn lại khoảng cách: d  ,
A    AH với AH    tại H H ? . H ? 
Bài toán cơ bản: Cho SH   HAB. Ta có d H ,SAB 1 2 
H ? 2  H ? 2 1 2
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 31 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
Với ?  S , ?  M , HM AB tại M 1 2
LƯU Ý: Nếu HSAB là tam diện vuông tại H . Tính d H ,SAB (không cần dùng điểm M ) 1 1 1 1 Ta có:    2
d H ,SAB H ? H ? H ? 1 2  2 2  3 2
Trong đó ?  S, ?  , A ?  B 1 2 3 
(Kỷ thuật trượt điểm quy về bài toán cơ bản) d A? , A   1 
d H ,  H ?1
Trong đó ?  M với M AH    1
Trở lại bài toán 36. Học sinh sẽ không cần sử dụng điểm D và lời giải (có thể không cần
dùng hình vẽ) mất vài giây ra đáp số. Hơn nữa học sinh mức TB cũng dễ dàng thấy được đáp số. Ta có: 0 SA  .
AB tan 60  a 3
Ta có: d AC, SB  d AC,SBx với Bx / / AC a 3   AS.AN d ,
A SBx 
với AN d  ,
A Bx  d B, AC   2 2 AS AN 2 a 15
Suy ra: d AC, SB  5
(Lưu ý lời giải trên điểm N chỉ mượn tạm chứ không cần dùng đến)
Câu 37. Cho hình chóp S.ABC có đáy là tam giác vuông tại A , AB  1cm , AC  3 cm . Tam giác
SAB SAC lần lượt vuông tại B và C . Khối cầu ngoại tiếp hình chóp S.ABC có thể tích bằng 5 5 3
cm . Tính khoảng cách từ C tới SAB . 6 5 5 3 3 A. cm . B. cm . C. cm . D. cm . 2 4 4 2 Lời giải
Tác giả : Nguyễn Thị Thu Hằng ; Fb: Nguyễn Thu Hằng. Chọn D Cách 1: Vì  
SBA SCA  90 suy ra trung điểm I của cạnh SA là tâm mặt cầu ngoại tiếp hình SA
chóp S.ABC với bán kính R  . 2 5 5 4 5 5 5
Thể tích khối cầu là V  3   R   R   SA  5 . 6 3 6 2
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 32 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
Gọi O là trung điểm BC , điểm D đối xứng với A qua O nên tứ giác ABDC là hình chữ nhật.
Dễ thấy CD SB , CD DB CD SD   1 .
SC DB , CD DB DB SD 2 .
Từ (1) (2)  SD   ABDC  2 2  SD
SA AD  5  4  1.
Gọi H là chân đường vuông góc của D lên cạnh SB .
d C,SAB  d D,SAB  DH .
Thật vậy AB BD ; AB SD AB  SDB  AB DH ; DH SB DH  SAB . 1 1 1 1 1 1 4 3        DH  . 2 2 2 DH SD DB 2 DH 1 3 3 2 3
Vậy khoảng cách từ C đến mặt phẳng SAB là cm . 2
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 33 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 Cách 2: Vì  
SBA SCA  90 suy ra trung điểm I của cạnh SA là tâm mặt cầu ngoại tiếp hình SA
chóp S.ABC với bán kính R  . 2 5 5 4 5 5 5
Thể tích khối cầu là V  3   R   R   SA  5 . 6 3 6 2 1
Gọi O là trung điểm BC , vì BI
C cân nên OI BC ; 2 2 OI IC OC  . 2
Mà O là tâm đường tròn ngoại tiếp AB
C OI   ABC   d C,SAB  2d  ,
O ABI  .
Gọi N là trung điểm AB nên ON AB , OI AB AB  ONI  .
  ABI   ONI  theo giao tuyến IN .
Kẻ OH IN OH   ABI   d C,SAB  2d  ,
O ABI   2OH . 1 1 1 4 16 3     4   OH  . 2 2 2 OH ON OI 3 3 4 3
Vậy khoảng cách từ C đến mặt phẳng SAB là cm . 2 1
Câu 38. Cho hàm số f x liên tục trên  thỏa mãn f 2x  3 f x , x    . Biết rằng
f x dx  1  . 0 2 Tính tích phân I
f x dx  . 1 A. I  5 . B. I  6 . C. I  3 . D. I  2 . Lời giải.
Tác giả: Nguyễn Mạnh Dũng ; Fb: Mạnh Dũng. Chọn A.
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 34 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 1 1 1 1 1
Ta có: 3  3.1  3. f x dx  3 f x dx f 2x dx
f 2x d 2x, x        . 2 0 0 0 0
Đặt 2x t  d 2x  dt , với x  0  t  0 ; x  1  t  2 . 1 2 2 1 1 1  3 
f 2x d 2x 
f t  dt
f x dx , x     
 (do hàm số f x liên tục trên  ). 2 2 2 0 0 0 2 1 2 
f x dx  6, x   
  f xdx f xdx  6, x      . 0 0 1 2  1
f x dx  6, x     . 1 2 
f x dx  5, x     . 1
Câu 38.1 Cho hàm số f x liên tục trên  thỏa mãn f mx  nf x  p , x
   m  0 . Biết rằng 1 m
f x dx q
q  0 . Tính tích phân I f x dx  . 0 1 Lời giải.
Tác giả: Nguyễn Mạnh Dũng ; Fb: Mạnh Dũng. n 1 n 1 n
1 f mx  p 1 f mx 1 p Ta có: n  .q
. f x dx  
f x dx   dx   dx  dx , x      . q q q q q q 0 0 0 0 0 1 1 p 1 1 1 pn
f mx d mx  x  
f mx d mx  , x     . mq q 0 mq q 0 0 1  p  
f mx d mx  n  .mq , x       . q 0  
Đặt mx t  d mx  dt , với x  0  t  0 ; x  1  t m . 1  p
f mx d mx  n  .mq , x       . q 0   m mp  
f t  dt f x dx n  .mq , x      
 (do hàm số f x liên tục trên  ). q 0 0   1 mp  
f x dx f x dx n  .mq , x        . q 0 1   mp   q
f x dx n  .mq , x       . q 1   mp  
f x dx n  .mq q   
nmq mp q , x    . q 1  
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 35 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 m
f x dx  nmq mp q , x     . 1 x 1
Câu 39. Tìm số đường tiệm cận của đồ thị hàm số y  .
4 3x 1  3x  5 A. 3. B. 2. C. 1. D. 0. Lời giải.
Tác giả: Trần Mạnh Tường; Fb: Trần Tuệ Minh. Chọn B.    x   2 16 3
1  9x  30x  25
Ta có: 4 3x 1  3x  5  0  4 3x 1  3x  5    x  1 3  x  5  0   1 
Tập xác định: D   ;  \     1  3  x   x  
1 4 3x 1  3x  5 1 
4 3x 1  3x  5 + Ta có: lim  lim  lim   x
 4 3x 1  3x  5 x  9 x  2 1 1 x 1 1     9  x   1
do đó đường thẳng x  1 là đường tiệm cận đứng của đồ thị hàm số. 1 1 x 1 1 1 + lim  lim x
  do đó đường thẳng y   là đường
x 4 3x 1  3x  5 x 3 1 5 3 3 4   3  2 x x x
tiệm cận ngang của đồ thị hàm số.
Kết luận: Đồ thị hàm số có hai tiệm cận.
Câu 40. Trong không gian Oxyz , lấy điểm C trên tia Oz sao cho OC  1 . Trên hai tia Ox, Oy lần lượt lấy hai điểm ,
A B thay đổi sao cho OA OB OC . Tìm giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp tứ diện . O ABC ? 6 6 6 A. . . B. 6.. C. . . D. . . 4 3 2 Lời giải.
Tác giả: Lê Anh Đông; Fb: Le Anh Đong. Chọn A.
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 36 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 Bốn điểm O, ,
A B,C tạo thành 1 tam diện vuông. 2 2 2
OA OB OC
Bán kính mặt cầu ngoại tiếp tứ diện . O ABC là R  . 2
Đặt OA a;OB b, a,b  0. Ta có a b  1  b  1 a . 2 2 2
OA OB OC 2 2 2 a b 1
a    a2 2 2 1 1 Vậy R    2 2 2 2  1 3    2 a       2 4      6   . 2 4 6 1 Vậy R
, tại a b  . . min 4 2
Câu 41. Cho hàm số y f x có đạo hàm cấp hai trên  . Biết f 0  3 , f 2  2018  và bảng xét
dấu của f  x như sau:
Hàm số y f x  2017  2018x đạt giá trị nhỏ nhất tại điểm x thuộc khoảng nào sau đây? 0 A.  ;   2017 . B. 2017;  . C. 0; 2 . D. 2017;0 .
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 37 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 Lời giải.
Tác giả: Giáp Văn Quân; Fb: quanbg. quan. Chọn A.
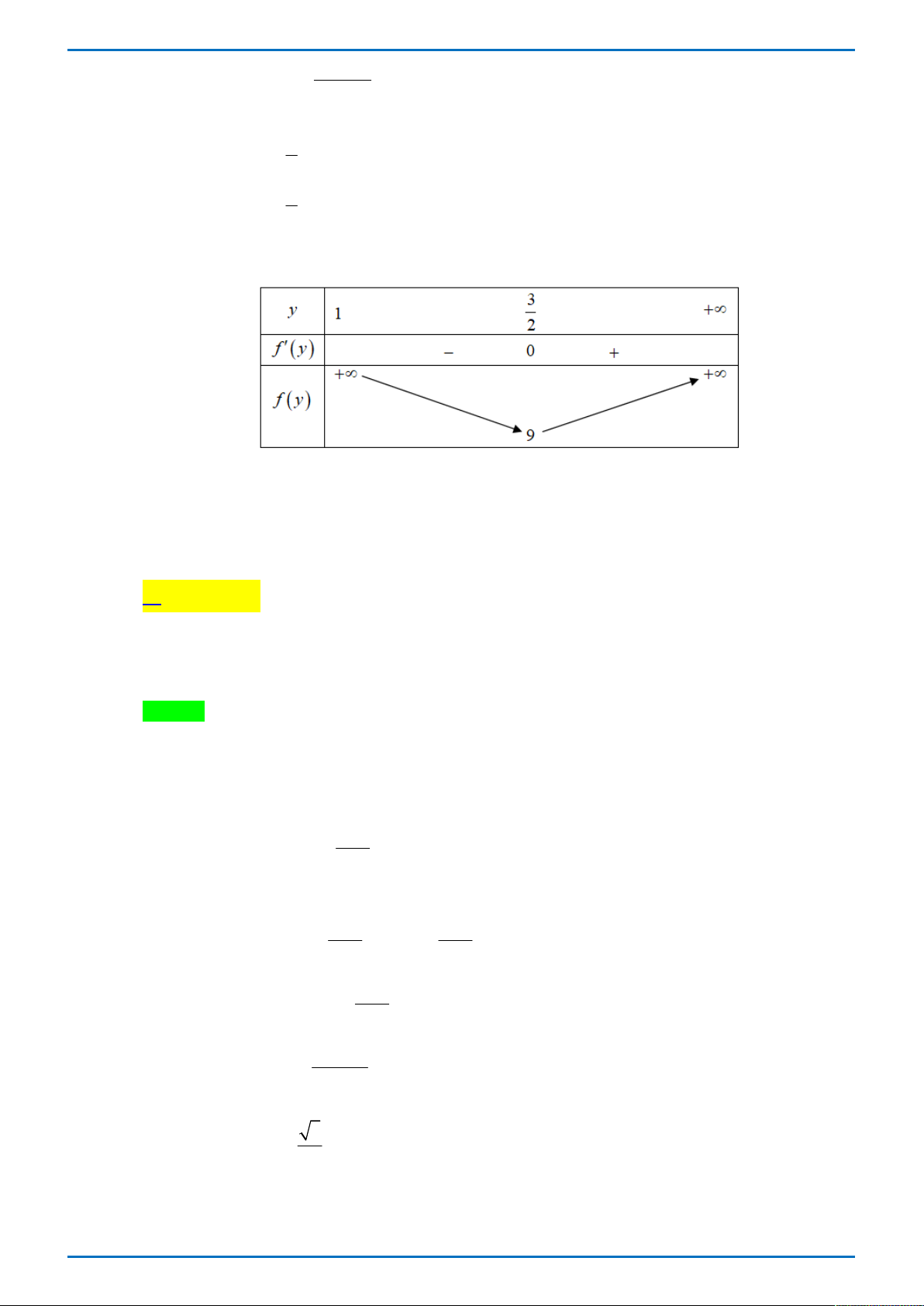
Dựa vào bảng xét dấu của f   x ta có bảng biến thiên của hàm sồ f  x
Đặt t x  2017 .
Ta có y f x  2017  2018x f t   2018t  2017.2018  g t  .
gt   f t   2018 .
Dựa vào bảng biến thiên của hàm số f  x suy ra phương trình gt  có một nghiệm đơn    ;
 0 và một nghiệm kép t  2 .
Ta có bảng biến thiên g t
Hàm số g t  đạt giá trị nhỏ nhất tại t    ;  0 . 0  
Suy ra hàm số y f x  2017  2018x đạt giá trị nhỏ nhất tại x mà 0 x  2017  ;  0  x  ;  2017  . 0   0  
Câu 42. Cho hàm số y f x có đạo hàm liên tục trên đoạn 0 
;1 và thỏa mãn f 0  0 . Biết 1 9 1  x 3 1 2
f x dx   và
f  x cos dx   . Tích phân
f x dx  bằng 2 2 4 0 0 0 6 2 4 1 A. . B. . C. . D. .     Lời giải Chọn A 1 1 1  2  2  3 Ta có: f (x) sin xdx   f (x).cos x f '(x).cos xdx    2  2  2 2 0 0 0 1 1 1 1    2 2 2 ( f (x)  3sin x) dx
f (x)dx  6 f (x) sin xdx  9 sin xdx  0     2 2 2 0 0 0 0 1 1   6
Từ đây ta suy ra f (x)  3sin x
f x dx  3sin xdx    . 2 2  0 0
PHÁT TRIỂN BÀI TOÁN CÂU 42
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 38 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 1 2
Câu 42.1. Cho hàm số f x có đạo hàm liên tục trên đoạn 0 
;1 thỏa mãn f  
1  0 ,  f  x dx  7    0 1 1 1 và 2
x f x dx   . Tích phân
f x dx  bằng 3 0 0 7 7 A. . B. 1. C. . D. 4 . 5 4 Lời giải Chọn A.  Nhận xét
- Ý tưởng sáng tác bài toán giống câu 50 trong đề minh họa của BGD năm 2018. Vì thầy
Nguyễn Việt Hải phân tích quá hay nên tôi trích dẫn lại nguyên văn nhận xét và ý tưởng đó 1 1 1 Từ giả thiết: 2  d   x f x x 2  3  d  1  x f x x . 3 0 0 1 Tính: 2
I  3x f x d  x . 0 u   f x du f    xdx Đặt:    . 2 3 dv  3x d  xv   x Ta có: 1 1 1 1 1 2
I  3x f x 3
dx x f x 3
x . f  x d  
x  1. f   1  0. f 0 3
x . f  x d  x 3   .   d  x f x x . 0 0 0 0 0 1 1 Mà: 2 3  d  1  x f x x 3  1   .   d  x f x x 0 0 1 1 1 1 3 2  .   d  1  x f x x 3  7 .   d  7  x f x x 3
 7x . f  x dx    f  x d    
x , (theo giả thiết: 0 0 0 0 1
f  x 2  dx  7    ). 0 1 1
 7x . f x+  f x 2 3  3   dx  0 
  7x + f  x d  x  0  f x   0 0 7 3
 7x + f  x  0  f  x 3
 7x f x 4   x C . 4 7 7 Với f   1  0 4
  .1  C  0  C  . 4 4 7 7
Khi đó: f x 4   x  . 4 4
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 39 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 1 1 1  7 7  5 7  x  7 Vậy: f x 4 dx   x  d    x     x   .  4 4  4 5 5 0 0   0  PHÂN TÍCH 1 1 3 3 1 3 1 x x x 1  2
x f (x)dx f x 1 3 d  f (x) |  df (x)  
x . f '(x)dx 0     3 3 3 3 0 0 0 0
Từ đây, chúng ta quan sát giả thiết bài toán: Ta thấy xuất hiện f x 2 '( ) và 3
x . f '(x) 2
Nghĩ ngay đến hằng đẳng thức f x  3 '( ) ax  
, như vậy số a  ? tương ứng với bài toán? 1 2
+ f '(x) dx   7 0 1 + 3
2ax . f '(x)dx    2a 0 1 2 2 a +  3 ax dx   7 0 1 2 2 a
Do đó số a chọn tương ứng là  f '(x)  3
ax dx  7  2a   0  a     7 . 7 0 7x 7 3  4
 . Suy ra f '(x)  7x f (x)   . 4 4 Vậy đáp chọn: A  NHẬN XÉT:
Vì đây là trắc nghiệm chỉ cần ĐS đúng do đó ta sử dụng kỷ thuật đồng nhất suy ra đáp số dễ dàng. 1 1
f '(x)2dx   7 và  3
7x f '(x)dx  
7 . Vì trắc nghiệm nên đồng nhất hai biểu thức dưới dấu 0 0 7x 7 3  4
tích phân. Suy ra f '(x)  7x f (x)    A . 4 4
 Hướng tiếp cận khác theo con đường BĐT. 1 1 2 1
+ Quan sát giả thiêt bài toán: f (1)  0,  f '(x) dx   7 và 2
x f (x)dx   . 3 0 0
+ Ta nghĩ đến đánh giá bằng BĐT: Thật vậy sử dụng kiến thức dấu tam thức bậc hai. Chúng ta
có kết quả BĐT Cauchy – Schawz b b b b t f x  2 2 2
dx t f x g x dx  2 2
g x dx  t. f x   g x dx  0,t         . a a a a
Suy ra: BĐT Cauchy – Schawz 2  bb b
f x g x  2 2 dx   
f xdx. g x   dx aa a
Do đó ta có hướng giải bài toán trên:
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 40 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 1 1 3 3 1 3 1 1 x x x 1  2
x f (x)dx
f xd  1 f (x) |  df (x)       3
x . f '(x)dx . 0 3 3 3 3 3 0 0 0 0 2 1   1 1  1 2 1 2 1 Ta suy ra:  3 3 
x f '  x dx   
x dx f 'x dx  . 9  3 9 9 0  0
Tương đương f x  3 ' k.x
Ý TƯỞNG SÁNG TẠO ĐỀ a a 2 2
Tạo hằng tích phân có dạng đẳng thức:  A Bdx  
0 Hoặc  A B Cdx   0 … 0 0 a a a a 2
Chọn a, A, B thích hợp tương ứng ta có bài toán. 0   A Bdx  2 A dx  2 . A Bdx      2 B dx 0 0 0 0
MỘT SỐ BÀI TOÁN TƯƠNG TỰ 1 2
Câu 42.2. Cho hàm số f x có đạo hàm liên tục trên đoạn 0 
;1 thỏa mãn f  
1  4 ,  f  x dx  36    0 1 1 1 và .   d   x f x x . Tích phân
f x dx  bằng 5 0 0 5 3 2 A. . B. . C. 4 . D. . 6 2 3 Lời giải Chọn B. 1 1 1 Từ giả thiết: .   d   x f x x  5 .   d  1  x f x x . 5 0 0 1 Tính: I  5 . x f x d  x . 0
u f x x
u f x d  d  Đặt:    5 . 2 dv  5 d x x v    x  2 1 1 1 5 5 Ta có: I  5 . x f x 2 dx
x . f x 2 
x . f  x d   x 2 2 0 0 0 1 5 5 1 5  . f   2 1 
x . f  x d  x 2  10  .   d
x f x x , (vì f   1  4 ) 2 2 2 0 0 1 1 5 1 18 Mà: I  5 .
x f x dx  1  2  1  10  .   d  x f x x 2  .   d   x f x x 2 5 0 0 0 1 1 1 1 2 2 2  10 .   d  36  x f x x 2
 10 x . f  x dx   f  x d    
x , (theo giả thiết:  f  x dx  36    ) 0 0 0 0
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 41 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 1 1  10  .
    f x 2 2     dx  0  x f x 2      10 
x f  x dx  0    f x   0 0 3 10x 2
 10x f  x  0  f  x 2
 10x f x   C 3 10.1 2 Với f   1  4  4   C C  . 3 3 3 10x 2
Khi đó: f x   . 3 3 1 1 1 3  10x 2  4  5x 2  3 Vậy:
f x dx   d    x   x    . 3 3 6 3 2 0 0     0 2 2
Câu 42.3 Cho hàm số f x có đạo hàm liên tục trên đoạn 0; 2 thỏa mãn f 2  3 ,  f  x dx  4    0 2 1 2 và 2  d   x f x x . Tích phân  d  f x x bằng 3 0 0 2 297 562 266 A. . B. . C. . D. . 115 115 115 115 Lời giải Chọn C. 2 1 2 Từ giả thiết: 2  d   x f x x 2  3  d  1  x f x x . 3 0 0 2 Tính: 2
I  3x f x d  x . 0 u   f x du f    xdx Đặt:    . 2 3 dv  3x d  xv   x 2 2 2 2 Ta có: 2
I  3x f x 3
dx x . f x 3
x . f  x d   x 3  24  .   d
x f x x , (vì f 2  3) 0 0 0 0 2 2 Mà: 2
I  3x f x dx  1  3  1  24  .   d  x f x x 0 0 2 2 4 3  .   d  23  x f x x 3  .   d  4  x f x x 23 0 0 2 2 4 1 2 
x . f  x dx   f  x 2 3  d  
x , (theo giả thiết:    d  4  f x x ) 23     0 0 0 2 2  4   4  
x . f  x   f  x 2 3  dx  0  3          d  0  f x x f x x 23         23  0 0
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 42 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 4 4 1 3 
x f  x  0  f  x 3 
x f x 4  x C 23 23 23 16 53
Với f 2  3  3   C C  . 23 23 1 53
Khi đó: f x 4  x  . 23 23 2 2 2  1 53   1 53  562 Vậy f x 4 dx x  d   5   x x x    .  23 23   115 23  115 0 0 0 1 2
Câu 42.4. Cho hàm số f x có đạo hàm liên tục trên đoạn 0 
;1 thỏa mãn f  
1  4 ,  f  x dx  5    0 1 1 1 và .
x f x dx    . Tích phân
f x dx  bằng 2 0 0 15 17 17 15 A. . B. . C. . D. . 19 4 18 4 Lời giải Chọn D.
du f x dx 1 u
  f x    Tính: I  .
x f x dx  . Đặt:    1 2 dv  d x x v x 0    2 1 1 1 1 1 1 Ta có: 2 I
x . f x 2 
x f  x dx  2  2 
x f  x dx  , (vì f   1  4 ). 2 0 2 2 0 0 1 1 1 1 1 Mà: .
x f x dx    2    2    d  x f x x 2 2 2 0 0 1 1 1 1 2 2 2    d  5  x f x x
, (theo giả thiết:  f  x dx  5  2  
)  x f  x dx   f  x d     x 0 0 0 0 1 1 2   2
x f  x   f  x 2    dx  0 
 .x f  x dx  0  f x   0 0 1  2
x f  x  0    2 f
x x f x 3  x C . 3 11 Với f   1  4  C  . 3 1 11
Khi đó: f x 3  x  . 3 3 1 1  1 11   1 11 1  15 Vậy f x 3 4 dx x  dx x x       .  3 3   12 3  0 4 0 0
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 43 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 2 2
Câu 42.5. Cho hàm số f x có đạo hàm liên tục trên đoạn 0; 2 thỏa mãn f 2  6 ,  f  x dx  7    0 2 17 2 và .
x f x dx   . Tích phân
f x dx  bằng 2 0 0 A. 8 . B. 6 . C. 7 . D. 5 . Lời giải Chọn A. 2 Tính: I  .
x f x dx  . 0         du
f x dx u f x  Đặt:    1 2 dv  d x x v x    2 2 1 2 1 2 1 Ta có: 2 I
x . f x 2 
x f  x dx  2  12 
x f  x dx
, (vì f 2  6 ). 2 0 2 2 0 0 2 17 2 17 1 Theo giả thiết: .
x f x dx   2   12    d  x f x x 2 2 2 0 0 2 2    d  7  x f x x 0 2 2 2  2
x f  x dx   f  x dx     0 0 2 2   2
x f  x   f  x   dx  0 0 2  f  x 2
. x f  x dx  0    0 1  2
x f  x  0  f x 2 
x f x 3  x C . 3 10
Với f 2  6  C  . 3 1 10
Khi đó: f x 3  x  . 3 3 2 2  1 10   1 10 2  Vậy f x 3 4 dx x  dx x x  8      .  3 3   12 3  0 0 0
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 44 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 3 2
Câu 42.6. Cho hàm số f x có đạo hàm liên tục trên đoạn 0; 
3 thỏa mãn f 3  6 ,  f  x dx  2    0 3 154 3 và 2 .  d   x f x x . Tích phân
f x dx  bằng 3 0 0 53 117 153 13 A. . B. . C. . D. . 5 20 5 5 Lời giải Chọn B. 3 Tính 2
I x . f x dx  . 0     
du f  x dx u f x  Đặt    1 . 2 3
dv x dx v x    3 3 1 3 1 3 1 Ta có 3 I
x . f x 3 
x f  x dx  3  54    d
x f x x , (vì f 3  6 ). 3 0 3 3 0 0 3 154 3 154 1 Theo giả thiết: 2 .  d   x f x x 3   54    d  x f x x 3 3 3 0 0 3 3 3 3 3 2 2    d  8  x f x x 3
x f  x dx  4  f  x d   3  
x  x f x  4  f x   dx  0 0 0 0 0 3    3
x  4 f  x dx  0  f x   . 0 3 x 4 x 3
x  4 f  x  0  f  x 
f x   C . 4 16 15
Với f 3  6  C  . 16 4 x 15
Khi đó: f x   . 16 16 3 3  1 15   1 15 3  117 Vậy f x 4 5 dx x  dx x x       .  16 16   80 16  0 20 0 0 1 2
Câu 42.7. Cho hàm số f x có đạo hàm liên tục trên đoạn 0 
;1 thỏa mãn f  
1  2 ,  f  x dx  8    0 1 1 và 3
x . f x dx  10  . Tích phân
f x dx  bằng 0 0 2 194 116 584 A.  . B. . C. . D. . 285 95 57 285
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 45 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 Lời giải Chọn C. 1 Tính: 3
I x . f x dx  . 0     
du f  x dx u f x  Đặt:    1 . 3 4
dv x dx v x    4 1 1 1 1 1 1 1 Ta có: 4 I
x . f x 4 
x f  x dx  4  
x f  x dx  , (vì f   1  2 ). 4 0 4 2 4 0 0 1 1 Theo giả thiết: 3
x . f x dx  10   4
x f  x dx  38  0 0 1 1 1 2 4  8.   d  38.8  x f x x 4
 8. x f  x dx  38.  f  x d     x 0 0 0 1 1
 8x f x  38 f x 2 4  4   dx  0   . 8
x  38 f  x dx  0  f x   0 0 4 4  4
8x  38 f  x  0  f  x 4  
x f x 5   x C . 19 95 194 Với f   1  2  C  . 95 4 194
Khi đó: f x 5   x  . 95 95 1 1  4 194   2 194 1  116 Vậy f x 5 6 dx   x  dx   x x       .  95 95   285 95  0 57 0 0 x  cos x
Câu 43. Biết F x là nguyên hàm của hàm số f x 
. Hỏi đồ thị của hàm số y F x có 2 x
bao nhiêu điểm cực trị? A. Vô số điểm. B. 0. C. 1. D. 2. Lời giải
Tác giả: Võ Minh Chung; Fb: Võ Minh Chung Chọn C. x  cos x x  cos x
Vì F x là nguyên hàm của hàm số f x  nên suy ra: F (
x)  f (x)  . 2 x 2 x x  cos x
x  cos x  0  Ta có: F (  x)  0   0    1 . 2  x x    1  ;  1 \   0 
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 46 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
Xét hàm số g(x)  x  cos x trên 1  ;1 , ta có : g (
x)  1 sin x  0, x  1  ;1 . Suy ra hàm số
g(x) đồng biến trên 1 
;1 . Vậy phương trình g(x)  x  cos x  0 có nhiều nhất một nghiệm trên 1  ;1 2 .
Mặt khác ta có: hàm số g(x)  x  cos x liên tục trên 0 
;1 và g 0  0  cos 0  1   0 ,
g(1)  1 cos  
1  0 nên g 0.g   1  0 . Suy ra x
 0;1 sao cho g x  0 3 . 0  0   Từ  
1 , 2 , 3 suy ra: phương trình F (
x)  0 có nghiệm duy nhất x  0 . Đồng thời vì x 0 0
là nghiệm bội lẻ nên F (
x) đổi qua x x . 0
Vậy đồ thị hàm số y F x có 1 điểm cực trị.
PHÂN TÍCH VÀ PHÁT TRIỂN CÂU 43: Cô Nguyễn Thị Bích Ngọc – Fb: Bích Ngọc.
PHÂN TÍCH: Bản chất bài toán là muốn khai thác định nghĩa nguyên hàm của một hàm số và
cách giải phương trình chứa hàm số hỗn hợp gồm đa thức và hàm số lượng giác. Phương trình
này sử dụng tính chất đơn điệu của hàm số dẫn đến số nghiệm tối đa là một, khi đó chỉ cần
nhẩm một nghiệm hoặc sử dụng định lí liên tục của hàm số suy ra phương trình có nghiệm duy nhất. 2 x e
Câu 43.1 Cho biết f x 9  t ln tdt
, tìm điểm cực trị của hàm số đã cho e A. x  2 B. x  0 C. x  1  D. x  6 Lời giải Chọn B
Gọi G x là một nguyên hàm của hàm số g x 9
x ln x . Theo định nghĩa:     2x f x
G e   G e    
x x    x f x G e G e e x9 2 2 4 ' ' .e .2 ' 2. 2 /
f (x)  0  x  0 . Suy ra chọn đáp án B. 2 x
Câu 43.2 Cho hàm số G(x)  sin tdt. 
Tính đạo hàm của hàm số G(x). 0 A. G (
x)  2xsin x B. G (
x)  2x cos x C. G (
x)  cos x D. G (
x)  2x sin x Lời giải Chọn A
Gọi F x là một nguyên hàm của hàm số f x  sin x . Theo định nghĩa:
G x  F  2
x   F 0
G x  F  2
x x F   2 ' ' .2 ' 0  2 . x sin x  2 .
x sin x . Chọn A
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 47 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 1
Câu 43.3 Biết F x là nguyên hàm của hàm số f x 2  cos x
x 1. Hỏi đồ thị của hàm số y F x 2
có bao nhiêu điểm cực trị? A. Vô số điểm. B. 0 . C. 1. D. 2 . Lời giải Chọn D 1 Ta có /
F (x)  f x 2  cos x x 1 . 2 /
f (x)   s inx  x ; //
f (x)   cos x 1  0 x   R . Suy ra hàm số /
f (x) đồng biến trên R , từ đó dẫn đến phương trình /
f (x)  0 có nhiều nhất một nghiệm. Mặt khác /
f (0)  0 suy ra x  0 là nghiệm duy nhất của phương trình / f (x)  0 . Do hàm số /
f (x) liên tục trên mỗi khoảng  ;
 0;0;  và vô nghiệm trên mỗi khoảng này nên dấu của /
f (x) không đổi trên mỗi khoảng trên. Mà / / f ( 1
 )  0; f (1)  0 suy ra / f (x)  0 x    ;  0 và / f (x)  0 x   0;  .
Vậy hàm số f (x) nghịch biến trên khoảng  ;
 0 và đồng biến trên khoảng 0;  . Mà
f (0)  0 nên phương trình f (x)  0 có nghiệm duy nhất x  0 hay phương trình / F (x)  0
có nghiệm duy nhất x  0 .
Vậy đồ thị của hàm số y F x có duy nhất một điểm cực trị. ux
BÀI TOÁN TỔNG QUÁT: Cho hàm số F x 
g t dt
. Tìm đạo hàm của hàm số F x . vx CHỨNG MINH:
Gọi G t  là nguyên hàm của hàm số g t  . Theo định nghĩa tích phân, ta có: uxF x 
g t dt G(u)  G v  . vx Suy ra: F (x)
G(u) G v      
  u .G (
u)  v .G (
v)  u .g(u)  v '.g(v) . ux   
Vậy, ta có công thức tổng quát: 
g t dt   u .g(u)  v '.g(v)   .  vx  
Câu 44. Tìm tất cả các giá trị thực của tham số m để phương trình 3m m e e   2 x   x  2 2 1
1 x 1 x  có nghiệm.  1   1   1   1  A. 0; ln 2   . B. ;  ln 2   . C. 0;   . D. ln 2;    .  2   2   e   2  Lời giải.
Tác giả: Trần Quốc Thép; Fb: Thép Trần Quốc. Chọn B.
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 48 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 2 t 1 Đặt 2 2 2 2
t x  1 x t  1 2x 1 x x 1 x  . 2 2 1 x x 1 Ta có t ' 
, t '  0  x  . 2 1 x 2 Vậy t   1  ; 2  .   2  t   m m 1 Phương trình trở thành 3 3m m 3 ee  2t 1 m   e
e t t e t   . (sử dụng hàm đặc 2   trưng). m 1
Phương trình có nghiệm khi và chi khi 1  e
2  m  ln 2  m  ( ;  ln 2] . 2
Câu 45. Tìm tập S tất cả các giá trị thực của tham số m để tồn tại duy nhất cặp số  ; x y  thỏa mãn 2 log
4x  4 y  6  m  1 và 2 2
x y  2x  4 y  1  0 . 2 2 x y 2   A. S  1;  1 .
B. S  5; 1;1;  5 . C. S   5  ;  5 .
D. S    7;  5; 1;1;5;  7 . Lời giải.
Tác giả: Nguyễn Đình Hải; Fb: Nguyen Dinh Hai. Chọn A. Ta có 2 log
4x  4 y  6  m  1 2 2 2
 4x  4 y  6  m x y  2 2 2 x y 2   2 2 2 2 2
x y  4x  4 y  8  m  0   x     y   2 2 2
m là một hình tròn C tâm I 2; 2 , 1 
bán kính R m với m  0 hoặc là điểm I 2; 2 với m  0 và 2 2
x y  2x  4 y 1  0 1
  x  2   y  2 1 2
 4 là một đường tròn C tâm J  1
 ; 2 , bán kính R  2 . 2  2
TH1: Với m  0 ta có: I 2; 2 C suy ra m  0 không thỏa mãn điều kiện bài toán. 2  TH2: Với m  0 .
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 49 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 2 log
4x  4 y  6  m  1 2 2  x y 2   Để hệ 
tồn tại duy nhất cặp số  ;
x y  thì hình tròn C và 1  2 2
x y  2x  4 y 1  0 
đường tròn C tiếp xúc ngoài với nhau 2 
IJ R R 2 2
 3  0  m  2  m  1  m  1  . 1 2
Câu 46. Cho hình trụ có đáy là hai đường tròn tâm O và O , bán kính đáy bằng chiều cao và bằng 2a .
Trên đường tròn đáy có tâm O lấy điểm A , trên đường tròn tâm O lấy điểm B . Đặt  là góc
giữa AB và đáy. Tính tan  khi thể tích khối tứ diện OO AB
đạt giá trị lớn nhất. 1 1 A. tan  2 . B. tan   . C. tan   . D. tan  1. 2 2 Lời giải
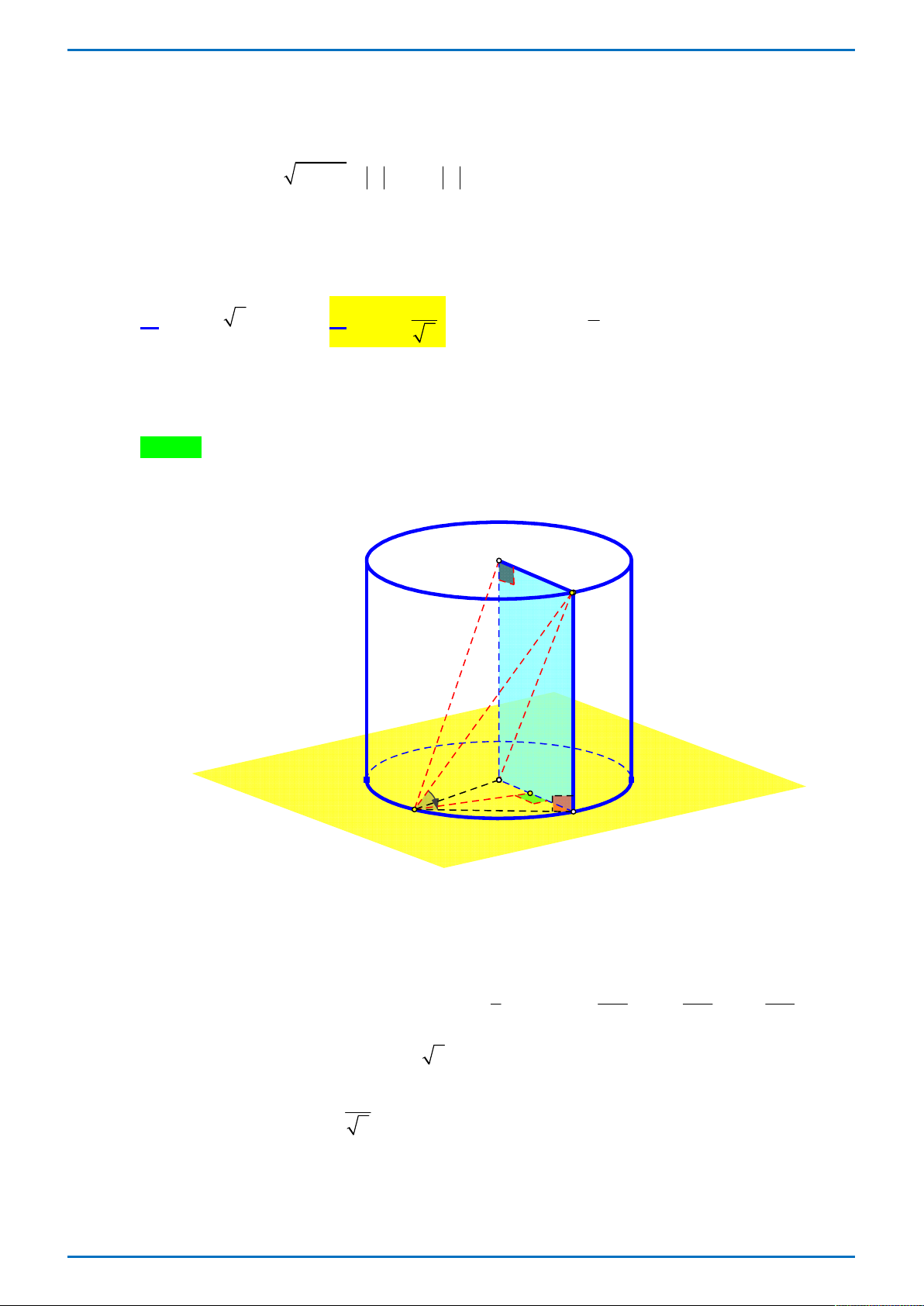
Tác giả: Nguyễn Việt Hải; Fb: Nguyễn Việt Hải Chọn B Cách 1: O' B O α H A D
Gọi D là hình chiếu vuông góc của B lên mặt phẳng O .
Kẻ AH OD , H OD . 1 2 2a 2 2a 3 4a
Ta có thể tích của khối chóp OO AB  : VAH.S  .AH  .AO  . OO AB  3 OO B  3 3 3 V
H O . Suy ra AD  2 2a . OO AB  max 1 Suy ra:  tan  tan BAD  . 2
Cách 2: Tác giả: Võ Thị Ngọc Ánh; Fb: Võ Ánh
Nhận xét: Nên thêm giả thiết AB chéo với OO ' để tứ diện OO AB tồn tại.
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 50 STRONG TEAM TOÁN VD-VDC
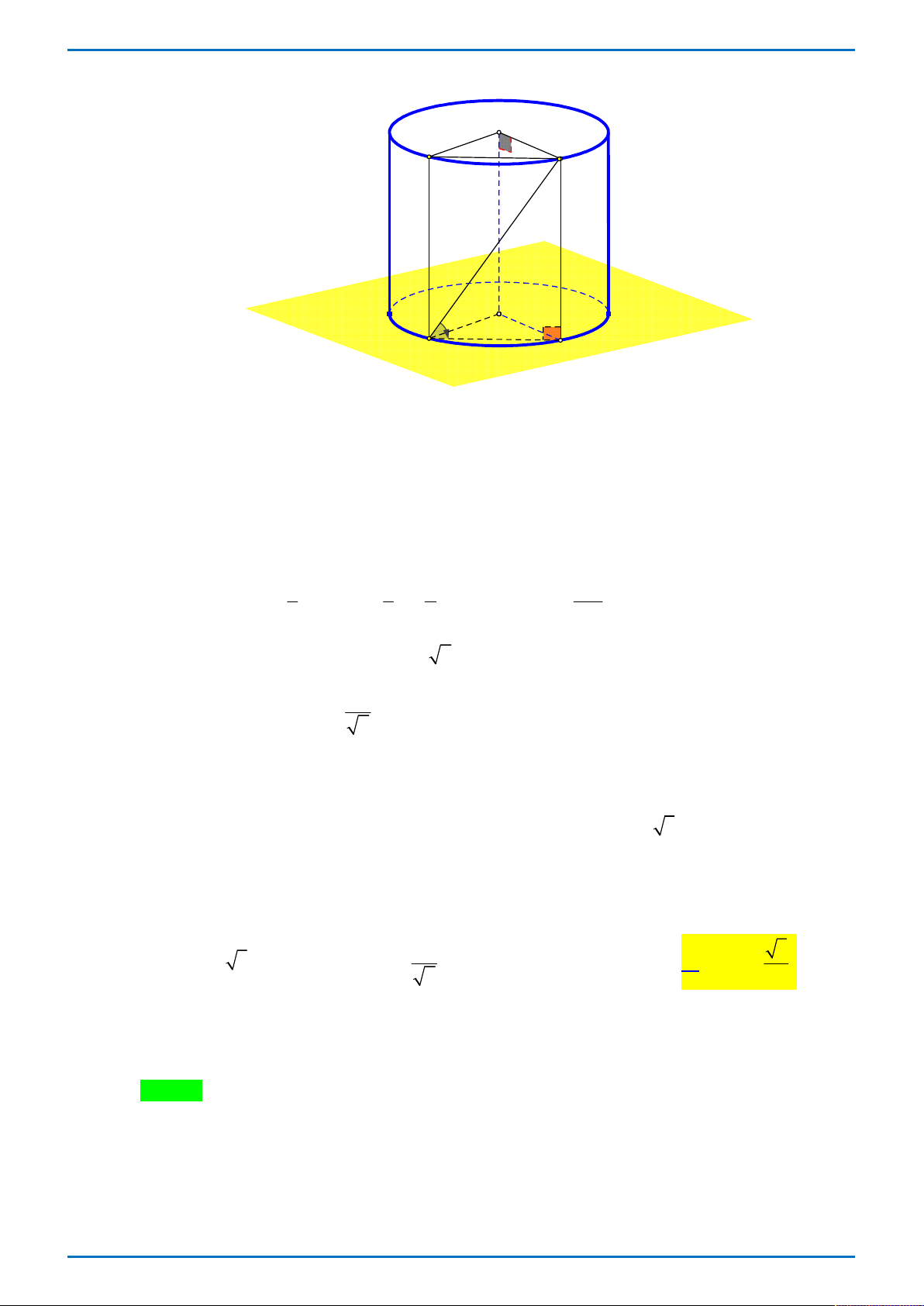
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 O' C B O α A D
Gọi D là hình chiếu vuông góc của B lên mặt phẳng chứa đường tròn O .
Gọi C là hình chiếu vuông góc của A lên mặt phẳng chứa đường tròn O ' . Ta có O ' .
CB OAD là một hình lăng trụ đứng.
Ta có thể tích của khối chóp OO AB  : 1 1 1  3 4a VV  2 . a S  .2 . a .2 .2 a . a sin AOD  . OO AB
O ' BC.OAD 3 OAD  3 2 3 VAOD   AD a . ABCD   0 90 2 2 O ' max 1 Suy ra:  tan  tan BAD  . 2
PHÂN TÍCH VÀ PHÁT TRIỂN CÂU 46: Tác giả: Võ Thị Ngọc Ánh; Fb: Võ Ánh
Câu 46.1. Cho hình trụ có đáy là hai đường tròn tâm O và O , bán kính đáy bằng chiều cao và bằng 2a .
Trên đường tròn đáy có tâm O lấy điểm A , D sao cho AD  2 3a ; gọi C là hình chiếu
vuông góc của D lên mặt phẳng chứa đường tròn O ' ; trên đường tròn tâm O lấy điểm B
( AB chéo với CD ) . Đặt  là góc giữa AB và đáy. Tính tan  khi thể tích khối tứ diện
CDAB đạt giá trị lớn nhất. 1 3 A. tan   3 . B. tan   . C. tan  1. D. tan  . 2 3 Lời giải
Tác giả: Võ Thị Ngọc Ánh; Fb: Võ Ánh Chọn D
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 51 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 B O' K C H α O A D
Gọi H là hình chiếu vuông góc của B lên mặt phẳng chứa đường tròn O .
Gọi K là hình chiếu vuông góc của A lên mặt phẳng chứa đường tròn O ' . Ta có HA .
D BKC là một hình lăng trụ đứng.
Ta có thể tích của tứ diện CDAB là 1 1 1 1 1 1 VV  .2 . a S  .2 . a . .
AD d H ; AD  .2 . a
.2a 3.d H ; AD . ABCD HAD.BKC HAD      3 3 3 2 3 2 V   d H ; AD
H là điểm chính giữa cung lớn 
AD của đường tròn O (1). ABCD max   max AD AD a Theo định lý sin ta có  2 3 3
  2.2a  sin AHD    nên  0 AHD  60 . sin AHD 4a 4a 2
Do đó (1) xảy ra khi AHD
đều  AH AD  2 3a . BH a Suy ra:  2 3 tan  tan BAH    . AH 2a 3 3
Câu 46.2. Cho hình trụ có đáy là hai đường tròn tâm O và O , bán kính đáy bằng chiều cao và bằng 2a .
Trên đường tròn đáy có tâm O lấy điểm A , D trên đường tròn tâm O lấy điểm B , C sao cho
AB//CD và AB không cắt OO ' . Tính AD để thể tích khối chóp O '.ABCD đạt giá trị lớn nhất. 4 3
A. AD  2 2a . B. AD  4a . C. AD a . D. AD  2a . 3 Lời giải
Tác giả: Võ Thị Ngọc Ánh; Fb: Võ Ánh Chọn A
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 52 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 B C O' O A D O1
Kẻ đường thẳng qua O ' song song với AB cắt mặt phẳng chứa đường tròn (O) tại O . 1 Lúc đó AO .
D BO 'C là một hình lăng trụ chiều cao bằng 2a . 1
Vì AD BC nên SS BO  'C OAD
Ta có thể tích của khối chóp O '.ABCD : 1 2 2 2 1  3 8a VV  .2 . a S  .2 . a S  .2 . a .2 .2 a . a sin AOD  . O ' ABCD 1
AO D.BO 'CBO ' 3 3 C 3 OAD 3 2 3 VAOD   AD a . ABCD   0 90 2 2 O ' max
Câu 47. Xét các số thực dương x , y thỏa mãn log x  log y  log  2 x y
. Tìm giá trị nhỏ nhất 1 1 1  2 2 2
P của biểu thức P x  3y . min 25 2 17 A. P  9 . B. P  8 . C. P  . D. P  . min min min 4 min 2 Lời giải.
Tác giả: Nguyễn Huỳnh Tấn Trung ; Fb: Nguyễn Huỳnh Tấn Trung. Chọn A. Ta có:
log x  log y  log  2 x y  log xy  log x y
xy x y 1   1  2  2 1 1 1  2 2 2 2 2 2  y x  
x y   2 1  y   y 1 ( Vì ; x y  0 ).  y 1  2 y 1
Ta có: P x  3y
 3y  4 y 1 . y 1 y 1 1
Xét hàm số: f y  4 y 1 ; y  1. y 1
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 53 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 1 Đạo hàm: /
f y  4  .  y  2 1  3 y  n  / f y 2  0   . 1
y  l  2 Bảng biến thiên. BÀI TOÁN TƯƠNG TỰ
Câu 47. 1 Cho x, y là các số thực dương thỏa mãn 2 log x  log y  log
x y . Gọi T là giá 2019 2019 2019   min
trị nhỏ nhất của biểu thức T  2x y . Mệnh đề nào dưới đây đúng? A. T  7;8 . B. T  6; 7 . C. T  5; 6 . D. T  8;9 . min   min   min   min   Lời giải.
Tác giả: Nguyễn Huỳnh Tấn Trung ; Fb: Nguyễn Huỳnh Tấn Trung. Chọn A. Ta có: 2 log x  log y  log x y 2  log xy  log x y 2
xy x y 2019 2019   2019 2019 2019   2  xy
y x   2 1  x   x 1 x  1  2 x 1
Ta có: T  2x y  2x   3x 1 . x 1 x 1 1
Xét hàm số: f x  3x 1 ; x  1 . x 1 1 Đạo hàm: /
f x  3  .  x  2 1 3 /
f x  0  x  1 (do x  1) . 3 Bảng biến thiên.
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 54 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 Do đó: T  4  2 3 . min
Câu 48. Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn có dạng abcd ,
trong đó 1  a b c d  9 . A. 0, 014 . B. 0, 0495 . C. 0, 079 . D. 0, 055 . Lời giải
Tác giả: Nguyễn Trường Giang; Fb: Giang Nguyen Chọn D
Chọn số tự nhiên có 4 chữ số bất kỳ có: n   9.10.10.10  9000 (cách).
Gọi A là biến cố: “Số được chọn có dạng abcd , trong đó 1  a b c d  9 ”. (*) Cách 1: Dùng tổ hợp
Nhận xét rằng với 2 số tự nhiên bất kỳ ta có: m n m n 1. x a   y b 1 Do đó nếu đặt:  z c  2  t   d  3 
Từ giả thuyết 1  a b c d  9 ta suy ra: 1  x y z t  12 (**).
Với mỗi tập con gồm 4 phần tử đôi một khác nhau được lấy ra từ 1, 2,...,  12 ta đều có được duy
nhất một bộ số thoả mãn (**) và do đó tương ứng ta có duy nhất một bộ số a, ,
b c, d  thoả mãn
(*). Số cách chọn tập con thoả tính chất trên là tổ hợp chập 4 của 12 phần tử, do đó: n A 4  C  495 . 12 n A 495
Vậy: P A    0, 055 . n  9000
Cách 2: Dùng tổ hợp lặp
Chọn số tự nhiên có 4 chữ số bất kỳ có: n   9.10.10.10  9000 (cách).
Mỗi tập con có 4 phần tử được lấy từ tập 1, 2,..., 
9 (trong đó mỗi phần tử có thể được chọn lặp
lại nhiều lần) ta xác định được một thứ tự không giảm duy nhất và theo thứ tự đó ta có được
một số tự nhiên có dạng abcd (trong đó 1  a b c d  9 ). Số tập con thoả tính chất trên là
số tổ hợp lặp chập 4 của 9 phần tử.
Do đó theo công thức tổ hợp lặp ta có: n A 4  C  495 . 94 1 
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 55 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019 n A 495
Vậy: P A    0, 055 . n  9000
Câu 49. Có tất cả bao nhiêu giá trị nguyên của tham số a thuộc khoảng 0; 2019 để n n 1 9  3  1 lim  ?
5n  9na 2187 A. 2011. B. 2018 . C. 2019 . D. 2012 . Lời giải
Tác giả: Lê Hữu Đức; Fb: Le Huu Duc ChọnD n  1  1 3 n n 1 9 3      3  1 Ta có: lim  lim 
5n  9na n a  5 9   9a    9  2 1 1 1  1  Suy ra   0  
 9a  4782969  a  log 4782969  a  7 a a   9 9 2187 9  2187 
Kết hợp điều kiện của bài toán ta được a  và 7  a  2019 nên có 2012 giá trị của a
Câu 50. Cho hàm số y f x có đạo hàm trên và có đồ thị là đường cong trong hình vẽ dưới. Đặt
g x  f f x 
 . Tìm số nghiệm của phương trình g x  0 . . A. 2 . B. 8 . C. 4 . D. 6 . Lời giải.
Tác giả: Lương Văn Huy; Fb: Lương Văn Huy. Chọn B.
f  x  0
Ta có: g x  f  xf   f x  0     * .
f   f x  0   
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 56 STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ CHUYÊN VĨNH PHÚC L3 – TỔ 4 – 2019
Theo đồ thị hàm số suy ra. x  0
f  x  0  
, với 2  a  3 . x  1  1 a
f x  0 ,  1
f   f x  0     .
f x  a , 2  1   Phương trình  
1 : f x  0 có 3 nghiệm phân biệt khác nghiệm phương trình * .
Phương trình 2 : f x  1
a có 3 nghiệm phân biệt khác nghiệm phương trình   1 và phương trình * .
Vậy phương trình ban đầu có 8 nghiệm phân biệt.
STRONG TEAM TOÁN VD-VDC- Nhóm toán Số 1 Việt Nam Trang 57
Document Outline

  • [toanmath.com] - Đề KSCL Toán 12 ôn thi THPTQG năm 2018 – 2019 trường chuyên Vĩnh Phúc lần 3
    • KS3-2018-2019_TOAN12_345
    • Chuyen Vinh Phuc-KSCL-Lan 3-2019-Ma de 678
  • [STRONG TEAM TOÁN VD-VDC]-Nhóm Toán Số 1 VN- Giải Chi Tiết Đề Chuyên Vĩnh Phúc Lần 3-2019