








Preview text:
ĐỀ THI THỬ THPT MÔN TOÁN 2023 PHÁT TRIỂN TỪ ĐỀ MINH HỌA-ĐỀ 8
Câu 1. Điểm M trong hình vẽ bên là điểm biểu diễn số phức nào? A. z = 2 − + i .
B. z =1− 2i .
C. z = 2 + i .
D. z =1+ 2i .
Câu 2. Tính đạo hàm của hàm số y = log 3x + 2 . 3 ( ) 1 1 3 3 A. y = ( . B. y = . C. y = . D. y = . 3x + 2) (3x + 2)ln3 (3x + 2)ln3 (3x + 2)
Câu 3. Tập xác định của hàm số
y = ( x − 2) là A. D = (− ;
2) . B. D = (2;+) . C. D = \
2 . D. D = (− ; 2. x
Câu 4. Tập nghiệm của bất phương trình 1 1 là 3 A. 0;+ ) . B. (− ;1 . C. (0;+ ) .
D. (−;0) .
Câu 5. Cho cấp số cộng (u với u = 2023 , công sai d = 3. Số hạng tổng quát của cấp số cộng là n ) 1
A. u = 2023 + 3n. B. u = 2019 + 3n . C. u = 2023+ 3 n − .
D. u = 2023+ 3 n + . n ( ) 1 n ( ) 1 n n
Câu 6. Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng ( ): 2x − y + z −1= 0 . Vectơ nào dưới đây không
là vectơ pháp tuyến của ( ) ? A. n(2;1; ) 1 . B. n = ( 2 − ;1;− )
1 . C. n = (2; 1 − ; )
1 . D. n = (4; 2 − ;2) .
Câu 7. Cho hàm số y = f (x) có bảng biến thiên dưới đây
Số nghiệm của phương trình 3 f (x) −5 =1 là A. 3 . B. 2 . C. 1. D. 4 . 5 5 5
Câu 8. Cho I = f
(x)dx = 4;J = g
(x)dx = 3. Khi đó K = 4 f
(x)−3g(x)dx bằng 1 1 1 A. 2 . B. 7 . C. 8 . D. 4 .
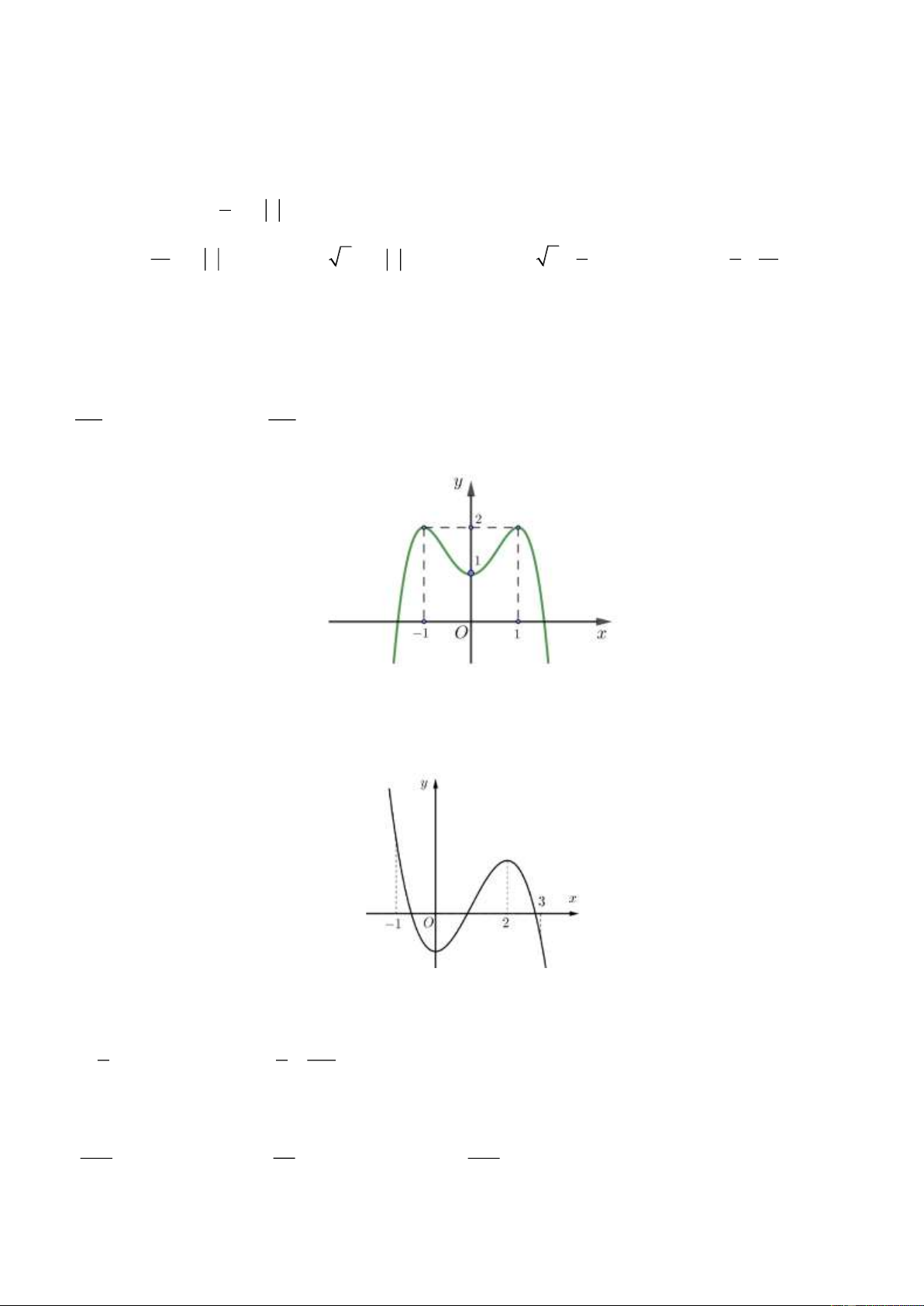
Câu 9. Đường cong hình bên là đồ thị của hàm số nào? Trang 1 y O x A. 2
y = x − 3x + 2 . B. 4 2
y = x − x + 2. C. 3
y = −x − 3x + 2 . D. 3
y = x − 3x + 2 .
Câu 10. Tính bán kính R của mặt cầu (S) : 2 2 2
x + y + z − 2x + 2 y − 2z − 3 = 0 .
A. R = 6 .
B. R = 2 .
C. R = 3 .
D. R = 6 .
Câu 11. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng ( P) có phương trình là x − z − 3 = 0 . Tính góc giữa
(P) và mặt phẳng (Oxy). A. 0 30 . B. 0 60 . C. 0 45 . D. 0 90 .
Câu 12. Cho số phức z thỏa mãn z −3+ i = 0 . Môđun của z bằng A. 4 . B. 10 . C. 3 . D. 10 .
Câu 13. Thể tích của khối hộp chữ nhật có ba kích thước là a , 3a , 5a bằng A. 2 15a . B. 3 15a .
C. 15a . D. 15 .
Câu 14. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B biết AB = a AC = 2a , SA ⊥ ( ABC ) và
SA = a 3 . Thể tích khối chóp S.ABC là 3 a 3 a 3 3a 3 3a A. . B. . C. . D. . 2 4 8 4
Câu 15. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu (S ) x + ( y − )2 2 2 :
1 + z = 2 . Trong các điểm cho dưới
đây, điểm nào nằm ngoài mặt cầu (S )? A. M (1;1; ) 1 .
B. N (0;1;0). C. P(1;0; ) 1 .
D. Q(1;1;0) .
Câu 16. Trong các số phức z = 2
− i , z = 2 − i , z = 5i , z = 4 có bao nhiêu số thuần ảo? 1 2 3 4 A. 4 . B. 1. C. 3 . D. 2 .
Câu 17. Diện tích xung quanh của hình trụ có độ dài đường sinh l và đường kính đáy a bằng
A. 2 al .
B. 4 al .
C. al .
D. 1 al . 2 x =1+ 3t
Câu 18. Trong không gian với hệ tọa độ Oxyz , điểm nào dưới đây thuộc đường thẳng d : y = 2
− + t (t ) . z = 3+5t
A. M (3;1;5) . B. N (1; 2 − ;3) . C. P(4; 1 − ; 2 − ) . D. Q( 2 − ; 1 − ; 2 − ) .
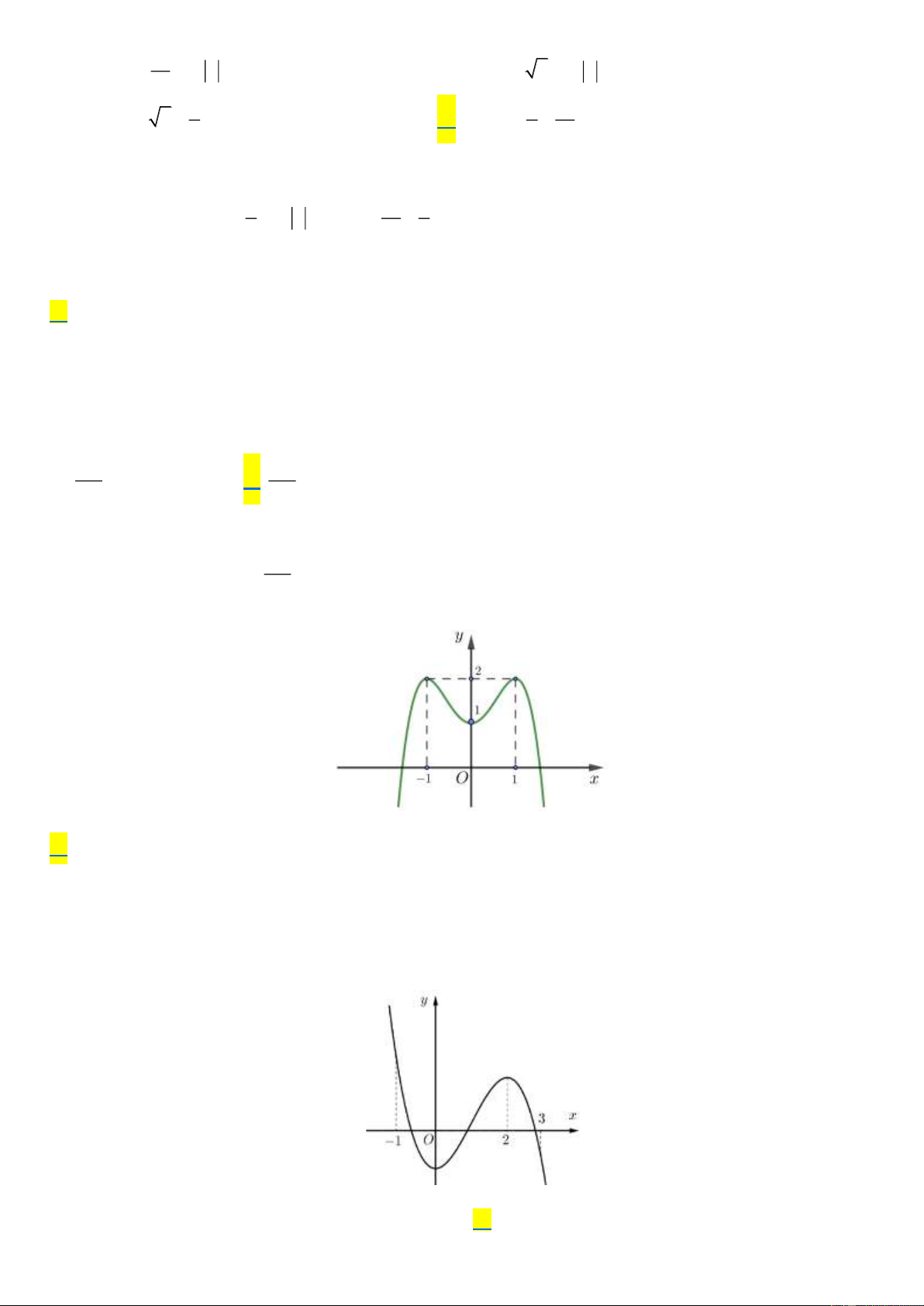
Câu 19. Cho hàm số y = f (x) có đồ thị như hình vẽ y 2 -2 1 -1 O 2 x -2
Hàm số đã cho đạt cực đại tại điểm nào dưới đây? A. x = 1 − .
B. x = 2 . C. x =1. D. x = 2 − . 2x +1
Câu 20. Các đường tiệm cận đứng và ngang của đồ thị hàm số y = là x −1 Trang 2
A. x = 2; y =1. B. x = 1 − ; y = 2 − .
C. x =1; y = 2 − .
D. x =1; y = 2 .
Câu 21. Tập nghiệm của bất phương trình log x +1 1 là 2 ( ) A. ( 1 − ;2) . B. ( ) ;1 − . C. ( 1 − ;+). D. ( 1 − ; ) 1 .
Câu 22. Trong hộp có 4 viên bi xanh, 5 viên bi đỏ, 6 viên bi vàng. Lấy ngẫu nhiên từ hộp 3 viên bi. Số cách chọn là A. 3 A . B. 3 C . C. 9 . D. 3 3 3
C + C + C . 15 15 4 5 6 Câu 23. Nếu f (x) 1 dx =
+ ln x + C thì x 1 1 1
A. f (x) = −
+ ln x . B. f (x) = x + ln x . C. ( ) 1 f x = − x + .
D. f ( x) = − . 2 x x 2 x x 2 2 Câu 24. Nếu f
(x)dx = 2 thì I = 3f
(x)−2dx bằng bao nhiêu? 1 1
A. I = 4 .
B. I =1.
C. I = 2 .
D. I = 3 .
Câu 25. Họ nguyên hàm của hàm số ( ) 3x f x = +1 là 3x 3x A. + C . B.
+ x + C .
C. 3x + x + C .
D. 3x ln x + x + C . ln 3 ln 3
Câu 26. Cho hàm số y = f (x) có đồ thị là đường cong trong hình bên.
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. (0; ) 1 .
B. (−;0) . C. (1;+ ) . D. ( 1 − ;0) .
Câu 27. Cho hàm số y = f ( )
x liên tục trên đoạn 1 − ;
3 và có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng?
A. Hàm số đạt cực tiểu tại x = 0 , cực đại tại x = 1
− . B. Hàm số có hai điểm cực tiểu là x = 0 , x = 3.
C. Hàm số có hai điểm cực đại là x = 1 − , x = 2 .
D. Hàm số đạt cực tiểu tại x = 0 , cực đại tại x = 2 .
Câu 28. Với các số thực dương a , b bất kì. Mệnh đề nào dưới đây đúng? a a ln a
A. ln = ln b − ln a . B. ln = .
C. ln(ab) = ln . a ln b .
D. ln(ab) = ln a + lnb . b b ln b
Câu 29. Cho hình phẳng giới hạn bởi các đường 3
y = x +1, y = 0, x = 0 , x = 1 quay xung quanh trục Ox . Tính thể
tích của khối tròn xoay tạo thành là 79 5 23 A. . B. . C. . D. 9 . 63 4 14
Câu 30. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy và SA = a . Góc giữa
hai mặt phẳng (ABC ) D và (SC ) D bằng Trang 3 A. 0 30 . B. 0 90 . C. 0 60 . D. 0 45 .
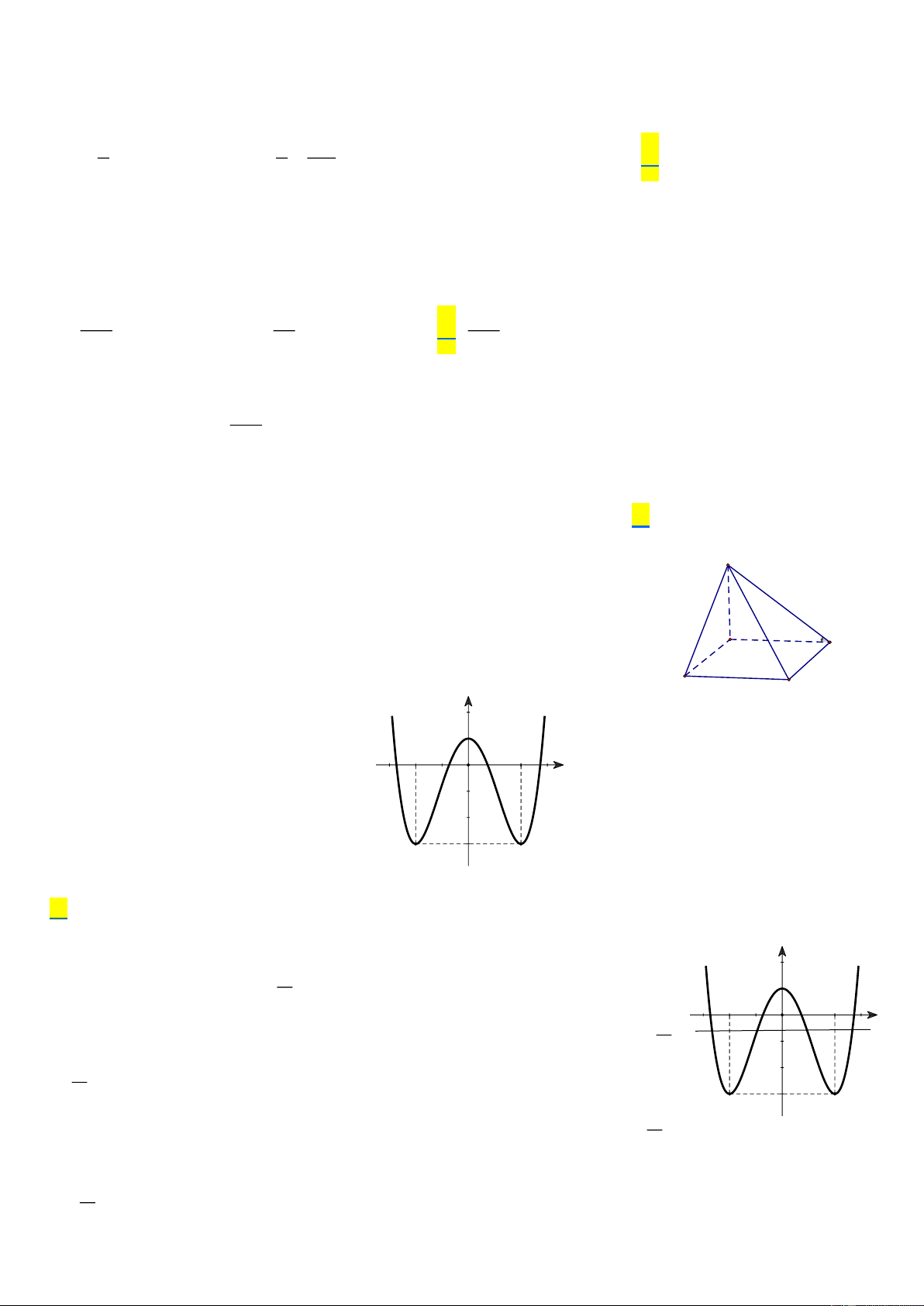
Câu 31. Cho hàm số bậc bốn y = f (x) có đồ thị như hình sau: y 1 -2 2 O x -3
Có bao nhiêu giá trị nguyên của tham số m để phương trình 2 f (x) + m = 0 có bốn nghiệm phân biệt?
A. 7 . B. 6 .
C. 8 . D. 5 .
Câu 32. Hàm số nào dưới đây đồng biến trên khoảng (− ; +) x − A. 4 2
y = x + 2x + 2 . B. 1 y = . C. 3
y = x + x − 5 . D. y = x + tan x . 2x +1
Câu 33. Một hộp đựng 9 viên bi trong đó có 4 viên bi đỏ và 5 viên bi xanh. Lấy ngẫu nhiên từ hộp 3 viên bi. Xác
suất để 3 viên bi lấy ra có ít nhất 2 viên bi màu xanh là A. 10 . B. 25 . C. 5 . D. 5 . 11 42 42 14 Câu 34. Gọi +
x , x là hai nghiệm của phương trình x x 1 4.4 −9.2
+8 = 0 . Khi đó, tích x .x bằng 1 2 1 2 A. 2. − B. 1. C. 2. . D. 1. −
Câu 35. Trong mặt phẳng tọa độ Oxy , tập hợp tất cả các điểm biểu diễn của số phức z thõa mãn z − 4 + i = 3 là
đường tròn có phương trình: 2 2 2 2 2 2 2 2
A. ( x − 4) + ( y + ) 1
= 9 . B. (x − 4) + ( y − ) 1
= 3. C. (x − 4) + ( y + ) 1 = 3.
D. ( x − 4) + ( y − ) 1 = 9.
Câu 36. Trong không gian Oxyz , cho ba điểm A(1;2; 2 − ), B( 2 − ;3; ) 1 ,C ( 1
− ;1;2) . Đường thẳng đi qua C và song
song với đường thẳng AB có phương trình chính tắc là − + + − + + + − − + − − A. x 1 y 1 z 2 = = . B. x 3 y 1 z 3 = = . C. x 1 y 1 z 2 = = . x y z D. 3 1 3 = = . 3 − 1 3 1 − 1 2 3 − 1 3 1 − 1 2
Câu 37. Trong không gian với hệ tọa độ Oxyz , điểm đối xứng của M (1; 2; 3) qua trục Ox có tọa độ là
A. (1; − 2; −3). B. (1; 0 0) . C. (0; 2; ) 3 . D. ( 1 − ; − 2; −3).
Câu 38. Cho hình chóp S.ABC . Biết SA vuông góc với mặt phẳng đáy, SA = a 3 và ABC
vuông tại B có cạnh
BC = a , AC = a 5 . Tính theo a khoảng cách từ B đến (SAC) . a a a a A. 2 21 . B. 21 . C. 2 5 D. 15 . 7 7 5 3
Câu 39. Số nghiệm nguyên dương của bất phương trình 3 2x + 2log x 4 là 3 A. 4 . B. 2 . C. 1. D. 3 .
Câu 40. Cho hàm số f (x) liên tục trên . Gọi F (x),G(x) là hai nguyên hàm của f (x) trên thỏa mãn 2023 x F ( ) 1 + G ( )
1 = 5 và F (0) + G(0) =1. Khi đó f dx bằng 2023 0 A. 2023. B. 2 . C. 4046 . D. 4 . 2023 2023
Câu 41. Cho hàm số f (x) 5 3
= x − mx + 5x + 2m + 3 ( m là tham số). Có bao nhiêu số nguyên m để hàm số f (x) có
4 điểm cực trị và tổng các giá trị cực trị nhỏ hơn 2023? A. 251. B. 250 . C. 248 . D. 247 Trang 4 +
Câu 42. Hai số phức 2023z 2023i
z , w thay đổi nhưng luôn thỏa mãn đẳng thức (1+ i) 2 z − 2iz −1 = + 2 − 2i . Giá w
trị lớn nhất của w là A. 2019 2 . B. 2019 2 . C. 2019 . D. Đáp án khác. 4 2
Câu 43. Cho hình lăng trụ đứng AB . C A B C
có đáy ABC là tam giác vuông tại A . AC = a , ACB = 60 . Đường
thẳng BC tạo với mặt phẳng ( ACC A
) một góc 30. Thể tích của khối lăng trụ AB . C A B C bằng 3 a 3 3 a 6 A. 3 a 3 . B. 3 a 6 . C. . D. . 3 3 3 x 4 + f x
Câu 44. Cho hàm số f (x) liên tục, không âm trên 0;
2 , thỏa f ( x) ( ) =
với mọi x 0;2 và 2 f ( x)
f (0) = 0. Tính diện tích hình phẳng giới hạn bởi hai đường 3 y = 4 + f (x) và 11 y = 4 A. 1. B. 2 . C. 21 . D. 2 .
Câu 45. Trên tập hợp các số phức, xét phương trình 2 z − (m − ) 2 2
1 z + m − 3 = 0 ( m là tham số thực). Gọi S là tập
hợp giá trị của m để phương trình đó có hai nghiệm z , z thỏa mãn z − z = 2 5 . Tính tổng các phần tử của tập 1 2 1 2 S . A. 5 . B. 4 . C. 9 . D. 1 − . 2 2 − + − − − +
Câu 46. Trong không gian x 1 y 2 z 1 x 1 y 1 z 2
Oxyz , cho hai đường thẳng d : = = và d : = = . Mặt 1 1 1 2 2 2 1 1
phẳng (P): x + ay +bz + c = 0, c 0 song song với d , d và khoảng cách từ d đến (P) gấp đôi khoảng cách từ 1 2 1
d đến ( P) . Giá trị của a + b + c bằng 2 A. 14. B. 6 . C. 4 − . D. −6 . Câu 47. Có bao nhiêu bộ ( ;x y) với , x y nguyên và 1 , x y 2023 thỏa mãn ( +
xy + x + y + ) 2 y 2x 1 2 4 8 log
2x + 3y − xy − 6 log ? 3 ( ) 2 y + 2 x − 3 A. 2022 . B. 2023. C. 4040 . D. 20222023 .
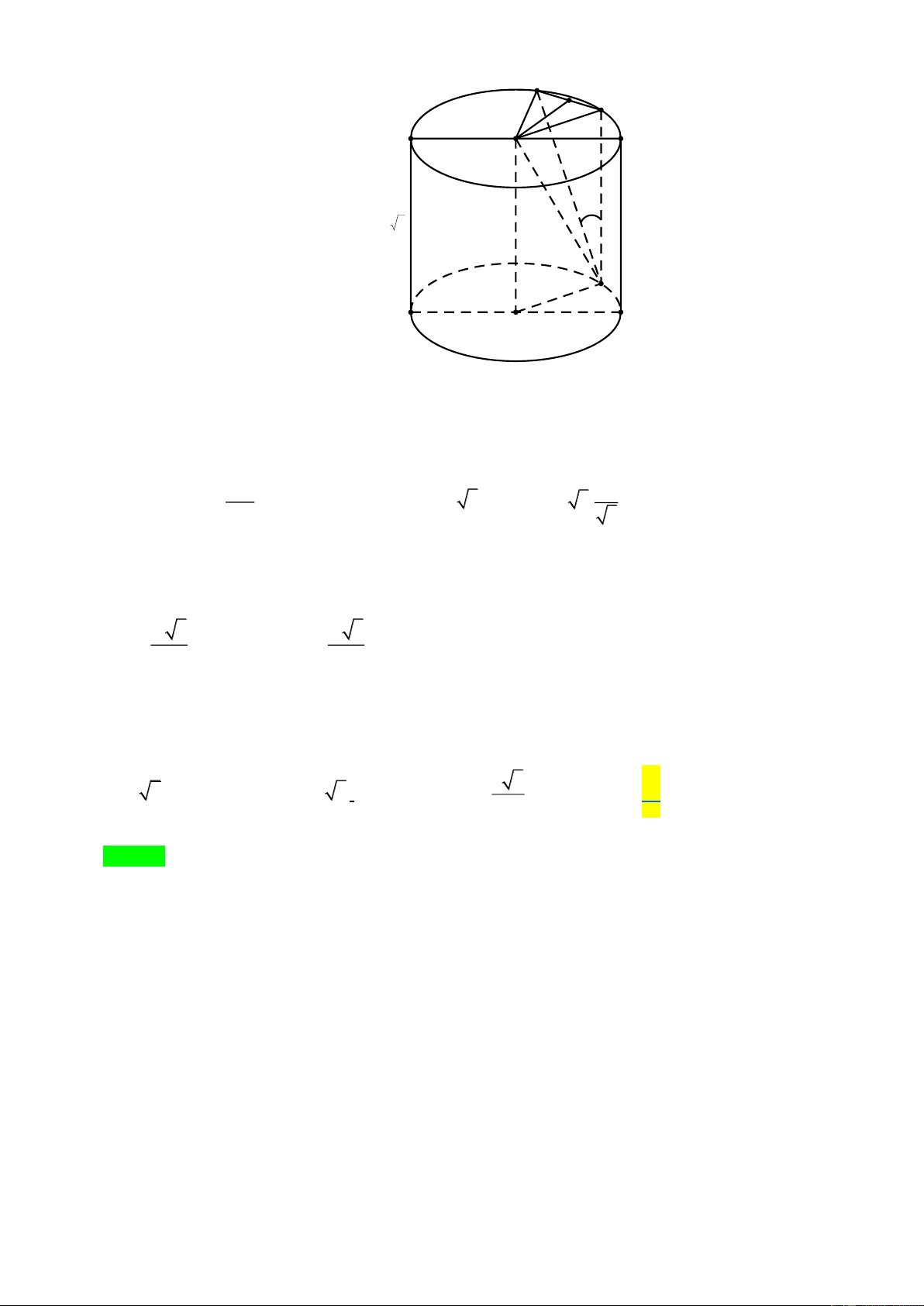
Câu 48. Cho hình trụ có bán kính R và chiều cao 3R . Hai điểm A , B lần lượt nằm trên hai đường tròn đáy sao
cho góc giữa AB và trục d của hình trụ bằng 30 . Tính khoảng cách giữa AB và trục của hình trụ. R A. ( R d AB, d ) = .
B. d ( A , B d ) = R .
C. d ( A ,
B d ) = R 3 . D. d ( AB d ) 3 , = . 2 2 Câu 49. 2 2 2
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S ) : ( x − 2) + ( y − ) 1 + (z − ) 1 = 4 và điểm M (2;2; )
1 . Một đường thẳng thay đổi qua M và cắt (S ) tại hai điểm ,
A B . Khi biểu thức
T = MA + 4MB đạt giá trị nhỏ nhất thì đoạn thẳng AB có giá trị bằng A. 4 3 . B. 2 3 . C. 5 3 . D. 4 . 2 Câu 50. 1 1 2 Cho hàm số 3 2
f (x) = − x +
(2m + 3)x − ( 2
m + 3m) x + . Có bao nhiêu giá trị nguyên của tham số m 3 2 3 thuộc [ 9
− ;9] để hàm số nghịch biến trên khoảng (1;2) ? A. 3. B. 2. C. 16. D. 9.
…………………..Hết…………………… Trang 5 ĐÁP ÁN 1 - A 2 - C 3 - B 4 - D 5 - C 6 - A 7 - C 8 - B 9 - D 10 - A 11 - C 12 - D 13 - B 14 - A 15 - C 16 - D 17 - C 18 - B 19 - A 20 - D 21 - D 22 - B 23 - D 24 - A 25 - B 26 - A 27 - D 28 - D 29 - C 30 - D 31 - A 32 - C 33 - B 34 - A 35 - A 36 - C 37 - A 38 - C 39 - D 40 - C 41 - C 42 - A 43 - B 44 - A 45 - B 46 - A 47 - C 48 - D 49 - D 50 - B LỜI GIẢI
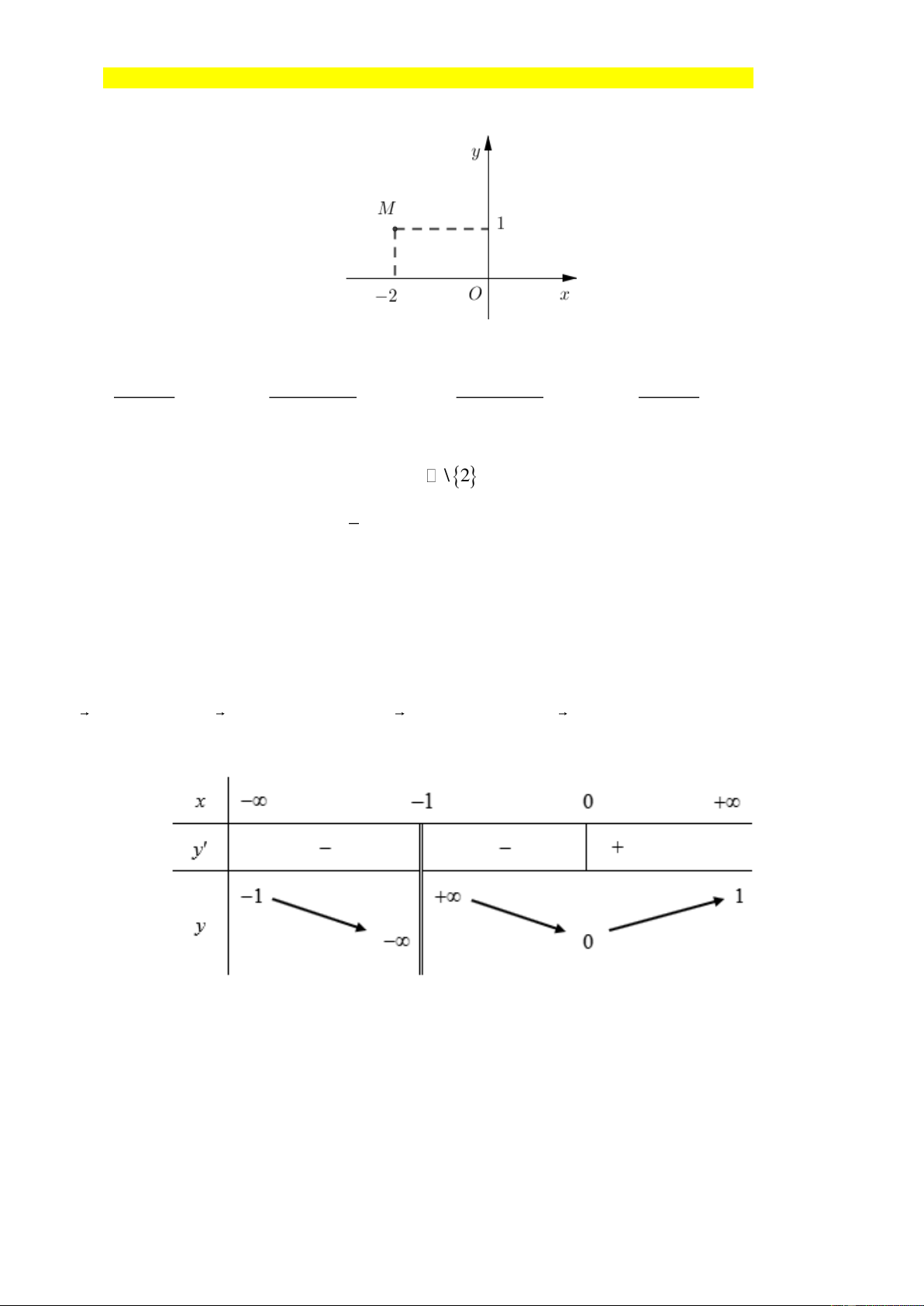
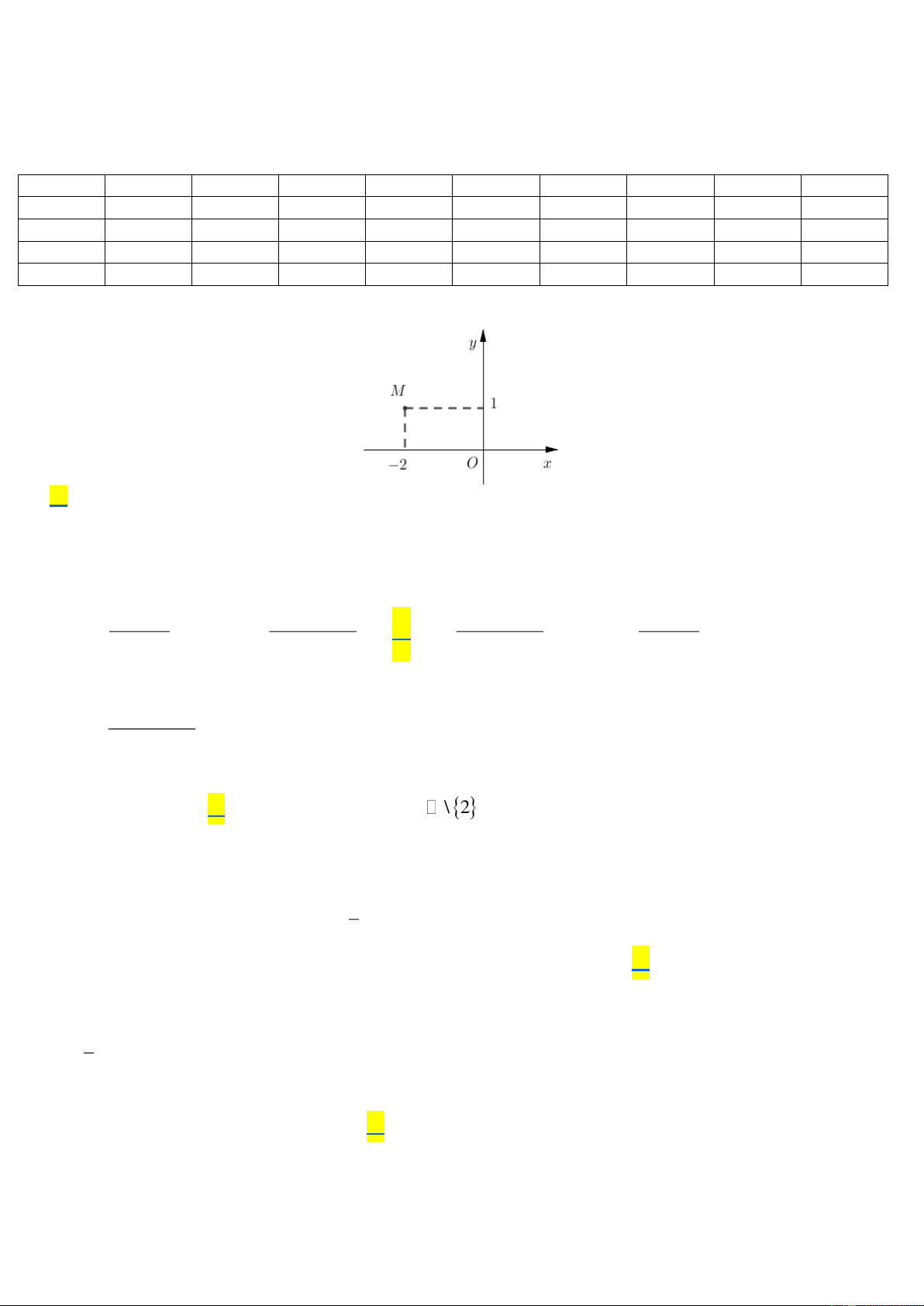
Câu 1. Điểm M trong hình vẽ bên là điểm biểu diễn số phức nào? A. z = 2 − + i .
B. z =1− 2i .
C. z = 2 + i .
D. z =1+ 2i . Lời giải Chọn A Điểm M( 2
− ;1) là điểm biểu diễn của số phức z = 2 − + i
Câu 2. Tính đạo hàm của hàm số y = log 3x + 2 . 3 ( ) 1 1 3 3 A. y = ( . B. y = . C. y = . D. y = . 3x + 2) (3x + 2)ln3 (3x + 2)ln3 (3x + 2) Lời giải Chọn C Ta có 3 y = ( 3x + 2) ln 3
Câu 3. Tập xác định của hàm số
y = ( x − 2) là A. D = (− ;
2) . B. D = (2;+) . C. D = \
2 . D. D = (− ; 2. Lời giải Chọn B
Điều kiện xác định x − 2 0 x 2 x
Câu 4. Tập nghiệm của bất phương trình 1 1 là 3 A. 0;+ ) . B. (− ;1 . C. (0;+ ) . D. (−;0) . Lời giải Chọn D x Ta có 1 1 x 0 3
Câu 5. Cho cấp số cộng (u với u = 2023 , công sai d = 3. Số hạng tổng quát của cấp số cộng là n ) 1
A. u = 2023 + 3n. B. u = 2019 + 3n . C. u = 2023+ 3 n − .
D. u = 2023+ 3 n + . n ( ) 1 n ( ) 1 n n Lời giải Chọn C
Theo công thức số hạng tổng quát của cấp số cộng ta có u = u + (n −1)d = 2023+ 3 n −1 n 1 ( ) Trang 6
Câu 6. Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng ( ): 2x − y + z −1= 0. Vectơ nào dưới đây không
là vectơ pháp tuyến của ( ) ? A. n(2;1; ) 1 . B. n = ( 2 − ;1;− )
1 . C. n = (2; 1 − ; )
1 . D. n = (4; 2 − ;2) . Lời giải Chọn A
() có một véc tơ pháp tuyến là n = (2; 1 − ; )
1 k(2;1;1), k .
Câu 7. Cho hàm số y = f (x) có bảng biến thiên dưới đây
Số nghiệm của phương trình 3 f (x) −5 =1 là A. 3 . B. 2 . C. 1. D. 4 . Lời giải Chọn B
Ta có 3 f (x) −5 =1 f (x) = 2. Dựa vào bảng biến thiên thấy đường thẳng y = 2 cắt đồ thị hàm số đã cho tại một
điểm duy nhất hay phương trình có hai nghiệm. 5 5 5
Câu 8. Cho I = f
(x)dx = 4;J = g
(x)dx = 3. Khi đó K = 4 f
(x)−3g(x)dx bằng 1 1 1 A. 2 . B. 7 . C. 8 . D. 4 . Lời giải Chọn B 5 5 5
Ta có K = 4 f
(x)−3g(x)dx = 4 f (x)dx−3 g(x)dx = 4.4−3.3 = 7 1 1 1
Câu 9. Đường cong hình bên là đồ thị của hàm số nào? y O x A. 2
y = x − 3x + 2 . B. 4 2
y = x − x + 2. C. 3
y = −x − 3x + 2 . D. 3
y = x − 3x + 2 . Lời giải Chọn D
Ta thấy đây là đồ thị đường cong bậc 3 có hệ số bậc ba dương.
Câu 10. Tính bán kính R của mặt cầu (S) : 2 2 2
x + y + z − 2x + 2 y − 2z − 3 = 0 .
A. R = 6 .
B. R = 2 .
C. R = 3 . D. R = 6 . Lời giải Chọn A
Mặt cầu (S ) có bánh kính R = 1+1+1+ 3 = 6 Trang 7
Câu 11. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng ( P) có phương trình là x − z − 3 = 0 . Tính góc giữa
(P) và mặt phẳng (Oxy). A. 0 30 . B. 0 60 . C. 0 45 . D. 0 90 . Lời giải Chọn C
(P) có một véc tơ pháp tuyến n(1;0;−1)
(Oxy) có một véc tơ pháp tuyến n'(0;0;1) Do đó ((P) (Oxy)) (n n ) 1 cos , cos , '
((P),(Oxy)) 45 = = = 2
Câu 12. Cho số phức z thỏa mãn z −3+ i = 0 . Môđun của z bằng A. 4 . B. 10 . C. 3 . D. 10 . Lời giải Chọn D
Ta có z − 3+ i = 0 z = 3− i z = 3+ i z = 10
Câu 13. Thể tích của khối hộp chữ nhật có ba kích thước là a , 3a , 5a bằng A. 2 15a . B. 3 15a .
C. 15a . D. 15 . Lời giải Chọn B Ta có 3 V = . a 3 .
a 5a =15a
Câu 14. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B biết AB = a AC = 2a , SA ⊥ ( ABC ) và
SA = a 3 . Thể tích khối chóp S.ABC là 3 a 3 a 3 3a 3 3a A. . B. . C. . D. . 2 4 8 4 Lời giải Chọn A 2
Theo pitago trong tam giác vuông 1 a 3 2 2 ABC BC =
AC − BA = a 3 S = A . B BC = ABC 2 2 3 Vậy 1 a V = S .SA = . S . ABC 3 ABC 2
Câu 15. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu (S ) x + ( y − )2 2 2 :
1 + z = 2 . Trong các điểm cho dưới
đây, điểm nào nằm ngoài mặt cầu (S )? A. M (1;1; ) 1 .
B. N (0;1;0). C. P(1;0; ) 1 . D. Q(1;1;0) . Lời giải Chọn C
(S) có tâm I(0;1;0), bán kính R = 2
Ta có IM = 2 = R , IN = 0 R , IP = 3 R , IQ =1 R .
Câu 16. Trong các số phức z = 2
− i , z = 2 − i , z = 5i , z = 4 có bao nhiêu số thuần ảo? 1 2 3 4 A. 4 . B. 1. C. 3 . D. 2 . Lời giải Chọn D
Trong các số phức đã cho có hai số là số thuần ảo đó là z = 2
− i và z = 5i 1 3
Câu 17. Diện tích xung quanh của hình trụ có độ dài đường sinh l và đường kính đáy a bằng
A. 2 al .
B. 4 al .
C. al . D. 1 al . 2 Lời giải Chọn C Trang 8
Hình trụ có độ dài đường sinh l và đường kính đáy a có diện tích xung quanh là S = 2 rl = al xq x =1+ 3t
Câu 18. Trong không gian với hệ tọa độ Oxyz , điểm nào dưới đây thuộc đường thẳng d : y = 2
− + t (t ) . z = 3+5t
A. M (3;1;5) . B. N (1; 2 − ;3) . C. P(4; 1 − ; 2 − ) . D. Q( 2 − ; 1 − ; 2 − ) . Lời giải Chọn B
Kiểm tra bằng cách thay toạ độ các điểm M, N, ,
P Q vào phương trình của d chỉ có toạ độ điểm N (1; 2 − ;3) làm
cho hệ phương trình có nghiệm duy nhất t = 0 , hay điểm N thuộc d .
Câu 19. Cho hàm số y = f (x) có đồ thị như hình vẽ y 2 -2 1 -1 O 2 x -2
Hàm số đã cho đạt cực đại tại điểm nào dưới đây? A. x = 1 − .
B. x = 2 . C. x =1. D. x = 2 − . Lời giải Chọn A
Từ đồ thị hàm số ta thấy hàm số đạt cực đại tại điểm x = 1 − . +
Câu 20. Các đường tiệm cận đứng và ngang của đồ thị hàm số 2x 1 y = là x −1
A. x = 2; y =1. B. 1 1 x = ; y = .
C. x =1; y = 2 − .
D. x =1; y = 2 . 2 2 Lời giải Chọn D
Đồ thị hàm số đã cho có tiệm cận đứng và ngang lần lượt là x =1; y = 2 .
Câu 21. Tập nghiệm của bất phương trình log x +1 1 là 2 ( ) A. ( 1 − ;2) . B. ( ) ;1 − . C. ( 1 − ;+). D. ( 1 − ; ) 1 . Lời giải Chọn D
Điều kiện x +1 0 x 1 −
Khi đó log x +1 1 x +1 2 x 1 2 ( )
Vậy tập nghiệm của bất phương trình là ( 1 − ; ) 1
Câu 22. Trong hộp có 4 viên bi xanh, 5 viên bi đỏ, 6 viên bi vàng. Lấy ngẫu nhiên từ hộp 3 viên bi. Số cách chọn là A. 3 A . B. 3 C . C. 9 . D. 3 3 3
C + C + C . 15 15 4 5 6 Lời giải Chọn B
Số cách lấy ra ba viên bi từ hộp chứa 15 viên bi là 3 C . 15 Câu 23. Nếu f (x) 1 dx =
+ ln x + C thì x Trang 9 1
A. f (x) = − + ln x .
B. f (x) = x + ln x . 2 x 1 1 C. ( ) 1 f x = − x + .
D. f ( x) = − . x 2 x x Lời giải Chọn D Ta có f x = ( f (x) x) ' ' 1 1 1 ( ) d = + ln x + C = − + 2 x x x 2 2 Câu 24. Nếu f
(x)dx = 2 thì I = 3f
(x)−2dx bằng bao nhiêu? 1 1
A. I = 4 .
B. I =1.
C. I = 2 . D. I = 3 . Lời giải Chọn A 2 2 2
Ta có I = 3 f
(x)−2dx = 3 f (x)dx−2 dx= 3.2−2 = 4 1 1 1
Câu 25. Họ nguyên hàm của hàm số ( ) 3x f x = +1 là 3x 3x A. + C . B.
+ x + C .
C. 3x + x + C .
D. 3x ln x + x + C . ln 3 ln 3 Lời giải Chọn B x Ta có ( ) = ( x f x dx + ) 3 3 1 dx = + x + C . ln 3
Câu 26. Cho hàm số y = f (x) có đồ thị là đường cong trong hình bên.
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. (0; ) 1 .
B. (−;0) . C. (1;+ ) . D. ( 1 − ;0) . Lời giải Chọn A
Từ đồ thị ta thấy hàm số đã cho đồng biến trên các khoảng (− ; − ) 1 và (0 ) ;1
Câu 27. Cho hàm số y = f ( )
x liên tục trên đoạn 1 − ;
3 và có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng?
A. Hàm số đạt cực tiểu tại x = 0 , cực đại tại x = 1
− . B. Hàm số có hai điểm cực tiểu là x = 0 , x = 3.
C. Hàm số có hai điểm cực đại là x = 1 − , x = 2 .
D. Hàm số đạt cực tiểu tại x = 0 , cực đại tại x = 2 . Trang 10 Lời giải Chọn D
Từ đồ thị ta thấy hàm số đạt cực tiểu tại x = 0 , cực đại tại x = 2 .
Câu 28. Với các số thực dương a , b bất kì. Mệnh đề nào dưới đây đúng? a a a
A. ln = ln b − ln a . B. ln ln = .
C. ln(ab) = ln . a ln b .
D. ln(ab) = ln a + lnb . b b ln b Lời giải Chọn D
Theo quy tắc logarit của một tích ta có ln(ab) = ln a + lnb .
Câu 29. Cho hình phẳng giới hạn bởi các đường 3
y = x +1, y = 0, x = 0 , x = 1 quay xung quanh trục Ox . Tính thể
tích của khối tròn xoay tạo thành là A. 79 . B. 5 . C. 23 . D. 9 . 63 4 14 Lời giải Chọn C 1
Ta có V = (x + )2 23 3 1 dx = 14 0
Câu 30. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy và SA = a . Góc giữa
hai mặt phẳng (ABC ) D và (SC ) D bằng A. 0 30 . B. 0 90 . C. 0 60 . D. 0 45 . Lời giải S Chọn D AD ⊥ CD Có
((SAD),( ABCD)) = SDA CD ⊥ SD A D
Tam giác SAD là tam giác vuông cân suy ra ((SAD),( ABCD)) = SDA = 45
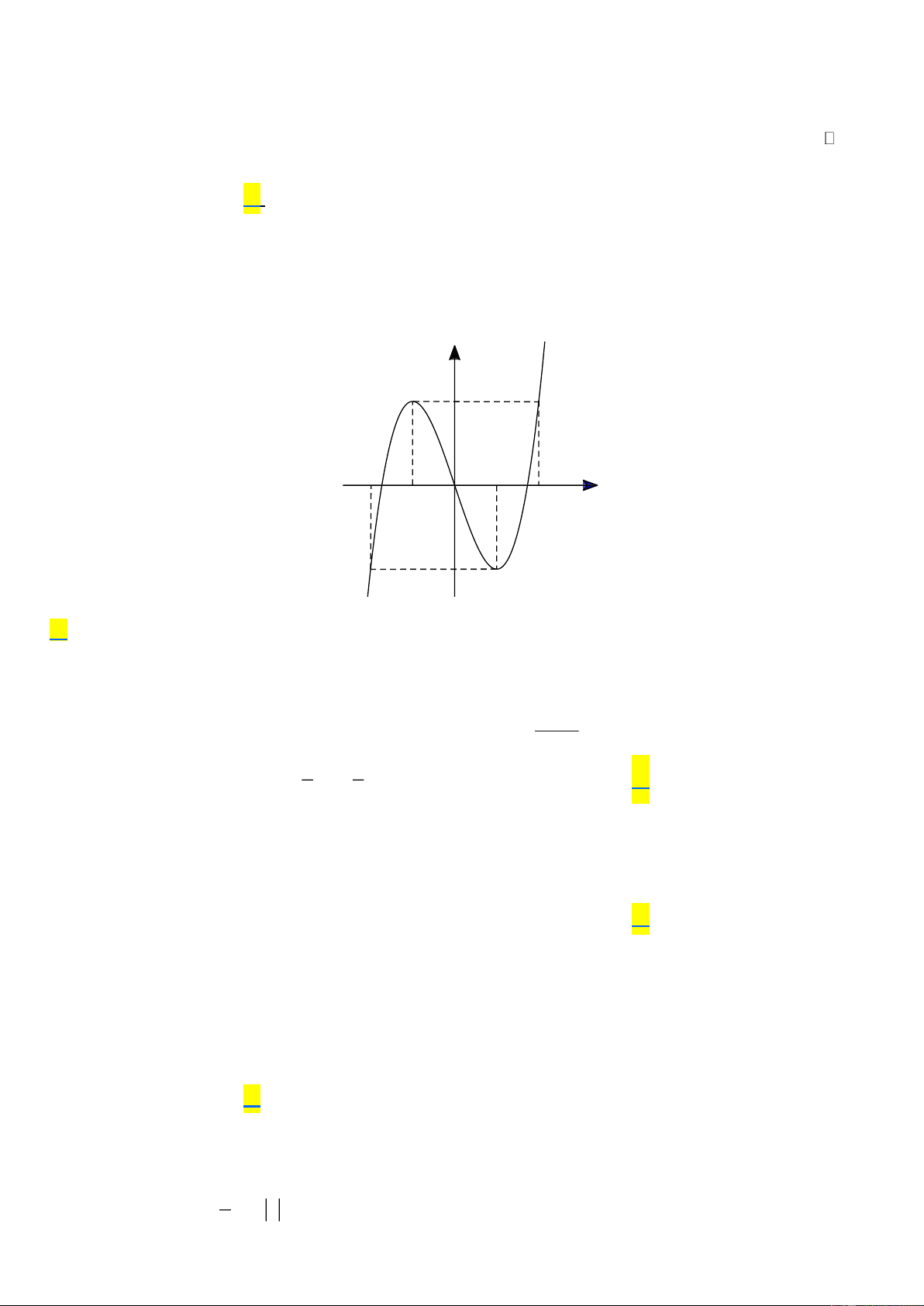
Câu 31. Cho hàm số bậc bốn y = f (x) có đồ thị như hình sau: B C y 1 -2 2 O x -3
Có bao nhiêu giá trị nguyên của tham số m để phương trình 2 f (x) + m = 0 có bốn nghiệm phân biệt?
A. 7 . B. 6 . C. 8 . D. 5 . Lời giải y Chọn A m 1
Ta có 2 f (x) + m = 0 f (x) = − 2 -2 2 m O x Vẽ đường thẳng y = − 2 m y = − 2 -3
Để phương trình đã cho có bốn nghiệm phân biệt khi và chỉ khi đường thẳng m y = − 2 cắt đồ thị hàm số y = f ( ) x
tại bốn điểm phân biệt. Quan sát đồ thị ta thấy m 3 − − 1 6
− −m 2 2 − m 6 2 Trang 11
Vậy có 7 giá trị nguyên của tham số thoả mãn bài toán.
Câu 32. Hàm số nào dưới đây đồng biến trên khoảng (− ; +) x − A. 4 2
y = x + 2x + 2 . B. 1 y = . C. 3
y = x + x − 5 . D. y = x + tan x . 2x +1 Lời giải Chọn C
Hàm số đồng biến trên (− ;
+) khi hàm được xác định trên (− ; +), suy ra loại B, D Xét hàm 4 2
y = x + 2x + 2 không đồng biến trên (− ; +) Xét hàm số 3
y = x + x − 5 có tập xác định (− ; +), 2
y ' = 3x +1 0, x (− ; ) Vậy chọn C
Câu 33. Một hộp đựng 9 viên bi trong đó có 4 viên bi đỏ và 5 viên bi xanh. Lấy ngẫu nhiên từ hộp 3 viên bi. Xác
suất để 3 viên bi lấy ra có ít nhất 2 viên bi màu xanh là A. 10 . B. 25 . C. 5 . D. 5 . 11 42 42 14 Lời giải Chọn B
Chọn 3 viên bi từ 9 viên bi suy ra n() 3 = C 9
Biến cố A chọn được ít nhất 2 viên bi màu xanh nên 2 1 3 n( )
A = C C + C 5 4 5 2 1 3 C C + C Vậy 25 5 4 5 P( ) A = = 3 C 42 9 Câu 34. Gọi +
x , x là hai nghiệm của phương trình x x 1 4.4 −9.2
+8 = 0 . Khi đó, tích x .x bằng 1 2 1 2 A. 2. − B. 1. C. 2. . D. 1. − Lời giải Chọn A t = 4 Đặt = 2x t
,t 0 , phương trình đã cho trở thành 2
4t −18t + 8 = 0 1 t = 2 Với = 4 2x t = 4 x = 2 1 Với 1 x 1 t = 2 = x = 1 − 2 2 2 Vậy x .x = 2 − 1 2
Câu 35. Trong mặt phẳng tọa độ Oxy , tập hợp tất cả các điểm biểu diễn của số phức z thõa mãn z − 4 + i = 3 là
đường tròn có phương trình: 2 2 2 2
A. ( x − 4) + ( y + ) 1 = 9 .
B. ( x − 4) + ( y − ) 1 = 3. 2 2 2 2
C. ( x − 4) + ( y + ) 1 = 3.
D. ( x − 4) + ( y − ) 1 = 9. Lời giải Chọn A Gọi 2 2
z = x + yi , khi đó z − 4 + i = 3 ( x − 4) + ( y + ) 1 = 9
Câu 36. Trong không gian Oxyz , cho ba điểm A(1;2; 2 − ), B( 2 − ;3; ) 1 ,C ( 1
− ;1;2) . Đường thẳng đi qua C và song
song với đường thẳng AB có phương trình chính tắc là x −1 y +1 z + 2 x − 3 y +1 z + 3 x +1 y −1 z − 2 x + 3 y −1 z − 3 A. = = . B. = = . C. = = . D. = = . 3 − 1 3 1 − 1 2 3 − 1 3 1 − 1 2 Lời giải Chọn C
Đường thẳng được xác định đi qua C ( 1
− ;1;2) và có véc tơ chỉ phương là u = AB = (−3;1;3) Trang 12 + − −
Vậy đường thẳng có phương trình chính tắc là x 1 y 1 z 2 = = 3 − 1 3
Câu 37. Trong không gian với hệ tọa độ Oxyz , điểm đối xứng của M (1; 2; 3) qua trục Ox có tọa độ là
A. (1; − 2; −3). B. (1; 0 0) . C. (0; 2; ) 3 . D. ( 1 − ; − 2; −3). Lời giải Chọn A
Hình chiếu của M (1; 2; 3) trên trục Ox là H(1;0;0)
M ' là điểm đối xứng của M (1; 2; 3) qua trục Ox khi chỉ khi H là trung điểm đoạn MM '
Vậy M '(1; − 2; − ) 3
Câu 38. Cho hình chóp S.ABC . Biết SA vuông góc với mặt phẳng đáy, SA = a 3 và ABC
vuông tại B có cạnh
BC = a , AC = a 5 . Tính theo a khoảng cách từ B đến (SAC) . a a a a A. 2 21 . B. 21 . C. 2 5 D. 15 . 7 7 5 3 Lời giải Chọn A S
Kẻ BH ⊥ AC tại H
Do SA ⊥ (ABC) SA ⊥ BH BH ⊥ (SAC) d( ,
B (SAC)) = BH
Theo pitago trong tam giác vuông ABC có 2 2 AB =
AC − BC = 2a
Trong tam giác vuông ABC tại B có BH là đường cao suy ra B . A BC 2 . a a 2 5a BH = = = H AC a 5 5 A C
Câu 39. Số nghiệm nguyên dương của bất phương trình 3 2x + 2log x 4 là 3 A. 4 . B. 2 . C. 1. D. 3 . B Lời giải
Điều kiện: x 0 Xét hàm số 3 ( ) = 2x f x
+ 2log x , xác định trên (0; ) + 3 x 3 Có đạo hàm 2 ln 2 2 f '(x) = + 0, x
0 , suy ra hàm số đồng biến trên (0; ) + 3 x ln 3
Mà f (3) = 4. Do đó bất phương trình có tập nghiệm (0;
3 . Vậy bất phương trình có 3 nghiệm nguyên dương.
Câu 40. Cho hàm số f (x) liên tục trên . Gọi F (x),G(x) là hai nguyên hàm của f (x) trên thỏa mãn 2023 x F ( ) 1 + G ( )
1 = 5 và F (0) + G(0) =1. Khi đó f dx bằng 2023 0 A. 2023. B. 2 . C. 4046 . D. 4 . 2023 2023 Lời giải
Ta có: G(x) = F (x) +C F ( ) 1 + G ( ) 1 = 5 2F ( ) 1 + C = 5 Theo giả thiết: F ( ) 1 − F (0) = . F ( ) + G ( ) = F ( ) 2 0 0 1 2 0 + C = 1 Đặt x 1 t = dt =
dx dx = 2023dt 2023 2023
+ x = 0 t = 0
+ x = 2023 t =1 Trang 13 2023 1 1 Khi đó x f dx = 2023 f
(t)dt = 2023 f
(x)dx = 2023F ( ) 1 − F (0) = 4046 . 2023 0 0 0
Câu 41. Cho hàm số f (x) 5 3
= x − mx + 5x + 2m + 3 ( m là tham số). Có bao nhiêu số nguyên m để hàm số f (x) có
4 điểm cực trị và tổng các giá trị cực trị nhỏ hơn 2023? A. 251. B. 250 . C. 248 . D. 247 Lời giải
Xét hàm số f (x) 5 3
= x − mx + 5x + 2m + 3, có tập xác định , 4 2
f '(x) = 5x − 3mx + 5
Để hàm số đã cho có 4 điểm cực trị khi và chỉ khi 4 2
f '(x) = 5x − 3mx + 5 = 0 có 4 nghiệm phân biệt, hay 10 m 3
Nhận thấy trong 4 nghiệm phân biệt x , x , x , x của phương trình f '( )
x = 0 thì ta có x = −x , x = −x 1 2 3 4 1 2 3 4
Do đó f (x ) + f (x ) + f (x ) + f x = 4 2m + 3 . Nên ta có 2011
8m +12 2023 m 1 2 3 ( 4) ( ) 8 Vậy 10 2011 m
, hay có 248 số nguyên thoả mãn bài toán. 3 8
Câu 42. Hai số phức z , w thay đổi nhưng luôn thỏa mãn đẳng thức ( z + i 1+ i) 2023 2023 2 z − 2iz −1 =
+ 2 − 2i . Giá trị lớn nhất của w là w A. 2019 2 . B. 2019 2 . C. 2019 . D. Đáp án khác. 4 2 Lời giải Chọn A 2 Ta có: 2
z − i = z + i nên 2
z − 2iz −1 = z − i = z + i . Như vậy: + 2 2023 2023 + 2023 z i z i 2 ( )
(1+i) z −2iz −1 =
+ 2 − 2i (1+ i) z + i = + 2 − 2i w w + + 2 2023(z i) ( z i 1+ i) 2
z + i + 2i − 2 =
z + i − 2 + ( 2 z + i + 2) 2023( ) i = . w w
Điều kiện: w 0 suy ra z + i 0 hay z + i 0 . 2023 z + i
Đặt t = z + i ,t 0ta có 2 t − 2 + ( 2 t + 2) ( ) i =
. Lấy môđun hai vế ta được: w ( z + i t t − 2) 2023 2 + (t + 2)2 =
(t − 2)2 + (t + 2)2 2023 2 2 2 2 = w w 2023t 2023t w = w = .
(t − )2 +(t + )2 4 2 2 2t + 8 2 2 2023t 2023 2 w w . 2 2t 4 Trang 14 Vậy 2023 2 max w = khi 4 4
2t = 8 t = 4 t = 2 z − i = 2 . 4
Câu 43. Cho hình lăng trụ đứng AB . C A B C
có đáy ABC là tam giác vuông tại A . AC = a , ACB = 60 . Đường
thẳng BC tạo với mặt phẳng ( ACC A
) một góc 30. Thể tích của khối lăng trụ AB . C A B C bằng 3 a 3 3 a 6 A. 3 a 3 . B. 3 a 6 . C. . D. . 3 3 Lời giải 2 a 3 A' C'
Tính được BC = 2a , AB = a 3 S = ABC 2 Đặt 2 2
AA' = x AC ' = a + x
Ta có BC tạo với mặt phẳng (BC ( ACC A )) 0 ', = AC ' B = 30
Trong tam giác vuông ABC ' có B' AB a 3 3 0 3 tan 30 = =
x = 2 2a V = a 6 . ' ' ' 2 2 AC ' + 3 ABC A B C a x A C B 3 +
Câu 44. Cho hàm số f (x) liên tục, không âm trên 0; 2 , thỏa f ( x) x 4 f ( x) = với 2 f ( x)
mọi x 0;2 và f (0) = 0. Tính diện tích hình phẳng giới hạn bởi hai đường 3 y = 4 + f (x) và 11 y = 4 A. 1. B. 2 . C. 21 . D. 2 . Lời giải 3 2 x 4 + f x
f ( x). f ( x) 2
f ( x). f ( x) 2 Ta có ( ) ( ) x f x = = x dx = + C 2 f ( x) 3 + f (x) 3 + f (x) 2 4 4 2
f ( x). f ( x) Đặt 3 2 3 2 2 tdt 2 2 t =
4 + f (x) t = 4 + f (x) 2tdt = 3 f (x) f '(x)dx 3 dx = = t = 4 + f (x) 3 + f (x) 3 t 3 3 4 Do đó ta có 2 x 3 4 + f ( x) 2 3 =
+ C , thay x = 0 ta được 4 C = suy ra 3 4 + f ( x) 2 = x + 2 3 2 3 4 Xét phương trình 11 3 11 3 4 + f ( x) 2 = x + 2 = x = 1 4 4 4 1 3 3
Vậy diện tích cần tìm là 2 S = − x dx = 1 4 4 1 −
Câu 45. Trên tập hợp các số phức, xét phương trình 2 z − (m − ) 2 2
1 z + m − 3 = 0 ( m là tham số thực). Gọi S là tập
hợp giá trị của m để phương trình đó có hai nghiệm z , z thỏa mãn z − z = 2 5 . Tính tổng các phần tử của tập 1 2 1 2 S . 9 1 A. 5 . B. 4 . C. . D. − . 2 2 Lời giải Có = (m − )2 2 ' 1 − m + 3 = 2 − m + 4 Trang 15 TH1: 1
' 0 m 2 thì phương trình có hai nghiệm thực, khi đó z − z = 2 5 2 2
− m + 4 = 2 5 m = − 1 2 2
TH2: ' = 0 z − z = 0 loại 1 2
TH3: ' 0 m 2khi đó phương trình có hai nghiệm phức z = m −1 i 2m − 4 z − z = 2 2m − 4 1,2 1 2 YCBT 9
2 2m − 4 = 2 5 m = 2
Vậy ta có tổng các phần tử của S là 4 − + − − − +
Câu 46. Trong không gian x 1 y 2 z 1 x 1 y 1 z 2
Oxyz , cho hai đường thẳng d : = = và d : = = . Mặt 1 1 1 2 2 2 1 1
phẳng (P): x + ay +bz + c = 0, c 0 song song với d , d và khoảng cách từ d đến (P) gấp đôi khoảng cách từ 1 2 1
d đến ( P) . Giá trị của a + b + c bằng 2 A. 14. B. 6 . C. 4 − . D. −6 . Lời giải
Do mặt phẳng (P): x + ay +bz + c = 0, c 0 song song với d , d , suy ra n = u ;u = 1; 3 − ;1 1 2 ( ) 1 2 Suy ra ( )
P : x −3y + z + m = 0 Lấy ( A 1; 2
− ;1)d , B(1;1; 2 − )d 1 2 m =
YCBT d ( A P ) = d (B P ) 0 , ( ) 2
, ( ) m + 8 = 2 m − 4 m =16
Do c 0 m =16 ( )
P : x −3y + z +16 = 0 . Vậy a + b + c = 14 Câu 47. Có bao nhiêu bộ ( ;x y) với , x y nguyên và 1 , x y 2023 thỏa mãn ( +
xy + x + y + ) 2 y 2x 1 2 4 8 log
2x + 3y − xy − 6 log ? 3 ( ) 2 y + 2 x − 3 A. 2022 . B. 2023. C. 4040 . D. 20222023 . Lời giải * x, y : x, y 2023 * x, y : x, y 2023
+ Điều kiện 2x +1 2 y . 0, 0
x 3, y 0 x − 3 y + 2 + −
BPT cho có dạng ( x − )( y − ) x 4 y 2 3 2 log
+1 + x + 4 y + 2 log +1 0 . 2 ( )( ) 3 x − 3 y + 2 x + 4 2
+ Xét y =1 thì thành −(x −3)log +1 + 3 x + 4 log
0, rõ ràng BPT này nghiệm đúng với 2 ( ) 3 x −3 3 mọi x 3 vì ( + − x − ) x 4 2 3 0;log
+1 log 0 +1 = 0;3 x + 4 0 ;log 0 . 2 2 ( ) ( ) 3 x −3 3
Như vậy trường hợp này cho ta đúng 2020 bộ ( ; x y) = ( , x )
1 với 4 x 2023, x .
+ Xét y = 2 thì thành 4(x + 4)log 1 0 , BPT này cũng luôn đúng với mọi x mà 4 x 2023, x . 3
Trường hợp này cho ta 2020 cặp ( ; x y) nữa.
+ Với y 2, x 3 thì VT ( ) * 0 nên không xảy ra.
Vậy có đúng 4040 bộ số ( ;
x y) thỏa mãn yêu cầu bài toán.
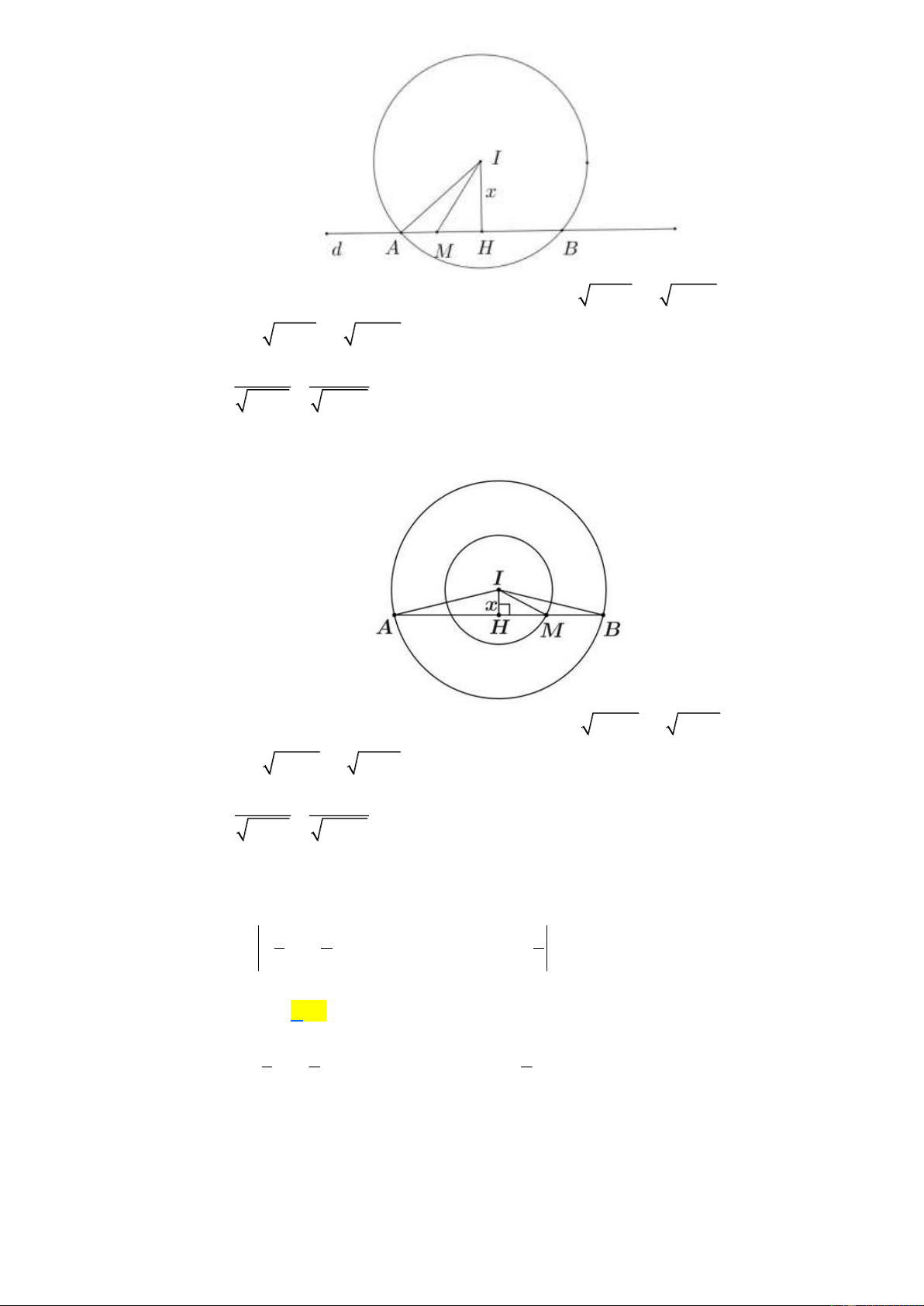
Câu 48. Cho hình trụ có bán kính R và chiều cao 3R . Hai điểm A , B lần lượt nằm trên hai đường tròn đáy sao
cho góc giữa AB và trục d của hình trụ bằng 30 . Tính khoảng cách giữa AB và trục của hình trụ. R R
A. d ( AB,d ) = .
B. d ( A , B d ) = R .
C. d ( A ,
B d ) = R 3 . D. d ( AB d ) 3 , = . 2 2 Trang 16 Lời giải A H C J 300 R 3 B R I
Gọi I , J là tâm của hai đáy (hình vẽ).
Từ B kẻ đường thẳng song song với trục d của hình trụ, cắt đường tròn đáy kia tại C . Khi đó, ( A , B d ) = (A ,
B BC) = ABC . Suy ra ABC = 30.
Xét tam giác ABC vuông tại C , ta có: AC tan ABC = AC = C .
B tan ABC = R 3.tan 30 = 1 R 3. = R . CB 3
Lại có d// ( ABC) và ( ABC) AB nên d (d, AB) = d (d,( ABC)) = d (J,( ABC)).
Kẻ JH ⊥ AC , H AC . Vì BC ⊥ JH nên JH ⊥ ( ABC) . Suy ra d (J,( ABC)) = JH .
Xét tam giác JAC ta thấy JA = JC = AC = R nên JAC là tam giác đều cạnh R . Khi đó chiều cao là R 3 R JH = . Vậy d (d AB) 3 , = . 2 2 Câu 49. 2 2 2
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S ) : ( x − 2) + ( y − ) 1 + (z − ) 1 = 4 và điểm M (2;2; )
1 . Một đường thẳng thay đổi qua M và cắt (S ) tại hai điểm ,
A B . Khi biểu thức
T = MA + 4MB đạt giá trị nhỏ nhất thì đoạn thẳng AB có giá trị bằng A. 4 3 . B. 2 3 . C. 5 3 . D. 4 . 2 Lời giải Chọn D
(S) có tâm I (2;1; ) 1 , bán kính R = 2 .
Ta có IM =1 R điểm M nằm trong mặt cầu (S ) và M nằm trên mặt cầu (S) tâm I , bán kính R = 1.
Gọi H là hình chiếu của I lên AB và đặt IH = x , vì IH IM =1 0 x 1.
TH1: MA MB. Trang 17
T = MA + 4MB = AH − MH + 4(MH + HB) = 3MH + 5AH 2 2
= 3 1− x + 5 4 − x .
Xét hàm số f (x) 2 2
= 3 1− x + 5 4 − x trên đoạn 0; 1 . − Ta có f (x) 3 5 = x − = 0 x = 0 . 2 2 1− x 4 − x Suy ra T
= 13 khi d đi qua I AB = 2R = 4. min
TH2: MA MB.
T = MA + 4MB = AH + MH + 4(BH − MH ) = 5AH − 3MH 2 2
= 5 4 − x − 3 1− x .
Xét hàm số f (x) 2 2
= 5 4 − x − 3 1− x trên đoạn 0; 1 . − Ta có f (x) 5 3 = x +
= 0 x = 0 0; 1 . 2 2 1− x 4 − x
Tìm được min f (x) = f (0) = 7 , khi d đi qua I AB = 2R = 4. 0; 1
● So sánh cả hai trường hợp thì ta có T
= 7 , khi d đi qua I AB = 2R = 4 . min Câu 50. 1 1 2 Cho hàm số 3 2
f (x) = − x +
(2m + 3)x − ( 2
m + 3m) x + . Có bao nhiêu giá trị nguyên của tham số m 3 2 3 thuộc [ 9
− ;9] để hàm số nghịch biến trên khoảng (1;2) ? A. 3. B. 2. C. 16. D. 9. Lời giải Xét hàm số 1 1 2 3 2
g(x) = − x +
(2m + 3)x − ( 2
m + 3m) x + 3 2 3 2
g x = −x + m + x − ( 2 ( ) (2 3) m + 3m)
Để f (x) nghịch biến trên khoảng (1;2) ta xét hai trường hợp sau:
Trường hợp 1: g( )
x nghịch biến và không âm trên khoảng (1;2) . Trang 18 2
−x + (2m + 3)x −( 2
m + 3m) 0, x (1;2)
g (x) 0, x (1;2) Tức là: 1 1 2 3 2 g(2) 0
− .2 + .(2m + 3).2 − ( 2
m + 3m).2 + 0 3 2 3
x m + 3, x (1;2) m 2 − x , m x
(1;2) m 2 m = 2 − . 2 2
− m − 2m + 4 0 2 − m 1
Trường hợp 2: g( )
x đồng biến và không dương trên khoảng (1;2) . 2
−x + (2m + 3)x −( 2
m + 3m) 0, x (1;2)
g (x) 0, x (1;2) Tức là: 1 1 2 3 2 g(2) 0
− .2 + .(2m + 3).2 − ( 2
m + 3m).2 + 0 3 2 3 1 − m 1
m x m + 3, x (1;2) m 1 m =1. 2 2
− m − 2m + 4 0 m 2 − Trang 19




