S SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT THANH HÓA NĂM HỌC 2025 - 2026 MÔN TOÁN
DỰ THẢO ĐỀ MINH HỌA
Thời gian làm bài.120 phút (Không kể thời gian giao đề)
Ngày thi. Ngày tháng năm 2024
Đề gồm có 02 trang, 15 câu
I. PHẦN TRẮC NGHIỆM (2,0 điểm, gồm 8 câu, mỗi câu 0,25 điểm)
Câu 1. Phương trình 3x − 9 = 0 có nghiệm là
A. x = 9 B. x = −3 C. x = 3 D. x = −9
Câu 2. Điều kiện của x để biểu thức 2x −1 xác định là.
A. x  0 B. x  1 C. 2x −1  0 D. 2x −1  0 1 1
Câu 3. Giá trị biểu thức + bằng: 2 + 5 2 − 5 1 A. B. 4 C. 1 D. −4 2
Câu 4. Đồ thị hàm số nào sau đây đi qua điểm có tọa độ (3; 3)? 1 1 A. 2 y = x B. 2 y = x C. 2 y = 3x D. 2 y = x 2 3
Câu 5. Cho tam giác ABC vuông tại A có AB = 3(cm) , AC = 4(cm) . Khẳng định nào sau đây là đúng? C 4 A 3 B 4 4 4 3 A. tan B = B. tan C = C. cot B = D. cot C = 3 3 3 4
Câu 6. Công thức tính thê tích khối cầu bán kính R là. A. 4 1 3 V = .  R B. 2 V = .R C. 3 V = .  R D. V = 2 R  3 3
Câu 7. Đo chiều cao (đơn vị cm) các em học sinh của một lớp, ta được một bảng tần số ghép nhóm như sau. Chiều cao (cm) 1  50 1 ; 58  ) 1  58 1 ; 6  ) 1 1  61 1 ; 64  ) 1  64 1 ; 67  ) Số học sinh 5 12 15 8
Số học sinh có chiều cao từ 158 cm đến dưới 161 cm là. A. 5 . B. 12 . C. 15 . D. 8 .
Câu 8. Bạn Nam gieo một con xúc xắc 10 lần liên tiếp thì thấy mặt 4 chấm xuất hiện 3 lần. Xác
suất thực nghiệm xuất hiện mặt 4 chấm là. 3 4 7 3 A. B. C. D. 10 10 10 14
II. PHẦN TỰ LUẬN (8,0 điểm) 2x + y = 5
Câu 9. (1,0 điểm) Giải hệ phương trình.  x − 3y = 1 − 2 2 x − 5
Câu 10. (1,0 điểm) Rút gọn biểu thức P = + +
với x  0; x  1 . x +1 x −1 x −1
Câu 11. (1,0 điểm) Tìm m để đồ thị hàm số 2
y = x và đường thẳng y = ( m + ) 2 2
1 x - m - 2 cắt
nhau tại 2 điểm phân biệt có hoành độ x ; x thỏa mãn điều kiện 3x x - 5 x + x + 7 = 0 1 2 ( 1 2 ) 1 2
Câu 12. (1,0 điểm)
Bác Việt chia số tiền 800 triệu đồng của mình cho hai khoản đầu tư. Sau một năm, tổng số tiền lãi
bác thu được là 54 triệu đồng. Lãi suất cho khoản đầu tư thứ nhất là 6% năm và khoản đầu tư thứ
hai là 8% năm. Tính số tiền bác Việt đầu tư cho mỗi khoản.
Câu 13. (1,0 điểm)
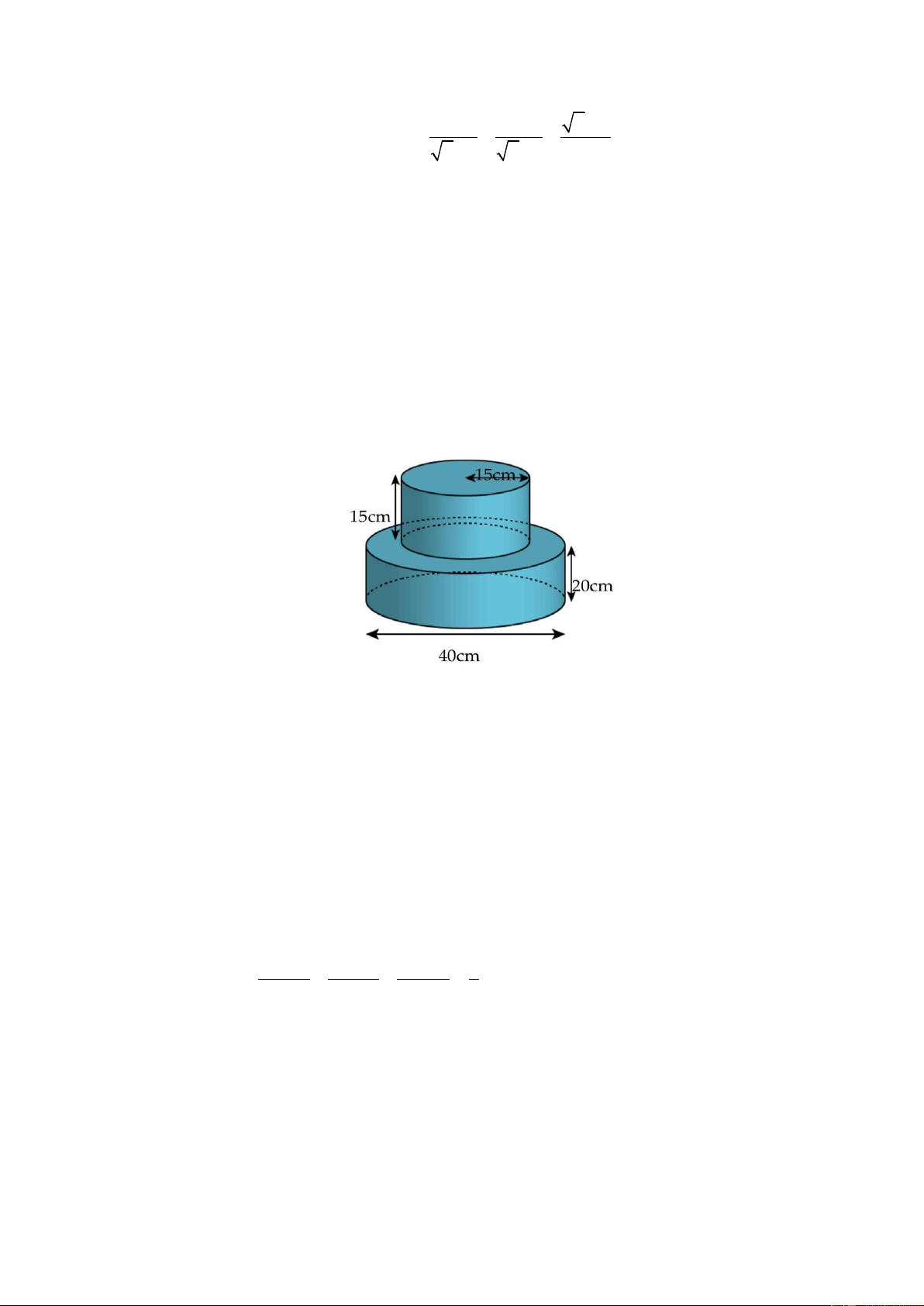
Một chiếc bánh ngọt được làm có hai tầng, tầng phía trên cao 15 cm , bán kính tầng trên là 15 cm ,
tầng dưới cao 20 cm , đường kính tầng dưới là 40 cm . Tính diện tích bề mặt của chiếc bánh có thể
dùng để trang trí? (mặt đáy của bánh sinh nhật không trang trí).
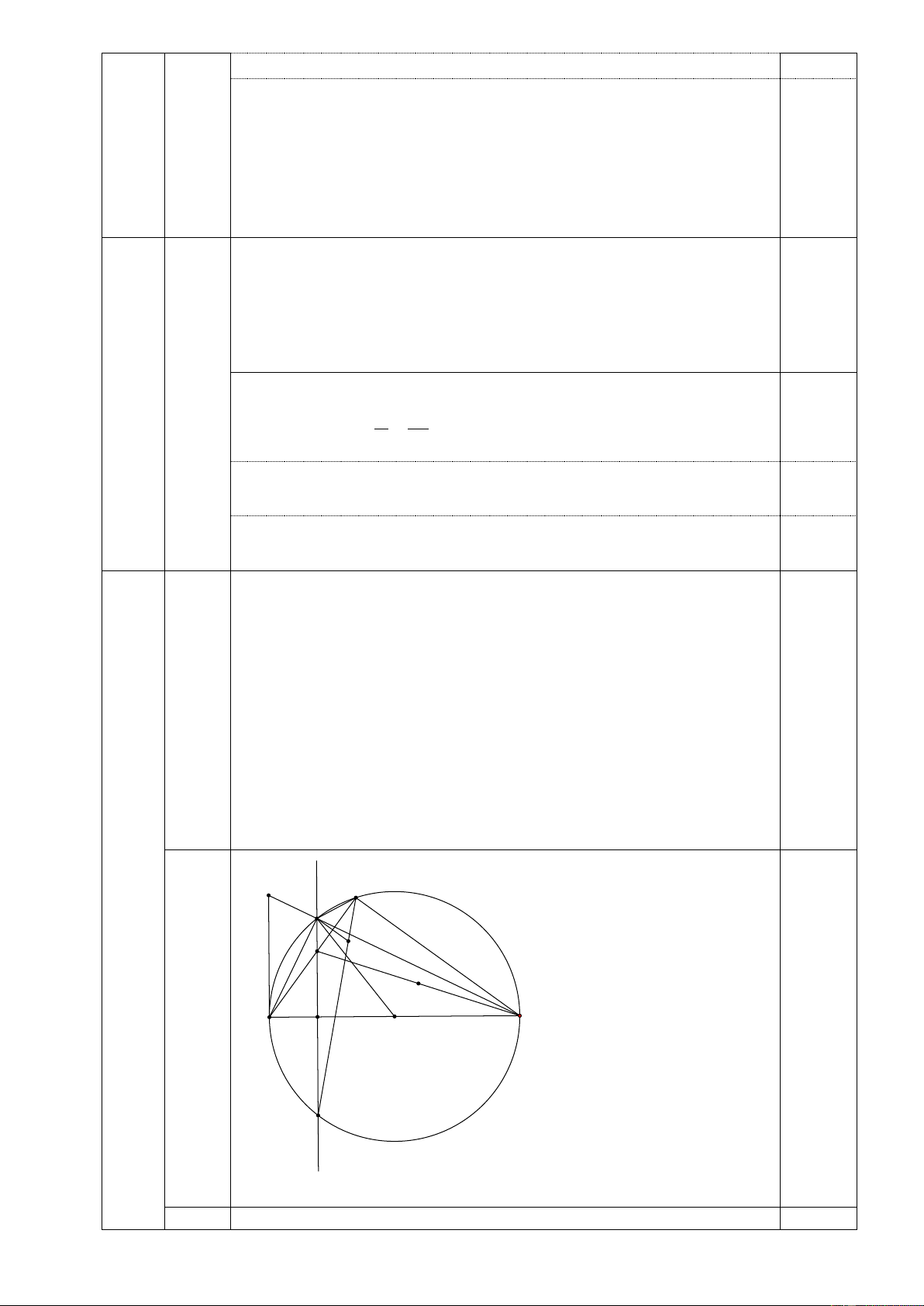
Câu 14. (2,5 điểm) Cho đường tròn tâm O đường kính AB = 2R , trên đoạn OA lấy điểm I (I  ;
A I  O) . Vẽ tia Ix ⊥ AB cắt (O) tại C . Lấy điểm E trên cung nhỏ BC ( E  B; E  C ) ,
AE cắt CI tại F , gọi D là giao điểm của BC với tiếp tuyến tại A của (O; R)
a) (1,0 điểm) Chứng minh rằng tứ giác BEFI là tứ giác nội tiếp.
b) (1,0 điểm) Chứng minh rằng AE.AF = C . B CD .
c) (0,5 điểm) Biết rằng AB = 2 AC , tia Iy là tia đối của tia Ix cắt đường tròn (O) tại điểm M . Tìm
giá trị lớn nhất của biểu thức S = 2025. . EB EC
Câu 15. (0,5 điểm) Cho ba số dương a,b,c thỏa mãn a + b + c = 12 . a b c 3 Chứng minh rằng. + +  2 2 2 b +16 c +16 a +16 8 ……..…..HẾT……….
HƯỚNG DẪN CHẤM ĐỀ THI MINH HỌA TUYỂN SINH VÀO LỚP 10 THPT MÔN TOÁN NĂM HỌC 2025 - 2026 Chú ý.
- Các cách làm khác nếu đúng vẫn cho điểm tối đa.
- Đối với câu 14 (Hình học).
+ Không vẽ hình, hoặc vẽ hình sai cơ bản thì không chấm;
+ Học sinh không chứng minh mà thừa nhận kết quả của ý trên để giải ý dưới thì không chấm điểm ý dưới.
- Các trường hợp khác tổ chấm thống nhất phương án chấm. ĐÁP ÁN
I. PHẦN TRẮC NGHIỆM (2,0 điểm gồm 8 câu, mỗi câu 0,25 điểm) Câu 1 2 3 4 5 6 7 8 Đáp án C C B D A A B D
II. PHẦN TỰ LUẬN (8,0 điểm) Câu Ý Nội dung Điểm
Giải phương trình. 2
x − 5x + 4 = 0 a
Vì a + b + c = 1− 5 + 4 = 0 0,25 c 0,5
Nên phương trình có hai nghiệm là x = 1 và x = = 4 1 2 a 2x - y =1
Giải hệ phương trình.  3  x + y = 4 b 9
Cộng từng vế hai phương trình của hệ ta được. 5x = 5 0,25 Suy ra. x = 1
Thay x = 1 vào phương trình thứ nhất của hệ, ta được. 0,25 2 1 . − y = 1 Suy ra. y = 1
Vậy hệ phương trình có nghiệm duy nhất (1 1 ; ) 0,25 2 2 x − 5 Cho P = + +
với x  0; x  1 . x +1 x −1 x −1
Rút gọn biểu thức P 2 2 x − 5 P = + + x +1 x −1 x −1 − 2 2 x 5 = + + 0,25 x +1 x −1
( x − )1( x + )1 2 ( x − ) 1 + 2 ( x + ) 1 + x − 5 = ( x − ) 1 ( x + ) 1 10
2 x − 2 + 2 x + 2 + x − 5 = ( x − ) 1 ( x + ) 1 5 x − 5 = ( x − ) 1 ( x + ) 1 0,25 5( x − ) 1 = ( x − ) 1 ( x + ) 1 5 P =
với x  0; x  1 x +1 0,25 5 Vậy P =
với x  0; x  1 x +1 Cho phương trình. 2
x − ( m −1)x − m = 0
a) Chứng tỏ rằng phương trình luôn có nghiệm x , x với mọi m. 1 2
b) Tìm m để phương trình luôn có nghiệm x , x thỏa mãn điều 1 2 kiện. 2 2 x x + x x − 3x x = −5 1 2 1 2 1 2 a 2 2 Ta có.  = (m − ) 2 1
+ 4m = m + 2m +1 = (m + ) 1 0,25 Vì (m + )2 1  0 với m
 nên   0 với m  0,25
Suy ra phương trình luôn có nghiệm x , x với mọi m. 0,25 1 2 11  b − + = = − x x m 1  1 2  a
Theo định lí Viet, ta có.  0,25 c
x  x = = −m 1 2  a Theo bài ra ta có. 2 2 x x + x x − 3x x = −5 1 2 1 2 1 2
x x ( x + x ) − 3x x + 5 = 0 1 2 1 2 1 2 b 0,25 −m (m − ) 1 + 3m = 5 − 2
m − 4m − 5 = 0
Giải phương trình trên ta được. 0,25
m = −1 (thỏa mãn) hoặc m = 5 (thỏa mãn) . Vậy m  1 − ;  5 là giá trị cần tìm.
Bác Việt chia số tiền 800 triệu đồng của mình cho hai khoản đầu
tư. Sau một năm, tổng số tiền lãi bác thu được là 54 triệu đồng.
Lãi suất cho khoản đầu tư thứ nhất là 6% năm và khoản đầu tư
thứ hai là 8% năm. Tính số tiền bác Việt đầu tư cho mỗi khoản?
Gọi lần lượt là số tiền hai khoản đầu tư của bác Việt lần lượt là
x ( triệu đồng) và y ( triệu đồng) với ( x, y  0 )
Tổng số tiền bác Việt đầu tư là 800 triệu đồng nên ta có phương trình 0,25 x + y = 800 (1) 12
Lãi suất cho khoản đầu tư thứ nhất là 6% năm và khoản đầu tư thứ hai
là 8% năm, nên ta có phương trình
0,06.x + 0,08.y = 54 (2) x + y = 800
Từ (1) và (2) ta có hệ phương trình  
0,06.x + 0,08.y = 54 0,25 x = 500
Giải hệ phương trình ta được  (thỏa mãn) y = 300
Vậy bác Việt đầu tư cho khoản thứ nhất và khoản thứ hai lần lượt là
500 triệu đồng và 300 triệu đồng 0,25
Nón Huế là một hình nón có đường kính đáy bằng 40cm , độ dài
đường sinh là 30cm . Người ta lát mặt xung quanh hình nón bằng
ba lớp lá khô. Tính diện tích diện tích bề mặt đã được lót lá để tạo
nên một chiếc nón Huế như vậy? (Kết quả làm tròn đến chữ số
thập phân thứ hai, theo đơn vị 2
cm , lấy   3 1 , 4 )
Chiếc nón Huế là một hình nón có đường kính đáy d = 40 (cm) , nên 0,25 13 bán kính đáy d 40 R = = = 20(cm) . 2 2 Vậy diện tích xung quanh của hình nón này là. 0,25
S =  Rl = , . . = ( 2 3 14 20 30 1884 cm ) .
Vì người ta lợp nón bằng 3 lớp lá, nên diện tích bề mặt đã được lót lá 0,25
để tạo nên một chiếc nón Huế sẽ là. . = ( 2 1884 3 5652 cm ) .
Cho đường tròn tâm
O đường kính AB = 2R , trên đoạn OA lấy điểm   . Vẽ tia ⊥ cắt (O) I (I ; A I O) Ix AB
tại C . Lấy điểm E
trên cung nhỏ BC (E  B; E  C ) , AE cắt CI tại F , gọi D là giao
điểm của BC với tiếp tuyến tại A của (O; R)
a) Chứng minh rằng tứ giác BEFI là tứ giác nội tiếp. =
b) Chứng minh rằng . AE.AF C . B CD .
c) Biết rằng AB = 2 AC , tia Iy là tia đối của tia Ix cắt đường
tròn (O) tại điểm M . Tìm giá trị lớn nhất của biểu thức S = 2025. . EB EC x E D C N F K A B I O M y 14
Chứng minh rằng tứ giác BEFI là tứ giác nội tiếp.
Gọi K là trung điểm của BF
Ta có. AEB = 90 ( góc nội tiếp chắn nửa đường tròn) 0,25 1
Do đó, BEF vuông tại E . suy ra. KE = BF (tính chất đường trung 2
tuyến trong tam giác vuông) ( ) 1 1 = 0,25
Xét tam giác vuông BIF , có KI
BF (tính chất đường trung tuyến 2 a trong tam giác vuông) (2) 1 0,5
Từ (1) và (2) suy ra KE = KI = KB = KF = BF 2
Suy ra, tứ giác BEFI nội tiếp đường tròn đường kính BF
Chứng minh rằng . AE.AF = CB.CD .
Vì ACB là góc nội tiếp chắn nửa đường tròn nên 0 ACB = 90 , suy ra 
ACB vuông tại A có CI là đường cao nên. 2 AC = AI .AB ( )1 0,25
Vì AD là tiếp tuyến của (O) nên AD ⊥ AB , suy ra ADB vuông ở A , b
có AC là đường cao nên. 2
AC = BC CD (2)
Mặt khác. AIF ∽ AEB (g.g) 0,25 AI AF Suy ra . =
, suy ra AI  AB = AE  AF (3) AE AB
Từ (1),(2) và (3) suy ra AE.AF = CB.CD 0,25
Biết rằng AB = 2AC và điểm E di chuyển trên cung nhỏ BC . Tìm giá
trị lớn nhất của biểu thức. S = 2025.EB.EC 1
Do AB = 2 AC và tam giác ABC vuông tại C nên sin ABC = , suy ra 2 0 ABC = 30 do đó. 0 BAC = 60 suy ra 0
BCM = BMC = 60 . Do đó tam
giác BCM đều suy ra 0 MEC = 60 .
Trên đoạn ME lấy N sao cho NE = EC , CEN đều, suy ra CE = CN . Xét B  EC; M  NC có. =  − =  CNM 180 CNE 120 ;
Do tứ giác BECM có bốn đỉnh nằm trên (O) nên tứ giác BECM nội 0,25 tiếp (O) , suy ra.
CEB = 180 − CMB = 120
CE = CN ; CMN = CBE ( 2 góc nội tiếp cùng chắn cung CE ), suy ra. c MCN = BCE Do đó. BEC 
= MNC suy ra BE = MN
BE + CE = MN + NE = ME  AB = 2R (Quan hệ đường kính và dây cung) .
Mà BE + CE  2 BE.CE ( áp dụng bất đẳng thức Cauchy) 0,25 2 BE.CE  R 2
S = 2025.BE.CE  2025R
Dấu bằng xảy ra khi BE = CE và ME = 2R hay E là điểm chính giữa cung nhỏ BC
Cho ba số dương a,b,c thỏa mãn a + b + c = 12 . a b c 3 Chứng minh rằng. + +  2 2 2 b +16 c +16 a +16 8 a b c A = + + 2 2 2 b +16 c +16 a +16 1  16a 16b 16c  =  + + A   2 2 2 16  b +16 c +16 a +16   a( 2 b +16) 2 − ab b ( 2 c +16) 2 − bc c ( 2 a +16 −  1 ) 2 ca A =  + +  15 2 2 2 16  b +16 c +16 a +16    2 2 2 1  ab bc ca  A = a − + b − + c −  2 2 2 16 b +16 c +16 a +16   0,25 2 2 2 1 1  ab bc ca  A =
( a + b + c ) −  + +  2 2 2 16 16 b +16 c +16 a +16   2 2 2 3 1  ab bc ca  A = −  + +  2 2 2 4 16 b +16 c +16 a +16  
Áp dụng bất đẳng thức Cô Si ta có. 2 2
b +16  2 16b = 8b 2 c +16  8c 2 a +16  8a Do đó. 2 2 2 3 1  ab bc ca  A  −  + +  4 64 2b 2c 2a   0,25 2 3
1 ( a + b + c ) A  − 4 64 6 2 3 1 12 A  − 4 64 6 3 A  8
Dấu bằng xảy ra khi a = b = c = 4