Đề minh họa thi TN THPT 2023 môn Toán trường THPT Phú Lâm – TP HCM

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề minh họa ôn thi tốt nghiệp THPT năm học 2022 – 2023 môn Toán trường THPT Phú Lâm, thành phố Hồ Chí Minh

18 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

27 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG THPT PHÚ LÂM
ĐỀ MINH HỌA
MÃ ĐỀ: 123
Họ, tên thí sinh:…………………………
Số Báo danh:…………………………….
ĐỀ THI TỐT NGHIỆP THPT QG
Năm học: 2022 - 2023
Môn: TOÁN – Khối 12
Thời gian làm bài: 90 phút
Ngày kiểm tra: 31/03/2023
Câu 1: Cho số phức
126=−−zi
. Phần thực và phần ảo của số phức
z
là?
A. Phần thực bằng
1−
và phần ảo bằng
26
. B. Phần thực bằng
1−
và phần ảo bằng
26i
.
C. Phần thực bằng
và phần ảo bằng
26
. D. Phần thực bằng
1−
và phần ảo bằng
26− i
.
Câu 2: Đạo hàm của hàm số
( )
2
2023
logy xx= +
là
A.
2
21+
+
x
xx
. B.
( )
2
21
.ln 2023
x
xx
+
+
. C.
2
1
+xx
D.
( )
2
1
.ln 2023xx+
.
Câu 3: Đạo hàm của hàm số
8
x
y =
là
A.
8
ln 8
x
y
′
=
. B.
8 ln 8
x
y
′
=
. C.
8 ln 8
x
yx
′
=
. D.
1
8
x
yx
−
′
=
.
Câu 4: Tìm tập nghiệm
S
của bất phương trình
1
1
50
5
x+
−>
.
A.
( )
;2S = −∞ −
. B.
( )
1;S = +∞
. C.
( )
1;S = − +∞
. D.
( )
2;S = − +∞
.
Câu 5: Cho cấp số cộng có số hạng đầu và công sai . Giá trị của bằng
A. . B. . C. . D. .
Câu 6: Trong không gian , cho mặt phẳng . Vectơ nào sau đây là vectơ pháp
tuyến của mặt phẳng ?
A. . B. . C. . D.
Câu 7: Số giao điểm của đồ thị
32
( ): 3 2 1Cyx x x=− ++
và đường thẳng
1y =
là
A. 0. B. 3. C. 1. D. 2.
Câu 8: Cho hàm số
( )
fx
có đạo hàm trên đoạn
[ 1; 2]−
và
( ) ( )
1 2023, 2 1.ff−= =−
Tích phân
( )
2
1
dfxx
−
′
∫
bằng:
A.
2024.
B.
2024.−
C.
1.
D.
2022.
Câu 9: Hàm số nào dưới đây có bảng biến thiên như sau:
( )
n
u
1
11u =
4d =
5
u
2816
27
15
26−
Oxyz
( )
:3 2 1 0P xy z+ − +=
( )
P
( )
4
3; 2;1n = −
( )
3
2;1; 3n = −
( )
1
3;1; 2n = −
( )
2
1; 2;1n = −
2
A.
42
2.yx x= −
B.
3
3.yx x=−+
C.
42
2.yx x=−+
D.
3
3.yx x= −
Câu 10: Trong không gian
Oxyz
, mặt cầu
( ) ( ) ( ) ( )
2 22
: 1 2 3 25Sx y z− +− +− =
có tọa độ tâm
I
và
bán kính
R
là
A.
( )
1; 2; 3 , 5
IR
=
. B.
(
)
1; 2; 3 , 5IR−=
. C.
( )
1; 2; 3 , 25IR−=
. D.
( )
1; 2; 3 , 25IR=
.
Câu 11: Cho điểm
( )
1,4,2M −−
và mặt phẳng
( )
: 5 14 0Pxy z
++ − =
. Tính khoảng cách từ
M
đến
()P
.
A.
23
B.
43
C.
63
D.
33
Câu 12: Cho số phức
z
thỏa mãn
(
)
1 14 2iz i
+=−
. Tổng phần thực và phần ảo của
z
bằng
A.
14.
B.
2.
C.
2.
−
D.
14.−
Câu 13: Thể tích của khối lăng trụ có diện tích đáy
2
2Sa=
, chiều cao
6ha=
là:
A.
3
12a
. B.
3
4
a
. C.
3
6a
. D.
3
36a
.
Câu 14: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA a=
và
SA
vuông góc với
mặt phẳng đáy. Thể tích khối chóp
.S ABCD
bằng
A.
3
6
a
. B.
3
2
3
a
. C.
3
a
. D.
3
3
a
.
Câu 15: Phương trình tiếp tuyến của đường cong
32
32yx x=+−
tại điểm có hoành độ
0
1x =
là
A.
97yx= +
. B.
97yx=−−
. C.
97
yx=−+
. D.
97yx= −
.
Câu 16 : Trong mặt phẳng Oxy , điểm M trong hình vẽ bên là điểm biểu diễn số phức z . Số phức
z
là
A.
2 i−−
. B.
12i−
. C.
2 i−+
. D.
2 i+
.
Câu 17: Cho hình trụ có bán kính đáy
r
và độ dài đường sinh
l
. Diện tích xung quanh
xq
S
của hình trụ
đã cho được tính theo công thức nào dưới đây?
A.
4
xq
S rl
π
=
. B.
2
xq
S rl
π
=
. C.
3
xq
S rl
π
=
. D.
xq
S rl
π
=
.
+
∞
∞
2
2
+
+
+
∞
∞
0
0
1
-1
y'
x
y
3
Câu 18: Trong không gian
Oxyz
, đường thẳng
134
:
13 2
xyz
d
−−+
= =
−
đi qua điểm nào dưới đây?
A.
(1; 3 2)
Q −
. B.
( 1; 3; 4)
M −−
. C.
(1; 3; 4)C −
. D.
( 1; 3; 2)N −−
.
Câu 19: Cho hàm số
42
y ax bx c=++
,
( )
,,abc R∈
có đồ thị là đường cong như hình bên. Điểm cực tiểu
của hàm số đã cho là:
A.
1x = −
. B.
2x =
. C.
1x =
. D.
0x =
.
Câu 20: Tiệm cận ngang của đồ thị hàm số
21
24
x
y
x
−
=
+
là đường thẳng có phương trình:
A.
2y = −
. B.
2
x = −
. C.
1x
=
. D.
1y =
.
Câu 21: Tập nghiệm của bất phương trình
2
13
3 27
x −
<
là
A.
( )
4;+∞
. B.
( )
4;4−
. C.
( )
;4−∞
. D.
( )
0;4
.
Câu 22: Có bao nhiêu số có năm chữ số khác nhau được tạo thành từ các chữ số 1,2,3,4,5,6?
A.
5
6
A
B.
6
P
. C.
5
6
C
. D.
5
P
.
Câu 23: Nguyên hàm của hàm số
( )
3
2 2023fx x= −
là:
A.
4
1
2023
2
x xC−+
. B.
4
4 2023x xC
−+
. C. . D. .
Câu 24: Cho hai tích phân
( )
5
2
d8
−
=
∫
fx x
và
( )
2
5
d3
−
=
∫
gx x
. Tính
( ) ( )
5
2
4 1d
−
= −−


∫
I f x gx x
A.
13
. B.
27
. C.
11−
. D.
3
.
Câu 25: (Khái niệm, tính chất, bảng nguyên hàm cơ bản). Cho
()Fx
là một nguyên hàm của hàm số
()fx
. Tìm
[ ]
2 ( ) 1dI fx x= +
∫
.
A.
2 ()I xF x x C= ++
. B.
2 ()I Fx x C= ++
.
C.
2 () 1I Fx C= ++
. D.
2 () 1
I xF x C= ++
.
Câu 26: Hàm số nào dưới đây có bảng biến thiên như sau:
4
1
4
xC+
3
4 2023−+x xC
4
A.
42
2.yx x= −
B.
3
3.yx x=−+
C.
42
2.yx x=−+
D.
3
3.yx x= −
Câu 27: Cho hàm số
( )
fx
có đạo hàm
( ) ( )( )
2023
' 1 4,
f x xx x x= − + ∀∈
. Số điểm cực trị của hàm
số đã cho là
A. 3. B. 4 . C. 2 . D. 1 .
Câu 28: Đặt
23
log 5, log 5ab= =
. Hãy biểu diễn
6
log 5
theo
a
và
b
.
A.
22
6
log 5
ab= +
. B.
6
log 5 ab= +
. C.
6
11
log 5
ab
= +
. D.
6
log 5
ab
ab
=
+
.
Câu 29: Gọi S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số:
3
3yx x= −
,
yx=
. Tính S.
A.
4S =
. B.
8
S =
. C.
2S =
. D.
0S =
.
Câu 30: Cho hình lăng trụ đứng
.ABC A B C
′′′
có tất cả các cạnh bằng nhau. Góc giữa hai đường thẳng
AB
′
và
CC
′
bằng
A.
30
o
. B.
90
o
. C.
60
o
. D.
45
o
.
Câu 31: Cho hàm số
( )
42
f x ax bx c=++
có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị
nguyên thuộc đoạn
[ ]
2;5−
của tham số
m
để phương trình
( )
fx m=
có đúng hai nghiệm phân biệt?
+
∞
∞
2
2
+
+
+
∞
∞
0
0
1
-1
y'
x
y
5
A.
1
. B.
6
. C.
7
. D.
5
.
Câu 32: Hàm số nào sau đây đồng biến trên
?
A.
42
yx x= −
. B.
3
yx x= −
. C.
1
2
x
y
x
−
=
+
. D.
3
yx x= +
.
Câu 33: Một đội thanh niên tình nguyện của trường gồm có học sinh nam và học sinh nữ. Chọn
ngẫu nhiên học sinh để cùng các giáo viên tham gia đo thân nhiệt cho học sinh khi đến trường. Xác
suất để chọn được học sinh trong đó số học sinh nam bằng số học sinh nữ bằng
A. . B. . C. . D. .
Câu 34: Nghiệm của phương trình
( ) ( )
33
log 2 1 1 log 1xx+=+ −
là
A.
4x =
. B.
2x = −
. C.
1x =
. D.
2x =
.
Câu 35: Gọi
1
z
là nghiệm phức có phần ảo âm của phương trình
2
2 50− +=zz
. Tọa độ điểm biểu diễn
số phức
1
74− i
z
trên mặt phẳng phức là
A.
( )
3; 2P
B.
( )
1; 2−N
C.
( )
3; 2−Q
D.
( )
1; 2M
Câu 36: Trong không gian
Oxyz
, phương trình mặt phẳng
( )
P
song song và cách đều hai đường thẳng
1
2
:
1 11
x yz
d
−
= =
−
và
2
12
:
21 1
xy z
d
−−
= =
−−
là
A.
( )
:2 2 1 0P yz− +=
. B.
( )
:2 2 1 0Pxz− +=
. C.
( )
:2 2 1 0Pxy− +=
. D.
( )
:2 2 1 0P yz− −=
Câu 37: Cho hình nón đỉnh
S
, đáy là đường tròn
( )
;5O
.Một mặt phẳng đi qua đỉnh của hình nón cắt
đường tròn đáy tại hai điểm
A
và
B
sao cho
8SA AB= =
. Tính khoảng cách từ
O
đến
( )
SAB
.
A.
22
. B.
3 13
4
. C.
32
7
. D.
13
2
.
Câu 38: Cho hình chóp
.S ABC
có
SA a=
và
SA
vuông góc với đáy. Biết đáy là tam giác vuông cân tại
A
và
2BC a=
. Tính khoảng cách từ
A
đến mặt phẳng
( )
SBC
.
A.
5
5
a
. B.
3
3
a
. C.
3a
.
D.
3
a
Câu 39: Có bao nhiêu giá trị nguyên của trong đoạn thỏa mãn bất phương trình sau
.
A. . B. . C. . D. .
Câu 40: Tập nghiệm của bất phương trình
21
1
(3 9)(3 ) 3 1 0
27
xx x+
− − −≤
chứa bao nhiêu số nguyên ?
A. 2. B. 3. C. 4. D. 5.
Câu 41: Cho hàm số
( )
fx
xác định trên
{ }
\ 1;1−
, thỏa mãn
( ) ( ) ( )
2
2
' ; 3 3 2ln2
1
fx f f
x
= −+ =
−
và
11
0
22
ff

−+ =


. Giá trị của biểu thức
( ) ( ) ( )
204Pf f f= −+ +
là:
A.
2ln2 ln5−
B.
6ln2 2ln3 ln5+−
C.
2ln2 2ln3 ln5+−
D.
6ln2 2ln5−
6
5
4
4
5
66
5
11
6
11
2
33
x
[ ]
0;2023
16 25 36 20 24 30
xxx xxx
++≤++
2023
3
2024
1
6
Câu 42:
Cho
( )
( )
2
2
2
2
2
1
ln
1
d
2 ln
ln
xxxx
a
Ix
bc
xx x
++ +
= = −
+
+
∫
với
a
,
b
,
c
là các số nguyên dương. Khẳng
định nào sau đây đúng ?
A.
26abc =
. B.
3abc =
. C.
11abc =
. D.
12abc =
.
Câu 43: Cho
( )
H
là hình phẳng giới hạn bởi parabol
2
3yx=
, cung tròn có phương trình
2
4yx= −
(với
02x≤≤
) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của
( )
H
là
A.
43
12
π
+
. B.
43
6
π
−
. C.
4 23 3
6
π
+−
. D.
53 2
3
π
−
.
Câu 44: Cho hai số phức
12
2 , 1 2.z iz i=+=−
Môđun của số phức
2022
1
2023
2
z
w
z
=
là
A.
5.w =
B.
3.w =
C.
3.w =
D.
5
.
5
=w
Câu 45: Cho hình trụ có thiết diện qua trục là một hình vuông. Thiết diện của hình trụ tạo bởi mặt phẳng
song song và cách trục một khoảng bằng
a
có diện tích bằng
2
83a
. Thể tích của khối trụ là
A.
3
16
3
a
π
. B.
2
16 a
π
. C.
3
16 a
π
. D.
3
32 a
π
.
Câu 46: Trong không gian Oxyz, cho điểm
( )
I 1; 2; 3 .−
Viết phương trình mặt cầu tâm I, cắt trục Ox tại
hai điểm A và B sao cho
AB 2 3.=
A.
( ) ( ) ( )
2 22
x 1 y 2 z 3 16.− ++ +− =
B.
( ) ( )
22
2
x1 y2 z3 2() 0.− ++ +− =
C.
( ) ( ) ( )
2 22
x 1 y 2 z 3 25.− ++ +− =
D.
( ) ( ) ( )
2 22
x 1 y 2 z 3 9.− ++ +− =
Câu 47: Cho hàm số liên tục trên và thỏa mãn Giá
trị của tích phân bằng
A. . B. . C. . D. .
Câu 48: Cho hàm số bậc ba
( )
y fx=
có đồ thị như hình vẽ, biết
( )
fx
đạt cực tiểu tại điểm
1x =
và
thỏa mãn
( )
1fx+


và
( )
1fx−


lần lượt chia hết cho
( )
2
1x −
và
( )
2
1x +
. Gọi
12
,SS
lần lượt là diện
tích như trong hình bên. Tính
21
28SS+
.
( )
fx
( )
4
2
0
tan . cos d 1,xf x x
π
=
∫
( )
2
2
ln
d 1.
ln
e
e
fx
x
xx
=
∫
( )
2
1
4
2
d=
∫
fx
Ix
x
2
3
4
7
A.
9
. B.
4
. C.
3
5
. D.
1
2
.
Câu 49: Cho hình chóp
.S ABC
có đáy là tam giác
ABC
vuông cân tại
C
và
SA
vuông góc với mặt
phẳng đáy. Cho
SC a=
, mặt phẳng
( )
SBC
tạo với mặt đáy một góc
α
. Thể tích khối chóp
.
S ABC
đạt
giá trị lớn nhất là
A.
3
16
a
. B.
3
3
27
a
. C.
3
3
48
a
. D.
3
2
24
a
.
Câu 50: Trong không gian Oxyz, cho mặt cầu
( ) ( ) ( ) ( )
2 22
: 2 3 1 16Sx y z− +− ++ =
và điểm
(
)
1; 1; 1 .A −−−
Xét các điểm M thuộc
( )
S
sao cho đường thẳng AM tiếp xúc với
( )
.S
M luôn thuộc một
mặt phẳng cố định có phương trình là
A.
3 4 20xy+ −=
. B.
3 4 20xy+ +=
.
C.
6 8 11 0xy+ +=
. D.
6 8 11 0
xy+ −=
.
………..Hết………
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG THPT PHÚ LÂM
ĐỀ CHÍNH THỨC
HƯỚNG DẪN CHẤM
Năm học: 2022 - 2023
Môn: TOÁN – Khối 12
Thời gian làm bài: 90 phút
Ngày kiểm tra: 31/03/2023
1
2
3
4
5
6
7
8
9
10
A
B
B
D
B
C
B
B
D
A
11
12
13
14
15
16
17
18
19
20
D
A
A
D
D
A
B
C
D
D
21
22
23
24
25
26
27
28
29
30
B
A
A
A
B
D
A
D
B
D
31
32
33
34
35
36
37
38
39
40
C
D
B
A
A
A
B
B
D
B
41
42
43
44
45
46
47
48
49
50
C
D
B
D
C
A
D
B
B
A
Câu 1: Cho số phức
126=−−zi
. Phần thực và phần ảo của số phức
z
là?
A. Phần thực bằng
1
−
và phần ảo bằng
26
. B. Phần thực bằng
1−
và phần ảo bằng
26i
.
C. Phần thực bằng
và phần ảo bằng
26
. D. Phần thực bằng
1−
và phần ảo bằng
26− i
.
Lời giải
Chọn A
126 126z iz i=−− ⇒ =−+
Vậy
z
có phần thực bằng
1−
và phần ảo bằng
26
.
Câu 2: Đạo hàm của hàm số
( )
2
2023
logy xx= +
là
A.
2
21+
+
x
xx
. B.
( )
2
21
.ln 2023
x
xx
+
+
. C.
2
1
+xx
D.
( )
2
1
.ln 2023xx+
.
Lời giải
Chọn B
Ta có
( )
( )
( ) ( )
2
2
2023
22
21
log
.ln 2023 .ln 2023
xx
x
y xx
xx xx
′
+
+
′

′
= += =

++
.
Câu 3: Đạo hàm của hàm số
8
x
y =
là
A.
8
ln 8
x
y
′
=
. B.
8 ln 8
x
y
′
=
. C.
8 ln 8
x
yx
′
=
. D.
1
8
x
yx
−
′
=
.
Lời giải
Chọn B
Ta có
( )
8 8 ln 8
xx
y
′
′
= =
.
Câu 4: Tìm tập nghiệm
S
của bất phương trình
1
1
50
5
x+
−>
.
A.
( )
;2S = −∞ −
. B.
( )
1;S = +∞
. C.
( )
1;S = − +∞
. D.
( )
2;S = − +∞
.
Lời giải
Chọn D
Bất phương trình tương đương
11
5 5 1 1 2.
x
xx
+−
> ⇔ + >− ⇔ >−
Câu 5: Cho cấp số cộng có số hạng đầu và công sai . Giá trị của bằng
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có : .
Câu 6: Trong không gian , cho mặt phẳng . Vectơ nào sau đây là vectơ pháp
tuyến của mặt phẳng ?
A. . B. . C. . D.
.
Lời giải
Chọn C
Từ phương trình mặt phẳng ta có vectơ pháp tuyến của là .
Câu 7: Số giao điểm của đồ thị
32
( ): 3 2 1Cyx x x=− ++
và đường thẳng
1y =
là
A. 0. B. 3. C. 1. D. 2.
Lời giải
Chọn B
Phương trình hoành độ giao điểm:
32 32
3211 320xx x xx x−++=⇔−+=
0
1
2
x
x
x
=
⇔=
=
.
Vậy có ba giao điểm.
Câu 8: Cho hàm số
( )
fx
có đạo hàm trên đoạn
[ 1; 2]−
và
( ) ( )
1 2023, 2 1.ff−= =−
Tích phân
( )
2
1
dfxx
−
′
∫
bằng:
A.
2024.
B.
2024.−
C.
1.
D.
2022.
Lời giải
( )
n
u
1
11u =
4d =
5
u
2816
27
15
26−
1
51
11
4 27
4
u
uu d
d
=
⇒=+ =
=
Oxyz
( )
:3 2 1 0P xy z+ − +=
( )
P
( )
4
3; 2;1n = −
( )
3
2;1; 3n = −
( )
1
3;1; 2n = −
( )
2
1; 2;1n = −
( )
P
( )
P
( )
1
3;1; 2n = −
Chọn B
Ta có:
( ) ( ) ( ) ( )
2
1
2
d 2 1 1 2023 2024
1
f x x fx f f
−
′
= = − − =−− =−
−
∫
.
Câu 9: Hàm số nào dưới đây có bảng biến thiên như sau:
A.
42
2.yx x= −
B.
3
3.
yx x=−+
C.
42
2.yx x=−+
D.
3
3.yx x= −
Lời giải
Chọn D
Hàm số có bảng biến thiên như trên, trong 4 đáp án đã cho phải là hàm bậc ba với
a 0.>
Câu 10: Trong không gian
Oxyz
, mặt cầu
( ) ( ) ( ) ( )
2 22
: 1 2 3 25Sx y z− +− +− =
có tọa độ tâm
I
và
bán kính
R
là
A.
( )
1; 2; 3 , 5IR=
. B.
( )
1; 2; 3 , 5IR−=
. C.
( )
1; 2; 3 , 25IR−=
. D.
( )
1; 2; 3 , 25IR=
.
Lời giải
Chọn A
Ta có, tọa độ tâm:
(
)
1; 2; 3
I
Bán kính:
25 5R = =
Câu 11: Cho điểm
( )
1,4,2
M −−
và mặt phẳng
( )
: 5 14 0Pxy z++ − =
. Tính khoảng cách từ
M
đến
()P
.
A.
23
B.
43
C.
63
D.
33
Lời giải
Chọn D
( )
( )
( )
( )
( )
2
22
1 4 5. 2 14
, 33
11 2
dM P
+−+ −−
= =
+ +−
Câu 12: Cho số phức
z
thỏa mãn
( )
1 14 2iz i+=−
. Tổng phần thực và phần ảo của
z
bằng
A.
14.
B.
2.
C.
2.−
D.
14.−
Lời giải
Chọn A
+
∞
∞
2
2
+
+
+
∞
∞
0
0
1
-1
y'
x
y
Ta có:
( )
14 2
1 14 2 6 8 6 8 .
1
i
iz i z z i z i
i
−
+ = − ⇔= ⇔=−⇒=+
+
Suy ra,
z
có phần thực bằng 6 và phần ảo bằng 8.
Do đó tổng phần thực và phần ảo của
z
bằng 14.
Câu 13: Thể tích của khối lăng trụ có diện tích đáy
2
2Sa=
, chiều cao
6ha=
là:
A.
3
12a
. B.
3
4a
. C.
3
6a
. D.
3
36a
.
Lời giải
Chọn A
3
. 12= =V Sh a
Câu 14: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA a=
và
SA
vuông góc với
mặt phẳng đáy. Thể tích khối chóp
.S ABCD
bằng
A.
3
6
a
. B.
3
2
3
a
. C.
3
a
. D.
3
3
a
.
Lời giải
Chọn D
Thể tích khối chóp
.S ABCD
là
3
2
11
..
33 3
a
V Bh a a= = =
.
Câu 15: Phương trình tiếp tuyến của đường cong
32
32yx x=+−
tại điểm có hoành độ
0
1x =
là
A.
97yx= +
. B.
97yx=−−
. C.
97yx=−+
. D.
97yx= −
.
Lời giải
Xét hàm
32 2
( ) 3 2 '( ) 3 6 '(1) 9.y fx x x f x x x f= = + −⇒ = + ⇒ =
Ta có
( )
00 0
1 2 1; 2xy M=⇒=⇒
.
Phương trình tiếp tuyến tại điểm
( )
0
1; 2M
có dạng:
( ) ( )
000
'( ) 2 9 1 9 7y y fx xx y x y x− = − ⇔−= − ⇔ = −
.
Câu 16 : Trong mặt phẳng , điểm trong hình vẽ bên là điểm biểu diễn số phức . Số phức là
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có .
Câu 17: Cho hình trụ có bán kính đáy
r
và độ dài đường sinh
l
. Diện tích xung quanh
xq
S
của hình trụ
đã cho được tính theo công thức nào dưới đây?
A.
4
xq
S rl
π
=
. B.
2
xq
S rl
π
=
. C.
3
xq
S rl
π
=
. D.
xq
S rl
π
=
.
Oxy
M
z
z
2 i−−
12i−
2 i−+
12i+
22z iz i=−+⇒ =−−
Lời giải
Chọn B
Công thức tính diện tích xung quanh của hình trụ có bán kính đáy
r
và độ dài đường sinh
l
là
2
xq
S rl
π
=
.
Câu 18: Trong không gian
Oxyz
, đường thẳng
134
:
13 2
xyz
d
−−+
= =
−
đi qua điểm nào dưới đây?
A.
(1; 3 2)
Q −
. B.
( 1; 3; 4)M −−
. C.
(1; 3; 4)
C
−
. D.
( 1; 3; 2)N −−
.
Lời giải
Chọn C
Thay tọa độ điểm
Q
vào đường thẳng
11 33 2 4
:
13 2
d
− − −+
= =
−
(sai) nên loại
Thay tọa độ điểm
M
vào đường thẳng
11 33 4 4
:
132
d
−− −− +
= =
−
(sai) nên loại
Thay tọa độ điểm
C
vào đường thẳng
11 33 4 4
:
13 2
d
− − −+
= =
−
(đúng) nên chọn
Thay tọa độ điểm
N
vào đường thẳng
11 33 2 4
:
132
d
−− −− +
= =
−
(sai) nên loại
Câu 19: Cho hàm số
42
y ax bx c=++
,
( )
,,
abc R∈
có đồ thị là đường cong như hình bên. Điểm cực tiểu
của hàm số đã cho là:
A.
1x = −
. B.
2x =
. C.
1x =
. D.
0x =
.
Lời giải
Chọn D
Nhìn vào đồ thị hàm số ta thấy hàm số có điểm cực tiểu là
0x =
.
Câu 20: Tiệm cận ngang của đồ thị hàm số
21
24
x
y
x
−
=
+
là đường thẳng có phương trình:
A.
2y
= −
. B.
2x = −
. C.
1
x =
. D.
1y =
.
Lời giải
Chọn D
Có:
1
2
21
lim lim lim 1
4
24
2
xx x
x
x
y
x
x
→+∞ →+∞ →+∞
−
−
= = =
+
+
và:
1
2
21
lim lim lim 1
4
24
2
xx x
x
x
y
x
x
→−∞ →−∞ →−∞
−
−
= = =
+
+
Vậy đồ thị hàm số
21
24
x
y
x
−
=
+
có tiệm cận ngang là đường thẳng có phương trình:
1y =
.
Câu 21: Tập nghiệm của bất phương trình
2
13
3 27
x −
<
là
A.
( )
4;+∞
. B.
( )
4;4−
. C.
( )
;4−∞
. D.
( )
0;4
.
Lời giải
Chọn B
Ta có:
22
13 13 3 2 2
3 27 3 3 13 3 16 4 4 4
xx
x xx x
−−
< ⇔ < ⇔ − <⇔ < ⇔ <⇔−<<
.
Tập nghiệm của bất phương trình đã cho là
( )
4;4S = −
.
Kết luận:
( )
4;4S = −
.
Câu 22: Có bao nhiêu số có năm chữ số khác nhau được tạo thành từ các chữ số 1,2,3,4,5,6?
A.
5
6
A
B.
6
P
. C.
5
6
C
. D.
5
P
.
Lời giải.
Chọn A
Số tự nhiên gồm năm chữ số khác nhau được tạo thành từ các chữ số 1,2,3,4,5,6 là một chỉnh
hợp chập 5 của 6 phần tử. Vậy có
5
6
A
số cần tìm.
Câu 23: Nguyên hàm của hàm số
( )
3
2 2023fx x= −
là:
A.
4
1
2023
2
x xC−+
. B.
4
4 2023x xC−+
. C. . D. .
Lời giải
Chọn A
.
Câu 24: Cho hai tích phân
( )
5
2
d8
−
=
∫
fx x
và
( )
2
5
d3
−
=
∫
gx x
. Tính
( ) ( )
5
2
4 1d
−
= −−


∫
I f x gx x
A.
13
. B.
27
. C.
11−
. D.
3
.
Lời giải
Chọn A
4
1
4
xC+
3
4 2023−+x xC
( )
3
2 2023 d−
∫
xx
4
2. 2023
4
=−+
x
xC
4
2023
2
=−+
x
xC
(
)
(
)
5
2
4 1d
−
= −−


∫
I f x gx x
( ) ( )
55 5
22 2
d4dd
−− −
=−−
∫∫ ∫
f x x gx x x
( ) ( )
5 55
2 22
d4 d d
− −−
=−−
∫ ∫∫
f x x gx x x
(
)
(
)
5 25
2 52
d4 d d
−
−−
=+−
∫ ∫∫
f x x gx x x
5
8 4.3
2
=+−
−
x
8 4.3 7=+−
13=
.
Câu 25: (Khái niệm, tính chất, bảng nguyên hàm cơ bản). Cho
()Fx
là một nguyên hàm của hàm số
()
fx
. Tìm
[
]
2 ( ) 1dI fx x= +
∫
.
A.
2 ()I xF x x C= ++
. B.
2 ()
I Fx x C
= ++
.
C.
2 () 1I Fx C= ++
. D.
2 () 1I xF x C= ++
.
Lời giải
Chọn B
Câu 26: Hàm số nào dưới đây có bảng biến thiên như sau:
A.
42
2.yx x= −
B.
3
3.yx x=−+
C.
42
2.yx x=−+
D.
3
3.yx x= −
Lời giải
Chọn D
Hàm số có bảng biến thiên như trên, trong 4 đáp án đã cho phải là hàm bậc ba với
a 0.>
Câu 27: Cho hàm số
( )
fx
có đạo hàm
( ) ( )( )
2023
' 1 4,f x xx x x= − + ∀∈
. Số điểm cực trị của hàm
số đã cho là
A. 3. B. 4 . C. 2 . D. 1 .
Lời giải
Chọn A
Câu 28: Đặt
23
log 5, log 5ab
= =
. Hãy biểu diễn
6
log 5
theo
a
và
b
.
A.
22
6
log 5 ab= +
. B.
6
log 5 ab= +
. C.
6
11
log 5
ab
= +
. D.
6
log 5
ab
ab
=
+
.
Lời giải
Chọn D
25
56
35
1
log 5 log 2
11
log 6 log 5
1
log 5 log 3
a
a b ab
a
a b ab a b
b
b
=⇒=
+
⇒ =+= ⇒ =
+
=⇒=
+
∞
∞
2
2
+
+
+
∞
∞
0
0
1
-1
y'
x
y
Câu 29: Gọi S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số:
3
3yx x= −
,
yx=
. Tính S.
A.
4
S =
. B.
8S
=
. C.
2S =
. D.
0S =
.
Lời giải
Chọn B
Phương trình hoành độ giao điểm của hai đồ thị là
33
2
3 40
0
x
x xx x x
x
= ±
−=⇔−=⇔
=
Vậy
( ) ( )
02
33
20
4 4 448S x x dx x x dx
−
= − + − =+=
∫∫
.
Câu 30: Cho hình lăng trụ đứng
.ABC A B C
′′′
có tất cả các cạnh bằng nhau. Góc giữa hai đường thẳng
AB
′
và
CC
′
bằng
A.
30
o
. B.
90
o
. C.
60
o
. D.
45
o
.
Lời giải
Chọn D
Ta có:
(;)(;) 45
o
AB CC AB BB AB B
′′ ′′ ′
= = =
.
Câu 31: Cho hàm số
( )
42
f x ax bx c=++
có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị
nguyên thuộc đoạn
[ ]
2;5−
của tham số
m
để phương trình
( )
fx m=
có đúng hai nghiệm phân biệt?
A.
1
. B.
6
. C.
7
. D.
5
.
Lời giải
Chọn C
Số nghiệm của phương trình
( )
fx m=
chính là số giao điểm của đồ thị hàm số
( )
y fx=
và
đường thẳng
//
:d y m d Ox

= ≡


Dựa vào đồ thị ta có phương trình
(
)
fx m=
có đúng hai nghiệm phân biệt khi và chỉ khi
2
1.
m
m
= −
>−
Mặt khác
[ ]
{ }
2;5 2;0;1; 2;3; 4;5mm∈− ⇒ ∈−
.
Suy ra có 7 giá trị thỏa mãn yêu cầu.
Câu 32: Hàm số nào sau đây đồng biến trên
?
A.
42
yx x= −
. B.
3
yx x= −
. C.
1
2
x
y
x
−
=
+
. D.
3
yx x= +
.
Lời giải
Chọn D
Xét
3
yx x= +
có
2
3 1 0;yx x
′
= +> ∀∈
. Vậy hàm số trên đồng biến trên
.
Câu 33: Một đội thanh niên tình nguyện của trường gồm có học sinh nam và học sinh nữ. Chọn
ngẫu nhiên học sinh để cùng các giáo viên tham gia đo thân nhiệt cho học sinh khi đến trường. Xác
suất để chọn được học sinh trong đó số học sinh nam bằng số học sinh nữ bằng
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có không gian mẫu .
Gọi là biến cố: “Chọn được học sinh trong đó số học sinh nam bằng số học sinh nữ”
.
Xác suất của biến cố A là:
6
5
4
4
5
66
5
11
6
11
2
33
( )
4
11
nCΩ=
A
4
( )
22
56
.nA CC⇒=
( )
( )
( )
22
56
4
11
.
5
.
11
nA
CC
PA
nC
= = =
Ω
Câu 34: Nghiệm của phương trình
( ) ( )
33
log 2 1 1 log 1xx+=+ −
là
A.
4x =
. B.
2x = −
. C.
1
x =
. D.
2x =
.
Lời giải
Chọn A
Điều kiện:
2 10
1
10
x
x
x
+>
⇔>
−>
.
Ta có:
(
) (
)
33
log 2 1 1 log 1xx+=+ −
(
) ( )
33
log 2 1 log 3 1xx⇔ += ⋅−


2 13 3xx⇔ += −
4
x⇔=
(nhận).
Câu 35: Gọi
1
z
là nghiệm phức có phần ảo âm của phương trình
2
2 50− +=zz
. Tọa độ điểm biểu diễn
số phức
1
74− i
z
trên mặt phẳng phức là
A.
( )
3; 2P
B.
( )
1; 2−N
C.
( )
3; 2−Q
D.
(
)
1; 2
M
Lời giải
Chọn A
Ta có
2
12
2 50
12
= +
− +=⇔
= −
zi
zz
zi
Theo yêu cầu của bài toán ta chọn
1
12= −zi
. Khi đó:
( )( )
22
1
74 12
74 74
32
12 1 2
−+
−−
= = = +
−+
ii
ii
i
zi
Vậy điểm biểu diễn của số phức là
( )
3; 2P
Câu 36: Trong không gian
Oxyz
, phương trình mặt phẳng
( )
P
song song và cách đều hai đường thẳng
1
2
:
1 11
x yz
d
−
= =
−
và
2
12
:
21 1
xy z
d
−−
= =
−−
là
A.
( )
:2 2 1 0P yz− +=
. B.
( )
:2 2 1 0Pxz− +=
. C.
( )
:2 2 1 0Pxy− +=
. D.
( )
:2 2 1 0P yz− −=
.
Lời giải
Chọn A
Ta có
( )
( )
1
1
qua 2; 0; 0
:
vtcp 1;1;1
A
d
u
= −

và
( )
( )
2
2
qua 0;1;2
:
vtcp 2;1;1
B
d
u
= −−

.
Mặt phẳng
( )
P
song song và cách đều hai đường thẳng
1
2
:
1 11
x yz
d
−
= =
−
và
2
12
:
21 1
xy z
d
−−
= =
−−
nên:
( )
P
có một véc tơ pháp tuyến là
( )
12
, 0;1; 1n uu

= = −


suy ra
( )
:0P yzD−+ =
Và
( )
(
)
( )
( )
,,dAP dB P=
1DD⇔=−
1
2
D⇔=
Vậy
( )
:2 2 1 0P yz− +=
.
Câu 37: Cho hình nón đỉnh
S
, đáy là đường tròn
( )
;5O
.Một mặt phẳng đi qua đỉnh của hình nón cắt
đường tròn đáy tại hai điểm
A
và
B
sao cho
8
SA AB
= =
. Tính khoảng cách từ
O
đến
( )
SAB
.
A.
22
. B.
3 13
4
. C.
32
7
. D.
13
2
.
Lời giải
Chọn B
Gọi
I
là trung điểm
AB
.
Ta có
( ) ( ) ( )
AB SO
AB SOI SAB SOI
AB OI
⊥
⇒⊥ ⇒ ⊥
⊥
.
Trong
( )
SOI
, kẻ
OH SI
⊥
thì
( )
OH SAB⊥
.
( )
( )
;d O SAB OH⇒=
.
Ta có:
2
22 2
8.5
5 39
5
SO SA OA

= − = −=


.
Ta có:
2
22 2
4.5
53
5
OI OA AI

= −=− =


.
Tam giác vuông
SOI
có:
22 2
1 1 1 3 13
4
OH
OH OI SO
=+ ⇒=
.
Vậy
( )
( )
3 13
;
4
d O SAB OH= =
.
Câu 38: Cho hình chóp
.S ABC
có
SA a=
và
SA
vuông góc với đáy. Biết đáy là tam giác vuông cân tại
A
và
2BC a=
. Tính khoảng cách từ
A
đến mặt phẳng
( )
SBC
.
A.
5
5
a
. B.
3
3
a
. C.
3a
.
D.
3
a
Lời giải
Chọn B
Gọi
E
là trung điểm của
BC
12
22
a
AE BC⇒= =
Kẻ
AH SE⊥
( )
AH SBC⇒⊥
AH⇒
là khoảng cách từ
A
đến mặt phẳng
( )
SBC
.
Có
2 2 2222
1 1 1 21 3 3
3
a
AH
AH AE SA a a a
= + =+=⇒ =
.
Câu 39: Có bao nhiêu giá trị nguyên của trong đoạn thỏa mãn bất phương trình sau
.
A. . B. . C. . D. .
Lời giải
Chọn D
Ta có
.
Vậy có 1 giá trị nguyên của
trong đoạn thỏa mãn bất phương trình.
Câu 40: Tập nghiệm của bất phương trình
21
1
(3 9)(3 ) 3 1 0
27
xx x+
− − −≤
chứa bao nhiêu số nguyên ?
A. 2. B. 3. C. 4. D. 5.
Lời giải
Chọn B
Điều kiện
11
3 10 3 1 1
xx
x
++
− ≥ ⇔ ≥ ⇔ ≥−
.
S
A
C
B
E
H
x
[ ]
0;2023
16 25 36 20 24 30
xxx xxx
++≤++
2023
3
2024
1
222
16 25 36 20 24 30 4 5 6 4 .5 4 .6 5 .6
x x x x x x x x x xx xx xx
+ + ≤ + + ⇔++≤ + +
( ) ( ) ( ) ( )
222
2 4 5 6 2.4 .5 2.4 .6 2.5 .6 0
x x x xx xx xx

⇔ ++ − + + ≤


( ) ( ) ( )
222
45 46 56 0
xx xx xx
⇔− +− +− ≤
[ ]
x
xx
x
xx
xx
x
4
1
5
450
4
4 6 0 1 x 0 0;2023
6
56 0
5
1
6

=


−=

⇔ −
=⇔ =⇔=∈




−=

=


x
[ ]
0;2023
Ta có
1x = −
là một nghiệm của bất phương trình.
Với
1
x
>−
, bất phương trình tương đương với
2
1
(3 9)(3 ) 0
27
xx
− −≤
.
Đặt
30
x
t = >
, ta có
2
1
( 9)( ) 0
27
tt−−≤
1
( 3)( 3)( ) 0
27
ttt⇔− + − ≤
3
1
3
27
t
t
≤−
⇔
≤≤
. Kết
hợp điều kiện
30
x
t = >
ta được nghiệm
1
3
27
t≤≤
1
33 3 1
27
x
x
⇔ ≤ ≤ ⇔− ≤ ≤
. Kết hợp
điều kiện
1x >−
ta được
11x−< ≤
suy ra trường hợp này bất phương trình có 2 nghiệm
nguyên.
Vậy bất phương trình đã cho có tất cả 3 nghiệm nguyên.
Câu 41: Cho hàm số
( )
fx
xác định trên
{ }
\ 1;1−
, thỏa mãn
( ) ( )
( )
2
2
' ; 3 3 2ln2
1
fx f f
x
= −+ =
−
và
11
0
22
ff

−+ =


. Giá trị của biểu thức
( )
( )
(
)
204
Pf f f= −+ +
là:
A.
2ln2 ln5−
B.
6ln2 2ln3 ln5+−
C.
2ln2 2ln3 ln5+−
D.
6ln2 2ln5−
Lời giải
Chọn C
( ) ( )
2
2 11 1
' ln
1 11 1
x
f x f x dx dx dx C
x xx x
−

= = =−=+

− −+ +

∫∫∫
Hay
( )
1
2
3
1
ln 1
1
11
ln ln 1 1
11
1
ln 1
1
x
C khi x
x
xx
f x C C khi x
xx
x
C kh i x
x
−

+>

+

−−
= + = + −< <
++
−

+ <−

+

Theo bài ra, ta có:
( ) ( )
13
2
3 3 2ln2
2ln2
11
0
0
22
ff
CC
C
ff
−+ =
+=
⇔


=
−+ =


Do đó
( )
( ) ( )
32 1
3
2 0 4 ln 3 ln 2 ln 2 2 ln 3 ln 5
5
f f f CC C−+ + = + + + + = + −
.
Câu 42:
Cho
( )
( )
2
2
2
2
2
1
ln
1
d
2 ln
ln
xxxx
a
Ix
bc
xx x
++ +
= = −
+
+
∫
với
a
,
b
,
c
là các số nguyên dương. Khẳng
định nào sau đây đúng ?
A.
26abc =
. B.
3abc =
. C.
11abc =
. D.
12abc =
.
Lời giải
Chọn D
Ta có
( ) ( )
( )
2
2
2
2
1
ln 1
d
ln
x x xx
Ix
xx x
+ ++
=
+
∫
( )
22
2
2
11
11
dd
ln
x
xx
x
xx x
+
= +
+
∫∫
( )
2
2
1
11
d
2
ln
x
x
xx x
+
= +
+
∫
.
Đặt
1
ln d d
x
tx x t x
x
+
=+ ⇒=
. Đổi cận
11xt=⇒=
và
2 2 ln 2xt= ⇒=+
.
Do đó
( )
2
2
1
11
d
2
ln
x
Ix
xx x
+
= +
+
∫
2 ln 2
2
1
11
d
2
t
t
+
= +
∫
2 ln 2
1
11
2 t
+
= = −
11
1
2 2 ln 2
= +−
+
31
2 2 ln 2
= −
+
.
Vậy
3.2.2 12abc = =
.
Câu 43: Cho
( )
H
là hình phẳng giới hạn bởi parabol
2
3yx=
, cung tròn có phương trình
2
4yx= −
(với
02x≤≤
) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của
( )
H
là
A.
43
12
π
+
. B.
43
6
π
−
. C.
4 23 3
6
π
+−
. D.
53 2
3
π
−
.
Lời giải
Chọn B
Phương trình hoành độ giao điểm của parabol
2
3yx=
và cung tròn
2
4yx= −
(với
02x≤≤
) lả
2 2 24
4 34 3 1x x xxx− = ⇔− = ⇔=
.
Diện tích của
(
)
H
là
12
1
2 23
0
01
33
34
33
S x dx x dx x I I= + − = += +
∫∫
với
2
2
1
4I x dx= −
∫
.
Đặt
2sinxt=
,
; 2cos .
22
t dx t dt
ππ

∈− ⇒ =


Đổi cận
1
6
xt
π
=⇒=
,
2
2
xt
π
= ⇒=
.
(
) ( )
2
2 22
22
6
6 66
4 4sin .2cos . 4cos . 2 1 cos 2 . 2 sin 2I t t dt t dt t dt x t
π
π ππ
π
π ππ
=− = =+=+
∫ ∫∫
23
32
π
= −
Vậy
3 32 34 3
3 332 6
SI
ππ
−
= += + − =
Câu 44: Cho hai số phức
12
2 , 1 2.z iz i
=+=−
Môđun của số phức
2022
1
2023
2
z
w
z
=
là
A.
5.w =
B.
3.w =
C.
3.w =
D.
5
.
5
=
w
Lời giải
Chọn D
1
2
2
12
zi
i
zi
+
= =
−
( )
( )
2022
2022
1010
1010
2022 2
11
2023
2 22
1 1 12 12 12
w . . . 1.
12 55 55 55
12 5
w
55 5

 
= = = = +=− +=+

 
−
 

=+=
zz
i i i ii
z zz i
i
Câu 45: Cho hình trụ có thiết diện qua trục là một hình vuông. Thiết diện của hình trụ tạo bởi mặt phẳng
song song và cách trục một khoảng bằng
a
có diện tích bằng
2
83a
. Thể tích của khối trụ là
A.
3
16
3
a
π
. B.
2
16 a
π
. C.
3
16 a
π
. D.
3
32 a
π
.
Lời giải
Chọn C
Gọi
R
là bán kính đáy hình trụ, do thiết diện qua trục là một hình vuông nên
2Rl =
.
Thiết diện của hình trụ tạo bởi mặt phẳng song song và cách trục một khoảng bằng
a
là hình
chữ nhật
DABC
khi đó
OI a=
với
I
là trung điểm
BC
ta có
22 22
2IC Ra BC Ra= −⇒ = −
.
Diện tích hình chữ nhật là
22 2
D
. 4 83
ABC
S AB BC R R a a= = −=
.
4 22 2
12 0R Ra a⇔− − =
( )( )
2 22 2
4 30R aR a⇔− + =
2Ra⇔=
từ đó
24hl R a= = =
.
Thể tích khối trụ là
23
16V Rh a
ππ
= =
.
Câu 46: Trong không gian Oxyz, cho điểm
( )
I 1; 2; 3 .−
Viết phương trình mặt cầu tâm I, cắt trục Ox tại
hai điểm A và B sao cho
AB 2 3.=
A.
( ) ( ) ( )
2 22
x 1 y 2 z 3 16.− ++ +− =
B.
( ) ( )
22
2
x1 y2 z3 2() 0.− ++ +− =
C.
( ) ( ) ( )
2 22
x 1 y 2 z 3 25.− ++ +− =
D.
( ) ( ) ( )
2 22
x 1 y 2 z 3 9.− ++ +− =
Lời giải
Chọn A
Gọi H là trung điểm
AB IH AB⇒⊥
tại
( )
( )
( )
I;Ox
I; AB
H IH d d⇒= =
Lấy
( )
( )
I,Ox
IM,i
M 2; 0;0 Ox IH d 3.
i


∈⇒= = =

Bán kính mặt cầu cần tìm là
22
R IA IH HA 4.== +=
Vậy phương trình mặt cầu cần tìm là
( ) ( ) ( )
2 22
x 1 y 2 z 3 16.− ++ +− =
Câu 47: Cho hàm số liên tục trên và thỏa mãn Giá
trị của tích phân bằng
A. . B. . C. . D. .
Lời giải
Chọn D
● Xét . Đặt
Suy ra
( )
fx
( )
4
2
0
tan . cos d 1,xf x x
π
=
∫
( )
2
2
ln
d 1.
ln
e
e
fx
x
xx
=
∫
( )
2
1
4
2
d=
∫
fx
Ix
x
2
3
4
( )
4
2
0
tan . cos d 1A xf x x
π
= =
∫
2
cos .tx=
2
d
d 2sin cos d 2cos tan d 2 .tan d tan d .
2
t
t x xx x xx t xx xx
t
= − = − = − → = −
Đổi cận:
Khi đó
● Xét Đặt
Suy ra
Đổi cận:
Khi đó
● Xét tích phân cần tính
Đặt suy ra Đổi cận:
Khi đó
Câu 48: Cho hàm số bậc ba
( )
y fx=
có đồ thị như hình vẽ, biết
( )
fx
đạt cực tiểu tại điểm
1x =
và
thỏa mãn
( )
1fx+


và
( )
1fx−


lần lượt chia hết cho
( )
2
1x −
và
( )
2
1x +
. Gọi
12
,SS
lần lượt là diện
tích như trong hình bên. Tính
21
28SS+
.
A.
9
. B.
4
. C.
3
5
. D.
1
2
.
Lời giải
01
.
1
42
xt
xt
π
=⇒=
= ⇒=
( ) ( )
( )
( )
1
111
2
111
1
222
111
1 d d d d 2.
222
ft ft fx fx
A t t xx
t t xx
==− = = ⇒=
∫∫∫∫
( )
2
2
ln
d 1.
ln
e
e
fx
Bx
xx
= =
∫
2
ln .ux=
2
2ln 2ln 2 d du
dd dd .
ln ln ln 2
x xu x
ux xx
x xx xx xx u
= = = ⇒=
2
1
.
4
xe u
xe u
=⇒=
= ⇒=
( )
( ) ( )
4 44
1 11
11
1 d d d 2.
22
fu fx fx
B u xx
u xx
== = ⇒=
∫ ∫∫
( )
2
1
2
2
d.
fx
Ix
x
=
∫
2,vx=
1
dd
2
.
2
xv
v
x
=
=
11
.
42
24
xv
xv
= ⇒=
=⇒=
( ) ( )
( ) ( )
44 1 4
11 1
1
22 2
dddd224.
fv fx fx fx
Ivxxx
vx xx
= = = + =+=
∫∫ ∫∫
Chọn B
Đặt
( )
32
f x ax bx cx d= + ++
theo giả thiết có
( ) ( ) ( )
( ) ( ) ( )
2
2
11
11
f x ax x m
f x ax x n
+= − +
−= + +
Do đó
(
)
( )
(
)
(
)
(
)
3
1
1 10
10
2
1 10
10 0
13
00
03
22
2
10
32 0
0
a
f
abcd
f
abcd b
fx x x
f
d
c
f
a bc
d
=
+=
+++ +=
− −=
−+−+ −= =

⇔ ⇔ ⇒=−

=
=

= −

′
=
+ +=

=
Ta có
(
)
3
0
13
0
22
3
x
fx x x
x
=
= −=⇔
= ±
1
S
là diện tích giới hạn bởi đồ thị
3
13
22
yx x= −
,
1y = −
,
0, 1xx= =
1
3
1
0
13 3
1
22 8
S xx⇒ = − +=
∫
( )
1
2
S
là diện tích giới hạn bởi đồ thị
2
13
32
yx x= −
,
0, 1, 3y xx= = =
3
3
2
1
131
222
S xx⇒= − =
∫
( )
2
Từ
( ) ( )
1,2
21
13
2 8 2. 8. 4
28
SS⇒ += +=
.
Câu 49: Cho hình chóp
.S ABC
có đáy là tam giác
ABC
vuông cân tại
C
và
SA
vuông góc
với mặt phẳng đáy. Cho
SC a
=
, mặt phẳng
( )
SBC
tạo với mặt đáy một góc
α
. Thể tích khối
chóp
.S ABC
đạt giá trị lớn nhất là
A.
3
16
a
. B.
3
3
27
a
. C.
3
3
48
a
. D.
3
2
24
a
.
Lời giải
Chọn B
Ta có
( ) ( )
( )
( )
,,SBC ABC SC AC SCA
α
= = =
Xét
SAC∆
vuông tại
A
có
.sin sin
.cos cos
SA SC a
AC SC a
αα
αα
= =
= =
2
.
1 11
.. .
3 32
S ABC ABC
V S SA AC SA
∆

⇒= =


( )
3
2
2
1
. cos . sin cos .sin .
66
a
aa
α α αα
= =
.S ABC
V
đạt giá trị lớn nhất khi và chỉ khi biểu thức
( )
22
cos .sin . 1 sin .sinP
αα α α
= = −
đạt giá trị lớn nhất.
Đặt
sint
α
=
. Vì
0 90
α
<<°
nên
0 sin 1
α
<<
01t⇒ <<
Ta có
(
)
(
)
23
1P ft t t t t
= = − =−+
xác định và liên tục trên
( )
0;1
.
( ) (
)
=
′′
=− +⇒ = ⇔
= −
2
3
(
3
31 0
3
(loai)
nha )
3
nt
ft t ft
t
Bảng biến thiên:
Dựa vào bảng biến thiên, ta có
( )
(
)
0;1
23
max
9
ft=
khi
3
3
t =
.
Vậy
33 3
. max
23 3
max . .
6 6 9 27
S ABC
aa a
VP= = =
khi và chỉ khi
3
sin
3
α
=
.
Câu 50: Trong không gian Oxyz, cho mặt cầu
( ) ( ) ( ) ( )
2 22
: 2 3 1 16Sx y z− +− ++ =
và điểm
( )
1; 1; 1 .A −−−
Xét các điểm M thuộc
( )
S
sao cho đường thẳng AM tiếp xúc với
( )
.S
M luôn thuộc một
mặt phẳng cố định có phương trình là
A.
3 4 20xy+ −=
. B.
3 4 20xy+ +=
.
C.
6 8 11 0xy+ +=
. D.
6 8 11 0xy+ −=
.
Lời giải
Chọn A
(
)
S
có tâm
( )
2; 3; 1 ;I −
bán kính
4R =
( ) ( )
1;1;1 3;4;0A IA−−− ⇒ =−−

, tính được
5IA =
.
Mặt phẳng cố định đi qua điểm H là hình chiếu của M xuống IA và nhận
( )
3; 4; 0IA =−−

làm
vectơ pháp tuyến.
Do hai tam giác MHI và AMI đồng dạng nên tính được
2
2
16
.
5
IM
IM IH IA IH
IA
= ⇒= =
, từ đó
tính được
16
25
IH IA=
 
tìm được
2 11
; ;1
25 25
H

−


Mặt phẳng cần tìm có phương trình là:
2 11
3 4 0 3 4 2 0.
25 25
x y xy

−−−−=⇔+−=


| 1/27
| | Tải xuống

Có thể bạn quan tâm:

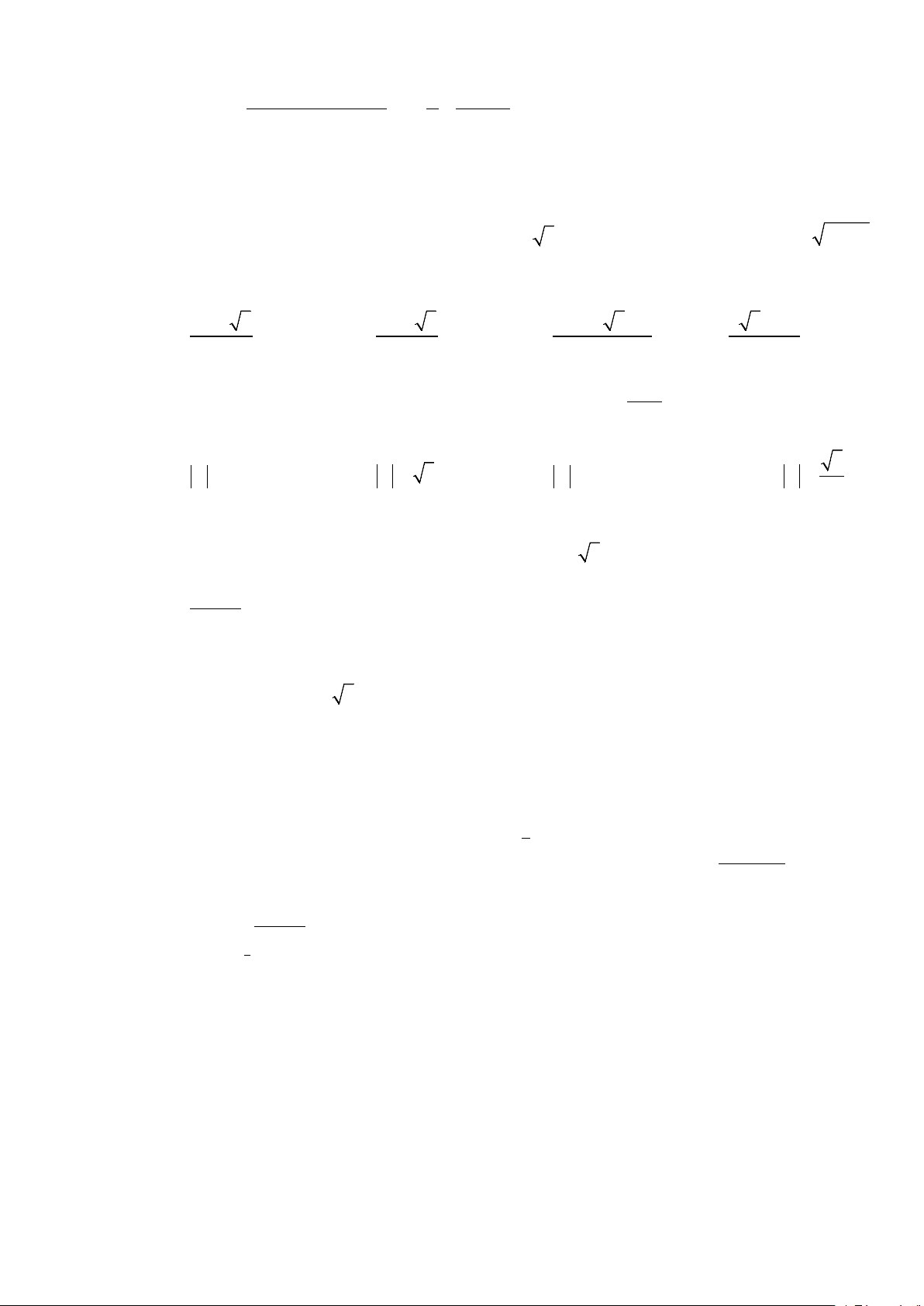
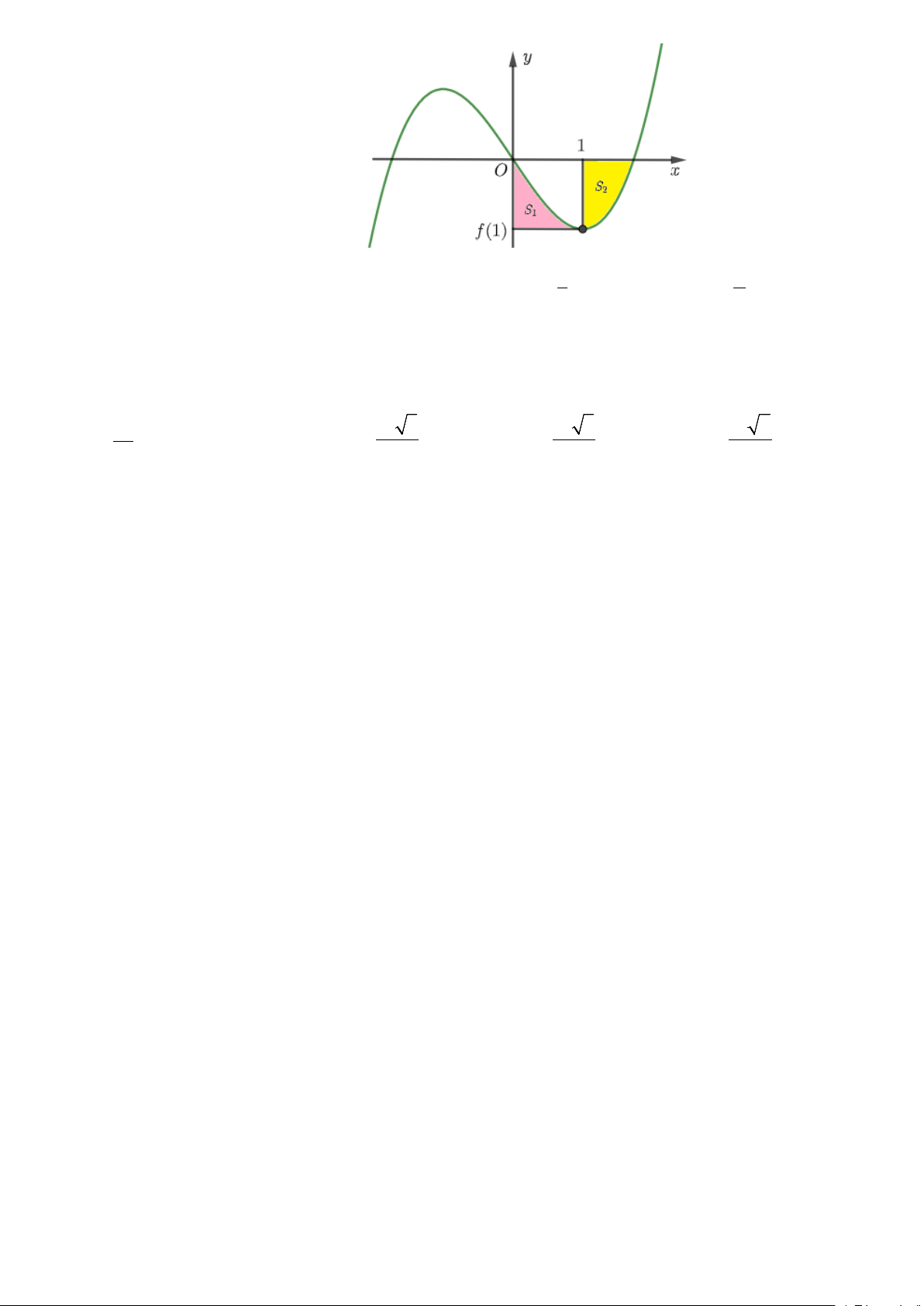
Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TỐT NGHIỆP THPT QG THÀNH PHỐ HỒ CHÍ MINH
Năm học: 2022 - 2023
TRƯỜNG THPT PHÚ LÂM
Môn: TOÁN – Khối 12
Thời gian làm bài: 90 phút ĐỀ MINH HỌA
Ngày kiểm tra: 31/03/2023 MÃ ĐỀ: 123
Họ, tên thí sinh:…………………………
Số Báo danh:…………………………….
Câu 1: Cho số phức z = 1
− − 2 6i . Phần thực và phần ảo của số phức z là?
A. Phần thực bằng 1
− và phần ảo bằng 2 6 . B. Phần thực bằng 1
− và phần ảo bằng 2 6i .
C. Phần thực bằng 1 và phần ảo bằng 2 6 .
D. Phần thực bằng 1 − và phần ảo bằng 2 − 6i .
Câu 2: Đạo hàm của hàm số y = log
( 2x + x là 2023 ) 2x +1 1 A. . B. 2x +1 . C. D. 1 . 2 x + x ( 2x + x).ln2023 2 x + x ( 2x + x).ln2023
Câu 3: Đạo hàm của hàm số 8x y = là x A. 8 y′ = . B. 8x y′ = ln8 . C. ′ = 8x y x ln8 . D. 1 8x y x − ′ = . ln8
Câu 4: Tìm tập nghiệm S của bất phương trình x 1+ 1 5 − > 0 . 5 A. S = ( ; −∞ − 2).
B. S = (1;+ ∞) . C. S = ( 1; − + ∞). D. S = ( 2; − + ∞).
Câu 5: Cho cấp số cộng (u u =11 d = 4 u
n ) có số hạng đầu 1 và công sai
. Giá trị của 5 bằng A. 2816 . B. 27 . C. 15 . D. 26 − .
Câu 6: Trong không gian Oxyz , cho mặt phẳng (P) :3x + y − 2z +1 = 0. Vectơ nào sau đây là vectơ pháp
tuyến của mặt phẳng (P) ? A. n = 3; 2 − ;1 n = 2 − ;1;3 n = 3;1; 2 − n = 1; 2 − ;1 2 ( ) 1 ( ) 3 ( ) 4 ( ) . B. . C. . D.
Câu 7: Số giao điểm của đồ thị 3 2
(C) : y = x − 3x + 2x +1 và đường thẳng y =1 là A. 0. B. 3. C. 1. D. 2.
Câu 8: Cho hàm số f (x) có đạo hàm trên đoạn [ −1;2] và f (− ) 1 = 2023, f (2) = 1. − 2 Tích phân f ′
∫ (x)dxbằng: 1 − A. 2024. B. 2024. − C. 1. D. 2022.
Câu 9: Hàm số nào dưới đây có bảng biến thiên như sau: 1 x ∞ -1 1 +∞ y' + 0 0 + +∞ 2 y 2 ∞ A. 4 2
y = x − 2x . B. 3
y = −x + 3 .x C. 4 2
y = −x + 2x . D. 3
y = x − 3 .x
Câu 10: Trong không gian Oxyz , mặt cầu (S ) (x − )2 + ( y − )2 + (z − )2 : 1 2
3 = 25 có tọa độ tâm I và bán kính R là
A. I (1;2;3), R = 5. B. I (1; 2
− ;3),R = 5. C. I (1;2; 3
− ), R = 25 . D. I (1;2;3),R = 25.
Câu 11: Cho điểm M (1, 4 − , 2
− ) và mặt phẳng (P) : x + y + 5z −14 = 0 . Tính khoảng cách từ M đến (P). A. 2 3 B. 4 3 C. 6 3 D. 3 3
Câu 12: Cho số phức z thỏa mãn (1+ i) z =14 − 2i . Tổng phần thực và phần ảo của z bằng A. 14. B. 2. C. 2. − D. 14. −
Câu 13: Thể tích của khối lăng trụ có diện tích đáy 2
S = 2a , chiều cao h = 6a là: A. 3 12a . B. 3 4a . C. 3 6a . D. 3 36a .
Câu 14: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA = a và SA vuông góc với
mặt phẳng đáy. Thể tích khối chóp S.ABCD bằng 3 3 3 A. a . B. 2a . C. a 3 a . D. . 6 3 3
Câu 15: Phương trình tiếp tuyến của đường cong 3 2
y = x + 3x − 2 tại điểm có hoành độ x =1 là 0
A. y = 9x + 7 . B. y = 9 − x − 7 . C. y = 9 − x + 7 .
D. y = 9x − 7 .
Câu 16 : Trong mặt phẳng Oxy , điểm M trong hình vẽ bên là điểm biểu diễn số phức z . Số phức z là A. 2 − − i .
B. 1− 2i . C. 2 − + i .
D. 2 + i .
Câu 17: Cho hình trụ có bán kính đáy r và độ dài đường sinh l . Diện tích xung quanh S của hình trụ xq
đã cho được tính theo công thức nào dưới đây?
A. S = π rl .
B. S = π rl .
C. S = π rl .
D. S = πrl . xq 3 xq 2 xq 4 xq 2
x −1 y − 3 z + 4
Câu 18: Trong không gian Oxyz , đường thẳng d : = =
đi qua điểm nào dưới đây? 1 3 2 −
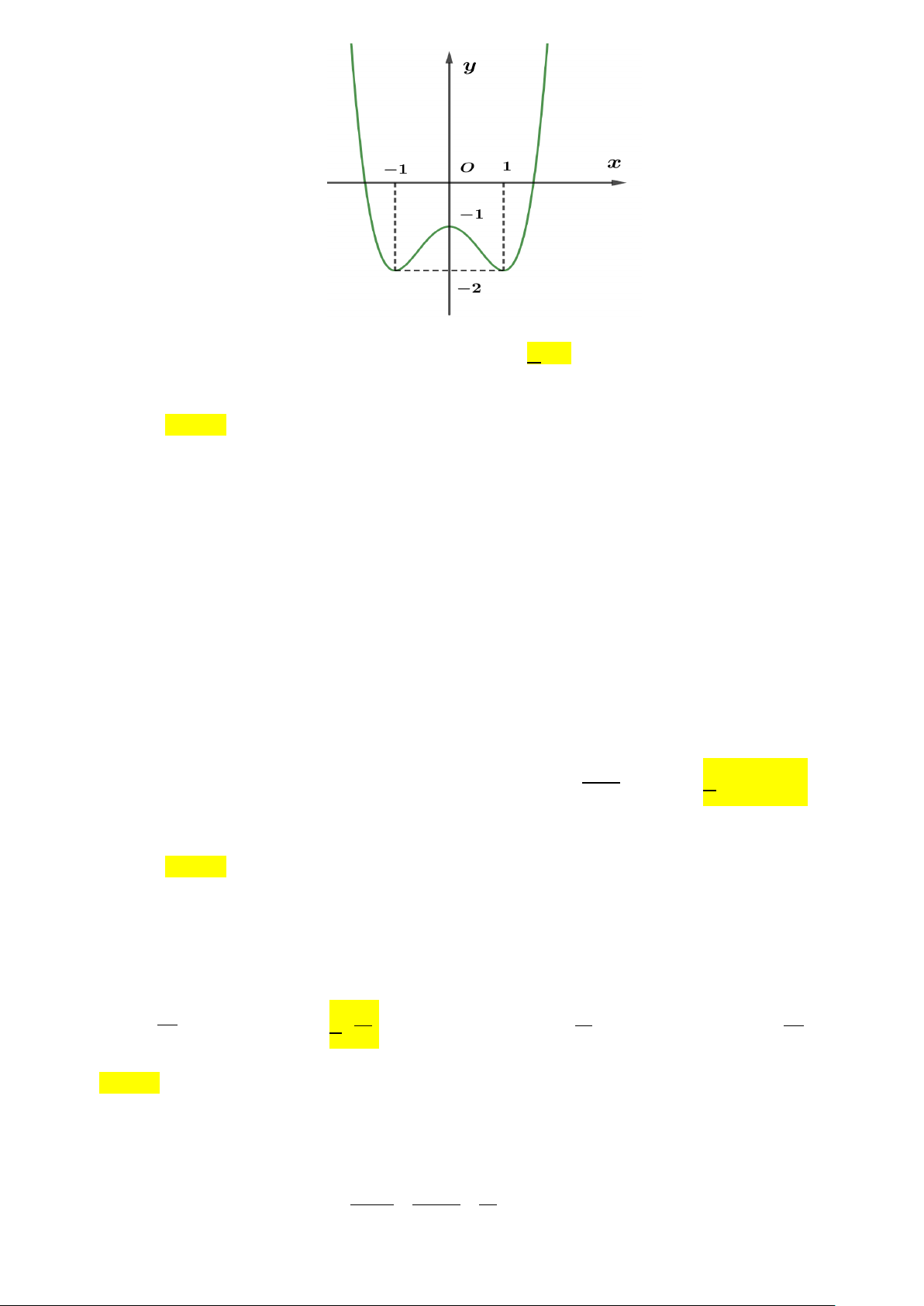
A. Q(1;3− 2) . B. M ( 1; − 3 − ;4) . C. C(1;3; 4 − ) . D. N( 1; − 3 − ;2) . Câu 19: Cho hàm số 4 2
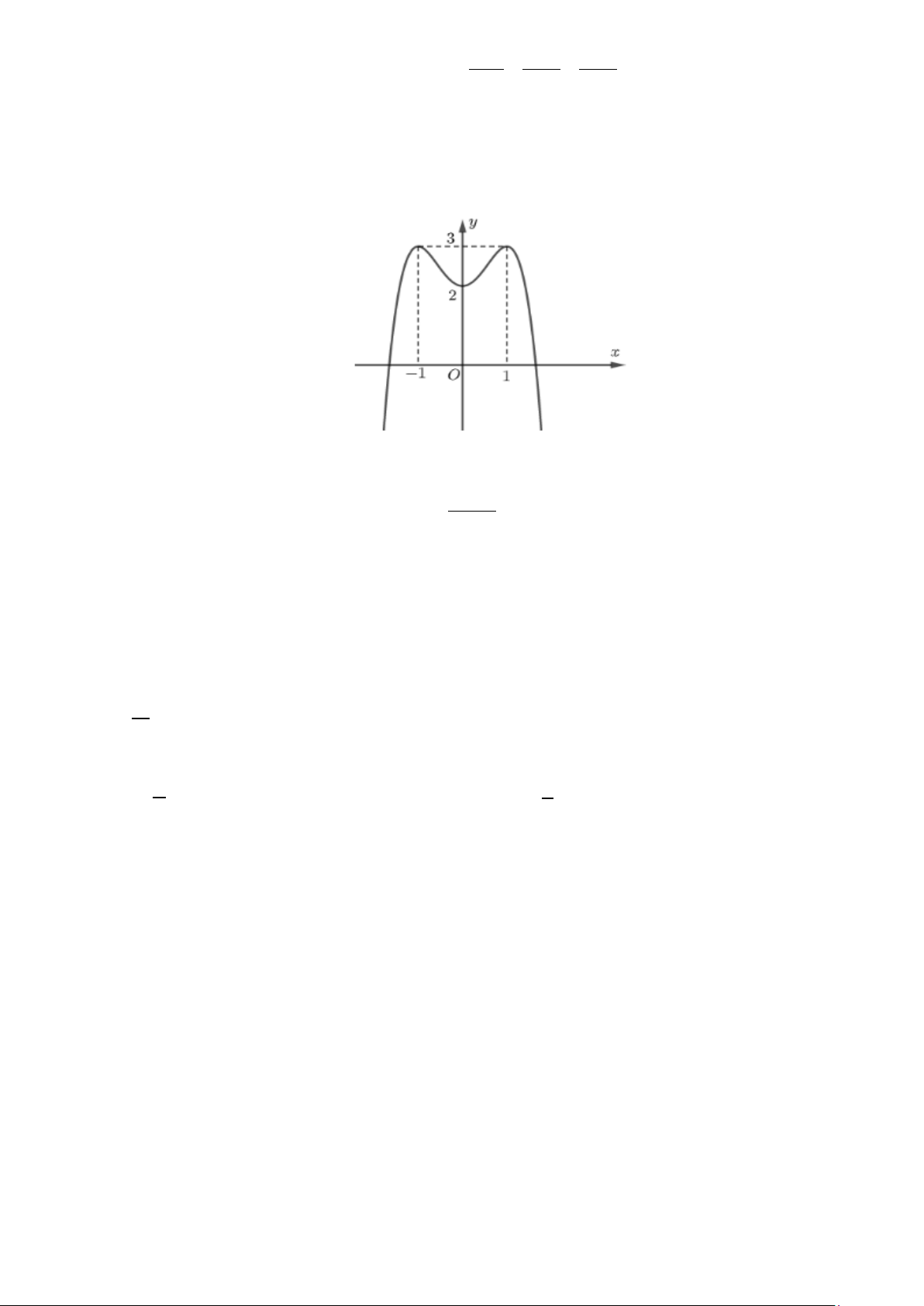
y = ax + bx + c , (a,b,c∈ R) có đồ thị là đường cong như hình bên. Điểm cực tiểu của hàm số đã cho là: A. x = 1 − . B. x = 2 . C. x =1. D. x = 0 .
Câu 20: Tiệm cận ngang của đồ thị hàm số 2x −1 y =
là đường thẳng có phương trình: 2x + 4 A. y = 2 − . B. x = 2 − . C. x =1. D. y =1.
Câu 21: Tập nghiệm của bất phương trình 2x 13 3 − < 27 là A. (4;+ ∞) . B. ( 4; − 4) .
C. (−∞;4) . D. (0;4).
Câu 22: Có bao nhiêu số có năm chữ số khác nhau được tạo thành từ các chữ số 1,2,3,4,5,6? A. 5 A B. P . C. 5 C .
D. P . 6 6 6 5
Câu 23: Nguyên hàm của hàm số f (x) 3 = 2x − 2023 là: 1 A. 4
x − 2023x + C . B. 4
4x − 2023x + C . C. 1 4
x + C . D. 3
4x − 2023x + C . 2 4 5 2 − 5
Câu 24: Cho hai tích phân ∫ f (x)dx = 8 và ∫ g(x)dx = 3. Tính I = 
∫  f (x)−4g(x)−1d  x 2 − 5 2 − A. 13. B. 27 . C. 11 − . D. 3.
Câu 25: (Khái niệm, tính chất, bảng nguyên hàm cơ bản). Cho F(x) là một nguyên hàm của hàm số
f (x) . Tìm I = [2 f (x) + ∫ ]1dx .
A. I = 2xF(x) + x + C .
B. I = 2F(x) + x + C .
C. I = 2F(x) +1+ C .
D. I = 2xF(x) +1+ C .
Câu 26: Hàm số nào dưới đây có bảng biến thiên như sau: 3 x ∞ -1 1 +∞ y' + 0 0 + +∞ 2 y 2 ∞ A. 4 2
y = x − 2x . B. 3
y = −x + 3 .x C. 4 2
y = −x + 2x . D. 3
y = x − 3 .x
Câu 27: Cho hàm số f (x) có đạo hàm f (x) = x(x − )(x + )2023 ' 1 4 , x
∀ ∈  . Số điểm cực trị của hàm số đã cho là A. 3. B. 4 . C. 2 . D. 1 .
Câu 28: Đặt a = log 5,b = log 5 . Hãy biểu diễn log 5 theo 2 3 6 a và b . A. 1 1 2 2
log 5 = a + b .
B. log 5 = a + b . C. log 5 = + . D. log 5 ab = . 6 6 6 a b 6 a + b
Câu 29: Gọi S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số: 3
y = x − 3x , y = x . Tính S. A. S = 4 .
B. S = 8. C. S = 2 . D. S = 0 .
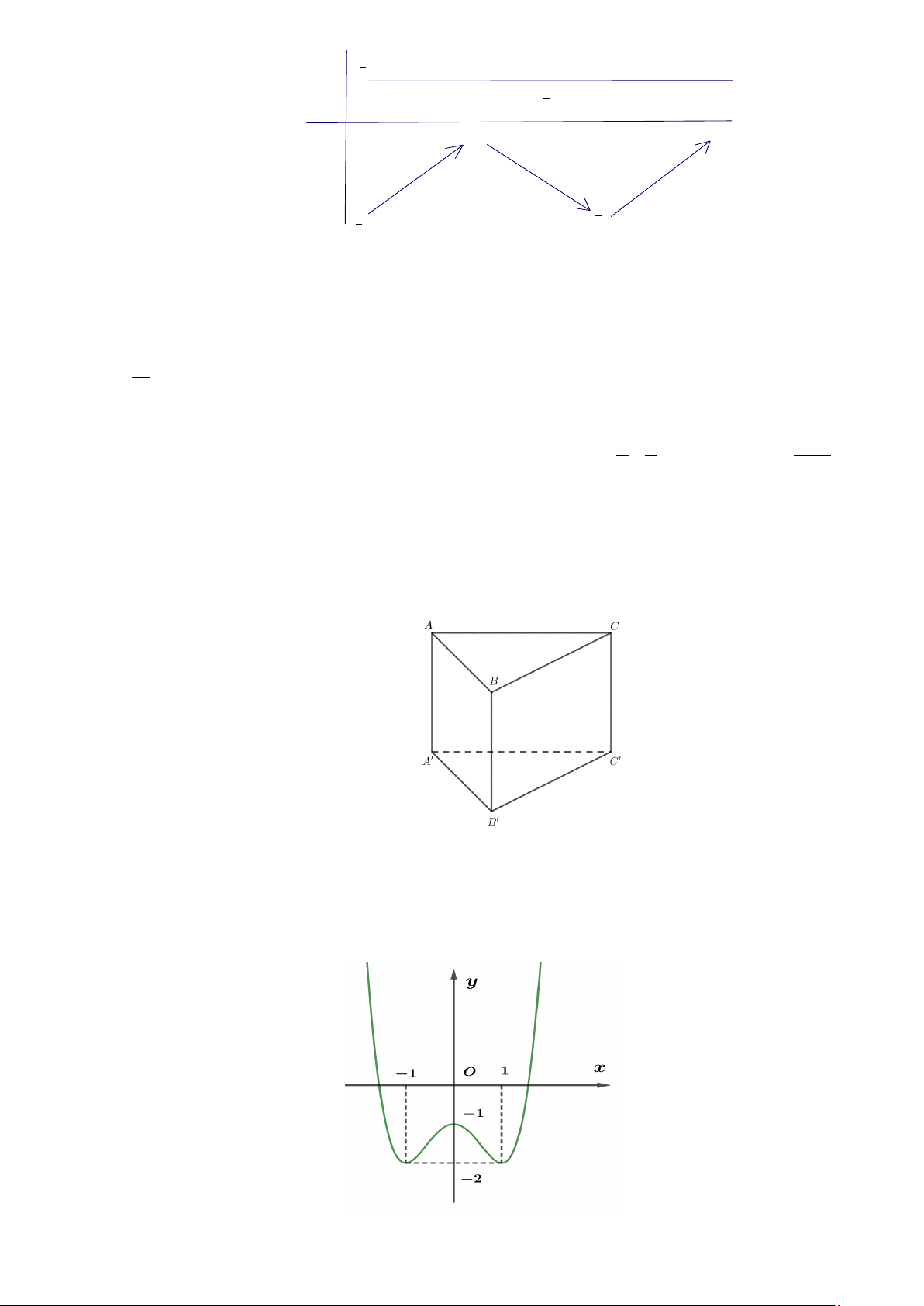
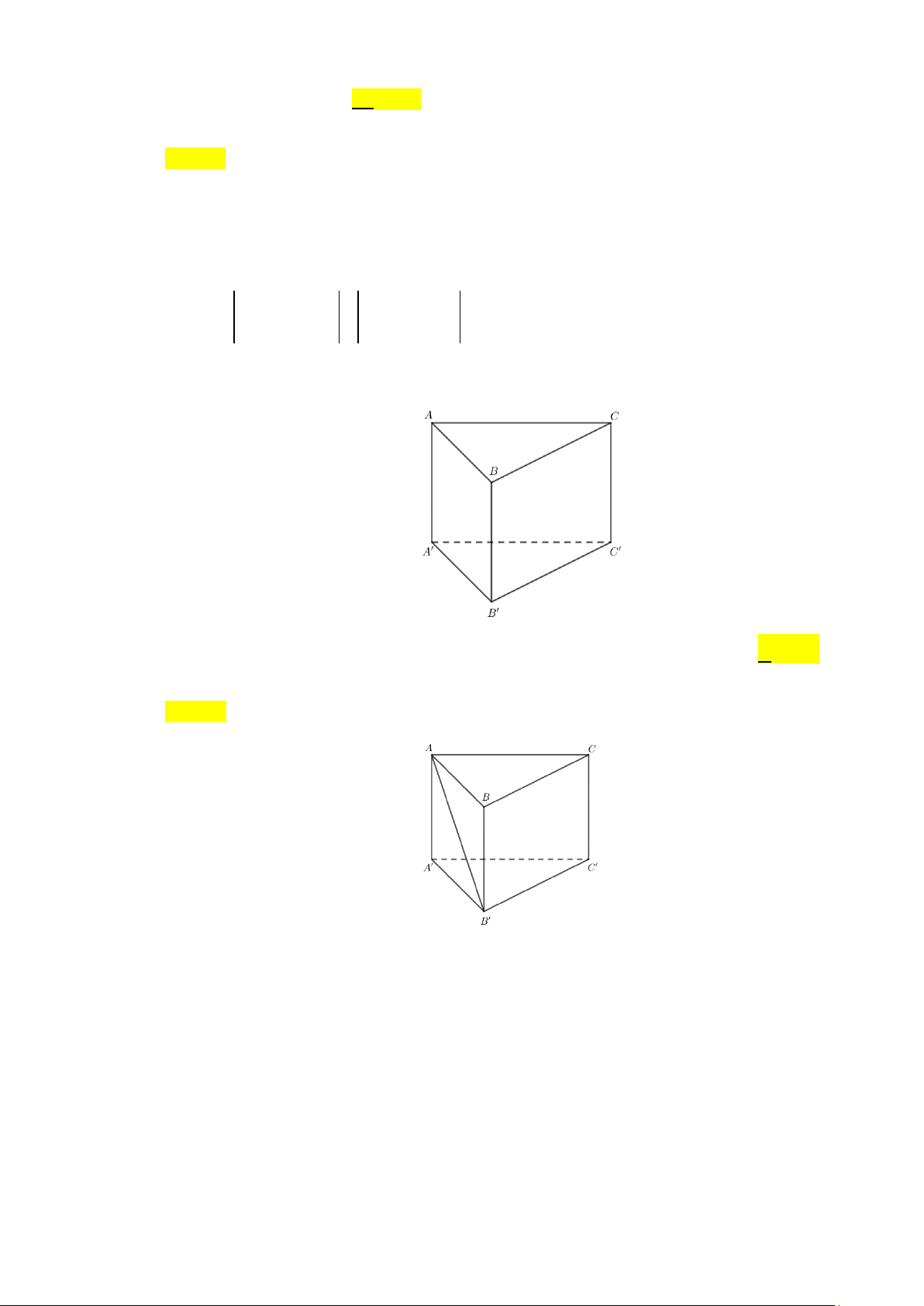
Câu 30: Cho hình lăng trụ đứng ABC.A′B C
′ ′ có tất cả các cạnh bằng nhau. Góc giữa hai đường thẳng
AB′ và CC′ bằng A. 30o . B. 90o . C. 60o . D. 45o .
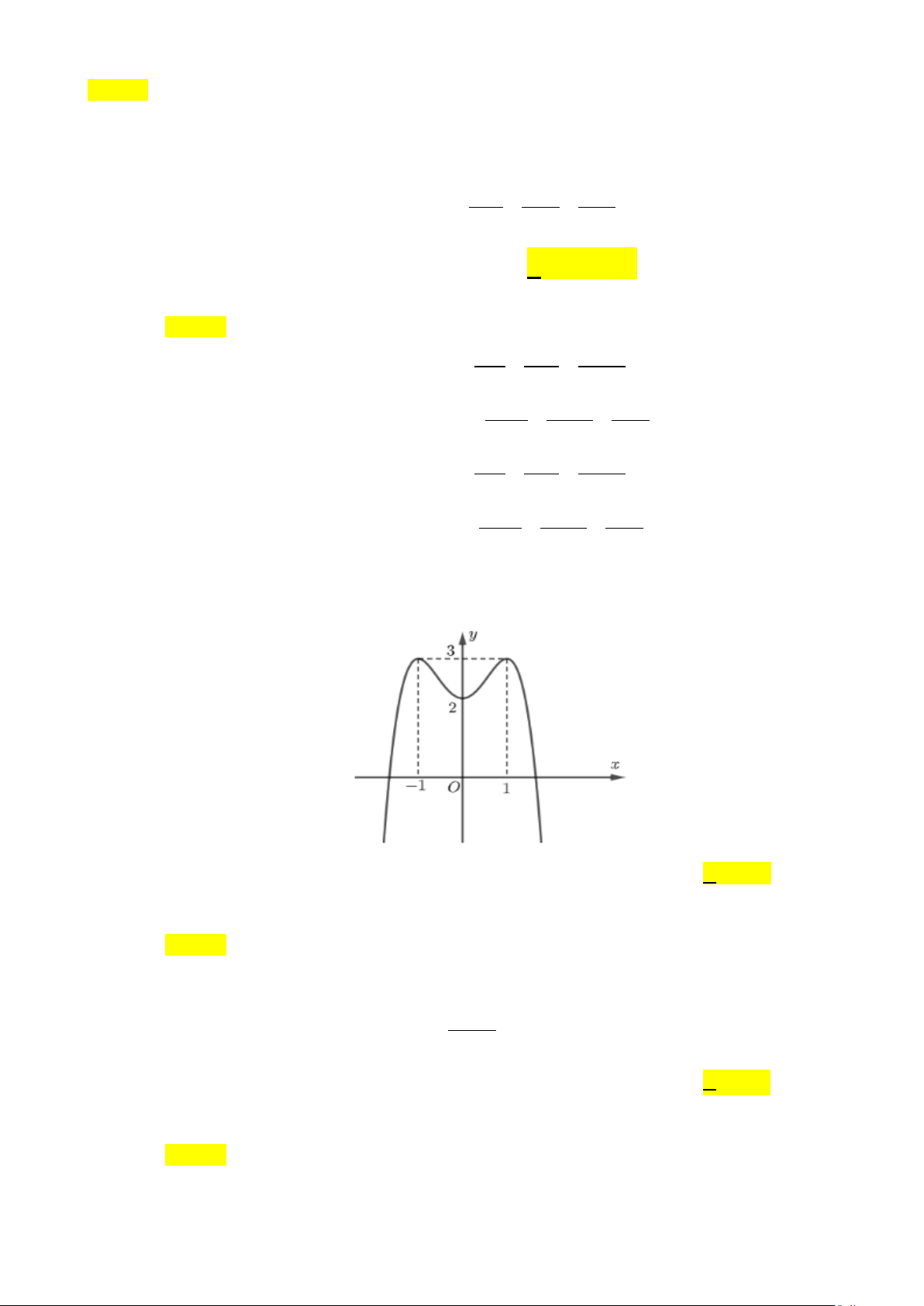
Câu 31: Cho hàm số ( ) 4 2
f x = ax + bx + c có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên thuộc đoạn [ 2;
− 5] của tham số m để phương trình f (x) = m có đúng hai nghiệm phân biệt? 4 A. 1. B. 6 . C. 7 . D. 5.
Câu 32: Hàm số nào sau đây đồng biến trên ? A. 4 2 y − = x − x . B. 3
y = x − x . C. x 1 y = . D. 3
y = x + x . x + 2
Câu 33: Một đội thanh niên tình nguyện của trường gồm có 6 học sinh nam và 5 học sinh nữ. Chọn
ngẫu nhiên 4 học sinh để cùng các giáo viên tham gia đo thân nhiệt cho học sinh khi đến trường. Xác
suất để chọn được 4 học sinh trong đó số học sinh nam bằng số học sinh nữ bằng A. 5 . B. 5 . C. 6 . D. 2 . 66 11 11 33
Câu 34: Nghiệm của phương trình log 2x +1 =1+ log x −1 3 ( ) 3 ( ) là
A. x = 4 . B. x = 2 − . C. x =1. D. x = 2 .
Câu 35: Gọi z là nghiệm phức có phần ảo âm của phương trình 2
z − z + = . Tọa độ điểm biểu diễn 1 2 5 0 −
số phức 7 4i trên mặt phẳng phức là z1
A. P(3;2) B. N (1; 2 − ) C. Q(3; 2 − ) D. M (1;2)
Câu 36: Trong không gian Oxyz , phương trình mặt phẳng (P) song song và cách đều hai đường thẳng x 2 : y z d − − − = = và x y 1 z 2 d : = = là 1 1 − 1 1 2 2 1 − 1 −
A. (P) : 2y − 2z +1 = 0 . B. (P) : 2x − 2z +1 = 0 . C. (P) : 2x − 2y +1 = 0 . D. (P) : 2y − 2z −1 = 0
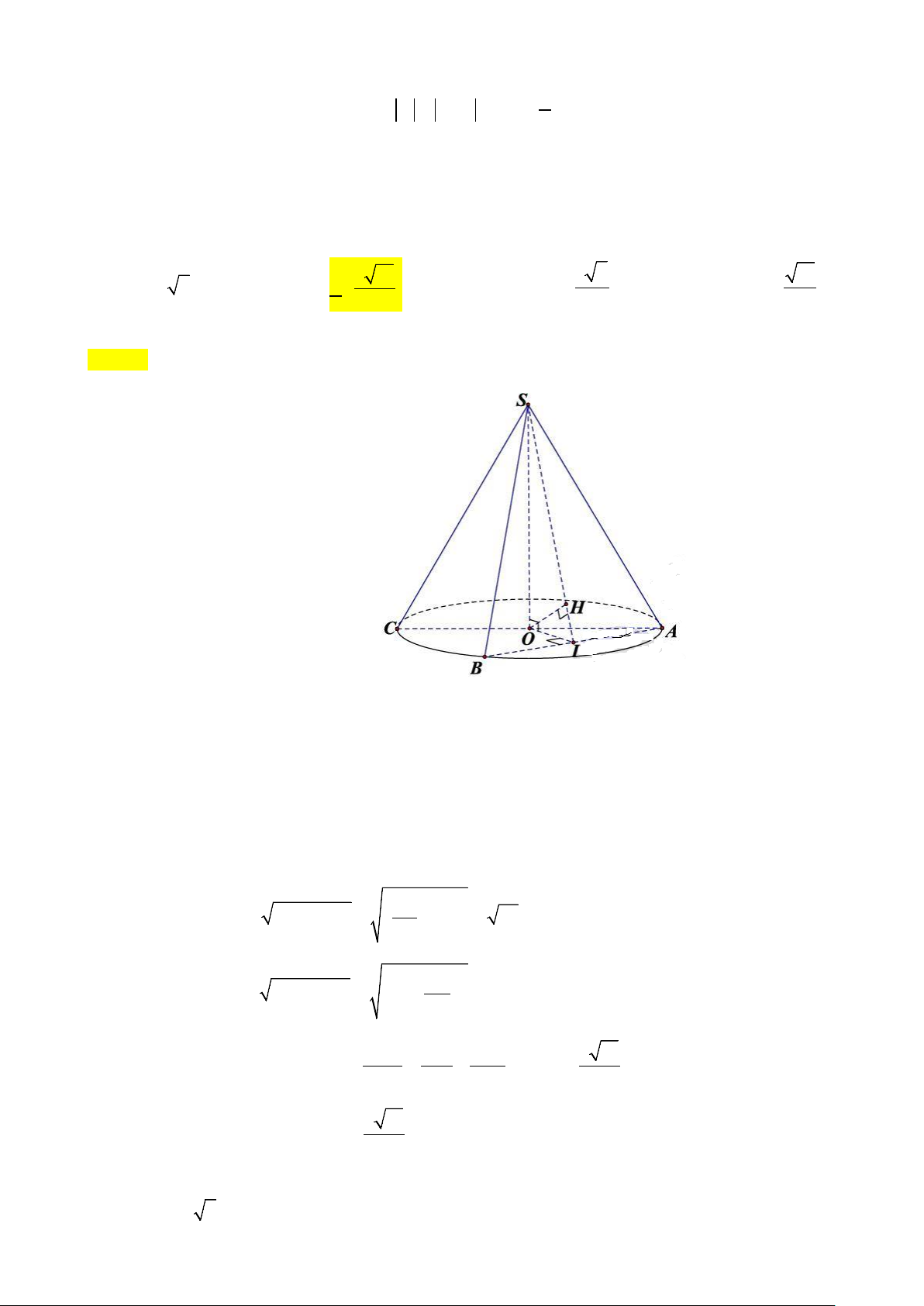
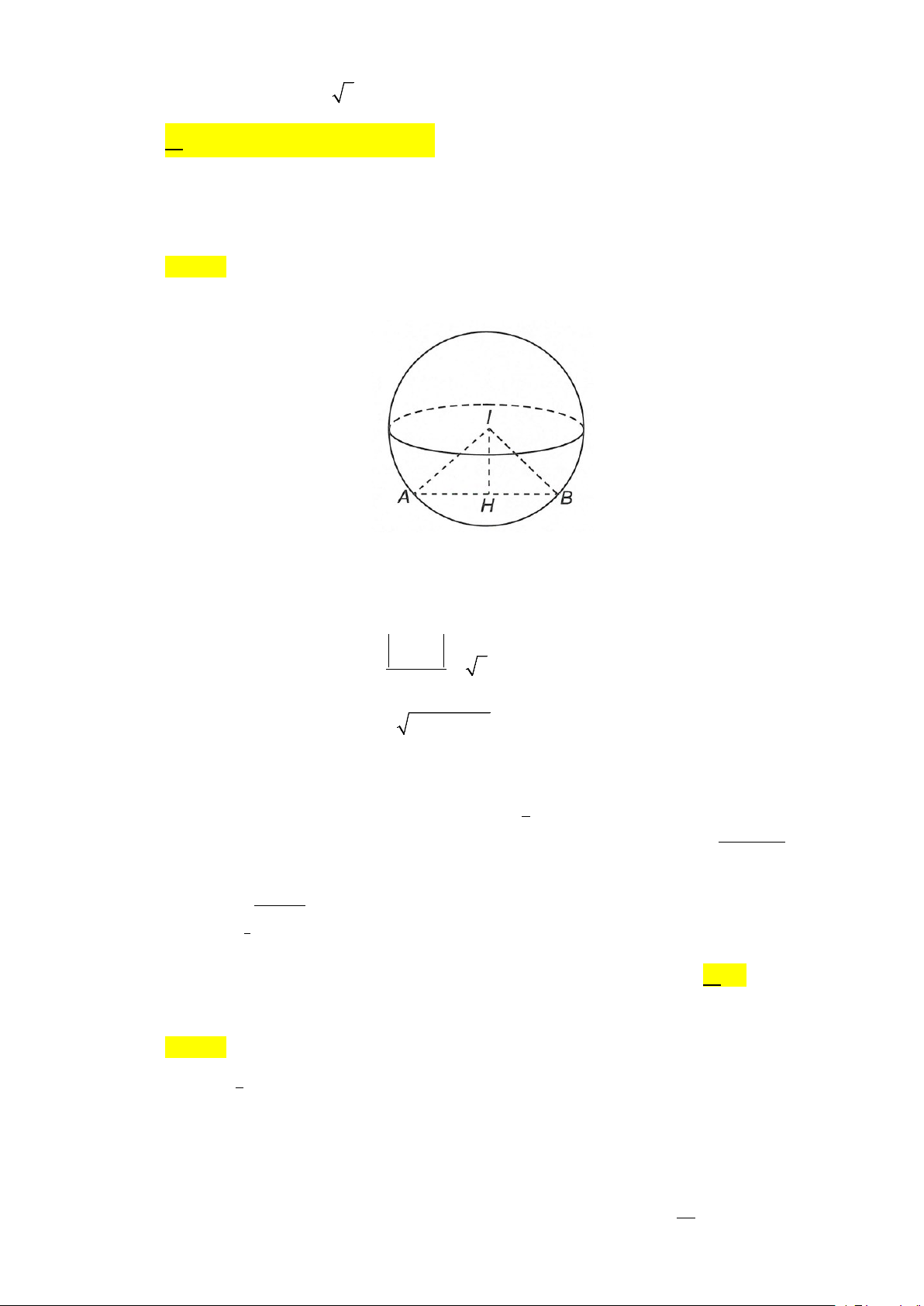
Câu 37: Cho hình nón đỉnh S , đáy là đường tròn ( ;
O 5) .Một mặt phẳng đi qua đỉnh của hình nón cắt
đường tròn đáy tại hai điểm A và B sao cho SA = AB = 8. Tính khoảng cách từ O đến (SAB) . 3 2 A. 2 2 . B. 3 13 . C. . D. 13 . 4 7 2
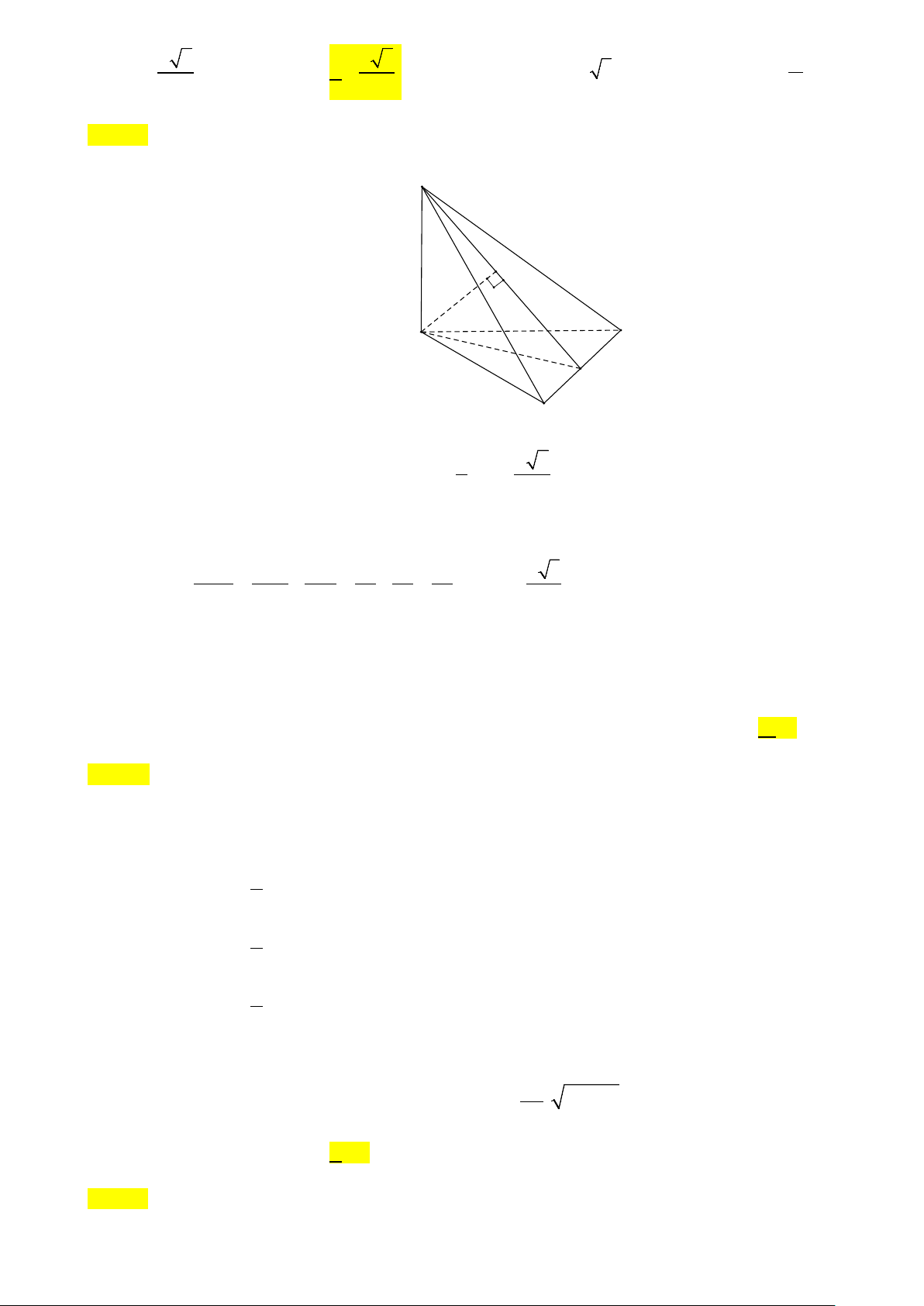
Câu 38: Cho hình chóp S.ABC có SA = a và SA vuông góc với đáy. Biết đáy là tam giác vuông cân tại
A và BC = a 2 . Tính khoảng cách từ A đến mặt phẳng (SBC). A. a 5 . B. a 3 . C. a a 3 . 5 3 D. 3
Câu 39: Có bao nhiêu giá trị nguyên của x trong đoạn [0; ]
2023 thỏa mãn bất phương trình sau
16x 25x 36x 20x 24x 30x + + ≤ + + . A. 2023. B. 3. C. 2024 . D. 1. x x 1
Câu 40: Tập nghiệm của bất phương trình 2 x 1 (3 9)(3 ) 3 + − −
−1 ≤ 0 chứa bao nhiêu số nguyên ? 27 A. 2. B. 3. C. 4. D. 5. Câu 41: Cho hàm số 2
f ( x) xác định trên  \ { 1; − }
1 , thỏa mãn f '( x) = ; f 3 − + f 3 = 2 ln 2 và 2 ( ) ( ) x −1  1   1  f − + f = 0    
. Giá trị của biểu thức P = f ( 2
− ) + f (0) + f (4) là:  2   2 
A. 2 ln 2 − ln 5
B. 6 ln 2 + 2 ln3− ln 5 C. 2 ln 2 + 2 ln3− ln 5 D. 6 ln 2 − 2 ln 5 5 2 2
x + (x + ln x)2 + x Câu 42: a 1 Cho I = dx = − ∫
với a , b , c là các số nguyên dương. Khẳng 2 x x + ln x 2 b + ln c 1 ( )2
định nào sau đây đúng ?
A. abc = 26.
B. abc = 3 .
C. abc =11.
D. abc =12 .
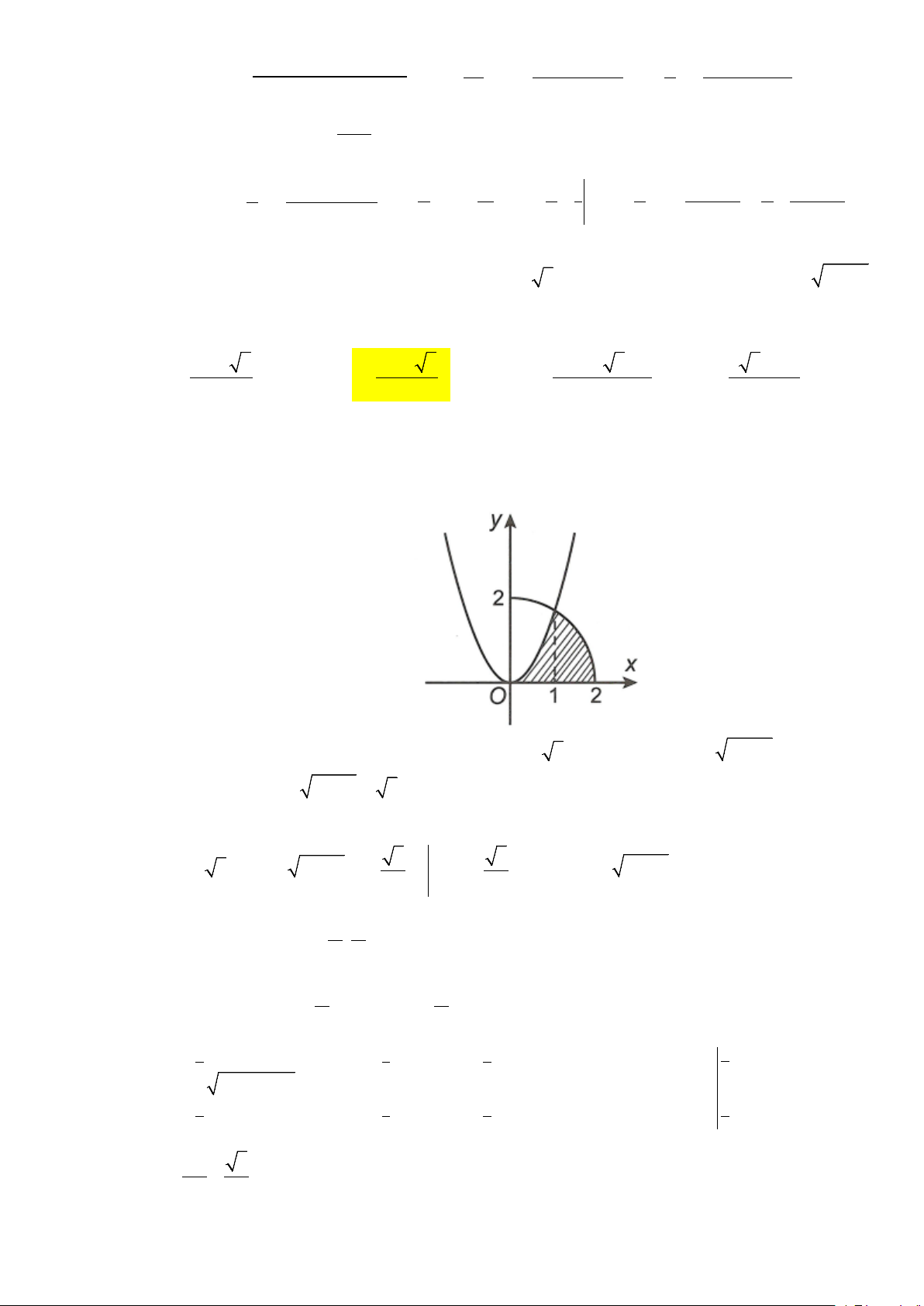
Câu 43: Cho (H ) là hình phẳng giới hạn bởi parabol 2
y = 3x , cung tròn có phương trình 2 y = 4 − x
(với 0 ≤ x ≤ 2) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của (H ) là π + π − π + − − π A. 4 3 . B. 4 3 . C. 4 2 3 3 . D. 5 3 2 . 12 6 6 3 2022
Câu 44: Cho hai số phức z = 2 + i, z =1− 2 .i Môđun của số phức z1 = là 1 2 w 2023 z2 5
A. w = 5.
B. w = 3.
C. w = 3. D. w = . 5
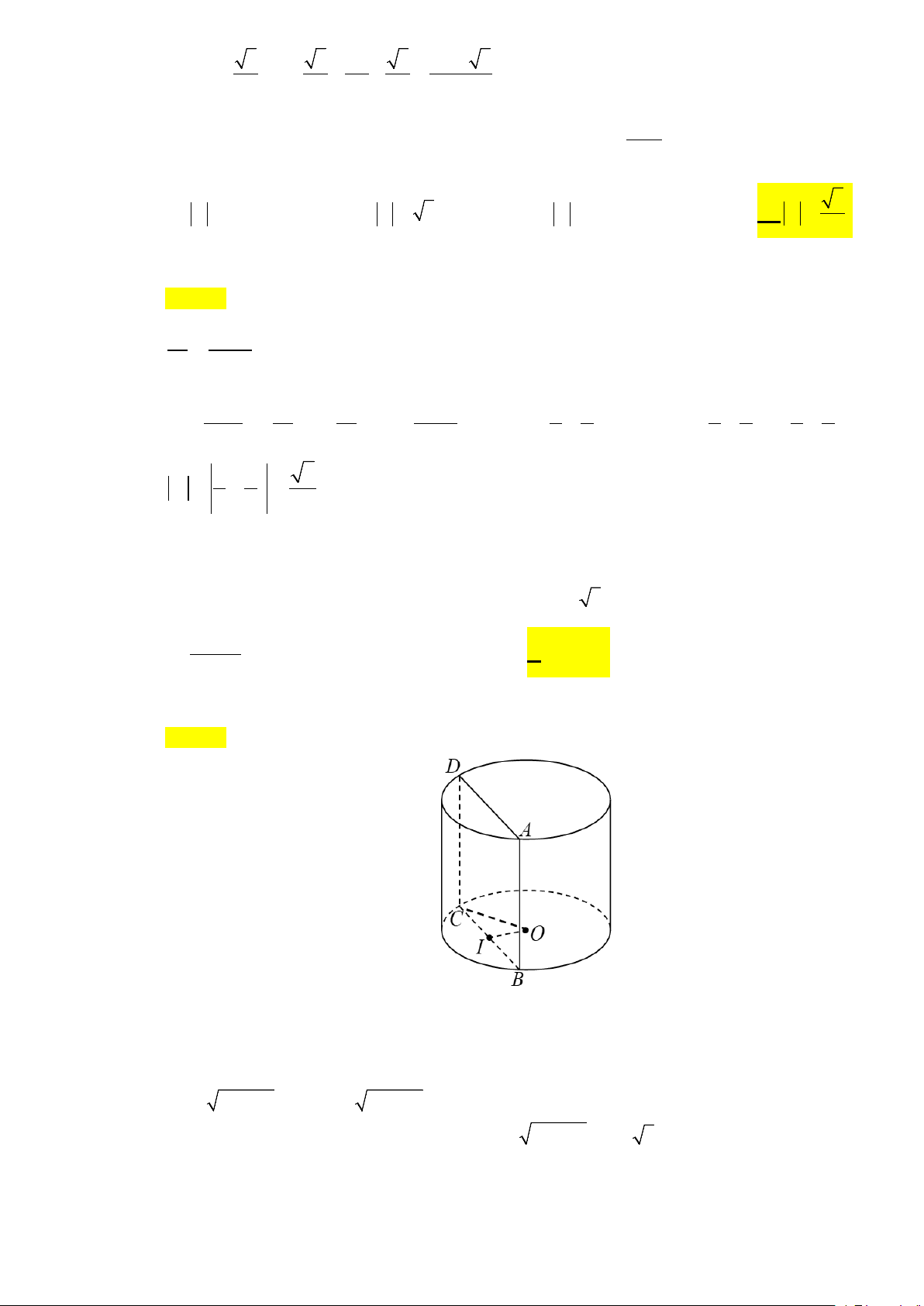
Câu 45: Cho hình trụ có thiết diện qua trục là một hình vuông. Thiết diện của hình trụ tạo bởi mặt phẳng
song song và cách trục một khoảng bằng a có diện tích bằng 2
8a 3 . Thể tích của khối trụ là 3
A. 16π a . B. 2 16πa . C. 3 16πa . D. 3 32πa . 3
Câu 46: Trong không gian Oxyz, cho điểm I(1; 2
− ;3). Viết phương trình mặt cầu tâm I, cắt trục Ox tại
hai điểm A và B sao cho AB = 2 3.
A. ( − )2 + ( + )2 + ( − )2 x 1 y 2 z 3 =16. B. ( − )2 2
x 1 + (y + 2) + (z −3)2 = 20.
C. ( − )2 + ( + )2 + ( − )2 x 1 y 2 z 3 = 25.
D. ( − )2 + ( + )2 + ( − )2 x 1 y 2 z 3 = 9. π 4 2 e f ( 2 ln x)
Câu 47: Cho hàm số f (x) liên tục trên  và thỏa mãn tan .x f ∫ ( 2 cos x)dx =1, dx =1. ∫ Giá x ln x 0 e 2 (2 ) trị của tích phân = d ∫ f x I x bằng 1 x 4 A. 1. B. 2 . C. 3. D. 4 .
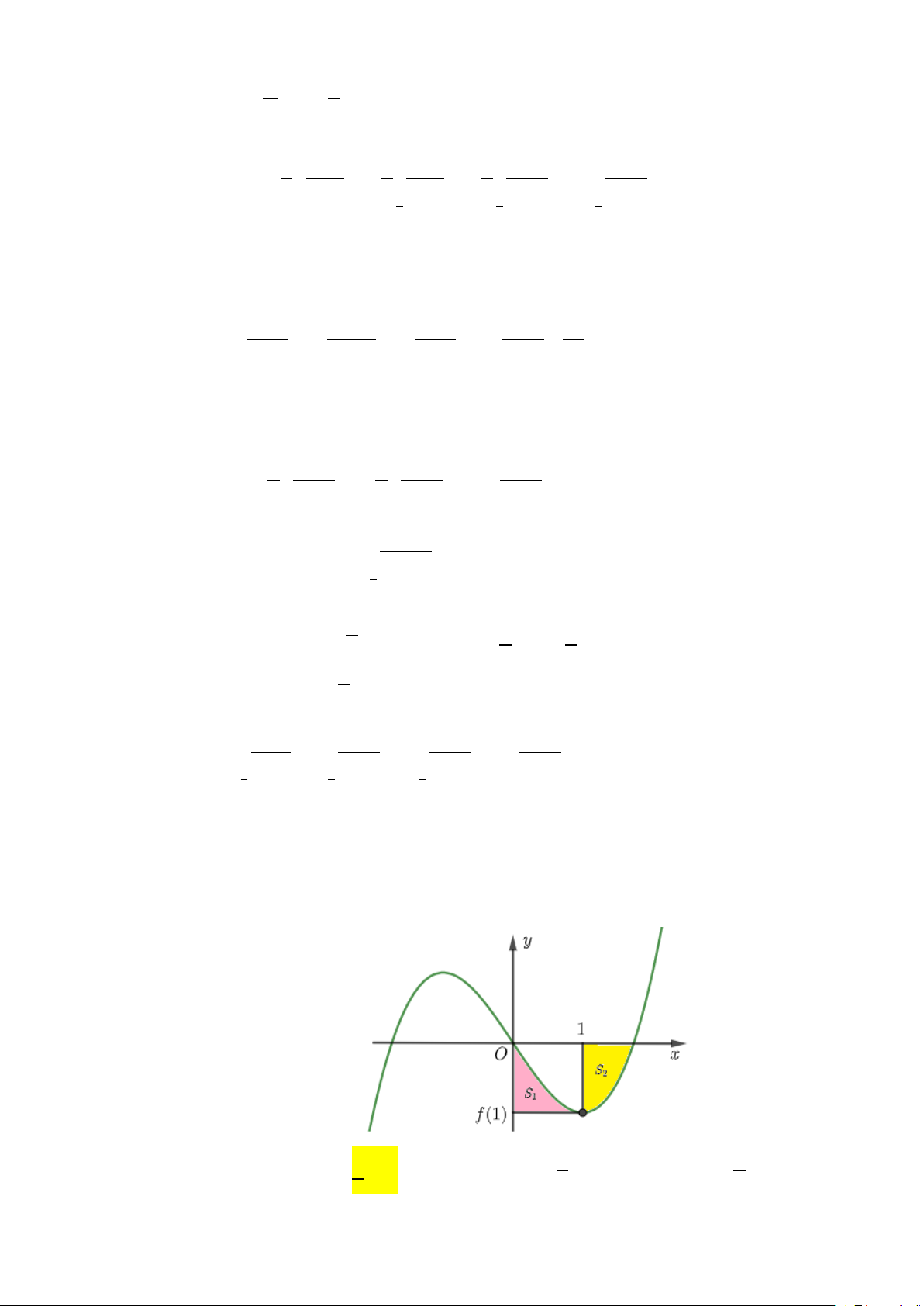
Câu 48: Cho hàm số bậc ba y = f (x) có đồ thị như hình vẽ, biết f (x) đạt cực tiểu tại điểm x =1 và
thỏa mãn  f (x) +1 
 và  f ( x) −1 
 lần lượt chia hết cho ( x − )2 1 và (x + )2
1 . Gọi S , S lần lượt là diện 1 2
tích như trong hình bên. Tính 2S + 8S . 2 1 6 A. 9. B. 4 . C. 3 . D. 1 . 5 2
Câu 49: Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại C và SA vuông góc với mặt
phẳng đáy. Cho SC = a , mặt phẳng (SBC) tạo với mặt đáy một góc α . Thể tích khối chóp S.ABC đạt giá trị lớn nhất là 3 3 3 3 A. a . B. a 3 . C. a 3 . D. a 2 . 16 27 48 24
Câu 50: Trong không gian Oxyz, cho mặt cầu (S ) (x − )2 + ( y − )2 + (z + )2 : 2 3 1 =16 và điểm A( 1; − 1; − − )
1 . Xét các điểm M thuộc (S ) sao cho đường thẳng AM tiếp xúc với (S ). M luôn thuộc một
mặt phẳng cố định có phương trình là
A. 3x + 4y − 2 = 0.
B. 3x + 4y + 2 = 0 .
C. 6x + 8y +11 = 0 .
D. 6x + 8y −11 = 0 . ………..Hết……… 7
SỞ GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM THÀNH PHỐ HỒ CHÍ MINH
Năm học: 2022 - 2023
TRƯỜNG THPT PHÚ LÂM
Môn: TOÁN – Khối 12
Thời gian làm bài: 90 phút ĐỀ CHÍNH THỨC
Ngày kiểm tra: 31/03/2023 1 2 3 4 5 6 7 8 9 10 A B B D B C B B D A 11 12 13 14 15 16 17 18 19 20 D A A D D A B C D D 21 22 23 24 25 26 27 28 29 30 B A A A B D A D B D 31 32 33 34 35 36 37 38 39 40 C D B A A A B B D B 41 42 43 44 45 46 47 48 49 50 C D B D C A D B B A
Câu 1: Cho số phức z = 1
− − 2 6i . Phần thực và phần ảo của số phức z là?
A. Phần thực bằng 1
− và phần ảo bằng 2 6 . B. Phần thực bằng 1
− và phần ảo bằng 2 6i .
C. Phần thực bằng 1 và phần ảo bằng 2 6 .
D. Phần thực bằng 1 − và phần ảo bằng 2 − 6i . Lời giải Chọn A z = 1
− − 2 6i ⇒ z = 1 − + 2 6i
Vậy z có phần thực bằng 1
− và phần ảo bằng 2 6 .
Câu 2: Đạo hàm của hàm số y = log
( 2x + x là 2023 ) 2x +1 1 A. . B. 2x +1 . C. D. 1 . 2 x + x ( 2x + x).ln2023 2 x + x ( 2x + x).ln2023 Lời giải Chọn B 2 ′ x x ′ + Ta có y′ =  ( 2 2x +1 log x + x  = = . 2023 ) ( ) 
( 2x + x).ln2023 ( 2x + x).ln2023
Câu 3: Đạo hàm của hàm số 8x y = là x A. 8 y′ = . B. 8x y′ = ln8 . C. ′ = 8x y x ln8 . D. 1 8x y x − ′ = . ln8 Lời giải Chọn B Ta có (8x) 8x y ′ ′ = = ln8 .
Câu 4: Tìm tập nghiệm S của bất phương trình x 1+ 1 5 − > 0 . 5 A. S = ( ; −∞ − 2).
B. S = (1;+ ∞) . C. S = ( 1; − + ∞). D. S = ( 2; − + ∞). Lời giải Chọn D
Bất phương trình tương đương x 1+ 1 5 5− > ⇔ x +1 > 1 − ⇔ x > 2. −
Câu 5: Cho cấp số cộng (u u =11 d = 4 u
n ) có số hạng đầu 1 và công sai
. Giá trị của 5 bằng A. 2816 . B. 27 . C. 15 . D. 26 − . Lời giải Chọn B u  =11 Ta có : 1 
⇒ u = u + 4d = 27 5 1 . d = 4
Câu 6: Trong không gian Oxyz , cho mặt phẳng (P) :3x + y − 2z +1 = 0. Vectơ nào sau đây là vectơ pháp
tuyến của mặt phẳng (P) ? A. n = 3; 2 − ;1 n = 2 − ;1;3 n = 3;1; 2 − n = 1; 2 − ;1 2 ( ) 1 ( ) 3 ( ) 4 ( ) . B. . C. . D. . Lời giải Chọn C
Từ phương trình mặt phẳng (P) ta có vectơ pháp tuyến của (P) là n = 3;1; 2 − 1 ( ) .
Câu 7: Số giao điểm của đồ thị 3 2
(C) : y = x − 3x + 2x +1 và đường thẳng y =1 là A. 0. B. 3. C. 1. D. 2. Lời giải Chọn B x = 0
Phương trình hoành độ giao điểm: 3 2 3 2
x −3x + 2x +1=1⇔ x −3x + 2x = 0  ⇔ x =1  . x =  2 Vậy có ba giao điểm.
Câu 8: Cho hàm số f (x) có đạo hàm trên đoạn [ −1;2] và f (− ) 1 = 2023, f (2) = 1. − Tích phân 2 f ′
∫ (x)dxbằng: 1 − A. 2024. B. 2024. − C. 1. D. 2022. Lời giải Chọn B 2 2 Ta có: f ′
∫ (x)dx = f (x) = f (2)− f (− )1 = 1 − − 2023 = 2024 − . − − 1 1
Câu 9: Hàm số nào dưới đây có bảng biến thiên như sau: x ∞ -1 1 +∞ y' + 0 0 + +∞ 2 y 2 ∞ A. 4 2
y = x − 2x . B. 3
y = −x + 3 .x C. 4 2
y = −x + 2x . D. 3
y = x − 3 .x Lời giải Chọn D
Hàm số có bảng biến thiên như trên, trong 4 đáp án đã cho phải là hàm bậc ba với a > 0.
Câu 10: Trong không gian Oxyz , mặt cầu (S ) (x − )2 + ( y − )2 + (z − )2 : 1 2
3 = 25 có tọa độ tâm I và bán kính R là
A. I (1;2;3), R = 5. B. I (1; 2
− ;3),R = 5. C. I (1;2; 3
− ), R = 25 . D. I (1;2;3),R = 25. Lời giải
Chọn A Ta có, tọa độ tâm: I(1;2;3) Bán kính: R = 25 = 5
Câu 11: Cho điểm M (1, 4 − , 2
− ) và mặt phẳng (P) : x + y + 5z −14 = 0 . Tính khoảng cách từ M đến (P). A. 2 3 B. 4 3 C. 6 3 D. 3 3 Lời giải Chọn D + − + − −
d (M (P)) 1 ( 4) 5.( 2) 14 , = = 3 3 2 2 1 +1 + ( 2 − )2
Câu 12: Cho số phức z thỏa mãn (1+ i) z =14 − 2i . Tổng phần thực và phần ảo của z bằng A. 14. B. 2. C. 2. − D. 14. − Lời giải Chọn A Ta có: ( + ) 14 − 2 1 =14 − 2 i i z i ⇔ z =
⇔ z = 6 −8i ⇒ z = 6 + 8 .i 1+ i
Suy ra, z có phần thực bằng 6 và phần ảo bằng 8.
Do đó tổng phần thực và phần ảo của z bằng 14.
Câu 13: Thể tích của khối lăng trụ có diện tích đáy 2
S = 2a , chiều cao h = 6a là: A. 3 12a . B. 3 4a . C. 3 6a . D. 3 36a . Lời giải Chọn A 3
V = S.h =12a
Câu 14: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA = a và SA vuông góc với
mặt phẳng đáy. Thể tích khối chóp S.ABCD bằng 3 3 3 A. a . B. 2a . C. a 3 a . D. . 6 3 3 Lời giải Chọn D 3
Thể tích khối chóp S.ABCD là 1 1 2 = = . . a V Bh a a = . 3 3 3
Câu 15: Phương trình tiếp tuyến của đường cong 3 2
y = x + 3x − 2 tại điểm có hoành độ x =1 là 0
A. y = 9x + 7 . B. y = 9 − x − 7 . C. y = 9 − x + 7 .
D. y = 9x − 7 . Lời giải Xét hàm 3 2 2
y = f (x) = x + 3x − 2 ⇒ f '(x) = 3x + 6x ⇒ f '(1) = 9.
Ta có x =1⇒ y = 2 ⇒ M 1;2 . 0 0 0 ( )
Phương trình tiếp tuyến tại điểm M 1;2 có dạng: 0 ( )
y − y = f '(x ) x − x ⇔ y − 2 = 9 x −1 ⇔ y = 9x − 7 . 0 0 ( 0 ) ( )
Câu 16 : Trong mặt phẳng Oxy , điểm M trong hình vẽ bên là điểm biểu diễn số phức z . Số phức z là A. 2 − − i . B. 1− 2i . C. 2 − + i . D. 1+ 2i . Lời giải Chọn A Ta có z = 2
− + i ⇒ z = 2 − − i .
Câu 17: Cho hình trụ có bán kính đáy r và độ dài đường sinh l . Diện tích xung quanh S của hình trụ xq
đã cho được tính theo công thức nào dưới đây?
A. S = π rl .
B. S = π rl .
C. S = π rl .
D. S = π rl . xq 3 xq 2 xq 4 xq Lời giải Chọn B
Công thức tính diện tích xung quanh của hình trụ có bán kính đáy r và độ dài đường sinh l là S = π rl . xq 2
x −1 y −3 z + 4
Câu 18: Trong không gian Oxyz , đường thẳng d : = =
đi qua điểm nào dưới đây? 1 3 2 −
A. Q(1;3− 2) . B. M ( 1; − 3 − ;4) . C. C(1;3; 4 − ) . D. N( 1; − 3 − ;2) . Lời giải Chọn C 1−1 3−3 2 − + 4
Thay tọa độ điểm Q vào đường thẳng d : = = (sai) nên loại 1 3 2 − 1 − −1 3 − − 3 4 + 4
Thay tọa độ điểm M vào đường thẳng d : = = (sai) nên loại 1 3 2 − 1−1 3−3 4 − + 4
Thay tọa độ điểm C vào đường thẳng d : = = (đúng) nên chọn 1 3 2 − 1 − −1 3 − − 3 2 + 4
Thay tọa độ điểm N vào đường thẳng d : = = (sai) nên loại 1 3 2 − Câu 19: Cho hàm số 4 2
y = ax + bx + c , (a,b,c∈ R) có đồ thị là đường cong như hình bên. Điểm cực tiểu của hàm số đã cho là: A. x = 1 − . B. x = 2 . C. x =1. D. x = 0 . Lời giải Chọn D
Nhìn vào đồ thị hàm số ta thấy hàm số có điểm cực tiểu là x = 0 .
Câu 20: Tiệm cận ngang của đồ thị hàm số 2x −1 y =
là đường thẳng có phương trình: 2x + 4 A. y = 2 − . B. x = 2 − . C. x =1. D. y =1. Lời giải Chọn D 1 2 2x 1 − − Có: lim = lim = lim x y =1 x→+∞
x→+∞ 2x + 4 x→+∞ 4 2 + x 1 2 2x 1 − − và: lim = lim = lim x y =1 x→−∞
x→−∞ 2x + 4 x→−∞ 4 2 + x Vậy đồ thị hàm số 2x −1 y =
có tiệm cận ngang là đường thẳng có phương trình: y =1. 2x + 4
Câu 21: Tập nghiệm của bất phương trình 2x 13 3 − < 27 là A. (4;+ ∞) . B. ( 4; − 4) .
C. (−∞;4) . D. (0;4). Lời giải Chọn B Ta có: 2 2 x 13 − x 13 − 3 2 2 3 < 27 ⇔ 3
< 3 ⇔ x −13 < 3 ⇔ x <16 ⇔ x < 4 ⇔ 4 − < x < 4.
Tập nghiệm của bất phương trình đã cho là S = ( 4; − 4). Kết luận: S = ( 4; − 4).
Câu 22: Có bao nhiêu số có năm chữ số khác nhau được tạo thành từ các chữ số 1,2,3,4,5,6? A. 5 A B. P . C. 5 C .
D. P . 6 6 6 5 Lời giải.
Chọn A Số tự nhiên gồm năm chữ số khác nhau được tạo thành từ các chữ số 1,2,3,4,5,6 là một chỉnh
hợp chập 5 của 6 phần tử. Vậy có 5 A số cần tìm. 6
Câu 23: Nguyên hàm của hàm số f (x) 3 = 2x − 2023 là: 1 A. 4
x − 2023x + C . B. 4
4x − 2023x + C . C. 1 4
x + C . D. 3
4x − 2023x + C . 2 4 Lời giải Chọn A 4 4 ∫( 3
2x − 2023)dx = 2. x − 2023x + C = x − 2023x + C . 4 2 5 2 − 5
Câu 24: Cho hai tích phân ∫ f (x)dx = 8 và ∫ g(x)dx = 3. Tính I = 
∫  f (x)−4g(x)−1d  x 2 − 5 2 − A. 13. B. 27 . C. 11 − . D. 3. Lời giải Chọn A 5 5 5 5 5 5 5 I = 
∫  f (x)−4g(x)−1d
x = ∫ f (x)dx − 4
∫ g(x)dx− d
∫ x = ∫ f (x)dx−4∫ g(x)dx− d ∫ x 2 − 2 − 2 − 2 − 2 − 2 − 2 − 5 2 − 5 5
= ∫ f (x)dx + 4∫ g (x)dx − d
∫ x = 8+ 4.3− x = 8+ 4.3−7 =13. 2 − 2 − 5 2 −
Câu 25: (Khái niệm, tính chất, bảng nguyên hàm cơ bản). Cho F(x) là một nguyên hàm của hàm số
f (x) . Tìm I = [2 f (x) + ∫ ]1dx .
A. I = 2xF(x) + x + C .
B. I = 2F(x) + x + C .
C. I = 2F(x) +1+ C .
D. I = 2xF(x) +1+ C . Lời giải Chọn B
Câu 26: Hàm số nào dưới đây có bảng biến thiên như sau: x ∞ -1 1 +∞ y' + 0 0 + +∞ 2 y 2 ∞ A. 4 2
y = x − 2x . B. 3
y = −x + 3 .x C. 4 2
y = −x + 2x . D. 3
y = x − 3 .x Lời giải Chọn D
Hàm số có bảng biến thiên như trên, trong 4 đáp án đã cho phải là hàm bậc ba với a > 0.
Câu 27: Cho hàm số f (x) có đạo hàm f (x) = x(x − )(x + )2023 ' 1 4 , x
∀ ∈  . Số điểm cực trị của hàm số đã cho là A. 3. B. 4 . C. 2 . D. 1 . Lời giải Chọn A
Câu 28: Đặt a = log 5,b = log 5 . Hãy biểu diễn log 5 theo 2 3 6 a và b . A. 1 1 2 2
log 5 = a + b .
B. log 5 = a + b . C. log 5 = + . D. log 5 ab = . 6 6 6 a b 6 a + b Lời giải Chọn D 1 a log 5 log 2  = ⇒ = 2 5 a  1 1  ⇒ log 6 a + b = + = ⇒ log 5 ab = 5 6 1 log 5 log 3 a b ab a + b b  = ⇒ = 3 5 b 
Câu 29: Gọi S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số: 3
y = x − 3x , y = x . Tính S. A. S = 4 .
B. S = 8. C. S = 2 . D. S = 0 . Lời giải Chọn B
Phương trình hoành độ giao điểm của hai đồ thị là x = 2 ± 3 3
x − 3x = x ⇔ x − 4x = 0 ⇔  x = 0 0 2
Vậy S = ∫ ( 3x −4x)dx + ∫( 3x −4x)dx = 4+ 4 = 8. 2 − 0
Câu 30: Cho hình lăng trụ đứng ABC.A′B C
′ ′ có tất cả các cạnh bằng nhau. Góc giữa hai đường thẳng
AB′ và CC′ bằng A. 30o . B. 90o . C. 60o . D. 45o . Lời giải Chọn D Ta có: ( ;′ )′ = ( ;′ )′ =  ′ = 45o AB CC AB BB AB B .
Câu 31: Cho hàm số ( ) 4 2
f x = ax + bx + c có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên thuộc đoạn [ 2;
− 5] của tham số m để phương trình f (x) = m có đúng hai nghiệm phân biệt? A. 1. B. 6 . C. 7 . D. 5. Lời giải Chọn C
Số nghiệm của phương trình f (x) = m chính là số giao điểm của đồ thị hàm số y = f (x) và //
đường thẳng d : y m d Ox = ≡   
Dựa vào đồ thị ta có phương trình f (x) = m có đúng hai nghiệm phân biệt khi và chỉ khi m = 2 −  m > 1. − Mặt khác m∈[ 2; − 5] ⇒ m∈{ 2; − 0;1;2;3;4; } 5 .
Suy ra có 7 giá trị thỏa mãn yêu cầu.
Câu 32: Hàm số nào sau đây đồng biến trên ? A. 4 2 y − = x − x . B. 3
y = x − x . C. x 1 y = . D. 3
y = x + x . x + 2 Lời giải Chọn D Xét 3
y = x + x có 2
y′ = 3x +1 > 0; x
∀ ∈. Vậy hàm số trên đồng biến trên .
Câu 33: Một đội thanh niên tình nguyện của trường gồm có 6 học sinh nam và 5 học sinh nữ. Chọn
ngẫu nhiên 4 học sinh để cùng các giáo viên tham gia đo thân nhiệt cho học sinh khi đến trường. Xác
suất để chọn được 4 học sinh trong đó số học sinh nam bằng số học sinh nữ bằng A. 5 . B. 5 . C. 6 . D. 2 . 66 11 11 33 Lời giải
Chọn B Ta có không gian mẫu n(Ω) 4 = C11.
Gọi A là biến cố: “Chọn được 4 học sinh trong đó số học sinh nam bằng số học sinh nữ” ⇒ n( A) 2 2 = C .C 5 6 . 2 2 n A C .C 5
Xác suất của biến cố A là: P( A) ( ) 5 6 = = = . 4 n(Ω) C 11 11
Câu 34: Nghiệm của phương trình log 2x +1 =1+ log x −1 3 ( ) 3 ( ) là
A. x = 4 . B. x = 2 − . C. x =1. D. x = 2 . Lời giải Chọn A 2x +1 > 0 Điều kiện:  ⇔ x >1. x −1 > 0
Ta có: log 2x +1 =1+ log x −1 3 ( ) 3 ( )
⇔ log 2x +1 = log 3⋅ x −1  3 ( ) 3  ( )
⇔ 2x +1 = 3x − 3 ⇔ x = 4 (nhận).
Câu 35: Gọi z là nghiệm phức có phần ảo âm của phương trình 2
z − z + = . Tọa độ điểm biểu diễn 1 2 5 0 −
số phức 7 4i trên mặt phẳng phức là z1
A. P(3;2) B. N (1; 2 − ) C. Q(3; 2 − ) D. M (1;2) Lời giải Chọn Az =1+ 2i Ta có 2
z − 2z + 5 = 0 ⇔  z = 1− 2i
Theo yêu cầu của bài toán ta chọn z =1− 2i . Khi đó: 1
7 − 4i 7 − 4i (7 − 4i)(1+ 2i) = = = 3+ 2i 2 2 z 1− 2i 1 + 2 1
Vậy điểm biểu diễn của số phức là P(3;2)
Câu 36: Trong không gian Oxyz , phương trình mặt phẳng (P) song song và cách đều hai đường thẳng x 2 : y z d − − − = = và x y 1 z 2 d : = = là 1 1 − 1 1 2 2 1 − 1 −
A. (P) : 2y − 2z +1 = 0 . B. (P) : 2x − 2z +1 = 0 . C. (P) : 2x − 2y +1 = 0 . D. (P) : 2y − 2z −1 = 0 . Lời giải Chọn A qua A(2;0;0) qua B(0;1;2) Ta có d : d : 1   và 2   . vtcpu = 1 − ;1;1  vtcpu = 2; 1 − ; 1 −  2 ( ) 1 ( )
Mặt phẳng (P) song song và cách đều hai đường thẳng x 2 : y z d − = = và 1 1 − 1 1 x y −1 z − 2 d : = = nên: 2 2 1 − 1 −   
(P) có một véc tơ pháp tuyến là n = u ,u  = 0;1; 1
− suy ra (P) : y − z + D = 0 1 2 ( )   Và d ( ,
A (P)) = d (B,(P)) ⇔ D = D −1 1 ⇔ D = 2
Vậy (P) : 2y − 2z +1 = 0 .
Câu 37: Cho hình nón đỉnh S , đáy là đường tròn ( ;
O 5) .Một mặt phẳng đi qua đỉnh của hình nón cắt
đường tròn đáy tại hai điểm A và B sao cho SA = AB = 8. Tính khoảng cách từ O đến (SAB) . 3 2 A. 2 2 . B. 3 13 . C. . D. 13 . 4 7 2 Lời giải Chọn B
Gọi I là trung điểm AB . AB ⊥ SO Ta có 
⇒ AB ⊥ (SOI ) ⇒ (SAB) ⊥ (SOI ) . AB ⊥ OI
Trong (SOI ) , kẻ OH ⊥ SI thì OH ⊥ (SAB) . ⇒ d ( ;
O (SAB)) = OH . 2 Ta có: 2 2 8.5 2 SO SA OA   = − = − 5 =   39 .  5  2 Ta có: 2 2 2  4.5 OI OA AI 5  = − = − =   3.  5  Tam giác vuông 1 1 1 3 13 SOI có: = + ⇒ OH = . 2 2 2 OH OI SO 4
Vậy d (O (SAB)) 3 13 ; = OH = . 4
Câu 38: Cho hình chóp S.ABC có SA = a và SA vuông góc với đáy. Biết đáy là tam giác vuông cân tại
A và BC = a 2 . Tính khoảng cách từ A đến mặt phẳng (SBC). A. a 5 . B. a 3 . C. a 3 . a 5 3 D. 3 Lời giải Chọn B S H A C E B
Gọi E là trung điểm của BC 1 a 2 ⇒ AE = BC = 2 2
Kẻ AH ⊥ SE ⇒ AH ⊥ (SBC) ⇒ AH là khoảng cách từ A đến mặt phẳng (SBC). Có 1 1 1 2 1 3 a 3 = + = + = ⇒ AH = . 2 2 2 2 2 2 AH AE SA a a a 3
Câu 39: Có bao nhiêu giá trị nguyên của x trong đoạn [0; ]
2023 thỏa mãn bất phương trình sau
16x 25x 36x 20x 24x 30x + + ≤ + + . A. 2023. B. 3. C. 2024 . D. 1. Lời giải Chọn D Ta có x x x x x x 2x 2x 2 16 25 36 20 24 30 4 5
6 x 4x.5x 4x.6x 5x.6x + + ≤ + + ⇔ + + ≤ + + 
(4x 5x)2 (4x 6x)2 (5x 6x ⇔ − + − + − )2
( x )2 ( x )2 ( x )2 2 4 5 6  ⇔ + + − ≤ 0 
 (2.4x.5x + 2.4x.6x + 2.5x.6x ) ≤ 0 .  x  4   =   1   5 x x 4 − 5 = 0   x  x x  4 4 6 0  ⇔ − = ⇔  =   1 ⇔ x = 0∈[0; ] 2023   6   x x 5 − 6 = 0   x  5   =   1  6  
Vậy có 1 giá trị nguyên của x trong đoạn [0; ]
2023 thỏa mãn bất phương trình. x x 1
Câu 40: Tập nghiệm của bất phương trình 2 x 1 (3 9)(3 ) 3 + − −
−1 ≤ 0 chứa bao nhiêu số nguyên ? 27 A. 2. B. 3. C. 4. D. 5. Lời giải Chọn B Điều kiện x 1+ x 1 3 1 0 3 + − ≥ ⇔ ≥ 1 ⇔ x ≥ 1 − . Ta có x = 1
− là một nghiệm của bất phương trình. Với x > 1
− , bất phương trình tương đương với 2x x 1 (3 − 9)(3 − ) ≤ 0. 27 1 t ≤ 3 − Đặt 3x t = > 0 , ta có 2 1
(t − 9)(t − ) ≤ 0 ⇔ (t − 3)(t + 3)(t − ) ≤ 0  ⇔ . Kết 27 27 1  ≤ t ≤ 3  27 1 1 hợp điều kiện 3x
t = > 0 ta được nghiệm ≤ t ≤ 3 ⇔ ≤ 3x ≤ 3 ⇔ 3
− ≤ x ≤1. Kết hợp 27 27 điều kiện x > 1 − ta được 1
− < x ≤1 suy ra trường hợp này bất phương trình có 2 nghiệm nguyên.
Vậy bất phương trình đã cho có tất cả 3 nghiệm nguyên. Câu 41: Cho hàm số 2
f ( x) xác định trên  \ { 1; − }
1 , thỏa mãn f '( x) = ; f 3 − + f 3 = 2 ln 2 và 2 ( ) ( ) x −1  1   1  f − + f = 0    
. Giá trị của biểu thức P = f ( 2
− ) + f (0) + f (4) là:  2   2 
A. 2 ln 2 − ln 5
B. 6 ln 2 + 2 ln3− ln 5 C. 2 ln 2 + 2 ln3− ln 5 D. 6 ln 2 − 2 ln 5 Lời giải Chọn C   −
f ( x) = f ∫ (x) 2 1 1 x 1 ' dx = dx = − dx = ln + C ∫ ∫ 2 x   −1
x −1 x +1 x +1   x −1 ln + C khi x > 1    1  x +1  −  − Hay ( ) x 1 1 x f x = ln + C = ln
+ C khi −1 < x < 1 2 x +1 1+ x    x −1 ln + C khi x < 1 −    3   x +1  f ( 3 − ) + f (3) = 2 ln 2 
C + C = 2 ln 2 Theo bài ra, ta có: 1 3   1   1 ⇔    f − + f = 0     C = 0 2   2   2 
Do đó f (− ) + f ( ) + f ( ) 3 2 0
4 = ln 3 + C + C + ln + C = 2 ln 2 + 2 ln 3 − ln 5 . 3 2 1 5 2 2
x + (x + ln x)2 + x Câu 42: a 1 Cho I = dx = − ∫
với a , b , c là các số nguyên dương. Khẳng 2 x x + ln x 2 b + ln c 1 ( )2
định nào sau đây đúng ?
A. abc = 26.
B. abc = 3 .
C. abc =11.
D. abc =12 . Lời giải Chọn D (x + ln x)2 2 + x(x + ) 1 2 2 2 Ta có I = dx ∫ 1 x +1 + = dx + dx ∫ ∫ 1 x 1 = + dx ∫ . 2 2 2 x 2 2 1
x (x + ln x)2
1 x ( x + ln x) 1
1 x ( x + ln x ) Đặt x +1
t = x + ln x ⇒ dt =
dx . Đổi cận x =1⇒ t =1 và x = 2 ⇒ t = 2 + ln 2 . x 2 2+ln 2 2+ln 2 Do đó 1 x +1 1 1 1 1 3 1 I = + dx = + dt ∫ = = − 1 1 = +1− = − .
2 ∫ x(x + ln x)2 2 2 t 2 t 2 2 + ln 2 2 2 + ln 2 1 1 1
Vậy abc = 3.2.2 =12 .
Câu 43: Cho (H ) là hình phẳng giới hạn bởi parabol 2
y = 3x , cung tròn có phương trình 2 y = 4 − x
(với 0 ≤ x ≤ 2) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của (H ) là π + π − π + − − π A. 4 3 . B. 4 3 . C. 4 2 3 3 . D. 5 3 2 . 12 6 6 3 Lời giải Chọn B
Phương trình hoành độ giao điểm của parabol 2
y = 3x và cung tròn 2 y = 4 − x
(với 0 ≤ x ≤ 2) lả 2 2 2 4
4 − x = 3x ⇔ 4 − x = 3x ⇔ x =1.
Diện tích của (H ) là 1 2 1 2 2 2 3 3 3 S = 3x dx + 4 − x dx = x + I = + I ∫ ∫ với 2 I = 4 − x dx 3 3 ∫ . 0 1 0 1  π π
Đặt x = 2sin t , t ;  ∈ −
⇒ dx = 2cost.dt  2 2    π π
Đổi cận x =1⇒ t = , x = 2 ⇒ t = . 6 2 π π π π 2 2 2 2 2 2 I =
4 − 4sin t.2cost.dt = 4cos t.dt = 2 ∫ ∫
∫ (1+cos2t).dt = (2x+sin2t) π π π π 6 6 6 6 2π 3 = − 3 2 π π − Vậy 3 3 2 3 4 3 S = + I = + − = 3 3 3 2 6 2022
Câu 44: Cho hai số phức z = 2 + i, z =1− 2 .i Môđun của số phức z1 = là 1 2 w 2023 z2 5
A. w = 5.
B. w = 3.
C. w = 3. D. w = . 5 Lời giải Chọn D z 2 + i 1 = = i z 1− 2i 2 2022 2022 zz  1 1  1 2   1 2  1 2 1 1 2022 w = =   . = i . = i . + i =   1 − . + i = + i 2023 ( 2)1010 ( )1010 zz z 1 2i 5 5  5 5  −     5 5 2 2 2 1 2 5 w = + i = 5 5 5
Câu 45: Cho hình trụ có thiết diện qua trục là một hình vuông. Thiết diện của hình trụ tạo bởi mặt phẳng
song song và cách trục một khoảng bằng a có diện tích bằng 2
8a 3 . Thể tích của khối trụ là 3
A. 16π a . B. 2 16πa . C. 3 16πa . D. 3 32πa . 3 Lời giải Chọn C
Gọi R là bán kính đáy hình trụ, do thiết diện qua trục là một hình vuông nên l = 2R .
Thiết diện của hình trụ tạo bởi mặt phẳng song song và cách trục một khoảng bằng a là hình
chữ nhật ABCD khi đó OI = a với I là trung điểm BC ta có 2 2 2 2
IC = R − a ⇒ BC = 2 R − a .
Diện tích hình chữ nhật là 2 2 2 S
= AB BC = R R − a = a . ABC . 4 8 3 D 4 2 2 2
⇔ R − R a −12a = 0 ⇔ ( 2 2 R − a )( 2 2 4
R + 3a ) = 0 ⇔ R = 2a từ đó h = l = 2R = 4a . Thể tích khối trụ là 2 3
V = π R h =16πa .
Câu 46: Trong không gian Oxyz, cho điểm I(1; 2
− ;3). Viết phương trình mặt cầu tâm I, cắt trục Ox tại
hai điểm A và B sao cho AB = 2 3.
A. ( − )2 + ( + )2 + ( − )2 x 1 y 2 z 3 =16. B. ( − )2 2
x 1 + (y + 2) + (z −3)2 = 20.
C. ( − )2 + ( + )2 + ( − )2 x 1 y 2 z 3 = 25.
D. ( − )2 + ( + )2 + ( − )2 x 1 y 2 z 3 = 9. Lời giải Chọn A
Gọi H là trung điểm AB ⇒ IH ⊥ AB tại H ⇒ IH = d( = d I;(AB)) (I;Ox)   IM,i Lấy M(2;0;0) Ox IH d   ∈ ⇒ = ( =  = 3. I,Ox) i
Bán kính mặt cầu cần tìm là 2 2 R = IA = IH + HA = 4.
Vậy phương trình mặt cầu cần tìm là ( − )2 + ( + )2 + ( − )2 x 1 y 2 z 3 =16. π 4 2 e f ( 2 ln x)
Câu 47: Cho hàm số f (x) liên tục trên  và thỏa mãn tan .x f ∫ ( 2 cos x)dx =1, dx =1. ∫ Giá x ln x 0 e 2 (2 ) trị của tích phân = d ∫ f x I x bằng 1 x 4 A. 1. B. 2 . C. 3. D. 4 . Lời giải Chọn D π 4 ● Xét A = tan . x f ∫ ( 2
cos x)dx =1. Đặt 2 t = cos . x 0 Suy ra 2 d d = 2 − sin cos d = 2 − cos tan d = 2 − .tan d  → tan d t t x x x x x x t x x x x = − . 2t
x = 0 ⇒ t =1 Đổi cận:  π 1 . x = ⇒ t =  4 2 1 2 1 f (t) 1 1 f (t) 1 1 f (x) 1 f (x) Khi đó 1 = A = − dt = dt = dx ⇒ dx = 2. 2 ∫ t 2 ∫ t 2 ∫ x ∫ x 1 1 1 1 2 2 2 2 e f ( 2 ln x) ● Xét B = dx =1. ∫ Đặt 2 u = ln . x x ln x e 2 Suy ra 2ln x 2ln x 2u dx du du = dx = dx = dx ⇒ = . x x ln x x ln x x ln x 2u
x = e ⇒ u =1 Đổi cận:  . 2
x = e ⇒ u = 4 4 1 f (u) 4 1 f (x) 4 f (x) Khi đó 1 = B = du = dx ⇒ dx = 2. ∫ ∫ ∫ 2 u 2 x x 1 1 1 2 f (2x)
● Xét tích phân cần tính I = d . x ∫1 x 2  1 dx = dv   1 1 x = ⇒ v =
Đặt v = 2x, suy ra  2  . Đổi cận:  4 2 . vx =
x = 2 ⇒ v = 4  2 4 f (v) 4 f (x) 1 f (x) 4 f (x) Khi đó I = dv = dx = dx + dx = 2 + 2 = 4. ∫ ∫ ∫ ∫ 1 v 1 x 1 x x 1 2 2 2
Câu 48: Cho hàm số bậc ba y = f (x) có đồ thị như hình vẽ, biết f (x) đạt cực tiểu tại điểm x =1 và
thỏa mãn  f (x) +1 
 và  f ( x) −1 
 lần lượt chia hết cho ( x − )2 1 và (x + )2
1 . Gọi S , S lần lượt là diện 1 2
tích như trong hình bên. Tính 2S + 8S . 2 1 A. 9. B. 4 . C. 3 . D. 1 . 5 2 Lời giải Chọn B
 f (x)+1= a(x − )2 1 (x + m) Đặt ( ) 3 2
f x = ax + bx + cx + d theo giả thiết có   f
 ( x) −1 = a ( x + )2 1 (x + n)   1  ( ) 1 +1 = 0 + + + +1 = 0 a f a b c d =   2     f (− ) 1 −1 = 0
−a + b − c + d −1 = 0 b  = 0 Do đó 1 3   ( ⇔  ⇔ 
⇒ f x = x − x f 0) ( ) 3 = 0 d = 0 3 2 2   = −  ′( ) c f 1 = 0 3
a + 2b + c =  0  2    d = 0 1 3 x = 0 Ta có f (x) 3
= x − x = 0 ⇔ 2 2  x = ± 3 1
S là diện tích giới hạn bởi đồ thị 1 3 3
y = x − x , 1 3 3 3 ⇒ S = x − x +1 = 1 y = 1
− , x = 0, x = 1 2 2 1 ∫ 2 2 8 0 ( )1
S là diện tích giới hạn bởi đồ thị 1 2 3
y = x − x , = = = 2
y 0, x 1, x 3 3 2 3 1 3 3 1 ⇒ S = x − x = 2 2 ∫ ( ) 2 2 2 1 Từ ( ) 1 ,(2) 1 3
⇒ 2S + 8S = 2. + 8. = 4 . 2 1 2 8
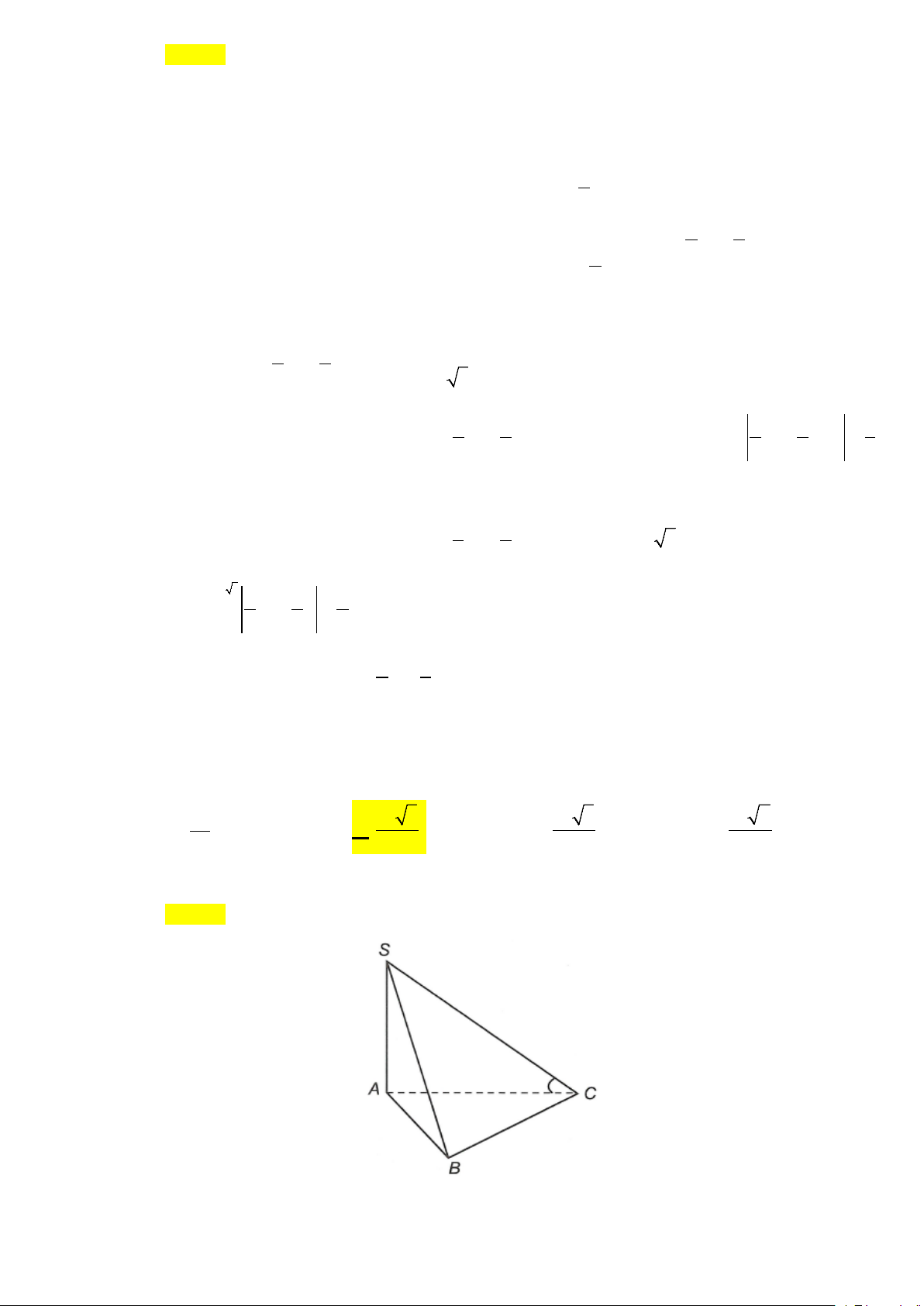
Câu 49: Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại C và SA vuông góc
với mặt phẳng đáy. Cho SC = a , mặt phẳng (SBC) tạo với mặt đáy một góc α . Thể tích khối
chóp S.ABC đạt giá trị lớn nhất là 3 3 3 3 A. a . B. a 3 . C. a 3 . D. a 2 . 16 27 48 24 Lời giải Chọn B
Ta có ((SBC) ( ABC))  =  (SC AC)=  , , SCA = α Xét S
∆ AC vuông tại A có
SA = SC.sinα = a sinα 
AC = SC.cosα = a cosα 1 1  1 2 V S  ⇒ = = ∆ SAAC SA S ABC ABC . . . . 3 3  2  3 1 = .(a cosα )2 a 2 .asinα = cos α.sinα. 6 6 V
đạt giá trị lớn nhất khi và chỉ khi biểu thức S.ABC 2 P = α α = ( 2
cos .sin . 1− sin α ).sinα đạt giá trị lớn nhất.
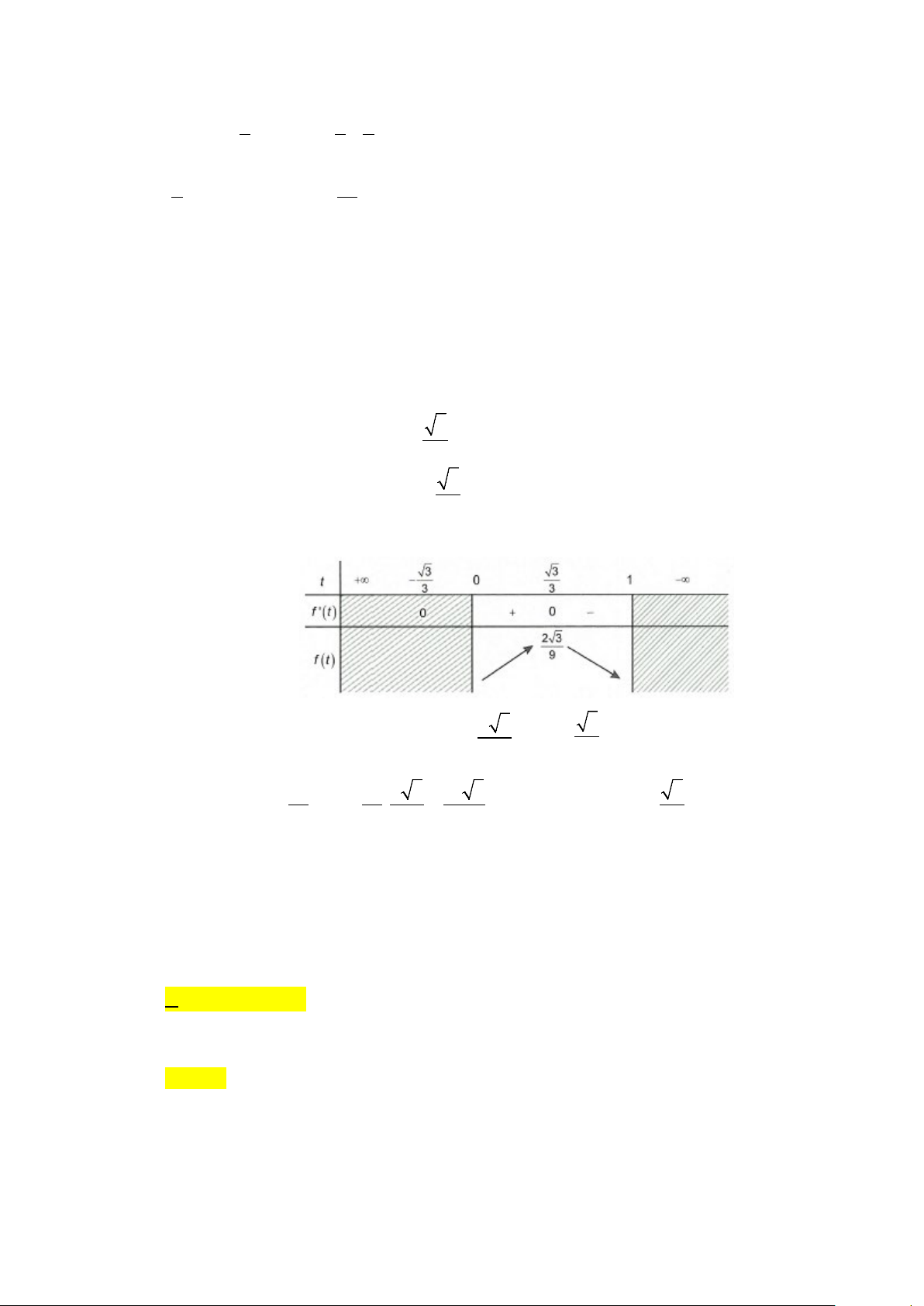
Đặt t = sinα . Vì 0 < α < 90° nên 0 < sinα <1 ⇒ 0 < t <1
Ta có P = f (t) = ( 2 − t ) 3 1 t = t
− + t xác định và liên tục trên (0; ) 1 .  3 t = (nhan)
f ′(t) = − 2t + ⇒ f ′(t) = ⇔  3 3 1 0  3 t = − (loai)  3 Bảng biến thiên:
Dựa vào bảng biến thiên, ta có f (t) 2 3 max = khi 3 t = . (0 ) ;1 9 3 3 3 3 Vậy a a 2 3 a 3 maxV = P = = khi và chỉ khi 3 sinα = . S ABC . . . max 6 6 9 27 3
Câu 50: Trong không gian Oxyz, cho mặt cầu (S ) (x − )2 + ( y − )2 + (z + )2 : 2 3 1 =16 và điểm A( 1; − 1; − − )
1 . Xét các điểm M thuộc (S )sao cho đường thẳng AM tiếp xúc với (S ). M luôn thuộc một
mặt phẳng cố định có phương trình là
A. 3x + 4y − 2 = 0.
B. 3x + 4y + 2 = 0 .
C. 6x + 8y +11 = 0 .
D. 6x + 8y −11 = 0 . Lời giải Chọn A
(S)có tâm I (2;3;− )1; bán kính R = 4  A( 1 − ; 1 − ;− ) 1 ⇒ IA = ( 3 − ; 4
− ;0) , tính được IA = 5 . 
Mặt phẳng cố định đi qua điểm H là hình chiếu của M xuống IA và nhận IA = ( 3 − ; 4 − ;0) làm vectơ pháp tuyến. 2
Do hai tam giác MHI và AMI đồng dạng nên tính được 2 IM 16
IM = IH.IA ⇒ IH = = , từ đó IA 5   tính được 16 IH = IA tìm được 2 11 H  ; ; 1 − 25 25 25   
Mặt phẳng cần tìm có phương trình là:  2   11 3 x 4 y  − − − −
= 0 ⇔ 3x + 4y − 2 =     0.  25   25 
Document Outline

  • ĐỀ MINH HỌA - Vien Banh Van
  • ĐÁP ÁN ĐỀ MINH HỌA - Vien Banh Van