ĐỀ ÔN TẬP GIỮA HKI - SỐ 4 (1)

LỚP TOÁN THẦY CHÍ 2007
ÔN TẬP: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT
ĐỀ ÔN TẬP GIỮA HKI L12 (TIẾP)
VÀ VẼ ĐỒ THỊ HÀM SỐ ĐỀ SỐ 4
VECTƠ VÀ HỆ TRỤC TỌA ĐỘ TRONG KHÔNG GIAN
PHẦN I: Trắc nghiệm nhiều phương án trả lời. Học sinh trả lời từ Câu 1 đến Câu 12.
Mỗi Câu chỉ chọn một phương án.
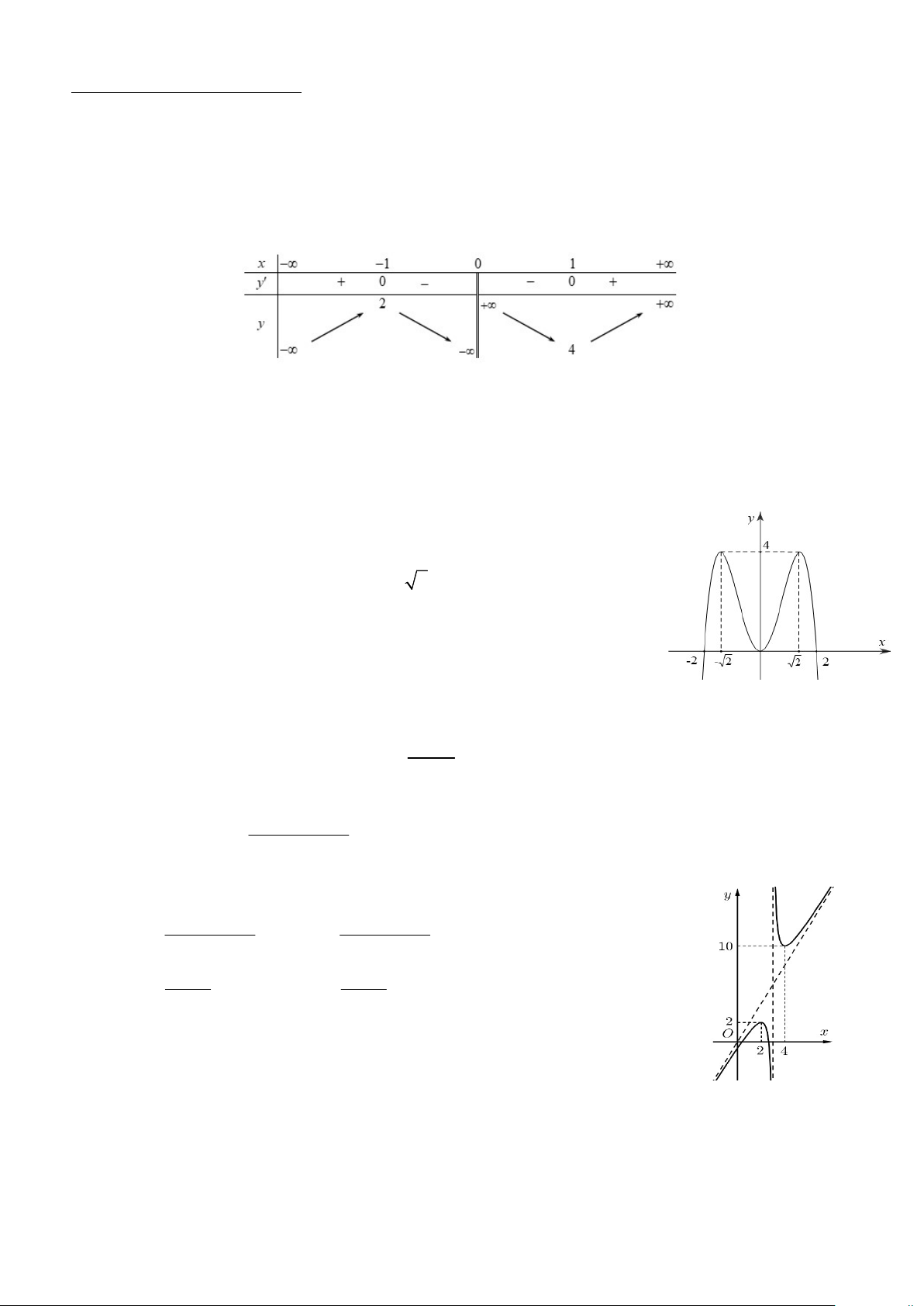
Câu 1. Cho hàm số y  f  x có bảng biến thiên như sau:
Hàm số nghịch biến trong khoảng nào? A. 1;  1 . B. 0;  1 . C. 4; . D.  ;  2 .
Câu 2. Cho hàm số f x có đạo hàm f x  x x   x  3 ' 1 4 , x
  . Số điểm cực tiểu của hàm số đã cho là A. 2 B. 3 C. 4 D. 1
Câu 3. Cho hàm số y  f  x có đồ thị như hình vẽ.
Giá trị lớn nhất của hàm số f x trên đoạn 0;2 là: A. Max f  x  2 . B. Max f  x  2 . 0;2 0;2 C. Max f  x  4 . D. Max f  x  0 . 0;2 0;2
Câu 4. Giá trị lớn nhất của hàm số 4 2
y  x  4x  9 trên đoạn 2;3 bằng A. 201 B. 2 C. 9 D. 54 2x  2
Câu 5. Tiệm cận đứng của đồ thị hàm số y  là x 1 A. x  2 . B. x 1. C. x  1 . D. x  2 . 2 4x  2x  5 Câu 6. Cho hàm số y 
. Đường tiệm cận xiên của hàm số là x  2 A. y  4x 10 . B. y  2x  3. C. y  2x 3 . D. y  4x 10.
Câu 7. Đồ thị sau là của hàm số nào dưới đây? 2 2x  6x  2 2 2x  6x  2 A. y  . B. y  . x  3 x  3 2 x  6 2 x  6 C. y  . D. y  . x  3 x  3
Câu 8. Đồ thị của hàm số 3
y  x  3x  2 cắt trục tung tại điểm có tung độ bằng A. 0 . B. 1. C. 2 . D. 2  . 
Câu 9. Cho hình hộp chữ nhật ABC .
D A' B 'C ' D ' . Khi đó, vectơ bằng vectơ AB là vectơ nào dưới đây?     A. D 'C '. B. BA . C. CD . D. B ' A' .
Câu 10.Cho hình lập phương ABC .
D A B C D . Gọi O là tâm của hình lập phương. Chọn đẳng thức đúng? 1 1 1 1
 1   
 1   
A. AO   AB  AD  AA .
B. AO   AB  AD  AA . 1  1  3 2
 1   
 2   
C. AO   AB  AD  AA .
D. AO   AB  AD  AA . 1  1  4 3
Câu 11.Trong không gian Oxyz , cho điểm A2; 3;5 . Tìm tọa độ A là điểm đối xứng với A qua trục Oy . A. A2;3;5 . B. A2;3; 5 . C. A2;3;5 . D. A2;3;5 .
Câu 12.Trên mặt phẳng toạ độ Oxy , cho tam giác ABC biết A1;3 , B 2;2, C 3;1 . Tính cosin góc A của tam giác. 2 1 2 1 A. cos A  B. cos A  C. cos A   D. cos A   17 17 17 17
PHẦN II: Trắc nghiệm lựa chọn đúng sai. Học sinh trả lời từ Câu 1 đến Câu 4.
Trong mỗi ý a), b), c), d) ở mỗi Câu, học sinh chọn đúng hoặc sai. Câu 1. Cho hàm số f ( ) x có đồ thị như sau:
a) Hàm số y  f (x) đồng biến trên khoảng (3;2)
b) Hàm số y  f (x) nghịch biến trên các khoảng (5; 3) và (2;5)
c) Hàm số y  f (x) có x  3  là điểm cực tiểu
d) Hàm số y  f (x) có x  2 là điểm cực đại 2x  3
Câu 2. Cho hàm số f (x) 
có đồ thị như hình vẽ. 2 5x 15x 10
Xét tính đúng sai của các mệnh đề sau: a) Đồ thị hàm số f ( )
x có ba đường tiệm cận.
b) Đường thẳng x 1, x  2 là hai đường tiệm cận đứng của đồ thị hàm số.
c) Đường thẳng x  0 là tiệm cận ngang của đồ thị hàm số.
d) Hàm số đã cho có hai điểm cực trị. 2 ax  bx  c Câu 3. Cho hàm số y 
có đồ thị là đường cong ở Hình. x  n
Xét tính đúng sai của các mệnh đề sau a) n  0 . b) a  0 . c) c  0 . d) b  0 .
Câu 4.Trong không gian với hệ tọa độ Oxyz , cho hình hộp ABCD ABCD  có
A4;6;5, B 5;7;4,C 5;6; 4
 , D2;0;2 . Xét tính đúng, sai của các mệnh đề sau:  a) Ta có: AB  1;1;  1 .
b) Tọa độ của điểm D là 4;5; 5  .
   
c) AA  BB  CC  DD
d) Tọa độ của điểm C là 1;3;  1
PHẦN III: Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ Câu 1 đến Câu 6
Câu 1. Cho bất phương trình 2
x  (m 1)x  m  2  0 , với m là tham số thực. Tìm giá trị lớn nhất của m
sao cho bất phương trình đã cho nghiệm đúng với mọi x [0; 4]. Đáp án:……………..
Câu 2. Người ta muốn làm một chiếc hộp hình hộp chữ nhật có đáy hình vuông và thể tích là 10l . Diện
tích toàn phần nhỏ nhất của hộp là bao nhiêu? (làm tròn kết quả đến hàng phần mười) Đáp án:……………..
Câu 3. Quan sát một đàn ong trong 20 tuần, người ta ước lượng được số lượng ong trong đàn bởi công 20000 thức P(t) 
, trong đó t là thời gian tính theo tuần kể từ khi bắt đầu quan sát, 0  t  20 . Tại 11000 t e
thời điểm nào thì số lượng ong của đàn tăng nhanh nhất (kết quả làm tròn đến hàng đơn vị của tuần)? Đáp án:……………..
Câu 4. Cho hình hộp ABCD ABCD 
có tất cả các mặt bên là hình thoi cạnh 2 6 , các góc  BAA   BAD DAA 60   
. Tính độ dài đường chéo AC. Đáp án:……………..   
Câu 5. Trong không gian với hệ tọa độ Oxyz , cho các vectơ a  (1; x 1;1),b  (2;1; 1),c(1;3; 3) , với x    
là số thực thay đổi. Đặt P |
 a  b |  | a  c | , tính giá trị nhỏ nhất của P (làm tròn kết quả đến hàng đơn vị) Đáp án:……………..
Câu 6. Xét các số thực dương ,
x y, z thỏa mãn x  y  z  4 và xy  yz  zx  5 . Giá trị nhỏ nhất của  1 1 1  biểu thức  3 3 3 x  y  z      bằng?  x y z  Đáp án:…………….. BẢNG ĐÁP ÁN PHẦN I 1.B 2.A 3.C 4.D 5.C 6.D 7.A 8.C 9.A 10.B 11.D 12.B BẢNG ĐÁP ÁN PHẦN II Câu 1 a) Đúng b) Đúng c) Đúng d) Đúng Câu 2 a) Đúng b) Đúng c) Sai d) Sai Câu 3 a) Sai b) Đúng c) Đúng d) Sai Câu 4 a) Đúng b) Đúng c) Đúng d) Sai BẢNG ĐÁP ÁN PHẦN III Câu 1: 1 Câu 2: 27,8 Câu 3: 7 Câu 4: 12 Câu 5: 8 Câu 6: 25