Đề thi chuyên đề Toán 12 lần 4 năm 2019 – 2020 trường THPT Liễn Sơn – Vĩnh Phúc

Đề thi chuyên đề Toán 12 lần 4 năm học 2019 – 2020 trường THPT Liễn Sơn – Vĩnh Phúc mã đề 132 gồm có 06 trang với 50 câu trắc nghiệm

24 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

28 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
Trang 1/6 - Mã đề thi 132
SỞ GD & ĐT VĨNH PHÚC
TRƯỜNG THPT LIỄN SƠN
(đề thi gồm có 06 trang)
ĐỀ THI KIỂM TRA CHUYÊN ĐỀ LẦN 4
MÔN TOÁN LỚP 12
Thời gian làm bài: 90 phút không kể thời gian giao đề
(50 câu trắc nghiệm)
Mã đề thi 132
(Thí sinh không được sử dụng tài liệu)
Họ, tên thí sinh:..................................................................... Số báo danh: .............................
Câu 1: Thể tích của khối lăng trụ có chiều cao bằng
h
và diện tích đáy bằng
B
là
A.
.
3
1
Bh
B.
.
6
1
Bh
C.
.Bh
D.
.3Bh
Câu 2: Cho cấp số nhân
có
1
2u = −
và công bội
3q =
. Giá trị của
11
u
là
A.
11
3072u =
.
B.
11
354294u = −
.
C.
11
118098u = −
.
D.
2
354294u =
.
Câu 3: Số điểm chung của đồ thị hàm số
42
yx7x6=−−
và đồ thị hàm số
3
y x 13x= −
là:
A. 4. B. 1. C. 2. D. 3.
Câu 4: Trong không gian
Oxyz
cho hai đường thẳng
12
x1t
x2 y2 z3
d : , d : y 1 2t
2 11
z 1t
= −
−+−
= = = +
−
=−+
và điểm
A(1;2;3).
Đường thẳng
∆
qua
A
vuông góc với
1
d
và cắt
2
d
có phương trình là:
A.
x1 y2 z3
.
1 35
−−−
= =
−−
B.
x1 y2 z3
.
135
−−−
= =
−−−
C.
x1 y2 z3
.
135
−−−
= =
D.
x1 y2 z3
.
13 5
−−−
= =
−
Câu 5: Cho hàm số
y f(x)
=
có
x
lim f (x) 3
→+∞
=
và
x
lim f (x) 3
→−∞
= −
. Khẳng định nào sau đây là đúng ?
A. Đồ thị hàm số đã cho không có tiệm cận ngang.
B. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng
y3=
và
y3= −
.
C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng
x3=
và
x3= −
.
Câu 6: Cho hàm số
fx
liên tục và có đạo hàm trên
0; ,
2


thỏa mãn hệ thức
3
tan .
cos
x
f x xf x
x

Biết rằng
3 3 ln 3
36
f f ab

 







 
trong đó
, .ab
Tính giá trị của biểu thức
.P ab
A.
4
.
9
P 
B.
2
.
9
P 
C.
7
.
9
P
D.
14
.
9
P
Câu 7: Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
( ) ( ) ( ) ( )
22 2
S : x 3 y 1 z 2 8.− ++ ++ =
Khi đó
tâm I và bán kính R của mặt cầu là
A.
(
)
I3;1;2,R 22−− =
B.
( )
I3;1;2,R 4−− =
C.
( )
I 3;1; 2 , R 2 2−=
D.
( )
I 3;1; 2 , R 4−=
Câu 8: Đồ thị hàm số
32
32yx x=−− +
có dạng nào dưới đây ?
Hình 1 Hình 2 Hình 3 Hình 4
Trang 2/6 - Mã đề thi 132
-3 -2
-1 1
-3
-2
-1
1
2
3
y
-3
-2
-1 1
2 3
-3
-2
-1
1
2
3
y
-3
-2
-1
1
-3
-2
-1
1
2
3
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
y
A. Hình 4. B. Hình 3. C. Hình 1. D. Hình 2.
Câu 9: Cho số phức
( )
1
z bi b=+∈
và
10z =
.Giá trị của b bằng
A. 3.
B.
3±
. C. –3.
D.
10
.
Câu 10: Đạo hàm của hàm số
( )
2
x
fx x= +
là
A.
( )
2
1
ln 2
x
fx
′
= +
. B.
(
)
2
2
ln 2 2
x
x
fx
′
= +
. C.
( )
2 ln 2 1
x
fx
′
= +
D.
( )
21
x
fx
′
= +
.
Câu 11: Giá trị nhỏ nhất của hàm số
54
2
4
+−= xxy
trên đoạn
[ ]
2;1−
là
A.
3.
B.
5.
C.
2.
D.
1.
Câu 12: Người ta muốn xây một bể chứa nước dạng khối hộp chữ
nhật trong một phòng tắm. Biết chiều dài, chiều rộng, chiều cao của
khối hộp đó lần lượt là
5m
;
1
m
;
2m
(người ta chỉ xây hai mặt thành
bể như hình vẽ bên). Biết mỗi viên gạch có chiều dài
20cm
, chiều
rộng
10cm
, chiều cao
5cm
. Hỏi người ta sử dụng ít nhất bao nhiêu
viên gạch để xây bể đó và thể tích thực của bể chứa bao nhiêu lít
nước? (Giả sử lượng xi măng và cát không đáng kể).
A. 1180 viên,
8820
lít. B. 1180 viên, 8800 lít.
C. 1182 viên, 8820 lít. D. 1180 viên, 8800 lít.
Câu 13: Tính môđun của số phức
( )
=+∈
,, .z a bi a b
A.
= +
22
.z ab
B.
= +
22
.za b
C.
= + .z ab
D.
= −
22
.
z ab
Câu 14: Cho chiếc trống như hình vẽ, có đường sinh là nửa elip được cắt bởi trục lớn với độ dài trục lớn
bằng 80 cm, độ dài trục bé bằng 60 cm và đáy trống là hình tròn có bán kính bằng 60 cm. Tính thể tích
V
của chiếc trống (kết quả làm tròn đến hàng đơn vị).
A.
3
344963cmV =
.
B.
3
344964cmV =
.
C.
3
208347cmV =
.
D.
3
208346cmV =
.
Câu 15: Họ nguyên hàm của hàm số
x
f (x) 3 cos x= −
là
A.
x
3
sinx C.
ln 3
−+
B.
x
3 ln 3 sinx C.−+
C.
x
3
sinx C.
ln 3
++
D.
x
3 ln 3 s inx C.++
Câu 16: Diện tích của mặt cầu bán kính 2a là
A.
2
4 a
π
.
B.
2
16 a
π
.
C.
2
16a
.
D.
2
4
3
a
π
.
1, 8 m
1dm
1
dm
3m
1, 3 m
Trang 3/6 - Mã đề thi 132
Câu 17: Phương trình tham số của đường thẳng d đi qua điểm
( )
1; 1; 2A −
và có vectơ chỉ phương
(1; 2; 3)u
= −
là
A.
1
:2
32
xt
dy t
zt
= +
= −
=−+
.
B.
1
:1
22
xt
dy t
zt
= +
=−−
= +
C.
1
: 13
25
x
dy t
zt
=
=−+
= −
.
D.
1
: 12
23
xt
dy t
zt
= +
=−+
= −
.
Câu 18: Một lớp học gồm có 20 học sinh nam và 15 học sinh nữ. Cần chọn ra 2 học sinh, 1 nam và 1
nữ để phân công trực nhật. Số cách chọn là
A.
2
35
A
. B. 300.
C.
2
35
C
. D. 35.
Câu 19: Một hình trụ có bán kính đáy bằng 3 và đường cao bằng 4. Tính diện tích xung quanh
xq
S
của
hình trụ.
A.
24
xq
S
π
=
.
B.
30
xq
S
π
=
.
C.
15
xq
S
π
=
.
D.
12
xq
S
π
=
.
Câu 20: Trong không gian Oxyz, cho điểm
( )
1; 2; 2A
và mặt phẳng
()
α
:
2 2 40
xyz
+ − −=
. Tính
khoảng cách
d
từ điểm
A
đến mặt phẳng
()
α
.
A.
1
.
3
d =
B.
1.
d
=
C.
13
.
3
d =
D.
3.d =
Câu 21: Bình có bốn đôi giày khác nhau gồm bốn màu: đen, trắng, xanh và đỏ. Một buổi sáng đi học, vì
vội vàng, Bình đã lấy ngẫu nhiên hai chiếc giày từ bốn đôi giày đó. Tính xác suất để Bình lấy được hai
chiếc giày cùng màu.
A.
1
4
.
B.
2
7
.
C.
1
14
D.
1
7
.
Câu 22: Rút gọn biểu thức
7
3
5
3
7
42
.
.
aa
A
aa
−
=
với
0a >
ta được kết quả
m
n
Aa
=
, trong đó
m
,
*
n∈
và
m
n
là
phân số tối giản. Khẳng định nào sau đây đúng?
A.
2
3 22mn−=
.
B.
22
43mn+=
.
C.
2
2 15mn+=
.
D.
22
25mn+=
.
Câu 23: Biết tiếp tuyến của đồ thị hàm số
42
2y ax bx=++
tại điểm A(-1;1) vuông góc với đường thẳng
2 3 0.xy
− +=
Tính
22
?ab−
A.
22
2.ab−=−
B.
22
13.ab−=
C.
22
5.ab−=−
D.
22
10.ab
−=
Câu 24: Trong không gian Oxyz cho
2OA k i j= −+

. Tọa độ điểm A là
A.
( 2; 1; 1)A
−
.
B.
( 2; 1; 1)A −−
.
C.
( )
1; 1; 2A −−
.
D.
( 1; 1; 2)A
−
.
Câu 25: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt đáy
và
2SA a
. Tìm số đo của góc giữa đường thẳng SC và mặt phẳng (SAB).
A.
0
30
.
B.
0
45
.
C.
0
60
.
D.
0
90
.
Câu 26: Tập nghiệm của phương trình
x1
4 10
−
−=
là
A.
B.
{ }
1.−
C.
{ }
1.
D.
{ }
2.
Câu 27: Tập nghiệm của bất phương trình
( )
0,5
log 1 1
x −>
là
A.
3
;
2

+∞


.
B.
3
1;
2


.
C.
3
;
2

−∞


.
D.
3
1;
2



.
Câu 28: Khi cắt khối nón (N) bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác
vuông cân có cạnh huyền bằng
2 3.a
Tính thể tích V của khối nón (N).
A.
3
36 .Va= π
B.
3
6.Va= π
C.
3
3.Va= π
D.
3
33 .Va= π
Trang 4/6 - Mã đề thi 132
Câu 29: Hàm số
2
1
2
log ( 1)
yx
= +
có tập giá trị là
A.
( ;0].−∞
B.
[1; ).+∞
C.
.
D.
[0; ).+∞
Câu 30: Cho ba số thực dương a, b, c và a khác 1. Khẳng định nào sau đây là sai?
A.
( )
log log log .
a aa
bc b c= +
B.
log
a
b
ab=
.
C.
log log
aa
bb
α
α
=
.
D.
ln
log
ln
a
a
b
b
=
.
Câu 31: Biết rằng tồn tại duy nhất bộ các số nguyên a, b, c sao cho
3
2
(4x 2) ln xdx a bln 2 c ln 3+ =++
∫
.
Giá trị của a + b + c bằng
A. 19 B. -19 C. 5 D. -5
Câu 32: Trong không gian
Oxyz
, một vectơ chỉ phương của đường thẳng
2
:1
1
xt
yt
z
=
∆ =−+
=
là
A.
( )
2; 1; 0 .m = −

B.
(
)
2;1;1 .
m
=

C.
( )
2; 1;1 .m = −

D.
( )
2; 1; 0 .m =−−

Câu 33: Kí hiệu
12
z ,z
là hai nghiệm phức của phương trình
2
z 4z 5 0− +=
. Phần thực
a
của số phức
22
12
wz z= +
bằng
A.
0.
B.
8.
C.
16.
D.
6.
Câu 34: Hàm số
3
2
1
3
x
y x mx=−+− +
nghịch biến trên khoảng
( )
0; +∞
khi và chỉ khi
A.
(
)
1;
m∈ +∞
.
B.
[
)
1;m
∈ +∞
.
C.
[
)
0;m∈ +∞
.
D.
( )
0;m∈ +∞
.
Câu 35: Cho hàm số
2
21
x
y
x
−
=
+
. Tìm mệnh đề đúng ?
A. Hàm số đồng biến trên khoảng
1
;
2

−∞ −


.
B. Hàm số luôn nghịch biến trên tập xác định
1
\
2
DR

= −


C. Hàm số nghịch biến trên khoảng
1
;
2

− +∞


.
D. Hàm số luôn đồng biến trên tập xác định
1
\
2
DR

= −


.
Câu 36: Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
(1; 0; 2),A
−
(1;1;1),B
( 0; 1; 2 )C −
. Biết rằng
mặt phẳng đi qua ba điểm
,,
ABC
có phương trình
7 0.xayczd+ + +=
Tính giá trị biểu thức
22 2
Sa c d=++
A.
29.
B.
59.
C.
26.
D.
35.
Câu 37: Cho hình trụ có hai đáy là hai hình tròn
( )
;OR
và
( )
';OR
. AB là một dây cung của đường tròn
(
)
;OR
sao cho tam giác
'O AB
là tam giác đều và mặt phẳng
( )
'O AB
tạo với mặt phẳng chứa đường
tròn
( )
;OR
một góc 60
0
. Tính theo R thể tích V của khối trụ đã cho.
A.
3
7
7
R
V
π
=
B.
3
35
5
R
V
π
=
C.
3
5
5
R
V
π
=
D.
3
37
7
R
V
π
=
Câu 38: Cho tứ diện ABCD có
000
; 60 ; 60 ; 90AB AC AD a BAC CAD DAB= = = = = =
. Khoảng cách
giữa hai đường thẳng AC và BD là
Trang 5/6 - Mã đề thi 132
A.
30
10
a
B.
2
a
C.
3
2
a
D.
2
2
a
Câu 39: Cho số phức
3
w
5
i
=
−
. Khi đó phần ảo của số phức w là:
A.
15
26
. B.
3
26
−
. C.
3
26
. D.
15
26
−
.
Câu 40: Cho hình lăng trụ đứng
.'' 'ABC A B C
có cạnh bên
'a2AA =
. Biết đáy ABC là tam giác vuông
có
BA BC a= =
, gọi M là trung điểm của BC. Tính khoảng cách giữa hai đường thẳng AM và B’C.
A.
( )
7
,'
7
a
d AM B C =
B.
(
)
3
,'
3
a
d AM B C =
C.
(
)
2
,'
2
a
d AM B C =
D.
( )
5
,'
5
a
d AM B C =
Câu 41: Cho hàm số
( )
y fx=
liên tục trên đoạn
[
]
a;b .
Diện tích của hình phẳng giới hạn bởi đồ thị
( ) ( )
C :y f x ,=
trục hoành,
hai đường thẳng
x a,=
xb=
(Hình vẽ bên dưới) được xác định bởi
công thức nào dưới đây?
A.
0b
a0
S f (x)dx f (x)dx.
= −
∫∫
B.
0b
a0
S f (x)dx f (x)dx.=−+
∫∫
C.
0b
a0
S f (x)dx f (x)dx.=−−
∫∫
D.
0b
a0
S f (x)dx f (x)dx.
= +
∫∫
Câu 42: Cho hàm số
y fx
liên tục trên
, có đồ thị như hình vẽ.
Có bao nhiêu giá trị của tham số
m
để phương
trình
3
2
2
4
3
25
mm
fx
fx

có 3 nghiệm phân biệt ?
A. 1. B. 5. C. 2. D. 0.
Câu 43: Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số
x
y e 4x
=−+
, trục hoành và hai đường thẳng
x 1; x 2= =
. Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục hoành.
A.
2
V 6e e=−−
.
B.
( )
2
V 6e e=π−+
.
C.
( )
2
V 6e e=π−−
.
D.
2
V 6e e=−+
.
Câu 44: Cho các số thực x, y dương và thỏa mãn
( )
22
2
22
log 2 1
22
2
log 2 log 8 .
3
xy
xy
xy
xy x
++
+
+≤
+
Tìm giá trị
nhỏ nhất của biểu thức
22
2
22
.
2
x xy y
P
xy y
−+
=
−
A.
1
.
2
B.
5
.
2
C.
3
.
2
D.
15
.
2
+
Câu 45: Gọi
x
,
y
là các số thực dương thỏa mãn điều kiện
( )
9 12 16
log log logx y xy= = +
và
2
x ab
y
−+
=
, với
a
,
b
là hai số nguyên dương. Tính
.P ab=
.
O
x
b
a
y
( )
y fx=
Trang 6/6 - Mã đề thi 132
A.
6
P =
.
B.
5P =
.
C.
8
P =
.
D.
4P =
.
Câu 46: Cho hàm số
( )
y fx=
liên tục trên R và
có đồ thị như hình bên. Phương trình
( )
2sinf xm=
có đúng ba nghiệm phân biệt thuộc
đoạn
[
]
;
ππ
−
khi và chỉ khi
A.
{ }
3;1m∈−
.
B.
( )
3;1m∈−
.
C.
[
)
3;1m∈−
.
D.
(
]
3;1m∈−
.
Câu 47: Cho hai hàm số
(
)
y fx=
và
( )
y gx=
là
hai hàm số liên tục trên
có đồ thị hàm số
( )
y fx
′
=
là đường cong nét đậm, đồ thị hàm số
(
)
y gx
′
=
là đường cong nét mảnh như hình vẽ. Gọi
ba giao điểm A, B, C của
( )
y fx
′
=
và
( )
y gx
′
=
trên hình vẽ lần lượt có hoành độ là a, b, c. Tìm giá
trị nhỏ nhất của hàm số
(
) ( ) ( )
hx f x gx
= −
trên
đoạn
[ ]
;?
ac
A.
[ ]
( ) ( )
;
min 0 .
ac
hx h=
B.
[ ]
( ) ( )
;
min .
ac
hx ha=
C.
[ ]
( ) ( )
;
min .
ac
hx hb=
D.
[ ]
( ) ( )
;
min .
ac
hx hc=
Câu 48: Trên mặt phẳng tọa độ Oxy, số phức nào dưới đây có điểm biểu diễn là
( )
1; 2M −
?
A.
12zi= +
.
B.
12zi
= −
.
C.
12zi
=−−
.
D.
12
zi=−+
.
Câu 49: Cho hàm số
( )
y fx=
có bảng biến thiên sau:
Tìm giá trị cực đại của hàm số
( )
y fx=
.
A.
5
.
B.
3−
.
C.
0
.
D.
1
.
Câu 50: Cho hàm số
( ) ( )
42
,,f x ax bx c a b c=++ ∈
và có bảng biến
thiên như hình vẽ bên. Số nghiệm thực dương của
phương trình
( )
2 30fx−=
là
A. 3. B. 1 . C. 4. D. 2.
----------- HẾT ----------
made cautron dapan
132 1 C
132 2 C
132 3 D
132 4 A
132 5 B
132 6 A
132 7 A
132 8 B
132 9 B
132 10 C
132 11 D
132 12 A
132 13 A
132 14 B
132 15 A
132 16 B
132 17 D
132 18 B
132 19 A
132 20 B
132 21 D
132 22 C
132 23 C
132 24 D
132 25 A
132 26 C
132 27 D
132 28 C
132 29 C
132 30 D
132 31 C
132 32 D
132 33 D
132 34 B
132 35 A
132 36 D
132 37 D
132 38 B
132 39 C
132 40 A
132 41 B
132 42 A
132 43 B
132 44 B
132 45 B
132 46 A
132 47 C
132 48 B
132 49 C
132 50 D
NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
https:/www.facebook.com/groups/toanvd. Trang 8
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
HƯỚNG DẪN GIẢI CHI TIẾT
ĐỀ THI CHUYÊN ĐỀ TOÁN 12 LẦN 4
NĂM HỌC 2019 – 2020
TRƯỜNG THPT LIỄN SƠN – VĨNH PHÚC
Câu 1: Thể tích của khối lăng trụ có chiều cao bằng
h
và diện tích đáy bằng
B
là
A.
1
3
Bh
. B.
1
6
Bh
. C.
Bh
. D.
3Bh
.
Lời giải
Chọn C
Câu 2: Cho cấp số nhân
n
u
có
1
2u 
và công bội
3q
. Giá trị của
11
u
là
A.
11
3072u
. B.
11
354294u 
. C.
11
118098u 
. D.
11
354294u
.
Lời giải
Chọn C
10 10
11 1
. 2.3 118098u u q
.
Câu 3: Số điểm chung của đồ thị hàm số
42
76y x x
và đồ thị hàm số
3
13y x x
là
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn A
Xét phương trình hoành độ giao điểm:
4 2 3
7 6 13x x x x
32
2 5 3 0x x x x
32
2
5 3 0
x
x x x
Xét hàm số
32
53f x x x x
2
3 2 5f x x x
1
0
5
3
x
fx
x

Bảng biến thiên:
Từ bảng biến thiên ta thấy hàm số
fx
có
.0
cd ct
yy
NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
https:/www.facebook.com/groups/toanvd. Trang 9
NHÓM TOÁN VD
– VDC
NHÓM
TOÁN VD
– VDC
đồ thị hàm số
y f x
cắt
Ox
tại 3 điểm phân biệt.
32
5 3 0x x x
có 3 nghiệm phân biệt.
Vậy số điểm chung của 2 đồ thị hàm số đã cho là
4
.
Câu 4: Trong không gian
Oxyz
, cho hai đường thẳng
1
2 2 3
:
2 1 1
x y z
d

;
2
1
:
12
1
xt
d
yt
zt


và điểm
1;2;3A
. Đường thẳng
qua
A
vuông góc với
1
d
và cắt
2
d
có phương trình là
A.
1 2 3
1 3 5
x y z


. B.
1 2 3
1 3 5
x y z

.
C.
1 2 3
1 3 5
x y z

. D.
1 2 3
1 3 5
x y z

.
Lời giải
Chọn A
Đường thẳng
1
d
có VTCP là
1
2; 1;1u 
.
Gọi
22
1 ;1 2 ; 1M d M d M t t t
;2 1; 4AM t t t
Do
22
. 0 3 3 0 1d u AM t t
.
Vậy đường thẳng
qua điểm
1;2;3A
có VTCP là
1; 3; 5AM
.
1 2 3
:
1 3 5
x y z

.
Câu 5: Cho hàm số
y f x
có
lim 3
x
fx

và
lim 3
x
fx


. Khẳng định nào sau đây là đúng?
A. Đồ thị hàm số đã cho không có tiệm cận ngang.
B. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng
3y
và
3y 
.
C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng
3x
và
3x 
.
Lời giải
Chọn B
lim 3
x
fx

TCN:
3y
.
lim 3
x
fx


TCN:
3y 
.
NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
https:/www.facebook.com/groups/toanvd. Trang 10
NHÓM TOÁN VD
– VDC
NHÓM
TOÁN VD
– VDC
Câu 6: Cho hàm số
fx
liên tục và có đạo hàm trên
0;
2



, thỏa mãn hệ thức
3
tan .
cos
x
f x x f x
x

. Biết rằng
3 3 ln3
36
f f a b

trong đó
;ab
.
Tính giá trị của biểu thức
P a b
.
A.
4
9
P 
. B.
2
9
P 
. C.
7
9
P
. D.
14
9
P
.
Lời giải
Chọn A
Ta có:
3
tan .
cos
x
f x x f x
x

2
cos . sin .
cos
x
x f x x f x
x
2
sin .
cos
x
x f x
x



33
2
66
sin .
cos
x
x f x dx dx
x






3
6
5 3 1
sin . ln
18
3
x f x


3 1 5 3 1
ln3
2 3 2 6 18 2
ff

53
3 ln3
3 6 9
ff

Vậy
5
;1
9
ab
54
1
99
P a b
.
Câu 7: Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
2 2 2
: 3 1 2 8 S x y z
. Khi đó
tâm
I
và bán kính
R
của mặt cầu là.
A.
3; 1; 2 , 2 2 IR
. B.
3; 1; 2 , 4 IR
.
C.
3;1;2 2 2IR
. D.
3;1;2 , 4IR
.
Lời giải
Chọn A
Tâm và bán kính của mặt cầu là
3; 1; 2 , 2 2 IR
Câu 8: Đồ thị hàm số
32
32 y x x
có dạng nào dưới đây
Hình 1
Hình 2
Hình 3
Hình 4
A. Hình 4. B. Hình 3. C. Hình 1. D. Hình 2.
Lời giải
Chọn B
NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
https:/www.facebook.com/groups/toanvd. Trang 11
NHÓM TOÁN VD
– VDC
NHÓM
TOÁN VD
– VDC
Đồ thị hàm số có hai điểm cực trị là
2; 2
và
0;2
nên hình 3 là dạng của đồ thị hàm số đã
cho
Câu 9: Cho số phức
1, z bi b
và
10z
. Giá trị của
b
bằng
A.
3
. B.
3
. C.
3
. D.
10
.
Lời giải
Chọn B
Ta có
2 2 2
10 1 10 1 10 9 3 z b b b b
Câu 10: Đạo hàm của hàm số
2
x
f x x
là
A.
2
' 1.
ln2
x
fx
B.
2
2
'.
ln2 2
x
x
fx
C.
' 2 ln2 1.
x
fx
D.
' 2 1.
x
fx
Lời giải
Chọn C
Câu 11: Giá trị nhỏ nhất của hàm số
42
45y x x
trên đoạn
1;2
là
A.
3.
B.
5.
C.
2.
D.
1.
Lời giải
Chọn D
Ta có:
3
0
' 4 8 ; ' 0
2
x
y x x y
x

Mà
1 2; 0 5; 2 1; 2 5f f f f
Vậy giá trị nhỏ nhất của hàm số
42
45y x x
trên đoạn
1;2
là
1.
Câu 12: Người ta muốn xây một bể nước dạng khối hộp chữ nhật trong một phòng tắm. Biết chiều dài,
chiều rộng, chiều cao của khối hộp đó lần lượt là
5 ;1 ;2m m m
(người ta chỉ xây hai mặt thành bể
như hình vẽ bên). Biết mỗi viên gạch có chiều dài
20 ,cm
chiều rộng
10cm
, chiều cao
5.cm
Hỏi
người ta sử dụng ít nhất bao nhiêu viên gạch để xây bể đó và thể tích thực của bể chứa bao nhiêu
lít nước? (Giả sử lượng xi măng và cát không đáng kể).
A.
1180
viên,
8820
lít. B.
1180
viên,
8800
lít.
C.
1182
viên,
8820
lít. D.
1180
viên,
8800
lít.
Lời giải
Chọn A
* Theo mặt nước của bể:
Số viên gạch xếp theo chiều dài của bể mỗi hàng là
500
25
20
x 
viên
NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
https:/www.facebook.com/groups/toanvd. Trang 12
NHÓM TOÁN VD
– VDC
NHÓM
TOÁN VD
– VDC
Số viên gạch xếp theo chiều cao của bể mỗi hàng là:
200
40.
5
Vậy tính theo chiều dài thì có
40 hàng gạch mỗi hàng
25
viên. Khi đó theo mặt nước của bể
25.40 1000N 
viên.
*Theo mặt bên của bể: ta thấy,nếu hàng mặt trước của bể đã được viên hoàn chỉnh đoạn nối
hao mặt thì ở mặt bên viên gạch còn lại sẽ được cắt đi còn
1
2
viên. Tức là mặt bên sẽ có
1 100 20
.40 .40 180
2 20

viên.
Vậy tổng số viên gạch là
1180
viên.
Khi đó thể tích bờ tường xây là
1180.2.10,5 1180
lít.
Vậy thể tích bể chứa nước là:
50.10.20 1180 8820
lít.
Câu 13: Tính môđun của số phức
,,z a bi a b
.
A.
22
z a b
. B.
22
z a b
. C.
z a b
. D.
22
z a b
.
Lời giải
Chọn A
Theo định nghĩa ta có
22
z a b
.
Câu 14: Cho chiếc trống như hình vẽ, có đường sinh là nửa elip được cắt bỡi trục lớn với độ dài trục lớn
bằng
80 cm
, độ dài trục bé bằng
60 cm
và đáy trống là hình tròn có bán kính bằng
60cm
. Tính
thể tích của chiếc trống (kết quả làm tròn đến hàng đơn vị).
A.
3
344963V cm
. B.
3
344964V cm
. C.
3
208347V cm
. D.
3
208346V cm
.
Lời giải
Chọn B
Ta
NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
https:/www.facebook.com/groups/toanvd. Trang 13
NHÓM TOÁN VD
– VDC
NHÓM
TOÁN VD
– VDC
Gắn hệ trục tọa độ như hình vẽ:
Ta có phương trình Elip:
22
22
40 60
1
40 30
xy

2
2
2
2
2
2
40
60 30 1
40
3
60 40 40
4
x
y
yx




2
2
3
60 40 40
4
yx
Khi đó
2
80
2
2
0
3
60 40 40 d
4
V x x



.
Sử dụng máy tính bỏ túi tính được
344963,6143V
Câu 15: Họ nguyên hàm của hàm số
3 cos
x
f x x
là
A.
3
sin
ln3
x
xC
. B.
3 ln3 sin
x
xC
. C.
3
sin
ln
x
xC
x

. D.
3 ln3 sin
x
xC
.
Lời giải
Chọn A
3 cos d
x
xx
3
sin
ln3
x
xC
.
Câu 16: Diện tích của mặt cầu bán kính
2a
là
A.
2
4 a
. B.
2
16 a
. C.
2
16a
. D.
2
4
3
a
.
Lời giải
Chọn B
Ta có:
2
22
4 4 . 2 16S r a a
.
NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
https:/www.facebook.com/groups/toanvd. Trang 14
NHÓM TOÁN VD
– VDC
NHÓM
TOÁN VD
– VDC
Câu 17: Phương trình tham số của đường thẳng
d
đi qua điểm
1; 1;2A
và có véc tơ chỉ phương
1;2; 3u 
là
A.
1
:2
32
xt
d y t
zt


B.
1
:1
22
xt
d y t
zt



C.
1
: 1 3
25
x
d y t
zt

D.
1
: 1 2
23
xt
d y t
zt


Lời giải
Chọn D
Câu 18: Một lớp học gồm có
20
học sinh nam và
15
học sinh nữ. Cần chọn ra
2
học sinh,
1
nam và
1
nữ để phân công trực nhật. Số cách chọn là
A.
2
35
A
B.
300
C.
2
35
C
D.
35
Lời giải
Chọn A
Có
20
cách chọn
1
học sinh nam.
Có
15
cách chọn
1
học sinh nữ.
Số cách chọn
1
nam và
1
nữ để phân công trực nhật là:
20.15 300.
Câu 19: Một hình trụ có bán kính đáy bằng 3 và đường cao bằng 4. Tính diện tích xung quanh
xq
S
của
hình trụ.
A.
24
xq
S
. B.
30
xq
S
. C.
15
xq
S
. D.
15
xq
S
.
Lời giải
Chọn A
+) Hình lăng trụ có độ dài đường sinh bằng đường cao nên diện tích xung quanh của hình trụ là
2 2 .3.4 24 .
xq
S rl
Câu 20: Trong không gian 𝑂𝑥𝑦𝑧, cho điểm
(1;2;2)A
và mặt phẳng
( ): 2 2 4 0x y z
. Tính khoảng
cách
d
từ điểm
A
đến mặt phẳng
()
.
A.
1
3
d
. B.
1d
. C.
13
3
d
. D.
3d
.
Lời giải
Chọn B
+) Ta có
1
1 2.2 2
14
4
;
4
.2
dA

.
Câu 21: Bình có bốn đôi giày khác nhau gồm bốn màu: đen, trắng, xanh và đỏ. Một buổi sáng đi học, vì
vội vàng, Bình đã lấy ngẫu nhiên hai chiếc giày từ bốn đôi giày đó. Tính xác suất để Bình lấy
được hai chiếc giày cùng màu.
NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
https:/www.facebook.com/groups/toanvd. Trang 15
NHÓM TOÁN VD
– VDC
NHÓM
TOÁN VD
– VDC
A.
1
4
. B.
2
7
. C.
1
14
. D.
1
7
.
Lời giải
Chọn D
+) Số phần tử không gian mẫu là
2
8
28nC
.
+) Gọi 𝐴 là biến cố: “Bình lấy được 2 chiếu cùng màu”. Ta có
4nA
cách.
Vậy
1
7
nA
PA
n

.
Câu 22: Rút gọn biểu thức
7
3
5
3
7
42
.
.
aa
A
aa
với
0a
ta được kết quả
m
n
Aa
, trong đó
*
,mn
và
m
n
là phân số tối giản. Khẳng định nào sau đây đúng?
A.
2
3 2 2mn
. B.
22
43mn
. C.
2
2 15mn
. D.
22
25mn
.
Lời giải
Chọn C
Ta có
7 5 7
26 2
3
54
3 3 3
4
2
77
2 26
7
42
4
77
..
2; 7 2 15.
.
.
a a a a a
A a a m n m n
aa
a a a
Câu 23: Biết tiếp tuyến của đồ thị hàm số
42
2y ax bx
tại điểm
1;1A
vuông góc với đường thẳng
2 3 0xy
. Tính
22
?ab
A.
22
2ab
. B.
22
13ab
. C.
22
5ab
. D.
22
10ab
.
Lời giải
Chọn C
Ta có
13
2 3 0
22
x y y x
có hệ số góc là
1
1
2
k
.
Mặt khác
4 2 3
( 2) 4 2y ax bx ax bx

, suy ra tiếp tuyến tại
1;1A
của đồ thị hàm số có
hệ số góc là
2
42k a b
.
Ta có hệ
12
22
1
.1
2
4 2 1
5
2
11
3
21
kk
a
ab
ab
y
b
ab



.
Câu 24: Trong không gian
Oxyz
cho
2OA k i j
. Tọa độ điểm
A
là
A.
2; 1;1A
. B.
2;1; 1A 
. C.
1; 1; 2A 
. D.
1;1;2A
.
Lời giải
Chọn D
NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
https:/www.facebook.com/groups/toanvd. Trang 16
NHÓM TOÁN VD
– VDC
NHÓM
TOÁN VD
– VDC
Ta có
2 1;1;2 1;1;2OA k i j OA A
.
Câu 25: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, cạnh bên
SA
vuông góc với
mặt đáy và
2SA a
. Tìm số đo của góc giữa đường thẳng
SC
và mặt phẳng
.SAB
A.
0
30
. B.
0
45
. C.
0
60
. D.
0
90
.
Lời giải
Chọn A
Chọn hệ trục tọa độ
Oxyz
như hình vẽ
Ta có
0;0;0 , 0;0;a 2 , a;a;0 , 0;a;0 .A O S C D
Đường thẳng
SC
có một véctơ chỉ phương là
; ; a 2 .SC a a
Mặt phẳng
SAB
có một véctơ pháp tuyến là
0; a;0 .AD
2
2 2 2
.
.
1
sin , .
2
..
2.
SC AD
aa
SC SAB
SC AD
a a a a
Vậy số đo của góc giữa đường thẳng
SC
và mặt phẳng
SAB
bằng
0
30 .
Câu 26: Tập nghiệm của phương trình
1
4 1 0
x

là
A.
0
. B.
1
. C.
1
. D.
2
.
Lời giải
Chọn C
NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
https:/www.facebook.com/groups/toanvd. Trang 17
NHÓM TOÁN VD
– VDC
NHÓM
TOÁN VD
– VDC
Ta có
11
4 1 0 4 1 1 0 1.
xx
xx

Câu 27: Tập nghiệm của bất phương trình
0,5
log 1 1x 
là
A.
3
;
2




. B.
3
1;
2


. C.
3
;
2




. D.
3
1;
2



.
Lời giải
Chọn D
Ta có
0,5
1 0 1
3
log 1 1 1 .
13
2
1
22
xx
xx
xx





Vậy tập nghiệm của bất phương trình đã cho là
3
1; .
2
S



Câu 28: Khi cắt khối nón
N
bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác
vuông cân có cạnh huyền bằng
23a
. Tính thể tích
V
của khối nón
N
.
A.
3
36Va
. B.
3
6Va
. C.
3
3Va
. D.
3
33Va
.
Lời giải
Chọn C
Gọi
S
là đỉnh hình nón, thiết diện qua trục là tam giác
SAB
.
Ta có
2 3 3
2
AB
AB a r h a
.
Vậy
2
23
11
. 3 . 3 3
33
V r h a a a
.
Câu 29: Hàm số
2
1
2
log 1yx
có tập giá trị là
A.
;0
. B.
1; 
. C. . D.
0;
.
O
S
A
B
NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
https:/www.facebook.com/groups/toanvd. Trang 18
NHÓM TOÁN VD
– VDC
NHÓM
TOÁN VD
– VDC
Lời giải
Chọn C
Hàm số
2
1
2
log 1yx
có tập giá trị là .
Câu 30: Cho ba số thực dương
,,a b c
và
a
khác
1
. Khẳng định nào sau đây là sai?
A.
log log log
a a a
bc b c
. B.
log
a
b
ab
.
C.
log log
aa
bb

. D.
ln
log
ln
a
a
b
b
.
Lời giải
Chọn D
Ta có:
+)
log log log
a a a
bc b c
nên A đúng.
+)
log
a
b
ab
nên B đúng.
+)
log log
aa
bb

nên C đúng.
+)
ln
log
ln
a
b
b
a
nên D sai.
Câu 31: Biết rằng tồn tại duy nhất các bộ số nguyên
,,abc
sao cho
3
2
(4 2)ln ln2 ln3x xdx a b c
Giá trị của
abc
bằng
A.
19
. B.
19
. C.
5
. D.
5
.
Lời giải
Chọn C
3 3 3
2 2 3
2
2 2 2
(4 2)ln ln 2 2 2 2 ln | 22xx xdx xd x x x x x dx
Vậy
3
2
7
(4 2)ln 7 12ln2 24ln3 12.
24
a
x xdx b
c

Do đó:
5.abc
Câu 32: Trong không gian
Oxyz
, một véc tơ chỉ phương của đường thẳng
2
:1
1
xt
yt
z
là
A.
2; 1;0m
. B.
2;1;1m
. C.
2; 1;1m
. D.
2; 1;0m 
.
Lời giải
Chọn D
NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
https:/www.facebook.com/groups/toanvd. Trang 19
NHÓM TOÁN VD
– VDC
NHÓM
TOÁN VD
– VDC
Từ phương trình tham số của đường thẳng
2
:1
1
xt
yt
z
ta có một véc tơ chỉ phương của đường
thẳng là
2; 1;0m 
Câu 33: Kí hiệu
1
z
và
2
z
là nghiệm phức của phương trình
2
4 5 0zz
. Phần thực
a
của số phức
22
12
w z z
bằng
A.
0
. B.
8
. C.
16
. D.
6
.
Lời giải
Chọn D
Xét phương trình
2
2
4 5 0
2
zi
zz
zi


Khi đó
22
12
6w z z
Câu 34: Hàm số
3
2
1
3
x
y x mx
nghịch biến trên
0;
khi và chỉ khi
A.
1;m
B.
1;m 
C.
0;m 
D.
0;m 
Lời giải.
Chọn B.
Ta có
3
22
12
3
x
y x mx y x x m
.
Theo bài ra
22
2 0, 0 2 , 0x x m x m x x x
.
Khảo sát hàm số
2
( ) 2 (0) 0; (1) 1g x x x g g
. Vậy điều kiện cần tìm là
1;m 
.
Câu 35: Cho hàm số
2
21
x
y
x
. Tìm mệnh đề đúng
A. Hàm số đồng biến trên khoảng
1
;
2




.
B. Hàm số luôn nghịch biến trên tập xác định
1
\
2
D



.
C. Hàm số nghịch biến trên khoảng
1
;
2




.
D. Hàm số luôn đồng biến trên tập xác định
1
\
2
D



.
Lời giải.
Chọn A.
NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
https:/www.facebook.com/groups/toanvd. Trang 20
NHÓM TOÁN VD
– VDC
NHÓM
TOÁN VD
– VDC
Ta có
2
2 5 1
0,
2 1 (2 1) 2
x
y y x
xx

.
Hàm số đã cho luôn đồng biến trên từng khoảng xác định.
Như vậy hàm số đồng biến trên khoảng
1
;
2




.
Câu 36: Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
(1;0; 2), (1;1;1), (0; 1;2)A B C
. Biết rằng
mặt phẳng đi qua ba điểm
,,A B C
có phương trình
70x ay cz d
. Tính giá trị biểu thức
2 2 2
S a c d
.
A. 29 B. 59 C. 26 D. 35
Lời giải.
Chọn D.
Ta có
(0;1;3)
(1;0; 2), (1;1;1), (0; 1;2)
( 1; 1;4)
AB
A B C
AC
Mặt phẳng
()ABC
có một véc tơ pháp tuyến là
, (7; 3;1) ( ):7( 1) 3 2 0 7 3 5 0AB AC ABC x y z x y z


.
Như vậy
2 2 2
3; 1; 5 35a b c a c d
.
Câu 37: Cho hình trụ có hai đáy là hai hình tròn
;OR
và
;OR
.
AB
là một dây cung của đường tròn
;OR
sao cho tam giác
O AB
là tam giác đều và mặt phẳng
O AB
tạo với mặt phẳng chứa
đường tròn
;OR
một góc
0
60
. Tính theo
R
thể tích
V
của khối trụ đã cho.
A.
3
7
7
R
V
. B.
3
35
5
R
V
. C.
3
5
5
R
V
. D.
3
37
7
R
V
.
Lời giải
Chọn D
60
0
R
h
I
O'
O
B
A
NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
https:/www.facebook.com/groups/toanvd. Trang 21
NHÓM TOÁN VD
– VDC
NHÓM
TOÁN VD
– VDC
Gọi
I
là trung điểm của đoạn
AB
suy ra
AB OO I
.
Ta có
;OI AB AB O I

nên góc giữa mặt phẳng
O AB
và mặt đáy bằng
0
60O IO
.
Suy ra
0
2 2 4
.
sin60 3
33
OO h
O I AB O I h

.
Và
0
.cot60
3
h
OI OO

.
Mặt khác ta có
2
2
2 2 2 2
1 4 3
4 3 3
7
hR
IB OI R h R h



.
Vậy
2
2
37
7
R
V R h

.
Câu 38: Tứ diện
ABCD
có
AB AC AD a
;
0
60BAC
;
0
60CAD
;
0
90DAB
. Khoảng cách giữa
hai đường thẳng
AC
và
BD
là
A.
30
10
a
. B.
2
a
. C.
3
2
a
. D.
2
2
a
.
Lời giải
Chọn C
Ta có tam giác
ABC
có
AB AC a
và
0
60BAC
nên tam giác
ABC
đều suy ra
BC a
.
Tương tự tam giác
ACD
cũng đều nên
CD a
.
Suy ra
..ABD CBD cc c
nên
0
90BCD BAD
và
,ABD CBD
vuông cân tại
A
và
C
.
Gọi
I
là trung điểm của đoạn
BD
.
Suy ra
22
2
2 2 2
BD AD AB a
AI CI
và
AI BD
,
CI BD
. Do đó
BD ACI
.
Trong mặt phẳng
ACI
kẻ
IK AC
ta cũng có
IK BD
nên
,IK d AC BD
.
Tam giác
ACI
cân tại
I
nên
K
là trung điểm
AC
.
Suy ra
2
2
2
2 2 2
2
4 2 2 2
AC a a a
IK AI AK AI







.
Vậy
,
2
a
d AC BD
.
Câu 39: Cho số phức
3
5
w
i
. Khi đó phần ảo của số phức
w
là:
A.
15
26
. B.
3
26
. C.
3
26
. D.
15
26
.
a
a
a
I
A
C
B
D
K
NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
https:/www.facebook.com/groups/toanvd. Trang 22
NHÓM TOÁN VD
– VDC
NHÓM
TOÁN VD
– VDC
Lời giải
Chọn C
Ta có
3 15 3
5 26 26
wi
i
.
Vậy phần ảo của số phức
w
là
3
26
.
Câu 40: Cho hình lăng trụ đứng
. ' ' 'ABC A B C
có cạnh bên
'2AA a
. Biết đáy
ABC
là tam giác vuông
có
BA BC a
, gọi
M
là trung điểm của
BC
. Tính khoảng cách giữa hai đường thẳng
AM
và
'BC
.
A.
7
,'
7
a
d AM B C
. B.
3
,'
3
a
d AM B C
.
C.
2
,'
2
a
d AM B C
. D.
5
,'
5
a
d AM B C
.
Lời giải
Chọn A
Kẻ
'MN B C
(
N
là trung điểm của
'BB
). Khi đó:
, ' ' , ; ;d AM B C d B C AMN d C AMN d B AMN
.
Kẻ
BH AM
, mà
AM BN AM BHN AMN BHN
theo giao tuyến
NH
. Kẻ
;BK NH BK AMN d B AMN BK
.
Ta có
2 2 2 2
. 5 . 7
57
BABM a BH BN a
BH BK
BA BM BH BN

.
Câu 41: Cho hàm số
y f x
liên tục trên đoạn
;ba
. Diện tích của hình phẳng giới hạn bởi đồ thị
:C y f x
, trục hoành, hai đường thẳng
,x a x b
(Hình vẽ bên dưới) được xác định bởi
công thức nào dươi đây?
NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
https:/www.facebook.com/groups/toanvd. Trang 23
NHÓM TOÁN VD
– VDC
NHÓM
TOÁN VD
– VDC
A.
0
0
b
a
S f x dx f x dx

. B.
0
0
b
a
S f x dx f x dx

.
C.
0
0
b
a
S f x dx f x dx

. D.
0
0
b
a
S f x dx f x dx

.
Lời giải
Chọn D
Diện tích của hình phẳng giới hạn bởi đồ thị
:C y f x
, trục hoành, hai đường thẳng
,x a x b
cho bởi công thức:
b
a
S f x dx
. Ta lại có:
x
a
0
b
fx
0
Do đó
0
0
b
a
S f x dx f x dx

.
Câu 42: Cho hàm số
y f x
liên tục trên , có đồ thị như hình vẽ.
Có bao nhiêu giá trị của tham số
m
để phương trình
3
2
2
4
3
25
mm
fx
fx

có
3
nghiệm
phân biệt?
A.
1
. B.
5
. C.
2
. D.
0
.
Lời giải
Chọn A
Ta có:
3
2 3 2 2
2
4
3 4 3 2 5
25
mm
f x m m f x f x
fx
.
Đặt
2
22
5
2 5 5
2
t
f x t t f x
, khi đó phương trình có dạng
2
3
3 3 3 3
1
4 4 . 8 8 2 2 *
2
t
m m t m m t t m m t t



. Xét hàm số
32
, ' 1 0,f u u u f u u u
nên phương trình
NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
https:/www.facebook.com/groups/toanvd. Trang 24
NHÓM TOÁN VD
– VDC
NHÓM
TOÁN VD
– VDC
2
2
22
2
45
5 4 5
2
* 2 5 2 2 5
22
45
2
m
fx
m
m t t m m f x f x
m
fx




.
Nhìn vào đồ thị của hàm số
y f x
, ta có phương trình có
3
nghiệm khi
2
5
22
2
2
45
4
37 37 37
2
4 5 32
4 2 2
45
0
2
m
m
m m m m
m


.
Câu 43: Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số
4
x
y e x
, trục hoành và hai đường thẳng
1, 2xx
. Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục
hoành.
A.
2
6V e e
. B.
2
6V e e
. C.
2
6V e e
. D.
2
6V e e
.
Lời giải
Chọn B.
Ta có
2
2
22
1
1
( 4 ) 2 6
xx
V e x dx e x e e
.
Câu 44: Cho các số thực dương
,xy
thỏa mãn
22
2
22
log 2 1
22
2
log 2 log 8
3
xy
xy
xy
xy x


. Tìm giá trị nhỏ nhất
của biểu thức:
22
2
22
2
x xy y
P
xy y

A.
1
2
B.
5
2
C.
3
2
D.
15
2
Lời giải
Chọn B Giả thiết được viết lại:
2 2 2 2 2
22
log log 3 2 1 3x y xy x x y xy
2 2 2 2 2 2
2 2 2
log 2 log 3 log 2 3x y x y xy x x xy
2
2 2 2 2 2
22
3
log 2 log 3
2
xy x
x y x y x xy
2
2 2 2 2 2
22
3
log 2 log 3
2
xy x
x y x y x xy
Xét hàm số
2
log 2f t t t
, dễ thấy hàm số luôn đồng biến với
0t
. Từ đó ta có:
2
22
3
2
xy x
xy

. Chia hai vế cho
2
y
, ta được:
2
3 2 0 1 2
x x x
y y y
NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
https:/www.facebook.com/groups/toanvd. Trang 25
NHÓM TOÁN VD
– VDC
NHÓM
TOÁN VD
– VDC
Biểu thức
P
được viết lại:
2
2
22
22
21
21
xx
yy
tt
P
x
t
y






, với
1;2t
.
Khảo sát hàm số
Pt
trên
1;2
ta tìm được
1;2
5
min
2
Pt
Câu 45: Gọi
,xy
là các số thực dương thỏa mãn điều kiện
9 12 16
log log logx y x y
và
2
x a b
y

, với
,ab
là hai số nguyên dương. Tính
P ab
.
A.
6P
. B.
5P
. C.
8P
. D.
4P
.
Lời giải
Chọn B
Giả sử
9 12 16
log log logx y x y t
.
Khi đó
9
12
16
t
t
t
x
y
xy

2
3 3 3 1 5
9 12 16 1 0
4 4 4 2
t t t
t t t

.
Do đó
1
9 3 1 5
5
5
12 4 2
t
t
t
a
x
ab
b
y




.
Câu 46: Cho hàm số
y f x
liên tục trên và có đồ thị như hình bên.
Phương trình
2sinf x m
có đúng ba nghiệm phân biệt thuộc đoạn
;

khi và chỉ khi:
A.
3;1m
. B.
3;1m
. C.
3;1m
. D.
3;1m
.
Lời giải
Chọn A
Đặt
2sintx
. Với
;x


2;2t
.
f t m
.
Số nghiệm của phương trình
f t m
là số giao điểm của
y f t
và
ym
.
NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
https:/www.facebook.com/groups/toanvd. Trang 26
NHÓM TOÁN VD
– VDC
NHÓM
TOÁN VD
– VDC
Dựa vào đồ thị ta thấy, để phương trình
f t m
có ba nghiệm thì có một nghiệm
sin x
thuộc
khoảng
1;1
, một nghiệm là
1
và một nghiệm là
1
. Như vậy đồ thị hàm số
y f t
cắt
đường thẳng
ym
tại hai điểm có hoành độ bằng
2
hoặc
2
. Khi đó
1m
,
3m 
.
Câu 47: Cho hai hàm số
y f x
và
y g x
là hai hàm số liên tục trên có đồ thị hàm số
y f x
là đường cong nét đậm, đồ thị hàm số
y g x
là đường cong nét mảnh như hình vẽ. Gọi ba
giao điểm
A
,
B
,
C
của
y f x
và
y g x
trên hình vẽ lần lượt có hoành độ là
a
,
b
,
c
.
Tìm giá trị nhỏ nhất của hàm số
h x f x g x
trên đoạn
;ac
?
A.
;
min 0
ac
h x h
. B.
;
min
ac
h x h a
. C.
;
min
ac
h x h b
. D.
;
min
ac
h x h c
.
Lời giải
Chọn C
Ta có:
h x f x g x

.
0
xa
h x x b
xc
.
;x b c
:
0f x g x


;x a b
:
0f x g x


.
Xét bảng biến thiên:
Từ bảng biến thiên ta có:
;
min
ac
h x h b
.
Câu 48: Trên mặt phẳng toạ độ
Oxy
, số phức nào dưới đây có điểm biểu diễn là
1; 2M
?
A.
12zi
. B.
12zi
. C.
12zi
. D.
12zi
.
–
O
x
y
A
B

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
https:/www.facebook.com/groups/toanvd. Trang 27
NHÓM TOÁN VD
– VDC
NHÓM
TOÁN VD
– VDC
Lời giải
Chọn B
Câu 49: Cho hàm số
y f x
có bảng biến thiên sau
Tìm giá trị cực đại của hàm số
y f x
.
A.
5
. B.
3
. C.
0
. D.
1
.
Lời giải
Chọn C
Từ bảng biến thiên ta có giá trị cực đại của hàm số là
0y
Câu 50: Cho hàm số
42
,,f x ax bx c a b c
và có bảng biến thiên như hình vẽ
Số nghiệm thực dương của phương trình
2 3 0fx
là
A.
3
. B.
1
. C.
4
. D.
2
.
Lời giải
Chọn D
Ta có
3
2 3 0
2
f x f x
Từ bảng biến thiên suy ra đường thẳng
3
2
y
cắt đồ thị hàm số tại 4 điểm trong đó có hai điểm
có hoành độ dương.
Vậy phương trình
2 3 0fx
có hai nghiệm dương phân biệt.
NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
https:/www.facebook.com/groups/toanvd. Trang 28
NHÓM TOÁN VD
– VDC
NHÓM
TOÁN VD
– VDC
| 1/28
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD & ĐT VĨNH PHÚC
ĐỀ THI KIỂM TRA CHUYÊN ĐỀ LẦN 4
TRƯỜNG THPT LIỄN SƠN MÔN TOÁN LỚP 12
(đề thi gồm có 06 trang)
Thời gian làm bài: 90 phút không kể thời gian giao đề
(50 câu trắc nghiệm) Mã đề thi 132
(Thí sinh không được sử dụng tài liệu)
Họ, tên thí sinh:..................................................................... Số báo danh: .............................
Câu 1: Thể tích của khối lăng trụ có chiều cao bằng h và diện tích đáy bằng B là 1 . Bh 1 . Bh C. . Bh D. 3 . Bh A. 3 B. 6
Câu 2: Cho cấp số nhân (u − q =
n ) có u = 2 và công bội
3. Giá trị của u là 1 11 A. u = 3072 . u = 354294 − . u = 118098 − . u = 354294 . 11 B. 11 C. 11 D. 2
Câu 3: Số điểm chung của đồ thị hàm số 4 2
y = x − 7x − 6 và đồ thị hàm số 3 y = x −13x là: A. 4. B. 1. C. 2. D. 3. x = 1− t x − 2 y + 2 z − 3 Câu 4:
Trong không gian Oxyz cho hai đường thẳng d : = = , d : y =1+ 2t 1 2 2 1 − 1 z = 1 − +  t
và điểm A(1;2;3). Đường thẳng ∆ qua A vuông góc với d và cắt d có phương trình là: 1 2 x −1 y − 2 z − 3 − − − = = . x 1 y 2 z 3 = = . A. 1 3 − 5 − B. 1 − 3 − 5 − x −1 y − 2 z − 3 − − − = = . x 1 y 2 z 3 = = . C. 1 3 5 D. 1 3 5 −
Câu 5: Cho hàm số y = f (x) có limf (x) = 3và limf (x) = 3
− . Khẳng định nào sau đây là đúng ? x→+∞ x→−∞
A. Đồ thị hàm số đã cho không có tiệm cận ngang.
B. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y = 3 và y = 3 − .
C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x = 3 và x = 3 − . Câu 6: Cho hàm số  x
f x liên tục và có đạo hàm trên 0; , 
thỏa mãn hệ thức f xtan xf x .  2  3 cos x Biết rằng   3 f     f    
   a 3 b ln 3 trong đó , a b  .
 Tính giá trị của biểu thức P a  . b  3 6 4 2 7 14 P   . P   . P  . P  . A. 9 B. 9 C. 9 D. 9
Câu 7: Trong không gian với hệ tọa độ Oxyz , cho mặt cầu ( ) ( − )2 + ( + )2 + ( + )2 S : x 3 y 1 z 2 = 8. Khi đó
tâm I và bán kính R của mặt cầu là I(3; 1 − ; 2 − ) A. I(3; 1 − ; 2 − ),R = 2 2 B. ,R = 4 I( 3 − ;1;2) C. I( 3 − ;1;2),R = 2 2 D. ,R = 4
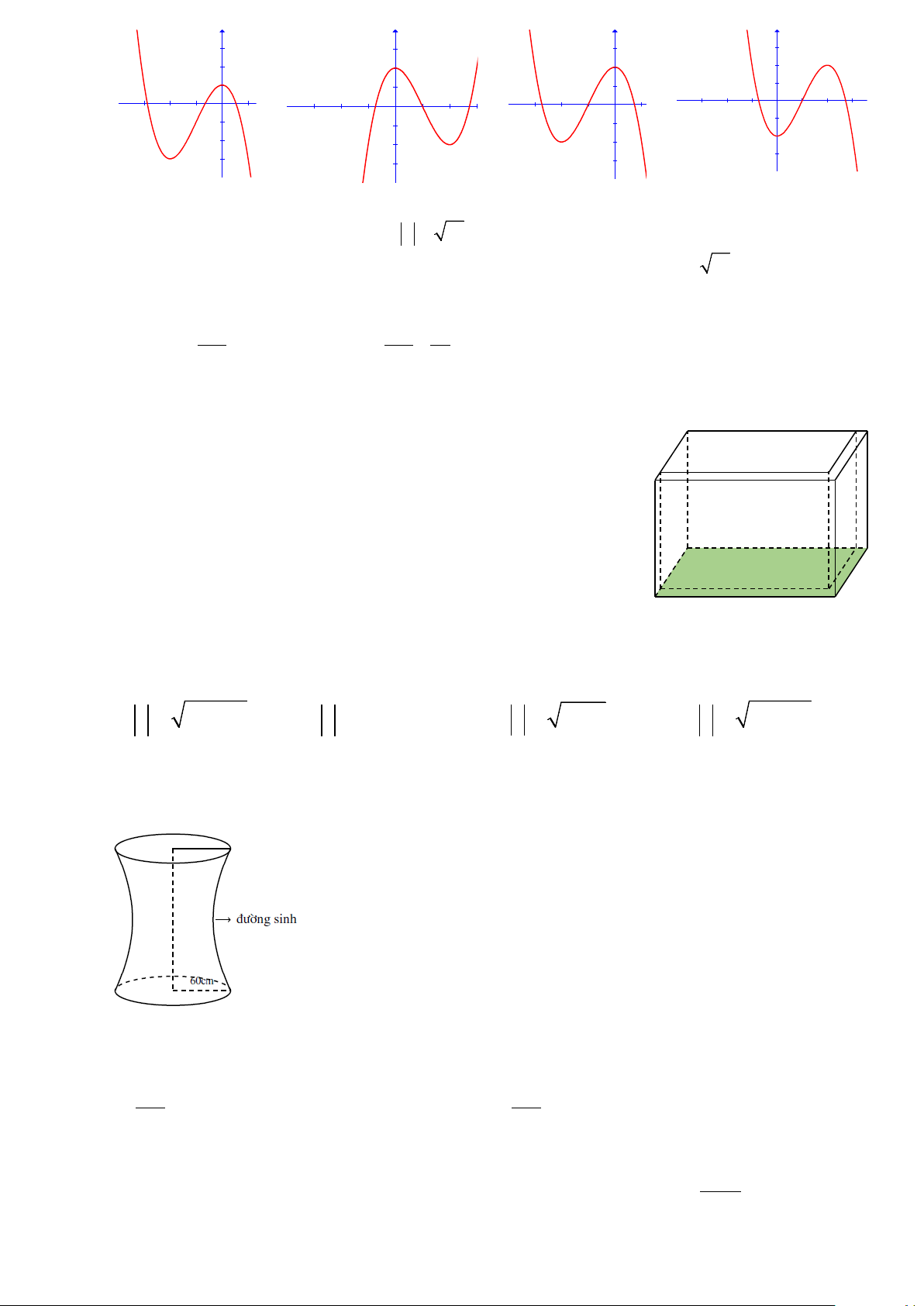
Câu 8: Đồ thị hàm số 3 2
y = −x − 3x + 2 có dạng nào dưới đây ? Hình 1 Hình 2 Hình 3 Hình 4
Trang 1/6 - Mã đề thi 132 y y y y 3 3 3 3 2 2 2 2 1 1 1 1 -3 -2 -1 1 -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -3 -2 -1 1 -1 -1 -1 -1 -2 -2 -2 -2 -3 -3 -3 -3 A. Hình 4. B. Hình 3. C. Hình 1. D. Hình 2.
Câu 9: Cho số phức z =1+ bi(b∈) và z = 10 .Giá trị của b bằng A. 3. B. 3 ± . C. –3. D. 10 .
Câu 10: Đạo hàm của hàm số ( ) = 2x f x + x là x x 2
A. f ′(x) 2 = +1. B. ′( ) 2 x f x = + . C. ′( ) = 2x f x ln 2 +1 D. ′( ) = 2x f x +1. ln 2 ln 2 2
Câu 11: Giá trị nhỏ nhất của hàm số 4 y = x − 4 2
x + 5 trên đoạn [− ; 1 2] là A. 3. B. 5. 1dm C. 2. D. 1.
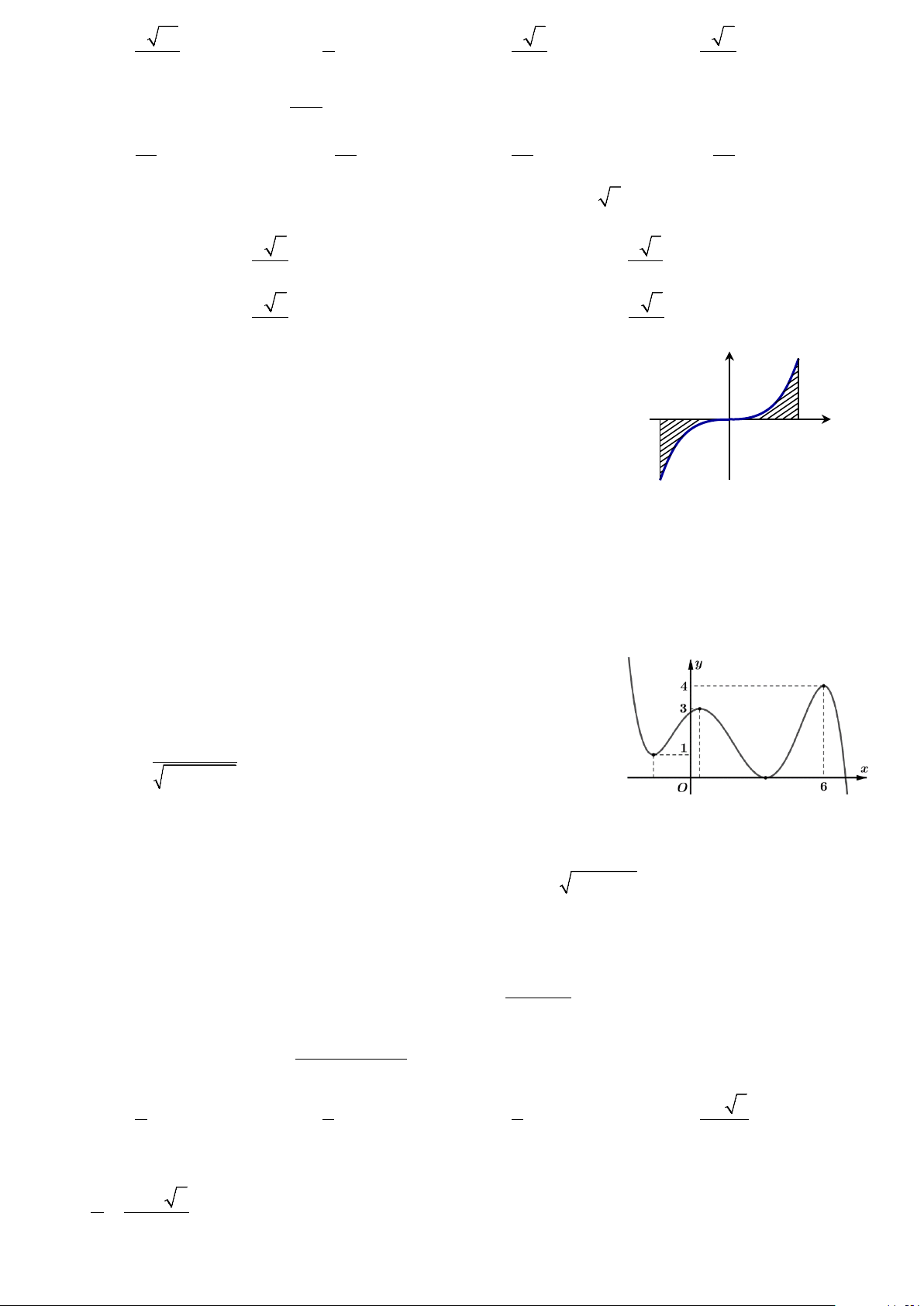
Câu 12: Người ta muốn xây một bể chứa nước dạng khối hộp chữ 1dm
nhật trong một phòng tắm. Biết chiều dài, chiều rộng, chiều cao của
khối hộp đó lần lượt là 5m ; 1m; 2m (người ta chỉ xây hai mặt thành
bể như hình vẽ bên). Biết mỗi viên gạch có chiều dài 20cm, chiều 1,8m
rộng 10cm , chiều cao 5cm. Hỏi người ta sử dụng ít nhất bao nhiêu
viên gạch để xây bể đó và thể tích thực của bể chứa bao nhiêu lít 1,3m
nước? (Giả sử lượng xi măng và cát không đáng kể). 3m
A. 1180 viên, 8820 lít. B. 1180 viên, 8800 lít.
C. 1182 viên, 8820 lít. D. 1180 viên, 8800 lít.
Câu 13: Tính môđun của số phức z = a + bi, ( , a b∈). z = 2 a + 2 b . z = 2 a + 2 b .
z = a + b. z = 2 a − 2 b . A. B. C. D.
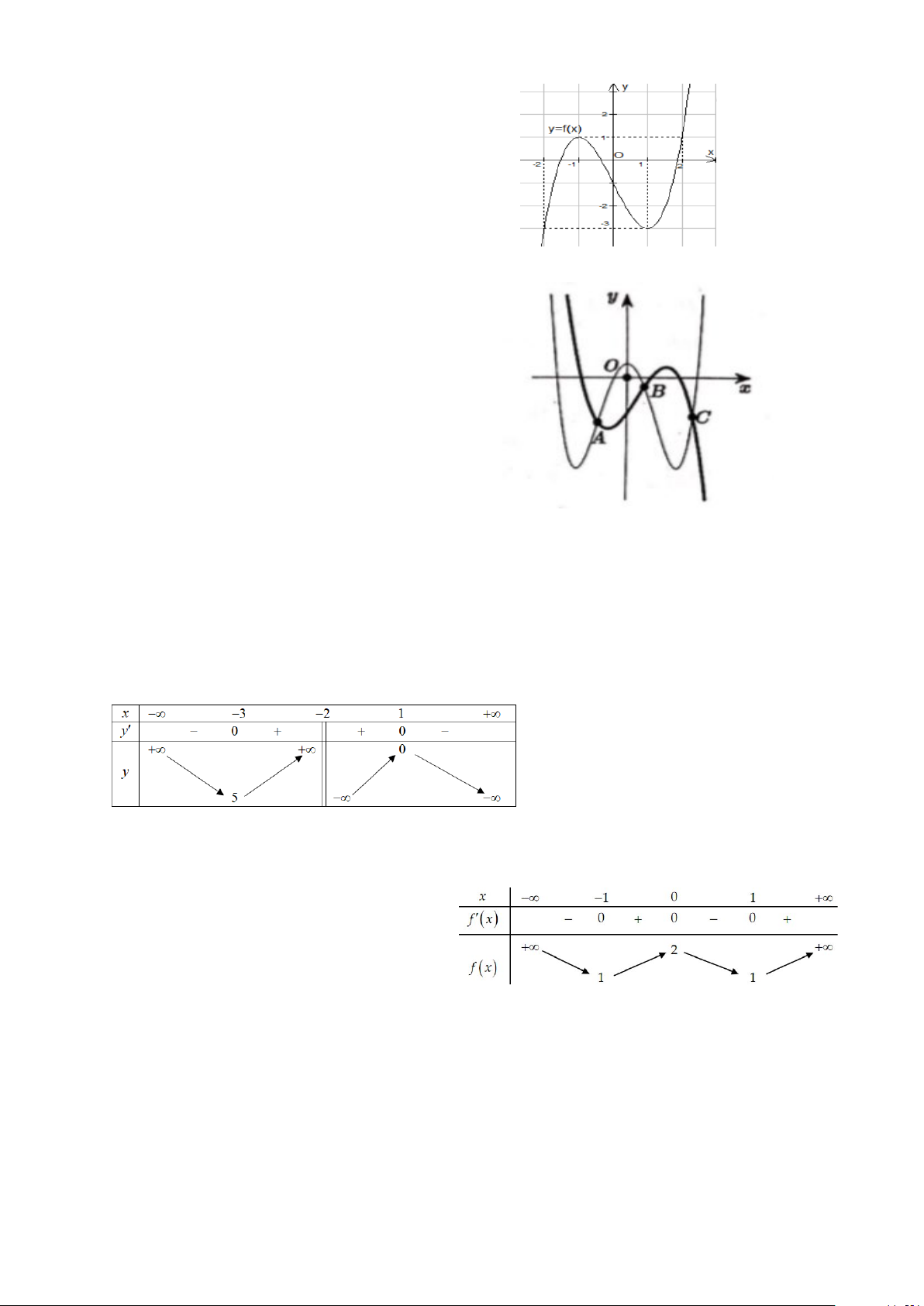
Câu 14: Cho chiếc trống như hình vẽ, có đường sinh là nửa elip được cắt bởi trục lớn với độ dài trục lớn
bằng 80 cm, độ dài trục bé bằng 60 cm và đáy trống là hình tròn có bán kính bằng 60 cm. Tính thể tích V
của chiếc trống (kết quả làm tròn đến hàng đơn vị). 3 3 3 3
A. V = 344963cm .
B. V = 344964cm .
C. V = 208347cm .
D. V = 208346cm .
Câu 15: Họ nguyên hàm của hàm số x f (x) = 3 − cos x là x 3 x − sinx + C. 3 B. x 3 ln3 − sinx + C. + sinx + C. D. x 3 ln3 + sinx + C. A. ln 3 C. ln 3
Câu 16: Diện tích của mặt cầu bán kính 2a là 2 4π a A. 2 4π a . B. 2 16π a . C. 2 16a . . D. 3
Trang 2/6 - Mã đề thi 132
Câu 17: Phương trình tham số của đường thẳng d đi qua điểm A(1; 1;
− 2) và có vectơ chỉ phương u = (1;2; 3) − là  x =1+ tx =1+ tx =1  x =1+ t d :    
y = 2 − t . d : y = 1 − − t d : y = 1 − + 3t . d : y = 1 − + 2t .     A. z = 3 − +  2t B. z = 2 +  2t C. z = 2 −  5t D. z = 2 −  3t
Câu 18: Một lớp học gồm có 20 học sinh nam và 15 học sinh nữ. Cần chọn ra 2 học sinh, 1 nam và 1
nữ để phân công trực nhật. Số cách chọn là 2 2 A. A . B. 300. C . D. 35. 35 C. 35
Câu 19: Một hình trụ có bán kính đáy bằng 3 và đường cao bằng 4. Tính diện tích xung quanh Sxq của hình trụ. A. S = π S = π S = π S = π xq 24 . B. xq 30 . C. xq 15 . D. xq 12 .
Câu 20: Trong không gian Oxyz, cho điểm A(1; 2; 2) và mặt phẳng (α): x+2y −2z −4 = 0 . Tính
khoảng cách d từ điểm A đến mặt phẳng (α) . 1 d = . 13 B. d =1. d = . D. d = 3. A. 3 C. 3
Câu 21: Bình có bốn đôi giày khác nhau gồm bốn màu: đen, trắng, xanh và đỏ. Một buổi sáng đi học, vì
vội vàng, Bình đã lấy ngẫu nhiên hai chiếc giày từ bốn đôi giày đó. Tính xác suất để Bình lấy được hai chiếc giày cùng màu. 1 . 2 . 1 1 . A. 4 B. 7 C. 14 D. 7 7 3 5 3 m
Câu 22: Rút gọn biểu thức a .a A =
với a > 0 ta được kết quả n
A = a , trong đó m , *
n∈ và m là 4 7 2 a . a− n
phân số tối giản. Khẳng định nào sau đây đúng? A. 2 3m − 2n = 2 . B. 2 2 m + n = 43. C. 2 2m + n =15. D. 2 2 m + n = 25.
Câu 23: Biết tiếp tuyến của đồ thị hàm số 4 2
y = ax + bx + 2 tại điểm A(-1;1) vuông góc với đường thẳng
x − 2y + 3 = 0. Tính 2 2 a − b ? A. 2 2 a − b = 2. − B. 2 2 a − b = 13. C. 2 2 a − b = 5. − D. 2 2 a − b = 10.   
Câu 24: Trong không gian Oxyz cho OA = 2k − i + j . Tọa độ điểm A là A. ( A 2; 1; − 1) . B. ( A 2 − ;1; 1 − ) . A(1; 1; − 2 − ) C. . D. ( A 1; − 1;2) .
Câu 25: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt đáy
và SA a 2 . Tìm số đo của góc giữa đường thẳng SC và mặt phẳng (SAB). A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 .
Câu 26: Tập nghiệm của phương trình x 1 4 − −1 = 0 là { } {− } { } { } A. 0 . B. 1 . C. 1 . D. 2 .
Câu 27: Tập nghiệm của bất phương trình log x −1 >1 là 0,5 ( )  3 ;  +∞  3   3   3    . 1;   . ; −∞   . 1;  . A.  2  B.  2  C.  2  D.  2 
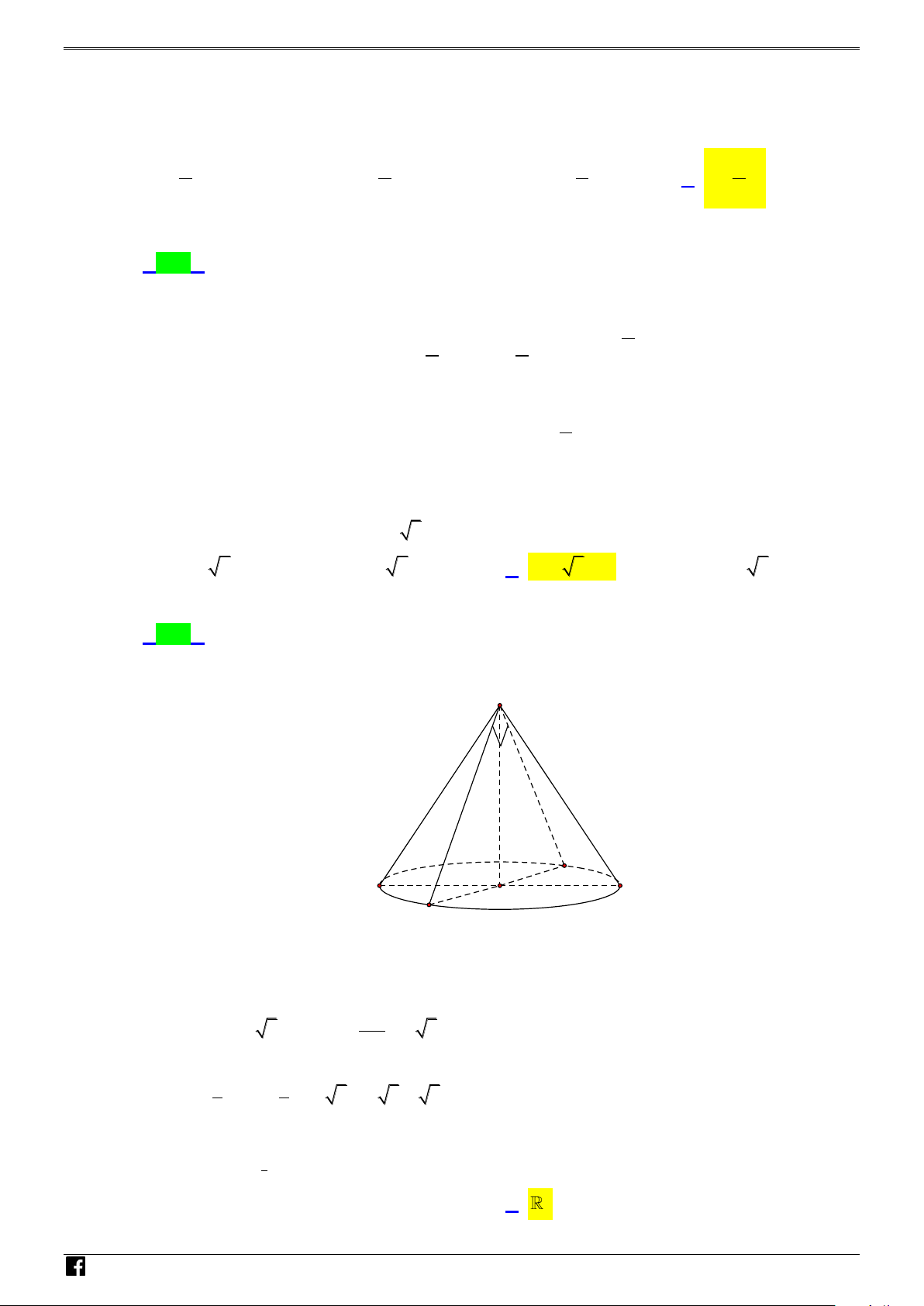
Câu 28: Khi cắt khối nón (N) bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác
vuông cân có cạnh huyền bằng 2a 3. Tính thể tích V của khối nón (N). A. 3 V = 3 6 a π . B. 3 V = 6 a π . C. 3 V = 3 a π . D. 3 V = 3 3 a π .
Trang 3/6 - Mã đề thi 132 Câu 29: Hàm số 2
y = log (x +1) có tập giá trị là 1 2 A. ( ; −∞ 0]. B. [1;+∞). C. .  D. [0;+∞).
Câu 30: Cho ba số thực dương a, b, c và a khác 1. Khẳng định nào sau đây là sai? log bc = b + c = a ( ) A. loga loga . B. logab a b . α ln a C. log b = α b . log b = . a loga D. a ln b 3
Câu 31: Biết rằng tồn tại duy nhất bộ các số nguyên a, b, c sao cho (4x + 2)ln xdx = a + bln 2 + cln 3 ∫ . 2
Giá trị của a + b + c bằng A. 19 B. -19 C. 5 D. -5 x = 2t
Câu 32: Trong không gian Oxyz , một vectơ chỉ phương của đường thẳng  ∆ : y = 1 − + t là z =1      m = (2; 1; − 0) m = (2;1 ) m = (2; 1; − ) m = ( 2 − ; 1; − 0) A. . B. ;1 . C. 1 . D. . Câu 33: Kí hiệu 1
z ,z2là hai nghiệm phức của phương trình 2
z − 4z + 5 = 0 . Phần thực a của số phức 2 2 w = 1 z + z2 bằng A. 0. B. 8. C. 16. D. 6. 3 Câu 34: Hàm số x 2 y = −
+ x − mx +1 nghịch biến trên khoảng (0;+∞) khi và chỉ khi 3 m∈(1;+∞) m∈[1;+∞) m∈[0;+∞) m∈(0;+∞) A. . B. . C. . D. . Câu 35: Cho hàm số x − 2 y = . Tìm mệnh đề đúng ? 2x +1
A. Hàm số đồng biến trên khoảng  1 ;  −∞ −  . 2   
B. Hàm số luôn nghịch biến trên tập xác định  1 D R \  = −   2
C. Hàm số nghịch biến trên khoảng  1 ;  − +∞  . 2   
D. Hàm số luôn đồng biến trên tập xác định  1 D R \  = −  .  2
Câu 36: Trong không gian với hệ tọa độ Oxyz , cho ba điểm ( A 1;0; 2
− ), B(1;1;1), C(0; 1; − 2) . Biết rằng
mặt phẳng đi qua ba điểm ,
A B,C có phương trình 7x + ay + cz + d = 0. Tính giá trị biểu thức 2 2 2
S = a + c + d A. 29. B. 59. C. 26. D. 35.
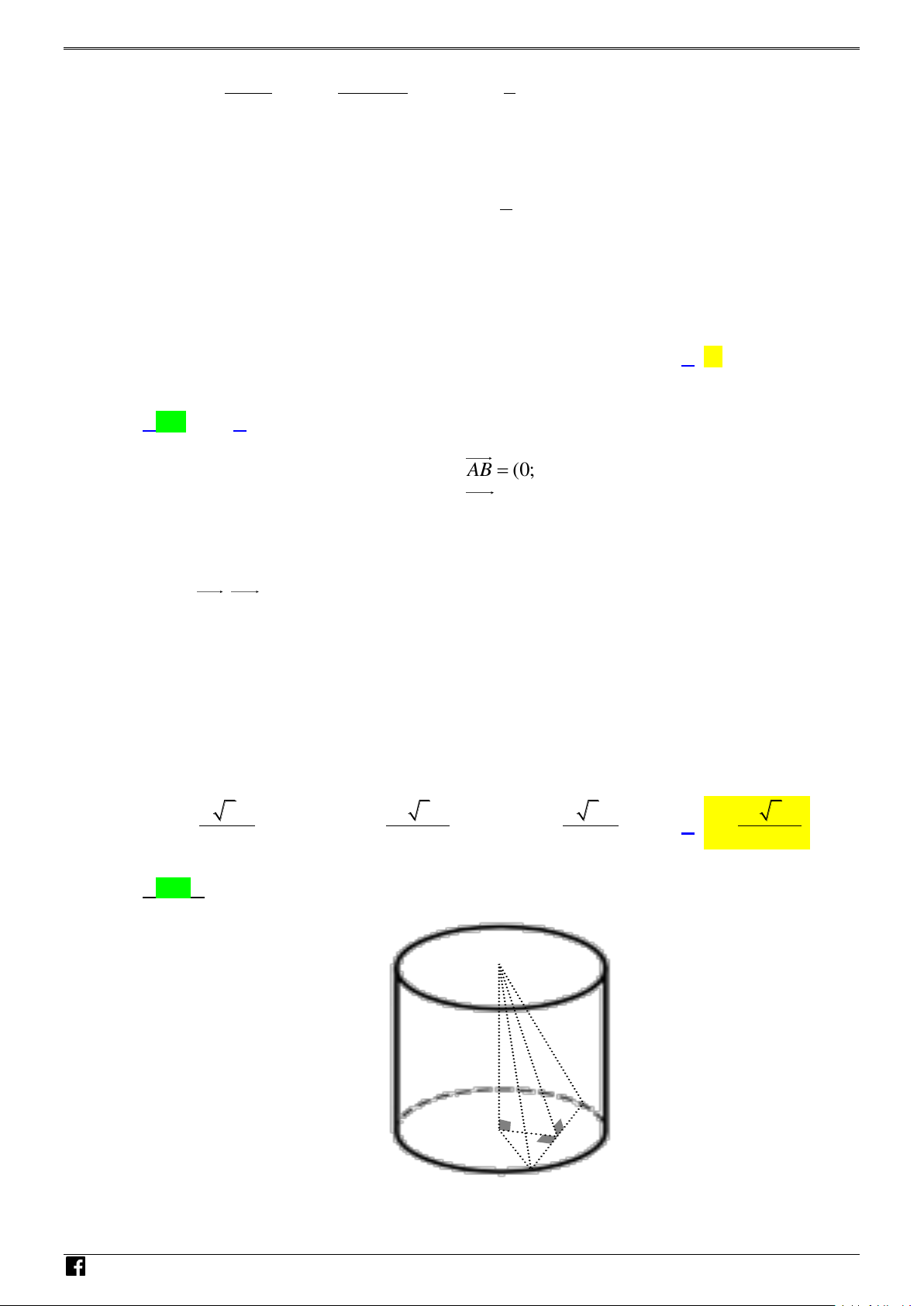
Câu 37: Cho hình trụ có hai đáy là hai hình tròn ( ;
O R) và (O'; R). AB là một dây cung của đường tròn ( ;
O R) sao cho tam giác O' AB là tam giác đều và mặt phẳng (O' AB) tạo với mặt phẳng chứa đường tròn ( ;
O R) một góc 600. Tính theo R thể tích V của khối trụ đã cho. 3 π 7R 3 π 3 π 3 π V = 3 5R V = 5R V = 3 7R V = A. 7 B. 5 C. 5 D. 7
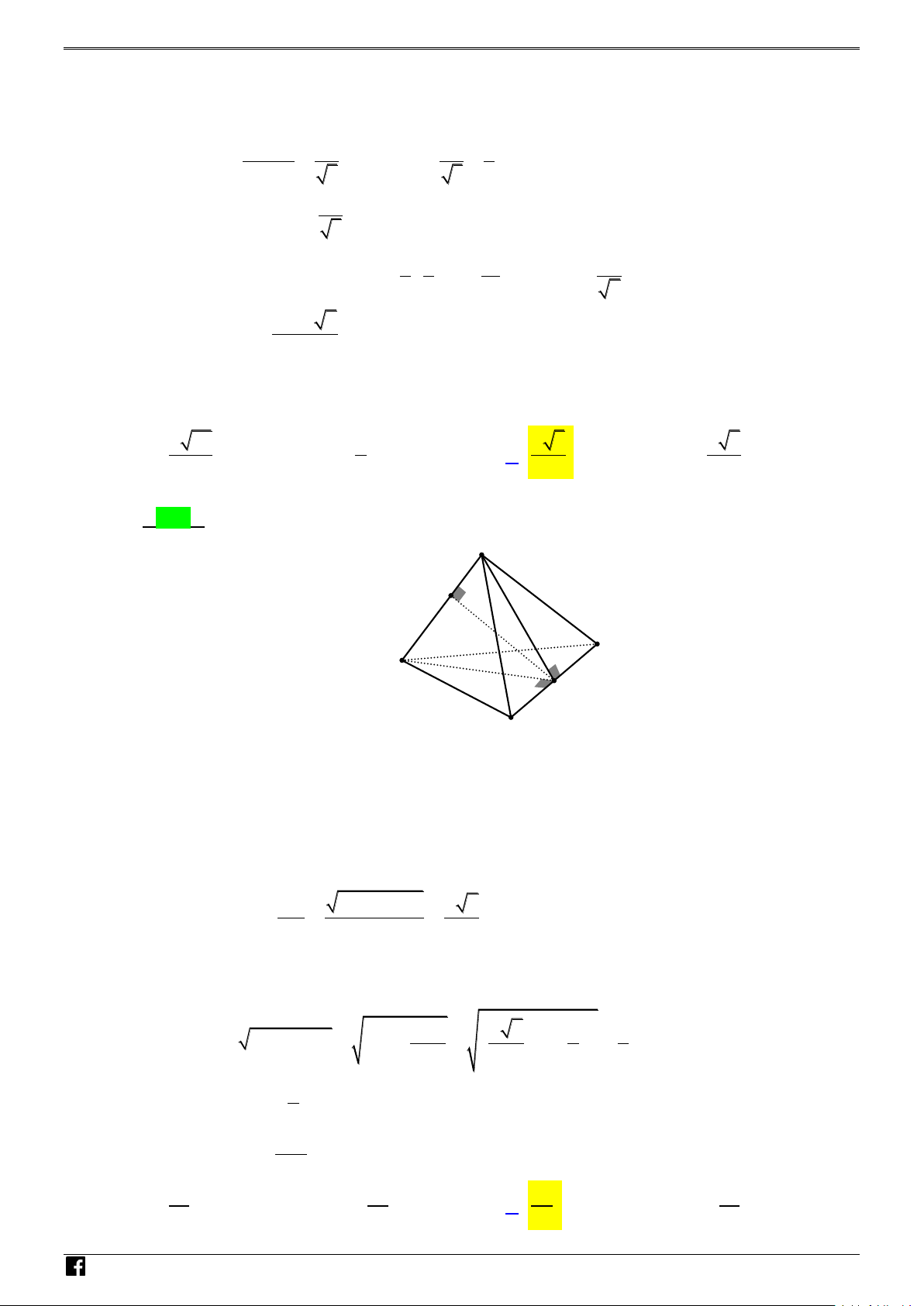
Câu 38: Cho tứ diện ABCD có = = =  0 =  0 =  0 AB AC AD ;
a BAC 60 ;CAD 60 ; DAB = 90 . Khoảng cách
giữa hai đường thẳng AC và BD là
Trang 4/6 - Mã đề thi 132 a 30 a a 3 a 2 A. 10 B. 2 C. 2 D. 2
Câu 39: Cho số phức 3 w =
. Khi đó phần ảo của số phức w là: 5 − i A. 15 . B. 3 − . C. 3 . D. 15 − . 26 26 26 26
Câu 40: Cho hình lăng trụ đứng ABC.A'B 'C ' có cạnh bên AA' = a 2 . Biết đáy ABC là tam giác vuông
có BA = BC = a , gọi M là trung điểm của BC. Tính khoảng cách giữa hai đường thẳng AM và B’C.
d ( AM B C) a 7 , ' =
d ( AM B C) a 3 , ' = A. 7 B. 3
d ( AM B C) a 2 , ' =
d ( AM B C) a 5 , ' = C. 2 D. 5
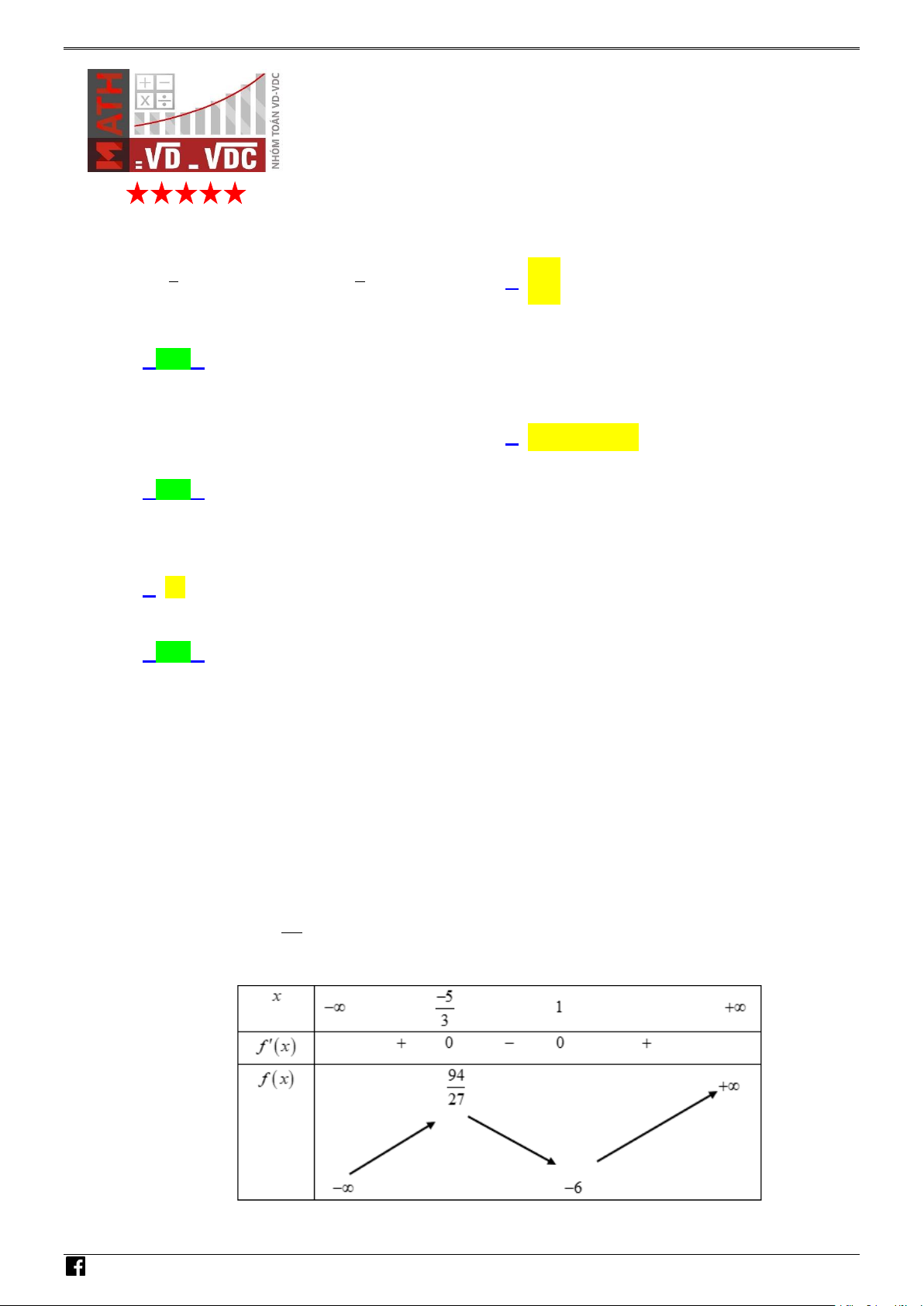
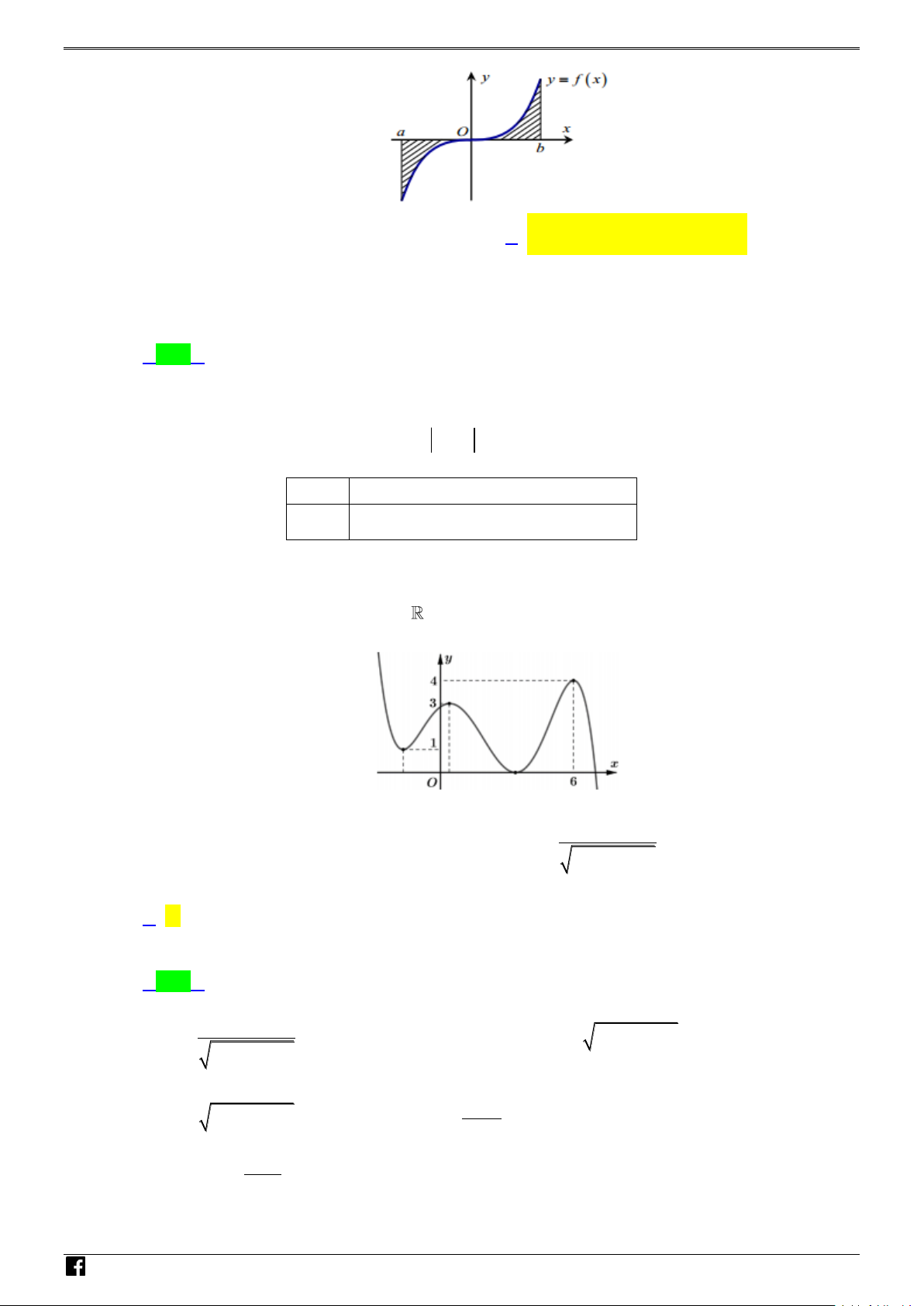
Câu 41: Cho hàm số y = f (x) liên tục trên đoạn [a;b]. y
y = f ( x)
Diện tích của hình phẳng giới hạn bởi đồ thị (C) : y = f (x), trục hoành, a O x b
hai đường thẳng x = a, x = b (Hình vẽ bên dưới) được xác định bởi
công thức nào dưới đây? 0 b 0 b S = f (x)dx − f (x)dx. ∫ ∫ S = − f (x)dx + f (x)dx. ∫ ∫ A. a 0 B. a 0 0 b 0 b S = − f (x)dx − f (x)dx. ∫ ∫ S = f (x)dx + f (x)dx. ∫ ∫ C. a 0 D. a 0
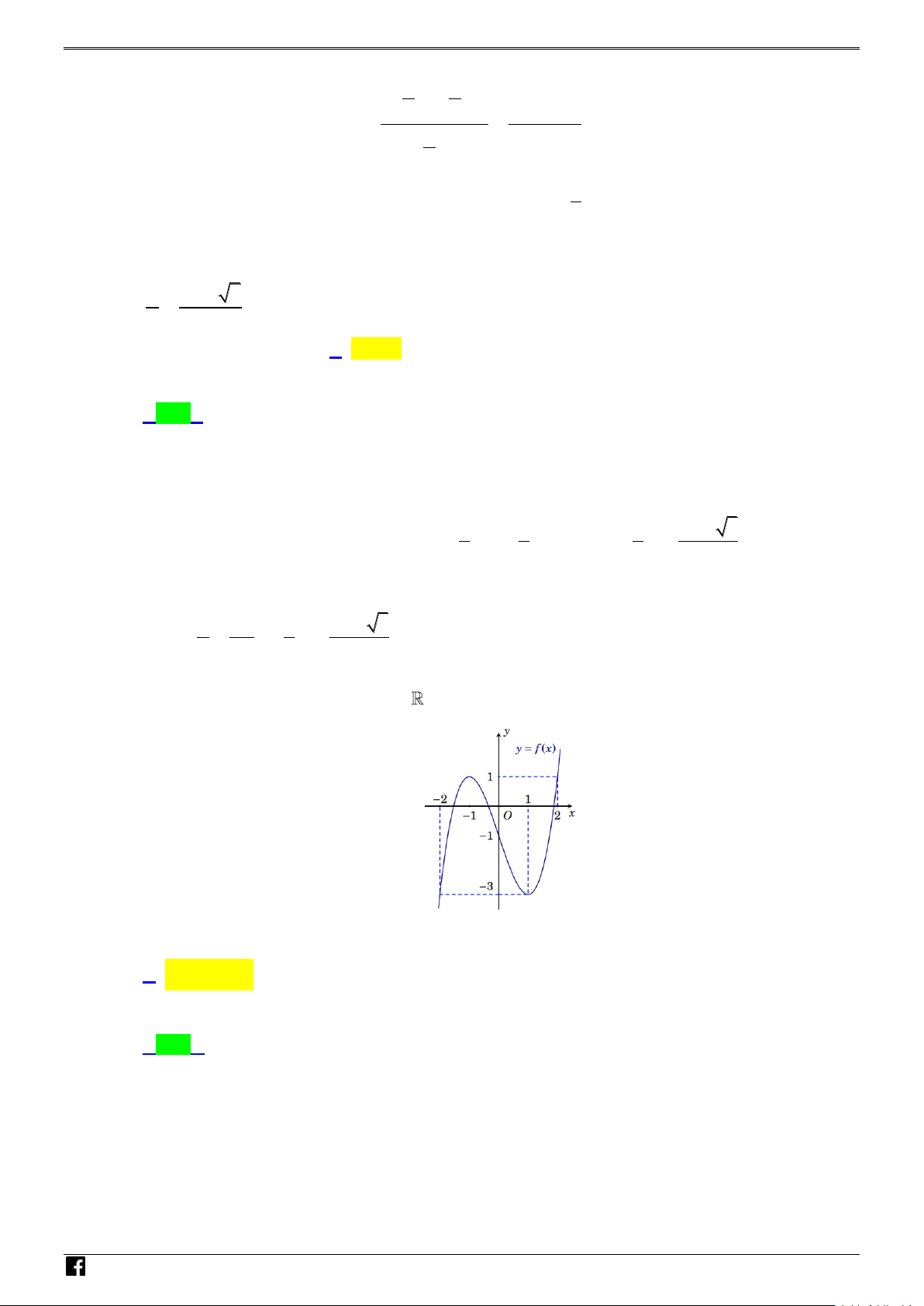
Câu 42: Cho hàm số y f x liên tục trên  , có đồ thị như hình vẽ.
Có bao nhiêu giá trị của tham số m để phương 3 trình 4m m 2
f x3 có 3 nghiệm phân biệt ? 2 2 f x5 A. 1. B. 5. C. 2. D. 0.
Câu 43: Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số x
y = −e + 4x , trục hoành và hai đường thẳng
x =1;x = 2 . Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục hoành. A. 2 V = 6 − e − e . = π( 2 V 6 − e + e) = π( 2 V 6 − e − e) = − + B. . C. . D. 2 V 6 e e . 2 2 x + y log ( 2 2 2 x +2 y + ) 1
Câu 44: Cho các số thực x, y dương và thỏa mãn log xy 2 + 2 ≤ log2 8 . Tìm giá trị 2 3xy + x 2 2
nhỏ nhất của biểu thức
2x − xy + 2y P = . 2 2xy − y 1 5 3 1+ 5 . . . . A. 2 B. 2 C. 2 D. 2
Câu 45: Gọi x , y là các số thực dương thỏa mãn điều kiện log x = log y = log x + y và 9 12 16 ( )
x −a + b =
, với a , b là hai số nguyên dương. Tính P = . a b . y 2
Trang 5/6 - Mã đề thi 132 A. P = 6. B. P = 5 . C. P = 8 . D. P = 4 .
Câu 46: Cho hàm số y = f (x) liên tục trên R và
có đồ thị như hình bên. Phương trình
f (2sin x) = m có đúng ba nghiệm phân biệt thuộc đoạn [ π − ;π ] khi và chỉ khi m∈{ 3 − ; } m∈( 3 − ; ) m∈[ 3 − ; ) m∈( 3 − ; ] A. 1 . B. 1 . C. 1 . D. 1 .
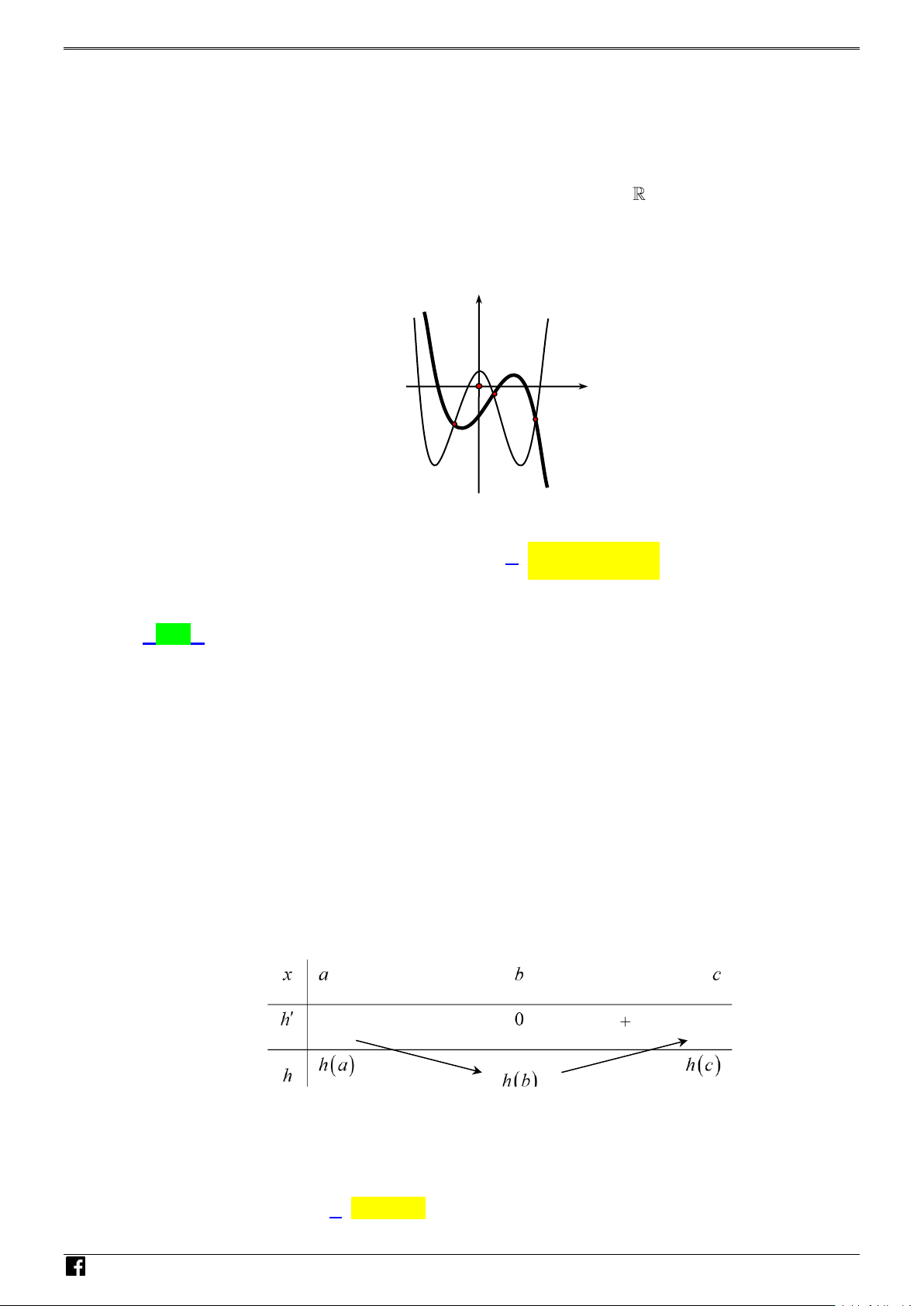
Câu 47: Cho hai hàm số y = f (x) và y = g (x) là
hai hàm số liên tục trên  có đồ thị hàm số
y = f ′( x) là đường cong nét đậm, đồ thị hàm số
y = g′( x) là đường cong nét mảnh như hình vẽ. Gọi
ba giao điểm A, B, C của y = f ′(x) và y = g′(x)
trên hình vẽ lần lượt có hoành độ là a, b, c. Tìm giá
trị nhỏ nhất của hàm số h(x) = f (x) − g (x) trên đoạn [ ; a c]?
min h( x) = h(0).
min h( x) = h(a).
min h( x) = h(b).
min h( x) = h(c). A. [ ;ac] B. [ ;ac] C. [a;c] D. [ ;ac]
Câu 48: Trên mặt phẳng tọa độ Oxy, số phức nào dưới đây có điểm biểu diễn là M (1; 2 − ) ?
A. z =1+ 2i .
B. z =1− 2i . C. z = 1 − − 2i . D. z = 1 − + 2i .
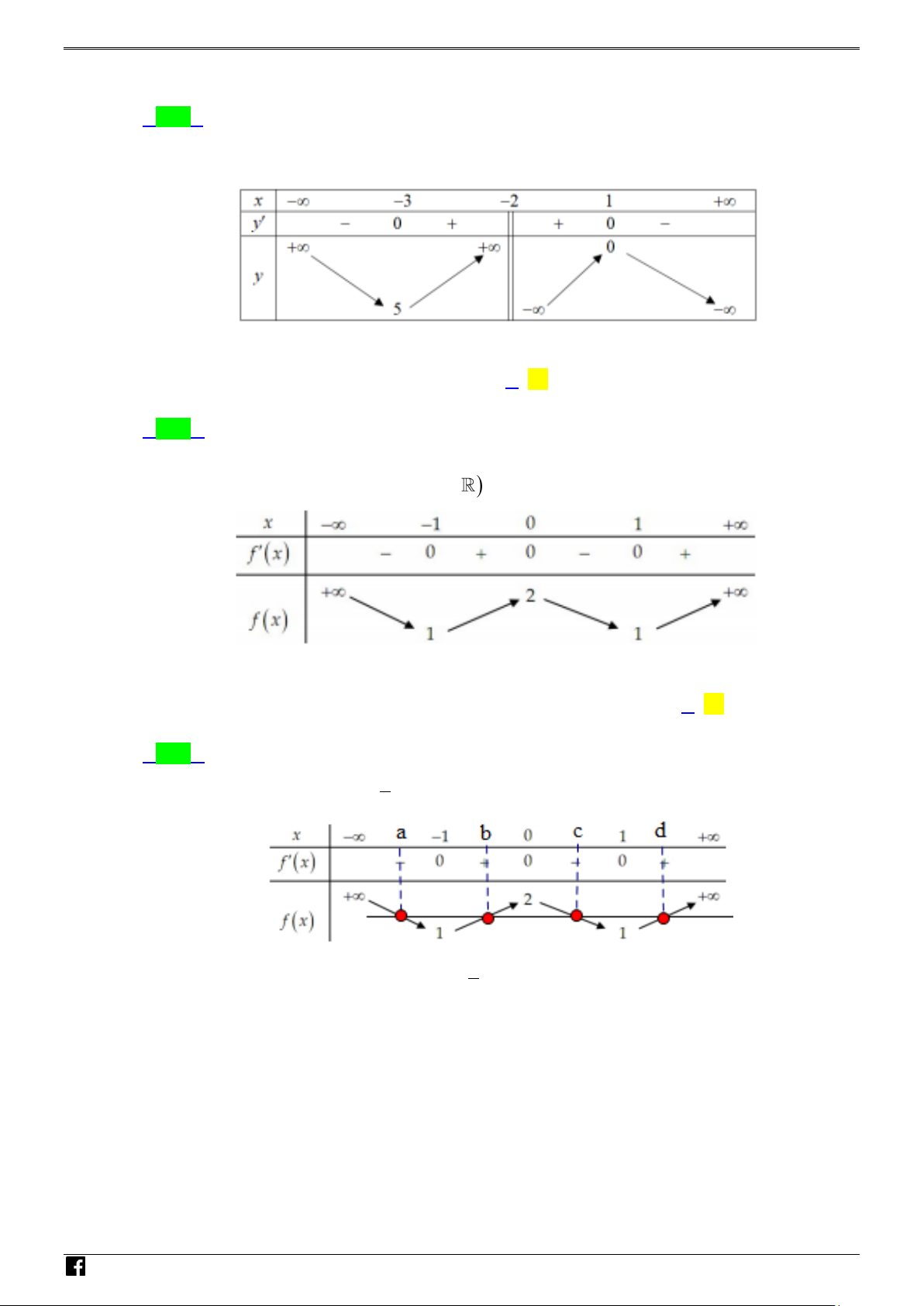
Câu 49: Cho hàm số y = f (x) có bảng biến thiên sau:
Tìm giá trị cực đại của hàm số y = f (x) . A. 5. B. 3 − . C. 0 . D. 1. Câu 50: Cho hàm số f (x) 4 2
= ax + bx + c(a,b,c∈) và có bảng biến
thiên như hình vẽ bên. Số nghiệm thực dương của
phương trình 2 f ( x) − 3 = 0 là A. 3. B. 1 . C. 4. D. 2. ----------- HẾT ----------
Trang 6/6 - Mã đề thi 132 made cautron dapan 132 1 C 132 2 C 132 3 D 132 4 A 132 5 B 132 6 A 132 7 A 132 8 B 132 9 B 132 10 C 132 11 D 132 12 A 132 13 A 132 14 B 132 15 A 132 16 B 132 17 D 132 18 B 132 19 A 132 20 B 132 21 D 132 22 C 132 23 C 132 24 D 132 25 A 132 26 C 132 27 D 132 28 C 132 29 C 132 30 D 132 31 C 132 32 D 132 33 D 132 34 B 132 35 A 132 36 D 132 37 D 132 38 B 132 39 C 132 40 A 132 41 B 132 42 A 132 43 B 132 44 B 132 45 B 132 46 A 132 47 C 132 48 B 132 49 C 132 50 D NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
HƯỚNG DẪN GIẢI CHI TIẾT
ĐỀ THI CHUYÊN ĐỀ TOÁN 12 LẦN 4 NĂM HỌC 2019 – 2020 N
TRƯỜNG THPT LIỄN SƠN – VĨNH PHÚC H Ó M T Câu 1:
Thể tích của khối lăng trụ có chiều cao bằng h và diện tích đáy bằng B là O Á 1 1 N A. Bh . B. Bh . C. Bh . D. 3Bh . 3 6 V D Lời giải – VDC Chọn C Câu 2:
Cho cấp số nhân u có u  2
 và công bội q  3. Giá trị của u là n  1 11
A. u  3072 . B. u  354294  . C. u  118098  .
D. u  354294 . 11 11 11 11 Lời giải Chọn C 10 10
u u .q  2  .3  1  18098. 11 1 Câu 3:
Số điểm chung của đồ thị hàm số 4 2
y x  7x  6 và đồ thị hàm số 3
y x 13x là A. 4 . B. 1. C. 2 . D. 3 . Lời giải Chọn A N
Xét phương trình hoành độ giao điểm: 4 2 3
x  7x  6  x 13x H 3 2 Ó
 x  2x x 5x 3  0 M x  2 T  O  3 2      Á x x 5x 3 0 N
Xét hàm số f x 3 2
x x 5x 3 V D f  x 2
 3x  2x 5 – VDC x 1  
f x  0  5  x   3 Bảng biến thiên:
Từ bảng biến thiên ta thấy hàm số f x có y .y  0 cd ct
https:/www.facebook.com/groups/toanvd. Trang 8 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
 đồ thị hàm số y f x cắt Ox tại 3 điểm phân biệt.  3 2
x x  5x  3  0 có 3 nghiệm phân biệt.
Vậy số điểm chung của 2 đồ thị hàm số đã cho là 4 . N x 1 t H x  2 y  2 z  3  Ó Câu 4:
Trong không gian Oxyz , cho hai đường thẳng d :  
; d :  y  1 2t và điểm 1 2 M T 2 1  1   z  1   t O A1; 2; 
3 . Đường thẳng  qua A vuông góc với d và cắt d có phương trình là Á 1 2 N x 1 y  2 z  3 x 1 y  2 z  3 V A.   . B.   . D 1 3  5  1  3  5  – x 1 y  2 z  3 x 1 y  2 z  3 VDC C.   . D.   . 1 3 5 1 3 5  Lời giải Chọn A
Đường thẳng d có VTCP là u  2;1;1 . 1   1 
Gọi M   d M d M 1 t ;1 2t ;1 t 2   2   AM   t
 ;2t 1;t  4
Do d    u .AM  0  3
t 3  0  t  1  . 2    2
Vậy đường thẳng  qua điểm A1; 2;3 có VTCP là AM  1; 3; 5 . N H Ó x y z  M   1 2 3 :   . 1 3  5  T O Á Câu 5:
Cho hàm số y f x có lim f x  3 và lim f x  3
 . Khẳng định nào sau đây là đúng? N x x V
A. Đồ thị hàm số đã cho không có tiệm cận ngang. D
B. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y  3 và y  3  . – VDC
C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x  3 và x  3  . Lời giải Chọn B
lim f x  3  TCN: y  3 . x
lim f x  3   TCN: y  3  . x
https:/www.facebook.com/groups/toanvd. Trang 9 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020    Câu 6: Cho hàm số
f x liên tục và có đạo hàm trên 0;   , thỏa mãn hệ thức  2    x       f x  tan .
x f  x  . Biết rằng 3 ff
a 3  bln 3    
trong đó a;b  . 3 cos x  3   6  N H
Tính giá trị của biểu thức P a b . Ó M T 4 2 7 14 A. P   . B. P   . C. P  . D. P  . 9 9 9 9 O Á Lời giải N V Chọn A D – x x VDC
Ta có: f x  tan .
x f  x   cos .
x f x  sin .
x f  x  3 cos x 2 cos x    x 3 3    x sin . x f  x    sin . x f 
x dx dx   2 cos x 2   cos x 6 6   sin . x f  x 5 3 1 3     ln   18 3 6 3    1    5 3 1        5 3 ff    ln3      3 ff    ln3     2  3  2  6  18 2  3   6  9 5 5 4 Vậy a  ; b  1
  P a b  1   . 9 9 9 2 2 2 Câu 7:
Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S  :x 3   y  
1   z  2  8 . Khi đó N
tâm I và bán kính R của mặt cầu là. H Ó A. I 3; 1  ; 2
 ,R  2 2 . B. I 3; 1  ; 2  ,R  4. M T C. I  3
 ;1;2R  2 2 . D. I  3  ;1;2,R  4 . O Á Lời giải N V Chọn A D – I 3; 1  ; 2  , R  2 2 VDC
Tâm và bán kính của mặt cầu là   Câu 8: Đồ thị hàm số 3 2
y  x  3x  2 có dạng nào dưới đây Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 4. B. Hình 3. C. Hình 1. D. Hình 2. Lời giải Chọn B
https:/www.facebook.com/groups/toanvd. Trang 10 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
Đồ thị hàm số có hai điểm cực trị là  2  ; 2
  và 0;2 nên hình 3 là dạng của đồ thị hàm số đã cho Câu 9:
Cho số phức z 1 bi,b  và z  10 . Giá trị của b bằng N H A. 3 . B. 3  . C. 3  . D. 10 . Ó M T Lời giải O Chọn B Á N V Ta có 2 2 2
z  10  1 b  10  1 b  10  b  9  b  3  D – VDC
Câu 10: Đạo hàm của hàm số    2x f xx là x x x
A. f x 2 '  1.
B. f x 2 2 '   . C. '  2x f x  ln 2 1. D. '  2x f x  1. ln 2 ln 2 2 Lời giải Chọn C
Câu 11: Giá trị nhỏ nhất của hàm số 4 2
y x  4x  5 trên đoạn  1  ;2 là A. 3. B. 5. C. 2. D. 1. Lời giải Chọn D N   H x 0     Ó Ta có: 3 y ' 4x 8 ; x y ' 0  M x   2 T O Mà f  
1  2; f 0  5; f 2  1; f 2  5 Á     N V     D
Vậy giá trị nhỏ nhất của hàm số 4 2 y x 4x
5 trên đoạn  1; 2 là 1. – VDC
Câu 12: Người ta muốn xây một bể nước dạng khối hộp chữ nhật trong một phòng tắm. Biết chiều dài,
chiều rộng, chiều cao của khối hộp đó lần lượt là 5 ; m 1 ;
m 2m (người ta chỉ xây hai mặt thành bể
như hình vẽ bên). Biết mỗi viên gạch có chiều dài 20 ,
cm chiều rộng 10cm , chiều cao 5 . cm Hỏi
người ta sử dụng ít nhất bao nhiêu viên gạch để xây bể đó và thể tích thực của bể chứa bao nhiêu
lít nước? (Giả sử lượng xi măng và cát không đáng kể).
A. 1180 viên, 8820 lít.
B. 1180 viên, 8800 lít.
C. 1182 viên, 8820 lít.
D. 1180 viên, 8800 lít. Lời giải Chọn A
* Theo mặt nước của bể: 500
Số viên gạch xếp theo chiều dài của bể mỗi hàng là x   25 viên 20
https:/www.facebook.com/groups/toanvd. Trang 11 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 200
Số viên gạch xếp theo chiều cao của bể mỗi hàng là:
 40. Vậy tính theo chiều dài thì có 5
40 hàng gạch mỗi hàng 25 viên. Khi đó theo mặt nước của bể N  25.40  1000 viên. N
*Theo mặt bên của bể: ta thấy,nếu hàng mặt trước của bể đã được viên hoàn chỉnh đoạn nối H Ó
hao mặt thì ở mặt bên viên gạch còn lại sẽ được cắt đi còn 1 viên. Tức là mặt bên sẽ có M T 2 1 100  20 O .40  .40  180 viên. Á 2 20 N V
Vậy tổng số viên gạch là 1180 viên. D –
Khi đó thể tích bờ tường xây là 1180.2.10,5 1180 lít. VDC
Vậy thể tích bể chứa nước là: 50.10.20 1180  8820 lít.
Câu 13: Tính môđun của số phức z a bi,  , a b   . A. 2 2
z a b . B. 2 2
z a b .
C. z a b . D. 2 2
z a b . Lời giải Chọn A Theo định nghĩa ta có 2 2
z a b .
Câu 14: Cho chiếc trống như hình vẽ, có đường sinh là nửa elip được cắt bỡi trục lớn với độ dài trục lớn
bằng 80 cm , độ dài trục bé bằng 60 cm và đáy trống là hình tròn có bán kính bằng 60 cm . Tính N
thể tích của chiếc trống (kết quả làm tròn đến hàng đơn vị). H Ó M T O Á N V D – VDC A. 3
V  344963cm . B. 3
V  344964 cm . C. 3
V  208347 cm . D. 3
V  208346 cm . Lời giải Chọn B Ta
https:/www.facebook.com/groups/toanvd. Trang 12 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 N H Ó M T O Á N V D –
Gắn hệ trục tọa độ như hình vẽ: VDC
x 402  y 602 Ta có phương trình Elip:  1 2 2 40 30 2      x y  602 40 2    30 1  2  40    3  y  60   40   x  402 2 4 3  y  60  40   x  402 2 4 80 2 Khi đó 3 V     60  40   x 402 2 dx  . N  4  0 H Ó M
Sử dụng máy tính bỏ túi tính được V  344963, 6143 T O
Câu 15: Họ nguyên hàm của hàm số    3x f x  cos x là Á N 3x 3x x x V A.
 sin x C .
B. 3 ln 3  sin x C . C.
 sin x C .
D. 3 ln 3  sin x C . D ln 3 ln x – Lời giải VDC Chọn A x
3x  cos xdx  
3 sin x C . ln 3
Câu 16: Diện tích của mặt cầu bán kính 2a là 2 4 a A. 2 4 a . B. 2 16 a . C. 2 16a . D. . 3 Lời giải Chọn B
Ta có: S   r    a2 2 2 4 4 . 2 16a .
https:/www.facebook.com/groups/toanvd. Trang 13 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
Câu 17: Phương trình tham số của đường thẳng d đi qua điểm A1; 1
 ;2 và có véc tơ chỉ phương u  1; 2; 3   là x  1 tx  1 tx  1 x  1 t N    
A. d :  y  2  t
B. d :  y  1 t
C. d :  y  1
  3t D. d : y  1   2t H Ó     z  3   2t z  2  2t z  2  5t z  2  3t M T     Lời giải O Á Chọn D N V D
Câu 18: Một lớp học gồm có 20 học sinh nam và 15 học sinh nữ. Cần chọn ra 2 học sinh, 1 nam và 1 –
nữ để phân công trực nhật. Số cách chọn là VDC A. 2 A B. 300 C. 2 C D. 35 35 35 Lời giải Chọn A
Có 20 cách chọn 1 học sinh nam.
Có 15 cách chọn 1 học sinh nữ.
Số cách chọn 1 nam và 1 nữ để phân công trực nhật là: 20.15  300.
Câu 19: Một hình trụ có bán kính đáy bằng 3 và đường cao bằng 4. Tính diện tích xung quanh S của xq hình trụ. N A. S  24 . B. S  30 . C. S 15 . D. S 15 . H xq xq xq xq Ó Lời giải M T O Chọn A Á N
+) Hình lăng trụ có độ dài đường sinh bằng đường cao nên diện tích xung quanh của hình trụ là V S
 2rl  2.3.4  24. D xq – VDC
Câu 20: Trong không gian 𝑂𝑥𝑦𝑧, cho điểm (
A 1; 2; 2) và mặt phẳng () : x  2y  2z  4  0 . Tính khoảng
cách d từ điểm A đến mặt phẳng ( ) . 1 13 A. d .
B. d  1. C. d  .
D. d  3. 3 3 Lời giải Chọn B 1 2.2  2.2  4 +) Ta có d  ; A    1. 1 4  4
Câu 21: Bình có bốn đôi giày khác nhau gồm bốn màu: đen, trắng, xanh và đỏ. Một buổi sáng đi học, vì
vội vàng, Bình đã lấy ngẫu nhiên hai chiếc giày từ bốn đôi giày đó. Tính xác suất để Bình lấy
được hai chiếc giày cùng màu.
https:/www.facebook.com/groups/toanvd. Trang 14 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 1 2 1 1 A. . B. . C. . D. . 4 7 14 7 Lời giải N Chọn D H Ó    M T
+) Số phần tử không gian mẫu là n   2 C 28 . 8 O
+) Gọi 𝐴 là biến cố: “Bình lấy được 2 chiếu cùng màu”. Ta có n A  4 cách. Á N V n A 1 D Vậy P A     . – n  7 VDC 7 3 5 3 m a .a m
Câu 22: Rút gọn biểu thức A
với a  0 ta được kết quả n
A a , trong đó * , m n  4 7 2 và a . an
là phân số tối giản. Khẳng định nào sau đây đúng? A. 2
3m  2n  2 . B. 2 2
m n  43. C. 2
2m n  15 . D. 2 2 m n  25. Lời giải Chọn C 7 5 7 3 5 4 26 2 3 3 3 4 a .a a .a a  Ta có 2 7 7 A     a
a m  2;n  7  2m n 15. 2 26 4 7 2 a . a  4 7 7 a .a a N
Câu 23: Biết tiếp tuyến của đồ thị hàm số 4 2
y ax bx  2 tại điểm A 1  ; 
1 vuông góc với đường thẳng HÓ
x  2y  3  0 . Tính 2 2 a b ? M T A. 2 2 a b  2  . B. 2 2
a b  13 . C. 2 2 a b  5  . D. 2 2
a b  10 . O Lời giải Á N V Chọn C D – 1 3 1 VDC
Ta có x  2 y  3  0  y x
có hệ số góc là k  . 2 2 1 2 Mặt khác 4 2 3
y  (ax bx  2)  4ax  2bx , suy ra tiếp tuyến tại A 1  ; 
1 của đồ thị hàm số có
hệ số góc là k  4  a  2b . 2 1 k .k  1   4
a  2b  1   a  2 1 2   Ta có hệ 2 2          . y    2 a b 5 1  1 b    3 
a b  2 1
Câu 24: Trong không gian Oxyz cho OA  2k i j . Tọa độ điểm A là A2; 1  ;  1 A 2  ;1;  1 A1; 1  ; 2   A 1  ;1;2 A. . B. . C. . D. . Lời giải Chọn D
https:/www.facebook.com/groups/toanvd. Trang 15 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
Ta có OA  2k i j OA   1  ;1;2  A 1  ;1;2.
Câu 25: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với
mặt đáy và SA a 2 . Tìm số đo của góc giữa đường thẳng SC và mặt phẳng SAB. N H A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 . Ó M T Lời giải O Chọn A Á N
Chọn hệ trục tọa độ Oxyz như hình vẽ V D – VDC N H Ó M T O
Ta có A O0;0;0, S 0;0;a 2 ,C a;a;0, D0;a;0. Á N V
Đường thẳng SC có một véctơ chỉ phương là SC  ; a ; a a 2 . D   – VDC
Mặt phẳng SAB có một véctơ pháp tuyến là AD  0; a;0.
SC SAB SC.AD . a a 1 sin ,    SC . .AD
a a  a 2 . 2 2 2 2 2 . a
Vậy số đo của góc giữa đường thẳng SC và mặt phẳng SAB bằng 0 30 . 
Câu 26: Tập nghiệm của phương trình x 1 4 1 0 là A.   0 . B.   1  . C.   1 . D.   2 . Lời giải Chọn C
https:/www.facebook.com/groups/toanvd. Trang 16 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020   Ta có x 1 x 1 4
1 0  4 1 x 1 0  x 1.
Câu 27: Tập nghiệm của bất phương trình log x 1 1 là 0,5   N  3   3   3   3  A. ; . B. 1; . C. ;  . D. 1; . H         Ó  2   2   2   2  M T Lời giải O Chọn D Á N V x 1 0 x 1 D   3 Ta có log x 1  1     1 x  . 0,5   – 1 3    VDC x 1 x 2    2  2  3 
Vậy tập nghiệm của bất phương trình đã cho là S  1; .    2 
Câu 28: Khi cắt khối nón  N  bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác
vuông cân có cạnh huyền bằng 2a 3 . Tính thể tích V của khối nón  N  . A. 3 V  3 6 a  . B. 3 V  6 a  . C. 3 V  3 a  . D. 3 V  3 3 a  . Lời giải Chọn C S N H Ó M T O Á N V D B – VDC O A
Gọi S là đỉnh hình nón, thiết diện qua trục là tam giác SAB . AB
Ta có AB  2a 3  r h   a 3 . 2 1 1 Vậy V rh  .  a 32 2 3 .a 3  3 a  . 3 3
Câu 29: Hàm số y  log  2
x 1 có tập giá trị là 1  2 A.  ;  0 .
B. 1;  . C. . D. 0;  .
https:/www.facebook.com/groups/toanvd. Trang 17 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 Lời giải Chọn C
Hàm số y  log  2
x 1 có tập giá trị là . 1  N H 2 Ó M T
Câu 30: Cho ba số thực dương a, ,
b c và a khác 1. Khẳng định nào sau đây là sai? A. log bc b c . B. log b a ab . a   log log O a a Á ln a N
C. log b   log b . D. log b  . a a a V ln b D Lời giải – VDC Chọn D Ta có:
+) log bc  log b  log c nên A đúng. a a a +) log b a a
b nên B đúng.
+) log b   log b nên C đúng. a a ln b +) log b  nên D sai. a ln a 3
Câu 31: Biết rằng tồn tại duy nhất các bộ số nguyên a, , b c sao cho
(4x  2) ln xdx a b ln 2  c ln 3  2
Giá trị của a b c bằng N A. 19 . B. 19  . C. 5 . D. 5  . H Ó Lời giải M T Chọn C O Á 3 3 3 N
(4x  2) ln xdx  ln xd    2
2x  2x   2 2x  2x 3 ln x |  2x  2 dx  2   V 2 2 2 D – a  7  VDC 3  Vậy
(4x  2) ln xdx  7  1  2ln 2 2  4ln3  b    1  2. 2 c  24 
Do đó: a b c  5. x  2t
Câu 32: Trong không gian Oxyz , một véc tơ chỉ phương của đường thẳng  :  y  1 t là z 1  A. m2; 1  ;0. B. m2;1;  1 . C. m2; 1  ;  1 . D. m 2  ; 1  ;0 . Lời giải Chọn D
https:/www.facebook.com/groups/toanvd. Trang 18 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020x  2t
Từ phương trình tham số của đường thẳng  :  y  1 t ta có một véc tơ chỉ phương của đường z 1  N thẳng là m 2  ; 1  ;0 H Ó M T
Câu 33: Kí hiệu z và z là nghiệm phức của phương trình 2
z  4z  5  0 . Phần thực a của số phức 1 2 2 2 O w  z  z bằng 1 2 Á N A. 0 . B. 8 . C. 16 . D. 6 . V Lời giải D – Chọn D VDC z  2  i Xét phương trình 2
z  4z  5  0   z  2  i Khi đó 2 2 w  z  z  6 1 2 3 x Câu 34: Hàm số 2 y  
x mx 1nghịch biến trên 0;khi và chỉ khi 3
A. m 1;
B. m 1;
C. m 0;
D. m 0; Lời giải. Chọn B. 3 N x Ta có 2 2 y  
x mx 1 y  x  2x m . H 3 Ó M T Theo bài ra 2 2
x  2x m  0, x
  0  m  x  2 , x x   0 . O Á N Khảo sát hàm số 2
g(x)  x  2x g(0)  0; g(1)  1. Vậy điều kiện cần tìm là m 1; V . D – VDC x  2
Câu 35: Cho hàm số y  . Tìm mệnh đề đúng 2x 1  1 
A. Hàm số đồng biến trên khoảng  ;     .  2   1 
B. Hàm số luôn nghịch biến trên tập xác định D  \   .  2  1 
C. Hàm số nghịch biến trên khoảng  ;    .  2   1 
D. Hàm số luôn đồng biến trên tập xác định D  \   .  2 Lời giải. Chọn A.
https:/www.facebook.com/groups/toanvd. Trang 19 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 x  2 5 1 Ta có y   y   0, x    2 2x 1 (2x  . 1) 2
Hàm số đã cho luôn đồng biến trên từng khoảng xác định. N H Ó  1 
Như vậy hàm số đồng biến trên khoảng  ;   . M T    2  O Á
Câu 36: Trong không gian với hệ tọa độ Oxyz , cho ba điểm ( A 1;0; 2  ), ( B 1;1;1),C(0; 1  ;2) . Biết rằng N
mặt phẳng đi qua ba điểm , A ,
B C có phương trình 7x ay cz d  0 . Tính giá trị biểu thức VD 2 2 2
S a c d . – VDC A. 29 B. 59 C. 26 D. 35 Lời giải. Chọn D. AB  (0;1;3) Ta có ( A 1;0; 2
 ), B(1;1;1),C(0; 1  ;2)   AC  ( 1  ; 1  ;4)
Mặt phẳng (ABC) có một véc tơ pháp tuyến là A , B AC  (7; 3
 ;1)  (ABC) : 7(x 1)  3y z  2  0  7x  3y z  5  0   . Như vậy 2 2 2 a  3
 ;b 1;c  5
  a c d  35. N  H
Câu 37: Cho hình trụ có hai đáy là hai hình tròn  ;
O R và O ; R . AB là một dây cung của đường tròn ÓM  ;
O R sao cho tam giác O A
B là tam giác đều và mặt phẳng O A
B tạo với mặt phẳng chứa TO đường tròn  ; O R một góc 0
60 . Tính theo R thể tích V của khối trụ đã cho. Á 3 3 3 3 N  7R 3 5R  5R 3 7R A. V  . B. V  . C. V  . D. V  . V 7 5 5 7 D – Lời giải VDC Chọn D O' h B O 600 I R A
https:/www.facebook.com/groups/toanvd. Trang 20 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
Gọi I là trung điểm của đoạn AB suy ra AB  OO I  .
Ta có OI A ; B AB O I
 nên góc giữa mặt phẳng O A
B và mặt đáy bằng 0 O IO  60 . OO 2h 2 4 Suy ra O I   
AB O I.  h . N 0 sin 60 3 3 3 H Ó h M T Và 0
OI OO .cot 60  . 3 O 2 2 1  4  h 3R Á Mặt khác ta có 2 2 2 2
IB OI R h   R h    . N 4  3  3 7 V 2 D 3 R 7 2    Vậy V R h . – 7 VDC 0 0 0
Câu 38: Tứ diện ABCD có AB AC AD a ; BAC  60 ; CAD  60 ; DAB  90 . Khoảng cách giữa
hai đường thẳng AC và BD là a 30 a a 3 a 2 A. . B. . C. . D. . 10 2 2 2 Lời giải Chọn C A a K a D a C I N H Ó B M    T
Ta có tam giác ABC có AB AC a và 0
BAC  60 nên tam giác ABC đều suy ra BC a . O
Tương tự tam giác ACD cũng đều nên CD a . Á N Suy ra ABD C
BD .c .cc nên 0
BCD BAD  90 và AB , D C
BD vuông cân tại A và C VD . –
Gọi I là trung điểm của đoạn BD . VDC 2 2 BD AD AB a 2
Suy ra AI CI   
và AI BD , CI BD . Do đó BD   ACI  . 2 2 2
Trong mặt phẳng  ACI  kẻ IK AC ta cũng có IK BD nên IK d AC, BD .
Tam giác ACI cân tại I nên K là trung điểm AC . 2 2 2 AC
a 2   a a Suy ra 2 2 2 IK AI AK AI           . 4 2    2  2 a
Vậy d AC,BD   . 2 3
Câu 39: Cho số phức w
. Khi đó phần ảo của số phức w là: 5  i 15 3 3 15 A. . B.  . C. . D.  . 26 26 26 26
https:/www.facebook.com/groups/toanvd. Trang 21 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 Lời giải Chọn C 3 15 3 Ta có w    i . 5  i 26 26 N 3 H
Vậy phần ảo của số phức w là . Ó 26 M T
Câu 40: Cho hình lăng trụ đứng AB .
C A' B 'C ' có cạnh bên AA'  a 2 . Biết đáy ABC là tam giác vuông OÁ
có BA BC a , gọi M là trung điểm của BC . Tính khoảng cách giữa hai đường thẳng AM N và B 'C . V D a a
A. d AM B C  7 , '  .
B. d AM B C  3 , '  . – 7 3 VDC a a
C. d AM B C  2 , '  .
D. d AM B C  5 , '  . 2 5 Lời giải Chọn A N H Ó M T O Á N V D Kẻ MN B 'C ( N là trung điểm của BB ' ). Khi đó: – VDC
d AM , B 'C  d B'C, AMN   d C; AMN   d  ;
B AMN  .
Kẻ BH AM , mà AM BN AM  BHN    AMN   BHN  theo giao tuyến NH . Kẻ
BK NH BK   AMN   d  ;
B AMN   BK . B . A BM a 5 BH.BN a 7 Ta có BH    BK   . 2 2 2 2  5  7 BA BM BH BN
Câu 41: Cho hàm số y f x liên tục trên đoạn  ;
a b. Diện tích của hình phẳng giới hạn bởi đồ thị
C: y f x , trục hoành, hai đường thẳng x  ,ax b (Hình vẽ bên dưới) được xác định bởi
công thức nào dươi đây?
https:/www.facebook.com/groups/toanvd. Trang 22 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 N H Ó M T 0 b 0 b A. S f
 xdxf
 xdx. B. S   f
 xdxf
 xdx. a 0 a 0 O Á 0 b 0 b S   f x dx f x dx S f x dx f x dx N C.       . D.       . a 0 a 0 V Lời giải D – VDC Chọn D
Diện tích của hình phẳng giới hạn bởi đồ thị C : y f x , trục hoành, hai đường thẳng b x  ,
a x b cho bởi công thức: S f
 xdx . Ta lại có: a x a 0 b f x  0  Do đó 0 S   f  xb dx f  xdx. a 0
Câu 42: Cho hàm số y f x liên tục trên
, có đồ thị như hình vẽ. N H Ó M T O Á N 3 V 4m m
Có bao nhiêu giá trị của tham số m để phương trình 2
f x  3 có 3 nghiệm D 2
2 f x  5 – VDC phân biệt? A. 1. B. 5 . C. 2 . D. 0 . Lời giải Chọn A 3 4m m Ta có: 2  f x 3
 3  4m m   2
f x  3 2
2 f x  5 . 2
2 f x  5  Đặ t 5 t
2 f x  5  t t  5  f x 2 2 2  , khi đó phương trình có dạng 2 2  t 1
4m  4m  
.t  8m  8m t t  2m3 3 3 3 3
 2m t t * . Xét hàm số  2  f u 3
u u f u 2 , '
u 1 0, u  nên phương trình
https:/www.facebook.com/groups/toanvd. Trang 23 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020  4m  5  f x  2   2    5  4m  5 2 
m t t   m   m f x 2
  f x 2 * 2 5 2 2 5     2 2      f x 2 4m 5   N  2 H Ó . M T
Nhìn vào đồ thị của hàm số y f x , ta có phương trình có 3 nghiệm khi O Á N 2  4m  5 V   4 5 D  2 37 37 m 37 2 2 2 
 4m  5  32  m   m    m  . – 2 4 2 2   VDC 4m 5   0  2
Câu 43: Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số x y e
  4x , trục hoành và hai đường thẳng
x  1, x  2 . Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục hoành. A. 2
V  6  e e . B. V    2
6  e e. C. V    2
6  e e . D. 2
V  6  e e . Lời giải Chọn B. 2 2 Ta có V   ( x e
  4x)dx     x 2 e
  2x     2
6  e e . 1 1 N 2 2 2 2 H x y log x 2 y 1  2   xy Ó
Câu 44: Cho các số thực dương , x y thỏa mãn log  2
 log 8 . Tìm giá trị nhỏ nhất 2 2 2  M 3xy x 2 2 T
2x xy  2 y O
của biểu thức: P  2 Á 2xy y N  V 1 5 3 1 5 A. B. C. D. D 2 2 2 2 – VDC Lời giải
Chọn B Giả thiết được viết lại: log  2 2
x y   log  2 3xy x  2 2
x  2y 1 3xy 2 2  log  2 2
x y   2 2 2
x y   log  2 3xy x  2
x  log 2  3xy 2 2 2 xy x
 log x y  2x y  2 3 2 2 2 2 2  log  x  3xy 2 2 2 xy x
 log x y  2x y  2 3 2 2 2 2 2  log  x  3xy 2 2 2
Xét hàm số f t   log t  2t , dễ thấy hàm số luôn đồng biến với t   0 . Từ đó ta có: 2 2 2 3xy xx   x x 2 2 x y  . Chia hai vế cho 2 y , ta được:  3  2  0  1  2     2  y   y y
https:/www.facebook.com/groups/toanvd. Trang 24 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 2  x x 2   2   2  y y 2t t  2
Biểu thức P được viết lại: P  
, với t 1;2. x 2t 1 2 1 y N H 5 Ó
Khảo sát hàm số P t  trên 1;2 ta tìm được min Pt   1;2 M T 2 O
Câu 45: Gọi x, y là các số thực dương thỏa mãn điều kiện log x  log y  log x y và 9 12 16   Á N xa b V 
, với a, b là hai số nguyên dương. Tính P ab . D y 2 – A. P  6 . B. P  5. C. P  8 . D. P  4 . VDC Lời giải Chọn B
Giả sử log x  log y  log
x y t . 9 12 16   x  9t  2t t t         Khi đó t t t 3 3 3 1 5  y  12t  9  12  16   1  0         .   4   4   4  2
x y  16tt x 9t  3  1   5 a  1 Do đó         ab  5. y 12t  4  2 b  5 N
Câu 46: Cho hàm số y f x liên tục trên
và có đồ thị như hình bên. H Ó M T O Á N V D – VDC
Phương trình f 2sin x  m có đúng ba nghiệm phân biệt thuộc đoạn  
 ;  khi và chỉ khi: A. m  3  ;  1 . B. m  3  ;  1 . C. m  3  ;  1 . D. m  3  ;  1 . Lời giải Chọn A
Đặt t  2sin x . Với x  
 ;   t  2  ;2.
f t  m .
Số nghiệm của phương trình f t   m là số giao điểm của y f t  và y m.
https:/www.facebook.com/groups/toanvd. Trang 25 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
Dựa vào đồ thị ta thấy, để phương trình f t   m có ba nghiệm thì có một nghiệm sin x thuộc khoảng  1  
;1 , một nghiệm là 1 và một nghiệm là 1
 . Như vậy đồ thị hàm số y f t cắt
đường thẳng y m tại hai điểm có hoành độ bằng 2 hoặc 2
 . Khi đó m 1, m  3  . N H
Câu 47: Cho hai hàm số y f x và y g x là hai hàm số liên tục trên có đồ thị hàm số y f  x ÓM T
là đường cong nét đậm, đồ thị hàm số y gx là đường cong nét mảnh như hình vẽ. Gọi ba O
giao điểm A , B , C của y f x và y gx trên hình vẽ lần lượt có hoành độ là a , b , c . ÁN V y D – VDC O B x  A
Tìm giá trị nhỏ nhất của hàm số hx  f x  g x trên đoạn  ; a c ?
A. min h x  h0 .
B. min h x  ha . C. min hx  hb . D. min hx  hc . a;c a;c a;c a;cLời giải Chọn C
Ta có: h x  f  x  g x . N H Ó x a M 
h x  0  x b . T  O x c  Á N V x   ;
b c : f  x  g x  0 D – VDC x   ;
a b : f  x  g x  0 . Xét bảng biến thiên: –
Từ bảng biến thiên ta có: min h x  hb . a;c
Câu 48: Trên mặt phẳng toạ độ Oxy , số phức nào dưới đây có điểm biểu diễn là M 1;  2 ?
A. z  1 2i .
B. z  1 2i . C. z  1   2i . D. z  1   2i .
https:/www.facebook.com/groups/toanvd. Trang 26 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 Lời giải Chọn B
Câu 49: Cho hàm số y f x có bảng biến thiên sau N H Ó M T O Á N V D –
Tìm giá trị cực đại của hàm số y f x . VDC A. 5 . B. 3  . C. 0 . D. 1. Lời giải Chọn C
Từ bảng biến thiên ta có giá trị cực đại của hàm số là y  0
Câu 50: Cho hàm số f x 4 2
ax bx c , a ,
b c   và có bảng biến thiên như hình vẽ
Số nghiệm thực dương của phương trình 2 f x  3  0 là N A. 3 . B. 1. C. 4 . D. 2 . H Ó Lời giải M Chọn D T O     Á
Ta có f xf x 3 2 3 0 2 N V D – VDC 3
Từ bảng biến thiên suy ra đường thẳng y
cắt đồ thị hàm số tại 4 điểm trong đó có hai điểm 2 có hoành độ dương.
Vậy phương trình 2 f x  3  0 có hai nghiệm dương phân biệt.
https:/www.facebook.com/groups/toanvd. Trang 27 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 N H Ó M T O Á N V D – VDC N H Ó M T O Á N V D – VDC
https:/www.facebook.com/groups/toanvd. Trang 28
Document Outline

  • de-thi-chuyen-de-toan-12-lan-4-nam-2019-2020-truong-thpt-lien-son-vinh-phuc.pdf
    • TOAN 123_TOÁN CHUYEN ĐỀ_132
    • TOAN 123_TOÁN CHUYEN ĐỀ_dapancacmade
  • 2037-TOANVDC.EDU.VN-TT-L12-THPT-LIEN-SON-VINH-PHUC-1920_PBX.pdf