Đề thi chuyên đề Toán 12 lần 4 năm 2022 – 2023 trường THPT Trần Phú – Vĩnh Phúc

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi chuyên đề môn Toán 12 lần 4 năm học 2022 – 2023 trường THPT Trần Phú, tỉnh Vĩnh Phúc

29 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

22 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
Trang 1/6 - Mã đề thi 101
SỞ GD&ĐT VĨNH PHÚC
TRƯỜNG THPT TRẦN PHÚ
ĐỀ THI CHUYÊN ĐỀ LẦN 4 NĂM HỌC 2022-2023
Môn thi: TOÁN 12
ĐỀ THI CHÍNH THỨC
Thời gian làm bài: 90 phút ( không kể thời gian phát đề)
(Đề thi có 6 trang)
Mã đề thi:101
Câu 1: Có 30 chiếc thẻ được đánh số từ 1 đến 30. Chọn ngẫu nhiên 2 thẻ. Xác suất để chọn được ít nhất
một thẻ đánh số nguyên tố bằng
A. 0,56 B. 0,41 C. 0,46 D. 0,52
Câu 2: Với
a
là số thực dương tùy ý,
3
2
a
bằng
A.
3
2
a
B.
2
3
C.
2
3
a
D.
3
2
Câu 3: Tập nghiệm
S
của bất phương trình
2
4
1
27
3
x
chứa bao nhiêu số nguyên
A. 3 B. 1 C. 2 D. Vô số
Câu 4: Cho cấp số cộng
n
u
có
1
11
u
và công sai
4
d
. Số hạng thứ ba bằng
A. 44 B. 176 C. 19 D. 15
Câu 5: Hàm số
3 2
1
( ) 2 2021
3
F x x x x
là một nguyên hàm của hàm số nào dưới đây
A.
2
4 3
1 2
2021
9 3 2
x
x x x C
. B.
2
4 3
1 2
2021
12 3 2
x
x x x C
.
C.
2
4 3
1 2
2021
9 3 2
x
x x x C
. D.
2
4 1
x x
.
Câu 6: Hàm số nào sau đây đồng biến trên
?
A.
3 2
3 1
y x x
B.
3 2
6 1
y x x x
C.
2
1
x
y
x
D.
4 2
2 1
y x x
Câu 7: Trong không gian
Oxyz
, cho hai mặt phẳng
: 2 2 1 0
P x y z
và
:2 2 3 0
Q x y z
.
Gọi
là góc giữa hai mặt phẳng
P
và
Q
. Tính
cos
.
A.
4
9
. B.
4
9
. C.
2
3
. D.
2
3
.
Câu 8: Cho hàm số
y f x
có đồ thị như hình vẽ
Số điểm cực trị của hàm số là
A. 1 B. 0 C. 3 D. 2
Câu 9: Cho hàm số
2
.2021
x x
f x e
. Chọn khẳng định đúng trong các khẳng định sau.
Trang 2/6 - Mã đề thi 101
A.
1 2 ln2021 0
f x x x
. B.
2
1 ln 2021 0
f x x
.
C.
2
1 ln 2021 0
f x x x
. D.
2
1 1 ln 2021 0
f x x
.
Câu 10: Cho hàm số y = f(x) có đồ thị như hình vẽ
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên [-1; 1] lần lượt là
A. -3 và -4 B. 1 và -4 C. 0 và -4 D. 1 và -1
Câu 11: Phương trình
2
4 6
5 5
x x
có bao nhiêu nghiệm thực?
A.
1
B.
3
C.
2
D.
0
Câu 12: Cho hàm số
y f x
có đồ thị như hình vẽ
Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên khoảng
1;3
.
B. Hàm số nghịch biến trên khoảng
1;1
.
C. Hàm số đồng biến trên khoảng
; 1

và
1;

.
D. Hàm số đồng biến trên khoảng
1;1 .
Câu 13: Đồ thị hàm số
2 3
1
x
y
x
có các đường tiệm cận đứng và tiệm cận ngang lần lượt là
A.
1
x
và
3
y
. B.
1
x
và
2
y
.
C.
2
x
và
1
y
. D.
1
x
và
2
y
.
Câu 14: Cho hình chóp tứ giác
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, cạnh bên
SA
vuông góc
với mặt phẳng đáy và
2
SA a
. Tính thể tích khối chóp
.
S ABCD
.
A.
3
2
3
a
B.
3
2
4
a
C.
3
2
a
D.
3
2
6
a
Câu 15: Đồ thị hàm số
2 1
1
x
y
x
cắt trục tung tại điểm có tung độ bằng
A.
1
2
B. 1 C.
1
D. 2
Câu 16: Nghiệm của phương trình
2
log (2 6) 3
x
là:
A.
6
x
B.
9
x
C.
8
x
D.
7
x
x
y
-1
-1
3
0
1
Trang 3/6 - Mã đề thi 101
Câu 17: Trong không gian
Oxyz
, cho mặt phẳng
: 4 3 1 0
P x y z
. Điểm nào dưới đây thuộc (P)
A. M(0; 2; -1) B. N(1; 1; -6) C. P(1; -6; 1) D. Q(0; 2; 1)
Câu 18: Cho hình trụ có diện tích xung quanh bằng
50
và độ dài đường sinh bằng đường kính của
đường tròn đáy. Tính bán kính
r
của đường tròn đáy.
A.
5 2
2
r
B.
5r
C.
5 2
2
r
D.
5
r
Câu 19: Cho
2
1
2
f t dt
và
2
1
1
g x dx
. Tính
2
1
2 3
I x f x g x dx
.
A.
17
2
I
. B.
7
I
. C.
5
I
. D.
11
2
I
.
Câu 20: Trong không gian
Ox
yz
, mặt cầu tâm
(1;0; 2)
I
bán kính
2
R
có phương trình
A.
2 2 2
( 1) ( 2) 2
x y y
B.
2 2 2
( 1) ( 2) 4
x y y
C.
2 2 2
( 1) ( 2) 4
x y y
D.
2 2 2
( 1) ( 2) 2
x y y
Câu 21: Tính nguyên hàm của hàm số
2
e
e 2
x
x
f x
.
A.
2
e 4ln e 2
x x
F x C
. B.
e 2ln e 2
x x
F x C
.
C.
e 2ln e 2
x x
F x C
. D.
ln e 2
x
F x C
.
Câu 22: Khối nón có bán kính đáy bằng 6, chiều cao bằng
1
, thể tích khối nón bằng
A. 12 B. 2 C. 6 D. 36
Câu 23: Với
a
,
b
là hai số thực dương thỏa mãn
log 11, log 13
a b
. Khi đó
2
log
ab
bằng
A. 46 B. 37 C. 180 D. 23
Câu 24: Trong không gian tọa độ
Oxyz
, Cho các điểm
(1;2; 3), (3;2;4)
M N
. Tọa độ vec tơ
MN
là
A.
4;4;1
B.
2;0;7
C.
2;0; 7
D.
1
2;2;
2
Câu 25: Có bao nhiêu cách chọn ra 2 học sinh từ một nhóm có 10 học sinh
A. 90 B. 20 C. 45 D. 8
Câu 26: Biết
3
( )
F x x C
là nguyên hàm của hàm số
( )
f x
trên tập số thực; Tính
3
1
( )
I f x dx
A. 23 B. 20 C. 26 D. 17
Câu 27: Trong không gian
Oxyz
, bán kính mặt cầu
S
:
2 2 2
2 2 4 2 0
x y z x y z
bằng.
A.
2 2
. B.
2
. C.
22
. D.
4
.
Câu 28: Cho hàm số
( )
y f x
liên tục trên
và có bảng xét dấu đạo hàm như sau:
.
Điểm cực đại của hàm số là
A. x = 0 B. x = -3 C. x = 1 D. x = 2
Câu 29: Cho u,v là hai hàm số có đạo hàm liên tục trên
;
a b
. Công thức nào sau đây là đúng:
Trang 4/6 - Mã đề thi 101
A.
. .
b b
a a
b
u dv uv v du
a
B.
. .
b b
a a
b
u dv uv u dv
a
C.
.
b
a
b
u dv uv
a
D.
. .
b b
a a
b
u dv uv v du
a
Câu 30: Đạo hàm của hàm số
1
3
x
y
bằng
A.
1
3
ln3
x
B.
1
3 .ln3
x
C.
(1 ).3
x
x
D.
1
1
3 .ln
3
x
Câu 31: Họ nguyên hàm của hàm số
1
sin 2
f x x
x
là
A.
1
ln cos 2
2
x x C
B.
1
ln cos 2
2
x x C
.
C.
2
1 1
cos 2
2
x C
x
. D.
1
ln cos 2
2
x x C
.
Câu 32: Nếu
4
1
dx 2
f x
và
4
1
dx 6
g x
thì
4
1
2 1 dx
f x g x
bằng
A. 2 B.
4
. C. 5 D. 3
Câu 33: Khối lập phương có thể tích bằng 64 cm
3
thì cạnh của hình lập phương đó bằng
A. 4 cm B. 8cm C. 6cm D. 16 cm
Câu 34: Đường cong trong hình vẽ là đồ thị của hàm số nào trong các hàm số sau:
A.
4 2
2
y x x
B.
4 2
2 2
y x x
.
C.
4 2
2 2
y x x
. D.
4 2
2 2
y x x
Câu 35: Trong không gian Oxyz, cho hai điểm A(1; 2; 2) và B(0, 2, 1). Mặt cầu có tâm thuộc trục
Ox
và
đi
qua hai điểm A, B có đường kính bằng
A.
2
B. 3 C. 6 D. 2
Câu 36: Cho hàm số
f x
liên tục trên
1;
và
3
0
1 d 8
f x x
. Tính
2
1
. d
I x f x x
.
A.
4
I
. B.
4
I
. C.
1
4
I
. D.
1
4
I
.
Câu 37: Cho hình chóp S.ABCD có ABCD là hình vuông cạnh bằng
4
, SA vuông góc với đáy. Góc giữa
SC và mặt (SBD) bằng
. Biết
3 10
cos
10
và tam giác SAC không cân. Thể tích khối chóp
S.ABCD bằng
A.
32 2
3
B.
128
3
C.
16
3
D.
16 2
3
Trang 5/6 - Mã đề thi 101
Câu 38: Xét hàm số
f x
liên tục trên đoạn
0;1
và thỏa mãn điều kiện
2 2
4 3 1 1 , 0;1
xf x f x x x . Tích phân
1
0
d
I f x x
bằng
A.
4
I
. B.
6
I
. C.
16
I
. D.
20
I
.
Câu 39: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng 2.
Khoảng cách từ A đến mặt phẳng (SCD) bằng:
A.
2
B.
3
C.
6
3
D.
2 6
3
Câu 40: Một ô tô đang chạy thì người lái đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều
với vận tốc
( ) 12 24 ( / )
v t t m s
trong đó
t
là khoảng thời gian tính bằng giây, kể từ lúc bắt
đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô di chuyển bao nhiêu mét?
A.
15
m
. B.
24
m
. C.
20
m
. D.
18
m
.
Câu 41: Tìm số nghiệm nguyên của bất phương trình
2 2
2 4 9 5 1
2021 2021 1 8 0
x x x x
x x
.
A.
. B.
5
. C.
. D.
8
.
Câu 42: Cho
f x
là hàm số bậc bốn. Biết
(4) 0
f
và đồ thị của hàm số
( )
f x
như hình vẽ. Hàm số
2
1
4
x
g x f x
có bao nhiêu điểm cực tiểu
A. 2 B. 1 C. 4 D. 3
Câu 43: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh bằng 2,
SA
vuông góc với mặt phẳng
ABCD
và
2 2
SA
.
Trang 6/6 - Mã đề thi 101
Góc giữa
SC
và mặt phẳng
ABCD
bằng:
A.
0
45
. B.
0
60
. C.
0
30
. D.
0
90
.
Câu 44: Có bao nhiêu giá trị nguyên của
m
để bất phương trình
2
3 3
log log
x m x m
nghiệm đúng với
mọi giá trị của
0;x

.
A.
. B.
. C.
4
. D.
.
Câu 45: Một thùng hình trụ có bán kính đáy bằng 2(m), bên trong thùng có chứa một lượng nước. Biết
rằng khi để thùng nằm ngang thì phần bề mặt nước là một hình vuông và mặt nước cách trục của
hình trụ một khoảng bằng
3
(m). Nếu để thùng thẳng đứng thì chiều cao của nước trong thùng
bằng:
A. 10,67(cm) B. 5,77 (cm) C. 33,3 (cm) D. 8,33 ( cm)
Câu 46: Có bao nhiêu số nguyên dương
a
để tồn tại đúng hai số thực
b
phân biệt, thỏa mãn điều kiện
2
2 2
4.log log 5 7 0
b
b b a
A. 48 B. 47 C. 49 D. 46
Câu 47: Tích phân
1
2
0
1
d
4 3
x
x x
có kết quả là.
A.
1 3
ln
3 2
. B.
1 3
ln
2 2
. C.
1 3
ln
2 2
. D.
3
ln
2
.
Câu 48: Cho hàm số y = f(x) có đạo hàm
2
'( ) ( 1)( 1) ( 2)
f x x x x
.Giá trị nhỏ nhất của hàm số
3 2
8 5 1
(2 1) 4 , [ 1; ]
3 3 2
y f x x x x
bằng
A.
(0) 1
f
B.
5
(1)
3
f
C.
( 1)
3
f
D.
1
(2)
3
f
Câu 49: Có bao nhiêu số nguyên
y
sao cho ứng với mỗi
y
có đúng 5 số nguyên
x
thỏa mãn:
2
log( 2 ) 2log(2 1) 0
x x y x
A. 75 B. 26 C. 27 D. 74
Câu 50: Trong không gian Oxyz cho mặt phẳng (P)
2 2 12 0
x y z
và mặt cầu (S):
2 2 2
2 4 2 5 0
x y z x y z
. Xét hai điểm M, N lần lượt thuộc (P) và (S) sao cho
MN
cùng
phương với vectơ
(1;1;1)
u
. Giá trị nhỏ nhất của MN bằng
A. 3 B.
9 3 1
C.
6 3
D. 2
(Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm)
----------- HẾT ----------
BẢNG ĐÁP ÁN
1.A
2.C
3.A
4.C
5.D
6.B
7.B
8.D
9.C
10.A
11.A
12.D
13.B
14.A
15.C
16.D
17.B
18.A
19.A
20.B
21.C
22.A
23.B
24.B
25.C
26.C
27.A
28.D
29.D
30.D
31.C
32.C
33.A
34.D
35.C
36.A
37.A
38.D
39.D
40.B
41.C
42.A
43.A
44.D
45.B
46.D
47.B
48.B
49.C
50.C
Câu 51: Có 30 chiếc thẻ được đánh số từ 1 đến 30. Chọn ngẫu nhiên 2 thẻ. Xác suất để chọn được ít nhất
một thẻ đánh số nguyên tố bằng?
A. . B. . C. . D. .
0,56
0,41
0,46
0,52
Lời giải
Chọn A
Tập hợp số số nguyên tố:
2;3;5;7;11;13;17;19;23;29
Số cách chọn 2 thẻ ngẫu nhiên:
2
30
Ω 435C
Gọi A là biến cố chọn được ít nhất một thẻ đánh số nguyên tố
biến cố chọn được không thẻ đánh số nguyên tố:
A
2
20
190C
190
1 1 0,56
435
A
A
P P
Câu 52: Với là số thực dương tùy ý, bằng:
a
3
2
a
A. . B. . C. . D. .
3
2
a
2
3
a
2
3
a
3
2
a
Lời giải
Chọn C
Câu 53: Tập nghiệm S của bất phương trình chứa bao nhiêu số nguyên
2
4
1
27
3
x
A. . B. . C. . D. Vô số.
3
1
2
Lời giải
Chọn A
2
4
2
1
27 4 3 1 1
3
1;0;1
x
x x
S
Câu 54: Cho cấp số cộng có và công sai . Số hạng thứ ba bằng
( )
n
u
1
11u
4d
A. . B. . C. . D. .
44
176
19
15
Lời giải
Chọn C
3 1
2 11 2.4 19u u d
Câu 55: Hàm số là một nguyên hàm của hàm số nào dưới đây
3 2
1
2 2021
3
F x x x x
A. . B. .
2
4 3
1 2
2021
9 3 2
x
x x x C
2
4 3
1 2
2021
12 3 2
x
x x x C
C. . D. .
2
4 3
1 2
2021
9 3 2
x
x x x C
2
4 1x x
Lời giải
Chọn D
Câu 56: Hàm số nào sau đây đồng biến trên ?
A. . B. . C. . D. .
3 2
3 1y x x
3 2
6 1y x x x
2
1
x
y
x
4 2
2 1y x x
Lời giải
Chọn B
Ta có: suy ra .
3 2
6 1y x x x
2
' 3 2 6y x x
Cho phương trình vô nghiệm. Do đó, .
2
' 0 3 2 6 0y x x
' 0,y x
Vậy hàm số đồng biến trên .
3 2
6 1y x x x
Câu 57: Trong không gian , cho hai mặt phẳng và .
Oxyz
: 2 2 1 0P x y z
: 2 2 3 0Q x y z
Gọi là góc giữa hai mặt phẳng và . Tính .
P
Q
cos
A. . B. . C. . D. .
4
9
4
9
2
3
2
3
Lời giải
Chọn B
Ta có vtpt và vtpt .
1; 2;2
P
n
2;2; 1
Q
n
Suy ra .
2 2
2 2 2 2
.
1.2 2 .2 2. 1
4
cos
9
.
1 2 2 . 2 2 1
P Q
P Q
n n
n n
Câu 58: Cho hàm số có đồ thị như hình vẽ
y f x
Số điểm cực trị của hàm số là
A. . B. . C. . D. .
1
0
3
2
Lời giải
Chọn D
Câu 59: Cho hàm số . Chọn khẳng định đúng trong các khẳng định sau.
2
.2021
x x
f x e
A. . B. .
1 2 ln 2021 0f x x x
2
1 ln 2021 0f x x
C. . D. .
2
1 ln 2021 0f x x x
2
1 1 ln 2021 0f x x
Lời giải
Chọn C
Ta có:
2 2
1 .2021 1 ln .2021 ln1
x x x x
f x e e
.
2
2
ln ln 2021 0 ln 2021 0
x x
e x x
Câu 60: Cho hàm số có đồ thị như hình vẽ
y f x
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên lần lượt là
1;1
A. và . B. và . C. và . D. và .
3
4
1
4
0
4
1
1
Lời giải
Chọn A
Câu 61: Phương trình có bao nhiêu nghiệm thực?
2
4 6
5 5
x x
A. B. C. D.
1
3
2
0
Lời giải
Chọn A
2
4 6
2
5 5 4 6 2 2
x x
x x x
Câu 62: Cho hàm số có đồ thị như hình vẽ.
( )y f x
Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên
1;3
B. Hàm số nghịch biến trên
1;1
C. Hàm số đồng biến trên và
; 1
1;
D. Hàm số đồng biến trên
1;1
Lời giải
Chọn D
Câu 63: Đồ thị hàm số có các đường tiệm cận đứng và tiệm cận ngang lần lượt là
2 3
1
x
y
x
A. và B. và
1x
3y
1x
2y
C. và D. và
2x
1y
1x
2y
Lời giải
Chọn B
Câu 64: Cho hình chóp tứ giác có đáy là hình vuông cạnh , cạnh bên vuông góc
SABCD
ABCD
a
SA
với mặt phẳng đáy và . Tính thể tích khối chóp
2SA a
SABCD
A. B. C. D.
3
2
3
a
3
2
4
a
3
2a
3
2
6
a
Lời giải
Chọn A
.
3
2
1 1 2
. 2.
3 3 3
ABCD
a
V SA S a a
Câu 65: Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng
2 1
1
x
y
x
A. B. C. D.
1
2
1
1
2
Lời giải
Chọn C
Cho .
0 1x y
Câu 66: Nghiệm của phương trình là
2
log 2 6 3x
A. B. C. D.
6x
9x
8x
7x
Lời giải
Chọn D
Ta có
3
2
log 2 6 3 2 6 2 7x x x
Câu 67: Trong không gian , cho mặt phẳng . Điểm nào dưới đây thuộc ?
Oxyz
: 4 3 1 0P x y z
P
A. B. C. D.
0;2; 1M
1;1; 6N
1; 6;1P
0;2;1Q
Lời giải
Chọn B
Câu 68: Cho hình trụ có diện tích xung quanh bằng và độ dài đường sinh bằng đường kính của
50
đường tròn đáy. Tính bán kính của đường tròn đáy
r
A. B. C. D.
5 2
2
r
5r
5 2
2
r
5r
Lời giải
Chọn A
Ta có
2l r
Theo đề .
2
25 5 2
50 2 50 2 .2 50
2 2
xq
S rh r r r r
Câu 69: Cho và . Tính
2
1
d 2f t t
2
1
d 1g x x
2
1
2 3 dI x f x g x x
A. B. C. D.
17
2
I
7
2
I
5
2
I
11
2
I
Lời giải
Chọn A
Ta có
2 2 2 2
1 1 1 1
3 17
2 3 d d 2 d 3 d 2.2 3 1
2 2
I x f x g x x x x f x x g x x
Câu 70: Trong không gian , mặt cầu tâm bán kính có phương trình
Oxyz
1;0; 2I
2R
A. B.
2 2
2
1 2 2x y z
2 2
2
1 2 4x y z
C. D.
2 2
2
1 2 4x y z
2 2
2
1 2 2x y z
Lời giải
Chọn B
Câu 71: Tính nguyên hàm của hàm số .
2
( )
2
x
x
e
f x
e
A. B.
2
( ) 4ln( 2) .
x x
F x e e C
( ) 2ln( 2) .
x x
F x e e C
C. D.
( ) 2ln( 2) .
x x
F x e e C
( ) ln( 2) .
x
F x e C
Lời giải
Chọn C
Ta có:
2
2
( ) ( ) 1 2ln( 2) .
2 2
x
x x x
x x
e
F x f x dx dx e dx e e C
e e
Câu 72: Khối nón có bán kính đáy bằng , chiều cao bằng , thể tích khối nón bằng
6
1
A. B. C. D.
12.
2.
6.
36.
Lời giải
Chọn B
Thể tích khối nón là:
2 2
1 1 1
. . .6 . 12.
3 3
V r h
Câu 73: Với là hai số thực dương thỏa mãn . Khi đó bằng
,a b
loga 11,logb 13
2
log( )ab
A. B. C. D.
46.
37.
180.
23.
Lời giải
Chọn A
Ta có:
2
log( ) loga 2logb 11 2.13 37.ab
Câu 74: Trong không gian tọa độ , cho các điểm . Tọa độ véc tơ là
Oxyz
(1;2; 3), (3;2;4)M N
MN

A. B. C. . D.
(4;4;1).
(2;0;7).
( 2;0; 7).
1
(2;2; ).
2
Lời giải
Chọn B
3 1;2 2;4 ( 3) 2;0;7 .MN

Câu 75: Có bao nhiêu cách chọn ra 2 học sinh từ một nhóm có 10 học sinh
A. 90 B. 20 C. 45 D. 8
Lời giải
Chọn C
Số cách chọn ra 2 học sinh từ một nhóm có 10 học sinh là .
2
10
45
C
Câu 76: Biết là nguyên hàm của hàm số trên tập số thực. Tính
3
F x x C
f x
3
1
dx
I f x
A. 23 B. 20 C. 26 D. 17
Lời giải
Chọn C
.
3
3
3
1
1
dx 26
I f x x
Câu 77: Trong không gian , bán kính mặt cầu bằng
Oxyz
2 2 2
: 2 2 4 2 0
S x y z x y z
A. B. C. D. 4
2 2
2
22
Lời giải
Chọn A
Bán kính mặt cầu bằng .
2 2 2
: 2 2 4 2 0
S x y z x y z
2 2 2
1 1 2 2 2 2
Câu 78: Cho hàm số liên tục trên và có bảng xét dấu đạo hàm như sau
y f x
Điểm cực đại của hàm số là
A. B. C. D.
0
x
3
x
1
x
2
x
Lời giải
Chọn D
Câu 79: Cho là hai hàm số có đạo hàm liên tục trên . Công thức nào sau đây là đúng?
,u v
;a b
A.
.
B.
.
d d
b b
b
a
a a
u v uv v u
d d
b b
b
a
a a
u v uv u v
C.
.
D.
.
d
b
b
a
a
u v uv
d d
b b
b
a
a a
u v uv v u
Lời giải
Chọn D
.
d d
b b
b
a
a a
u v uv v u
Câu 80: Đạo hàm của hàm số bằng
1
3
x
y
A.
.
B.
.
C.
.
D.
.
1
3
ln3
x
1
3 .ln 3
x
1 .3
x
x
1
1
3 .ln
3
x
Lời giải
Chọn D
.
1 1 1 1
1
3 1 .3 .ln3 3 .ln 3 3 .ln
3
x x x x
y x
Câu 81: Họ nguyên hàm của hàm số là
1
sin 2f x x
x
A.
.
B. .
1
ln cos 2
2
x x C
1
ln cos 2
2
x x C
C.
.
D.
.
2
1 1
cos2
2
x C
x
1
ln cos 2
2
x x C
Lời giải
Chọn C
.
2
1 1 1
sin 2 d cos2
2
x x x C
x x
Câu 82: Nếu và thì bằng
4
1
d 2f x x
4
1
d 6g x x
4
1
2 1 df x g x x
A.
.
B.
.
C.
.
D.
.
2
4
5
3
Lời giải
Chọn C
.
4 4 4 4
1 1 1 1
2 1 d 2 d d 1 d 2. 2 6 3 5f x g x x f x x g x x x
Câu 83: Một khối lập phương có thể tích bằng . Độ dài mỗi cạnh của khối lập phương đó bằng
3
64cm
A. . B. . C. . D. .
4cm
8cm
6cm
16cm
Lời giải
Chọn A
Giả sử khối lập phương có độ dài mỗi cạnh bằng .
a
Ta có . Suy ra .
3
64a
4a
Câu 84: Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào trong các hàm số dưới đây?
A. . B. . C. . D. .
4 2
2y x x
4 2
2 2y x x
4 2
2 2y x x
4 2
2 2y x x
Lời giải
Chọn D
Từ đồ thị ta có đây là đồ thị hàm số bậc trùng phương với hệ số và cắt trục tung tại
4
0a
điểm có tung độ - 2.
Câu 85: Trong không gian , cho hai điểm , . Mặt cầu có tâm thuộc trục Ox và
Oxyz
1;2;2A
0;2;1B
đi qua hai điểm A,B có đường kính bằng
A. . B. . C. . D. .
2
3
6
2
Lời giải
Chọn C
Gọi là tâm mặt cầu
;0;0I a Ox
2
2 2 2 2 2
1 2 2 2 1 2IA IB a a a
Đường kính mặt cầu
2
2 2
2. 2. 1 2 2 6d IA a
Câu 86: Cho hàm số liên tục trên và . Tính
f x
1; 
3
0
1 d 8
f x x
2
1
. d .
I x f x x
A. B. C. D.
4.I
4. I
1
.
4
I
1
.
4
I
Lời giải
Chọn A
Đặt
2
1 1 2 d d t x t x t t x
Khi đó,
3 2 2
0 1 1
1 d 8 .2 d 8 . d 4.
f x x f t t t t f t t
Vậy
4.I
Câu 87: Cho hình chóp có là hình vuông cạnh bằng vuông góc với đáy. Góc
.S ABCD
ABCD
4, SA
giữa và mặt bằng . Biết và tam giác không cân. Thể tích khối
SC
SBD
3 10
cos
10
SAC
chóp bằng
.S ABCD
A. B. C. D.
32 2
.
3
128
.
3
16
.
3
16 2
.
3
Lời giải
Chọn A
O
C
A
D
B
S
H
Gọi là tâm hình vuông , là hình chiếu của trên .
O
ABCD
H
C
SO
Khi đó .
3 10
,
10
SH
CH SBD SC SBD CSO
SC
2 2
2 2
2
2
3 10
10
3 10
10
8 3 10
1
10
32
SO OH
SC
SA AO OH
SA AC
SA OH
SA
Lại có đồng dạng nên
SAO
CHO
2
. . 8 2
SO AO
SO OH AO SO OH
CO OH
Từ (1) và (2) suy ra
2
2
2
4 2
2 2
2
8
8
8
3 10
8
40 256 0
10
32
32
SA
SA
SA
SA SA
SA AC
SA
loaïi
2
.
2 2
1 1 32 2
. .4 .2 2 .
3 3 3
S ABCD ABCD
SA
V S SA
Câu 88: Xét hàm số liên tục trên đoạn và thoả mãn điều kiện
f x
0;1
Tích phân bằng
2 2
4 3 1 1 , 0;1 . xf x f x x x
1
0
d
I f x x
A. B. C. D.
.
4
I
.
6
I
.
16
I
.
20
I
Lời giải
Chọn D
nên
2 2
4 3 1 1 , 0;1 xf x f x x x
1 1 1
2 2
0 0 0
4 d 3 1 d 1 d
xf x x f x x x x
Mà
1 1
2 2 2
0 0
1 1 1
0 0 0
4 d 2 d 2
3 1 d 3 1 d 1 3 d 3 , 1
xf x x f x x I
f x x f x x f t t I t x
Xét
1
2
0
1 d
J x x
Đặt
sin d 2cos d x t x t t
Khi đó,
2 2
2
0 0
1 cos2 1 1
1 sin cos d d sin 2 .
2
2 2 4 4
0
t
J t t t t t t
Do đó
5 .
4 20
I I
Câu 89: Cho hình chóp tứ giác đều có tất cả các cạnh bằng
.S ABCD
2.
Khoảng cách từ đến mặt phẳng là
A
SCD
A. B. C. D.
2
3.
6
3
2 6
3
Lời giải
Chọn D
Gọi là giao điểm của và thì do hình chóp có tất cả các cạnh bằng
O
AC
BD
SO ABCD
nhau nên hình chiếu từ đỉnh xuống mặt phẳng đáy trùng với tâm của đáy.
S
Do:
,
2 , 2 ,
,
d A SCD
AC
d A SCD d O SCD
d O SCD OC
Hạ . Vì
, OE CD OH SE
CD OE
CD SOE CD OH
CD SO
Mà
,OH SE OH SCD d O SCD OH
Do là hình vuông nên và là trung điểm nên
ABCD
1
1
2
OE CD
E
CD
1.CE DE
2 2 2 2
3, 2SE SC CE SO SE OE
. 6 2 6
, 2 .
3 3
SO OE
OH d A SCD OH
SE
Câu 90: Một ô tô đang chạy thì người lái đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều
với vận tốc trong đó là khoảng thời gian tính bằng giây, kể từ lúc bắt
12 24 /v t t m s
t
đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô di chuyển được bao nhiêu mét?
A. B. C. D.
15m
24 .m
20 .m
18 .m
Lời giải
Chọn B
Thời gian từ lúc xe đạp phanh đến lúc dừng hẳn là:
0 12 24 0 2v t t t s
Từ lúc đạp phanh đến khi dừng hẳn, ô tô di chuyển được:
2
0
12 24 24S t dt m
Câu 91: Tìm số nghiệm nguyên của bất phương trình .
2 2
2 4 9 5 1
2021 2021 1 8 0
x x x x
x x
A. B. C. D.
7.
5.
6.
8.
Lời giải
Chọn C
Đặt
2 2 2
2 4 9, 5 1 9 8 1 8a x x b x x a b x x x x
Khi đó:
2021 2021 0 2021 2021
a b a b
b a a b
Xét hàm số:
2021 2021 .ln2021 1 0
x x
f x x f x x
Hàm số đơn điệu tăng mà
2 2
2 4 9 5 1 1 8 0 1 8f a f b a b x x x x x x x
Nên bất phương trình có nghiệm nguyên.
6
Câu 92: Cho là hàm số bậc bốn. Biết và đồ thị của hàm số như hình vẽ. Hàm số
f x
4 0f
f x
có bao nhiêu điểm cực tiểu
2
1
4
x
g x f x
A. . B. . C. . D. .
2
1
4
3
Lời giải
Chọn A
Gọi , .
2
1
4
x
h x f x
2
x
h x f x
, .
2
0 0
2
4
x
x
h x f x x
x
2
0
2 4
2
x
x
h x f x
x
Ta có ; .
2
4
4 4 1 3
4
h f
4
2
d 0 4 2h x x h h
Bảng biến thiên
Dựa vào BBT ta có 2 điểm cực tiểu.
Câu 93: Cho hình chóp có đáy là hình vuông cạnh bằng , vuông góc với mặt
.S ABCD
ABCD
2
SA
phẳng và . Góc giữa và mặt phẳng bằng:
ABCD
2 2SA
SC
ABCD
A. . B. . C. . D. .
o
45
0
60
0
30
0
90
Lời giải
Chọn A
Có
;SC ABCD SCA
Xét , .
SCA
0
2 2
tan 1 45
2 2
SA
SCA SCA
AC
Câu 94: Có bao nhiêu giá trị nguyên của để bất phương trình nghiệm đúng với
m
2
3 3
log logx m x m
mọi giá trị của .
0;x 
A. . B. . C. . D. .
7
6
4
5
Lời giải
Chọn D
Đặt , bpt trở thành .
3
logt x
2
2
1 0 TM
0, 0 4
4 0
a
t mt m t m
m m
Vậy có 5 giá trị nguyên của thỏa mãn.
m
Câu 95: Một thùng hình trụ có bán kính đáy bằng , bên trong thùng có chứa một lượng nước. Biết
2 m
rằng khi để thùng nằm ngang thì phần bề mặt nước là một hình vuông và mặt nước cách trục của
hình trụ một khoảng bằng . Nếu để thùng thẳng đứng thì chiều cao của nước trong thùng
3 m
bằng:
A. (cm). B. (cm). C. (cm). D. (cm).
10,67
5,77
33,3
8,33
Lời giải
Chọn B
Ta (m).
2 2
2 2 2AB HA OA OH
2h
Ta có nên tam giác đều nên , khi đó hình viên phân giới hạn
OA OB AB
AOB
60AOB
bởi dây cung và cung nhỏ có diện tích là .
AB
AB
2
2
60 2 3 2
2 3
360 4 3
Vậy khi để thùng thẳng đứng, chiều cao của nước trong thùng là .
2
3 2
3
0,0577
4
m
Câu 96: Có bao nhiêu số nguyên dương để tồn tại đúng hai số thực phân biệt, thỏa mãn điều kiện
a
b
.
2
2 2
4log log 5 7 0
b
b b a
A. . B. . C. . D. .
48
47
49
46
Lời giải
Chọn D
.
7
7
2
2
5
2 2
4
2
7
0, log
0, log
log 1
2
4log log 5 7 0
5
log
2
4
log
7
b
b
b b a
b b a
b
b
b b a
b
b
b a
a
Để tồn tại đúng hai số thực phân biệt .
b
5
4
5
2
4
7
2 log 2 7 49 3;4;...;48a a a
Câu 97: Tích phân có kết quả là
1
2
0
1
d
4 3
x
x x
A. . B. . C. . D. .
1 3
ln
3 2
1 3
ln
2 2
1 3
ln
2 2
3
ln
2
Lời giải
Chọn B
Ta có
1 1 1
2
0 0 0
1
1 1 1 1 1 1 1
d d d ln
0
4 3 1 3 2 1 3 2 3
x
x x x
x x x x x x x
1 1 1 1 3
ln ln ln
2 2 3 2 2
Câu 98: Cho hàm số có đạo hàm . Giá trị nhỏ nhất của hàm số
y f x
2
1 1 2f x x x x
bằng
3 2
8 5 1
2 1 4 , 1;
3 3 2
y f x x x x
A. . B. . C. . D. .
0 1f
5
1
3
f
1
1
3
f
1
2
3
f
Lời giải
Chọn B
Ta có
2 2
2 2 1 8 8 16 1 2 1 8 1y f x x x x x x x x
2
8 1 4 2 1x x x x
Khi đó trên thì
1
1;
2
0 0y x
Ta có bảng biến thiên trên
1
1;
2
Vậy .
1
1;
2
5
min 1
3
y f
Câu 99: Có bao nhiêu số nguyên sao cho ứng với mỗi có đúng số nguyên thỏa mãn:
y
y
5
x
?
2
log 2 2log 2 1 0x x y x
A. . B. . C. . D. .
75
26
27
74
Lời giải
Chọn C
Điều kiện .
1
2
x
Ta có
2
2
2
2 2
2
log 2 2log 2 1 0
log 2 log 2 1
2 4 4 1
3 6 1.
x x y x
x x y x
x x y x x
y x x
Đặt với , ta có .
2
3 6 1f x x x
1
2
x
6 6 0 1f x x x
Lập bảng biến thiên
Ứng với mỗi có đúng số nguyên thỏa mãn
y
5
x
.
5 6 46 73y f x f y f y
Vậy có số nguyên thỏa yêu cầu bài toán.
27
y
Câu 100: Trong không gian cho mặt phẳng và mặt cầu
Oxyz
: 2 2 12 0P x y z
. Xét hai điểm , lần lượt thuộc và sao cho
2 2 2
: 2 4 2 5 0S x y z x y z
M
N
P
S
cùng phương với véc-tơ . Giá trị nhỏ nhất của bằng
MN
1;1;1u
MN
A. . B. . C. . D. .
3
9 3 1
6 3
2
Lời giải
Chọn C
Mặt cầu có tâm
2 2 2
2 2 2
: 2 4 2 5 0 1 2 1 1S x y z x y z x y z
, bán kính .
1;2;1I
1R
Ta có nên và không giao nhau.
2 2 2
2 2 12
d , 3
1 2 2
I I I
x y z
I P R
P
S
Gọi là góc tạo bởi và mặt phẳng .
MN
P
Gọi là hình chiếu của lên mặt phẳng .
H
N
P
Mặt khác cùng phương với véc-tơ và suy ra
MN
1;1;1u
1; 2;2
P
n
.
1
sin
3 3
P
P
u n
u n
Khi đó .
min
d , 1
3 1
6 3
1
sin sin sin
3 3
I P
NH
NH
MN
| 1/22
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD&ĐT VĨNH PHÚC
ĐỀ THI CHUYÊN ĐỀ LẦN 4 NĂM HỌC 2022-2023
TRƯỜNG THPT TRẦN PHÚ Môn thi: TOÁN 12
ĐỀ THI CHÍNH THỨC
Thời gian làm bài: 90 phút ( không kể thời gian phát đề) (Đề thi có 6 trang) Mã đề thi:101 Câu 1:
Có 30 chiếc thẻ được đánh số từ 1 đến 30. Chọn ngẫu nhiên 2 thẻ. Xác suất để chọn được ít nhất
một thẻ đánh số nguyên tố bằng A. 0,56 B. 0,41 C. 0,46 D. 0,52 Câu 2:
Với a là số thực dương tùy ý, 3 2 a bằng 3 2a 2 3a A. 2 a B. C. 3 a D. 3 2 2 x 4 1 Câu 3:
Tập nghiệm S của bất phương trình      27 
chứa bao nhiêu số nguyên 3 A. 3 B. 1 C. 2 D. Vô số Câu 4:
Cho cấp số cộng u có u  11 và công sai d  4 . Số hạng thứ ba bằng n  1 A. 44 B. 176 C. 19 D. 15 1 Câu 5: Hàm số 3 2 F (x) 
x  2x x  2021 là một nguyên hàm của hàm số nào dưới đây 3 2 1 2 x 2 1 2 x A. 4 3 x x
 2021x C . B. 4 3 x x
 2021x C . 9 3 2 12 3 2 2 1 2 x C. 4 3 x x
 2021x C . D. 2 x  4x 1. 9 3 2 Câu 6:
Hàm số nào sau đây đồng biến trên  ? x  2 A. 3 2
y x  3x 1 B. 3 2
y x x  6x 1 C. y D. 4 2
y x  2x 1 x 1 Câu 7:
Trong không gian Oxyz , cho hai mặt phẳng  P : x  2 y  2z 1  0 và Q :2x  2y z  3  0 .
Gọi  là góc giữa hai mặt phẳng  P và   Q . Tính cos  . 4 4 2 2 A.  . B. . C. . D.  . 9 9 3 3 Câu 8:
Cho hàm số y f x có đồ thị như hình vẽ
Số điểm cực trị của hàm số là A. 1 B. 0 C. 3 D. 2 Câu 9: Cho hàm số   2 x  .2021x f x e
. Chọn khẳng định đúng trong các khẳng định sau.
Trang 1/6 - Mã đề thi 101
A. f x  1  x  2x ln 2021  0 .
B. f x 2
 1  x ln 2021  0 .
C. f x 2
1  x x ln 2021  0 .
D. f x 2
 1  1 x ln 2021  0 .
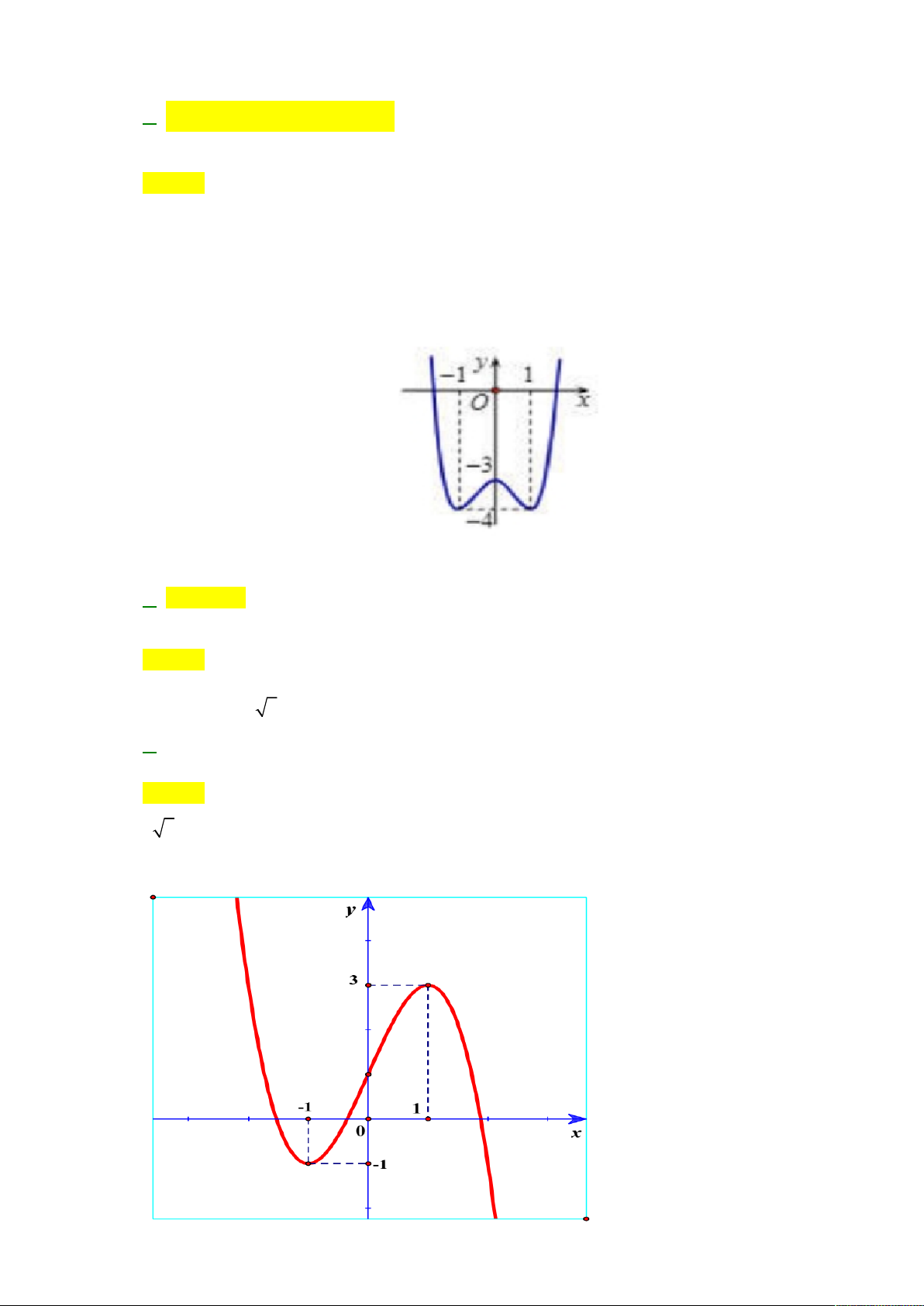
Câu 10: Cho hàm số y = f(x) có đồ thị như hình vẽ
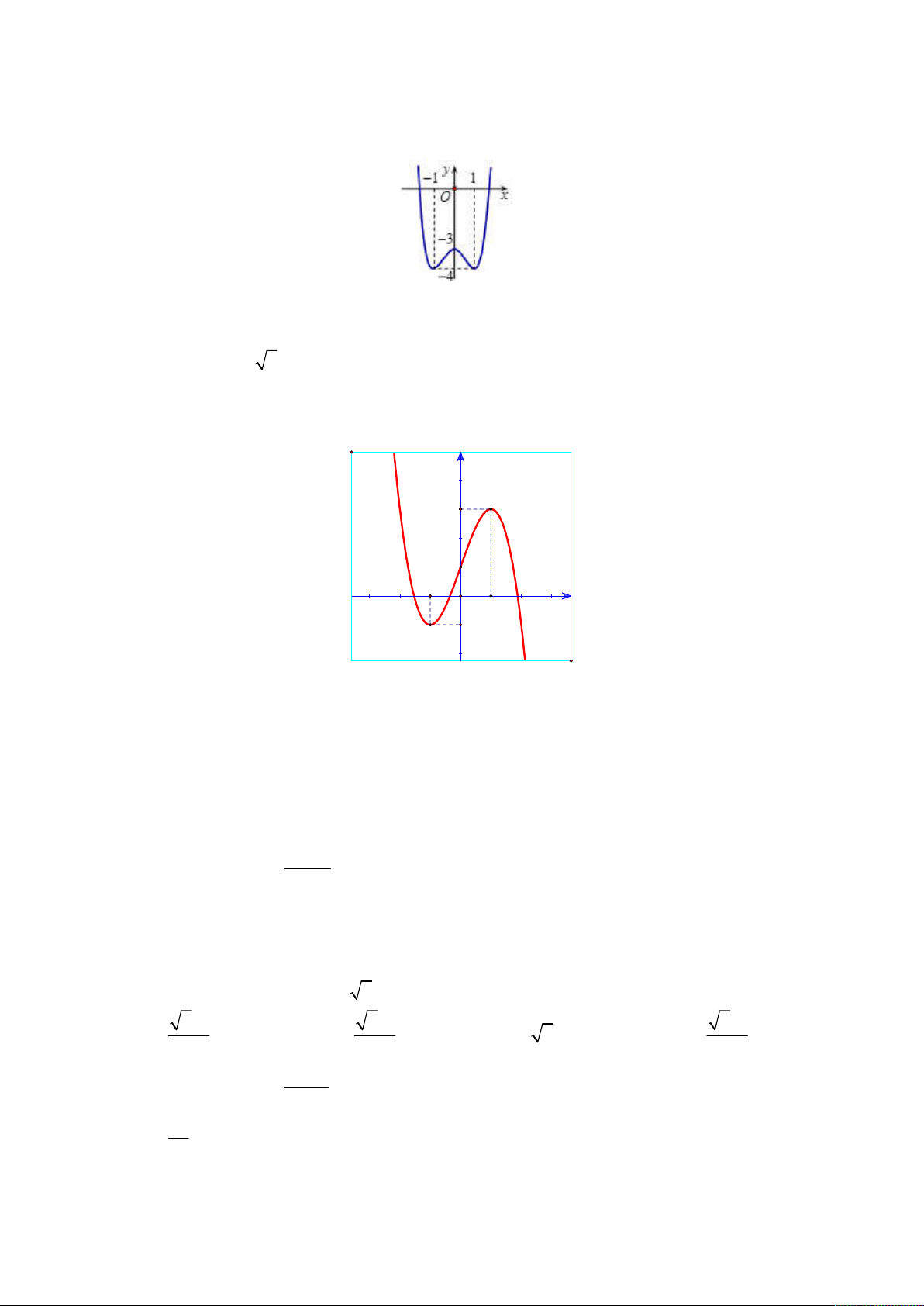
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên [-1; 1] lần lượt là A. -3 và -4 B. 1 và -4 C. 0 và -4 D. 1 và -1 2 x 4 x6
Câu 11: Phương trình  5
 5 có bao nhiêu nghiệm thực? A. 1 B. 3 C. 2 D. 0
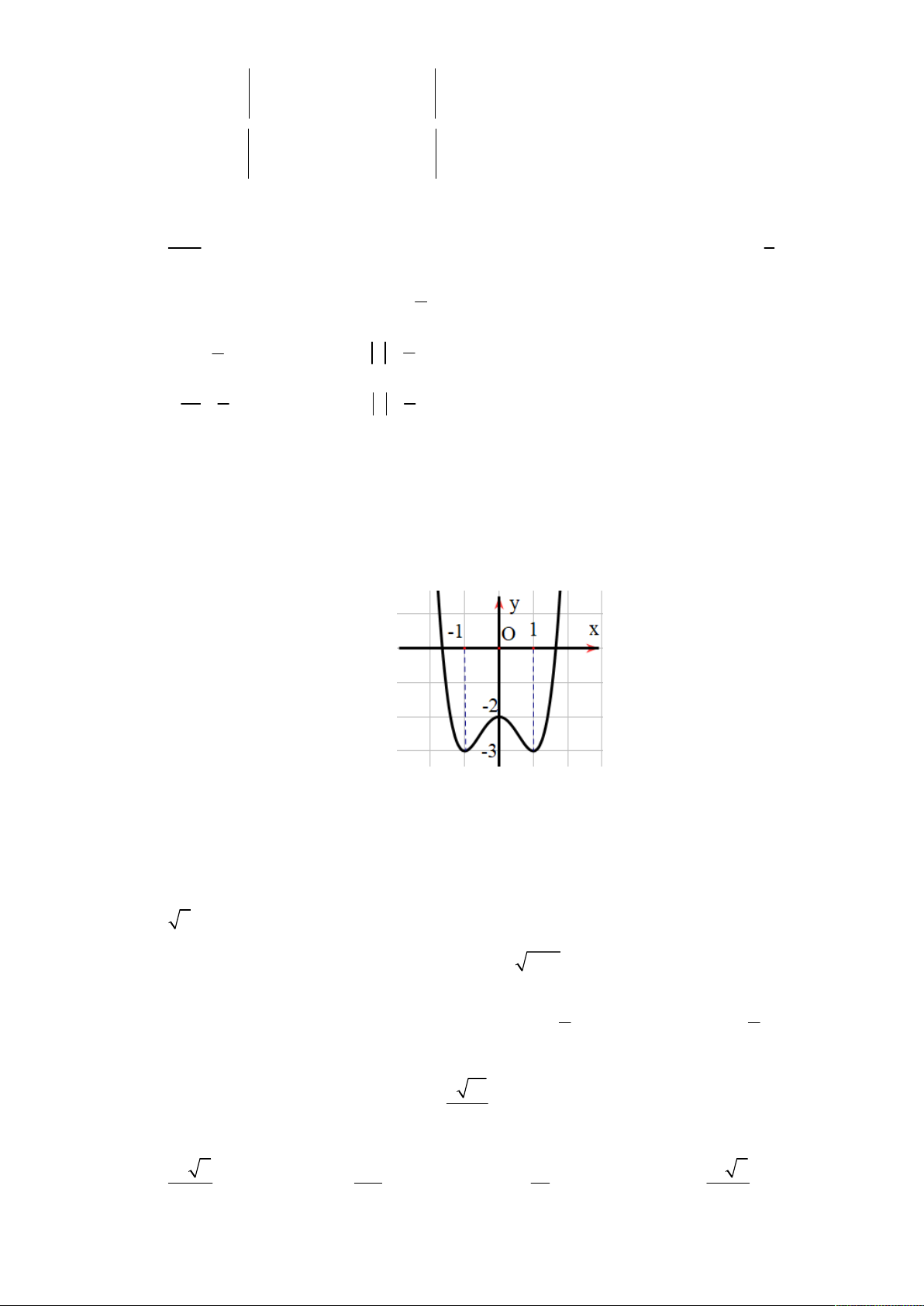
Câu 12: Cho hàm số y f x có đồ thị như hình vẽ y 3 -1 1 0 x -1
Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên khoảng  1  ;  3 .
B. Hàm số nghịch biến trên khoảng  1  ;  1 .
C. Hàm số đồng biến trên khoảng  ;    1 và 1;  .
D. Hàm số đồng biến trên khoảng  1  ;  1 . 2x  3
Câu 13: Đồ thị hàm số y
có các đường tiệm cận đứng và tiệm cận ngang lần lượt là x 1
A. x  1 và y  3 .
B. x  1 và y  2 .
C. x  2 và y  1. D. x  1  và y  2 .
Câu 14: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc
với mặt phẳng đáy và SA  2a . Tính thể tích khối chóp S.ABCD . 3 2a 3 2a 3 2a A. B. C. 3 2a D. 3 4 6 2x 1
Câu 15: Đồ thị hàm số y
cắt trục tung tại điểm có tung độ bằng x 1 1 A. B. 1 C. 1 D. 2 2
Câu 16: Nghiệm của phương trình log (2x  6)  3 là: 2 A. x  6 B. x  9 C. x  8 D. x  7
Trang 2/6 - Mã đề thi 101
Câu 17: Trong không gian Oxyz , cho mặt phẳng  P : 4x  3y z 1  0 . Điểm nào dưới đây thuộc (P) A. M(0; 2; -1) B. N(1; 1; -6) C. P(1; -6; 1) D. Q(0; 2; 1)
Câu 18: Cho hình trụ có diện tích xung quanh bằng 50 và độ dài đường sinh bằng đường kính của
đường tròn đáy. Tính bán kính r của đường tròn đáy. 5 2 5 2 A. r B. r  5  C. r D. r  5 2 2 2 2 2 Câu 19: Cho
f t dt  2 
và g xdx  1   . Tính I
x  2 f x  3g x dx    . 1 1  1  17 7 5 11 A. I  . B. I  . C. I  . D. I  . 2 2 2 2
Câu 20: Trong không gian Oxyz , mặt cầu tâm I (1; 0; 2) 
bán kính R  2 có phương trình A. 2 2 2
(x 1)  y  ( y  2)  2 B. 2 2 2
(x 1)  y  ( y  2)  4 C. 2 2 2
(x 1)  y  ( y  2)  4 D. 2 2 2
(x 1)  y  ( y  2)  2 2 e x
Câu 21: Tính nguyên hàm của hàm số f x   . e x  2 A.   2
 e x 4lnex F x   2 C .
B.    ex  2lnex F x  2 C .
C.    ex 2lnex F x   2 C. D.    ln ex F x  2   C . 1
Câu 22: Khối nón có bán kính đáy bằng 6, chiều cao bằng
, thể tích khối nón bằng  A. 12 B. 2 C. 6 D. 36
Câu 23: Với a , b là hai số thực dương thỏa mãn log a  11, log b  13 . Khi đó  2 log ab  bằng A. 46 B. 37 C. 180 D. 23 
Câu 24: Trong không gian tọa độ Oxyz , Cho các điểm M (1; 2; 3), N (3; 2; 4) . Tọa độ vec tơ MN là  1  A. 4;4  ;1 B. 2;0;7 C.  2  ; 0; 7   D. 2; 2;    2 
Câu 25: Có bao nhiêu cách chọn ra 2 học sinh từ một nhóm có 10 học sinh A. 90 B. 20 C. 45 D. 8 3 Câu 26: Biết 3
F (x)  x C là nguyên hàm của hàm số f (x) trên tập số thực; Tính I f (x)dx  1 A. 23 B. 20 C. 26 D. 17 2 2 2
Câu 27: Trong không gian Oxyz , bán kính mặt cầu  S  : x y z  2x  2y  4z 2  0 bằng. A. 2 2 . B. 2 . C. 22 . D. 4 .
Câu 28: Cho hàm số y f (x) liên tục trên  và có bảng xét dấu đạo hàm như sau: .
Điểm cực đại của hàm số là A. x = 0 B. x = -3 C. x = 1 D. x = 2
Câu 29: Cho u,v là hai hàm số có đạo hàm liên tục trên  ;
a b . Công thức nào sau đây là đúng:
Trang 3/6 - Mã đề thi 101 b b b b b b
A. u.dv uv  . v du  
B. u.dv uvu.dv   a a a a a a b b b b b
C. u.dv uv
D. u.dv uv  . v du   a a a a a
Câu 30: Đạo hàm của hàm số 1  3 x y bằng 1 3 x      A. B. 1 3 . x ln 3 C. (1 ).3 x x D. 1 x 1 3 .ln     ln 3 3 1
Câu 31: Họ nguyên hàm của hàm số f x   sin 2x là x 1 1 A. ln x  cos 2 x C B. ln x  cos 2x C . 2 2 1 1 1 C.  
cos 2x C . D. ln x  cos 2x C . 2 x 2 2 4 4 4 Câu 32: Nếu
f x dx  2  
và g x dx  6  
thì 2 f x  g x 1 dx    bằng 1 1 1 A. 2 B. 4  . C. 5 D. 3
Câu 33: Khối lập phương có thể tích bằng 64 cm3 thì cạnh của hình lập phương đó bằng A. 4 cm B. 8cm C. 6cm D. 16 cm
Câu 34: Đường cong trong hình vẽ là đồ thị của hàm số nào trong các hàm số sau: A. 4 2
y x  2x B. 4 2
y x  2x  2 . C. 4 2
y  x  2x  2 . D. 4 2
y x  2x  2
Câu 35: Trong không gian Oxyz, cho hai điểm A(1; 2; 2) và B(0, 2, 1). Mặt cầu có tâm thuộc trục Ox và đi
qua hai điểm A, B có đường kính bằng A. 2 B. 3 C. 6 D. 2 3 2
Câu 36: Cho hàm số f x liên tục trên  1  ;   và f
  x 1dx  8 . Tính I  .x f xdx  . 0 1 1 1 A. I  4 . B. I  4  . C. I  . D. I   . 4 4
Câu 37: Cho hình chóp S.ABCD có ABCD là hình vuông cạnh bằng 4 , SA vuông góc với đáy. Góc giữa 3 10
SC và mặt (SBD) bằng  . Biết cos 
và tam giác SAC không cân. Thể tích khối chóp 10 S.ABCD bằng 32 2 128 16 16 2 A. B. C. D. 3 3 3 3
Trang 4/6 - Mã đề thi 101
Câu 38: Xét hàm số f x liên tục trên đoạn 0; 
1 và thỏa mãn điều kiện 1 xf  2
x   f   x 2 4 3 1  1 x , x  0  ;1 . Tích phân I
f x dx  bằng 0     A. I  . B. I  . C. I  . D. I  . 4 6 16 20
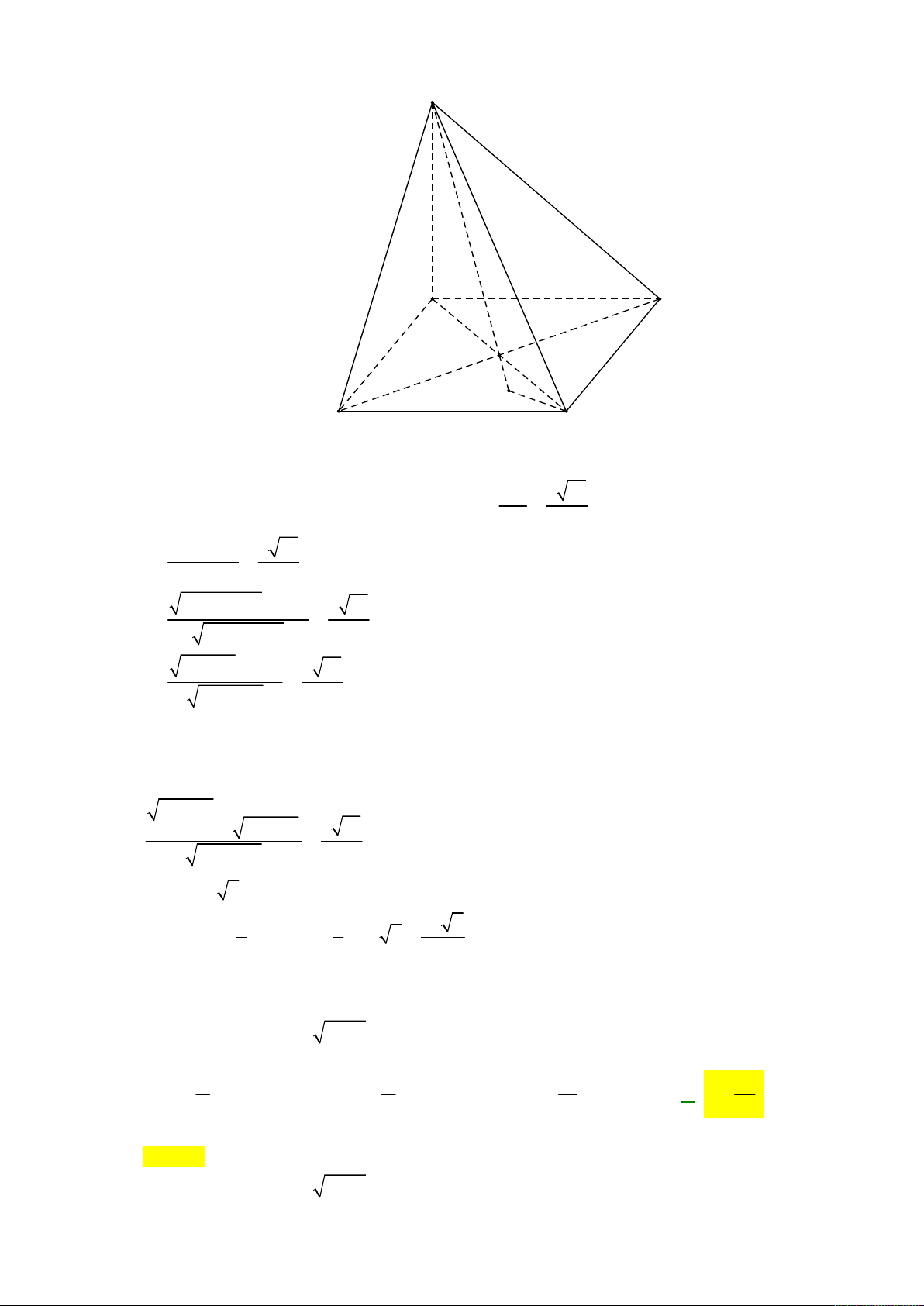
Câu 39: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng 2.
Khoảng cách từ A đến mặt phẳng (SCD) bằng: 6 2 6 A. 2 B. 3 C. D. 3 3
Câu 40: Một ô tô đang chạy thì người lái đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều
với vận tốc v(t)  12t  24 (m / s) trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt
đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô di chuyển bao nhiêu mét? A. 15m . B. 24m . C. 20m . D. 18m.
Câu 41: Tìm số nghiệm nguyên của bất phương trình 2 2 2 x 4 x9 x 5 x 1 2021 2021     x  
1 8  x  0 . A. 7 . B. 5 . C. 6 . D. 8 .
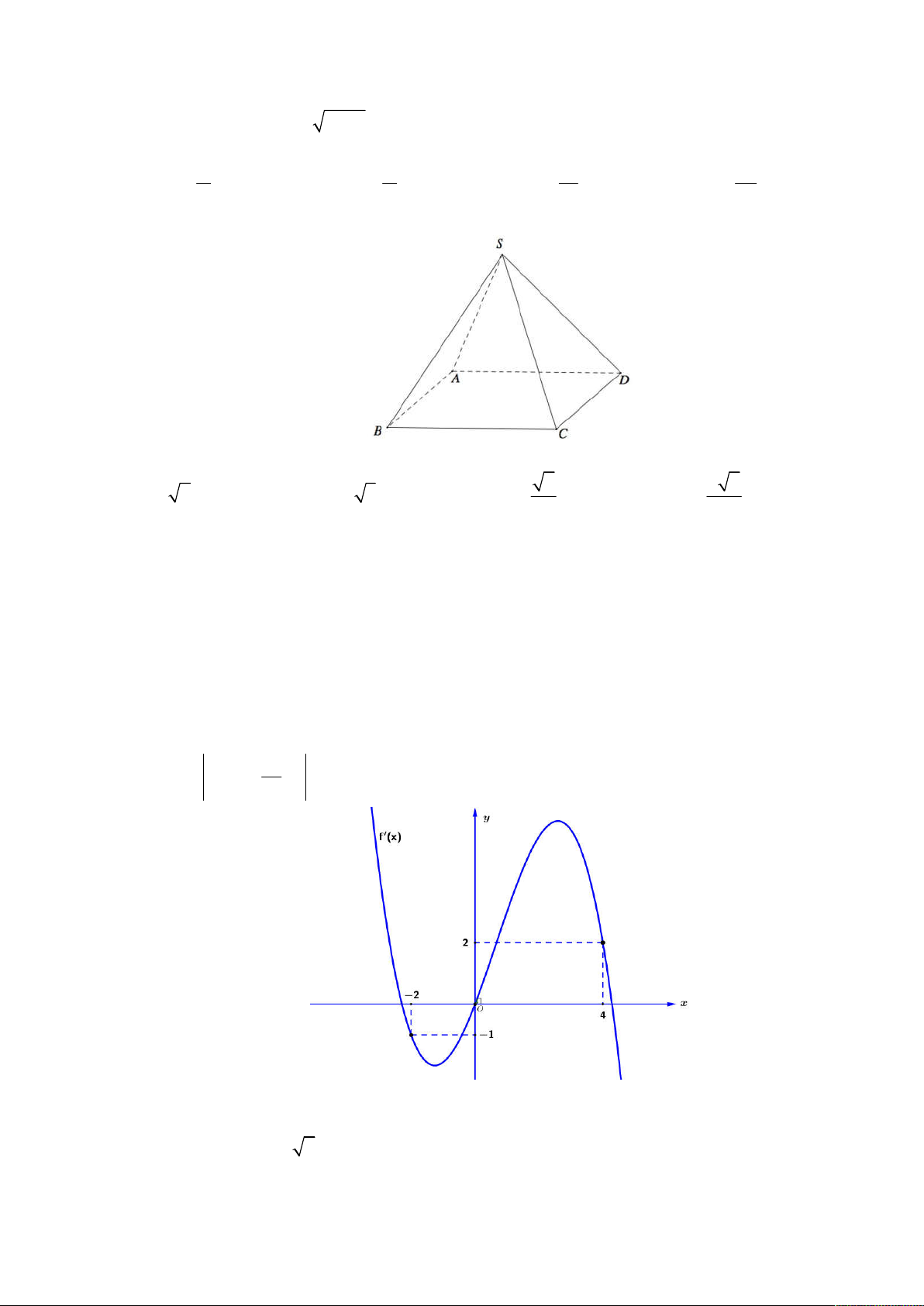
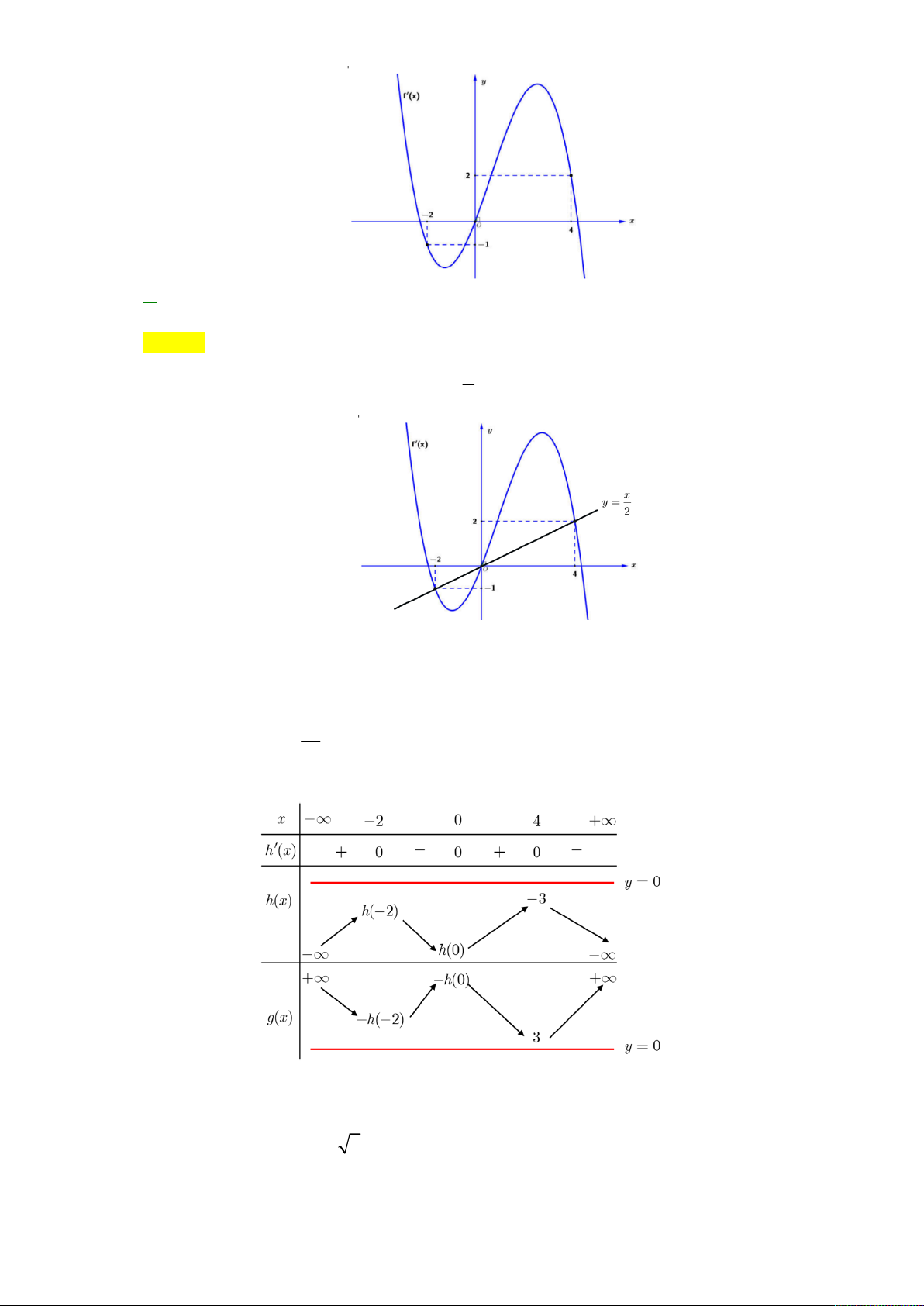
Câu 42: Cho f x là hàm số bậc bốn. Biết f (4)  0 và đồ thị của hàm số f ( x) như hình vẽ. Hàm số 2 x
g x   f x  
 1 có bao nhiêu điểm cực tiểu 4 A. 2 B. 1 C. 4 D. 3
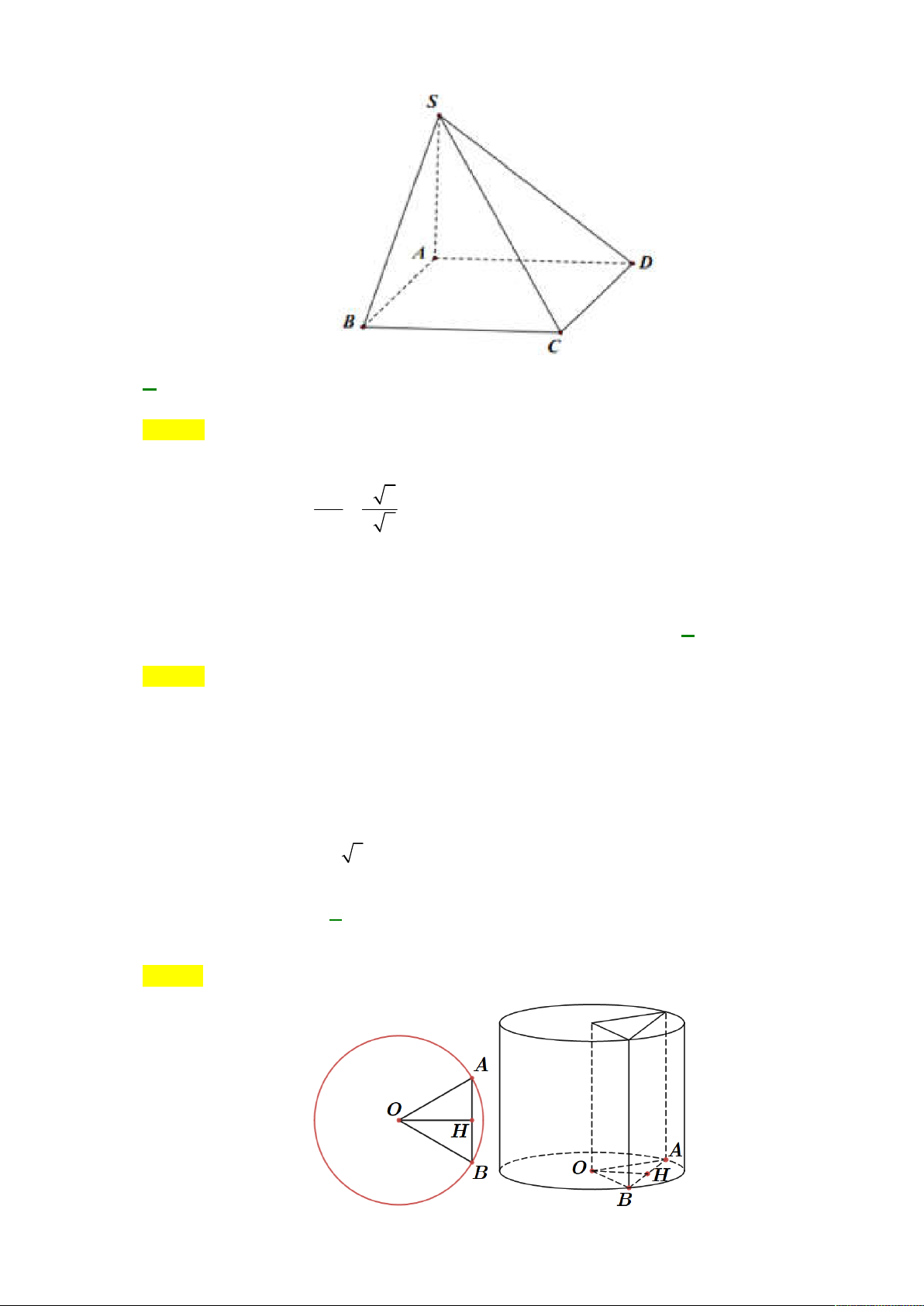
Câu 43: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2, SA vuông góc với mặt phẳng
ABCD và SA  2 2 .
Trang 5/6 - Mã đề thi 101
Góc giữa SC và mặt phẳng  ABCD bằng: A. 0 45 . B. 0 60 . C. 0 30 . D. 0 90 .
Câu 44: Có bao nhiêu giá trị nguyên của m để bất phương trình 2
log x mlog x m nghiệm đúng với 3 3
mọi giá trị của x  0;  . A. 7 . B. 6 . C. 4 . D. 5 .
Câu 45: Một thùng hình trụ có bán kính đáy bằng 2(m), bên trong thùng có chứa một lượng nước. Biết
rằng khi để thùng nằm ngang thì phần bề mặt nước là một hình vuông và mặt nước cách trục của
hình trụ một khoảng bằng 3 (m). Nếu để thùng thẳng đứng thì chiều cao của nước trong thùng bằng: A. 10,67(cm) B. 5,77 (cm) C. 33,3 (cm) D. 8,33 ( cm)
Câu 46: Có bao nhiêu số nguyên dương a để tồn tại đúng hai số thực b phân biệt, thỏa mãn điều kiện  2 4.log  log  5 7b b ba  0 2 2  A. 48 B. 47 C. 49 D. 46 1 1 Câu 47: Tích phân dx  có kết quả là. 2 x  4x  3 0 1 3 1 3 1 3 3 A. ln . B. ln . C.  ln . D. ln . 3 2 2 2 2 2 2
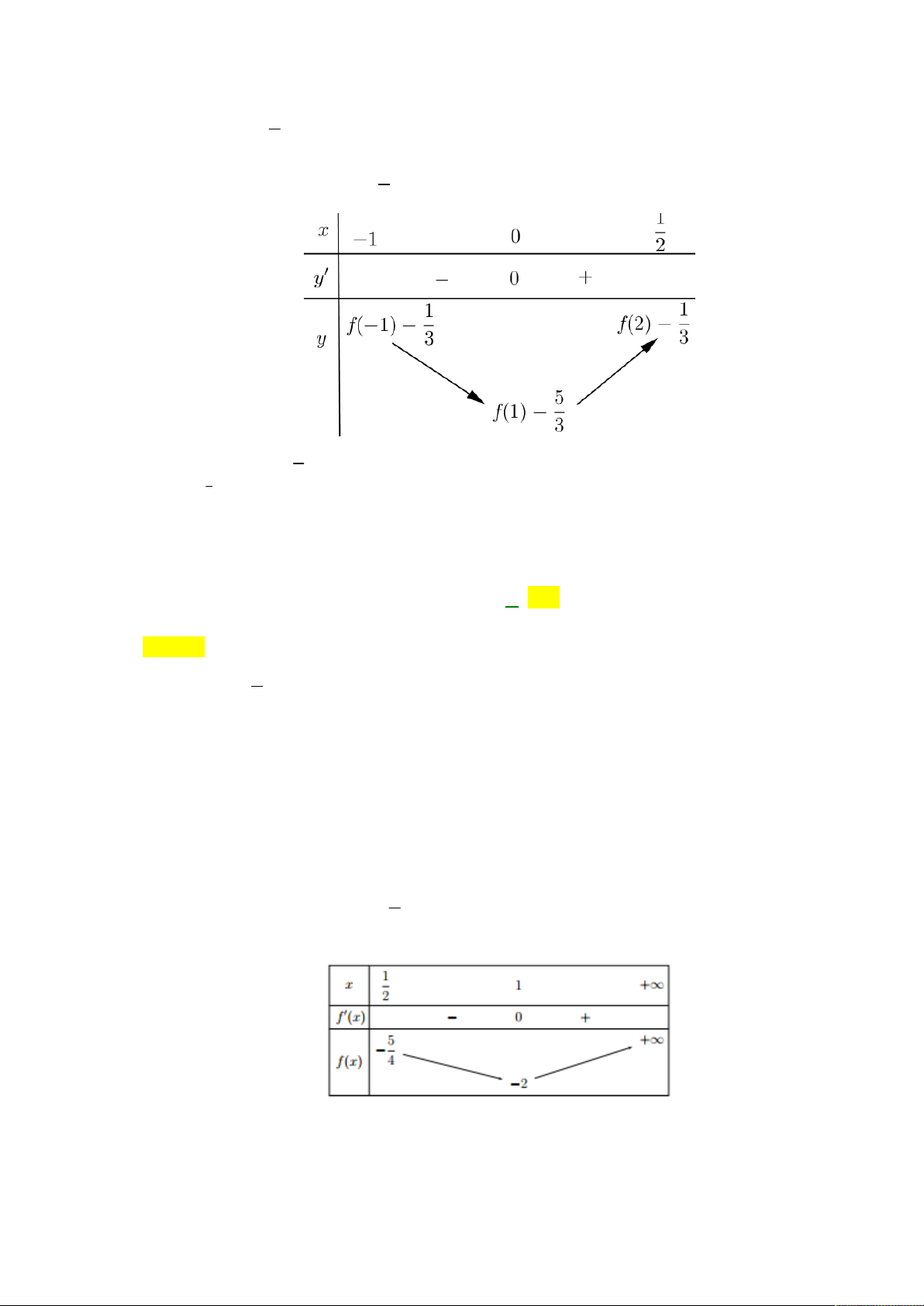
Câu 48: Cho hàm số y = f(x) có đạo hàm 2
f '(x)  (x 1)(x 1) (x  2) .Giá trị nhỏ nhất của hàm số 8 5 1 3 2
y f (2x 1) 
x  4x  , x [ 1; ] bằng 3 3 2 5 1 1 A. f (0) 1 B. f (1)  C. f (1)  D. f (2)  3 3 3
Câu 49: Có bao nhiêu số nguyên y sao cho ứng với mỗi y có đúng 5 số nguyên x thỏa mãn: 2
log(x  2x y)  2 log(2x 1)  0 A. 75 B. 26 C. 27 D. 74
Câu 50: Trong không gian Oxyz cho mặt phẳng (P) x  2 y  2z 12  0 và mặt cầu (S):  2 2 2
x y z  2x  4 y  2z  5  0 . Xét hai điểm M, N lần lượt thuộc (P) và (S) sao cho MN cùng 
phương với vectơ u  (1;1;1) . Giá trị nhỏ nhất của MN bằng A. 3 B. 9 3 1 C. 6 3 D. 2
(Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm) ----------- HẾT ----------
Trang 6/6 - Mã đề thi 101 BẢNG ĐÁP ÁN 1.A 2.C 3.A 4.C 5.D 6.B 7.B 8.D 9.C 10.A 11.A 12.D 13.B 14.A 15.C 16.D 17.B 18.A 19.A 20.B 21.C 22.A 23.B 24.B 25.C 26.C 27.A 28.D 29.D 30.D 31.C 32.C 33.A 34.D 35.C 36.A 37.A 38.D 39.D 40.B 41.C 42.A 43.A 44.D 45.B 46.D 47.B 48.B 49.C 50.C
Câu 51: Có 30 chiếc thẻ được đánh số từ 1 đến 30. Chọn ngẫu nhiên 2 thẻ. Xác suất để chọn được ít nhất
một thẻ đánh số nguyên tố bằng? A. 0,56 . B. 0, 41. C. 0, 46 . D. 0,52 . Lời giải Chọn A
Tập hợp số số nguyên tố: 2;3;5;7;11;13;17;19;23;2  9
Số cách chọn 2 thẻ ngẫu nhiên: 2 Ω  C  435 30
Gọi A là biến cố chọn được ít nhất một thẻ đánh số nguyên tố
A biến cố chọn được không thẻ đánh số nguyên tố: 2 C  190 20 190
P  1 P  1  0,56 A A 435
Câu 52: Với a là số thực dương tùy ý, 3 2 a bằng: 3 2a 2 3a A. 2 a . B. . C. 3 a . D. . 3 2 Lời giải Chọn C 2 x 4  1 
Câu 53: Tập nghiệm S của bất phương trình
 27 chứa bao nhiêu số nguyên    3  A. 3 . B. 1. C. 2 . D. Vô số. Lời giải Chọn A 2 x 4  1  2
 27  x  4  3  1   x  1    3  S   1  ;0;  1
Câu 54: Cho cấp số cộng (u ) có u  11và công sai d  4 . Số hạng thứ ba bằng n 1 A. 44 . B. 176 . C. 19 . D. 15 . Lời giải Chọn C
u u  2d  11 2.4  19 3 1 1
Câu 55: Hàm số F x 3 2
x  2x x  2021 là một nguyên hàm của hàm số nào dưới đây 3 2 1 2 x 2 1 2 x A. 4 3 x x
 2021x C . B. 4 3 x x
 2021x C . 9 3 2 12 3 2 2 1 2 x C. 4 3 x x
 2021x C . D. 2 x  4x 1. 9 3 2 Lời giải Chọn D
Câu 56: Hàm số nào sau đây đồng biến trên  ? x A. 3 2
y x  3x 1. B. 3 2
y x x  6x  2 1. C. y  . D. 4 2
y x  2x 1. x 1 Lời giải Chọn B Ta có: 3 2
y x x  6x 1 suy ra 2
y '  3x  2x  6 . Cho 2
y '  0  3x  2x  6  0 phương trình vô nghiệm. Do đó, y '  0, x    . Vậy hàm số 3 2
y x x  6x 1 đồng biến trên  .
Câu 57: Trong không gian Oxyz , cho hai mặt phẳng P : x  2y  2z 1  0 và Q : 2x  2y z  3  0 .
Gọi là góc giữa hai mặt phẳng P và Q . Tính cos. 4 2 2 A.  4 . B. . C. . D.  . 9 9 3 3 Lời giải Chọn B  
Ta có vtpt n  1; 2  ;2 n   Q 2;2; 1 P  và vtpt .   n .n     P Q 1.2  2.2 2.  1 4
Suy ra cos     . n . n P Q 1   2
 2  2 . 2  2   2 2 2 2 2 9 1
Câu 58: Cho hàm số y f x có đồ thị như hình vẽ
Số điểm cực trị của hàm số là A. 1. B. 0 . C. 3 . D. 2 . Lời giải Chọn D
Câu 59: Cho hàm số   2 x  .2021x f x e
. Chọn khẳng định đúng trong các khẳng định sau.
A. f x 1  x  2x ln 2021  0 .
B. f x 2
1  x ln 2021  0 .
C. f x 2
1  x x ln 2021  0 .
D. f x 2
1  1 x ln 2021  0 . Lời giải Chọn C Ta có:   2 x x      2 1 .2021 1 ln x.2021x f x e e ln1 2 x x 2
 ln e  ln 2021  0  x x ln 2021  0 .
Câu 60: Cho hàm số y f x có đồ thị như hình vẽ
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên  1  ;  1 lần lượt là A. 3  và 4  . B. 1 và 4  . C. 0 và 4  . D. 1 và 1. Lời giải Chọn A x x
Câu 61: Phương trình   2 4 6 5
 5 có bao nhiêu nghiệm thực? A. 1 B. 3 C. 2 D. 0 Lời giải Chọn A
  2x4x6 2 5
 5  x  4x  6  2  x  2 
Câu 62: Cho hàm số y f (x) có đồ thị như hình vẽ.
Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên  1  ;3
B. Hàm số nghịch biến trên  1  ;  1
C. Hàm số đồng biến trên  ;   
1 và 1;
D. Hàm số đồng biến trên  1  ;  1 Lời giải Chọn D 2x  3
Câu 63: Đồ thị hàm số y
có các đường tiệm cận đứng và tiệm cận ngang lần lượt là x 1
A. x  1 và y  3 
B. x  1 và y  2
C. x  2 và y  1 D. x  1  và y  2 Lời giải Chọn B
Câu 64: Cho hình chóp tứ giác SABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc
với mặt phẳng đáy và SA a 2 . Tính thể tích khối chóp SABCD 3 2a 3 2a 3 2a A. B. C. 3 2a D. 3 4 6 Lời giải Chọn A 3 1 1 a 2 2 V S . A Sa 2.a . 3 ABCD 3 3 2x 1
Câu 65: Đồ thị hàm số y
cắt trục tung tại điểm có tung độ bằng x 1 1  A. B. 1 C. 1  D. 2 2 Lời giải Chọn C
Cho x  0  y  1  .
Câu 66: Nghiệm của phương trình log 2x  6  3 2   là A. x  6 B. x  9 C. x  8 D. x  7 Lời giải Chọn D
Ta có log 2x  6 3
 3  2x  6  2  x  7 2
Câu 67: Trong không gian Oxyz , cho mặt phẳng P : 4x  3y z 1  0 . Điểm nào dưới đây thuộc P ?
A. M 0;2;  1 B. N 1;1; 6   C. P 1; 6  ;  1 D. Q 0;2;  1 Lời giải Chọn B
Câu 68: Cho hình trụ có diện tích xung quanh bằng 50 và độ dài đường sinh bằng đường kính của
đường tròn đáy. Tính bán kính r của đường tròn đáy 5 2 A. r B. r  5 2 5 C. r D. r  5 2 2 Lời giải Chọn A
Ta có l  2r 25 5 2 Theo đề 2
S  50 2 rh  50 2 r.2r  50r   r  . xq 2 2 2 2 2 f
 tdt  2
g xdx  1  
I  x  2 f  
x3g x d  xCâu 69: Cho 1  và 1  . Tính 1  17 A. I  7 B. I  5 C. I  11 D. I  2 2 2 2 Lời giải Chọn A 2 2 2 2 3 17
Ta có I  x  2 f  
x3g x d  x  d x x  2 f  
 xdx3 g
 xdx   2.23 1  2 2 1  1  1  1 
Câu 70: Trong không gian Oxyz , mặt cầu tâm I 1;0; 2
  bán kính R  2 có phương trình
A. x  2  y   z  2 2 1 2  2
B. x  2  y   z  2 2 1 2  4
C. x  2  y   z  2 2 1 2  4
D. x  2  y   z  2 2 1 2  2 Lời giải Chọn B 2 x e
Câu 71: Tính nguyên hàm của hàm số f (x)  . x e  2 A. 2 ( ) x   4ln( x F x e e  2)  C. B. ( ) x   2ln( x F x e e  2)  C. C. ( ) x   2ln( x F x e e  2)  C. D. ( )  ln( x F x e  2)  C. Lời giải Chọn C 2 x e  2 
Ta có: F(x)  f (x)dx dx  1 x x
e dx e  2ln( x e  2)  C.    x   e  2 xe  2  1
Câu 72: Khối nón có bán kính đáy bằng 6 , chiều cao bằng , thể tích khối nón bằng A. 12. B. 2. C. 6. D. 36. Lời giải Chọn B 1 1 1 Thể tích khối nón là: 2 2
V .r .h .6 .  12. 3 3
Câu 73: Với a,b là hai số thực dương thỏa mãn loga  11,logb  13. Khi đó 2 log(ab ) bằng A. 46. B. 37. C. 180. D. 23. Lời giải Chọn A Ta có: 2
log(ab )  loga 2logb  11 2.13  37. 
Câu 74: Trong không gian tọa độ Oxyz , cho các điểm M (1; 2; 3
 ), N(3;2;4) . Tọa độ véc tơ MN là A. (4; 4;1). B. (2;0;7). C. ( 2  ;0; 7  1 ). . D. (2; 2; ). 2 Lời giải Chọn B 
MN  3 1;2  2;4  ( 3  )  2;0;7.
Câu 75: Có bao nhiêu cách chọn ra 2 học sinh từ một nhóm có 10 học sinh A. 90 B. 20 C. 45 D. 8 Lời giải Chọn C
Số cách chọn ra 2 học sinh từ một nhóm có 10 học sinh là 2 C  45. 10 3 Câu 76: Biết   3
F x x C là nguyên hàm của hàm số f x trên tập số thực. Tính I f  xdx 1 A. 23 B. 20 C. 26 D. 17 Lời giải Chọn C 3 I f  x 3 3 dx  x  26. 1 1
Câu 77: Trong không gian Oxyz , bán kính mặt cầu   2 2 2
S : x y z  2x  2y  4z 2  0 bằng A. 2 2 B. 2 C. 22 D. 4 Lời giải Chọn A
Bán kính mặt cầu   2 2 2
S : x y z  2x  2y  4z 2  0 bằng 2 2 2 1 1  2  2  2 2 .
Câu 78: Cho hàm số y f x liên tục trên  và có bảng xét dấu đạo hàm như sau
Điểm cực đại của hàm số là A. x  0 B. x  3  C. x  1 D. x  2 Lời giải Chọn D
Câu 79: Cho u,v là hai hàm số có đạo hàm liên tục trên a;b . Công thức nào sau đây là đúng? b b b b A. d b u v uv  d v u b .
B. u v uv u v .   d d   a a a a a a b b b C. ud b v uv b .
D. u v uv v u .  d d   a a a a a Lời giải Chọn D b b d b u v uv  d v u .   a a a
Câu 80: Đạo hàm của hàm số 1 3 x y   bằng 1x A. 3 x  1 1x  . B. 3 .ln 3 . C. 1 .3 x x   1 . D. 3 .ln .   ln 3  3  Lời giải Chọn D    
y   xxxx 1 1
3   1 x 1 1 1 .3 .ln 3  3  .ln 3  3 .ln   .  3 
Câu 81: Họ nguyên hàm của hàm số f x 1   sin 2x là x A. 1
ln x  cos 2x  1 C .
B. ln x  cos 2x C . 2 2 C. 1 1   cos 2x  1
C . D. ln x  cos 2x C . 2 x 2 2 Lời giải Chọn C  1  1 1
 sin 2x dx    cos 2x C   . 2  xx 2 4 4 4 Câu 82: Nếu f
 x dx  2  và g
 x dx  6  thì 2 f
 x gx1 dx bằng  1 1 1 A. 2 . B. 4  . C. 5 . D. 3 . Lời giải Chọn C 4 4 4 4 2 f
 x gx1 dx  2 f
 x dxg
 x dx 1 dx  2.   2    6  3  5 . 1 1 1 1
Câu 83: Một khối lập phương có thể tích bằng 3
64cm . Độ dài mỗi cạnh của khối lập phương đó bằng A. 4cm . B. 8cm . C. 6cm . D. 16cm . Lời giải Chọn A
Giả sử khối lập phương có độ dài mỗi cạnh bằng a . Ta có 3
a  64 . Suy ra a  4 .
Câu 84: Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào trong các hàm số dưới đây? A. 4 2
y x  2x . B. 4 2
y x  2x  2 . C. 4 2
y  x  2x  2 . D. 4 2
y x  2x  2 . Lời giải Chọn D
Từ đồ thị ta có đây là đồ thị hàm số bậc 4 trùng phương với hệ số a  0 và cắt trục tung tại điểm có tung độ - 2.
Câu 85: Trong không gian Oxyz , cho hai điểm A1;2;2 , B0;2; 
1 . Mặt cầu có tâm thuộc trục Ox và
đi qua hai điểm A,B có đường kính bằng A. 2 . B. 3 . C. 6 . D. 2 . Lời giải Chọn C Gọi I  ;
a 0;0Ox là tâm mặt cầu
IA IB  a  2 2 2 2 2 2
1  2  2  a  2 1  a  2
Đường kính mặt cầu d IA  a  2 2 2 2. 2. 1  2  2  6 3 2
Câu 86: Cho hàm số f x liên tục trên  1
 ; và  f x 1dx  8 . Tính I  .
x f xd .x 0 1 1 1 A. I  4. B. I  4  . C. I  . D. I   . 4 4 Lời giải Chọn A Đặt 2
t x 1  t x 1 2tdt  dx 3 2 2
Khi đó,  f x 1dx  8   f t.2tdt  8  t.
f tdt  4. 0 1 1 Vậy I  4.
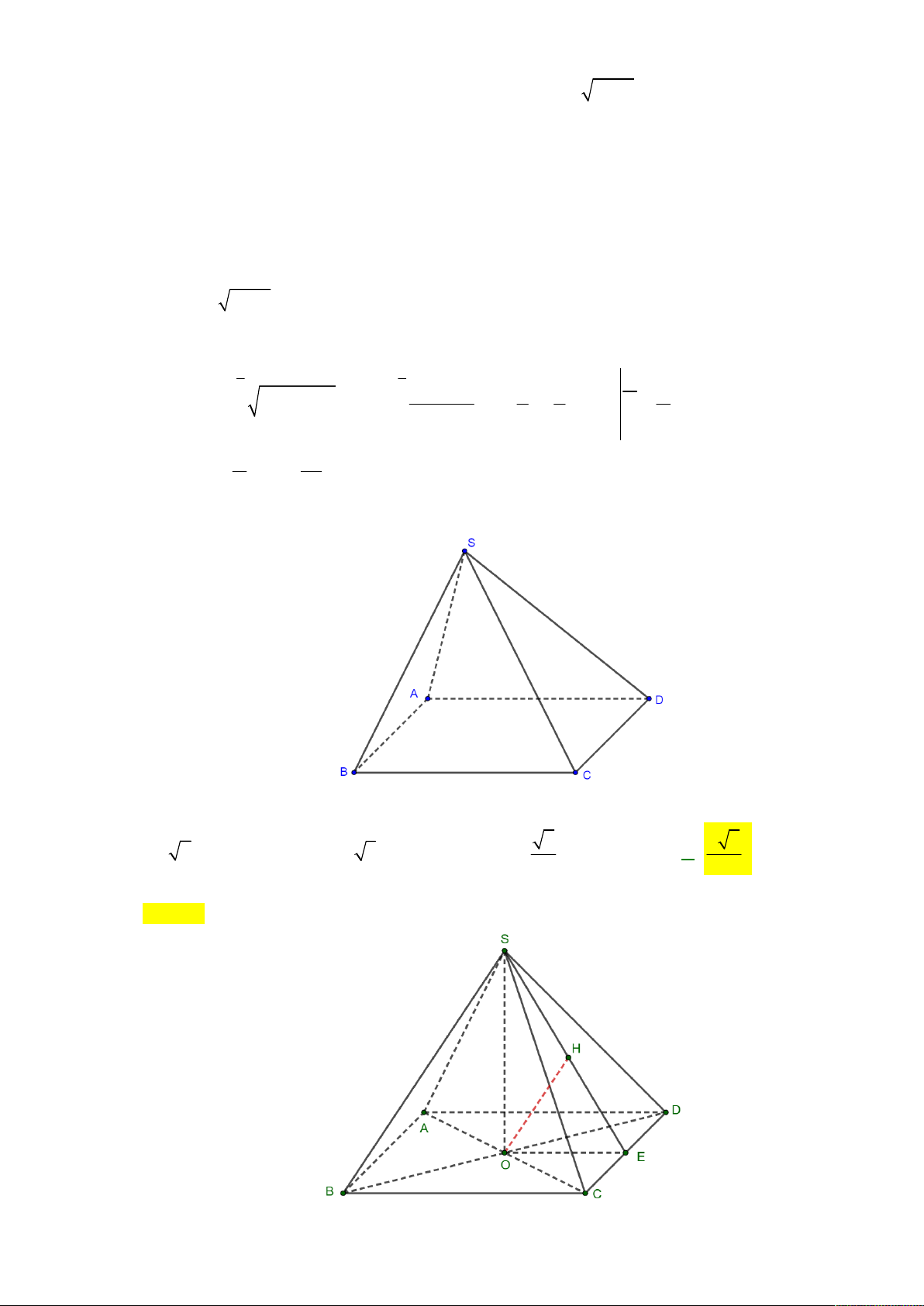
Câu 87: Cho hình chóp S.ABCD có ABCD là hình vuông cạnh bằng 4, SA vuông góc với đáy. Góc
giữa SC và mặt SBD bằng 3 10 . Biết cos
và tam giác SAC không cân. Thể tích khối 10
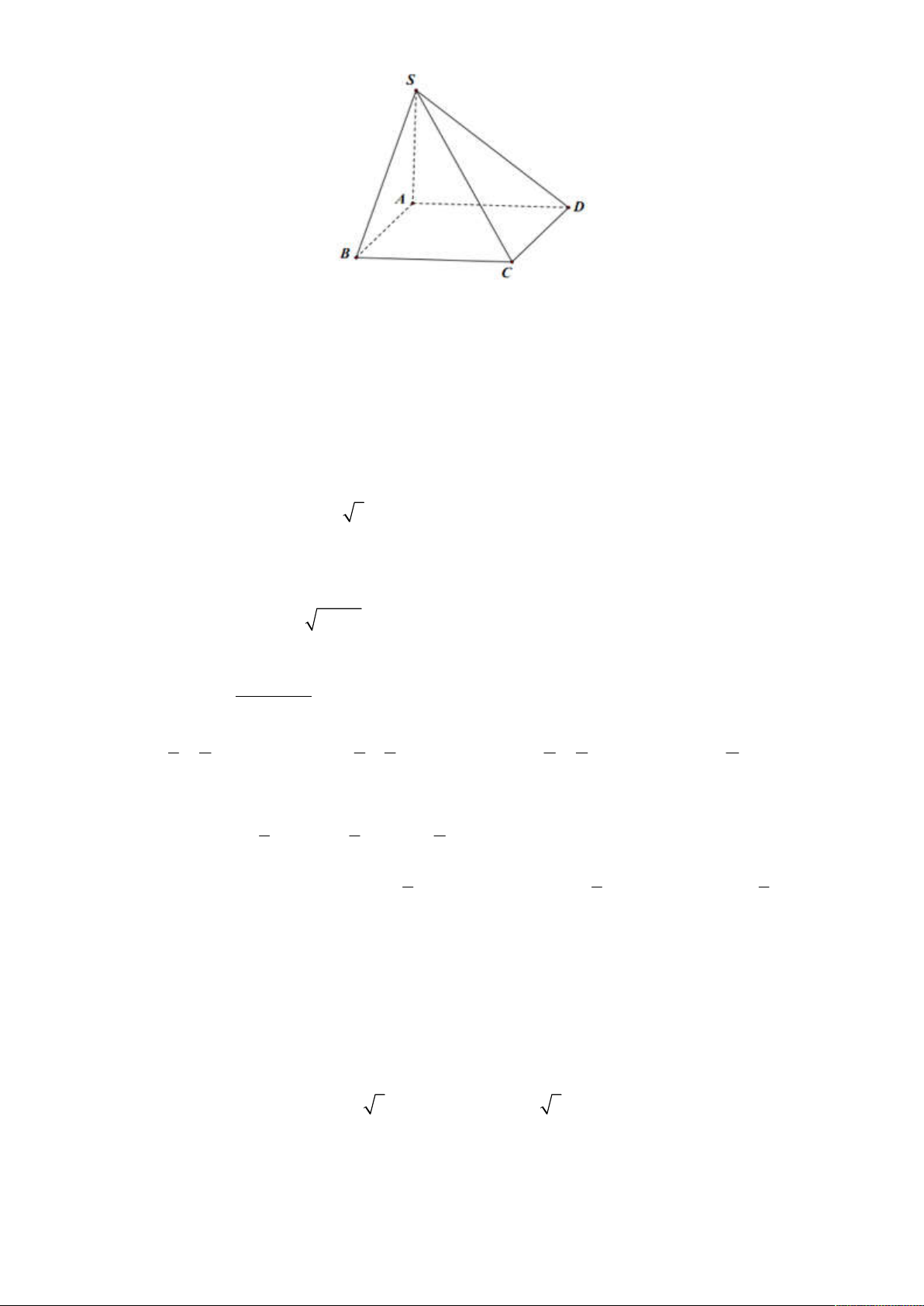
chóp S.ABCD bằng 32 2 128 16 16 2 A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn A S A B O H D C
Gọi O là tâm hình vuông ABCD , H là hình chiếu của C trên SO . SH
Khi đó CH  SBD  SC SBD     3 10 , CSO   . SC 10 SO OH 3 10   SC 10 2 2
SA AO OH 3 10   2 2 SA AC 10 2 SA  8  OH 3 10     1 2 SA  32 10 SO AO
Lại có SAO đồng dạng CHO nên 2   S .
O OH AO S . O OH  8 2 CO OH Từ (1) và (2) suy ra 2 8 SA  8  2 2 SA  8 3 10 SA  8 4 2 
SA  40SA  256  0   2 2 2 SA  32 10 SA  32   AC loaïi  SA  2 2 1 1 32 2 2  VS .SA  .4 .2 2  . S.ABCD 3 ABCD 3 3
Câu 88: Xét hàm số
f x liên tục trên đoạn 0; 
1 và thoả mãn điều kiện 1 xf  2
x   f   x 2 4 3 1
 1 x ,x 0; 
1 . Tích phân I   f xdx bằng 0 A. I  . B. I  . C. I  . D. I  . 4 6 16 20 Lời giải Chọn D xf  2
x   f   x 2 4 3 1
 1 x ,x 0;  1 nên 1 4
xf x  1 1 2 dx  3
f 1 x 2 dx  1 x d  x 0 0 0 Mà 1 4  xf x  1
2 dx  2 f  2xd 2x  2I 0 0 1 1 1 3
f 1 xdx  3
  f 1 xd1 x  3 f tdt  3I, t 1 x 0 0 0 1 Xét 2 J  1 x d  x 0
Đặt x  sin t  dx  2costdt 2 2 1 cos2  1 1  Khi đó,  1  sin 2cos d  d  t  sin 2  t J t t t t t  2  . 2  2 4  4 0 0 0 Do đó 5I   I  . 4 20
Câu 89: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng 2.
Khoảng cách từ A đến mặt phẳng SCD là A. 6 2 6 2  B. 3. C. D.  3 3 Lời giải Chọn D
Gọi O là giao điểm của AC và BD thì SO   ABCD do hình chóp có tất cả các cạnh bằng
nhau nên hình chiếu từ đỉnh S xuống mặt phẳng đáy trùng với tâm của đáy. d  ,
A SCD AC Do:     d  2 d  ,
A SCD  2d O, SCD O,SCD     OC CD OE
Hạ OE CD, OH SE . Vì 
CD  SOE  CD OH CD SO
Mà OH SE OH  SCD  d O,SCD  OH 1
Do ABCD là hình vuông nên OE CD  1 và E là trung điểm CD nên CE DE  1. 2 2 2 2 2
SE SC CE  3, SO SE OE  2 S . O OE 6  OH  
d A SCD 2 6 ,  2OH  . SE 3 3
Câu 90: Một ô tô đang chạy thì người lái đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều
với vận tốc vt  1
 2t  24 m / s trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt
đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô di chuyển được bao nhiêu mét? A. 15m B. 24 . m C. 20 . m D. 18 . m Lời giải Chọn B
Thời gian từ lúc xe đạp phanh đến lúc dừng hẳn là: vt  0  1
 2t  24  0  t  2s 2
Từ lúc đạp phanh đến khi dừng hẳn, ô tô di chuyển được: S   1
 2t  24dt  24m 0
Câu 91: Tìm số nghiệm nguyên của bất phương trình 2 2 2 x 4 x9 x 5x1 2021  2021  x   1 8  x  0 . A. 7. B. 5. C. 6. D. 8. Lời giải Chọn C Đặt 2 2 2
a  2x  4x  9, b x  5x 1  a b x  9x  8   x   1  x  8
Khi đó: 2021a  2021b      0  2021a   2021b b a ab
Xét hàm số:    2021x      2021 .x f x x f x ln 20211  0 x
 Hàm số đơn điệu tăng mà
f a  f b 2 2
a b  2x  4x  9  x  5x 1  x  
1  x  8  0  1  x  8
Nên bất phương trình có 6 nghiệm nguyên.
Câu 92: Cho f x là hàm số bậc bốn. Biết f 4  0 và đồ thị của hàm số f  x như hình vẽ. Hàm số 2      x g x f x
1 có bao nhiêu điểm cực tiểu 4 A. 2 . B. 1. C. 4 . D. 3 . Lời giải Chọn A 2 x x
Gọi hx  f x 
1, hx  f x  . 4 2 x  2    x xx  
h x  0  f x   
  x  0 , hx   f x 2 0   . 2  2  2  x  4 x  4  2 4 4
Ta có h4  f 4  1  3
 ; hxdx  0  h4  h 2    . 4 2  Bảng biến thiên
Dựa vào BBT ta có 2 điểm cực tiểu.
Câu 93: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2 , SA vuông góc với mặt
phẳng  ABCD và SA  2 2 . Góc giữa SC và mặt phẳng  ABCD bằng: A. o 45 . B. 0 60 . C. 0 30 . D. 0 90 . Lời giải Chọn A
Có SC; ABCD   SCA SA 2 2 Xét SCA, tan  SCA    1  0 SCA  45 . AC 2 2
Câu 94: Có bao nhiêu giá trị nguyên của m để bất phương trình 2
log x m log x m nghiệm đúng với 3 3
mọi giá trị của x 0; . A. 7 . B. 6 . C. 4 . D. 5 . Lời giải Chọn D a 1 0 TM 2  
Đặt t  log x , bpt trở thành t mt m  0, t       0  m  4 . 3 2
  m  4m  0
Vậy có 5 giá trị nguyên của m thỏa mãn.
Câu 95: Một thùng hình trụ có bán kính đáy bằng 2m , bên trong thùng có chứa một lượng nước. Biết
rằng khi để thùng nằm ngang thì phần bề mặt nước là một hình vuông và mặt nước cách trục của
hình trụ một khoảng bằng 3 m . Nếu để thùng thẳng đứng thì chiều cao của nước trong thùng bằng: A. 10,67 (cm). B. 5,77 (cm). C. 33,3 (cm). D. 8,33 (cm). Lời giải Chọn B Ta 2 2
AB  2HA  2 OA OH  2  h  2 (m).
Ta có OA OB AB nên tam giác AOB đều nên 
AOB  60 , khi đó hình viên phân giới hạn 2 60 2 3 2
bởi dây cung AB và cung nhỏ AB có diện tích là 2 2    3 . 360 4 3  2    3 2   3
Vậy khi để thùng thẳng đứng, chiều cao của nước trong thùng là   0,0577m. 4
Câu 96: Có bao nhiêu số nguyên dương a để tồn tại đúng hai số thực b phân biệt, thỏa mãn điều kiện  2 4log  log  5 7b b ba  0 2 2  . A. 48 . B. 47 . C. 49 . D. 46 . Lời giải Chọn D b
  0,b  log a 7 b
  0,b  log a 7  log b 1   b  2   
4log b  log b  5
7b a  0     2 2  2 2  5 5  . log b  4  2  b  2 4    7b a b  log a  7 5  5 
Để tồn tại đúng hai số thực b phân biệt 4 2 4
 2  log a  2  7
a  49  a  3;4;...;48 7  . 1 1 Câu 97: Tích phân dx có kết quả là  2x 4x3 0 1 3 1 3 1 3 A. ln . B. ln . C.  3 ln . D. ln . 3 2 2 2 2 2 2 Lời giải Chọn B 1 1 1 1 1 1  1 1  1 x 1 1 Ta có dx  dx   dx  ln    2   x  4x  3 x 1 x  3
2  x 1 x  3  2 x  3 0 0 0    0 1  1 1  1 3  ln  ln  ln   2  2 3  2 2
Câu 98: Cho hàm số y f x có đạo hàm f  x   x   x  2 1
1  x  2 . Giá trị nhỏ nhất của hàm số  
y f 2x   8 5 1 3 2
1  x  4x  , x  1  ; bằng 3 3  2   
A. f 0 1. B. f   5 1  .
C. f   1 1  . D. f   1 2  . 3 3 3 Lời giải Chọn B
Ta có y  f  x   2 2 2 2
1  8x  8x  16x x   1 2x  
1  8x x   1
xx   2 8
1 4x  2x   1  1  Khi đó trên 1  ; thì  
y  0  x  0  2   1 
Ta có bảng biến thiên trên 1  ;  2    5
Vậy min y f   1  .  1  3 1  ;  2  
Câu 99: Có bao nhiêu số nguyên y sao cho ứng với mỗi y có đúng 5 số nguyên x thỏa mãn:  2
log x  2x y 2log2x   1  0 ? A. 75 . B. 26 . C. 27 . D. 74 . Lời giải Chọn C 1 Điều kiện x  . 2 Ta có log  2
x  2x y  2log2x   1  0
 logx  2x y  log2x  2 2 1 2 2
x  2x y  4x  4x 1 2
y  3x  6x 1. 1
Đặt f x 2
 3x  6x 1 với x  , ta có f x  6x  6  0  x 1. 2 Lập bảng biến thiên
Ứng với mỗi y có đúng 5 số nguyên x thỏa mãn
y f x  f 5  y f 6  46  y  73.
Vậy có 27 số nguyên y thỏa yêu cầu bài toán.
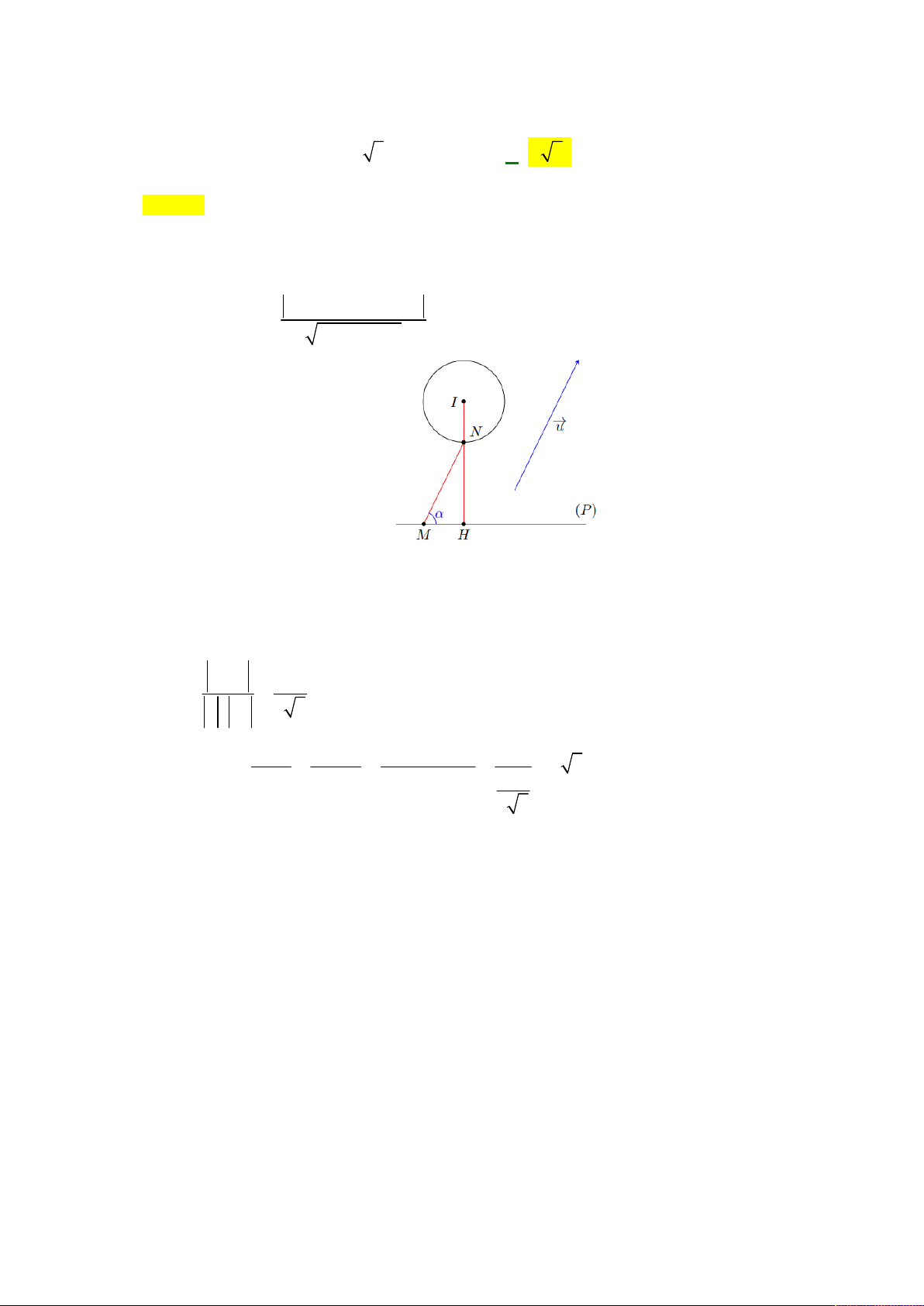
Câu 100: Trong không gian Oxyz cho mặt phẳng P : x  2y  2z 12  0 và mặt cầu S 2 2 2
: x y z  2x  4y  2z  5  0 . Xét hai điểm M , N lần lượt thuộc P và S  sao cho  
MN cùng phương với véc-tơ u  1;1; 
1 . Giá trị nhỏ nhất của MN bằng A. 3. B. 9 3 1. C. 6 3 . D. 2 . Lời giải Chọn C
Mặt cầu S x y z x y z     x  2   y  2   z  2 2 2 2 : 2 4 2 5 0 1 2 1  1 có tâm I  1  ;2; 
1 , bán kính R  1 .
x  2y  2z 12
Ta có d I,P I I I
 3  R nên P và S  không giao nhau. 2 2 2 1  2  2
Gọi là góc tạo bởi MN và mặt phẳng P .
Gọi H là hình chiếu của N lên mặt phẳng P .   
Mặt khác MN cùng phương với véc-tơ u  1;1;  1 và n  1; 2  ;2 P  suy ra   u nP 1
sin    . u n 3 3 P NH NH d I, P 1 3 1 min    Khi đó MN      6 3 . sin sin sin 1 3 3
Document Outline

  • de-thi-chuyen-de-toan-12-lan-4-nam-2022-2023-truong-thpt-tran-phu-vinh-phuc
  • 34. ĐỀ THI THỬ TN THPT 2023 - MÔN TOÁN - THPT-TRẦN-PHÚ-VĨNH-PHÚC-L4 (Bản word kèm giải).Image.Marked