Đề thi cuối học kỳ 2 Toán 7 năm 2023 – 2024 trường THCS Đa Tốn – Hà Nội

PHÒNG GD&ĐT GIA LÂM ĐỀ KIỂM TRA CUỐI HỌC KỲ II
TRƯỜNG THCS ĐA TỐN NĂM HỌC 2023-2024
Môn: TOÁN – Lớp 7( Tiết 135+136)
Thời gian: 90 phút (không kể thời gian giao đề) ĐỀ 1
I. TRẮC NGHIỆM (3,0 điểm). Chọn phương án trả lời đúng của mỗi câu hỏi sau: Câu 1: Nếu a c  thì b d A. .
a b  .cd . B. . a c  . b d . C. . a d  . b c.
D. b  d .
Câu 2: Trong các công thức sau, công thức nào phát biểu: Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 2?
A. y = x + 2. 2 B. y = . C. y = 2 . x D. 2 y = x . x Câu 3: Đa thức 3 4 2 6x 5
+ x –3x + 4 sắp xếp theo lũy thừa giảm dần của biến là: A. 3 4 2
6x + 5x – 3x 4 + B. 4 2 3
5x –3x + 4 + 6x C. 4 3 2 5x 6 + x + 4 –3x D. 4 3 2 5x 6 + x –3x + 4
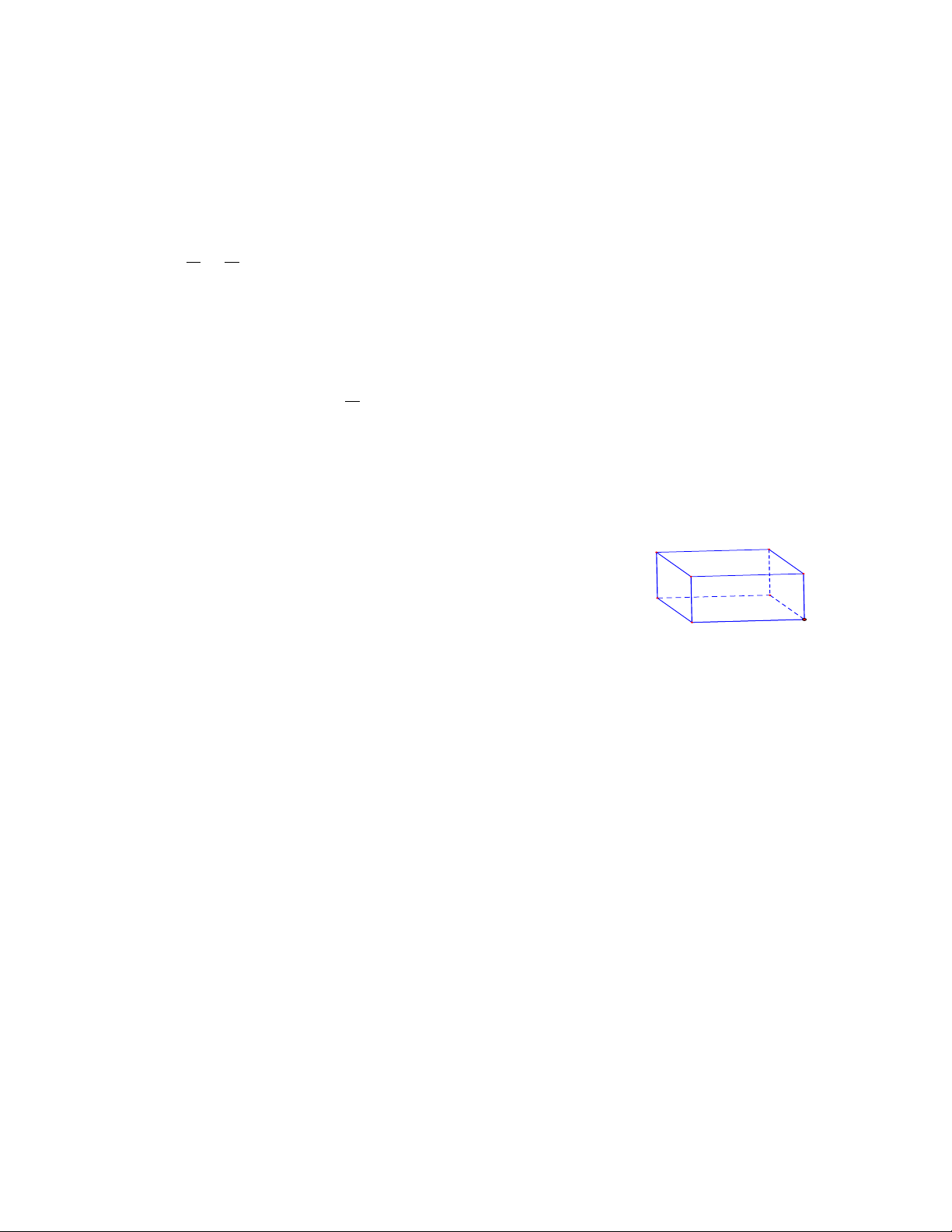
Câu 4: Quan sát hình hộp chữ nhật ABC .
D MNPQ , những cạnh có A D
độ dài bằng cạnh AB là: B C
A. BC,CD, DA . B. MN, DC, PQ Q M
C. AM , BN,CP, DQ . D. MQ, PQ . P N
Câu 5: Đa thức nào là đa thức một biến? A. 2
27x y − 3xy +15. B. 2 x − 6x + 9 . C. 3
8x − y + 8. D. 3
yz − 2x y + 5.
Câu 6: Tích của hai đơn thức 2
6x và 2x là: A. 3 12 − x . B. 3 12x . C. 2 12x . D. 3 8x .
Câu 7: Nghiệm của đa thức P(x) = x + 3là: A. x = 0 . B. x =1. C. x = 3. D. x = 3 −
Câu 8: Một hộp bút màu có các màu: màu xanh, màu vàng, màu đỏ, màu đen, màu hồng, màu cam.
Hỏi nếu rút bất kỳ một cây bút màu thì có thể xảy ra mấy kết quả? A. 3. B. 4. C. 5. D.6.
Câu 9: Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của một tam giác? A. 7 cm;9 cm;18 cm
B. 2 cm;5 cm;7 cm
C. 6 cm;11 cm;13 cm
D. 1 cm;7 cm;9 cm
Câu 10: Trong các biến cố sau, biến cố nào là biến cố chắc chắn?
A. “Trong điều kiện thường, nước đun đến 1000C sẽ sôi”
B. “Tháng hai dương lịch năm sau có 31 ngày”
C. “Khi gieo hai con xúc xắc thì tổng số chấm xuất hiện trên hai con xúc xắc là 8”
D. “Ngày 19/5/2023 tại thị xã Hoàng Mai sẽ có mưa”. Câu 11: Cho A
∆ BC có ˆA = 56 ;° ˆ = ° ˆ
B 42 ;C = 82° , khẳng định nào sau đây đúng về quan hệ giữa các cạnh của A ∆ BC ?
A. BC > AC > AB .
B. AB > AC > BC .
C. AB > BC > AC .
D. BC > AB > AC .
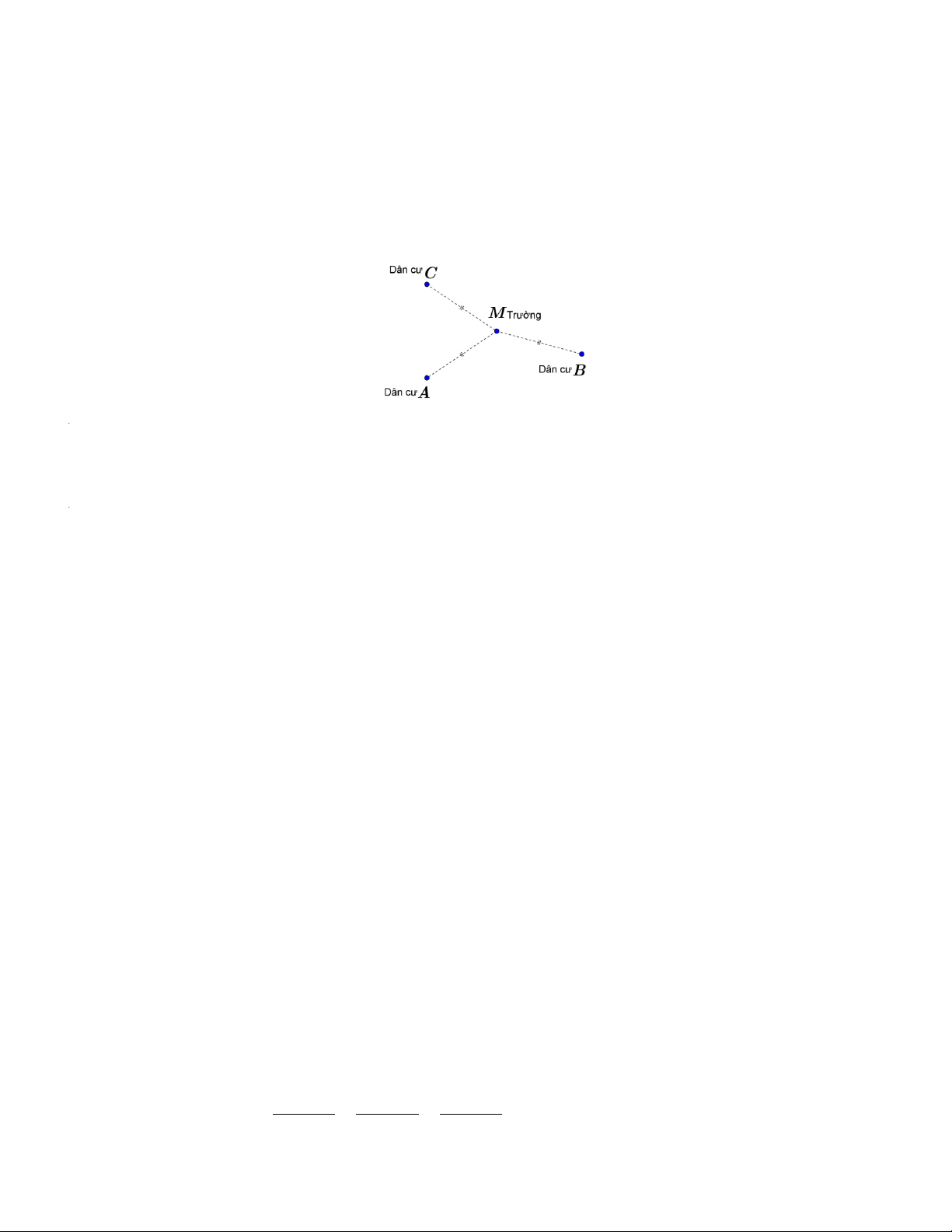
Câu 12: Trên bản đồ quy hoạch của một khu dân cư có ba điểm dân cư ,
A B,C . Xác định địa điểm
M xây dựng trường học sao cho trường học này cách đều ba điểm của dân cư đó.
m A. Điểm M cần tìm là giao điểm của hai đường trung trực của hai đoạn AB, AC .
B. Điểm M cần tìm là giao điểm của hai đường trung tuyến của A ∆ BC .
C. Điểm M cần tìm là giao điểm của hai đường cao của A ∆ BC .
m D. Điểm M cần tìm là giao điểm của hai đường phân giác của A ∆ BC .
II. TỰ LUẬN (7,0 điểm):
Bài 1. (1,5 điểm) Thực hiện phép tính: a) x( 2
3 x − 5x + 7) b) ( 5 6 9
3x + 9x +12x ):(3x) c) (x + )( x + ) 2 1 3 5 − 3x
Bài 2. ( 1 điểm ) Trong đợt tham gia hội trại kỉ niệm ngày thành lập Đoàn do liên đội trường THCS
Đa Tốn tổ chức, ba lớp 7A, 7B, 7C có tham gia làm gian hàng. Sau buổi bán hàng mỗi lớp đã lãi
được một số tiền. Biết số tiền lãi của ba lớp 7A, 7B, 7C tỉ lệ với 4, 5 và 2 và số tiền lãi của lớp 7A
nhiều hơn lớp 7C là 150 nghìn đồng. Hãy tính số tiền lãi mà ba lớp đã nhận được.
Bài 3.( 1,5 điểm ) Cho hai đa thức: A(x ) = 3 x + 2 x + x − 3 2
x + 3 và B (x ) = 2 x − x − 1 .
a) Thu gọn và cho biết bậc, hệ số cao nhất, hệ số tự do của A(x );
b) Tính B(1) . Tính C (x ) = A(x ) + B (x )
c) Tính D x = x B x + 2 ( )
. ( ) x + x − 1 và tìm nghiệm của D(x).
Bài 4. (2,5 điểm) Cho A
∆ BC cân tại A, kẻ AH vuông góc với BC tại H. a/ Chứng minh: A ∆ HB = A
∆ HC và AH là tia phân giác của  BAC .
b/ Từ H kẻ HM ⊥ AB , HN ⊥ AC ( M ∈AB, N ∈AC ). Chứng minh: MB = NC .
c) Trên tia đối của tia HM lấy điểm P sao cho H là trung điểm MP. Chứng minh: CP // AB.
d) Tia AH cắt MN tại K, NP cắt BC tại E, NH cắt ME tại Q. Chứng minh: P, Q, K thẳng hàng.
Bài 5 .(0,5 điểm): Tìm tất cả các số nguyên dương x, y, z thỏa mãn:
2z − 4x 3x − 2y 4y − 3z = = và 2 2
200 < y + z < 450. 3 4 2 - HẾT-
PHÒNG GD&ĐT GIA LÂM ĐỀ KIỂM TRA CUỐI HỌC KỲ II
TRƯỜNG THCS ĐA TỐN NĂM HỌC 2023-2024
Môn: TOÁN – Lớp 7( Tiết 135+136)
Thời gian: 90 phút (không kể thời gian giao đề) ĐỀ 2
I. TRẮC NGHIỆM (3,0 điểm). Chọn phương án trả lời đúng của mỗi câu hỏi sau: c
Câu 1. Nếu 3 = (d ≠ 0) thì: 2 d
A. 3c = 2 d .
B. 3 d = 2c.
C. 3: d = 2 : c .
D. cd = 6 . 3 −
Câu 2: Nếu y =
thì ta nói đại lượng y tỉ lệ nghịch với đại lượng x theo hệ số tỉ lệ là: x A. x B. -3 C. 3 D. 1 − Câu 3: Đa thức 12 5 6
7x − x + 6x +10 sắp xếp theo lũy thừa tăng dần của biến là: A. 5 6 12
10 + x + 6x + 7x B. 5 6 12
10 + x + 6x − 7x C. 5 6 12
10 − x + 6x + 7x D. 5 6 12
10 − x − 6x + 7x
Câu 4: Phát biểu nào sau đây đúng về hình hộp chữ nhật:
A. Có 6 mặt, 8 đỉnh và 12 cạnh.
B. Có 6 mặt, 8 cạnh và 12 đỉnh.
C. Có các mặt bên là hình chữ nhật bằng nhau
D. Có các cạnh bằng nhau
Câu 5: Trong các đa thức sau, đa thức một biến là A. 3 3 x + y . B. 3 x + 8 .
C. (x + y)(x − y) . D. ( − )3 x y .
Câu 6: Tích của hai đơn thức 2
5x và 3x là: A. 2 15x . B. 3 15x . C. 2 5x . D. 3 3x .
Câu 7: Nghiệm của đa thức P(x) =15x − 3 là: A. 1 − . B. 1 . C.5 . D. 5 − . 5 5
Câu 8: Gieo một con xúc xắc đồng chất được chế tạo cân đối. Số kết quả có thể xảy ra: A. 4. B. 5. C. 6. D. 7.
Câu 9: . Bộ ba số nào là độ dài ba cạnh của một tam giác?
A. 4𝑐𝑐𝑐𝑐, 5𝑐𝑐𝑐𝑐, 10𝑐𝑐𝑐𝑐.
B. 5𝑐𝑐𝑐𝑐, 5𝑐𝑐𝑐𝑐, 12𝑐𝑐𝑐𝑐.
C. 11𝑐𝑐𝑐𝑐, 11𝑐𝑐𝑐𝑐, 20𝑐𝑐𝑐𝑐.
D. 9𝑐𝑐𝑐𝑐, 20𝑐𝑐𝑐𝑐, 11𝑐𝑐𝑐𝑐.
Câu 10: "Khi gieo đồng xu thì được mặt sấp" là:
A. Biến cố ngẫu nhiên.
B. Biến cố chắc chắn.
C. Biến cố không thể.
D. Không phải là biến cố.
Câu 11: ∆𝐴𝐴𝐴𝐴𝐴𝐴 có 𝐴𝐴̂ = 900, 𝐴𝐴� =300 thì quan hệ giữa ba cạnh AB, AC, BC là:
A. BC > AC > AB. B. AC > AB > BC. C. AB > AC > BC. D. BC > AB > AC.
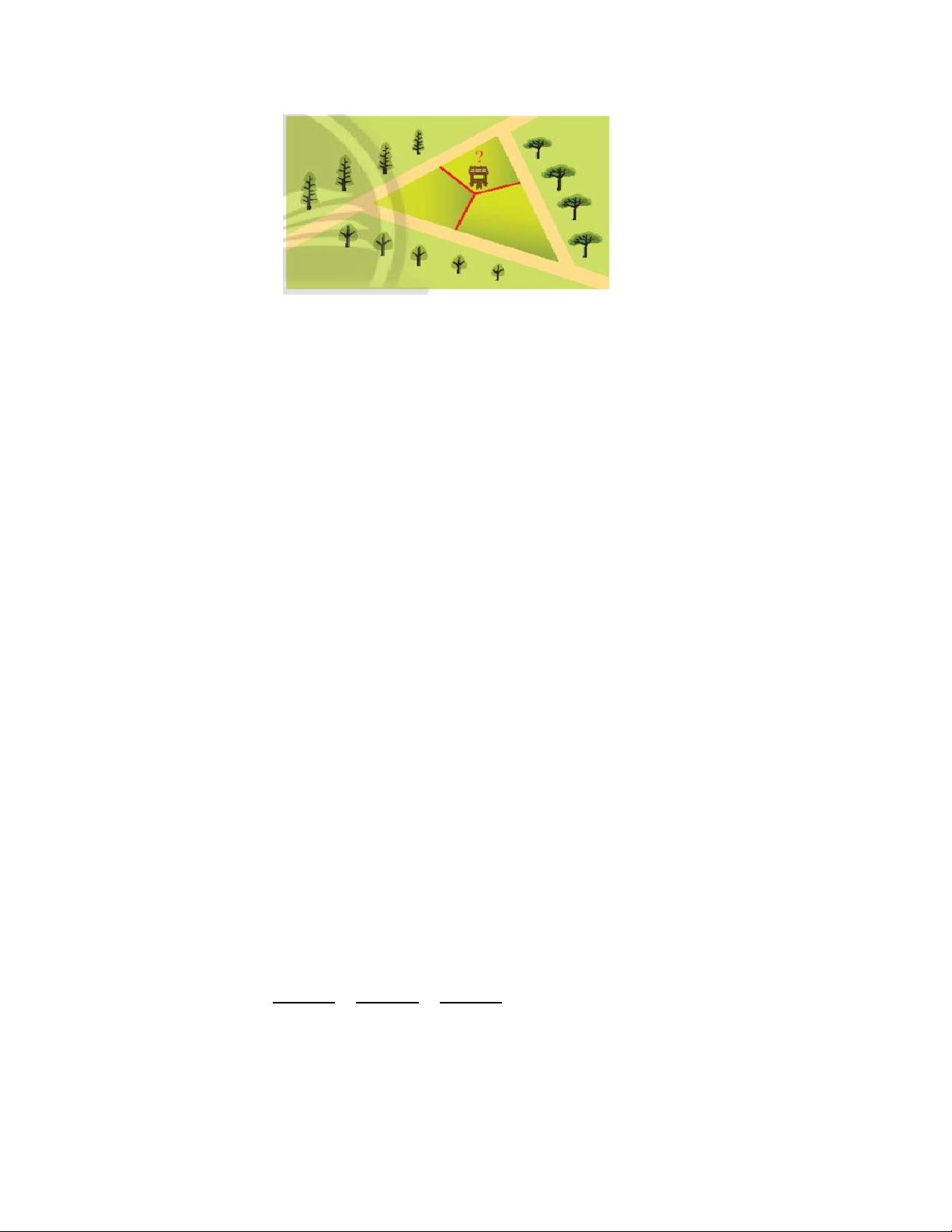
Câu 12: Một nông trại nằm trên mảnh đất hình tam giác có ba cạnh tường rào tiếp giáp với ba con
đường (hình bên). Hỏi phải đặt trạm quan sát ở đâu để nó cách đều ba cạnh tường rào?
A. Đặt trạm quan sát ở giao điểm của ba đường trung tuyến.
B. Đặt trạm quan sát ở giao điểm của ba đường phân giác.
C. Đặt trạm quan sát ở giao điểm của ba đường trung trực.
D. Đặt trạm quan sát ở giao điểm của ba đường cao.
II. TỰ LUẬN (7,0 điểm):
Bài 1. (1,5 điểm) Thực hiện phép tính: a) x( 2
2 x + 3x − 5) b) ( 4 6 8
x + x + x ) ( 2 4 2 12
: 2x ) c) (x + )( x + ) 2 1 2 1 − 2x
Bài 2. ( 1 điểm ) Trong đợt tham gia hội trại kỉ niệm ngày thành lập Đoàn do liên đội trường THCS
Đa Tốn tổ chức, ba lớp 7D, 7E, 7G có tham gia làm gian hàng. Sau buổi bán hàng mỗi lớp đã lãi
được một số tiền. Biết số tiền lãi của ba lớp 7D, 7E, 7G tỉ lệ với 5, 4 và 3 và số tiền lãi của lớp 7D
nhiều hơn lớp 7G là 100 nghìn đồng. Hãy tính số tiền lãi mà ba lớp đã nhận được.
Bài 3.( 1,5 điểm ) Cho hai đa thức: A(x ) = 4 x + 2 x − x − 4 3
x + 4 và B (x ) = 2 x + x − 3 .
a) Thu gọn và cho biết bậc, hệ số cao nhất, hệ số tự do của A(x );
b) Tính B(2) .Tính C (x ) = A(x ) + B (x )
c) Tính D x = x B x − 2 ( )
. ( ) x + 3x − 1và tìm nghiệm của D(x).
Bài 4. (2,5 điểm) Cho ∆OAB cân tại O, kẻ OM vuông góc với AB tại M.
a/ Chứng minh: ∆OMA = ∆OMB và OM là tia phân giác của  AOB .
b/ Từ M kẻ ME ⊥ OA , MF ⊥ OB ( E ∈OA, F ∈OB ). Chứng minh: AE = BF .
c) Trên tia đối của tia ME, lấy điểm H sao cho M là trung điểm HE. Chứng minh: BH // OA.
d) Tia OM cắt EF tại K, FH cắt AB tại I, EI cắt MF tại Q. Chứng minh: K, Q, H thẳng hàng.
Bài 5 : (0,5 điểm): Tìm tất cả các số nguyên dương x, y, z thỏa mãn:
2z − 4x 3x − 2y 4y − 3z = = và 2 2
200 < y + z < 450. 3 4 2 - HẾT -
PHÒNG GD & ĐT GIA LÂM
TRƯỜNG THCS ĐA TỐN
HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KỲ II NĂM HỌC 2023 - 2024 MÔN TOÁN 7
+) Điểm toàn bài để lẻ đến 0,25.
+) Các cách làm khác nếu đúng vẫn cho điểm tương ứng với biểu điểm của hướng dẫn chấm.
+) Các tình huống phát sinh trong quá trình chấm do Hội đồng chấm thi quy định, thống nhất bằng biên bản. Đề 1 Đề 2 Biểu điểm
Phần I: Trắc nghiệm (3đ) 1 2 3 4 5 6 1 2 3 4 5 6 Mỗi ý C C D B B B B B C A B B chọn 7 8 9 10 11 12 7 8 9 10 11 12 đúng: D D C A C A B C C A D B 0,25 đ
Phần II: Tự luận ( 7đ)
Bài 1 a) x( 2x − x + ) 3 2 3 5
7 = 3x −15x + 21x
a) x( 2x +3x − ) 3 2 2
5 = 2x + 6x −10x 0,5 ( 1,5 b) ( 5 6 9
3x + 9x +12x ):(3x) 4 6 8 2 đ)
b)(4x + 2x +12x ):(2x ) 0,5 4 5 8
= x + 3x + 4x 2 4 6
= 2x + x + 6x
c (x + )( x + ) 2 ) 1 3 5 − 3x c)(x + ) 1 (2x + ) 2 1 − 2x = 8x + 5 2 2
= 2x + 3x +1− 2x 0,5 = 3x +1
Bài 2 Gọi số tiền lãi mà ba lớp 7A, 7B, 7C nhận Gọi số tiền lãi mà ba lớp 7D, 7E, 7G 0,25 (1đ)
được lần lượt là x, y , z ( x, y, z > 0, nghìn nhận được lần lượt là x, y , z ( đồng)
x, y, z > 0, nghìn đồng) Theo đề bài ta có Theo đề bài ta có x y z 0,25 = = x y z
và x − z =150
= = và x − z =100 4 5 2 5 4 3
Áp dụng tính chất dãy tỉ số bằng nhau ta
Áp dụng tính chất dãy tỉ số bằng nhau có: ta có:
x y z x − z 150 − = = = = = 75 x y z x z 100 = = = = = 50 0,25 4 5 2 4 − 2 2 5 4 3 5 − 3 2 x = 75.4 = 300(TM) x = 250(TM) y = 75.5 = 375 (TM) y = 200 (TM) z = 75.2 = 150 (TM) z = 150 (TM)
Vậy số tiền lãi ba lớp nhận được là 300;
Vậy số tiền lãi ba lớp nhận được là 0,25 375; 150 nghìn đồng. 250; 200; 150 nghìn đồng. Bài 3 3 2 3 A x x 2x x x 3 4 2 4 A x x 3x x x 4 0,5 đ (1,5 a) ( ) = + + − + a) ( ) = + − − + = 2 2x + x + 3 = 2 3x − x + 4 0,25
điểm) Bậc: 2 ; HSCN :2, HSTD : 3 Bậc: 2 ; HSCN :3, HSTD : 4 b) B(1) = -1 b) B(2) = 3 2 (
A x) + B(x) = 3x + 2 2 (
A x) + B(x) = 4x +1 0,25 0,25
c) D x = x B x + 2 x + x − = 3 ( ) . ( ) 1 x − 1 c)
D x = x B x − 2 x + x − = 3 ( ) . ( ) 3 1 x − 1 0,25
D(x) = 0 suy ra x = 1
D(x) = 0 suy ra x = 1 Bài 4 Cho A
∆ BC cân tại A, kẻ AH vuông góc Cho ∆OAB cân tại O, kẻ OM vuông 2.5 đ (2,5 với BC tại H. góc với AB tại M.
điểm) a/ Chứng minh: A ∆ HB = A ∆ HC và AH
a/ Chứng minh: ∆OMA = ∆OMB và là tia phân giác của  BAC
OM là tia phân giác của  AOB . b/ Từ H kẻ HM ⊥ AB ,
b/ Từ M kẻ ME ⊥ OA , MF ⊥ OB
HN ⊥ AC ( M ∈AB, N ∈AC ). Chứng
( E ∈OA, F ∈OB ). Chứng minh: minh: MB = NC AE = BF .
c) Trên tia đối của tia HM lấy điểm P sao c) Trên tia đối của tia ME, lấy điểm H
cho H là trung điểm MP. Chứng minh: CP sao cho M là trung điểm HE. Chứng // AB. minh: BH // OA.
d) Tia AH cắt MN tại K, NP cắt BC tại E, d) Tia OM cắt EF tại K, FH cắt AB tại
NH cắt ME tại Q. Chứng minh: P, Q, K
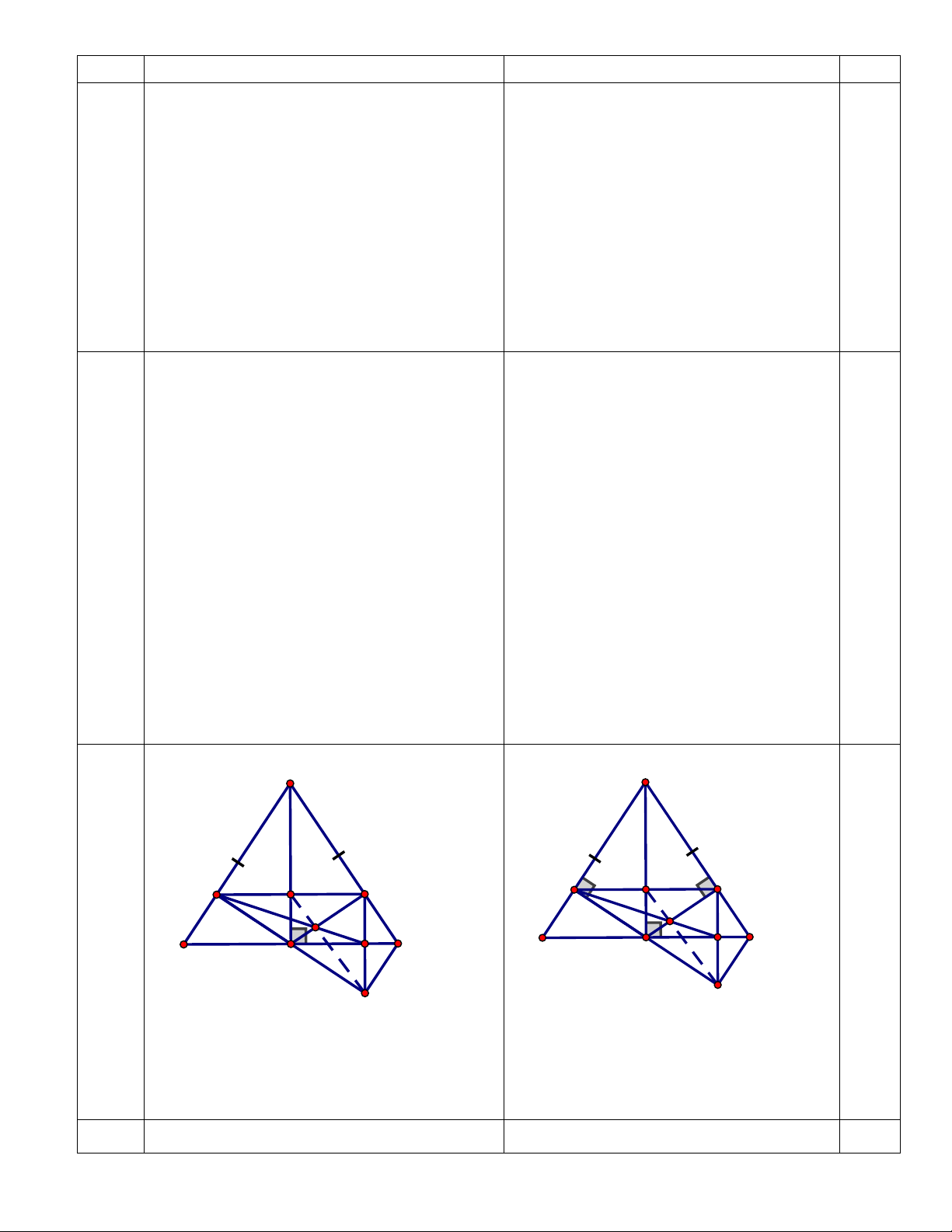
I, EI cắt MF tại Q. Chứng minh: K, Q, thẳng hàng. H thẳng hàng. 0.25 A O đ (vẽ hình đúng M N E F đến K K câu a Q Q A I B B E H C M H P a) Chứng minh A ∆ BH = A ∆ CH a) Chứng minh O ∆ MA = O ∆ MB 0.5đ
và AH là phân giác của góc BAC
và OM là phân giác của góc AOB 0.25 đ
b) Chứng minh: MB = NC b) Chứng minh: AE = BF . 0.5 đ c) Chứng minh: CP // AB. c) Chứng minh: BH // OA. 0,5 đ
d) Chứng minh đúng P, Q, K thẳng hàng. d) Chứng minh đúng P, Q, K thẳng 0,5 đ hàng.
Bài 5 2z − 4x 3x − 2y 4y − 3z = = 0,25 (0,5đ) 3 4 2 đ
6z −12x 12x −8y 8y − 6z ⇔ = = 9 16 4
Áp dụng tính chất của dãy tỉ số bằng nhau:
6z −12x 12x −8y 8y − 6z = = = 0 9 16 4
Do đó 6z =12x = 8y
Đặt 6z =12x = 8y = 24k (k ∈*) ⇒ ( ;x y; z) = (2k;3k;4k) 0,25 Theo giả thiết 2 2 2 2
200 < y + z < 450 ⇒ 200 < 9k +16k < 450 đ 2
⇒ 200 < 25k < 450 ⇒ k ∈{3; } 4
Từ đó tìm được ( ;x y; z)∈ ( { 6;9;12);(8;12;16)}
Document Outline

• Câu 8: Một hộp bút màu có các màu: màu xanh, màu vàng, màu đỏ, màu đen, màu hồng, màu cam. Hỏi nếu rút bất kỳ một cây bút màu thì có thể xảy ra mấy kết quả?