NXH Trang 1/5
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
KỲ THI THPT QUỐC GIA NĂM 2019
TRƯỜNG ISCHOOL NHA TRANG
Bài thi: Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề
(Đề thi có 05 trang)
Câu 1. Cho hàm số y = f(x) có đồ thị như hình bên, mệnh đề nào sau đây đúng ?
A. Hàm số nghịch biến trên khoảng
( )
;0 .−∞
B. Hàm số đồng biến trên khoảng
( )
1;1 .−
C. Hàm số đồng biến trên khoảng (–1; 3).
D. Hàm số nghịch biến trên khoảng
(
)
0; .+∞
Câu 2. Cho hàm số y = f(x) có bảng biến thiên như hình bên. Mệnh đề nào sau đây đúng ?
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị cực tiểu bằng
1
.
C. Hàm số đat cực đại tại
2x = −
và đạt cực
tiểu tại x = 1.
D. Hàm số đạt giá trị lớn nhất bằng 5 và giá trị
nhỏ nhất bằng –1.
Câu 3. Thể tích của khối hộp chữ nhật có ba kích thước a, 2a, 3a bằng
A.
3
2a
. B.
3
6a
. C.
3
36a
. D.
3
5a
.
Câu 4. Trong không gian Oxyz, cho
(1; 2;3)
a
= −
và
(3; 0; 4)b =
. Tính
.ab
.
A. 15. B. 36. C. 9. D. 5.
Câu 5. Với a và b là hai số thực dương và a ≠ 1,
log
a
a
b
bằng
A.
1 2log
a
b
+
. B.
1
1 log
2
a
b+
. C.
11
log
22
a
b−
. D.
1
1 log
2
a
b−
.
Câu 6. Cho
5
1
() 5f x dx
=
∫
và
3
1
() 7
f x dx =
∫
, tính
5
3
()
f x dx
∫
.
A.
2−
.
B. 12. C. 2. D.
12−
.
Câu 7. Cho hình nón có bán kính đáy bằng 5 và đường sinh bằng 12. Diện tích xung quanh của hình nón đó
bằng
A.
30 .
π
B.
120 .
π
C.
60 .
π
D. 60.
Câu 8. Phương trình
3
21
51
xx−+
=
có bao nhiêu nghiệm?
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 9. Trong không gian Oxyz, phương trình của mặt phẳng đi qua điểm A(2;6; –3) và song song với mặt
phẳng (Oxy) là
A. y - 6 = 0. B. z +3=0. C. x – 2 = 0. D. x + y – 8 = 0.
Câu 10. Tìm
(sin 2 1)x dx+
∫
.
A.
cos 2xxC++
. B.
1
cos 2
2
xC−+
. C.
1
cos 2
2
xxC++
. D.
1
cos 2
2
xxC
− ++
.
Câu 11. Trong không gian Oxyz, cho đường thẳng d :
22
3
35
xt
yt
zt
= +
= −
=−+
. Phương trình chính tắc của d là
A.
233
.
2 35
xyz−++
= =
−
B.
23
.
2 35
x yz+−
= =
−
C.
.
2 35
xyz
= =
−
D.
23
.
2 35
x yz−+
= =
−
Câu 12. Trong các mệnh đề sau đây, mệnh đề nào sai ?
ĐỀ THI ĐỀ XUẤT
NXH Trang 2/5
A.
!
(0 ).
!( )!
k
n
n
C kn
knk
= ≤≤
−
B.
!
(1 ).
( )!
k
n
n
A kn
nk
= ≤≤
−
C.
! (0 ).
kk
nn
C kA k n= ≤≤
D. P
n
= n! (n ≥ 1).
Câu 13. Cho cấp số nhân (u
n
) có
17
1
, 32
2
uu=−=−
. Giá trị của công bội q bằng
A.
1
.
2
±
B.
2.
±
C.
4.
±
D.
1.
±
Câu 14. Cho số phức
25
34
z
i
=
+
. Điểm biểu diễn hình học số phức liên hợp của z trong mặt phẳng Oxy là
A.
( )
3; 4−
. B.
( )
2; 3−
. C.
( )
3; 2−
. D.
(
)
3; 4
.
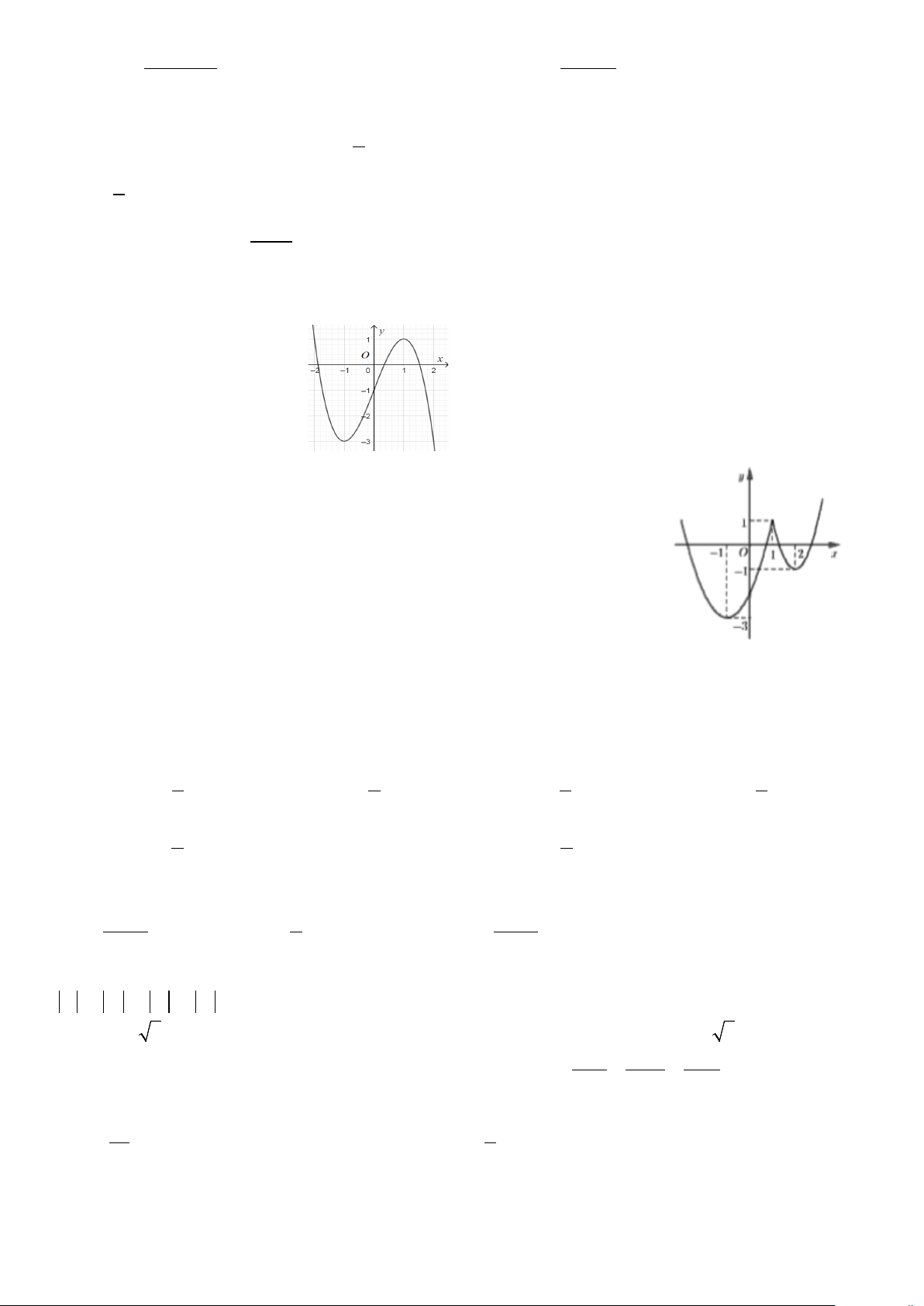
Câu 15. Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau đây ?
A.
42
1=−+ −y xx
.
B.
3
1
=− +−y xx
.
C.
3
31=−+ −
yx x
.
D.
3
35=−+yx x
.
Câu 16. Cho hàm số
( )
=y fx
liên tục trên đoạn
[ ]
1;2
−
và có đồ thị như hình
vẽ bên.Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho
trên đoạn
[ ]
1;2−
. Giá trị của
Mm−
bằng
A. –3.
B. 1.
C. 3.
D. 4.
Câu 17. Cho hàm số
()y fx=
có đạo hàm
23
( ) ( 1)( 2)fx x x
′
=−+
,
xR∀∈
. Hàm số có bao nhiêu điểm cực trị ?
A. 3. B. 2. C. 5. D. 1.
Câu 18. Cho số phức
2 (, )
z a bi a b=+∈
. Khi đó phần thực của số phức
(2 )(3 )w zi i=+−
bằng
A.
6 2 1.ab++
B.
2 12 3.ab−+ +
C.
6 4 1.ab++
D.
2 6 3.ab−++
Câu 19. Trong không gian
,Oxyz
cho hai điểm
( 1; 2;1), (0; 2;3).AB−
Phương trình mặt cầu
()S
đường kính
AB
là
A.
( ) ( )
2
22
15
( ): 2 2 .
24
Sx y z
+ +− +− =
B.
(
) ( )
2
22
15
( ): 2 2 .
24
Sx y z
− ++ ++ =
C.
( ) ( )
2
22
1
( ) : 2 2 5.
2
Sx y z
+ +− +− =
D.
( ) ( )
2
22
1
( ) : 2 2 5.
2
Sx y z
− ++ ++ =
Câu 20. Đặt
2
log 6 a=
, khi đó log
3
18 bằng
A.
21
.
1
a
a
+
−
B.
1
2.
a
+
C.
21
.
1
a
a
−
−
D. 2 – 3a.
Câu 21. Kí hiệu
1234
,,,zzzz
là bốn nghiệm phức của phương trình
42
4 5 0.zz+ −=
Giá trị của
2222
1234
zzzz+++
bằng
A.
2 2 5.+
B. 12. C. 0. D.
2 5.+
Câu 22. Trong không gian
Oxyz
, khoảng cách giữa đường thẳng
123
:
22 3
xy z
d
+−+
= =
−
và mặt phẳng
( ): 2 2 5 0Px y z− + −=
bằng
A.
16
.
3
B. 2. C.
5
.
3
D. 3.
Câu 23. Tập nghiệm của bất phương trình
2
2
28
xx−
<
là
A.
( 1; 3)−
. B.
(3; )+∞
. C.
( ; 1)−∞ −
. D.
( ; 1) (3; )−∞ − ∪ +∞
.
NXH Trang 3/5
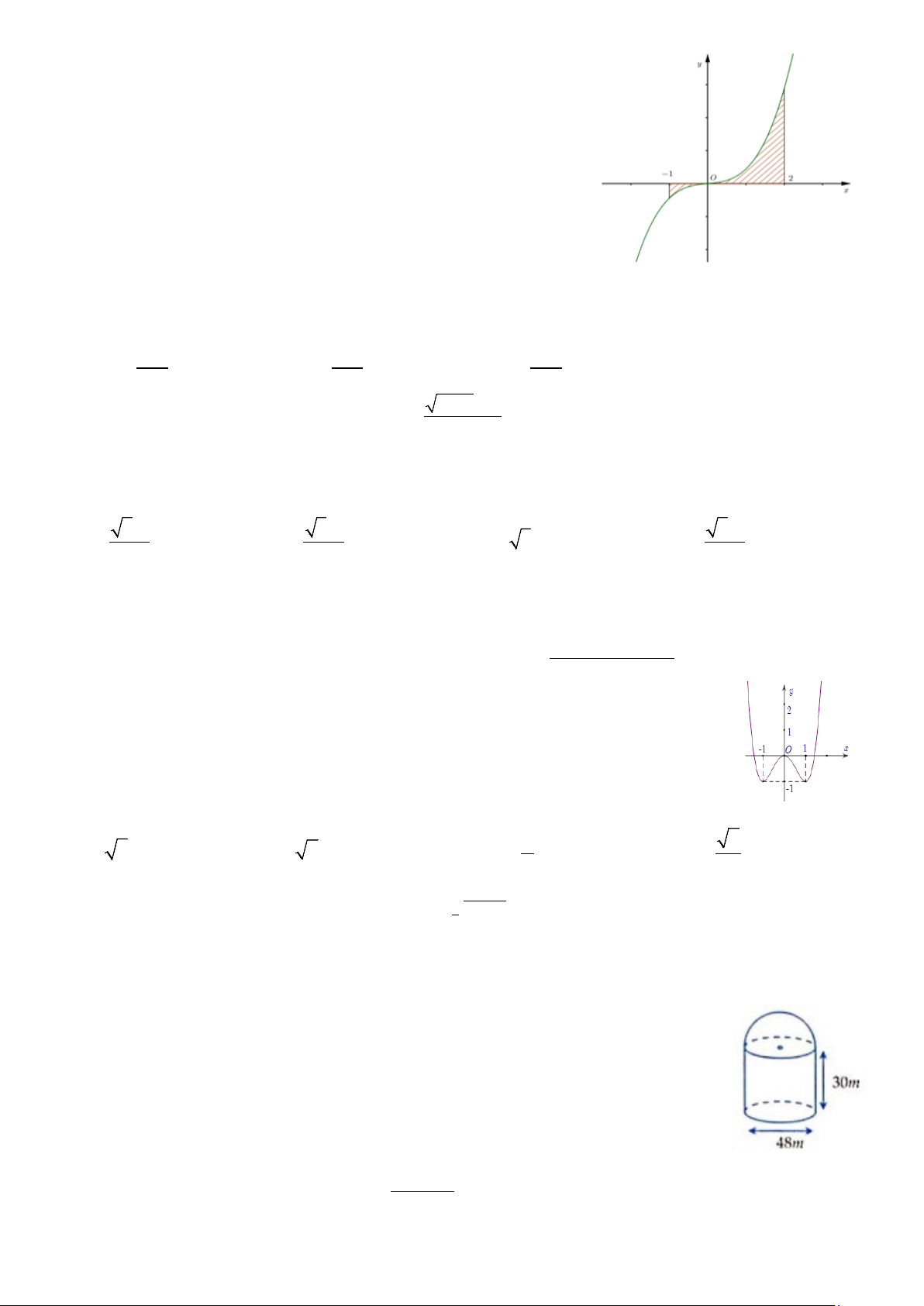
Câu 24. Gọi
S
là diện tích hình phẳng
( )
H
giới hạn
bởi các đường:
( )
, y fx=
trục hoành và hai đường thẳng
1, 2
xx=−=
trong hình vẽ bên.
Đặt
( )
(
)
02
12
10
, .S f x dx S f x dx
−
= =
∫∫
Mệnh đề nào sau đây đúng?
A.
12
.SS S= +
B.
12
.
S SS=−−
C.
12
.SSS= −
D.
21
.SS S= −
Câu 25. Cho hình chữ nhật ABCD có AB = a, BC = 2a. Gọi M, N lần lượt là trung điểm của AB và CD. Thể
tích của khối trụ tạo thành khi quay hình chữ nhật ABCD quanh trục MN bằng
A.
3
.
6
a
V
π
=
B.
3
.
2
a
V
π
=
C.
3
.
4
a
V
π
=
D.
3
2.Va
π
=
Câu 26. Số tiệm cận đứng của đồ thị hàm số
2
42x
xx
y
là
A. 3. B. 0. C. 2. D. 1.
Câu 27. Cho khối chóp
.S ABC
có đáy là tam giác đều cạnh 2a,
(
)
SA ABC⊥
,
SA a=
. Thể tích của khối
chóp đã cho bằng
A.
3
3
4
a
. B.
3
3
6
a
. C.
3
3a
. D.
3
3
3
a
.
Câu 28. Hàm số
3
2 34
5
xx
y
+−
=
có đạo hàm
A.
3
2 34
' 5 ln 5.
xx
y
+−
=
B.
3
2 2 34
' (6 3)5 ln 5.
xx
yx
+−
= +
C.
3
2 2 34
' (6 3)5 .
xx
yx
+−
= +
D.
3
2 2 34
(6 3)5
'.
ln 5
xx
x
y
+−
+
=
Câu 29. Cho hàm số
y fx
liên tục trên
và có đồ thị như hình vẽ bên. Số nghiệm
thực của phương trình
5 40
fx
là
A. 4 B. 3 C. 2 D. 0
Câu 30. Cho hình lập phương ABCD.A’B’C’D’. Tang của góc giữa hai mặt phẳng (A’BD) và (ABCD) bằng
A.
3
. B.
2
. C.
1
2
. D.
2
2
.
Câu 31. Số nghiệm nguyên của bất phương trình
1
2
31
log 1
1
x
x
+
≥−
+
là
A. 1. B. 2 C. 3. D. 4.
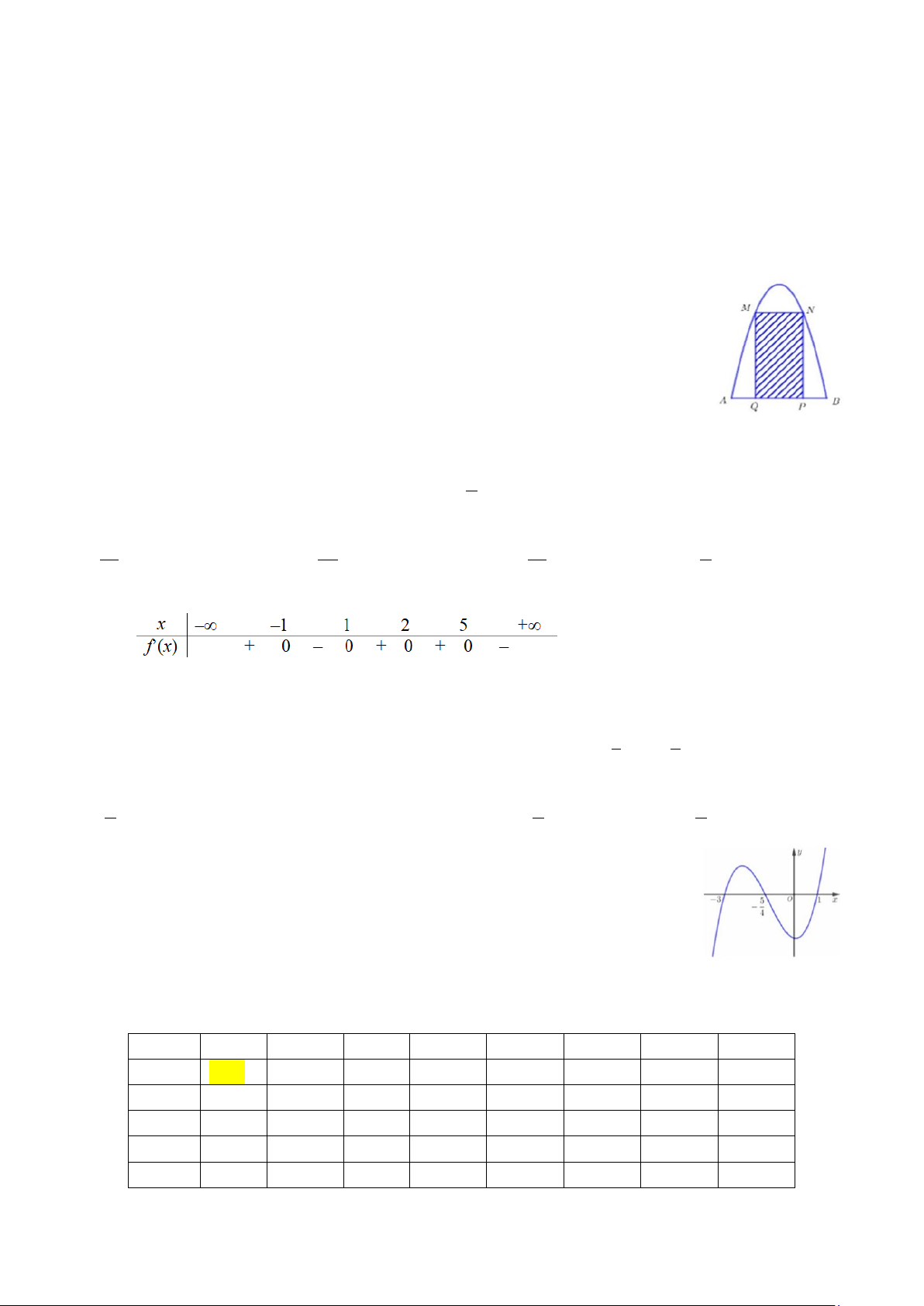
Câu 32. Một cái tháp có thân là hình trụ và mái là một nửa hình cầu. Người ta muốn
sơn toàn bộ mặt ngoài của tháp (kể cả mái). Tính diện tích S cần sơn (làm tròn đến
mét vuông).
A.
( )
2
8143 .Sm=
B.
(
)
2
11762 .Sm
=
C.
( )
2
12667 .Sm=
D.
( )
2
23524 .Sm=
Câu 33. Họ nguyên hàm của hàm số
( )
2
()
1
x
x
e
fx
e
=
+
là

NXH Trang 4/5
A.
2
1
x
C
e
+
+
. B.
2
1
x
C
e
−
+
+
. C.
1
1
x
C
e
−
+
+
. D.
1
1
x
C
e
+
+
.
Câu 34. Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại A, AB = a, cạnh bên
'2AA a=
. Gọi M là trung điểm của BC. Khoảng cách giữa hai đường thẳng AM và B’C bằng
A.
2.a
B.
3
.
4
a
C.
2
.
2
a
D.
.
2
a
Câu 35. Trong không gian Oxyz, cho điểm
( )
1; 0; 2A
và đường thẳng
11
:
112
x yz
d
−+
= =
. Phương trình
đường thẳng
∆
đi qua A, vuông góc và cắt d là
A.
12
.
111
x yz−−
= =
B.
12
.
11 1
x yz−−
= =
−
C.
12
.
221
x yz−−
= =
D.
12
.
1 31
x yz−−
= =
−
Câu 36. Tìm các giá trị thực của tham số m để đồ thị hàm số
32
( 1) 3 ( 1) 2y x mx=−− + −−
có hai điểm cực
trị cách đều gốc tọa độ.
A.
1
.
3
m
= ±
B.
1
.
2
m
= ±
C.
5.
m = −
D.
5.m =
Câu 37. Cho số phức z thỏa mãn
1 2; (1 3 ) 2z w iz−= = + +
.Tập hợp điểm biểu diễn các số phức
w
là một
đường tròn, bán kính của đường tròn đó bằng
A. 5. B. 3. C. 4. D. 2.
Câu 38. Cho
0
2
1
3 51 2
ln
23
xx
dx a b
x
−
+−
= +
−
∫
với a, b là các số hữu tỉ. Tính
2.ab+
A. 60. B. 50. C. 30. D. 40.
Câu 39. Cho hàm số
()y fx
=
có bảng xét dấu đạo hàm như sau
Bất phương trình
2
2
()
xx
fx e m
−
<+
đúng với mọi
(0; 2)x ∈
khi và chỉ khi
A.
1
(1) .mf
e
>−
B.
1
(1) .mf
e
≥−
C.
(0) 1.mf>−
D.
(0) 1.mf≥−
Câu 40. Có hai dãy ghế đối diện nhau, mỗi dãy có bốn ghế. Xếp ngẫu nhiên 8 học sinh, gồm 4 nam và 4 nữ,
ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi
đối diện với một học sinh nữ và không có hai học sinh cùng giới ngồi cạnh nhau bằng
A.
8
.
35
B.
1
.
35
C.
2
.
35
D.
4
.
35
Câu 41. Trong không gian Oxyz, cho hai điểm A(3;1;1), B(7;3;9) và mặt phẳng (P): x + y + z + 3 = 0. Điểm
M (x; y; z) thuộc (P) sao cho
MA MB+
đạt giá trị nhỏ nhất. Giá trị của x + y + z bằng
A. – 3. B. 3. C. 0. D. 2.
Câu 42. Cho số phức z không phải là số thực và
2
2
24
24
zz
zz
−+
++
là số thực. Có bao nhiêu số phức z thỏa mãn
2
?zz zz z++−=
A.0. B. 2. C. 4. D. 8.
Câu 44. Ông A vay ngân hàng 200 triệu đồng với lãi suất 0,6% một tháng theo thỏa thuận: Sau đúng một
tháng kể từ ngày vay thì ông bắt đầu trả nợ và đều đặn cứ mỗi tháng ông A sẽ trả cho ngân hàng 9 triệu đồng
Câu 43. Cho hàm số
()y fx=
xác định trên
và có đồ thị như hình vẽ bên. Có bao
nhiêu giá trị nguyên của tham số m để phương trình
( )
44
4 sin cosf x xm
+=
có
nghiệm?
A. 2. B. 4. C. 3. D. 5.
NXH Trang 5/5
cho đến khi hết nợ (biết rằng, tháng cuối cùng có thể trả dưới 9 triệu đồng). Hỏi sau bao nhiêu tháng thì ông
A trả hết nợ cho ngân hàng ?
A. 22 tháng. B. 23 tháng. C. 24 tháng. D. 25 tháng.
Câu 45. Trong không gian Oxyz, cho điểm E(1;1;1), mặt cầu
2 22
( ): 4Sx y z++=
và mặt phẳng
( ) : 3 5z 3 0.Px y
− + −=
Gọi ∆ là đường thẳng đi qua E, nằm trong (P) và cắt (S) tại hai điểm A, B sao cho
OAB là tam giác đều. Phương trình của ∆ là
A.
12
1.
1
xt
yt
zt
= +
= +
= +
B.
14
1 3.
1
xt
yt
zt
= +
= +
= +
C.
12
1.
1
xt
yt
zt
= +
= −
= −
D.
1
1.
12
xt
yt
zt
= +
= +
= −
Câu 46. Một chiếc cổng có hình dạng là một Parabol có khoảngcách giữa hai chân
cổng là 8m. Người ta treo một tấm phông hình chữ nhật có hai đỉnh M, N nằm trên
Parabol và hai đỉnh P, Q nằm trên mặt đất như hình vẽ bên. Ở phần phía ngoài phông
(phần không kẻ) người ta mua hoa để trang trí với chi phí 200.000 đồng/m
2
,
biết MN = 4m, MQ = 6m. Hỏi số tiền để mua hoa trang trí gần với số tiền nào sau đây?
A. 3.434.300 đồng. B. 3.373.400 đồng.
C. 3.437.300 đồng. D. 3.733.300 đồng.
Câu 47. Cho khối lăng trụ ABC.A’B’C’ có thể tích bằng 2. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh
AA’và BB’ sao cho M là trung điểm của AA’và
2
'.
3
BN BB=
Đường thẳng CM cắt đường thẳng C’ A ’ tại P
và đường thẳng CN cắt đường thẳng C’B’ tại Q. Thể tích khối đa diện lồi A’MPB’NQ bằng
A.
13
.
18
B.
23
.
9
C.
7
.
18
D.
5
.
9
Câu 48. Cho hàm số
()fx
có bảng xét dấu của đạo hàm như sau
Hàm số
3
3 ( 3) 12y fx x x= +−+
nghịch biến trên khoảng nào sau đây ?
A.
( )
; 1.−∞ −
B.
( )
1; 0 .−
C.
( )
0; 2 .
D.
( )
2; .+∞
Câu 49. Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số
25 3 2 2
11
( ) 10 ( 20)
53
f x m x mx x m m x= − + − −−
đồng biến trên
. Tổng giá trị của tất cả các phần tử thuộc S bằng
A.
3
.
2
B.
2.−
C.
5
.
2
D.
1
.
2
Câu 50. Cho hàm số
432
() (,,, , )
f x ax bx cx dx m a b c d m= + + ++ ∈
.
Hàm số
'( )y fx=
có đồ thị như hình vẽ bên. Tập nghiệm của phương trình
()fx m=
có số phần tử là
A. 1. B. 2.
C. 3. D. 4.
--------------HẾT--------------
ĐÁP ÁN
1. B
7. C
13. B
19. A
25. B
31. B
37. C
43. D
49. D
2. C
8. B
14. D
20. C
26. D
32. A
38. D
44. C
50. C
3. B
9. B
15. C
21. B
27. D
33. C
39. A
45. C
4. A
10. D
16. D
22. A
28. B
34. D
40. B
46. D
5. D
11. D
17. A
23. A
29. A
35. B
41. A
47. B
6. A
12. C
18. C
24. D
30. B
36. B
42. B
48. D

NTP Trang 1/5
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
KỲ THI THPT QUỐC GIA NĂM 2019
TRƯỜNG THPT ĐOÀN THỊ ĐIỂM
Bài thi: Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề
(Đề thi có 05 trang)
Câu 1. Hàm số
42
3y xx=−− +
đồng biến trên khoảng nào dưới đây?
A.
(0; )+∞
. B.
( ;0)−∞
. C.
( ;1)
−∞
. D.
( 2; 2)−
.
Câu 2. Cho hàm số
4
mx
y
xm
+
=
+
với
m
là tham số . Gọi
S
là tập hợp tất cả các giá trị nguyên của
m
để hàm số nghịch biến trên từng khoảng xác định. Số phần tử của
S
là
A.
3
. B.
5
. C.
2
. D. Vô số.
Câu 3. Cho hàm số
()
y fx=
có bảng biến
thiên như hình vẽ. Số điểm cực trị của hàm
số
()y fx=
là
A.
0.
B.
1.
C.
2.
D.
3
.
x
y’
y
+
−∞
+∞
+∞
–1
0
1
0 00 +
––
1
1
2
+∞
Câu 4. Tất cả các giá trị nguyên của tham số
m
để đồ thị hàm số
42
22y x mx m=−+
có 3 điểm cực
trị cùng với gốc tọa độ
O
tạo thành bốn đỉnh của một hình vuông là
A.
1m = −
. B.
4m
= −
. C.
1m
=
. D.
4m =
.
Câu 5. Giá trị nhỏ nhất của hàm số
4
yx
x
= +
trên
[
]
1; 4
bằng
A.
5
. B.
2
. C.
4−
. D.
4
.
Câu 6. Cho hàm số
2
1
mx
y
x
=
+
với
m
là tham số thực. Tất cả các giá trị của
m
để
[ ]
[ ]
0;2
0;2
2
min max
3
yy
+=
là
A.
1m =
. B.
1m = −
. C.
{ }
1;1m
∈−
. D.
{ }
0;1m ∈
.
Câu 7. Trong bốn hàm số dưới đây, đồ thị của hàm số nào có tiệm cận ngang?
A.
32
2yx x= −
. B.
42
25y xx=−+
. C.
2
41yx x= −−
. D.
2
9y x xx= +−
.
Câu 8. Tập hợp tất cả các giá trị thực của tham số thực
m
để đồ thị hàm số
( )
2
2
4
1
x
y
x m xm
−
=
−+ +
có
hai tiệm cận đứng phân biệt là
A.
{
}
\ 2;1; 2−
. B.
{ }
\1
. C.
{ }
\ 2;2−
. D.
( )
1; +∞
.
Câu 9. Đường cong như của hình vẽ bên là đồ thị của
hàm số nào dưới đây?
A.
42
1yx x
=−+
.
B.
32
1yx x=−+
.
C.
32
31yx x=−+ −
.
D.
32
31yx x=−+
.
2
-2
-1
1
O
x
y
Câu 10. Số điểm chung Đồ thị hàm số
42
22yx x=−+
và đồ thị hàm số
2
4yx=−+
là
A. 0. B. 1. C. 2. D. 4.
ĐỀ THI ĐỀ XUẤT

NTP Trang 2/5
Câu 11. Một vật chuyển động theo quy luật
32
1
9
2
s tt=−+
, với
t
(giây) là khoảng thời gian tính từ
lúc vật bắt đầu chuyển động và
s
(mét) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi
trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được
bằng
A. 216 (m/s). B. 30 (m/s). C. 400 (m/s). D. 54 (m/s).
Câu 12. Phương trình tiếp tuyến
∆
của đồ thị hàm số
4
yx x= +
tại điểm có hoành độ bằng 1 là
A.
: 55yx∆=−
. B.
: 53yx∆=−
. C.
: 57yx∆=+
. D.
: 53
yx∆ =−−
.
Câu 13. Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
(
)
3
2
2
() 2 2f x x mx= ++
xác định với
mọi
x ∈
?
A.
5
. B.
4
. C.
7
. D.
9
.
Câu 14. Cho
, ab
là hai số thực dương. biểu thức
24
log 2log
Pa b= −
bằng
A.
( )
2
logP ab=
. B.
2
log
a
P
b
=
. C.
2
2
log
a
P
b
=
. D.
2
4
log
a
P
b
=
.
Câu 15. Biết hàm số
(
)
2
ln 1
()
x
fx
x
+
=
có
( )
(1) ln 2 ,
f a b ab
′
=+∈
. Tính
S ab= +
.
A.
1S =
. B.
0
S =
. C.
2S =
. D.
1S
= −
.
Câu 16. Tập nghiệm bất phương trình
( ) ( )
2
23 23
xx+
− >+
là
A.
( )
1;− +∞
. B.
( )
;2−∞ −
. C.
( )
2;− +∞
D.
( )
;1−∞ −
.
Câu 17. Gọi
S
là tổng tất cả các nghiệm của phương trình
( )
2
log 3.2 1 2 1
x
x−= +
. Tổng
S
bằng
A.
0
S =
. B.
1S
= −
. C.
3
2
S =
. D.
1
2
S =
.
Câu 18. Tập hợp tất cả các giá trị thực của tham số
m
để phương trình
1
93
xx
m
+
−=
có nghiệm
thực là
A.
9
4
m ≥−
. B.
0m >
. C.
1m ≤−
. D.
5
8
m ≥
.
Câu 19. Số lượng của loại vi khuẩn A trong một phòng thí nghiệm được tính theo công thức
( ) (0)2
t
st s=
, trong đó
(0)s
là số lượng vi khuẩn A lúc ban đầu,
()st
là số lượng vi khuẩn A có sau
t
phút. Biết sau 3 phút thì số lượng vi khuẩn A là 625 nghìn con. Hỏi sau bao lâu, kể từ lúc bắt đầu,
số lượng vi khuẩn A là 10 triệu con?
A. 48 phút. B. 19 phút. C. 7 phút. D. 12 phút.
Câu 20. Nguyên hàm của hàm số
2
( ) cosfx x=
là
A.
2
11
cos sin 2
22
xdx x x C
=−+
∫
. B.
2
11
cos sin 2
22
xdx x x C
=++
∫
.
C.
( )
2
1
cos sin 2
2
xdx x x C=++
∫
. D.
( )
2
1
cos 2sin 2
2
xdx x x C=++
∫
.
Câu 21. Biết
2
()Fx x=
là một nguyên hàm của hàm số
2
()
x
f xe
. Nguyên hàm của hàm số
2
()
x
f xe
′
là
A.
22
() 2
x
f x e dx x x C
′
=−+ +
∫
. B.
22
()
x
f x e dx x x C
′
=− ++
∫
.
C.
22
() 2 2
x
f x e dx x x C
′
= −+
∫
. D.
22
() 2 2
x
f x e dx x x C
′
=− ++
∫
.

NTP Trang 3/5
Câu 22. Biết
4
0
() 5f x dx =
∫
. Tính
3
2
1
2
(2 1)I f x dx
−
= +
∫
.
A.
5
2
I =
. B.
10I =
. C.
4I =
. D.
0I =
.
Câu 23. Biết
b
là số thực dương thỏa mãn
( )
1
25 4
b
x dx
−=
∫
. Mệnh đề nào dưới đây đúng?
A.
( )
5;6b∈
. B.
( )
6;7b
∈
. C.
( )
4;b∈ +∞
. D.
( )
0;3b∈
.
Câu 24. Biết
(
)
2
1
ln 7 ln 2 ,
31
dx
a b ab
x
=+∈
+
∫
. Mệnh đề nào dưới đây đúng?
A.
( )
1; 0ab∈−
. B.
( )
0;1ab∈
. C.
(
)
1; 2
ab∈
. D.
(
)
2;3
ab∈
.
Câu 25. Gọi
V
là thể tích của khối tròn xoay sinh ra khi cho hình phẳng giới hạn bởi các đường
2
1 , 0y xy=−=
quay quanh trục
Ox
. Khẳng định nào sau đây đúng?
A.
( )
1
2
1
1V x dx
−
= −
∫
. B.
( )
1
2
1
1V x dx
π
−
= −
∫
.
C.
1
2
1
1V x dx
π
−
= −
∫
. D.
1
2
1
1V x dx
−
= −
∫
.
Câu 26. Tính diện tích
S
của hình phẳng giới hạn bởi các đường
2
2 , 2y x xx y=− + +=
.
A.
4,5S =
. B.
1
7
S =
. C.
1
5
S =
. D.
1
6
S =
.
Câu 27. Cho số phức
12zi= +
. Tìm phần ảo của số phức
2w zz= +
.
A. Phần ảo của
w
bằng 2. B. Phần ảo của
w
bằng
2i
.
C. Phần ảo của
w
bằng
2−
. D. Phần ảo của
w
bằng
2i
−
.
Câu 28. Gọi
A
và
B
là hai điểm trong mặt phẳng biểu diễn hai nghiệm phức phân biệt của phương
trình
2
6 12 0zz++=
. Tính độ dài của đoạn thẳng
AB
.
A.
12AB =
. B.
3AB =
. C.
23AB =
. D.
3
AB =
.
Câu 29. Cho số phức
( )
,z a bi a b=+∈
thỏa mãn
( )
1 2 32iz z i++=+
. Tính
Pab= +
.
A.
1
2
P =
. B.
1P =
. C.
1P
= −
. D.
1
2
P = −
.
Câu 30. Xét số phức
z
thỏa mãn
( )
10
12 2
iz i
z
+ = −+
. Mệnh đề nào dưới đây đúng?
A.
3
2
2
z<<
. B.
2z >
. C.
1
2
z <
. D.
13
22
z<<
.
Câu 31. Số hạng chứa
4
x
trong khai triển của biểu thức
( )
7
3
x+
là
A.
44
7
Cx
. B.
44
7
27Cx
. C.
4
7
27C
. D.
4
27x
.
Câu 32. Gieo một con súc sắc cân đối và đồng chất sáu lần liên tiếp. Xác suất để số chấm xuất hiện
trong sáu lần gieo là sáu số tự nhiên phân biệt, đồng thời tổng số chấm xuất hiện trong hai lần gieo
liên tiếp bất kì là một số tự nhiên có một chữ số bằng
A.
323
324
. B.
1
324
. C.
161
162
. D.
1
162
.
Câu 33. Tất cả các giá trị thực của tham số
m
để phương trình
2
cos cos 1 0x xm− + −=
có nghiệm
thực là

NTP Trang 4/5
A.
5
1;
4
m
∈−
. B.
5
;1
4
m
∈−
. C.
5
;
4
m
∈ +∞
. D.
5
;
4
m
∈ −∞
.
Câu 34.
2
2
23
lim
6
x
xx
x
→−∞
−+
−
bằng
A.
1
. B.
1
−
. C.
2
. D.
2−
.
Câu 35. Tập nghiệm của bất phương trình
54 2xx+≤+
bằng
A.
[
)
1;
+∞
. B.
4
;0
5
−
. C.
[ ]
4
; 0 1; 2
5
−∪
. D.
[
)
4
; 0 1;
5
− ∪ +∞
.
Câu 36. Cho tam giác
ABC
có
5, 6, 7AB AC BC= = =
. Gọi
M
là trung điểm của cạnh
AC
. Tính
bán kính
R
của đường tròn ngoại tiếp tam giác
ABM
.
A.
5 42
12
R =
. B.
5
12
R =
. C.
42
12
R =
. D.
12
5
R =
.
Câu 37. Cho hình chóp đều
.
S ABCD
có độ dài cạnh bên bằng
3a
và độ dài cạnh đáy bằng
2a
.
Thể tích của khối chóp
.S ABCD
bằng
A.
3
23
3
a
. B.
3
22a
. C.
3
2
3
a
. D.
3
22
3
a
.
Câu 38. Cho hình hộp chữ nhật
.ABCD A B C D
′′′′
có đáy ABCD là hình vuông. Biết diện tích toàn
phần của hình hộp đó bằng 32. Thể tích lớn nhất
0
V
của khối hộp chữ nhật
.ABCD A B C D
′′′′
bằng
A.
0
56 3
9
V =
. B.
0
70 3
9
V =
. C.
0
64 3
9
V =
. D.
0
80 3
9
V =
.
Câu 39. Tính thể tích
V
của khối nón có bán kính đáy bằng 3 và diện tích xung quanh bằng
15
π
.
A.
12V
π
=
. B.
20V
π
=
. C.
36V
π
=
. D.
60V
π
=
.
Câu 40. Một hình trụ có diện tích toàn phần là
6
π
và có thiết diện cắt bởi mặt phẳng qua trục là hình
vuông. Thể tích
V
của khối trụ tạo nên bởi hình trụ đã cho bằng
A.
4V
π
=
. B.
8
V
π
=
. C.
6V
π
=
. D.
2V
π
=
.
Câu 41. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
AB a=
,
3, 4
AD a SA a= =
và
SA
vuông góc với
()ABCD
. Tính bán kính
R
của mặt cầu ngoại tiếp hình chóp
.S ABCD
.
A.
2Ra=
. B.
5Ra=
. C.
3Ra=
. D.
Ra=
.
Câu 42. Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
B
và
()SA ABC⊥
. Biết
2SB a=
,
BC a=
và thể tích của khối chóp
.S ABC
là
3
3
a
. Khoảng cách
h
từ
A
đến
( )
SBC
bằng
A.
ha=
. B.
3
a
h =
. C.
2
a
h =
. D.
3
2
a
h =
.
Câu 43. Cho lăng trụ đều
.ABC A B C
′′′
có cạnh bên bằng
3a
, cạnh đáy bằng
2a
.Góc giữa hai mặt
phẳng
( )
A BC
′
và
( )
ABC
bằng
A.
0
90
. B.
0
60
. C.
0
45
. D.
0
30
.
Câu 44. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ): 2 3 8 0Px y z+ − +=
. Vectơ nào
dưới đây là một vectơ pháp tuyến của
()P
?
A.
( )
1
1; 2; 3n = −
. B.
( )
2
1; 2; 3n =
C.
( )
3
1; 2; 3n =−−
. D.
(
)
4
1;2;3n = −−
.
Câu 45. Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
( )
0;1; 1A −
và
( )
2; 1; 3B −
.Phương trình
mặt phẳng trung trực của đoạn thẳng
AB
là
A.
2 30xy z−+ −=
. B.
2 30xy z−+ +=
C.
30xz+−=
. D.
30xz++=
.
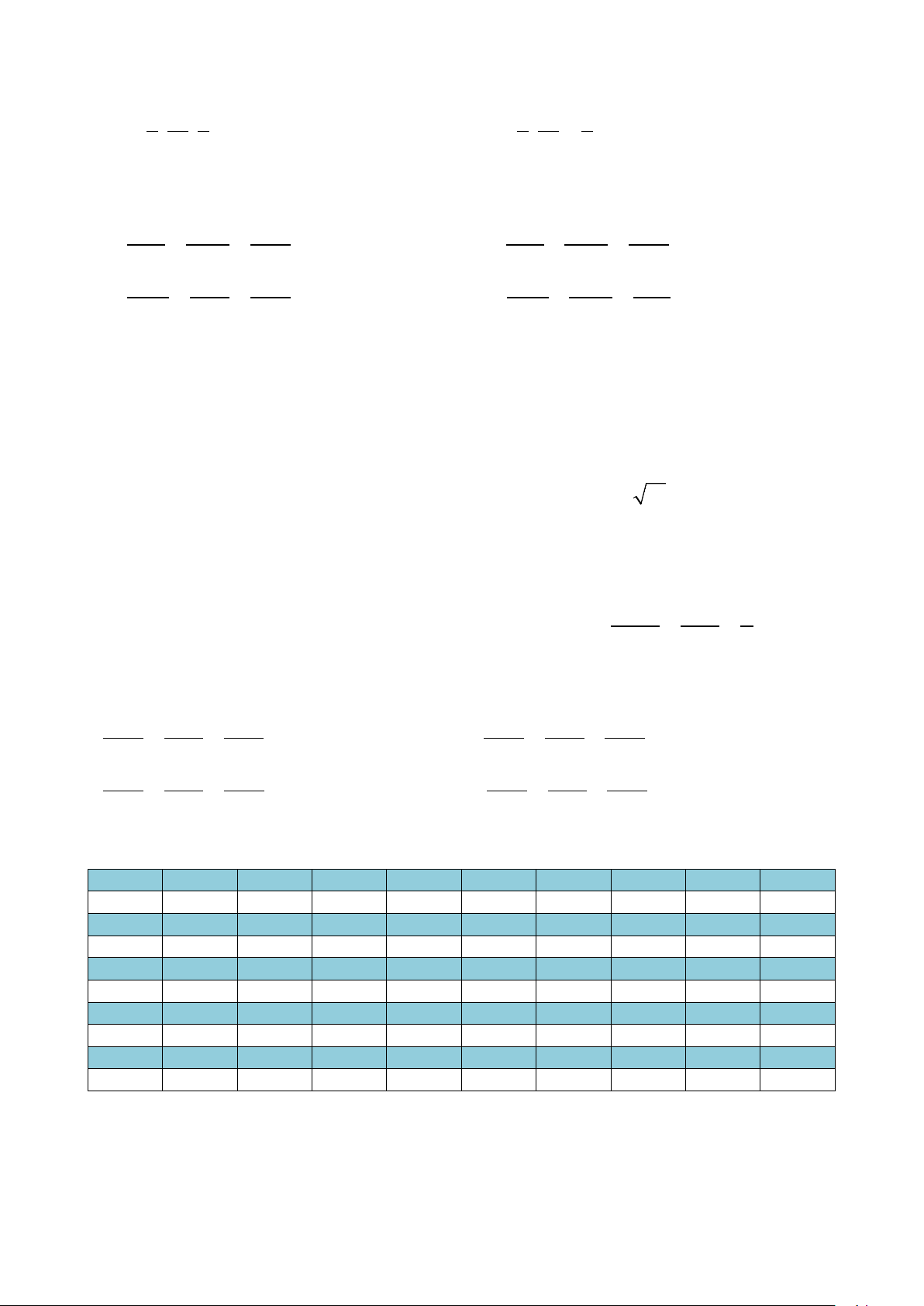
NTP Trang 5/5
Câu 46. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
1; 2; 3M
và mặt phẳng
( ): 2 0Pxyz−++=
. Tọa độ điểm
H
là hình chiếu vuông góc của
M
lên mặt phẳng
()
P
là
A.
1 10 5
;;
333
H
−
. B.
( )
3; 0;5H
. C.
5 10 1
;;
33 3
H
−
. D.
( )
1; 0;1H −
.
Câu 47. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
1; 2; 4M −−
và mặt phẳng
( ):5 6 0P xyz−++=
. Phương trình của đường thẳng
d
đi qua
M
và vuông góc với
()
P
là
A.
124
:
5 11
xy z
d
++−
= =
−
. B.
124
:
1 15
xy z
d
++−
= =
−
.
C.
214
:
5 11
x yz
d
+ +−
= =
−
. D.
4 21
:
5 11
xyz
d
−++
= =
−
.
Câu 48. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
2;2;2
M
. Phương trình mặt cầu đường
kính
OM
là
A.
( ) ( ) ( )
2 22
1 1 1 12xyz−+−+−=
. B.
(
) ( ) ( )
2 22
1 1 13xyz−+−+−=
.
C.
( ) ( ) ( )
2 22
1 1 13xyz+++++=
. D.
( ) ( ) ( )
2 22
1 1 1 12xyz+++++=
.
Câu 49. Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
( ) ( )
1;1;1 , 4;1; 0AB
và
( )
1; 4; 1C −−
. Mặt
phẳng
()
P
chứa đường thẳng
AB
và khoảng cách từ
C
đến
( )
P
bằng
14
. Phương trình mặt phẳng
(P) là
A.
( )
: 2 3 20Px y z− + −=
. B.
( )
: 2 3 20Px y z− + +=
.
C.
( )
:230
Px y z+−=
. D.
( )
: 2 3 40Px y z− − +=
.
Câu 50. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
13 1
:
1 14
x yz
d
−+
= =
−
và mặt cầu
( )
2 22
: 2 4 6 67 0Sx y z x y z++−− −−=
. Qua
d
dựng các tiếp diện tới
( )
S
, tiếp xúc với
( )
S
tại các
điểm
, TT
′
. Phương trình đường thẳng
TT
′
là
A.
815
15 1
x yz− −−
= =
−
. B.
815
15 1
x yz− +−
= =
−−
.
C.
815
151
x yz− −+
= =
. D.
815
1 51
x yz− −−
= =
−−
.
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
Câu 6
Câu 7
Câu 8
Câu 9
Câu 10
B
A
D
C
D
C
D
A
D
C
Câu 11
Câu 12
Câu 13
Câu 14
Câu 15
Câu 16
Câu 17
Câu 18
Câu 19
Câu 20
D
B
C
B
B
A
B
A
C
B
Câu 21
Câu 22
Câu 23
Câu 24
Câu 25
Câu 26
Câu 27
Câu 28
Câu 29
Câu 30
D
A
C
A
B
D
A
C
C
D
Câu 31
Câu 32
Câu 33
Câu 34
Câu 35
Câu 36
Câu 37
Câu 38
Câu 39
Câu 40
B
D
A
B
D
A
D
C
A
D
Câu 41
Câu 42
Câu 43
Câu 44
Câu 45
Câu 46
Câu47
Câu 8
Câu 49
Câu 50
B
A
C
A
A
A
A
B
A
A
NTP Trang 1/6
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
KỲ THI THPT QUỐC GIA NĂM 2019
TRƯỜNG THPT NGUYỄN HUỆ
Bài thi: Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề
(Đề thi có 06 trang)
Câu 1. Khối trụ có bán kính đáy là r và độ dài chiều cao là h có thể tích khối trụ đã cho bằng
A.
2
2
rh
π
. B.
2
rh
π
. C.
2
1
3
rh
π
. D.
2
rh
π
.
Câu 2. Cho hàm số
( )
y fx=
liên tục trên
và có bảng biến thiên như hình dưới đây
x
−∞
0
4
3
+∞
'y
+
0
−
0
+
y
1
+∞
−∞
5
27
−
Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực đại tại
1
x =
. B. Hàm số đạt cực đại bằng 1.
C. Hàm số đạt cực tiểu bằng
4
3
. D. Hàm số đạt cực tiểu tại
5
27
x = −
.
Câu 3. Trong không gian Oxyz, cho mặt phẳng
(
)
: 2 3 10 0P x yz− +− =
. Điểm nào dưới đây thuộc mặt
phẳng
( )
P
?
A.
( )
2;1; 2M
. B.
( )
2; 2;0N
. C.
(
)
1; 2; 0
E
. D.
( )
2; 2;0
−F
.
Câu 4. Cho hàm số
( )
y fx=
xác định và liên tục trên R, có bảng biến thiên như sau
x
−∞
1−
1
+∞
'y
+
0
−
0
+
y
−∞
2
1−
+∞
Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
( )
;1 .−∞
B. Hàm số đồng biến trên khoảng
( )
; 1.−∞ −
C. Hàm số nghịch biến trên khoảng
( )
1; .+∞
D. Hàm số đồng biến trên khoảng
( )
1; .− +∞
Câu 5. Nghiệm của phương trình
( )
2019
log 5 13x −=
là
A.
13
2019 5x = +
. B.
2019
13 5x = −
. C.
13
2019 5
x = −
. D.
2019
13 5x = +
.
Câu 6. Hàm số
( )
2
x
Fx e=
là nguyên hàm của hàm số nào trong các hàm số dưới đây?
A.
( )
2
2
x
f x xe=
. B.
( )
2
2
1
x
f x xe= −
. C.
( )
2x
fx e=
. D.
( )
2
2
x
e
fx
x
=
.
Câu 7. Tiệm cận ngang của đồ thị hàm số
1
24
x
y
x
+
=
−
có phương trình là
A.
2y =
B.
1y = −
. C.
1
2
y =
. D.
1
4
y = −
.
Câu 8. Cho hàm số
( )
y fx=
xác định và liên tục trên
, có
( ) ( )
8 20; 4 12.ff= =
(
)
8
4
'.
∫
f x dx
bằng
A. 4. B. 32. C. 8. D. 16.
ĐỀ THI ĐỀ XUẤT
NTP Trang 2/6
Câu 9. Trong không gian với hệ tọa độ Oxyz, trong các phương trình sau phương trình nào là phương trình
của mặt cầu?
A.
2 22
2 4 10xyz xz+ + − + −=
. B.
22
3 2 4 10xz x y z+ + − + −=
.
C.
2 22
2 4 4 10x y z xy y z+ + + − + −=
. D.
2 22
2 2 4 80xyz x yz+ + − + − +=
.
Câu 10. Cho khối lăng trụ đều
.'' '
ABC A B C
có tất cả các cạnh bằng 2a. Thể tích khối lăng trụ đã cho bằng
A.
3
23a
. B.
3
3
2
a
. C.
3
23
3
a
. D.
3
3a
.
Câu 11. Nguyên hàm của hàm số
2
1
3=−+yx x
x
là
A.
32
3
ln .
32
xx
xC−− +
B.
32
2
31
.
32
xx
C
x
− ++
C.
32
3
ln .
32
xx
xC−−+
D.
32
3
ln .
32
xx
xC−+ +
Câu 12. Trong không gian Oxyz, cho điểm
(
)
3; 9; 6
M −
. Gọi
123
,,MMM
lần lượt là hình chiếu vuông góc
của M trên các trục tọa độ Ox, Oy, Oz. Mặt phẳng
( )
123
MMM
có phương trình là
A.
0
396
x yz
++=
−
. B.
1
396
xy z
++=
−−
. C.
1
396
x yz
++=
−
. D.
1
132
x yz
++=
−
.
Câu 13. Đường cong trong hình vẽ bên là đồ thị của hàm
số nào dưới đây?
A.
42
2yx x= −
. B.
21
1
x
y
x
+
=
−
.
C.
3
3yx x=−+
. D.
24
2y xx= −
.
Câu 14. Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng
1
12
:
21 2
x yz
d
−+
= =
−
,
2
21
:
2 12
x yz
d
+−
= =
−−
. Vị trí tương đối của hai đường thẳng đã cho là
A. Chéo nhau. B. Trùng nhau. C. Song song. D. Cắt nhau .
Câu 15. Cho số phức
z a bi= +
với
2
,,1
ab i∈=−
. Môđun của z tính bằng công thức nào sau đây?
A.
.z ab
= +
B.
.z ab
= +
C.
22
.z ab= +
D.
22
.zab= +
Câu 16. Cho cấp số cộng
( )
n
u
có
1
11u =
và công sai
4d =
.
99
u
bằng
A. 401. B. 403. C. 404. D. 402.
Câu 17. Gọi
12
,zz
là các nghiệm của phương trình
2
2 50zz− +=
.
22
12
Pz z= +
bằng
A. 10. B. 5. C. 12. D. 4.
Câu 18. Giá trị thực của p và q thỏa mãn
( )
3 2 3 98p q ii i+−=−
( i là đơn vị ảo) bằng
A.
2, 4
pq= = −
. B.
5
3,
2
pq= = −
. C.
4, 4
pq= = −
. D.
11
3,
2
pq= = −
.
Câu 19. Giá trị lớn nhất của hàm số
2
22
1
xx
y
x
++
=
+
trên đoạn
1
;2
2
−
bằng
A.
5
2
. B.
2
. C.
10
3
. D.
3
.
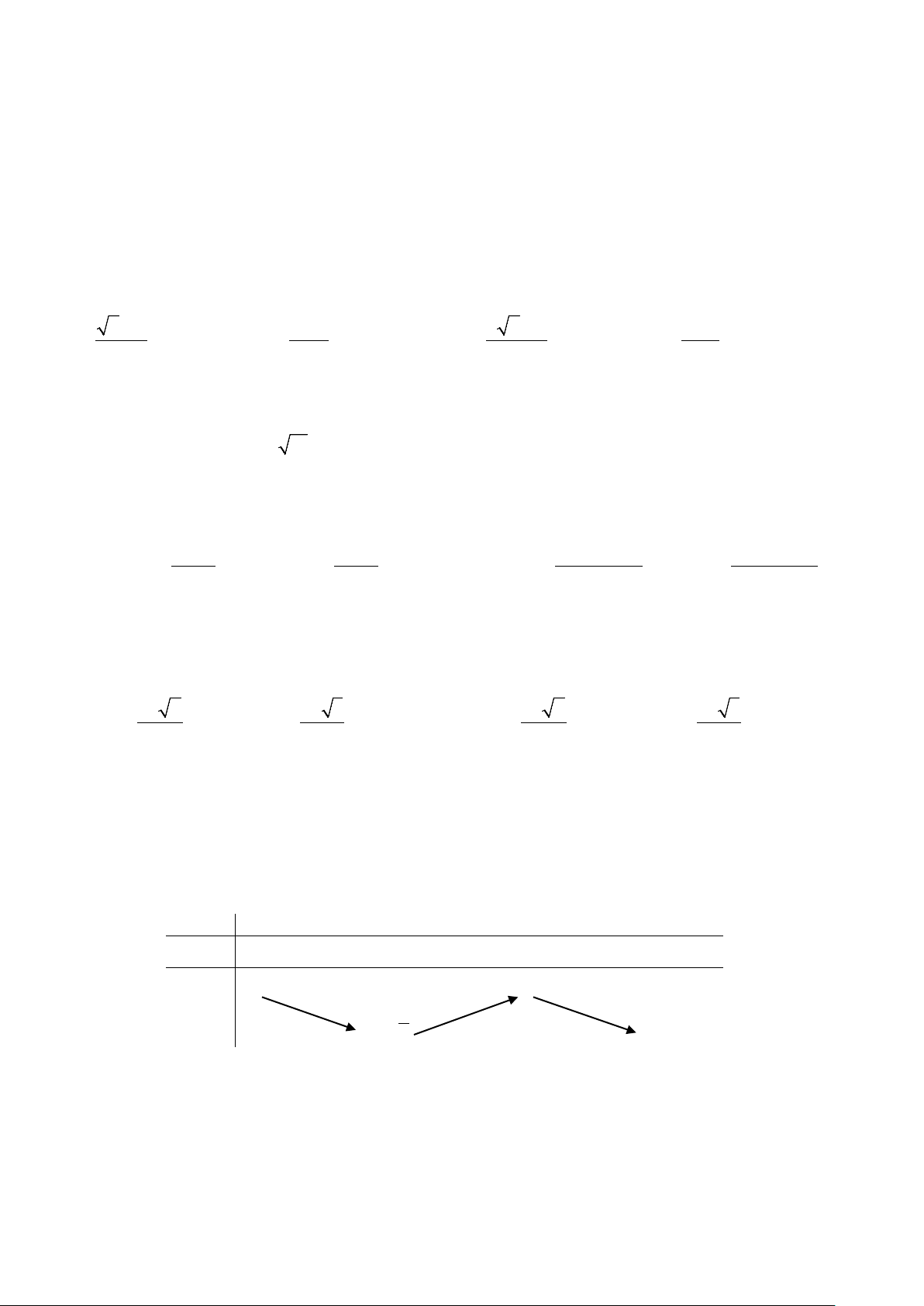
NTP Trang 3/6
Câu 20. Biết rằng
4
a
x=
và
16
b
y
=
. Khi đó xy bằng
A.
64
ab
. B.
2
4
ab
+
. C.
2
4
ab
. D.
2
16
ab
+
.
Câu 21. Có bao nhiêu số hạng trong khai triển nhị thức
( )
2018
57x −
thành đa thức ?
A. 2019. B. 2020. C. 2018. D. 2017.
Câu 22. Cho hàm số y=
(
)
fx
có đạo hàm
( ) ( ) ( )
24
' 12f x xx x=+−
với mọi
x ∈
. Số điểm cực trị của
hàm số y= f(x) là
A. 0. B. 3. C. 2. D. 1.
Câu 23. Cho khối nón có bán kính đáy bằng r và độ dài đường sinh bằng 3 lần bán kính đáy. Thể tích của
khối nón đã cho bằng
A.
3
2
3
r
π
. B.
3
2
3
r
π
. C.
3
22
3
r
π
. D.
3
8
3
r
π
.
Câu 24. Trong không gian Oxyz, cho điểm
( )
1; 2; 3M
−
. Gọi I là hình chiếu vuông góc của M trên trục Ox.
Phương trình mặt cầu tâm I bán kính IM là
A.
( )
2
22
1 13.x yz−++=
B.
( )
2
22
1 13.
x yz
−++=
C.
( )
2
22
1 13.
x yz+ ++=
D.
( )
2
22
1 17.x yz+ ++=
Câu 25. Đạo hàm của hàm số
( )
2
log 2 1yx
= +
là
A.
1
'.
21
y
x
=
+
B.
2
'.
21
y
x
=
+
C.
( )
1
'.
2 1 ln 2
y
x
=
+
D.
( )
2
'.
2 1 ln 2
y
x
=
+
Câu 26. Tập nghiệm của bất phương trình
2
2
6 216
−
≤
xx
là
A.
[ ]
1; 3−
. B.
(
]
;1
−∞ −
. C.
[
)
3; +∞
. D.
(
] [
)
; 1 3;−∞ − ∪ +∞
.
Câu 27. Khối tứ diện đều cạnh
a
có thể tích bằng
A.
.3
2
.
6
a
B.
.3
3
.
12
a
C.
.3
2
.
12
a
D.
.3
3
.
6
a
Câu 28. Một người gửi tiết kiệm số tiền 80 000 000 đồng với lãi suất là 6,9%/năm. Biết rằng tiền lãi hàng
năm được nhập vào tiền gốc, hỏi sau đúng 5 năm người đó có rút được cả gốc và lãi số tiền gần với con số
nào dưới đây?
A. 107 667 000 đồng. B. 105 370 000 đồng. C. 111 680 000 đồng. D. 116 570 000 đồng.
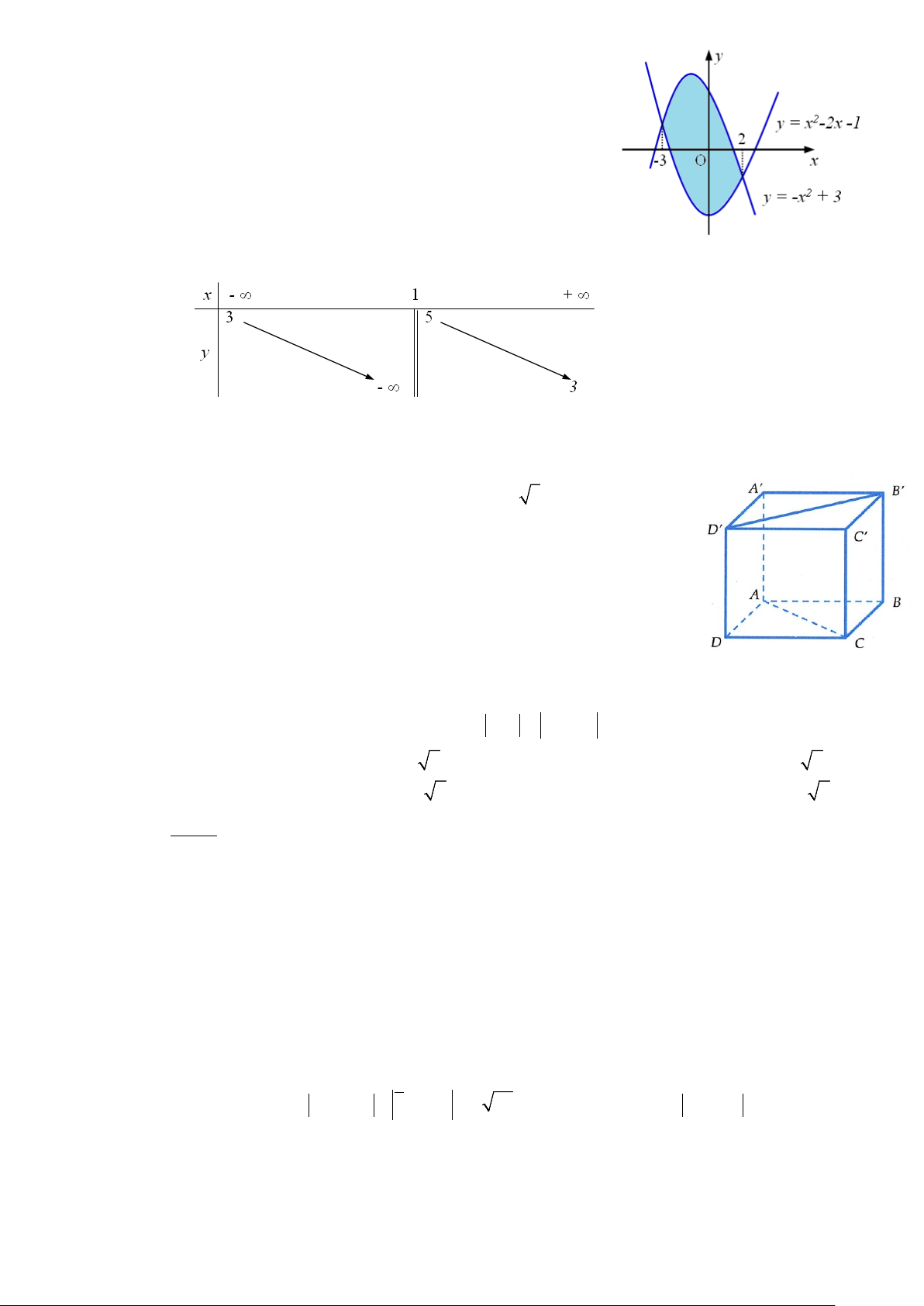
Câu 29. Cho hàm số
(
)
y fx=
có bảng biến thiên như sau
x
−∞
1
3
+∞
( )
'fx
−
0 + 0
−
( )
fx
+∞
1
1
3
−
−∞
Số nghiệm thực của phương trình
( )
4 23 10fx− +=
là
A. 1. B. 3. C. 2. D. 0.
NTP Trang 4/6
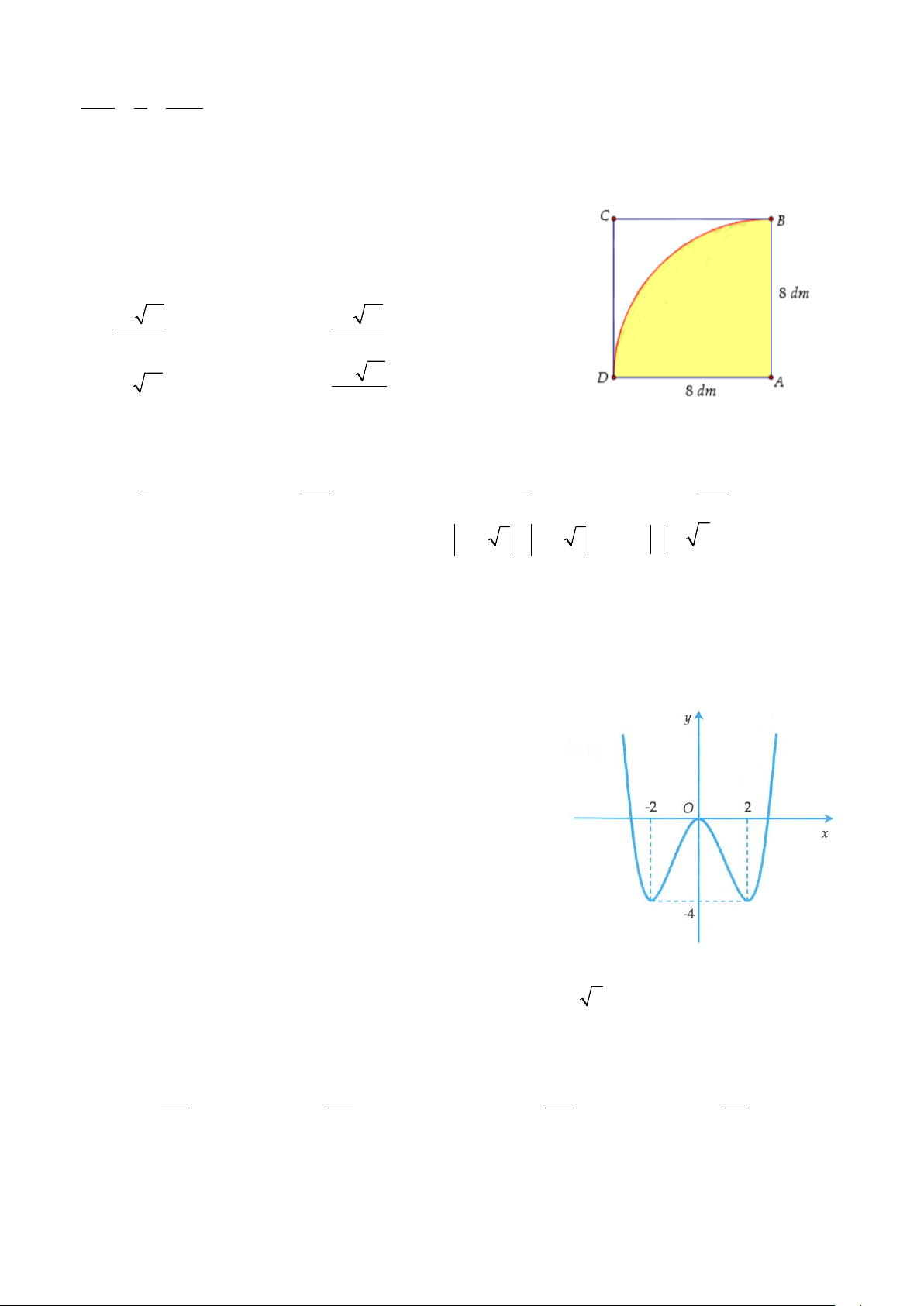
Câu 30. Diện tích phần tô đậm trong hình vẽ bên được tính theo công
thức nào dưới đây?
A.
( )
2
2
3
2 24
−
−−
∫
x x dx
. B.
( )
2
3
22
−
−+
∫
x dx
.
C.
( )
2
3
22
−
−
∫
x dx
. D.
(
)
2
2
3
2 24
−
− ++
∫
x x dx
.
Câu 31. Cho hàm số
( )
fx
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A. 1. B. 3. C. 2 . D. 4.
Câu 32. Cho hình hộp chữ nhật
.'' ' '
ABCD A B C D
có
3AB a=
và
AD a=
(tham
khảo hình vẽ). Góc giữa hai đường thẳng
''BD
và AC bằng
A. 90°. B. 30°.
C. 45°. D. 60°.
Câu 33. Tổng bình phương các nghiệm thực của phương trình
( )
3
1
2 32
x
x
−
+
=
bằng
A. 20. B. 4. C. 2. D. 6.
Câu 34. Tìm tập hợp điểm biểu diễn số phức z thỏa mãn
( )
1z i iz−= +
là
A. Đường tròn tâm I(0; 1), bán kính
2R
=
. B. Đường tròn tâm I(1; 0), bán kính
2R =
.
C. Đường tròn tâm I(-1; 0), bán kính
2R =
. D. Đường tròn tâm I(0; -1), bán kính
2
R =
.
Câu 35. Cho
5
2
3
ln 5 ln 3 ln 2
dx
abc
xx
=++
−
∫
với a, b, c là các số hữu tỷ. Giá trị của (
2
32
bc a+−
) bằng
A.
2−
. B. 6. C. 3. D. 0.
Câu 36. Diện tích hình phẳng giới hạn bởi các đường
1, 2, 0x xy=−= =
và parabol
(
)
2
:
P y ax bx c= ++
bằng 15. Biết
( )
P
có đỉnh
( )
1; 2I
là điểm cực tiểu. Tính
.T abc=+−
A. T = -8. B. T = -2. C. T = 14. D. T = 3.
Câu 37. Trong không gian với hệ tọa độ Oxyz, cho hình chóp tứ giác đều S. ABCD biết
( ) (
) ( )
1;0;0 , 5;0;0 , 5;4;0AB C
và chiều cao hình chóp bằng 6. Gọi
( )
;;
I abc
là điểm cách đều 5 đỉnh của
hình chóp (với c > 0). Tính giá trị của
2 3.Ta b c=++
A.
41.T =
B.
14.T =
C.
23.T =
D.
32.
T =
Câu 38. Cho số phức z thỏa mãn
1 3 5 2 65z iz i−+ + + + =
. Giá trị nhỏ nhất của
2zi++
đạt được khi
z a bi= +
với a, b là các số thực dương. Giá trị của (
23ba+
) bằng
A. 19. B. 16. C. 24. D. 13.
NTP Trang 5/6
Câu 39. Trong không gian Oxyz, cho mặt cầu
( ) ( ) ( ) ( )
2 22
: 2 5 3 27Sx y z−+−+−=
và đường thẳng
12
:
212
x yz
d
−−
= =
. Mặt phẳng
( )
P
chứa đường thẳng d và cắt mặt cầu
(
)
S
theo giao tuyến là đường tròn
có bán kính nhỏ nhất. Phương trình của
( )
P
là
0ax by z c+ −+=
.Mệnh đề nào dưới đây đúng ?
A.
1
abc++=
. B.
6abc
++=−
. C.
6abc++=
. D.
2
abc++=
.
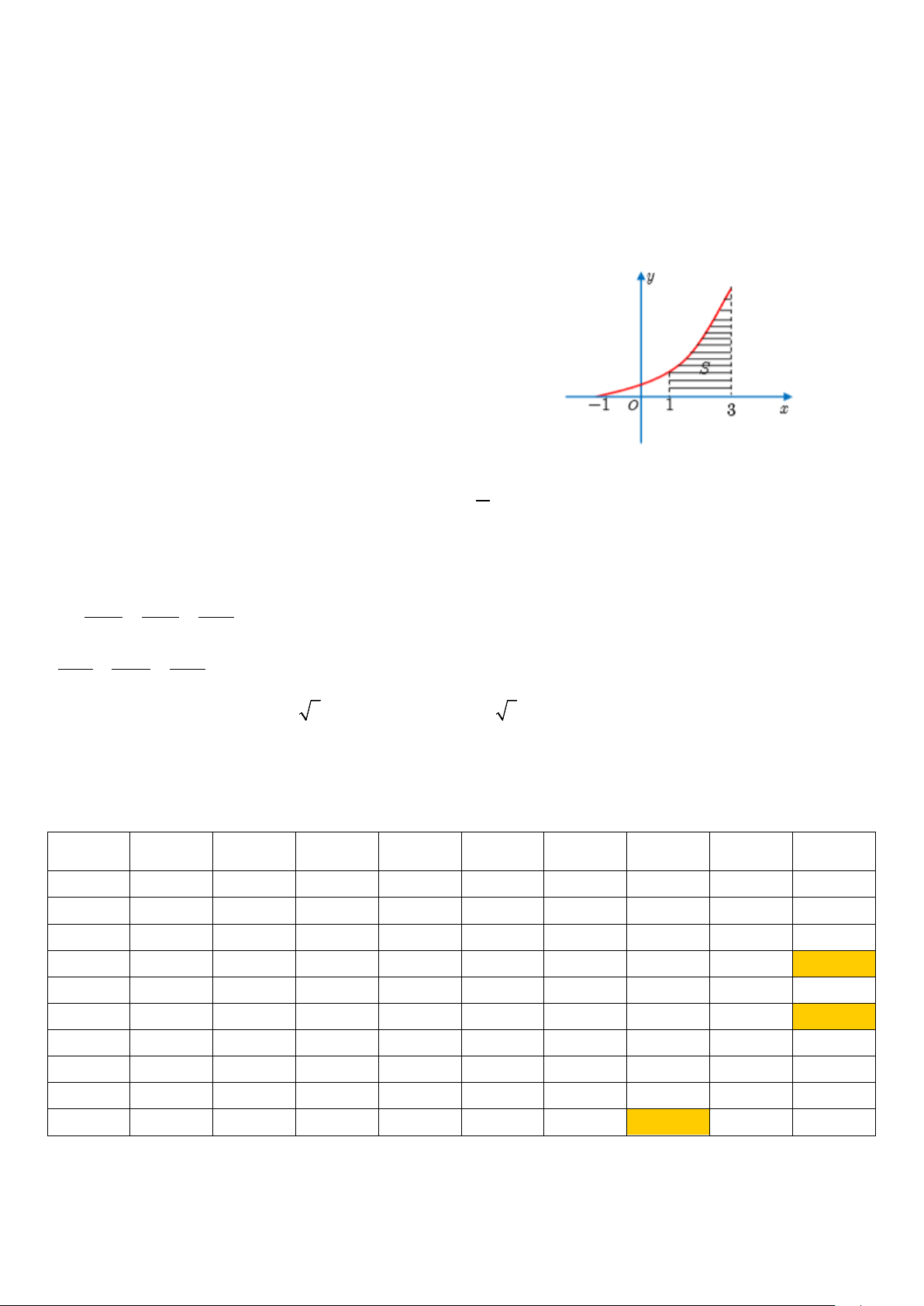
Câu 40. Từ miếng tôn hình vuông ABCD cạnh bằng 8 dm,
người ta cắt ra hình quạt tâm A bán kính AB = 8 dm (như
hình vẽ) để cuộn thành chiếc phễu hình nón (khi đó AB trùng
AD). Tính thể tích V của khối nón tạo thành bằng
A.
3
8 15
.
3
V dm
π
=
B.
3
8 15
.
5
V dm
π
=
C.
3
8 15 .V dm
π
=
D.
3
4 15
.
3
V dm
π
=
Câu 41. Chọn ngẫu nhiên một số tự nhiên nhỏ hơn 300. Gọi A là biến cố “số được chọn không chia hết cho
3”. Xác suất của biến cố A bằng
A.
2
.
3
B.
124
.
300
C.
1
.
3
D.
99
.
300
Câu 42. Có bao nhiêu số phức z thỏa mãn điều kiện
5 56
zi zi+ +− =
và
z5=
?
A. 3. B. 4. C. 2 . D. 0.
Câu 43. Trong không gian Oxyz, cho ba điểm
(
) ( ) ( )
0;1; 2 , 2; 2;1 , 2;0;1AB C−−
và mặt phẳng
( )
α
có
phương trình
2 2 30x yz+ +−=
. Biết rằng tồn tại duy nhất điểm
( )
;;M abc
thuộc mặt phẳng
( )
α
sao cho
MA MB MC= =
. Mệnh đề nào dưới đây đúng?
A.
20abc
+−=
. B.
2 3 4 41abc+−=
. C.
50abc++=
. D.
30
a bc+ +=
.
Câu 44. Cho hàm số
( )
y fx=
liên tục trên
và hàm số
( )
'y fx=
có đồ thị như hình bên. Bất phương trình
( ) ( )
( )
3 4 5 25
fx m fx m
fx m
++
+ ≤ ++
nghiệm đúng với mọi
( )
1; 2x ∈−
khi và chỉ khi
A.
( ) ( )
1 12f mf− − < <−
.
B.
( ) ( )
2 11f mf− < <− −
.
C.
( ) ( )
1 12f mf− − ≤ ≤−
.
D.
( ) ( )
2 11f mf− ≤ ≤− −
.
Câu 45. Cho hình chóp S. ABC có đáy
ABC∆
vuông cân ở B,
( )
2, ,AC a SA ABC SA a=⊥=
. Gọi G là
trọng tâm của
SBC∆
, mp
( )
α
đi qua AG và song song với BC chia khối chóp thành hai phần. Gọi V là thể
tích của khối đa diện không chứa đỉnh S. Tính V.
A.V=
3
5
.
54
a
B.V=
3
4
.
9
a
C. V=
3
2
.
9
a
D.V=
3
4
.
27
a
Câu 46. Ông Chính gửi 200 triệu đồng vào một ngân hàng với lãi suất 7%/năm. Biết rằng nếu không rút tiền
ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm tiếp theo và từ
năm thứ hai trở đi, mỗi năm ông gửi thêm vào tài khoản với số tiền 20 triệu đồng. Hỏi sau 18 năm số tiền
NTP Trang 6/6
ông Chính nhận được cả gốc lẫn lãi là bao nhiêu? Giả định trong suốt thời gian gửi lãi suất không thay đổi
và ông Chính không rút tiền ra (kết quả được làm tròn đến hàng nghìn).
A. 1. 686. 898. 000 VNĐ. B. 743. 585. 000 VNĐ.
C. 739. 163. 000 VNĐ. D. 1. 335. 967. 000 VNĐ.
Câu 47. Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng
( )
1000;1000−
để hàm số
( ) ( )
32
2 32 1 6 1 1yx mxmmx=− + + ++
đồng biến trên khoảng
( )
2; +∞
?
A. 999 B. 1001 C. 1998 D. 998
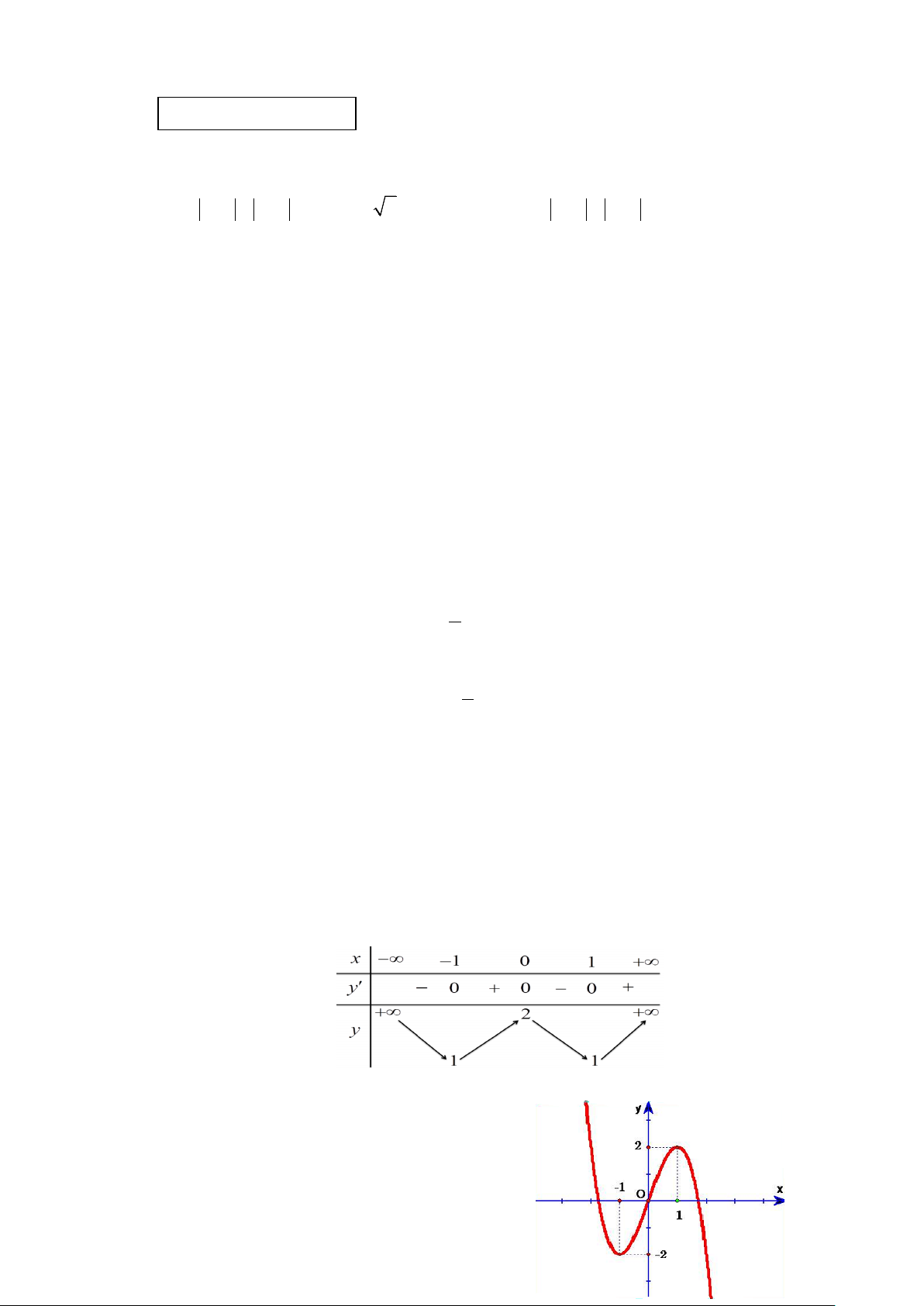
Câu 48. Cho hàm số
( )
y fx
=
liên tục trên
và hàm số
( )
( )
23
y gx xf x= =
có đồ thị trên đoạn
[
]
1; 3
−
như hình vẽ.
Biết miền hình phẳng được tô sọc kẻ có diện tích S = 6. Tính
tích phân
( )
27
1
.I f x dx=
∫
A. I = 2. B. I = 12.
C. I = 24. D. I = 18.
Câu 49. Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng
( )
2019;2019−
để hàm số
32
sin 3cos sin 1y x xm x=− −−
đồng biến trên đoạn
0;
2
π
.
A. 2020. B. 2019. C. 2028. D. 2018.
Câu 50. Trong không gian Oxyz, cho tam giác ABC có
( )
3; 2;3C
, đường cao AH nằm trên đường thẳng
1
233
:
11 2
xyz
d
− −−
= =
−
và đường phân giác trong BD của góc B nằm trên đường thẳng
2
d
có phương trình
143
1 21
xy z
−−−
= =
−
. Diện tích tam giác ABC bằng
A. 4. B.
23
. C.
43
. D. 8.
-------------------------------------HẾT ------------------------------------
ĐÁP ÁN ĐỀ ÔN TẬP KỲ THI THPT QUỐC GIA NĂM 2019 – MÔN TOÁN
Câu
Đáp án
Câu
Đáp án
Câu
Đáp án
Câu
Đáp án
Câu
Đáp án
1
D
11
D
21
A
31
C
41
A
2
B
12
C
22
D
32
D
42
B
3
D
13
D
23
C
33
A
43
B
4
B
14
C
24
B
34
D
44
D
5
A
15
C
25
D
35
B
45
A
6
A
16
B
26
A
36
A
46
D
7
C
17
A
27
C
37
B
47
B
8
C
18
A
28
C
38
B
48
D
9
A
19
C
29
B
39
C
49
B
10
A
20
B
30
D
40
A
50
B
NTP Trang 1/5
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
KỲ THI THPT QUỐC GIA NĂM 2019
TRƯỜNG THPT TRẦN BÌNH TRỌNG
Bài thi: Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề
(Đề thi có 05 trang)
Câu 1. Hàm số nào trong các hàm số sau đây là hàm số lẻ?
A.
11
yx x
= ++ −
. B.
yx=
. C.
11
yx x
= +− −
. D.
42
21
y xx
= ++
.
Câu2 .Trong mặt phẳng tọa độ Oxy, bán kính của đường tròn tâm I(0 ;-2) và tiếp xúc với đường thẳng
d :
3 4 23 0xy−−=
là
A. 3 . B. 5 . C.15 . D.4 .
Câu 3. Phương trình
cos 0
xm−=
( m là tham số thực) vô nghiệm khi và chỉ khi
A.
1
1
m
m
<−
>
. B.
1
m ≥
. C.
11m−≤ ≤
. D.
1m <
.
Câu 4. Một hộp đựng 7 bi xanh, 5 bi đỏ, 4 bi vàng. Có bao nhiêu cách lấy 7 viên bi đủ cả 3 màu, trong đó có
3 bi xanh và nhiều nhất 2 bi đỏ ?
A.
2100.
B.
95.
C.
2835.
D.
2800.
Câu 5. Trong các khẳng định sau khẳng định nào đúng?
sin 0
.sin 3 cos 2 1 2sin cos 2 .
sin 1
=
+=+ ⇔
=
x
Ax x xx
x
B.
sin 3 cos 2 1 2sin cos 2x x xx+=+
⇔
sin 0
.
sin 1
=
= −
x
x
C.
sin 3 cos 2 1 2sin cos 2x x xx+=+
⇔
sin 0
1
sin
2
x
x
=
=
.
D.
sin 3 cos 2 1 2sin cos 2x x xx+=+
⇔
sin 0
1
sin
2
x
x
=
= −
.
Câu 6. Cho hình chóp S.ABCD có đáy là hình bình hành. Giao tuyến của (SAB) và (SCD) là
A. Đường thẳng qua S và song song với CD .
B. Đường thẳng qua S và song song với AD.
C.Đường thẳng SO với O là tâm hình bình hành ABCD .
D. Đường thẳng qua S và cắt AB.
Câu7. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA ^ (ABCD). AE và AF là các đường cao
của tam giác SAB và SAD. Khẳng định nào dưới đây đúng?
A. SC ^ (AFB). B. SC ^ (AEC). C. SC ^ (AED). D. SC ^ (AEF).
Câu 8. Cho hàm số
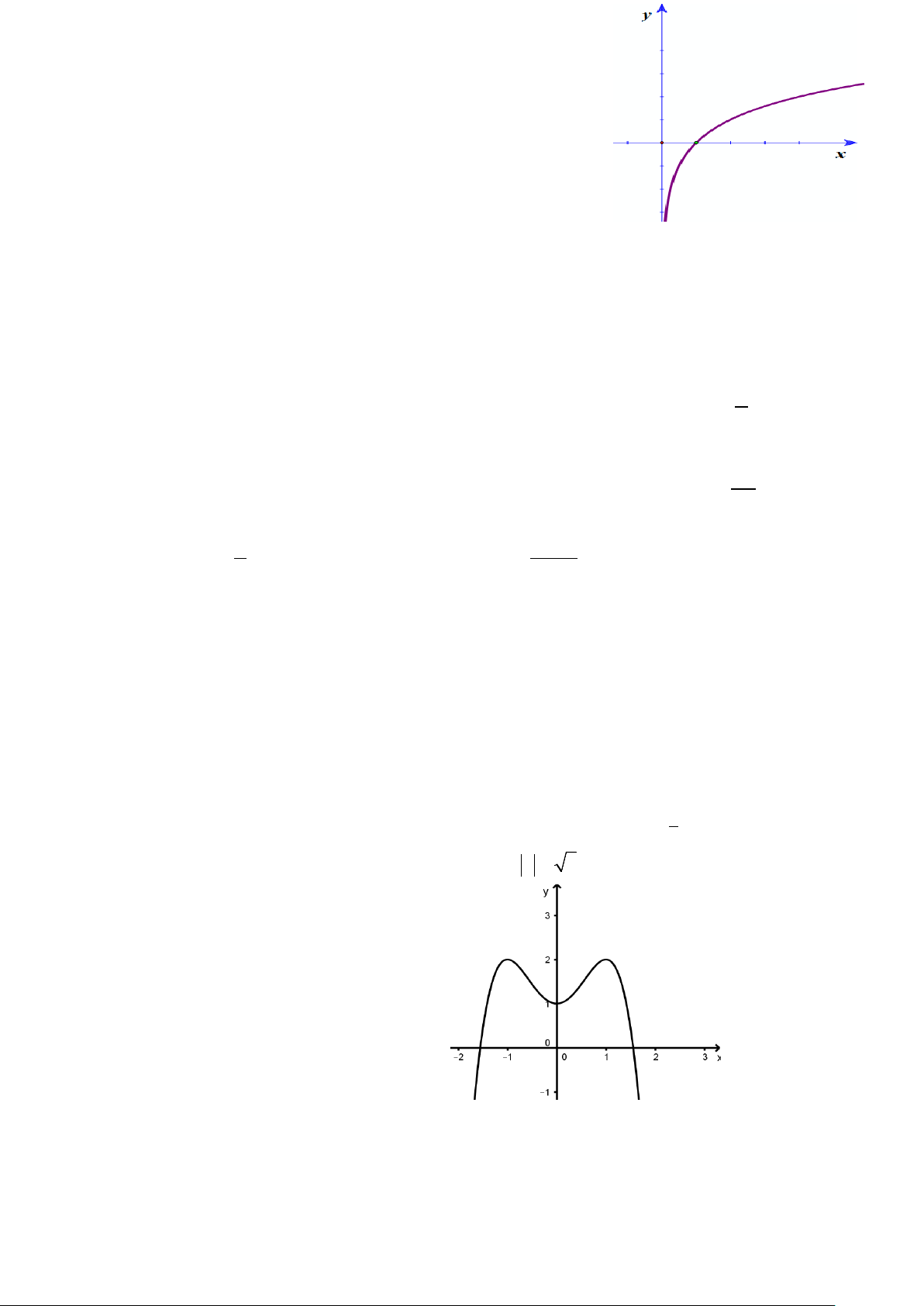
(
)
y fx=
liên tục trên
và có bảng biến thiên như sau
Mệnh đề nào dưới đây sai ?
A.
0
1x = −
là điểm cực tiểu của hàm số.
B. Hàm số đồng biến trên khoảng
( )
1; 0−
.
C.
( )
0; 2M
là điểm cực đại của đồ thị hàm số.
D. Hàm số có 5 điểm cực trị.
ĐỀ THI ĐỀ XUẤT
NTP Trang 2/5
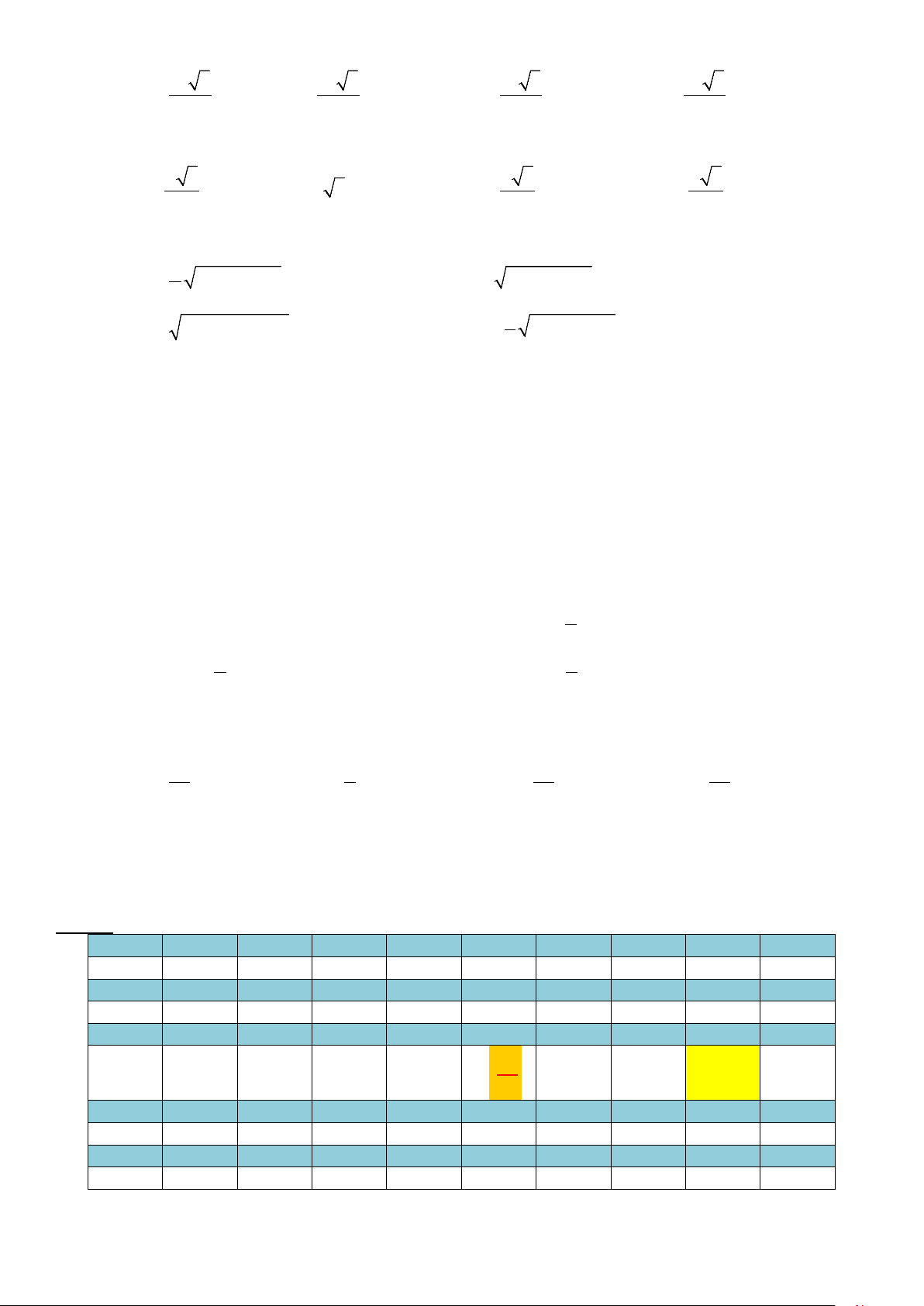
Câu 9. Cho hàm số
()y fx=
có đồ thị như hình bên.
Giá trị nhỏ nhất của hàm số trên [-1;1] bằng
A.
-1. B. 1.
C.
-2. D.
không tồn tại.
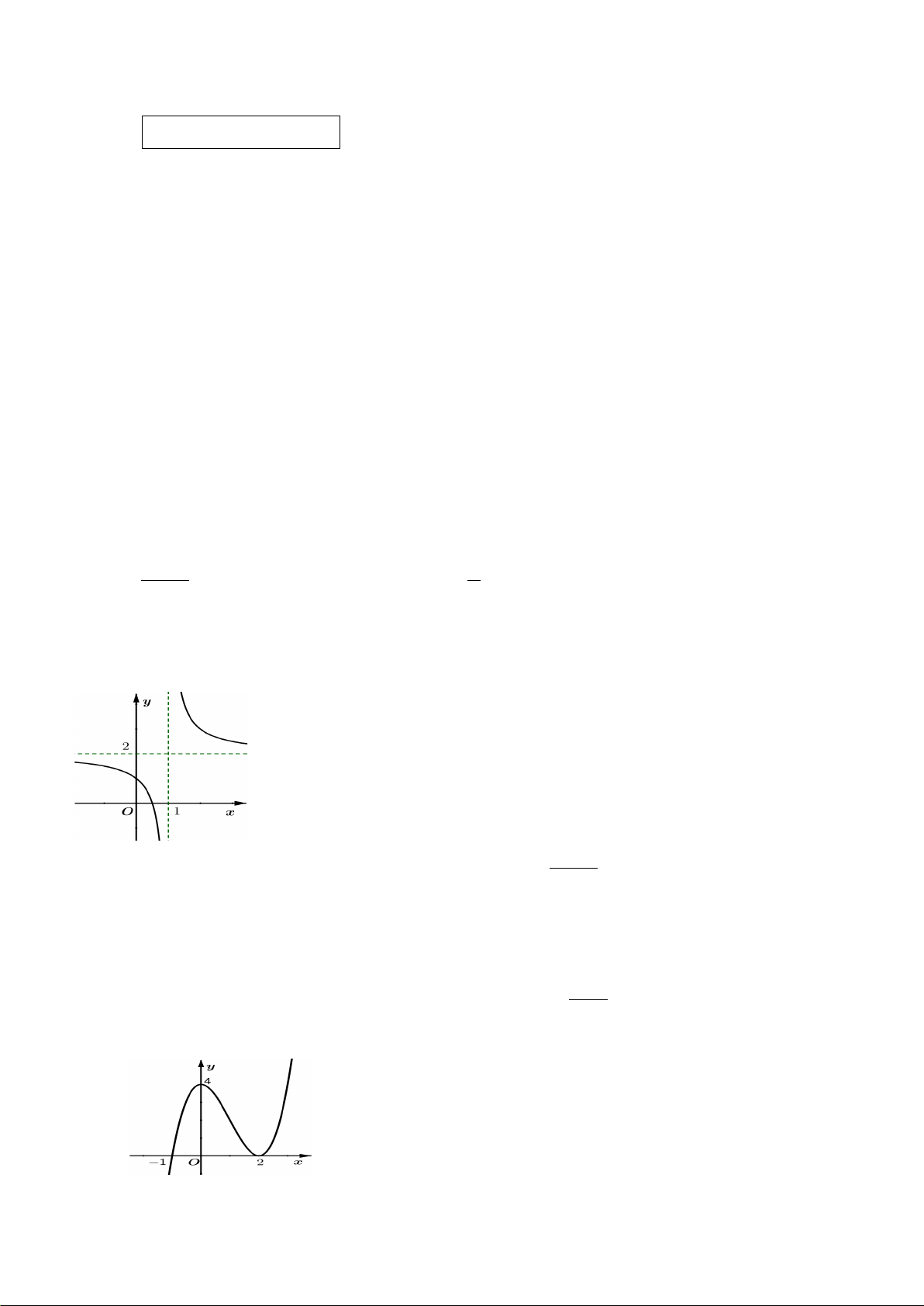
Câu 10. Hình bên là đồ thị của hàm số
2
logyx
=
. Đường thẳng
1y =
cắt đồ thị hàm số
2
logyx=
tại bao
nhiêu điểm ?
A.
0. B. 3.
C.
2. D.1.
Câu 11. Trong các hàm số sau, hàm số nào nghịch biến trên
?
A.
3
logyx=
. B.
( )
0,5
x
y =
. C.
21yx= +
. D.
4
x
y
−
π
=
.
Câu 12. Đạo hàm của hàm số
2x
ye=
là
A.
2
'
x
ye=
. B.
'2
x
ye=
. C.
2
'2
x
ye
=
. D.
2
'
2
x
e
y =
.
Câu 13. Khẳng định nào dưới đây sai?
A.
1
ln dxx C
x
= +
∫
. B.
2
1
d tan
cos
x xC
x
= +
∫
.
C.
sin d cos
xx x C=−+
∫
. D.
ed e
xx
xC= +
∫
.
Câu 14. Cho hàm số
( )
y fx=
liên tục trên đoạn
[ ]
;ab
. Gọi
D
là hình phẳng giới hạn bởi đồ thị hàm số
( )
y fx
=
, trục hoành và hai đường thẳng
xa=
,
xb=
( )
ab<
. Thể tích khối tròn xoay tạo thành khi quay
D
quanh trục hoành được tính theo công thức nào sau đây?
A.
( )
2
d
b
a
V fx x= π
∫
. B.
( )
2
2d
b
a
V f xx= π
∫
. C.
( )
22
d
b
a
V f xx= π
∫
. D.
(
)
2
d
b
a
V f xx= π
∫
.
Câu 15. Phần ảo của số phức
34zi= −
là
A. 3. B. -4. C. 4. D. -4i.
Câu 16[1]. Cho số phức
12zi= −
. Khẳng định nào sau đây là khẳng định đúng ?
A. z có điểm biểu diễn là M(1;2). B. Số phức liên hợp là
12zi=−+
.
C. Phần thực của z bằng -2. D.
5z
=
.
Câu 17. Đồ thị ở hình bên là đồ thị của hàm số
nào dưới đây?
A.
32
31yx x=−+
.
B.
42
21yx x=−+ +
.
C.
4
1yx=−+
.
D.
42
21
yx x=++
.
Câu 18. Cho hàm
()y fx=
có đạo hàm trên R và có
( ) ( )
( )
2
' 1 32fx x x x=− −+
. Số điểm cực đại của
hàm số là
A. 0. B. 1. C. 2. D. 3.
Câu 19. Đồ thị của hàm số nào sau đây có ba đường tiệm cận ?

NTP Trang 3/5
A.
1
12
x
y
x
−
=
+
. B.
2
1
4
x
y
x
+
=
−
. C.
2
3
1
x
y
x
+
=
+
. D.
32
31yx x=−+
.
Câu 20. Cho hàm số
21
1
x
y
x
−
=
+
có đồ thị
( )
C
và đường thẳng
: 2 1.dy x= −
Hoành độ giao điểm của (C) và
(d) là
A.
1
1;
2
xx= =
. B.
1; 1xx=−=
. C.
1
0;
2
xx= =
. D.
1
;2
2
xx
=−=
.
Câu 21. Tính tổng tất cả các nghiệm thực của phương trình
2
ln(2 x 5 x 4) ln 2 0+ +− =
bằng
A.
3
2
. B.
5
2
−
. C. 3. D. 5.
Câu 22. Số nghiệm thực nguyên âm của bất phương trình
83
4
25
5 16
x−−
≥
là
A. 1. B.2 . C.5. D. 12 .
Câu 23. Giá trị nhỏ nhất của hàm số
3
3y x xm=−− +
(m là tham số thực ) trên đoạn
[ ]
0;1
là
A. m . B.
4
m −
. C.
4
m +
. D.
2
m
.
Câu 24. Tất cả giá trị thực của tham số m để hàm số
32
32y x x mx=− +−
đạt cực tiểu tại
2x
=
là
A.
0
m >
. B.
0m =
. C.
0m <
. D.
0m ≠
.
Câu 25. Cho hàm số
( )
fx
xác định trên
2
\
3
thỏa mãn
( )
3
32
fx
x
′
=
−
,
( )
12f =
. Giá trị của biểu thức
( ) ( )
13ff−+
bằng
A.
4 ln 35
+
. B.
2 ln15+
. C.
3 ln 25+
. D.
1 ln 45+
.
Câu 26. Diện tích của hình phẳng giới hạn bởi đồ thị hàm số
21
yx= −
, trục hoành và hai đường thẳng
1; 3xx=−=
có giá trị bằng
A. 2. B. 12. C. 8. D.
17
2
.
Câu 27. Tập hợp điểm biểu diễn của số phức
z x yi= +
thõa mãn
11z zi+ = −+
là
A. đường tròn tâm O(0;0) bán kính bằng 1. B. đường thẳng
20xy+−=
.
C. đường thẳng
4 2 10xy
− −=
. D. hình tròn tâm I(1;1) bán kính bằng 3.
Câu 28.Tập hợp tất cả giá trị thực của tham số
m
để phương trình
3
3 10
x xm− − +=
có ba nghiệm thực
phân biệt, trong đó có đúng hai nghiệm dương là
A.
11m−< <
. B.
11m−< ≤
. C.
13m−< <
. D.
11m−≤ ≤
.
Câu 29. Tìm
m
để hàm số
( )
2
6 2ln 3 3y x x x mx= + + +− −
đồng biến trên
( )
1;− +∞
A.
0m ≤
. B.
5≤m
. C.
0m ≥
. D.
4m ≥−
.
Câu 30. Tổng giá trị tất cả các nghiệm thực của phương trình
3 9 81 243
2
log .log .log .log
5
xx x x=
bằng
A.
82
9
. B.
80
9
. C.
9
. D.
0
.
Câu 31. Biết tích phân
( )
2
2
0
2 1 cosI x xdx
π
= −
∫
=
2
1
2
c
ab
ππ
−−
. Giá trị ( a+b+c ) bằng
A. 5/3 . B. 7. C. 12. D. -7.
Câu 32. Cho số phức
z x yi
= +
( )
,xy
∈
thỏa mãn
( )
2 10z iz i+ +− + =
và
3z >
. Tính
2P xy= +
.
A.
12P =
. B.
5P = −
. C.
3P =
. D.
10P =
.
Câu 33. Tất cả giá trị thực của tham số
m
để bất phương trình
( ) ( )
22
22
log 2 3 log 1x x mx+> + +
có tập
nghiệm
là
A.
22m−< <
. B.
22m <
. C.
22 22m− <<
. D.
22m−≤ ≤
.
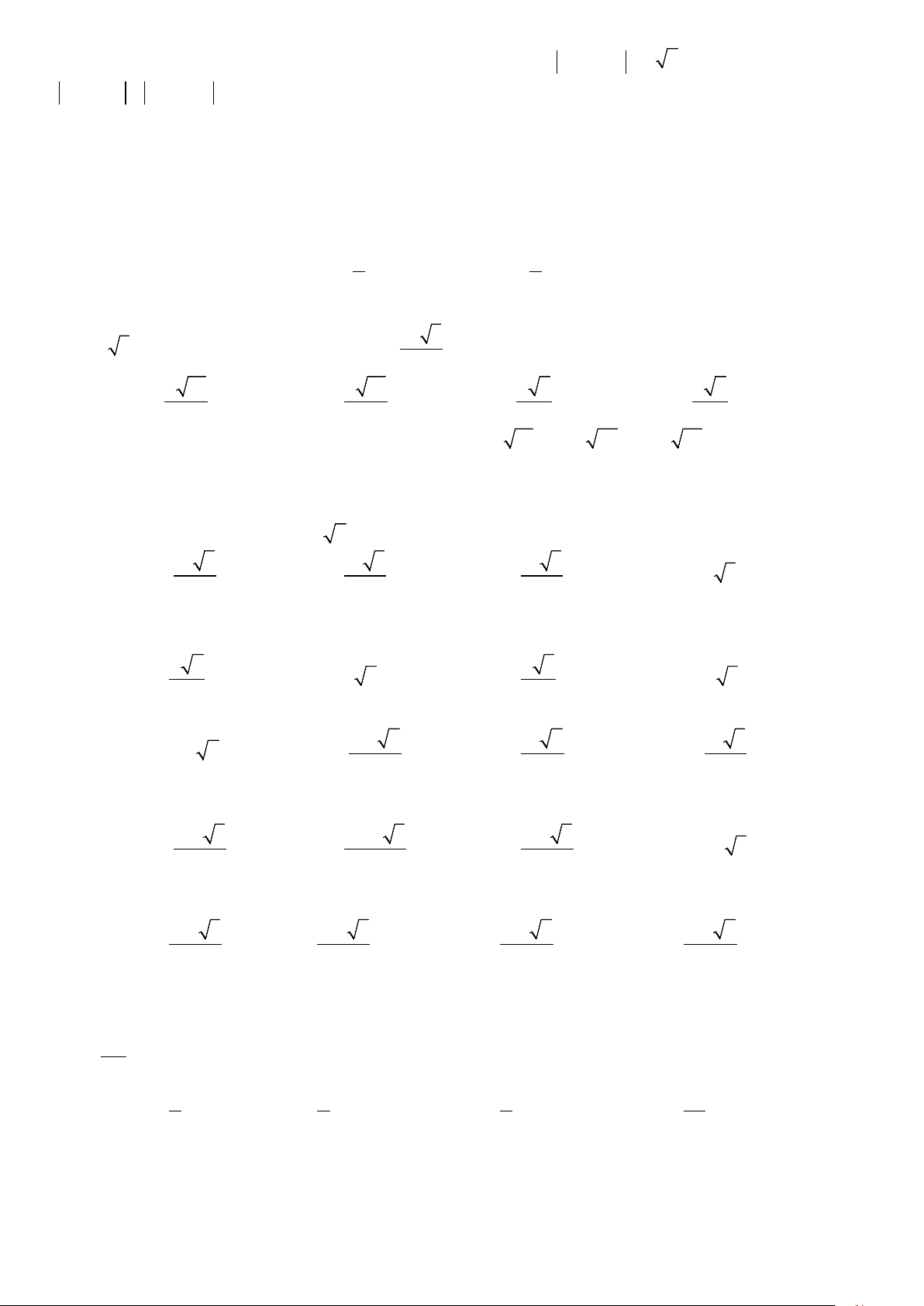
NTP Trang 4/5
Câu 34. Xét các số phức
z x yi= +
( )
,xy∈
thỏa mãn
2 3 22
zi+− =
. Tính
3P xy= −
khi
16 72z iz i++ + − −
đạt giá trị lớn nhất.
A.
1P =
B.
17P = −
C.
3
P =
D.
7
P =
Câu 35. Cho hàm số có đồ thị
(
)
32
:3 4
m
C y x x mx m= − + +−
và đường thẳng
:3dy x
= −
. Đường thẳng
d
cắt đồ thị
( )
m
C
tại ba điểm phân biệt
,,AI B
(theo thứ tự hoành độ từ nhỏ đến lớn). Tiếp tuyến tại
,AB
của
( )
m
C
lần lượt cắt
( )
m
C
tại điểm thứ hai là
M
và
N
. Tham số
m
thuộc khoảng nào dưới đây để tứ giác
AMBN
là hình thoi.
A.
( )
5; 4−
. B.
3
;2
2
. C.
3
;4
2
. D.
( )
2;5
.
Câu 36.Cho khối chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc với đáy và
3SA a=
. Biết diện tích tam giác SAB bằng
2
3
2
a
, khoảng cách từ điểm B đến mặt phẳng (SAC) bằng
A.
10
5
a
. B.
10
3
a
. C.
2
2
a
. D.
2
3
a
.
Câu 37. Cho hình hộp chữ nhật ABCD.A
1
B
1
C
1
D
1
có
11
13, 29, 38BD BA CA= = =
. Thể tích của khối
hộp ABCD.A
1
B
1
C
1
D
1
bằng
A. 10 . B. 15. C. 20. D. 30.
Câu 38. Cho hình chóp S.ABCD có đáy là hình chữ nhật tâm O với AB = 2a, BC = a. Các cạnh bên của
hình chóp đều bằng nhau và bằng
2a
. Thể tích khối chóp S.ABCD bằng
A.
3
3
3
a
. B.
3
3
4
a
. C.
3
3
2
a
. D.
3
3a
.
Câu 39. Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
2
a
, góc hợp bởi cạnh bên với mặt phẳng
đáy bằng
60
o
. chiều cao của khối chóp
.S ABCD
bằng
A.
6
2
a
. B.
6a
. C.
3
2
a
. D.
3a
.
Câu 40. Thể tích của khối tứ diện đều cạnh 2a bằng
A.
3
22a
. B.
3
22
3
a
. C.
3
2
12
a
. D.
3
3
3
a
.
Câu 41. Một tứ diện đều cạnh a có một đỉnh trùng với đỉnh hình nón, ba đỉnh còn lại nằm trên đường tròn
đáy của hình nón. Khi đó diện tích xung quanh của hình nón bằng
A.
2
3
2
aπ
. B.
2
23
3
aπ
. C.
2
3
3
aπ
. D.
2
3aπ
.
Câu 42. Cho hình lập phương ABCD.A’B’C’D’ có cạnh đáy bằng a. Một hình nón có đỉnh là tâm của hình
vuông ABCD và có đường tròn đáy ngoại tiếp hình vuông A’B’C’D’. Diện tích xung quanh của hình nón đó
bằng A.
2
3
3
aπ
. B.
2
3
2
aπ
. C.
2
6
2
aπ
. D.
2
2
2
aπ
.
Câu 43.Trong không gian cho hình vuông ABCD có cạnh bằng a. Gọi H, K lần lượt là trung điểm của DC
và AB. Khi quay hình vuông đó xung quanh trục HK ta được một hình trụ tròn xoay (H). Gọi S
xq
, V lần
lượt là diện tích xung quanh của hình trụ tròn xoay (H) và khối trụ tròn xoay được giới hạn bởi hình trụ (H).
Tỉ số
xq
V
S
bằng
A.
4
a
. B.
2
a
C.
3
a
D.
2
3
a
Câu 44. Cho hình trụ có các đáy là hai hình tròn tâm O và O’. Bán kính đáy bằng chiều cao và bằng a. Trên
đường tròn O lấy điểm A, trên đường tròn O’ lấy điểm B sao cho AB=2a. Thể tích khối tứ diện OO’AB tính
NTP Trang 5/5
theo a bằng
A.
3
3
12
a
. B.
3
3
4
a
. C.
3
3
8
a
. D.
3
3
6
a
.
Câu 45. Một hình trụ có bán kính đáy là a. A và B là 2 điểm trên 2 đường tròn đáy sao cho AB = 2a và tạo
với trục của hình trụ một góc 30
0
. chiều cao của hình trụ đã cho bằng
A.
3
2
a
. B.
3a
. C.
3
3
a
. D.
3
6
a
.
Câu 46. Cho tứ diện OABC có OA,OB,OC đôi một vuông góc nhau và OA = a,OB = b, OC= c. Bán kính
của mặt cầu (S) ngoại tiếp tứ diện OABC bằng
A.
222
1
2
abc++
. B.
222
abc
++
.
C.
222
2( )abc++
. D.
222
1
3
abc++
.
Câu 47. Phương trình mặt phẳng qua M(2; -3; 4) và cách điểm A(0; 1; -2) một khoảng lớn nhất là
A.
2 30xyz+−+=
.
B.
2 90xy z+− +=
.
C.
2 2 10
xy z
− − +=
. D.
2 3 20 0xyz−+−=
.
Câu 48. Trong các khẳng định sau, khẳng định nào sai ?
A. Mặt phẳng (P):
2 40xy z−+ −=
và mặt phẳng (Q):
2 10xy z− + +=
song song.
B. Mặt phẳng (P):
2 40xy z−+ −=
và mặt phẳng (Q):
3 2 10xyz− − +=
vuông góc.
C. Mặt phẳng (R):
320xyz
−+=
đi qua gốc toạ độ.
D. Mặt phẳng (H):
40xy+=
song song với trục Oz.
Câu 49. Tất cả giá trị thực của tham số m để mặt phẳng
2 40x my mz
+ + +=
tiếp xúc với mặt cầu
222
(1)( 3)(2)1xyz− ++ +− =
là
A.
14
mm=∨=
. B.
3
1
2
mm=−∨ =
.
C.
3
4
2
mm=−∨ =
. D.
1
2
2
mm=−∨ =
.
Câu 50. Trong không gian Oxyz, cho
( )
P
:
10xyz− ++=
,
( )
1;1;1A
,
( )
0;1; 2B
,
( )
2;0;1C −
và
( ) (
)
;;
M abc P∈
sao cho
22 2
2
S MA MB MC= ++
đạt giá trị nhỏ nhất. giá trị
(3 2 )++a bc
bằng
A.
25
4
. B.
7
4
.
C.
25
4
−
. D.
25
2
−
.
ĐÁP ÁN – HƯỚNG DẪN GIẢI
ĐỀ THI THAM KHẢO TN THPT QUỐC GIA NĂM HỌC 2018 – 2019
Đáp án
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
Câu 6
Câu 7
Câu 8
Câu 9
Câu 10
C
A
A
D
C
A
D
D
C
D
Câu 11
Câu 12
Câu 13
Câu 14
Câu 15
Câu 16
Câu 17
Câu 18
Câu 19
Câu 20
B
C
A
D
B
D
B
A
B
C
Câu 21
Câu 22
Câu 23
Câu 24
Câu 25
Câu 26
Câu 27
Câu 28
Câu 29
Câu 30
B
A
B
B
A
D
17
2
C
A
B
5≤m
A
Câu 31
Câu 32
Câu 33
Câu 34
Câu 35
Câu 36
Câu 37
Câu 38
Câu 39
Câu 40
B
D
A
B
A
C
D
A
B
B
Câu 41
Câu 42
Câu 43
Câu 44
Câu 45
Câu 46
Câu47
Câu 8
Câu 49
Câu 50
C
B
A
A
B
A
D
D
C
B
VĐL Trang
1/5
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
KỲ THI THPT QUỐC GIA NĂM 2019
TRƯỜNG THPT KHÁNH SƠN
Bài thi: Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Câu 1. Trong các phát biểu sau, phát biểu nào là mệnh đề đúng?
A.
π
là một số hữu tỉ. B. Tổng của hai cạnh một tam giác lớn hơn cạnh thứ ba.
C. Bạn có chăm học không? D. Con thì thấp hơn cha.
Câu 2. Cho ba đường thẳng
1
:3 –2 5 0dx y+=
,
2
:2 4 –7 0dxy+=
,
3
:3 4 –1 0dxy+=
. Phương trình
đường thẳng
d
đi qua giao điểm của
1
d
và
2
d
, và song song với
3
d
là :
A.
24 32 – 53 0xy+=
. B.
24 32 53 0xy+ +=
. C.
24 – 32 53 0xy+=
. D.
24 – 32 – 53 0xy =
.
Câu 3. Công thức nghiệm của phương trình lượng giác
sin sinx
α
=
là
A.
2xk
απ
= +
. B.
xk
απ
= +
. C.
2
2
xk
xk
απ
πα π
= +
=−+
. D.
2
2
xk
xk
απ
απ
= +
=−+
.
Câu 4. Cho sáu chữ số
4
,
5
,
6
,
7
,
8
,
9
. Hỏi có bao nhiêu số gồm
3
chữ số khác nhau được thành lập từ
6
chữ số đó ?
A. 120. B. 180. C. 256. D. 216.
Câu 5. Một đa giác có
740
đường chéo. Số cạnh của đa giác đó bằng:
A.
15
. B.
20
. C.
30
. D.
40
.
Câu 6.
1
1
lim
21
x
x
x
→
−
+
có giá trị là bao nhiêu? A.
0.
B.
1
.
2
C.
.
−∞
D.
.+∞
Câu 7. Cho hình hộp chữ nhật
.ABCD A B C D
′′′′
. Khi đó, vectơ bằng vectơ
AB
là vectơ nào dưới đây?
A.
CD
. B.
BA
′′
. C.
DC
′′
. D.
BA
.
Câu 8. Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây?
A.
42
2.yx x= −
B.
3
2 1.yx x=−− +
C.
21
.
1
x
y
x
−
=
−
D.
2
2 3.yx x
=+−
Câu 9. Cho hàm số
42
21
y xx= +−
. Số điểm cực trị của hàm số là
A. 1. B. 2. C. 3. D. 4.
Câu 10. Hàm số nào sau đây có điểm cực đại và điểm cực tiểu?
A.
32
3 1.yx x=−− +
B.
32
2 7 1.yx x x=− ++
C.
1
.
1
x
y
x
+
=
−
D.
42
2 1.yx x=++
Câu 11. Cho hàm số
( )
y fx=
có đồ thị như hình vẽ
Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên khoảng
( )
;4 .
−∞
B. Hàm số nghịch biến trên khoảng
( )
2;4
.
C. Hàm số đồng biến trên khoảng
( )
0;+∞
. D. Hàm số nghịch biến trên khoảng
( )
0;2
.
ĐỀ THI ĐỀ XUẤT

VĐL Trang
2/5
Câu 12. Số đường tiệm cận của đồ thị hàm số
2
2
1
32
x
y
xx
+
=
++
là
A. 2. B. 1. C. 0. D. 3.
Câu 13. Cho hàm số
32
3 (3 1)y x mx m=−+ − +
. Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
đã cho có cực đại và cực tiểu đối xứng nhau qua đường thẳng
: 8 74 0dx y+−=
?
A.
2
. B.
3
. C.
1
. D.
4
.
Câu 14. Cho hàm số
( )
y fx
=
liên tục trên
{ }
\ 0; 1−
thỏa mãn điều kiện
( )
1 2ln 2
f = −
và
( ) ( ) ( )
2
1. 'xx f x f x x x+ +=+
. Biết
( )
2 ln 3f ab= +
( )
,ab Q∈
. Tính
22
?ab+=
A.
3
4
. B.
13
4
. C.
1
2
. D.
9
2
.
Câu 15. Tập xác định của hàm số
( )
3yx
π
= −
là
A.
[
)
3;D = +∞
. B.
(
)
3;
D = +∞
. C.
{ }
\3D =
. D.
.
Câu 16. Bất phương trình
21 3xx
ee
++
≥
có tập nghiệm là
A.
(
]
;2−∞
. B.
( )
;2−∞
. C.
[
)
2;+∞
. D.
(
)
2;+∞
.
Câu 17. Bất phương trình
( ) ( )
12
2
log 3 2 log 6 5 0xx−+ − <
có tập nghiệm là
A.
(
)
;1−∞
. B.
6
1;
5
. C.
( )
1; +∞
. D.
6
1;
5
.
Câu 18. Bất phương trình
21
1
11
3. 12
33
xx
+
+>
có tập nghiệm
(
)
;S ab
=
. Giá trị của biểu thức
3 10Pa b= +
bẳng A.
3P = −
. B.
4P = −
. C.
5P =
. D.
2P =
.
Câu 19. Tìm tất cả giá trị của tham số
m
để phương trình
( )
2
21
2
log 1 log 0x mx m x+ +++ =
có nghiệm duy
nhất A.
[
)
{ }
1; 3 2 3+∞ ∪ −
. B.
( )
;1−∞ −
. C.
(
]
{ }
;1 23 3−∞ − ∪ − +
. D.
( )
1;1−
.
Câu 20. Tập nghiệm của bất phương trình
3.9 10.3 3 0
xx
− +≤
có dạng
[ ]
;S ab=
, trong đó
,ab
là các số
nguyên. Giá trị của biểu thức
52Pab= −
bằng A.
43
3
. B.
8
3
. C.
3
. D.
7−
.
Câu 21. Trong tất cả các mệnh đề dưới đây. Mệnh đề sai là
A.
ln
x
x
a
a dx C
a
= +
∫
. B.
1
1
n
n
x
x dx C
n
+
= +
+
∫
. C.
sin cosxdx x C= +
∫
. D.
0dx C=
∫
.
Câu 22. Nguyên hàm
( )
Fx
của hàm số
( )
1
13
fx
x
=
−
là
A.
( )
1
ln 1 3
3
Fx x C= −+
.B.
( )
1
ln 1 3
3
Fx x C=− −+
. C.
( )
ln 1 3
Fx x C=− −+
. D.
( )
ln 1 3Fx x C= −+
.
Câu 23. Cho
( ) ( )
25
11
2, 19f x dx f x dx= =
∫∫
. Khi đó
( )
5
2
f x dx
∫
nhận kết quả bằng
A.
17
. B.
21
. C.
17−
. D.
21−
.
VĐL Trang
3/5
Câu 24. Cho hàm số
( )
3
3
x
fx e
+
=
có một nguyên hàm là hàm số
( )
Fx
thỏa mãn
( )
02Fe=
. Khi đó giá trị của
( )
3F
bằng A.
2
ee+
. B.
2
3
3
ee+
. C.
2
3ee−
. D.
2
3
2
ee−
.
Câu 25. Cho
( )
0
24 5
a
x dx
−=
∫
. Giá trị của
a
thỏa mãn là A.
{ }
1; 4−
. B.
{ }
1; 5−
. C.
{
}
1
−
. D.
{
}
5
.
Câu 26. Cho hình phẳng
( )
H
được giới hạn bởi đồ thị các hàm số
ln , 0y x xy= =
và hai đường thẳng
1,x xe= =
. Quay hình phẳng
(
)
H
xung quanh trục
Ox
ta được một khối tròn xoay có thể tích bằng
A.
3
21
9
e −
. B.
3
1
9
e +
. C.
3
21
9
e
+
. D.
3
21
3
e
+
.
Câu 27. Cho
( )
1
1 3ln ln
e
xx
m
I dx
xn
+
= =
∫
, trong đó
,
mn
là các số nguyên, phân số
m
n
tối giản. Giá trị
mn−
A.
18−
. B.
19−
. C.
20−
. D.
17−
.
Câu 28. Từ một tấm tôn hình bán nguyệt có bán kính
3R cm=
người ta cắt ra một hình chữ nhật như hình vẽ.
Tính diện tích
S
của hình viên phân cung
AB
(kết qủa làm tròn đến hành phần trăm) sao cho diện tích hình chữ
nhật là lớn nhất
A.
2
2,57
S cm≈
. B.
2
2,75
S cm
≈
. C.
2
1, 28S cm≈
. D.
2
2,58
S cm
≈
.
Câu 29. Xác định phần ảo của số phức
18 12
zi
= −
. A.
12
−
. B.
18
. C.
12
. D.
12i
−
.
Câu 30. Tính môđun số phức nghịch đảo của số phức
( )
2
12zi= −
. A.
1
5
. B.
5
. C.
1
25
. D.
1
5
.
Câu 31. Cho hai số phức
1
23zi= +
,
2
45zi=−−
. Số phức
12
zz z= +
là
A.
22zi= +
. B.
22
zi=−−
. C.
22zi= −
. D.
22
zi
=−+
.
Câu 32. Điểm
A
trong hình vẽ bên là điểm biểu diễn của số phức
z
.
Khi đó mệnh đề nào sau đây là đúng?
A.
2zi= +
B.
12zi
= +
C.
22zi= +
D.
2zi= −
Câu 33. Tìm số phức
z
thỏa mãn
( )( )
1 12 32 0iz i i− +− −+ =
.
A.
43
zi= −
. B.
35
22
zi= +
. C.
43
zi= +
. D.
53
22
zi= +
.
Câu 34. Cho
2 4 6 2016 2018
1 iii i i abi+++++ + =+
với
,ab∈
. Tính giá trị của
3H ab= −
.
A.
0H =
. B.
3H =
. C.
2
. D.
3030H =
.
Câu 35. Cho số phức
z
thỏa mãn
1z =
. Giá trị lớn nhất của biểu thức
1 21Pz z=++ −
bằng
VĐL Trang
4/5
A.
5
. B.
65
. C.
25
. D.
45
.
Câu 36. Hình mười hai mặt đều có bao nhiêu cạnh?
A.
30
. B.
20
. C.
12
. D.
18
.
Câu 37. Hình nào dưới đây không phải là hình đa diện?
A. . B. C. D.
Câu 38. Số hình đa diện lồi trong các hình dưới đây là
A.
3
B.
0
C.
1
D.
2
.
Câu 39. Cho khối chóp tam giác đều. Nếu tăng cạnh đáy lên hai lần và giảm chiều cao đi bốn lần thì thể tích của
khối chóp đó sẽ:
A. Không thay đổi. B. Tăng lên hai lần. C. Giảm đi ba lần. D. Giảm đi hai lần.
Câu 40. Cho lăng trụ đứng
.ABC A B C
′′′
có đáy
ABC
là tam giác vuông cân tại
A
và
2BC a=
, mặt phẳng
( )
A BC
′
tạo với đáy một góc
60°
. Thể tích của khối lăng trụ
.ABC A B C
′′′
là
A.
3
6
.
4
a
V =
B.
3
3
.
4
a
V =
C.
3
6
.
12
a
V =
D.
3
3
.
3
a
V =
Câu 41. Cho hình chóp
.
S ABC
có đáy là tam giác vuông cân tại
B
, có
.AB a=
Gọi
I
là trung điểm
AC
.
Hình chiếu của
S
lên mặt phẳng
( )
ABC
là điểm
H
thỏa mãn
3BI IH=
và góc giữa
SI
với đáy là
30°
.
Khoảng cách giữa hai đường thẳng
AB
và
SI
bằng
A.
10
.
10
a
B.
5
.
5
a
C.
10
.
30
a
D.
5
.
15
a
Câu 42. Một hình trụ có bán kính đáy
(
)
5 cm
r =
, chiều cao
( )
7 cmh =
. Diện tích xung quanh của hình trụ này
là: A.
( )
2
35 cm
π
. B.
( )
2
70 cm
π
. C.
( )
2
70
cm
3
π
. D.
( )
2
35
cm
3
π
.
Câu 43. Cho hình vuông
ABCD
cạnh
( )
8 cm
. Gọi
,MN
lần lượt là trung điểm của
AB
và
CD
. Quay hình
vuông
ABCD
xung quanh
MN
. Diện tích xung quanh của hình trụ tạo thành là:
A.
( )
2
64 cm
π
. B.
( )
2
32 cm
π
. C.
( )
2
96 cm
π
. D.
( )
2
126 cm
π
.
Câu 44. Cho hình chữ nhật
ABCD
có
AB a=
và góc
30BDC
= °
. Quay hình chữ nhật này xung quanh cạnh
AD
. Diện tích xung quanh của hình trụ được tạo thành là:
A.
2
3 a
π
. B.
2
23a
π
. C.
2
2
3
a
π
. D.
2
a
π
.
Câu 45. Một hình trụ có diện tích xung quanh bằng
4
π
và có chiều cao bằng đường kính đáy. Thể tích khối trụ
tương ứng bằng: A.
2
π
. B.
π
. C.
3
π
. D.
4
π
.
Câu 46. Trong không gian với hệ toạ độ
Oxyz
, cho mặt phẳng (P) có phương trình
3 2 10x yz+ −+=
. Mặt
phẳng (P) có một vectơ pháp tuyến là

VĐL Trang
5/5
A.
(3; 2;1)n
. B.
( 2; 3;1)n
−
. C.
(3; 2; 1)n −
. D.
(3;2;1)n −−
.
Câu 47. Trong không gian với hệ tọa độ
Oxyz
, cho ba vectơ
( )
1; 1; 0
a = −
,
( )
2;1; 1b
= −
,
( )
;0; 2 1cm m
= −
.
Khi đó để ba vectơ
,,abc
đồng phẳng thì giá trị của tham số thực
m
bằng bao nhiêu?
A.
7
3
m =
. B.
1
2
m
=
. C.
3
7
m =
. D.
2
7
m =
.
Câu 48. Trong không gian với hệ tọa độ
Oxyz
cho mặt cầu
( )
S
tâm
( )
2; 3; 0I −
và tiếp xúc với mặt phẳng
( )
: 2 2 1 0.xy z
α
− + −=
Phương trình của mặt cầu
( )
S
là
A.
( ) ( ) ( )
22
2
: 2 3 4.Sx y z− ++ +=
B.
( ) ( ) ( )
22
2
: 2 3 2.Sx y z− ++ +=
C.
( ) ( ) ( )
22
2
: 2 3 4.Sx y z+ +− +=
D.
( ) ( ) ( )
22
2
: 2 3 2.Sx y z+ +− +=
Câu 49. Trong không gian với hệ trục tọa độ
Oxyz
, cho điểm
1; 4; 3G
. Viết phương trình mặt phẳng cắt các
trục
,,
Ox Oy Oz
lần lượt tại
,,ABC
sao cho
G
là trọng tâm tứ diện
OABC
?
A.
0
4 16 12
xy z
++=
. B.
1
4 16 12
xy z
++=
. C.
1
3 12 9
xyz
+ +=
. D.
0
3 12 9
xyz
+ +=
.
Câu 50. Trong không gian hệ trục toạ độ
Oxyz
, cho 2 đường thẳng
1
1
:
2 11
xy z
d
−
= =
−
,
2
11
:
121
x yz
d
−+
= =
.
Viết phương trình mặt phẳng
( )
α
vuông góc với
1
d
, cắt
Oz
tại
A
và cắt
2
d
tại
B
(có tọa nguyên) sao cho
21AB
=
.
A.
( )
:10 5 5 1 0xyz
α
− + +=
. B.
( )
:4 2 2 1 0xyz
α
− + +=
.
C.
( )
:2 1 0xyz
α
− ++=
. D.
( )
:2 2 0xyz
α
−++=
.
BẢNG ÐÁP ÁN
1B
2A
3C
4A
5D
6A
7C
8C
9A
10A
11D
12D
13C
14D
15B
16C
17B
18A
19C
20D
21C
22B
23A
24C
25B
26C
27B
28A
29A
30D
31B
32D
33B
34A
35C
36A
37C
38C
39A
40A
41A
42B
43A
44C
45A
46C
47C
48A
49C
50C

VĐL Trang
1/5
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
KỲ THI THPT QUỐC GIA NĂM 2019
TRƯỜNG THPT NGUYỄN VĂN TRỖI
Bài thi: Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Câu 1: Cho hàm số
()
y fx=
liên tục trên và có bảng biến thiên sau.
x
2
'
y
y
61
Hỏi
()
y fx=
đồng biến trên khoảng nào?
A.
( )
3;− +∞
. B.
( )
64;
− +∞
. C.
( )
;61−∞
. D.
( )
;3
−∞ −
.
Câu 2: Tìm tiệm cận đứng của đồ thị hàm số
2
1
x
y
x
−
=
−
. A.
1x =
. B.
2x = −
. C.
1
y =
. D.
2y
= −
.
Câu 3: Điểm cực đại của hàm số
2
2 61
42
xx
y
x
++
=
−
là A.
1x = −
. B.
1
1;
2
−
. C.
2x =
. D.
7
2;
2
.
Câu 4: Tìm giá trị lớn nhất của hàm số
1yx x= +−
trên
[ ]
1; 3−
. A.
3
4
−
. B.
5
4
. C.
1
. D.
1−
.
Câu 5: Số điểm chung của đồ thị hàm số
42
2yx x=+−
và đường thẳng
2y = −
là
A. 0. B. 1. C. 3. D. 4.
Câu 6: Cho hàm số
( )
y fx=
liên tục trên
và có bảng xét dấu đạo hàm
(
)
'fx
như sau
x
−∞
1−
2 3 5
+∞
( )
'fx
−
0
−
0
+
0
+
0
−
Khẳng định nào sau đây đúng?
A. Hàm số đạt cực tiểu tại
1x = −
. B. Hàm số đạt cực đại tại
5
x =
.
C. Hàm số có bốn điểm cực trị. D. Hàm số có hai điểm cực đại.
Câu 7: Tìm tất cả các tham số thực
m
để hàm số
3
2
() 5
3
mx
y f x mx x= = + −+
có cực đại và cực tiểu.
A.
1m <−
hay
0
m >
. B.
1m ≤−
hay
0m ≥
. C.
10m
−≤ ≤
. D.
10m−< <
.
Câu 8: Cho hàm số
()y fx=
liên tục trên và có đồ thị như hình vẽ.
Tìm tất cả các tham số thực
m
để phương trình
() 3 0fx m−=
có đúng một nghiệm âm.
A.
2
3
m ≤
hay
4
3
m =
. B.
2
3
m <
. C.
2m ≤
hay
4m =
. D.
2
m
<
.
Câu 9: Tìm tích tất cả các tham số thực
m
để tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
1
21
mx
y fx
xm
−
= =
++
cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện tích bằng 3.
A.
3
2
. B.
3
2
−
. C.
1
2
−
. D.
1
2
.
Câu 10: Tìm tập xác định của hàm số
3
4
()y fx x
−
= =
.
ĐỀ THI ĐỀ XUẤT

VĐL Trang
2/5
A.
( )
;0−∞
. B.
(
)
0;
+∞
. C.
[
)
0; +∞
. D.
(
]
;0−∞
.
Câu 11: Cho hàm số
() a
x
y fx= =
, với
0, 1aa
>≠
có đồ thị như sau.
Tìm tập nghiệm của bất phương trình
1
()
4
fx
≤
.
A.
[
)
2; +∞
. B.
[
)
2;5
. C.
(
]
3; 2−
. D.
(
]
;2
−∞
.
Câu 12: Tính tổng các nghiệm của phương trình
2
22
log 3log 2 0
xx− +=
. A. 6. B. 5. C.
9
2
. D.
9
4
.
Câu 13: Giải bất phương trình
21
39
x
−
≤
.
A.
13
22
x−≤≤
. B.
13
22
x
−<<
. C.
1
2
x ≤−
hay
3
2
x ≥
. D.
1
2
x <−
hay
3
2
x
>
.
Câu 14: Cho hàm số
1
()
22
x
fx=
+
. Tính tổng
( ) ( ) ( ) ( )
( )
2 2018 2017 ... 2018 2019Sf f f f= − + − ++ +
.
A.
2019
S =
. B.
2018S =
. C.
2018 2S =
. D.
2019 2S =
.
Câu 15: Cho dãy số
162log
12
,
x
12
log
,
y
12
log
,
z
12
log
,
1250log
12
là một cấp số cộng. Tìm
x
.
A. 434. B. 270. C. 706. D. 450.
Câu 16: Cho phương trình
( )( )
8 log log 7log 6log 2019 0
nm n m
xx x x− − −=
với
,mn
là các số nguyên lớn hơn 1.
Tìm
mn
+
để tích các nghiệm của phương trình là giá trị nguyên nhỏ nhất.
A. 12. B. 20. C. 24. D. 48.
Câu 17: Cho hàm số
()fx
có đạo hàm liên tục trên khoảng
K
và
()
gx
là hàm số liên tục trên
K
. Khẳng định
nào sau đây sai?
A.
'() ()f x dx f x c= +
∫
, với
c ∈
. B.
() ()af x dx a f x dx
=
∫∫
, với
a ∈
.
C.
[ ]
() () () ()f x g x dx f x dx g x dx+= +
∫ ∫∫
. D.
[ ]
() () () ()f x g x dx f x dx g x dx−= −
∫ ∫∫
.
Câu 18: Cho hàm số
2
() 2y fx x= = −
. Khẳng định nào sau đây đúng?
A.
222
11
2
() () ()f x dx f x dx f x dx= −
∫∫∫
. B.
1 21
2
22
() () ()f x dx f x dx f x dx
− −−
−
−−
= +
∫ ∫∫
.
C.
222
2
22
() () ()f x dx f x dx f x dx
−−
= +
∫ ∫∫
. D.
2 11
2 22
() () ()f x dx f x dx f x dx
−−
= −
∫ ∫∫
.
Câu 19: Cho
5
0
() 5f x dx =
∫
và
( )
5
0
12g x dx =
∫
. Tính
5
0
1
2 () ()
3
I f x g x dx
= −
∫
.
A.
6I =
. B.
30I =
. C.
1I =
. D.
14
I =
.
Câu 20: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
1
()
2
x
y f x xe= =
, trục hoành và hai đường thẳng
3, 1xx=−=−
. A.
3
12
ee
−
. B.
3
12
2
ee
−
. C.
3
11
ee
−
D.
3
11
2
ee
−
.
Câu 21: Cho hàm số
32
() 3 3y fx x x x= =−+ + −
có đồ thị
( )
C
. Gọi
( )
∆
là tiếp tuyến với
( )
C
tại
( )
2; 1M −
Tính diện tích hình phẳng giới hạn bởi
( )
C
và
(
)
∆
biết rằng 1 đơn vị độ dài trên trục
Ox
bằng
3cm
và trên trục
Oy
bằng
8cm
. A.
( )
2
625
12
cm
. B.
( )
2
1250 cm
. C.
( )
2
6875
6
cm
. D.
( )
2
1070 cm
.

VĐL Trang
3/5
Câu 22: Trong không gian
Oxyz
, cho vật thể
()T
nằm giữa hai mặt phẳng
0x =
và
1x =
. Thiết diện của
()T
bị
cắt bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
[ ]
0;1x ∈
là một tam giác đều cạnh
4 ln(1 )x+
.
Tính thể tích của
()
T
.
A.
(
)
4 3 2ln 2 1
−
. B.
(
)
4 3 2ln 2 1
+
. C.
( )
8 3 2ln 2 1−
. D.
( )
8 3 2ln 2 1+
.
Câu 23: Cho hai số phức
1
z a bi= +
và
2
z c di= +
, với
,,,abcd∈
. Khẳng định nào sau đây đúng?
A.
12
( )( )z z ac bdi+=+++
. B.
12
( )( )z z a d b ci+=+++
.
C.
12
( )( )z z a d b ci−=−+−
. D.
12
(c ) (d )z z a bi− =−+−
.
Câu 24: Trên mặt phẳng
Oxy
, cho
,MN
lần lượt là điểm biểu diễn hai số phức
12
,zz
.
Tính
12
zz+
.
A.
2 i−
. B.
12i−+
. C.
43i−
. D.
34i−+
.
Câu 25: Cho
12
,zz
là hai nghiệm phức của phương trình
2
5 6 20zz+ +=
. Tính
12
zz+
.
A.
10
5
. B.
2 10
5
. C.
1
5
. D.
6
5
.
Câu 26: Cho số phức
(
)
2 5 .(3 )z ii= −
. Tìm môđun của
z
. A.
3 29
. B.
3 21
. C. 9. D. 21.
Câu 27: Trong mặt phẳng tọa độ
Oxy
, tìm tập hợp điểm biểu diễn số phức
( )
w 34iz i=++
, biết số phức
z
thỏa
23z −=
.
A. Đường tròn tâm
(
)
6;9I
, bán kính
15R =
. B. Hình tròn tâm
( )
6; 9I −−
, bán kính
15R =
.
C. Hình tròn tâm
( )
6;9I
, bán kính
25R =
. D. Đường tròn tâm
( )
6; 9I −−
, bán kính
25R =
.
Câu 28: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành và chiều cao hình chóp
15h cm=
. Biết diện
tích của tam giác
BCD
là
2
20cm
. Hỏi thể tích khối chóp
.S ABCD
?
A.
3
100cm
. B.
3
200
cm
. C.
3
300cm
. D.
3
600cm
.
Câu 29: Cho hình lăng trụ đứng có đáy là hình thang như hình vẽ.
Thể tích của khối lăng trụ đó là A.
4725
. B.
6300
. C.
14175
. D.
18900
.
Câu 30: Cho hình chóp
ABCS.
,
M
là trung điểm của cạnh
SA
và
N
là điểm trên cạnh
SC
sao cho
NCSN
3=
. Tính tỉ số thể tích giữa hai khối chóp
BMNA.
và
ABCS.
. A.
3
8
. B.
2
5
. C.
1
3
. D.
3
4
.
Câu 31: Cho lăng trụ
'''. CBAABC
có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc của điểm
'A
lên mặt
phẳng
( )
ABC
trùng với trọng tâm của tam giác
ABC
. Biết khoảng cách giữa hai đường thẳng
'
AA
và
BC
bằng
3
4
a
. Tính thể tích của khối lăng trụ đó. A.
3
3
12
a
. B.
3
3
6
a
. C.
3
3
3
a
. D.
3
3
24
a
.
Câu 32: Một nhà sản xuất muốn làm một chiếc hộp dạng hình hộp chữ nhật không nắp có đáy là hình vuông và
tổng diện tích các mặt là
2
108dm
.

VĐL Trang
4/5
Xác định chiều cao
h
sao cho thể tích của chiếc hộp lớn nhất.
A.
6dm
. B.
3
dm
. C.
32dm
. D.
62
dm
.
Đã sửa lại đáp án là B. 3dm
Câu 33: Cho khối nón có bán kính đáy là
2
a
và chiều cao
6a
. Tính thể tích
V
của khối nón đó.
A.
3
6
a
π
B.
3
8
Va
π
=
. C.
3
24Va
π
=
. D.
3
48 a
π
.
Câu 34: Cho khối trụ như hình vẽ.
Diện tích toàn phần
tp
S
của hình trụ là
A.
2
22
tp
S rh r
ππ
= +
. B.
2
2
tp
S rh r
ππ
= +
. C.
2
2
tp
S rh r
ππ
= +
. D.
2
tp
S rh r
ππ
= +
.
Câu 35: Cho hình lập phương cạnh
a
. Một hình nón có đỉnh là tâm của hình vuông
ABCD
và có đường tròn
đáy ngoại tiếp hình vuông
'''' DCBA
. Tính diện tích xung quanh của hình nón đó.
A.
3
3
2
a
π
. B.
2
2
2
a
π
. C.
2
3
2
a
π
. D.
2
6
2
a
π
.
Câu 36: Trong không gian
Oxyz
, cho
34OM i k= −
. Tìm tọa độ của điểm
M
.
A.
( )
3; 0; 4M −
. B.
( )
3; 4; 0M −
. C.
( )
0; 3; 4M −
. D.
( )
4;0;3M −
.
Câu 37: Trong không gian
Oxyz
, cho mặt phẳng
( )
: 2 50xy
α
− +=
. Tọa độ một vectơ pháp tuyến của
( )
α
là
A.
( )
1; 2; 0−
. B.
( )
1; 0; 2−
. C.
(
)
2; 5; 0
−
. D.
( )
2;0;5−
.
Câu 38: Trong không gian
Oxyz
, cho mặt cầu
( )
S
qua điểm
( )
0; 2;5A
và có tâm
( )
1; 3; 2I −
. Viết phương trình
mặt cầu
(
)
S
.
A.
( )
( )
(
)
222
13251xyz
− +− ++ =
. B.
( )
( )
22
2
2 5 51xy z
+− +− =
.
C.
( ) ( ) ( )
222
1 1 7 51xyz++++− =
. D.
( ) ( ) ( )
222
1 3 2 51xyz+ ++ +− =
.
Câu 39: Trong không gian
Oxyz
, cho hai điểm
( )
1; 3; 2A −
và
( )
0; 4;3
B
. Viết phương trình đường thẳng
AB
.
A.
43
11 5
xy z−−
= =
−
. B.
115
11 5
xyz+−−
= =
−
. C.
115
13 2
xyz+−−
= =
−
. D.
43
13 2
xy z−−
= =
−
.
Câu 40: Trong không gian
Oxyz
, cho điểm
( )
2; 3;1M −
và mặt phẳng
( )
: 3 20
Px yz− +−=
. Tìm điểm đối
xứng
'M
của
M
qua
( )
P
.
A.
2 39 35
'; ;
11 11 11
M
−
. B.
42 27 81
' ;;
11 11 11
M
−
. C.
46 105 13
' ;;
11 11 11
M
−
−
. D.
96 171 9
' ;;
11 11 11
M
−
.
Câu 41: Trong không gian
Oxyz
, cho tam giác
ABC
có
( 2;0; 1)A −−
,
(1;2;7)B −−
và
(5;14;1)C −−
. Viết phương
trình đường phân giác trong góc .
A.
127
2 8 18
xy z−++
= =
−
. B.
9 41
12 7
xyz+−−
= =
−
. C.
127
1 49
xy z+−−
= =
−−
. D.
127
94 1
xy z−++
= =
−
.
Câu 42: Trong không gian
Oxyz
, cho điểm
( )
2;1;1H −
. Viết phương trình mặt phẳng cắt các trục
,,Ox Oy Oz
lần
lượt tại
,,ABC
sao cho
H
là trực tâm của tam giác
ABC
.
A.
2 30xy z+− +=
. B.
2 60xyz−−+=
. C.
2 2 60xyz− − +=
. D.
2 30x yz− ++=
.
VĐL Trang
5/5
Câu 43: Trong không gian
Oxyz
, cho
(1;1; 0)A
,
(3; 5; 2)
B
và mặt phẳng
(
)
: 2 70
x yz
α
− +−=
. Phương trình
mặt phẳng đi qua hai điểm
,
AB
và vuông góc với
( )
α
là
A.
10xz−−=
. B.
10xz−+=
. C.
0
xy
−=
. D.
0
xy
+=
.
Câu 44: Khẳng định nào sau đây đúng?
A.
sinyx=
là hàm số chẵn. B.
cosyx=
là hàm số lẻ. C.
tanyx=
là hàm số lẻ. D.
cotyx=
là hàm số chẵn.
Câu 45: Bỏ ngẫu nhiên 6 lá thư vào 6 phong bì đã viết sẵn tên người nhận. Tính xác suất để lá thư thứ nhất đến
đúng người nhận. A.
720
1
. B.
6
1
. C.
30
1
. D.
5
1
.
(1.5 !)/6 !=1/6.
Câu 46: Mệnh đề nào sau đây sai?
A. Hàm số
3
1yx= −
liên tục trên . B. Hàm số
1
x
y
x
=
−
liên tục trên
( )
1; +∞
.
C. Hàm số
sinyx
=
liên tục trên . D. Hàm số
tan
yx
=
liên tục trên
(
)
0;
π
.
Câu 47: Cho hình lăng trụ tam giác
.'' 'ABC A B C
.
G
và
'G
lần lượt là trọng tâm hai tam giác
ABC
và
'''ABC
.
Khẳng định nào sau đây sai?
A.
'/ /( ' ')AA BCC B
. B.
'C'/ /(ABC)A
. C.
GG'/ /(ACC'A')
. D.
CG/ /(AB'C')
.
Câu 48: Cho hình chóp
ABC
S.
có đáy
ABC
là tam giác đều cạnh
2
a
,
( )
ABCSA ⊥
,
4
a
SA =
. Tính góc tạo bởi
hai mặt phẳng
( )
SBC
và
( )
ABC
.
A.
0
45
. B.
0
60
. C.
0
30
. D.
0
90
.
Câu 49: Khẳng định nào sau đây đúng?
A.
5 52 2
xx x x+ −≥ −+⇔≥
. B.
22
54 3
5 43
11
xx
xx
xxxx
+
+< ⇔ >
−− −−
.
C.
( )
2
11
2
xx
x
x
+
<⇔ <
+
. D.
2
22xx xx−≥⇔−≥
.
Câu 50: Trong mặt phẳng
Oxy
, cho ba điểm
( )
( )
2; 2 , 4; 1
AB−
và
( )
4; 2C −−
. Viết phương trình đường tròn
ngoại tiếp tam giác
ABC
.
A.
2
2
3 65
24
xy
++ =
. B.
2
2
3 65
22
xy
++ =
. C.
2
2
3 65
24
xy
+ +=
. D.
2
2
3 65
22
xy
+ +=
.
ĐÁP ÁN
1 D
2A
3 A
4 B
5B
6B
7A
8A
9B
10B
11A
12A
13A
14A
15B
16A
17B
18D
19A
20A
21B
22 A
23A
24A
25B
26A
27A
28B
29C
30A
31A
32B
33B
34A
35C
36A
37A
38A
39A
40A
41A
42B
43A
44C
45B
46D
47D
48C
49B
50A
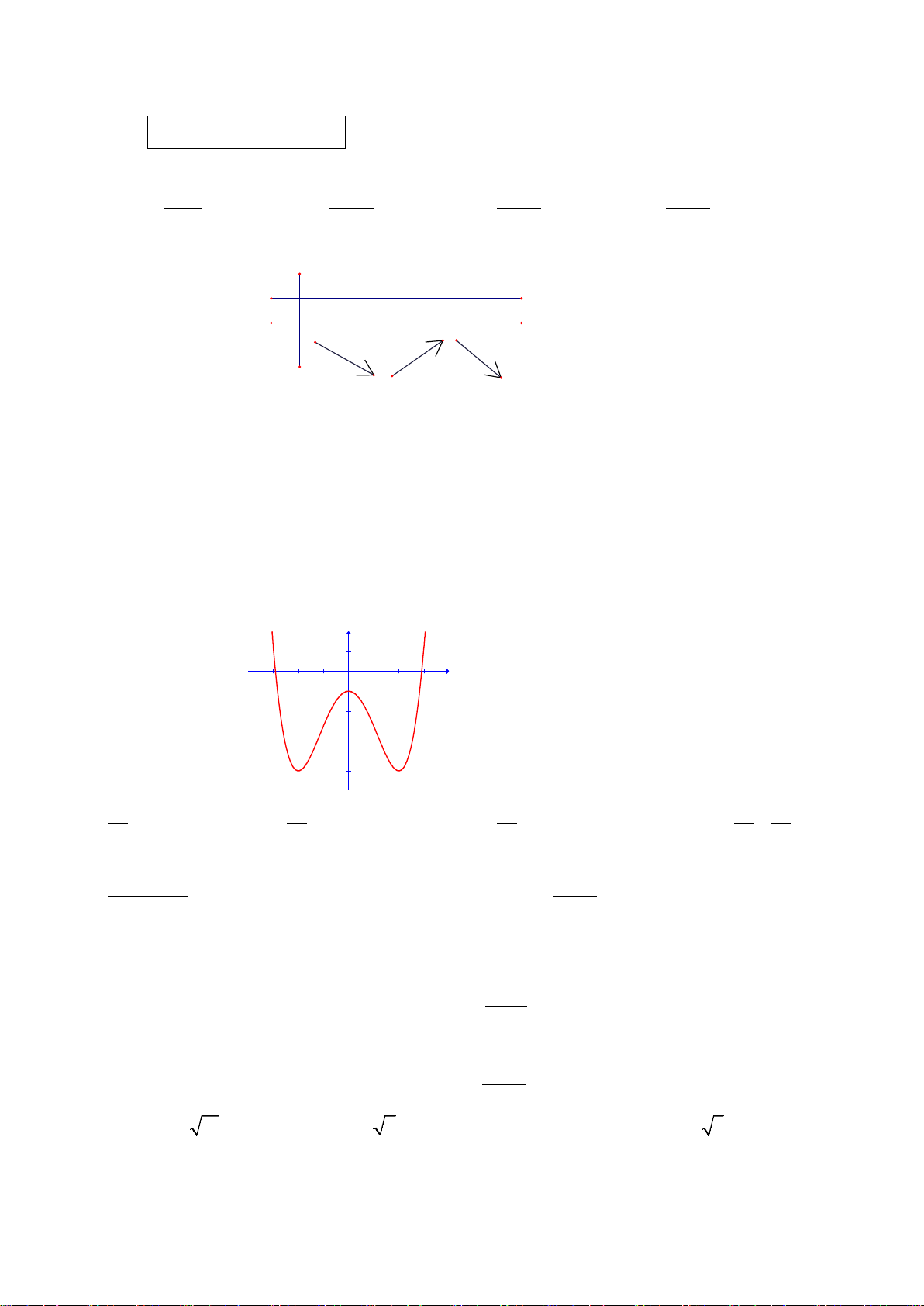
VĐL Trang
1/5
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
KỲ THI THPT QUỐC GIA NĂM 2019
TRƯỜNG PT HERMANN GMEINER
Bài thi: Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Câu 1. Hàm số nào sau đây có đường tiệm cận đứng là
2x =
và tiệm cận ngang là
2y
=
A.
2
.
2
x
y
x
+
=
−
B.
21
.
2
x
y
x
+
=
+
C.
12
.
2
x
y
x
−
=
−
D.
12
.
2
x
y
x
+
=
−
Câu 2. Khoảng đơn điệu của hàm số có bảng biến thiên:
--
+
∞
-
∞
3
+
--
+
∞
-1
-
∞
0
0
2
0
y
y'
x
A. Hàm số đồng biến trên
(
)
1; 3
−
và nghịch biến trên
( ) ( )
;0 ; 2; .−∞ +∞
B. Hàm số đồng biến trên
( )
0; 2
và nghịch biến trên
( ) ( )
;0 ; 2; .−∞ +∞
C. Hàm số đồng biến trên
( ) ( )
;0 ; 2;−∞ +∞
và nghịch biến trên
( )
0; 2
.
D. Hàm số đồng biến trên
( )
0; 2
và nghịch biến trên
(
) (
)
; 1 ; 3; .−∞ − +∞
Câu 3. Tìm giá trị nhỏ nhất m của hàm số
32
21yx x x= − ++
trên
[ ]
2;3−
.
A.
13m =
. B.
17m
= −
. C.
18m =
. D.
12m =
.
Câu 4. Đồ thị sau đây là của hàm số nào?
-3 -2 -1 1 2 3
-5
-4
-3
-2
-1
1
x
y
A.
4
2
1.
4
x
yx= −−
B.
4
2
1.
4
x
yx=−+−
C.
4
2
2 1.
4
x
yx=−−
D.
42
1
42
xx
y =−−
.
Câu 5. Trong các hàm số sau, hàm số nào chỉ có một cực đại mà không có cực tiểu?
A.
2
45
2
xx
y
x
+−
=
+
. B.
32
3 61yx x x=+ −+
. C.
21x
y
x
−
=
. D.
42
5y xx
=−− +
.
Câu 6. Phương trình tiếp tuyến của đường cong (C):
3
2yx x= −
tại điểm có hoành độ
1x = −
là:
A.
2.yx=−−
B.
2.yx= +
C.
2.yx=−+
D.
2.yx
= −
Câu 7. Tìm các giá trị của tham số m sao cho hàm số
2x
y
xm
−
=
−
đồng biến trên khoảng
(0;1)
.
A.
2m ≤
. B.
0m ≤
. C.
12m≤<
. D.
0m ≤
hoặc
12m≤<
.
Câu 8. Gọi
, AB
là các giao điểm của đồ thị hàm số
21
3
x
y
x
+
=
−
và đường thẳng
7 19yx= −
. Độ dài của đoạn
thẳng
AB
là A.
13.
B.
10 2.
C.
4.
D.
2 5.
Câu 9. Tìm tập xác định D của hàm số
22
( 1)yx
−
= −
.
A.
( ;1).D = −∞
B.
(1; ).D = +∞
C.
D ( ; 1] [-1; ).= −∞ − ∪ +∞
D.
\ { 1} .
D = ±
ĐỀ THI ĐỀ XUẤT

VĐL Trang
2/5
Câu 10. Rút gọn biểu thức
( )
( )
7 +1 2- 7
2+2
2-2
a .a
a>0
a
( )
0a >
. A.
4
Pa=
. B.
Pa=
.C.
5
Pa=
. D.
5
Pa
−
=
.
Câu 11. Cho các số thực dương
, ab
với
1a ≠
. Khẳng định nào sau đây là đúng?
A.
( ) ( )
1
log log
2
a
a
ab ab=
. B.
( )
2
log 2 2log
a
a
ab b= +
. C.
(
)
( )
2
log 2log
a
a
ab ab
=
. D.
( )
log 2 2log
a
a
ab b
= +
.
Câu 12. Cho hàm số
( )
2
2
log 3 2
y xx
= ++
. Khẳng định nào sau đây là đúng?
A. Hàm số luôn đồng biến trên
(
) ( )
2 ; 1;−∞ − − +∞
. B. Hàm số luôn đồng biến trên
( )
2; 1−−
.
C. Hàm số luôn đồng biến trên R. D. Hàm số luôn nghịch biến trên
( ) ( )
2 ; 1;−∞ − − +∞
.
Câu 13. Cho
log 1, log 4
aa
bc=−=−
. Giá trị của
( )
4
3
3
log
a
ab
c
bằng A.
31
.
3
B.
7
.
3
−
C.
29
.
3
D.
19
.
3
Câu 14. Với giá trị nào của m để bất phương trình:
0233).1(29 >−−+− mm
x
x
có nghiệm đúng với mọi số
thực : A.
2.m ≠
B.
.m ∈∅
C.
3
.
2
m ≤−
D.
( )
5 23;5 23.m ∈−− −+
Câu 15. Anh A gửi tiết kiệm ngân hàng X một số tiền là 500 triệu đồng theo hình thức: Có kì hạn 3 tháng (sau 3
tháng mới được rút tiền), lãi suất 5 %/năm, lãi nhập gốc (sau 3 tháng anh A không rút tiền ra thì tiền lãi sẽ nhập
vào gốc ban đầu). Hỏi: Để có số tiền ít nhất là 561 triệu đồng thì anh A phải gửi bao nhiêu tháng?
A. 30. B. 28. C. 27. D. 29.
Câu 16. Nguyên hàm của hàm số
2
() 3 2
fx x x
=++
là:
A.
3
2
2
2.
33
x
x xC+ ++
B.
32
3
3 2.
2
x x xC+ ++
C.
3
2
3
.
32
x
x xC+ ++
D.
3
2
3
2.
32
x
x xC+ ++
Câu 17. Cho
( ) ( )
,Fx Gx
lần lượt là một nguyên hàm của
( ) ( )
,f x gx
trên tập
K ⊂
và
,
kh∈
. Kết luận nào
sau đây là sai?
A.
( ) ( ) ( ) ( )
fxgxdxFxGxC± =±+
∫
. B.
( ) ( ) ( ) ( )
kf x hg x dx kF x hG x C± =±+
∫
.
C.
( ) (
) ( )
( )
..f x g x dx F x G x C
= +
∫
. D.
( ) ( )
',F x fx x K
= ∀∈
.
Câu 18. Giả sử
( )
1
0
7f x dx =
∫
và
( )
1
0
6g x dx
= −
∫
. Khi đó,
( )
1
0
2 3()I f x g x dx
= −
∫
bằng
A. I = - 4. B. I = 32. C. I = 22. D. I = - 37.
Câu 19. Cho biết
24
11
() 2; () 7f x dx f x dx
−−
=−=
∫∫
. Khi đó
4
2
()f x dx
∫
có kết quả là :
A. -9. B. −5. C. 9. D. 5.
Câu 20. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
32
32yx x x=−+
, trục tung, trục hoành, đường
thẳng
3
2
x =
. A.
1
2
. B.
9
64
. C.
23
64
. D. 0.
Câu 21. Cho
( )
2
4
sin= +
m
fx x
π
. Tìm tham số m để nguyên hàm
( )
Fx
của
( )
fx
thỏa
( )
0 1,
48
= =
FF
ππ
A.
3
4
m = −
. B.
5
4
m = −
. C.
1
4
=m
. D.
1
4
m = −
.
Câu 22. Tính diện tích
S
của hình phẳng
H
nằm trong phần tư thứ nhất và được giới hạn bởi đồ thị hàm số
=
3
yx
,
yx=
, và đường thẳng
=y 8x
được kết quả là: A.12. B.15,75. C.6,75. D.4.
Câu 23. Phần thực a và phần ảo b của số phức liên hợp của số phức
13zi= −
là
A. a=1, b=-3. B. a=1, b=-3i. C. a=1, b=3. D. a=-, b=1.

VĐL Trang
3/5
Câu 24. Cho hai số phức
(
)
0
z a bi; z' a' b'i z'=+=+ ≠
Khẳng định nào đúng?
A.
+−
=
+
22
z (a bi)(a ' b ' i)
.
z' a' b'
B.
++
=
+
22
z (a bi)(a ' b ' i)
.
z' a' b'
C.
+−
=
+
22
z (a bi)(a bi)
.
z' a' b'
D.
++
=
+
22
z (a bi)(a ' b ' i)
.
z' a b
Câu 25. Cho số phức
( )
35 4 2 1z ii= − +−
. Modun của số phức z là:
A. 2. B.
14 10 .i−
C.
4 6.
D.
2 74.
Câu 26. Cho
s
ố phức z thỏa mãn:
z( i) i
+=+
12 74
.Tính
ω
= +zi2
.
A.
ω
= .5
B.
ω
= .3
C.
ω
= .5
D.
ω
= .29
Câu 27. Cho hai số phức
( )( ) ( )( )
12
1 2 3, 1 3 2 .z ii z i i= − − = −− +
Mệnh đề nào dưới đây là đúng?
A.
12
..zz∈
B.
1
2
.
z
z
∈
C.
12
..zz∈
D.
12
.zz−∈
Câu 28. Tập hợp điểm biểu diễn số phức
−=z 2i 3
là đường tròn tâm I. Tất cả giá trị m sao cho khoảng cách từ
điểm I đến d :
3x 4y-m=0+
bằng
1
5
là:
A.
7; 9mm=−=
. B.
8; 8mm= = −
. C.
7; 9mm
= =
. D.
8; 9mm
= =
.
Câu 29. Giả sử
12
, z
z
là hai nghiệm của phương trình
2
2z 5 0z − +=
và A, B là các điểm biểu diễn của
12
, z
z
.
Tọa độ trung điểm của đoạn thẳng AB là
A.
(
)
0;1
. B.
( )
1; 0
. C.
(
)
0; 1
−
. D.
( )
1; 0−
.
Câu 30. Số cạnh của hình bát diện đều là A. 12. B. 8. C. 24. D. 32.
Câu 31. Cho khối lăng trụ tam giác có các cạnh đáy là 10cm, 17cm, 21cm, chiều cao của khối lăng trụ bằng trung
bình cộng của các cạnh đáy. Tính thể tích của khối lăng trụ.
A. 6720cm
3
. B. 448cm
3
. C. 1344cm
3
. D. 3500cm
3
.
Câu 32. Cho hình chóp
S.ABC
có đáy
ABC
là tam giác vuông tại
B
,
AB a
,
BC a 3
,
SA
vuông góc
với mặt đáy. Biết góc giữa
SC
và
ABC
bằng
0
60
. Thể tích khối chóp
S.ABC
bằng:
A.
3
3
.
a
B.
3
.a
C.
3
.
2a
D.
3
.3a
Câu 33. Cho hình chóp tam giác đều S.ABC. Góc giữa cạnh bên và mặt đáy bằng 60
0
.
Gọi D là giao điểm của
SA với mp qua BC và vuông góc với SA. Khi đó tỉ số thể tích của hai khối chóp S.DBC và S.ABC là:
A.
5
8
. B.
1
2
. C.
3
8
. D.
8
3
.
Câu 34. Một hình nón có bán kính đường tròn đáy là R=25cm và độ dài đường cao là h=20cm. Tính diện tích
xung quanh của hình nón đã cho.
A.
375
cm
π
. B.
750
cm
π
. C.
500
cm
π
. D.
125 41 cm
π
.
Câu 35. Diện tích toàn phần của một hình trụ nội tiếp khối lập phương có thể tích 216 là:
A.
27
tp
s
π
=
. B
54
tp
s
π
=
. C.
45
tp
s
π
=
. D.
42
tp
s
π
=
.
Câu 36. Một lon sữa hình trụ tròn xoay có chiều cao là 10cm, đường kính đáy là 6cm. Nhà sản xuất muốn tiết
kiệm chi phí sản suất vỏ lon mà không làm thay đổi thể tích của lon sữa nên đã hạ chiều cao của lon sữa xuống
còn 8cm. Tính bán kính của lon sữa mới. A.
45
2
. B.
45
. C.
65
. D.
45
4
.
Câu 37. Trong không gian cho ba véctơ
( ) (
) ( )
1;1; 0 , 1;1; 0 , 1;1;1a bc=−= =
. Mệnh đề nào sau đây đúng:
A.
=
. 1.ac
B.
,ab
cùng phương. C.
( )
=
2
os ; .
6
c bc
D.
++=
0.abc

VĐL Trang
4/5
Câu 38. Cho đường thẳng d có phương trình tham số là :
22
3
35
xt
yt
zt
= +
= −
=−+
. Phương trình nào sau đây là phương trình
chính tắc của d ?
A.
23
.
2 35
x yz−+
= =
−
B.
23
.
2 35
x yz+−
= =
−
C. x - 2 = y = x + 3. D. x + 2 = y = x – 3.
Câu 39. Cho đường thẳng d đi qua điểm M(2,3 ,0) và song song mặt phẳng (P) : 3x – 2y +z + 1 = 0
và vuông góc với đường thẳng d
’
:
113
234
xyz
−++
= =
. Phương trình tham số của đường thẳng d là :
A.
2 11
3 10 .
13
xt
yt
zt
= −
= −
=
B.
23
3 2.
13
xt
yt
zt
= +
= −
= +
C.
22
3 3.
4
xt
yt
zt
= +
= +
=
D.
2
3.
3
xt
yt
zt
= −
= +
=
Câu 40. Trong không gian
,Oxyz
cho mặt phẳng
22
: 10 0
xy zP
và điểm
2 ; 1 ; 3I
. Phương
trình mặt cầu
( )
S
tâm
I
cắt mặt phẳng
( )
P
theo một đường tròn
( )
C
có bán kính bằng 4 là
A.
22 2
2 1 3 25.xyz
B.
22 2
2 1 3 7.xyz
C.
22 2
2 1 3 9.
x yz
D.
22 2
2 1 3 25.xyz
Câu 41. Trong không gian với hệ toạ độ
,Oxyz
cho mặt phẳng
Px yz( ): 3 1 0+ −−=
và các điểm
A(1;0;0)
;
B(0; 2;3)
−
. Viết phương trình đường thẳng
d
nằm trong mặt phẳng
( )
P
đi qua
A
và cách
B
một
khoảng lớn nhất.
A.
1
: 2.
3
xt
dy t
zt
= +
=
= −
B.
1
:.
xt
dy t
zt
= +
= −
=
C.
17
: 2.
xt
dy t
zt
= +
=
=
D.
17
: 2.
xt
dy t
zt
= +
= −
=
Câu 42. Cho
0, 0xy
thay đổi và thỏa mãn điều kiện
22
()xy x y x y xy
. Tìm giá trị lớn nhất của
biểu thức
33
11
A
xy
A.
12
B.
16
C.
8
D.
4
Câu 43. Trong mặt phẳng tọa độ Oxy cho đường tròn
22
( ): 1Cx y
. Đường tròn
()C
tiếp xúc với đường
thẳng nào dưới đây?
A.
3 4 50xy
B.
10xy
C.
0xy
D.
3 4 10xy
Câu 44. Cho cấp số cộng
( )
n
u
với
33
17
=u
và
65
33
=
u
, khi đó công sai của CSC bằng:
A. 1. B. 2. C. 3. D.
2
.
Câu 45. Hệ số của
7
x
trong khai triển biểu thức
9
2x
là A.
7
9
4C
. B.
2
9
2C
. C.
7
9
C
. D.
2
9
C
.
Câu 46. Tìm hệ số không chứa x trong khai triển:
15
2
3
x
x
A.
10 10
15
3C
. B.
99
15
3C
. C.
12 10
15
3C
. D.
11 11
15
3
C
.
Câu 47. Một người có
7
cái áo và
11
cái cà vạt. Hỏi có bao nhiêu cách để chọn ra một chiếc áo và cà vạt?
A.
7
. B.
18
. C.
77
. D.
11
.
Câu 48. Một hộp có
5
bi đen và
4
bi trắng. Chọn ngẫu nhiên
2
bi. Tính xác suất
2
bi được chọn đều cùng màu.
A.
1
.
4
B.
1
.
9
C.
4
9
. D.
5
.
9
Câu 49. Giá trị của
2
2
4
34
lim
4
x
xx
xx
bằng: A.
5
.
4
B.
5
.
4
C.
1
.
D.
1
.
VĐL Trang
5/5
Câu 50. Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông tâm O cạnh bằng 2 cm,
2
SO cm
. Tính
góc giữa
SA
và
()ABCD
. A.
0
30
. B.
0
45
. C.
0
60
. D.
0
90 .
ĐÁP ÁN.
1D
2B
3B
4C
5D
6B
7D
8B
9D
10C
11D
12A
13C
14C
15A
16D
17C
18B
19C
20C
21A
22B
23C
24A
25D
26A
27A
28C
29B
30A
31C
32B
33A
34D
35B
36A
37C
38A
39A
40D
41D
42B
43A
44B
45A
46A
47C
48C
49A
50B
---------------------------------Hết--------------------------------------
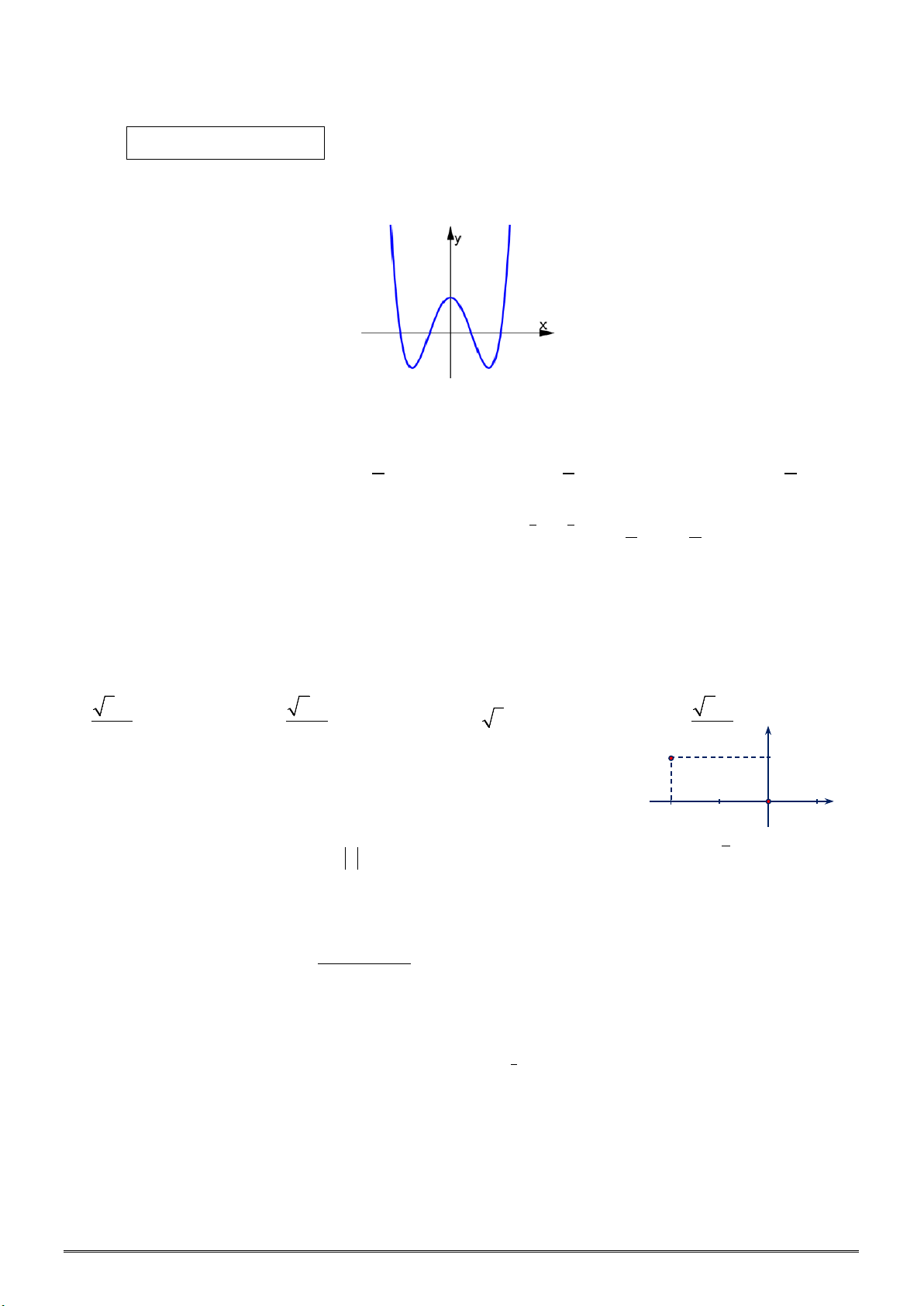
LTAD Trang 1/17
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
KỲ THI THPT QUỐC GIA NĂM 2019
TRƯỜNG THPT NGÔ GIA TỰ
Bài thi: Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Câu 1. Cho hàm số
42
cy ax
bx++=
có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
A.
0, 0, 0.
abc>>>
B.
0, 0, 0.
abc><>
C.
0, 0, 0.
abc<>>
D.
0, 0, 0.abc
><<
Câu 2. Cho hai số thực
x
,
y
thoả mãn phương trình
2 34x i yi+=+
. Khi đó giá trị của
x
và
y
là:
A.
3
x =
,
2y =
. B.
3
xi=
,
1
2
y
=
. C.
3x =
,
1
2
y =
. D.
3
x =
,
1
2
y = −
.
Câu 3. Cho
,ab
là các số thực dương,
1b ≠
thỏa mãn
5
3
7
4
a a>
,
35
log log
47
bb
<
. Mệnh đề nào dưới
đây là đúng?
A.
0 log 1.
a
b
<<
B.
log 1.
a
b >
C.
log 0.
b
a <
D.
0 log 1.
b
a<<
Câu 4. Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
,
a SA
vuông góc với mặt đáy
, SD
tạo
với mặt phẳng
( )
SAB
một góc bằng
30
. Tính thể tích
V
của khối chóp.
A.
3
3
.
3
a
B.
3
6
.
18
a
C.
3
3.a
D.
3
6
.
3
a
Câu 5. Điểm
M
trong hình vẽ bên là điểm biểu diễn số phức
A.
2zi=−+
. B.
12zi= −
.
C.
2zi= +
. D.
1 2.zi= +
Câu 6. Cho số phức
z
thỏa mãn
2z
=
. Tập hợp điểm biểu diễn số phức
( )
12w iz i=−+
là
A. Một đường tròn. B. Một đường thẳng.
C. Một Elip. D. Một parabol hoặc hyperbol.
Câu 7. Tìm
m
để hàm số
( )
34mx
y
xm
++
=
+
nghịch biến trên khoảng
( )
;1−∞
.
A.
(
)
4;1 .m ∈−
B.
[ ]
4;1 .m ∈−
C.
( )
4; 1 .m ∈− −
D.
(
]
4; 1 .m
∈− −
Câu 8. Số nghiệm của phương trình
( )
( )
2
1
3
3
4llog 2 3og 0x x x++ +=
là
A.
2.
B.
0.
C.
1.
D.
3.
Câu 9. Cho hàm số phù hợp với bảng biến thiên sau. Phát biểu nào sau đây đúng?
O
x
y
2−
1
M
ĐỀ THI ĐỀ XUẤT

LTAD Trang 2/17
A. Hàm số đạt cực đại tại điểm
1.
x
=
B. Hàm số đạt cực đại tại điểm
0.x
=
C. Hàm số đạt cực đại tại điểm
1.x = −
D. Hàm số không có điểm cực đại.
Câu 10. Một hình trụ có bán kính đáy
4
cm
và có thiết diện qua trục là một hình vuông. Tính thể tích
V
của khối trụ đó.
A.
( )
3
180 .V cm
π
=
B.
( )
3
64 .V cm
π
=
C.
( )
3
128 .V cm
π
=
D.
( )
3
256 .V cm
π
=
Câu 11. Số đường tiệm cận ngang của đồ thị hàm số
2
1
23
yx x x+ ++ +=
là
A.
1.
B.
0.
C.
3.
D.
2.
Câu 12. Cho hình chóp
.
S ABC
có đáy là tam giác vuông tại
B
, hai mặt bên
SAB
và
SAC
cùng
vuông góc với đáy,
2
SB a=
,
AB BC a
= =
. Bán kính của mặt cầu ngoại tiếp hình chóp
.S ABC
là
A.
6
.
2
a
R =
B.
5
.
2
a
R =
C.
2.
Ra=
D.
3
.
2
a
R =
Câu 13. Cho cấp số nhân
( )
n
u
có
2
2u = −
và
5
54.
u =
Tính tổng
100
số hạng đầu tiên của cấp số nhân
đã cho.
A.
100
100
13
.
4
S
−
=
B.
100
100
31
.
2
S
−
=
C.
100
100
31
.
6
S
−
=
D.
100
100
13
.
6
S
−
=
Câu 14. Cho tam giác
ABC
vuông tại
A
với
,2
AB a AC a= =
quay xung quanh cạnh
AB
ta được
một khối nón tròn xoay có đường sinh
l
bằng bao nhiêu ?
A.
5.
la
=
B.
3.la=
C.
3.la=
D.
2 2.la=
Câu 15. Tìm tập xác định của hàm số
( )
1
3
log 3 .yx= −
A.
( )
3; .D = +∞
B.
(
]
3; 4 .D =
C.
[
)
4; .D = +∞
D.
(
]
0; 4 .D =
Câu 16. Kí hiệu
1
z
,
2
z
,
3
z
,
4
z
là bốn nghiệm của phương trình
42
60zz+ −=
. Tính
1234
Sz z z z=+++
.
A.
23S =
. B.
( )
22 3S = −
. C.
22S =
. D.
( )
22 3S = +
.
Câu 17. Cho
2
logam=
và
log 8
m
Am=
, với
01m<≠
. Khẳng định nào sau đây là đúng?
A.
(
)
3.A aa= −
B.
(
)
3.A aa= +
C.
3
.
a
A
a
−
=
D.
3
.
a
A
a
+
=
Câu 18. Diện tích ba mặt của hình hộp chữ nhật lần lượt là
222
15 ,24 ,40cm cm cm
. Thể tích của khối
hộp đó là
A.
3
120 .cm
B.
3
140 .cm
C.
3
150 .cm
D.
3
100 .cm
Câu 19. Với các số thực dương
,1ab≠
, ta có các đồ thị hàm số
, log
x
b
y ay x= =
được cho như hình
vẽ bên. Mệnh đề nào sau đây đúng?
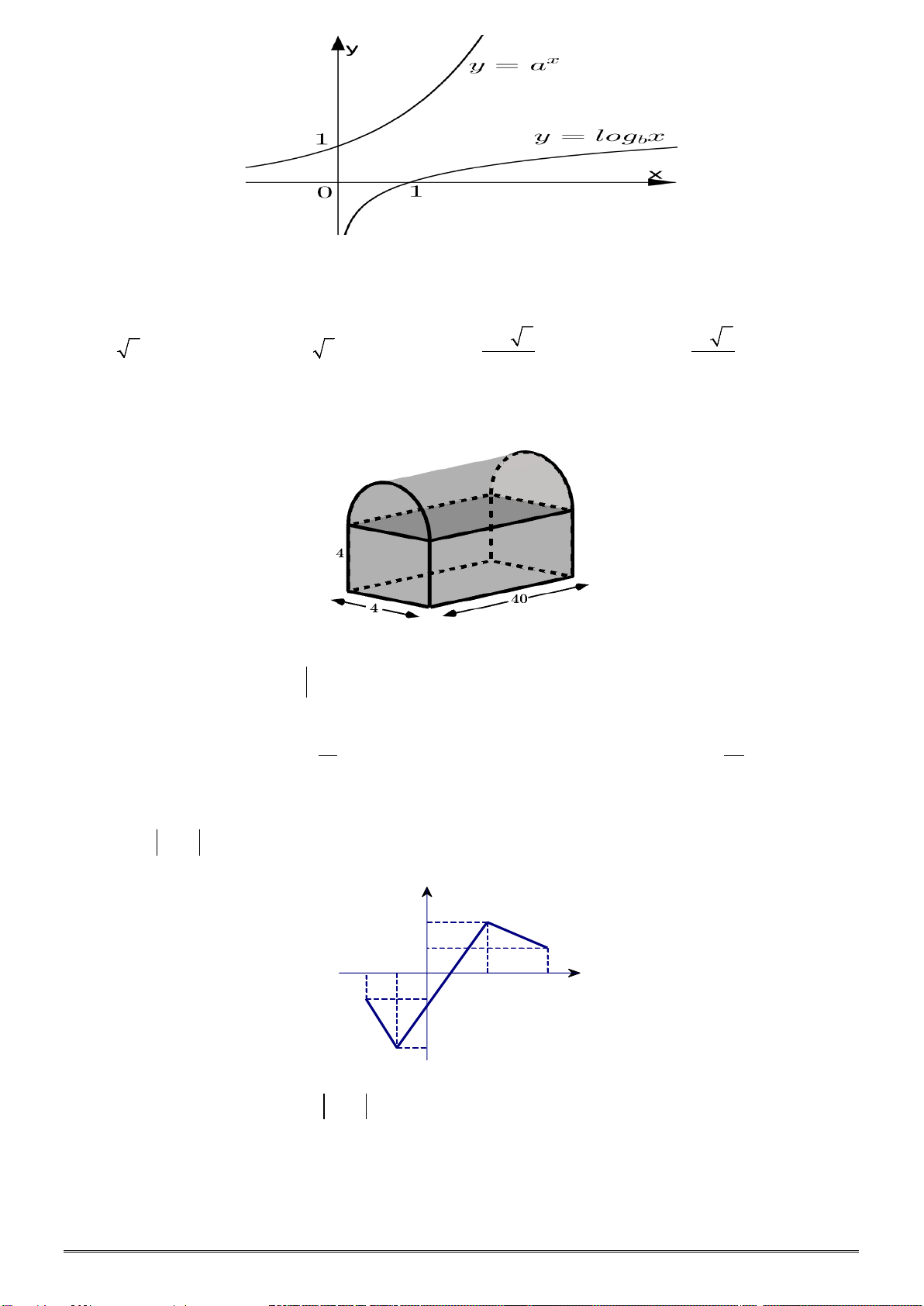
LTAD Trang 3/17
A.
1.ab<<
B.
1.
ba<<
C.
1.ab<<
D.
1.ba<<
Câu 20. Cho hình lăng trụ tam giác đều có cạnh đáy bằng
2a
và có các mặt bên đều là hình vuông.
Thể tích khối lăng trụ đã cho bằng
A.
3
3 2.
a
B.
3
2 3.a
C.
3
22
.
3
a
D.
3
2
.
2
a
Câu 21. Một thùng thư, được thiết kế như hình vẽ bên, phần phía trên là nữa hình trụ. Thể tích của
thùng đựng thư là
A.
640 160 .
π
+
B.
640 80 .
π
+
C.
640 40 .
π
+
D.
320 80 .
π
+
Câu 22. Cho tập
22
4 12 7 3 0.xxxXx x
Tính tổng bình phương
S
các phần tử
của tập
.X
A.
6.S
B.
15
.
2
S
C.
14.S
D.
73
.
4
S
Câu 23. Cho hàm số
( )
y fx=
có đồ thị trên đoạn
[
]
2; 4
−
như hình vẽ. Tìm giá trị lớn nhất
M
của
hàm số
( )
y fx=
trên đoạn
[ ]
2; 4−
.
A.
2.M =
B.
( )
0.Mf
=
C.
3.M =
D.
1.M =
Câu 24. Cho hình chóp tam giác đều
.S ABC
có cạnh bên bằng
2a
, góc giữa cạnh bên và mặt đáy bằng
30°
. Tính khoảng cách từ
S
đến mặt phẳng
( )
.ABC
2
-1
-1
-3
-2
1
4
2
y
x
O

LTAD Trang 4/17
A.
.a
B.
2.a
C.
3
.
2
a
D.
.
2
a
Câu 25. Phương trình đường tròn
( )
C
có tâm
( )
1; 2I
và tiếp xúc với đường thẳng
: –2 7 0xy∆ +=
là:
A.
( ) ( )
22
16
1 –2 .
5
xy++ =
B.
( ) ( )
22
16
1 –2 .
5
xy−+ =
C.
( ) ( )
22
4
1 2.
5
xy− +− =
D.
( ) ( )
22
1 – 2 5.xy−+ =
Câu 26. Trong không gian
,Oxyz
cho đường thẳng
85
:
4 21
xyz
d
+−
= =
−
. Khi đó vectơ chỉ phương của
đường thẳng
d
có tọa độ là
A.
( )
4; 2;1−
. B.
( )
4; 2; 1
−
. C.
( )
4; 2; 1−−
D.
( )
4; 2;1
.
Câu 27. Tìm nguyên hàm
( ) ( )
sinF x x x dx= +
∫
biết
( )
0 19F =
.
A.
( )
2
cos 20.Fx x x=++
B.
( )
2
cos 20.Fx x x=−+
C.
( )
2
1
cos 20.
2
Fx x x=++
D.
( )
2
1
cos 20.
2
Fx x x=−+
Câu 28. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
B
,
3AB =
,
4BC =
, đường thẳng
SA
vuông góc với mặt phẳng
( )
ABC
, biết
4SA =
. Gọi
, MN
lần lượt là chiều cao của A lên cạnh
SB
và
SC
. Thể tích khối tứ diện
AMNC
là
A.
768
.
41
B.
128
.
41
C.
384
.
41
D.
256
.
41
Câu 29. Trong không gian với hệ tọa độ
Oxyz
, cho tam giác
ABC
có đỉnh
( )
2; 2; 2C −
và trọng tâm
( )
1;1; 2G −
. Tìm tọa độ các đỉnh
, AB
của tam giác
ABC
, biết
A
thuộc mặt phẳng
( )
Oxy
và điểm
B
thuộc trục
Oz
A.
(
) ( )
1;1; 0 , 0; 0; 4 .AB
−
B.
( ) ( )
1; 1; 0 , 0; 0; 4 .AB−−
C.
( ) ( )
1;0;1 , 0;0; 4 .AB−
D.
( )
( )
4; 4;0 , 0;0;1 .AB−
Câu 30. Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
0;10
và
( )
10
0
d7fx x=
∫
và
( )
6
2
d3
fx x=
∫
. Tính
( ) ( )
2 10
06
ddP fx x fx x= +
∫∫
.
A.
7P =
. B.
4P = −
. C.
4P =
. D.
10
P =
.
Câu 31. Biết rằng
0
cos
x
e xdx ae b
π
π
= +
∫
trong đó
,ab∈
. Tính
?P ab= +
A.
1.P =
B.
0.P =
C.
1
.
2
P = −
D.
1.P = −
Câu 32. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )
: 2 10 0P xyz−+− =
và đường thẳng
2 11
:
21 1
x yz
d
+ −−
= =
−
. Đường thẳng
Δ
cắt
( )
P
và
d
lần lượt tại
M
và
N
sao cho
( )
1; 3; 2A

LTAD Trang 5/17
là trung điểm
MN
. Tính độ dài đoạn
MN
.
A.
4 33MN =
. B.
2 26,5MN =
. C.
4 16,5MN =
. D.
2 33MN =
.
Câu 33. Tìm mệnh đề sai trong các mệnh đề sau.
A.
4
3
d
4
+
=
∫
xC
xx
. B.
1
d ln= +
∫
x xC
x
. C.
sin d cos= −
∫
xx C x
. D.
( )
2e d 2 e= +
∫
xx
xC
.
Câu 34. Cho hình lăng trụ
.ABC A B C
′′′
có đáy
ABC
là tam giác đều cạnh
a
. Hình chiếu vuông góc
của
A
′
xuống
( )
ABC
là trung điểm của
AB
. Mặt bên
( )
ACC A
′′
tạo với đáy góc
45°
. Tính thể tích khối
lăng trụ
.ABC A B C
′′′
.
A.
3
3
.
3
a
B.
3
23
.
3
a
C.
3
3
.
16
a
D.
3
.
16
a
Câu 35. Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
(
)
( )
( )
1; 2; 1 , 2;1;1 , 0;1; 2
A BC−
. Gọi
( )
;;H abc
là trực tâm của tam giác
ABC
. Giá trị của
abc++
bằng
A.
4.
B.
5.
C.
6.
D.
7.
Câu 36. Cho hàm số
( )
(
)
3 22 2
2 32y x mx m x m m C=− + − ++
Khi tham số thực
m
thay đổi nhận thấy
đồ thị
( )
C
luôn tiếp xúc với một parabol cố định
( )
P
. Gọi tọa độ đỉnh của parabol
( )
P
là
( )
;.
II
Ix y
Khi
đó giá trị
2
II
Tx y= −
là
A.
1.
B.
3.−
C.
4.
D.
5.
Câu 37. Cho hình lăng trụ
.'' 'ABC A B C
có các mặt bên đều là hình vuông cạnh
.
a
Gọi
, , DEF
lần
lượt là trung điểm của các cạnh
, ' ', ' '.BC A C C B
Khoảng cách giữa hai đường thẳng
DE
và
'
AB
bằng
A.
2
.
3
a
B.
2
.
4
a
C.
3
.
4
a
D.
5
.
4
a
Câu 38. Cho hàm số
( )
2
1gx x= +
và hàm số
( )
32
3 1.fx x x=−+
Tìm
m
để phương trình
( )
0f gx m−=
có 4 nghiệm phân biệt.
A.
3 1.m
− < ≤−
B.
3 1.m
− ≤ ≤−
C.
1.m >−
D.
3 1.
m− < <−
Câu 39. Cho hàm số
( )
y fx
=
có đồ thị
(
)
y fx
′
=
cắt trục
Ox
tại ba điểm có hoành độ
abc<<
như
hình vẽ.
Khẳng định nào dưới đây có thể xảy ra?
A.
( ) ( ) ( )
.
fa fb fc>>
B.
( ) ( ) ( )
.fb fa fc>>
C.
( ) ( ) ( )
.
fc fa fb>>
D.
( ) ( ) ( )
.fc fb fa>>
Câu 40. Cho hình vuông
1
V
có chu vi bằng
1.
Người ta nối các trung điểm của các cạnh một cách thích
hợp để có hình vuông
2
V
(tham khảo hình vẽ bên). Từ hình vuông
2
V
tiếp tục làm như trên ta được dãy
các hình vuông
123
, , ,...VV V
Tổng chu vi các hình vuông đó bằng
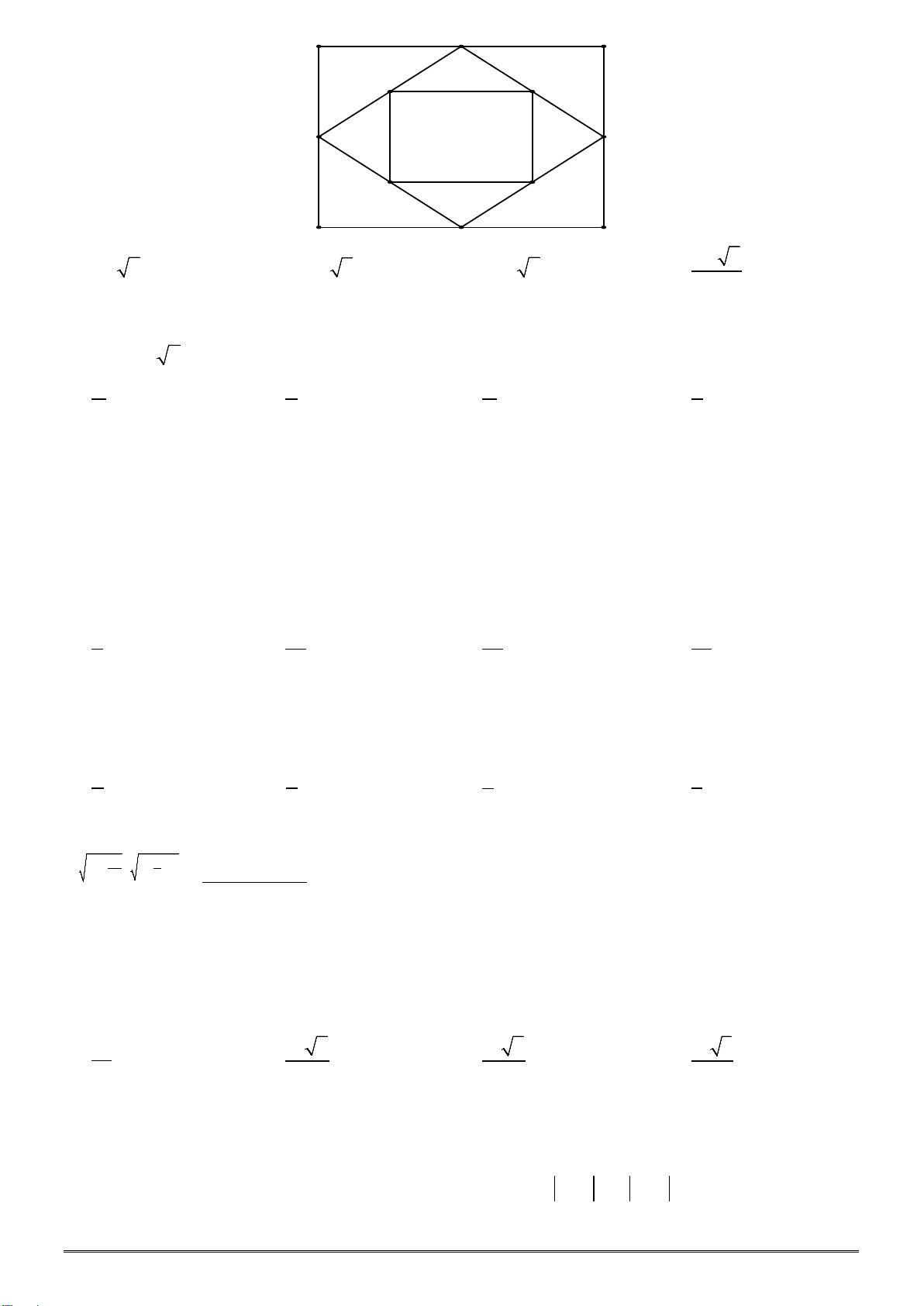
LTAD Trang 6/17
A.
2 2.+
B.
(
)
42 2.
+
C.
6 2 2.+
D.
32
.
2
+
Câu 41. Thể tích của khối tròn xoay thu được khi quay quanh trục
Ox
hình phẳng giới hạn bởi đồ thị
hàm số
e
x
yx=
, trục hoành và đường thẳng
1x =
là:
A.
( )
2
e1
4
π
+
. B.
( )
2
1
e1
4
+
. C.
( )
4
e1
4
π
−
. D.
( )
4
1
e1
4
−
.
Câu 42. Ông Bách dự định đầu tư khoản tiền
20
triệu đồng vào một dự án với lãi suất tăng dần:
3,35%
/năm trong
3
năm đầu,
3,75%
/năm tong
2
năm kế tiếp và
4,8%
/năm ở
5
năm cuối. Khoản tiền
mà ông Bách nhận được (cả vốn và lãi) cuối năm thứ
10
là
A.
25
triệu. B.
30
triệu. C.
35
triệu. D.
40
triệu.
Câu 43. Một chuồng có
3
con thỏ trắng và
4
con thỏ nâu. Người ta bắt ngẫu nhiên lần lượt từng con
ra khỏi chuồng cho đến khi nào bắt được cả
3
con thỏ trắng mới thôi. Xác suất để cần phải bắt đến ít nhất
5
con thỏ là
A.
4
.
5
B.
4
.
35
C.
29
.
35
D.
31
.
35
Câu 44. Cho parabol
( )
2
:Pyx=
và hai điểm
A
,
B
thuộc
(
)
P
sao cho
2AB
=
. Tìm giá trị lớn nhất
của diện tích hình phẳng giới hạn bởi parabol
( )
P
và đường thẳng
AB
.
A.
3
2
. B.
4
3
. C.
3
4
. D.
5
6
.
Câu 45. Có bao nhiêu giá trị nguyên dương của
m
nhỏ hơn
2018
để phương trình
2
2
11
32
4
1
x xm
x
x
x mx x
e
x
+ − ++
++
=
+
có nghiệm thực dương?
A.
2016.
B.
2017.
C.
2018.
D.
2019.
Câu 46. Cho hình vuông
ABCD
cạnh
,a
trên đường thẳng vuông góc với
(
)
ABCD
tại
A
ta lấy điểm
S
di động. Hình chiếu vuông góc của
A
lên
,SB SD
lần lượt là
,.HK
Thể tích lớn nhất của tứ diện
ACHK
bằng
A.
3
.
6
a
B.
3
2
.
12
a
C.
3
6
.
32
a
D.
3
3
.
16
a
Câu 47. Cho hàm số
( )
y fx=
có đạo hàm, liên tục trên
.
Gọi
12
, dd
lần lượt là tiếp tuyến của đồ
thị hàm số
( )
4
y fx=
và
( ) ( )
3
65y gx xf x= = −
tại điểm có hoành độ bằng
1.
Biết rằng hai đường
thẳng
12
, dd
có tích hệ số góc bằng
6,−
giá trị nhỏ nhất của
( ) ( )
3
1 312Qf f=−+
bằng
A.
3.
B.
4.
C.
5.
D.
2.
LTAD Trang 7/17
Câu 48. Cho các số thực
, ,
abc
thỏa
( ) ( ) ( )
2
222
log 4 4 4 .
2
abc
aabbcc
abc
++
= −+ −+ −
+++
Giá trị lớn
nhất của biểu thức
23abc
P
abc
++
=
++
bằng
A.
4 30
.
3
+
B.
8 30
.
3
+
C.
6 30
.
3
+
D.
12 30
.
3
+
Câu 49. Cho số phức
z
thỏa mãn
24zizi− ≤−
và
33 1
zi
−− =
. Giá trị lớn nhất của biểu thức
2Pz
= −
là:
A.
13 1+
. B.
10 1+
. C.
13
. D.
10
.
Câu 50. Biết rằng đồ thị hàm số
( )
432
y f x ax bx cx dx e= = + + ++
(với
,,, ,abcde
∈
và
0; 0ab≠≠
) cắt trục hoành tại
4
điểm phân biệt. Khi đó đồ thị hàm số
( ) ( ) ( ) ( )
2
.0gx f x f x f x
′ ′′
=−=
cắt trục hoành tại bao nhiêu điểm?
A.
0.
B.
2.
C.
4.
D.
6.
−−−−−−−−−− HẾT −−−−−−−−−−
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
Câu 6
Câu 7
Câu 8
Câu 9
Câu 10
B
C
C
A
A
A
D
C
B
C
Câu 11
Câu 12
Câu 13
Câu 14
Câu 15
Câu 16
Câu 17
Câu 18
Câu 19
Câu 20
A
B
D
A
B
D
D
A
C
B
Câu 21
Câu 22
Câu 23
Câu 24
Câu 25
Câu 26
Câu 27
Câu 28
Câu 29
Câu 30
B
C
C
A
B
A
D
B
A
C
Câu 31
Câu 32
Câu 33
Câu 34
Câu 35
Câu 36
Câu 37
Câu 38
Câu 39
Câu 40
D
C
B
C
A
D
C
D
C
A
Câu 41
Câu 42
Câu 43
Câu 44
Câu 45
Câu 46
Câu47
Câu 8
Câu 49
Câu 50
A
B
D
B
D
D
D
B
C
A
LTAD Trang 8/17
ĐÁP ÁN CHI TIẾT
Câu 1. Vì đồ thị hàm số có hai điểm cực trị và
( )
0
lim
,0
x
fx
ab
→±∞
= +∞⇒ > <
.
Mặt khác điểm cực đại của đồ thị hàm số có tung độ dương
0c⇒>
. Chọn B.
đường thẳng
Câu 2. Lời giải Từ
2 34x i yi+=+
3
24
x
y
=
⇒
=
3
1
2
x
y
=
⇔
=
. Vậy
3x =
,
1
3
y =
.
Câu 3. Ta có:
5
3
7
4
1
a
a
a
;
35
log log 0 1
47
bb
b
. Vậy
log 0.
b
a <
Chọn C.
Câu 4. Chú ý rằng
0
30DSA
do đó Chọn A.
Câu 5. Lời giải Chọn A Điểm
( )
2;1M −
biểu diễn số phức
2zi=−+
.
Câu 6. Lời giải Chọn A
Ta có:
( )
12w iz i=−+
( )
21w i iz⇔−=−
(
)
21
w i iz
⇒−=−
2 22wi⇔−=
.
Do đó, tập hợp điểm biểu diễn số phức
w
là đường tròn tâm
( )
0; 2I
và bán kính
22
.
Câu 7. Ta có tập xác định
{ }
\Dm= −
và
( )
2
2
3
'
4mm
y
xm
+−
=
+
Hàm số nghịch biến trên khoảng
(
)
;1−∞
khi
( )
(
]
2
4;1
3 40
;1
1
4
1
m
m
m
m
m
m
∈−
+
⇔⇔
−<
∈− −
≤−
≤−
. Chọn D.
Câu 8. Điều kiện:
2
0
4
0
2 30
40
3
2
x
xx
x
x
x
x
*
Ta có :
( )
( )
( )
( )
22
33
13
3
log 2 3 04 log 4 loglog 2 3
xx xxxx+= +⇔++ +=
.
22
1
4 2 3 2 30
3
x
xx x xx
x
. Kết hợp với
*
, ta được
1x
. Chọn C.
Câu 9. Vì
'y
đổi dấu từ dương sang âm khi đi qua điểm
0x =
nên đây là điểm cực đại. Chọn B.
Câu 10. Hình trụ có bán kính
4
r =
và chiều cao
22
2 8 .8 1.4
28hr V h
r= =⇒= = =
ππ π
. Chọn C.
Câu 11. Hàm số có tập xác định
D =
Ta có:
(
)
( )
22
2
2
2213
lim , lim lim 1 3 lim
13
2
2
x xx x
xx xx
y y x xx
x xx
→+∞ →−∞ →−∞ →−∞
+− +
= +∞ = + + + =
+−
+
+
+ +
+
2
2
lim 0
1 2
3
x
x xx
→−∞
−
= = ⇒
+− ++
Đồ thị hàm số có TCN
0y =
. Chọn A.
Câu 12. Ta có
( ) ( )
SAB ABC⊥
và
( ) ( )
SAC ABC⊥
, mà
( ) (
)
SAB SAC SA∩=
.
Suy ra
( )
.SA ABC⊥
Gọi
I
là trung điểm của
SC
.
Ta có
SAC∆
vuông tại
A
nên
.IS IA IC= =
Do
( )
BC SAB SBC⊥ ⇒∆
vuông tại
B
nên
.IS IB IC= =
Do đó
I
là tâm của mặt cầu ngoại tiếp hình chóp
.S ABC
.
Vì vậy:
22
5
.
22 2
SC SB BC a
R
+
= = =
Chọn B.
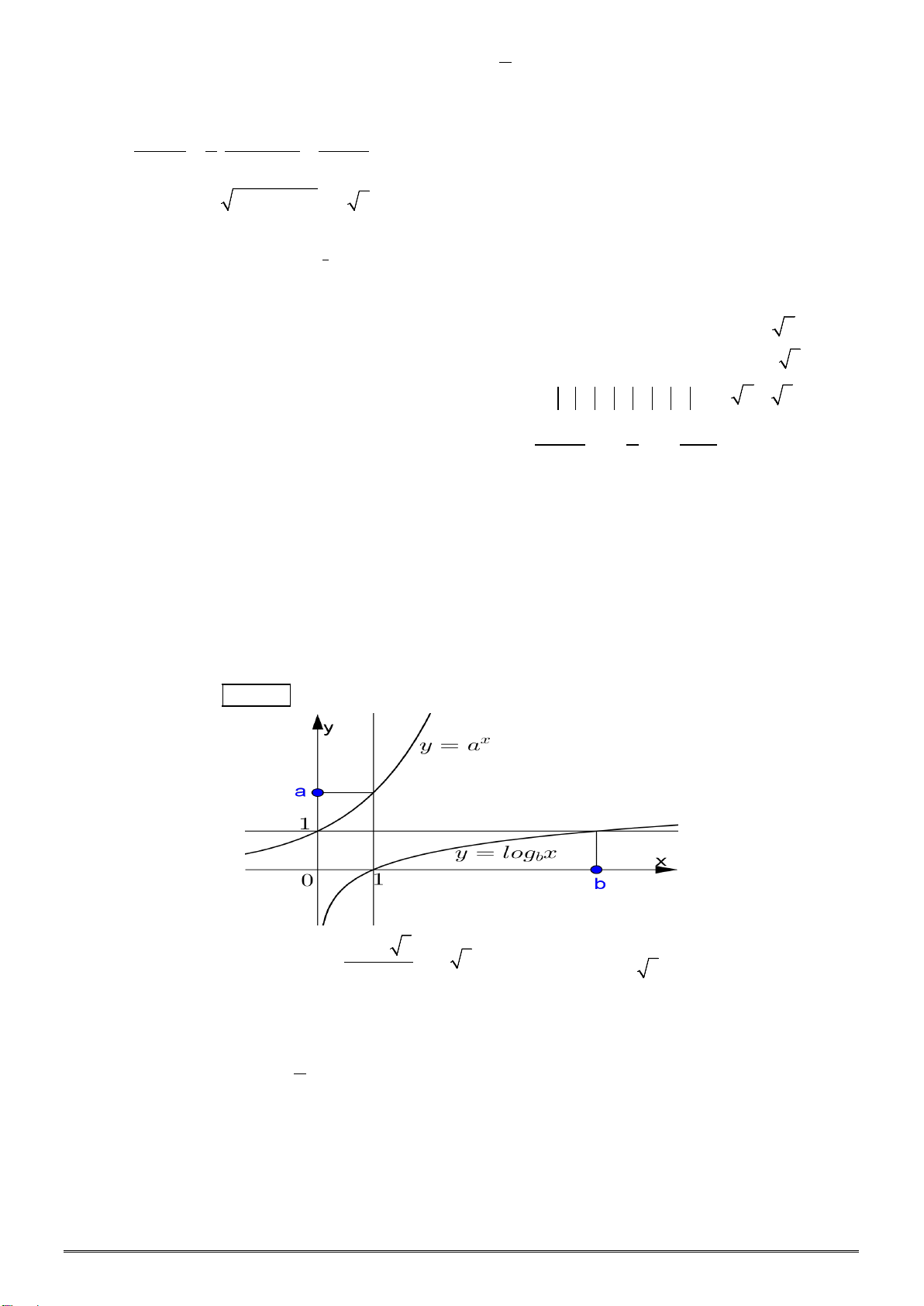
LTAD Trang 9/17
Câu 13. Ta có
21
1
4 33
51 1
2
2
.
3
54 . 2
3
u uq
u
u uq uqq q
q
−= =
=
⇔
= = = = −
= −
Khi đó
(
)
(
)
100
100 100
100 1
13
1 2 13
..
1 31 3 6
−−
−−
= = = ⇒
− −−
q
Su
q
Chọn D.
Câu 14.
22
5.
l BC AB AC a
== +=
Chọn A.
Câu 15. Điều kiện xác định
( )
1
3
log 3 0x −≥
30
31
x
x
−>
⇔
−≤
3
4
x
x
>
⇔
≤
.
Vậy tập xác định hàm số là
(
]
3; 4D
=
. Chọn B.
Câu 16. L ời giải Chọn D a có:
42
60zz+ −=
2
2
2
3
z
z
=
⇔
= −
2
3
z
zi
= ±
⇔
= ±
.
Kí hiệu
1
z
,
2
z
,
3
z
,
4
z
là bốn nghiệm của phương trình, ta có:
1234
Sz z z z=+++
(
)
22 3
= +
.
Câu 17. Ta có
2
3 33
log 8 log 8 log 3log 2 1 1 1 .
log
m mm m
a
Am m
ma a
+
= = + = += += +=
Chọn D.
Câu 18. Gọi kích thước ba cạnh của hình hộp chữ nhật là
( )
;;abc cm
.
Vì các mặt là các hình chữ nhật nên diện tích ba mặt lần lượt là:
( )
2
15
24 15.24.40 120.
40
ab
bc abc abc
ac
=
=⇒ = ⇒=
=
Vậy thể tích của hình hộp chữ nhật là:
3
120 .V abc cm
= =
Chọn A.
Câu 19. Đầu tiên chúng ta kẻ thêm các đường thẳng
1x =
và
1y =
như hình vẽ dưới đây. Từ đây ta
nhận xét được rằng:
1 ab<<
. Chọn C.
Câu 20. Từ giả thiết, ta có
( )
2
2
3
day
day
23
3
. 2 3.
4
2
a
Sa
VSh a
ha
= =
→ = =
=
Chọn B.
Câu 21. Thể tích phần phía dưới là
1
4.4.40 640.V = =
Thể tích phần bên trên là
( )
2
2
1
2 .40 80 .
2
V
ππ
=×=
Vậy
12
640 80 .VVV
π
=+= +
Chọn B.
LTAD Trang 10/17
Câu 22. Lời giải: Ta có
2
2
2
2
2
40 2
7 3 0 10 1 .
1
7 30
2
1
3
42
2
x
xx
xx x
x
x
x
x
xx
x
Suy ra
22 2
2 1 3 14.S
Chọn C.
Câu 23. Từ đồ thị hàm số
( )
y fx=
trên đoạn
[ ]
2; 4−
ta suy ra đồ thị hàm số
(
)
fx
trên
[ ]
2; 4−
như
hình vẽ.
Do đó
[
]
(
)
2;4
max 3fx
−
=
tại
1.x = −
Chọn C.
Câu 24. Ta có hình vẽ sau
Gọi
G
là tâm tam giác đều
ABC
thì
( )
SG ABC⊥
,
30SAG = °
.
Ta có
sin
SG
SAG
SA
=
1
22
SG
a
⇒=
SG a⇒=
⇒
Chọn A.
Câu 25.
Lời giải:
( )
( )
[ ]
( )
( ) ( )
22
1; 2
16
: :1 2 .
147
4
5
;
14 5
I
C Cx y
R dI
→−
∆
+− =
−+
= = =
+
Chọn B.
Câu 26. Lời giải Chọn A
Vectơ chỉ phương của đường thẳng
d
có tọa độ là
( )
4; 2; 1−
.
Câu 27. Ta có:
( ) ( )
sin dFx x x x= +
∫
2
cos
2
x
xC=−+
. Mà
( )
0 19 1 19FC= ⇔− + =
20C⇔=
.
Chọn D.
Câu 28. Ta có hình vẽ sau:
O
x
y
2
4
1
-2
3
-1
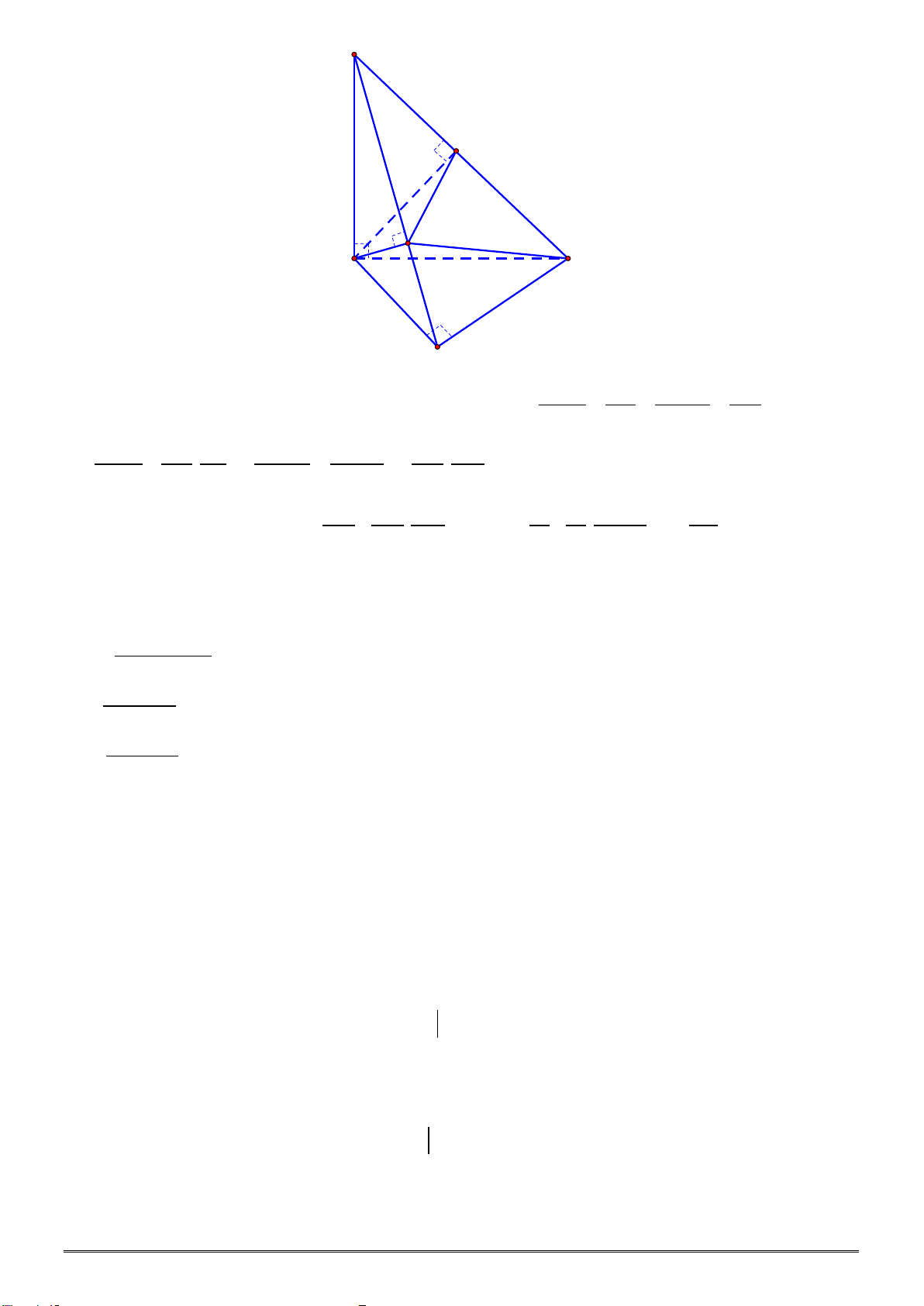
LTAD Trang 11/17
M
N
A
C
B
S
. ..
.
A MNC S AMC S AMN
V VV= −
Mặt khác:
2
.
22
.
.
S AMC
S ABC
V
SM SM SB SA
V SB SB SB
= = =
.
Và
22
.
2 2 22
.
..
. ..
S AMN
S ABC
V
SM SN SM SB SN SC SA SA
V SB SC SB SC SB SC
= = =
Do đó:
2 2 2 22 2
. .. .
2 2 2 2 22 2
4 4 4 128
. . . .8
5 5 4 5 41
A MNC S AMC S AMN S ABC
SA SA SA
V VV V
SB SB SC
=−=− =− =
+
. Chọn B.
Câu 29. Giả sử
( ) ( ) ( )
; ; 0 , 0;0; .
AA B
A x y Oxy B z Oz∈∈
Vì
( )
1;1; 2
G −
là trọng tâm của tam giác
ABC
nên
( )
(
) ( )
02
1
3
1
02
1 1 1;1; 0 , 0; 0; 4 .
3
4
02
2
3
A
A
A
A
B
B
x
x
y
yA B
z
z
+ +−
−=
= −
++
= ⇒ =⇒−
=
++
=
Chọn A.
Câu 30. Chọn C
Ta có
(
)
10
0
d7fx x
=
∫
( ) ( ) ( )
2 6 10
026
d d d7fx x fx x fx x⇔++ =
∫∫∫
( ) ( )
2 10
06
d d 734fx x fx x⇔ + =−=
∫∫
.Vậy
4P =
.
Câu 31. Ta có:
0
cos
x
I e xdx ae b
π
π
= = +
∫
Đặt:
cos sin
xx
u x du xdx
dv e dx v e
= = −
⇒
= =
1
0
0
.cos sin
xx
I
I e x e xdx
π
π
⇒= +
∫
1
e eI
π
=− −+
Ta sẽ đi tính
1
0
sin
x
I e xdx
π
=
∫
.
Đặt:
sin cos
xx
u x du xdx
dv e dx v e
= =
⇒
= =
1
0
0
.sin cos
xx
I
I e x e xdx
π
π
⇒= −
∫
I= −
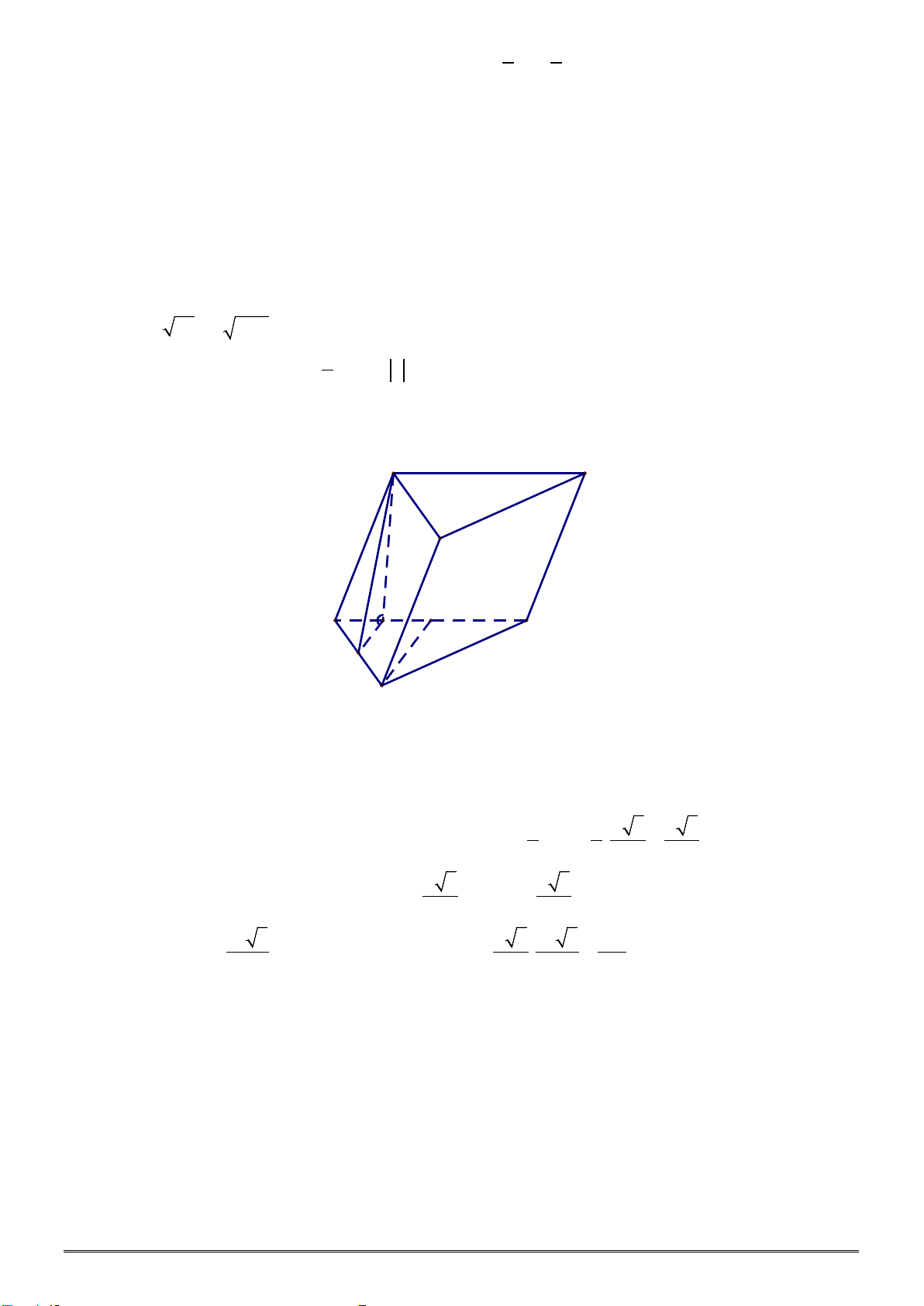
LTAD Trang 12/17
Vậy:
0
cos
x
I e xdx e e I
π
π
= =− −−
∫
11
2
22
I eeI e
ππ
⇒ =− −⇒ =− −
.
1ab+=−
. Chọn D.
Câu 32. Lời giải Chọn C
Vì
Δ
Nd= ∩
nên
Nd∈
, do đó
(
)
2 2 ;1 ;1
N ttt
−+ + −
.
Mà
(
)
1; 3; 2A
là trung điểm
MN
nên
2 4 2,
2 5,
2 3.
M AN M
M AN M
M AN M
x xx x t
y yy y t
z zz z t
=−=−
= −⇔ =−
=−=+
Vì
( )
ΔMP
= ∩
nên
( )
MP
∈
, do đó
(
)
( )
( )
2 4 2 5 3 10 0 2
ttt t− −−++−=⇔=−
.
Suy ra
(
)
8; 7;1
M
và
( )
6; 1; 3N −−
.
Vậy
2 66 4 16,5MN = =
.
Câu 33. Chọn B Ta có
1
d ln= +
∫
x xC
x
.
Câu 34. Ta có hình vẽ sau:
I
M
H
C
B
A'
B'
C'
A
Gọi
H
,
M
,
I
lần lượt là trung điểm các cạnh
AB
,
AC
,
AM
.
Do
( )
A H ABC A H AC
′′
⊥ ⇒⊥
. Có
// ,HI BM BM AC HI AC⊥ ⇒⊥
Do đó
( )
AC A HI AC A I
′′
⊥ ⇒⊥
, suy ra góc giữa hai mặt phẳng
( )
ACC A
′′
và
( )
ABC
là góc giữa
AI
′
và
IH
, tức là góc
45A IH
′
= °
. Có
1 13 3
.
2 22 4
aa
IH BM= = =
.
Trong tam giác
A HI
′
có
33
.tan .tan 45
44
aa
A H IH A IH
′′
= = °=
.
Diện tích đáy
2
3
4
ABC
a
S =
. Vậy
23
.
3 33
..
4 4 16
ABC A B C ABC
aa a
V AH S
′′′
′
= = =
⇒
Chọn C.
Câu 35. Ta có
( )
( )
1; 2; 1
2; 1; 1
AH a b c
BH a b c
=−− +
=− −−
và
(
)
( )
( )
( )
1; 1; 2
1; 1; 3 , 1; 5; 2
2;0;1
AB
AC AB AC
BC
= −
=−− ⇒ =−−−
= −
.
Do
H
là trực tâm của tam giác
ABC
( ) ( )
( ) ( ) ( )
( ) (
) ( )
.0
2 1 10
. 0 1 21 13 1 0
1 15 22 1 0
,. 0
AH BC
ac
BH AC a b c
ab c
AB AC AH
=
− −+ +=
⇔ = ⇔− − − − + − =
− −− − − +=
=
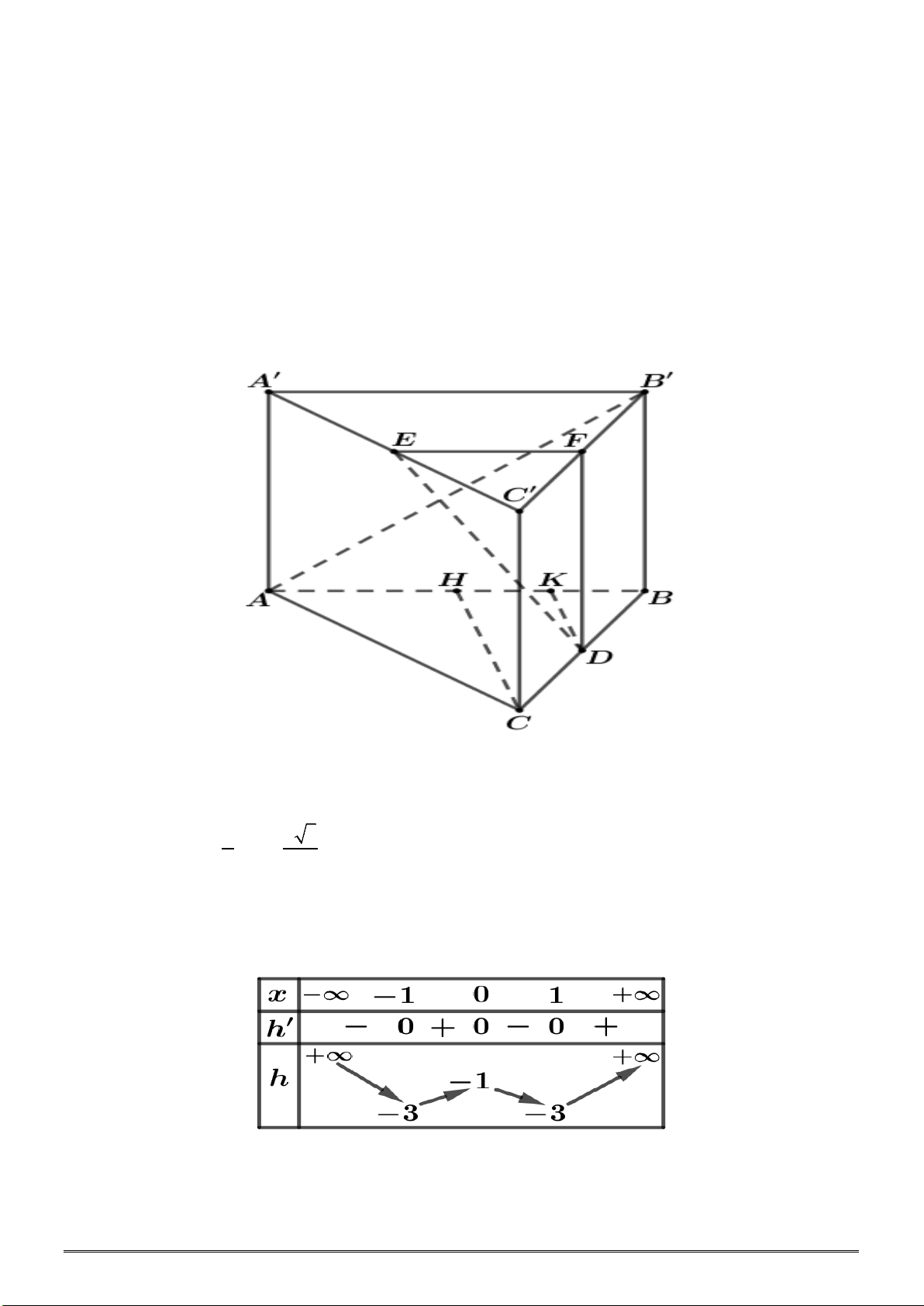
LTAD Trang 13/17
23 2
30 1
52 9 1
ac a
ab c b
abc c
− +=− =
⇔−−+ = ⇔ =
−− − =− =
. Do đó
4
abc++=
. Chọn A.
Câu 36. Để
( )
C
tiếp xúc
(
)
P
thì phương trình hoành độ giao điểm phải có nghiệm bội 2 trở nên. Tức
là hàm số
( )
y fx=
sẽ được phân tích dưới dạng:
( ) ( )
( )
( ) ( ) ( )
(
)
3
2
1
2
2
23
f x x x ax bx c
f x x x x x ax bx c
=− + ++
=− − + ++
trong
đó các hệ số thực
,,abc
là cố định không phụ thuộc vào tham số
m
.
Ta có
( )
( ) ( )
2
3 22 2 2
2 3 2 1 1 21y x mx m x m m x m x x x= − + − + + = −− ++ − −
Suy ra parabol cố định là:
( )
2
: 21
Pyx x=−−
Đỉnh
( )
1; 2I −
25
II
xy⇒− =
⇒
Chọn D.
Câu 37. Ta có hình vẽ sau:
Từ giả thiết suy ra lăng trụ đã cho là lặng trụ đứng và hai mặt đáy là những tam giác đều cạnh
.a
Kẻ
( )
CH AB H AB⊥∈
và
( )
.DK AB K AB⊥∈
Ta chứng minh được
DK
là đoạn vuông góc chung của
DE
và
AB
′
nên
[
]
13
;.
24
a
d DE AB DK CH
′
= = =
Chọn C.
Câu 38. Ta có
( )
( ) ( )
( )
32
2 2 62
13 11 3 1 .m f gx x x x x hx= = + − + += − −=
Đạo hàm
( ) (
)
5
0
6 6 0; 0 .
1
x
hx x x hx
x
=
′′
= −= =⇔
= ±
Bảng biến thiên như hình trên. Yêu cầu bài toán
3 1.m → − < < −
Chọn D.
Câu 39. Từ đồ thị của
( )
y fx
′
=
ta có bảng biến thiên như sau
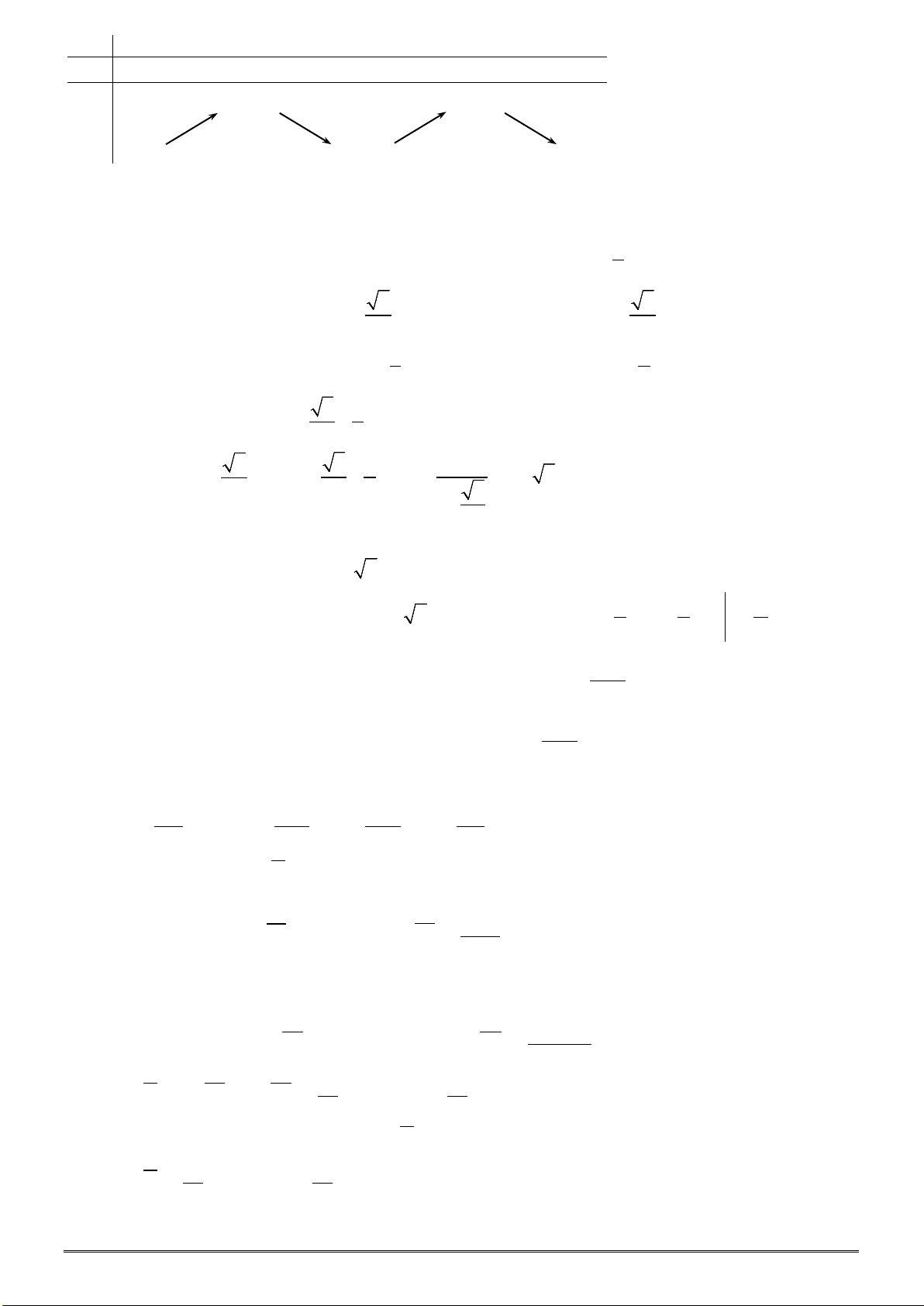
LTAD Trang 14/17
Từ bảng biến thiên ta có
( ) ( ) ( ) ( )
,fa fb fc fb>>
(
( )
fb
là số nhỏ nhất) nên phương án C có thể xảy
ra
⇒
Chọn C.
Câu 40. Hình vuông
1
V
có chu vi bằng
1 →
cạnh hình vuông bằng
1
.
4
Từ đó tính được cạnh hình vuông
2
V
là
2
8
→
chu vi hình vuông
2
V
là
2
.
2
Tương tự tính được cạnh hình vuông
3
V
là
1
8
→
chu vi hình vuông
3
V
là
1
.
2
Tổng chu vi các hình vuông:
21
1 ...
22
+ ++
Đây là tổng của cấp số nhân lùi vô hạn với số hạng đầu
1
1,u =
công bội
2
2
q = →
21 1
1 ... 1. 2 2.
22
2
1
2
+ ++= =+
−
Chọn A.
Câu 41. L ời giải Chọn A
Xét phương trình hoành độ giao điểm
e0
x
x
=
0x⇔=
.
Thể tích khối tròn xoay thu được là:
( )
1
2
0
ed
x
V xx
π
=
∫
1
2
0
ed
x
xx
π
=
∫
1
22
0
11
ee
24
xx
x
π
= −
( )
2
e1
4
π
= +
.
Câu 42. Số tiền ông Bách nhận được sau
3
năm đầu là
3
1
3, 35
20. 1 .
100
T
= +
Số tiền ông Bách nhận được sau
2
năm tiếp theo là
2
21
3, 75
.1 .
100
TT
= +
Số tiền ông Bách nhận được vào cuối năm thứ
10
là
5 3 25
32
4,8 3, 35 3, 75 4,8
.1 20.1 .1 .1 30
100 100 100 100
TT
=+=+ + +
triệu đồng. Chọn B.
Câu 43. Xét biến cố đối
A : ''
bắt được 3 thỏ trắng trong 3 hoặc 4 lần
''
.
• Trường hợp 1: Bắt được 3 con thỏ trắng trong 3 lần đầu:
Ta có
( )
7.6.5n Ω=
và
( )
1
A 3!.n =
Suy ra
( )
1
3!
A.
7.6.5
P =
• Trường hợp 2: Bắt được 3 con thỏ trắng trong 4 lần đầu:
lần 4 bắt được con trắng; lần 1, 2 và 3 bắt được 2 con trắng và 1 con nâu.
Ta có
( )
7.6.5.4n Ω=
và
( )
12
2 43
A . .3!.n CC=
Suy ra
( )
12
43
2
. .3!
A.
7.6.5.4
CC
P =
Suy ra
( ) ( ) ( )
( )
12
4 31
AA A A.
35 35
PP P P= + = → =
Chọn D.
Cách 2: Ta mô tả không gian của biến cố
A
như sau
{ }
TTT; TNNN; NTNN; NNTN
Suy ra
( )
( )
4 31
A A.
35 35
PP= → =
Câu 44. L ời giải Chọn B
x
−∞
a
b
c
+∞
y
′
+
0
−
0
+
0
−
y
−∞
( )
fa
(
)
fb
( )
fc
−∞
LTAD Trang 15/17
x
y
y=x
2
O
1
A
B
Gọi
( )
2
;Aaa
và
( )
2
;B bb
là hai điểm thuộc
( )
P
sao cho
2AB =
.
Không mất tính tổng quát giả sử
ab
<
.
Theo giả thiết ta có
2AB =
nên
(
)
( )
2
2
22
4ba b a
−+− =
( ) ( )
22
14ba ba
⇔− − +=
.
Phương trình đường thẳng đi qua hai điểm
A
và
B
là
(
)
y b a x ab=+−
.
Gọi
S
là diện tích hình phẳng giới hạn bởi parabol
( )
P
và đường thẳng
AB
ta có
( )
2
d
b
a
S a b x ab x x
= + −−
∫
( )
23
23
b
a
xx
a b abx
=+ −−
( )
3
6
ba−
=
.
Mặt khác
( )
( )
22
14
ba ba
− − +=
nên
2ba ba
− =−≤
do
( )
2
11ba− +≥
.
Vậy
( )
3
3
2
66
ba
S
−
= ≤
. Vậy
max
4
3
S =
.
Câu 45. Phương trình
2
2
2
2
1
1
1
2
2
1
2
2
1
11
.
1
x
x
x
xm
xx
xm
x
xm
e
x
x e x me
xx
x
e
x
+
+
++
++
++
⇔ = ⇔ + = ++
+
Xét hàm
( )
t
f t te=
với
0
t ≥
và đi đến kết quả
2
2
11
x xm
xx
+ =++
2
1
2
BBT
2
do 0
11
2 2 0 0.
tx
x
x
m x x tt m
xx
=+≥
>
⇔ = + − + − → − − ≥ → ≥
Mà
m
là số nguyên dương nhỏ hơn
2020
nên
{ }
1;2;3...2016;2019 .=m
Chọn B.
Câu 46. Tham khảo hình vẽ. Ta sẽ sử dụng công thức
( ) ( )
1
.. ,.sin,.
6
V abd ab ab
=
Đặt
( )
0.SA x x= >
Tính được
2
22
2
,
xa
KH
ax
=
+
2
22
.
ax
IH
ax
=
+
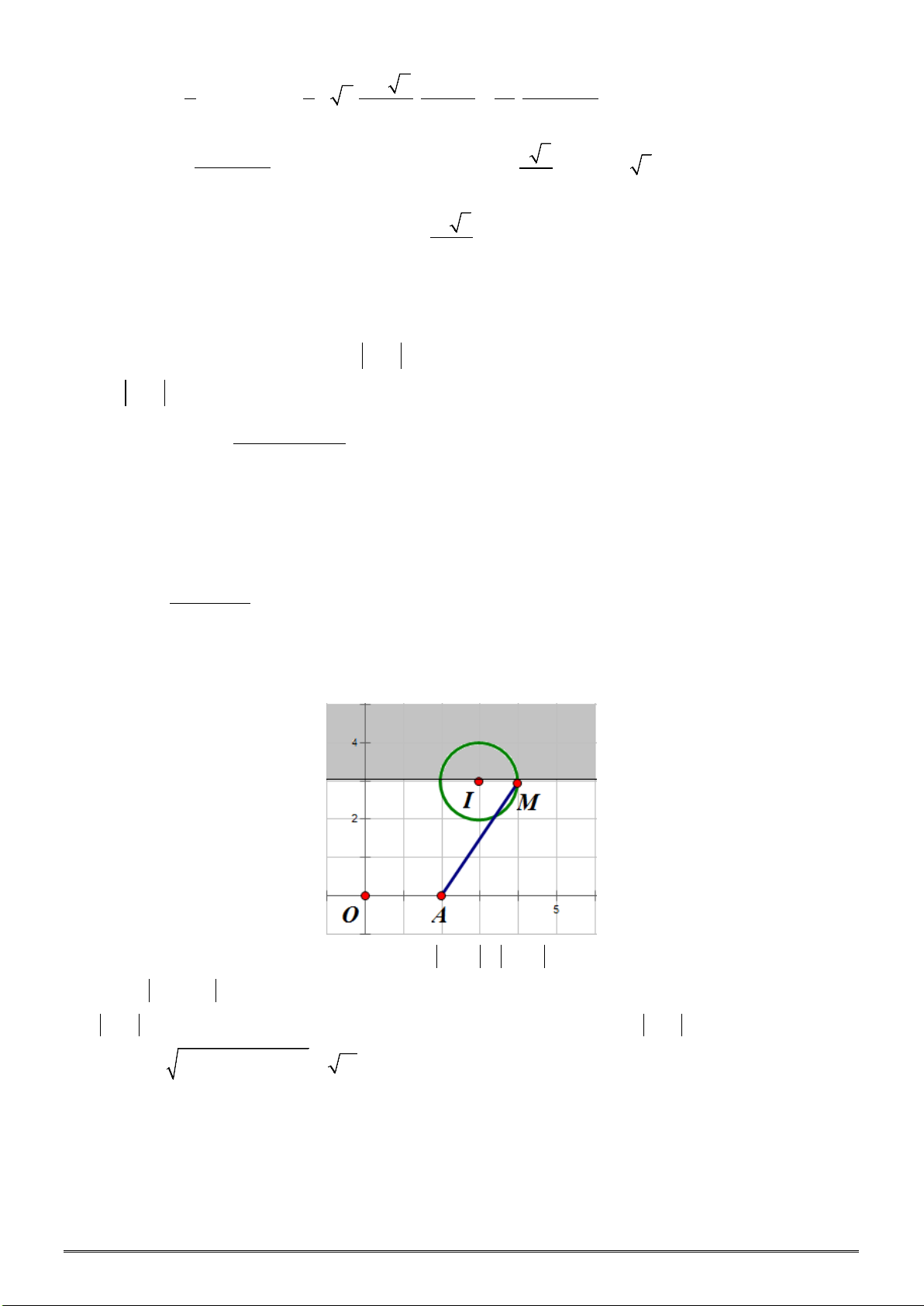
LTAD Trang 16/17
Chứng minh được
( )
,HI d KH AC=
và
.AC HK⊥
Khi đó
1
..
6
ACHK
V AC KH HI=
(
)
2 2 43
2
2222
22
12
. 2. . . .
63
xa ax a x
a
axax
ax
= =
++
+
Xét hàm
( )
(
)
3
2
22
x
fx
x a
=
+
trên
( )
0; ,+∞
ta có
(
)
( )
0;
33
max
16
fx
a
+∞
=
khi
3.
xa=
Suy ra thể tích khối tứ diện lớn nhất bằng
3
max
3
.
16
a
V =
Chọn D.
Câu 47. Ta có
( )
1
41kf
′
=
và
( ) ( )
2
3 1 6 1.kf f
′
= +
Theo giả thiết ta có
( ) ( ) ( )
2
12
. 6 24 1 12 1 . 1 6 0.kk f f f
′′
=−⇔ + + =
Điều kiện để tồn tại
( )
1f
′
thì
( )
0 1 2.f∆≥ ⇔ ≥
Đặt
( )
1tf=
với
2.t ≥
Khi đó
(
)
[
)
( )
3
2;
3 2 min 4.
Q ft t t ft
+∞
= = − +≥ =
Chọn B.
Câu 48. Ta có
( ) (
)
( )
2
222
log 4 4 4
2
abc
aabbcc
abc
++
= −+ −+ −
+++
( ) ( )
(
)
222 222
22
log 4 4 4 4 4 4 log 2 2.
abc abc abc abc
⇔ ++ + ++ = +++++++
Xét hàm
( )
2
logft t t= +
với
0t >
ta đi đến kết quả
222
444 2abcabc++ =+++
( ) ( ) ( )
222
2 2 2 10.abc⇔−+−+−=
Ta lại có
(
) ( )
( )
23
1230.
abc
P P aP bP c
abc
++
= ⇔− +− +− =
++
Đến đây ta dùng điều kiện để mặt phẳng
và mặt cầu có điểm chung. Chọn C.
Câu 49. Lời giải Chọn C
Gọi
( )
;M xy
là điểm biểu diễn số phức
z
ta có:
24
zizi− ≤−
( ) ( )
22
22
24xy xy⇔+− ≤+−
3y⇔≤
;
33 1zi
−− =
⇔
điểm M nằm trên đường tròn tâm
( )
3; 3I
và bán kính bằng 1. Biểu thức
2P z AM=−=
trong đó
( )
2;0A
, theo hình vẽ thì giá trị lớn nhất của
2Pz= −
đạt được khi
( )
4;3M
nên
( ) ( )
22
max 4 2 3 0 13P = − +− =
.
Câu 50. Gọi các hoành độ giao điểm của đồ thị hàm số
( )
y fx=
và trục hoành là
1234
, , , .xx xx
Suy
ra
(
) ( )( )( )(
)
1234
.fx axx xx xx xx=−−−−
Đạo hàm
( ) ( )( )( ) ( )( )( )
234 134
fx axx xx xx axx xx xx
′
=−−−+−−−
( )( )( ) ( )( )( )
124 123
.axx xx xx axx xx xx+−−−+−−−

LTAD Trang 17/17
• Ta có
( )
( ) ( )
( )
(
)
22
. 0,
ii iii i
gx fx f x fx fx x
′ ′′ ′
= − = >∀
⇒
( )
0gx=
không có nghiệm
.
i
x
• Xét
,
i
xx≠
ta có
(
) (
) ( )
4
1
1234
1111 1
.
i
i
f x fx fx
xx xx xx xx xx
=
′
= +++ =
−−−− −
∑
( )
(
)
(
)
(
)
44
11
11
ii
ii
fx fx
fx x x fx x x
= =
′
′
′′
⇒= ⇒ =
−−
∑∑
( ) ( ) ( )
( )
( )
2
4
22
1
.
1
0,
i
i
f xfx f x
x
xx
fx
=
′′ ′
−
⇒ =− <∀
−
∑
hay
( ) ( ) ( )
2
. 0,
i
f x f xfx x x
′ ′′
− > ∀≠
Vậy trong mọi trường hợp phương trình
(
)
0
gx
=
đều vô nghiệm. Chọn A.

LTAD Trang 1/6
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
KỲ THI THPT QUỐC GIA NĂM 2019
TRƯỜNG THPT TRẦN HƯNG ĐẠO
Bài thi: Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Câu 1: Trong không gian
,Oxyz
cho ba điểm
( )
0;0; 2 ,A
( )
3; 0;1
B
và
( )
8; 2; 0 .C
Viết phương trình mặt phẳng
( )
P
đi qua ba điểm
,AB
và
.C
A.
3 6 0.xy z−+ +=
B.
4 8 0.xy z−+ −=
C.
3 6 0.xy z−+ −=
D.
3 0.xy z−+ =
Câu 2: Tìm nguyên hàm của hàm số
(
)
(
)
2018
32
1 3.
fx x x
= +
A.
(
)
( )
2018
3
1
.
2018
x
f x dx C
+
= +
∫
B.
( )
( )
2019
3
.
2019
x
f x dx C= +
∫
C.
( )
( )
2019
3
1
.
2019
x
f x dx C
+
= +
∫
D.
( )
2018
4
.
4
x
f x dx x C
=++
∫
Câu 3: Tính đạo hàm của hàm số
( )
5
2
2 1.yx= +
A.
( )
4
2
' 20 2 1 .yx
= +
B.
(
)
4
2
' 20 2 1 .y xx= +
C.
( )
5
2
' 20 2 1 .y xx= +
D.
( )
4
2
' 52 1 .yx= +
Câu 4: Tìm nguyên hàm của hàm số
( )
1
.fx x
x
= −
A.
( )
2
2
1
.
2
x
f x dx C
x
=++
∫
B.
( )
2
ln .
2
x
f x dx x C=−+
∫
C.
( )
2
ln .
2
x
f x dx x C
=++
∫
D.
( )
2
ln .f x dx x x C=−+
∫
Câu 5: Giải phương trình
2 5.
x
=
A.
2
log 5.x =
B.
0.x =
C.
1.
x =
D.
5
log 2.x =
Câu 6: Trong không gian
,Oxyz
cho
2 5 7.aijk=−+
Chọn mệnh đề đúng.
A.
( )
2;0;0 .a = −
B.
( )
2;5;7 .a =
C.
( )
2;0;7 .a =
D.
( )
2; 5;7 .a = −
Câu 7: Trong không gian
,Oxyz
cho hai điểm
( )
0; 3; 2 ,A −
( )
1; 0;1 .B
Viết phương trình của đường thẳng
d
đi
qua hai điểm
A
và
.B
A.
1
3
1.
xt
yt
zt
= +
=
= −
B.
1
3
1.
xt
yt
zt
= +
=
= +
C.
0
33
2.
x
yt
z
=
=−+
=
D.
1
33
2.
xt
yt
zt
= +
=−+
= −
Câu 8: Tính giá trị của biểu thức
( ) ( )
2018 2019
16 255 16 255 .P =− ⋅+
A.
1.P = −
B.
16 255.
P = +
C.
1.P =
D.
16 255.
P = −
Câu 9: Cho hàm số
42
23yx x=−+ −
, gọi
CT
y
là giá trị cực tiểu của hàm số. Tìm
.
CT
y
A.
0.
CT
y =
B.
1.
CT
y =
C.
3.
CT
y = −
D.
2.
CT
y = −
ĐỀ THI ĐỀ XUẤT
LTAD Trang 2/6
y
Câu 10: Trong không gian
,Oxyz
cho
(
)
1; 3; 4u
= −
và
(
)
0; 3; 7 .v
= −
Tìm tọa độ của vectơ
.uv−
A.
( )
1; 6;11 .uv
−= −
B.
( )
1; 0;11 .uv−=
C.
( )
1; 0; 3 .uv−= −
D.
( )
1;6;3.
uv−= −−
Câu 11: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi,
3, 6AC a BD a= =
và
.SA a=
Các mặt phẳng
( )
SAB
và
( )
SAC
cùng vuông góc với mặt phẳng
( )
.ABCD
Tính thể tích
V
của khối chóp
..
S ABCD
A.
3
3.
Va=
B.
3
6.
Va=
C.
3
9.
Va=
D.
3
18 .
Va
=
Câu 12: Xét hàm số
( )
1
fx
x
=
trên đoạn
[ ]
1;1 .−
Mệnh đề nào dưới đây đúng?
A. Giá trị lớn nhất của hàm số
( )
fx
trên đoạn
[ ]
1;1−
là
1.−
B. Giá trị lớn nhất của hàm số
( )
fx
trên đoạn
[ ]
1;1
−
là
0.
C. Hàm số
( )
fx
trên đoạn
[ ]
1;1−
không tồn tại giá trị lớn nhất.
D. Giá trị lớn nhất của hàm số
( )
fx
trên đoạn
[
]
1;1−
là
1.
Câu 13: Cho một tấm nhôm hình vuông cạnh
40
cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông
bằng nhau, mỗi hình vuông có cạnh bằng
x
cm , rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp
không nắp.
Tìm
x
để hộp nhận được có thể tích lớn nhất.
A.
6.x =
B.
20.x =
C.
20
.
3
x
=
D.
2.
x
=
Câu 14: Trong không gian
,Oxyz
cho hai vectơ
( )
1; 0;1a =
và
( )
1;1; 0 .b =
Tính góc của hai vecơ
a
và
.b
A.
( )
, 90 .
o
ab
=
B.
( )
, 45 .
o
ab =
C.
( )
, 60 .
o
ab =
D.
( )
, 30 .
o
ab =
Câu 15: Cho hàm số
( )
y fx
=
có đạo hàm trên
và có bảng biến thiên như sau.
Chọn mệnh đề đúng.
A. Hàm số đạt cực đại tại
3.x =
B. Hàm số đạt cực đại tại
4.x =
C. Hàm số đạt cực đại tại
1.x = −
D. Hàm số đạt cực đại tại
2.x =
Câu 16: Cho hình chữ nhật
ABCD
có
2,AB a=
6.AD a=
Tính thể tích
V
của khối trụ được tạo thành khi
quay hình chữ nhật
ABCD
quanh cạnh
.AB
A.
3
18 .Va
π
=
B.
3
6.Va
π
=
C.
3
24 .Va
π
=
D.
3
72 .Va
π
=
Câu 17: Số mặt của khối đa diện đều loại
{ }
3, 4
là
A.
8.
B.
6.
C.
3.
D.
4.
Câu 18: Cho hàm số
( )
y fx=
là hàm số bậc ba và có đồ thị như hình vẽ dưới đây.

LTAD Trang 3/6
Tìm tất cả các giá trị của tham số
m
để phương trình
( )
fx m
=
có ba nghiệm phân biệt.
A.
[ ]
2;2 .m ∈−
B.
(
] [
)
; 2 2; .m ∈ −∞ − ∪ +∞
C.
( ) ( )
; 2 2; .m ∈ −∞ − ∪ +∞
D.
( )
2;2 .m ∈−
Câu 19: Trong không gian
,Oxyz
cho mặt cầu
( )
S
có tâm
( )
3;1; 3I −
và bán kính
2.R =
Viết phương trình
mặt cầu
(
)
.S
A.
( ) ( ) ( )
222
3 1 3 2.x yz
− +− ++ =
B.
(
) (
) (
)
222
3 1 3 2.x yz− +− ++ =
C.
( ) ( ) ( )
222
3 1 3 2.x yz+ ++ +− =
D.
( ) ( ) ( )
222
3 1 3 2.x yz+ ++ +− =
Câu 20: Tính tổng
S
của cấp số nhân lùi vô hạn
( )
,
n
u
với
1
.
4
n
n
u =
A.
1
.
3
S = −
B.
1
.
3
S =
C.
4
.
3
S =
D.
4
.
3
S
= −
Câu 21: Cho hàm số
( )
y fx=
có đạo hàm trên
và
( ) ( )
' 1.f x xx= −
Chọn mệnh đề đúng.
A. Hàm số nghịch biến trên khoảng
( )
0;1 .
B. Hàm số nghịch biến trên khoảng
( )
;0−∞
và
( )
1; .+∞
C. Hàm số nghịch biến trên khoảng
( )
;1 .−∞
D. Hàm số nghịch biến trên khoảng
( )
0; .+∞
Câu 22: Tìm số các đường tiệm cận (tiệm cận ngang, tiệm cận đứng) của đồ thị hàm số
2
2
4
.
56
x
y
xx
−
=
−+
A.
2.
B.
3.
C.
1.
D.
4.
Câu 23: Cho tứ diện
ABCD
có
,.AB CD AC BD
⊥⊥
Gọi
α
là góc giữa hai đường thẳng
AD
và
.BC
Tính
.
α
A.
0
90 .
α
=
B.
0
30 .
α
=
C.
0
60 .
α
=
D.
0
45 .
α
=
Câu 24: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông. Đường thẳng
SA
vuông góc với hai đường
thẳng
AB
và
.BC
Chọn mệnh đề đúng.
A.
( )
.SC ABCD⊥
B.
( )
.SD ABCD⊥
C.
( )
.SA ABCD
⊥
D.
( )
.
SB ABCD⊥
Câu 25: Biết rằng đồ thị sau đây là của một trong bốn hàm số được cho bốn phương án. Hỏi hàm số đó là hàm số
nào ?
A.
3
3.yx x= −
B.
3
3 1.yx x=−−
C.
3
3 1.yx x=−+
D.
3
3.yx x=−+

LTAD Trang 4/6
Câu 26: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên đoạn
[ ]
1; 3
thỏa mãn
(
)
( )
3
1
21' 5x f x dx
−=
∫
và
(
)
( )
5 3 1 7.ff
−=
Tính
(
)
3
1
.I f x dx=
∫
A.
1.I
=
B.
2.I =
C.
7.I
=
D.
6.I
=
Câu 27: Cho số phức
4 3.zi= −
Tìm
.z
A.
7.
z
=
B.
5.z =
C.
7.z =
D.
25.z =
Câu 28: Tìm nguyên hàm của hàm số
( )
.fx x=
A.
( )
2
.
3
f x dx x x C= +
∫
B.
( )
3
.
2
f x dx x C= +
∫
C.
( )
2
.
3
f x dx x C= +
∫
D.
(
)
3
.
2
f x dx x x C
= +
∫
Câu 29: Viết công thức tính thể tích
V
của khối tròn xoay được tạo ra khi quay hình thang cong giới hạn bởi đồ
thị hàm số
(
)
y fx=
, trục hoành và hai đường thẳng
,xa=
xb=
( )
ab<
, xung quanh trục hoành.
A.
( )
.
b
a
V f x dx
π
=
∫
B.
( )
2
.
b
a
V f x dx
π
=
∫
C.
( )
.
b
a
V f x dx=
∫
D.
( )
2
.
b
a
V f x dx=
∫
Câu 30: Trong không gian
,Oxyz
cho ba điểm
( )
3;0;0 ,A
( )
0;5;0B
và
( )
0;0;7 .C
Viết phương trình theo đoạn
chắn của mặt phẳng
( )
α
đi qua ba điểm
,A
B
và
.C
A.
1.
357
xyz
++=−
B.
0.
357
xyz
++=
C.
1.
357
xyz
++=
D.
1.
357
xyz
−−=
Câu 31: Cho hình nón có đáy là đường tròn có bán kính
Ra=
và chiều cao
2.ha=
Tính độ dài đường sinh
l
của hình nón.
A.
3.la
=
B.
3.
la=
C.
5.la=
D.
5.la=
Câu 32: Cho
22
log 5, log 7.ab= =
Hãy biểu diễn
2
log 274400
theo
a
và
.b
A.
2
log 274400 2 3 2.
ab= ++
B.
2
log 274400 5.ab=++
C.
2
log 274400 2 3 .ab
= +
D.
2
log 274400 2 3 5.ab= ++
Câu 33: Tìm tất cả các giá trị của tham số
m
để hàm số
( )
32
1 31
yx m x x=−+ +−
đồng biến trên
.
A.
( ) ( )
; 4 2; .m ∈ −∞ − ∪ +∞
B.
[ ]
4;2 .
m ∈−
C.
( )
4;2 .m∈−
D.
(
] [
)
; 4 2; .m ∈ −∞ − ∪ +∞
Câu 34: Tìm tập xác định
D
của hàm số
( )
7
2
2 9 7.y xx= −+
A.
7
\ 1; .
2
D
=
B.
( )
7
;1 ; .
2
D
= −∞ ∪ +∞
C.
7
1; .
2
D
=
D.
( )
0; .D = +∞
Câu 35: Trong không gian
,Oxyz
cho hai mặt phẳng
( )
P
và
( )
Q
lần lượt có phương trình
8 10 2 4 0x yz+ − −=
và
4 5 2 0.x yz+ −−=
Chọn mệnh đề đúng.

LTAD Trang 5/6
A. Hai mặt phẳng
( )
P
và
( )
Q
cắt nhau và
( )
(
)
,
M PM Q∈∈
với
( )
0;0; 2 .M −
B. Hai mặt phẳng
( )
P
và
( )
Q
trùng nhau.
C. Hai mặt phẳng
( )
P
và
(
)
Q
song song.
D. Hai mặt phẳng
( )
P
và
(
)
Q
cắt nhau và
(
)
( )
,.O PO Q∈∈
Câu 36: Biết rằng đường thẳng
:dy x=
cắt đồ thị hàm số
2
21
x
y
x
+
=
+
tại hai điểm phân biệt
,.MN
Gọi
M
là
điểm có hoành độ dương. Viết phương trình tiếp tuyến của của đồ thị hàm số
2
21
x
y
x
+
=
+
tại điểm
.M
A.
4.yx= −
B.
12
.
33
yx=−+
C.
.yx=
D.
14
.
33
yx=−+
Câu 37: Trên mặt phẳng tọa độ
,
Oxy
cho các điểm
,A
,B
C
lần lượt biểu diễn các số phức
2 4,
i
+
i
và
1 bi+
(
b∈
). Tìm giá trị thực của
b
để ba điểm
,A
,B
C
thẳng hàng.
A.
25
.
6
b = −
B.
5
.
2
b =
C.
11
.
2
b =
D.
23
.
6
b =
Câu 38: Cho số thực dương
a
thỏa mãn
( )
0
8 4 0.
a
x dx
−=
∫
Tìm
.a
A.
2.a =
B.
1
.
2
a =
C.
4.a =
D.
1.a =
Câu 39: Cho hình lăng trụ tứ giác đều
.'' ' 'ABC D A B C D
với
2
AB a
=
và
' 3.AA a=
Tính thể tích
V
của khối
lăng trụ tứ giác
. ' ' ' '.ABCD A B C D
A.
3
4.Va=
B.
3
3.Va
=
C.
3
.Va=
D.
3
12 .Va=
Câu 40: Cho hình hộp
.'' ' 'ABCD A B C D
biết rằng tứ giác
ABCD
là hình thoi và
0
120 .BAD =
Gọi
α
là góc
giữa hai vectơ
BA
và
' '.BC
Tính
.
α
A.
0
45 .
α
=
B.
0
60 .
α
=
C.
0
90 .
α
=
D.
0
120 .
α
=
Câu 41: Cho hàm số
1
.
1
x
y
x
−
=
+
Chọn mệnh đề đúng.
A. Hàm số nghịch biến trên
.
B. Hàm số đồng biến trên
.
C. Hàm số nghịch biến trên các khoảng
( )
;1−∞ −
và
( )
1; .− +∞
D. Hàm số đồng biến trên các khoảng
(
)
;1−∞ −
và
( )
1; .− +∞
Câu 42: Bạn Nam tổ chức trò chơi có kết quả là một dãy số gồm
5
số đôi một khác nhau không kể thứ tự được
lấy trong
11
quả cầu được đánh số từ
1
đến
11.
Hỏi có bao nhiêu kết quả có thể xuất hiện trong trò chơi này ?
A.
55440
kết quả. B.
161051
kết quả. C.
120
kết quả. D.
462
kết quả.
Câu 43: Tìm số nghiệm nguyên
n
của bất phương trình
( )
2
11
33
log 3 12 log .xx x−− + ≤
A.
1.n =
B.
7.n =
C.
9.n =
D.
2n =
Câu 44: Cho số phức
z
thỏa mãn
3 1.zz i−=−
Tính môđun của số phức
( )
1.wz i= −
A.
8.w =
B.
10.w =
C.
4 2.
w =
D.
5 2.w =
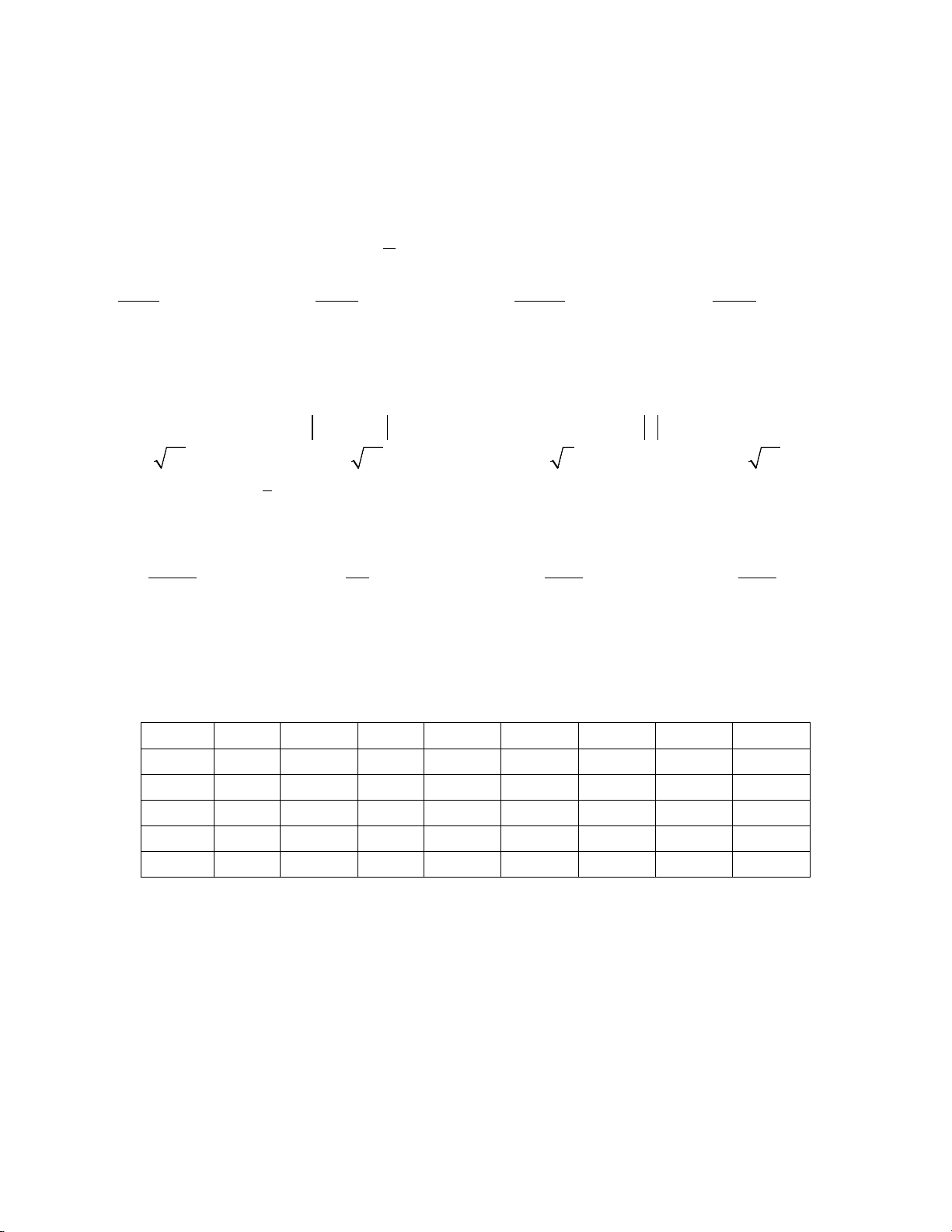
LTAD Trang 6/6
Câu 45: Cho tứ diện
OABC
có
,
OA OB OB OC⊥⊥
và
.OC OA⊥
Gọi
H
là hình chiếu vuông góc của
O
trên mặt phẳng
( )
.
ABC
Chọn mệnh đề đúng.
A.
H
là trọng tâm của tam giác
.
ABC
B.
H
là trung điểm của đoạn thẳng
.AC
C.
H
là trung điểm của đoạn thẳng
.BC
D.
H
là trực tâm của tam giác
.ABC
Câu 46: Cho hàm số
42
2y x mx m=−+
với
m
là tham số. Biết rằng,
0
mm=
là giá trị duy nhất để đồ thị hàm
số có ba điểm cực trị tạo thành một tam giác nhận gốc tọa độ làm trọng tâm. Chọn mệnh đề đúng.
A.
(
]
0
2;3 .m ∈
B.
(
]
0
1; 2 .
m ∈
C.
(
]
0
1; 0 .m
∈−
D.
(
]
0
0;1 .m ∈
Câu 47: Cho dãy số
()
n
u
xác định bởi
1
1
2
u =
và
1
2
nn
uu n
−
= +
với mọi
2.
n
≥
Khi đó
50
u
bằng
A.
5101
.
2
B.
5097
.
2
C.
10193
.
2
D.
2549
.
2
Câu 48: Trong không gian
,
Oxyz
cho điểm
( )
3;3;3A
và mặt phẳng
( )
: 2 2 14 0.
P x yz+ +− =
Xét
M
là điểm
thay đổi thuộc
( )
,P
giá trị nhỏ nhất của
22
2MO MA+
là
A.
26.
B.
89.
C.
45.
D.
24.
Câu 49: Cho số phức
z
thỏa mãn
2 3 2.zi+− =
Tìm giá trị nhỏ nhất
m
của
.z
A.
13 2.m = −
B.
13.m =
C.
5 2.m = +
D.
13 2.m = +
Câu 50: Tính tích phân
(
)
2
0
1 cos sin
n
I x xdx
π
= −
∫
(
n
là số tự nhiên,
1
n ≥
).
A.
1
.
21
I
n
=
−
B.
1
.
2
I
n
=
C.
1
.
1
I
n
=
−
D.
1
.
1
I
n
=
+
ĐÁP ÁN
1. C
7. A
13. C
19. A
25. C
31. C
37. B
43. D
49. A
2. C
8. B
14. C
20. B
26. A
32. D
38. D
44. D
50. D
3. B
9. C
15. C
21. A
27. B
33. B
39. D
45. D
4. B
10. A
16. D
22. A
28. A
34. B
40. B
46. B
5. A
11. A
17. A
23. A
29. B
35. B
41. D
47. B
6. D
12. C
18. D
24. C
30. C
36. D
42. D
48. C
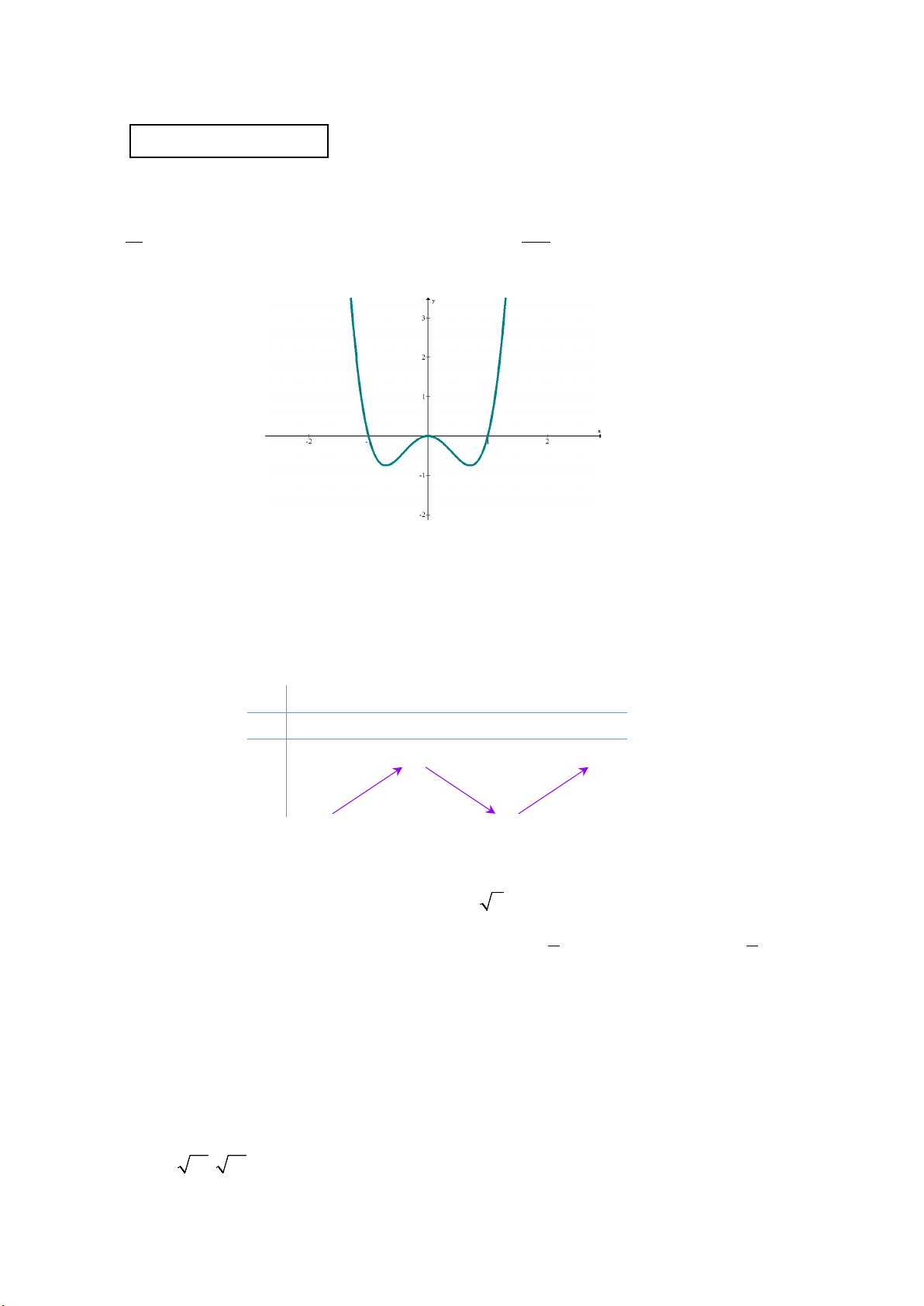
LTAD Trang 1/7
x
– ∞
-1
1
+ ∞
y'
+
0
–
0
+
y
– ∞
1
0
+ ∞
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
KỲ THI THPT QUỐC GIA NĂM 2019
TRƯỜNG THPT PHAN BỘI CHÂU
Bài thi: Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Câu 1. Thể tích của khối chóp có đường cao bằng
a
và diện tích đáy bằng
2
2
a
là
A.
3
3
a
. B.
3
a
. C.
3
2
3
a
. D.
3
2a
.
Câu 2. Cho hàm số
( )
y fx=
liên tục trên
và có đồ thị như hình vẽ sau:
Hỏi hàm số có bao nhiêu điểm cực đại?
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 3. Trong không gian
( )
Ox
yz
, cho
( ) ( )
1; 2;3 , 2;3;1uv= = −
. Tính
.uv
?
A.
.7uv= −
. B.
.7uv
=
. C.
. 11uv=
. D.
. 11uv= −
.
Câu 4. Cho hàm số
( )
y fx=
liên tục trên
và có bảng biên thiên như sau:
Hỏi hàm số nghịch biến trên khoảng nào?
A.
(
) ( )
; 1 1;−∞ − ∪ +∞
. B.
( ) ( )
; 1,1;
−∞ − +∞
. C.
( )
1;1−
. D.
( )
0; 2
.
Câu 5. Với số thực
a
dương và khác
1
,
( )
2
log 4
a
bằng
A.
2
2 2log a−
. B.
2
2 2log a+
. C.
2
1
2 log
2
a−
. D.
2
1
2 log
2
a+
.
Câu 6. Cho
( ) ( )
55
03
3, 8f x dx f x dx= =
∫∫
, tính
( )
3
0
f x dx
∫
.
A.
( )
3
0
5f x dx = −
∫
. B.
( )
3
0
5f x dx =
∫
. C.
( )
3
0
11f x dx =
∫
. D.
( )
3
0
11f x dx = −
∫
.
Câu 7. Tính diện tích xung quanh của khối nón, biết chiều cao
3h =
, bán kính đáy
4r =
.
A.
40
π
. B.
20
π
. C.
16
π
. D.
48
π
.
Câu 8. Tập nghiệm của phương trình
2
3
2 16
x +
=
là
A.
{ }
13; 13S = −
. B.
{ }
13S =
. C.
{ }
1S =
. D.
{ }
1;1S = −
.
ĐỀ THI ĐỀ XUẤT

LTAD Trang 2/7
Câu 9. Trong không gian
( )
Ox
yz
, mặt phẳng có phương trình nào sau đây là mặt phẳng song
song với trục
Oy
?
A.
( )
:2 3 0P xz−=
. B.
30y −=
. C.
2 10xz+−=
. D.
0y =
.
Câu 10. Họ nguyên hàm của hàm số
( )
sin 2 2fx x x= −
là
A.
2
1
cos 2
2
xx c− −+
. B.
2
1
cos 2
2
xx c−+
. C.
2
2cos 2
2
x
xc− −+
. D.
2
2cos 2
2
x
xc−+
.
Câu 11. Trong không gian
( )
Oxyz
, cho đường thẳng
2
: 13
3
xt
yt
zt
= −
∆=+
=−−
. Vectơ nào sau đây là vectơ
chỉ phương của đường thẳng
∆
?
A.
( )
2; 6; 2u = −−
. B.
( )
2; 6; 2
u
=−−
. C.
( )
2; 6; 2u = −
. D.
( )
2;6; 2u =
.
Câu 12. Cho 2 số nguyên dương
k
và
n
thỏa
kn≤
. Mệnh đề nào sau đây là mệnh đề đúng?
A.
!
!
k
n
n
A
k
=
. B.
( )
!
!
k
n
n
A
nk
=
−
. C.
( )
!
!!
k
n
n
A
knk
=
−
. D.
(
)
!
!
k
n
nk
A
k
−
=
.
Câu 13. Cho cấp số nhân
( )
n
u
có số hạng đầu
1
2u =
và số hạng thứ hai
2
1
u =
. Hỏi số hạng thứ tư
của
( )
n
u
bằng bao nhiêu?
A.
4
1
16
u
=
. B.
4
1
2
u =
. C.
4
1
8
u =
. D.
4
1
4
u
=
.
Câu 14. Cho số phức
2zi= −
được biểu diễn bởi điểm
M
. Hỏi
OM
bằng bao nhiêu?
A.
3OM =
. B.
3OM =
. C.
5OM =
. D.
5OM =
.
Câu 15. Đồ thị của hàm số
21
3
x
y
x
−
=
+
có bao nhiêu đường tiệm cận?
A.
3
. B.
0
. C.
1
. D.
2
.
Câu 16. Đường cong trong hình vẽ dưới đây là đồ thị của hàm số nào?
A.
3
3yx x=−+
. B.
42
4yx x=−+
. C.
1
x
y
x
=
−
. D.
3
3yx x
= −
.
Câu 17. Cho hàm số
( )
fx
liên tục trên
và có đạo hàm
( ) ( )( )( )
12 13fx x x x
′
=− +−
. Hỏi hàm
số
( )
fx
có bao nhiêu điểm cực đại?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 18. Tìm số thực
a
để số phức
24z ai=+−
, với
i
là đơn vị ảo, có môđun bằng
5
.
A.
1; 5aa=−=
. B.
1; 5aa= = −
. C.
7; 11aa= = −
. D.
7; 11aa=−=
.
Câu 19. Trong không gian
( )
Oxyz
, viết phương trình mặt cầu đường kính
AB
, biết
( ) ( )
2;1; 4 , 4;5;6AB−
.
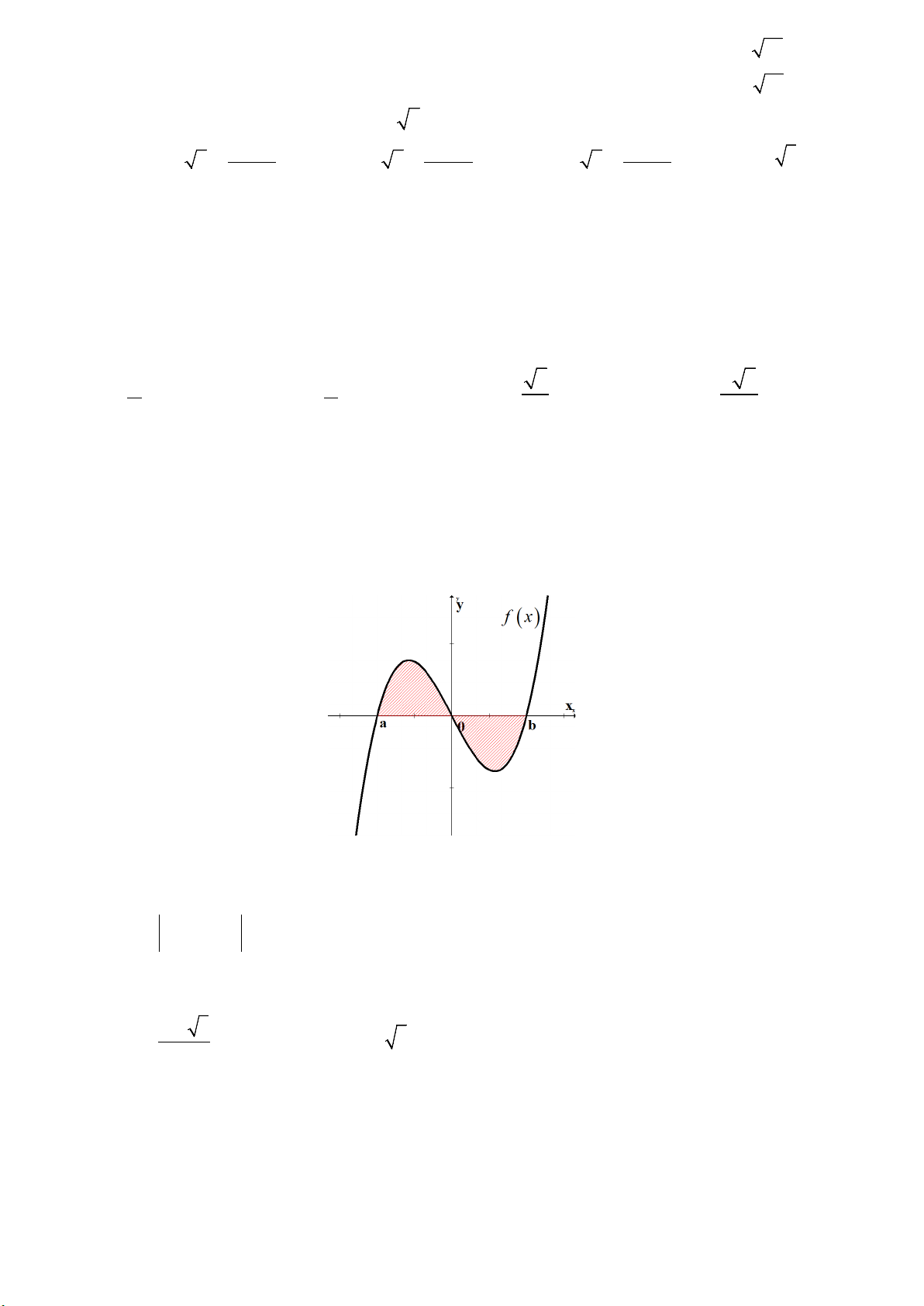
LTAD Trang 3/7
A.
( ) ( ) (
)
222
1 3 5 14xyz+ +− +− =
. B.
( )
(
) (
)
222
1 3 5 14
xyz
+ +− +− =
.
C.
( ) ( ) (
)
222
1 3 5 14xyz
− ++ ++ =
. D.
(
) ( ) ( )
222
1 3 5 14xyz
− ++ ++ =
.
Câu 20. Cho
5
log 3 b=
. Tính
25
log 15 5
theo
b
.
A.
25
32
log 15 5
2
b+
=
. B.
25
34
log 15 5
4
b+
=
. C.
25
32
log 15 5
4
b+
=
. D.
25
log 15 5 3 2b
= +
.
Câu 21. Biết phương trình
2
4 50
zz
− +=
có 2 nghiệm phức
12
,zz
, trong đó
1
z
có phần ảo âm.
Tính
12
2zz+
.
A.
12
26
zz i
+=+
. B.
12
26zz i+=−
. C.
12
2 63zz i
+=+
. D.
12
2 63zz i
+=−
.
Câu 22. Trong không gian
( )
Oxyz
, tính côsin của góc giữa hai mặt phẳng
(
)
: 30
Pxyz−−+=
và
(
)
:2 2 0Qx+=
.
A.
1
6
. B.
1
3
. C.
3
3
. D.
23
3
.
Câu 23. Tập nghiệm của bất phương trình
( )
2
2
log 3 2
xx+>
là
A.
( ) ( )
; 4 1;S = −∞ − ∪ +∞
. B.
( )
4;1S = −
.
C.
(
) ( )
; 1 4;S = −∞ − ∪ +∞
. D.
( )
1; 4S = −
.
Câu 24. Cho hàm số
( )
y fx=
liên tục trên
và có đồ thị như hình vẽ sau.
Diện tích của hình phẳng được gạch chéo trong hình vẽ được tính bằng công thức nào dưới đây?
A.
( ) ( )
0
0
b
a
S f x dx f x dx= +
∫∫
. B.
(
)
b
a
S f x dx=
∫
.
C.
( )
b
a
S f x dx=
∫
. D.
( ) ( )
0
0
b
a
S f x dx f x dx= −
∫∫
.
Câu 25. Cho hình chữ nhật
ABCD
có
,2
AB a AC a= =
. Tính thể tích của khối trụ có được bằng
cách quay hình chữ nhật
ABCD
quanh cạnh
AD
.
A.
3
3
3
a
V
π
=
. B.
3
3
Va
π
=
. C.
3
3Va
π
=
. D.
3
Va
π
=
.
Câu 26. Cho hàm số có bảng biến thiên được cho dưới đây.
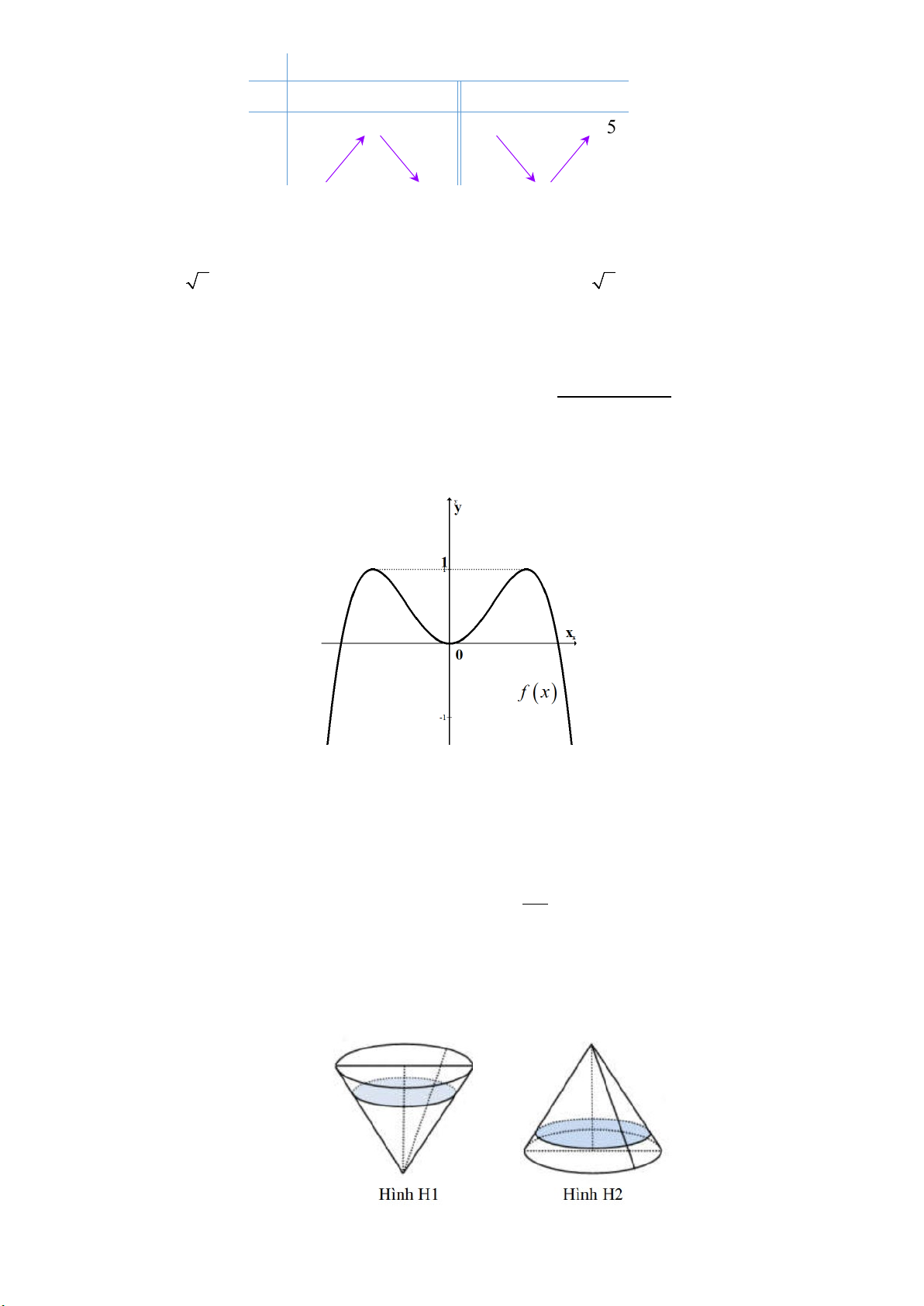
LTAD Trang 4/7
Hỏi tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đó bằng bao nhiêu?
A.
2
. B.
3
. C.
1
. D.
4
.
Câu 27. Khối lập phương có diện tích mỗi mặt bên bằng
2
4a
, có thể tích là
A.
3
82Va=
. B.
3
64Va=
. C.
3
16 2Va=
. D.
3
8Va=
.
Câu 28. Đạo hàm của hàm số
2
34
2
xx
y
−
=
là
A.
(
)
2
34
6 42
xx
yx
−
′
= −
. B.
( )
2
34
6 4 2 ln 2
xx
yx
−
′
= −
.
C.
64
2 ln 2
x
y
−
′
=
. D.
( )
2
34
6 42
ln 2
xx
x
y
−
−
′
=
.
Câu 29. Cho hàm số
( )
y fx
=
liên tục trên
có đồ thị như hình vẽ dưới đây.
Tìm tất cả các giá trị của
m
để phương trình
(
)
20fx m
−=
có 4 nghiệm phân biệt.
A.
02m<<
. B.
02m≤≤
. C.
01
m<<
. D.
01m≤≤
.
Câu 30. Cho hình lập phương
.ABCD A B C D
′′′′
. Góc giữa hai đường thẳng
AC
′′
và
AD
′
bằng
A.
45
o
. B.
30
o
. C.
90
o
. D.
60
o
.
Câu 31. Phương trình
64.9 84.12 27.16 0
xxx
−+=
có tích các nghiệm bằng
A.
2
. B.
1−
. C.
27
64
. D.
1
.
Câu 32. Một cái phễu có dạng hình nón, chiều cao của phễu là
20
cm. Người ta đổ một lượng
nươc vào phễu sao cho chiều cao của cột nước trong phễu bằng
10
cm (Hình 1). Nếu bịt kín
miệng phễu và lật ngược phễu lên (Hình 2) thì chiều cao của cột nước trong phễu gần bằng giá
trị nào sau đây.
x
– ∞
-1
0
1
+ ∞
y'
+
0
–
–
0
+
y
– ∞
1
– ∞
+ ∞
0
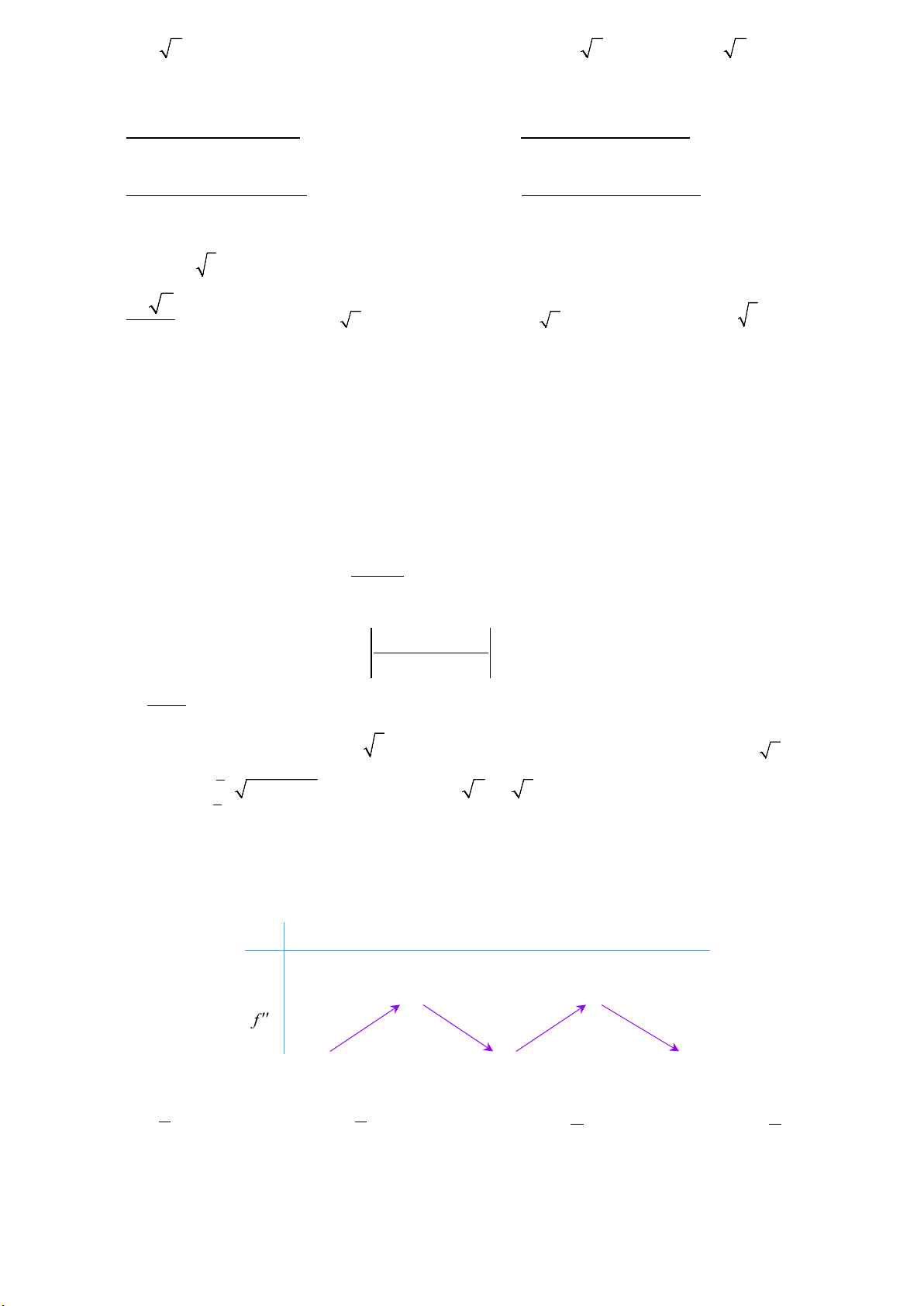
LTAD Trang 5/7
A.
3
7
. B.
1
. C.
( )
3
20 10 7−
. D.
( )
3
20 7 10−
.
Câu 33. Họ nguyên hàm của hàm số
( ) ( )
sin 2 1fx x x= +
là
A.
2
2 2 cos 2 sin 2
4
xx x x
c
−−
+
. B.
2
cos 2 sin 2
4
xx x x
c
−− +
+
.
C.
2
2 2 cos 2 sin 2
4
xx x x
c
−+
+
. D.
2
cos 2 2sin 2
4
xx x x
c
−− +
+
.
Câu 34. Cho hình lăng trụ đứng
.ABC A B C
′′′
có cạnh bên bằng
3a
, đáy là tam giác đều có chu
vi bằng
63a
. Tính khoảng cách từ
C
′
đến mp
( )
A BC
′
.
A.
32
2
a
. B.
32
a
. C.
62
a
. D.
23a
.
Câu 35. Đường thẳng vuông góc chung của hai đường thẳng
1
33
:2
3
xt
dy
zt
= +
=
=−−
và
2
46
:1
32
xt
dy t
zt
=−+
= +
= −
có phương trình là:
A.
1
2
23
xt
y
zt
= +
= −
= +
. B.
1
2
23
xt
y
zt
= +
=
= +
. C.
1
2
23
xt
y
zt
= +
=
=−−
. D.
1
2
23
xt
y
zt
= +
=
=−+
.
Câu 36. Tìm
m
để hàm số
1
3
x
y
xm
−
=
+
đồng biến trên khoảng
( )
;1−∞ −
và
( )
6; +∞
.
A.
3m >−
. B.
33
m−< ≤
. C.
3 18m−< ≤
. D.
3 18m−< <
.
Câu 37. Cho số phức
z
thỏa mãn
( )
2 31
4
iz i
zi
− −−
=
−
. Biết tập hợp điểm biểu diễn số phức
1
w
1
iz
=
+
trên mặt phẳng tọa độ là một đường tròn. Tìm bán kính
R
của đường tròn đó.
A.
4R =
. B.
45R =
. C.
8
R =
. D.
22R =
.
Câu 38. Biết
( )
(
)
2
6
1 2sin 1 cos 2 3 , ,
x xdx a b c abc
π
π
+ − =++ ∈
∫
. Tính
465aba++
.
A.
1
. B.
1
−
. C.
11
. D.
11−
.
Câu 39. Cho hàm số
( )
y fx
=
có đạo hàm cấp hai trên
,
( )
'0 0f
=
và
( )
fx
′′
có bảng biến
thiên như sau
Tìm
m
để hàm số
( )
sin 2y f x x mx= −+
đồng biến trên
( )
0;3
.
A.
1
2
m ≥
. B.
1
2
m ≤
. C.
3
2
m
≥−
. D.
3
2
m ≤−
.
Câu 40. Cho hai dãy ghế đối diện nhau, mỗi dãy gồm 4 ghế. Xếp 4 nam, 4 nữ vào hai dãy ghế
đó, biết mỗi bạn ngồi vào 1 ghế. Hỏi có bao nhiêu cách xếp sao cho số nữ ở hai dãy ghế bằng
nhau?
x
– ∞
0
2
3
+ ∞
– ∞
3
2
5
– ∞

LTAD Trang 6/7
A.
1728
. B.
144
. C.
41.472
. D.
20.736
.
Câu 41. Trong không gian tọa độ
( )
Oxyz
, cho mặt phẳng
(
)
P
đi qua điểm
( )
2;1; 4
M
và cắt 3 tia
,,
Ox Oy Oz
lần lượt tại 3 điểm
,,ABC
sao cho
4OB OC=
. Khi
OABC
V
nhỏ nhất, mặt phẳng
( )
P
có phương trình:
10ax by cz+ + −=
. Tính
111
abc
++
?
A.
37
102
. B.
303
8
. C.
21
. D.
7
3
.
Câu 42. Tìm số phức
z
thỏa
13z =
và
2 21z i zi+ − = +−
A.
32zi= ±
. B.
32zi= −
. C.
23
zi= ±
. D.
32
zi=±−
.
Câu 43. Cho hàm số
( )
y fx=
liên tục trên
và có đồ thị như hình vẽ dưới đây.
Tập hợp tất cả các giá trị thực của
m
để phương trình
( )
x
fe m=
có nghiệm trên khoảng
( )
ln 2; +∞
là
A.
( )
0; +∞
. B.
( )
4;0−
. C.
[
)
4;
− +∞
. D.
( )
4;− +∞
.
Câu 44. Một người gởi vào ngân hàng
100
triệu đồng với kì hạn 3 tháng, lãi suất
2%
một quý
theo hình thức lãi kép. Sau đúng 6 tháng, người đó gửi thêm
100
triệu đồng với kì hạn và lãi
suất như trước đó. Tổng số tiền người đó nhận được 1 năm sau gởi tiền gần nhất với kết quả
nào sau đây?
A.
210
triệu đồng. B.
220
triệu đồng. C.
212
triệu đồng. D.
216
triệu đồng.
Câu 45. Trong không gian
( )
Oxyz
, cho hai mặt phẳng
( )
: 60Pxyz−−+=
;
( )
:2 3 2 1 0Qxyz+ − +=
. Gọi
( )
S
là mặt cầu cắt mặt phẳng
( )
P
theo giao tuyến là đường tròn
tâm
( )
1; 2; 3H −
, bán kính
8r =
và cắt mặt phẳng
( )
Q
theo giao tuyến là đường tròn có bán
kính lớn nhất. Phương trình mặt cầu
( )
S
là:
A.
( ) ( ) ( )
22
2
: 1 23Sx y z+− ++ =
. B.
( ) (
) (
)
22
2
: 1 2 67Sx y z+− +− =
.
C.
( ) ( ) ( )
22
2
: 1 2 64Sx y z++ +− =
. D.
( ) (
) ( )
22
2
: 1 2 64Sx y z++ ++ =
.
Câu 46. Cho khối lập phương có cạnh bằng
a
. Gọi
O
′
là điểm đối xứng của tâm
O
của khối
lập phương qua mặt phẳng
( )
ABCD
′′′′
. Tính thể tích phần khối chóp tứ giác
.O ABCD
′
nằm
ngoài khối lập phương.
A.
3
2
a
. B.
3
54
a
. C.
3
8
a
. D.
3
6
a
.
Câu 47. Cho số phức
z
thỏa mãn
5z =
. Giá trị nhỏ nhất, giá trị lớn nhất của biểu thức
22
8 6 4 10z iz i−− + −−
lần lượt là:
A.
66
và
466
. B.
5
và
15
. C.
82
và
482
. D.
41
và
241
.

LTAD Trang 7/7
Câu 48. Trong không gian với hệ tọa độ
Oxyz
, cho 3 thẳng
1
11
:
1 21
x yz
d
−−
= =
−
;
2
21
:
13 2
x yz
d
−+
= =
−−
;
3
123
:
211
xy z
d
+−+
= =
. Đường thẳng
d
vuông góc với
3
d
; cắt hai
đường thẳng
12
,dd
theo một đoạn thẳng có độ dài nhỏ nhất là?
A.
23
. B.
10
. C.
3
. D.
2 10
.
Câu 49. Biết đồ thị hàm số
( )
32
f x ax bx cx d= + ++
cắt trục hoành tại ba điểm phân biệt có
hoành độ
123
,,xxx
. Tính giá trị của biểu thức
( )
( )
( )
123
111
T
fx fx fx
=++
′′′
.
A.
1
3
T =
. B.
3T =
. C.
1T =
. D.
0T =
.
Câu 50. Cho hàm số
( )
y fx=
có bảng xét dấu đạo hàm như sau:
x
−∞
3−
1
3
+∞
(
)
fx
′
−
0
+
0
−
0
+
Bất phương trình
( )
2
2xx
fx e m
−
<+
đúng với mọi
( )
0; 2x ∈
khi và chỉ khi
A.
( )
1
1
mf
e
>−
. B.
( )
1
1mf
e
≥−
. C.
( )
01mf>−
. D.
( )
01mf≥−
.
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
C
A
B
C
D
A
B
D
C
A
11
12
13
14
15
16
17
18
19
20
C
B
D
C
D
A
C
B
A
C
21
22
23
24
25
26
27
28
29
30
A
C
A
D
B
A
D
B
A
D
31
32
33
34
35
36
37
38
39
40
A
C
C
A
D
B
A
B
A
C
41
42
43
44
45
46
47
48
49
50
B
D
D
C
B
B
A
C
D
A
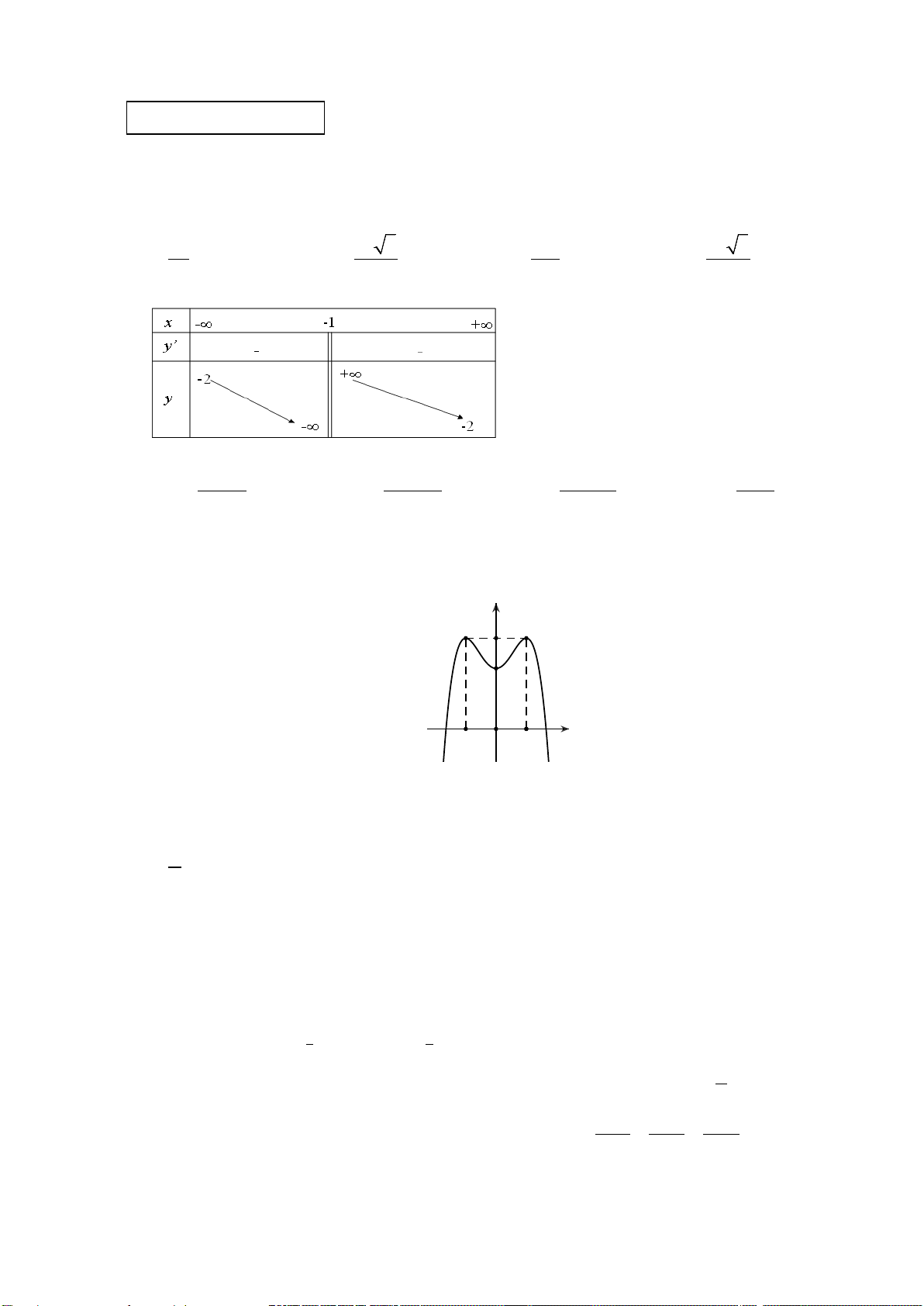
THTTH Trang 1/6
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
KỲ THI THPT QUỐC GIA NĂM 2019
TRƯỜNG THPT HOÀNG VĂN THỤ
Bài thi: Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề
(Đề thi có 06 trang)
Câu 1. Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh bằng
a
, cạnh bên
SB
vuông góc với mặt
phẳng
(
)
ABC
,
2=SB a
. Tính thể tích khối chóp
.S ABC
.
A.
3
4
a
. B.
3
3
6
a
. C.
3
3
4
a
. D.
3
3
2
a
.
Câu 2. Cho hàm số
()y fx
=
có bảng biến thiên như sau
Bảng biến thiên trong hình vẽ là của hàm số
A.
4
22
x
y
x
−
=
+
. B.
24
1
x
y
x
−−
=
+
. C.
23
1
x
y
x
−+
=
+
. D.
2
1
x
y
x
−
=
+
.
Câu 3. Trong không gian
Oxyz
, cho hai điểm
( )
1;1; 2A −
và
( )
2; 2;1B
. Vectơ
AB
có tọa độ là
A.
(
)
3; 3; 1−
. B.
( )
1; 1; 3−−−
. C.
( )
3;1;1
. D.
( )
1;1; 3
.
Câu 4. Hàm số
()y fx=
có đồ thị như hình vẽ dưới.
Hàm số đã cho nghịch biến trên
A.
(2 ; 3).
. B.
(0 ; 1).
. C.
( ; 1) (1 ; ).−∞ − ∪ + ∞
. D.
( 1; 0).−
.
Câu 5. Với
a
và
b
là hai số thực dương tùy ý,
2
log( )ab
bằng
A.
1
log log .
2
ab+
. B.
2log log .ab+
. C.
2log log .ab−
. D.
2(log log ).ab+
.
Câu 6. Cho
( )
2
0
d3I fx x
= =
∫
. Khi đó
( )
2
0
4 3dJ fx x= −
∫
bằng
A.
2
. B.
6
. C.
8
. D.
4
.
Câu 7. Tính thể tích
V
của khối trụ có bán kính đáy và chiều cao đều bằng
2
.
A.
4
π
=V
. B.
12
π
=V
. C.
16
π
=V
. D.
8
π
=V
.
Câu 8. Bất phương trình
( ) ( )
11
22
log 2 1 log 5xx−≥ −
có tập nghiệm là
A.
[
)
2; +∞
. B.
[
)
2;5
. C.
(
]
;2−∞
. D.
1
;2
2
.
Câu 9. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
113
:
2 12
xyz
d
−++
= =
−
. Một véctơ chỉ
phương của đường thẳng
d
là
A.
( )
2;1; 2u
. B.
( )
1; 1; 3u −−
. C.
( )
2;1;2u −−−
. D.
( )
2;1; 2u −−
.
x
y
O
2
3
-1
1
ĐỀ THI ĐỀ XUẤT
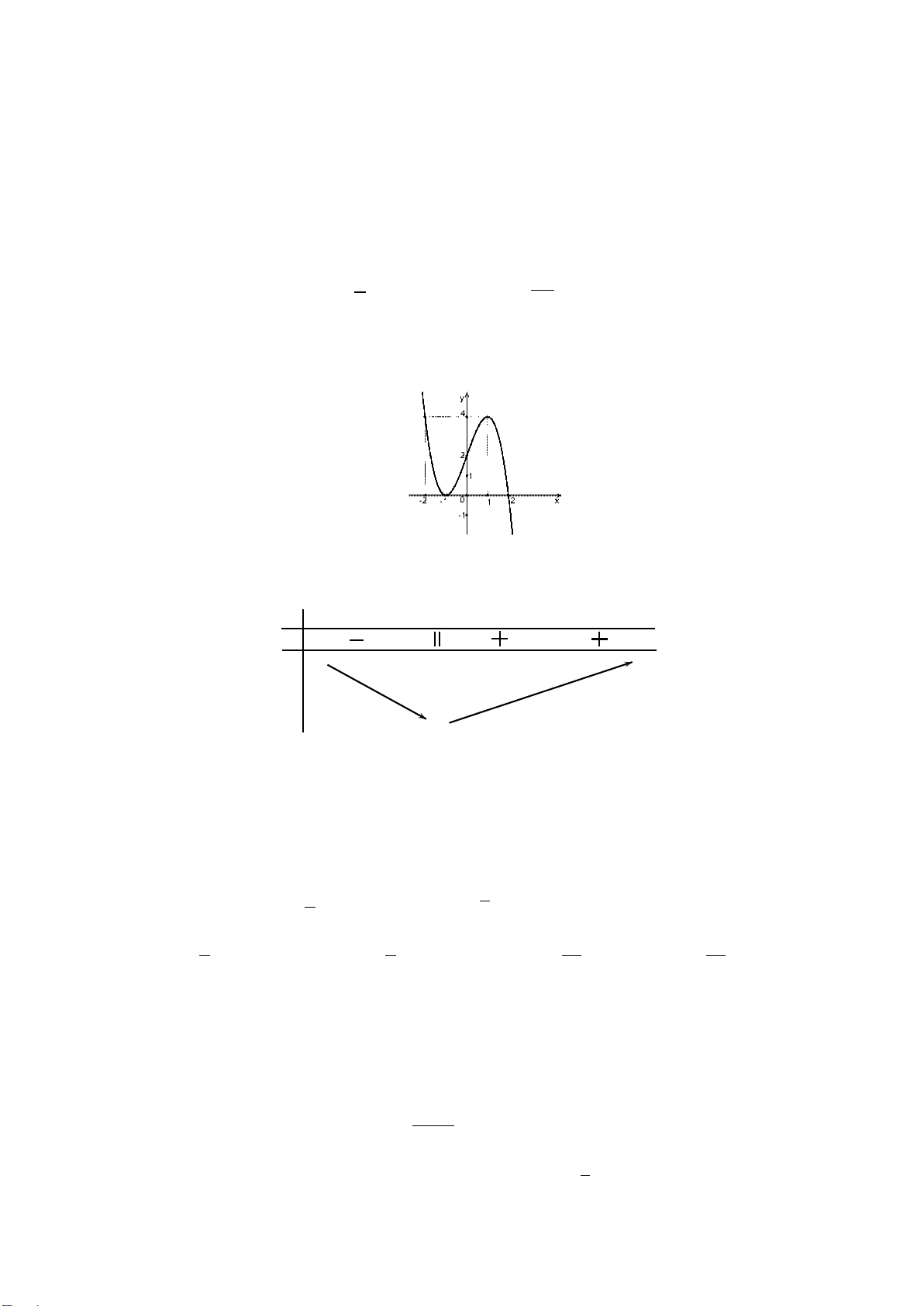
THTTH Trang 2/6
Câu 10. Họ các nguyên hàm của hàm số
( )
sin 2fx x x= +
là
A.
2
cos
xx C
− ++
. B.
2
cos xx C++
. C.
cos 2xC++
. B.
cos 2xC− ++
.
Câu 11. Trong không gian
( )
Oxyz
, mặt phẳng
( )
: 2 30Px yz− +−=
có một vectơ pháp tuyến là:
A.
( )
1; 2;1n −
. B.
( )
1; 2;1
n
. C.
( )
1;2;3
n −−
. B.
( )
1;1; 3n −
.
Câu 12. Để đi từ A đến C bắt buộc phải đi qua B. Từ A đến B có 3 cách để đi, từ B đến C có 4 cách để
đi. Hỏi có bao nhiêu cách để đi từ A đến C mà chỉ qua B một lần?
A.
12
. B.
7
. C.
4
3
. D.
3
4
.
Câu 13. Cho cấp số nhân
n
u
có
1
3u
và
2
6u
. Khi đó công bội của cấp số nhân
n
u
bằng
A.
2
. B.
1
2
. C.
1
2
. D.
2
.
Câu 14. Phần ảo của số phức
18 12zi
= −
là
A.
12i
−
. B.
12
−
. C.
18
. D.
12
.
Câu 15. Đường cong trong hình bên là đồ thị của hàm số nào dưới đây?
A.
3
32
yx x=−+ +
. B.
3
31yx x=−+
. C.
3
31
yx x
=−+ +
. D.
42
1yx x=−+
.
Câu 16. Cho hàm số
( )
y fx=
xác định, liên tục trên
và có bảng biến thiên như sau
.
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có giá trị nhỏ nhất bằng −1. B. Hàm số có giá trị cực tiểu bằng 0.
C. Hàm số không xác định tại
1x = −
. D. Hàm số có đúng hai cực trị.
Câu 17. Cho hàm số
()fx
có đạo hàm
2
( ) ( 1)( 1), .fx xx x x
′
= − + ∀∈
Số điểm cực trị của hàm số
đã cho là
A. 1. B. 2. C. 3. D. 4.
Câu 18. Cho số phức
1
1
3
zi= −
. Tính số phức
3w iz z= +
.
A.
8
3
w =
. B.
8
3
wi= +
. C.
10
3
wi= +
. D.
10
3
.
Câu 19. Trong không gian với hệ tọa độ
Oxyz
, phương trình mặt cầu
( )
S
có tâm
( )
1; 2;1I −
và tiếp
xúc với mặt phẳng
( ): 2 2 2 0Px y z− − −=
là
A.
( ) ( ) ( )
2 22
1 2 13xy z+ +− ++ =
. B.
( ) ( ) ( )
2 22
1 2 19xy z+ +− ++ =
.
C.
(
) ( ) ( )
2 22
1 2 13
xy z+ +− +− =
. D.
( ) ( ) ( )
2 22
1 2 19
xy z+ +− +− =
.
Câu 20. Cho
2
log 6 m=
. Khi đó
48
log 16
a
mb
=
+
. Tính giá trị của
.P ab=
A.
12P =
. B.
20P =
. C.
10P =
. D.
8P =
.
Câu 21. Cho số phức
z a bi= +
( )
,ab∈
thỏa mãn :
( )
23 19z iz i−+ =−
. Giá trị của
1ab +
là
A.
1−
. B. 0. C. 1. D.
2−
.
-1
+
∞
+
∞
+
∞
0
0
-1
-
∞
y'
y
x
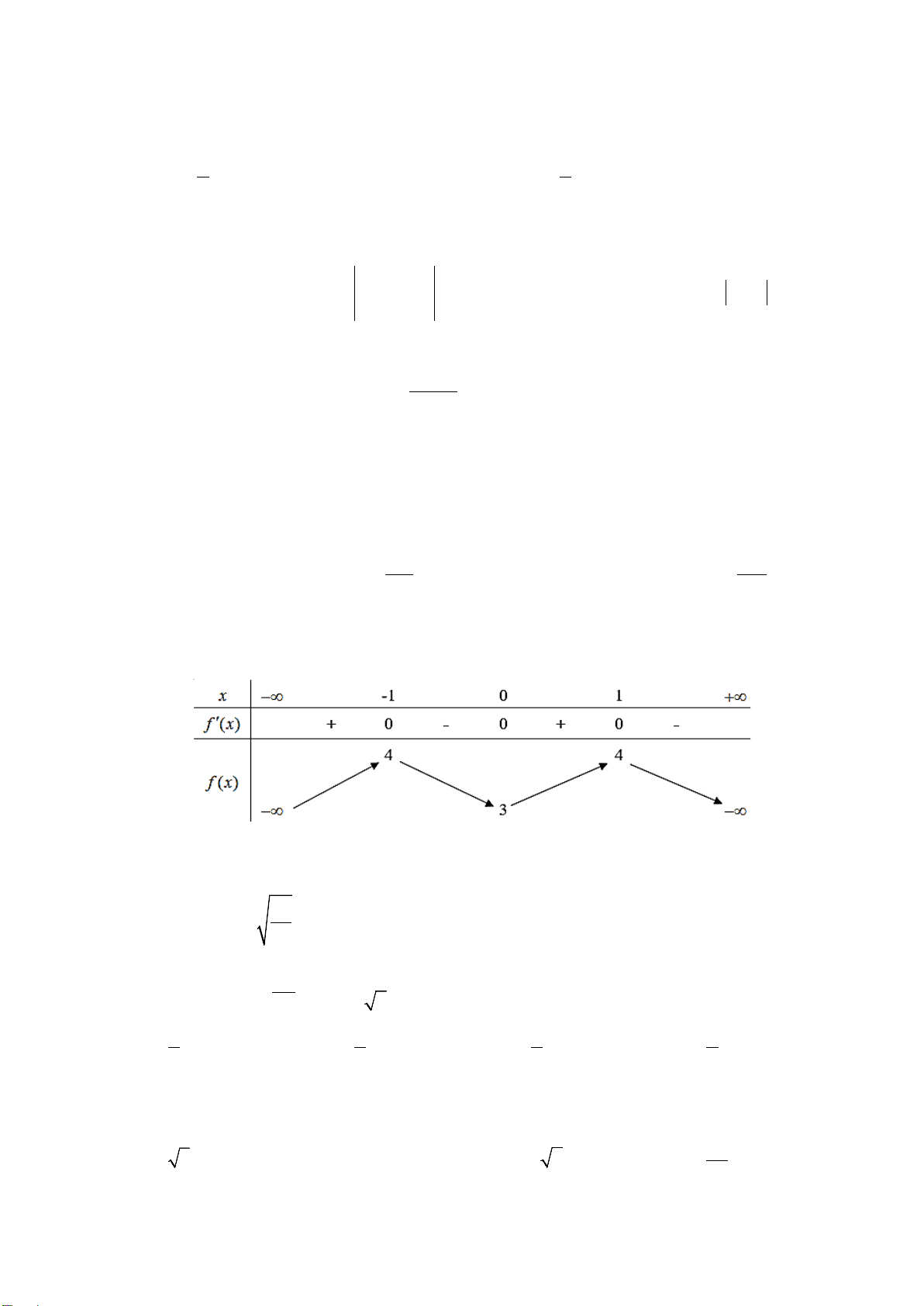
THTTH Trang 3/6
Câu 22. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
( )
:22 0x y zm
α
+ + +=
và điểm
( )
1;1;1
A
. Khi đó
m
nhận giá trị nào sau đây để khoảng cách từ điểm A đến mặt phẳng
( )
α
bằng 1?
A.
−
2. B. 8. C.
−
2 hoặc
8−
. D.
2
hoặc
8
.
Câu 23. Phương trình
32
39
−
=
x
có nghiệm là
A.
4
3
=x
. B.
3=x
. C.
3
4
=x
. D.
5=x
.
Câu 24. Cho hàm số
y fx
liên tục trên
; công thức tính diện tích hình thang cong giới hạn bởi
đồ thị hàm số
y fx
và các đường thẳng
0; ; y x ax b
ab
là
A.
2
d
b
a
fx x
. B.
d
b
a
fx x
. C.
d
b
a
fx x
. D.
d
b
a
fx x
.
Câu 25. Thể tích của khối nón có chiều cao bằng
4
và bán kính bằng 3 bằng
A.
48
π
. B.
12
π
. C.
36
π
. D.
16
π
.
Câu 26. Gọi
( )
C
là đồ thị của hàm số
24
3
x
y
x
−
=
−
. Trong các mệnh đề sau, mệnh đề nào sai ?
A.
( )
C
có đúng
1
tiệm cận ngang. B.
( )
C
có đúng
1
trục đối xứng.
C.
( )
C
có đúng
1
tâm đối xứng. D.
( )
C
có đúng
1
tiệm cận đứng.
Câu 27. Cho tứ diện
ABCD
có các cạnh
,,BA BC BD
đôi một vuông góc với nhau,
3,BA a=
2
BC BD a= =
. Gọi
M
và
N
lần lượt là trung điểm của
AB
và
AD
. Tính thể tích khối chóp
.C BDNM
.
A.
3
8=Va
. B.
3
3
2
=
a
V
. C.
3
=Va
. D.
3
2
3
=
a
V
.
Câu 28. Tìm tất cả các giá trị thực của tham số
m
để hàm số
( )
2
2
log 4y x xm= −+
xác định trên
.
A.
4m >
. B.
4m <
. C.
4m ≥
. D.
4m ≤
.
Câu 29. Cho hàm số
()y fx=
có bảng biến thiên như sau
Số nghiệm thực của phương trình
() 4 0fx−=
là
A. 1. B. 2. C. 3. D. 4.
Câu 30. Cho lăng trụ
.ABC A B C
′′′
có đáy
ABC
là tam giác đều cạnh
a
và
7
.
12
AA AB AC a
′′′
= = =
Tính góc giữa hai mặt phẳng
()
ABB A
′′
và
( ).ABC
A.
0
75
. B.
0
30
. C.
0
45
. D.
0
60
.
Câu 31. Phương trình
( )
21
7
1
8 0,25. 2
x
x
x
−
+
=
có tổng các nghiệm bằng
A.
4
7
. B.
2
3
. C.
9
7
. D.
1
2
.
Câu 32. Người ta đặt được vào trong một hình nón hai khối cầu có bán kính lần lượt là
a
và
2a
sao
cho các khối cầu đều tiếp xúc với mặt xung quanh của hình nón, hai khối cầu tiếp xúc với nhau và khối
cầu lớn tiếp xúc với đáy của hình nón. Bán kính đáy của hình nón đã cho là
A.
5a
. B.
3a
. C.
22a
. D.
8
3
a
.
Câu 33. Tìm một nguyên hàm
( )
Fx
của hàm số
( ) ( )
48 7 .lnxfx x= −
, biết
( )
15F =
.

THTTH Trang 4/6
A.
( )
( )
22
24 7 .ln 12 7 5Fx x x x x x= − − +−
. B.
( )
( )
22
24 7 .ln 12 7 5Fx x x x x x= − − ++
.
C.
( )
( )
22
24 7 .ln 12 7 9Fx x x x x x= − − ++
. D.
( )
(
)
22
24 7 .ln 12 7 10Fx x x x x x
= − − ++
.
Câu 34. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
B
,
3AB a=
,
4
BC a=
và
( )
SA ABC⊥
. Góc giữa đường thẳng
SC
và mặt phẳng
( )
ABC
bằng
60°
. Gọi
M
là trung điểm của
cạnh
AC
. Khoảng cách giữa hai đường thẳng
AB
và
SM
bằng
A.
10 3
79
a
. B.
5
2
a
. C.
53a
. D.
53
79
a
.
Câu 35. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )
: 2 10 0P xyz−+− =
và đường thẳng
2 11
:
21 1
x yz
d
+ −−
= =
−
. Đường thẳng
∆
cắt
( )
P
và
d
lần lượt tại
M
và
N
sao cho
( )
1; 3; 2A
là
trung điểm
MN
. Tính độ dài đoạn
MN
.
A.
2 10MN =
. B.
2 66
MN =
. C.
66
MN =
. D.
10
MN =
.
Câu 36. Tìm tất cả các giá trị thực của tham số m để hàm số
( )
32
11
23
33
y xx m x
=− −+ − −
nghịch
biến trên
( )
1; +∞
.
A.
3m ≤
. B.
3m ≥
. C.
2m ≤
. D.
2m ≥
.
Câu 37. Cho hai số phức
12
z ,z
thỏa mãn
22
11 2 2
z 20 z 10i z 20 z 10i− +− = − +−
và
11
z 20 z 10i 10 5
− +− =
. Giá trị lớn nhất của
12
zz
−
là
A. 20. B. 40. C. 30. D.
10 5.
.
Câu 38. Cho
0m >
. Tìm điều kiện của tham số
m
để
1
0
1
1
2
dx
xm
≥
+
∫
A.
1
4
m >
. B.
0m >
. C.
1
0
4
m≤≤
. D.
1
4
m ≤
.
Câu 39. Cho hàm số
(
)
y fx
=
liên tục trên
. Biết rằng hàm số
( )
y fx
′
=
có đồ thị như hình vẽ.
Hàm số
( )
2
5y fx= −
nghịch biến trên khoảng nào sau đây?
A.
( )
1; 0−
. B.
( )
1;1−
. C.
( )
0;1
. D.
( )
1; 2
.
Câu 40. Một nhóm gồm
10
học sinh trong đó có hai bạn A và B, đứng ngẫu nhiên thành một hàng.
Xác suất để hai bạn A và B đứng cạnh nhau là
A.
1
10
. B.
1
4
. C.
2
5
. D.
1
5
.
Câu 41. Trong không gian
Oxyz
cho
( )
1; 2; 1A −
,
( )
3;1; 2B −
,
( )
2; 3; 3C
−
và mặt phẳng
( )
: 2 2 30Px y z− + −=
.
( )
;;M abc
là điểm thuộc mặt phẳng
( )
P
sao cho biểu thức
22 2
MA MB MC++
có giá trị nhỏ nhất. Xác định
abc
++
.
A.
3−
. B.
2−
. C.
2
. D.
3
.
Câu 42. Cho số phức
z
thoả mãn
34 5zi−− =
. Gọi
M
và
m
là giá trị lớn nhất và giá trị nhỏ nhất
của biểu thức
22
2P z zi=+ −−
. Tính môđun của số phức
.w M mi= +
A.
2315w =
. B.
1258w =
. C.
3 137w =
. D.
2 309w =
.
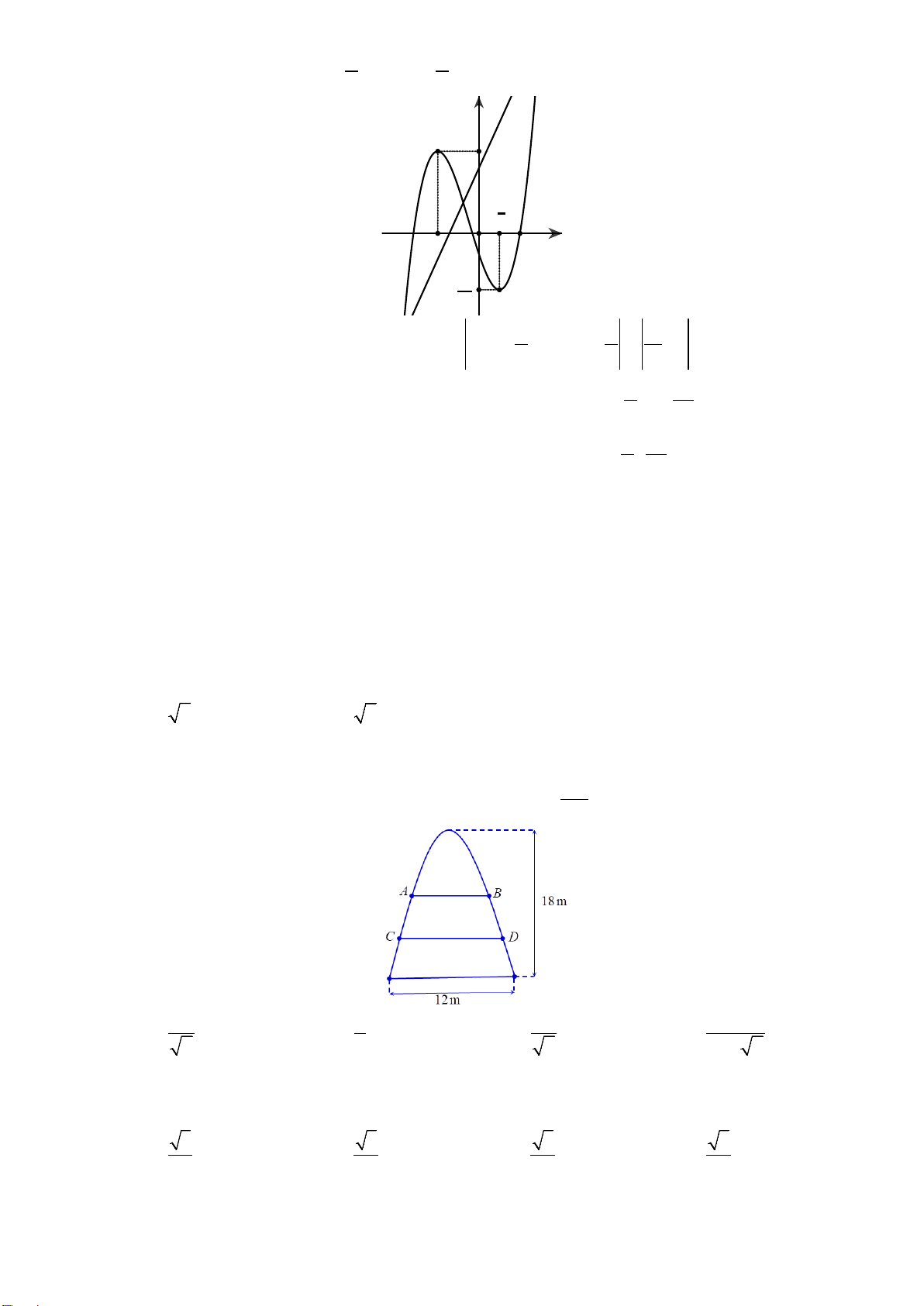
THTTH Trang 5/6
Câu 43. Đồ thị hàm số
32
31
23
22
yx x x= + −−
như hình sau
Tìm tất cả các giá trị thực của
m
để phương trình
32
31
23 1
2 22
m
x xx+ −−= −
có đúng 4 nghiệm.
A.
.m ∈∅
. B.
3 19
( 2 ; ) ( ; 6).
44
m ∈− − ∪
.
C.
6
m =
hoặc
2.m = −
. D.
3 19
2, , , 6 .
44
m
∈− −
.
Câu 44. Vào ngày 1/1, cô Phong mua một ngôi nhà làm văn phòng giá mua 200 triệu đồng với sự thoả
thuận thanh toán như sau: Trả ngay 10% số tiền. Số còn lại trả dần hàng năm bằng nhau trong 5 năm
song phải chịu lãi suất 6%/năm của số nợ còn lại (theo phương thức lãi kép). Thời điểm tính trả lãi
hàng năm là cuối năm (31/12). Số tiền phải trả hàng năm là
m
triệu đồng để lần cuối cùng là vừa hết
nợ. Vậy giá trị của
m
gần nhất với giá trị nào sau đây?
A. 42,730 triệu đồng. B. 42,630 triệu đồng. C. 42,720 triệu đồng. D. 42,620 triệu đồng.
Câu 45. Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
(
)
1;1; 2A
,
( )
1; 0; 4B −
,
( )
0; 1; 3C −
và
điểm
M
thuộc mặt cầu
( ) ( )
2
22
: 11Sx y z+ +− =
. Khi biểu thức
22 2
MA MB MC++
đạt giá trị nhỏ
nhất thì độ đài đoạn
AM
bằng
A.
2
. B.
6
. C.
6
. D.
2
.
Câu 46. Một cổng chào có dạng hình Parabol chiều cao
18 m
, chiều rộng chân đế
12 m
. Người ta
căng hai sợi dây trang trí
AB
,
CD
nằm ngang đồng thời chia hình giới hạn bởi Parabol và mặt đất
thành ba phần có diện tích bằng nhau (xem hình vẽ bên). Tỉ số
AB
CD
bằng
A.
1
2
. B.
4
5
. C.
3
1
2
. D.
3
122+
.
Câu 47. Cho hình lăng trụ đều
.ABC A B C
′′′
có tất cả các cạnh bằng
1
. Gọi
E
,
F
lần lượt là trung
điểm
AA
′
và
BB
′
; đường thẳng
CE
cắt đường thẳng
CA
′′
tại
E
′
, đường thẳng
CF
cắt đường thẳng
'CB
′
tại
F
′
. Thể tích khối đa diện
EFABEF
′′′′
bằng
A.
3
6
. B.
3
2
. C.
3
3
. D.
3
12
.
2
-1
-
11
8
1
2
O
x
y
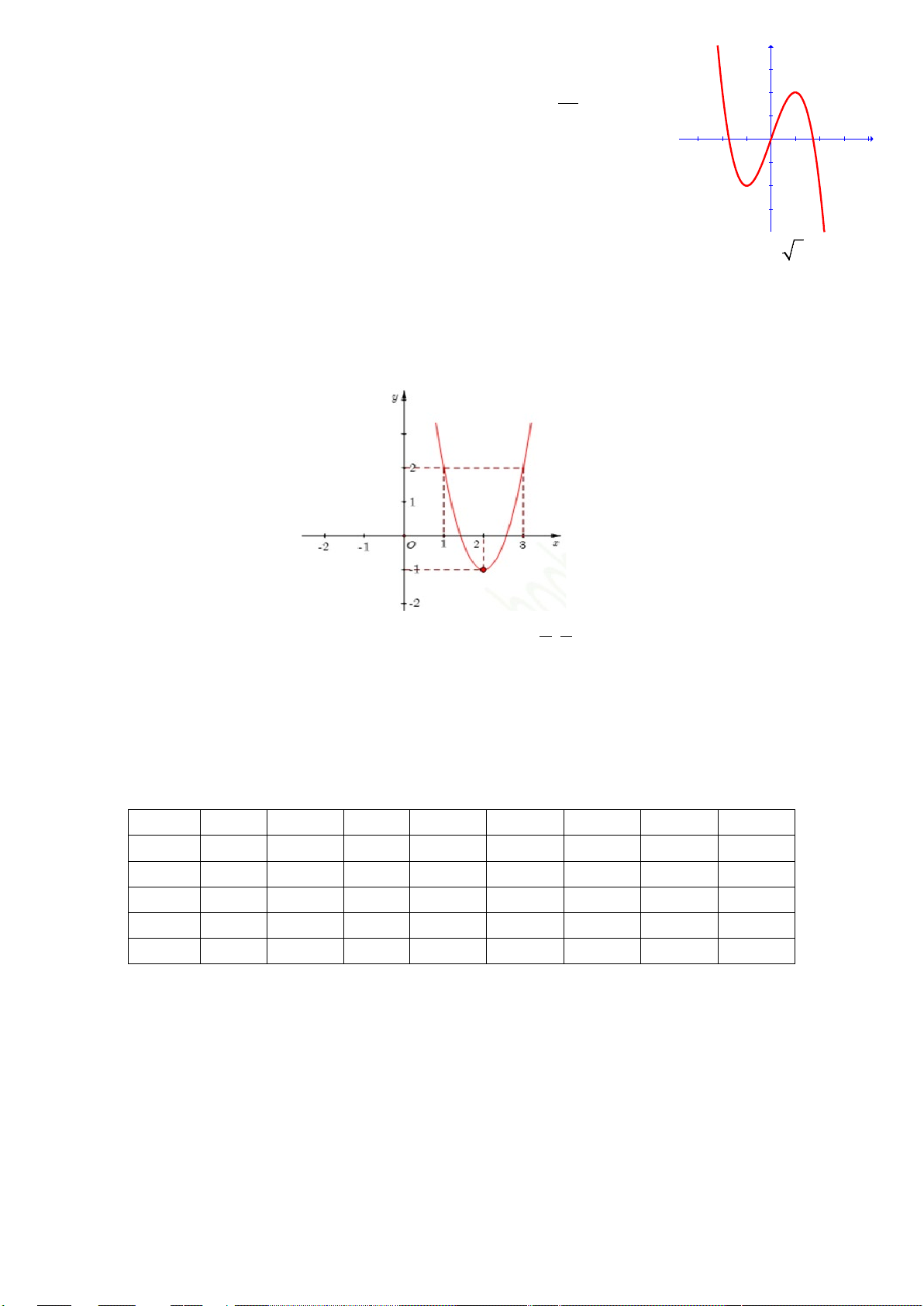
THTTH Trang 6/6
Câu 48. Cho hàm số
( )
y fx
=
liên tục và có đạo hàm
( )
'fx
trên
. Hình
bên là đồ thị của hàm số
( )
'y fx=
. Hàm số
( )
(
)
2
2018
2
x
gx f x
= +−
đạt
cực đại tại điểm nào trong các điểm sau đây ?
A.
2x = −
.
B.
0
x
=
.
C.
1x = −
.
D.
1x
=
.
Câu 49. Tìm tất cả các giá trị thực của tham số
m
để hàm số
(
)
2
6 2ln 3 3
y x x x mx= + + +− −
đồng
biến trên
( )
3;
− +∞
.
A.
0m
≤
. B.
4m ≤
. C.
0m ≥
. D.
4
m ≥−
.
Câu 50 . Cho hàm số
( )
fx
có đạo hàm là hàm số
( )
fx
′
trên
. Biết rằng hàm số
( )
22y fx
′
= −+
có đồ thị như hình vẽ bên dưới. Hàm số
( )
fx
nghịch biến trên khoảng nào?
A.
( )
;2−∞
. B.
( )
1;1−
. C.
35
;
22
. D.
( )
2; +∞
.
-------HẾT-------
ĐÁP ÁN
1. B
7. D
13. D
19. D
25. B
31. C
37. D
43. B
49. B
2. C
8. D
14. B
20. A
26. B
32. C
38. C
44. A
50. B
3. D
9. D
15. A
21. A
27. B
33. D
39. C
45. A
4. D
10. A
16. A
22. C
28. A
34. A
40. D
46. C
5. B
11. A
17. B
23. A
29. B
35. B
41. D
47. A
6. B
12. A
18. A
24. D
30. D
36. A
42. B
48. A
-3 -2 -1 1 2
3 4
-3
-2
-1
1
2
3
O
.
.
x
y
.
.
.
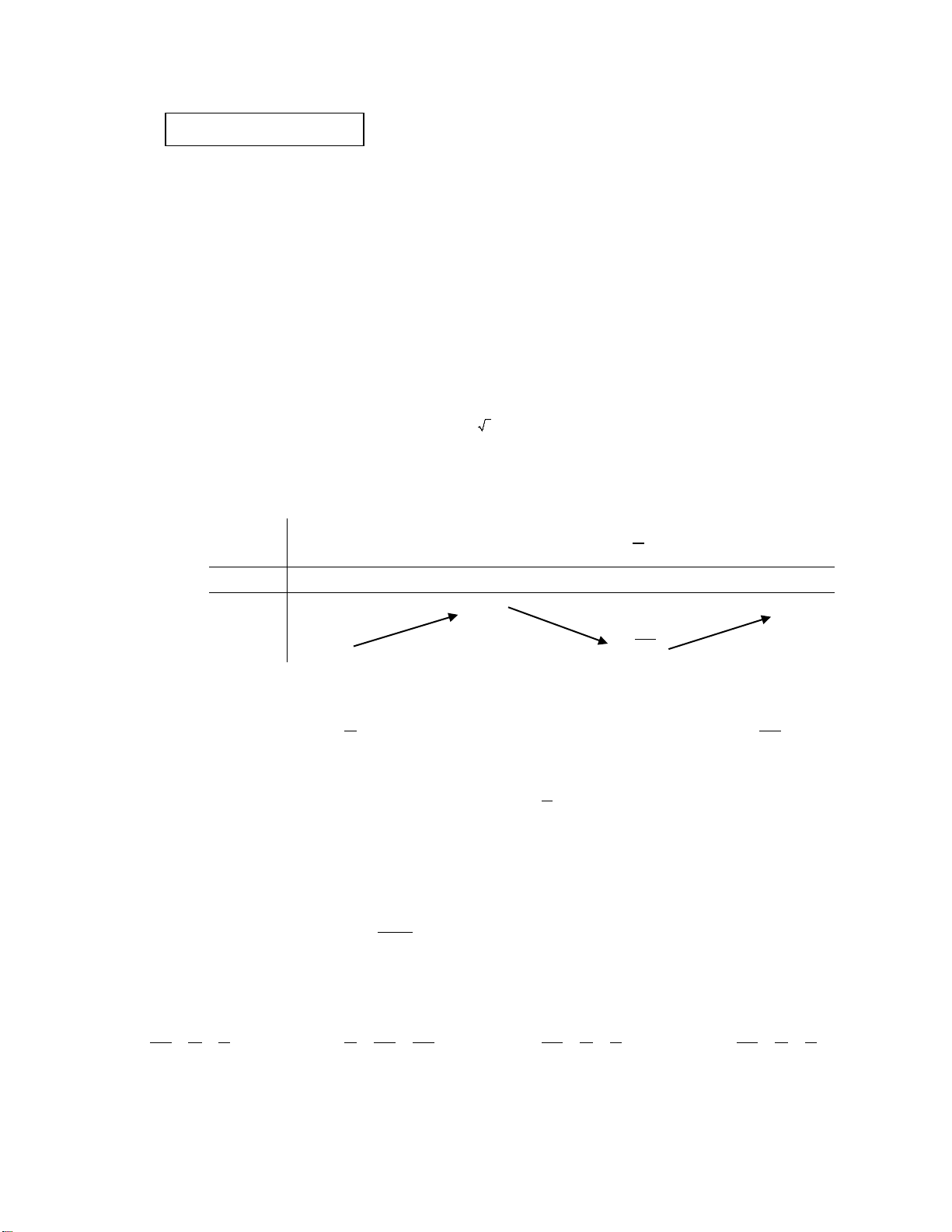
THTTH Trang 1/6
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
KỲ THI THPT QUỐC GIA NĂM 2019
TRƯỜNG THPT NGUYỄN THỊ MINH KHAI
Bài thi: Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề
(Đề thi có 06 trang)
Câu 1. Trong không gian Oxyz, cho mặt phẳng
( )
: 2 3 10 0P x yz− +− =
. Điểm nào dưới đây thuộc mặt
phẳng
( )
P
?
A.
( )
1
2;1; 2M
. B.
( )
2
2; 2;0
M
. C.
( )
3
1; 2; 0M
. D.
( )
4
2; 2; 0M −
.
Câu 2. Số giao điểm của đồ thị hàm số
42
95y xx
=−−
với trục hoành là
A. 3. B. 0. C. 1. D. 4.
Câu 3. Nghiệm của phương trình
( )
2019
log 5 13x −=
là
A.
13
2019 5x = +
. B.
2019
13 5
x
= −
. C.
13
2019 5x = −
. D.
2019
13 5x
= +
.
Câu 4. Cho hai số phức
1
34zi= −
và
2
13zi= +
. Hiệu số phức
1
z
và
2
z
bằng
A.
4 i−
. B.
27
i−
. C.
2 i−
. D.
47
i−
.
Câu 5. Tìm tập xác định của hàm số
(
)
3
2
28yx x= −−
.
A.
. B.
(
] [
)
; 2 4;−∞ − ∪ +∞
. C.
{ }
\ 2; 4−
. D.
(
) (
)
; 2 4;−∞ − ∪ +∞
.
Câu 6. Cho hàm số
( )
y fx=
liên tục trên
và có bảng biến thiên như hình dưới đây:
x
−∞
0
4
3
+∞
'y
+
0
−
0
+
y
1
+∞
−∞
5
27
−
Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực đại tại
1x =
. B. Hàm số đạt cực đại bằng 1.
C. Hàm số đạt cực tiểu bằng
4
3
. D. Hàm số đạt cực tiểu tại
5
27
x = −
.
Câu 7. Khối trụ có bán kính đáy là r và độ dài chiều cao là h có thể tích bằng
A.
2
2 rh
π
. B.
2
rh
π
. C.
2
1
3
rh
π
. D.
2
rh
π
.
Câu 8. Cho cấp số nhân
( )
n
a
có số hạng đầu bằng 3 và công bội
2q =
. Giá trị của
5
a
bằng
A. 96. B. 48. C. 13. D. 11.
Câu 9. Họ nguyên hàm của hàm số
( )
4
5
x
fx x e= −
là
A.
3
20
x
xeC
−+
. B.
51
1
1
x
x eC
x
+
−+
+
. C.
31
20
x
x xe C
−
−+
. D.
5 x
xeC−+
.
Câu 10. Trong không gian Oxyz, cho điểm
( )
3; 9; 6M −
. Gọi
123
,,
MMM
lần lượt là hình chiếu vuông góc
của M trên các trục tọa độ Ox, Oy, Oz. Mặt phẳng
( )
123
MMM
có phương trình là
A.
0
396
x yz
++=
−
. B.
1
396
xy z
++=
−−
. C.
1
396
x yz
++=
−
. D.
1
132
x yz
++=
−
.
Câu 11. Biết rằng
4
a
x=
và
16
b
y=
. Khi đó xy bằng
A.
64
ab
. B.
2
4
ab+
. C.
2
4
ab
. D.
2
16
ab+
.
ĐỀ THI ĐỀ XUẤT
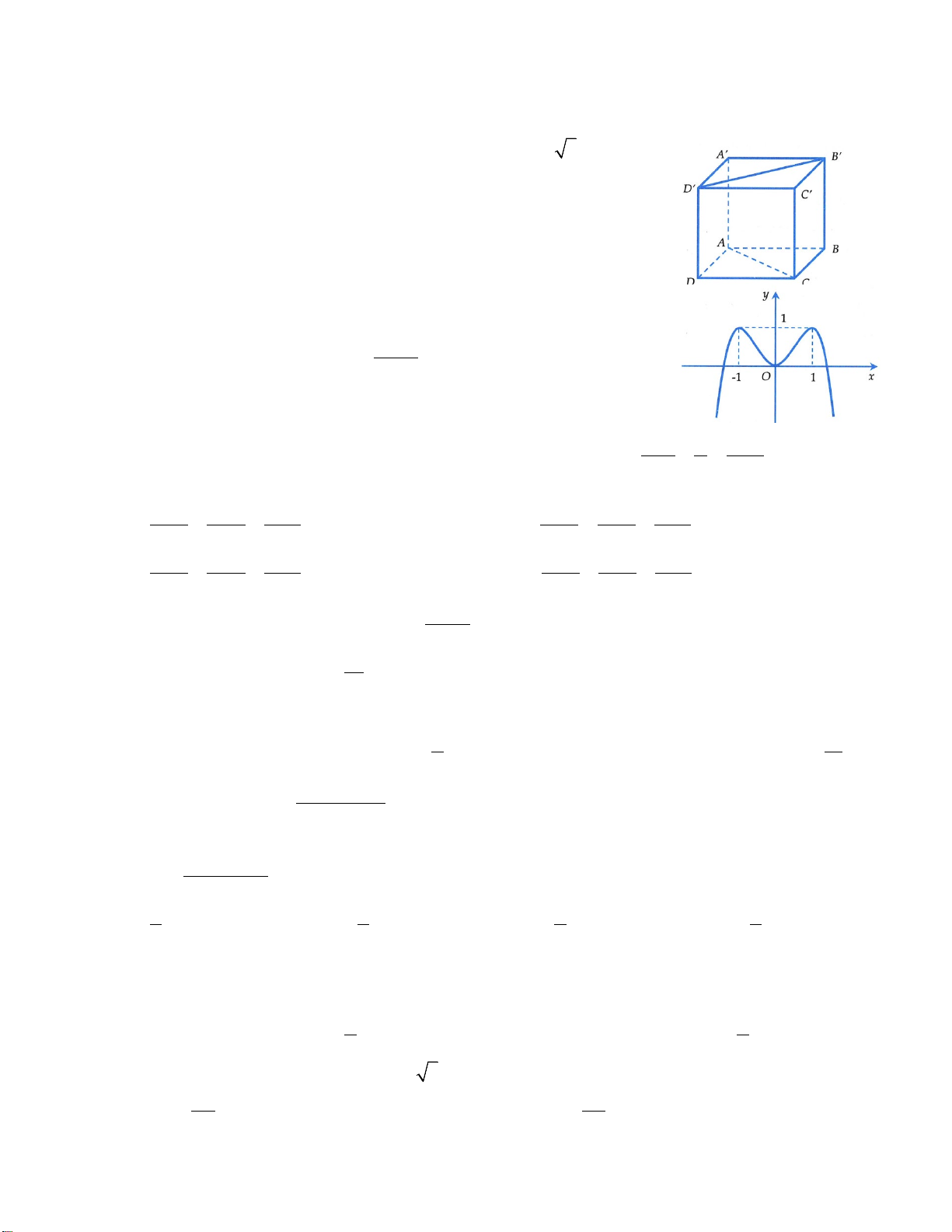
THTTH Trang 2/6
Câu 12. Cho
( )
4
0
2018f x dx =
∫
. Giá trị
(
) (
)
22
02
22f x dx f x dx
−
+−
∫∫
bằng
A. 4036. B. 3027. C. 0. D.
1009−
.
Câu 13. Cho hình hộp chữ nhật
.'' ' 'ABCD A B C D
có
3AB a=
và
AD a=
(tham khảo hình vẽ bên ). Góc giữa hai đường thẳng
''BD
và AC bằng
A. 90°. B. 30°.
C. 45°. D. 60°.
Câu 14. Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
42
2yx x= −
. B.
21
1
x
y
x
+
=
−
.
C.
3
3yx x=−+
. D.
24
2y xx= −
.
Câu 15. Trong không gian Oxyz, cho điểm
(
)
2;5;3I
và đường thẳng
12
:
212
x yz
d
−−
= =
. Đường thẳng Δ
đi qua I và vuông góc với hai đường thẳng OI, d có phương trình là
A.
253
7 28
xyz+ ++
= =
−−
. B.
253
87 2
xyz−−−
= =
−−
.
C.
253
72 8
xyz+ ++
= =
−
. D.
253
72 8
xyz−−−
= =
−
.
Câu 16. Giá trị nhỏ nhất của hàm số
( )
2
3
1
x
fx
x
+
=
−
trên
[
]
2; 4
bằng
A. 6. B.
19
3
. C. 2. D. 7.
Câu 17. Tìm các số thực p và q thỏa mãn
( )
3 2 3 98
p q ii i+− =−
với i là đơn vị ảo.
A.
2, 4pq= = −
. B.
5
3,
2
pq= = −
. C.
4, 4pq
= = −
. D.
11
3,
2
pq= = −
.
Câu 18. Đồ thị hàm số
2
2
6 51
2 95
xx
y
xx
−+
=
+−
có bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
A. 2. B. 3. C. 4. D. 1.
Câu 19.
( )
2
0
cos 3 1
lim
x
x
x
→
−
bằng
A.
9
2
. B.
3
2
−
. C.
2
3
−
. D.
9
2
−
.
Câu 20. Trong không gian Oxyz, cho hai mặt phẳng
( )
:2 2 4 0
P xy z−+ −=
và
( )
:2 2 5 0Q xy z−+ +=
.
Mặt cầu
( )
S
tiếp xúc với hai mặt phẳng
(
)
P
và
( )
Q
có bán kính bằng
A. 3. B.
3
2
. C. 9. D.
1
2
.
Câu 21. Nghiệm của phương trình
2sin 3 0x +=
là
A.
2
2,
3
x kk
π
π
=±+ ∈
. B.
5
2,
6
x kk
π
π
=±+ ∈
.
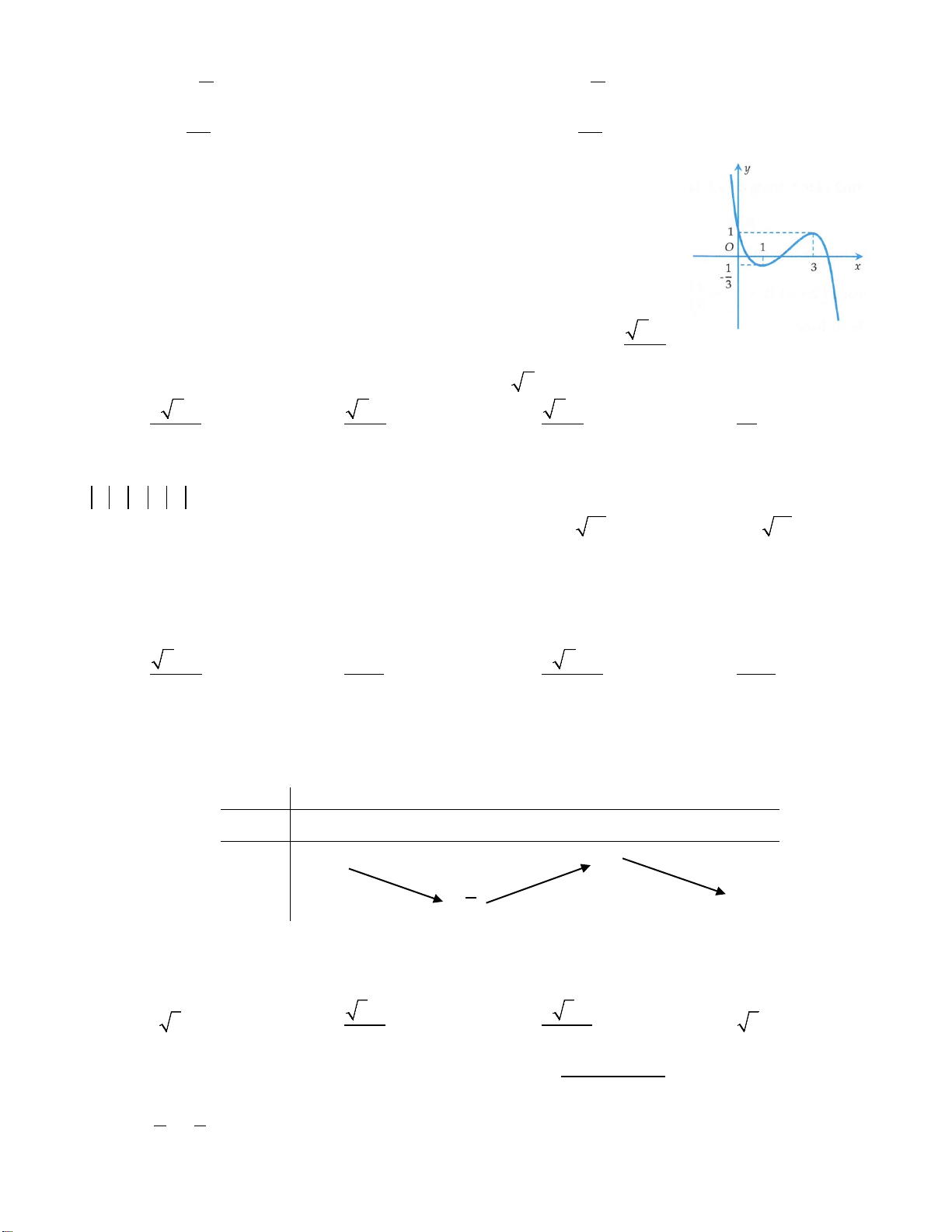
THTTH Trang 3/6
C.
2
3
,
2
3
xk
k
xk
π
π
π
π
=−+
∈
4
= +
. D.
2
6
,
7
2
6
xk
k
xk
π
π
π
π
=−+
∈
= +
.
Câu 22. Cho hàm số
( )
y fx
=
có đạo hàm trên
và đồ thị hàm số
( )
'
y fx=
như hình bên. Số điểm cực trị của hàm số
(
)
( )
2019 2018 13gx f x x= −+
là
A. 0. B. 1.
C. 2. D. 3.
Câu 23. Biết rằng khối tứ diện đều cạnh bằng k thì có thể tích bằng
3
2
12
k
.
Cho hình lập phương
.'' ' 'ABCD A B C D
có cạnh bằng
2a
. Tính theo a thể tích khối tứ diện
''ACB D
.
A.
3
22
3
a
. B.
3
2
6
a
. C.
3
2
2
a
. D.
3
3
a
.
Câu 24. Biết rằng phương trình
( )
( )
2
3 2 10 0z zz+ −+ =
có ba nghiệm phức là
123
,,zzz
. Giá trị của
123
zzz++
bằng
A. 5. B. 23. C.
3 2 10+
. D.
3 10+
.
Câu 25. Trong mặt phẳng Oxy, đường tròn
( )
22
: 4 6 12 0Cx y x y+++−=
có tâm là
A.
(
)
2; 3I −−
B.
( )
2;3I
C.
( )
4;6I
D.
( )
4; 6
I −−
Câu 26. Cho khối nón có bán kính đáy bằng r và độ dài đường sinh bằng 3 lần bán kính đáy. Thể tích của
khối nón đã cho bằng
A.
3
2
3
r
π
. B.
3
2
3
r
π
. C.
3
22
3
r
π
. D.
3
8
3
r
π
.
Câu 27. Tổng bình phương các nghiệm của phương trình
( )
3
1
2 32
x
x
−
+
=
bằng
A. 20. B. 4. C. 2. D. 6.
Câu 28. Cho hàm số
( )
y fx=
có bảng biến thiên như sau:
x
−∞
1
3
+∞
( )
'fx
−
0 + 0
−
( )
fx
+∞
1
1
3
−
−∞
Số nghiệm thực của phương trình
( )
4 23 10fx− +=
là
A. 1. B. 3. C. 2. D. 0.
Câu 29. Cho khối lăng trụ đều
.'' 'ABC A B C
có tất cả các cạnh bằng 2a. Thể tích khối lăng trụ đã cho bằng
A.
3
23a
. B.
3
3
2
a
. C.
3
23
3
a
. D.
3
3a
.
Câu 30. Cho
(
)
Fx
là một nguyên hàm của hàm số
( )
2
2
6 13 11
2 52
xx
fx
xx
++
=
++
và thỏa mãn
( )
27F =
. Biết
rằng
15
ln 2 ln 5
22
F ab
=++
, trong đó a, b là các số nguyên. Tính trung bình cộng của a và b.
A. 10. B. 8. C. 5. D. 3.
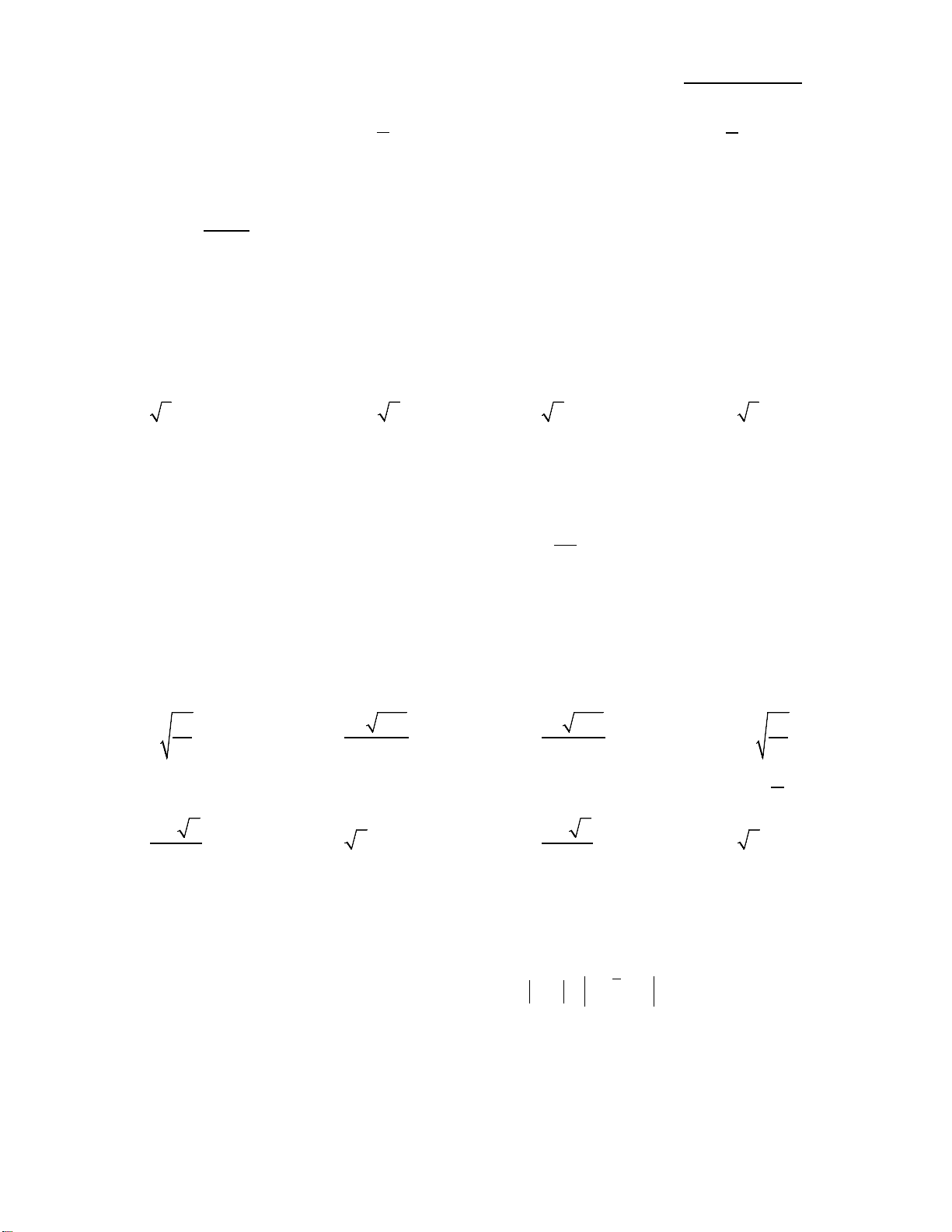
THTTH Trang 4/6
Câu 31. Biết rằng tập hợp tất cả các giá trị của tham số m để hàm số
(
)
2
221x xm
fx
xm
++ −
=
−
đồng biến
trên nửa khoảng
[
)
2; +∞
và
;
a
S
b
= −∞
, trong đó a, b là các số nguyên dương và
a
b
là phân số tối giản.
Giá trị của
3
ab−
bằng
A. 11. B. 23. C. 7. D. 19.
Câu 32. Cho
5
2
3
ln 5 ln 3 ln 2
dx
abc
xx
=++
−
∫
với a, b, c là các số hữu tỷ. Giá trị của
2
32bc a
+−
bằng
A.
2−
. B. 0. C. 3. D. 6.
Câu 33. Cho hình trụ
( )
T
có chiều cao bằng đường kính đáy, hai đáy là các hình tròn
( )
;Or
và
(
)
';
Or
.
Gọi A là điểm di động trên đường tròn
( )
;Or
và B là điểm di động trên đường tròn
( )
';Or
sao cho AB
không là đường sinh của hình trụ
( )
T
. Khi thể tích khối tứ diện
'OO AB
đạt giá trị lớn nhất thì đoạn thẳng
AB có độ dài bằng
A.
3r
. B.
( )
22r+
. C.
6r
. D.
5
r
.
Câu 34. Các loài cây xanh trong quá trình quang hợp sẽ nhận được một lượng nhỏ cacbon 14 (một đồng vị
cacbon). Khi một bộ phận của cây đó bị chết thì hiện tượng quang hợp cũng sẽ ngưng và nó sẽ không nhận
thêm cacbon 14 nữa. Lượng cacbon 14 của bộ phận đó sẽ phân hủy một cách chậm chạp, chuyển hóa thành
nitơ 14. Gọi
( )
Pt
là số phần trăm cacbon 14 còn lại trong một bộ phận của một cây sinh trưởng từ t năm
trước đây thì
( )
Pt
được cho bởi công thức
( ) (
) ( )
5750
100. 0,5 %
t
Pt =
. Phân tích một mẫu gỗ từ một công
trình kiến trúc cổ, người ta thấy lượng cacbon 14 còn lại trong gỗ là 45,78 (%). Hãy xác định niên đại của
công trình kiến trúc đó.
A. 6482 năm. B. 6481 năm. C. 6428 năm. D. 6248 năm.
Câu 35. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu vuông góc của S lên mặt
phẳng
(
)
ABCD
trùng với trọng tâm G của tam giác ABD. Đường thẳng SD tạo với mặt phẳng
( )
ABCD
một góc 60°. Khoảng cách giữa hai đường thẳng AB và SC bằng
A.
15
19
a
. B.
2 285
57
a
. C.
9 285
19
a
. D.
5
3
17
a
.
Câu 36. Cho x, y là các số thực thỏa mãn
(
)
9 12 16
log log log 2x y xy= = +
. Giá trị của tỷ số
x
y
là
A.
22
2
+
. B.
21+
. C.
22
2
−
. D.
21−
.
Câu 37. Trong không gian Oxyz, cho ba điểm
( ) ( ) ( )
0;1; 2 , 2; 2;1 , 2;0;1AB C−−
và mặt phẳng
(
)
α
có
phương trình
2 2 30x yz+ +−=
. Biết rằng tồn tại duy nhất điểm
( )
;;M abc
thuộc mặt phẳng
(
)
α
sao cho
MA MB MC= =
. Đẳng thức nào sau đây đúng?
A.
20abc+−=
. B.
2 3 4 41abc+−=
. C.
50abc++=
. D.
30a bc+ +=
.
Câu 38. Tập hợp điểm biểu diễn các số phức z thỏa mãn
22zi zz i−= −+
là
A. một đường thẳng. B. một đường elip. C. một parabol. D. một đường tròn.
Câu 39. Cho d là đường thẳng đi qua điểm
( )
1; 3A −
và có hệ số góc m. Gọi S là tập hợp các giá trị của
tham số m để đường thẳng d cắt đồ thị
( )
C
của hàm số
3
31yx x=−+
tại ba điểm phân biệt A, B, C sao
cho tiếp tuyến với đồ thị
( )
C
tại B và C cắt nhau tại điểm I nằm trên đường tròn đường kính BC. Tính
tổng bình phương các phần tử thuộc tập hợp S.

THTTH Trang 5/6
A.
16
9
. B.
34
9
. C.
38
9
. D.
34
3
.
Câu40: Trong mặt phẳng Oxy, cho biết điểm
( )
;M ab
(
0
a >
) thuộc đường thẳng
3
:
2
xt
d
yt
= +
= +
và cách
đường thẳng
:2 3 0
xy∆ −−=
một khoảng
25
. Khi đó
ab+
là:
A. 21 B. 23 C. 22 D. 20
Câu 41. Trong không gian Oxyz, cho mặt cầu
( ) ( ) ( ) ( )
2 22
: 2 5 3 27Sx y z−+−+−=
và đường thẳng
12
:
212
x yz
d
−−
= =
. Mặt phẳng
( )
P
chứa đường thẳng d và cắt mặt cầu
( )
S
theo giao tuyến là đường tròn
có bán kính nhỏ nhất. Nếu phương trình của
( )
P
là
0
ax by z c+ −+=
thì
A.
1abc++=
. B.
6abc++=−
. C.
6abc++=
. D.
2abc++=
.
Câu 42. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với
2, 2 3AB AD= =
. Mặt bên SAB là
tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng
( )
ABCD
. Gọi M, N, P lần lượt là trung
điểm của các cạnh SA, CD,CB. Tính côsin góc tạo bởi hai mặt phẳng
( )
MNP
và
( )
SCD
.
A.
2 435
145
. B.
11 145
145
. C.
2 870
145
. D.
3 145
145
.
Câu 43. Bệnh máu khó đông ở người do đột biến gen lặn nằm trên nhiễm sắc thể giới tính X, alen trội
tương ứng quy định người bình thường. Một gia đình có người chồng bình thường còn người vợ mang gen
dị hợp về tính trạng trên. Họ dự định sinh 2 người con, giả thiết rằng mỗi lần sinh chỉ sinh được một người
con, xác suất để cả 2 người con không bị bệnh máu khó đông là bao nhiêu?
A.
9
16
. B.
15
16
. C.
1
4
. D.
3
4
.
Câu 43 nội dung thiên về môn Sinh học
Câu 44. Cho hàm số
( )
y fx=
liên tục trên
và hàm số
( )
'y fx=
có đồ thị như hình bên. Bất phương trình
( ) ( )
( )
3 4 5 25
fx m fx m
fx m
++
+ ≤ ++
nghiệm đúng với mọi
( )
1; 2
x ∈−
khi và chỉ khi
A.
( ) ( )
1 12f mf− − < <−
.
B.
( ) ( )
2 11f mf− < <− −
.
C.
( ) ( )
1 12f mf− − ≤ ≤−
.
D.
( ) ( )
2 11f mf− ≤ ≤− −
.
Câu 45. Trong không gian Oxyz, cho điểm
( )
2; 3; 4
M −
. Gọi
( )
P
là
mặt phẳng đi qua M và cắt các trục
' ,' ,'x Ox y Oy z Oz
lần lượt tại các điểm D, E, F sao cho
( )
2
2 22 0OD OE m m OF= = −+ ≠
, trong đó m là tham số thực. Gọi S là tập hợp các giá trị của m để chỉ có
đúng ba mặt phẳng
( )
P
thỏa mãn yêu cầu trên.
Tập hợp S có bao nhiêu tập hợp con khác rỗng?
A. 7. B. 3. C. 15. D. 4.
Câu 46. Cho
( )
fx
là hàm đa thức thỏa mãn
( ) ( )
43 2
1 5 12 4 f x xf x x x x x− − = − + − ∀∈
. Gọi M và m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
y fx=
trên tập
{ }
42
| 10 9 0Dx x x= ∈ − +≤
.
Giá trị của
21 6 2019mM++
bằng
A. 2235. B. 2319. C. 3045. D. 3069.

THTTH Trang 6/6
Câu 47. Cho hình phẳng D giới hạn bởi các đường
(
)
(
)
2
2 sin 1 cos
sin cos
xx xx x
y
xx x
+ −−
=
+
, trục hoành và hai
đường thẳng
0x
=
và
4
x
π
=
. Biết rằng diện tích của hình phẳng D bằng
( )
2
4
ln 2 ln 4
16
ab
ππ
π
+
++ +
, với
a, b là các số hữu tỷ. Mệnh đề nào dưới đây đúng?
A.
2 12ab+=
. B.
26ab−=−
. C.
2 12ab−=−
. D.
26ab
+=
.
Câu 48. Cho số phức z thỏa mãn
1 3 5 2 65
z iz i
−+ + + + =
. Giá trị nhỏ nhất của
2zi
++
đạt được khi
z a bi
= +
với a, b là các số thực dương. Giá trị của
23ba+
bằng
A. 19. B. 16. C. 24. D. 13.
Câu 49. Trong hệ trục tọa độ Oxyz, cho tam giác ABC có
( )
3; 2;3C
, đường cao AH nằm trên đường thẳng
1
233
:
11 2
xyz
d
− −−
= =
−
và đường phân giác trong BD của góc B nằm trên đường thẳng
2
d
có phương
trình
143
1 21
xy z−−−
= =
−
. Diện tích tam giác ABC bằng
A. 4. B.
23
. C.
43
. D. 8.
Câu 50. Cho hàm số
( )
y fx=
có đạo hàm trên
và đồ thị
(
)
C
. Tiếp tuyến của đồ thị
( )
C
tại điểm
( )
2; m
có phương trình là
46yx
= −
. Tiếp tuyến của các đồ thị hàm số
(
)
y f fx=
và
( )
2
3 10yfx= −
tại điểm có hoành độ bằng 2 có phương trình lần lượt là
y ax b= +
và
y cx d= +
. Tính giá trị của biểu thức
432S a c bd= +−+
.
A.
26
S = −
. B.
176S =
. C.
178S =
. D.
174
S =
.
-------HẾT-------
ĐÁP ÁN
1. D
2. C
3. A
4. B
5. D
6. B
7. D
8. B
9. D
10. C
11. B
12. B
13. D
14. D
15. D
16. A
17. A
18. A
19. D
20. B
21. C
22. D
23. A
24. C
25. A
26. C
27. A
28. B
29. A
30. D
31. C
32. D
33. C
34. B
35. A
36. D
37. B
38. C
39. B
40. B
41. B
42. B
43. A
44. A
45. A
46. A
47. A
48. B
49. B
50. D
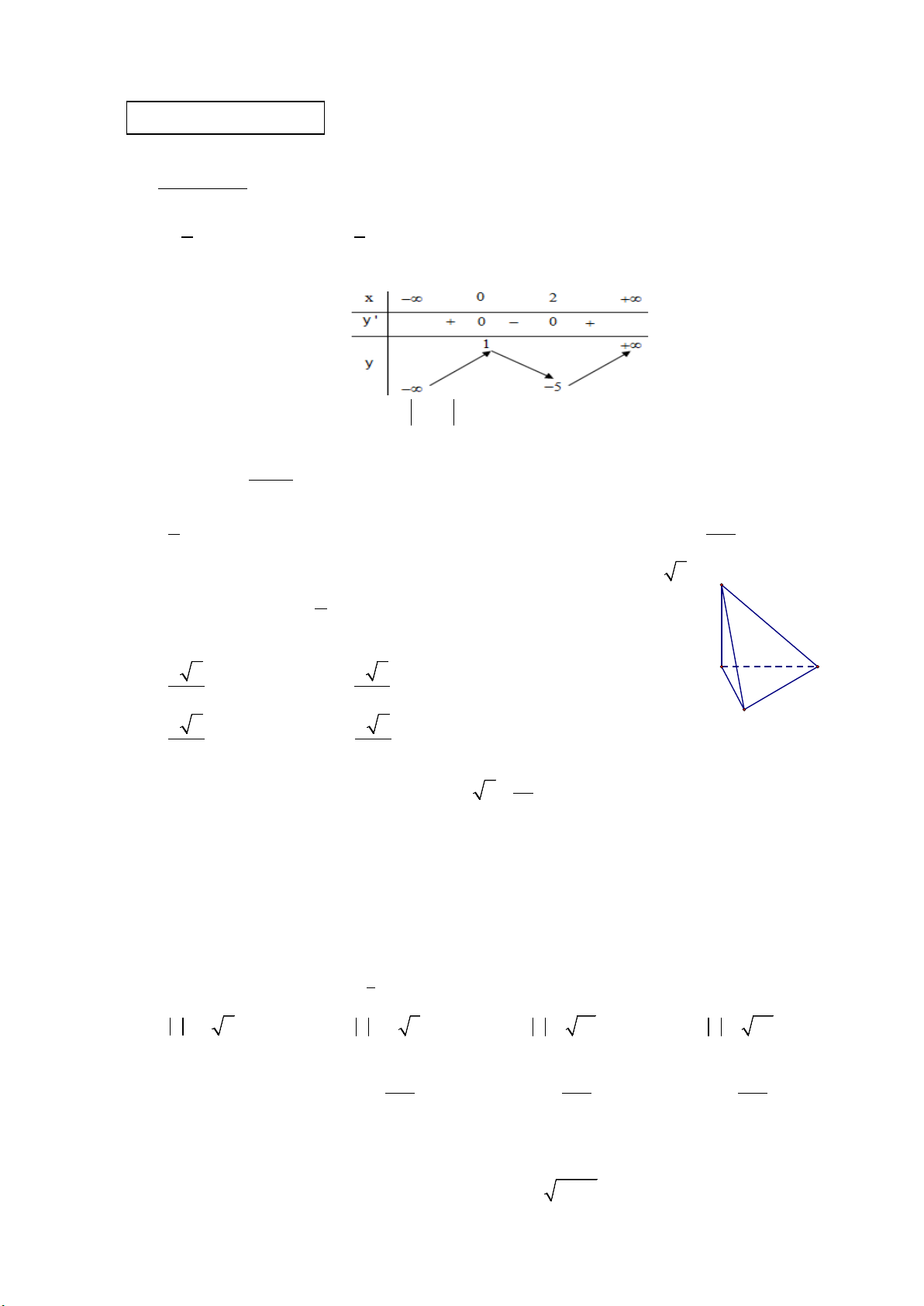
THTTH Trang 1/6
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
KỲ THI THPT QUỐC GIA NĂM 2019
TRƯỜNG THPT LÝ TỰ TRỌNG
Bài thi: Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề
(Đề thi có 06 trang)
Câu 1.
45
4
32
lim
5 32
x
xx
xx
→−∞
−
++
bằng:
A.
2
5
−
. B.
3
5
. C.
−∞
. D.
+∞
.
Câu 2. Cho hàm số
(
)
y fx=
xác định, liên tục trên
và có bảng biến thiên như hình dưới đây.
Số nghiệm thực của phương trình
(
)
3 70
fx−=
là
A. 0. B. 4. C. 5. D. 6.
Câu 3. Tính tích phân
1
2
0
2
1
x
dx
x +
∫
ta được kết quả là
A.
1
2
. B.
ln 2
. C. 1. D.
ln 2
2
.
Câu 4. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
B
,
2AB a=
.
SA
vuông góc với đáy và
2
a
SA =
(tham khảo hình vẽ bên). Tính khoảng cách từ
điểm
A
đến mặt phẳng
()SBC
.
A.
2
12
a
. B.
2
2
a
.
C.
2
3
a
. D.
2
6
a
.
Câu 5. Tìm số hạng không chứa
x
trong khai triển
4
1
n
xx
x
+
với
0x >
, nếu biết rằng
21
44
nn
CC−=
.
A. 165. B. 238. C. 485. D. 525.
Câu 6. Có 12 học sinh gồm 5 học sinh lớp A, 4 học sinh lớp B và 3 học sinh lớp C. Hỏi có bao nhiêu cách
chọn 4 học sinh đi làm nhiệm vụ mà 4 người này không thuộc quá 2 trong 3 lớp trên?
A. 242. B. 2525. C. 215. D. 225.
Câu 7. Cho tam giác
ABC
có
( ) ( ) (
)
1; 1 , 2;5 , 4; 3A BC−−
. Lập phương trình đường thẳng chứa đường
trung tuyến xuất phát từ đỉnh A của tam giác
ABC
.
A.
5 3 20xy+ −=
. B.
4 50xy− −=
. C.
0xy+=
. D.
20xy−−=
.
Câu 8. Tính môđun của số phức
z
biết
(2 1)(3 i)zi=−+
.
A.
52z =
.
B.
25z =
.
C.
10z =
.
D.
26z =
.
Câu 9. Một khối lăng trụ có chiều cao 2a và diện tích đáy bằng
2
2.
a
Tính thể tích khối lăng trụ.
A.
3
4Va=
. B.
3
4
3
a
V =
. C.
3
2
3
a
V =
. D.
2
4
3
a
V =
.
Câu 10. Tìm khoảng đồng biến của hàm số
32
3 9.
yx x x=−+ +
A.
( )
1; 3
. B.
( )
3; 1−−
. C.
( )
1; 3−
. D.
( )
;−∞ +∞
.
Câu 11. Gọi
D
là hình phẳng giới hạn bởi đồ thị hàm số
2
1yx= −
và trục hoành. Thể tích của khối
tròn xoay tạo thành khi quay
D
quanh trục hoành là
A
C
B
S
ĐỀ THI ĐỀ XUẤT

THTTH Trang 2/6
A.
3
2
π
. B.
4
3
π
. C.
3
4
π
. D.
2
3
π
.
Câu 12. Trong các mệnh đề sau, hãy tìm mệnh đề sai.
A. Hàm số
3
2yx x= ++
không có cực trị. B. Hàm số
42
23yx x=+−
có ba điểm cực trị.
C. Hàm số
1
1
yx
x
= +
+
có hai cực trị. D. Hàm số
32
231
yx x
=+−
có hai điểm cực trị.
Câu 13. Cho các số thực
0ab<<
. Mệnh đề nào sau đây sai?
A.
( )
( ) (
)
2
22
ln ln lnab a b= +
. B.
( )
( )
1
ln ln ln
2
ab a b
= +
.
C.
ln ln ln
a
ab
b
= −
. D.
( ) ( )
2
22
ln ln ln
a
ab
b
= −
.
Câu 14. Chọn mệnh đề đúng?
A.
sin(3 5 ) 5cos(3 5 ) .
x dx x C− = −+
∫
. B.
1
sin(3 5 ) cos(3 5 ) .
5
x dx x C− =− −+
∫
.
C.
1
sin(3 5 ) cos(5 3) .
5
x dx x C
− = −+
∫
. D.
1
sin(3 5 ) cos(3 5 ) .
3
x dx x C− =− −+
∫
.
Câu 15. Trong không gian Oxyz, cho đường thẳng
1
: 23( )
5
x
d y ttR
zt
=
=+∈
= −
. Vectơ nào dưới đây là vectơ
chỉ phương của
d
?
A.
( )
1
0; 3; 1 .u = −
. B.
( )
2
1; 3; 1 .u = −
. C.
(
)
3
1;3;1.u = −−
. D.
( )
4
1; 2; 5 .u =
.
Câu 16. Tập nghiệm của bất phương trình
( )
( )
2
log 25 log 10+>xx
là
A.
{ }
\5
. B.
. C.
(
)
0; +∞
. D.
( ) ( )
0; 5 5;∪ +∞
.
Câu 17. Đồ thị hàm số
1
1
x
y
x
+
=
−+
là đường cong trong hình nào dưới đây?
A. . B. . C. . D. .
Câu 18. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):
6 3 20xyz+ − +=
và đường thẳng
112
:
31 2
xyz
d
−−−
= =
−
. Tọa độ giao điểm D của đường thẳng d và mặt phẳng (P) là
A.
( )
5; 3; 6D −
. B.
( )
1; 3; 7D
. C.
( )
4;0; 0D
. D.
( )
2; 2; 4D −
.
Câu 19. Cho hình nón có diện tích xung quanh bằng
2
3 a
π
và độ dài đường sinh bằng
3a
. Bán kính đáy
của hình nón đã cho bằng
A.
3a
. B.
a
. C.
2a
. D.
3
2
a
.
Câu 20. Biết rằng hàm số
1
2
ax
y
bx
+
=
−
có tiệm cận đứng là
2x =
và tiệm cận ngang là
3
y =
. Hiệu
2−ab
có giá trị là:
A. 4. B. 5. C. 1. D. 0.
Câu 21. Cho hàm số
=−+
32
33yx x
.Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm
số trên đoạn
1; 3
.Tính giá trị T = M + m.
A.
2.
. B.
4.
. C.
3.
. D.
0.
.
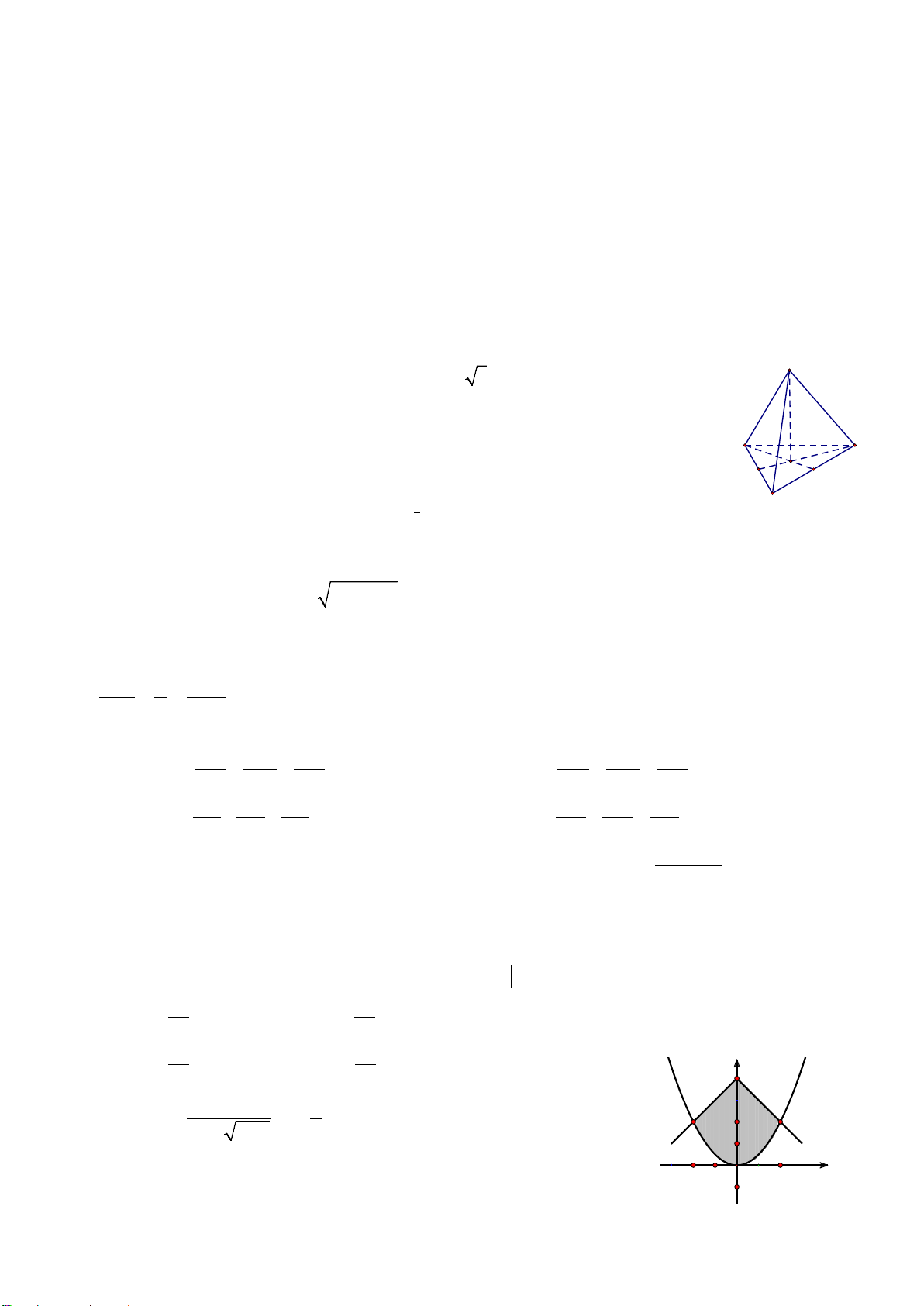
THTTH Trang 3/6
Câu 22. Gọi
1
z
là nghiệm phức có phần ảo dương của phương trình
2
8 25 0zz−+=
. Giả sử
2
1
(, )z a bi a b=+∈
.Khi đó tổng
ab+
bằng
A.
31
.
B.
7−
.
C.
24
.
D.
7
.
Câu 23. Sau Tết Mậu Tuất, bé An được tổng tiền lì xì là 12 triệu đồng. Bố An gửi toàn bộ số tiền trên của
con vào ngân hàng với lãi suất ban đầu là 5%/năm, tiền lãi hàng năm được nhập vào gốc và sau một năm
thì lãi suất tăng lên 0,2% so với năm trước đó. Hỏi sau 5 năm tổng số tiền của bé An trong ngân hàng là
bao nhiêu ?
A. 13,5 triệu đồng. B. 15,6 triệu đồng. C. 16,7 triệu đồng. D. 14,5 triệu đồng.
Câu 24. Trong không gian với hệ tọa độ Oxyz, cho điểm
( )
1; 1; 2A −
. Phương trình mặt phẳng (Q) đi qua
các hình chiếu của điểm A trên các trục tọa độ là
A.
( )
: 2 20Qxy z
−+ −=
. B.
( )
:2 2 2 0Q x yz− +−=
.
C.
( )
:1
11 2
xyz
Q
++ =
−−
. D.
( )
: 2 60Qxy z−+ +=
.
Câu 25. Cho hình chóp
.
S ABC
có
3SA SB SC a= = =
và đáy
ABC
là tam giác đều
cạnh bằng
a
(tham khảo hình vẽ bên). Góc giữa đường thẳng
SA
và mặt phẳng đáy
gần đúng với kết quả nào nhất trong các kết quả sau?
A.
0
65
. B.
0
70
.
C.
0
74
. D.
0
83
.
Câu 26. Phương trình
1
31
3
log (3 1) 2 log 2
x
x
+
−= +
có hai nghiệm; gọi hai nghiệm đó là
12
,xx
. Tính tổng
12
27 27
xx
S = +
A.
180S
=
. B.
45S =
. C.
9S
=
. D.
252S =
.
Câu 27. Bất phương trình
( 1) ( 2) 0
x xx+ +≥
có tập nghiệm là:
A.
[
)
0; { 2}S = +∞ ∪ −
. B.
[
)
2;
S = − +∞
. C.
[
)
0;S = +∞
. D.
( )
1;S = − +∞
.
Câu 28. Trong không gian
,Oxyz
cho mặt phẳng
( )
: 2 4 0P x yz
+ +−=
và đường thẳng
12
: .
213
x yz
d
++
= =
Viết phương trình đường thẳng
∆
nằm trong mặt phẳng
( )
P
, đồng thời cắt và
vuông góc với đường thẳng
d
.
A.
111
:
5 1 3
xyz−+
=
−
−
∆=
−
. B.
111
:
5 13
xyz−−−
∆==
−
.
C.
111
:
5 13
xyz−−−
∆==
−−
. D.
111
: .
5 12
xyz−+−
∆==
−
.
Câu 29. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số
2
sin
cos
mx
y
x
−
=
nghịch biến trên
khoảng
0;
6
π
?
A. 0. B. 2. C. 1. D. Vô số.
Câu 30. Diện tích hình phẳng giới hạn bởi đường
4yx= −
và một parabol như hình vẽ bằng:
A.
28
3
. B.
22
3
.
C.
26
3
. D.
25
3
.
Câu 31. Cho
3
0
ln 2 ln 3
3
42 1
xa
dx b c
x
=++
++
∫
, với
,,abc∈
. Giá trị của
biểu thức
T abc=++
bằng :
A. 1. B. 2. C. 7. D. 9.
O
M
A
C
B
S
x
y
-1
4
2
1
-2
-1
2
1
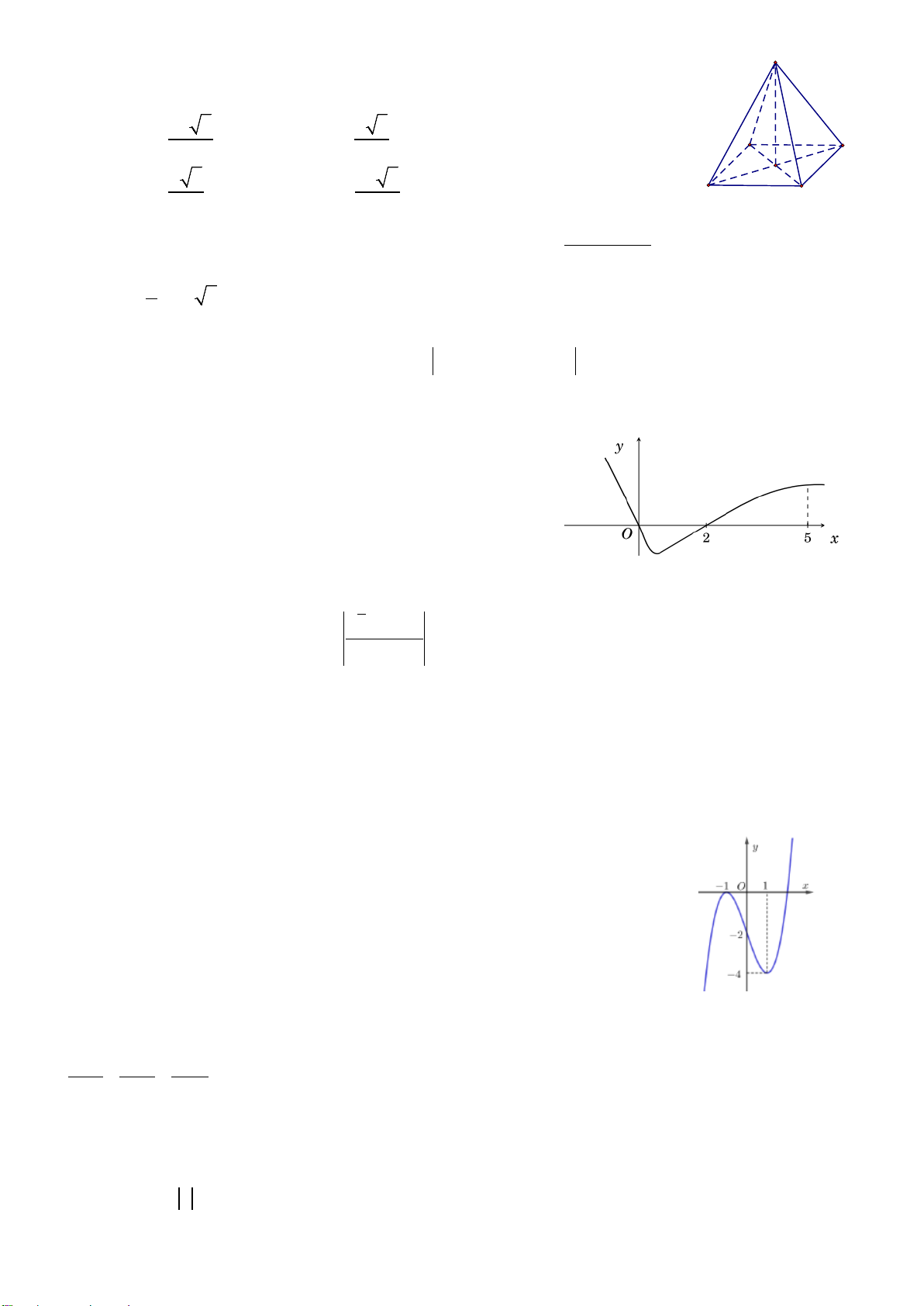
THTTH Trang 4/6
Câu 32. Cho hình chóp
.S ABCD
có đáy là hình vuông
ABCD
tâm O có cạnh
AB a=
đường cao SO vuông góc với mặt đáy và
SO a=
(tham khảo hình vẽ
bên). Khoảng cách giữa
SC
và
AB
là:
A.
25
7
a
. B.
5
7
a
.
C.
5
5
a
. D.
25
5
a
.
Câu 33. Biết
121 2
,( )
xx x x>
là hai nghiệm của phương trình
2
2
7
4 41
log 4 1 6
2
xx
xx
x
−+
+ +=
và
(
)
12
1
2
4
x x ab+= −
với a, b là hai số nguyên dương. Tính
ab+
.
A.
16.
ab
+=
. B.
11.ab+=
. C.
14.ab+=
. D.
13.ab+=
.
Câu 34. Biết giá trị lớn nhất của hàm số
( )
32
3 72 90fx x x x m=+ − ++
trên đoạn
[ ]
5;5−
là 2018. Trong
các khẳng định dưới đây, khẳng định nào đúng?
A.
1600 1700m<<
. B.
1618m <
. C.
1500 1600
m
<<
. D.
400m =
.
Câu 35. Cho hàm số
(
)
fx
có đạo hàm là
( )
.fx
′
Đồ thị hàm số
( )
y fx
′
=
được cho như hình bên. Biết rằng
( ) ( ) ( ) (
)
0325.ffff+=+
Giá trị nhỏ nhất, giá trị lớn nhất
của
( )
fx
trên đoạn
[ ]
0;5
lần lượt là
A.
( ) ( )
2, 5ff
. B.
(
) ( )
0, 5
ff
.
C.
( ) ( )
2, 0ff
. D.
( ) ( )
1, 5ff
.
Câu 36. Cho số phức z thỏa mãn :
23
3
zz i
zi
−+
=
+
. Tập hợp các điểm M biểu diễn số phức z trên mặt
phẳng phức là
A. Một parabol. B. Một đường thẳng. C. Một đường tròn. D. Một elip.
Câu 37. Cho hàm số
32
31yx x=++
có đồ thị
( )
C
. Đường thẳng đi qua điểm
( )
3;1
−A
và có hệ số góc
bằng k. Xác định k để đường thẳng đó cắt đồ thị tại 3 điểm khác nhau
A.
01<<k
. B.
0>k
. C.
09<≠k
. D.
19<<k
.
Câu 38. Cho hàm số
( )
=y fx
có đạo hàm trên
. Đường cong trong hình vẽ dưới đây là đồ thị của hàm
số
( )
'=
y fx
(
( )
'=y fx
liên tục trên
). Xét hàm số
( )
( )
2
2= −gx f x
.
Mệnh đề nào dưới đây sai?
A. Hàm số
(
)
gx
nghịch biến trên
( )
;2−∞ −
.
B. Hàm số
( )
gx
đồng biến trên
( )
2; +∞
.
C. Hàm số
( )
gx
nghịch biến trên
(
)
1; 0−
.
D. Hàm số
(
)
gx
nghịch biến trên
( )
0; 2
.
Câu 39. Trong không gian
Oxyz
, viết phương trình mặt phẳng
( )
P
đi qua điểm
(1; 2;3)M
và cắt các
trục
Ox
,
Oy
,
Oz
lần lượt tại ba điểm
,,ABC
khác với gốc tọa độ
O
sao cho biểu thức
22 2
111
OA OB OC
++
có giá trị nhỏ nhất.
A.
2 3 14 0xyz+ +−=
. B.
2 3 11 0xyz+ +−=
.
C.
3 2 10 0x yz+ +− =
. D.
3 2 14 0x yz+ +− =
.
Câu 40. Cho hàm số
( ) ( ) ( )
32
21 2 2f x x m x mx=− − +− +
. Tìm tất cả các giá trị thực của tham số m để
hàm số
( )
y fx=
có 5 điểm cực trị
O
C
A
B
D
S
THTTH Trang 5/6
A.
5
2
4
m<<
. B.
5
2
4
m≤≤
. C.
5
2
4
m−< <
. D.
5
2
4
m−< <
.
Câu 41. Trong không gian
Oxyz
, gọi
d
là đường thẳng đi qua
( )
2;1; 0A
, song song với mặt phẳng
(
)
:0
Pxyz
−−=
và có tổng khoảng cách từ các điểm
(
)
( )
0; 2;0 , 4; 0;0MN
tới đường thẳng
d
có giá trị
nhỏ nhất. Vecto chỉ phương
u
của
d
có tọa độ là
A.
( )
1; 0;1
. B.
(
)
2;1;1
. C.
(
)
3; 2;1
. D.
( )
0;1; 1−
.
Câu 42. Cho hình chóp tứ giác đều
.S ABC D
có khoảng cách từ điểm
A
đến
mặt phẳng
( )
SCD
bằng 4 (tham khảo hình vẽ bên). Gọi V là thể tích khối chóp
.S ABC D
, tính giá trị nhỏ nhất của V.
A.
32 3
. B.
83
.
C.
16 3
. D.
16 3
3
.
Câu 43. Cho số phức
( )
,
12
im
zm
mm i
−
= ∈
−−
. Tìm giá trị nhỏ nhất của số thực
k sao cho tồn tại m để
1zk+≤
.
A.
51
2
k
−
=
.
B.
0k
=
.
C.
51
2
k
+
=
.
D.
1k =
.
Câu 44. Trong không gian
Oxyz
, cho điểm
( )
1; 2; 3A −
và mặt phẳng
( )
:2 2 9 0P x yz+ −+=
. Đường
thẳng
d
đi qua
A
có vectơ chỉ phương
( )
3; 4; 4u
= −
cắt
( )
P
tại
B
. Điểm
M
thay đổi trong
(
)
P
sao
cho
M
luôn nhìn đoạn
AB
dưới một góc vuông. Khi độ dài
MB
lớn nhất, đường thẳng
MB
đi qua điểm
nào trong các điểm sau?
A.
(
)
3; 2; 7
J −
. B.
( )
2; 1; 3H −−
. C.
( )
3; 0;15
K
. D.
( )
1; 2; 3I −−
.
Câu 45. Cho hình chóp
.
S ABCD
có đáy ABCD là hình thang cân,
222 2
AD AB BC CD a= = = =
. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với
mặt phẳng (ABCD). Gọi
, MN
lần lượt là trung điểm của
SB
và
CD
(tham khảo
hình vẽ bên). Tính cosin góc giữa
MN
và
( )
SAC
, biết thể tích khối chóp S.ABCD
bằng
3
3
4
a
.
A.
5
10
. B.
3 310
20
.
C.
310
20
. D.
35
10
.
Câu 46. Cho
,ab
là các số thực và
( )
(
)
2017 2 2018
ln 1 sin 2.= ++ + +f x a x x bx x
Biết
( )
log 6
56=
c
f
, tính
giá trị của biểu thức
(
)
log 5
6
= −
c
Pf
với
01<≠c
A.
2= −P
. B.
6=P
. C.
4=P
. D.
2=P
.
Câu 47. Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
2 22
( ) : ( 1) ( 2) ( 3) 27Sx y z− ++ +− =
. Gọi
()
α
là mặt phẳng đi qua hai điểm
(0; 0; 4), B(2;0;0)A −
và cắt
()S
theo giao tuyến là đường tròn
()C
sao
cho khối nón có đỉnh là tâm của
()S
và đáy là đường tròn
()C
có thể tích lớn nhất. Biết rằng
( ) : ax by z c 0
α
+ −+ =
. Tính
P abc=−+
A.
8P =
. B.
0P =
. C.
2P =
. D.
4P
= −
.
Câu 48. Có bao nhiêu giá trị nguyên của
m
để phương trình
3
3
log ( 3) log 9 16
x
xm
+
++ =
có hai nghiệm
thỏa mãn:
12
2 xx−< <
A.
15
. B.
17
. C.
14
. D.
16
.
O
C
A
D
B
S
N
M
C
A
D
S
B
THTTH Trang 6/6
Câu 49. Cho hình hộp
.'' ' 'ABCD A B C D
. Gọi
O
là tâm của
ABCD
;
,MN
lần lượt là trung điểm của
''AB
và
''AD
. Tỉ số thể tích của khối
'DA AB
và
'''OMND C B
bằng
A.
4
9
. B.
4
7
. C.
5
7
. D.
3
7
.
Câu 50. Hình trụ (T) được sinh ra khi quay hình chữ nhật ABCD quanh cạnh AB. Biết
22
AC a
=
và
0
45ACB =
. Diện tích toàn phần
tp
S
của hình trụ (T) là
A.
2
16
tp
Sa
π
=
. B.
2
10
tp
Sa
π
=
. C.
2
12
tp
Sa
π
=
. D.
2
8
tp
Sa
π
=
-------HẾT-------
ĐÁP ÁN
1D
2B
3B
4C
5A
6D
7D
8A
9A
10C
11B
12B
13B
14C
15A
16D
17D
18D
19B
20C
21A
22A
23B
24B
25B
26A
27A
28C
29C
30A
31A
32D
33C
34A
35A
36A
37C
38D
39ª
40A
41A
42C
43A
44D
45C
46A
47D
48A
49B
50A
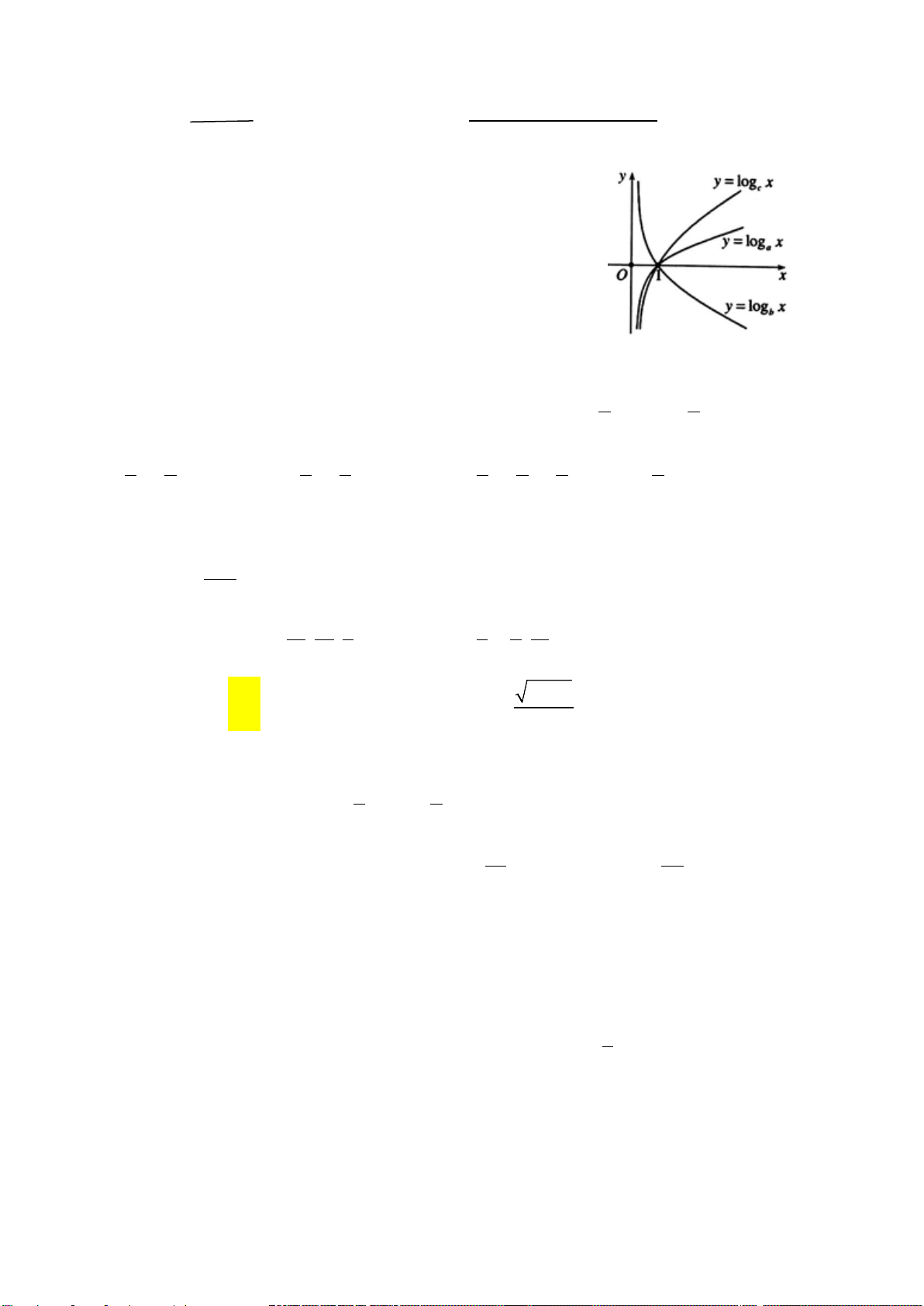
NTTL Trang 1/9
TRƯỜNG THPT CHUYÊN ĐỀ NGHỊ ĐỀ THI THPT QUỐC GIA NĂM 2019
LÊ QUÝ ĐÔN MÔN TOÁN – THỜI GIAN LÀM BÀI : 90 PHÚT
Câu 1: Cho số thực dương a, b, c khác 1. Đồ thị các hàm số
abc
y log x, y log x, y log x
= = =
được cho trong hình vẽ bên.
Tìm khẳng định đúng.
A.
bca
<<
B.
abc
<<
C.
acb<<
D.
bac
<<
Câu 2: Biết
( )
Fx
là một nguyên hàm của hàm số
( )
2x
fx e=
và
( )
3
F0
2
=
. Tính
1
F
2
A.
11
F e2
22
= +
B.
11
F e1
22
= +
C.
111
Fe
222
= +
D.
1
F 2e 1
2
= +
Câu 3: Trong không gian với hệ tọa độ Oxyz, cho 2 điểm
(
) ( )
A 3; 2; 1 , B 5; 4;3
−
. M là điểm thuộc tia đối
của tia BA sao cho
AM
2
BM
=
. Tìm tọa độ của điểm M.
A.
( )
7;6;7
B.
13 10 5
;;
3 33
C.
5 2 11
;;
3 33
−−
D.
( )
13;11;5
Câu 4: Tìm tất cả các tiệm cận ngang của đồ thị hàm số
2
x3
y
x
+
=
A.
y1=
B.
y1= −
C.
x1
= −
và
x1=
D.
y1= −
và
y1=
Câu 5: Tìm chu kì của hàm số
22
y sin x .cos x
55
=
A.
T = π
B.
T2
= π
C.
5
T
2
π
=
D.
2
T
3
π
=
Câu 6: Cho hàm số
32
y x 3x 4=−− +
. Mệnh đề nào dưới đây đúng.
A. Hàm số nghịch biến trên khoảng
(
)
2;0−
B. Hàm số đồng biến trên khoảng
( )
0; +∞
C. Hàm số đồng biến trên khoảng
( )
;2−∞ −
D. Hàm số đồng biến trên khoảng
( )
2;0−
Câu 7: Tìm tập hợp tất cả các giá trị của tham số thực m để hàm số
32
1
y x mx 4x m
3
= + +−
đồng biến trên
khoảng
( )
;−∞ +∞
A.
(
]
;2−∞ −
B.
[
)
2; +∞
C.
[ ]
2; 2−
D.
( )
;2−∞
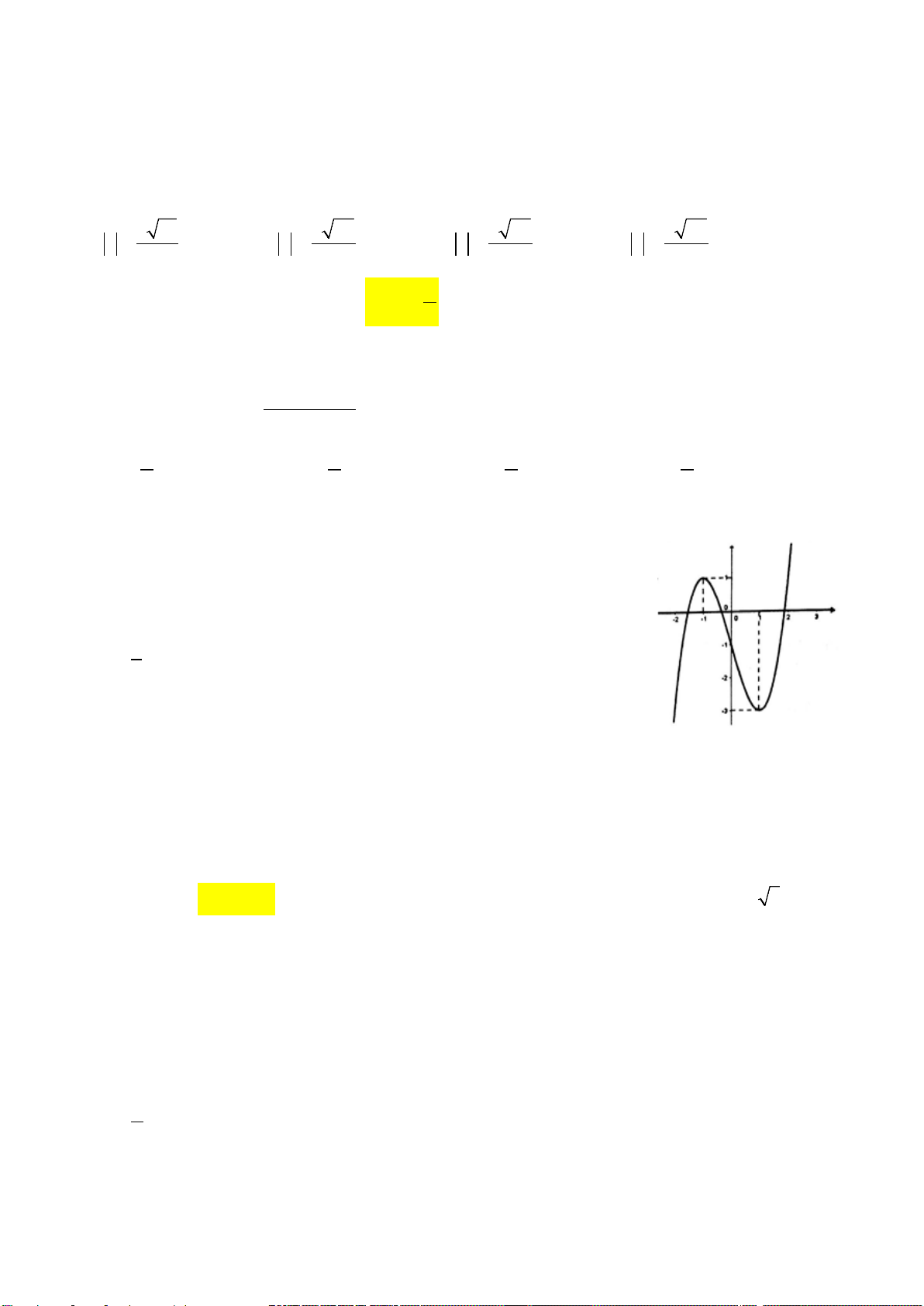
NTTL Trang 2/9
Câu 8: Cho hàm số
( )
32
y f x x ax bx c= =+ ++
đạt cực tiểu bằng – 3 tại điểm
x1=
và đồ thị hàm số cắt
trục tung tại điểm có tung độ là 2. Tính đạo hàm cấp một của hàm số tại
x3= −
A.
( )
f' 3 0−=
B.
(
)
f' 3 2−=
C.
( )
f' 3 1−=
D.
(
)
f' 3 2
−=−
Câu 9: Tính môđun của số phức z thỏa mãn
( )
5 2i z 3 4i
−+ =−+
A.
5 31
z
31
=
B.
5 29
z
29
=
C.
5 28
z
28
=
D.
5 27
z
27
=
Câu 10: Tìm giá trị nhỏ nhất của hàm số
4
yx
x
= +
trên khoảng
( )
0; +∞
A.
( )
0;
min y 2
+∞
=
B.
( )
0;
min y 4
+∞
=
C.
(
)
0;
min y 0
+∞
=
D.
( )
0;
min y 3
+∞
=
Câu 11: Giải phương trình
sin x cos x
1 sin 2x
cos x sin x
+
= +
−
A.
xk
4
xk
π
= +π
= π
B.
x k2
4
x k2
π
=−+ π
= π
C.
xk
4
x k2
π
=− +π
= π
D.
xk
4
xk
π
=− +π
= π
Câu 12: Đường cong trong hình bên là đồ thị của một hàm số được liệt kê ở
bốn phương án A,B,C,D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
32
y x 3x 3x 1
=− −−
B.
3
1
y x 3x 1
3
= +−
C.
32
y x 3x 3x 1=+ −−
D.
3
y x 3x 1=−−
Câu 13: Đồ thị của hàm số
32
y x 2x 2=−+
và đồ thị hàm số
2
yx 2= +
có tất cả bao nhiêu điểm chung.
A. 4 B. 1 C. 0 D. 2
Câu 14: Tìm giá trị tham số m để đường thẳng
( )
d : mx y m 0
−+ =
cắt đường cong
( )
32
C : y x 3x 4=−+
tại
ba điểm phân biệt lần lượt là A, B và
( )
C 1; 0−
sao cho tam giác AOB có diện tích bằng
55
. (Với O là
gốc tọa độ).
A.
m5=
B.
m3=
C.
m4=
D.
m6=
Câu 15: Cho các số thực dương a, b khác 1. Biết rằng đường thẳng
y2=
cắt đồ thị của các hàm số
xx
y a ,y b= =
và trục tung lần lượt tại A, B và C sao cho C nằm giữa A và B và
AC 2BC=
. Khẳng định
nào dưới đây đúng.
A.
a
b
2
=
B.
b 2a=
C.
2
ba
−
=
D.
2
ba=
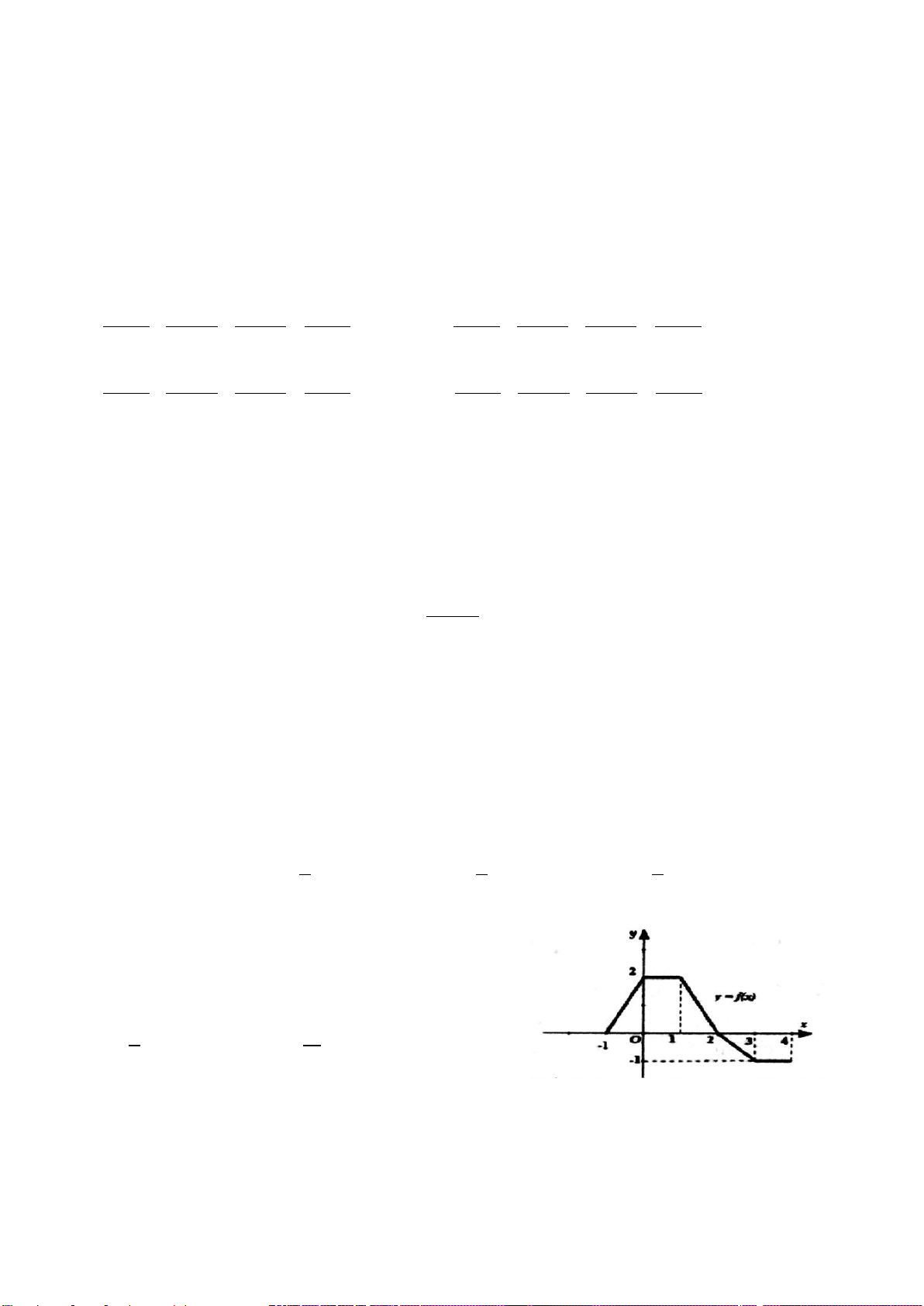
NTTL Trang 3/9
Câu 16: Khi ánh sáng qua một môi trường (chẳng hạn như không khí, nước, sương mù,...) cường độ sẽ giảm
dần theo quãng đường truyền x, theo công thức
( )
x
0
I x Ie
−µ
=
trong đó
0
I
là cường độ của ánh sáng khi bắt
đầu truyền vào môi trường và
µ
là hệ số hấp thu của môi trường đó. Biết rằng nước biển có hệ số hấp thu
1, 4µ=
và người ta tính được rằng khi đi từ độ sâu 2m xuống đến độ sâu 20m thì cường độ ánh sáng giảm
10
l.10
lần. Số nguyên nào sau đây gần với l nhất?
A. 8 B. 9 C. 10 D. 90
Câu 17: Cho hai số thực a, b dương khác 1. Mệnh đề nào dưới đây đúng?
A.
23
aa
aa
1118
log b log b log b log b
++=
B.
23
aa
aa
1114
log b log b log b log b
++=
C.
23
aa
aa
1116
log b log b log b log b
++=
D.
23
aa
aa
1117
log b log b log b log b
++=
Câu 18: Một người gửi ngân hàng 50 triệu đồng với lãi suất 4% một tháng, sau mỗi tháng tiền lãi được nhập
vào vốn. Hỏi sau một năm người đó rút tiền thì tổng số tiền nhận được là bao nhiêu?
A.
( )
12
50. 1,004
(triệu đồng) B.
(
)
12
50. 1 12.0,04+
(triệu đồng)
C.
(
)
12
50. 1 0,04+
(triệu đồng) D. 50.1,004 (triệu đồng)
Câu 19: Giải bất phương trình
( )
( )
x
x
42
18 2
log 18 2 log 1 *
8
−
− ≤−
.
A.
2
1 log 7 x 4+ ≤≤
B.
3
1 log 7 x 4+ ≤≤
C.
2
1 log 5 x 4+ ≤≤
D.
2
log 7 x 4≤≤
Câu 20: Gọi
12
x , x
là hai nghiệm của phương trình
( )
3
log x x 2 1+=
. Tính
22
12
xx+
.
A.
22
12
xx4+=
B.
22
12
xx6+=
C.
22
12
xx8+=
D.
22
12
x x 10
+=
Câu 21: Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình
xx
4 3.2 2 m 0− +− =
có nghiệm
thuộc khoảng
( )
0; 2
.
A.
( )
0; +∞
B.
1
;8
4
−
C.
1
;6
4
−
D.
1
;2
4
−
Câu 22: Cho đồ thị hàm số
( )
y fx=
có đồ thị trên đoạn
[ ]
1; 4−
như hình vẽ dưới. Tính tích phân
( )
4
1
I f x dx
−
=
∫
A.
5
I
2
=
B.
11
I
2
=
C.
I5=
D.
I3=
Câu 23: Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính diện tích S của mặt cầu ngoại tiếp hình lập
phương ABCD.A’B’C’D’.
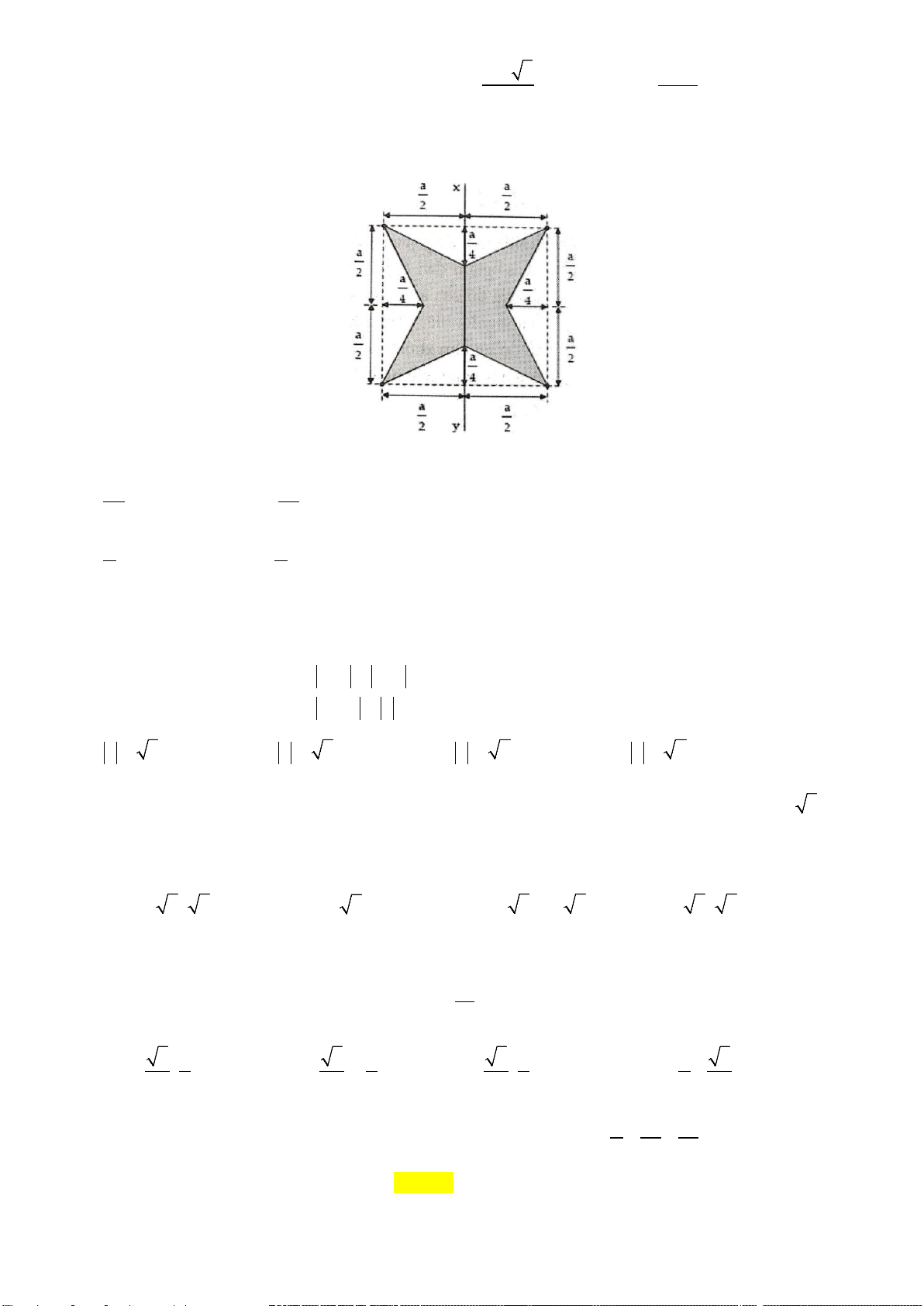
NTTL Trang 4/9
A.
2
Sa= π
B.
2
S 3a= π
C.
2
a3
S
2
π
=
D.
2
4a
S
3
π
=
Câu 24: Bên trong hình vuông cạnh a, dựng hình sao bốn cánh đều như hình vẽ bên (các kích thước cần
thiết cho như ở trong hình).
Tính thể tích của khối tròn xoay sinh ra khi quay hình sao đó quanh trục Oy.
A.
3
5
a
48
π
B.
3
5
a
16
π
C.
3
a
6
π
D.
3
a
8
π
Câu 25: Cho khối nón có đường sinh bằng 5 và diện tích đáy bằng
9π
. Tính thể tích V của khối nón.
A.
V 12= π
B.
V 24
= π
C.
V 36= π
D.
V 45= π
Câu 26: Xét số phức z thỏa mãn
zi z1
z 2i z
−= −
−=
. Mệnh đề nào sau đây là đúng?
A.
z5>
B.
z5=
C.
z2=
D.
z2<
Câu 27: Cho hàm số
(
)
fx
có đạo hàm
( )
f' x
liên tục trên
[ ]
a;b
và
( )
fb 5=
và
(
)
b
a
f ' x dx 3 5=
∫
. Tính
( )
fa
.
A.
( )
( )
fa 5 5 3= −
B.
( )
fa 35=
C.
( )
( )
fa 53 5= −
D.
( )
( )
fa 3 5 3= −
Câu 28: Kí hiệu
0
z
là nghiệm phức có phần ảo âm của phương trình
2
z z10++=
. Tìm trên mặt phẳng tọa
độ điểm nào dưới đây là điểm biểu diễn số phức
0
i
w
z
=
?
A.
31
M;
22
−
B.
31
M;
22
−−
C.
31
M;
22
D.
13
M;
22
−−
Câu 29: Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng
( ) ( )
xy z
P: 1a 0
a 2a 3a
++= >
cắt ba trục
Ox, Oy, Oz lần lượt tại 3 điểm A, B, C. Tính thể tích V của khối tứ diện OABC.

NTTL Trang 5/9
A.
3
Va=
B.
3
V 3a=
C.
3
V 2a
=
D.
3
V 4a
=
Câu 30: Với
[
)
(
]
m 1; 0 0;1
∈− ∪
, mặt phẳng
( )
2
P : 3mx 5 1 m y 4mz 20 0+ − + +=
luôn cắt mặt phẳng
( )
Oxz
theo giao tuyến là đường thẳng
m
∆
. Hỏi khi m thay đổi thì các giao tuyến
m
∆
có kết quả nào sau
đây?
A. Cắt nhau B. Song song C. Chéo nhau D. Trùng nhau
Câu 31: Trong không gian với hệ trục Oxyz, cho điểm
( )
I 0; 3; 0
−
. Viết phương trình của mặt cầu tâm I và
tiếp xúc với mặt phẳng
( )
Oxz
.
A.
( )
2
22
x y3 z 3++ +=
B.
( )
2
22
x y3 z 3+− +=
C.
( )
2
22
x y3 z 3+− +=
D.
( )
2
22
x y3 z 9
++ +=
Câu 32: Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
x y z1
d:
12 1
+
= =
−−
và
x1 y2 z
d'
2 42
−−
= = =
−
. Viết phương trình mặt phẳng (Q) chứa hai đường thẳng d và d’.
A. Không tồn tại
(
)
Q
B.
( )
Q : y 2z 2 0− −=
C.
( )
Q : x y 2 0
−−=
D.
( )
Q:2y4z10− + +=
Câu 33: Cho hình chóp S.ABCD, có đáy ABCD là hình thoi tâm O và thể tích bằng 8. Tính thể tích V của
hình chóp SOCD.
A.
V3=
B.
V4=
C.
V5=
D.
V2=
Câu 34: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
( )
:2x 2y z 3 0α − −+=
và điểm
( )
M 1; 2;13−
. Tính khoảng cách từ điểm M đến mặt phẳng
( )
α
.
A.
( )
( )
4
d M,
3
α=
B.
( )
( )
2
d M,
3
α=
C.
( )
( )
5
d M,
3
α=
D.
( )
( )
d M, 4α=
Câu 35: Cho hình chóp S.ABC có đáy là tam giác vuông cân ở A, cạnh
BC 2 3a
=
. Tam giác SBC cân tại
S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Biết thể tích khối chóp là
3
a
, tính góc giữa SA và
mặt phẳng (SBC).
A.
6
π
B.
3
π
C.
4
π
D.
3
arctan
2
Câu 36: Cho hình hộp chữ nhật ABCD.A’B’C’D’ có các kích thước là
AB 2, AD 3, AA’ 4= = =
. Gọi (N)
là hình nón có đỉnh là tâm của mặt ABB’A’ và đường tròn đáy là đường tròn ngoại tiếp hình chữ nhật
CDD’C’. Tính thể tích V của hình nón (N).
A.
13
3
π
B.
5π
C.
8π
D.
25
6
π

NTTL Trang 6/9
Câu 37: Cho lăng trụ đều ABC.A’B’C’ có cạnh đáy bằng 2a, diện tích xung quanh bằng
2
6 3a
Thể tích
của khối lăng trụ là:
A.
3
1
Va
3
=
B.
3
3
Va
4
=
C.
3
Va
=
D.
3
V 3a
=
Câu 38: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
( ) ( ) ( ) ( )
22 2
S:x 1 y 1 z 2 4
−+−++ =
và điểm
( )
A 1;1; 1−
. Ba mặt phẳng thay đổi đi qua A và đôi một vuông góc với nhau, cắt mặt cầu (S) theo ba giao
tuyến là các đường tròn
( ) (
) (
)
123
C,C ,C .
Tính tổng diện tích của ba đường tròn
( ) ( ) ( )
123
C,C ,C .
A.
4π
B.
12π
C.
11π
D.
3π
Câu 39: Cho số phức w và hai số thực a, b. Biết
1
z w 2i= +
và
2
z 2w 3= −
là hai nghiệm phức của phương
trình
2
z az b 0+ +=
. Tính
12
Tz z= +
A.
T 2 13
=
B.
2 97
T
3
=
C.
2 85
T
3
=
D.
T 4 13=
Câu 40: Trong khai triển
( )
n
x 2x
22
−
+
, tổng hệ số của số hạng thứ hai và số hạng thứ ba là 36, số hạng thứ 3
lớn gấp 7 lần số hạng thứ hai. Tìm x?
A.
1
x
3
=
B.
1
x
2
=
C.
1
x
2
= −
D.
1
x
3
= −
Câu 41: Cho số phức z thỏa mãn
z2 z2 6
++−=
. Tìm giá trị nhỏ nhất của biểu thức
2
P z3 z
=+−
:
A. -3 B. 2 C. -1 D. -4
Câu 42: Trong mặt phẳng tọa độ, cho hình chữ nhật (H) có một cạnh nằm trên trục hoành, và có hai đỉnh
trên một đường chéo là
(
)
A 1; 0−
và
( )
C a; a
, với
a0>
. Biết rằng đồ thị hàm số
yx=
chia hình (H)
thành hai phần có diện tích bằng nhau. Tìm a.
A.
a9=
B.
a4
=
C.
1
a
2
=
D.
a3=
Câu 43: Gọi
(
)
Va
là thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox hình phẳng giới hạn bởi các
đường
1
y , y 0, x 1
x
= = =
và
( )
x aa 1= >
. Tìm
( )
a
lim V a
→+∞
.
A.
( )
a
lim V a
→+∞
= π
B.
( )
2
a
lim V a
→+∞
= π
C.
( )
a
lim V a 3
→+∞
= π
D.
( )
a
lim V a 2
→+∞
= π
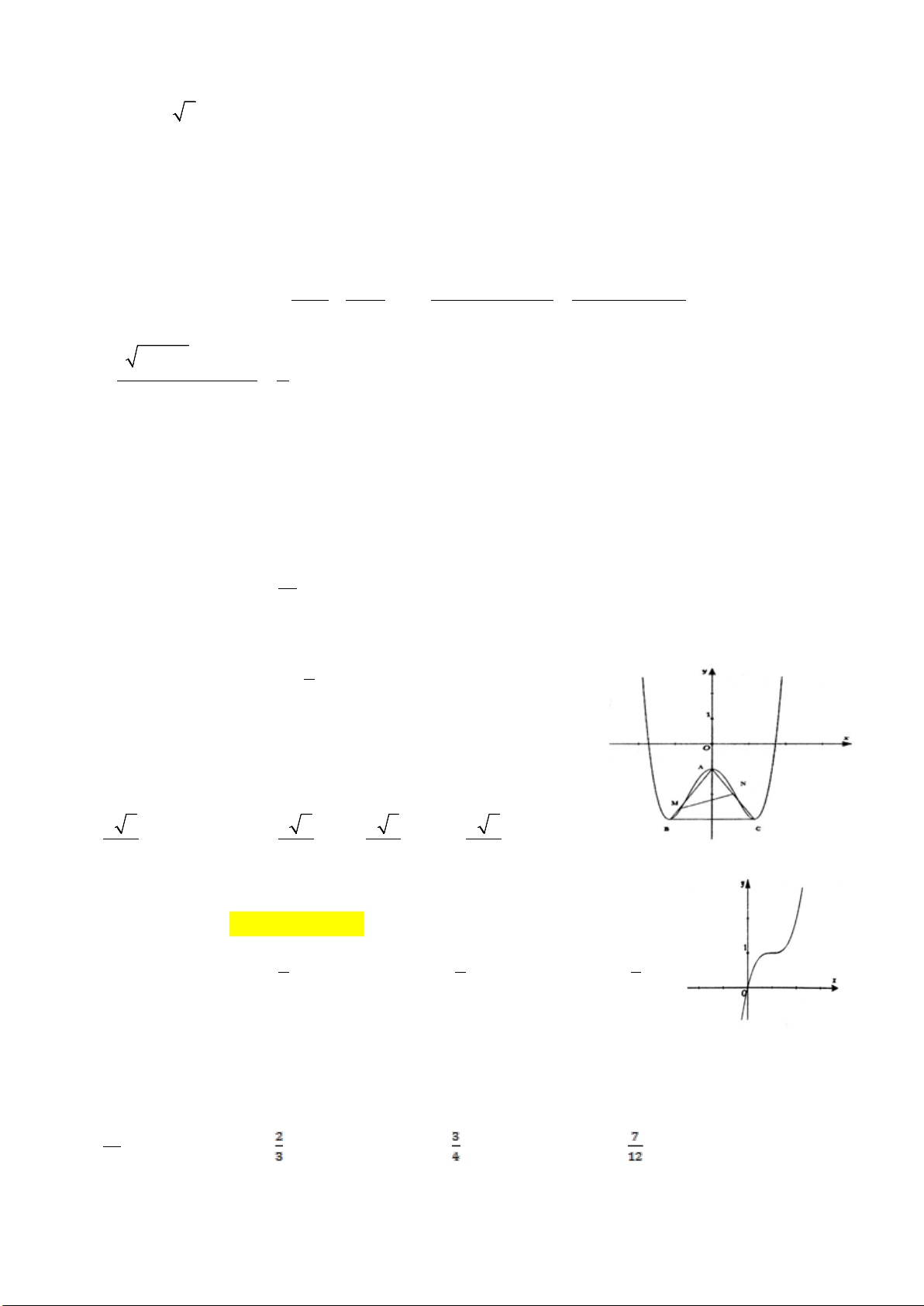
NTTL Trang 7/9
Câu 44: Cho x, y là các số thực thỏa mãn
( ) ( )
44
log x y log x y 1++ −≥
. Biết giá trị nhỏ nhất của biểu thức
P 2x y= −
là
( )
a b 1 a,b<∈
. Giá trị
22
ab+
là:
A.
22
a b 18+=
B.
22
ab8+=
C.
22
a b 13+=
D.
22
a b 20+=
Câu 45: Có bao nhiêu số tự nhiên có 6 số sao cho trong mỗi số tự nhiên đó chữ số đứng sau lớn hơn chữ số
đứng trước nó.
A. 60480 B. 84 C. 151200 D. 210
Câu 46: Cho hàm số
(
)
(
)
( )
( )
( )
(
)
nn 3
11 1
f n ... , n N*
1.2.3 2.3.4 n. n 1 . n 2 4 n 1 n 2
+
= + ++ = ∈
+ + ++
. Kết quả giới
hạn
(
)
(
)
( )
2
2n 1 1 f n
a
lim b Z
5n 1 b
+−
= ∈
+
. Giá trị của
22
ab+
là:
A. 101 B. 443 C. 363 D. 402
Câu 47: Cho hàm số
(
)
( )
32 2
fxx mm1xmm
= − ++ + +
có đồ thị cắt trục hoành tại ba điểm có hoành độ
123
x ,x ,x
. Biết m là số nguyên dương, giá trị nhỏ nhất của biểu thức
222
1 23
Pxxx=++
gần giá trị nào sau đây
nhất:
A. 2 B.
13
2
C. 6 D. 12
Câu 48: Cho đồ thị hàm số
42
9
y x 3x 1
8
= −−
có ba điểm cực trị A, B,
C như hình vẽ. Biết M, N lần lượt thuộc AB, AC sao cho đoạn thẳng
MN chia tam giác ABC thành hai phần bằng nhau. Giá trị nhỏ nhất của
MN là:
A.
26
3
B.
22
3
C.
25
3
D.
27
3
Câu 49: Cho hàm số bậc 3
32
y ax bx cx d= + ++
có đồ thị như hình vẽ. Giá trị
nhỏ nhất của biểu thức
2 2
P a c b1= + ++
là :
A. 1 B.
1
5
C.
5
8
D.
1
3
Câu 50: Gieo hai hột súc sắc màu xanh và trắng. Gọi x là số nút hiện ra trên hột
xanh và y là số nút hiện ra trên hột trắng. Gọi A là biến cố
( )
xy<
và B là biến cố
5xy8<+<
. Khi đó
( )
PA B∪
có giá trị là:
A.
11
8
B. C. D.

NTTL Trang 8/9
Đáp án
1-A
2-B
3-A
4-D
5-C
6-D
7-C
8-A
9-B
10-B
11-D
12-D
13-D
14-A
15-C
16-B
17-C
18-C
19-A
20-D
21-C
22-A
23-B
24-A
25-A
26-C
27-A
28-B
29-A
30-B
31-D
32-B
33-D
34-A
35-B
36-B
37-D
38-C
39-B
40-D
41-A
42-D
43-A
44-C
45-B
46D-
47-C
48-A
49-C
50-D
LỜI GIẢI CHI TIẾT
Câu 1: Đáp án A
Xét đường thẳng
1y =
cắt 3 đồ thị lần lượt từ trái sang phải tại các điểm
( )
,1Bb
,
( )
c,1C
,
( )
a,1A
.
Vậy ta có
bca
<<
.
Câu 2: Đáp án B
Ta có
2x 2x
1
e dx e C
2
= +
∫
mà
( )
3
F0
2
=
nên
0
1
e C C1
2
+⇒=
Do đó
( )
2x
1
Fx e C
2
= +
. Vậy
11
F e1
22
= +
.
Câu 3: Đáp án A.
M là điểm thuộc tia đối của tia BA sao cho
AM
2
BM
=
nên B là trung điểm của AM.
( )
M
M
M
M
M
M
3x
5
2
x7
2y
4 y 6 M 7;6;7
2
z7
1z
3
2
+
=
=
+
⇒= ⇒ =⇒
=
−+
=
Câu 4: Đáp án D.
Ta có:
22
xx
x3 x3
lim 1; lim 1
xx
→+∞ →−∞
++
= = −
Vậy hàm số có hai tiệm cận ngang là
y1= −
và
y1=
Câu 5: Đáp án C.
Ta biến đổi
2 2 14
y sin x .cos x sin x
5 5 25
= =
.
Do đó f là hàm số tuần hoàn với chu kì
25
T
4
2
5
ππ
= =
Câu 6: Đáp án D.
NTTL Trang 9/9
2
x2
y' 3x 6x, y' 0
x0
= −
=−− =⇔
=
Lập bảng biến thiên, hàm số đồng biến trên khoảng
( )
2;0 .−
Câu 7: Đáp án C.
Ta có:
2
y' x 2mx 4.=++
(Dethithpt.com)
Hàm số đồng biến trên khoảng
( )
;−∞ +∞
khi và chỉ khi
( )
y ' 0, x ; .≥ ∀ ∈ −∞ +∞
2
'm 40 2m2⇔∆ = − ≤ ⇔− ≤ ≤
Câu 8: Đáp án A.
Ta có:
( )
2
y' f ' x 3x 2ax b.= =++
Theo giả thiết
( )
(
)
( )
f'1 0
2a b 3 0
a3
f1 3 a b c 4 0
b9
c2
f0 2
=
++=
=
⇒ =−⇔ + ++ = ⇒
= −
=
=
Thử lại
( )
2
y' f ' x 3x 6x 9= = +−
và
( ) ( )
y '' f '' 6x 6 f '' 1 12 0= +⇒ =>
nên hàm số đạt cực tiểu tại
x1=
.
Suy ra
(
) ( ) ( )
2
f ' 3 3. 3 2a. 3 b 0
= − + −+=
Câu 9: Đáp án B.
Ta có
(
)
3 4i 23 14 5 29
5 2i z 3 4i z i z
5 2i 29 29 29
−+
−+ =−+ ⇒ = = − ⇒ =
−+
Câu 10: Đáp án B.
Cách 1: Ta có
2
22
4x4
y' 1 ; y' 0 x 2
xx
−
=− = =⇒=±
Lập bảng biến thiên của hàm số trên khoảng
( )
0; .+∞
Nhận thấy hàm số chỉ đạt cực tiểu tại điểm
x2=
và
CT
y4=
nên
( )
0;
min y 4
+∞
=
Cách 2: Áp dụng BĐT Cauchy cho 2 số
4x
x 2 x. 4 min y 4 x 2
x4
+≥ =⇐ =⇔=
Câu 11: Đáp án D.
Phương trình tương đương:
( )( )
2
sin x cos x
1 sin 2x sin x cos x cos x sin x cos x sin x
cos x sin x
+
=+ ⇔+ = − +
−
( )( )
sin x cos x 0
xk
sin x cos x 1 cos 2x 0
4
cos 2x 1
xk
π
+=
=− +π
⇔+ − =⇔ ⇔
=
= π
Câu 12: Đáp án D.

NTTL Trang 10/9
Ta có:
32
x1
y x 3x 1 y' 3x 3 y' 0
x1
=
= − −⇐ = −⇒ = ⇔
= −
Câu 13: Đáp án D.
Ta có:
32 2 32
x0
x2x2x2 x3x0
x3
=
− += +⇔ − =⇔
=
nên có hai điểm chung.
Câu 14: Đáp án A.
Ta có:
( )
2
m
d O;d
m1
=
+
Do
( )
( )
( ) ( )
32 2
2
x1
x 3x 4mxm x1x 4x4m 0
x 2 mm 0
= −
− += + ⇒ + − +− =⇔
−= >
Nên
( ) ( )
3
A 2 m;3m m m , B 2 m;3m m m AB 4m 4m
+ + − − ⇒= +
Theo giả thiết
3
AOB
2
1m
S 55 4m 4m. 55 mm 55 m 5
2
m1
= ⇔ + = ⇔ = ⇒=
+
Câu 15: Đáp án C.
Ta có
( )
( ) (
)
ab
A log 2; 2 , B log 2; 2 , C 0; 2
Ta có:
( ) (
)
ab
CA log 2;0 , CB log 2;0
= =
Vì C nằm giữa A và B và
AC 2BC=
nên
CA 2CB= −
1
2
1
2
2
a ba
b
log 2 2log 2 log 2 2log 2 a b b a
−
−
⇔=− ⇔= ⇔=⇔=
Câu 16: Đáp án B.
Ta có:
- Ở độ sâu 2m:
( )
2,8
0
I 2 Ie
−
=
- Ở độ sâu 20m:
( )
28
0
I 2 Ie
−
=
Theo giả thiết
( )
( )
10 2,8 10 28 10 25,2
I 2 l.10 .I 20 e l.10 .e l 10 .e 8,79.
− −−
= ⇒ = ⇒= ≈
Câu 17: Đáp án C.
Ta có:
23
aa a
aa
aa
1111 1 1 6
11
log b log b log b log b log b
log b log b
23
++=++=
Câu 18: Đáp án C.
Theo công thức lãi kép ta được
( )
12
12
T 50 1 0,04= +
(triệu đồng)
Chú ý bài này không thực tế vì không có ngân hàng nào có lãi cao như vậy.
Câu 19: Đáp án A.
Điều kiện
18 2x 0−>
, ta có:
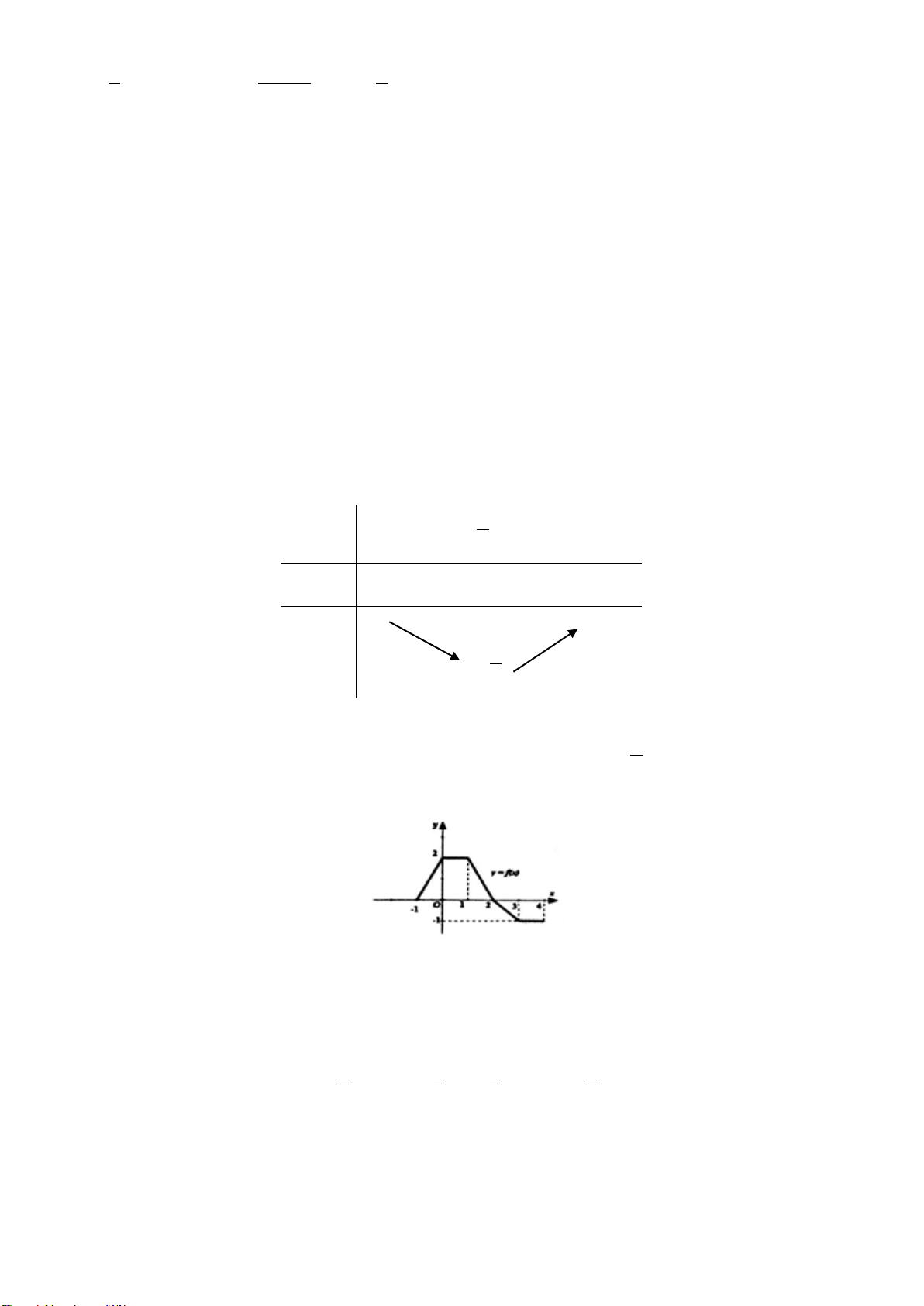
NTTL Trang 11/9
( )
( )
( ) ( )
x
x xx
22 2 2
1 18 2 1
* log 18 2 log 1 log 18 2 log 18 2 3 1
2 82
−
⇔ − ≤− ⇔ − − − ≤−
( ) ( ) ( )
( )
2
x x2 x
22 2
log 18 2 3log 18 2 2 t 3t 2 0 t log 18 2
⇔ − − − ≤− ⇔ − + ≤ = −
( ) (
)
xx
2 22 2
1 t 2 1 log 18 2 2 log 2 log 18 2 log 4
⇔≤≤ ⇔≤ − ≤ ⇔ ≤ − ≤
x xx
2 18 2 4 16 2 14 14 2 16⇔ ≤ − ≤ ⇔− ≤− ≤− ⇔ ≤ ≤
Suy ra
2
1 log 7 x 4+ ≤≤
(thỏa mãn điều kiện của phương trình).
Câu 20: Đáp án D.
Điều kiện
x2
x0
<−
>
. Khi đó
( )
1
3
2
x3
log x x 2 1
x1
= −
+=⇔
=
. Vậy
22
12
x x 10+=
.
Câu 21: Đáp án C.
Đặt
( ) (
)
x
t 2 , x 0;2 t 1;4= ∈ ⇒∈
và
2
t 3t 2 m.− +=
Bảng biến thiên của hàm
(
) ( )
2
f t t 3t 2, t 1;4=−+ ∈
t
1
3
2
4
( )
f' t
-
0 +
(
)
ft
0
1
4
−
6
Dựa vào bảng biến thiên, phương trình có nghiệm thuộc khoảng
(
)
0; 2
khi
1
m6
4
−≤ <
Câu 22: Đáp án
Gọi
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
A 1;0 , B 0;2 , C 1;2 , D 2;0 , E 3; 1 , F 4; 1 , H 1;0 , K 3;0 , L 4;0 .− −−
Ta có:
4 24
1 12
I f (x)dx f (x)dx f (x)dx
−−
= = +
∫∫∫
ABO OBCH HCD DKE EFLK
1 11 5
S S S S S .2.1 2.1 .2.1 .1.1 1.1
2 22 2
= + + − − = ++ − −=
Câu 23: Đáp án
Gọi O, O' lần lượt là tâm các hình vuông ABCD và A'B'C'D'. I là trung điểm đoạn OO'. Khi đó bán kính r
của mặt cầu ngoại tiếp hình lập phương ABCD.A'B'C'D' là:
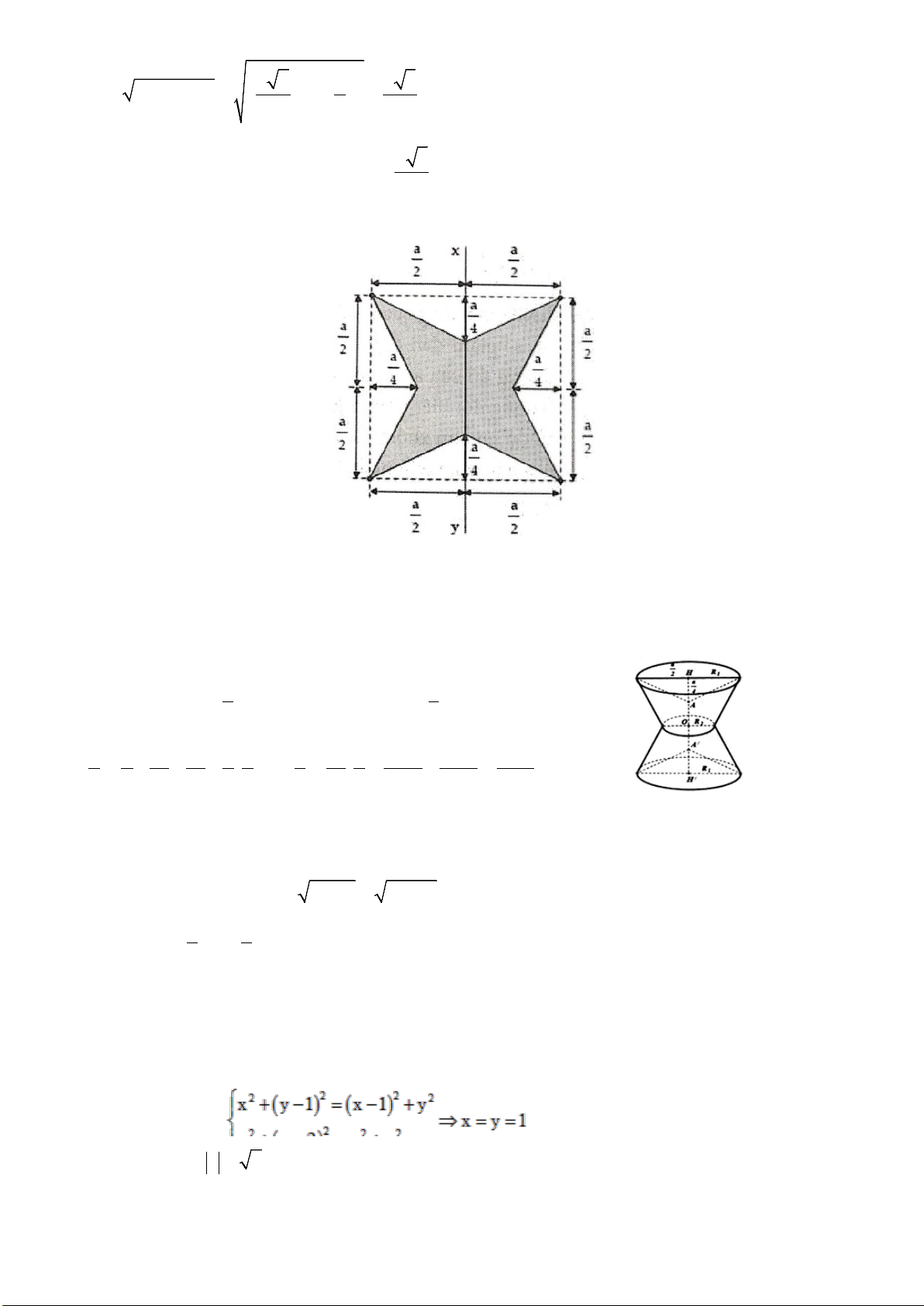
NTTL Trang 12/9
2
2
22
a2 a a3
r IA OA OI
2 22
== += + =
Vậy diện tích S của mặt cầu là S=
2
22
a3
4r 4 3a
2
π=π =π
Câu 24: Đáp án
Khi quay hình sao đó quanh trục Oy sinh ra hai khối có thể tích bằng nhau.
Gọi V là thể tích khối hình sao tròn xoay cần tính, V
nón
lần lượt là thể tịch khối nón có chiều cao AH, V
c
là
thể tích khối nón cụt có bán kính đáy lớn là R
1
và bán kính đáy nhỏ là R
2
Ta thấy:
( )
22 2
C non 1 2 1 2 1
11
V 2(V V 2. . .OH R R R R . .R .AH
33
= − = π + + −π
22 2 3 3 3
1 a a a aa 1 a a 7a 2a 5a
2. . . . . 2. . . . .
2 2 4 6 2 4 3 2 4 48 48 48
πππ
= π ++ − π = − =
Câu 25: Đáp án A.
Gọi diện tích đáy là S, ta có
2
S r 9 r3=π = π⇒ =
Gọi h là chiều cao khối nón
22 22
h lr 53 4= −= −=
Vậy thể tích
11
V Bh .9 .4 12
33
= = π= π
Câu 26: Đáp án C.
Đặt
( )
z x yi, x, y .=+∈
Ta có hệ phương trình
Do đó
z1i= +
nên
z2
=
Câu 27: Đáp án A.

NTTL Trang 13/9
Ta có
( ) ( ) ( ) ( )
b
b
a
a
f ' x dx f x f b f a 3 5= = = =
∫
Suy ra
( ) ( )
( )
fa fb 35 5 35 5 5 3= −=−= −
Câu 28: Đáp án B.
Ta có
2
1,2 0
13 13
z z10 z i z i
22 22
++=⇔ =−± ⇒ =−−
Vậy
i 31 3 1
w iM ;
22 2 2
13
i
22
= =− −⇒ − −
−−
Câu 29: Đáp án A.
Ta có
(
) (
)
( )
A a; 0;0 , B 0; 2a; 0 , C 0;0;3a OA a, OB 2a, OC 3a.⇒= = =
Vậy
3
OBC
1 11
V S .OA . .OB.OC.OA a
3 32
= = =
Câu 30: Đáp án B.
( )
m
P
có vector pháp tuyến
(
)
2
n 3m;5 1 m ; 4m= −
( )
Oxz
có vector pháp tuyến
( )
j 0;1; 0=
( )
m
P
cắt
( )
Oxz
khi và chỉ khi
2
m0
1m 0
≠
= ≥
hay
[
) (
]
m 1; 0 0;1∈− ∪
Suy ra vecto chỉ phương của giao tuyến
m
∆
là
( )
u 4m; 0; 3m
= −
cùng phương với vecto
(
)
[
)
(
]
u ' 4;0; 3 , m 1;0 0;1= − ∀ ∈− ∪
Vì vecto
u'
không phụ thuộc vào m nên các giao tuyến
m
∆
là song song với nhau.
Câu 31: Đáp án D.
Mặt phẳng
( )
Oxz : y 0=
nên
( )
( )
d I, Oxz 3.=
Vậy phương trình của mặt cầu là
( )
2
22
x y3 z 9++ +=
Câu 32: Đáp án B.
Ta có: Hai vector chỉ phương của hai đường thẳng là cùng phương nên hai đường thẳng luôn đồng phẳng.
(Dethithpt.com)
( ) ( ) ( )
M 0;0; 1 d, M ' 1;2;0 d ' MM ' 1; 2;1−∈ ∈ ⇒ =
Vector chỉ phương của đường thẳng d là
( )
u 1;2;1= −−
Vector pháp tuyến của mặt phẳng
( ) ( )
Q : n MM '; u 0;2; 4
= = −
Phương trình mặt phẳng
( )
Q : y 2z 2 0.− −=
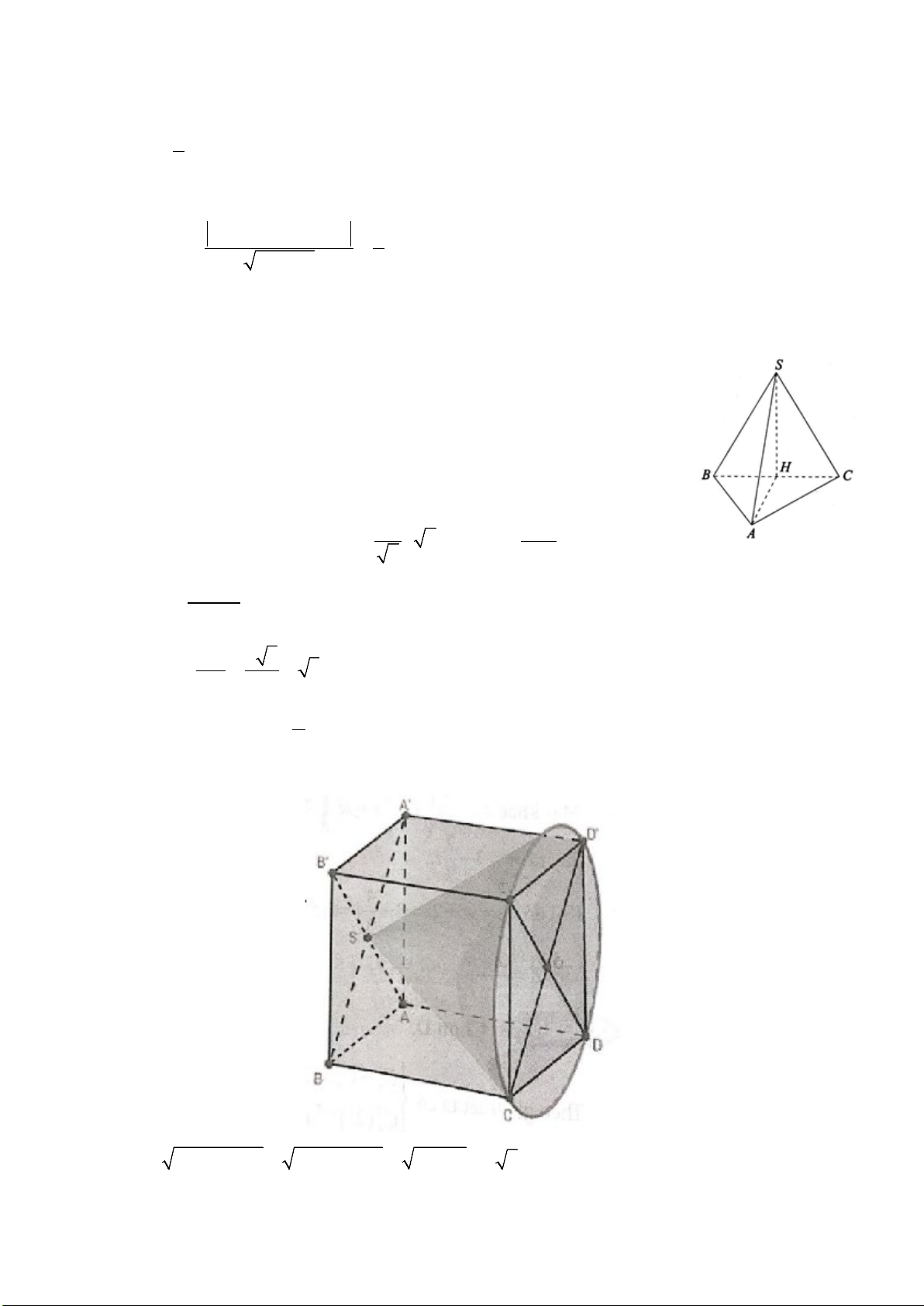
NTTL Trang 14/9
Câu 33: Đáp án D.
Ta có hai hình chóp có cùng chiều cao mà
ABCD OCD
S 4S .=
Do đó
S.OCD S.ABCD
1
V V2
4
= =
Câu 34: Đáp án A.
Ta có:
( )
( )
( )
2.1 2 2 13 3
4
d M,
3
441
−−− +
α= =
++
Câu 35: Đáp án B.
Gọi H là trung điểm BC, ta chứng minh được SH là đường cao của hình chóp và
(
)
AH SBC .
⊥
Do đó, hình chiếu vuông góc của SA lên
( )
SBC
là SH hay
(
)
( )
(
)
SA, SBC SA;SH
=
.
Tam giác ABC vuông cân tại A nên
BC
AB a 6
2
=
và
2
2
ABC
AB
S 3a
2
=
Đường cao
SBAC
ABC
3V
SH a
S
= =
Do đó,
AH a 3
tan ASH 3
SH a
= = =
Vậy
(
)
(
)
( )
SA; SBC SA;SH
3
π
= =
Câu 36: Đáp án B.
Ta có:
2 2 2 2 22
D 'C DD ' DC AA ' AB 4 2 2 5= + = + = +=
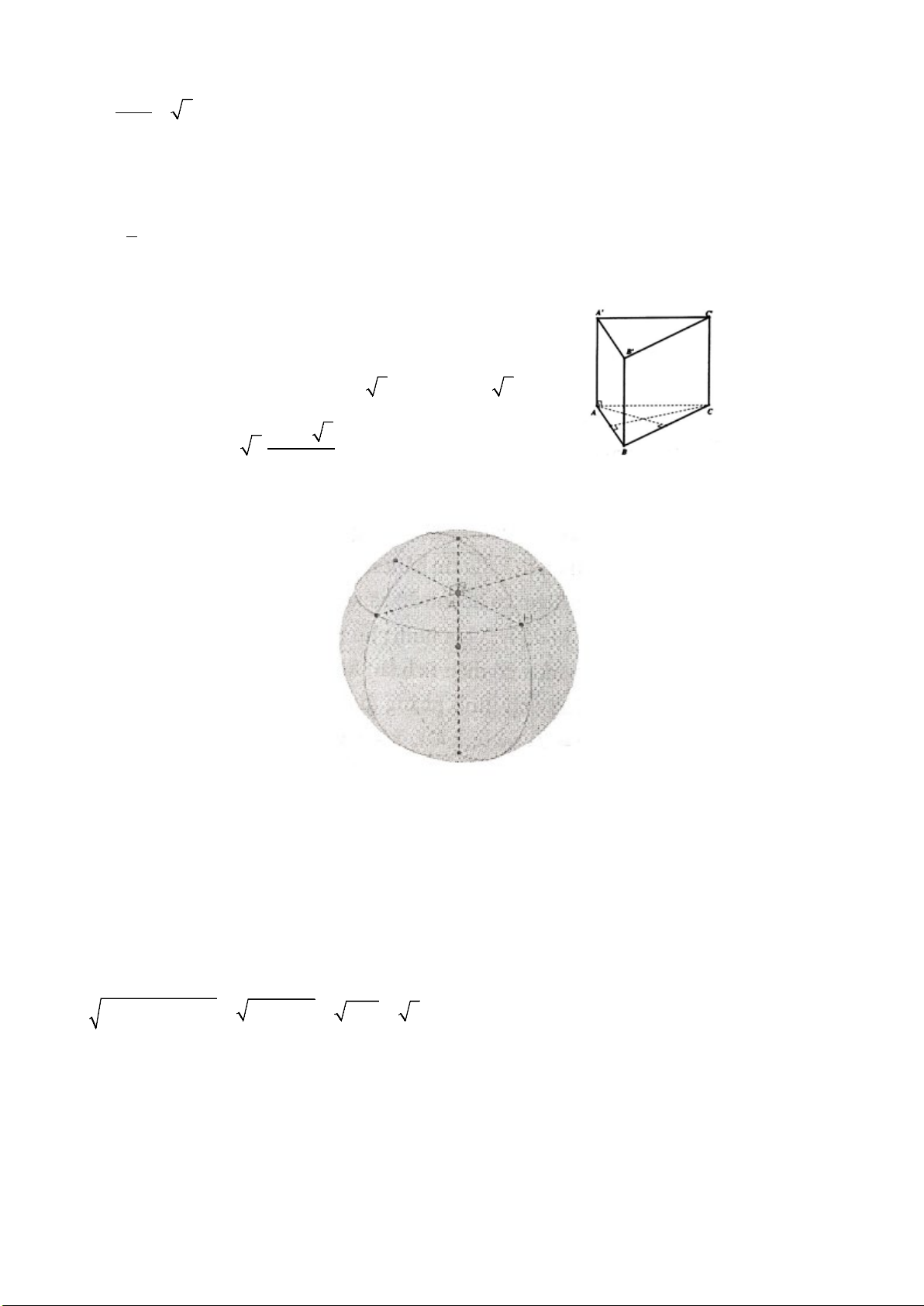
NTTL Trang 15/9
Đường tròn đáy là đường tròn ngoại tiếp hình chữ nhật CDD’C’ nên có đường kính là D’C. Suy ra bán kính
đáy
D'C
r5
2
= =
Chiều cao của hình nón là SO (với O là tâm của hình chữ nhật CDD’C’)
h SO AD 3⇒= = =
.
Vậy
2
1
V rh 5
3
=π=π
Câu 37: Đáp án D.
Do ABC.A’B’C’ là lăng trụ đều nên
ABB’A’ ACC’A’ BCC’B’
SSS
= =
2
xq ABB'A '
S 3S 3AB.AA ' 6a.AA ' 6 3a AA ' a 3⇒= = = = ⇔ =
.
Do đó
( )
2
3
ABC
2a 3
V AA '.S a 3. 3a
4
= = =
Câu 38: Đáp án C.
Mặt cầu
(
) ( ) ( )
( )
22 2
S:x 1 y 1 z 2 4
−+−++ =
có tâm và bán kính
R2=
Xét ba mặt phẳng thay đổi đi qua A và đôi một vuông góc với nhau, cắt mặt cầu (S) theo ba giao tuyến là
các đường tròn
( ) ( ) ( )
123
C ,C ,C
lần lượt là
( ) ( )
( )
1 23
P : x 1, P : y 1, P : z 1.= = = −
Gọi
123
r , r , r
lần lượt là bán
kính của các đường tròn giao tuyến của mặt cầu (S) với ba mặt phẳng
( ) ( ) ( )
123
P,P,P.
Vì
( ) ( )
12
P,P,
đi qua tâm
(
)
I 1;1; 2−
nên
( )
12 3
r r R 2, IA P= = = ⊥
nên
( )
( )
22 2 2
33
r R d I, P R IA 4 1 3= − = − = −=
Tổng diện tích của ba hình tròn
( ) ( ) ( )
123
C ,C ,C
là
222
123 1 2 3
S S S .r .r .r 11+ + =π +π +π = π
Câu 39: Đáp án B.
Đặt
w x yi= +
với
x,y R∈
Ta có
( ) ( ) ( ) ( )
12
z z x yi 2i 2x 2yi 3 3x 3 3y 2 i a+ = ++ + + −= −+ + =−
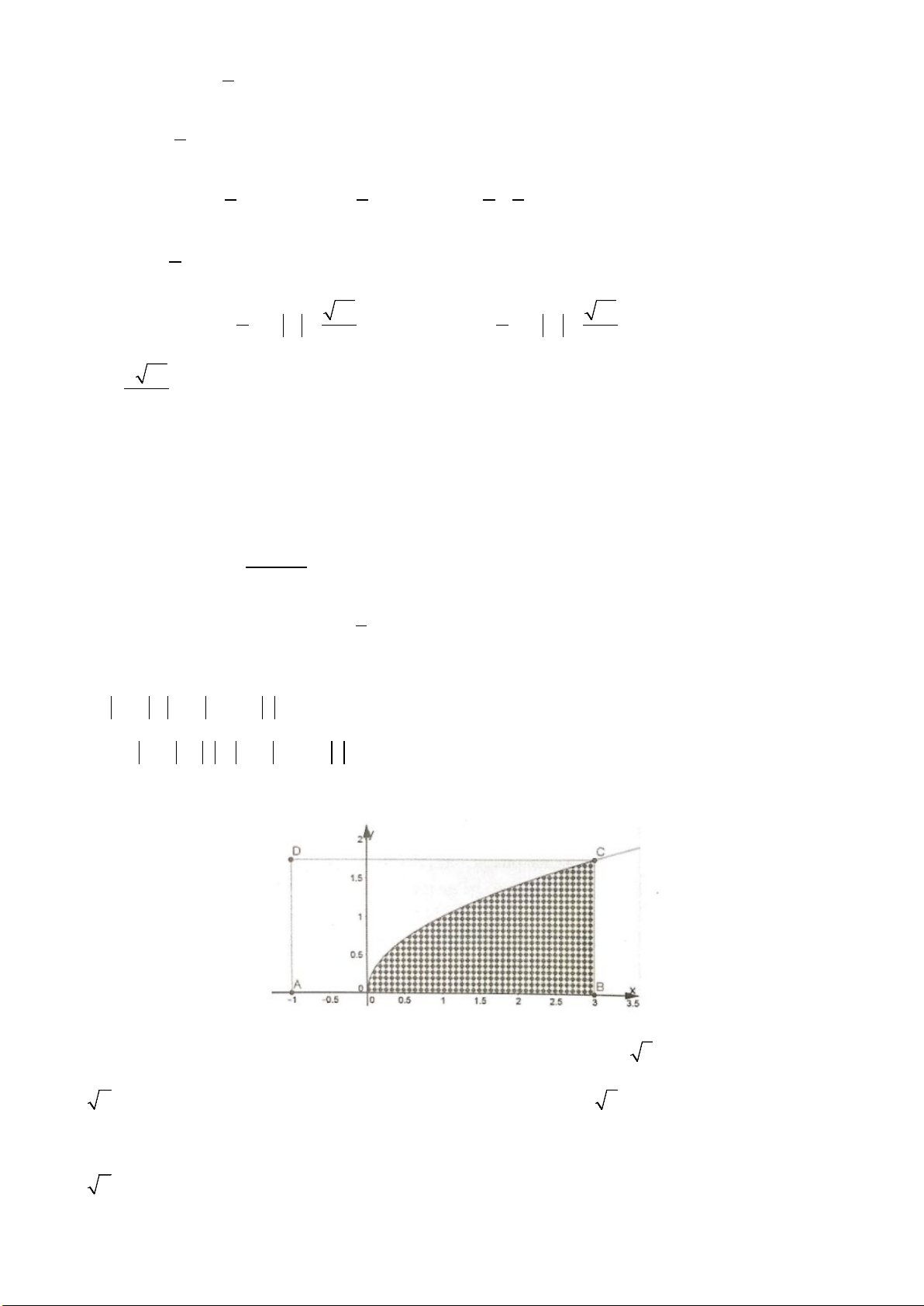
NTTL Trang 16/9
2
3y 2 0 y
3
⇒ +=⇔=−
Khi đó
2
wx i
3
= −
Mặc khác
( )
2
12
2 4 44
z .z x i 2i 2x 3 i 2x 3x x 3 i b x 3
3 3 33
= − + −− = − + + − = ⇒ =
Suy ra
2
w3 i
3
= −
Khi đó
1 12 2
4 97 4 97
zw2i3iz ;z2w33iz
33 33
= + =+ ⇒ = = −=− ⇒ =
Vậy
2 97
T
3
=
Câu 40: Đáp án D.
Theo giả thiết ta có
( )
( ) ( ) (
) ( )
( )
12
nn
n2 2 n1 1
2 x 2x 1 x 2x
nn
C C 36 1
C 2 .2 7C 2 .2 2
−−
−−
+=
=
Phương trình (1) cho
( )
2
nn 1
n 36 n n 72 0
2
−
+ = ⇒ +− =
. Giải ra
n8
=
Thay
n8=
vào
( )
2x 5x 1
1
2 :2 2 x
3
+
= ⇒=−
Câu 41: Đáp án A.
Ta có:
z2 z2 6
3z++−=⇒
≤
Do đó
( )
22
P z3 z z3 3z 3 3=+−=++−−≥−
dấu bằng xảy ra khi
z3= −
Câu 42: Đáp án D.
Gọi ABCD là hình chữ nhật với AB nằm trên trục Ox,
( )
A 1; 0−
và
( )
C a; a
. Nhận thấy đồ thị hàm số
yx=
cắt trục hoành tại điểm có hoành độ bằng 0 và đi qua
( )
C a; a
. Do đó nó chia hình chữ nhật
ABCD ra làm 2 phần có diện tích lần lượt là
12
S , S
. Gọi
1
S
là diện tích hình phẳng giới hạn bởi các đường
yx=
và trục Ox,
x0, xa
= =
và
2
S
là diện tích phần còn lại. Ta tính lần lượt
12
S , S
.
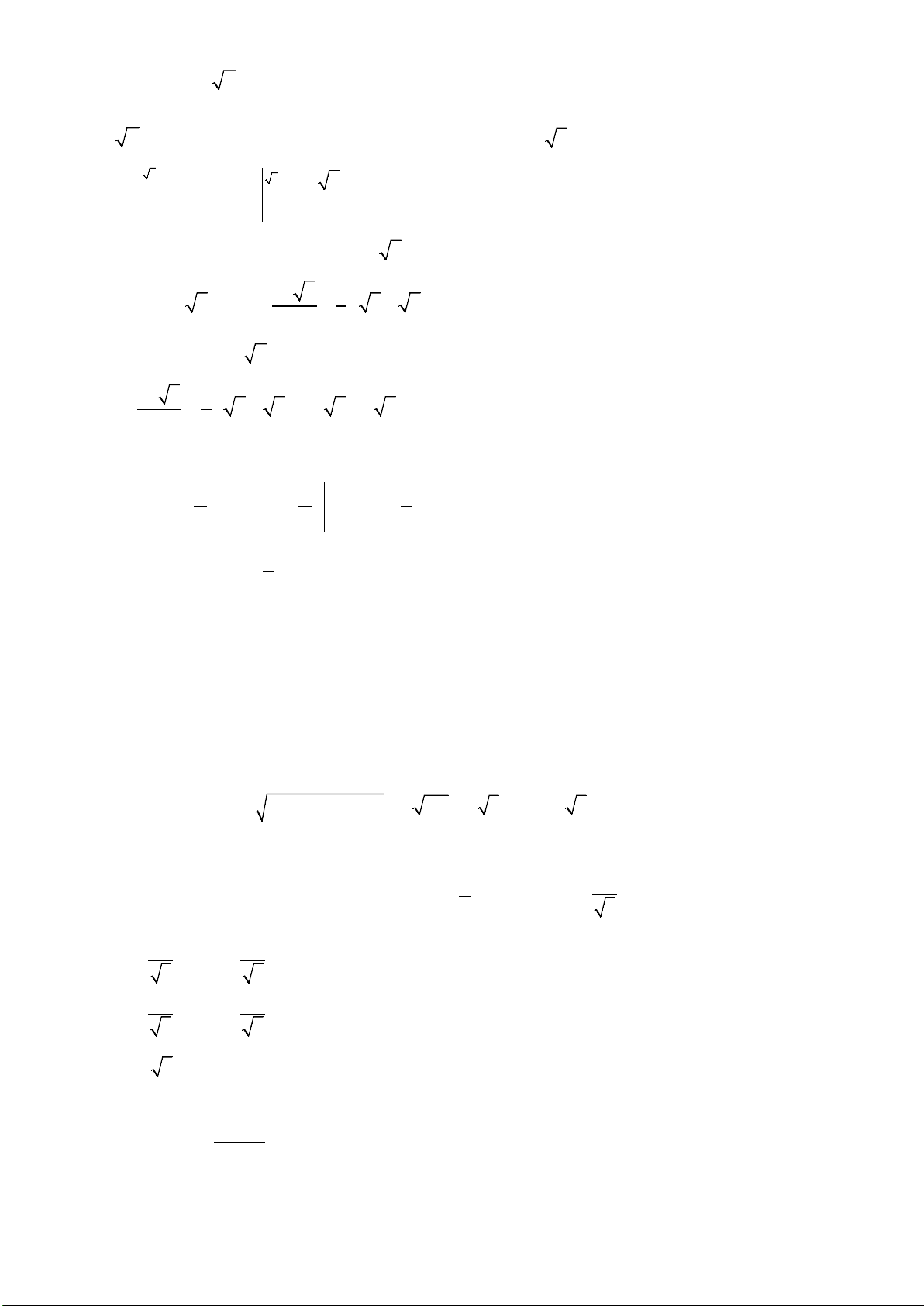
NTTL Trang 17/9
Tính diện tích
a
1
0
S xdx=
∫
Đặt
2
t x t x 2tdt dx= ⇒=⇒ =
; khi
x0 t0;xa t a.=⇒= =⇒=
Do đó
a
3
a
2
1
0
0
2t 2a a
S 2t dt
33
= = =
∫
Hình chữ nhật ABCD có
AB a 1; AD a=+=
nên
( )
2 ABCD 1
2a a 1
S S S aa 1 aa a
33
= − = +− = +
Do đó đồ thị hàm số
yx=
chia hình (H) thành hai phần có diện tích bằng nhau nên
(
)
12
2a a 1
S S aa a aa 3a a 3doa 0
33
= ⇔ = + ⇔ = ⇔= >
Câu 43: Đáp án A.
Ta có
( )
2
a
a
1
1
1 11
V a dx 1
x xa
=π =π− =π −
∫
.
Vậy
( )
aa
1
lim V a lim 1
a
→+∞ →+∞
= π− =π
Câu 44: Đáp án C.
Từ giả thiết ta có
( )( )
( )( )
4
xy0 xy0
xy0 xy0
xyxy 4
log x y x y 1
+> +>
−> ⇔ −>
+ −≥
+ −≥
Áp dụng bất đẳng thức Cauchy cho hai số dương
( )
xy+
và
( )
3x y−
ta được:
( ) ( ) (
)( )
2P x y 3x y 23x y x y 23.4 43 P 23= + + − ≥ − + ≥ = ⇒=
Dấu “=” xảy ra
(
)
( )
( )
( )
( )
( )
2
x y 3x y
x y 3x y
x y 3x y
2
4
xy
xyxy 4
xy
33
+= −
+= −
+= −
⇔ ⇔⇔
−=
+ −=
−=
(do
xy>
)
64
xy x
33
22
xy y
33
+= =
⇔⇔
−= =
Vậy
min
P 23=
, do đó
22
a b 13+=
Câu 45: Đáp án B.
Số đang xét có dạng
( )
a0
abcdef, a,b,c,d,e,f 1;2;3;...;9
abcdef
≠
⇒∈
<<<<<
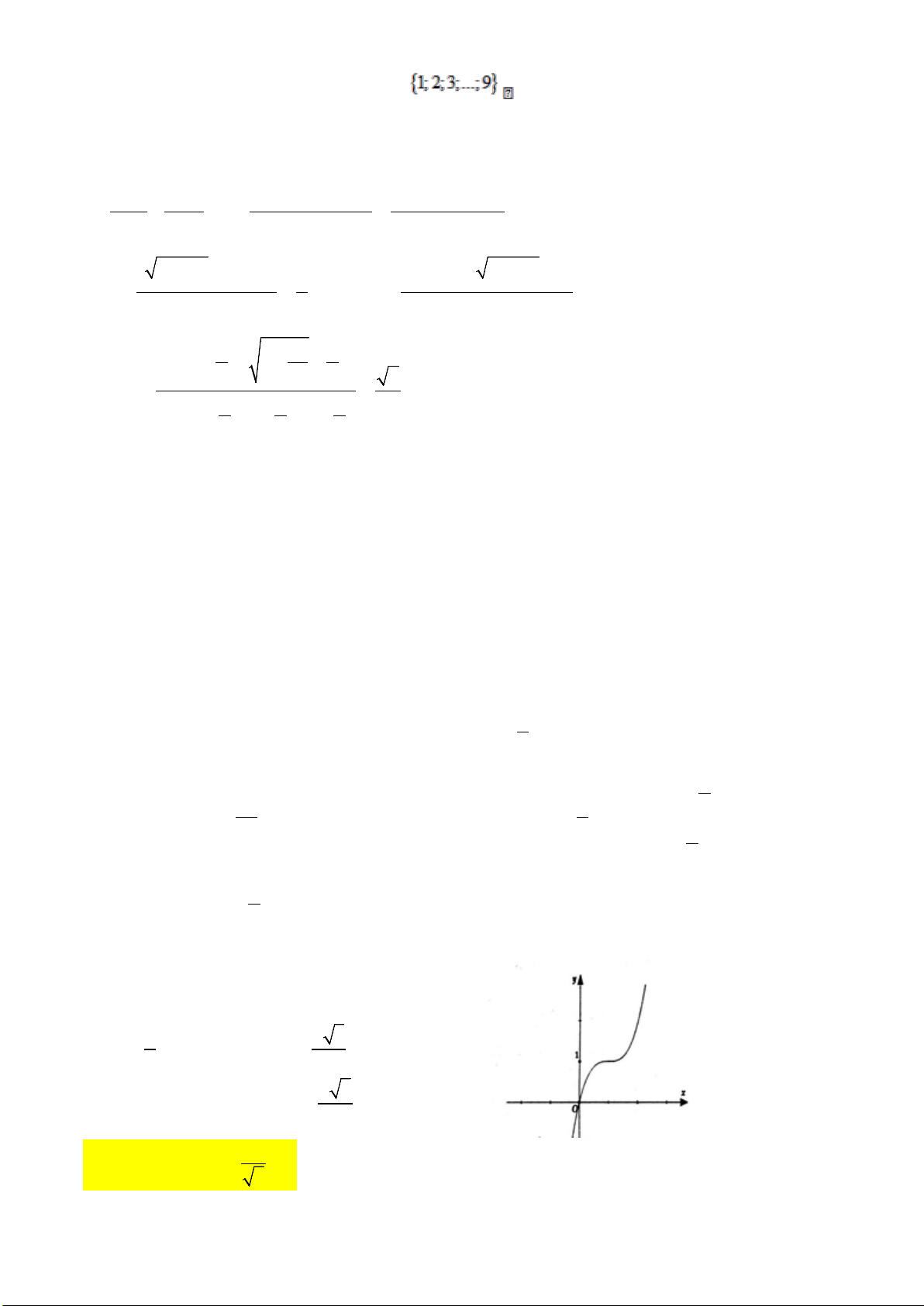
NTTL Trang 18/9
Mỗi bộ gồm 6 chữ số khác nhau lấy trong tập chỉ cho ta một số thỏa mãn điều kiện trên. Do
đó số các số tìm được là
6
9
C 84=
Câu 46: Đáp án D.
Ta có:
( )
(
)
( )
(
)( )
nn 3
11 1
...
1.2.3 2.3.4 n. n 1 . n 2 4 n 1 n 2
+
+ ++ =
+ + ++
Do đó
(
)
( )
( )
( )
(
)
(
)( )( )
22
2n 1 1 f n n n 3 2n 1 1
a
lim b lim
5n1 b 4n1n25n1
+− + +−
= ∈
+ ++ +
3
2
3
3 11
n1 2
n nn
2
lim
121
20
4n 1 1 5
nn n
+ +−
= =
+++
Suy ra
22
a b 402+=
Câu 47: Đáp án C.
Ta có
( )
( )
32 2
x1
fxx mm1xmm0 xm
x m1
=
= − ++ + +=⇔ =
=−−
Do đó
( )
2 22 2
1 23
P x x x 2 m m 1 .
= + + = ++
( )
( )
22
f ' x 3x m m 1= − ++
nên hàm số luôn có hai điểm cực trị.
Đường thẳng đi qua hai điểm cực trị có phương trình là
( )
22
2
y mm1xmm
3
=− ++ + +
Ta có:
( )
( )
32
22 2
CĐ CT
3
m
43
2
0 mm1 mm 0 mm 0
1
27 4
m
.
2
yy
<−
<⇔− + + + + <⇔ + −>⇔
>
Do m nguyên dương nên
1
m
2
<
suy ra
min P 6=
Câu 48: Đáp án A.
Ta có:
3
x0
y1
9 23
y' x 6x 0 x y 3
23
y3
23
x
3
=
= −
= −=⇔ = ⇒=−
= −
= −
Do đó
4
ABBCCA a
3
= = = =

NTTL Trang 19/9
Đặt
AM x, AN y= =
từ giả thiết
2
AMN
ABC
S
AM AN 1 a
. xy
S AB AC 2 2
= =⇒=
Ta có
2
2 22
a
MN x y xy
2
=+−≥
do đó
min
a2 26
MN
23
= =
Câu 49: Đáp án C.
Hàm số đồng biến trên tập xác định khi và chỉ khi
2
2
b
' b 3ac 0 ac
3
∆= − ≤ ⇔ ≥
Lúc này
2
2b 5
P 2acb1 b1
38
≥ + +≥ + +≥
Câu 50: Đáp án D.
Không gian mẫu co 36 phần tử.
Số phần tử của biến cố A là
36 6
15
2
−
=
Biến cố
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
{ }
B 1;6;6,1;1;5;5,1,2;4;4,2;2,5;5,2;3,3;3,4; 4,3=
Biến cố giao A và B gồm các phần tử
( ) ( )
( ) ( ) ( )
{ }
1; 6 ; 1; 5 ; 2; 4 ; 2, 5 ; 3, 4
Vậy
( )
15 11 5 7
P AB
36 12
+−
=∪= =
.
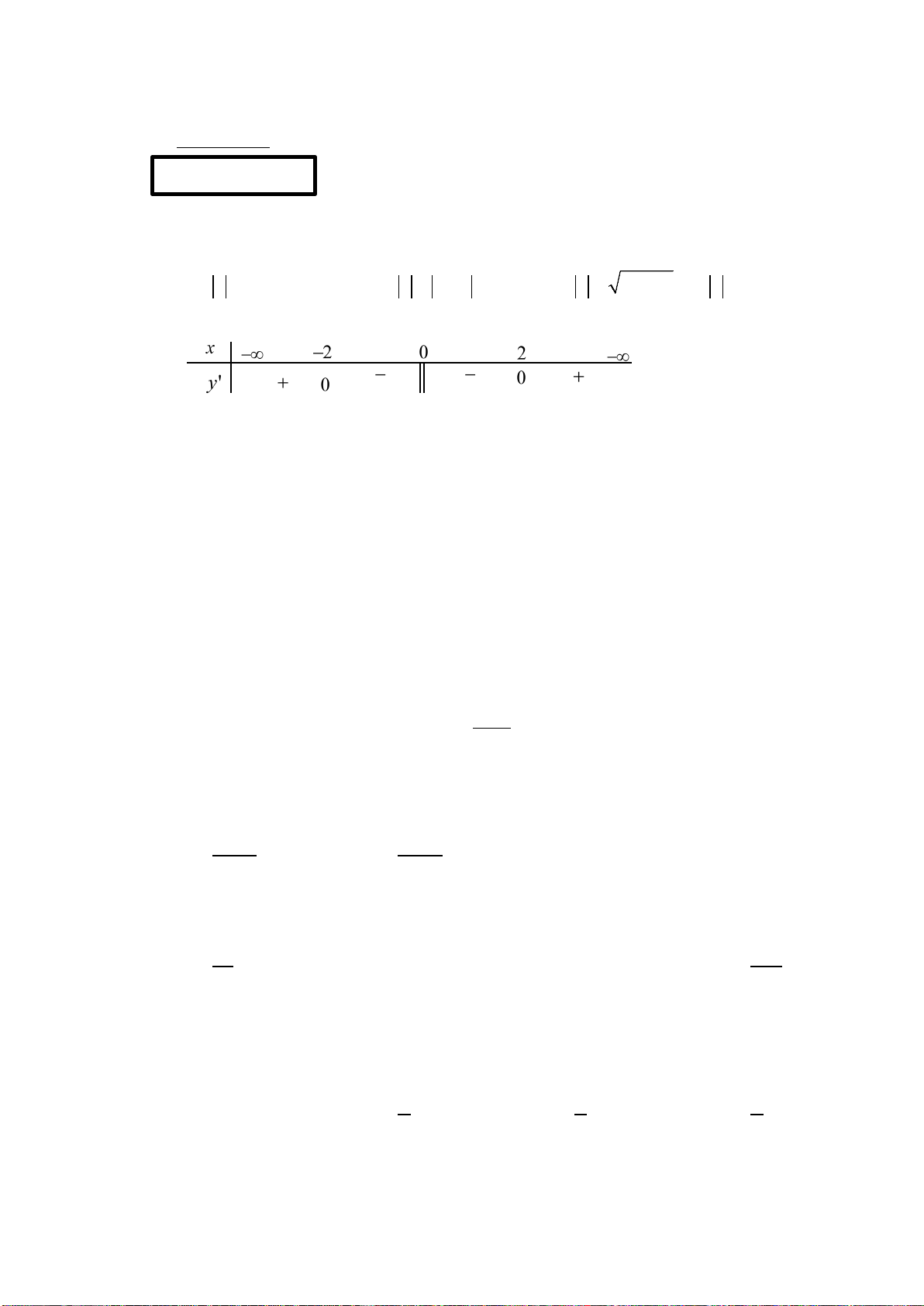
NTTL Trang 1/29
SỞ GD&ĐT KHÁNH HÒA ĐỀ ÔN TẬP THI THPT QUỐC GIA NĂM 2019
TRƯỜNG THPT TÔ VĂN ƠN Môn: Toán, thời gian 90 phút
(Không kể thời gian giao đề)
Câu 1: Cho số phức
z a bi= +
với
,ab∈
. Môđun của z tính theo công thức nào sau đây?
A.
.z ab
= +
B.
.z ab= +
C.
22
.z ab= +
D
22
.
zab
= +
Câu 2: Cho hàm số có bảng xét dấu đạo hàm như sau
Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
( ; 2).−∞ −
B. Hàm số đồng biến trên khoảng
( 2; 0).−
C. Hàm số đồng biến trên khoảng
( ; ).−∞ +∞
D. Hàm số nghịch biến trên khoảng
(0; 2).
Câu 3: Điểm cực đại của hàm số
32
31yx x
=−−
là
A.
5.x
= −
B.
0.x =
.
C.
1.x = −
D.
2.x =
Câu 4: Giá trị nhỏ nhất của hàm số
42
81
yx x=−+
trên
[ ]
1; 3
là
A.
15.−
B.
10.
C.
23.−
D.
6.−
Câu 5: Số tiệm cận đứng của đồ thị hàm số
1
1
x
y
x
+
=
−
là
A.
3.
B.
1.
C.
2.
D.
0.
Câu 6: Cho khối trụ có chiều cao bằng 2a và bán kính đáy bằng a. Thể tích của khối trụ đã cho
bằng
A.
3
2
3
a
π
. B.
3
4
3
a
π
. C.
3
2 a
π
. D.
3
a
π
.
Câu 7: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
và đường cao là
2.a
Thể tích của khối
chóp
.
S ABCD
là
A.
3
.
3
a
B.
3
.
a
C.
3
2.
a
D.
3
2
.
3
a
Câu 8: Cho
()
n
u
là cấp số cộng có số hạng đầu là
1
2u =
và công sai
3
d =
. Tính số hạng
2
.u
A.
2
5.u =
B.
2
6.u =
C.
2
4.u =
D.
2
9.u =
Câu 9: Gieo đồng xu cân đối và đồng chất một lần. Xác suất để đồng xu xuất hiện mặt sấp là
A.
1.
B.
1
.
4
C.
1
.
8
D.
1
.
2
Câu 10: Trong không gian Oxyz cho
(2; 0; 1), (0; 2; 3)MN−−
.Tọa độ trung điểm của đoạn
thẳng
MN
là
(Đề gồm 7 trang)

NTTL Trang 2/29
A.
( )
1; 1; 1 .−
B.
( )
2; 2; 2 .−
C.
( )
1; 1; 2 .−−
D.
( )
1; 1; 2 .−
Câu 11: Trong không gian Oxyz, gọi
()
α
là mặt phẳng cắt ba trục tọa độ tại ba điểm
( )
8;0;0 ,M
( )
0; 2; 0N −
và
( )
0; 0; 4P
. Phương trình của mặt phẳng
()
α
là
A.
4 2 8 0.xyz
− + −=
B.
4 2 0.xyz
−+=
C.
1
4 12
xyz
+ +=
−
. D.
0
8 24
xyz
+ +=
−
.
Câu 12: Cho
,,abc
là các số dương,
1a ≠
. Mệnh đề nào sau đây là đúng?
A.
log ( . ) log log
a aa
bc b c= +
. B.
log ( ) log log
a aa
bc b c
+= +
.
C.
log ( . ) log . log
a aa
bc b c=
. D.
log ( ) log . log
a aa
bc b c+=
.
Câu 13: Tính đạo hàm của hàm số
log
a
yx=
(
0,0 1xa> <≠
).
A.
( )
'
log
ln
a
x
x
a
=
. B.
( )
'
1
log
.ln
a
x
xa
=
.
C.
(
)
'
1
log
.log
a
x
xa
=
. D.
( )
'
1
log
.ln
a
x
ax
=
.
Câu 14: Phương trình
( )
2
log 1 3x −=
có nghiệm là
A.
7x =
. B.
9x =
. C.
8x =
. D.
10x =
.
Câu 15: Tập xác định của hàm số
( )
3
2
2yx x
= −
là:
A.
( ) ( )
;0 2;D = −∞ ∪ +∞
. B.
(
] [
)
;0 2;D = −∞ ∪ +∞
.
C.
( )
0;2D =
. D. R.
Câu 16: Cho
2
log 5
a=
. Tính
4
log 1250
theo
a.
A.
4
14
log 1250
2
a−
=
. B.
4
14
log 1250
2
a
+
=
.
C.
4
34
log 1250
2
a−
=
. D.
4
34
log 1250
2
a+
=
.
Câu 17: Trong không gian Oxyz, cho mặt cầu
( ) ( ) ( )
22
2
: 2 19Sx y z− + ++ =
. Điểm nào sau
đây thuộc mặt cầu
( )
S
?
A.
( )
2;0; 1 .M −
B.
( )
1; 0; 1 .N −−
C.
( )
2; 1; 1 .P −
D.
( )
2; 0;1Q
Câu 18: Trong không gian Oxyz, phương trình của mặt cầu có tâm
( )
1; 2; 3I −
và tiếp xúc với
mặt phẳng Oyz là
A.
( ) ( ) ( )
2 22
1 2 3 1.xy z− ++ ++ =
B.
( ) ( ) ( )
2 22
1 2 3 13.xy z+ +− +− =
C.
( ) ( ) ( )
2 22
1 2 3 1.xy z+ +− +− =
D.
( )
(
) ( )
2 22
1 2 3 13.xy z− ++ ++ =
Câu 19: Biết
( )
3; 4K −
là điểm biểu diễn số phức z trên mặt phẳng tọa độ Oxy. Điểm nào sau
đây biểu diễn số phức
|| .w zz= −
A.
( )
2; 4 .M
B.
( )
2; 4 .N −−
C.
( )
2; 4 .P −
D.
( )
2;4 .Q −
NTTL Trang 3/29
Câu 20: Gọi
12
,
zz
là hai nghiệm phức của phương trình
22
2 40z zm− + +=
. Tìm các giá trị
thực của tham số m thỏa mãn
12
111
.
4zz
+=
A.
2.m =
B.
2.m
= −
C.
2, 2.mm= = −
D.
0.
m =
Câu 21: Trong không gian Oxyz, mặt phẳng (P) song song với mặt phẳng
(
)
: 2 2 30
Qx y z
− + −=
và cách điểm
( )
3;1;1M
một khoảng bằng 2 có phương
trình là:
A.
2 2 9 0;xyz− + −=
2 2 3 0.xyz− + +=
B.
2 2 9 0;xyz− + +=
2 2 3 0.xyz− + +=
C.
2 2 9 0;xyz− + −=
2 2 3 0.xyz
− + −=
D.
2 2 1 0;xyz
− + −=
2 2 3 0.xyz
− + +=
Câu 22: Trong không gian Oxyz, viết phương trình hình chiếu vuông góc của đường thẳng
d:
xt
yt
zt
4
3
7
2
2
=
=−+
=
trên mặt phẳng
Px y z: 2 50− ++=
.
A.
4 16
11
13
2
2 10
xt
yt
zt
= −
= −
= +
. B.
4
11
2
2
xt
yt
zt
= +
= +
= +
C.
46
11
3
2
2
xt
yt
z
= +
= +
=
. D.
4 16
11
13
2
2 10
xt
yt
zt
= +
= +
= +
Câu 23: Cho hình nón tròn xoay, một thiết diện qua trục của hình nón là một tam giác đều cạnh
bằng
.a
Thể tích của khối nón này bằng
A.
3
3
8
a
. B.
3
3
12
a
π
. C.
3
3
6
a
π
. D.
3
3
24
a
π
.
Câu 24: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên đoạn
[ ]
1; 2−
và
( ) ( )
2 2 1 5.ff= −=
Tính
( )
2
/
1
.f x dx
−
∫
A.
5.
B.
10.
C.
5
.
2
D.
5
.
2
−
Câu 25: Cho hàm số
()y fx=
có đồ thị là đường cong ở hình vẽ bên. Có bao
nhiêu giá trị nguyên của tham số
m
để phương trình
() 2 0fx m+=
có bốn nghiệm phân biệt.
A.
0.
B.
1.
C.
2.
D.
3.
Câu 26: Họ nguyên hàm của hàm số
1
sinyx
x
= +
là
A.
cos .ln x xC−+
B.
cos .ln x xC++
C.
2
1
cos .xC
x
−+ +
D.
2
1
cos .xC
x
−− +
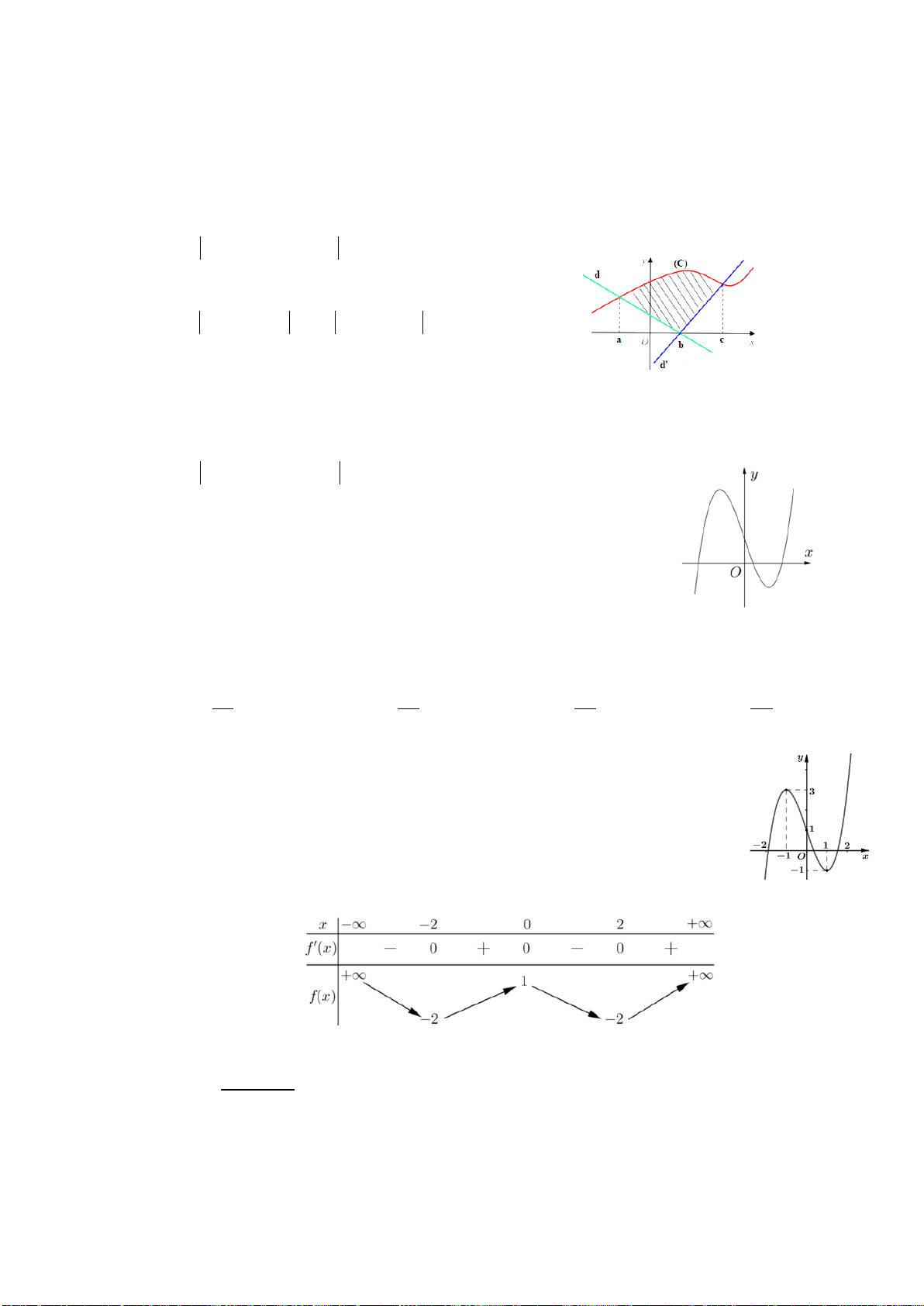
NTTL Trang 4/29
Câu 27: Cho hình phẳng D giới hạn bởi đường
( ) ( )
:C y fx=
, hai đường thẳng
d:
(
)
y gx=
và d’:
( )
y hx=
(tham khảo hình vẽ). Diện tích hình phẳng D được tính
theo công thức nào sau đây?
A.
c
a
() () ()f x g x h x dx−−
∫
B.
bc
ab
() () () () .
f x g x dx f x h x dx
− −−
∫∫
C.
bc
ab
[() ()] [() ()] .f x g x dx f x h x dx− +−
∫∫
D.
c
a
() () () .f x g x h x dx++
∫
Câu 28: Đường cong trong hình vẽ là đồ thị của hàm số nào sau đây?
A.
3
1.y xx=− −+
B.
3
1.yx x= ++
C.
3
3 1.yx x=−+
D.
3
3 1.yx x=−+ +
Câu 29: Gọi
S
là tập hợp các số tự nhiên gồm
6
chữ số khác nhau được
lập từ các số
{
}
0;1;2;3;4;8
. Chọn ngẫu nhiên từ tập
S
một số. Tính xác suất chọn
được số có tổng ba chữ số cuối gấp đôi tổng của ba chữ số đầu.
A.
7
.
31
B.
1
.
10
C.
1
.
12
D.
1
.
60
Câu 30: Cho hàm số
( )
y fx=
có đạo hàm trên
R
. Đồ thị hàm số
( )
y fx
′
=
như hình vẽ. Tìm tất cả các giá trị của
m
để hàm số
( ) ( )
y g x f x mx= = −
đồng biến trên
[ ]
2;1 .
−
A.
1.
m ≥
B.
1.m
≤−
C.
3.m
≤
D.
2.m ≥
Câu 31: Cho hàm số
( )
y fx=
có bảng biến thiên sau
Tổng số các đường tiệm cận ngang và đường tiệm cận đứng của đồ thị hàm số
( )
1
2
y
fx
=
+
là
A. 1. B. 2. C. 3. D. 4.
NTTL Trang 5/29
Câu 32: Họ nguyên hàm của hàm số
2
()
11
x
fx
x
=
++
là
A.
22
1 ln(1 1) .x xC+− + + +
B.
22
1 ln 1 1 .x xC++ + ++
C.
2
ln 1 1 .xC+ ++
D.
22
11
1 ln(1 1) .
22
x xC+− + + +
Câu 33: Trong không gian cho khối lăng trụ đều
.'''ABC A B C
, có tất cả các cạnh bằng
2
a
.
Gọi
,MN
lần lượt là trung điểm của các cạnh
', 'AA BB
. Tính khoảng cách từ
'
A
đến mặt phẳng
(' )C MN
theo
.a
A.
.
2
a
B.
23
.
3
a
C.
3
.
3
a
D.
2
.
2
a
Câu 34: Trong không gian cho khối chóp
.,S ABCD
có đáy là hình chữ nhật,
, 3,AB a AD a= =
M
là trung điểm
BC
. Cạnh
SA
vuông góc mặt phẳng
ABCD
,
3.SA a
=
Tính khoảng cách từ
M
đến mặt phẳng
( ).SBD
A.
21
.
7
a
B.
15
.
6
a
C.
15
.
10
a
D.
15
.
9
a
Câu 35: Cho
( )
1
3
2
2
0
1
( 1) , .
x
x
e
I x dx e me n m n Q
e
−
+
=+ =++ ∈
∫
Khi đó
mn
+
bằng
A.
1
.
2
B.
1
.
4
C.
2.
D.
1
.
2
−
Câu 36: Tìm số phức
z
biết
34
zz i
+=+
.
A.
7
4
6
zi= +
. B.
3z =
. C.
7
4
6
zi
=−+
. D.
34zi=−+
Câu 37: Một khúc gỗ có dạng khối nón có bán kính đáy bằng, chiều cao
3
m
h
=
và
1mr =
.
Một người muốn chế tác khúc gỗ đó thành một khúc gỗ có dạng hình khối trụ như
hình vẽ sao cho thể tích khối trụ lớn nhất. Gọi
V
là thể tích lớn nhất
đó. Tính
.V
A.
( )
4
27
2
mV
π
=
. B.
( )
4
9
2
mV
π
=
.
C.
(
)
4
3
2
mV
π
=
. D.
( )
2
9
2
mV
π
=
.
Câu 38: Cho hình chóp
.S ABCD
có đáy là hình vuông tâm O cạnh
a
.
Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy.
Khoảng cách từ O đến mặt phẳng (SCD) là
2
4
a
. Tính thể tích khối
chóp
.S ABCD
.
A.
3
a
. B.
3
3
3
a
. C.
3
3
6
a
. D.
3
3
a
.

NTTL Trang 6/29
Câu 39: Nghiệm của bất phương trình
5
2
xx
ee
−
+<
là
A.
ln 2
ln 2.
x
x
<−
>
B.
ln 2 ln 2.
x− <<
C.
1
2
2.
x
x
<
>
D.
1
2.
2
x<<
Câu 40: Tìm số phức
z
thỏa
13 3z iz i−+ = + −
và
3zi−−
nhỏ nhất.
A.
1 3.zi= +
B.
1 3.zi=−+
C.
2 2.
zi= +
D.
2 2.zi= −
Câu 41: Cho hàm số
(
) ( )
42
0y f x ax bx c a
= =++ ≠
có
( )
( ) (
)
;0
min 1fx f
−∞
= −
. Tìm giá trị
nhỏ nhất của hàm số
(
)
y fx=
trên đoạn
1
;2 .
2
A.
8.ca
+
B.
7
.
16
a
c −
C.
9
.
16
a
c
+
D.
.
ca
−
Câu 42: Trong không gian Oxyz, cho tam giác ABC với
( )
1; 2; 5A
,
( )
1; 4; 3B
,
( )
5; 2; 1
C
và
mặt phẳng
( ): 3 0.
Pxyz−−−=
Gọi M là một điểm thay đổi trên mặt phẳng (P).
Tìm giá trị nhỏ nhất của biểu thức
F MA MB MC
222
=++
.
A.
553
min
9
F =
. B.
553
min
3
F =
. C.
min 65F =
. D.
9
min
553
F =
.
Câu 43: Trong không gian Oxyz, cho mặt cầu
( )
2 22
: 2 4 2 30Sx y z x y z+ + − + + −=
Và đường thẳng
11
:.
2 11
xyz
d
−+
= =
−
Mặt phẳng
( ): 1 0P ax by cz
+ + +=
chứa d
cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có bán kính nhỏ nhất. Tính giá trị
biểu thức
4 3 2.T abc=++
A.
9.
T =
B.
5.
T =
C.
1.T =
D.
5.
T = −
Câu 44: Cho hàm số
( )
y fx
=
xác định trên
R
và có hàm số
( )
( )
(
)
(
)
/2 2
1 2 2 2.f x x x x mx m= − − − ++
Có bao nhiêu giá trị nguyên của tham
số
m
để hàm số
( )
2y fx= +
có đúng ba điểm cực trị?
A.
2.
B.
3.
C.
4.
D.
5.
Câu 45: Cho hàm số
( )
32
f x ax bx cx d
= + ++
có đồ thị như hình vẽ.
Tìm số tiệm cận đứng của đồ thị hàm số
( )
( )
( ) ( )
2
2
32 1
.
xx x
gx
xf x fx
−+ −
=
−
A. 3. B. 4.
C. 5 D. 6.
Câu 46: Cho hàm số
31
1
x
y
x
+
=
+
có đồ thị
( )
C
. Gọi A, B là hai điểm
thuộc
( )
C
sao cho tiếp tuyến của
( )
C
tại A, B song song với
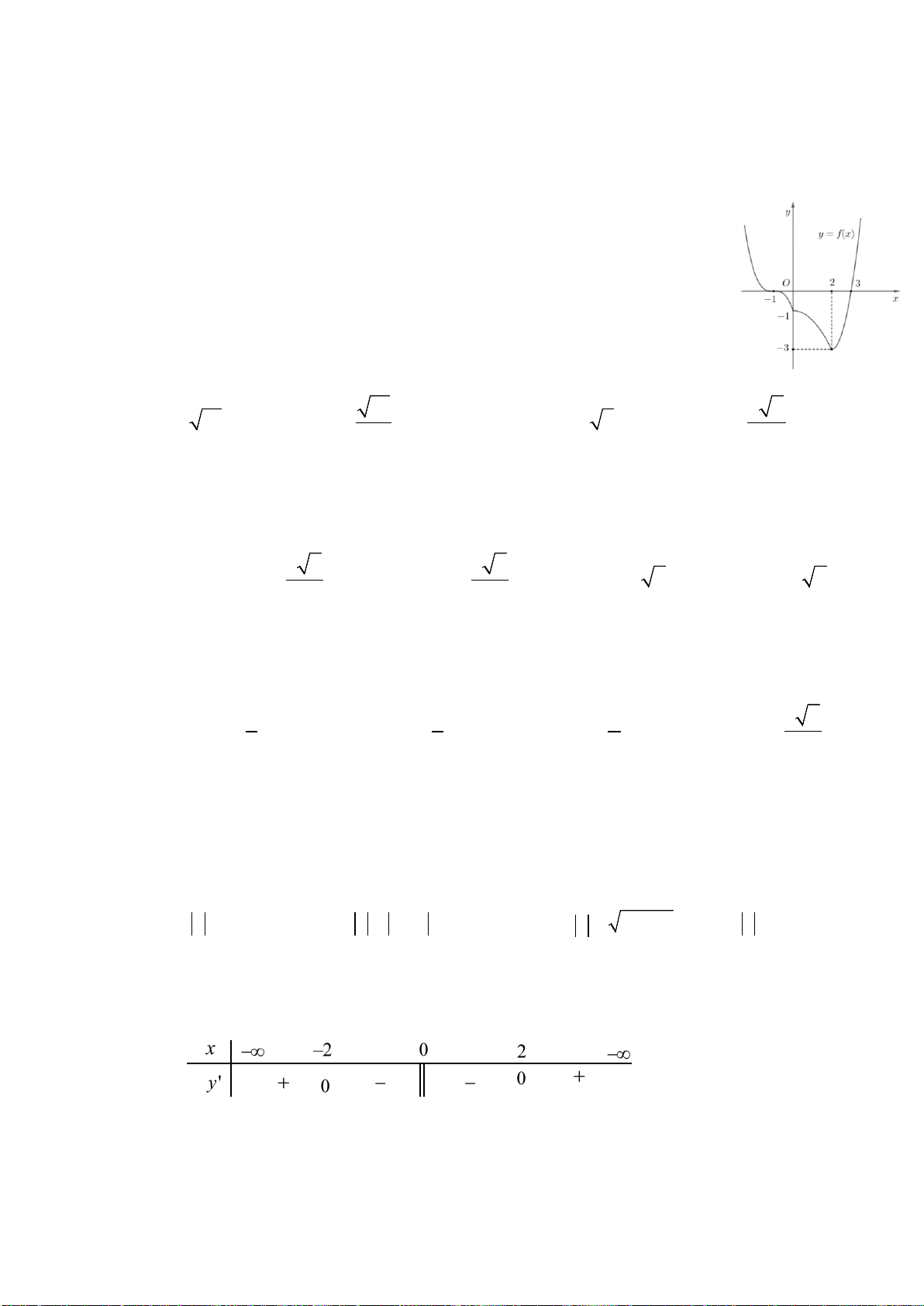
NTTL Trang 7/29
nhau. Các tiếp tuyến này lần lượt cắt tiệm cận đứng, tiệm cận ngang của
(
)
C
tại M, N
(tham khảo hình vẽ). Tứ giác AMNB có chu vi nhỏ nhất bằng bao nhiêu?
A.
16.
B.
8.
C.
20.
D.
12.
Câu 47: Cho hàm số
(
)
y fx=
liên tục trên
R
và có đồ thị như hình vẽ. Tìm tất
cả các giá trị thực của tham số
m
để bất phương trình
( )
32
2 32fx x x m+> +
nghiệm đúng với mọi
( )
1; 3 .x ∈
A.
10.
m
<−
B.
5.m <−
C.
3.m <−
D.
2.
m <−
Câu 48: : Cho
,ab
là hai số thực dương thỏa mãn
22
1ab+>
và
( )
22
log 1.
ab
ab
+
+≥
Tìm giá trị lớn nhất của biểu thức:
2 4 3.
P ab=+−
A.
10.
B.
10
.
2
C.
25
. D.
52
.
2
Câu 49: Cho hàm số
( )
(
)
32
3 29 6
y x m x m xm= + + − + ++
có đồ thị
( )
C
. Tìm tất cả các
giá trị thực của tham số
m
để
(
)
C
có hai điểm cực trị sao cho khoảng cách từ gốc tọa
độ
O
đến đường thẳng nối hai điểm cực trị là lớn nhất.
A.
32
6.
2
m =−±
B.
32
3.
2
m =−±
C.
3 6 2.
m =−±
D.
6 6 2.
m =−±
Câu 50: Cho đoạn thẳng AB cố định trong không gian và có độ dài
2
AB =
. Qua các điểm A và
B lần lượt kẻ các đường thẳng Ax và By chéo nhau thay đổi nhưng luôn vuông góc với
đoạn thẳng AB. Trên các đường thẳng đó lần lượt lấy các điểm M, N sao cho
23AM BN+=
. Tính thể tích
V
lớn nhất của khối tứ diện ABMN.
A.
1
3
V =
. B.
3
8
V =
. C.
1
2
V
=
. D.
32
4
V =
.
-------------HẾT-------------
Họ và tên học sinh……………………….............Số báo danh: ……............
Cán bộ coi thi không giải thích gì thêm.
ĐÁP ÁN
Câu 1: Cho số phức với . Môđun của z tính theo công thức nào sau đây?
A. B. C. D
Hướng dẫn giải.
Đáp án C.
()y fx=
Câu 2: Cho hàm số có bảng xét dấu đạo hàm như sau
Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
( ; 2).−∞ −
B. Hàm số đồng biến trên khoảng
( 2;0).−
z a bi
= +
,ab∈
.z ab= +
.z ab= +
22
.z ab= +
22
.zab= +

NTTL Trang 8/29
C. Hàm số đồng biến trên khoảng
( ; ).
−∞ +∞
D. Hàm số nghịch biến trên khoảng
(0;2).
Hướng dẫn giải.
Đáp án. D.
Câu 3: Điểm cực đại của hàm số
32
31yx x=−−
là
A.
5.x = −
B.
0.
x =
C.
1.x = −
D.
2.x =
Hướng dẫn giải.
Đáp án. B.
Câu 4: Giá trị nhỏ nhất của hàm số
42
81yx x=−+
trên
[ ]
1; 3
là
A.
15.−
B.
10.
C.
23.−
D.
6.−
Hướng dẫn giải.
Đáp án A.
Câu 5: Số tiệm cận đứng của đồ thị hàm số
1
1
x
y
x
+
=
−
là
A.
3.
B.
1.
C.
2.
D.
0.
Hướng dẫn giải.
Đáp án B.
Câu 6: Cho khối trụ có chiều cao bằng 2a và bán kính đáy bằng a . Thể tích của khối trụ đã cho
bằng
A.
3
2
3
a
π
. B.
3
4
3
a
π
. C.
3
2 a
π
. D.
3
a
π
.
Hướng dẫn giải.
3
.2V Bh a
π
= =
Đáp án C.
Câu 7: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
và đường cao là
2.a
Thể tích của khối
chóp
.S ABCD
là
A.
3
.
3
a
B.
3
.a
C.
3
2.a
D.
3
2
.
3
a
Hướng dẫn:
1
3
V Bh
=
Đáp án: D.

NTTL Trang 9/29
Câu 8: Cho
()
n
u
là cấp số cộng có số hạng đầu là
1
2u
=
và công sai
3d =
. Tính số hạng
2
.u
A.
2
5.u
=
B.
2
6.u
=
C.
2
4.u
=
D.
2
9.u
=
Hướng dẫn giải.
Cho
()
n
u
là cấp số cộng có số hạng đầu là
1
2u =
và công sai
3d =
. Khi đó:
21
2 3 5.u ud= + =+=
Đáp án A.
Câu 9: Gieo đồng xu cân đối và đồng chất một lần. Xác suất để đồng xu xuất hiện mặt sấp là
A.
1.
B.
1
.
4
C.
1
.
8
D.
1
.
2
Hướng dẫn giải.
Gieo đồng xu cân đối và đồng chất một lần.
Xác suất để đồng xu xuất hiện mặt sắp là
1
.
2
P =
Đáp án D.
Câu 10: Trong không gian Oxyz cho
(2; 0; 1), (0; 2; 3)MN−−
. Tọa độ trung điểm của đoạn
thẳng
MN
là
A.
( )
1; 1; 1 .−
B.
( )
2; 2; 2 .−
C.
( )
1; 1; 2 .−−
D.
( )
1; 1; 2 .−
Hướng dẫn giải :
( )
2002 13
( ; ; ) I 1; 1;1
22 2
I
+ − −+
⇒−
.
Đáp án A.
Câu 11: Trong không gian Oxyz, gọi là mặt phẳng cắt ba trục tọa độ tại ba điểm
( )
8;0;0 ,M
( )
0; 2; 0 ,N −
và
( )
0; 0; 4P
. Phương trình của mặt phẳng là
A.
4 2 8 0.xyz− + −=
B.
4 2 0.xyz−+=
C.
1
4 12
xyz
+ +=
−
. D.
0
8 24
xyz
+ +=
−
.
Hướng dẫn giải.
()
α
()
α

NTTL Trang 10/29
1 4 2 8 0.
8 24
xyz
xyz
+ + =⇔− + −=
−
Đáp án A.
Câu 12:
Cho
,,
abc
là các số dương,
1a ≠
. Công thức nào sau đây là đúng?
A.
log ( . ) log log
a aa
bc b c= +
. B.
log ( ) log log
a aa
bc b c+= +
.
C.
log ( . ) log . log
a aa
bc b c
=
. D.
log ( ) log . log
a aa
bc b c+=
.
Hướng dẫn:
Đáp án A
Câu 13: Đạo hàm của hàm số
log
a
yx=
( )
0, 0 1xa> <≠
là
A.
( )
'
log
ln
a
x
x
a
=
. B.
( )
'
1
log
.ln
a
x
xa
=
. C.
( )
'
1
log
.log
a
x
xa
=
. D.
( )
'
1
log
a.ln
a
x
x
=
.
Hướng dẫn:
Đáp án B
Câu 14: Phương trình
( )
2
log 1 3x −=
có nghiệm là
A.
7x =
. B.
9x =
. C.
8x =
. D.
10
x
=
.
Hướng dẫn:
( )
2
log 1 3 1 8 9.x xx− = ⇔ −= ⇔ =
Đáp án B
Câu 15: Tập xác định của hàm số
( )
3
2
2yx x
= −
là:
A.
( ) (
)
;0 2;D = −∞ ∪ +∞
. B.
(
] [
)
;0 2;D = −∞ ∪ +∞
.
C.
( )
0;2D =
. D. R.
Hướng dẫn:
TXĐ của
( )
3
2
2yx x= −
là
2
2
20
0.
x
xx
x
>
− >⇔
<

NTTL Trang 11/29
Đáp án A
Câu 16: Cho
2
log 5 a
=
. Tính
4
log 1250
theo
a.
A.
4
14
log 1250
2
a−
=
. B.
4
14
log 1250
2
a+
=
.
C.
4
34
log 1250
2
a
−
=
. D.
4
34
log 1250
2
a
+
=
.
Hướng dẫn:
(
)
4
2
22
4
2
22
log 2.5
log 1250 1 4log 5 1 4
log 1250 .
log 4 log 2 2 2
a++
= = = =
Cách khác: Sử dụng máy tính CASIO
Đáp án B
Câu 17: Trong không gian Oxyz, cho mặt cầu
( ) ( ) ( )
22
2
: 2 19Sx y z
− + ++ =
. Điểm nào sau
đây thuộc mặt cầu (S) ?
A.
( )
2;0; 1 .M −
B.
( )
1; 0; 1 .N −−
C.
( )
2; 1; 1 .P −
D.
( )
2; 0;1
Q
Hướng dẫn giải :
( )
( )
22
2
12 0 11 9
−− + +−+ =
nên
( )
1; 0; 1 ( )NS− −∈
.
Đáp án B.
Câu 18: Trong không gian Oxyz, phương trình của mặt cầu có tâm
( )
1; 2; 3I −
và tiếp xúc với
mặt phẳng Oyz là
A.
(
) ( )
( )
2 22
1 2 3 1.
xy z− ++ ++ =
B.
( ) ( )
( )
2 22
1 2 3 13.xy z+ +− +− =
C.
(
) ( )
( )
2 22
1 2 3 1.
xy z+ +− +− =
D.
( ) ( ) ( )
2 22
1 2 3 13.xy z− ++ ++ =
Hướng dẫn giải :
Mặt cầu cần tìm có tâm
( )
1; 2; 3I −
, bán kính
( )
; 11R d I Oyz= =−=
nên có phương trình
( ) ( )
( )
2 22
1 2 3 1.xy z+ +− +− =
Đáp án C.
Câu 19: Biết
( )
3; 4K −
là điểm biểu diễn số phức z trên mặt phẳng tọa độ Oxy. Khi đó điểm
nào sau đây biểu diễn số phức
||w zz= −

NTTL Trang 12/29
A.
(
)
2; 4 .M
B.
( )
2; 4 .N −−
C.
( )
2; 4 .P −
D.
( )
2;4 .Q −
Hướng dẫn giải.
Ta có
34zi= −
nên
5.
z
=
Do đó
2 4.
w i
= +
Đáp án A.
Câu 20: Gọi
12
,
zz
lần lượt là hai nghiệm phức của phương trình
22
2 40z zm− + +=
. Tìm
các giá trị thực của tham số m thỏa mãn
12
111
.
4zz
+=
A.
2.
m =
B.
2.m = −
C.
2, 2.
mm= = −
D.
0.m =
Hướng dẫn giải.
12
1 2 12
2
111 1
44
21
2.
44
zz
z z zz
m
m
+
+=⇔ =
⇔ =⇔=±
+
Đáp án C.
Câu 21: Trong không gian Oxyz, mặt phẳng (P) song song với mặt phẳng
( )
: 2 2 30Qx y z− + −=
và cách điểm
( )
3;1;1M
một khoảng bằng 2 có phương
trình là:
A.
2 2 9 0;xyz− + −=
2 2 3 0.
xyz− + +=
B.
2 2 9 0;xyz− + +=
2 2 3 0.
xyz
− + +=
C.
2 2 9 0;xyz− + −=
2 2 3 0.xyz− + −=
D.
2 2 1 0;xyz− + −=
2 2 3 0.xyz− + +=
Hướng dẫn giải
Vì (P) // (Q) nên
(
)
( ): 2 2 0 3 .Px y zD D− + + = ≠−
( )
( )
9
;2
3
D
dM P
D
= −
= ⇔
=
.
Vậy có hai mặt phẳng là :
2 2 9 0;xyz− + −=
2 2 3 0.xyz− + +=
Đáp án A.
Câu 22: Trong không gian Oxyz, viết phương trình hình chiếu vuông góc của đường thẳng

NTTL Trang 13/29
d:
trên mặt phẳng .
A.
4 16
11
13
2
2 10
xt
yt
zt
= −
= −
= +
. B.
4
11
2
2
xt
yt
zt
= +
= +
= +
. C.
46
11
3
2
2
xt
yt
z
= +
= +
=
. D.
4 16
11
13
2
2 10
xt
yt
zt
= +
= +
= +
Hướng dẫn giải.
Gọi ⇒ .
Ta có .
Gọi là hình chiếu vuông góc của B trên (P). Ta tìm được .
Gọi ∆ là hình chiếu vuông góc của d trên (P) ⇒ ∆ đi qua A và H
⇒ Phương trình của ∆: .
Cách khác: Sử dụng máy tính CASIO.
4 16
11
13
2
2 10
xt
yt
zt
= +
= +
= +
Đáp án D.
Câu 23: [2] Cho hình nón tròn xoay, một thiết diện qua trục của hình nón là một tam giác đều
cạnh bằng . Thể tích của khối nón này bằng
A.
3
3
8
a
. B.
3
3
12
a
π
. C.
3
3
6
a
π
. D.
3
3
24
a
π
.
Hướng dẫn giải.
xt
yt
zt
4
3
7
2
2
=
=−+
=
Px y z: 2 50
− ++=
Ad P()= ∩
A
11
4; ;2
2
B dB P
33
0; ;0 , 0; ;0 ( )
22
−∈ −∉
Hxyz(;;)
H
47 4
;;
36 3
−−
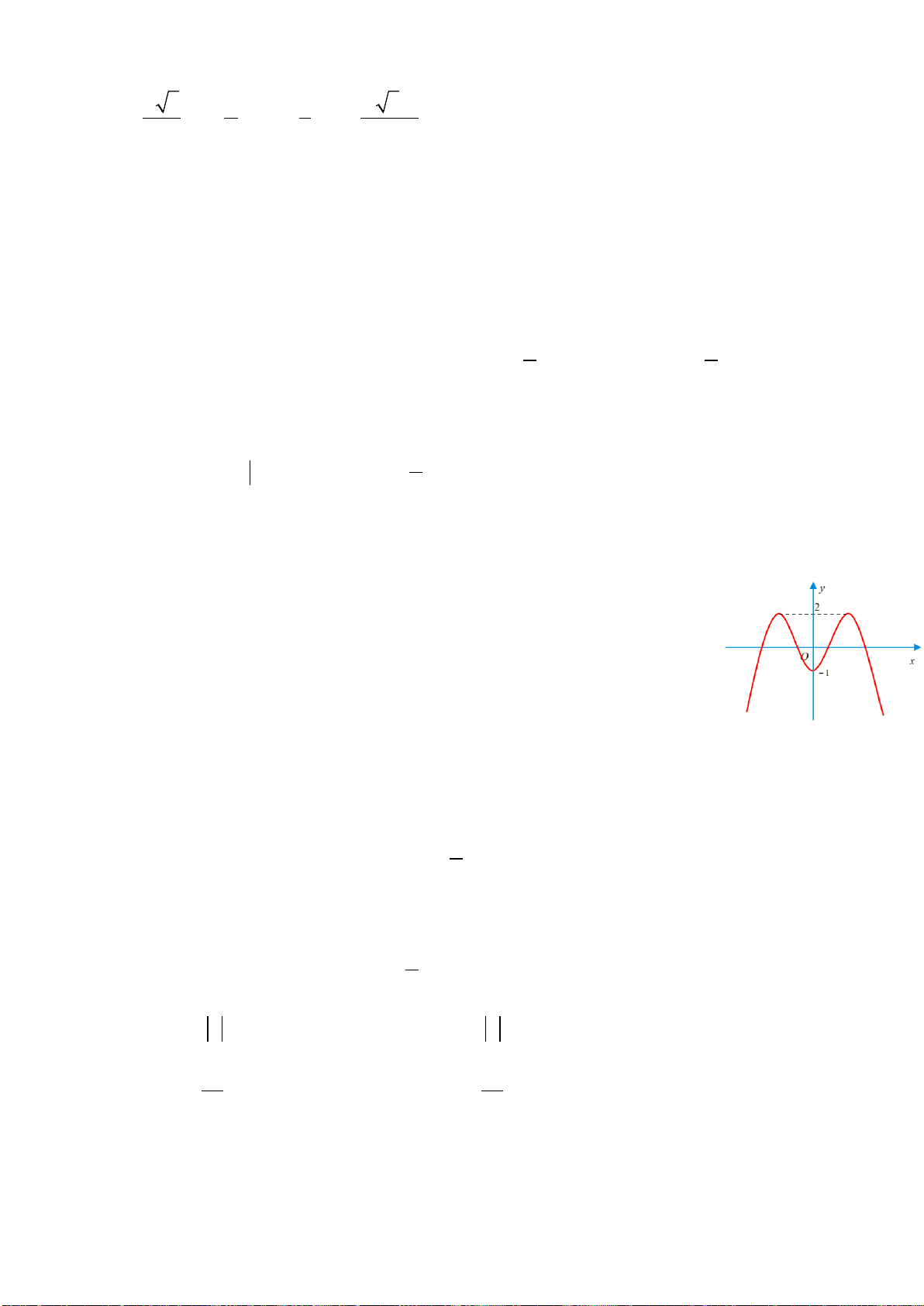
NTTL Trang 14/29
Đáp án D.
Câu 24: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên đoạn
[ ]
1; 2−
và
( )
(
)
2 2 1 5.
ff= −=
Tính
( )
2
/
1
.f x dx
−
∫
A.
5.
B.
10.
C.
5
.
2
D.
5
.
2
−
Hướng dẫn giải
2
2
1
1
5
'() () (2) (1) .
2
df x x fx f f
−
−
= = − −=
∫
Đáp án: C
Câu 25: Cho hàm số
()y fx=
có đồ thị là đường cong ở hình vẽ bên. Có bao
nhiêu giá trị nguyên của tham số
m
để phương trình
() 2 0
fx m+=
có bốn nghiệm phân biệt.
A.
0.
B.
1.
C.
2.
D.
3.
Hướng dẫn giải.
() 2 0 () 2fx m fx m+=⇔ =−
Yêu cầu bài toán trở thành
1
1 2 2 1 0.
2
m mm− <− < ⇔ > >− → =
Đáp án B.
Câu 26: Họ nguyên hàm của hàm số
1
sinyx
x
= +
là
A.
cos .ln x xC−+
B.
cos .ln x xC++
C.
2
1
cos .xC
x
−+ +
D.
2
1
cos .xC
x
−− +
Hướng dẫn giải
3
3 13
, ..
2 2 3 24
aa a
h r V Bh
π
= =⇒= =
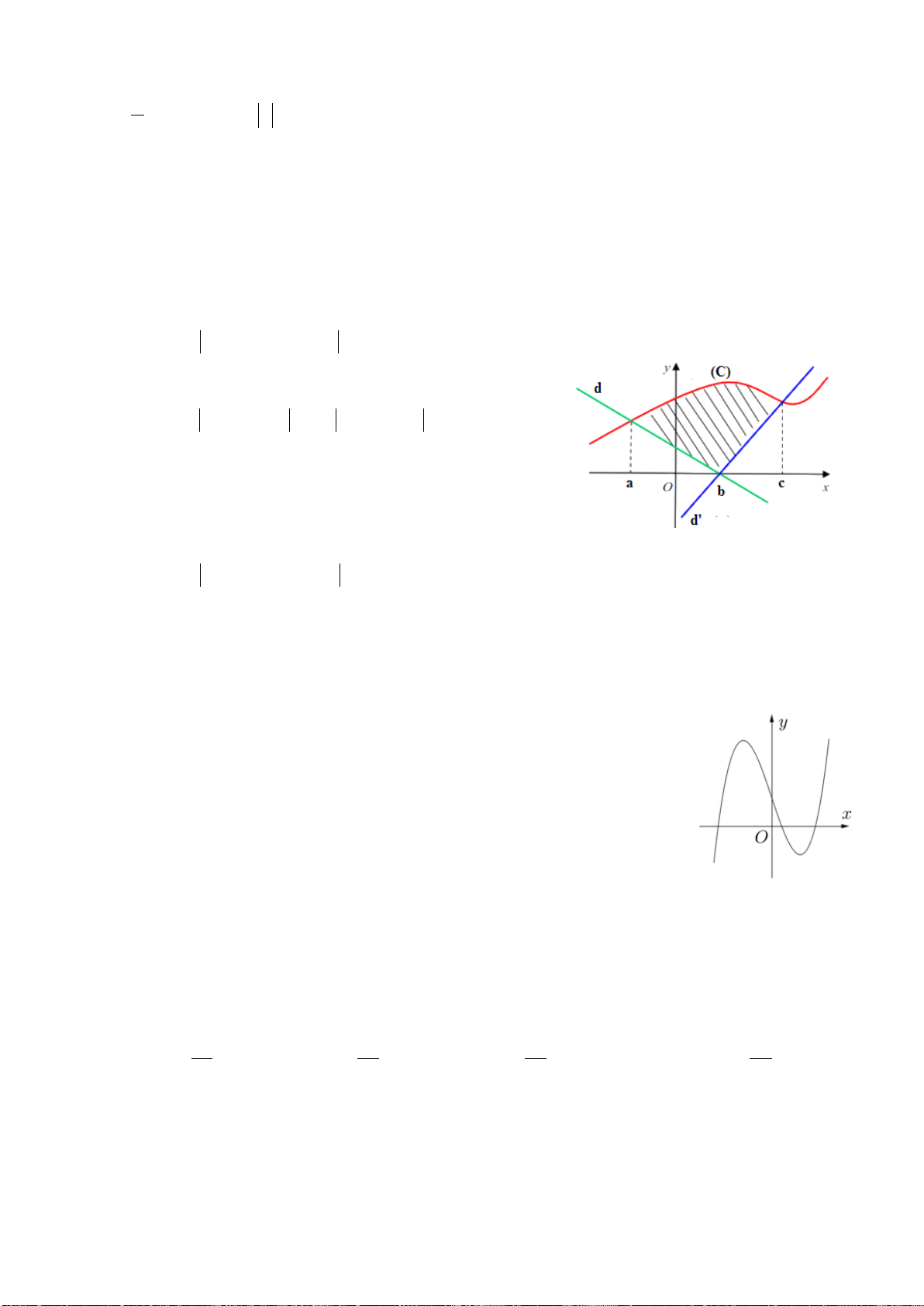
NTTL Trang 15/29
1
( sin cos .)d =lnxx x xC
x
+ −+
∫
Đáp án: A
Câu 27: Cho hình phẳng D giới hạn bởi đường
( ) ( )
:C y fx=
, hai đường thẳng d:
( )
y gx
=
và d’:
(
)
y hx=
(tham khảo hình vẽ). Diện tích hình phẳng D được tính theo công thức nào sau
đây?
A.
c
a
() () ()f x g x h x dx−−
∫
B.
bc
ab
() () () () .f x g x dx f x h x dx− −−
∫∫
C.
bc
ab
[() ()] [() ()] .f x g x dx f x h x dx
− +−
∫∫
D.
c
a
() () () .
f x g x h x dx++
∫
Đáp án: C
Câu 28: Đường cong trong hình vẽ là đồ thị của hàm số nào sau đây?
A.
3
1.
y xx=− −+
B.
3
1.yx x
= ++
C.
3
3 1.yx x=−+
D.
3
3 1.yx x
=−+ +
Hướng dẫn giải.
Dựa vào đồ thị hàm số, hệ số
0a >
nên loại hai phương án A và D.
Đồ thị hàm số có hai điểm cực trị :
2
30b ac
−>
nên đáp án là C.
Câu 29: Gọi
S
là tập hợp các số tự nhiên gồm
6
chữ số khác nhau được lập từ các số
{ }
0;1;2;3;4;8
. Chọn ngẫu nhiên từ tập
S
một số. Tính xác suất chọn được số có tổng
ba chữ số cuối gấp đôi tổng của ba chữ số đầu.
A.
7
.
31
B.
1
.
10
C.
1
.
12
D.
1
.
60
Hướng dẫn giải.
B: “Chọn được số thỏa yêu cầu đề bài.”
( ) 5.5! 600.n
Ω
= =
( ) 60.nB =
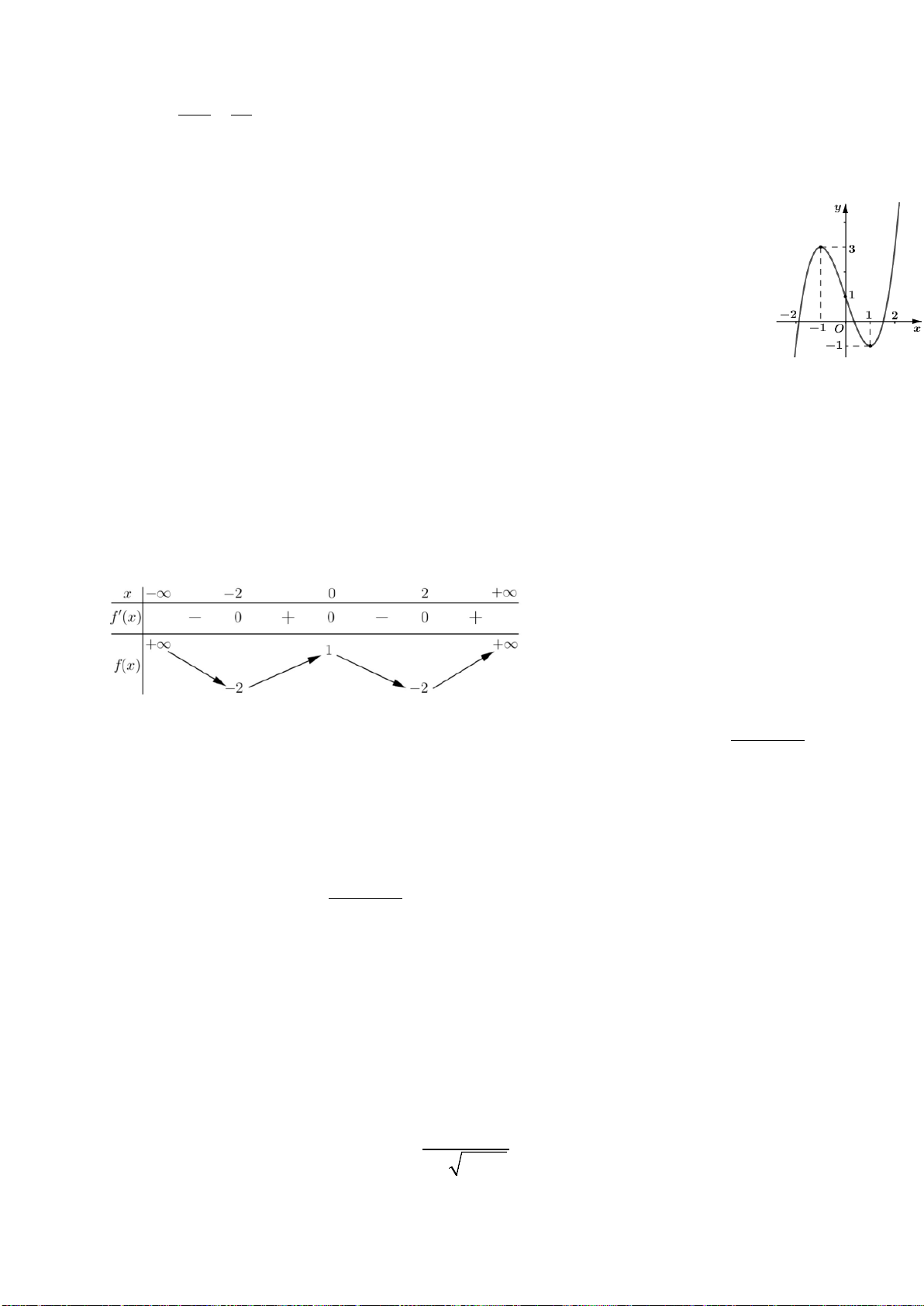
NTTL Trang 16/29
60 1
() .
600 10
PB
= =
Đáp án B.
Câu 30: Cho hàm số
(
)
y fx=
có đạo hàm trên
R
. Đồ thị hàm số
( )
y fx
′
=
như
hình vẽ. Tìm tất cả các giá trị của
m
để hàm số
( ) ( )
y g x f x mx
= = −
đồng biến trên
[ ]
2;1 .
−
A.
1.m ≥
B.
1.m ≤−
C.
3.m ≤
D.
2.
m ≥
Hướng dẫn giải.
Ta có
( ) ( )
//
.gx f x m= −
Dựa vào đồ thị, ta được
1.m−≥
Đáp án B.
Câu 31: Cho hàm số
( )
y fx
=
có bảng biến thiên sau
Tổng số các đường tiệm cận ngang và đường tiệm cận đứng của đồ thị hàm số
( )
1
2
y
fx
=
+
là
A. 1. B. 2. C. 3. D. 4.
Hướng dẫn giải.
( )
( )
1
0
2
x fx
fx
→ ±∞ ⇒ → +∞ ⇒ →
+
suy ra tiệm cận ngang là
0.y =
Ta có
( )
2
2
2
x
fx
x
= −
=−⇔
=
Do đó
22
lim , lim
xx
yy
++
→− →
= +∞ = +∞
. Suy ra có 2 tiệm cận đứng.
Đáp án là C
Câu 32: Họ nguyên hàm của hàm số
2
()
11
x
fx
x
=
++
là

NTTL Trang 17/29
A.
22
1 ln(1 1) .
x xC
+− + + +
B.
22
1 ln 1 1 .x xC++ + ++
C.
2
ln 1 1 .xC+ ++
D.
22
11
1 ln(1 1) .
22
x xC+− + + +
Hướng dẫn giải.
Đặt
2 22
11t x t x tdt xdx
= +⇒ = +⇒ =
1
(1 ) ln(1 )
11
t
dt dt t t C
tt
= − =− ++
++
∫∫
Vậy
22
2
1 ln(1 1) .
11
x
dx x x C
x
= +− + + +
++
∫
Đáp án: A
Câu 33: Trong không gian cho khối lăng trụ đều
.'''
ABC A B C
, có tất cả các cạnh bằng
2a
.
Gọi
,MN
lần lượt là trung điểm của các cạnh
', '
AA BB
. Tính khoảng cách từ
'A
đến mặt phẳng
(' )
C MN
theo
.a
A.
.
2
a
B.
23
.
3
a
C.
3
.
3
a
D.
2
.
2
a
Hướng dẫn giải.(Đã sửa)
'
2
.
3
C MN ABC
SS=
'. ' '. ' ' . ' ' '
11
26
11
.2. . ( ',( ' )) 2 .
36
3
( ', ( ' )) .
2
A C MN C A B NM ABC A B C
ABC ABC
VV V
S d A C MN a S
a
d A C MN
= =
→=
→=
Đáp án E.
3
2
a
.

NTTL Trang 18/29
Câu 34: Trong không gian cho khối chóp
.,S ABCD
có đáy là hình chữ nhật.
, 3,AB a AD a
= =
M
là trung điểm
BC
. Cạnh
SA
vuông góc mặt phẳng
ABCD
,
3.SA a=
Tính khoảng cách từ
M
đến mặt phẳng
( ).SBD
A.
21
.
7
a
B.
15
.
6
a
C.
15
.
10
a
D.
15
.
9
a
Hướng dẫn giải.
1 15
( ,( )) ( ,( )) .
2 10
a
d M SBD d A SBD= =
Đáp án C.
Câu 35: Cho
( )
1
3
2
2
0
1
( 1) , .
x
x
e
I x dx e me n m n Q
e
−
+
=+ =++ ∈
∫
Khi đó
mn+
bằng
A.
1
.
2
B.
1
.
4
C.
2.
D.
1
.
2
−
Hướng dẫn giải
11
3
2
2
00
1
( 1). ( 1).( )
x
xx
x
e
I x dx x e e dx
e
−
+
=+ =++
∫∫
Đặt
2
2
1
1
()
2
xx
xx
du dx
ux
ve e
dv e e dx
−
−
=
= +
⇒
= −
= +
1
22 2
0
1 3 53
() .
2 4 44
[]
xx x
I xe e e e e
−− −
= − − =−+
Ta có:
53 1
;.
44 2
m n mn
=− = ⇒ +=−
Đáp án: D
Câu 36: Tìm số phức
z
biết .
A. . B. . C. . D.
.
Hướng dẫn giải.
Ta có
25
34 .
6
z zi z=−+ ⇒=
34zz i+=+
7
4
6
zi= +
3z
=
7
4
6
zi=−+
34zi=−+
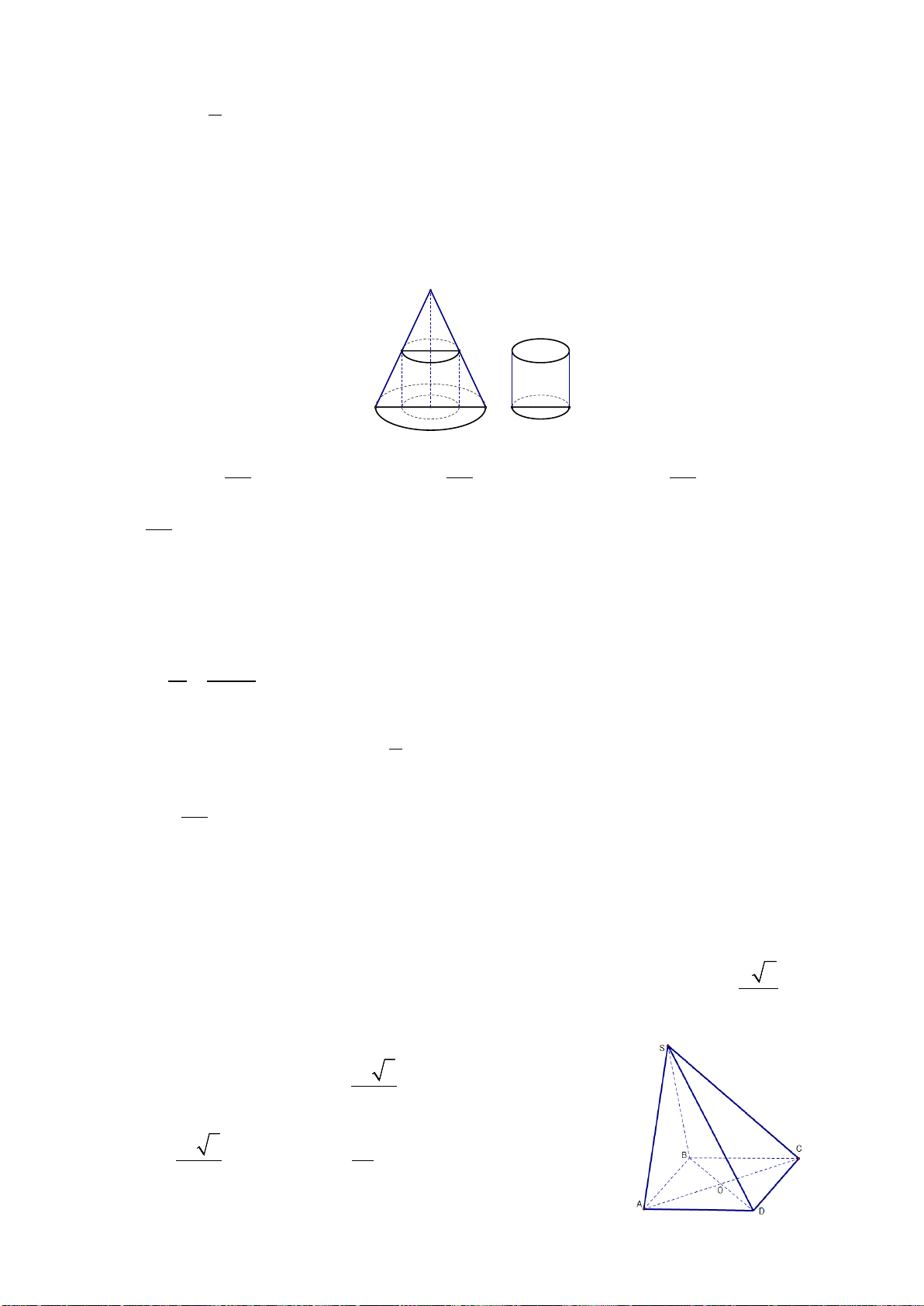
NTTL Trang 19/29
Suy ra
7
4.
6
zi=−+
Đáp án C.
Câu 37: Một khúc gỗ có dạng khối nón có bán kính đáy bằng , chiều cao
3 m,h =
1mr =
. Một
người muốn chế tác khúc gỗ đó thành một khúc gỗ có dạng hình khối trụ như hình vẽ
sao cho thể tích khối trụ lớn nhất. Gọi
V
là thể tích lớn nhất đó. Tính
V
.
A.
( )
4
27
2
m
V
π
=
. B.
( )
4
9
2
mV
π
=
. C.
( )
4
3
2
mV
π
=
. D.
( )
2
9
2
mV
π
=
.
Hướng dẫn giải.
Khối trụ có bán kính đáy là
/
,
r
chiều cao
/
.h
Khi đó
//
//
33.
r hh
hr
rh
−
= ⇒=−
/2 / / /
2
(3 3 ) 0 .
3
Vr r V r
π
= − ⇒ =⇒=
Vậy
( )
4
9
2
mV
π
=
Đáp án B.
Câu 38: Cho hình chóp
.S ABCD
có đáy là hình vuông tâm O cạnh
a
. Tam giác SAB cân tại S và nằm
trong mặt phẳng vuông góc với đáy. Khoảng cách từ O đến mặt phẳng (SCD) là
2
4
a
. Tính
thể tích khối chóp
.S ABCD
.
A.
3
a
. B.
3
3
3
a
.
C.
3
3
6
a
. D.
3
3
a
.

NTTL Trang 20/29
Hướng dẫn:
I
là trung điểm AB. Ta có
()SI ABCD
⊥
2
( ;( )) 2 ( ;( ))
2
a
d I ABCD d O ABCD= =
SI a
⇒=
3
3
a
V⇒=
Đáp án: D
Câu 39: Nghiệm của bất phương trình
5
2
xx
ee
−
+<
là
A.
ln 2
ln 2.
x
x
<−
>
B.
ln 2 ln 2.x− <<
C.
1
2
2.
x
x
<
>
D.
1
2.
2
x<<
Hướng dẫn giải.
2
5
2 5 20
2
1
2
2
ln2<x<ln2.
xx x x
x
ee e e
e
−
+ < ⇔ − +<
⇔ < < ⇔−
Đáp án B.
Câu 40: Tìm số phức
z
thỏa
13 3
z iz i−+ = + −
và
3
zi−−
nhỏ nhất .
A .
1 3.zi= +
B.
1 3.zi
=−+
C.
2 2.
zi= +
D.
2 2.zi
= −
Hướng dẫn giải.
Gọi
( )
( ) (
)
1; 3 , 3; 1 , 3; 1 .
E NI−−
(
)
;
M xy
là điểm biểu diễn số phức
z
.
Ta có
ME MN=
và
MI
nhỏ nhất
Do đó M là hình chiếu của I trên trung trực
.
EN
Suy ra
( )
2;2 .
M
Đáp án C.
Câu 41: Cho hàm số
( ) ( )
42
0y f x ax bx c a= =++ ≠
có
( )
( ) ( )
;0
min 1
fx f
−∞
= −
. Tìm giá trị
nhỏ nhất của hàm số
( )
y fx=
trên đoạn
1
;2 .
2

NTTL Trang 21/29
A.
8.
ca+
B.
7
.
16
a
c
−
C.
9
.
16
a
c
+
D.
.ca−
Hướng dẫn giải.
Nếu
0
a
<
,
( )
lim
x
fx
→−∞
= −∞
nên không có giá trị nhỏ nhất trên
( )
;0 .−∞
Do đó
0.a >
Mặt khác
( )
/
10f
−=
. Suy ra
2.ba= −
Ta được
(
)
42
2.
f x ax ax c=−+
Hơn nữa,
(
)
/
0
01
1
x
fx x
x
=
=⇔=−
=
Do vậy
( ) ( ) (
)
1
;2
2
1
min min , 1 , 2
2
7
; ;8 .
16
fx f f f
a
c cac a ca
=
=− −+ =−
Đáp án D.
Câu 42: Trong không gian Oxyz, cho tam giác ABC với
(
)
1; 2; 5A
,
( )
1; 4; 3B
,
( )
5; 2; 1C
và
mặt phẳng
( ) : 3 0.Pxyz−−−=
Gọi M là một điểm thay đổi trên mặt phẳng (P).
Tìm giá trị nhỏ nhất của biểu thức .
A.
553
min
9
F =
. B.
553
min
3
F
=
. C.
min 65F =
. D.
9
min
553
F =
.
Hướng dẫn giải.
Gọi G là trọng tâm của ∆ABC ⇒ G ;
Ta có
222 2
3MG GA GB GC= +++
F nhỏ nhất ⇔ MG
2
nhỏ nhất ⇔ M là hình chiếu của G lên (P) .
F MA MB MC
222
=++
78
; ;3
33
GA GB GC
222
56 32 104 64
99 9 3
+ + =++ =
( ) ( ) ( )
F MA MB MC MG GA MG GB MG GC
222
222
=++=+++ ++

NTTL Trang 22/29
Vậy F nhỏ nhất bằng .
Đáp án A.
Câu 43: Trong không gian Oxyz, cho mặt cầu
(
)
2 22
: 2 4 2 30
Sx y z x y z+ + − + + −=
Và đường thẳng
11
:.
2 11
xyz
d
−+
= =
−
Mặt phẳng
( ): 1 0P ax by cz+ + +=
chứa d cắt mặt cầu
(S) theo giao tuyến là đường tròn (C) có bán kính nhỏ nhất. Tính giá trị biểu thức
4 3 2.T abc=++
A.
9.T =
B.
5.T =
C.
1.T =
D.
5.T = −
Hướng dẫn giải.
Tâm
( )
1; 2; 1I −−
, bán kính
3R =
của mặt cầu (S).
Bán kính đường tròn giao tuyến
(
)
( )
22
;r R d IP
= −
.
Để bán kính
r
nhỏ nhất thì
( )
( )
;dI P
lớn nhất.
Gọi H là hình chiếu của I lên d ; K là hình chiếu của I lên (P).
Ta có d(I,(P))= IK IH
Do đó d(I,(P))
max
AK = AH K H
Mặt phẳng (P) đi qua
(1; 1; 0)H −
và nhận
( )
0;1;1IH
làm véctơ pháp tuyến
Do đó
( ) : 1 0.Pyz++=
Đáp án B.
Câu 44: Cho hàm số
( )
y fx=
xác định trên
R
và có hàm số
( )
( )
( )
( )
/2 2
1 2 2 2.f x x x x mx m= − − − ++
Có bao nhiêu giá trị nguyên của tham
số
m
để hàm số
( )
2y fx= +
có đúng ba điểm cực trị?
A.
2.
B.
3.
C.
4.
D.
5.
Hướng dẫn giải.
MG d G P
78
33
33
19
( ,( ))
111 33
− −−
= = =
++
2
19 64 553
3.
39
33
+=
≤
⇔
⇔
≡

NTTL Trang 23/29
Số điểm cực trị của hàm số
( )
2y fx
= +
bằng số điểm cực trị của hàm số
(
)
.y fx=
Để hàm số
( )
2y fx= +
có đúng ba điểm cực trị thì
( )
2
2 20g x x mx m
= − + +=
vô nghiệm,
nghiệm kép hoặc có nghiệm
1, 2.±
TH1.
( )
2
2 20g x x mx m
= − + +=
vô nghiệm, nghiệm kép
/2
20
1 2.
mm
m
∆
⇔ = − −≤
⇔− ≤ ≤
TH2.
( )
2
2 20g x x mx m= − + +=
có nghiệm
1, 2.±
Suy ra
( )
( )
(
)
/
1
0
2
10
1
10
3
20
2
m
m
g
m
g
m
g
m
∆
≤−
≥
≥
−=
⇔
= −
=
=
=
=
Thử lại
1
3
5
x
m
x
=
= ⇒
=
,nhận
1, 2mm
=−=
,m=3
Vậy có 5 giá trị nguyên của
m
là
1, 0, 1, 2, 3−
Câu 45: Đáp án C. [4] Cho hàm số
( )
32
f x ax bx cx d
= + ++
có đồ thị như
hình vẽ. Tìm số tiệm cận đứng của đồ thị hàm số
(
)
( )
( ) (
)
2
2
32 1xx x
gx
xf x fx
−+ −
=
−
A. 3. B. 4.
C. 5 D. 6.
Hướng dẫn giải.
0x =
không là tiệm cận đứng của đồ thị hàm số vì biểu thức
1x
−
không có nghĩa.
( ) ( )
( )
( )
2
0
0
1
fx
f x fx
fx
=
−=⇔
=
( )
( )
( )
1
2
0;1
0
20 2
xx
fx
xx
= ∈
= ⇔
− =⇔=
1
xx=
không là tiệm cận đứng
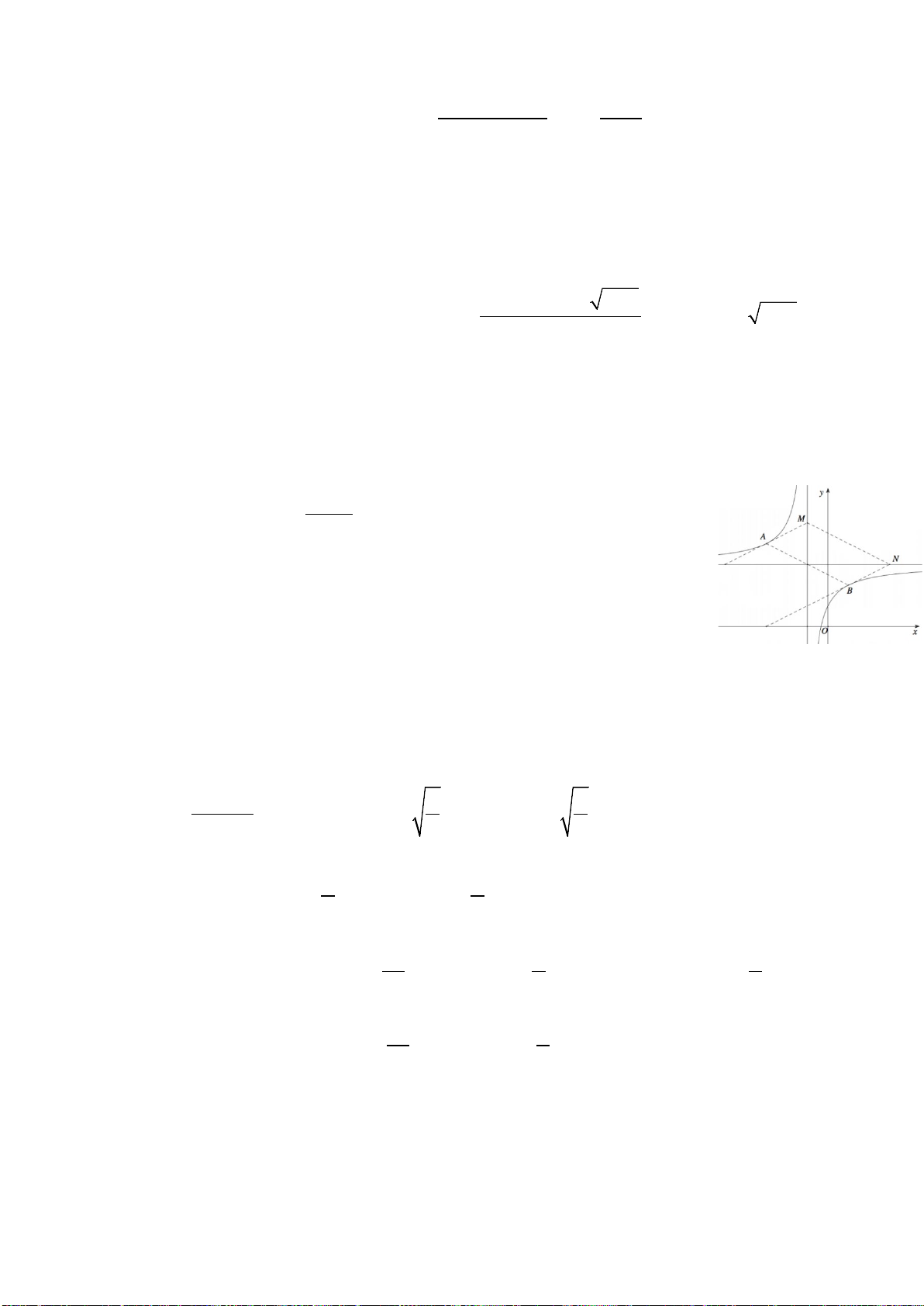
NTTL Trang 24/29
2x =
là tiệm cận đứng vì
( )
(
)(
)
(
)
2
22 2
12
1
lim lim lim .
2
2
xx x
xx
x
gx
x
x
++ +
→→ →
−−
−
= = = +∞
−
−
( ) ( )
(
)
2
3
1
1 1; 2
2;
x
fx x x
xx
=
=⇔=∈
= ∈ +∞
1x
=
không là tiệm cận đứng vì
( )
( )( )
( )
11 1
12 1
lim lim lim 2 1 0
1
xx x
xx x
gx x x
x
++ +
→→ →
−− −
= = − −=
−
23
,xxxx= =
là các tiệm cận đứng của đồ thị hàm số.
Vậy có 3 tiệm cận đứng của đồ thị hàm số.
Đáp án B.
Câu 46: Cho hàm số
31
1
x
y
x
+
=
+
có đồ thị
( )
C
. Gọi A, B là hai điểm thuộc
( )
C
sao cho tiếp tuyến của
( )
C
tại A, B song song với nhau. Các
tiếp tuyến này lần lượt cắt tiệm cận đứng, tiệm cận ngang của
(
)
C
tại M, N (tham khảo hình vẽ). Tứ giác AMNB có chu vi nhỏ nhất
bằng bao nhiêu?
A.
16.
B.
8.
C.
20.
D.
12.
Hướng dẫn giải.
Hoành độ của hai điểm A, B là nghiệm của phương trình
( )
/
2
2 22
0 1 1 0.
1
y k k x aa
kk
x
= ⇔ = > ⇔ =−± =−± = >
+
Tọa độ điểm
22
1 ;3 , 1 ;3 .Aa Ba
aa
−− + −+ −
Phương trình tiếp tuyến tại A là
( )
2
22
13y xa
aa
= ++ ++
. Suy ra điểm
4
1; 3
M
a
−+
Phương trình tiếp tuyến tại B là
( )
2
22
13y xa
aa
= +− +−
. Suy ra điểm
( )
2 1; 3Na−
Ta có
AB MN=
. Do đó tứ giác AMNB là hình bình hành.
Chu vi của hình bình hành là

NTTL Trang 25/29
(
)
22 2
22 2
16 4 4
2 2 4 6 12.
AB AM a a a
aa a
+ = ++ + = +≥
Dấu “=” xảy ra khi
2.
a =
Đáp án D.
Câu 47: Cho hàm số
( )
y fx=
liên tục trên
R
và có đồ thị như hình vẽ. Tìm tất cả các giá trị
thực của tham số
m
để bất phương trình
( )
32
2 32fx x x m+> +
nghiệm đúng với
mọi
(
)
1; 3 .
x
∈
A.
10.m
<−
B.
5.m <−
C.
3.m
<−
D.
2.m <−
Hướng dẫn giải.
( ) ( )
( )
( )
( )
32
32
1; 3
3
, 1; 3
22
3
min , ( ) .
22
xx
ycbt m f x x
xx
m g x gx f x
−
⇔ < + − ∀∈−
⇔< = + −
Quan sát đồ thị hàm số, ta có
( )
( )
( )
1; 3
min 2 3.fx f
−
= = −
Mặt khác
( )
( ) ( )
1; 3
min 2 2,hx h
−
= = −
( )
32
3
.
22
xx
hx= −
Vậy
5.m <−
Đáp án B.
Câu 48: : Cho
,ab
là hai số thực dương thỏa mãn
22
1
ab+>
và
(
)
22
log 1.
ab
ab
+
+≥
Tìm giá trị lớn
nhất của biểu thức:
2 4 3.P ab=+−
A.
10.
B.
10
.
2
C.
25
. D.
52
.
2
Hướng dẫn giải.
Ta có
( )
22
22
22
1 11
log 1 1.
2 22
ab
a b a b do a b
+
+ ≥⇔ − + − ≤ + >

NTTL Trang 26/29
22
1 1 11
2 4 3 2 4 20 10.
2 2 22
P ab a b a b
= + −= − + − ≤ − + − ≤
Vậy giá trị lớn nhất
10.
P
=
Đáp án A.
Câu 49: Cho hàm số
( ) ( )
32
3 29 6y x m x m xm= + + − + ++
có đồ thị
( )
C
. Tìm tất cả các giá
trị thực của tham số
m
để
( )
C
có hai điểm cực trị sao cho khoảng cách từ gốc tọa độ
O
đến đường thẳng nối hai điểm cực trị là lớn nhất.
A.
32
6.
2
m =−±
B.
32
3.
2
m =−±
C.
3 6 2.
m =−±
D.
6 6 2.m =−±
Hướng dẫn giải.
Điều kiện có cực trị
( )
( )
2
3 32 9 0mm+ + +>
Phương trình đường thẳng qua hai điểm cực trị là
22
28 28
: 89
93 93
mm mm
yx
∆
=− −− + ++
∆
luôn đi qua điểm có tọa độ
( )
1; 1 .M
( )
;2d O OM
∆
≤=
. Dấu “=” xảy ra khi
OM
∆
⊥
hay
2
2 8 32
8 .1 1 6 .
93 2
mm
m
− − − =−⇔ =−±
Đáp án A.
Câu 50: Cho đoạn thẳng AB cố định trong không gian và có độ dài
2AB =
. Qua các điểm A và B lần
lượt kẻ các đường thẳng Ax và By chéo nhau thay đổi nhưng luôn vuông góc với đoạn thẳng
AB. Trên các đường thẳng đó lần lượt lấy các điểm M, N sao cho
23
AM BN+=
. Tính
thể tích
V
lớn nhất của khối tứ diện ABMN.
A.
1
3
V
=
. B.
3
8
V =
. C.
1
2
V =
. D.
32
4
V =
.
Hướng dẫn:
Đặt
;AM x BN y= =
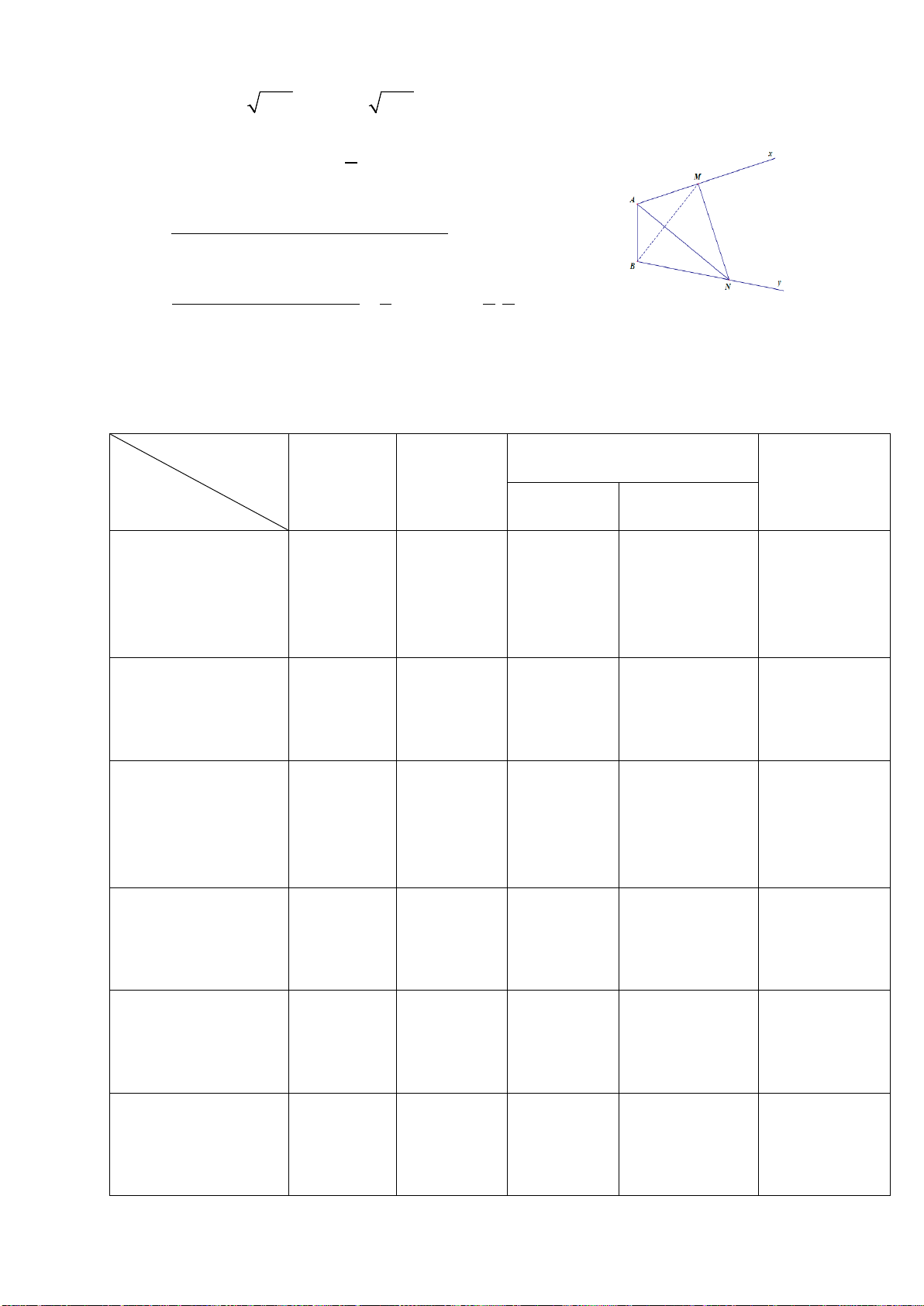
NTTL Trang 27/29
Ta có
2 22a b ab+≥
3 22
ab⇔≥
9
8
ab⇔≤
. . ( ; )sin( ; )
6
AM BN d AM BN AM BN
V =
2 . sin( ; ) 1
63
AM BN AM BN
V ab
⇔= ≤
19
.
38
V⇔≤
Đáp án: B
Mức độ
Chủ đề
Nhận biết Thông hiểu
Vận dụng
Tổng
Thấp
cao
Ứng dụng đạo hàm
khảo sát hàm số
Tỉ lệ :28 %
4
0,8
2
0,4
2
0,4
6
0,6
14
2,8
Mũ - Logarit
Tỉ lệ : 14 %
2
0,4
3
0,6
1
0,2
1
0,2
7
1,4
Nguyên hàm - Tích
phân
Tỉ lệ : 10 %
1
0,2
2
0,4
2
0,4
5
1,0
Số phức
Tỉ lệ : 10 %
1
0,2
2
0,4
2
0,4
5
1,0
Dãy số - Cấp số
Tỉ lệ : 2 %
1
0,2
1
0,2
Quan hệ vuông góc
Tỉ lệ : 4 %
2
0,4
2
0,4
NTTL Trang 28/29
Mức độ
Chủ đề
Nhận biết Thông hiểu
Vận dụng
Tổng
Thấp
cao
Khối đa diện, thể tích
khối đa diện
Tỉ lệ : 6 %
1
0,2
1
0,2
1
0,2
3
0,6
Khối tròn xoay, thể
tích khối tròn xoay
Tỉ lệ : 6 %
1
0,2
1
0,2
1
0,2
3
0,6
Hình học giải tích
Oxyz
Tỉ lệ : 16 %
2
0,4
3
0,6
1
0,2
2
0,4
8
1,6
Tổ hợp - Xác suất
Tỉ lệ : 6 %
1
0,2
1
0,2
2
0,4
Tổng
100 %
14
2,8
13
2,6
13
2,6
10
2,0
50
10,0

NTTL Trang 29/29
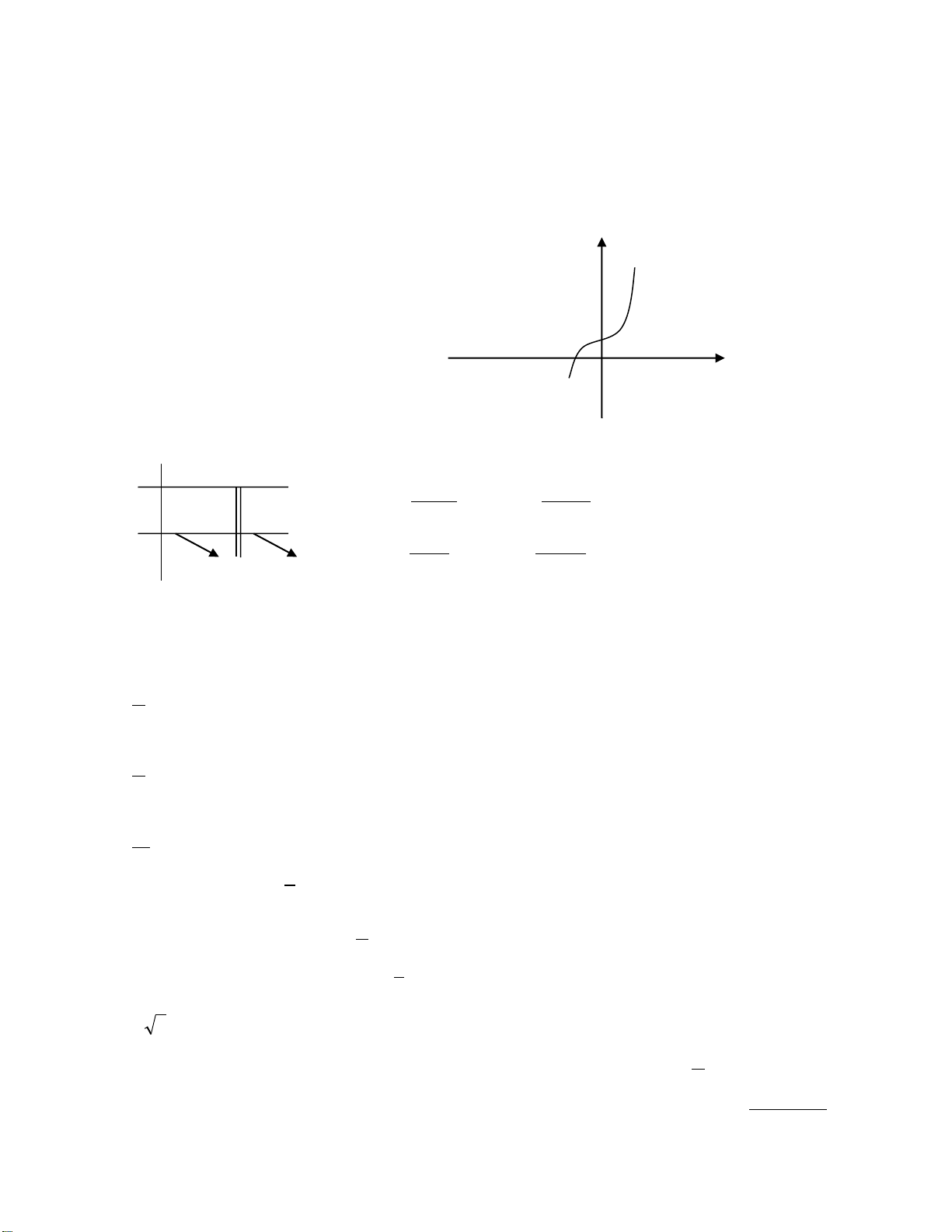
NTTL Trang 1/10
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
ĐỀ ÔN THI THPT QUỐC GIA NĂM 2019
TRƯỜNG THPT LÊ HỒNG PHONG
Bài thi: TOÁN
Đề thi có 07 trang
(Thời gian làm bài: 90 phút, không kể thời gian phát đề)
Câu 1: Đồ thi hàm số nào sau đây có hình dạng như hình vẽ bên
Câu 2: Hàm số nào sau đây có bảng biến thiên như hình bên
Câu 3: Trong các tiếp tuyến tại các điểm trên đồ thị hàm số
32
32yx x=−+
, tiếp tuyến có hệ số
góc nhỏ nhất bằng:
A. - 3 B. 3 C. - 4 D. 0
Câu 4: Đường thẳng y = m cắt đồ thị hàm số
3
32yx x
=−+
tại 3 điểm phân biệt khi :
A.
04m
<<
B.
04m
≤<
C.
04
m<≤
D.
4m >
Câu 5. Hàm số
32
3y x x mx=−+
đạt cực tiểu tại x = 2 khi :
A.
0
m =
B.
0m ≠
C.
0
m >
D.
0
m <
Câu 6: Hàm số
32
1
( 1) ( 1) 1
3
y xmxmx= ++ +++
đồng biến trên tập xác định của nó khi:
A.
1m >−
B.
10m−≤ ≤
C.
0m <
D.
10
m−< <
Câu 7: Xác định m để hàm số y =
3
1
x
3
+ (m + 1)x
2
+ 4x + 7 có độ dài khoảng nghịch biến bằng
2
5
A. m = -2, m = 4 B. m = 1, m = 3 C. m = 0, m = -1 D. m = 2, m = -4
Câu 8: Viết phương trình đường thẳng qua hai điểm cực trị của đồ thị hàm số y =
2
54
2
+
−+
x
xx
−∞
2
21 23
..
22
3 27
..
22
xx
Ay By
xx
xx
Cy Dy
xx
−
−−
= =
−+
+−
= =
−−
−∞
−
−
+∞
'y
x
y
2
2
+∞
O
y
x
1
3
3
3
3
. 31
. 31
. 31
. 31
Ay x x
By x x
Cy x x
Dy x x
−
=++
=−+
=−− +
=−+ +

NTTL Trang 1/10
A. y = 4x + 1 B. y = x – 5 C. y = 4x – 5 D. y = 8x +1
Câu 9: Giá trị nhỏ nhất của hàm số y =
46 +−
− xx
đạt tại x
0
, tìm x
0
.
A. x
0
= -
10
B. x
0
= - 4 C. x
0
= 6 D. x
0
=
10
Câu 10: Một hành lang giữa hai nhàcó hình dạng của một lăng trụ đứng. Hai mặt bênABA’B’ và
ACA’C’??? là hai tấm kính hình chữ nhật dài 20 m , rộng 5m. Gọi x (mét) là độ dài của cạnh BC.
Hình lăng trụ có thể tích lớn nhất bằng bao nhiêu ?
A. Thể tích lớn nhất
3
250( )Vm
=
B. Thể tích lớn nhất
3
5 2( )Vm=
C. Thể tích lớn nhất
3
50( )Vm=
D. Thể tích lớn nhất
3
2500( )Vm=
Câu 11: Xác định tất cả giá trị m để đồ thị hàm số y =
1
42
2
−
+−
x
xx
cắt đường thẳng y = m (x-4) tại hai
điểm phân biệt.
A. m < -2, m >
3
2
, m ≠1 B. m ≠ 1 C. ∀ m D. – 2 < m <
3
2
, m ≠ 0
Câu 12: Tính N = log
49
32 nếu log
2
14 = m
A. N = 3m + 1 B. N = 3m – 2 C. N =
5
22
m −
D. N =
1
1m
−
Câu 13: Cho hàm số f(x) =
2
2 lnxx+
. Tính f’(1)
A.
3
B. -
3
C. 1 D. 0
Câu 14: Tìm giới hạn
2 32
0
lim
x
x
ee
x
+
→
−
A. e
2
B. 3e
2
C. -3e
2
D.–e
2
Câu 15: Tập nghiệm của phương trình
2
31
3
log (4 ) 2log (4 ) 15xx−− −=
là:
A. {5; -3} B. {
971
243
; -23} C. {3
5
; 3
-3
} D. {-239;
107
27
}
Câu 16: Giải bất phương trình log
2
(x
2
– 4x + 5) ≤ 4
A. -7 ≤ x < -1 B. -3 ≤ x < -1 hoặc 5 < x ≤ 7 C. -3 ≤ x ≤ 7 D. Vô nghiệm
(đáp án đúng là:
2 15 2 15x− ≤≤+
)
Câu 17: Giải hệ phương trình
2(log log ) 5
8
yx
xy
xy
+=
=
A. (4; 16), (2; 4) B. (2; 4), (4; 3) C. (1; 4), (4; 2) D. (2; 4), (4; 2)

NTTL Trang 1/10
Câu 18: Tìm miền xác định của các hàm số y =
2
log (4 ) 1x−−
.
A. (-
∞
; 4) B. (-
∞
; 2) C. (-
∞
; 21] D. [2; 4)
(đáp án đúng là:
(
]
;2x ∈ −∞
)
Câu 19: Gọi M = log
3
4 và N = log
4
1
3
. Bất đẳng thức nào sau đây đúng?
A. M > N > 1 B. M > 0 > N C. 1 > M > N D. 0 > M > N
Câu 20: Khẳng định nào sau đây đúng?
A.
( )
!
!!
k
n
k
C
nnk
=
−
. B.
( )
!
!
k
n
k
C
nk
=
−
. C.
( )
!
!
k
n
n
C
nk
=
−
. D.
( )
!
!!
k
n
n
C
knk
=
−
.
Câu 21: Phương trình
( )( )
8
512 1024 16 4 512 1024x xx x− + −= + − −
có bao nhiêu nghiệm?
A.
4
nghiệm. B.
3
nghiệm. C.
8
nghiệm. D.
2
nghiệm.
Câu 22: Tính tích phân I =
5
2
0
sin xdx
π
∫
A.
5
6
B.
3
5
C.
8
15
D.
5
12
Câu 23: Tính tích phân I =
2
2
0
sin 3x os 2xdx
c
π
∫
.
A.
2
3
B.
5
42
−
C.
4
7
D.
1
21
−
Câu 24: Tính diện tích hình phẳng giới hạn bởi các đường y = x
3
– 6x
2
+ 12x – 8, trục tung và
đường thẳng y = 1.
A. S =
16
3
B.
27
4
S
=
C. S =
2
5
D. S =
141
5
Câu 25: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y =
21
2
x
x
+
−
; tiệm cận ngang và hai
đường thẳng x = 3; x = e + 2 được tính bằng:
A.
2
3
2x 1
x
2
e
d
x
+
+
−
∫
B.
2
3
5
x
2
e
d
x
+
−
∫
C.
2
3
ln 2
e
x
+
−
D. 5 – e
Câu 26: Tính thể tích vật thể giới hạn bởi các đường: x
2
+ y – 5 = 0 và x + y – 3 = 0 khi quay
quanh trục Ox.
A. 2
π
B.
53
15
π
C.
153
5
π
D.
31
13
π

NTTL Trang 1/10
Câu 27: Thể tích của vật thể tròn xoay tạo ra khi quay quanh trục Ox hình giới hạn bởi các
đường y =
3
3
x
; y = x
2
được tính bằng công thức nào sau đây?
A.
16
7
π
B.
81
5
π
C.
347
21
π
D.
486
35
π
Câu 28: Cho tập hợp
1; 2;3; 4;5;6;7;8;9A
. Gọi
S
là tập hợp các số tự nhiên có 4 chữ số lập
từ các chữ số thuộc tập
A
. Chọn ngẫu nhiên một số từ
S
, xác suất để số được chọn chia hết cho
6
bằng
A.
9
.
28
B.
4
.
27
C.
4
.
9
D.
1
.
9
Câu 29: Tính i
2009
A.-1 B. 1 C. –i D. i
Câu 30: Tính:
54
43
i
i
−
−
A.
32
25 25
i
−
B.
41 8
25 25
i
−
C. -
41 8
25 25
i
−+
D.
41
25 25
i
−−
Câu 31: Cho số phức
z
thỏa mãn:
( )
3
13
1
i
z
i
+
=
−
. Tìm môđun của
z iz+
.
A.
42
. B.
4
. C.
82
. D.
8
.
Câu 32: Xác định tập hợp điểm biểu diễn số phức z trên mặt phẳng phức thỏa
zi
zi
−
+
là số thực
A. Đường tròn phương trình x
2
+ y
2
= 1 bỏ đi điểm (0; -1)
B. Hyperbol phương trình x
2
– y
2
= - 1 bỏ đi điểm (0; -1)
C. Trục tung bỏ đi điểm (0; -1)
D. Trục hoành bỏ đi điểm (0; -1)
Câu 33: Kí hiệu
0
z
là nghiệm phức có phần thực âm và phần ảo dương của phương trình
2
2 10 0zz++=
. Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn số phức
2017
0
wi z=
?
A.
( )
3; 1M −
. B.
( )
3; 1M
. C.
( )
3; 1M −
. D.
( )
3; 1M −−
.
Câu 34: Giải phương trình trong tập số phức z
2
– (5 + 2i)z + 10i = 0
A. z = 5 2i B. z = 5, z = 2i C. z = 2, z = -5i D. z = -2 5i

NTTL Trang 1/10
Câu 35: Cho hình hộp chữ nhật ABCD.A’B’C’D’ với AB = 5dm, AD = 10dm và đường chéo
AC’ hợp với đáy một góc
ϕ
sao cho sin
ϕ
=
2
3
. Tính thể tích hình hộp.
A. 220dm
3
B. 300dm
3
C. 410dm
3
D. 500dm
3
Câu 36: Cho hình lập phương ABCD. A'B'C'D' cạnh bằng
2
3
a
dm. Thể tích của hình lập
phương bằng.
A.
3
2a 2
27
dm
3
. B.
3
2a 3
27
dm
3
. C.
2
2a 2
27
dm
3
. D.
3
2a 3
9
dm
3
.
Câu 37: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=16
3
dm, AD=30
3
dm
và SA=SB=SC=SD. Biết góc giữa SA và đáy bằng 30
0
. Tính thể tích hình chóp S.ABCD
A. 9 580dm
3
B. 8 160dm
3
C. 7 250dm
3
D. 4 320dm
3
Câu 38: Cho hình chóp SABCD có đáy là hình vuông cạnh a, mặt bên (SAB) là tam giác đều
nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ điểm A đến mặt phẳng
(SCD) bằng
A.
21
7
a
B. a C.
21
14
a
D.
21a
Câu 39: Cho hình chóp tứ giác đều với cạnh bên bằng 2
3
cm có đỉnh trùng với đỉnh hình nón.
Biết rằng cạnh bên hình chóp hợp với đáy một góc 60
0
và đáy hình chóp ngoại tiếp đường tròn
đáy hình nón. Tính thể tích khối nón.
A.
3
2
π
cm
3
B.
7
π
cm
3
C.
10
π
cm
3
D.
13
π
cm
3
Câu 40: Một hình trụ có bán kính đáy 2cm và có thiết diện qua trục là một hình vuông. Tính diện
tích xung quanh của hình trụ
A. 8
π
cm
2
B. 4
π
cm
2
C. 16
π
cm
2
D. 2
π
cm
2
Câu 41: Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Xác định bán kính mặt cầu ngoại
tiếp hình chóp S.ABCD
A.
2
4
a
B.
2
2
a
C.
3
2
a
D.
2
a
Câu 42: Cho cấp số cộng
( )
n
u
thỏa mãn
4
46
10
26
u
uu
=
+=
có công sai là
A.
3d = −
. B.
3d =
. C.
5d =
. D.
6d =
.

NTTL Trang 1/10
Câu 43: Viết phương trình mặt phẳng đi qua điểm A (1; -3; 5) và chứa đường thẳng d:
12
251
xy z−+
= =
−
A. 31x + 13y + 3z – 7 = 0 B. 2x + 3y – 4z + 3 = 0
C. 27x + 29y – 13z + 10 = 0 D. 14x – 15y – 10z + 3 = 0
Câu 44: Tìm toạ độ điểm đối xứng của điểm A(-3; 2; 5) qua mặt phẳng (P): 2x+3y–5z–13=0
A. (1; 8; -5) B. (2; -4; 3) C. (7; 6; -4) D. (0; 1; -3)
Câu 45: Viết phương trình mặt phẳng (P) chứa hai đường thẳng d
1
:
123
231
xy z−+−
= =
và d
2
:
22
43
3
xt
yt
zt
=−+
= +
= +
A. x + 2y – 5z + 12 = 0 B. 7x + 2y – z + 3 = 0
C. 2x + y – 7z + 21 = 0 D. 2x – y + 7z + 5 = 0
Câu 46: Viết phương trình mặt phẳng (P) qua A(-2; -3; 1) và vuông góc với đường thẳng d:
2z 5 0
20
x
yz
+ −=
++=
A. 3x – 2y – 4z + 1 = 0 B. 2x – y – z + 2 = 0
C. 2x + y – z + 8 = 0 D. 5x – 11y – 3z + 1 = 0
Câu 47: Viết phương trình mặt phẳng (Q) chứa đường thẳng d:
21
1 21
x yz−−
= =
và vuông góc với mặt phẳng (P): 2x + y = 0
A. 3x–2y–7=0 B. x–2y+3z=0 C. 2x+y–4z=0 D. 3y+2z+7=ư0
Câu 48: Tính khoảng cách từ điểm M(2; 3; 3) đến đường thẳng
111
41 3
xyz−−−
= =
−
A.
15
B.
10
C. 3 D. 4
Câu 49: Viết phương trình mặt phẳng (Q) chứa đường thẳng d có phương trình
234
231
xyz− +−
= =
và vuông góc với mặt phẳng (Oyz)
A. x + y – 2z + 4 = 0 B. y – 3z + 15 = 0
C. x + 4y – 7 = 0 D. 3x + y – z + 2 = 0

NTTL Trang 1/10
Câu 50: Viết phương trình đường thẳng d qua M(1; -2; 3) và vuông góc với hai đường thẳng
d
1:
2x 0
10
yz
xy
−−=
+ −=
, d
2
:
1
2
13
xt
yt
zt
= −
= +
= +
A.
1
2
3
xt
yt
z
= +
=−+
=
B.
13
2
3
xt
yt
zt
= +
=−+
= +
C.
1
22
33
xt
yt
zt
= −
=−−
= −
D.
1
2
3
x
yt
zt
=
=−+
= +
-------HẾT---------
Câu
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
ĐA
A
A
A
A
A
B
D
D
C
A
A
C
D
C
B
E.
D
E.
B
D
Câu
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
ĐA
B
C
D
B
B
C
D
B
D
A
C
C
D
B
D
A
B
A
A
C
Câu
41
42
43
44
45
46
47
48
49
50
ĐA
B
B
A
A
C
C
B
C
B
A
HƯỚNG DẪN CHẤM
1A
2A
3A Hệ số góc tại điểm uốn là nhỏ nhất
4A
5A
'(2) 0
''(2) 0
y
y
=
>
6B Hàm số đồng biến trên tập xác định trên R
0
'0
0
a
y
>
≥⇔
∆≤
7D
2
' 2( 1) 4yx m x=+ ++
Điều kiện có khoảng nghịch biến là
1
'0
3
m
m
>
∆> ⇔
<−

NTTL Trang 1/10
Khoảng nghịch biến
(
)
12
;xx
với
12
,xx
là nghiệm của
'0y =
, có độ dài bằng
25
. Khi đó
12
25
xx
−=
( ) ( )
22
1 2 1 2 12
20 4 20x x x x xx⇔− =⇔+ − =
8A
9C
10A
23
5x 100 ( )
V xm= −
(0 10)x<<
. Hình lăng trụ có thể tích lớn nhất khi
5 2( )xm=
Suy ra max V =250
3
m
11A
12C
13D
14C
15B
16B
17D
18C
19B
20D
21B
22B
23D
24B
25B
2
3
5ln 2 5
e
Sx
+
= −=
26C
27D
28B
29D
30A
31C
32C
22
22
1 2x
( 1)
zi x y i
zi x y
− + −−
=
+ ++
là số thực khi phần ảo bằng 0
22
2x
0
( 1)xy
−
⇔=
++
33D
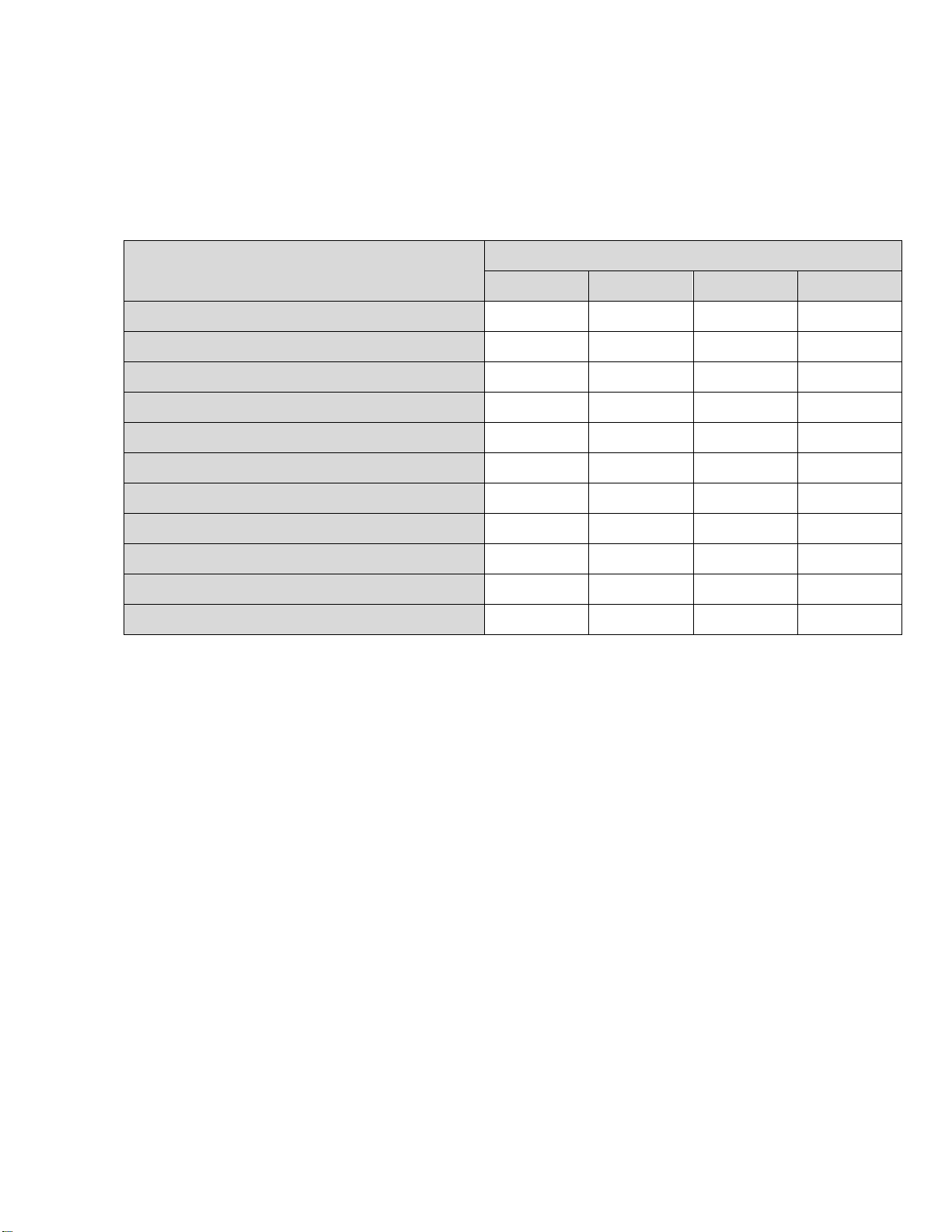
NTTL Trang 1/10
34B
35D
36A;37B;38A;39A;40C;41B;42B;43A;44A;45C;46C;47B;48C;49B;50A
CHỦ ĐỀ
MỨC ĐỘ
1
2
3
4
HÀM SỐ
3
4
2
1
MŨ – LÔGARIT
2
2
2
0
NGUYÊN HÀM – TÍCH PHÂN
2
1
2
1
SỐ PHỨC
1
2
2
1
KHỐI ĐA DIỆN
1
2
1
1
KHỐI TRÒN XOAY
1
1
1
0
HỆ TỌA ĐỘ OXYZ
3
3
1
1
GIỚI HẠN - TỎ HỢP – XÁC SUẤT
1
1
1
0
CSC-CSN
1
0
0
0
PHƯƠNG TRÌNH – BẤT PHƯƠNG TRÌNH
0
1
0
0
TỈ LỆ
30%
40%
20%
10%

NTTL Trang 1/10
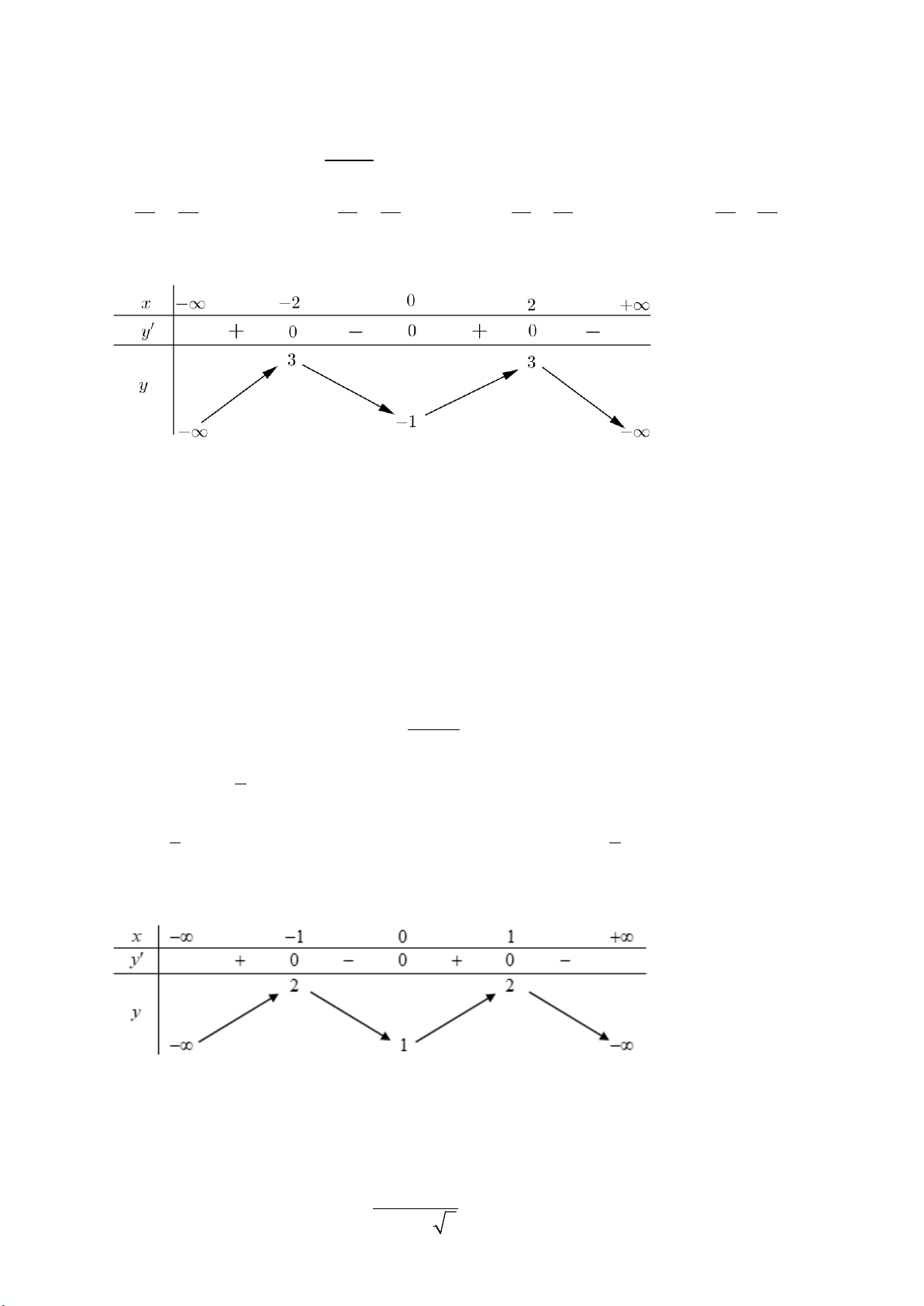
HĐT
Câu 1: Dạng a+bi của số phức
1
32i
là số phức nào dưới đây?
A.
32
13 13
i
B.
32
13 13
i
C.
32
13 13
i
D.
32
13 13
i
Câu 2: Cho hàm số
y fx
có bảng biến thiên như sau
Hàm số
y fx
nghịch biến trên khoảng nào dưới đây?
A.
;2
. B.
2; 0
. C.
0; 2
. D.
0;
.
Câu 3: Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1
:2
2
xt
dy t
zt
. Trong các điểm sau
điểm nào thuộc đường thẳng
d
?
A.
.2; 2;1A
B.
1;4;3A
. C.
4; 2; 7A
. D.
0; 2; 3A
.
Câu 4: Tập xác định của hàm số
7
25
log
1
x
y
x
là
A.
5
;1 ;
2
B.
\1R
C.
5
1;
2
. D.
5
;1 ;
2
Câu 5: Cho hàm số
y fx
có bảng biến thiên như hình vẽ sau.
Khẳng định nào sau đây đúng?
A.
2
C
x
Đ
. B.
2
CT
y
. C.
1
CT
y
. D.
0
C
y
Đ
.
Câu 6: Khối đa diện đều loại {3;5} có bao nhiêu đỉnh?
A. 12 B. 30 C. 4 D. 20
Câu 7: Tập xác định của hàm số
2 sin 5
cot 3
x
y
x
là
SỞ GD&ĐT KHÁNH HÒA
TRƯỜNG THPT HÀ HUY TẬP
ĐỀ THPT QUỐC GIA NĂM 2019
Môn: Toán
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
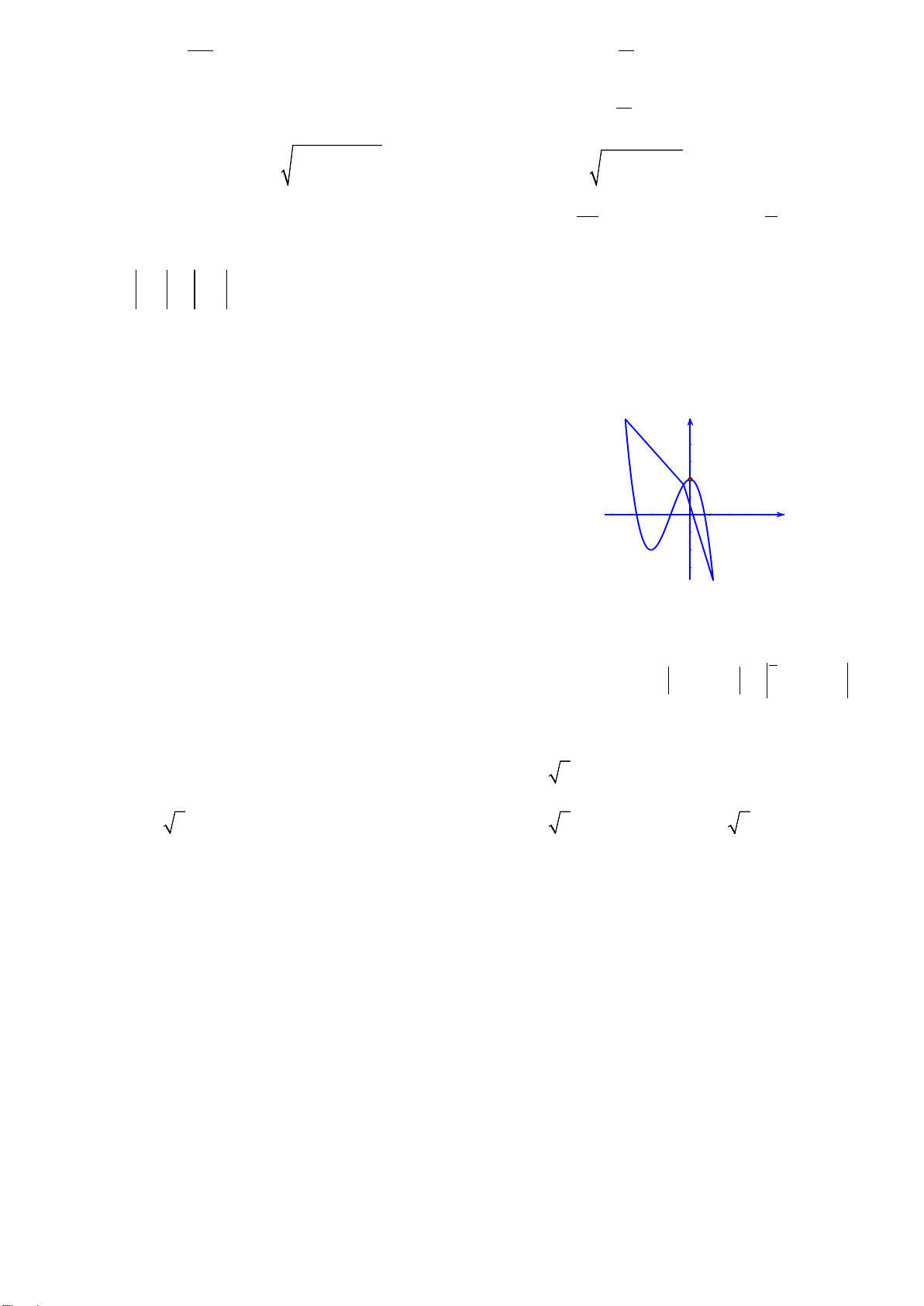
HĐT
A. D=R\
|
4
k
kZ
π
∈
B. D=R\
,|
6
k k kZ
π
ππ
+∈
C.
D=
{
}
|
k kZ
π
∈
. D. D=R\
,|
2
k k kZ
π
ππ
+∈
Câu 8: Biết hàm số
4
2
3
35y xx
có đạo hàm
2
3
. 3 5 (, )y ax b x x a b R
. Tính
ab
.
A.
1ab
B.
11ab
C.
44
3
ab
D.
4
3
ab
Câu 9: Cho hình vuông
ABCD
, khẳng định nào sau đây đúng?
A.
AB BC
. B.
AC BD
.
C.
AB
và
AC
cùng hướng. D.
AB CD
.
Câu 10: Giá trị lớn nhất của hàm số
42
45fx x x
trên đoạn
2; 3
bằng
A.
5
. B.
50
. C.
1
. D.
122
.
Câu 11: Đường cong trong hình bên là đồ thị của hàm số nào
dưới đây?
x
y
2
O
1
A.
32
32yxx
. B.
42
22yx x
.
C.
32
32yx x
. D.
32
32
yxx
.
Câu 12: Trên mặt phẳng tọa độ, tập hợp điểm biểu diển số phức
z
thỏa mãn
2 32z iz i
A. là đường thẳng
2 80xy
. B. là đường thẳng
10 2 8 0xy
.
C. là đường thẳng
10280xy
. D. là đường thẳng
10280xy
.
Câu 13: Cho hình lập phương
.''''
ABCD A B C D
có cạnh
2a
.Khi quay tam giác vuông
''AA C
xung
quanh cạnh góc vuông
'AA
ta được hình nón tròn xoay có diện tích xung quanh bằng
A.
2
6a
. B.
2
2 a
.
C.
2
26
a
. D.
2
6a
.
Câu 14: Trong không gian với hệ tọa độ
Oxyz
,trong các phương trình sau có bao nhiêu phương trình là
phương trình của mặt cầu?
222
1: 4 2 6 0x yz xyz
222
2: 2 0x y z xyz
22
3: 6 2 2 5 0xz xyz
222
4: 2 6 4 5 0x yz xyz
A. 3. B. 4. C. 2. D. 1.
Câu 15: Cho hình bình hành
ABCD
tâm
I
. Kết luận nào sau đây sai?(
u
T
là ký hiệu phép tịnh tiến theo
véc tơ
u
)
A.
()
AB
TD C
. B.
()
CD
TB A
. C.
()
AI
TI C
. D.
()
ID
TI B
.
Câu 16: Trong không gian với hệ tọa độ
Oxyz
,Tọa độ giao điểm
A
của mặt phẳng
: 2 60Px yz
với trục
Oy
là
A.
6; 0; 0 .A
B.
0; 3; 0A
. C.
0; 6; 0A
. D.
0; 0; 1A
.
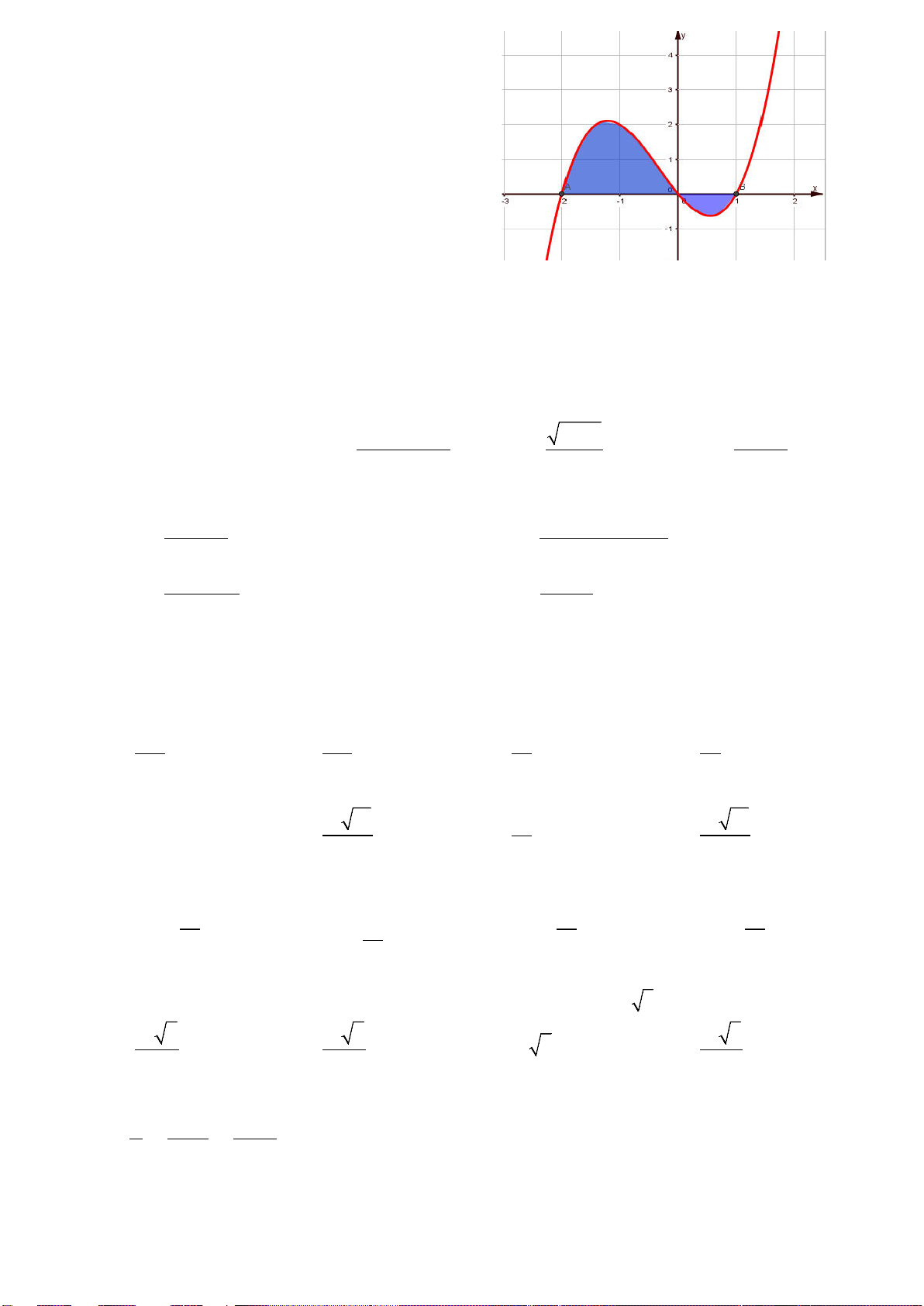
HĐT
Câu 17: Cho đồ thị hàm số
y fx
có đồ thị như
hình bên. Diện tích hình phẳng (phần tô đậm trong
hình) là
A.
01
20
S f x dx f x dx
B.
0
2
S f x dx
C.
21
00
S f x dx f x dx
D.
01
20
S f x dx f x dx
Câu 18: Đồ thị của hàm số nào dưới đây không có đường tiệm cận đứng ?
A.
log 1 .
yx
B.
2
32
.
2
xx
y
x
C.
3
.
2
x
y
x
D.
23
.
2
x
y
x
Câu 19: Trong bốn giới hạn sau đây, giới hạn nào có kết quả bằng 0?
A.
3
2
1
lim
2
n
nn
B.
2
3
21 3
lim
2
nn
nn
C.
21
lim
3.2 3
n
nn
D.
23
lim
12
n
n
Câu 20:
G
ọi
1
z
và
2
z
là các nghiệm phức của phương trình
2
2 50zz
. Tính
44
12
Pz z
A.
14
B.
14i
C.
14
i
D.
14
Câu 21: Một bình chứa 16 viên bi trong đó có 7 viên bi trắng, 6 viên bi đen và 3 viên bi đỏ. Lấy ngẫu
nhiên trong bình đó 3 viên bi. Tính xác suất sao cho cả 3 viên bi được lấy ra không có viên nào màu đỏ.
A.
143
.
280
B.
1
.
560
C.
1
16
. D.
1
.
28
Câu 22: Tính thể tich của khối chóp tam giác đều có cạnh đáy bằng a, cạnh bên bằng 2a.
A.
3
a
. B.
3
11
4
a
. C.
3
4
a
. D.
3
11
12
a
.
Câu 23: Phương trình
2
log 2 log 4x x xm
có nghiệm duy nhất khi và chỉ khi
A.
17
4
4
m
m
B.
17
4
m
C.
17
4
4
m
m
D.
17
4
4
m
m
Câu 24: Tính thể tích của khối lăng trụ tam giác đều có cạnh đáy bằng
2a
, cạnh bên bằng
2a
.
A.
3
3
3
a
B.
3
3
2
a
C.
3
3a
D.
3
6
2
a
Câu 25: Trong không gian với hệ tọa độ
Oxyz
, cho điểm
4; 3; 2
M
và đường thẳng
13
( ') :
112
xy z
d
. Phương trình đường thẳng
d
qua
M
, vuông góc và cắt
( ')d
là
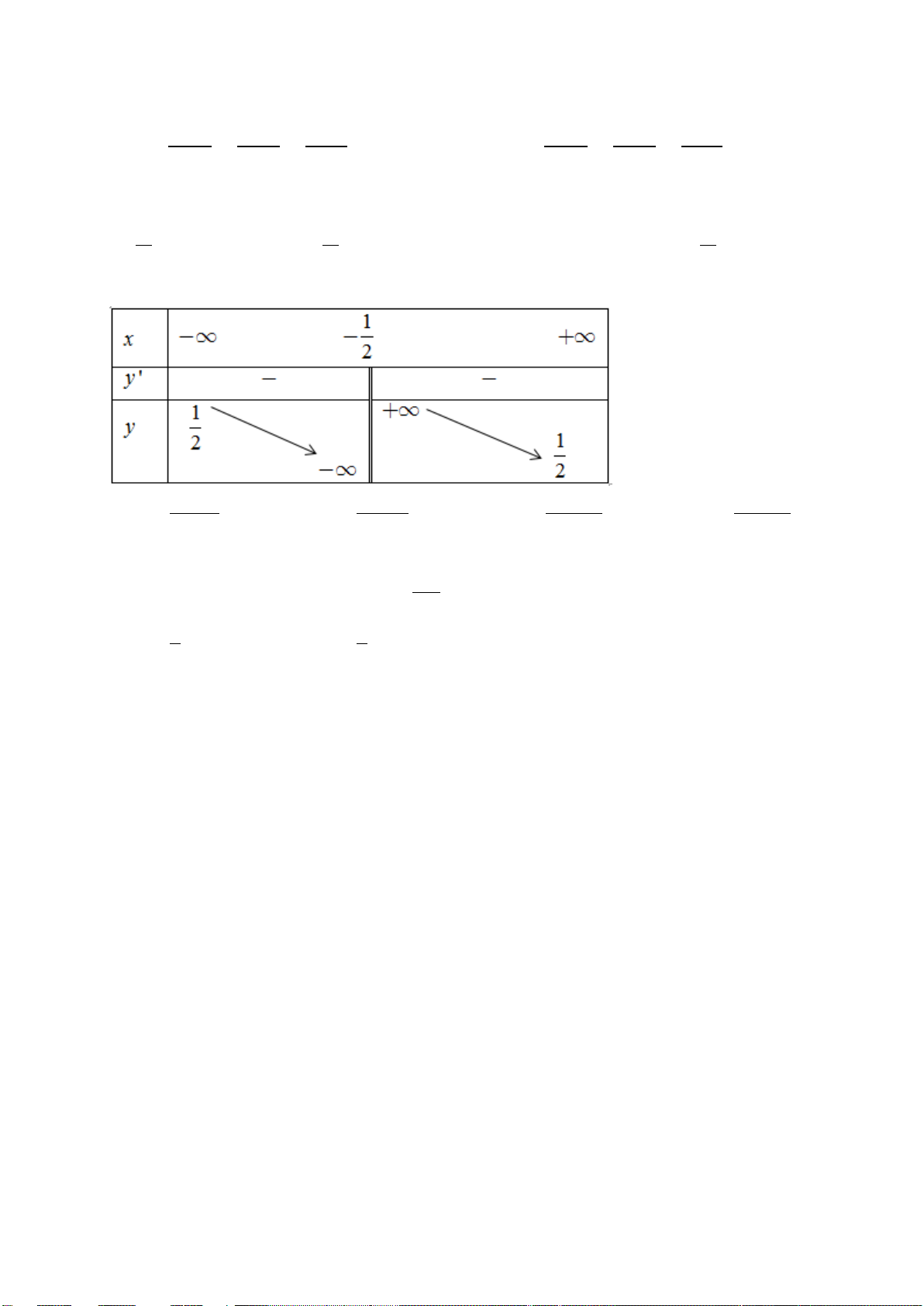
HĐT
A.
4
( ): 3 5
22
xt
dy t
zt
. B.
( ): 1 5
32
xt
dy t
zt
.
C.
432
( ):
241
xyz
d
. D.
432
( ): .
212
xyz
d
Câu 26: Cho hình lăng trụ
.'''ABC A B C
có thể tích là
V
. Gọi G là trọng tâm của tam giác
ABC
. Thể
tich của khối chóp
.'''GA B C
tính theo
V
là
A.
6
V
. B.
3
V
. C.
V
. D.
2
V
.
Câu 27: Bảng phía dưới là bảng biến thiên của hàm số nào sau đây?
A.
21
2
x
y
x
. B.
4
21
x
y
x
. C.
3
21
x
y
x
. D.
2
21
x
y
x
.
Câu 28: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành tâm
O
. Gọi
P
là trung điểm của
OD
,
I
là điểm thuộc đoạn
SD
, đặt
SD
k
ID
. Xác định
k
để
//IP SBC
.
A.
5
2
k
. B.
1
2
k
. C.
3k
.
D.
4k
.
Câu 29: Trong các đa diện sau, đa diện nào luôn nội tiếp được trong một mặt cầu:
A. Hình lăng trụ. B. Hình chóp tứ giác. C. Hình chóp ngũ giác. D. Hình hộp chữ nhật.
Câu 30: Ông An có một mảnh đất hình chữ nhật chiều dài gấp 3 lần chiều rộng nằm ở góc phần tư hai
con đường vuông góc giao nhau. Vì do nhu cầu đi lại của người dân nên chính quyền đã mở rộng hai con
đường đó về phía đất của ông An, nên chiều dài và chiều rộng của mảnh đất giảm đi 5m. Sau khi làm
đường xong mảnh đất của ông An vẫn là hình chử nhất có chiều dài gấp 4 lần chiều rộng. Hỏi diện tích
sau khi mở đường của mảnh đất là bao nhiêu?
A.
2
675 .Sm
B.
2
100 .Sm
C.
2
400 .Sm
D.
2
120 .Sm
Câu 31: Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
3; 2; 1 0; 2, ;1 2, 1; ; 0BA C
. Phương
trình mặt phẳng
ABC
là
A.
4 3 4 2 0.xyz
B.
4 3 4 10 0xyz
.
C.
4 3 4 10 0xyz
. D.
4 3 4 20xyz
.
Câu 32: Đẳng thức nào sau đây là đẳng thức đúng?
A.
8
(1 ) 16i
B.
8
(1 ) 16ii
C.
8
(1 ) 16i
D.
8
(1 ) 16ii
Câu 33: Trong không gian với hệ tọa độ
Oxyz
, phương trình mặt cầu tâm
1; 1; 0
I
và tiếp xúc với mặt
phẳng
:2 2 3 0P x yz
là
A.
22
2
1 1 1.
x yz
B.
22
2
11 1x yz
.
C.
22
2
11 9x yz
. D.
22
2
11 9x yz
.
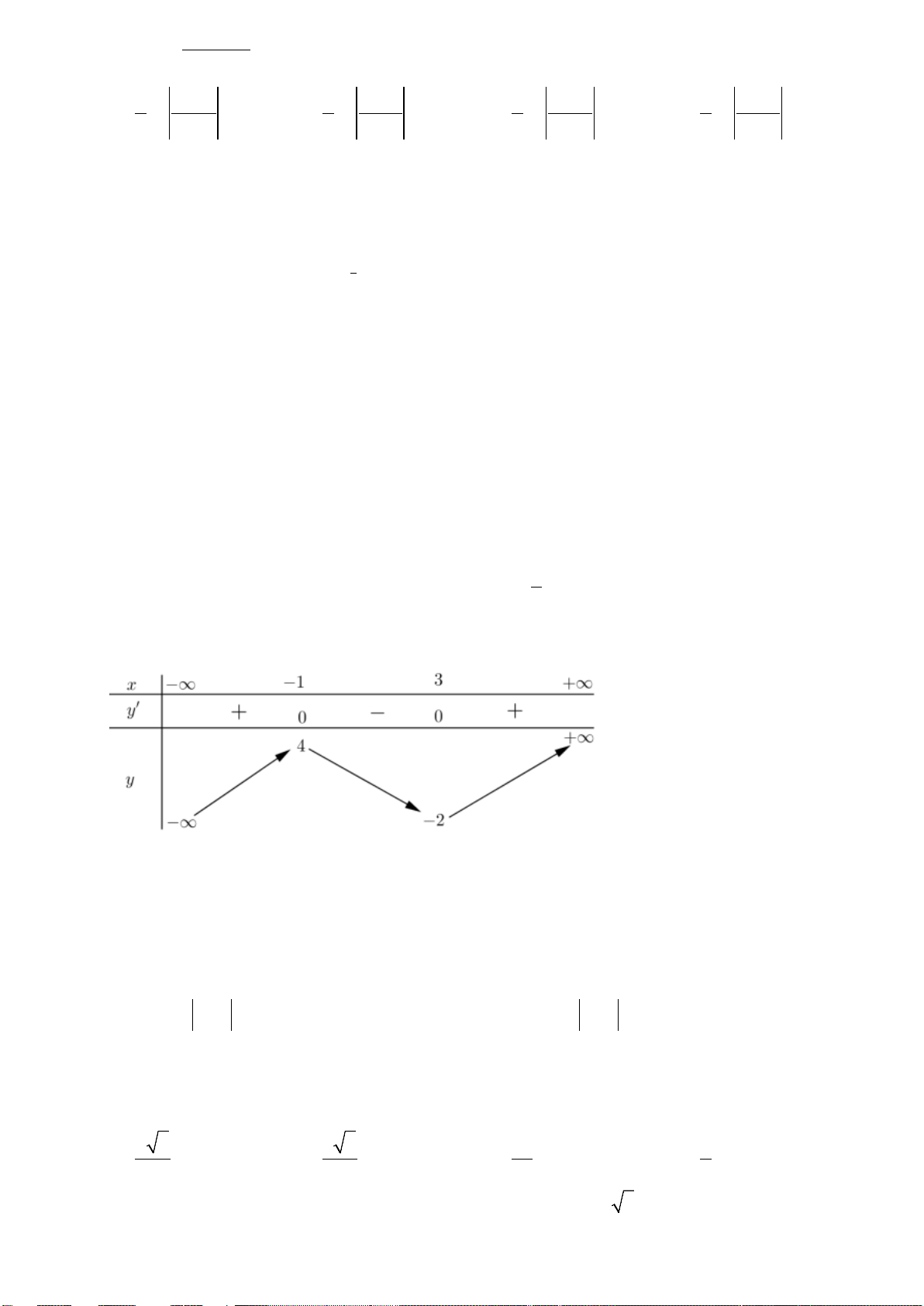
HĐT
Câu 34:
1
3
dx
xx
là
A.
1
ln
33
x
C
x
. B.
13
ln
3
x
C
x
. C.
13
ln
3
x
C
x
. D.
1
ln
33
x
C
x
.
Câu 35: Cho
,,
abc
là ba số thực thỏa mãn:
10cb a
. Mệnh đề nào dưới đây đúng ?
A.
log log 0
bb
ca
B.
log 0 log
bb
ac
C.
0log log
bb
a
c
D.
log 0 log
bb
a
c
Câu 36: Cho bất phương trình
1
5
log 2 3 1
x
. Hỏi có bao nhiêu số nguyên
x
thỏa mãn bất phương
trình đã cho?
A.
0
B.
1
C.
2
D.
3
Câu 37: Nếu cho
2
1
2f x dx
thì
2
1
32I f x dx
bằng
A.
2
I
. B.
3I
. C.
4
I
. D.
2I
.
Câu 38: Cho hàm số
fx
liên tục trên
và
4
2
2f x dx
. Mệnh đề nào sau đây là sai?
A.
2
1
22f x dx
B.
3
3
12
f x dx
C.
2
1
21f x dx
D.
6
0
1
21
2
f x dx
Câu 39: Cho hàm số
( )
y fx=
có bảng biến thiên như sau.
.
Số nghiệm của phương trình
( )
20fx−=
bằng
A.
0
.
B.
2
.
C.
1
.
D.
3
.
Câu 40: Diện tích
S
của hình phẳng giới hạn bởi đồ thị hàm số
y fx
liên tục trên
;ab
,
trục hoành và
hai đường thẳng
,x ax ba b
bằng
A.
b
a
S f x dx
B.
b
a
S f x dx
C.
b
a
S f x dx
D.
2
b
a
S f x dx
Câu 41: Cho hình lăng trụ đứng
.'''ABC A B C
có đáy
ABC
là tam giác cân,
AB AC a
, góc
0
120BAC
, mặt phẳng
( ' ')AB C
tạo với đáy một góc
0
60
. Tính khoảng cách giữa đường thẳng
AC
và mặt phẳng
(''')ABC
A.
3
2
a
. B.
3
6
a
. C.
3
2
a
. D.
2
a
Câu 42: Tính thể tích hình trụ có bán kính đáy R và chiều cao bằng
3R
.
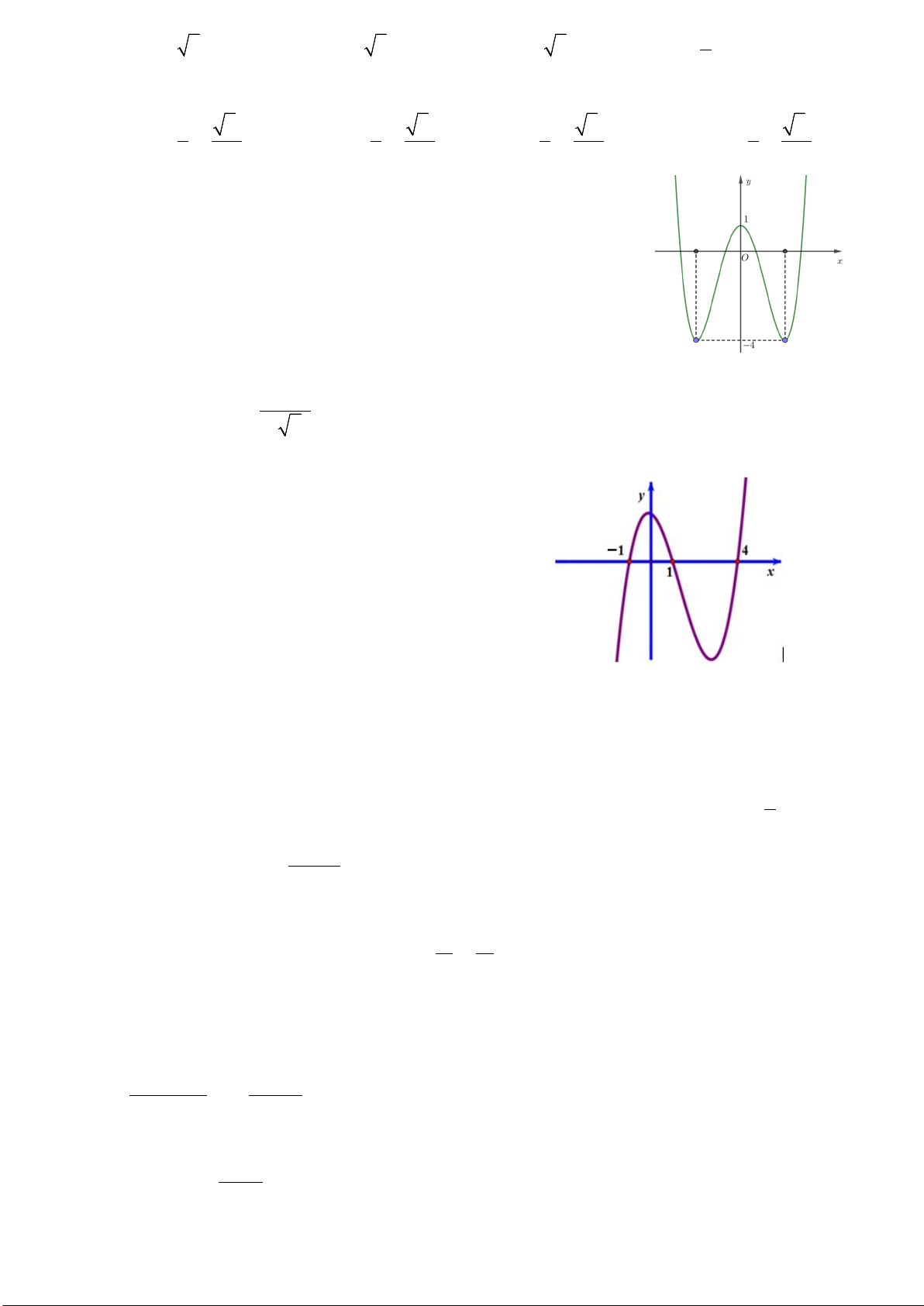
HĐT
A.
3
43
R
.
B.
3
43
R
. C.
3
3R
. D.
3
4
3
R
.
Câu 43: Tập nghiệm của phương trình :
22
( 9)( 1) 0
z zz
trên tập hợp số phức là
A.
13
3;
22
i
B.
13
3;
22
i
i
C.
13
3;
22
i
D.
13
3;
22
i
i
Câu 44: Cho hàm số
42
ax xy fx b c
có đồ thị như hình
vẽ bên. Số nghiệm của phương trình
30
fx
bằng
A.
3
. B.
1
. C.
2
. D.
4
.
Câu 45: Biết
4
4
1
21
..
2
x
x
K e dx a e b e
x
, với
,ab
. Tính
33
Sa b
A.
9S
. B.
7S
. C.
2S
. D.
3
S
.
Câu 46: Cho hàm số
( )
y fx=
. Hàm số
( )
y fx
′
=
có
đồ thị như hình vẽ bên. Hàm số
( )
4yf x= −
đồng biến
trên khoảng nào sau đây?
A.
3; 5
. B.
4;
. C.
0;3
. D.
;0
.
Câu 47: Tìm tất cả các giá trị thực của tham số
m
để phương trình
51
x
mx
có hai nghiệm phân
biệt.
A.
0m
B.
ln 5
0
m
m
C.
5
1
m
m
D.
1
5
0
m
m
.
Câu 48: Cho hàm số
21
1
x
y
x
có đồ thị
C
. Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
để đường thẳng
:dy x m
cắt
C
tại hai điểm phân biệt
,AB
sao cho tiếp tuyến với
C
tại
A
và
B
lần lượt có hệ số góc là
12
,kk
thoả mãn
2018 2018
1 2 12
12
11
2 2018k k kk
kk
. Tổng các giá trị của
tất cả các phần tử của
S
bằng
A.
2018
B.
3
C.
0
D.
6
Câu 49: Cho
,xy
là các số thực dương thỏa mãn
21xy x
. Giá trị nhỏ nhất của biểu thức
52
2
ln
xy
yx
yx
S
bằng
lnab
. Tính
ab
.
A.
8
. B.
15
C.
18
D.
11
Câu 50: Biết
2
1
0
1
ln 2 ln 3, , ,
2
x
dx a b c a b c
x
. Đẳng thức nào sau đây đúng?
A.
27abc
B.
25abc
C.
25abc
D.
27abc

HĐT
-----------------------------------------------
----------- HẾT ----------
ĐÁP ÁN ĐỀ THPT QUỐC GIA NĂM 2019 - Môn: Toán
1
2
3
4
5
6
7
8
9
10
C
B
A
A
C
A
B
D
A
B
11
12
13
14
15
16
17
18
19
20
A
B
C
C
D
B
D
A
C
A
21
22
23
24
25
26
27
28
29
30
A
D
C
C
C
B
B
D
D
C
31
32
33
34
35
36
37
38
39
40
D
A
A
B
D
C
C
A
D
A
41
42
43
44
45
46
47
48
49
50
A
C
B
D
B
C
B
D
C
B

HĐT Trang 1/6
SỞ GIÁO DỤC & ĐÀO TẠO KHÁNH HÒA
TRƯỜNG THPT PHẠM VĂN ĐỒNG
ĐỀ THI THỬ THI THPTQG NĂM 2019
Môn thi: TOÁN
Thời gian : 90 phút (không kể thời gian phát đề )
Câu 1: Hàm số
32
6 2019yx x=−+
đồng biến trên khoảng nào dưới đây ?
A.
( )
5; +∞
B.
( )
0; 4
C.
(
)
1; 5−
D.
( )
;5−∞
Câu 2: Tìm số tiệm cận của đồ thị hàm số
2 2019
1
x
y
x
+
=
+
.
A. 1 B. 0 C. 2 D. 3
Câu 3: Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
32
2 3 12 2yx x x=+−+
trên đoạn
[
]
1; 2−
. Tính M – m.
A.
10
B.
20
C.
9
D.
27
Câu 4: Cho đồ thị hàm số y = f(x) như hình vẽ.
Mệnh đề nào dưới đây đúng ?
A. Hàm số đạt cực đại tại x = 0
B. Hàm số đạt cực tiểu tại x = 0
C. Hàm số có cực đại bằng 0
D. Đồ thị hàm số có hai điểm cực đại
Câu 5: Cho
a
là số thực dương khác 1. Giá trị của biểu thức
( )
5
log .
a
aa
bằng
A.
6
5
B.
4
C.
5
6
D.
4
1
Câu 6: Tập xác định D của hàm số
= −
1
3
( 1)yx
là
A. D = (1; +∞) B. D = R\{1} C. D = R D. D = (1;+ ∞)
Câu 7: Tìm tập nghiệm của phương trình
2
5 625
x
=
.
A.
{ }
2S = ±
B.
{ }
2S = ±
C.
{ }
4S =
D.
{ }
2S =
Câu 8: Tìm nguyên hàm của hàm số
( )
5
5
x
fx x= +
.
A.
56
5
(5 ) .
ln 5 6
x
xx
x dx C
+ = ++
∫
B.
5
51
(5 ) .5 .
ln
xx
x
x dx x C
x
−
+ = ++
∫
C.
5 14
(5 ) .5 5 .
xx
x dx x x C
−
+ = ++
∫
D.
5
5
5
(5 ) .
ln 5 ln
x
x
x
x dx C
x
+ =++
∫
Câu 9: Tính tích phân I =
4
0
1
dx
x +
∫
.
A. I = ln3 B. I = ln4 C. I = ln2. D. I = ln 5.
Câu 10: Phần ảo của số phức
4
32
23
zi
i
=−+
+
là
A. -
38
13
B.
47
13
C.
38
13
D.
38
13
i
Câu 11:
Thể tích V của khối hộp chữ nhật có ba kích thước lần lượt
3, 4,5
bằng
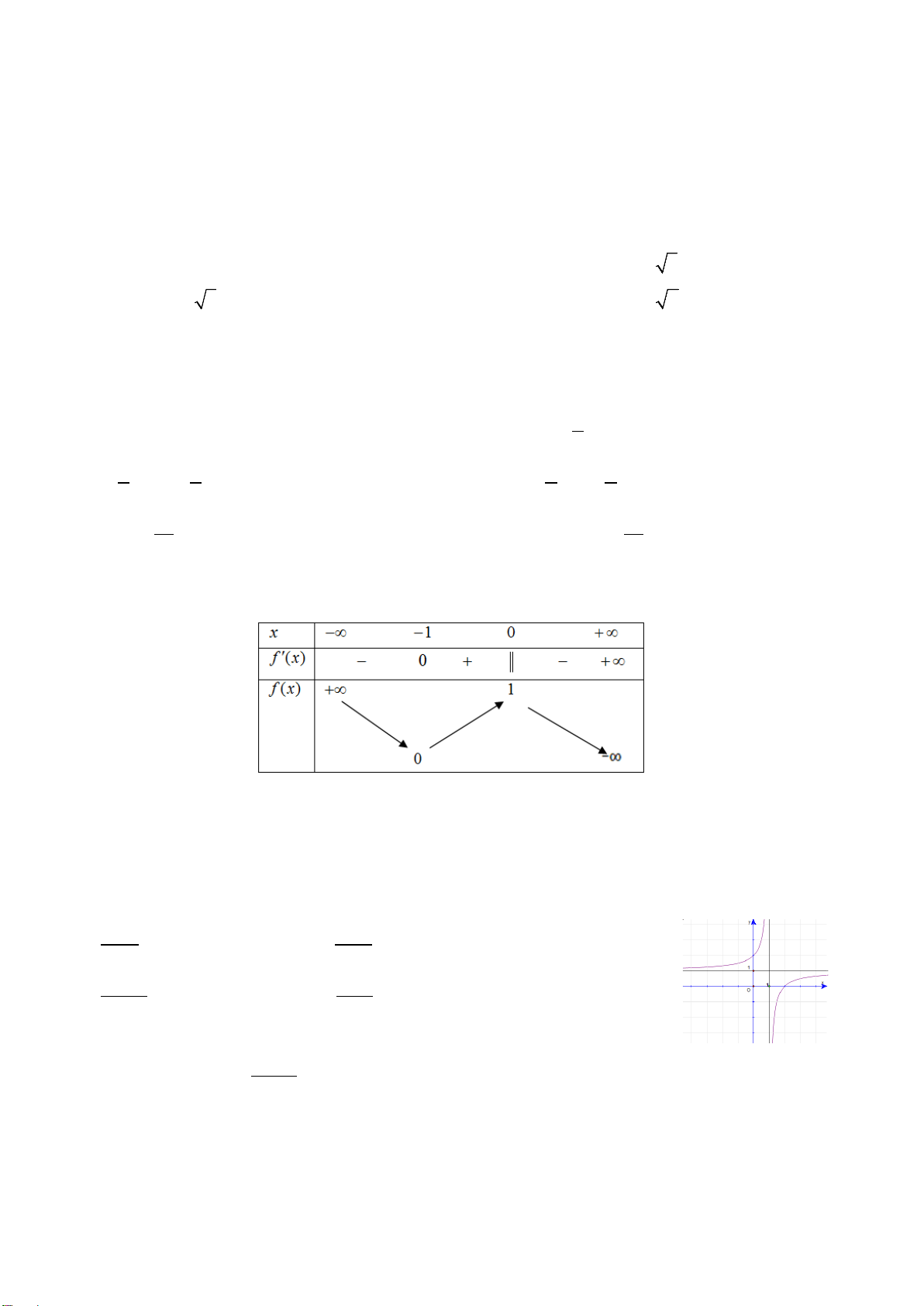
HĐT Trang 2/6
A.
120.V =
B.
60.V =
C.
17.V =
D.
30.V
=
Câu 12: Trong không gian với hệ tọa độ Oxyz, cho véc tơ
345di jk=−+
. Mệnh đề nào dưới đây
đúng ?
A.
(
)
3; 4; 5
d
= −
B.
(
)
3;4;5
d
= −−
C.
(
)
3; 4; 5
d
=−−
D.
( )
3; 4;5d =
Câu 13: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu có phương trình:
( ) ( ) (
)
2 22
1 2 4 20.xy z− ++ +− =
Tìm tọa độ tâm
I
và bán kính
R
của mặt cầu.
A.
( )
1; 2;4 , 20.IR−=
B.
( )
1; 2; 4 , 2 5.IR−− =
C.
( )
1; 2; 4 , 2 5.IR−=
D.
( )
1; 2; 4 , 5 2 .IR−− =
Câu 14: Giả sử có 6 bông hoa khác nhau và 4 lọ khác nhau. Hỏi có bao nhiêu cách cắm 4 bông hoa
vào 4 lọ đã cho ( mỗi lọ cắm một bông)?
A.
15.
B.
720.
C.
30.
D.
360.
Câu 15: Tìm công bội
q
và số hạng
1
u
của cấp số nhân, biết
2
1
4
u =
và
5
16u =
.
A.
1
11
; .
22
qu=−=−
B.
1
11
; .
22
qu= =
C.
1
1
4; .
16
qu= =
D.
1
1
4; .
16
qu=−=−
Câu 16 : Cho hàm số
()
y fx=
xác định, lên tục trên R và có bảng biến thiên như sau
Phương trình
( )
0fx=
có bao nhiêu nghiệm ?
A.
2
B.
3
C.
1
D.
0
Câu 17: Đường cong trong hình bên là đồ thị của một trong bốn hàm số dưới đây.
Hàm số đó là hàm số nào ?
A.
2
1
x
y
x
−
=
−
B.
3
1
x
y
x
−
=
−
C.
23
1
x
y
x
−
=
−
D.
3
1
x
y
x
−
=
+
Câu 18: Cho hàm số
1
2
x
y
ax
+
=
−
có đồ thị là (C). Biết rằng tiếp tuyến của (C) tại điểm
1; 2M
song
song với đường thẳng d:
3 40xy+−=
. Tính
a
.
A.
0a =
B.
2a =
C.
1a = −
D.
1a =
Câu 19: Phương trình
( )
( )
2
log 1 log 3xx+= +
có mấy nghiệm ?
A. 0 B. 2 C. 1 D. 3
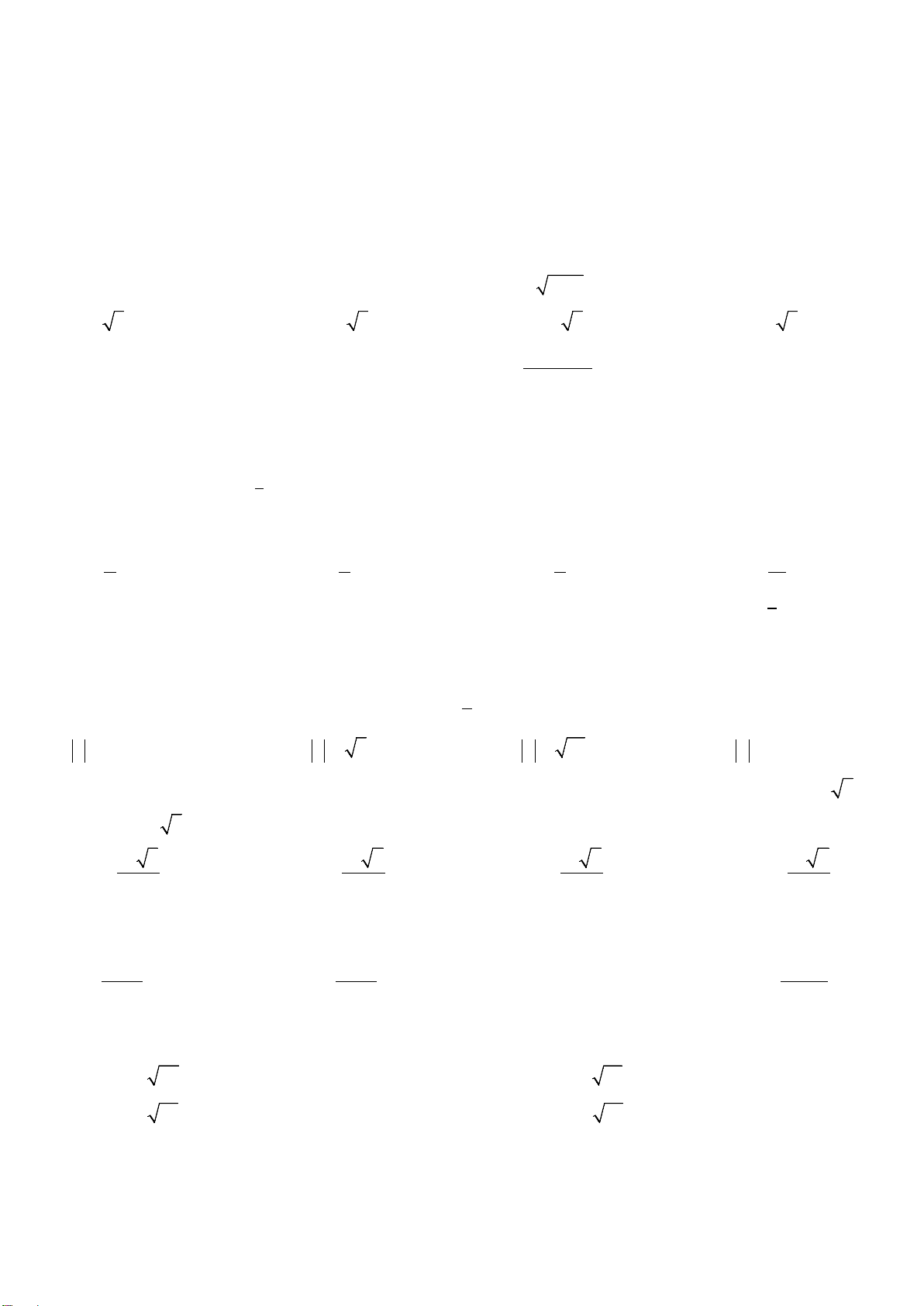
HĐT Trang 3/6
Câu 20: Tìm tập nghiệm S của bất phương trình
( )
( )
2
ln 1 ln 7
xx+< +
.
A.
( ) ( )
; 2 3;S = −∞ − ∪ +∞
B.
(
)
7;
S
= − +∞
C.
(
)
7; 1S
=−−
D.
(
)
2;3S = −
Câu 21: Một lượng vi khuẩn ban đầu có 100 con nhưng sau 3 giờ đã tăng lên đến 8000 con. Biết
rằng tốc độ phát triển tỉ lệ thuận với số lượng của chúng. Số lượng vi khuẩn sau 5 giờ là bao nhiêu ?
A. 13333 con B. 39664 con C. 13166 con D. 148530 con
Câu 22: Tính thể tích V của vật thể nằm giữa hai mặt phẳng vuông góc với trục Ox lần lượt tại
0
x =
và
x
π
=
, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng tùy ý vuông góc với trục Ox tại
điểm có hoành độ
( )
0xx
π
≤≤
là một tam giác đều cạnh là
2 sin x
.
A.
3V =
B.
23V =
. C.
33V
=
. D.
43V
=
.
Câu 23: Cho
( )
Fx
là một nguyên hàm của hàm số
( )
2
42
1
x
fx
xx
+
=
++
và
(
)
2 ln 81
F
−=
. Tính
( )
2F
.
A.
(
) (
)
2 2 ln 7 ln 3F = +
. B.
( )
2 2ln 7 ln 9F = −
.
C.
(
)
2 ln 7 ln 9F
= −
.
D.
( )
2 ln 9F =
.
Câu 24: Cho tích phân
4
2
0
tanI xdx a b
π
π
= = +
∫
. Tính
S ab
= +
.
A. S =
1
4
B. S =
5
4
C. S =
3
4
D. S =
11
4
Câu 25: Cho số phức
35zi=−+
. Điểm nào dưới đây là điểm biểu diễn của số phức
z
trên mặt
phẳng tọa độ ?
A.
( )
3; 5M −−
B.
( )
3; 5N −
C.
( )
3; 5P
D.
(
)
3; 5Q
−
Câu 26: Tính môđun của số phức z biết:
( )
1 2 3 8 10
iz z i+ − =−+
.
A.
10.z
=
B.
5.z =
C.
10.z =
D.
5.
z =
Câu 27: Cho khối chóp
.S ABC
có
( )
,SA ABC⊥
tam giác
ABC
vuông tại
B
, biết rằng
5SB a=
, 3.AB a AC a
= =
Tính thể tích V của khối chóp
.S ABC
.
A.
V =
3
3
3
a
B.
V
=
3
6
6
a
C.
V
=
3
6
4
a
D.
V
=
3
2
3
a
Câu 28: Cho hình lăng trụ tam giác đều ABC. A'B'C' có tất cả các cạnh đều bằng
a
. Tính diện tích
S của mặt cầu ngoại tiếp hình lăng trụ theo
a
.
A.
2
7
3
a
S
π
=
. B.
2
5
3
a
S
π
=
. C.
2
3
Sa
π
=
. D.
2
11
3
a
S
π
=
.
Câu 29: Một hình nón tròn xoay có đường cao
20h cm=
, bán kính đáy
25r cm=
. Tính diện tích
xung quanh S của hình nón.
A. S =
( )
2
125 40 cm
π
B. S =
( )
2
124 41 cm
π
C. S =
( )
2
120 41 cm
π
D. S =
( )
2
125 41
cm
π
Câu 30: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I thuộc trục Oz, biết rằng mặt
phẳng (Oxy) và mặt phẳng (P) :
2z =
lần lượt cắt (S) theo hai đường tròn có bán kính bằng 2 và 8.
Phương trình nào dưới đây là phương trình của mặt cầu (S).

HĐT Trang 4/6
A.
22 2
( 26) 260xy z+ +− =
B.
22 2
( 10) 260xy z+ +− =
C.
22 2
( 6) 260xy z
+ +− =
D.
22 2
( 16) 260xy z+ +− =
Câu 31: Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A(2;0;0), B(0;3;1), C(-3;6;4). Gọi M là
điểm nằm trên đoạn BC sao cho MB = 2MC. Tính độ dài đoạn thẳng AM.
A.
35
B.
52
C.
53
D.
25
Câu 32: Trong không gian với hệ tọa độ Oxyz, tìm tọa độ giao điểm
M
của đường
thẳng
43
: 63
xt
yt
zt
= +
∆ =−−
=
và mặt phẳng
( ):2 4 3 2 0Pxyz+ − −=
.
A.
( )
2;0; 2
M −−
B.
(
)
10; 12; 2
M
−
C.
( )
4;3;1
M −−
D.
(
)
1; 3; 4
M
Câu 33: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
12
:
12 3
xy z
d
++
= =
và mặt phẳng
( )
: 2 2 30
Px y z+ − +=
. Tìm tọa độ điểm
M
thuộc
d
, biết hoành độ của
M
âm và khoảng cách từ
M
đến
()P
bằng 2.
A.
( )
1;3;5M −−−
B.
( )
2;3;1M −−−
C.
( )
2;5;8M −−−
D.
( )
1;5;7M −−−
Câu 34: Rút gọn biểu thức
( )
12 1
2 ... 1
nn
nn n n
A C C n C nC
−
= + ++ − +
*
()
nN
∈
.
A.
( )
1
1 .2
n
An
−
= −
. B.
( )
1
1 .2
n
An
+
= +
. C.
1
.2
n
An
−
=
. D.
1
.2
n
An
+
=
.
Câu 35: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật biết
AB a=
,
3AD a=
.
( )
SA ABCD⊥
, và
5SA a=
. Gọi
O
là giao điểm của
AC
và
BD
. Gọi
α
là góc giữa đường thẳng
SO
và mặt phẳng
( )
ABCD
. Tính
tan .
α
.A.
tan 5
α
=
. B.
10
tan
2
α
=
C.
5
tan
2
α
=
D.
tan 10.
α
=
Câu 36: Cho hàm số
32
1y x x mx=−+ +
có cực đại tại
0
11
;
22
x
∈−
. Mệnh đề nào dưới đây đúng ?
A.
1
0
3
m≤<
B.
71
44
m−≤ ≤
C.
71
43
m
−< <
D.
1
1
5
m
−≤ <
Câu 37: Cho hàm số
( )
y fx=
có đồ thị như hình vẽ.
Tìm tất cả các giá trị thực của tham số
m
để phương trình
( )
2
10fx m m− + +=
có 5 nghiệm phân biệt.
A.
( )
0;1m ∈
B.
m ∈∅
C.
1m =
D.
2m =
hoặc
1m = −
Câu 38: Tìm tất cả các giá trị thực của tham số m để hàm số
2
44
log
mm
yx
+−
=
luôn đồng biến trên
tập xác định của nó.
A.
(
)
5;1m ∈−
B.
( )
( )
; 5 1;m ∈ −∞ − ∪ +∞
C.
(
)
;1m ∈ −∞
D.
( )
5;m ∈ − +∞

HĐT Trang 5/6
Câu 39: Cho bất phương trình
+
+ + − ++ >
1
.4 (4 2)(6 2 5) (6 2 5) 0
x xx
mm
. Tìm tất cả giá trị thực
của tham số m để bất phương trình nghiệm đúng với mọi
(
)
∈ −∞
;0x
.
A.
+
>
13
2
m
B.
−
>
13
2
m
C.
−
≥
13
2
m
D.
+
≥
13
2
m
Câu 40: Cho số phức
z
thỏa mãn
31z −≤
và
3zi
−≤
. Gọi
12
;zz
lần lượt là số phức z có môđun
lớn nhất và bé nhất . Tính tổng phần thực và phần ảo của
12
2zz+
bằng :
A. 6 B. 10 C. 8 D. 4
Câu 41: Tính thể tích V của khối trụ ngoại tiếp hình lập phương có cạnh bằng a.
A.
3
Va
π
=
. B.
3
2
a
V
π
=
. C.
3
6
a
V
π
=
. D.
3
4
a
V
π
=
.
Câu 42: Trong không gian với hệ tọa độ Oxyz, cho các điểm A (0; 1; 2), B(2; -2; 1), C(-2; 0; 1) và
mặt phẳng
( ):2 2 3 0P x yz+ +−=
. Gọi M là điểm thuộc mặt phẳng
()P
sao cho MA = MB = MC.
Tính
OM
.
A.
62
. B.
70
. C.
38
. D.
46.
Câu 43: Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng
( ): 3 1 0Px yz+ −−=
và các điểm
(1;0;0)A
;
(0; 2;3)B −
. Phương trình nào dưới đây là phương trình đường thẳng d nằm trong
()
P
đi
qua
A
và khoảng cách từ
B
đến
()
P
lớn nhất?
A.
1
1
2
xt
yt
zt
= +
= −
=
B.
1xt
yt
zt
= +
=
=
C.
1xt
yt
zt
= −
= −
= −
D.
= −
=
= −
xt
yt
zt
17
2
Câu 44: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
biết
( )
SA ABCD
⊥
, Đặt
SA x
=
.
Tìm
x
để hai mặt phẳng
( )
SBC
và
( )
SCD
tạo với nhau góc
60
o
.
A.
3
2
a
x =
B.
xa=
C.
2
a
x =
D.
2
xa=
Câu 45: Cho số thực
a
thỏa mãn:
3
.
4
a
π
π
<<
Biết bốn điểm
( ) ( ) (
) ( )
2 22 2
cos ;cos , cot ;cot , sin ;sin , tan ;tanP a aQ a aR a aS a a
là các đỉnh của một hình thang.
Tính
sin 2 .a
A.
sin 2 2 2 2.a = −
B.
sin 2 3 2 5.a = −
C.
sin 2 3 3 6.a = −
D.
sin 2 1 3.a = −
Câu 46: Cho hàm số
( )
y fx=
có đạo hàm
( ) ( )
( )
2
2
f ' x x 1 x 2x ,=−−
với mọi
x.∈
Có bao nhiêu giá
trị nguyên dương của tham số thực m để hàm số
( )
2
y f x 8x m= −+
có 5 điểm cực trị ?
A. 16 B.15 C.
17
D.
18
Câu 47:
Nhà hàng có cấu trúc vỏ hình parabol chất liệu tre nứa , nằm
trên quần đảo Cát Bà (Hải Phòng) do công ty kiến trúc Vo
Trong Nghia Architects thiết kế. Nhìn mặt trước mặt sau của
mỗi lều là hình parabol, biết rằng mặt sàn hình chữ nhật chiều
rộng 3m, chiều sâu 6m, chiều
cao từ mặt sàn lên đỉnh của
parabol là 3m.

HĐT Trang 6/6
Tính thể tích V phần không gian bên trong của mỗi lều.
A.
( )
3
18Vm=
B.
(
)
3
36
Vm=
C.
( )
3
6Vm=
D.
( )
3
12Vm=
Câu 48: Cho số phức
z a bi= +
với
0a ≤
thỏa mãn
22zi
−≤
và
22
14z zi+−−≤
. Gọi (H) là tập
hợp điểm biểu diễn của số phức
z
. Tính diện tích của (H).
A.
4
3
S
π
=
B.
4
S
π
=
C.
3
2
S
π
=
D.
2S
π
=
Câu 49: Tìm tất cả các giá trị thực của tham số
m
để phương trình
2sin cos 1xm x m+=−
có
nghiệm
;
22
x
ππ
∈−
.
A.
31m−≤ ≤
. B.
26m−≤ ≤
. C.
13m≤≤
D.
13m−≤ ≤
.
Câu 50: Cho hàm số
(
)
3
32fx x x m
= − ++
. Có bao nhiêu số nguyên dương
2018m
<
sao cho với
mọi bộ ba số thực
[
]
, , 1; 2
abc
∈−
thì
( ) ( ) (
)
,,fa fb fc
là độ dài ba cạnh một tam giác nhọn ?
A. 2009. B. 2013. C. 2017. D. 2008.
ĐÁP ÁN ĐỀ THPT QUỐC GIA NĂM 2019 - Môn: Toán
1
2
3
4
5
6
7
8
9
10
A
C
B
A
A
A
B
A
D
A
11
12
13
14
15
16
17
18
19
20
B
A
C
D
C
A
A
D
B
D
21
22
23
24
25
26
27
28
29
30
D
B
A
C
A
A
D
A
D
D
31
32
33
34
35
36
37
38
39
40
B
A
A
C
A
C
D
B
B
C
41
42
43
44
45
46
47
48
49
50
B
A
D
B
A
B
B
C
D
D

HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Hàm số
32
6 2019yx x
=−+
đồng biến trên khoảng nào dưới đây ?
A.
( )
5; +∞
B.
( )
0; 4
C.
( )
1; 5−
D.
( )
;5−∞
Đáp án : A
Lời giải: Dựa vào bảng biến thiên
Câu 2: Tìm số tiệm cận của đồ thị hàm số
2 2019
1
x
y
x
+
=
+
.
A. 1 B. 0 C. 2 D. 3
Đáp án : C
Lời giải: Hàm số bậc nhất/bậc nhất
Câu 3: Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
32
2 3 12 2
yx x x
=+−+
trên
đoạn
[ ]
1; 2−
. Tính M – m bằng:
A.
10
B.
20
C.
9
D.
27
Đáp án : B
Lời giải: Dựa vào bảng biến thiên hoặc bấm máy tính
Câu 4: Cho đồ thị hàm số y = f(x) như hình vẽ.
Mệnh đề nào dưới đây đúng ?
A. Hàm số đạt cực đại tại x = 0
B. Hàm số đạt cực tiểu tại x = 0
C. Hàm số có cực đại bằng 0
D. Đồ thị hàm số có hai điểm cực đại
Đáp án : A
Lời giải: Dựa vào hình vẽ
Câu 5: Cho a là số thực dương khác 1. Tính
( )
5
log .
a
aa
bằng:
A.
6
5
B.
4
C.
5
6
D.
4
1
Đáp án : A
Lời giải:
( )
16
5
55
6
log log . log
5
aa a
a a aa a
= = =
Câu 6: Tập xác định D của hàm số
= −
1
3
( 1)yx
.
A. D = (1; +∞) B. D = R\{1} C. D = R D. D = (1;+ ∞)
Đáp án: A
Lời giải:
Điều kiện x -1 > 0 suy ra x > 1
Câu 7: Tìm tập nghiệm của phương trình
2
5 625
x
=
.
A.
{ }
2S = ±
B.
{ }
2S = ±
C.
{ }
4S =
D.
{ }
2S =

Đáp án : B
Lời giải:
22
42
5 625 5 5 4 2
xx
xx
= ⇔ = ⇔ =⇔=±
Câu 8: Tìm nguyên hàm của hàm số
( )
5
5
x
fx x
= +
.
A.
6
5
5
(5 ) .
ln 5 6
x
x
x
x dx C
+ = ++
∫
B.
5
51
(5 ) .5 .
ln
xx
x
x dx x C
x
−
+ = ++
∫
C.
5 14
(5 ) .5 5 .
xx
x dx x x C
−
+ = ++
∫
D.
5
5
5
(5 ) .
ln 5 ln
x
x
x
x dx C
x
+ =++
∫
Đáp án : A
Lời giải: Dựa vào định nghĩa nguyên hàm
Câu 9: Tính tích phân I =
4
0
1
dx
x +
∫
.
A. I = ln3 B. I = ln4 C. I = ln2. D. I = ln 5.
Đáp án : D
Lời giải:
( )
4
4
0
0
ln 1 | ln 5 ln1 ln 5
1
dx
x
x
= += −=
+
∫
Câu 10: Số phức
4
32
23
zi
i
=−+
+
có phần ảo bằng:
A. -
38
13
B.
47
13
C.
38
13
D.
38
13
i
Đáp án : A
Lời giải: Dùng máy tính
4 47 38
z 3 2i i
2 3i 13 13
=−+ = −
+
. Phần ảo: -
38
13
Câu 11:
Thể tích V của khối hộp chữ nhật có ba kích thước lần lượt
3, 4,5
là
A.
120.V =
B.
60.
V =
C.
17.V =
D.
30.V
=
Đáp án : B
Lời giải:
Thể tích khối hộp chữ nhật có ba kích thước lần lượt
3, 4,5
là: V = 3.4.5=60
Câu 12: Trong không gian với hệ tọa độ Oxyz, cho
345di jk
=−+
. Mệnh đề nào dưới đây đúng ?
A.
( )
3; 4; 5d = −
B.
( )
3;4;5d
= −−
C.
( )
3; 4; 5d =−−
D.
( )
3; 4;5d =
Đáp án : A
Lời giải:
345di jk=−+
. Tọa độ của vectơ
d
là :
( )
3; 4; 5d
= −
Câu 13: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu có phương trình
( ) ( ) ( )
2 22
1 2 4 20.xy z− ++ +− =
Tìm tọa độ tâm I và bán kính R của mặt cầu.
A.
( )
1; 2;4 , 20.IR−=
B.
( )
1; 2; 4 , 2 5.IR−− =
C.
( )
1; 2; 4 , 2 5.IR−=
D.
( )
1; 2; 4 , 5 2 .IR
−− =
Đáp án : C
Lời giải:
( )
1; 2; 4 , 2 5.IR−=
Câu 14: Có bao nhiêu cách xếp khác nhau cho 6 người ngồi vào 4 chỗ trên một bàn dài ?
A.
15.
B.
720.
C.
30.
D.
360.
Đáp án : D
Lời giải: Số cách xếp khác nhau cho 6 người ngồi vào 4 chỗ trên một bàn dài là một chỉnh hợp chập 4 của 6
phần tử.Suy ra có
4
6
360
A
cách.
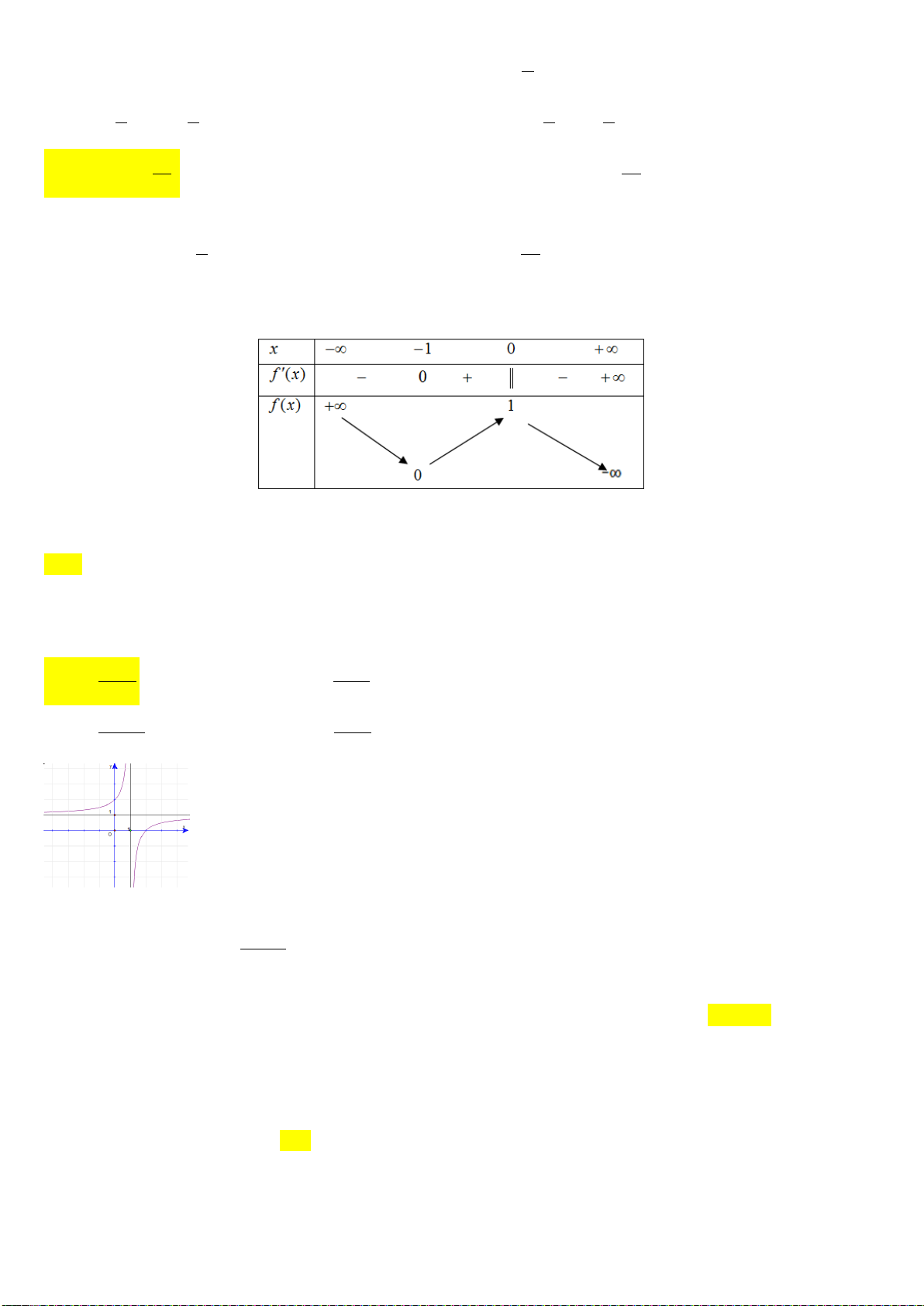
Câu 15: Tìm công bội
q
và số hạng
1
u
của cấp số nhân có
2
1
4
u =
;
5
16
u
=
.
A.
1
11
; .
22
qu
=−=−
B.
1
11
; .
22
qu= =
C.
1
1
4; .
16
qu
= =
D.
1
1
4; .
16
qu=−=−
Đáp án : C
Lời giải:
43
21 51 1
11
; 16 64 4
4 16
u uq u uq q q u= = = = ⇒ = ⇒=⇒ =
Câu 16 : Cho hàm số
()
y fx=
xác định, lên tục trên R và có bảng biến thiên như sau
Phương trình
( )
0fx=
có bao nhiêu nghiệm ?
A.
2
B.
3
C.
1
D.
0
Đáp án : A
Câu 17: Đường cong trong hình bên là đồ thị của một trong bốn hàm số dưới đây.
Hàm số đó là hàm số nào ?
A.
2
1
x
y
x
−
=
−
B.
3
1
x
y
x
−
=
−
C.
23
1
x
y
x
−
=
−
D.
3
1
x
y
x
−
=
+
Đáp án : A
Câu 18: Cho hàm số
1
2
x
y
ax
+
=
−
có đồ thị là (C). Biết rằng tiếp tuyến của (C) tại điểm
1; 2M
song song
với đường thẳng d:
3 40xy+−=
. Tính a.
A.
0
a =
B.
2a =
C.
1a
= −
D.
1a =
Đáp án : D
Câu 19: Phương trình
( )
( )
2
log 1 log 3xx+= +
có mấy nghiệm ?
A. 0 B. 2 C. 1 D. 3
Đáp án : B
Lời giải:
2
3
30
2
2
1
13
1
x
x
x
x
x
xx
x
>−
+>
=
⇔⇔
=
= −
+= +
= −

Câu 20: Tìm tập nghiệm S của bất phương trình
( )
( )
2
ln 1 ln 7
xx+< +
.
A.
( ) ( )
; 2 3;S = −∞ − ∪ +∞
B.
( )
7;
S = − +∞
C.
( )
7; 1
S
=−−
D.
(
)
2;3S = −
Đáp án : D
Lời giải:
2
2
10
23
23
17
x xR
x
x
xx
+> ∈
⇔ ⇔− < <
−< <
+< +
Câu 21: Một lượng vi khuẩn ban đầu có 100 con nhưng sau 3 giờ đã tăng lên đến 8000 con. Biết rằng tốc độ
phát triển tỉ lệ thuận với số lượng của chúng. Số lượng vi khuẩn sau 5 giờ là bao nhiêu ?
A. 13333 con B. 39664 con C. 13166 con D. 148530 con
Đáp án : D
Lời giải: Ta có
0
rt
t
N Ne=
trong đó
t
N
số lượng tại thời điểm t,
0
N
số lượng ban đầu ,
r
tỉ lệ tăng
Tại thời điểm
3t =
ta có
.3 .3
ln 80
8000 100. 80
3
rr
ee r
= ⇒ = ⇒=
Tại thời điểm
5t =
ta có
ln 80
5.
3
5
100. 148530Ne= ≈
Câu 22: Tính thể tích V của vật thể nằm giữa hai mặt phẳng
0x =
và
x
π
=
, biết rằng thiết diện của vật thể
bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ
( )
0xx
π
≤≤
là một tam giác đều cạnh là
2 sin x
.
A.
3V =
B.
23V =
. C.
33
V =
. D.
43
V =
.
Đáp án : B
Lời giải: Diện tích thiết diện S(x) được cho bởi:
( )
2
a3
S x 3sinx
4
= =
.
Khi đó, thể tích vật thể được cho bởi:
(
)
00
0
V S x dx 3 sin x.dx 3 cos x 2 3
π
ππ
= = =−=
∫∫
.
Câu 23: Cho
( )
Fx
là một nguyên hàm của hàm số
( )
2
42
1
x
fx
xx
+
=
++
và
( )
2 ln 81F −=
. Tính
( )
2F
.
A.
( )
( )
2 2 ln 7 ln 3
F = +
. B.
(
)
2 2ln 7 ln 9
F = −
.
C.
(
)
2 ln 7 ln 9F
= −
.
D.
( )
2 ln 9F =
.
Đáp án : A
Lời giải:
( )
( )
2
2
22
dx x 1
4x 2
dx 2 2ln x x 1 C
x x1 x x1
++
+
= = ++ +
++ ++
∫∫
( ) ( )
2
F 2 ln 81 2ln 2 2 1 C ln 81 C 2ln 3
− = ⇔ − −+ + = ⇔ =
⇒
( ) ( ) ( )
2
F 2 2ln 2 2 1 2ln 3 2ln7 2ln 3 2 ln7 ln 3
= +++=+= +
Câu 24: Cho tích phân
4
2
0
tanI xdx a b
π
π
= = +
∫
. Tính
S ab= +
.
A. S =
1
4
B. S =
5
4
C. S =
3
4
D. S =
11
4
Đáp án : C
Lời giải:

( )
44
2
4
2
0
00
1 1 13
tan xdx 1 dx tan x x 1 a b a 1, b S a b 1
cos x 4 4 4 4
ππ
π
π−
= − = − = − = + π⇒ = = ⇒ = + = − =
∫∫
Câu 25: Cho số phức
35
zi=−+
. Điểm nào dưới đây là điểm biểu diễn của số phức
z
trên mặt phẳng tọa
độ ?
A.
(
)
3; 5
M
−−
B.
(
)
3; 5
N
−
C.
( )
3; 5P
D.
( )
3; 5Q −
Đáp án : A
Lời giải:
z 3 5i z 3 5i=−+ ⇒ =−− ⇒
Điểm biểu diễn của
z
trên mặt phẳng tọa độ Oxy là :
( )
3; 5
M −−
Câu 26: Tính môđun của số phức z biết:
( )
1 2 3 8 10iz z i+ − =−+
.
A.
10.z =
B.
5.z =
C.
10.z =
D.
5.z =
Đáp án : A
Lời giải:
Gọi
z a bi
= +
( )( ) ( )
( )
( )
1 2i a bi 3 a bi 8 10i
a 2b 2a b i 3a 3bi 8 10i
2a 2b 2a 4b 8 10i
2a 2b 8 a 3
2a 4b 10 b 1
+ + − − =−+
⇔ − + + − + =−+
⇔− − + + =− +
−− =− =
⇔⇔
+= =
z a bi 3 i z 10⇒ = + = +⇒ =
Câu 27: Cho khối chóp
.S ABC
có
( )
,SA ABC⊥
tam giác
ABC
vuông tại
B
, biết rằng
5SB a=
, 3.
AB a AC a= =
Tính thể tích V của khối chóp
.S ABC
.
A.
V =
3
3
3
a
B.
V
=
3
6
6
a
C.
V
=
3
6
4
a
D.
V
=
3
2
3
a
Đáp án : D
Lời giải:
ABC∆
vuông tại B có
22
BC AC AB a 2= −=
SAB∆
vuông tại A có
22
SA SB AB 2a= −=
3
1 1 1 1 a2
V .SA. AB.BC .2a. .a .a 2
32 32 3
= = =
Câu 28: Cho hình lăng trụ tam giác đều ABC, A'B'C' có tất cả các cạnh đều bằng a. Tính diện tích S của mặt
cầu ngoại tiếp hình lăng trụ theo a.
A.
2
7
3
a
S
π
=
. B.
2
5
3
a
S
π
=
. C.
2
3Sa
π
=
. D.
2
11
3
a
S
π
=
.
Đáp án : A
Lời giải:
Gọi G, G
’
lần lượt là trọng tâm tam giác ABC và A
’
B
’
C
’
, I là trung điểm của GG
’
ta có bán kính
mặt cầu ngoại tiếp lăng trụ tam giác đều ABC. A'B'C' là
22
21
6
a
R IG AG= +=
Diện tích mặt cầu là:
22
7
4
3
SRa
ππ
= =
Câu 29: Một hình nón tròn xoay có đường cao
20h cm=
, bán kính đáy
25r cm=
. Gọi S là diện tích xung
quanh hình nón. Tính S.

A. S =
( )
2
125 40 cm
π
B. S =
( )
2
124 41 cm
π
C. S =
(
)
2
120 41 cm
π
D. S =
(
)
2
125 41 cm
π
Đáp án : D
Lời giải:
22
5 41l hr= +=
Tính diện tích xung quanh hình nón đã cho là:
s rl
π
= =
( )
2
125 41 cm
π
Câu 30: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I thuộc trục Oz, biết rằng mặt phẳng
(Oxy) và mặt phẳng (P) :
2
z =
lần lượt cắt (S) theo hai đường tròn có bán kính bằng 2 và 8. Phương trình
nào dưới đây là phương trình của mặt cầu (S).
A.
22 2
( 26) 260xy z+ +− =
B.
22 2
( 10) 260xy z+ +− =
C.
22 2
( 6) 260xy z+ +− =
D.
22 2
( 16) 260xy z+ +− =
Đáp án : D
Lời giải: Từ giả thiết ta có vô số mặt cầu (S) thoả YCBT. Gọi (S
0
) là mặt cầu có tâm
Im
0
(0;0; )
thuộc trục
Oz. Khi đó mp(Oxy) và mp(P) cắt (S
0
) theo 2 đường tròn tâm
OO
1
(0;0;0)≡
, bán kính
R
1
2
=
và tâm
O
2
(0;0;2)
, bán kính
R
2
8=
.
Gọi R là bán kính mặt cầu thì
Rm
m mm
Rm
2
22
22
2
22
2
4 64 ( 2) 16
82
= +
⇒+ = + − ⇒ =
=+−
⇒
R 2 65=
và
I
0
(0;0;16)
.Suy ra mặt cầu (S) có tâm
I(0; 0;16)
(a, b ∈ R), bán kính
R 2 65
=
.
Vậy phương trình mặt cầu (S):
+ +− =xy z
22 2
( 16) 260
Câu 31: Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A(2;0;0), B(0;3;1), C(-3;6;4). Gọi M là điểm nằm
trên đoạn BC sao cho MB = 2MC. Tính độ dài đoạn AM.
A.
35AM =
B.
52AM =
C.
53AM =
D.
25AM =
Đáp án : B
Lời giải: M là điểm nằm trên đoạn BC sao cho MB = 2MC nên
2
( 3)
3
2
22
3 .3 5 ( 2;5;3) AM 5 2
33
3
2
1 .3
3
x
x
BM BC y y M
z
z
= −
= −
= ⇔⇔ − = ⇔ = ⇒ − ⇒ =
=
−=
Câu 32: Tìm giao điểm M của đường thẳng
43
: 63
xt
yt
zt
= +
∆ =−−
=
và mặt phẳng
( ):2 4 3 2 0Px yz
+ − −=
.
A.
( )
2;0; 2
M −−
B.
( )
10; 12; 2M −
C.
( )
4;3;1M −−
D.
( )
1; 3; 4
M
Đáp án : A
Lời giải: Tọa độ giao điểm M của d và (P) là nghiệm của hệ
43
63
2(4 3 ) 4( 6 3 ) 3 2 0 2
2 4 3 20
( 2; 0; 2)
xt
yt
t tt t
zt
xyz
M
= +
=−−
⇒ + + −− − − = ⇔=−
=
+ − −=
⇒−−

Câu 33: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
12
:
12 3
xy z
d
++
= =
và mặt phẳng
( )
: 2 2 30Px y z+ − +=
. Tìm điểm M có hoành độ âm thuộc d sao cho khoảng cách từ M đến (P) bằng 2.
A.
( )
1;3;5M −−−
B.
( )
2;3;1
M −−−
C.
( )
2;5;8M −−−
D.
( )
1;5;7M −−−
Đáp án : A
Lời giải:
Ptts d:
1 2, (; 1 2; 2 3),
23
xt
y tMd t t t
zt
=
=−+ ∈ ⇒ −+ −+
=−+
2( 1 2 ) 2( 2 3 ) 3
( ,) 2 2
3
1 (1;3;5)
11 (11;21;31)
tt t
dMP
tM
tM
+ −+ − −+ +
=⇔=
=−⇒ − − −
⇔
= ⇒
( )
1;3;5M −−−
Câu 34: Rút gọn biểu thức
( )
12 1
2 ... 1
nn
nn n n
A C C n C nC
−
= + ++ − +
*
()nN∈
.
A.
(
)
1
1 .2
n
An
−
= −
. B.
(
)
1
1 .2
n
An
+
= +
. C.
1
.2
n
An
−
=
. D.
1
.2
n
An
+
=
.
Đáp án : C
Lời giải:
Ta có:
( )
n
0 1 2 2 n1 n1 n n
nn n n n
1 x C Cx Cx ... C x Cx
−−
+ = + + ++ +
. (1)
Lấy đạo hàm theo x hai vế của (1), ta được:
( ) ( )
n1
1 2 n1 n2 n n1
nn n n
n 1 x C 2C x ... n 1 C x nC x
−
−− −
+ = + ++ − +
. (2)
Thay x = 1 vào (2), ta được:
( )
n1 1 2 n1 n n1
nn n n
n.2 C 2C ... n 1 C nC A n.2
− −−
= + ++ − + ⇔ =
Câu 35: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật
AB a=
,
3AD a=
,
( )
SA ABCD⊥
,
5SA a=
. Gọi
O
là giao điểm của
AC
và
BD
. Gọi
α
là góc giữa
SO
và mặt phẳng
( )
ABCD
.
Tính
tan .
α
.
A.
tan 5
α
=
. B.
10
tan
2
α
=
C.
5
tan
2
α
=
D.
tan 10.
α
=
Đáp án : A
Lời giải:
Vì SO có hình chiếu lên (ABCD) là AO nên góc giữa
SO
và mặt phẳng
( )
ABCD
là góc
SOA
22
2AC AB BC a AO a= + =⇒=
; Trong
;tan 5
SA
SAO SOA
AO
∆==
Câu 36: Cho hàm số
32
1y x x mx=−+ +
có cực đại tại
0
11
;
22
x
∈−
. Mệnh đề nào dưới đây đúng ?
A.
1
0
3
m≤<
B.
71
44
m−≤ ≤
C.
71
43
m−< <
D.
1
1
5
m−≤ <
Đáp án : C
Lời giải:
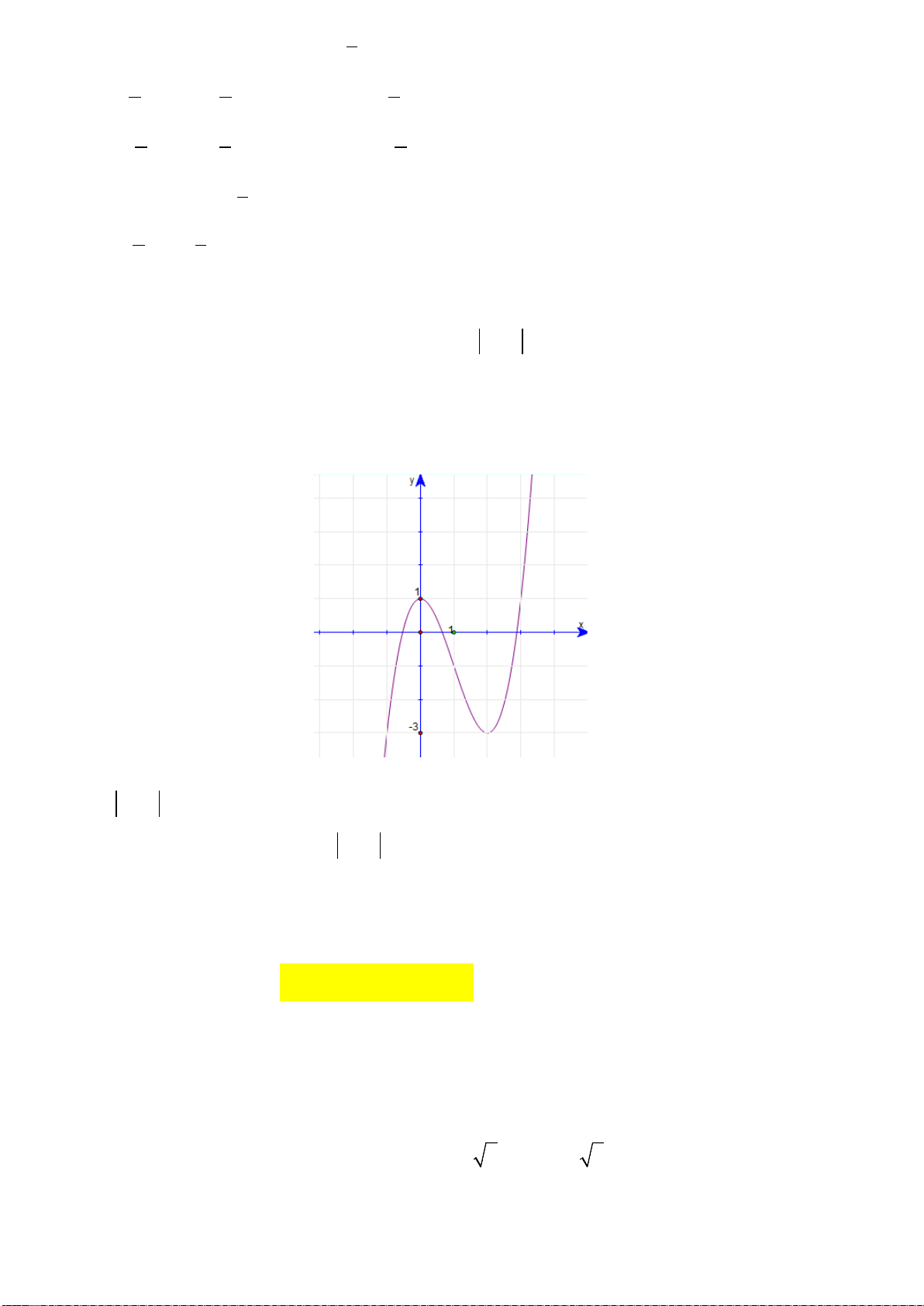
2
1
' 3 2 ;'13 0
3
y x xm m m= − + ∆= − > ⇔ <
TH1:
13 1
'( ) 0 1 0
24 4
13 7
'( ) 0 1 0
24 4
y mm
y mm
≤ −+ ≤ ≤
⇔⇔
− > + + > >−
TH2: Tương tự ta có
1
3
m <
Kết luận:
71
43
m−< <
Câu 37: Cho hàm số
( )
y fx=
có đồ thị như hình vẽ.
Tìm tất cả các giá trị thực của tham số m để phương trình
( )
2
10fx m m− + +=
có 5 nghiệm phân biệt.
A.
( )
0;1m ∈
B.
m ∈∅
C.
1m
=
D.
2; 1mm= = −
Đáp án : D
Lời giải:
( )
2
1fx m m= −−
Dựa vào đồ thị của hàm số
( )
y fx=
, phương trình có 5 nghiệm phân biệt khi và chỉ khi
22
11 2 0mm mm−−=⇔ −−=
. Vậy
2; 1mm= = −
Câu 38: Tìm tất cả các giá trị thực của tham số m để hàm số
2
44
log
mm
yx
+−
=
luôn đồng biến trên tập xác
định.
A.
( )
5;1m ∈−
B.
( ) ( )
; 5 1;m ∈ −∞ − ∪ +∞
C.
( )
;1m
∈ −∞
D.
( )
5;m∈ − +∞
Đáp án : B
Lời giải: Tập xác định
( )
0;D = +∞
Khi đó
2
44
y log
mm
x
+−
=
luôn đồng biến trên tập xác định thì
22
5
4 41 4 50
1
m
mm mm
m
<−
+−>⇔+−>⇔
>
Câu 39: Cho bất phương trình
+
+ + − ++ >
1
.4 (4 2)(6 2 5) (6 2 5) 0
x xx
mm
. Tìm tất cả giá trị tham số
m để bất phương trình nghiệm đúng với mọi
( )
∈ −∞;0x
.

A.
+
>
13
2
m
B.
−
>
13
2
m
C.
−
≥
13
2
m
D.
+
≥
13
2
m
Đáp án : B
( )
( ) (
)
(
)
1
.4 4 2 6 25 6 25 0
35 35
.4 4 2 0
22
xx
x
xx
mm
mm
+
+ + − ++ >
−+
⇔++ + >
Đặt
35
2
x
t
−
=
ĐK
0t >
Bất phương trình trở thành
( ) ( )
2
1
4 42 0 42 4 10mmt mtmt
t
+ + + > ⇔ + + +>
(*)
Bất pt nghiệm đúng mọi x < 0 thì bpt (*) nghiệm đúng mọi t > 1
Khi đó ta có TH1 :
( )
2
1
4 20
13 13
2
22
13 13
4 4 20
22
m
m
m
mm
m
−
>
+>
−+
⇔ ⇔ <<
−+
− −<
<<
TH2 :
( )
12
2
3
8
4 2 4 10
1
1
41
2
1
1
42 4
4 4 20
4
13
2
13
2
13
2
13
2
m
mm
m
tt
m
m
m
mm
m
m
m
m
m
−
>
+ + +>
<−
<<
−
⇔ < ⇔ ⇔ >−
+
− −>
>−
−
<
−
<
+
>
+
>
Vậy
−
>
13
2
m
Câu 40: Cho số phức
z
thỏa mãn
31z −≤
;
3zi−≤
. Gọi
12
;zz
lần lượt là số phức z có môđun lớn nhất và
bé nhất . Tính tổng phần thực và phần ảo của
12
2zz+
bằng :
A. 6 B. 10 C. 8 D. 4
Đáp án : C
Lời giải:
31z
−≤
suy ra điểm biễu diễn của z thuộc hình tròn tâm I( 3;0) bán kính r=1
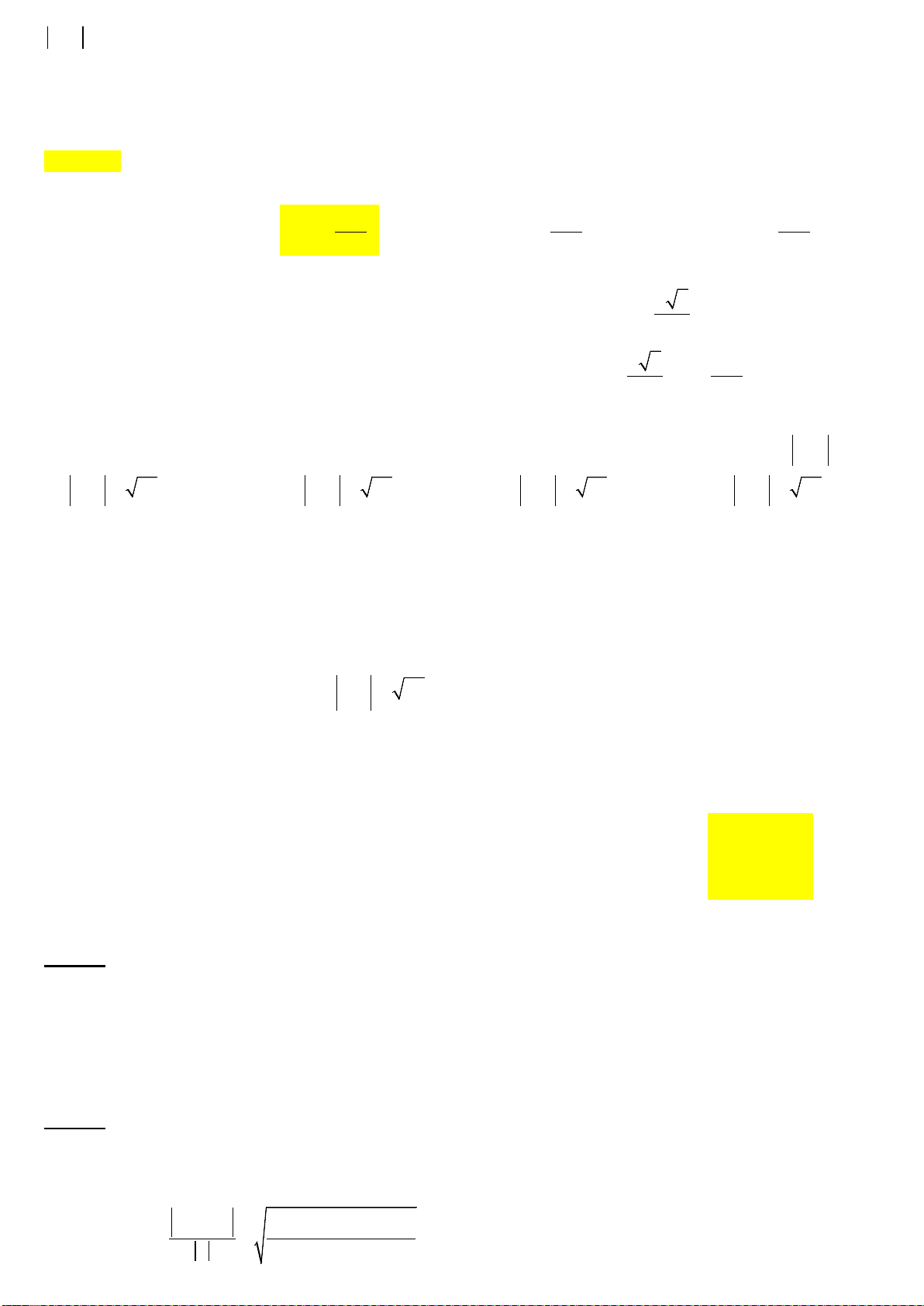
3zi−≤
suy ra điểm biễu diễn của z thuộc hình tròn tâm M(0;1) bán kính R=3
Khi đó z có điểm biểu diễn là giao của 2 đường tròn, điểm có khoảng cách lớn nhất , nhỏ nhất với O lần lượt
là A( 1;3) và B(0;2)
Vậy
1 2 12
1 3i; 2 2 5 3z z zz i=+ =⇒+ =+
Đáp án : 8
Câu 41: Tính thể tích V của khối trụ ngoại tiếp hình lập phương có cạnh bằng a.
A.
3
Va
π
=
. B.
3
2
a
V
π
=
. C.
3
6
a
V
π
=
. D.
3
4
a
V
π
=
.
Đáp án : B
Lời giải: Khối trụ ngoại tiếp hình lập phương có cạnh bằng a có bán kính đáy là
2
2
a
Thể tích V của khối trụ ngoại tiếp hình lập phương có cạnh bằng a là:
2
3
2
22
aa
Va
π
π
= =
Câu 42: Trong không gian với hệ tọa độ Oxyz, cho các điểm A (0; 1; 2), B(2; -2; 1), C(-2; 0; 1) và mặt
phẳng
( ):2 2 3 0P x yz+ +−=
. Gọi M là điểm thuộc mặt phẳng (P) sao cho MA = MB = MC. Tính
OM
.
A.
62OM =
. B.
70OM =
. C.
38OM =
. D.
46.OM =
Đáp án : A
Lời giải:
MA=MB nên M thuộc mặt phẳng trung trực của đoạn thẳng AB .Mp trung trực của AB là
2 3 20x yz
− −−=
MB=BC nên M thuộc mặt phẳng trung trực của đoạn thẳng BC. Mp trung trực của BC là
2 10xy− −=
(
)
(
)
∈ ⇒ + +−=
−−= =
⇒ − −−= ⇔ = ⇒ =
+ +−= =−
M x;y;z P 2x 2y z 3 0
2x y 1 0 x 2
2x 3y z 2 0 y 3 OM 62
2x 2x z 3 0 z 7
Câu 43: Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng
( ): 3 1 0Px yz+ −−=
và các điểm
(1;0;0)A
;
(0; 2;3)
B −
. Phương trình nào dưới đây là phương trình đường thẳng d nằm trong (P) đi qua A và
cách B một khoảng lớn nhất.
A.
1
1
2
xt
yt
zt
= +
= −
=
B.
1xt
yt
zt
= +
=
=
C.
1xt
yt
zt
= −
= −
= −
D.
= −
=
= −
xt
yt
zt
17
2
Đáp án : D
Lời giải:
Cách 1: Vì điểm A, B và mặt phẳng (P) cố định, nên khoảng cách từ B đến (d) đạt Max khi A là hình chiếu
của B lên đường thẳng d. Khi đó VTCP của d là
( )
, 7, 2, 1
p
d
u n AB
= =−−
Vậy PT (d):
17
2
xt
yt
zt
= −
=
= −
Cách 2: Ta có:
AP(1;0;0) ( )∈
. Gọi VTCP của đường thẳng d là:
u abc a b c
222
( ; ; ), 0= ++≠
Ta có:
⊂ ⇔ =⇔=+
P
d P un c a b() . 0 3
AB ( 1; 2; 3)=−−
;
= + −− −+
d
uAB ababab, (2 9;4 3;2 )
⇒
++
= =
++
u AB
a ab b
dBd
u
a ab b
22
22
,
24 56 91
(,)
2 6 10
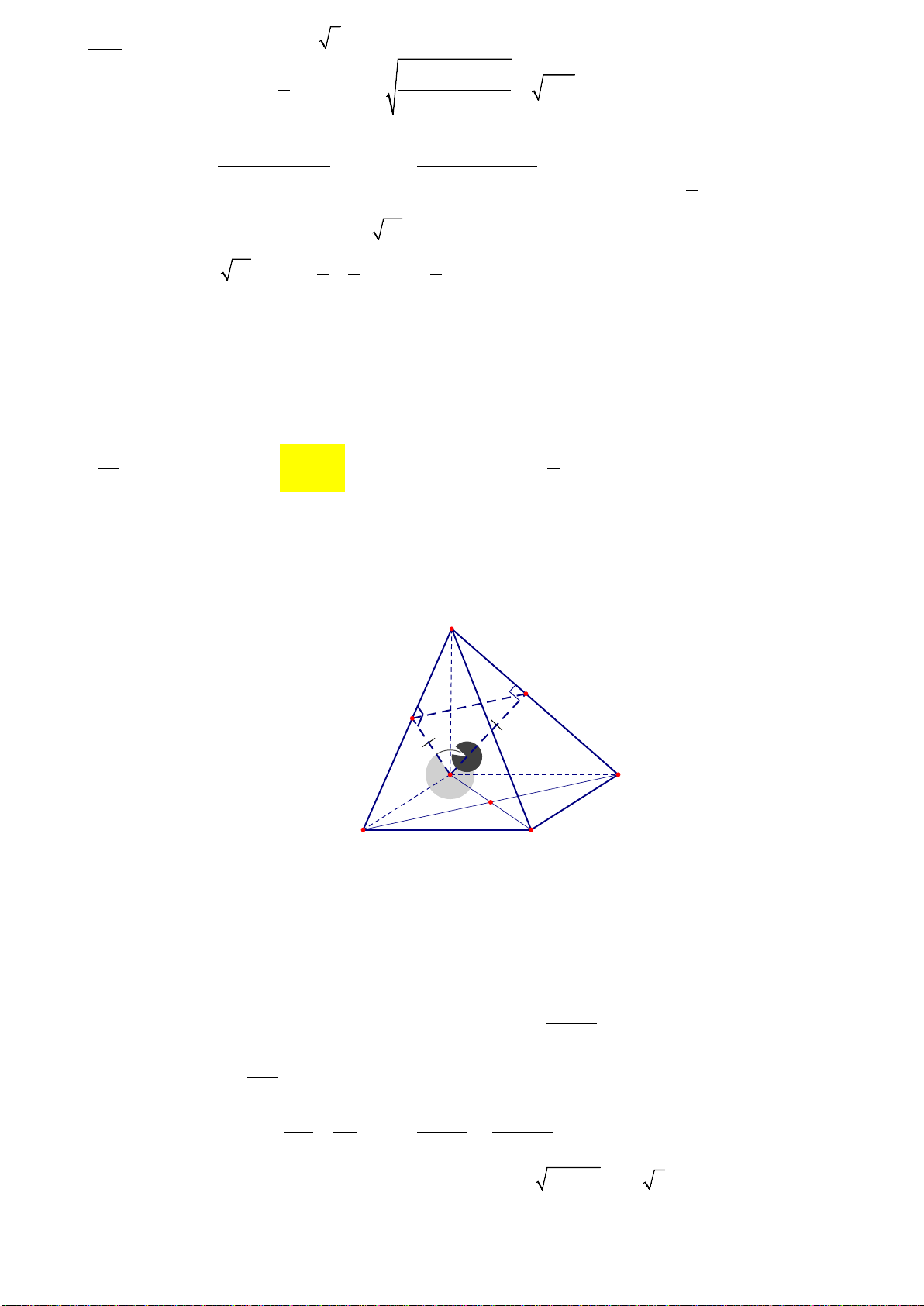
+TH1: Nếu b = 0 thì
=dBd(,) 23
+TH2: Nếu
b 0≠
. Đặt
a
t
b
=
⇒
++
= =
++
tt
dBd f t
tt
2
2
24 56 91
( , ) ()
2 6 10
Xét hàm số
= −
++ + +
= =>= =⇔
++ ++
= −
t
tt t t
ft fx fx
tt tt
t
22
''
22
7
24 56 91 32 116 14
2
() () , () 0
1
2 6 10 (2 6 10)
8
Lập bbt ta suy ra được
= ≤
dBd f t( , ) ( ) 14
= ⇔=− = ⇔ =−
a
dBd t a b
b
77
max( ( , )) 14
22
.Chọn b = 2⇒ a =-7 , c =-1
⇒ Phương trình đường thẳng d:
= −
=
= −
xt
yt
zt
17
2
Câu 44: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
biết
( )
SA ABCD
⊥
,
SA x=
.
Tìm
x
để hai mặt phẳng
( )
SBC
và
( )
SCD
tạo với nhau góc
60
o
.
A.
3
2
a
x =
B.
xa=
C.
2
a
x =
D.
2xa=
Đáp án : B
Lời giải:
a
a
x
60
o
J
C
A
B
D
S
I
* Trong
(
)
SAB
dựng
AI SB⊥
ta chứng minh được
( )
AI SBC⊥
(1)
Trong
( )
SAD
dựng
AJ SD⊥
ta chứng minh được
( )
AJ SCD⊥
(2)
Từ (1) và (2) ⇒góc
(
)
( )
( ),( ) ,SBC SCD AI AJ IAJ= =
* Ta chứng minh được
AI AJ=
. Do đó, nếu góc
60
o
IAJ =
thì
AIJ∆
đều ⇒
AI AJ IJ= =
SAB∆
vuông tại
A
có
AI
là đường cao ⇒
..AI SB SA AB=
⇒
.SA AB
AI
SB
=
(3)
Và có
2
.SA SI SB=
⇒
2
SA
SI
SB
=
(4)
Ta chứng minh được
//IJ BD
⇒
IJ SI
BD SB
=
⇒
.SI BD
IJ
SB
=
(4)
=
2
2
.SA BD
SB
(5)
Thế (3)&(5) vào
AI IJ=
⇒
.SA BD
AB
SB
=
⇔
..AB SB SA BD=
⇔
22
. .2a x a xa+=
⇔
22 2
2xa x
+=
⇔
xa=

Câu 45: Cho
3
.
4
a
π
π
<<
Biết bốn điểm
(
) (
) ( ) ( )
2 22 2
cos ;cos , cot ;cot , sin ;sin , tan ; tan
P a aQ a aR a aS a a
là các đỉnh của một hình thang. Tính
sin 2 .
a
A.
sin 2 2 2 2.a = −
B.
sin 2 3 2 5.a = −
C.
sin 2 3 3 6.a = −
D.
sin 2 1 3.a
= −
Đáp án : A
Lời giải: Bốn điểm
22 22
( ; ), ( ; ), ( ; ), ( ; )Bbb Ccc Dd d Eee
là bốn đỉnh của một hình thang, giả sử BC // DE.
Khi đó
22 2 2
.
BC DE
cb ed
k k cb ed
cb ed
−−
= ⇒ = ⇔+=+
−−
Với
3
,
4
a
π
π
<<
ta có
cot 1 cos 0 sin
cot 1 tan 0 sin
a aa
a aa
<− < < <
<− < < <
Do đó điều kiện để bốn điểm
( ) ( ) ( ) (
)
2 22 2
cos ;cos , cot ;cot , sin ;sin , tan ;tan
P a aQ a aR a aS a a
là các đỉnh
của một hình thang là
sin cot tan cos sin cos cot tan 0aa aa aaaa+=+⇔−+−=
(
)
22
cos sin sin cos
sin cos 0 1 0 sin cos 0
sin cos sin cos
a a aa
aa aa
aa aa
−+
⇔ − + = ⇔− = − >
2
1
sin cos sin cos sin 2 1 sin 2 sin 2 2 2 2 (sin 2 0).
4
aa a a a a a a⇔ =+⇒ =+ ⇒ =− <
*Chú ý hệ số góc của đường thẳng nối hai điểm A, B là
.
BA
AB
BA
yy
k
xx
−
=
−
Câu 46: Cho hàm số
( )
y fx=
có đạo hàm
(
) (
)
( )
2
2
f ' x x 1 x 2x ,=−−
với mọi
x.∈
Có bao nhiêu giá trị
nguyên dương của tham số
m
để hàm số
(
)
2
y f x 8x m
= −+
có 5 điểm cực trị ?
A. 16 B.15 C.
17
D.
18
Đáp án : B
Lời giải: Ta có
( )
( )
( )
( )
( )
( )
2
2
x4
g' x 2x 8 f ' x 8x m 0 I .
f ' x 8x m 0 *
=
= − −+ =⇔
−+ =
Mà
( ) ( )
( )
( ) ( )
22
2
f'x x1 x 2x x1.xx2;x= − − = − − ∀∈
Suy ra
( )
( ) ( )( )
( )
( )
( )
2
2
2 22 2
2
x 8x m 1 0 1
* x 8x m 1 x 8x m x 8x m 2 0 x 8x m 0 2
x 8x m 2 0 3
− + −=
⇔ −+− −+ −+−=⇔ −+=
− + −=
Qua các nghiệm của phương trình (1) (nếu có) thì
( )
g' x
đều không đổi dấu. Do đó ta không xét phương
trình (1).
Để hàm số đã cho có 5 điểm cực trị khi và chỉ khi phương trình (2); (3) có 2 nghiệm phân biệt khác 4.
16 m 0
16 m 2 0
m 16
16 m 0
18 m 0
−>
− +>
⇔ ⇔<
−+≠
−+≠
Kết hợp
*
m∈⇒
có 15 gia trị
m
cần tìm.
Câu 47:
Nhà hàng có cấu trúc vỏ hình parabol chất liệu tre nứa , nằm trên quần đảo Cát Bà (Hải Phòng) do công ty
kiến trúc Vo Trong Nghia Architects thiết kế. Nhìn mặt trước mặt sau của mỗi lều là hình parabol, biết rằng
mặt sàn hình chữ nhật chiều rộng 3m, chiều sâu 6m, chiều cao từ mặt sàn lên đỉnh của parabol là 3m.
Tính thể tích V phần không gian bên trong của mỗi lều.

A.
( )
3
18Vm=
B.
( )
3
36Vm
=
C.
( )
3
6
Vm=
D.
( )
3
12
Vm
=
Đáp án : B
Lời giải: Giả sử mặt sàn hình chữ nhật là ABCD, trong đó AB=3m, BC= 6m. I là đỉnh parabol.
Gọi O là trung điểm AB. Chọn hệ trục tọa độ Oxy sao cho gốc O, trục Ox trùng AB, Oy trùng OI
Khi đó parabol có phương trình
=−+
2
4
y x3
3
.Diện tích mặt trước của lều là
=−+ =
∫
3
2
2
0
4
S 2 x 3 dx 6
3
2
m
Thể tích cần tìm là
( )
= =
2
V 6.S 36 m
Câu 48: Cho số phức
z a bi
= +
với
0a ≤
thỏa mãn
22zi−≤
;
22
14z zi+−−≤
. Tính diện tích S phần
giới hạn bởi điểm biểu diễn của số phức z và trục Oy.
A.
4
3
S
π
=
B.
4S
π
=
C.
3
2
S
π
=
D.
2S
π
=
Đáp án : C
Lời giải:
Gọi z= x+yi ( x, y số thực)
22
14z zi+−−≤
Suy ra z có điểm biểu diễn là nửa mặt phẳng bờ
20xy++≤
kể cả đường thẳng
20xy
++=
( phần chứa O)
22
zi−≤
suy ra điểm biễu diễn của z thuộc hình tròn tâm I( 0;2) bán kính R=2
Phần diện tích là
3 33
4
8 82
tron
S
ππ
= =
Câu 49: Tìm tất cả các giá trị thực của tham số m để phương trình
2sin cos 1xm x m+=−
có nghiệm
;
22
x
ππ
∈−
.
A.
31m−≤ ≤
. B.
26m−≤ ≤
. C.
13m≤≤
D.
13m−≤ ≤
.
Đáp án : D
Lời giải:
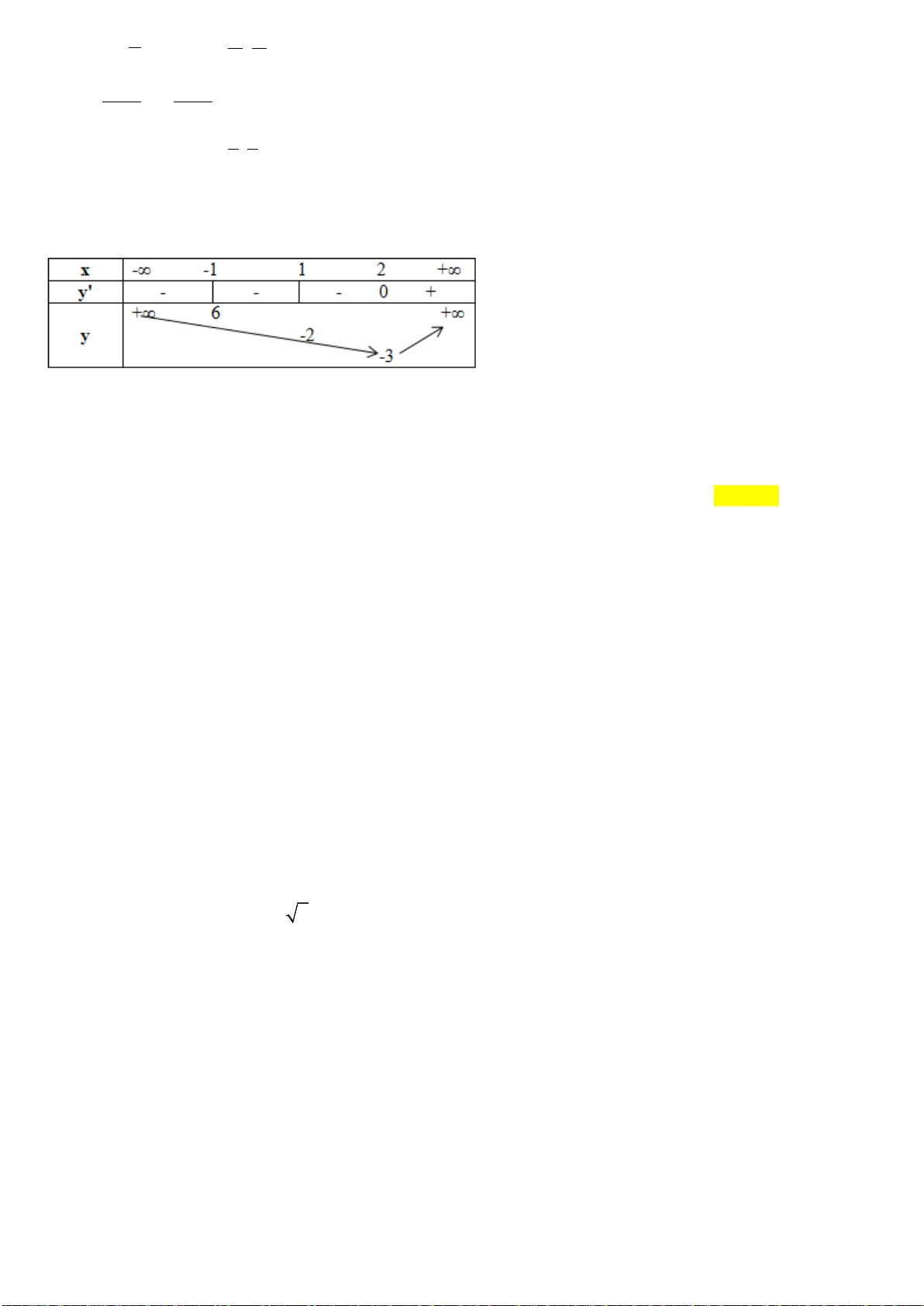
Đặt
tan
2
x
t =
, để
;
22
x
ππ
∈−
thì
[ ]
1;1t ∈−
.
(
)
2
22
22
21
2 14
t 11
1
p
1
tt
m m t m mt m m t
tt
⇔
−
+ =−⇔ +− =−+−
++
2
4 12tt m+⇔ −=
Để (1) có nghiệm
x;
22
ππ
∈−
( )
2⇔
có nghiệm
t 1; 1
∈−
.
( )
2
2 t 4t 1 2m⇔ − +=
là phương trình hoành độ giao
điểm của
(
)
2
(P) : y t 4t 1
d : y 2m, d Ox
=−+
=
, số nghiệm của phương trình (2) là số giao điểm của (P) và d.
Bảng biến thiên của hàm số
2
y t 4t 1=−+
Dựa vào BBT ta có để yêu cầu bài toán xảy ra thì
13m−≤ ≤
Câu 50: Cho hàm số
( )
3
32
fx x x m= − ++
. Có bao nhiêu số nguyên dương
2018m <
sao cho với mọi bộ
ba số thực
[ ]
, , 1; 2abc∈−
thì
( ) ( ) ( )
,,fa fb fc
là độ dài ba cạnh một tam giác nhọn ?
A. 2009. B. 2013. C. 2017. D. 2008.
Đáp án : D
Lời giải:
Với m nguyên dương, ta có
2
() 3 3; () 0 1; 1.
fx x fx x x= − =⇔=− =
′′
Khi đó
{ } { }
[ 1;2]
min ( ) min ( 1), (1), (2) min 4, , 4 0.f x f f f m mm m
−
= − = + +=>
{ } { }
[ 1;2]
max ( ) max ( 1), (1), (2) max 4, , 4 4f x f f f m mm m
−
= − = + +=+
Điều kiện cần có để
( ), ( ), ( )
fa fb fc
là độ dài ba cạnh một tam giác nhọn là
222
( ) ( ) ( ).fa fb fc+>
Chọn
(
)
(
)
2
2
[ 1;2] [ 1;2]
[ 1;2] [ 1;2]
( ) ( ) min ( ), ( ) max ( ) 2 min ( ) max ( ) 0.fa fb fx fc fx fx fx
−−
−−
== =⇒ −>
Ngược lại nếu
(
)
(
)
2
2
[ 1;2]
[ 1;2]
2 min ( ) max ( ) 0fx fx
−
−
−>
thì
(
)
(
)
2
2
222
[ 1;2]
[ 1;2]
( ) ( ) ( ) 2 min ( ) max ( ) 0.
f a f b f c fx fx
−
−
+−≥ − >
Vậy điều kiện cần và đủ để mọi bộ ba số thực
, , [ 1; 2]abc∈−
thì
( ), ( ), ( )fa fb fc
là độ dài ba cạnh một tam
giác là
(
)
(
)
2
2
[ 1;2]
[ 1;2]
2 min ( ) max ( ) 0.
fx fx
−
−
−>
Vậy
22
2 ( 4) 4 4 2 9,656.
mm m> + ⇒ >+ ≈
Vậy
{ }
10,11,..., 2017m ∈
có tất cả 2008 số nguyên dương thoả mãn.

Trang 15/15
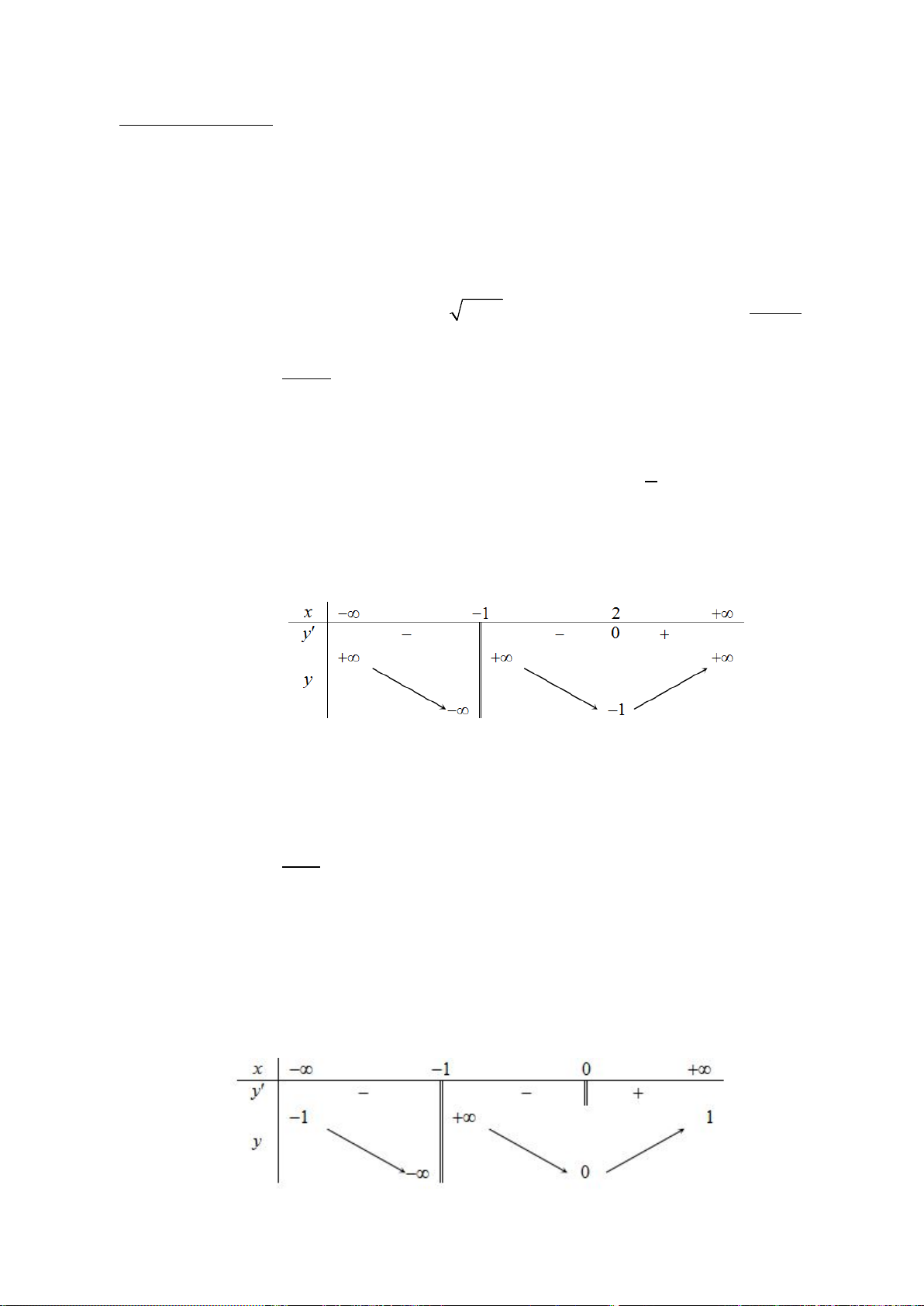
HĐT Trang 1/7
SỞ GD&ĐT KHÁNH HÒA
TRƯỜNG THPT
NGUYỄN THIỆN THUẬT
ĐỀ THI THAM KHẢO
(Đề thi có 07 trang)
KỲ THI TRUNG HỌC PHỔ THÔNG QUỐC GIA NĂM 2019
Bài thi: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Câu 1: Trong các hàm số dưới đây, hàm số nào có đồ thị đi qua điểm
(
)
1; 0M
?
A.
42
32yx x=−+
. B.
( )
12yx x=−−
. C.
32
33yx x=+−
. D.
2
22
1
x
y
x
−
=
−
.
Câu 2: Cho hàm số
21
1
x
y
x
+
=
−
. Khẳng định nào sau đây là khẳng định sai?
A. Hàm số không xác định tại điểm
1
x =
.
B. Hàm số nghịch biến trên
.
C. Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng
1
2
x = −
.
D. Đồ thị hàm số có tiệm cận đứng là
1x =
.
Câu 3: Cho hàm số
()fx
xác định trên
{ }
\1−
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như hình vẽ. Hỏi mệnh đề nào dưới đây sai?
A. Hàm số không có đạo hàm tại điểm
1x = −
.
B. Hàm số đạt cực trị tại điểm
2x =
.
C. Đồ thị hàm số có tiệm cận ngang là
1y = −
.
D. Đồ thị hàm số có tiệm cận đứng là
1x = −
.
Câu 4: Cho hàm số
3
1
y
x
=
−
. Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên mỗi khoảng
( ;1)−∞
và
(1; )+∞
.
B. Đồ thị hàm số có hai đường tiệm cận.
C. Hàm số có một cực trị.
D. Hàm số nghịch biến trên
{ }
\1
.
Câu 5. Cho hàm số
( )
y fx=
có bảng biến thiên
Hàm số
( )
y fx=
có bảng biến thiên trên là hàm số nào dưới đây?
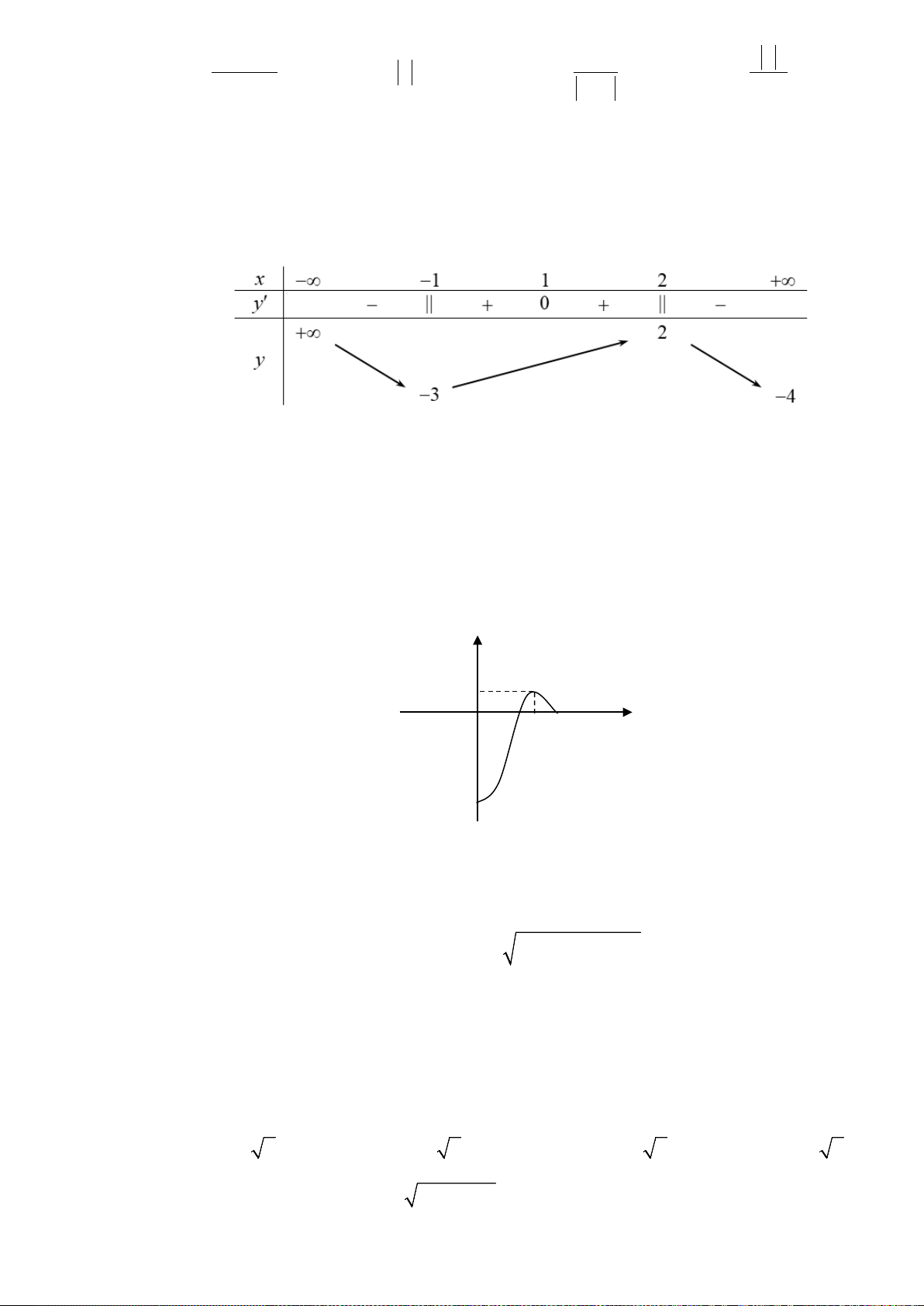
HĐT Trang 2/7
A.
( )
1
1
y
xx
=
+
. B.
(
)
1.
y xx
= +
C.
1
x
y
x
=
+
. D.
1
x
y
x
=
+
.
Câu 6. Cho hàm số
(
)
32
y f x ax bx cx d= = + ++
,
0
a ≠
. Khẳng định nào sau đây đúng?
A.
(
)
lim
x
fx
→−∞
= +∞
. B. Đồ thị hàm số luôn cắt trục hoành.
C. Hàm số luôn tăng trên
. D. Hàm số luôn có cực trị.
Câu 7. Cho hàm số
(
)
y fx=
liên tục trên
và có bảng biến thiên như sau:
Trong các mệnh đề sau, mệnh đề nào sai?
A. Hàm số có hai điểm cực trị.
B. Hàm số đạt giá trị lớn nhất bằng
2
và giá trị nhỏ nhất bằng
3−
.
C. Đồ thị hàm số có đúng một đường tiệm cận.
D. Hàm số nghịch biến trên các khoảng
( )
;1−∞ −
,
( )
2;+∞
.
Câu 8: Cho hàm số
( )
y fx=
có đạo hàm
(
)
fx
′
liên tục trên đoạn
[ ]
0;5
và đồ thị hàm số
( )
y fx
′
=
trên đoạn
[ ]
0;5
được cho như hình bên.
Tìm mệnh đề đúng
A.
( ) ( ) ( )
053fff= <
. B.
( ) ( ) ( )
305fff<=
.
C.
( ) ( )
(
)
305
fff<<
. D.
( ) ( )
(
)
350
fff<<
.
Câu 9: Cho
( )
32
3 61fx x x x=− −+
. Phương trình
(
)
(
)
( )
11 2f fx fx+ += +
có số nghiệm thực
là
A.
4
. B.
6
. C.
7
. D.
9
.
Câu 10: Cho hàm số
( )
( )
3 22 2
21 2 2 4y x m x m mx m
=−−+ − +
có đồ thị
(
)
C
và đường thẳng
: 48dy x= +
. Đường thẳng
d
cắt đồ thị
(
)
C
tại ba điểm phân biệt có hoành độ
123
,,xx x
. Tìm
giá trị lớn nhất
max
P
của biểu thức
333
1 23
Pxxx=++
.
A.
max
16 2 6P = −
. B.
max
16 2 8P = −
. C.
max
23 6 2P = −
. D.
max
24 6 2P = −
.
Câu 11: Phương trình
sin 2
2017 sin 2 cos
x
xx= +−
có bao nhiêu nghiệm thực trong
[ ]
5 ;2017
ππ
−
?
A. vô nghiệm. B.
2017
. C.
2022
. D.
2023
.
5−
3
5
1
x
O
y

HĐT Trang 3/7
Câu 12: Hàm số nào dưới đây có tập xác định là khoảng
( )
0;+∞
?
A.
( )
ln 1yx= +
B.
1
2
yx=
C.
x
ye=
D.
3
yx x
= −
Câu 13: Cho
,
ab
là các số thực dương,
1b ≠
. Nếu
3
2
3
2
aa
>
và
34
log log
45
bb
<
thì
A.
1, 1
ab>>
. B.
1, 0 1
ab> <<
.
C.
0 1, 0 1
ab<< <<
. D.
0 1, 1
ab<< >
.
Câu 14. Trong các mệnh đề sau. Mệnh đề nào sai?
A. Hàm số
x
ye=
không chẵn cũng không lẻ.
B. Hàm số
(
)
2
ln 1
y xx= ++
không chẵn cũng không lẻ.
C. Hàm số
x
ye=
có tập giá trị là
( )
0;
+∞
.
D. Hàm số
(
)
2
ln 1
y xx= ++
có tập xác định là
.
Câu 15. Cho hai hàm số
(
)
log
a
y fx x
= =
và
(
)
x
y gx a= =
(
,1 0aR a∈ ≠>
). Xét các mệnh đề sau:
I. Đồ thị của hai hàm số
( )
fx
và
( )
gx
luôn cắt nhau tại một điểm.
II. Hàm số
( ) ( )
f x gx+
đồng biến khi
1a
>
, nghịch biến khi
01a<<
.
III. Đồ thị hàm số
( )
fx
nhận trục
Oy
làm tiệm cận.
IV. Chỉ có đồ thị hàm số
( )
fx
có tiệm cận.
Số mệnh đề đúng là
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 16: Giải bất phương trình
( )
2
4 2 .log 1 0
x
x
− +≥
.
A.
0x
≥
B.
12x−< ≤
C.
02x≤≤
D.
12x−≤ ≤
Câu 17. Một người mua một căn hộ chung cư với giá
500
triệu đồng. Người đó trả trước số tiền là
100
triệu đồng. Số tiền còn lại người đó thanh toán theo hình thức trả góp với lãi suất tính trên tổng
số tiền còn nợ là
0,5%
mỗi tháng. Kể từ ngày mua, sau đúng mỗi tháng người đó trả số tiền cố
định là
4
triệu đồng (cả gốc lẫn lãi). Thời gian (làm tròn đến hàng đơn vị) để người đó trả hết nợ
là
A.
136
tháng. B.
140
tháng. C.
139
tháng. D.
133
tháng.
Câu 18: Xét các số thực dương
,ab
thỏa mãn
(
)
12
5
9
1
log log loga b ab= = +
. Mệnh đề nào dưới đây
đúng?
A.
( )
3;9
a
b
∈
B.
( )
9;16
a
b
∈
C.
( )
2;3
a
b
∈
D.
( )
0;2
a
b
∈
Câu 19: Xét
a
và
b
là hai số thực dương tùy ý. Đặt
( )
1000
2
22
1000logx ab= +
,
( )
2
1000
1
log
1000
y ab= +
. Mệnh đề nào dưới đây đúng?
A.
21xy− ≥−
B.
21xy− ≤−
C.
21xy− >−
D.
21xy− <−
Câu 20. Khẳng định nào sau đây sai?
A.
0dxC=
∫
. B.
5
4
d
5
x
xx C= +
∫
. C.
1
d lnx xC
x
= +
∫
. D.
ed e
xx
xC= +
∫
.
Câu 21:
0
3
1
d
1
x
x
−
−
∫
bằng
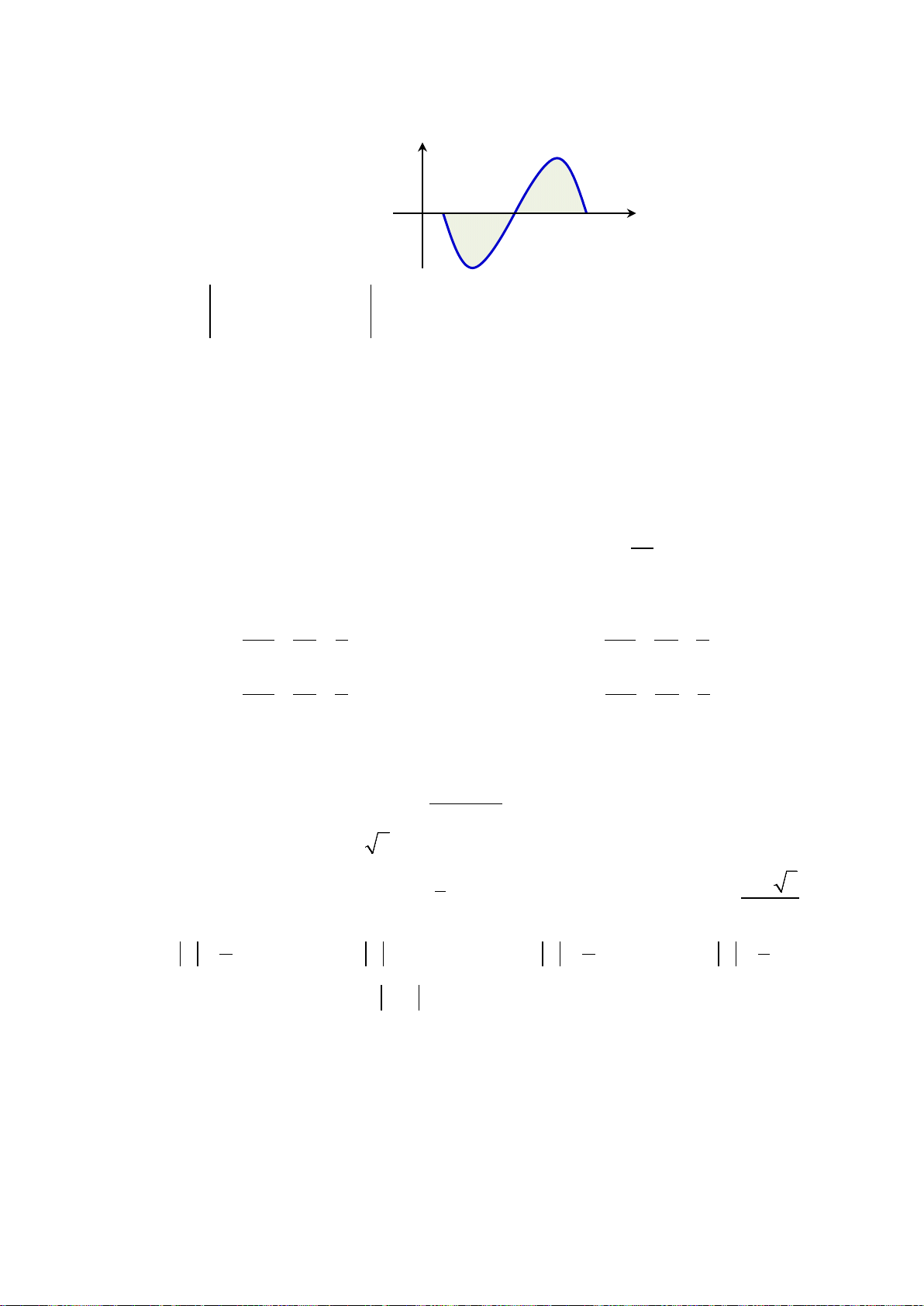
HĐT Trang 4/7
A.
2ln 2
−
. B.
2ln 2 1−
. C.
ln 2
. D.
2ln 2
.
Câu 22: Kí hiệu
S
là diện tích hình phẳng giới hạn bởi đồ thị hàm số
( )
y fx=
, trục hoành, đường
thẳng
, x ax b= =
(như hình bên). Hỏi khẳng định nào dưới đây là khẳng định đúng?
A.
( ) (
)
d d.
cb
ac
S fx x fx x= +
∫∫
B.
(
) ( )
d d.
cb
ac
S fx x fx x= +
∫∫
C.
(
)
(
)
dd
cb
ac
S fx x fx x=−+
∫∫
. D.
( )
d.
b
a
S fx x=
∫
Câu 23: Một vật chuyển động với vận tốc
(
)
vt
(
)
m/s
có gia tốc
( ) ( )
2 10at v t t
′
= =−+
( )
2
m/s
. Vận
tốc ban đầu của vật là
5 m/s
. Tính vận tốc của vật sau
5
giây.
A.
30 m/s
. B.
25 m/s
. C.
20 m/s
. D.
15 m/s
.
Câu 24: Tìm một nguyên hàm
( )
Fx
của hàm số
( ) ( )
2
, ;0
b
f x ax a b x
x
=+ ∈≠
, biết rằng
( )
11F −=
,
( )
14F =
,
( )
10
f
=
.
A.
( )
2
3 37
424
x
Fx
x
= ++
. B.
( )
2
3 37
424
x
Fx
x
= −−
.
C.
(
)
2
3 37
244
x
Fx
x
= +−
. D.
( )
2
3 31
222
x
Fx
x
= −−
.
Câu 25: Phần ảo của số phức
23zi= −
là
A.
3
i−
. B.
3
. C.
3−
. D.
3i
.
Câu 26: Cho số phức
z
thỏa mãn
( )
( )
21 2
2 78
1
i
iz i
i
+
++ =+
+
. Môđun của số phức
12
wz i= +−
là
A.
7
. B.
7
. C.
25
. D.
4
.
Câu 27: Cho số phức
z
thoả mãn
( )
1 2 19iz z i−−=+
. Tìm môđun của số phức
13i
w
z
+
=
.
A.
2
5
w =
. B.
5w =
. C.
5
2
w =
. D.
1
5
w =
.
Câu 28. Cho các số phức
z
thoả mãn
5zi−=
. Biết rằng tập hợp điểm biểu diễn số phức
1w iz i= +−
là đường tròn. Tính bán kính của đường tròn đó.
A.
9a⇒=−
. B.
22r =
. C.
4r =
. D.
5r =
.
Câu 29: Cho số phức
z a bi= +
( )
,ab∈
. Biết tập hợp các điểm
A
biểu diễn hình học số phức
z
là
đường tròn
(
)
C
có tâm
( )
4;3I
và bán kính
3R =
. Đặt
M
là giá trị lớn nhất,
m
là giá trị nhỏ
nhất của
4 31F ab= +−
. Tính giá trị
Mm+
.
A.
63Mm+=
. B.
48Mm+=
. C.
50Mm+=
. D.
41Mm+=
.
Câu 30. Hình đa diện đều có tất cả các mặt là ngũ giác có bao nhiêu cạnh?
A.
60
. B.
20
. C.
12
. D.
30
.
O
a
c
b
x
y
( )
y fx=
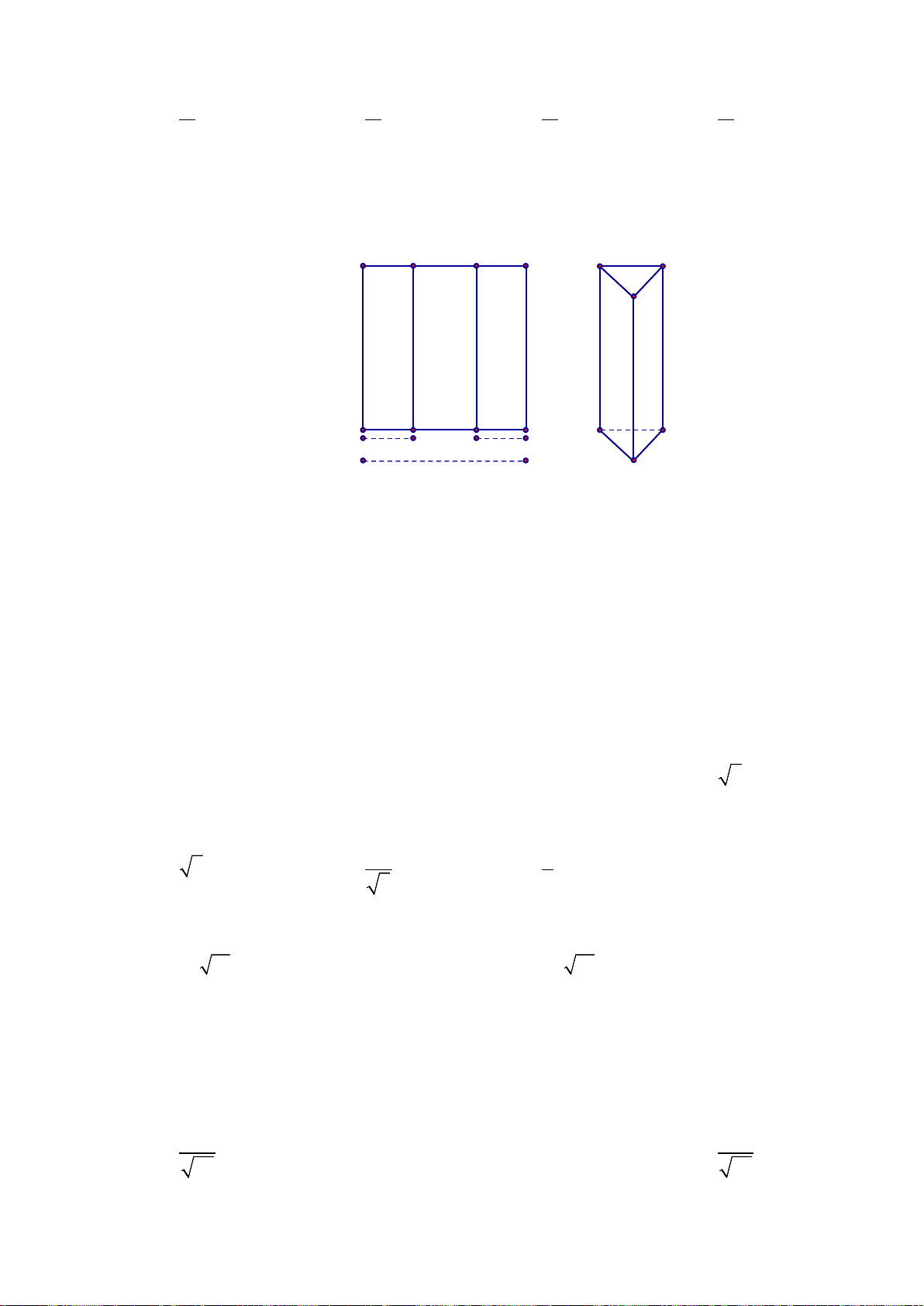
HĐT Trang 5/7
Câu 31. Cho hình chóp
.S ABCD
có thể tích
V
. Gọi
M
,
N
lần lượt là trung điểm của
SA
,
MC
. Thể
tích của khối chóp
.N ABCD
là
A.
6
V
. B.
4
V
. C.
2
V
. D.
3
V
.
Câu 32: Một tấm kẽm hình vuông
ABCD
có cạnh bằng
30 cm
. Người ta gập tấm kẽm theo hai cạnh
EF
và
GH
cho đến khi
AD
và
BC
trùng nhau như hình vẽ bên để được một hình lăng trụ
khuyết hai đáy.
Giá trị của
x
để thể tích khối lăng trụ lớn nhất là
A.
( )
5 cmx =
. B.
( )
9 cm
x =
. C.
( )
8 cm
x =
. D.
( )
10 cmx =
.
Câu 33: Chỉ ra khẳng định sai trong các khẳng định sau.
A. Khối lăng trụ có đáy có diện tích đáy là
B
, đường cao của lăng trụ là
h
, khi đó thể tích khối
lăng trụ là
V Bh=
B. Diện tích xung quanh của mặt nón có bán kính đường tròn đáy
r
và đường sinh
l
là
S rl
π
=
C. Mặt cầu có bán kính là
R
thì thể tích khối cầu là
3
4VR
π
=
D. Diện tích toàn phần của hình trụ có bán kính đường tròn đáy
r
và chiều cao của trụ
l
là
( )
2
tp
S rl r
π
= +
Câu 34: Một hình trụ có bán kính đáy bằng
r
và khoảng cách giữa hai đáy bằng
3
r
. Một hình nón có
đỉnh là tâm mặt đáy này và đáy trùng với mặt đáy kia của hình trụ. Tính tỉ số diện tích xung
quanh của hình trụ và hình nón.
A.
3
B.
1
3
C.
1
3
D. 3
Câu 35: Một hình nón có đường cao
4h cm=
, bán kính đáy
5r cm=
. Tính diện tích xung quanh của hình
nón đó.
A.
5 41
π
. B.
15
π
. C.
4 41
π
. D.
20
π
.
Câu 36: Trong không gian với hệ tọa độ
Oxyz
, hình chiếu vuông góc
'M
của điềm
(1; 1; 2)M −
trên
trục
Oy
có tọa độ là
A.
(0; 1; 0)−
. B.
(1;0;0)
. C.
(0;0;2)
. D.
(0;1; 0)
.
Câu 37: Khoảng cách từ điểm
( )
0;2;1A
đến mặt phẳng
( )
:2 3 5 0P xy z−+ +=
bằng
A.
6
14
. B.
6
. C.
4
. D.
4
14
.
A
E
G
B
E
G
A
B
D
F
H
C
F
H
D
C
x
x
30 cm

HĐT Trang 6/7
Câu 38: Cho đường thẳng
113
:
211
xyz
d
++−
= =
và mặt phẳng
( )
: 2 – 5 0P x yz+ +=
. Góc giữa
d
và
( )
P
là
A.
30
°
. B.
45°
. C.
60°
. D.
90°
.
Câu 39: Trong không gian với hệ tọa độ
Oxyz
, cho điểm
(
)
3; 2; 1M −
. Hình chiếu vuông góc của điểm
M
lên trục
Oz
là điểm
A.
( )
3
3;0;0M
. B.
( )
4
0;2;0M
. C.
( )
1
0;0; 1M −
. D.
( )
2
3; 2; 0M
.
Câu 40: Trong không gian với hệ tọa độ
Oxyz
, cho hai mặt phẳng
( )
:2 3 5 0P x my z+ + −=
và
( )
: 8 6 20Q nx y z− − +=
. Tìm giá trị của các tham số
m
,
n
để
( )
P
và
( )
Q
song song.
A.
4, 3mn=−=
. B.
4, 3
mn= =
. C.
4, 4mn=−=
. D.
4, 4
mn= = −
.
Câu 41: Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
( )
(
) ( )
22
2
: 3 1 10
Sx y z
+ + +− =
. Mặt
phẳng nào trong các mặt phẳng dưới đây cắt mặt cầu
( )
S
theo giao tuyến là đường tròn có bán
kính bằng
3
?
A.
( )
1
: 2 2 80
Px y z
+ − +=
. B.
( )
1
: 2 2 80Px y z+ − −=
.
C.
( )
1
: 2 2 20Px y z+ − −=
. D.
( )
1
: 2 2 40Px y z+ − −=
.
Câu 42: Trong không gian với hệ toạ độ
Oxyz
, cho mặt cầu
( ) ( ) ( ) ( )
222
:1 3 24Sx y z− +− +− =
. Gọi
( )
0 00
;;Nx y z
là điểm thuộc
( )
S
sao cho khoảng cách từ điểm
N
đến mặt phẳng
( )
Oxz
lớn
nhất. Giá trị của biểu thức
0 00
Px y z=++
bằng
A.
6
. B.
8
. C.
5
. D.
4
.
Câu 43: Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
1; 1; 2A
và mặt phẳng
( )
(
)
: 1 10P m x y mz
− + + −=
, với
m
là tham số thực. Cho biết có một giá trị duy nhất
0
m
của
m
để khoảng cách từ điểm
A
đến mặt phẳng
( )
P
là lớn nhất. Khẳng định nào sau đây
đúng ?
A.
0
26m<<
B.
0
7 11m
<<
. C.
0
22m−< <
. D.
0
62m− < <−
.
Câu 44: Nhân ngày 8/3 trường THPT Nguyễn Thiện Thuật tổ chức giải bóng đá nữ gồm 11 lớp tham gia,
trong đó có 10 lớp mỗi lớp có một đội tham gia, riêng lớp 12A1 có hai đội tham gia. Ban tổ chức
tiến hành bốc thăm ngẫu nhiên để chia thành hai bảng đấu, mỗi bảng
6
đội. Xác suất để
2
đội
của lớp 12A1 ở cùng một bảng là
A.
4
11
P =
. B.
3
22
P =
. C.
5
11
P =
. D.
5
22
P =
.
Câu 45: Một đề thi trắc nghiệm gồm
50
câu, mỗi câu có
4
phương án trả lời trong đó chỉ có
1
phương
án đúng, mỗi câu trả lời đúng được
0,2
điểm. Một thí sinh làm bài bằng cách chọn ngẫu nhiên
1
trong
4
phương án ở mỗi câu. Tính xác suất để thí sinh đó được
6
điểm.
A.
20 30
1 0,25 .0,75−
. B.
30 20
0,25 .0,75
. C.
20 30
0,25 .0,75
. D.
30 20 20
50
0,25 .0,75 C
.
Câu 46. Cho cấp số nhân
( )
1
; 1, 2
n
uu q
= =
. Hỏi số
1024
là số hạng thứ mấy?
A.
11
. B.
9
. C.
8
. D.
10
.
Câu 47: Cho hình chóp
.S ABC
có
( )
SA ABC⊥
và đáy
ABC
vuông ở
A
. Khẳng định nào sau đây sai?
A.
( ) ( )
SAB ABC⊥
.
B.
( ) ( )
SAB SAC⊥
.
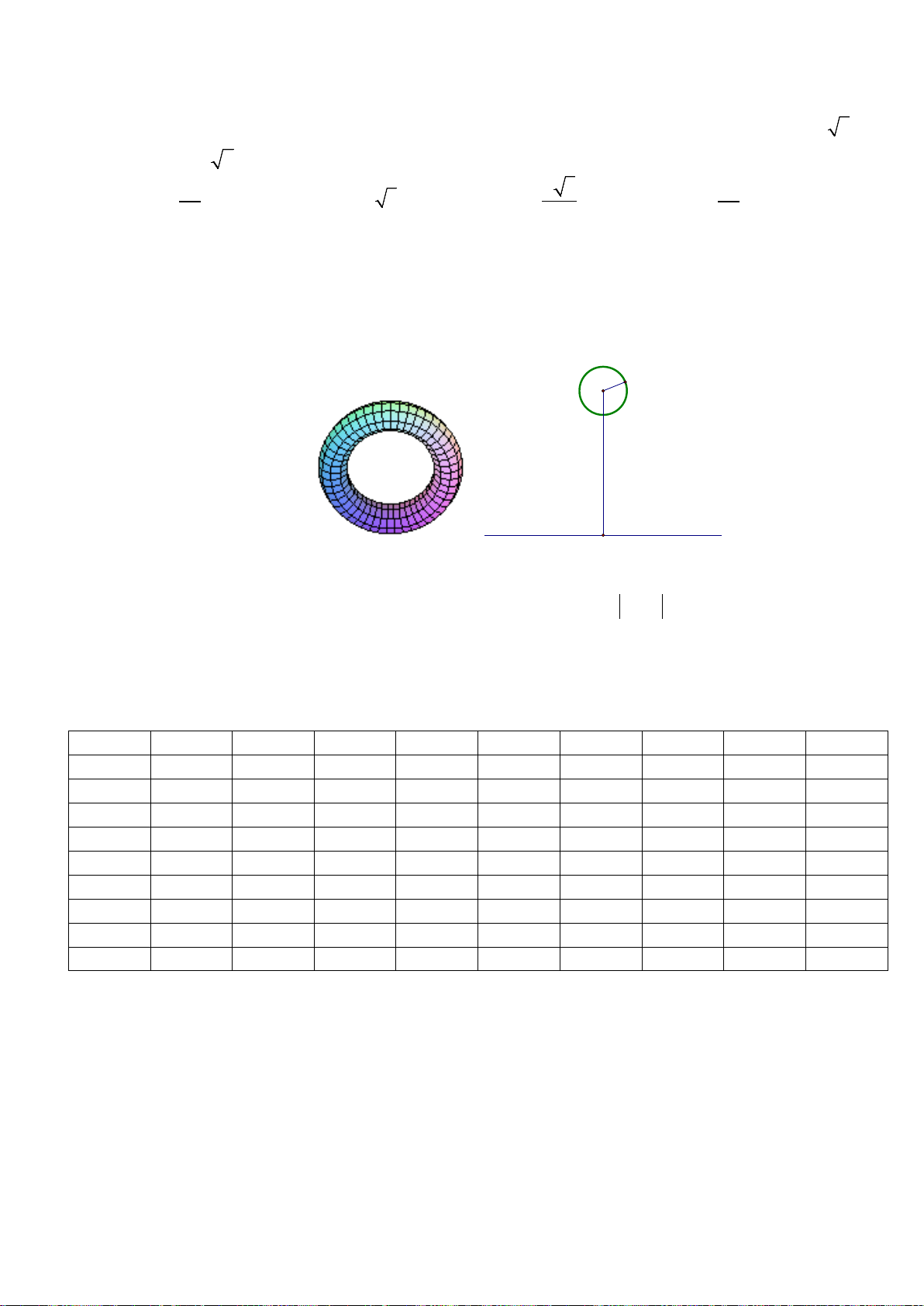
HĐT Trang 7/7
C. Vẽ
,
AH BC H BC⊥∈
⇒ góc
AHS
là góc giữa hai mặt phẳng
(
)
SBC
và
(
)
ABC
.
D. Góc giữa hai mặt phẳng
( )
SBC
và
( )
SAC
là góc
SCB
.
Câu 48. Cho hình chóp
S.
ABCD
có
( )
SDA ABC⊥
, đáy
ABCD
là hình chữ nhật với
5AC a=
và
2.BC a=
Tính khoảng cách giữa hai đường thẳng
SD
và
BC
.
A.
3
4
a
. B.
3a
. C.
3
2
a
. D.
2
3
a
.
Câu 49: Người ta làm một chiếc phao bơi như hình vẽ (với bề mặt xung quanh có được bằng cách quay
đường tròn
( )
C
quanh trục
d
). Biết rằng
30 cmOI =
,
5 cmR
=
. Tính thể tích
V
phần
không gian bên trong của chiếc phao.
(
C
)
d
R
I
O
A.
23
1500 cmV
π
=
. B.
23
9000 cmV
π
=
. C.
3
1500 cmV
π
=
. D.
3
9000 cmV
π
=
.
Câu 50: Tìm giá trị tham số thực
a
để bất phương trình:
( )
2
4 21x x ax+ ≤ ++
có nghiệm.
A.
a∀∈
. B. Không có
a
C.
4a ≥−
. D.
4a ≤−
.
BẢNG ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
A
B
C
B
D
B
B
D
A
B
11
12
13
14
15
16
17
18
19
20
D
B
D
B
C
C
C
D
A
C
21
22
23
24
25
26
27
28
29
30
D
C
A
A
C
D
A
D
B
D
31
32
33
34
35
36
37
38
39
40
B
D
C
A
A
A
A
A
C
D
41
42
43
44
45
46
47
48
49
50
A
B
A
D
D
A
D
B
A
C

LTB Trang 1/7
TRƯỜNG THPT LẠC LONG QUÂN
TỔ: TOÁN-TIN
ĐỀ ĐỀ XUẤT
KÌ THI THPT QUỐC GIA NĂM 2019
BÀI THI MÔN: TOÁN.
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Câu 1: Cho số phức
32zi= −
.
Phần ảo của số phức liên hợp của
z
là
A. 2i. B. -2i. C. 2. D. -2.
Câu 2: Cho hàm số
3
1
y
x
=
+
có đồ thị là
( )
C
. Mệnh đề nào sau đây đúng ?
A.
( )
C
có tiệm cận ngang là
3.y =
B.
( )
C
chỉ có một tiệm cận.
C.
( )
C
có tiệm cận ngang là
0.y =
D.
( )
C
có tiệm cận đứng là
1.x
=
Câu 3: Cho tập hợp
{ }
0;1; 2;3; 4;5;6;7;8;9M =
có
10
phần tử. Số tập con gồm
2
phần tử của
M
và không chứa phần tử
1
là
A.
2
9
A
. B.
2
9
C
. C.
2
10
C
. D.
2
9
.
Câu 4: Hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
B
,
SA
vuông góc với mặt phẳng
đáy. Thể tích khối tứ diện
SABC
được tính theo công nào sau đây ?
A.
1
.
3
SAB
V SA S
∆
=
. B.
1
.
3
SAC
V SA S
∆
=
. C.
1
.
3
SAB
V BC S
∆
=
. D.
1
.
3
SCB
V SA S
∆
=
.
Câu 5: Cho hàm số
( )
fx
có đạo hàm
( )
( ) ( ) ( )
23
1 12fx x x x
′
=+−−
. Hàm số
(
)
fx
đồng biến
trên khoảng nào dưới đây ?
A.
( )
;1
−∞ −
. B.
(
)
1;1−
. C.
( )
2; +∞
. D.
( )
1; 2
.
Câu 6: Mệnh đề nào sau đây đúng?
A.
d
2.
x
xc
x
= +
∫
B.
2d 2 .
xx
xc= +
∫
C.
2
d1
.
x
c
xx
= +
∫
D.
d
ln .
1
x
xc
x
= +
+
∫
Câu 7: Cho hàm số
( )
y fx=
có bảng biến thiên như hình vẽ bên. Mệnh đề nào sau đây sai?
A. Hàm số đã cho đồng biến trên khoảng
( )
2; +∞
.
B. Hàm số đã cho đồng biến trên khoảng
( )
3; +∞
.
C. Hàm số đã cho đồng biến trên khoảng
( )
;1−∞
.
D. Hàm số đã cho nghịch biến trên khoảng
( )
0; 3
.
Câu 8: Giả sử
,xy
là các số thực dương. Mệnh đề nào sau đây sai?
A.
2 22
log log log .
x
xy
y
= −
B.
(
)
2 22
1
log log log .
2
xy x y= +
C.
2 22
log log log .xy x y= +
D.
( )
2 22
log log log .xy x y+= +
x
−∞
1
2
+∞
y
′
+
0
−
||
+
y
−∞
3
0
+∞
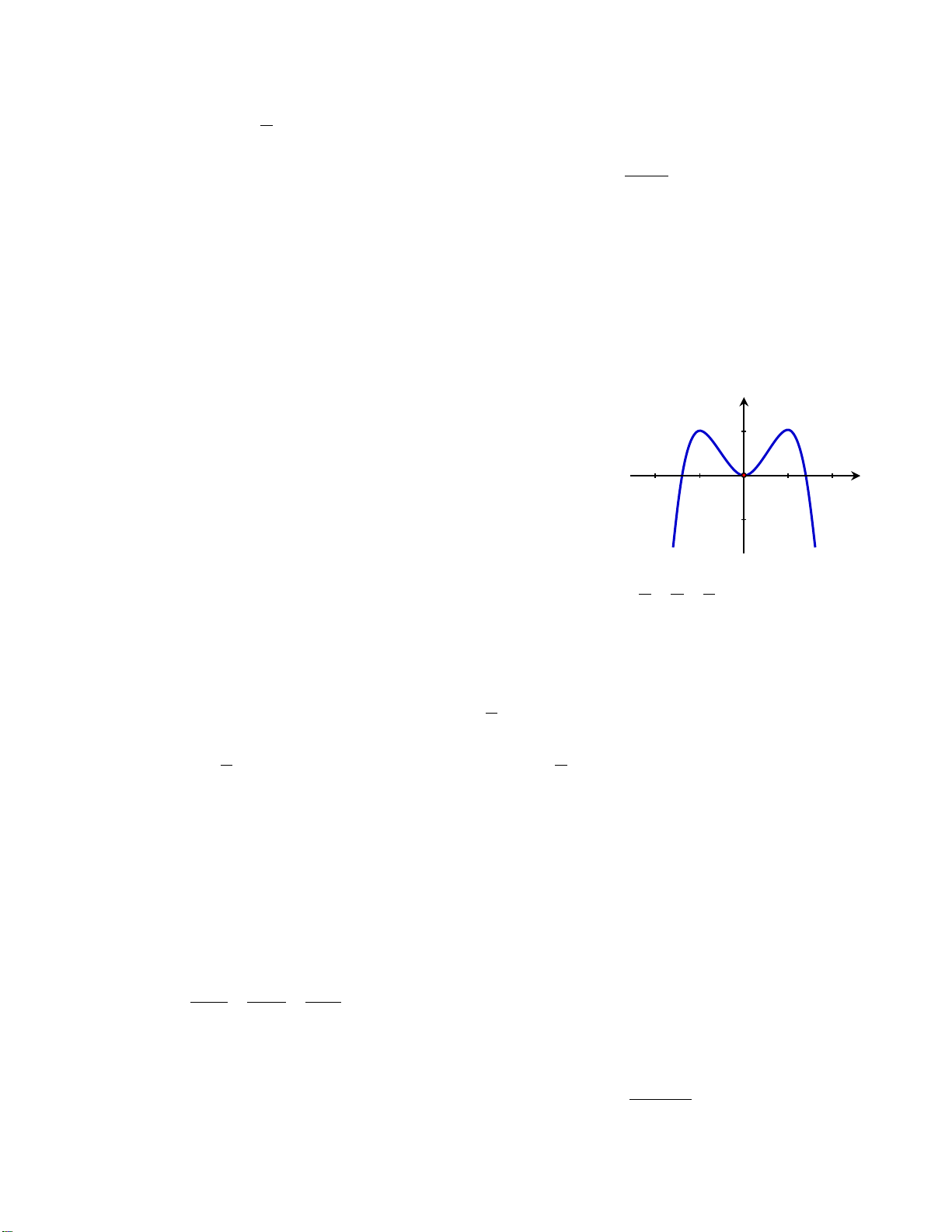
LTB Trang 2/7
Câu 9: Tìm nguyên hàm của hàm số
( )
2
.
x
fx e=
A.
22
1
d
2
xx
ex e C= +
∫
. B.
22
d
xx
e xe C
= +
∫
.
C.
22
d2
xx
ex e C= +
∫
. D.
21
2
d
21
x
x
e
ex C
x
+
= +
+
∫
.
Câu 10: Trong không gian với hệ tọa độ
,Oxyz
cho điểm
( )
;;M abc
. Mệnh đề nào sau đây sai?
A. Điểm
M
thuộc
Oz
khi và chỉ khi
0.ab= =
B. Khoảng cách từ
M
đến
(
)
Oxy
bằng
c
.
C. Tọa độ hình chiếu của
M
lên
Ox
là
( )
;0;0a
.
D. Tọa độ
OM
là
( )
;;abc
.
Câu 11: Cho hàm số
()y fx=
có đồ thị như hình vẽ bên. Biết rằng
()fx
là một trong bốn phương
án A, B, C, D đưa ra dưới đây. Tìm
()fx
.
A.
42
() 2fx x x= −
. B.
42
() 2fx x x= +
.
C.
42
() 2 1fx x x=−+ −
. D.
42
() 2
fx x x
=−+
.
Câu 12: Trong không gian với hệ tọa độ
Oxyz
, đường thẳng
:
112
xyz
∆==
vuông góc với mặt
phẳng nào trong các mặt phẳng sau ?
A.
( )
: 0.
Pxyz++=
B.
( )
: 0.xyz
β
+−=
C.
( )
: 2 0.xy z
α
++ =
D.
( )
: 2 0.Qxy z+− =
Câu 13: Nghiệm của bất phương trình
5
2
xx
ee
−
+<
là
A.
1
2
x <
hoặc
2x >
. B.
1
2
2
x<<
.
C.
ln 2 ln 2x− <<
. D.
ln 2x <−
hoặc
ln 2x >
.
Câu 14: Hình trụ có bán kính đáy bằng
,a
chu vi của thiết diện qua trục bằng
10 .a
Thể tích của
khối trụ đã cho bằng
A.
3
5.a
π
B.
3
.
a
π
C.
3
3.a
π
D.
3
4.a
π
Câu 15: Trong không gian với hệ toạ độ
Oxyz
, cho đường thẳng
∆
nằm trong mặt phẳng
( )
: 30xyz
α
++−=
đồng thời đi qua điểm
( )
1; 2; 0M
và cắt đường thẳng
223
:
211
xyz
d
−−−
= =
. Một vectơ chỉ phương của
∆
là
A.
( )
1;1; 2u = −
. B.
( )
1; 0; 1u = −
. C.
( )
1; 1; 2u = −−
. D.
( )
1; 2;1u = −
.
Câu 16: Tìm tất cả các giá trị của tham số
a
để đồ thị hàm số
2
32
x
y
x
a
ax
+
+
=
có 3 đường tiệm cận.
O
x
y
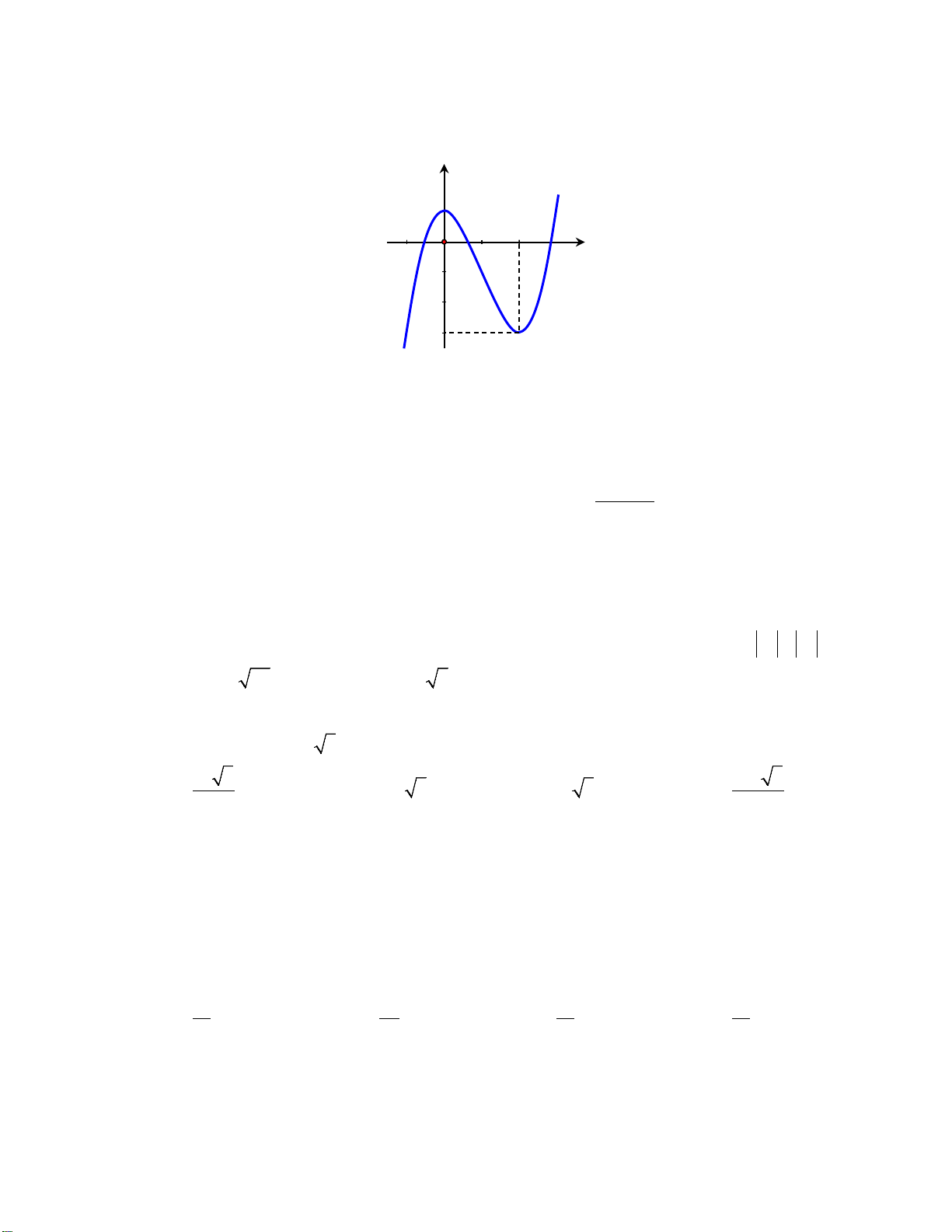
LTB Trang 3/7
A.
0, 1a a≠ ≠±
. B.
0, 1a a≠ ≠−
. C.
, 10aa< ≠−
. D.
0a
>
.
Câu 17: Cho hàm số
32
y ax bx cx d= + ++
có đồ thị trong hình bên. Hỏi phương trình
32
10ax bx cx d
+ + + +=
có bao nhiêu nghiệm ?
A.Phương trình không có nghiệm. B.Phương trình có đúng một nghiệm.
C.Phương trình có đúng hai nghiệm. D.Phương trình có đúng ba nghiệm.
Câu 18: Tọa độ đỉnh I của Parabol
2
23yx x=−+
là
A.
(1; 2)I
. B.
(1; 3)I −
. C.
( 1; 0)I −
. D.
(1; 0)I
.
Câu 19: Cho hàm số
( )
y fx=
liên tục trên
và thỏa mãn
(
)
1
ln
d.
e
fx
xe
x
=
∫
Mệnh đề nào sau đây
đúng ?
A.
( )
1
0
d 1.fx x=
∫
B.
( )
1
0
d.fx x e=
∫
C.
( )
0
d 1.
e
fx x=
∫
D.
( )
0
d.
e
fx x e=
∫
Câu 20: Gọi
12
,zz
là các nghiệm phức của phương trình
2
2 50zz+ +=
. Tính
22
12
Mz z
= +
.
A.
2 34M =
.
B.
45M
=
C.
12M =
D.
10M =
Câu 21: Cho hình chóp đều
.S ABCD
có cạnh đáy bằng
2a
, khoảng cách giữa hai đường thẳng
SA
và
CD
bằng
3a
. Thể tích khối chóp đều
.S ABCD
bằng
A.
3
3
3
a
. B.
3
43a
. C.
3
3a
. D.
3
43
3
a
.
Câu 22: Một người gửi vào ngân hàng một khoản tiền
T
theo hình thức lãi kép với lãi suất
0,6%
mỗi tháng. Biết sau
15
tháng người đó có số tiền cả vốn lẫn lãi là
10
triệu đồng. Hỏi số
tiền
T
gần với số tiền nào nhất trong các số sau ?
A.
9.145.000
. B.
9.141.769
. C.
9.141.000
. D.
9.141.900
.
Câu 23: Một hộp chứa
11
quả cầu trong đó có
5
quả màu xanh và
6
quả màu đỏ. Lấy ngẫu nhiên
lần lượt
2
quả cầu từ hộp đó. Tính xác suất để
2
lần đều lấy được quả cầu màu xanh.
A.
5
11
. B.
9
55
. C.
4
11
. D.
2
11
.
O
2
x
y
3
−
1
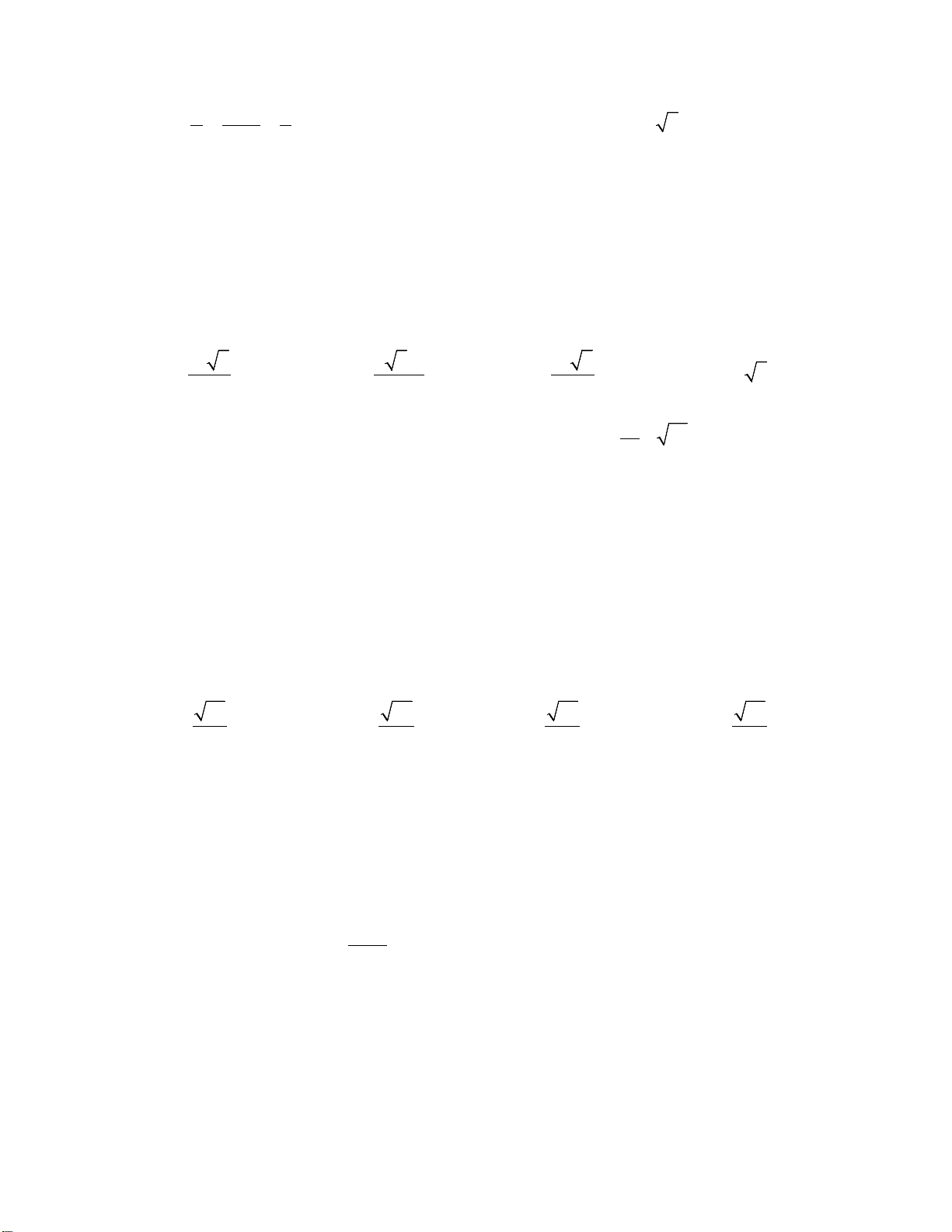
LTB Trang 4/7
Câu 24: Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
( )
S
có tâm
I
thuộc đường thẳng
3
:
112
xy z+
∆= =
. Biết rằng mặt cầu
(
)
S
có bán kính bằng
22
và cắt mặt phẳng
(
)
Oxz
theo một đường tròn có bán kính bằng
2
. Tìm tọa độ của điểm
I
.
A.
( ) ( )
5;2;10 , 0; 3;0II−
. B.
(
)
(
)
1; 2; 2 , 0; 3;0II
−−
.
C.
( ) ( )
1; 2; 2 , 5;2;10II−
. D.
( )
( )
1; 2; 2 , 1; 2; 2II− −−
.
Câu 25: Cho lăng trụ đứng
.
ABC A B C
′′′
có đáy là tam giác vuông tại
A
,
AC a
=
,
60ACB = °
.
Đường chéo
BC
′
của mặt bên
( )
BCC B
′′
tạo với mặt phẳng
( )
AA C C
′′
một góc
30°
. Tính
thể tích của khối lăng trụ theo
a
.
A.
3
6
2
a
. B.
3
26
3
a
. C.
3
6
3
a
. D.
3
6a
.
Câu 26: Tìm hệ số của số hạng chứa
8
x
trong khai triển của
5
3
1
n
x
x
+
, biết
n
là số nguyên
dương thỏa mãn
(
)
1
43
73
nn
nn
CC n
+
++
−=+
.
A.
495
. B.
313
. C.
1303
. D.
13129
Câu 27: Tìm tập
S
của bất phương trình:
2
3 .5 1
xx
<
.
A.
(
]
5
log 3; 0−
. B.
[
)
3
log 5; 0
. C.
( )
5
log 3; 0−
. D.
( )
3
log 5; 0
.
Câu 28: Cho hình chóp
.S ABC D
có đáy
ABCD
là hình thoi cạnh
a
,
0
120ABC =
, tam giác
SAB
đều và nằm trong mặt phẳng vuông góc với đáy. Tính bán kính mặt cầu ngoại tiếp hình
chóp
.S ABC
.
A.
41
6
a
. B.
37
6
a
. C.
39
6
a
. D.
35
6
a
.
Câu 29: Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
( ) ( )
( ) ( )
2 22
: 1 2 3 25Sx y z++−+−=
và
mặt phẳng
( )
:2 2 0xy zm
α
+− + =
. Tìm các giá trị của
m
để
( )
α
và
( )
S
không có điểm
chung.
A.
9m <−
hoặc
21m >
. B.
9 21
m−< <
.
C.
9 21m−≤ ≤
. D.
9
m ≤−
hoặc
21m ≥
.
Câu 30: Tìm
m
để hàm số
32
1
2(2 ) 2(2 ) 5
3
m
y x mx mx
−
= −− +− +
nghịch biến trên tập xác định.
A.
25m<<
. B.
2m >−
. C.
1m =
. D.
23m≤≤
.
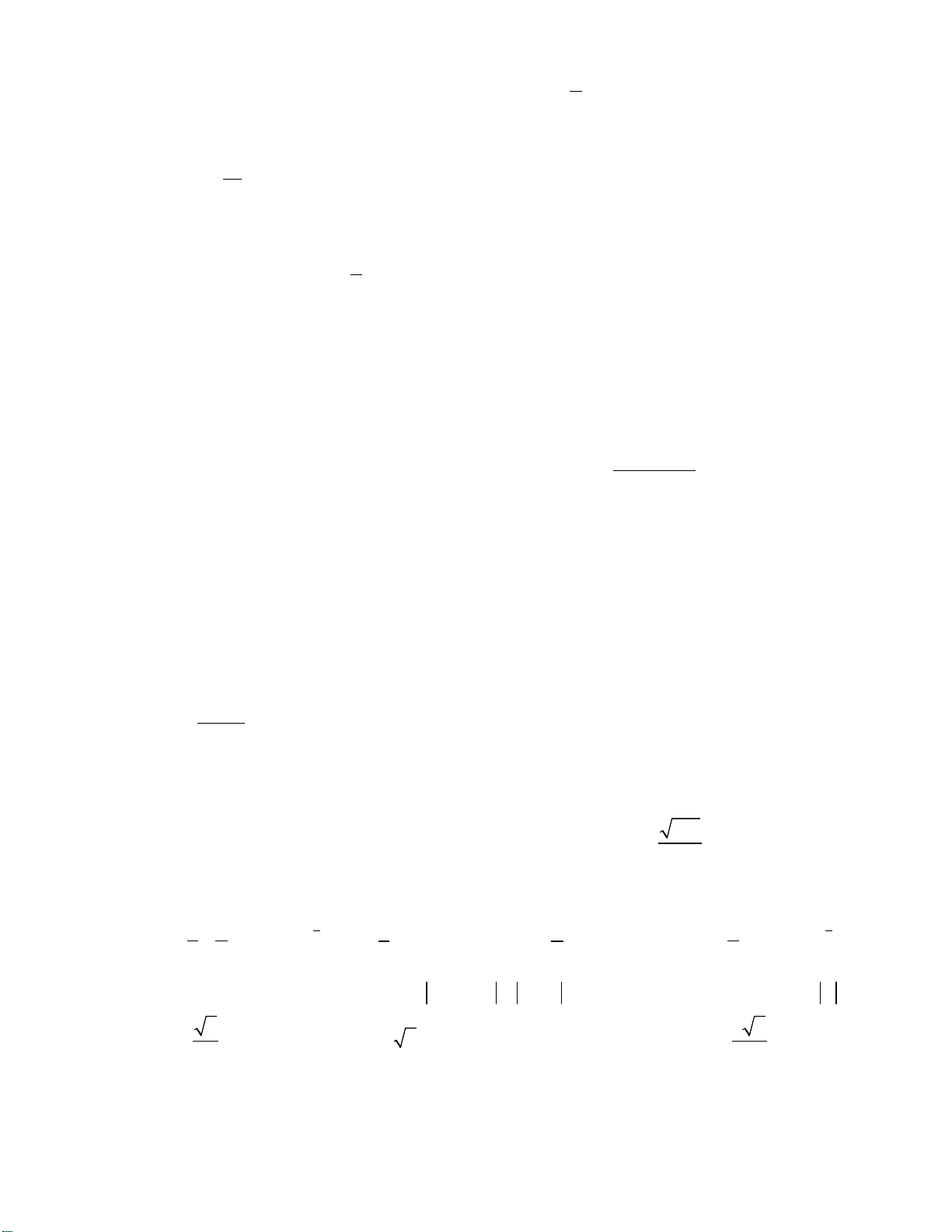
LTB Trang 5/7
Câu 31: Cho hình phẳng
( )
H
giới hạn bởi các đường
1
1y
x
= +
,
0
y =
,
1
x
=
,
xk=
( )
1k >
. Gọi
V
là thể tích của khối tròn xoay sinh ra khi quay hình
(
)
H
xung quanh trục
Ox
. Tìm
k
để
15
ln16
4
V
π
= +
.
A.
2
ke=
. B.
2
ke=
. C.
4k =
. D.
8
k =
.
Câu 32: Biết rằng
1
0
1
cos 2 d ( sin 2 cos 2 )
4
x xx a b c
= ++
∫
với
,,abc∈
. Mệnh đề nào sau đây là đúng ?
A.
21abc++=−
. B.
20a bc
+ +=
. C.
0abc−+=
. D.
1abc++=
.
Câu 33: Trong mặt phẳng (Oxy), cho tam giác ABC có
(0;1) , ( 1;3) , (2; 2)AB C−
. Phương trình
đường cao hạ từ đỉnh A của tam giác ABC là
A.
31
yx= +
. B.
31yx=−+
. C.
31yx=−−
. D.
31
yx= −
.
Câu 34:
Tìm tất cả các giá trị của tham số
m
để phương trình
( )
3
2
log 1
xm
x
−=
+
có hai nghiệm thực
phân biệt.
A.
01 m−< ≠
. B.
1
m >−
. C. Không tồn tại
m
. D.
10m−< <
.
Câu 35: Tìm tập hợp tất cả các giá trị tham số
m
sao cho phương trình
22
21 22
4 .2 3 2 0
xx xx
mm
−+ −+
− + −=
có bốn nghiệm thực phân biệt.
A.
( )
;1−∞
. B.
( ) ( )
;1 2;−∞ ∪ +∞
. C.
[
)
2; +∞
. D.
( )
2; +∞
.
Câu 36: Giá trị của tham số thực
m
thuộc vào khoảng nào để để giá trị lớn nhất của hàm số
1mx
y
xm
+
=
−
trên đoạn
[1; 2]
bằng
2−
?
A.
( )
3; 1−−
. B.
( )
2; 4
. C.
( )
4;6
. D. Không tồn tại.
Câu 37: Cho hàm số
( )
fx
xác định trên
( )
0; +∞
thỏa mãn
( )
ln x
fx
x
′
=
,
( )
11
f =
. Giá trị của
biểu thức
( ) ( )
2018f e f+
bằng
A.
( )
( )
3
2
82
ln 2018
33
+
. B.
( )
8
ln 2018
3
+
. C.
( )
2
ln 2018
3
+
. D.
( )
( )
3
2
2
ln 2018
3
.
Câu 38: Cho các số phức
,
zw
thỏa mãn
2 2 4, 1z i z i w iz+− = − = +
. Giá trị nhỏ nhất của
w
là
A.
2
2
. B.
22
. C.
2
. D.
32
2
.
Câu 39: Cho hàm số
()y fx=
có đồ thị hàm số
'( 2) 2y fx= −+
như hình vẽ bên
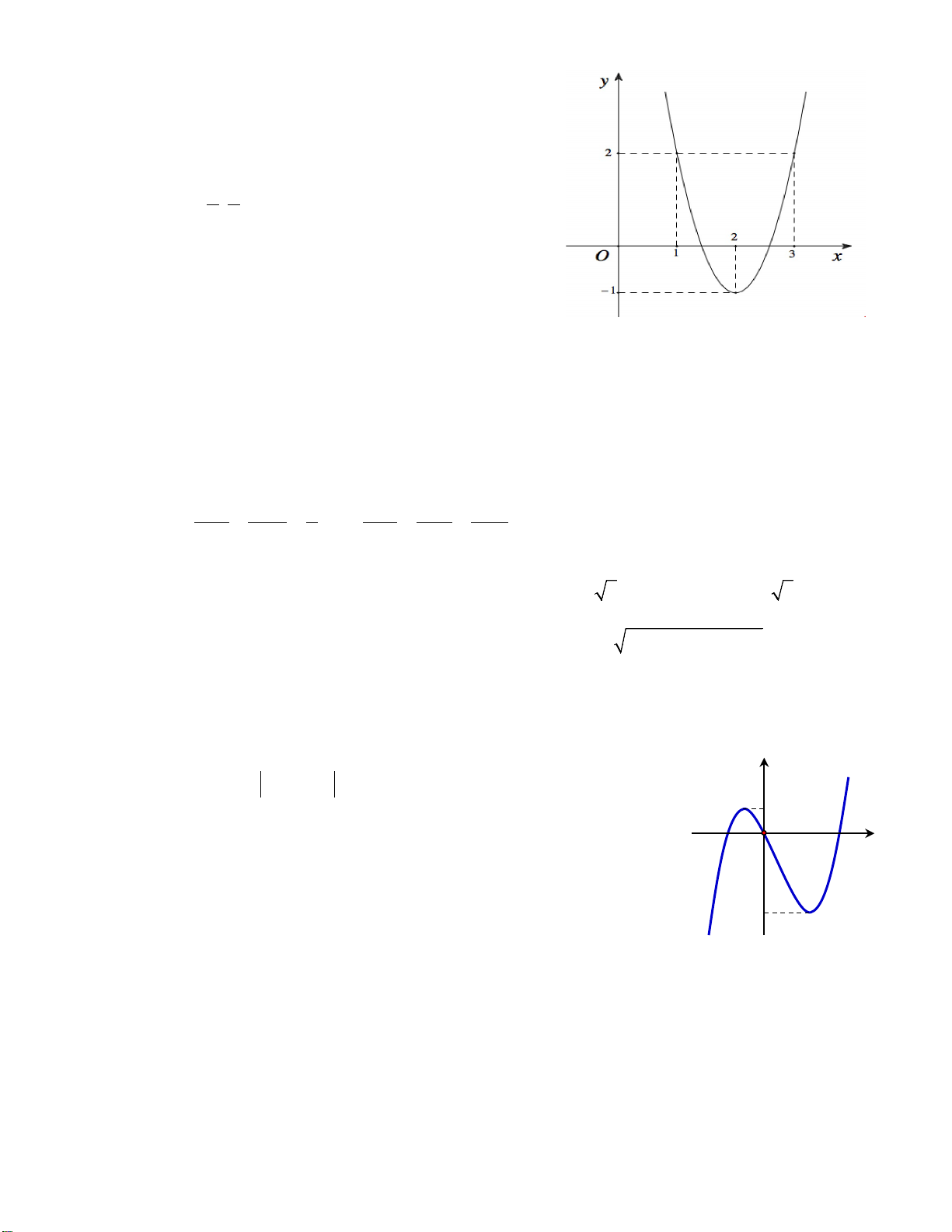
LTB Trang 6/7
Hàm số
()y fx=
nghịch biến trên khoảng nào
dưới đây ?
A.
( )
;2 .−∞
B.
( )
1;1 .−
C.
35
;.
22
D.
(
)
2; .+∞
Câu 40: Cho hàm số
3
12 12yx x=−+
có đồ thị
( )
C
và điểm
( )
;4Am−
. Gọi
S
là tập hợp tất cả các
giá trị thực của
m
nguyên thuộc khoảng
( )
6;5−
để từ
A
kẻ được ba tiếp tuyến với đồ thị
(
)
C
. Tổng tất cả các phần tử nguyên của
S
bằng
A.
2
. B.
9
. C.
3
. D.
4
.
Câu 41: Trong không gian với hệ trục tọa độ
Oxyz
, cho điểm
( )
3; 3; 2M −
và hai đường thẳng
1
12
:
1 31
xy z
d
−−
= =
;
2
112
:
12 4
xyz
d
+−−
= =
−
. Đường thẳng
d
qua
M
cắt
12
,dd
lần lượt
A
và
B
. Tính độ dài đoạn thẳng
AB
.
A.
2AB =
. B.
3AB =
. C.
6AB =
. D.
5
AB =
.
Câu 42: Cho dãy số
( )
n
u
thỏa mãn:
( )
52 52
log 2log 2 1 log 2log 1uu uu−=+−+
và
1
3
nn
uu
−
=
,
1n∀≥
. Giá trị lớn nhất của
n
để
100
7
n
u <
bằng
A.
192
. B.
191
. C.
176
. D.
177
.
Câu 43: Cho hàm số bậc ba
( )
y fx=
có đồ thị như hình bên. Tất cả các giá trị của tham số
m
để
hàm số
( )
y fx m= +
có ba điểm cực trị là
A.
1m ≤−
hoặc
3m ≥
. B.
3
m ≤−
hoặc
1m ≥
.
C.
1m = −
hoặc
3m =
. D.
13m
≤≤
.
Câu 44: Trong không gian
,Oxyz
cho hai điểm
( )
1; 3; 2A −−
,
( )
3; 7; 18
B −−
và mặt phẳng
( )
:2 1 0P xyz− ++=
. Điểm
( )
;;M abc
thuộc
( )
P
sao cho mặt phẳng
( )
ABM
vuông góc
với
( )
P
và
22
246.MA MB+=
Tính
3 2 4.S abc=++
A.
12
. B.
12−
. C.
10
. D.
10−
.
x
y
O
3−
1

LTB Trang 7/7
Câu 45: Cho hình lập phương
.ABCD A B C D
′′′′
có cạnh bằng
a
. Gọi
O
là tâm hình vuông
ABCD
.
S
là điểm đối xứng với
O
qua
CD
. Thể tích của khối đa diện
ABCDSA B C D
′′′′
bằng
A.
3
6
a
B.
3
7
6
a
C.
3
a
D.
3
2
3
a
Câu 46: Với hai số phức
1
z
và
2
z
thỏa mãn
12
86+=+zz i
và
12
2−=zz
. Tìm giá trị lớn nhất
của
12
= +Pz z
A.
5 35= +
P
. B.
2 26=P
. C.
46=P
. D.
34 3 2= +
P
.
Câu 47: Cho hình chóp tứ giác đều
.
SABCD
có cạnh đáy bằng
1,
cạnh bên hợp với mặt đáy một
góc
0
60.
Khoảng cách từ
O
đến mặt phẳng
SBC
bằng
A.
1
.
2
B.
2
.
2
C.
7
.
2
D.
42
.
14
Câu 48: Cho mặt cấu
1
()S
có tâm
1
3; 2; 2I
bán kính
1
2R
, mặt cấu
2
()
S
có tâm
2
(1; 0; 1)I
bán
kính
2
1
R
.Mặt phẳng
( )
P
đồng thời tiếp xúc với
1
()S
và
2
()
S
và cắt đoạn
12
II
có dạng
20x by cz d+ + +=
. Tính
T bcd=++
.
A.
5−
. B.
3−
. C.
1
−
. D.
2
.
Câu 49: Cho
cos 1x ≠±
. Gọi
24 2
1 cos cos ... cos ...
n
S xx x=++++ +
Khi đó
S
có biểu thức thu gọn
là:
A.
2
sin x
. B.
2
cos x
. C.
2
1
cos
x
. D.
2
1
sin x
.
Câu 50: Cho hàm số
(
)
fx
có đạo hàm liên tục trên
0;
2
π
thỏa mãn
( ) ( ) ( )
22
2
00
0 0, sin
4
ππ
π
′
= = =
∫∫
f f x dx xf x dx
. Tích phân
( )
2
0
π
∫
f x dx
bằng
A.
4
π
. B.
2
π
. C.
2
. D.
1
.
----------HẾT---------
CÂU 34 ĐÁP ÁN B. FILE GỐC ĐÁP ÁN C
CÂU 49 ĐÁP ÁN D. FILT GỐC ĐÁP ÁN A
BẢNG ĐÁP ÁN

LTB Trang 8/7
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
C
C
B
C
D
A
D
D
A
B
D
C
C
C
A
B
D
A
B
D
D
B
D
C
D
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
A
C
C
A
D
C
C
A
B
D
B
A
A
B
A
B
A
A
B
B
B
D
B
D
D
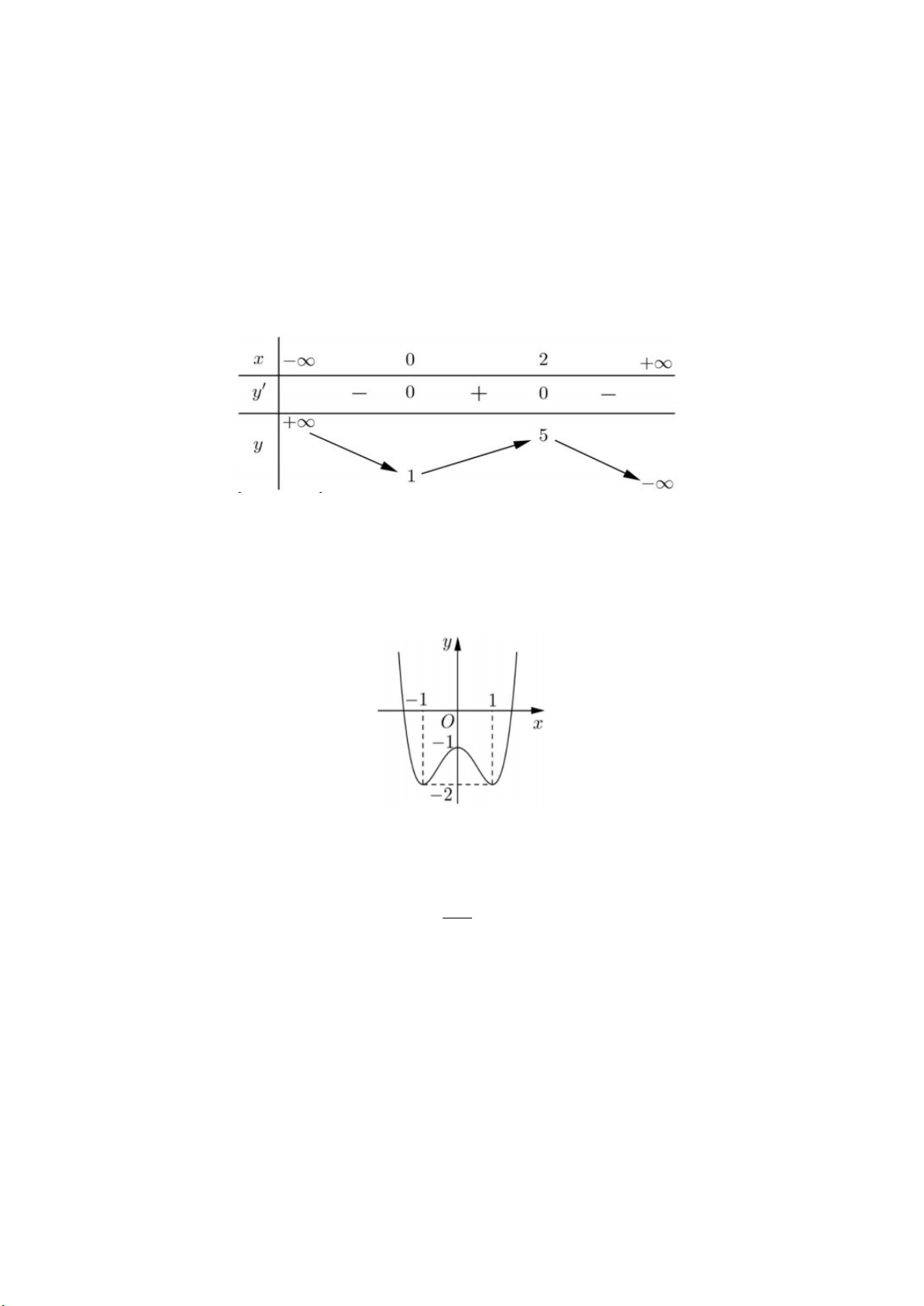
LTB Trang 1/6
Trường THPT Hoàng Hoa Thám ĐỀ THI THỬ THPT QUỐC GIA NĂM 2018- 2019
Tổ Toán Môn: Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Họ và tên thí sinh:………………………………………………
Số báo danh:………………………………………………….…
Câu 1: Tính thể tích của khối hộp chữ nhật có các kích thước lần lượt là
3 ,4 ,5aaa
.
A.
3
12a
B.
3
20a
C.
3
60
a
D.
3
10a
Câu 2: Cho hàm số
()y fx=
có bảng biến thiên như sau
Giá trị cực tiểu của hàm số đã cho bằng
A. 0 B. 1 C. 2 D. 5
Câu 3: Trong không gian Oxyz, cho điểm
(1; 2;3)A −
. Tìm tọa độ điểm B thỏa mãn
0OA OB+=
.
A.
( 1; 2; 3)B −−
B.
(1; 2;3)B
C.
( 1; 0; 3)
B −−
D.
(1;0;3)B
Câu 4: Cho hàm số
()y fx=
có đồ thị như hình vẽ bên dưới.
Khẳng định nào dưới đây sai?
A. Hàm số có một điểm cực đại. B. Hàm số có giá trị nhỏ nhất bằng
2−
.
C. Hàm số có giá trị lớn nhất bằng
1−
. D. Hàm số đồng biến trên khoảng
( 1; 0)
−
.
Câu 5: Với
,ab
là hai số thực dương tùy ý,
2
log
10
b
a
bằng
A.
2log log 1ba−+
B.
2log log 1ab−−
C.
2log log 1ab−+
D.
2log log 1ba−−
Câu 6: Cho hàm số
()y fx=
có đạo hàm liên tục trên đoạn
[ ]
1; 2
và
(1) 3, (2) 1ff=−=
.
Tính
2
1
'( )I f x dx
=
∫
.
A.
2I = −
B.
2I =
C.
4I =
D.
4I = −
Câu 7: Thể tích của khối trụ có bán kính đáy
ra=
và chiều cao
3ha=
là
A.
3
a
B.
3
3
π
a
C.
3
9a
D.
3
6a
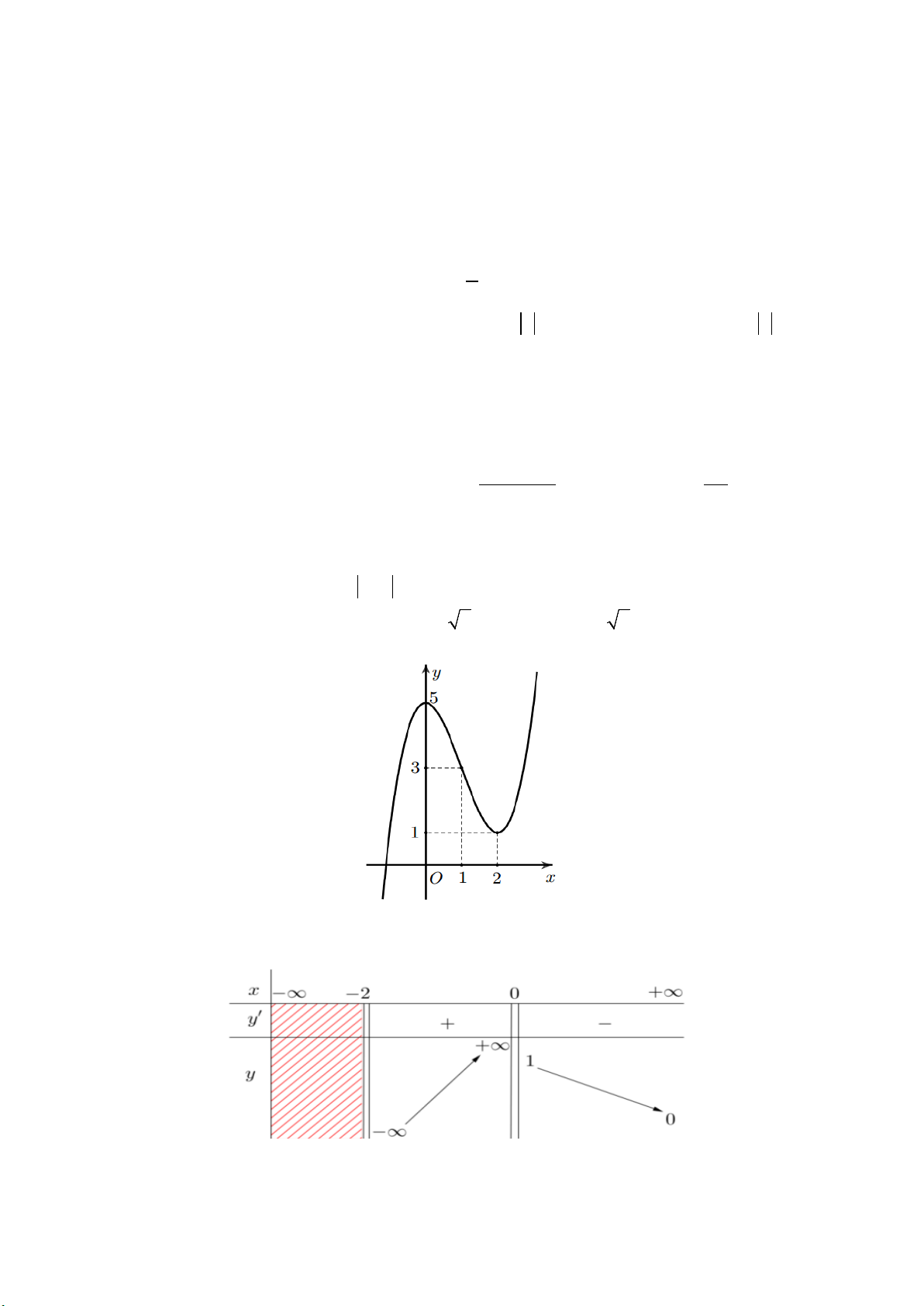
LTB Trang 2/6
Câu 8: Tập nghiệm của phương trình
2
31
22
xx
−+
=
là
A.
{ }
0
B.
{ }
0;3
C.
{ }
1; 3
D.
{ }
0; 3−
Câu 9: Trong không gian Oxyz, trục Ox có phương trình là
A.
0
0
x
y
zt
=
=
=
B.
0
0
x
yt
z
=
=
=
C.
0
0
xt
y
z
=
=
=
D.
0x
yt
zt
=
=
=
Câu 10: Họ nguyên hàm của hàm số
2
( ) sinfx x
x
= +
là
A.
cos 2lnx xC++
B.
cos 2lnx xC−++
C.
cos 2lnx xC−+
D.
cos 2lnx xC−+ +
Câu 11: Trong không gian Oxyz, điểm
(0;0;0)O
cách mặt phẳng nào dưới đây một khoảng bằng 2?
A.
2 20xyz−+−=
B.
2 2 20xy z−+ −=
C.
2 60xyz
−+−=
D.
2 2 60xy z−− −=
Câu 12: Với
,nk
là hai số nguyên dương tùy ý và
kn≤
, mệnh đề nào dưới đây sai?
A.
n
nn
PA=
B.
kk
nn
A kC=
C.
!
( )!. !
k
n
n
C
nkk
=
−
D.
!
k
k
n
n
A
C
k
=
Câu 13: Cho cấp số cộng
()
n
u
có số hạng đầu
1
3u =
và
15
14uu+=
. Tìm công sai d của cấp số cộng.
A.
1d =
B.
3d =
C.
2d =
D.
4d =
Câu 14: Cho số phức
12zi= −
. Tính
zi
+
.
A.
1
B.
2
C.
22
D.
2
Câu 15: Đường cong ở hình bên dưới là đồ thị của hàm số nào sau đây?
A.
32
35yx x=−+
B.
32
35yx x=−−
C.
32
35yx x=−+ +
D.
42
35yx x
=−+
Câu 16: Cho hàm số
()y fx=
có bảng biến thiên như sau
Hỏi phương trình
() 1 0fx−=
có bao nhiêu nghiệm?
A. 1 B. 2 C. 0 D. 3
LTB Trang 3/6
Câu 17: Cho hàm số
23
(1 )(3 ) ,()= − +∀
′
∈fx x x xx
. Hàm số
()fx
đạt cực đại tại điểm
A.
0x
=
B.
1
x =
C.
3x = −
D.
1x
=
và
3x = −
Câu 18: Tìm các số thực
,
xy
thỏa mãn
(1 ) (1 ) 2x iy i−+ +=
A.
1, 1
xy= = −
B.
0, 2
xy= =
C.
1, 1xy= =
D.
1, 1xy=−=−
Câu 19: Trong không gian Oxyz, cho hai điểm
(2;0; 2)M
và
( 2; 4; 0)N −
. Phương trình mặt cầu đường
kính MN là
A.
22 2
( 2) ( 2) 20
x yz− + +− =
B.
22 2
( 2) ( 2) 36x yz− + +− =
C.
2 22
( 2) ( 1) 20xy z
+− +− =
D.
2 22
( 2) ( 1) 9+− +− =xy z
Câu 20: Đặt
2
log 10 a=
. Khi đó
25
log 16
bằng
A.
2
( 1)a
+
B.
2
( 1)
a −
C.
2( 1)
a −
D.
2( 1)
a +
Câu 21: Kí hiệu
12
,zz
là hai nghiệm của phương trình
2
2 10zz−+=
. Tính tổng
12
Tz z= +
.
A.
1
2
T =
B.
2
2
T =
C.
2T =
D.
2T =
Câu 22: Trong không gian Oxyz, tính khoảng cách giữa đường thẳng
3
:
22 3
xyz−
∆==
và mặt phẳng
( ): 2 2 0Px y z+−=
.
A.
1
B.
3
2
C.
2
3
D.
2
Câu 23: Tập nghiệm của bất phương trình
2
log (3 2) 3x
+<
là
A.
( ;2)−∞
B.
2
;2
3
−
C.
( ;2−∞ ]
D.
2
;2
3
Câu 24: Thể tích của vật thể tròn xoay khi quay hình phẳng giới hạn bởi đồ thị hàm số
2
2y xx
= −
,
trục Ox xung quanh trục Ox là
A.
16
15
π
B.
4
3
π
C.
20
3
π
D.
64
15
π
Câu 25: Cho khối trụ có độ dài đường sinh và đường kính đáy đều bằng 2a. Thể tích của khối trụ đã
cho bằng
A.
3
2 a
π
B.
3
4 a
π
C.
3
8 a
π
D.
3
3 a
π
Câu 26: Cho hàm số
()y fx=
có bảng biến thiên như sau
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A.
1
B. 3 C. 2 D. 4
1
2
+
∞
∞
∞
3
+
∞
f(x)
x
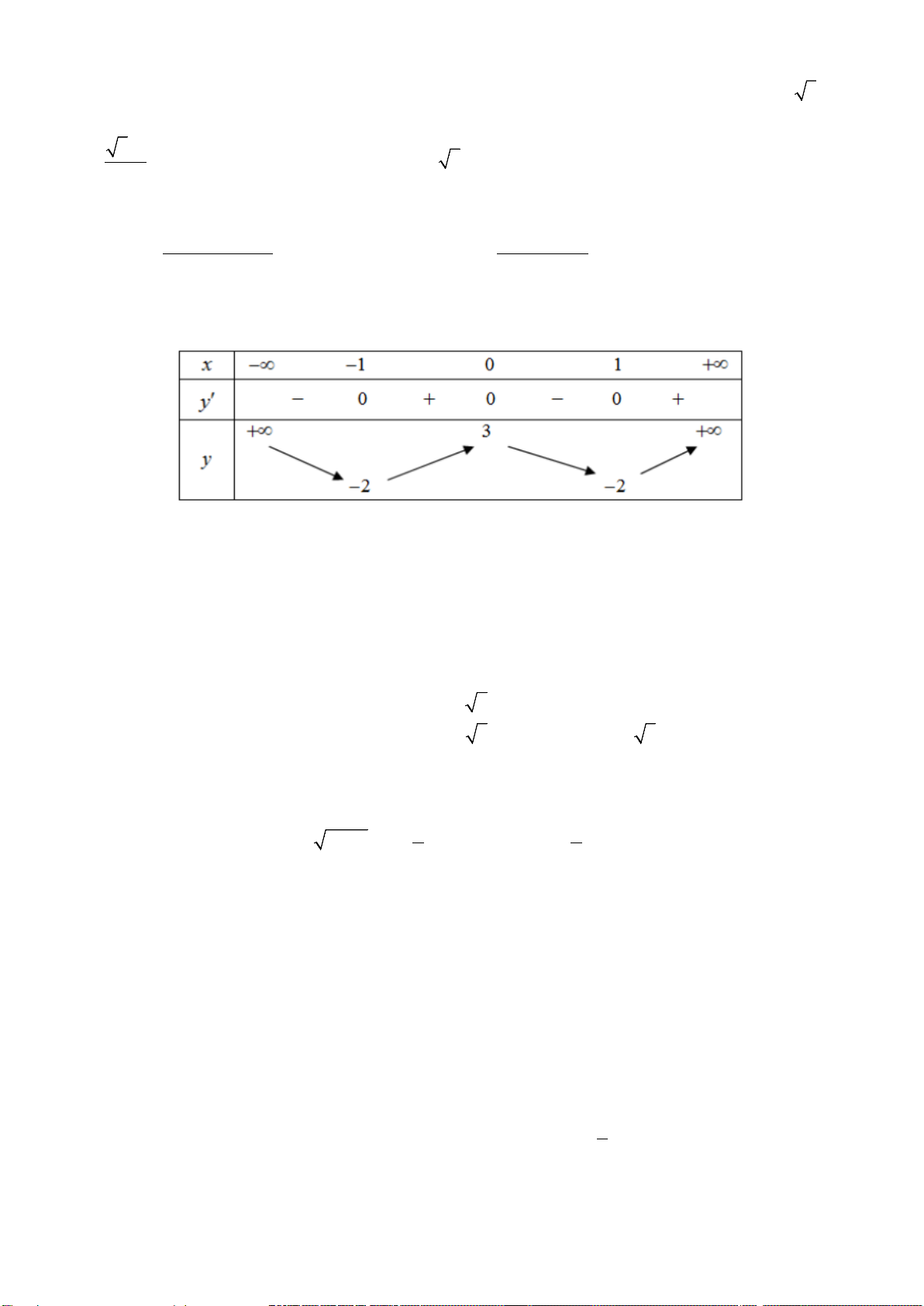
LTB Trang 4/6
Câu 27: Cho khối lăng trụ tam giác đều có cạnh đáy bằng 2a và khoảng cách giữa hai đáy bằng
3a
.
Thể tích của khối lăng trụ đã cho bằng
A.
3
3
3
a
B.
3
a
C.
3
3
a
D.
3
3a
Câu 28: Hàm số
2
2
() 5
xx
fx
−
=
có đạo hàm
A.
2
2
(2 2 ).5
()
ln 5
xx
x
fx
−
−
′
=
B.
2
2
5
()
(2 2 ).ln 5
xx
fx
x
−
′
=
−
C.
2
22 1
( ) (2 ).5 .ln 5
xx
fx xx
−−
′
= −
D.
2
2
( ) (2 2 ).5 .ln 5
xx
fx x
−
′
= −
Câu 29: Cho hàm số
()
y fx=
có bảng biến thiên như sau
Hỏi phương trình
() 3 0fx
+=
có bao nhiêu nghiệm thực?
A. 1 B. 4 C. 0 D. 3
Câu 30: Cho tứ diện đều ABCD. Góc giữa hai đường thẳng BC và AD bằng
A. 30
0
B. 45
0
C. 60
0
D. 90
0
Câu 31: Tổng tất cả các nghiệm của phương trình
2 2.5 2 10
xx x
+=+
bằng
A. 1 B. 4 C. 7 D. 3
Câu 32: Cho hình trụ có chiều cao
5ha=
. Một mặt phẳng (P) song song và cách trục một khoảng
2
a
cắt hình trụ theo một thiết diện có diện tích bằng
2
10 5
a
. Tính bán kính đáy r của hình trụ.
A.
2ra=
B.
3ra=
C.
5ra=
D.
3ra=
Câu 33: Họ nguyên hàm của hàm số
( 2)
x
y xe= +
là
A.
2
( 1)
x
x ex−+
B.
2
( 1)
x
x exC− ++
B.
2
( 2)
x
x exC− ++
D.
2
( 2)
x
x ex−+
Câu 34: Biết bất phương trình
3
51
5
xx−<+
có tập nghiệm là
( )
1
;;
5
ab
∪ +∞
với a, b là các số
hữu tỉ và
ab<
. Tính
4ab+
.
A. 1 B. 3 C.
2
D. 5
Câu 35: Trong không gian Oxyz, cho đường thẳng
1
:2
32
xt
yt
zt
= −
∆=+
= −
. Hình chiếu vuông góc của đường
thẳng
∆
trên mặt phẳng (Oyz) có phương trình là:
A.
0
3
12
x
yt
zt
=
= −
= +
B.
0
3
12
x
yt
zt
=
= +
= +
C.
0
1
32
x
yt
zt
=
= −
= +
D.
0
1
32
x
yt
zt
=
= −
= −
Câu 36: Tập hợp tất cả các giá trị thực của tham số m để hàm số
32
1
2 (2 1) 1
3
y x x mx= − + −+
đồng
biến trên khoảng
(
)
2;− +∞
là:
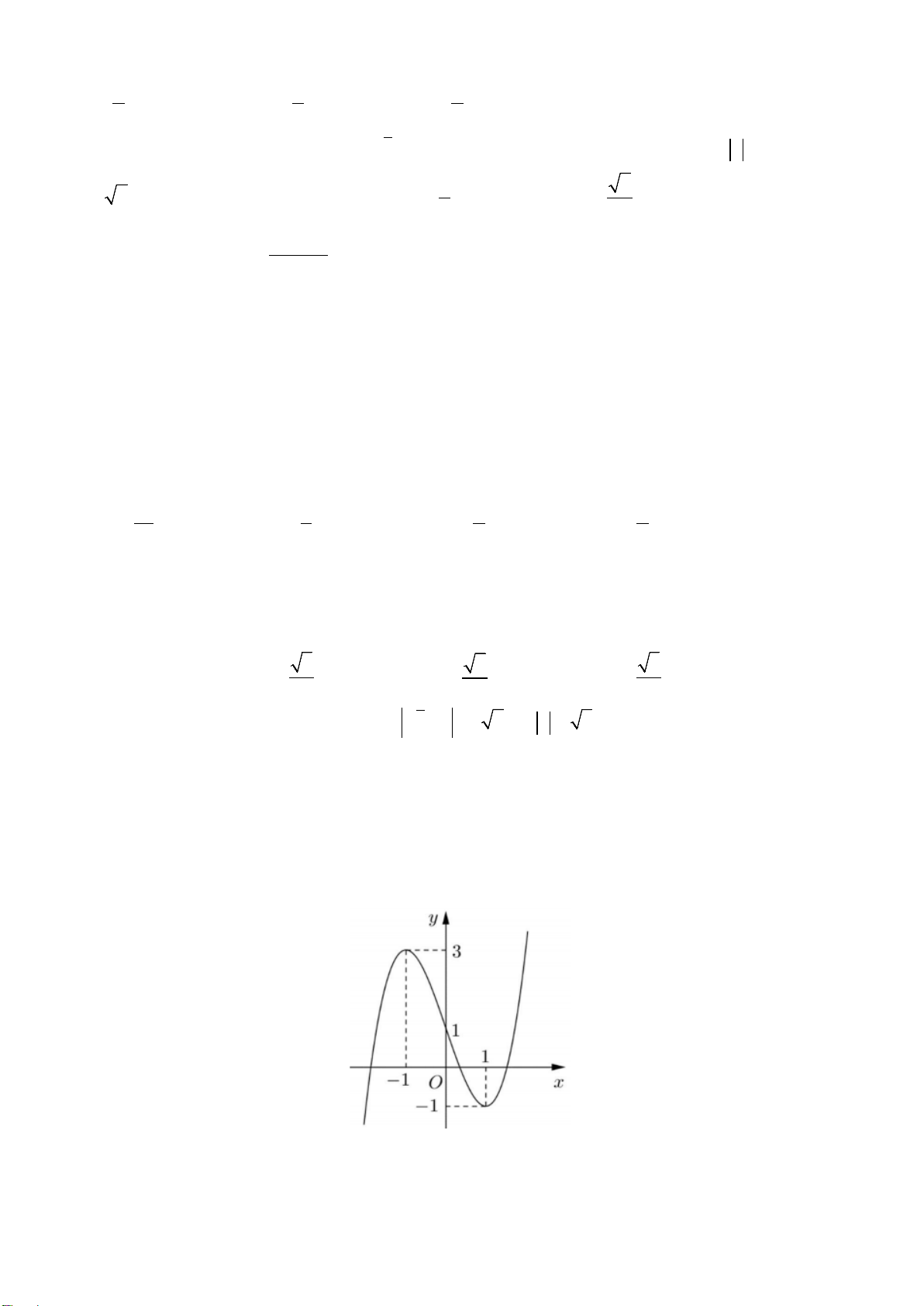
LTB Trang 5/6
A.
5
;
4
+∞
B.
5
;
4
− +∞
C.
5
;
2
+∞
D.
[
)
0;
+∞
Câu 37: Cho số phức z thỏa mãn
( 1)( )z zi
+−
là một số thực. Tìm giá trị nhỏ nhất của
z
.
A.
2
B.
1
C.
1
2
D.
2
2
Câu 38: Cho tích phân
1
2
2
0
3
ln 2 ln 3
( 3)
x
dx a b c
x
+
=++
+
∫
với a, b, c là các số hữu tỉ. Giá trị của biểu
thức
abc++
bằng
A.
3−
B.
5
C.
4−
D.
0
Câu 39: Một quả bóng cao su được thả từ độ cao 100m. Mỗi lần chạm đất, quả bóng nảy lên ba phần
tư độ cao của lần rơi trước đó. Tính tổng các khoảng cách rơi và nảy của quả bóng từ lúc thả quả bóng
cho đến lúc quả bóng không nảy nữa.
A.
700m
B.
350m
C.
400m
D.
666
m
Câu 40: Tính diện tích S hình phẳng giới hạn bởi đồ thị
()P
của hàm số
2
23yx x
và hai tiếp
tuyến của parabol tại hai điểm
(0;3)A
và
(2;3)B
.
A.
14
3
S =
B.
1
3
S =
C.
3
2
S
=
D.
2
3
S =
Câu 41: Trong không gian với hệ tọa độ Oxyz, cho ba điểm
( )
2;0; 0A
,
( )
0; 2;0
B
,
(
)
0;0; 2
C
.
Biết rằng tập hợp các điểm
M
thỏa mãn
( )
.0MA MA MB MC++ =
là một mặt cầu. Tính bán kính
r của mặt cầu đó.
A.
1r
=
B.
5
.
2
r =
C.
6
.
3
r =
D.
3
.
2
r =
Câu 42: Có bao nhiêu số phức z thỏa mãn
. 52
zz z
+=
và
5
z
=
.
A. 1 B. 2 C. 3 D. 4
Câu 43: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có trọng tâm
( 2; 1)G −−
; phương
trình cạnh
AB
là
4 15 0xy++ =
và phương trình cạnh
AC
là
2 5 30xy+ +=
. Viết phương trình
đường thẳng BC.
A.
2 30xy
− −=
B.
2 50
xy+ +=
C.
20xy−=
D.
2 40
xy++=
Câu 44: Cho hàm số
()y fx=
có đồ thị như hình vẽ.
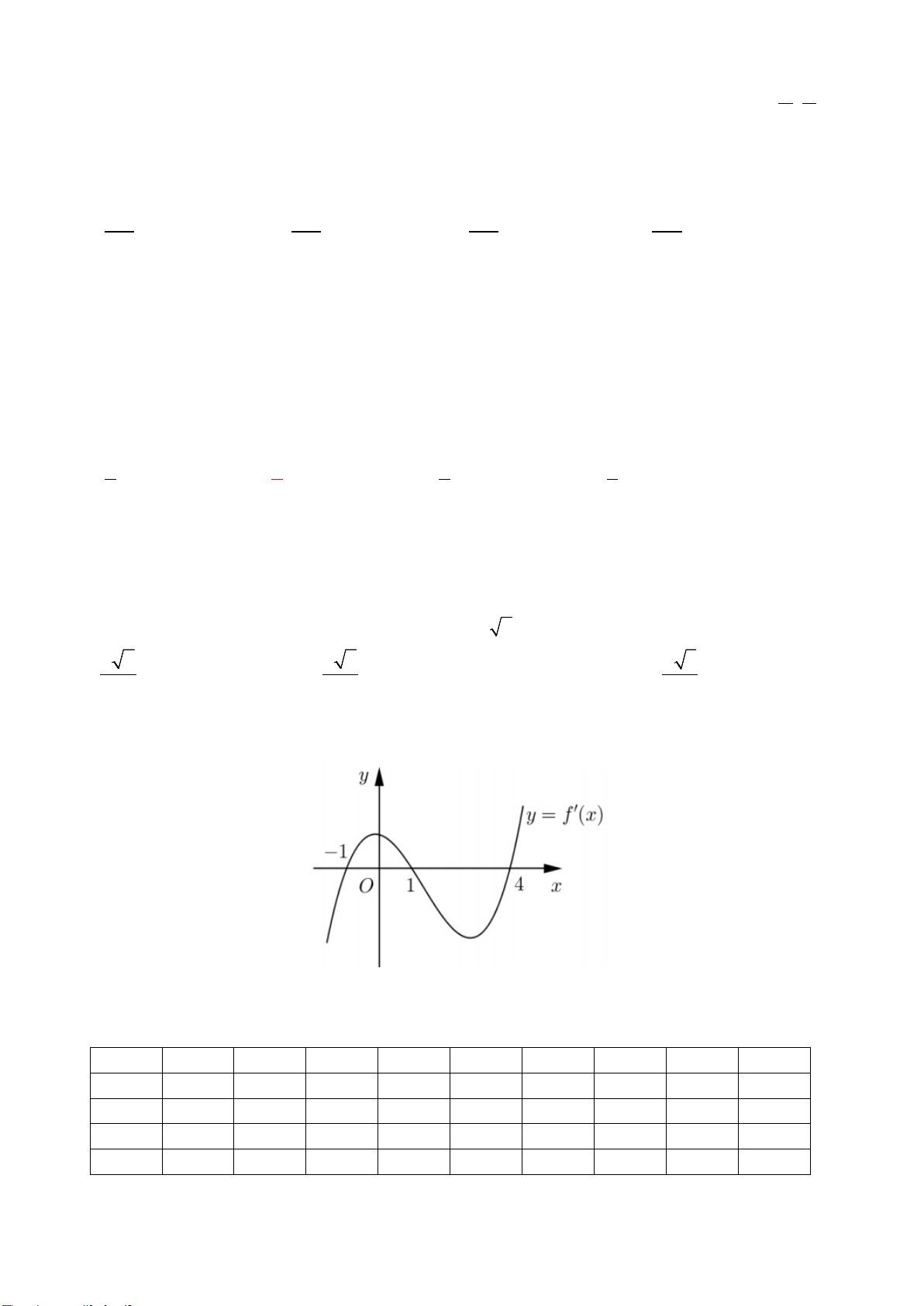
LTB Trang 6/6
Hỏi có bao nhiêu số nguyên m để phương trình
(
)
cos 1
fx m−=
có nghiệm thuộc khoảng
;
22
−
ππ
.
A. Vô số B. 2 C. 3 D. 4
Câu 45: Có 30 tấm thẻ được đánh số từ 1 đến 30. Rút ngẫu nhiên 3 tấm thẻ. Tính xác suất để tổng các
số ghi trên ba thẻ là một số chia hết cho 3.
A.
68
203
B.
68
205
C.
67
203
D.
67
205
Câu 46: Trong không gian Oxyz, cho mặt cầu
++=
222
( ): 9Sx y z
, điểm
(1;1; 2)M
và mặt phẳng
++− =
( ): 4 0Pxyz
. Gọi
∆
là đường thẳng đi qua điểm
,M
nằm trong mặt phẳng (P) và cắt mặt
cầu (S) tại hai điểm A, B sao cho độ dài đoạn thẳng AB nhỏ nhất. Biết rằng
∆
có một vectơ chỉ phương
=
(1; ; )u ab
. Tính giá trị của biểu thức
= +
T ab
.
A.
=
0T
B.
= −1T
C.
= 1
T
D.
= −2T
Câu 47: Cho khối tứ diện ABCD. Gọi M, N, P, Q, R lần lượt là trung điểm của các cạnh AB, AC, AD,
BC và BD. Tỉ số thể tích của khối lăng trụ MNP.BQR và khối tứ diện ABCD là
A.
3
7
B.
3
4
C.
1
2
D.
3
5
Câu 48: Cho hàm số
92 5 3 2 4
( ) ( ) (3 7 4 ) 11f x x m mx m m mx=+− + − + +
( m là tham số).
Hỏi có bao nhiêu giá trị nguyên của tham số m để hàm số đồng biến trên
.
A. Vô số B. 2 C. 5 D. 11
Câu 49: Cho hình lập phương
.'' ' 'ABCD A B C D
cạnh a. Lấy điểm M thuộc đoạn thẳng
'AD
, điểm N
thuộc đoạn thẳng
BD
sao cho
(0 2)AM DN x x a= = <<
. Tìm x để đoạn thẳng MN ngắn nhất.
A.
2
2
a
B.
2
3
a
C.
a
D.
3
3
a
Câu 50: Cho hàm số
432
()f x ax bx cx dx e= + + ++
trong đó
,,, ,abcde∈
. Biết rằng đồ thị hàm số
()
y fx
′
=
có đồ thị như hình vẽ bên dưới.
Hỏi tập nghiệm của phương trình
()
fx abcde=+++ +
có tất cả bao nhiêu phần tử ?
A. 2 B. 4 C. 5 D. 3
ĐÁP ÁN
1C
2B
3A
4C
5D
6C
7B
8B
9C
10D
11D
12B
13C
14D
15A
16A
17B
18C
19D
20B
21D
22D
23B
24A
25A
26C
27D
28D
29C
30D
31A
32B
33B
34D
35A
36C
37D
38C
39A
40D
41C
42B
43A
44B
45A
46B
47B
48B
49B
50D
LTB Trang 1/8
SỞ GIÁO DỤC & ĐÀO TẠO KHÁNH HÒA
TRƯỜNG THPT LÊ THÁNH TÔN
ĐỀ ÔN TẬP THI THPT QUỐC GIA
NĂM HỌC 2018 - 2019
MÔN: TOÁN
Thời gian làm bài: 90 phút (không kể thời gian phát đề).
Câu 1: Cho hàm số
()
y fx=
có bảng biến thiên như sau.
x
−∞
1
−
3
+∞
y'
+
0
−
0
+
2
+∞
y
−∞
3−
Mệnh đề nào dưới đây sai ?
A. Hàm số có hai điểm cực trị. B. Hàm số có giá trị cực đại bằng
2
.
C. Hàm số có giá trị cực đại bằng
1−
. D. Hàm số đạt cực tiểu tại
3x
=
.
Câu 2: Tìm nguyên hàm của hàm số
( ) sin 2fx x=
.
A.
cos 2
sin 2
2
x
xdx C= +
∫
. B.
sin 2 cos 2xdx x C=−+
∫
.
C.
sin 2 2cos 2xdx x C= +
∫
. D.
cos 2
sin 2
2
x
xdx C=−+
∫
.
Câu 3: Cho hai số phức
1
23zi= +
và
2
34zi= −
. Tìm số phức
12
zz z= +
.
A.
5zi= +
. B.
75zi= −
. C.
17zi= −
. D.
5zi= −
.
Câu 4: Cho
a
là số thực dương khác
1
. Tính
log 2
a
Ia
=
.
A.
4I =
. B.
1
4
I
=
. C.
2I =
. D.
4I = −
.
Câu 5: Cho hàm số
1
1
x
y
x
−
=
+
. Mệnh đề nào dưới đây đúng ?
A. Hàm số đồng biến trên
{ }
\1−
.
B. Hàm số đồng biến trên khoảng
( )
;1−∞
và
(
)
1; +∞
.
C. Hàm số nghịch biến trên khoảng
( )
;1−∞ −
và
(
)
1;− +∞
.
D. Hàm số đồng biến trên khoảng
( )
;1−∞ −
và
( )
1;− +∞
.
Câu 6: Tính giới hạn sau:
3
2
0
11
L lim
x
xx
x
→
+− +
=
.
A.
1
2
L = −
. B.
1
2
L =
. C.
1L
=
. D.
1L = −
.
Câu 7:Cho phương trình
cos 2 sin 2 0xx+ +=
. Khi đặt
sintx
=
, ta được phương trình nào dưới đây ?
A.
2
2 10tt++=
. B.
10t +=
. C.
2
2 30tt− ++ =
. D.
2
2 20tt− ++ =
.
Câu 8:Tìm số đường tiệm cận của đồ thị hàm số
2
3
1
32
x
y
xx
−
=
−+
?
A.
3
. B.
2
. C.
1
. D.
4
.
Câu 9: Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào ?

LTB Trang 2/8
A.
32
32yx x=−+
. B.
42
52
yx x
=−+
.
C.
42
52yx x=++
. D.
42
52yx x=−+ +
.
Câu 10: Hàm số nào sau đây là hàm số chẵn ?
A.
sinyx=
. B.
cosyx=
. C.
tanyx=
. D.
cotyx
=
.
Câu 11: Tìm nghiệm thực của phương trình
( )
3
log 1 2x +=
.
A.
2x =
. B.
7x =
. C.
8x =
. D.
26x =
.
Câu 12: Số phức nào dưới đây là số thuần ảo ?
A.
27zi= +
. B.
5z = −
. C.
1
z
i
=
. D.
2
zi=
.
Câu 13: Cho hình lăng trụ tam giác đều
.'' 'ABC A B C
có
',AA a=
'C 3Aa=
. Tính thể tích
V
của lăng
trụ
.'' 'ABC A B C
.
A.
3
33
2
Va
=
. B.
3
3
6
Va=
. C.
3
3
2
Va=
. D.
3
6
4
Va=
.
Câu 14: Tìm tập xác định
D
của hàm số
( )
2
3
log 2 5 2y xx= −+
.
A.
( )
( )
; 2 1 2 1;D = −∞ − + +∞
. B.
1
;2
2
D
=
.
C.
( )
1
2 1; 2; 2 1
2
D
=−+
. D.
( )
1
; 2;
2
D
= −∞ +∞
.
Câu 15: Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
3; 4; 2I −
. Lập phương trình mặt cầu tâm
I
và
tiếp xúc với trục
Oz
.
A.
( ) (
) ( )
222
3 4 2 25xyz− +− ++ =
. B.
( )
( ) (
)
2 22
3 4 2 20xyz+ ++ +− =
.
C.
( ) ( ) ( )
222
3 4 25xyz− +− ++ =
. D.
(
) ( ) ( )
222
3 4 24xyz− +− ++ =
.
Câu 16: Cho số phức
1zi
=−+
. Điểm nào dưới đây là điểm biểu diễn của số phức
( )
w2
iz= +
trên mặt
phẳng tọa độ .
A.
( )
1; 3
M −−
. B.
( )
3;1N −
. C.
( )
1; 3
P
. D.
( )
3; 1Q −
.
Câu 17: Cho mặt phẳng (P) : 2x + y - 2z - 1 = 0 và đường thẳng d :
23
1 23
x yz−+
= =
−
. Phương trình mặt
phẳng chứa d và vuông góc với (P) là :
A.
5 8 14 0xy z++ + =
. B.
8 5 13 0x yz+++=
.
C.
8 5 31 0xyz+++=
. D.
5 80xy z++ =
.
Câu 18: Cho
3
2
2
8
ln 2 ln 5
2
x
dx a b
xx
+
= +
+−
∫
với
,a
b
là các số thực nguyên. Mệnh đề nào sau đây đúng ?
A.
3ab+=
. B.
2 11ab−=
. C.
5ab−=
. D.
2 11ab+=
.
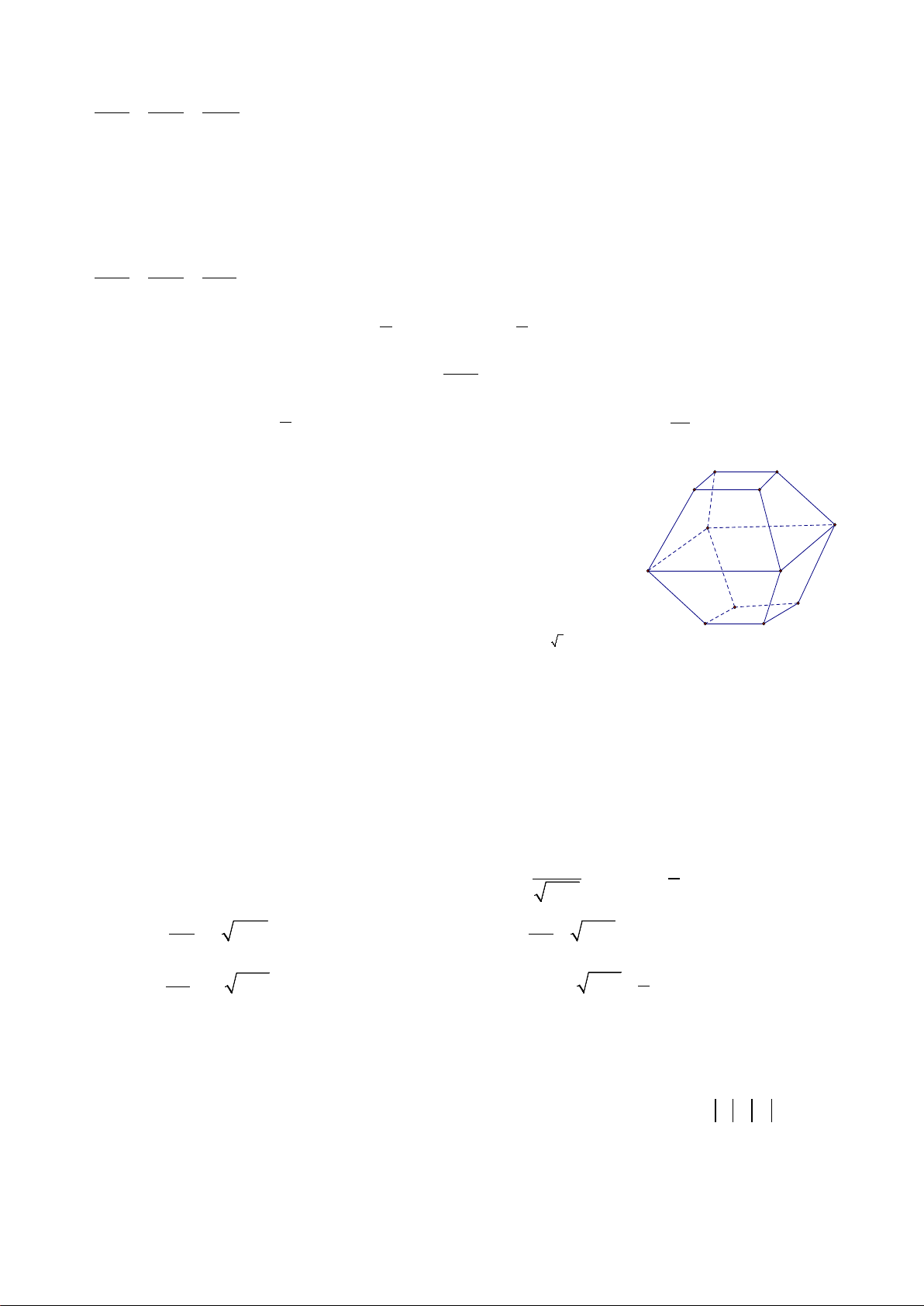
LTB Trang 3/8
Câu 19: Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )
: 20xyz
α
+−−=
và đường thẳng
( )
112
:
211
xyz
d
+−−
= =
. Phương trình nào dưới đây là phương trình mặt phẳng chứa đường thẳng
( )
d
và
vuông góc với mặt phẳng
( )
α
.
A.
2 40xy z++ −=
. B.
2 3 70
x yz
− −+=
.
C.
2 3 70x yz
− −−=
. D.
20xyz+−+=
.
Câu 20: Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )
2
: 10x m y mz
α
−+ + +=
và đường thẳng
( )
111
:
23 1
xyz
d
−+−
= =
−
. Tìm tất cả các giá trị thực của tham số
m
để
( )
d
song song với
( )
α
.
A.
1m =
. B.
1m =
hoặc
2
3
m = −
. C.
2
3
m
= −
. D. Không tồn tại
m
.
Câu 21: Tìm giá trị nhỏ nhất
m
của hàm số
1
1
yx
x
= +
−
trên đoạn
[ ]
3; 5
.
A.
3
m
=
. B.
7
2
m =
. C.
2m =
. D.
21
4
m
=
.
Câu 22: Hình đa diện trong hình vẽ bên có bao nhiêu mặt ?
A. 8. B. 11. C. 12. D. 10.
Câu 23:Tìm tập nghiệm thực
S
của bất phương trình
22
3
3
log log 3 0xx− +≥
.
A.
(
] [
)
;1 3;S = −∞ +∞
. B.
(
] [
)
0;3 27;
S = +∞
.
C.
(
] [
)
;3 27;
S = −∞ +∞
. D.
[
]
3; 27
S
=
.
Câu 24: Tìm số hạng chứa
7
x
trong khai triển nhị thức Niu- tơn:
( ) ( )
6
72
42Px x x x=+−
.
A.
16
. B.
7
16x
. C.
8−
. D.
7
8x−
.
Câu 25: Cho các số thực dương
,a
,b
c
khác
1
thỏa mãn điều kiện
log 2;log 3
ab
bc
= =
. Tính giá trị của
biểu thức
2
log log ( )
ab
P c ac= +
.
A.
10P =
. B.
7P =
. C.
11P
=
. D.
13P
=
.
Câu 26:Cho
()Fx
là một nguyên hàm của hàm số
2
2
()
1
x
fx e
x
= +
+
và
1
(0)
2
F
=
. Tìm
( )
Fx
.
A.
( )
2
41
2
x
e
Fx x
=++
. B.
( )
2
11
2
x
e
Fx x= + +−
.
C.
( )
(
)
2
4 11
2
x
e
Fx x= + +−
. D.
(
)
2
5
21
2
x
Fx e x= + +−
.
Câu 27: Cho hình trụ có thiết diện qua trục là một hình vuông có diện tích bằng
2
2a
. Tính diện tích toàn
phần
tp
S
của hình trụ đó.
A.
2
3
tp
Sa
π
=
. B.
2
2
tp
Sa
π
=
. C.
2
8
tp
Sa
π
=
. D.
2
5
tp
Sa
π
=
.
Câu 28: Kí hiệu
1
,z
2
z
là hai nghiệm phức của phương trình
2
2 3 50xx
+ +=
. Tính
12
Pz z= +
.
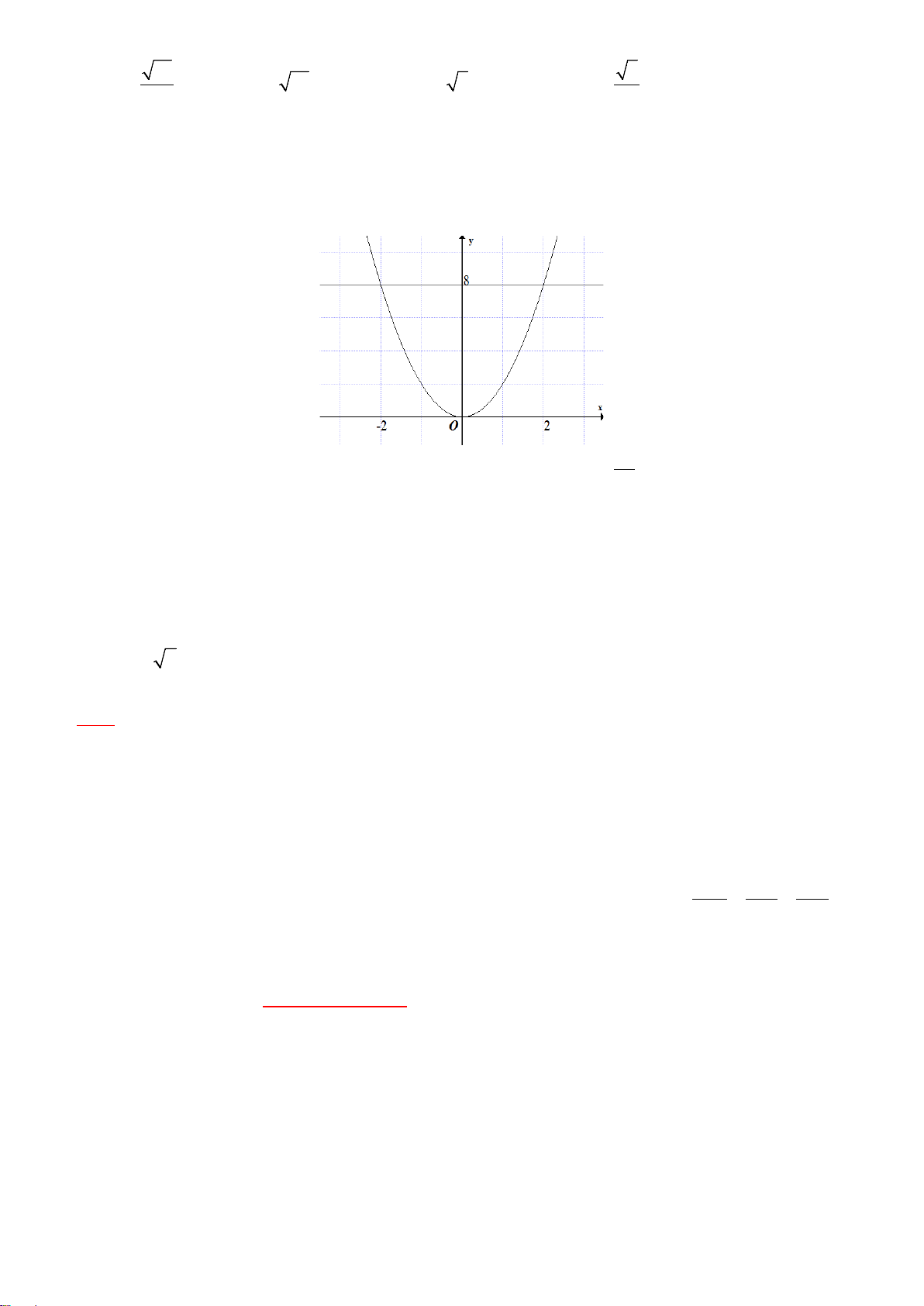
LTB Trang 4/8
A.
10
2
P =
. B.
10P =
. C.
5
P =
. D.
5
2
P =
.
Câu 29: Tế bào E. Coli trong điều kiện nuôi cấy thích hợp cứ
20
phút lại phân đôi một lần. Nếu có
6
10
tế
bào này thì sau bao lâu sẽ phân chia thành
6
512.10
tế bào.
A.
3
giờ. B.
6
giờ. C.
9
giờ. D.
8
giờ.
Câu 30: Cho hàm số bậc hai
()y fx=
có đồ thị như hình bên. Tính thể tích
V
của khối tròn xoay tạo thành
khi quay hình phẳng giới hạn bởi đồ thị của hàm số
( )
y fx=
và đường thẳng
8y =
quanh trục tung.
A.
16V
π
=
. B.
8V
π
=
. C.
32V
π
=
. D.
64
3
V
π
=
.
Câu 31:Cho hình chóp
.
S ABCD
có đáy là hình chữ nhật với
2,AB a=
AD a=
. Tam giác
SAD
vuông cân
tại
S
và nằm trong mặt phẳng vuông góc với đáy. Tính diện tích
S
của mặt cầu ngoại tiếp hình chóp
.S ABCD
.
A.
2
4Sa
π
=
. B.
2
Sa
π
=
. C.
2
20Sa
π
=
. D.
2
5
Sa
π
=
.
Câu 32: Tìm các giá trị thực của tham số
m
để phương trình
22
24
log log 3 2 0xm x m− + −=
có hai nghiệm
thực
1
,x
2
x
thỏa mãn
12
4xx =
.
A.
2m = −
. B.
2m =
. C.
2m = −
. D.
2m = ±
.
Câu 33: Cho hàm số
( ) ( )
32
2 1 15ymx mxmx= − + ++ +
với
m
là tham số. Gọi
S
là tập hợp tất cả các giá
trị thực nguyên của
m
để hàm số nghịch biến trên khoảng
( )
;−∞ +∞
. Tính tổng các phần tử của
S
.
A.
5
. B.
5−
. C.
10
. D.
10−
.
Câu 34:Xét các số nguyên dương
,a
b
sao cho phương trình
.4 .2 7 0
xx
ab
+ +=
có hai nghiệm phân biệt
1
,x
2
x
và phương trình
7.9 .3 0
xx
ba+ +=
có hai nghiệm phân biệt
3
,x
4
x
thỏa mãn
12 34
xx xx+<+
. Tìm giá
trị nhỏ nhất
min
S
của
2S ab= +
.
A.
min
35S =
. B.
min
29S =
. C.
min
28S =
. D.
min
31S =
.
Câu 35:Trong không gian với hệ tọa độOxyz, cho điểm M(2;3;-1) và đường thẳng
415
:
1 22
x yz
d
tọa độ hình chiếu vuông góc của M trên (d)
A.
( )
2; 5;1
H
. B. H(4;1;5). C. H(2;3;-1). D. H(1;-2;2).
Câu 36: Trong không gian với hệ tọa độ 0xyz, cho mặt phẳng (P): 2x + 3y + z – 11 = 0. mặt cầu (S) có tâm
I(1; -2; 1) và tiếp xúc với (P) tại H. tọa độ tiếp điểm H là.
A. H(2;3;-1). B. H(5;4;3). C. H(1;2;3). D. H(3;1;2).
Câu 37: Tìm tập hợp tất cả các giá trị thực của tham số
m
để hàm số
( )
2
2
log 1
x
y e ex m= − +−
có tập xác
định là
.
A.
1m >
. B.
1m <−
. C.
1m ≤−
. D.
1m ≥
.
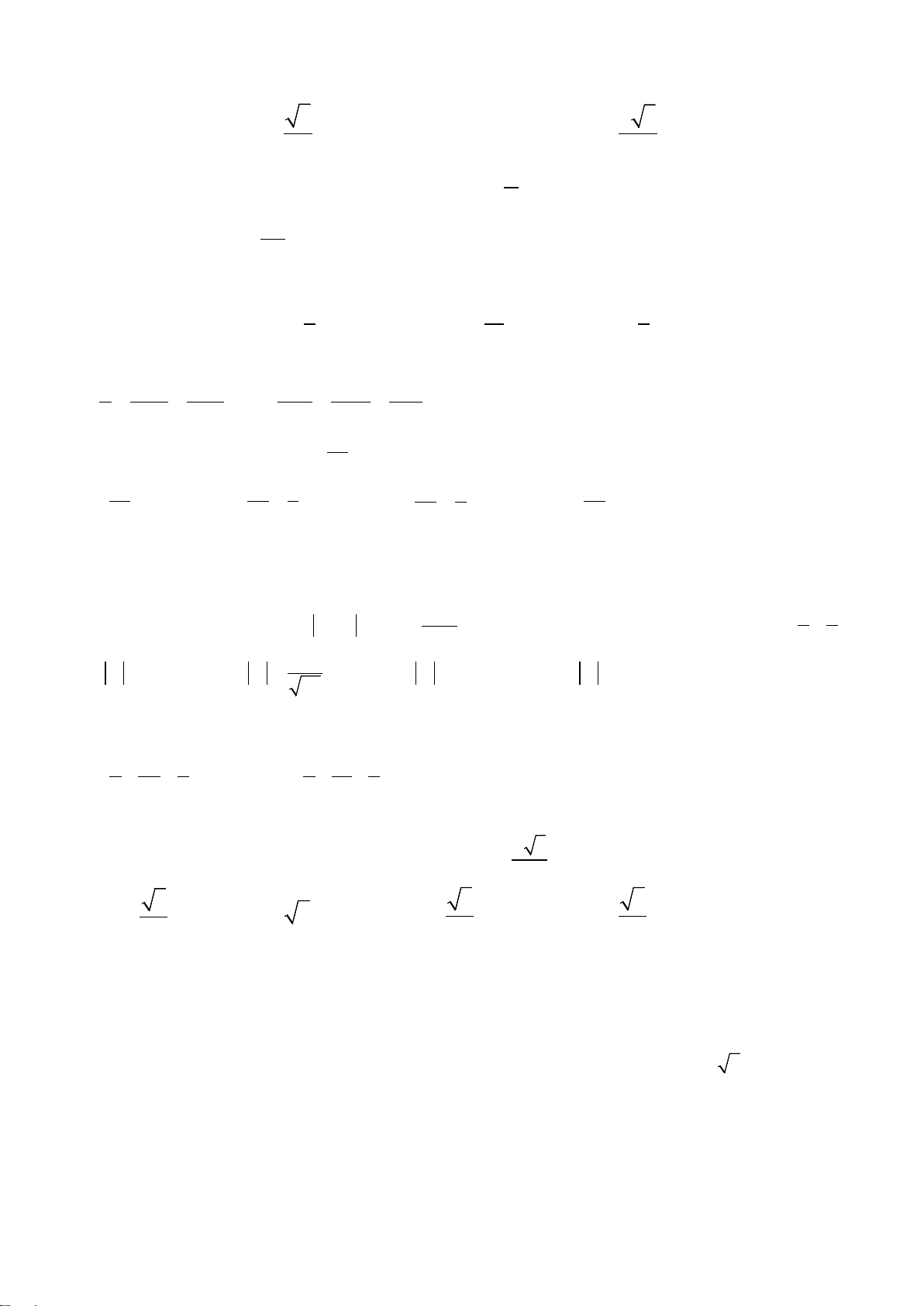
LTB Trang 5/8
Câu 38: Trong không gian cho tam giác đều
ABC
cạnh bằng
2a
. Tính thể tích V của khối tròn xoay nhận
được khi quay tam giác
ABC
quanh cạnh
AB
.
A.
3
Va
π
=
. B.
3
3
3
Va
π
=
. C.
3
2Va
π
=
. D.
3
23
3
Va
π
=
.
Câu 39: Tính tổng các nghiệm của phương trình
2
2sin 2sin cos
4
x xx
π
−+ =
trên đoạn
[ ]
;
ππ
−
.
A.
0
. B.
2
3
π
−
. C.
π
. D.
π
−
.
Câu 40: Tìm tập giá trị
K
của hàm số
( )
2
cos3 3 sin cosy x xx=+−
.
A.
[ ]
2;5K = −
. B.
5
;3
2
K
= −
. C.
19
2;
4
K
= −
. D.
5
;2
2
K
= −
.
Câu 41:Trong không gian với hệ tọa độ
Oxyz
, cho hai đường thẳng
( )
1
32
:
21 1
xy z
d
−+
= =
−
,
( )
2
121
:
3 12
xy z
d
+−−
= =
−
và điểm
( )
1; 1; 2I −
. Đường thẳng
( )
∆
đi qua
I
và cắt
( )
1
d
,
( )
2
d
lần lượt tại
A
,
B
. Tính
IA
IB
.
A.
3
IA
IB
=
. B.
1
3
IA
IB
=
. C.
1
2
IA
IB
=
. D.
2
IA
IB
=
.
Câu 42: Ba xạ thủ
,A
,B
C
cùng bắn vào một bia. Xác suất để bắn trúng đích của xạ thủ
A
là
0,8
; xạ thủ
B
là
0,6
; xạ thủ
C
là
0,5
. Tính xác suất
P
để có ít nhất một xạ thủ bắn trúng đích.
A.
0, 24P =
. B.
0,96P =
. C.
0, 26P =
. D.
0,72P
=
.
Câu 43: Cho số phức
z
thỏa mãn
8 10zi
+=
và
6
z
z −
là số thuần ảo. Tính modun của số phức
93
w
2z
= +
.
A.
w5
=
. B.
18
w
73
=
. C.
w3=
. D.
w6=
.
Câu 44: Gọi
()
α
là mặt phẳng cắt ba trục tọa độ tại 3 điểm M (8; 0; 0), N(0; -2; 0) , P(0; 0; 4). Phương trình
của mặt phẳng
()
α
là:
A.
0
8 24
xyz
+ +=
−
. B.
1
4 12
xyz
+ +=
−
. C.x – 4y + 2z – 8 = 0. D.x – 4y + 2z = 0.
Câu 45: Cho hình chóp
.S ABC
có đáy làtam giác đều,
SA a=
, hai mặt phẳng
( )
,SAB
( )
SAC
cùng vuông
góc với đáy. Khoảng cách từ
A
đến mặt phẳng
( )
SBC
bằng
3
2
a
.Tính thể tích V của hình chóp
.S ABC
.
A.
3
3
3
Va=
. B.
3
3Va=
. C.
3
3
12
Va
=
. D.
3
3
4
Va=
.
Câu 46: Mặt phẳng
( )
P
đi qua
( )
0;1; 1
A −
và nhận
( )
2;1; 2n = −
làm vectơ pháp tuyến có phương trình tổng
quát là.
A.
2 2 30xy z−+ +=
. B.
2 2 30xy z+− −=
.
C.
2 2 30xy z+− +=
. D.
2 2 30xy z−+ −=
.
Câu 47: Cho tứ diện
ABCD
có
AB a
=
; diện tích các tam giác
,
ABC
ABD
thứ tự là
2
3a
,
2
a
; góc giữa
hai mặt phẳng
( )
,ABC
( )
ABD
bằng
0
45
.Tính thể tích V của tứ diện
ABCD
.
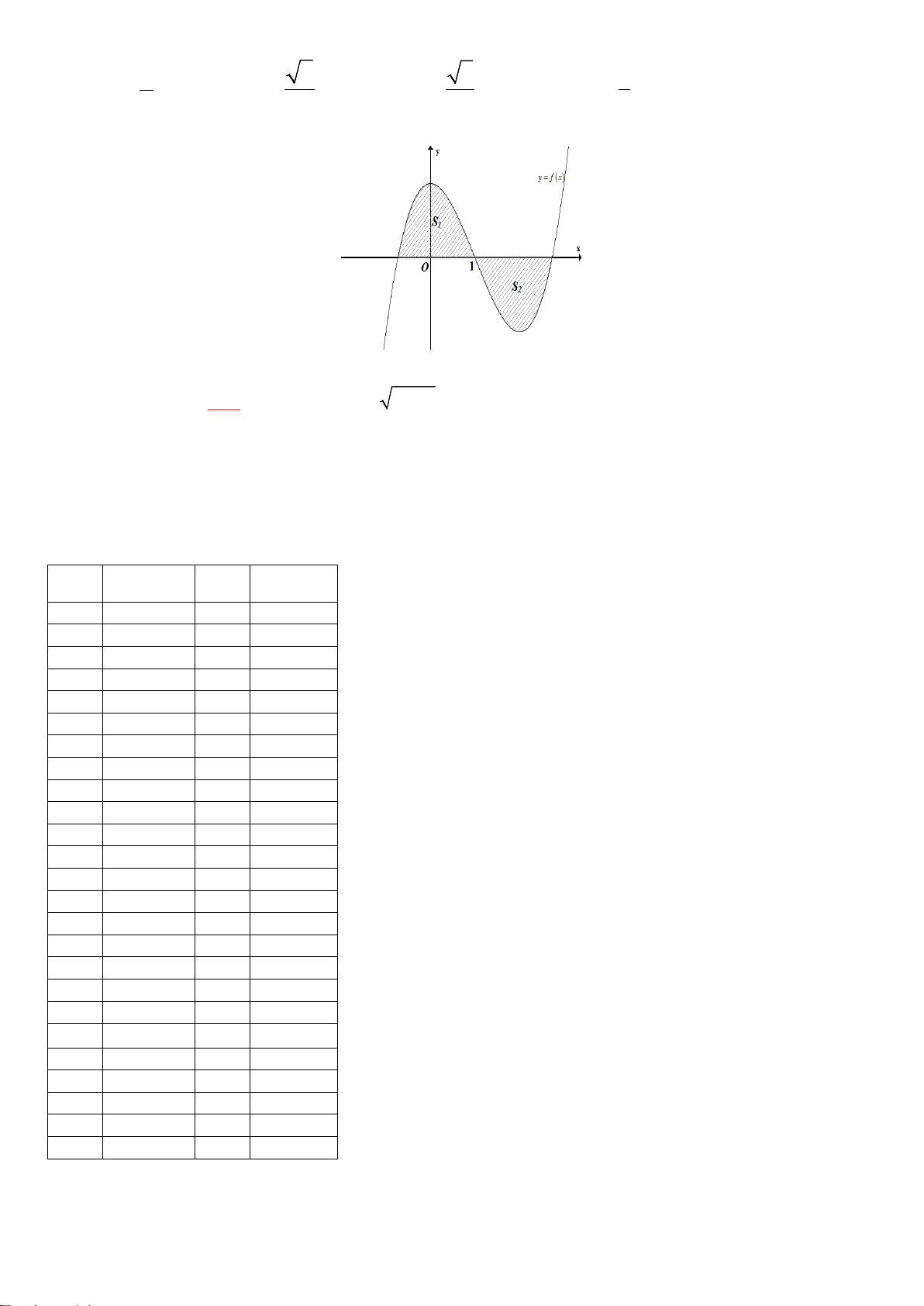
LTB Trang 6/8
A.
3
1
2
Va=
. B.
3
6
3
Va=
. C.
3
6
9
Va=
. D.
3
1
3
Va
=
.
Câu 48:Cho hàm số
()y fx=
có đồ thị như hình dưới đây. Biết
12
SS=
. Khẳng định nào sau đây đúng ?
A.
( ) (
)
6 40ff+ −=
. B.
( ) ( )
5 50ff+ −=
. C.
( ) ( )
4 60ff+ −=
. D.
(
) (
)
4 60
ff− −=
.
Câu 49: Số nghiệm thực của phương trình
2
3 32xx−=−
.
A. 1. B. 0. C. 2. D. 3.
Câu 50: Cho đường thẳng
: 3 10
dx y
− +=
. Tọa độ một vectơ chỉ phương
u
của đường thẳng d là.
A.
( )
1; 3u = −
. B.
( )
3;1
u =
. C.
( )
3;1u = −
. D.
( )
3; 1u = −
.
---- HẾT ----
Câu
Đáp án
Câu
Đáp án
1
C
26
C
2
D
27
A
3
D
28
B
4
A
29
A
5
D
30
A
6
A
31
D
7
C
32
C
8
A
33
D
9
B
34
10
B
35
A
11
C
36
D
12
C
37
A
13
C
38
C
14
D
39
D
15
A
40
C
16
A
41
C
17
B
42
B
18
B
43
A
19
B
44
C
20
C
45
A
21
B
46
B
22
D
47
B
23
B
48
A
24
D
49
B
25
A
50
B
LTB Trang 7/8
Mức độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Vận dụng cao
1. Phương trình
chứa ẩn dưới dấu
căn
Câu 49
2. Phương trình
đường thẳng trong
mặt phẳng tọa độ
Oxy
Câu 50
3. Tập giá trị của
hàm số lượng giác
Câu 40
4. Giới hạn của
hàm số, dạng vô
định
0
0
Câu 6
5. Phương tŕnh
lượng giác
Câu 7
Câu 39
6. Tính chẵn, lẻ của
hàm số lượng giác
Câu 10
7. Nhị thức Newton
Câu 24
8. Xác suất của
biến cố
Câu 42
9. Sự đồng biến,
nghịch biến của
hàm số
Câu 5
Câu 33
10. Cực trị của hàm
số
Câu 1
11. giá trị lớn nhất,
giá trị nhỏ nhất của
hàm số
Câu 21
Câu 34
12. Tiệm cận của
đồ thị
Câu 8
13. Đồ thị của hàm
số
Câu 9
14. Các phép tính
về lũy thừa, logarit
Câu 4
Câu 25
15. Phương trình
logarit
Câu 11
Câu 32
16. Bất phương
trình logarit
Câu 23
17. Tập xác định
của hàm số logarit
Câu 14
Câu 37
18. Hàm số mũ
Câu 29
Câu 36
19. Họ nguyên hàm
Câu 2
Câu 26
20. Tích phân hàm
Câu 18

LTB Trang 8/8
số phân thức hữu tỉ
21. Diện tích hình
phẳng
Câu 48
22. Thể tích khối
tròn xoay
Câu 30
23. Số phức thuần
ảo
Câu 12
24. Môdun của số
phức
Câu 43
25. Phép cộng số
phức
Câu 3
26. Biểu diễn số
phức
Câu 16
27. Phương trình
bậc II trên tập
Câu 28
28. Hình đa diện,
khối đa diện
Câu 22
29. Thể tích khối
chóp
Câu 45
Câu 47
30. Thể tích khối
lăng trụ
Câu 13
31. Mặt cầu ngoại
tiếp khối chóp
Câu 31
32. Diện tích hình
trụ tròn xoay
Câu 27
33. Thể tích khối
nón tròn xoay
Câu 38
34. Phương trình
mặt phẳng
Câu 46
Câu 19
Câu 44
Câu 17
35. Vị trí tương đối
của 2 mặt phẳng
Câu 20
36. Vị trí tương đối
của 2 đường thẳng
Câu 41
37. Phương trình
mặt cầu
Câu 36
Câu 15
Tổng số câu: 50
Tổng số điểm: 10
Tỉ lệ: 100%
11
2,2 (điểm)
22%
15
3,0 (điểm)
30%
21
4,2 (điểm)
42%
3
0,6 (điểm)
6%

Trang 9/6

BVC Trang 1/5
MA TRẬN ĐỀ ÔN THI QUỐC GIA NĂM 2019
LỚP
CHỦ ĐỀ
NB
TH
VD
VDC
GHI
CHÚ
LỚP 12
Ứng dụng đạo
hàm kháo sát hàm
số
C8, C11 C9,C12,C13 C10,C15 C14
Mũ - Logarit
C17,C18,
C20
C16,C19 C21
Nguyên hàm –
Tích phân
C23,
C25, C28
C22, C24,
C27
C26
Số phức C29
C30, C31,
C32
C33 C34
Khối đa diện, thể
tích khối đa diện
C35, C36 C38 C42
Khối tròn xoay,
thể tích khối tròn
xoay
C37, C40, C41
Hình học giải tích
Oxyz
C39, C43
C44, C45,
C46
C49
C48,
C50
Lớp 11
Lượng giác
C3
Tổ hợp – Xác suất
C4
Dãy số - Cấp số
Giới hạn, liên tục
C6
Đạo hàm và ứng
dụng
Phép biến hình
Quan hệ song
song
C5
Quan hệ vuông
góc
C7
Lớp 10
Bất đẳng thức
C1
Phương trình –
bất phương trình
C2
Hình học giải tích
Oxy
Tỉ lệ
15( 30%)
20( 40%)
10(
20%)
5(10%)

BVC Trang 2/5
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
KỲ THI THPT QUỐC GIA NĂM 2019
TRƯỜNG THPT NGUYỄN CHÍ THANH
Bài thi: Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề
(Đề thi có 05 trang)
Câu 1. Suy luận nào sau đây đúng?
A.
d
a
ac b
b
cd
>
>
⇒>
. B.
ab
ab
cd
cd
>
⇒>
>
.
C.
––d
a
acb
b
cd
>
⇒
>
>
. D.
0
0
d
a
a
d
b
b
c
c
>>
⇒
>
>>
.
Câu 2. Tập nghiệm của bất phương trình:
2
2
9
0
3 10
x
xx
−
≥
+−
là
A.
[ ] [ ]
5; 3 2; 3−−∪
. B.
(
] [
)
5; 3 2; 3−−∪
. C.
(
]
(
]
5; 3 2; 3−−∪
. D.
( ) ( )
5; 3 2; 3−− ∪
.
Câu 3. Công thức nghiệm của phương trình
sin sin
x
α
=
là:
A.
2; 2, .x k x k kZ
αππαπ
=+ =−+ ∈
. B.
2; 2, .x k x k kZ
απ απ
= + =−+ ∈
.
C.
2; 2, .x k x k kZ
αππαπ
=+ =++ ∈
. D.
; ,.x kx kkZ
απ παπ
=+ =−+ ∈
.
Câu 4. Từ các chữ số
1, 2,3, 4,5
có thể lập được bao nhiêu số tự nhiên có 5 chữ số đôi một khác nhau
và chia hết cho 5?
A. 24. B. 256. C. 120. D. 3125.
Câu 5. Cho hình chóp
.S ABCD
, đáy là hình thang, đáy lớn
AB
, giao tuyến của mặt
( )
SAD
và
( )
SBC
là:
A. SK với
K AB CD= ∩
. B. SK với
K AC BD= ∩
.
C. SK với
K AD BC= ∩
. D. Sx với
//Sx AB
.
Câu 6. Cho
,0aa
∈≠
. Khi đó
2
2
2
lim 3
1
x
x
ax
→+∞
−
=
−
thì giá trị của a bằng :.
A. – 1. B. 1. C. 2. D.
1
3
.
Câu 7. Cho hình chóp
.S ABCD
có đáy là hình vuông tâm
O
, cạnh bằng
a
. Cho biết hai mặt bên
( )
( )
, SAB SAD
cùng vuông góc với đáy
( )
ABCD
và
2SA a=
. Khoảng cách từ
A
đến mặt
phẳng
( )
SBD
bằng:
A.
10
5
a
. B.
5
5
a
. C.
2
3
a
. D.
10
15
a
.
Câu 8. Đồ thị ở hình bên là đồ thị của hàm số nào?
ĐỀ THI ĐỀ XUẤT
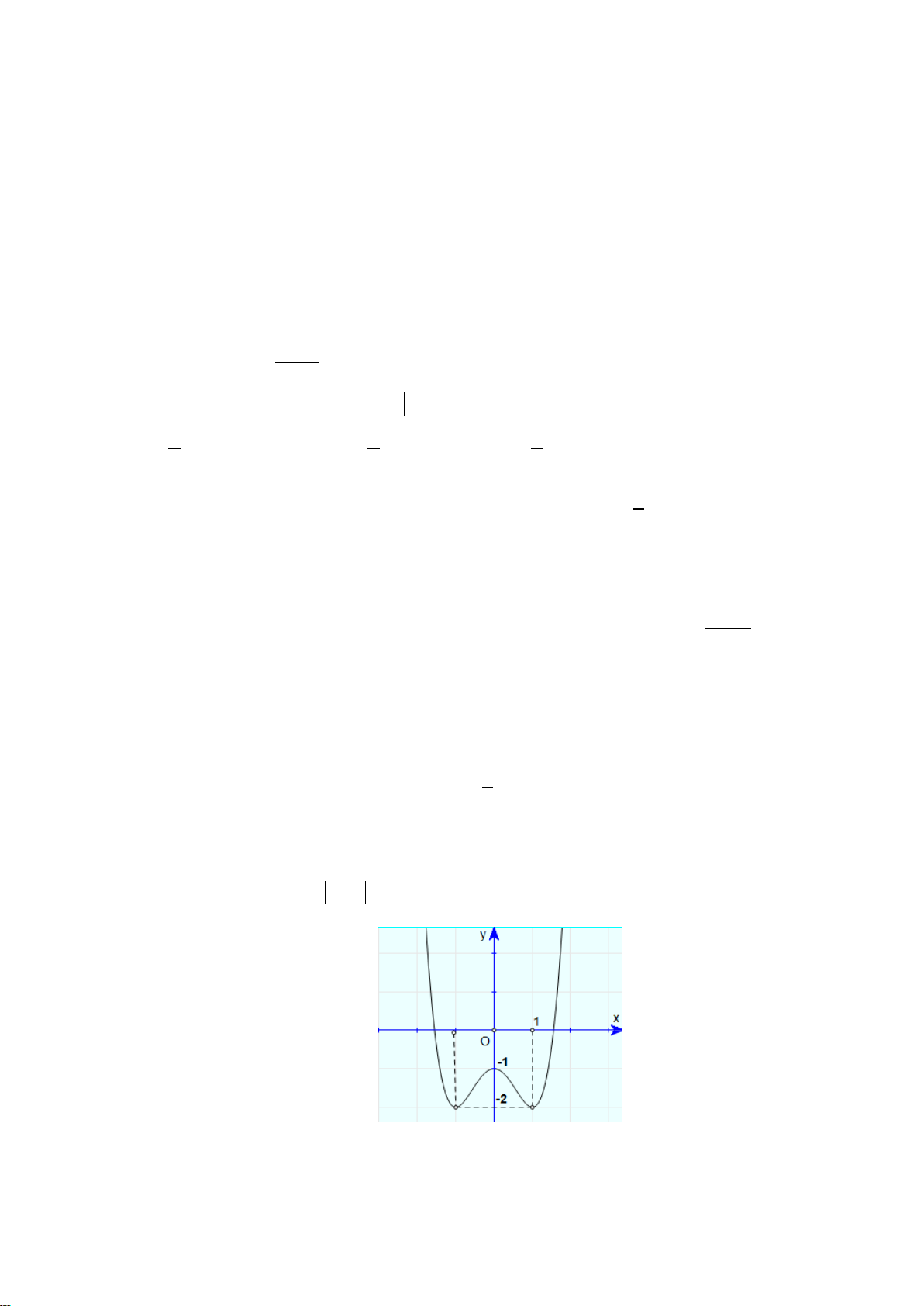
BVC Trang 3/5
A.
42
1
3
2
yx x=−−
. B.
42
1
23
4
yxx= −−
.
C.
42
23yx x=−−
. D.
42
23
yx x=−+ −
.
Câu 9. Cho hàm số
2x 1
2x 1
y
+
=
−
có đồ thị (H). Gọi
12
, xx
là hoành độ giao điểm của (H) với đường
thẳng
20xy−+=
. Khi đó
21
xx−
bằng
A.
5
2
. B.
5
2
−
. C.
1
2
. D. 1.
Câu 10. Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số
(
)
32
1
12
3
y xx m x
= ++ − +
có hai
điểm cực trị đều nằm bên trái trục tung.
A.
12m<<
. B.
1m >
. C.
2m <
. D.
1m <
.
Câu 11. Đường thẳng nào dưới đây là đường tiệm cận ngang của đồ thị hàm số
32
1
x
y
x
−
=
−
?
A.
1x =
. B.
3y =
. C.
2x = −
. D.
2y = −
.
Câu 12. Hàm số
( )
fx
có đạo hàm
( ) ( )
( )
2
2
' 12fx xx x=++
. Số cực trị của hàm số là:
A. 1. B. 2. C. 0. D. 3.
Câu 13. Với giá trị nào của tham số m thì hàm số
32
1
21
3
y x x mx= + −−
đồng biến trên R.
A.
4
m <−
. B.
4m >−
. C.
4m ≥−
. D.
4m ≤−
.
Câu 14. Cho hàm số
()y fx=
có đồ thị như hình vẽ bên. Tìm tất cả các giá trị
của
m
để phương trình
()fx m=
có hai nghiệm thực phân biệt?
A.
0m =
hoặc
2m >
. B.
2m = −
hoặc
1m >−
.
C.
1m
>−
. D.
2m >
.
Câu 15. Cho hàm số xác định trên , liên tục trên các khoảng
( )
y fx=
{ }
\1−
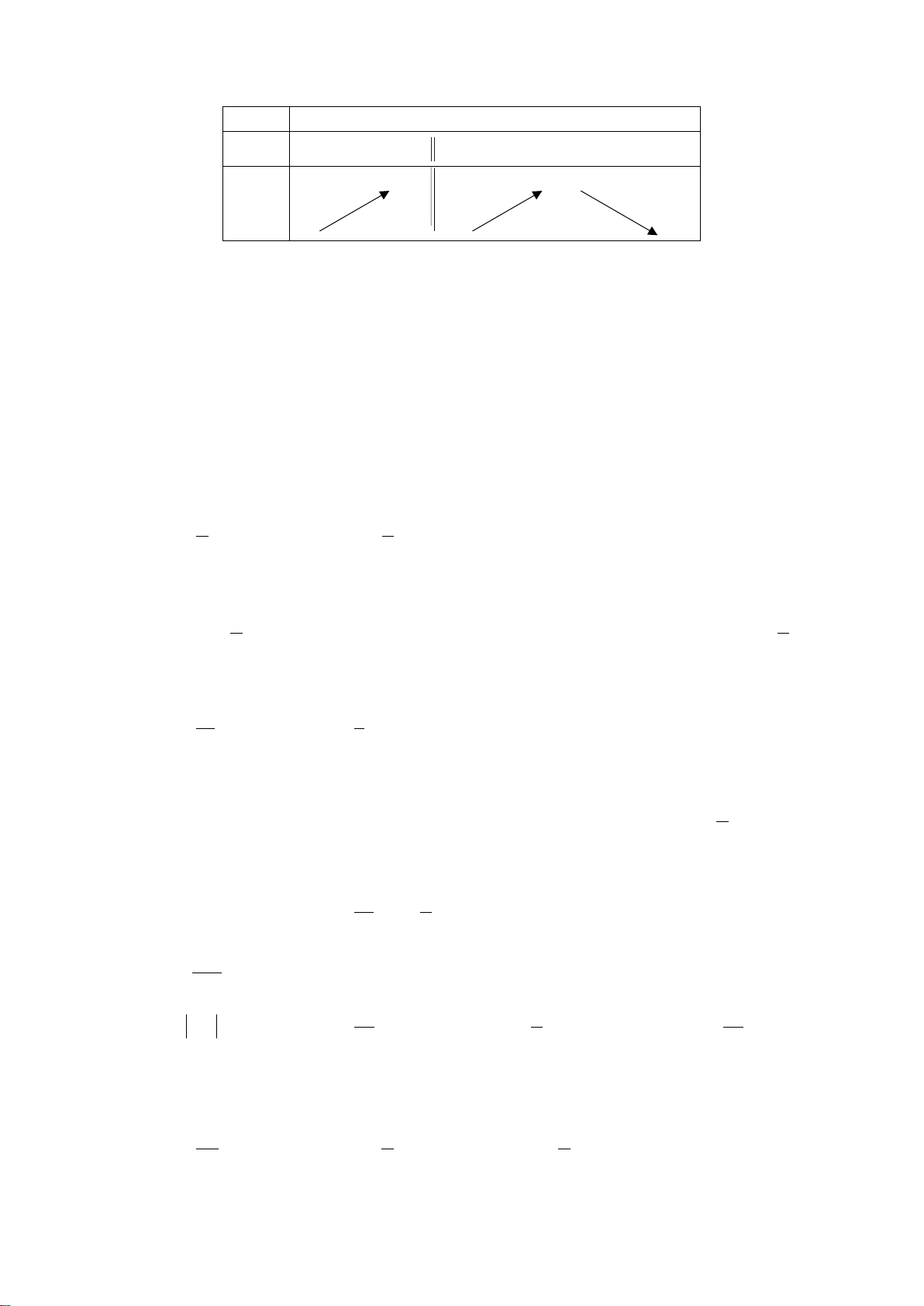
BVC Trang 4/5
xác định của nó và có bảng biến thiên như hình vẽ:
Khẳng định nào sau đây là đúng?
A. Đồ thị hàm số có 3 tiệm cận.
B. Phương trình có 3 nghiệm thực phân biệt thì .
C. Giá trị lớn nhất của hàm số là .
D. Hàm số đồng biến trên .
Câu 16. Hàm số
2
ln( 4 3)y xx
= −+ −
có tập xác định là:
A.
( ;1) (3; )−∞ ∪ +∞
. B.
( )
0; +∞
. C.
( ;0)−∞
. D.
(1; 3)
.
Câu 17. Phương trình
32
39
x
−
=
có nghiệm là:
A.
4
3
x =
. B.
3
4
x =
. C.
3x =
. D.
5x =
.
Câu 18. Cho hàm số
( )
(
)
2
ln 4fx x x= −
chọn khẳng định đúng trong các khẳng định sau:
A.
( )
1
'5
2
f =
. B.
( )
'2 1f
=
. C.
(
)
'2 0
f =
. D.
(
)
6
'1
5
f
−=
.
Câu 19. Bất phương trình
( )
2
log 3 1 3x −>
có nghiệm là:
A.
10
3
x >
. B.
1
3
3
x<<
. C.
3x <
. D.
3x >
.
Câu 20. Tập nghiệm của phương trình
22
log ( 3) log ( 1) 3xx−+ −=
bằng:
A.
{ }
1; 5−
. B.
{ }
5
. C.
{ }
6
. D.
7
2
.
Câu 21. Nghiệm của bất phương trình
32.4 18.2 1 0
xx
− +<
là:
A.
41x
− < <−
. B.
11
16 2
x
<<
. C.
24x<<
. D.
14x<<
.
Câu 22. Tìm
ln x
dx
x
∫
có kết quả là:
A.
ln ln xC+
. B.
( )
2
ln 1
2
x
xC−+
. C.
2
1
ln
2
xC+
. D.
2
ln
2
x
C+
.
Câu 23. Tính tích phân
2
0
cos sinI x xdx
π
=
∫
bằng:
A.
2
3
I
−
=
. B.
2
3
I =
. C.
3
2
I =
. D.
0I =
.
Câu 24. Tìm khẳng định sai trong số các khẳng định sau:
x
−∞
1−
1
+∞
y
′
+
+
0
−
y
1
+∞
−∞
2
1
( )
fx m=
( )
1; 2 .
m ∈
2.
( )
;1 .−∞

BVC Trang 5/5
A.
11
00
sin(1 ). sin .x dx x dx
−=
∫∫
. B.
2
00
sin . 2 sin .
2
x
dx x dx
π
π
=
∫∫
.
C.
0
2
1
(1 ) . 0x dx
−
+=
∫
. D.
1
2007
1
2
.(1 ).
2009
x x dx
−
+=
∫
.
Câu 25. Tính tích phân:
0
cos dI x xx
π
=
∫
bằng:
A. I =
2−
. B. I = 2. C. I = 0. D. I = 1.
Câu 26. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
2yx x= −
và đồ thị hàm số
2
y xx=−+
bằng:
A.
12S =
. B.
10
3
S =
. C.
9
8
S =
. D.
6S =
.
Câu 27. Cho hình phẳng giới hạn bởi các đường
2
1yx= −
và
0y =
quay xung quanh trục
Ox
. Thể tích
của khối tròn xoay tạo thành bằng:
A.
16
5
V
π
=
. B.
6
15
V
π
=
. C.
6
5
V
π
=
. D.
16
15
V
π
=
.
Câu 28. Thể tích
V
của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị hàm
số
( )
y fx=
trục
Ox
và hai đường thẳng
(), x ax b a b
= = <
, xung quanh trục
Ox
là:
A.
2
()
b
a
V f x dx
π
=
∫
. B.
2
()
b
a
V f x dx=
∫
. C.
()
b
a
V f x dx
π
=
∫
. D.
()
b
a
V f x dx=
∫
.
Câu 29. Số phức
23zi= +
được biểu diễn điểm trên mặt phẳng tọa độ
Oxy
là:
A. M(2; -3). B. M (-2; -3). C. M (2; 3). D. M (-2; 3).
Câu 30. Cho số phức
25zi= +
. Số phức
w iz z= +
là:
A.
73wi= −
. B.
33wi=−−
. C.
37wi= +
. D.
77
wi=−−
.
Câu 31. Trong tập số phức
, phương trình
4
1
1
i
z
= −
+
có nghiệm là:
A.
2zi= −
. B.
3 2zi= +
. C.
5 - 3zi=
. D.
1 2zi= +
.
Câu 32.
G
ọi
1
z
và
2
z
lần lượt là nghiệm của phương trình:
2
2 50zz+ +=
. Tính
12
zz= +
A.
25
. B. 10. C. 3. D. 6
.
Câu 33.
G
ọi
1
z
và
2
z
là các nghiệm của phương trình
2
4 90zz− +=
. Gọi M, N là các điểm biểu diễn
của
1
z
và
2
z
trên mặt phẳng phức. Khi đó độ dài của MN là:
A.
4MN =
. B.
5MN =
. C.
25MN = −
. D.
25MN =
.
Câu 34. Cho số phức
( )
,z x yi x y=+∈
thỏa mãn
24 2z izi−− = −
và
minmz=
. Tính mô đun
số phức
( )
w m x yi=−+
.
A.
26w =
. B.
23w =
. C.
32w =
. D.
5w =
.
Câu 35. Cho khối chóp
.S ABCD
có đáy là hình chữ nhật có chiều rộng
2a
, chiều dài
3a
. Chiều cao
của khối chóp là
4a
. Thể tích khối chóp
.S ABCD
tính theo
a
là:

BVC Trang 6/5
A.
3
8Va
=
. B.
3
24Va=
. C.
3
9Va=
. D.
3
40Va=
.
Câu 36. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng
a
là:
A.
3
3
2
Va=
. B.
3
2
4
Va=
. C.
3
3
4
Va=
. D.
3
2
3
Va=
.
Câu 37. Một hình trụ có diện tích xung quanh bằng
4
π
và thiết diện qua trục là hình vuông. Thể tích
khối trụ tương ứng bằng
A.
2
π
. B.
π
. C.
3
π
. D.
4
π
.
Câu 38. Cho lăng trụ tam giác đều
.
ABC A B C
′′′
có cạnh đáy bằng
2a
, khoảng cách từ
A
đến mặt
phẳng
(
)
A BC
′
bằng
6
2
a
. Khi đó thể tích lăng trụ bằng:
A.
3
Va=
. B.
3
3Va=
. C.
3
4
3
Va=
. D.
3
43
3
Va
=
.
Câu 39. Trong không gian
Oxyz
, mặt phẳng
(
)
P
đi qua
( )
1 ; 4 ; 3
A −−
và song song mặt phẳng
( )
: 2 3 5 0Q xy z+− −=
, có phương trình là :
A.
2 3 11 0xy z+− − =
. B.
2 3 17 0
xy z+− + =
.
C.
2 3 70xy z+− +=
. D.
2 3 10
xy z+ − +=
.
Câu 40. Một hình nón có đường kính đáy là
2a
, chiều cao của hình nón bằng
3a
. Tính thể tích của
khối nón là:
A.
2
6Va
π
=
. B.
3
3
Va
π
=
. C.
3
Va
π
=
. D.
3
4Va
π
=
.
Câu 41. Cho hình chóp
.S ABCD
có tất cả các cạnh đều bằng
a
. Xác định bán kính mặt cầu ngoại tiếp
hình chóp
.S ABCD
.
A.
2
4
a
. B.
2
2
a
. C.
3
2
a
. D.
2
a
.
Câu 42. Với một tấm bìa hình vuông, người ta cắt bỏ ở mỗi góc tấm bìa một hình vuông cạnh 12 cm rồi
gấp lại thành một hình hộp chữ nhật không có nắp. Nếu dung tích của cái hộp đó là 4800
3
cm
thì cạnh tấm bìa có độ dài là
A. 42 cm. B. 36 cm. C. 44 cm. D. 38 cm.
Câu 43. Trong không gian với hệ tọa độ
Oxyz
, mặt cầu có tâm
( )
1; 2; 0I −
đường kính bằng 10 có
phương trình là:
A.
2 22
( 1) ( 2) 25x yz+ +− +=
. B.
2 22
( 1) ( 2) 100x yz
+ +− +=
.
C.
2 22
( 1) ( 2) 25x yz− ++ +=
. D.
2 22
( 1) ( 2) 100x yz− ++ +=
.
Câu 44. Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
( ) ( )
0;1;1 а 1; 2; 3A vB
Viết phương trình
của mặt phẳng (P) đi qua
A
và vuông góc với đường thẳng
AB
.
A.
2 60
xy z++ −=
. B.
2 30xy z++ −=
.
C.
3 4 70xyz+ + −=
. D.
3 4 26 0
xyz++−=
.
Câu 45. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng (P):
2 2 30x yz+ −−=
và điểm
( )
1; 2 3I
−
. Mặt cầu (S) tâm I và tiếp xúc mp(P) có phương trình:
A.
2 22
():(1)( 2)(3)4Sx y z++−+−=
. B.
2 22
( ) : ( 1) ( 2) ( 3) 16Sx y z− +− ++ =
;.

BVC Trang 7/5
C.
2 22
():(1)( 2)(3) 4Sx y z− +− ++ =
. D.
2 22
():(1)( 2)(3) 2Sx y z− +− ++ =
.
Câu 46. Giá trị của m nào để cặp mặt phẳng sau vuông góc.
( ) ( )
:2 2 90; :6 100x my mz x y z
αβ
+ + −= −−− =
A.
34m =
. B.
-4
m =
. C.
4
m
=
. D.
2
m
=
.
Câu 47. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
∆
đi qua điểm
( )
1; 2; 3A
và vuông góc
với mặt phẳng
4 3 7 10xyz+ − +=
. Phương trình tham số của đường thẳng
∆
là:
A.
14
23
37
xt
yt
zt
=−+
=−+
=−−
. B.
14
23
37
xt
yt
zt
= +
= +
= −
. C.
13
24
37
xt
yt
zt
= +
= −
= −
. D.
18
26
3 14
xt
yt
zt
=−+
=−+
=−−
.
Câu 48. Đường tròn giao tuyến của mặt cầu (S) tâm
( )
3;1;4I −−
, bán kính
4R =
và mặt phẳng
( )
: 2 2 3 0.P x yz− −−=
Tâm H của đường tròn là điểm nào sau đây:
A. H(1;1;3). B. H (1;1;-3). C. H (-1;1;3). D. H (-3;1;1).
Câu 49. Cho mặt phẳng
( )
: 2 2 10 0Px y z+ +−=
và đường thẳng d:
12
15
2
xt
yt
zt
= +
=−+
= −
. Điểm nằm trên d sao
cho khoảng cách từ điểm đó đến mặt phẳng (P) bằng 1 là:
A.
( )
98
3;4;1 ; ;1;
55
. B.
( )
89
3; 4;1 ; 0; ;
55
.
C.
( )
89
1; 4; 3 ; ; ; 0
55
. D.
( )
98
3; 4;1 ; ;0;
55
−
−
.
Câu 50. Trong không gian với hệ toạ độ
Oxyz
,cho
( )
: 4 2 60Px y z+ − −=
,
( )
: 2 4 60Qx y z− + −=
.
Lập phương trình mặt phẳng
(
)
α
chứa giao tuyến của
( ) ( )
,PQ
và cắt các trục tọa độ tại các
điểm
,,ABC
sao cho hình chóp
.O ABC
là hình chóp đều.
A.
60xyz+++=
. B.
60xyz++−=
. C.
60xyz+−−=
. D.
30xyz++−=
.
--------------------Hết--------------------
BẢNG ĐÁP ÁN
1.D
2.C
3.A
4.A
5.C
6.D
7.A
8.C
9.A
10.A
11.D
12.A
13.D
14.A
15.B
16.D
17.A
18.C
19.D
20.B
21.A
22.C
23.B
24.C
25.A
26.C
27.D
28.A
29.C
30.B
31.D
32.A
33.D
34.A
35.A
36.C
37.A
38.B
39.A
40.C
41.B
42.C
43.A
44.B
45.C
46.C
47.B
48.B
49.A
50.B
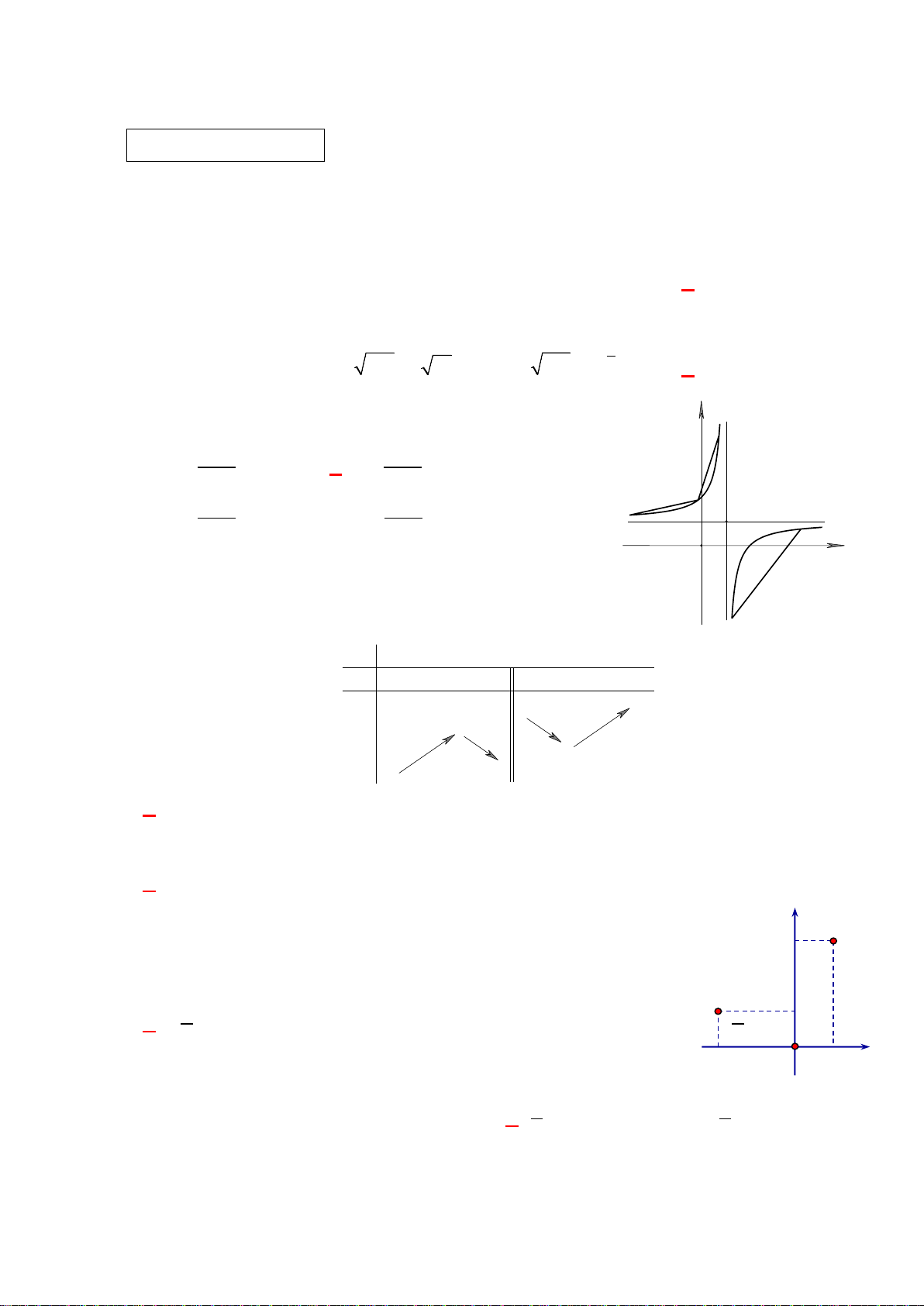
BVC Trang 1/5
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
KỲ THI THPT QUỐC GIA NĂM 2019
TRƯỜNG THPT NGUYỄN TRÃI
Bài thi: Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề
(Đề thi có 05 trang)
Câu 1. Hàm số
32
35yx x=−+
đồng biến trên khoảng nào dưới đây?
A.
(
)
0; 2
.
B.
(
)
0;
+∞
.
C.
( )
;2−∞
.
D.
( ,0)−∞
và
( )
2; +∞
.
Câu 2. Với
α
là số thực bất kỳ, mệnh đề nào sau đây sai?
A.
( )
2
10 100
αα
=
. B.
( )
10 10
α
α
=
. C.
2
10 10
α
α
=
. D.
( )
2
2
10 10
αα
=
.
Câu 3. Đường cong trong hình vẽ bên là đồ thị của một trong bốn
hàm số sau. Hỏi đó là đồ thị của hàm số nào?
A.
2
1
x
y
x
−
=
+
. B.
2
.
1
x
y
x
−
=
−
.
C.
2
2
x
y
x
+
=
−
. D.
2
.
1
x
y
x
+
=
−
.
Câu 4. Cho hàm số
()y fx=
có bảng biến thiên như hình vẽ bên.
Hàm số
()
y fx=
nghịch biến trên khoảng nào trong các
khoảng sau đây?
+
∞
+
∞
−
∞
−
∞
0
−
−
−
1
x
y'
y
−
∞
+
∞
0
0
+
1
+
A.
( 1; 0)−
. B.
( 1; 1)−
. C.
( ; 1)−∞ −
. D.
(0; )+∞
.
Câu 5. Trong không gian
Oxyz
, điểm
( )
3; 4; 2M −
thuộc mặt phẳng nào trong các mặt phẳng sau?
A.
( )
: 70Rxy+−=
. B.
( )
: 50S xyz+++=
.
C.
( )
: 10Qx−=
. D.
( )
: 20Pz−=
.
Câu 6. Trong mặt phẳng
Oxy
, cho các điểm
,AB
như hình vẽ bên. Trung
điểm của đoạn thẳng
AB
biểu diễn số phức.
A.
1
2
2
i−+
. B.
12i−+
. C.
2 i−
. D.
1
2
2
i−
.
Câu 7. Tất cả các nguyên hàm của hàm số
( )
cos 2fx x=
là:
A.
2sin 2xC+
. B.
sin 2xC+
. C.
1
sin 2
2
xC+
. D.
1
sin 2
2
xC−+
.
Câu 8. Cho hình hộp đứng
.ABCD A B C D
′′′′
có cạnh bên
AA h
′
=
và diện tích tam giác
ABC
bằng
S
.
Thể tích của khối hộp
.ABCD A B C D
′′′′
bằng:
O
x
y
2−
1
1
3
B
A
2
2
1
1
O
x
y
ĐỀ THI ĐỀ XUẤT
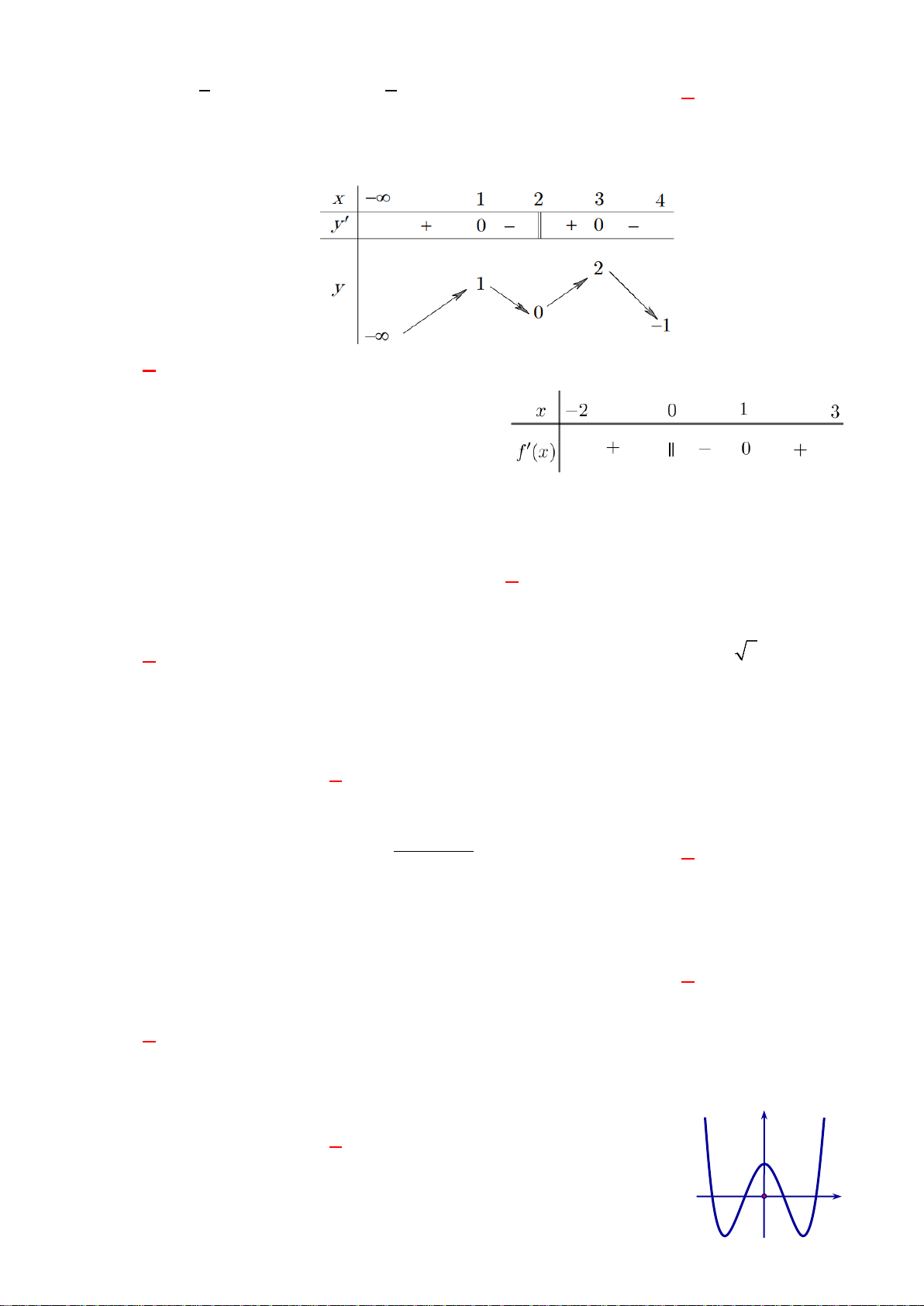
BVC Trang 2/5
A.
1
3
V Sh
=
. B.
2
3
V Sh=
. C.
V Sh=
. D.
2V Sh
=
.
Câu 9. Cho hàm số
( )
y fx=
có tập xác định
(
]
;4−∞
và có bảng biến thiên như hình vẽ bên. Số điểm
cực trị của hàm số đã cho là
A.
3
. B.
2
. C.
4
. D.
5
.
Câu 10. Cho hàm số
( )
y fx=
xác định và liên tục
trên
[ ]
2; 3−
và có bảng xét dấu đạo hàm như
hình bên.
Mệnh đề nào sau đây là đúng về hàm số đã
cho?
A. Đạt cực tiểu tại
2x = −
. B. Đạt cực đại tại
1
x =
.
C. Đạt cực tiểu tại
3x =
. D. Đạt cực đại tại
0
x =
.
Câu 11. Cho hình trụ có bán kính đáy bằng
R
, chiều cao bằng
h
. Biết rằng hình trụ đó có diện tích
toàn phần gấp đôi diện tích xung quanh. Mệnh đề nào sau đây đúng?
A.
Rh=
. B.
2Rh=
. C.
2hR=
. D.
2
hR=
.
Câu 12. Trong không gian
Oxyz
, một vectơ chỉ phương của đường thẳng
2
:1
1
xt
yt
z
=
∆ =−+
=
là
A.
( )
2; 1;1m
= −
. B.
( )
2; 1; 0n =−−
. C.
( )
2; 1; 0v = −
. D.
( )
2;1;1u =
.
Câu 13. Cho
k
,
n
( )
kn<
là các số nguyên dương. Mệnh đề nào sau đây sai?
A.
!.
kk
nn
A kC=
. B.
( )
!
!. !
k
n
n
C
k nk
=
−
. C.
k nk
nn
CC
−
=
. D.
!.
kk
nn
A nC=
.
Câu 14. Trong không gian
Oxyz
, cho hai mặt phẳng
( )
: 2 10x yz
α
+ −−=
và
( )
:2 4 2 0x y mz
β
+ − −=
. Tìm
m
để
( )
α
và
( )
β
song song với nhau.
A.
1m =
. B.
2m =
. C.
2m = −
. D. Không tồn tại
m
.
Câu 15. Giả sử
a
,
b
là các số thực dương bất kỳ. Mệnh đề nào sau đây sai?
A.
( ) ( )
22
log 10 1 log logab a b=++
. B.
(
) ( )
2
log 10 2 2logab ab= +
.
C.
( ) ( )
2
log 10 2 1 log logab a b=++
. D.
( ) ( )
22
log 10 2 logab ab
= +
.
Câu 16. Đường cong ở hình bên là đồ thị của hàm số nào sau đây?
A.
2
31yx x=−+
. B.
42
31yx x=−+
.
C.
42
31yx x
=−+ +
. D.
32
31yx x=−+
.
Câu 17. Cho hàm số
( ) ( )
3
log 2 1fx x= +
. Giá trị của
( )
0f
′
bằng
O
x
y
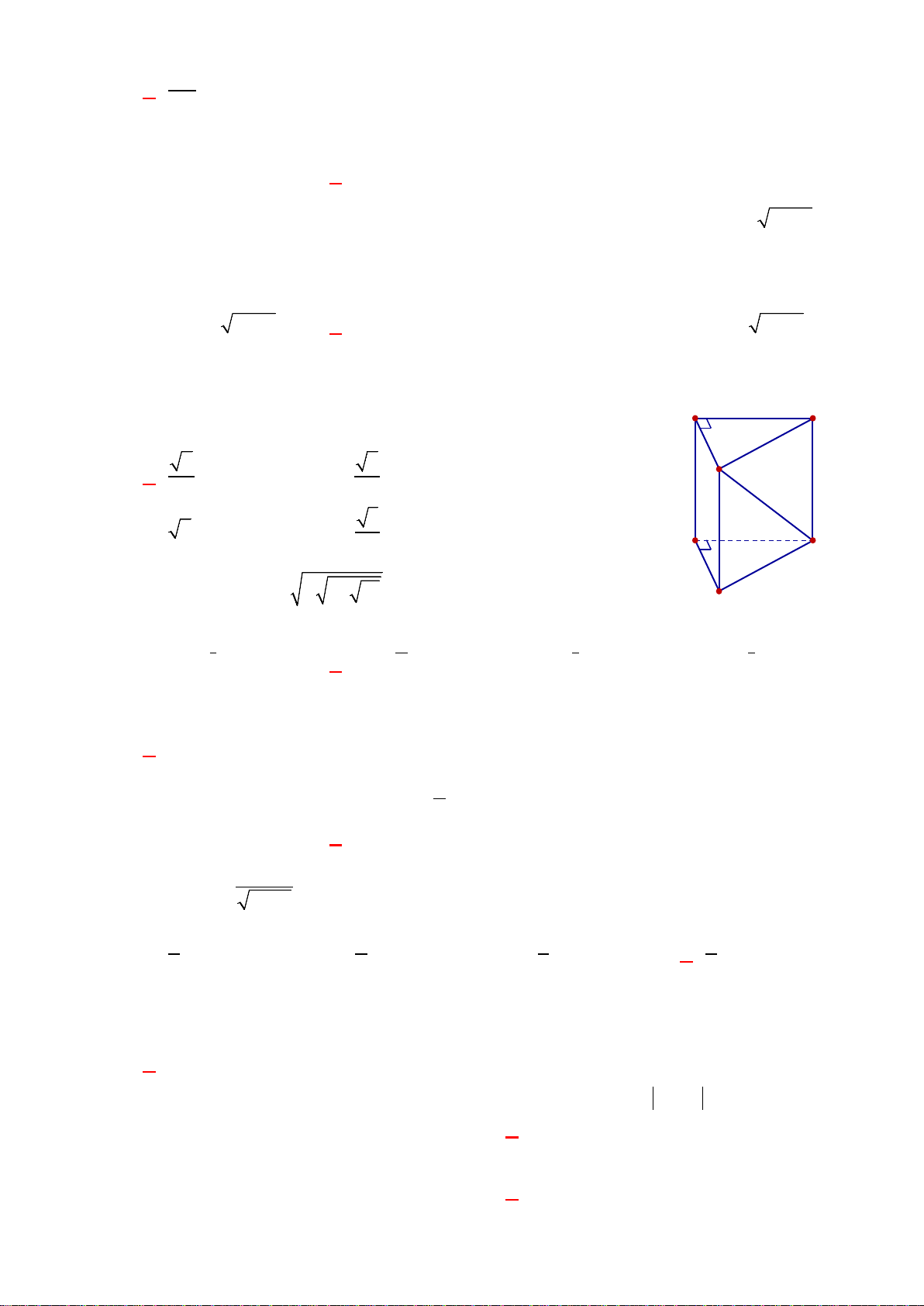
BVC Trang 3/5
A.
2
ln 3
. B.
0
. C.
2ln 3
. D.
2
.
Câu 18. Trong không gian
Oxyz
, cho điểm
( )
1; 2; 3M
. Hình chiếu của
M
lên trục
Oy
là điểm
A.
( )
1; 0; 3P
. B.
(
)
0; 2;0Q
. C.
( )
1;0;0R
. D.
( )
0;0;3S
.
Câu 19. Cho hình phẳng
(
)
D
được giới hạn bởi các đường
0x =
,
1x =
,
0
y =
và
21yx= +
. Thể
tích
V
của khối tròn xoay tạo thành khi quay
( )
D
xung quanh trục
Ox
được tính theo công
thức?
A.
1
0
2 1dV xx=π+
∫
. B.
( )
1
0
2 1dV xx
=π+
∫
. C.
( )
1
0
2 1dV xx= +
∫
. D.
1
0
2 1dV xx= +
∫
.
Câu 20. Cho hình lăng trụ đứng
.ABC A B C
′′′
có đáy
ABC
là tam giác vuông cân tại
,A
AB AA a
′
= =
(tham khảo hình vẽ bên). Tính tang của góc giữa đường thẳng
BC
′
và mặt phẳng
( )
ABB A
′′
.
A.
2
2
. B.
6
3
.
C.
2
. D.
3
3
.
Câu 21. Cho biểu thức
4
3
23
..=P xx x
, với
0>x
. Mệnh đề nào dưới đây
đúng?
A.
1
2
=Px
. B.
13
24
=Px
. C.
1
4
=Px
. D.
2
3
=Px
.
Câu 22. Trong không gian
Oxyz
, cho điểm
(
)
1; 0; 1M
−
. Mặt phẳng
( )
α
đi qua
M
và chứa trục
Ox
có
phương trình là
A.
0
y =
. B.
0xz+=
. C.
10yz++=
. D.
0xyz++=
.
Câu 23. Giá trị nhỏ nhất của hàm số
4
1yx
x
=++
trên đoạn
[ ]
3; 1
−−
bằng
A.
5
. B.
4−
. C.
6−
. D.
5−
.
Câu 24. Tích phân
1
0
d
31
x
x +
∫
bằng
A.
4
3
. B.
3
2
. C.
1
3
. D.
2
3
.
Câu 25. Cho hàm số
( )
y fx=
có đạo hàm
( )
2
2, .fx x xx
′
= − ∀∈
Hàm số
( )
2y fx= −
đồng biến
trên khoảng
A.
( )
0; 2
. B.
( )
2; +∞
. C.
( )
;2−∞ −
. D.
( )
2;0−
.
Câu 26. Gọi
1
z
,
2
z
là các nghiệm của phương trình
2
8 25 0zz−+=
. Giá trị
12
zz−
bằng
A.
8
. B.
5
. C.
6
. D.
3
.
Câu 27. Phương trình bậc hai nào sau đây có nghiệm
12i+
?
A.
2
2 30zz− +=
. B.
2
2 50zz+ +=
. C.
2
2 50zz− +=
. D.
2
2 30zz+ +=
.
A
C
B
A
′
C
′
B
′
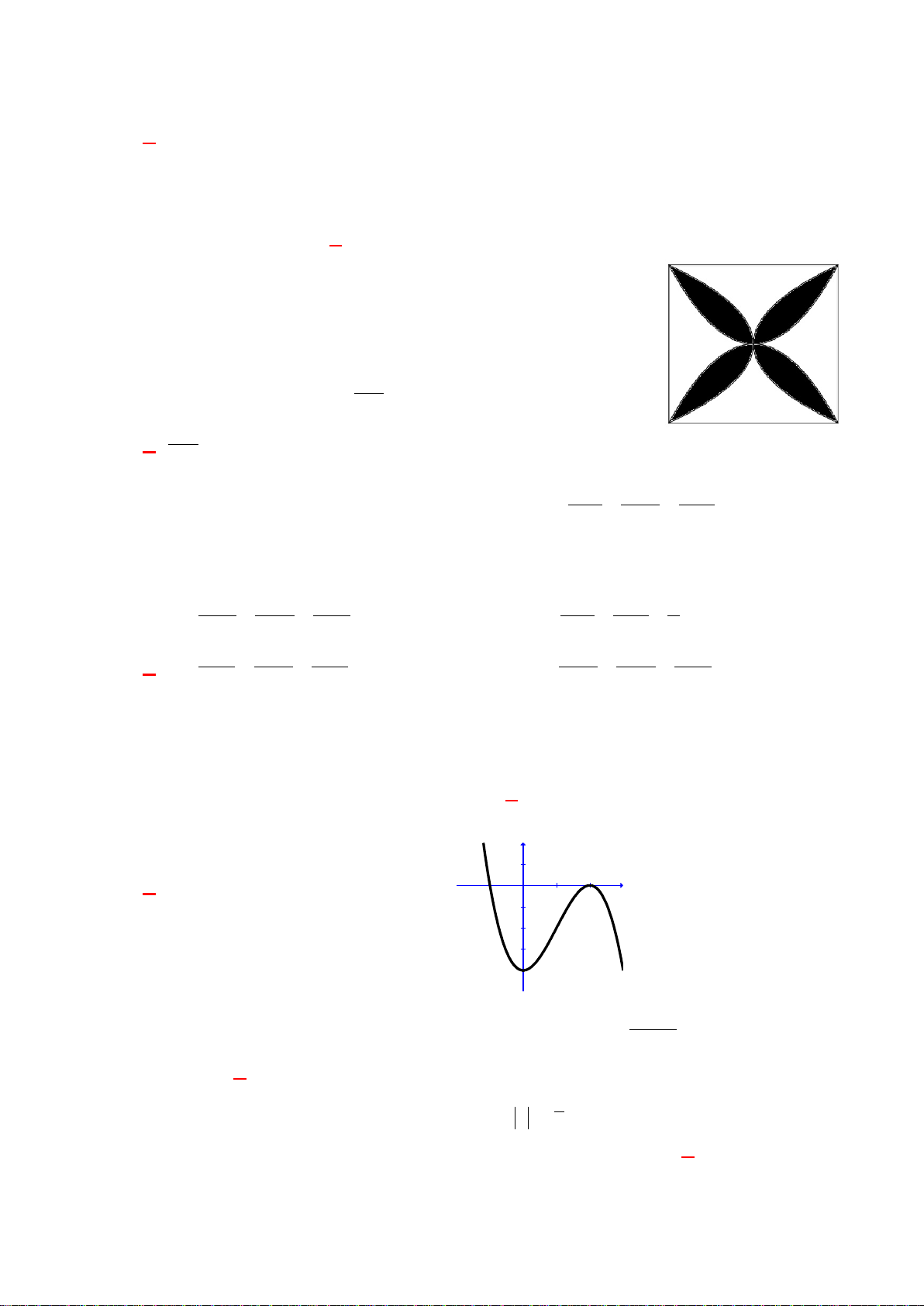
BVC Trang 4/5
Câu 28. Biết
a
là số thực dương bất kì để bất phương trình
91
x
ax
≥+
nghiệm đúng với mọi
x ∈
.
Mệnh đề nào sau đây là đúng?
A.
(
34
10 ;10a
∈
. B.
(
23
10 ;10
a
∈
. C.
(
2
0;10a
∈
. D.
(
)
4
10 ;+∞
.
Câu 29. Cho
(
)
fx
liên tục trên
và thỏa mãn
(
)
2 16f
=
,
( )
1
0
2d 2f xx=
∫
. Tích phân
( )
2
0
dxf x x
′
∫
bằng?
A.
30
. B.
28
. C.
36
. D.
16
.
Câu 30. Một viên gạch hoa hình vuông cạnh
40
cm
. Người thiết kế đã sử
dụng bốn đường parabol có chung đỉnh tại tâm viên gạch để tạo ra
bốn cánh hoa (được tô mầu sẫm như hình vẽ bên).
Diện tích mỗi cánh hoa của viên gạch bằng
A.
2
800cm
. B.
2
800
cm
3
.
C.
2
400
cm
3
. D.
2
250cm
.
Câu 31. Trong không gian
Oxyz
, cho đường thẳng
123
:
121
xy z
d
−−−
= =
và mặt phẳng
( )
: 20xyz
α
+−−=
. Trong các đường thẳng sau, đường thẳng nào nằm trong mặt phẳng
( )
α
,
đồng thời vuông góc và cắt đường thẳng
d
?
A.
2
244
:
1 23
xyz−−−
∆==
−
. B.
4
11
:
3 21
xyz−−
∆==
−
.
C.
3
525
:
3 21
xyz−−−
∆==
−
. D.
1
244
:
32 1
xyz+++
∆==
−−
.
Câu 32. Một người gửi tiền tiết kiệm
200
triệu đồng vào một ngân hàng với kỳ hạn một năm và lãi suất
8,25%
một năm, theo thể thức lãi kép. Sau
3
năm tổng số tiền cả gốc và lãi người đó nhận
được là (làm tròn đến hàng nghìn)
A.
124, 750
triệu đồng. B.
253,696
triệu đồng.
C.
250,236
triệu đồng. D.
224, 750
triệu đồng.
Câu 33. Đồ thị sau đây là của hàm số nào?
A.
32
34yx x=−+ −
.
B.
3
34yx x=−−
.
C.
32
34yx x=−− −
.
D.
3
34yx x=−−
.
Câu 34. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
1mx
y
xm
+
=
+
đồng biến trên khoảng
( )
1; +∞
. A.
1.m >
. B.
1m <−
hoặc
1m >
. C.
1m ≥
. D.
1 1.m−< <
.
Câu 35. Có bao nhiêu số phức
z
thỏa mãn điều kiện
2
2
zzz= +
?
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 36. Hàm số
( )
4
2
41yx
−
= −
có tập xác định là :
-1 1 2
-4
-3
-2
-1
1
x
y
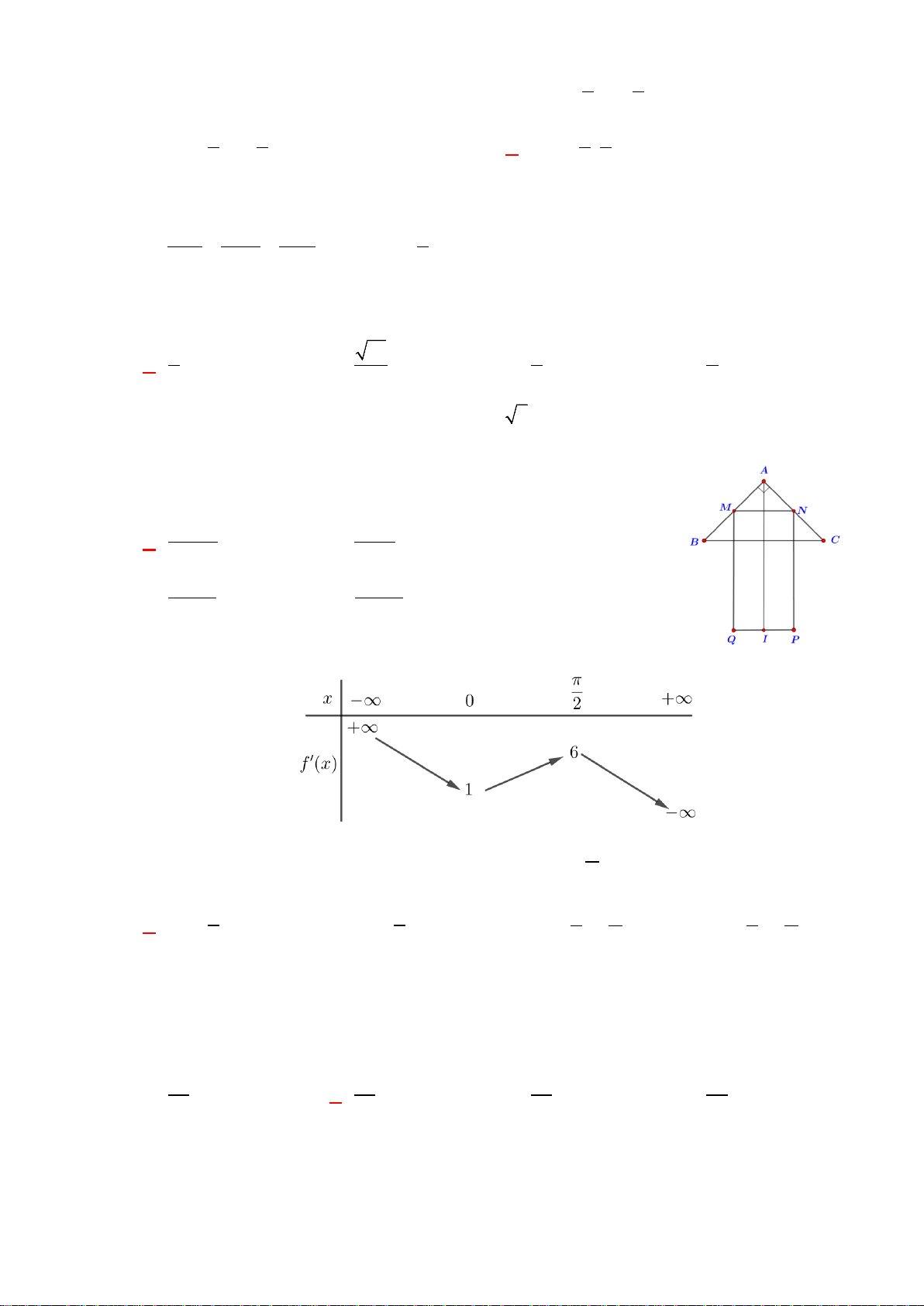
BVC Trang 5/5
A.
. B.
11
;;
22
−∞ − ∪ +∞
.
C.
11
;;
22
−∞ ∪ +∞
. D.
11
\;
22
−
.
Câu 37. Trong không gian
Oxyz
, cho mặt phẳng
(
)
: 2 2 2 0,xy z
α
+− −=
đường thẳng
123
:
122
xy z
d
+++
= =
và điểm
1
;1;1 .
2
A
Gọi
∆
là đường thẳng nằm trong mặt phẳng
( )
α
,
song song với
d
đồng thời cách
d
một khoảng bằng 3. Đường thẳng
∆
cắt mặt phẳng
(
)
Oxy
tại điểm
.B
Độ dài đoạn thẳng
AB
bằng.
A.
7
2
. B.
21
2
. C.
7
3
. D.
3
2
.
Câu 38. Cho tam giác vuông cân
ABC
có
2
AB AC a
= =
và hình chữ nhật
MNPQ
với
2MQ MN=
được xếp chồng lên nhau sao cho
M
,
N
lần lượt là trung điểm của
AB
,
AC
(như hình vẽ).
Tính thể tích
V
của vật thể tròn xoay khi quay mô hình trên quanh
trục
AI
, với
I
là trung điểm
PQ
.
A.
3
17
24
a
π
. B.
3
5
6
a
π
.
C.
3
11
8
a
π
. D.
3
11
24
a
π
.
Câu 39. Cho hàm số
y fx
. Hàm số
y fx
có bảng biến thiên như sau
Bất phương trình
cos
23
x
fx m
đúng với mọi
0;
2
x
khi và chỉ khi
A.
1
02
3
mf
. B.
1
02
3
mf
. C.
1
1
32
mf
. D.
1
1
32
mf
.
Câu 40. Có hai dãy ghế đối diện nhau, mỗi dãy có bốn ghế. Xếp ngẫu nhiên 8 học sinh, gồm 4 nam và 4
nữ, ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học
sinh nam đều ngồi đối đối diện với một học sinh nữ và không có hai học sinh cùng giới ngồi
cạnh nhau bằng
A.
8
35
. B.
1
35
. C.
2
35
. D.
4
35
.
Câu 41. Trong không gian với hệ tọa độ
Oxyz
, cho tam giác
ABC
với
2; 1; 3A
,
1; 1; 2B
,
3; 6; 1C
. Điểm
;;M xyz
thuộc mặt phẳng
Oyz
sao cho
22 2
MA MB MC
đạt giá trị
nhỏ nhất. Tính giá trị của biểu thức
P xyz
.
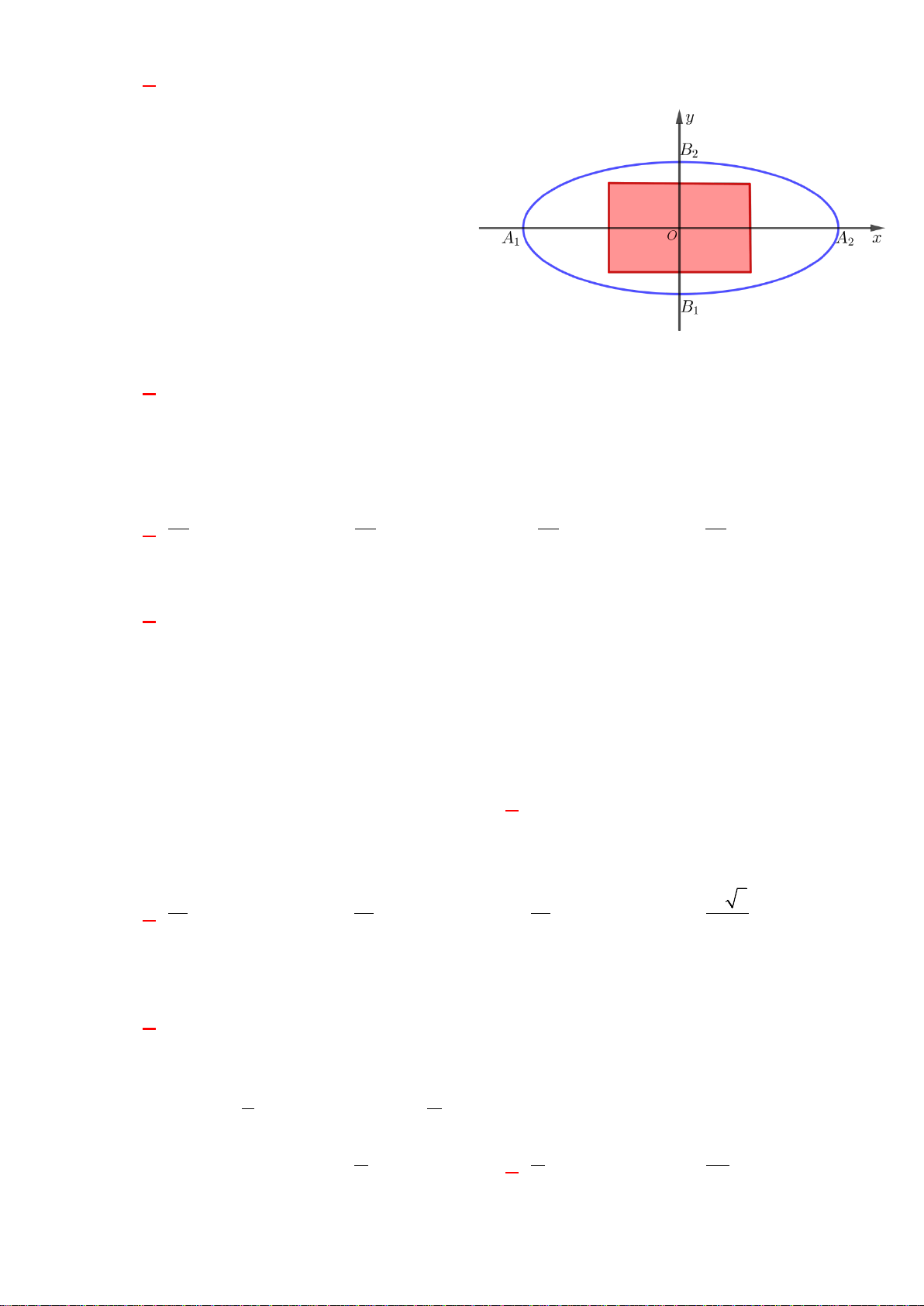
BVC Trang 6/5
A.
0P
. B.
2
P
. C.
6
P
. D.
2
P
.
Câu 42. Một mặt bàn hình elip có chiều dài là 120
cm, chiều rộng là là 60 cm. Anh Phượng
muốn gắn đá hoa cương và dán gạch tranh
trên mặt bàn theo hình (phần đá hoa cương
bên ngoài và điểm nhấn bên trong là bộ
tranh gồm 2 miếng gạch với kích thước
mỗi miếng là 25 cm x 40 cm). Biết rằng đá
hoa cương có giá và bộ tranh gạch có giá
lần lượt là 600.000 vnđ/
2
m
và
300.000
vnđ/bộ. Hỏi số tiền để gắn đá hoa cương
và dán gạch tranh theo cách trên gần nhất với số tiền nào dưới đây?
A.
519.000
đồng. B.
610.000
đồng. C.
639.000
đồng. D.
279.000
đồng.
Câu 43. Cho khối chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Gọi
M
trên cạnh
SC
sao
cho
2.
MC MS
=
,
G
là trọng tâm tam giác
BCD
. Tính thể tích khối tứ diện
BMGD
biết khối
chóp
.S ABCD
có thể tích bằng
3
a
.
A.
3
9
a
. B.
3
2
a
. C.
3
12
a
. D.
3
4
a
.
Câu 44. Đơn giản biểu thức ta được
(
)
22 2
1 sin cot 1 cot sin
n
x x x xm− +− = +
. Khi đó m+n bằng
A. 2. B. 4. C. 1. D. 3.
Câu 45. Trong không gian
Oxyz
, cho điểm
2; 1; 3E
, mặt phẳng
:2 2 3 0P x yz
và mặt
cầu
222
: 3 2 5 36Sx y z
. Gọi
là đường thẳng đi qua
E
, nằm trong
P
và cắt
S
tại hai điểm có khoảng cách nhỏ nhất. Biết
có một vectơ chỉ phương
00
2018; ;u yz
. Tính
00
.Tz y
A.
0
T
. B.
2018T
. C.
2018T
. D.
1009
T
.
Câu 46. Cho hình lăng trụ đứng
.ABC A B C
′′′
có đáy
ABC
là tam giác vuông,
AB BC a= =
. Biết rằng
góc giữa hai mặt phẳng
( )
ACC
′
và
( )
AB C
′′
bằng
60
°
. Tính thể tích khối chóp
.B ACC A
′ ′′
.
A.
3
3
a
. B.
3
6
a
. C.
3
2
a
. D.
3
3
3
a
.
Câu 47. . Trong mặt phẳng với hệ tọa độ
Oxy
, xác định tọa độ tâm
I
của đường tròn
22
( ): 2 4 1 0Cx y x y+ − + +=
.
A.
(1; 2)I −
. B.
( 2; 4)I −
. C.
( 1; 2)I
−
. D.
(2; 4)I −
.
Câu 48. Cho hàm số
( )
y fx
=
có đạo hàm liên tục trên đoạn
[ ]
0;1
và
( ) ( )
0 10ff+=
. Biết
( ) ( ) ( )
11
2
00
1
d , cos d
22
f xx fx xx
π
π
′
= =
∫∫
. Tính
( )
1
0
dfx x
∫
.
A.
π
. B.
1
π
. C.
2
π
. D.
3
2
π
.

BVC Trang 7/5
Câu 49. Xét các số phức z và w thỏa mãn
| 1 3|| 2|z izi−− ≤ +
và
|w 1 3 | |w 2 |ii++ ≤ −
. Giá trị nhỏ nhất
của
| w|Pz= −
là
A.
3
13
. B.
3 26
13
. C.
26
4
. D.
13 1
2
+
.
Câu 50. Giả sử
1
z
,
2
z
là hai trong số các số phức
z
thỏa mãn
21iz i+ −=
và
12
2zz−=
. Giá trị lớn
nhất của
12
zz+
bằng
A.
4
. B.
23
. C.
32
. D.
3
.
----------HẾT----------
BẢNG ĐÁP ÁN
1.D
2.D
3.B
4.A
5.A
6.A
7.C
8.D
9.A
10.D
11.A
12.B
13.D
14.D
15.A
16.B
17.A
18.B
19.B
20.A
21.B
22.A
23.B
24.D
25.A
26.C
27.C
28.A
29.B
30.C
31.C
32.B
33.A
34.A
35.D
36.D
37.A
38.A
39.A
40.B
41.A
42.A
43.A
44.A
45.C
46.A
47.A
48.C
49.B
50.A

BVC Trang 1/6
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
KỲ THI THPT QUỐC GIA NĂM 2019
TRƯỜNG THPT NGUYỄN THÁI HỌC
Bài thi: Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề
(Đề thi có 06 trang)
Câu 1. Cho tứ diện
SABC
có các cạnh
,,SA SB SC
đôi một vuông góc với nhau. Biết
3, 4, 5
SA a SB a SC a= = =
Tính theo a thể tích V của khối tứ diện
SABC
A.
3
20Va=
. B.
3
10Va
=
. C.
3
5
2
a
V =
. D.
3
5Va=
.
Câu 2. Hàm số
32
3 34yx x x=− +−
có bao nhiêu điểm cực trị?
A. 1. B. 2. C. 0. D. 3.
Câu 3. Tính góc giữa hai vectơ
( 1;1; 0)a = −
;
(2;1;2)b = −−
A. 30
0
. B. 60
0
. C. 120
0
. D. 135
0
.
Câu 4. Hàm số
32
35yx x=−+
đồng biến trên khoảng nào dưới đây?
A.
(0; 2)
. B.
(0; )
+∞
.
C.
( ;2)−∞
.
D.
( ,0)
−∞
và
(2; )+∞
.
Câu 5. Đạo hàm của hàm số
1
2
3
(1 3 )
yx x= −+
A.
( )
1
3
2 13xx−+
. B.
( )
2
3
2 13xx
−
−+
. C.
( )
2
3
1
2 13
3
xx
−
−+
. D.
( )
1
3
1
2 13
3
xx−+
.
Câu 6. Cho biết I =
2ln
7ln
ln
152
1
2
1
2
2
CBe
Adx
x
x
x
+
+=
−+
+
∫
−
.Tính
S ABC=++
.
A.
4
15
=S
.
B.
4
15
−=S
.
C.
4
17
=S
.
D.
4
17
−=S
.
Câu 7. Một mặt cầu có bán kính
R
có thể tích là:
A.
2
4
3
R
π
. B.
3
4
3
R
π
. C.
3
2
3
R
π
. D.
3
4 R
π
.
Câu 8. Tìm tập nghiệm của phương trình:
2
( 2 1) 2 1
x
−=+
.
A.
{ }
1−
. B.
{ }
1
. C.
−
2
1
. D.
2
1
.
Câu 9. Cho
( ) ( )
1; 2; 4 ; 1; 0; 2AB−−
. Mặt phẳng trung trực của đoạn
AB
có phương trình tổng quát là:
A.
–4 0xyz++ =
. B.
–4 0xyz−+ =
. C.
40xyz−−+=
. D.
0xyz−−=
.
Câu 10. Tính
sin xdxx
∫
.
A.
cos – sinx x xC+
. B.
cos sin –x x xC+
. C.
– cos – sinx x xC+
. D.
– cos sin –x x xC+
.
Câu 11. Đường thẳng
d
đi qua điểm
( )
2;1; 4A −
và vuông góc với mặt phẳng
( )
:– 30Pxz+=
có
phương trình
A.
2
1.
4
xt
yt
z
=−+
= −
=
B.
2
1.
4
xt
yt
z
=−+
= +
=
C.
4
1.
6
xt
y
zt
=−+
=
= −
D.
1
1.
3
xt
y
zt
=−+
=
= +
ĐỀ THI ĐỀ XUẤT

BVC Trang 2/6
Câu 12. Có
7
bông hồng đỏ,
8
bông hồng vàng và
10
bông hồng trắng, các bông hồng khác nhau từng
đôi một. Hỏi có bao nhiêu cách lấy
3
bông hồng có đủ ba màu.
A.
319
. B.
3014
. C.
310
. D.
560
.
Câu 13. Trong các dãy số sau đây, dãy số nào là một cấp số cộng?
A.
2
1, 1
n
un n=+≥
. B.
2, 1
n
n
un= ≥
. C.
1, 1
n
u nn=+≥
. D.
2 3, 1
n
u nn=−≥
.
Câu 14. Cho số phức
34zi= −
. Mệnh đề nào dưới đây sai?
A. Phần thực và phần ảo của lần lượt là 3 và .
B. Môđun của số phức là 5.
C. Số phức liên hợp của là .
D. Biểu diễn số phức lên mặt phẳng tọa độ là điểm
( )
3; 4M −
.
Câu 15. Đường cong ở hình dưới là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số
nào?
A.
32
2 61y xx x= −++
.
B.
32
2 6 61yx x x= − ++
.
C.
32
2 6 61yx x x= − −+
.
D.
32
2 6 61y xxx=− − −+
.
Câu 16. Giá trị nhỏ nhất của hàm số
3
35yx x
=−+
trên đoạn
[ ]
2; 4
là:
A.
[ ]
2;4
min 3y
=
. B.
[ ]
2;4
min 7y =
. C.
[ ]
2;4
min 5y
=
. D.
[ ]
2;4
min 0y =
.
Câu 17. Gọi S là tập các giá trị dương của tham số
m
sao cho hàm số
32
3 27 3 2y x mx x m=− + +−
đạt
cực trị tại
12
,xx
thỏa mãn
12
5
xx−≤
. Biết
(
]
;S ab=
. Tính
2T ba= −
.
A.
51 6T = +
. B.
61 3T = +
. C.
61 3T
= −
. D.
51 6T
= −
.
Câu 18. Tìm phần ảo của số phức
z
biết
2
(3 )(3 )z ii
=+−
.
A. . B. . C. . D. .
Câu 19. Mặt cầu
(
)
S
có tâm là
( )
1; 0; 3I −
và đi qua điểm
( )
1;3;3M −
có phương trình là:
A.
( ) ( )
22
2
1 3 49x yz+ ++− =
. B.
( ) (
)
22
2
1 37x yz− + ++ =
.
C.
2 22
2 6 – 39 0xyz xz++−+ =
. D.
2 22
2 6 39 0xyz xy++−+ +=
.
Câu 20. Khẳng định nào sau đây đúng.
A. Hàm số
1
2
x
y
=
đồng biến trên R. B. Hàm số
2
x
y
−
=
đồng biến trên R.
C. Hàm số
2
x
y =
đồng biến trên R. D. Hàm số
x
ye=
nghịch biến trên R.

BVC Trang 3/6
Câu 21. Cho số phức
12zi= +
. Điểm nào dưới đây là điểm biểu diễn của số phức
w z iz= +
trên mặt
phẳng tọa độ?
A.
M(3 ; 3)
. B.
( )
2;3N
. C.
( )
3; 3P −
. D.
(
)
3; 2
Q
.
Câu 22. Cho hai mặt phẳng
( )
(
)
,
PQ
cắt nhau theo giao tuyến là đường thẳng
d
. Đường thẳng
a
song
song với cả hai mặt phẳng
( ) ( )
,PQ
. Khẳng định nào sau đây đúng?
A.
,ad
trùng nhau. B.
,
ad
chéo nhau. C.
a
song song
d
. D.
,ad
cắt nhau.
Câu 23. Tìm số nghiệm nguyên của bất phương trình
2
log (9 ) 3x−≤
.
A.
8
. B.
7
. C.
6
. D.
9
.
Câu 24. Tính diện tích hình phẳng
( )
H
giới hạn bởi các đường:
2
2yx x= −
và
2
4
yx x
=−+
.
A. 7.
B. 8.
C. 9.
D. 10.
Câu 25. Cho tam giác
ABO
vuông tại
O
, có góc
30 ,
o
A AB a
= =
. Quay tam giác
ABO
quanh trục
AO
ta được một hình nón có diện tích xung quanh bằng:
A.
2
2
a
π
. B.
2
a
π
. C.
4
2
a
π
. D.
2
2 a
π
.
Câu 26. Đồ thị hàm số
23
1
x
y
x
−
=
−
có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:
A.
1x =
và
2y =
. B.
2x =
và
1y
=
. C.
1x
=
và
3y
= −
. D.
1x = −
và
2
y =
.
Câu 27. Cho khối hộp
.ABCD A B C D
′′′′
có thể tích bằng
2018
. Gọi
M
là trung điểm của cạnh
AB
. Mặt
phẳng
( )
MB D
′′
chia khối chóp
.ABCD A B C D
′′′′
thành hai khối đa diện. Tính thể tích phần
khối đa diện chứa đỉnh
A
.
A.
5045
6
. B.
7063
6
. C.
10090
17
. D.
7063
12
.
Câu 28. Đạo hàm của hàm số
2
3
log log(2 1)y x xx= + −−
A.
2
1 41
. ln 3 (2 1)
x
x xx
−
+
−−
. B.
2
ln 3 ln10
(2 1)x xx
+
−−
.
C.
2
1 41
.ln3 (2 1).ln10
x
x xx
−
+
−−
. D.
2
1 21
.ln3 (2 1).ln10
x
x xx
−
+
−−
.
Câu 29. Giá trị của
m
làm cho phương trình
2
( 2) 2 3 0m x mx m− − + +=
có hai nghiệm dương phân biệt
là
A.
6m >
. B.
6m <
và
2m ≠
.
C.
26m<<
hoặc
3m <−
. D.
0m <
hoặc
26m<<
.
Câu 30. Cho hình chóp
SABC
có đáy
ABC
là tam giác vuông tại
,B SA
vuông góc với mặt phẳng
( ),ABC AH
là đường cao trong tam giác
SAB
Trong các khẳng định sau, khẳng định nào là
khẳng định sai?
A.
AH AC⊥
. B.
AH BC⊥
. C.
SA BC⊥
. D.
AH SC⊥
.
Câu 31. Tìm tập nghiệm của phương trình:
2
26
log 2 log 2 1
log 2 1
xx
x
+ +=
−
.

BVC Trang 4/6
A.
{
}
5
. B.
{ }
50
. C.
{ }
500
. D.
1000
2
e
.
Câu 32. Một mp
( )
P
vuông góc với trục của một khối trụ
T
, thiết diện
( )
P
với khối trụ
T
là:
A. Hình vuông. B. Hình tam giác. C. Hình chữ nhật. D. Hình tròn.
Câu 33. Tìm một nguyên hàm
( )
Fx
của hàm số
( )
sin 2
fx x=
nếu
( )
01
F =
.
A.
2
3
2
cos
2
1
+
−
x
. B.
2
1
2cos
2
1
+x
. C.
2
1
2cos
2
1
+− x
. D.
12cos +x
.
Câu 34. Cho hình chóp
.S ABC
có tam giác
ABC
vuông tại
A
, tam giác
SAC
vuông cân tại
S
. Biết
,2
AB a AC a
= =
,
( ) ( )
SAC ABC⊥
. Tính diện tích mặt cầu ngoại tiếp hình chóp
.S ABC
.
A.
2
2 a
π
. B.
2
4
a
π
. C.
2
5 a
π
. D.
2
3 a
π
.
Câu 35. Cho mặt phẳng
( )
:0Pxyz++=
. Hình chiếu vuông góc của
( )
0;1; 2A
lên mặt phẳng
( )
P
là
điểm:
A.
( )
1; 0;1M −
. B.
(
)
2;0; 2
N
−
. C.
( )
1;1; 0H −
. D.
( )
2; 2;0−
.
Câu 36. Cho hàm số
()y fx=
đồng biến trên khoảng
(;)
ab
Mệnh đề nào sau đây sai?
A. Hàm số
( 1)y fx
= +
đồng biến trên khoảng
(;)
ab
.
B. Hàm số
() 1y fx=−+
nghịch biến trên khoảng
(;)
ab
.
C. Hàm số
() 1y fx= +
đồng biến trên khoảng
(;)ab
.
D. Hàm số
() 1y fx=−−
nghịch biến trên khoảng
(;)ab
.
Câu 37. Cho số phức
( )( )
2 3 1–z ii= +
. Tính tổng phần thực và phần ảo của số phức
z
.
A. 6. B. 5. C. 4. D. - 4.
Câu 38. Cho hình phẳng (H) giới hạn bởi các đường
0 ;
2
sin ; ; y xy x x
π
π
= = ==
. Thể tích của vật
thể tròn xoay sinh ra khi quay hình (H) quanh trục
Ox
bằng:
A.
)(
2
2
đvtt
π
.
B.
)(
2
đvtt
π
.
C.
)(
4
đvtt
π
.
D.
)(
4
2
đvtt
π
.
Câu 39. Cho hai số thực x, y thay đổi thỏa mãn điều kiện
22
2xy+=
. Gọi M, m lần lượt là giá trị lớn
nhất và giá trị nhỏ nhất của biểu thức
( )
33
23P x y xy= +−
. Giá trị của của
Mm+
bằng
A.
4−
. B.
1
2
−
. C.
6−
. D.
142−
.
Câu 40. Một hộp đựng 11 tấm thẻ được đánh số từ 1 đến 11. Chọn ngẫu nhiên 4 tấm thẻ từ hộp đó. Gọi P
là xác suất để tổng các số ghi trên 4 tấm thẻ ấy là một số lẻ. Khi đó P bằng:
A.
1
12
. B.
16
33
. C.
10
33
. D.
2
11
.
Câu 41. Cho
( ) ( )
1; 3; 0 ; 3; 5; 4AB−− −
. Mặt cầu (S) nhận
AB
làm đường kính có phương trình là:
A.
2 22
2 8 4 12 0xyz xyz++−+−+=
. B.
2 22
2 8 – 4 15 0xyz xyz++−+ −=
.
C.
2 22
2 8 4 12 0xyz xyz+++−++=
. D.
2 22
2 8 – 4 15 0xyz xyz++++ +=
.
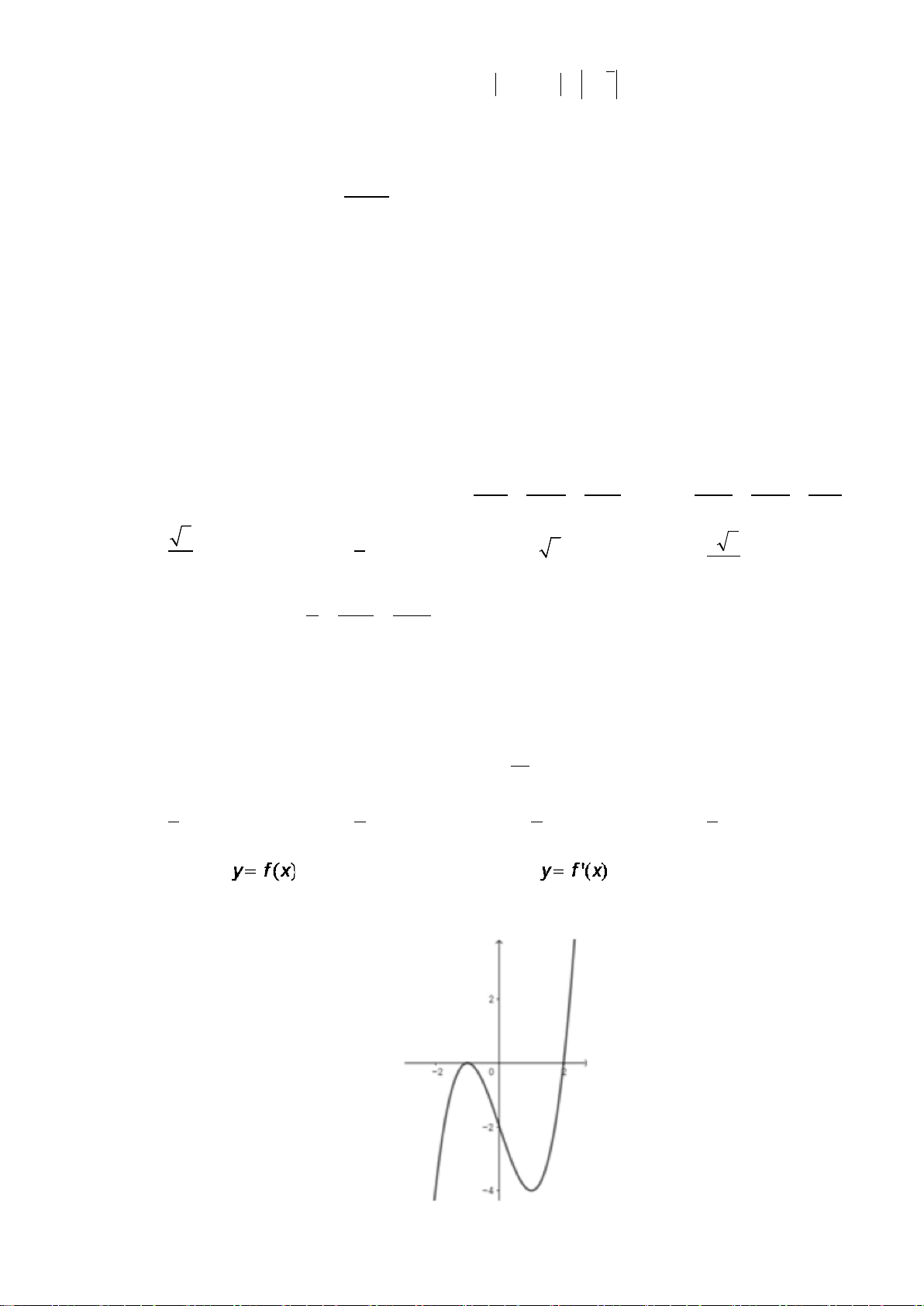
BVC Trang 5/6
Câu 42. Tập hợp các điểm biểu diễn số phức z thỏa mãn
13 1
ziz++ = −
là:
A. Đường thẳng
4 6 –9 0
xy+=
. B. Đường thẳng
4 6 90
xy+ +=
.
C. Đường thẳng
6 4 90xy+ +=
. D. Đường thẳng
6 4 –9 0xy−=
.
Câu 43. Biết rằng đồ thị hàm số
21x
y
x
+
=
và đồ thị hàm số
2
1yx x= ++
c ắt nhau tại hai điểm, ký hiệu
(
) (
)
11 2 2
;,,
xy x y
là tọa độ hai điểm đó. Tìm
12
.
yy+
A.
12
0yy+=
. B.
12
2.yy+=
. C.
12
6.yy+=
. D.
12
4
yy
+=
.
Câu 44. Một người muốn có 1 tỉ tiền tiết kiệm sau 6 năm gửi ngân hàng bằng cách bắt đầu từ ngày
01/01/2019 đến 31/12/2024, vào ngày 01/01 hàng năm người đó gửi vào ngân hàng một số tiền
bằng nhau với lãi suất ngân hàng là 7% /1 năm (tính từ ngày 01/01 đến ngày 31/12) và lãi suất
hàng năm được nhập vào vốn. Hỏi số tiền mà người đó phải gửi vào ngân hàng hàng năm là
bao nhiêu (với giả thiết lãi suất không thay đổi và số tiền được làm tròn đến đơn vị đồng)?
A. 130 650 280 (đồng). B. 30 650 000 (đồng).
C. 139 795 799 (đồng). D. 139 795 800 (đồng).
Câu 45. Tính khoảng cách giữa hai đường thẳng (d
1
):
123
213
xy z
−−+
= =
và (d
2
):
2 31
.
123
xyz− +−
= =
A.
3
.
3
B.
8
.
3
C.
83
.
D.
3
38
.
Câu 46. Cho đường thẳng (d):
1
2
1
1
2
−
−
=
−
=
zyx
và điểm
( )
1; 1; 2A −
. Tìm điểm H nằm trên (d) sao cho
độ dài
AH
ngắn nhất:
A.
( )
0;1;2H −−
. B.
(
)
0;1; 2
H
. C.
( )
0;1; 2H −
. D.
(
)
0; 1; 2
H
−
.
Câu 47. Cho hình chóp
SABC
có
A
′
,
B
′
lần lượt là trung điểm của
SA
,
SB
. Gọi
1
V
,
2
V
lần lượt là thể
tích của khối chóp
SABC
′′
và
SABC
. Tính tỉ số
1
2
V
V
.
A.
1
8
. B.
1
4
. C.
1
2
. D.
1
3
.
Câu 48. Cho hàm số có đạo hàm trên R và có đồ thị như hình vẽ.
Xét hàm số
(
)
(
)
2
2gx f x= −
.

BVC Trang 6/6
Mệnh đề nào sau đây sai?
A. Hàm số nghịch biến trên .
B. Hàm số đồng biến trên .
C. Hàm số nghịch biến trên .
D. Hàm số nghịch biến trên .
Câu 49. Tìm tất cả các giá trị thực của tham số m sao cho phương trình
2
4
3 1 12 1x mx x−+ += −
có
hai nghiệm thực phân biệt.
A.
31m
≤<
. B.
1
2
3
m−< ≤
. C.
1
1
4
m−≤ ≤
. D.
1
0
3
m≤<
.
Câu 50. Phương trình
42
83
xx m− +=
có bốn nghiệm phân biệt khi:
A.
13 3m−<<
. B.
3m ≤
. C.
13m >−
. D.
13 3
m−≤≤
.
BẢNG ĐÁP ÁN
1.B
2.C
3.D
4.D
5.B
6.A
7.B
8.C
9.B
10.D
11.C
12.D
13.D
14.C
15.B
16.B
17.C
18.D
19.C
20.C
21.A
22.C
23.A
24.C
25.A
26.A
27.D
28.C
29.C
30.A
31.C
32.D
33.A
34.C
35.A
36.A
37.C
38.D
39.B
40.B
41.A
42.B
43.D
44.A
45.D
46.B
47.B
48.D
49.D
50.A
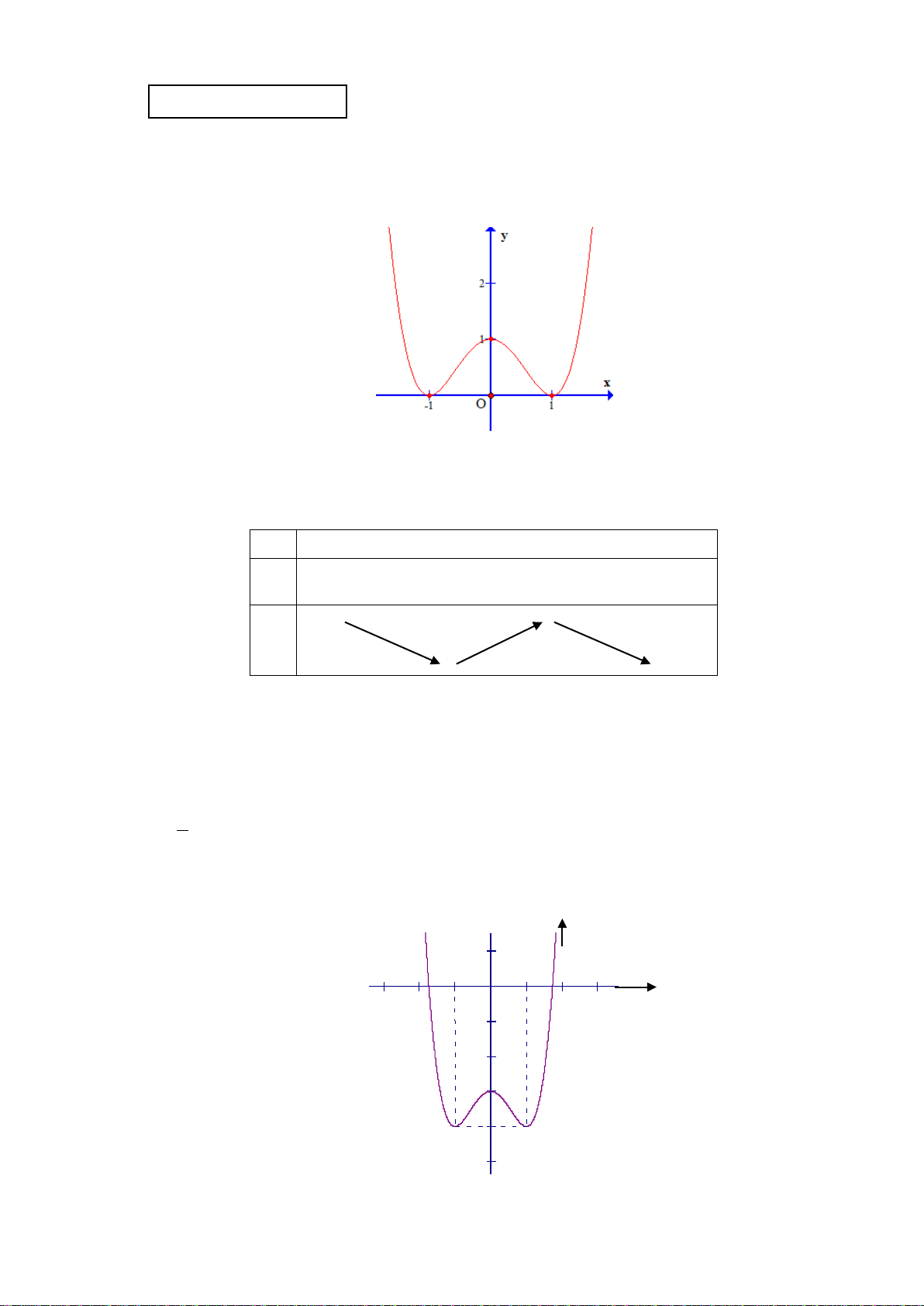
Trang 1/7
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
KỲ THI THPT QUỐC GIA NĂM 2019
TRƯỜNG THPT HUỲNH THÚC KHÁNG
Bài thi: Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề
(Đề thi có 07 trang)
Câu 1: Cho hàm số
(
)
y fx=
liên tục trên R và có đồ thị như hình vẽ bên. Trong các khẳng định
sau khẳng định nào là đúng?
A.
( )
fx
nghịch biến trên
( )
1; +∞
.
B.
( )
fx
đồng biến trên
( )
;1−∞ −
C.
( )
fx
nghịch biến trên
( )
1; 0−
.
D.
(
)
fx
nghịch biến trên
(
)
0;1
Câu 2: Cho hàm số
( )
y fx=
liên tục trên R và có bảng biến thiên như hình vẽ .
x
−∞
-1 3
+∞
y
’
- 0 + 0 -
y
+∞
6
0
−∞
Hàm số đạt cực tiểu tại điểm nào sau đây?.
A. x= -1. B. x=3. C. x= 0. D. x= 6.
Câu 3: Hàm số nào có đồ thị dưới đây ?
A.
42
3 3.
yx x=−−
B.
42
1
3 3.
4
y xx=− +−
C.
42
2 3.
yx x=−−
D.
42
2 3.yx x=+−
-2
-4
O
-3
-1
1
x
y
ĐỀ THI ĐỀ XUẤT
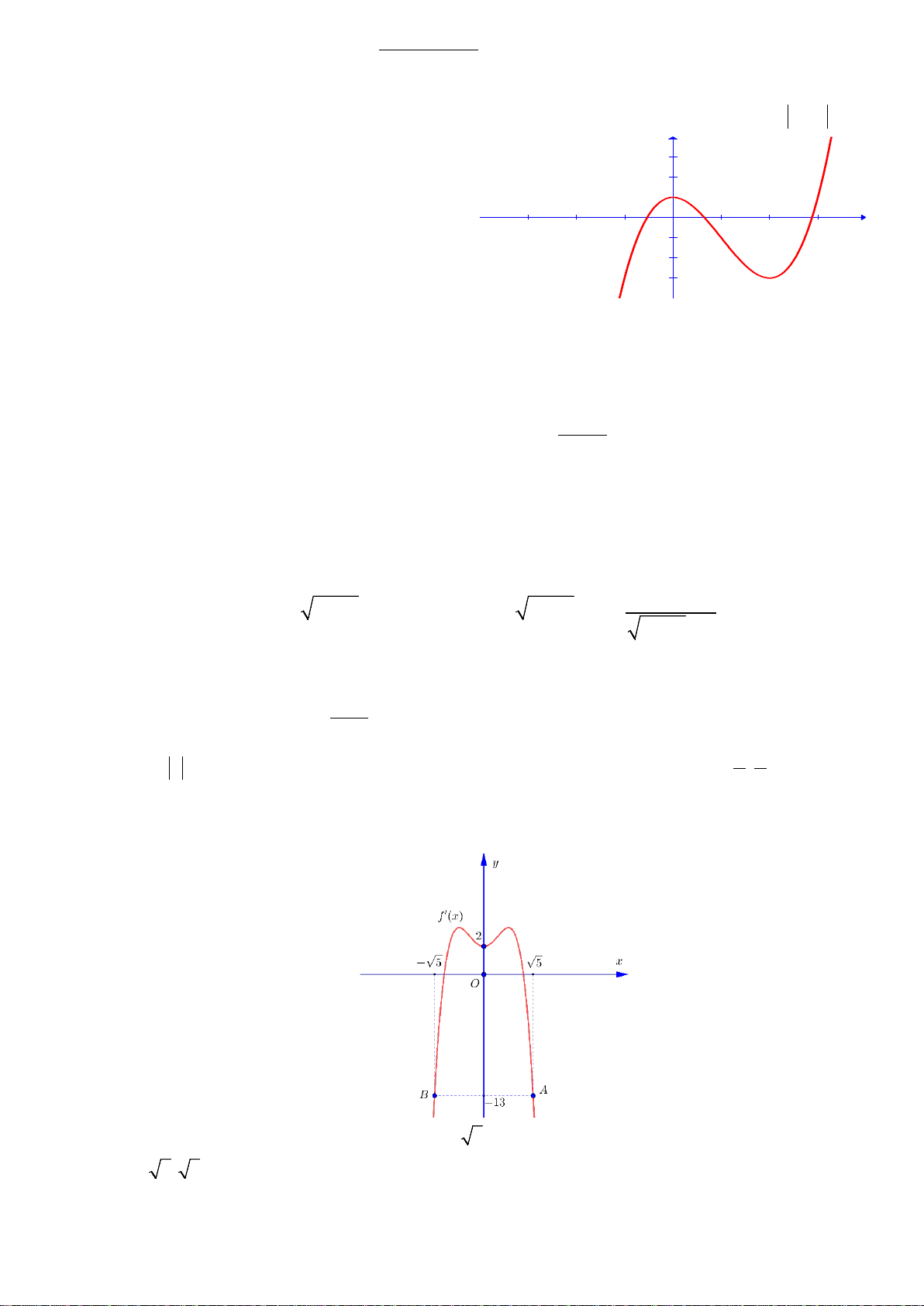
Trang 2/7
Câu 4: Gọi (C) là đồ thị hàm số
2
2
2
5 23
xx
y
xx
++
=
− −+
Số đường tiệm cận của đồ thị hàm số là
A. 1. B. 2. C. 3. D. 4.
Câu 5: Cho hàm số
()
y fx=
có đồ thị như hình vẽ .Khi đó trên đoạn
[ ]
0;3
hàm số
()y fx=
đạt
giá trị nhỏ nhất và giá trị lớn nhất lần lượt là
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
A.
0 3. vа
B.
-3 3. vа
C.
0 1.vа
D.
-3 1.vа
Câu 6: Tìm tất cả các giá trị thực của tham số
m
để hàm số
32
3 3(2 1) 1y x mx m x
=− + −+
có hai
điểm cực trị.
A.
1.
m ≠
B.
1.
m >
C.
1.m <
D.
1.m =
Câu 7: Tìm tất cả các giá trị của tham số để hàm số
xm
y
x1
+
=
+
đồng biến trên từng khoảng xác
định.
A. m < 1. B . m > 1. C. m < -1. D.
1.m ≠
Câu 8: Tìm tất cả các giá trị thực của tham số m để phương trình
03
24
=+−
mxx
có ba nghiệm
thực phân biệt .
A. m = -3. B. m = - 4. C. m = 0 . D. m = 4.
Câu 9: Cho hàm số
(
)
(
)
3
2 22
2
6m
y x 1 x m 2x 2x x 1 1 1.
x 1x
−
= +− − − ++ + −
++
Có tất cả bao
nhiêu giá trị nguyên dương của tham số m để hàm số nghịch biến trên R?
A. 2. B. 3. C. 5. D. vô số.
Câu 10: Cho hàm số
( )
1
2
x
fx
x
+
=
−
. Có tất cả bao nhiêu giá trị nguyên của
m
để đồ thị hàm số
(
)
(
)
gx f x m= +
cắt trục hoành tại
2
điểm phân biệt có hoành độ thuộc đoạn
33
;
22
−
?
A.
0
.
B.
2
.
C.
4
.
D.
6
.
Câu 11: Cho hàm số
( )
=
y fx
có đồ thị
( )
′
=y fx
như hình vẽ:
Xét hàm số
( ) ( )
3
2 2 4 3 65= + −− −gx f x x x m
( )
∈m
. Điều kiện cần và đủ để
( )
0≤gx
với
5; 5
∀∈−
x
là
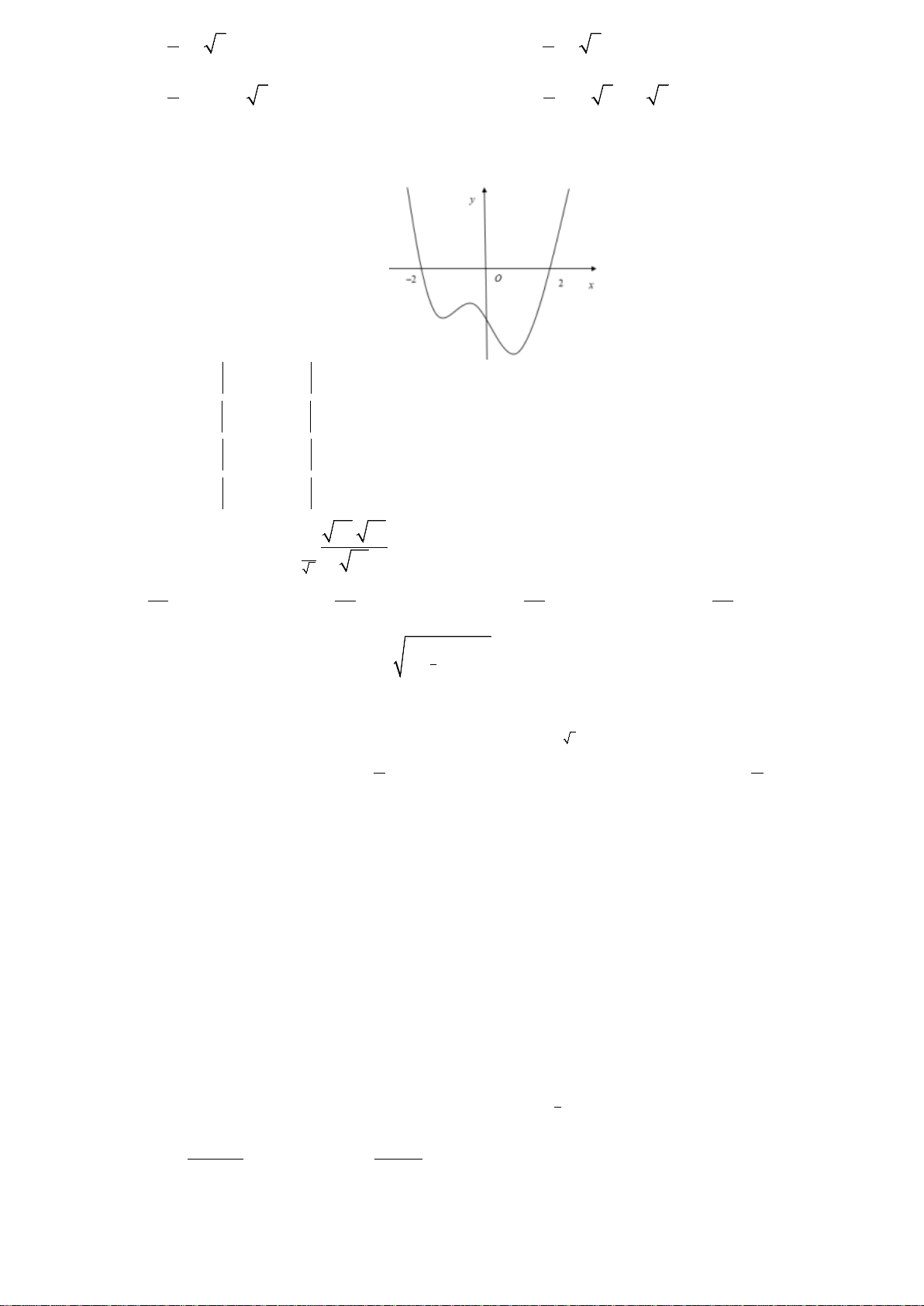
Trang 3/7
A.
( )
2
5
3
≥mf
.
B.
( )
2
5
3
≤mf
.
C.
( )
2
0 25
3
≤−mf
.
D.
( )
2
5 45
3
≥ −−mf
.
Câu 12: Cho hàm số
( )
y fx=
xác định, liên tục trên
và có
( )
20
f −<
và đồ thị hàm số
( )
fx
′
như hình vẽ bên.Khẳng định nào sau đây là khẳng định sai ?
A. Hàm số
( )
2018
1yf x= −
nghịch biến trên khoảng
( )
;2−∞ −
.
B. Hàm số
( )
2018
1yf x= −
có hai cực tiểu.
C. Hàm số
( )
2018
1yf x= −
có hai cực đại và một cực tiểu.
D. Hàm số
( )
2018
1yf x= −
đồng biến trên khoảng
(
)
2; +∞
.
Câu 13: Giá trị của
(
)
3
3
25
4
1
5
3
a
a.a
P log , a 0,a 1
a
= >≠
là
A.
53
20
−
.
B.
79
20
−
.
C.
62
15
−
. D.
34
15
−
.
Câu 14: Tập xác định của hàm số
( )
1
2
log 2yx= −
là
A.
(
]
2;3 .
B.
[
)
3; .+∞
C.
( )
;2 .−∞
D.
( )
2;3 .
Câu 15: Tập nghiệm của bất phương trình
( ) ( )
3
3
2log 1 log 2 1 2xx−+ −≤
là
A.
(
]
1; 2 .S =
B.
1
;2 .
2
S
= −
C.
[ ]
1; 2 .S =
D.
1
;2 .
2
S
= −
Câu 16: Số nghiệm của phương trình
9 5.3 7 0
xx
− −=
là
A. 0. B. 1.
C. 2. D. Vô nghiệm.
Câu 17: Một người lần đầu gửi vào ngân hàng 100 triệu đồng với kì hạn 3 tháng, lãi suất 2% một
quý theo hình thức lãi kép. Sau 6 tháng, người đó gửi thêm 100 triệu đồng với kỳ hạn và lãi suất
như trước đó.Tổng số tiền người đó nhận được sau 1 năm sau khi gửi thêm tiền, gần nhất với kết
quả nào sau đây?
A. 220.859 triệu. B. 212.283 triệu. C. 216.486 triệu. D. 208.08 triệu.
Câu 18: Tìm tất cả các giá trị thực của tham số m để bất phương trình
( ) ( )
22
55
1 log 1 log 4x mx x m+ +≥ + +
có tập nghiệm là R
A.
(
]
2;3 .m ∈
B.
(
]
2;3 .m ∈−
C.
[
)
2;3 .m ∈
D.
[
)
2;3 .m ∈−
Câu 19: Biết
()Fx
là một nguyên hàm của hàm số
1
3
()
x
fx e
+
=
và
( )
02Fe
=
. Tính
( )
3F
.
A.
( )
2
17
3
9
ee
F
+
=
. B.
( )
2
5
3
3
ee
F
+
=
. C.
( )
2
3F ee= +
. D.
( )
2
33F ee= −
.

Trang 4/7
Câu 20: Cho các tích phân
24
02
() 3, () 5
f x dx f x dx= =
∫∫
.Tính
2
0
(2 ) .I f x dx=
∫
A.
= 2I
. B.
= 3I
.
C.
=
4I
.
D.
= 8I
.
Câu 21: Cho hàm số
()fx
liên tục trên
[
)
1;− +∞
và
8
0
( 1) 10+=
∫
f x dx
. Tính
3
1
.()=
∫
I xf xdx
.
A.
5I
. B.
10I
. C.
20I
. D.
40I
.
Câu 22: Cho hình phẳng D giới hạn bởi đồ thị
2
2yx x= −
và trục Ox. Thể tích khối tròn xoay khi
quay hình phẳng D quanh trục Ox bằng
A.
32
5
π
. B.
16
5
π
. C.
32
15
π
. D.
16
.
15
π
Câu 23: Tính tích phân
π
π
π
−
+
= =
−
∫
cos x
c
I dx
x x ab
2
4
2
4
1
ln
2sin cos 3
.Khi đó
++abc
bằng
A. 8. B. 7. C. 6. D. 5.
Câu 24: Một người chạy trong thời gian 1 giờ, vận tốc v [km/h] phụ thuộc thời gian t [h] có đồ thị
là một phần của đường parabol với đỉnh
1
;8
2
I
và trục đối xứng song song với trục tung như
hình bên. Tính quãng đường s người đó chạy được trong khoảng thời gian 45 phút, kể từ khi bắt
đầu chạy.
A.
4,0 (km).s =
B.
2,3 (km).s
=
C.
4,5 (km)s =
.
D.
5,3 (km)s =
.
Câu 25: Tìm phần ảo của số phức
z
thỏa mãn
23zz i+=+
.
A.
3−
. B.
1−
. C.
1
3
. D.
1
.
Câu 26: Phương trình
2
50zz
++=
có hai nghiệm
12
;
zz
trên tập hợp số phức. Tính giá trị của
biểu thức
22
12
Pz z= +
A.
10P
=
. B.
9P = −
. C.
37
2
P = −
. D.
11P =
.
Câu 27: . Tập hợp tất cả các điểm biểu diễn các số phức
z
thỏa mãn:
24zi
+−=
là đường tròn có
tâm
I
và bán kính
R
lần lượt là:
A.
( )
2; 1I
−−
;
4R =
. B.
( )
2; 1I −−
;
2R =
. C.
( )
2; 1I −
;
4R =
. D.
( )
2; 1I −
;
1R =
.
Câu 28: Cho số phức
z
thỏa mãn
11zi−− =
, số phức
w
thỏa mãn
23 2wi−− =
. Tìm giá trị nhỏ
nhất của
zw−
.
A.
13 3−
B.
17 3−
C.
17 3+
D.
13 3+
Câu 29: Cho hình lăng trụ đứng
.ABC A B C
′′′
có đáy
ABC
là tam giác vuông cân tại
A
,
AB a=
và
3AA a
′
=
. Thể tích khối lăng trụ
.ABC A B C
′′′
bằng
A.
3
33
2
a
. B.
3
33
a
. C.
3
3
2
a
. D.
3
3
6
a
.
Câu 30: Cho
( )
H
là khối chóp tứ giác đều có tất cả các cạnh bằng
2
a
. Thể tích của
( )
H
bằng
A.
3
4
5
a
. B.
3
43
3
a
. C.
3
42
3
a
. D.
3
4
3
a
.
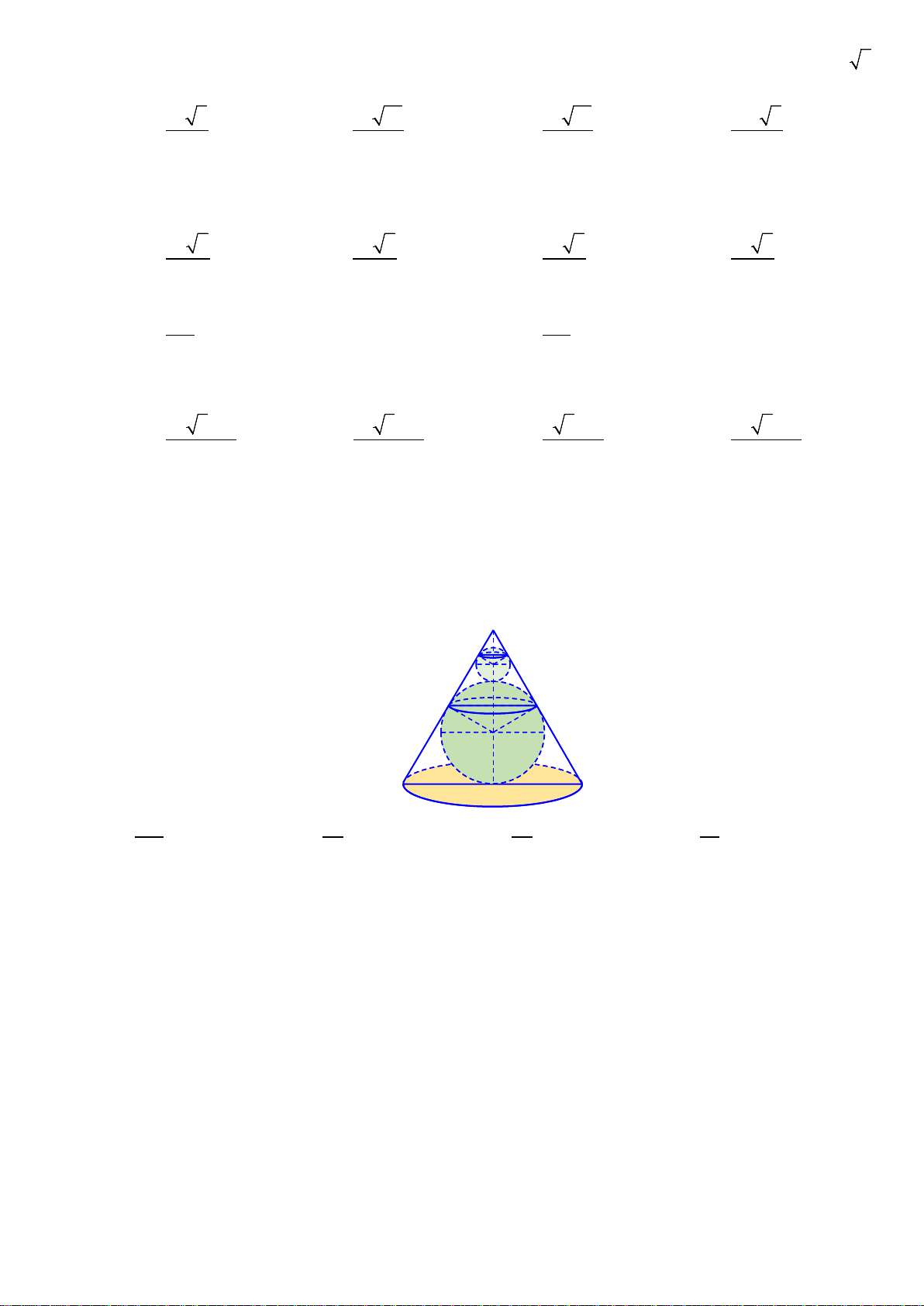
Trang 5/7
Câu 31: Cho hình chóp
.S ABCD
có đáy là hình thang vuông tại
A
và
B
,
AB BC a= =
,
2
AD a
=
.
Hình chiếu của
S
lên mặt phẳng
( )
ABCD
trùng với trung điểm cạnh
AB
. Biết rằng
5SC a=
.
Tính theo
a
thể tích
V
của khối chóp
.S ABCD
.
A.
3
5
4
a
V =
B.
3
15
3
a
V =
. C.
3
15
4
a
V =
. D.
3
25
3
a
V =
.
Câu 32: Cho hình chóp tứ giác đều
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, cạnh bên tạo
với đáy một góc
60°
. Gọi
M
là trung điểm của
SC
. Mặt phẳng đi qua
AM
và song song với
BD
cắt
SB
tại
E
và cắt
SD
tại
F
. Tính thể tích
V
khối chóp
.S AEMF
.
A.
3
6
36
a
V
=
. B.
3
6
9
a
V =
. C.
3
6
6
a
V =
. D.
3
6
18
a
V
=
.
Câu 33:
Hình nón có bán kính đáy
8 cmr =
, đường sinh
10 cml =
. Thể tích khối nón là
A.
( )
3
192
cm
3
V
π
=
. B.
( )
3
128 cmV
π
=
. C.
( )
3
128
cm
3
V
π
=
. D.
( )
3
192 cm
V
π
=
.
Câu 34: Cho hình lăng trụ tam giác đều
.ABC A B C
′′′
có độ dài cạnh đáy bằng
a
và chiều cao bằng
2a
. Tính thể tích
V
của khối cầu ngoại tiếp hình lăng trụ
..ABC A B C
′′′
A.
3
32 3
27
a
V
π
=
. B.
3
32 3
9
a
V
π
=
. C.
3
83
27
a
V
π
=
. D.
3
32 3
81
a
V
π
=
.
Câu 35: Người ta chế tạo ra một món đồ chơi cho trẻ em theo các công đoạn như sau: Trước tiên,
chế tạo tra một mặt nón tròn xoay có góc ở đỉnh là
2 60
β
= °
bằng thủy tinh trong suốt. Sau đó đặt
hai quả cầu nhỏ bằng thủy tinh có bán kính lớn, nhỏ khác nhau sao cho 2 mặt cầu tiếp xúc với
nhau và đều tiếp xúc với mặt nón. Quả cầu lớn tiếp xúc với cả mặt đáy của mặt nón. Cho biết
chiều cao của mặt nón bằng
9cm.
Bỏ qua bề dày của những lớp vỏ thủy tinh, hãy tính tổng thể
tích của hai khối cầu.
A.
( )
3
112
.
3
cm
π
B.
( )
3
40
.
3
cm
π
C.
( )
3
25
.
3
cm
π
D.
( )
3
10
.
3
cm
π
Câu 36: Trong không gian
Oxyz
cho ba vectơ
(
) (
) ( )
1; 1; 2 , 3; 0; 1 , 2; 5;1abc=− = −=−
, vectơ
mabc=+−
có tọa độ là
A.
( )
6;0; 6−
. B.
( )
6;6;0−
.
C.
( )
6; 6;0−
. D.
( )
0;6; 6−
.
Câu 37: Trong không gian
Oxyz
, mặt cầu
( ) ( ) ( )
22
2
:1 2 9Sx y z− ++ +=
có tâm là
A.
( )
1; 2; 0 .I −
B.
( )
1; 2; 0 .I −
C.
(
)
1; 2; 0 .I
D.
( )
1; 2; 0 .I −−
Câu 38: Trong không gian
Oxyz
Trong không gian với hệ toạ độ
Oxyz
, cho ba điểm
( )
1; 2;1A −
,
( )
1;3;3B −
,
( )
2; 4;2C −
. Một vectơ pháp tuyến
n
của mặt phẳng
( )
ABC
là
A.
( )
9;4; 1n = −
. B.
( )
9;4;1n
=
.
C.
( )
4;9; 1n = −
. D.
( )
1; 9; 4n = −
.
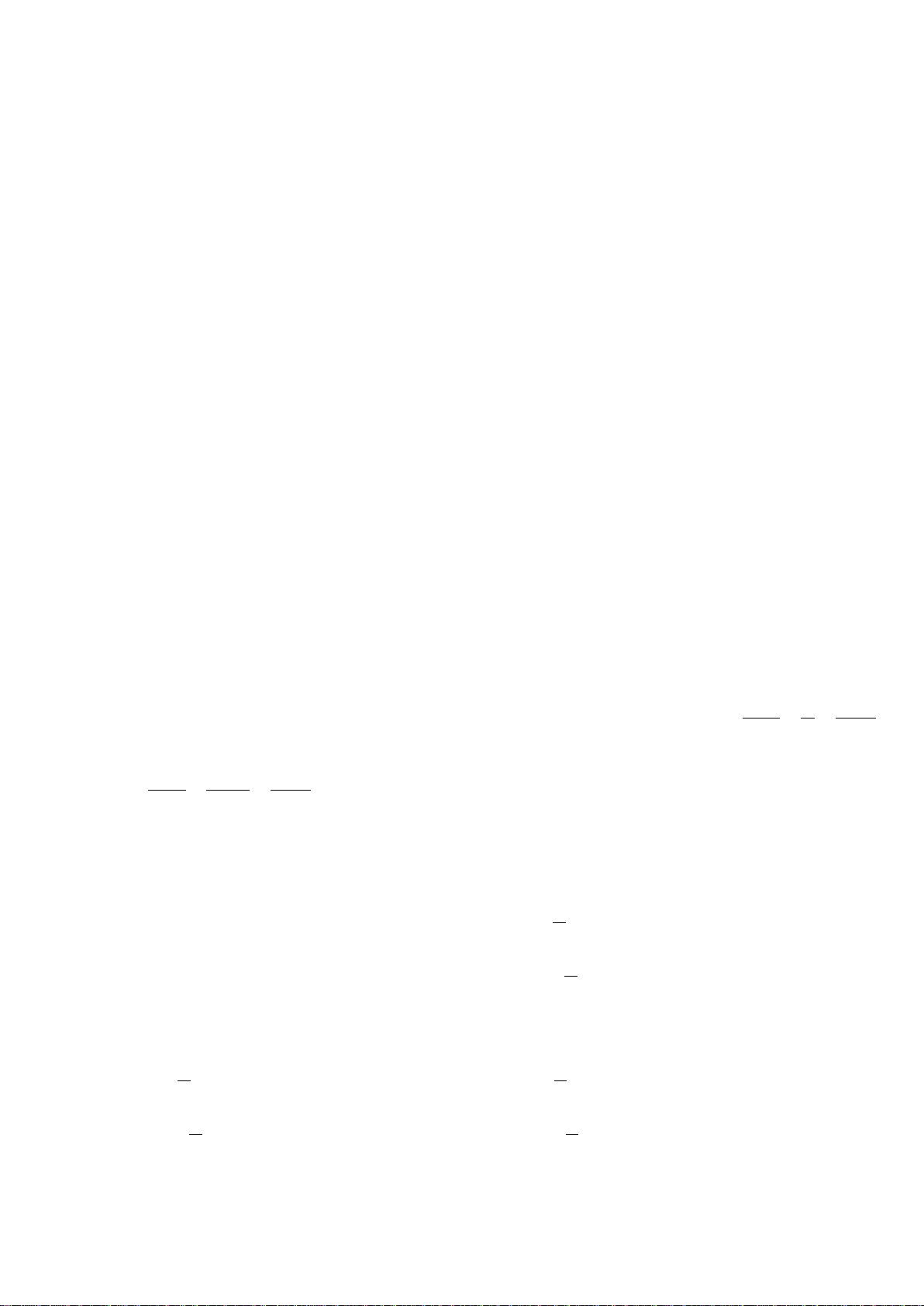
Trang 6/7
Câu 39: Cho hai điểm
(
)
1; 0; 3
A
−
và
( )
3; 2;1
B
. Phương trình mặt cầu đường kính AB là
A.
2 22
4 2 2 0.x yz x y z
++−− + =
B.
2 22
4 2 2 0.xyz xyz
+++− + =
C.
2 22
2 6 0.x y z xyz
+ + − −+−=
D.
2 22
4 2 2 6 0.xyz x yz
+ + − − + +=
Câu 40: Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng
( )
α
đi qua
(
)
2; 1; 4
A −
,
( )
3; 2; 1
B −
và vuông góc với mặt phẳng
( )
: 2 30Qxy z++ −=
. Phương trình mặt phẳng
(
)
α
là
A.
5 3 4 90xyz+ − +=
. B.
3 5 21 0xyz+−+=
.
C.
2 30xy z++ −=
. D.
5340
xyz+−=
.
Câu 41: Trong không gian với hệ tọa độ
12
, dd
cho tam giác
ABC
có
( ) ( ) ( )
2;1; 2 , 4; 1;1 , 0; 3;1ABC−− −
. Phương trình
d
đi qua trọng tâm của tam giác
ABC
và vuông
góc với mặt phẳng
d
là
A.
2
1 2.
2
xt
yt
zt
= +
=−−
= −
B.
2
1 2.
2
xt
yt
zt
=−+
=−−
= −
C.
2
1 2.
2
xt
yt
zt
= +
= −
= −
D.
2
1 2.
2
xt
yt
zt
= +
= +
=
Câu 42: Trong không gian với hệ trục tọa độ
Oxyz
, cho điểm
(1; 2;3).M
Gọi
()
α
là mặt phẳng
chứa trục
Oy
và cách
M
một khoảng lớn nhất. Phương trình của
()
α
là
A.
30xz+=
. B.
20xz
+=
.
C.
30
xz−=
. D.
0x =
.
Câu 43: Trong không gian với hệ tọa độ
2
32
12
xt
yt
zt
= +
=−−
=−+
cho hai đường thẳng
1
12
:
21 1
x yz
d
−+
= =
−
và
2
122
:
13 2
xy z
d
−+−
= =
−
. Gọi
∆
là đường thẳng song song với
( )
: 70Pxyz++−=
và cắt
12
, dd
lần lượt tại hai điểm
,AB
sao cho
AB
ngắn nhất. Phương trình của đường thẳng
∆
là
A.
12
5.
9
xt
y
zt
= −
=
=−+
B.
6
5
.
2
9
2
xt
y
zt
= −
=
=−+
C.
6
5
.
2
9
2
x
yt
zt
=
= −
=−+
D.
62
5
.
2
9
2
xt
yt
zt
= −
= +
=−+
Câu 44: Từ các chữ số 1, 2, 3, 4, 5 có thể lập được số các số có 3 chữ số đôi một khác nhau là
A. 60 B. 30 C. 125 D. 25
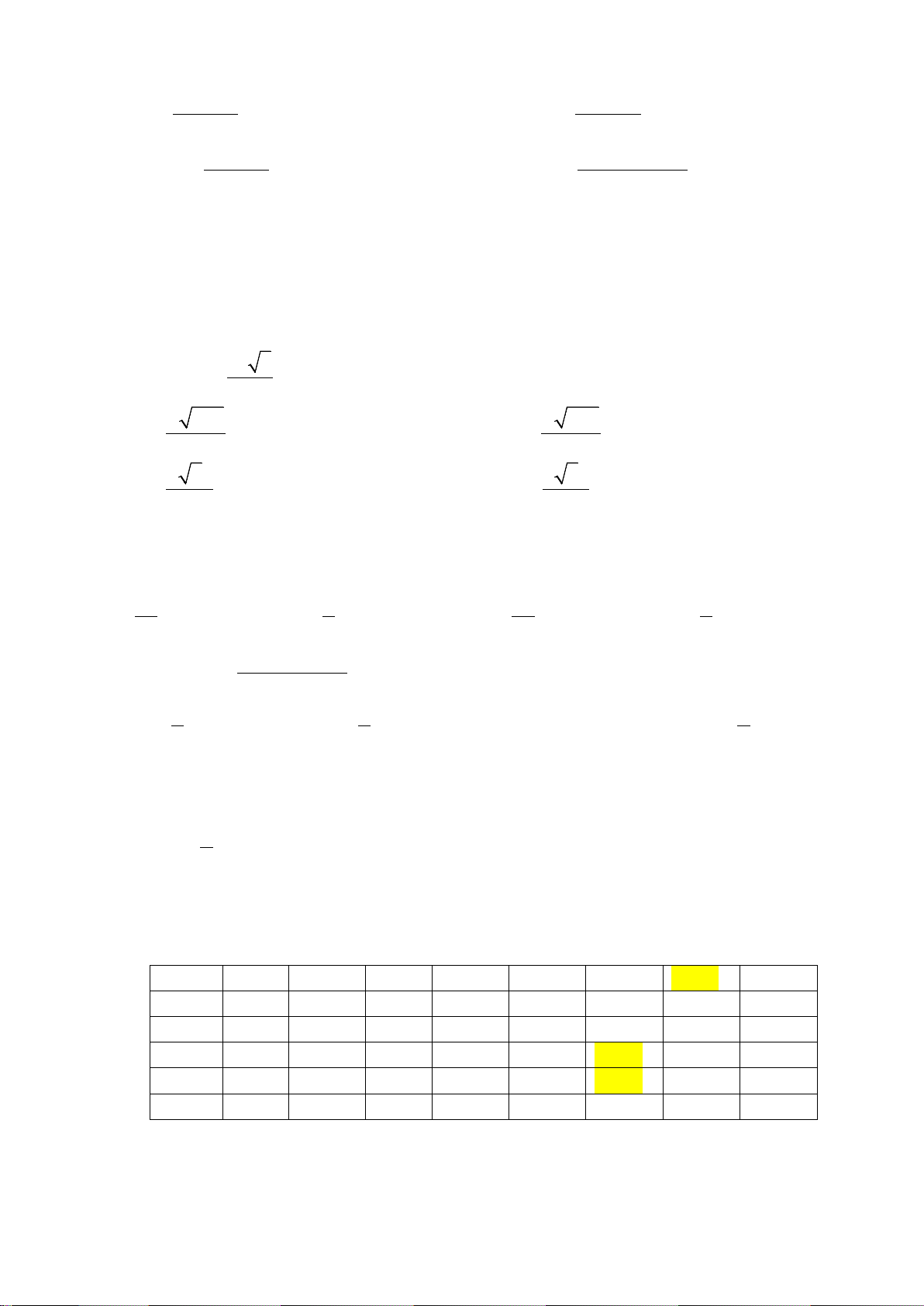
Trang 7/7
Câu 45: Cho dãy số
1
1
5
nn
u un
+
=
= +
u
. Số hạng tổng quát của dãy số trên là
A.
( )
1
2
n
nn
u
−
=
. B.
(
)
1
5
2
n
nn
u
−
= +
.
C.
( )
1
5
2
n
nn
u
+
= +
. D.
( )( )
12
5
2
n
nn
u
++
= +
.
Câu 46: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt
phẳng
( )
ABCD
,
2SA a
=
. Gọi F là trung điểm SC, tính góc
ϕ
giữa hai đường thẳng BF và AC.
A.
0
60
ϕ
=
. B.
0
90
ϕ
=
. C.
0
30
ϕ
=
. D.
0
45
ϕ
=
.
Câu 47: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh a, góc
0
120
BAD
=
. Các
mặt phẳng
( )
SAB
và
( )
SAD
cùng vuông góc với mặt đáy. Gọi M là trung điểm SD, thể tích khối
chóp S.ABCD là
3
3
3
a
. Hãy tính khoảng cách h từ M tới mặt phẳng
( )
SBC
theo
A.
228
38
a
h
=
. B.
228
19
a
h =
.
C.
25
5
a
h
=
. D.
25
19
a
h =
.
Câu 48: Có hai hộp cùng chứa các quả cầu. Hộp thứ nhất có 7 quả cầu đỏ, 5 quả cầu xanh. Hộp
thứ hai có 6 quả cầu đỏ, 4 quả cầu xanh. Từ mỗi hộp lấy ra ngẫu nhiên 1 quả cầu. xác suất để 2
quả cầu lấy ra cùng màu là
A.
31
60
. B.
1
6
. C.
27
50
. D.
1
3
.
Câu 49: Tính
sin 3cos
cos 2sin
aa
F
aa
−
=
+
biết
tan 3a = −
.
A.
6
5
=F
. B.
1
6
=
F
. C.
3
= −F
. D. F=
2
3
−
.
Câu 50: Tìm tất cả giá trị thực của tham số
m
để bất phương trình
(
) ( )
2
12 10
mx m x x+ +− −>
nghiệm đúng với mọi
[ ]
2;1x ∈−
.
A.
3
0
2
m<<
. B.
0m >
. C.
3m <
. D.
2m <−
.
--------------HẾT--------------
ĐÁP ÁN
1. D
7. A
13. B
19. D
25. B
31. C
37.A
43. B
49. A
2. A
8. C
14. A
20. C
26. B
32. D
38. A
44. A
50. A
3. C
9. B
15. A
21. A
27. A
33. B
39. A
45. B
4. C
10. C
16. B
22. D
28. B
34. A
40. A
46. B
5. A
11. A
17. A
23. A
29. C
35. A
41. A
47. A
6. A
12. C
18. A
24. C
30. C
36. C
42. A
48. A
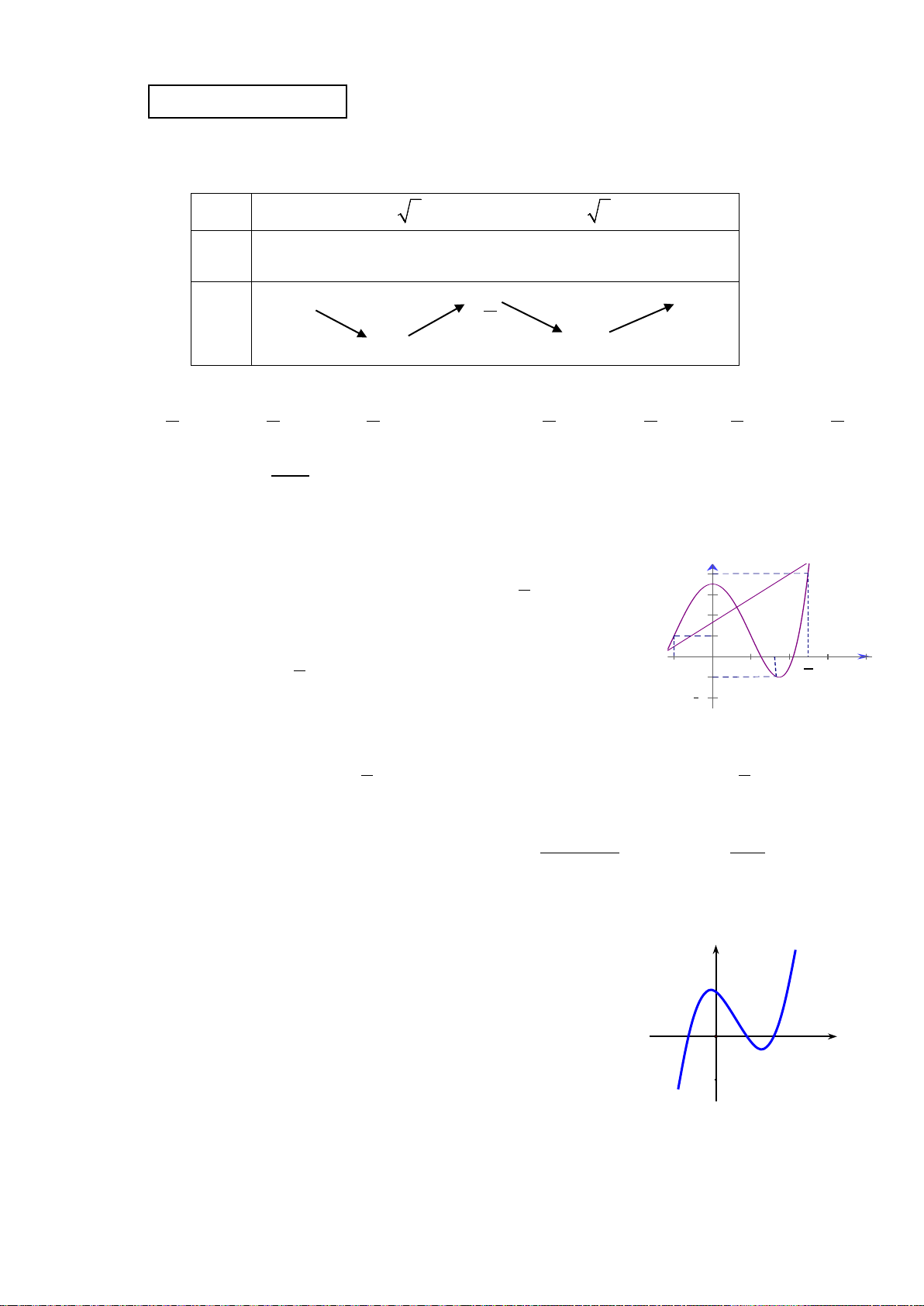
Trang 1/6
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
KỲ THI THPT QUỐC GIA NĂM 2019
TRƯỜNG THPT TRẦN CAO VÂN
Bài thi: Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề
(Đề thi có 06 trang)
Câu 1: Bảng biến thiên sau đây là của hàm số nào.
x
−∞
−
3
0
3
+∞
'y
−
0
+
0
−
0
+
y
+∞
5
2
+∞
−2
−2
A.
= −+
42
13
3
42
yxx
B.
=−+
42
1
2
4
y xx
C.
= −+
42
15
2
22
yxx
D.
= −+
42
15
3
22
yxx
Câu 2: Cho hàm số
2
3
x
y
x
−
=
+
A. Hs đồng biến trên
( ; 3)
−∞ −
và
( 3; )
− +∞
B. Hs đồng biến trên khoảng
(
)
;
−∞ ∞
C. Hs nghịch biến trên
( ; 3)
−∞ −
và
( 3; )− +∞
D. Hs nghịch biến trên khoảng
(
)
;−∞ ∞
Câu 3: Cho hàm số
( )
xfy =
xác định, liên tục trên
−
2
3
;
1
và có đồ thị
là đường cong như hình vẽ. Giá trị lớn nhất
M
và giá trị nhỏ nhất
m
của hàm số
(
)
xf
trên
−
2
3
;1
là:
4
2
2
-1
y
1
4
3
2
-1
O
x
A.
1,4 == mM
. B.
1
,
2
7
−
==
mM
. C.
1
,4 −== mM
. D.
1
,
2
7
−==
mM
.
Câu 4: Hàm số nào sau đây đồng biến trên
A.
32
31
yx x x=−+−
B.
3
33
yx x=−+
C.
2
28
1
xx
y
x
+−
=
−
D.
1
x
y
x
=
+
Câu 5: Đồ thị hình bên là của hàm số nào?
A.
42
22
yx x=−+ +
. B.
42
22yx x=−+
. C.
42
42yx x=−+
. D.
42
23yx x=−+
.
Câu 6: Cho hàm số
( )
y fx=
xác định và có đạo hàm
( )
fx
′
. Đồ thị
của hàm số
( )
fx
′
như hình dưới đây. Khẳng định nào sau đây là
đúng?
A. Hàm số
( )
y fx=
đồng biến trên khoảng
( )
;2−∞
.
B. Hàm số
( )
y fx=
đồng biến trên khoảng
( )
;1−∞ −
.
C. Hàm số
( )
y fx=
có ba điểm cực trị.
O
x
y
1−
1
2
2
2−
ĐỀ THI ĐỀ XUẤT
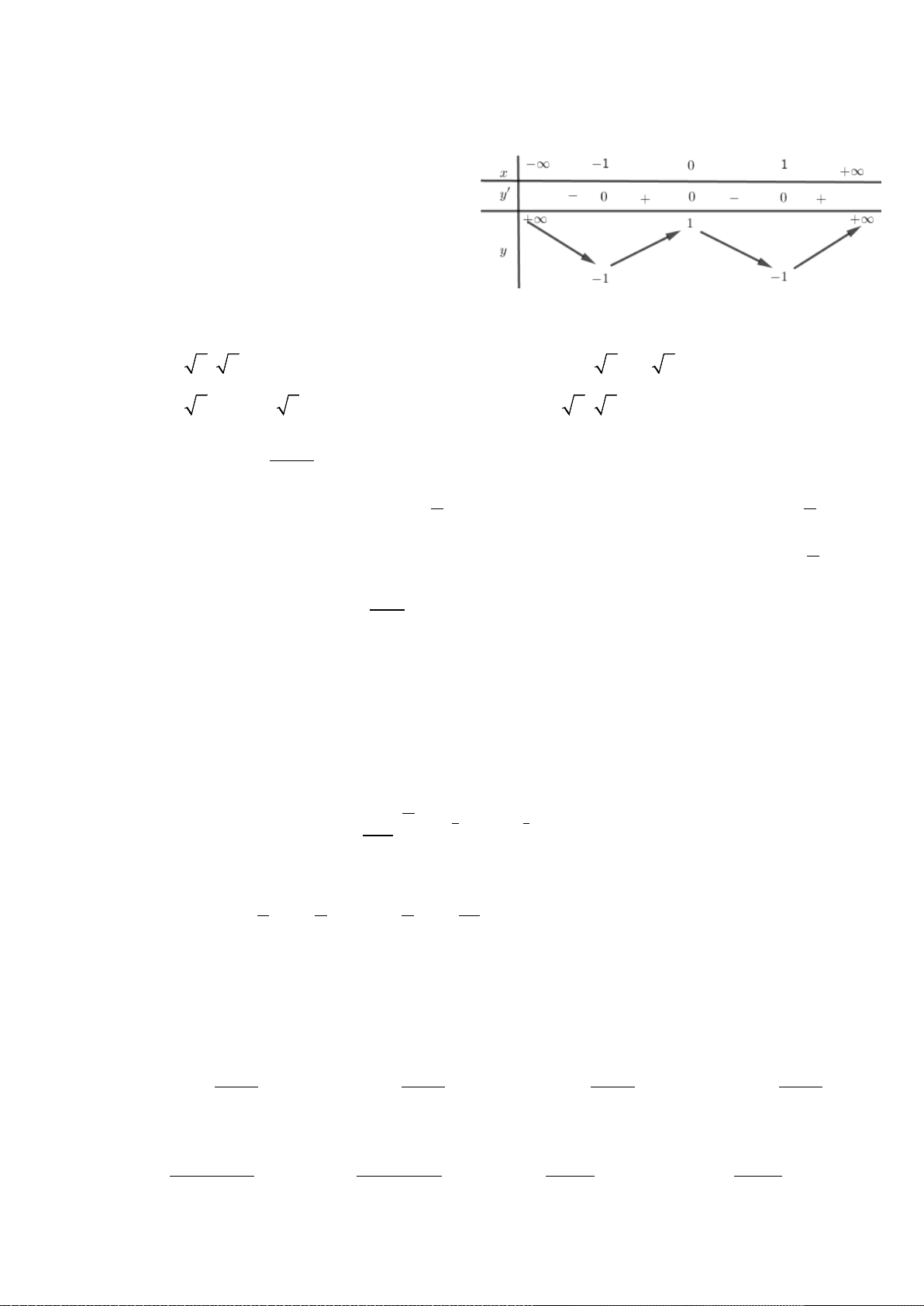
Trang 2/6
D. Hàm số
(
)
y fx=
nghịch biến trên khoảng
( )
0;1
.
Câu 7: Tìm tất cả các giá trị của tham số m sao cho hàm số
32
33 1y x x mx=++ −
đồng biến trên
.
Chọn kết quả đúng:
A.
1
m ≥
B.
1m >
C.
1m <
D.
1m ≤
Câu 8: Cho hàm số
(
)
y fx
=
có tập xác định
là
và có bảng biến thiên như hình vẽ. Tìm
tất cả các giá trị của m để phương trình
( )
2
10fx m+ −=
có nhiều nghiệm nhất.
A.
( )
2; 2m ∈−
B.
( ) ( )
; 2 2;m ∈ −∞ − ∪ + ∞
C.
( )
( )
2; 0 0; 2m ∈− ∪
D.
2; 2m
∈−
Câu 9: Cho hàm số
31
21
x
y
x
+
=
−
. Khẳng định nào sau đây đúng?
A. Đồ thị hàm số có tiệm cận ngang là
3
2
y =
B. Đồ thị hàm số có tiệm cận đứng là
3
2
x =
C. Đồ thị hàm số có tiệm cận đứng là x= 1 D. Đồ thị hàm số có tiệm cận ngang là
1
2
y =
Câu 10: Tìm m để đồ thị hàm số
1
x
y
x
=
−
cắt đường thẳng
y xm=−+
tại 2 điểm phân biệt.
A.
4
0
m
m
>
<
. B.
04m<<
. C.
m∀∈
.
D.
4
0
m
m
≥
≤
.
Câu 11: Cho hàm số
32
32yx x x=−+
với đồ thị
( )
C
. Đường thẳng nào sau đây là tiếp tuyến của
( )
C
tại
(
)
10M;
?
A.
y x.= −
B.
2y x.
=
C.
1y x.=−+
D.
22y x.= −
Câu 12: Tính giá trị biểu thức
1
1
3
4
2
3
4
1
16 2 .64 .
625
A
−
−
= +−
A. 14 B. 12 C. 11 D. 10
Câu 13: Tính
12 8 9
log log ... log log .
2 3 9 10
P = + ++ +
A.
2.P =
B.
0.P =
C.
1.P =
D.
1.P = −
Câu 14: Hàm số
2
2
log ( 5 6)y xx= −+ −
có tập xác định là:
A.
( )
2;3
B.
( )
;2−∞
C.
( )
3; +∞
D.
( ) ( )
; 2 3;−∞ ∪ +∞
Câu 15: Biết
23
log 3; log 7ab
= =
. Tính
24
log 14
theo a,b
A.
24
1
log 14
3
ab
a
+
=
+
. B.
24
1
log 14
3
ab
a
−
=
+
. C.
24
3
log 14
1
a
ab
+
=
+
. D.
24
3
log 14
1
a
ab
+
=
−
.
Câu 16: Đạo hàm của hàm số
( )
2
log 1= +
x
ye
là
A.
( )
'
1 ln 2
=
+
x
x
e
y
e
B.
( )
2
'
2 1 ln 2
=
+
x
x
y
C.
2 ln 2
'
21
=
+
x
x
y
D.
ln 2
'
1
=
+
x
x
e
y
e
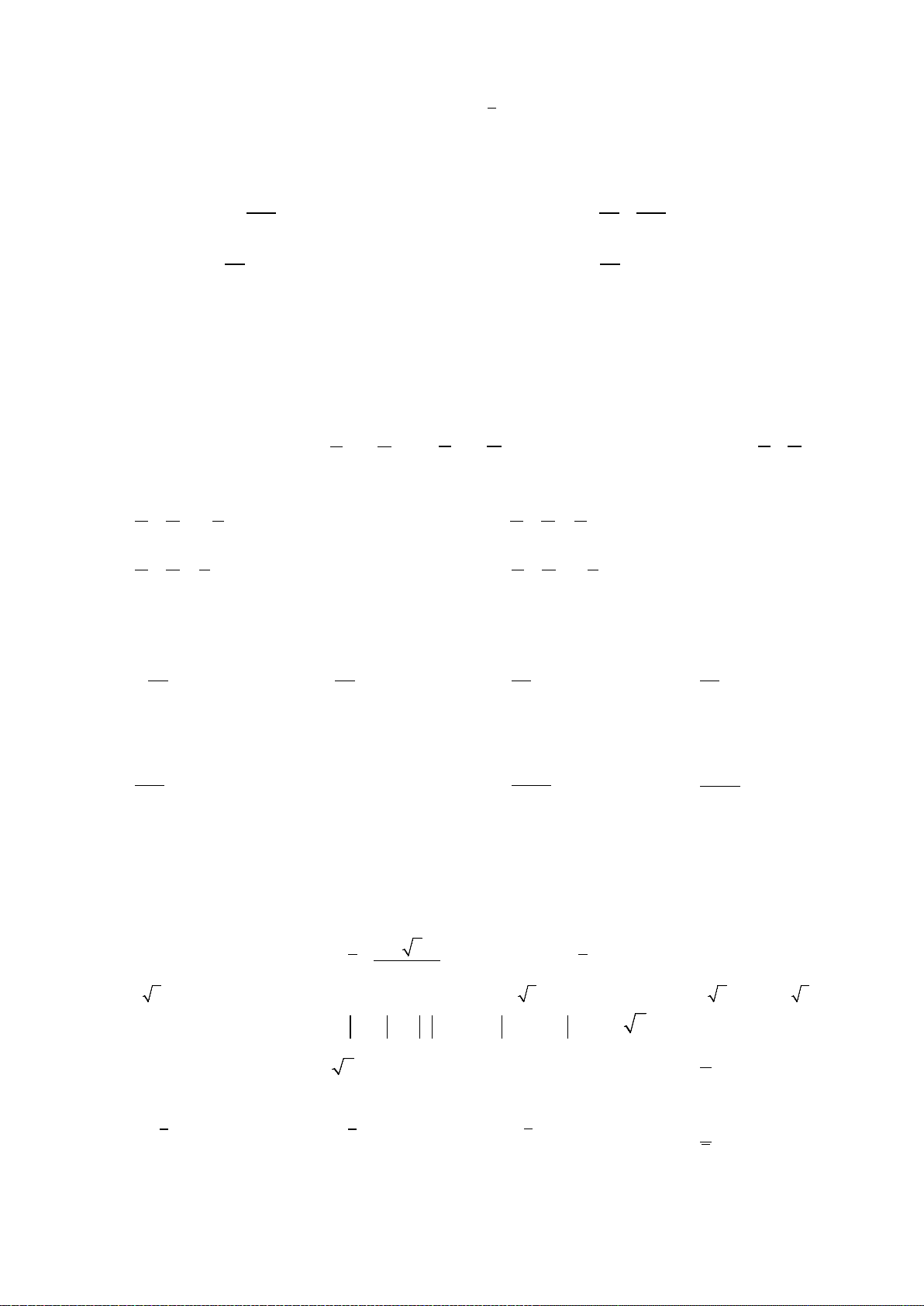
Trang 3/6
Câu 17: Phương trình sau
22
log ( 5) log ( 2) 3xx−+ +=
có nghiệm là:
A.
6
x =
B.
3x =
C.
6; 1xx= =
D.
8
x =
Câu 18: Tìm tập nghiệm
S
của bất phương trình
(
)
[
]
02loglog
3
6
>−x
π
.
A.
( )
5;∞−=S
. B.
( )
5;3=S
. C.
( )
∞+= ;5S
. D.
( )
1;4−=S
.
Câu 19: Nguyên hàm của hàm số
( )
2
x
fx x= +
là:
A.
(
)
2
1
ln 2
x
fx x C
=++
∫
d
. B.
(
)
2
2
2 ln 2
x
x
fx x C=++
∫
d
.
C.
( )
2
2 ln 2
2
x
x
fx x C=++
∫
d
. D.
( )
2
2
2
x
x
fx x C= ++
∫
d
.
Câu 20: Biết một nguyên hàm của hàm số
( )
y fx=
là
( )
2
41Fx x x=++
. Khi đó, giá trị của hàm số
( )
y fx=
tại
3x =
là
A.
( )
36f =
. B.
( )
3 10f =
.
C.
( )
3 22f =
. D.
( )
3 30f =
.
Câu 21: Biết rằng
23
1
ln d
e
ac
x xx e
bd
= +
∫
, với
a
b
và
c
d
là hai phân số tối giản. Khi đó,
ac
bd
+
bằng bao
nhiêu?
A.
1
9
ac
bd
+=−
. B.
1
9
ac
bd
+=
.
C.
1
3
ac
bd
+=
. D.
1
3
ac
bd
+=−
.
Câu 22: Biết rằng
( )
22
3 dx=e cos 3 sin 2
xx
I e cos x a x b x c= ++
∫
, trong đó a, b , c là các hằng số. Khi đó,
tổng
ab+
có giá trị là:
A.
1
13
−
. B.
5
13
−
. C.
5
13
D.
1
13
Câu 23: Một vật chuyển động với vận tốc 10m/s thì tăng tốc với gia tốc được tính theo thời gian t là
( )
2
a t 3t t= +
. Tính quảng đường vật đi được trong khoảng 10s kể từ khi bắt đầu tăng tốc.
A.
130
3
km
.
B.
130
km
.
C.
3400
3
km
.
D.
4300
3
km
.
Câu 24: Một người có mảnh đất hình tròn có bán kính 5m, người này tính trồng cây trên mảnh đất đó,
biết mỗi mét vuông trồng cây thu hoạch được giá 100 nghìn. Tuy nhiên cần có khoảng trống để dựng chòi
và đồ dùng nên người này căng sợi dây 6m sao cho 2 đầu mút dây nằm trên đường tròn xung quanh mảnh
đất. Hỏi người này thu hoạch được bao nhiêu tiền (tính theo đơn vị nghìn và bỏ phần số thập phân).
A.
3722
B.
7445
C.
7446
D.
3723
Câu 25: Cho số phức z thỏa mãn:
3
(1 3 )
1
i
z
i
−
=
−
. Tìm môđun của
z iz+
.
A.
82
` B.
83
C.
42
D.
43
Câu 26: Cho số phức
z
thỏa mãn
32zz−=
và
max 1 2 2z i ab−+ = +
. Tính
ab+
.
A.
4
. B.
42
. C.
3
. D.
4
3
.
Câu 27: Cho z là một số phức tùy ý khác 0. Khẳng định nào sau đây sai?
A.
zz
−
là số ảo B.
zz+
là số thực C.
z.z
là số thực D.
z
z
là số ảo
Câu 28: Biết rằng phương trình
( )
2
z bz c 0 b,c+ += ∈
có một nghiệm phức là
1
z 1 2i= +
. Khi đó
A.
bc0+=
B.
bc3
+=
C.
bc2+=
D.
bc7+=

Trang 4/6
Câu 29: Tập hợp các điểm trong mặt phẳng biểu diễn số phức Z thoả mãn điều kiện:
2 z i z z 2i−= −+
là:
A. Một đường tròn. B. Một đường thẳng. C. Một đường Elip. D. Một đường Parabol
Câu 30: Cho tứ diện ABCD. Gọi B’ và C’ lần lượt là trung điểm của AB và AC. Khi đó tỉ số thể tích của
khối tứ diện AB’C’D và khối tứ diện ABCD bằng:
A.
1
2
B.
1
4
C.
1
6
D.
1
8
Câu 31: Cho khối chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
a
. Hai mặt bên
SAB
và
SAC
cùng vuông góc với đáy. Tính thể tích khối chóp biết
3SC a
, hãy chọn đáp án đúng?
A.
3
3
2
a
B.
3
6
12
a
C.
3
26
9
a
D.
3
3
4
a
Câu 32: Cho hình chóp
.
S ABCD
có đáy là hình thang vuông tại
A
và
D
,
, 2,AB BC a AD a= = =
cạnh
bên
SA
vuông góc với đáy,
= .
SA a
Tính khoảng cách từ điểm
B
đến mặt phẳng
( ).SCD
A.
6
4
a
B.
26
3
a
C.
6
3
a
D.
6
6
a
Câu 33: Trong không gian, cho hình nón bán kính đáy là 4a, chiều cao là 3a. Diện tích xung quanh của
hình nón là.
A.
2
20 aπ
. B.
2
15 aπ
C.
2
16 aπ
D.
2
12 aπ
Câu 34: Cho hình hộp chữ nhật
.ABCD A B C D
′′′ ′
có
2AB a=
,
3AD a
=
và
4AA a
′
=
. Tính thể tích
V
của khối trụ ngoại tiếp hình hộp chữ nhật đã cho.
A.
3
144π
13
a
V =
. B.
3
13π
Va=
. C.
3
24πVa=
. D.
3
13Va
=
.
Câu 35: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi cạnh
a
,
0
120ABC =
, tam giác
SAB
đều và
nằm trong mặt phẳng vuông góc với đáy. Tính bán kính mặt cầu ngoại tiếp hình chóp
.
S ABC
.
A.
41
6
a
B.
37
6
a
C.
39
6
a
D.
35
6
a
Câu 36: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ( d) có phương trình:
= +
= −
=
12
5
xt
yt
z
Véc tơ nào dưới đây là một véc tơ chỉ phương của (d)?
A.
( )
= −
1
2; 1; 5 .u
B.
( )
= −
2
2; 1; 0 .u
C.
( )
=
3
1; 0; 5 .u
D.
( )
= −
4
1; 1; 5 .
u
Câu 37: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (4;-1;1 ) và B (3;1;-1 ).
Viết phương trình của mặt phẳng (P) đi qua AB và song song với trục Ox.
A.
0
+=xy
B.
0++=
xyz
C.
0
+=yz
D.
0+=xz
Câu 38: Tìm giao điểm của
31
:
1 12
x yz
d
−+
= =
−
và
( )
:2 7 0P xyz−−−=
A.
(
)
3; 1; 0M
−
B.
( )
0;2; 4M −
C.
( )
6; 4;3M −
D.
( )
1; 4; 2M
Câu 39: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
1
x1 y2 z3
d:
1 21
−−−
= =
−
và
2
x 1 kt
d: y t
z 1 2t
= +
=
=−+
. Tìm giá trị của k để
1
d
cắt
2
d
A.
k1= −
B.
k0=
C.
k1=
D.
1
k
2
= −

Trang 5/6
Câu 40: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
( ) ( ) ( )
22
2
: 1 1 2.Sx y z−++ +=
Tìm tâm I và
tính bán kính của mặt cầu (S).
A.
( )
I 1;1; 0−
và
R 2.
=
B.
( )
I 1;1; 0−
và
R 2.=
C.
( )
I 1; 1; 0−
và
R 2.
=
D.
( )
I 1; 1; 0−
và
R 2.=
Câu 41: Mặt phẳng (P) chứa đường thẳng d:
11
213
x yz−+
= =
và vuông góc với mặt phẳng
(Q): 2x y z 0+−=
có phương trình là:
A.
2 10xy+ −=
B.
20x yz
− +=
C.
2 10xy− −=
D.
20
x yz
+ +=
Câu 42: Trong không gian với hệ tọa độ
,Oxyz
cho mặt phẳng
:2 2 1 0 P xy z
và đường thẳng
13
Δ:
2 13
y
xz
. Phương trình đường thẳng
d
đi qua điểm
2; 1; 5B
song song với
P
và
vuông góc với
Δ
là
A.
1
25
52 4
y
xz
. B.
1
25
52 4
y
xz
.
C.
2
54
2 15
y
xz
. D.
2
54
2 15
y
xz
.
Câu 43: Trong không gian với hệ tọa độ
Oxyz
, cho điểm
(1;2;3)M
. Mặt phẳng
()
P
qua
M
cắt các tia
,,Ox Oy Oz
lần lượt tại
,,
ABC
sao cho thể tích khối tứ diện nhỏ nhất có phương trình là:
A.
++=6320xyz
.
B.
++−=6 3 2 18 0xyz
C.
++−=2 3 14 0xyz
.
D.
++−=60xyz
.
Câu 44: Tìm nghiệm của phương trình
2
2cos cos 3 0xx− −=
.
A.
2,
2
x kk
π
π
=−+ ∈
B.
2
,.
3
arccos 2
2
xk
k
xk
ππ
π
= +
∈
=±+
C.
2
2
,.
3
arccos 2
2
xk
k
xk
π
π
π
=−+
∈
=±+
D.
2,x kk
ππ
=+∈
.
Câu 45: Gieo 3 con xúc sắc. Tính xác suất P để 3 số hiện ra có thể sắp xếp để tạo thành 3 số tự nhiên liên
tiếp .
A. P=
2
9
. B. P=
1
9
. C. P=
1
54
. D. P=
1
12
.
Câu 46: Cho tứ diện ABCD các điểm M,N lần lượt là trung điểm BC và BD. Gọi d là giao tuyến của hai
mp (AMN) và (ACD). Khi đó ta có:
A. d//BC B. d//MD C. d//CN D. d//CD
Câu 47: Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
, ,B AB a=
cạnh bên
SA
vuông góc
với đáy và
2.SA a
=
Gọi
M
là trung điểm của
.AB
Khoảng cách giữa
SM
và
BC
bằng bao nhiêu?
A.
2
3
a
B.
2
a
C.
3
3
a
D.
3
2
a
Câu 48: Cho cấp số cộng:
2; 5; 8; 11; 14;........
−−−− −
Tìm công sai
d
A.
3d =
. B.
3d = −
. C.
3d = −
. D.
3d =
.
Câu 49: Cho đường tròn
( )
22
: 8 6 21 0Cx y x y+−++=
và đường thẳng
: 10dx y+ −=
. Xác định tọa độ
các đỉnh
A
của hình vuông
ABCD
ngoại tiếp
( )
C
biết
Ad∈
.
Trang 6/6
A.
( )
2, 1A −
hoặc
( )
6, 5
A −
. B.
( )
2, 1A −
hoặc
( )
6,5A
.
C.
( )
2,1A
hoặc
( )
6, 5A −
. D.
( )
2,1A
hoặc
( )
6,5A
.
Câu 50: Tìm tất cả các giá trị thực của tham số m sao cho pt:
2
4
3 1 12 1x mx x−+ += −
có hai nghiệm
thực phân biệt.
A.
1
1
3
m≤<
B.
1
1
4
m−≤ ≤
C.
1
0
3
m≤<
D.
1
2
3
m
−< ≤
--------------HẾT--------------
ĐÁP ÁN
1. D
7. A
13. D
19. B
25. A
31. B
37. C
43. B
49. A
2. A
8. A
14. A
20. B
26. A
32. D
38. A
44. D
50. C
3. C
9. A
15. A
21. C
27. D
33. B
39. B
45. B
4. A
10. A
16. A
22. C
28. B
34. B
40. D
46. D
5. B
11. C
17. A
23. D
29. D
35. C
41. C
47. A
6. C
12. B
18. B
24. B
30. B
36. B
42. A
48. B
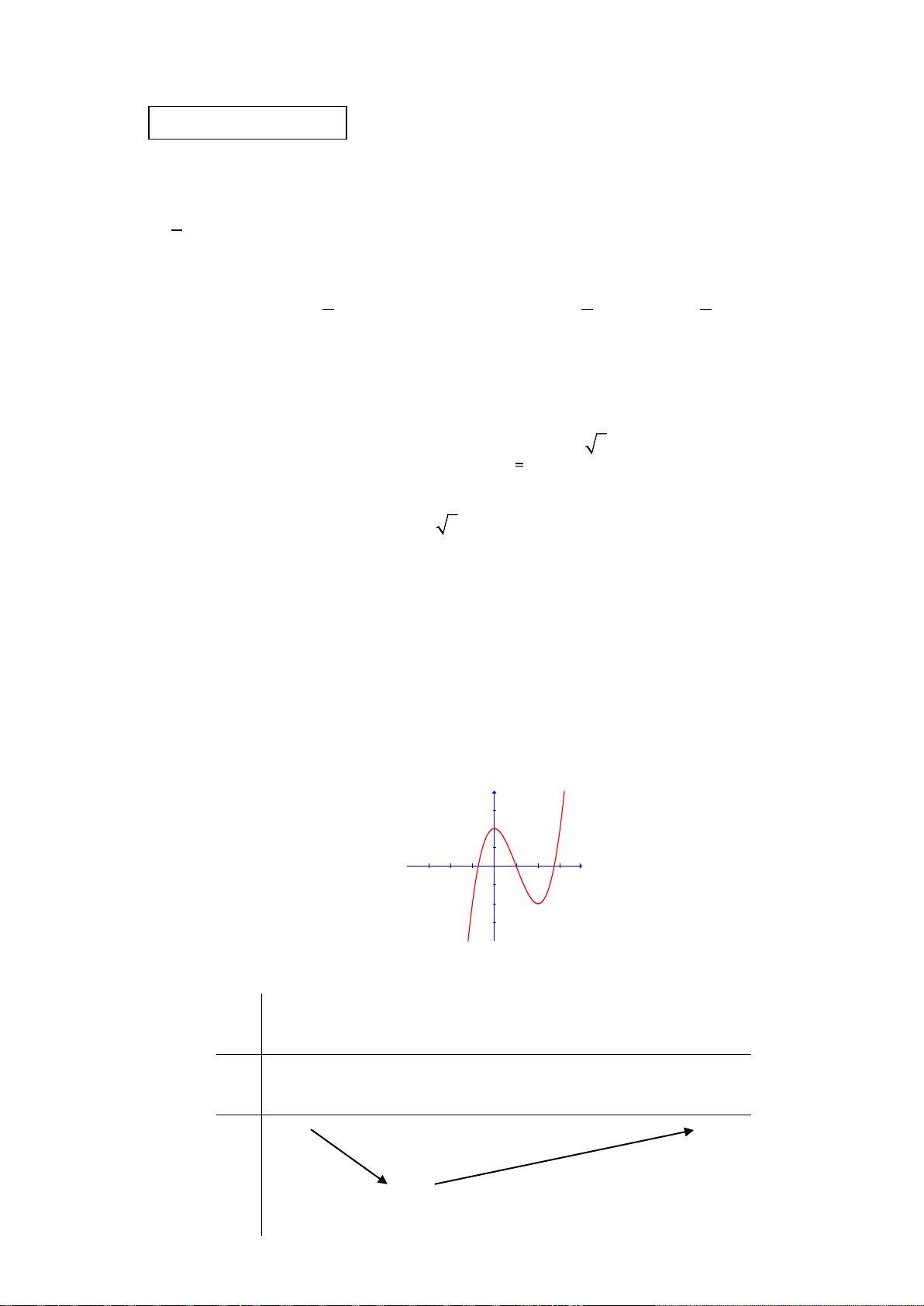
Trang 1/5
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
KỲ THI THPT QUỐC GIA NĂM 2019
TRƯỜNG THPT TRẦN QUÝ CÁP
Bài thi: Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề
(Đề thi có 05 trang)
Câu 1: Tập nghiệm của bất phương trình:
2
2 50xx− + −>
A.
1
\
3
B.
C.
Φ
D.
{ }
\3−
Câu 2: Cho phương trình
cos 4 3 5xm= −
. Tìm
m
để phương trình đã cho có nghiệm.
A.
11m
−≤ ≤
B.
4
2
3
m≤≤
C.
4
2
3
m−≤ ≤
D.
4
3
3
m≤≤
Câu 3: Gieo ngẫu nhiên một con súc sắc cân đối đồng chất 3 lần liên tiếp. Số phần tử của không
gian mẫu là:
A. 216 B. 18 C. 36 D. 261
Câu 4: Kí hiệu R là tập số thực, C là tập số phức. Tìm khẳng định sai?
A.
RC⊂
B.
21 7 3zi= −
C.
1z = −
không phải là số phức D.
,z z zC= ∀∈
Câu 5: Cho khối nón có bán kính đáy
3
r =
và chiều cao
4h =
. Thể tích của khối nón đã cho
bằng:
A.
12π
B.
12
C.
4π
D.
4
Câu 6: Cho mặt phẳng
( )
P : 2x 3y 4z 2016−+=
. Vectơ nào sau đây là một vectơ pháp tuyến của
mặt phẳng (P) ?
A.
( )
n 2; 3; 4=−−
B.
( )
n 2; 3; 4
= −
C.
( )
n 2; 3; 4
=−−
D.
( )
n 2;3; 4= −
Câu 7: Đường cong trong hình dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
3
31
yx x=−+ +
B.
32
32yx x=−+
C.
32
32yx x
=++
D.
32
32yx x=−+ +
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
Câu 8: Cho hàm số
()y fx=
xác định, liên tục trên và có bảng biến thiên :
x
-∞
2−
0
+∞
y
’
- || + 0 +
y
+∞
+ ∞
4−
ĐỀ THI ĐỀ XUẤT
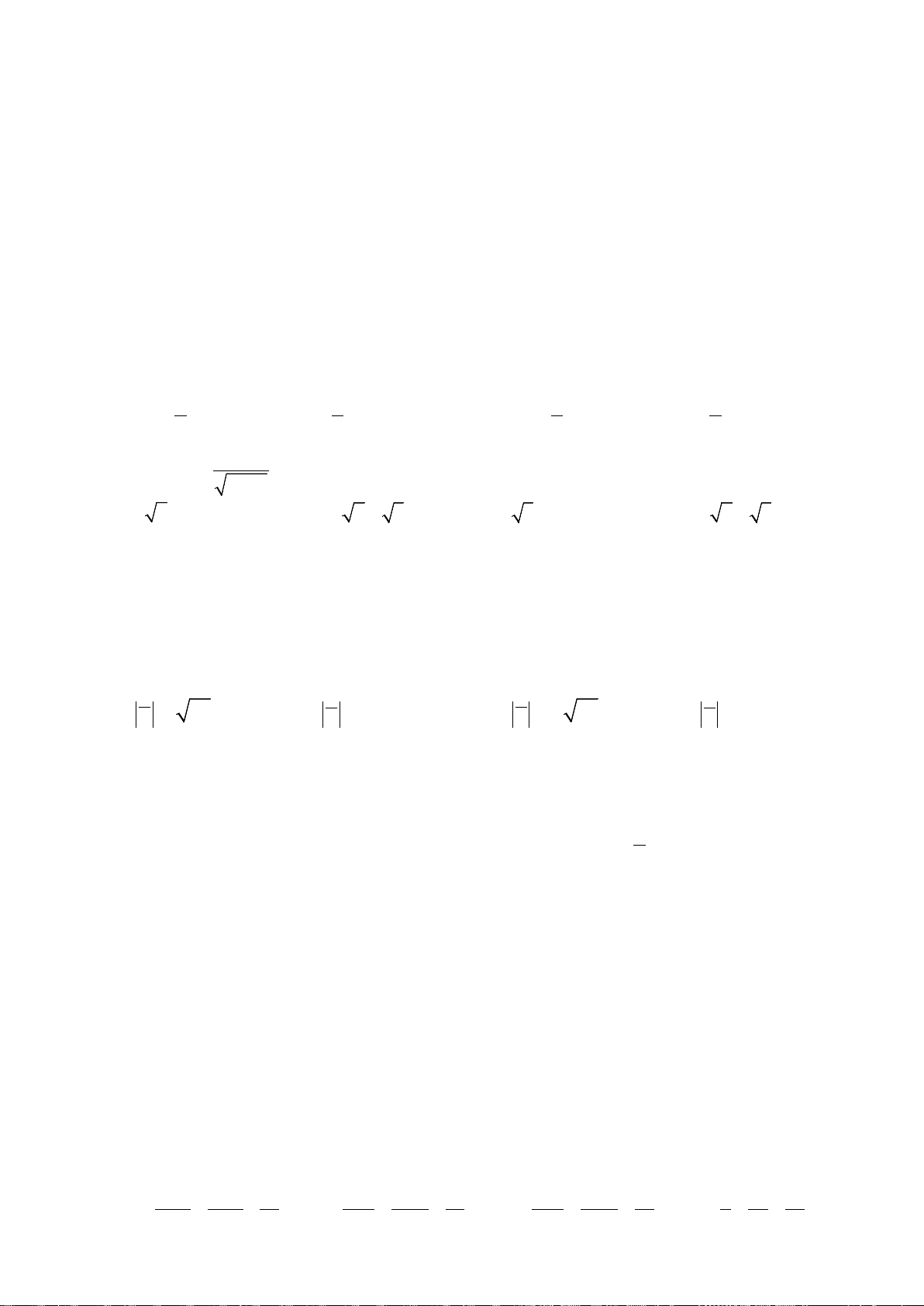
Trang 2/5
Khẳng định nào sau đây là khẳng định sai ?
A. Hàm số có đúng hai cực trị. B. Hàm số có giá trị nhỏ nhất bằng
4−
.
C. Hàm số có giá trị cực tiểu bằng
4
−
. D. Hàm số đồng biến trên khoảng
( 2; )
− +∞
Câu 9: Cho
(2,1, 3)a =
,
(4, 3,5)
b
= −
,
( 2, 4, 6)
c −
.Tọa độ của vectơ
2u a bc=+−
là
A.
(10,9,6)
B.
(12, 9, 7)−
C.
(10, 9, 6)−
D.
(12, 9, 6)−
Câu 10: Cho hàm số
()y fx=
có
( 2)
lim ( )
x
fx
+
→−
= +∞
và
2
lim ( )
x
fx
−
→
= +∞
.Chọn mệnh đề đúng ?
A. Đồ thị hàm số đã cho không có tiệm cận đứng.
B. Đồ thị hàm số đã cho có đúng một tiệm cận đứng.
C. Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng y = 2 và y = −2.
D. Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng x = 2 và x = −2.
Câu 11: Tập xác định hàm số
2
log (4 3 )yx= −
A.
4
;
3
−∞
B.
4
;
3
+∞
C.
3
;
4
−∞
D.
3
;
4
+∞
Câu 12: Tính
3
2
2
1
xdx
x −
∫
A.
22
B.
22 3−+
C.
3
D.
22 3−
Câu 13: Mệnh đề nào sau đây sai:
A. Nếu
a >1
thì
log log 0
aa
M N MN
> ⇔ >>
B. Nếu
0 < a < 1
thì
log log 0
aa
M N MN> ⇔< <
C. Nếu
M, N >0, 0< a 1≠
thì
log log .log
a aa
MN M N=
D. Nếu
0 < a <1
thì
log 2018 log 2019
aa
>
Câu 14: Cho số phức z = 1+3i .Khi đó môđun số phức liên hợp của z là :
A.
10z =
.
B.
10z =
.
C.
2 10z =
.
D.
3z =
.
Câu 15: Khi tăng độ dài tất cả các cạnh của một khối hộp chữ nhật lên gấp đôi thì thể tích khối
hộp tương ứng sẽ:
A. tăng 2 lần B. tăng 4 lần C. tăng 6 lần D. tăng 8 lần
Câu 16: Tổng 3 hệ số của 3 số hạng đầu tiên trong khai triển
2
2
n
x
x
−
bằng 97. Hạng tử của khai
triển chứa
4
x
là:
A.
4
1020x
B.
4
1120x
C.
4
1792x
D.
4
448x
Câu 17: Phương trình nào là phương trình tham số của đường thẳng x–y+2 = 0:
A.
2
xt
yt
=
= +
B.
2
x
yt
=
=
C.
3
1
xt
yt
= +
= +
D.
3
xt
yt
=
= −
Câu 18: Cắt hình chóp tứ giác bằng một mặt phẳng, thiết diện không thể là hình nào sau đây:
A. Tam giác. B. Tứ giác. C. Ngũ giác. D. Lục giác.
Câu 19: Cho hình chữ nhật ABCD cạnh AB = 4, AD = 2. Gọi M, N là trung điểm các cạnh AB và
CD. Cho hình chữ nhật quay quanh MN, ta được hình trụ tròn xoay có thể tích bằng
A.
4π
B.
8π
C.
16π
D.
32π
Câu 20: Đường thẳng d đi qua điểm A(1; -2;0) và vuông góc với mp
− −+=(P) : 2x 3y z 2 0
có
phương trình chính tắc:
A.
23
:
1 21
xy z
d
−+
= =
−−
B.
12
:
2 31
xy z
d
−+
= =
−−
C.
12
:
12 3
xy z
d
−+
= =
−−
D.
:
231
xy z
d = =
−−
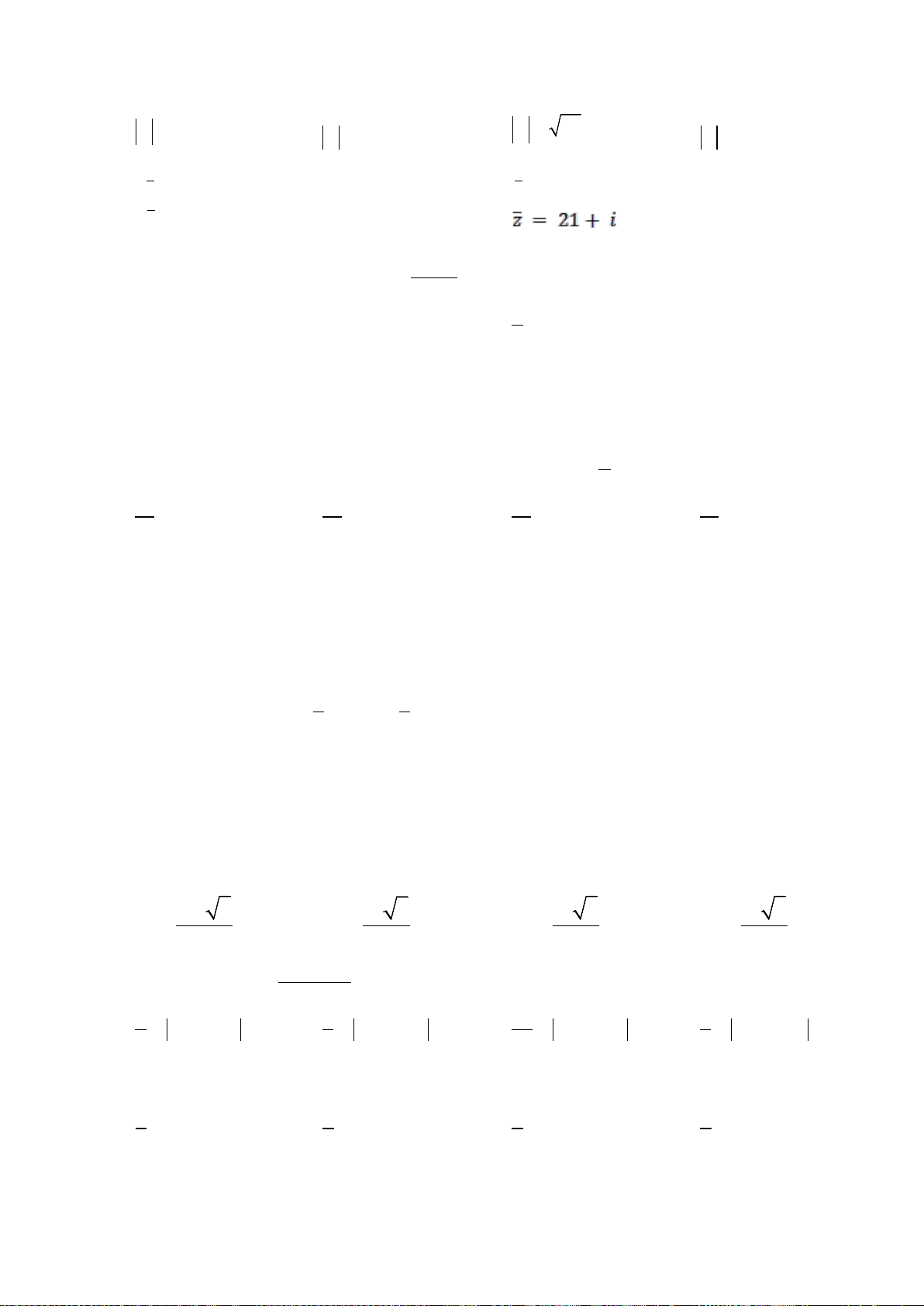
Trang 3/5
Câu 21: Viết phương trình mặt phẳng qua
( ) ( )
1; 1; 2 , 3;1; 4
MN
−
và song song với trục Ox.
A.
3 4 4 70
xyz+ + −=
B.
0
yz+=
C.
4 10xz−+=
D.
30yz−+=
Câu 22: Cho số phức z có phần ảo âm và thỏa mãn
− +=zz
2
4 60
. Mô đun của số phức:
ω
= −z
23
A.
=w 3
B.
4w
=
C.
=w 24
D.
5w =
Câu 23: Tìm số phức liên hợp của z = (3 + 2i)[(2 – i) + (3 – 2i)]
A.
21zi= −
B.
21zi= +
C.
1 21zi= −
D.
Câu 24: Giá trị nhỏ nhất của hàm số
23
2
x
y
x
+
=
−
trên đoạn
[ ]
2;1−
là :
A.
5.−
B.
4−
C.
1
4
D.
6−
Câu 25: Gọi
00
M( ; )xy
là giao điểm của đường thẳng
32yx= +
và đồ thị hàm số
32
32yx x x= −+−
,với
0
0x
<
. Tìm
0
y
?
A.
0
2y =
. B.
0
11y =
. C.
0
4y = −
. D.
0
2y = −
.
Câu 26: Cho F(x) là một nguyên hàm của f(x). Biết
2
()
3
b
a
f x dx =
∫
, F(b) = 5. Tính F(a)?
A.
14
5
B.
13
3
C.
17
3
D.
12
3
Câu 27: Điểm cực đại của đồ thị hàm số
3
31yx x+
=−+
là :
A.
(1; 3)
. B.
(1; 5)
. C.
( 1; 1)−−
. D.
( 1; 3)−−
.
Câu 28: Cho hàm số
3
34
yx x=−+ +
có đồ thị (C). Tìm phương trình tiếp tuyến của (C) tại giao
điểm của (C) với trục tung.
A.
34yx=−+
. B.
2y =
. C.
34yx
= −
. D.
34yx= +
.
Câu 29: Bất phương trình :
2
1 21
33
() > ()
55
xx x−+ −
có tập nghiệm dạng
( ; ).S ab=
Hỏi
?
ba−=
A. 4 B. 2 C. 3 D. 1
Câu 30: Số nghiệm của phương trình
2
2 53
7 =1
xx−+
là :
A. 0 B. 1 C. 2 D. 3
Câu 31: Cho khối chóp S.ABCD có đáy là hình vuông tâm O,
AB a
.Hình chiếu vuông góc của
S trên mặt phẳng ABCD trùng với trung điểm OA. Góc giữa mặt phẳng (SCD) và mặt phẳng
(ABCD) bằng
0
60
. Tính thể tích V của khối chóp S.ABCD:
A.
3
3a 3
V
4
B.
3
a3
V
8
C.
3
a3
V
4
D.
3
a3
V
12
Câu 32: Hàm số
=
+
cos
()
5sin 6
x
fx
x
có nguyên hàm là
A.
1
ln 5sin 6
5
x +
B.
1
ln 5sin 6
5
xC++
C.
1
ln 5sin 6
5
xC
−
++
D.
1
ln 5cos 6
5
xC++
Câu 33: Cho tứ diện ABCD. Gọi B’ và C’ lần lượt là trung điểm của AB và AC. Khi đó tỉ số thể
tích của khối tứ diện AB’C’D và khối tứ diện ABCD bằng:
A.
1
2
B.
1
4
C.
1
6
D.
1
8

Trang 4/5
Câu 34: Cho đường thẳng (∆) :
1
22
3
= +
= −
= +
xt
yt
zt
(t∈R). Điểm M nào sau đây thuộc đường thẳng (∆):
A. M(1; –2; 3) B. M(2; 0; 4) C. M(1; 2; – 3) D. M(2; 1; 3)
Câu 35: Tính tích phân
2
2
1
I 2x x 1dx
= −
∫
bằng cách đặt
2
u x 1.= −
Mệnh đề nào dưới đây đúng?
A.
3
0
I 2 udu.=
∫
B.
2
1
I udu.=
∫
C.
3
0
I udu.=
∫
D.
2
1
1
I udu.
2
=
∫
Câu 36: Tìm
( )
2
. 1 3 5 ... 2 1
lim
21
nn
n
+++ + −
+
ta được:
A.
1
2
B.
0
C.
+∞
D.1
Câu 37: Tìm tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều kiện :
2 |z – 1 – 2i| = |3i + 1 – 2
|
A. Đường thẳng 2x + 14y – 5 = 0 B. Đường thẳng: 6x + 1 = 0
C. Đường thẳng: 2x – y + 1 = 0 D. Parabol: 2x = y
2
Câu 38: Xét một hộp bóng bàn có dạng hình hộp chữ nhật. Biết rằng hộp chứa vừa khít ba quả
bóng bàn được xếp theo chiều dọc, các quả bóng bàn có kích thước như nhau. Phần không gian
còn trống trong hộp chiếm (giá trị gần đúng nhất)
A.
47,6%
B.
65,1%
C.
82,6%
D.
83,3%
Câu 39: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
1
13
:2
2
xt
dy t
z
= +
=−+
=
,
2
12
:
2 12
xy z
d
−+
= =
−
và mặt phẳng
( ):2 2 3 0Px yz+−=
. Phương trình nào dưới đây là phương
trình mặt phẳng đi qua giao điểm của
1
d
và (P), đồng thời vuông góc với
2
d
.
A.
2 2 22 0xy z
−+ + =
B.
2 2 13 0xy z−+ + =
C.
2 2 13 0xy z−+ − =
D.
2 2 22 0xy z
++ − =
Câu 40: Có bao nhiêu giá trị nguyên của
m
để hàm số
3 22
1
(23) 57
3
y x m x mx m= − + + −+
luôn
đồng biến trên tập xác định của nó ?
A. 1 B. 2. C. 4. D. 3.
Câu 41: Diện tích của hình phẳng giới hạn bởi
( )
2
: =
Cyx
và
(
)
:
=dy x
là:
A.
2
3
B.
4
3
C.
5
3
D.
1
3
Câu 42: Tìm tất cả các giá trị của m để đồ thị hàm số
32
1
( 2) (2 4) 1
3
yxmx mxm= − + + + −+
có hai
điểm cực trị nằm cùng một phía đối với trục tung ?
A.
0m >
B.
2m >−
C.
0m ≥
D.
20m−< <
Câu 43: Cho tứ diện ABCD có đáy là tam giác vuông tại C. AB vuông góc với đáy, AB=4, BC =
3.Khoảng cách từ điểm B đến mặt phẳng (ACD) là.
A.
12
5
. B.
3
5
. C.
6
5
. D.
12
15
.
Câu 44: Anh An mong muốn sau 5 năm sẽ có 2 tỷ để mua nhà. Hỏi anh An phải gởi vào ngân
hàng một khoảng tiền tiết kiệm như nhau hằng năm gần nhất với giá trị nào sau đây, biết lãi suất
ngân hàng
8%
/năm và lãi hằng năm nhập vào vốn.
A. 358,2 triệu B. 315,7 triệu C. 333,3 triệu D. 400 triệu
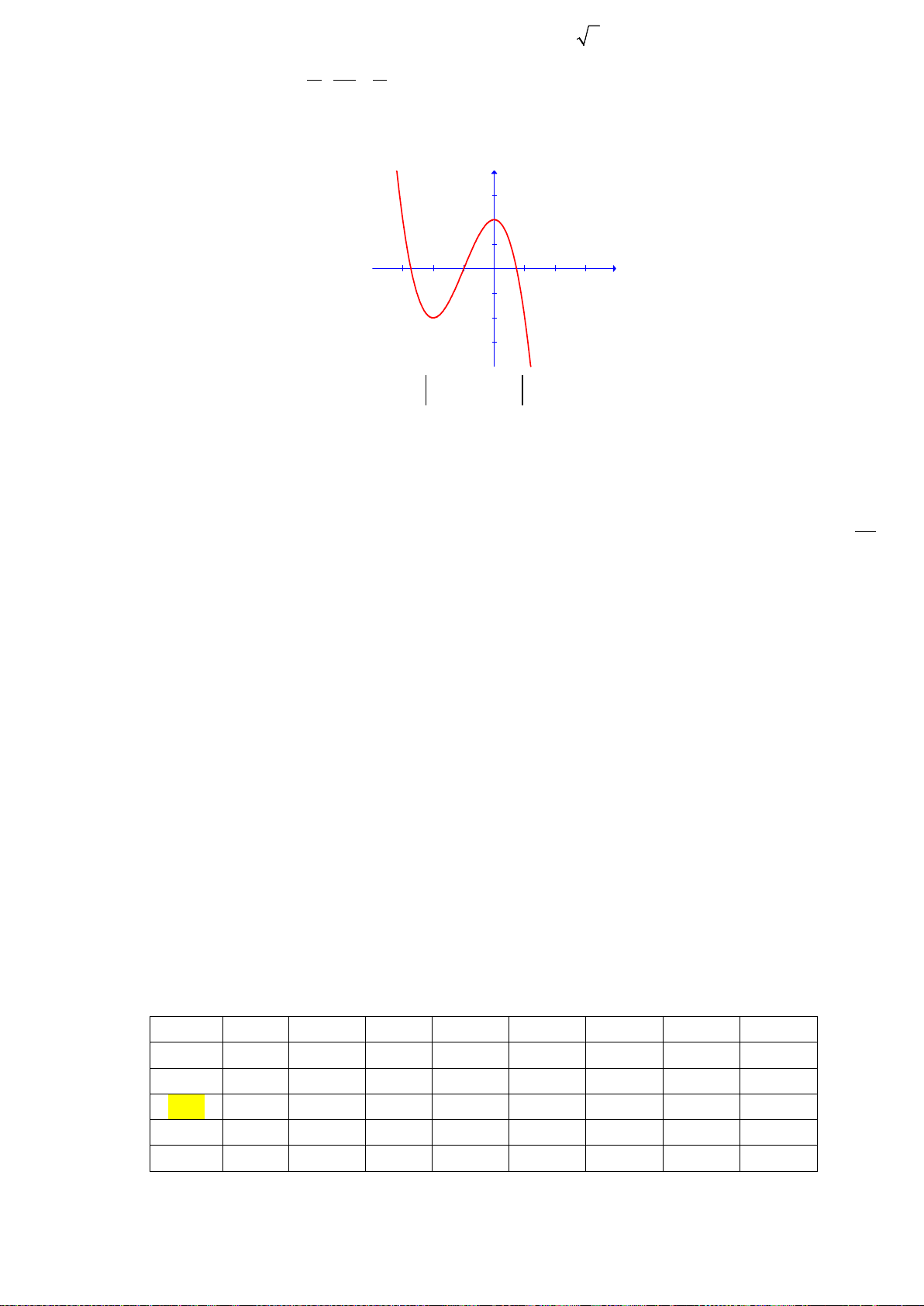
Trang 5/5
Câu 45: Thể tích vật thể hình phẳng giới hạn bởi đồ thị
cosyxx
=
và
0; / 4yx
π
= =
quay xung
quanh trục Ox có giá trị là
2
1
8
ab
ππ π
+−
khi đó a + b là?
A. 4. B. 8. C. 10. D. 6.
Câu 46: Đồ thị sau đây là của hàm số
32
32
yx x
=−− +
:
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
Với giá trị nào của m thì phương trình
32
3 2 42 0
xx m
+ − +− =
có 6 nghiệm phân biệt. ?
A.
13m
<<
. B.
23m≤≤
. C.
23m<<
. D.
02m<<
.
Câu 47: Một khay đá viên gồm 8 ngăn nhỏ có dạng là các hình chóp cụt với miệng và đáy là hình
vuông (kích thước của miệng lớn hơn của đáy). Kích thước của khay đá (dài x rộng x cao) là
160x80x25 (đơn vị mm), khoảng cách giữa các ngăn đá là không đáng kể. Biết góc giữa mặt bên
của mỗi ngăn và mặt phẳng miệng là 80
0
, hãy tính tổng thể tích của 8 ngăn đá (lấy tan80
0
=
17
3
và kết quả cuối cùng làm tròn đến hàng phần trăm)
A. 254,64 ml B. 284,46 ml C. 524,16 ml D. 542,16 ml
Câu 48: Có bao nhiêu giá trị nguyên dương của tham số m để phương trình
16 2 12 2 9 0.()
xx x
m
− +− =
có nghiệm dương?
A. 1 B. 2 C. 3 D. 4
Câu 49: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
2 22
( ): 9Sx y z++=
, điểm
(1;1; 2)M
và mặt phẳng
( ): 4 0Pxyz++−=
. Gọi
∆
là đường thẳng đi qua M, thuộc (P) và cắt (S) tại hai
điểm A, B sao cho AB nhỏ nhất. Biết rằng
∆
có một vectơ chỉ phương là
(1; ; )u ab
. Tính
t ab= −
A.
2T = −
B.
1
T =
C.
1T = −
D.
0T =
Câu 50: Một ô tô xuất phát với vận tốc
1
( ) 2 10( / )vt t ms= +
. Sau khi đi được khoảng thời gian
1
t
thì
gặp chướng ngại vật và tài xế đạp phanh gấp với vận tốc
2
( ) 20 4 ( / )v t tm s= −
và đi thêm một
khoảng
2
t
nửa thì dừng lại. Biết rằng thời gian từ lúc đạp phanh đến lúc xe dừng hẳn là 4s. Quãng
đường xe đi được sau khi đạp phanh là bao nhiêu?
A. 57 m B. 47 m C. 60 m D. 50 m
--------------HẾT--------------
ĐÁP ÁN
1. C
7. B
13. C
19. B
25. C
31. C
37. A
43. A
49. C
2. B
8. A
14. A
20. B
26. B
32. B
38. D
44. B
50. A
3. A
9. B
15. D
21. D
27. A
33. B
39. C
45. C
4. C
10. D
16. B
22. A
28. D
34. B
40. D
46. C
5. C
11. A
17. A
23. A
29. D
35. C
41. D
47. A
6. C
12. D
18. D
24. A
30. C
36. A
42. A
48. B
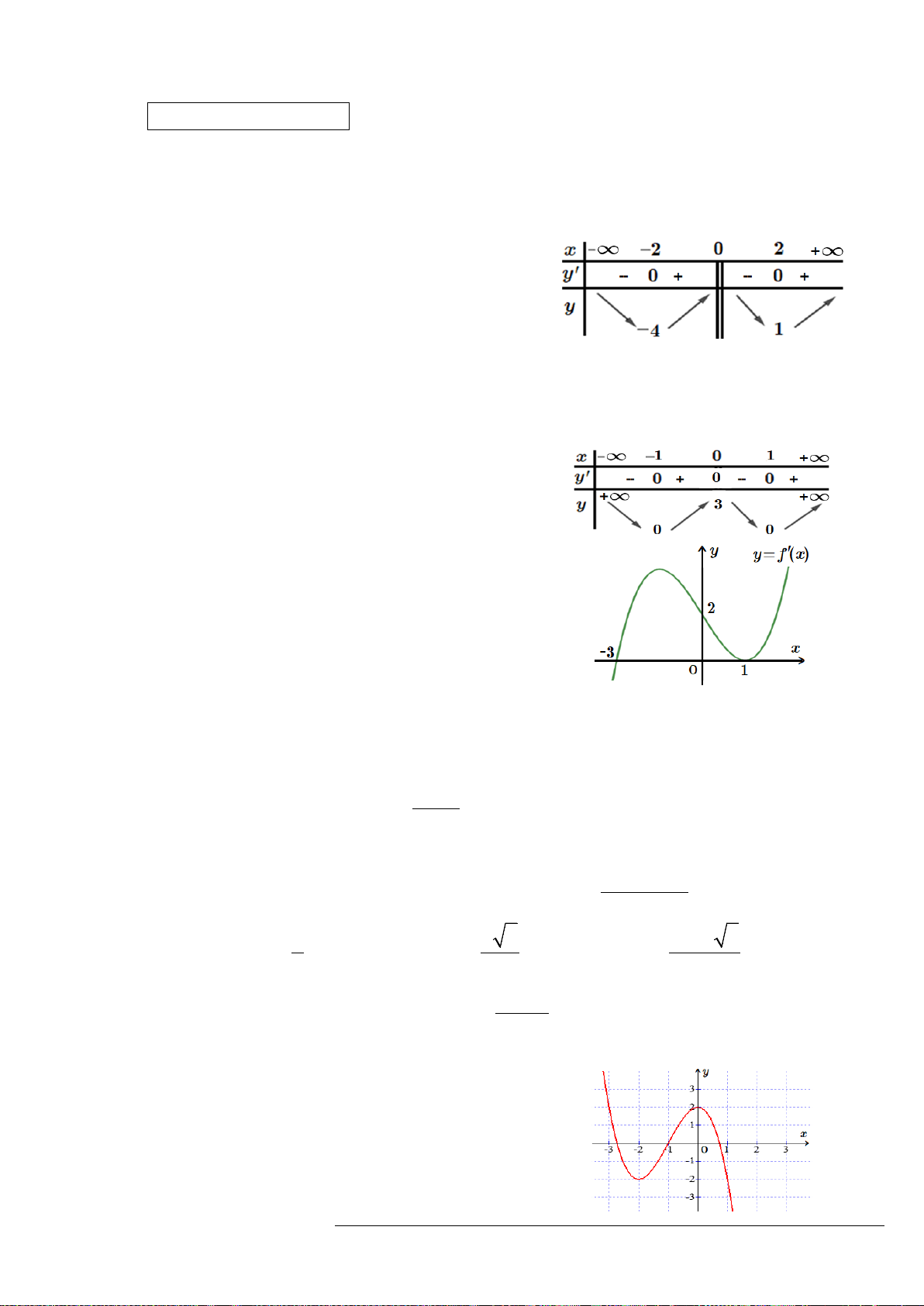
NTC
Trang 1/5
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
TRƯỜNG PT. DTNT TỈNH
KỲ THI THPT QUỐC GIA NĂM 2019
Bài thi: Toán
ĐỀ THI ĐỀ XUẤT
Thời gian làm bài: 90 phút, (không kể thời gian phát đề)
(Đề thi có 05 trang)
Câu 1. Cho hàm số
()y fx
liên tục trên
và có bảng biến thiên như hình vẽ dưới đây. Khẳng định
nào sau đây không đúng ?
A. Hàm số đồng biến trên
( 2; 1)
B. Hàm số đồng biến trên
( 2; 0)
và
(2; )
C. Hàm số đồng biến trên
( 2; 0) (2; )
D. Hàm số nghịch biến trên
( ; 2)
và
(0; 2)
Câu 2. Hàm số
32
3yx x
nghịch biến trên khoảng nào sau đây ?
A.
(0; 2)
B.
( ; 0)
C.
(2; )
D.
( 4; 0)
Câu 3. Cho hàm số
()y fx
có bảng biến thiên như hình bên. Mệnh đề nào dưới đây sai ?
A. Hàm số có ba điểm cực trị.
B. Hàm số có hai điểm cực tiểu.
C. Hàm số có giá trị cực đại bằng
0
.
D. Hàm số có giá trị cực đại bằng
3
.
Câu 4. Cho hàm số
()y fx
liên tục và có đạo hàm
trên
K
. Biết hình bên là đồ thị của hàm số
()y fx
trên
K
. Tìm số điểm cực trị của hàm số
()y fx
.
A.
0
B.
1
C.
2
D.
3
Câu 5. Cho hàm số
()y fx
có đạo hàm
22 2
( ) ( 1) ( 2)f x xx x
với mọi
x
. Tìm số điểm cực
trị của đồ thị hàm số
()y fx
dã cho.
A.
1
B.
2
C.
3
D.
4
Câu 6. Tìm giá trị nhỏ nhất của hàm số
3
1
x
y
x
trên đoạn
[ 1; 0 ]
.
A.
2
B.
3
C.
4
D.
3
Câu 7. Tính tổng giá trị lớn nhất à giá trị nhỏ nhất của hàm số
2
21
1
x
y
xx
.
A.
0
B.
8
3
C.
47
3
D.
4 27
3
Câu 8. Tìm số đường tiệm cận của độ thị hàm số
21x
y
x
.
A.
0
B.
1
C.
2
D.
3
Câu 9. Hàm số
32
31yxx
có đồ thị như hình
bên. Tìm
m
để phương trình
32
31 0xx m
có ba nghiệm phân biệt.
A.
31m
B.
22m
C.
13m
D.
31m

NTC
Trang 2/5
Câu 10. Hàm số
3
y ax bx c
có đồ thị như hình bên. Tìm mệnh đề
đúng.
A.
0; 0 & 0ab c
B.
0; 0 & 0ab c
C.
0; 0 & 0ab c
D.
0; 0 & 0ab c
Câu 11. Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng nếu trên mỗi đơn vị diện tích
của mặt hồ có
n
con cá thì trung bình mỗi con cá sau một vụ cân nặng
( ) 480 20Pn n
(gam). Hỏi
phải thả bao nhiêu cá trên một đơn vị diện tích của mặt hồ để cuối vụ thu hoạch được nhiều cá nhất?
A.
11
B.
12
C.
13
D.
14
Câu 12. Đơn giản biểu thức
51
5
1
.Pa
a
.
A.
a
B.
251
a
C.
5
a
D.
125
a
Câu 13. Hàm số nào sau đây không phải là hàm số lũy thừa?
A.
2
x
y
B.
1
2
yx
C.
yx
D.
2
yx
Câu 14. Tìm khẳng định sai trong các khẳng định sau.
A.
ln 0 1xx
B.
3
log 0 0 1xx
C.
11
33
log log 0a b ab
D.
11
22
log log 0a b ab
Câu 15. Tìm tập xác định của hàm số
22
( 1)yx
.
A.
B.
\ { 1}
C.
\ ( 1; 1)
D.
\ [ 1; 1]
Câu 16. Tìm số nghiệm của phương trình
1
4 2.2 4 0
xx
.
A.
0
B.
1
C.
2
D.
3
Câu 17. Tìm tập nghiệm của bất phương trình
11
55
log (2 7) log ( 1)
xx
.
A.
B.
( 1; 2)
C.
( ; 1)
D.
( 1; )
Câu 18. Tìm tập nghiệm của bất phương trình
2
0,7 6
log (log ) 0
4
xx
x
.
A.
(8; )
B.
( 4; 3) (8; )
C.
( 4; 3) (8; )
D.
( 4; 3) [8; )
Câu 19. Khẳng định nào sau đây sai ?
A.
sin d cosxx x C
B.
d
xx
exe C
C.
1
d lnx xC
x
D.
1
d , ( 1)
1
x
xx C
Câu 20. Hàm số hàm số
()fx
có đạo hàm trên đoạn
[2;8]
và thỏa mãn
(2) 10; (8) 2029ff
. Giá trị
của tích phân
8
2
( )dfx x
là
A.
2019
B.
2018
C.
2017
D.
2019
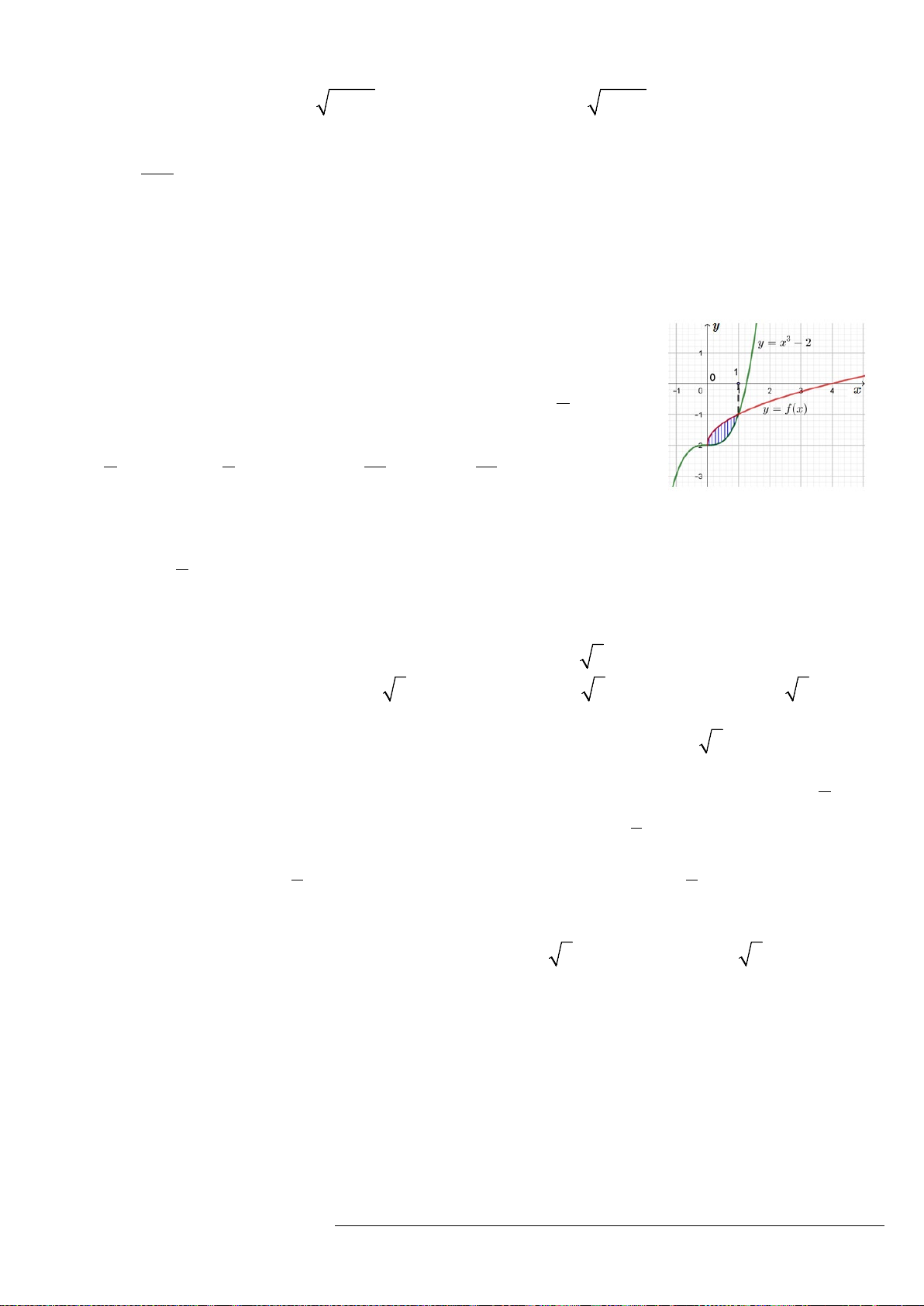
NTC
Trang 3/5
Câu 21. Cho tích phân
6
1
3dI xx x
và phép đổi biến
3tx
. Tìm mệnh đề sai.
A.
232
5
I
B.
3
42
2
( 3 )dI t tt
C.
3
42
2
(2 6 ) dI t tt
D.
3
42
2
(2 6 ) d
I x xx
Câu 22. Giả sử tích phân
1
0
(2 3) d
x
x e x ae b
, (với
, ab
). Tìm mệnh đề đúng.
A.
3ab
B.
2ab
C.
21
ab
D.
22
28
ab
Câu 23. Cho biết hình bên là đồ thị của hai hàm số
()y fx
và
3
2yx
. Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm
số trên (phần gạch chéo trong hình) biết rằng
1
0
4
( )d
3
fx x
.
A.
5
3
B.
5
4
C.
5
12
D.
11
12
Câu 24. Một ô tô đang chạy với vận tốc
10 ( / )
ms
thì tăng tốc và chuyển động nhanh dần đều với gia
tốc
2
() 1 ( / )
3
t
at m s
. Tính quãng đường mà ô tô đi được sau
6
giây kể từ khi bắt đầu tăng tốc.
A.
58 ( )m
B.
90 ( )m
C.
100 ( )
m
D.
246 ( )m
Câu 25. Gọi
a
là phần thực và
b
phần ảo của số phức
3 22
zi
, ta có
A.
3, 2
ab
B.
3, 2ab
C.
3, 2 2ab
D.
3, 2 2ab
Câu 26. Cho số phức
( 1) ( 2)zm m i
, (với
m
). Tìm
m
để
| | 5
z
.
A.
m
B.
01m
C.
10m
D.
0
m
hoặc
1
2
m
Câu 27. Cho số phức
z a bi
, (với
, ab
) thỏa mãn
(1 ) 2 3 2iz z i
. Tính
()ab
.
A.
1
B.
1
2
C.
1
D.
1
2
Câu 28. Tìm nghiệm phức của phương trình
2
2 30zz
.
A.
1; 3zz
B.
12zi
C.
12zi
D.
22zi
Câu 29. Tìm
m
để phương trình
2
(2 ) 2 0z mz
có một nghiệm
1zi
.
A.
0m
B.
2m
C.
4m
D.
4m
Câu 30. Cho khối đa diện đều loại
{ ; }pq
. Chỉ số
p
cho ta biết
A. số đỉnh của đa diện B. số mặt của đa diện
C. số cạnh của đa diện D. số cạnh của mỗi mặt
Câu 31. Khối đa diện đều nào sau đây có mặt không phải là tam giác đều?
A. Tứ diện đều B. Bát diện đều C. 12 mặt đều D. 20 mặt đều

NTC
Trang 4/5
Câu 32. Tứ diện
ABCD
có
AD
vuông góc với mặt phẳng
()ABC
và
3 (cm); 5 (cm)AB BC
;
4 (cm)AC AD
. Tính thể tích khối tứ diện đó.
A.
3
8 ( )m
B.
3
16 ( )
m
C.
3
12 ( )m
D.
3
15
8
()m
Câu 33. Cho hình lăng trụ
.ABC A B C
có đáy
ABC
là tam giác đều với
AB a
và
3
2
a
AA
.
Biết hình chiếu vuông góc của
A
lên mặt phẳng
()
ABC
trùng với trung điểm của
BC
. Tính thể tích
của khối lăng trụ đó.
A.
3
a
B.
3
2
3
a
C.
3
. 1, 5a
D.
3
32
8
a
Câu 34. Tính diện tích xung quanh của hình nón tròn xoay có chiều cao
8 (c m)
h
và bán kính đáy
6 (c m)r
.
A.
2
0, 6 (dm )
B.
2
1, 2 ( d m )
C.
2
12 (dm )
D.
2
60 (dm )
Câu 35. Tính đường kính mặt cầu ngoại tiếp hình lập phương
.ABCD A B C D
có cạnh bằng
3
a
.
A.
3
B.
2
a
C.
3a
D.
3
2
a
Câu 36. Trong không gian với hệ toạ độ
()Oxyz
cho hai vectơ
( 1; 3; 2)u
và
(2; 1; 1)v
. Tìm
tọa độ của vectơ
3
xu v
.
A.
(5; 6; 5)
B.
(6; 6; 1)
C.
( 5; 6; 1)
D.
(1; 4; 3)
Câu 37. Trong không gian với hệ toạ độ
()Oxyz
, tìm
m
để phương trình sau là phương trình mặt cầu.
222 2
2( 2) 4 2 5 9 0x y z m x my mz m
A.
m
B.
1m
C.
51m
D.
5m
hoặc
1m
Câu 38. Trong không gian với hệ toạ độ
()Oxyz
, cho mặt phẳng
()Q
cắt ba trục
, , Ox Oy Oz
theo thứ
tự tại
( 2; 0; 0), (0; 3; 0), (0; 0; 1)A BC
. Điểm nào trong các điểm sau không thuộc
()
Q
?
A.
( 2; 3; 1)M
B.
(4; 3; 1)M
C.
(6; 6; 2)M
D.
( 2; 3; 1)M
Câu 39. Trong không gian với hệ toạ độ
()
Oxyz
, gọi
, , N PQ
lần lượt là điểm đối xứng của điêm
( 1; 2; 3)M
qua các mặt phẳng
( ), ( )Oxy Oxz
và
()Oyz
. Tìm phương trình mặt phẳng
()NPQ
.
A.
6 3 2 60xyz
B.
63260xyz
C.
62360xyz
D.
6 3 2 60
xyz
Câu 40. Trong không gian với hệ toạ độ
()Oxyz
cho điểm
(2; 2; 4)A
và mặt phẳng
( ): 4Pxyz
.
Tìm phương trình mặt phẳng
()Q
song song với
()P
đồng thời cắt hai tia
, Ox Oy
tại hai điểm
, BC
sao cho tam giác
ABC
có diện tích bằng 6.
A.
( ): 2 0Qx yz
B.
( ): 6 0Qx yz
C.
( ): 2 0Qx yz
D.
( ): 8 0Qx yz
Câu 41. Trong không gian với hệ toạ độ
()Oxyz
, gọi
12
, MM
lần lượt là hình chiếu vuông góc của
điểm
(1; 2; 3)M
lên các trục
, Ox Oy
. Một vectơ chỉ phương của đường thẳng
12
MM
có tọa độ là
A.
( 1; 2; 0)
B.
(0; 2; 0)
C.
(1;0;0)
D.
(1; 2; 0)

NTC
Trang 5/5
Câu 42. Trong không gian với hệ toạ độ
()Oxyz
, tìm phương trình đường thẳng đi qua
( 1; 2; 3)I
và
song song với đường thẳng
13
( ):
2 21
x yz
.
A.
123
2 21
xyz
B.
123
2 21
xy z
C.
123
2 21
xy z
D.
123
22 1
xyz
Câu 43. Trong không gian
()Oxyz
, gọi
()
là đường thẳng song song với
12
( ): 3
14
xt
yt
zt
đồng
thời cắt cả hai đường thẳng
1
223
( ):
31 1
xyz
d
và
2
321
( ):
12 2
xyz
d
. Điểm nào
trong số các điểm sau thuộc
()
?
A.
12; 4( ; 17)
M
B.
;3(5 3);M
C.
;1(6 5);M
D.
; 2;(1 130)M
Câu 44. Hình chóp
.S ABC
có
, , SA SB SC
vuông góc với nhau từng đôi một và
, 2
SA a SB a
,
3SC a
. Tính khoảng cáh từ
S
đến mặt phẳng
()ABC
.
A.
5
6
a
B.
6
5
a
C.
6
7
a
D.
7
6
a
Câu 45. Cho tứ diện
OABC
có
, , OA OB OC
đôi một vuông góc với nhau và
OA OB OC
. Gọi
M
là trung điểm
BC
. Tính góc giữa hai đường thẳng
AB
và
OM
.
A.
30
B.
45
C.
60
D.
90
Câu 46. Cho tập hợp
M
có
10
phần tử. Tìm số tập con gồm hai phần tử của
M
.
A.
2
10
B.
2
10
A
C.
8
10
A
D.
2
10
C
Câu 47. Một hộp có
10
viên bi màu trắng,
20
viên bi màu xanh và
30
viên bi màu đỏ. Tính số cách
chọn ngẫu nhiên hai trong số các viên bi thuộc hộp đó.
A.
60
B.
1770
C.
3540
D.
3600
Câu 48. Cho cấp số cộng
()
n
u
có số hạng đầu
1
15u
và công sai
5d
. Tính tổng
15
số hạng đầu
của cấp số cộng đó.
A.
100
B.
200
C.
300
D.
400
Câu 49. Tìm giá trị nhỏ nhất của hàm số
2
()
21
x
fx
x
, (với
1x
).
A.
2
B.
5
2
C.
3
D.
22
Câu 50. Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
2 23y x mx m
có tập xác
định
?
A.
3
B.
4
C.
5
D.
6
NTC
Trang 6/5
ĐÁP ÁN
01C
02A
03C
04B
05A
06B
07A
08C
09B
10D
11B
12A
13A
14C
15B
16B
17A
18C
19A
20A
21B
22C
23C
24B
25D
26C
27C
28C
29A
30D
31C
32A
33D
34A
35C
36A
37D
38A
39B
40A
41A
42A
43A
44C
45C
46D
47B
48C
49B
50C

NTC
Trang 1/5
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
TRƯỜNG GDTX & NH NHA TRANG
KỲ THI THPT QUỐC GIA NĂM 2019
Bài thi: Toán
ĐỀ THI ĐỀ XUẤT
Thời gian làm bài: 90 phút, (không kể thời gian phát đề)
(Đề thi có 05 trang)
01. Gọi
S
là tập hợp các giá trị của
m
để đồ thị hàm số
42
21y x mx
có ba điểm cực trị và
đường tròn đi qua ba điểm cực trị này có bán kính
1R
. Tính tổng các phần tử của
S
.
A.
51
B.
15
2
C.
52
D.
25
2
02. Cho
0 & 2aa
. Tính
2
2
log
4
a
a
.
A.
2
B.
1
2
C.
2
D.
1
2
03. Một đội văn nghệ có
10
người gồm
6
nam và
4
nữ. Cần chọn ra một bạn nam và một bạn nữ
để hát song ca. Hỏi có bao nhiêu cách chọn?
A.
1
B.
10
C.
24
D.
2
10
C
04. Cho biết bất phương trình
2
(5 2)
log (5 2) 3 log 4
x
x
có tập nghiệm
(log ; )
a
Sb
, trong
đó
,
ab
là các số nguyên dương nhỏ hơn
6
và
1a
. Tính
(2 3 )ab
.
A.
7
B.
11
C.
16
D.
18
05. Một người gửi
200
triệu vào ngân hàng với lãi suất
7% /
năm theo hình thức lãi kép. Và sau
mỗi năm người đó lại gửi thêm vào
20
triệu. Tính số tiền người đó nhận được sau 18 năm.
A.
739 163 000
B.
743 585 000
C.
1 335 967 000
D.
1 686 898 000
06. Cho hình chóp
.S ABCD
có đáy là hình vuông có cạnh bằng
a
, chiều cao
SA x
. Góc giữa
()SBC
và mặt đáy bằng
60
. Tìm
x
.
A.
3a
B.
3
2
a
C.
3
3
a
D.
6
2
a
07. Tính tổng các hệ số trong khai triển
2019
( ) (1 2 )Px x
.
A.
1
B.
1
C.
2019
D.
2019
08. Cho hình chóp
.S ABCD
có thể tích
V
. Lấy điểm
A
trên cạnh
SA
sao cho
3SA SA
. Mặt
phẳng qua
A
và song song với mặt đáy của hình chóp cắt các cạnh
, , SB SC SD
lần lượt tại
, , BC D
. Tính theo
V
thể tích khối chóp
.SABCD
.
A.
3
V
B.
9
V
C.
27
V
D.
81
V
09. Tính chiều cao của một khối chóp có đáy là tam giác đều cạnh bằng
a
và thể tích
3
0, 25Va
.
A.
3a
B.
3
2
a
C.
23a
D.
3
3
a

NTC
Trang 2/5
10. Tìm phần thực và phần ảo của số phức
z
biết rằng điểm
M
trong hình vẽ bên
là điểm biểu diễn của nó.
A. Phần thực là
4
và phần ảo là
3
B. Phần thực là
3
và phần ảo là
4i
C. Phần thực là
3
và phần ảo là
4
D. Phần thực là
4
và phần ảo là
3i
11. Tìm
m
để phương trình
1
4 .2 2 0
xx
mm
có hai nghiệm
12
,xx
thỏa mãn
12
3xx
.
A.
1m
B.
2
m
C.
3m
D.
4m
12. Giải phương trình
32
4 16
x
.
A.
3x
B.
3
4
x
C.
5x
D.
4
3
x
13. Hàm số
()fx
liên tục trên
và thoả mãn
8 12 8
14 4
( )d 9; ( )d 3 & ( )d 5fx x fx x fx x
.
Tính
12
1
( )dfx x
.
A.
1
B.
7
C.
11
D.
17
14. Trong không gian
()Oxyz
, cho mặt cầu tâm
(;;)
Iabc
bán kính
1R
, tiếp xúc mặt phẳng
()Oxz
. Tìm khẳng định đúng
A.
| | 1a
B.
| | 1b
C.
| | 1
c
D.
1abc
15. Trong không gian
()Oxyz
, cho tìm phương trình mặt cầu tâm
(1; 2; 3)I
và cắt trục
Ox
tại hai
điểm
&AB
sao cho
23AB
.
A.
222
( 1) ( 2) ( 3) 16xyz
B.
222
( 1) ( 2) ( 3) 9xy z
C.
222
( 1) ( 2) ( 3) 25xy z
D.
222
( 1) ( 2) ( 3) 2 3xyz
16. Tìm họ nguyên hàm của hàm số
42
()fx x x
.
A.
42
x xC
B.
53
xxC
C.
3
42x xC
D.
53
11
53
x xC
17. Tam giác đều
ABC
có cạnh bằng
a
. Tính diện tích xung quanh của hình nón tạo thành khi
quay tam giác
ABC
quanh đường cao
AH
của nó.
A.
2
a
B.
2
2
a
C.
2
2 a
D.
2
3
4
a
18. Xét các số phức
z
thỏa mãn
| 2 1 | 4zi
. Biết rằng tập hợp các điểm biểu diễn các số phức
(12 5 ) 3w iz i
là một đường tròn tâm
I
bán kính
r
. Tìm khẳng định đúng.
A.
(32;2) & 52Ir
B.
( 32; 2) & 2 13Ir
C.
( 22; 16) & 52Ir
D.
( 22; 16) & 2 13Ir
19. Cho tứ diện
ABCD
. Trên cạnh
AB
lần lượt lấy hai điểm
, MN
tùy ý (
M
khác
N
). Xét vị trí
tương đối của hai đường thẳng
& CM DN
.
A. cắt nhau B. chéo nhau C. song song D. đồng phẳng

NTC
Trang 3/5
20. Tìm tổng các nghiệm của phương trình
35 35 4 2 7xx x
.
A.
1
B.
5
C.
10
D.
51
21. Tìm tập nghiệm của phương trình
33
log (2 1) log ( 1) 1xx
.
A.
{1}S
B.
{2}S
C.
{3}S
D.
{4}S
22. Cho hình trụ có bán kính đáy
R
và chiều cao
3hR
. Hai điểm
, AB
lần lượt nằm trên hai
đường tròn đáy sao cho góc giữa
AB
và trục của hình trụ bằng
30
. Tính khoảng cách giữa
AB
và
trục của hình trụ.
A.
R
B.
2
R
C.
3R
D.
3
2
R
23. Tính thể tích của khối chóp tứ giác đều có cạnh đáy bằng
a
và cạnh bên tạo với mặt đáy một
góc
60
.
A.
3
3
2
a
B.
3
3
6
a
C.
3
6
2
a
D.
3
6
6
a
24. Tìm
m
để hàm số
32
1
21
3
y mx x x m
nghịch biến trên
.
A.
m
B.
0
m
C.
;0m
D.
1
;
2
m
25. Tính chiều cao của khối trụ có thể tích lớn nhất nội tiếp trong hình cầu có bán kính
R
cho trước.
A.
3R
B.
3
3
R
C.
23
3
R
D.
43
3
R
26. Trong không gian
()Oxyz
, gọi
I
là hình chiếu vuông góc của
(1; 2; 3)M
lên trục
Ox
. Tìm
phương trình cầu tâm
I
bán kính
IM
.
A.
222
( 1) 13x yz
B.
222
( 1) 13x yz
C.
222
( 1) 17x yz
D.
222
( 1) 13x yz
27. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
24yx x
lần lượt là
A.
2 & 0
B.
3 & 2
C.
4 & 2
D.
2 & 2
28. Tính đạo hàm của hàm số
2
log (2 1)yx
.
A.
1
21
y
x
B.
2
21
y
x
C.
ln 2
2(2 1)
y
x
D.
2
(2 1) ln 2
y
x
29. Tính diện tích hình phẳng giới hạn bởi các đồ thị hàm số
3
3yx x
và
yx
.
A.
0
B.
2
C.
4
D.
8
30. Cho hàm số
()fx
thỏa mãn
(0) 2f
và
42
(). ()fx f x x x
. Tính
2
(2)f
.
A.
313
15
B.
323
15
C.
324
15
D.
332
15
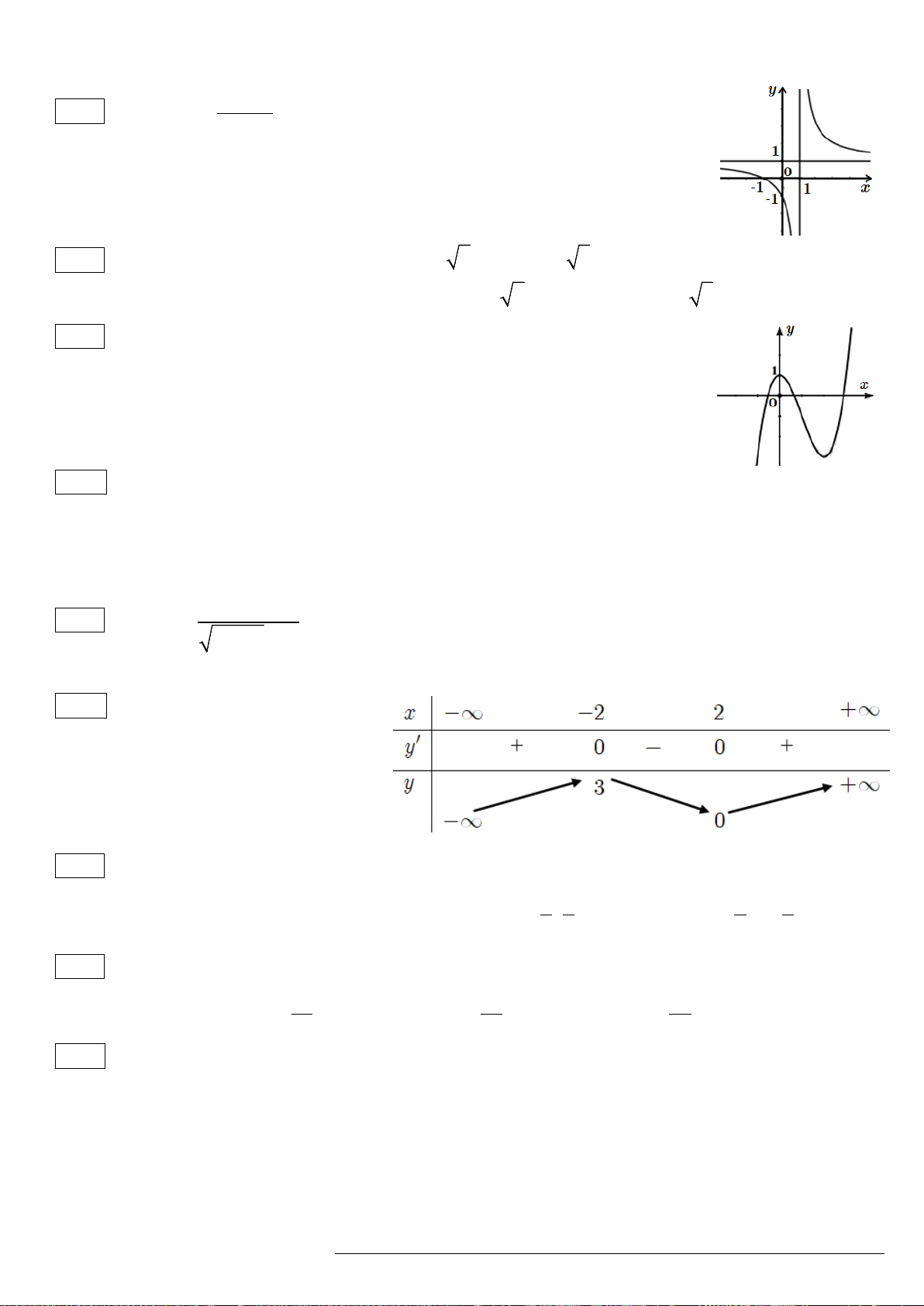
NTC
Trang 4/5
31. Hàm số
ax b
y
cx d
có đồ thị như hình bên. Tìm mệnh đề đúng.
A.
0 yx
B.
0 yx
C.
0 1yx
D.
0 1yx
32. Cho hai số phức
12
, zz
thỏa mãn
12
| | 2 3 & | | 3 2zz
. Tính
22
12 12
| || |zz zz
.
A.
50
B.
60
C.
20 3
D.
30 2
33. Tìm hàm số có đồ thị như hình bên.
A.
32
31yx x
B.
32
31
yxx
C.
42
21yx x
D.
42
21yxx
34. Trong không gian
()Oxyz
, cho ba điểm
(1; 1; 2), ( 2; 0; 3), (0; 1; 2)AB C
. Gọi
(;;)Mabc
là
điểm thuộc mặt phẳng
()Oxy
sao cho biểu thức
(. 2. 3 .)
MA MB MB MC MC MA
đạt giá trị nhỏ
nhất. Tính
(12 12 )a bc
.
A.
1
B.
1
C.
3
D.
3
35. Tính
2
23
lim
1
x
x
xx
.
A.
0
B.
1
C.
1
D.
36. Hàm số
()y fx
có BBT như
hình bên. Tính tổng giá trị cực đại và
giá trị cực tiểu của nó.
A.
0
B.
1
C.
2
D.
3
37. Tìm tập xác định của hàm số
24
(4 1)yx
.
A.
B.
(0; )
C.
11
\;
22
D.
11
;;
22
38. Tìm giá trị nhỏ nhất của hàm số
42
13yx x
trên đoạn
[ 2; 3]
.
A.
13
B.
51
2
C.
51
4
D.
49
4
39. Gọi
V
là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị các hàm số
2
3, 0, 0 & 2yx y x x
quanh trục
Ox
. Tìm mệnh đề đúng.
A.
2
2
0
( 3) dVx x
B.
2
2
0
( 3) dV xx
C.
2
22
0
( 3) dVx x
D.
2
22
0
( 3) dVxx

NTC
Trang 5/5
40. Hàm số
()fx
liên tục trên
và thỏa mãn
2
0
( )d 2018fx x
. Tính
2
0
( )dxf x x
.
A.
1008
B.
1009
C.
2017
D.
2019
41. Chọn ngẫu nhiên một số tự nhiên nhỏ hơn
300
. Tính xác suất để “số được chọn không chia hết
cho
3
”.
A.
1
3
B.
2
3
C.
99
300
D.
124
300
42. Tìm điều kiện để hàm số
42
, ( 0)y ax bx c a
có ba cực trị.
A.
0b
B.
0c
C.
0ab
D.
0ab
43. Trong không gian
()Oxyz
, tìm tâm của mặt cầu
2 22
( ) : ( 3) ( 1) ( 1) 2Sx y z
.
A.
(3; 1; 1)I
B.
(3; 1; 1)I
C.
( 3; 1; 1)I
D.
( 3; 1; 1)I
44. Tìm
m
để hàm số
3 22
1
( 4) 3
3
y x mx m x
đạt cực đại tại
3x
.
A.
1m
B.
1
m
C.
5m
D.
{1;5}
m
45. Số phức nào sau đây là số thuần ảo?
A.
2z
B.
3zi
C.
23zi
D.
3zi
46. Gọi
0
x
là một nghiệm của phương trình
sin cos 2(sin cos ) 2xx x x
. Tính
0
(3 sin 2 )x
.
A.
0
B.
2
C.
3
D.
2
3
2
47. Tính diện tích
S
của mặt cầu và thể tích
V
của khối cầu có bán kính
3 (cm)r
.
A.
23
18 (cm ) & 36 (cm )S V
B.
23
18 (cm ) &
108
(cm )S V
C.
23
36 (cm ) & 36 (cm )S V
D.
23
36 (cm ) &
108
(cm )S V
48. Trong không gian
()Oxyz
, cho hai điểm
(2; 4; 3), (2; 2; 7)AB
. Tìm tọa độ trung điểm của
AB
.
A.
(1; 3; 2)
B.
(2; 1; 5)
C.
(2; 1; 5)
D.
(2; 6; 4)
49. Tính
2
1
1
d
32
x
x
.
A.
ln 2
B.
1
ln 2
3
C.
2 ln 2
D.
2
ln 2
3
50. Tính đạo hàm của hàm số
3
21yx x
.
A.
2
2yx
B.
2
32yx
C.
2
32yxx
D.
2
3 21yxx
ĐÁP ÁN
01B
02A
03C
04C
05C
06A
07B
08C
09A
10C
11D
12D
13B
14B
15A
16D
17B
18C
19B
20B
21D
22D
23D
24A
25C
26B
27D
28D
29D
30D
31D
32B
33A
34B
35C
36D
37A
38C
39D
40B
41B
42D
43D
44C
45B
46C
47C
48B
49D
50B

NTC
Trang 6/5
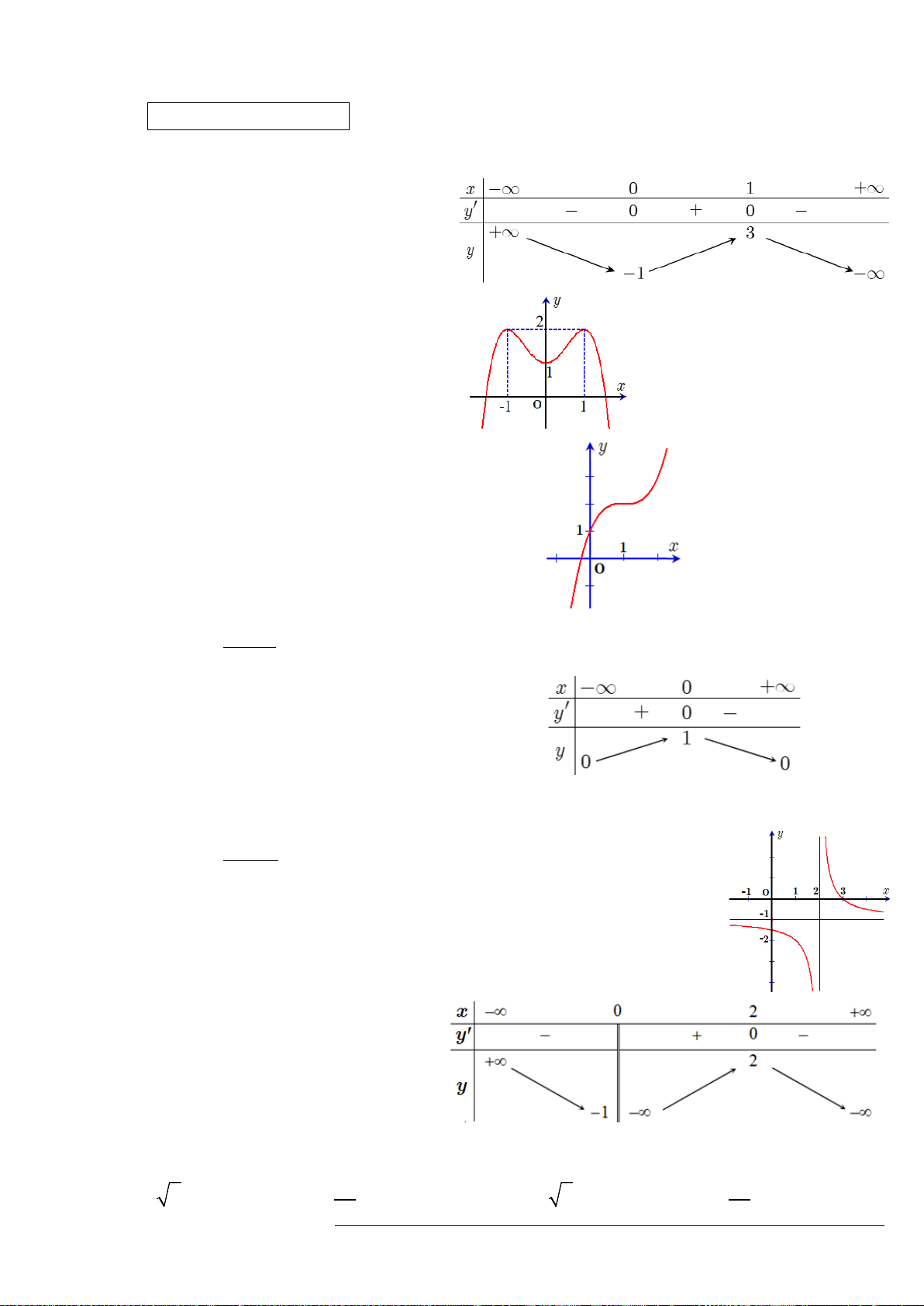
NTC
Trang 1/5
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
TRƯỜNG THPT TÔN ĐỨC THẮNG
KỲ THI THPT QUỐC GIA NĂM 2019
Bài thi: Toán
ĐỀ THI ĐỀ XUẤT
Thời gian làm bài: 90 phút, (không kể thời gian phát đề)
(Đề thi có 05 trang)
Câu 1. Tìm khoảng đồng biến của hàm số
()
fx
biết nó có bảng biến thiên như hình bên.
A.
(0; 1)
B.
( 1; 3)
C.
( ; 0)
D.
(0; )
Câu 2. Tìm điểm cực tiểu của hàm số
()y fx
biết nó có đồ thị như hình bên.
A.
0x
B.
1
x
C.
2x
D.
1x
Câu 3. Hình bên là đồ thị của hàm số nào sau đây?
A.
3
31yx x
B.
32
31
yxx
C.
23
13
y xx
D.
32
3 31yx x x
Câu 4. Hàm số
2
1
1
y
x
có bảng biến thiên như hình bên. Tìm khẳng định đúng.
A. Hàm số có giá trị lớn nhất bằng
0
B. Hàm số có giá trị lớn nhất bằng
1
C. Hàm số có giá trị nhỏ nhất bằng
0
D. Hàm số không có GTLN & GGTNN
Câu 5. Tìm số điểm cực trị của hàm số
()fx
biết đạo hàm của nó
42
( ) (2 1) ( 1)fx x x x
.
A.
0
B.
1
C.
2
D.
3
Câu 6. Hàm số
ax b
y
xc
có đồ thị như hình bên. Tính
(2 )
a bc
.
A.
0
B.
1
C.
2
D.
3
Câu 7. Hàm số
()y fx
có bảng biến thiên
như hình bên. Tìm
m
để phương trình
() 0fx m
có ba nghiệm phân biệt.
A.
( 1; 2)
B.
( 2; 1)
C.
[ 1; 2)
D.
( 2; 1]
Câu 8. Tìm
m
để hàm số
32
22y x mx x
đồng biến trên khoảng
( 2; 0)
.
A.
23m
B.
13
2
m
C.
23m
D.
13
2
m
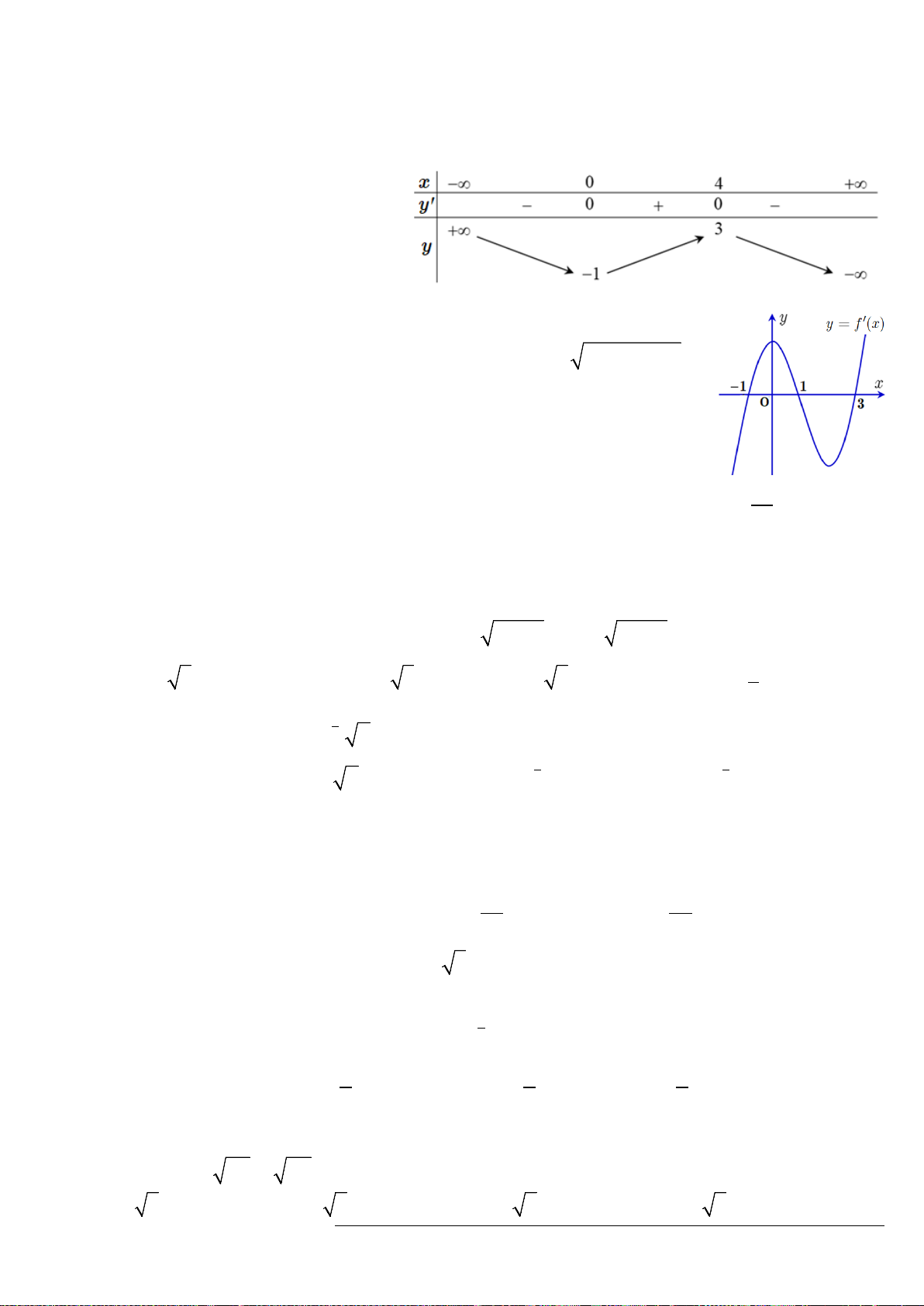
NTC
Trang 2/5
Câu 9. Gọi
a
là số thực lớn nhất để bất phương trình
22
2 ln( 1) 0
xx axx
nghiệm đúng
với mọi
x
. Tìm mênh đề đúng.
A.
3](2;a
B.
7](6;a
C.
(8; )a
D.
(6 ];5a
Câu 10. Hàm số
()y fx
có bảng biến
thiên như hình bên. Tìm số nghiệm thực
của phương trình
2
(4 ) 2fx x
.
A.
0
B.
2
C.
4
D.
6
Câu 11. Cho hàm số bậc bốn
()y fx
và hình bên là đồ thị của hàm số đạo
hàm
()y fx
của nó. Tìm số điểm cực đại của hàm số
2
( 2 2)y fx x
.
A.
1
B.
2
C.
3
D.
4
Câu 12. Hàm số
()y fx
có đạo hàm trên
và thỏa mãn
4
2
2
(1) (, 2 01 )f fx x x x
x
.
Khi đó, phương trình
() 0fx
A. có
1
nghiệm trên
(0; 1)
. B. có
1
nghiệm trên
(1; 2)
.
C. có
1
nghiệm trên
(2; 5)
. D. có đúng
3
nghiệm trên
(0; )
.
Câu 13. Tìm
m
để phương trình
3 22
2 1 11
mm
ee x x x x
có nghiệm.
A.
ln 2m
B.
0 ln 2m
C.
ln 2m
D.
1
0 m
e
Câu 14. Rút gọn biểu thức
1
3
6
.Pxx
, (với
0x
).
A.
2
Px
B.
Px
C.
1
8
Px
D.
2
9
Px
Câu 15. Biết bất phương trình
22
( 2 2)( 2 4) 15xx xx
tập nghiệm là
[;]
ab
. Tính
()ab
.
A.
1
B.
2
C.
1
D.
2
Câu 16. Cho
2
log 5a
. Tính
8
log 25
theo
a
.
A.
2a
B.
3a
C.
2
3
a
D.
3
2
a
Câu 17. Tìm tập nghiệm của bất phương trình
1
3
3
55
x
x
.
A.
( ; 0)
B.
( ; 5)
C.
(0; )
D.
( 5; )
Câu 18. Tìm tập xác định của hàm số
5
3
(2 3 )yx
.
A.
B.
2
;
3
C.
2
\
3
D.
2
;
3
Câu 19. Biết phương trình
21 1
3
log (3 3 1)
xx
x
có hai nghiệm
12
,
xx
(với
12
xx
). Tính giá trị
của biểu thức
12
33
xx
P
.
A.
13
B.
13
C.
23
D.
23
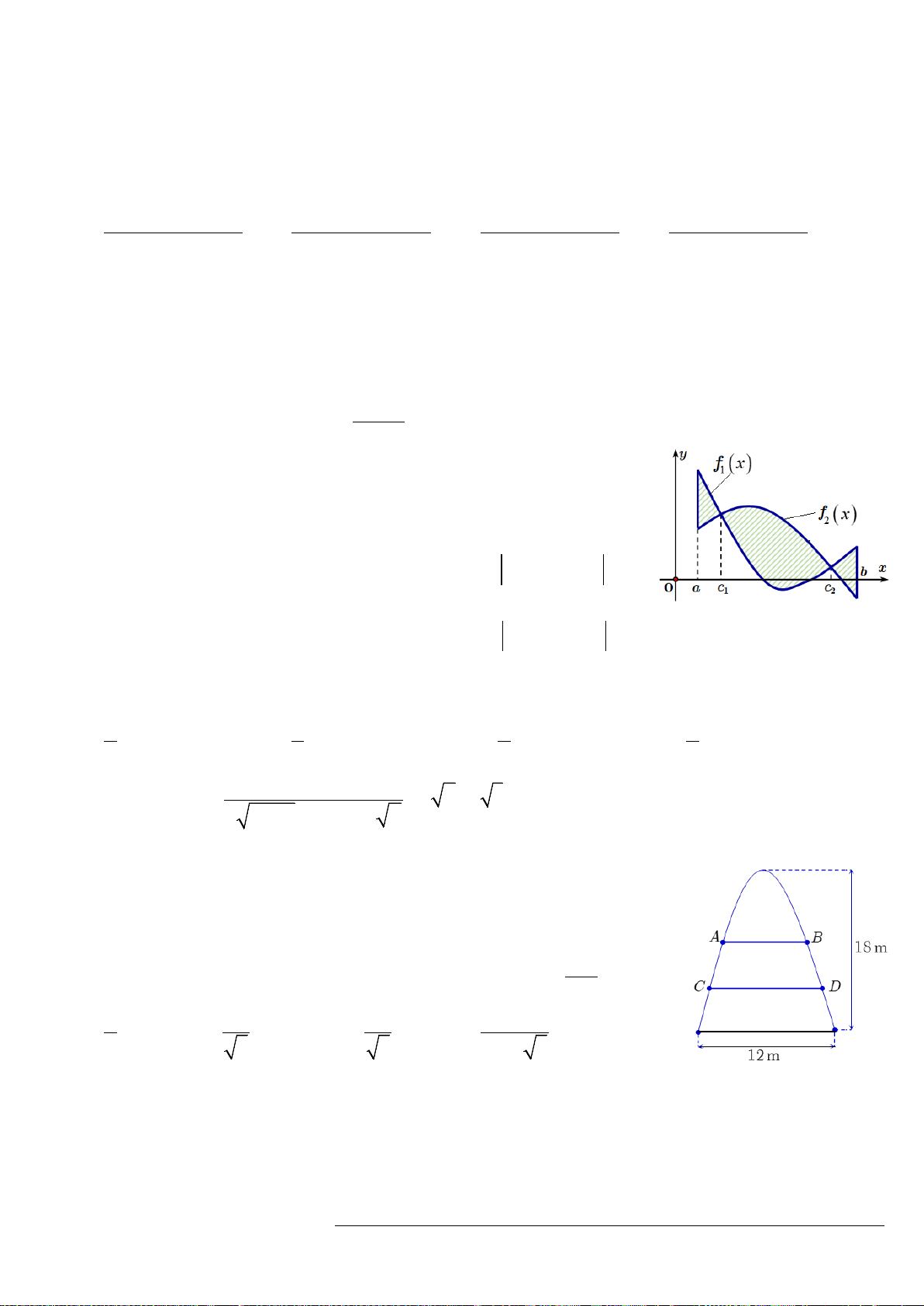
NTC
Trang 3/5
Câu 20. Nhằm giúp đỡ sinh viên có hoàn cảnh khó khăn, Ngân hàng Chính sách xã hội địa phương đã
hỗ trợ bạn sinh viên A vay
20
triệu đồng với lãi suất
12% /
năm và ngân hàng chỉ bắt đầu tính lãi sau
khi bạn A kết thúc khóa học của mình. Bạn A đã hoàn thành khóa học và đi làm với mức lương
5, 5
triệu đồng/tháng, bạn A dự tính sẽ trả hết nợ gốc lẫn lãi suất cho ngân hàng trong
36
tháng. Hỏi số tiền
mỗi tháng mà bạn A phải trả cho ngân hàng là bao nhiêu (triệu)?
A.
2
2
1,12 20 0,12
(1,12 1) 12
B.
3
3
1,12 36 0,12
(1,12 1) 12
C.
2
2
1,12 36 0,12
(1,12 1) 12
D.
3
3
1,12 20 0,12
(1,12 1) 12
Câu 21. Cho
( )d 7
b
a
fx x
và
( )d 3
b
a
gx x
. Tính
[() ()]d
b
a
fx gx x
.
A.
4
B.
10
C.
10
D.
21
Câu 22. Hàm số
( ) cos 3Fx x
là một nguyên hàm của hàm số nào sau đây ?
A.
( ) 3 sin 3fx x
B.
sin 3
()
3
x
fx
C.
( ) sin 3fx x
D.
( ) 3 sin 3fx x
Câu 23. Cho hình phẳng
()
H
giới hạn bởi đồ thị của hai hàm số
12
(), ()
yfxyfx
và hai đường thẳng
,
x ax b
(phần gạch chéo
trên hình). Tìm công thức tính diện tích của hình
()
H
.
A.
12
[() ()]d
b
a
fx fx x
B.
12
() ()d
b
a
fx fx x
C.
21
( )d ( )d
bb
aa
fxx fxx
D.
12
() ()d
b
a
fx fx x
Câu 24. Cho biết
2 22
d
x xx
xe x axe be C
, (với
a
,
b
là các số hữu tỉ). Tính
ab
.
A.
1
4
B.
1
8
C.
1
4
D.
1
8
Câu 25. Cho biết
2
1
d
2 ( 2)
x
a bc
xx x x
, (với
, , *
abc
). Tính
()abc
.
A.
2
B.
8
C.
22
D.
46
Câu 26. Một cổng chào có dạng hình parabol với chiều cao
18 (m)
, bề
rộng chân đế
12 (m)
. Người ta căng hai sợi dây trang trí
AB
và
CD
nằm
song song với mặt đất, đồng thời chia hình giới hạn bởi parabol và mặt đất
thành ba phần có diện tích bằng nhau (như hình vẽ). Tính tỉ số
AB
CD
.
A.
4
5
B.
1
2
C.
3
1
2
D.
3
1 22
Câu 27. Trong mặt phẳng
()
Oxy
, điểm
(2; 3)M
biểu diễn số phức nào sau đây ?
A.
23zi
B.
23zi
C.
32zi
D.
32zi
Câu 28. Cho hai số phức
1
23zi
và
2
35zi
. Tìm tổng phần thực và phần ảo của số phức
12
wz z
.
A.
0
B.
3
C.
3
D.
12i

NTC
Trang 4/5
Câu 29. Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
4 11 0zz
. Tính
22
12
2zz
.
A.
14
B.
18
C.
22
D.
33
Câu 30. Gọi
w
là số phức tùy ý thỏa
| | 2z
. Biết tập hợp điểm biểu diễn số phức
3 12zw i
là
một đường tròn. Tìm tâm và bán kính của đường tròn đó.
A.
(1; 2)I
và
2R
B.
( 1; 2)
I
và
2R
C.
(1; 2)I
và
6R
D.
( 1; 2)I
và
6R
Câu 31. Cho hai số phức
1
z
,
2
z
thỏa mãn
11 2
5
1 2 3 3 2 1 17
2
z iz i z i
. Tìm giá
trị lớn nhất của biểu thức
12 1
12
Pzz z i
.
A.
2 17
B.
3 41
C.
17 41
D.
17 41
Câu 32. Tìm tiêu cự của elip
22
( ) : 4 8 32
Ex y
.
A.
2
B.
4
C.
23
D.
42
Câu 33. Hình chóp
.S ABCD
có đáy là hình chữ nhật với
& 2AB a AD a
. Biết
()
SA BCD
,
góc giữa
& ( )SC ABD
bằng
60
. Thể tích khối chóp
.S ABCD
đã cho.
A.
3
3
a
B.
3
2a
C.
3
32a
D.
3
6a
Câu 34. Hình chóp
.
S ABCD
có đáy là hình vuông cạnh bằng
a
, chiều cao
SA x
. Tìm
x
để hai
mặt phẳng
( ) & ( )SBC SCD
tạo với nhau một góc
60
.
A.
xa
B.
2
a
x
C.
2xa
D.
3
2
a
x
Câu 35. Cho hình nón có chiều cao
h
, bán kính đáy
r
và độ dài đường sinh
l
. Tìm khẳng định đúng.
A.
xq
S rh
B.
2
xq
S rh
C.
()
tp
S rr l
D.
2
1
.
3
V rh
Câu 36. Tính diện tích toàn phần của hình trụ có bán kính đáy
a
và đường cao
3
a
.
A.
2
3
a
B.
2
(1 3)a
C.
2
2 ( 3 1)a
D.
2
2 (1 3 )a
Câu 37. Xét một hình chữ nhật có các cạnh thay đổi thay đổi và có diện tích bằng
2
961 (m
)
nội tiếp trong một đường tròn. Gọi
S
là diện tích của phần hình phẳng
nằm trong hình tròn nhưng nằm ngoài hình chữ nhật. Tìm giá trị nhỏ nhất của
S
.
A.
2
961 961 ) (m
B.
2
480, 5 961 ) (m
C.
2
1922 961 ) (m
D.
2
1892 946 ) (m
Câu 38. Trong không gian
()Oxyz
, cho ba điểm
(1; 0; 3), (2; 3; 4) & ( 3; 1; 2)AB C
. Tọa độ điểm
D
sao cho tứ giác
ABCD
là hình bình hành.
A.
(4; 2; 9)
B.
(4; 2; 9)
C.
(4; 2; 9)
D.
( 4; 2; 9)
Câu 39. Trong không gian
()Oxyz
, tìm vectơ chỉ phương của đường thẳng
124
( ):
23 1
xyz
d
.
A.
(2; 3; 1)u
B.
(2; 3; 1)u
C.
(1; 2; 4)u
D.
( 1; 2; 4)u
Câu 40. Trong không gian
()Oxyz
, điểm nào sau đây không thuộc mặt phẳng
( ):2 3 1x yz
?
A.
( 2; 1; 8)M
B.
(4; 2; 1)N
C.
(3; 1; 3)P
D.
(1; 2; 5)Q

NTC
Trang 5/5
Câu 41. Trong không gian
()
Oxyz
, tìm phương trình mặt cầu tâm
(1; 1; 1)
I
và tiếp xúc với mặt phẳng
( ) : 2 2 10 0xy z
.
A.
2 22
( 1) ( 1) ( 1) 1xyz
B.
222
( 1) ( 1) ( 1) 3xyz
C.
222
( 1) ( 1) ( 1) 1xyz
D.
2 22
( 1) ( 1) ( 1) 9xyz
Câu 42. Trong không gian
()
Oxyz
, cho ba điểm
(1; 2; 3), ( 4; 2; 5) & ( 2; 2 1; 1)A B Mm n
thẳng
hàng. Tính
()mn
.
A.
2
B.
2
C.
4
D.
4
Câu 43. Trong không gian
()Oxyz
, tìm phương trình mặt phẳng chứa điểm
(1; 2; 3)M
và đường thẳng
( ):
1 11
xyz
d
.
A.
235 0xyz
B.
2 3 5 70xyz
C.
523 0xyz
D.
5 2 3 10
xyz
Câu 44. Trong không gian
()Oxyz
, hai mặt phẳng
( ) & ( )PQ
chứa đường thẳng
2
( ):
2 14
x yz
d
đồng thời tiếp xúc với mặt cầu
2 22
( ) : ( 1) ( 2) ( 1) 2Sx y z
lần lượt tại hai điểm
M
và
N
.
Tính độ dài đoạn thẳng
MN
.
A.
4
B.
22
C.
6
D.
43
3
Câu 45. Có bốn lá thư với nội dung khác nhau được bỏ vào bốn phong bì có ghi bốn địa chỉ khác nhau.
Một em nhỏ vô tình đã lấy bốn lá thư đó ra, tuy nhiên khi bỏ vô lại thì em đó lại không nhớ thư nào cần
bỏ vào phong bì nào, và cuối cùng em ấy lại bỏ một cách ngẫu nhiên bốn lá thư vào bốn phong bì trên.
Tính xác suất để có “ít nhất một lá thư bỏ đúng phong bì như ban đầu”.
A.
1
3
B.
1
4
C.
5
8
D.
1
24
Câu 46. Cho hình lập phương
.ABCD A B C D
có cạnh bằng
a
. Tính số đo góc giữa hai đường
thẳng
BD
và
AD
.
A.
30
B.
45
C.
60
D.
90
Câu 47. Hình chóp
.S ABCD
có đáy là hình vuông, hình chiếu vuông góc của
S
lên mặt phẳng
()
ABC
là trung điểm của
AB
. Biết
3
&
2
a
AB a SD
, tính khoảng cách từ
A
đến
()SBD
.
A.
3
a
B.
2
3
a
C.
3
2
a
D.
3
3
a
Câu 48. Tính số cách xếp
4
học sinh vào một dãy ghế dài có
4
chỗ ngồi.
A.
4
B.
8
C.
16
D.
24
Câu 49. Gọi
S
là tập hợp các số tự nhiên có
3
chữ số khác nhau được tạo thành từ
0; 1; 2; 3; 4{ ; 5}
.
Chọn ngẫu nhiên một số từ tập
S
, tính xác suất để số được chọn có chữ số cuối gấp đôi chữ số đầu.
A.
1
5
B.
2
25
C.
4
5
D.
23
25
Câu 50. Tìm số hạng thứ
10
của một cấp số cộng có số hạng tổng quát là
23
n
un
.
A.
20
B.
23
C.
140
D.
280
NTC
Trang 6/5
ĐÁP ÁN
01A
02A
03D
04B
05B
06D
07B
08C
09B
10C
11A
12B
13C
14B
15D
16C
17D
18B
19A
20D
21A
22D
23B
24D
25B
26C
27B
28C
29D
30C
31C
32B
33B
34C
35C
36D
37B
38D
39B
40C
41D
42B
43C
44D
45C
46C
47B
48D
49B
50B
Bấm Tải xuống để xem toàn bộ.




