Đề thi diễn tập THPT Quốc gia 2019 môn Toán sở GD&ĐT Đồng Tháp

Đề thi diễn tập THPT Quốc gia 2019 môn Toán sở GD&ĐT Đồng Tháp có mã đề 172 (đề gốc), đề được biên soạn theo dạng trắc nghiệm khách quan với 50 câu hỏi và bài toán

20 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

15 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
Trang 1/15 - Mã đề 172
SỞ GIÁO DỤC VÀ ĐÀO TẠO
TỈNH ĐỒNG THÁP
________________
ĐỀ GỐC
(Đề gồm có trang)
THI DIỄN TẬP THPT QUỐC GIA NĂM 2019
Môn: TOÁN
Ngày kiểm tra: 16/5/2019
Thời gian làm bài: 50 phút, không kể thời gian phát đề
Mã đề thi
172
Họ và tên: ……………………………………………..……….. Lớp: ……………
Câu 1. Hàm số
()yfx
với đồ thị như hình vẽ có bao nhiêu điểm cực trị?
A.
3
. B.
1
. C.
2
. D.
4
.
Hướng dẫn giải
3
Câu 2. Cho hàm số
()yfx
có bảng biến thiên như hình vẽ. Tìm mệnh đề đúng?
A. Hàm số
()yfx
đồng biến trên khoảng
(1;1)
.
B. Hàm số
()yfx
nghịch biến trên khoảng
(;1)
.
C. Hàm số
()yfx
đồng biến trên khoảng
(2;2)
.
D. Hàm số
()yfx
nghịch biến trên khoảng .
Hướng dẫn giải
Hàm số đồng biến trên
(1;1)
.
Câu 3. Đường cong trong hình vẽ là đồ thị của hàm số nào?
A.
3
3yx x
. B.
3
3yx x
. C.
2
1yxx
.
D.
42
1yx x
.
Hướng dẫn giải
3
3yx x
Câu 4. Đồ thị hàm số
()yfx
với bảng biến thiên như hình vẽ có tổng số đường tiệm cận ngang và tiệm
cận đứng bằng bao nhiêu?
1;
Trang 2/15 - Mã đề 172
A.
2
. B.
0
. C.
1
. D.
3
.
Hướng dẫn giải
2
Câu 5. Biến đổi biểu thức
2
3
.Aaa
(với
a
là số thực dương khác 1) về dạng lũy thừa với số mũ hữu
tỷ ta được
A.
7
6
Aa
. B.
2
Aa
. C.
Aa
. D.
7
2
Aa
.
Hướng dẫn giải
7
6
Aa
Câu 6. Phương trình
6.4 13.6 6.9 0
xxx

có tập nghiệm
A.
{1,1}S 
. B.
23
{,}
32
S
. C.
{0, 1}S
. D.
{1}S
.
Hướng dẫn giải
{1,1}S 
Câu 7. Họ các nguyên hàm của hàm số
3
2
1
() 4fx x
x

là
A.
4
1
()Fx x C
x

. B.
2
1
() 12Fx x C
x

.
C.
4
1
()Fx x C
x

. D.
42
() lnFx x x C
.
Hướng dẫn giải
4
1
()Fx x C
x

Câu 8. Cho số phức
2
(1 ) (1 2 )zi i
. Số phức
z
có phần ảo là
A.
2
. B.
4
. C.
2
. D.
2i
.
Hướng dẫn giải
2z
Câu 9. Tổng
2
11 1
33 3
n
S  
có giá trị là
A.
1
2
. B.
1
3
. C.
1
4
. D.
1
9
.
Hướng dẫn giải
1
2
S
Câu 10. Cho hình chóp tứ giác
.S ABCD
có đáy
ABCD
là hình vuông cạnh bằng
a
,

SA ABCD
và
3.SA a
Thể tích của khối chóp
.S ABCD
là
A.
3
Va
. B.
3
6Va
. C.
3
3Va
. D.
3
2Va
.
Hướng dẫn giải
Trang 3/15 - Mã đề 172
3
Va
Câu 11. Một khối nón tròn xoay có độ dài đường sinh
13 ( )lcm
và bán kính đáy
5( ).rcm
Khi đó thể
tích khối nón bằng
A.
3
100 ( )Vcm
. B.
3
300 ( )Vcm
.
C.
3
325
()
3
Vcm
. D.
3
20 ( )Vcm
.
Hướng dẫn giải
3
100 ( )Vcm
Câu 12. Trong không gian với hệ toạ độ
,Oxyz
mặt phẳng ()P đi qua các điểm
( 1;0;0)A
,
(0 ; 2 ; 0)B
,
(0 ; 0 ; 2)C
có phương trình là
A.
220
x
yz
. B.
220
x
yz
.
C.
220
x
yz
. D.
220
x
yz
.
Hướng dẫn giải
1
12 2
xyz


220
x
yz
Câu 13. Trong không gian với hệ trục toạ độ
,Oxyz
mặt phẳng đi qua

1;4;3M và vuông góc với trục
Oy
có phương trình là
A.
40y 
. B.
10
x

. C.
30z 
. D.
40y 
.
Hướng dẫn giải
Mặt phẳng cần tìm có VTPT là
(0 ;1; 0)j
nên phương trình mặt phẳng là:
0( 1) 1( 4) 0(z 3) 0 y 4 0xy
.
Câu 14. Tổ hợp chập
k của
n
phần tử được tính bởi công thức
A.
!
!( )!
n
kn k
. B.
!
()!
n
nk
. C.
!
!
n
k
. D.
!n
.
Hướng dẫn giải
Công thức:
!
!( )!
k
n
n
C
kn k
Câu 15. Cho hàm số
()yfx có đồ thị ()yfx
như hình vẽ. Hàm số có bao nhiêu điểm cực trị?
A.
1
. B.
2
. C.
0
. D.
3
.
Hướng dẫn giải
Đạo hàm
()
f
x
đổi dấu khi đi qua chỉ 1 điểm nên có 1 cực trị.
Câu 16. Gọi
,
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1
()
1
x
fx
x
trên đoạn
3; 5
. Khi đó
M
m
bằng
Trang 4/15 - Mã đề 172
A.
1
2
. B.
7
2
. C.
2
. D.
3
8
.
Hướng dẫn giải
3
(3) 2, (5)
2
ff
Vậy
1
2
Mm
.
Câu 17. Cho
5
log 2 m
,
3
log 5 n
. Tính
25 9
log 2000 log 675A 
theo
,.mn
A.
32
A
mn . B. 32
A
mn . C. 32
A
mn . D. 32
A
mn .
Hướng dẫn giải
22
34 32
25 9
53
log 2000 log 675 log (5 .2 ) log (3 .5 )A 
5533
343233
log 5 log 2 log 3 log 5 2
222222
mn
32mn
Câu 18. Đạo hàm của hàm số
2
lnyx x là
A.
2ln
1
x
y
x

. B. 12lnyx
 . C.
2
1
ln
y
x
x

. D. 12lnyxx
 .
Hướng dẫn giải
22
2
( ln ) (ln ) 1 2ln (ln ) 1 lnyx xx x xx x
x


Câu 19. Tập nghiệm
S
của bất phương trình
2
1
5
25
x
x



là
A.
(2 ; )S . B. (1 ; )S . C. (;1)S  . D. (;2)S  .
Hướng dẫn giải
Ta có:
222
1
555222
25
x
xxx
xxx





Câu 20. Hàm số
5
cos
()
sin
x
fx
x
có một nguyên hàm ()Fx bằng
A.
4
1
2019
4sin x

. B.
4
1
2019
4sin x
.
C.
4
4
2018
sin x
. D.
4
4
2018
sin x
.
Hướng dẫn giải
5
cos
()
sin
x
F
xdx
x
. Đặt
554
cos 1
sin cos
sin 4
xdt
txdt xdx dx C
xtt


Vậy một nguyên hàm là:
4
1
4sin
x
Câu 21. Cho hàm số
()yfx liên tục trên
. Nếu
5
1
2() 2fxdx
và
3
1
() 7fxdx
thì
5
3
()
f
xdx
có giá
trị bằng
A.
6
. B.
9
. C.
9
. D.
5
.
Hướng dẫn giải
535 553
113 311
() () () () () () 1 7 6f x dx f x dx f x dx f x dx f x dx f x dx
 
Trang 5/15 - Mã đề 172
Câu 22. Gọi
1
z
là nghiệm phức có phần ảo âm của phương trình
2
230zz. Điểm biểu diễn hình học
của số phức
1
z
là
A.

1; 2M 
. B.
(1; 2)M
. C.
(1; 2)M 
. D.

1; 2
M
i
.
Hướng dẫn giải
2
12
230
12
zi
zz
zi



Nghiệm phức có phần ảo âm là
12 (1;2)ziM
.
Câu 23.
Số phức z thỏa
23z6 0zi i
có phần ảo là
A.
4
. B.
3
. C.
2
. D.
1
.
Hướng dẫn giải
Gọi
(, )zxyixy
. Ta có:
2( ) 3 ( ) 6 0 2 3 6 ( 3 2 1) 0
x
yi i x yi i x y x y i 
2360 3
3210 4
xy x
xy y




Vậy phần ảo là
4.y
Câu 24. Cho hình chóp tứ giác đều
.SABCD
có cạnh đáy bằng
a
và chiều cao bằng
2.a
Diện tích xung
quanh của hình nón đỉnh
S và đáy là hình tròn nội tiếp hình vuông
A
BCD bằng
A.
2
17
4
a
. B.
2
15
4
a
. C.
2
15
2
a
. D.
2
17
2
a
.
Hướng dẫn giải
Theo giả thiết, bán kính hình tròn nội tiếp hình vuông ABCD là
2
a
r
Gọi
M là trung điểm của AB nên
lSM
là độ dài đường sinh của hình chóp.
Gọi
O là tâm của hình vuông ABCD suy ra
22
17
2
a
lSM SO OM
.
Vậy
2
17 17
..
22 4
xq
aa a
Srl


.
Câu 25.
Trong không gian
,Oxyz
cho tam giác
A
BC
với
(4;9; 9),A 
(2 ;12; 2)B
và
(2;1;5)Cm mm
. Tìm giá trị của m để tam giác
A
BC vuông tại .B
A.
4m 
. B.
4m
. C.
3m 
. D.
3m
.
Hướng dẫn giải
Ta có:
(6;7;3), ( 4; 11; 7).BA BC m m m 
 
Mặt khác:
.0BA BC
 
nên
4.m 
Câu 26.
Trong không gian với hệ tọa độ
,Oxyz
cho điểm

2;1;1A và mặt phẳng
():2 2 1 0Pxyz . Mặt cầu tâm
A
tiếp xúc với mặt phẳng ()P có phương trình
A.
222
(2)(1)(1)4xyz
. B.
222
(2)(1)(1)9xyz
.
C.
222
(2)(1)(1)3xyz. D.
222
(2)(1)(1)5xyz.
Hướng dẫn giải
Bán kính mặt cầu là:



2
22
2.2 1 2.1 1
;2
212
rdAP



.
Trang 6/15 - Mã đề 172
Vậy được phương trình mặt cầu:
222
2114xyz
.
Câu 27.
Trong không gian
,Oxyz
đường thẳng đi qua hai điểm
(1 ; 1 ; 2)A
và
(3;2;1)B
có phương
trình tham số là
A.
14
13( )
2
xt
ytt
zt



. B.
43
32( )
1
xt
ytt
zt



.
C.
14
13( )
2
xt
ytt
zt



. D.
4
3( )
12
xt
ytt
zt



.
Hướng dẫn giải
Đường thẳng
d
đi qua hai điểm
1; 1; 2A và
3; 2;1B có vectơ chỉ phương

4;3; 1AB 

hay

4; 3;1u 
.
Phương trình đường thẳng
14
:13
2
x
t
dy t
zt



.
Câu 28.
Gọi d là tiếp tuyến có hệ số góc nhỏ nhất của đồ thị hàm số
32
2
4911.
3
yxxx
Hỏi đường
thẳng
d đi qua điểm nào dưới đây?
A.
2
5;
3
P



. B.
2
5;
3
M



. C.
5
2;
3
P



. D.
5
2;
3
P



.
Hướng dẫn giải
Ta có
2
289yxx

,
48yx


Tiếp tuyến
d có hệ số góc nhỏ nhất là tiếp tuyến tại điểm uốn của đồ thị hàm số
11
2;
3
U



.
Phương trình

11
:22
3
dy y x

17
3
yx
Vậy
d
đi qua điểm
2
5;
3
P



.
Câu 29.
Có bao nhiêu điểm
M
thuộc đồ thị
()C
của hàm số
2
2
x
y
x
sao cho khoảng cách từ điểm
M
đến tiệm cận ngang bằng
5
lần khoảng cách từ
M
đến tiệm cận đứng?
A.
2
. B.
1
. C.
3
. D.
4
.
Hướng dẫn giải
Gọi

2
;
2
a
M
aC
a



với
2a
.
Ta có:

2
24
52 152 5 444
22
a
aaaa
aa
 

.
2
10 2 5
520160
5
aa a

.
Vậy có hai điểm cần tìm.
Trang 7/15 - Mã đề 172
Câu 30. Tìm tất cả các giá trị thực của tham số
m
để phương trình

22
22
(log ) log 3 0xxm
có
nghiệm

1;8 .x
A.
26m
. B.
69m
. C.
36m
. D.
23m
.
Hướng dẫn giải
Đặt
2
tlogx
. Vì

1;8x
nên

0;3t
. Phương trình


2
2
22
log log 3 0xxm
trở thành
22
23 0 23tt m mtt
,

0;3t
. Ta có bảng biến thiên của hàm số
2
23mt t
:
t
m
m
0
3
1
0
3
6
2
Vậy:

2;6m
.
Câu 31. Tính diện tích
S
của miền hình phẳng giới hạn bởi đồ thị của hàm số
32
() ,f x ax bx c
các
đường thẳng
1, 2xx
và trục hoành (miền gạch chéo cho trong hình vẽ).
A.
51
8
S
. B.
52
8
S
. C.
50
8
S
. D.
53
8
S
.
Hướng dẫn giải
Hình phẳng giới hạn bởi đồ thị của hàm số
32
()f x ax bx c
, các đường thẳng
1x 
,
2x
và
trục hoành được chia thành hai phần:
Miền
1
D
là hình chữ nhật có hai kích thước lần lượt là
1
và
3
1
3S
.
Miền
2
D
gồm:

32
1
1; 2
f x ax bx c
y
xx


.

C
đi qua
3
điểm

1;1A
,

0;3B
,

2;1C
nên đồ thị

C
có phương trình

32
13
3
22
fx x x
2
32
2
1
13 27
31d
22 8
Sxx x




.
Vậy diện tích hình phẳng cần tìm là
12
51
8
SS S
.
Trang 8/15 - Mã đề 172
Câu 32. Cho hàm số
()yfx
liên tục trên
0;1
và thỏa mãn

23
6
() 6 .
31
fx xf x
x

Tính
1
0
() .
f
xdx
A.
4
. B.
2
. C.
1
. D.
6
.
Hướng dẫn giải


23
6
6
31
fx xfx
x


1
0
d
f
xx

1
23
0
6d
x
fx x
1
0
6
d
31
x
x
Đặt
32
d3dtx t xx
, đổi cận 00
x
t, 11
x
t.
Ta có:

1
23
0
6d
x
fx x

1
0
2d
f
tt

1
0
2d
f
xx
,
1
0
6
d4
31
x
x
.
Vậy

1
0
d
f
xx

1
0
2d4
f
xx

1
0
d4fxx
Câu 33.
Tìm phần thực và phần ảo của số phức
 
210
11...1.zi i i
A.
Phần thực của z là
31
, phần ảo của z là
33
. B. Phần thực của z là
31
, phần ảo của z là
33i .
C.
Phần thực của z là 33, phần ảo của z là 31. D. Phần thực của z là 33, phần ảo của z là
31i
.
Hướng dẫn giải
Số phức cần tìm là tổng của 10 số hạng đầu tiên của cấp số nhân có số hạng đầu tiên là
1 i
và
công bội
1qi
.
Do đó:








10
10
5
2
1
5
55
11 1
1
.1. .11
111
1.12 1 12.
1 1 32 31 33 .
ii
q
zu i i
qii
ii ii
ii i








 

Câu 34.
Số phức
(, )zabiab
là số phức có môđun nhỏ nhất trong tất cả các số phức thỏa điều
kiện
32ziz i, khi đó giá trị
.zz
bằng
A.
1
5
. B.
5
. C.
3
. D.
3
25
.
Hướng dẫn giải
Gọi
,zabi
khi đó
Ta có:
2
22 22 2
211
(1 2 ) 5 4 1 5
555
ab b b b b b

 


22
1
..
5
zz a b
Câu 35.
Cho hình chóp tam giác đều
.SABC
cạnh đáy bằng
2a
và chiều cao bằng
3.a
Tính khoảng
cách từ tâm
O
của đáy
A
BC
đến một mặt bên.

222
2
32 3 2 1ziz i a b a b 
484 12ab a b
Trang 9/15 - Mã đề 172
A.
30
10
a
. B.
5
2
a
. C.
23
3
a
. D.
10
5
a
.
Hướng dẫn giải
Gọi
d
là khoảng cách từ
O
đến
()mp SBC
.
Ta có:

22
2222
11 1 1910
333
12 3
3
.
32
daaa
a
a




Vậy khoảng cách từ
O
đến mặt bên là:
30
.
10
a
d
Câu 36. Cho hình chóp
.SABCD
có đáy
ABCD
là hình chữ nhật có
2, 4,AB a AD a
()SA ABCD
và cạnh
SC
tạo với đáy góc
o
60 .
Gọi
M
là trung điểm của
,BC
N
là điểm trên
cạnh
AD
sao cho
.DN a
Khoảng cách giữa
MN
và
SB
là
A.
2 285
19
a
. B.
285
19
a
. C.
295
19
a
. D.
8
19
a
.
Hướng dẫn giải
Lấy
K
trên
AD
sao cho
AK a
thì
MN
//

SBK
.
25AC a
.

,dMNSB


,dMN SBK


,dN SBK


2,dASBK
.
Vẽ
AE BK
tại
E
,
AH SE
tại
H
.
Ta có

SAE SBK
,

SAE SBK SE
,
AH SE

AH SBK


,dASBK AH
.
.3SA AC 215a
.
22 2
111
AH SA AE

222
111
SA AK AB


2
22
111
4
215
aa
a


2
22
111
4
215
aa
a

285
19
a
AH

,dMNSB
2285
19
a
.
Câu 37. Cho hình lăng trụ tam giác đều
.
ABC A B C

có tất cả các cạnh bằng
a
. Gọi
,MN
lần lượt là
trung điểm của các cạnh
AB
và
.BC

Mặt phẳng
()AMN
cắt cạnh
BC
tại
.P
Tính thể tích của
khối đa diện
.MBPA B N

A.
3
73
96
a
. B.
3
3
24
a
. C.
3
3
12
a
. D.
3
73
32
a
.
Trang 10/15 - Mã đề 172
Hướng dẫn giải
Khối chóp
.S ABN

có diện tích đáy
2
3
8
a
S
và chiều cao
2ha
nên
3
3
12
SAB N
a
V
. Ta có:
3
13
896
SMBP SA B N
a
VV


.
Vậy:
33 3
3373
12 96 96
aa a
VMBPABN


.
Câu 38.
Cho tứ diện
SABC
có đáy
A
BC
là tam giác vuông tại
B
với
3, 4,
A
BaBCa
()SA ABC
và cạnh bên SC tạo với đáy góc
0
60 . Tính thể tích khối cầu ngoại tiếp
SABC
.
A.
3
500
3
a
V
. B.
3
5
3
a
V
. C.
3
50
3
a
V
. D.
3
3
a
V
.
Hướng dẫn giải
Ta có:
SAC
vuông tại S (*).
()
BC AB
BC SAB BC SB SBC
BC SA
 
vuông tại B (**)
Từ (*) và (**)
Tâm mặt cầu ngoại tiếp khối chóp S.ABC là trung điểm đoạn SC.
Ta có: AC
22
5.
A
BBC a
Mà
0
1
cos60 2 10
2
AC
SC AC a
SC

5
2
SC
R
a
Vậy
3
3
4 500
33
a
VR

.
Câu 39.
Trong không gian với hệ trục tọa độ
,Oxyz
mặt phẳng ():2 5 0Pxyz tiếp xúc với mặt
cầu
22 2
( ) : ( 3) ( 1) ( 2) 24Sx y z tại điểm
(; ;).
M
abc
Tính giá trị biểu thức
.Tabc
A.
2T
. B.
2T 
. C.
10T
. D.
4T 
.
Hướng dẫn giải
Gọi
là đường thẳng qua tâm
(3;1; 2)I
của mặt cầu và vuông góc
()mp P
.
Ta được
32
:1
2
x
t
yt
zt



.
M
là giao điểm của
và
()mp P
.
Xét:
2(32)(1 )(2 )50 2tt t t
Vậy:
(1;3;0) 2.MT
Câu 40.
Trên giá sách có
4
quyển sách Toán,
3
quyển sách Lí và
2
quyển sách HóA. Lấy ngẫu nhiên
3
quyển sách. Tính xác suất sao cho ba quyển lấy ra có ít nhất một quyển sách Toán.
P
S
M
N
C
B
A'
B'
C'
A
Trang 11/15 - Mã đề 172
A.
37
42
. B.
5
42
. C.
10
21
. D.
42
37
.
Hướng dẫn giải
Số phần tử của không gian mẫu
3
9
84nC .
Gọi
A
là biến cố sao cho ba quyển lấy ra có ít nhất một quyển sách Toán
A
là biến cố sao cho ba quyển lấy ra không có sách Toán

3
5
10nA C
.
P
A

1
P
A
10
1
84

37
42
.
Câu 41.
Tìm tất cả các giá trị thực của tham số
m
sao cho đường thẳng đi qua hai điểm cực trị của đồ thị
hàm số
32
73yx mx x
vuông góc với đường thẳng
9
1.
8
yx
A.
5m  . B. 6m  . C. 12m  . D. 10m  .
Hướng dẫn giải
Đạo hàm
2
32 7yxmx

. Đồ thị hàm số có hai điểm cực trị khi
0y
có hai nghiệm phân biệt
2
0210m

.
Hệ số góc đường thẳng đi qua hai điểm cực trị là
22
2142
(21 )
939
km m

.
Ycbt

22
5
29
21 . 1 25
5
98
m
mm
m


.
Câu 42.
Cho hàm số
()yfx
có đạo hàm trên
và có đồ thị hàm số
()yfx
như hình vẽ. Hàm số
(3 )yf x đồng biến trên khoảng nào?
A.
(1;2)
. B.
(2; 1)
. C.
(2 ; )
. D.
(;1)
.
Hướng dẫn giải
Đặt
() (3 )gx f x
ta có
'( ) '(3 )gx f x
Xét
(2;1) 3 (4;5) (3 ) 0 () 0xxfxgx


hàm số
()ygx
nghịch biến trên
(2;1)
Xét
(1;2) 3 (1;4) (3 ) 0 () 0xxfxgx


hàm số
()ygx
đồng biến trên
(1;2)
Câu 43.
Cho hàm số ()yfx xác định trên
và hàm số ()yfx
có đồ thị như hình vẽ. Tìm số điểm
cực trị của hàm số

2
3yfx
.
Trang 12/15 - Mã đề 172
A.
3
. B.
1
. C.
5
. D.
2
.
Hướng dẫn giải
Quan sát đồ thị ta có
()yfx
đổi dấu từ âm sang dương qua
2x 
nên hàm số

yfx
có một
điểm cực trị là
2x 
.
Ta có
 
/
222
2
0
0
'32.'30321
2
31
x
x
yfx xfx x x
x
x





.
Mà
2x 
là nghiệm kép, còn các nghiệm còn lại là nghiệm đơn nên hàm số

2
3yfx
có ba
cực trị.
Câu 44. Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số

42
23 1yx m x m
có ba
điểm cực trị tạo thành một tam giác đều.
A.
3
3
3
2
m 
. B.
3
3
3
2
m 
. C.
3
3
3
2
m 
. D.
3
3
3
2
m 
.
Hướng dẫn giải
Ta có:

3
'4 22 3yx mx
.
2
0
'0
32
2
x
y
m
x

Để hàm số có 3 điểm cực trị thì
32 3
0.
22
m
m

Điểm cực trị của đồ thị hàm số là:

22
3 2 4 8 13 3 2 4 8 13
0; 1 , ; , C ;
24 24
mmm mmm
Am B

 




Ta thấy
AB AC
nên để
ABC
đều thì
AB BC
2
2
12 9 4 3 2
4.
42
mm m






4
32
32
3.
16 2
m
m

33
3
32 23 3.
2
mm
Câu 45.
Một hình trụ có thể tích
3
16 cm
. Khi đó bán kính đáy
R
bằng bao nhiêu để diện tích toàn phần
của hình trụ nhỏ nhất?
A.
2Rcm
.
B.
1, 6Rcm
.
C.
Rcm
.
D.
16
Rcm
.
Hướng dẫn giải
Ta có
2
2
16
16VRh h
R


.
Để ít tốn nguyên liệu nhất thì diện tích toàn phần của lọ phải nhỏ nhất. Ta có:
Trang 13/15 - Mã đề 172
222 2
3
tp
2
32 16 16 16 16
22 2 2 32.. 24SRRhR R R
RRR RR


 .
Dấu “
” xảy ra

2
16
22cmRR
R

.
Câu 46.
Khi xây dựng nhà, chủ nhà cần làm một bể nước (không nắp) bằng gạch có dạng hình hộp có đáy
là hình chữ nhật chiều dài
()dm
và chiều rộng
()rm
với 2.dr Chiều cao bể nước là
()hm
và
thể tích bể là
3
2( ).m Hỏi chiều cao bể nước bằng bao nhiêu thì chi phí xây dựng là thấp nhất?
A.
3
4
()
9
m
. B.
22
()
33
m
. C.
3
3
()
2
m
. D.
3
2
()
3
m
.
Hướng dẫn giải
Gọi
(0)xx
là chiều rộng của đáy suy ra thể tích bể nước là
2
2
1
2. 2Vxh h
x

Diện tích xung quanh hồ và đáy bể là:

22
6
6. 2 2 0Sxhx xx
x

Xét hàm số

2
6
2
f
xx
x

với
0.x
Hàm số đạt giá trị nhỏ nhất tại
3
3
.
2
x
Vậy chiều cao cần xây là

3
2
2
3
11 4
.
9
3
2
hm
x




Câu 47.
Một người mỗi đầu tháng đều đặn gửi vào ngân hàng một khoản tiền T theo hình thức lãi kép với
lãi suất
0,6%
mỗi tháng. Biết đến cuối tháng thứ
15
thì người đó có số tiền là
10
triệu đồng. Hỏi
số tiền T gần với số tiền nào nhất trong các số sau?
A.
635000
. B.
535000
. C.
613000
. D.
643000
.
Hướng dẫn giải
Bài toán tổng quát “Một người, hàng tháng gửi vào ngân hàng số tiền là
a
đồng, biết lãi suất hàng
tháng là
.m
Sau
n
tháng, người tiền mà người ấy có là
 
.1 1.1
n
n
a
Tmm
m



”.
Áp dụng công thức với
15; 0,6%
10000000
n
nm
T


15
10000000.0,6%
635000
10,6% 110,6%
a



đồng
Câu 48.
Cho hình lăng trụ đều
.
A
BC ABC

có tất cả các cạnh bằng
1
. Gọi
,EF
lần lượt là trung điểm
A
A
và ,BB
đường thẳng
CE
cắt đường thẳng CA

tại
E
, đường thẳng
CF
cắt đường thẳng
CB

tại
.F
Thể tích khối đa diện
EFBAEF

bằng
A.
3
6
. B.
3
2
. C.
3
3
. D.
3
12
.
Hướng dẫn giải
Trang 14/15 - Mã đề 172
Thể tích khối lăng trụ đều
.
A
BC A B C

là
.
33
..1
44
ABC A B C ABC
VSAA


.
Gọi
M
là trung điểm
A
B
CM ABB A

 và
3
2
CM
. Do đó, thể tích khối chóp
.C ABFE
là:
..
1
.
3
C ABFE C ABFE
VSCH
113 3
.1. .
322 12

.
Thể tích khối đa diện
A
BCEFC

là:
..
A
B C EFC ABC A B C C ABFE
VV V
 

333
412 6

.
Do
A
là trung điểm
CE

nên:
,'2,'d E BCCB d A BCCB
 
3
2. 3
2

.
'CC F F B F FB C C
SSS

 1
FBC FB C C BCC B
SS S

 .
Thể tích khối chóp
.
E
CC F

là


.
1
., '
3
ECCF CCF
VSdEBCCB


13
.1. 3
33

.
Thể tích khối đa diện
E
FABEF

bằng
.
E
FA B E F E CC F A B C EFC
VVV
  

333
366

.
Câu 49.
Trong không gian với hệ tọa độ
,Oxyz
cho 2 điểm
(0;0; 3), (2;0; 1)AB
và mặt phẳng
():3 8 7 1 0.Pxyz Tìm
(; ;) ()
M
abc P
thỏa mãn
22
2
M
AMB nhỏ nhất, tính
.Tabc
A.
35
183
T 
. B.
131
61
T 
. C.
85
61
T
. D.
311
183
T
.
Hướng dẫn giải
Gọi
I
sao cho
45
20 ;0;
33
IA IB I







2
2
222
2
2
222
22222 222
2.
2.
23 22 3 2
MA MA MI IA MI IA MI IA
MB MB MI IB MI IB MI IB
M
AMBMIIAIBMIIAIBMIIAIB



 
  

Suy ra
22
min
2MA MB
khi
M
I
bé nhất hay
M
là hình chiếu của
I
trên
.
P
M
F'
E'
F
E
B
C
A'
C'
B'
A
Trang 15/15 - Mã đề 172
Tìm được tọa độ
283 104 214 35
;; .
183 183 183 183
MT





Câu 50.
Trong không gian với hệ tọa độ
,Oxyz
cho (1;0;0), (2; 1;2), ( 1;1; 3).AB C Viết phương
trình mặt cầu có tâm thuộc trục
,Oy
đi qua
A
và cắt mặt phẳng
()
A
BC
theo một đường tròn có
bán kính nhỏ nhất.
A.
2
22
15
24
xy z




. B.
2
22
15
24
xy z




.
C.
2
22
19
24
xy z




. D.
2
22
19
24
xy z




.
Hướng dẫn giải
Mặt phẳng

A
BC có phương trình:
10xyz
. Gọi
S là mặt cầu có tâm
IOy
và cắt

A
BC
theo một đường tròn bán kính r nhỏ nhất.
Vì
IOy
nên
0; ;0 ,It
gọi
H
là hình chiếu của
I
lên

A
BC
khi đó là có bán kính đường tròn
giao của

A
BC và
S là
22
.rAH IA IH
Ta có:


22
22 2
1
21 2 22
1, , 1 .
33
3
t
tt tt
IA t IH d I ABC r t
 

Do đó, r nhỏ nhất khi và chỉ khi
1
.
2
t
Khi đó
2
15
0; ; 0 ,
24
IIA



.
Vậy phương trình mặt cầu cần tìm là:
2
22
15
24
xy z




.
------------- HẾT -------------
| 1/15
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
THI DIỄN TẬP THPT QUỐC GIA NĂM 2019 TỈNH ĐỒNG THÁP Môn: TOÁN ________________
Ngày kiểm tra: 16/5/2019 ĐỀ GỐC
Thời gian làm bài: 50 phút, không kể thời gian phát đề
(Đề gồm có t rang) Mã đề thi 172
Họ và tên: ……………………………………………..……….. Lớp: ……………
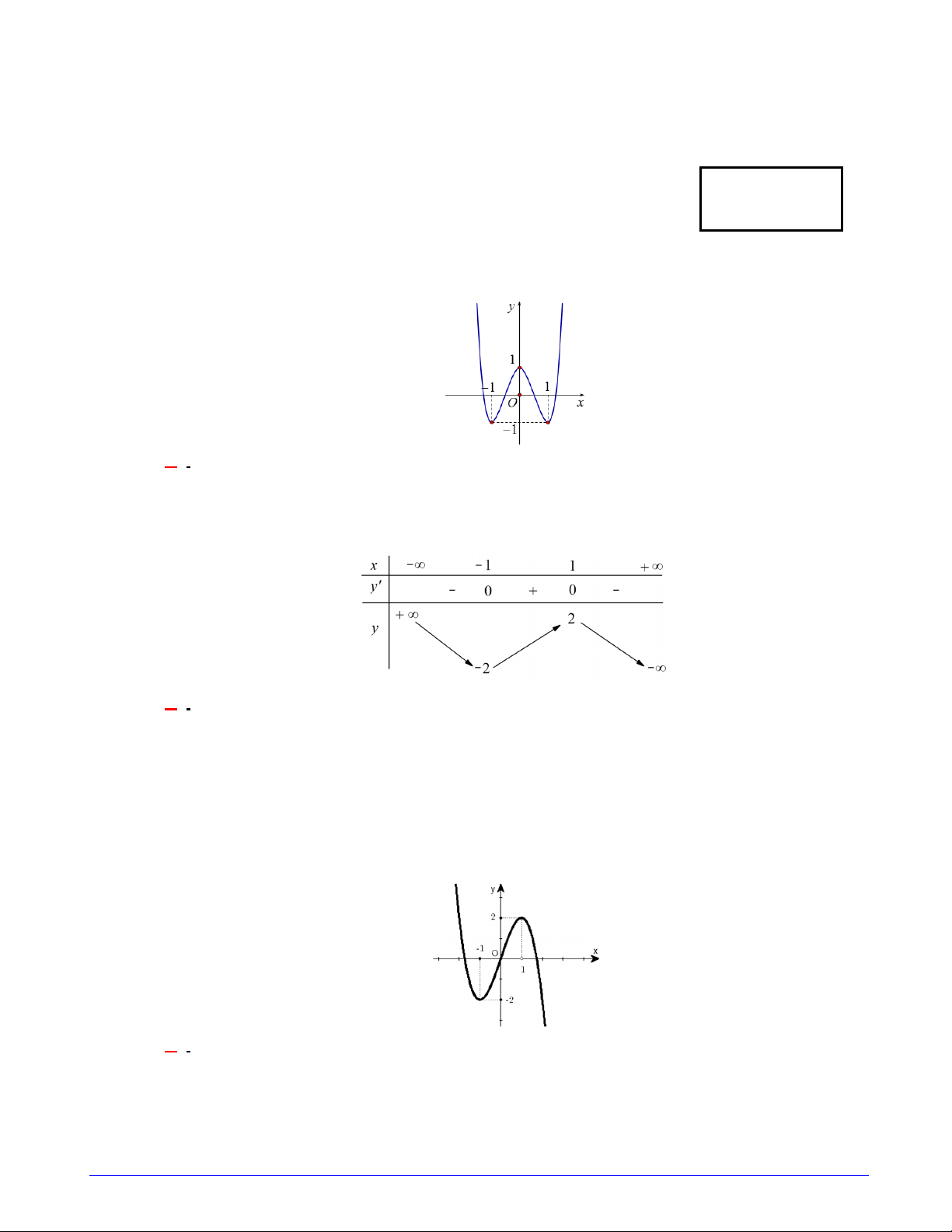
Câu 1. Hàm số y f (x) với đồ thị như hình vẽ có bao nhiêu điểm cực trị? A. 3. B. 1 . C. 2 . D. 4 . Hướng dẫn giải 3
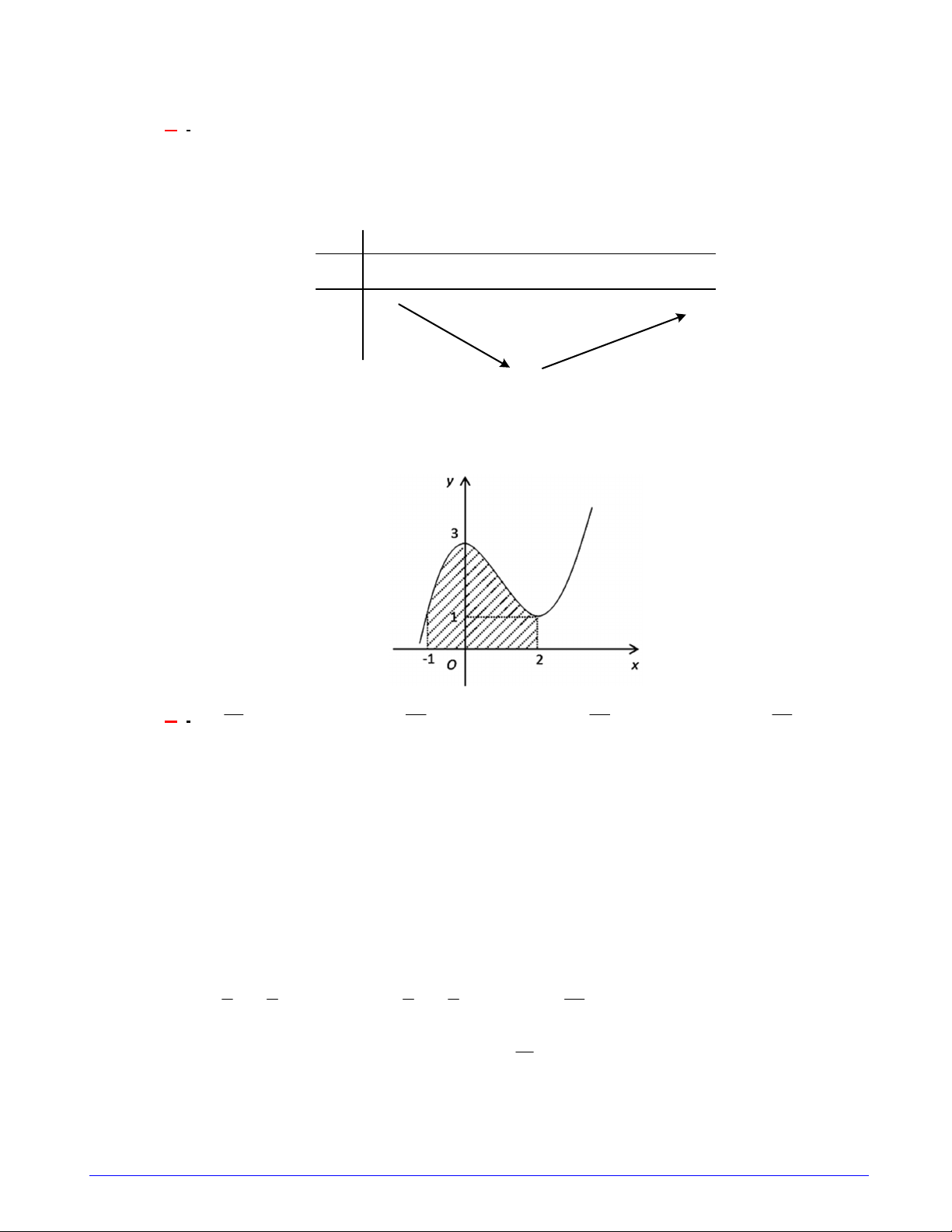
Câu 2. Cho hàm số y f (x) có bảng biến thiên như hình vẽ. Tìm mệnh đề đúng?
A. Hàm số y f (x) đồng biến trên khoảng ( 1  ;1).
B. Hàm số y f (x) nghịch biến trên khoảng ( ;1) .
C. Hàm số y f (x) đồng biến trên khoảng ( 2  ; 2) .
D. Hàm số y f (x) nghịch biến trên khoảng  1  ; . Hướng dẫn giải
Hàm số đồng biến trên (1;1) .
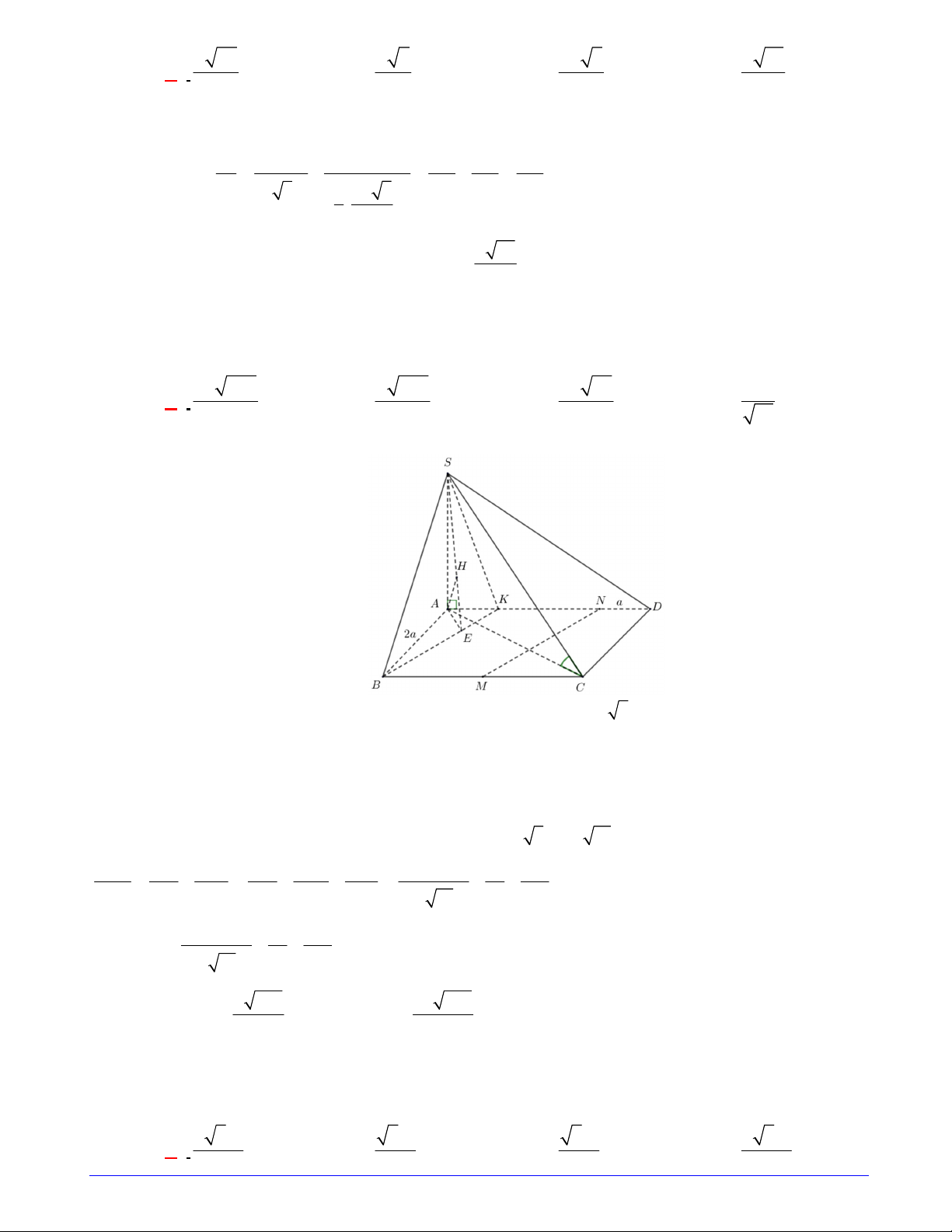
Câu 3. Đường cong trong hình vẽ là đồ thị của hàm số nào? A. 3
y  x  3x . B. 3
y x  3x . C. 2
y  x x 1. D. 4 2
y x x 1. Hướng dẫn giải 3
y  x  3x
Câu 4. Đồ thị hàm số y f (x) với bảng biến thiên như hình vẽ có tổng số đường tiệm cận ngang và tiệm
cận đứng bằng bao nhiêu? Trang 1/15 - Mã đề 172 A. 2 . B. 0 . C. 1 . D. 3. Hướng dẫn giải 2
Câu 5. Biến đổi biểu thức 3 2
A a. a (với a là số thực dương khác 1) về dạng lũy thừa với số mũ hữu tỷ ta được 7 7 A. 6
A a . B. 2
A a .
C. A a . D. 2
A a . Hướng dẫn giải 7 6 A a
Câu 6. Phương trình 6.4x 13.6x 6.9x  
 0 có tập nghiệm 2 3 A. S  { 1  ,1}.
B. S  { , }.
C. S  {0, 1}.
D. S  {1}. 3 2 Hướng dẫn giải S  { 1  ,1} 1
Câu 7. Họ các nguyên hàm của hàm số 3
f (x)  4x  là 2 x A. 4 1
F (x)  x   C . B. 2 1
F (x)  12x   C . x x C. 4 1
F (x)  x   C . D. 4 2
F (x)  x  ln x C . x Hướng dẫn giải 4 1
F (x)  x   C x
Câu 8. Cho số phức 2
z  (1 i) (1 2i) . Số phức z có phần ảo là A. 2 . B. 4 . C. 2 . D. 2i . Hướng dẫn giải z  2 1 1 1
Câu 9. Tổng S     
  có giá trị là 2 3 3 3n 1 1 1 1 A. . B. . C. . D. . 2 3 4 9 Hướng dẫn giải 1 S 2
Câu 10. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng a , SA   ABCD và SA  3 .
a Thể tích của khối chóp S.ABCD là A. 3
V a . B. 3
V  6a . C. 3
V  3a . D. 3
V  2a . Hướng dẫn giải Trang 2/15 - Mã đề 172 3 V a
Câu 11. Một khối nón tròn xoay có độ dài đường sinh l  13 (cm) và bán kính đáy r  5 (cm). Khi đó thể
tích khối nón bằng A. 3
V  100 (cm ) . B. 3
V  300 (cm ) . 325 C. 3 V   (cm ) . D. 3
V  20 (cm ) . 3 Hướng dẫn giải 3
V  100 (cm )
Câu 12. Trong không gian với hệ toạ độ Oxyz, mặt phẳng (P) đi qua các điểm ( A 1  ; 0 ; 0) ,
B(0 ; 2 ; 0) , C(0 ; 0 ;  2) có phương trình là
A. 2x y z  2  0 .
B. 2x y z  2  0 .
C. 2x y z  2  0 .
D. 2x y z  2  0 . Hướng dẫn giải x y z  
 1  2x y z  2  0 1  2 2 
Câu 13. Trong không gian với hệ trục toạ độ Oxyz, mặt phẳng đi qua M 1; 4 ; 3 và vuông góc với trục
Oy có phương trình là
A. y  4  0 .
B. x 1  0 .
C. z  3  0 .
D. y  4  0 . Hướng dẫn giải
Mặt phẳng cần tìm có VTPT là j  (0 ;1; 0) nên phương trình mặt phẳng là:
0(x 1) 1( y  4)  0(z 3)  0  y 4  0 .
Câu 14. Tổ hợp chập k của n phần tử được tính bởi công thức n! n! n! A. . B. . C. . D. n!.
k!(n k)! (n k)! k! Hướng dẫn giải n k ! Công thức: C n
k!(n k)!
Câu 15. Cho hàm số y f (x) có đồ thị y f (
x) như hình vẽ. Hàm số có bao nhiêu điểm cực trị? A. 1 . B. 2 . C. 0 . D. 3. Hướng dẫn giải Đạo hàm f (
x) đổi dấu khi đi qua chỉ 1 điểm nên có 1 cực trị. x 1
Câu 16. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f (x)  trên đoạn x 1
3; 5. Khi đó M m bằng Trang 3/15 - Mã đề 172 1 7 3 A. . B. . C. 2 . D. . 2 2 8 Hướng dẫn giải 3
f (3)  2, f (5)  2 1
Vậy M m  . 2
Câu 17. Cho log 2  m , log 5  n . Tính A  log 2000  log 675 theo , m . n 5 3 25 9
A. A  3  2m n .
B. A  3  2m n .
C. A  3  2m n .
D. A  3  2m n . Hướng dẫn giải 3 4 3 2
A  log 2000  log 675  log (5 .2 )  log (3 .5 ) 2 2 25 9 5 3 3 4 3 2 3 3
 log 5  log 2  log 3  log 5   2m   n  3 2m n 5 5 3 3 2 2 2 2 2 2
Câu 18. Đạo hàm của hàm số 2
y x  ln x là 2ln x 2 A. y  1 .
B. y  1 2ln x .
C. y  1 .
D. y  1 2x ln x . x x ln x Hướng dẫn giải 2 2 2
y  (x  ln x)  x  (ln x)  1 2 ln x(ln x)  1 ln x x   x  1 x
Câu 19. Tập nghiệm S của bất phương trình 2 5    là  25 
A. S  (2 ;  ) .
B. S  (1;  ) .
C. S  ( ;1) .
D. S  ( ; 2) . Hướng dẫn giải    x 1 x Ta có: 2 x2 2 5   5
 5 x x  2  2x x  2    25  cos x
Câu 20. Hàm số f (x) 
có một nguyên hàm F (x) bằng 5 sin x 1 1 A.   2019 . B.  2019 . 4 4sin x 4 4sin x 4 4  C.  2018. D.  2018. 4 sin x 4 sin x Hướng dẫn giải cos x cos x dt 1 F (x)  dx
. Đặt t  sin x dt  cos xdx dx     C   5 sin x 5 5 4 sin x t 4t 1
Vậy một nguyên hàm là:  4 4sin x 5 3 5
Câu 21. Cho hàm số y f (x) liên tục trên  . Nếu 2 f (x)dx  2 
và f (x)dx  7 
thì f (x)dx  có giá 1 1 3 trị bằng A. 6  . B. 9  . C. 9 . D. 5 . Hướng dẫn giải 5 3 5 5 5 3
f (x)dx f (x)dx f (x)dx f (x)dx f (x)dx f (x)dx  1 7  6        1 1 3 3 1 1 Trang 4/15 - Mã đề 172
Câu 22. Gọi z là nghiệm phức có phần ảo âm của phương trình 2
z  2z  3  0 . Điểm biểu diễn hình học 1
của số phức z là 1 A. M  1  ;  2. B. M ( 1  ; 2) . C. M ( 1  ;  2) . D. M  1
 ;  2i . Hướng dẫn giải z  1   2i 2
z  2z  3  0   z  1   2i
Nghiệm phức có phần ảo âm là z  1
  2i M ( 1  ;  2) .
Câu 23. Số phức z thỏa 2z  3iz  6  i  0 có phần ảo là A. 4 . B. 3. C. 2 . D. 1 . Hướng dẫn giải
Gọi z x yi (x, y  ) . Ta có:
2(x yi)  3i(x yi)  6  i  0  2x  3y  6  (3x  2 y 1)i  0
 2x  3y  6  0  x  3     3
x  2y 1  0  y  4
Vậy phần ảo là y  4.
Câu 24. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng 2 . a Diện tích xung
quanh của hình nón đỉnh S và đáy là hình tròn nội tiếp hình vuông ABCD bằng 2  a 17 2  a 15 2  a 15 2  a 17 A. . B. . C. . D. . 4 4 2 2 Hướng dẫn giải a
Theo giả thiết, bán kính hình tròn nội tiếp hình vuông ABCD là r  2
Gọi M là trung điểm của AB nên l SM là độ dài đường sinh của hình chóp. a 17
Gọi O là tâm của hình vuông ABCD suy ra 2 2
l SM SO OM  . 2 2 a a 17  a 17
Vậy S   rl  . .  . xq 2 2 4
Câu 25. Trong không gian Oxyz, cho tam giác ABC với ( A 4
 ; 9 ;  9), B(2 ;12 ;  2) và
C(m  2 ;1 m ; m  5). Tìm giá trị của m để tam giác ABC vuông tại . B A. m  4  .
B. m  4 . C. m  3  .
D. m  3. Hướng dẫn giải  
Ta có: BA  (6; 7; 3), BC  (m  4; m 11; m  7).  Mặt khác: .
BA BC  0 nên m  4. 
Câu 26. Trong không gian với hệ tọa độ Oxyz, cho điểm A2;1;  1 và mặt phẳng
(P) : 2x y  2z 1  0 . Mặt cầu tâm A tiếp xúc với mặt phẳng (P) có phương trình A. 2 2 2
(x  2)  ( y 1)  (z 1)  4 . B. 2 2 2
(x  2)  ( y 1)  (z 1)  9 . C. 2 2 2
(x  2)  ( y 1)  (z 1)  3 . D. 2 2 2
(x  2)  ( y 1)  (z 1)  5 . Hướng dẫn giải 2.2 1 2.11
Bán kính mặt cầu là: r d  ; A P   2 . 2   2 2 2 1  2 Trang 5/15 - Mã đề 172
Vậy được phương trình mặt cầu:  x  2   y  2   z  2 2 1 1  4 .
Câu 27. Trong không gian Oxyz, đường thẳng đi qua hai điểm (1
A ; 1; 2) và B( 3  ; 2 ;1) có phương trình tham số là x 1 4t
x  4  3t   A. y  1
  3t (t  ) . B. y  3
  2t (t  ) . z  2  t   z  1 t  x 1 4tx  4  t   C. y  1
  3t (t  ) . D. y  3
  t (t  ). z  2  t   z  1 2tHướng dẫn giải 
Đường thẳng d đi qua hai điểm A1; 1;
 2 và B3;2; 
1 có vectơ chỉ phương AB   4;  3;  1  hay u  4; 3  ;  1 . x  1 4t
Phương trình đường thẳng d : y  1 3t . z  2 t  2
Câu 28. Gọi d là tiếp tuyến có hệ số góc nhỏ nhất của đồ thị hàm số 3 2
y x  4x  9x 11. Hỏi đường 3
thẳng d đi qua điểm nào dưới đây?  2   2   5   5  A. P 5 ;    . B. M 5  ;   . C. P 2 ;    . D. P 2 ;   .  3   3   3   3  Hướng dẫn giải Ta có 2
y  2x  8x  9 , y  4x  8  11 
Tiếp tuyến d có hệ số góc nhỏ nhất là tiếp tuyến tại điểm uốn của đồ thị hàm số U 2;    .  3 
Phương trình d y y  x   11 : 2 2  17  y x  3 3  2 
Vậy d đi qua điểm P 5;    .  3  x  2
Câu 29. Có bao nhiêu điểm M thuộc đồ thị (C) của hàm số y
sao cho khoảng cách từ điểm M x  2
đến tiệm cận ngang bằng 5 lần khoảng cách từ M đến tiệm cận đứng? A. 2 . B. 1 . C. 3. D. 4 . Hướng dẫn giải a  2  Gọi M ; a  
 C  với a  2.  a  2  a  2 4 Ta có: 5 a  2  1  5 a  2   5 2
a  4a  4  4 . a  2 a  2 10  2 5 2
 5a  20a 16  0  a  . 5
Vậy có hai điểm cần tìm. Trang 6/15 - Mã đề 172
Câu 30. Tìm tất cả các giá trị thực của tham số m để phương trình 2 (log x)  log  2
x  3  m  0 có 2 2 
nghiệm x 1; 8.
A. 2  m  6 .
B. 6  m  9 .
C. 3  m  6 .
D. 2  m  3. Hướng dẫn giải
Đặt t  log x . Vì x 1; 8 nên t 0; 
3 . Phương trình log x2  log  2
x  3  m  0 trở thành 2 2  2 2 2
t  2t  3  m  0  m t  2t  3 , t 0 ; 
3 . Ta có bảng biến thiên của hàm số 2
m t  2t  3 : t 0 1 3 m  0  3 6 m 2
Vậy: m 2;6 .
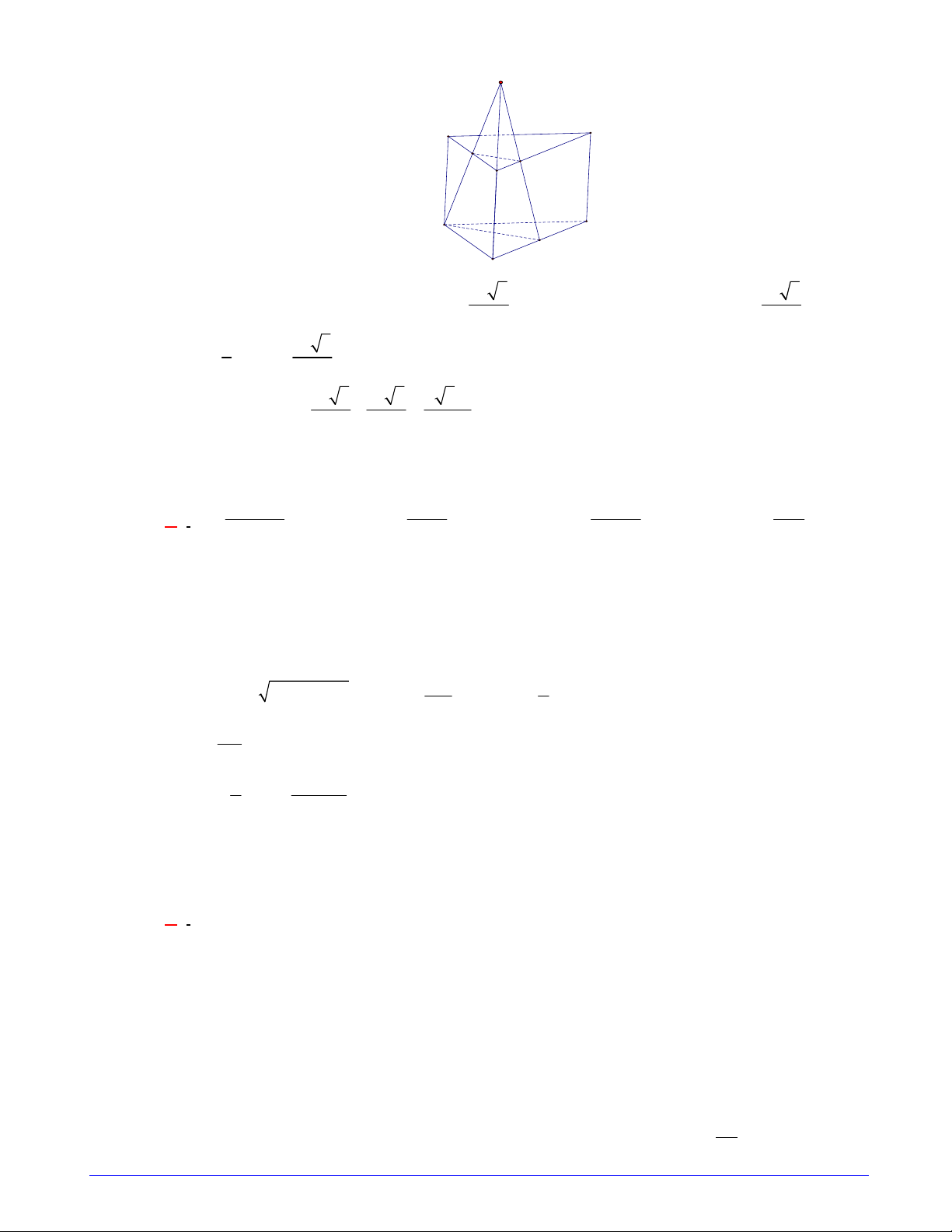
Câu 31. Tính diện tích S của miền hình phẳng giới hạn bởi đồ thị của hàm số 3 2
f (x)  ax bx c, các
đường thẳng x  1,
x  2 và trục hoành (miền gạch chéo cho trong hình vẽ). 51 52 50 53 A. S  . B. S  . C. S  . D. S  . 8 8 8 8 Hướng dẫn giải
Hình phẳng giới hạn bởi đồ thị của hàm số 3 2
f (x)  ax bx c , các đường thẳng x  1  , x  2 và
trục hoành được chia thành hai phần:
Miền D là hình chữ nhật có hai kích thước lần lượt là 1 và 3  S  3. 1 1  f x 3 2
ax bx c
Miền D gồm: y 1 . 2
x  1; x  2 
C đi qua 3 điểm A 1;  
1 , B 0;3 , C 2; 
1 nên đồ thị C  có phương trình 2  1 3  27 f x 1 3 3 2
x x  3 3 2  S
x x  3 1 dx     . 2 2 2  2 2  8 1  51
Vậy diện tích hình phẳng cần tìm là S S S  . 1 2 8 Trang 7/15 - Mã đề 172 6
Câu 32. Cho hàm số y f (x) liên tục trên 0 ;  1 và thỏa mãn 2
f (x)  6x f  3 x   . Tính 3x 1 1 f (x)d . x 0 A. 4 . B. 2 . C. 1. D. 6 . Hướng dẫn giải 1 1 1 6 f x 6 2  6x f  3 x  
f xdx   2 6x f  3 x dx   dx  3x 1 3x 1 0 0 0 Đặt 3 2
t x  dt  3x dx , đổi cận x  0  t  0 , x  1 t 1. 1 1 1 1 6 Ta có: 2 6x f  3 x dx   2 f
 tdt  2 f  xdx, dx  4  . 3x 1 0 0 0 0 1 1 1
Vậy f xdx   2 f
 xdx4  f
 xdx  4 0 0 0
Câu 33. Tìm phần thực và phần ảo của số phức z    i    i2     i10 1 1 ... 1 .
A. Phần thực của z là 31, phần ảo của z là 33. B. Phần thực của z là 31, phần ảo của z là 33i .
C. Phần thực của z là 33, phần ảo của z là 31. D. Phần thực của z là 33, phần ảo của z là 31i . Hướng dẫn giải
Số phức cần tìm là tổng của 10 số hạng đầu tiên của cấp số nhân có số hạng đầu tiên là 1 i và
công bội q  1 i . Do đó: 10 10 1 q   ii z u .
 1 i 1 1  1  5  2 .  .1 1 i    1  1 q 1 1 i   i    
 1 i.12i5  1i 5 5 1 2 .i
 1 i1 32i  31 33 .i
Câu 34. Số phức z a bi (a,b  ) là số phức có môđun nhỏ nhất trong tất cả các số phức thỏa điều
kiện z  3i z  2  i , khi đó giá trị . z z bằng 1 3 A. . B. 5 . C. 3. D. . 5 25 Hướng dẫn giải
Gọi z a bi, khi đó z i z   i a  b  2  a  2  b  2 2 3 2 3 2 1
 4a  8b  4  a  1 2b 2   Ta có: 2 2 2 2 2 2 1 1
a b  (1 2b)  b  5b  4b 1  5 b       5  5 5 1 2 2
z.z a b  . 5
Câu 35. Cho hình chóp tam giác đều S.ABC cạnh đáy bằng 2a và chiều cao bằng a 3. Tính khoảng
cách từ tâm O của đáy ABC đến một mặt bên. Trang 8/15 - Mã đề 172 a 30 a 5 2a 3 a 10 A. . B. . C. . D. . 10 2 3 5 Hướng dẫn giải
Gọi d là khoảng cách từ O đến mp(SBC) . 1 1 1 1 9 10 Ta có:      2 da 32 2 2 2 2   3a 3a 3 1 2 3 a a  .  3 2   a 30
Vậy khoảng cách từ O đến mặt bên là: d  . 10
Câu 36. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB  2a, AD  4a,
SA  (ABCD) và cạnh SC tạo với đáy góc o
60 . Gọi M là trung điểm của BC, N là điểm trên
cạnh AD sao cho DN  .
a Khoảng cách giữa MN và SB là 2a 285 a 285 2a 95 8a A. . B. . C. . D. . 19 19 19 19 Hướng dẫn giải
Lấy K trên AD sao cho AK a thì MN // SBK  . AC  2a 5 .
d MN, SB  d MN,SBK   d N,SBK   2d  ,
A SBK  .
Vẽ AE BK tại E , AH SE tại H .
Ta có SAE  SBK  , SAE SBK   SE , AH SE
AH  SBK   d  ,
A SBK   AH . SA AC. 3  2a 15 . 1 1 1   1 1 1    1 1 1    2 2 2 AH SA AE 2 2 2 SA AK AB  2 2 2 4 2 15 a a a 1 1 1      2 2 2 4 2 15 a a a a 285  a AH   2 285
d MN, SB  . 19 19
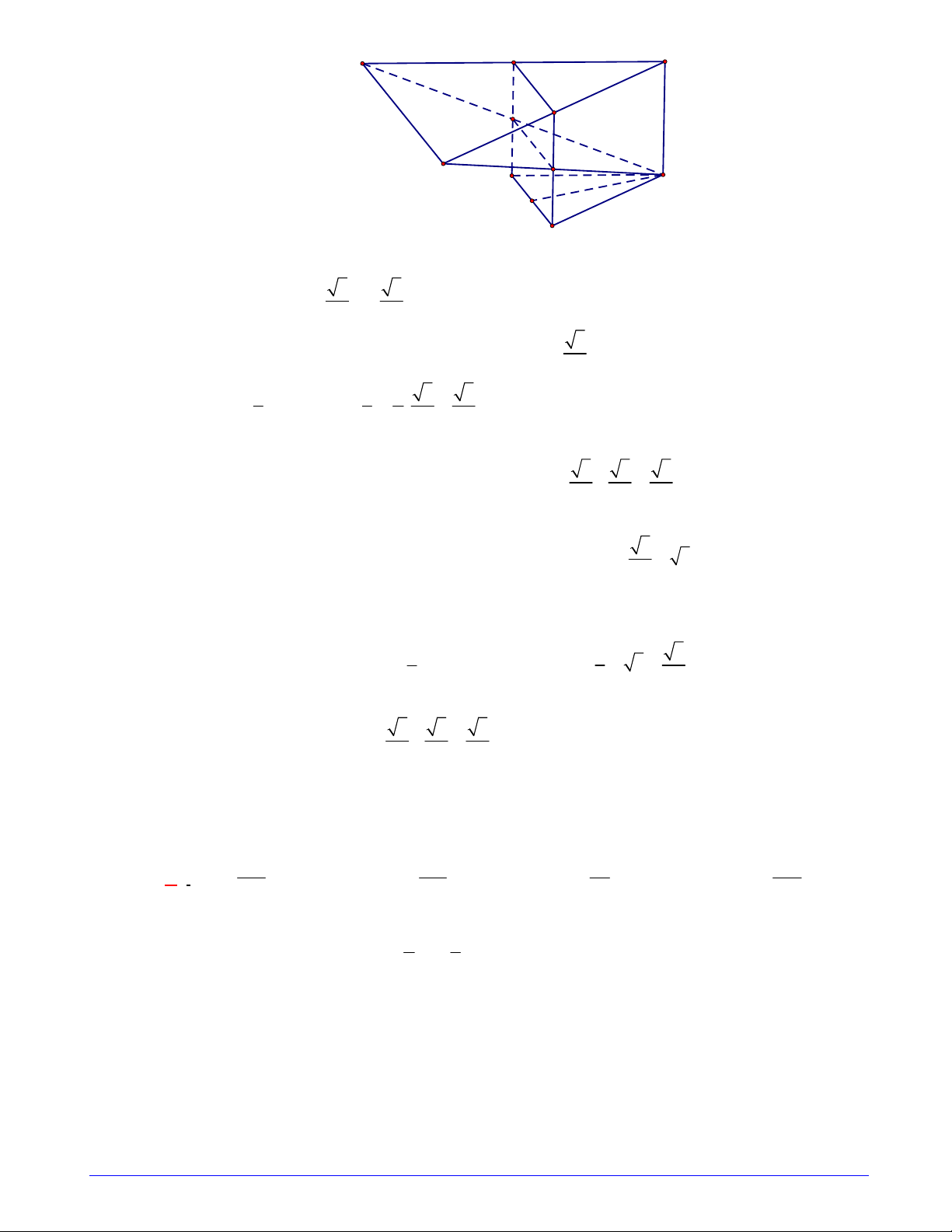
Câu 37. Cho hình lăng trụ tam giác đều ABC.AB C
  có tất cả các cạnh bằng a . Gọi M , N lần lượt là
trung điểm của các cạnh AB và B C
 . Mặt phẳng (AMN) cắt cạnh BC tại .
P Tính thể tích của
khối đa diện MBPAB N  . 3 7 3a 3 3a 3 3a 3 7 3a A. . B. . C. . D. . 96 24 12 32 Trang 9/15 - Mã đề 172 Hướng dẫn giải S A C M P B C' A' N B' 2 a 3 3 a 3
Khối chóp S.A BN
 có diện tích đáy S
và chiều cao h  2a nên V  . Ta có: 8 SAB N  12 3 1 a 3 VV  . SMBP 8 SAB N 96 3 3 3 a 3 a 3 7 3a
Vậy: VMBPAB N     . 12 96 96
Câu 38. Cho tứ diện SABC có đáy ABC là tam giác vuông tại B với AB  3a, BC  4a, SA  ( ABC)
và cạnh bên SC tạo với đáy góc 0
60 . Tính thể tích khối cầu ngoại tiếp SABC . 3 500 a 3 5 a 3 50 a 3  a A. V  . B. V  . C. V  . D. V  . 3 3 3 3 Hướng dẫn giải Ta có: SAC  vuông tại S (*). BC AB
BC  (SAB)  BC SB S
BC vuông tại B (**) BC   SA
Từ (*) và (**)  Tâm mặt cầu ngoại tiếp khối chóp S.ABC là trung điểm đoạn SC. AC 1 Ta có: AC 2 2
AB BC  5 . a Mà 0
 cos 60   SC  2AC  10a SC 2 SCR   5a 2 3 4 500 a Vậy 3 V   R  . 3 3
Câu 39. Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng (P) : 2x y z  5  0 tiếp xúc với mặt cầu 2 2 2
(S) : (x  3)  ( y 1)  (z  2)  24 tại điểm M (a ; b ; c). Tính giá trị biểu thức
T a b  . c
A. T  2 .
B. T  2 .
C. T  10 .
D. T  4 . Hướng dẫn giải
Gọi  là đường thẳng qua tâm I (3;1;  2) của mặt cầu và vuông góc mp(P) .
x  3  2t
Ta được  :  y 1 t . M là giao điểm của  và mp(P) . z  2   t
Xét: 2(3  2t)  (1 t)  (2  t)  5  0  t  2
Vậy: M (1; 3 ; 0)  T  2.
Câu 40. Trên giá sách có 4 quyển sách Toán, 3 quyển sách Lí và 2 quyển sách HóA. Lấy ngẫu nhiên 3
quyển sách. Tính xác suất sao cho ba quyển lấy ra có ít nhất một quyển sách Toán. Trang 10/15 - Mã đề 172 37 5 10 42 A. . B. . C. . D. . 42 42 21 37 Hướng dẫn giải
Số phần tử của không gian mẫu n  3  C  84 . 9
Gọi A là biến cố sao cho ba quyển lấy ra có ít nhất một quyển sách Toán
A là biến cố sao cho ba quyển lấy ra không có sách Toán  nA 3  C 10 . 5
P A 1 10
P A 1 37  . 84 42
Câu 41. Tìm tất cả các giá trị thực của tham số m sao cho đường thẳng đi qua hai điểm cực trị của đồ thị 9 hàm số 3 2
y x mx  7x  3 vuông góc với đường thẳng y x 1. 8 A. m  5  . B. m  6  . C. m  12  . D. m  10  . Hướng dẫn giải Đạo hàm 2
y  3x  2mx  7 . Đồ thị hàm số có hai điểm cực trị khi y  0 có hai nghiệm phân biệt 2
   0  m  21  0 . 2 14 2
Hệ số góc đường thẳng đi qua hai điểm cực trị là 2 2 k   m   (21 m ) . 9 3 9 2 9 m  5 Ycbt   2 21 m  2 .  1   m  25  . 9 8 m   5 
Câu 42. Cho hàm số yf (x) có đạo hàm trên  và có đồ thị hàm số yf (
x) như hình vẽ. Hàm số
y f (3  x) đồng biến trên khoảng nào? A. ( 1  ; 2). B. ( 2  ; 1).
C. (2 ;  ) .
D. ( ;1) . Hướng dẫn giải
Đặt g(x)  f (3  x) ta có g '(x)   f '(3  x)
Xét x  (2; 1)  3  x  (4;5)  f (
 3  x)  0  g (x)  0
 hàm số y g(x) nghịch biến trên (2;1)
Xét x  (1; 2)  3  x  (1; 4)  f (
 3  x)  0  g (x)  0
 hàm số y g(x) đồng biến trên (1;2)
Câu 43. Cho hàm số y f (x) xác định trên  và hàm số y f (
x) có đồ thị như hình vẽ. Tìm số điểm
cực trị của hàm số y f  2 x  3 . Trang 11/15 - Mã đề 172 A. 3. B. 1 . C. 5 . D. 2 . Hướng dẫn giải
Quan sát đồ thị ta có y f (
x) đổi dấu từ âm sang dương qua x  2
 nên hàm số y f x có một
điểm cực trị là x  2  . x  0 x  0 /  Ta có y '  f   2
x  3  2 .x f '   2x 3 2
 0  x  3  2     x  1   .  2 x  3  1 x  2   Mà x  2
 là nghiệm kép, còn các nghiệm còn lại là nghiệm đơn nên hàm số y f  2 x  3 có ba cực trị.
Câu 44. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 4
y x   m   2 2
3 x m 1 có ba
điểm cực trị tạo thành một tam giác đều. 3 3 3 3 A. 3 m   3 . B. 3 m   3 . C. 3
m    3 . D. 3
m    3 . 2 2 2 2 Hướng dẫn giải x  0 Ta có: 3
y '  4x  22m  3 x . y ' 0    3  2m 2 x   2 3  2m 3
Để hàm số có 3 điểm cực trị thì  0  m  . 2 2
 Điểm cực trị của đồ thị hàm số là: 2 2            
A m   3 2m 4m 8m 13 3 2m 4m 8m 13 0; 1 , B  ; ,C  ;   2 4   2 4      2 2
12m  9  4m  3  2m
Ta thấy AB AC nên để ABC đều thì AB BC     4. 4 2     m4 3 2 3  2m   3 3. 3 3
 3  2m  2 3  m   3. 16 2 2
Câu 45. Một hình trụ có thể tích 3
16 cm . Khi đó bán kính đáy R bằng bao nhiêu để diện tích toàn phần
của hình trụ nhỏ nhất? 16
A. R  2 cm .
B. R  1,6 cm .
C. R   cm . D. R cm . Hướng dẫn giải 16 Ta có 2
V   R h  16  h  . 2 R
Để ít tốn nguyên liệu nhất thì diện tích toàn phần của lọ phải nhỏ nhất. Ta có: Trang 12/15 - Mã đề 172 32 16 16 16 16 2 2 2 2 3
S  2 R  2 Rh  2 R   2 R    3 2 R . .  24 . tp 2 R R R R R 16 Dấu “  ” xảy ra 2  2 R
R  2cm . R
Câu 46. Khi xây dựng nhà, chủ nhà cần làm một bể nước (không nắp) bằng gạch có dạng hình hộp có đáy
là hình chữ nhật chiều dài d (m) và chiều rộng r (m) với d  2r. Chiều cao bể nước là h (m) và thể tích bể là 3
2(m ). Hỏi chiều cao bể nước bằng bao nhiêu thì chi phí xây dựng là thấp nhất? 4 2 2 3 2 A. 3 (m) . B. (m) . C. 3 (m) . D. 3 (m) . 9 3 3 2 3 Hướng dẫn giải 1
Gọi x (x  0) là chiều rộng của đáy suy ra thể tích bể nước là 2
V  2x .h  2  h  2 x 6
Diện tích xung quanh hồ và đáy bể là: 2 2 S  6 .
x h  2x   2x x  0 x 6 3
Xét hàm số f x 2
  2x với x  0.Hàm số đạt giá trị nhỏ nhất tại 3 x  . x 2 1 1 4
Vậy chiều cao cần xây là 3 h    m . 2   2 x 9  3  3    2 
Câu 47. Một người mỗi đầu tháng đều đặn gửi vào ngân hàng một khoản tiền T theo hình thức lãi kép với
lãi suất 0,6% mỗi tháng. Biết đến cuối tháng thứ 15 thì người đó có số tiền là 10 triệu đồng. Hỏi
số tiền T gần với số tiền nào nhất trong các số sau? A. 635000. B. 535000 . C. 613000. D. 643000. Hướng dẫn giải
Bài toán tổng quát “Một người, hàng tháng gửi vào ngân hàng số tiền là a đồng, biết lãi suất hàng a tháng là .
m Sau n tháng, người tiền mà người ấy có là T  .  m    m n 1 n 1 .1  m   ”.
n 15;m  0,6%
Áp dụng công thức với  T  10000000  n 10000000.0,6%  a   635000 đồng
1 0,6%15 11 0,6%  
Câu 48. Cho hình lăng trụ đều ABC.AB C
  có tất cả các cạnh bằng 1. Gọi E, F lần lượt là trung điểm
AA và BB , đường thẳng CE cắt đường thẳng C A
  tại E , đường thẳng CF cắt đường thẳng C B
  tại F . Thể tích khối đa diện EFB A  E F   bằng 3 3 3 3 A. . B. . C. . D. . 6 2 3 12 Hướng dẫn giải Trang 13/15 - Mã đề 172 E' A' C' E B' F' F A C M B
Thể tích khối lăng trụ đều ABC.A BC   là 3 3 V        S .AA .1 . ABC.A B C ABC 4 4 3
Gọi M là trung điểm AB CM   ABB A   và CM
. Do đó, thể tích khối chóp C.ABFE 2 1 là: V  1 1 3 3 S .CH  .1. .  . C.ABFE C. 3 ABFE 3 2 2 12
Thể tích khối đa diện AB CEFC là: V   3 3 3       V    V . A B C EFC ABC.A B C C.ABFE 4 12 6
Do A là trung điểm C E   nên:
d E ,BCC B  '  3
2d A ,BCC B  '  2.  3 . 2 S         S S S S   S   1. CC F F B'F FB CCFBC FB C C BCC B
Thể tích khối chóp E .CC F   là 1 1 3 V        
S  .d E , BCC B ' .1. 3 . E .CC F CC F    3 3 3
Thể tích khối đa diện EFAB EF   bằng 3 3 3 V          V    V . EFA B E F E .CC F AB CEFC  3 6 6
Câu 49. Trong không gian với hệ tọa độ Oxyz, cho 2 điểm (
A 0 ; 0 ;  3), B(2 ; 0 ; 1) và mặt phẳng
(P) : 3x  8y  7z 1  0. Tìm M (a ; b ; c)  (P) thỏa mãn 2 2
MA  2MB nhỏ nhất, tính
T a b  . c 35 131 85 311 A. T   . B. T   . C. T  . D. T  . 183 61 61 183 Hướng dẫn giải    4 5 
Gọi I sao cho IA  2IB  0  I ;0;     3 3  2     2
MA MA  MI IA2 2 2
MI IA  2MI.IA 2     2
MB MB  MI IB2 2 2
MI IB  2MI.IB
   2 2 2 2 2
MA  2MB  3MI IA  2IB  2MI IAIB 2 2 2
 3MI IA  2IB Suy ra  2 2
MA  2MB  khi MI bé nhất hay M là hình chiếu của I trên P. min Trang 14/15 - Mã đề 172  283 1  04 214  35
Tìm được tọa độ M ; ;  T   .    183 183 183  183
Câu 50. Trong không gian với hệ tọa độ Oxyz, cho (
A 1; 0 ; 0), B(2 ; 1; 2), C( 1
 ;1;  3). Viết phương
trình mặt cầu có tâm thuộc trục Oy, đi qua A và cắt mặt phẳng ( ABC) theo một đường tròn có
bán kính nhỏ nhất. 2  1  5 2  1  5 A. 2 2 x y   z    . B. 2 2 x y   z    .  2  4  2  4 2  1  9 2  1  9 C. 2 2 x y   z    . D. 2 2 x y   z    .  2  4  2  4 Hướng dẫn giải
Mặt phẳng  ABC có phương trình: x y z 1  0 . Gọi S  là mặt cầu có tâm I Oy và cắt
ABC theo một đường tròn bán kính r nhỏ nhất.
Vì I Oy nên I 0;t;0, gọi H là hình chiếu của I lên  ABC khi đó là có bán kính đường tròn
giao của  ABC và S  là 2 2
r AH IA IH . t 1 t  2t 1 2t  2t  2
Ta có: IA t 1, IH d I, ABC 2 2 2 2 2 
r t 1  . 3 3 3 1  1  5
Do đó, r nhỏ nhất khi và chỉ khi t  . Khi đó 2 I 0; ;0 , IA    . 2  2  4 2  1  5
Vậy phương trình mặt cầu cần tìm là: 2 2 x y   z    .  2  4
------------- HẾT ------------- Trang 15/15 - Mã đề 172