Đề thi HK2 Toán 10 năm 2018 – 2019 trường Lê Hồng Phong – Khánh Hòa

SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
KIỂM TRA HỌC KỲ II - KHỐI 10
TRƯỜNG THPT LÊ HỒNG PHONG NĂM HỌC 2018-2019 Môn thi: TOÁN Đề thi có 03 trang Ngày thi: 09/5/2019
(Thời gian làm bài: 90 phút, không kể thời gian phát đề) Mã đề 246
Họ và tên thí sinh:……………………………..SBD:…………..Phòng thi:…………
A. PHẦN TRẮC NGHIỆM ( 24 câu – 6 điểm) π
Câu 1. Cho < α < π . Kết quả đúng là: 2
A. sinα > 0; cosα > 0 .
B. sinα < 0 ; cosα < 0 .
C. sinα > 0 ; cosα < 0 .
D. sinα < 0 ; cosα > 0 .
Câu 2. Cho tam giác ABC . Trung tuyến m được tính theo công thức a 2 2 2 2 2 2 2 2 2 2 2 2 A. 2 b c a m + = + . B. 2 b c a m + = − . C. 2 a c b m + = − . D. 2 b c a m + = − . a 2 4 a 2 4 a 2 4 a 4 2 
Câu 3. Đường thẳng đi qua A( 1;
− 2), nhận n = (2; 4
− ) làm véctơ pháp tuyến có phương trình là:
A. x – 2y – 4 = 0.
B. x + y + 4 = 0 . C. – 2
x + y – 4 = 0 .
D. x – 2y + 5 = 0 .
Câu 4. Đường tròn 2 2
x  y 6x8y  0 có bán kính bằng bao nhiêu? A. 10. B. 25. C. 5. D. 10 .
Câu 5. Tìm phương trình chính tắc của elip nếu nó có tiêu cự bằng 6 và trục lớn bằng 10? 2 2 2 2 2 2 2 2
A. x + y =1. B. x y − =1.
C. x + y =1.
D. x + y =1. 25 9 25 16 25 16 100 81 3
 x + 3 > 2x + 3
Câu 6. Tập nghiệm của hệ bất phương trình là: 1   − x > 0 A. S = ( 1; − 0) . B. S = ( 1; − ) 1 .
C. S = (1;+∞) . D. S = (0; ) 1 .
Câu 7. Phương trình tham số của đường thẳng đi qua hai điểm A(2;3); B(3; ) 1 là: x = 3 − t x = 2 + 2t x = 2 + t x = 1 − + 2t A.  . B.  . C.  . D.  . y = 1+ 2t y = 3 + t y = 3 + 2t y = 2 + 3t
Câu 8. Cho bảng xét dấu: x −∞ 2 +∞ f (x) + 0 −
Hàm số có bảng xét dấu như trên là:
A. f (x) =16x −8
B. f (x) = −x − 2
C. f (x) = 8 − 4x
D. f (x) = 2 − 4x
Câu 9. Rút gọn biểu thức sin x + sin 3x A = 2cos x
A. A = sin 4 .x
B. A = sin .x
C. A = sin 2 .x
D. A = cos 2 .x
Câu 10. Cho b < 0 , chọn phép biến đổi đúng
A.bx − b ≤ 0 ⇔ x ≤1.
B.bx − b ≤ 0 ⇔ x ≥1.
C.bx − b ≤ 0 ⇔ x ≤ 1. −
D.bx − b ≤ 0 ⇔ x ≥ 1. − 2 Câu 11. +
Số nghiệm nguyên của bất phương trình x 2x 8 ≤ là x −1 x −1 A. 6 . B. 7 . C. 4 . D. 3 .
Câu 12. Cặp số (1; – )
1 là nghiệm của bất phương trình nào sau đây?
A. x + y – 3 > 0.
B. –x – y < 0.
C. x + 3y +1< 0 .
D. –x – 3y –1< 0 .
Câu 13. Trên đường tròn bán kính r = 20 , độ dài của cung có số đo π rad là: 2
Mã đề 246 -Trang 1/3 A. π l = . B. 40 l = . C. l = 5π .
D.l =10π . 40 π
Câu 14. Chọn khẳng định sai trong các khẳng định sau: A. 2 2
cos 2a = cos a − sin a . B. 2
cos 2a =1− 2cos a . C. 2
cos 2a =1− 2sin a . D. 2
cos 2a = 2cos a −1.
Câu 15. Điểm O(0;0) không thuộc miền nghiệm của hệ bất phương trình nào sau đây?
x + 3y − 6 < 0 x + 3y ≥ 0 x + 3y < 0
x + 3y − 6 < 0 A.  . B.  . C.  . D.  .
2x + y + 4 > 0
2x + y − 4 < 0
2x + y + 4 > 0
2x + y + 4 ≥ 0
Câu 16. Cung có số đo 5π rad đổi sang đơn vị độ bằng 3 A. 0 300 . B. 0 5 . C. 0 600 . D. 0 270 .
Câu 17. Cho tam giác ABC có =  0 =  0
AB 5; A 30 , B = 70 . Độ dài của cạnh BC có giá trị gần nhất với giá trị nào dưới đây A. 2,5. B. 2,6. C. 9,8. D. 5,2.
Câu 18. Cho đường tròn (C) 2
: x + ( y + 2)2 =16 và đường thẳng d : 6x −8y − 46 = 0. Đường thẳng ∆ song
song với đường thẳng d và cắt đường tròn theo một dây cung có độ dài bằng 2 7 . Đường thẳng ∆
chắn trên hai trục tọa độ một tam giác vuông có diện tích bằng A. 15. B. 49 . C. 6. D. 7 . 2 24 3 2 Câu 19. − − + −
Cho hai hàm số f (x) x 4 = và g (x) x 7x 10 =
có tập xác định theo thứ tự lần lượt là 1− x (3− x)2019
D , D . Tập hợp D ∪ D là tập nào sau đây 1 2 1 2 A. [2;4]\{ } 3 . B. [1;5]. C. (2;5]\{ } 3 . D. (1;5].
Câu 20. Cho tan(2a + b + )
1 = 2;tan (b −3a + 2020) =10 . Giá trị của tan(2019 −5a) bằng A. 7 − . B. 7 . C. 8 − . D. 8 . 15 15 21 21
Câu 21. Cho hai điểm A(2;0); B(1;2) . Tập hợp các điểm N thỏa mãn NA = 2NB là đường tròn (C) có
tâm I (a;b) bán kính R . Giá trị của 2
a + b + R thuộc khoảng nào sau đây A. (0; ) 1 . B. (8;9). C. (5;6). D. (6;8).
Câu 22. Cho tan x + cot x = m . Biết 4 4 4 3 2
tan x + cot x = am + bm + cm + dm + e(a,b,c,d,e∈) , tính giá trị
của T = a + b + c + d + e là A. T = 1. − B. T =1. C. T = 2. − D. T = 2. 2
x − 2(2m − 3) x + 4m − 3
Câu 23. Bất phương trình
< 0 có tập nghiệm là tập số thực  khi và chỉ khi 2 −x + 4x − 5 m∈( ;
a b) . Chọn khẳng định đúng
A. b −3a = 0.
B. b − 2a = 0.
C. b + a = 5.
D. b + a = 3.
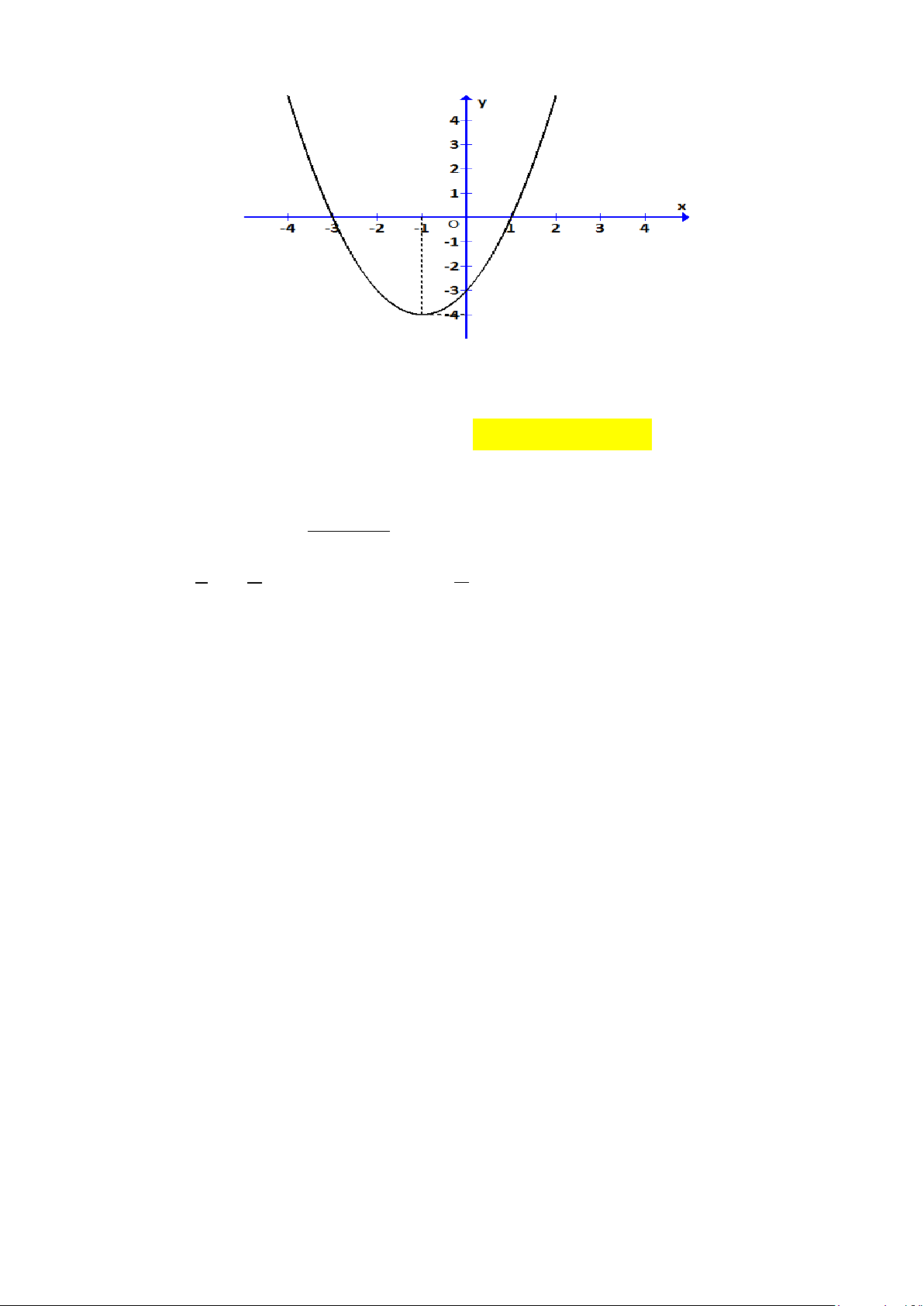
Câu 24. Cho hàm số y = f (x) có đồ thị là parabol ( hình bên)
Mã đề 246 -Trang 2/3
Tập nghiệm S của bất phương trình (x − ) f ( 2 3 . x ) > 0 là A. S = ( ; −∞ 3 − ) ∪(1;3). B. S = ( 1; − ) 1 ∪(3;+∞). C. S = ( 3 − ; ) 1 ∪(3;+∞). D. S = ( ; −∞ − ) 1 ∪(1;3).
B. PHẦN TỰ LUẬN ( 4 điểm)
Bài 1. Giải bất phương trình sau: x − 2 ≥ 0 2 x − 4x + 3 Bài 2. Cho 4 π  π
sin a = với < a < π . Tính cos ; a tan  a − 5 2 6   
Bài 3. Cho tam giác ABC có cạnh = =  0
CB 7, AC 10,C = 60 . Tính cạnh AB và diện tích tam giác ABC.
Bài 4. Viết phương trình đường tròn có đường kính AB với A( 1; − 4), B( 3 − ;6)
----------------HẾT----------------
( Giám thị coi thi không giải thích gì thêm)
Mã đề 246 -Trang 3/3
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
KIỂM TRA HỌC KỲ II - KHỐI 10
TRƯỜNG THPT LÊ HỒNG PHONG NĂM HỌC 2018-2019 Môn thi: TOÁN Đề thi có 03 trang Ngày thi: 09/5/2019
(Thời gian làm bài: 90 phút, không kể thời gian phát đề) Mã đề 357
Họ và tên thí sinh:……………………………..SBD:…………..Phòng thi:…………
A. PHẦN TRẮC NGHIỆM ( 24 câu – 6 điểm)
Câu 1. Tìm phương trình chính tắc của elip nếu nó có tiêu cự bằng 6 và trục lớn bằng 10? 2 2 2 2 2 2 2 2
A. x + y =1.
B. x + y =1.
C. x + y =1. D. x y − = 1. 25 9 25 16 100 81 25 16 3
 x + 3 > 2x + 3
Câu 2. Tập nghiệm của hệ bất phương trình là: 1   − x > 0 A. S = (0; ) 1 . B. S = ( 1; − ) 1 .
C. S = (1;+∞) . D. S = ( 1; − 0) .
Câu 3. Điểm O(0;0) không thuộc miền nghiệm của hệ bất phương trình nào sau đây? x + 3y < 0 x + 3y ≥ 0
x + 3y − 6 < 0
x + 3y − 6 < 0 A.  . B.  . C.  . D.  .
2x + y + 4 > 0
2x + y − 4 < 0
2x + y + 4 > 0
2x + y + 4 ≥ 0
Câu 4. Đường tròn 2 2
x  y 6x8y  0 có bán kính bằng bao nhiêu? A. 10. B. 25. C. 5. D. 10 . 2 +
Câu 5. Số nghiệm nguyên của bất phương trình x 2x 8 ≤ là x −1 x −1 A. 4 . B. 3. C. 6 . D.7 .
Câu 6. Phương trình tham số của đường thẳng đi qua hai điểm A(2;3); B(3; ) 1 là: x = 2 + 2t x = 1 − + 2t x = 2 + t x = 3 − t A.  . B.  . C.  . D.  . y = 3+ t y = 2 + 3t y = 3 + 2t y =1+ 2t
Câu 7. Cho bảng xét dấu: x −∞ 2 +∞ f (x) + 0 −
Hàm số có bảng xét dấu như trên là:
A. f (x) = 8− 4x
B. f (x) =16x −8
C. f (x) = −x − 2
D. f (x) = 2 − 4x
Câu 8. Cho b < 0 , chọn phép biến đổi đúng
A.bx − b ≤ 0 ⇔ x ≤1.
B.bx − b ≤ 0 ⇔ x ≥1.
C.bx − b ≤ 0 ⇔ x ≤ 1. −
D.bx − b ≤ 0 ⇔ x ≥ 1. −
Câu 9. Chọn khẳng định sai trong các khẳng định sau: A. 2
cos 2a =1− 2sin a . B. 2 2
cos 2a = cos a − sin a . C. 2
cos 2a =1− 2cos a . D. 2
cos 2a = 2cos a −1.
Câu 10. Cặp số (1; – )
1 là nghiệm của bất phương trình nào sau đây?
A. x + y – 3 > 0.
B. –x – 3y –1< 0 .
C. –x – y < 0.
D. x + 3y +1< 0 .
Câu 11. Cung có số đo 5π rad đổi sang đơn vị độ bằng 3 A. 0 5 . B. 0 270 . C. 0 600 . D. 0 300 .
Câu 12. Cho tam giác ABC . Trung tuyến m được tính theo công thức a 2 2 2 2 2 2 2 2 2 2 2 2 A. 2 b c a m + = + . B. 2 b c a m + = − . C. 2 a c b m + = − . D. 2 b c a m + = − . a 2 4 a 2 4 a 2 4 a 4 2
Mã đề 357 -Trang 1/3 π
Câu 13. Cho < α < π . Kết quả đúng là: 2
A. sinα > 0; cosα > 0 .
B. sinα < 0 ; cosα < 0 .
C. sinα > 0 ; cosα < 0 .
D. sinα < 0 ; cosα > 0 .
Câu 14. Trên đường tròn bán kính r = 20 , độ dài của cung có số đo π rad là: 2 A. π l = . B. 40 l = . C. l = 5π .
D.l =10π . 40 π
Câu 15. Rút gọn biểu thức sin x + sin 3x A = 2cos x
A. A = sin 4 .x
B. A = sin 2 .x
C. A = cos 2 .x
D. A = sin .x 
Câu 16. Đường thẳng đi qua A( 1;
− 2), nhận n = (2; 4
− ) làm véctơ pháp tuyến có phương trình là:
A. x – 2y + 5 = 0 .
B. x + y + 4 = 0 .
C. x – 2y – 4 = 0 .
D. – x + 2y – 4 = 0 . 2 Câu 17. − − + −
Cho hai hàm số f (x) x 4 = và g (x) x 7x 10 =
có tập xác định theo thứ tự lần lượt là 1− x (3− x)2019
D , D . Tập hợp D ∪ D là tập nào sau đây 1 2 1 2 A.[2;4]\{ } 3 . B.(1;5]. C. (2;5]\{ } 3 . D. [1;5].
Câu 18. Cho tan(2a + b + )
1 = 2;tan (b −3a + 2020) =10 . Giá trị của tan(2019 −5a) bằng A. 8 − . B. 7 7 . C. 8 . D. − . 21 15 21 15
Câu 19. Cho tam giác ABC có =  0 =  0
AB 5; A 30 , B = 70 . Độ dài của cạnh BC có giá trị gần nhất với giá trị nào dưới đây A. 2,5. B. 2,6. C. 9,8. D. 5,2. 2
x − 2(2m − 3) x + 4m − 3
Câu 20. Bất phương trình
< 0 có tập nghiệm là tập số thực  khi và chỉ khi 2 −x + 4x − 5 m∈( ;
a b) . Chọn khẳng định đúng
A. b −3a = 0.
B. b − 2a = 0.
C. b + a = 5.
D. b + a = 3.
Câu 21. Cho tan x + cot x = m . Biết 4 4 4 3 2
tan x + cot x = am + bm + cm + dm + e(a,b,c,d,e∈) , tính giá trị
của T = a + b + c + d + e là A. T = 2. B.T = 1. − C.T = 2. − D.T =1.
Câu 22. Cho hai điểm A(2;0); B(1;2) . Tập hợp các điểm N thỏa mãn NA = 2NB là đường tròn (C) có tâm I ( ;
a b) bán kính R . Giá trị của 2
a + b + R thuộc khoảng nào sau đây A. (0; ) 1 . B. (8;9). C. (5;6). D. (6;8).
Câu 23. Cho đường tròn (C) 2
: x + ( y + 2)2 =16 và đường thẳng d : 6x −8y − 46 = 0. Đường thẳng ∆ song
song với đường thẳng d và cắt đường tròn theo một dây cung có độ dài bằng 2 7 . Đường thẳng ∆
chắn trên hai trục tọa độ một tam giác vuông có diện tích bằng A. 7 . B. 6. C. 49 . D. 15. 3 24 2
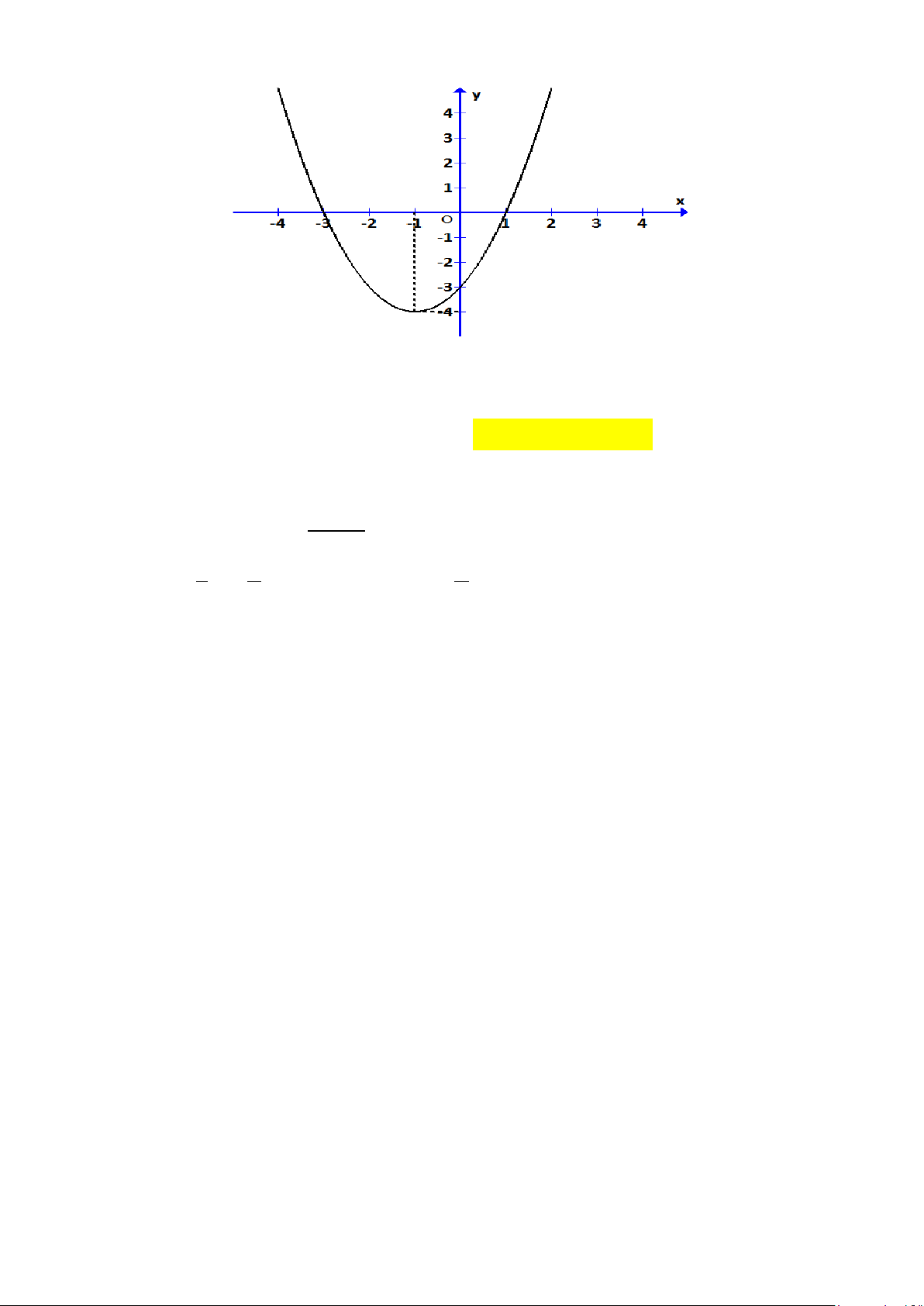
Câu 24. Cho hàm số y = f (x) có đồ thị là parabol ( hình bên)
Mã đề 357 -Trang 2/3
Tập nghiệm S của bất phương trình (x − ) f ( 2 3 . x ) > 0 là A. S = ( ; −∞ 3 − ) ∪(1;3). B. S = ( 1; − ) 1 ∪(3;+∞). C. S = ( 3 − ; ) 1 ∪(3;+∞). D. S = ( ; −∞ − ) 1 ∪(1;3).
B. PHẦN TỰ LUẬN ( 4 điểm)
Bài 1. Giải bất phương trình sau: x −1 ≤ 0 2 x − 2x Bài 2. Cho 3 π  π
sin a = với < a < π . Tính cos ; a tan  a − 5 2 3   
Bài 3 . Cho tam giác ABC có cạnh = =  0
CB 8, AC 10,C =120 . Tính cạnh AB và diện tích tam giác ABC.
Bài 4 .Viết phương trình đường tròn có đường kính AB với A(1;4), B( 3 − ;6)
----------------HẾT----------------
( Giám thị coi thi không giải thích gì thêm)
Mã đề 357 -Trang 3/3
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
KIỂM TRA HỌC KỲ II - KHỐI 10
TRƯỜNG THPT LÊ HỒNG PHONG NĂM HỌC 2018-2019 Môn thi: TOÁN
HƯỚNG DẪN CHẤM-MÃ ĐỀ 246 I. TỰ LUẬN Nội dung Điểm
BÀI 1 .Giải bất phương trình sau: x − 2 ≥ 0 1,0 2 x − 4x + 3
Đk: x ≠ 1, x ≠ 3 2
x − 2 = 0 ⇔ x = 2; x − 4x + 3 = 0 ⇔ x = 1∨ x = 3 BXD x −∞ 1 2 3 +∞ x − 2 - | - 0 + | + 0,25 0,25 2 x − 4x + 3 + 0 - | - 0 + 0,25 VT - || + 0 - || +
Vậy: T = (1,2 ∪(3,+∞  ) 0,25 BÀI 2. π Cho 4 sin 1,0
a = với < a < π . Tính  π cos ; a tan  a  − 5 2 6    2 9 3 cos a 2x 0,25 = ⇒ cos a = − 25 5 tan π − tan a  π  6 48 + 25 3 2x 0,25 tan − a = =  6    π 11 1+ tan . a tan 6
BÀI 3 . Cho tam giác ABC có cạnh = =  0
CB 7, AC 10,C = 60 . Tính cạnh AB và 1,0 diện tích tam giác ABC 2 2 2 = + −  2.CB.
.cos = 49 +100 − 2.7.10.cos60o AB CB AC AC C = 79 0,25 0,25 ⇒ AB = 79 1 =  1 o 35 3 S C .
B AC.sin C = .7.10.sin 60 = 2 2 2 0,25 0,25
BÀI 4 .Viết phương trình đường tròn có đường kính AB với A( 1; − 4), B( 3 − ;6) 1,0 Tâm I ( 2; − 5)  0,25x2 IA = (1;− ) 1 , R = IA = 2
Phương trình đường tròn là: (x + )2 + (y − )2 2 5 = 2 0,50
( Học sinh giải cách khác đúng vẫn cho điểm tương ứng với từng ý của câu)
II. TRẮC NGHIỆM: Mỗi câu đúng được 0,25 điểm Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Đáp án C B D C C D A C C B D C D B C Câu 16 17 18 19 20 21 22 23 24
Đáp án A A B D D C A A B
HƯỚNG DẪN CHẤM - MÃ ĐỀ 357 I. TỰ LUẬN Nội dung Điểm
BÀI 1 .Giải bất phương trình sau: x −1 ≤ 0 1,0 2 x − 2x
Đk x ≠ 0, x ≠ 2 2
x −1 = 0 ⇔ x = 1; x − 2x = 0 ⇔ x = 0 ∨ x = 2 BXD x −∞ 0 1 2 +∞ x −1 - | - 0 + | + 0,25 0,25 2 x − 2x + 0 - | - 0 + 0,25 VT - || + 0 - || +
Vậy T = (−∞,0)∪ 1,  2  ) 0,25 BÀI 2. π Cho 3 sin 1,0
a = với < a < π . Tính  π cos ; a tan  a  − 5 2 3    2 16 4 cos a 2x 0,25 = ⇒ cos a = − 25 5 tan π − tan a  π  3 48 + 25 3 2x 0,25 tan − a = = −  3    π 11 1+ tan . a tan 6
BÀI 3 . Cho tam giác ABC có cạnh = =  0
CB 8, AC 10,C =120 . Tính cạnh AB và 1,0 diện tích tam giác ABC 2 2 2 = + −  2.CB.
.cos = 64 +100 − 2.8.10.cos120o AB CB AC AC C = 244 0,25 0,25 ⇒ AB = 2 61 1 =  1 . .sin = .8.10.sin120o S CB AC C = 20 3 2 2 0,25 0,25
BÀI 4 .Viết phương trình đường tròn có đường kính AB với A(1;4), B( 3 − ;6) 1,0 Tâm I ( 1; − 5)  0,25x2 IA = (2;− ) 1 , R = IA = 5
Phương trình đường tròn là: (x + )2 + (y − )2 1 5 = 5 0,50
( Học sinh giải cách khác đúng vẫn cho điểm tương ứng với từng ý của câu)
II. TRẮC NGHIỆM: Mỗi câu đúng được 0,25 điểm Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Đáp án B A A C B D A B C D D B C D B Câu 16 17 18 19 20 21 22 23 24
Đáp án A B C A A B C C B
SỞ GIÁO DỤC VÀ ĐÀO TẠO KHÁNH HÒA
ĐỀ KIỂM TRA HỌC KỲ II
TRƯỜNG THPT LÊ HỒNG PHONG
NĂM HỌC 2018 – 2019
Môn- lớp: Toán – 10
MA TRẬN NHẬN THỨC Mức nhận thức Chủ đề 1 2 3 4 Cộng TN TL TN TL TN TL TN TL Hệ thức Cho tam lượng Nhận biết giác. Tính Ứng dụng 1,5 trong công thức cạnh và định lí sin điểm tam giác diện tích ( 5 tiết) Số câu: 1 Số câu: 1 Số câu: 1 3 câu - Viết pttq của Quỷ tích đường Nhận biết thẳng đi Viết - Tương
Đường các yếu tố qua điểm phương giao
thẳng, cơ bản của và có trình đường 2,5 đường đường VTPT đường thẳng và điểm tròn, thẳng, - Lập tròn có đường Elip đường tròn phương đường tròn ( 9 tiết) trình kính của elip Số câu: 2 Số câu: 2 Số câu: 1 Số câu: 1 Số câu: 1 7 câu - Biết được -Tìm Giải Bất Tập xác Tìm m; Bất bảng xét nghiệm phương định hàm ứng dụng phương dấu của bpt trình dạng số đồ thị trình, hàm số. chứa thương dấu nhị - Nghiệm điều 2,75 thức, của HBPT. kiện điểm
dấu đa - Phép biến
thức và đổi tương ứng đương. dụng
( 10 tiết ) Số câu: 3 Số câu: 1 Số câu: 1 Số câu: 1 Số câu: 2 8 câu Bất phương - Nghiệm
trình,hệ của hệ bất 0,5 bất PT bậc nhất điểm
phương một ẩn, hai trình ẩn bậc nhất 2 ẩn ( 2 tiết) Số câu: 2 2 câu - Quy đổi góc giữa 2 - Áp đơn vị độ và dụng rad. được - Tính độ CTLG dài cung để tính Lượng tròn. Rút gọn Biến đổi giá trị Biến đổi 3,0 LG giác - Nhận biết biểu thức biểu thức điểm của
( 10 tiết) góc phần tư một -Nhận biết biểu các công thức thức lượng giác Số câu: 4 Số câu: 1 Số câu: 1 Số câu: 1 Số câu: 1 11câu Số câu: 12 Số Số câu: Số 28 câu:4
Số câu: 3 Số câu: 4 Số câu: 1 4 câu: câu Tổng Số Số Số điểm:
điểm: Số điểm: Số điểm: điểm: Số điểm: Số 10,0 3,0 - 30% 1,0 -
3,0 - 30% 1,0- 10% 1,0 - 1,0 – điểm: điểm 10% 10% 10% 0 -0%
Document Outline

• đề 246
• đề 357
• HƯỚNG DẪN CHẤM
• ma trận10 HKI II