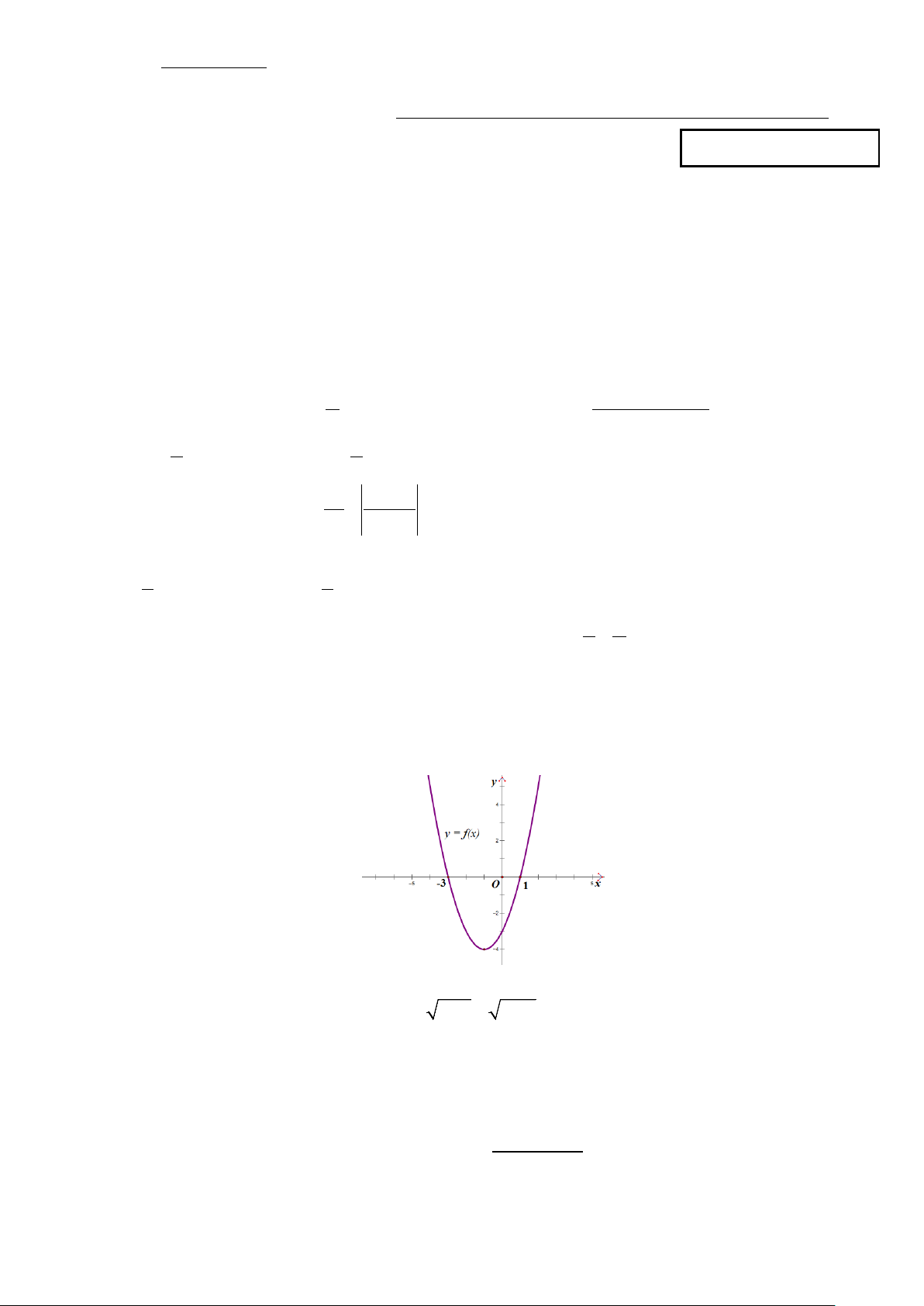
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA CHẤT LƯỢNG HỌC KÌ II BẮC GIANG NĂM HỌC 2019 - 2020
MÔN: TOÁN LỚP 10 THPT
Thời gian làm bài: 90 phút, không kể thời gian giao đề
(Đề gồm có 02 trang) Mã đề: 101
PHẦN I. TRẮC NGHIỆM (5,0 điểm)
Câu 1: Tập hợp nghiệm của bất phương trình 2x + 4 ≤ x + 6 là A. ( ; −∞ 2 − ]. B. ( ;2 −∞ ]. C. [6;+∞). D. [ 6; − +∞).
Câu 2: Tập hợp nghiệm của bất phương trình 2
x + 2x ≤ 0 là A. ( ; −∞ 2
− ]∪[0;+∞) . B. [0;+∞). C. ( 2; − 0). D. [ 2; − 0].
Câu 3: Trong mặt phẳng với hệ trục tọa độ Oxy , cho tam giác ABC với A( 1;
− 3); B(5;4) và C (5;− ) 1 .
Tìm tọa độ trọng tâm G của tam giác ABC . A. G(2; ) 1 . B. G(3;2). C. G(2;3). D. G(9;6).
Câu 4: Cho góc α thỏa mãn π α − α
− < α < 0 và tanα = 2 − . Tính 3cos 2sin P = . 2 3sinα + 2cosα A. 7 P = − . B. 1 P = . C. P = 8. D. P = 2. − 4 4 2
Câu 5: Bất phương trình 2 1 2x −1 4x + +
− 6 ≤ 0 có tập hợp nghiệm là [ ; a b]∪[ ; c d] (với 2 x x a, ,
b c, d ∈ ). Khi đó tổng S = a + b + c + d có giá trị bằng A. 3 − . B. 3 . C. 0. D. 2. 2 2
Câu 6: Trong mặt phẳng với hệ trục tọa độ Oxy , đường thẳng : x y ∆
+ = 1 đi qua điểm nào trong các 3 2 điểm cho dưới đây ? A. M (0;3). B. Q(0;2). C. P(2;0). D. N (3;2).
Câu 7: Cho hàm số bậc hai ( ) 2
f x = ax + bx + c xác định trên và có đồ thị là hình vẽ bên dưới. Tìm tất
cả các giá trị của tham số m để bất phương trình f (x) − m +1≤ 0 nghiệm đúng với x ∀ ∈[ 3 − ; ] 1 .
A. m∈(−∞ ] ;1 . B. m∈(−∞ ) ;1 .
C. m∈[1;+∞).
D. m∈(1;+∞).
Câu 8: Điều kiện xác định của phương trình x −1 + 3− x = 2 là A. x∈[1; ] 3 . B. x∈( ; −∞ ] 3 .
C. x∈[1;+∞). D. x∈(1;3).
Câu 9: Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình 2 2
x −8x + m − 9 = 0 có
hai nghiệm dương phân biệt. Tổng các phần tử của S bằng A. 4. B. 0. C. 4. − D. 12. 2
Câu 10: Cho cos x + sin x ≠ 0. Rút gọn biểu thức 2cos x 1 P − = ta được cos x + sin x
A. P = cos x − sin .x B. P = −cos x − sin .x
C. P = sin x − cos .x D. P = cos x + sin .x Trang 1/2 - Mã đề 101 x = 3 + 2t
Câu 11: Trong mặt phẳng với hệ trục tọa độ Oxy , cho đường thẳng ∆ :
(t ∈). Véctơ có tọa y = 4 − t
độ nào sau đây là một véctơ chỉ phương của đường thẳng ∆ ? A. (2; ) 1 . B. (2;− ) 1 . C. ( 1; − 2). D. (3;4).
Câu 12: Trong mặt phẳng với hệ trục tọa độ Oxy , điểm đối xứng với điểm M ( 1;
− 2) qua gốc tọa độ là điểm nào sau đây ? A. Q(2; ) 1 . B. N (1;2). C. E (2;− ) 1 . D. P(1; 2 − ).
Câu 13: Tập hợp tất cả các giá trị của tham số m để phương trình 2
x − 2mx + 9 = 0 vô nghiệm là A. [ 3 − ; ] 3 . B. ( 6; − 6). C. ( 3 − ;3). D. [ 6; − 6].
Câu 14: Trong mặt phẳng với hệ trục tọa độ Oxy , cho đường tròn (C) 2
: x + ( y − 2)2 = 9 , tọa độ tâm của đường tròn đã cho là A. (0; 2 − ). B. (1;2). C. (2;0). D. (0;2).
Câu 15: Tìm tất cả các giá trị của tham số m để bất phương trình 2 x − 2(m + ) 1 x + 3(m + ) 1 ≥ 0 nghiệm
đúng với mọi x∈ . A. m∈( 1;
− 2). B. m∈( 2; − ] 1 . C. m∈( ; −∞ − ]
1 ∪[2;+∞). D. m∈[ 1; − 2].
Câu 16: Trong mặt phẳng với hệ trục tọa độ Oxy , cho đường thẳng ∆ có phương trình x + 2y − 3 = 0.
Khoảng cách từ điểm M ( 1; − 3
− ) đến đường thẳng ∆ bằng A. 2 5. B. 8 . C. 4 . D. 10. 5 5
Câu 17: Trong mặt phẳng với hệ trục tọa độ Oxy , bán kính R của đường tròn có phương trình 2 2
x + y − 4x + 6y −12 = 0 là A. R = 8. B. R =12. C. R = 5. D. R =1.
Câu 18: Số nghiệm của phương trình 2
3x − 2x + 4 = 2x −1 là A. 3. B. 0. C. 1. D. 2.
Câu 19: Cho tam giác ABC có AB = 3c ; m BC = 5c ; m góc
ABC =120°. Độ dài cạnh AC bằng A. 19c . m
B. ( 34−15 3)c .
m C. ( 34+15 3)c .
m D. 7c . m
Câu 20: Cho góc α thỏa mãn : π 1
0 ≤ α ≤ ; sinα = . Tính cosα . 2 3 A. 2 2 cosα = . B. 2 cosα = . C. 8 cosα = . D. 2 2 cosα = − . 3 3 9 3
PHẦN II. TỰ LUẬN (5,0 điểm)
Câu 1. (3,0 điểm). Giải các bất phương trình sau:
a. 2x − 4 ≤ 0. b. 2
−x − 2x + 3 ≤ x + 3 . −x +1
Câu 2. (1,5 điểm).
Trong mặt phẳng với hệ trục tọa độ Oxy , cho tam giác ABC với A( 1; − )
1 , B(2;5) và C (5;− ) 1 .
a. Viết phương trình tổng quát của đường thẳng ∆ chứa cạnh AB .
b. Viết phương trình đường tròn đường kính AC .
Câu 3. (0,5 điểm). Cho tam giác nhọn ABC có AB = ;
c BC = a;CA = b ; bán kính đường tròn ngoại tiếp
tam giác là R và G là trọng tâm. Đặt = α = β GAC ;GCB
;GBA = γ . Chứng minh rằng: 1 1 1 ( 2 2 2
3 a + b + c ) R + + = . tanα tan β tanγ abc
-------------------------------Hết--------------------------------
Họ và tên học sinh: ............................................. Số báo danh:........................................................... Trang 2/2 - Mã đề 101
Document Outline
- Toan 10 _101




