Đề thi học kỳ 2 Toán 12 năm 2020 – 2021 trường THPT Lê Quý Đôn – Quảng Ngãi

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra học kỳ 2 môn Toán 12 năm học 2020 – 2021 .Mời bạn đọc đón xem.

40 20 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 12

Môn: Toán 12

Thông tin:

20 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Mã đề 132
Trang 1/6
TRƯỜNG THPT LÊ QUÝ ĐÔN
TỔ TOÁN
Đề thi gồm 06 trang
KIỂM TRA HỌC KỲ II NĂM HỌC 2020-2021
Môn: Toán – Lớp 12
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ, tên thí sinh:……………………………………………………
Số báo danh: ………………………………………………………
Câu 1: Chọn khẳng định đúng trong các khẳng định sau.
A.
f x g x dx f x dx g x dx





.
B.
.
f x g x dx f x dx g x dx





.
C.
f x g x dx f x dx g x dx





.
D.
f x g x dx f x dx g x dx





Câu 2: Họ nguyên hàm của hàm số
cos
fx x
trên
là
A.
sin Cx
. B.
cos Cx
. C.
sin Cx
. D.
cos Cx
.
Câu 3: Cho hàm số
(
)
fx
liên tục trên đoạn
[ ]
;ab
và
k
là hằng số tùy ý. Mệnh đề nào dưới đây đúng?
A.
.
bb
aa
k f x dx k f x dx

. B.
..
bb
aa
k f x dx k f x dx

.
C.
..
b bb
a aa
k f x dx kdx f x dx

. D.
.
bb
aa
k f x dx f kx dx

.
Câu 4: Cho hàm số
(
)
fx
liên tục và không âm trên đoạn
[
]
;ab
.
Diện tích của hình thang cong giới hạn bởi đồ thị hàm số
( )
y fx=
, trục hoành và hai đường thẳng
,x ax b= =
được tính theo công thức nào dưới đây? (Hình bên)
A.
b
a
S f x dx
. B.
2
b
a
S f x dx




.
C.
b
a
S f x dx
. D.
b
a
S f x dx
Câu 5: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
;ab
. Diện tích
S
của hình phẳng giới hạn bởi đồ thị
hàm số
( )
fx
, trục hoành và hai đường thẳng
,x ax b= =
được tính theo công thức
A.
b
a
S f x dx
. B.
b
a
S f x dx
. C.
b
a
S f x dx
. D.
b
a
S f x dx
.
Câu 6: Thể tích
V
của khối tròn xoay khi quay hình phẳng giới hạn bởi đồ thị hàm số
( )
y fx=
, trục
Ox
và hai đường thẳng
,x ax b= =
(
ab<
) quanh trục
Ox
được tính theo công thức
A.
2
b
a
V f x dx
. B.
b
a
V f x dx
. C.
b
a
V f x dx
. D.
2
b
a
V f x dx
.
a
b
f(x)
y
x
O
A
B
Mã đề thi 132
Mã đề 132
Trang 2/6
Câu 7: Cho hai hàm số
( )
y fx
=
và
( )
y gx=
liên tục trên đoạn
[
]
;
ab
. Diện tích
S
của hình phẳng
giới hạn bởi hai đồ thị hàm số đó và các đường thẳng
,x ax b= =
được tính theo công thức
A.
b
a
S f x g x dx




. B.
b
a
S f x g x dx
.
C.
b
a
S f x g x dx
. D.
b
a
S f x g x dx




.
Câu 8: Phần ảo của số phức
23zi= +
là
A.
3i
. B.
2
. C.
2i
. D.
3
.
Câu 9: Tính môđun của số phức
( )
,
z a bi a b=+∈
.
A.
22
z ab
. B.
22
za b
. C.
z ab
. D.
z ab
.
Câu 10: Số phức liên hợp của số phức
23zi
= +
là
A.
23i
. B.
32
i
. C.
32i
. D.
23i
.
Câu 11: Trên mặt phẳng tọa độ điểm biểu diễn số phức
12zi
là điểm nào trong các điểm sau? (hình
vẽ bên)
A.
.
M
B.
.
N
C.
.P
D.
.Q
Câu 12: Cho hai số phức
1
23zi= +
và
2
12zi= −
. Tính
12
zz+
A.
3 i
. B.
32i
. C.
35i
. D.
35i
.
Câu 13: Tính số phức
( )
2.z ii= +
A.
12i
. B.
12i
. C.
12i
. D.
12i
.
Câu 14: Tìm tất cả các căn bậc hai của
4−
.
A.
2i
. B.
2
. C.
2
và
2−
. D.
2i
và
2i−
.
Câu 15: Trong không gian Oxyz, tích vô hướng của hai véc tơ
( )
1; 2; 3a = −

và
( )
3;2;1
b
= −−
bằng
A. 2. B. -4. C. 4. D. -2.
Câu 16: Trong không gian Oxyz, điểm nào dưới đây thuộc mặt phẳng
( )
: 2 3 20xyz
α
− + −=
?.
A.
( )
1; 2; 3M −
. B.
( )
1;2;1N −−
. C.
( )
1; 2;1
P
−
. D.
( )
1; 2;1Q −
.
Câu 17: Trong không gian Oxyz, mặt phẳng nào dưới đây song song với mặt phẳng
( )
:2 3 1 0x yz
α
+ −+=
?
A.
4 6 2 20
xyz+ − +=
. B.
2 3 10x yz+ +−=
.
C.
4 6 2 20xyz− − + +=
. D.
5 10xy z+ + +=
.
Câu 18: Trong không gian Oxyz, điểm nào dưới đây không thuộc đường thẳng
11
:
323
x yz
d
−+
= =
?
A. M(1; 0; -1). B. N(4; 2; 2). C. P(7; 4; -7). D. Q(-2; -2; -4).
Mã đề 132
Trang 3/6
Câu 19: Trong không gian Oxyz, đường thẳng
2
:1
2
xt
dy t
zt
= +
= −
=
có một véc tơ chỉ phương
u
là
A.
(
)
1; 1; 0
u = −
. B.
( )
2; 1; 2u =
. C.
(
)
1; 1; 2
u = −
. D.
(
)
2; 1; 0
u
=
.
Câu 20: Trong không gian Oxyz, đường thẳng đi qua điểm M(3; -2; 1) và nhận véc tơ
( )
4; 3; 5u = −
làm
véc tơ chỉ phương có phương trình tham số là
A.
34
23
15
xt
yt
zt
= +
=−−
= +
. B.
43
32
5
xt
yt
zt
= +
=−−
= +
. C.
34
23
15
xt
yt
zt
= +
= −
= +
. D.
34
23
15
xt
yt
zt
= +
=−−
= −
.
Câu 21: Họ tất cả các nguyên hàm của hàm số
2x
fx e
là
A.
2
1
2
x
eC
. B.
2x
eC
. C.
2
2
x
eC
. D.
2
2.
x
xe C
.
Câu 22: Nếu đặt
2
tx
=
thì tích phân
2
2
0
.
x
x e dx
∫
trở thành tích phân nào trong các tích phân sau?
A.
4
0
t
e dt
. B.
2
0
1
2
t
e dt
. C.
4
0
1
2
t
e dt
. D.
2
0
t
e dt
.
Câu 23: Tính tích phân
1
0
2
x
I dx=
∫
A.
2
ln 2
. B.
ln 2
. C.
2.ln 2
. D.
1
ln 2
.
Câu 24: Cho tích phân
3
1
.lnI x xdx=
∫
. Chọn đẳng thức đúng trong các đẳng thức sau
A.
3
2
3
1
1
ln
2
x
I x xdx



. B.
3
2
3
1
1
1
ln
22
x
I x xdx



.
C.
3
3
2
1
1
x lnI x xdx
. D.
3
3
2
1
1
1
x ln
2
I x xdx
.
Câu 25: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
;ac
có đồ thị
như hình vẽ bên, biết
( )
2
b
a
f x dx = −
∫
và
( )
3
c
b
f x dx =
∫
. Tính diện tích
S
của hình phẳng được
tô đậm.
A.
1S
. B.
3.S
C.
5S
. D.
7.S
O
a
b
c
x
y
( )
y fx=
Mã đề 132
Trang 4/6
Câu 26: Tính diện tích
S
hình phẳng giới hạn bởi đồ thị hàm số
2
4yx
= −
, trục hoành và hai đường
thẳng
0, 1xx= =
.
A.
11
3
S 
. B.
8
3
S
. C.
11
3
S
. D.
5
3
S
.
Câu 27: Trong các số phức sau số phức nào là số thuần ảo?
A.
2zi
. B.
3zi
. C.
2z
. D.
zi
.
Câu 28: Biết rằng tập hợp các số phức
z
thỏa mãn điều kiện
12z −=
là một đường tròn. Tìm tọa độ
tâm đường tròn đó.
A.
1; 0
. B.
1; 0
. C.
0;1
. D.
0; 1
.
Câu 29: Tìm số phức
z
thỏa mãn điều kiện
2 34zz i+=+
.
A.
34zi
. B.
14zi
. C.
14zi
. D.
34zi
.
Câu 30: Cho số phức
z
thỏa mãn điều kiện
. 12iz i= +
. Phần thực của số phức
z
bằng
A.
1
. B.
1
. C.
2
. D.
2
.
Câu 31: Gọi
12
,zz
là hai nghiệm phức của phương trình
2
2 50zz+ +=
. Tính
12
zz+
A.
5
. B.
13
. C.
2 13
. D.
25
.
Câu 32: Trong không gian Oxyz, mặt cầu
( )
222
: 2 4 20Sx y z x y+ + + − −=
có bán kính bằng
A. 2. B.
3
. C.
6
. D.
7
.
Câu 33: Trong không gian Oxyz, mặt phẳng (Oxy) có một véc tơ pháp tuyến
n
là
A.
(
)
1;1; 0n
=
. B.
( )
1;0;0n =
. C.
( )
0; 1; 0n =
. D.
( )
0; 0; 1n =
.
Câu 34: Khoảng cách từ điểm
( )
1; 2; 3M
đến mặt phẳng
( )
:x 2 2 1 0P yz+ + −=
bằng
A.
7
3
. B.
5
3
. C.
2
3
. D.
10
3
.
Câu 35: Trong không gian Oxyz, đường thẳng đi qua hai điểm
( ) ( )
1; 2; 3 , N 3; 4;5M −
có phương trình
tham số là
A.
2
3
14
xt
yt
zt
= +
= +
= +
. B.
12
22
38
xt
yt
zt
= +
= +
= +
. C.
3
4
54
xt
yt
zt
= +
= −
= +
. D.
12
22
38
xt
yt
zt
= −
= −
=−+
.
Câu 36: Chọn khẳng định đúng trong các khẳng định sau.
A.
1
1 11
2
x dx x x C 
. B.
2
11
3
x dx x x C 
.
C.
1
11
2
x dx x x C 
. D.
2
1 11
3
x dx x x C 
.
Câu 37: Biết rằng số phức
( )
,z a bi a b=+∈
thỏa mãn
.z 2. 6 3iz i+=+
. Tính
ab−
A.
2
. B.
4
. C.
3
. D.
1
.
Mã đề 132
Trang 5/6
Câu 38: Tính thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi các đường
2
1,0
y xy
=−=
quanh trục
Ox
.
A.
4
3
. B.
4
3
. C.
16
15
. D.
16
.
15
Câu 39: Tính tích phân
(
)
4
1
xf x
I dx
x
+
=
∫
biết rằng
( )
2
1
2f x dx =
∫
A.
7
I
. B.
5
I
. C.
8I
. D.
9
I
.
Câu 40: Cho số phức
z
thỏa mãn điều kiện
2
.3
z
zi
i
+=
. Mệnh đề nào sau đây đúng?
A.
01z
. B.
12z
. C.
23z
. D.
34
z
.
Câu 41: Gọi
0
z
là nghiệm phức có phần ảo dương của phương trình
42
60zz+ −=
. Tính
0
.iz
A.
3
. B.
3
. C.
2.i
. D.
2.i
.
Câu 42: Trong không gian Oxyz, cho hai điểm A(1;-2;0), B(-3;6;2). Mặt cầu đường kính AB có phương
trình là
A.
( ) ( ) ( )
2 22
1 2 1 21xy z+ +− +− =
. B.
( ) ( )
( )
2 22
1 2 1 21xy z− ++ ++ =
.
C.
( ) ( ) ( )
2 22
1 2 19xy z+ +− +− =
. D.
( ) ( ) ( )
2 22
1 2 19xy z− ++ ++ =
.
Câu 43: Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc và SA = 2, SB = 4. Gọi điểm M là
trung điểm của SB. Biết khoảng cách từ điểm M đến mặt phẳng (ABC) bằng
2
3
. Tính độ dài
cạnh SC.
A. SC = 2. B. SC = 4. C. SC = 6. D. SC = 8.
Câu 44: Trong không gian Oxyz, cho hai đường thẳng
42
:2
13
xt
dy t
zt
= +
= −
= −
và
:
22
3
43
xt
dy t
zt
= −
= +
= +
/
//
/
Xét vị trí tương đối của
d
và
'
d
.
A. d trùng với d’. B. d song song với d’. C. d cắt d’. D. d chéo d’.
Câu 45: Trong không gian Oxyz, cho điểm A(2; 1; 3) và đường thẳng
112
:
1 22
xyz+−−
∆==
−
. Gọi
( )
; ;3u ab=
là một véc tơ chỉ phương của đường thẳng d đi qua điểm A, vuông góc với đường
thẳng
∆
và cắt trục Oy. Tính
ab+
A. -6. B. 6. C. 4. D. -4.
Câu 46: Biết diện tích hình phẳng giới hạn bởi đường thẳng
y mx=
(
m
là tham số dương) và đồ thị
hàm số
2
yx
=
bằng
1
. Chọn khẳng định đúng trong các khẳng định sau.
A.
01m
. B.
12m
. C.
23m
. D.
34m
.
Mã đề 132
Trang 6/6
Câu 47: Cho hàm số
( )
fx
liên tục trên
thỏa mãn
( )
sin .cos
2
fx f x x x
π

+ −=


và
(
)
00
f =
. Tính
tích phân
( )
2
0
.'
I x f x dx
π
=
∫
.
A.
1
4
I 
. B.
1
4
I
. C.
3
4
I 
. D.
1
2
I 
.
Câu 48: Cho số phức
z
thỏa
(
)
2
1 .z
12
13
i
i
i
z
z
−
+
= ++
, giá trị của
z
bằng
A.
10
10
. B.
2 10
10
. C.
3 10
10
. D.
2 10
5
.
Câu 49: Biết rằng tập hợp các điểm biểu diễn số phức
( )
1
w2
2
iz
z
z
+
= ≠−
+
là một đường thẳng. Giá trị
lớn nhất của biểu thức
4Pz i= −
là
A.
6
. B.
7
. C.
5
. D.
8
.
Câu 50: Trong không gian Oxyz, cho điểm M(1; 1; 2) và đường thẳng
1
:
1
x
d yt
zt
=
=
= −
. Xét mặt phẳng (P)
chứa đường thẳng d và cách điểm M một khoảng lớn nhất. Giả sử mặt phẳng (P) có phương
trình dạng
10ax by cz+ + −=
. Tính
T abc=++
.
A. T = 0. B. T = 2. C. T = 4. D. T = 6.
-----------Hết-----------
Mã đề 468
Trang 1/6
TRƯỜNG THPT LÊ QUÝ ĐÔN
TỔ TOÁN
Đề thi gồm 06 trang
KIỂM TRA HỌC KỲ II NĂM HỌC 2020-2021
Môn: Toán – Lớp 12
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ, tên thí sinh:……………………………………………………
Số báo danh: ………………………………………………………
Câu 1: Họ nguyên hàm của hàm số
cosfx x
trên
là
A.
sin xC

. B.
sin xC
. C.
cos xC

. D.
cos
xC
Câu 2: Chọn khẳng định đúng trong các khẳng định sau.
A.
f x g x dx f x dx g x dx





.
B.
.f x g x dx f x dx g x dx





.
C.
f x g x dx f x dx g x dx





.
D.
f x g x dx f x dx g x dx





.
Câu 3: Cho hàm số
( )
fx
liên tục và không âm trên đoạn
[ ]
;ab
.
Diện tích của hình thang cong giới hạn bởi đồ thị hàm số
( )
y fx
=
, trục hoành và hai đường thẳng
,x ax b= =
được tính theo công thức nào dưới đây? (Hình bên)
A.
b
a
S f x dx
. B.
b
a
S f x dx
.
C.
2
b
a
S f x dx




. D.
b
a
S f x dx
Câu 4: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
;ab
. Diện tích
S
của hình phẳng giới hạn bởi đồ thị
hàm số
( )
fx
, trục hoành và hai đường thẳng
,x ax b= =
được tính theo công thức
A.
b
a
S f x dx
. B.
b
a
S f x dx

. C.
b
a
S f x dx
. D.
b
a
S f x dx
.
Câu 5: Thể tích
V
của khối tròn xoay khi quay hình phẳng giới hạn bởi đồ thị hàm số
( )
y fx=
, trục
Ox
và hai đường thẳng
,x ax b= =
(
ab<
) quanh trục
Ox
được tính theo công thức
A.
b
a
V f x dx
. B.
2
b
a
V f x dx

. C.
2
b
a
V f x dx
. D.
b
a
V f x dx
.
Câu 6: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
;ab
và
k
là hằng số tùy ý. Mệnh đề nào dưới đây đúng?
A.
..
bb
aa
k f x dx k f x dx

. B.
.
bb
aa
k f x dx k f x dx

.
C.
.
bb
aa
k f x dx f kx dx

. D.
..
b bb
a aa
k f x dx kdx f x dx

.
a
b
f(x)
y
x
O
A
B
Mã đề thi 468
Mã đề 468
Trang 2/6
Câu 7: Cho hai hàm số
(
)
y fx=
và
( )
y gx=
liên tục trên đoạn
[ ]
;ab
. Diện tích
S
của hình phẳng
giới hạn bởi hai đồ thị hàm số đó và các đường thẳng
,x ax b= =
được tính theo công thức
A.
b
a
S f x g x dx
. B.
b
a
S f x g x dx




.
C.
b
a
S f x g x dx




. D.
b
a
S f x g x dx

.
Câu 8: Tính số phức
(
)
1.z ii
= +
A.
1 i
. B.
1 i
. C.
1 i
. D.
1
i
.
Câu 9: Phần ảo của số phức
23zi= −
là
A.
3
. B.
2
. C.
2i
. D.
3i
.
Câu 10: Tính môđun của số phức
( )
,z a bi a b
=+∈
.
A.
z ab
. B.
z ab
. C.
22
z ab
. D.
22
za b
.
Câu 11: Số phức liên hợp của số phức
32zi= −
là
A.
23i
. B.
32i
. C.
32i
. D.
23i
.
Câu 12: Trên mặt phẳng tọa độ điểm biểu diễn số phức
2
zi
là điểm nào trong các điểm sau? (hình vẽ
bên)
A.
.M
B.
.N
C.
.P
D.
.Q
Câu 13: Cho hai số phức
1
27zi
= +
và
2
12zi= −
. Tính
12
zz
+
A.
32i
. B.
32i
. C.
35i
. D.
35i
.
Câu 14: Tìm tất cả các căn bậc hai phức của
9−
.
A.
3
i
và
3i−
. B.
3
. C.
3
và
3−
. D.
3i
.
Câu 15: Trong không gian Oxyz, tích vô hướng của hai véc tơ
( )
1;2;3a = −−

và
( )
3; 1; 4b = −
bằng
A. 7. B. -7. C. 5. D. -5.
Câu 16: Trong không gian Oxyz, điểm nào dưới đây thuộc mặt phẳng
( )
: 2 3 20xyz
α
− − +=
?.
A.
( )
1;1; 0M
. B.
( )
2; 3; 2
N
−
. C.
( )
2; 3; 2
P −−
. D.
( )
1;2;1Q
−−
.
Câu 17: Trong không gian Oxyz, đường thẳng đi qua điểm M(4; -3; 5) và nhận véc tơ
( )
3; 2;1u = −
làm
véc tơ chỉ phương có phương trình tham số là
A.
34
23
15
xt
yt
zt
= +
=−−
= +
. B.
43
32
5
xt
yt
zt
= +
=−−
= +
. C.
34
23
15
xt
yt
zt
= +
= −
= +
. D.
43
32
5
xt
yt
zt
= +
=−+
= +
.
Mã đề 468
Trang 3/6
Câu 18: Trong không gian Oxyz, mặt phẳng nào dưới đây trùng với mặt phẳng
( )
:2 3 4 0x yz
α
− −+=
?
A.
( )
:4 6 2 8 0xyz
α
− + + +=
. B.
2 3 40x yz+ +−=
.
C.
3 3 20
xy z++ +=
. D.
( )
:4 6 2 8 0xyz
α
− + + −=
.
Câu 19: Trong không gian Oxyz, đường thẳng
2
:1
3
xt
dy t
zt
=
= −
= +
có một véc tơ chỉ phương
u
là
A.
( )
2;1; 3u =
. B.
( )
2; 1;1u = −
. C.
( )
0;1; 3u =
. D.
( )
0; 1;1
u
= −
.
Câu 20: Trong không gian Oxyz, điểm nào dưới đây thuộc đường thẳng
11
:
323
x yz
d
−+
= =
?
A. M(1; 2; -1). B. N(4; 2; 2). C. P(7; 4; -7). D. Q(-2; -2; 5).
Câu 21: Tính tích phân
1
0
3
x
I dx=
∫
A.
1
ln 3
. B.
2.ln 3
. C.
2
ln 3
. D.
ln 3
.
Câu 22: Họ tất cả các nguyên hàm của hàm số
4x
fx e
là
A.
4
4
x
xe C
. B.
4
4
x
eC
. C.
4
1
4
x
eC
. D.
4x
eC
.
Câu 23: Nếu đặt
2
tx=
thì tích phân
2
2
1
.
x
x e dx
∫
trở thành tích phân nào trong các tích phân sau?
A.
4
1
1
2
t
e dt
. B.
4
1
t
e dt
. C.
2
1
1
2
t
e dt
. D.
2
1
t
e dt
.
Câu 24: Cho tích phân
2
1
.lnI x xdx=
∫
. Chọn đẳng thức đúng trong các đẳng thức sau
A.
2
2
2
1
1
x lnI x xdx
. B.
2
2
2
1
1
1
x ln
2
I x xdx
.
C.
2
2
2
1
1
ln
2
x
I x xdx



. D.
2
2
2
1
1
1
ln
22
x
I x xdx



.
Câu 25: Tìm số phức
z
thỏa mãn điều kiện
26zz i+=+
.
A.
1zi
. B.
1zi
. C.
2zi
. D.
2zi
.
Câu 26: Cho số phức
z
thỏa mãn điều kiện
.1iz i=−−
. Phần thực của số phức
z
bằng
A.
1
. B.
1
. C.
2
. D.
2
.
Câu 27: Gọi
12
,zz
là hai nghiệm phức của phương trình
2
2 30zz+ +=
. Tính
12
zz+
A.
23
. B.
3
. C.
25
. D.
5
.
Mã đề 468
Trang 4/6
Câu 28: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
;ac
có đồ thị
như hình vẽ bên, biết
( )
3
b
a
f x dx = −
∫
và
( )
4
c
b
f x dx =
∫
. Tính diện tích
S
của hình phẳng được
tô đậm.
A.
1S
. B.
3S
.
C.
4
S
. D.
7S
Câu 29: Tính diện tích
S
hình phẳng giới hạn bởi đồ thị hàm số
2
3yx
= −
, trục hoành và hai đường
thẳng
0, 1
xx
= =
.
A.
11
3
S
. B.
8
3
S
. C.
5
3
S
. D.
8
3
S 
.
Câu 30: Trong các số phức sau số phức nào là số thuần ảo?
A.
3zi
. B.
1zi
. C.
13zi
. D.
3
z
.
Câu 31: Biết rằng tập hợp các số phức
z
thỏa mãn điều kiện
12
z
+=
là một đường tròn. Tìm tọa độ
tâm đường tròn đó.
A.
1; 0
. B.
1; 0
. C.
0;1
. D.
0; 1
.
Câu 32: Trong không gian Oxyz, mặt cầu
( )
222
: 4 6 20Sx y z x y
+ + + − −=
có bán kính bằng
A.
11
. B. 3. C.
15
. D.
14
.
Câu 33: Trong không gian Oxyz, mặt phẳng (Oxz) có một véc tơ pháp tuyến
n
là
A.
( )
1;0;0
n =
. B.
( )
0;1; 0n =
. C.
( )
0; 0;1n =
. D.
( )
1; 0;1n =
.
Câu 34: Khoảng cách từ điểm
( )
1; 2; 3M
đến mặt phẳng
( )
: 2 2 60Px y z+ + −=
bằng
A.
. B.
5
3
. C.
2
3
. D.
10
3
.
Câu 35: Trong không gian Oxyz, đường thẳng đi qua hai điểm
( ) ( )
1; 2;3 , N 3; 4;5M −
có phương trình
tham số là
A.
12
26
32
xt
yt
zt
= +
=−+
= −
. B.
2
13
4
xt
yt
zt
= +
= +
= +
. C.
1
23
3
xt
yt
zt
= +
=−−
= +
. D.
3
43
5
xt
yt
zt
= +
= +
=−+
.
Câu 36: Tính thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi các đường
2
4 ,0y xy=−=
quanh trục
Ox
.
A.
512
15
. B.
512
15
. C.
32
3
. D.
32
3
.
O
a
b
c
x
y
( )
y fx=
Mã đề 468
Trang 5/6
Câu 37: Chọn khẳng định đúng trong các khẳng định sau.
A.
1
2 22
2
x dx x x C 
. B.
1
22
2
x dx x x C 
.
C.
2
2 22
3
x dx x x C 
. D.
2
22
3
x dx x x C 
.
Câu 38: Tính tích phân
( )
4
1
xf x
I dx
x
+
=
∫
biết rằng
( )
2
1
1f x dx =
∫
A.
7I
. B.
5I
. C.
8I
. D.
9I
.
Câu 39: Biết rằng số phức
( )
,z a bi a b=+∈
thỏa mãn
2 15 6iz z i+=+
. Tính
ab−
A.
6
. B.
7
. C.
8
. D.
9
.
Câu 40: Cho số phức
z
thỏa mãn điều kiện
2
.4
z
zi
i
+=
. Mệnh đề nào sau đây đúng?
A.
01z
. B.
12z

. C.
23z
. D.
34z
.
Câu 41: Gọi
0
z
là nghiệm phức có phần ảo dương của phương trình
42
60zz− −=
. Tính
0
.iz
A.
3i
. B.
3i
. C.
2
. D.
2
.
Câu 42: Trong không gian Oxyz, cho hai điểm A(1;-2;0), B(3;6;-2). Mặt cầu đường kính AB có phương
trình là
A.
( ) ( ) ( )
2 22
2 2 1 18xyz++++−=
. B.
( ) ( ) ( )
2 22
2 2 1 18xyz−+−++=
.
C.
( ) ( ) ( )
2 22
2 2 1 10xyz++++−=
. D.
( ) ( ) (
)
2 22
2 2 1 10xyz−+−++=
.
Câu 43: Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc và SA = 3, SC = 6. Gọi điểm M là
trung điểm của SC. Biết khoảng cách từ điểm M đến mặt phẳng (ABC) bằng 1. Tính độ dài
cạnh SB.
A. SB = 8. B. SB = 6. C. SB = 4. D. SB = 3.
Câu 44: Trong không gian Oxyz, cho hai đường thẳng
42
:2
13
xt
dy t
zt
= −
= +
= +
và
22
:3
13
xt
dy t
zt
= +
= −
= −
/
//
/
Xét vị trí tương đối của
d
và
'd
.
A. d trùng với d’. B. d song song với d’. C. d cắt d’. D. d chéo d’.
Câu 45: Trong không gian Oxyz, cho điểm A(2; 1; 3) và đường thẳng
112
:
12 2
xyz+−−
∆==
−
. Gọi
( )
;1; cua=
là một véc tơ chỉ phương của đường thẳng d đi qua điểm A, vuông góc với đường
thẳng
∆
và cắt trục Ox. Tính
ac+
A. -5. B. 5. C. 7. D. -7.
Câu 46: Biết diện tích hình phẳng giới hạn bởi đường thẳng
y mx=
(
m
là tham số dương) và đồ thị
hàm số
2
yx=
bằng
2
. Chọn khẳng định đúng trong các khẳng định sau.
A.
01m
. B.
12m
. C.
23m
. D.
34m
.
Mã đề 468
Trang 6/6
Câu 47: Cho hàm số
( )
fx
liên tục trên
thỏa mãn
( )
2sin .cos
2
fx f x x x
π

+ −=


và
( )
00f =
.
Tính tích phân
( )
2
0
.'I x f x dx
π
=
∫
.
A.
1
4
I 
. B.
1
4
I
. C.
3
4
I 
. D.
1
2
I 
.
Câu 48: Cho số phức
z
thỏa
( )
2
1 .z
1
13
i
i
i
z
z
−
+
= ++
, giá trị của
z
bằng
A.
10
10
. B.
2 10
10
. C.
3 10
10
. D.
2 10
5
.
Câu 49: Biết rằng tập hợp các điểm biểu diễn số phức
( )
1
w2
2
iz
z
z
+
= ≠−
+
là một đường thẳng. Giá trị
lớn nhất của biểu thức
5Pzi= −
là
A.
6
. B.
7
. C.
5
. D.
8
.
Câu 50: Trong không gian Oxyz, cho điểm M(1; 1; 2) và đường thẳng
1
:1
x
dy t
zt
=
= +
=
. Xét mặt phẳng (P)
chứa đường thẳng d và cách điểm M một khoảng lớn nhất. Giả sử mặt phẳng (P) có phương
trình dạng
10
ax by cz+ + −=
. Tính
T abc=++
.
A. T = 0. B. T = 2. C. T = 4. D. T = 6.
------Hết--------
Mã đề 672
Trang 1/6
TRƯỜNG THPT LÊ QUÝ ĐÔN
TỔ TOÁN
Đề thi gồm 06 trang
KIỂM TRA HỌC KỲ II NĂM HỌC 2020-2021
Môn: Toán – Lớp 12
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ, tên thí sinh:……………………………………………………
Số báo danh: ………………………………………………………
Câu 1: Cho hàm số
( )
fx
liên tục trên đoạn
[
]
;ab
và
k
là hằng số tùy ý. Mệnh đề nào dưới đây đúng?
A.
.
bb
aa
k f x dx f kx dx

. B.
..
b bb
a aa
k f x dx kdx f x dx

.
C.
.
bb
aa
k f x dx k f x dx

. D.
..
bb
aa
k f x dx k f x dx

Câu 2: Chọn khẳng định đúng trong các khẳng định sau.
A.
.f x g x dx f x dx g x dx





.
B.
f x g x dx f x dx g x dx





.
C.
f x g x dx f x dx g x dx





.
D.
f x g x dx f x dx g x dx





.
Câu 3: Họ nguyên hàm của hàm số
sinfx x
trên
là
A.
sin
xC

. B.
sin xC
. C.
cos xC
. D.
cos
xC
.
Câu 4: Cho hai hàm số
( )
y fx=
và
( )
y gx=
liên tục trên đoạn
[
]
;ab
. Diện tích
S
của hình phẳng
giới hạn bởi hai đồ thị hàm số đó và các đường thẳng
,x ax b= =
được tính theo công thức
A.
b
a
S f x g x dx




. B.
b
a
S f x g x dx
.
C.
b
a
S f x g x dx
. D.
b
a
S f x g x dx




.
Câu 5: Thể tích
V
của khối tròn xoay khi quay hình phẳng giới hạn bởi đồ thị hàm số
( )
y fx=
, trục
Ox
và hai đường thẳng
,x ax b= =
(
ab<
) quanh trục
Ox
được tính theo công thức
A.
2
b
a
V f x dx
. B.
b
a
V f x dx
. C.
2
b
a
V f x dx
. D.
b
a
V f x dx
.
Câu 6: Cho hàm số
( )
fx
liên tục và không âm trên đoạn
[ ]
;
ab
.
Diện tích của hình thang cong giới hạn bởi đồ thị hàm số
( )
y fx=
, trục hoành và hai đường thẳng
,x ax b= =
được tính theo công thức nào dưới đây? (Hình bên)
A.
b
a
S f x dx
. B.
b
a
S f x dx
.
C.
b
a
S f x dx
. D.
2
b
a
S f x dx




a
b
f(x)
y
x
O
A
B
Mã đề thi 672
Mã đề 672
Trang 2/6
Câu 7: Cho hàm số
(
)
fx
liên tục trên đoạn
[ ]
;ab
. Diện tích
S
của hình phẳng giới hạn bởi đồ thị
hàm số
( )
fx
, trục hoành và hai đường thẳng
,x ax b= =
được tính theo công thức
A.
b
a
S f x dx
. B.
b
a
S f x dx
. C.
b
a
S f x dx
. D.
b
a
S f x dx

.
Câu 8: Phần ảo của số phức
32zi= +
là
A.
3i
. B.
2
. C.
2i
. D.
3
.
Câu 9: Tìm tất cả các căn bậc hai phức của
16−
.
A.
4i
. B.
4i
và
4i−
. C.
4
. D.
4
và
4−
.
Câu 10: Tính môđun của số phức
( )
,z a bi a b=+∈
.
A.
z ab
. B.
22
z ab
. C.
z ab
. D.
22
za b

.
Câu 11: Số phức liên hợp của số phức
32
zi
= +
là
A.
23i
. B.
32i
. C.
32i
. D.
23i
Câu 12: Trên mặt phẳng tọa độ điểm biểu diễn số phức
2zi

là điểm nào trong các điểm sau? (hình vẽ
bên)
A.
.M
B.
.N
C.
.P
D.
.Q
Câu 13: Cho hai số phức
1
23zi= −
và
2
12zi= −
. Tính
12
zz+
A.
32
i
. B.
32
i
. C.
35i
. D.
35i
.
Câu 14: Tính số phức
( )
3.z ii= +
A.
13i
. B.
13i
. C.
13i
. D.
13i
.
Câu 15: Trong không gian Oxyz, tích vô hướng của hai véc tơ
( )
1; 2; 3a = −

và
( )
3; 2; 1b
=−−
bằng
A. 2. B. -4. C. 4. D. 2.
Câu 16: Trong không gian Oxyz, điểm nào dưới đây thuộc mặt phẳng
( )
: 2 3 20x yz
α
+ − −=
?
A.
( )
0; 0;1M
. B.
( )
2; 0; 0
N
−
. C.
( )
2; 3; 2P −
. D.
( )
2; 3; 2Q
.
Câu 17: Trong không gian Oxyz, mặt phẳng nào dưới đây cắt mặt phẳng
( )
:2 3 1 0
x yz
α
− −+=
?
A.
( )
:4 6 2 1 0xyz
α
− + − −=
. B.
( )
:4 6 2 1 0xyz
α
− + + −=
.
C.
( )
:4 6 2 1 0xyz
α
− + + +=
. D.
( )
:2 3 1 0x yz
α
− −+=
.
Câu 18: Trong không gian Oxyz, đường thẳng
12
:
3
xt
d yt
zt
= −
=
= +
có một véc tơ chỉ phương
u
là
A.
( )
1;1; 3u =
. B.
( )
1; 0; 3u =
. C.
( )
2; 0;1u = −
. D.
( )
2;1;1u = −
.
Mã đề 672
Trang 3/6
Câu 19: Trong không gian Oxyz, đường thẳng đi qua điểm M(3; 2; 1) và nhận véc tơ
(
)
4; 3; 5
u
= −
làm
véc tơ chỉ phương có phương trình tham số là
A.
43
32
5
xt
yt
zt
= +
=−+
= +
. B.
43
32
5
xt
yt
zt
= +
=−−
= +
. C.
34
23
15
xt
yt
zt
= +
= −
= +
. D.
34
23
15
xt
yt
zt
= +
= −
= −
.
Câu 20: Trong không gian Oxyz, điểm nào dưới đây không thuộc đường thẳng
11
:
323
x yz
d
+−
= =
?
A. M(-1; 0; 1). B. N(-4; -2; -2). C. P(-7; -4; 7). D. Q(2; 2; 4).
Câu 21: Họ tất cả các nguyên hàm của hàm số
3x
fx e
là
A.
3
3
x
xe C
. B.
3
3
x
eC
. C.
3x
eC
. D.
3
1
3
x
eC
.
Câu 22: Nếu đặt
2
tx=
thì tích phân
2
3
0
.
x
x e dx
∫
trở thành tích phân nào trong các tích phân sau?
A.
9
0
t
e dt
. B.
3
0
1
2
t
e dt
. C.
9
0
1
2
t
e dt
. D.
3
0
t
e dt
.
Câu 23: Tính tích phân
1
0
5
x
I dx=
∫
A.
3
ln 5
. B.
3 ln 5
. C.
ln 5
. D.
4
ln 5
.
Câu 24: Cho tích phân
3
2
.ln
I x xdx=
∫
. Chọn đẳng thức đúng trong các đẳng thức sau
A.
3
3
2
2
2
1
x ln
2
I x xdx
. B.
3
3
2
2
2
x lnI x xdx
.
C.
3
2
3
2
2
1
ln
22
x
I x xdx



. D.
3
2
3
2
2
ln
2
x
I x xdx



Câu 25: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
;ac
có đồ thị
như hình vẽ bên, biết
( )
1
b
a
f x dx = −
∫
và
( )
2
c
b
f x dx =
∫
. Tính diện tích
S
của hình phẳng được
tô đậm.
A.
1S
. B.
3S
.
C.
2S
. D.
5S
Câu 26: Tính diện tích
S
hình phẳng giới hạn bởi đồ thị hàm số
2
5yx= −
, trục hoành và hai đường
thẳng
0, 1xx= =
.
A.
14
3
S
. B.
8
3
S
. C.
11
3
S
. D.
14
3
S
.
O
a
b
c
x
y
(
)
y fx=
Mã đề 672
Trang 4/6
Câu 27: Trong các số phức sau số phức nào là số thuần ảo?
A.
2
z
. B.
2zi
. C.
13zi
. D.
1
zi

.
Câu 28: Tìm số phức
z
thỏa mãn điều kiện
2 35
zz i
+=+
.
A.
25
zi
. B.
25
zi
. C.
15zi
. D.
15zi
.
Câu 29: Cho số phức
z
thỏa mãn điều kiện
.2iz i
=−+
. Phần thực của số phức
z
bằng
A.
1
. B.
1
. C.
2
. D.
2
.
Câu 30: Biết rằng tập hợp các số phức
z
thỏa mãn điều kiện
21z
−=
là một đường tròn. Tìm tọa độ
tâm đường tròn đó.
A.
0; 2
. B.
0; 2
. C.
2; 0
. D.
2; 0
.
Câu 31: Gọi
12
,zz
là hai nghiệm phức của phương trình
2
2 70zz+ +=
. Tính
12
zz+
A.
5
. B.
27
. C.
7
. D.
25
.
Câu 32: Khoảng cách từ điểm
(
)
1; 2; 3
M
đến mặt phẳng
( )
: 2 2 40
Px y z
+ + −=
bằng
A.
. B.
5
3
. C.
2
3
. D.
10
3
.
Câu 33: Trong không gian Oxyz, mặt cầu
(
)
222
: 2 6 20Sx y z x y+ + + − −=
có bán kính bằng
A.
11
. B.
12
. C.
8
. D. 4.
Câu 34: Trong không gian Oxyz, mặt phẳng (Oyz) có một véc tơ pháp tuyến
n
là
A.
( )
1;0;0n =
. B.
( )
0; 1; 0n =
. C.
( )
0; 0;1n =
. D.
( )
0;1;1n =
.
Câu 35: Trong không gian Oxyz, đường thẳng đi qua hai điểm
( ) ( )
1; 2;3 , N 3;4;5M −
có phương trình
tham số là
A.
12
3
4
xt
yt
zt
= +
= +
= +
. B.
14
22
32
xt
yt
zt
=−+
= +
= −
. C.
32
4
5
xt
yt
zt
= +
= −
= +
. D.
14
22
32
xt
yt
zt
= +
= +
= +
.
Câu 36: Chọn khẳng định đúng trong các khẳng định sau.
A.
2
22
3
x dx x x C 
. B.
1
2 22
2
x dx x x C

.
C.
1
22
2
x dx x x C 
. D.
2
2 22
3
x dx x x C 
.
Câu 37: Tính thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi các đường
2
9 ,0y xy=−=
quanh trục
Ox
.
A.
36
. B.
1296
5
. C.
1296
5
. D.
36.
Câu 38: Tính tích phân
(
)
4
1
xf x
I dx
x
+
=
∫
biết rằng
( )
2
1
3f x dx =
∫
A.
7I
. B.
5I
. C.
8I
. D.
9I
.
Mã đề 672
Trang 5/6
Câu 39: Biết rằng số phức
( )
,z a bi a b=+∈
thỏa mãn
2. 19 5iz z i+=+
. Tính
ab−
A.
6
. B.
7
. C.
8
. D.
9
.
Câu 40: Cho số phức
z
thỏa mãn điều kiện
2
.6
z
zi
i
+=
. Mệnh đề nào sau đây đúng?
A.
01z
. B.
12z
. C.
23z
. D.
34
z
.
Câu 41: Gọi
0
z
là nghiệm phức có phần ảo dương của phương trình
42
3 10 0
zz+ −=
. Tính
0
.iz
A.
5
. B.
5
. C.
2i
. D.
2
i
.
Câu 42: Trong không gian Oxyz, cho hai điểm A(-1;-2;0), B(-3;6;-2). Mặt cầu đường kính AB có
phương trình là
A.
( ) ( ) ( )
2 22
2 2 1 18xyz− ++ +− =
. B.
( ) ( ) ( )
2 22
2 2 1 10xyz− ++ +− =
.
C.
(
) (
) ( )
2 22
2 2 1 18
xyz+ +− ++ =
. D.
( ) ( ) ( )
2 22
2 2 1 10xyz+ +− ++ =
.
Câu 43: Trong không gian Oxyz, cho hai đường thẳng
32
: 23
1
xt
dy t
zt
= +
= −
=−+
và
14
: 56
42
xt
dy t
zt
=−−
= +
= −
/
//
/
Xét vị trí tương đối của
d
và
'd
.
A. d cắt d’. B. d chéo d’. C. d trùng với d’. D. d song song với d’.
Câu 44: Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc và SC = 4, SB = 8. Gọi điểm M là
trung điểm của SB. Biết khoảng cách từ điểm M đến mặt phẳng (ABC) bằng
4
3
. Tính độ dài
cạnh SA.
A. SA = 2. B. SA = 4. C. SA = 6. D. SA = 8.
Câu 45: Biết diện tích hình phẳng giới hạn bởi đường thẳng
y mx=
(
m
là tham số dương) và đồ thị
hàm số
2
yx=
bằng
5
. Chọn khẳng định đúng trong các khẳng định sau.
A.
01m
. B.
12m
. C.
23m
. D.
34m
.
Câu 46: Trong không gian Oxyz, cho điểm A(3; 2; 1) và đường thẳng
11
112
:
2
xyz−+−
∆==
−
. Gọi
( )
3; ; cub=
là một véc tơ chỉ phương của đường thẳng d đi qua điểm A, vuông góc với đường
thẳng
∆
và cắt trục Oz. Tính
bc+
A. 3. B. -5. C. -3. D. 5.
Câu 47: Cho số phức
z
thỏa
(
)
2
1 .z
12
13
i
i
i
z
z
+
+
= ++
, giá trị của
z
bằng
A.
10
10
. B.
2 10
10
. C.
3 10
10
. D.
2 10
5
.
Mã đề 672
Trang 6/6
Câu 48: Biết rằng tập hợp các điểm biểu diễn số phức
( )
1
w2
2
iz
z
z
+
= ≠−
+
là một đường thẳng. Giá trị
lớn nhất của biểu thức
3Pzi= −
là
A.
6
. B.
7
. C.
5
. D.
8
.
Câu 49: Cho hàm số
(
)
fx
liên tục trên
thỏa mãn
(
)
3sin .cos
2
fx f x x x
π

+ −=


và
(
)
00f =
. Tính
tích phân
( )
2
0
.'I x f x dx
π
=
∫
.
A.
1
4
I 
. B.
1
4
I
. C.
3
4
I 
. D.
1
2
I 
.
Câu 50: Trong không gian Oxyz, cho điểm M(1; 2; 1) và đường thẳng
:1
2
xt
dy t
z
=
= −
=
. Xét mặt phẳng (P)
chứa đường thẳng d và cách điểm M một khoảng lớn nhất. Giả sử mặt phẳng (P) có phương
trình dạng
10ax by cz+ + +=
. Tính
T abc=++
.
A. T = 3. B. T = 2. C. T = 1. D. T = 0
-------Hết-------
Trang 1/1
TRƯỜNG THPT LÊ QUÝ ĐÔN
TỔ TOÁN
ĐÁP ÁN KIỂM TRA CUỐI KỲ II NĂM 2020-2021
MÃ ĐỀ 132
1.D
2.C
3.B
4.D
5.C
6.D
7.C
8.D
9.A
10.D
11.C
12.A
13.C
14.D
15.A
16.B
17.C
18.C
19.C
20.A
21.A
22.C
23.D
24.B
25.C
26.C
27.D
28.B
29.C
30.C
31.D
32.D
33.D
34.D
35.A
36.D
37.C
38.D
39.A
40.B
41.B
42.A
43.A
44.A
45.B
46.B
47.A
48.C
49.A
50.B
MÃ ĐỀ 468
1.B
2.A
3.A
4.D
5.B
6.A
7.A
8.B
9.A
10.C
11.B
12.B
13.C
14.A
15.B
16.C
17.B
18.D
19.B
20.B
21.C
22.C
23.A
24.D
25.D
26.B
27.A
28.D
29.B
30.A
31.A
32.C
33.B
34.B
35.B
36.A
37.C
38.B
39.B
40.C
41.D
42.B
43.D
44.B
45.C
46.C
47.D
48.B
49.B
50.A
MÃ ĐỀ 672
1.D
2.B
3.C
4.B
5.C
6.B
7.A
8.B
9.B
10.B
11.C
12.A
13.D
14.D
15.C
16.D
17.A
18.D
19.C
20.C
21.D
22.C
23.D
24.C
25.B
26.A
27.B
28.D
29.A
30.D
31.B
32.A
33.B
34.A
35.A
36.D
37.C
38.D
39.C
40.D
41.A
42.C
43.D
44.B
45.D
46.A
47.A
48.C
49.C
50.C
HD GIẢI MỘT SỐ CÂU VẬN DỤNG CAO TRONG MÃ ĐỀ 132
Câu 47. Cho hàm số
( )
fx
liên tục trên
thỏa mãn
( )
sin .cos
2
fx f x x x
π

+ −=


và
( )
00f =
. Tính
tích phân
( )
2
0
.'I x f x dx
π
=
∫
.
A.
1
4
I 
. B.
1
4
I
. C.
3
4
I 
. D.
1
2
I 
.
HD
+ Thay
0
vào biểu giả thiết
( )
sin .cos
2
fx f x x x
π

+ −=


(1) ta được
(
)
00
2
ff
π

= =


+ Tích phân
( ) ( ) ( ) ( )
2 22
2
0
0 00
.' .I x f x dx x f x f x dx f x dx
π ππ
π
= =−=
∫ ∫∫
+ Lấy tích phân hai vế biểu thức (1) ta được
( )
22 2
00 0
sin .cos
2
f x dx f x dx x xdx
ππ π
π

+ −=


∫∫ ∫
( )
22
00
2 sin .cosf x dx x xdx
ππ
⇔=
∫∫
(do
( )
22
00
2
f x dx f x dx
ππ
π

= −


∫∫
)
Câu 48. Cho số phức
z
thỏa
( )
2
1 .z
12
13
i
i
i
z
z
−
+
= ++
, giá trị của
z
bằng
Trang 2/1
A.
10
10
. B.
2 10
10
. C.
3 10
10
. D.
2 10
5
.
HD
+ Nhân hai vế giả thiết với
z
ta được
( ) ( )
12 1 13.i i iz+ =−++
(chú ý
2
.zz z=
)
Câu 49. Biết rằng tập hợp các điểm biểu diễn số phức
(
)
1
w2
2
iz
z
z
+
= ≠−
+
là một đường thẳng. Giá trị
lớn nhất của biểu thức
4Pz i
= −
là
A.
6
. B.
7
. C.
5
. D.
8
.
HD
+ Trước tiên ta chứng minh kq:
12 1 2
..zz z z=
Thật vậy đặt
1
z a bi= +
và
2
z c di= +
Khi đó
( ) (
)
12
.z z ac bd ad bc i=−++
( ) ( )
( ) ( ) ( ) ( )
2 2 2 2 22
12
.z z ac bd ad bc ac bd ad bc⇒ = − ++ = + + +
( ) ( ) (
)(
)
222 222 2222
12
.
acd bcd abcd zz= ++ += + +=
+ Đặt
w x yi
= +
.
Từ giả thiết
( ) ( )
[
]
(
)
1
w w2 1 w 12 12
2
iz
z iz z i w z x yi i x yi
z
+
= ⇒ + =+⇒ −=− ⇒ + −=− +
+
(1)
+ Lấy modun hai vế biểu thức (1) ta được
(
)
( ) ( )
2 22
2
1 12 2zx y x y
+ − = − +−
( ) ( )
2
22 2 2
21 4 4 41zxyy xyx⇒ + − += + − +
(2)
+ Từ (2) suy ra:
- Nếu
2
4z
≠
thì tập hợp các điểm biểu diễn số phức
w
là đường tròn.
-Nếu
2
4z =
thì tập hợp các điểm biểu diễn số phức
w
là đường thẳng thỏa mãn đề bài.
Suy ra
2z =
+
4 46Pz i z i=− ≤+ =
. Dấu “=” xảy ra khi
2zi= −
. Vậy GTLN của P bằng
6
Câu 50. Trong không gian Oxyz, cho điểm M(1; 1; 2) và đường thẳng
1
:
1
x
d yt
zt
=
=
= −
. Xét mặt phẳng (P)
chứa đường thẳng d và cách điểm M một khoảng lớn nhất. Giả sử mặt phẳng (P) có phương trình dạng
10ax by cz
+ + −=
. Tính
T abc=++
.
A. T = 0. B. T = 2. C. T = 4. D. T = 6.
HD
+ Gọi H là hình chiếu vuông góc của M lên đường thẳng d. Khi đó mp (P) thỏa ycbt đi qua vuông góc với
MH tại H.
+ Tìm tọa độ điểm H sau đó viết ptmp (P)
-------Hết-------
| 1/20
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT LÊ QUÝ ĐÔN
KIỂM TRA HỌC KỲ II NĂM HỌC 2020-2021 TỔ TOÁN
Môn: Toán – Lớp 12
Đề thi gồm 06 trang
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ, tên thí sinh:…………………………………………………… Mã đề thi 132
Số báo danh: ………………………………………………………
Câu 1: Chọn khẳng định đúng trong các khẳng định sau. A. f
  xgx  dx f .  
 xdx g  xdxB. f
  xgx  dx f .  
 xdx. g  xdxC. f
  xgx  dx f .  
 xdx g  xdxD. f
  xgx  dx f  
 xdx g  xdx
Câu 2: Họ nguyên hàm của hàm số f x  cosx trên  là
A. sinx  C . B. cosx  C . C. sinx  C .
D. cosx  C .
Câu 3: Cho hàm số f (x) liên tục trên đoạn [ ;
a b] và k là hằng số tùy ý. Mệnh đề nào dưới đây đúng? b b b b A. k.f
xdx k f  xdx . B. k.f
xdx k. f
 xdx . a a a a b b b b b C. k.f
xdx kdx. f   xdx . D. k.f
xdx f
 kxdx . a a a a a
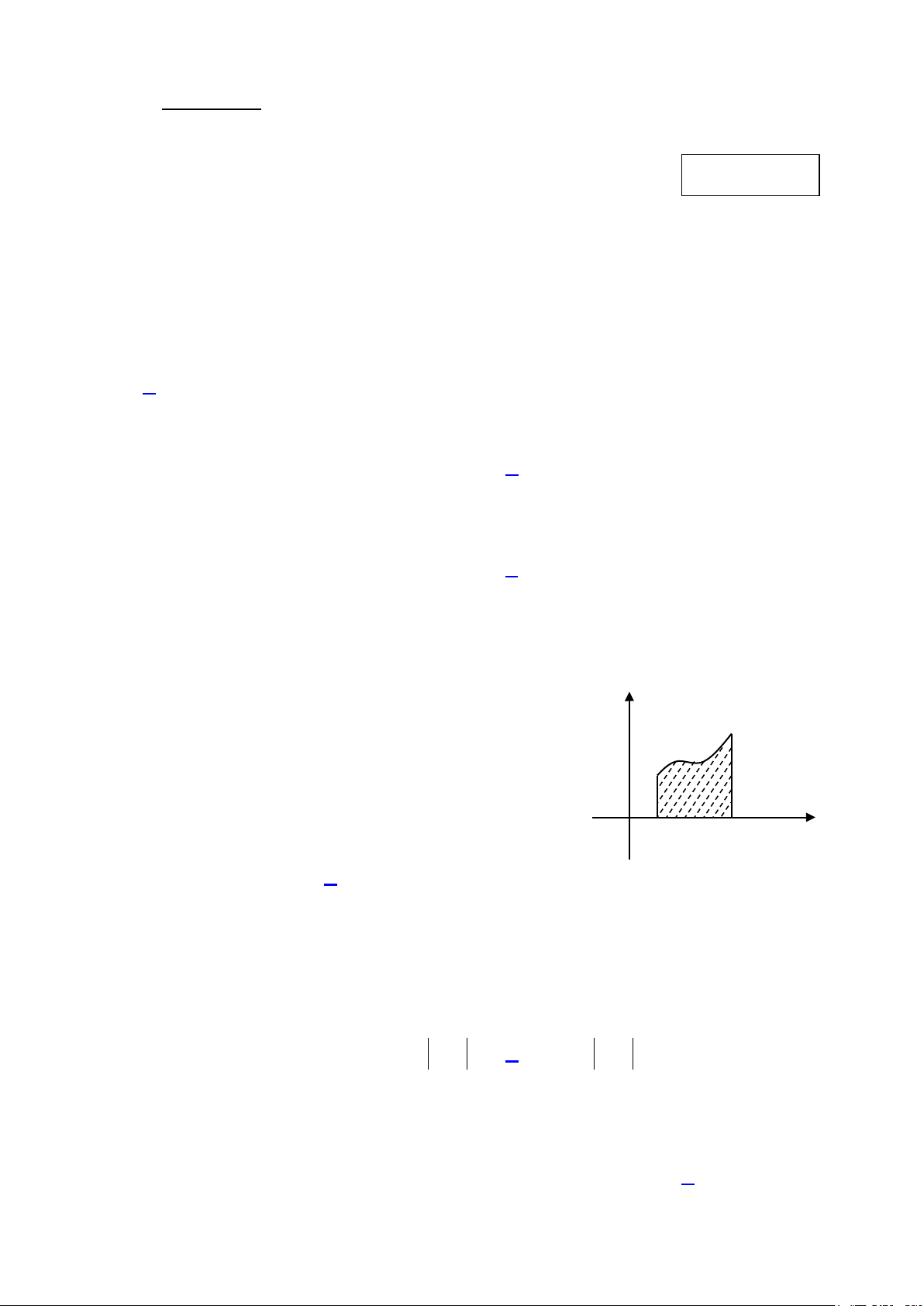
Câu 4: Cho hàm số f (x) liên tục và không âm trên đoạn [a;b]. y
Diện tích của hình thang cong giới hạn bởi đồ thị hàm số B
y = f (x) , trục hoành và hai đường thẳng x = a, x = b f(x)
được tính theo công thức nào dưới đây? (Hình bên) A b b x A. S   f
 xdx . B. Sf   x2   dx   O a b a a. b b C. S   f
 xdx . D. S f  xdx a a
Câu 5: Cho hàm số f (x) liên tục trên đoạn [ ;
a b]. Diện tích S của hình phẳng giới hạn bởi đồ thị
hàm số f (x) , trục hoành và hai đường thẳng x = a, x = b được tính theo công thức b b b b A. S f
 xdx . B. S   f
 xdx . C. S f
 xdx . D. S   f  xdx . a a a a
Câu 6: Thể tích V của khối tròn xoay khi quay hình phẳng giới hạn bởi đồ thị hàm số y = f (x) , trục
Ox và hai đường thẳng x = a, x = b ( a < b ) quanh trục Ox được tính theo công thức b b b b A. 2 V f
 xdx . B. V f
 xdx . C. V   f
 xdx . D. 2 V   f  xdx . a a a a Mã đề 132 Trang 1/6
Câu 7: Cho hai hàm số y = f (x) và y = g (x) liên tục trên đoạn [a;b]. Diện tích S của hình phẳng
giới hạn bởi hai đồ thị hàm số đó và các đường thẳng x = a, x = b được tính theo công thức b b A. Sf
  xgx   dx   . B. S   f
 xgxdx . aa b b C. S f
 xgxdx . D. Sf
  xgx    dx   . a a
Câu 8: Phần ảo của số phức z = 2 + 3i là A. 3i . B. 2 . C. 2i . D. 3 .
Câu 9: Tính môđun của số phức z = a + bi (a,b∈) . A. 2 2
z a b . B. 2 2
z a b .
C. z a b .
D. z a b .
Câu 10: Số phức liên hợp của số phức z = 2 + 3i là
A. 2  3i . B. 3  2i . C. 3  2i . D. 2  3i .
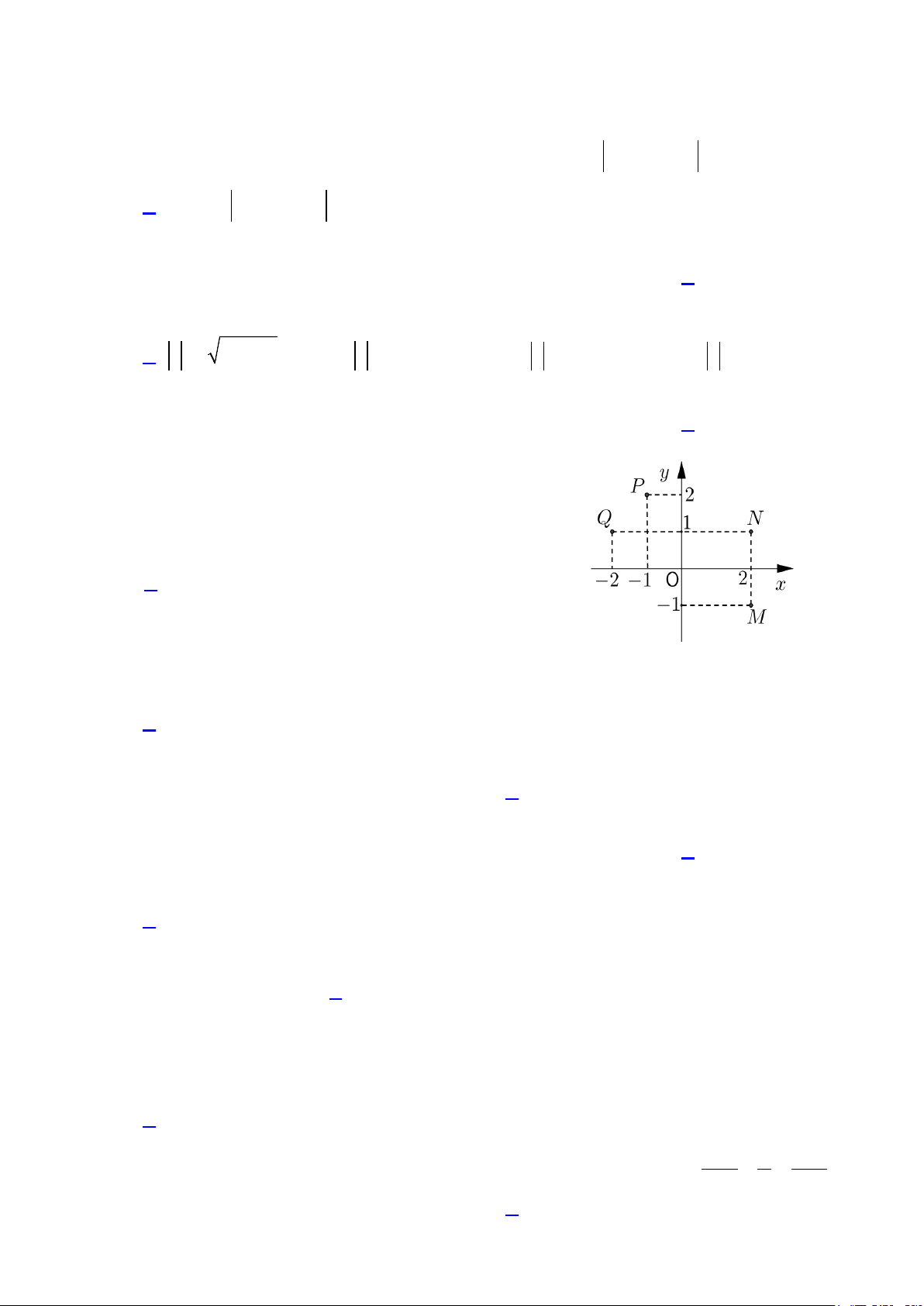
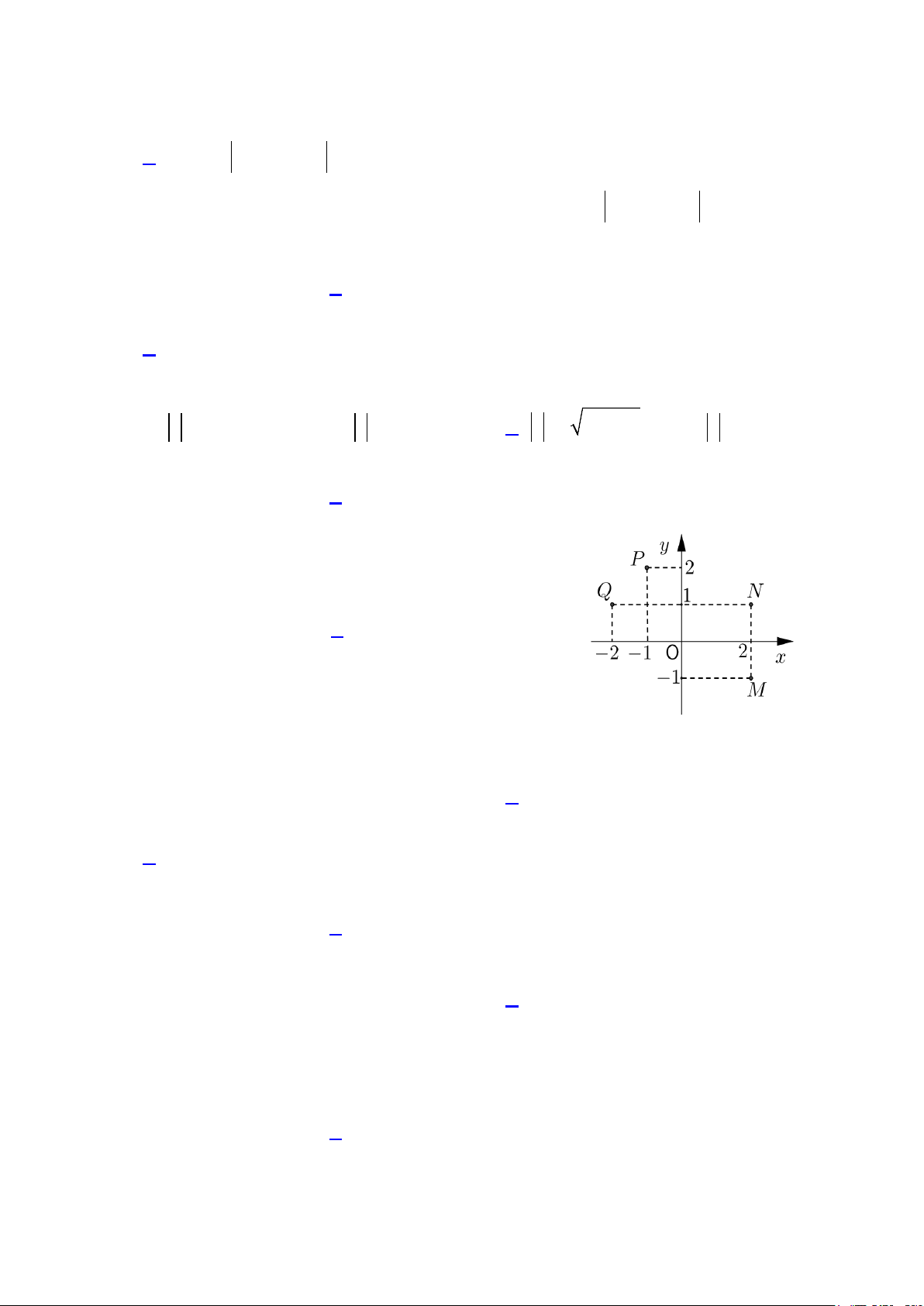
Câu 11: Trên mặt phẳng tọa độ điểm biểu diễn số phức
z  1 2i là điểm nào trong các điểm sau? (hình vẽ bên) A. M. B. N. C. . P D. . Q
Câu 12: Cho hai số phức 1z = 2 + 3i và z2 =1− 2i . Tính 1z + z2 A. 3  i . B. 3  2i . C. 3  5i . D. 3  5i .
Câu 13: Tính số phức z = (2 + i).i A. 1  2i . B. 1  2i .
C. 1  2i .
D. 1  2i .
Câu 14: Tìm tất cả các căn bậc hai của 4 − . A. 2i . B. 2 . C. 2 và 2 − .
D. 2i và 2 − i .  
Câu 15: Trong không gian Oxyz, tích vô hướng của hai véc tơ a = (1;2; 3 − ) và b = (3; 2 − ;− ) 1 bằng A. 2. B. -4. C. 4. D. -2.
Câu 16: Trong không gian Oxyz, điểm nào dưới đây thuộc mặt phẳng (α ): x − 2y + 3z − 2 = 0 ?. A. M (1; 2 − ;3) . B. N (1; 2 − ;− ) 1 . C. P(1; 2 − ; ) 1 . D. Q( 1; − 2; ) 1 .
Câu 17: Trong không gian Oxyz, mặt phẳng nào dưới đây song song với mặt phẳng
(α ):2x +3y − z +1= 0?
A. 4x + 6y − 2z + 2 = 0.
B. 2x + 3y + z −1= 0 . C. 4
− x − 6y + 2z + 2 = 0.
D. x + y + 5z +1= 0. − +
Câu 18: Trong không gian Oxyz, điểm nào dưới đây không thuộc đường thẳng x 1 y z 1 d : = = ? 3 2 3 A. M(1; 0; -1). B. N(4; 2; 2). C. P(7; 4; -7). D. Q(-2; -2; -4). Mã đề 132 Trang 2/6 x = 2 + t
Câu 19: Trong không gian Oxyz, đường thẳng d :  y =1−t có một véc tơ chỉ phương u là   z = 2t     A. u = (1; 1; − 0) .
B. u = (2;1;2) . C. u = (1; 1; − 2) .
D. u = (2;1;0) . 
Câu 20: Trong không gian Oxyz, đường thẳng đi qua điểm M(3; -2; 1) và nhận véc tơ u = (4; 3; − 5) làm
véc tơ chỉ phương có phương trình tham số là x = 3 + 4tx = 4 + 3tx = 3+ 4tx = 3 + 4t A.     y = 2 − − 3t . B. y = 3 − − 2t .
C. y = 2 −3t . D. y = 2 − − 3t .  z =1+     5t z = 5 +  t z =1+  5t z =1−  5t
Câu 21: Họ tất cả các nguyên hàm của hàm số   2x f x e là A. 1 2x e C . B. 2x e C . C. 2 2 x e C . D. 2 2 . x x e C 2 . Câu 22: Nếu đặt 2
t = x thì tích phân 2 2 . x x e dx ∫
trở thành tích phân nào trong các tích phân sau? 0 4 2 4 2 A. t 1 1 e dt  . B. t e dt  . C. t e dt  . D. t e dt  0 2 0 2 0 0 .
Câu 23: Tính tích phân 1 = 2x I dx ∫ 0 A. 2 . B. ln2 . C. 2.ln2. D. 1 ln 2 ln 2 .
Câu 24: Cho tích phân 3 I = . x ln xdx ∫
. Chọn đẳng thức đúng trong các đẳng thức sau 1 3  3 2  3  2  3 A. x  x  1 I   ln x    xdx I   ln x    xdx   . B. .  2  1   2  2 1 1 1 C. 1
I  x lnx3 3 2  xdx  .
D. I  x lnx3 3 2  xdx  1 1 1 2 1 . y
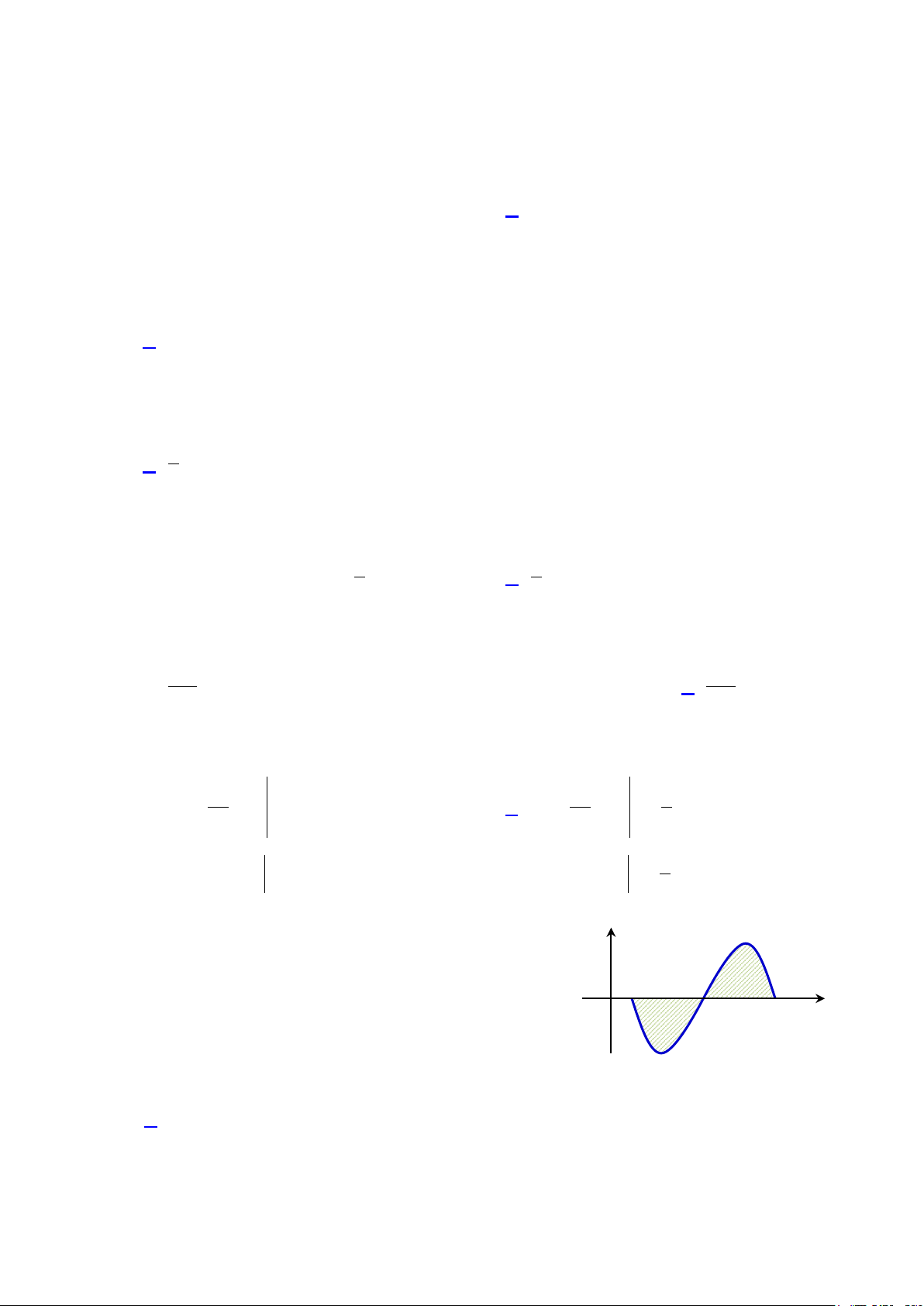
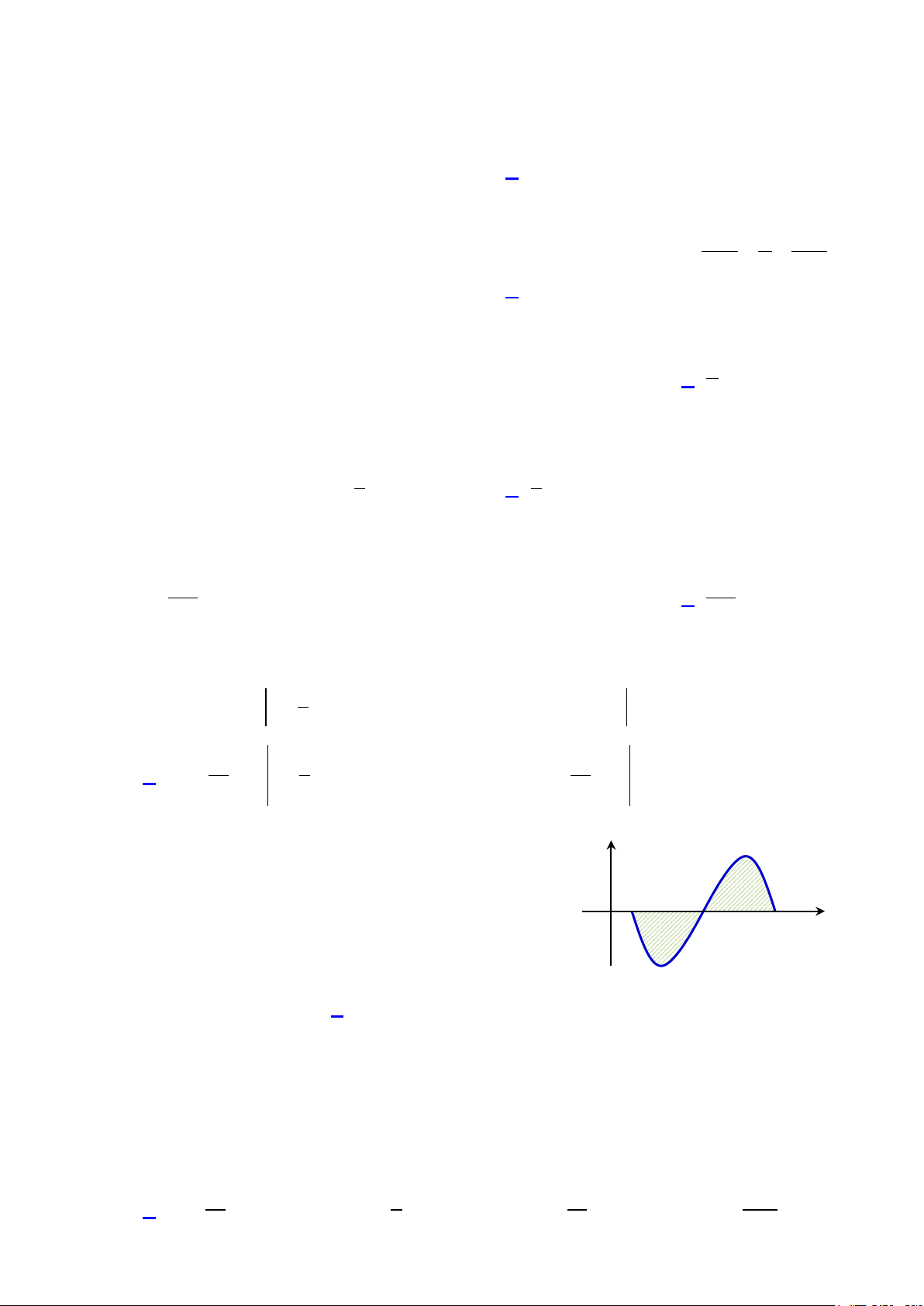
Câu 25: Cho hàm số f (x) liên tục trên đoạn [ ; a c] có đồ thị như hình vẽ bên, biết
b f (x)dx = 2 − ∫ và a O a b c x c f
∫ (x)dx = 3. Tính diện tích S của hình phẳng được b y = f (x) tô đậm. A. S  1. B. S  3. C. S  5 .
D. S  7. Mã đề 132 Trang 3/6
Câu 26: Tính diện tích S hình phẳng giới hạn bởi đồ thị hàm số 2
y = x − 4 , trục hoành và hai đường
thẳng x = 0, x =1. A. 11 S   . B. 8 S  . C. 11 S  . D. 5 S  . 3 3 3 3
Câu 27: Trong các số phức sau số phức nào là số thuần ảo?
A. z  2  i .
B. z  3  i . C. z  2 .
D. z i .
Câu 28: Biết rằng tập hợp các số phức z thỏa mãn điều kiện z −1 = 2 là một đường tròn. Tìm tọa độ tâm đường tròn đó. A. 1;  0 . B. 1;  0 . C. 0; 1. D. 0;  1 .
Câu 29: Tìm số phức z thỏa mãn điều kiện 2z + z = 3+ 4i .
A. z  3  4i .
B. z  1  4i .
C. z  1  4i .
D. z  3  4i .
Câu 30: Cho số phức z thỏa mãn điều kiện .iz =1+ 2i . Phần thực của số phức z bằng A. 1. B. 1. C. 2 . D. 2.
Câu 31: Gọi 1z, z2 là hai nghiệm phức của phương trình 2
z + 2z + 5 = 0 . Tính 1z + z2 A. 5 . B. 13 . C. 2 13 . D. 2 5 .
Câu 32: Trong không gian Oxyz, mặt cầu (S ) 2 2 2
: x + y + z + 2x − 4y − 2 = 0 có bán kính bằng A. 2. B. 3 . C. 6 . D. 7 . 
Câu 33: Trong không gian Oxyz, mặt phẳng (Oxy) có một véc tơ pháp tuyến n là     A. n = (1;1;0). B. n = (1;0;0). C. n = (0;1;0). D. n = (0;0; ) 1 .
Câu 34: Khoảng cách từ điểm M (1;2;3) đến mặt phẳng (P) : x+ 2y + 2z −1 = 0 bằng A. 7 . B. 5 . C. 2 . D. 10 3 3 3 3 .
Câu 35: Trong không gian Oxyz, đường thẳng đi qua hai điểm M (1;2; 3
− ), N(3;4;5) có phương trình tham số là x = 2 + tx =1+ 2tx = 3 + tx =1− 2t A.      y = 3 + t .
B. y = 2 + 2t .
C. y = 4 −t .
D. y = 2 − 2t . z =1+     4t z = 3+  8t z = 5 +  4t z = 3 − +  8t
Câu 36: Chọn khẳng định đúng trong các khẳng định sau. A. 1 x  1dx  
x  1 x 1 C . B. 2
x  1dx x x  1 C. 2 3 C. 1 2
x  1dx x x  1 C  . D. x  1dx  
x  1 x 1 C . 2 3
Câu 37: Biết rằng số phức z = a + bi (a,b∈) thỏa mãn .iz+ 2.z = 6 + 3i . Tính a −b A. 2 . B. 4 . C. 3 . D. 1. Mã đề 132 Trang 4/6
Câu 38: Tính thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi các đường 2
y =1− x , y = 0 quanh trục Ox .   A. 4 . B. 4 . C. 16 . D. 16 . 3 3 15 15 4
x + f ( x)
Câu 39: Tính tích phân I = dx ∫ biết rằng 2 f ∫ (x)dx = 2 1 x 1 A. I  7 . B. I  5. C. I  8 . D. I  9.
Câu 40: Cho số phức z thỏa mãn điều kiện 2z + z .i = 3. Mệnh đề nào sau đây đúng? i
A. 0  z  1.
B. 1  z  2.
C. 2  z  3 .
D. 3  z  4 .
Câu 41: Gọi z0 là nghiệm phức có phần ảo dương của phương trình 4 2
z + z − 6 = 0. Tính .iz0 A. 3 . B.  3 . C. 2.i . D.  2.i .
Câu 42: Trong không gian Oxyz, cho hai điểm A(1;-2;0), B(-3;6;2). Mặt cầu đường kính AB có phương trình là
A. ( x + )2 + ( y − )2 + ( z − )2 1 2 1 = 21.
B. (x − )2 + ( y + )2 + (z + )2 1 2 1 = 21.
C. (x + )2 + ( y − )2 + (z − )2 1 2 1 = 9.
D. (x − )2 + ( y + )2 + (z + )2 1 2 1 = 9 .
Câu 43: Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc và SA = 2, SB = 4. Gọi điểm M là
trung điểm của SB. Biết khoảng cách từ điểm M đến mặt phẳng (ABC) bằng 2 . Tính độ dài 3 cạnh SC. A. SC = 2. B. SC = 4. C. SC = 6. D. SC = 8. x = 4 + 2t
x = 2 − 2t/
Câu 44: Trong không gian Oxyz, cho hai đường thẳng d :  y = 2 −t và d / :  y = 3+ t/    z =1− 3t
z = 4 + 3t/
Xét vị trí tương đối của d và d ' . A. d trùng với d’.
B. d song song với d’. C. d cắt d’. D. d chéo d’. + − − Câu 45: x y z
Trong không gian Oxyz, cho điểm A(2; 1; 3) và đường thẳng 1 1 2 ∆ : = = . Gọi 1 2 − 2 u =( ;a ;3
b ) là một véc tơ chỉ phương của đường thẳng d đi qua điểm A, vuông góc với đường
thẳng ∆ và cắt trục Oy. Tính a + b A. -6. B. 6. C. 4. D. -4.
Câu 46: Biết diện tích hình phẳng giới hạn bởi đường thẳng y = mx ( m là tham số dương) và đồ thị hàm số 2
y = x bằng 1. Chọn khẳng định đúng trong các khẳng định sau.
A. 0  m  1.
B. 1  m  2 .
C. 2  m  3 .
D. 3  m  4 . Mã đề 132 Trang 5/6
Câu 47: Cho hàm số f (x) liên tục trên  π
 thỏa mãn f (x) f x + − =   sin .
x cos x và f (0) = 0. Tính  2  π tích phân = 2 I . x f ' ∫ (x)dx . 0 A. 1 I   . B. 1 I  . C. 3 I   . D. 1 I   . 4 4 4 2 1+ 2i (1− i).z
Câu 48: Cho số phức z thỏa =
+1+ 3i , giá trị của z bằng 2 z z A. 10 . B. 2 10 . C. 3 10 . D. 2 10 . 10 10 10 5
Câu 49: Biết rằng tập hợp các điểm biểu diễn số phức 1+ w iz = (z ≠ 2
− ) là một đường thẳng. Giá trị 2 + z
lớn nhất của biểu thức P = z − 4i là A. 6. B. 7 . C. 5. D. 8 .  x =1
Câu 50: Trong không gian Oxyz, cho điểm M(1; 1; 2) và đường thẳng d :  y = t . Xét mặt phẳng (P)  z =1− t
chứa đường thẳng d và cách điểm M một khoảng lớn nhất. Giả sử mặt phẳng (P) có phương
trình dạng ax + by + cz −1= 0 . Tính T = a + b + c . A. T = 0. B. T = 2. C. T = 4. D. T = 6.
-----------Hết----------- Mã đề 132 Trang 6/6 TRƯỜNG THPT LÊ QUÝ ĐÔN
KIỂM TRA HỌC KỲ II NĂM HỌC 2020-2021 TỔ TOÁN
Môn: Toán – Lớp 12
Đề thi gồm 06 trang
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ, tên thí sinh:…………………………………………………… Mã đề thi 468
Số báo danh: ………………………………………………………
Câu 1: Họ nguyên hàm của hàm số f x  cosx trên  là
A. sin x C .
B. sinx C .
C. cosx C .
D. cosx C
Câu 2: Chọn khẳng định đúng trong các khẳng định sau. A. f
  xgx  dx f .  
 xdx g  xdxB. f
  xgx  dx f .  
 xdx. g  xdxC. f
  xgx  dx f .  
 xdx g  xdxD. f
  xgx  dx f  
 xdx g  xdx  .
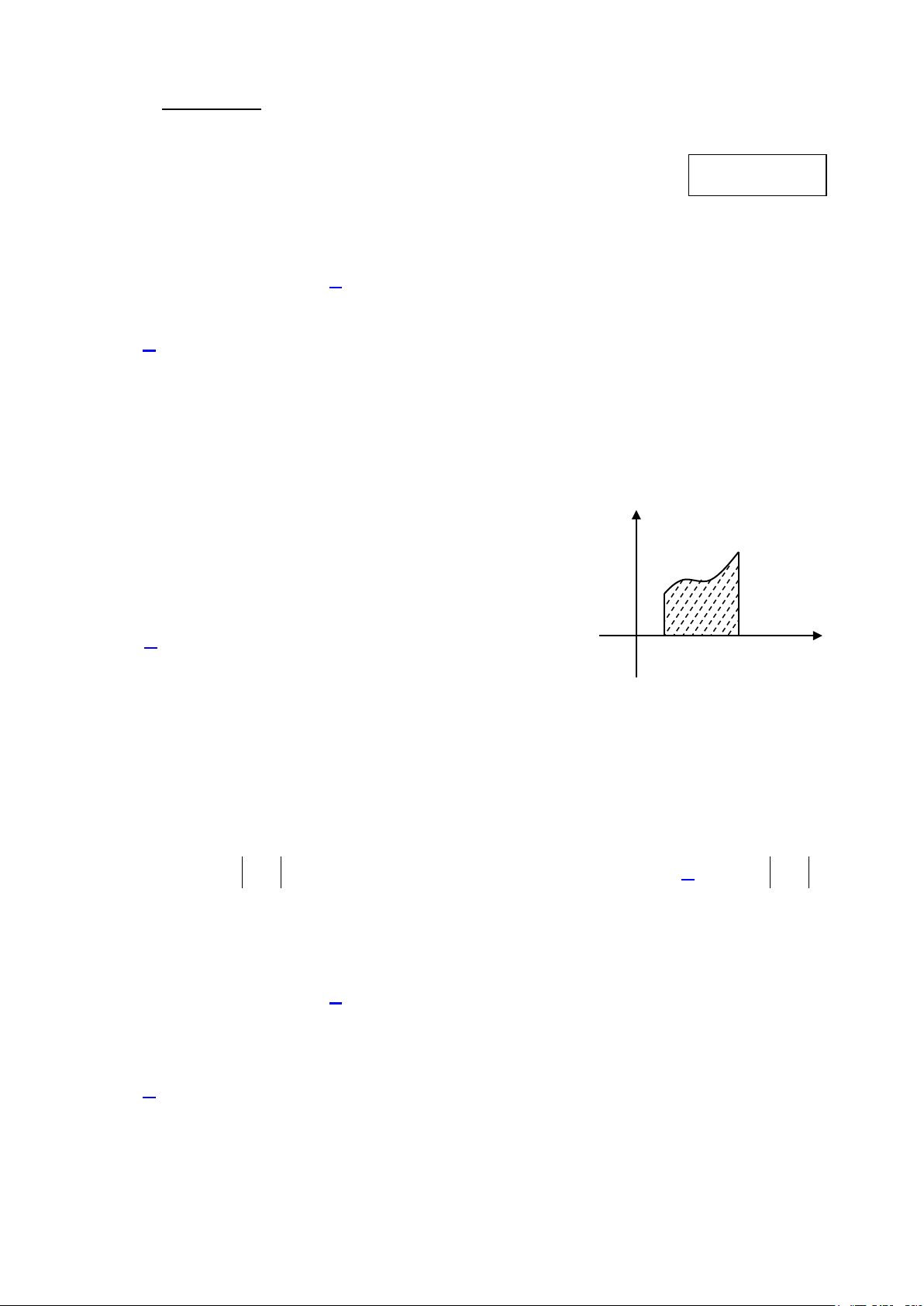
Câu 3: Cho hàm số f (x) liên tục và không âm trên đoạn [ ; a b]. y
Diện tích của hình thang cong giới hạn bởi đồ thị hàm số B
y = f (x) , trục hoành và hai đường thẳng x = a, x = b f(x)
được tính theo công thức nào dưới đây? (Hình bên) A b b x A. S f
 xdx . B. S   f  xdx O a a a . b b b C. Sf   x2   dx   . D. S   f  xdx aa
Câu 4: Cho hàm số f (x) liên tục trên đoạn [a;b]. Diện tích S của hình phẳng giới hạn bởi đồ thị
hàm số f (x) , trục hoành và hai đường thẳng x = a, x = b được tính theo công thức b b b b A. S   f
 xdx . B. S   f
 xdx . C. S f
 xdx . D. S f  xdx . a a a a
Câu 5: Thể tích V của khối tròn xoay khi quay hình phẳng giới hạn bởi đồ thị hàm số y = f (x) , trục
Ox và hai đường thẳng x = a, x = b ( a < b ) quanh trục Ox được tính theo công thức b b b b A. V   f
 xdx . B. 2 V   f
 xdx . C. 2 V f
 xdx . D. V f
 xdx . a a a a
Câu 6: Cho hàm số f (x) liên tục trên đoạn [ ;
a b] và k là hằng số tùy ý. Mệnh đề nào dưới đây đúng? b b b b A. k.f
xdx k. f  xdx . B. k.f
xdx k f
 xdx . a a a a b b b b b C. k.f
xdx f
 kxdx . D. k.f
xdx kdx. f   xdx . a a a a a Mã đề 468 Trang 1/6
Câu 7: Cho hai hàm số y = f (x) và y = g (x) liên tục trên đoạn [ ;
a b]. Diện tích S của hình phẳng
giới hạn bởi hai đồ thị hàm số đó và các đường thẳng x = a, x = b được tính theo công thức b b A. S f
 xgxdx . B. Sf
  xgx    dx   . a ab b C. Sf
  xgx   dx   . D. S   f
 xgxdx . aa
Câu 8: Tính số phức z = (1+ i).i A. 1  i . B. 1  i . C. 1  i . D. 1  i .
Câu 9: Phần ảo của số phức z = 2 − 3i là A. 3. B. 2 . C. 2i . D. 3i .
Câu 10: Tính môđun của số phức z = a + bi (a,b∈) .
A. z a b .
B. z a b . C. 2 2
z a b . D. 2 2
z a b .
Câu 11: Số phức liên hợp của số phức z = 3− 2i là
A. 2  3i . B. 3  2i . C. 3  2i . D. 2  3i .
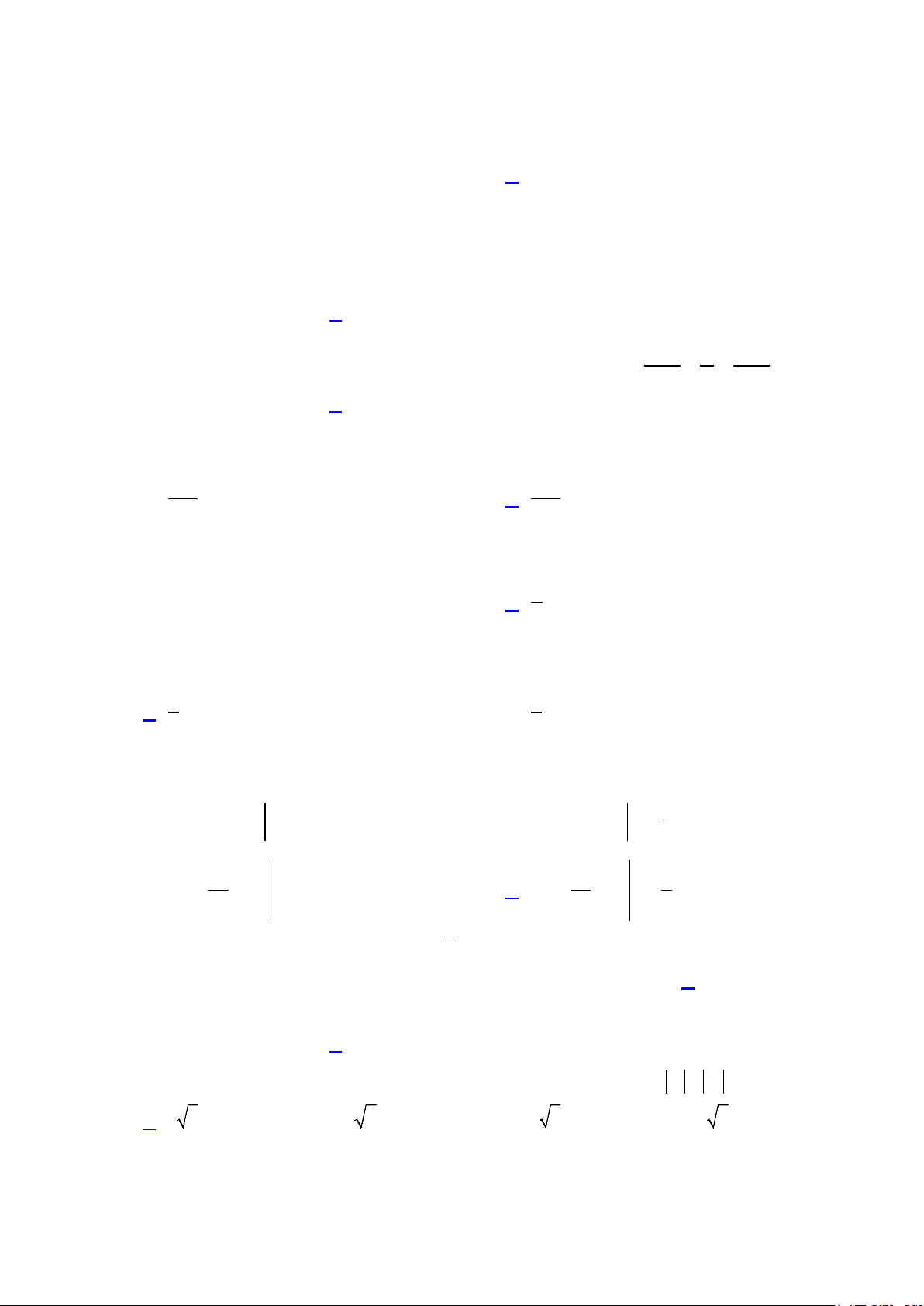
Câu 12: Trên mặt phẳng tọa độ điểm biểu diễn số phức
z  2i là điểm nào trong các điểm sau? (hình vẽ bên) A. M. B. N. C. . P D. . Q
Câu 13: Cho hai số phức 1z = 2 + 7i và z2 =1− 2i . Tính 1z + z2 A. 3  2i . B. 3  2i . C. 3  5i . D. 3  5i .
Câu 14: Tìm tất cả các căn bậc hai phức của 9 − .
A. 3i và 3 − i . B. 3 . C. 3 và 3 − . D. 3i .  
Câu 15: Trong không gian Oxyz, tích vô hướng của hai véc tơ a = (1; 2 − ; 3 − ) và b = (3; 1; − 4) bằng A. 7. B. -7. C. 5. D. -5.
Câu 16: Trong không gian Oxyz, điểm nào dưới đây thuộc mặt phẳng (α ): x − 2y −3z + 2 = 0 ?. A. M (1;1;0) . B. N ( 2 − ;3;2) . C. P( 2 − ;3; 2 − ) . D. Q(1; 2 − ;− ) 1 . 
Câu 17: Trong không gian Oxyz, đường thẳng đi qua điểm M(4; -3; 5) và nhận véc tơ u = (3; 2 − ; ) 1 làm
véc tơ chỉ phương có phương trình tham số là x = 3+ 4tx = 4 + 3tx = 3+ 4tx = 4 + 3t A.     y = 2 − − 3t . B. y = 3 − − 2t .
C. y = 2 −3t . D. y = 3 − + 2t .  z =1+     5t z = 5 +  t z =1+  5t z = 5 +  t Mã đề 468 Trang 2/6
Câu 18: Trong không gian Oxyz, mặt phẳng nào dưới đây trùng với mặt phẳng
(α ):2x −3y − z + 4 = 0 ? A. (α ): 4
− x + 6y + 2z +8 = 0 .
B. 2x + 3y + z − 4 = 0 .
C. 3x + y + 3z + 2 = 0. D. (α ): 4
− x + 6y + 2z −8 = 0.  x = 2t
Câu 19: Trong không gian Oxyz, đường thẳng d :  y =1−t có một véc tơ chỉ phương u là  z = 3+ t    
A. u = (2;1;3) . B. u = (2; 1; − ) 1 .
C. u = (0;1;3) . D. u = (0; 1; − ) 1 . Câu 20: − +
Trong không gian Oxyz, điểm nào dưới đây thuộc đường thẳng x 1 y z 1 d : = = ? 3 2 3 A. M(1; 2; -1). B. N(4; 2; 2). C. P(7; 4; -7). D. Q(-2; -2; 5).
Câu 21: Tính tích phân 1 = 3x I dx ∫ 0 A. 1 . B. 2.ln 3 . C. 2 . D. ln 3 ln 3 ln 3 .
Câu 22: Họ tất cả các nguyên hàm của hàm số   4x f x e là A. 4 1 4 x xe C . B. 4 4 x e C . C. 4x e C . D. 4x e C 4 . Câu 23: Nếu đặt 2
t = x thì tích phân 2 2 . x x e dx ∫
trở thành tích phân nào trong các tích phân sau? 1 4 4 2 2 A. 1 t 1 e dt  . B. t e dt  . C. t e dt  . D. t e dt  2 1 1 2 1 1 .
Câu 24: Cho tích phân 2 I = . x ln xdx ∫
. Chọn đẳng thức đúng trong các đẳng thức sau 1 A. 1
I  x lnx2 2 2  xdx  .
B. I  x lnx2 2 2  xdx. 1 1 1 2 1 2  2 2  2  2  2 C. x  x  1 I   ln x    xdx I   ln x    xdx   . D.   2  1   2  2 1 . 1 1
Câu 25: Tìm số phức z thỏa mãn điều kiện 2z + z = 6 + i .
A. z  1  i .
B. z  1  i .
C. z  2  i .
D. z  2  i .
Câu 26: Cho số phức z thỏa mãn điều kiện .iz = 1
− − i . Phần thực của số phức z bằng A. 1. B. 1. C. 2 . D. 2. Câu 27: Gọi + + = z + z 1
z , z2 là hai nghiệm phức của phương trình 2 z 2z 3 0 . Tính 1 2 A. 2 3 . B. 3 . C. 2 5 . D. 5 . Mã đề 468 Trang 3/6 y
Câu 28: Cho hàm số f (x) liên tục trên đoạn [ ; a c] có đồ thị như hình vẽ bên, biết
b f (x)dx = 3 − ∫ và a O a b c x c f
∫ (x)dx = 4. Tính diện tích S của hình phẳng được b y = f (x) tô đậm. A. S  1.
B. S  3 . C. S  4 .
D. S  7
Câu 29: Tính diện tích S hình phẳng giới hạn bởi đồ thị hàm số 2
y = x − 3, trục hoành và hai đường
thẳng x = 0, x =1. A. 11 S  . B. 8 S  . C. 5 S  . D. 8 S   . 3 3 3 3
Câu 30: Trong các số phức sau số phức nào là số thuần ảo?
A. z  3i .
B. z  1  i .
C. z  1  3i . D. z  3 .
Câu 31: Biết rằng tập hợp các số phức z thỏa mãn điều kiện z +1 = 2 là một đường tròn. Tìm tọa độ tâm đường tròn đó. A. 1;  0 . B. 1;  0 . C. 0; 1. D. 0;  1 .
Câu 32: Trong không gian Oxyz, mặt cầu (S ) 2 2 2
: x + y + z + 4x − 6y − 2 = 0 có bán kính bằng A. 11 . B. 3. C. 15 . D. 14 . 
Câu 33: Trong không gian Oxyz, mặt phẳng (Oxz) có một véc tơ pháp tuyến n là     A. n = (1;0;0). B. n = (0;1;0). C. n = (0;0; ) 1 . D. n = (1;0; ) 1 .
Câu 34: Khoảng cách từ điểm M (1;2;3) đến mặt phẳng (P) : x + 2y + 2z − 6 = 0 bằng A. 7 . B. 5 . C. 2 . D. 10 3 3 3 3 .
Câu 35: Trong không gian Oxyz, đường thẳng đi qua hai điểm M (1; 2;
− 3), N(3;4;5) có phương trình tham số là x =1+ 2tx = 2 + tx =1+ tx = 3 + t A.     y = 2 − + 6t .
B. y =1+ 3t . C. y = 2 − − 3t .
D. y = 4 + 3t .  z = 3−     2t z = 4 +  t z = 3+  t z = 5 − +  t
Câu 36: Tính thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi các đường 2
y = 4 − x , y = 0 quanh trục Ox . A. 512  . B. 512 . C. 32 . D. 32 15 15 3 3 . Mã đề 468 Trang 4/6
Câu 37: Chọn khẳng định đúng trong các khẳng định sau. A. 1 x  2dx  
x 2 x 2 C . B. 1
x  2dx x x  2 C. 2 2 C. 2 x  2dx  
x 2 x 2 C . D. 2
x  2dx x x  2 C  . 3 3 4
x + f ( x)
Câu 38: Tính tích phân I = dx ∫ biết rằng 2 f ∫ (x)dx =1 1 x 1 A. I  7 . B. I  5. C. I  8 . D. I  9.
Câu 39: Biết rằng số phức z = a + bi (a,b∈) thỏa mãn iz + 2z =15 + 6i . Tính a − b A. 6. B. 7 . C. 8 . D. 9.
Câu 40: Cho số phức z
z thỏa mãn điều kiện 2 + z .i = 4 . Mệnh đề nào sau đây đúng? i
A. 0  z  1.
B. 1  z  2.
C. 2  z  3 .
D. 3  z  4 . Câu 41: Gọi z − − =
0 là nghiệm phức có phần ảo dương của phương trình 4 2 z z 6 0 . Tính .iz0 A. 3i . B.  3i . C. 2 . D.  2 .
Câu 42: Trong không gian Oxyz, cho hai điểm A(1;-2;0), B(3;6;-2). Mặt cầu đường kính AB có phương trình là
A. (x + )2 + ( y + )2 + (z − )2 2 2 1 =18.
B. (x − )2 + ( y − )2 + (z + )2 2 2 1 =18.
C. (x + )2 + ( y + )2 + (z − )2 2 2 1 =10 .
D. (x − )2 + ( y − )2 + (z + )2 2 2 1 =10.
Câu 43: Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc và SA = 3, SC = 6. Gọi điểm M là
trung điểm của SC. Biết khoảng cách từ điểm M đến mặt phẳng (ABC) bằng 1. Tính độ dài cạnh SB. A. SB = 8. B. SB = 6. C. SB = 4. D. SB = 3. x = 4 − 2t
x = 2 + 2t/
Câu 44: Trong không gian Oxyz, cho hai đường thẳng d :  /
y = 2 + t và d :  y = 3 − t/ z =1+   3t
z =1− 3t/
Xét vị trí tương đối của d và d '.
A. d trùng với d’.
B. d song song với d’. C. d cắt d’. D. d chéo d’. + − − Câu 45: x y z
Trong không gian Oxyz, cho điểm A(2; 1; 3) và đường thẳng 1 1 2 ∆ : = = . Gọi 1 2 2 −
u =( ;a1;c) là một véc tơ chỉ phương của đường thẳng d đi qua điểm A, vuông góc với đường
thẳng ∆ và cắt trục Ox. Tính a + c A. -5. B. 5. C. 7. D. -7.
Câu 46: Biết diện tích hình phẳng giới hạn bởi đường thẳng y = mx ( m là tham số dương) và đồ thị hàm số 2
y = x bằng 2 . Chọn khẳng định đúng trong các khẳng định sau.
A. 0  m  1.
B. 1  m  2 .
C. 2  m  3 .
D. 3  m  4 . Mã đề 468 Trang 5/6
Câu 47: Cho hàm số f (x) liên tục trên  thỏa mãn f (x) f  π x + − =   2sin .
x cos x và f (0) = 0.  2  π Tính tích phân = 2 I . x f ' ∫ (x)dx . 0 A. 1 I   . B. 1 I  . C. 3 I   . D. 1 I   . 4 4 4 2 1+ i (1− i).z
Câu 48: Cho số phức z thỏa =
+1+ 3i , giá trị của z bằng 2 z z A. 10 . B. 2 10 . C. 3 10 . D. 2 10 . 10 10 10 5
Câu 49: Biết rằng tập hợp các điểm biểu diễn số phức 1+ w iz = (z ≠ 2
− ) là một đường thẳng. Giá trị 2 + z
lớn nhất của biểu thức P = z − 5i là A. 6. B. 7 . C. 5. D. 8 .  x =1
Câu 50: Trong không gian Oxyz, cho điểm M(1; 1; 2) và đường thẳng d : y =1+ t . Xét mặt phẳng (P)   z = t
chứa đường thẳng d và cách điểm M một khoảng lớn nhất. Giả sử mặt phẳng (P) có phương
trình dạng ax + by + cz −1= 0 . Tính T = a + b + c . A. T = 0. B. T = 2. C. T = 4. D. T = 6. ------Hết-------- Mã đề 468 Trang 6/6 TRƯỜNG THPT LÊ QUÝ ĐÔN
KIỂM TRA HỌC KỲ II NĂM HỌC 2020-2021 TỔ TOÁN
Môn: Toán – Lớp 12
Đề thi gồm 06 trang
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ, tên thí sinh:…………………………………………………… Mã đề thi 672
Số báo danh: ………………………………………………………
Câu 1: Cho hàm số f (x) liên tục trên đoạn [ ;
a b] và k là hằng số tùy ý. Mệnh đề nào dưới đây đúng? b b b b b A. k.f
xdx f
 kxdx . B. k.f
xdx kdx. f
 xdx . a a a a a b b b b C. k.f
xdx k f  xdx . D. k.f
xdx k. f
 xdx a a a a
Câu 2: Chọn khẳng định đúng trong các khẳng định sau. A. f
  xgx  dx f .  
 xdx. g  xdxB. f
  xgx  dx f .  
 xdx g  xdxC. f
  xgx  dx f .  
 xdx g  xdxD. f
  xgx  dx f  
 xdx g  xdx  .
Câu 3: Họ nguyên hàm của hàm số f x  sinx trên  là
A. sin x C .
B. sinx C .
C. cosx C .
D. cosx C .
Câu 4: Cho hai hàm số y = f (x) và y = g (x) liên tục trên đoạn [ ;
a b]. Diện tích S của hình phẳng
giới hạn bởi hai đồ thị hàm số đó và các đường thẳng x = a, x = b được tính theo công thức b b A. Sf
  xgx    dx   . B. S f
 xgxdx . aa b b C. S   f
 xgxdx . D. Sf
  xgx   dx   . a a
Câu 5: Thể tích V của khối tròn xoay khi quay hình phẳng giới hạn bởi đồ thị hàm số y = f (x) , trục
Ox và hai đường thẳng x = a, x = b ( a < b ) quanh trục Ox được tính theo công thức b b b b A. 2 V f
 xdx . B. V   f
 xdx . C. 2 V   f
 xdx . D. V f  xdx . a a a a
Câu 6: Cho hàm số f (x) liên tục và không âm trên đoạn [a;b]. y
Diện tích của hình thang cong giới hạn bởi đồ thị hàm số B
y = f (x) , trục hoành và hai đường thẳng x = a, x = b f(x)
được tính theo công thức nào dưới đây? (Hình bên) A b b x A. S   f
 xdx . B. S f  xdx O a a a . b b b C. S   f
 xdx . D. Sf   x2   dx   a a Mã đề 672 Trang 1/6
Câu 7: Cho hàm số f (x) liên tục trên đoạn [a;b]. Diện tích S của hình phẳng giới hạn bởi đồ thị
hàm số f (x) , trục hoành và hai đường thẳng x = a, x = b được tính theo công thức b b b b A. S f
 xdx . B. S f
 xdx . C. S   f
 xdx . D. S   f  xdx . a a a a
Câu 8: Phần ảo của số phức z = 3+ 2i là A. 3i . B. 2 . C. 2i . D. 3 .
Câu 9: Tìm tất cả các căn bậc hai phức của 16 − . A. 4i .
B. 4i và 4 − i . C. 4 . D. 4 và 4 − .
Câu 10: Tính môđun của số phức z = a + bi (a,b∈) .
A. z a b . B. 2 2
z a b .
C. z a b . D. 2 2
z a b .
Câu 11: Số phức liên hợp của số phức z = 3+ 2i là
A. 2  3i . B. 3  2i . C. 3  2i .
D. 2  3i
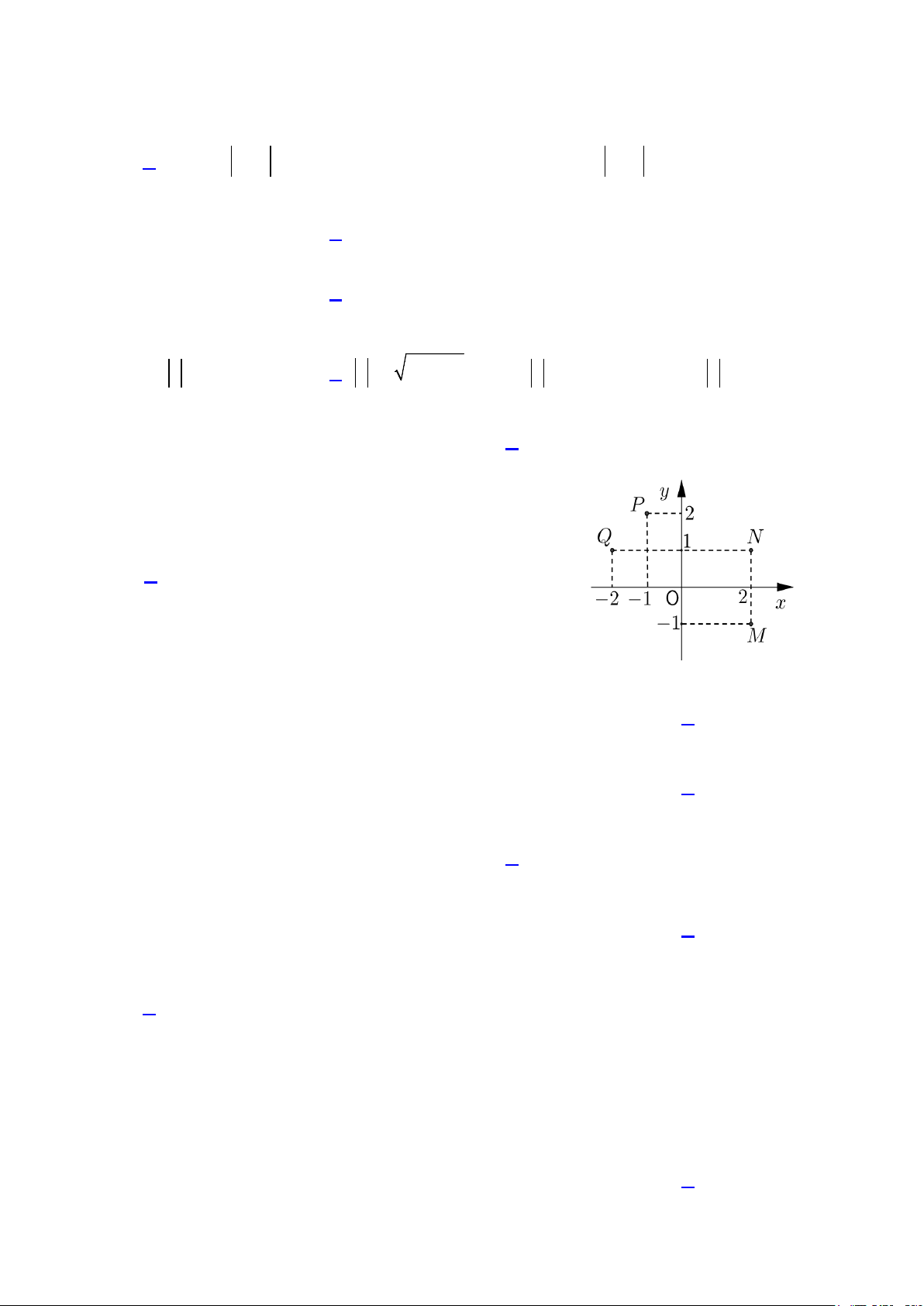
Câu 12: Trên mặt phẳng tọa độ điểm biểu diễn số phức
z  2i là điểm nào trong các điểm sau? (hình vẽ bên) A. M. B. N. C. . P D. . Q
Câu 13: Cho hai số phức 1z = 2 −3i và z2 =1− 2i . Tính 1z + z2 A. 3  2i . B. 3  2i . C. 3  5i . D. 3  5i .
Câu 14: Tính số phức z = (3+ i).i A. 1  3i . B. 1  3i .
C. 1  3i .
D. 1  3i .  
Câu 15: Trong không gian Oxyz, tích vô hướng của hai véc tơ a = ( 1; − 2;3) và b = ( 3; − 2;− ) 1 bằng A. 2. B. -4. C. 4. D. 2.
Câu 16: Trong không gian Oxyz, điểm nào dưới đây thuộc mặt phẳng (α ): x + 2y −3z − 2 = 0 ? A. M (0;0; ) 1 . B. N ( 2 − ;0;0). C. P(2;3; 2 − ) . D. Q(2;3;2).
Câu 17: Trong không gian Oxyz, mặt phẳng nào dưới đây cắt mặt phẳng (α ): 2x −3y − z +1= 0? A. (α ): 4
− x + 6y − 2z −1= 0 . B. (α ): 4
− x + 6y + 2z −1= 0 . C. (α ): 4
− x + 6y + 2z +1= 0 .
D. (α ): 2x −3y − z +1= 0. x =1− 2t
Câu 18: Trong không gian Oxyz, đường thẳng d : y = t có một véc tơ chỉ phương u là   z = 3+ t    
A. u = (1;1;3) .
B. u = (1;0;3) . C. u = ( 2 − ;0; ) 1 . D. u = ( 2 − ;1 ) ;1 . Mã đề 672 Trang 2/6
Câu 19: Trong không gian Oxyz, đường thẳng đi qua điểm M(3; 2; 1) và nhận véc tơ u = (4; 3; − 5) làm
véc tơ chỉ phương có phương trình tham số là x = 4 + 3tx = 4 + 3tx = 3+ 4tx = 3 + 4t A.     y = 3 − + 2t . B. y = 3 − − 2t .
C. y = 2 −3t .
D. y = 2 −3t .  z = 5+     t z = 5 +  t z =1+  5t z =1−  5t Câu 20: + −
Trong không gian Oxyz, điểm nào dưới đây không thuộc đường thẳng x 1 y z 1 d : = = ? 3 2 3 A. M(-1; 0; 1). B. N(-4; -2; -2). C. P(-7; -4; 7). D. Q(2; 2; 4).
Câu 21: Họ tất cả các nguyên hàm của hàm số   3x f x e là A. 3 1 3 x xe C . B. 3 3 x e C . C. 3x e C . D. 3x e C 3 . Câu 22: Nếu đặt 2
t = x thì tích phân 3 2 . x x e dx ∫
trở thành tích phân nào trong các tích phân sau? 0 9 3 9 3 A. t 1 1 e dt  . B. t e dt  . C. t e dt  . D. t e dt  0 2 0 2 0 0 .
Câu 23: Tính tích phân 1 = 5x I dx ∫ 0 A. 3 . B. 3 ln 5 . C. ln 5. D. 4 ln 5 ln 5 .
Câu 24: Cho tích phân 3 I = .xln xdx ∫
. Chọn đẳng thức đúng trong các đẳng thức sau 2 A. I   x 3 3 2 1 x ln  xdx  .
B. I  x lnx3 3 2  xdx. 2 2 2 2 2 3  3 2  3  2  3 C. x  1 xI   ln x    xdx I   ln x    xdx   . D.   2  2 2  2  2  2 2 y
Câu 25: Cho hàm số f (x) liên tục trên đoạn [ ; a c] có đồ thị như hình vẽ bên, biết
b f (x)dx = 1 − ∫ và a O a b c x c f
∫ (x)dx = 2. Tính diện tích S của hình phẳng được b y = f (x) tô đậm. A. S  1.
B. S  3 . C. S  2 .
D. S  5
Câu 26: Tính diện tích S hình phẳng giới hạn bởi đồ thị hàm số 2
y = x − 5, trục hoành và hai đường
thẳng x = 0, x =1.  A. 14 S  . B. 8 S  . C. 11 S  . D. 14 S  . 3 3 3 3 Mã đề 672 Trang 3/6
Câu 27: Trong các số phức sau số phức nào là số thuần ảo? A. z  2 .
B. z  2i .
C. z  1  3i .
D. z  1  i .
Câu 28: Tìm số phức z thỏa mãn điều kiện 2z + z = 3+ 5i .
A. z  2  5i .
B. z  2  5i .
C. z  1  5i .
D. z  1  5i .
Câu 29: Cho số phức z thỏa mãn điều kiện .iz = 2
− + i . Phần thực của số phức z bằng A. 1. B. 1. C. 2 . D. 2.
Câu 30: Biết rằng tập hợp các số phức z thỏa mãn điều kiện z − 2 =1 là một đường tròn. Tìm tọa độ tâm đường tròn đó. A. 0;  2 . B. 0;  2 . C. 2;  0 . D. 2;  0 . Câu 31: Gọi + + = z + z 1
z , z2 là hai nghiệm phức của phương trình 2 z 2z 7 0. Tính 1 2 A. 5 . B. 2 7 . C. 7 . D. 2 5 .
Câu 32: Khoảng cách từ điểm M (1;2;3) đến mặt phẳng (P) : x + 2y + 2z − 4 = 0 bằng A. 7 . B. 5 . C. 2 . D. 10 3 3 3 3 .
Câu 33: Trong không gian Oxyz, mặt cầu (S ) 2 2 2
: x + y + z + 2x − 6y − 2 = 0 có bán kính bằng A. 11 . B. 12 . C. 8 . D. 4. 
Câu 34: Trong không gian Oxyz, mặt phẳng (Oyz) có một véc tơ pháp tuyến n là     A. n = (1;0;0). B. n = (0;1;0). C. n = (0;0; ) 1 . D. n = (0;1 ) ;1 .
Câu 35: Trong không gian Oxyz, đường thẳng đi qua hai điểm M ( 1
− ;2;3), N(3;4;5) có phương trình tham số là x =1+ 2tx = 1 − + 4tx = 3 + 2tx =1+ 4t A.      y = 3 + t .
B. y = 2 + 2t .
C. y = 4 −t .
D. y = 2 + 2t .  z = 4+     t z = 3−  2t z = 5 +  t z = 3+  2t
Câu 36: Chọn khẳng định đúng trong các khẳng định sau. A. 2 1
x  2dx x x  2 C  . B. x  2dx  
x  2 x  2 C . 3 2 C. 1 2
x  2dx x x  2 C  . D. x  2dx  
x  2 x  2 C . 2 3
Câu 37: Tính thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi các đường 2
y = 9 − x , y = 0 quanh trục Ox . A.  36. B. 1296 . C. 1296 . D. 36. 5 5 4
x + f ( x)
Câu 38: Tính tích phân I = dx ∫ biết rằng 2 f ∫ (x)dx = 3 1 x 1 A. I  7 . B. I  5. C. I  8 . D. I  9. Mã đề 672 Trang 4/6
Câu 39: Biết rằng số phức z = a + bi (a,b∈) thỏa mãn iz + 2.z =19 + 5i . Tính a − b A. 6. B. 7 . C. 8 . D. 9.
Câu 40: Cho số phức z
z thỏa mãn điều kiện 2 + z .i = 6 . Mệnh đề nào sau đây đúng? i
A. 0  z  1.
B. 1  z  2.
C. 2  z  3 .
D. 3  z  4 . Câu 41: Gọi z + − =
0 là nghiệm phức có phần ảo dương của phương trình 4 2 z
3z 10 0 . Tính .iz0 A.  5 . B. 5 . C. 2i . D.  2i .
Câu 42: Trong không gian Oxyz, cho hai điểm A(-1;-2;0), B(-3;6;-2). Mặt cầu đường kính AB có phương trình là
A. (x − )2 + ( y + )2 + (z − )2 2 2 1 =18.
B. (x − )2 + ( y + )2 + (z − )2 2 2 1 =10.
C. (x + )2 + ( y − )2 + (z + )2 2 2 1 =18.
D. (x + )2 + ( y − )2 + (z + )2 2 2 1 =10 . x = 3+ 2tx = 1 − − 4t/
Câu 43: Trong không gian Oxyz, cho hai đường thẳng d : y = 2 −3t và d / :  y = 5+ 6t/   z = 1 − + t
z = 4 − 2t/
Xét vị trí tương đối của d và d '. A. d cắt d’. B. d chéo d’.
C. d trùng với d’.
D. d song song với d’.
Câu 44: Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc và SC = 4, SB = 8. Gọi điểm M là
trung điểm của SB. Biết khoảng cách từ điểm M đến mặt phẳng (ABC) bằng 4 . Tính độ dài 3 cạnh SA. A. SA = 2. B. SA = 4. C. SA = 6. D. SA = 8.
Câu 45: Biết diện tích hình phẳng giới hạn bởi đường thẳng y = mx ( m là tham số dương) và đồ thị hàm số 2
y = x bằng 5. Chọn khẳng định đúng trong các khẳng định sau.
A. 0  m  1.
B. 1  m  2 .
C. 2  m  3 .
D. 3  m  4 . − + − Câu 46: x y z
Trong không gian Oxyz, cho điểm A(3; 2; 1) và đường thẳng 1 1 2 ∆ : = = . Gọi 1 2 − 1
u =(3; ;bc)là một véc tơ chỉ phương của đường thẳng d đi qua điểm A, vuông góc với đường
thẳng ∆ và cắt trục Oz. Tính b + c A. 3. B. -5. C. -3. D. 5. 1+ 2i (1+ i).z
Câu 47: Cho số phức z thỏa =
+1+ 3i , giá trị của z bằng 2 z z A. 10 . B. 2 10 . C. 3 10 . D. 2 10 . 10 10 10 5 Mã đề 672 Trang 5/6
Câu 48: Biết rằng tập hợp các điểm biểu diễn số phức 1+ w iz = (z ≠ 2
− ) là một đường thẳng. Giá trị 2 + z
lớn nhất của biểu thức P = z − 3i là A. 6. B. 7 . C. 5. D. 8 .
Câu 49: Cho hàm số f (x) liên tục trên  thỏa mãn f (x) f  π x + − =   3sin .
x cos x và f (0) = 0. Tính  2  π tích phân = 2 I . x f ' ∫ (x)dx . 0 A. 1 I   . B. 1 I  . C. 3 I   . D. 1 I   . 4 4 4 2  x = t
Câu 50: Trong không gian Oxyz, cho điểm M(1; 2; 1) và đường thẳng d : y =1−t . Xét mặt phẳng (P)   z = 2
chứa đường thẳng d và cách điểm M một khoảng lớn nhất. Giả sử mặt phẳng (P) có phương
trình dạng ax + by + cz +1= 0 . Tính T = a + b + c . A. T = 3. B. T = 2. C. T = 1. D. T = 0 -------Hết------- Mã đề 672 Trang 6/6 TRƯỜNG THPT LÊ QUÝ ĐÔN
ĐÁP ÁN KIỂM TRA CUỐI KỲ II NĂM 2020-2021 TỔ TOÁN MÃ ĐỀ 132 1.D 2.C 3.B 4.D 5.C 6.D 7.C 8.D 9.A 10.D 11.C 12.A 13.C 14.D 15.A 16.B 17.C 18.C 19.C 20.A 21.A 22.C 23.D 24.B 25.C 26.C 27.D 28.B 29.C 30.C 31.D 32.D 33.D 34.D 35.A 36.D 37.C 38.D 39.A 40.B 41.B 42.A 43.A 44.A 45.B 46.B 47.A 48.C 49.A 50.B MÃ ĐỀ 468 1.B 2.A 3.A 4.D 5.B 6.A 7.A 8.B 9.A 10.C 11.B 12.B 13.C 14.A 15.B 16.C 17.B 18.D 19.B 20.B 21.C 22.C 23.A 24.D 25.D 26.B 27.A 28.D 29.B 30.A 31.A 32.C 33.B 34.B 35.B 36.A 37.C 38.B 39.B 40.C 41.D 42.B 43.D 44.B 45.C 46.C 47.D 48.B 49.B 50.A MÃ ĐỀ 672 1.D 2.B 3.C 4.B 5.C 6.B 7.A 8.B 9.B 10.B 11.C 12.A 13.D 14.D 15.C 16.D 17.A 18.D 19.C 20.C 21.D 22.C 23.D 24.C 25.B 26.A 27.B 28.D 29.A 30.D 31.B 32.A 33.B 34.A 35.A 36.D 37.C 38.D 39.C 40.D 41.A 42.C 43.D 44.B 45.D 46.A 47.A 48.C 49.C 50.C
HD GIẢI MỘT SỐ CÂU VẬN DỤNG CAO TRONG MÃ ĐỀ 132
Câu 47. Cho hàm số f (x) liên tục trên  π
 thỏa mãn f (x) f x + − =   sin .
x cos x và f (0) = 0. Tính  2  π tích phân = 2 I . x f ' ∫ (x)dx . 0 A. 1 I   . B. 1 I  . C. 3 I   . D. 1 I   . 4 4 4 2 HD + Thay  π
0 vào biểu giả thiết f (x) f x + − =     sin .
x cos x (1) ta được f (0) = f π =   0  2   2  π π π π + Tích phân = 2 I . x f ' ∫
(x)dx = .xf (x) 2 − 2 f ∫ (x) = 2 dx f ∫ (x)dx 0 0 0 0 π π π  π
+ Lấy tích phân hai vế biểu thức (1) ta được  2 f ∫ (x) + 2 − = 2 dx f ∫  xdx sin . x cos xdx ∫ 0 0 0  2  π π ⇔ 2 2 f ∫ (x) = 2 dx sin . x cos xdx ∫ 0 0 π π  π (do  2 f ∫ (x) = 2 dx f −
∫  xdx ) 0 0  2  1+ 2i (1− i).z
Câu 48. Cho số phức z thỏa =
+1+ 3i , giá trị của z bằng 2 z z Trang 1/1 A. 10 . B. 2 10 . C. 3 10 . D. 2 10 . 10 10 10 5 HD
+ Nhân hai vế giả thiết với z ta được 1+ 2i = (1−i) + (1+ 3i).z (chú ý 2
z.z = z )
Câu 49. Biết rằng tập hợp các điểm biểu diễn số phức 1+ w iz = (z ≠ 2
− ) là một đường thẳng. Giá trị 2 + z
lớn nhất của biểu thức P = z − 4i là A. 6. B. 7 . C. 5. D. 8 . HD
+ Trước tiên ta chứng minh kq: 1z.z2 = 1z . z2 Thật vậy đặt 1z = a + bi và z2 = c + di
Khi đó 1z.z2 = (ac −bd ) + (ad + bc)i
⇒ z .z = (ac − bd )2 + (ad + bc)2 = (ac)2 + (bd )2 + (ad )2 + (bc)2 1 2 2 = a ( 2 2 c + d ) 2 + b ( 2 2 c + d ) = ( 2 2 a + b )( 2 2
c + d ) = 1z . z2
+ Đặt w = x + yi . + Từ giả thiết 1 w iz =
⇒ w (2 + z) =1+ iz ⇒ z (w − i) =1− 2w ⇒ z[x + yi − i] =1− 2(x + yi) (1) 2 + z
+ Lấy modun hai vế biểu thức (1) ta được 2 z x + ( y − )2 1 = (1− 2x)2 + ( 2 − y)2 2 ⇒ z ( 2 2
x + y − y + ) = ( 2 2 2 1
4x + 4y − 4x + ) 1 (2) + Từ (2) suy ra: - Nếu 2
z ≠ 4 thì tập hợp các điểm biểu diễn số phức w là đường tròn. -Nếu 2
z = 4 thì tập hợp các điểm biểu diễn số phức w là đường thẳng thỏa mãn đề bài. Suy ra z = 2
+ P = z − 4i ≤ z + 4i = 6 . Dấu “=” xảy ra khi z = 2
− i . Vậy GTLN của P bằng 6  x =1
Câu 50. Trong không gian Oxyz, cho điểm M(1; 1; 2) và đường thẳng d :  y = t . Xét mặt phẳng (P)  z =1− t
chứa đường thẳng d và cách điểm M một khoảng lớn nhất. Giả sử mặt phẳng (P) có phương trình dạng
ax + by + cz −1= 0 . Tính T = a + b + c . A. T = 0. B. T = 2. C. T = 4. D. T = 6. HD
+ Gọi H là hình chiếu vuông góc của M lên đường thẳng d. Khi đó mp (P) thỏa ycbt đi qua vuông góc với MH tại H.
+ Tìm tọa độ điểm H sau đó viết ptmp (P) -------Hết------- Trang 2/1
Document Outline

  • ĐỀ 1-CUỐI KỲ 2-KHỐI 12 (NĂM 20-21)
  • ĐỀ 2-CUỐI KỲ 2-KHỐI 12 (NĂM 20-21)
  • ĐỀ 3-CUỐI KỲ 2-KHỐI 12 (NĂM 20-21)
  • BẢNG ĐÁP ÁN-CUỐI KỲ 2-KHỐI 12 (NĂM 20-21)