Đại học Quốc gia TpHCM Trường Đại học KHTN
ĐỀ THI CƠ HỌC 1 (Khóa 2013)
Năm học: 2013 - 2014 – Thời gian: 90 phút
Sinh viên không sử dụng tài liệu
Câu 1: Một chất điểm chuyển động với vận tốc thay đổi theo quãng đường với quy
luật sau: v = α√s, với α là hằng số dương. Biết rằng s = 0 tại thời điểm t = 0. Hãy tìm
quãng đường vật đi được s và vận tốc v của chất điểm như hàm của thời gian.
Câu 2: Một viên đạn có khối lượng m được bắn thẳng đứng từ mặt đất với vận tốc ban
đầu bằng vo (lúc t = 0). Cho biết lực cản của không khí lên viên đạn có độ lớn tỉ lệ với
vận tốc của viên đạn với hệ số tỉ lệ là 𝜂 (hằng số dương). Hãy xác định thời điểm t lúc
viên đạn đạt được độ cao cực đại. Từ kết quả thu được hãy suy ra thời điểm này trong
trường hợp không có lực cản (𝜂 = 0).
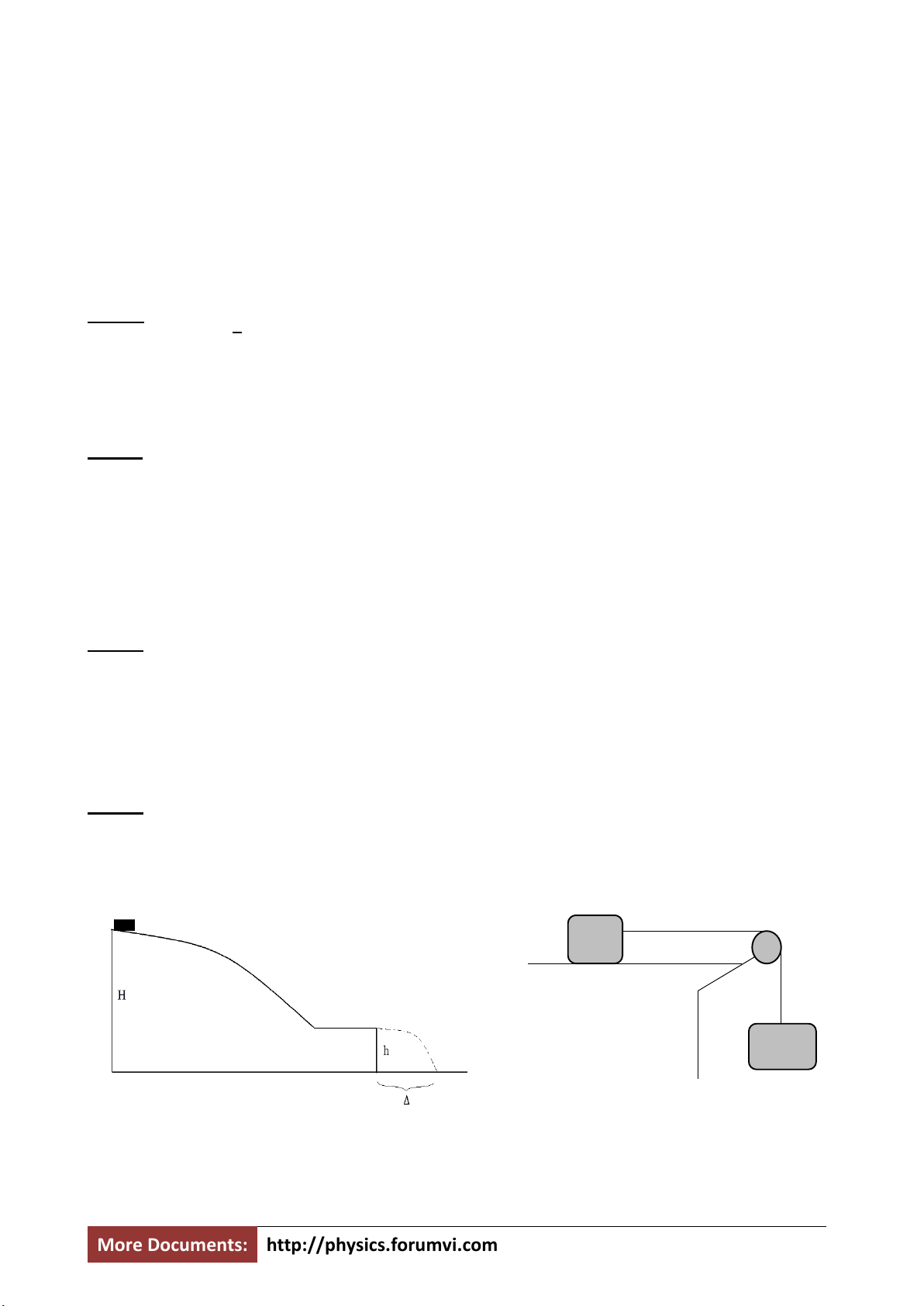
Câu 3: Một vật nhỏ với vận tốc ban đầu vo = 0, trượt xuống từ một vị trí ở độ cao H
của một ngọn đồi. Phần cuối của ngọn đồi là một đoạn thẳng nằm ngang có bờ dốc
thẳng đứng ở độ cao h (hình 1). Hỏi h phải bằng bao nhiêu để vật nhỏ bay ra được một
khoảng cách s là xa nhất. Bỏ qua lực ma sát của đất và lực cản của không khí.
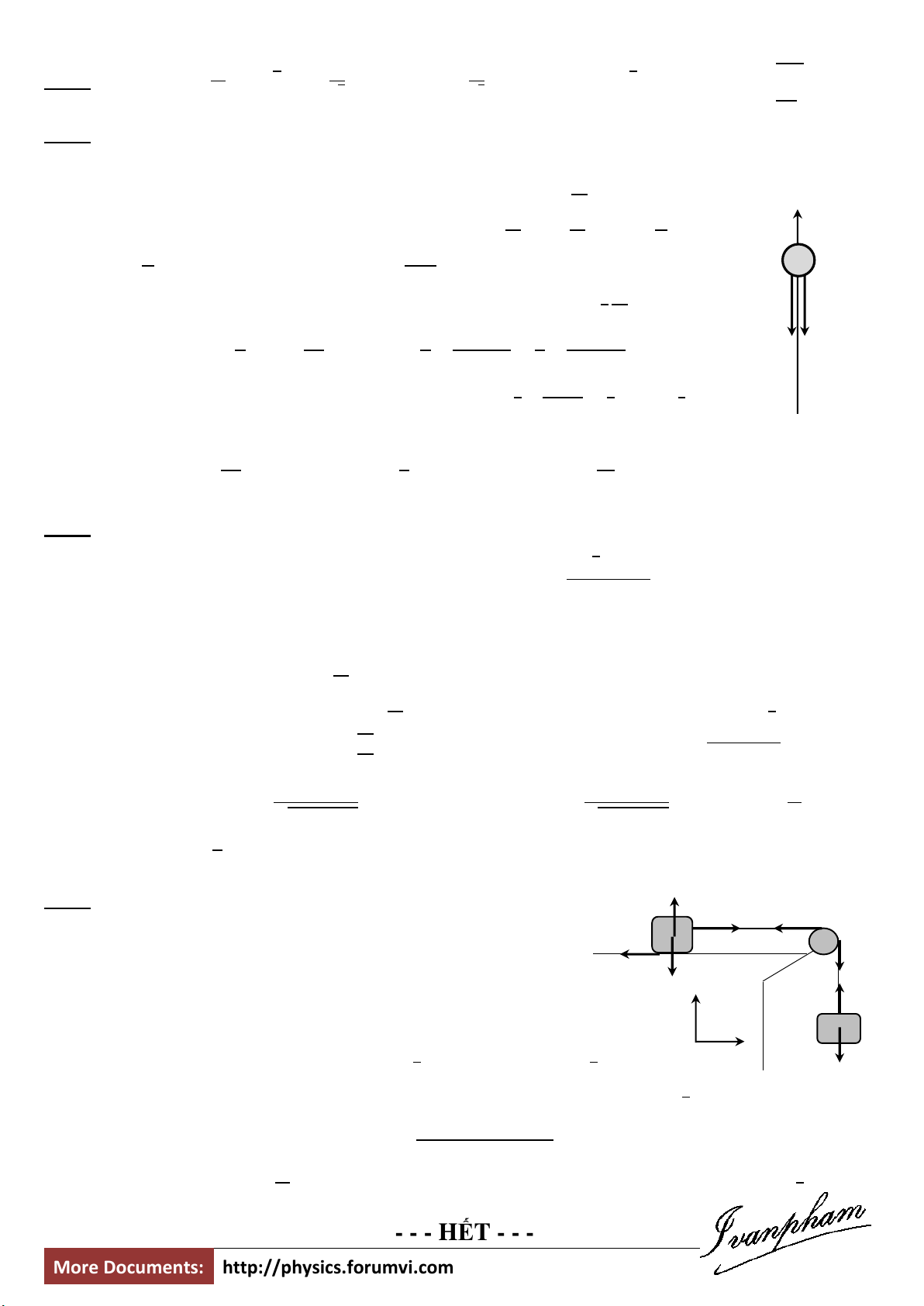
Câu 4: Cho hai vật m1 và m2 mắc qua ròng rọc (xem hình 2). Ròng rọc có khối lượng
M và dạng đĩa tròn đồng chất. Hệ số ma sát giữa vật m1 và mặt nằm ngang là k. Lúc t
= 0, vật m2 bắt đầu hạ xuống. Hãy xác định đoạn dịch chuyển của hai vật sau t giây. M m1 m2 Hình 1 Hình 2 - - - HẾT - - -
More Documents: http://physics.forumvi.com s = α2t2 s t 4 Câu 1:
Ta có: v = ds = α√s ⟹ ds = αdt ⟹ ∫ ds = α ∫ dt ⟹ 2√s = αt ⟹ { dt √s 0 √s 0 v = α2t 2 Câu 2:
Lực cản của không khí lên viên đạn: F ⃗⃗ c = −ηv⃗
(Dấu “–” cho thấy lực cản F
⃗⃗ c và vận tốc v⃗ luôn ngược chiều nhau)
Áp dụng định luật II Newton: P
⃗ + F⃗⃗ c = ma⃗ ⟺ P⃗ − ηv⃗ = m dv⃗ dt 𝐯⃗ dv
Chọn chiều dương (+) như hình vẽ, ta có: – mg – ηv = m ⟹ dv = −g − η v dt dt m
Đặt λ = η, phương trình trở thành: dt = − dv m g+λv du
Đặt u = g + λv ⟹ du = λdv nên phương trình trở thành: dt = − 1 λ u t 1 g+λv du 1 g + λv 1 g + λv ⟹ ∫ dt = − ∫ ⟹ t = − ln = ln o 𝐏⃗ 𝐅⃗⃗⃗ 𝐦𝐬 0 λ u g+λv λ g + λv λ g + λv o o
Khi viên đạn đạt độ cao Hmax thì v = 0 ⟹ t(Hmax) = 1 ln g+λvo = 1 ln (1 + λ v λ g λ g o) 𝐎
Trường hợp không có lực cản không khí: η = 0 ⟹ λ = 0 dv 1 0 v ⟹ dt′ = − ⟹ t′(H ∫ dv ⟹ t′(H o g max) = − g max) = v g o Câu 3:
Cơ năng của vật ở đầu ngọn dốc: Wđ = Uđ = mgH 1
Cơ năng của vật ở cuối đoạn dốc nằm ngang: Ws = Us + Ts = mgh + mv′2 2
Áp dụng định luật bảo toàn cơ năng, ta có: Wđ = Ws ⟹ 𝐯′ = √𝟐𝐠(𝐇 − 𝐡) ax = 0 v′ox = v′
Lúc này ta có bài toán ném ngang với: a
⃗ { ay = −g và v′⃗ { v′oy = 0 x t
Theo Ox: v′x = v′ox = v′ ⟹ dx = v′ ⟹ ∫ dx = v′ ∫ dt ⟹ 𝐱 = 𝐯′𝐭 dt 0 0 y t
Theo Oy: v′y = v′oy − gt = −gt ⟹ dy = −gt ⟹ ∫ dy = −g ∫ tdt ⟹ 𝐲 = 𝐡 − 𝟏 𝐠𝐭𝟐 dt h 0 𝟐
Khi vật chạm đất: 𝑦 = 0 ⟹ t = √2h ⟹ Tầm bay xa: 𝐋 = 𝐱 g
𝐦𝐚𝐱 = 𝐯′𝐭 = 𝟐√𝐡(𝐇 − 𝐡) H − 2h H − 2h 𝐇 ⟹ Đạo hàm L′ =
. Để Lmax thì L′ = 0 ⟺ = 0 ⟺ 𝐡 = √h(H − h) √h(H − h) 𝟐 H
Kết luận: Với h = thì vật bay ra được khoảng cách xa nhất là L 2 max = H. 𝐍 ⃗⃗⃗ Câu 4:
Định luật II cho vật m ⃗⃗ ⃗⃗ ⃗⃗⃗⃗ ⃗⃗ 𝟏 1: P1 + N1 + Fms + T1 = m1a ⃗ 1⃗ m ⃗⃗ ⃗⃗⃗ 1 𝐓𝟏 𝐓′𝟏 Chiếu lên Oy: N M
1 = P1 = m1g ⟹ Fms = kN1 = km1g. 𝐅⃗⃗⃗ Chiếu lên Ox: T 𝐦𝐬
1 – Fms = m1a1 ⟹ 𝐓𝟏 = 𝐦𝟏(𝐚𝟏 + 𝐤𝐠) (1) 𝐓 ⃗⃗′⃗⃗ 𝟐
Định luật II cho vật m ⃗⃗ ⃗⃗ 2: P2 + T2 = m2a ⃗ 2 ⃗ 𝐏 ⃗⃗ 𝟏 y 𝐓 ⃗⃗ Chiếu lên Oy: T 𝟐
2 – P2 = – m2a2 ⟹ 𝐓𝟐 = 𝐦𝟐(𝐠 − 𝐚𝟐) (2)
Chuyển động của ròng rọc: M ⃗⃗⃗ ⃗⃗⃗ 1 + M2 = Iβ ⃗ m2 1 1 O
Chiếu lên chiều chuyển động: R(T x ⃗⃗ 2' – T1') = MR2β ⟹ T MRβ 𝐏 2 2' – T1' = 2 𝟐 𝟏
Sợi dây không co giãn nên: T1 = T1', T2 = T2' và a1 = a2 = a = βR ⟹ T2 – T1 = 𝐌𝐚 (3) 𝟐 𝟐𝐠(𝐦
Từ (1), (2)và (3)giải ra ta được: 𝐚 = 𝟐 − 𝐤𝐦𝟏)
𝐌 + 𝟐(𝐦𝟏 + 𝐦𝟐) s t
Tại thời điểm t: v = at = ds ⟹ ds = atdt ⟹ ∫ ds = a ∫ tdt ⟹ Độ dịch chuyển: 𝐬 = 𝟏 𝐚𝐭𝟐 dt 0 0 𝟐 - - - HẾT - - -
More Documents: http://physics.forumvi.com