Đề thi học sinh giỏi Toán 6 năm 2023 – 2024 phòng GD&ĐT Lương Tài – Bắc Ninh

UBND HUYỆN LƯƠNG TÀI
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP HUYỆN
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2023 - 2024
Môn thi: Toán - Lớp 6
Thời gian: 120 phút (không kể thời gian giao đề)
Ngày thi: 09 tháng 4 năm 2024
I. PHẦN CHUNG (dành cho tất cả các thí sinh)
Bài 1. (2,0 điểm) Thực hiện phép tính bằng cách hợp lí nhất (nếu có thể):
1) 56⋅712 − 7⋅50⋅80 − 7⋅12⋅8; 2) 0 3  1 4 5 5 : 6 2 2  + − ⋅ ; (− )2024 1 6 9 11   3) 1 1 1 1 1 + + + ...+ + . 2⋅6 4⋅9 6⋅12 36⋅57 38⋅60
Bài 2. (2,5 điểm) 1) Tìm x , biết: a) x x 1 2 3 5 3 + ⋅ + ⋅ = 153;
b) x + 2035 x + 2036 x + 2037 x + 2038 + = + . 11 12 13 14
2) Tìm cặp số nguyên (x; y) thỏa mãn 2xy − x − y = 2 .
Bài 3. (1,5 điểm)
1) Cho a ; b là các số nguyên dương thỏa mãn a + 7 ; b + 2025 cùng chia hết cho 6 . Chứng minh
rằng 4a + a + b chia hết cho 6 .
2) Tìm số tự nhiên n có hai chữ số, biết rằng 2n +1 và 3n +1 đều là các số chính phương.
Bài 4. (2,0 điểm)
1) Một khu vườn hình chữ nhật có chiều dài 20m , chiều rộng bằng 3 chiều dài. Người ta làm 4
một lối đi xung quanh vườn rộng 1m , phần còn lại để trồng cây. Tính diện tích phần trồng cây.
2) Cho đoạn thẳng AB có độ dài 6cm . Lấy điểm M nằm giữa hai điểm A và B . Gọi I và K
lần lượt là trung điểm của AM và BM . Tính độ dài đoạn thẳng IK .
3) Cho a + b + c = 2024 và 1 1 1 1 + + = . Tính a b c M = + + .
a + b b + c c + a 2024
b + c c + a a + b II. PHẦN RIÊNG
1. Dành cho thí sinh bảng A
Bài 5. (2,0 điểm)
1) Cho k là số tự nhiên khác 0 . Chứng minh rằng tồn tại số tự nhiên có dạng 1011k −1 chia hết cho 2024 .
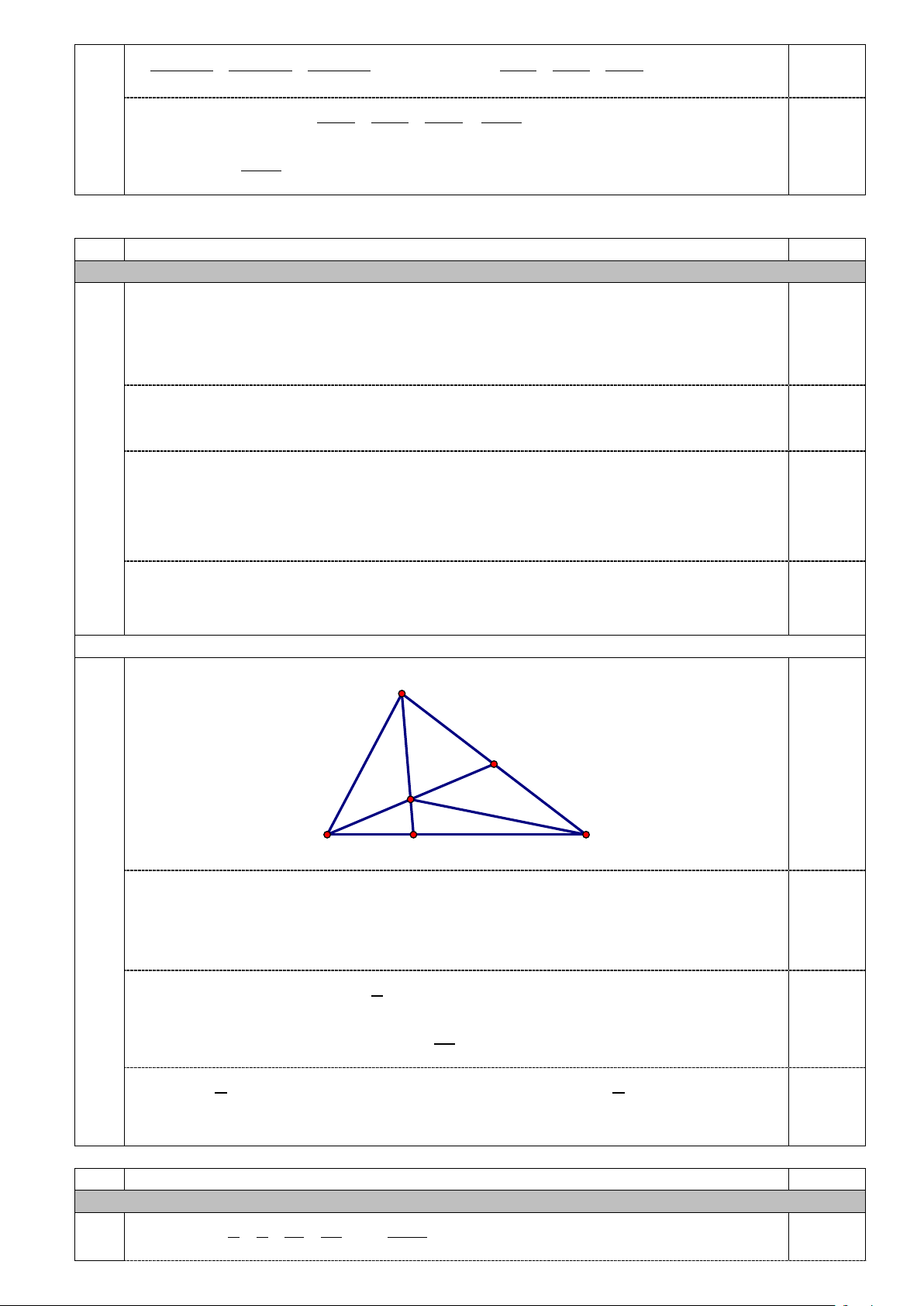
2) Cho tam giác ABC có diện tích bằng 2
60cm . Trên cạnh BC lấy điểm M sao cho 1
BM = BC , trên cạnh AC lấy điểm N sao cho 1
AN = AC . Gọi I là giao điểm của AM và 3 2
BN . Tính diện tích tam giác AIN .
2. Dành cho thí sinh bảng B
Bài 5. (2,0 điểm) 1) Cho 3 8 15 24 2499 B = + + + +...+
. Chứng tỏ rằng giá trị của B không phải là số tự nhiên. 4 9 16 25 2500
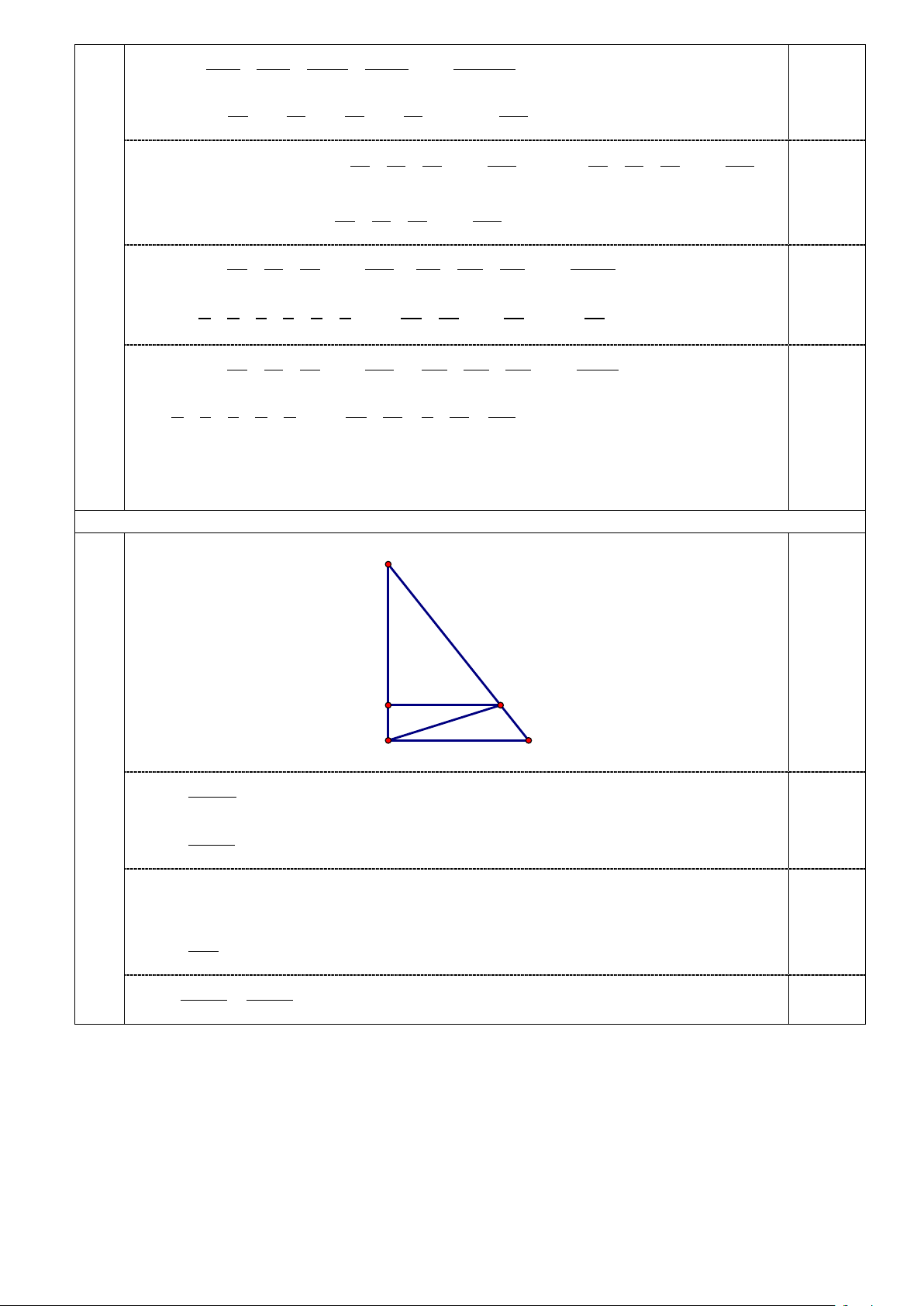
2) Cho tam giác ABC vuông tại A , AB = 50cm , AC = 40cm . Một đường thẳng song song với
AC cắt AB và BC lần lượt tại D và E , AD =10cm . Tính DE .
---------- Hết ----------
(Đề thi có 01 trang)
Họ và tên thí sinh:.................................................................. ; Số báo danh:.................... UBND HUYỆN LƯƠNG TÀI HƯỚNG DẪN CHẤM
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP HUYỆN Năm học 2023-2024
Môn thi: Toán - Lớp 6 Bài
Lời giải sơ lược Điểm 1.1. (0,5 điểm)
56⋅712 − 7⋅50⋅80 − 7⋅12⋅8 = 56⋅712 − 56⋅500 − 56⋅12 0,25
= 56⋅(712 − 500 −12) = 56⋅200 =11 200 0,25 1.2. (0,75 điểm) 0 3  1 4 5 5 : 6 2 2  + − ⋅ (− )2024 1 6 9 11    37 22 27 1:3  = + − ⋅  6 9 11  0,25   1  37  6 = + − 3 6  0,25   2 1 3 1 = + = = 6 6 6 2 0,25 1.3. (0,75 điểm) 1 1 1 1 1 + + + ...+ + 2 ⋅6 4⋅9 6⋅12 36⋅57 38⋅60 1  1 1 1 1 1  ...  = ⋅ + + + + + 2 3 0,25 1 2 2 3 3 4 18 19 19 20  ⋅ ⋅ ⋅ ⋅ ⋅ ⋅  1  1 1 1 1 1 1 1 1 1 1 ...  = − + − + − + + − + − 2 3 2 2 3 3 4 18 19 19 20  ⋅ 0,25   1  1 1 19 19 1  = − = ⋅ = 6 20  0,25   6 20 120 2.1.a. (0,75) x x 1 2 3 5 3 + ⋅ + ⋅ = 153 2 3x 15 3x ⋅ + ⋅ = 153 0,25 17 3x ⋅ = 153 0,25 3x = 9 0,25 Vậy x = 2 2.1.b. (0,75 điểm)
x + 2035 x + 2036 x + 2037 x + 2038 + = + 11 12 13 14  x + 2035   x + 2036   x + 2037   x + 2038 1  1  1  1 − + − = − + −  11 12 13 14  0,25        
x + 2024 x + 2024 x + 2024 x + 2024 + − − = 0 11 12 13 14 0,25 (x ) 1 1 1 1 2024  + + − − =   0 11 12 13 14  0,25 x + 2024 = 0 Vậy x = 2024 − 2.2. (1,0 điểm)
2xy − x − y = 2 x(2y − ) 1 − y = 2 0,25 2x(2y − ) 1 − (2y − ) 1 = 5 0,25
(2x − )1(2y − )1 = 5 0,25
Vì x nguyên nên 2x −1 là ước của 5. Ta có bảng sau: 2x −1 5 − 1 − 1 5 2y −1 1 − 5 − 5 1 x 2 − 0 1 3 0,25 y 0 2 − 3 1
Vậy các cặp số nguyên (x; y) phải tìm là ( 2;
− 0) ; (0;− 2) ; (1;3) ; (3 ) ;1 . 3.1. (0,75 điểm)
Vì a + 7 ; b + 2025 chia hết cho 6 nên a và b đều là số lẻ
⇒ a + b chia hết cho 2
Do 4 nguyên dương nên 4a chia hết cho 2 0,25
⇒ 4a + a + b chia hết cho 2 ( ) 1
Vì a + 7 ; b + 2025 chia hết cho 6
⇒ a + 7 + b + 2025 chia hết cho 6 ⇒ (a + b + ) 1 + 2031 chia hết cho 3 0,25
⇒ a + b +1 chia hết cho 3 (vì 2031 chia hết cho 3)
Vì 4 chia cho 3 dư 1 nên 4a chia cho 3dư 1 4a ⇒ −1 chia hết cho 3 ⇒ + +1+ 4a a b −1 chia hết cho 3 0,25
⇒ 4a + a + b chia hết cho 3 (2) Từ ( )
1 , (2) và (2,3) =1 nên 4a + a + b chia hết cho 6 . 3.2. (0,75 điểm)
Vì n là số tự nhiên có hai chữ số nên 10 ≤ n ≤ 99 ⇒ 21≤ 2n +1≤199 0,25
Mà 2n +1 là số chính phương lẻ nên 2n +1∈{25;49;81;121; } 169 0,25 ⇒ n∈{12;24;40;60; } 84
⇒ 3n +1∈{37;73;121;181; } 253 0,25
Mà 3n +1 là số chính phương nên 3n +1 =121. Vậy n = 40 4.1. (0,75 điểm)
Chiều rộng khu vườn là 3 20⋅ =15(m) 0,25 4 Sau khi làm lối đi thì:
Chiều dài phần đất trồng cây là 20 − 2⋅1 =18(m) 0,25
Chiều rộng phần đất trồng cây là 15 − 2⋅1 =13(m)
Vậy diện tích phần đất trồng cây là 2 18⋅13 = 234(m ) 0,25 4.2. (0,75 điểm) A I M K B 0,25
Vì M nằm giữa A và B nên AM + BM = AB = 6(cm) 0,25
Mà AM = 2IM ; BM = 2KM (do I và K lần lượt là trung điểm của AM và BM )
Suy ra 2(IM + KM ) = 6 hay 2IK = 6. Vậy IK = 3cm. 0,25 4.3. (0,5 điểm) a b c  a 1  b 1  c M 1 = + + = + + + + + −       3 0,25
b + c c + a a
+ b  b + c   c + a   a + b 
a + b + c a + b + c a + b + c (a b c) 1 1 1 + + 3 + +  = − = + + −   3 b + c c + a a + b
 b + c c + a a + b 
Mà a + b + c = 2024 và 1 1 1 1 + + =
a + b b + c a + c 2024 1 0,25 ⇒ M = 2024⋅ − 3 =1− 3 = 2 − . Vậy M = 2 − . 2024 II. PHẦN RIÊNG
1. Dành cho thí sinh bảng A Bài
Lời giải sơ lược Điểm 5.1. (1,0 điểm)
Xét dãy số 10111; 10112; 10113; … ; 10112025 (có 2025 số)
Vì trong phép chia số tự nhiên cho 2024 thì có 2024 loại số dư 0,25
(dư 0; dư 1; dư 2; …; dư 2023)
Suy ra trong 2025 số thuộc dãy trên, luôn tồn tại ít nhất 2 số có cùng số dư khi chia 0,25
cho 2024 (theo nguyên lý Đirichlet, vì 2025 : 2024 = 1 dư 1)
Gọi hai số đó là 1011m và 1011m+k ( * ,
m k ∈ ;m < m + k ≤ 2025)
Vì hai số 1011m và 1011m+k có cùng số dư khi chia cho 2024 0,25
=> hiệu (1011m+k – 1011m) 2024 => 1011m.(1011k – 1) 2024
Mà 1011m và 2024 là hai số nguyên tố cùng nhau (do ƯCLN(1011,2024) = 1) 0,25
=> 1011k – 1 2024. Vậy tồn tại số 1011k – 1  2024 với k * ∈  5.2. (1,0 điểm) A N 0,25 I B M C
Tam giác ABN và tam giác CBN có chung chiều cao từ B , đáy AN = NC nên S = S
⇒ chiều cao kẻ từ A của tam giác ABN bằng chiều cao kẻ từ C của ABN CBN tam giác 0,25
CBN (do chung đáy BN ) nên S
= S (do chiều cao ứng với đáy chung ABI CBI BI bằng nhau)
Tương tự, ta chỉ ra được 1 S = S hay S = S = S ACI 2 ABI 2 ABI 2 ACI CBI 0,25 Do đó: S = S = S nên 60 2 S = = ACI 30(cm ) ABC 4 ABI 2 ACI 2 Mà 1 S
= S (do có chung chiều cao kẻ từ C và đáy 1 AN = AC ). AIN 2 ACI 2 0,25 Vậy 2 S = . AIN 15cm
2. Dành cho thí sinh bảng B Bài
Lời giải sơ lược Điểm 5.1. (1,0 điểm) Ta có : 3 8 15 24 2499 B = + + + + ...+ (có 49 phân số) 0,25 4 9 16 25 2500 4 −1 9 −1 16 −1 25 −1 2500 −1 = + + + + ...+ 4 9 16 25 2500 1 1 1 1 1 = 1− +1− +1− +1− + .....+1− 2 2 2 2 2 2 3 4 5 50  1 1 1 1   1 1 1 1 (1 1 1 .... 1) ...   49  ...  = + + + + − + + + + = − + + + +  2 2 2 2 2 2 2 2  2 3 4 50   2 3 4 50  49 so hang1  0,25 = 49 – A với A = 1 1 1 1 + + + ...+ 2 2 2 2 2 3 4 50 Ta có: A = 1 1 1 1 + + + ...+ < 1 1 1 1 + + + ...+ 2 2 2 2 2 3 4 50 1.2 2.3 3.4 49.50 0,25 A < 1 1 1 1 1 1 1 1 1− + − + − + −....+ − = 1  1 1 1do 0 − < > 2 2 3 3 4 4 49 50 50 50    Lại có A = 1 1 1 1 + + + ...+ > 1 1 1 1 + + + ...+ 2 2 2 2 2 3 4 50 2.3 3.4 4.5 50.51 A > 1 1 1 1 1 1 1 1 1 49 − + − + −....+ − = − = > 0 2 3 3 4 4 50 51 2 51 101 0,25
Do đó: 0 < A <1 mà B = 49 – A => 48 < B < 49 mà 48 và 49 là hai số tự nhiên
liên tiếp => giá trị của B không phải là số tự nhiên
Vậy giá trị của B không phải là số tự nhiên. 5.2. (1,0 điểm) B 0,25 E D A C 40 50 2 S ⋅ = = ABC 1000(cm ) 2 40 10 0,25 2 S ⋅ = = AEC 200(cm ) 2 2 S = − = ABE 1000 200 800(cm ) S = S
(do chung chiều cao từ E , đáy AB bằng 5AD ) ABE 5 ADE 0,25 800 2 S = = ADE 160(cm ) 5 2S ⋅ ADE 2 160 DE = =
= 32(cm) . Vậy DE = 32cm . 0,25 AD 10 Chú ý:
1. Học sinh làm đúng đến đâu giám khảo cho điểm đến đó, tương ứng với thang điểm.
2. HS trình bày theo cách khác mà đúng thì giám khảo cho điểm tương ứng với thang
điểm. Trong trường hợp mà hướng làm của HS ra kết quả nhưng đến cuối còn sai sót thì giám
khảo trao đổi với tổ chấm để giải quyết.
3. Tổng điểm của bài thi không làm tròn.
-----------Hết-----------
Document Outline

• ĐỀ THI CHỌN HỌC SINH GIỎI CẤP HUYỆN
• UBND HUYỆN LƯƠNG TÀI
• PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
• Môn thi: Toán - Lớp 6