Đề thi khảo sát Toán 12 năm 2023 lần 1 trường THPT Thái Phiên – Hải Phòng

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi khảo sát chất lượng môn Toán 12 năm 2023 lần 1 trường THPT Thái Phiên, thành phố Hải Phòng

35 18 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

26 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
SỞ GD&
ĐT HẢI PHÒNG
TRƯỜNG THPT THÁI PHIÊN
ĐỀ THI LẦN 1
Câu 1: Cho hàm số xác định và liên tục trên có đồ thị như hình vẽ bên. Tìm giá trị nhỏ hất
( )
y f x=
và giá trị lớn nhất của hàm số trên đoạn .
m
M
( )
y f x=
[ ]
2;2-
A. . B. . C. . D. .
5, 0m M=- =
2, 2m M=- =
1, 0m M=- =
5, 1m M=- =-
Câu 2: Tìm họ nguyên hàm của hàm số .
( )
sin 2023f x x=
A. . B. . C. . D. .
2023cos2023x C+
cos2023x
2023
C- +
Câu 3: Trong không gian , điểm nào dưới đây nằm trên mặt phẳng ?
Oxyz
( )
: 2 2 0P x y z- + - =
A. . B. . C. . D. .
( )
1;1; 1M -
( )
1; 1; 1N - -
( )
1; 2;2Q -
( )
2; 1; 1P - -
Câu 4: Cho hàm số có bảng biến thiên như sau:
( )
y f x=
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. . B. . C. . D. .
( )
1;0-
( )
0;1
( )
1;1-
( )
; 1-¥ -
Câu 5: Cho một cấp số cộng có số hạng đầu và công sai , số hạng tổng quát được xác định bởi
1
u
d
n
u
công thức
A. . B. . C. . D. .
1
.
n
u d n u= +
( )
1
1
n
u u n d= + -
( )
1
1
n
u d n u= + -
1
.
n
u u n d= +
Câu 6: Tập nghiệm của bất phương trình là
2
log 0x <
A. . B. . C. . D. .
( )
0;1
( )
;1-¥
( )
1;+¥
( )
0;+¥
Câu 7: Tính đạo hàm của hàm số
17
x
y
-
=
A. . B. . C. . D. .
17
x
y
-
¢
=-
17 ln17
x
y
-
¢
=-
Câu 8: Cho hình phẳng được giới hạn bởi các đường và . Thể tích
( )
D
0, , 0x x y= = p =
siny x=-
của khối tròn xoay tạo thành khi quay xung quanh trục được tính theo công thức
V
( )
D
Ox
A. . B. .
0
sin dV x x
p
= p
ò
2
0
sin dV x x
p
= p
ò
KỲ THI KHẢO SÁT CHẤT LƯỢNG KHỐI 12 NĂM 2023
Bài thi: TOÁN
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
C. .D. .
( )
0
sin dV x x
p
= p -
ò
2
0
sin dV x x
p
=
ò
Câu 9: Cho hàm số có bảng biến thiên như hình vẽ. Điểm cực đại của hàm số đã cho là
( )
f x
A. . B. . C. . D. .
3x =
3x = -
1x =
2x = -
Câu 10: Cho khối lăng trụ đứng có đáy là tam giác đều cạnh , chiều cao . Khi đó thể
. ' ' 'ABC A B C
a
h
tích khối lăng trụ là
A. . B. . C. . D. .
2
3
6
a h
2
3
12
a h
2
4
a h
2
3
4
a h
Câu 11: Cho hàm xác định trên có bảng xét dấu như sau
( )
f x
( )
'f x
Số điểm cực trị của hàm số đã cho là
A. . B. . C. . D. .
3
0
2
1
Câu 12: Cho hàm có đạo hàm liên tục trên đồng thời . Tính
( )
f x
[ ]
2;3
( ) ( )
2 2, 3 5f f= =
( )
3
2
'f x dx
ò
bằng
A. . B. . C. . D. .
10
3
3-
7
Câu 13: Đường cong trong hình bên dưới là đồ thị của hàm số nào?
A. . B. . C. . D. .
3
3 1y x x= - +
3
3 1y x x=- + +
4 2
1y x x= - +
2
1y x x=- + -
Câu 14: Trong không gian , cho hai điểm , . Véc tơ có toạ độ là
Oxyz
( )
1;1; 2A -
( )
2;2;1B
AB

A. . B. . C. . D. .
( )
3;1;1
( )
1;1;3
( )
3;3; 1-
( )
1; 1; 3- - -
Câu 15: Hàm số có tập xác định là
( )
4
2
1 4y x
-
= -
A. . B. . C. . D. .
1 1
\ ;
2 2
ì ü
ï ï
ï ï
-
í ý
ï ï
ï ï
î þ
1 1
;
2 2
æ ö
÷
ç
-
÷
ç
÷
ç
è ø
( )
0;+¥
Câu 16: Nếu thì bằng
( ) ( )
2 3
1 2
d 3, d 1f x x f t t= =-
ò ò
( )
3
1
df x x
ò
A. . B. . C. . D. .
2-
2
3
4
Câu 17: Cho hàm số có bảng biến thiên như hình vẽ. Tìm mệnh đề đúng?
4 2
y ax bx c= + +
A. . B. . C. . D. .
4 2
2 3y x x= - -
4 2
2 3y x x=- - -
4 2
2 3y x x= - +
4 2
2 3y x x=- + -
Câu 18: Cho hàm số có báng biến thiên như sau:
( )
y f x=
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
A. 2. B. 3. C. 4. D. 1.
Câu 19: Từ các số , , , , có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số đôi một khác nhau.
1
2
3
4
5
A. . B. . C. . D. .
16
24
120
720
Câu 20: Khối lăng trụ ngũ giác có tất cả bao nhiêu cạnh?
A. . B. . C. . D. .
15
25
10
20
Câu 21: Đường cong trong hình sau là đồ thị hàm số nào
A. . B. . C. . D. .
2
log (2 )y x=
2
x
y =
1
1
2
y x= +
( )
2
x
y =
Câu 22: Thể tích của khối trụ có độ dài đường sinh và bán kính đáy
bằng
l
r
A. . B. . C. . D. .
4V rl= p
V rl= p
1
3
V rl= p
2
V l r= p
Câu 23: Gọi lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình nón. Tìm mệnh
, ,l h r
đề đúng
A. . B. . C. . D. .
2
xq
1
3
S r h= p
xq
S rl= p
xq
S rh= p
xq
2S rl= p
Câu 24: Cho mặt phẳng . Khi đó một vectơ pháp tuyến của
là
( )
: 2 3 4 1 0x y za - - + =
( )
a
A. . B. . C. . D. .
( )
2;3;4n = -
( )
2;3;1n = -
( )
2;3; 4n = -
( )
2; 3;4n = -
Câu 25: Thể tích của khối chóp có diện tích đáy bằng và chiều cao bằng là
V
S
h
A. . B. . C. . D. .
V Sh=
1
3
V Sh=
3V Sh=
1
2
V Sh=
Câu 26: Số nghiệm phương trình là
2
2 7 5
2 1
x x- +
=
A. . B. . C. . D. .
0
1
2
3
Câu 27: Họ các nguyên hàm của hàm số là
( )
2
2
3f x x x
x
= - +
A. . B. .
( )
3
2
3
2ln
3 2
x
F x x x C= + + +
( )
3
2
3
2ln
3 2
x
F x x x C= - + +
C. . D. .
( )
2
2
2 3F x x C
x
= - - +
( )
3
2
3
2ln
3 2
x
F x x x C= - + +
Câu 28: Trong không gian , hình chiếu vuông góc của điểm trên trục có tọa độ là
Oxyz
( )
3;5;2A
Ox
A. . B. . C. . D. .
( )
3;0;0
( )
0;0;2
( )
0;5;2
( )
0;5;0
Câu 29: Cho là một nguyên hàm của hàm số . Hàm số có bao nhiêu
( )
F x
( )
( )
2
3
e 4
x
f x x x= -
( )
F x
điểm cực trị?
A. . B. . C. . D. .
1
4
2
3
Câu 30: Hàm số nào dưới đây đồng biến trên khoảng
( )
;-¥ +¥
A. . B. . C. . D. .
3
y x x= +
3
3y x x= - -
1
3
x
y
x
+
=
+
1
2
x
y
x
-
=
-
Câu 31: Cho tích phân . Tìm mệnh đề đúng
5
2
1
.e d
x
I x x=
ò
A. . B. .
5
2 5 2
1
1
1 1
e | e d
2 2
x x
I x x= -
ò
5
2 5 2
1
1
1
e | e d
2
x x
I x x= -
ò
C. . D.
5
2 5 2
1
1
e | e d
x x
I x x= -
ò
5
5
1
1
1 1
e | e d
2 2
x x
I x x= -
ò
Câu 32: Có hai hộp bút chì màu, các bút chì khác nhau. Hộp thứ nhất có bút chì màu đỏ và bút chì
5
7
màu xanh. Hộp thứ hai có bút chì màu đỏ và bút chì màu xanh. Chọn ngẫu nhiên mỗi hộp
8
4
một cây bút chì. Xác suất để chọn một cây bút chì màu đỏ và một bút chì màu xanh là
A. . B. . C. . D. .
17
36
7
12
19
36
5
12
Câu 33: Tìm giá trị thực của tham số để hàm số đạt cực đại tại .
m
( )
3 2 2
1
4 3
3
y x mx m x= - + - +
3x =
A. . B. . C. . D. .
1m =
1m =-
1; 5m m= =
5m =
Câu 34: Cho hàm số . Tính .
( )
( )
2
3
log 1f x x= +
( )
1f
¢
-
A. Không tồn tại . B. .
( )
1f
¢
-
( )
1
1
2ln 3
f
¢
- =
C. . D. .
( )
1
1
ln3
f
¢
- =
( )
1 1.f x
¢
- = -
Câu 35: Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn bằng ( là tham
1
x m
y
x
+
=
+
[ ]
1;2
8
m
số thực). Khẳng định nào sau đây là đúng?
A. . B. . C. . D. .
8 10m< <
0 4m< <
4 8m< <
10m >
Câu 36: Trong không gian cho hai điểm và . Mặt phẳng trung trực đoạn có
( )
1; 1;2A -
( )
3;3;0B
AB
phương trình là
A. . B. . C. . D. .
2 0x y z+ - - =
2 0x y z+ - + =
2 3 0x y z+ - - =
2 3 0x y z+ - + =
Câu 37: Cho hàm số có đáy là hình vuông cạnh , là tâm đáy. Hình chiếu vuông
.S ABCD
ABCD
2a
O
góc của xuống là trung điểm của , biết . Gọi là góc
S
( )
ABCD
H
OA
( )
( )
, 60SD ABCD = °
a
giữa và . Tìm mệnh đề đúng.
( )
mp SCD
( )
mp ABCD
A. . B. . C. . D. .
( )
tan 0;1a Î
( )
tan 3;4a Î
( )
tan 2;3a Î
( )
tan 1;2a Î
Câu 38: Cho hình chóp có đáy là hình thoi với . Gọi là trọng
.S ABCD
ABCD
2 , 2 2AC a BD a= =
H
tâm tam giác , biết rằng các mặt phẳng và cùng vuông góc với mặt phẳng
ABD
( )
SHC
( )
SHD
. Khoảng cách từ đến mặt phẳng bằng
( )
ABCD
C
( )
SHD
A. . B. . C. . D. .
4 19
38
a
38
19
a
4 38
19
a
19
38
a
Câu 39: Cho hàm số đồng biến trên liên tục, nhận giá trị dương trên
( )
y f x=
( ) ( )
0; , y f x+¥ =
thỏa mãn và . Tính .
( )
0;+¥
( )
4
3
9
f =
( ) ( ) ( )
2
' 1 .f x x f x
é ù
= +
ë û
( )
8f
A. . B. . C. . D. .
( )
1
8
16
f =
( )
8 64f =
( )
8 49f =
( )
8 256f =
Câu 40: Cho các số thực dương x,y thỏa mãn .
2
2
5
2 5
10 3
9
10
xy y
x xy
+
-
æ ö
æ ö
÷
÷
ç
ç
£
÷
÷
ç
ç
÷
÷
ç
÷
ç
è ø
è ø
Hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của biểu thức bằng
x
y
A. . B. . C. . D.
5
2
1
4
1
5
5
4
Câu 41: Cho hàm số trùng phương có đồ thị như hình vẽ.
4 2
axy bx c= + +
Hỏi đồ thị hàm số có tổng cộng bao nhiêu tiệm cận đứng?
( )( )
( ) ( )
2 2
2
4 2
2 3
x x x
y
f x f x
- +
=
é ù
+ -
ë û
A. . B. . C. . D.
3
4
5
2
Câu 42: Có bao nhiêu số nguyên dương m nhỏ hơn 20 thỏa mãn phương trình có
( )
log log 10
m x
mx m+ =
đúng hai nghiệm thực phân biệt.
A. . B. . C. . D.
11
13
12
10
Câu 43: Cho tứ diện có . Góc giữa hai mặt phẳng
ABCD
2 2
4 , 6 , = 3
ABC ABD
S cm S cm AB cm
D D
= =
và bằng . Thể tích của tứ diện đã cho bằng
( )
ABC
( )
ABD
60°
A. . B. . C. . D. .
3
2 3 cm
3
2 3
3
cm
3
4 3
3
cm
3
8 3
3
cm
Câu 44: Cho hình nón đỉnh , đường cao , và là hai điểm thuộc đường tròn đáy sao cho khoảng
S
SO
A
B
cách từ đến mặt bằng và . Độ dài đường sinh của hình
O
( )
SAB
3
3
a
0 0
30 , 60SAO SAB= =
nón theo bằng
a
A. . B. . C. . D. .
2 3a
5a
2a
3a
Câu 45: Cho hàm số , có đồ thị như hình sau:
( )
y f x=
( )
y g x=
Khi đó tổng số nghiệm của hai phương trình và là
( )
( )
0f g x =
( )
( )
0g f x =
A. . B. . C. . D. .
26
25
22
21
Câu 46: Cho hàm số có với là tham số thực. Hỏi
( )
y f x=
( ) ( )
( )
2
1 2 1 ,f x x x x mx x
¢
= + - + " Î
m
có tất cả bao nhiêu số nguyên không vượt quá sao cho hàm số có
m
2023
( )
( )
2
1g x f x= -
7
điểm cực trị?
A. . B. . C. . D. .
2021
2022
2020
2023
Câu 47: Cho hàm số liên tục trên thỏa mãn . Giá trị tích phân
( )
y f x=
1
;3
3
é ù
ê ú
ê ú
ë û
( )
3
1
f x x f x x
x
æ ö
÷
ç
+ × = -
÷
ç
÷
ç
è ø
bằng
3
2
1
3
( )
d
f x
I x
x x
=
+
ò
A. . B. . C. . D. .
3
4
16
9
2
3
8
9
Câu 48: Cho hàm số có ba điểm cực trị là , và .
( )
4 3 2
2f x x ax bx cx d= + + + +
( )
, , ,a b c d Î
1-
1
3
Gọi là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số .
( )
y g x=
( )
y f x=
Diện tích hình phẳng giới hạn bởi hai đường và bằng
( )
y f x=
( )
y g x=
A. . B. . C. . D. .
182
15
265
15
128
15
256
15
Câu 49: Trong các nghiệm thỏa mãn bất phương trình . Giá trị lớn nhất của
( )
;x y
( )
2 2
2
log 2 1
x y
x y
+
+ ³
biểu thức bằng
2T x y= +
A. . B. . C. . D. .
9
9
4
9
2
9
8
Câu 50: Tìm để giá trị lớn nhất của hàm số trên đoạn là nhỏ nhất. Giá trị
m
3
3 2 1y x x m= - + -
[ ]
0;2
của thuộc khoảng nào?
m
A. . B. . C. . D. .
( )
0;1
2
;2
3
æ ö
÷
ç
÷
ç
÷
ç
è ø
[ ]
1;0-
3
; 1
2
æ ö
÷
ç
- -
÷
ç
÷
ç
è ø
HẾT
BẢNG ĐÁP ÁN
1.D
2.D
3.B
4.A
5.B
6.A
7.C
8.B
9.D
10.D
11.C
12.B
13.A
14.B
15.A
16.B
17.A
18.B
19.C
20.A
21.B
22.D
23.B
24.A
25.B
26.C
27.D
28.A
29.D
30.A
31.A
32.C
33.A
34.C
35.A
36.C
37.D
38.C
39.C
40.B
41.B
42.B
43.D
44.C
45.C
46.A
47.D
48.D
49.C
50.A
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 51: Cho hàm số xác định và liên tục trên có đồ thị như hình vẽ bên. Tìm giá trị nhỏ hất
( )
y f x=
và giá trị lớn nhất của hàm số trên đoạn .
m
M
( )
y f x=
[ ]
2;2-
A. . B. . C. . D. .
5, 0m M=- =
2, 2m M=- =
1, 0m M=- =
5, 1m M=- =-
Lời giải
Chọn D.
Câu 52: Tìm họ nguyên hàm của hàm số .
( )
sin 2023f x x=
A. . B. . C. . D. .
2023cos2023x C+
cos2023x
2023
C- +
Lời giải
Chọn D.
Câu 53: Trong không gian , điểm nào dưới đây nằm trên mặt phẳng ?
Oxyz
( )
: 2 2 0P x y z- + - =
A. . B. . C. . D. .
( )
1;1; 1M -
( )
1; 1; 1N - -
( )
1; 2;2Q -
( )
2; 1; 1P - -
Lời giải
Chọn B.
Câu 54: Cho hàm số có bảng biến thiên như sau:
( )
y f x=
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. . B. . C. . D. .
( )
1;0-
( )
0;1
( )
1;1-
( )
; 1-¥ -
Lời giải
Chọn A
.
Câu 55: Cho một cấp số cộng có số hạng đầu và công sai , số hạng tổng quát được xác định bởi
1
u
d
n
u
công thức
A. . B. . C. . D. .
1
.
n
u d n u= +
( )
1
1
n
u u n d= + -
( )
1
1
n
u d n u= + -
1
.
n
u u n d= +
Lời giải
Chọn B.
Ta có .
( )
1
1
n
u u n d= + -
Câu 56: Tập nghiệm của bất phương trình là
2
log 0x <
A. . B. . C. . D. .
( )
0;1
( )
;1-¥
( )
1;+¥
( )
0;+¥
Lời giải
Chọn A.
Ta có .
2
log 0 0 1x x< Û < <
Tập nghiệm của bất phương trình là .
2
log 0x <
( )
0;1
Câu 57: Tính đạo hàm của hàm số
17
x
y
-
=
A. . B. . C. . D. .
17
x
y
-
¢
=-
17 ln17
x
y
-
¢
=-
Lời giải
Chọn C.
Ta có .
17 17 ln17
x x
y y
- -
¢
= Þ = -
Câu 58: Cho hình phẳng được giới hạn bởi các đường và . Thể tích
( )
D
0, , 0x x y= = p =
siny x= -
của khối tròn xoay tạo thành khi quay xung quanh trục được tính theo công thức
V
( )
D
Ox
A. . B. .
0
sin dV x x
p
= p
ò
2
0
sin dV x x
p
= p
ò
C. .D. .
( )
0
sin dV x x
p
= p -
ò
2
0
sin dV x x
p
=
ò
Lời giải
Chọn B.
Ta có .
( )
2
2
0 0
sin d sin dV x x x x
p p
= p - = p
ò ò
Câu 59: Cho hàm số có bảng biến thiên như hình vẽ. Điểm cực đại của hàm số đã cho là
( )
f x
A. . B. . C. . D. .
3x =
3x = -
1x =
2x = -
Lời giải
Chọn D.
Câu 60: Cho khối lăng trụ đứng có đáy là tam giác đều cạnh , chiều cao . Khi đó thể
. ' ' 'ABC A B C
a
h
tích khối lăng trụ là
A. . B. . C. . D. .
2
3
6
a h
2
3
12
a h
2
4
a h
2
3
4
a h
Lời giải
Chọn D.
.
2
3
.
4
a h
S h S= =
Câu 61: Cho hàm xác định trên có bảng xét dấu như sau
( )
f x
( )
'f x
Số điểm cực trị của hàm số đã cho là
A. . B. . C. . D. .
3
0
2
1
Lời giải
Chọn C.
Câu 62: Cho hàm có đạo hàm liên tục trên đồng thời . Tính
( )
f x
[ ]
2;3
( ) ( )
2 2, 3 5f f= =
( )
3
2
'f x dx
ò
bằng
A. . B. . C. . D. .
10
3
3-
7
Lời giải
Chọn B.
.
( ) ( ) ( )
3
2
' 3 2 5 2 3f x dx f f= - = - =
ò
Câu 63: Đường cong trong hình bên dưới là đồ thị của hàm số nào?
A. . B. . C. . D. .
3
3 1y x x= - +
3
3 1y x x=- + +
4 2
1y x x= - +
2
1y x x=- + -
Lời giải
Chọn A.
Quan sát đồ thị ta nhận thấy đồ thị là của hàm số bậc 3 có hệ số chứa dương.
3
x
Câu 64: Trong không gian , cho hai điểm , . Véc tơ có toạ độ là
Oxyz
( )
1;1; 2A -
( )
2;2;1B
AB

A. . B. . C. . D. .
( )
3;1;1
( )
1;1;3
( )
3;3; 1-
( )
1; 1; 3- - -
Lời giải
Chọn B.
Ta có .
( ) ( )
; ; 1;1;3
B A B A B A
AB x x y y z z= - - - =

Câu 65: Hàm số có tập xác định là
( )
4
2
1 4y x
-
= -
A. . B. . C. . D. .
1 1
\ ;
2 2
ì ü
ï ï
ï ï
-
í ý
ï ï
ï ï
î þ
1 1
;
2 2
æ ö
÷
ç
-
÷
ç
÷
ç
è ø
( )
0;+¥
Lời giải
Chọn A.
Hàm số đã cho xác định khi và .
2
1
1 4 0
2
x x- ¹ Û ¹-
1
2
x ¹
Vậy tập xác định của hàm số là .
1 1
\ ;
2 2
ì ü
ï ï
ï ï
-
í ý
ï ï
ï ï
î þ
Câu 66: Nếu thì bằng
( ) ( )
2 3
1 2
d 3, d 1f x x f t t= =-
ò ò
( )
3
1
df x x
ò
A. . B. . C. . D. .
2-
2
3
4
Lời giải
Chọn B.
Tích phân không phụ thuộc vào biến số nên . Do đó
( ) ( )
3 3
2 2
d d 1f t t f x x= = -
ò ò
..
( ) ( ) ( ) ( )
3 2 3
1 1 2
d d d 3 1 2f x x f x x f x x= + = + - =
ò ò ò
Câu 67: Cho hàm số có bảng biến thiên như hình vẽ. Tìm mệnh đề đúng?
4 2
y ax bx c= + +
A. . B. . C. . D. .
4 2
2 3y x x= - -
4 2
2 3y x x=- - -
4 2
2 3y x x= - +
4 2
2 3y x x=- + -
Lời giải
Chọn A.
Dựa vào bảng biến thiên ta có . Loại đáp án
0a >
,B D
Đồ thị hàm số đi qua điểm nên chọn đáp án .
(0; 3)-
A
Câu 68: Cho hàm số có báng biến thiên như sau:
( )
y f x=
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
A. 2. B. 3. C. 4. D. 1.
Lời giải
Chọn B.
Nhìn bảng biến thiên ta thấy là TCĐ của đồ thị hàm số
( )
0
lim
x
f x
-
®
=-¥ Þ
0x =
Ta có
là TCN của đồ thị hàm số
( )
lim 3 3
x
f x y
®+¥
= Þ =
là TCN của đồ thị hàm số
( )
lim 1 1
x
f x y
®-¥
= Þ =
Vậy hàm số có 3 tiệm cận.
Câu 69: Từ các số , , , , có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số đôi một khác nhau.
1
2
3
4
5
A. . B. . C. . D. .
16
24
120
720
Lời giải
Chọn C.
Mỗi số tự nhiên có 5 chữ số khác nhau lập từ 5 chữ số đã cho là một hoán vị của 5 phần tử. Nên
số số tự nhiên cần tìm là số.
5! 120=
Câu 70: Khối lăng trụ ngũ giác có tất cả bao nhiêu cạnh?
A. . B. . C. . D. .
15
25
10
20
Lời giải
Chọn A.
Khối lăng trụ ngũ giác có 10 cạnh đáy và 5 cạnh bên nên khối lăng trụ ngũ giác có tất cả 15
cạnh.
Câu 71: Đường cong trong hình sau là đồ thị hàm số nào
A. . B. . C. . D. .
2
log (2 )y x=
2
x
y =
1
1
2
y x= +
( )
2
x
y =
Lời giải
Chọn B.
Câu 72: Thể tích của khối trụ có độ dài đường sinh và bán kính đáy
bằng
l
r
A. . B. . C. . D. .
4V rl= p
V rl= p
1
3
V rl= p
2
V l r= p
Lời giải
Chọn D.
Câu 73: Gọi lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình nón. Tìm mệnh
, ,l h r
đề đúng
A. . B. . C. . D. .
2
xq
1
3
S r h= p
xq
S rl= p
xq
S rh= p
xq
2S rl= p
Lời giải
Chọn B.
Câu 74: Cho mặt phẳng . Khi đó một vectơ pháp tuyến của
là
( )
: 2 3 4 1 0x y za - - + =
( )
a
A. . B. . C. . D. .
( )
2;3;4n = -
( )
2;3;1n = -
( )
2;3; 4n = -
( )
2; 3;4n = -
Lời giải
Chọn A.
Mặt phẳng có vectơ pháp tuyến là .
( )
: 2 3 4 1 0x y za - - + =
( )
2; 3; 4n = - -
Suy ra cũng là một vectơ pháp tuyến của .
( )
2;3;4n = -
( )
a
Câu 75: Thể tích của khối chóp có diện tích đáy bằng và chiều cao bằng là
V
S
h
A. . B. . C. . D. .
V Sh=
1
3
V Sh=
3V Sh=
1
2
V Sh=
Lời giải
Chọn B.
.
1
3
V Sh=
Câu 76: Số nghiệm phương trình là
2
2 7 5
2 1
x x- +
=
A. . B. . C. . D. .
0
1
2
3
Lời giải
Chọn C.
.
2
2 7 5 2 2
2
1
2 1 2 7 5 log 1 2 7 5 0
5
2
x x
x
x x x x
x
- +
é
=
ê
= Û - + = Û - + = Û ê
ê
=
ê
ë
Vậy phương trình có 2 nghiệm phân biệt.
Câu 77: Họ các nguyên hàm của hàm số là
( )
2
2
3f x x x
x
= - +
A. . B. .
( )
3
2
3
2ln
3 2
x
F x x x C= + + +
( )
3
2
3
2ln
3 2
x
F x x x C= - + +
C. . D. .
( )
2
2
2 3F x x C
x
= - - +
( )
3
2
3
2ln
3 2
x
F x x x C= - + +
Lời giải
Chọn D.
.
3
2 2
2 3
3 d 2ln
3 2
x
x x x x x C
x
æ ö
÷
ç
- + = - + +
÷
ç
÷
ç
è ø
ò
Câu 78: Trong không gian , hình chiếu vuông góc của điểm trên trục có tọa độ là
Oxyz
( )
3;5;2A
Ox
A. . B. . C. . D. .
( )
3;0;0
( )
0;0;2
( )
0;5;2
( )
0;5;0
Lời giải
Chọn A.
Đường thẳng chứa trục có 1 vectơ chỉ phương .
Ox
( )
1;0;0i =
Gọi là hình chiếu của điểm trên trục ; .
H
( )
3;5;2A
Ox
( )
;0;0H aÞ
( )
3; 5; 2AH a= - - -

.
. 0 3 0 3
AH i
AH i a a
Þ ^
Þ = Û - = Û =


Vậy .
( )
3;0;0H
Câu 79: Cho là một nguyên hàm của hàm số . Hàm số có bao nhiêu
( )
F x
( )
( )
2
3
e 4
x
f x x x= -
( )
F x
điểm cực trị?
A. . B. . C. . D. .
1
4
2
3
Lời giải
Chọn D.
Ta có ,
( ) ( )
( )
2
3
e 4
x
F x f x x x
¢
= = -
( )
( )
2
3
0 e 4 0
x
F x x x
¢
= Û - =
3
0
4 0
1
x
x x
x
é
=
ê
Û - = Û
ê
= ±
ë
Suy ra hàm số có điểm cực trị.
( )
F x
3
Câu 80: Hàm số nào dưới đây đồng biến trên khoảng
( )
;-¥ +¥
A. . B. . C. . D.
3
y x x= +
3
3y x x= - -
1
3
x
y
x
+
=
+
1
2
x
y
x
-
=
-
Lời giải
Chọn A.
Ta có , luôn đồng biến trên .
2
3 1 0y x
¢
= + >
x" Î
3
y x xÞ = +
Câu 81: Cho tích phân . Tìm mệnh đề đúng
5
2
1
.e d
x
I x x=
ò
A. . B. .
5
2 5 2
1
1
1 1
e | e d
2 2
x x
I x x= -
ò
5
2 5 2
1
1
1
e | e d
2
x x
I x x= -
ò
C. . D.
5
2 5 2
1
1
e | e d
x x
I x x= -
ò
5
5
1
1
1 1
e | e d
2 2
x x
I x x= -
ò
Lời giải
Chọn A.
Đặt .
5
2 5 2
1
2
2
1
d
1 1
e | e d
1
2 2
e
e d
2
x x
x
x
du x
u x
I x x
v
dv x
ì
=
ï
ì
ï
=
ï
ï
ï
Þ Þ = -
í í
ï ï
=
=
ï ï
î
ï
î
ò
Câu 82: Có hai hộp bút chì màu, các bút chì khác nhau. Hộp thứ nhất có bút chì màu đỏ và bút chì
5
7
màu xanh. Hộp thứ hai có bút chì màu đỏ và bút chì màu xanh. Chọn ngẫu nhiên mỗi hộp
8
4
một cây bút chì. Xác suất để chọn một cây bút chì màu đỏ và một bút chì màu xanh là
A. . B. . C. . D. .
17
36
7
12
19
36
5
12
Lời giải
Chọn C.
Ta có .
( )
1 1
12 12
. 144n C CW = =
Gọi là biến cố chọn được một cây bút chì màu đỏ và một bút chì màu xanh.
A
Khi đó .
( )
1 1 1 1
5 4 7 8
76n A C C C C= + =
( )
( )
( )
76 19
144 36
n A
P A
n
Þ = = =
W
Câu 83: Tìm giá trị thực của tham số để hàm số đạt cực đại tại .
m
( )
3 2 2
1
4 3
3
y x mx m x= - + - +
3x =
A. . B. . C. . D. .
1m =
1m =-
1; 5m m= =
5m =
Lời giải
Chọn A.
Có ; .
( )
2 2
2 4y x mx m
¢
= - + -
2 2y x m
¢¢
= -
Để hàm số đạt cực đại tại thì
3x =
( )
( )
3 0
3 0
y
y
ì
¢
=
ï
ï
í
¢¢
ï
<
ï
î
.
( )
2 2
2
1
3 2 .3 4 0
6 5 0
1
5
3
2.3 2 0
3
m
m m
m m
m
m
m
m
m
ì
é
=
ï
ï
ì
ì
ê
ï
- + - =
ï
- + =
ï
ï
ï ï
ê
Û Û Û Û =
=
í í í
ë
ï ï ï
<
- <
ï ï ï
î
î
ï
<
ï
î
Câu 84: Cho hàm số . Tính .
( )
( )
2
3
log 1f x x= +
( )
1f
¢
-
A. Không tồn tại . B. .
( )
1f
¢
-
( )
1
1
2ln 3
f
¢
- =
C. . D. .
( )
1
1
ln3
f
¢
- =
( )
1 1.f x
¢
- = -
Lời giải
Chọn C.
Ta có .
( )
( )
( )
( )
( ) ( )
2
2
3
2 2
1
2
log 1
1 ln 3 1 ln 3
x
x
f x x
x x
¢
+
¢
¢
= + = =
+ +
Suy ra .
( )
( )
2
2 1
1
ln3
( 1) 1 ln3
f
-
¢
- = = -
- +
Câu 85: Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn bằng ( là tham
1
x m
y
x
+
=
+
[ ]
1;2
8
m
số thực). Khẳng định nào sau đây là đúng?
A. . B. . C. . D. .
8 10m< <
0 4m< <
4 8m< <
10m >
Lời giải
Chọn A.
Tập xác định của hàm số . Ta có .
{ }
\ 1D = -
( )
2
1
1
m
y
x
-
¢
=
+
.
( ) ( )
1 2
1 ; 2
2 3
m m
f f
+ +
= =
và .
[ ]
( ) ( ) ( )
{ }
1;2
min min 1 ; 2f x f f=
[ ]
( ) ( ) ( )
{ }
1;2
max ax 1 ; 2f x m f f=
Nên theo đề ta có
[ ]
( )
[ ]
( )
1;2
1;2
max +min 8f x f x =
2 1 5 7
8 8
3 2 6
m m m+ + +
Û + = Û =
.
41
5 7 48
5
m mÛ + = Û =
Câu 86: Trong không gian cho hai điểm và . Mặt phẳng trung trực đoạn có
( )
1; 1;2A -
( )
3;3;0B
AB
phương trình là
A. . B. . C. . D. .
2 0x y z+ - - =
2 0x y z+ - + =
2 3 0x y z+ - - =
2 3 0x y z+ - + =
Lời giải
Chọn C.
Gọi là trung điểm suy ra .
I
AB
( )
2;1;1I
Mặt phẳng trung trực đoạn qua và nhận có dạng
AB
( )
2;1;1I
( ) ( )
2;4; 2 2 1;2; 1AB = - = -

.
( ) ( ) ( )
1. 2 2. 1 1. 1 0 2 3 0x y z x y z- + - - - = Û + - - =
Câu 87: Cho hàm số có đáy là hình vuông cạnh , là tâm đáy. Hình chiếu vuông
.S ABCD
ABCD
2a
O
góc của xuống là trung điểm của , biết . Gọi là góc
S
( )
ABCD
H
OA
( )
( )
, 60SD ABCD = °
a
giữa và . Tìm mệnh đề đúng.
( )
mp SCD
( )
mp ABCD
A. . B. . C. . D. .
( )
tan 0;1a Î
( )
tan 3;4a Î
( )
tan 2;3a Î
( )
tan 1;2a Î
Lời giải
Chọn D.
Ta có ,
( )
( )
, 60SD ABCD SDH= = °
.
2 2
2 10
2 2 2 2 ,
2 2
a a
AB a AC BD a OD a OH DH OH OD= Þ = = Þ = = Þ = + =
.
30
.tan 60
2
a
SH HDÞ = ° =
Kẻ , .
( ) ( )
( )
,HI CD SCD ABCD SIH^ Þ =
3 3 3
4 4 2
HI CH a
HI AD
AD CA
= = Þ = =
Do đó .
( )
30
tan tan 1;2
3
SH
SIH
HI
a = = = Î
Câu 88: Cho hình chóp có đáy là hình thoi với . Gọi là trọng
.S ABCD
ABCD
2 , 2 2AC a BD a= =
H
tâm tam giác , biết rằng các mặt phẳng và cùng vuông góc với mặt phẳng
ABD
( )
SHC
( )
SHD
. Khoảng cách từ đến mặt phẳng bằng
( )
ABCD
C
( )
SHD
A. . B. . C. . D. .
4 19
38
a
38
19
a
4 38
19
a
19
38
a
Lời giải
Chọn C.
Các mặt phẳng và cùng vuông góc với mặt phẳng nên .
( )
SHC
( )
SHD
( )
ABCD
( )
SH ABCD^
Kẻ .
( ) ( )
( )
,CK HD SH CK CK SHD d C SHD CK^ Þ ^ Þ ^ Þ =
Kẻ .
2 2
. 4 38
4 4
19
HO OD a
OI HD CK OI
OH OD
^ Þ = = =
+
Câu 89: Cho hàm số đồng biến trên liên tục, nhận giá trị dương trên
( )
y f x=
( ) ( )
0; , y f x+¥ =
thỏa mãn và . Tính .
( )
0;+¥
( )
4
3
9
f =
( ) ( ) ( )
2
' 1 .f x x f x
é ù
= +
ë û
( )
8f
A. . B. . C. . D. .
( )
1
8
16
f =
( )
8 64f =
( )
8 49f =
( )
8 256f =
Lời giải
Chọn C.
Ta có .
( ) ( ) ( )
( )
( )
2
'
' 1 . 1
f x
f x x f x x
f x
é ù
= + Þ = +
ë û
Suy ra
.
( )
( )
( ) ( ) ( ) ( ) ( )
8 8
3 3
8
3
'
1
1
38 19
2 8 3 8 7 8 49
3 3
f x
dx dx
x
f x
f x f f f f
=
+
Þ = Û - = Û = Û =
ò ò
Câu 90: Cho các số thực dương x,y thỏa mãn .
2
2
5
2 5
10 3
9
10
xy y
x xy
+
-
æ ö
æ ö
÷
÷
ç
ç
£
÷
÷
ç
ç
÷
÷
ç
÷
ç
è ø
è ø
Hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của biểu thức bằng
x
y
A. . B. . C. . D.
5
2
1
4
1
5
5
4
Lời giải
Chọn B.
2
5
2
2 2
( )
5
2 5 2 5
2
10 3 10 10
9 9 9
10
xy y
xy y
x xy x xy
+
-
+
- -
æ ö
æ ö æ ö æ ö
÷
÷ ÷ ÷
ç
ç ç ç
£ Û £
÷
÷ ÷ ÷
ç
ç ç ç
÷
÷ ÷ ÷
ç ç ç
÷
ç
è ø è ø è ø
è ø
2
2
2 2
( 5 )
2 5
2
4 9 5 0
(4 5 )( ) 0
4 5 0
5
0
4
4 5 0
1
0
xy y
x xy
x xy y
x y x y
x y
x
x y
y
x
x y
y
x y
- +
Û - £
Û - + £
Û - - £
é
ì
- £
ï
ì
ï
ï
ê
ï
£
í
ï
ê
ï
- ³
ï
ï
î
ï
ê
Û Û
í
ê
ï
ì
- ³
ï
ê
ï
ï
³
ï
í
ê
ï
ï
- £
ï
ê î
ï
î
ë
Vậy
5
min 1;max
4
x x
y y
= =
Nên .
5 1
max min 1
4 4
x x
y y
- = - =
Câu 91: Cho hàm số trùng phương có đồ thị như hình vẽ.
4 2
axy bx c= + +
Hỏi đồ thị hàm số có tổng cộng bao nhiêu tiệm cận đứng?
( )( )
( ) ( )
2 2
2
4 2
2 3
x x x
y
f x f x
- +
=
é ù
+ -
ë û
A. . B. . C. . D.
3
4
5
2
Lời giải
Chọn B.
( )( )
( ) ( )
( )( )
( ) ( )
2
2 2
2 2
4 2
2 2
2 3 2 3
x x x
x x x
y
f x f x f x f x
- +
- +
= =
é ù é ù
+ - + -
ë û ë û
Xét
( ) ( )
2
( ) 1
2 3 0
( ) 3.
f x
f x f x
f x
é
=
é ù
ê
+ - = Û
ë û
ê
=-
ë
1
1
0
( ) 1 2
2
x
f x x x
x x
é
=
ê
ê
= Û = <-
ê
ê
= >
ë
Có 3 tiệm cận đứng
2( )
( ) 3
2
x l
f x
x
é
=-
ê
=- Û
ê
=
ë
Có 1 tiệm cận đứng
Vậy tổng cộng có 4 đường tiệm cận đứng.
Câu 92: Có bao nhiêu số nguyên dương m nhỏ hơn 20 thỏa mãn phương trình có
( )
log log 10
m x
mx m+ =
đúng hai nghiệm thực phân biệt.
A. . B. . C. . D.
11
13
12
10
Lời giải
Chọn B.
( )
( )
10
10
10
log log 10 log 10
10 ( log ) 10 .10
.10 .log( .10 ) 10 .10 (1)
x
x
x
m x
x x
x x x
mx m mx m m
mx m m
m m
+ = Û + =
Û + =
Û =
10 ;log( .10 )
.10 .10 10 log( .10 ) log
log 10
x x
a b x x
x
a m b
a b a b m m x
m x
= =
= Þ = Þ = = +
Þ = -
'
'
( ) 10
( ) 10 .ln10 1
( ) 0 log(ln10)
x
x
g x x
g x
g x x
= -
= -
= Û =-
Để phương trình có hai nghiệm thì
{ }
0.8
log 0.8 10 6.72
7;8;....19
m m
m
Þ > Þ > =
Þ Î
Vậy có 13 số.
Câu 93: Cho tứ diện có . Góc giữa hai mặt phẳng
ABCD
2 2
4 , 6 , = 3
ABC ABD
S cm S cm AB cm
D D
= =
và bằng . Thể tích của tứ diện đã cho bằng
( )
ABC
( )
ABD
60°
A. . B. . C. . D. .
3
2 3 cm
3
2 3
3
cm
3
4 3
3
cm
3
8 3
3
cm
Lời giải
Chọn D.
A
B
D
C
H
K
Gọi là chân đường cao của tứ diện hạ từ đỉnh và trong , kẻ với
H
ABCD
C
( )
ABC
CK AB^
. Khi đó, và .
K ABÎ
( ) ( )
( )
0
, 60ABC ABD CKH= =
h CH=
Do đó,
2
8 4 3
sin
3 3
ABC
S
CK = = CH = CK. CKH
AB
D
Þ =
Vậy .
3
1 8 3
. cm
3 3
ABCD ABD
V S CH
D
= =
Câu 94: Cho hình nón đỉnh , đường cao , và là hai điểm thuộc đường tròn đáy sao cho khoảng
S
SO
A
B
cách từ đến mặt bằng và . Độ dài đường sinh của hình
O
( )
SAB
3
3
a
0 0
30 , 60SAO SAB= =
nón theo bằng
a
A. . B. . C. . D. .
2 3a
5a
2a
3a
Lời giải
Chọn C.
Gọi là trung điểm của nên trong , kẻ (với
K
AB
( ) ( )
SOK SABÞ ^
( )
SOK
OH SK^
) thì .
H SKÎ
( )
( )
3
;
3
a
d O SAB OH= =
Ta có, tam giác đều nên và lại có .
SAB
3
2
SK = SA
sin
2
SA
SO = SA. SAO =
Xét tam giác vuông tại có
SOK
O
.
2 2 2 2 2
1 1 1 6 1
2 2SA a l a
OH SO OK SA OH
= + Þ = Þ = Þ =
Câu 95: Cho hàm số , có đồ thị như hình sau:
( )
y f x=
( )
y g x=
Khi đó tổng số nghiệm của hai phương trình và là
( )
( )
0f g x =
( )
( )
0g f x =
A. . B. . C. . D. .
26
25
22
21
Lời giải
Chọn C.
Ta có và .
( )
( )
( )
( )
( )
( )
1 1
2 2
3 3
4 4
5 5
3 2
2 1
0 1 2
2 3
4 5
x a a
x a a
f x x a a
x a a
x a a
é
= - < <-
ê
ê
= - < <-
ê
ê
= Û = < <
ê
ê
= < <
ê
ê
= < <
ê
ë
( )
( )
( )
6 6
7 7
2 1
0 0 1
3
x a a
g x x a a
x
é
= - < <-
ê
ê
= Û = < <
ê
ê
=
ê
ë
Khi đó , phương trình này có nghiệm.
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
1 1
2 2
3 3
4 4
5 5
3 2
2 1
0 1 2
2 3
4 5
g x a a
g x a a
f g x g x a a
g x a a
g x a a
é
= - < <-
ê
ê
= - < <-
ê
ê
= Û = < <
ê
ê
= < <
ê
ê
= < <
ê
ë
11
, phương trình này có nghiệm.
( )
( )
( )
( )
( )
6
7
0
3
f x a
g f x f x a
f x
é
=
ê
ê
= Û =
ê
ê
=
ê
ë
11
Vậy tổng số nghiệm của hai phương trình và là .
( )
( )
0f g x =
( )
( )
0g f x =
22
Câu 96: Cho hàm số có với là tham số thực. Hỏi
( )
y f x=
( ) ( )
( )
2
1 2 1 ,f x x x x mx x
¢
= + - + " Î
m
có tất cả bao nhiêu số nguyên không vượt quá sao cho hàm số có
m
2023
( )
( )
2
1g x f x= -
7
điểm cực trị?
A. . B. . C. . D. .
2021
2022
2020
2023
Lời giải
Chọn A.
( )
( )
( )
( ) ( ) ( ) ( )
2
2 2 2 2 2 2
1 2 1 2 1 1 2 1 1g x f x g x xf x x x x x m x
é ù
¢ ¢
= - Þ = - = - - - - +
ê ú
ë û
Ta có .
( )
0g x
¢
=
( ) ( )
2
2
2
2 2
0
1 0
0
1 2 1 1 0
x
x
x
x m x
é
=
ê
ê
- =
ê
Û
ê
=
ê
ê
ê
- - - + =
ê
ë
( ) ( )
2
2 2
0
1
1 2 1 1 0
x
x
x m x
é
=
ê
ê
ê
Û = ±
ê
ê
- - - + =
ê
ë
Để hàm số có điểm cực trị thì phương trình
( )
( )
2
1g x f x= -
7
( ) ( )
2
2 2
1 2 1 1 0x m x- - - + =
phải có đơn nghiệm phân biệt khác , .
4
0x =
1x = ±
Xét phương trình
( ) ( )
2
2 2
1 2 1 1 0x m x- - - + =
Đặt , khi đó ta được phương trình với .
2
1t x= -
2
2 1 0t mt- + =
1t ³-
Với ta có hai nghiệm ,
1t >-
x
Với ta có nghiệm ,
1t =-
0x =
Với phương trình vô nghiệm.
1t <-
Nên để có đơn nghiệm phân biệt khi và chỉ khi phương trình
( ) ( )
2
2 2
1 2 1 1 0x m x- - - + =
4
có hai nghiệm phân biệt .
2
2 1 0t mt- + =
0 1t¹ >-
Ta có .
2
1
2 1 0 2t mt m t
t
- + = Û = +
Xét hàm số , ta có .
( )
1
h t t
t
= +
( )
2
1
1 0 1h t t
t
¢
= - = Û = ±
Bảng biến thiên:
Từ bảng biến thiên, phương trình có hai nghiệm phân biệt khi
2
2 1 0t mt- + =
0 1t¹ >-
.
2m >
Câu 97: Cho hàm số liên tục trên thỏa mãn . Giá trị tích phân
( )
y f x=
1
;3
3
é ù
ê ú
ê ú
ë û
( )
3
1
f x x f x x
x
æ ö
÷
ç
+ × = -
÷
ç
÷
ç
è ø
bằng
3
2
1
3
( )
d
f x
I x
x x
=
+
ò
A. . B. . C. . D. .
3
4
16
9
2
3
8
9
Lời giải
Chọn D.
Ta có .
( )
( )
3
2
1 1 1
1
1
f x
f x x f x x f x
x x x x x
æ ö æ ö
÷ ÷
ç ç
+ × = - Û + × = -
÷ ÷
ç ç
÷ ÷
ç ç
è ø è ø
+ +
Suy ra
( ) ( )
3 3 3
2
1 1 1
3 3 3
( ) 1 1
d d 1 d . *
1
f x
x f x x x
x x x x
æ ö
÷
ç
+ × = -
÷
ç
÷
ç
è ø
+ +
ò ò ò
Đặt suy ra và .
1
t
x
=
2
1
d dx t
t
=-
1 1
1 1
t
x
t x t
= Û =
+ +
Đổi cận . Khi đó
1
3
3
1
3
3
x t
x t
ì
ï
ï
= Þ =
ï
ï
ï
í
ï
ï
= Þ =
ï
ï
ï
î
.
( )
( )
1
3 3
3
2 2
1 1
3
3 3
1 1 1
d d d
1 1
f t
t
f x f t t t I
x x t t t t
æ ö
÷
ç
× = - × × = =
÷
ç
÷
ç
è ø
+ + +
ò ò ò
Do đó .
( )
16 8
* 2
9 9
I IÛ = Û =
Câu 98: Cho hàm số có ba điểm cực trị là , và .
( )
4 3 2
2f x x ax bx cx d= + + + +
( )
, , ,a b c d Î
1-
1
3
Gọi là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số .
( )
y g x=
( )
y f x=
Diện tích hình phẳng giới hạn bởi hai đường và bằng
( )
y f x=
( )
y g x=
A. . B. . C. . D. .
182
15
265
15
128
15
256
15
Lời giải
Chọn D.
Hàm số có ba điểm cực trị là , và nên
( )
4 3 2
2f x x ax bx cx d= + + + +
( )
, , ,a b c d Î
1-
1
3
( )
( )
( )
1 0
3 2 8 8
1 0 3 2 8 4
27 6 216 24.
3 0
f
a b c a
f a b c b
a b c c
f
ì
¢
- =
ï
ì ì
- + = = -
ï ï
ï
ï ï
ï
ï ï
ï
ï ï
¢
= Û + + = - Û = -
í í í
ï ï ï
ï ï ï
+ + = - =
ï ï ï
¢
=
ï ï
î î
ï
î
Suy ra .
( )
4 3 2
2 8 4 24f x x x x x d= - - + +
( )
1
Ta có .
( )
3 2
8 24 8 24f x x x x
¢
= - - +
Khi đó
( ) ( ) ( ) ( )
.f x g x f x r x
¢
= +
Ta có . Suy ra .
( ) ( )
( ) ( )
( ) ( )
1 1
2 2
3 3
f x r x
f x r x
f x r x
ì
=
ï
ï
ï
ï
=
í
ï
ï
ï
=
ï
î
2
( ) ( ) 8 16 6r x g x x x d= +=- + +
Đồ thị đi qua ba điểm cực trị của đồ thị hàm số nên phương trình
( )
y g x=
( )
y f x=
( ) ( ) ( )
1
1 2
3.
x
f x g x x
x
é
=-
ê
ê
= Û =
ê
ê
=
ë
Từ và suy ra .
( )
1
( )
2
( ) ( ) ( )( ) ( )
2
2 1 1 3f x g x x x x- = + - -
Diện tích hình phẳng giới hạn bởi hai đường và bằng
( )
y f x=
( )
y g x=
.
( ) ( ) ( )( ) ( )
3
1
2
3
1
2 1
256
15
1 3 df x g x dx x x x x
- -
+ - =-- =
ò ò
Câu 99: Trong các nghiệm thỏa mãn bất phương trình . Giá trị lớn nhất của
( )
;x y
( )
2 2
2
log 2 1
x y
x y
+
+ ³
biểu thức bằng
2T x y= +
A. . B. . C. . D. .
9
9
4
9
2
9
8
Lời giải
Chọn C.
Ta có:
( )
( )
( )
2 2
2 2
2 2
2
2 2
2 2
2 1
1
2 2
log 2 1
0 2 1
2
2 2
x y
x y
x y x y
x y
x y
x y x y
+
é
ì
ï
+ >
ï
ê
í
ê
ï
+ ³ +
êï
î
+ ³ Û
ê
ì
ê
ï
< + <
ï
ê
í
ê
ï
+ £ +
ï
ê
î
ë
TH1: Khi đó:
( )
2
2
2 2
1 9
2 2 1 2 .
8
2 2
x y x y x y
æ ö
÷
ç
+ £ + Û - + - £
÷
ç
÷
÷
ç
è ø
( ) ( )
2
2
2
1 1 9 1 1 9
2 2 1 2 2 1 2
4 2 4
2 2 2 2 2
Cauchy schwarz
x y x y x y
-
é ù
æ ö æ ö
æ ö
ê ú
÷ ÷
÷
ç ç
ç
+ = - + - + £ + - + - +
÷ ÷
÷
ç ç
ç
ê ú
÷ ÷
÷
ç
÷ ÷
ç ç
è ø
è ø è ø
ê ú
ë û
9
2
£
TH2:
2 2
0 2 2 1T x y x y< = + £ + <
Vậy GTLN của khi .
9
2
T =
( )
1
; 2;
2
x y
æ ö
÷
ç
=
÷
ç
÷
ç
è ø
Câu 100: Tìm để giá trị lớn nhất của hàm số trên đoạn là nhỏ nhất. Giá trị
m
3
3 2 1y x x m= - + -
[ ]
0;2
của thuộc khoảng nào?
m
A. . B. . C. . D. .
( )
0;1
2
;2
3
æ ö
÷
ç
÷
ç
÷
ç
è ø
[ ]
1;0-
3
; 1
2
æ ö
÷
ç
- -
÷
ç
÷
ç
è ø
Lời giải
Chọn A.
Đặt . Nên:
( ) ( )
3 2
3 2 1 3 3f x x x m f x x
¢
= - + - Þ = -
( )
( )
( )
1 0;2
0
1 0;2
x
f x
x
é
= Î
ê
¢
= Û
ê
=- Ï
ê
ë
Có:
( ) ( ) ( )
1 2 3 0 2 1 2 2 1f m f m f m= - < = - < = +
( )
[ ]
{ }
0;2
max max 2 1 , 2 3f x m mÞ = + -
TH1: thì:
( )
[ ]
0;2
max 2 1f x m= +
( ) ( )
2 2
1
2 1 2 3 2 1 2 3 16 8 .
2
m m m m m m+ ³ - Û + ³ - Û ³ Û ³
Với GLTN của hàm số trên đoạn đạt GTNN là: khi
1
2 1 2
2
m m³ Þ + ³ Þ
[ ]
0;2
2
1
.
2
m =
TH2: thì:
( )
[ ]
0;2
max 2 3f x m= -
( ) ( )
2 2
1
2 3 2 1 2 3 2 1 16 8 .
2
m m m m m m- ³ + Û - ³ + Û £ Û £
Với GTLN của hàm số trên đoạn đạt GTNN là: khi
1
2 3 2
2
m m£ Þ - ³ Þ
[ ]
0;2
2
1
.
2
m =
Vậy giá trị lớn nhất của hàm số trên đạt GTNN là: khi
[ ]
0;2
2
1
.
2
m =
HẾT
| 1/26
| | Tải xuống

Có thể bạn quan tâm:

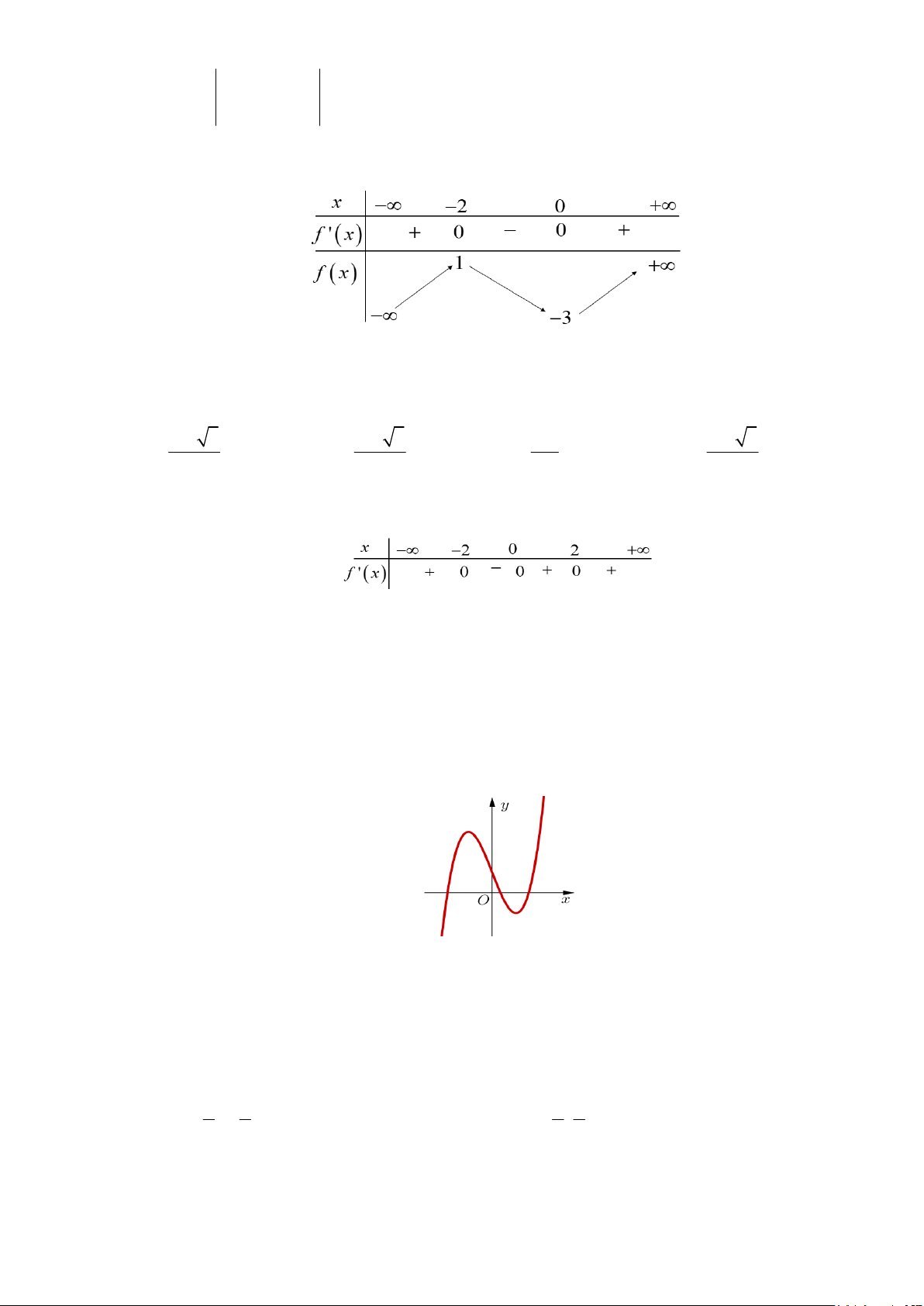
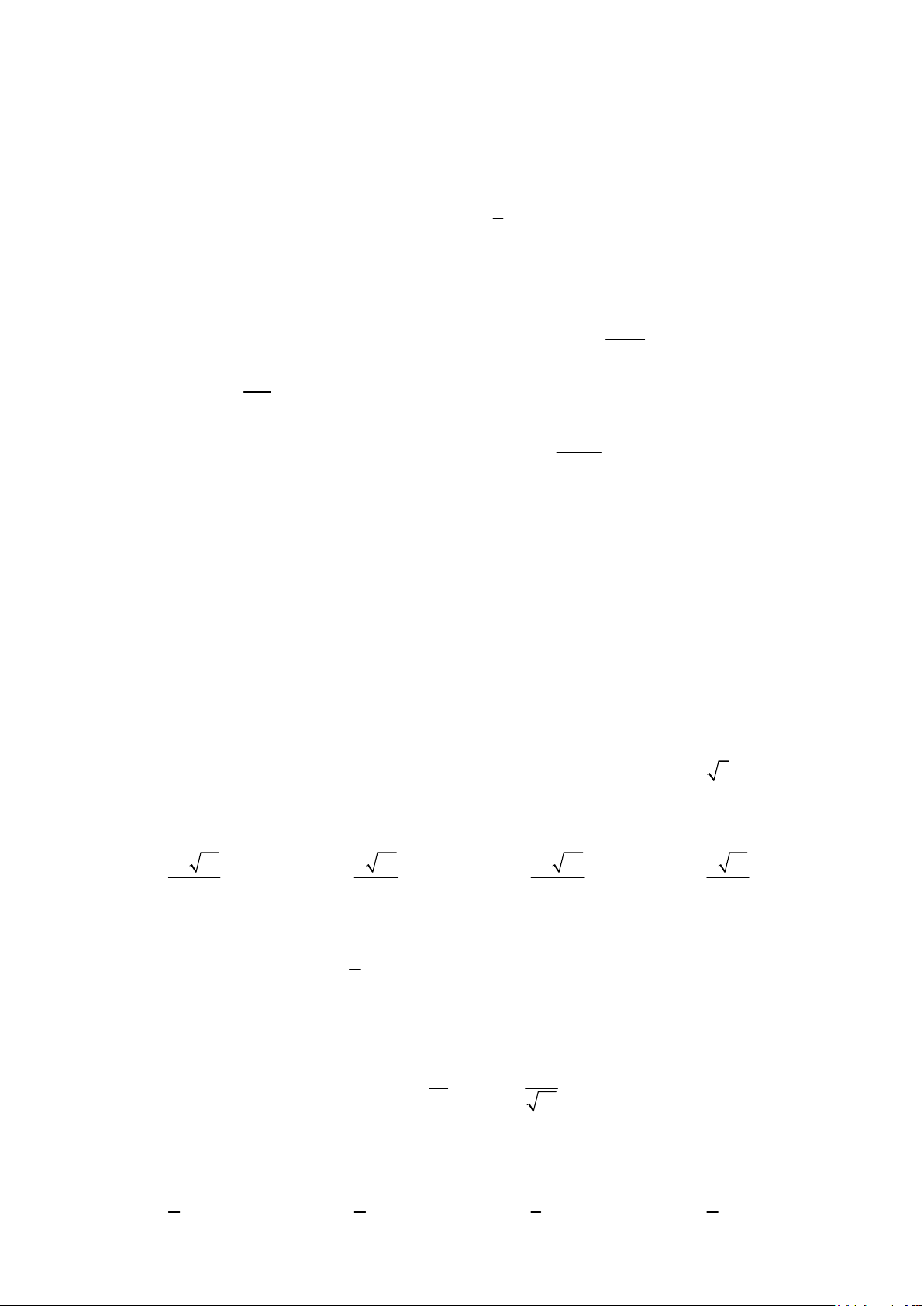
Preview text:

SỞ GD&ĐT HẢI PHÒNG
KỲ THI KHẢO SÁT CHẤT LƯỢNG KHỐI 12 NĂM 2023
TRƯỜNG THPT THÁI PHIÊN Bài thi: TOÁN ĐỀ THI LẦN 1
Thời gian làm bài: 90 phút (không kể thời gian giao đề) Câu 1:
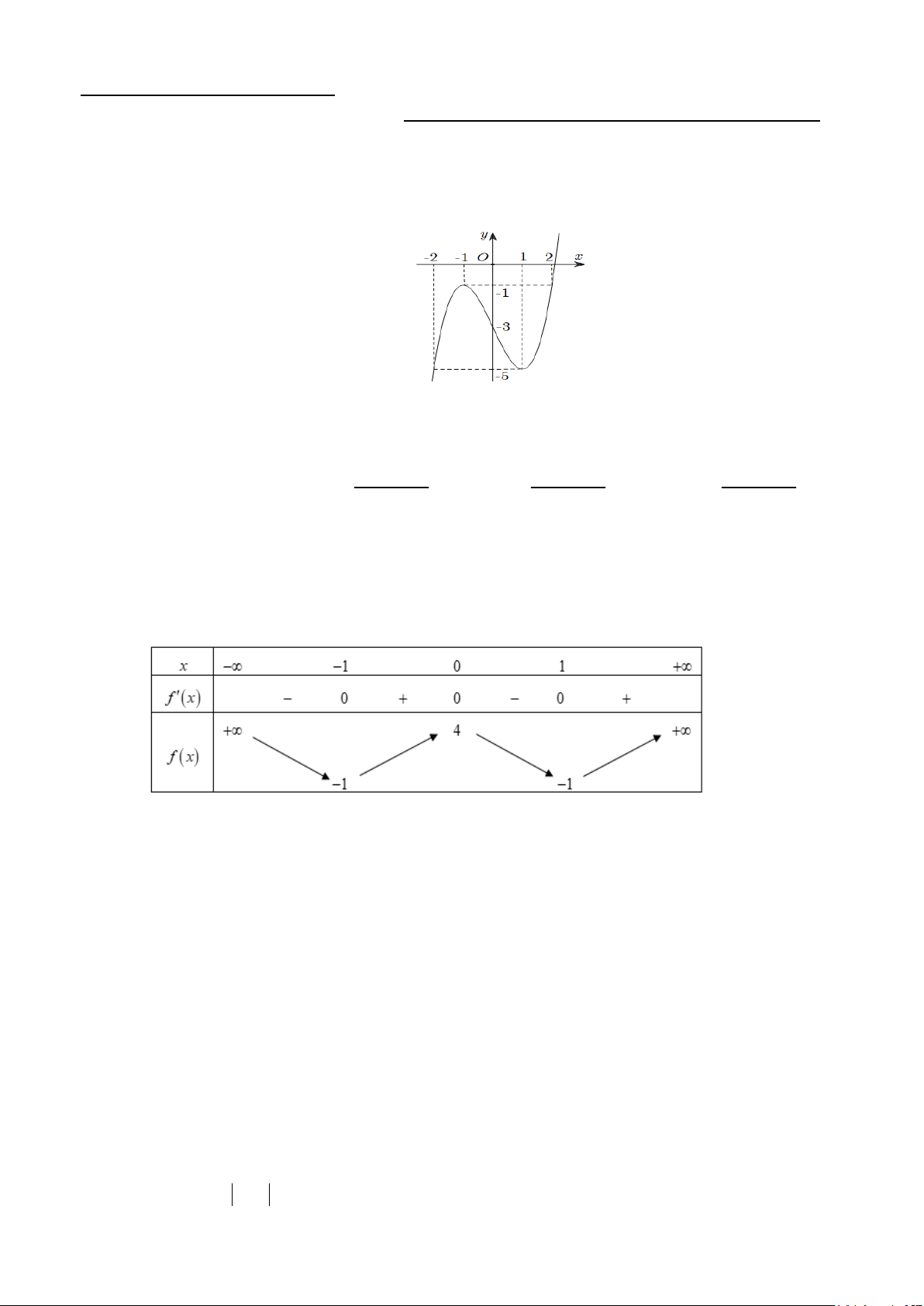
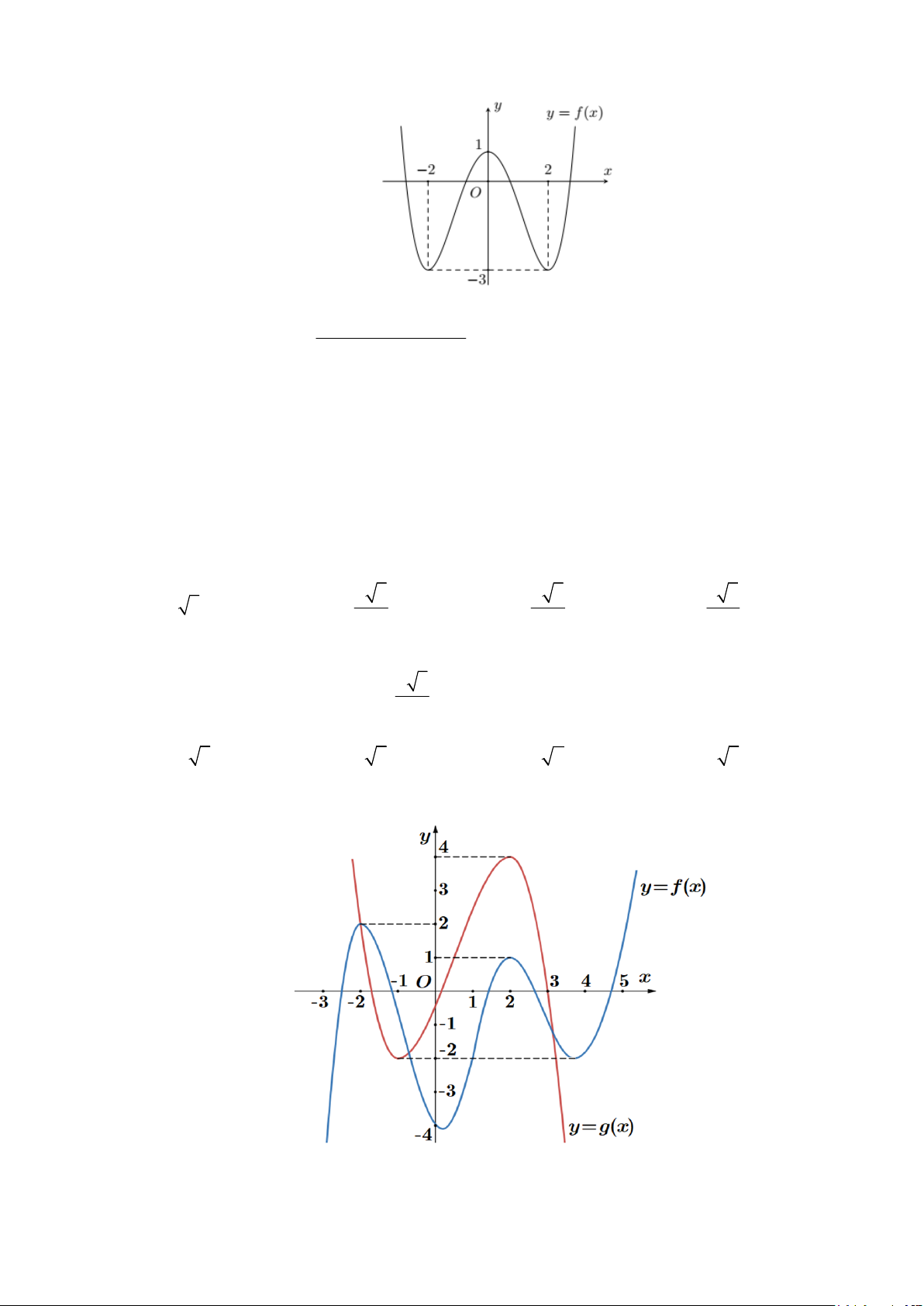
Cho hàm số y = f (x) xác định và liên tục trên  có đồ thị như hình vẽ bên. Tìm giá trị nhỏ hất
m và giá trị lớn nhất M của hàm số y = f (x) trên đoạn [-2;2].
A. m = -5, M = 0 .
B. m = -2, M = 2 .
C. m = -1, M = 0 .
D. m = -5, M = -1. Câu 2:
Tìm họ nguyên hàm của hàm số f (x)= sin 2023x.
A. 2023cos 2023x + cos2023x C . B. + cos2023x C . C. + cos2023x C . D. - +C . 2023 2024 2023 Câu 3:
Trong không gian Oxyz , điểm nào dưới đây nằm trên mặt phẳng (P): 2x- y + z -2 = 0 ? A. M (1;1;- ) 1 . B. N (1;-1;- ) 1 . C. Q(1;-2;2). D. P(2;-1;- ) 1 . Câu 4:
Cho hàm số y = f (x) có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. (-1;0) . B. (0; ) 1 . C. (-1; ) 1 . D. (- ; ¥ - ) 1 . Câu 5:
Cho một cấp số cộng có số hạng đầu u và công sai d , số hạng tổng quát u được xác định bởi 1 n công thức
A. u = d + . n u .
B. u = u + n-1 d
u = d + n- u u = u + . n d n ( )1 n 1 ( ) . C. . D. . n 1 1 n 1 Câu 6:
Tập nghiệm của bất phương trình log x < 0 là 2 A. (0; ) 1 . B. (- ; ¥ ) 1 . C. (1;+¥). D. (0;+¥). Câu 7:
Tính đạo hàm của hàm số 17 x y - = A. 1 .17 x y x - - ¢ =- . B. 17 x y - ¢ =- . C. 17 x y - ¢ =- ln17 . D. 17 x y - ¢ = ln17 . Câu 8:
Cho hình phẳng (D) được giới hạn bởi các đường x = 0, x = ,
p y = 0 và y =-sin x . Thể tích
V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức p p
A. V = p sin x dx . B. V = p sin d x x . ò 2 ò 0 0 p p
C. V = p ò (-sin x)dx .D. 2 V = sin d x x . ò 0 0 Câu 9:
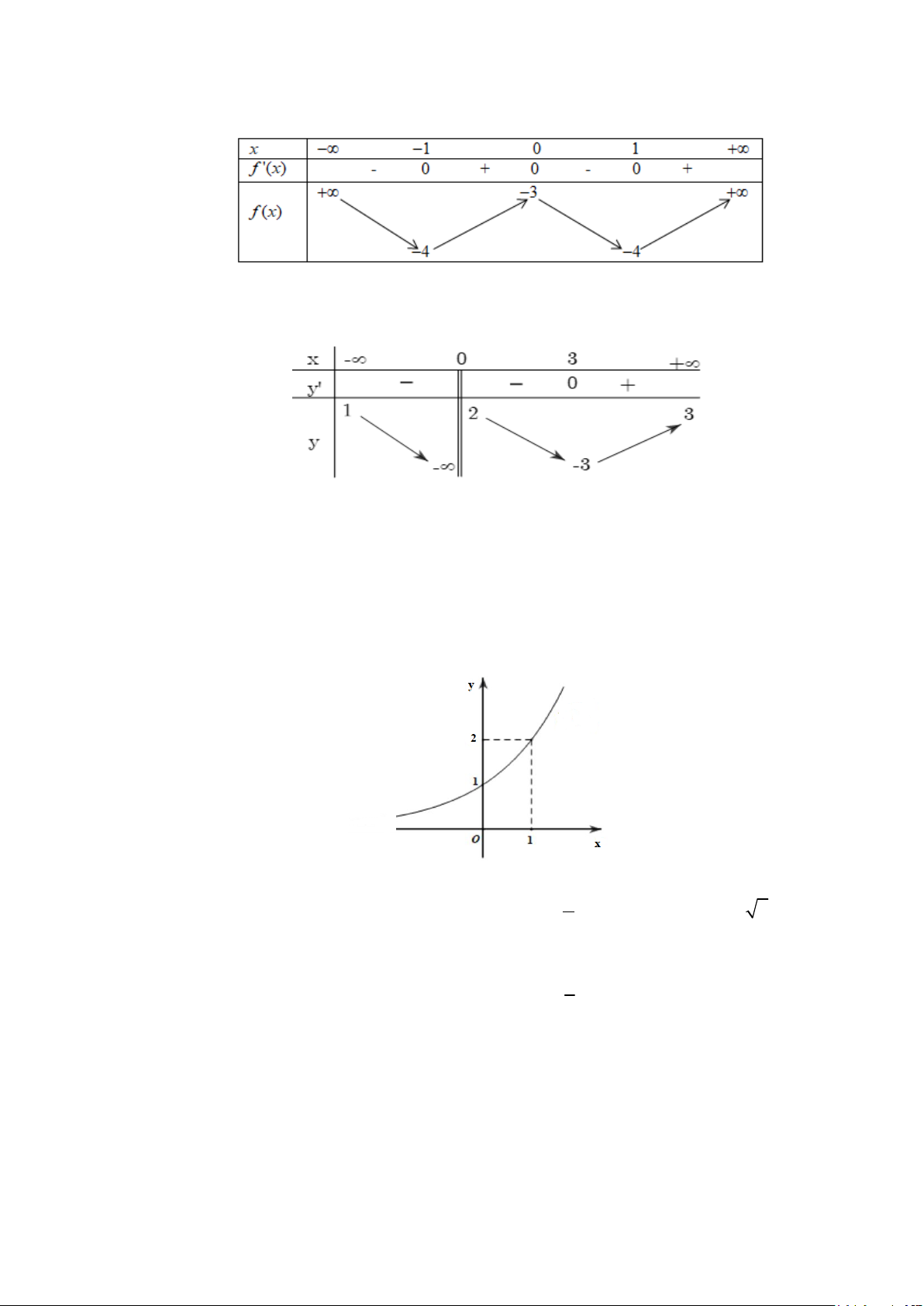
Cho hàm số f (x) có bảng biến thiên như hình vẽ. Điểm cực đại của hàm số đã cho là A. x = 3. B. x = -3. C. x = 1 . D. x = -2.
Câu 10: Cho khối lăng trụ đứng ABC.A' B 'C ' có đáy là tam giác đều cạnh a , chiều cao h . Khi đó thể tích khối lăng trụ là 2 a h 3 2 a h 3 2 a h 2 a h 3 A. . B. . C. . D. . 6 12 4 4
Câu 11: Cho hàm f (x) xác định trên  có bảng xét dấu f '(x) như sau
Số điểm cực trị của hàm số đã cho là A. 3 . B. 0 . C. 2 . D. 1. 3
Câu 12: Cho hàm f (x) có đạo hàm liên tục trên [2; ]
3 đồng thời f (2)= 2, f ( ) 3 = 5. Tính f ' ò (x)dx 2 bằng A. 10 . B. 3 . C. -3 . D. 7 .
Câu 13: Đường cong trong hình bên dưới là đồ thị của hàm số nào? A. 3
y = x -3x +1. B. 3
y = -x +3x +1. C. 4 2
y = x - x +1. D. 2
y = -x + x-1. 
Câu 14: Trong không gian Oxyz , cho hai điểm A(1;1;-2), B(2;2; )
1 . Véc tơ AB có toạ độ là A. (3;1; ) 1 . B. (1;1; ) 3 . C. (3;3;- ) 1 . D. (-1;-1;- ) 3 . -
Câu 15: Hàm số y = - x có tập xác định là ( ) 4 2 1 4 ìï1 1ü ï ï æ ö A.  \ ; ï í - ý . B.  1 1 . C. ç- ; ÷ ç ÷. D. 0;+¥ . ï2 2 ï ï î þ çè 2 2÷ø ( ) 2 3 3 Câu 16: Nếu f
ò (x)dx=3, f
ò (t)dt =-1 thì f ò (x)dx bằng 1 2 1 A. -2 . B. 2 . C. 3 . D. 4 . Câu 17: Cho hàm số 4 2
y = ax +bx +c có bảng biến thiên như hình vẽ. Tìm mệnh đề đúng? A. 4 2
y = x -2x -3. B. 4 2
y = -x -2x -3. C. 4 2
y = x -2x +3 . D. 4 2
y = -x + 2x -3.
Câu 18: Cho hàm số y = f (x)có báng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là: A. 2. B. 3. C. 4. D. 1.
Câu 19: Từ các số 1, 2 , 3 , 4 , 5 có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số đôi một khác nhau. A. 16 . B. 24 . C. 120 . D. 720 .
Câu 20: Khối lăng trụ ngũ giác có tất cả bao nhiêu cạnh? A. 15 . B. 25 . C. 10 . D. 20 .
Câu 21: Đường cong trong hình sau là đồ thị hàm số nào x
A. y = log (2x) . B. 2x y = 1 .
C. y = x +1. D. y = 2 . ( ) 2 2
Câu 22: Thể tích của khối trụ có độ dài đường sinh l và bán kính đáy r bằng
A. V = 4 r p l . B. V = r p 1 l . C. V = r p l . D. 2 V = l r p . 3
Câu 23: Gọi l, ,
h r lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình nón. Tìm mệnh đề đúng 1 A. 2 S = r p h . B. S = r p l . C. S = r p h.
D. S = 2 r p l . xq 3 xq xq xq
Câu 24: Cho mặt phẳng (a): 2x-3y-4z +1= 0 . Khi đó một vectơ pháp tuyến của (a) là     A. n =(-2;3;4). B. n = (-2;3; ) 1 . C. n =(2;3;-4). D. n = (2;-3;4).
Câu 25: Thể tích V của khối chóp có diện tích đáy bằng S và chiều cao bằng h là A. V = 1 Sh .
B. V = Sh . C. V = 1 3Sh .
D. V = Sh . 3 2
Câu 26: Số nghiệm phương trình 2 2 x 7 - x+5 2 =1 là A. 0 . B. 1. C. 2 . D. 3 . 2
Câu 27: Họ các nguyên hàm của hàm số f (x) 2 = x -3x + là x 3 x 3 3 x 3 A. F (x) 2
= + x +2ln x +C . B. F (x) 2
= - x +2ln x +C . 3 2 3 2 2 3 x 3
C. F (x)= 2x-3- +C . D. F (x) 2
= - x +2ln x +C . 2 x 3 2
Câu 28: Trong không gian Oxyz , hình chiếu vuông góc của điểm A(3;5;2) trên trục Ox có tọa độ là A. (3;0;0). B. (0;0;2). C. (0;5;2). D. (0;5;0).
Câu 29: Cho F (x) là một nguyên hàm của hàm số f (x) 2 x 3
= e x -4x . Hàm số F (x) có bao nhiêu ( ) điểm cực trị? A. 1. B. 4 . C. 2 . D. 3 .
Câu 30: Hàm số nào dưới đây đồng biến trên khoảng (- ; ¥ +¥) x + x -1 A. 3
y = x + x . B. 3 y = -x - 1 3x . C. y = . D. y = . x +3 x -2 5
Câu 31: Cho tích phân 2 = .e x I x
dx . Tìm mệnh đề đúng ò1 5 1 5 1 x 1 A. 2 5 2 = e | - e x I x dx . B. 2 x 5 2 = e | - e x I x dx . 1 ò ò 2 2 1 2 1 1 5 5 1 x 1 C. 2 x 5 2 = e | - e x I x dx . D. 5 = e | - ex I x dx 1 ò 1 ò 2 2 1 1
Câu 32: Có hai hộp bút chì màu, các bút chì khác nhau. Hộp thứ nhất có 5 bút chì màu đỏ và 7 bút chì
màu xanh. Hộp thứ hai có 8 bút chì màu đỏ và 4 bút chì màu xanh. Chọn ngẫu nhiên mỗi hộp
một cây bút chì. Xác suất để chọn một cây bút chì màu đỏ và một bút chì màu xanh là 17 7 19 5 A. . B. . C. . D. . 36 12 36 12 1
Câu 33: Tìm giá trị thực của tham số m để hàm số 3 2 2
y = x -mx + m -4 x +3 đạt cực đại tại x = 3. ( ) 3 A. m =1. B. m = -1.
C. m =1;m = 5 . D. m = 5 .
Câu 34: Cho hàm số f (x) 2
= log x +1 . Tính f ¢(- ) 1 . 3 ( )
A. Không tồn tại f ¢(- ) 1 . B. f ¢(- ) 1 1 = . 2ln 3 C. f ¢(- ) 1 1 = . D. f ¢(- ) 1 = -1.x . ln 3 x + m
Câu 35: Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y =
trên đoạn [1;2] bằng 8 ( m là tham x +1
số thực). Khẳng định nào sau đây là đúng?
A. 8 < m <10 .
B. 0 < m < 4 .
C. 4 < m <8. D. m >10 .
Câu 36: Trong không gian cho hai điểm A(1;-1;2) và B(3;3;0). Mặt phẳng trung trực đoạn AB có phương trình là
A. x + y - z -2 = 0 .
B. x + y - z + 2 = 0 . C. x + 2y - z -3 = 0 . D. x + 2y - z +3 = 0 .
Câu 37: Cho hàm số S.ABCD có đáy ABCD là hình vuông cạnh 2a , O là tâm đáy. Hình chiếu vuông
góc của S xuống (ABCD) là trung điểm H của OA , biết (SD (ABCD) = °. Gọi a là góc )  , 60
giữa mp(SCD) và mp(ABCD). Tìm mệnh đề đúng. A. tan a Î(0; ) 1 . B. tan a Î(3;4). C. tan a Î(2; ) 3 . D. tan a Î(1;2).
Câu 38: Cho hình chóp S.ABCD có đáy ABCD là hình thoi với AC = 2a, BD = 2a 2 . Gọi H là trọng
tâm tam giác ABD , biết rằng các mặt phẳng (SHC) và (SHD) cùng vuông góc với mặt phẳng
(ABCD). Khoảng cách từ C đến mặt phẳng (SHD) bằng 4a 19 a 38 4a 38 a 19 A. . B. . C. . D. . 38 19 19 38
Câu 39: Cho hàm số y = f (x) đồng biến trên (0;+¥), y = f (x) liên tục, nhận giá trị dương trên ( 2
0;+¥) thỏa mãn f ( ) 4
3 = và é f '(x)ù =(x + )
1 . f (x). Tính f . 9 ë û ( ) 8 A. f ( ) 1 8 = . B. f ( ) 8 = 64 . C. f ( ) 8 = 49 . D. f ( ) 8 = 256 . 16 2 2 2 x 5 - xy xy+5 1 æ 0ö æ 3 y ö
Câu 40: Cho các số thực dương x,y thỏa mãn ç ÷ ç ÷ £ç ÷ ç ÷ . çè 9 ÷ø çè 10÷ø x
Hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của biểu thức bằng y 5 1 1 5 A. . B. . C. . D. 2 4 5 4
Câu 41: Cho hàm số trùng phương 4 2
y = ax +bx +c có đồ thị như hình vẽ.
( 2x- )4( 2x +2x)
Hỏi đồ thị hàm số y =
có tổng cộng bao nhiêu tiệm cận đứng?
é f (x) 2ù +2 f (x)-3 ë û A. 3 . B. 4 . C. 5 . D. 2
Câu 42: Có bao nhiêu số nguyên dương m nhỏ hơn 20 thỏa mãn phương trình log +log m =10x mx m có ( )
đúng hai nghiệm thực phân biệt. A. 11. B. 13 . C. 12. D. 10
Câu 43: Cho tứ diện ABCD có 2 2 S = 4 cm , S
= 6 cm , AB = 3 cm . Góc giữa hai mặt phẳng A D BC A D BD
(ABC) và (ABD) bằng 60°. Thể tích của tứ diện đã cho bằng 2 3 4 3 8 3 A. 3 2 3 cm . B. 3 cm . C. 3 cm . D. 3 cm . 3 3 3
Câu 44: Cho hình nón đỉnh S , đường cao SO , A và B là hai điểm thuộc đường tròn đáy sao cho khoảng a 3
cách từ O đến mặt (SAB) bằng và  0 SAO  0
= 30 , SAB = 60 . Độ dài đường sinh của hình 3 nón theo a bằng A. 2a 3 . B. a 5 . C. a 2 . D. a 3 .
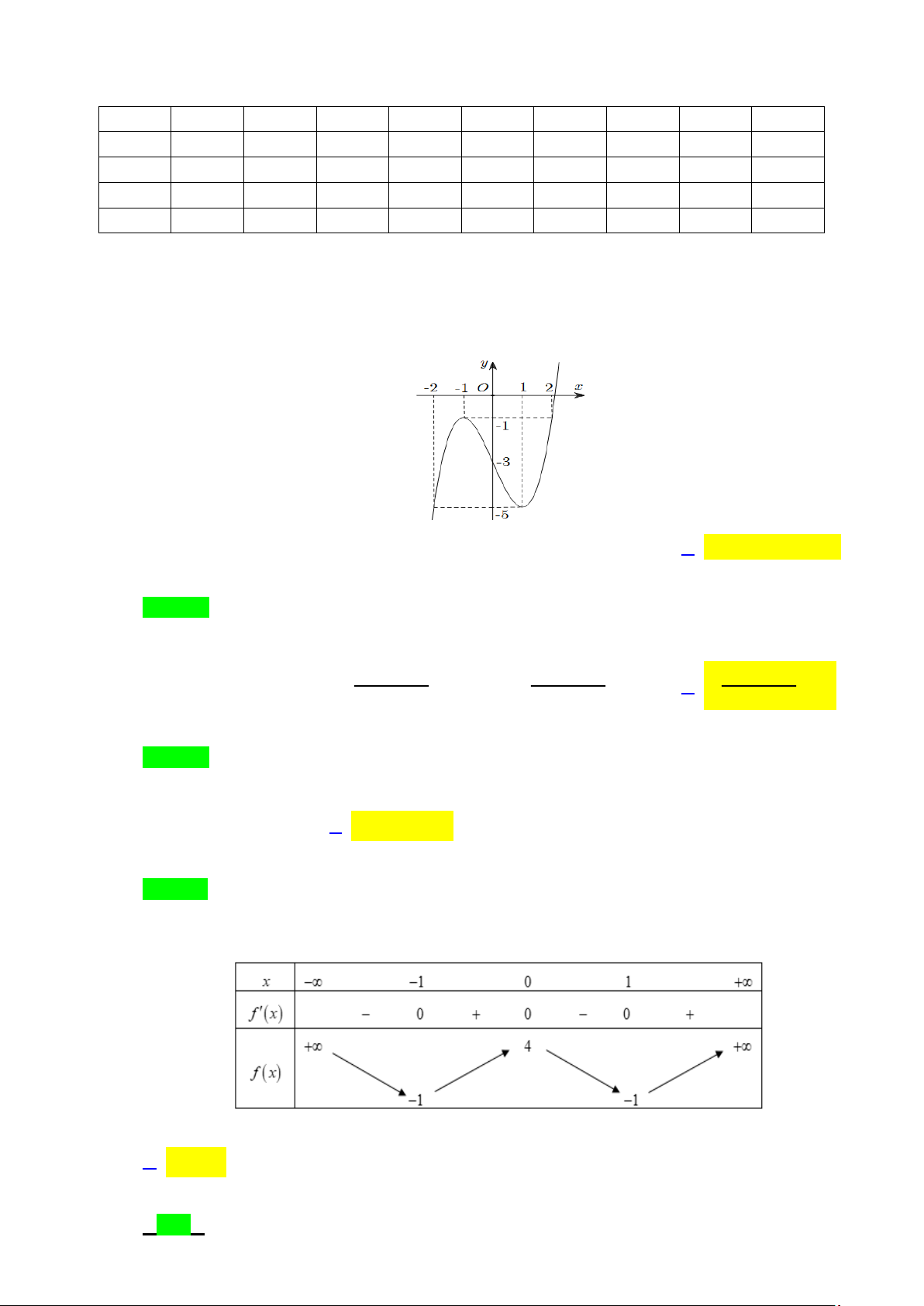
Câu 45: Cho hàm số y = f (x), y = g(x) có đồ thị như hình sau:
Khi đó tổng số nghiệm của hai phương trình f (g(x) = và g( f (x) = là ) 0 ) 0 A. 26 . B. 25 . C. 22 . D. 21.
Câu 46: Cho hàm số y = f (x) có f ¢(x)= x(x + ) 2
1 x -2mx +1 , "x Î  với m là tham số thực. Hỏi ( )
có tất cả bao nhiêu số nguyên m không vượt quá 2023 sao cho hàm số g (x) 2 = f x -1 có 7 ( ) điểm cực trị? A. 2021. B. 2022 . C. 2020 . D. 2023. é ù æ1ö
Câu 47: Cho hàm số y = 1
f (x) liên tục trên ê ;3ú thỏa mãn f (x) 3 + x× f ç ÷
ç ÷= x - x . Giá trị tích phân ê3 ë úû çèx÷ø 3 f (x) I = dx bằng 2 ò x +x 1 3 3 16 2 8 A. . B. . C. . D. . 4 9 3 9
Câu 48: Cho hàm số f (x) 4 3 2
= 2x + ax +bx +cx + d (a, ,bc,d Î ) có ba điểm cực trị là 1 - , 1 và 3.
Gọi y = g(x) là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số y = f (x).
Diện tích hình phẳng giới hạn bởi hai đường y = f (x) và y = g(x) bằng 182 265 128 256 A. . B. . C. . D. . 15 15 15 15
Câu 49: Trong các nghiệm ( ;x y) thỏa mãn bất phương trình log 2x + y ³1 2 2 x +2 y (
) . Giá trị lớn nhất của
biểu thức T = 2x + y bằng 9 9 9 A. 9 . B. . C. . D. . 4 2 8
Câu 50: Tìm m để giá trị lớn nhất của hàm số 3
y = x -3x + 2m-1 trên đoạn [0;2] là nhỏ nhất. Giá trị
của m thuộc khoảng nào? æ2 ö æ ö A. (0; ) 1 . B. ç ; 2÷ ç ÷. C. - 3 1;0 . D. ç- ; ç -1÷÷. çè3 ÷ø [ ] çè 2 ÷ø  HẾTBẢNG ĐÁP ÁN 1.D 2.D 3.B 4.A 5.B 6.A 7.C 8.B 9.D 10.D 11.C 12.B 13.A 14.B 15.A 16.B 17.A 18.B 19.C 20.A 21.B 22.D 23.B 24.A 25.B 26.C 27.D 28.A 29.D 30.A 31.A 32.C 33.A 34.C 35.A 36.C 37.D 38.C 39.C 40.B 41.B 42.B 43.D 44.C 45.C 46.A 47.D 48.D 49.C 50.A
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 51: Cho hàm số y = f (x) xác định và liên tục trên  có đồ thị như hình vẽ bên. Tìm giá trị nhỏ hất
m và giá trị lớn nhất M của hàm số y = f (x) trên đoạn [-2;2].
A. m = -5, M = 0 .
B. m = -2, M = 2 .
C. m = -1, M = 0 .
D. m = -5, M = -1. Lời giải Chọn D.
Câu 52: Tìm họ nguyên hàm của hàm số f (x)= sin 2023x.
A. 2023cos 2023x + cos2023x C . B. + cos2023x C . C. + cos2023x C . D. - +C . 2023 2024 2023 Lời giải Chọn D.
Câu 53: Trong không gian Oxyz , điểm nào dưới đây nằm trên mặt phẳng (P): 2x- y + z -2 = 0 ? A. M (1;1;- ) 1 . B. N (1;-1;- ) 1 . C. Q(1;-2;2). D. P(2;-1;- ) 1 . Lời giải Chọn B.
Câu 54: Cho hàm số y = f (x) có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. (-1;0) . B. (0; ) 1 . C. (-1; ) 1 . D. (- ; ¥ - ) 1 . Lời giải Chọn A .
Câu 55: Cho một cấp số cộng có số hạng đầu u và công sai d , số hạng tổng quát u được xác định bởi 1 n công thức
A. u = d + . n u .
B. u = u + n-1 d
u = d + n- u u = u + . n d n ( )1 n 1 ( ) . C. . D. . n 1 1 n 1 Lời giải Chọn B.
Ta có u = u + n-1 d n 1 ( ) .
Câu 56: Tập nghiệm của bất phương trình log x < 0 là 2 A. (0; ) 1 . B. (- ; ¥ ) 1 . C. (1;+¥). D. (0;+¥). Lời giải Chọn A.
Ta có log x < 0 Û 0 < x <1. 2
Tập nghiệm của bất phương trình log x < 0 là (0; ) 1 . 2
Câu 57: Tính đạo hàm của hàm số 17 x y - = A. 1 .17 x y x - - ¢ =- . B. 17 x y - ¢ =- . C. 17 x y - ¢ =- ln17 . D. 17 x y - ¢ = ln17 . Lời giải Chọn C.
Ta có =17-x Þ ¢ = -17-x y y ln17 .
Câu 58: Cho hình phẳng (D) được giới hạn bởi các đường x = 0, x = ,
p y = 0 và y =-sin x . Thể tích
V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức p p
A. V = p sin x dx . B. V = p sin d x x . ò 2 ò 0 0 p p
C. V = p ò (-sin x)dx .D. 2 V = sin d x x . ò 0 0 Lời giải Chọn B. p p
Ta có V = pò (-sin x)2 2 dx = p sin d x x . ò 0 0
Câu 59: Cho hàm số f (x) có bảng biến thiên như hình vẽ. Điểm cực đại của hàm số đã cho là A. x = 3. B. x = -3. C. x = 1 . D. x = -2. Lời giải Chọn D.
Câu 60: Cho khối lăng trụ đứng ABC.A' B 'C ' có đáy là tam giác đều cạnh a , chiều cao h . Khi đó thể tích khối lăng trụ là 2 a h 3 2 a h 3 2 a h 2 a h 3 A. . B. . C. . D. . 6 12 4 4 Lời giải Chọn D. 2 a h 3 S = . h S = . 4
Câu 61: Cho hàm f (x) xác định trên  có bảng xét dấu f '(x) như sau
Số điểm cực trị của hàm số đã cho là A. 3 . B. 0 . C. 2 . D. 1. Lời giải Chọn C. 3
Câu 62: Cho hàm f (x) có đạo hàm liên tục trên [2; ]
3 đồng thời f (2)= 2, f ( ) 3 = 5. Tính f ' ò (x)dx 2 bằng A. 10 . B. 3 . C. -3 . D. 7 . Lời giải Chọn B. 3 f '
ò (x)dx= f ( )3- f (2)=5-2=3. 2
Câu 63: Đường cong trong hình bên dưới là đồ thị của hàm số nào? A. 3
y = x -3x +1. B. 3
y = -x +3x +1. C. 4 2
y = x - x +1. D. 2
y = -x + x-1. Lời giải Chọn A.
Quan sát đồ thị ta nhận thấy đồ thị là của hàm số bậc 3 có hệ số chứa 3 x dương. 
Câu 64: Trong không gian Oxyz , cho hai điểm A(1;1;-2), B(2;2; )
1 . Véc tơ AB có toạ độ là A. (3;1; ) 1 . B. (1;1; ) 3 . C. (3;3;- ) 1 . D. (-1;-1;- ) 3 . Lời giải Chọn B. 
Ta có AB =(x - x ; y - y ; z - z = B A B A B A ) (1;1; )3. -
Câu 65: Hàm số y = - x có tập xác định là ( ) 4 2 1 4 ìï1 1ü ï ï æ ö A.  \ ; ï í - ý . B.  1 1 . C. ç- ; ÷ ç ÷. D. 0;+¥ . ï2 2 ï ï î þ çè 2 2÷ø ( ) Lời giải Chọn A. 1
Hàm số đã cho xác định khi 2
1-4x ¹ 0 Û x ¹ - 1 và x ¹ . 2 2 ìï1 1ü ï ï
Vậy tập xác định của hàm số là  \ ; í - ý . ï2 2 ï ï î þ 2 3 3 Câu 66: Nếu f
ò (x)dx=3, f
ò (t)dt =-1 thì f ò (x)dx bằng 1 2 1 A. -2 . B. 2 . C. 3 . D. 4 . Lời giải Chọn B. 3 3
Tích phân không phụ thuộc vào biến số nên f
ò (t)dt = f
ò (x)dx=-1. Do đó 2 2 3 2 3 f
ò (x)dx= f
ò (x)dx+ f ò (x)dx 3 = +(- ) 1 = 2 .. 1 1 2 Câu 67: Cho hàm số 4 2
y = ax +bx +c có bảng biến thiên như hình vẽ. Tìm mệnh đề đúng? A. 4 2
y = x -2x -3. B. 4 2
y = -x -2x -3. C. 4 2
y = x -2x +3 . D. 4 2
y = -x + 2x -3. Lời giải Chọn A.
Dựa vào bảng biến thiên ta có a > 0 . Loại đáp án B, D
Đồ thị hàm số đi qua điểm (0;-3) nên chọn đáp án A .
Câu 68: Cho hàm số y = f (x)có báng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là: A. 2. B. 3. C. 4. D. 1. Lời giải Chọn B.
Nhìn bảng biến thiên ta thấy lim f (x = -¥ Þ x = 0 - )
là TCĐ của đồ thị hàm số x®0 Ta có
lim f (x)= 3 Þ y = 3 là TCN của đồ thị hàm số x®+¥
lim f (x)=1Þ y =1là TCN của đồ thị hàm số x®-¥
Vậy hàm số có 3 tiệm cận.
Câu 69: Từ các số 1, 2 , 3 , 4 , 5 có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số đôi một khác nhau. A. 16 . B. 24 . C. 120 . D. 720 . Lời giải Chọn C.
Mỗi số tự nhiên có 5 chữ số khác nhau lập từ 5 chữ số đã cho là một hoán vị của 5 phần tử. Nên
số số tự nhiên cần tìm là 5!=120 số.
Câu 70: Khối lăng trụ ngũ giác có tất cả bao nhiêu cạnh? A. 15 . B. 25 . C. 10 . D. 20 . Lời giải Chọn A.
Khối lăng trụ ngũ giác có 10 cạnh đáy và 5 cạnh bên nên khối lăng trụ ngũ giác có tất cả 15 cạnh.
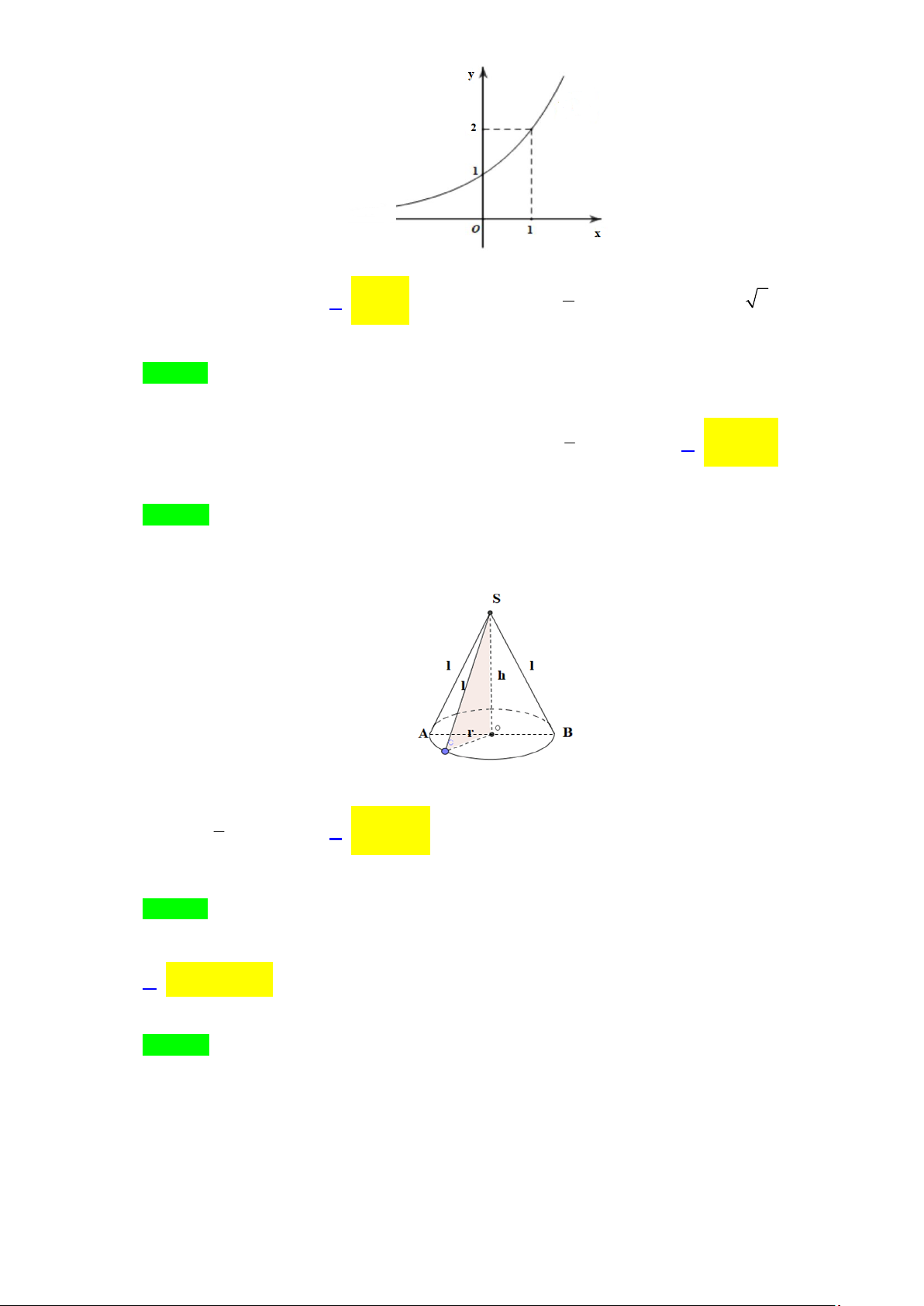
Câu 71: Đường cong trong hình sau là đồ thị hàm số nào x
A. y = log (2x) . B. 2x y = 1 .
C. y = x +1. D. y = 2 . ( ) 2 2 Lời giải Chọn B.
Câu 72: Thể tích của khối trụ có độ dài đường sinh l và bán kính đáy r bằng
A. V = 4 r p l . B. V = r p 1 l . C. V = r p l . D. 2 V = l r p . 3 Lời giải Chọn D.
Câu 73: Gọi l, ,
h r lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình nón. Tìm mệnh đề đúng 1 A. 2 S = r p h . B. S = r p l . C. S = r p h.
D. S = 2 r p l . xq 3 xq xq xq Lời giải Chọn B.
Câu 74: Cho mặt phẳng (a): 2x-3y-4z +1= 0 . Khi đó một vectơ pháp tuyến của (a) là     A. n =(-2;3;4). B. n = (-2;3; ) 1 . C. n =(2;3;-4). D. n = (2;-3;4). Lời giải Chọn A. 
Mặt phẳng (a): 2x-3y-4z +1= 0 có vectơ pháp tuyến là n =(2;-3;-4). 
Suy ra n =(-2;3;4) cũng là một vectơ pháp tuyến của (a).
Câu 75: Thể tích V của khối chóp có diện tích đáy bằng S và chiều cao bằng h là A. V = 1 Sh .
B. V = Sh . C. V = 1 3Sh .
D. V = Sh . 3 2 Lời giải Chọn B. 1 V = Sh . 3
Câu 76: Số nghiệm phương trình 2 2 x 7 - x+5 2 =1 là A. 0 . B. 1. C. 2 . D. 3 . Lời giải Chọn C. éx =1 2 ê 2 x 7 - x+5 2 2 2
=1Û 2x -7x +5 = log 1Û 2x -7x +5 = 0 Û ê 5 . 2 êx = êë 2
Vậy phương trình có 2 nghiệm phân biệt. 2
Câu 77: Họ các nguyên hàm của hàm số f (x) 2 = x -3x + là x 3 x 3 3 x 3 A. F (x) 2
= + x +2ln x +C . B. F (x) 2
= - x +2ln x +C . 3 2 3 2 2 3 x 3
C. F (x)= 2x-3- +C . D. F (x) 2
= - x +2ln x +C . 2 x 3 2 Lời giải Chọn D. 3 æ 2ö x 3 2 2 çx
ò ç -3x+ ÷÷ dx= - x +2ln x +C . çè x÷ø 3 2
Câu 78: Trong không gian Oxyz , hình chiếu vuông góc của điểm A(3;5;2) trên trục Ox có tọa độ là A. (3;0;0). B. (0;0;2). C. (0;5;2). D. (0;5;0). Lời giải Chọn A. 
Đường thẳng chứa trục Ox có 1 vectơ chỉ phương i =(1;0;0). 
Gọi H là hình chiếu của điểm A(3;5;2) trên trục Ox Þ H ( ;
a 0;0); AH =(a-3;-5;-2).   Þ AH ^ i .  
Þ AH.i = 0 Û a-3= 0 Û a = 3 Vậy H (3;0;0).
Câu 79: Cho F (x) là một nguyên hàm của hàm số f (x) 2 x 3
= e x -4x . Hàm số F (x) có bao nhiêu ( ) điểm cực trị? A. 1. B. 4 . C. 2 . D. 3 . Lời giải Chọn D. éx = 0
Ta có F ¢(x)= f (x) 2 x 3 = e x -4x , ( ) ¢( ) 2 x F x = Û ( 3 0 e x -4x)= 0 3
Û x -4x = 0 Û êêx=±1 ë
Suy ra hàm số F (x) có 3 điểm cực trị.
Câu 80: Hàm số nào dưới đây đồng biến trên khoảng (- ; ¥ +¥) x + x -1 A. 3
y = x + x . B. 3 y = -x - 1 3x . C. y = . D. y = x +3 x -2 Lời giải Chọn A. Ta có 2
y¢ = 3x +1> 0 , "x Î  3
Þ y = x + x luôn đồng biến trên  . 5
Câu 81: Cho tích phân 2 = .e x I x
dx . Tìm mệnh đề đúng ò1 5 1 5 1 x 1 A. 2 5 2 = e | - e x I x dx . B. 2 x 5 2 = e | - e x I x dx . 1 ò ò 2 2 1 2 1 1 5 5 1 x 1 C. 2 x 5 2 = e | - e x I x dx . D. 5 = e | - ex I x dx 1 ò 1 ò 2 2 1 1 Lời giải Chọn A. ìïdu = dx 5 u ìï = x ï 1 x 1 Đặt 2 5 2 ï ï í Þí Þ I = x - x ò x 1 e | e xd . 2 2 x 1 ïdv ï = e dx v ï î ï = e 2 2 1 ïî 2
Câu 82: Có hai hộp bút chì màu, các bút chì khác nhau. Hộp thứ nhất có 5 bút chì màu đỏ và 7 bút chì
màu xanh. Hộp thứ hai có 8 bút chì màu đỏ và 4 bút chì màu xanh. Chọn ngẫu nhiên mỗi hộp
một cây bút chì. Xác suất để chọn một cây bút chì màu đỏ và một bút chì màu xanh là 17 7 19 5 A. . B. . C. . D. . 36 12 36 12 Lời giải Chọn C. Ta có n( ) 1 1 W = C .C =144. 12 12
Gọi A là biến cố chọn được một cây bút chì màu đỏ và một bút chì màu xanh. n A 76 19 Khi đó n( ) 1 1 1 1
A = C C +C C = 76 Þ P( ) ( ) A = = = . 5 4 7 8 n( ) W 144 36 1
Câu 83: Tìm giá trị thực của tham số m để hàm số 3 2 2
y = x -mx + m -4 x +3 đạt cực đại tại x = 3. ( ) 3 A. m =1. B. m = -1.
C. m =1;m = 5 . D. m = 5 . Lời giải Chọn A. Có 2 2
y¢ = x -2mx + m -4 ; y¢ = 2x-2m . ( ) ìï y¢ ï ( ) 3 = 0
Để hàm số đạt cực đại tại x = 3thì íïy¢ ï ( ) 3 < 0 î ìïém =1 2 3 ìï -2 . m 3+ ï ( 2 m - ) 2 4 = 0
ìïm -6m+5= 0 ï ï ïêï Û í Û í
Û íêm = 5 Û m =1. ë ï 2.3 ï -2m < 0 ï m î ï < 3 ï î ïïm ï < 3 î
Câu 84: Cho hàm số f (x) 2
= log x +1 . Tính f ¢(- ) 1 . 3 ( )
A. Không tồn tại f ¢(- ) 1 . B. f ¢(- ) 1 1 = . 2ln 3 C. f ¢(- ) 1 1 = . D. f ¢(- ) 1 = -1.x . ln 3 Lời giải Chọn C. 2 x 1 ¢ ¢ + 2x Ta có f ¢(x) 2 = log x +1 = = . ( 3( ) ( )
( 2x + )1ln3 ( 2x + )1ln3 -2 1 Suy ra f ¢(- ) 1 = =- . ( 2 (-1) + ) 1 ln 3 ln 3 x + m
Câu 85: Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y =
trên đoạn [1;2] bằng 8 ( m là tham x +1
số thực). Khẳng định nào sau đây là đúng?
A. 8 < m <10 .
B. 0 < m < 4 .
C. 4 < m <8. D. m >10 . Lời giải Chọn A. 1-m
Tập xác định của hàm số D =  \ {- } 1 . Ta có y¢ = . (x+ )2 1 ( ) 1+m + = f ( ) 2 m f 1 ; 2 = . 2 3
min f (x)= min f 1 ; f 2 max f (x)= a
m x f 1 ; f 2 1;2 { ( ) ( )} 1;2 { ( ) ( ) và . } [ ] [ ] +m +m m +
Nên theo đề ta có max f (x)+min f (x)= 2 1 5 7 8 Û + = 8 Û = 8 [1;2] [1;2] 3 2 6 41
Û 5m+7 = 48 Û m = . 5
Câu 86: Trong không gian cho hai điểm A(1;-1;2) và B(3;3;0). Mặt phẳng trung trực đoạn AB có phương trình là
A. x + y - z -2 = 0 .
B. x + y - z + 2 = 0 . C. x + 2y - z -3 = 0 . D. x + 2y - z +3 = 0 . Lời giải Chọn C.
Gọi I là trung điểm AB suy ra I (2;1; ) 1 . 
Mặt phẳng trung trực đoạn AB qua I (2;1; )
1 và nhận AB = (2;4;-2)= 2(1;2;- ) 1 có dạng
1 (.x-2)+ 2 (.y- ) 1 -1 (.z - )
1 = 0 Û x + 2y - z -3 = 0 .
Câu 87: Cho hàm số S.ABCD có đáy ABCD là hình vuông cạnh 2a , O là tâm đáy. Hình chiếu vuông
góc của S xuống (ABCD) là trung điểm H của OA , biết (SD (ABCD) = °. Gọi a là góc )  , 60
giữa mp(SCD) và mp(ABCD). Tìm mệnh đề đúng. A. tan a Î(0; ) 1 . B. tan a Î(3;4). C. tan a Î(2; ) 3 . D. tan a Î(1;2). Lời giải Chọn D.
Ta có (SD,(ABCD) = SDH = 60°, )   2a 10a 2 2
AB = 2a Þ AC = BD = 2a 2 Þ OD = 2a,OH =
Þ DH = OH +OD = . 2 2 30a Þ SH = H . D tan 60° = . 2 HI CH a
Kẻ HI ^ CD Þ (SCD),(ABCD) = 3 3 3 SIH , = = Þ HI = AD = . )  AD CA 4 4 2 SH 30 Do đó tan a = tan  SIH = = Î(1;2). HI 3
Câu 88: Cho hình chóp S.ABCD có đáy ABCD là hình thoi với AC = 2a, BD = 2a 2 . Gọi H là trọng
tâm tam giác ABD , biết rằng các mặt phẳng (SHC) và (SHD) cùng vuông góc với mặt phẳng
(ABCD). Khoảng cách từ C đến mặt phẳng (SHD) bằng 4a 19 a 38 4a 38 a 19 A. . B. . C. . D. . 38 19 19 38 Lời giải Chọn C.
Các mặt phẳng (SHC) và (SHD) cùng vuông góc với mặt phẳng (ABCD)nên SH ^(ABCD).
Kẻ CK ^ HD Þ SH ^ CK Þ CK ^(SHD)Þ d (C,(SHD) = CK . ) H . O OD 4a 38
Kẻ OI ^ HD Þ CK = 4OI = 4 = . 2 2 OH +OD 19
Câu 89: Cho hàm số y = f (x) đồng biến trên (0;+¥), y = f (x) liên tục, nhận giá trị dương trên ( 2
0;+¥) thỏa mãn f ( ) 4
3 = và é f '(x)ù =(x + )
1 . f (x). Tính f . 9 ë û ( ) 8 A. f ( ) 1 8 = . B. f ( ) 8 = 64 . C. f ( ) 8 = 49 . D. f ( ) 8 = 256 . 16 Lời giải Chọn C. 2 f ' x
Ta có é f '(x)ù =(x + ) 1 . f (x) ( ) Þ = x +1 . ë û f (x) Suy ra 8 f '(x) 8 1 dx = dx ò ò f x x +1 3 ( ) 3 . Þ f (x) 8 38 =
Û f ( )- f ( ) 19 2 8 3 = Û f ( ) 8 = 7 Û f ( ) 8 = 49 3 3 3 2 2 2 x 5 - xy xy+5 1 æ 0ö æ 3 y ö
Câu 90: Cho các số thực dương x,y thỏa mãn ç ÷ ç ÷ £ç ÷ ç ÷ . çè 9 ÷ø çè 10÷ø x
Hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của biểu thức bằng y 5 1 1 5 A. . B. . C. . D. 2 4 5 4 Lời giải Chọn B. 2 xy 5 + y 2 2 2 -( ) 2 x 5 - xy xy+5 y 2 x 5 - xy æ ö æ ö 2 10 3 1 æ 0ö 1 æ 0ö ç ÷ ç ÷ £ç ÷ ç ÷ Û ç ÷ çè ÷ø ç ÷ ç ÷ £ç ÷ è ÷ø çè ÷ ç ÷ 9 10 9 ø çè 9 ÷ø 2 ( - xy +5y ) 2 Û 2x -5xy £ 2 2 2
Û 4x -9xy +5y £ 0
Û (4x-5y)(x- y) £ 0 éìï4x-5y £0 ï ì ê ï x 5 í ï £ êïx ï - y ³ 0 ï î ï y 4 ê ï Û Û ê í ìï4x ê -5y ³ 0 ï x ï ï íê ï ³1 x êï - y £0 ï ï y î ï ë î x x 5 Vậy min =1;max = y y 4 x x 5 1 Nên max -min = -1= . y y 4 4
Câu 91: Cho hàm số trùng phương 4 2
y = ax +bx +c có đồ thị như hình vẽ.
( 2x- )4( 2x +2x)
Hỏi đồ thị hàm số y =
có tổng cộng bao nhiêu tiệm cận đứng?
é f (x) 2ù +2 f (x)-3 ë û A. 3 . B. 4 . C. 5 . D. 2 Lời giải Chọn B.
( 2x- )4( 2x +2x)
x(x-2)(x + 2)2 y = =
é f (x) 2ù +2 f (x)-3 é f (x) 2ù +2 f (x)-3 ë û ë û é f (x) =1
Xét é f (x) 2ù + 2 f (x)-3= 0 Û ê ë û ê f (x) =-3. ë éx = 0 ê
f (x) =1Û êx = x <-2 1 êêx= x >2 1 ë Có 3 tiệm cận đứng éx =-2(l)
f (x) = -3 Û êêx =2 ë Có 1 tiệm cận đứng
Vậy tổng cộng có 4 đường tiệm cận đứng.
Câu 92: Có bao nhiêu số nguyên dương m nhỏ hơn 20 thỏa mãn phương trình log +log m =10x mx m có ( )
đúng hai nghiệm thực phân biệt. A. 11. B. 13 . C. 12. D. 10 Lời giải Chọn B. log(mx+log m m ) x 10
=10 Û mx + mlog m =10 x x x 10
Û10 (mx + mlog m) =10 .10 x Û ( . m 10x ) x x 10 .log( .
m 10 ) =10 .10 x (1) 10x = a;log( .
m 10x ) = b . a 10a = .
b 10b Þ a = b Þ10x = log( .
m 10x ) = log m + x
Þ log m =10x - x
g(x) =10x - x '
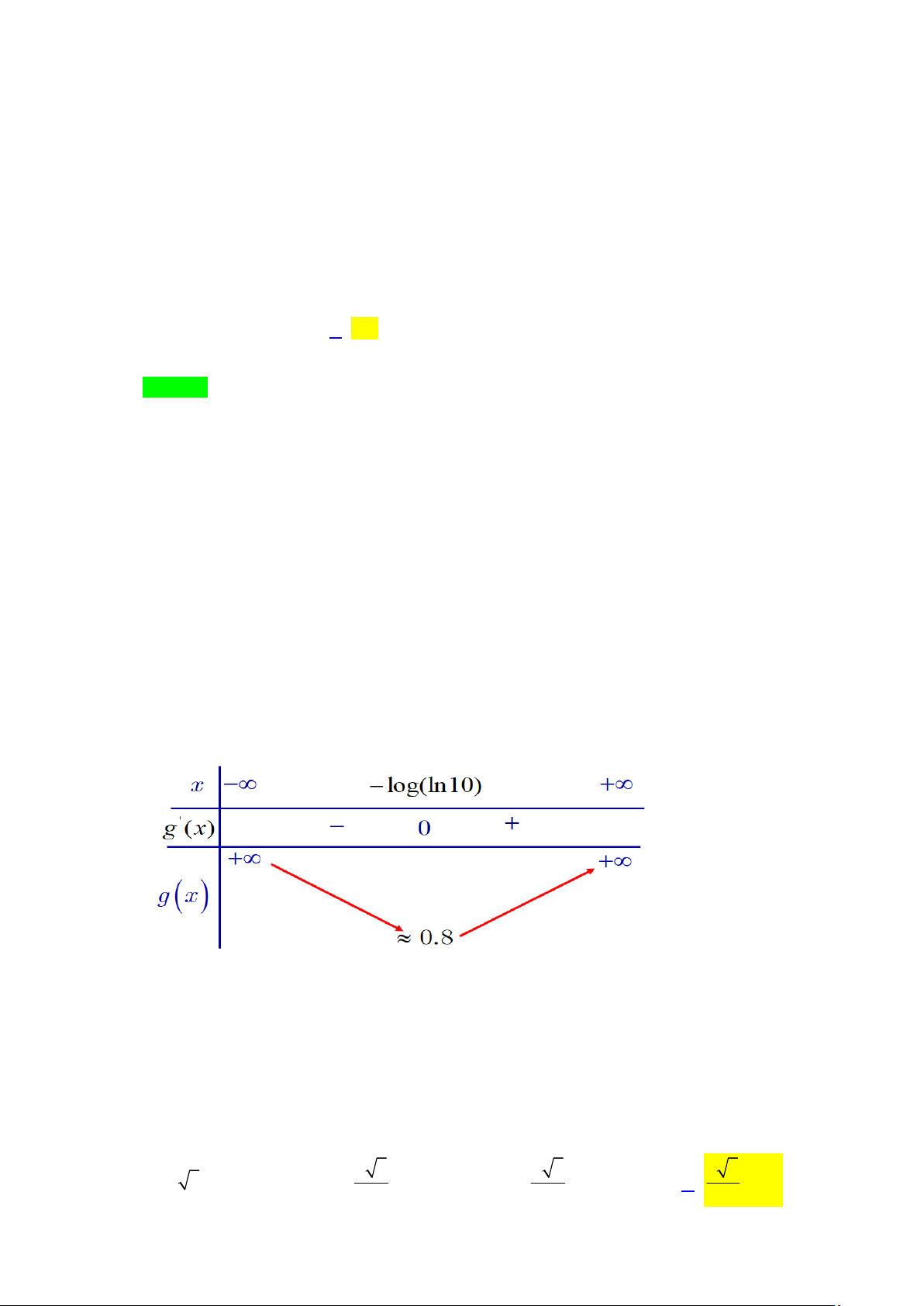
g (x) =10x.ln10-1 '
g (x) = 0 Û x = -log(ln10) 0.8
Þ log m > 0.8 Þ m >10 = 6.72
Để phương trình có hai nghiệm thì ÞmÎ{7;8;....1 }9 Vậy có 13 số.
Câu 93: Cho tứ diện ABCD có 2 2 S = 4 cm , S
= 6 cm , AB = 3 cm . Góc giữa hai mặt phẳng A D BC A D BD
(ABC) và (ABD) bằng 60°. Thể tích của tứ diện đã cho bằng 2 3 4 3 8 3 A. 3 2 3 cm . B. 3 cm . C. 3 cm . D. 3 cm . 3 3 3 Lời giải Chọn D. C A D H K B
Gọi H là chân đường cao của tứ diện ABCD hạ từ đỉnh C và trong (ABC), kẻ CK ^ AB với
K Î AB . Khi đó, ( ( ABC) (ABD)
 =CKH = và h=CH . )  0 , 60 2S 8 4 3 Do đó, A D BC CK =
= Þ CH = CK s.in CKH = AB 3 3 1 8 3 Vậy 3 V = S .CH = cm . ABCD 3 A D BD 3
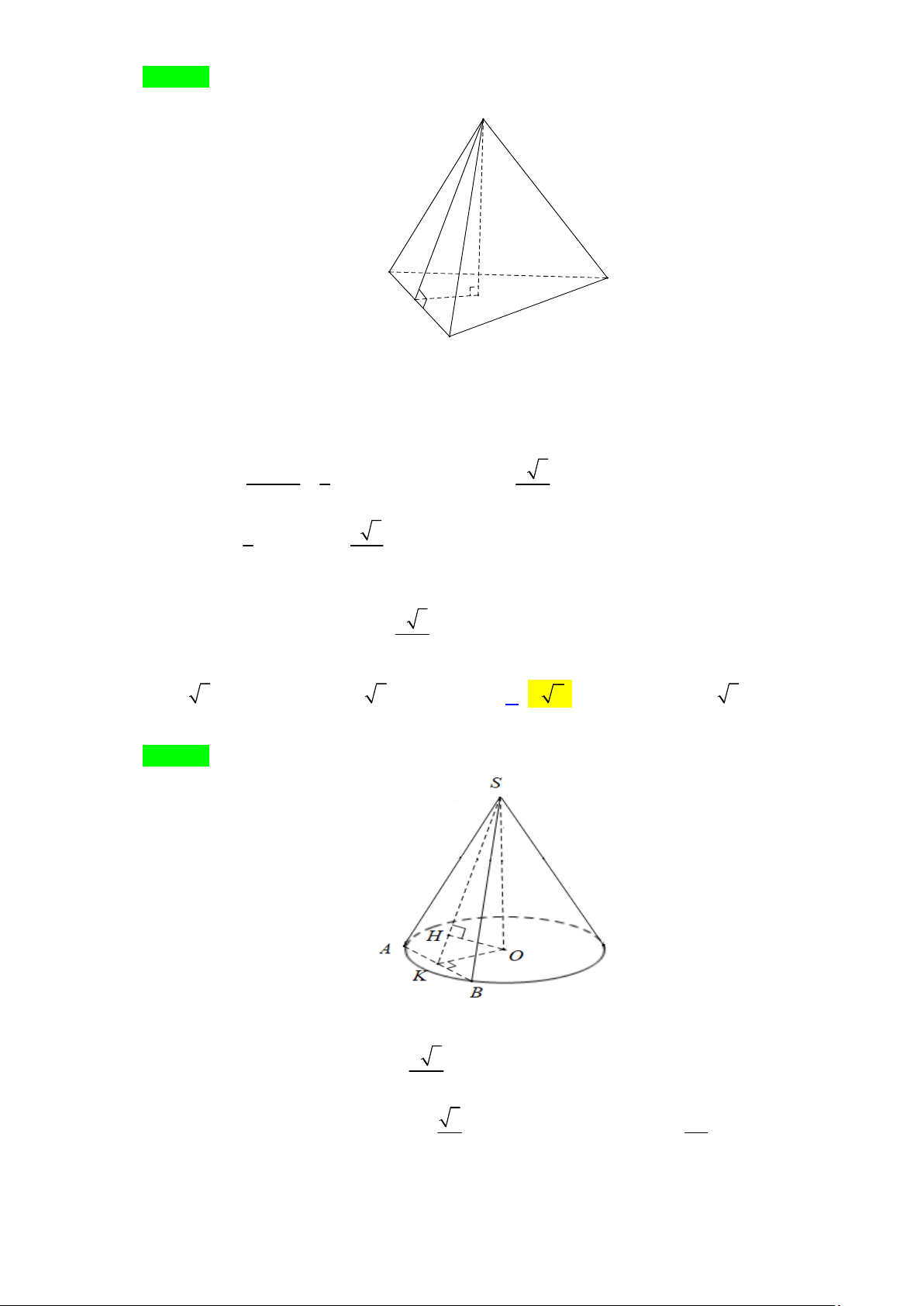
Câu 94: Cho hình nón đỉnh S , đường cao SO , A và B là hai điểm thuộc đường tròn đáy sao cho khoảng a 3
cách từ O đến mặt (SAB) bằng và  0 SAO  0
= 30 , SAB = 60 . Độ dài đường sinh của hình 3 nón theo a bằng A. 2a 3 . B. a 5 . C. a 2 . D. a 3 . Lời giải Chọn C.
Gọi K là trung điểm của AB Þ(SOK)^(SAB) nên trong (SOK), kẻ OH ^ SK (với a
H Î SK ) thì d (O (SAB) = OH = . ) 3 ; 3 3 SA
Ta có, tam giác SAB đều nên SK = SA
và lại có SO = SA s.in  SAO = . 2 2
Xét tam giác SOK vuông tại O có 1 1 1 6 1 = + Þ =
Þ SA = a 2 Þ l = a 2 . 2 2 2 2 2 OH SO OK SA OH
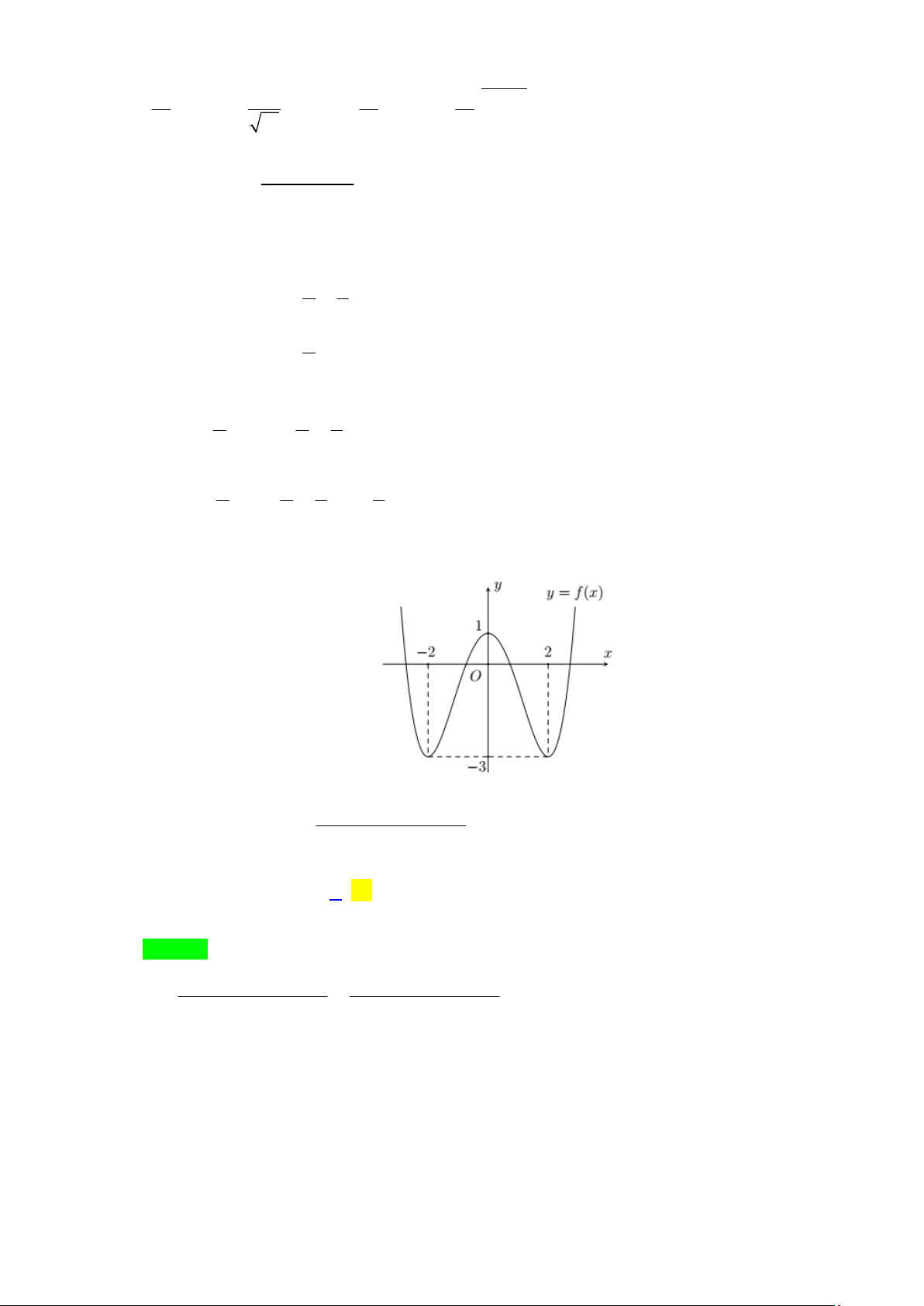
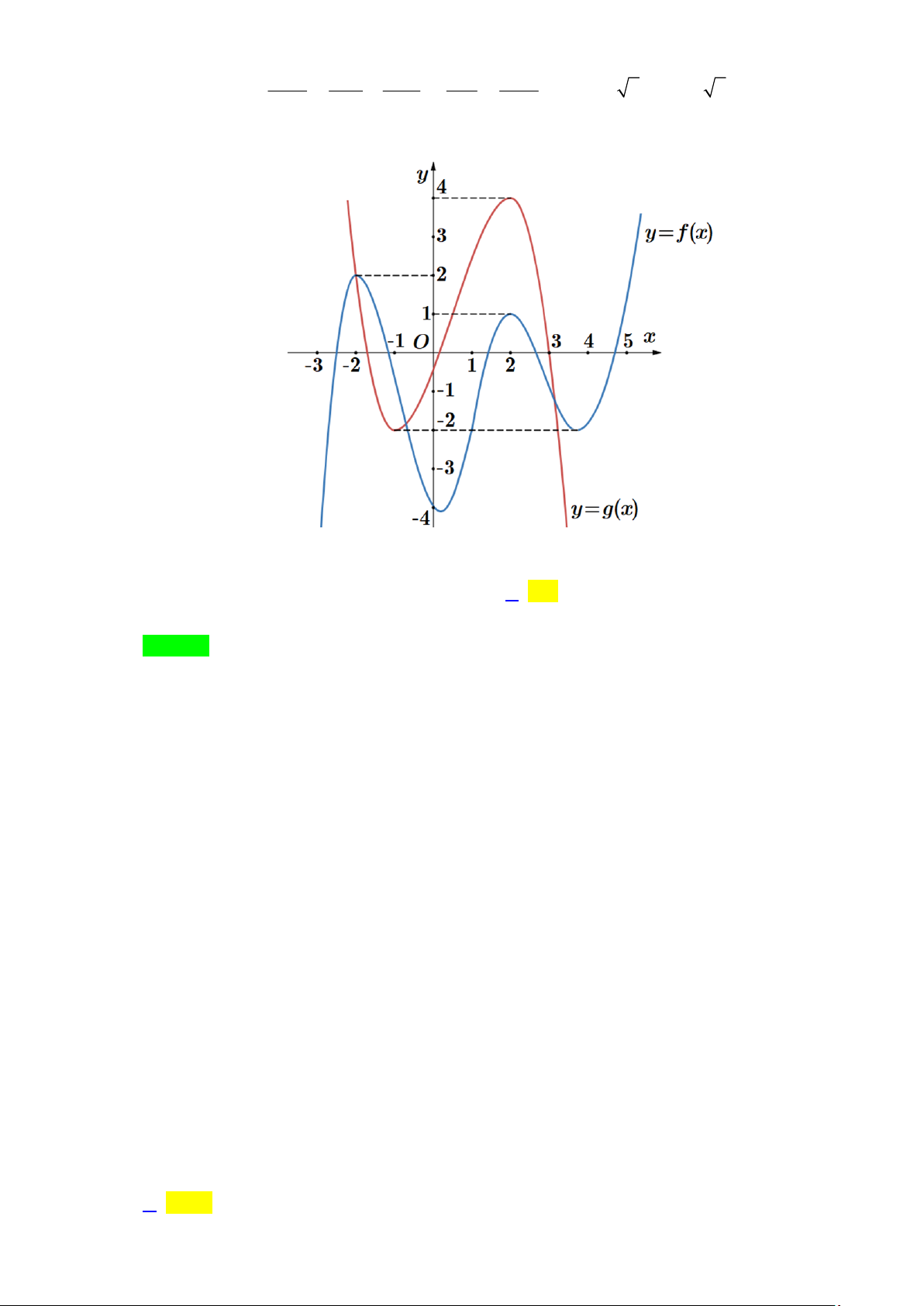
Câu 95: Cho hàm số y = f (x), y = g(x) có đồ thị như hình sau:
Khi đó tổng số nghiệm của hai phương trình f (g(x) = và g( f (x) = là ) 0 ) 0 A. 26 . B. 25 . C. 22 . D. 21. Lời giải Chọn C.
éx = a -3< a <-2 1 ( 1 )
êêx=a -2<a <-1
éx = a -2< a <-1 6 ( 6 ) 2 ( 2 ) ê ê Ta có f (x) 0 ê = Û x = a 1< a < 2
g (x)= 0 Û êx = a 0 < a <1 7 ( 7 ) 3 ê ( 3 ) và . ê ê x ê = a 2 < a < 3 ê x ê = 3 4 ( 4 ) ê ë x ê = a 4 < a < 5 5 ( 5 ) ë
ég(x)= a -3<a <-2 1 ( 1 )
êêg(x)=a -2<a <-1 2 ( 2 ) ê
Khi đó f (g(x) 0 ê = Û g ê (x)= a 1< a < 2 11 3 ( 3
) , phương trình này có nghiệm.
êgê(x)=a 2<a <3 4 ( 4 )
êgê(x)=a 4<a <5 5 ( 5 ) ë
é f (x)= a6 ê
g ( f (x) = 0 Û ê f (x)= a , phương trình này có 11 nghiệm. ) 7 êê fê (x)=3 ë
Vậy tổng số nghiệm của hai phương trình f (g(x) = và g( f (x) = là 22 . ) 0 ) 0
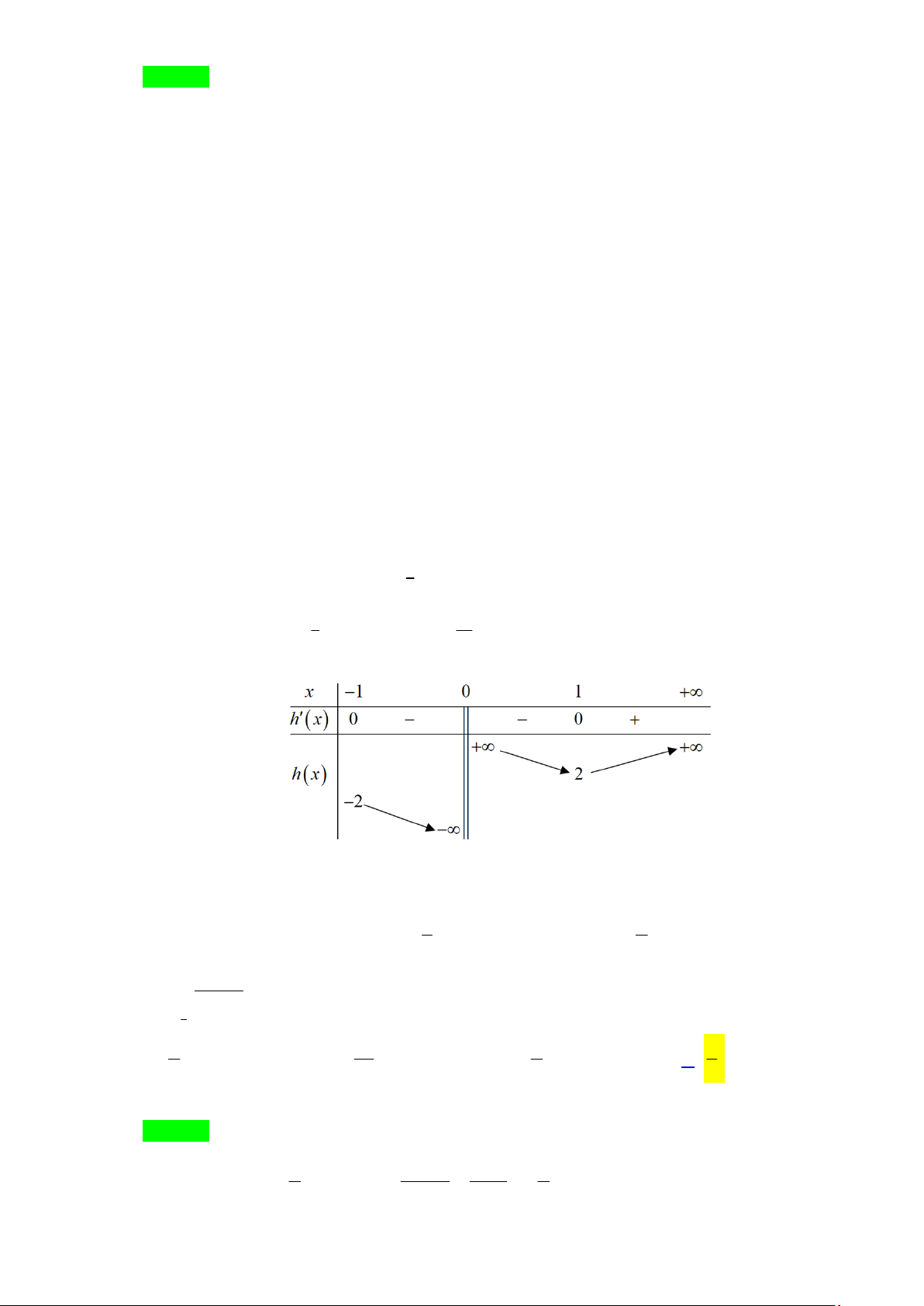
Câu 96: Cho hàm số y = f (x) có f ¢(x)= x(x + ) 2
1 x -2mx +1 , "x Î  với m là tham số thực. Hỏi ( )
có tất cả bao nhiêu số nguyên m không vượt quá 2023 sao cho hàm số g (x) 2 = f x -1 có 7 ( ) điểm cực trị? A. 2021. B. 2022 . C. 2020 . D. 2023. Lời giải Chọn A.
g (x)= f (x - )Þ g (x)= xf (x - )= x(x - )x (éx ê - )2 2 2 2 2 2 - m( 2 1 2 1 2 1 1 2 x - ) 1 +1ù ¢ ¢ ú ë û éx = 0 ê é 2 êx -1= 0 êx = 0 ê ê
Ta có g¢(x)= 0 Û ê Û ê 2 x = ±1 . x ê = 0 ê 2 ê (êê ( 2x ê - ë
)1 -2m( 2x- )1+1=0 x - êë )2 2 1 -2m( 2 x - ) 1 +1= 0 2
Để hàm số g (x) 2
= f x -1 có 7 điểm cực trị thì phương trình 2 2
x -1 -2m x -1 +1= 0 ( ) ( ) ( )
phải có 4 đơn nghiệm phân biệt khác x = 0 , x = ±1. 2
Xét phương trình ( 2x - ) - m( 2 1 2 x - ) 1 +1= 0 Đặt 2
t = x -1, khi đó ta được phương trình 2t -2mt +1= 0 với t ³-1.
Với t > -1 ta có hai nghiệm x ,
Với t = -1 ta có nghiệm x = 0 ,
Với t <-1 phương trình vô nghiệm. 2 Nên để 2 2
x -1 -2m x -1 +1= 0 có 4 đơn nghiệm phân biệt khi và chỉ khi phương trình ( ) ( ) 2
t -2mt +1= 0 có hai nghiệm phân biệt 0 ¹ t >-1. 1 Ta có 2
t -2mt +1= 0 Û 2m = t + . t 1 Xét hàm số ( ) 1
h t = t + , ta có h¢(t)=1- = 0 Û t = ±1. t 2 t Bảng biến thiên:
Từ bảng biến thiên, phương trình 2
t -2mt +1= 0 có hai nghiệm phân biệt 0 ¹ t >-1 khi m > 2 . é ù æ1ö
Câu 97: Cho hàm số y = 1
f (x) liên tục trên ê ;3ú thỏa mãn f (x) 3 + x× f ç ÷
ç ÷= x - x . Giá trị tích phân ê3 ë úû çèx÷ø 3 f (x) I = dx bằng 2 ò x +x 1 3 3 16 2 8 A. . B. . C. . D. . 4 9 3 9 Lời giải Chọn D. æ1ö f x 1 æ1ö Ta có f (x) 3 ( ) + x× f ç ÷ ç ÷= x - x Û + × f ç ÷ çè ÷ ç ÷= x-1. 2 xø x + x x +1 çè x÷ø 3 3 3 f (x) 1 æ1ö Suy ra dx + × f ç ÷ ò ò ç ÷dx = x -1 d . x * 2 ò ( ) ( ) x + x x +1 çè x÷ø 1 1 1 3 3 3 1 1 t
Đặt t = suy ra dx = - 1 1 dt và x = Û = . x 2 t t x +1 t +1 ìï 1 ïx = Þ t = 3 ï Đổi cận ï 3 ï . Khi đó íï 1 ïx ï = 3Þ t = ïïî 3 1 3 3 3 1 æ1ö t f t × f ç ÷ ò ç ÷dx = - × f ò (t) 1 ( ) × dt = dt = I . 2 2 ò x +1 çè x÷ø t +1 t t +t 1 3 1 3 3 Do đó ( ) 16 8 * Û 2I = Û I = . 9 9
Câu 98: Cho hàm số f (x) 4 3 2
= 2x + ax +bx +cx + d (a, ,bc,d Î ) có ba điểm cực trị là 1 - , 1 và 3.
Gọi y = g(x) là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số y = f (x).
Diện tích hình phẳng giới hạn bởi hai đường y = f (x) và y = g(x) bằng 182 265 128 256 A. . B. . C. . D. . 15 15 15 15 Lời giải Chọn D. Hàm số f (x) 4 3 2
= 2x + ax +bx +cx + d (a, ,bc,d Î ) có ba điểm cực trị là 1 - , 1 và 3 nên ìï f ¢(- )1= 0 3 ì ï
ï a-2b+c = 8 ìïa =-8 ï ï ï ï f í ¢( ) 1 = 0 Û 3 ï a í +2b+c =-8 Û b ïí =-4 ï ï ï ï ï ï ï f ¢ ï ( ) 3 = 0
ï27a +6b+c =-216 c ï = 24. î ïî ïî Suy ra f (x) 4 3 2
= 2x -8x -4x + 24x + d . ( ) 1 Ta có f ¢(x) 3 2
= 8x -24x -8x + 24 .
Khi đó f (x)= g(x). f ¢(x)+ r(x)
ìï f (x = r x 1 ) ( 1) ïï Ta có ï f í (x = r x 2
r(x) = g(x) = -8x +16x +6+ d 2 ) ( 2). Suy ra .
ïïïfï (x =r x 3 ) ( 3) î
Đồ thị y = g(x) đi qua ba điểm cực trị của đồ thị hàm số y = f (x) nên phương trình éx =-1 ê
f (x)= g(x) Û êx =1 (2) êêx=3. ë Từ ( )
1 và (2) suy ra f (x)- g(x)= (x + )(x- )2 2 1 1 (x- ) 3 .
Diện tích hình phẳng giới hạn bởi hai đường y = f (x) và y = g(x) bằng 3 3 f
ò (x)-g(x) 256 dx = 2
ò (x+ )1(x- )21(x- )3dx= . 15 -1 -1
Câu 99: Trong các nghiệm ( ;x y) thỏa mãn bất phương trình log 2x + y ³1 2 2 x +2 y (
) . Giá trị lớn nhất của
biểu thức T = 2x + y bằng 9 9 9 A. 9 . B. . C. . D. . 4 2 8 Lời giải Chọn C. 2 2
éìïx +2y >1 ïê 1 íê 2 2 ( ) ï2x
êï + y ³ x +2y Ta có: log 2x y 1 î + ³ Û 2 2 ê x +2 y ( ) 2 2 0
ìêï < x +2y <1 ïê 2 í 2 2 ( ) êï2x
ïê + y £ x +2y îë 2 æ 1 ö 9
TH1: x + 2y £ 2x + y Û (x- )2 2 2 1 +ç 2y ÷ ç - ÷ £ . Khi đó: çè 2 2 ÷ø 8 2 Cauchy-schwarz æ ö é æ ö æ ö ù
2x + y = 2(x- ) 1 1 9 1 1 + ç 2y ÷ ç - ÷+ £ ç2 ç ÷ ç + ÷÷ (êx- è ÷ø çè ÷ê )2 1 9 2 1 +ç 2y ÷ ú ç - ÷ + 2 2 2 4 2ø çè 2 2 ÷ ú ø 4 êë úû 9 £ 2 TH2: 2 2
0 <T = 2x + y £ x + 2y <1 9 æ ö
Vậy GTLN của T = khi (x y) 1 ; =ç2; ÷ ç ÷. 2 çè 2÷ø
Câu 100: Tìm m để giá trị lớn nhất của hàm số 3
y = x -3x + 2m-1 trên đoạn [0;2] là nhỏ nhất. Giá trị
của m thuộc khoảng nào? æ2 ö æ ö A. (0; ) 1 . B. ç ; 2÷ ç ÷. C. - 3 1;0 . D. ç- ; ç -1÷÷. çè3 ÷ø [ ] çè 2 ÷ø Lời giải Chọn A. éx =1Î 0;2 Đặt f (x) 3
= x - x + m- Þ f ¢(x) 2 3 2 1
= 3x -3 . Nên: f ¢(x) ( ) = 0 ê Û êxê=-1Ï(0;2) ë Có: f ( )
1 = 2m-3< f (0)= 2m-1< f (2)= 2m+1
Þ max f (x) = max{ 2m+1 , 2m-3} [0;2]
TH1: max f (x) = 2m+1 thì: [0;2]
m + ³ m- Û ( m+ )2 ³( m- )2 1 2 1 2 3 2 1 2
3 Û16m ³8 Û m ³ . 2 1 1
Với m ³ Þ 2m +1 ³ 2 Þ GLTN của hàm số trên đoạn [0;2] đạt GTNN là: 2 khi m = . 2 2
TH2: max f (x) = 2m-3 thì: [0;2]
m- ³ m + Û ( m- )2 ³( m+ )2 1 2 3 2 1 2 3 2
1 Û16m £8 Û m £ . 2 1 1
Với m £ Þ 2m-3 ³ 2 ÞGTLN của hàm số trên đoạn [0;2] đạt GTNN là: 2 khi m = . 2 2 1
Vậy giá trị lớn nhất của hàm số trên [0;2] đạt GTNN là: 2 khi m = . 2  HẾT