Đề Thi Olympic Toán 7 Thị Xã Hoàng Mai 2025-2026 Có Đáp Án

UBND THỊ XÃ HOÀNG MAI
ĐỀ THI OLYMPIC NĂM HỌC 2025-2026
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO ĐỀ CHÍNH THỨC Môn: Toán 7
(Đề thi gồm 01 trang)
Thời gian làm bài: 150 phút,
không kể thời gian giao đề
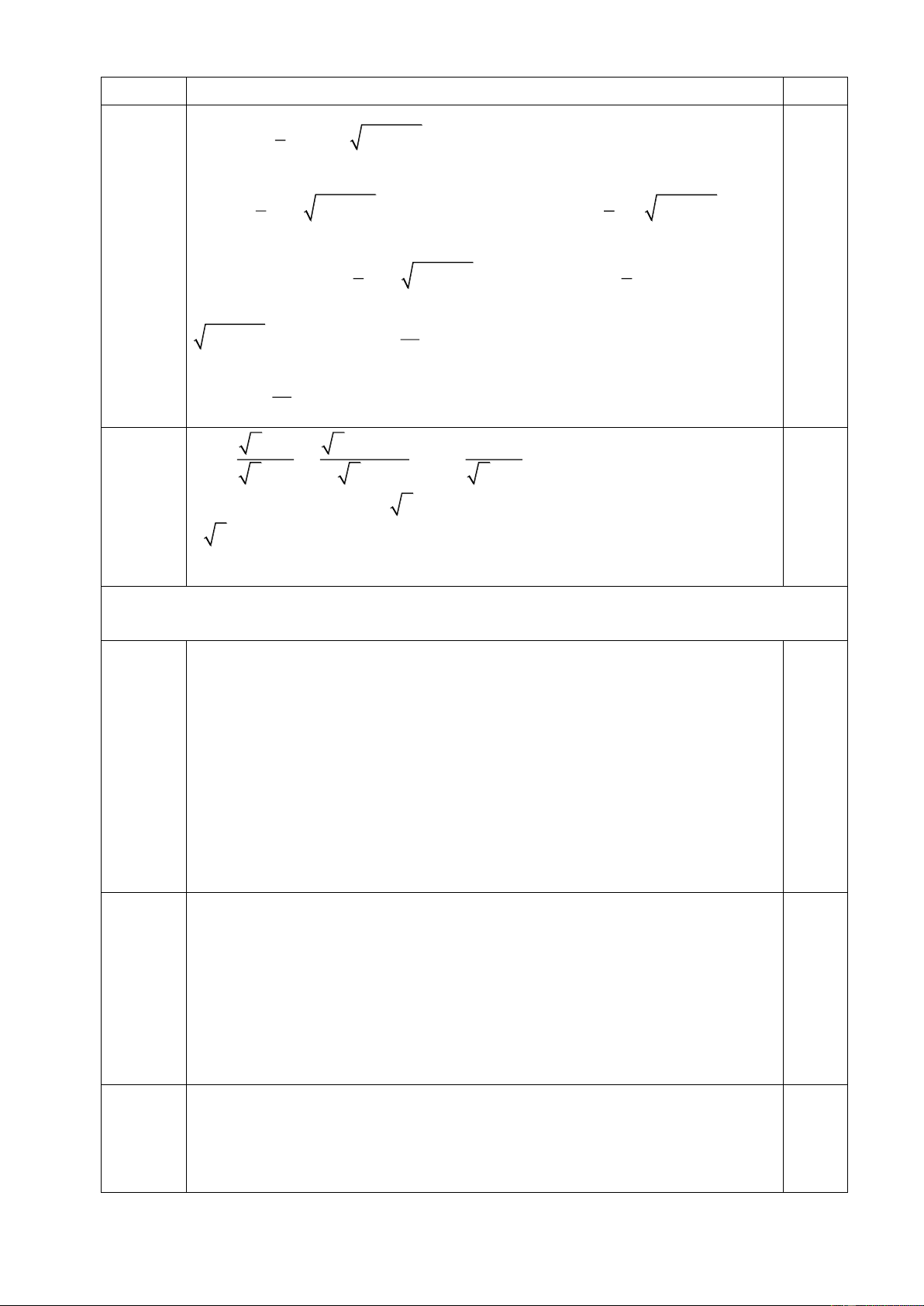
Câu 1. (4,5 điểm) Tính giá trị các biểu thức sau. 12 12 10 10 2 .13 + 2 .65 3 .11 + 3 .5 a) A = + 10 9 2 .104 3 .16 2 æ ö æ ö ç 1 1 1 ÷ ç 64 4 2 æ ö = ç ÷ ç ç ÷ 4 ÷ b) ÷ B 1 - + - ç ÷: ç - + ç ÷ - ÷ ç ÷ ç ç ÷ ÷ 2 ç 49 ÷ è ø ç 2 7 ç ç è7÷ ø 343 49 (7 7) ÷ ÷ è ø 1 3 1 5 3 5 3 c) C = + + + + + + 3 7 2.7 2.13 13.4 4.21 21.6
Câu 2. (3,5 điểm) x + x + x + x + a) Tìm x biết: 4 3 2 1 + = + . 2020 2021 2022 2023 2 æ 1ö b) Tìm x, y biết: ç ÷ 2 ç x - ÷ + 3y + 12 £ 0 ç ÷ . çè 6÷ ø x + c) Tìm số nguyên x để 1 P = là một số nguyên. x - 3
Câu 3. (4,0 điểm)
a) Ông Ba gửi ngân hàng 100 triệu, lãi suất 8% trên 1 năm. Hỏi sau 36 tháng số
tiền cả gốc và lãi ông Ba thu được là bao nhiêu ? (Biết nếu tiền lãi không rút ra thì
tiền lãi đó sẽ nhập vạ̀o vốn để tính lãi cho các kì hạn tiếp theo).
b) Biết x + 1 và 2x + 1 đồng thời là các số chính phương. Chứng minh x 12 .
c) Cho hai đa thức: f (x) = (x - 1)(x + 3) và 3 2 (
g x ) = x - ax + b - 3 . Xác định hệ
số a, b của đa thức (
g x ) biết nghiệm của đa thức f (x ) cũng là nghiệm của đa thức ( g x ) .
Câu 4. (6,0 điểm)
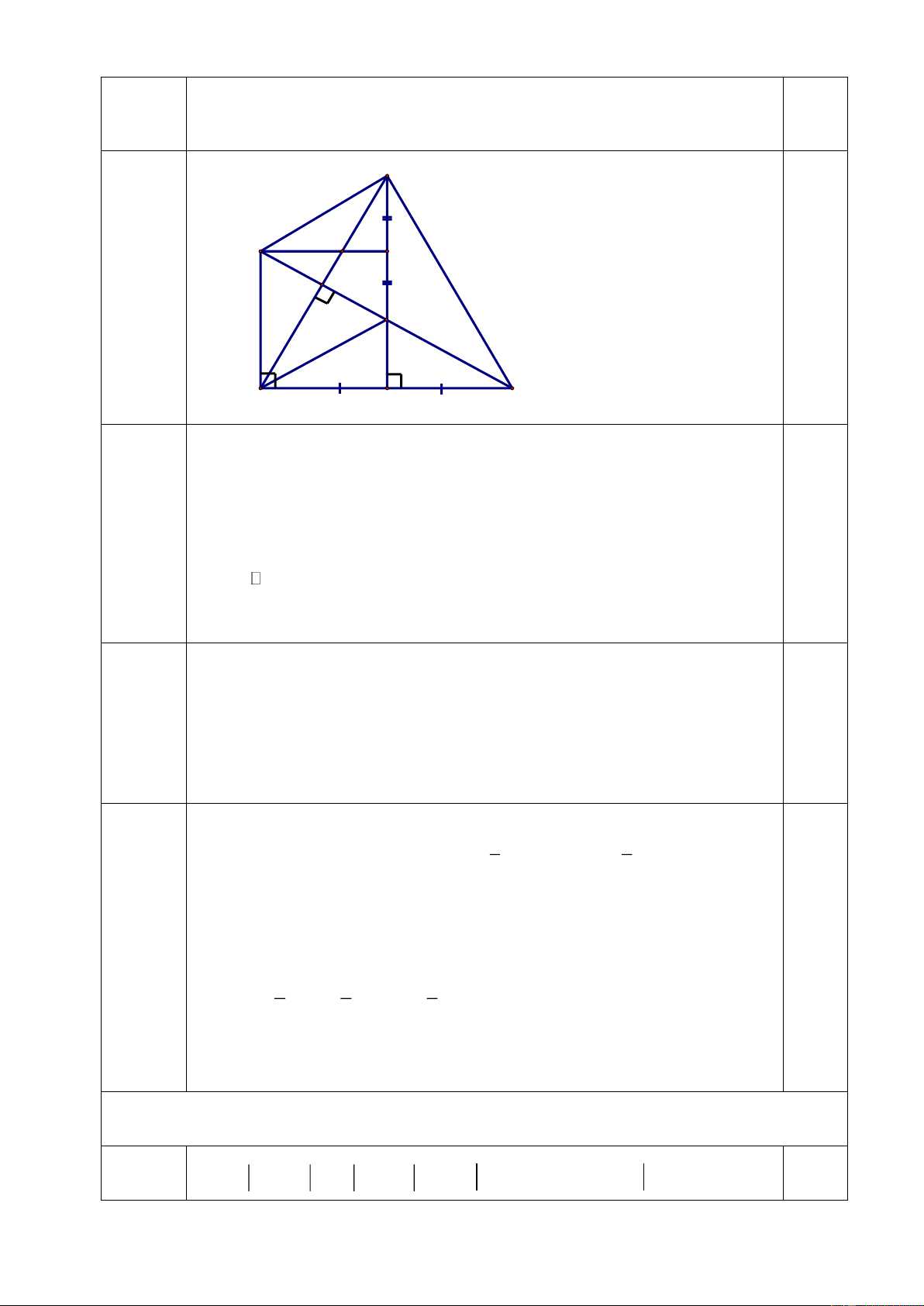
Cho tam giác A BC vuông tại B có 0
C = 60 , kẻ đường cao BK (K Î A C ). Vẽ
đường thẳng d là trung trực của A B cắt cạnh A B tại N , cắt cạnh A C tại M , cắt tia
B K của tam giác A BC tại E .
a) Chứng minh DANM = DBNM và M là trung điểm của A C .
b) Chứng minh điểm E cách đều MB và BC . c) Vẽ điểm 1
D thuộc đoạn B E sao cho ED =
EB , gọi I là trung điểm của ME 3
. Chứng minh ba điểm C , D , I thẳng hàng.
Câu 5. (2,0 điểm)
Tìm giá trị nhỏ nhất của biểu thức:M = 7x – 5y + 2z – 3x + xy + yz + zx - 2000 . --- Hết ---
(Thí sinh không dùng tài liệu, cán bộ coi thi không giải thích gì thêm) thTrang 1
Họ và tên thí sinh: ………………………………………………… Số báo danh: ………… UBND THỊ XÃ HOÀNG MAI
HƯỚNG DẪN CHẤM THI OLYMPIC
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO Năm học 2025-2026
(Hướng dẫn chấm gồm 04 trang) Môn: Toán 7 Câu Nội dung Điểm Câu 1 (4,5 điểm) 12 10 2 .78 3 .16 A = + 1.0 a 10 9 2 .104 3 .16 = 3 + 3 = 6 0,5 1 1 1 1 1 1 1 - + - 2 1 49 - + - 2 3 49 (7 7) 0.5 7 7 7 B = = 2 æ ö 8 4 4 4 64 4 2 ç ÷ 4 - + - - + ç ÷ - 2 3 ç ÷ ç ÷ 2 7 7 7 2 7 è7ø 343 b 1 1 1 1 - + - 2 3 1 7 7 7 = = æ 1.0 1 1 1 ö 4 ç ÷ 4. 1 ç - + - ÷ ç 2 3 ÷ çè 7 7 7 ÷ ø 1 3 1 5 3 5 3 P = + + + + + + 3 7 2.7 2.13 13.4 4.21 21.6 æ 1 3 1 5 3 5 3 ö ç ÷ 0.5 = 4ç + + + + + + ÷ ç ÷ çè3.4 4.7 7.8 8.13 13.16 16.21 21.24÷ ø 4 æ 3 7 4 8 7 13 8 16 13 21 16 24 21ö - - - - - - - ç ÷ c = 4ç + + + + + + ÷ ç ÷ çè 0.5 3.4 4.7 7.8 8.13 13.16 16.21 21.24 ÷ ø 1 æ 1 1 1 1 1 1 1 1 1 1 1 1 1 ö ç ÷ = 4ç - + - + - + - + - + - + - ÷ ç ÷ çè3 4 4 7 7 8 8 13 13 16 16 21 21 24÷ ø 1 æ 1 ö ç ÷ 21 7 = 4ç - ÷= 4. = 0.5 ç ÷ çè3 24÷ø 3.24 6 Câu 2 (3,5 điểm) x + 4 x + 3 x + 2 x + 1 + = + 2020 2021 2022 2023 x + 4 x + 3 x + 2 x + 1 Û + 1 + + 1 = + 1 + + 1 0.5 2020 2021 2022 2023 x + 2024 x + 2024 x + 2024 x + 2024 Û + = + = 0 a 2020 2021 2022 2023 æ 1 1 1 1 ö ç ÷ 0.5 Û (x + 2024)ç + - - ÷= 0 ç ÷ 202 çè 0 2021 2022 2023÷ ø æ ö Û 1 1 1 1 ç ÷ x + 2024 = 0 vì ç + - - ¹ 0÷ ç ÷ 2 çè 020 2021 2022 2023 ÷ ø thTrang 2 Û x = - 2024 0.5 2 æ 1ö ç ÷ Vì 2 ç x - ÷ ³ 0 ç ÷
; 3y + 12 ³ 0 ; do đó: çè 6÷ ø 2 æ 1ö ç ÷ æ ö ç ÷ 0.5 2 ç x - ÷ + 3y + 12 ³ 0 ç ÷ . Theo đề bài thì 1 2 ç x - ÷+ 3y + 12 £ 0 . ç ç ÷ è 6÷ ø çè 6÷ ø 2 b æ ö Từ đó suy ra: 1 ç ÷ 2 ç x - ÷ + 3y + 12 = 0 ç ÷ Khi đó 1 2x - = 0 và çè 6÷ ø 6 1
3y + 12 = 0 suy ra x = và 0.5 y = - 4 12 Vậy 1 x = và y = - 4 12 x + 1 x - 3 + 4 4 P = = = 1 + 0.5 x - 3 x - 3 x - 3 c
Để P là số nguyên thì ( x - 3 ) là ước của 4, tức là 0.5
( x - 3) Î {± 1; ± 2; ± } 4
Vậy giá trị x cần tìm là 1 ; 4 ; 16 ;25 ; 49 Câu 3 (4,0 điểm) 36 tháng = 3 năm
Năm đầu, ông lãi được số tiền là
100 000 000⋅8%=8 000 000 (đồng) 0.25
Năm thứ 2, ông lãi được số tiền là a
(100 000 000+8 000 000).8%=8 640 000 (đồng) 0.25
Năm thứ 3, ông lãi được số tiền là
(100 000 000+8 000 000+8 640 000).8%=9 331 200 (đồng) 0.25
Sau 36 tháng, ông Ba rút ra cả vốn cả lãi là
100 000 000 + 8 000 000 + 8 640 000 + 9 331 200=125 971 200 (đồng) 0.25
Vì 2x + 1 là số chính phương lẻ nên 2x + 1 chia cho 8 dư 1, suy ra 2x
chia hết cho 8, nên x chia hết cho 4 (1) 0.5
Ta có (x + 1) + (2x + 1) = 3x + 2 chia cho 3 dư 2 b 0.5
Mà số chính phương chia cho 3 dư 0 hoặc 1 nên x + 1 và 2x + 1 chia
cho 3 cùng dư 1, nên x chia hết cho 3 (2) 0.5
Từ (1), (2), (3;4) = 1 nên x chia hết cho 3.4 = 12 0.5
HS biết tìm nghiệm của f (x) = (x - 1)(x + 3) = 0 Û x = 1, x = - 3 0.5 c
Nghiệm của f (x) cũng là nghiệm của 3 2 (
g x ) = x - ax + b - 3 nên: Thay x = 1 vào (
g x ) ta có: 1 - a + b - 3 = 0 thTrang 3 Thay x = - 3 vào (
g x ) ta có: - 27 - 9a - 3b - 3 = 0
Từ đó HS biến đổi và tính được: a = - 3, b = - 1 0.5 Câu 4 E (6,0 điểm) C D I K M B N A ìï MA = MB ï c/m ï
D A NM = D BNM (c-g-c) Þ í ï 1.0 MA B = MB A ïïî
c/m CMB = MA B + MBA (góc ngoài tại đỉnh M của DA BM ) a Þ 0.5
CMB = MA B + MBA = 2MA B = MCB .
Do đó BMC cân tại M nên MB = MC .
Mặt khác MB = MA (do DA NM = DBNM ) 0.5
Suy ra MA = MC hay M là trung điểm của A C . 0.5 c/m: Tam giác °
B MC cân tại M , lại có BCM = 60 nên là tam giác đều. 0.5
D BCM là tam giác đều nên đường cao BK đồng thời là đường trung b
tuyến, đường phân giác. 1.0
Do E nằm trên đường phân giác BK của CB M nên E cách đều MB , B C . 0.5
c/m DEA B cân tại E . 1 ° 1 và A BE A BM MBK MA B MBC 30 60° 60° = + = + = + = nên 2 2 D EA B đều 0.5
Do đó chân đường vuông góc K của A xuống BE cũng là trung điểm
của cạnh BE hay BK = KE . c 0.5
Trong tam giác CME , điểm D thuộc trung tuyến EK 1 1 2 và ED = EB = 2 × EK = EK . 3 3 3
Do đó D là trọng tâm của tam giác ECM .
Do CI là đường trung tuyến của tam giác ECM nên CI đi qua D . 0.5
Do đó C , D , I thẳng hàng. Câu 5 (2,0 điểm)
Ta có 7x – 5y ³ 0; 2z – 3x ³ 0 và xy + yz + zx - 2000 ³ 0 thTrang 4
Nên M = 7x – 5y + 2z – 3x + xy + yz + zx - 2000 ³ 0 0.5
Mà M = 0 khi và chỉ khi
7x – 5y + 2z – 3x + xy + yz + zx - 2000 = 0 ì
ïïï 7 – 5 = 0 Û 7 = 5 x y x y x y Û = ï ï 5 7 ïï Û í 2 – 3 = 0 Û 2 = 3 z x z x z x Û = ï 3 2 ï
ïï xy + yz + zx - 2000 = 0 Û xy + yz + zx = 2000 ï 0.5 ï îïï x
é = 20, y = 28, z = 30 Từ đó tìm được ê x
ê = - 20, y = - 28, z = - 30 0.5 êë
Vậy GTNN của M = 0 Û (x,y,z)= (20;28;30)
hoặc (x,y, z ) = (- 20;- 28;- 30) 0.5
Lưu ý: HS làm cách khác đúng vẫn cho điểm tối đa cho câu đó. ---Hết--- thTrang 5