






Preview text:
TR◊ÕNG THPT CHUYÊN QUANG TRUNG
ó THI TH€ THPT 2019 - 2020 T TOÁN
MÔN: TOÁN, LŒP 12, LÜN 4 ( ∑ thi có 6 trang)
ThÌi gian làm bài: 90 phút Mã ∑ thi 111
Câu 1. Nghiªm cıa ph˜Ïng trình log5(x 2) = 2 là A 27. B 9. C 34. D 12.
Câu 2. Trong không gian vÓi hª to§ Î Oxyz, ph˜Ïng trình chính t≠c cıa ˜Ìng thØng i qua i∫m M(2; 1; 3)
và có véctÏ chø ph˜Ïng ~u(1; 2; 4) là x y 1 z x 2 y z 3 A + 2 + 3 + 1 1 = 2 = 4 · B 1 = 2 = 4 · x 1 y 2 z x y z 4 C + 4 + 1 + 2 2 = 1 = 3 · D 2 = 1 = 3 ·
Câu 3. Trong không gian vÓi hª tÂa Î Oxyz, ph˜Ïng trình cıa ˜Ìng thØng d i qua i∫m A(1; 2; 5) và
vuông góc vÓi m∞t phØng (P) : 2x + 3y 4z + 5 = 0 là 8 8 8 8 >> > > > >x = 1 + 2t >x = 1 + 2t >x = 2 + t x = 2 + t > >> >> >> A d : < < < < >y = 2 + 3t B d : y = 2 + 3t C d : y = 3 + 2t D d : y = 3 + 2t > > > > > > > > > > :z > > = 5 4t. >:z = 5 + 4t. :z = 4 5t. >:z = 4 + 5t. 1
Câu 4. MÎt hình nón có diªn tích xung quanh b¨ng 2⇡ cm2 và bán kính áy r = cm. Tìm Î dài ˜Ìng sinh 2 cıa hình nón. A 1 cm. B 4 cm. C 2 cm. D 3 cm.
Câu 5. HÂ tßt c£ các nguyên hàm cıa hàm sË f (x) = 2x + 2020 là A 2x2 + C. B x2 + 2020x + C. C x2 + C. D 2x2 + 2020x + C.
Câu 6. T™p nghiªm cıa bßt ph˜Ïng trình 3x2+2x > 27 là
A ( 1; 3) [ (1; +1). B ( 1; 1) [ (3; +1). C ( 1; 3). D ( 3; 1). 2x 3
Câu 7. Cho hàm sË y =
có Á th‡ là (C). Mªnh ∑ nào sau ây là úng? x + 1
A (C) có tiªm c™n ngang là y = 2.
B (C) chø có mÎt tiªm c™n.
C (C) có tiªm c™n ˘ng là x = 1.
D (C) có tiªm c™n ngang x = 2.
Câu 8. Diªn tích toàn ph¶n cıa hình l™p ph˜Ïng c§nh 3a là A 72a2. B 54a2. C 36a2. D 9a2.
Câu 9. Th∫ tích khËi l´ng trˆ có diªn tích áy B và chi∑u cao h là 1 4 A Bh. B Bh. C Bh. D 3Bh. 3 3
Câu 10. Trong không gian vÓi hª tÂa Î Oxyz, cho m∞t c¶u (S ) : x2 + y2 + z2 + 2x 2z 7 = 0. Bán kính cıa m∞t c¶u ã cho b¨ng p p A 7. B 3. C 9. D 15.
Câu 11. T¯ các ch˙ sË 2, 3, 4, 5 có th∫ l™p ˜Òc bao nhiêu sË gÁm 4 ch˙ sË? A 24. B 16. C 120. D 256.
Câu 12. Trong không gian vÓi hª tÂa Î Oxyz, m∞t phØng (P) : x 3z + 5 = 0 có mÎt vectÏ pháp tuy∏n là A ~n1 = (1; 3; 5). B ~n4 = (0; 2; 3). C ~n3 = (1; 0; 3). D ~n2 = (1; 3; 0).
Câu 13. Cho hai sË ph˘c z1 = 1 + 2i và z2 = 2 3i. Ph¶n £o cıa sË ph˘c w = 3z1 2z2 là A 1. B 11. C 12. D 12i. Trang 1/6 Mã ∑ 111
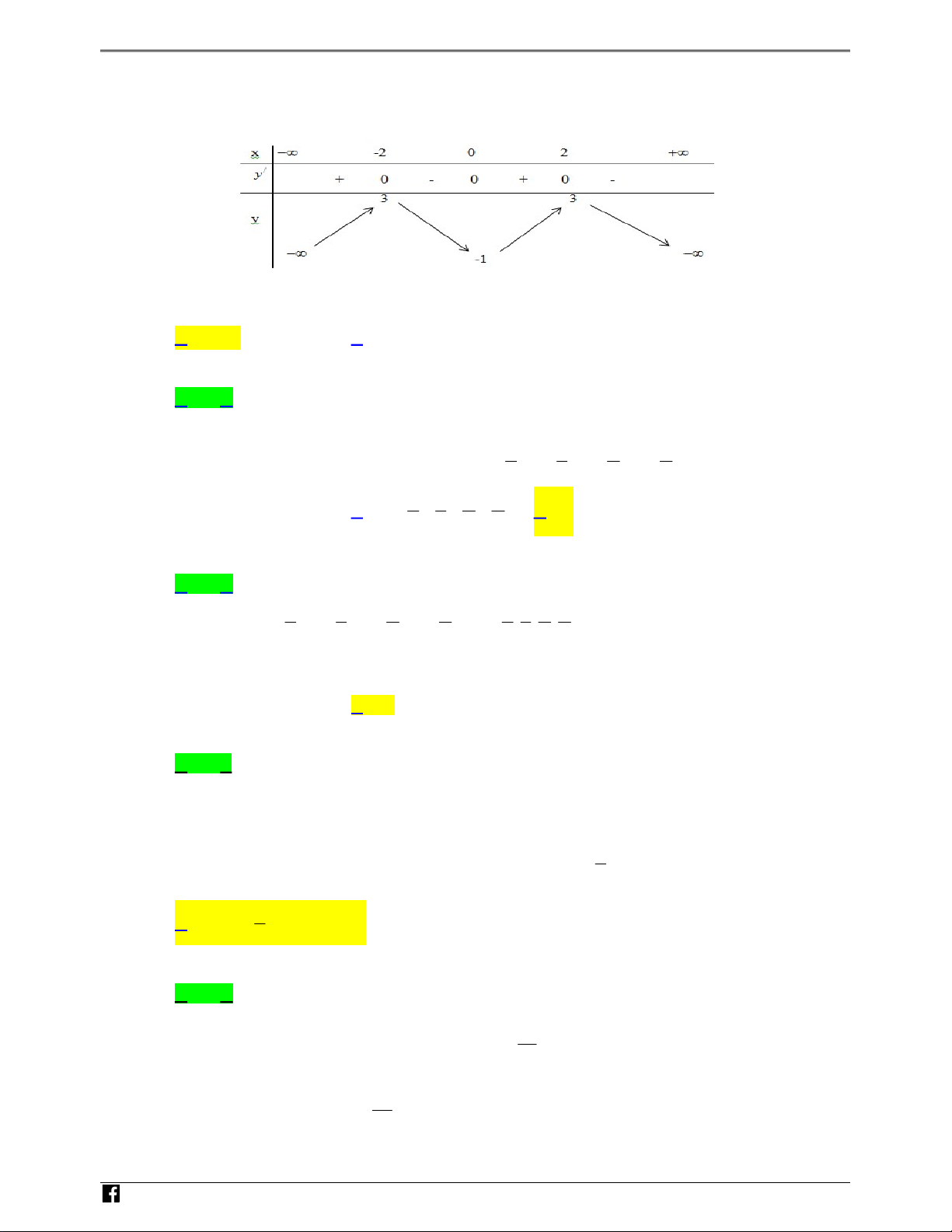
Câu 14. Cho hàm sË y = f (x) xác ‡nh trên R, có b£ng bi∏n thiên nh˜ sau x 1 2 0 2 +1 y0 + 0 0 + 0 3 3 y 1 1 1
Hàm sË y = f (x) Áng bi∏n trên kho£ng nào d˜Ói ây? A (0; 2). B ( 1; 0). C ( 1; 3). D ( 1; 3). a b c d
Câu 15. Cho các sË d˜Ïng a, b, c, d. Bi∫u th˘c M = log b¨ng b + log c + log d + log a a b c d! A 1. B log . C 0. D log(abcd). b + c + d + a
Câu 16. Cho cßp sË cÎng (un) có sË h§ng ¶u u1 = 3 và công sai d = 2. Khi ó u5 có giá tr‡ b¨ng A 15. B 11. C 14. D 12. Z
Câu 17. Tìm nguyên hàm F(x) =
(x + sin x) dx bi∏t F(0) = 1. 1 A F(x) = x2 cos x + 20. B F(x) = x2 cos x. 2 1 C F(x) = x2 cos x 2 + 2. D F(x) = x2 + cos x + 20.
Câu 18. Mô un cıa sË ph˘c z = 3 4i b¨ng p A 100. B 5. C 14. D 5. Câu 19. y
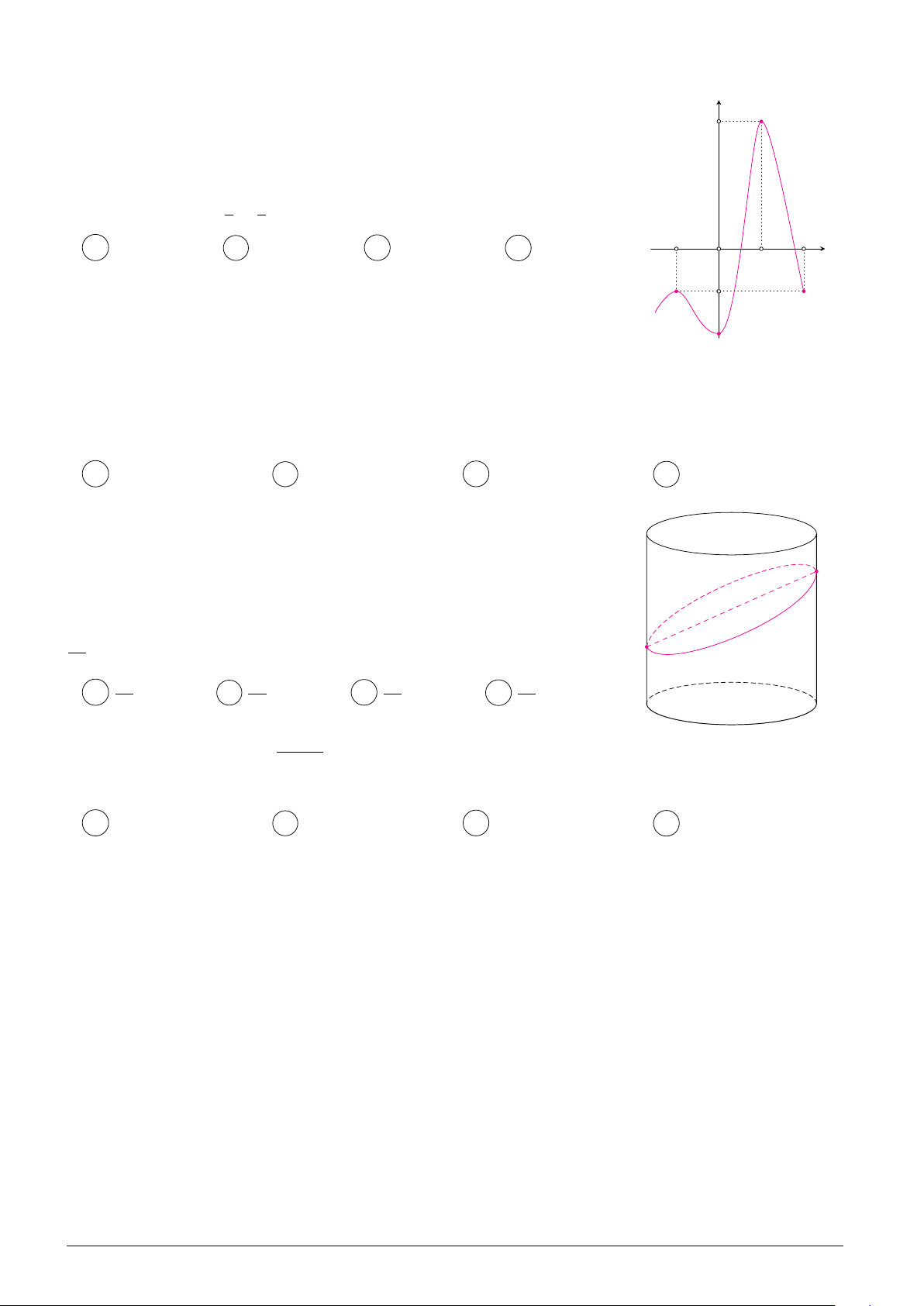
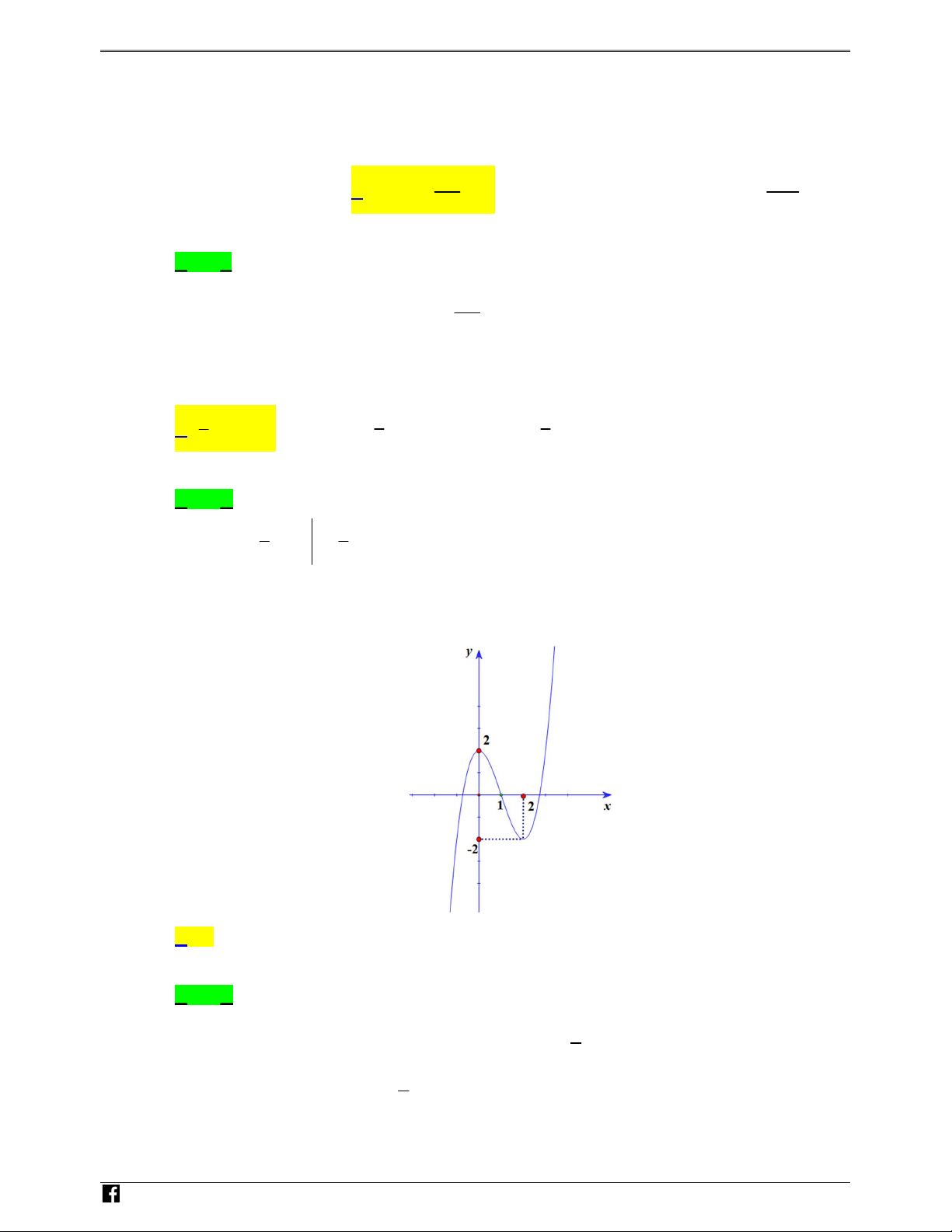
˜Ìng cong trong hình v≥ bên là Á th‡ cıa hàm sË nào d˜Ói ây? A y = x3 3x2 1. B y = x3 + 3x2 1. O x C y = x4 3x2 1. D y = x4 + 3x2 1. 1
Câu 20. KhËi c¶u có bán kính R = 4 có th∫ tích là 64⇡ 256⇡ A . B 64⇡. C . D 12⇡. 3 3
Câu 21. Trong các Øng th˘c sau, Øng th˘c nào sai? ⇣ ⌘ ⇣ ⌘ ⇣ ⌘ A ln 2e2 = 2 + ln 2. B ln(2e) = 1 + ln 2. C ln e2 = 2. D ln e2 = 1.
Câu 22. Cho hàm sË y = f (x) có b£ng bi∏n thiên x 1 1 0 1 +1 y0 + 0 + 0 2 3 y 1 1 1 2
H‰i hàm sË có bao nhiêu c¸c tr‡? A 3. B 1. C 2. D 4. Trang 2/6 Mã ∑ 111
Câu 23. Trong không gian vÓi hª tÂa Î Oxyz, kho£ng cách t¯ i∫m A(1; 2; 3) ∏n m∞t phØng (P) : x + 3y 4z + 9 = 0 là p p 17 p 26 4 26 A p · B 8. C 26 13 · D 13 ·
Câu 24. Cho sË ph˘c z = 1 + 2i. i∫m nào d˜Ói ây là i∫m bi∫u diπn cıa sË ph˘c w = z + iz trên m∞t phØng to§ Î? A N(2; 3). B M(3; 3). C Q(3; 2). D P( 3; 3).
Câu 25. Trong không gian vÓi hª tÂa Î Oxyz, ph˜Ïng trình m∞t phØng qua hai i∫m A(0; 1; 1), B( 1; 0; 2)
và vuông góc vÓi m∞t phØng (P) : x y + z + 1 = 0 là A y z 2 = 0. B y + z + 2 = 0. C y + z 2 = 0. D y + z 2 = 0.
Câu 26. Tìm nguyên hàm cıa hàm sË f (x) = 3x. Z Z 3x Z Z 3x+1 A 3xdx = 3x+1 + C. B 3x dx = 3x dx 3xdx ln 3 + C. C = 3x ln 3+C. D = x + 1 + C. 2 Z Câu 27. Tích phân e3x 1 dx b¨ng 1 1 ⇣ ⌘ 1 ⇣ ⌘ 1 A e5 e2 . B e5 . C e5 e2. D e5 e2. 3 3 + e2 3 Câu 28. y y = f (x) 2
Cho hàm sË f (x) = ax3 + bx2 + cx + d, (a, b, c, d 2 R) có Á th‡ nh˜ hình v≥ bên.
SË nghiªm th¸c cıa ph˜Ïng trình 4. f (x) + 3 = 0 là O 2 A 3. B 0. C 1. D 2. x 2
Câu 29. T™p nghiªm cıa bßt ph˜Ïng trình log1 (x 3) log1 4 là 2 2 A S = [7; +1). B S = (3; 7]. C S = ( 1; 7]. D S = [3; 7].
Câu 30. Tìm giá tr‡ lÓn nhßt cıa hàm sË y = x3 2x2 7x + 1 trên o§n [ 2; 1]. A 4. B 6. C 5. D 3.
Câu 31. Cho hàm sË y = 2x4 6x2 có Á th‡ (C). SË giao i∫m cıa Á th‡ (C) và ˜Ìng thØng y = 4 là A 4. B 2. C 0. D 1. Câu 32. A0 D0
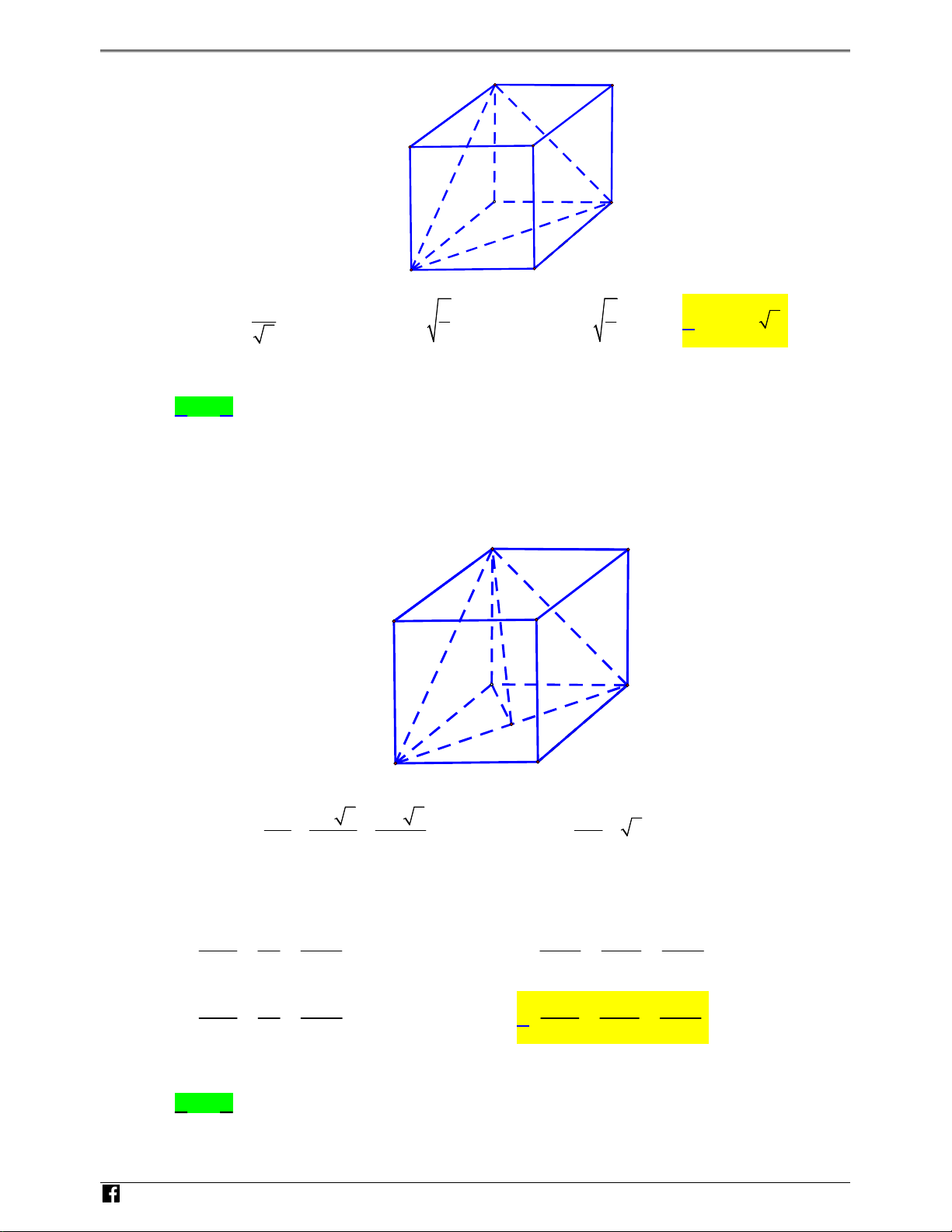
Cho hình l™p ph˜Ïng ABCD.A0B0C0D0. GÂi ' là góc gi˙a hai m∞t phØng B0 (A0BD) và (ABC). Tính tan C0 '. r r 1 2 3 p A tan ' = p · B tan ' = 2. A 2 3· C tan ' = 2· D tan ' = D B C
Câu 33. Trong không gian vÓi hª tÂa Î Oxyz, cho i∫m hai i∫m A(1; 0; 2) và B(3; 1; 3). ˜Ìng thØng AB có ph˜Ïng trình là x 1 y z 2 x 3 y z A + 1 + 2 2 = 1 = 5 · B 2 = 1 = 5 · Trang 3/6 Mã ∑ 111 x y z x y 1 z 7 C + 1 + 2 + 1 2 = 1 = 5 · D 2 = 1 = 5 ·
Câu 34. GÂi z là nghiªm ph˘c có ph¶n £o âm cıa ph˜Ïng trình (z 2)2 + 1 = 0. Mô un cıa sË ph˘c z .i b¨ng p p A 5. B 2. C 5. D 2. 8 >>x = t >
Câu 35. Trong không gian vÓi hª tÂa Î Oxyz, cho i∫m A(2; 0; 3) và ˜Ìng thØng : <>y = 1 + 3t M∞t >>:z = 5 t.
phØng i qua A và vuông góc vÓi có ph˜Ïng trình là A x + 3y z = 0. B x 3y + z + 1 = 0. C 3y z 3 = 0. D x + 3y z 5 = 0.
Câu 36. MÎt hình trˆ có bán kính áy b¨ng r và có thi∏t diªn qua trˆc là mÎt hình vuông. Khi ó diªn tích
toàn ph¶n cıa hình trˆ ó là A 4⇡r2. B 6⇡r2. C 2⇡r2. D 8⇡r2.
Câu 37. Có 8 chi∏c gh∏ ˜Òc kê thành mÎt hàng ngang. X∏p ng®u nhiên 8 hÂc sinh, gÁm 3 hÂc sinh lÓp A, 3
hÂc sinh lÓp B và 2 hÂc sinh lÓp C, ngÁi vào hàng gh∏ ó, sao cho mÈi gh∏ có úng mÎt hÂc sinh. Xác sußt a
∫ có úng 2 hÂc sinh lÓp A ngÁi c§nh c§nh nhau b¨ng vÓi a, b b
2 N, (a, b) = 1. Khi ó giá tr‡ a + b là A 43. B 93. C 101. D 21.
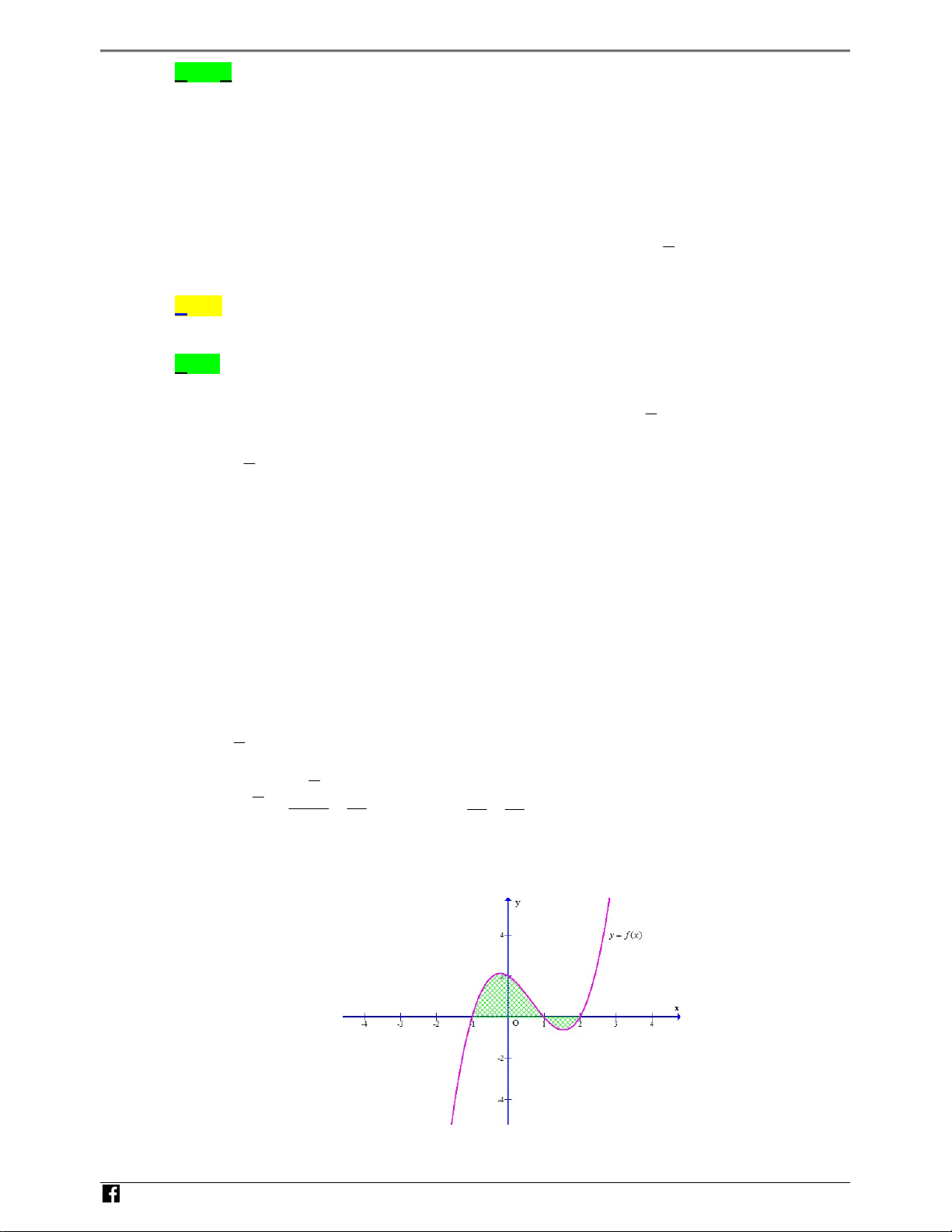
Câu 38. GÂi S là diªn tích mi∑n hình phØng ˜Òc g§ch chéo trong hình v≥ bên. Công th˘c tính S là 2 Z 1 Z 2 Z y A S = f (x)dx. B S = f (x)dx f (x)dx. y = f (x) 1 1 1 1 Z 2 Z 2 Z C S O = f (x)dx + f (x)dx. D S = f (x)dx. x 1 1 2 1 1 1
Câu 39. Cho z1, z2 là hai nghiªm ph˘c cıa ph˜Ïng trình z2 + 2z + 5 = 0, trong ó z1 là sË ph˘c có ph¶n £o âm. Khi ó z1 + 3z2 b¨ng A 4 + 4i. B 4 + 4i. C 4 4i. D 4 4i. Câu 40. S
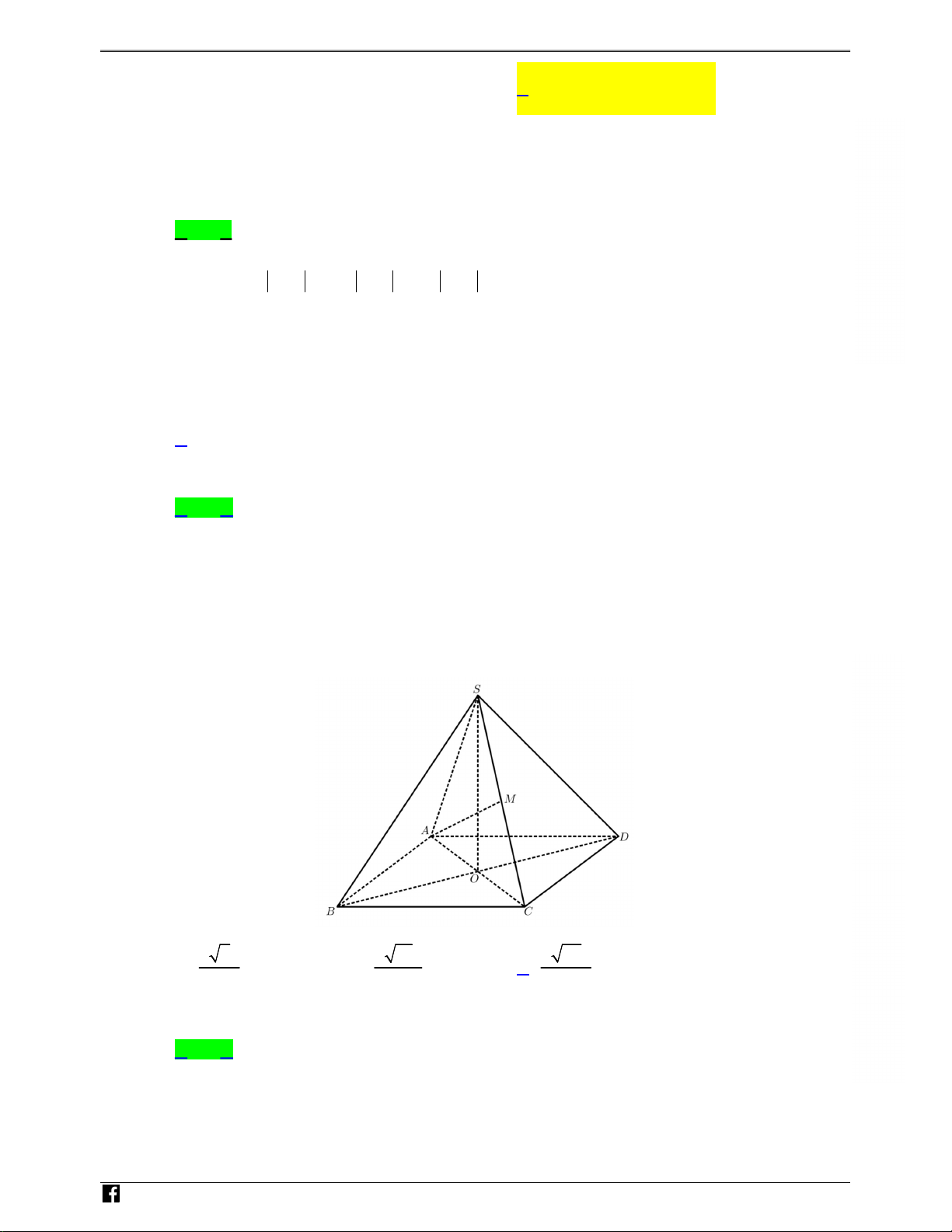
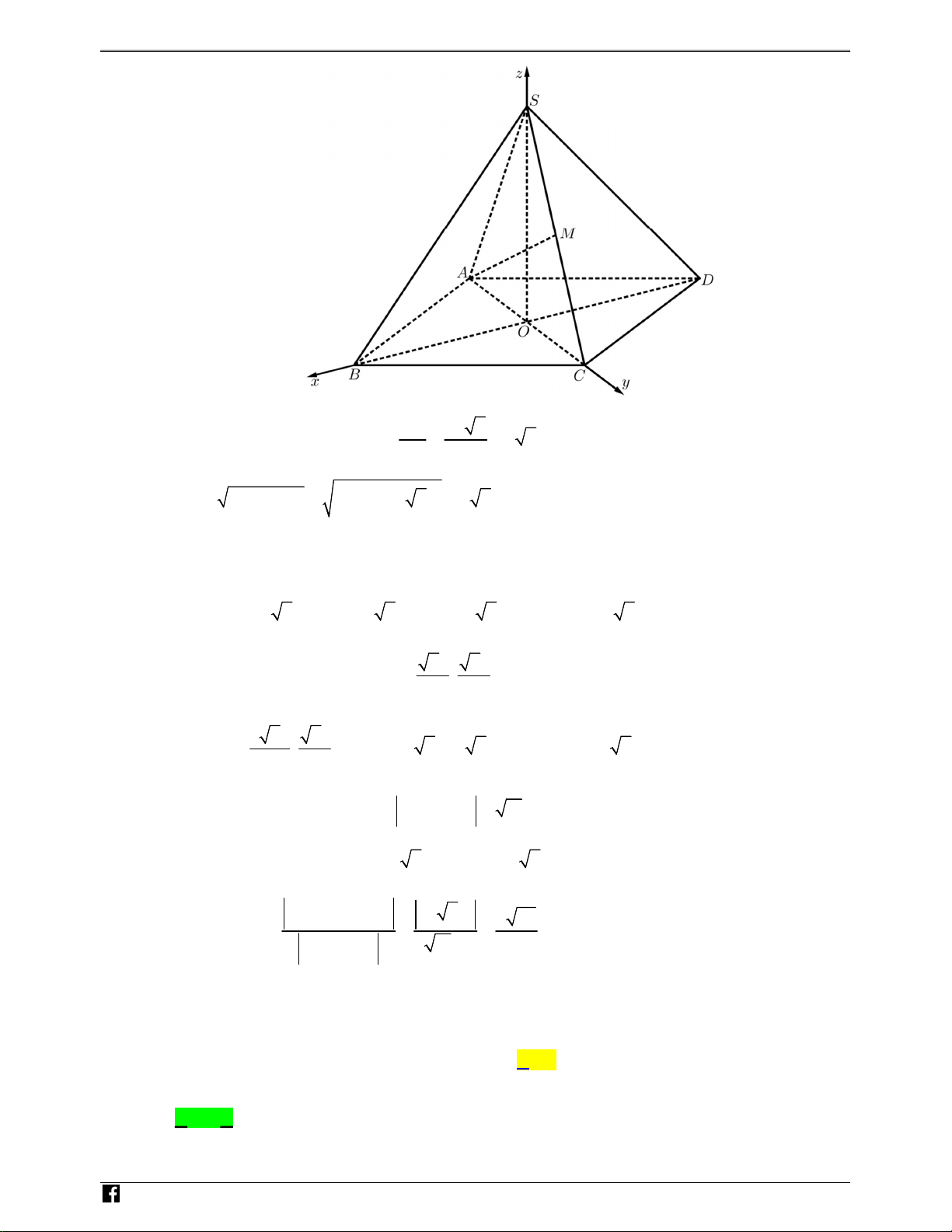
Cho hình chóp ∑u S.ABCD, S A = AB = 2a (minh hÂa nh˜ hình
bên). GÂi M là trung i∫m cıa S C. Kho£ng cách gi˙a hai ˜Ìng thØng AM và CD b¨ng p p p M 2 2a 2 10a 2 22a A A 3 · B 9 · C 11 · D a. D O B C
Câu 41. Cho hàm sË y = ax4 + bx2 + c, vÓi a, b, c là các sË th¸c, a , 0. Bi∏t lim y = +1, hàm sË có 3 c¸c x!+1
tr‡ và ph˜Ïng trình y = 0 vô nghiªm. H‰i trong ba sË a, b, c có bao nhiêu sË d˜Ïng? A 0. B 3. C 2. D 1.
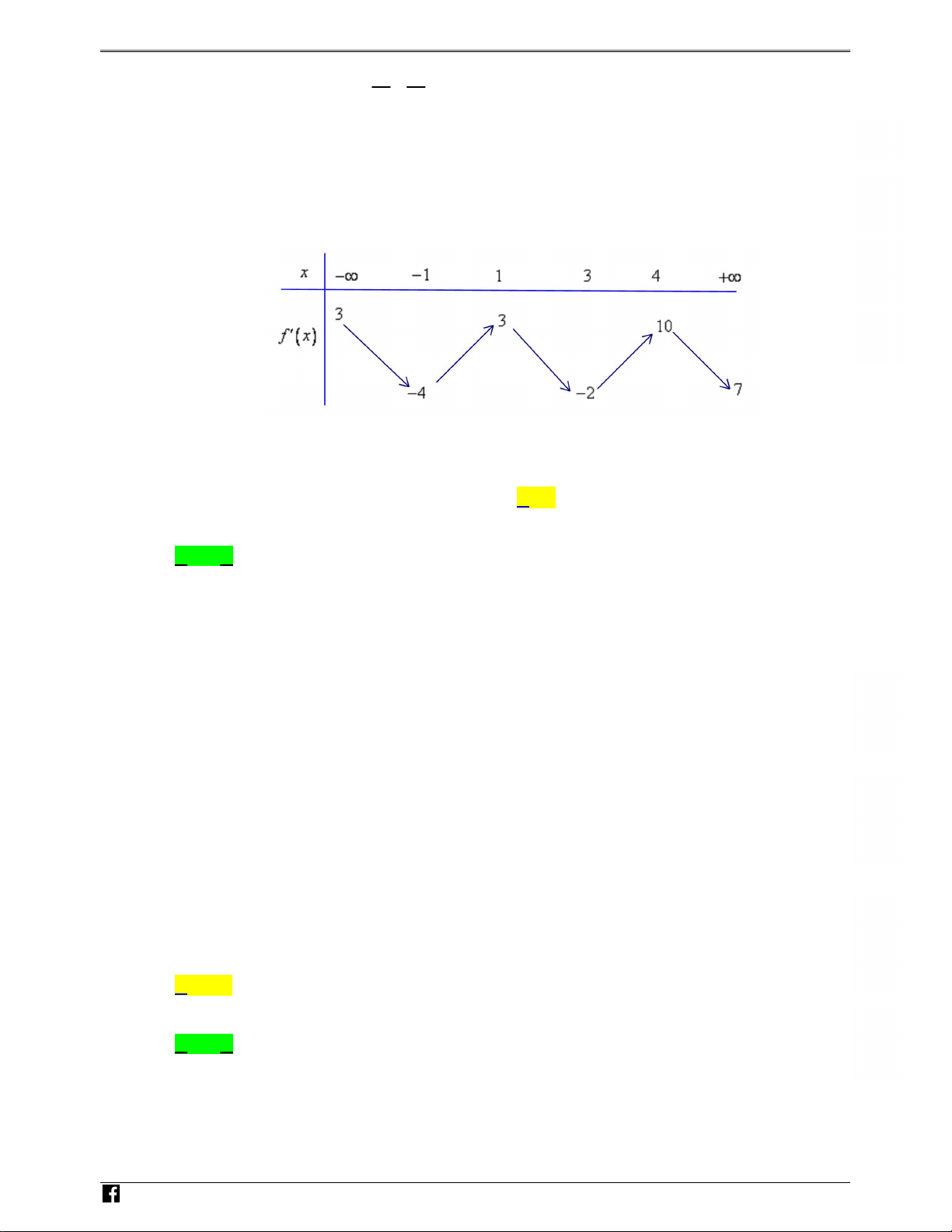
Câu 42. Cho hàm sË y = f (x) có §o hàm liên tˆc trên R và có b£ng bi∏n thiên cıa y0 nh˜ sau. Trang 4/6 Mã ∑ 111 x 1 1 1 3 4 +1 3 3 10 y0 4 2 7
Có bao nhiêu giá tr‡ nguyên cıa m ∫ hàm sË g(x) = f (x) mx ngh‡ch bi∏n trên kho£ng ( 1; 3), Áng thÌi Áng bi∏n trên (4, +1)? A 4. B 3. C 5. D 6.
Câu 43. SË ca nhiπm Covid-19 trong cÎng Áng mÎt tønh vào ngày th˘ x trong mÎt giai o§n ˜Òc ˜Óc
tính theo công th˘c f (x) = A.erx, trong ó A là sË ca nhiπm ngày ¶u cıa giai o§n, r là t lª gia t´ng sË
ca nhiπm hàng ngày cıa giai o§n ó và trong cùng mÎt giai o§n thì r không Íi. Giai o§n th˘ nhßt tính t¯
ngày tønh ó có 9 ca bªnh ¶u tiên và không dùng biªn pháp phòng chËng lây nhiπm nào thì ∏n ngày th˘ 6
sË ca bªnh cıa tønh là 180 ca. Giai o§n th˘ hai (k∫ t¯ ngày th˘ 7 tr i) tønh ó áp dˆng các biªn pháp phòng
chËng lây nhiπm nên t lª gia t´ng sË ca nhiπm hàng ngày gi£m i 10 l¶n so vÓi giai o§n tr˜Óc. ∏n ngày
th˘ 6 cıa giai o§n hai thì sË ca m≠c bªnh cıa tønh ó g¶n nhßt vÓi sË nào sau ây? A 242. B 90. C 16. D 422. Câu 44. A0 D0
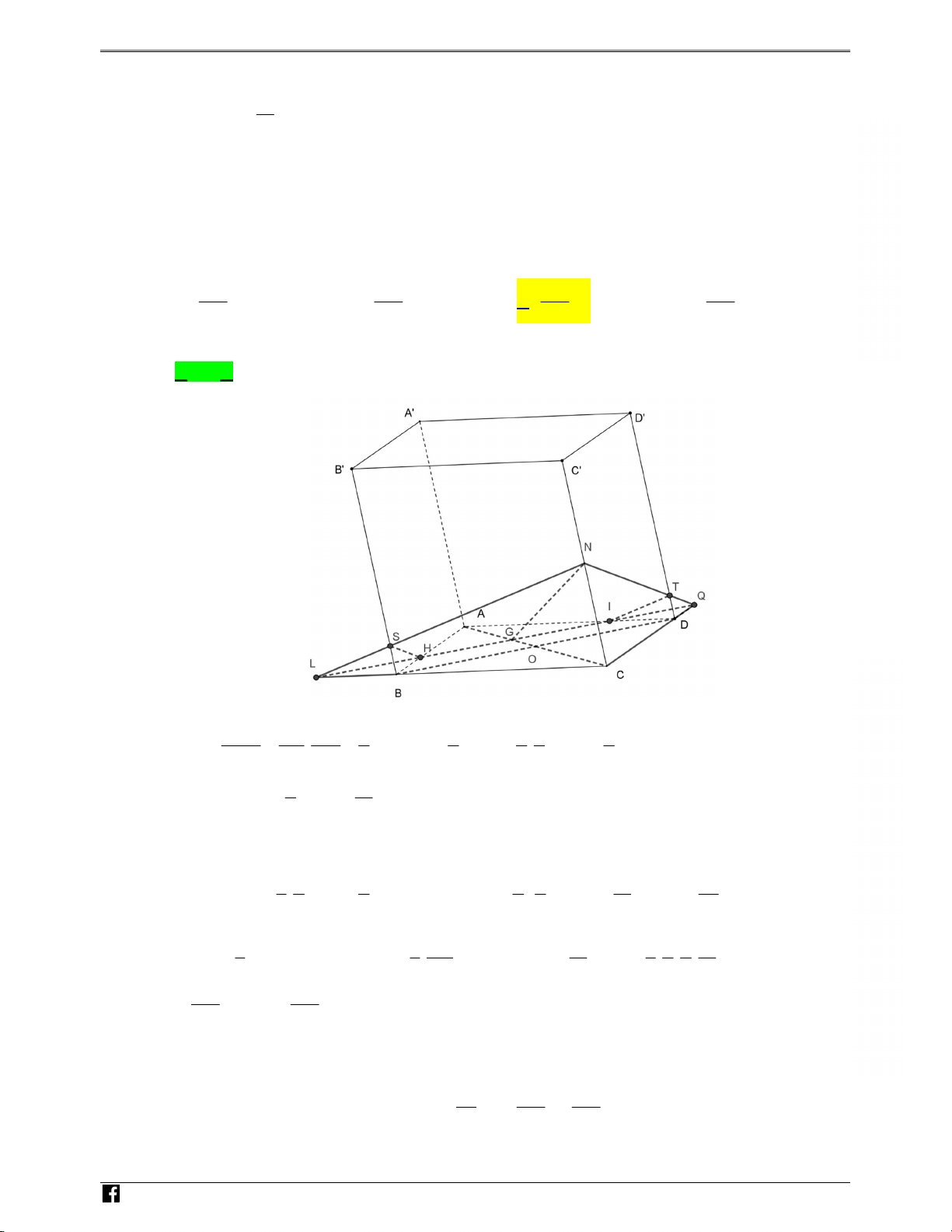
Cho hình hÎp ABCD.A0B0C0D0 có th∫ tích là V. MÎt m∞t phØng C0
(Q) i qua trÂng tâm cıa tam giác ABD và trung i∫m CC0 B0
Áng thÌi (Q) song song vÓi BD. M∞t phØng (Q) chia khËi hÎp
ABCD.A0B0C0D0 thành hai ph¶n. Th∫ tích cıa ph¶n ch˘a ønh A0 b¨ng N 181 187 185 191 A A V. B V. C V. D V. D G 216 216 216 216 O B C
Câu 45. Cho hàm sË y = f (x) có §o hàm và liên tˆc trên o§n [0; 1] th‰a mãn
f (0) = 2 và f 0(x).ef(x) x2 2 = 2x, 8x 2 [0; 1]. 1 Z Tính giá tr‡ cıa f (x) dx. 0 5 7 A 3· B 3. C 3· D 2.
Câu 46. Xét các sË th¸c d˜Ïng a, b, c > 1 vÓi a > b th‰a 4 loga c + logb c = 25 logab c. Giá tr‡ nh‰ nhßt cıa
bi∫u th˘c P = logb a + loga c + logc b b¨ng 17 A 5. B 3. C 8. D 2 · Câu 47. Trang 5/6 Mã ∑ 111 y 6
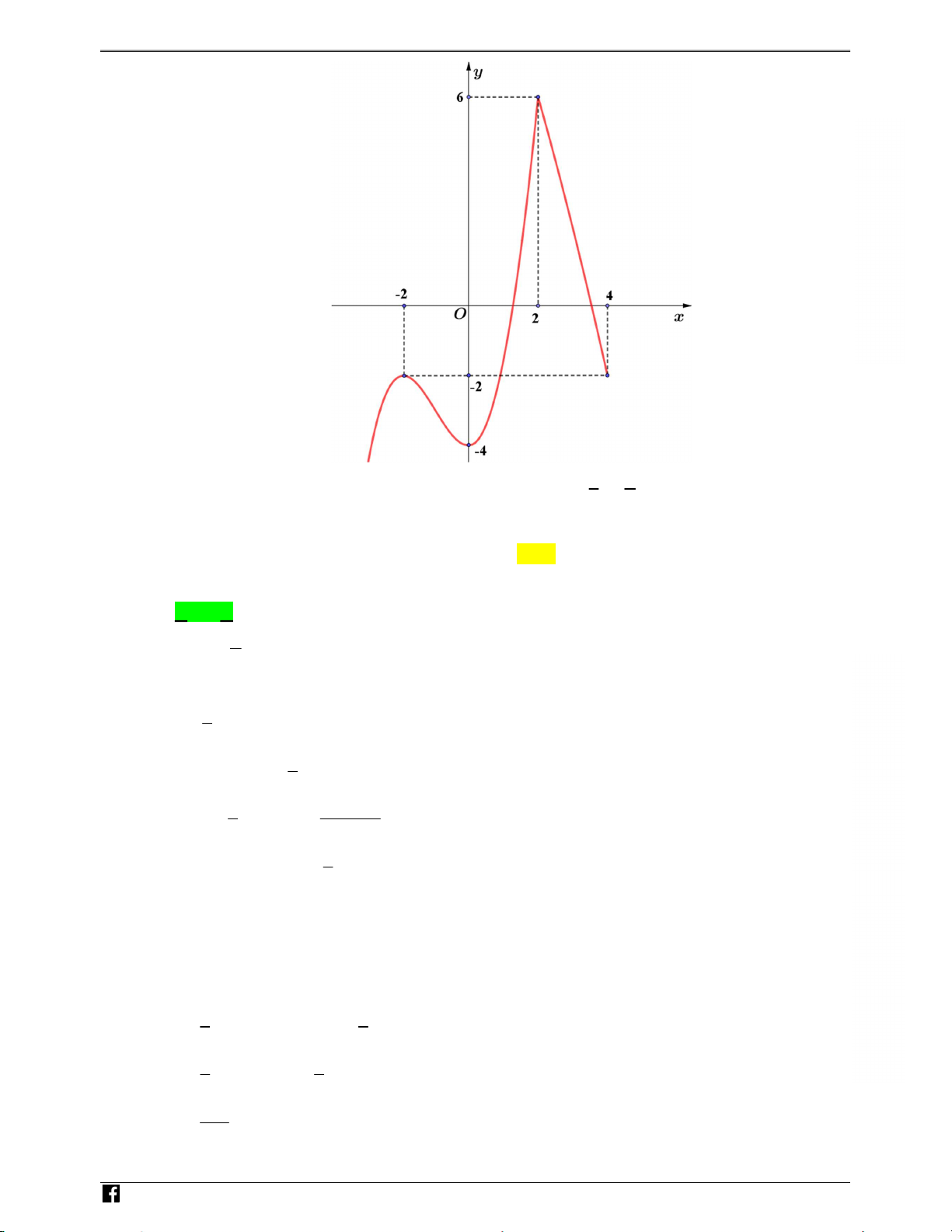
Cho hàm sË y = f (x) có Á th‡ nh˜ hình v≥ bên. Có bao nhiêu sË nguyên cıa tham 1 ✓ x ◆ sË m ∫ ph˜Ïng trình f 3
2 + 1 + x = m có nghiªm thuÎc [ 2,2]? A 7. B 6. C 8. D 5. 2 O 4 2 x 2 4
Câu 48. Có bao nhiêu bÎ sË (a; b; c) vÓi a, b 2 { 1; 0; 1; 2; 3; 4; 5} và c > 1 là sË th¸c th‰a mãn loga(b + c) = 2 log10 c. A 8. B 10. C 6. D 12. Câu 49.
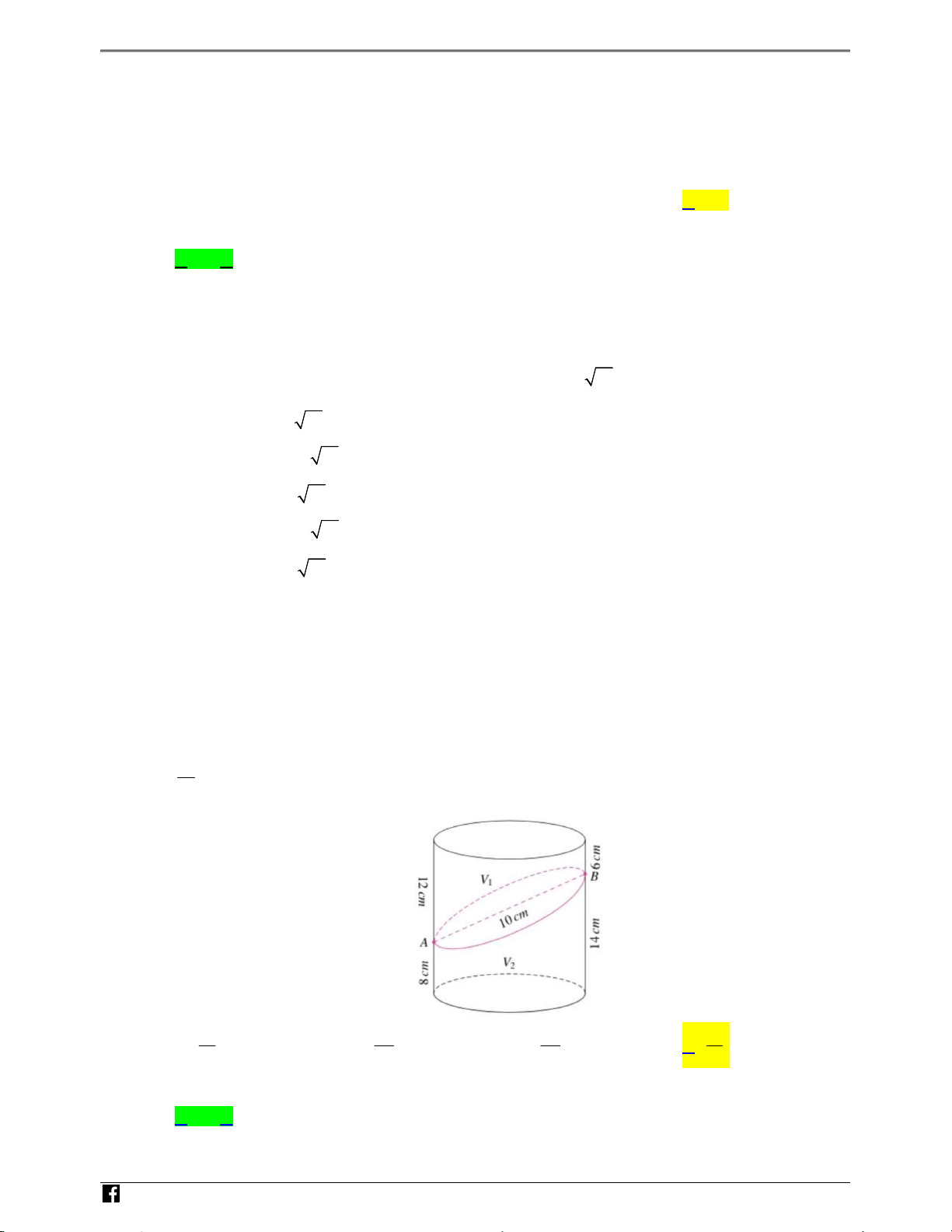
Cho khËi trˆ có chi∑u cao 20 cm. C≠t khËi trˆ bi mÎt m∞t phØng ˜Òc thi∏t
diªn là hình elip có Î dài trˆc lÓn b¨ng 10 cm. Thi∏t diªn chia khËi trˆ ban cm 6 12
¶u thành hai n˚a, n˚a trên có th∫ tích V V B
1, n˚a d˜Ói có th∫ tích V2 (nh˜ hình cm 1
v≥). Kho£ng cách t¯ mÎt i∫m thuÎc thi∏t diªn g¶n áy d˜Ói nhßt và i∫m
thuÎc thi∏t diªn xa áy d˜Ói nhßt tÓi áy d˜Ói là 8 cm và 14 cm. Tính tø sË 10 cm V cm 1 A 14 V · 2 V 6 9 11 9 cm 2 A 11· B 20· C 20· D 11· 8 x
Câu 50. Cho hàm sË f (x) + m
= 2x + 1· GÂi S là t™p hÒp các sË nguyên d˜Ïng m 7 sao cho vÓi mÂi bÎ sË th¸c
a, b, c 2 [2; 3] thì | ln f (a)|, | ln f (b)|, | ln f (c)| là Î dài ba c§nh cıa mÎt tam giác. TÍng tßt c£ các ph¶n t˚ cıa S là A 10. B 15. C 16. D 14.
- - - - - - - - - - HòT- - - - - - - - - - Trang 6/6 Mã ∑ 111 NHÓM TOÁN VD – VDC NĂM HỌC 2019 - 2020 BẢNG ĐÁP ÁN 1.A 2.B 3.A 4.B 5.B 6.A 7.A 8.B 9.A 10.B N 11.D 12.C 13.C 14.A 15.C 16.B 17.C 18.B 19.D 20.C H 21.D 22.C 23.D 24.B 25.C 26.B 27.A 28.A 29.B 30.C Ó 31.B 32.D 33.D 34.C 35.B 36.B 37.A 38.B 39.A 40.C M 41.C 42.C 43.A 44.C 45.C 46.B 47. C 48.D 49.D 50.C TO Á N LỜI GIẢI CHI TIẾT V D
Câu 1: Nghiệm của phương trình log x 2 2 là 5 – V A. 27 . B. 9 . C. 34. D. 12 . D Lời giải C Chọn A Điều kiện: x 2 . Ta có: log x 2 2
2 x 2 5 x 27 (nhận). 5
Câu 2: Trong không gian với hệ tọa độ Oxyz , phương trình chính tắc của đường thẳng đi qua điểm M 2; 1
;3 và có vectơ chỉ phương u 1;2;4 là x 2 y 1 z 3 x 2 y 1 z 3 A. . B. . 1 2 4 1 2 4 x 1 y 2 z 4 x 1 y 2 z 4 C. . D. . 2 1 3 2 1 3 Lời giải Chọn B N H
Phương trình chính tắc của đường thẳng đi qua điểm M 2; 1
;3 và có vectơ chỉ phương Ó M x 2 y 1 z 3 u 1; 2 ; 4 có dạng . TO 1 2 4 Á N
Câu 3: Trong không gian với hệ tọa độ Oxyz , phương trình của đường thẳng d đi qua điểm V M 1;2; 5
và vuông góc với mặt phẳng P : 2x 3y 4z 5 0 là D – V x 1 2t x 1 2t x 2 t x 2 t D A. d : y 2 3t . B. d : y 2 3t . C. d : y 3 2t . D. d : y 3 2t . C z 5 4t z 5 4t z 4 5t z 4 5t Lời giải Chọn A
Ta có: mặt phẳng P : 2x 3y 4z 5 0 có vectơ pháp tuyến n 2;3; 4 .
Vì d vuông góc với mặt phẳng P nên d nhận n 2;3; 4
là một vectơ chỉ phương.
Khi đó phương trình đường thẳng d đi qua M 1;2; 5
và vuông góc với mặt phẳng P là:
https://www.facebook.com/groups/toanvd.vdc Trang 9 NHÓM TOÁN VD – VDC NĂM HỌC 2019 - 2020 x 1 2t d : y 2 3t . N z 5 4t H Ó 1 M
Câu 4: Một hình nón có diện tích xung quanh bằng 2
2cm và bán kính đáy r c . m Tìm độ dài 2 TO
đường sinh của hình nón. Á N A. 1cm . B. 4cm . C. 2cm . D. 3 cm . V Lời giải D – Chọn B V D 1 C
Diện tích xung quanh hình nón S . r.l 2 . .l 2 l 4 cm 2
Câu 5: Họ tất cả các nguyên hàm của hàm số f x 2x 2020 là. A. 2 2x C . B. 2 x 2020x C . C. 2 x C . D. 2 2x 2020x C . Lời giải Chọn B F x x 2 2 2020 dx x 2020x C
Câu 6: Tập nghiệm của bất phương trình 2x2 3 x 27 là A. ;
3 1; . B. ; 1 3; . C. 1 ; 3 . D. 3 ; 1 . Lời giải Chọn A N 2 2 x 2x x 2 x 3 2 3 27 3 3 x 2x 3 H Ó x 3 M 2
x 2x 3 0 x 1 TO Á
Vậy tập nghiệm của bất phương trình là S ; 3 1; N V 2x 3 D Câu 7: Cho hàm số y
có đồ thị là C . Mệnh đề nào sau đây là đúng? – V x 1
A. C có tiệm cận ngang là y 2 .
B. C chỉ có một tiệm cận. D C
C. C có tiệm cận đứng là x 1.
D. C có tiệm cận ngang là x 2 . Lời giải Chọn A 2x 3 2x 3 Ta có: lim y lim 2; lim y lim
2 nên đường thẳng y 2 là tiệm cận x x x 1 x x x 1
ngang của đồ thị hàm số. 2x 3 2x 3 lim y lim ; lim y lim
nên đường thẳng x 1 là tiệm cận x 1 x 1 x 1 x 1 x 1 x 1
đứng của đồ thị hàm số. Vậy các đáp án B, C, D sai.
Câu 8: Diện tích toàn phần của hình lập phương cạnh 3a là A. 2 72a . B. 2 54a . C. 2 36a . D. 2 9a .
https://www.facebook.com/groups/toanvd.vdc Trang 10 NHÓM TOÁN VD – VDC NĂM HỌC 2019 - 2020 Lời giải Chọn B N
Diện tích toàn phần của hình lập phương cạnh 3a là S S a2 2 6 6. 3 54a . tp mb H Ó M
Câu 9: Thể tích của khối lăng trụ có diện tích đáy B và chiều cao h là TO 1 4 A. Bh . B. Bh . C. Bh . D. 3Bh . Á 3 3 N V Lời giải D Chọn A – V
Thể tích của khối lăng trụ có diện tích đáy B và chiều cao h là V Bh . D C
Câu 10: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S 2 2 2
: x y z 2x 2z 7 0. Bán
kính của mặt cầu đã cho bằng A. 7 . B. 3 . C. 9 . D. 15 . Lời giải Chọn B
S x y z x z x 2 y z 2 2 2 2 2 2 : 2 2 7 0 1 1 3 .
Vậy bán kính của mặt cầu đã cho bằng 3 .
Câu 11: Từ các chữ số 2,3, 4,5 có thể lập được bao nhiêu số gồm 4 chữ số? A. 24 . B. 16 . C. 120 . D. 256 . N Lời giải H Ó Chọn D M TO
Gọi số cần tìm dạng abcd. Á N
Khi đó, a có 4 cách chọn, b có 4 cách chọn, c có 4 cách chọn, d có 4 cách chọn. V D
Theo quy tắc nhân có 4.4.4.4 256 số. – V
Câu 12: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : x 3z 5 0 có một vec tơ pháp D C tuyến là A. n 1; 3;5 . B. n 0; 2; 3 . 4 1 C. n 1;0; 3 . D. n 1;3;0 . 2 3 Lời giải Chọn C
Câu 13: Cho hai số phức z 1 2i; z 2 3i . Phần ảo của số phức w 3z 2z là 1 2 1 2 A. 1. B. 11. C. 12 . D. 12i Lời giải Chọn C
https://www.facebook.com/groups/toanvd.vdc Trang 11 NHÓM TOÁN VD – VDC NĂM HỌC 2019 - 2020
Ta có w 3z 2z 3(1 2i) 2(2 3i) 1
12i nên phần ảo của w 1 2 là: 12
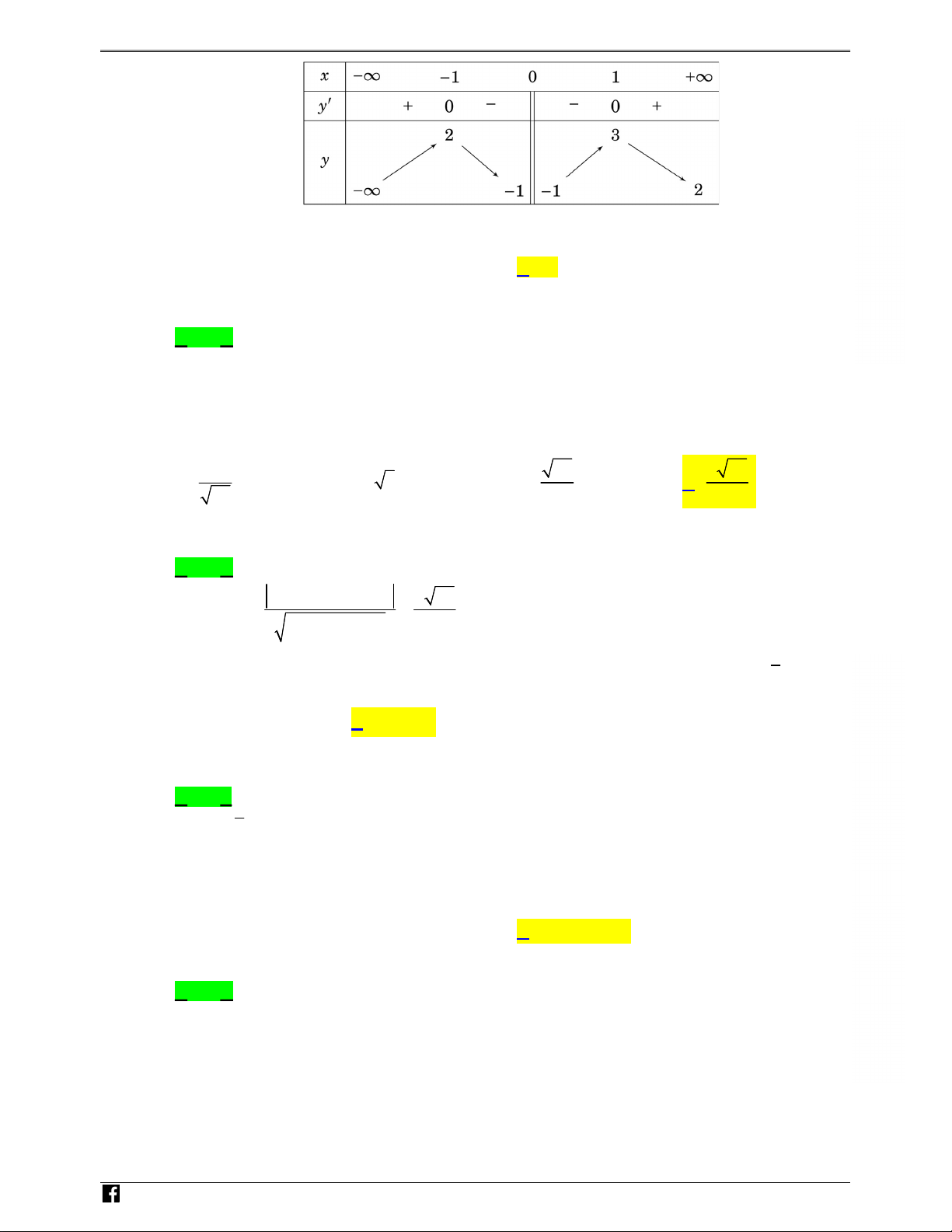
Câu 14: Cho hàm số y f (x) xác định trên R , có bảng biến thiên như sau: N H Ó M TO Á N V D – Hàm số y f (x)
đồng biến trên khoảng nào dưới đây? V D A. (0; 2) . B. (;0) . C. (1;3) . D. (;3) C Lời giải Chọn A.
Từ bảng biến thiên ta có hàm số y f (x) đồng biến trên (0; 2) a b c d
Câu 15: Cho các số dương a,b, .
c d . Biểu thức M log log log log bằng b c d a a b c d A. 1. B. log . C. 0 . D. 12 b c d a Lời giải Chọn C a b c d a b c d
Ta có: M log log log log log . . . log(1) 0 b c d a b c d a N
Câu 16: Cho cấp số cộng n
u có số hạng đầu u và công sai d 2 . Khi đó H 1 3 5 u có giá trị bằng Ó A. 15 . B. 11. C. 14 . D. 12 . M Lời giải TO Á Chọn B N Ta có u u d . 5 1 4 3 4.2 11 V D
Câu 17: Tìm nguyên hàm F x x sin xdx biết F 0 1. – V 1 D A. F x 2 x cos x 20 . B. F x 2 x cos x . C 2 1 C. F x 2 x cos x 2 . D. F x 2 x cos x 20 . 2 Lời giải Chọn C 2 x
Ta có F x x sin xdx xdx sin xdx cos x C . 2 2 0
Mặt khác ta có F 0 1
cos0 C 1 C 2. 2
https://www.facebook.com/groups/toanvd.vdc Trang 12 NHÓM TOÁN VD – VDC NĂM HỌC 2019 - 2020 2 x Vậy F x cos x 2 . 2 N
Câu 18: Môđun của số phức z 3 4i bằng H Ó A. 100 . B. 5 . C. 14 . D. 5 . M TO Lời giải Á Chọn B N V D Ta có z 2 2 3 4 5 . – V
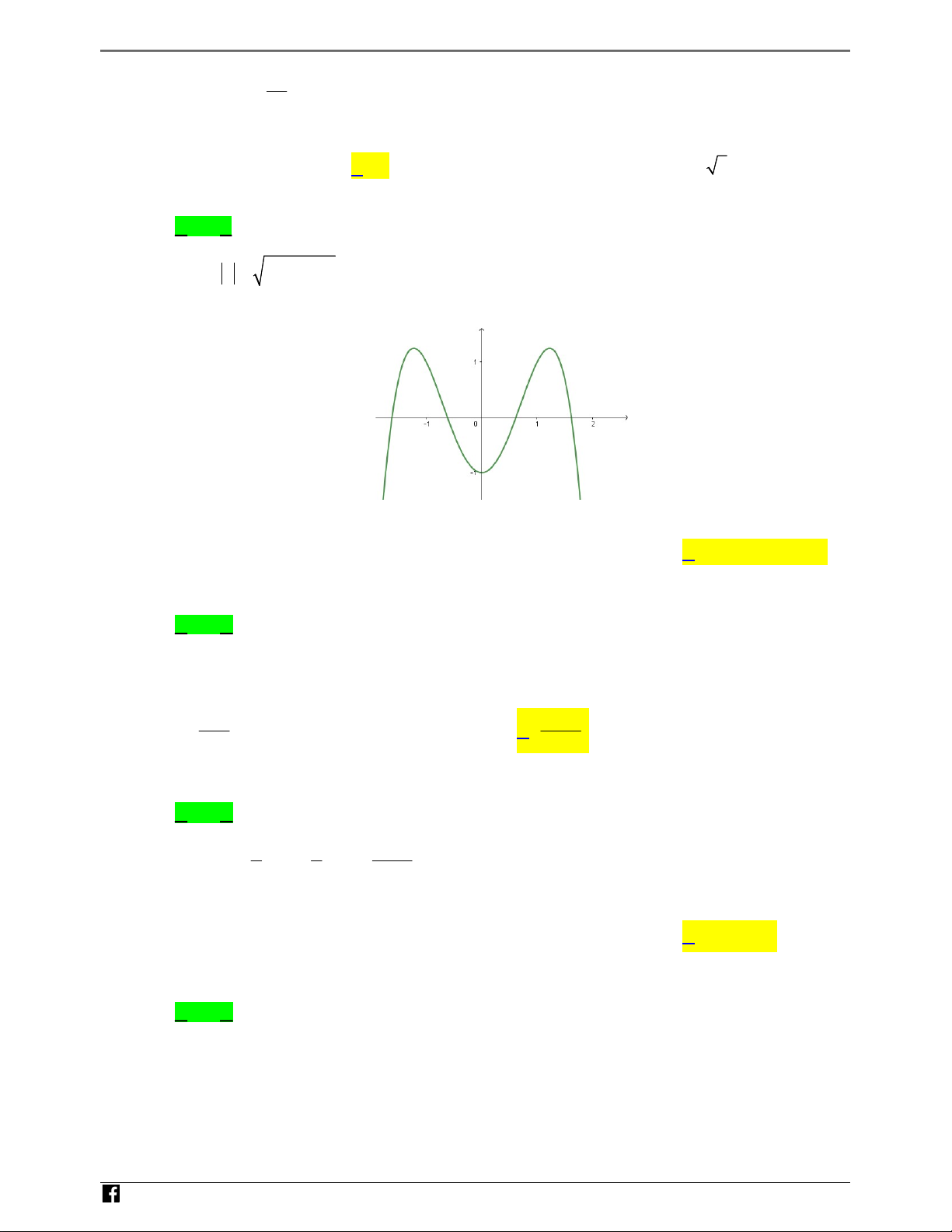
Câu 19: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây D C A. 3 2 y x 3x 1 . B. 3 2 y x 3x 1 . C. 4 2 y x 3x 1. D. 4 2 y x 3x 1. Lời giải Chọn D
Dựa vào đồ thị ta thấy đây là hàm bậc 4 trùng phương có hệ số a 0 N H Ó
Câu 20: Khối cầu có bán kính R 4 có thể tích là M 64 256 A. . B. 64 . C. . D. 12 . TO 3 3 Á N Lời giải V D Chọn C – V 4 4 256 D Ta có 3 3 V R .4 3 3 3 C
Câu 21: Trong các đẳng thức sau, đẳng thức nào sai? A. 2
ln 2e 2 ln 2 . B. ln2e 1 ln 2. C. 2 ln e 2 . D. 2 ln e 1 Lời giải Chọn D Ta có 2
ln e 2 nên D là đáp án sai
Câu 22: Cho hàm số y f x có bảng biến thiên
https://www.facebook.com/groups/toanvd.vdc Trang 13 NHÓM TOÁN VD – VDC NĂM HỌC 2019 - 2020 N H Ó M TOÁ
Hỏi hàm số có bao nhiêu cực trị? N V A. 3 . B. 1. C. 2 . D. 4 . D – V Lời giải D C Chọn C
Hàm số đã cho có hai cực trị y 2 và y 3 .
Câu 23: Trong không gian với hệ tọa độ Oxyz , khoảng cách từ điểm A1; 2 ;3 đến mặt phẳng
P: x 3y 4z 9 0 là 17 26 4 26 A. . B. 8 . C. . D. . 26 13 13 Lời giải Chọn D
d A P 1 3 2 4.3 9 4 26 , . 2 2 2 13 1 3 4 N
Câu 24: Cho số phức z 1 2i . Điểm nào dưới đây là điểm biểu diễn của số phức w z iz trên mặt H Ó phẳng tọa độ? M A. N 2;3 . B. M 3;3 . C. Q3;2 . D. P 3 ;3 . TO Á Lời giải N V Chọn B D
w z iz 3 3i điểm biểu diễn là M 3;3 . – VD
Câu 25: Trong không gian Oxyz , phương trình mặt phẳng đi qua A0;1; 1 , B 1 ;0;2 và vuông góc C
với mặt phẳng P : x y z 1 0 là A. y z 2 0 . B. y z 2 0 . C. y z 2 0. D. y z 2 0 . Lời giải Chọn C
Gọi mặt phẳng cần tìm là mặt phẳng Q .
Vì mặt phẳng P : x y z 1 0 nên ta có nP 1;1; 1 . Ta có A0;1; 1 , B 1
;0;2 AB1;1; 1
Do Q đi qua A0;1; 1 , B 1
;0;2 và vuông góc với P : x y z 1 0 nên Q đi qua
https://www.facebook.com/groups/toanvd.vdc Trang 14 NHÓM TOÁN VD – VDC NĂM HỌC 2019 - 2020 A0;1;
1 và nhận n n ; AB n 0; 2; 2 là một vectơ pháp tuyến. Q P Q
Vì vậy phương trình Q là 0 x 0 2 y 1 2z
1 0 y z 2 0 N H
Câu 26: Tìm nguyên hàm của hàm số 3x f x . Ó x x 1 M x 3 x 3 A. x x 1 3 dx C x x 3 dx C 3 dx 3 C dx C T . B. . C. 3 3 ln 3 . D. . ln 3 x 1 O Á N Lời giải V Chọn B D – x 3x V
Theo bảng nguyên hàm ta có : 3 dx C . D ln 3 C 2 Câu 27: Tích phân 3x 1 e dx bằng 1 1 1 1 A. 5 2 e e . B. 5 2 e e . C. 5 2 e e . D. 5 2 e e . 3 3 3 Lời giải Chọn A 2 2 x 1 x 1 3 1 3 1 e dx e 5 2 e e . 3 3 1 1 Câu 28: Cho hàm số 3 2 y
f x ax bx cx d a;b;c;d có đồ thị như hình vẽ bên. Số
nghiệm của phương trình 4 f x 3 0 là N H Ó M TO Á N V D – VDC A. 3 . B. 0 . C. 1. D. 2 . Lời giải Chọn A
Số nghiệm của phương trình f x f x 3 4 3 0
chính là số giao điểm của đồ thị hàm 4 3
số f x và đường thẳng y . 4
https://www.facebook.com/groups/toanvd.vdc Trang 15 NHÓM TOÁN VD – VDC NĂM HỌC 2019 - 2020 3
Quan sát đồ thị hàm số ta thấy đồ thị hàm số f x cắt đường thẳng y tại 3 điểm phân 4 biệt. N H Ó
Vậy phương trình 4 f x 3 0 có ba nghiệm. M TO
Câu 29: Tập nghiệm của bất phương trình log x 3 log 4 là 1 1 2 2 Á N A. S 7; . B. S 3;7. C. S ; 7. D. S 3;7. V D Lời giải – V Chọn B D x 3 0 C
Ta có: log x 3 log 4 3 x 7 . 1 1 x 3 4 2 2
Vậy bất phương trình đã cho có tập nghiệm S 3;7.
Câu 30: Tìm giá trị lớn nhất của hàm số 3 2
y x 2x 7x 1 trên đoạn 2 ; 1 . A. 4 . B. 6 . C. 5 . D. 3 . Lời giải Chọn C x 1 2 ; 1 Ta có : ' 2 y 3x 4x 7 . y ' 0 7 . x 2; 1 3 y 1 5 ; y 2 1 ; y 1 7 max y 5 . 1;2 N H Ó Câu 31: Cho hàm số 4 2
y 2x 6x có đồ thị (C) . Số giao điểm của đồ thị (C) với đường thẳng y 4 M là TO A. 4 . B. 2 . C. 0 . D. 1. Á N Lời giải V D Chọn B – V
Ta có phương trình hoành độ giao điểm là D C 3 17 2 x (vn) 2 3 17 4 2 4 2
2x 6x 4 2x 6x 4 0 x . 3 17 2 2 x 2
Vậy số giao điểm của đồ thị (C) với đường thẳng y 4 là 2.
Câu 32: Cho hình lập phương ABC . D AB C D
, Gọi là góc giữa hai mặt phẳng ABD và ABC. Tính tan .
https://www.facebook.com/groups/toanvd.vdc Trang 16 NHÓM TOÁN VD – VDC NĂM HỌC 2019 - 2020 A' D' N B' H C' Ó M TO A D Á N V D B C – V 1 2 3 A. tan . B. tan . C. tan . D. tan 2 . D 2 3 2 C Lời giải Chọn D
Gọi O là tâm hình vuông ABCD , ta có AO là hình chiếu vuông góc của AO lên mặt phẳng AO B D ( ABCD) . Khi đó ta có suy ra A O A . A O B D A' D' B' C' N A H Ó D M TO O Á B C N V D AC AB 2 AA 2 AA – V Ta có AO . tan tan A OA 2 . 2 2 2 AO D C
Câu 33: Trong không gian Oxyz , cho hai điểm A1;0;2 và B3;1;3. Đường thẳng AB có phương trình là x 1 y z 2 x 3 y 1 z 2 A. . B. . 2 1 5 2 1 5 x 1 y z 2 x 1 y 1 z 7 C. . D. . 2 1 5 2 1 5 Lời giải Chọn D AB2; 1 ; 5
https://www.facebook.com/groups/toanvd.vdc Trang 17 NHÓM TOÁN VD – VDC NĂM HỌC 2019 - 2020 x 1 2t AB: y t N z 2 5t H Ó M Thay tọa độ điểm 1
;1;7 thỏa mãn nên chon đáp án D. TO Á
Câu 34: Gọi Z là nghiệm phức có phần ảo âm của phương trình z 2
2 1 0 . Môđun của số phức N 0 V z .i bằng 0 D – A. 5 . B. 2 . C. 5 . D. 2 . V D C Lời giải Chọn C z 22 1 0 z 22 1 z 2 i z 2i z 2 i z 2i
z 2 i Z .i 2 i i 2i 1 2i 1 5 . 0 0 N x t H
Câu 35: Trong không gian với hệ tọa độ A 2;0; 3
và đường thẳng : y 1 3t . Ó Oxyz , cho điểm M z 5t TO
Mặt phẳng đi qua A và vuông góc có phương trình là Á A. x 3y z 0 .
B. x 3y z 1 0 . C. 3y z 3 0 .
D. x 3y z 5 0 . N V D Lời giải – V Chọn B D C
Đường thẳng có véc tơ chỉ phương u 1 ;3; 1
Mặt phẳng P vuông góc với đường thẳng nên P có véc tơ pháp tuyến u 1 ;3; 1 .
Mặt phẳng P đi qua A2;0; 3
có phương trình là: 1
x 2 3 y 0 1z 3 0 x 3y z 1 0 hay x 3y z 1 0
Câu 36: Một hình trụ có bán kính đáy là r và có thiết diện qua trục là một hình vuông. Khi đó diện tích
toàn phần của hình trụ đó là A. 2 4 r . B. 2 6 r . C. 2 2 r . D. 2 8 r . Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 18 NHÓM TOÁN VD – VDC NĂM HỌC 2019 - 2020 Chọn B
Thiết diện qua trục của hình trụ là hình vuông nên h d 2r . N H
Diện tích toàn phần của hình trụ là 2 2 2
S 2 rh 2 r 2 r.2r 2 r 6 r . tp Ó M
Câu 37: Có 8 chiếc ghế được kê thành một hàng ngang. Xếp ngẫu nhiên 8 học sinh, gồm 3 học sinh lớp TO
A, 3 học sinh lớp B và 2 học sinh lớp C, ngồi vào hàng ghế đó, sao cho mỗi ghế có đúng một Á a N
học sinh. Xác suất để có đúng 2 học sinh lớp A ngồi cạnh nhau bằng
với a,b , (a;b) 1. V b D
Khi đó giá trị a b là – A. 43 . B. 93 . C. 101. D. 21. V D Lời giải C Chọn A
Không gian mẫu: n 8! 40320 .
Gọi A là biến cố có đúng 2 học sinh lớp A ngồi cạnh nhau. Khi đó A là biến cố: Không có 2
học sinh nào của lớp A ngồi cạnh nhau hoặc 3 học sinh lớp A ngồi cạnh nhau. * Tính n( ) A .
Trường hợp không có 2 học sinh nào của lớp A ngồi cạnh nhau:
+ Xếp 5 học sinh (3 học sinh lớp B, 2 học sinh lớp C) thành hàng ngang có 5! cách. Khi đó tạo
ra 6 vị trí để có thể xếp 3 học sinh lớp A.
+ Chọn 3 vị trí từ 6 vị trí và xếp 3 học sinh lớp A có: 3 C .3! cách. 6 Do đó có 3
5!.C .3! 14400 cách trong trường hợp này. 6
Trường hợp 3 học sinh lớp A ngồi cạnh nhau:
+ Xem 3 học sinh lớp A như một phần tử cùng với 5 học sinh còn lại (3 học sinh lớp B, 2 học N
sinh lớp C) là 6 phần tử. Xếp thành hàng ngang có 6! cách. H Ó
+ Trong bộ 3 học sinh lớp A có 3! cách sắp xếp. M
Do đó có: 6!.3! 4320 cách trong trường hợp này. TO Vậy: n A 18720. Á N n A V 13 13 15 Suy ra: P A P( ) A 1 . D n 28 28 28 – V
Khi đó: a 15,b 28 a b 43. D C
Câu 38: Gọi S là diện tích miền hình phẳng được gạch chéo trong hình vẽ bên. Công thức tính S là
https://www.facebook.com/groups/toanvd.vdc Trang 19 NHÓM TOÁN VD – VDC NĂM HỌC 2019 - 2020 2 1 2 A. S f (x)dx . B. S f (x)dx f (x)dx . 1 1 1 N 1 2 2 H
C. S f (x)dx f (x)dx S f (x)dx Ó . D. . M 1 1 1 T Lời giải O Á Chọn B N V 2 1 2 1 2 D Ta có: S f (x) dx f (x) dx f (x) dx f (x)dx f (x)dx – 1 1 1 1 1 V D (Vì f (x) 0, x 1 ; 1 và f (x) 0, x 1;2 ) C
Câu 39: Cho z , z là hai nghiệm phức của phương trình 2
z 2z 5 0, trong đó z là số phức có 1 2 1
phần ảo âm. Khi đó z 3z bằng 1 2 A. 4 4i . B. 4 4i . C. 4 4i . D. 4 4i . Lời giải Chọn A Phương trình 2
z 2z 5 0 có hai nghiệm z 1 2i, z 1 2 .i 1 2 z 3z 1 2i 3. 1 2i 4 4 .i 1 2
Câu 40: Cho hình chóp đều S.ABCD, SA AB 2a (minh họa như hình bên dưới). Gọi M là trung
điểm của SC. Khoảng cách giữa hai đường thẳng AM và CD bằng N H Ó M TO Á N V D – VDC 2 2a 2 10a 2 22a A. . B. . C. . D. a . 3 9 11 Lời giải Chọn C
https://www.facebook.com/groups/toanvd.vdc Trang 20 NHÓM TOÁN VD – VDC NĂM HỌC 2019 - 2020 N H Ó M TOÁN VD – VDC AC 2a 2
ABCD là hình vuông AO a 2. 2 2
SO SA AO a a 2 2 2 2 2 2 a 2.
Gắn hệ trục tọa độ với O là gốc tọa độ, OB nằm trên trục Ox, OC nằm trên trục Oy, SO nằm trên trục O . z
Ta có A0; 2a;0, C 0; 2a;0, D 2a;0;0, S 0;0; 2a. 2a 2a N
Vì M là trung điểm SC M 0; ; . H 2 2 Ó M TO
3 2a 2a AM 0; ; , AC 0;2 2a;0
CD 2a; 2a;0, . Á 2 2 N V 2 2 2 2 D AM ,CD a ; a ;3a AM ,CD 11a . – V
2 2 2 3 D AM ,CD .AC a .0
a .2 2a3a .0 2 2a . C
3 AM ,CD.AC 2 2a d AM CD 2 22 , . a 2 AM ,CD 11a 11 Câu 41: Cho hàm số 4 2
y ax bx c , với a,b, c là các số thực, a 0 . Biết lim y , hàm số có 3 x
điểm cực trị và phương trình y 0 vô nghiệm. Hỏi trong ba số a,b, c có bao nhiêu số dương. A. 0 . B. 3 . C. 2 . D. 1. Lời giải Chọn C
https://www.facebook.com/groups/toanvd.vdc Trang 21 NHÓM TOÁN VD – VDC NĂM HỌC 2019 - 2020 b c 4
lim y lim ax 1 a 0 2 4 x x x x
Hàm số có 3 điểm cực trị ab 0 b 0 . N H
Phương trình y 0 vô nghiệm, suy ra đồ thị nằm phía trên trục Ox y 0 c 0 . Ó M
Vậy có hai số dương đó là a, c . TO Á Câu 42: Cho hàm số y
f x có đạo hàm liên tục trên và có bảng biến thiên của f x như sau: N V D – V D C
Có bao nhiêu số nguyên của m để hàm số g x f x mx nghịch biến trên khoảng ; 3 ,
đồng thời đồng biến trên khoảng 4; ? A. 4 . B. 3 . C. 5 . D. 6 . Lời giải Chọn A
Ta có gx f x m
Để hàm số nghịch biến trên khoảng ; 3 thì gx 0, x ;
3 f x , m x ; 3 m 3 N H
Để hàm số đồng biến trên khoảng 4; thì Ó M g x 0, x
4; f x , m x
4; m 7 . TO
m3;7 m3;4;5;6;
7 . Vậy có 5 giá trị nguyên của m . Á N
Câu 43: Số ca nhiễm Covid-19 trong cộng đồng ở một tỉnh vào ngày thứ x trong một giai đoạn được V r x D
tính theo công thức f x . .
A e trong đó A là số ca nhiễm ngày đầu của giai đoạn, r là tỉ lệ –
gia tăng số ca nhiễm hằng ngày của giai đoạn đó và trong cùng một giai đoạn thì r không đổi. V D
Giai đoạn thứ nhất tính từ ngày tỉnh đó có 9 ca bệnh đầu tiên và không dùng biện pháp phòng C
chống lây nhiễm nào thì đến ngày thứ 6 số ca bệnh của tỉnh là 180 ca. Giai đoạn hai (kể từ
ngày thứ 7 trở đi) tỉnh đó áp dụng biện pháp phòng chống lây nhiễm nên tỷ lệ gia tăng số ca
hằng ngày giảm đi 10 lần so với giai đoạn trước. Đến ngày thứ 6 của giai đoạn hai thì số ca
bệnh của tỉnh đó gần nhất với số nào sau đây? A. 242 . B. 90 . C. 16 . D. 422 . Lời giải Chọn A
Gọi r là tỉ lệ gia tăng số ca nhiễm của giai đoạn một. 1
Gọi A là số ca nhiễm ngày đầu của giai đoạn một. 1 Theo giả thiết ta có: 6. 1r 6. 1 180 . 180 9. r A e e r 0,5 1 1
https://www.facebook.com/groups/toanvd.vdc Trang 22 NHÓM TOÁN VD – VDC NĂM HỌC 2019 - 2020
Gọi r là tỉ lệ gia tăng số ca nhiễm của giai đoạn hai. 2 r Suy ra 1 r 0,05 . 2 10 N H
Đến ngày thứ 6 của giai đoạn hai thì số ca bệnh của tỉnh đó Ó 6. 2 r 6.0,05 M 180.e 180.e 243. T Câu 44: Cho hình hộp ABC . D A B C
D có thể tích V . Một mặt phẳng Q đi qua trọng tâm của tam O Á
giác ABD và trung điểm CC ' đồng thời Q song song với BD . Mặt phẳng Q chia khối N V hộp ABC . D A B C
D thành hai phần. Thể tích của phần chứa A bằng D – 181 187 185 191 A. V . B. V . C. V . D. V . V 216 216 216 216 D C Lời giải Chọn C N H Ó M TO S AI AH 4 4 4 1 2 Ta có AIH . S S . S S S AB AC 9 AIH 9 ABC 9 2 ABCD 9 ABCD Á ABC N 1 1 V S S S S . IDQ HBL AHK ABCD D 4 18 – V
Gọi h là chiều cao của hình hộp. D C 1 h h h 7 1 4 Ta có V . .S . S S S S V NCLQ CLQ 2 BCDIH HBL 2 ABCD ABCD 3 2 6 6 9 18 27 1 1 LS 1 1 1 h 1 V d S, ABCD .S . d N, ABCD . S . . . S S .LBH HBL 3 3 LN 18 ABCD 3 4 2 18 ABCD . 1 V . h S 432 ABCD 432
Gọi V là thể tích cần tìm. 1 4 V 185 Suy ra V V V 2V V V 2 V . 1 N.CLQ S .HBL 27 432 216
https://www.facebook.com/groups/toanvd.vdc Trang 23 NHÓM TOÁN VD – VDC NĂM HỌC 2019 - 2020
Câu 45: Cho hàm số y f x có đạo hàm và liên tục trên đoạn 0; 1 thoả mãn
f 0 2 và f x f x 2 x 2 ' .e 2x,x 0; 1 . N 1 H Tính giá trị của f x . dx Ó M 0 TO 5 7 A. . B. 3 . C. . D. 2 . Á 3 3 N Lời giải V D Chọn C – x x x f x x f x x f x 2 2 x 2 V Ta có: f ' x .e e .2x f ' x .e dx e .2xdx e e C D C
Thay x C f x 2 0 0 x 2 1 7 Suy ra f x dx 3 0
Câu 46: Xét các số thực dương a,b, c 1 với a b thoả 4log c log c 25log . c Giá trị nhỏ nhất a b ab
của biểu thức P log a log c log b bằng b a c 17 A. 5 . B. 3 . C. 8 . D. . 2 Lời giải Chọn B x log a c 1 Đặt log c , với x y 0 . y log ab b x y c N H 1 1 1 x y Ó
Ta có : 4log c log c c a b 4 25log 4 25. ab x y x y y 4x (loaïi) M TO x 1 1 Á Suy ra P . y Với x 4y : P 4 y 3 . y x 4 y N V D
Vậy giá trị nhỏ nhất của biểu thức P log a log c log b bằng 3. b a c – V
Câu 47: Cho hàm số y f (x) có đồ thị như hình vẽ bên. D C
https://www.facebook.com/groups/toanvd.vdc Trang 24 NHÓM TOÁN VD – VDC NĂM HỌC 2019 - 2020 N H Ó M TOÁN VD – VDC 1 x
Có bao nhiêu số nguyên của tham số m để phương trình f 1 x m có nghiệm thuộc 3 2 [-2; 2]? A. 7 . B. 6. C. 8 . D. 5 . Lời giải Chọn C x Đặt t 1 ta có: 2 N H
Vì x [ 2;2] t [0;2] Ó M 1
Và f t 2(t 1) . m TO 3 1 Á Xét hàm g(t)
f t 2(t 1) trên đoạn [0;2] : N 3 V 1 f '(t) 6 D g '(t) f 't 2 0 t [0;2] – 3 3 V 1 D Như vậy hàm g(t)
f t 2(t 1) là hàm đồng biến trên [0;2] C 3
Để phương trình ban đầu có nghiệm x [-2;2] thì phương trình phải có nghiệm t [0; 2]. Khi đó: min g(t) m max g(t) [0;2] [0;2] g(0) m g(2) 1 1
f (0) 2(0 1) m f (2) 2(2 1) 3 3 1 1
(4) 2 m .6 2 3 3 10 m 4 3
https://www.facebook.com/groups/toanvd.vdc Trang 25 NHÓM TOÁN VD – VDC NĂM HỌC 2019 - 2020
Vì m Z nên m 3;2;1;0;1;2;3; 4 .
Vậy có tất cả 8 giá trị nguyên m thỏa mãn yêu cầu bài toán. N
Câu 48: Có bao nhiêu bộ số (a; ;
b c) với a,b 1;0;1;2;3;4;
5 và c 1 là số thực thỏa mãn H Ó ? M log (b c) 2log c a 10 TO A. 8 . B. 10 . C. 6 . D. 12. Á Lời giải N V Chọn D D b c 0 b c 0 –
Theo giả thiết: c 1 V log (b c) 2log c 0 a 1 a 10 D t C b c a
Đặt log (b c) 2log c t(t 0) , ta thu được hệ: a 10 c t 10 t Suy ra: t a b 10
Trường hợp 1: a 10 a 2; 3 t Khi đó: t
b a 10 0(t 0) b 1
Trường hợp 2: a 10 a 4; 5 t Khi đó: t
b a 10 0(t 0) b1;2;3;4; 5
Với mỗi giá trị dương của t ta thu được 1 giá trị của c.
Vậy có tất cả 12 bộ số (a; ;
b c) thỏa mãn yêu cầu bài toán.
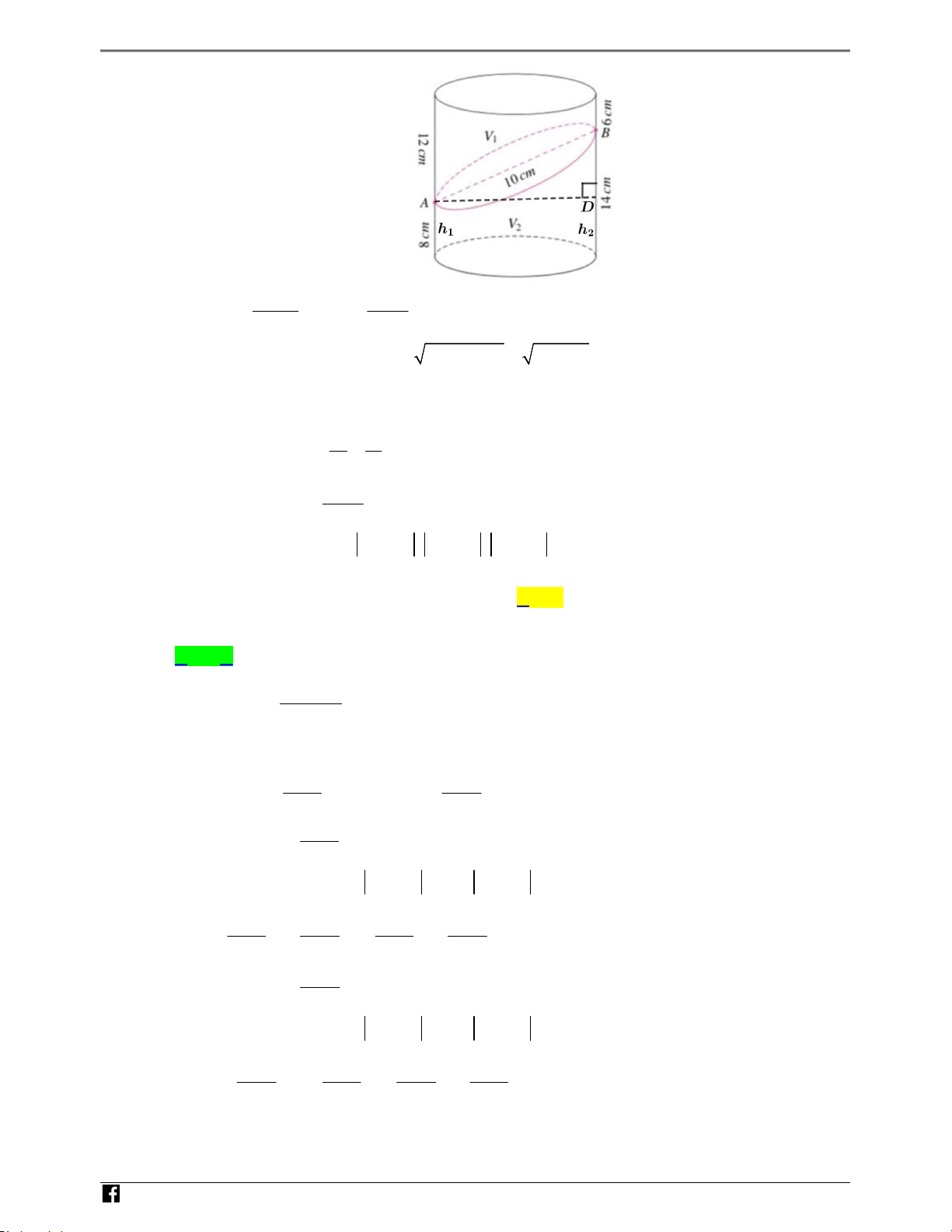
Câu 49: Cho khối trụ có chiều cao 20cm . Cắt khối trụ bởi một mặt phẳng được thiết diện là hình elip có N H
độ dài trục lớn bằng 10cm. Thiết diện chia khối trụ ban đầu thành hai nửa, nửa trên có thể tích Ó M
V , nửa dưới có thể tích V (như hình vẽ). Khoảng cách từ một điểm thuộc thiết diện gần đáy 1 2 TO
dưới nhất và điểm thuộc thiết diện xa đáy dưới nhất tới đáy dưới là 8cm và 14cm. Tính tỉ số Á V1 N . V V 2 D – V D C 6 9 11 9 A. . B. . C. . D. . 11 20 20 11 Lời giải Chọn D
https://www.facebook.com/groups/toanvd.vdc Trang 26 NHÓM TOÁN VD – VDC NĂM HỌC 2019 - 2020 N H Ó M TO Á N V D – h h 8 14 2 1 2 2 2 V V R R 11 R . 2 D 2 2 C AED vuông tại D có 2 2 2 2 2R=AD E A D E
10 6 8 R 4 . 2 V r .h 320 2 V 4 .11 176 2 V 9 1 V V V 144 1 2 V 11 2 m
Câu 50: Cho hàm số f x 2
. Gọi S là tập hợp các số nguyên dương m 7 sao cho với mọi bộ 2x 1 số thực a, , b c 2;
3 thì ln f a , ln f b , ln f c là độ dài ba cạnh của một tam giác. Tổng
tất cả các phần tử của S là A. 10 . B. 15 . C. 16 . D. 14 . Lời giải Chọn C N H 1 2m Ó Ta có f x M 2x 2 1 TO Vì m ,
m 7 f x 0 x 2; 3 Á N 3 m 2 m min f x 0; max f x 0 . V 2; 3 7 2; 3 5 D – V 3 m Trường hợp 1: ln 0 m 4 . 7 D C
Yêu cầu bài toán 2 min ln f x max ln f x 2; 3 2; 3 2 3 m 2 m 3 m 2 m 2ln ln 2
5m 19mp 53 0 m {6;7} 7 5 7 5 2 m Trường hợp 2: ln 0 m 3 . 7
Yêu cầu bài toán 2 min ln f x max ln f x 2; 3 2; 3 2 2 m 3 m 2 m 3 m 2 ln ln m {1;2} . 5 7 5 7
Vậy tổng các giá trị của m là 16.
-------------------- HẾT --------------------
https://www.facebook.com/groups/toanvd.vdc Trang 27
Document Outline
- de-thi-thu-thpt-2020-mon-toan-lan-4-truong-chuyen-quang-trung-binh-phuoc
- TOANVDC.EDU.VN-THI-THỬ-CHUYÊN-QUANG-TRUNG-L4-NĂM-2020