Đề thi thử THPT Quốc gia 2019 môn Toán sở GD và ĐT Bắc Ninh

Đề thi thử THPT Quốc gia 2019 môn Toán sở GD và ĐT Bắc Ninh, đề được biên soạn với hình thức và cấu trúc đề tương tự với đề minh họa THPT Quốc gia môn Toán năm 2019 do Bộ Giáo dục và Đào tạo đề xuất

23 12 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Trang 1/6 - Mã đề 101

SỞ GDĐT BẮC NINH

PHÒNG QUẢN LÝ CHẤT LƯỢNG

¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯

ĐỀ THI THỬ THPT QUỐC GIA NĂM 2019

Bài thi: Toán

Thời gian làm bài: 90 phút (không kể thời gian giao đề)

(Đề có 50 câu trắc nghiệm)

¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯

Họ và tên thí sinh:..................................................... Số báo danh :...................

Câu 1. Trong không gian với hệ tọa độ

Oxyz

, phương trình mặt phẳng

 



đi qua điểm

 

0; 1; 0A 

;





2; 0; 0

;

 

0; 0; 3C

là

213

xyz



. B.

2 13

xyz

 



. C.

123

x yz





. D.

2 13

xyz

 



Câu 2. Gọi

là hai nghiệm phức của phương trình

2 3 30zz 

. Giá trị của biểu thức

zz

bằng

. B.



. C.

. D.



Câu 3. Tập xác định của hàm số

 

32 3yx x x



   

là









; \3D

   

. B.

   

 

;1 2; \ 3

D     

 

; \ 1; 2D    

. D.

   

;1 2;D     

Câu 4. Cho hàm

 

y fx

có

 

22f 

 

35f 

; hàm số

 

y fx





liên tục trên

2; 3







. Khi đó

 

dfxx





bằng

. B.

3

. C.

. D.

Câu 5. Bất phương trình

   

log 3 2 log 6 5xx 

có tập nghiệm là

 

;ab

. Tổng

ab

bằng

. B.

. C.

. D.

Câu 6. Cho hàm số

 

y fx

có bảng biến thiên như sau:

Tập tất cả các giá trị của tham số

để phương trình

 

fx m

có ba nghiệm phân biệt là

 

4; 

. B.

 

;2 

. C.

2; 4









. D.

 

2; 4

Câu 7. Số đường tiệm cận của đồ thị hàm số





là

. B.

. C.

. D.

Câu 8. Hàm số

34yx x 

nghịch biến trên khoảng nào sau đây?



. B.

 

;2 

. C.

 

0; 

. D.

 

2; 0



1













2



Mã đề 101

Trang 2/6 - Mã đề 101

-1

-3

-4

Câu 9. Trong không gian với hệ trục tọa độ

Oxyz

, cho hai vectơ





4; 5; 3a

 



 

2; 2; 1b 



. Tìm tọa độ

của vectơ

2xa b

 





2; 3; 2

x 



. B.

 

0; 1; 1x 



. C.





0; 1; 1

x 



. D.

 

8; 9;1x 



Câu 10. Họ nguyên hàm của hàm số

 

cos 2fx x

là

sin 2

cos 2 d

xx C



. B.

cos 2 d sin 2xx x C



sin 2

cos 2 d

xx C

 



. D.

cos 2 d 2 sin 2xx x C



Câu 11. Cho hàm số



với

01a

. Mệnh đề nào sau đây SAI?

A. Đồ thị hàm số

ya

và đồ thị hàm số

log

yx

đối xứng nhau qua đường thẳng



B. Hàm số

ya

có tập xác định là



và tập giá trị là

 

0; 

C. Hàm số

ya

đồng biến trên tập xác định của nó khi

1a 

D. Đồ thị hàm số

ya

có tiệm cận đứng là trục tung.

Câu 12. Đường cong trong hình vẽ bên là đồ thị của một hàm số trong

bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây.

Hỏi đó

là h

àm số nào?

2yx x

. B.

yx x

  

3yx x

. D.

23yx x

 

Câu 13. Cho hình lăng trụ

.ABC A B C



có đáy

ABC

là tam giác

đều cạnh





. Biết rằng hình chiếu vuông góc của



lên

 

ABC

là trung điểm

. Thể tích của khối lăng trụ

.ABC A B C



là

. B.

3 2

. C.

. D.

Câu 14. Trong không gian với hệ tọa độ

Oxyz

, phương trình đường thẳng

đi qua điểm

 

1; 2; 1A

và

vuông góc với mặt phẳng

 

: 2 10Px y z 

có dạng

121

1 21

xyz







. B.

1 21

x yz







121

xyz





. D.

2 42

x yz







Câu 15. Trong các hàm số

       

log ; ; ; 3

f x xg x hx x k x











   













có bao nhiêu hàm số

đồng biến trên



. B.

. C.

. D.

Câu 16. Số giá trị nguyên của tham số

để phương trình để phương trình

 

sin 1 cos 2 1xm x m  

có

nghiệm là

. B.

. C.

. D.

Câu 17. Một hình nón có độ dài đường sinh bằng đường kính đáy. Diện tích hình tròn đáy của hình nón

bằng

9

. Tính đường cao

của hình nón.

h 

. B.

33h 

h 

. D.

3h 

Trang 3/6 - Mã đề 101

Câu 18. Trong không gian, cho các mệnh đề sau:

Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.

.II

Hai mặt phẳng phân biệt chứa hai đường thẳng song song cắt nhau theo giao tuyến song song với hai

đường thẳng đó.

.III

Nếu đường thẳng

song song với đường thẳng

, đường thẳng

nằm trên mặt phẳng

 

thì

song

song với

 

.IV

Qua điểm

không thuộc mặt phẳng

 



, kẻ được đúng một đường thẳng song song với

 



Số mệnh đề đúng là

. B.

. C.

. D.

Câu 19. Tập hợp điểm biểu diễn số phức

thỏa mãn điều kiện

12 1zi 

là

A. đường tròn

 

1; 2I

, bán kính

1R 

. B. đường tròn

 

1; 2I 

, bán kính

1R 

C. đường tròn

 

1; 2I 

, bán kính

R 

. D. đường tròn

 

1; 2I 

, bán kính

1R 

Câu 20. Kí hiệu

là số các tổ hợp chập

của

phần tử

 

1 kn

. Mệnh đề nào sau đây đúng?

 

kn k





. B.

 





. C.

 

nn k





. D.

 





Câu 21. Cho hàm số

 

y fx

liên tục, đồng biến trên đoạn

;.ab







Khẳng định nào sau đây đúng?

A. Hàm số đã cho có cực trị trên đoạn

;.ab







B. Hàm số đã cho có giá trị lớn nhất, giá trị nhỏ nhất trên khoảng





C. Phương trình

 

0fx

có nghiệm duy nhất thuộc đoạn

;.ab







D. Hàm số đã cho có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn

;.ab







Câu 22. Cho hình chóp

.S ABCD

có đáy là hình bình hành. Gọi

là trung điểm của

. Mặt

phẳng

 

MNCD

chia hình chóp đã cho thành hai phần. Tỉ số thể tích hai phần là (số bé chia số lớn)

. B.

. C.

. D.

Câu 23. Trong không gian với hệ tọa độ

Oxyz

, mặt cầu

 

có tâm

 

3; 3; 1I



và đi qua điểm

 

5; 2; 1A 

có phương trình là



    

2 22

5 2 15xyz

   

. B.

     

2 22

3 3 1 25xyz   

     

2 22

3 3 15xyz   

. D.

 

   

2 22

3 3 15xyz   

Câu 24. Cho lăng trụ tam giác đều

.ABC A B C



có độ dài cạnh đáy bằng

, góc giữa đường thẳng



và mặt phẳng

 

ABC

bằng

60º

. Tính thể tích

của khối trụ ngoại tiếp lăng trụ đã cho.

3Va



. B.





. C.





. D.





Câu 25. Cho hàm số

 

y fx

liên tục trên



, có đạo hàm

  



() 1 2fx x x x



 

. Hỏi hàm số

 

y fx

có bao nhiêu điểm cực trị?

. B.

. C.

. D.

Câu 26. Tích giá trị lớn nhất và giá trị nhỏ nhất của hàm số



trên đoạn







bằng

. B.

. C.

. D.

Trang 4/6 - Mã đề 101

Câu 27. Cho hình chóp

.S ABC

có đáy là tam giác vuông tại

, biết





SA ABC

và

2 , 3AB a AC a

4SA a

. Tính khoảng cách

từ điểm

đến mặt phẳng

 

SBC

d 

. B.

6 29



. C.

12 61

d 

. D.

d 

Câu 28. Cho hàm số

 

,y fx y gx

liên tục trên đoạn

 

;ab a b









. Hình phẳng

giới hạn bởi đồ thị

hai hàm số

 





y fx y gx



và hai đường thẳng

,x ax b

có diện tích là

   

S fx gx x





. B.

   

S fx gx x











   

S f x gx x



. D.

   

S fx gx x



Câu 29. Số phức

58zi

có phần ảo là

. B.

8

. D.

8i

Câu 30. Biểu thức





0xxx

viết dưới dạng lũy thừa với số

mũ hữu tỉ là

. B.

. D.

Câu 31. Cho

 

y fx



là

hàm đa thức bậc

, có đồ thị hàm số

 

y fx





như hình vẽ. Hàm số

 

5 2 4 10yf x x x 

đồng

biến trong khoảng nào trong các khoảng sau đây?

 

3; 4

. B.









































. D.





















Câu 32. Cho hàm số





y fx

liên tục trên

 

\ 1; 0

thỏa mãn

 

1 2 ln 2 1f 



 



 

12 1xx f x x fx xx



   

 

\ 1; 0x 



. Biết





2 ln 3f ab

, với

,ab

là hai số hữu

tỉ. Tính

Ta b



. B.

T 

. C.

T 

. D.

0T 

Câu 33.

Cho hàm số bậc ba

 

y fx

có đồ thị như hình vẽ. Có bao

nhiêu giá trị nguyên của tham số

thuộc đoạn

0; 9







sao cho bất

phương trình

         

2 16.2 4 16 0

f x fx m f x fx m fx 

  

có nghiệm





1; 1x 

. B.

. D.

Câu 34. Cho

,,,abcd

là các số nguyên dương,

1, 1ac

thỏa mãn

log ,log

bd

và

9ac

. Khi đó,

bd

bằng

(

)

-2

-1

. B.

. C.

. D.

Trang 5/6 - Mã đề 101

Câu 35. Cho hàm số

–8 8yx x x

có đồ thị





và hàm số





8y x ax b

  

(với

,ab 

) có

đồ thị

 

. Biết đồ thị hàm số

 

cắt

 

tại

điểm có hoành độ nằm trong đoạn

1; 5









. Khi

đạt giá

trị nhỏ nhất thì tích

bằng

729

. B.

375

. C.

225

. D.

384

Câu 36. Gọi

là tập các số tự nhiên có

chữ số đôi một khác nhau. Lấy ngẫu nhiên ra từ

hai số. Tính

xác suất để lấy được hai số mà các chữ số có mặt ở hai số đó giống nhau.

5823

. B.

5823

. C.

7190

. D.

1941

Câu 37. Cho hàm số

 

y fx

liên tục trên



và

   

2 16, d 4f fx x



. Tính

I xf x



























144

I 

. B.

12I 

. C.

112I 

. D.

28I 

Câu 38. Cho tứ diện

ABCD

có



90ºDAB CBD

;



; 5; 135AB a AC a ABC 



. Biết góc giữa

hai mặt phẳng

   

,ABD BCD

bằng



. Thể tích của tứ diện

ABCD

là

. B.

. C.

. D.

Câu 39. Trong mặt phẳng với hệ tọa độ

Oxy

, cho hình

 

giới hạn bởi các đường

2,yx

2, 4y xx 

; hình





là tập hợp tất cả các điểm

 

;M xy

thỏa mãn các điều kiện:

16;xy

   

24;24x yx y   

. Khi quay









quanh

ta được các khối tròn

xoay có thể tích lần lượt là

,VV

. Khi đó, mệnh đề nào sau đây là đúng?

2VV

. B.

VV

. C.

48VV 



. D.

4VV

Câu 40. Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

   

1; 2;1 , 3; 4; 0AB

, mặt phẳng

 

: 46 0P ax by cz 

. Biết rằng khoảng cách từ

,AB

đến mặt phẳng

 

lần lượt bằng

và

. Giá

trị của biểu thức

T abc 

bằng

3

. B.

6

. C.

. D.

Câu 41. Cho hình chóp

.S ABC

có

vuông góc với

 

ABC



, 2, 45º

AB a AC a BAC 

. Gọi

,BC

lần lượt là hình chiếu vuông góc của

lên

,SB SC

. Thể tích khối cầu ngoại tiếp hình chóp

.A BCC B

bằng

a

. B.

2a

. C.

a

. D.



Câu 42. Cho các số phức

,zw

khác

thỏa mãn

0zw

và

13 6

z w zw





. Khi đó

bằng

. B.

. C.

. D.

Câu 43. Ông Nam dự định gửi vào ngân hàng một số tiền với lãi suất

6, 6%

/năm. Biết rằng nếu không rút

tiền khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho năm tiếp

theo. Tính số tiền tối thiểu

triệu đồng

 

x  

ông Nam gửi vào ngân hàng để sau

năm số tiền lãi đủ

mua một chiếc xe gắn máy trị giá

triệu đồng.

191

triệu đồng. B.

123

triệu đồng. C.

124

triệu đồng. D.

145

triệu đồng.

Trang 6/6 - Mã đề 101

Câu 44. Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

112

12 1

xyz







và mặt phẳng

 

:2 2 1 0P xy z 

. Gọi



là hình chiếu của đường thẳng

lên mặt phẳng

 

, vectơ chỉ phương

của đường thẳng



là

 

5; 16; 13u 

 

. B.

 

5;4;3u 

 

. C.

 

5;16; 13u

 

. D.





5;16; 13

u 



Câu 45. Trong không gian với hệ tọa độ

Oxyz

, cho điểm

     

4;0;0 , 0;4;0 , 0;0;A B Sc

và đường thẳng

111

112

xyz





. Gọi



lần lượt là hình chiếu vuông góc của

lên

,SA SB

. Khi góc giữa

đường thẳng

và mặt phẳng





OA B



lớn nhất, mệnh đề nào sau đây đúng?

 

8; 6c  

. B.





9; 8

 

. C.

 

0; 3c 

. D.

17 15

;









 













Câu 46. Cho hàm số





y fx



có đồ thị như hình

vẽ. Biết tất cả các điểm cực trị của hàm số

 

y fx



là

2; 0; 2; ; 6a

với

46a

. Số điểm

cực trị của hàm số

 

3y fx x



là

. B.

. D.

Câu 47. Cho hai số thực

,xy

thỏa mãn

(

)

-2









 



2 32

log 8 16 log 5 1 2 log log 2 8 .

yy x x y





     





Gọi

là tập các giá trị nguyên của tham số

để giá trị lớn nhất của biểu thức

P xym 

không

vượt quá

. Hỏi

có bao nhiêu tập con không phải là tập rỗng?

2047

. B.

16383

. C.

16384

. D.

Câu 48. Cho tích phân



  

2 ln 1 d ln 2I x x xa

  



trong đó

là các số nguyên dương.

Tổng

ab

bằng

. B.

. C.

. D.

Câu 49. Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

   

: 1 2 10P mx m y z m   

, với

là tham số. Gọi

 



là tập hợp các điểm

là hình chiếu vuông góc của điểm

 

3; 3; 0H

trên

 

. Gọi

,ab

lần lượt là khoảng cách lớn nhất, khoảng cách nhỏ nhất từ

đến một điểm thuộc

 



. Khi đó,

ab

bằng

. B.

. C.

. D.

Câu 50. Cho số phức

thỏa mãn

 

1 1 3 32iz i  

. Giá trị lớn nhất của biểu thức

2 6 23

Pz i z i  

bằng

. B.

 

15 1 6

. C.

. D.

10 3 15

------ HẾT ------

Câu

101 102

103 104 105 106 107 108

109 110

111 112

D A D A A D A A

A C

D B B C C A A B

D B

B B C

A A

D D D D A

A B B

D D

D C C D B

D D A

A B

C C C B D

D B D

A C

B B A A A

D C C

D A

C D B C A

D C C

A C

A C B D C

B C

B B

C A

C B B D

A D

A B

B C

C A D D

D C

C C

B C

C A

D A C A A B A C A

B A

B D D A A A C D D

C A

D D D A B A A B A

D B

D C A D C D A C C

D B

C C C A C D B A D

C B

B D A C C A B B C

B C

B C A A B B D C C

A C

C D C A B D D B D C C A

A D A D

D B C D B D A A

D C

A A A D B B

C B B C

A C

A C B C D D

D C B A

D B

C A C C A A

C B A C

D A

A B D D A C

D C D C

A C

D C B C A A

A D A A

A A

A B D C A A

A B B B

C A

C C A C C B

C B C A

A A

D B D B B D

C D D C

B D C C A C

A D B B B

D C C B D B

B C D D A

B A A A A C

D A B D C

A D C C A D C B

A A D

A D A B D D D D

A C A

C D C C C C A D

B B B

C C C C D D D B

B A A

A B A D C C A A

A B C

C A C

C B D C D A A D C

D A B

B A B C D C D B D

D D C

B C B C C C D B B

B D A

A D A B A C B B D

D B A

C A B C B B D B D

D B C

D A B C A A A A A

C B B

D B D B C A B A C

D D A

D A C A D B A C C

D C C

B C A D A B C D D

C A A D D C D A A A B B

B A D C B A A C B A

D C

D D B A B C A D B D C D

D C D D D B C B D A C B

C A A C B B C A C D C C

ĐÁP ÁN TOÁN

Câu

113 114

115 116 117 118 119 120

121 122

123 124

C B C D B C D D

C D

C D A B A A D D

B D

C A D

A B

D C B A A

C D D

A C

C D B D C

B B B

B A

D D B D B

A A B

A C

A C D B D

D C D

B C

C B D B A

A A B

C B

B C C C A

A A

B C

D A D D

D C

B D

D A B A

D B

B C

C D

D A

D A B C C C C A B

D C

B C A B B B A C A

C D

C B B C C C B A D

C A

C D D B A D A A C

D D

D A A A B D A C B

B D

B C A D D C B C B

D C

C B A B D B D D B

C B

D D D D A A D A C B A B

D A D D

D B C A A A D D

B C

D A A C C D

B A B A

D B

C A C A B B

B D B B

A C

C B D C B D

D B B D

B A

A D C C A B

A D A B

C C

A C D D C D

D D B A

C D

D A C C A C

A A A C

D D

D D C D B C

B B B D

C C

C B A C B D

D C B A

D B C B A C

C D D A C

D A D D A D

C C B B C

C C C A C B

C C C B B

B A C D A B A B

A C B

A A C C B B C D

A D A

C C C B D A D A

A C D

C A D C B B B B

C A A

B B D A A C B D

A D B

C B B

A D B A C A A D B

C B C

A D C A B A C B C

D D A

B B D C D A C C C

D D B

A D A C A D B D C

A D D

B C A A B A D B A

B B D

C A B A D A B C A

A D B

B A B B B B C D D

A A D

A A D C A D C C B

B A A

D A B B C B C B D

B B D A A B C D C D C C

B D C D C D A C D D

A D

C C D D C A A D A C C D

D A D C B C D D A D B A

C D C B D C A B B C C C

ĐÁP ÁN TOÁN

NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019

https://www.facebook.com/groups/toanvd.vdc Trang 8

NHÓM TOÁN VD – VDC

BẢNG ĐÁP ÁN

1.D 2.D 3.B 4.A 5.D 6.D 7.D 8.D 9.B 10.A

11.D 12.D 13.B 14.D 15.D 16.C 17.B 18.B 19.C 20.A

21.D 22.A 23.D 24.D 25.A 26.A 27.C 28.A 29.B 30.D

31.B 32.A 33.A 34.A 35.B 36.A 37.C 38.D 39.D 40.B

41.D 42.D 43.C 44.D 45.D 46.B 47.B 48.D 49.D 50.C

LỜI GIẢI CHI TIẾT

Câu 1.

Trong không gian với hệ tọa độ

, phương trình mặt phẳng





đi qua điểm





0; 1;0A  ;



2;0;0B ;





0;0;3C là

213



. B.

213

xyz





. C.

123

xyz





. D.

213





Lời giải

Chọn D

Câu 2.

Gọi

là hai nghiệm phức của phương trình

2330zz. Giá trị của biểu thức

zz

bằng

. B.



. C.

. D.



Lời giải

Chọn D

Vì

,zz là hai nghiệm của phương trình

2330zz

nên theo viet ta có

















Mà



12 12 12

339

22.

224

zz zz zz



    





Câu 3. Tập xác định của hàm số



32 3yx x x





là:









;\3D 

. B.













;1 2; \ 3D   



;\1;2D 

. D.

 

;1 2;D   

Lời giải

Chọn B

Ta có hàm số xác định khi

320































Suy ra tập xác định













;1 2; \ 3D   

NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019

https://www.facebook.com/groups/toanvd.vdc Trang 9

NHÓM TOÁN VD – VDC

Câu 4. Cho hàm số





yfx

có



22f 





35f 

; hàm số



x



liên tục trên





2;3

. Khi đó



fxdx





bằng:

. B.

3

. C.

. D.

Lời giải

Chọn A

Ta có

'( ) ( ) (3) (2) 5 2 3fxdx fx f f



Câu 5. Bất phương trình

 

log32log65

x 

có tập nghiệm là





;ab

. Tổng

ab

bằng

. B.

. C.

. D.

Lời giải

Chọn D

Bất phương trình đã cho tương đương với:

65 0

3265

























Vậy bất phương trình có tập nghiệm









, suy ra:

















Câu 6. Cho hàm số





yfx có bảng biến thiên như sau:

Tập tất cả các giá trị của tham số

m để phương trình



xm

có ba nghiệm phân biệt là



4;  . B.





;2  . C.





2; 4 . D.





2; 4 .

Lời giải

Chọn D

Số nghiệm của phương trình





xm bằng số giao điểm của đồ thị hàm số





yfx với

đường thẳng

m

Từ bảng biến thiên suy ra phương trình có ba nghiệm phân biệt khi

24m 

Câu 7. Số đường tiệm cận của đồ thị hàm số





là

NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019

https://www.facebook.com/groups/toanvd.vdc Trang 10

NHÓM TOÁN VD – VDC

A. 2 . B. 4 . C.

. D. 1.

Lời giải

Chọn D

Tập xác định của hàm số

D  

Có:

lim lim 0 lim

xx x

  







Đồ thị hàm số có đường tiệm cận ngang

0y 

Câu 8. Hàm số

34yx x  nghịch biến trên khoảng nào sau đây?

A.  . B.





;2 

. C.





0; 

. D.





2;0

Lời giải

Chọn D

Tập xác định của hàm số

D  

Có:

'3 6;'0

yxxy





 







Dấu của









'0 ;2 0;yx ;





'0 2;0yx

Câu 9. Trong không gian với hệ trục tọa độ

Oxyz

, cho hai vectơ





4;5; 3a  







2; 2;1b 



. Tìm tọa

độ của vectơ

ab

 





2;3; 2x 



. B.



0;1; 1x 



. C.



0; 1;1x 



. D.



8;9;1x 



Lời giải

Chọn B









4;5; 3

2. 0;1; 1

2. 4; 4;2

xa b



 



  











 



 Vậy



0;1; 1x 



Câu 10. Họ nguyên hàm của hàm số



cos 2

xx là:

sin 2

cos 2 d

xC



. B. cos 2 d sin 2

xxC



sin 2

cos 2 d

xC 



. D. cos 2 d 2sin 2

xxC



Lời giải

Chọn A

Cách 1



Vì

 

sin 2 2.cos 2

Cxfx 

nên B sai.

 Vì



sin 2 1

.2.cos 2 cos 2

Cxxfx



    





nên C sai.

NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019

https://www.facebook.com/groups/toanvd.vdc Trang 11

NHÓM TOÁN VD – VDC

-1

-3

-4

 Vì

 

2.sin 2 2.2.cos 2 4.cos2

Cxxfx  

nên D sai.

 Vì



sin 2 1

.2.cos 2 cos 2

Cxxfx



  





nên họ nguyên hàm của hàm số



cos 2

xx là

sin 2

cos 2 d

xC



Cách 2





cos2 d . cos2 .d 2 .sin2

xxxxC



 Vậy họ nguyên hàm của hàm số



cos 2

xx là

sin 2

cos 2 d

xC



Câu 11. Cho hàm số

a với

01a

. Mệnh đề nào sau đây sai?

A. Đồ thị hàm số

a và đồ thị hàm số log

x đối xứng nhau qua đường thẳng .

x

B. Hàm số

ya có tập xác định là  và tập giá trị là

(0; )

C. Hàm số

ya đồng biến trên tập xác định của nó khi

1a 

D. Đồ thị hàm số

ya có tiệm cận đứng là trục tung.

Lời giải

Chọn D

+ Hàm số

a có tập xác định là  và tập giá trị là

(0; )

Hàm số

ya đồng biến trên tập xác định của nó khi

1a 

và nghịch biến trên tập xác định

của nó khi

01a

+ Đồ thị hàm số

a có tiệm cận ngang là trục hoành và không có tiệm cận đứng.

+ Đồ thị hàm số

ya và đồ thị hàm số log

yx đối xứng nhau qua đường thẳng .

x

Câu 12.

Đường cong trong hình vẽ bên là đồ thị của một trong bốn hàm số được liệt kê ở bốn phương

án dưới đây. Hỏi đó là hàm số nào?

2yx x

. B.

33yx x  

. C.

3yx x

. D.

23yx x 

Lời giải

Chọn D

+ Ta có:

lim





, suy ra loại B.

+ Từ hình vẽ bên ta thấy đồ thị hàm số đạt cực đại tại

(0; 3)

suy ra loại A.

+ Đồ thị hàm số đạt cực tiểu tại

(1;4)

suy ra loại C.

NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019

https://www.facebook.com/groups/toanvd.vdc Trang 12

NHÓM TOÁN VD – VDC

Câu 13. Cho hình lăng trụ

.ABC A B C



có đáy

ABC

là tam giác đều cạnh





. Biết rằng hình

chiếu vuông góc của



lên



ABC

là trung điểm

. Thể tích của khối lăng trụ

.ABC A B C



là

. B.

. D.

Lời giải

Chọn B

Gọi

là trung điểm của

,BC

khi đó

AM BC AM

và



AM ABC



Trong tam giác vuông

'AAM

có:

A M AA AM



Vậy, thể tích khối lăng trụ là:

6332

'. .

24 8

ABC

aa a

VAMS

 



Câu 14. Trong không gian với hệ tọa độ

Oxyz

, phương trình đường thẳng

đi qua điểm



1; 2;1

và

vuông góc với mặt phẳng



:2 10Px yz

có dạng

121

xy z







. B.

121

xyz







121

xy z





242

xyz







Lời giải

Chọn D

Do đường thẳng

vuông góc với mặt phẳng



nên

nhận của véc tơ pháp tuyến của



là



1; 2;1n 



làm véc tơ chỉ phương. Vì thế loại đáp án C.

Trong các đáp án A, B, D chỉ có đáp án D là đường thẳng

đi qua điểm



1; 2;1 .

Vậy chọn D.

Câu 15. Trong các hàm số

   

log ; ; ; 3

fx x gx hx x kx





 





có bao nhiêu hàm

số đồng biến trên



NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019

https://www.facebook.com/groups/toanvd.vdc Trang 13

NHÓM TOÁN VD – VDC

A. 2 . B.

. C. 4 . D. 1.

Lời giải

Chọn D

Ta có:

 

log 0, 0

ln 2

fx x f x x





 

111

3ln0,

222

gx g x x x



 



     

 

 



 

0, 0

hx x h x x x





  

 

323ln30,0

kx k x x x



  

Vậy có một hàm số













đồng biến trên



Câu 16. Số giá trị nguyên của tham số

để phương trình để phương trình



sin 1 cos 2 1xm x m   có

nghiệm là

. B.

. C.

. D.

Lời giải

Chọn C

Phương trình





sin 1 cos 2 1xm x m   có nghiệm khi và chỉ khi

 

11213210 1

mmmm m



  

. Vậy





0;1m  .

Câu 17. Một hình nón có độ dài đường sinh bằng đường kính đáy. Diện tích hình tròn đáy của hình nón

bằng



. Tính đường cao

của hình nón.

h 

. B. 33h  . C.

h 

. D. 3h  .

Lời giải

Chọn B

Ta có diện tích đáy

93.Sr r





Do đó

26.lr

Mặt khác ta có

222 22222

6327 33.lhr hlr h

Câu 18. Trong không gian, cho các mệnh đề sau:

Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.

.II

Hai mặt phẳng phân biệt chứa hai đường thẳng song song cắt nhau theo giao tuyến song

song với hai đường thẳng đó.

.III

Nếu đường thẳng

song song với đường thẳng

, đường thẳng

nằm trên mặt phẳng



thì

song song với



NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019

https://www.facebook.com/groups/toanvd.vdc Trang 14

NHÓM TOÁN VD – VDC

.IV

Qua điểm

không thuộc mặt phẳng





, kẻ được đúng một đường thẳng song song với





Số mệnh đề

đúng là

. B.

. C.

. D.

Lời giải

Chọn B

I. Sai vì hai đường thẳng đó có thể chéo nhau.

II. Sai vì hai giao tuyến có thể trùng nhau.

III. Sai vì hai đường thẳng đó có thể cùng nằm trên mp

()

P .

IV. Sai vì có thể kẻ được vô số đường thẳng song song mp

()

P .

Câu 19. Tập hợp điểm biểu diễn số phức z thỏa mãn điều kiện

|12|1 zi

là

A. Đường tròn





1; 2I , bán kính

1R

. B. Đường tròn





1; 2I , bán kính

1R

C. Đường tròn



1; 2I

, bán kính 1R . D. Đường tròn





1; 2I

, bán kính 1R .

Lời giải

Chọn C

Giả sử



,, zxyixy . Ta có:

   

|12|1| 12 i|1 1 2 1         zi x y x y .

Vậy tập hợp điểm biểu diễn số phức

z là đường tròn tâm



1; 2I

, bán kính 1R .

Câu 20. Kí hiệu

là số các tổ hợp chập

của

phần tử

(1 )kn

. Mệnh đề nào sau đây đúng?

!( )!

knk





. B.

!( )!

kn k





. C.

!( )!

kn k





. D.

()!





Lời giải

Chọn A

Công thức:

!( )!

kn k





Câu 21. Cho hàm số



yfx

liên tục, đồng biến trên đoạn



;.ab

Khẳng định nào sau đây đúng?

A. Hàm số đã cho có cực trị trên đoạn



;.ab

B. Hàm số đã cho có giá trị lớn nhất, giá trị nhỏ nhất trên khoảng





;.ab

C. Phương trình





0fx có nghiệm duy nhất thuộc đoạn



;.ab

D. Hàm số đã cho có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn



;.ab

Lời giải

Chọn D

Hàm số





yfx liên tục, đồng biến trên đoạn



;ab ta có bảng biến thiên trên đoạn



;ab

như sau:

NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019

https://www.facebook.com/groups/toanvd.vdc Trang 15

NHÓM TOÁN VD – VDC

Dựa vào bảng biến thiên ta có:

Hàm số đã cho có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn



;ab là:



;

max ( ) ( ); min ( ) ( )

xfb fxfa

Trên



;ab hàm số không có cực trị.

Trên khoảng





;ab không thể kết luận được giá trị lớn nhất và giá trị nhỏ nhất.

Trên





;ab

chưa thể kết luận được phương trình





0fx

có nghiệm duy nhất thuộc đoạn



;ab

vì không xác định được dấu của

()

và

()

Câu 22. Cho hình chóp

.SABCD

có đáy là hình bình hành. Gọi

là trung điểm của

. Mặt

phẳng





NCD chia hình chóp đã cho thành hai phần. Tỉ số thể tích hai phần là (số bé chia số

lớn)

. B.

. C.

. D.

Lời giải

Chọn A

Gọi

là thể tích khối chóp

.SABCD

Ta có:

...

2. 2.

S ABCD S ABC S ACD

VVVV

(do các hình chóp này có cùng đường cao là khoảng

cách từ S đên (ABCD) và

2. 2.

BCD ABC ACD

SSS





)

là trung điểm của

suy ra

;

SM SN

SA SB



Ta lại có:

NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019

https://www.facebook.com/groups/toanvd.vdc Trang 16

NHÓM TOÁN VD – VDC

.......

......

.. .

.. .. 111113

.. . .

2 . . 2 . . 222 22 8

33 35

.. ..

88 88

S MNCD S MNC S MCD S MNC S MCD S MNC S MCD

S ABCD S ABCD S ABCD S ABCD S ABC S ACD

S MNCD S ABCD ABCDMN S MNCD

VVVVVVV

VVVVVV

SM SN SC SM SC SD

SA SB SC SA SC SD

VVVVVVVVV







  

S MNCD

ABCDMN



Câu 23. Trong không gian với hệ tọa độ

, mặt cầu



S có tâm





3; 3;1I  và đi qua điểm





5; 2;1A  có phương trình là

 

222

5215xyz

. B.



222

33125xyz



222

3315xyz

. D.



222

3315xyz

Lời giải

Chọn D

Gọi

là bán kính của mặt cầu





S . Do mặt cầu





S có tâm là





3; 3;1I  và đi qua

nên

RIA

hay

 

222

53 23 11R 

5 .

Do đó phương trình mặt cầu





S là



222

3315xyz

Câu 24. Cho lăng trụ tam giác đều

BC A B C



có độ dài cạnh đáy bằng

, góc giữa đường thẳng



và mặt phẳng





BC bằng

60º

. Tính thể tích

của khối trụ ngoại tiếp lăng trụ đã cho.

3Va



 . B.





. C.





. D.





Lời giải

Chọn D

Ta có



BABC



 nên

là hình chiếu vuông góc của



. Do đó



BABC





BAB











Xét tam giác vuông

BAB



có

tan 60BB a





3a .

NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019

https://www.facebook.com/groups/toanvd.vdc Trang 17

NHÓM TOÁN VD – VDC

Gọi

,OO



lần lượt là tâm của đường tròn ngoại tiếp tam giác



nên





OO ABC





và

3OO BB a





là đường cao của khối trụ ngoại tiếp hình lăng trụ.

Do tam giác

và



đều nên

,OO



là trọng tâm tam giác



Do đáy là tam giác đều cạnh

a nên bán kính đường tròn đáy là

RAM



Khi đó thể tích của khối cầu ngoại tiếp hình lăng trụ là

VRh





..3











Câu 25. Cho hàm số





yfx

liên tục trên

 , có đạo hàm

 

() 1 2



 

fx xx x

. Hỏi hàm số





yfx có bao nhiêu điểm cực trị?

. B.

. C.

. D.

Lời giải

Chọn A

Ta có:

 

() 0 1 2 0



   

fx x x x















Qua nghiệm

1

(nghiệm bội chẵn)





không đổi dấu



hàm số có 2 cực trị.

Câu 26. Tích giá trị lớn nhất và giá trị nhỏ nhất của hàm số

yx

trên đoạn







bằng

. B.

. C.

. D.

Lời giải

Chọn A

Ta có:

yx

xác định

;2 .









22 2







;

01;2











yx .

 

117

13 25.



   





ff f

Suy ra







MMaxy ;







mMiny Vậy

.15.Mm

Câu 27. Cho hình chóp

.SABC

có đáy là tam giác vuông tại

, biết





SA ABC và

2, 3,

BaACa

4SA a

. Tính khoảng cách

từ điểm

đến mặt phẳng





SBC .



. B.

629



. C.

12 61



. D.



Lời giải

NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019

https://www.facebook.com/groups/toanvd.vdc Trang 18

NHÓM TOÁN VD – VDC

Chọn C

Vẽ

AH BC

. Ta có:



SA BC SA ABC



AH BC

Nên



BC SAH



, mà



BC SBC



, Do đó

 

SBC SAH



Lại có



SBC SAH SH



Vẽ

AK SH



AK SBC



Như vậy



,dASBC AK





22 22 2 2

111111

AK SA AH SA AB AC

  

 



11161 1261

144 61

 

Câu 28. Cho hàm số

 

,

yfxygx

liên tục trên đoạn





; 

ab a b

. Hình phẳng

giới hạn bởi

đồ thị hai hàm số

 

,

yfxygx

và hai đường thẳng

,xaxb

có diện tích là

 

d



Sfxgxx

. B.

 

d







Sfxgxx

 







Sfxgxx

. D.

 

d



Sfxgxx

Lời giải

Chọn A

Câu 29.

Số phức

58zi

có phần ảo là

. B.

8

. C.

. D.

8 i

Lời giải

Chọn B

Ta có:

58zi

nên phần ảo của số phức là

8

Câu 30. Biểu thức



0xxx

viết dưới dạng lũy thừa với số mũ hữu tỉ là:

. B.

. C.

. D.

Lời giải

NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019

https://www.facebook.com/groups/toanvd.vdc Trang 19

NHÓM TOÁN VD – VDC

Chọn D

Ta có

412

xx x x

Câu 31. Cho hàm số



yfx



là hàm đa thức bậc 4, có đồ thị hàm số



yfx



như hình vẽ. Hàm số



52 4 10yf x x x

đồng biến trong các khoảng nào sau đây?



3;4

. B.







. C.







. D.







Lời giải

Chọn B

Ta có

 



'2'528102'522525

yf xx f x x

        

Ta có

 

'0 '52 252 50*

yfx x

 

. Đặt

52tx

khi đó

  

*'250'25

ft t ft t



. Từ đồ thị trên ta có:

0105212

txx    

NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019

https://www.facebook.com/groups/toanvd.vdc Trang 20

NHÓM TOÁN VD – VDC

Câu 32. Cho hàm số





yfx

liên tục trên





\1;0

thỏa mãn





12ln21f 

 

12 1xx f x x f x xx









\1;0x 

. Biết



2ln3fab

, với

,ab

là hai

số hữu tỉ. Tính

Ta b.

T 

. B.

T 

. C.

T 

. D.

0T 

Lời giải

Chọn A

Ta có:

 

12 1xx f x x f x xx





 

22 2

.() 1 . .()

(1) 1 (1) 1

xxxx

f x fx f x fx

xxxx





   



 

222 2

.. 1

111 1 1

xxx x

xfxdxdxxdx

xxx x x

 



 

 



  



 





.ln1.

xxxC





Thay



vào 2 vế ta được:

 

.1 ln2 1 2ln212 1.

fCfCC        

Thay

2x 

vào 2 vế ta được:

 

433

.21ln3 2 ln3.

344

ff   

Từ đó

ab

Vậy

Ta b





Câu 33. Cho hàm số bậc ba





yfx có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số

thuộc đoạn





0;9 sao cho bất phương trình

    

216.24160

fxfxm fxfxm fx 

 có

nghiệm





1;1x  ?

. B.

. C.

. D.

Lời giải

Chọn A

y =

(x)

-2

1-1

NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019

https://www.facebook.com/groups/toanvd.vdc Trang 21

NHÓM TOÁN VD – VDC

         

  



 



 



22 2 2

22 2

2 16.2 4 16 0 2 2 16.2 16 0

2 . 2 1 16. 2 1 0 4 16 . 2 1 0

f x fx m f x fx m fx f x fx m fx f x fx m

fx f x fx m f x fx m fx f x fx m

   

  





Vì

  

1;1 2; 2xfx  



4160



Để bất phương trình

    

216.24160

fxfxm fxfxm fx 



có nghiệm



1;1x 

thì

 

210

fxfxm

 có nghiệm





1;1x 

 

0fx fxm có nghiệm



1;1x 

 

xfxm có nghiệm



1;1x 

Đặt













;1;1 2;2fx tx t 

Phương trình

 

xfxm

có nghiệm



1;1x 

khi và chỉ khi phương trình

ttm

có nghiệm





2; 2t 

Xét



ttt với





2; 2t  .Có

 

'21;'0

gt t gt t 

Ta có bảng biến thiên của



t trên khoảng





2; 2

Dựa vào bảng biến thiên ta thấy

ttm có nghiệm



2; 2t 

6m

Vì





0;9m 





0;5m . Vậy có

giá trị của

để bất phương trình có nghiệm thuộc





1;1 .

Câu 34. Cho

,,,abcd

là các số nguyên dương,

1; 1ac

thoa mãn

log ;log

bd

và

9ac

Khi đó

bd

bằng

. B.

. C.

. D.

Lời giải

Chọn A

Ta có:

log log

baabab  

NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019

https://www.facebook.com/groups/toanvd.vdc Trang 22

NHÓM TOÁN VD – VDC

Vì:

log log

dccdcd  

Lại có:













24 2 2

35 35 35

99.9ac b d b d b d     

Vì

,,,abcd

nguyên dương nên

;bd

nguyên dương

,bd

nguyên dương

1125

bd b





 





















. Vậy

93bd

Câu 35. Cho hàm số

88yx x x 

có đồ thị



C và hàm số





8yx axb  (với

,ab

) có

đồ thị



. Biết đồ thị hàm số



C cắt



tại các điểm có hoành độ nằm trong đoạn



1; 5 .

Khi

đạt giá trị nhỏ nhất thì tích

bằng

729

. B. 375 . C. 225 . D. 384 .

Lời giải

Chọn B

Xét phương trình hoành độ giao điểm của hai đồ thị



và



32 2

88 8

xxx axb 

Khi đó ta có phương trình





90*xxaxb có

nghiệm thuộc



1; 5 .

Đặt



xx xaxb .

Ta có





318

xx xa



, khi đó để





* có các nghiệm thuộc



1; 5 thì



0fx



 có

nghiệm thuộc



1; 5 .

Xét hàm số



318

xx x

15x 

có bảng biến thiên

Khi đó

15 27a

Xét

15a 

thì





* có nghiệm

5x 

nên

25b 

Thử lại phương trình



91525 1 50xx x x x 

thỏa mãn. Vậy

375ab 

Câu 36. Gọi

là tập các số tự nhiên có

chữ số đôi một khác nhau. Lấy ngẫu nhiên từ

ra hai số.

Tính xác suất để lấy được hai số mà các chữ số có mặt ở hai số đó giống nhau.

5823

. B.

5823

. C.

7190

. D.

1941

Lời giải

Chọn A

Ta có số các số tự nhiên có

chữ số đôi một khác nhau là

9.9.8 648

, trong đó có

9.8.7 504

số không chứa chữ số

NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019

https://www.facebook.com/groups/toanvd.vdc Trang 23

NHÓM TOÁN VD – VDC

Khi đó

648

C

Trường hợp 1: Xét các số tự nhiên có

chữ số đôi một khác nhau và không chứa chữ số

Khi đó số cách chọn ra được hai số mà các chữ số có mặt ở hai số đó giống nhau là

504 5

(vì

mỗi số được kể 2 lần).

Trường hợp 2: Xét có số tự nhiên có

chữ số đôi một khác nhau và chứa chữ số

. Khi đó số

cách chọn ra được hai số mà các chữ số có mặt ở hai số đó giống nhau là

144 3

Vậy xác suất để lấy đươc hai số mà các chữ số có mặt giống nhau là

11 11

5045 1443

648

5823

CC CC





Câu 37. Cho hàm số





yfx liên tục trên



và

 

216, d 4ffxx



. Tính

Ixf x













A. 144I  . B. 12I  . C. 112I  . D.

28I 

Lời giải

Chọn C

Đặt

vf x













































Khi đó

Ixf x













22d

ffx

 



 

 



128 2 d











Đặt

t 

, khi đó

  

422

000

d2 d2 d8

fxfttfxx



 







Vậy

128 2.8 112I 

Câu 38. Cho tứ diện

ABCD

có



90DAB CBDº ;



; 5; 135AB a AC a ABC 



. Biết góc giữa hai

mặt phẳng









BD BCD bằng



. Thể tích của tứ diện

BCD

là

. B.

. C.

. D.

Lời giải

Chọn D

NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019

https://www.facebook.com/groups/toanvd.vdc Trang 24

NHÓM TOÁN VD – VDC

Dựng



DH ABC

Ta có

BA DA

BA AH

BA DH













. Tương tự

BC DB

BC BH

BC DH













Tam giác

có

AB a



45ABH 

AB

vuông cân tại

AH AB a

Áp dụng định lý cosin, ta có

Ca

Vậy



112

sin 2

2222

ABC

SBABCCBAaa



     

Dựng

EDA

FDB















HE DAB và





HF DBC .

Suy ra











,,DBA DBC HE HF EHF

và tam giác

HEF

vuông tại

Đặt

DH x

, khi đó









Suy ra



cos

HE x a

EHF x a



 



Vậy

ABCD ABC

VDHS



   .

Câu 39. Trong mặt phẳng với hệ tọa độ

, cho hình



H giới hạn bởi các đường

2,yx

2, 4yxx 

; hình





là tập hợp tất cả các điểm



;

thỏa mãn các điều kiện:

16;xy

 

24;24xyxy 

. Khi quay



H ,





H quanh

ta được các

khối tròn xoay có thể tích lần lượt là

,VV

. Khi đó, mệnh đề nào sau đây là đúng?

2VV

. B.

VV

. C.

48VV





. D.

4VV

Lời giải

Chọn D

NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019

https://www.facebook.com/groups/toanvd.vdc Trang 25

NHÓM TOÁN VD – VDC

Hình phẳng



Khi cho



H quay quanh trục

, ta có



216Vxdx







Hình phẳng





Khi cho





H quay quanh trục

, ta có

. 4 2. . 2 64 .





 

Vậy

4.VV

Câu 40. Trong không gian với hệ tọa độ

, cho hai điểm









1; 2;1 , 3; 4;0AB, mặt phẳng



:460Paxbycz. Biết rằng khoảng cách từ

đến mặt phẳng



lần lượt bằng

và

. Giá trị của biểu thức

Tabc

bằng

3

. B.

6

. C.

. D.

Lời giải

Chọn B

Gọi

lần lượt là hình chiếu vuông góc của

lên mặt phẳng



Ta có

3,AB 

6AH 

3BH 

Suy ra

nằm cùng một phía của mặt phẳng



Lại có

66AB BK AK AH  

Suy ra

thẳng hàng và

là trung điểm của



5; 6; 1H

Vậy mặt phẳng



đi qua



5;6; 1H  và có vtpt





2; 2; 1AB 



có phương trình

NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019

https://www.facebook.com/groups/toanvd.vdc Trang 26

NHÓM TOÁN VD – VDC

2( 5) 2( 6) 1(z 1) 0 2 x 2 y z 23 0 4 4 2 46 0xy xyz        

Vậy

4, 4, 2abc  

nên

6.Tabc

Câu 41. Cho hình chóp

.SABC

có

vuông góc với





,2,45AB a AC a BAC º. Gọi

,BC lần lượt là hình chiếu vuông góc của

lên

,SB SC

. Thể tích khối cầu ngoại tiếp hình

chóp

BCC B bằng



. B.



. C.



. D.



Lời giải

Chọn D

Tam giác ABC có



,2,45ºABaACa BAC BCa== ==

ABC

vuông cân ở B.

Ta có:



BC AB

BC SAB BC AB

BC SA





 







Ta có:



111

AB BC

B SBC AB B C

AB SB





 







Vì các tam giác

B C ABC AC C là các tam giác vuông chung cạnh huyền AC



,,,,

BBCC cùng thuộc mặt cầu đường kính AC.

Do đó khối cầu ngoại tiếp chóp

.ABCC B có tâm H là trung điểm AC và

AC a

R 

Vậy thể tích khối cầu cần tìm là:





Câu 42. Cho các số phức

,zw

khác

thỏa mãn

0zw

và

13 6

zwzw





. Khi đó

bằng

. B.

. C. 3 . D.

Lời giải

Chọn D

Ta có:

13 6

zwzw













36wz w zz w zw 

w2 3 0zw z  



w2zz 







w2.ziz 

NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019

https://www.facebook.com/groups/toanvd.vdc Trang 27

NHÓM TOÁN VD – VDC



12 3

12.

w1 2.

w2.

w1 2.

12 3

12.

ziz















































Câu 43.

Ông Nam dự định gửi vào ngân hàng một số tiền với lãi suất

6,6%

/năm. Biết rằng nếu không

rút tiền khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi

cho năm tiếp theo. Tính số tiền tối thiểu

triệu đồng





x ông Nam gửi vào ngân hàng để

năm số tiền lãi đủ mua một chiếc xe gắn máy trị giá

triệu đồng.

191

triệu đồng. B.

123

triệu đồng. C.

124

triệu đồng. D.

145

triệu đồng.

Lời giải

Chọn C

Với lãi suất

6,6

100

r

Theo giả thiết ta có:



1 26.10 124 xrx x

triệu đồng.

Câu 44.

Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

112

12 1







xyz

và mặt phẳng





:2 2 1 0 Pxyz

. Gọi



là hình chiếu của đường thẳng

lên mặt phẳng



, vectơ chỉ

phương của đường thẳng



là





5; 16; 13



. B.





5; 4; 3



. C.





5;16;13



. D.





5;16; 13



Lời giải

Chọn D

Gọi





Q là mặt phẳng chứa

và vuông góc với





vectơ pháp tuyến



; 5;4;3







 

QdP

nun

là hình chiếu của đường thẳng

lên mặt phẳng



nên





' dP.

Do đó









' dPQ hay



;5;16;13







 

dPQ

unn

Câu 45. Trong không gian với hệ tọa độ

, cho điểm













4;0; 0 , 0;4; 0 , 0;0;

BSc và đường

thẳng

111

112





. Gọi



lần lượt là hình chiếu vuông góc của

lên

,SA SB

Khi góc giữa đường thẳng

và mặt phẳng





OA B



lớn nhất, mệnh đề nào sau đây đúng?



8; 6c   . B.



9; 8c   . C.





0;3c  . D.

17 15

;



 





Lời giải

Chọn D

Ta có:





1; 1; 2

u 



và





4; 4;0AB 



SA SB

SOA SOB A B AB

SA SB









 







NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019

https://www.facebook.com/groups/toanvd.vdc Trang 28

NHÓM TOÁN VD – VDC

Xét

SOA

222 2

416

AA OA

OA AA SA AA AS

SA SA c c









 



222

'4 0 4

16 4 16

'0 0 0 ;0;

16 16 16

'0 0

ccc



 













 











 









416

;0; ;0;4

16 16

OA u c







 













;16;16;4c 4;4;

OA B

Bu n c















Gọi













;coscos;

OA B

dOAB un











22 2 2 2

4.1 4.1 .2

cos

112.4 4







 



  

Xét hàm số









8432

fc f c











;

















Bảng biến thiên

  

max 8

fc f



max cos 1





khi

8c 

Câu 46. Cho hàm số





yfx có đồ thị như hình vẽ. Biết tất cả các điểm cực trị của hàm số





yfx

là

2,0, 2, , 6a

với

46a

. Số điểm cực trị của hàm số





fx x là

. B.

. C.

. D.

Lời giải

Chọn B

Ta có



562

'6 6 3

xxfxx



 

y =

(x)

-2

NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019

https://www.facebook.com/groups/toanvd.vdc Trang 29

NHÓM TOÁN VD – VDC



62 62

32320

660

03030

32 32

330

36 360

xx xx

yxxxx

fx x

xx xx

xxaxxa

xx xx











 









     















 



 



 



Xét

 

62 2 2 2

320 1 20 1xx x x x 

là nghiệm kép.

Xét



62 24

30 30

xx xx







  









với

0x 

là nghiệm kép.

Xét









62 2 2 2

320 1 20 2 2xx x x x x 

Xét

xa.

Đặt

0tx, Pt

3tta 

Ta có đồ thị hàm số





tt t

Số nghiệm của phương trình

3tta

số giao điểm của đường thẳng

a

và đồ thị



4;6a 

3tta

có 1 nghiệm duy nhất

2txx





 

Xét





62 2

360 2xx x x



 

 

Ta thấy:

0x 

là nghiệm bội 3 nên là cực trị.

1x 

là nghiệm bội 3 nên là cực trị.

2, 3, ,xxx x





    là nghiệm đơn nên là cực trị.

Vậy hàm số





fx x có 11 điểm cực trị.

Câu 47. Cho hai số thực

thỏa mãn:



 

232

log 8 16 log 5 1 2log log 2 8 .

yy x x y



      





NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019

https://www.facebook.com/groups/toanvd.vdc Trang 30

NHÓM TOÁN VD – VDC

Gọi

là tập các giá trị nguyên của tham số m để giá trị lớn nhất của biểu thức

xym không vượt quá

. Hỏi

có bao nhiêu tập con không phải là tập rỗng?

2047

. B.

16383

. C.

16384

. D.

Lời giải

Chọn B

Điều kiện:





4; 1;5yx  



 

 





   

232

2 2

232

32 3 2

log 8 16 log 5 1 2 log log 2 8

log 4 log 5 1 2log log 4. 4

2log 4 log 4 2log 5 1 log 5 1

yy x x y

yxx y

y y xx xx



      





  





 





Xét hàm số









2log log , 0;ft t t t

 

21121

',0,0;

t.ln 3 t .ln 2 t ln 3 ln 2

ft t



  

















 

2222

451 454 4291fy f x x y xx y x









;

xy C

tâm



4; 2 , 3IR

và

OM x y

Ta có

min max

,OM OI R OM OI R 



25 3 25 3 2

25 3 10

10 2 5 7 2 5 7

25 3 10

mxym m

     



 



   



 





Vậy





2; 1;0...;10;11S   có 14 số nguyên.Số tập con khác rỗng của S là

2 1 16383

Câu 48. Cho tích phân



2ln 1d ln2Ix xxa

   



trong đó

là các số nguyên dương.

Tổng

ab

bằng

. B.

. C.

. D.

Lời giải

Chọn D

NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019

https://www.facebook.com/groups/toanvd.vdc Trang 31

NHÓM TOÁN VD – VDC



2ln 1dIx xx 



. Đặt



ln 1

dv dx

dv x dx

vxxC





























Chọn

31 3

22 2

Cvxx  

 





1 1

0 0

2ln1d 2 n1 d

22 21

177

4ln2 3 4ln2 ln2

22 4

Ix xx xxlx x





    









 







4; 4 20ab ab  

Câu 49. Trong không gian với hệ tọa độ

, cho mặt phẳng









:1210Pmx m yz m 

, với

là tham số. Gọi





là tập hợp các điểm

là hình chiếu vuông góc của điểm



3; 3; 0H

trên



. Gọi

,ab

lần lượt là khoảng cách lớn nhất, khoảng cách nhỏ nhất từ

đến một điểm thuộc





 . Khi đó,

ab

bằng

A. 52. B. 33. C. 82. D. 42.

Lời giải

Chọn D

Ta có:













:1210 2(1)0Pmx m yz m mxy yz       

Suy ra



luôn chứa đường thẳng

dyt





















 



Gọi

là hình chiếu vuông góc của

(3;3;0)H

lên đường thẳng

, ta tìm được

(1;1; 0)K

Tam giác

là tam giác vuông tại

và

Hd

nên





T là đường tròn có tâm





2; 2;0I là trung điểm của

, bán kính

R 

và nằm trong mặt phẳng



Q đi qua

, vuông góc với

Phương trình mặt phẳng



:0Qxyz và 22OI  , suy ra



OQ và

ở ngoài





T .

Gọi

là giao điểm của

và



T (với

là điểm nằm giữa

và

Ta có

OA OH OB, suy ra 2aOAOIR, 32bOBOIR .

Câu 50. Cho số phức z thỏa mãn





11332iz i . Giá trị lớn nhất của biểu thức

2623

zi z i 

bằng

A. 56. B.





15 1 6

. C. 65. D. 10 3 15 .

Lời giải

Chọn C

NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019

https://www.facebook.com/groups/toanvd.vdc Trang 32

NHÓM TOÁN VD – VDC

Ta có



11332123iz i z i 

nên tập hợp điểm

biểu diễn số phức

là

đường tròn tâm

(1; 2)I

, bán kính

3R 

Cách 1: Gọi

(2;1), (2;3)AB

, suy ra

32, 2AI BI

và 3IA IB



Khi đó:

  

22 2 2

MA MB MI IA MI IB  

  

27 6 . 6 11 2 .

IIB MIIB  

 

Hướng 1:

 

27 6 . 2 33 6 . 1 2 27 33 6 5PMIIB MIIB    

 

Hướng 2: Đặt

2. 62cos(.), 62;62tMIIB MIIBt



 



  



27 3 6(11 )

ttft  . Ta có



ft t

Và





62;62

62; 62; 65

max f t max f f f f









 

 



 

 



Cách 2: Đặt

12, 1az ib i 

Ta có



2222

2393..

23 . .

ziabab abab

ziabababab



      





      





222222

2323 33 41260ziz iababa b        

Khi đó







32.3 12 33 65Pa b ab a b ab        .

….………………………HẾT…………………………

Xin chân thành cảm ơn tất cả các quý thầy cô tham gia dự án này. Chúc thầy cô thật nhiều

sức khỏe, luôn thành công trong mọi công việc và luôn bình an hạnh phúc bên gia đình.

Hẹn gặp lại quý thầy, cô ở các dự án tiếp theo. Thân chào.

Ban quản trị nhóm VD-VDC.

Bấm Tải xuống để xem toàn bộ.

| 1/33

| | Tải xuống

Preview text:

SỞ GDĐT BẮC NINH
ĐỀ THI THỬ THPT QUỐC GIA NĂM 2019
PHÒNG QUẢN LÝ CHẤT LƯỢNG Bài thi: Toán
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
(Đề có 50 câu trắc nghiệm)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Họ và tên thí sinh:..................................................... Số báo danh :................... Mã đề 101
Câu 1. Trong không gian với hệ tọa độ Oxyz , phương trình mặt phẳng  đi qua điểm A0;1;  0 ; B 2;0;  0 ; C 0;0;  3 là A. x y z x y z x y z x y z    1 . B.    0 . C.    1. D.    1 . 2 1 3 2 1 3 1 2 3 2 1 3
Câu 2. Gọi z , z là hai nghiệm phức của phương trình 2
2z  3z  3  0 . Giá trị của biểu thức 2 2 z  z 1 2 1 2 bằng A. 3 . B. 9 . C.  3 . D. 9 . 18 8 4 3
Câu 3. Tập xác định của hàm số 
y  x  x    x   2 2 5 3 2 3 là A. D   ;     \   3 . B. D   ;   1  2;   \   3 . C. D   ;     \ 1;2. D. D   ;   1  2;   .
Câu 4. Cho hàm y  f x có f 2  2 , f 3  5 ; hàm số y  f x liên tục trên 2;3   . Khi đó 3 f 
 xdx bằng 2 A. 3 . B. 3. C. 10 . D. 7 .
Câu 5. Bất phương trình log 3x  2  log 6  5x có tập nghiệm là a;b. Tổng a b bằng 2   2   A. 8 . B. 28 . C. 26 . D. 11 . 3 15 5 5
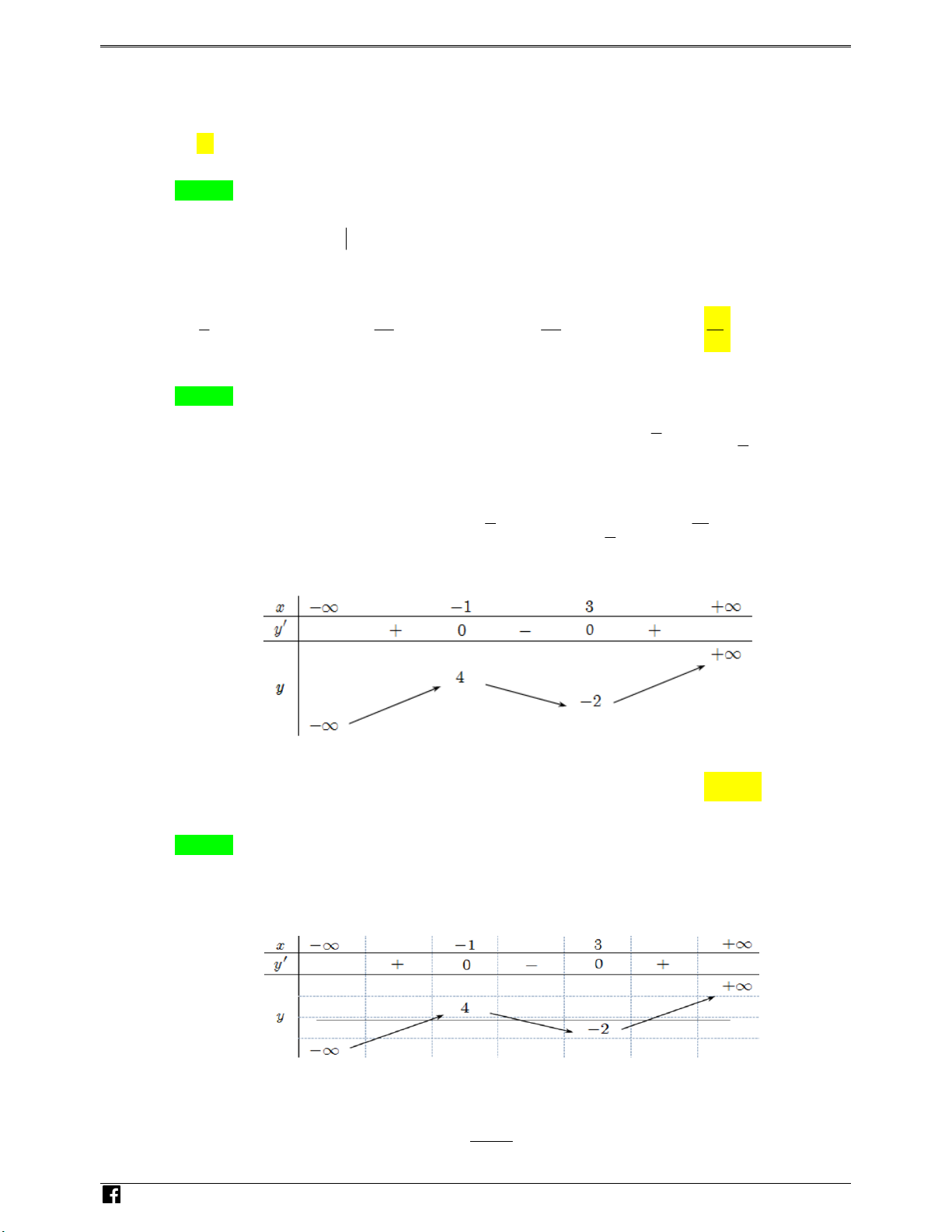
Câu 6. Cho hàm số y  f x có bảng biến thiên như sau: x  1 3  y  0  0   y 4 2 
Tập tất cả các giá t rị của tham số m để phương trình f x  m có ba nghiệm phân biệt là
A. 4;. B.  ;  2. C.  2;4    . D. 2;4.
Câu 7. Số đường tiệm cận của đồ thị hàm số x y  là 2 x  9 A. 2 . B. 4 . C. 3 . D. 1. Câu 8. Hàm số 3 2
y  x  3x  4 nghịch biến trên khoảng nào sau đây? A.  . B.  ;  2.
C. 0;. D. 2;0. Trang 1/6 - Mã đề 101  
Câu 9. Trong không gian với hệ trục tọa độ Oxyz , cho hai vectơ a  4;5;3, b  2;2;  1 . Tìm tọa độ   
của vectơ x  a  2b .    A. 
x  2;3;2.
B. x  0;1;  1 .
C. x  0;1;  1 .
D. x  8;9;  1 .
Câu 10. Họ nguyên hàm của hàm số f x  cos2x là A. sin 2x cos 2xdx  C  .
B. cos2xdx  sin2x C  . 2 C. sin 2x cos 2xdx   C  .
D. cos2xdx  2 sin2x C  . 2 Câu 11. Cho hàm số x
y  a với 0  a  1 . Mệnh đề nào sau đây SAI?
A. Đồ thị hàm số x
y  a và đồ thị hàm số y  log x đối xứng nhau qua đường thẳng y  x . a B. Hàm số x
y  a có tập xác định là  và tập giá trị là 0;   . y C. Hàm số x
y  a đồng biến trên tập xác định của nó khi a  1 .
D. Đồ thị hàm số x
y  a có tiệm cận đứng là trục tung. -1 O 1 x
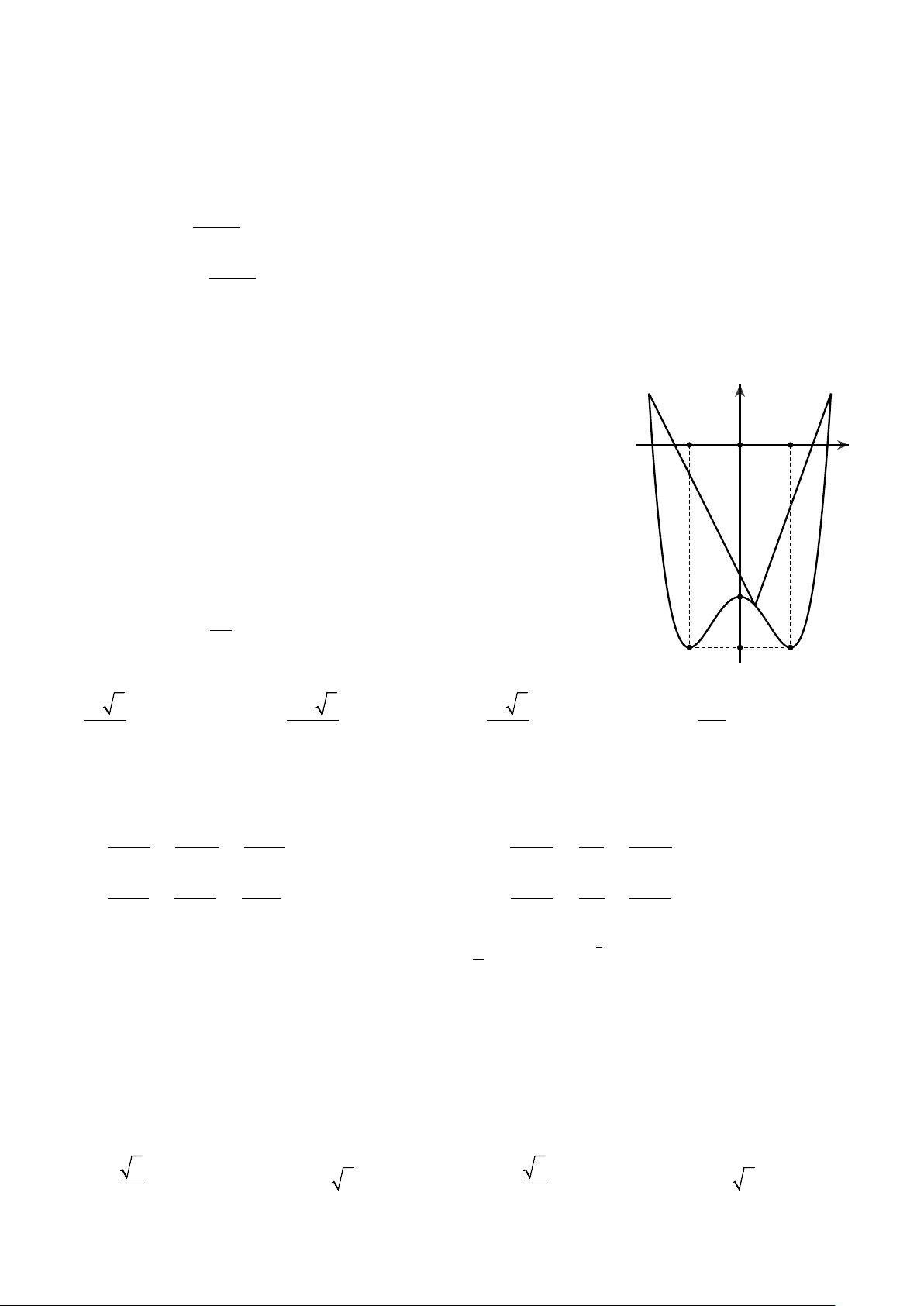
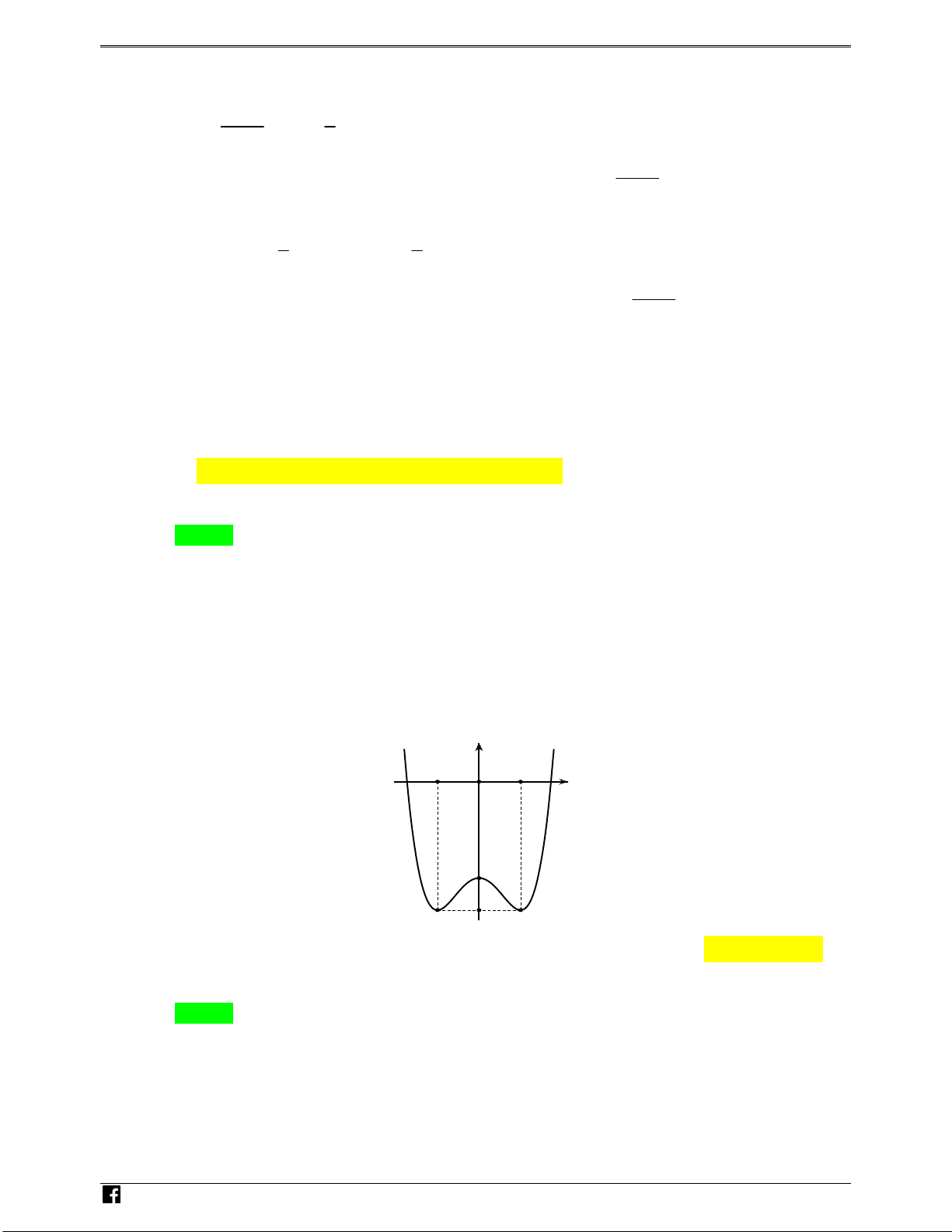
Câu 12. Đường cong trong hình vẽ bên là đồ thị của một hàm số trong
bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào? A. 4 2
y  x  2x . B. 4 2 y  x
  3x  3 . C. 4 2
y  x  x  3 . D. 4 2
y  x  2x  3 .    -3
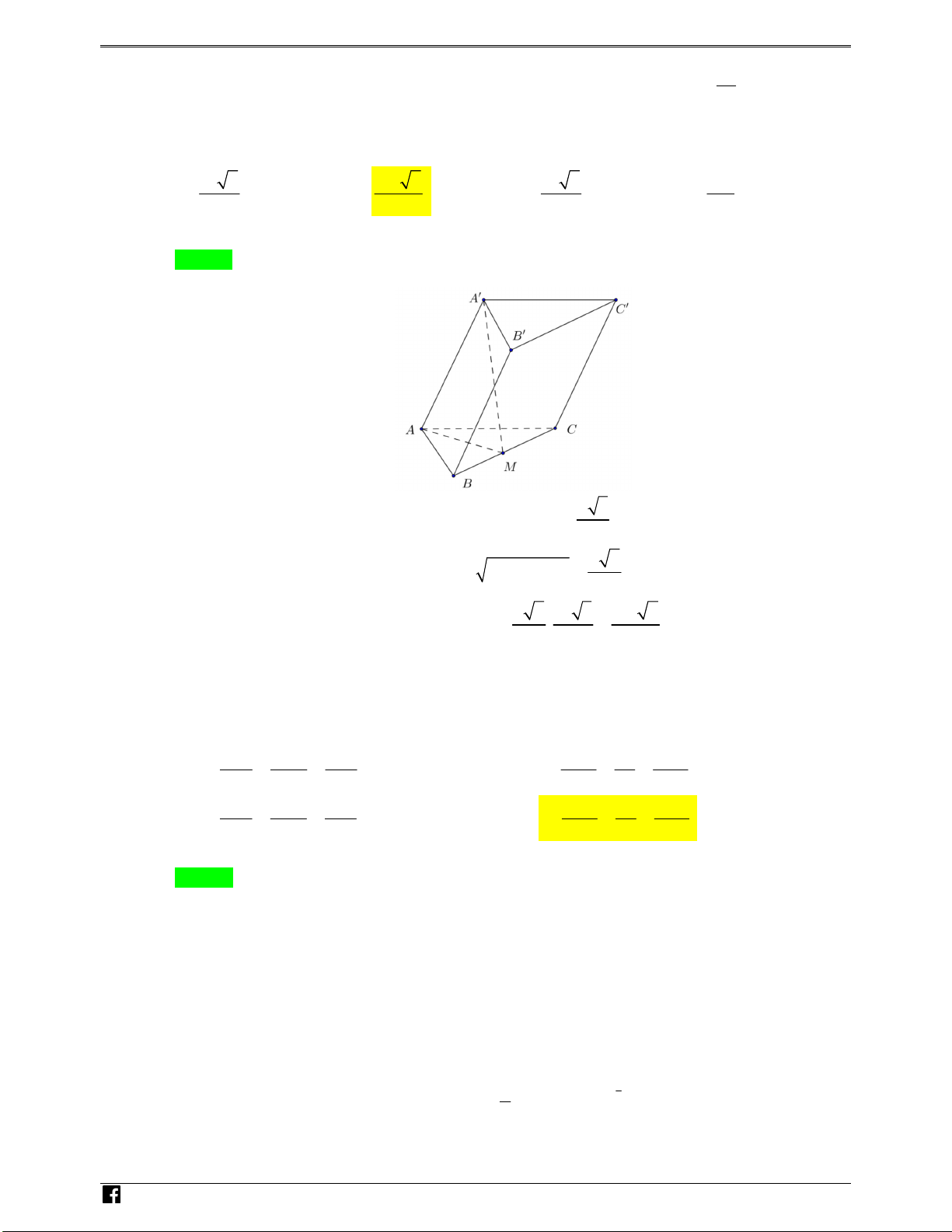
Câu 13. Cho hình lăng trụ ABC.A B C có đáy ABC là tam giác đều cạnh a a , 3 AA 
. Biết rằng hình chiếu vuông góc của A -4 2
lên ABC  là trung điểm BC . Thể tích của khối lăng trụ ABC.AB C   là 3 3 3 3
A. a 2 .
B. 3a 2 . C. a 6 . D. 2a . 8 8 2 3
Câu 14. Trong không gian với hệ tọa độ Oxyz , phương trình đường thẳng d đi qua điểm A1;2;  1 và
vuông góc với mặt phẳng P :x  2y  z 1  0 có dạng A. x  1 y  2 z  1 x  y z  d :   . B. 2 2 d :   . 1 2 1 1 2 1 C. x  1 y  2 z  1 x  y z  d :   . D. 2 2 d :   . 1 2 1 2 4 2 3 x 1  1  
Câu 15. Trong các hàm số      1 log ;      ;     3  ;  3x f x x g x h x x k x có bao nhiêu hàm số 2   2 2 đồng biến trên  ? A. 2 . B. 3 . C. 4 . D. 1.
Câu 16. Số giá trị nguyên của tham số m để phương trình để phương trình sinx  m  
1 cos x  2m  1 có nghiệm là A. 0 . B. 3 . C. 2 . D. 1.
Câu 17. Một hình nón có độ dài đường sinh bằng đường kính đáy. Diện tích hình tròn đáy của hình nón
bằng 9 . Tính đường cao h của hình nón. A. 3 h  .
B. h  3 3 C. 3 h  . D. h  3 . 2 3 Trang 2/6 - Mã đề 101
Câu 18. Trong không gian, cho các mệnh đề sau:
I. Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.
II. Hai mặt phẳng phân biệt chứa hai đường thẳng song song cắt nhau theo giao tuyến song song với hai đường thẳng đó.
III. Nếu đường thẳng a song song với đường thẳng b , đường thẳng b nằm trên mặt phẳng P thì a song song với P.
IV . Qua điểm A không thuộc mặt phẳng , kẻ được đúng một đường thẳng song song với . Số mệnh đề đúng là A. 2 . B. 0 . C. 1. D. 3 .
Câu 19. Tập hợp điểm biểu diễn số phức z thỏa mãn điều kiện z  1  2i  1 là
A. đường tròn I 1;2, bán kính R  1.
B. đường tròn I 1;2, bán kính R  1.
C. đường tròn I 1;2, bán kính R  1.
D. đường tròn I 1;2, bán kính R  1.
Câu 20. Kí hiệu k
C là số các tổ hợp chập k của n phần tử 1  k  n. Mệnh đề nào sau đây đúng? n A. k n ! k k ! k k ! k n ! C  . B. C  . C. C  . D. C  . n
k !n  k! n n k! n
n !n  k! n n k!
Câu 21. Cho hàm số y  f x liên tục, đồng biến trên đoạn a;b.
  Khẳng định nào sau đây đúng?
A. Hàm số đã cho có cực trị trên đoạn a;b.  
B. Hàm số đã cho có giá trị lớn nhất, giá trị nhỏ nhất trên khoảng a;b.
C. Phương trình f x  0 có nghiệm duy nhất thuộc đoạn a;b.  
D. Hàm số đã cho có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn a;b.  
Câu 22. Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M , N là trung điểm của SA, SB . Mặt
phẳng MNCD chia hình chóp đã cho thành hai phần. Tỉ số thể tích hai phần là (số bé chia số lớn) A. 3 . B. 3 . C. 1 . D. 4 . 5 4 3 5
Câu 23. Trong không gian với hệ tọa độ Oxyz , mặt cầu S có tâm I 3;3;  1 và đi qua điểm A5;2;  1 có phương trình là A.  2 2 2
x  2  y  2  z  2 5 2 1  5 .
B. x  3  y  3  z   1  25 . C.  2 2 2
x  2  y  2  z  2 3 3 1  5 .
D. x  3  y  3  z   1  5 .
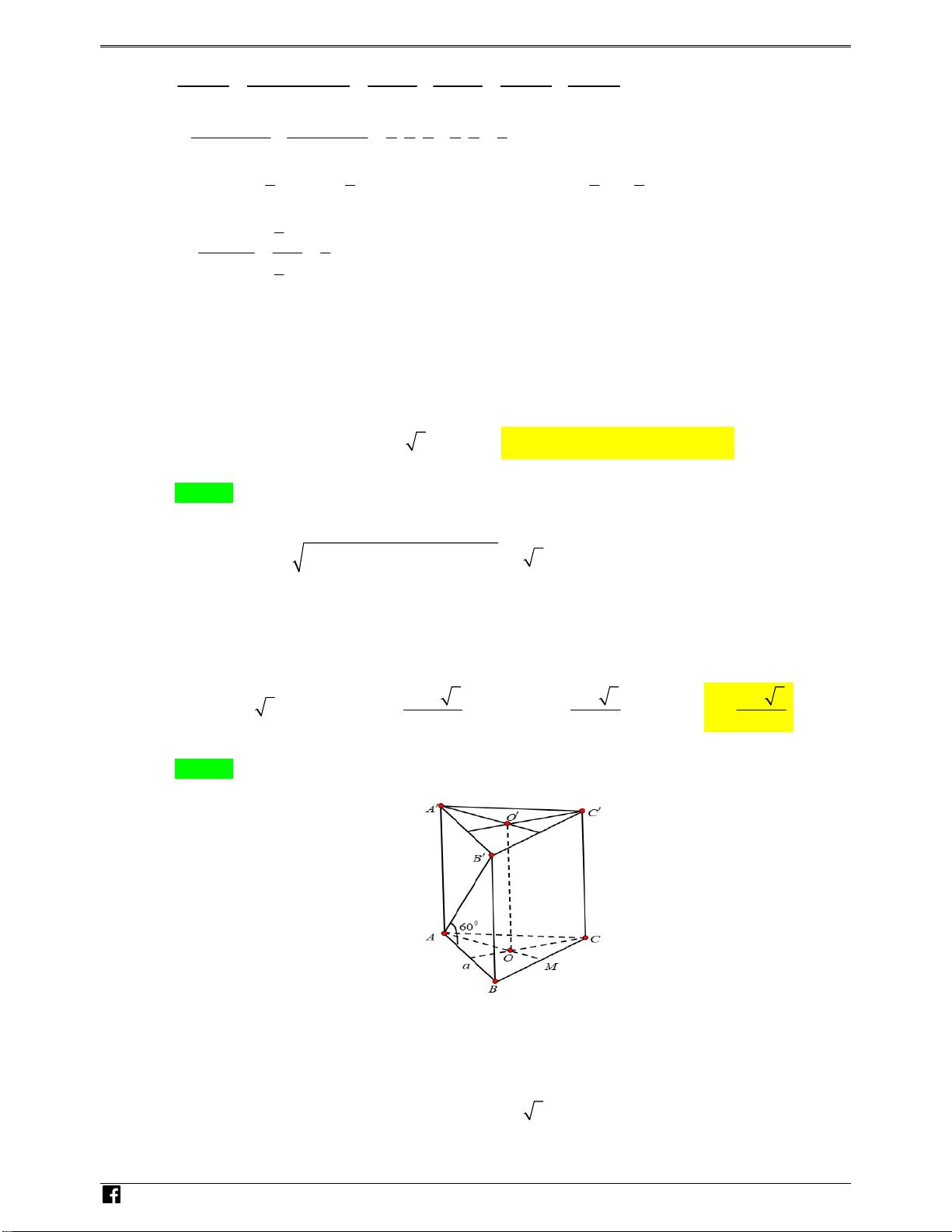
Câu 24. Cho lăng trụ tam giác đều ABC.AB C
  có độ dài cạnh đáy bằng a , góc giữa đường thẳng AB
và mặt phẳng ABC  bằng 60º . Tính thể tích V của khối trụ ngoại tiếp lăng trụ đã cho. 3 3 3 A.    3 4a 3 a 3 a 3
V  a  3 . B. V  . C. V  . D. V  . 3 9 3 Câu 25. Cho hàm số 2
y  f x liên tục trên  , có đạo hàm 3 f (
 x)x x   1 x  
2 . Hỏi hàm số y  f x
có bao nhiêu điểm cực trị? A. 2 . B. 0 . C. 1. D. 3 .  
Câu 26. Tích giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2 2
y  x  trên đoạn 1  ;2 bằng x 2    A. 15 . B. 8 . C. 51 . D. 85 . 4 4 Trang 3/6 - Mã đề 101
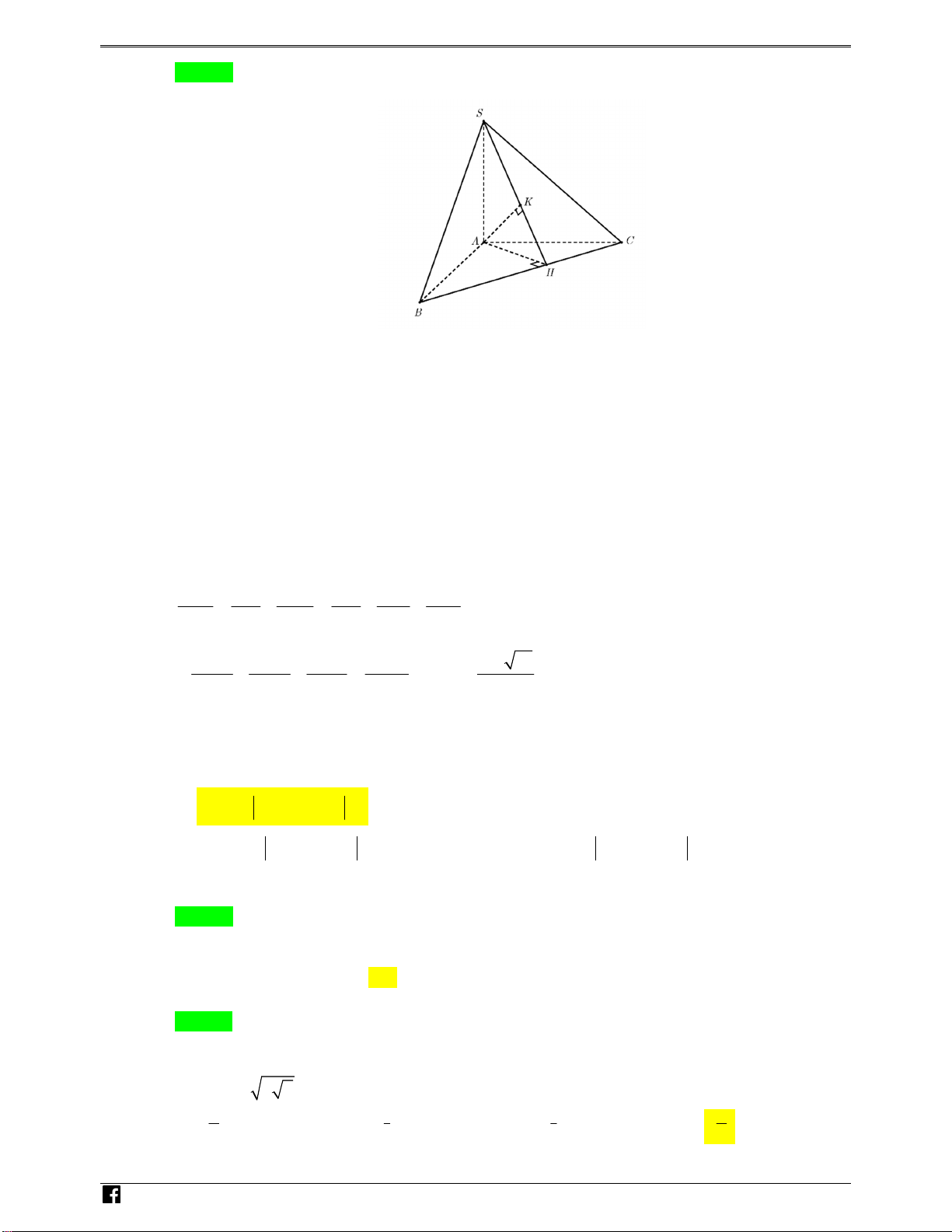
Câu 27. Cho hình chóp S.ABC có đáy là tam giác vuông tạiA , biết SA  ABC  và AB  2a,
AC  3a , SA  4a . Tính khoảng cách d từ điểm A đến mặt phẳng SBC . A. 2a a a a d  . B. 6 29 d  . C. 12 61 d  . D. 43 d  . 11 29 61 12
Câu 28. Cho hàm số y  f x,y  g x liên tục trên đoạn a;b 
. Hình phẳng D giới hạn bởi đồ thị 
 a  b 
hai hàm số y  f x,y  g xvà hai đường thẳng x  a,x  b có diện tích là A. b b S  f x  g x x  . B. S f x g x    x  . D     d D    d   a a  C. b a S   f x  g x x  . D. S  f x  g x x  . D    d D    d a b
Câu 29. Số phức z  5  8i có phần ảo là A. y 5 . B. 8 . C. 8 . D. 8i . 5
Câu 30. Biểu thức 3 4
x x x  0 viết dưới dạng lũy thừa với số mũ hữu tỉ là 1 1 A. 12 x . B. 7 x . 3 5 5 C. 4 x . D. 12 x .
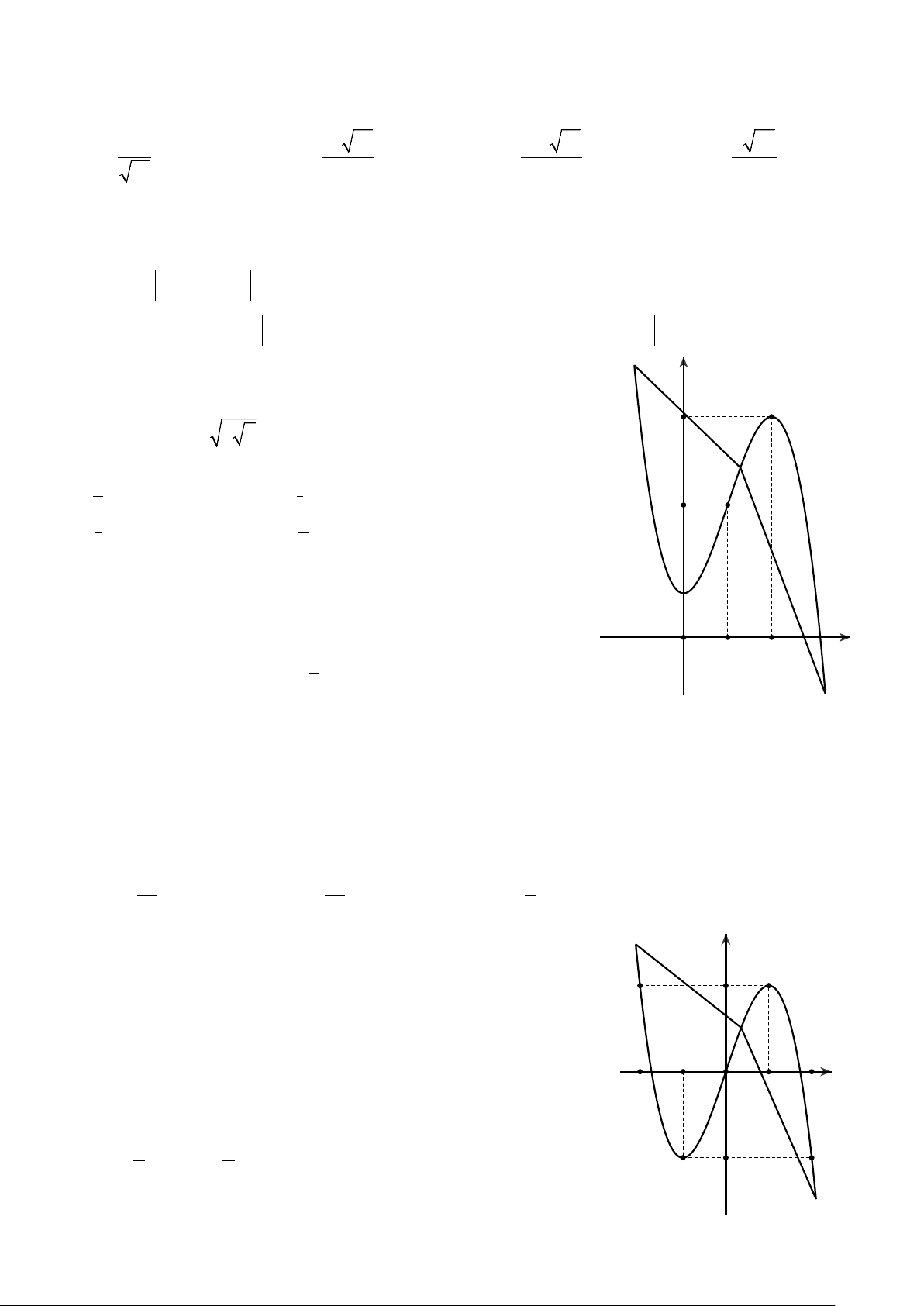
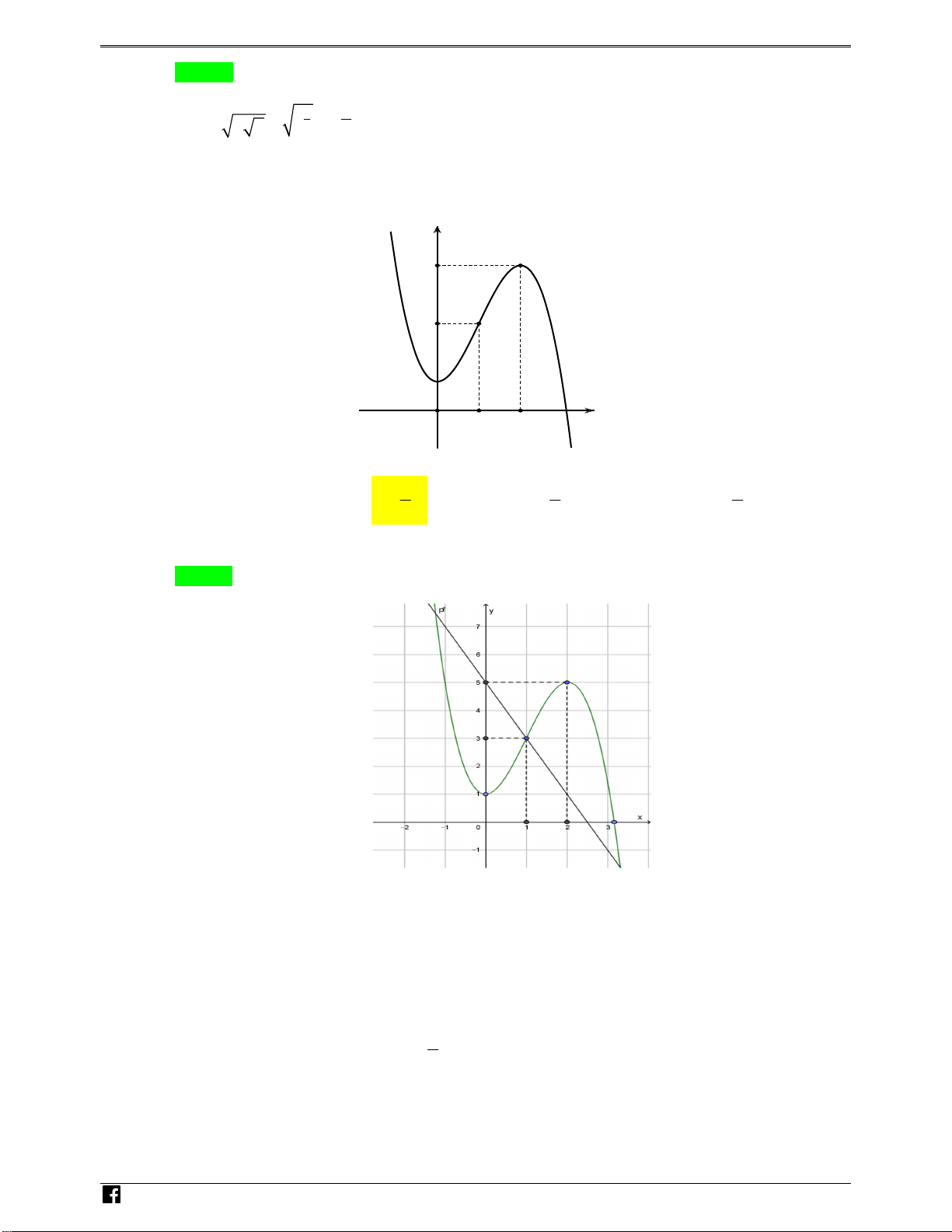
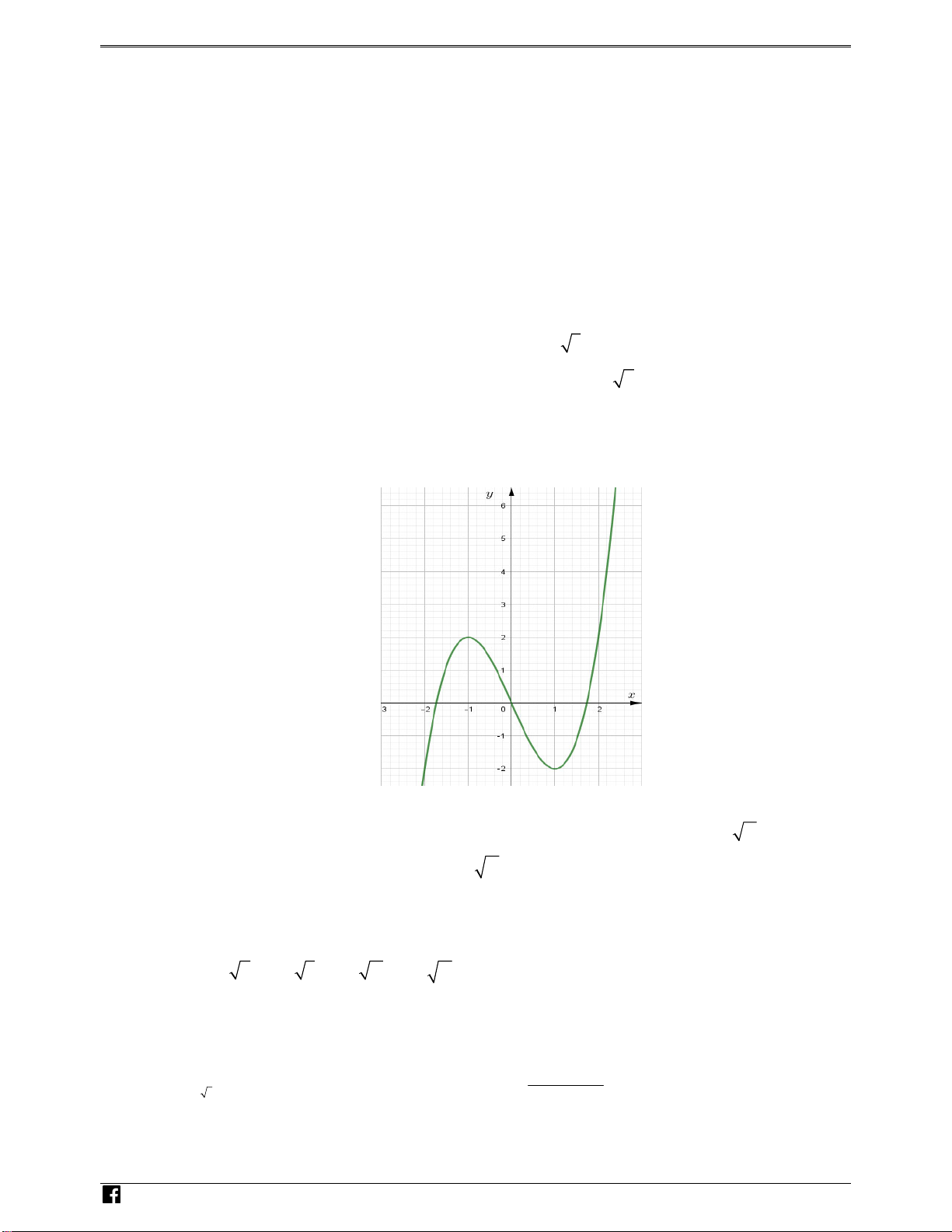
Câu 31. Cho y  f x là hàm đa thức bậc 4 , có đồ thị hàm số
y  f xnhư hình vẽ. Hàm số y  f   x 2
5 2  4x  10x 1 đồng
biến trong khoảng nào trong các khoảng sau đây?   O 1 2 x A. 3;4. B. 5 2  ;   .  2     C. 3  ;2    . D. 3 0; . 2   2
Câu 32. Cho hàm số y  f x liên tục trên  \ 1;  0 thỏa mãn f   1  2 ln 2  1 , x x  
1 f x  x  2f x  x x  
1 , x   \ 1; 
0 . Biết f 2  a b ln 3 , với a,b là hai số hữu tỉ. Tính 2
T  a b . A. 3 T   . B. 21 T  . C. 3 T  . D. T  0 . 16 16 2
Câu 33. Cho hàm số bậc ba y  f x có đồ thị như hình vẽ. Có bao y
nhiêu giá trị nguyên của tham số m thuộc đoạn 0;9  sao cho bất   2
phương trình 2fxfx 2 m 
f xf x m  f x 2  16.2  4  16  0 có nghiệm x  1;  1 ? 2 A. 6. B. 8 . -1 O 1 x C. -2 5 . D. 7 .
Câu 34. Cho a, , b ,
c d là các số nguyên dương, a  1,c  1 thỏa mãn 3 5
log b  , log d  và a c  9 . Khi đó, b d bằng a 2 c 4 -2 y = f(x) A. 93. B. 9. C. 13 . D. 21 . Trang 4/6 - Mã đề 101 Câu 35. Cho hàm số 3 2
y  x – 8x  8x 2
có đồ thị C  và hàm số y  x  8 ax b (với a,b   ) có
đồ thị P. Biết đồ thị hàm số C  cắt P tại 3 điểm có hoành độ nằm trong đoạn 1;5 
 . Khi a đạt giá
trị nhỏ nhất thì tích ab bằng A. 729. B. 375 . C. 225 . D. 384 .
Câu 36. Gọi A là tập các số tự nhiên có 3 chữ số đôi một khác nhau. Lấy ngẫu nhiên ra từ A hai số. Tính
xác suất để lấy được hai số mà các chữ số có mặt ở hai số đó giống nhau. A. 41 . B. 35 . C. 41 . D. 14 . 5823 5823 7190 1941 2 4   Câu 37. Cho hàm số x
y  f x liên tục trên  và f 2  16, f
 xdx  4 . Tính I  xf  dx   . 2 0 0
A. I  144 .
B. I  12 .
C. I  112 . D. I  28.
Câu 38. Cho tứ diện ABCD có  
DAB  CBD  90º ; 
AB  a;AC  a 5;ABC  135 . Biết góc giữa
hai mặt phẳng ABD,BCD bằng 30. Thể tích của tứ diện ABCD là 3 3 3 3 A. a . B. a . C. a . D. a . 2 3 2 3 2 6
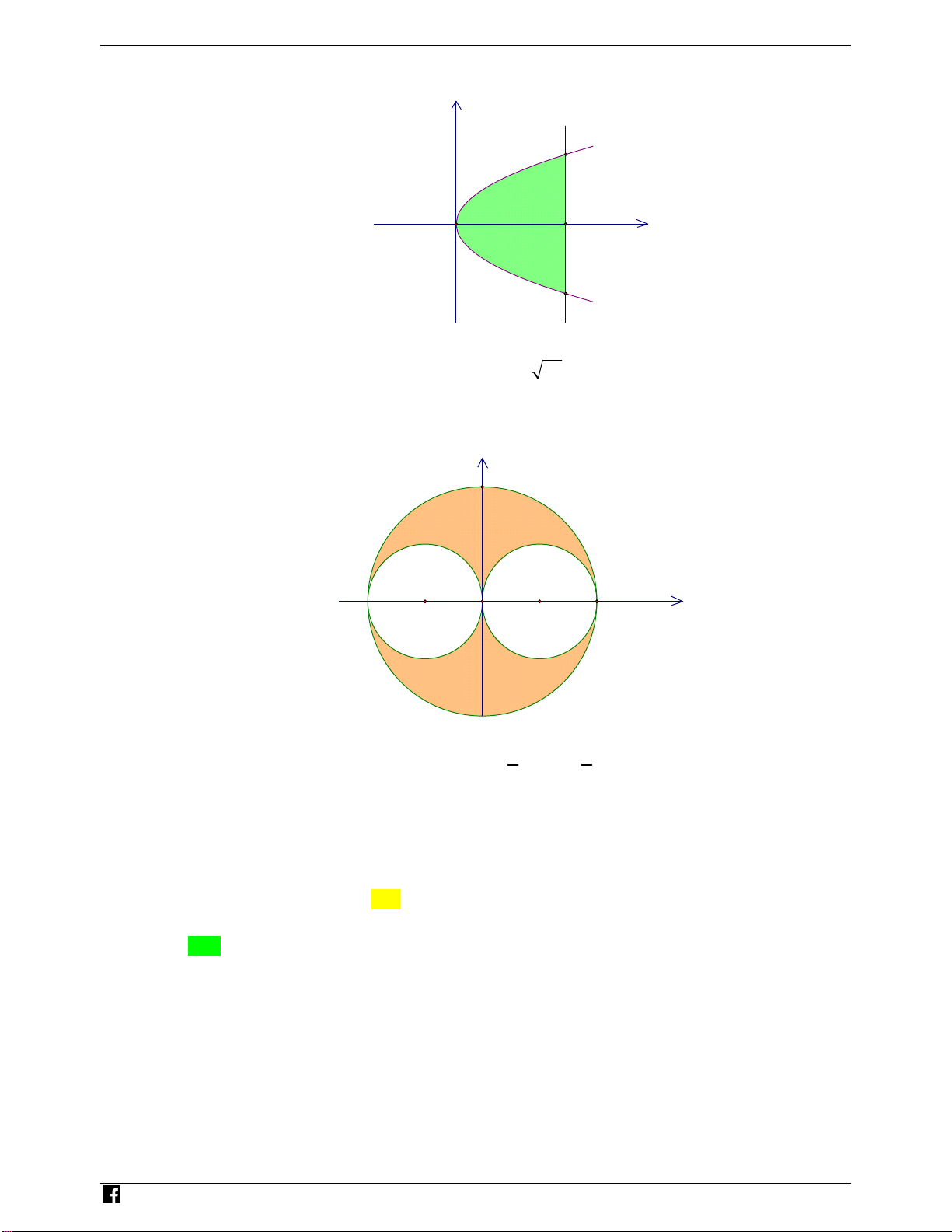
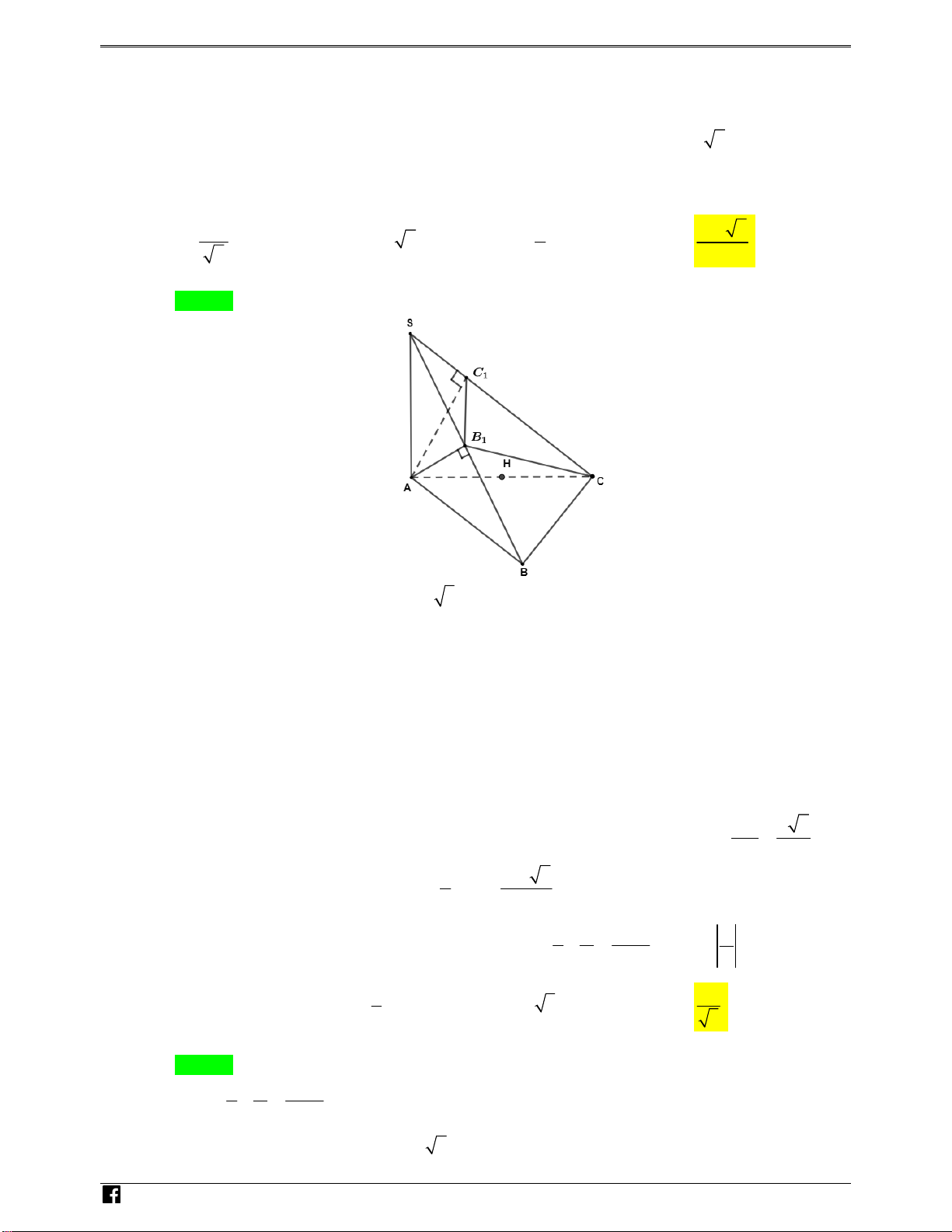
Câu 39. Trong mặt phẳng với hệ tọa độ Oxy , cho hình H giới hạn bởi các đường y  2x, 1 
y   2x,x  4 ; hình H là tập hợp tất cả các điểm M x;y thỏa mãn các điều kiện: 2  2 2 2 2
x  y  16; x   2
 y  x   2 2 4;
2  y  4 . Khi quay H , H quanh Ox ta được các khối tròn 2  1 
xoay có thể tích lần lượt là V ,V . Khi đó, mệnh đề nào sau đây là đúng? 1 2
A. V  2V .
B. V V .
C. V V  48 .
D. V  4V . 2 1 1 2 1 2 2 1
Câu 40. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A1;2;  1 ,B 3;4;  0 , mặt phẳng
P:ax by cz  46  0. Biết rằng khoảng cách từ ,
A B đến mặt phẳng P lần lượt bằng 6 và 3 . Giá
trị của biểu thức T  a b  c bằng A. 3. B. 6. C. 3 . D. 6.
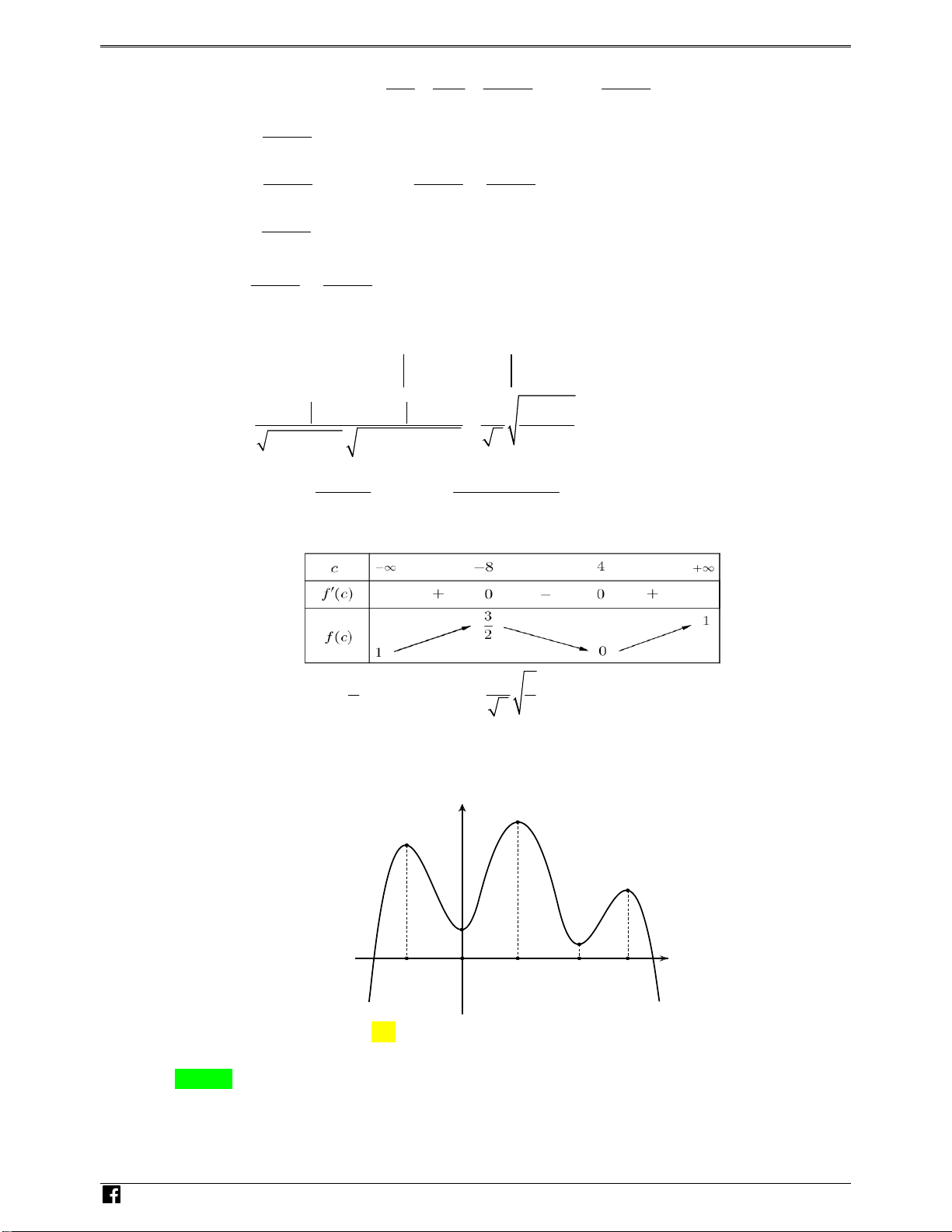
Câu 41. Cho hình chóp S.ABC có SA vuông góc với ABC , 
AB  a,AC  a 2,BAC  45º . Gọi
B ,C lần lượt là hình chiếu vuông góc của A lên S ,
B SC . Thể tích khối cầu ngoại tiếp hình chóp 1 1 . ABCC B bằng 1 1 3 3 A. a  . B. 3 4 a  2 a  2 . C. 3 a  . D. . 2 3 3
Câu 42. Cho các số phức z,w khác 0 thỏa mãn z  w  0 và 1 3 6   . Khi đó z bằng z w z  w w A. 3 . B. 1 . C. 3 . D. 1 . 3 3
Câu 43. Ông Nam dự định gửi vào ngân hàng một số tiền với lãi suất 6,6% /năm. Biết rằng nếu không rút
tiền khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho năm tiếp
theo. Tính số tiền tối thiểu x triệu đồng x   ông Nam gửi vào ngân hàng để sau 3 năm số tiền lãi đủ
mua một chiếc xe gắn máy trị giá 26 triệu đồng.
A. 191triệu đồng.
B. 123 triệu đồng.
C. 124 triệu đồng.
D. 145 triệu đồng. Trang 5/6 - Mã đề 101
Câu 44. Trong không gian với hệ tọa độ x  y  z 
Oxyz , cho đường thẳng 1 1 2 d :   và mặt phẳng 1 2 1
P:2x y  2z 1  0. Gọi d là hình chiếu của đường thẳng d lên mặt phẳng P, vectơ chỉ phương
của đường thẳng d là    
A. u 5;16;13 .
B. u 5; 4; 3 .
C. u 5;16;13 .
D. u 5;16;13 . 1   4   2   3  
Câu 45. Trong không gian với hệ tọa độ Oxyz , cho điểm A4;0  ;0 ,B 0;4 
;0 ,S 0;0;c và đường thẳng x  1 y  1 z  1 d :  
. Gọi A ,B lần lượt là hình chiếu vuông góc của O lên S , A SB . Khi góc giữa 1 1 2
đường thẳng d và mặt phẳng OAB lớn nhất, mệnh đề nào sau đây đúng?  
A. c  8;  6 .
B. c  9; 8.
C. c  0;  3 . D. 17 15 c     ;     .  2 2 
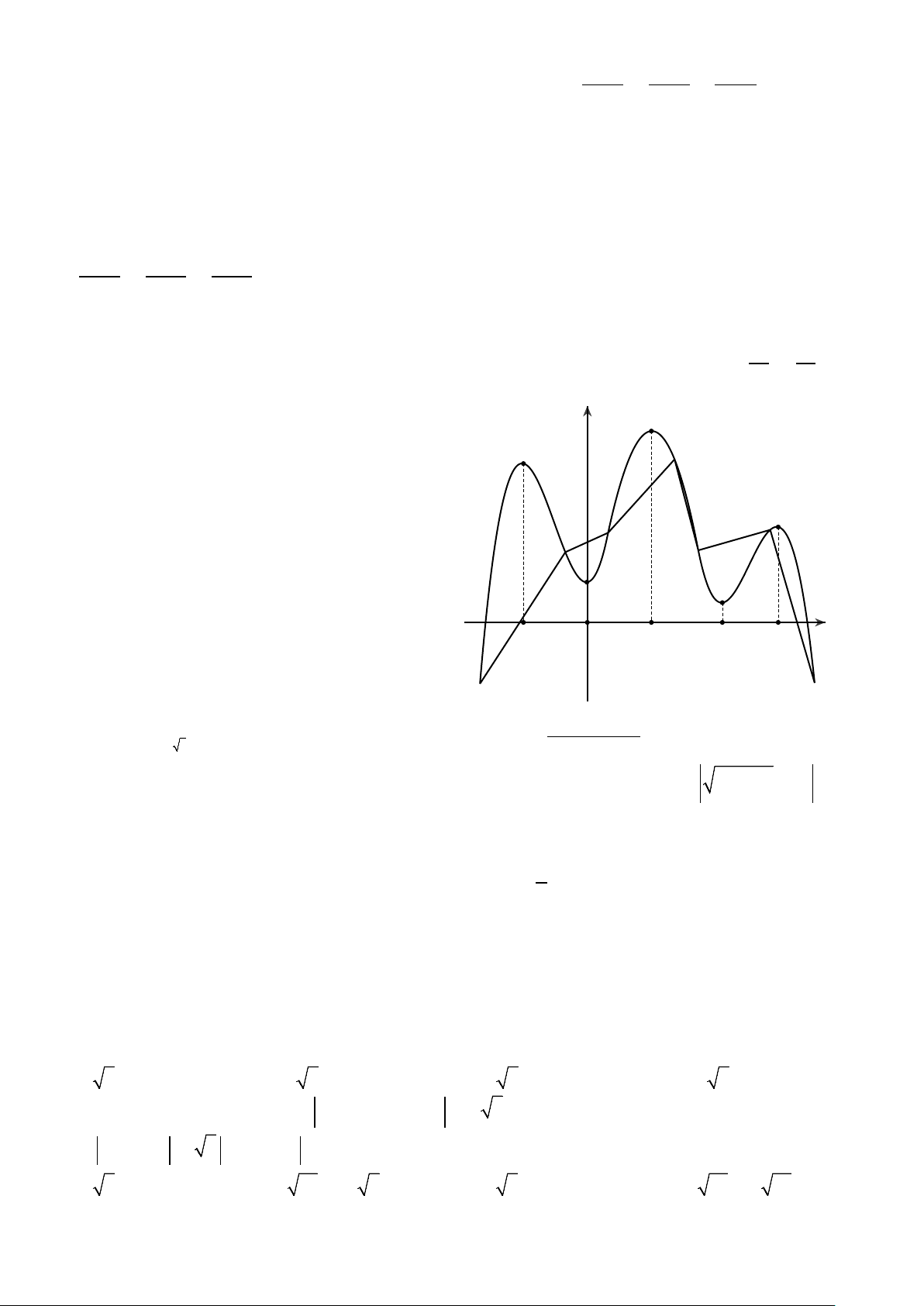
Câu 46. Cho hàm số y  f x có đồ thị như hình y
vẽ. Biết tất cả các điểm cực trị của hàm số
y  f x là 2;0;2;a;6 với 4  a  6. Số điểm
cực trị của hàm số y  f  6 2
x  3x  là A. 8 . B. 11. C. 9. D. 7 . -2 O 2 a 6 x y = f(x)
Câu 47. Cho hai số thực x,y thỏa mãn 5  4x  x log y 8y 16
log  5 x 1 x        2 log  log 2y  8 . 3      2    2 2 2 3 2  3
Gọi S là tập các giá trị nguyên của tham số m để giá trị lớn nhất của biểu thức 2 2
P  x  y  m không
vượt quá 10 . Hỏi S có bao nhiêu tập con không phải là tập rỗng? A. 2047 . B. 16383 . C. 16384 . D. 32 . 1
Câu 48. Cho tích phân I  x   x   7 2 ln
1 dx  a ln 2  
trong đó a , b là các số nguyên dương. b 0 Tổng 2 a  b bằng A. 8 . B. 16 . C. 12 . D. 20 .
Câu 49. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P : mx  m  
1 y  z  2m  1  0 , với
m là tham số. Gọi  là tập hợp các điểm H là hình chiếu vuông góc của điểm H 3;3;0 trên P. Gọi m
a,b lần lượt là khoảng cách lớn nhất, khoảng cách nhỏ nhất từ O đến một điểm thuộc . Khi đó, a b bằng A. 5 2 . B. 3 3 . C. 8 2 . D. 4 2 .
Câu 50. Cho số phức z thỏa mãn 1  iz  1 3i  3 2 . Giá trị lớn nhất của biểu thức
P  z  2  i  6 z  2  3i bằng A. 5 6 .
B. 15 1 6. C. 6 5 . D. 10  3 15 .
------ HẾT ------ Trang 6/6 - Mã đề 101 ĐÁP ÁN TOÁN Câu 101 102 103 104 105 106 107 108 109 110 111 112 1 D D A D A A D A A D A C 2 D D B B C C A A B A D B 3 B B C A A A C D D D D A 4 A B B B D D C D C C D B 5 D D A C A B A C C C B D 6 D B D C A C D B B A A A 7 D C C D D A D C D B C A 8 D C C B A C C A C B D C 9 B C D B B B C A C B B D 10 A D B A B A B C C A D D 11 D C D C C A B C D C A B 12 D A C A A B A C A B A A 13 B D D A A A C D D C A D 14 D D D A B A A B A D B D 15 D C A D C D A C C D B A 16 C C C A C D B A D C B B 17 B D A C C A B B C B C C 18 B C A A B B D C C A C B 19 C D C A B D D B D C C A 20 A D A D D B C D B D A A 21 D C A A A D B B C B B C 22 A C A C B C D D D C B A 23 D B C A C C A A C B A C 24 D A A B D D A C D C D C 25 A C D C B C A A A D A A 26 A A A B D C A A A B B B 27 C A C C A C C B C B C A 28 A A D B D B B D C D D C 29 B D C C A C A D B B B C 30 D C C B D B B C D D A A 31 B A A A A C D A B D C D 32 A A D C C A D C B A A D 33 A A D A B D D D D A C A 34 A C D C C C C A D B B B 35 B C C C C D D D B B A A 36 A A B A D C C A A A B C 37 C A C C B D C D A A D C 38 D A B B A B C D C D B D 39 D D C B C B C C C D B B 40 B D A A D A B A C B B D 41 D B A C A B C B B D B D 42 D B C D A B C A A A A A 43 C B B D B D B C A B A C 44 D D A D A C A D B A C C 45 D C C B C A D A B C D D 46 C A A D D C D A A A B B 47 B A D C B A A C B A D C 48 D D B A B C A D B D C D 49 D C D D D B C B D A C B 50 C A A C B B C A C D C C ĐÁP ÁN TOÁN Câu 113 114 115 116 117 118 119 120 121 122 123 124 1 D C B C D B C D D B C D 2 B C D A B A A D D B B D 3 C A D C A B D D C B A A 4 C D D B A C D C D B D C 5 B B B C B A A D D B D B 6 A A B B A C B A C D B D 7 D C D B B C D C B D B A 8 A A B D C B D B C C C A 9 A A A A A D B C D A D D 10 D C B D C B B D D A B A 11 D B B B C C C D A D A C 12 D A B C C C C A B D C D 13 B C A B B B A C A C D D 14 C B B C C C B A D C A C 15 C D D B A D A A C D D D 16 D A A A B D A C B B D B 17 B C A D D C B C B D C D 18 C B A B D B D D B C B C 19 D D D D A A D A C B A B 20 D A D D D B C A A A D D 21 B C D A A C C D B A B A 22 D B C A C A B B B D B B 23 A C C B D C B D D B B D 24 B A A D C C A B A D A B 25 C C A C D D C D D D B A 26 C D D A C C A C A A A C 27 D D D D C D B C B B B D 28 C C C B A C B D D C B A 29 D B C B A C C D D A C B 30 D A D D A D C C B B C B 31 C C C A C B C C C B B A 32 D B A C D A B A B A C B 33 D A A C C B B C D A D A 34 D C C C B D A D A A C D 35 C C A D C B B B B C A A 36 A B B D A A C B D A D B 37 C B B A D B A C A A D B 38 C B C A D C A B A C B C 39 D D A B B D C D A C C C 40 D D B A D A C A D B D C 41 A D D B C A A B A D B A 42 B B D C A B A D A B C A 43 A D B B A B B B B C D D 44 A A D A A D C A D C C B 45 B A A D A B B C B C B D 46 B B D A A B C D C D C C 47 B D C D C D A C D D A D 48 C C D D C A A D A C C D 49 D A D C B C D D A D B A 50 C D C B D C A B B C C C NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 BẢNG ĐÁP ÁN 1.D 2.D 3.B 4.A 5.D 6.D 7.D 8.D 9.B 10.A 11.D 12.D 13.B 14.D 15.D 16.C 17.B 18.B 19.C 20.A NHÓM 21.D 22.A 23.D 24.D 25.A 26.A 27.C 28.A 29.B 30.D 31.B 32.A 33.A 34.A 35.B 36.A 37.C 38.D 39.D 40.B 41.D 42.D 43.C 44.D 45.D 46.B 47.B 48.D 49.D 50.C TOÁN VD –
LỜI GIẢI CHI TIẾT
Câu 1. Trong không gian với hệ tọa độ Oxyz , phương trình mặt phẳng   đi qua điểm A0;1;0 ; VDC
B 2;0;0 ; C 0;0;3 là x y z x y z x y z x y z A.    1. B.    0 . C.   1. D.   1. 2 1 3 2 1  3 1  2 3 2 1  3 Lời giải Chọn D Câu 2. Gọi 
  . Giá trị của biểu thức 1
z , z là hai nghiệm phức của phương trình 2 2z 3z 3 0 2 2 2  bằng 1 z z2 3 9 9 A. . B.  . C. 3 . D.  . 18 8 4 Lời giải Chọn D  NHÓM T 3     1 z z2 Vì  z ,    nên theo viet ta có 2 .
1 z là hai nghiệm của phương trình 2 2z 3z 3 0 2   3  1 z z2  2 OÁN VD – VDC 2   Mà 2 2 3 3 9
z  z  z  z  2z z      2.   . 1 2  1 2 2 1 2  2    2 4 3
Câu 3. Tập xác định của hàm số y   2 x  x  5 3
2  x  32 là:
A. D  ; \  3 .
B. D    ;1  2; \  3 .
C. D  ; \ 1;2 . D. D    ;1  2;. Lời giải Chọn B x  1 2 
Ta có hàm số xác định khi x  3x  2  0    x  2 x  3  0  x  3
Suy ra tập xác định D    ;1  2; \  3
https://www.facebook.com/groups/toanvd.vdc Trang 8 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019
Câu 4. Cho hàm số y  f  x có f 2  2 , f 3  5 ; hàm số y  f  x liên tục trên 2;  3 . Khi đó 3 f 
 xdx bằng: 2 A. 3. B. 3 . C. 10 . D. 7 . NHÓM Lời giải Chọn A TOÁN VD – Ta có 3 3
f '(x)dx  f (x)  f (3)  f (2)  5  2  3  2 2
Câu 5. Bất phương trình log 3x  2  log 6  5 có tập nghiệm là  ;
a b . Tổng  bằng 2   2  x a b 8 28 26 11 A. . B. . C. . D. . VDC 3 15 5 5 Lời giải Chọn D  6 6  5x  0  
Bất phương trình đã cho tương đương với: x 6    5  1 x  . 3
 x  2  6  5x 5 x 1 a  1
Vậy bất phương trình có tập nghiệm  6   11 S  1; , suy ra:   a  b  . 5  6   b  5  5
Câu 6. Cho hàm số y  f  x có bảng biến thiên như sau: NHÓM T OÁN VD – VDC
Tập tất cả các giá trị của tham số m để phương trình f x  m có ba nghiệm phân biệt là
A. 4; . B.  ;  2   . C.  2;  4. D. 2;4 . Lời giải Chọn D
Số nghiệm của phương trình f x  m bằng số giao điểm của đồ thị hàm số y  f x với
đường thẳng y  m.
Từ bảng biến thiên suy ra phương trình có ba nghiệm phân biệt khi 2  m  4 . x
Câu 7. Số đường tiệm cận của đồ thị hàm số y  là 2 x  9
https://www.facebook.com/groups/toanvd.vdc Trang 9 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 A. 2 . B. 4 . C. 3 . D. 1. Lời giải Chọn D
Tập xác định của hàm số D   NHÓM 1 x x x    TOÁN VD – Có: lim lim 0 lim . 2 2
x x  9 x 9
x x  9 1 2 x
Đồ thị hàm số có đường tiệm cận ngang y  0 VDC Câu 8. Hàm số 3 2
y  x  3x  4 nghịch biến trên khoảng nào sau đây? A.  . B.  ;  2   .
C. 0;. D. 2;0 . Lời giải Chọn D
Tập xác định của hàm số D   x  0 Có: 2
y '  3x  6x; y '  0   x  2 
Dấu của y' : y '  0  x  ;  2
  0; ; y '  0  x 2  ;0  
Câu 9. Trong không gian với hệ trục tọa độ Oxyz , cho hai vectơ a   4;  5; 3
  , b  2; 2;   1 . Tìm tọa   
độ của vectơ x  a  2b .     NHÓM T
A. x  2;3; 2
  . B. x  0;1; 
1 . C. x  0; 1  ;  1 . D. x   8;  9;  1 . Lời giải Chọn B   OÁN VD – VDC a   4;  5; 3         
 x  a  2.b  0;1;  1 . 2.b   4; 4  ;2
 Vậy x  0;1;  1 .
Câu 10. Họ nguyên hàm của hàm số f  x  cos 2x là: sin 2x A. cos 2 d x x   C  . B. cos 2 d
x x  sin 2x  C 2  . sin 2x C. cos 2 d x x    C  . D. cos 2 d
x x  2sin 2x  C 2  . Lời giải Chọn A Cách 1  Vì  x  C / sin 2
 2.cos 2x  f x nên B sai. /  Vì  sin 2x  1   C    
.2.cos 2x  cos 2x  f x nên C sai.  2  2
https://www.facebook.com/groups/toanvd.vdc Trang 10 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019  Vì  x  C / 2.sin 2
 2.2.cos 2x  4.cos 2x  f x nên D sai. /  Vì  sin 2x  1  C   
.2.cos 2x  cos 2x  f x  2  2 NHÓM
nên họ nguyên hàm của hàm số x
f  x  cos 2x là sin 2 cos 2 d x x   C  . 2 Cách 2 TOÁN VD – 1 1  cos 2 d x x  . cos 2 . x d  
2x  .sin 2x C . 2 2
 Vậy họ nguyên hàm của hàm số x
f  x  cos 2x là sin 2 cos 2 d x x   C  . 2 VDC Câu 11. Cho hàm số x
y  a với 0  a  1. Mệnh đề nào sau đây sai?
A. Đồ thị hàm số x
y  a và đồ thị hàm số y  log x đối xứng nhau qua đường thẳng y  . x a B. Hàm số x
y  a có tập xác định là  và tập giá trị là (0; ) . C. Hàm số x
y  a đồng biến trên tập xác định của nó khi a  1.
D. Đồ thị hàm số x
y  a có tiệm cận đứng là trục tung. Lời giải Chọn D + Hàm số x
y  a có tập xác định là  và tập giá trị là (0; ) . + Hàm số x
y  a đồng biến trên tập xác định của nó khi a  1 và nghịch biến trên tập xác định
của nó khi 0  a  1.
+ Đồ thị hàm số x
y  a có tiệm cận ngang là trục hoành và không có tiệm cận đứng. NHÓM T + Đồ thị hàm số x
y  a và đồ thị hàm số y  log x đối xứng nhau qua đường thẳng y  . x a
Câu 12. Đường cong trong hình vẽ bên là đồ thị của một trong bốn hàm số được liệt kê ở bốn phương
án dưới đây. Hỏi đó là hàm số nào? y OÁN VD – VDC -1 O 1 x -3 -4 A. 4 2
y  x  2x . B. 4 2
y  x  3x  3. C. 4 2
y  x  x  3. D. 4 2
y  x  2x  3 . Lời giải Chọn D
+ Ta có: lim y   , suy ra loại B. x
+ Từ hình vẽ bên ta thấy đồ thị hàm số đạt cực đại tại (0;3) suy ra loại A.
+ Đồ thị hàm số đạt cực tiểu tại (1; 4)suy ra loại C.
https://www.facebook.com/groups/toanvd.vdc Trang 11 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 a
Câu 13. Cho hình lăng trụ ABC.AB C
  có đáy ABC là tam giác đều cạnh a , 3 AA  . Biết rằng hình 2
chiếu vuông góc của A lên  ABC là trung điểm BC . Thể tích của khối lăng trụ ABC.AB C   NHÓM T là 3 a 2 3 3a 2 3 a 6 3 2a A. . B. . C. . D. . 8 8 2 3 OÁN VD Lời giải Chọn B – VDC Gọi a
M là trung điểm của BC, khi đó 3
AM  BC, AM 
và A'M   ABC. 2 Trong tam giác vuông a A' AM có: 2 2 6 A' M  ' AA  AM  2 2 3
Vậy, thể tích khối lăng trụ là:
a 6 a 3 3a 2
V  A'M .S   .  ABC . 2 4 8 NHÓM
Câu 14. Trong không gian với hệ tọa độ Oxyz , phương trình đường thẳng d đi qua điểm A1;2;  1 và
vuông góc với mặt phẳng P :x  2y  z 1  0 có dạng TOÁN VD – VDC
x 1 y  2 z 1 x  2 y z  2 A. d :   . B. d :   . 1 2  1 1 2  1
x 1 y  2 z 1 x  2 y z  2 C. d :   . D. d :   . 1 2 1 2 4  2 Lời giải Chọn D
Do đường thẳng d vuông góc với mặt phẳng P nên d nhận của véc tơ pháp tuyến của P  là n  1; 2  ; 
1 làm véc tơ chỉ phương. Vì thế loại đáp án C.
Trong các đáp án A, B, D chỉ có đáp án D là đường thẳng d đi qua điểm A1;2;  1 . Vậy chọn D. 3 x 1  1  1 
Câu 15. Trong các hàm số    log x ; g  x   ; hx 3  x ; k x    3x f x có bao nhiêu hàm 2   2  2 
số đồng biến trên  ?
https://www.facebook.com/groups/toanvd.vdc Trang 12 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 A. 2 . B. 3. C. 4 . D. 1. Lời giải Chọn D NHÓM Ta có: 1    TOÁN VD –
+ f x log x f x   0, x   0. 2   xln2 3 3 x 1  x 1  +     g  x 1    g  x 2 1 1  3
 x   ln  0, x     .  2   2  2 VDC 1 2  + hx 1 3
 x  hx 3  x  0, x   0 . 3 +   2 x     2 3  2 3x k x k x x ln 3  0, x   0. 3 x 1  Vậy có một hàm số   g  x 1   đồng biến trên  . 2   
Câu 16. Số giá trị nguyên của tham số m để phương trình để phương trình sin x  m  
1 cos x  2m 1 có nghiệm là A. 0 . B. 3 . C. 2 . D. 1. Lời giải Chọn C NHÓM T
Phương trình sin x  m  
1 cos x  2m 1 có nghiệm khi và chỉ khi 2 2 2 1  OÁN VD – VDC 1 m   1  2m  
1  3m  2m 1 0 
 m 1. Vậy m0;  1 . 3
Câu 17. Một hình nón có độ dài đường sinh bằng đường kính đáy. Diện tích hình tròn đáy của hình nón
bằng 9 . Tính đường cao h của hình nón. 3 3 A. h  . B. h  3 3 h  . D. h  3 . 2 . C. 3 Lời giải Chọn B Ta có diện tích đáy 2
S   r  9  r  3. Do đó l  2r  6. Mặt khác ta có 2 2 2 2 2 2 2 2
l  h  r  h  l  r  6  3  27  h  3 3.
Câu 18. Trong không gian, cho các mệnh đề sau:
I. Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.
II. Hai mặt phẳng phân biệt chứa hai đường thẳng song song cắt nhau theo giao tuyến song
song với hai đường thẳng đó.
III. Nếu đường thẳng a song song với đường thẳng b , đường thẳng b nằm trên mặt phẳng
P thì a song song với P .
https://www.facebook.com/groups/toanvd.vdc Trang 13 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019
IV. Qua điểm A không thuộc mặt phẳng   , kẻ được đúng một đường thẳng song song với   .
Số mệnh đề đúng là NHÓM A. 2 . B. 0 . C. 1. D. 3 . Lời giải TOÁN VD – Chọn B
I. Sai vì hai đường thẳng đó có thể chéo nhau.
II. Sai vì hai giao tuyến có thể trùng nhau.
III. Sai vì hai đường thẳng đó có thể cùng nằm trên mp(P) .
IV. Sai vì có thể kẻ được vô số đường thẳng song song mp(P) . VDC
Câu 19. Tập hợp điểm biểu diễn số phức z thỏa mãn điều kiện | z 1 2i |1 là
A. Đường tròn I 1;2 , bán kính R 1. B. Đường tròn I  1;
  2 , bán kính R 1.
C. Đường tròn I  1;
 2 , bán kính R 1. D. Đường tròn I 1; 2 , bán kính R 1. Lời giải Chọn C
Giả sử z  x  yi, x, y  . Ta có:
z   i    x      y    x  2   y  2 | 1 2 | 1 | 1 2 i | 1 1 2 1.
Vậy tập hợp điểm biểu diễn số phức z là đường tròn tâm I  1;
 2 , bán kính R 1.
Câu 20. Kí hiệu k
C là số các tổ hợp chập k của n phần tử (1 k  n) . Mệnh đề nào sau đây đúng? n n k k n k ! k ! k ! k ! A. C  . B. C  . C. C  . D. C  . n n n n NHÓM T
k !(n  k)!
k !(n  k)!
k !(n  k)! (n  k)! Lời giải Chọn A OÁN VD – VDC Công thức: n k ! C  . n
k!(n  k)!
Câu 21. Cho hàm số y  f  x liên tục, đồng biến trên đoạn a;b. Khẳng định nào sau đây đúng?
A. Hàm số đã cho có cực trị trên đoạn a;b.
B. Hàm số đã cho có giá trị lớn nhất, giá trị nhỏ nhất trên khoảng a;b.
C. Phương trình f  x  0 có nghiệm duy nhất thuộc đoạn a;b.
D. Hàm số đã cho có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn a;b. Lời giải Chọn D
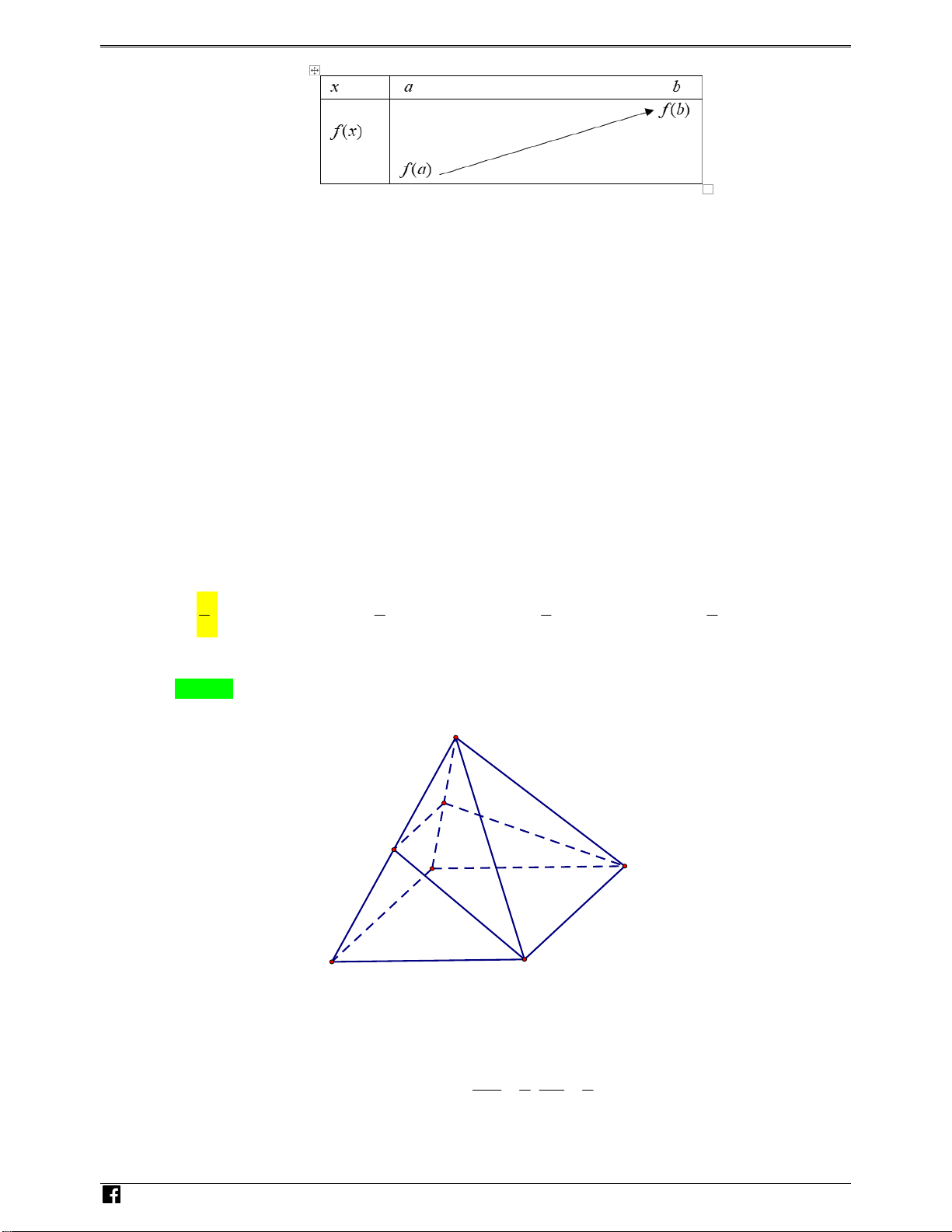
Hàm số y  f x liên tục, đồng biến trên đoạn a;b ta có bảng biến thiên trên đoạn a;b như sau:
https://www.facebook.com/groups/toanvd.vdc Trang 14 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 NHÓM TOÁN VD –
Dựa vào bảng biến thiên ta có:
Hàm số đã cho có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn a;b là:
max f (x)  f (b); min f (x)  f (a) . a;b a;b VDC
Trên a;b hàm số không có cực trị. Trên khoảng  ;
a b không thể kết luận được giá trị lớn nhất và giá trị nhỏ nhất. Trên  ;
a b chưa thể kết luận được phương trình f  x  0 có nghiệm duy nhất thuộc đoạn
a;b vì không xác định được dấu của f (a) và f (b).
Câu 22. Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M , N là trung điểm của SA , SB . Mặt
phẳng MNCD chia hình chóp đã cho thành hai phần. Tỉ số thể tích hai phần là (số bé chia số lớn) 3 3 1 4 A. . B. . C. . D. . 5 4 3 5 Lời giải NHÓM T Chọn A S OÁN VD – VDC M N A D B C
Gọi V là thể tích khối chóp S.ABCD . Ta có: V  V  V
 V (do các hình chóp này có cùng đường cao là khoảng S ABCD 2. S ABC 2. . . S.ACD
cách từ S đên (ABCD) và S  S  S ) ABCD
2. ABC 2. ACD  SM SN
M , N là trung điểm của SA , SB suy ra 1 1  ;  . SA 2 SB 2 Ta lại có:
https://www.facebook.com/groups/toanvd.vdc Trang 15 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 V V V V V V V S.MNCD S.MNC S.MCD S.MNC S.MCD S.MNC S.MCD      V V V V V V S ABCD S ABCD S ABCD S ABCD 2 S ABC 2 . . . . . S.ACD
SM .SN.SC SM .SC.SD 1 1 1 1 1 3    . .  .  . 2 . SA . SB SC 2 .
SA SC.SD 2 2 2 2 2 8 NHÓM 3 3 3 5  V  V  V  V  V V
 V  V  V. S MNCD . S ABCD . ABCDMN S MNCD . . . . . 8 8 8 8 TOÁN VD – 3.V VS MNCD 8 3 .    . V 5 ABCDMN 5 .V 8 VDC
Câu 23. Trong không gian với hệ tọa độ Oxyz , mặt cầu S  có tâm I 3; 3;   1 và đi qua điểm A5; 2  ;  1 có phương trình là
A.  x  2   y  2   z  2 5 2 1  5.
B. x  2   y  2  z  2 3 3 1  25 .
C.  x  2   y  2   z  2 3 3 1  5 .
D. x  2   y  2  z  2 3 3 1  5. Lời giải Chọn D
Gọi R là bán kính của mặt cầu S  . Do mặt cầu S  có tâm là I 3; 3;   1 và đi qua A nên
R  IA hay R    2    2    2 5 3 2 3 1 1  5 .
Do đó phương trình mặt cầu S  là x  2   y  2  z  2 3 3 1  5.
Câu 24. Cho lăng trụ tam giác đều ABC.AB C
  có độ dài cạnh đáy bằng a , góc giữa đường thẳng AB
và mặt phẳng  ABC bằng 60º . Tính thể tích V của khối trụ ngoại tiếp lăng trụ đã cho. NHÓM T 3 4a  3 3 a  3 3 a  3 A. 3 V  a  3 . B. V  . C. V  . D. V  . 3 9 3 Lời giải OÁN VD – VDC Chọn D
Ta có BB   ABC nên AB là hình chiếu vuông góc của AB. Do đó  AB , ABC
  AB , AB   B AB  60o  .
Xét tam giác vuông B A  B có 0
BB  a tan 60  a 3 .
https://www.facebook.com/groups/toanvd.vdc Trang 16 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 Gọi ,
O O lần lượt là tâm của đường tròn ngoại tiếp tam giác ABC , AB C
  nên OO   ABC
và OO  BB  a 3 là đường cao của khối trụ ngoại tiếp hình lăng trụ.
Do tam giác ABC và AB C   đều nên ,
O O là trọng tâm tam giác ABC , AB C   . NHÓM
Do đáy là tam giác đều cạnh a nên bán kính đường tròn đáy là TOÁN VD – 2 a a R  .AM = 2 3 . 3  . 3 3 2 3 2 3  
Khi đó thể tích của khối cầu ngoại tiếp hình lăng trụ là 2 a 3  a 3
V   R h  .  .a 3    .  3  3 VDC
Câu 25. Cho hàm số y  f  x liên tục trên  , có đạo hàm 3
f (x)  x  x  2
1 x  2. Hỏi hàm số
y  f  x có bao nhiêu điểm cực trị? A. 2 . B. 0 . C. 1. D. 3. Lời giải Chọn A x  0 Ta có: 3
f (x)  0  x  x  2
1 x  2  0 x 1  . x    2
Qua nghiệm x  1 (nghiệm bội chẵn) f x không đổi dấu  hàm số có 2 cực trị.  
Câu 26. Tích giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2 2
y  x  trên đoạn 1 ;2 bằng x 2  NHÓM T  51 85 A. 15 . B. 8 . C. . D. . 4 4 Lời giải OÁN VD – VDC Chọn A Ta có: +) 2 2  
y  x  xác định 1 x  ;2 . x  2    3 +) 2 2 2 2      x   y x ; 1
y  0  x  1 ;2 . 2 2 x x 2    +) f    1  17 1  3 f   f 2    5.  2  4
Suy ra M  Max y  5 ; m  Min y  3. Vậy M .m 15. 1;2 1   ;2 2    2   
Câu 27. Cho hình chóp S.ABC có đáy là tam giác vuông tại A , biết SA   ABC  và
AB  2a, AC  3a, SA  4a . Tính khoảng cách d từ điểm A đến mặt phẳng SBC  . 2 6 29 12 61 43 A.  a d . B.  a d . C.  a d . D.  a d . 11 29 61 12 Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 17 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 Chọn C NHÓM T OÁN VD – VDC
Vẽ AH  BC . Ta có: SA  BC SA   ABC , AH  BC
Nên BC  SAH  , mà BC  SBC , Do đó SBC  SAH  .
Lại có SBC SAH   SH
Vẽ AK  SH  AK  SBC
Như vậy d A,
 SBC   AK  1 1 1 1 1 1      2 2 2 2 2 2 AK SA AH SA AB AC 1 1 1 61 12a 61 NHÓM      AK 
4a2 2a2  2 3a  2 144a 61 TOÁN VD – VDC
Câu 28. Cho hàm số y  f  x, y  g  x liên tục trên đoạna;ba  b . Hình phẳng D giới hạn bởi
đồ thị hai hàm số y  f x, y  g x và hai đường thẳng x  a, x  b có diện tích là A. S  f  x  b g x x . B. S   b f x g x x. D a       d  D  d  a C. S   f  x  b g x x . D. S  f  x  a g x x . D  d D  d a b Lời giải Chọn A
Câu 29. Số phức z  5  8i có phần ảo là A. 5 .
B. 8 . C. 8 . D. 8i . Lời giải Chọn B
Ta có: z  5 8i nên phần ảo của số phức là 8
Câu 30. Biểu thức 3 4
x x  x  0 viết dưới dạng lũy thừa với số mũ hữu tỉ là: 1 1 5 5 A. 12 x . B. 7 x . C. 4 x . D. 12 x . Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 18 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 Chọn D 5 5 Ta có 3 3 4 4 12
x x  x  x NHÓM T
Câu 31. Cho hàm số y  f  x là hàm đa thức bậc 4, có đồ thị hàm số y  f ' x như hình vẽ. Hàm số
y  f   x 2
5 2  4x 10x đồng biến trong các khoảng nào sau đây? y OÁN VD 5 – VDC 3 1 O 1 2 x  5   3   3  A. 3;4 . B.  2; . C.  ;2 . D. 0; . 2       2   2  Lời giải Chọn B NHÓM TOÁN VD – VDC Ta có y '  2
 f '5  2x 8x 10  2
  f '5  2x  25  2x 5
Ta có y '  0  f '5 2x  25 2x  5  0 * . Đặt t  5  2x khi đó
*  f 't  2t 5  0  f 't  2
 t  5 . Từ đồ thị trên ta có: 5
0  t 1  0  5  2x 1  2  x  2
https://www.facebook.com/groups/toanvd.vdc Trang 19 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019
Câu 32. Cho hàm số y  f  x liên tục trên  \ 1  ;  0 thỏa mãn f   1  2ln 2 1, x  x  
1 f x  x  2 f x  xx   1 , x    \ 1  ; 
0 . Biết f 2  a  bln 3 , với a,b là hai số hữu tỉ. Tính 2
T  a  b . NHÓM 3 21 3 A. T   . B. T  . C. T  . D. T  0 . 16 16 2 TOÁN VD – Lời giải Chọn A
Ta có: xx  
1 f x  x  2 f x  xx   1 2 2 2    x  2 x      x  2 . ( ) 1 . x  . ( ) x f x f x f x f x  2 VDC x(x 1) x 1 (x 1) x 1 ' ' 2 2 2 2  x       f  x x x   f   x x 1 . . dx  dx  x   1 dx    x 1  x 1  x 1  x 1  x 1       2 2 x  .   x f x 
 x  ln x 1  C. x 1 2 Thay 1 1
x  1 vào 2 vế ta được: . f  
1    ln 2  C  f  
1  2ln 2 1 2C  C 1. 2 2 Thay 4 3 3
x  2 vào 2 vế ta được: . f 2 1 ln 3 f 2   ln 3. Từ đó 3 3 a  ; b  . 3 4 4 4 4 Vậy 2 3 
T  a  b  . 16 NHÓM T
Câu 33. Cho hàm số bậc ba y  f  x có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số 2 2
m thuộc đoạn 0;9 sao cho bất phương trình f x f xm
f x f xm f x 2 16.2  4
16  0 có OÁN VD – VDC nghiệm x 1;   1 ? y 2 2 -2 -1 O 1 x -2 y = f(x) A. 6 . B. 8 . C. 5 . D. 7 . Lời giải Chọn A
https://www.facebook.com/groups/toanvd.vdc Trang 20 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 2
f x f x 2 m
f x f xm f x 2
f  x f  xm 2 f x 2
f  x f  x 2 16.2  4 16  0  2  2 16.2 m 16  0 2 f x 2
f x f x  2 .2 m   2
f x f x 1 16.2 m   f x 1  0  4 16 2
f x f x .2 m  1  0 NHÓM Vì x  1;  
1  f x 2  ;2 f x  4 16  0
Để bất phương trình 2fx f x 2 m
f x f xm f x 2 16.2  4
16  0 có nghiệm x 1;   1 thì TOÁN VD – 2
f x f x 2
m 1  0 có nghiệm x 1;   1 2
 f x  f x  m  0 có nghiệm x 1;   1 2
 f x  f x  m có nghiệm x 1;   1 VDC
Đặt f x  t; x 1  ;  1  t  2  ;2 Phương trình 2
f  x  f  x  m có nghiệm x  1;  
1 khi và chỉ khi phương trình 2t t  m
có nghiệm t  2;  2 Xét   2
g t  t  t với t  2;
 2 . Có g t  t  g t 1 ' 2 1; '  0  t  2
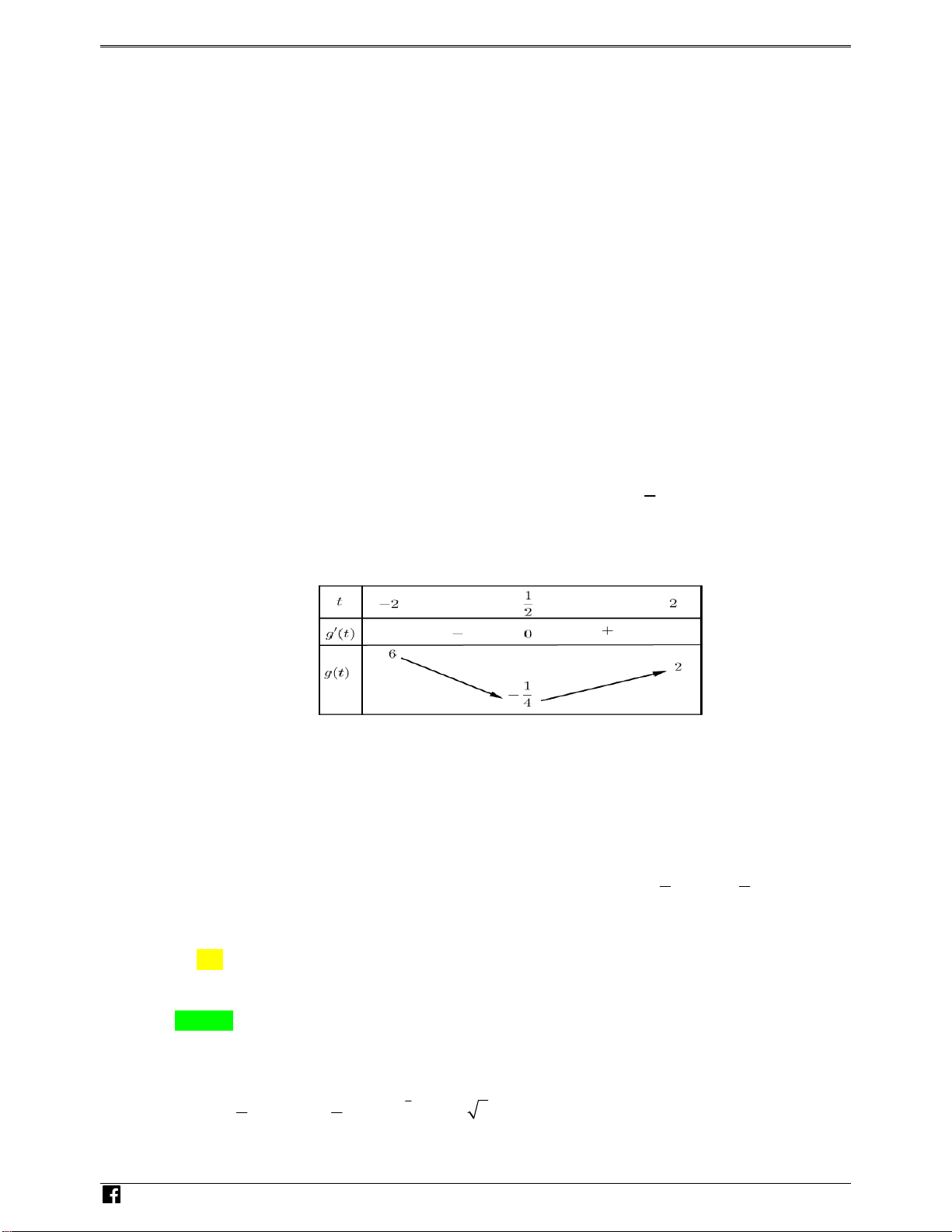
Ta có bảng biến thiên của g t trên khoảng 2;2 NHÓM T OÁN VD – VDC
Dựa vào bảng biến thiên ta thấy 2t t  m có nghiệm t  2;  2  m  6.
Vì m0;9  m0; 
5 . Vậy có 6 giá trị của m để bất phương trình có nghiệm thuộc  1;   1 .
Câu 34. Cho a, , b ,
c d là các số nguyên dương, a  1;c  1 thoa mãn 3 5 log b 
d  và a  c  9 . a ;log 2 c 4
Khi đó b  d bằng A. 93 . B. 9 . C. 13 . D. 21. Lời giải Chọn A Ta có: 2 3 2 2 3 3 log b  
a   a  b  a  b a log 2 b 3
https://www.facebook.com/groups/toanvd.vdc Trang 21 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 4 5 4 4 Vì: 5 5 log d  
c   c  d  c  d c log 4 d 5 2 4 2 2
Lại có: a  c   3 5
b  d    3 5 b  d  3 5 9 9
. b  d   9 NHÓM Vì a, , b ,
c d nguyên dương nên 2 4 3 5
b ; d nguyên dương 3 5
 b, d nguyên dương TOÁN VD – 2 3 5 3
 b  d  1  b   5 b  125      
. Vậy b  d  93 . 2 2 3 5 5      d  32 b d 9 d 4 Câu 35. Cho hàm số 3 2
y  x  8x  8x có đồ thị C  và hàm số 2
y  x  8  a x  b (với a,b ) có VDC
đồ thị P . Biết đồ thị hàm số C cắt P tại các điểm có hoành độ nằm trong đoạn 1;5 .
Khi a đạt giá trị nhỏ nhất thì tích ab bằng A. 72
 9 . B. 375. C. 225 . D. 384  . Lời giải Chọn B
Xét phương trình hoành độ giao điểm của hai đồ thị C và P 3 2 2
x  8x  8x  x  8  a x  b
Khi đó ta có phương trình 3 2
x  9x  ax  b  0 * có 3 nghiệm thuộc  1;  5 . Đặt f x 3 2
 x  9x  ax  b .
Ta có f x 2
 3x 18x  a , khi đó để * có các nghiệm thuộc 1;5 thì f x  0 có nghiệm thuộc  1;  5 .
Xét hàm số g x  x  x ,   x  có bảng biến thiên NHÓM T   2 3 18 1 5 OÁN VD – VDC
Khi đó 15  a  27 .
Xét a  15 thì * có nghiệm x  5 nên b  25. Thử lại phương trình 3 2
x  9x 15x  25   x  
1 x 52  0 thỏa mãn. Vậy ab  375.
Câu 36. Gọi A là tập các số tự nhiên có 3 chữ số đôi một khác nhau. Lấy ngẫu nhiên từ A ra hai số.
Tính xác suất để lấy được hai số mà các chữ số có mặt ở hai số đó giống nhau. 41 35 41 14 A. . B. . C. . D. . 5823 5823 7190 1941 Lời giải Chọn A
Ta có số các số tự nhiên có 3 chữ số đôi một khác nhau là 9.9.8  648 , trong đó có 9.8.7  504
số không chứa chữ số 0 .
https://www.facebook.com/groups/toanvd.vdc Trang 22 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 Khi đó 2   . 648 C
Trường hợp 1: Xét các số tự nhiên có 3 chữ số đôi một khác nhau và không chứa chữ số 0 . 1 1 C .C 504 5 NHÓM
Khi đó số cách chọn ra được hai số mà các chữ số có mặt ở hai số đó giống nhau là (vì 2
mỗi số được kể 2 lần). TOÁN VD –
Trường hợp 2: Xét có số tự nhiên có 3 chữ số đôi một khác nhau và chứa chữ số 0 . Khi đó số 1 1
cách chọn ra được hai số mà các chữ số có mặt ở hai số đó giống nhau là C . 144 3 C . 2
Vậy xác suất để lấy đươc hai số mà các chữ số có mặt giống nhau là VDC 1 1 1 1 C .C C . 504 5 144 3 C  2 2 41 P   2 C 5823 648 2 4  x 
Câu 37. Cho hàm số y  f  x liên tục trên  và f 2 16, f
 xdx  4. Tính I  xf    dx.  2  0 0 
A. I  144 .
B. I  12 .
C. I  112 . D. I  28 . Lời giải Chọn C u   x du  dx Đặt     . d  x    x  v  f    dx v  2 f      2    2  NHÓM T 4 4 4 4 Khi đó  x   x   x   x  I  xf 
  dx  2xf    2 f   dx   128  2 f   dx  .  2   2   2  2 0  0 0  0  OÁN VD – VDC 4 2 2 Đặt x  x 
t  , khi đó f dx  2 f 
 tdt  2 f
 xdx    8 . 2  2 0  0 0
Vậy I 128  2.8 112 .
Câu 38. Cho tứ diện ABCD có  
DAB  CBD  90º ;  AB  ;
a AC  a 5; ABC 135 . Biết góc giữa hai
mặt phẳng  ABD,BCD bằng 30 . Thể tích của tứ diện ABCD là 3 a 3 a 3 a 3 a A. . B. . C. . D. . 2 3 2 3 2 6 Lời giải Chọn D
https://www.facebook.com/groups/toanvd.vdc Trang 23 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 NHÓM TOÁN VD – VDC
Dựng DH   ABC . BA  DA BC  DB Ta có 
 BA  AH . Tương tự   BC  BH . BA  DH BC  DH
Tam giác AHB có AB  a ,  o
ABH  45  HAB vuông cân tại A  AH  AB  a .
Áp dụng định lý cosin, ta có BC  a 2 . 2 Vậy 1  1 2 a S
  BA BC 
CBA   a  a   . ABC sin 2 2 2 2 2 HE  DA Dựng 
 HE  DAB và HF  DBC . HF  DB NHÓM T
Suy ra DBA DBC   HE HF   , ,
 EHF và tam giác HEF vuông tại E . OÁN VD – VDC Đặt ax xa 2
DH  x , khi đó HE  , HF  . 2 2 a  x 2 2 2a  x 2 2 Suy ra  HE 3 x  2 cos a EHF     x  a . 2 2 HF 4 2x  2a 3 Vậy 1 a V   DH  S  . ABCD 3 AB  C 6
Câu 39. Trong mặt phẳng với hệ tọa độ Oxy , cho hình H giới hạn bởi các đường y  2x, 1 
y   2x, x  4 ; hình H là tập hợp tất cả các điểm M  ;
x y thỏa mãn các điều kiện: 2  2 2
x  y  16;  x  2 2
 y  x  2 2 2 4;
2  y  4 . Khi quay H , H quanh 2  1  Ox ta được các
khối tròn xoay có thể tích lần lượt là V ,1 2
V . Khi đó, mệnh đề nào sau đây là đúng? A. V  2 .  .
V V  48 . V  4 . 2 1 V B. 2 V 1 V C. 1 2 D. 2 1 V Lời giải Chọn D
https://www.facebook.com/groups/toanvd.vdc Trang 24 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019
Hình phẳng H1 y NHÓM TOÁN VD – O 4 x VDC 4 Khi cho  2 H quay quanh trục V   2x dx 16 . 1  Ox , ta có 1   0
Hình phẳng H2  y O 4 x NHÓM T H2 OÁN VD – VDC Khi cho  4 4 H quay quanh trục
V  . 4  2. . 2  64. Vậy V  4V . 2  Ox , ta có 3 3 2 3 3 2 1
Câu 40. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A1;2; 
1 , B3;4;0 , mặt phẳng
P:ax by  cz  46  0. Biết rằng khoảng cách từ ,
A B đến mặt phẳng P lần lượt bằng 6
và 3. Giá trị của biểu thức T  a  b  c bằng A. 3 . B. 6 . C. 3 . D. 6 . Lời giải Chọn B
Gọi H, K lần lượt là hình chiếu vuông góc của ,
A B lên mặt phẳng P .
Ta có AB  3, AH  6 , BH  3 Suy ra ,
A B nằm cùng một phía của mặt phẳng P
Lại có 6  AB  BK  AK  AH  6 Suy ra ,
A B, H thẳng hàng và B là trung điểm của AH  H 5;6;  1 
Vậy mặt phẳng P đi qua H 5;6; 
1 và có vtpt AB  2;2;  1 có phương trình
https://www.facebook.com/groups/toanvd.vdc Trang 25 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019
2(x 5)  2(y  6) 1(z1)  0  2x 2 y z 23  0  4
 x  4y  2z  46  0 Vậy a  4,  b  4,  c  2      nên T a b c 6.
Câu 41. Cho hình chóp S.ABC có SA vuông góc với  ABC , 
AB  a, AC  a 2, BAC  45º . Gọi NHÓM B ,
SB SC . Thể tích khối cầu ngoại tiếp hình 1 1
C lần lượt là hình chiếu vuông góc của A lên , chóp . A BC 1 C 1 B bằng TOÁN VD – 3  a 4 3  a 2 A. . B. 3  a 2 . C. 3  a . D. . 2 3 3 Lời giải Chọn D VDC Tam giác ABC có  AB = ,
a AC = a 2,BAC = 45º BC = a  ABC vuông cân ở B. BC  AB Ta có:
  BC  SAB  BC  A . 1 B BC  SA  NHÓM T AB  BC Ta có: 1   A    . 1 B SBC 1 AB 1 B C  1 AB SB  OÁN VD – VDC Vì các tam giác A  B C, ABC  ,
là các tam giác vuông chung cạnh huyền AC 1 1 AC C  ,
A B , B,C , 1
1 C cùng thuộc mặt cầu đường kính AC.
Do đó khối cầu ngoại tiếp chóp AC a .
A BCC B có tâm H là trung điểm AC và 2 R   . 1 1 2 2 3
Vậy thể tích khối cầu cần tìm là: 4 3  a 2 V   R  . 3 3
Câu 42. Cho các số phức z, w khác 0 thỏa mãn z  w  0 và 1 3 6  
. Khi đó z bằng z w z  w w 1 1 A. 3. B. . C. 3 . D. . 3 3 Lời giải Chọn D Ta có: 1 3 6  
 wz  w  3z z  w  6zw 2 2
 w  2zw  3z  0 z w z  w  z  2 2
w  2z  z     i z2 2 w 2 .
https://www.facebook.com/groups/toanvd.vdc Trang 26 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019  z z 1 1       w     
z  w  2 .iz 1 2i.z w
1 2i.z 1 2i 3         .
z    i z NHÓM w 2 . w  
1 2i.z  z z 1 1     w 1 
2i.z 1 2i 3  TOÁN VD –
Câu 43. Ông Nam dự định gửi vào ngân hàng một số tiền với lãi suất 6,6% /năm. Biết rằng nếu không
rút tiền khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi
cho năm tiếp theo. Tính số tiền tối thiểu x triệu đồng x ông Nam gửi vào ngân hàng để
sau 3 năm số tiền lãi đủ mua một chiếc xe gắn máy trị giá 26 triệu đồng. VDC
A. 191triệu đồng.
B. 123 triệu đồng.
C. 124triệu đồng.
D. 145 triệu đồng. Lời giải Chọn C Với lãi suất 6,6 r  . 100
Theo giả thiết ta có: x  r3 6 1
 x  26.10  x 124 triệu đồng. x  y  z 
Câu 44. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng 1 1 2 d :   và mặt phẳng 1 2 1 
P:2x  y  2z 1 0 . Gọi d là hình chiếu của đường thẳng d lên mặt phẳng P , vectơ chỉ
phương của đường thẳng d là    
A. u 5;16;13 . u 5; 4; 3 . u 5;16;13 . u 5;16;13 . 3   B. 2   C. 4   D. 1   Lời giải NHÓM T Chọn D
Gọi Q là mặt phẳng chứa d và vuông góc với P .    OÁN VD – VDC
 vectơ pháp tuyến n  u n . Q d ;   P 5;4;3  
Do d ' là hình chiếu của đường thẳng d lên mặt phẳng P nên d '  P.   
Do đó d '  PQ hay u  n n . d P ;   Q 5;16;13 '    
Câu 45. Trong không gian với hệ tọa độ Oxyz , cho điểm A4;0;0, B0;4;0, S 0;0;c và đường    thẳng
x 1 y 1 z 1 d :  
. Gọi A , B lần lượt là hình chiếu vuông góc của O lên , SA SB . 1 1 2
Khi góc giữa đường thẳng d và mặt phẳng OA B
  lớn nhất, mệnh đề nào sau đây đúng?  17 15  A. c  8;  6
  . B. c 9;  8
  . C. c0;3 . D. c   ;  . 2 2    Lời giải Chọn D  Ta có: u  và AB   4;  4;0 d 1;1;2 '    Do SA SB SO  A  S  OB  
 AB / / AB SA  SB
https://www.facebook.com/groups/toanvd.vdc Trang 27 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 2 4    Xét AA OA 4 16 SOA : 2
OA  AA .SA     AA  AS 2 2 2 2 SA SA 4  c c 16  16 x ' 4  0  4  2   c 16 NHÓM  2  16  4c 16    ' 0  0  0   ;0; c y A 2   2 2  c 16   c 16 c 16   16 TOÁN VD – z ' 0  c  0  2    c 16  2  4c 16       ;0; c OA   u   ; c 0;4 2 2    c 16 c 16 OA    
  AB;u        n c OA 16;16; 4c OAB 4;4;  VDC     Gọi      d;OA B
   cos  cosu n d ; OA B      4.1 4.1 .2 c 2 c  42  cos   2 2 2 2 2
1 1  2 . 4  4  c 2 2 6 c  32 2 c  4 8 2
c  4c  32 c 
Xét hàm số f c     f  c  ; f c 4  0  2   c  32   2 c  322 c  8  Bảng biến thiên NHÓM T 
f c  f   3 max 8      2 3 max cos  1 khi c  8 . 2 6 2
Câu 46. Cho hàm số y  f  x có đồ thị như hình vẽ. Biết tất cả các điểm cực trị của hàm số y  f  x OÁN VD – VDC là 2,
 0,2,a,6 với 4  a  6 . Số điểm cực trị của hàm số y  f  6 2
x  3x  là y -2 O 2 a 6 x y = f(x) A. 8 . B. 11. C. 9 . D. 7 . Lời giải Chọn B Ta có y   5
x  x f  6 2 ' 6 6 x  3x 
https://www.facebook.com/groups/toanvd.vdc Trang 28 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 x  0 x  0  4  2 x  1 x  1    6 2  6 2 x  3x  2
 x  3x  2  0 5
6x  6x  0   6 2 6 2 NHÓM y  0           f    x 3x 0 x 3x 0 6 2
x  3x   0   6 2 6 2
x  3x  2 x  3x    2  6 2  6 2
x  3x  a x  3x  a  0 TOÁN VD –   6 2 6 2
x  3x  6 x  3x  6    0
Xét x  x    x  2 6 2 2  2x   2 3 2 0 1
2  0  x 1 là nghiệm kép. x  0 x  0
Xét x  3x  0  x x 3 2 6 2 2 4  0   
với x  0 là nghiệm kép. VDC  4 4 x  3 x   3
Xét x  x    x  2 6 2 2  2x   2 3 2 0 1
2  0  x  2  x   2 Xét 6 2
x  3x  a . Đặt 2
t  x  0, Pt 3 2
 t 3t  a
Ta có đồ thị hàm số f t 3  t  3t NHÓM T OÁN VD – VDC
Số nghiệm của phương trình 3 2
t  3t  a  số giao điểm của đường thẳng y  a và đồ thị Do a 4;6  3 2
t  3t  a có 1 nghiệm duy nhất 2
t    2  x    x    Xét 6 2 2
x  3x  6  0  x    2  x        Ta thấy:
+ x  0 là nghiệm bội 3 nên là cực trị.
+ x  1 là nghiệm bội 3 nên là cực trị. + 4
x   2, x   3, x    , x    là nghiệm đơn nên là cực trị.
Vậy hàm số y  f  6 2
x  3x  có 11 điểm cực trị.
Câu 47. Cho hai số thực x, y thỏa mãn: 5  4 log  8 16  log  5  1   2log x  x y y x x  log 2y  8 . 3  2  2 2    3 2  2 3
https://www.facebook.com/groups/toanvd.vdc Trang 29 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019
Gọi S là tập các giá trị nguyên của tham số m để giá trị lớn nhất của biểu thức 2 2 P 
x  y  m không vượt quá 10. Hỏi S có bao nhiêu tập con không phải là tập rỗng?
A. 2047 . B. 16383 .
C. 16384. D. 32 . NHÓM Lời giải Chọn B
Điều kiện: y  4; x  1  ;5 TOÁN VD – 5  4 log  8 16  log  5  1   2log x  x y y x x  log 2y  8 3  2  2 2    3 2  2 3  x  x
 log  y  42  log 5 x1 x 5 1    2log  log 4.   y  42 3 2 3 2 3 2 2 VDC
 2log y  4  log y  4  2log  5  x 1 x   log  5  x 1  3   2   3    2   x
Xét hàm số f t  2log t  log t , t   0; 3 2      f t 2 1 1 2 1 '     ,  0, t  0;   
t.ln 3 t.ln 2 t  ln 3 ln 2 
 f  y  2  f   x  x   y  2 2 4 5 1
4  5 4x  x   y  42  x  22  9  1  M  ;
x yC tâm I  4;  2, R  3 và 2 2
OM  x  y NHÓM T OÁN VD – VDC
Ta có OM  OI  R,   min OMmax OI R 2 2
2 5  3 m  x  y  m  2 5  3 m2
2 5  3 m 10 P  10  
 2 5  7  m  2 5  7
2 5  3 m  1  0 Vậy S   2  ; 1  ;0...;10 
;11 có 14 số nguyên.Số tập con khác rỗng của S là 14 2 116383 1 7
Câu 48. Cho tích phân I   x  2ln  x  
1 dx  a ln 2  
trong đó a , b là các số nguyên dương. b 0 Tổng 2 a  b bằng A. 8 . B. 16 . C. 12. D. 20 . Lời giải Chọn D
https://www.facebook.com/groups/toanvd.vdc Trang 30 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019  1 1    ln    1 dv  dx u x  
I   x  2ln  x    1 dx . Đặt x 1    dv   x  2dx 1 0  2
v  x  2x  C  2 NHÓM Chọn 3 1 2 3
C   v  x  2x  2 2 2 TOÁN VD – 1 1 1     x  x  I
x  2ln  x   1 3 1 3 2 1 dx  x  2x 
l n  x      1    dx   2 2  2 x 1 0 0 0   1 2 1  x  7 7
 4ln 2    3x  4ln 2   aln 2  VDC 2  2  4 b 0 2
 a  4;b  4  a  b  20
Câu 49. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P : mx  m  
1 y  z  2m 1  0 , với m
là tham số. Gọi  là tập hợp các điểm H là hình chiếu vuông góc của điểm H 3;3;0 trên m
P . Gọi a,b lần lượt là khoảng cách lớn nhất, khoảng cách nhỏ nhất từ O đến một điểm thuộc
. Khi đó, a  b bằng
A. 5 2 . B. 3 3 . C. 8 2 . D. 4 2 . Lời giải Chọn D
Ta có: P: mx  m  
1 y  z  2m 1  0  mx  y  2  (y  z 1)  0 . x  2  t NHÓM T
x  y  2  0 Suy ra  
P luôn chứa đường thẳng d :   y  t .
 y  z 1  0 z    1 t
Gọi K là hình chiếu vuông góc của H(3;3;0) lên đường thẳng d , ta tìm được K(1;1;0) . OÁN VD – VDC
Tam giác HH K là tam giác vuông tại H và HH  d nên T  là đường tròn có tâm m m m HK
I 2;2;0 là trung điểm của HK , bán kính R 
 2 và nằm trong mặt phẳng Q đi qua 2
H , vuông góc với d .
Phương trình mặt phẳng Q : x  y  z  0 và OI  2 2 , suy ra OQ và O ở ngoài T . Gọi ,
A B là giao điểm của OI và T  (với A là điểm nằm giữa O và I ).
Ta có OA  OH  OB , suy ra a  OA  OI  R  2 , b  OB  OI  R  3 2 . m
Câu 50. Cho số phức z thỏa mãn 1 i z 1 3i  3 2 . Giá trị lớn nhất của biểu thức
P  z  2  i  6 z  2  3i bằng A. 5 6 . B. 15 1 6. C. 6 5 . D. 10  3 15 . Lời giải Chọn C
https://www.facebook.com/groups/toanvd.vdc Trang 31 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019
Ta có 1 i z 13i  3 2  z 1 2i  3 nên tập hợp điểm M biểu diễn số phức z là
đường tròn tâm I(1;2) , bán kính R  3.     NHÓM Cách 1: Gọi (
A 2; 1), B(2;3) , suy ra AI  3 2, BI  2 và IA  3IB .      
Khi đó: P  MA2 
MB2  MI  IA2  MI IB2 6 6 TOÁN VD –    
 27  6MI.IB  6 11 2MI.IB .    
Hướng 1: P  27  6MI.IB  2 33  6MI.IB  1 227  33  6 5 . VDC    
Hướng 2: Đặt t  2MI.IB  6 2 cos(MI.IB),t   6  2;6 2   .
P  27  3t  6(11 t)  f t . Ta có f t 7 '  0  t  . 3    Và  
max f t  max  f   f   7 7
6 2 ; 6 2 ; f    f    6 5 .  6  2;6 2     3   3 
Cách 2: Đặt a  z 1 2i,b 1 i . 2 2 2 2
 z  2  i  a 3b  a 9 b 3 
 .ab .ab Ta có  2 2 2 2
 z  2  3i  a  b  a  b  
 .ab .ab NHÓM T 2 2 2 2 2 2
 z  2  i  3 z  2  3i  a  3b  3 a  b  4 a 12 b  60 .
Khi đó P  a  b 
a  b     2 2 3 2. 3
1 2 a  3b  3 a  b   6 5 . OÁN VD – VDC
….………………………HẾT…………………………
Xin chân thành cảm ơn tất cả các quý thầy cô tham gia dự án này. Chúc thầy cô thật nhiều
sức khỏe, luôn thành công trong mọi công việc và luôn bình an hạnh phúc bên gia đình.
Hẹn gặp lại quý thầy, cô ở các dự án tiếp theo. Thân chào.
Ban quản trị nhóm VD-VDC.
https://www.facebook.com/groups/toanvd.vdc Trang 32
Document Outline

[toanmath.com] - Đề thi thử THPT Quốc gia 2019 môn Toán sở GD và ĐT Bắc Ninh.pdf
- de 101
- Dap an Toan
  - Toán
88-TOANVD.EDU.VN-SGD-BẮC-NINH-18-19.pdf

Đề thi thử THPT Quốc gia 2019 môn Toán sở GD và ĐT Bắc Ninh

Thông tin :

Tài liệu liên quan:

Chuyên đề đọc đồ thị hàm số mức thông hiểu giải chi tiết

TOP 205 câu trắc nghiệm vận dụng cao phương pháp tọa độ trong không gian Oxyz (có đáp án và lời giải)

TOP 100 câu trắc nghiệm số phức vận dụng cao (có đáp án và lời giải)

Đề ôn thi TN THPT môn Toán 2021 chuẩn cấu trúc đề minh họa -Đề 13 (có lời giải chi tiết và đáp án)

Bộ đề thi thử tốt nghiệp THPT 2023 môn Toán (có lời giải chi tiết)