Đề thi thử THPT Quốc gia 2019 môn Toán sở GD&ĐT Hưng Yên

Đề thi thử THPT Quốc gia 2019 môn Toán sở GD&ĐT Hưng Yên có mã đề 617 gồm 06 trang với 50 câu trắc nghiệm dạng 04 đáp án

17 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

30 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$1$,$Mã$617$
Câu 1. [2H3-2.1.1] Trong không gian với hệ tọa độ , lập phương trình của các mặt phẳng song
song với mặt phẳng và cách một khoảng bằng .
A. ; . B. .
C. ; . D. ; .
Câu 2. [2D4-5.2-3] Cho số phức thỏa mãn . Gọi và lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của biểu thức . Tính .
A. . B. . C. . D. .
Câu 3. [1D5-2.1-2] Cho . Tính .
A. . B. . C. . D. .
Câu 4. [2D3-2.1-2] Biết , với , , , . Tính tổng .
A. . B. . C. . D. .
Câu 5. [2H3-1.1-1] Trong không gian , cho mặt phẳng có phương trình . Một
vectơ pháp tuyến của mặt phẳng có tọa độ là
A. . B. . C. . D. .
Câu 6. [2D2-4.4-4] Cho các số thực sao cho và thỏa mãn điều kiện
Tìm giá trị nhỏ nhất của biểu thức .
A. . B. . C. . D. .
Câu 7. [2H1-3.2-2] Cho lăng trụ có đáy là tam giác đều cạnh , độ dài cạnh bên
bằng , hình chiếu của đỉnh trên mặt phẳng trùng với trọng tâm của tam giác
. Thể tích khối lăng trụ bằng
A. . B. . C. . D. .
Oxyz
( )
:30xyz
b
+-+=
( )
b
3
60xyz+-+=
0xyz+-=
60xyz+-+=
60xyz--+=
0xyz--=
60xyz+++=
0xyz++=
1z =
M
m
2
11Pz z z=++ -+
.Mm
13 3
4
39
4
33
13
4
( )
32 1
,
4
41 4141
x ax b
x
xxx
¢
--
æö
=">
ç÷
---
èø
a
b
16-
4-
1-
3
1
2
dln
x
Ixabc
x
+
==+
ò
c Î !
9c <
Sabc=++
7S =
5S =
8S =
6S =
Oxyz
( )
P
3470xz-+=
( )
P
( )
3; 0; 4-
( )
3; 4; 7--
( )
3; 0; 7
( )
3; 4; 7-
,, ,abmn
20mn+<
( )
( )
( )
22
22
4
2
2
log 9 1 log 3 2
9 .3 .3 ln 2 2 1 81
mn
mn
ab a b
mn
-
--
+
ì
++=+ +
ï
í
éù
ï
++++=
ëû
î
( ) ( )
22
Pambn=-+-
25 2-
52-
25
.' ' 'ABC A B C
ABC
2
3
a
'A
( )
ABC
ABC
.' ' 'ABC A B C
3
3
36
a
3
3
6
a
3
3
12
a
3
3
24
a
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HƯNG
YÊN
ĐỀ CHÍNH THỨC
KỲ
THI THỬ THPT QUỐC GIA NĂM 2019
MÔN: TOÁN
Ngày thi: 11/04/2019
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ
và tên thí sinh: .....................................................
Số báo danh: ..............................................................
MÃ
ĐỀ: 617
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$2$,$Mã$617$
Câu 8. [2H1-3.4-3] Cho hình chóp có vuông góc với mặt phẳng . Tứ giác
là hình vuông cạnh , . Gọi là hình chiếu vuông góc của trên . Tính
khoảng cách từ đến mặt phẳng .
A. . B. . C. . D. .
Câu 9 . [2D1-5.6-2] Cho hàm số có đồ thị . Tìm số tiếp tuyến của đồ thị song
song với đường thẳng .
A. . B. . C. 3. D. 0.
Câu 10 . [2D1-4.1-1] Đồ thị hàm số có các đường tiệm cận đứng, tiệm cận ngang lần lượt là:
A. . B. .
C. . D. .
Câu 11. [2D1-5.8-4] Cho các hàm số và
thỏa mãn . Các hàm số và có đồ thị
như hình vẽ bên.
Tập nghiệm của phương trình có số phần tử là
A. 4. B. 2. C. 1. D. 3.
Câu 12. [2D1-1.1-1] Trong các hàm số sau, hàm số nào đồng biến trên ?
A. . B. . C. . D. .
Câu 13. [2H3-2.3-2] Trong không gian với hệ tọa độ , viết phương trình mặt phẳng đi qua hai
điểm , và vuông góc với mặt phẳng : .
A. . B. . C. . D. .
Câu 14. [2D1-2.4-2] Cho hàm số với là tham số thực. Tìm tất cả
các giá trị của để hàm số có điểm cực đại và điểm cực tiểu nằm trong khoảng .
A. . B. . C. . D. .
Câu 15. [2D3-3.3-1] Cho hàm số liên tục trên . Gọi là hình phẳng giới hạn bởi đồ thị
hàm số , trục hoành và hai đường thẳng , . Thể tích khối tròn xoay tạo
thành khi quay quanh trục hoành được tính theo công thức
.S ABCD
SA
( )
ABCD
ABCD
2SA a=
H
A
SB
H
( )
SCD
45
5
a
45
25
a
25
5
a
85
25
a
32
32yx x=- +
( )
C
( )
C
: 9 25dy x=-
1
31
2
x
y
x
-+
=
+
2, 3xy=- =-
2, 3xy=- =
2, 1xy=- =
2, 1xy==
( )
43 2
f x mx nx px qx r=++++
( )
32
g x ax bx cx d=+++
( )
,, ,,,,,,mn pqrabcdÎ !
( ) ( )
00fg=
( )
yfx
¢
=
( )
gx
¢
( ) ( )
fx gx=
!
2
21yx x=+-
42
2yx x=-
3
2 2019yx x=+-
21
3
x
y
x
-
=
+
Oxyz
( )
P
( )
2;1;1A
( )
1; 2; 3B ---
( )
Q
0xyz++=
0xyz--=
30xy+-=
10xy--=
40xyz++-=
( ) ( )
32
23 1 6 21yx m x m x=+ - + --
m
m
( )
2; 3-
( ) { }
1; 4 \ 3m Î-
( )
3; 4m Î
( )
1; 3m Î
( )
1; 4m Î-
( )
yfx=
[ ]
3; 4
D
( )
yfx=
3x =
4x =
D
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$3$,$Mã$617$
A. . B. . C. . D. .
Câu 16. [2H3-1.4-3] Trong không gian với hệ tọa độ , cho ba điểm , ,
và mặt phẳng . Gọi là điểm thuộc sao
cho đạt giá trị nhỏ nhất. Tính tổng .
A. . B. . C. . D. .
Câu 17. [2D3-2.4-3] Cho hàm số có đạo hàm liên tục trên và có đồ thị như hình vẽ.
Giá trị của biểu thức bằng
A. . B. . C. . D. .
Câu 18. [2D3-2.4-2] Cho hàm số có đạo hàm liên tục trên đoạn và thỏa mãn ,
. Tính tích phân .
A. . B. . C. . D. .
Câu 19. [2H1-3.2-2] Cho khối chóp có thể tích là . Gọi , lần lượt là trung điểm ,
Tính theo thể tích của khối chóp .
A. . B. . C. . D. .
Câu 20. [2D1-5.4-3] Có bao nhiêu giá trị âm của tham số để phương trình
có hai nghiệm thực phân biệt
A. . B. . C. Vô số. D. .
Câu 21: [2D1-3.1-2] Cho hàm số với là tham số thực. Giả sử là giá trị dương của
tham số
để hàm số có giá trị nhỏ nhất trên đoạn
bằng . Giá trị
thuộc khoảng nào
trong các khoảng cho dưới đây?
A. . B. . C. . D. .
Câu 22: [0H1-2.1-2] Cho tứ diện có là trung điểm của đoạn thẳng nối trung điểm của hai
cạnh đối diện và là số thực dương không đổi. Tập hợp các điểm trong không gian thỏa
mãn hệ thức
là
A. mặt cầu tâm
bán kính . B. mặt cầu tâm
bán kính .
C. mặt cầu tâm
bán kính . D. mặt cầu tâm
bán kính .
( )
4
2
3
dVfxx
p
=
ò
( )
4
22
3
dVfxx
p
=
ò
( )
4
3
dVfxx=
ò
( )
4
2
3
dVfxx=
ò
Oxyz
( )
1; 4; 5A
( )
3; 4; 0B
( )
2; 1; 0C -
( )
: 3 3 2 29 0Pxyz+--=
( )
;;Mabc
( )
P
22 2
3MA MB MC++
abc++
8
10
10-
8-
( )
yfx=
!
( ) ( )
42
00
'2d '2dIfx xfx x=-++
òò
2-
10
( )
fx
[ ]
0;2
( )
02f =
( ) ( )
2
0
24.'d4xfxx-=
ò
( )
2
0
dIfxx=
ò
2I =
2I =-
6I =
6I =-
.S ABC
V
B
¢
C
¢
AB
AC
V
.S AB C
¢¢
1
3
V
1
2
V
1
12
V
1
4
V
m
22
2019 2019mmxx++=
1
2
8
xm
y
x
-
=
+
m
o
m
m
[ ]
0; 3
3-
o
m
( )
20; 25
( )
5; 6
( )
6; 9
( )
2; 5
ABCD
O
M
MA MB MC MD a++ + =
!!!" !!!" !!!!" !!! !"
O
3
a
r =
O
4
a
r =
O
ra=
O
2
a
r =
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$4$,$Mã$617$
Câu 23. [2D1-2.1-1] Cho hàm số có đạo hàm . Số điểm cực trị của hàm
số đã cho là
A. 3. B. 5. C. 2. D. 1.
Câu 24. [2D3-3.5-2] Một vật chuyển động với vận tốc thì tăng tốc với gia tốc
, trong đó là khoảng thời gian tính bằng giây kể từ lúc bắt đầu tăng tốc.
Hỏi quãng đường vật đi được trong 12 giây kể từ lúc bắt đầu tăng tốc bằng bao nhiêu mét?
A. . B. . C. D. .
Câu 25. [2H2-1.2-1] Hai khối nón có cùng thể tích. Một khối nón có bán kính đáy bằng và chiều cao
bằng , khối nón còn lại có bán kính đáy bằng và chiều cao bằng . Khi đó
A. . B. . C. . D. .
Câu 26. [1D1-2.1-1] Phương trình có 1 nghiệm là
A. . B. . C. . D. .
Câu 27. [2D3-3.4-2] Có một cốc thủy tinh hình trụ, bán kính trong lòng đáy cốc là , chiều cao trong
lòng cốc là đang đựng một lượng nước. Tính thể tích lượng nước trong cốc, biết rằng khi
nghiêng cốc nước vừa lúc chạm miệng cốc thì ở đáy cốc, mực nước trùng với đường kính đáy.
A. . B. . C. . D. .
Câu 28. [2D1-5.8-1] Điểm thuộc đồ thị hàm số nào dưới đây?
A. . B. . C. . D. .
Câu 29. [2D3-1.1-1] Họ nguyên hàm của hàm số là
A. . B. . C. . D. .
Câu 30. [2H1-3.4-1] Cho hình lập phương . Góc giữa hai mặt phẳng và
bằng
A. . B. . C. . D. .
Câu 31. [2D4-1.3-2] Trên mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn số phức sao cho là số
thuần ảo.
A. Hai đường thẳng và .
B. Trục .
C. Trục .
D. Hai đường thẳng và , bỏ đi điểm .
Câu 32. [2D4-1.3-1] Cho số phức . Phần ảo của
là
( )
yfx=
( )
2
2
4
,0
3
x
fx x
x
-
¢
="¹
10 /ms
( )
( )
22
1
2/
3
at t t m s=+
t
1272 m
456 m
1172 m
1372 m
R
2R
2
h
x =
3
2
h
x =
3
4
xh=
4
h
x =
sin cos 1xx+=
2
p
p
2
3
p
4
p
4cm
12cm
3
128 cm
p
3
256 cm
3
256 cm
p
3
128 cm
( )
1;Me
x
ye=
lnyx=
2
yx
-
=
2
x
y
-
=
( )
1
1
fx
x
=
-
ln 1xC-+
( )
2
1
1
C
x
-+
-
2ln 1xC-+
( )
ln 1xC-+
.ABCD A B C D
¢¢¢¢
( )
ABCD
( )
ABCD
¢¢¢¢
45°
60°
0°
90°
2
z
yx=
yx=-
Ox
Oy
yx=
yx=-
( )
0;0O
35zi=-
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$5$,$Mã$617$
A. . B. . C.
. D.
.
Câu 33. [2D2-5.6-2] Một người gửi triệu đồng vào ngân hàng theo thể thức lãi kép với lãi suất
năm, kì hạn một năm. Hỏi sau 5 năm người đó rút cả vốn lẫn lãi được số tiền gần với số
nào nhất trong các số tiều sau? (biết lãi suất hàng năm không đổi) .
A. triệu đồng. B. triệu đồng. C. triệu đồng. D. triệu đồng.
Câu 34. [2D1-5.1-1] Hàm số nào sau đây có đồ thị như hình vẽ ?
A. . B. . C. . D. .
Câu 35. [2D1-5.3-3] Số giá trị nguyên của thuộc khoảng để phương trình
có bốn nghiệm phân biệt là
A. . B. . C. . D. .
Câu 36. [2H1-1.2-1] Hình chóp tứ giác có tất cả bao nhiêu cạnh
A. . B. . C. . D. .
Câu 37. [2D3-3.1-2] Cho hàm số có đạo hàm liên tục trên . Đồ thị của hàm số
được cho như hình vẽ. Diện tích các hình phẳng , lần lượt là và .
Biết , tính .
A. . B. . C. . D. .
Câu 38. [2D1-1.5-2] Cho các mệnh đề:
1. Nếu hàm số liên tục trên và thì tồn tại sao cho
.
2. Nếu hàm số liên tục trên và thì phương trình có
nghiệm.
3. Nếu hàm số liên tục, đơn điệu trên và thì phương trình
có nghiệm duy nhất trên .
5-
5i-
5
3
50
6,5% /
73
53,3
64,3
68, 5
42
2yx x=-
42
21yx x=- -
32
2yx x x=- +
42
2yx x=- +
m
( )
2019; 2019-
22
21 2 2
4 .2 3 2 0
xx xx
mm
-+ -+
-+-=
2017
2016
4035
4037
20
12
8
( )
yfx=
[ ]
1; 2-
( )
yfx
¢
=
( )
K
( )
H
5
12
8
3
( )
19
1
12
f -=
( )
2f
( )
23
2
6
f =
( )
2
2
3
f =-
( )
2
2
3
f =
( )
11
2
6
f =
( )
yfx=
( )
;ab
( ) ( )
.0fa fb<
( )
0
;xabÎ
( )
0
0fx =
( )
yfx=
[ ]
;ab
( ) ( )
.0fa fb<
( )
0fx=
( )
yfx=
[ ]
;ab
( ) ( )
.0fa fb<
( )
0fx=
( )
;ab
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$6$,$Mã$617$
Trong ba mệnh đề trên
A. Có đúng hai mệnh đề sai. B. Cả ba mệnh đề đều đúng.
C. Cả ba mệnh đề đều sai. D. Có đúng một mệnh đề sai.
Câu 39. [2D4-2.4-2] Cho số phức thỏa mãn . Biết tập hợp các điểm biểu diễn số phức
là một đường tròn. Tìm bán kính của đường tròn đó.
A. . B. . C. . D. .
Câu 40. [2H3-1.1-1] Trong không gian với hệ tọa độ , cho hai điểm và . Tọa
độ của vectơ là
A. . B. . C. . D. .
Câu 41. [2H3-1.1-1] Trong không gian với hệ trục , cho tam giác có , ,
. Gọi là trọng tâm của tam giác đó. Tổng bằng
A. . B. . C. . D. .
Câu 42. [2D2-4.1-1] Điều kiện xác định của hàm số là
A. . B. . C. . D.
.
Câu 43. [2H2-2.3-3] Cho tứ diện đều có cạnh bằng . Thể tích của khối cầu tiếp xúc với tất cả
các cạnh của tứ diện bằng
A. . B. . C. . D. .
Câu 44. [2H2-2.7-1] Trong không gian , phương trình mặt cầu tâm , bán kính là
A. . B. .
C. . D. .
Câu 45. [1D5-2.1-1] Đạo hàm của hàm số là
A. . B. . C. . D. .
Câu 46. [2D2-6.1-2] Tập nghiệm của bất phương trình là
A. . B. . C. . D. .
Câu 47. [1D2-5.5-2] Đội tuyển học sinh giỏi Toán của trường THPT X có học sinh trong đó có
bạn Minh Anh. Lực học của các học sinh là như nhau. Nhà trường chọn ngẫu nhiên học sinh
đi thi. Tìm xác suất để Minh Anh được chọn đi thi.
A. . B. . C. . D. .
Câu 48. [2D1-3.1-2] Tìm giá trị nhỏ nhất của hàm số trên đoạn .
A. . B. . C. . D. .
Câu 49. [1D2-2.1-1] Trong tủ quần áo của bạn An có chiếc áo khác nhau và chiếc quần khác nhau.
Hỏi bạn An có bao nhiêu cách để chọn 1 bộ quần áo để mặc?
A. . B. . C. . D. .
Câu 50. [2D1-5.8-1] Cho hàm số có đồ thị như hình vẽ. Tìm kết luận đúng trong các kết luận
sau.
5z =
( )
12wizi=+ +
r
5r =
10r =
5r =
25r =
Oxyz
( )
3; 0; 2A -
( )
1; 4; 2B
AB
!!!"
( )
1; 2; 2-
( )
2; 4; 4-
( )
2; 2; 0
( )
4; 4; 0
Oxyz
ABC
( )
3; 3; 2A
( )
1; 2; 0B -
( )
1; 1; 2C -
( )
000
;;Gx y z
000
xyz++
9
1
3
2
3
-
3
( )
2
log 1yx=-
1x ¹
1x >
1x <
x"Î!
ABCD
ABCD
3
3
24
a
3
2
24
a
p
3
22
9
a
3
3
8
a
p
Oxyz
( )
1; 2; 3I -
2R =
( ) ( ) ( )
222
1234xy z++- ++ =
( ) ( ) ( )
222
1232xy z++- ++ =
( ) ( ) ( )
222
1234xy z-++ +- =
( ) ( ) ( )
222
1232xy z-++ +- =
2
lnyxx=+
1
yx
x
¢
=+
1
2yx
x
¢
=+
1
2yx
x
¢
=-
3
1
3
x
y
x
¢
=+
21
2
1
3
x+
æö
>
ç÷
èø
( )
;0-¥
( )
0; +¥
1
;
2
æö
-¥ -
ç÷
èø
1
;
2
æö
-+¥
ç÷
èø
12
1
7
4
7
3
7
1
2
9
yx
x
=+
[ ]
2;4
[ ]
2;4
13
min
2
y =
[ ]
2;4
25
min
4
y =
[ ]
2;4
min 6y =
[ ]
2;4
min 6y =-
3
27
64
12
( )
yfx=
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$7$,$Mã$617$
A. Hàm số có điểm cực tiểu .
B. Hàm số không có cực trị .
C. Phương trình vô nghiệm.
D. Hàm số đồng biến trên khoảng .
----
----- HẾT ---------
( )
yfx=
1x =
( )
yfx=
( )
0fx=
( )
yfx=
( )
;0-¥
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$8$,$Mã$617$
LỜI GIẢI CHI TIẾT
Câu 1. [2H3-2.3-1] Trong không gian với hệ tọa độ , lập phương trình của các mặt phẳng song
song với mặt phẳng và cách một khoảng bằng .
A. ; . B. .
C. ; . D. ; .
Lời giải
Tác giả: Giáp Minh Đức; Fb: Giáp Minh Đức
Chọn A
Gọi là mặt phẳng cần tìm. Ta có .
Do nên phương trình của mặt phẳng có dạng: , với .
Ta có (thỏa mãn).
Vậy phương trình của các mặt phẳng cần tìm là và .
Câu 2. [2D4-5.2-3] Cho số phức thỏa mãn . Gọi và lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của biểu thức . Tính .
A. . B. . C. . D. .
Lời giải
Tác giả: Giáp Minh Đức; Fb: Giáp Minh Đức
Chọn A
Giả sử , .
Do . Suy ra .
Ta có . Thay vào ta được:
.
Xét hàm số
Ta có .
Bảng biến thiên của hàm số trên
Oxyz
( )
:30xyz
b
+-+=
( )
b
3
60xyz+-+=
0xyz+-=
60xyz+-+=
60xyz--+=
0xyz--=
60xyz+++=
0xyz++=
( )
a
( ) ( )
0; 0; 3A
b
Î
( ) ( )
//
ab
( )
a
0xyzm+-+ =
3m ¹
( ) ( )
( )
,3d
ab
=
( )
( )
,3dA
a
Û=
3
3
3
m -
Û=
6
33
0
m
m
m
=
é
Û-=Û
ê
=
ë
60xyz+-+=
0xyz+-=
1z =
M
m
2
11Pz z z=++ -+
.Mm
13 3
4
39
4
33
13
4
zxyi=+
( )
,xy RÎ
1z =
22
1xyÛ+=
22
1xyÛ+=
[ ]
,1;1xyÎ-
2
.1zz z==
P
( )
2
1.111.111Pz z zzz z zz z z zzz z zz=++ -+ =++ -+ =++ +-=+++-
( )
2
2
1212221xyx xx=+++-= ++-
( )
2221yfx x x==++-
( )
1
2221 1
2
1
2221 1
2
x x khi x
yfx
x x khi x
ì
+- + -£<
ï
ï
==
í
ï
++ - ££
ï
î
( )
11
21
2
22
11
21
2
22
khi x
x
fx
khi x
x
ì
--<<
ï
+
ï
¢
=
í
ï
+<£
ï
+
î
( )
1
1
2
'0
1
20
22
x
fx
x
ì
-< <
ï
ï
=Û
í
ï
-=
ï
+
î
1
1
2
1
22
2
x
x
ì
-< <
ï
ï
Û
í
ï
+=
ï
î
7
8
xÛ=-
( )
fx
[ ]
1; 1-
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$9$,$Mã$617$
Suy ra
Vậy .
Câu 3. [1D5-2.1-2] Cho . Tính .
A. . B. . C. . D. .
Lời giải
Tác giả: Lưu Thị Thủy; Fb: thuy.luu.33886
Chọn C
Ta có
.
Suy ra , . Vậy .
Câu 4. [2D3-2.1-2] Biết , với , , , . Tính tổng .
A. . B. . C. . D. .
Lời giải
Tác giả: Lưu Thị Thủy; Fb: thuy.luu.33886
Chọn A
Ta có .
Mà , với , , , . Suy ra , , .
Vậy .
Câu 5. [2H3-1.1-1] Trong không gian , cho mặt phẳng có phương trình . Một
vectơ pháp tuyến của mặt phẳng có tọa độ là
A. . B. . C. . D. .
Lời giải
Tác giả: Nguyễn Hoàng Hưng ; Fb: Nguyễn Hưng
Chọn A
Ta có: .
Suy ra một vectơ pháp tuyến của mặt phẳng có tọa độ là .
Câu 6. [2D2-4.4-4] Cho các số thực sao cho và thỏa mãn điều kiện
3
13
4
3
3
+
1
x
y'
y
1
0
7
8
1
2
+
[ ]
( )
[ ]
( )
1;1
1;1
min 3
14
max
3
mfx
Mfx
-
-
ì
==
ï
í
ï
==
î
13 3
.
4
Mm=
( )
32 1
,
4
41 4141
x ax b
x
xxx
¢
--
æö
=">
ç÷
---
èø
a
b
16-
4-
1-
( ) ( )
( )
( )
2
32 4 1 32 4 1
32
41
41
xx x x
x
x
x
¢
¢
¢
-----
-
æö
=
ç÷
-
èø
-
( )
2
24 1 3 2 .
41
41
xx
x
x
----
-
=
-
( ) ( )
( )
24 1 23 2
4141
xx
xx
----
=
--
( )
44
4141
x
xx
--
=
--
4a =-
4b =
1
a
b
=-
3
1
2
dln
x
Ixabc
x
+
==+
ò
c Î !
9c <
Sabc=++
7S =
5S =
8S =
6S =
3
1
2
d
x
Ix
x
+
=
ò
3
1
2
1dx
x
æö
=+
ç÷
èø
ò
( )
3
2ln
1
xx=+
22ln3=+
lnIabc=+
c Î !
9c <
2a =
2b =
3c =
7Sabc=++=
Oxyz
( )
P
3470xz-+=
( )
P
( )
3; 0; 4-
( )
3; 4; 7--
( )
3; 0; 7
( )
3; 4; 7-
3470 3470xz xz-+=Û-+-=
( )
P
( )
3; 0; 4-
,, ,abmn
20mn+<
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$10$,$Mã$617$
Tìm giá trị nhỏ nhất của biểu thức .
A. . B. . C. . D. .
Lời giải
Tác giả: Nguyễn Hoàng Hưng ; Fb: Nguyễn Hưng
Chọn A
Ta có:
.
Gọi , suy ra thuộc đường tròn có tâm , bán kính .
Lại có
,
Với thỏa mãn , ta có:
+)
+) .
Suy ra
Do đó .
Gọi , suy ra thuộc đường thẳng có phương trình .
Ta có: .
đường thẳng không cắt đường tròn .
Do đó ngắn nhất khi là hình chiếu của điểm trên đường thẳng và điểm là giao
điểm của đoạn thẳng với đường tròn .
Lúc đó .
Vậy giá trị nhỏ nhất của bằng .
( )
( )
( )
22
22
4
2
2
log 9 1 log 3 2
9 .3 .3 ln 2 2 1 81
mn
mn
ab a b
mn
-
--
+
ì
++=+ +
ï
í
éù
ï
++++=
ëû
î
( ) ( )
22
Pambn=-+-
25 2-
52-
25
( )
( )
( )
( )
22 22
2222
log 9 1 log 3 2 log 9 log 2 3 2ab a b ab a b++=+ + Û ++= +
éù
ëû
( ) ( )
22
22
96 4 3 2 4ab ab a bÛ++=+Û- +- =
( )
;Hab
H
( )
C
( )
3; 2I
2R =
( )
4
2
2
9 .3 .3 ln 2 2 1 81
mn
mn
mn
-
--
+
éù
++++=
ëû
( )
( )
4
2
2
2
3 ln 2 2 1 81
mn
mn
mn
-
æö
-++
ç÷
+
èø
éù
Û++++=
ëû
( )
1
,mn"
20mn+<
( ) ( )
( )
4
2
2
44
2 2 2 . 4 3 81
22
mn
mn
mn mn
mn mn
-
æö
-++
ç÷
+
èø
--
æö
-++ ³-+ =Þ ³
éù
ç÷
ëû
++
èø
( )
2
ln 2 2 1 ln1 0mn
éù
++ + ³ =
ëû
( )
( )
4
2
2
2
3 ln 2 2 1 81
mn
mn
mn
-
æö
-++
ç÷
+
èø
éù
++++³
ëû
( )
( )
4
2
1220
2
220
mn
mn
mn
mn
-
ì
-+=
ï
ÛÛ++=
+
í
ï
++=
î
( )
;Kmn
K
D
220xy++=
( ) ( )
22
PambnHK=-+-=
( )
22
2.3 2 2
,252
21
dI
++
D= = >
+
Þ
D
( )
C
HK
K
D
H
IK
( )
C
25 2HK IK IH=-= -
P
25 2-
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$11$,$Mã$617$
Câu 7. [2H1-3.2-2] Cho lăng trụ có đáy là tam giác đều cạnh , độ dài cạnh bên
bằng , hình chiếu của đỉnh trên mặt phẳng trùng với trọng tâm của tam giác
. Thể tích khối lăng trụ bằng
A. . B. . C. . D. .
Lời giải
Tác giả:Nguyễn Thị Anh Đào; Fb:Đào Nguyễn
Chọn C
Gọi là trọng tâm của tam giác .
Do tam giác đều cạnh nên .
Mặt khác do .
Vậy thể tích lăng trụ là .
Câu 8. [2H1-3.4-3] Cho hình chóp có vuông góc với mặt phẳng . Tứ giác
là hình vuông cạnh , . Gọi là hình chiếu vuông góc của trên . Tính
khoảng cách từ đến mặt phẳng .
A. . B. . C. . D. .
Lời giải
Chọn D
.' ' 'ABC A B C
ABC
2
3
a
'A
( )
ABC
ABC
.' ' 'ABC A B C
3
3
36
a
3
3
6
a
3
3
12
a
3
3
24
a
H
ABC
ABC
3
3
a
AH =
( )
''A H ABC A H AH^Þ^
22
22
43
''
993
aaa
A H AA AHÞ= -= -=
.' ' 'ABC A B C
23
.'' '
33
'. .
3 4 12
ABC A B C ABC
aa a
VAHS
D
===
.S ABCD
SA
( )
ABCD
ABCD
2SA a=
H
A
SB
H
( )
SCD
45
5
a
45
25
a
25
5
a
85
25
a
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$12$,$Mã$617$
Ta có
Ta có:
, (do ).
Gọi là hình chiếu vuông góc của trên .
Ta có .
Vì .
Ta có .
Vậy .
Câu 9 . [2D1-5.6-2] Cho hàm số có đồ thị . Tìm số tiếp tuyến của đồ thị song
song với đường thẳng .
A. . B. . C. 3. D. 0.
Lời giải
Tác giả: Nguyễn Huyền ; Fb: Huyen Nguyen.
Chọn A
Vì tiếp tuyến song song với đường thẳng nên hệ số góc tiếp tuyến .
Gọi là tiếp điểm . Ta có: .
Tiếp tuyến đi qua và có hệ số góc có phương trình .
Tiếp tuyến đi qua và có hệ số góc có phương trình (loại vì
.
Vậy có tiếp tuyến thỏa mãn yêu cầu bài toán.
Câu 10 . [2D1-4.1-1] Đồ thị hàm số có các đường tiệm cận đứng, tiệm cận ngang lần lượt là:
A. . B. .
C. . D. .
Lời giải
Tác giả: Nguyễn Huyền ; Fb: Huyen Nguyen.
Chọn A
.
Vì nên đồ thị hàm số nhận là tiệm cận đứng.
Vì nên đồ thị hàm số nhận là tiệm cận ngang.
Câu 11. [2D1-5.8-4] Cho các hàm số và
thỏa mãn . Các hàm số và có đồ thị
như hình vẽ bên.
22
2
222
44
..
45
SH SA a
SH SB SA
SB SB a a
=Þ= = =
+
( )
( )
( )
,( )
4
.
5
,
d H SCD
SH
SB
d B SCD
==
( )
( )
( )
( )
( )
( )
44
,.,.,
55
d H SCD d B SCD d A SCDÞ= =
( )
//AB SCD
A
SD
( )
CD SAD CD AI^Þ^
( ) ( )
( )
,
AI SD
AI SCD d A SCD AI
AI CD
^
ì
Þ^ Þ =
í
^
î
.25
..
5
SA AD a
AI SD SA AD AI
SD
=Þ= =
( )
( )
485
,.
5 25
a
d H SCD AI==
32
32yx x=- +
( )
C
( )
C
: 9 25dy x=-
1
: 9 25dy x=-
9k =
( )
00
;Mx y
( )
0
fx k
¢
=
2
00
369xxÛ-=
0
0
1
3
x
x
=-
é
Û
ê
=
ë
( )
( )
1; 2
3; 2
M
M
-
é
Û
ê
ê
ë
1
d
( )
1; 2M --
9k =
97yx=+
2
d
( )
3; 2M
9k =
9 25yx=-
2
ddº
1
31
2
x
y
x
-+
=
+
2, 3xy=- =-
2, 3xy=- =
2, 1xy=- =
2, 1xy==
{ }
\2D =-!
2
31
lim
2
x
x
x
+
®-
-+
= +¥
+
2x =-
31
lim 3
2
x
x
x
®±¥
-+
=-
+
3y =-
( )
43 2
f x mx nx px qx r=++++
( )
32
g x ax bx cx d=+++
( )
,, ,,,,,,mn pqrabcdÎ !
( ) ( )
00fg=
( )
yfx
¢
=
( )
gx
¢
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$13$,$Mã$617$
Tập nghiệm của phương trình có số phần tử là
A. 4. B. 2. C. 1. D. 3.
Lời giải
Tác giả:Thu Trang ; Fb: Nguyễn Thị Thu Trang
Chọn B
+ Từ đồ thị hàm số .
+ .
+ Ta có .
Mặt khác từ đồ thị hai hàm số và ta có
hay .
Từ và ta suy ra .
+ Phương trình
.
Phương trình có đúng một nghiệm thực khác 0.
Vậy phương trình đã cho có 2 nghiệm thực phân biệt.
Câu 12. [2D1-1.1-1] Trong các hàm số sau, hàm số nào đồng biến trên ?
A. . B. . C. . D. .
Lời giải
Tác giả:Thu Trang ; Fb: Nguyễn Thị Thu Trang
Chọn C
Cách 1: (Trắc nghiệm).
+ Hàm số và với không đồng biến trên .
Loại A, B.
( ) ( )
fx gx=
( )
yfx
¢
=
0mÞ¹
( ) ( )
00fg rd=Þ=
( ) ( ) ( ) ( )
32
43 2fx gx mx nax pbxqc
¢¢
-=+-+-+-
( )
1
( )
yfx
¢
=
( )
gx
¢
( ) ( ) ( ) ( )( )
4112fx gx mx x x
¢¢
-=+--
( ) ( )
32
4848fx gx mx mx mx m
¢¢
-=--+
( )
2
( )
1
( )
2
( )
( )
38
24
8
na m
pb m
qc m
-=-
ì
ï
-=-
í
ï
-=
î
( ) ( )
43 2 32
f x g x mx nx px qx r ax bx cx d=Û++++=+++
43 2 32
mx nx px qx ax bx cxÛ+++=++
( ) ( )
32
0xmx n ax p bx q c
éù
Û+-+-+-=
ëû
32
8
28 0
3
m
xmx x mx m
æö
Û--+=
ç÷
èø
32
32
0
8
280
8
3
280
3
x
mx x x x
xxx
=
é
æö
ê
Û--+=Û
ç÷
ê
--+=
èø
ë
32
8
280
3
xxx--+=
!
2
21yx x=+-
42
2yx x=-
3
2 2019yx x=+-
21
3
x
y
x
-
=
+
2
y ax bx c=++
42
y ax bx c=++
,, , 0abc aι!
!
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$14$,$Mã$617$
+ Hàm số với có tập xác định nên hàm số không
đồng biến trên . Loại D.
Vậy chọn C.
Cách 2: (Tự luận).
+ Hàm số có .
nên hàm số không đồng biến trên .
+ Hàm số có .
nên hàm số không đồng biến trên .
+ Hàm số có nên hàm số đồng biến trên .
+ Hàm số có TXĐ nên hàm số không đồng biến trên .
Câu 13. [2H3-2.3-2] Trong không gian với hệ tọa độ , viết phương trình mặt phẳng đi qua hai
điểm , và vuông góc với mặt phẳng : .
A. . B. . C. . D. .
Lời giải
Tác giả: Phạm Thị Phương Thúy; Fb: thuypham
Chọn C
.
Một vectơ pháp tuyến của là .
Vì nên là một vectơ pháp tuyến của .
Vậy phương trình là: .
Câu 14. [2D1-2.4-2] Cho hàm số với là tham số thực. Tìm tất cả
các giá trị của để hàm số có điểm cực đại và điểm cực tiểu nằm trong khoảng .
A. . B. . C. . D. .
Lời giải
Tác giả: Phạm Thị Phương Thúy; Fb: thuypham
Chọn A
Xét hàm số
Ta có .
.
+) Hàm số có 2 điểm cực trị có 2 nghiệm phân biệt .
+) Hàm số có điểm cực đại và điểm cực tiểu nằm trong khoảng
.
Kết hợp điều kiện , ta được .
Câu 15. [2D3-3.3-1] Cho hàm số liên tục trên . Gọi là hình phẳng giới hạn bởi đồ thị
hàm số , trục hoành và hai đường thẳng , . Thể tích khối tròn xoay tạo
thành khi quay quanh trục hoành được tính theo công thức
ax b
y
cx d
+
=
+
,,, , 0abcd cι!
\
d
D
c
ìü
=-
íý
îþ
!
!
2
21yx x=+-
22yx
¢
=+
01yx
¢
>Û>-
2
21yx x=+-
!
42
2yx x=-
( )
32
444 1yxxxx
¢
=-= -
10
0
1
x
y
x
-< <
é
¢
>Û
ê
>
ë
42
2yx x=-
!
3
2 2019yx x=+-
2
320,yx x
¢
=+>"Î!
!
21
3
x
y
x
-
=
+
{ }
\3D =-!
!
Oxyz
( )
P
( )
2;1;1A
( )
1; 2; 3B -- -
( )
Q
0xyz++=
0xyz--=
30xy+-=
10xy--=
40xyz++-=
( )
3; 3; 4AB =- - -
!!!"
( )
Q
( )
( )
1; 1; 1
Q
n =
!
( )
( ) ( )
P AB
PQ
É
ì
ï
í
^
ï
î
( )
( )
,1;1;0
Q
n AB n
éù
==-
ëû
!"""!"""!
( )
P
( )
P
( ) ( ) ( )
1211010 10xyz xy-- -+ -=Û--=
( ) ( )
32
23 1 6 21yx m x m x=+ - + --
m
m
( )
2; 3-
( ) { }
1; 4 \ 3m Î-
( )
3; 4m Î
( )
1; 3m Î
( )
1; 4m Î-
( ) ( )
32
23 1 6 21yx m x m x=+ - + --
( ) ( )
2
66 16 2yx mxm
¢
=+ -+ -
( )
2
1
0120
2
x
yxmxm
xm
=-
é
¢
=Û + - + -=Û
ê
=-
ë
0y
¢
Û=
21mÛ- ¹-
3mÛ¹
( )
2; 3-
213
14
22 3
m
m
-<-<
ì
ÛÛ-<<
í
-< - <
î
3m ¹
( ) { }
1; 4 \ 3m Î-
( )
yfx=
[ ]
3; 4
D
( )
yfx=
3x =
4x =
D
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$15$,$Mã$617$
A. . B. . C. . D. .
Lời giải
Tác giả: Ngô Quốc Tuấn; Fb: Quốc Tuấn
Chọn A
Thể tích khối tròn xoay tạo thành khi quay quanh trục hoành là: .
Câu 16. [2H3-1.4-3] Trong không gian với hệ tọa độ , cho ba điểm , ,
và mặt phẳng . Gọi là điểm thuộc sao
cho đạt giá trị nhỏ nhất. Tính tổng .
A. . B. . C. . D. .
Lời giải
Tác giả: Ngô Quốc Tuấn; Fb: Quốc Tuấn
Chọn A
Gọi là điểm thỏa mãn .
Khi đó: .
Ta có:
.
Suy ra đạt giá trị nhỏ nhất nhỏ nhất là hình chiếu của lên .
Phương trình đường thẳng đi qua và vuông góc với là .
Tọa độ của điểm thỏa mãn hệ phương trình
. Vậy .
Câu 17. [2D3-2.4-3] Cho hàm số có đạo hàm liên tục trên và có đồ thị như hình vẽ.
Giá trị của biểu thức bằng
A. . B. . C. . D. .
Lời giải
Tác giả: Trần Thị Thúy; Fb: Thúy Minh
Chọn C
( )
4
2
3
dVfxx
p
=
ò
( )
4
22
3
dVfxx
p
=
ò
( )
4
3
dVfxx=
ò
( )
4
2
3
dVfxx=
ò
D
( )
4
2
3
dVfxx
p
=
ò
Oxyz
( )
1; 4; 5A
( )
3; 4; 0B
( )
2; 1; 0C -
( )
: 3 3 2 29 0Pxyz+--=
( )
;;Mabc
( )
P
22 2
3MA MB MC++
abc++
8
10
10-
8-
( )
;;
HHH
Hx y z
30HA HB HC++ =
!!!" !!!" !!! " "
( )
( )
( ) ( )
1332 0
2
4431 0 1
1
530
HH H
H
HH H H
H
HH H
xx x
x
yy y y
z
zz z
-+-+ - =
ì
=
ì
ï
ï
-+-+-- =Û =
íí
ïï
=
-+- +- =
î
î
( )
2;1;1HÛ
( ) ( ) ( )
22 2
22 2
33TMA MB MC MHHA MHHB MHHC=++ = + + + + +
!!!!" !!!" !!!!" !!!" !!!!" !!!"
( )
222 2
5323MH HA HB HC MH HA HB HC=++++ ++
!!!!" !!!" !!!" !!!"
222 2
53MH HA HB HC=+++
T
Û
MH
Û
M
H
( )
P
d
( )
2;1;1H
( )
P
( )
23
13,
12
xt
ytt
zt
=+
ì
ï
=+ Î
í
ï
=-
î
!
M
23 5
13 4
12 1
3 3 2 29 0 1
xt x
yt y
zt z
xyz t
=+ =
ìì
ïï
=+ =
ïï
Û
íí
=- =-
ïï
ïï
+--= =
îî
Þ
( )
5; 4; 1M -
8abc++=
( )
yfx=
!
( ) ( )
42
00
'2d '2dIfx xfx x=-++
òò
2-
10
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$16$,$Mã$617$
Cách 1:
Đặt , .
Tính : Đặt .
Đổi cận:
Ta có: .
Tính : Đặt .
Đổi cận:
Ta có: .
Vậy: .
Cách 2:
.
Câu 18. [2D3-2.4-2] Cho hàm số có đạo hàm liên tục trên đoạn và thỏa mãn ,
. Tính tích phân .
A. . B. . C. . D. .
Lời giải
Tác giả: Trần Thị Thúy; Fb: Thúy Minh
Chọn A
Ta có: .
Đặt
Nên .
Theo giả thiết ta có: .
Câu 19. [2H1-3.2-2] Cho khối chóp có thể tích là . Gọi , lần lượt là trung điểm ,
Tính theo thể tích của khối chóp .
A. . B. . C. . D. .
Lời giải
Tác giả: LêHoa; Fb:LêHoa
Chọn D
( )
4
1
0
'2dIfx x=-
ò
( )
2
2
0
'2dIfx x=+
ò
1
I
2d dux u x=-Þ =
( ) ( )
22
1
22
'd 'dIfuufxx
--
==
òò
( ) ( ) ( ) ( )
2
2
22224fx f f
-
==--=--=
2
I
2ddvx v x=+Þ =
( ) ( )
44
2
22
'd 'dIfvvfxx==
òò
( ) ( ) ( )
4
2
42422fx f f==-=-=
12
42 6II I=+ =+=
( ) ( ) ( ) ( ) ( ) ( )
42 4 2
00 0 0
'2d '2d '2d2 '2d 2Ifx xfx xfx x fx x=-++=--+++
òò ò ò
( ) ( ) ( ) ( )
( )
( ) ( )
( )
42
00
222242fx fx f f f f=-++= --+ -
( )
( )
( )
22 426=-- +-=
( )
fx
[ ]
0;2
( )
02f =
( ) ( )
2
0
24.'d4xfxx-=
ò
( )
2
0
dIfxx=
ò
2I =
2I =-
6I =
6I =-
( ) ( )
2
0
24.'d4xfxx-=
ò
( )
24
d'd
ux
vfxx
=-
ì
ï
í
=
ï
î
( )
d 2dux
vfx
=
ì
ï
Þ
í
=
ï
î
( ) ( ) ( ) ( ) ( )
22
2
0
00
24.' d 24. 2 dxfxxxfx fxx-=--
òò
( )
4. 0 2fI=-
82I=-
482 2 4 2II I=- Û = Û =
.S ABC
V
B
¢
C
¢
AB
AC
V
.S AB C
¢¢
1
3
V
1
2
V
1
12
V
1
4
V
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$17$,$Mã$617$
Ta có .
Câu 20. [2D1-5.4-3] Có bao nhiêu giá trị âm của tham số để phương trình
có hai nghiệm thực phân biệt
A. . B. . C. Vô số. D. .
Lời giải
Tác giả: LêHoa; Fb:LêHoa
Chọn A
Cách 1:
Đặt
.
Ta được hệ (*)
Trường hợp 1: .
Khi đó (*)
phương trình vô nghiệm.
Trường hợp 2:
Thay vào (*) thỏa mãn. Vậy (*) có nghiệm .
Với ta có .
Phương trình có hai nghiệm thực phân biệt
có 2 nghiệm thỏa mãn
. Do âm nên có một giá trị thỏa mãn.
Cách 2: Lưu Thêm
Ta có
, .
C'
B'
C
A
B
S
.
.
1
. .sin
.1
2
1
.4
. .sin
2
SABC ABC
SABC ABC
AB AC A
VS
AB AC
V S AB AC
AB AC A
¢¢ ¢¢
D
D
¢¢
¢¢
== = =
..
11
44
SABC SABC
VVV
¢¢
Þ= =
m
22
2019 2019mmxx++=
1
( )
( )
2
2
2019 0
0
tmxt
ax a
ì
=+³
ï
í
=³
ï
î
2019
2019
mt a
ma t
ì
+=
ï
í
+=
ï
î
2019 2019mt ma atÞ+-+=-
at¹
2019 2019
ta
at
mt ma
-
Û=-
++ +
1
1
2019 2019mt ma
Û=-
++ +
at=
at=
at=
2019ama=+
2
2019amaÛ= +
2
2019 0aa mÛ-- =
22
2019 2019mmxx++=
2
2019 0aa mÛ-- =
12
,aa
12
12
0
0
aa
aa
=>
é
ê
<<
ë
( )
0
0
1. 2019 0
S
m
éD=
ì
í
ê
>
Û
î
ê
ê
-<
ë
1
4.2019
0
m
m
é
=-
ê
Û
ê
>
ë
m
1
4.2019
m =-
22 24
2019 2019 2019 2019mmxx mmxx++=Û++=
( )
2242
2019 2019mx mx x xÛ++ +=+
( )
1
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$18$,$Mã$617$
Xét hàm số ; .
Ta có hàm số đồng biến trên khoảng
và , .
Do đó
.
Ta có BBT hàm số
Phương trình đã cho có hai nghiệm thực phân biệt
Do âm nên có một giá trị thỏa mãn.
Câu 21: [2D1-3.1-2] Cho hàm số với là tham số thực. Giả sử là giá trị dương của
tham số
để hàm số có giá trị nhỏ nhất trên đoạn
bằng . Giá trị
thuộc khoảng nào
trong các khoảng cho dưới đây?
A. . B. . C. . D. .
Lời giải
Tác giả: Võ Thanh Hải; Fb:Võ Thanh Hải
Chọn D
* Tập xác định .
* Ta có , suy ra hàm số đã cho đồng biến trên đoạn .
Do đó .
* Theo yêu cầu bài toán ta có: .
Câu 22: [0H1-2.1-2] Cho tứ diện có là trung điểm của đoạn thẳng nối trung điểm của hai
cạnh đối diện và là số thực dương không đổi. Tập hợp các điểm trong không gian thỏa
mãn hệ thức
là
A. mặt cầu tâm
bán kính . B. mặt cầu tâm
bán kính .
( )
2
ft t t=+
( )
1
'210,
2
ft t t=+>">-
( )
2
ft t t=+
1
;
2
æö
- +¥
ç÷
èø
2
1
2019 ;
2
mx
æö
+ Î - +¥
ç÷
èø
2
1
;
2
x
æö
Î - +¥
ç÷
èø
( )
1
(
)
( )
22 22
2019 2019fmxfx mxxÛ+=Û+=
24 42
2019 2019mx x m x xÛ+=Û=-
( )
42
gx x x=-
1
2019
4
0
m
m
é
=-
ê
Û
ê
>
ë
m
1
4.2019
m =-
2
8
xm
y
x
-
=
+
m
o
m
m
[ ]
0; 3
3-
o
m
( )
20; 25
( )
5; 6
( )
6; 9
( )
2; 5
{ }
\8D =-!
( )
2
2
8
0, 8
8
m
yx
x
+
¢
=>"¹-
+
[ ]
0; 3
[ ]
( )
2
0;3
min 0
8
m
yy==-
( )
2
0
0
26 2;5
3
26
8
m
m
m
m
m
>
ì
>
ì
ïï
ÛÛ=Î
íí
-=-
=±
ï
î
ï
î
ABCD
O
M
MA MB MC MD a++ + =
!!!" !!!" !!!!" !!! !"
O
3
a
r =
O
4
a
r =
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$19$,$Mã$617$
C. mặt cầu tâm
bán kính . D. mặt cầu tâm
bán kính .
Lời giải
Tác giả: Võ Thanh Hải; Fb:Võ Thanh Hải
Chọn B
* Gọi lần lượt là trung điểm của . Theo giả thiết là trung điểm của nên suy
ra
là trọng tâm của tứ diện .
* Ta có
.
Vậy tập hợp các điểm trong không gian là mặt cầu tâm
bán kính .
Câu 23. [2D1-2.1-1] Cho hàm số có đạo hàm . Số điểm cực trị của hàm
số đã cho là
A. 3. B. 5. C. 2. D. 1.
Lời giải
Tác giả: Trần Bạch Mai ; Fb: Bạch Mai
Chọn C
Ta có ; .
Nhận thấy đổi dấu qua 2 nghiệm nên hàm số có 2 điểm cực trị.
Câu 24. [2D3-3.5-2] Một vật chuyển động với vận tốc thì tăng tốc với gia tốc
, trong đó là khoảng thời gian tính bằng giây kể từ lúc bắt đầu tăng tốc.
Hỏi quãng đường vật đi được trong 12 giây kể từ lúc bắt đầu tăng tốc bằng bao nhiêu mét?
A. . B. . C. D. .
Lời giải
Tác giả: Trần Bạch Mai; Fb: Bạch Mai
Chọn A
Ta có: .
Vận tốc khi bắt đầu tăng tốc là : .
Vận tốc của vật là .
Quãng đường vật đi được trong 12 giây kể từ lúc bắt đầu tăng tốc:
O
ra=
O
2
a
r =
O
P
Q
B
D
C
A
,PQ
,AB CD
O
PQ
O
ABCD
MA MB MC MD a++ + =
!!!" !!!" !!!!" !!! !"
4
4
a
OM a OMÛ=Û=
!!!!"
M
O
4
a
r =
( )
yfx=
( )
2
2
4
,0
3
x
fx x
x
-
¢
="¹
( )
2
2
4
3
x
fx
x
-
¢
=
( )
2
0
2
x
fx
x
=
é
¢
=Û
ê
=-
ë
( )
fx
¢
2x =±
( )
yfx=
10 /ms
( )
( )
22
1
2/
3
at t t m s=+
t
1272 m
456 m
1172 m
1372 m
( ) ( )
3
22
1
dt 2 dt =
39
t
vt at t t t C
æö
==+ ++
ç÷
èø
òò
10 /ms
( )
0 10 10vC=Û=
( )
3
2
10
9
t
vt t=++
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$20$,$Mã$617$
.
Câu 25. [2H2-1.2-1] Hai khối nón có cùng thể tích. Một khối nón có bán kính đáy bằng và chiều cao
bằng , khối nón còn lại có bán kính đáy bằng và chiều cao bằng . Khi đó
A. . B. . C. . D. .
Lời giải
Tác giả: Trương Thanh Nhàn; Fb: Trương Thanh Nhàn.
Chọn D
Gọi là thể tích của khối nón có bán kính đáy bằng và chiều cao bằng ; là thể tích khối
nón còn lại. Ta có .
Do hai khối nón có cùng thể tích nên ta có .
Câu 26. [1D1-2.1-1] Phương trình có 1 nghiệm là
A. . B. . C. . D. .
Lời giải
Tác giả: Trương Thanh Nhàn; Fb: Trương Thanh Nhàn.
Chọn A
Xét Ta có nên là một nghiệm của phương trình đã cho .
Câu 27. [2D3-3.4-2] Có một cốc thủy tinh hình trụ, bán kính trong lòng đáy cốc là , chiều cao trong
lòng cốc là đang đựng một lượng nước. Tính thể tích lượng nước trong cốc, biết rằng khi
nghiêng cốc nước vừa lúc chạm miệng cốc thì ở đáy cốc, mực nước trùng với đường kính đáy.
A. . B. . C. . D. .
Lời giải
Tác giả: Võ Tự Lực; Fb: Võ Tự Lực
Chọn D
( )
12 12
3
2
00
dt = 10 dt = 1272 m
9
t
vt t
æö
++
ç÷
èø
òò
R
2R
2
h
x =
3
2
h
x =
3
4
xh=
4
h
x =
1
V
R
2
V
2
1
1
;
3
VRh
p
=
( )
2
2
2
14
2
33
VRxRx
pp
==
12
VV=
22
14
33
Rh Rx
pp
Û=
4
h
xÛ=
sin cos 1xx+=
2
p
p
2
3
p
4
p
( )
sin cos .fx x x=+
1
2
f
p
æö
=
ç÷
èø
2
x
p
=
4cm
12cm
3
128 cm
p
3
256 cm
3
256 cm
p
3
128 cm
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$21$,$Mã$617$
+) Chọn hệ trục tọa độ như hình vẽ.
là bán kính đáy cốc, là chiều cao của cốc.
+) Thiết diện cắt bởi mặt phẳng vuông góc với trục tại điểm có hoành độ là
một tam giác vuông tại có độ dài cạnh và
.
+) Diện tích thiết diện là .
+) Thể tích khối nước trong cốc là .
Chú ý: Có thể tính thể tích hình trên bằng công thức tính nhanh .
+) Với , thể tích cần tìm .
Câu 28. [2D1-5.8-1] Điểm thuộc đồ thị hàm số nào dưới đây?
A. . B. . C. . D. .
Lời giải
Tác giả: Võ Tự Lực; Fb:Võ Tự Lực
Chọn A
Thay tọa độ của điểm lần lượt vào các phương trình , , ,
, nhận thấy tọa độ thỏa mãn phương trình .
Vậy điểm thuộc đồ thị hàm số .
Câu 29. [2D3-1.1-1] Họ nguyên hàm của hàm số là
A. . B. . C. . D. .
Lời giải
Tác giả:Vũ Thị Thúy; Fb: Vũ Thị Thúy
Chọn A
Có .
Vậy họ nguyên hàm của hàm số là .
Oxy
4cmR =
12 cmh =
Ox
( )
44xx-£ £
ABC
B
22 2
16BC R x x=-=-
22 2 2
12
. 16 . 3 16
4
h
BA R x x x
R
=- =- = -
( )
( )
22 2
13
16 .3 16 16
22
Sx x x x=- -=-
( )
2
cm
( )
4
2
4
3
16
2
V x dx
-
=-
ò
3
4
3
16 128
4
23
x
x
æö
=- =
ç÷
-
èø
( )
3
cm
2
2
3
VRh=
4R =
cm
12h =
cm
2
2
.4 .12 128
3
V ==
3
cm
( )
1;Me
x
ye=
lnyx=
2
yx
-
=
2
x
y
-
=
( )
1;Me
x
ye=
lnyx=
2
yx
-
=
2
x
y
-
=
( )
1;Me
x
ye=
( )
1;Me
x
ye=
( )
1
1
fx
x
=
-
ln 1xC-+
( )
2
1
1
C
x
-+
-
2ln 1xC-+
( )
ln 1xC-+
( )
11
dd1ln1
11
xxxC
xx
=-=-+
--
òò
( )
1
1
fx
x
=
-
ln 1xC-+
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$22$,$Mã$617$
Câu 30. [2H1-3.4-1] Cho hình lập phương . Góc giữa hai mặt phẳng và
bằng
A. . B. . C. . D. .
Lời giải
Tác giả: Vũ Thị Thúy; Fb: Vũ Thị Thúy
Chọn C
Vì nên góc giữa hai mặt phẳng và bằng .
Câu 31. [2D4-1.3-2] Trên mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn số phức sao cho là số
thuần ảo.
A. Hai đường thẳng và .
B. Trục .
C. Trục .
D. Hai đường thẳng và , bỏ đi điểm .
Lời giải
Tác giả: Nguyễn Văn Diệu; Fb: dieuptnguyen
Chọn A
+) Gọi với . Khi đó .
+) là số thuần ảo khi và chỉ khi .
Vậy tập hợp điểm biểu diễn số phức là hai đường thẳng và .
Câu 32. [2D4-1.3-1] Cho số phức . Phần ảo của
là
A. . B. . C.
. D.
.
Lời giải
Tác giả: Nguyễn Văn Diệu; Fb: dieuptnguyen
Chọn A
Cho số phức với . Khi đó được gọi là phần ảo của .
Vậy là phần ảo của số phức .
Câu 33. [2D2-5.6-2] Một người gửi triệu đồng vào ngân hàng theo thể thức lãi kép với lãi suất
năm, kì hạn một năm. Hỏi sau 5 năm người đó rút cả vốn lẫn lãi được số tiền gần với số
nào nhất trong các số tiều sau? (biết lãi suất hàng năm không đổi) .
A. triệu đồng. B. triệu đồng. C. triệu đồng. D. triệu đồng.
Lời giải
Tác giả: Bùi Quý Minh; Fb: Minh Bùi
Chọn D
Gọi số tiền ban đầu là . Lãi suất tính theo năm là .
Hết năm thứ nhất số tiền cả vốn và lãi là: .
Hết năm thứ hai số tiền cả vốn và lãi là: .
Hết năm thứ ba số tiền cả vốn và lãi là: .
.ABCD A B C D
¢¢¢¢
( )
ABCD
( )
ABCD
¢¢¢¢
45°
60°
0°
90°
( ) ( )
//ABCD A B C D
¢¢¢¢
( )
ABCD
( )
ABCD
¢¢¢¢
0°
2
z
yx=
yx=-
Ox
Oy
yx=
yx=-
( )
0;0O
zxyi=+
,xyÎ !
( )
2
222222
22zxyixxyiyixyxyi=+ =+ + =-+
2
z
22
0
yx
xy
yx
=
é
-=Û
ê
=-
ë
z
yx=
yx=-
35zi=-
5-
5i-
5
3
zxyi=+
,xyÎ !
y
5-
35zi=-
50
6,5% /
73
53,3
64,3
68, 5
A
r
( )
.1AAr A r+= +
( ) ( ) ( )
2
11.1ArArrAr++ + = +
( ) ( ) ( )
22 3
11.1Ar ArrAr++ + = +
C'
B'
A'
D
C
B
A
D'
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$23$,$Mã$617$
Từ đó suy ra sau năm số tiền cả vốn và lãi là: .
Thay số với ta được số tiền là (triệu đồng ) .
Câu 34. [2D1-5.1-1] Hàm số nào sau đây có đồ thị như hình vẽ ?
A. . B. . C. . D. .
Lời giải
Tác giả: Bùi Quý Minh; Fb: Minh Bùi
Chọn A
+) Đồ thị hàm số có ba cực trị nên không thể là hàm bậc ba loại đáp án C .
+) loại đáp án B .
+) loại đáp án D .
Vậy đáp án A đúng.
Câu 35. [2D1-5.3-3] Số giá trị nguyên của thuộc khoảng để phương trình
có bốn nghiệm phân biệt là
A. . B. . C. . D. .
Lời giải
Tác giả: Vũ Việt Tiến, FB: Vũ Việt Tiến
Chọn B
Cách 1:
+) Ta có .
Đặt . Ta có . Suy ra .
Phương trình trở thành: .
+) Phương trình có bốn nghiệm phân biệt khi và chỉ khi phương trình có hai nghiệm
phân biệt , thỏa mãn .
Theo định lý Vi-et ta có .
+) Khi đó .
( )
1
n
Ar+
50; 6,5%; 5Ar n== =
( )
5
5
50 1 6,5% 68,5A =+ »
42
2yx x=-
42
21yx x=- -
32
2yx x x=- +
42
2yx x=- +
Þ
( )
00f =
Þ
( )
x
lim f x
®+¥
= +¥
Þ
m
( )
2019; 2019-
22
21 2 2
4 .2 3 2 0
xx xx
mm
-+ -+
-+-=
2017
2016
4035
4037
22
21 2 2
4 .2 3 2 0
xx xx
mm
-+ -+
-+-=
( )
2
2
221
21
2 2 .2 3 2 0
xx
xx
mm
-+
-+
Û- +-=
( )
1
2
21
2
xx
t
-+
=
( )
2
2
1
21 0
2221,
x
xx
tx
-
-+
==³="
1t ³
( )
1
2
2. 3 2 0tmtm-+-=
( )
2
( )
1
( )
2
1
t
2
t
12
1tt>>
( )( ) ( )
2
12 1212
12 12
0320
110 10
22
mm
tt tttt
tt tt
¢
ì
D> - + >
ì
ï
ï
Û- ->Û -++>
íí
ïï
+> +>
î
î
( )
3
12
12
2
.32
tt m
tt m
+=
ì
í
=-
î
( )
3
2
320
2
32210 2
1
22
1
mm
m
mm m
m
m
m
ì
-+>
ì>
é
ï
ï
ê
Û--+>Û Û>
<
íí
ë
ïï
>
>
î
î
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$24$,$Mã$617$
Mà nguyên và nên ta có .
Vậy có giá trị nguyên của thỏa mãn bài toán.
Cách 2: Đặng Ân
+) Ta có .
Đặt . Ta có . Suy ra .
Phương trình trở thành: .
Vì không là nghiệm của nên .
Xét hàm số trên khoảng .
; .
Ta có bảng biến thiên
Phương trình có bốn nghiệm phân biệt có hai nghiệm phân biệt lớn hơn 1 .
Mà nguyên và nên ta có .
Vậy có giá trị thỏa mãn bài toán.
Câu 36. [2H1-1.2-1] Hình chóp tứ giác có tất cả bao nhiêu cạnh
A. . B. . C. . D. .
Lời giải
Tác giả: Vũ Việt Tiến, FB: Vũ Việt Tiến
Chọn D
Hình chóp tứ giác (ví dụ như hình vẽ trên) có cạnh bên và cạnh đáy nên có tất cả cạnh.
Chú ý: Chóp -giác có cạnh.
m
( )
2019;2019m -Î
{ }
3;4;...;2018m Î
2016
m
22
21 2 2
4 .2 3 2 0
xx xx
mm
-+ -+
-+-=
( )
2
2
221
21
2 2 .2 3 2 0
xx
xx
mm
-+
-+
Û- +-=
( )
1
2
21
2
xx
t
-+
=
( )
2
2
1
21 0
2221,
x
xx
tx
-
-+
==³="
1t ³
( )
1
( )
22
2. 3 2 0 2 3. 2tmtm t mt-+-=Û- =-
( )
2
3
2
t =
( )
2
( )
2
2
2
23
t
m
t
-
Û=
-
( )
*
2
2
23
t
y
t
-
=
-
( )
1; +¥
( )
2
2
264
23
tt
y
t
-+
¢
=
-
1
0
2
t
y
t
=
é
¢
=Û
ê
=
ë
( )
1
( )
*Û
2mÛ>
m
( )
2019; 2019m -Î
{ }
3; 4;...; 2018m Î
2016
m
20
12
8
8
2n
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$25$,$Mã$617$
Câu 37. [2D3-3.1-2] Cho hàm số có đạo hàm liên tục trên . Đồ thị của hàm số
được cho như hình vẽ. Diện tích các hình phẳng , lần lượt là và .
Biết , tính .
A. . B. . C. . D. .
Lời giải
Tác giả:Trần Quôc Khang; Fb:Bi Trần
Chọn B
Gọi , lần lượt là diện tích hình phẳng , .
.
Câu 38. [2D1-1.5-2] Cho các mệnh đề:
1. Nếu hàm số liên tục trên và thì tồn tại sao cho
.
2. Nếu hàm số liên tục trên và thì phương trình có
nghiệm.
3. Nếu hàm số liên tục, đơn điệu trên và thì phương trình
có nghiệm duy nhất trên .
Trong ba mệnh đề trên
A. Có đúng hai mệnh đề sai. B. Cả ba mệnh đề đều đúng.
C. Cả ba mệnh đề đều sai. D. Có đúng một mệnh đề sai.
( )
yfx=
[ ]
1; 2-
( )
yfx
¢
=
( )
K
( )
H
5
12
8
3
( )
19
1
12
f -=
( )
2f
( )
23
2
6
f =
( )
2
2
3
f =-
( )
2
2
3
f =
( )
11
2
6
f =
1
S
2
S
( )
K
( )
H
( )
( )
0
1
1
2
2
0
5
5
dx
12
12
8
8
dx
3
3
fx
S
S
fx
-
ì
ì
¢
=
ï
=
ï
ïï
Û
íí
ïï
=
¢
-=
ï
ï
î
î
ò
ò
( ) ( )
( ) ( )
5
01
12
8
02
3
ff
ff
ì
--=
ï
ï
Û
í
ï
-=
ï
î
( ) ( )
58 9
21
12 3 4
ffÞ--=-=-
( ) ( )
9 19 9 2
21
4 12 4 3
ffÞ=--=-=-
( )
yfx=
( )
;ab
( ) ( )
.0fa fb<
( )
0
;xabÎ
( )
0
0fx =
( )
yfx=
[ ]
;ab
( ) ( )
.0fa fb<
( )
0fx=
( )
yfx=
[ ]
;ab
( ) ( )
.0fa fb<
( )
0fx=
( )
;ab
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$26$,$Mã$617$
Lời giải
Tác giả:Trần Quôc Khang; Fb:Bi Trần
Chọn D
Định lí: “Nếu hàm số liên tục trên và thì tồn tại ít nhất một
điểm sao cho ”.
Mệnh đề 1: SAI ở giả thiết .
Mệnh đề 2: Nếu hàm số liên tục trên và thì tồn tại ít nhất một
điểm sao cho hay là nghiệm của phương trình nên mệnh đề 2
ĐÚNG.
Mệnh đề 3: Nếu hàm số liên tục, đơn điệu trên và thì đồ thị
hàm số cắt trục tại duy nhất một điểm thuộc khoảng nên có
nghiệm duy nhất trên . Do đó mệnh đề 3 ĐÚNG.
Câu 39. [2D4-2.4-2] Cho số phức thỏa mãn . Biết tập hợp các điểm biểu diễn số phức
là một đường tròn. Tìm bán kính của đường tròn đó.
A. . B. . C. . D. .
Lời giải
Tác giả: Phạm Thị Thuần ; Fb: Phạm Thuần
Chọn C
Cách 1:
Ta có . Khi đó .
Đặt . Khi đó (*) trở thành .
Vậy tập hợp các điểm biểu diễn số phức là đường tròn có bán kính .
Cách 2: Lưu Thêm
Gọi là điểm biểu biểu diễn số phức .
Ta có
, với .
Vậy tập hợp các điểm biểu diễn số phức là đường tròn tâm , bán kính .
Câu 40. [2H3-1.1-1] Trong không gian với hệ tọa độ , cho hai điểm và . Tọa
độ của vectơ là
A. . B. . C. . D. .
Lời giải
Tác giả: Phạm Thị Thuần ; Fb: Phạm Thuần
Chọn B
Ta có: .
Câu 41. [2H3-1.1-1] Trong không gian với hệ trục , cho tam giác có , ,
. Gọi là trọng tâm của tam giác đó. Tổng bằng
A. . B. . C. . D. .
Lời giải
Tác giả: Nguyễn Tình; Fb:Gia Sư Toàn Tâm
Chọn D
( )
yfx=
[ ]
;ab
( ) ( )
.0fa fb<
( )
;cabÎ
( )
0fc=
( )
;ba
( )
yfx=
[ ]
;ab
( ) ( )
.0fa fb<
( )
;cabÎ
( )
0fc=
c
( )
0fx=
( )
yfx=
[ ]
;ab
( ) ( )
.0fa fb<
( )
yfx=
Ox
( )
;ab
( )
0fx=
( )
;ab
5z =
( )
12wizi=+ +
r
5r =
10r =
5r =
25r =
( )
12
12
wi
wiziz
i
-
=+ +Û=
+
55
12
wi
z
i
-
=Û =
+
5wiÛ-=
wxyi=+
( )
2
,, 1xy iÎ=-!
( )
2
22
515x iy i x y+-=Û + - =
w
5r =
M
w
( ) ( )
12 12wiziwiiz=+ +Û-=+
( )
12 12. 5.5 5wi iz izÞ-=+ =+ = =
5MIÞ=
( )
0;1I
w
( )
0;1I
5r =
Oxyz
( )
3; 0; 2A -
( )
1; 4; 2B
AB
!!!"
( )
1; 2; 2-
( )
2; 4; 4-
( )
2; 2; 0
( )
4; 4; 0
( ) ( )
;; 2;4;4
BAB ABA
AB x x y y z z=- - -=-
!!!"
Oxyz
ABC
( )
3; 3; 2A
( )
1; 2; 0B -
( )
1; 1; 2C -
( )
000
;;Gx y z
000
xyz++
9
1
3
2
3
-
3
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$27$,$Mã$617$
Vì là trọng tâm nên ta có: .
Câu 42. [2D2-4.1-1] Điều kiện xác định của hàm số là
A. . B. . C. . D.
.
Lời giải
Tác giả: Nguyễn Tình; Fb: Gia Sư Toàn Tâm
Chọn B
Điều kiện xác định: .
Câu 43. [2H2-2.3-3] Cho tứ diện đều có cạnh bằng . Thể tích của khối cầu tiếp xúc với tất cả
các cạnh của tứ diện bằng
A. . B. . C. . D. .
Lời giải
Tác giả: Đặng Mai Hương; Fb: maihuongpla
Chọn B
Gọi là trọng tâm tứ diện . Ta chứng minh là tâm mặt cầu tiếp xúc với tất cả các
cạnh của tứ diện .
Gọi , , , , , lần lượt là trung điểm các cạnh , , , , , .
Ta có G là trung điểm của các đoạn .
cân tại . Tương tự ta có .
Ta có: .
Suy ra .
G
ABCD
( )
( )
0
0
0
311
1
3
321
2
3
20 2
0
3
x
y
z
+- +
ì
==
ï
ï
++
ï
==
í
ï
ï
++-
==
ï
î
000
120 3xyzÞ++=++=
( )
2
log 1yx=-
1x ¹
1x >
1x <
x"Î!
10 1xx-> Û >
ABCD
ABCD
3
3
24
a
3
2
24
a
p
3
22
9
a
3
3
8
a
p
G
ABCD
G
M
N
P
Q
R
S
AB
CD
BC
AD
AC
BD
,,MN PQ RS
ACD BCD AN BN NABD=DÞ=ÞD
N MN ABÞ^
MN CD^
2
2
22
32
242
aaa
PQ RS MN AN AM
æö
== = - = -=
ç÷
ç÷
èø
( ) ( )
12
,,CD
24
a
d G AB d G MN===
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$28$,$Mã$617$
Chứng minh tương tự ta có .
Vậy là tâm mặt cầu tiếp xúc với tất cả các cạnh của tứ diện .
Bán kính mặt cầu . Suy ra thể tích khối cầu là .
Câu 44. [2H2-2.7-1] Trong không gian , phương trình mặt cầu tâm , bán kính là
A. . B. .
C. . D. .
Lời giải
Tác giả: Đặng Mai Hương; Fb: maihuongpla@gmail.com
Chọn C
Mặt cầu tâm , bán kính có phương trình là .
Câu 45. [1D5-2.1-1] Đạo hàm của hàm số là
A. . B. . C. . D. .
Lời giải
Tác giả: Trần Lê Hương Ly; Fb: Trần Lê Hương Ly
Chọn B
Ta có .
Câu 46. [2D2-6.1-2] Tập nghiệm của bất phương trình là
A. . B. . C. . D. .
Lời giải
Tác giả: Trần Lê Hương Ly; Fb: Trần Lê Hương Ly
Chọn C
Ta có: .
Vậy tập nghiệm của bất phương trình đã cho là .
Câu 47. [1D2-5.5-2] Đội tuyển học sinh giỏi Toán của trường THPT X có học sinh trong đó có
bạn Minh Anh. Lực học của các học sinh là như nhau. Nhà trường chọn ngẫu nhiên học sinh
đi thi. Tìm xác suất để Minh Anh được chọn đi thi.
A. . B. . C. . D. .
Lời giải
Tác giả: Phùng Hoàng Cúc ; Fb: Phùng Hoàng Cúc
Chọn B
Không gian mẫu
Gọi biến cố A: “Minh Anh được chọn trong học sinh được chọn đi thi.”
+ Chọn Minh Anh đi thi có cách.
+ Chọn bạn trong bạn còn lại có cách.
Suy ra .
Vậy xác suất để Minh Anh được chọn đi thi là: .
( ) ( ) ( ) ( )
2
,AC ,AD ,BD ,BC
4
a
dG dG dG dG====
G
ABCD
2
4
a
R =
3
3
3
4422
3 3 4 24
aa
VR
p
pp
æö
== =
ç÷
ç÷
èø
Oxyz
( )
1; 2; 3I -
2R =
( ) ( ) ( )
222
1234xy z++- ++ =
( ) ( ) ( )
222
1232xy z++- ++ =
( ) ( ) ( )
222
1234xy z-++ +- =
( ) ( ) ( )
222
1232xy z-++ +- =
( )
1; 2; 3I -
2R =
( ) ( ) ( )
222
1234xy z-++ +- =
2
lnyxx=+
1
yx
x
¢
=+
1
2yx
x
¢
=+
1
2yx
x
¢
=-
3
1
3
x
y
x
¢
=+
1
2yx
x
¢
=+
21
2
1
3
x+
æö
>
ç÷
èø
( )
;0-¥
( )
0; +¥
1
;
2
æö
-¥ -
ç÷
èø
1
;
2
æö
-+¥
ç÷
èø
21 21 0
222
1
333
xx++
æö æö æö
>Û >
ç÷ ç÷ ç÷
èø èø èø
210xÛ+<
1
2
xÛ<-
1
;
2
æö
-¥ -
ç÷
èø
12
1
7
4
7
3
7
1
2
( )
4
7
nCW=
1
3
3
6
C
( )
3
6
1. 20nA C==
( )
( )
( )
20 4
35 7
nA
PA
n
===
W
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$29$,$Mã$617$
Câu 48. [2D1-3.1-2] Tìm giá trị nhỏ nhất của hàm số trên đoạn .
A. . B. . C. . D. .
Lời giải
Tác giả: Phùng Hoàng Cúc ; Fb: Phùng Hoàng Cúc
Chọn C
Ta có .
Khi đó .
Ta có .
.
.
Suy ra: .
Câu 49. [1D2-2.1-1] Trong tủ quần áo của bạn An có chiếc áo khác nhau và chiếc quần khác nhau.
Hỏi bạn An có bao nhiêu cách để chọn 1 bộ quần áo để mặc?
A. . B. . C. . D. .
Lời giải
Tác giả: Lê Bá Phi ; Fb:Lee Bas Phi
Chọn D
Chọn một bộ quần áo, cần thực hiện liên tiếp hai hành động:
Hành động 1 - chọn áo: có 4 cách chọn.
Hành động 2 - chọn quần: ứng với mỗi cách chọn áo có 3 cách chọn quần.
Vậy số cách chọn một bộ quần áo là: (cách).
Câu 50. [2D1-5.8-1] Cho hàm số có đồ thị như hình vẽ. Tìm kết luận đúng trong các kết luận
sau.
A. Hàm số có điểm cực tiểu .
B. Hàm số không có cực trị .
C. Phương trình vô nghiệm.
D. Hàm số đồng biến trên khoảng .
Lời giải
Tác giả: Lê Bá Phi ; Fb:Lee Bas Phi
Chọn A
Dựa vào đồ thị ta thấy:
Hàm số có hai điểm cực trị B sai.
9
yx
x
=+
[ ]
2;4
[ ]
2;4
13
min
2
y =
[ ]
2;4
25
min
4
y =
[ ]
2;4
min 6y =
[ ]
2;4
min 6y =-
2
22
99
1
x
y
xx
-
¢
=- =
[ ]
[ ]
32;4
0
32;4
x
y
x
é
=Î
¢
=Û
ê
=- Ï
ë
( )
9 13
22
22
f =+ =
( )
9
33 6
3
f =+ =
( )
9 25
44
44
f =+ =
[ ]
2;4
min 6y =
3
27
64
12
4 . 3 12=
( )
yfx=
( )
yfx=
1x =
( )
yfx=
( )
0fx=
( )
yfx=
( )
;0-¥
( )
yfx=
Þ
Sản$phẩm$của$STRONG$TEAM$TOÁN$VD$VDC Đề$SGD$Hưng$Yên$Lần$1$Năm$2019
STRONG$TEAM$TOÁN$VD-VDC-$Group$toán$Số$1$VN-$Làm$1,2$câu$nhận$lại$hàng$ngàn$câu/tuần$$$$$P$30$,$Mã$617$
Đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt nên phương trình có 3
nghiệm phân biệt C sai.
Hàm số đồng biến trên các khoảng và D sai.
Hàm số đạt cực đại tại , đạt cực tiểu tại A đúng.
--------- STRONG TEAM TOÁN VD VDC ----------
( )
yfx=
( )
0fx=
Þ
( )
yfx=
( )
;1-¥ -
( )
1; +¥
Þ
( )
yfx=
1x =-
1x =
Þ
| 1/30
| | Tải xuống

Có thể bạn quan tâm:

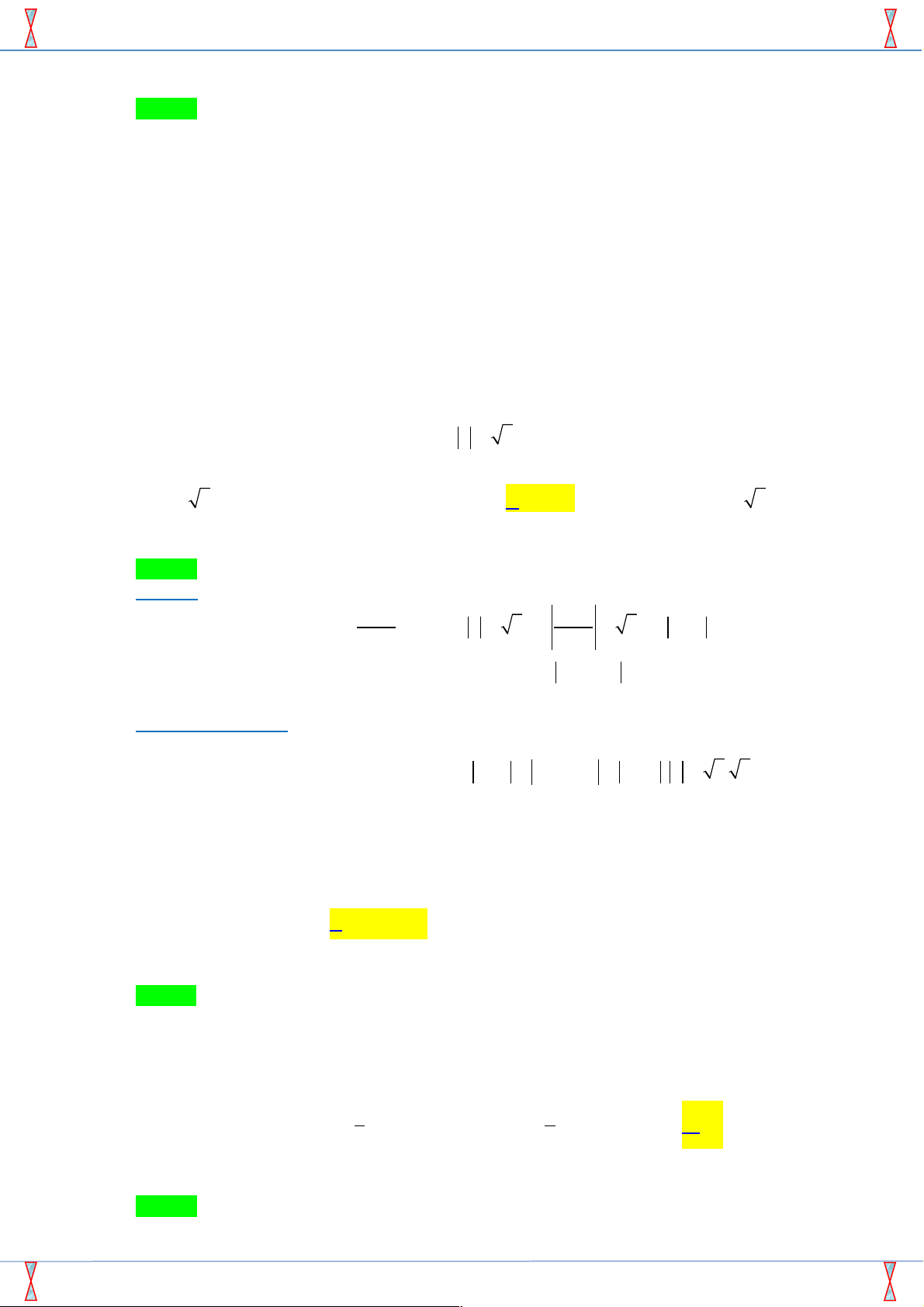
Preview text:

Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI THỬ THPT QUỐC GIA NĂM 2019 HƯNG YÊN MÔN: TOÁN Ngày thi: 11/04/2019 ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ và tên thí sinh: .....................................................
Số báo danh: .............................................................. MÃ ĐỀ: 617
Câu 1. [2H3-2.1.1] Trong không gian với hệ tọa độ Oxyz , lập phương trình của các mặt phẳng song
song với mặt phẳng (b ) : x + y - z + 3 = 0 và cách (b ) một khoảng bằng 3 .
A. x + y - z + 6 = 0 ; x + y - z = 0 .
B. x + y - z + 6 = 0 .
C. x - y - z + 6 = 0 ; x - y - z = 0 .
D. x + y + z + 6 = 0 ; x + y + z = 0 .
Câu 2. [2D4-5.2-3] Cho số phức z thỏa mãn z = 1. Gọi M và m lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của biểu thức 2
P = z +1 + z - z +1 . Tính M .m . 13 3 39 13 A. . B. . C. 3 3 . D. . 4 4 4 æ 3 2x ¢ - ö ax - b 1 a
Câu 3. [1D5-2.1-2] Cho = , x " > . Tính . ç ÷ è 4x -1 ø (4x - ) 1 4x -1 4 b A. 16 - . B. 4 - . C. 1 - . D. 4 . 3 x + 2 Câu 4.
[2D3-2.1-2] Biết I =
dx = a + b ln c , với , ,
, c < . Tính tổng S = a + b + c . ò a b c Î ! 9 x 1
A. S = 7 . B. S = 5. C. S = 8.
D. S = 6 .
Câu 5. [2H3-1.1-1] Trong không gian Oxyz , cho mặt phẳng (P) có phương trình 3x - 4z + 7 = 0. Một
vectơ pháp tuyến của mặt phẳng (P) có tọa độ là A. ( 3; - 0;4) . B. (3; 4 - ; 7 - ). C. (3;0;7) . D. (3; 4 - ;7). Câu 6.
[2D2-4.4-4] Cho các số thực a, , b ,
m n sao cho 2m + n < 0 và thỏa mãn điều kiện ìlog ( 2 2
a + b + 9 = 1+ log 3a + 2b 2 ) 2 ( ) ï í 4 - 9- ï .3 m - .3 n
m+n + ln é(2m + n + 2)2 2 +1ù = 81 î ë û
Tìm giá trị nhỏ nhất của biểu thức = ( - )2 + ( - )2 P a m b n . A. 2 5 - 2 . B. 2 . C. 5 - 2 . D. 2 5 .
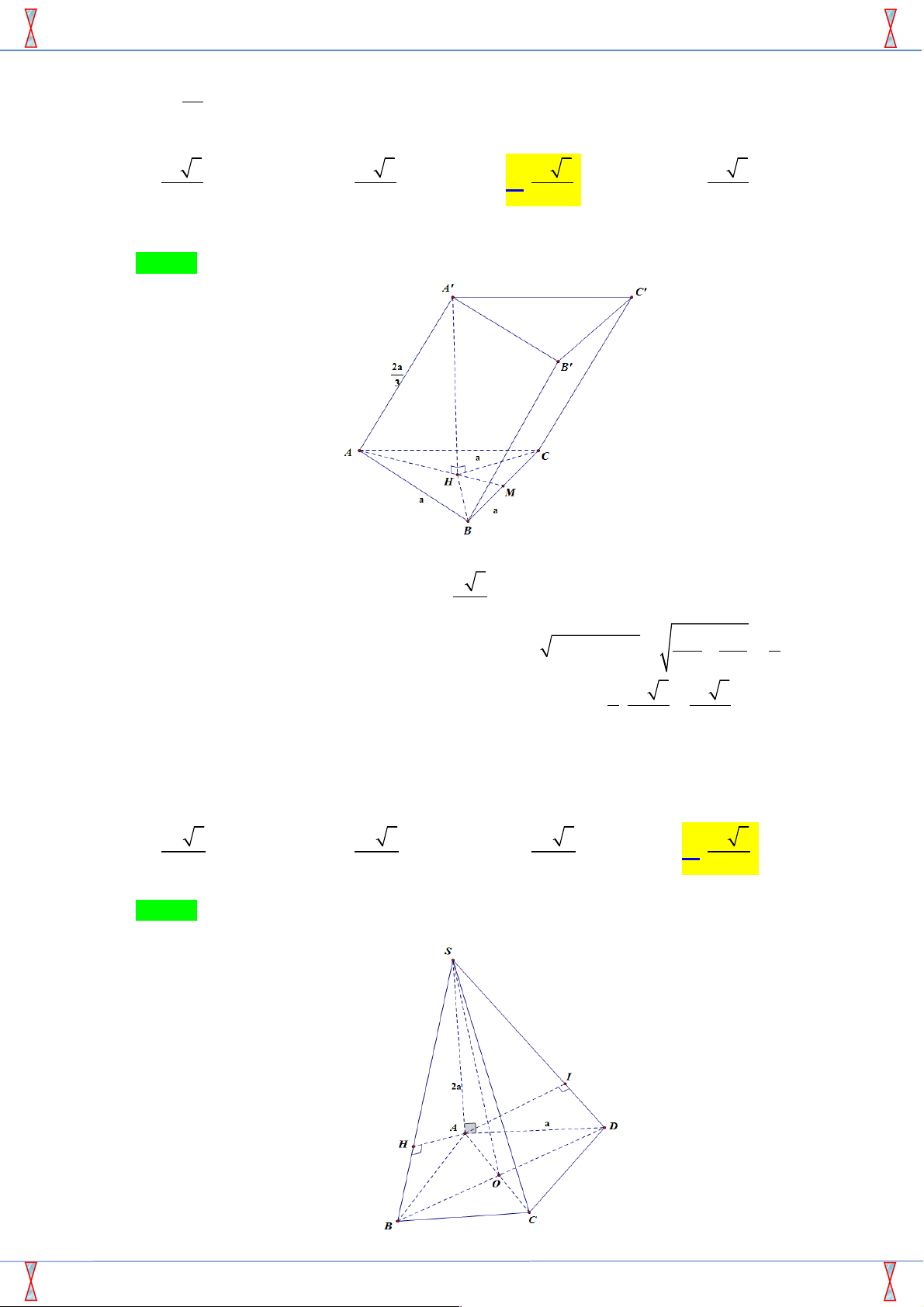
Câu 7. [2H1-3.2-2] Cho lăng trụ ABC.A' B 'C ' có đáy ABC là tam giác đều cạnh a , độ dài cạnh bên 2a bằng
, hình chiếu của đỉnh A' trên mặt phẳng ( ABC) trùng với trọng tâm của tam giác 3
ABC . Thể tích khối lăng trụ ABC.A' B 'C ' bằng 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 36 6 12 24
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 1 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019
Câu 8. [2H1-3.4-3] Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng ( ABCD) . Tứ giác
ABCD là hình vuông cạnh a , SA = 2a . Gọi H là hình chiếu vuông góc của A trên SB . Tính
khoảng cách từ H đến mặt phẳng (SCD) . 4a 5 4a 5 2a 5 8a 5 A. . B. . C. . D. . 5 25 5 25
Câu 9 . [2D1-5.6-2] Cho hàm số 3 2
y = x - 3x + 2 có đồ thị (C). Tìm số tiếp tuyến của đồ thị (C) song
song với đường thẳng d : y = 9x - 25. A. 1. B. 2 . C. 3. D. 0. 3 - x +1
Câu 10 . [2D1-4.1-1] Đồ thị hàm số y =
có các đường tiệm cận đứng, tiệm cận ngang lần lượt là: x + 2 A. x = 2, - y = -3 . B. x = 2, - y = 3. C. x = 2, - y = 1.
D. x = 2, y = 1.
Câu 11. [2D1-5.8-4] Cho các hàm số ( ) 4 3 2
f x = mx + nx + px + qx + r và ( ) 3 2
g x = ax + bx + cx + d ( , m ,
n p, q, r, a, ,
b c, d Î ! ) thỏa mãn f (0) = g (0) . Các hàm số y = f ¢( x) và g¢( x) có đồ thị như hình vẽ bên.
Tập nghiệm của phương trình f ( x) = g ( x) có số phần tử là A. 4. B. 2. C. 1. D. 3.
Câu 12. [2D1-1.1-1] Trong các hàm số sau, hàm số nào đồng biến trên ! ? x - A. 2
y = x + 2x -1. B. 4 2
y = x - 2x . C. 3
y = x + 2x - 2 1 2019 . D. y = . x + 3
Câu 13. [2H3-2.3-2] Trong không gian với hệ tọa độ Oxyz , viết phương trình mặt phẳng (P) đi qua hai điểm A(2;1; ) 1 , B ( 1; - 2
- ;- 3) và vuông góc với mặt phẳng (Q) : x + y + z = 0.
A. x - y - z = 0 .
B. x + y - 3 = 0 .
C. x - y -1 = 0.
D. x + y + z - 4 = 0 .
Câu 14. [2D1-2.4-2] Cho hàm số 3
y = x + (m - ) 2 2 3
1 x + 6(m - 2) x -1 với m là tham số thực. Tìm tất cả
các giá trị của m để hàm số có điểm cực đại và điểm cực tiểu nằm trong khoảng ( 2; - 3) . A. m Î( 1; - 4) \{ } 3 . B. m Î(3;4) . C. m Î(1;3). D. m Î( 1; - 4) .
Câu 15. [2D3-3.3-1] Cho hàm số y = f ( x) liên tục trên [3;4]. Gọi D là hình phẳng giới hạn bởi đồ thị
hàm số y = f ( x) , trục hoành và hai đường thẳng x = 3, x = 4 . Thể tích khối tròn xoay tạo
thành khi quay D quanh trục hoành được tính theo công thức
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 2 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019 4 4 4 4 A. 2 V = p f ò (x)dx. B. 2 2 V = p f
ò (x)dx. C. V = f ò (x)dx. D. 2 V = f ò (x)dx. 3 3 3 3
Câu 16. [2H3-1.4-3] Trong không gian với hệ tọa độ Oxyz , cho ba điểm A(1;4;5), B(3;4;0) , C (2; 1
- ;0) và mặt phẳng (P) :3x + 3y - 2z - 29 = 0. Gọi M (a; ;
b c) là điểm thuộc (P) sao cho 2 2 2
MA + MB + 3MC đạt giá trị nhỏ nhất. Tính tổng a + b + c . A. 8 . B. 10 . C. 10 - . D. 8 - .
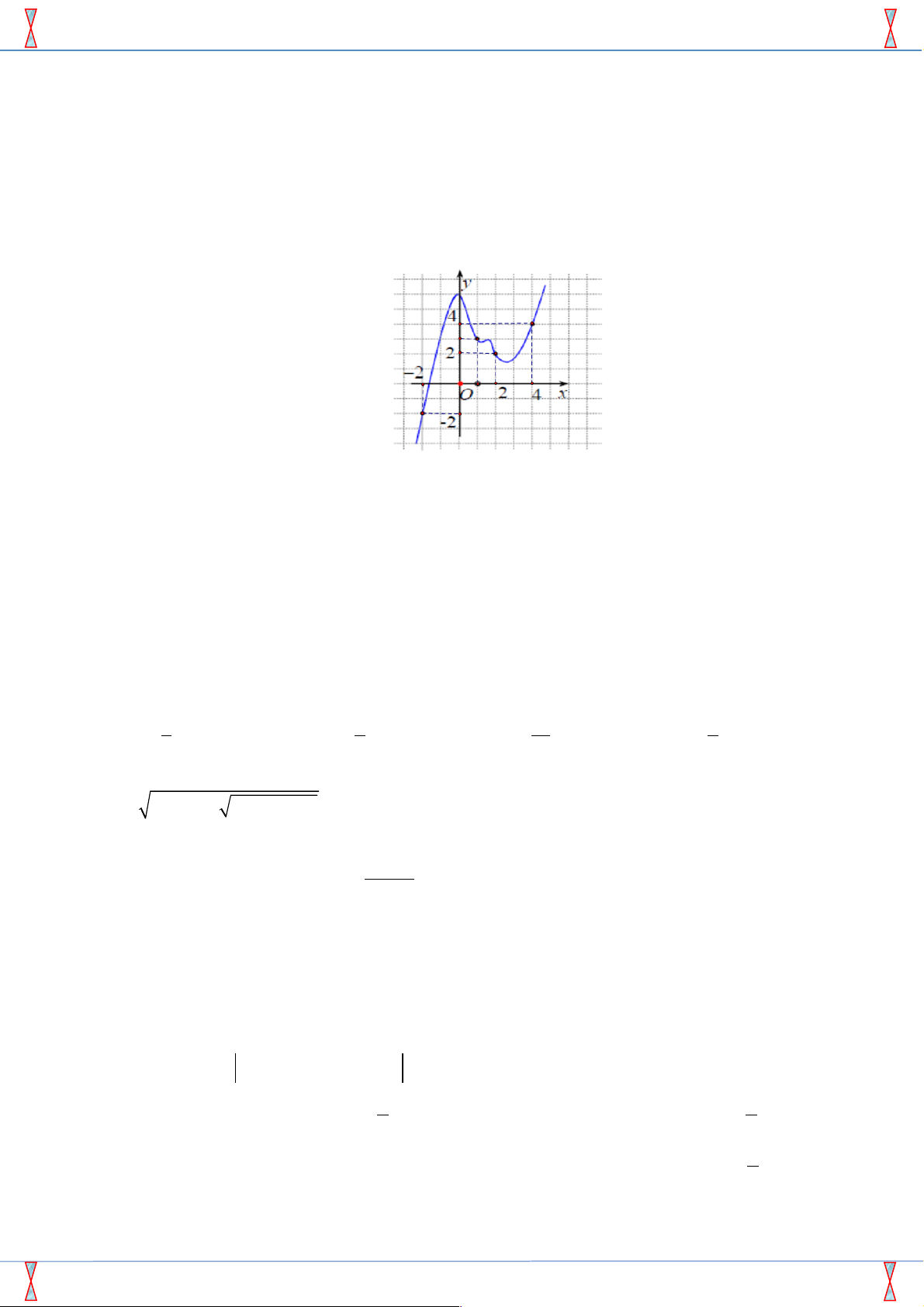
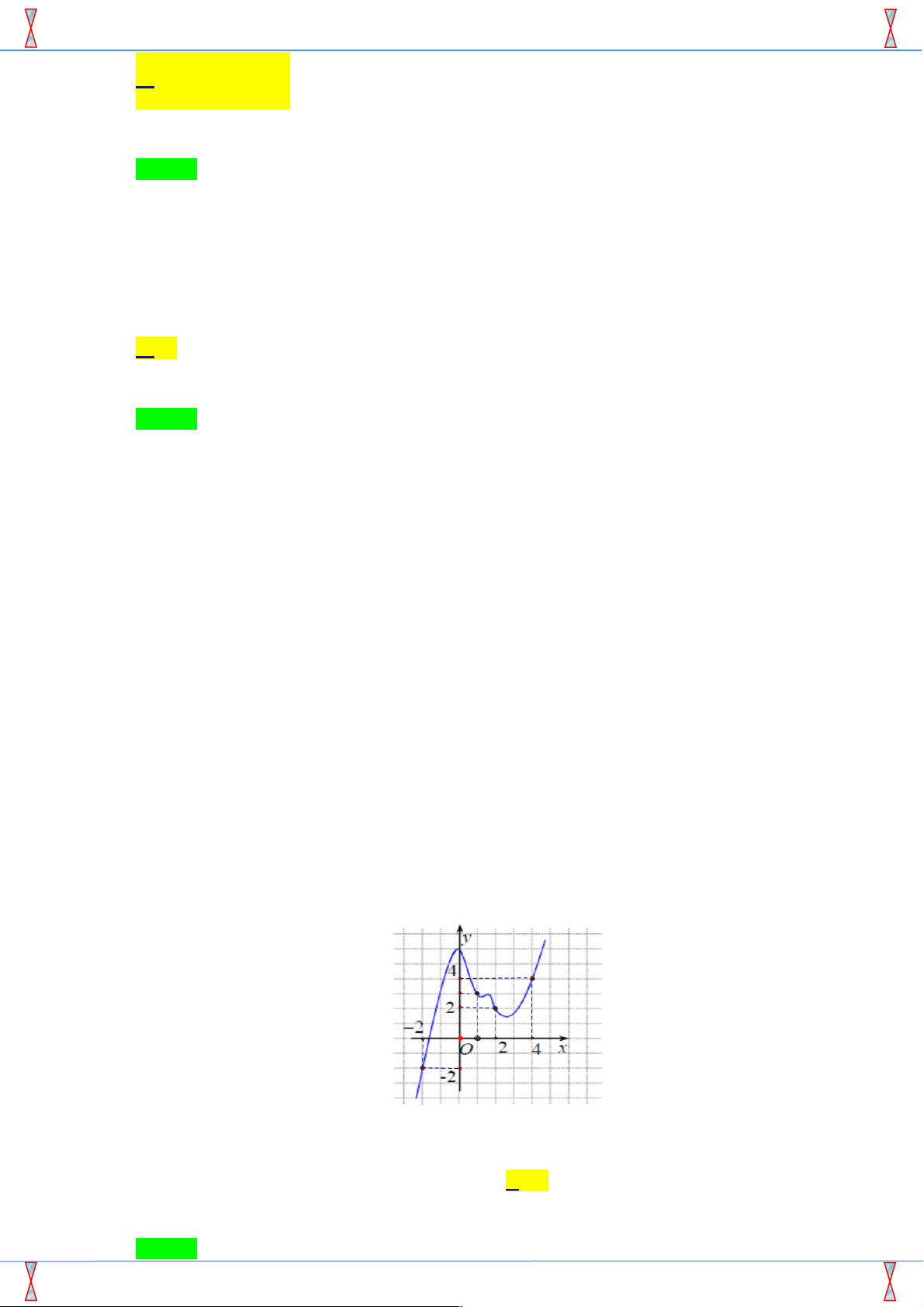
Câu 17. [2D3-2.4-3] Cho hàm số y = f ( x) có đạo hàm liên tục trên ! và có đồ thị như hình vẽ. 4 2
Giá trị của biểu thức I = f '
ò (x-2)dx+ f '
ò (x+ 2)dx bằng 0 0 A. 2 - . B. 2 . C. 6 . D. 10 .
Câu 18. [2D3-2.4-2] Cho hàm số f ( x) có đạo hàm liên tục trên đoạn [0;2] và thỏa mãn f (0) = 2 , 2 2
ò(2x-4).f '(x)dx = 4 . Tính tích phân I = f ò (x) dx. 0 0 A. I = 2 . B. I = 2 - . C. I = 6 . D. I = 6 - .
Câu 19. [2H1-3.2-2] Cho khối chóp S.ABC có thể tích là V . Gọi B¢, C¢ lần lượt là trung điểm AB , AC
Tính theo V thể tích của khối chóp S.AB C ¢ ¢ . 1 1 1 1 A. V . B. V . C. V . D. V . 3 2 12 4
Câu 20. [2D1-5.4-3] Có bao nhiêu giá trị âm của tham số m để phương trình 2 2
2019m + 2019m + x = x có hai nghiệm thực phân biệt A. 1. B. 0 . C. Vô số. D. 2 . 2 x - m
Câu 21: [2D1-3.1-2] Cho hàm số y =
với m là tham số thực. Giả sử m là giá trị dương của x + 8 o
tham số m để hàm số có giá trị nhỏ nhất trên đoạn [0; ] 3 bằng 3
- . Giá trị mo thuộc khoảng nào
trong các khoảng cho dưới đây? A. (20;25) . B. (5;6). C. (6;9) . D. (2;5) .
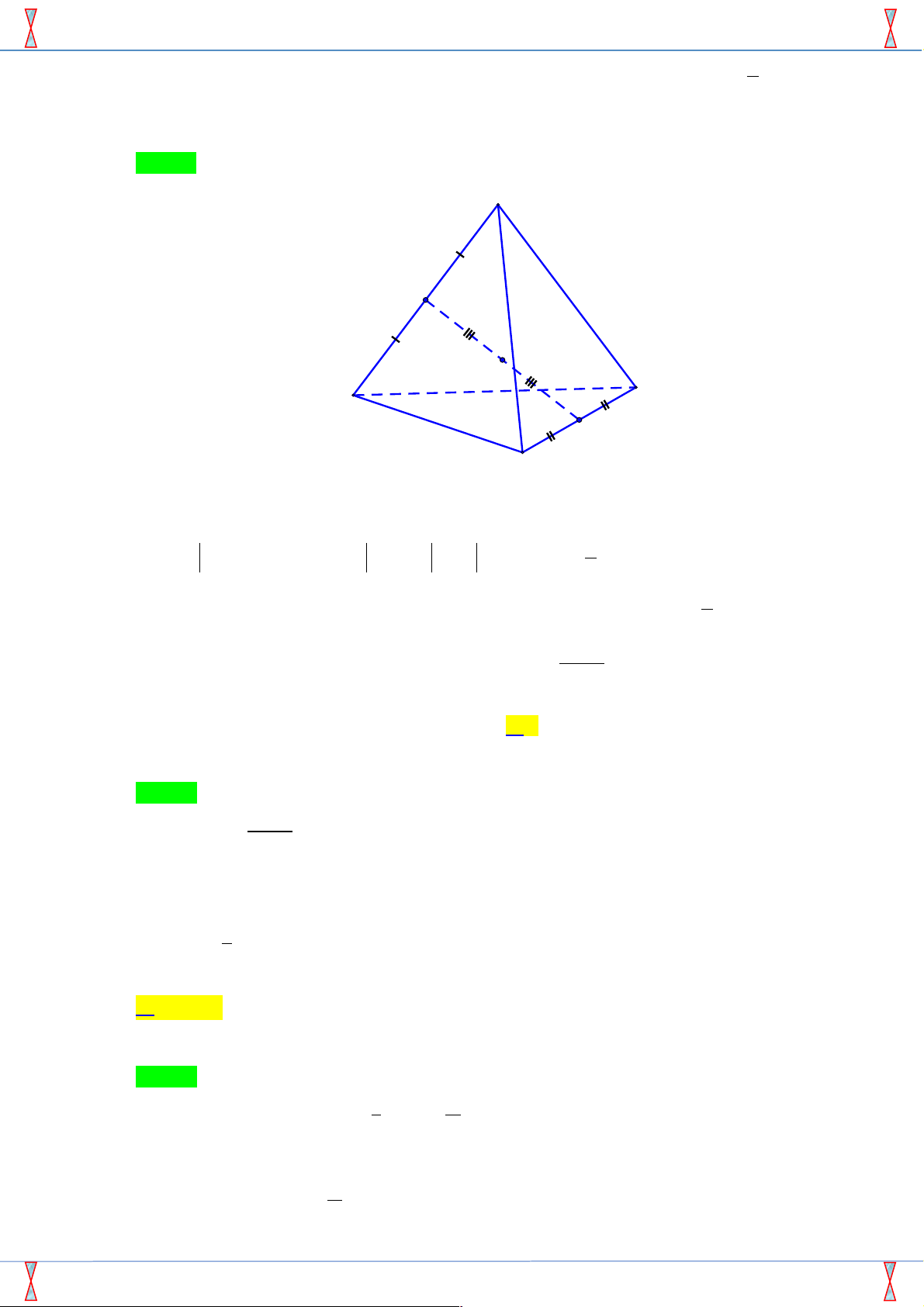
Câu 22: [0H1-2.1-2] Cho tứ diện ABCD có O là trung điểm của đoạn thẳng nối trung điểm của hai
cạnh đối diện và a là số thực dương không đổi. Tập hợp các điểm M trong không gian thỏa !!!" !!!" !!!!" !!!!"
mãn hệ thức MA + MB + MC + MD = a là a a
A. mặt cầu tâm O bán kính r = .
B. mặt cầu tâm O bán kính r = . 3 4 a
C. mặt cầu tâm O bán kính r = a .
D. mặt cầu tâm O bán kính r = . 2
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 3 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019 2 x - 4
Câu 23. [2D1-2.1-1] Cho hàm số y = f ( x) có đạo hàm f ¢( x) = , x
" ¹ 0 . Số điểm cực trị của hàm 2 3x số đã cho là A. 3. B. 5. C. 2. D. 1.
Câu 24. [2D3-3.5-2] Một vật chuyển động với vận tốc 10 m / s thì tăng tốc với gia tốc a (t) 1 2 = 2t + t ( 2
m / s ), trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu tăng tốc. 3
Hỏi quãng đường vật đi được trong 12 giây kể từ lúc bắt đầu tăng tốc bằng bao nhiêu mét? A. 1272 m . B. 456 m . C. 1172 m
D. 1372 m .
Câu 25. [2H2-1.2-1] Hai khối nón có cùng thể tích. Một khối nón có bán kính đáy bằng R và chiều cao
bằng h , khối nón còn lại có bán kính đáy bằng 2R và chiều cao bằng x . Khi đó h h h A. x = 3 . B. x = 3 .
C. x = h . D. x = . 2 2 4 4
Câu 26. [1D1-2.1-1] Phương trình sin x + cos x = 1 có 1 nghiệm là p p p A. . B. p 2 . C. . D. . 2 3 4
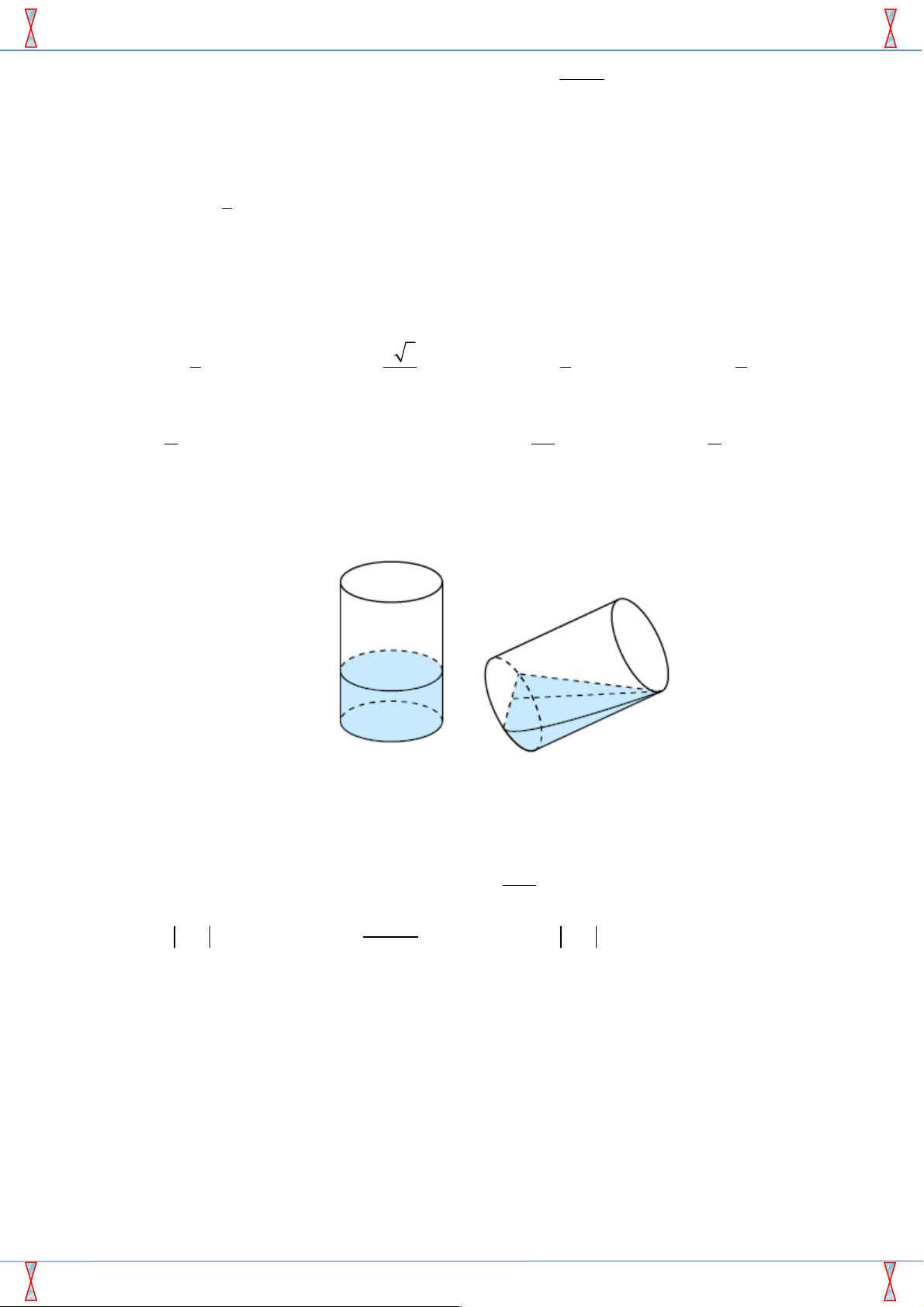
Câu 27. [2D3-3.4-2] Có một cốc thủy tinh hình trụ, bán kính trong lòng đáy cốc là 4cm , chiều cao trong
lòng cốc là 12cm đang đựng một lượng nước. Tính thể tích lượng nước trong cốc, biết rằng khi
nghiêng cốc nước vừa lúc chạm miệng cốc thì ở đáy cốc, mực nước trùng với đường kính đáy. A. 3 128p cm . B. 3 256cm . C. 3 256p cm . D. 3 128cm .
Câu 28. [2D1-5.8-1] Điểm M (1;e) thuộc đồ thị hàm số nào dưới đây? A. x y = e .
B. y = ln x . C. 2 y x- = . D. 2 x y - = .
Câu 29. [2D3-1.1-1] Họ nguyên hàm của hàm số f ( x) 1 = là x -1 1
A. ln x -1 + C . B. - + C .
C. 2ln x -1 + C . D. ln ( x - ) 1 + C . (x - )2 1
Câu 30. [2H1-3.4-1] Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ . Góc giữa hai mặt phẳng ( ABCD) và ( A¢B C ¢ D ¢ ¢) bằng A. 45° . B. 60° . C. 0° . D. 90° .
Câu 31. [2D4-1.3-2] Trên mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn số phức z sao cho 2 z là số thuần ảo.
A. Hai đường thẳng y = x và y = -x . B. Trục Ox . C. Trục Oy .
D. Hai đường thẳng y = x và y = -x , bỏ đi điểm O (0;0).
Câu 32. [2D4-1.3-1] Cho số phức z = 3 - 5i . Phần ảo của z là
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nh ận lại hàng ngàn câu/tuần P 4 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019 A. 5 - . B. 5 - i . C. 5. D. 3.
Câu 33. [2D2-5.6-2] Một người gửi 50 triệu đồng vào ngân hàng theo thể thức lãi kép với lãi suất
6,5% / năm, kì hạn một năm. Hỏi sau 5 năm người đó rút cả vốn lẫn lãi được số tiền gần với số
nào nhất trong các số tiều sau? (biết lãi suất hàng năm không đổi) . A. 73triệu đồng.
B. 53,3 triệu đồng.
C. 64,3triệu đồng.
D. 68,5 triệu đồng.
Câu 34. [2D1-5.1-1] Hàm số nào sau đây có đồ thị như hình vẽ ? A. 4 2
y = x - 2x . B. 4 2
y = x - 2x -1. C. 3 2
y = x - 2x + x . D. 4 2
y = -x + 2x .
Câu 35. [2D1-5.3-3] Số giá trị nguyên của m thuộc khoảng ( 2019 - ; 2019) để phương trình 2 2 x -2x 1 + x -2 x+2 4 - .2 m
+ 3m - 2 = 0 có bốn nghiệm phân biệt là A. 2017 . B. 2016 . C. 4035 . D. 4037 .
Câu 36. [2H1-1.2-1] Hình chóp tứ giác có tất cả bao nhiêu cạnh A. 6 . B. 20 . C. 12 . D. 8 .
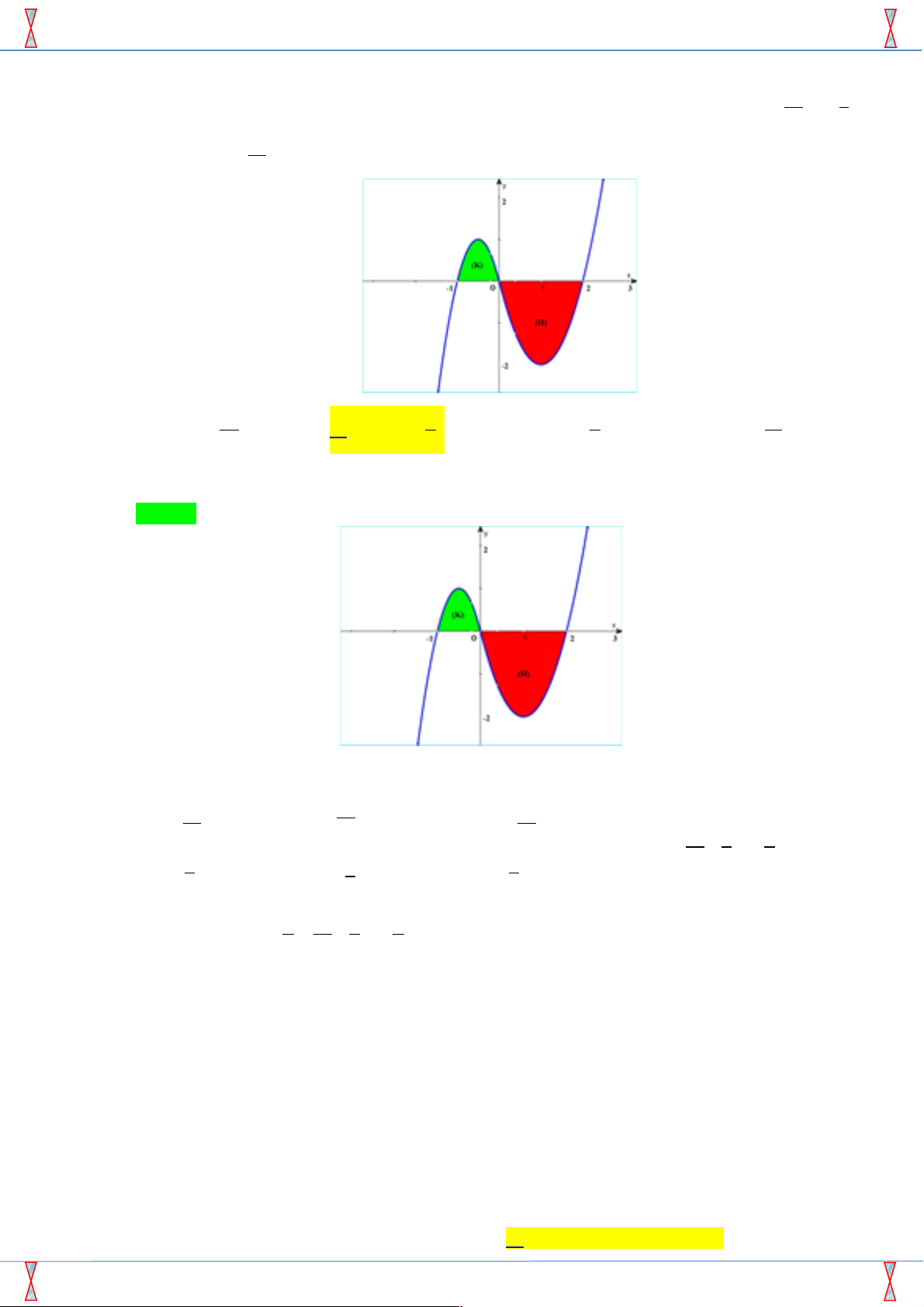
Câu 37. [2D3-3.1-2] Cho hàm số y = f ( x) có đạo hàm liên tục trên [ 1;
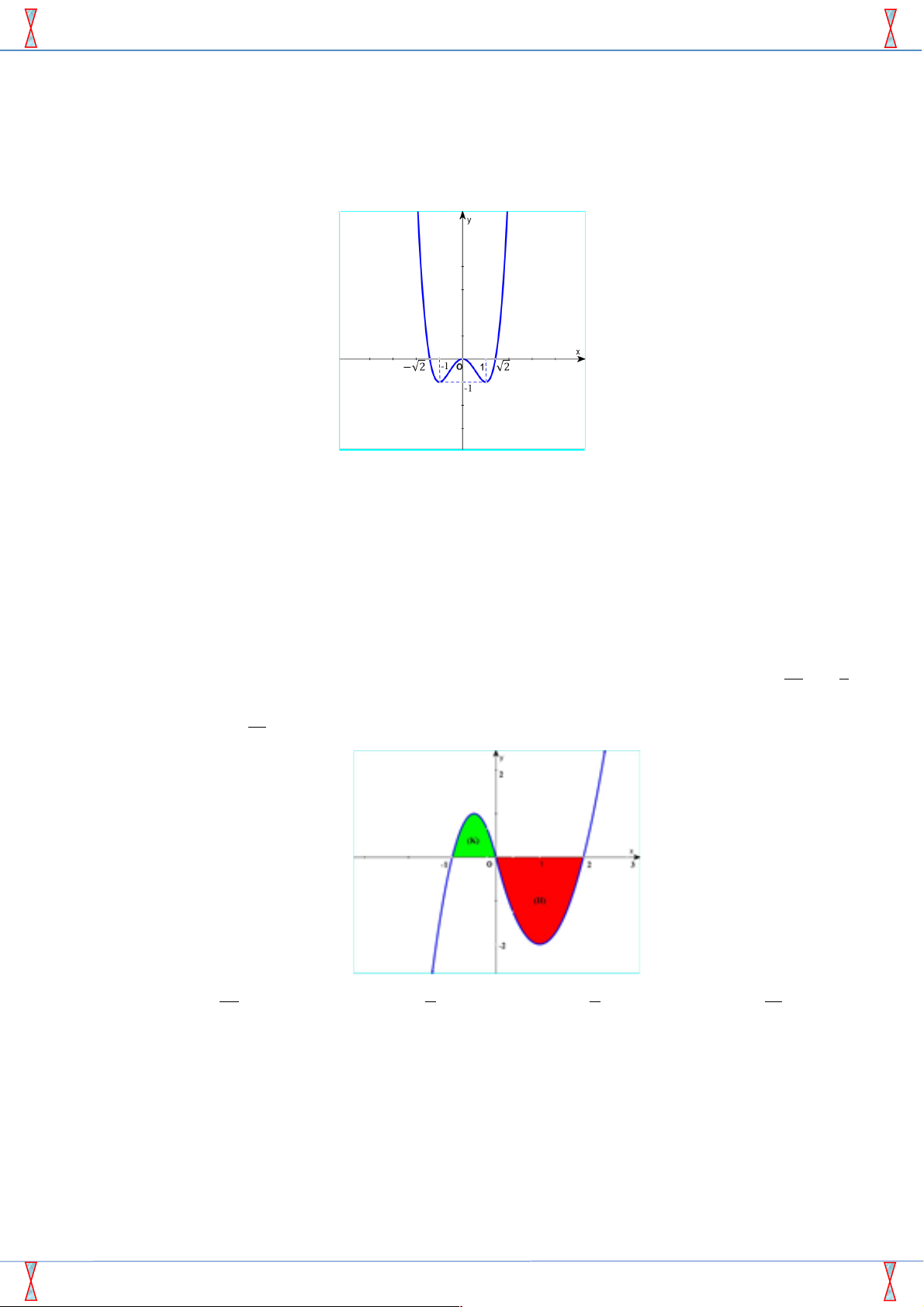
- 2]. Đồ thị của hàm số 5 8
y = f ¢( x) được cho như hình vẽ. Diện tích các hình phẳng (K ) , (H ) lần lượt là và . 12 3 Biết f (- ) 19 1 = , tính f (2) . 12 A. f ( ) 23 2 = . B. f ( ) 2 2 = - . C. f ( ) 2 2 = . D. f ( ) 11 2 = . 6 3 3 6
Câu 38. [2D1-1.5-2] Cho các mệnh đề:
1. Nếu hàm số y = f ( x) liên tục trên (a;b) và f (a). f (b) < 0 thì tồn tại x Î a;b 0 ( ) sao cho f ( x = 0 0 ) .
2. Nếu hàm số y = f ( x) liên tục trên [a;b] và f (a). f (b) < 0 thì phương trình f ( x) = 0 có nghiệm.
3. Nếu hàm số y = f ( x) liên tục, đơn điệu trên [ ;
a b] và f (a). f (b) < 0 thì phương trình
f ( x) = 0 có nghiệm duy nhất trên ( ; a b).
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 5 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019
Trong ba mệnh đề trên
A. Có đúng hai mệnh đề sai.
B. Cả ba mệnh đề đều đúng.
C. Cả ba mệnh đề đều sai.
D. Có đúng một mệnh đề sai.
Câu 39. [2D4-2.4-2] Cho số phức z thỏa mãn z = 5 . Biết tập hợp các điểm biểu diễn số phức
w = (1+ 2i) z + i là một đường tròn. Tìm bán kính r của đường tròn đó. A. r = 5 . B. r = 10 . C. r = 5 . D. r = 2 5 .
Câu 40. [2H3-1.1-1] Trong không gian với hệ tọa độ Oxyz , cho hai điểm A(3;0; 2
- ) và B(1;4;2). Tọa !!!"
độ của vectơ AB là A. ( 1; - 2;2) . B. ( 2; - 4;4). C. (2;2;0). D. (4;4;0).
Câu 41. [2H3-1.1-1] Trong không gian với hệ trục Oxyz , cho tam giác ABC có A(3;3;2) , B( 1; - 2;0) , C (1;1; 2
- ) . Gọi G(x ; y ; z x + y + z 0 0
0 ) là trọng tâm của tam giác đó. Tổng bằng 0 0 0 1 2 A. 9 . B. . C. - . D. 3 . 3 3
Câu 42. [2D2-4.1-1] Điều kiện xác định của hàm số y = log x -1 2 ( ) là A. x ¹ 1. B. x > 1. C. x < 1. D. x " Î ! .
Câu 43. [2H2-2.3-3] Cho tứ diện đều ABCD có cạnh bằng a . Thể tích của khối cầu tiếp xúc với tất cả
các cạnh của tứ diện ABCD bằng 3 3a 3 2p a 3 2 2a 3 3p a A. . B. . C. . D. . 24 24 9 8
Câu 44. [2H2-2.7-1] Trong không gian Oxyz , phương trình mặt cầu tâm I (1; 2
- ;3), bán kính R = 2 là
A. ( x + )2 + ( y - )2 + ( z + )2 1 2 3 = 4 .
B. ( x + )2 + ( y - )2 + ( z + )2 1 2 3 = 2 .
C. ( x - )2 + ( y + )2 + ( z - )2 1 2 3 = 4 .
D. ( x - )2 + ( y + )2 + ( z - )2 1 2 3 = 2 .
Câu 45. [1D5-2.1-1] Đạo hàm của hàm số 2
y = ln x + x là 1 3 1 x A. y¢ = + 1 x . B. y¢ = + 1 2x .
C. y¢ = - 2x . D. y¢ = + . x x x x 3 2 x 1 2 + æ ö
Câu 46. [2D2-6.1-2] Tập nghiệm của bất phương trình >1 là ç ÷ è 3 ø æ 1 ö æ 1 ö A. ( ;0 -¥ ). B. (0;+ ¥). C. ; -¥ - . D. - ;+ ¥ . ç ÷ ç ÷ è 2 ø è 2 ø
Câu 47. [1D2-5.5-2] Đội tuyển học sinh giỏi Toán 12 của trường THPT X có 7 học sinh trong đó có
bạn Minh Anh. Lực học của các học sinh là như nhau. Nhà trường chọn ngẫu nhiên 4 học sinh
đi thi. Tìm xác suất để Minh Anh được chọn đi thi. 1 4 3 1 A. . B. . C. . D. . 7 7 7 2 9
Câu 48. [2D1-3.1-2] Tìm giá trị nhỏ nhất của hàm số y = x + trên đoạn [2;4]. x 13 25 A. min y = . B. min y = . C. min y = 6 . D. min y = 6 - . [2;4] 2 [2;4] 4 [2;4] [2;4]
Câu 49. [1D2-2.1-1] Trong tủ quần áo của bạn An có 4 chiếc áo khác nhau và 3 chiếc quần khác nhau.
Hỏi bạn An có bao nhiêu cách để chọn 1 bộ quần áo để mặc? A. 7 . B. 27 . C. 64 . D. 12 .
Câu 50. [2D1-5.8-1] Cho hàm số y = f ( x) có đồ thị như hình vẽ. Tìm kết luận đúng trong các kết luận sau.
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 6 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019
A. Hàm số y = f ( x) có điểm cực tiểu x =1.
B. Hàm số y = f ( x) không có cực trị.
C. Phương trình f ( x) = 0 vô nghiệm.
D. Hàm số y = f ( x) đồng biến trên khoảng (-¥;0) .
--------- HẾT ---------
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 7 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019
LỜI GIẢI CHI TIẾT
Câu 1. [2H3-2.3-1] Trong không gian với hệ tọa độ Oxyz , lập phương trình của các mặt phẳng song
song với mặt phẳng (b ) : x + y - z + 3 = 0 và cách (b ) một khoảng bằng 3 .
A. x + y - z + 6 = 0 ; x + y - z = 0 .
B. x + y - z + 6 = 0 .
C. x - y - z + 6 = 0 ; x - y - z = 0.
D. x + y + z + 6 = 0 ; x + y + z = 0 . Lời giải
Tác giả: Giáp Minh Đức; Fb: Giáp Minh Đức Chọn A
Gọi (a ) là mặt phẳng cần tìm. Ta có A(0;0;3)Î(b ) .
Do (a ) / / (b ) nên phương trình của mặt phẳng (a ) có dạng: x + y - z + m = 0, với m ¹ 3. m - 3 ém = 6
Ta có d ((a ),(b )) = 3 Û d ( , A (a )) = 3 Û = 3 Û m - 3 = 3 Û (thỏa mãn). ê 3 ëm = 0
Vậy phương trình của các mặt phẳng cần tìm là x + y - z + 6 = 0 và x + y - z = 0 .
Câu 2. [2D4-5.2-3] Cho số phức z thỏa mãn z = 1. Gọi M và m lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của biểu thức 2
P = z +1 + z - z +1 . Tính M .m . 13 3 39 13 A. . B. . C. 3 3 . D. . 4 4 4 Lời giải
Tác giả: Giáp Minh Đức; Fb: Giáp Minh Đức Chọn A
Giả sử z = x + yi , ( x, y Î R) . Do z = 1 2 2 Û x + y = 1 2 2
Û x + y = 1. Suy ra x, y Î[ 1 - ; ] 1 . Ta có 2
z.z = z = 1. Thay vào P ta được: 2
P = z +1 + z - z + z.z = z +1 + z (z -1+ z) = z +1 + z . z + z -1 = z +1 + z + z -1 = ( x + )2 2
1 + y + 2x -1 = 2x + 2 + 2x -1 .
Xét hàm số y = f ( x) = 2x + 2 + 2x -1 ì 1
2x + 2 - 2x +1 khi 1 - £ x < ïï
Ta có y = f ( x) 2 = í . 1
ï 2x + 2 + 2x -1 khi £ x £1 ïî 2 ì 1 1
- 2 khi -1< x < ïï + f ¢( x) 2x 2 2 = í 1 1 ï + 2 khi < x £ 1 ïî 2x + 2 2 ì 1 1 - < x < ì 1 ï 1 - < x < ï ïï 7 f ( x) 2 ' = 0 Û 2 í Û í Û x = - 1 ï - 2 = 0 1 ï 8 2x + 2 = ïî 2x + 2 ïî 2
Bảng biến thiên của hàm số f ( x) trên [ 1; - ] 1
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 8 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019 7 1 x 1 1 8 2 y' + 0 + 13 3 y 4 3 3
ìm = min f (x) = 3 ï [ 1; - ] 1 Suy ra íïM = f ( x) 14 max = î [ 1; - ] 1 3 13 3 Vậy M .m = . 4 æ 3 2x ¢ - ö ax - b 1 a
Câu 3. [1D5-2.1-2] Cho = , x " > . Tính . ç ÷ è 4x -1 ø (4x - ) 1 4x -1 4 b A. 16 - . B. 4 - . C. 1 - . D. 4 . Lời giải
Tác giả: Lưu Thị Thủy; Fb: thuy.luu.33886 Chọn C ¢ ¢ - x - - ( - x) 2 2 4 1 3 2 .
æ - x ¢ö (3 - 2x) 4x -1 - (3 - 2x)( 4x -1 3 2 ) Ta có = 4x -1 ç ÷ = è 4x -1 ø ( 4x-1)2 4x -1 2 - (4x - ) 1 - 2(3- 2x) - - = 4x 4 = . (4x - )1 4x -1 (4x - )1 4x -1 a Suy ra a = 4 - , b = 4 . Vậy = 1 - . b 3 x + 2 Câu 4.
[2D3-2.1-2] Biết I =
dx = a + b ln c , với , ,
, c < . Tính tổng S = a + b + c . ò a b c Î ! 9 x 1 A. S = 7 . B. S = 5. C. S = 8.
D. S = 6 . Lời giải
Tác giả: Lưu Thị Thủy; Fb: thuy.luu.33886 Chọn A 3 x + 2 3 æ 2 ö Ta có I = dx = 1+ dx = ( x + x) 3 2ln = 2 + 2ln 3 . ò òç ÷ x è x ø 1 1 1
Mà I = a + b ln c , với a , b , c Î ! , c < 9 . Suy ra a = 2, b = 2 , c = 3.
Vậy S = a + b + c = 7 .
Câu 5. [2H3-1.1-1] Trong không gian Oxyz , cho mặt phẳng (P) có phương trình 3x - 4z + 7 = 0. Một
vectơ pháp tuyến của mặt phẳng (P) có tọa độ là A. ( 3; - 0;4) . B. (3; 4 - ; 7 - ). C. (3;0;7) . D. (3; 4 - ;7). Lời giải
Tác giả: Nguyễn Hoàng Hưng ; Fb: Nguyễn Hưng Chọn A
Ta có: 3x - 4z + 7 = 0 Û 3
- x + 4z - 7 = 0 .
Suy ra một vectơ pháp tuyến của mặt phẳng (P) có tọa độ là ( 3; - 0;4) . Câu 6.
[2D2-4.4-4] Cho các số thực a, , b ,
m n sao cho 2m + n < 0 và thỏa mãn điều kiện
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 9 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019 ìlog ( 2 2
a + b + 9 = 1+ log 3a + 2b 2 ) 2 ( ) ï í 4 - 9- ï .3 m - .3 n
m+n + ln é(2m + n + 2)2 2 +1ù = 81 î ë û
Tìm giá trị nhỏ nhất của biểu thức = ( - )2 + ( - )2 P a m b n . A. 2 5 - 2 . B. 2 . C. 5 - 2 . D. 2 5 . Lời giải
Tác giả: Nguyễn Hoàng Hưng ; Fb: Nguyễn Hưng Chọn A Ta có: log ( 2 2
a + b + 9) =1+ log (3a + 2b) Û log ( 2 2
a + b + 9 = log é2 3a + 2b ù 2 2 2 ) 2 ë ( )û
Û a + b + = a + b Û (a - )2 + (b - )2 2 2 9 6 4 3 2 = 4 .
Gọi H (a;b) , suy ra H thuộc đường tròn (C) có tâm I (3;2) , bán kính R = 2 . 4 - Lại có -m -n m+n + é( m + n + )2 2 9 .3 .3 ln 2 2 +1ù = 81 ë û ( æ - ö - m+n) 4 2 +ç ÷ è m+n ø Û + é( m + n + )2 2 3 ln 2 2 +1ù = 81, ë û ( )1 Với " ,
m n thỏa mãn 2m + n < 0 , ta có: 4 - æ 4 æ - ö - m+n + - ç ÷ ö +) -(2 + ) + ³ 2 é- ë (2 + ) ( ) 4 2 è 2 ù. = 4 Þ 3 m+n m n m n ø ³ 81 û ç ÷ 2m + n è 2m + n ø
+) é( m + n + )2 ln 2 2 +1ù ³ ln1 = 0 . ë û ( æ - ö - m+n) 4 2 +ç ÷ Suy ra
è m+n ø + é( m + n + )2 2 3 ln 2 2 +1ù ³ 81 ë û ì - ï- m + n = Do đó ( ) ( ) 4 2 1 Û í
2m + n Û 2m + n + 2 = 0 .
ïî2m+ n + 2 = 0 Gọi K ( ;
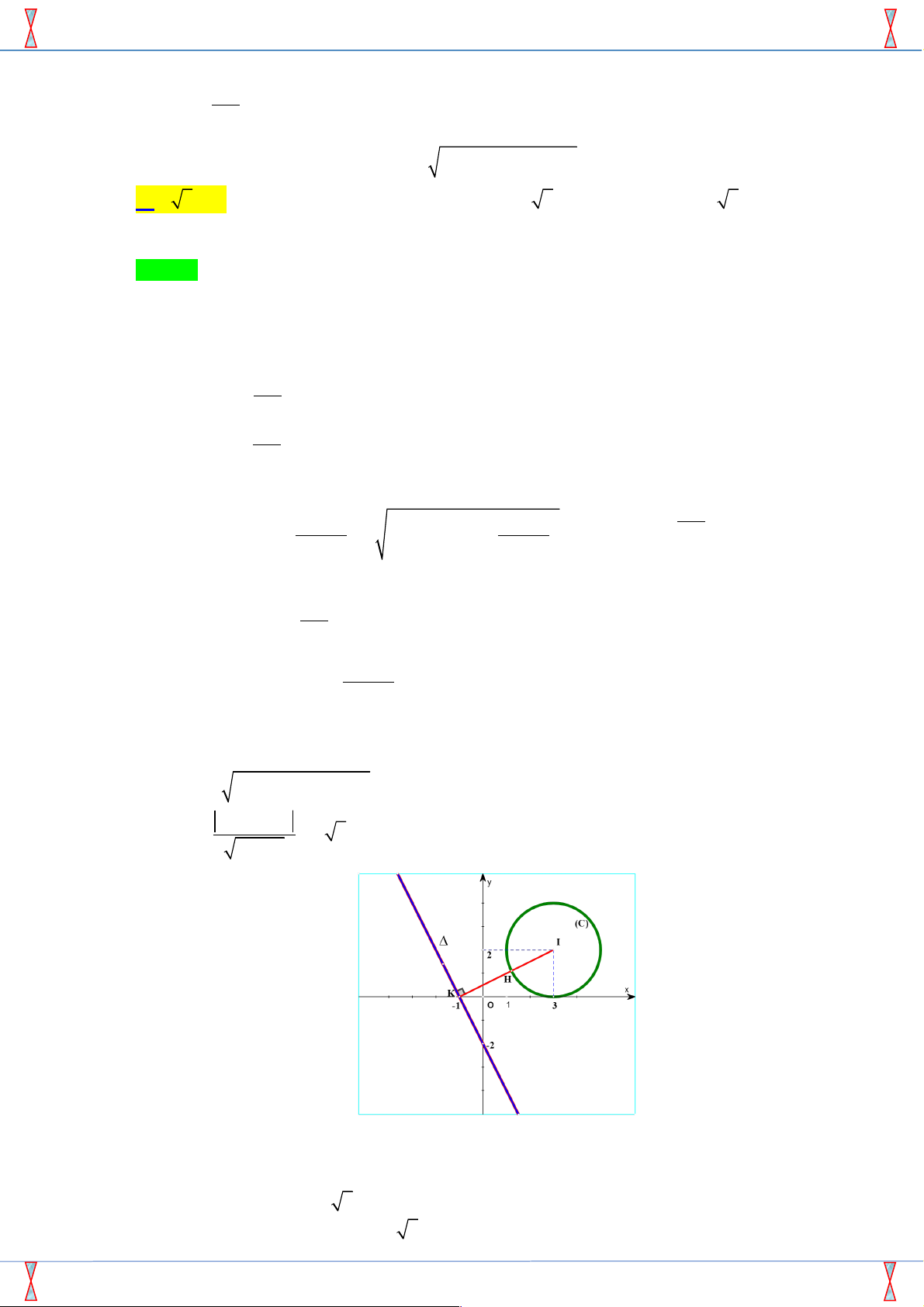
m n), suy ra K thuộc đường thẳng D có phương trình 2x + y + 2 = 0. Ta có: = ( - )2 + ( - )2 P a m b n = HK . + + d (I D) 2.3 2 2 , =
= 2 5 > 2 Þ đường thẳng D không cắt đường tròn (C). 2 2 2 +1
Do đó HK ngắn nhất khi K là hình chiếu của điểm I trên đường thẳng D và điểm H là giao
điểm của đoạn thẳng IK với đường tròn (C).
Lúc đó HK = IK - IH = 2 5 - 2 .
Vậy giá trị nhỏ nhất của P bằng 2 5 - 2 .
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 10 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019
Câu 7. [2H1-3.2-2] Cho lăng trụ ABC.A' B 'C ' có đáy ABC là tam giác đều cạnh a , độ dài cạnh bên 2a bằng
, hình chiếu của đỉnh A' trên mặt phẳng ( ABC) trùng với trọng tâm của tam giác 3
ABC . Thể tích khối lăng trụ ABC.A' B 'C ' bằng 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 36 6 12 24 Lời giải
Tác giả:Nguyễn Thị Anh Đào; Fb:Đào Nguyễn Chọn C
Gọi H là trọng tâm của tam giác ABC . a 3
Do tam giác ABC đều cạnh a nên AH = . 3 2 2 4a 3a a
Mặt khác do A' H ^ ( ABC) Þ A' H ^ AH 2 2
Þ A' H = AA' - AH = - = . 9 9 3 2 3 a a 3 a 3
Vậy thể tích lăng trụ ABC.A' B 'C ' là V = A' H.S = . = .
ABC.A'B 'C ' ABC D 3 4 12
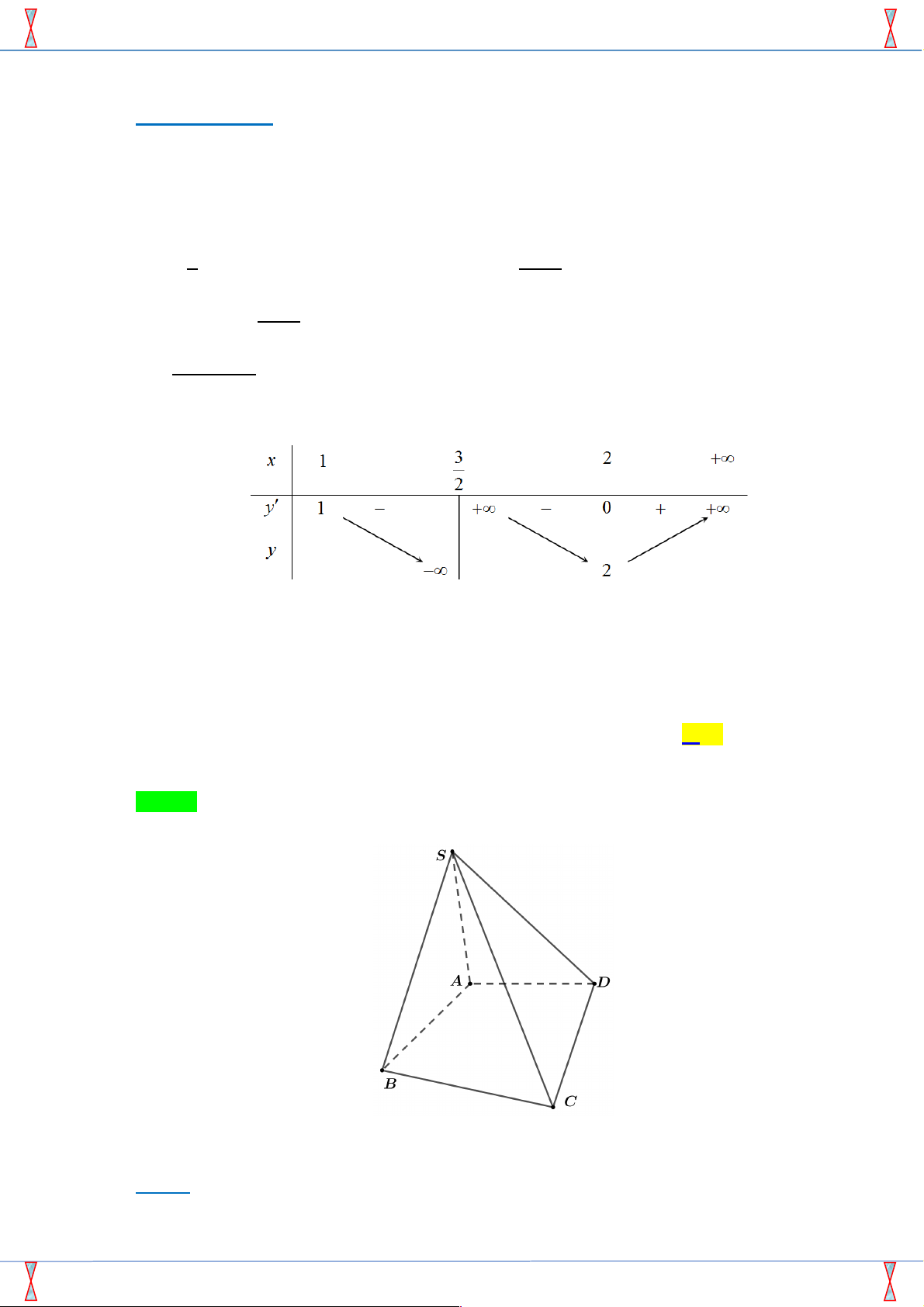
Câu 8. [2H1-3.4-3] Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng ( ABCD) . Tứ giác
ABCD là hình vuông cạnh a , SA = 2a . Gọi H là hình chiếu vuông góc của A trên SB . Tính
khoảng cách từ H đến mặt phẳng (SCD) . 4a 5 4a 5 2a 5 8a 5 A. . B. . C. . D. . 5 25 5 25 Lời giải Chọn D
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 11 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019 2 2 SH SA 4a 4 Ta có 2
SH.SB = SA Þ = = = . 2 2 2 SB SB 4a + a 5
d (H,(SCD)) SH 4 Ta có: = =
d (B,(SCD)) . SB 5
Þ d (H (SCD)) 4
= d (B (SCD)) 4 , . , = .d ( ,
A (SCD)) , (do AB// (SCD)). 5 5
Gọi I là hình chiếu vuông góc của A trên SD .
Ta có CD ^ (SAD) Þ CD ^ AI . ìAI ^ SD Vì í
Þ AI ^ (SCD) Þ d ( ,
A (SCD)) = AI . îAI ^ CD . SA AD 2a 5 Ta có AI.SD = . SA AD Þ AI = = . SD 5 a
Vậy d (H (SCD)) 4 8 5 , = .AI = . 5 25
Câu 9 . [2D1-5.6-2] Cho hàm số 3 2
y = x - 3x + 2 có đồ thị (C). Tìm số tiếp tuyến của đồ thị (C) song
song với đường thẳng d : y = 9x - 25. A. 1. B. 2 . C. 3. D. 0. Lời giải
Tác giả: Nguyễn Huyền ; Fb: Huyen Nguyen. Chọn A
Vì tiếp tuyến song song với đường thẳng d : y = 9x - 25 nên hệ số góc tiếp tuyến k = 9 . éx = 1 - éM ( 1; - 2)
Gọi M ( x ; y
f ¢( x = k 2 Û 3x - 6x = 9 0 Û Û ê 0 ) 0
0 ) là tiếp điểm . Ta có: . 0 0 êx = 3 ë êM ë (3;2) 0
Tiếp tuyến d đi qua M ( 1; - 2
- ) và có hệ số góc k = 9 có phương trình y = 9x + 7. 1
Tiếp tuyến d đi qua M (3;2) và có hệ số góc k = 9 có phương trình y = 9x - 25 (loại vì 2 d º d . 2
Vậy có 1 tiếp tuyến thỏa mãn yêu cầu bài toán. 3 - x +1
Câu 10 . [2D1-4.1-1] Đồ thị hàm số y =
có các đường tiệm cận đứng, tiệm cận ngang lần lượt là: x + 2 A. x = 2, - y = -3 . B. x = 2, - y = 3. C. x = 2, - y = 1.
D. x = 2, y = 1. Lời giải
Tác giả: Nguyễn Huyền ; Fb: Huyen Nguyen. Chọn A D = ! \{- } 2 . 3 - x +1 Vì lim
= +¥ nên đồ thị hàm số nhận x = 2 - là tiệm cận đứng. x 2+ ®- x + 2 3 - x +1 Vì lim = 3
- nên đồ thị hàm số nhận y = 3
- là tiệm cận ngang. x®±¥ x + 2
Câu 11. [2D1-5.8-4] Cho các hàm số ( ) 4 3 2
f x = mx + nx + px + qx + r và ( ) 3 2
g x = ax + bx + cx + d ( , m ,
n p, q, r, a, ,
b c, d Î ! ) thỏa mãn f (0) = g (0) . Các hàm số y = f ¢( x) và g¢( x) có đồ thị như hình vẽ bên.
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 12 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019
Tập nghiệm của phương trình f ( x) = g ( x) có số phần tử là A. 4. B. 2. C. 1. D. 3. Lời giải
Tác giả:Thu Trang ; Fb: Nguyễn Thị Thu Trang Chọn B
+ Từ đồ thị hàm số y = f ¢( x) Þ m ¹ 0 .
+ f (0) = g (0) Þ r = d .
+ Ta có f ¢( x) - g¢( x) 3
= mx + (n - a) 2 4 3
x + 2( p - b) x + q - c ( ) 1 .
Mặt khác từ đồ thị hai hàm số y = f ¢( x) và g¢( x) ta có f ¢( x) - g¢( x) = 4m( x + ) 1 ( x - ) 1 (x - 2)
hay f ¢( x) - g¢( x) 3 2
= 4mx - 8mx - 4mx + 8m (2) . 3
ì (n - a) = -8m ï Từ ( )
1 và (2) ta suy ra í2( p - b) = -4m .
ïq -c = 8m î + Phương trình ( ) = ( ) 4 3 2 3 2 f x
g x Û mx + nx + px + qx + r = ax + bx + cx + d 4 3 2 3 2
Û mx + nx + px + qx = ax + bx + cx æ 8m 3 Û ö
x émx + (n - a) 2
x + ( p - b) x + q - cù = 0 3 2 Û x mx -
x - 2mx + 8m = 0 ë û ç ÷ è 3 ø éx = 0 æ 8 3 2 ö mx x x 2x 8 0 ê Û - - + = Û ç ÷ 8 . 3 2 è 3 ø
êx - x - 2x + 8 = 0 ë 3 8 Phương trình 3 2
x - x - 2x + 8 = 0 có đúng một nghiệm thực khác 0. 3
Vậy phương trình đã cho có 2 nghiệm thực phân biệt.
Câu 12. [2D1-1.1-1] Trong các hàm số sau, hàm số nào đồng biến trên ! ? x - A. 2
y = x + 2x -1. B. 4 2
y = x - 2x . C. 3
y = x + 2x - 2 1 2019 . D. y = . x + 3 Lời giải
Tác giả:Thu Trang ; Fb: Nguyễn Thị Thu Trang Chọn C
Cách 1: (Trắc nghiệm). + Hàm số 2
y = ax + bx + c và 4 2
y = ax + bx + c với a, ,
b c Î ! , a ¹ 0 không đồng biến trên ! . Loại A, B.
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 13 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019 ax + b ì d ü + Hàm số y = với a, ,
b c, d Î ! ,c ¹ 0 có tập xác định D = ! \ í- ý nên hàm số không cx + d î c þ
đồng biến trên ! . Loại D. Vậy chọn C. Cách 2: (Tự luận). + Hàm số 2
y = x + 2x -1 có y¢ = 2x + 2.
y¢ > 0 Û x > -1 nên hàm số 2
y = x + 2x -1 không đồng biến trên ! . + Hàm số 4 2
y = x - 2x có 3
y¢ = x - x = x ( 2 4 4 4 x - ) 1 . é 1 - < x < 0 y¢ > 0 Û nên hàm số 4 2
y = x - 2x không đồng biến trên ! . ê ëx > 1 + Hàm số 3
y = x + 2x - 2019 có 2
y¢ = 3x + 2 > 0, x
" Î ! nên hàm số đồng biến trên ! . 2x -1 + Hàm số y = có TXĐ D = ! \{- }
3 nên hàm số không đồng biến trên ! . x + 3
Câu 13. [2H3-2.3-2] Trong không gian với hệ tọa độ Oxyz , viết phương trình mặt phẳng (P) đi qua hai điểm A(2;1; ) 1 , B ( 1; - 2
- ;- 3) và vuông góc với mặt phẳng (Q) : x + y + z = 0.
A. x - y - z = 0 .
B. x + y - 3 = 0 .
C. x - y -1 = 0.
D. x + y + z - 4 = 0 . Lời giải
Tác giả: Phạm Thị Phương Thúy; Fb: thuypham Chọn C !!!" AB = ( 3; - - 3; 4 - ) . !
Một vectơ pháp tuyến của (Q) là n(Q) = (1;1; ) 1 . ( ì P ï ) É AB ! """! """! Vì í
nên n = é AB, n ù = (1; 1 - ;0 (P) Q
) là một vectơ pháp tuyến của . ( ï P ë ( ) û î ) ^ (Q)
Vậy phương trình (P) là: 1( x - 2) -1( y - ) 1 + 0( z - )
1 = 0 Û x - y -1 = 0 .
Câu 14. [2D1-2.4-2] Cho hàm số 3
y = x + (m - ) 2 2 3
1 x + 6(m - 2) x -1 với m là tham số thực. Tìm tất cả
các giá trị của m để hàm số có điểm cực đại và điểm cực tiểu nằm trong khoảng ( 2; - 3) . A. m Î( 1; - 4) \{ } 3 . B. m Î(3;4) . C. m Î(1;3). D. m Î( 1; - 4) . Lời giải
Tác giả: Phạm Thị Phương Thúy; Fb: thuypham Chọn A Xét hàm số 3
y = x + (m - ) 2 2 3
1 x + 6(m - 2) x -1 Ta có 2
y¢ = 6x + 6(m - )
1 x + 6(m - 2) . éx = 1 - 2
y¢ = 0 Û x + (m - )
1 x + m - 2 = 0 Û . ê ëx = 2 - m
+) Hàm số có 2 điểm cực trị Û y¢ = 0 có 2 nghiệm phân biệt Û 2 - m ¹ 1 - Û m ¹ 3.
+) Hàm số có điểm cực đại và điểm cực tiểu nằm trong khoảng ( 2; - 3) ì 2 - < 1 - < 3 Û í Û 1 - < m < 4 . î 2 - < 2 - m < 3
Kết hợp điều kiện m ¹ 3 , ta được m Î( 1; - 4) \{ } 3 .
Câu 15. [2D3-3.3-1] Cho hàm số y = f ( x) liên tục trên [3;4]. Gọi D là hình phẳng giới hạn bởi đồ thị
hàm số y = f ( x) , trục hoành và hai đường thẳng x = 3, x = 4 . Thể tích khối tròn xoay tạo
thành khi quay D quanh trục hoành được tính theo công thức
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 14 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019 4 4 4 4 A. 2 V = p f ò (x)dx. B. 2 2 V = p f
ò (x)dx. C. V = f ò (x)dx. D. 2 V = f ò (x)dx. 3 3 3 3 Lời giải
Tác giả: Ngô Quốc Tuấn; Fb: Quốc Tuấn Chọn A 4
Thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành là: 2 V = p f ò (x)dx. 3
Câu 16. [2H3-1.4-3] Trong không gian với hệ tọa độ Oxyz , cho ba điểm A(1;4;5), B(3;4;0), C (2; 1
- ;0) và mặt phẳng (P) :3x + 3y - 2z - 29 = 0. Gọi M (a; ;
b c) là điểm thuộc (P) sao cho 2 2 2
MA + MB + 3MC đạt giá trị nhỏ nhất. Tính tổng a + b + c . A. 8 . B. 10 . C. 10 - . D. 8 - . Lời giải
Tác giả: Ngô Quốc Tuấn; Fb: Quốc Tuấn Chọn A !!!" !!!" !!!" "
Gọi H ( x ; y ; z
HA + HB + 3HC = 0 H H
H ) là điểm thỏa mãn . 1
ì - x + 3 - x + 3 - x = H H (2 H ) 0 ìx = 2 H ï ï
Khi đó: í4 - y + 4 - y + 3 - - y = Û íy = Û H (2;1; ) 1 H H ( 1 H ) 0 1 . H ï ï 5 - z + î (-z )+3(-z ) = 0 z = 1 î H H H H !!!!" !!!" 2 !!!!" !!!" 2 !!!!" !!!" 2 Ta có: 2 2 2
T = MA + MB + 3MC = (MH + HA) + (MH + HB) + 3(MH + HC) !!!!" !!!" !!!" !!!" 2 2 2 2
= 5MH + HA + HB + 3HC + 2MH (HA+ HB +3HC) 2 2 2 2
= 5MH + HA + HB + 3HC .
Suy ra T đạt giá trị nhỏ nhất Û MH nhỏ nhất Û M là hình chiếu của H lên (P). ìx = 2 + 3t ï
Phương trình đường thẳng d đi qua H (2;1; )
1 và vuông góc với (P) là íy =1+ 3t ,(t Î ! ). ïz =1- 2t î
Tọa độ của điểm M thỏa mãn hệ phương trình ìx = 2 + 3t ìx = 5 ï ïy 1 3t ï = + ïy = 4 í Û í Þ M (5;4;- )
1 . Vậy a + b + c = 8 . z = 1- 2t z = 1 - ï ï 3
ïî x +3y - 2z - 29 = 0 t ïî =1
Câu 17. [2D3-2.4-3] Cho hàm số y = f ( x) có đạo hàm liên tục trên ! và có đồ thị như hình vẽ. 4 2
Giá trị của biểu thức I = f '
ò (x-2)dx+ f '
ò (x+ 2)dx bằng 0 0 A. 2 - . B. 2 . C. 6 . D. 10 . Lời giải
Tác giả: Trần Thị Thúy; Fb: Thúy Minh Chọn C
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 15 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019 Cách 1: 4 2
Đặt I = f ' x - 2 dx I = f ' x + 2 dx 2 ò ( ) 1 ò ( ) , . 0 0
Tính I : Đặt u = x - 2 Þ du = dx . 1 Đổi cận: 2 2 Ta có: I =
f ' u du =
f ' x dx = f ( x) 2 = f 2 - f 2 - = 2 - -2 = 4 2 - ( ) ( ) ( ) 1 ò ( ) ò ( ) . 2 - 2 -
Tính I : Đặt v = x + 2 Þ dv = dx . 2 Đổi cận: 4 4
Ta có: I = f ' v dv = f ' x dx = f ( x) 4 = f 4 - f 2 = 4 - 2 = 2 2 ( ) ( ) 2 ò ( ) ò ( ) . 2 2
Vậy: I = I + I = 4 + 2 = 6 . 1 2 4 2 4 2
Cách 2: I = f '
ò (x-2)dx+ f '
ò (x+ 2)dx = f '
ò (x-2)d(x-2)+ f ' ò (x+2)d(x+2) 0 0 0 0
= f (x - 2) 4 + f (x + 2) 2 = f 2 - f 2 -
+ f 4 - f 2 = (2 -( 2 - )) + (4 - 2) = 6 0 0 ( ( ) ( )) ( ( ) ( )) .
Câu 18. [2D3-2.4-2] Cho hàm số f ( x) có đạo hàm liên tục trên đoạn [0;2] và thỏa mãn f (0) = 2 , 2 2
ò(2x-4).f '(x)dx = 4 . Tính tích phân I = f ò (x) dx. 0 0 A. I = 2 . B. I = 2 - . C. I = 6 . D. I = 6 - . Lời giải
Tác giả: Trần Thị Thúy; Fb: Thúy Minh Chọn A 2
Ta có: ò(2x - 4).f '(x)dx = 4 . 0 u ì = 2x - 4 ï ìdu = 2dx ï Đặt í Þ í ïdv = f ' î (x)dx ïv = f î (x) 2 2
Nên ò(2x - 4).f '(x)dx = (2x - 4).f (x) 2 - 2 f
ò (x)dx = 4.f (0)-2I = 8-2I . 0 0 0
Theo giả thiết ta có: 4 = 8 - 2I Û 2I = 4 Û I = 2 .
Câu 19. [2H1-3.2-2] Cho khối chóp S.ABC có thể tích là V . Gọi B¢, C¢ lần lượt là trung điểm AB , AC
Tính theo V thể tích của khối chóp S.AB C ¢ ¢ . 1 1 1 1 A. V . B. V . C. V . D. V . 3 2 12 4 Lời giải
Tác giả: LêHoa; Fb:LêHoa Chọn D
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 16 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019 S C B B' C' A
1 AB .¢AC .¢sin A V ¢ ¢ ¢ ¢ S 1 1 D ¢ ¢ AB .AC 1 Ta có S.AB C AB C 2 = = = = Þ V = = ¢ ¢ V V . V S 1 . AB AC 4 S.AB C S. 4 ABC 4 S.ABC A D BC . AB AC.sin A 2
Câu 20. [2D1-5.4-3] Có bao nhiêu giá trị âm của tham số m để phương trình 2 2
2019m + 2019m + x = x có hai nghiệm thực phân biệt A. 1. B. 0 . C. Vô số. D. 2 . Lời giải
Tác giả: LêHoa; Fb:LêHoa Chọn A Cách 1: 2 t
ìï = 2019m + x (t ³ 0) Đặt í . 2 ïa = x î (a ³ 0)
ìï 2019m +t = a Ta được hệ í
Þ 2019m + t - 2019m + a = a - t (*)
ïî 2019m + a = t
Trường hợp 1: a ¹ t . t - a Khi đó (*) Û = a - t
2019m + t + 2019m + a 1 Û = 1
- phương trình vô nghiệm.
2019m + t + 2019m + a
Trường hợp 2: a = t
Thay vào (*) thỏa mãn. Vậy (*) có nghiệm a = t .
Với a = t ta có a = 2019m + a 2
Û a = 2019m + a 2
Û a - a - 2019m = 0 . Phương trình 2 2
2019m + 2019m + x = x có hai nghiệm thực phân biệt éa = a > 0 2
Û a - a - 2019m = 0 có 2 nghiệm a , a thỏa mãn 1 2 1 2
êa < 0 < a ë 1 2 éìD = 0 é 1 êí m = - Û ê 1 êîS > 0 Û
4.2019 . Do m âm nên có một giá trị m = - thỏa mãn. ê 4.2019 1. ê ë ( 2019 - m) < 0 ëm > 0 Cách 2: Lưu Thêm Ta có 2 2 2 4
2019m + 2019m + x = x Û 2019m + 2019m + x = x Û ( 2 m + x ) 2 4 2 2019
+ 2019m + x = x + x , ( ) 1 .
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 17 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019 Xét hàm số ( ) 2
f t = t + t ; f (t) 1 '
= 2t +1 > 0, t " > - . 2 æ ö Ta có hàm số ( ) 2 f t = t + 1
t đồng biến trên khoảng - ; +¥ ç ÷ è 2 ø æ 1 ö æ 1 ö và 2
2019m + x Î - ;+¥ , 2 x Î - ;+¥ . ç ÷ ç ÷ è 2 ø è 2 ø Do đó ( ) 1 Û f ( 2
m + x ) = f ( 2x ) 2 2 2019
Û 2019m + x = x 2 4 4 2
Û 2019m + x = x Û 2019m = x - x . Ta có BBT hàm số ( ) 4 2
g x = x - x é 1 2019m = -
Phương trình đã cho có hai nghiệm thực phân biệt ê Û 4 ê ëm > 0 1
Do m âm nên có một giá trị m = - thỏa mãn. 4.2019 2 x - m
Câu 21: [2D1-3.1-2] Cho hàm số y =
với m là tham số thực. Giả sử m là giá trị dương của x + 8 o
tham số m để hàm số có giá trị nhỏ nhất trên đoạn [0; ] 3 bằng 3
- . Giá trị mo thuộc khoảng nào
trong các khoảng cho dưới đây? A. (20;25) . B. (5;6). C. (6;9) . D. (2;5) . Lời giải
Tác giả: Võ Thanh Hải; Fb:Võ Thanh Hải Chọn D
* Tập xác định D = ! \{- } 8 . 2 m + 8 * Ta có y¢ = > 0, x " ¹ 8
- , suy ra hàm số đã cho đồng biến trên đoạn [0; ] 3 . (x +8)2 2 m
Do đó min y = y (0) = - . [0 ] ;3 8 ìm > 0 ï ìm > 0 ï
* Theo yêu cầu bài toán ta có: 2 í Û í Û m = 2 6 m Î(2;5) . - = 3 - ï ïîm = 2 ± 6 î 8
Câu 22: [0H1-2.1-2] Cho tứ diện ABCD có O là trung điểm của đoạn thẳng nối trung điểm của hai
cạnh đối diện và a là số thực dương không đổi. Tập hợp các điểm M trong không gian thỏa !!!" !!!" !!!!" !!!!"
mãn hệ thức MA + MB + MC + MD = a là a a
A. mặt cầu tâm O bán kính r = .
B. mặt cầu tâm O bán kính r = . 3 4
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 18 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019 a
C. mặt cầu tâm O bán kính r = a .
D. mặt cầu tâm O bán kính r = . 2 Lời giải
Tác giả: Võ Thanh Hải; Fb:Võ Thanh Hải Chọn B A P O B D Q C
* Gọi P,Q lần lượt là trung điểm của AB,CD . Theo giả thiết O là trung điểm của PQ nên suy
ra O là trọng tâm của tứ diện ABCD . !!!" !!!" !!!!" !!!!" !!!!" a
* Ta có MA + MB + MC + MD = a Û 4OM = a Û OM = . 4 a
Vậy tập hợp các điểm M trong không gian là mặt cầu tâm O bán kính r = . 4 2 x - 4
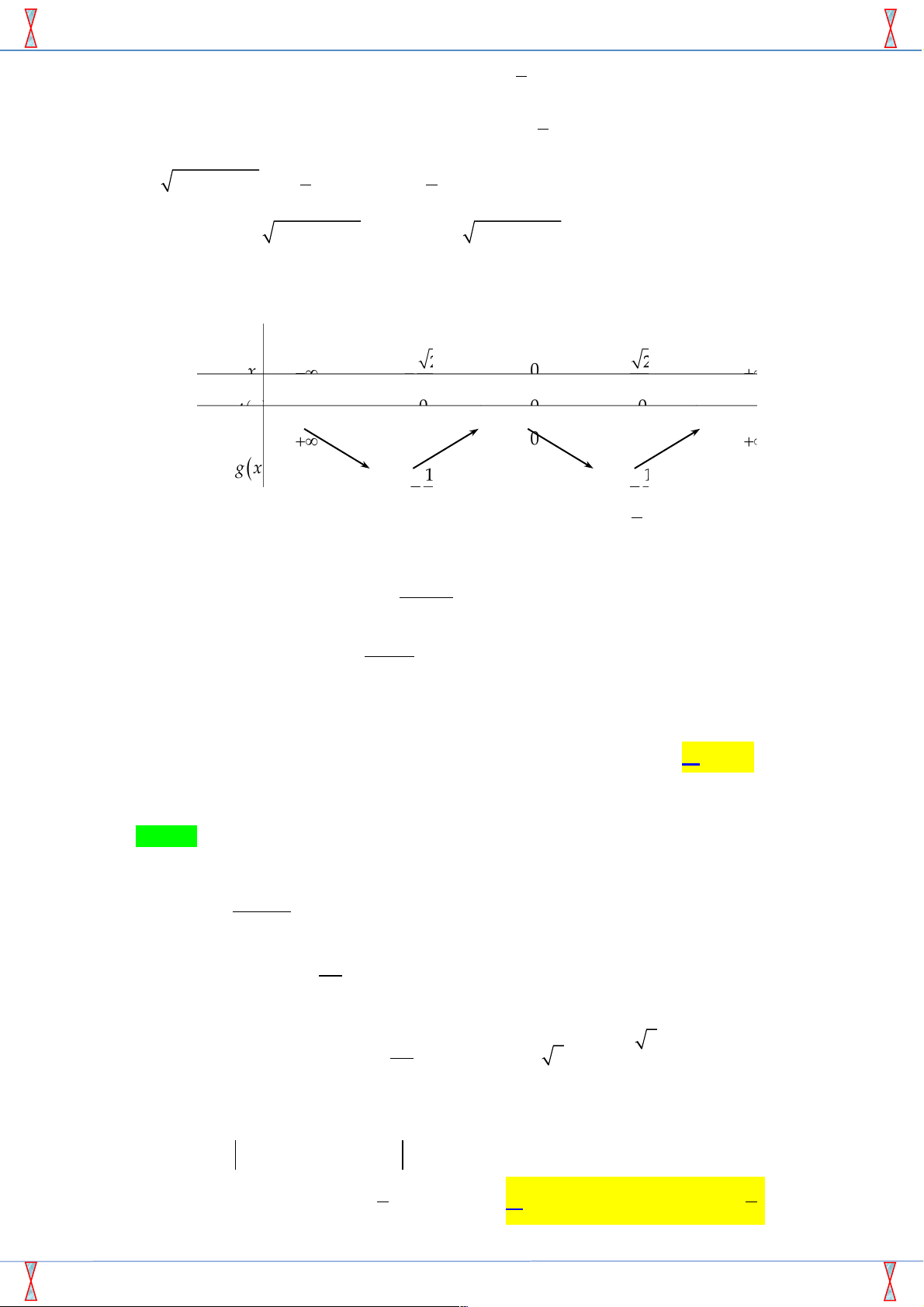
Câu 23. [2D1-2.1-1] Cho hàm số y = f ( x) có đạo hàm f ¢( x) = , x
" ¹ 0 . Số điểm cực trị của hàm 2 3x số đã cho là A. 3. B. 5. C. 2. D. 1. Lời giải
Tác giả: Trần Bạch Mai ; Fb: Bạch Mai Chọn C 2 x - 4 éx =
Ta có f ¢( x) = ; f ¢( x) 2 = 0 Û . 2 3x ê ëx = 2 -
Nhận thấy f ¢( x) đổi dấu qua 2 nghiệm x = 2
± nên hàm số y = f (x) có 2 điểm cực trị.
Câu 24. [2D3-3.5-2] Một vật chuyển động với vận tốc 10 m / s thì tăng tốc với gia tốc a (t) 1 2 = 2t + t ( 2
m / s ), trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu tăng tốc. 3
Hỏi quãng đường vật đi được trong 12 giây kể từ lúc bắt đầu tăng tốc bằng bao nhiêu mét? A. 1272 m . B. 456 m . C. 1172 m
D. 1372 m . Lời giải
Tác giả: Trần Bạch Mai; Fb: Bạch Mai Chọn A 3 æ 1 ö t
Ta có: v (t) = a ò (t) 2 2 dt = 2t + t dt = + t + C . òç ÷ è 3 ø 9
Vận tốc khi bắt đầu tăng tốc là 10 m / s : v (0) =10 Û C =10 . 3 t
Vận tốc của vật là v (t) 2 = + t +10 . 9
Quãng đường vật đi được trong 12 giây kể từ lúc bắt đầu tăng tốc:
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 19 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019 12 12 3 æ ö v ò (t) t 2
dt =ò ç +t +10 dt = 1272 m ÷ . è 9 0 0 ø
Câu 25. [2H2-1.2-1] Hai khối nón có cùng thể tích. Một khối nón có bán kính đáy bằng R và chiều cao
bằng h , khối nón còn lại có bán kính đáy bằng 2R và chiều cao bằng x . Khi đó h h h A. x = 3 . B. x = 3 .
C. x = h . D. x = . 2 2 4 4 Lời giải
Tác giả: Trương Thanh Nhàn; Fb: Trương Thanh Nhàn. Chọn D
Gọi V là thể tích của khối nón có bán kính đáy bằng R và chiều cao bằng h ; V là thể tích khối 1 2 1 1 4 nón còn lại. Ta có 2 V = p R ;
h V = p 2R x = p R x 2 ( )2 2 . 1 3 3 3 1 4 h
Do hai khối nón có cùng thể tích nên ta có V = V 2 2
Û p R h = p R x Û x = . 1 2 3 3 4
Câu 26. [1D1-2.1-1] Phương trình sin x + cos x = 1 có 1 nghiệm là p p p A. . B. p 2 . C. . D. . 2 3 4 Lời giải
Tác giả: Trương Thanh Nhàn; Fb: Trương Thanh Nhàn. Chọn A æ p ö p
Xét f ( x) = sin x + cos . x Ta có f
= 1 nên x = là một nghiệm của phương trình đã cho . ç ÷ è 2 ø 2
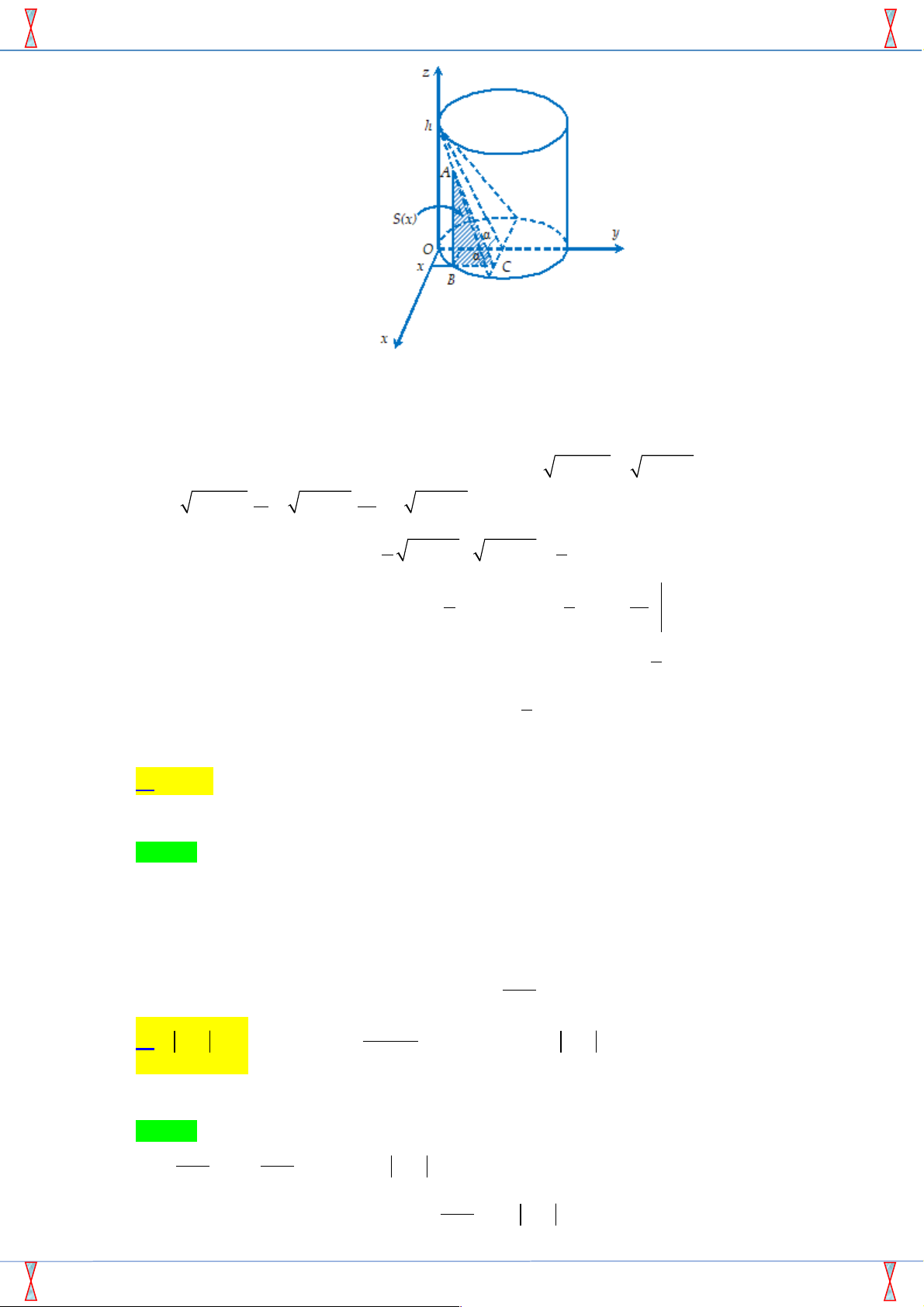
Câu 27. [2D3-3.4-2] Có một cốc thủy tinh hình trụ, bán kính trong lòng đáy cốc là 4cm , chiều cao trong
lòng cốc là 12cm đang đựng một lượng nước. Tính thể tích lượng nước trong cốc, biết rằng khi
nghiêng cốc nước vừa lúc chạm miệng cốc thì ở đáy cốc, mực nước trùng với đường kính đáy. A. 3 128p cm . B. 3 256cm . C. 3 256p cm . D. 3 128cm . Lời giải
Tác giả: Võ Tự Lực; Fb: Võ Tự Lực Chọn D
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 20 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019
+) Chọn hệ trục tọa độ Oxy như hình vẽ.
R = 4 cm là bán kính đáy cốc, h = 12 cm là chiều cao của cốc.
+) Thiết diện cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x ( 4 - £ x £ 4) là
một tam giác ABC vuông tại B có độ dài cạnh 2 2 2
BC = R - x = 16 - x và h 12 2 2 2 2
BA = R - x . = 16 - x . = 3 16 - x . R 4 1 3
+) Diện tích thiết diện là S ( x) 2 2 =
16 - x .3 16 - x = ( 2 16 - x ) ( 2 cm ). 2 2 4 3 3 3 æ x ö 4
+) Thể tích khối nước trong cốc là V = ò ( 2 16 - x )dx = 16x ç - ÷ = 128 ( 3 cm ) . 2 2 è 3 4 - 4 - ø 2
Chú ý: Có thể tính thể tích hình trên bằng công thức tính nhanh 2 V = R h . 3 2
+) Với R = 4 cm , h = 12 cm thể tích cần tìm 2 V = .4 .12 = 128 3 cm . 3
Câu 28. [2D1-5.8-1] Điểm M (1;e) thuộc đồ thị hàm số nào dưới đây? A. x y = e .
B. y = ln x . C. 2 y x- = . D. 2 x y - = . Lời giải
Tác giả: Võ Tự Lực; Fb:Võ Tự Lực Chọn A
Thay tọa độ của điểm M (1;e) lần lượt vào các phương trình x
y = e , y = ln x , 2 y x- = , 2 x y - =
, nhận thấy tọa độ M (1;e) thỏa mãn phương trình x y = e .
Vậy điểm M (1;e) thuộc đồ thị hàm số x y = e .
Câu 29. [2D3-1.1-1] Họ nguyên hàm của hàm số f ( x) 1 = là x -1 1
A. ln x -1 + C . B. - + C .
C. 2ln x -1 + C . D. ln ( x - ) 1 + C . (x - )2 1 Lời giải
Tác giả:Vũ Thị Thúy; Fb: Vũ Thị Thúy Chọn A 1 1 Có dx = d ò ò (x - )
1 = ln x -1 + C . x -1 x -1
Vậy họ nguyên hàm của hàm số f ( x) 1 =
là ln x -1 + C . x -1
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 21 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019
Câu 30. [2H1-3.4-1] Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ . Góc giữa hai mặt phẳng ( ABCD) và ( A¢B C ¢ D ¢ ¢) bằng A. 45° . B. 60° . C. 0° . D. 90° . Lời giải
Tác giả: Vũ Thị Thúy; Fb: Vũ Thị Thúy Chọn C C' A' D' B' D C A B
Vì ( ABCD) // ( A B ¢ C ¢ D
¢ ¢) nên góc giữa hai mặt phẳng ( ABCD) và ( A¢B C ¢ D ¢ ¢) bằng 0°.
Câu 31. [2D4-1.3-2] Trên mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn số phức z sao cho 2 z là số thuần ảo.
A. Hai đường thẳng y = x và y = -x . B. Trục Ox . C. Trục Oy .
D. Hai đường thẳng y = x và y = -x , bỏ đi điểm O (0;0). Lời giải
Tác giả: Nguyễn Văn Diệu; Fb: dieuptnguyen Chọn A
+) Gọi z = x + yi với x , y Î ! . Khi đó z = ( x + yi)2 2 2 2 2 2 2
= x + 2xyi + y i = x - y + 2xyi . é y = x +) 2
z là số thuần ảo khi và chỉ khi 2 2 x - y = 0 Û . ê ë y = -x
Vậy tập hợp điểm biểu diễn số phức z là hai đường thẳng y = x và y = -x .
Câu 32. [2D4-1.3-1] Cho số phức z = 3 - 5i . Phần ảo của z là A. 5 - . B. 5 - i . C. 5. D. 3. Lời giải
Tác giả: Nguyễn Văn Diệu; Fb: dieuptnguyen Chọn A
Cho số phức z = x + yi với x , y Î ! . Khi đó y được gọi là phần ảo của z . Vậy 5
- là phần ảo của số phức z = 3 - 5i .
Câu 33. [2D2-5.6-2] Một người gửi 50 triệu đồng vào ngân hàng theo thể thức lãi kép với lãi suất
6,5% / năm, kì hạn một năm. Hỏi sau 5 năm người đó rút cả vốn lẫn lãi được số tiền gần với số
nào nhất trong các số tiều sau? (biết lãi suất hàng năm không đổi) . A. 73triệu đồng.
B. 53,3 triệu đồng.
C. 64,3triệu đồng.
D. 68,5 triệu đồng. Lời giải
Tác giả: Bùi Quý Minh; Fb: Minh Bùi Chọn D
Gọi số tiền ban đầu là A . Lãi suất tính theo năm là r .
Hết năm thứ nhất số tiền cả vốn và lãi là: A + .
A r = A(1+ r) .
Hết năm thứ hai số tiền cả vốn và lãi là: A( + r) + A( + r) r = A( + r)2 1 1 . 1 .
Hết năm thứ ba số tiền cả vốn và lãi là: A( + r)2 + A( + r)2 r = A( + r)3 1 1 . 1 .
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 22 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019
Từ đó suy ra sau n năm số tiền cả vốn và lãi là: (1+ )n A r .
Thay số với A = 50; r = 6,5%; n = 5 ta được số tiền là A = 50 1+ 6,5% » 68,5 5 ( )5 (triệu đồng ) .
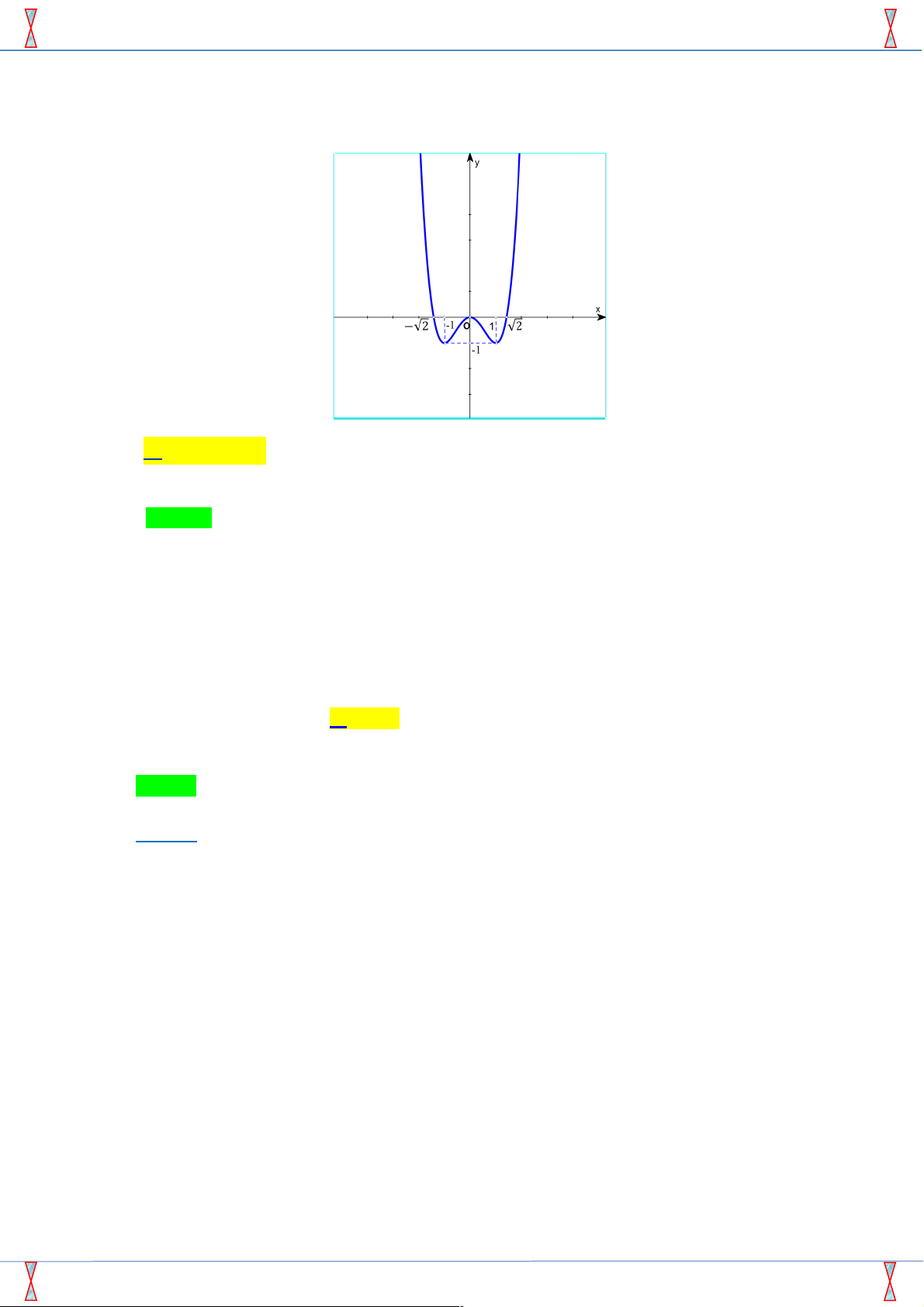
Câu 34. [2D1-5.1-1] Hàm số nào sau đây có đồ thị như hình vẽ ? A. 4 2
y = x - 2x . B. 4 2
y = x - 2x -1. C. 3 2
y = x - 2x + x . D. 4 2
y = -x + 2x . Lời giải
Tác giả: Bùi Quý Minh; Fb: Minh Bùi Chọn A
+) Đồ thị hàm số có ba cực trị nên không thể là hàm bậc ba Þ loại đáp án C .
+) f (0) = 0 Þ loại đáp án B .
+) lim f ( x) = +¥ Þ loại đáp án D . x®+¥
Vậy đáp án A đúng.
Câu 35. [2D1-5.3-3] Số giá trị nguyên của m thuộc khoảng ( 2019 - ; 2019) để phương trình 2 2 x -2x 1 + x -2 x+2 4 - .2 m
+ 3m - 2 = 0 có bốn nghiệm phân biệt là A. 2017 . B. 2016 . C. 4035 . D. 4037 . Lời giải
Tác giả: Vũ Việt Tiến, FB: Vũ Việt Tiến Chọn B Cách 1: 2 2 x -2x 1 + 2 +) Ta có 2 2 x -2x 1 + x -2x+2 4 - .2 m + 3m - 2 = ( ) 0 x -2x 1 2 2 .2 m + Û - + 3m - 2 = 0 . ( ) 1 Đặt 2 2 1 2x x t - + = . Ta có x -2 x 1 + (x- )2 2 1 0 t = 2 = 2 ³ 2 =1, x " . Suy ra t ³1. Phương trình ( ) 1 trở thành: 2 t - 2 .
m t + 3m - 2 = 0 . (2) +) Phương trình ( )
1 có bốn nghiệm phân biệt khi và chỉ khi phương trình (2) có hai nghiệm 2 ìD¢ > 0
ìm - 3m + 2 > 0 ï ï
phân biệt t , t thỏa mãn t > t > 1 Û (
í t -1 t -1 > 0 Û t
í t - t + t +1 > 0 (3) 1 )( 2 ) 1 2 ( 1 2 ) . 1 2 1 2 t ï t 2 t ï + > + t > 2 î 1 2 î 1 2 t ì + t = 2m
Theo định lý Vi-et ta có 1 2 í .
t .t = 3m - 2 î 1 2 2
ìm - 3m + 2 > 0 ìém > 2 ï ï +) Khi đó (3) 3 í m 2 2m 1 0 ê Û - -
+ > Û íëm <1 Û m > 2 . ï2m 2 ï > î îm > 1
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 23 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019
Mà m nguyên và m Î( 2019 -
;2019) nên ta có mÎ{3;4;...; } 2018 .
Vậy có 2016 giá trị nguyên của m thỏa mãn bài toán. Cách 2: Đặng Ân 2 2 x -2x 1 + 2 +) Ta có 2 2 x -2x 1 + x -2x+2 4 - .2 m + 3m - 2 = ( ) 0 x -2x 1 2 2 .2 m + Û - + 3m - 2 = 0 . ( ) 1 Đặt 2 2 1 2x x t - + = . Ta có x -2 x 1 + (x- )2 2 1 0 t = 2 = 2 ³ 2 =1, x " . Suy ra t ³1. Phương trình ( ) 1 trở thành: 2
t - m t + m - = Û ( t - ) 2 2 . 3 2 0 2
3 .m = t - 2 (2) . 3 2 t - 2
Vì t = không là nghiệm của (2) nên (2) Û m = (*) . 2 2t - 3 2 t - 2 Xét hàm số y = trên khoảng (1;+¥) . 2t - 3 2 2t - 6t + 4 ét = 1 y¢ = ; y¢ = 0 Û . ( ê 2t - 3)2 ët = 2 Ta có bảng biến thiên Phương trình ( )
1 có bốn nghiệm phân biệt Û (*) có hai nghiệm phân biệt lớn hơn 1 Û m > 2.
Mà m nguyên và m Î( 2019 -
; 2019) nên ta có mÎ{3;4;...; } 2018 .
Vậy có 2016 giá trị m thỏa mãn bài toán.
Câu 36. [2H1-1.2-1] Hình chóp tứ giác có tất cả bao nhiêu cạnh A. 6 . B. 20 . C. 12 . D. 8 . Lời giải
Tác giả: Vũ Việt Tiến, FB: Vũ Việt Tiến Chọn D
Hình chóp tứ giác (ví dụ như hình vẽ trên) có 4 cạnh bên và 4 cạnh đáy nên có tất cả 8 cạnh.
Chú ý: Chóp n -giác có 2n cạnh.
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 24 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019
Câu 37. [2D3-3.1-2] Cho hàm số y = f ( x) có đạo hàm liên tục trên [ 1;
- 2]. Đồ thị của hàm số 5 8
y = f ¢( x) được cho như hình vẽ. Diện tích các hình phẳng (K ) , (H ) lần lượt là và . 12 3 Biết f (- ) 19 1 = , tính f (2) . 12 A. f ( ) 23 2 = . B. f ( ) 2 2 = - . C. f ( ) 2 2 = . D. f ( ) 11 2 = . 6 3 3 6 Lời giải
Tác giả:Trần Quôc Khang; Fb:Bi Trần Chọn B
Gọi S , S lần lượt là diện tích hình phẳng (K ) , (H ) . 1 2 0 ì ì = ï f ¢ ò (x ì 5 S ) 5 5 dx = ï f (0) - f (- ) 1 = 1 ï ï 12 12 ï 1 - ï 12 í Û í Û í
Þ f ( ) - f (- ) 5 8 9 2 1 = - = - 2 8 ï ï 8 8 12 3 4 S =
ï f (0)- f (2) = 2 - f ¢ ò (x)dx = ïî 3 ï 3 ï î î 3 0
Þ f ( ) = f (- ) 9 19 9 2 2 1 - = - = - . 4 12 4 3
Câu 38. [2D1-1.5-2] Cho các mệnh đề:
1. Nếu hàm số y = f ( x) liên tục trên (a;b) và f (a). f (b) < 0 thì tồn tại x Î a;b 0 ( ) sao cho f ( x = 0 0 ) .
2. Nếu hàm số y = f ( x) liên tục trên [a;b] và f (a). f (b) < 0 thì phương trình f ( x) = 0 có nghiệm.
3. Nếu hàm số y = f ( x) liên tục, đơn điệu trên [ ;
a b] và f (a). f (b) < 0 thì phương trình
f ( x) = 0 có nghiệm duy nhất trên ( ; a b).
Trong ba mệnh đề trên
A. Có đúng hai mệnh đề sai.
B. Cả ba mệnh đề đều đúng.
C. Cả ba mệnh đề đều sai.
D. Có đúng một mệnh đề sai.
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 25 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019 Lời giải
Tác giả:Trần Quôc Khang; Fb:Bi Trần Chọn D
Định lí: “Nếu hàm số y = f ( x) liên tục trên [ ;
a b] và f (a). f (b) < 0 thì tồn tại ít nhất một
điểm c Î(a;b) sao cho f (c) = 0 ”.
Mệnh đề 1: SAI ở giả thiết ( ; a b) .
Mệnh đề 2: Nếu hàm số y = f ( x) liên tục trên [ ;
a b] và f (a). f (b) < 0 thì tồn tại ít nhất một
điểm c Î(a;b) sao cho f (c) = 0 hay c là nghiệm của phương trình f ( x) = 0 nên mệnh đề 2 ĐÚNG.
Mệnh đề 3: Nếu hàm số y = f ( x) liên tục, đơn điệu trên [a;b] và f (a). f (b) < 0 thì đồ thị
hàm số y = f ( x) cắt trục Ox tại duy nhất một điểm thuộc khoảng (a;b) nên f ( x) = 0 có nghiệm duy nhất trên ( ;
a b). Do đó mệnh đề 3 ĐÚNG.
Câu 39. [2D4-2.4-2] Cho số phức z thỏa mãn z = 5 . Biết tập hợp các điểm biểu diễn số phức
w = (1+ 2i) z + i là một đường tròn. Tìm bán kính r của đường tròn đó. A. r = 5 . B. r = 10 . C. r = 5 . D. r = 2 5 . Lời giải
Tác giả: Phạm Thị Thuần ; Fb: Phạm Thuần Chọn C Cách 1: w - i w - i
Ta có w = (1+ 2i) z + i Û z = . Khi đó z = 5 Û
= 5 Û w - i = 5 . 1+ 2i 1+ 2i
Đặt w = x + yi ( 2
x, y Î ! , i = - )
1 . Khi đó (*) trở thành x + iy - i = Û x + ( y - )2 2 2 5 1 = 5 .
Vậy tập hợp các điểm biểu diễn số phức w là đường tròn có bán kính r = 5 . Cách 2: Lưu Thêm
Gọi M là điểm biểu biểu diễn số phức w .
Ta có w = (1+ 2i) z + i Û w - i = (1+ 2i) z Þ w - i = (1+ 2i) z = 1+ 2i . z = 5. 5 = 5
Þ MI = 5 , với I (0; ) 1 .
Vậy tập hợp các điểm biểu diễn số phức w là đường tròn tâm I (0; ) 1 , bán kính r = 5 .
Câu 40. [2H3-1.1-1] Trong không gian với hệ tọa độ Oxyz , cho hai điểm A(3;0; 2
- ) và B(1;4;2). Tọa !!!"
độ của vectơ AB là A. ( 1; - 2;2) . B. ( 2; - 4;4). C. (2;2;0). D. (4;4;0) . Lời giải
Tác giả: Phạm Thị Thuần ; Fb: Phạm Thuần Chọn B !!!"
Ta có: AB = ( x - x ; y - y ; z - z ) = (-2;4;4 B A B A B A ) .
Câu 41. [2H3-1.1-1] Trong không gian với hệ trục Oxyz , cho tam giác ABC có A(3;3;2) , B( 1; - 2;0) , C (1;1; 2
- ) . Gọi G(x ; y ; z x + y + z 0 0
0 ) là trọng tâm của tam giác đó. Tổng bằng 0 0 0 1 2 A. 9 . B. . C. - . D. 3 . 3 3 Lời giải
Tác giả: Nguyễn Tình; Fb:Gia Sư Toàn Tâm Chọn D
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 26 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019 ì 3 + (- ) 1 +1 x = = 1 ï 0 3 ï ï 3 + 2 +1
Vì G là trọng tâm ABC D nên ta có: íy = = 2
Þ x + y + z = 1+ 2 + 0 = 3. 0 3 0 0 0 ï ï 2 + 0 + ( 2 - ) ïz = = 0 0 î 3
Câu 42. [2D2-4.1-1] Điều kiện xác định của hàm số y = log x -1 2 ( ) là A. x ¹ 1. B. x > 1. C. x < 1. D. x " Î ! . Lời giải
Tác giả: Nguyễn Tình; Fb: Gia Sư Toàn Tâm Chọn B
Điều kiện xác định: x -1 > 0 Û x > 1.
Câu 43. [2H2-2.3-3] Cho tứ diện đều ABCD có cạnh bằng a . Thể tích của khối cầu tiếp xúc với tất cả
các cạnh của tứ diện ABCD bằng 3 3a 3 2p a 3 2 2a 3 3p a A. . B. . C. . D. . 24 24 9 8 Lời giải
Tác giả: Đặng Mai Hương; Fb: maihuongpla Chọn B
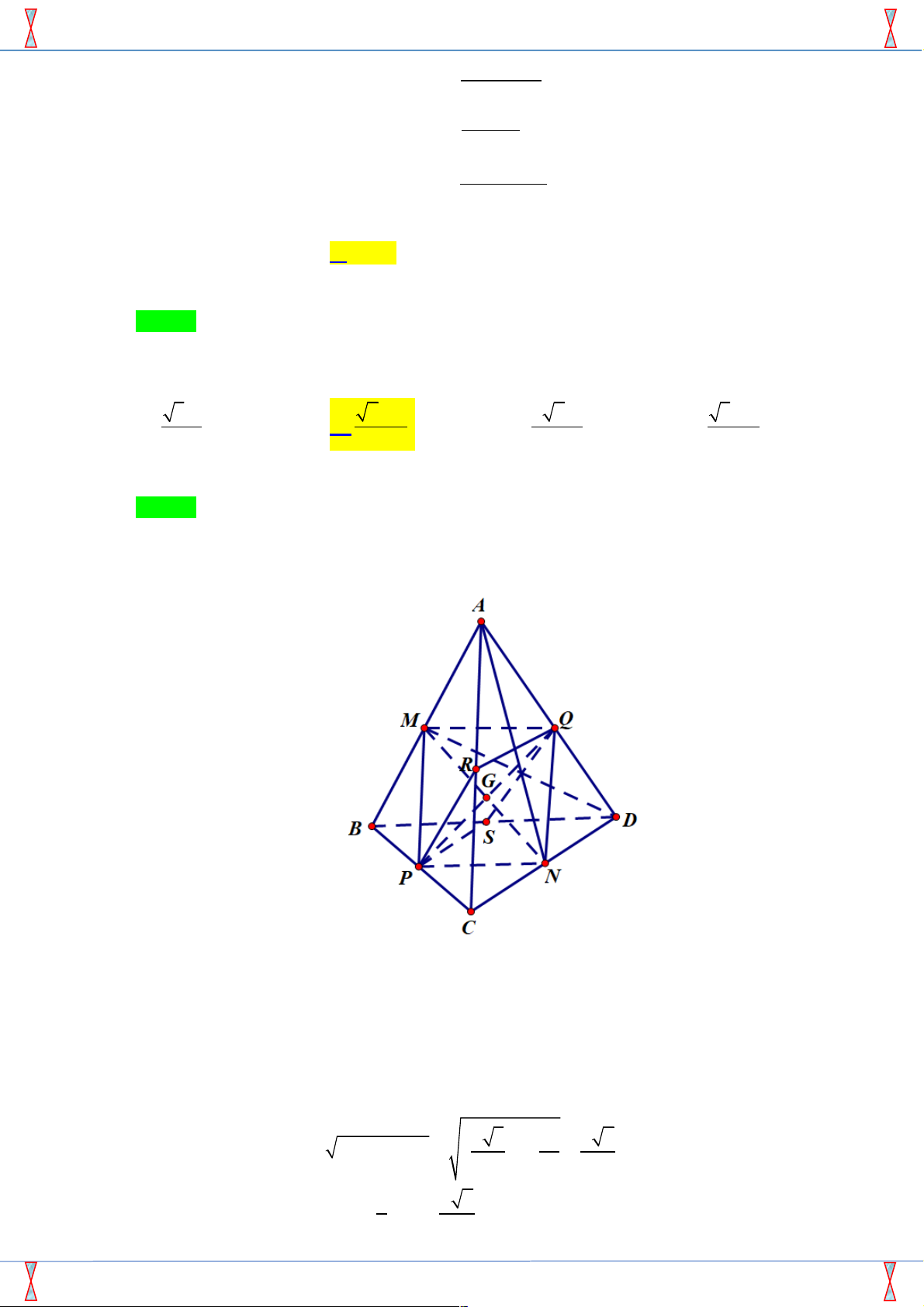
Gọi G là trọng tâm tứ diện ABCD . Ta chứng minh G là tâm mặt cầu tiếp xúc với tất cả các cạnh của tứ diện .
Gọi M , N , P , Q , R , S lần lượt là trung điểm các cạnh AB , CD, BC , AD , AC , BD.
Ta có G là trung điểm của các đoạn MN, PQ, RS . ACD D = BCD D
Þ AN = BN Þ N
D AB cân tại N Þ MN ^ AB . Tương tự ta có MN ^ CD . 2 2 æ a 3 ö a a 2 Ta có: 2 2
PQ = RS = MN = AN - AM = ç ÷ - = . ç 2 ÷ 4 2 è ø a
Suy ra d (G AB) = d (G ) 1 2 , ,CD = MN = . 2 4
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 27 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019 a
Chứng minh tương tự ta có d (G ) = d (G ) = d (G ) = d (G ) 2 , AC , AD , BD , BC = . 4
Vậy G là tâm mặt cầu tiếp xúc với tất cả các cạnh của tứ diện ABCD . 3 a 2 3 4 4 æ a 2 ö 2p a
Bán kính mặt cầu R =
. Suy ra thể tích khối cầu là 3 V = p R = p ç ÷ = . 4 3 3 ç 4 ÷ 24 è ø
Câu 44. [2H2-2.7-1] Trong không gian Oxyz , phương trình mặt cầu tâm I (1; 2
- ;3), bán kính R = 2 là
A. ( x + )2 + ( y - )2 + ( z + )2 1 2 3 = 4 .
B. ( x + )2 + ( y - )2 + ( z + )2 1 2 3 = 2 .
C. ( x - )2 + ( y + )2 + ( z - )2 1 2 3 = 4 .
D. ( x - )2 + ( y + )2 + ( z - )2 1 2 3 = 2 . Lời giải
Tác giả: Đặng Mai Hương; Fb: maihuongpla@gmail.com Chọn C
Mặt cầu tâm I (1; 2
- ;3), bán kính R = 2 có phương trình là (x - )2 + ( y + )2 + (z - )2 1 2 3 = 4 .
Câu 45. [1D5-2.1-1] Đạo hàm của hàm số 2
y = ln x + x là 1 3 1 x A. y¢ = + 1 x . B. y¢ = + 1 2x .
C. y¢ = - 2x . D. y¢ = + . x x x x 3 Lời giải
Tác giả: Trần Lê Hương Ly; Fb: Trần Lê Hương Ly Chọn B 1
Ta có y¢ = + 2x . x 2 x 1 2 + æ ö
Câu 46. [2D2-6.1-2] Tập nghiệm của bất phương trình >1 là ç ÷ è 3 ø æ 1 ö æ 1 ö A. ( ;0 -¥ ). B. (0;+ ¥). C. ; -¥ - . D. - ;+ ¥ . ç ÷ ç ÷ è 2 ø è 2 ø Lời giải
Tác giả: Trần Lê Hương Ly; Fb: Trần Lê Hương Ly Chọn C 2 x 1 + 2 x 1 + 0 æ 2 ö æ 2 ö æ 2 ö Ta có: > 1 Û > Û 2x +1 < 1 0 Û x < - . ç ÷ ç ÷ ç ÷ è 3 ø è 3 ø è 3 ø 2 æ 1 ö
Vậy tập nghiệm của bất phương trình đã cho là ; -¥ - . ç ÷ è 2 ø
Câu 47. [1D2-5.5-2] Đội tuyển học sinh giỏi Toán 12 của trường THPT X có 7 học sinh trong đó có
bạn Minh Anh. Lực học của các học sinh là như nhau. Nhà trường chọn ngẫu nhiên 4 học sinh
đi thi. Tìm xác suất để Minh Anh được chọn đi thi. 1 4 3 1 A. . B. . C. . D. . 7 7 7 2 Lời giải
Tác giả: Phùng Hoàng Cúc ; Fb: Phùng Hoàng Cúc Chọn B Không gian mẫu n(W) 4 = C7
Gọi biến cố A: “Minh Anh được chọn trong 4 học sinh được chọn đi thi.”
+ Chọn Minh Anh đi thi có 1 cách.
+ Chọn 3 bạn trong 6 bạn còn lại có 3 C cách. 6 Suy ra n( A) 3 =1.C = 20 . 6 n A 20 4
Vậy xác suất để Minh Anh được chọn đi thi là: P ( A) ( ) = = = . n(W) 35 7
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 28 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019 9
Câu 48. [2D1-3.1-2] Tìm giá trị nhỏ nhất của hàm số y = x + trên đoạn [2;4]. x 13 25 A. min y = . B. min y = . C. min y = 6 . D. min y = 6 - . [2;4] 2 [2;4] 4 [2;4] [2;4] Lời giải
Tác giả: Phùng Hoàng Cúc ; Fb: Phùng Hoàng Cúc Chọn C 2 9 x - 9 Ta có y¢ = 1- = . 2 2 x x é x = 3Î[2;4] Khi đó y¢ = 0 Û ê . x = 3 - Ï ë [2;4] Ta có f ( ) 9 13 2 = 2 + = . 2 2 f ( ) 9 3 = 3 + = 6 . 3 f ( ) 9 25 4 = 4 + = . 4 4 Suy ra: min y = 6 . [2;4]
Câu 49. [1D2-2.1-1] Trong tủ quần áo của bạn An có 4 chiếc áo khác nhau và 3 chiếc quần khác nhau.
Hỏi bạn An có bao nhiêu cách để chọn 1 bộ quần áo để mặc? A. 7 . B. 27 . C. 64 . D. 12 . Lời giải
Tác giả: Lê Bá Phi ; Fb:Lee Bas Phi Chọn D
Chọn một bộ quần áo, cần thực hiện liên tiếp hai hành động:
Hành động 1 - chọn áo: có 4 cách chọn.
Hành động 2 - chọn quần: ứng với mỗi cách chọn áo có 3 cách chọn quần.
Vậy số cách chọn một bộ quần áo là: 4 . 3 = 12 (cách).
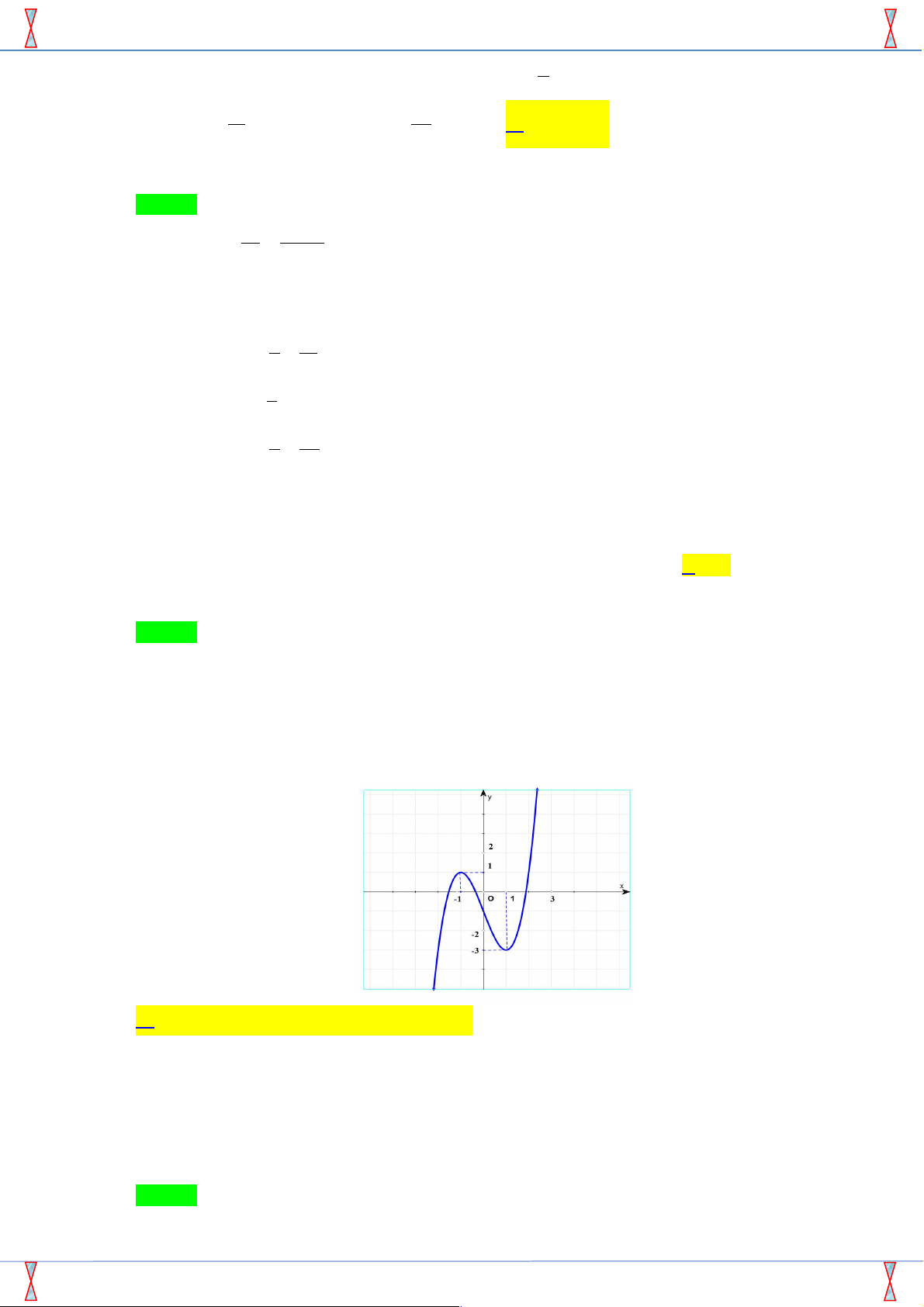
Câu 50. [2D1-5.8-1] Cho hàm số y = f ( x) có đồ thị như hình vẽ. Tìm kết luận đúng trong các kết luận sau.
A. Hàm số y = f ( x) có điểm cực tiểu x =1.
B. Hàm số y = f ( x) không có cực trị.
C. Phương trình f ( x) = 0 vô nghiệm.
D. Hàm số y = f ( x) đồng biến trên khoảng (-¥;0) . Lời giải
Tác giả: Lê Bá Phi ; Fb:Lee Bas Phi Chọn A
Dựa vào đồ thị ta thấy:
Hàm số y = f ( x) có hai điểm cực trị Þ B sai.
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 29 , Mã 617
Sản phẩm của STRONG TEAM TOÁN VD VDC
Đề SGD Hưng Yên Lần 1 Năm 2019
Đồ thị hàm số y = f ( x) cắt trục hoành tại 3 điểm phân biệt nên phương trình f ( x) = 0 có 3
nghiệm phân biệt Þ C sai.
Hàm số y = f ( x) đồng biến trên các khoảng (-¥;- ) 1 và (1;+ ¥) Þ D sai.
Hàm số y = f ( x) đạt cực đại tại x = 1
- , đạt cực tiểu tại x =1 Þ A đúng.
--------- STRONG TEAM TOÁN VD VDC ----------
STRONG TEAM TOÁN VD-VDC- Group toán Số 1 VN- Làm 1,2 câu nhận lại hàng ngàn câu/tuần P 30 , Mã 617