Đề thi thử THPT Quốc gia 2019 môn Toán trường THPT chuyên Hà Tĩnh

Đề thi thử THPT Quốc gia 2019 môn Toán trường THPT chuyên Hà Tĩnh có mã đề 001, đề gồm 06 trang với 50 câu trắc nghiệm dạng 04 đáp án, đề thi có đáp án và lời giải chi tiết.

33 17 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

78 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
Trang 1/6-Mã đề 001
SỞ GD - ĐT HÀ TĨNH
TRƯỜNG THPT CHUYÊN
ĐỀ THI CHÍNH THỨC
(Đề thi gồm có 6 trang)
KỲ THI THỬ TRUNG HỌC PHỔ THÔNG QUỐC GIA 2019
Môn thi : Toán
Thời gian làm bài: 90 phút
(50 câu trắc nghiệm)
Họ, tên thí sinh:.........................................................................
Số báo danh: .............................................................................
Câu 1: Cho các hàm số
( ),gf x x
liên tục trên có
5
1
2 ( ) 3g(x) 5;f x dx
5
1
3 ( ) 5g(x) 21f x dx

.
Tính
5
1
( ) g(x) .f x dx
A.
5
B.
1
C.
D.
1
Câu 2: Với
,kn
là hai số nguyên dương tùy ý thỏa mãn
,kn
mệnh đề nào dưới đây sai?
A.
!
!( )!
k
n
n
C
k n k
B.
!C
kk
nn
Ak
C.
1
1
C
k k k
n n n
CC

D.
!A
kk
nn
Ck
Câu 3: Cho số phức
3 2 .zi
Tìm phần ảo của số phức
w (1 2 )iz
A.
4
B.
7
C.
4
D.
4i
Câu 4: Trong không gian với hệ tọa độ
,Oxyz
cho mặt phẳng
()
:
2 0.xy
Mệnh đề nào dưới đây đúng?
A.
()
//
mp Oxy
B.
()
//
Oz
C.
()Oz
D.
()Oy
Câu 5: Hàm số nào sau đây nghịch biến trên
?
A.
3
32y x x
B.
42
22y x x
C.
32
2 4 1y x x x
D.
32
2 5 2y x x x
Câu 6: Biết
()Fx
là một nguyên hàm của hàm số
( ) sin
x
f x e x

thỏa mãn
(0) 0F
. Tìm
( )?Fx
A.
( ) cos 2
x
F x e x
B.
( ) cos
x
F x e x
C.
( ) cos 2
x
F x e x
D.
( ) cos 2
x
F x e x
Câu 7: Cho hàm số
()y f x
liên tục trên
R
và có bảng biến thiên như hình bên. Tìm khẳng định đúng
A. Hàm số có giá trị nhỏ nhất bằng 0 và giá trị lớn nhất bằng 1
B. Hàm số đạt cực đại tại
0x
và đạt cực tiểu tại
1x 
C. Đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt
D. Hàm số có đúng một cực trị
Câu 8: Trong không gian với hệ tọa độ
,Oxyz
phương trình nào sau đây không phải là phương trình mặt cầu?
A.
2 2 2
2x 2 2 2 4 6 5 0y z x y z
B.
2 2 2
x 2 0y z x y z
-
-
+
x
-
∞
+
∞
-
∞
+
∞
0
-1
0
0
1
Mã đề thi: 001
Trang 2/6-Mã đề 001
C.
2 2 2
x 3 7 5 1 0y z x y z
D.
2 2 2
x 3 4 3 7 0y z x y z
Câu 9: Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng
3a
. Thể tích khối lăng trụ đã cho bằng
A.
3
9
4
a
B.
3
3
4
a
C.
3
3
4
a
D.
3
33
4
a
Câu 10:
Đường cong trong hình vẽ bên là đồ thị của một trong 4 hàm số
dưới đây. Hỏi hàm số đó là hàm số nào?
A.
4
2
1
4
x
yx
B.
4
2
21
4
x
yx
C.
4
2
1
4
x
yx
D.
42
1
42
xx
y
Câu 11: Cho
01a
;
,0bc
thỏa mãn
log 3
a
b
;
log 2
a
c 
. Tính
32
log a .
a
bc
A.
18
B.
7
C.
10
D.
8
Câu 12: Cho hình trụ có đường cao bằng
5
và đường kính đáy bằng
8.
Tính diện tích xung quanh của hình trụ
đó.
A.
40
B.
20
C.
80
D.
160
Câu 13: Cho cấp số nhân
()
n
u
có số hạng đầu
1
3;u
công bội
2.q 
Tính tổng 10 số hạng đầu tiên của
()
n
u
.
A.
513
B.
1023
C.
513
D.
1023
Câu 14: Trong không gian với hệ tọa độ
,Oxyz
cho hai điểm
(1; 2;0);A
(3;2; 8)B
. Tìm một véctơ chỉ
phương của đường thẳng
.AB
A.
u
(1;2; 4)
B.
u
(2;4;8)
C.
u
( 1;2; 4)
D.
u
(1; 2; 4)
Câu 15: Cho
0 1,0 1ab
;
, 0,xy
m
. Trong các mệnh đề sau, mệnh đề nào sai?
A.
log log log
a a b
x b x
B.
log ( ) log log
a a a
xy x y
C.
log
log
log
a
a
a
x
x
yy
D.
1
log log
m
a
a
xx
m
Câu 16: Gọi
(C)
là đồ thị hàm số
2
21
x
y
x
. Trong các mệnh đề sau, mệnh đề nào sai?
A.
(C)
có tiệm cận ngang là
1
2
y
B.
(C)
có đúng một trục đối xứng
C.
(C)
có tiệm cận đứng là
1
2
x
D.
(C)
có đúng một tâm đối xứng
Câu 17: Cho hình chóp
SABCD
có đáy là hình vuông cạnh
2a
. Tam giác
SAC
vuông cân tại
S
và nằm
trong mặt phẳng vuông góc với đáy. Tính thể tích khối cầu ngoại tiếp hình chóp
SABCD
.
Trang 3/6-Mã đề 001
A.
3
2
3
a
B.
3
43a
C.
3
4
3
a
D.
3
4 a
Câu 18: Trong không gian
Oxyz
cho điểm
A(1; 2;3)
và hai đường thẳng
1
13
:
2 1 1
x y z
d


;
2
: 1 , 2 , 1d x t y t z
. Viết phương trình đường thẳng
đi qua
A
, vuông góc với cả
1
d
và
2
.d
A.
1
2
3
xt
yt
zt


B.
2
12
33
xt
yt
zt

C.
1
2
3
xt
yt
zt


D.
12
2
33
xt
yt
zt


Câu 19: Cho hình chóp
SABCD
có đáy
ABCD
là hình chữ nhật,
;3AB a AD a
,
( ),SA ABCD
SC
tạo
với đáy một góc
0
45
. Gọi
M
là trung điểm cạnh
SB
,
N
là điểm trên cạnh
SC
sao cho
1
2
SN NC
. Tính
thể tích khối chóp
.SAMN
A.
3
3
9
a
B.
3
3
18
a
C.
3
3
12
a
D.
3
3
6
a
Câu 20: Diện tích hình phẳng giới hạn bởi các đường
3
, 10y x y x
và trục Ox là
A.
32
B.
26
C.
36
D.
40
Câu 21: Biết
12
log 27 a
. Tính
6
log 16
theo
.a
A.
4(3 )
3
a
a
B.
4(3 )
3
a
a
C.
3
4(3 )
a
a
D.
3
4(3 )
a
a
Câu 22: Biết rằng đồ thị hàm số
32
2 5 3 2y x x x
chỉ cắt đường thẳng
34yx
tại một điểm duy nhất
;M a b
. Tổng
ab
bằng
A.
6
B.
3
C. 6 D. 3
Câu 23: Biết rằng phương trình
2
33
5log log 9 1 0xx
có hai nghiệm là
12
,xx
. Tìm khẳng định đúng?
A.
5
12
x3x
B.
12
5
1
3
xx
C.
12
1
5
xx
D.
12
1
5
xx 
Câu 24: Gọi
12
,zz
là hai nghiệm phức của phương trình:
2
5 7 0.zz
Tính
22
12
| | | |P z z
A.
47
B.
56
C.
14
D.
27
Câu 25: Cho khối nón có thiết diện qua trục là tam giác cân có một góc
0
120
và cạnh bên bằng
a
. Tính thể
tích khối nón.
A.
3
8
a
B.
3
3
8
a
C.
3
3
24
a
D.
3
4
a
Câu 26: Tìm tập xác định của hàm số
1
2
3
y ( 3 2) .xx
Trang 4/6-Mã đề 001
A.
\ 1;2
B.
( ;1) (2; )
C.
1;2
D.
Câu 27: Tập nghiệm của bất phương trình
1
2
log (2 1) 0x 
là
A.
1
;0
4



B.
(0; )
C.
1
;
2




D.
1
;0
2



Câu 28: Cho hình chóp
SABCD
có đáy là hình thoi cạnh
0
2 , 60 , 3a ABC SA a
và
()SA ABCD
. Tính
góc giữa
SA
và
( ).mp SBD
A.
0
60
B.
0
90
C.
0
30
D.
0
45
Câu 29: Biết
2
1
ln 2
dx bln c
(1 ) 1 1
e
xa
x e e
, với
,,abc
. Tính
abc
A.
1
B.
1
C.
D.
2
Câu 30: Có bao nhiêu tiếp tuyến của đồ thị hàm số
32
32y x x
đi qua điểm
3;2A
?
A. 3 B. 0 C. 1 D. 2
Câu 31: Gọi
,Mm
tương ứng là giá trị lớn nhất và nhỏ nhất của hàm số
2cos 1
cos 2
x
y
x
. Khi đó ta có:
A.
90Mm
B.
90Mm
C.
90Mm
D.
0Mm
Câu 32: Trong không gian
Oxyz
, viết phương trình mặt cầu tâm
( 1;3;0)I
và tiếp xúc với mặt phẳng
( ):2 2 11 0.P x y z
A.
2 2 2
( 1) ( 3) 4x y z
B.
2 2 2
( 1) ( 3) 4x y z
C.
2 2 2
( 1) ( 3) 2x y z
D.
2 2 2
4
( 1) ( 3)
9
x y z
Câu 33: Cho số phức
z
thỏa mãn :
(1 2 ) (2 3 ) 4 12z i z i i
. Tìm tọa độ điểm
M
biểu diễn số phức
z
.
A.
(3;1)M
B.
(3; 1)M
C.
( 1;3)M
D.
(1;3)M
Câu 34: Cho các hàm số
,y f x
,y g x
3
1
fx
y
gx
. Hệ số góc của các tiếp tuyến của các đồ thị các
hàm số đã cho tại điểm có hoành độ
1x
bằng nhau và khác 0. Khẳng định nào dưới đây là khẳng định đúng?
A.
1 3.f 
B.
13f 
C.
11
1.
4
f 
D.
11
1.
4
f 
Câu 35: Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy
2,4,n
3n
điểm phân biệt (các điểm
không trùng với các đỉnh của tam giác). Tìm n, biết rằng số tam giác có các đỉnh thuộc
6n
điểm đã cho là
247
.
A.
6
B.
8
C.
7
D.
5
Trang 5/6-Mã đề 001
Câu 36: Cho hàm số
fx
liên tục trên . Biết
ln2
0
(e 1) 5
x
f dx
và
3
2
23
3.
1
x f x
dx
x
Tính
3
2
.I f x dx
A.
2I
B.
4I
C.
2I 
D.
8I
Câu 37: Cho khối hộp
' ' ' 'ABCDA B C D
có thể tích
V
. Các điểm
,,M N P
thỏa mãn
2 , 3 'AM AC AN AB
,
4'AP AD
. Tính thể tích khối chóp
AMNP
theo
V
.
A.
6V
B.
8V
C.
12V
D.
4V
Câu 38: Số phức
z
thỏa mãn
15z 
,
1 1 5
17z
z

và
z
có phần ảo dương. Tìm tổng phần thực và phần ảo
của
.z
A. 2 B. 4 C.
6
D. 8
Câu 39: Trong không gian với hệ tọa độ Oxyz, cho điểm
1;2;2A
và đường thẳng
6 1 5
:
2 1 1
x y z
d

.
Tìm tọa độ điểm B đối xứng với A qua d.
A.
3;4; 4B 
B.
2; 1;3B
C.
3;4; 4B
D.
3; 4;4B
Câu 40: Ông An có một khu đất hình elip với độ dài trục lớn 10 m và độ dài trục bé 8 m. Ông An muốn chia
khu đất thành hai phần, phần thứ nhất là một hình chữ nhật nội tiếp elip dùng để xây bể cá cảnh và phần còn lại
dùng để trồng hoa. Biết chi phí xây bể cá là 1000000 đồng trên
2
1m
và chi phí trồng hoa là 1200000 đồng trên
2
1m
. Hỏi ông An có thể thiết kế xây dựng như trên với tổng chi phí thấp nhất gần nhất với số nào sau đây?
A. 67398224 đồng B. 67593346 đồng C. 63389223 đồng D. 67398228 đồng
Câu 41: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
5 7 12
:
2 2 1
x y z
d

và
: 2 3 3 0mp x y z
. Gọi
M
là giao điểm của d với
, A thuộc d sao cho
14AM
. Tính khoảng
cách từ A đến
.mp
A. 2 B. 3 C. 6 D.
14
Câu 42: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2 4 2 2
2019 1y m x m m x
có đúng một
cực trị?
A. 2019 B. 2020 C. 2018 D. 2017
Câu 43: Gọi
S
là tập tất cả các giá trị của tham số m để đồ thị hàm số
3
3 2 2
3 2 4 3 2y x x x x mx
có tiệm cận ngang. Tổng các phần tử của
S
là
A.
2
B.
2
C.
3
D. 3
Câu 44: Cho hàm số
2
lnf x x x
. Tính
1 2 2019
P ... .
f f f
e e e
Trang 6/6-Mã đề 001
A.
2020
P
2019
B.
2019
P
2020
C.
2019
P e
D.
2019
P
2020

Câu 45: Cho các số phức
12
,zz
thỏa mãn phương trình
2 3 5zi
và
12
6zz
. Biết tập hợp các điểm M
biểu diễn số phức
12
w z z
là một đường tròn. Tính bán kính đường tròn đó.
A.
8R
B.
4R
C.
22R
D.
2R
Câu 46: Cho các số thực
,xy
thay đổi thỏa mãn
22
1x y xy
và hàm số
32
2 3 1f t t t
. Gọi
,Mm
tương ứng là giá trị lớn nhất và nhỏ nhất của
52
4
xy
Qf
xy





. Tổng
Mm
bằng
A.
4 3 2
B.
4 5 2
C.
4 4 2
D.
4 2 2
Câu 47: Trong các khối chóp tứ giác đều S.ABCD mà khoảng cách từ A đến mp(SBC) bằng 2a, khối chóp có
thể tích nhỏ nhất bằng
A.
3
23a
B.
3
2a
C.
3
33a
D.
3
43a
Câu 48: Tổng tất cả các giá trị của tham số
m
để phương trình
2
2
2
2
2
3
1
3 log 2 2
xx
x
m
x
x
xm

có đúng
ba nghiệm phân biệt là
A.
3
B.
2
C.
3
D.
2
Câu 49: Cho các số thực
,,abc
thỏa mãn
2 2 2
2 4 4a b c a b
. Tính
23P a b c
khi biểu thức
2 2 7a b c
đạt giá trị lớn nhất.
A.
7
B.
3
C.
3
D.
7
Câu 50: Cho cấp số cộng
n
a
, cấp số nhân
n
b
thỏa mãn
2 1 2 1
0, 1a a b b
và hàm số
3
3f x x x
sao cho
21
2f a f a
và
2 2 2 1
log 2 logf b f b
. Tìm số nguyên dương
n
nhỏ nhất sao cho
2019 .
nn
ba
A. 17 B. 14 C. 15 D. 16
-----------------------------------HẾT-------------------------
mamon made cautron dapan
Toán 001 1
D
Toán 001
2 D
Toán 001 3 C
Toán 001 4
C
Toán 001
5 C
Toán 001 6
A
Toán 001 7
B
Toán 001
8 D
Toán 001 9 A
Toán 001 10
B
Toán 001
11 D
Toán 001 12 A
Toán 001 13
B
Toán
001 14 A
Toán 001 15 C
Toán 001 16
B
Toán 001 17 C
Toán 001 18 D
Toán 001 19 B
Toán 001 20 C
Toán 001 21 A
Toán 001 22 D
Toán 001 23 A
Toán 001 24 C
Toán 001 25 A
Toán 001 26 B
Toán 001 27 D
Toán 001 28 C
Toán 001 29 B
Toán 001 30 D
Toán 001 31 A
Toán 001 32 A
Toán 001 33 B
Toán 001 34 C
Toán 001 35 C
Toán 001 36 B
Toán 001 37 B
Toán 001 38 D
Toán 001 39 D
Toán 001 40 A
Toán 001 41 B
Toán 001 42 A
Toán 001 43 A
Toán 001 44 B
Toán 001 45 A
Toán 001 46 C
Toán 001 47 A
Toán 001 48 C
Toán 001 49 B
Toán 001 50 D
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậpht
tps://facebook.com/groups/900248096852019?ref=share Trang 1
Bản quyền thuộc tập thể thầy cô nhóm STRONG TEAM TOÁN VD-VDC
Nhóm làm 1-2 câu/ tuần nhận lại cả ngàn câu đã qua phản biện 3-4 lần! Mời thầy cô tham gia nhóm!
Câu 1. Cho các hàm số
 
,fx gx
liên tục trên
có
 
5
1
23d5fx gx x


;

5
1
35d21fx gx x



. Tính
 
5
1
dfx gx x


.
A.
5
. B.
1
. C.
5
. D.
1
.
Câu
2. Với
,kn
là hai số nguyên dương tùy ý thỏa mãn
,kn
mệnh đề nào dưới đây sai?
A
.

!
!!
k
n
n
C
knk
. B.
!.
kk
nn
AkC
.
C.
1
1
kk k
nn n
CC C

. D.
!.
kk
nn
CkA
.
Câu 3. Cho số phức
32zi
. Tìm phần ảo của số phức

w12iz
A.
4
. B.
7
. C.
4
. D.
4i
.
Câu
4. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
:20xy

. Mệnh đề nào dưới đây
đúng?
A.

// Oxy
. B.

//Oz
. C.

Oz
. D.

Oy
.
Câu
5. Hàm số nào sau đây nghịch biến trên
?
A.
3
32yx x. B.
42
22yx x .
C.
32
241yx x x . D.
32
252yx x x .
Câu
6. Biết

Fx
là một nguyên hàm của hàm số

sin
x
fx e x

thỏa mãn

00F
. Tìm

Fx
?
A.

cos 2
x
Fx e x

. B.

cos
x
Fx e x

.
C.

cos 2
x
Fx e x

. D.

cos 2
x
Fx e x
.
Câu
7. Cho hàm số

yfx
liên tục trên
và có bảng biến thiên như hình bên. Tìm khẳng định
đúng
A. H
àm số có giá trị nhỏ nhất bằng
0
và giá trị lớn nhất bằng 1.
B. Hà
m số đạt cực đại tại
0x
và đạt cực tiểu tại
1x 
.
C.
Đ
ồ thị hàm số cắt trục hoành tại 3 điểm phân biệt.
D. H
àm số có đúng một cực trị.
Câu 8. Trong không gian với hệ tọa độ
Oxyz
, phương trình nào sau đây không phải phương trình mặt
cầu ?
THPT CHUYÊN HÀ TĨNH
(Đề thi có 6 trang)
NĂM HỌC 2018 - 2019
MÔN: TOÁN
Thời gian: 90 phút
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 2
A.
222
22224650xyzxyz. B.
222
20xyz xyz.
C.
222
37510xyz xyz
. D.
222
34 370xyz xy z
.
Câu 9. Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng
3a . Thể tích khối lăng trụ đã cho bằng
A.
3
9
4
a
. B.
3
3
4
a
. C.
3
3
4
a
. D.
3
33
4
a
.
Câu 10. Đường cong trong hình vẽ dưới đây là đồ thị của một trong bốn hàm số đã cho. Hỏi hàm số đó là
hàm số nào?
A.
4
2
21
4
x
yx
. B.
4
2
1
4
x
yx
. C.
4
2
1
4
x
yx
. D.
42
1
42
xx
y 
.
Câu 12 . Cho hình trụ có đường cao bằng
5
và đường kính đáy bằng
8
. Tính diện tích xung quanh của
hình trụ đó.
A.
40
. B.
20
. C.
80
. D.
160
.
Câu 13. Cho cấp số nhân

n
u
có số hạng đầu
1
3u
, công bội
2q 
. Tính tổng
10
số hạng đầu tiên
của

n
u
.
A.
513
. B.
1023
. C.
513
. D.
1023
.
Câu 14. Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm

1; 2;0A
;

3;2; 8B
. Tìm một vectơ
chỉ phương của đường thẳng
AB
.
A.

1;2; 4u 
. B.

2;4;8u
. C.

1;2; 4u 
. D.

1; 2; 4u 
.
Câu 15. Cho
01,01;,0,abxym
. Trong các mệnh đề sau, mệnh đề nào sai?
A. log log .log
aab
xbx . B.

log . log log
aab
xy x y
.
C.
log
log
log y
a
a
a
x
x
y
. D.
1
log log
m
a
a
xx
m
.
Câu 16. Gọi

C
là đồ thị hàm số
2
21
x
y
x
. Trong các mệnh đề sau, mệnh đề nào sai?
A.

C
có tiệm cận ngang là
1
2
y
. B.

C
có một trục đối xứng.
C.

C
có tiệm cận đứng là
1
2
x
. D.

C
có một tâm đối xứng.
Câu 17. Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
2a
. Tam giác
SAC
vuông cân tại
S
và
nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối cầu ngoại tiếp hình chóp
.SABCD
.
A.
3
2
3
a
. B.
3
43
a . C.
3
4
3
a
. D.
3
4
a
.
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 3
Câu 18. Trong không gian
,Oxyz
cho điểm
()
1; 2; 3A -
và hai đường thẳng
1
13
:;
211
xyz
d
-+
==
-
2
1
:2
1
x
t
dy t
z
ì
=-
ï
ï
ï
ï
=
í
ï
ï
=
ï
ï
î
. Viết phương trình đường thẳng D đi qua
A
vuông góc với
1
d
và
2
.d
A.
1
2
3
x
t
y
t
zt



B.
2
12
33
x
t
y
t
zt



. C.
1
2
3
x
t
y
t
zt



. D.
12
2
33
x
t
y
t
zt



Câu 19.
Cho hình chóp .S ABCD có đáy
A
BCD là hình chữ nhật,
;3;
A
B a AD a SA ABCD
và
SC
tạo với đáy một góc
0
45
. Gọi
M
là trung điểm cạnh
SB
,
N
là điểm trên cạnh
SC
sao cho
1
2
SN NC
. Tính thể tích khối chóp
.SAMN
.
A.
3
3
9
a
. B.
3
3
18
a
. C.
3
3
12
a
. D.
3
3
6
a
.
Câu 20. Diện tích hình phẳng giới hạn bởi các đường
3
,10yxy x và trục
Ox
là
A.
32
. B.
26
. C.
36
. D.
40
.
Câu 21 . Biết
12
log 27 a . Tính
6
log 16 theo a
A.
43
3
a
a
. B.
43
3
a
a
. C.

3
43
a
a
. D.

3
43
a
a
.
Câu 22. Biết rằng đồ thị hàm số
32
2532yx x x chỉ cắt đường thẳng
34yx
tại một điểm
duy nhất

;
M
ab. Tổng của ab bằng
A.
6
. B.
3
. C.
6
. D.
3
.
Câu 23. Biết rằng phương trình

2
33
5log log 9 1 0xx có hai nghiệm là
12
,
x
x
. Tìm khẳng định đúng?
A.
5
12
3xx
. B.
12
5
1
3
xx
. C.
12
1
5
xx
. D.
12
1
5
xx 
.
Câu 24 . Gọi
12
,zz là hai nghiệm phức của phương trình
2
570zz
. Tính
22
12
Pz z
.
A.
47
.
B. 56 . C. 14. D.
27
.
Câu 25. Cho khối nón có thiết diện qua trục là tam giác cân có một góc
120
o
và cạnh bên bằng a . Tính
thể tích khối nón.
A.
3
8
a
. B.
3
8
a
. C.
3
3
24
a
. D.
3
4
a
.
Câu 26. Tập xác định của hàm số

1
2
3
32yx x
là
A.
\1;2 . B.
;1 2; 
. C.
1; 2 . D.
.
Câu 27. Tập nghiệm của bất phương trình
()
1
2
log 2 1 0x +>
là:
A.
1
;0 .
4



B.

0; .
C.
1
;.
2




D.
1
;0 .
2



Câu 28. Cho hình chóp .S ABCD có đáy là hình thoi cạnh 2a ,
60ABC , 3SA a và

SA ABCD
. Tính góc giữa
SA
và
mp SBD
.
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 4
A.
60
. B.
90
. C.
30
. D.
45
.
Câu 29. Biết

e
2
1
ln 2
dln
e+1 e+1
1
xa
x
bc
x

với
,,abc
. Tính abc.
A. 1 . B. 1. C. 3 . D. 2 .
Câu 30. Có bao nhiêu tiếp tuyến của đồ thị hàm số
32
32yx x đi qua điểm
3; 2A
?
A.
3
. B.
0
. C.
1
. D.
2
.
Câu 31. Gọi
,
M
m
tương ứng là giá trị lớn nhất và nhỏ nhất của hàm số
2cos 1
cos 2
x
y
x
. Khi đó ta có
A.
90Mm. B. 90Mm. C. 90Mm. D. 0Mm.
Câu 32 .
Trong không gian
Oxyz
, viết phương trình mặt cầu tâm

1;3;0I và tiếp xúc với mặt phẳng

:2 2 11 0Pxyz .
A.

22
2
134xyz
.
B.

22
2
134xyz
.
C.

22
2
132xyz
.
D.

22
2
4
13
9
xyz
.
Câu 33. Cho số phức z thoả mãn
12 23 412zizi i
. Tìm toạ độ điểm
M
biểu diễn số
phức
z .
A.

3;1M
. B.
3; 1M
. C.
1;3M
. D.
1;3M
.
Câu 34. Cho các hàm số
 

3
,,
1
fx
yfxygxy
gx

. Hệ số góc của các tiếp tuyến của các đồ thị
hàm số đã cho tại điểm có hoành độ
1
x
bằng nhau và khác 0. Khẳng định nào dưới đây là
khẳng định đúng?
A.
13f  . B.
13f  . C.

11
1
4
f  .
D.

11
1
4
f  .
Câu 35. Trên các cạnh
, ,
A
BBCCA
của tam giác
A
BC
lần lượt lấy
2, 4,
(
)
3nn> điểm phân biệt
(các điểm không trùng với các đỉnh của tam giác). Tìm
n biết rằng số tam giác có các đỉnh
thuộc
6n+ điểm đã cho là 247
A.6 . B.
7
. C.
5
. D.
8
.
Câu 36. Cho hàm số

f
x
liên tục trên
. Biết

ln 2
0
e1d 5
x
fx
và

3
2
23
d3
1
xfx
x
x
. Tính

3
2
dIfxx
.
A.
2I
. B.
4I
. C.
2I 
. D.
8I
.
Câu 37. Cho khối hộp
A
BCDABCD

có thể tích
V
. Các điểm
,,
M
NP
thỏa mãn 2
A
MAC

,
3
A
NAB
 
, 4
A
PAD

. Tính thể tích khối chóp
A
MNP
theo
V
.
A. 6V . B. 8V . C. 12V . D. 4V .
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 5
Câu 38. Cho số phức
z
thỏa mãn
15z 
,
11 5
17z
z
 và
z
có phần ảo dương. Tìm tổng phần thực
và phần ảo của
z
.
A. 2 . B. 4 . C.
6
. D.
8
.
Câu 39. Trong không gian với hệ tọa độ
Ox
y
z
, cho điểm
1;2;2A và đường thẳng
615
:
211
xyz
d


. Tìm tọa độ điểm
B đối xứng với
A
qua d .
A.
3;4; 4B  . B.
2; 1;3B . C.
3;4; 4B . D.
3; 4;4B .
Câu 40. Ông An có một khu đất hình elip với độ dài trục lớn
10
m và độ dài trục bé
8
m. Ông An muốn
chia khu đất thành hai phần, phần thứ nhất là một hình chữ nhật nội tiếp elip dùng để xây bể cá
cảnh và phần còn lại dùng để trồng hoa. Biết chi phí xây bể cá là
1000000 đồng trên
2
1m
và chi
phí trồng hoa là
1200000
đồng trên
2
1m
. Hỏi ông An có thể thiết kế xây dựng như trên với tổng
chi phí thấp nhất gần nhất với số nào sau đây?
A.
67398224
đồng. B.
67593346
đồng. C.
63389223
đồng. D.
67398228
đồng.
Câu 41. Trong không gian với hệ tọa độ
Ox
y
z
, cho đường thẳng
5712
:
22 1
xyz
d


và mặt phẳng
:2330xyz

. Gọi
M
là giao điểm của
d
với
,
A
thuộc
d
sao cho 14AM .
Tính khoảng cách từ
A
đến

.
A. 2. B. 3. C. 6. D. 14 .
Câu 42 . Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số
24 2 2
2019 1ymx m mx
có
đúng một điểm cực trị.
A.
2019
. B.
2020
.
C.
2018
. D.
2017
.
Câu 43. Gọi
S
là tập tất cả các giá trị của tham số m để đồ thị hàm số
3
32 2
32432
y
xx xx mx
có tiệm cận ngang. Tổng các phần tử của
S
là
A.
2
. B.
2
.
C.
3
. D.
3
.
Câu 44.
Cho hàm số
2
ln
f
xxx
. Tính

1 2 2019
P...
ff f
ee e .
A.
2020
P
2019
.
B.
2019
P
2020
.
C.
2019
P e
. D.
2019
P
2020
 .
Câu 45. Cho các số phức
1
z ,
2
z thỏa mãn phương trình
23 5zi
và
12
6zz
. Biết rằng tập hợp
các điểm biểu diễn số phức
12
wz z là một đường tròn. Tính bán kính đường tròn đó.
A.
8R
. B.
4R
. C. 22R . D.
2R
.
Câu 46. Cho các số thực
x
,
y
thay đổi thỏa mãn
22
1
x
yxy và hàm số
32
231ft t t
.
Gọi
M
,
m
tương ứng là giá trị lớn nhất và nhỏ nhất của
52
4
xy
Qf
xy





. Tổng
M
m
bằng
A.
432
. B.
452
. C.
442
. D.
422
.
Câu 47. Trong các khối chóp tứ giác đều .S ABCD mà khoảng cách từ
A
đến mp
()SBC
bằng 2a , khối
chóp có thể tích nhỏ nhất bằng
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 6
A.
3
23a . B.
3
2a . C.
3
33a . D.
3
43a .
Câu 48. Tổng tất cả các giá trị của tham số m để phương trình
2
2
212
23
3log22
xx xm
xx
xm



có
đúng ba nghiệm phân biệt là
A.
3
. B.
2
. C.
3
. D.
2
.
Câu 49. Cho các số thực ,,abc thỏa mãn
222
244abc ab . Tính
23Pa b c
khi biểu
thức
227ab c
đạt giá trị lớn nhất.
A. 7P . B. 3P . C. 3P  . D. 7P  .
Câu 50. Cho cấp số cộng

n
a
, cấp số nhân

n
b
thoả mãn
21
0aa,
21
1bb và hàm số
3
3
f
xx x
sao cho
21
2
f
a
f
a
và
22 21
log 2 log
f
b
f
b
. Tìm số nguyên
dương
n nhỏ nhất sao cho
2019
nn
ba
A. 17. B. 14. C. 15. D. 16.
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 7
PHÂN TÍCH BÌNH LUẬN ĐỀ THI THỬ ĐẠI HỌC CHUYÊN HÀ TĨNH
Câu 1.
Cho các hàm số
 
,
f
x
g
x
liên tục trên
có
 
5
1
23d5fx gx x



;
 
5
1
35d21fx gx x


. Tính
 
5
1
d
f
xgx x


.
A. 5 . B. 1. C. 5. D. 1 .
Lời giải
Tác giả: Lê Hữu Đức; Fb: Le Huu Duc
Chọn D
Đặt

5
1
dIfxx
;

5
1
d
J
gx x
Ta có
23 5
35 21
IJ
IJ


2
3
I
J

 
5
1
d1fx gx x I J



.
Câu 1.1. Cho các hàm số
 
,
f
x
g
x
liên tục trên
có

5
2
d8fx x
và

2
5
d3gx x
. Tính
 
5
2
41dIfxgx x


.
A.
11
. B.
13
. C.
27
. D.
3
.
Lời giải
Chọn B
Ta có:
 
5
2
41dIfxgx x



 
52
5
2
25
d4 d
f
xx gxxx


84.3 52 13
.
Câu 1.2. Cho các hàm số
 
,
f
x
g
x liên tục trên có
 
3
1
32d1
f
xgxx

;
 
3
1
2d3fx gx x


. Tính

1
0
21d
f
xx
.
A.
5
7
.
B.
10
7
.
C.
11
14
.
D.
5
14
.
Lời giải
Tác giả: Lê Hữu Đức; Fb: Le Huu Duc
Chọn D
Đặt

3
1
dIfxx
;

3
1
d
J
gx x
Ta có
32 1
23
IJ
IJ


5
7
11
7
I
J

 
13
01
15
21d d
214
fx x ftt

.
Câu 2. Với
,kn
là hai số nguyên dương tùy ý thỏa mãn
,kn
mệnh đề nào dưới đây sai?
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 8
A.

!
!!
k
n
n
C
knk
. B. !.
kk
nn
A
kC .
C.
1
1
kk k
nn n
CC C
. D. !.
kk
nn
CkA .
Lời giải
Tác giả: Lục Minh Tân; Fb: Lục Minh Tân
Chọn D

!
.
!. ! !
k
k
n
n
A
n
C
knk k

Câu 2.1. Với
,kn
là hai số nguyên dương tùy ý thỏa mãn
,kn
mệnh đề nào dưới đây sai?
A.
knk
nn
CC
. B.
11
1
kk k
nn n
CC C


.
C.
!
k
n
n
P
C
k
. D.
!
k
k
n
n
A
C
k
.
Lời giải
Tác giả: Lục Minh Tân; Fb: Lục Minh Tân
Chọn C

!1
.!.
!. ! !
kkkk
nnnn
n
CAAkC
knk k

Câu 2.2. Với
,kn
là hai số nguyên dương tùy ý thỏa mãn
4 kn
mệnh đề nào dưới đây sai?
A.
4321
1234
.
kkkkkk
nnnnnn
CCCCCC


 B.

2
!
.
2! 2!
k
n
n
C
knk

C.

!
.
!
k
n
n
A
nk
D.
!. .
kk
nn
AkC
Lời giải
Tác giả: Lục Minh Tân; Fb: Lục Minh Tân
Chọn B



2
!!
.
2! 2!
2! 2 !
k
n
nn
C
knk
knk



Câu 3. Cho số phức
32zi
. Tìm phần ảo của số phức
w12iz
A.
4
. B.
7
. C.
4
. D.
4i
.
Lời giải
Tác giả: Nguyễn Thị Thơm; Fb: Thom nguyen
Chọn C
Ta có

w12 1232 74iz i i i  . Số phức w có phần ảo bằng
4
Câu 3.1. Cho số phức 32zi . Tìm phần ảo của số phức
w1iz
A.
1
. B.
5
. C.
1
. D.i .
Lời giải
Tác giả: Nguyễn Thị Thơm; Fb: Thom nguyen
Chọn C
Ta có

w1 1 32 5iz i i i 
. Số phức w có phần ảo bằng
1
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 9
Câu 3.2. Cho số phức
32zi
. Tìm phần ảo của số phức liên hợp của
w2iz
A.
1
. B.
5
. C.
1
. D.i .
Lời giải
Tác giả: Nguyễn Thị Thơm; Fb: Thom nguyen
Chọn C
Ta có
w2 2 32 8iz i i i  . Số phức liên hợp của
w
có phần ảo bằng 1 .
Câu 4. Trong không gian với hệ tọa độ
Ox
y
z
, cho mặt phẳng
:20xy
. Mệnh đề nào dưới đây
đúng?
A.
// Ox
y
. B.
//Oz
. C.
Oz
. D.
Oy
.
Lời giải
Tác giả: Nguyễn Bảo Mai; Fb: Bao An
Chọn C

đi qua điểm
0;0; 0O nên loại phương án A và B.
có một vectơ pháp tuyến là
1; 2; 0n 
và
.0nk
nên
Oz
.
Câu 4.1.
Trong không gian với hệ tọa độ
Ox
y
z
, cho mặt phẳng
:230xy

. Mệnh đề nào dưới
đây đúng?
A.
// Oxy
. B.
//Oz
. C.
Oz
. D.
Oz
.
Lời giải
Chọn B
có một vectơ pháp tuyến là
1; 2; 0n 
và nên
//Oz
hoặc
Oz
.

không đi qua điểm
0;0;0O nên
//Oz
.
Câu 4.2. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
:2 3 0z

. Mệnh đề nào dưới đây
đúng?
A.
Ox
y
. B.
//Oz
. C.
Oz
. D.
Oz
.
Lời giải
Chọn D
có một vectơ pháp tuyến là
0;0; 2n
cùng phương với
0;0;1k
và nên
không
đi qua điểm
0;0; 0O
nên
Oz
.
Câu 5. Hàm số nào sau đây nghịch biến trên
?
A.
3
32yx x. B.
42
22yx x .
C.
32
241yx x x . D.
32
252yx x x .
Lời giải
Tác giả: Phạm Văn Tuấn; Fb: Phạm Tuấn
Chọn C
Xét hàm số
3
32yx x có hệ số
10a 
nên hàm số không thể nghịch biến trên
loại
đáp án A.
Xét hàm số
42
22yx x
là hàm số bậc 4 trùng phương nên hàm số không thể nghịch biến
trên
loại đáp án B.
Xét hàm số
32
241yx x x có
2
3440yxx
 ,
x
hàm số nghịch biến
trên
.
Câu 5.1. Hàm số nào sau đây đồng biến trên
?
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 10
A.
21yx
.
B.
3
31yx x.
C.
2
1yx. D.
3
31yx x.
Lời giải
Tác giả: Phạm Văn Tuấn; Fb: Phạm Tuấn
Chọn D
Xét hàm số
21yx
có
20y

hàm số nghịch biến trên
.
Xét hàm số
3
31yx x có
2
33yx
;
1
0
1
x
y
x


hàm số không thể đồng biến
trên
.
Xét hàm số
2
1yx có
2yx
;
00yx

hàm số không thể đồng biến trên
.
Xét hàm số
3
31yx x có
2
330yx
, x
hàm số luôn đồng biến trên .
Câu 6. Biết
Fx là một nguyên hàm của hàm số

sin
x
f
xe x
 thỏa mãn

00F . Tìm

Fx?
A.
cos 2
x
Fx e x
 . B.
cos
x
Fx e x
 .
C.
cos 2
x
Fx e x

. D.
cos 2
x
Fx e x
.
Lời giải
Tác giả: Phạm Thị Thu Trang; Fb: Trang Phạm
Chọn A
Ta có
dsinddsindcos
xx x
F
x fxx e xxex xxe xC



.
Lại có
0
00 cos0 0 2FeCC  .
Vậy
cos 2
x
Fx e x

.
Câu 6.1. Cho hàm số

2
4
sin
m
f
xx
. Giá trị của tham số để nguyên hàm
Fx
của hàm số
f
x
thỏa mãn điều kiện
01F
và
48
F



là:
A.
4
3
m .
B.
3
4
m .
C.
3
4
m .
D.
4
3
m .
Lời giải
Tác giả: Phạm Thị Thu Trang; Fb: Trang Phạm
Chọn C
Ta có
22
44
sin d d sin d





mm
x
xxxx

411
sin 2
24

m
x
xxC
.
Giải hệ

01
1
1
411
3
..sin
4244 2 8
4
48
F
C
C
m
C
m
F











.
Câu 7. Cho hàm số
yf
x
liên tục trên
và có bảng biến thiên như hình bên. Tìm khẳng định
đúng
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 11
A. Hàm số có giá trị nhỏ nhất bằng
0
và giá trị lớn nhất bằng 1.
B. Hàm số đạt cực đại tại
0x
và đạt cực tiểu tại
1x 
.
C. Đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt.
D. Hàm số có đúng một cực trị.
Lời giải
Tác giả: Nguyễn Thị Thanh Vân; Fb: Thanh Van
Chọn B
Theo bảng biến thiên ta có

fx
đổi dấu từ âm sang dương khi qua
1x 
nên hàm số

fx
đạt cực tiểu tại
1x 
;

fx
đổi dấu từ dương sang âm khi qua
0x
nên hàm số

fx
đạt cực đại tại
0x
.
Câu 7.1 Cho hàm số

yfx
xác định và liên tục trên

\1
và có bảng biến thiên như sau:
Khẳng định nào sau đây là sai?
A. Giá trị nhỏ nhất của hàm số trên đoạn

0;4
bằng
2
.
B. Hàm số đạt cực tiểu tại
3x
.
C. Đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt.
D. Hàm số nghịch biến trên khoảng

;3
.
Lời giải
Tác giả: Nguyễn Thị Thanh Vân; Fb: Thanh Van
Chọn D
Vì hàm số không xác định tại
1x 
thuộc khoảng

;3
nên hàm số không đơn điệu trên
khoảng đó.
Câu 8. Trong không gian với hệ tọa độ
Oxyz
, phương trình nào sau đây không phải phương trình mặt
cầu ?
A.
222
22224650xyzxyz. B.
222
20xyz xyz.
C.
222
37510xyz xyz. D.
222
34 370xyz xy z
.
Phân tích:
Nhận dạng bài toán: Bài toán nhận dạng phương trình mặt cầu.
Kiến thức cần nhớ: Phương trình mặt cầu là phương trình có dạng:
222
222 01xyz axbyczd
với điều kiện
222
0abcd
.
Phương pháp giải:
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 12
- Bước 1: Kiểm tra phương trình đã cho có đúng dạng chưa? Lưu ý: Ở phương trình (1) hệ số
của
222
,,
x
yz bằng nhau và bằng 0k đều có thể đưa về dạng (1) bằng cách chia cả 2 vế của
phương trình cho
k .
- Bước 2: Kiểm tra điều kiện
222
0abcd
( đặc biệt: nếu 0d thì
222
0abcd
luôn luôn đúng ), rồi kết luận.
Lời giải
Tác giả: Vũ Nga; Fb: Nga Vu
Chọn D
- Cả 4 đáp án đều có dạng (1).
- Đáp án A, B, C đều thỏa mãn điều kiện
222
0abcd
và ở đáp án D có
3
2
a ,
2b ,
3
2
a
,
7d
222
0abcd
( không thỏa mãn ).
Câu 8.1 Trong không gian với hệ tọa độ
Oxyz
, phương trình nào sau đây không phải phương trình mặt
cầu ?
A.
222
33320xyzx. B.
222
210xyz xyz.
C.
222
8210xyz xy. D.
222
24670xyz xyz.
Lời giải
Tác giả: Vũ Nga; Fb: Nga Vu
Chọn D
- Phương trình ở đáp án D không đúng dạng (1) do hệ số của
222
,,
x
yz không bằng nhau.
Câu 8.2 Gọi
S
là tập hợp tất cả các giá trị nguyên của m để phương trình

222 2
2242710xyz m xmymzm
là phương trình mặt cầu. Số phần tử của
S
là
A.
6
. B.
7
. C.
4
. D.
5
.
Lời giải
Tác giả: Vũ Nga; Fb: Nga Vu
Chọn D
Phương trình

222 2
2242710xyz m xmymzm
là phương trình mặt cầu

2
22 2
24 7 10mmmm
2
450mm
15m có 5 giá trị
nguyên thỏa mãn.
Câu 9. Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng 3a . Thể tích khối lăng trụ đã cho bằng
A.
3
9
4
a
. B.
3
3
4
a
. C.
3
3
4
a
. D.
3
33
4
a
.
Lời giải
Tác giả: Vũ Danh Được; Fb: Danh Được Vũ
Chọn A
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 13
Xét khối lăng trụ tam giác đều
.ABC A B C

có tất cả các cạnh bằng 3a .
Khi đó
2
33
4
ABC
a
S
. Do đó thể tích khối lăng trụ đã cho bằng
23
339
3.
44
aa
Va

.
Câu 9.1. Cho khối lăng trụ đứng
.ABCD A B C D

có
BB a
, đáy
ABCD
là hình thoi với
2, 3AC a BD a
. Thể tích khối lăng trụ
.ABCD A B C D

là
A.
3
3a
. B.
3
3
2
a
. C.
3
3
3
a
. D.
3
23a
.
Lời giải
Tác giả: Vũ Danh Được; Fb: Danh Được Vũ
Chọn A
B
'
C'
A
C
B
A
'
C'
D'
B'
C
A
A
'
D
B
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 14
Ta có
2
1
.. 3
2
ABCD
SACBDa

.
Do đó thể tích khối lăng trụ đã cho bằng
23
.3 3Vaa a.
Câu 10. Đường cong trong hình vẽ dưới đây là đồ thị của một trong bốn hàm số đã cho. Hỏi hàm số đó
là hàm số nào?
A.
4
2
21
4
x
yx

. B.
4
2
1
4
x
yx

. C.
4
2
1
4
x
yx

. D.
42
1
42
xx
y

.
Lời giải
Tácgiả:Quỳnh Giao; Fb:QGiaoDo
Chọn A
Vì đồ thị hàm số có bề lõm quay lên trên và có ba điểm cực trị là
2x = 0x =
và
2x =-
nên
chọn đáp án A
Phát triển
Câu 10.1. Trong các hình vẽ sau, hình nào biểu diễn đồ thị hàm số
42
23yx x=- + +
A. . B. .
C. . D. .
Lời giải
Tácgiả:Quỳnh Giao; Fb:QGiaoDo
Chọn A
Hàm số đã cho có ba điểm cực trị là
1; 0xx==
và
1x =-
đồng thời có bề lõm quay xuống
dưới nên chọn A
Câu 11. Cho
01; ,0abc
thỏa mãn log 3 ; log 2
aa
bc. Tính

32
log
a
ab c .
A.
18
. B.
7
. C.
10
. D.
8
.
Lời giải
Tác giả: Phạm Thanh My ; Fb: Thanh My Phạm
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 15
Chọn D
Ta có
32 3 2
1
log log log log 3 2log log 8
2
aaaaaa
ab c a b c b c
Câu 11.1. Cho
01; ,0abc
thỏa mãn

2
2
27
log 3 ; log
2
a
a
bbc
. Tính
3
log
a
ab
c
.
A.
2
. B.
3
2
.
C.
105
2
.
D.
11
2
.
Lời giải
Tác giả: Phạm Thanh My ; Fb: Thanh My Phạm
Chọn B
Ta có
2
log 3 log 6
a
a
bb

2
15 27 3
log 2 log log log
222
aaaa
bc b c c
3
133
log log log log 1 2
322
aaaa
ab
abc
c

Câu 12 . Cho hình trụ có đường cao bằng
5
và đường kính đáy bằng
8
. Tính diện tích xung quanh của
hình trụ đó.
A. 40
. B. 20
. C. 80
. D. 160
.
Lời giải
Tác giả: Trần Thị Thơm; Fb: Tranthom
Chọn A
Gọi
h,l
và r lần lượt là đường cao, đường sinh và bán kính đáy của hình trụ.
Ta có:
4, 5rhl
.
Ta có: 2 2 40
xq
Srlrh

.
Câu 12.1 Diện tích toàn phần của hình trụ có đường kính và đường sinh cùng bằng
4
cm là
A.
2
16cm . B.
2
24 cm . C.
2
16 2 cm
.
D.
2
32 2 cm
.
Lời giải
Tác giả: Trần Thị Thơm; Fb: Tranthom
Chọn B
Gọi
l
và r lần lượt là đường sinh và bán kính đáy của hình trụ.
Ta có:
2, 4rl
.
Diện tích toàn phần của hình trụ là
2
22
tp
Srlr
2
24 cm
.
Câu 12.2 Trong không gian, cho hình chữ nhật
A
BCD
có
1
A
B
và
2
A
D
. Gọi
,
M
N
lần lượt là
trung điểm của
A
D
và
BC
. Quay hình chữ nhật đó xung quanh trục
M
N
, ta được một hình
trụ. Tính diện tích toàn phần
S
tp
của hình trụ đó.
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 16
A.
4
tp
S
. B.
2
tp
S
. C.
6
tp
S
. D.
10
tp
S
.
Lời giải
Tác giả: Trần Thị Thơm; Fb: Tranthom
Chọn A
Gọi
l
và
r
lần lượt là đường sinh và bán kính đáy của hình trụ.
Ta có:
1, 1
2
AD
rlAB
.
Diện tích toàn phần của hình trụ là
2
22
tp
Srlr

4
.
Câu 13. Cho cấp số nhân

n
u
có số hạng đầu
1
3u
, công bội
2q 
. Tính tổng
10
số hạng đầu tiên
của

n
u
.
A.
513
. B.
1023
. C.
513
. D.
1023
.
Lời giải
Tác giả: Nguyễn Thị Thu Trang 215; Fb: Trang Nguyễn
Chọn B
Áp dụng công thức

1
1
1
n
n
uq
S
q
, ta có


10
10
31 2
1023
12
S





.
Câu 13.1. Cho cấp số nhân

n
u
có số hạng đầu
1
2u
, công bội
1
3
q 
. Khi đó
2
6561
là số hạng thứ
A.
10
. B.
9
. C.
8
. D.
7
.
Lời giải
Tác giả: Nguyễn Thị Thu Trang 215; Fb: Trang Nguyễn
Chọn B
Áp dụng công thức
1
1
n
n
uuq
, ta có
1
21
2.
6561 3
n



1
11
6561 3
n




18n 9n
.
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 17
Câu 13.2. Cho cấp số nhân

n
u có công bội
2q
, tổng 10 số hạng đầu tiên bằng
1023
2
. Tìm số
hạng đầu
1
u
của cấp số nhân

n
u .
A.
1
2u  . B.
1
1
2
u 
. C.
1
1
2
u
. D.
1
2u .
Lời giải
Tác giả: Nguyễn Thị Thu Trang 215; Fb: Trang Nguyễn
Chọn B
Áp dụng công thức

1
1
1
n
n
uq
S
q
, ta có


1
1
1
n
n
Sq
u
q

1
10
1023
12
1
2
12 2
u


.
Câu 14. Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
1; 2;0A ;

3;2; 8B . Tìm một vectơ
chỉ phương của đường thẳng
A
B
.
A .

1;2; 4u 
. B.
2;4;8u
. C.
1;2; 4u 
. D.
1; 2; 4u 
.
Tác giả: Nguyễn Ngọc Chi; Fb: Nguyễn Ngọc Chi
Lời giải
Chọn A
Ta có
2;4; 8AB 

, vậy đường thẳng
A
B
có một vectơ chỉ phương là

1;2; 4u 
.
Câu 14.1. Trong không gian với hệ tọa độ
Oxyz
, cho
23 5
OA i j k

;
24OB j k

. Tìm một vectơ
chỉ phương của đường thẳng
A
B
.
A .
2;5; 1u 
. B.
2;3; 5u 
. C.
2; 5; 1u 
. D.
2;5; 9u 
.
Tác giả: Nguyễn Ngọc Chi; Fb: Nguyễn Ngọc Chi
Lời giải
Chọn A
Ta có
23 5
OA i j k

2;3; 5Avà
24
OB j k


0; 2; 4B.
Ta có

2; 5;1AB 

, hay đường thẳng
A
B có một vectơ chỉ phương là
2;5; 1u 
.
Câu 15. Cho 01,01;,0,abxym . Trong các mệnh đề sau, mệnh đề nào sai?
A. log log .log
aab
x
bx . B.

log . log log
aab
x
yxy
.
C.
log
log
log y
a
a
a
x
x
y
. D.
1
log log
m
a
a
x
x
m
.
Lời giải
Tác giả: Nguyễn Tất Thành; Fb: Thanh Nguyen
Chọn C
Ta có:
log log log y
aaa
x
x
y

.
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 18
Câu 15.1 .Với các số thực , dương bất kì, . Mệnh đề nào dưới đây đúng?
A. B.
C. D.
Lời giải
Tác giả: Nguyễn Tất Thành; Fb: Thanh Nguyen
Chọn B
Ta có:

log . log log
aab
xy x y
.
Câu 15.2 .Cho , . Biểu diễn của theo và là
A. . B. . C. . D. .
Lời giải
Tác giả: Nguyễn Tất Thành; Fb: Thanh Nguyen
Chọn B
Ta có .
Câu 16. Gọi

C
là đồ thị hàm số
2
21
x
y
x
. Trong các mệnh đề sau, mệnh đề nào sai?
A.

C
có tiệm cận ngang là
1
2
y
. B.

C
có một trục đối xứng.
C.

C
có tiệm cận đứng là
1
2
x
. D.

C
có một tâm đối xứng.
Lời giải
Tác giả: Nguyễn Mạnh Dũng; Fb: Mạnh Dũng
Chọn B
Tập xác định
D
1
\
2



.
Ta có:
21
lim lim
212
xx
x
y
x
 


C
có tiệm cận ngang
1
2
y
A đúng.
11
22
2
lim lim
21
xx
x
y
x

 

 
 


C
có tiệm cận đứng
1
2
x
C đúng.
11
;
22
I



là tâm đối xứng của đồ thị D đúng.

C
có 2 trục đối xứng là
1
2
y
và
1
2
x
B sai.
Câu 16.1. Gọi

C
là đồ thị hàm số
2
24
4
x
y
x
. Khẳng định nào sau đây là đúng?
A.

C
có 2 tiệm cận đứng là
2; 2xx
. B.

C
không có tiệm cận đứng.
C.

C
có tiệm cận ngang là
2y
. D.

C
có 1 tiệm cận đứng là
2x
.
x
y 1y
2
2
2
log
log
log
x
x
yy



222
log log log
xy
x
y


2
222
log 2 log log
xy
x
y

222
log log log
xy
x
y

2
log 5a
2
log 9b
2
40
log
3
P
a
b
32
P
ab
1
3
2
P
ab
3
2
a
P
b
3
P
ab
2
40
log
3
P
22
log 40 log 3
22 2
1
log 8 log 5 log 9
2

1
3
2
ab
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 19
Lời giải
Chọn D
Tập xác định
D
\2;2
.
Ta có:
2
24
lim lim 0
4
xx
x
y
x
 

C
có tiệm cận ngang
0y
A sai.
Giải phương trình :
2
2
40
2
x
x
x


.
2
22
24
lim lim
4
xx
x
y
x



C có tiệm cận đứng
2x
B sai.
Tuy nhiên
 
22
22
24 24 1
lim lim
442
xx
xx
xx

 



2x  không thể là tiệm cận đứng của

C
C sai.
Câu 16.2. Có bao nhiêu giá trị m để đồ thị hàm số
2
1
4
x
y
x
mx

có đúng 1 tiệm cận đứng?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn C
Ta có:
10 1xx
.
TH1:
2
40xmx
có nghiệm kép. 0
m

2
16 0m
4
4
m
m

.
TH2:
2
40xmx
có 2 nghiệm phân biệt trong đó có 1 nghiệm là
1x 
.

2
0
140
m
m


4
4
5
m
m
m

5m
.
Vậy có 3 giá trị của
m để đồ thị hàm số
2
1
4
x
y
x
mx

có đúng 1 tiệm cận đứng.
Nhận xét admin :
Đặt
2
4fx x mx
. Yêu cầu bài toán

0
44
10
5
mm
f
m




Câu 17. Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh 2a . Tam giác
SAC
vuông cân tại
S
và
nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối cầu ngoại tiếp hình chóp
.S ABCD
.
A.
3
2
3
a
. B.
3
43
a . C.
3
4
3
a
. D.
3
4
a
.
Lời giải
Tác giả: Nguyễn Đình Hải ; Fb:Nguyen Dinh Hai
Chọn C
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 20
Gọi
O
là giao điểm của hai đường chéo
AC
và
BD
.
Ta có
90ABC ,
90ADC và
90ASC suy ra các đỉnh
B
,
D
,
S
cùng nhìn đoạn thẳng
AC
dưới một góc vuông nên
O
là tâm mặt cầu ngoại tiếp chóp
.SABCD
và
2

AC
ROA a
.
Vậy
33
44
33

VR a
.
Câu 17.1 (THPTQG năm 2017 Mã đề 104) Cho hình chóp
.S ABCD
có đáy là hình chữ nhật với
3AB a
,
4BC a
,
12SA a
và
SA
vuông góc với đáy. Tính bán kính
R
của mặt cầu ngoại
tiếp hình chóp
.SABCD
.
A.
5
2
a
R
. B.
17
2
a
R
. C.
13
2
a
R
. D.
6Ra
.
Lời giải
Chọn C
Ta có:
22
5AC AB BC a
Vì
SA AC
nên
22
13SC SA AC a
Nhận thấy:

BC AB
BC SB
BC SA
.Tương tự:
CD SD
Do các điểm
,A
,B
D đều nhìn đoạn thẳng
SC
dưới một góc vuông nên gọi
I
là trung điểm
của đoạn thẳng
SC
thì
I
là tâm mặt cầu ngoại tiếp hình chóp
.SABCD
.
O
D
A
B
C
S
12a
4a
3a
I
O
C
A
D
B
S
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 21
Vậy
13
22

SC a
R
.
Câu 17.2 (THPT QG 2017 Mã đề 105) Cho tứ diện
ABCD
có tam giác
BCD
vuông tại
C
,
AB
vuông
góc với mặt phẳng
BCD
,
5AB a
,
3BC a
và
4CD a
. Tính bán kính
R
của mặt cầu
ngoại tiếp tứ diện
ABCD
.
A.
52
3
a
R
. B.
53
3
a
R
. C.
52
2
a
R
. D.
53
2
a
R
.
Lời giải
Chọn C
Tam giác
BCD
vuông tại
C
nên áp dụng định lí Pitago, ta được
5BD a
.
Tam giác
ABD
vuông tại
B
nên áp dụng định lí Pitago, ta được
52.AD a
Vì
B
và
C
cùng nhìn
AD
dưới một góc vuông nên tâm mặt cầu ngoại tiếp tứ diện
ABCD
là
trung điểm
I
của
AD
. Bán kính mặt cầu này là:
52
.
22

AD a
R
Câu 17.3 (Đề tham khảo lần 2 2017) Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
32,a
cạnh bên bằng
5.a
Tính bán kính
R
của mặt cầu ngoại tiếp hình chóp
..SABCD
A. 3Ra. B.
2Ra
. C.
25
8
a
R
. D.
2Ra
.
Lời giải
Chọn C
Gọi
O
là tâm hình vuông
ABCD
,
G
là trung điểm
SD
,
,GI SD I SO
.
Ta có cạnh đáy bằng
32a
nên
32.2 6BD a a
,
3OD a
.
Xét
SOD
vuông tại
O
ta có:
22
4SO SD OD a
Ta có
SOD SGI
∽
(g-g), suy ra

2
125
4. 5
28

SO SD a
aR a R
SG SI
.
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 22
Câu 18. Trong không gian
,Oxyz
cho điểm
()
1; 2; 3A -
và hai đường thẳng
1
13
:;
211
xyz
d
-+
==
-
2
1
:2
1
x
t
dy t
z
ì
=-
ï
ï
ï
ï
=
í
ï
ï
=
ï
ï
î
. Viết phương trình đường thẳng D đi qua
A
vuông góc với
1
d
và
2
.d
A.
1
2
3
x
t
y
t
zt



B.
2
12
33
x
t
y
t
zt



. C.
1
2
3
x
t
y
t
zt



. D.
12
2
33
x
t
y
t
zt



Lời giải
Tác giả: Văn Bùi Vũ ; Fb: Van Tuan Vu
Chọn D
Đường thẳng
1
d có vtcp
(
)
1
2; 1;1u =-

, đường thẳng
2
d có vtcp
()
2
1; 2; 0u =-

.
Đường thẳng
D
vuông góc với
1
d
và
2
d
nên nhận
(
)
12
,2;1;3uuu
éù
==--
êú
ëû

hoặc
()
2;1; 3u =-
làm vectơ chỉ phương.
Phương trình đường thẳng
12
:2.
33
x
t
yt
zt
ì
=+
ï
ï
ï
ï
D=-+
í
ï
ï
=-
ï
ï
î
Câu 18.1 Trong không gian
,Ox
y
z
cho điểm
()
1; 1; 2A - và hai đường thẳng
1
12
:;
21 1
xy z
d
-+
==
2
1
:12
25
x
t
dy t
zt
ì
=+
ï
ï
ï
ï
=+
í
ï
ï
=- -
ï
ï
î
. Viết phương trình đường thẳng
D
đi qua
A
vuông góc với
1
d và
2
.d
A.
45
32
57
x
t
y
t
zt



B.
17
111
23
x
t
y
t
zt



. C.
1
12
2
x
y
t
zt


. D.
7
11
32
x
t
y
t
zt



Lời giải
Tác giả: Văn Bùi Vũ ; Fb: Van Tuan Vu
Chọn B
Đường thẳng
1
d có vtcp
(
)
1
2;1;1u =

, đường thẳng
2
d có vtcp
(
)
2
1; 2; 5u =-

.
Đường thẳng
D
vuông góc với
1
d và
2
d nên nhận
()
12
,7;11;3uuu
éù
==-
êú
ëû

làm vectơ chỉ
phương.
Phương trình đường thẳng
17
:111.
23
x
t
yt
zt
ì
=-
ï
ï
ï
ï
D=-+
í
ï
ï
=+
ï
ï
î
Câu 18.2 Trong không gian
,Oxyz
cho điểm
(
)
2;1;0M
và đường thẳng
11
:
211
x
yz
d
-+
==
-
. Viết
phương trình đường thẳng
D
đi qua điểm
M
cắt và vuông góc với đường thẳng
.d
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 23
A.
21
.
141
xyz

B.
21
.
141
xyz

C.
21
.
241
xyz

D.
21
.
142
xyz


Lời giải
Tác giả: Văn Bùi Vũ ; Fb: Van Tuan Vu
Chọn D
Gọi
()
12;1 ;Nt tt+-+-
là giao điểm của đường thẳng
D
và đường thẳng
.d
Lúc đó đường thẳng
D
nhận
()
21; 2;MN t t t=---

làm vectơ chỉ phương.
Mặt khác
D
vuông góc với đường thẳng
d
nên ta có:
()
2
22 1 2 0 .
3
ttt t-+-+==
Với
2
3
t =
đường thẳng
D
nhận
142
;;
333
MN
æö
÷
ç
=--
÷
ç
÷
ç
èø

hoặc
()
1; 4; 2u =--
làm vtcp.
Phương trình đường thẳng
21
:.
142
xy z--
D==
--
Câu 19. Cho hình chóp
.SABCD
có đáy
ABCD
là hình chữ nhật,

;3;AB a AD a SA ABCD
và
SC
tạo với đáy một góc
0
45
. Gọi
M
là trung điểm cạnh
SB
,
N
là điểm trên cạnh
SC
sao
cho
1
2
SN NC
. Tính thể tích khối chóp
.SAMN
.
A.
3
3
9
a
. B.
3
3
18
a
. C.
3
3
12
a
. D.
3
3
6
a
.
Lời giải
Tác giả: Nguyễn Văn Nghĩa ; Fb: Nghĩa Văn Nguyễn
Chọn B
Vì
SA ABCD
nên
AC
là hình chiếu vuông góc của
SC
lên
mp ABCD
, suy ra



;;goc SC mp ABCD goc SC AC SCA
và
0
45SCA
Tính được
22
2AC AB BC a
và

tan 2
SA
SCA SA a
AC

Khi đó
3
.
13
.
33
S ABC ABC
a
VSAS

Ta lại có
3
..
.
.
11 1 3
.. .
23 6 6 18
SAMN SABC
SAMN
S ABC
VV
SM SN SA a
V
VSBSCSA

45
0
N
M
a3
a
S
D
C
B
A
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 24
Câu 19.1 Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
;3;
A
D a AB a SA ABCD
và
SC
tạo với đáy một góc
0
30
. Gọi
M
là trung điểm cạnh
SB
,
N
là điểm trên cạnh
SC
sao
cho
1
3
SN NC
. Tính thể tích khối chóp
.SAMN
.
A.
3
8
a
. B.
3
3
24
a
. C.
3
24
a
. D.
3
3
8
a
.
Lời giải
Tác giả: Nguyễn Văn Nghĩa ; Fb: Nghĩa Văn Nguyễn
Chọn C
Vì

SA ABCD
nên
AC
là hình chiếu vuông góc của
SC
lên

mp ABCD
, suy ra



;;goc SC mp ABCD goc SC AC SCA
và
0
30SCA
Tính được
22
2AC AB BC a
và

23
tan
3
SA a
SCA SA
AC

Khi đó
3
.
1
.
33
S ABC ABC
a
VSAS

Ta lại có
3
..
.
.
11 1
.. .
24 8 8 24
SAMN SABC
SAMN
SABC
VV
SM SN SA a
V
VSBSCSA

Câu 19.2 Cho hình chóp
.SABCD
có đáy
ABCD
là hình chữ nhật,

;3;AD a AB a SA ABCD
và
SC
tạo với đáy một góc
0
45
. Gọi
M
là trung điểm cạnh
SB
,
N
là điểm trên cạnh
SC
sao
cho
2
3
SN NC
. Tính thể tích khối chóp
.AMNCB
.
A.
3
43
15
a
. B.
3
3
15
a
. C.
3
23
3
a
. D.
3
3
3
a
.
Lời giải
Tác giả: Nguyễn Văn Nghĩa ; Fb: Nghĩa Văn Nguyễn
Chọn A
30
0
N
M
a
a3
S
D
C
B
A
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 25
Vì
SA ABCD
nên
AC
là hình chiếu vuông góc của
SC
lên
mp ABCD
, suy ra



;;goc SC mp ABCD goc SC AC SCA
và
0
45SCA
Tính được
22
2AC AB BC a
và

tan 2
SA
SCA SA a
AC

Khi đó
3
.
13
.
33
S ABC ABC
a
VSAS

Ta lại có
3
..
.
.
12 1 3
.. .
25 5 5 15
SAMN SABC
SAMN
SABC
VV
SM SN SA a
V
VSBSCSA

Suy ra
33 3
...
3343
315 15
A MNCB S ABC S AMN
aa a
VVV
 
Câu 20. Diện tích hình phẳng giới hạn bởi các đường
3
,10yxy x và trục
Ox
là
A.
32
. B.
26
. C.
36
. D.
40
.
Lời giải
Tác giả: Giáp Văn Quân ; Fb: quanbg.quan
Chọn C
Dựa đồ thị hàm số ta có diện tích hình phẳng

210
3
02
x10x36Sxd xd

.
45
0
N
M
a
a3
S
D
C
B
A
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 26
Câu 20.1 Diện tích hình phẳng là phần bị gạch chéo trong hình vẽ sau là
A. . B. . C. . D. .
Lời giải
Tác giả: Giáp Văn Quân ; Fb: quanbg.quan
Chọn D
Dựa vào đồ thị ta có diện tích hình phẳng :

4
4
2
0
10
x2x
3
Sxd xd

.
Câu 21 . Biết
12
log 27 a . Tính
6
log 16 theo
a
A.

43
3
a
a
. B.

43
3
a
a
. C.

3
43
a
a
. D.

3
43
a
a
.
Lời giải
Tác giả:Lê Thị Phương Liên; Fb: Phuonglien Le
Chọn A
Ta có
2
12 2
2
log 27 2
log 27 log 3
log 12 3
a
aa
a
 
.
Suy ra

2
6
22
43
log 16
4
log 16
log 6 1 log 3 3
a
a


Câu 21.1 Biết
21
log 49 a . Tính
63
log 81 theo
a
A.

42
2
a
a
. B.

42
2
a
a
. C.

4
42
a
a
. D.

42
4
a
a
.
Câu 22. Biết rằng đồ thị hàm số
32
2532yx x x chỉ cắt đường thẳng
34yx
tại một điểm
duy nhất

;Mab
. Tổng của
ab
bằng
A.
6
. B.
3
. C.
6
. D.
3
.
Lời giải
Tác giả: Đoàn Thị Hường; Fb: Đoàn Thị Hường
Chọn D
8
3
11
3
7
3
10
3
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 27
Tọa độ giao điểm là nghiệm của hệ
32
2532
34
yx x x
yx


32
342 5 32
34
xxxx
yx



32
25620
34
xxx
yx


1
2
5
2
x
y
.
Vậy
1
2
5
2
a
b
3ab
.
Câu 22.1. Biết rằng đường thẳng 23
y
x và đồ thị hàm số
32
23yx x x
có hai điểm chung
phân biệt
A
và
B
, biết điểm
;
BB
Bx y
có hoành độ âm. Tìm
BB
x
y .
A.
6
BB
xy
. B.
3
BB
xy
. C.
5
BB
xy
. D.
1
BB
xy
.
Lời giải
Tác giả: Đoàn Thị Hường; Fb: Đoàn Thị Hường
Chọn A
Hoành độ giao điểm
,
A
B
là nghiệm của phương trình
32 32
0
2323 0
1
x
xxxxxx
x
 

.
Vì
015 6
BBBBB
xx y xy
.
Câu 22.2. Gọi
,
M
N
là giao điểm của đường thẳng
31
y
x
và đường cong
25
1
x
y
x
. Khi đó hoành
độ trung điểm
I
của đoạn thẳng
M
N bằng
A.
2
3
.
B.
2
3
.
C.
1
3
.
D.
1
3
.
Lời giải
Tác giả: Đoàn Thị Hường; Fb: Đoàn Thị Hường
Chọn D
Hoành độ giao điểm
,
M
N
là nghiệm của phương trình

2
1
1
25
31
25 131
3240
1
x
x
x
x
xx x
xx
x




1
.
Dễ thấy
1
có hai nghiệm
12
,
x
x và
12
2
3
xx
và do đó
21
323
MN
MN I
xx
xx x

.
Câu 23. Biết rằng phương trình

2
33
5log log 9 1 0xx
có hai nghiệm là
12
,
x
x . Tìm khẳng định
đúng?
A.
5
12
3xx
. B.
12
5
1
3
xx
. C.
12
1
5
xx
. D.
12
1
5
xx 
.
Lời giải
Tác giả: Đoàn Thị Hường; Fb: Đoàn Thị Hường
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 28
Chọn A
Điều kiện:
0x
.
Ta có

22
33 33
5log log 9 1 0 5log log 1 0 1xx xx
.
Đặt
3
log
x
t
phương trình

1
trở thành

2
5102tt
.
Dễ thấy phương trình
2
có hai nghiệm
12
,tt và
12
1
5
tt
và do đó phương trình

1
có hai
nghiệm
12
,
x
x
thỏa mãn
31 32
1
log log
5
xx

312
1
log
5
xx
1
5
5
12
33xx .
Câu 23. 1. Biết rằng phương trình
2
42 10
xx

có hai nghiệm là
12
,
x
x . Tìm khẳng định đúng?
A.
12
0xx
. B.
12
1xx
. C.
12
4xx
. D.
12
2xx
.
Lời giải
Tác giả: Đoàn Thị Hường; Fb: Đoàn Thị Hường
Chọn A
Ta có

22
4 2 10 2 4.2 10 1
xx x x
 .
Đặt

20
x
tt
phương trình

1
trở thành

2
4102tt
.
Dễ thấy phương trình
2
có hai nghiệm
12
,0tt và
12
1tt và do đó phương trình

1
có hai
nghiệm
12
,
x
x thỏa mãn
12 12
12
2.2 1 2 1 0
xx xx
xx
  .
( Học sinh có thể sử dụng máy tính cho câu 23 và pt23.1)
Câu 23.2 Cho phương trình

2
93
12log 3 1 log 3 0 1xm xm (
m
là tham số ). Giả sử
0
mm
là
giá trị thỏa mãn phương trình có hai nghiệm
1
x
,
2
x
thỏa mãn
12
.3xx . Mệnh đề nào sau đây
đúng ?
A.
0
12m. B.
0
34m. C.
0
3
0
2
m.
D.
0
23m.
Lời giải
Tác giả: Đoàn Thị Hường; Fb: Đoàn Thị Hường
Chọn C
Ta có:
2
93
12log 3 1 log 3 0 1xm xm
Đk:
0x


2
2
3
3
12 log 3 1 log 3 0xm xm

2
33
1
12 log 3 1 log 3 0
2
xm xm




2
33
3log 3 1 log 3 0xm xm
Đặt
3
logtx . Khi đó phương trình
1 trở thành
2
331 302tmtm
Phương trình đã cho có hai nghiệm
12
,
x
x thỏa mãn
12
.3xx

312
log . 1xx
31 32 1 2
log log 1 1xx tt
(Với
131
logtx và
232
logtx )
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 29
Áp dụng hệ thức Vi-et cho phương trình

2
ta có
12
31 2
11 1
33
bm
tt m
a


.
Thử lại phương trình

2
dễ thấy
0
2
3
mm
phương trình

2
có hai nghiệm.
Vậy
0
3
0
2
m
là mệnh đề đúng.
Câu 24 . Gọi
12
,zz là hai nghiệm phức của phương trình
2
570zz
. Tính
22
12
Pz z
.
A.
47
. B.
56
. C.
14
. D.
27
.
Lời giải
Chọn C
Phương trình
2
570zz
có hai nghiệm
53
2
i
z
và
53
2
i
z
Suy ra
22
12
14Pz z
.
Câu 24.1. Gọi
12
,zz là hai nghiệm phức của phương trình
2
470zz
. Tính
33
12
Pz z
.
A.
20
. B.
20
. C. 14 7 . D. 28 7 .
Câu 25. Cho khối nón có thiết diện qua trục là tam giác cân có một góc
120
o
và cạnh bên bằng
a
. Tính
thể tích khối nón.
A.
3
8
a
. B.
3
8
a
. C.
3
3
24
a
. D.
3
4
a
.
Lời giải
Tác giả: Giáp Văn Quân ; Fb: quanbg.quan
Chọn A
Ta có: tam giác
ABC
vuông tại
A
,
60
o
ABC ,
BC a
.
Do đó hình nón có độ dài đường sinh
la
,
Bán kính đáy
3
.sin60
2
o
a
rACBC

Đường cao hình nón
22
2
a
hlr
Thể tích khối nón
3
2
1
r.
38
a
Vh

.
Câu 25.1 Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng .
Tính diện tích xung quanh của hình nón.
a
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 30
A.
2
2
4
a
. B.
2
2
2
a
. C.
2
2a
. D.
2
22
3
a
.
Lời giải
Tác giả: Giáp Văn Quân ; Fb: quanbg.quan
Chọn B
Thiết diện qua trục là một tam giác vuông cạnh a nên đường sinh của hình nón là và bán
kính đáy là
2
2
a
nên ta có
2
2
r
2
xq
a
Sl

.
Câu 26. Tập xác định của hàm số

1
2
3
32yx x
là
A.

\1;2
. B.

;1 2; 
. C.

1; 2
. D.
.
Lời giải
Tác giả: Nguyễn Văn Nghĩa ; Fb: Nghĩa Văn Nguyễn
Chọn B
+ Vì
1
3
không là số nguyên nên điều kiện là

2
320 ;1 2;xx x
+ Chọn B
Câu 26.1 Tập xác định của hàm số

3
2
32yx x
là
A.

\1;2
. B.

;1 2; 
. C.

1; 2
. D.
.
Lời giải
Tác giả: Nguyễn Văn Nghĩa ; Fb: Nghĩa Văn Nguyễn
Chọn A
+ Vì
3
là số nguyên âm nên điều kiện là
2
320 \1;2xx x
+ Chọn A
Câu 26.2 Tập xác định của hàm số

21
2
23
e
yxx
 là
A.
3
\;1
2



. B.

3
;1;
2

 


. C.
3
;1
2



. D.
.
Lời giải
Tác giả: Nguyễn Văn Nghĩa ; Fb: Nghĩa Văn Nguyễn
Chọn C
+ Vì
21e
không là số nguyên nên điều kiện là
2
3
230 ;1
2
xx x




+ Chọn C
Câu 27. Tập nghiệm của bất phương trình
()
1
2
log 2 1 0x +>
là:
A.
1
;0 .
4



B.

0; .
C.
1
;.
2




D.
1
;0 .
2



a
a
O
a
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 31
Lời giải
Tác giả: Văn Bùi Vũ ; Fb: Van Tuan Vu
Chọn D
Ta có:
()
1
2
1
log 2 1 0 0 2 1 1 0.
2
xxx
+>< +<-<<
Tập nghiệm của bất phương trình:
1
;0 .
2
S
æö
÷
ç
=-
÷
ç
÷
ç
èø
Câu 27.1 Tập nghiệm của bất phương trình
(
)
2
1
2
log 5 7 0xx-+>
là:
A.

;2 3;
B.
;2
C.
2;3
D.
3; 
Lời giải
Tác giả: Văn Bùi Vũ ; Fb: Van Tuan Vu
Chọn C
Ta có:
(
)
222
1
2
log 5 7 0 0 5 7 1 5 6 0xx xx xx-+><-+<-+<
23.x<<
Tập nghiệm của bất phương trình:
()
2;3 .S =
Câu 27.2 Tập nghiệm của bất phương trình
2
log 1 3x
là.
A.
1;9S
B.
9;S 
C.
1; 9 .S
D.

;9S
Lời giải
Tác giả: Văn Bùi Vũ ; Fb: Van Tuan Vu
Chọn A
Ta có:
()
2
log 1 3 0 1 8 1 9.xxx-<<-<<<
Tập nghiệm của bất phương trình:
(
)
1; 9 .S =
Câu 28.
Cho hình chóp
.S ABCD
có đáy là hình thoi cạnh
2a
,
60ABC , 3SA a và

SA ABCD
. Tính góc giữa
SA
và
mp SBD
.
A.
60
. B.
90
. C.
30
. D.
45
.
Lời giải
Tác giả: Nguyễn Đình Hải ; Fb:Nguyen Dinh Hai
Chọn C
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 32
Ta có


BD AC
BD SAC
BD SA
mà

BD SBD

SAC SBD
và

SAC SBD SO
suy ra



,,SA SBD SA SO ASO
vì tam giác
SAO
vuông tại
A
.
Ta có tam giác
ABC
đều cạnh
2a
1
2
 OA AC a
.
Xét tam giác vuông
SAO
ta có:
1
tan
3

OA
ASO
SA
30ASO .
Vậy


,30SA SBD
.
Câu 28.1 (THPT QUỐC GIA 2018 - MÃ ĐỀ 102) Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng đáy và
2SA a
. Góc giữa đường thẳng
SC
và mặt phẳng
đáy bằng
A.
45
. B.
60
. C.
30
. D.
90
.
Lời giải
Chọn A
Do

SA ABCD
nên góc giữa đường thẳng
SC
và mặt phẳng đáy bằng góc
SCA .
Ta có
2SA a
,
2AC a
tan
SA
SCA
AC
1
45SCA .
Vậy góc giữa đường thẳng
SC
và và mặt phẳng đáy bằng bằng
45
.
Câu 28.2 (Tham khảo 2018) Cho hình chóp tứ giác đều
.SABCD
có tất cả các cạnh bằng
a
. Gọi
M
là
trung điểm của
SD
(tham khảo hình vẽ bên). Tan của góc giữa đường thẳng
BM
và mặt phẳng

ABCD
bằng
O
D
A
B
C
S
D
A
B
C
S
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 33
A.
2
2
. B.
3
3
. C.
2
3
. D.
1
3
.
Lời giải
Chọn D
Gọi
O
là tâm của hình vuông. Ta có

SO ABCD
và
2
2
2
22

aa
SO a
Gọi
M
là trung điểm của
OD
ta có
//MH SO
nên
H
là hình chiếu của
M
lên mặt phẳng

ABCD
và
12
24

a
MH SO
.
Do đó góc giữa đường thẳng
BM
và mặt phẳng
()ABCD
là
MBH
.
Khi đó ta có
2
1
4
tan
3
32
4

a
MH
MBH
BH
a
.
Vậy tang của góc giữa đường thẳng
BM
và mặt phẳng

ABCD
bằng
1
3
Câu 28.3 (THPT Chuyên - ĐH Vinh - Lần 3 - 2018)Cho hình chóp
.SABCD
có đáy
ABCD
là hình
chữ nhật, cạnh
,3AB a AD a
. Cạnh bên
2SA a
và vuông góc với mặt phẳng đáy. Góc
giữa
SB
và mặt phẳng

SAC
bằng
A
B
C
D
S
M
M
O
B
A
D
C
S
H
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 34
A.
30
. B.
60
. C.
45
. D.
75
.
Lời giải
Chọn A
Vẽ

BH AC BH SAC
Suy ra góc giữa
SB
và mặt phẳng

SAC
là
BSH
..33
22

BA BC a a a
BH
AC a
22
3SB SA AB a
1
sin
2

BH
BSH
SB
30BSH .
Câu 29. Biết

e
2
1
ln 2
dln
e+1 e+1
1
xa
xbc
x

với
,,abc
. Tính
abc
.
A.
1
. B.
1
. C.
3
. D.
2
.
Lời giải
Tác giả: Nguyễn Mạnh Dũng; Fb: Mạnh Dũng
Chọn B
Đặt

2
ln
1
dd
1
ux
vx
x
1
dd
1
1
ux
x
v
x
.


ee
2
11
e
ln ln 1
dd
1
11
1
xx
xx
xxx
x



=
e
1
111
d
e+1 1
x
xx




.
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 35
=


e
1
ln ln 1
1
e+1
xx
=

1
1lne1 ln1ln2
e+1

.
=
12
ln 1
e+1 e 1

=
2
ln
e+1 e+1
a
bc
1; 1; 1 1a b c abc
.
Câu 29.1. Biết . Giá trị của là
A. . B. . C. . D. .
Lời giải
Chọn B
Nhận xét: Do chưa thể áp dụng các công thức nguyên hàm cơ bản, quan sát mẫu thấy rằng có
thể áp dụng công thức hạ bậc : .
Ta có: .
, .
Câu 29.2. Cho hàm số . Họ nguyên hàm của hàm số trên là
A. . B. .
C. . D. .
Lời giải
Chọn D
Phương pháp: Áp dụng phương pháp nguyên hàm từng phần.
Đặt .
Đặt .
Đặt .
.
(với ).
Câu 30. Có bao nhiêu tiếp tuyến của đồ thị hàm số
32
32yx x đi qua điểm

3; 2A
?
A.
3
. B.
0
. C.
1
. D.
2
.
Lời giải
Tác giả: Nguyễn Tất Thành; Fb: Thanh Nguyen
Chọn D
Ta có:
2
36yxx
 .
1
d.tan
1cos
x
x
aC
xb

Sab
11 22
2
1cos
cos
22
x
x
2
1 cos 2cos
2
x
x
22
111
dddtan1.tan
1cos 2 2 2
2cos cos
22
xx x
x
xCC
xx
x





1a 2b 12 1Sab
esin
x
yx
11
ecos esin
22
xx
x
xC
11
ecos esin
22
xx
x
xC
11
ecos esin
22
xx
x
xC
11
ecos esin
22
xx
x
xC
esin d
x
Ixx
e
dsind
x
u
vxx
ded
cos
x
ux
vx

e cos e cos d
xx
Ixxx
1
1
e
dcosd
x
u
vxx
1
1
ded
sin
x
ux
vx
ecos esin esin d
xx x
Ixxxx
1
ecos esin
xx
x
xC I
1
2ecosesin
xx
I
xxC
11
ecos esin
22
xx
IxxC
1
1
2
CC
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 36
Giả sử
00
;BC Bx
y

32
00 0
32yx x .
Phương trình tiếp tuyến
T của
C tại B là
32 2
00 0 0 0
3236yx x x xxx
.

T
đi qua
3; 2A
nên
32 2
00 0 0 0
232363
x
xxxx .
32
000
21218 0xxx
0
0
0
3
x
x
.
Khi đó hai tiếp tuyến là:
2y
hoặc
925yx
.
Vậy có 2 tiếp tuyến của đồ thị hàm số đi qua
3; 2A
.
Câu 30.1. Cho hàm số
2
1
1
x
x
y
x

có đồ thị
C . Viết phương trình tiếp tuyến của
C xuất phát từ
(1;3)M
.
A.
31yx
;
3yx
. B.
13y
;
3yx
. C.
3y
;
31yx
. D.
3y
;
3yx
.
Lời giải
Tác giả: Nguyễn Tất Thành; Fb: Thanh Nguyen
Chọn D
Ta có
2
2
2
(1)
x
x
y
x
. Gọi
00
(; )
M
xy là tọa độ tiếp điểm của tiếp tuyến
d
với
C
2
00
0
0
1
1
xx
y
x


22
00 00
0
2
00
21
:()
(1) 1
xx xx
dy x x
xx



Cách 1:
22
00 00
0
2
00
21
3(1)
(1) 1
xx xx
Md x
xx



22 2
0000000
3( 1) ( 2 )( 1) ( 1)( 1)xxxxxxx
2
00 0 0
1
2520 2,
2
xx x x
Với
0
2x  Phương trình tiếp tuyến
3y
.
Với
0
1
2
x 
Phương trình tiếp tuyến
3yx
.
Cách 2: Gọi d là đường thẳng đi qua
(1;3)M
, có hệ số góc
k
, khi đó phương trình
d
có dạng:
(1)3ykx
.
d
tiếp xúc đồ thị
C tại điểm có hoành độ
0
x
khi hệ phương trình sau có nghiệm
0
x
:
2
00
0
0
2
00
2
0
1
(1)3 (1)
1
2
(2)
(1)
xx
kx
x
xx
k
x


Thế
2
vào
1
ta được:
22
00 0 0
0
2
00
12
(1)3
1(1)
xx x x
x
xx



STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 37
2
00 0 0
1
2520 2,
2
xx x x
.
Với
0
20xk Phương trình tiếp tuyến
3y
.
Với
0
1
3
2
xk
Phương trình tiếp tuyến
3yx
.
Câu 30.2. Cho hàm số:
42
2yx x có đồ thị là

C
. Tìm những điểm
M
trên trục
Oy
để từ
M
kẻ
được
4
tiếp tuyến đến

C
.
A.

0;Mm
với
01m
. B.

0;Mm
với
1
1
3
m
.
C.

0;Mm
với
2
0
3
m
. D.

0;Mm
với
1
0
3
m
.
Lời giải
Tác giả: Nguyễn Tất Thành; Fb: Thanh Nguyen
Chọn D

00
0; ; ;MOy M mB C Bxy
42
00 0
2yx x
.
Phương trình tiếp tuyến

T
của

C
tại
B
là


42 3
00 00 0
244yx x x xxx
.

T
đi qua

0;Mm
nên


42 4 42
00 000 00
244 32 0*mx x x x x x xm
.
Khi
1m 
thì tiếp tuyến có 2 tiếp điểm là

11;
và

11;
.
Vậy từ

0;Mm
kẻ được
4
tiếp tuyến đến đồ thị

C
khi và chỉ khi phương trình

*
có
4
nghiệm
phân biệt khác
1
.
Đặt
2
0
Xx
ta có phương trình

2
32 0**XXm
Phương trình

*
có
4
nghiệm phân biệt khác
1
khi và chỉ khi

**
có
2
nghiệm phân biệt khác 1
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 38
13 0
0
1
3
0
2
3
0
3
10
m
m
P
m
S
m





Vậy từ những điểm
0;
M
m với
1
0
3
m kẻ được
4 tiếp tuyến đến đồ thị
C của hàm số đã cho.
Câu 31.
Gọi
,
M
m
tương ứng là giá trị lớn nhất và nhỏ nhất của hàm số
2cos 1
cos 2
x
y
x
. Khi đó ta có
A.
90Mm
. B.
90Mm
. C.
90Mm
. D.
0Mm
.
Lời giải
Chọn A
Đặt

cos 1xtt
ta có
21
()
2
t
ft
t
, với

1;1t
.


2
5
0
2
ft
t

với

1;1t hàm số nghịch biến trên
1; 1
.

1;1
1
Max ( ) ( 1)
3
Mftf
 và

-1;1
Min ( ) (1) 3mftf.
Vậy
90Mm.
Nên chọn A.
Câu 31.1. Gọ i
,
M
m
tương ứng là giá trị lớn nhất và nhỏ nhất của hàm số
sin 1
32sin
x
y
x
. Khi đó ta có
A. 2019 2Mm. B. 2019 2019Mm.
C.
230Mm
. D.
1Mm
.
Lời giải
Chọn A
Đặt

sin 1xtt
ta có
1
()
32
t
ft
t
với
1; 1t
éù
"Î-
ëû
.


2
5
0
32
ft
t

với

1;1t
hàm số đồng biến trên
1;1
.

-1;1
Max ( ) (1) 2Mftf
và

-1;1
Min ( ) ( 1) 0mftf
.
Vậy
2019 2Mm
.
Nên chọn A.
Câu 31.2. Gọi S là tập tất cả các giá trị nguyên của m để giá trị lớn nhất của hàm số
sin
32sin
x
m
y
x
thuộc đoạn
2; 2
éù
-
ëû
. Khi đó số phần tử của S là
A.
11
. B. 10. C. Vô số. D. 9.
Lời giải
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 39
Chọn A
Đặt

sin 1xtt
ta có
()
23
tm
ft
t

với
1; 1t
éù
"Î-
ëû
.
Ta có


2
23
23
m
ft
t

.
Do
mZÎ
nên ta xét hai trường hợp sau
+TH1:
1m thì hàm số đồng biến trên
1;1
.

-1;1
Max ( ) (1) 1ft f m.
Xét

12;2 3 1mm
. Vậy
{}
0; 1m Î
.
+TH2:
2m
thì hàm số nghịch biến trên
1;1
.

-1;1
1
Max ( ) ( 1)
5
m
ft f
.
Xét

1
2; 2 9 11
5
m
m
 . Vậy
{}
9; 8; 7; 6; 5; 4; 3; 2m Î--------
.
Vậy tập
S
có
11
phần tử.
Nên chọn A.
Nhận xét của Admin tổ 4:
Cách khác liên quan đến bản chất Max, Min của hàm số:
Để giá trị lớn nhất của hàm số
sin
32sin
x
m
y
x
thuộc đoạn
2; 2
éù
-
ëû


2,
sin
32sin
sin
32
1
2
si
:2
n
xm
x
xm
x
x
x


65sin ,
:63sin
m
x
xx
mx


19 m
.
Câu 32 . Trong không gian
Oxyz
, viết phương trình mặt cầu tâm

1;3;0I và tiếp xúc với mặt phẳng

:2 2 11 0Pxyz .
A.

22
2
13 4xyz
. B.

22
2
134xyz
.
C.

22
2
132xyz. D.

22
2
4
13
9
xyz
.
Lời giải
Tác giả: Nguyễn Thị Thu Trang 215; Fb: Trang Nguyễn
Chọn A
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 40
Vì mặt cầu tiếp xúc mặt phẳng

P nên có bán kính


,rdIP


2
22
213011
212


2
.
Vậy phương trình mặt cầu là:

22
2
13 4xyz
.
Câu PT 32.1. Trong không gian
Oxyz
, viết phương trình mặt cầu tâm

1; 1;2I
và tiếp xúc với đường
thẳng
1
:3
12
x
t
yt
zt



.
A.

222
11211xyz
. B.

222
112121xyz
.
C.

22 2
11211xyz
. D.

22 2
1 1 2 121xyz
.
Lời giải
Tác giả: Nguyễn Thị Thu Trang 215; Fb: Trang Nguyễn
Chọn A
Gọi

1;3;12
H
tt t
là hình chiếu của
I
trên đường thẳng
, suy ra

;4 ; 2 1IH t t t

.
Đường thẳng
có một véc tơ chỉ phương

1; 1;2u

.
Theo bài ra, ta có
.0uIH

44 20tt t 1t
.
Suy ra

2;2;3H
, khi đó mặt cầu có bán kính 11r .
Vậy phương trình mặt cầu cần tìm là:

222
11211xyz
.
Câu PT 32.2. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu

S
có tâm

1; 1;1I
và mặt phẳng

:2 2 1 0Pxyz
. Biết mặt phẳng

P
cắt mặt cầu

S
theo giao tuyến là một đường
tròn có bán kính bằng
3
. Viết phương trình của mặt cầu

S .
A.

222
11113xyz
. B.

222
111169xyz
.
C.

222
11113xyz
. D.

222
1 1 1 169xyz
.
Lời giải
Tác giả: Nguyễn Thị Thu Trang 215; Fb: Trang Nguyễn
Chọn A
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 41
Giả sử đường tròn giao tuyến của mặt phẳng

P
và mặt cầu

S
có tâm
H
, bán kính
HM
.


,IH d I P

2
22
2121
2
212



.
Bán kính của mặt cầu

S
là
rIM
22
32
13
.
Vậy phương trình của mặt cầu

S
:

222
11113xyz
.
Diện tích toàn phần của hình trụ là
2
22
tp
Srlr

4
.
Câu 33. Cho số phức
z
thoả mãn

12 23 412zizi i 
. Tìm toạ độ điểm
M
biểu diễn số
phức
z
.
A.

3;1M
. B.

3; 1M
. C.

1;3M
. D.

1;3M
.
Lời giải
Tác giả: Trần Thị Thơm; Fb: Tranthom
Chọn B
Giả sử

,zabiab
. Suy ra
zabi
.
Khi đó:

12 23 412zizi i
 

12 23 412abi i abi i i

53 412ab a bi i 
43
5312 1
ab a
ab b






.
Do đó điểm
M
biểu diễn số phức
z
có toạ độ là

3; 1
.
PT 33.1 Cho số phức
z
thoả mãn

13 3 57iz z i
. Điểm nào sau đây trong các điểm
,,,MNPQ
biểu diễn cho số phức
z
?
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 42
A. Điểm
M
. B. Điểm
N
. C. Điểm
P
. D. Điểm
Q
.
Lời giải
Tác giả: Trần Thị Thơm; Fb: Tranthom
Chọn B
Giả sử

,zabiab
. Suy ra
zabi
.
Khi đó:

13 3 57iz z i

13357iabi abi i

23 34 57ab abi i 
23 5 1
347 1
ab a
ab b






.
Do đó điểm biểu diễn cho số phức
z
có toạ độ là

1;1
là điểm
N
trên hình vẽ.
PT 33.2 Cho số phức
z
thoả mãn

23 1 28iz iz i
. Khoảng cách từ điểm biểu diễn cho số
phức
z
trên mặt phẳng toạ độ
Oxy
đến điểm

1;2M
bằng
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Tác giả: Trần Thị Thơm; Fb: Tranthom
Chọn A
Giả sử

,zabiab
. Suy ra
zabi
.
Khi đó:

23 1 28iz iz i


23 1 28i a bi i a bi i

23428ab a bi i
220
348 2
ab a
ab b






.
Do đó điểm
N
biểu diễn cho số phức
z
có toạ độ là

0;2
.
Ta có khoảng cách cần tìm là
1MN
.
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 43
Câu 34. Cho các hàm số
 


3
,,
1
fx
yfxygxy
gx

. Hệ số góc của các tiếp tuyến của các đồ thị
hàm số đã cho tại điểm có hoành độ
1
x
bằng nhau và khác 0. Khẳng định nào dưới đây là
khẳng định đúng?
A.
13f  . B.
13f  . C.

11
1
4
f  .
D.

11
1
4
f  .
Lời giải
Tác giả: Phạm Thanh My ; Fb: Thanh My Phạm
Chọn C
Đặt


3
1
fx
yhx
gx

Ta có


2
'1' 3
'
1
fxgx gxfx
hx
gx





Theo bài ra ta có
'1 '1 '1 0fgh


  
  
 
2
2
2
2
'1 1 1 '1 1 3
'1
11
11 1 12
1113
11111
11
244
fg gf
h
g
ggf
fgg
fg
 











PT 34.1. Cho tiếp tuyến của các đồ thị hàm số
 

3
,,
1
fx
yfxygxy
gx

lần lượt tạo với chiều
dương của trục
Ox
các góc
000
60 ,60 ,30 . Khẳng định nào dưới đây là khẳng định đúng?
A.

9
1
4
f  .
B.

9
1
4
f  .
C.

27
1
4
f  .
D.

27
1
4
f  .
Lời giải
Tác giả: Phạm Thanh My ; Fb: Thanh My Phạm
Chọn D
Đặt


3
1
fx
yhx
gx

Ta có


2
'1' 3
'
1
fxgx gxfx
hx
gx





Theo bài ra ta có
  
1
'1 '1 3, '1
3
fg h
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 44


 

  
  
 

2
2
2
2
2
'1 1 1 '1 1 3
'1
11
311 313
1
3
11
11 31316
31 1 17
12727
31 1
24 4
9
1
4
fg gf
h
g
gf
g
ggf
fgg
fg
f
 




 













Câu 35. Trên các cạnh
, ,
A
BBCCA
của tam giác
A
BC
lần lượt lấy
2, 4,
(
)
3nn>
điểm phân biệt
(các điểm không trùng với các đỉnh của tam giác). Tìm
n biết rằng số tam giác có các đỉnh
thuộc
6n +
điểm đã cho là
247
A.6 . B.
7
. C.
5
. D.
8
.
Lời giải
Tácgiả:Quỳnh Giao; Fb:QGiaoDo
Chọn B
Lấy ba điểm phân biệt không thẳng hàng sẽ tạo thành một tam giác nên số tam giác tạo thành
là:
333
64
247 7
nn
CCC n
+
--= =
Phát triển
Câu 35.1.
Cho tam giác
A
BC
, gọi
S
là tập hợp gồm 4 đường thẳng song song với
A
B
, 6 đường thẳng
song song với
BC
và 8 đường thẳng song song với
A
C
. Hỏi có bao nhiêu hình bình hành được
tạo thành từ các đường thẳng thuộc tập
S
A. 2712 . B.
678
. C.
652
. D.
2436
.
Lời giải
Tácgiả:Quỳnh Giao; Fb:QGiaoDo
Chọn B
Ta chia tập
S
thành 3 nhóm, nhóm 1 gồm 4 đường thẳng song song với
A
B
, nhóm 2 gồm
6 đường thẳng song song với
BC
, nhóm 3 gồm 8 đường thẳng song song với
A
C
. Khi đó cứ 2
đường thẳng thuộc nhóm này và hai đường thẳng thuộc nhóm khác sẽ tạo thành một hình bình
hành. Khi đó số hình bình hành là:
22 22 22
46 86 48
...678CC CC CC++=
Câu 36. Cho hàm số
f
x
liên tục trên
. Biết

ln 2
0
e1d 5
x
fx
và

3
2
23
d3
1
xfx
x
x
. Tính

3
2
dIfxx
.
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 45
A.
2I
. B.
4I
. C.
2I 
. D.
8I
.
Lời giải
Tác giả: Vũ Danh Được; Fb: Danh Được Vũ
Chọn B
Đặt
d
e1ded d
1
xx
t
ttxx
t

.
Đổi cận
02;ln23
x
tx t
.
Do đó

ln 2 3 3
022
e1d5 d5 d5
11
x
ft fx
fx t x
tx



.
Ta có

33 3
22 2
23 221
dd2d3
11 1
x fx x fx fx
xxfxx
xx x






.
Suy ra

3
2
2d3284
1
fx
IxII
x

.
PT 36.1. Cho hàm số
()
f
x
liên tục trên
thỏa mãn
(2 ) 4 ( )
f
x
f
xx
, x . Biết rằng
1
0
()d 1
f
xx
. Tính tích phân
2
1
()d
I
fx x
.
A.
9I
. B.
6I
. C.
5I
. D.
8I
.
Lời giải
Tác giả: Vũ Danh Được; Fb: Danh Được Vũ
Chọn B
Ta có

1
0
2d
Kf
xx

1
0
4d
f
xxx




11
00
4dd
f
xx xx

17
4
22

.
Đặt
2d2dtx t x
. Đổi cận 00;12xtxt .

2
0
1
d
2
Kf
tt

2
0
d7
f
tt

2
0
d7fx x
.
 
212
001
ddd
f
xx
f
xx
f
xx

2
1
()d
I
fx x
 
21
00
dd
f
xx
f
xx

716
.
Câu 37. Cho khối hộp
A
BCDABCD

có thể tích V . Các điểm
,,
M
NP
thỏa mãn 2
A
MAC

,
3
A
NAB
 
, 4
A
PAD

. Tính thể tích khối chóp
A
MNP theo V .
A.
6V
. B.
8V
. C.
12V
. D.
4V
.
Phân tích:
Nhận dạng bài toán: Đây là bài toán tính thể tích khối đa diện thông qua tỉ số thể tích.
Kiến thức cần nhớ: Cho khối chóp
.SABC
. Trên các đường thẳng
,,SA SB SC
lần lượt
lấy ba điểm
,,
A
BC

khác
S
. Ta có:
.
.
..
S ABC
S ABC
V
SA SB SC
VSASBSC


.
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 46
Lời giải
Tác giả: Vũ Nga; Fb: Nga Vu
Chọn B
Ta có:
.
.
..
AMNP
ACBD
V
AM AN AP
VACABAD


2.3.4 24
..
24
AMNP ACBD
VV

 .
Mà:
.....
ACBD ABCDABCD A ABD ABBC ADDC CCBD
VV VVVV
 

1
4.
63
V
VV
.
8
AMNP
VV.
Câu PT 37.1 Cho khối hộp
ABCDABCD

có thể tích
V
. Lấy điểm
M
đối xứng với
A
qua
C
, điểm
N
đối xứng với
A
qua
B
, điểm
P
thỏa mãn
AP k AD
 
. Tìm
k
để thể tích khối chóp
AMNP
bằng
2
V
.
A.
3
8
k
. B.
3
8
k 
. C.
1
2
k
. D.
1
2
k 
.
Lời giải
Tác giả: Vũ Nga; Fb: Nga Vu
Chọn B
Ta có:
.
.
..
AMNP
ACBD
V
AM AN AP
VACABAD


2.2. 4kk
..
4
AMNP ACBD
VkV


.
Mà:
.....
ACBD ABCDABCD A ABD ABBC ADDC CCBD
VV VVVV
 

1
4.
63
V
VV
.
4
3
AMNP
VkV
.
.
3
28
ACBD
V
Vk


.
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 47
Câu PT 37.2 Cho khối lăng trụ tam giác
ABCA B C

có thể tích
V
. Điểm
M
là trung điểm của
AB
.
Mặt phẳng

CBM

chia khối lăng trụ thành hai khối đa diện có thể tích là
1
V
và
2
V , biết
1
V
là
khối chứa điểm
A
. Tính
2
V theo
V
.
A.
2
7
12
V
. B.
2
5
12
V
. C.
2
5
6
V
. D.
2
17
24
V
.
Lời giải
Tác giả: Vũ Nga; Fb: Nga Vu
Chọn B
Do
// (ABC)CB

nên

CBM

cắt
AC
tại điểm
N
thỏa mãn
//MN B C

N
là trung điểm
AC
.
Dễ thấy 3 đường
,,CN BM AA

đồng quy tại
S
và
..
1
8
S AMN S ABC
VV

1.
7
8
SABC
VV


.
Gọi
,hS
lần lượt là chiều cao và diện tích đáy của khối lăng trụ
ABCA B C

, ta có:


.
112
;..2.
333
SABC
VdSABCShSV



, vậy
1
7
12
VV
2
5
12
VV
.
Câu 38. Cho số phức
z
thỏa mãn
15z 
,
11 5
17z
z

và
z
có phần ảo dương. Tìm tổng phần thực
và phần ảo của
z
.
A.
2
. B.
4
. C.
6
. D.
8
.
Lời giải
Tác giả: Nguyễn Thị Thanh Vân; Fb: Thanh Van
Chọn D
Gọi
zabi

,,0ab Rb
.
Ta có
15z 

2
2
125ab

22
2241ab a
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 48
11 5
17z
z

115
17abi abi


22
25
17
a
ab


22
34
02
5
ab a
Trừ vế - vế của

1 cho
2 ta có 53ab 8ab.
PT 38.1 Cho số phức
z
thỏa mãn 15z  ,
11 5
17z
z

và
z
có phần ảo âm. Tìm tổng phần thực và
phần ảo của
z
.
A.
2
. B.
4
. C.6 . D.8 .
Lời giải
Tác giả: Nguyễn Thị Thanh Vân; Fb: Thanh Van
Chọn A
Gọi zabi
,,0ab Rb.
Ta có
15z 

2
2
125ab
22
2241ab a
11 5
17z
z

115
17abi abi


22
25
17
a
ab


22
34
02
5
ab a
Trừ vế - vế của

1
cho
2
ta có
53ab
2ab
.
PT 38.2 Cho số phức z thỏa mãn 25z  ,
1110
41z
z
 và
z có phần ảo dương. Tìm tổng phần thực
và phần ảo của
z .
A. 2 . B.1. C.9. D.8 .
Lời giải
Tác giả: Nguyễn Thị Thanh Vân; Fb: Thanh Van
Chọn C
Gọi
zabi
,,0ab Rb
.
Ta có
25z 

2
2
225ab 
22
4211ab a
1110
41z
z

1110
41abi abi


22
210
41
a
ab


22
41
02
5
ab a
Trừ vế - vế của

1
cho
2
ta có 54ab 9ab .
Câu 39. Trong không gian với hệ tọa độ
Ox
y
z
, cho điểm
1;2;2A
và đường thẳng
615
:
211
xyz
d

. Tìm tọa độ điểm
B
đối xứng với
A
qua
d
.
A.
3;4; 4B 
. B.
2; 1;3B
. C.
3;4; 4B
. D.
3; 4;4B
.
Lời giải
Tác giả: Phạm Thị Thu Trang; Fb: Trang Phạm
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 49
Chọn D
Từ phương trình đường thẳng d ta có véc tơ chỉ phương của d là
2;1;1u
Gọi
H
là hình chiếu của
A
trên d , suy ra
6 2 ;1 ;5 5 2 ; 1 ;3
H
tt t AH t t t

. Khi đó
.0AH u AH u 
 

25 2 1 3 0 2tttt
.
Với
2t 
thì

2; 1;3H
.
Gọi
B
là điểm đối xứng với
A
qua
d
thì
H
là trung điểm

3; 4;4AB B
.
Câu PT 39.1. Trong không gian với hệ tọa độ
Ox
y
z
, cho đường thẳng
615
:
211
xyz
d

 và mặt
phẳng
:2 3 4 0Pxyz
. Viết phương trình đường thẳng d
là hình chiếu vuông góc của
d trên
P
.
A.
6
25
23
x
t
yt
zt



.
B.
6
25
23
xt
yt
zt


.
C.
6
25
23
x
t
yt
zt



.
D.
6
25
23
x
t
yt
zt



.
Lời giải
Tác giả: Phạm Thị Thu Trang; Fb: Trang Phạm
Chọn A
Gọi
Id P
, khi đó toạ độ điểm
I
là nghiệm của hệ phương trình:

62 3
10
0; 2;2
52
23 40 2
xt t
yt x
I
zt y
xyz z












.
Lấy

6;1;5
A
d , gọi
là đường thẳng đi qua
A
và vuông góc với
P
suy ra PT đường thẳng
có dạng:
62
13
5
x
t
yt
zt



. Gọi
JP
, ta tính được
18 29 23
;;;
777
J




.
Khi đó đường thẳng
d
đi qua 2 điểm
,IJ
có PTTS là:
6
25
23
x
t
yt
zt



.
Nhận xét Admin tổ 4 – Strong
Bài 39 + 39.1 đều có điều chung là cần tìm hình chiếu của
1
điểm tới
1
mặt. Ta có thể giải nhanh:
Cho
:
0ax by cz d
;;
A
mnk
. Gọi
H
là hình chiếu của
A
lên
.
Khi đó

222
;;
am bn ck d
h
abc
H
mahnbhkch




STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 50
Câu 39: Ta có
d
qua

6;1;5M
; VTCP

2;1;1u
.

P
qua
A
,
d
có phương trình:

2112120xy z
260xyz
H
là hình chiếu của
M
lên

P

2; 1;3H
B
đối xứng với
A
qua
H

3; 4;4B
Câu 39.1

Id P

0; 2;2I

6;1;5A
d
H
là hình chiếu của
A
lên

P
18 29 23
;;
777
H




.
d
qua
IH
:
6
25
23
xt
yt
zt



Câu 40. Ông An có một khu đất hình elip với độ dài trục lớn
10
m và độ dài trục bé
8
m. Ông An muốn
chia khu đất thành hai phần, phần thứ nhất là một hình chữ nhật nội tiếp elip dùng để xây bể cá
cảnh và phần còn lại dùng để trồng hoa. Biết chi phí xây bể cá là
1000000
đồng trên
2
1m
và chi
phí trồng hoa là
1200000
đồng trên
2
1m
. Hỏi ông An có thể thiết kế xây dựng như trên với tổng
chi phí thấp nhất gần nhất với số nào sau đây?
A.
67398224
đồng. B.
67593346
đồng. C.
63389223
đồng. D.
67398228
đồng.
Lời giải
Tác giả:Phạm Văn Tuấn ; Fb: Phạm Tuấn
Chọn A
Gắn mảnh vườn hình elip của ông An vào hệ trục tọa độ như hình vẽ. Độ dài trục lớn 10m và độ dài
trục bé bằng 8m nên ta có
5a
và
4b
.
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 51
Phương trình của elip là:

22
:1
25 16
xy
E 
.
Diện tích của elip là:

20
E
Sab

.
Hình chữ nhật
A
BCD
nội tiếp elip. Đặt
2
A
Bx
05x
2
81
25
x
AD
.
Diện tích hình chữ nhật
A
BCD là:
2
16 1
25
ABCD
x
Sx
.
Diện tích phần còn lại trồng hoa là:
2
20 16 1
25
hoa
x
Sx
 .
Tổng chi phí xây dựng là:
22
16000000. 1 1200000. 20 16 1
25 25
x
x
Tx x





2
24000000 3200000 1
25
x
x

.
Mặt khác ta có:
22
2
1
25 25
16000000. 1 16000000. 8000000
525 2
xx
xx


.
2
24000000 3200000 1 24000000 8000000 67398223.69
25
x
Tx

 .
Dấu
"" xảy ra khi
2
52
1
525 2
xx
x

(thỏa mãn).
Vậy tổng chi phí thiết kế xây dựng thấp nhất gần với số
67398224 .
Câu 40.1. Một cái hồ rộng có hình chữ nhật. Tại một góc nhỏ của hồ người ta đóng một cái cọc ở vị trí
K
cách bờ
A
B là 1
m
và cách bờ
A
C là 8
m
, rồi dùng một cây sào ngăn một góc nhỏ của hồ
để thả bèo (như hình vẽ). Tính chiều dài ngắn nhất của cây sào để cây sào có thể chạm vào
2
bờ
A
B
,
A
C
và cây cọc
K
(bỏ qua đường kính của sào).
A.
565
4
. B. 55. C. 92. D.
571
4
.
Lời giải
Tác giả:Phạm Văn Tuấn ; Fb: Phạm Tuấn
Chọn B
K
A
C
B
P
Q
E
F
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 52
Đặt
AP a
,
AQ b

,0ab
. Gọi
E
và
F
lần lượt là hình chiếu vuông góc của
K
xuống
AB
và
AC
. Suy ra
1
KE
,
8KF
.
Ta có:
KE PK
AQ PQ
;
KF QK
AP PQ
1
KF KE
AP AQ

hay
81
1
ab

.
(Hoặc có thể dùng phép tọa độ hóa: Gán

0;0A
,

0;Pa
,

;0Qb
. Khi đó

1; 8K
.
Phương trình đường thẳng
:1
xy
PQ
ba

. Vì
PQ
đi qua
K
nên
18
1
ba

.)
Cách 1:
Ta có:
222
PQ a b. Vì
81
1
ab

8kk
k
ab

0k
.
22 2 2
8kk
abk a b
ab




22
44
22
kk kk
ab
aa bb




2
3
2
3
316 3
4
k
k.
Suy ra
PQ
nhỏ nhất
22
ab
nhỏ nhất
2
2
4
2
81
1
k
a
a
k
b
b
ab


250
10
5
k
a
b

.
Vậy giá trị nhỏ nhất của
PQ
là
22
ab
125 55
. Từ đó suy ra chiều dài ngắn nhất của
cây sào để cây sào có thể chạm vào
2
bờ
AB
,
AC
và cây cọc
K
là 55.
Cách 2:
Vì
81
1
ab

8
a
b
a

với
8a
. Khi đó
222
PQ a b
2
2
8
a
a
a




với
8a
.
Xét hàm số

2
2
8
a
fa a
a




với
8a
.
Ta có


2
28
2.
8
8
a
fa a
a
a



3
3
288
8
aa
a



;

0fa
10a
.
BBT của

fa
:
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 53
Vậy GTNN của

fa
là
125
khi
10a
.
Từ đó suy ra chiều dài ngắn nhất của cây sào để cây sào có thể chạm vào
2
bờ
AB
,
AC
và
cây cọc
K
là
125 5 5
.
Câu 41. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
5712
:
22 1
xyz
d


và mặt phẳng

:2330xyz

. Gọi
M
là giao điểm của
d
với

,
A
thuộc
d
sao cho
14AM
.
Tính khoảng cách từ
A
đến

.
A. 2. B. 3. C. 6. D.
14
.
Lời giải
Tác giả: Nguyễn Bảo Mai; Fb: Bao An
Chọn B

có một vectơ pháp tuyến là

1; 2; 3n 
và
d
có một vectơ chỉ phương là

2; 2; 1u 
.
Gọi
là góc giữa

và
d
,
H
là hình chiếu của
A
trên

.
Ta có
sin
AH
AM

 
22
22 22
1.2 2.2 3 1
9
sin 14. 14. 3
14.3
12 3 22 1
AH AM



PT 41.1. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
5712
:
22 1
xyz
d


và mặt phẳng

:2330xyz

. Gọi
M
là giao điểm của
d
với

,
A
thuộc
d
và cách

một
khoảng bằng 3. Tính độ dài đoạn thẳng
AM
.
A.
214
3
. B. 3. C.
214
. D.
14
.
Lời giải
Chọn D

có một vectơ pháp tuyến là

1; 2; 3n 
và
d
có một vectơ chỉ phương là

2; 2; 1u 
.
Gọi
là góc giữa

và
d
,
H
là hình chiếu của
A
trên

.
Ta có
sin
AH
AM

 
22
22 22
3
14
sin
1.2 2.2 3 1
12 3 22 1
AH
AM


 
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 54
PT 41.2. Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
S
có tâm
A
thuộc đường thẳng
5712
:
22 1
xyz
d


và cắt mặt phẳng
:2330xyz

theo một đường tròn có bán
kính bằng
5
. Biết rằng giao điểm
M
của d với

cũng thuộc
S , tính bán kính của
S .
A.
214
3
. B. 3. C. 214. D. 14 .
Lời giải
Chọn D

có một vectơ pháp tuyến là
1; 2; 3n 
và d có một vectơ chỉ phương là

2; 2; 1u 
.
Gọi
là góc giữa
và
d
,
H
là hình chiếu của
A
trên
.
Ta có
5MH và
.
3
sin
14
.
nd
nd

5
cos
14
.
Mà
cos
M
H
A
M
5
14
cos
5
14
MH
AM

.
Câu 42 . Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số
24 2 2
2019 1ymx m mx
có
đúng một điểm cực trị.
A.
2019
. B.
2020
.
C.
2018
. D.
2017
.
Lời giải
Tác giả: Nguyễn Thị Thơm; Fb: Thom nguyen
Chọn C
Xét 0m thì
1
y
đồ thị hàm số không có cực trị.
Xét
0m
Để đồ thị hàm số có 1 cực trị
22
2019 0 0 2019mm m m
Do
m nguyên nên có 2018 giá trị của m .
PT 42.1 Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số
24 2 2
57ymx m mx
có
đúng một điểm cực trị.
A.
20
. B.
5
.
C.
4
. D.
7
.
Lời giải
Tác giả: Nguyễn Thị Thơm; Fb: Thom nguyen
Chọn D
Xét 0m thì
1
y
đồ thị hàm số không có cực trị.
Xét
0m
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 55
Để đồ thị hàm số có 1 cực trị
22
500 5mm m m
Do
m
nguyên nên có 4 giá trị của
m
.
PT 42.2 Tính tổng các giá nguyên của tham số m để đồ thị hàm số
24 2 2
11 20ymx m mx có
đúng một điểm cực trị.
A.
20
. B.
55
.
C. 45 . D.10.
Lời giải
Tác giả: Nguyễn Thị Thơm; Fb: Thom nguyen
Chọn B
Xét
0m
thì
1
y
đồ thị hàm số không có cực trị.
Xét
0m
Để đồ thị hàm số có 1 cực trị

22
11 0 0 11mm m m
Do
m
nguyên nên
1;2;3;4;5;6; 7;8;9;10m
Tổng các giá trị của
m
bằng55.
Câu 43. Gọi S là tập tất cả các giá trị của tham số
m
để đồ thị hàm số
3
32 2
32432
y
xx xx mx có tiệm cận ngang. Tổng các phần tử của S là
A.
2
. B.
2
.
C.
3
. D.
3
.
Lời giải
Tác giả: Lục Minh Tân; Fb: Lục Minh Tân
Chọn A
33 2 2
lim lim 3 2 4 3 2
xx
yxxxxmx
 


3
32 2
lim 3 2 2 4 3 2 1
x
x
xxxxxmx


Ta có:
33 2
lim 3 2 1
x
xx x


;
2
3
lim 2 4 3 2
4
x
xxx


*
33 2 2
lim lim 3 2 4 3 2
xx
yxxxxmx
 


33 2 2
lim 3 2 2 4 3 2 3
x
x
xxxxxmx


Ta có:
33 2
lim 3 2 1
x
xx x


;
2
3
lim 2 4 3 2
4
x
xxx


* Đồ thị hàm số có tiệm cận ngang
lim
x
y

hoặc
lim
x
y

hữu hạn
10 1
30 3
mm
mm






Câu PT 43.1. Gọi S là tập tất cả các giá trị của tham số m để đồ thị hàm số
33 2 2
8522572
2
m
yxx xx x
 có tiệm cận ngang. Tích các phần tử của
S
là
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 56
A.
8
. B.
84
.
C.
21
. D.
21
.
Lời giải
Tác giả: Lục Minh Tân; Fb: Lục Minh Tân
Chọn B
*
3
32 2
lim lim 8 5 2 25 7 2
2
xx
m
yxxxxx
 




33 2 2
lim 8 5 2 2 5 25 7 2 3
2
x
m
x
xxxxx x








Ta có:
33 2
5
lim 8 5 2 2
12
x
xx x

;
2
7
lim 5 25 7 2
10
x
xxx


*
33 2 2
lim lim 8 5 2 25 7 2
2
xx
m
y
xx xx x
 




3
32 2
lim 8 5 2 2 5 25 7 2 7
2
x
m
x
xxxxx x








Ta có:
33 2
5
lim 8 5 2 2
12
x
xx x


;
2
7
lim 5 25 7 2
10
x
xxx


* Đồ thị hàm số có tiệm cận ngang
lim
x
y

hoặc
lim
x
y

hữu hạn
30
6
2
14
70
2
m
m
mm




Câu PT 43.2. Gọi
S
là tập tất cả các giá trị của tham số m để đồ thị hàm số
3
232
95364352
y
xx xxx mx
có tiệm cận ngang. Tổng bình phương tất cả các
phần tử của
S
là
A.
10
. B. 15.
C.
50
. D. 51.
Lời giải
Tác giả: Lục Minh Tân; Fb: Lục Minh Tân
Chọn C
3
232
lim lim 9 5 3 64 3 5 2
xx
y
xx xxx mx
 

3232
lim 9 5 3 3 4 64 3 5 2 ( 1)
x
x
xxxxxxmx


Ta có:
2
5
lim 9 5 3 3
6
x
xx x


,
33 2
1
lim 4 64 3 5 2
16
x
xxxx


*
3
232
lim lim 9 5 3 64 3 5 2
xx
y
xx xxx mx
 

3
232
lim 9 5 3 3 4 64 3 5 2 ( 7)
x
x
xxxxxxmx


Ta có:
2
5
lim 9 5 3 3
6
x
xx x


,
33 2
1
lim 4 64 3 5 2
16
x
xxxx


STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 57
* Đồ thị hàm số có tiệm cận ngang
lim
x
y

hoặc
lim
x
y

hữu hạn
10 1
70 7
mm
mm






Câu 44. Cho hàm số

2
ln
f
xxx
. Tính

1 2 2019
P...
ff f
ee e .
A.
2020
P
2019
. B.
2019
P
2020
. C.
2019
P e . D.
2019
P
2020
 .
Lời giải
Tác giả: Lê Hữu Đức; Fb: Le Huu Duc
Chọn B
TXĐ:

D;10;
Ta có

11
,D
1
fx
ex
x
x

Suy ra

1
1
1
2
f
e 


2
2019
11
23
...
11
2019 2020
f
f
e
e



1 2 2019
12019
P ... 1
2020 2020
ff f
ee e
Nhận xét: Câu 44 học sinh có thể dùng máy tính đề tính biểu thức P
Câu PT 44.1. Cho hàm số
2
log 2
f
xxx
. Tính

1 3 5 2019
P 10 10 10 ... 10
fff f
 .
A.
1010
P
2021
. B.
2022
P
2021
. C.
2021
P10
. D.
2020
P
2021
.
Lời giải
Tác giả: Lê Hữu Đức; Fb: Le Huu Duc
Chọn A
TXĐ:
D;20;
Ta có

11 1
10 , D
22
fx
x
xx




Suy ra

1
11
10 1
23
f




STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 58



3
5
2019
11 1
10
23 5
11 1
10
25 7
...
11 1
10
2 2019 2021
f
f
f













135 2019
1 1 1010
P 10 10 10 ... 10 1
2 2021 2021
ff f f




Câu PT 44.2.
Tính
2 3 2019
11 1
P...
log 2019! log 2019! log 2019!

A.
P 2019
. B.
P1
. C.
P0
. D.
P2019!
.
Lời giải
Tác giả: Lê Hữu Đức; Fb: Le Huu Duc
Chọn B
2 3 2019
11 1
P ...
log 2019! log 2019! log 2019!

2019! 2019! 2019!
log 2 log 3 ... log 2019
2019!
log 2.3...2019 1
Câu PT 44.3.
Cho số tự nhiên n , biết biểu thức
23
22
22 2
1 1 1 1 120
...
log log log log log
n
x
xx xx
 luôn
đúng

0; \ 1x . Giá trị
n
thuộc khoảng nào sau đây?
A.

19;25
. B.

14;17
. C.

6;10
. D.

11;14
.
Lời giải
Tác giả: Lê Hữu Đức; Fb: Le Huu Duc
Chọn B
Ta có
23
23
2
22 2
111 1
... log 2 log 2 log 2 ... log 2
log log log log
n
n
xx x x
xxx x


2
1
1 2 3 ... log 2
2log
x
nn
n
x

.
Do đó phương trình đã cho tương đương

2
15 /
1
120 240 0
16
2
ntm
nn
nn
nl


.
Vậy

14;17n
.
Câu 45. Cho các số phức
1
z ,
2
z thỏa mãn phương trình
23 5zi
và
12
6zz
. Biết rằng tập hợp
các điểm biểu diễn số phức
12
wz z là một đường tròn. Tính bán kính đường tròn đó.
A. 8R . B.
4R
. C. 22R . D.
2R
.
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 59
Lời giải
Tác giả: Lương Văn Huy ; Fb: Lương Văn Huy
Chọn A
Giả sử
A
,
B
lần lượt là các điểm biểu diễn số phức
1
z ,
2
z trên mặt phẳng tọa độ
Oxy
. Theo giả thiết ta
có
A
, B thuộc đường tròn tâm
2;3I , bán kính
5r
và
6AB
.
Gọi
M
là trung điểm của
A
B
khi đó
M
cũng là điểm biểu diễn số phức
12
22
zz
w
u

.
Lại có
2
22 22
16 4
2
AB
IM IA AM r IM




.
Vậy
M
thuộc đường tròn tâm
2;3I bán kính
'4r
.
Suy ra các điểm biểu diễn số phức
12
2wz z u là một đường tròn bán kính 28Rr

Câu 46. Cho các số thực
x
,
y
thay đổi thỏa mãn
22
1
x
yxy và hàm số
32
231ft t t
.
Gọi
M
,
m
tương ứng là giá trị lớn nhất và nhỏ nhất của
52
4
xy
Qf
xy





. Tổng
M
m
bằng
A.
432
. B.
452
. C.
442
. D.
422
.
Lời giải
Tác giả: Trần Thị Thanh Thủy; Fb: Song tử mắt nâu
Chọn C
Ta có:
22
1
x
yxy
2
2
3
1
24
yy
x




. Ta đặt:
52
4
xy
t
xy



45 2tx y x y
51420txtyt
.


3
53324
22
yy
tx t t




.
Áp dụng bất đẳng thức Bunhiacopxki, ta có:




2
2
2
2
2 2
33
24 5 3 3 5 3 3
22 24
yy yy
ttx t t t x


 




 


 





2
22
24 5 3 3 .1tt t




2
12 24 0tt
22t
.
Xét hàm số
32
231ft t t
với
22t
.
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 60
Có:
2
66ft t

nên

2
0
0660
1
t
ft t t
t
 
.
Ta có:
2542f 
,
01f
,
10f
,
2542f 
Do đó
01Mf
,

2542mf .
Vậy
442Mm
.
Bài toán gốc: Cho
22
ax by cxy d. Tìm MGT
111
222
ax by c
t
ax by c


Phương pháp giải:
Cách 1. Lượng giác hóa (Song Tử Mắt Nâu)
Ta có:
22
22
'' '' 1ax by cxy d a x b y c x d y
Đặt
''sin sin
''cos cos
ax by x m
cx d y y n





Suy ra:
111
222
sin cos
ax by c
tABC
ax by c




Ta có:
22 2
A
BC
suy ra MGT của t .
Cách 2. (Một cách nhìn khác đồng nhất hệ số Ng.Việt Hải)

111
222
ax by c
tAmxnyBkxqyC
ax by c



Chọn
,,,mnkq
sao cho

22
22
mx n
y
kx q
y
ax b
y
cx
y

22
22
22
mk a
nqb
mn kq c



Áp dụng BĐT Bunhiacoxki ta có:
222
CABd
suy ra MGT của t .
Câu PT 46.1. Cho 2 số
,
x
y
thỏa mãn
22
514
x
yxy và hàm số bậc ba
yf
x
có đồ thị như
hình vẽ. Gọi
,
M
m
tương ứng là giá trị lớn nhất và nhỏ nhất của
233
44
xy
Pf
xy





.
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 61
Tích
.Mm
bằng
A.
1436
1331
B.
3380
1331
C.
1436
1331
D.
1944
1331
Lời giải
Tác giả: Trần Thị Thanh Thủy; Fb: Song tử mắt nâu
Chọn C
Dễ thấy

3
3fx x x
Từ

2
22 2
514 2 1xy xyxyy
Đặt
2sin sin 2xy x cos
y cos y cos







. Khi đó
Xét


2sin 2 3 3
233
44 sin 2 4 4
cos cos
xy
t
xy cos cos






2sin 3
sin 2 4
cos
cos




Ta có:

sin 2 4 2sin 3tcos cos



2sin 1 2 4 3ttcost



*
Phương trình

*
có nghiệm

22 2
22143ttt
2
2
11
t

Khi đó

3
3Pft t t
với
2
2
11
t

Dễ dàng tìm được
2M
,
718
1331
m
. Vậy
1436
.
1331
Mm
Câu PT 46.2. Cho các số thực
,xy
thay đổi thỏa mãn
22
521xyxy
và hàm số

42
22ft t t
Gọi
,Mm
là giá trị lớn nhất và giá trị nhỏ nhất của
1
32
xy
Qf
xy





.
Tổng
Mm
A.
43 2
. B.
83 2
. C.
66
. D.
93 17
Lời giải
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 62
Tác giả: Trần Thị Thanh Thủy; Fb: Song tử mắt nâu
Chọn C
Ta có:
22
521
x
yxy

2
2
41xy y
Đặt
1
32
xy
t
xy


32 1tx y x y
21 1 2ttxyty
Áp dụng bất đẳng thức Bunhiacopxki, ta có:
 

2
222
22
21 1 2 1 4t t xy ty t t xy y 


22
2
21 1ttt
2
260 3 0tt t
Xét hàm số
42
22ft t t với
30t
Có:

3
44
f
ttt

, nên

0
01
1
t
ft t
t

02, 11, 365ff f
Do đó

365; 11Mf mf 
Vậy:
66Mm
Câu PT 46.3. Cho các số thực
,,
x
yz
thỏa mãn
8
5
xy yz zx
xyz


và hàm số
2
45
f
xx x
Gọi
,
M
m
là giá trị lớn nhất và giá trị nhỏ nhất của

f
x . Tổng
M
m
A.
3
. B.
28
9
.
C.
19
9
.
D.
2
Lời giải
Tác giả: Trần Thị Thanh Thủy; Fb: Song tử mắt nâu
Chọn A
Viết lại điều kiện:
8
5
xy yz zx
xyz


8
5
zy x y z
yz x


85
5
yz x x
yz x



*
Vì
,,
x
yz
thỏa mãn

* nên
,yz
là hai nghiệm của phương trình
22
5850TxTxx
**
Điều kiện có nghiệm của phương trình
**
là:

2
22
5485 031070xxxxx
7
1
3
x
Xét hàm số
2
45
f
xx x
với
7
1
3
x
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 63
Có

24fx x

nên

02fx x


710
12;21;
39
fff




Do đó

12, 21Mf mf
.
Vậy
3Mm
.
Câu 47. Trong các khối chóp tứ giác đều
.S ABCD
mà khoảng cách từ
A
đến mp
()SBC
bằng
2a
, khối
chóp có thể tích nhỏ nhất bằng
A.
3
23a
. B.
3
2a
. C.
3
33a
. D.
3
43a
.
Lời giải
Tác giả : Võ Thị Ngọc Ánh ; Fb: Võ Ánh
Chọn A.
Gọi I là trung điểm của AD; K là trung điểm của CB, O là tâm của hình chữ nhật ABCD.
Trong tam giác SOK kẻ đường cao OL.
Ta có
(;( ))dO SBC OL
và
11
(;( )) (;( )) (;( ))
22
d O SBC d I SBC d A SBC a
.
Suy ra
OL a
.
Đặt
OK x
,
xa
suy ra độ dài cạnh đáy hình chóp đều
.S ABCD
là
2x
.
Xét trong tam giác
SOK
vuông tại O có OL là đường cao, ta có
22 22
22 22222 22
22
11111xa ax ax
OS
OS OL OK a x a x x a
xa

Suy ra thể tích khối chóp
.SABCD
là
3
2
22 22
14
4. .
33
ax a x
Vx
xa xa


K
I
O
C
A
B
D
S
L
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 64
Đặt
3
22
4
() .
3
ax
fx
xa


22 2 3
22 2
22
22
22 22
3.
23
44
'( ) . .
33
x
xx a x
xx a
aa
xa
fx
xa
xa xa



6
'( ) 0
2
a
fx x
.
Bảng biến thiên:
Suy ra

33
;
6
Min Min ( ) 12 2 3
2
xa
a
Vfxf aa






PT 47.1 Trong các khối chóp tam giác đều
.S ABC
mà khoảng cách từ
A
đến mp
()SBC
bằng
3a
, khối
chóp có thể tích nhỏ nhất bằng
A.
3
63a
. B.
3
9
2
a
. C.
3
9a
. D.
3
12 3a
.
Tác giả : Võ Thị Ngọc Ánh ; Fb: Võ Ánh
Lời giải
Chọn B.
G
M
A
C
B
S
H
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 65
Gọi M là trung điểm của BC; G là trọng tâm tam giác đều ABC. Trong tam giác SGM kẻ đường cao
GH.
Ta có
(;( ))dG SBC GH
và
1
(G;( )) ( ;( ))
3
dSBC dASBCa
. Suy ra
GH a
.
Gọi
GM x
,
xa
suy ra độ dài cạnh đáy của tam giác ABC là
2
3. 2 3
3
xx
.
Xét trong tam giác
SGM
vuông tại G có GH là đường cao, ta có
22 22
2222222 22
22
11111xa ax ax
SG
GS GH GM a x a x x a
xa

Suy ra thể tích khối chóp
.S ABC
là

3
2
22 22
13
.2 3 . . 3.
34
ax x
Vx a
xa xa


Đặt
3
22
() 3.
x
fx a
xa


22 2 3
22 2
22
22
22 22
3.
23
'( ) 3 . 3 .
x
xx a x
xx a
xa
fx a a
xa
xa xa



6
'( ) 0
2
a
fx x
.
Bảng biến thiên:
Suy ra

3
;
69
Min Min ( )
22
xa
aa
Vfxf






Câu 48. Tổng tất cả các giá trị của tham số m để phương trình

2
2
212
23
3log22
xx xm
xx
xm



có
đúng ba nghiệm phân biệt là
A.
3
. B.
2
. C.
3
. D.
2
.
Lời giải
Tác giả: Lưu Huyền Trang ; Fb: Lưu Huyền Trang
Chọn C
Ta có
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 66





2
2
2
2
212
23
23
22
2
22
223
3log22
ln 2 2
3
ln 2 3
3
ln 2 3 .3 ln 2 2 .3
xx xm
xx
xx
xm
xm
xx
xm
xm
xx
xx xm











Xét
ln .3 , 2
t
f
ttt
 
1
3ln 3ln3 0, 2
tt
f
tt t
t

Vậy hàm số
f
t
đồng biến .


2
2
2
2
2
23 2 2
232 2
212
12 1
4122
fx x f xm
xx xm
xx xm
xm
xx m





Điều kiện cần để phương trình có 3 nghiệm là :
Th1 :
1
có nghiệm kép
1
2
m
 thử lại ta thấy thỏa mãn
Th2 :
2
có nghiệm kép
3
2
m
 thử lại ta thấy thỏa mãn
Th3 :
1
và
2
có nghiệm chung
x
m .Thế
1
vào ta có 1m 
Ta có

13
13
22


Bình luận : Bài toán là sự giao thoa giữa phương pháp sử dụng tính đơn điệu hàm số với biện luận
nghiệm .
Câu 48.1 Tìm các giá trị m để phương trình
sin 5 cos 5
sin 5 cos 10
3log 5
xxm
xx
m


 có nghiệm .
A. 66m . B. 55m . C.56 56m. D. 65m.
Lời giải
Tác giả: Lưu Huyền Trang ; Fb: Lưu Huyền Trang
Chọn C
Ta có :




sin 5 cos 5
sin 5 cos 10
sin 5 cos 10
5
5
sin 5 cos 10
3log 5
ln 5
3
3
ln sin 5 cos 10
3.lnsin5cos103.ln5
xxm
xx
xx
m
m
xx
m
m
xx
xx m








STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 67
Xét
ln .3 , 5
t
f
ttt
 
1
3ln 3ln3 0, 5
tt
f
tt t
t

Vậy hàm số
f
t đồng biến .
sin 5 cos 10 5
sin 5 cos 10 5
sin 5 cos 5
fx x fm
xxm
xxm



Mà
6sin 5cos 6xx
Vậy để phương trình có nghiệm ta phải có
56 56m
Câu 49. Cho các số thực ,,abc thỏa mãn
222
244abc ab. Tính
23Pa b c
khi biểu
thức
227ab c
đạt giá trị lớn nhất.
A.
7P
. B.
3P
. C.
3P 
. D.
7P 
.
Lời giải
Tác giả: Nguyễn Ngọc Hiệp; Fb: Nguyễn Ngọc Hiệp
Chọn B
Cách 1: phương pháp đại số.
Ta có:

22
222 2
244 1 2 9abc ab a b c
.
Áp dụng bất đẳng thức giá trị tuyệt đối và bất đẳng thức BCS, ta có kết quả sau:
 

22 2
222
227212211212211
1 2 2 1 2 11 20.
BCS
ab c a b c a b c
abc
 



Đẳng thức xảy ra khi:


22
2
21 220
3
12
3
212
2
12 9
ab c
a
ab c
b
c
abc








Khi đó:

2332.33.23.Pa b c
Cách 2: phương pháp hình học.
Trong không gian
Oxyz
, gọi mặt cầu

S có tâm

1; 2; 0I , bán kính
3R
. Khi đó:

22
2222
:1 2 9 244.Sx y z xyz xy
và mặt phẳng

:2 2 7 0Pxyz .
Gọi

;;
M
abc
, ta có:


227
;
3
ab c
dM P

.
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 68
Vì

222
244abc ab M S
.
Bài toán đã cho trở thành: Tìm

M
S sao cho


;dM P
lớn nhất.
Gọi
là đường thẳng qua
I
và vuông góc

P
12
:2
2
x
t
yt
zt



.
Điểm
M
cần tìm chính là 1 trong 2 giao điểm của với

12
:3;3;2, 1;1;2SM M
.
Ta có:






12 1
20 2 20
;; ;
33 3
dM P dM P MaxdM P M M 
.
Vậy

2332.33.23.Pa b c
Phân tích: Khi quan sát 2 cách giải, đối với giáo viên ta sẽ dễ chọn Cách 1 vì ngắn gọn và tiết kiệm thời
gian. Tuy nhiên học sinh không nhiều em đã từng được tiếp cận bất đẳng thức BCS. Đối với
Cách 2, về mặt trình bày có thể dài hơi, nhiều tính toán hơn nhưng đó chỉ là những bước tính
toán khá cơ bản, một học sinh khá nếu nhận ra ý đồ tác giả thì việc giải bài toán cũng không
mất quá nhiều thời gian. Bài toán sẽ dễ hơn nếu đề bài chỉ yêu cầu tìm Min hoặc Max của biểu
thức
227ab c
.
Câu PT 49.1. Cho ba số thực dương ,,abc thỏa mãn
222
24610abc abc và
2ac
.
Tính giá trị biểu thức
32Pabc
khi
222
14 8 18Qa b c a b c
đạt giá trị lớn
nhất.
A. 10. B.
10
. C. 12. D. 12 .
Lời giải
Tác giả: Nguyễn Ngọc Hiệp; Fb: Nguyễn Ngọc Hiệp
Chọn D
Gọi
S
là mặt cầu tâm

1; 2; 3I
, bán kính 24R . Khi đó:

222
: 2 4 6 10.Sx y z x y z
Gọi
P
là mặt phẳng có phương trình 2
x
z và điểm

7;4; 9K
.
Với

;;
M
abc
. Theo giả thiết ta có:

M
S
và
 
M
PMS P
.
Hơn nữa:

222
222 2
14 8 18 7 4 9 146 146Qa b c a b c a b c KM
.
Bài toán trở thành: Tìm
M
nằm trên đường tròn giao tuyến của mặt cầu

S
và mặt phẳng

P
sao cho
K
M
lớn nhất.
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 69

P
có VTPT

1; 0;1n
.
Gọi
là đường thẳng qua
K
và vuông góc

7
:4
9
xt
Py
zt



.
Gọi
H
là hình chiếu của
K
lên mặt phẳng
 
9;4; 7PH PH
.
Ta có:
22 2
KM KH HM
, mà
KH
không đổi nên
KM
lớn nhất khi
HM
lớn nhất.
Gọi
d
là đường thẳng qua
I
và vuông góc

1
:2
3
xt
Pdy
zt



.
Gọi
J
là tâm đường tròn giao tuyến của

S
và

PJ
là hình chiếu của
I
lên

P

0; 2;2Jd P J
.
Phương trình đường thẳng
3
:22.
23
xt
HJ y t
zt


Gọi
,AB
là các giao điểm của
HJ
và

3; 4; 5 , 3; 0; 1SA B
.
Ta có:
422 222HA HB
.
Vậy

422 3;4;5MaxHM M A
. Khi đó:
32 12
Pabc

.
B
P
A
J
I
H
K
M
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 70
Câu 50. Cho cấp số cộng
n
a
, cấp số nhân

n
b
thoả mãn
21
0aa,
21
1bb và hàm số
3
3
f
xx x
sao cho

21
2
f
a
f
a
và
22 21
log 2 log
f
b
f
b
. Tìm số nguyên
dương
n nhỏ nhất sao cho 2019
nn
ba
A. 17. B. 14. C. 15. D. 16.
Lời giải
Tác giả: Nguyễn Trường Giang; Fb: Giang Nguyen
Chọn D
Xét hàm số
3
3
f
xx x
với
[0, )x 
. Ta có

2
330 1fx x x

từ đó ta suy ra bảng
biến thiên của

f
x trên
[0, )
như sau:
x
0
1

f
x
- 0 +

f
x
0

2
Vì
2
0a nên
 
212
220fa fa fa
(1)
Giả sử
1
1a , vì

f
x đồng biến trên
[1, )
nên
21
f
afa suy ra
11
2
f
afa vô lý. Vậy
1
[0,1)a
do đó
1
0fa
(2).
Từ (1) và (2) ta có:

1
0
1
2
0
0
1
1
fa
a
a
fa

Vậy số hạng tổng quát của dãy cấp số cộng
n
a
là
1
n
an
.
Một cách tương tự, đặt
121
logtb và
222
logtb suy ra
21
2
f
tft , vì
12
1 bb nên
12
0 tt,
theo lập luận trên ta có:
1211
2222
0log 0 1
1log 1 2
tbb
tbb






Vậy số hạng tổng quát của dãy cấp số nhân
n
b
là
1
2
n
n
b
.
Do đó
1
2019 2 2019 1
n
nn
ba n

(*). Trong 4 đáp án 16n là số nguyên dương nhỏ nhất thỏa
(*).
STRONG TEAM TOÁN VD-VDC PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địachỉtruycậphttps://facebook.com/groups/900248096852019?ref=share Trang 71
| 1/78
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD - ĐT HÀ TĨNH
KỲ THI THỬ TRUNG HỌC PHỔ THÔNG QUỐC GIA 2019 TRƯỜNG THPT CHUYÊN Môn thi : Toán
Thời gian làm bài: 90 phút
ĐỀ THI CHÍNH THỨC
(50 câu trắc nghiệm)
(Đề thi gồm có 6 trang) Mã đề thi: 001
Họ, tên thí sinh:.........................................................................
Số báo danh: ............................................................................. 5 5
Câu 1: Cho các hàm số f (x), g  x liên tục trên
có  2 f (x) 3g(x)dx  5
 ; 3f (x) 5g(x)dx  21. 1  1  5
Tính   f (x)  g(x)d .x 1  A. 5  B. 1 C. 5 D. 1 
Câu 2: Với k, n là hai số nguyên dương tùy ý thỏa mãn k  ,
n mệnh đề nào dưới đây sai? n k ! A. C B. k
A k !Ck C. k k 1
C C   Ck D. k
C k !Ak n
k !(n k)! n n n n n 1 n n
Câu 3: Cho số phức z  3  2 .
i Tìm phần ảo của số phức w  (1 2i)z A.  4 B. 7 C. 4 D. 4i
Câu 4: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng ( ) : x  2y  0. Mệnh đề nào dưới đây đúng?
A. ( ) // mp Oxy
B. ( ) // Oz
C. Oz  ( )
D. Oy  ( )
Câu 5: Hàm số nào sau đây nghịch biến trên ? A. 3
y x  3x  2 B. 4 2
y x  2x  2 C. 3 2
y  x  2x  4x 1 D. 3 2
y  x  2x  5x  2 Câu 6: Biết 
F (x) là một nguyên hàm của hàm số ( ) x f x e
 sin x thỏa mãn F(0)  0 . Tìm F(x)? A. ( ) x F x e   cos x  2 B. ( ) x F x e   cos x C. ( ) x F x e  cos x  2 D. ( ) x F x e   cos x  2
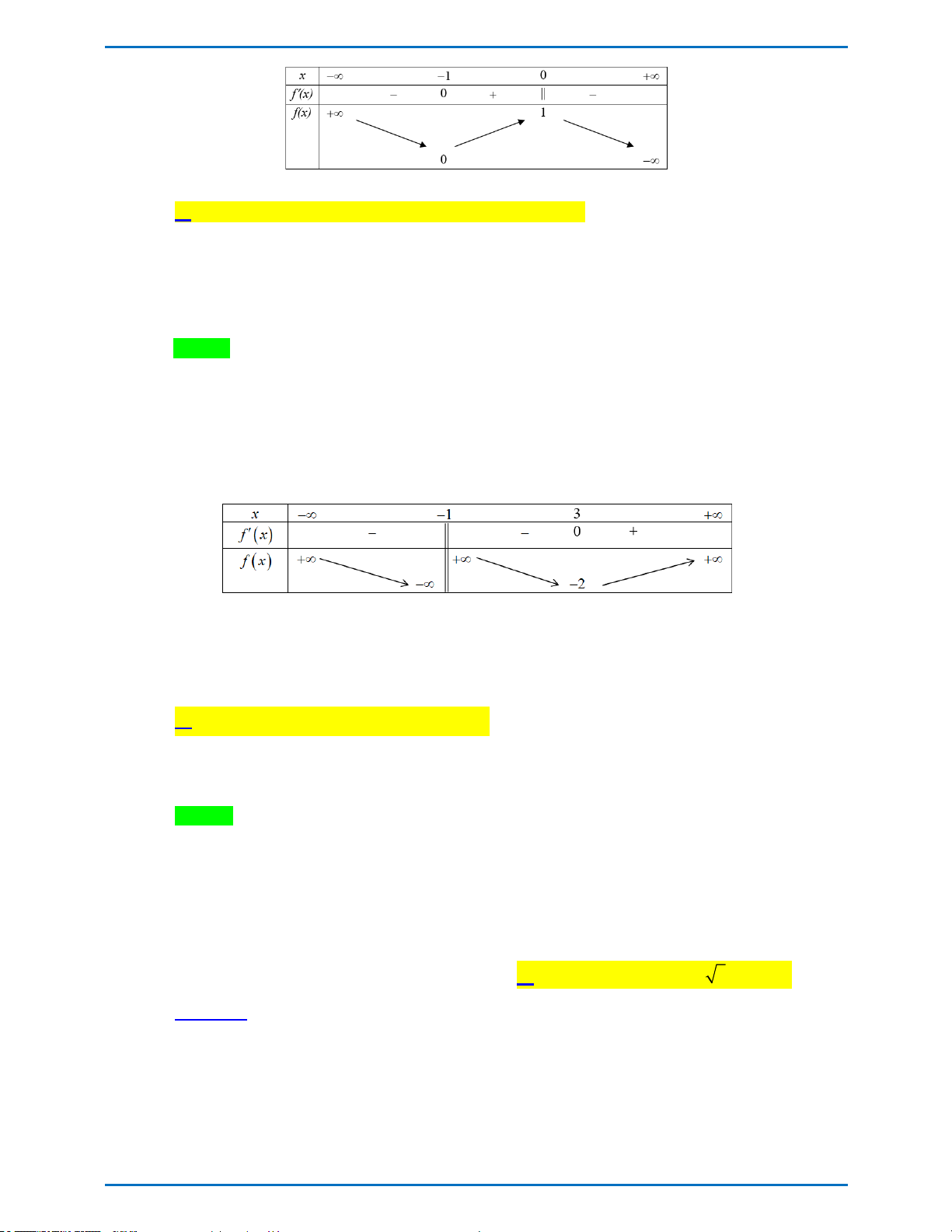
Câu 7: Cho hàm số y f (x) liên tục trên R và có bảng biến thiên như hình bên. Tìm khẳng định đúng
A. Hàm số có giá trị nhỏ nhất bằng 0 và giá trị lớn nhất bằng 1 x -∞ -1 0 +∞
B. Hàm số đạt cực đại tại x  0 và đạt cực tiểu tại x  1  - 0 + -
C. Đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt +∞ 1
D. Hàm số có đúng một cực trị -∞ 0
Câu 8: Trong không gian với hệ tọa độ Oxyz, phương trình nào sau đây không phải là phương trình mặt cầu? A. 2 2 2
2 x  2y  2z  2x  4y  6z  5  0 B. 2 2 2
x  y z  2x y z  0
Trang 1/6-Mã đề 001 C. 2 2 2
x  y z  3x  7 y  5z 1  0 D. 2 2 2
x  y z  3x  4y  3z  7  0
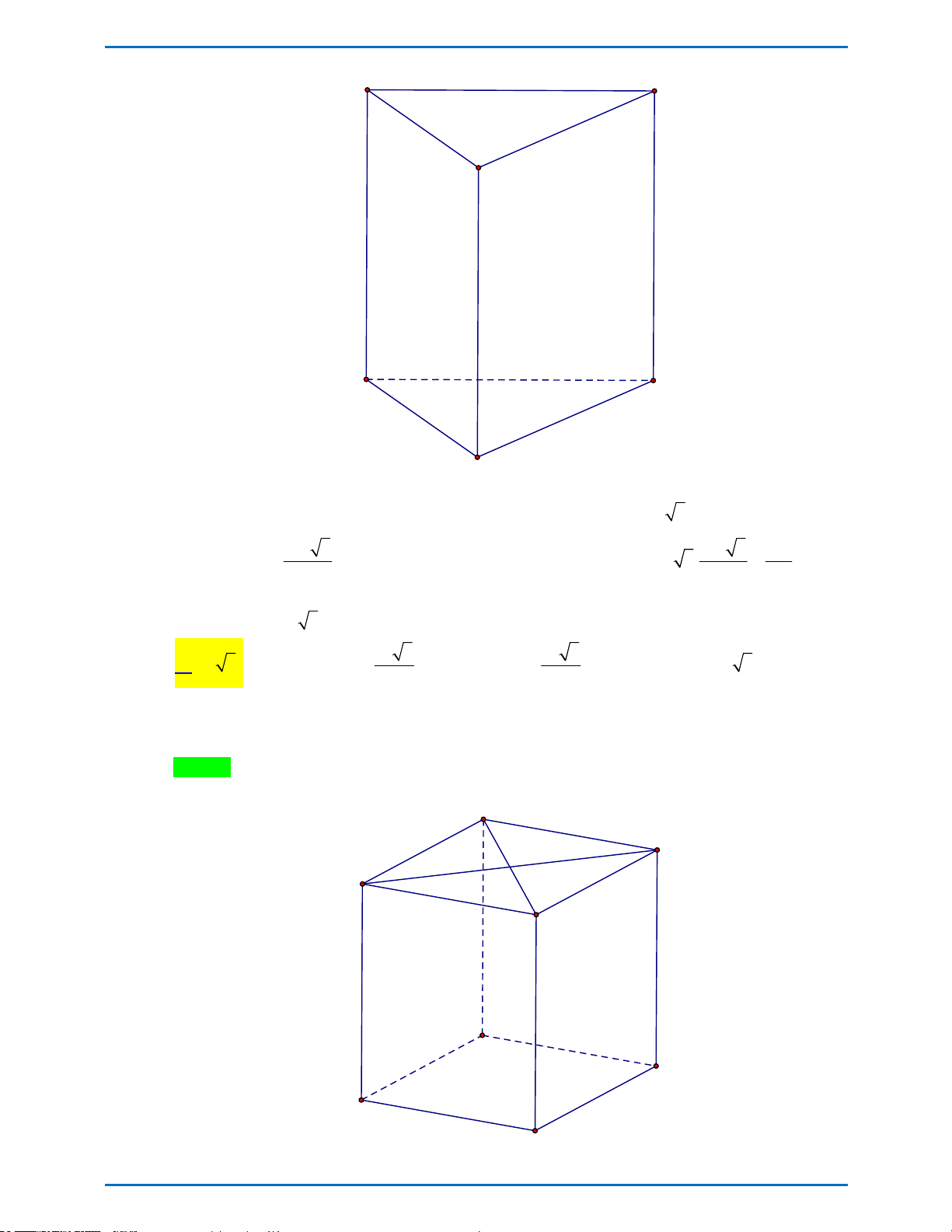
Câu 9: Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng a 3 . Thể tích khối lăng trụ đã cho bằng 3 9a 3 3a 3 a 3 3 3a 3 A. B. C. D. 4 4 4 4 Câu 10:
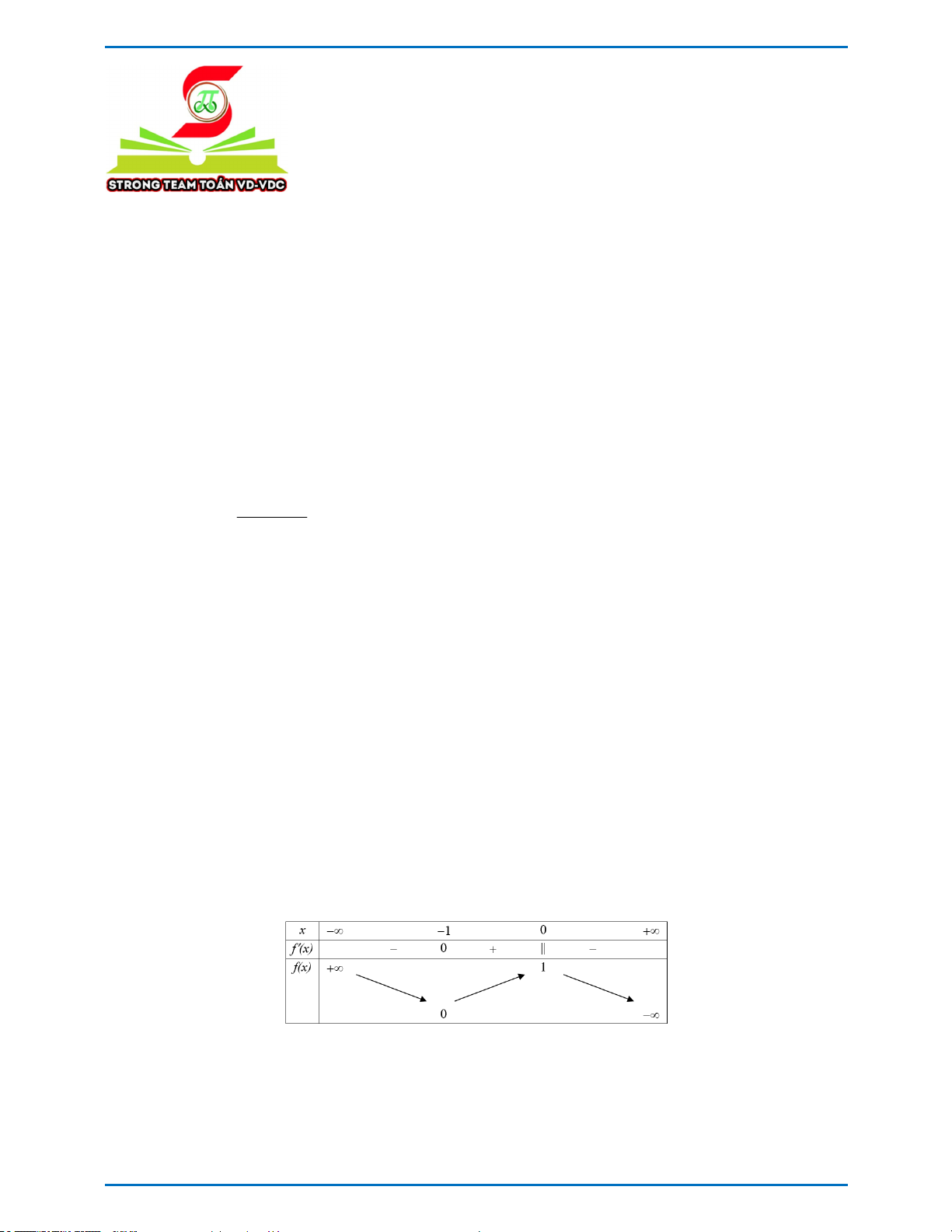
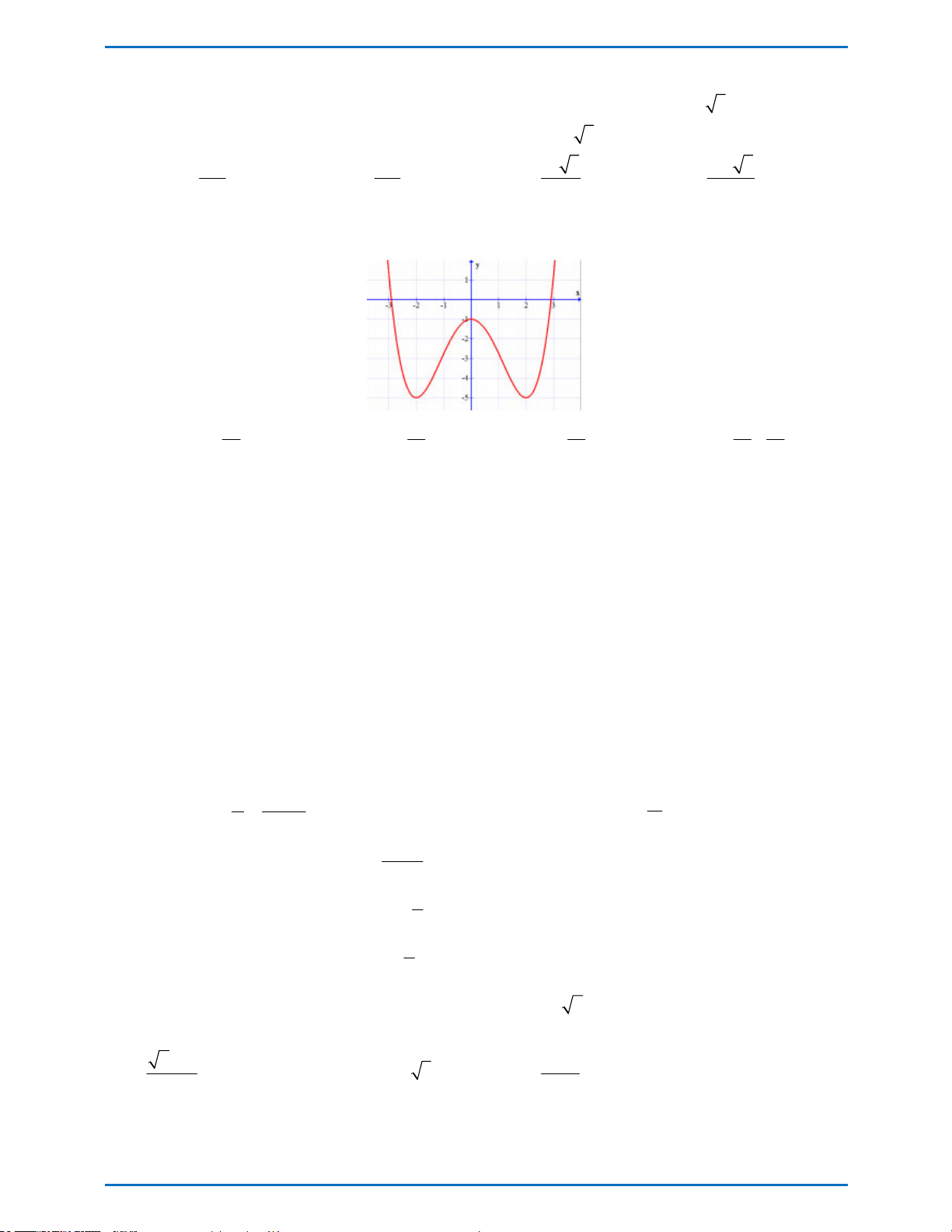
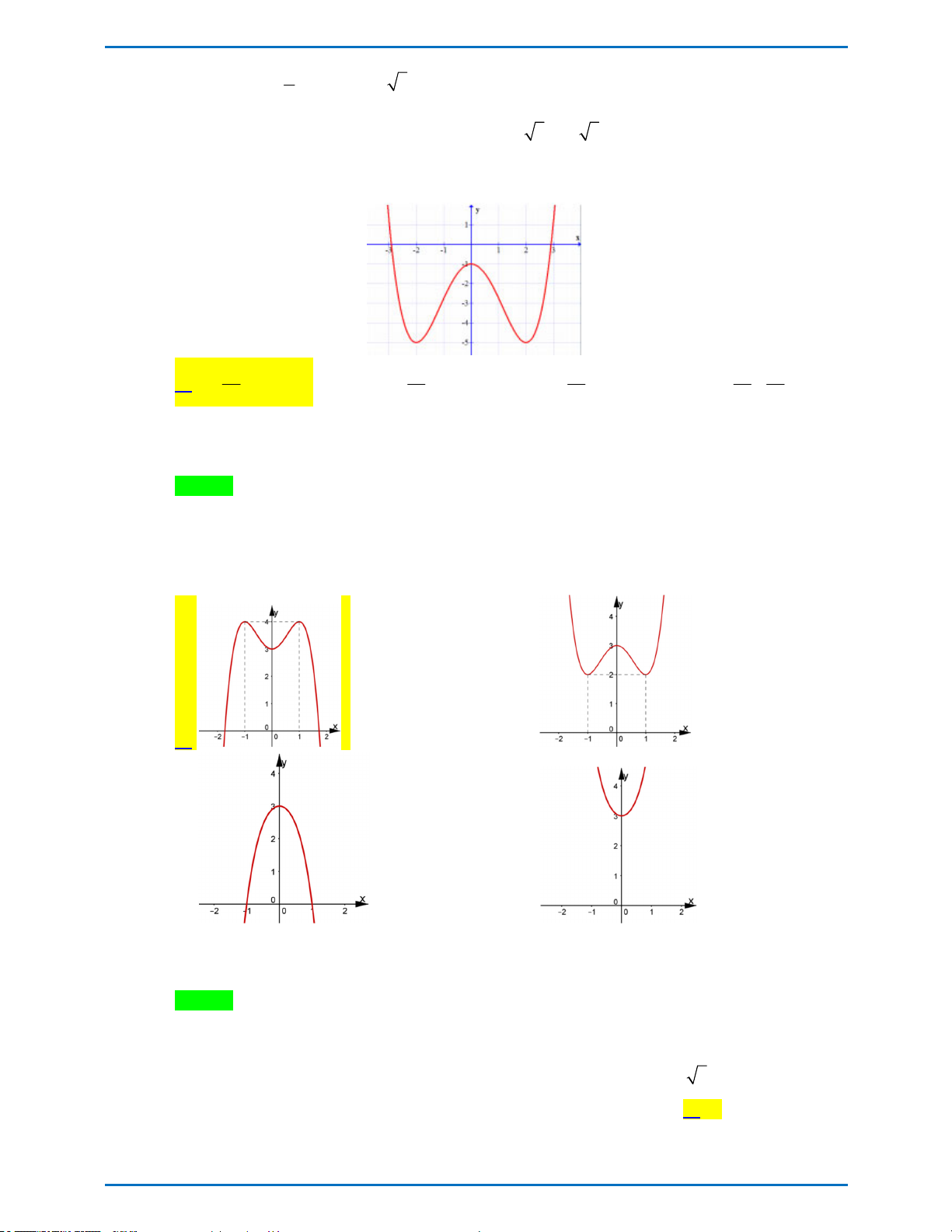
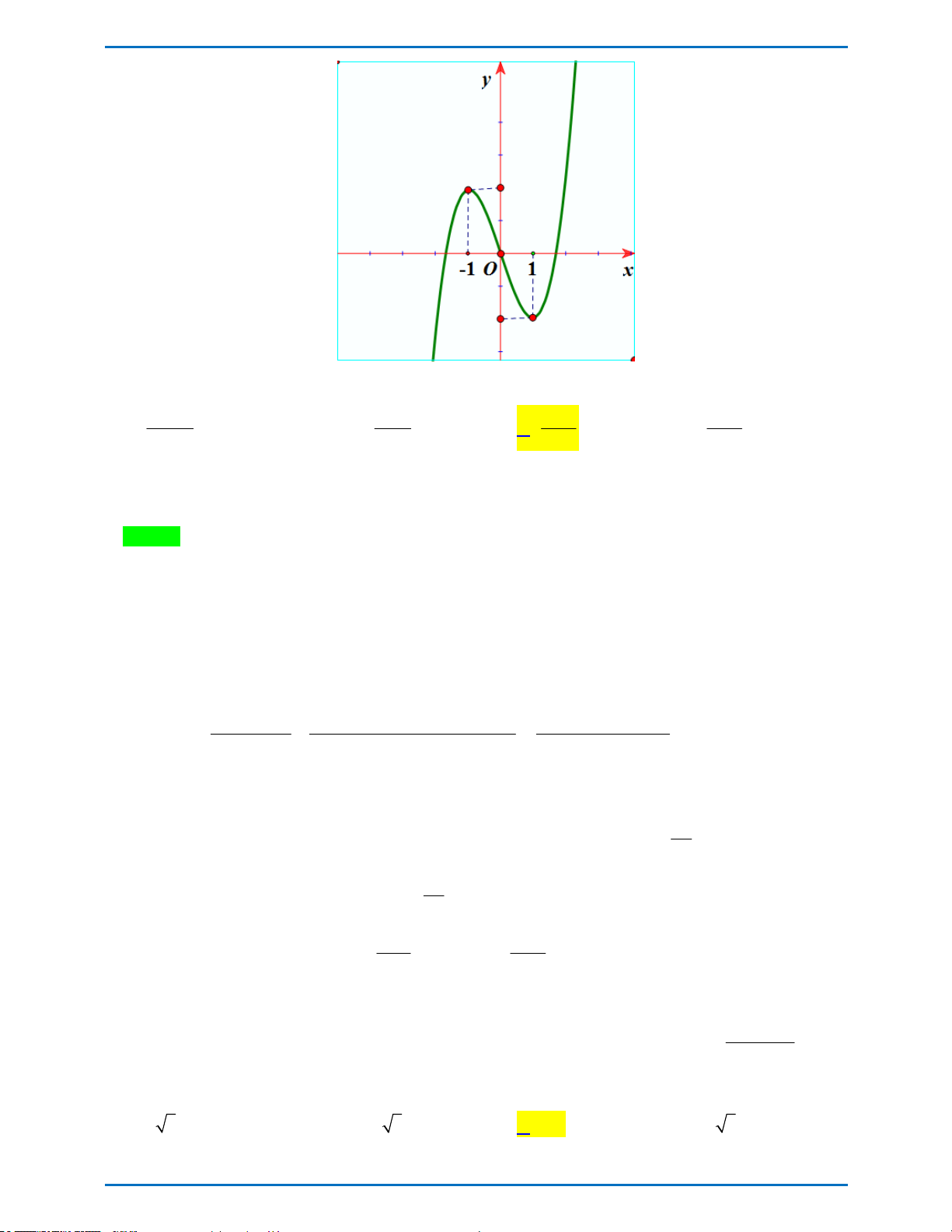
Đường cong trong hình vẽ bên là đồ thị của một trong 4 hàm số
dưới đây. Hỏi hàm số đó là hàm số nào? 4 x 4 x A. 2 y    x 1 B. 2 y   2x 1 4 4 4 x 4 2 x x C. 2 y   x 1 D. y   1 4 4 2
Câu 11: Cho 0  a  1 ; ,
b c  0 thỏa mãn log b  3 ; log c  2  . Tính b c a  3 2 log a . a a A. 18  B. 7 C. 10 D. 8
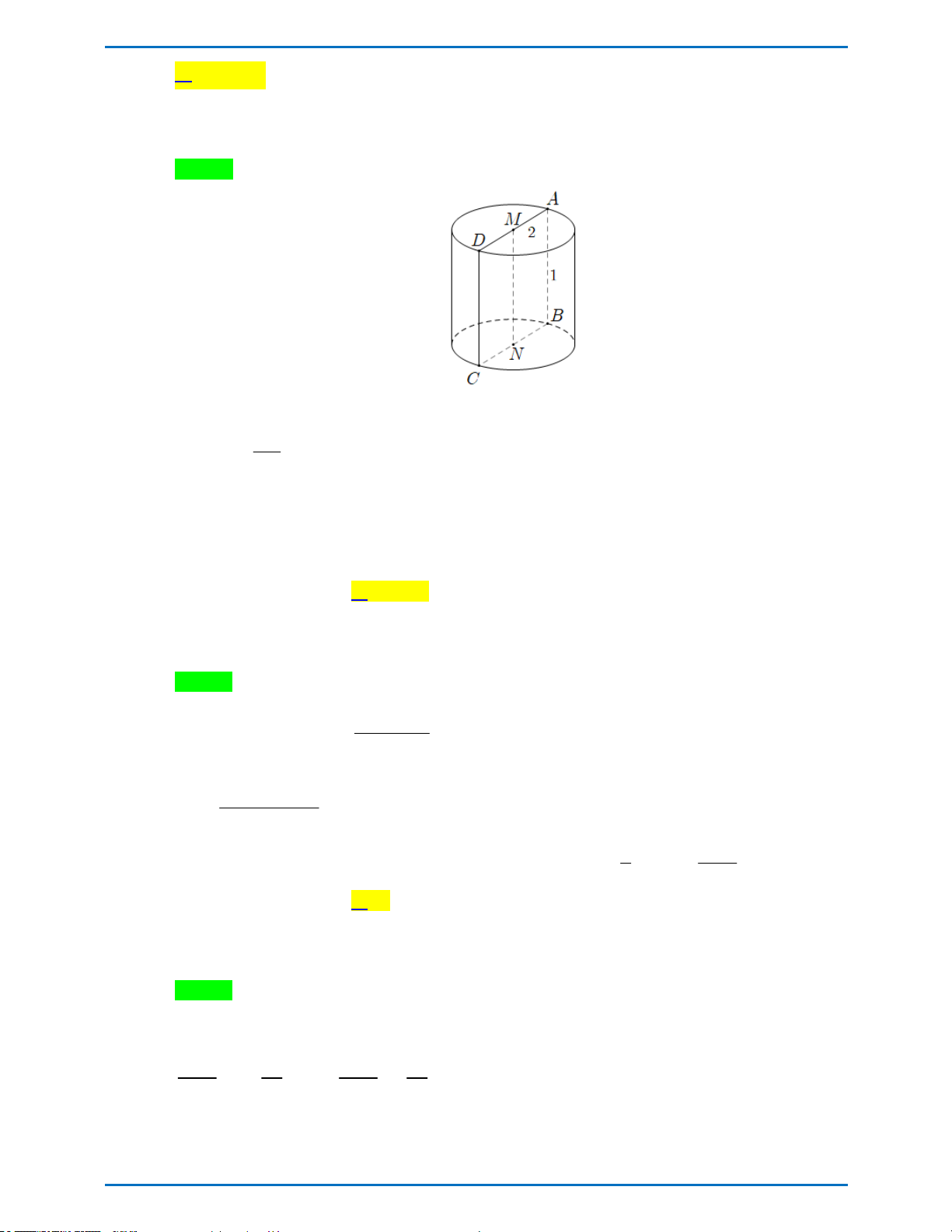
Câu 12: Cho hình trụ có đường cao bằng 5 và đường kính đáy bằng 8. Tính diện tích xung quanh của hình trụ đó. A. 40 B. 20 C. 80 D. 160
Câu 13: Cho cấp số nhân (u ) có số hạng đầu u  3; công bội q  2.
 Tính tổng 10 số hạng đầu tiên của n 1 (u ) . n A. 513  B. 1023  C. 513 D. 1023
Câu 14: Trong không gian với hệ tọa độ Oxyz, cho hai điểm ( A 1; 2  ;0); B(3;2; 8
 ) . Tìm một véctơ chỉ
phương của đường thẳng . AB A. u (1; 2; 4  ) B. u (2; 4;8) C. u ( 1  ;2; 4  ) D. u (1; 2  ; 4  )
Câu 15: Cho 0  a  1, 0  b  1; , x y  0, m
. Trong các mệnh đề sau, mệnh đề nào sai?
A. log x  log b  log x
B. log (xy)  log x  log y a a b a a a x log x 1 C. log aD. log x x m log a y log y a a m a x
Câu 16: Gọi (C) là đồ thị hàm số 2 y
. Trong các mệnh đề sau, mệnh đề nào sai? 2x 1
A. (C) có tiệm cận ngang là 1 y
B. (C) có đúng một trục đối xứng 2
C. (C) có tiệm cận đứng là 1 x
D. (C) có đúng một tâm đối xứng 2
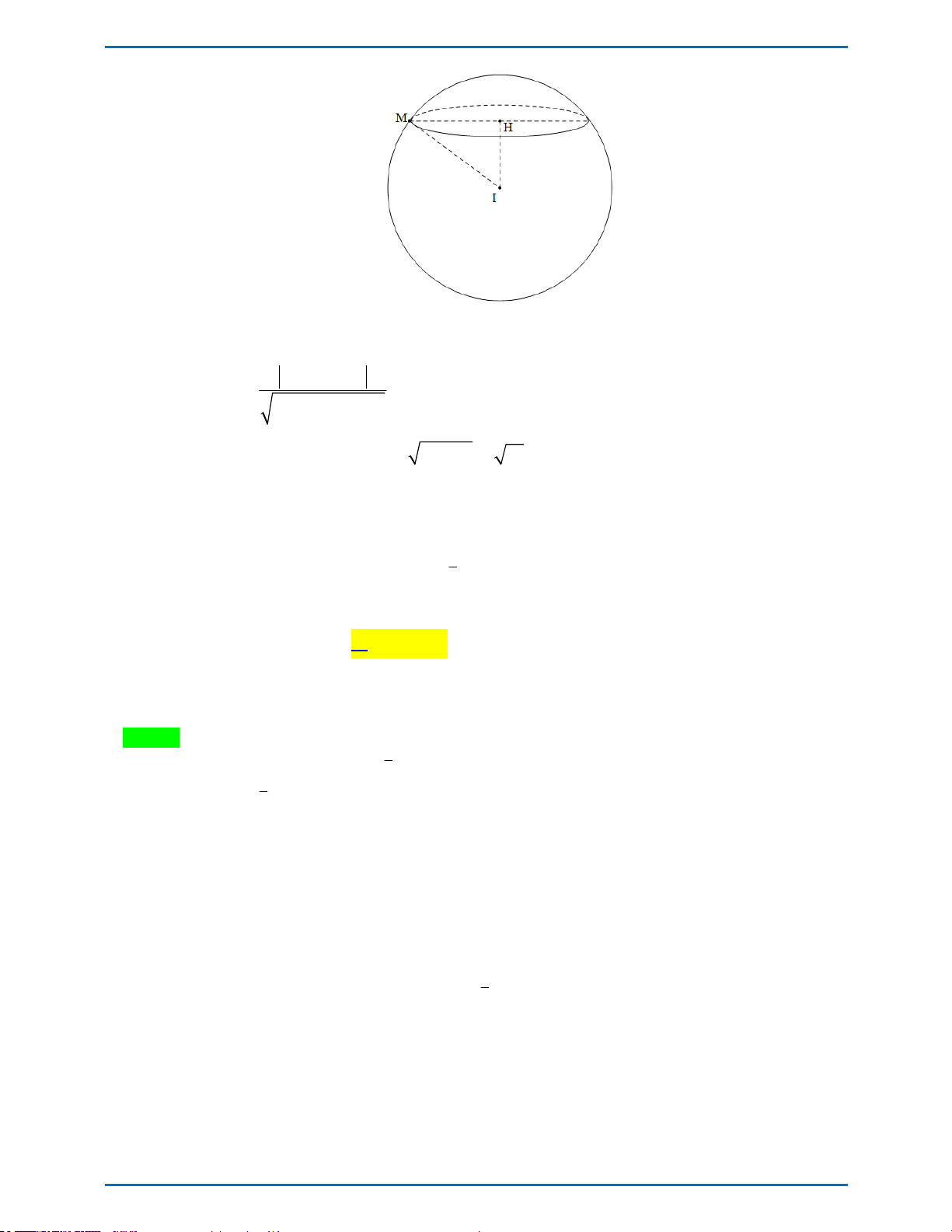
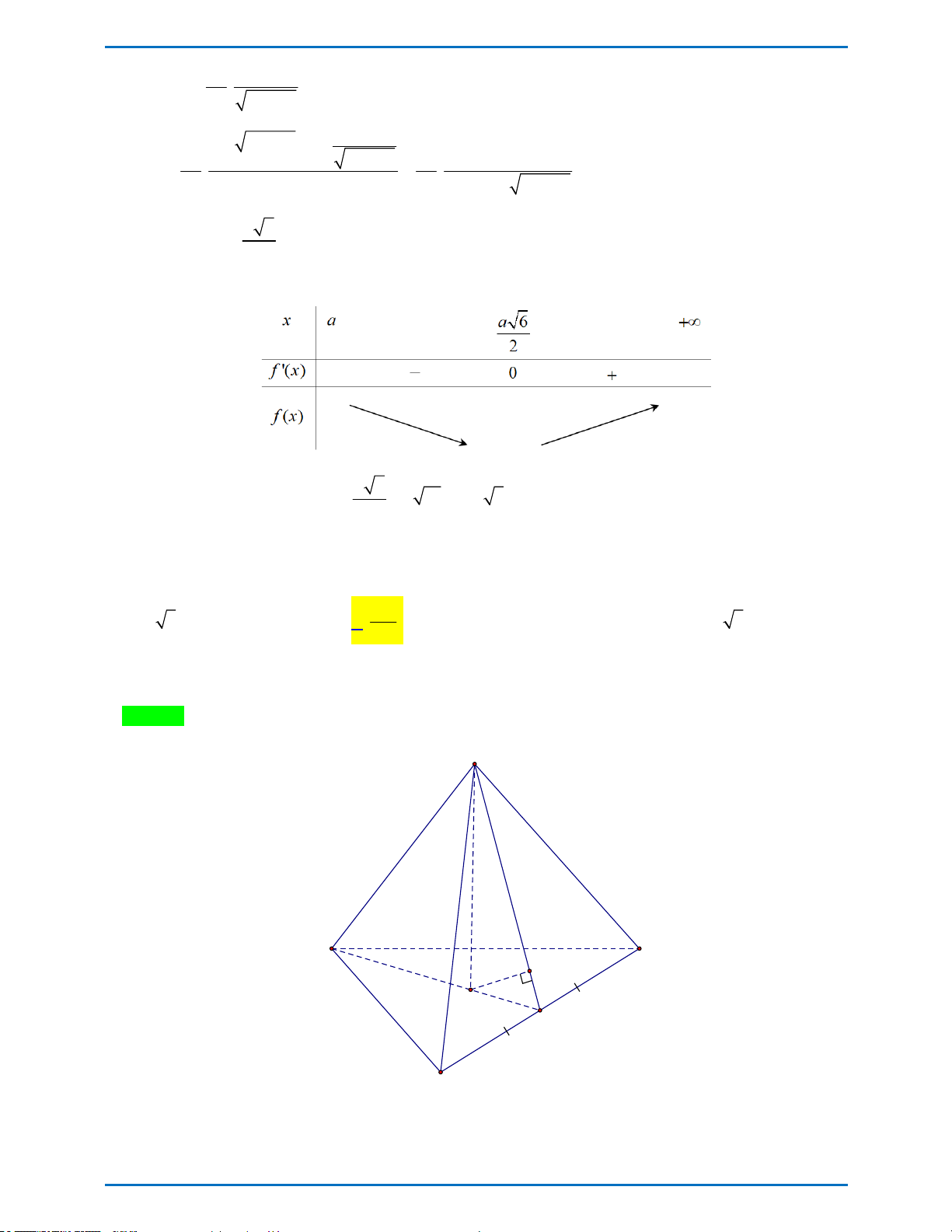
Câu 17: Cho hình chóp SABCD có đáy là hình vuông cạnh a 2 . Tam giác SAC vuông cân tại S và nằm
trong mặt phẳng vuông góc với đáy. Tính thể tích khối cầu ngoại tiếp hình chóp SABCD .
Trang 2/6-Mã đề 001 3 2 a 3 4 a A. B. 3 4 a 3 C. D. 3 4 a 3 3 x 1 y z  3
Câu 18: Trong không gian Oxyz cho điểm A(1; 2
 ;3) và hai đường thẳng d :   ; 1 2 1  1
d : x  1 t, y  2t, z  1 . Viết phương trình đường thẳng  đi qua A , vuông góc với cả d và d . 2 1 2 x  1 tx  2   tx  1 tx  1 2t     A. y  2   t B. y  1   2t C. y  2   t D. y  2   t     z  3  tz  3  3tz  3  tz  3  3t
Câu 19: Cho hình chóp SABCD có đáy ABCD là hình chữ nhật, AB  ;
a AD a 3 , SA  (ABC ) D , SC tạo với đáy một góc 1 0
45 . Gọi M là trung điểm cạnh SB , N là điểm trên cạnh SC sao cho SN NC . Tính 2
thể tích khối chóp SAMN. 3 a 3 3 a 3 3 a 3 3 a 3 A. B. C. D. 9 18 12 6
Câu 20: Diện tích hình phẳng giới hạn bởi các đường 3
y x , y  10  x và trục Ox là A. 32 B. 26 C. 36 D. 40
Câu 21: Biết log 27  a . Tính log 16 theo . a 12 6 4(3  a) 4(3  a) 3  a 3  a A. B. C. D. 3  a 3  a 4(3  a) 4(3  a)
Câu 22: Biết rằng đồ thị hàm số 3 2
y  2x  5x  3x  2 chỉ cắt đường thẳng y  3
x  4 tại một điểm duy nhất M  ;
a b . Tổng a b bằng A. 6  B. 3  C. 6 D. 3
Câu 23: Biết rằng phương trình 2
5log x  log 9x 1  0 có hai nghiệm là x , x . Tìm khẳng định đúng? 3 3   1 2 1 1 1 A. 5 x x  3 B. x x
C. x x D. x x   1 2 1 2 5 1 2 1 2 3 5 5
Câu 24: Gọi z , z là hai nghiệm phức của phương trình: 2
z  5z  7  0. Tính 2 2
P | z |  | z | 1 2 1 2 A. 4 7 B. 56 C. 14 D. 2 7
Câu 25: Cho khối nón có thiết diện qua trục là tam giác cân có một góc 0
120 và cạnh bên bằng a . Tính thể tích khối nón. 3  a 3 3 a 3  a 3 3  a A. B. C. D. 8 8 24 4 1
Câu 26: Tìm tập xác định của hàm số 2 3
y  (x  3x  2) .
Trang 3/6-Mã đề 001 A. \ 1;  2 B. ( ;  1) (2; )  C. 1; 2 D.
Câu 27: Tập nghiệm của bất phương trình log (2x 1)  0 là 1 2  1   1   1  A.  ; 0   B. (0; )  C.  ;    D.  ; 0    4   2   2 
Câu 28: Cho hình chóp SABCD có đáy là hình thoi cạnh 0 2 , a A
BC  60 , SA a 3 và SA  (ABC ) D . Tính
góc giữa SA và mp(SB ) D . A. 0 60 B. 0 90 C. 0 30 D. 0 45 e ln x a 2 Câu 29: Biết dx   bln  c  , với , a ,
b c  . Tính a b c 2 (1 x) e 1 e 1 1 A. 1  B. 1 C. 3 D. 2
Câu 30: Có bao nhiêu tiếp tuyến của đồ thị hàm số 3 2
y x  3x  2 đi qua điểm A3; 2 ? A. 3 B. 0 C. 1 D. 2 x
Câu 31: Gọi M , m tương ứng là giá trị lớn nhất và nhỏ nhất của hàm số 2 cos 1 y  . Khi đó ta có: cos x  2
A. 9M m  0
B. 9M m  0
C. M  9m  0
D. M m  0
Câu 32: Trong không gian Oxyz , viết phương trình mặt cầu tâm I ( 1
 ;3;0) và tiếp xúc với mặt phẳng ( )
P : 2x y  2z 11  0. A. 2 2 2
(x 1)  ( y  3)  z  4 B. 2 2 2
(x 1)  ( y  3)  z  4 4 C. 2 2 2
(x 1)  ( y  3)  z  2 D. 2 2 2
(x 1)  ( y  3)  z  9
Câu 33: Cho số phức z thỏa mãn : z(1 2i)  z(2  3i)   4 12i . Tìm tọa độ điểm M biểu diễn số phức z . A. M (3;1) B. M (3; 1  ) C. M ( 1  ;3) D. M (1;3) f x  3
Câu 34: Cho các hàm số y f x, y g x, y
. Hệ số góc của các tiếp tuyến của các đồ thị các g x 1
hàm số đã cho tại điểm có hoành độ x 1 bằng nhau và khác 0. Khẳng định nào dưới đây là khẳng định đúng? A. f   1  3  . B. f   1  3  C. f   11 1   . D. f   11 1   . 4 4
Câu 35: Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy 2, 4, n n  3 điểm phân biệt (các điểm
không trùng với các đỉnh của tam giác). Tìm n, biết rằng số tam giác có các đỉnh thuộc n  6 điểm đã cho là 247 . A. 6 B. 8 C. 7 D. 5
Trang 4/6-Mã đề 001 ln 2
3 2x  3 f x
Câu 36: Cho hàm số f x liên tục trên . Biết (ex f 1)dx  5  và dx  3.  Tính x 1 0 2 3 I f
 xd .x 2 A. I  2 B. I  4 C. I  2  D. I  8
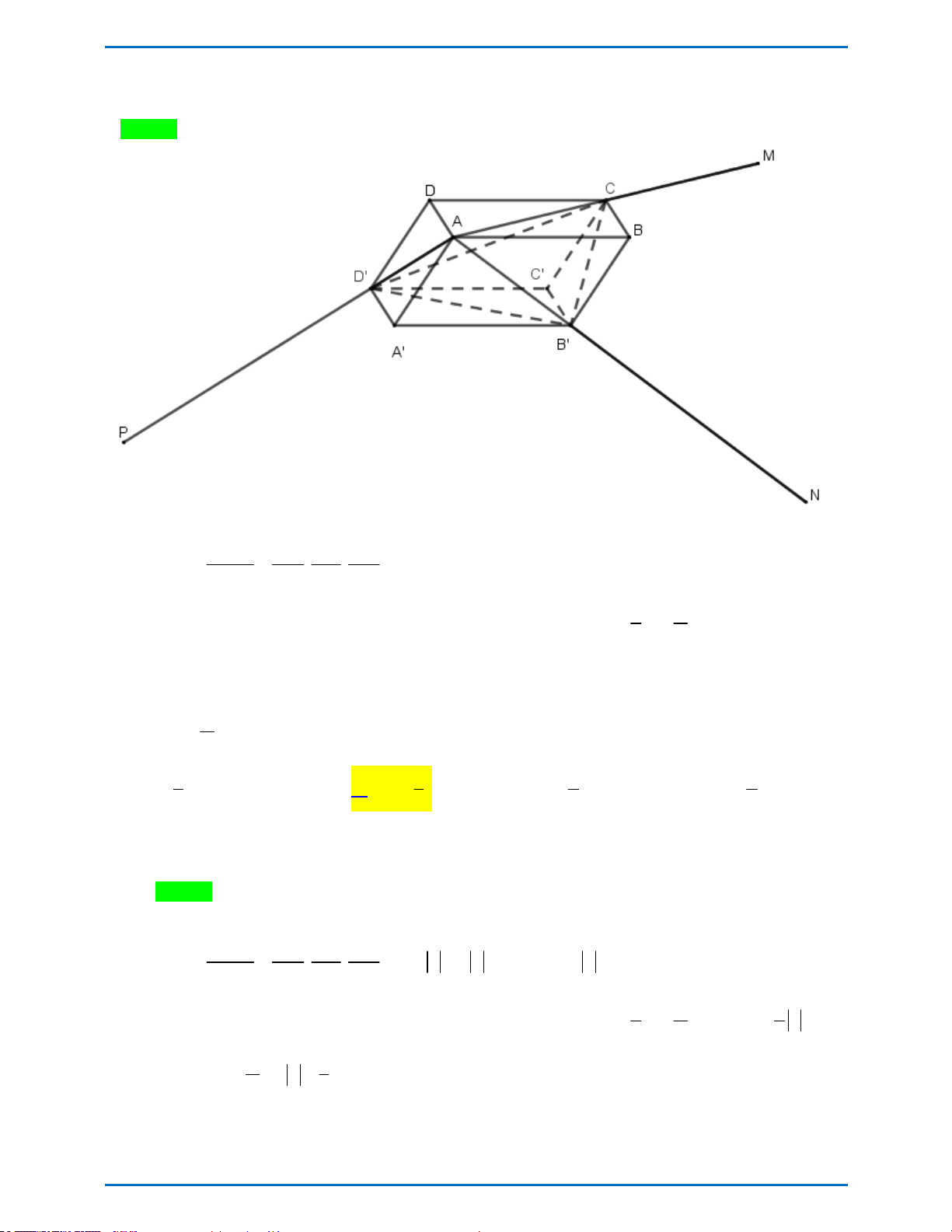
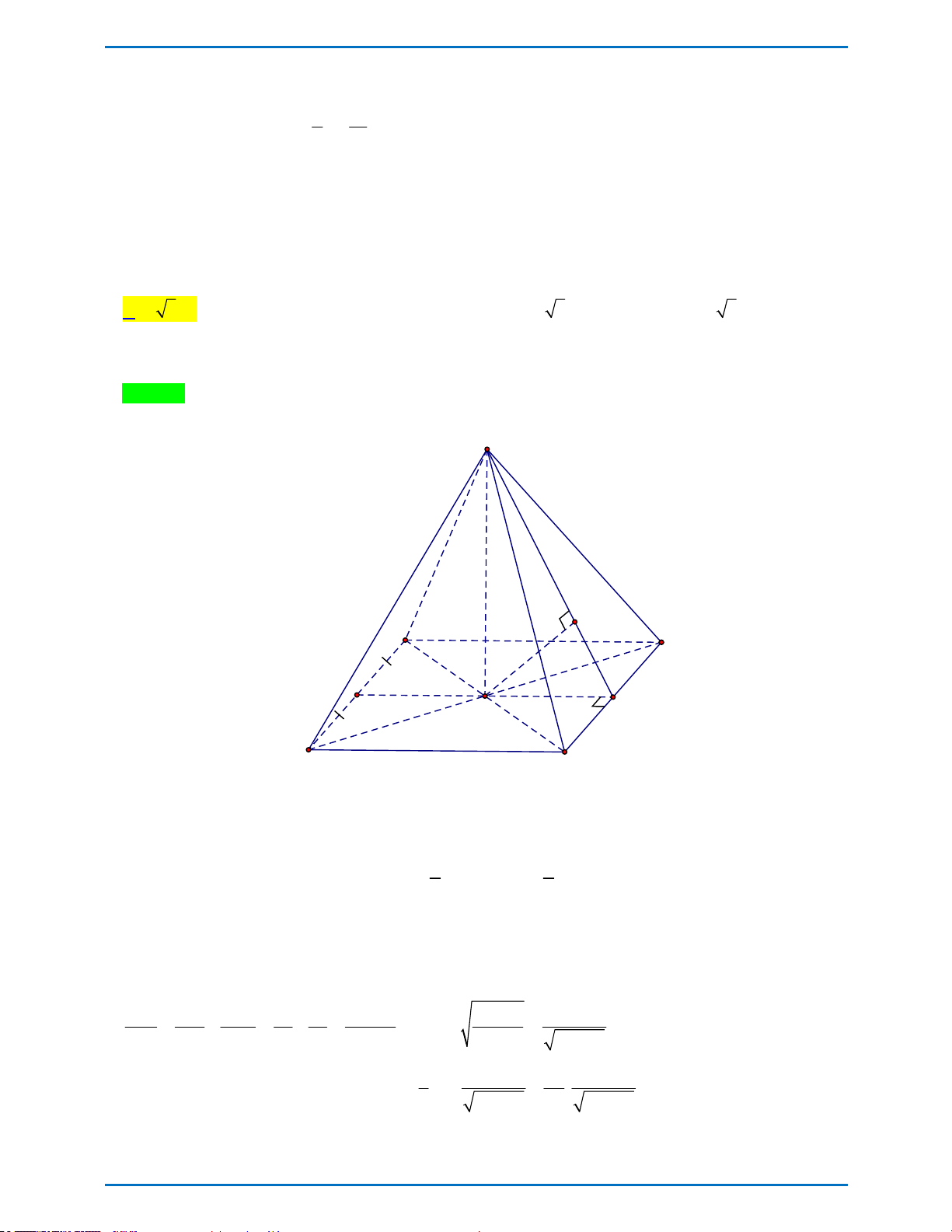
Câu 37: Cho khối hộp ABCDA' B 'C ' D ' có thể tích V . Các điểm M , N, P thỏa mãn AM  2AC, AN  3AB '
, AP  4AD ' . Tính thể tích khối chóp AMNP theo V . A. 6V B. 8V C. 12V D. 4V 1 1 5
Câu 38: Số phức z thỏa mãn z 1  5 ,  
và z có phần ảo dương. Tìm tổng phần thực và phần ảo z z 17 của z . A. 2 B. 4 C. 6 D. 8 x y z
Câu 39: Trong không gian với hệ tọa độ Oxyz, cho điểm A1;2;2 và đường thẳng 6 1 5 d :   . 2 1 1
Tìm tọa độ điểm B đối xứng với A qua d. A. B  3  ;4; 4   B. B 2; 1  ;3 C. B 3; 4; 4   D. B 3; 4  ;4
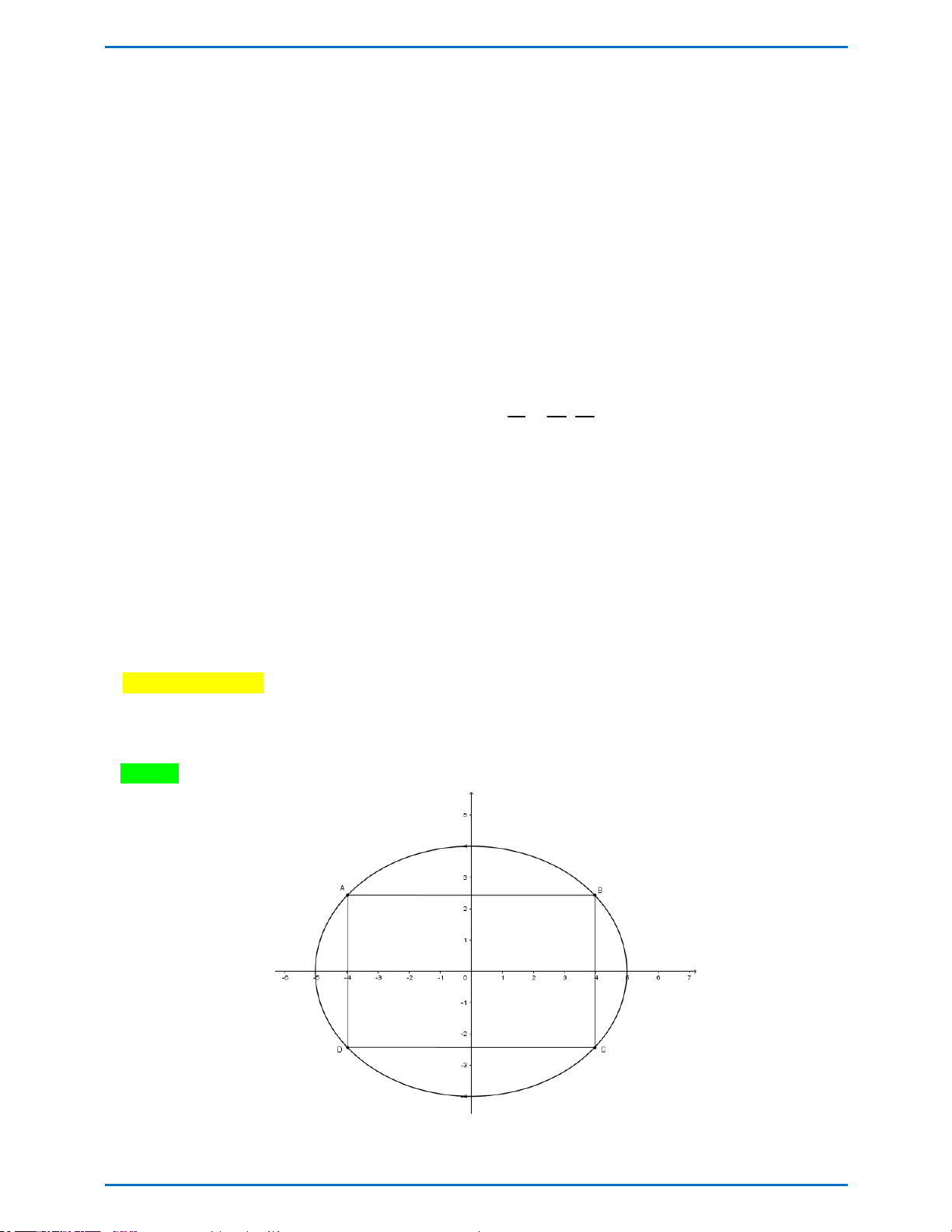
Câu 40: Ông An có một khu đất hình elip với độ dài trục lớn 10 m và độ dài trục bé 8 m. Ông An muốn chia
khu đất thành hai phần, phần thứ nhất là một hình chữ nhật nội tiếp elip dùng để xây bể cá cảnh và phần còn lại
dùng để trồng hoa. Biết chi phí xây bể cá là 1000000 đồng trên 2
1m và chi phí trồng hoa là 1200000 đồng trên 2
1m . Hỏi ông An có thể thiết kế xây dựng như trên với tổng chi phí thấp nhất gần nhất với số nào sau đây? A. 67398224 đồng B. 67593346 đồng C. 63389223 đồng D. 67398228 đồng x y z
Câu 41: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng 5 7 12 d :   2 2 1  và
mp   :x  2y  3z  3  0 . Gọi M là giao điểm của d với   , A thuộc d sao cho AM  14 . Tính khoảng
cách từ A đến mp  . A. 2 B. 3 C. 6 D. 14
Câu 42: Có bao nhiêu giá trị nguyên của tham số m để hàm số 2 4
y m x   2 m m 2 2019
x 1 có đúng một cực trị? A. 2019 B. 2020 C. 2018 D. 2017
Câu 43: Gọi S là tập tất cả các giá trị của tham số m để đồ thị hàm số 3 3 2 2 y
x  3x  2  4x  3x  2  mx
có tiệm cận ngang. Tổng các phần tử của S là A. 2  B. 2 C. 3  D. 3 f   1 f 2 f 2019
Câu 44: Cho hàm số f x    2
ln x x . Tính P  ee ... e .
Trang 5/6-Mã đề 001 2020 2019 2019 A. P  B. P  C. 2019 P  e D. P   2019 2020 2020
Câu 45: Cho các số phức z , z thỏa mãn phương trình z  2  3i  5 và z z  6 . Biết tập hợp các điểm M 1 2 1 2
biểu diễn số phức w z z là một đường tròn. Tính bán kính đường tròn đó. 1 2 A. R  8 B. R  4 C. R  2 2 D. R  2
Câu 46: Cho các số thực ,
x y thay đổi thỏa mãn 2 2
x y xy  1 và hàm số f t  3 2
 2t 3t 1 . Gọi M ,m    
tương ứng là giá trị lớn nhất và nhỏ nhất của 5x y 2 Q f
 . Tổng M m bằng
x y  4  A. 4  3 2 B. 4  5 2 C. 4   4 2 D. 4   2 2
Câu 47: Trong các khối chóp tứ giác đều S.ABCD mà khoảng cách từ A đến mp(SBC) bằng 2a, khối chóp có
thể tích nhỏ nhất bằng A. 3 2 3a B. 3 2a C. 3 3 3a D. 3 4 3a 2    
Câu 48: Tổng tất cả các giá trị của tham số x 2x 1 2 x m
m để phương trình 3  log   có đúng 2 2 x m 2 x 2x3 ba nghiệm phân biệt là A. 3 B. 2  C. 3  D. 2
Câu 49: Cho các số thực a, , b c thỏa mãn 2 2 2
a b c  2a  4b  4 . Tính P a  2b  3c khi biểu thức
2a b  2c  7 đạt giá trị lớn nhất. A. 7 B. 3 C. 3  D. 7 
Câu 50: Cho cấp số cộng a , cấp số nhân b thỏa mãn a a  0,b b 1 và hàm số f x 3  x 3x n n  2 1 2 1
sao cho f a  2  f a và f log b  2  f log b . Tìm số nguyên dương n nhỏ nhất sao cho 2 2   2 1 2   1 b  2019a . n n A. 17 B. 14 C. 15 D. 16
-----------------------------------HẾT-------------------------
Trang 6/6-Mã đề 001 mamon made cautron dapan Toán 001 1 D Toán 001 2 D Toán 001 3 C Toán 001 4 C Toán 001 5 C Toán 001 6 A Toán 001 7 B Toán 001 8 D Toán 001 9 A Toán 001 10 B Toán 001 11 D Toán 001 12 A Toán 001 13 B Toán 001 14 A Toán 001 15 C Toán 001 16 B Toán 001 17 C Toán 001 18 D Toán 001 19 B Toán 001 20 C Toán 001 21 A Toán 001 22 D Toán 001 23 A Toán 001 24 C Toán 001 25 A Toán 001 26 B Toán 001 27 D Toán 001 28 C Toán 001 29 B Toán 001 30 D Toán 001 31 A Toán 001 32 A Toán 001 33 B Toán 001 34 C Toán 001 35 C Toán 001 36 B Toán 001 37 B Toán 001 38 D Toán 001 39 D Toán 001 40 A Toán 001 41 B Toán 001 42 A Toán 001 43 A Toán 001 44 B Toán 001 45 A Toán 001 46 C Toán 001 47 A Toán 001 48 C Toán 001 49 B Toán 001 50 D
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 THPT CHUYÊN HÀ TĨNH
(Đề thi có 6 trang)
NĂM HỌC 2018 - 2019 MÔN: TOÁN Thời gian: 90 phút
Bản quyền thuộc tập thể thầy cô nhóm STRONG TEAM TOÁN VD-VDC
Nhóm làm 1-2 câu/ tuần nhận lại cả ngàn câu đã qua phản biện 3-4 lần! Mời thầy cô tham gia nhóm! 5
Câu 1. Cho các hàm số
f x, g x liên tục trên  có 2 f
  x3gxdx  5   ; 1  5 5 3 f
  x5gxdx  21  . Tính  f
  x gxdx  . 1  1  A. 5  . B. 1. C. 5 . D. 1.
Câu 2. Với k, n là hai số nguyên dương tùy ý thỏa mãn k n, mệnh đề nào dưới đây sai? n k ! A. C  . B. k
A k !. k C . k k k C C
C . D. k
C k !. k A . n k  ! n k ! n n C. 1 n n n 1  n n
Câu 3. Cho số phức z  3  2i . Tìm phần ảo của số phức w  1 2iz A. 4  . B. 7 . C. 4 . D. 4i .
Câu 4. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng   : x  2y  0. Mệnh đề nào dưới đây đúng?
A.   // Oxy .
B.   //Oz .
C. Oz    .
D. Oy    .
Câu 5. Hàm số nào sau đây nghịch biến trên  ? A. 3
y x  3x  2 . B. 4 2
y x  2x  2 . C. 3 2
y  x  2x  4x 1. D. 3 2
y  x  2x  5x  2 .
Câu 6. Biết F x là một nguyên hàm của hàm số    x
f x e  sin x thỏa mãn F 0  0 . Tìm F x ? A.    x
F x  e  cos x  2 . B.    x
F x  e  cos x . C.   x
F x e  cos x  2 . D.   x
F x  e  cos x  2 .
Câu 7. Cho hàm số y f x liên tục trên  và có bảng biến thiên như hình bên. Tìm khẳng định đúng
A. Hàm số có giá trị nhỏ nhất bằng 0 và giá trị lớn nhất bằng 1.
B. Hàm số đạt cực đại tại x  0 và đạt cực tiểu tại x  1  .
C. Đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt.
D. Hàm số có đúng một cực trị.
Câu 8. Trong không gian với hệ tọa độ Oxyz , phương trình nào sau đây không phải phương trình mặt cầu ?
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 1
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 A. 2 2 2
2x  2y  2z  2x  4y  6z  5  0 . B. 2 2 2
x y z  2x y z  0 . 2 2 2
C. x y z  3x  7 y  5z 1  0 . D. 2 2 2
x y z  3x  4y  3z  7  0 .
Câu 9. Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng a 3 . Thể tích khối lăng trụ đã cho bằng 3 9a 3 3a 3 a 3 3 3a 3 A. . B. . C. . D. . 4 4 4 4
Câu 10. Đường cong trong hình vẽ dưới đây là đồ thị của một trong bốn hàm số đã cho. Hỏi hàm số đó là hàm số nào? 4 x 4 x 4 x 4 2 x x A. 2 y   2x 1 . B. 2 y    x 1 . C. 2 y   x 1 . D. y   1 . 4 4 4 4 2
Câu 12 . Cho hình trụ có đường cao bằng 5 và đường kính đáy bằng 8 . Tính diện tích xung quanh của hình trụ đó. A. 40 . B. 20 . C. 80 . D. 160 .
Câu 13. Cho cấp số nhân u có số hạng đầu u  3 , công bội q  2 . Tính tổng 10 số hạng đầu tiên n  1 của u . n A. 513  . B. 1023  . C. 513. D. 1023 .
Câu 14. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A1; 2;0 ; B3;2;8 . Tìm một vectơ
chỉ phương của đường thẳng AB .    
A. u  1;2; 4 .
B. u  2;4;8 . C. u   1;  2; 4 .
D. u  1; 2; 4 .
Câu 15. Cho 0  a  1, 0  b  1; x, y  0, m   . Trong các mệnh đề sau, mệnh đề nào sai?
A. log x  log . b log x . B. log x y x y . a  .  log log a a b a b x log x 1 C. log a  . D. log x x . m log a y log y a a m a x  2
Câu 16. Gọi C là đồ thị hàm số y
. Trong các mệnh đề sau, mệnh đề nào sai? 2x 1 1
A. C có tiệm cận ngang là y  .
B. C có một trục đối xứng. 2 1
C. C có tiệm cận đứng là x  .
D. C có một tâm đối xứng. 2
Câu 17. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a 2 . Tam giác SAC vuông cân tại S và
nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối cầu ngoại tiếp hình chóp S.ABCD . 3 2 a 3 4 a A. . B. 3 4 a 3 . C. . D. 3 4 a . 3 3
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 2
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 x -1 y z + 3
Câu 18. Trong không gian Oxyz, cho điểm A(1; 2 - ; )
3 và hai đường thẳng d : = = ; 1 2 -1 1 ìïx =1-t ïï
d :íy = 2t . Viết phương trình đường thẳng D đi qua A vuông góc với d và d . 2 ï 1 2 ïïz =1 ïî x  1 tx  2   tx 1 tx  1 2t     A.y  2
  t B. y  1
  2t . C.y  2   t . D.y  2   t z  3 t     z  3  3tz  3  tz  3  3t
Câu 19. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  ;
a AD a 3; SA   ABCD và
SC tạo với đáy một góc 0
45 . Gọi M là trung điểm cạnh SB , N là điểm trên cạnh SC sao cho 1
SN NC . Tính thể tích khối chóp S.AMN . 2 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 9 18 12 6
Câu 20. Diện tích hình phẳng giới hạn bởi các đường 3
y x , y  10  x và trục Ox là A. 32 . B. 26 . C. 36 . D. 40 .
Câu 21 . Biết log 27  a . Tính log 16 theo a 12 6 43  a 43 a 3  a 3  a A. . B. . C. . D. . 3  a 3  a 43  a 43  a
Câu 22. Biết rằng đồ thị hàm số 3 2
y  2x  5x  3x  2 chỉ cắt đường thẳng y  3x  4 tại một điểm
duy nhất M a;b . Tổng của a b bằng A. 6 . B. 3 . C. 6 . D. 3.
Câu 23. Biết rằng phương trình 2
5log x  log 9x 1  0 có hai nghiệm là x , x . Tìm khẳng định đúng? 3 3   1 2 1 A. 5 1 1 x x  3 . B. x x  .
C. x x  .
D. x x   . 1 2 1 2 5 3 1 2 5 1 2 5
Câu 24 . Gọi z , z là hai nghiệm phức của phương trình 2
z  5z  7  0 . Tính 2 2
P z z . 1 2 1 2 A. 4 7 . B. 56 . C. 14 . D. 2 7 .
Câu 25. Cho khối nón có thiết diện qua trục là tam giác cân có một góc 120o và cạnh bên bằng a . Tính thể tích khối nón. 3  a 3 a 3  a 3 3  a A. . B. . C. . D. . 8 8 24 4
Câu 26. Tập xác định của hàm số y  x x  1 2 3 3 2 là A.  \ 1;  2 . B.   ;1  2;  . C. 1;2 . D.  .
Câu 27. Tập nghiệm của bất phương trình log 2x +1 > 0 là: 1 ( ) 2  1   1   1  A.  ;0 .  
B. 0;. C.  ; .   D.  ;0 .    4   2   2 
Câu 28. Cho hình chóp S.ABCD có đáy là hình thoi cạnh 2a , 
ABC  60 , SA a 3 và
SA   ABCD . Tính góc giữa SA và mpSBD .
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 3
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 A. 60 . B. 90 . C. 30 . D. 45. e ln x a 2 Câu 29. Biết dx   b ln  c
với a,b, c   . Tính a b c . 1 x2 e+1 e+1 1 A. 1. B. 1. C. 3 . D. 2 .
Câu 30. Có bao nhiêu tiếp tuyến của đồ thị hàm số 3 2
y x  3x  2 đi qua điểm A3;2 ? A. 3 . B. 0 . C. 1. D. 2 . 2cos x 1
Câu 31. Gọi M,m tương ứng là giá trị lớn nhất và nhỏ nhất của hàm số y  . Khi đó ta có cos x  2
A. 9M m  0 .
B. 9M m  0 .
C. M  9m  0 .
D. M m  0 .
Câu 32 . Trong không gian Oxyz , viết phương trình mặt cầu tâm I  1;
 3;0 và tiếp xúc với mặt phẳng
P: 2x y  2z 11 0.
A. x  2   y  2 2 1 3  z  4 .
B. x  2   y  2 2 1 3  z  4 .
C. x  2   y  2 2 1 3  z  2 .
D. x  2   y  2 2 4 1 3  z  . 9
Câu 33. Cho số phức z thoả mãn z 1 2i  z 2  3i  4
 12i . Tìm toạ độ điểm M biểu diễn số phức z . A. M 3;  1 .
B. M 3;  1 . C. M  1;  3 .
D. M 1;3 . f x  3
Câu 34. Cho các hàm số y f x, y g x   , y
. Hệ số góc của các tiếp tuyến của các đồ thị g x 1
hàm số đã cho tại điểm có hoành độ x  1 bằng nhau và khác 0. Khẳng định nào dưới đây là khẳng định đúng? A. f   1  3  . B. f   1  3  . C. f   11 1   . D. f   11 1   . 4 4
Câu 35. Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy 2, 4, n(n > ) 3 điểm phân biệt
(các điểm không trùng với các đỉnh của tam giác). Tìm n biết rằng số tam giác có các đỉnh
thuộc n +6 điểm đã cho là 247 A. 6 . B. 7 . C. 5 . D. 8 . ln 2
3 2x  3 f x
Câu 36. Cho hàm số f x liên tục trên  . Biết  ex f   1 dx  5 và dx  3  . Tính x 1 0 2 3 I f  xdx . 2 A. I  2 . B. I  4 . C. I  2  .
D. I  8 .  
Câu 37. Cho khối hộp ABCDA BCD
  có thể tích V . Các điểm M , N , P thỏa mãn AM  2AC ,    
AN  3AB , AP  4AD . Tính thể tích khối chóp AMNP theo V . A. 6V . B. 8V . C. 12V . D. 4V .
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 4
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 1 1 5
Câu 38. Cho số phức z thỏa mãn z 1  5 ,  
và z có phần ảo dương. Tìm tổng phần thực z z 17
và phần ảo của z . A. 2 . B. 4 . C. 6 . D.8 .
Câu 39. Trong không gian với hệ tọa độ Oxyz , cho điểm A 1;2;2  và đường thẳng x  6 y 1 z  5 d :  
. Tìm tọa độ điểm B đối xứng với A qua d . 2 1 1 A. B  3;  4; 4  .
B. B 2;1;3  .
C. B 3;4; 4  .
D. B 3; 4;4  .
Câu 40. Ông An có một khu đất hình elip với độ dài trục lớn 10 m và độ dài trục bé 8 m. Ông An muốn
chia khu đất thành hai phần, phần thứ nhất là một hình chữ nhật nội tiếp elip dùng để xây bể cá
cảnh và phần còn lại dùng để trồng hoa. Biết chi phí xây bể cá là 1000000 đồng trên 2 1m và chi
phí trồng hoa là 1200000 đồng trên 2
1m . Hỏi ông An có thể thiết kế xây dựng như trên với tổng
chi phí thấp nhất gần nhất với số nào sau đây? A. 67398224 đồng. B. 67593346 đồng. C. 63389223 đồng. D. 67398228 đồng. x  5 y  7 z 12
Câu 41. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 2 2 1 
 : x  2y 3z 3  0. Gọi M là giao điểm của d với   , A thuộc d sao cho AM  14 .
Tính khoảng cách từ A đến   . A. 2. B. 3. C. 6. D. 14 .
Câu 42 . Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số 2 4
y m x   2 m m 2 2019 x 1có
đúng một điểm cực trị. A. 2019 . B. 2020 . C. 2018 . D. 2017 .
Câu 43. Gọi S là tập tất cả các giá trị của tham số m để đồ thị hàm số 3 3 2 2
y x  3x  2  4x  3x  2  mx có tiệm cận ngang. Tổng các phần tử của S là A. 2  . B. 2 . C. 3 . D. 3 .
Câu 44. Cho hàm số f x    2
ln x x . Tính f   1 f 2 f 2019 P  ee ... e . 2020 2019 2019 A. P  . B. P  . C. 2019 P  e . D. P   . 2019 2020 2020
Câu 45. Cho các số phức z , z thỏa mãn phương trình z  2  3i  5 và z z  6 . Biết rằng tập hợp 1 2 1 2
các điểm biểu diễn số phức w z z là một đường tròn. Tính bán kính đường tròn đó. 1 2 A. R  8 . B. R  4 . C. R  2 2 . D. R  2 .
Câu 46. Cho các số thực x , y thay đổi thỏa mãn 2 2
x y xy  1 và hàm số f t  3 2
 2t  3t 1.
 5x y  2 
Gọi M , m tương ứng là giá trị lớn nhất và nhỏ nhất của Q f   . Tổng
x y  4 
M m bằng A. 4  3 2 . B. 4  5 2 . C. 4   4 2 . D. 4   2 2 .
Câu 47. Trong các khối chóp tứ giác đều S.ABCD mà khoảng cách từ A đến mp (SBC) bằng 2a , khối
chóp có thể tích nhỏ nhất bằng
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 5
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 A. 3 2 3a . B. 3 2a . C. 3 3 3a . D. 3 4 3a . 2
Câu 48. Tổng tất cả các giá trị của tham số m để phương trình x 2x 1  2 3 xm  log
2 x m  2 có 2 x 2 x3  
đúng ba nghiệm phân biệt là A. 3 . B. 2  . C. 3  . D. 2 .
Câu 49. Cho các số thực a,b,c thỏa mãn 2 2 2
a b c  2a  4b  4 . Tính P a  2b  3c khi biểu
thức 2a b  2c  7 đạt giá trị lớn nhất. A. P  7 . B. P  3 . C. P  3  . D. P  7  .
Câu 50. Cho cấp số cộng a , cấp số nhân b thoả mãn a a  0 , b b  1 và hàm số n n  2 1 2 1 f x 3
x  3x sao cho f a  2  f a và f log b  2  f log b . Tìm số nguyên 2 2   2 1 2   1
dương n nhỏ nhất sao cho b  2019a n n A. 17. B. 14. C. 15. D. 16.
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 6
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
PHÂN TÍCH BÌNH LUẬN ĐỀ THI THỬ ĐẠI HỌC CHUYÊN HÀ TĨNH 5
Câu 1. Cho các hàm số
f x, g x liên tục trên  có 2 f
  x3gxdx  5   ; 1  5 5 3 f
  x5gxdx  21  . Tính  f
  x gxdx  . 1  1  A. 5  . B. 1. C. 5 . D. 1. Lời giải
Tác giả: Lê Hữu Đức; Fb: Le Huu Duc Chọn D 5 5 Đặt I f
 xdx; J g  xdx 1  1
2I  3J  5  I  2 5 Ta có      f
  x gxdx I J  1  . 3 
I  5J  21 J  3  1  5 2 
Câu 1.1. Cho các hàm số f x, g x liên tục trên  có f
 xdx  8 và g
 xdx  3. Tính 2 5 5 I   f
  x4gx1dx  . 2  A. 11. B. 13 . C. 27 . D. 3 . Lời giải Chọn B 5 5 2
Ta có: I   f  5
  x  4g x 1 dx   f
 xdx4 g
 xdxx 84.352 13. 2  2  2  5 3
Câu 1.2. Cho các hàm số f x, g x liên tục trên  có 3 f
 x2gxdx 1  ; 1 3 1 2 f
 x gxdx  3  
. Tính f 2x   1dx . 1 0 5  10 11 5 A. . B.  . C. . D.  . 7 7 14 14 Lời giải
Tác giả: Lê Hữu Đức; Fb: Le Huu Duc Chọn D 3 3 Đặt I f
 xdx ; J g  xdx 1 1  5 I   3
I  2J 1  1 3 1 5 Ta có 7   
f 2x   1 dx
f tdt     .
2I J  3  11  2 14 J  0 1  7
Câu 2. Với k, n là hai số nguyên dương tùy ý thỏa mãn k n, mệnh đề nào dưới đây sai?
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 7
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 n k ! A. C  . B. k
A k !. k C . k k k C C
C . D. k
C k !. k A . n k  ! n k ! n n C. 1 n n n 1  n n Lời giải
Tác giả: Lục Minh Tân; Fb: Lục Minh Tân Chọn D n! k A k n C   n
k n k . !. ! k!
Câu 2.1. Với k, n là hai số nguyên dương tùy ý thỏa mãn k n, mệnh đề nào dưới đây sai? P k A A. k n k C C   . B. k k 1  k 1 C CC  . k n C  . D. k n C  . n n n n n 1  C. n k ! n k ! Lời giải
Tác giả: Lục Minh Tân; Fb: Lục Minh Tân Chọn C n k ! 1 k k k C  
A A k C n
k n k  . !. !. ! k ! n n n
Câu 2.2. Với k, n là hai số nguyên dương tùy ý thỏa mãn 4  k n mệnh đề nào dưới đây sai? A. k4 k 3 k 2 k 1  k k CCCCCC . B. n k ! 2 C  . n n n 1  n2 n3 n4 n
k  2!n k  2! C. n k ! A D. k
A k !. k C . n
n k  .! n n Lời giải
Tác giả: Lục Minh Tân; Fb: Lục Minh Tân Chọn B n n k ! ! 2 C   n
k  2 !n k  2! k   n k   . 2 ! 2 !
Câu 3. Cho số phức z  3  2i . Tìm phần ảo của số phức w  1 2iz A. 4  . B. 7 . C. 4 . D. 4i . Lời giải
Tác giả: Nguyễn Thị Thơm; Fb: Thom nguyen Chọn C
Ta có w  1 2iz  1 2i3 2i  7  4i . Số phức w có phần ảo bằng 4
Câu 3.1. Cho số phức z  3  2i . Tìm phần ảo của số phức w  1 iz A. 1  . B. 5 . C.1. D. i . Lời giải
Tác giả: Nguyễn Thị Thơm; Fb: Thom nguyen Chọn C
Ta có w  1 iz  1 i3 2i  5  i . Số phức w có phần ảo bằng 1
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 8
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Câu 3.2. Cho số phức z  3  2i . Tìm phần ảo của số phức liên hợp của w  2  iz A. 1  . B. 5 . C.1. D. i . Lời giải
Tác giả: Nguyễn Thị Thơm; Fb: Thom nguyen Chọn C
Ta có w  2  iz  2  i3 2i  8  i . Số phức liên hợp của w có phần ảo bằng 1  .
Câu 4. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng   : x  2y  0. Mệnh đề nào dưới đây đúng?
A.   // Oxy .
B.   //Oz .
C. Oz    .
D. Oy    . Lời giải
Tác giả: Nguyễn Bảo Mai; Fb: Bao An Chọn C
  đi qua điểm O0;0;0 nên loại phương án A và B.      
có một vectơ pháp tuyến là n  1; 2
 ;0 và n.k  0 nên Oz   .
Câu 4.1. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng   : x  2y  3  0 . Mệnh đề nào dưới đây đúng?
A.   // Oxy .
B.   //Oz .
C. Oz    .
D.    Oz . Lời giải Chọn B   
có một vectơ pháp tuyến là n  1; 2
 ;0 và nên   //Oz hoặc Oz   .
  không đi qua điểm O0;0;0 nên //Oz .
Câu 4.2. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng   : 2z  3  0. Mệnh đề nào dưới đây đúng?
A.    Oxy.
B.   //Oz .
C. Oz    .
D.    Oz . Lời giải Chọn D     
có một vectơ pháp tuyến là n  0;0;2 cùng phương với k  0;0;  1 và nên   không
đi qua điểm O0;0;0 nên    Oz .
Câu 5. Hàm số nào sau đây nghịch biến trên  ? A. 3
y x  3x  2 . B. 4 2
y x  2x  2 . C. 3 2
y  x  2x  4x 1. D. 3 2
y  x  2x  5x  2 . Lời giải
Tác giả: Phạm Văn Tuấn; Fb: Phạm Tuấn Chọn C Xét hàm số 3
y x  3x  2 có hệ số a  1  0 nên hàm số không thể nghịch biến trên   loại đáp án A. Xét hàm số 4 2
y x  2x  2 là hàm số bậc 4 trùng phương nên hàm số không thể nghịch biến
trên   loại đáp án B. Xét hàm số 3 2
y  x  2x  4x 1 có 2 y  3
x  4x  4  0 , x
   hàm số nghịch biến trên  .
Câu 5.1. Hàm số nào sau đây đồng biến trên  ?
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 9
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
A. y  x 2 1. B. 3
y x  3x 1. C. 2 y x 1. D. 3
y x  3x 1. Lời giải
Tác giả: Phạm Văn Tuấn; Fb: Phạm Tuấn Chọn D
Xét hàm số y  x 2 1 có y   2  0  hàm số nghịch biến trên  . x  1 Xét hàm số 3
y x  3x 1 có 2
y  3x  3 ; y  0  
 hàm số không thể đồng biến x  1  trên  . Xét hàm số 2
y x 1 có y  2x ; y  0  x  0  hàm số không thể đồng biến trên  . Xét hàm số 3
y x  3x 1 có 2
y  3x  3  0 , x
    hàm số luôn đồng biến trên  .
Câu 6. Biết F x là một nguyên hàm của hàm số    x
f x e  sin x thỏa mãn F 0  0 . Tìm F x ? A.    x
F x  e  cos x  2 . B.    x
F x  e  cos x . C.   x
F x e  cos x  2 . D.   x
F x  e  cos x  2 . Lời giải
Tác giả: Phạm Thị Thu Trang; Fb: Trang Phạm Chọn A
Ta có      d   x sin d  x  d  sin d  x F x f x x e x x e x
x x  e  cos x C   . Lại có F   0
0  0  e  cos 0  C  0  C  2 . Vậy   x
F x  e  cos x  2 . 4m
Câu 6.1. Cho hàm số f x 2 
 sin x . Giá trị của tham số để nguyên hàm F x của hàm số f x     
thỏa mãn điều kiện F 0  1 và F    là:  4  8 4 3 3 4 A. m   . B. m  . C. m   . D. m   . 3 4 4 3 Lời giải
Tác giả: Phạm Thị Thu Trang; Fb: Trang Phạm Chọn C  4m  4m 4m 1 1 Ta có 2 2  sin x dx  dx  sin d     x x
x x  sin 2x C .      2 4 F 0 1 C  1 C  1   
Giải hệ       4m  1  1     3 . F  .  .  sin  C m        4  8   4 2 4 4 2 8  4
Câu 7. Cho hàm số y f x liên tục trên  và có bảng biến thiên như hình bên. Tìm khẳng định đúng
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 10
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
A. Hàm số có giá trị nhỏ nhất bằng 0 và giá trị lớn nhất bằng 1.
B. Hàm số đạt cực đại tại x  0 và đạt cực tiểu tại x  1  .
C. Đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt.
D. Hàm số có đúng một cực trị. Lời giải
Tác giả: Nguyễn Thị Thanh Vân; Fb: Thanh Van Chọn B
Theo bảng biến thiên ta có
f  x đổi dấu từ âm sang dương khi qua x  1
 nên hàm số f x đạt cực tiểu tại x  1  ;
f  x đổi dấu từ dương sang âm khi qua x  0 nên hàm số f x đạt cực đại tại x  0 .
Câu 7.1 Cho hàm số y f x xác định và liên tục trên  \  1
 và có bảng biến thiên như sau:
Khẳng định nào sau đây là sai?
A. Giá trị nhỏ nhất của hàm số trên đoạn 0;4 bằng 2  .
B. Hàm số đạt cực tiểu tại x  3 .
C. Đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt.
D. Hàm số nghịch biến trên khoảng  ;3   . Lời giải
Tác giả: Nguyễn Thị Thanh Vân; Fb: Thanh Van Chọn D
Vì hàm số không xác định tại x  1  thuộc khoảng  ;3
  nên hàm số không đơn điệu trên khoảng đó.
Câu 8. Trong không gian với hệ tọa độ Oxyz , phương trình nào sau đây không phải phương trình mặt cầu ? A. 2 2 2
2x  2y  2z  2x  4y  6z  5  0 . B. 2 2 2
x y z  2x y z  0 . C. 2 2 2
x y z  3x  7 y  5z 1  0 . D. 2 2 2
x y z  3x  4y  3z  7  0 . Phân tích: 
Nhận dạng bài toán: Bài toán nhận dạng phương trình mặt cầu. 
Kiến thức cần nhớ: Phương trình mặt cầu là phương trình có dạng: 2 2 2
x y z  2ax  2by  2cz d  0   1 với điều kiện 2 2 2
a b c d  0 .  Phương pháp giải:
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 11
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
- Bước 1: Kiểm tra phương trình đã cho có đúng dạng chưa? Lưu ý: Ở phương trình (1) hệ số của 2 2 2
x , y , z bằng nhau và bằng k  0 đều có thể đưa về dạng (1) bằng cách chia cả 2 vế của
phương trình cho k .
- Bước 2: Kiểm tra điều kiện 2 2 2
a b c d  0 ( đặc biệt: nếu d  0 thì 2 2 2
a b c d  0
luôn luôn đúng ), rồi kết luận. Lời giải
Tác giả: Vũ Nga; Fb: Nga Vu Chọn D
- Cả 4 đáp án đều có dạng (1). 3
- Đáp án A, B, C đều thỏa mãn điều kiện 2 2 2
a b c d  0 và ở đáp án D có a  , b  2 , 2 3 a  , d  7 2 2 2
a b c d  0 ( không thỏa mãn ). 2
Câu 8.1 Trong không gian với hệ tọa độ Oxyz , phương trình nào sau đây không phải phương trình mặt cầu ? A. 2 2 2
3x  3y  3z  2x  0 . B. 2 2 2
x y z  2x y z 1  0 . C. 2 2 2
x y z  8x  2y 1  0 . D. 2 2 2
x y z  2x  4y  6z  7  0 . Lời giải
Tác giả: Vũ Nga; Fb: Nga Vu Chọn D
- Phương trình ở đáp án D không đúng dạng (1) do hệ số của 2 2 2
x , y , z không bằng nhau.
Câu 8.2 Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình 2 2 2
x y z  m   2 2
2 x  4my  2mz  7m 1  0 là phương trình mặt cầu. Số phần tử của S là A. 6 . B. 7 . C. 4 . D. 5 . Lời giải
Tác giả: Vũ Nga; Fb: Nga Vu Chọn D Phương trình 2 2 2
x y z  m   2 2
2 x  4my  2mz  7m 1  0 là phương trình mặt cầu  m  2 2 2
m m   2 2 4 7m   1  0 2
 m  4m  5  0  1
  m  5  có 5 giá trị nguyên thỏa mãn.
Câu 9. Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng a 3 . Thể tích khối lăng trụ đã cho bằng 3 9a 3 3a 3 a 3 3 3a 3 A. . B. . C. . D. . 4 4 4 4 Lời giải
Tác giả: Vũ Danh Được; Fb: Danh Được Vũ Chọn A
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 12
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 A B C A' B' C'
Xét khối lăng trụ tam giác đều ABC.A BC
  có tất cả các cạnh bằng a 3 . 2 3a 3 2 3 3a 3 9a Khi đó S
. Do đó thể tích khối lăng trụ đã cho bằng V a 3.  . ABC 4 4 4
Câu 9.1. Cho khối lăng trụ đứng ABC . D A BCD
  có BB  a , đáy ABCD là hình thoi với
AC  2a, BD a 3 . Thể tích khối lăng trụ ABC . D A BCD   là 3 a 3 3 a 3 A. 3 a 3 . B. . C. . D. 3 2a 3 . 2 3 Lời giải
Tác giả: Vũ Danh Được; Fb: Danh Được Vũ Chọn A B C A D B' C' A' D'
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 13
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 1 Ta có 2 S
 .AC.BD a 3 . ABCD 2
Do đó thể tích khối lăng trụ đã cho bằng 2 3 V  . a a 3  a 3 .
Câu 10. Đường cong trong hình vẽ dưới đây là đồ thị của một trong bốn hàm số đã cho. Hỏi hàm số đó là hàm số nào? 4 x 4 x 4 x 4 2 x x A. 2 y   2x 1 . B. 2 y    x 1 . C. 2 y   x 1 . D. y   1 . 4 4 4 4 2 Lời giải
Tácgiả:Quỳnh Giao; Fb:QGiaoDo Chọn A
Vì đồ thị hàm số có bề lõm quay lên trên và có ba điểm cực trị là x = 2 x = 0 và x = 2 - nên chọn đáp án A Phát triển
Câu 10.1. Trong các hình vẽ sau, hình nào biểu diễn đồ thị hàm số 4 2
y = -x + 2x + 3 A. . B. . C. . D. . Lời giải
Tácgiả:Quỳnh Giao; Fb:QGiaoDo Chọn A
Hàm số đã cho có ba điểm cực trị là x = 1; x = 0 và x = 1
- đồng thời có bề lõm quay xuống dưới nên chọn A
Câu 11. Cho 0  a  1; b,c  0 thỏa mãn log b  3 ; log c  2 . Tính  3 2 log a b c . aa a A. 18  . B. 7 . C. 10 . D. 8 . Lời giải
Tác giả: Phạm Thanh My ; Fb: Thanh My Phạm
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 14
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 Chọn D Ta có 1 log a b c a b c   b c a  3 2  3 2 log log log 3 2log log 8 a a a a 2 a 27 3 a b
Câu 11.1. Cho 0  a  1; b, c  0 thỏa mãn 2
log b  3 ; log b c  . Tính log . 2 a a   2 a c 3 105 11 A. 2 . B. . C. . D. . 2 2 2 Lời giải
Tác giả: Phạm Thanh My ; Fb: Thanh My Phạm Chọn B Ta có
log b  3  log b  6 2 a a log b c   b c   c a  15 27 3 2  2log log log 2 a a 2 a 2 3 a b 1 3 3 log
 log a  log b  log c  1 2   a a c 3 a a 2 2
Câu 12 . Cho hình trụ có đường cao bằng 5 và đường kính đáy bằng 8 . Tính diện tích xung quanh của hình trụ đó. A. 40 . B. 20 . C. 80 . D. 160 . Lời giải
Tác giả: Trần Thị Thơm; Fb: Tranthom Chọn A
Gọi h,l và r lần lượt là đường cao, đường sinh và bán kính đáy của hình trụ.
Ta có: r  4, h l  5 .
Ta có: S  2 rl  2 rh  40 . xq
Câu 12.1 Diện tích toàn phần của hình trụ có đường kính và đường sinh cùng bằng 4 cm là A. 2 16cm . B. 2 24cm . C. 2 16 2 cm . D. 2 32 2 cm . Lời giải
Tác giả: Trần Thị Thơm; Fb: Tranthom Chọn B
Gọi l và r lần lượt là đường sinh và bán kính đáy của hình trụ.
Ta có: r  2,l  4 .
Diện tích toàn phần của hình trụ là 2
S  2 rl  2 r   2 24 cm  . tp
Câu 12.2 Trong không gian, cho hình chữ nhật ABCD có AB  1 và AD  2 . Gọi M , N lần lượt là
trung điểm của AD và BC . Quay hình chữ nhật đó xung quanh trục MN , ta được một hình
trụ. Tính diện tích toàn phần Stp của hình trụ đó.
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 15
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 A. S  4 . B. S  2 . C. S  6 .
D. S  10 . tp tp tp tp Lời giải
Tác giả: Trần Thị Thơm; Fb: Tranthom Chọn A
Gọi l và r lần lượt là đường sinh và bán kính đáy của hình trụ. AD Ta có: r
 1,l AB  1. 2
Diện tích toàn phần của hình trụ là 2
S  2 rl  2 r  4 . tp
Câu 13. Cho cấp số nhân u có số hạng đầu u  3 , công bội q  2 . Tính tổng 10 số hạng đầu tiên n  1 của u . n A. 513  . B. 1023  . C. 513. D. 1023 . Lời giải
Tác giả: Nguyễn Thị Thu Trang 215; Fb: Trang Nguyễn Chọn B u 1 nq 1  
Áp dụng công thức S  , ta có n 1 q 3 1    2  10  S     1023. 10 1 2 1 2
Câu 13.1. Cho cấp số nhân u có số hạng đầu u  2 , công bội q   . Khi đó là số hạng thứ n  1 3 6561 A. 10 . B. 9 . C. 8. D. 7 . Lời giải
Tác giả: Nguyễn Thị Thu Trang 215; Fb: Trang Nguyễn Chọn B Áp dụng công thức n 1 u u q   , ta có n 1 n 1 2  1    n 1     1 1 2.  
    n 1 8  n  9 . 6561  3  6561  3 
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 16
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 1023
Câu 13.2. Cho cấp số nhân u có công bội q  2 , tổng 10 số hạng đầu tiên bằng  . Tìm số n  2
hạng đầu u của cấp số nhân u . n  1 1 1 A. u  2  . B. u   . C. u  . D. u  2 . 1 1 2 1 2 1 Lời giải
Tác giả: Nguyễn Thị Thu Trang 215; Fb: Trang Nguyễn Chọn B u 1 nq 1  
Áp dụng công thức S  , ta có n 1 q 1023 Sq  1 2 n 1  1 u  2  u    . 1 1 nq  1 10 1 2 2
Câu 14. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A1; 2;0 ; B3;2;8 . Tìm một vectơ
chỉ phương của đường thẳng AB .    
A. u  1;2; 4 .
B. u  2;4;8 . C. u   1;  2; 4 .
D. u  1; 2; 4 .
Tác giả: Nguyễn Ngọc Chi; Fb: Nguyễn Ngọc Chi Lời giải Chọn A  
Ta có AB  2;4;8 , vậy đường thẳng AB có một vectơ chỉ phương là u  1;2; 4 .       
Câu 14.1. Trong không gian với hệ tọa độ Oxyz , cho OA  2i  3 j  5k ; OB  2 j  4k . Tìm một vectơ
chỉ phương của đường thẳng AB .    
A. u  2;5;  1 .
B. u  2;3; 5 . C. u   2;   5; 
1 . D. u  2;5; 9 .
Tác giả: Nguyễn Ngọc Chi; Fb: Nguyễn Ngọc Chi Lời giải Chọn A       
Ta có OA  2i  3 j  5k A2;3; 5   và OB  2
j  4k B0; 2;  4  .   Ta có AB   2;   5; 
1 , hay đường thẳng AB có một vectơ chỉ phương là u  2;5;  1 .
Câu 15. Cho 0  a  1, 0  b  1; x, y  0, m   . Trong các mệnh đề sau, mệnh đề nào sai?
A. log x  log . b log x . B. log x y x y . a  .  log log a a b a b x log x 1 C. log a  . D. log x x . m log a y log y a a m a Lời giải
Tác giả: Nguyễn Tất Thành; Fb: Thanh Nguyen Chọn C x Ta có: log  log x  log y . a a a y
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 17
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Câu 15.1 .Với các số thực x, y dương bất kì, y  1 . Mệnh đề nào dưới đây đúng?  x  log x A. 2 log   
B. log xy  log x  log y 2  
2  y  log y 2 2 2 C. log  2
x y  2log x  log y
log xy  log x  log y 2   2  D. 2 2 2 2 Lời giải
Tác giả: Nguyễn Tất Thành; Fb: Thanh Nguyen Chọn B Ta có: log  .
x y  log x  log y . a a b 40
Câu 15.2 .Cho a  log 5 , b  log 9 . Biểu diễn của P  log
theo a và b là 2 2 2 3 a
A. P  3  a  1 2b .
B. P  3  a  3 b . C. P  .
D. P  3  a b . 2 2b Lời giải
Tác giả: Nguyễn Tất Thành; Fb: Thanh Nguyen Chọn B 40 1 Ta có P  log
 log 40  log 3  log 8  log 5  1
log 9  3  a b . 2 3 2 2 2 2 2 2 2 x  2
Câu 16. Gọi C là đồ thị hàm số y
. Trong các mệnh đề sau, mệnh đề nào sai? 2x 1 1
A. C có tiệm cận ngang là y  .
B. C có một trục đối xứng. 2 1
C. C có tiệm cận đứng là x  .
D. C có một tâm đối xứng. 2 Lời giải
Tác giả: Nguyễn Mạnh Dũng; Fb: Mạnh Dũng Chọn B 1 
Tập xác định D   \   . 2 x  2 1 1 Ta có: lim y  lim 
 C có tiệm cận ngang y   A đúng. x
x 2x 1 2 2 x  2 1 lim y  lim  
 C có tiệm cận đứng x   C đúng. 1  1      2x 1 2 xx      2   2   1 1  I ; 
 là tâm đối xứng của đồ thị  D đúng.  2 2   1 1
C có 2 trục đối xứng là y  và x   B sai. 2 2 2x  4
Câu 16.1. Gọi C là đồ thị hàm số y
. Khẳng định nào sau đây là đúng? 2 x  4
A. C có 2 tiệm cận đứng là x  2; x  2 .
B. C không có tiệm cận đứng.
C. C có tiệm cận ngang là y  2 .
D. C có 1 tiệm cận đứng là x  2 .
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 18
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 Lời giải Chọn D
Tập xác định D   \ 2  ;  2 . 2x  4 Ta có: lim y  lim  0
 C có tiệm cận ngang y  0  A sai. 2 x
x x  4 x  2 Giải phương trình : 2 x  4  0   . x  2 2x  4 lim y  lim  
 C có tiệm cận đứng x  2  B sai.   2 x2 x2 x  4 2x  4 2x  4 1 Tuy nhiên lim  lim    x  2
 không thể là tiệm cận đứng của C x  2 x  4 x  2 2 2 x  4 2  C sai. x 1
Câu 16.2. Có bao nhiêu giá trị m để đồ thị hàm số y
có đúng 1 tiệm cận đứng? 2 x mx  4 A. 1. B. 2 . C. 3 . D. 4 .
Lời giải Chọn C
Ta có: x 1  0  x  1  . m  4  TH1: 2
x mx  4  0 có nghiệm kép.    0 2  m 16  0  . m  m  4 TH2: 2
x mx  4  0 có 2 nghiệm phân biệt trong đó có 1 nghiệm là x  1  .     0 m 4  m           m 4 m 5 .    2 1  m  4  0 m   5 x 1
Vậy có 3 giá trị của m để đồ thị hàm số y
có đúng 1 tiệm cận đứng. 2 x mx  4 Nhận xét admin :   0
m  4  m  4
Đặt f x 2
x mx  4 . Yêu cầu bài toán    f    1 0    m  5
Câu 17. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a 2 . Tam giác SAC vuông cân tại S và
nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối cầu ngoại tiếp hình chóp S.ABCD . 3 2 a 3 4 a A. . B. 3 4 a 3 . C. . D. 3 4 a . 3 3 Lời giải
Tác giả: Nguyễn Đình Hải ; Fb:Nguyen Dinh Hai Chọn C
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 19
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 S A B O D C
Gọi O là giao điểm của hai đường chéo AC và BD . Ta có  ABC  90 ,  ADC  90 và 
ASC  90 suy ra các đỉnh B , D , S cùng nhìn đoạn thẳng
AC dưới một góc vuông nên O là tâm mặt cầu ngoại tiếp chóp S.ABCD và   AC R OAa . 2 4 4 Vậy 3 3
V   R   a . 3 3
Câu 17.1 (THPTQG năm 2017 Mã đề 104) Cho hình chóp S.ABCD có đáy là hình chữ nhật với
AB  3a , BC  4a , SA  12a và SA vuông góc với đáy. Tính bán kính R của mặt cầu ngoại
tiếp hình chóp S.ABCD . 5 17 13 A. a R . B. a R . C. a R .
D. R  6a . 2 2 2 Lời giải Chọn C S 12a I A D 3a O B 4a C Ta có: 2 2
AC AB BC  5a
Vì SA AC nên 2 2
SC SA AC  13a BC AB Nhận thấy: 
BC SB .Tương tự: CD SD BC SA Do các điểm ,
A B, D đều nhìn đoạn thẳng SC dưới một góc vuông nên gọi I là trung điểm
của đoạn thẳng SC thì I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD .
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 20
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 SC 13a Vậy R   . 2 2
Câu 17.2 (THPT QG 2017 Mã đề 105) Cho tứ diện ABCD có tam giác BCD vuông tại C , AB vuông
góc với mặt phẳng BCD , AB  5a , BC  3a và CD  4a . Tính bán kính R của mặt cầu
ngoại tiếp tứ diện ABCD . 5 2 5 3 5 2 5 3 A. a R . B. a R . C. a R . D. a R . 3 3 2 2 Lời giải Chọn C
Tam giác BCD vuông tại C nên áp dụng định lí Pitago, ta được BD  5a .
Tam giác ABD vuông tại B nên áp dụng định lí Pitago, ta được AD  5a 2.
Vì B và C cùng nhìn AD dưới một góc vuông nên tâm mặt cầu ngoại tiếp tứ diện ABCD là AD 5a 2
trung điểm I của AD . Bán kính mặt cầu này là: R   . 2 2
Câu 17.3 (Đề tham khảo lần 2 2017) Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 3 2a, cạnh bên bằng 5 .
a Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC . D 25
A. R  3a .
B. R  2a . C. a R .
D. R  2a . 8 Lời giải Chọn C
Gọi O là tâm hình vuông ABCD , G là trung điểm SD , GI SD, I SO .
Ta có cạnh đáy bằng 3 2a nên BD  3 2 .
a 2  6a , OD  3a .
Xét SOD vuông tại O ta có: 2 2
SO SD OD  4a SO SD 1 25a
Ta có SOD∽SGI (g-g), suy ra   4 .
a R  5a2  R  . SG SI 2 8
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 21
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 x -1 y z + 3
Câu 18. Trong không gian Oxyz, cho điểm ( A 1; 2 - ; )
3 và hai đường thẳng d : = = ; 1 2 -1 1 ìïx =1-t ïï
d :íy = 2t . Viết phương trình đường thẳng D đi qua A vuông góc với d và d . 2 ï 1 2 ïïz =1 ïî x  1 tx  2   tx 1 tx 1 2t     A.y  2
  t B. y  1
  2t . C.y  2   t . D.y  2   t z  3 t     z  3  3tz  3  tz  3  3tLời giải
Tác giả: Văn Bùi Vũ ; Fb: Van Tuan Vu Chọn D  
Đường thẳng d có vtcp u = 2;-1;1 , đường thẳng d có vtcp u = -1;2;0 . 2 ( ) 1 ( ) 1 2    
Đường thẳng D vuông góc với d và d nên nhận u éu ,u ù = = 2 - ; 1 - ;3 ê hoặc u = (2;1;- ) 3 1 2 ( ) 1 2 ú ë û làm vectơ chỉ phương. ìïx =1+ 2t ïï
Phương trình đường thẳng : D íy = -2 + t. ïïïz =3-3t ïî x y -1 z + 2
Câu 18.1 Trong không gian Oxyz, cho điểm ( A 1; 1 - ; )
2 và hai đường thẳng d : = = ; 1 2 1 1 ìïx =1+ t ïï
d :íy =1+ 2t . Viết phương trình đường thẳng D đi qua A vuông góc với d và d . 2 ï 1 2 ïïz = 2 - -5t ïî x  4   5tx  1 7tx 1 x  7   t     A.y  3
  2t B. y  1
 11t . C.y  1
  2t . D.y 11 t z  5   7t     z  2  3tz  2  tz  3  2tLời giải
Tác giả: Văn Bùi Vũ ; Fb: Van Tuan Vu Chọn B  
Đường thẳng d có vtcp u = 2;1;1 , đường thẳng d có vtcp u = 1;2;-5 . 2 ( ) 1 ( ) 1 2   
Đường thẳng D vuông góc với d và d nên nhận u éu ,u ù = = 7 - ;11;3 ê làm vectơ chỉ 1 2 ( ) 1 2 ú ë û phương. ìïx =1-7t ïï
Phương trình đường thẳng : D íy = 1 - +11t. ïïïz = 2+3t ïî x -1 y +1 z
Câu 18.2 Trong không gian Oxyz, cho điểm M (2;1;0)và đường thẳng d : = = . Viết 2 1 -1
phương trình đường thẳng D đi qua điểm M cắt và vuông góc với đường thẳng d.
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 22
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 x  2 y 1 z x  2 y 1 z A.   . B.   . 1 4 1 1 4  1 x  2 y 1 z x  2 y 1 z C.   . D.   . 2 4  1 1 4  2  Lời giải
Tác giả: Văn Bùi Vũ ; Fb: Van Tuan Vu Chọn D
Gọi N (1+ 2t; 1 - + t; t
- ) là giao điểm của đường thẳng D và đường thẳng d. 
Lúc đó đường thẳng D nhận MN = (2t -1;t - 2; t
- ) làm vectơ chỉ phương.
Mặt khác D vuông góc với đường thẳng d nên ta có: ( t - ) 2 2 2
1 + t - 2 + t = 0  t = . 3 2  æ1 4 2ö 
Với t = đường thẳng D nhận MN = çç ;- ; ÷
- ÷ hoặc u = (1;-4;-2) làm vtcp. 3 çè3 3 3÷ø x - 2 y -1 z
Phương trình đường thẳng D : = = . 1 -4 -2
Câu 19. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a; AD a 3; SA   ABCD và
SC tạo với đáy một góc 0
45 . Gọi M là trung điểm cạnh SB , N là điểm trên cạnh SC sao 1
cho SN NC . Tính thể tích khối chóp S.AMN . 2 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 9 18 12 6 Lời giải
Tác giả: Nguyễn Văn Nghĩa ; Fb: Nghĩa Văn Nguyễn Chọn B S N M a A B 450 a 3 D C
Vì SA   ABCD nên AC là hình chiếu vuông góc của SC lên mpABCD , suy ra
goc SC mp ABCD  gocSC AC  ; ;  SCA và  0 SCA  45 SA Tính được 2 2
AC AB BC  2a và  tan SCA   SA  2a AC 3 1 a 3 Khi đó VS . A SS.ABC 3 ABC 3 3 V SM SN SA 1 1 1 V a 3
Ta lại có S.AMN S.  . .  . ABC   V   S. V SB SC SA 2 3 6 AMN 6 18 S.ABC
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 23
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Câu 19.1 Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AD a; AB a 3; SA   ABCD và
SC tạo với đáy một góc 0
30 . Gọi M là trung điểm cạnh SB , N là điểm trên cạnh SC sao 1
cho SN NC . Tính thể tích khối chóp S.AMN . 3 3 a 3 a 3 3 a 3 a 3 A. . B. . C. . D. . 8 24 24 8 Lời giải
Tác giả: Nguyễn Văn Nghĩa ; Fb: Nghĩa Văn Nguyễn Chọn C S N M a 3 A B 300 a D C
Vì SA   ABCD nên AC là hình chiếu vuông góc của SC lên mpABCD , suy ra
goc SC mp ABCD  gocSC AC  ; ;  SCA và  0 SCA  30 SA a Tính được 2 2
AC AB BC  2a và  SCA 2 3 tan   SA AC 3 3 1 a Khi đó VS . A SS.ABC 3 ABC 3 3 V SM SN SA 1 1 1 V a
Ta lại có S.AMN S.  . .  . ABC  V   S. V SB SC SA 2 4 8 AMN 8 24 S.ABC
Câu 19.2 Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AD a; AB a 3; SA   ABCD và
SC tạo với đáy một góc 0
45 . Gọi M là trung điểm cạnh SB , N là điểm trên cạnh SC sao 2
cho SN NC . Tính thể tích khối chóp . A MNCB . 3 3 4a 3 3 a 3 3 2a 3 3 a 3 A. . B. . C. . D. . 15 15 3 3 Lời giải
Tác giả: Nguyễn Văn Nghĩa ; Fb: Nghĩa Văn Nguyễn Chọn A
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 24
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 S N M a 3 A B 450 a D C
Vì SA   ABCD nên AC là hình chiếu vuông góc của SC lên mpABCD , suy ra
goc SC mp ABCD  gocSC AC  ; ;  SCA và  0 SCA  45 SA Tính được 2 2
AC AB BC  2a và  tan SCA   SA  2a AC 3 1 a 3 Khi đó VS . A SS.ABC 3 ABC 3 3 V SM SN SA 1 2 1 V a 3
Ta lại có S.AMN S.  . .  . ABC   V   S. V SB SC SA 2 5 5 AMN 5 15 S.ABC 3 3 3 a 3 a 3 4a 3 Suy ra VVV    . A MNCB S.ABC S .AMN 3 15 15
Câu 20. Diện tích hình phẳng giới hạn bởi các đường 3
y x , y  10  x và trục Ox là A. 32 . B. 26 . C. 36 . D. 40 . Lời giải
Tác giả: Giáp Văn Quân ; Fb: quanbg.quan Chọn C 2 10
Dựa đồ thị hàm số ta có diện tích hình phẳng 3 S x x d    10 x x d  36 . 0 2
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 25
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Câu 20.1 Diện tích hình phẳng là phần bị gạch chéo trong hình vẽ sau là 8 11 7 10 A. . B. . C. . D. . 3 3 3 3 Lời giải
Tác giả: Giáp Văn Quân ; Fb: quanbg.quan Chọn D 4 4 10
Dựa vào đồ thị ta có diện tích hình phẳng : S x x d  x  2 x d    . 2 3 0
Câu 21 . Biết log 27  a . Tính log 16 theo a 12 6 43 a 43 a 3  a 3  a A. . B. . C. . D. . 3  a 3  a 43  a 43  aLời giải
Tác giả:Lê Thị Phương Liên; Fb: Phuonglien Le Chọn A log 27 2a Ta có 2 log 27  a   a  log 3  . 12 2 log 12 3  a 2 log 16 4 4 3 a 2   Suy ra log 16    6 log 6 1 log 3 3 a 2 2
Câu 21.1 Biết log 49  a . Tính log 81 theo a 21 63 42  a 42  a 4  a 42  a A. . B. . C. . D. . 2  a 2  a 42  a 4  a
Câu 22. Biết rằng đồ thị hàm số 3 2
y  2x  5x  3x  2 chỉ cắt đường thẳng y  3x  4 tại một điểm
duy nhất M a;b . Tổng của a b bằng A. 6 . B. 3 . C. 6 . D. 3. Lời giải
Tác giả: Đoàn Thị Hường; Fb: Đoàn Thị Hường Chọn D
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 26
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 3 2
y  2x  5x  3x  2 3 2  3
x  4  2x  5x  3x  2
Tọa độ giao điểm là nghiệm của hệ      y  3  x  4  y  3  x  4  1 x  3 2
2x  5x  6x  2  0  2    .  y  3  x  4 5 y   2  1 a   Vậy 2 
a b  3. 5 b   2
Câu 22.1. Biết rằng đường thẳng y  2x  3 và đồ thị hàm số 3 2
y x x  2 x  3 có hai điểm chung
phân biệt A và B , biết điểm Bx ; y có hoành độ âm. Tìm x y . B B B B
A. x y  6  .
B. x y  3  .
C. x y  5  .
D. x y  1  . B B B B B B B B Lời giải
Tác giả: Đoàn Thị Hường; Fb: Đoàn Thị Hường Chọn A
Hoành độ giao điểm ,
A B là nghiệm của phương trình  x  0 3 2 3 2
x x  2x  3  2x  3  x x  0   . x  1
Vì x  0  x  1   y  5
  x y  6  . B B B B B 2x  5
Câu 22.2. Gọi M , N là giao điểm của đường thẳng y  3x 1 và đường cong y  . Khi đó hoành x 1
độ trung điểm I của đoạn thẳng MN bằng 2 2 1 1 A. . B.  . C.  . D. . 3 3 3 3 Lời giải
Tác giả: Đoàn Thị Hường; Fb: Đoàn Thị Hường Chọn D
Hoành độ giao điểm M , N là nghiệm của phương trình 2x  5  x  1  x  1 3  x 1       1 . x 1 2x  5  
x  13x   2 1 3
x  2x  4  0 2 2 x x 1 Dễ thấy  
1 có hai nghiệm x , x và x x  và do đó M N
x x   x   . 1 2 1 2 3 M N 3 I 2 3
Câu 23. Biết rằng phương trình 2
5log x  log 9x 1  0 có hai nghiệm là x , x . Tìm khẳng định 3 3   1 2 đúng? 1 A. 5 1 1 x x  3 . B. x x  .
C. x x  .
D. x x   . 1 2 1 2 5 3 1 2 5 1 2 5 Lời giải
Tác giả: Đoàn Thị Hường; Fb: Đoàn Thị Hường
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 27
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 Chọn A
Điều kiện: x  0 . Ta có 2
5log x  log 9x 2
1 0  5log x  log x 1 0 1 . 3 3 3 3  
Đặt log x t phương trình   1 trở thành 2
5t t 1  0 2 . 3 1
Dễ thấy phương trình 2 có hai nghiệm t ,t và t t  và do đó phương trình   1 có hai 1 2 1 2 5 1 1 1
nghiệm x , x thỏa mãn log x  log x   log x x  5 5  x x  3  3 . 3  1 2  1 2 3 1 3 2 5 5 1 2
Câu 23. 1. Biết rằng phương trình x x2 4  2
1  0 có hai nghiệm là x , x . Tìm khẳng định đúng? 1 2
A. x x  0 . B. x x  1 .
C. x x  4 . D. x x  2 . 1 2 1 2 1 2 1 2 Lời giải
Tác giả: Đoàn Thị Hường; Fb: Đoàn Thị Hường Chọn A Ta có x x2 2 4  2
1 0  2 x  4.2x 1 0   1 .
Đặt 2x t t  0 phương trình   1 trở thành 2
t  4t 1  0 2 .
Dễ thấy phương trình 2 có hai nghiệm t ,t  0 và t t  1 và do đó phương trình   1 có hai 1 2 1 2
nghiệm x , x thỏa mãn  1 x 2 x 1 x 2
2 .2  1  2 x  1  x x  0 . 1 2 1 2
( Học sinh có thể sử dụng máy tính cho câu 23 và pt23.1)
Câu 23.2 Cho phương trình 2
12log x  3m 1 log x m  3  0
1 ( m là tham số ). Giả sử m m là 9   3   0
giá trị thỏa mãn phương trình có hai nghiệm x , x thỏa mãn x .x  3 . Mệnh đề nào sau đây 1 2 1 2 đúng ? 3
A. 1  m  2 .
B. 3  m  4 .
C. 0  m  .
D. 2  m  3 . 0 0 0 2 0 Lời giải
Tác giả: Đoàn Thị Hường; Fb: Đoàn Thị Hường Chọn C Ta có: 2
12 log x  3m 1 log x m  3  0 1 Đk: x  0 9   3    12 2
log x  3m 1 log x m  3  0 2    3 3 2  1   12
log x  3m 1 log x m  3  0  3    3  2  2
 3log x  3m 1 log x m  3  0 3   3
Đặt t  log x . Khi đó phương trình   1 trở thành 2
3t  3m  
1 t m  3  0 2 3
Phương trình đã cho có hai nghiệm x , x thỏa mãn x .x  3  log x .x 1 3  1 2  1 2 1 2
 log x  log x  1  t t 1 3 1 3 2 1 2
(Với t  log x và t  log x ) 1 3 1 2 3 2
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 28
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 b  3m 1 2
Áp dụng hệ thức Vi-et cho phương trình 2 ta có t t 1  1  1  m  . 1 2 a 3 3 2
Thử lại phương trình 2 dễ thấy m   m phương trình 2 có hai nghiệm. 0 3 3
Vậy 0  m  là mệnh đề đúng. 0 2
Câu 24 . Gọi z , z là hai nghiệm phức của phương trình 2
z  5z  7  0 . Tính 2 2
P z z . 1 2 1 2 A. 4 7 . B. 56 . C. 14 . D. 2 7 . Lời giải Chọn C 5  i 3 5  i 3 Phương trình 2
z  5z  7  0 có hai nghiệm z  và z  2 2 Suy ra 2 2
P z z  14 . 1 2
Câu 24.1. Gọi z , z là hai nghiệm phức của phương trình 2
z  4z  7  0 . Tính 3 3
P z z . 1 2 1 2 A. 20  . B. 20 . C. 14 7 . D. 28 7 .
Câu 25. Cho khối nón có thiết diện qua trục là tam giác cân có một góc 120o và cạnh bên bằng a . Tính thể tích khối nón. 3 a 3 a 3  a 3 3 a A. . B. . C. . D. . 8 8 24 4 Lời giải
Tác giả: Giáp Văn Quân ; Fb: quanbg.quan Chọn A
Ta có: tam giác ABC vuông tại A ,  60o ABC  , BC a .
Do đó hình nón có độ dài đường sinh l a , a o 3
Bán kính đáy r AC BC.sin 60  2 a Đường cao hình nón 2 2
h l r  2 3 1 a Thể tích khối nón 2
V   r .h  . 3 8
Câu 25.1 Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng a .
Tính diện tích xung quanh của hình nón.
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 29
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 2  a 2 2  a 2 2 2 a 2 A. . B. . C. 2  a 2 . D. . 4 2 3 Lời giải
Tác giả: Giáp Văn Quân ; Fb: quanbg.quan Chọn B a a O
Thiết diện qua trục là một tam giác vuông cạnh a nên đường sinh của hình nón là a và bán a 2 2  a 2 kính đáy là
nên ta có S   rl  . 2 xq 2
Câu 26. Tập xác định của hàm số y  x x  1 2 3 3 2 là A.  \ 1;  2 . B.  
;1  2;  . C. 1;2 . D.  . Lời giải
Tác giả: Nguyễn Văn Nghĩa ; Fb: Nghĩa Văn Nguyễn Chọn B 1
+ Vì không là số nguyên nên điều kiện là 2
x  3x  2  0  x  ;   1  2; 3 + Chọn B 
Câu 26.1 Tập xác định của hàm số y  x x   3 2 3 2 là A.  \ 1;  2 . B.  
;1  2;  . C. 1;2 . D.  . Lời giải
Tác giả: Nguyễn Văn Nghĩa ; Fb: Nghĩa Văn Nguyễn Chọn A + Vì 3
 là số nguyên âm nên điều kiện là 2
x  3x  2  0  x   \ 1;  2 + Chọn A e
Câu 26.2 Tập xác định của hàm số y   x x  2 1 2 2 3 là  3   3   3  A.  \  ;1. B. ;  1;    . C. ;1 . D.  .  2     2   2  Lời giải
Tác giả: Nguyễn Văn Nghĩa ; Fb: Nghĩa Văn Nguyễn Chọn C  3  
+ Vì 2e 1 không là số nguyên nên điều kiện là 2
2x x  3  0  x  ;1    2  + Chọn C
Câu 27. Tập nghiệm của bất phương trình log 2x +1 > 0 là: 1 ( ) 2  1   1   1  A.  ;0 .  
B. 0;. C.  ; .   D.  ;0 .    4   2   2 
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 30
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 Lời giải
Tác giả: Văn Bùi Vũ ; Fb: Van Tuan Vu Chọn D 1
Ta có: log 2x +1 > 0  0 < 2x +1<1  - < x < 0. 1 ( ) 2 2 æ 1 ö
Tập nghiệm của bất phương trình: S = ç- ç ;0÷÷. ç è 2 ÷ø
Câu 27.1 Tập nghiệm của bất phương trình log ( 2
x - 5x + 7 > 0 là: 1 ) 2 A.  ;2
  3;  B.  ;
 2 C. 2;3 D. 3;  Lời giải
Tác giả: Văn Bùi Vũ ; Fb: Van Tuan Vu Chọn C Ta có: log ( 2 x - 5x + 7) 2 2
> 0  0 < x - 5x + 7 <1  x - 5x + 6 < 0  2 < x < 3. 1 2
Tập nghiệm của bất phương trình: S = (2; ) 3 .
Câu 27.2 Tập nghiệm của bất phương trình log x 1  3 là. 2  
A. S  1;9
B. S  9; C. S  1;9. D. S   ;9 Lời giải
Tác giả: Văn Bùi Vũ ; Fb: Van Tuan Vu Chọn A
Ta có: log x -1 < 3  0 < x -1< 8  1< x < 9. 2 ( )
Tập nghiệm của bất phương trình: S = (1; ) 9 .
Câu 28. Cho hình chóp S.ABCD có đáy là hình thoi cạnh 2a , 
ABC  60 , SA a 3 và
SA   ABCD . Tính góc giữa SA và mpSBD . A. 60 . B. 90 . C. 30 . D. 45. Lời giải
Tác giả: Nguyễn Đình Hải ; Fb:Nguyen Dinh Hai Chọn C
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 31
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 S A B O D C BD AC Ta có
  BD  SAC mà BD  SBD  SAC  SBD và BD SA
SACSBD  SO suy ra SA SBD  SA SO  , ,
ASO vì tam giác SAO vuông tại A . 1
Ta có tam giác ABC đều cạnh 2a OA AC a . 2 OA
Xét tam giác vuông SAO ta có:  1 tan ASO     ASO  30 . SA 3 Vậy  ,
SA SBD  30.
Câu 28.1 (THPT QUỐC GIA 2018 - MÃ ĐỀ 102) Cho hình chóp S.ABCD có đáy là hình vuông cạnh
a , SA vuông góc với mặt phẳng đáy và SA  2a . Góc giữa đường thẳng SC và mặt phẳng đáy bằng A. 45 . B. 60. C. 30 . D. 90 . Lời giải Chọn A S D A B C
Do SA   ABCD nên góc giữa đường thẳng SC và mặt phẳng đáy bằng góc  SCA.
Ta có SA  2a , AC  2a   tan  SA SCA 1   SCA  45 . AC
Vậy góc giữa đường thẳng SC và và mặt phẳng đáy bằng bằng 45 .
Câu 28.2 (Tham khảo 2018) Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a . Gọi M là
trung điểm của SD (tham khảo hình vẽ bên). Tan của góc giữa đường thẳng BM và mặt phẳng ABCD bằng
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 32
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 S M A D B C 2 3 2 1 A. . B. . C. . D. . 2 3 3 3 Lời giải Chọn D S M A D H O B C 2 a a 2
Gọi O là tâm của hình vuông. Ta có SO   ABCD và 2 SO a   2 2
Gọi M là trung điểm của OD ta có MH / /SO nên H là hình chiếu của M lên mặt phẳng  1 2 ABCD và   a MH SO . 2 4
Do đó góc giữa đường thẳng BM và mặt phẳng ( ABCD) là  MBH . a 2 MH 1 Khi đó ta có  4 tan MBH    . BH 3a 2 3 4 1
Vậy tang của góc giữa đường thẳng BM và mặt phẳng  ABCD bằng 3
Câu 28.3 (THPT Chuyên - ĐH Vinh - Lần 3 - 2018)Cho hình chóp S.ABCD có đáy ABCD là hình
chữ nhật, cạnh AB a, AD  3a . Cạnh bên SA  2a và vuông góc với mặt phẳng đáy. Góc
giữa SB và mặt phẳng SAC bằng
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 33
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 A. 30 . B. 60. C. 45 . D. 75 . Lời giải Chọn A
Vẽ BH AC BH  SAC
Suy ra góc giữa SB và mặt phẳng SAC là  BSH . BA BC . a a 3 a 3 BH    AC 2a 2 2 2
SB SA AB a 3  BH 1 sin BSH     BSH  30 . SB 2 e ln x a 2 Câu 29. Biết dx   b ln  c
với a,b, c   . Tính a b c . 1 x2 e+1 e+1 1 A. 1. B. 1. C. 3 . D. 2 . Lời giải
Tác giả: Nguyễn Mạnh Dũng; Fb: Mạnh Dũng Chọn Bu  ln x  1 du  dx   x Đặt 1   . dv  dx   1    1 x2 v   1 x e e ln x ln x e 1 e 1  1 1  dx    dx     dx .   =   1 x2 1 x 1 x 1 x e +1  x x 1 1 1   1
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 34
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 1 1 = 
 ln x lnx   1  e =  1 ln e   1  ln1 ln 2 . e +1 1 e +1 1 2 a 2 =   ln 1 =  b ln
c a  1; b  1; c  1 a b c  1. e +1 e 1 e+1 e+1 1 x Câu 29.1. Biết dx  .
a tan  C . Giá trị của   là  S a b 1 cos x b A. 1. B. 1. C. 2 . D. 2  . Lời giải Chọn B
Nhận xét: Do chưa thể áp dụng các công thức nguyên hàm cơ bản, quan sát mẫu thấy rằng có x 1 cos x x
thể áp dụng công thức hạ bậc : 2 cos  2  1 cos x  2cos . 2 2 2 1 1 1  x x x Ta có: dx  dx  d
 tan  C  1.tan  C .      1 cos x 2 x 2 x  2  2 2 2 cos cos 2 2
a 1, b  2  S a b 1 2  1  .
Câu 29.2. Cho hàm số  ex y
sin x . Họ nguyên hàm của hàm số trên là 1 x 1 A. e cos  ex x sin x  1 x 1 C .
B.  e cos  ex x sin x C . 2 2 2 2 1 x 1 C. e cos  ex x sin x  1 x 1 C .
D.  e cos  ex x sin x C . 2 2 2 2 Lời giải Chọn D
Phương pháp: Áp dụng phương pháp nguyên hàm từng phần. Đặt  ex I
sin x dx .    ex u d  ex u dx Đặt   
  ex cos  ex I x cos x dx . 
dv  sin x dx
v   cos x   ex u d  ex u dx Đặt 1  1   .
dv  cos x dxv  sin x 1  1
  ex cos  ex sin  ex I x x
sin x dx  ex cos  ex x
sin x C I .  1  1 2  ex  cos  ex I x sin x  1 x 1
C    e cos  ex I x
sin x C (với C C ). 1 2 2 1 2
Câu 30. Có bao nhiêu tiếp tuyến của đồ thị hàm số 3 2
y x  3x  2 đi qua điểm A3;2 ? A. 3 . B. 0 . C. 1. D. 2 . Lời giải
Tác giả: Nguyễn Tất Thành; Fb: Thanh Nguyen Chọn D Ta có: 2
y  3x  6x .
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 35
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Giả sử B C  Bx ; y 3 2
y x  3x  2 . 0 0  0 0 0
Phương trình tiếp tuyến T  của C tại B là y   3 2
x  3x  2   2 3x  6x x x . 0 0 0 0   0 
T đi qua A3;2 nên 2  3 2
x  3x  2   2 3x  6x 3  x . 0 0 0 0   0  x  0  3 2
2x 12x 18x  0 0  . 0 0 0 x  3  0
Khi đó hai tiếp tuyến là: y  2 hoặc y  9x  25 .
Vậy có 2 tiếp tuyến của đồ thị hàm số đi qua A3;2 . 2 x x 1
Câu 30.1. Cho hàm số y
có đồ thị C . Viết phương trình tiếp tuyến của C xuất phát từ x 1 M( 1  ;3) .
A. y  3x 1; y  3  x .
B. y 13; y  3
x . C. y  3; y  3
x 1. D. y  3; y  3  x . Lời giải
Tác giả: Nguyễn Tất Thành; Fb: Thanh Nguyen Chọn D 2 x  2x 2 x x 1 Ta có y 
. Gọi M (x ; y ) là tọa độ tiếp điểm của tiếp tuyến d với C 0 0  y  2 (x 1) 0 0 0 x 1 0 2 2 x  2x x x 1 0 0 0 0 d : y  (x x )  2 0 (x 1) x 1 0 0 2 2 x  2x x x 1 Cách 1: 0 0 0 0
M d  3  ( 1   x )  2 0 (x 1) x 1 0 0 2 2 2
 3(x 1)  (x  2x )(x 1)  (x 1)(x x 1) 0 0 0 0 0 0 0 1 2
 2x  5x  2  0  x  2, x  0 0 0 0 2
 Với x  2  Phương trình tiếp tuyến y  3. 0 1  Với x
 Phương trình tiếp tuyến y  3  x . 0 2
Cách 2: Gọi d là đường thẳng đi qua M ( 1
 ;3) , có hệ số góc k , khi đó phương trình d có dạng:
y k(x 1)  3.
d tiếp xúc đồ thị C tại điểm có hoành độ x khi hệ phương trình sau có nghiệm x : 0 0 2  x x 1 0 0
k(x 1)  3 (1)  0  x 1 0  2  x  2x 0 0  k (2) 2 (x 1)  0 2 2 x x 1 x  2x Thế 2 vào   1 ta được: 0 0 0 0  (x 1)  3 2 0 x 1 (x 1) 0 0
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 36
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 1 2
 2x  5x  2  0  x  2, x  . 0 0 0 0 2
 Với x  2  k  0  Phương trình tiếp tuyến y  3. 0 1
 Với x   k  3
  Phương trình tiếp tuyến y  3  x . 0 2
Câu 30.2. Cho hàm số: 4 2
y x  2x có đồ thị là C . Tìm những điểm M trên trục Oy để từ M kẻ
được 4 tiếp tuyến đến C . 1
A. M 0;m với 0  m 1.
B. M 0;m với 1   m  . 3 2 1
C. M 0;m với 0  m  .
D. M 0;m với 0  m  . 3 3 Lời giải
Tác giả: Nguyễn Tất Thành; Fb: Thanh Nguyen Chọn D
M Oy M 0;m; B C  Bx ; y 4 2
y x  2x . 0 0  0 0 0
Phương trình tiếp tuyến T  của C tại B là y   4 2
x  2x    3 4x  4x x x . 0 0 0 0   0 
T đi qua M 0;m nên m  4 2
x  2x    4
4x  4x x  4 2
 3x  2x m  0 * . 0 0 0 0 0 0 0  
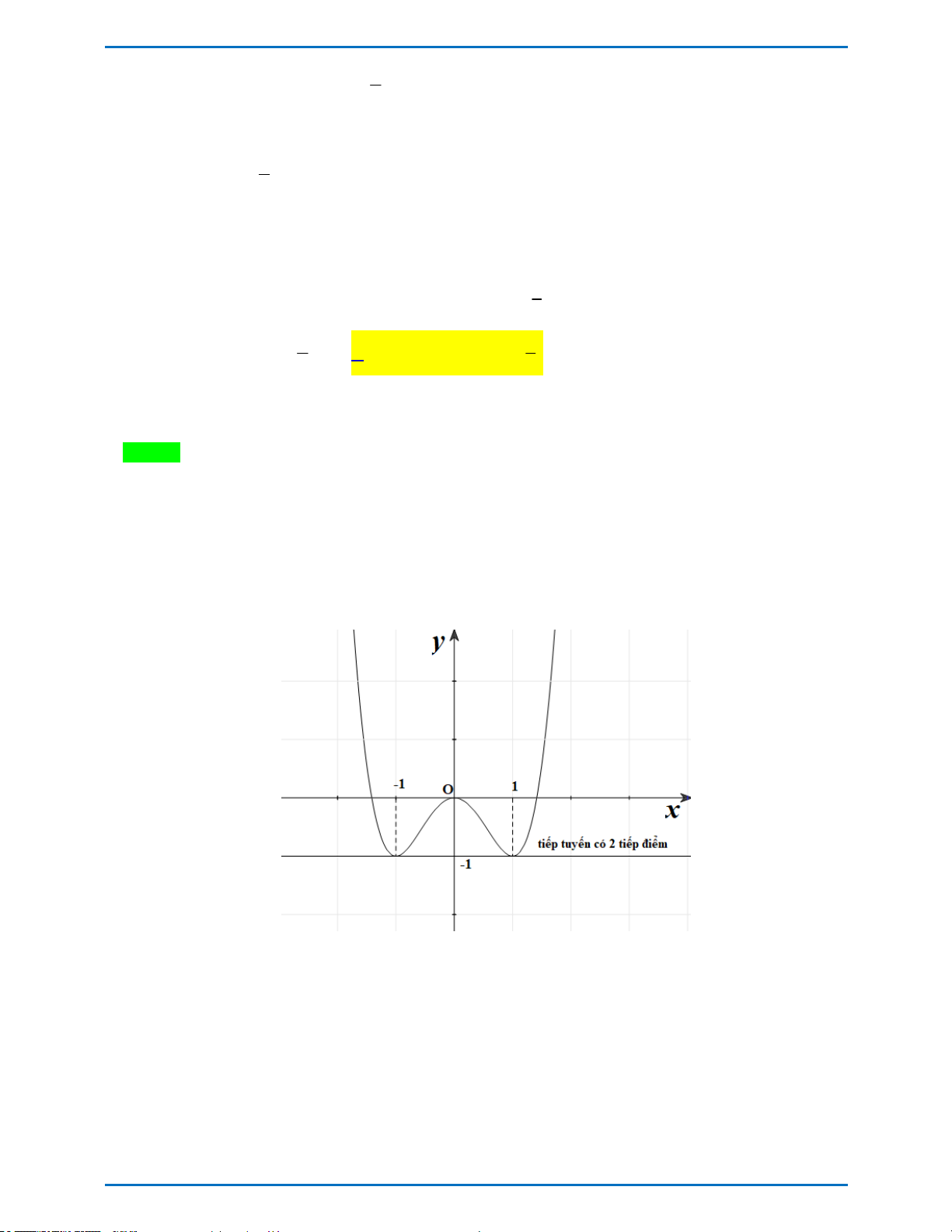
Khi m  1 thì tiếp tuyến có 2 tiếp điểm là 1;  1 và 1;1 .
Vậy từ M 0;m kẻ được 4 tiếp tuyến đến đồ thị C khi và chỉ khi phương trình   * có 4 nghiệm phân biệt khác 1. Đặt 2
X x ta có phương trình 2
3X  2X m  0  ** 0
Phương trình * có 4 nghiệm phân biệt khác 1 khi và chỉ khi  
** có 2 nghiệm phân biệt khác 1
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 37
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
  1 3m  0  mP   0  3 1    0  m  2 3 S   0  3 1    m  0 1
Vậy từ những điểm M 0;m với 0  m  kẻ được 4 tiếp tuyến đến đồ thị C của hàm số đã cho. 3 2cos x 1
Câu 31. Gọi M,m tương ứng là giá trị lớn nhất và nhỏ nhất của hàm số y  . Khi đó ta có cos x  2
A. 9M m  0 .
B. 9M m  0 .
C. M  9m  0 .
D. M m  0 . Lời giải Chọn A 2t 1
Đặt cos x t t  
1 ta có f (t)  , với t   1  ;  1 . t  2  f t 5   0 với t   1  ; 
1  hàm số nghịch biến trên  1  ;  1 . t  22 1
M  Max f (t)  f ( 1
 )  và m  Min f (t)  f (1)  3  . 1; 1 3 -1; 1
Vậy 9M m  0 . Nên chọn A. sin x 1
Câu 31.1. Gọi M,m tương ứng là giá trị lớn nhất và nhỏ nhất của hàm số y  . Khi đó ta có 3  2sin x
A. M  2019m  2 .
B. M  2019m  20  19 .
C. 2M  3m  0 .
D. M m  1. Lời giải Chọn A t 1
Đặt sin x t t  
1 ta có f (t)  với "t Î é-1;1ù 3  2t ë û . f t 5   0 với t   1  ; 
1  hàm số đồng biến trên  1  ;  1 . 3 2t2
M  Max f (t)  f (1)  2 và m  Min f (t)  f ( 1  )  0 . -1; 1 -1; 1
Vậy M  2019m  2 . Nên chọn A. sin x m
Câu 31.2. Gọi S là tập tất cả các giá trị nguyên của m để giá trị lớn nhất của hàm số y  3  2sin x thuộc đoạn é-2; 2ù ë
û . Khi đó số phần tử của S là A. 11. B. 10 . C. Vô số. D. 9 . Lời giải
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 38
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 Chọn A t m
Đặt sin x t t  
1 ta có f (t)  với "t Î é-1;1ù 2  t  3 ë û . 2m  3
Ta có f t  .  2  t  32
Do m Î Z nên ta xét hai trường hợp sau +TH1: m   1
 thì hàm số đồng biến trên  1  ;  1 .
 Max f (t)  f (1)  m 1. -1; 1 Xét m 1 2  ;2  3
  m 1. Vậy m Î{0; } 1 . +TH2: m   2
 thì hàm số nghịch biến trên  1  ;  1 . m 1
 Max f (t)  f ( 1  )  . -1; 1 5 m 1 Xét  2;  2  9
  m 11. Vậy m Î{-9; 8 - ; 7 - ; 6; - 5 - ; 4; - 3 - ;- } 2 . 5
Vậy tập S có 11 phần tử. Nên chọn A.
Nhận xét của Admin tổ 4:
Cách khác liên quan đến bản chất Max, Min của hàm số: sin x m
Để giá trị lớn nhất của hàm số y  thuộc đoạn é-2; 2ù 3  2sin x ë û
 sin x m  2 , x      1   3 2sin x   sin x m x :  2  2  3  2sin x
m  6  5sin x , x     
x   : m  6   3sin x  9   m  1.
Câu 32 . Trong không gian Oxyz , viết phương trình mặt cầu tâm I  1;
 3;0 và tiếp xúc với mặt phẳng
P: 2x y  2z 11 0.
A. x  2   y  2 2 1
3  z  4 . B. x  2   y  2 2 1 3  z  4 .
C. x  2   y  2 2 1
3  z  2 . D. x  2   y  2 2 4 1 3  z  . 9 Lời giải
Tác giả: Nguyễn Thị Thu Trang 215; Fb: Trang Nguyễn Chọn A
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 39
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 2  1  3  0 11
Vì mặt cầu tiếp xúc mặt phẳng P nên có bán kính r d I,P   2 . 2   2 2 2 1  2
Vậy phương trình mặt cầu là:  x  2   y  2 2 1 3  z  4 .
Câu PT 32.1. Trong không gian Oxyz , viết phương trình mặt cầu tâm I 1;1;2 và tiếp xúc với đường x  1 t
thẳng  : y  3  t . z 1 2t
A. x  2   y  2   z  2 1 1 2  11.
B. x  2   y  2   z  2 1 1 2  121.
C. x  2   y  2   z  2 1 1 2  11.
D. x  2   y  2   z  2 1 1 2  121. Lời giải
Tác giả: Nguyễn Thị Thu Trang 215; Fb: Trang Nguyễn Chọn A 
Gọi H 1 t ;3  t ;1 2t là hình chiếu của I trên đường thẳng  , suy ra IH  t ;4  t ; 2t   1 .
Đường thẳng  có một véc tơ chỉ phương u    1; 1;2.  
Theo bài ra, ta có u .IH  0  t t  4  4t  2  0  t  1  .
Suy ra H 2;2;3 , khi đó mặt cầu có bán kính r  11 .
Vậy phương trình mặt cầu cần tìm là:  x  2   y  2   z  2 1 1 2  11.
Câu PT 32.2. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S  có tâm I 1;1;  1 và mặt phẳng
P:2x y  2z 1 0. Biết mặt phẳng P cắt mặt cầu S theo giao tuyến là một đường
tròn có bán kính bằng 3. Viết phương trình của mặt cầu S  .
A. x  2   y  2   z  2 1 1 1  13 .
B. x  2   y  2   z  2 1 1 1  169 .
C. x  2   y  2   z  2 1 1 1  13.
D. x  2   y  2   z  2 1 1 1  169 . Lời giải
Tác giả: Nguyễn Thị Thu Trang 215; Fb: Trang Nguyễn Chọn A
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 40
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Giả sử đường tròn giao tuyến của mặt phẳng P và mặt cầu S  có tâm H , bán kính HM . 2 1 2 1
IH d I,P   2 . 2   2 2 2 1  2
Bán kính của mặt cầu S  là r IM 2 2  3  2  13 .
Vậy phương trình của mặt cầu S  :  x  2   y  2   z  2 1 1 1  13 .
Diện tích toàn phần của hình trụ là 2
S  2 rl  2 r  4 . tp
Câu 33. Cho số phức z thoả mãn z 1 2i  z 2  3i  4
 12i . Tìm toạ độ điểm M biểu diễn số phức z . A. M 3;  1 .
B. M 3;  1 . C. M  1;  3 .
D. M 1;3 . Lời giải
Tác giả: Trần Thị Thơm; Fb: Tranthom Chọn B
Giả sử z a bi a,b   . Suy ra z a bi .
Khi đó: z 1 2i  z 2  3i  4  12i
 a bi1 2i  a bi2  3i  4  12i
 a b  5a  3bi  4  12i
a b  4  a  3     . 5
a  3b  12 b  1 
Do đó điểm M biểu diễn số phức z có toạ độ là 3;  1 .
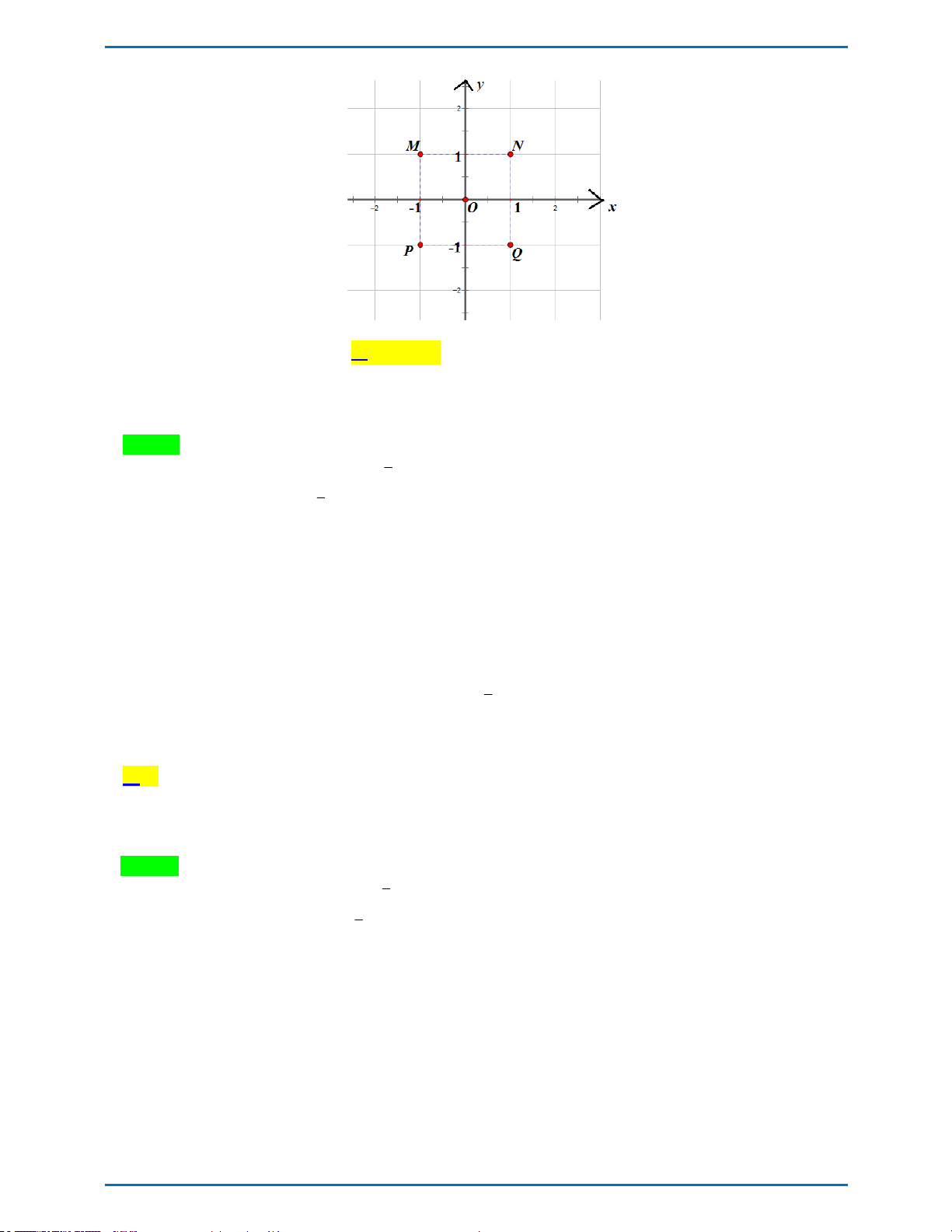
PT 33.1 Cho số phức z thoả mãn 1 3iz  3z  5
  7i . Điểm nào sau đây trong các điểm
M , N , P,Q biểu diễn cho số phức z ?
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 41
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 A. Điểm M . B. Điểm N . C. Điểm P . D. Điểm Q . Lời giải
Tác giả: Trần Thị Thơm; Fb: Tranthom Chọn B
Giả sử z a bi a,b   . Suy ra z a bi .
Khi đó: 1 3iz  3z  5   7i
 1 3ia bi  3a bi  5   7i  2
a  3b  3a  4bi  5   7i  2
a  3b  5  a  1     . 3
a  4b  7 b   1
Do đó điểm biểu diễn cho số phức z có toạ độ là 1; 
1 là điểm N trên hình vẽ.
PT 33.2 Cho số phức z thoả mãn 2i  3 z  1 iz  2
  8i . Khoảng cách từ điểm biểu diễn cho số
phức z trên mặt phẳng toạ độ Oxy đến điểm M 1;2 bằng A. 1. B. 2 . C. 3 . D. 4 . Lời giải
Tác giả: Trần Thị Thơm; Fb: Tranthom Chọn A
Giả sử z a bi a,b   . Suy ra z a bi .
Khi đó: 2i  3 z  1 iz  2   8i
 2i  3a bi  1 ia bi  2   8i
 2a b  3a  4bi  2   8i
2a b  2  a  0     . 3
a  4b  8 b   2
Do đó điểm N biểu diễn cho số phức z có toạ độ là 0;2 .
Ta có khoảng cách cần tìm là MN  1.
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 42
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 f x  3
Câu 34. Cho các hàm số y f x, y g x   , y
. Hệ số góc của các tiếp tuyến của các đồ thị g x 1
hàm số đã cho tại điểm có hoành độ x  1 bằng nhau và khác 0. Khẳng định nào dưới đây là khẳng định đúng? A. f   1  3  . B. f   1  3  . C. f   11 1   . D. f   11 1   . 4 4 Lời giải
Tác giả: Phạm Thanh My ; Fb: Thanh My Phạm Chọn C f x  3
Đặt y hx    g x 1
f ' x g x 1  g ' x f x  3
Ta có h ' x            g x 2 1  
Theo bài ra ta có f '  1  g '  1  h '  1  0        h   f '  1 g    1 1 g '    1 f    1 3 ' 1    g   2 1 1    g    2 1 1  g
 1  f    1 2  f   2 1  g   1  g   1  3 2  
f     g   1 11 11 1 1      2    4 4 f x  3
PT 34.1. Cho tiếp tuyến của các đồ thị hàm số y f x, y g x   , y
lần lượt tạo với chiều g x 1
dương của trục Ox các góc 0 0 0
60 ,60 ,30 . Khẳng định nào dưới đây là khẳng định đúng? A. f   9 1   . B. f   9 1   . C. f   27 1   . D. f   27 1   . 4 4 4 4 Lời giải
Tác giả: Phạm Thanh My ; Fb: Thanh My Phạm Chọn D f x  3
Đặt y hx    g x 1
f ' x g x 1  g ' x f x  3
Ta có h ' x            g x 2 1  
Theo bài ra ta có f    g    h   1 ' 1 ' 1 3, ' 1  3
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 43
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019        h   f '  1 g    1 1 g '    1 f    1 3 ' 1    g   2 1 1   1 3 g  
1 1  3  f   1  3       3 g   2 1 1    g    2 1 1  3g    1  3 f   1  6  3 f   2 1  g   1  g   1  7 2  
f     g   1 27 27 3 1 1      2    4 4  f   9 1   4
Câu 35. Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy 2, 4, n(n > ) 3 điểm phân biệt
(các điểm không trùng với các đỉnh của tam giác). Tìm n biết rằng số tam giác có các đỉnh
thuộc n +6 điểm đã cho là 247 A. 6 . B. 7 . C. 5 . D. 8 . Lời giải
Tácgiả:Quỳnh Giao; Fb:QGiaoDo Chọn B
Lấy ba điểm phân biệt không thẳng hàng sẽ tạo thành một tam giác nên số tam giác tạo thành là: 3 3 3 C
-C -C = 247  n = 7 n+6 4 n Phát triển
Câu 35.1. Cho tam giác ABC , gọi S là tập hợp gồm 4 đường thẳng song song với AB , 6 đường thẳng
song song với BC và 8 đường thẳng song song với AC . Hỏi có bao nhiêu hình bình hành được
tạo thành từ các đường thẳng thuộc tập S A. 2712 . B. 678 . C. 652 . D. 2436 . Lời giải
Tácgiả:Quỳnh Giao; Fb:QGiaoDo Chọn B
Ta chia tập S thành 3 nhóm, nhóm 1 gồm 4 đường thẳng song song với AB , nhóm 2 gồm
6 đường thẳng song song với BC , nhóm 3 gồm 8 đường thẳng song song với AC . Khi đó cứ 2
đường thẳng thuộc nhóm này và hai đường thẳng thuộc nhóm khác sẽ tạo thành một hình bình
hành. Khi đó số hình bình hành là: 2 2 2 2 2 2
C .C +C .C +C .C = 678 4 6 8 6 4 8 ln 2
3 2x  3 f x
Câu 36. Cho hàm số f x liên tục trên  . Biết  ex f   1 dx  5 và dx  3  . Tính x 1 0 2 3 I f  xdx . 2
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 44
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 A. I  2 . B. I  4 . C. I  2  . D. I  8 . Lời giải
Tác giả: Vũ Danh Được; Fb: Danh Được Vũ Chọn B t x x d
Đặt t  e 1  dt  e dx  dx  . t 1
Đổi cận x  0  t  2; x  ln 2  t  3 . ln 2 3 3 f t f x Do đó f  ex       1 dx  5  dt  5  dx  5   . t 1 x 1 0 2 2
3 2x  3 f x 3 2x  2   1 f x 3  f x  Ta có dx  dx  2 f    x    dx  3  . x 1 x 1 x 1 2 2 2   3 f x Suy ra 2I
dx  3  2I  8  I  4  . x 1 2 1
PT 36.1. Cho hàm số f (x) liên tục trên  thỏa mãn f (2x)  4 f (x)  x , x   . Biết rằng f (x)dx  1 0 2
. Tính tích phân I f (x)dx  . 1 A. I  9 . B. I  6 . C. I  5 . D. I  8 . Lời giải
Tác giả: Vũ Danh Được; Fb: Danh Được Vũ Chọn B 1 1 1 1 Ta có K f
 2xdx  4f
 x xdx   4 f
 xdx d x x  1 7  4   . 2 2 0 0 0 0
Đặt t  2x  dt  2dx . Đổi cận x  0  t  0; x  1  t  2 . 2 1 2 2 K f
 tdt f
 tdt  7  f
 xdx  7. 2 0 0 0 2 1 2 2 2 1 f
 xdx f
 xdxf
 xdx I f (x)dx   f
 xdxf
 xdx  71 6. 0 0 1 1 0 0  
Câu 37. Cho khối hộp ABCDA BCD
  có thể tích V . Các điểm M , N , P thỏa mãn AM  2AC ,    
AN  3AB , AP  4AD . Tính thể tích khối chóp AMNP theo V .
A. 6V . B. 8V . C. 12V . D. 4V . Phân tích:
 Nhận dạng bài toán: Đây là bài toán tính thể tích khối đa diện thông qua tỉ số thể tích.
 Kiến thức cần nhớ: Cho khối chóp S.ABC . Trên các đường thẳng SA, SB , SC lần lượt V       SA SB SC
lấy ba điểm A, B,C khác S . Ta có: S.A B C  . . . V SA SB SC S .ABC
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 45
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 Lời giải
Tác giả: Vũ Nga; Fb: Nga Vu Chọn B V AM AN AP
Ta có: A.MNP  . .  2.3.4  24  V  24V . V   . A MNP . A CB D     AC AB AD . A CB D V Mà: V      1        V    
V    V V V V 4. V V 8V . . A CB D ABCDA B C D . A A B D . A B BC . A D DC C.C BD   6 3 . A MNP
Câu PT 37.1 Cho khối hộp ABCDA BCD
  có thể tích V . Lấy điểm M đối xứng với A qua C , điểm  
N đối xứng với A qua B , điểm P thỏa mãn AP k AD . Tìm k để thể tích khối chóp AMNP V bằng . 2 3 3 1 1 A. k  . B. k   . C. k  . D. k   . 8 8 2 2 Lời giải
Tác giả: Vũ Nga; Fb: Nga Vu Chọn B V AM AN AP
Ta có: A.MNP  . .
 2.2. k  4 k V  4 k V . V   . A MNP . A CB D     AC AB AD . A CB D V 4 Mà: V      1        V    
V    V V V V 4. V V k V . . A CB D ABCDA B C D . A A B D . A B BC . A D DC C.C BD   6 3 . A MNP 3 V 3  V      k . . A CB D 2 8
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 46
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
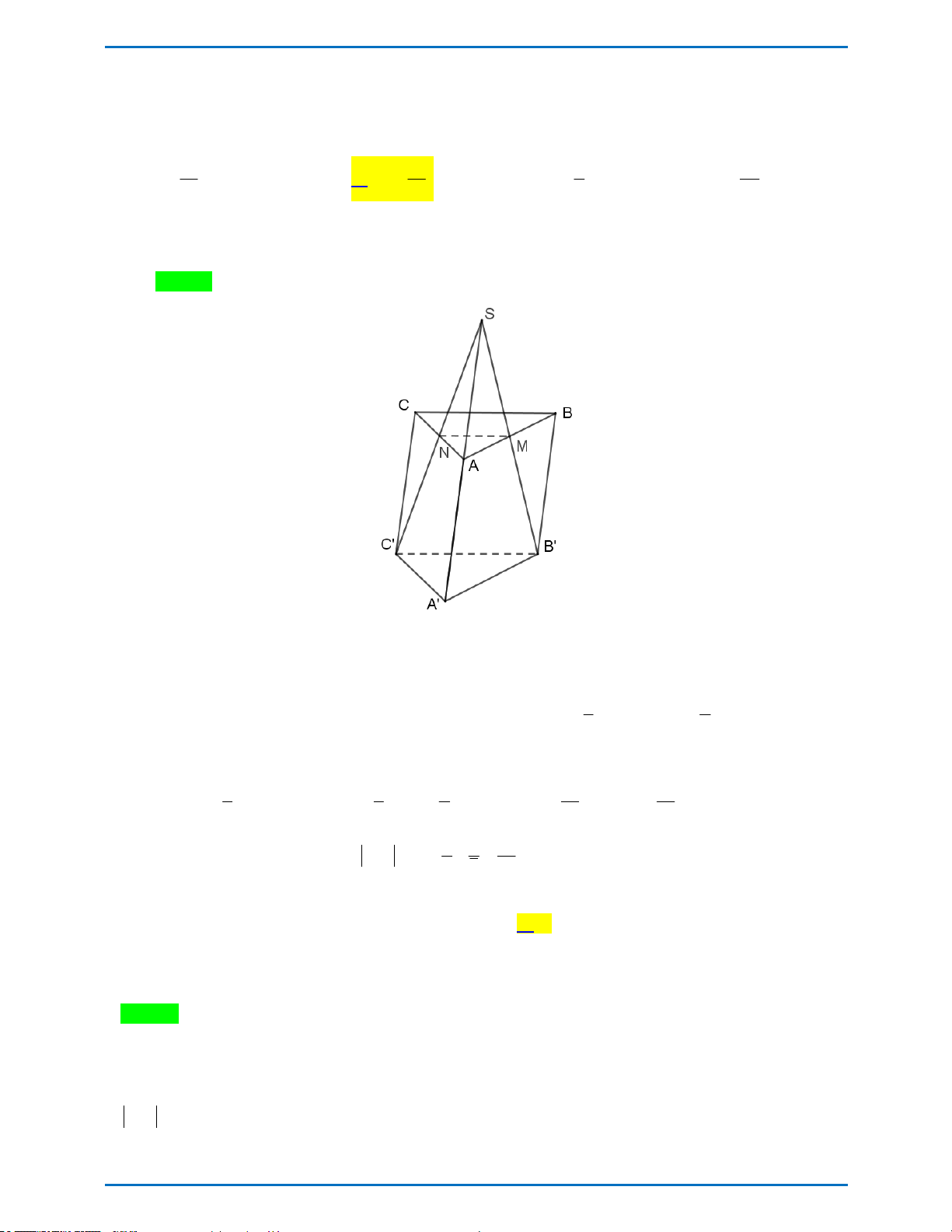
Câu PT 37.2 Cho khối lăng trụ tam giác ABCA BC
  có thể tích V . Điểm M là trung điểm của AB . Mặt phẳng C BM
  chia khối lăng trụ thành hai khối đa diện có thể tích là V và V , biết V là 1 2 1
khối chứa điểm A . Tính V theo V . 2 7 5 5 17 A. V  . B. V  . C. V  . D. V  . 2 12 2 12 2 6 2 24 Lời giải
Tác giả: Vũ Nga; Fb: Nga Vu Chọn B Do C B
  // (ABC) nên C BM
  cắt AC tại điểm N thỏa mãn MN // B C
   N là trung điểm AC . 1 7
Dễ thấy 3 đường C N  , B M
 , AA đồng quy tại S và VVV V . S.AMN S. 8 AB C   1 .
8 S AB C Gọi ,
h S lần lượt là chiều cao và diện tích đáy của khối lăng trụ ABCA BC   , ta có: 1 1 2 7 5 V              d S ; A B C .S .2 . h S V , vậy V V V V . S.A B C    3 3 3 1 12 2 12 1 1 5
Câu 38. Cho số phức z thỏa mãn z 1  5 ,  
và z có phần ảo dương. Tìm tổng phần thực z z 17
và phần ảo của z .
A. 2 . B. 4 . C. 6 . D.8 . Lời giải
Tác giả: Nguyễn Thị Thanh Vân; Fb: Thanh Van Chọn D
Gọi z a bi a,bR,b  0 . Ta có
z 1  5  a  2 2 1  b  25 2 2
a b  2a  24   1
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 47
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 1 1 5   1 1 5    2a 5   34 2 2  a b a  0 2 z z 17
a bi a bi 17 2 2 a b 17 5
Trừ vế - vế của  
1 cho 2 ta có a  5  b  3  a b  8. 1 1 5
PT 38.1 Cho số phức z thỏa mãn z 1  5 ,  
và z có phần ảo âm. Tìm tổng phần thực và z z 17 phần ảo của z .
A. 2 . B. 4 . C. 6 . D.8 . Lời giải
Tác giả: Nguyễn Thị Thanh Vân; Fb: Thanh Van Chọn A
Gọi z a bi a,bR,b  0 . Ta có
z 1  5  a  2 2 1  b  25 2 2
a b  2a  24   1 1 1 5   1 1 5    2a 5   34 2 2  a b a  0 2 z z 17
a bi a bi 17 2 2 a b 17 5
Trừ vế - vế của  
1 cho 2 ta có a  5  b  3
  a b  2 . 1 1 10
PT 38.2 Cho số phức z thỏa mãn z  2  5 ,  
và z có phần ảo dương. Tìm tổng phần thực z z 41
và phần ảo của z .
A. 2 . B.1. C. 9 . D.8 . Lời giải
Tác giả: Nguyễn Thị Thanh Vân; Fb: Thanh Van Chọn C
Gọi z a bi a,bR,b  0 . Ta có
z  2  5  a  2 2 2  b  25 2 2
a b  4a  21   1 1 1 10   1 1 10    2a 10   41 2 2  a b a  0 2 z z 41
a bi a bi 41 2 2 a b 41 5
Trừ vế - vế của  
1 cho 2 ta có a  5  b  4  a b  9 .
Câu 39. Trong không gian với hệ tọa độ Oxyz , cho điểm A 1;2;2  và đường thẳng x  6 y 1 z  5 d :  
. Tìm tọa độ điểm B đối xứng với A qua d . 2 1 1 A. B  3;  4; 4  .
B. B 2;1;3  .
C. B 3;4; 4  .
D. B 3; 4;4  . Lời giải
Tác giả: Phạm Thị Thu Trang; Fb: Trang Phạm
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 48
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 Chọn D
Từ phương trình đường thẳng d ta có véc tơ chỉ phương của d là u 2;1;1  
Gọi H là hình chiếu của A trên d , suy ra H 6  2t ;1 t ;5  t  AH 5  2t ;1 t ;3 t . Khi đó    
AH u AH.u  0  25  2t   1
  t  3 t  0  t  2  . Với t  2
 thì H 2;1;3 .
Gọi B là điểm đối xứng với A qua d thì H là trung điểm AB B 3; 4;4  . x  6 y 1 z  5
Câu PT 39.1. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt 2 1 1
phẳng P : 2x  3y z  4  0. Viết phương trình đường thẳng d là hình chiếu vuông góc của
d trên P . x  6  tx  6tx  6tx  6  t     A.y  2   5t . B. y  2   5t . C. y  2   5t . D. y  2   5t . z  23t     z  2  3tz  2  3tz  2  3tLời giải
Tác giả: Phạm Thị Thu Trang; Fb: Trang Phạm Chọn A
Gọi I d  P , khi đó toạ độ điểm I là nghiệm của hệ phương trình:
x  6  2t t   3    y 1 t    x  0   
I  0; 2;2  . z  5  t y  2   
2x 3y z  4  0 z  2
Lấy A6;1;5 d , gọi  là đường thẳng đi qua A và vuông góc với P suy ra PT đường thẳng 
x  6  2t   18 29 23 
có dạng: y 1 3t . Gọi J   P , ta tính được J  ; ; ;   .   7 7 7  z  5  t  x  6  t
Khi đó đường thẳng d đi qua 2 điểm I , J có PTTS là: y  2   5t . z  23t
Nhận xét Admin tổ 4 – Strong
Bài 39 + 39.1 đều có điều chung là cần tìm hình chiếu của 1 điểm tới 1 mặt. Ta có thể giải nhanh:
Cho   : ax by cz d  0
Am;n;k . Gọi H là hình chiếu của A lên   . 
am bn ck d h    Khi đó 2 2 2 
a b cH
 m ah;n bh;k ch
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 49
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Câu 39: Ta có d qua M 6;1;5 ; VTCP u  2;1;  1 .
P qua A ,  d có phương trình: 2 x  
1 1 y  2 1 z  2  0
 2x y z  6  0
H là hình chiếu của M lên P  H 2;1;3
B đối xứng với A qua H B 3; 4;4 Câu 39.1
I d P  I 0; 2;2
A6;1;5  d  18 29 23 
H là hình chiếu của A lên P  H  ; ;   .  7 7 7  x  6  t  
d qua IH : y  2   5t z  23t
Câu 40. Ông An có một khu đất hình elip với độ dài trục lớn 10 m và độ dài trục bé 8 m. Ông An muốn
chia khu đất thành hai phần, phần thứ nhất là một hình chữ nhật nội tiếp elip dùng để xây bể cá
cảnh và phần còn lại dùng để trồng hoa. Biết chi phí xây bể cá là 1000000 đồng trên 2 1m và chi
phí trồng hoa là 1200000 đồng trên 2
1m . Hỏi ông An có thể thiết kế xây dựng như trên với tổng
chi phí thấp nhất gần nhất với số nào sau đây? A. 67398224 đồng. B. 67593346 đồng. C. 63389223 đồng. D. 67398228 đồng. Lời giải
Tác giả:Phạm Văn Tuấn ; Fb: Phạm Tuấn Chọn A
Gắn mảnh vườn hình elip của ông An vào hệ trục tọa độ như hình vẽ. Độ dài trục lớn 10m và độ dài
trục bé bằng 8m nên ta có a  5 và b  4 .
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 50
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 2 2 x y
Phương trình của elip là: E :  1. 25 16
Diện tích của elip là: S       ab 20 . E 2 x
Hình chữ nhật ABCD nội tiếp elip. Đặt AB  2x 0  x  5  AD  8 1 . 25 2 x
Diện tích hình chữ nhật ABCD là: S  16x 1 . ABCD 25 2 x
Diện tích phần còn lại trồng hoa là: S  20 16x 1 . hoa 25
Tổng chi phí xây dựng là: 2 2 xx
T  16000000.x 1
1200000. 20 16x 1  25  25    2 x
 24000000  3200000x 1 . 25 2 2 x x 2 1 x x Mặt khác ta có: 25 25 16000000. 1 16000000.  8000000 . 5 25 2 2 x
T  24000000  3200000x 1
 24000000  8000000  67398223.69. 25 2 x x 5 2
Dấu "  " xảy ra khi  1  x  (thỏa mãn). 5 25 2
Vậy tổng chi phí thiết kế xây dựng thấp nhất gần với số 67398224 .
Câu 40.1. Một cái hồ rộng có hình chữ nhật. Tại một góc nhỏ của hồ người ta đóng một cái cọc ở vị trí
K cách bờ AB là 1 m và cách bờ AC là 8 m , rồi dùng một cây sào ngăn một góc nhỏ của hồ
để thả bèo (như hình vẽ). Tính chiều dài ngắn nhất của cây sào để cây sào có thể chạm vào 2
bờ AB , AC và cây cọc K (bỏ qua đường kính của sào). 5 65 5 71 A. . B. 5 5 . C. 9 2 . D. . 4 4 Lời giải
Tác giả:Phạm Văn Tuấn ; Fb: Phạm Tuấn Chọn B B P K E A F Q C
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 51
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Đặt AP a , AQ b a,b  0 . Gọi E và F lần lượt là hình chiếu vuông góc của K xuống
AB và AC . Suy ra KE  1, KF  8 . KE PK KF QK KF KE 8 1 Ta có:  ;    1 hay  1. AQ PQ AP PQ AP AQ a b
(Hoặc có thể dùng phép tọa độ hóa: Gán A  0;0 , P  0;a,Q   ;0
b . Khi đó K  1;8 . x y 1 8
Phương trình đường thẳng PQ : 
1. Vì PQ đi qua K nên  1.) b a b a Cách 1: 8 1 Ta có: 2 2 2
PQ a b . Vì   8k k 1    k k   0 . a b a b  8k   k  4k 4k   k k 2 k 2 2 2 2  
a b k a   b      2 2  a    b       3 2 3  3 16k  3 .  a   b   a a   2b 2b  4  4k 2 a   a  k  250  k  Suy ra PQ nhỏ nhất 2 2
a b nhỏ nhất 2  b    a 10 . 2b    b  5 8 1    1 a b
Vậy giá trị nhỏ nhất của PQ là 2 2
a b  125  5 5 . Từ đó suy ra chiều dài ngắn nhất của
cây sào để cây sào có thể chạm vào 2 bờ AB , AC và cây cọc K là 5 5 . Cách 2: 8 1 a 2  a  Vì   1  b
với a  8. Khi đó 2 2 2
PQ a b 2  a    với a  8. a b a  8  a  8  2  a
Xét hàm số f a 2  a    với a  8.  a 8  3     2a 8  2a a 8 8
Ta có f a  2a  .   
; f a  0  a 10 .
a  8 a 82 a 83
BBT của f a :
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 52
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Vậy GTNN của f a là 125 khi a 10 .
Từ đó suy ra chiều dài ngắn nhất của cây sào để cây sào có thể chạm vào 2 bờ AB , AC và
cây cọc K là 125  5 5 . x  5 y  7 z 12
Câu 41. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 2 2 1 
 : x  2y 3z 3  0. Gọi M là giao điểm của d với   , A thuộc d sao cho AM  14 .
Tính khoảng cách từ A đến   . A. 2. B. 3. C. 6. D. 14 . Lời giải
Tác giả: Nguyễn Bảo Mai; Fb: Bao An Chọn B    
có một vectơ pháp tuyến là n  1;2; 3
  và d có một vectơ chỉ phương là u  2;2;  1 .
Gọi  là góc giữa   và d , H là hình chiếu của A trên   . AH 1.2  2.2   3    1 9 Ta có sin 
AH AM sin  14.  14.  3 AM    2    2 2 2 2 2 14.3 1 2 3 2 2 1 x  5 y  7 z 12
PT 41.1. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 2 2 1 
 : x  2y 3z 3  0. Gọi M là giao điểm của d với   , A thuộc d và cách   một
khoảng bằng 3. Tính độ dài đoạn thẳng AM . 2 14 A. . B. 3. C. 2 14 . D. 14 . 3 Lời giải Chọn D    
có một vectơ pháp tuyến là n  1;2; 3
  và d có một vectơ chỉ phương là u  2;2;  1 .
Gọi  là góc giữa   và d , H là hình chiếu của A trên   . AH AH 3 Ta có sin   AM    14 AM sin 1.2  2.2   3    1 1  2   3
 2 2  2   2 2 2 2 2 1
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 53
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
PT 41.2. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S  có tâm A thuộc đường thẳng x  5 y  7 z 12 d :  
và cắt mặt phẳng   : x  2y  3z  3  0 theo một đường tròn có bán 2 2 1 
kính bằng 5 . Biết rằng giao điểm M của d với   cũng thuộc S  , tính bán kính của S  . 2 14 A. . B. 3. C. 2 14 . D. 14 . 3 Lời giải Chọn D    
có một vectơ pháp tuyến là n  1;2; 3
  và d có một vectơ chỉ phương là u  2;2;  1 .
Gọi  là góc giữa   và d , H là hình chiếu của A trên   .  n.d 3 5
Ta có MH  5 và sin      cos  . n . d 14 14 MH MH Mà cos  5  AM    14 . AM cos 5 14
Câu 42 . Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số 2 4
y m x   2 m m 2 2019 x 1có
đúng một điểm cực trị. A. 2019 . B. 2020 . C. 2018 . D. 2017 . Lời giải
Tác giả: Nguyễn Thị Thơm; Fb: Thom nguyen Chọn C
Xét m  0 thì y  1đồ thị hàm số không có cực trị. Xét m  0
Để đồ thị hàm số có 1 cực trị 2  m  2
m  2019m  0  0  m  2019
Do m nguyên nên có 2018 giá trị của m .
PT 42.1 Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số 2 4
y m x   2 m m 2 5 x  7 có
đúng một điểm cực trị. A. 20 . B. 5 . C. 4 . D. 7 . Lời giải
Tác giả: Nguyễn Thị Thơm; Fb: Thom nguyen Chọn D
Xét m  0 thì y  1đồ thị hàm số không có cực trị. Xét m  0
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 54
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Để đồ thị hàm số có 1 cực trị 2  m  2
m  5m  0  0  m  5
Do m nguyên nên có 4 giá trị của m .
PT 42.2 Tính tổng các giá nguyên của tham số m để đồ thị hàm số 2 4
y m x   2 m m 2 11 x  20 có
đúng một điểm cực trị. A. 20 . B. 55 . C. 45 . D.10 . Lời giải
Tác giả: Nguyễn Thị Thơm; Fb: Thom nguyen Chọn B
Xét m  0 thì y  1đồ thị hàm số không có cực trị. Xét m  0
Để đồ thị hàm số có 1 cực trị 2  m  2
m 11m  0  0  m 11
Do m nguyên nên m 1;2;3;4;5;6;7;8;9;1  0
Tổng các giá trị của m bằng 55 .
Câu 43. Gọi S là tập tất cả các giá trị của tham số m để đồ thị hàm số 3 3 2 2
y x  3x  2  4x  3x  2  mx có tiệm cận ngang. Tổng các phần tử của S là A. 2  . B. 2 . C. 3 . D. 3 . Lời giải
Tác giả: Lục Minh Tân; Fb: Lục Minh Tân Chọn A y           3 3 2 2 lim lim x 3x 2 4x 3x 2 mx x x              3 3 2 2 lim x 3x 2 x 2x 4x 3x 2 m  1 x x  3 Ta có: 3 3 2 lim
x  3x  2  x  ; lim x x x    x  2 2 4 3 2    1 x 4 * y           3 3 2 2 lim lim x 3x 2 4x 3x 2 mx x x  
x x   x x
x x   m x x  3 3 2 2 lim 3 2 2 4 3 2  3  3 Ta có: 3 3 2 lim
x  3x  2  x  ; lim x x x   x  2 2 4 3 2    1 x 4 m 1  0 m 1
* Đồ thị hàm số có tiệm cận ngang  lim y hoặc lim y hữu hạn     x x m  3  0 m  3 
Câu PT 43.1. Gọi S là tập tất cả các giá trị của tham số m để đồ thị hàm số m 3 3 2 2
y  8x  5x  2  25x  7x  2 
x có tiệm cận ngang. Tích các phần tử của S là 2
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 55
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 A. 8 . B. 84  . C. 21. D. 21  . Lời giải
Tác giả: Lục Minh Tân; Fb: Lục Minh Tân Chọn B m  * 3 3 2 2 lim y  lim
8x  5x  2  25x  7x  2  x   x x  2    m   3 3 2 2  lim
8x  5x  2  2x  5x  25x  7x  2   3 x     x   2   5 7 Ta có: lim
x x   x   ; lim x x x   x  2 5 25 7 2  x  3 3 2 8 5 2 2  12 10  m  * 3 3 2 2 lim y  lim
8x  5x  2  25x  7x  2  x   x x  2    m   3 3 2 2  lim
8x  5x  2  2x  5x  25x  7x  2  7  x     x   2   5 7 Ta có: lim
x x   x   ; lim x x x    x  2 5 25 7 2  x  3 3 2 8 5 2 2  12 10  m 3  0  m  6 
* Đồ thị hàm số có tiệm cận ngang  lim y hoặc lim y hữu hạn 2     x x m  m  14 7   0  2
Câu PT 43.2. Gọi S là tập tất cả các giá trị của tham số m để đồ thị hàm số 2 3 3 2
y  9x  5x  3  64x  3x  5x  2  mx có tiệm cận ngang. Tổng bình phương tất cả các
phần tử của S là A. 10 . B. 15 . C. 50 . D. 51. Lời giải
Tác giả: Lục Minh Tân; Fb: Lục Minh Tân Chọn C y            2 3 3 2 lim lim 9x 5x 3 64x 3x 5x 2 mx x x               2 3 3 2 lim 9x
5x 3 3x 4x 64x 3x
5x 2 (m 1)x x   1 lim
x x   x  lim x
x x x    x  3 3 2 4 64 3 5 2  x  5 2 9 5 3 3  Ta có: 6 , 16 * y            2 3 3 2 lim lim 9x 5x 3 64x 3x 5x 2 mx x x               2 3 3 2 lim 9x
5x 3 3x 4x 64x 3x
5x 2 (m 7)x x  1 lim
x x   x  lim x
x x x    x  3 3 2 4 64 3 5 2  x  5 2 9 5 3 3  Ta có: 6 , 16
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 56
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 m 1  0 m 1
* Đồ thị hàm số có tiệm cận ngang  lim y hoặc lim y hữu hạn     x x m  7  0 m  7
Câu 44. Cho hàm số f x    2
ln x x . Tính f   1 f 2 f 2019 P  ee ... e . 2020 2019 2019 A. P  . B. P  . C. 2019 P  e . D. P   . 2019 2020 2020 Lời giải
Tác giả: Lê Hữu Đức; Fb: Le Huu Duc Chọn B TXĐ: D   ;    1 0; Ta có f x 1 1 e   , x   D x x 1 Suy ra f  1 1 e  1 2 f 2 1 1 e   2 3 ... f 2019 1 1 e   2019 2020 f   1 f 2 f 2019 1 2019 P  ee  ... e  1  2020 2020
Nhận xét: Câu 44 học sinh có thể dùng máy tính đề tính biểu thức P
Câu PT 44.1. Cho hàm số f x    2
log x  2x . Tính f   1 f 3 f 5 f 2019 P  10 10 10 ...10 . 1010 2022 2020 A. P  . B. P  . C. 2021 P  10 . D. P  . 2021 2021 2021 Lời giải
Tác giả: Lê Hữu Đức; Fb: Le Huu Duc Chọn A TXĐ: D   ;  2   0;   Ta có f x 1 1 1 10   , x   D   2  x x  2    Suy ra f   1 1 1 10  1   2  3 
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 57
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 f 3 1  1 1  10     2  3 5  f 5 1  1 1  10     2  5 7  ... f 2019 1  1 1  10     2  2019 2021 f   1 f 3 f 5 f 2019 1  1  1010 P  10 10 10  ...10  1    2  2021 2021 1 1 1
Câu PT 44.2. Tính P   ... log 2019! log 2019! log 2019! 2 3 2019 A. P  2019 . B. P  1. C. P  0. D. P  2019!. Lời giải
Tác giả: Lê Hữu Đức; Fb: Le Huu Duc Chọn B 1 1 1 P    ...  log 2  log 3  ...  log 2019 log 2019! log 2019! log 2019! 2019! 2019! 2019! 2 3 2019  log 2.3...2019  1 2019!   1 1 1 1 120
Câu PT 44.3. Cho số tự nhiên n , biết biểu thức   ...  luôn
log x log x log x log x x n log 2 3 2 2 2 2 2 đúng x
 0;  \ 
1 . Giá trị n thuộc khoảng nào sau đây? A. 19;25 . B. 14;17 . C. 6;10 . D. 11;14 . Lời giải
Tác giả: Lê Hữu Đức; Fb: Le Huu Duc Chọn B 1 1 1 1 Ta có 2 3   ...
 log 2  log 2  log 2  ... log 2n log log log log x x x x x x x x 2 3 2 2 2 2n  
     nn n  1 1 2 3 ... log 2  . x 2log x 2 n n   1
n  15 t / m 2  
Do đó phương trình đã cho tương đương
 120  n n  240  0   . 2 n  16  l
Vậy n 14;17 .
Câu 45. Cho các số phức z , z thỏa mãn phương trình z  2  3i  5 và z z  6 . Biết rằng tập hợp 1 2 1 2
các điểm biểu diễn số phức w z z là một đường tròn. Tính bán kính đường tròn đó. 1 2 A. R  8 . B. R  4 . C. R  2 2 . D. R  2 .
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 58
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 Lời giải
Tác giả: Lương Văn Huy ; Fb: Lương Văn Huy Chọn A
Giả sử A , B lần lượt là các điểm biểu diễn số phức z , z trên mặt phẳng tọa độ Oxy . Theo giả thiết ta 1 2 có
A , B thuộc đường tròn tâm I 2;3 , bán kính r  5 và AB  6. z z w
Gọi M là trung điểm của AB khi đó M cũng là điểm biểu diễn số phức 1 2 u   . 2 2 Lại có 2 2 2 2 2  AB
IM IA AM r  16  IM  4   .  2 
Vậy M thuộc đường tròn tâm I 2;3 bán kính r '  4.
Suy ra các điểm biểu diễn số phức w z z  2u là một đường tròn bán kính R  2r  8 1 2
Câu 46. Cho các số thực x , y thay đổi thỏa mãn 2 2
x y xy  1 và hàm số f t  3 2
 2t  3t 1.
 5x y  2 
Gọi M , m tương ứng là giá trị lớn nhất và nhỏ nhất của Q f   . Tổng
x y  4 
M m bằng A. 4  3 2 . B. 4  5 2 . C. 4   4 2 . D. 4   2 2 . Lời giải
Tác giả: Trần Thị Thanh Thủy; Fb: Song tử mắt nâu Chọn C 2 2  y  3y 5x y  2 Ta có: 2 2
x y xy  1  x   1   . Ta đặt: t   2  4 x y  4
t x y  4  5x y  2  t  5 x  t 1 y  4t  2  0 .   y    x      t   3y t 5 3 3  2  4t .  2  2
Áp dụng bất đẳng thức Bunhiacopxki, ta có: 2 2 2           
t  t   y x      t
 3y  t      t  2 2 2 y 3y 2 4 5 3 3 5 3 3  x        2  2     2  4    t  t    t 2 2 2 2 4 5 3 3        .1   2
 12t  24t  0   2  t  2 .
Xét hàm số f t  3 2
 2t  3t 1 với  2  t  2 .
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 59
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 t  0
Có: f t  2
 6t  6 nên f t 2
 0  6t  6t  0   . t 1
Ta có: f  2  5
  4 2 , f 0  1, f  
1  0 , f  2  5   4 2
Do đó M f 0  1 , m f  2  5  4 2 .
Vậy M m  4   4 2 .
a x b y c Bài toán gốc: Cho 2 2
ax by cxy d . Tìm MGT 1 1 1 t
a x b y c 2 2 2 Phương pháp giải:
Cách 1. Lượng giác hóa (Song Tử Mắt Nâu)
Ta có: ax by cxy d  a x b y2  c x d y2 2 2 ' ' ' '  1
a ' x b ' y  sin x msin Đặt   
c ' x d ' y  cos
y n cos
a x b y c Suy ra: 1 1 1 t
Asin  B cos  C
a x b y c 2 2 2 Ta có: 2 2 2
A B C suy ra MGT của t .
Cách 2. (Một cách nhìn khác đồng nhất hệ số Ng.Việt Hải)    a x b y c 1 1 1 t
Amx ny  Bkx qy  C
a x b y c 2 2 2
 Chọn m, n, k, q sao cho   2   2 2 2 mx ny
kx qy ax by cxy 2 2
m k a  2 2
 n q b
2mn  2kq c
 Áp dụng BĐT Bunhiacoxki ta có: 2   2 2 C
A B d suy ra MGT của t .
Câu PT 46.1. Cho 2 số x, y thỏa mãn 2 2
x  5y  1 4xy và hàm số bậc ba y f x có đồ thị như
 2x  3y  3 
hình vẽ. Gọi M , m tương ứng là giá trị lớn nhất và nhỏ nhất của P f   .
 x  4y  4 
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 60
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Tích M .m bằng 1436  3380 1436 1944 A. B. C. D. 1331 1331 1331 1331 Lời giải
Tác giả: Trần Thị Thanh Thủy; Fb: Song tử mắt nâu Chọn C
Dễ thấy f x 3  x  3x
Từ x y   xy   x y2 2 2 2 5 1 4 2  y  1
x  2y  sin
x  sin  2cos Đặt    . Khi đó  y cos y cos 2x  3y  3
2sin  2cos   3cos  3
2sin  cos  3 Xét t   
x  4y  4 sin  2cos   4cos  4 sin  2cos  4
Ta có: t sin  2cos  4  2sin  cos  3  t  2sin  1 2tcos  4t  3 * 2
Phương trình * có nghiệm  t  2   t  2   t  2 2 2 1 4 3  2  t  11 2 
Khi đó P f t 3
t  3t với 2   t  11 718 1436
Dễ dàng tìm được M  2 , m  . Vậy M .m 1331 1331
Câu PT 46.2. Cho các số thực x, y thay đổi thỏa mãn 2 2
x  5y  2xy  1 và hàm số
x y 1  f t 4 2
t  2t  2 Gọi M , m là giá trị lớn nhất và giá trị nhỏ nhất của Q f   .
x  3y  2  Tổng M m A. 4 3  2 . B. 8 3  2 . C. 66 . D. 9 3 17 Lời giải
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 61
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Tác giả: Trần Thị Thanh Thủy; Fb: Song tử mắt nâu Chọn C Ta có: 2 2
x  5y  2xy  1   x y2 2  4y  1 x y 1 Đặt t
t x  3y  2  x y 1  2t   1  t  
1  x y  2ty x  3y  2
Áp dụng bất đẳng thức Bunhiacopxki, ta có:  t  2   2 2
t   x y 2  ty  
t 2 t  xy2 2 2 2 1 1 2 1
 4y    t    t   2 2 1 1  t 2
 2t  6t  0  3   t  0
Xét hàm số f t 4 2
t  2t  2 với 3   t  0 t  0
Có: f t 3
 4t  4t , nên f t 0     t  1   t 1 
f 0  2, f   1  1, f  3    65
Do đó M f  3
   65;m f   1  1
Vậy: M m  66
xy yz zx  8
Câu PT 46.3. Cho các số thực x, y, z thỏa mãn 
và hàm số f x 2
x  4x  5
x y z  5
Gọi M , m là giá trị lớn nhất và giá trị nhỏ nhất của f x . Tổng M m 28 19 A. 3 . B. . C. . D. 2 9 9 Lời giải
Tác giả: Trần Thị Thanh Thủy; Fb: Song tử mắt nâu Chọn A
xy yz zx  8
zy  8  xy z
yz  8  x5  x
Viết lại điều kiện:        *
x y z  5
y z  5  x
y z  5  x
Vì x, y, z thỏa mãn  
* nên y, z là hai nghiệm của phương trình 2
T    x 2 5
T  8  5x x  0   **
Điều kiện có nghiệm của phương trình   ** là:     7 x2   2  x x  2 5 4 8 5
 0  3x 10x  7  0  1  x  3 7
Xét hàm số f x 2
x  4x  5 với 1  x  3
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 62
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Có f  x  2x  4 nên f  x  0  x  2   f    f   7 10 1 2; 2  1; f     3  9
Do đó M f  
1  2, m f 2 1.
Vậy M m  3 .
Câu 47. Trong các khối chóp tứ giác đều S.ABCD mà khoảng cách từ A đến mp (SBC) bằng 2a , khối
chóp có thể tích nhỏ nhất bằng A. 3 2 3a . B. 3 2a . C. 3 3 3a . D. 3 4 3a . Lời giải
Tác giả : Võ Thị Ngọc Ánh ; Fb: Võ Ánh Chọn A. S L A B I K O D C
Gọi I là trung điểm của AD; K là trung điểm của CB, O là tâm của hình chữ nhật ABCD.
Trong tam giác SOK kẻ đường cao OL. 1 1
Ta có d (O;(SBC))  OL và d( ;
O (SBC))  d(I;(SBC))  d( ;
A (SBC))  a . 2 2
Suy ra OL a .
Đặt OK x , x a suy ra độ dài cạnh đáy hình chóp đều S.ABCD là 2x .
Xét trong tam giác SOK vuông tại O có OL là đường cao, ta có 2 2 2 2 1 1 1 1 1 x a a x ax       OS   2 2 2 2 2 2 2 2 2 2 2 OS OL OK a x a x x a x a 3 1 ax 4a x
Suy ra thể tích khối chóp S.ABCD là 2 V  4x .  . 2 2 2 2 3 x a 3 x a
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 63
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 3 4a x Đặt f (x)  . 2 2 3 x a 2 2 2 3 x 3x
x a x . 2 4a x a 4a x  2 2 2 2 2x  3a f '(x)  .  . 2 2 3 x a 3  2 2 x a  2 2 x a a 6
f '(x)  0  x  . 2 Bảng biến thiên:  a 6  Suy ra 3 3
MinV  Min f (x)  f
  12a  2 3a x   a;  2   
PT 47.1 Trong các khối chóp tam giác đều S.ABC mà khoảng cách từ A đến mp (SBC) bằng 3a , khối
chóp có thể tích nhỏ nhất bằng 3 9a A. 3 6 3a . B. . C. 3 9a . D. 3 12 3a . 2
Tác giả : Võ Thị Ngọc Ánh ; Fb: Võ Ánh Lời giải Chọn B. S A C H G M B
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 64
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Gọi M là trung điểm của BC; G là trọng tâm tam giác đều ABC. Trong tam giác SGM kẻ đường cao GH. 1
Ta có d (G;(SBC))  GH và d(G;(SBC))  d( ;
A (SBC))  a . Suy ra GH a . 3 2
Gọi GM x , x a suy ra độ dài cạnh đáy của tam giác ABC là 3 . x  2x 3 . 3
Xét trong tam giác SGM vuông tại G có GH là đường cao, ta có 2 2 2 2 1 1 1 1 1 x a a x ax       SG   2 2 2 2 2 2 2 2 2 2 2 GS GH GM a x a x x a x a 1 3 ax x
Suy ra thể tích khối chóp S.ABC là V  .2x 3 3 2 . .  3 . a 2 2 2 2 3 4 x a x a 3 x
Đặt f (x)  3 . a 2 2 x a 2 2 2 3 x 3x
x a x . 2 x   2 2 2 2 2x  3a x af '(x)  3 . a  3 . a 2 2 x a  2 2 x a  2 2 x a a 6
f '(x)  0  x  . 2 Bảng biến thiên: 3  a 6  9a
Suy ra MinV  Min f (x)  f    x   a;  2  2   2
Câu 48. Tổng tất cả các giá trị của tham số m để phương trình x 2x 1  2 3 xm  log
2 x m  2 có 2 x 2 x3  
đúng ba nghiệm phân biệt là A. 3 . B. 2  . C. 3  . D. 2 . Lời giải
Tác giả: Lưu Huyền Trang ; Fb: Lưu Huyền Trang Chọn C Ta có
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 65
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 2 x 2 x 1  2 3 xm  log 2 x m  2 2 x 2x3   2 x 2 x3 3
ln 2 x m  2   2 xm 2 3 ln  2
x  2x  3  ln  2
x  2x  3 2x2x3 .3
 ln 2 x m  2 2xm2 .3
Xét    ln  .3t f t t , t   2   1
 3t  ln  3t f t t ln 3  0, t   2 t
Vậy hàm số f t đồng biến . f  2
x  2x  3  f 2 x m  2 2
x  2x  3  2 x m  2 2
x  2x 1  2 x m 2 x  1   2m   1   2
x  4x  1 2m  2
Điều kiện cần để phương trình có 3 nghiệm là : 1  Th1 :  
1 có nghiệm kép  m
thử lại ta thấy thỏa mãn 2 3 
Th2 : 2 có nghiệm kép  m
thử lại ta thấy thỏa mãn 2 Th3 :  
1 và 2 có nghiệm chung  x m .Thế   1 vào ta có m  1  1  3  Ta có     1  3  2 2
Bình luận : Bài toán là sự giao thoa giữa phương pháp sử dụng tính đơn điệu hàm số với biện luận nghiệm .
Câu 48.1 Tìm các giá trị m để phương trình sinx 5cosxm 5 3  log m  5 có nghiệm .
sin x 5 cos x 1  0  
A. 6  m  6 . B. 5   m  5 .
C. 5  6  m  5  6 .
D.  6  m  5 . Lời giải
Tác giả: Lưu Huyền Trang ; Fb: Lưu Huyền Trang Chọn C Ta có :
sin x 5 cos xm 5 3  log m  5
sin x 5 cos x 1  0  
sin x 5 cos x 1  0 3 ln  m  5   m 5 3
ln sin x  5 cos x 10
sin x 5 cos x 1  0  3
.ln sin x  5 cos x 10 m 5  3 .ln  m  5
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 66
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Xét    ln  .3t f t t , t   5   1
 3t  ln  3t f t t ln 3  0, t   5 t
Vậy hàm số f t đồng biến .
f sin x  5 cos x 10  f m  5
 sin x  5 cos x 10  m  5
 sin x  5 cos x  5  m
Mà  6  sin x  5 cos x  6
Vậy để phương trình có nghiệm ta phải có 5  6  m  5  6
Câu 49. Cho các số thực a,b,c thỏa mãn 2 2 2
a b c  2a  4b  4 . Tính P a  2b  3c khi biểu
thức 2a b  2c  7 đạt giá trị lớn nhất. A. P  7 . B. P  3 . C. P  3  . D. P  7  . Lời giải
Tác giả: Nguyễn Ngọc Hiệp; Fb: Nguyễn Ngọc Hiệp Chọn B
Cách 1: phương pháp đại số.
Ta có: a b c a b   a  2  b  2 2 2 2 2 2 4 4 1 2  c  9 .
Áp dụng bất đẳng thức giá trị tuyệt đối và bất đẳng thức BCS, ta có kết quả sau:
2a b  2c  7  2a  
1  b  2  2c 11  2a  
1  b  2  2c 11 BCS   a  2
1  b  22  c  2 1   2  2 2 2 2  11  20.     2a  
1  b  2  2c  0  a  3
a 1 b  2 c
Đẳng thức xảy ra khi:     b   3 2 1 2         a    c 2 2 1  b  22 2  c  9
Khi đó: P a  2b  3c  3  2.3  3. 2    3.
Cách 2: phương pháp hình học.
Trong không gian Oxyz , gọi mặt cầu S  có tâm I 1;2;0 , bán kính R  3. Khi đó:
S x  2   y  2 2 2 2 2 : 1
2  z  9  x y z  2x  4y  4.
và mặt phẳng P : 2x y  2z  7  0.
a b c  Gọi M  ; a ;
b c, ta có: d M P 2 2 7 ;  . 3
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 67
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 Vì 2 2 2
a b c  2a  4b  4  M S  .
Bài toán đã cho trở thành: Tìm M S  sao cho d M ;P lớn nhất. x  1 2t
Gọi  là đường thẳng qua I và vuông góc P   : y  2  t . z  2  t
Điểm M cần tìm chính là 1 trong 2 giao điểm của  với S  : M 3;3; 2  , M 1  ;1;2 . 1   2   20 2 20
Ta có: d M ; P
d M ; P   Maxd M ; P   M M . 1    2      1 3 3 3
Vậy P a  2b  3c  3  2.3  3. 2    3.
Phân tích: Khi quan sát 2 cách giải, đối với giáo viên ta sẽ dễ chọn Cách 1 vì ngắn gọn và tiết kiệm thời
gian. Tuy nhiên học sinh không nhiều em đã từng được tiếp cận bất đẳng thức BCS. Đối với
Cách 2, về mặt trình bày có thể dài hơi, nhiều tính toán hơn nhưng đó chỉ là những bước tính
toán khá cơ bản, một học sinh khá nếu nhận ra ý đồ tác giả thì việc giải bài toán cũng không
mất quá nhiều thời gian. Bài toán sẽ dễ hơn nếu đề bài chỉ yêu cầu tìm Min hoặc Max của biểu
thức 2a b  2c  7 .
Câu PT 49.1. Cho ba số thực dương a,b,c thỏa mãn 2 2 2
a b c  2a  4b  6c  10 và a c  2 .
Tính giá trị biểu thức P  3a  2b c khi 2 2 2
Q a b c 14a  8b 18c đạt giá trị lớn nhất. A. 10. B. 10  . C. 12. D. 12  . Lời giải
Tác giả: Nguyễn Ngọc Hiệp; Fb: Nguyễn Ngọc Hiệp Chọn D
Gọi S  là mặt cầu tâm I 1; 2
 ;3 , bán kính R  24 . Khi đó: S 2 2 2
: x y z  2x  4y  6z  10.
Gọi P là mặt phẳng có phương trình x z  2 và điểm K 7;4; 9  . Với M  ; a ;
b c. Theo giả thiết ta có: M S  và M P  M S  P . Hơn nữa:
Q a b c a b c  a  2  b  2  c  2 2 2 2 2 14 8 18 7 4
9 146  KM 146 .
Bài toán trở thành: Tìm M nằm trên đường tròn giao tuyến của mặt cầu S  và mặt phẳng
P sao cho KM lớn nhất.
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 68
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019 I B H A J M P K
P có VTPT n  1;0; 1. x  7  t
Gọi  là đường thẳng qua K và vuông góc P   :  y  4 .
z  9  t
Gọi H là hình chiếu của K lên mặt phẳng P  H    P  H 9;4; 7  . Ta có: 2 2 2
KM KH HM , mà KH không đổi nên KM lớn nhất khi HM lớn nhất. x  1 t
Gọi d là đường thẳng qua I và vuông góc P  d :  y  2 . z  3 t
Gọi J là tâm đường tròn giao tuyến của S  và P  J là hình chiếu của I lên P
J d  P  J 0; 2;  2 . x  3t
Phương trình đường thẳng HJ :  y  2   2t. z  2 3t  Gọi ,
A B là các giao điểm của HJ và S   A 3;  4
 ;5,B3;0;  1 .
Ta có: HA  4 22  HB  2 22 .
Vậy MaxHM  4 22  M A3;4;5 . Khi đó: P  3a  2b c  1  2.
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 69
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Câu 50. Cho cấp số cộng a , cấp số nhân b thoả mãn a a  0 , b b 1 và hàm số n n  2 1 2 1 f x 3
x  3x sao cho f a  2  f a và f log b  2  f log b . Tìm số nguyên 2 2   2 1 2   1
dương n nhỏ nhất sao cho b  2019a n n A. 17. B. 14. C. 15. D. 16. Lời giải
Tác giả: Nguyễn Trường Giang; Fb: Giang Nguyen Chọn D
Xét hàm số f x 3
x  3x với x [0, ) . Ta có f x 2
 3x  3  0  x  1
 từ đó ta suy ra bảng
biến thiên của f x trên [0, ) như sau: x 0 1  f  x - 0 +
f x 0  2 
Vì a  0 nên f a  2
  f a f a  2  0 (1) 2   1  2  2
Giả sử a  1, vì f x đồng biến trên [1,) nên f a f a suy ra f a  2  f a vô lý. Vậy 1   1 2   1 1
a [0,1) do đó f a  0 (2). 1  1  f  a  0   1  a 0 Từ (1) và (2) ta có: 0     f  a  1 a  1 2   1
Vậy số hạng tổng quát của dãy cấp số cộng a là a n  . n  1 n
Một cách tương tự, đặt t  log b và t  log b suy ra f t  2  f t , vì 1 b b nên 0  t t , 2   1 1 2 1 2 2 2 1 2 1 2
theo lập luận trên ta có: t   0 log b  0 b  1 1 2 1 1      t  1 log b  1 b  2  2  2 2  2
Vậy số hạng tổng quát của dãy cấp số nhân b là 1 b 2n  . n n Do đó n 1 b 2019a 2   
 2019 n  (*). Trong 4 đáp án n 16 là số nguyên dương nhỏ nhất thỏa n n  1 (*).
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 70
STRONG TEAM TOÁN VD-VDC
PHÂN TÍCH-BÌNH LUẬN ĐỀ THI THPTQG CHUYÊN HÀ TĨNH – T4 –2019
Địa chỉ truy cập https://facebook.com/groups/900248096852019?ref=share Trang 71
Document Outline

  • [toanmath.com] - Đề thi thử THPT Quốc gia 2019 môn Toán trường THPT chuyên Hà Tĩnh
    • [toanmath.com] - Đề thi thử THPT Quốc gia 2019 môn Toán trường THPT chuyên Hà Tĩnh
    • Dap-an-Toan
      • Table1
  • PHÂN-TÍCH-BÌNH-LUẬN-THPT-CHUYÊN-HÀ-TĨNH T4-2019