Đề thi thử THPT Quốc gia môn Toán năm 2019 sở GD&ĐT Cao Bằng

Giới thiệu đến quý thầy, cô giáo cùng các em học sinh khối 12 đề thi thử THPT Quốc gia môn Toán năm 2019 sở GD&ĐT Cao Bằng, đề thi có mã đề 003 gồm 9 trang

14 7 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

32 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 1
SỞ GD&ĐT CAO BẰNG
ĐỀ THI THỬ THPT QUỐC GIA NĂM HỌC 2018 - 2019
Môn: TOÁN
-------------------------------------------------
Thời gian: 90 phút (Không kể thời gian phát đề)
Họ và tên thí sinh:...........................................SBD:............................................
MÃ ĐỀ
003
Câu 1: Trong không gian
Oxyz
, cho đường thẳng
1 4 3
:
1 2 3
x y z
d
. Véctơ nào sau
đây không phải là véctơ chỉ phương của đường thẳng
d
?
A.
1;2;3a
. B.
3; 6; 9a
. C.
1; 2; 3a
. D.
2;4;3a
.
Câu 2: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
3 2
3 1y x x
B.
3 2
3 1y x x
C.
3 2
3 1y x x
D.
3 2
3 1y x x
Câu 3: Cho hàm số
y f x
có bảng biến thiên như sau
Hàm số có bao nhiêu điểm cực trị?
A.
1
.
B.
2
.
C.
4
.
D.
3
.
Câu 4: Diện tích mặt cầu bán kính
R
bằng
A.
2
4
3
R
. B.
2
4 R
. C.
2
2 R
. D.
2
R
.
Câu 5: Tập xác định
D
của hàm số
5
2y x
là
x
– ∞ -1 1 + ∞
y'
+ 0 – +
y
– ∞
3
-1
+ ∞
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 2
A.
\ 2D
. B.
D
. C.
2;D 
. D.
2;D
.
Câu 6: Nghiệm của phương trình
3 3
log 1 log 3x x
là
A.
3x
. B.
4x
. C.
2x
. D.
1x
.
Câu 7: Điểm nào ở hình vẽ bên biểu diễn cho số phức
3 2z i
?
A.
Q
. B.
P
.
C.
N
. D.
M
.
Câu 8: Cho hàm số
y f x
có đồ thị như hình vẽ bên. Hàm số đã cho nghịch biến trên khoảng
nào dưới đây?
A.
; 1
. B.
0;1
.
C.
1;1
. D.
1;0
.
Câu 9: Trong không gian
Oxyz
, cho
2; 3;1AB

và điểm
1; 2;4A
. Khi đó tọa độ của điểm
B
là
A.
3;5; 5B
. B.
1; 1; 3B
. C.
3; 5;5B
. D.
1;1;3B
.
Câu 10: Cho cấp số nhân
n
u
có số hạng đầu
1
2u
và công bội
2q
. Giá trị
5
u
là
A.
32
. B.
16
. C.
6
. D.
32
.
Câu 11: Trong không gian
Oxyz
, mặt phẳng
: 3 0P x y z
đi qua điểm nào dưới đây?
A.
1; 1; 1M
. B.
1;1;1N
. C.
3;0; 0P
. D.
0;0; 3Q
.
Câu 12: Từ 10 điểm phân biệt trong mặt phẳng, có thể tạo ra ba nhiêu véctơ khác véctơ
0
?
A.
2
10
A
. B.
20
. C.
10
2
. D.
2
10
C
.
Câu 13: Họ nguyên hàm của hàm số
2
1
x
f x e
là
3
y
x
Q
P
N
M
-2
2
-2
2
3
O
1
O 1
-1
2
y
x
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 3
A.
2
1
2
x
F x e C
. B.
2x
F x x e C
.
C.
2
1
2
x
F x x e C
. D.
2 1
2
x
F x x xe C
.
Câu 14: Một hình hộp chữ nhật có ba kích thước là
, ,a b c
. Thể tích
V
của khối hộp chữ nhật đó
bằng
A.
a c b
. B.
abc
. C.
a b c
. D.
1
3
abc
.
Câu 15: Cho hàm số
f x
liên tục trên
, biết
8
0
7f x dx
và
5
0
5f x dx
. Khi đó
8
5
f x dx
bằng
A.
12
. B.
2
. C.
2
. D.
12
.
Câu 16: Cho hàm số
3
2
x
y
x
có đồ thị
C
. Gọi
I
là giao điểm của hai đường tiệm cận của
C
. Khi đó tọa độ của điểm
I
là
A.
3;0I
. B.
1;2I
. C.
2;1I
. D.
3
0;
2
I
.
Câu 17: Cho vật thể giới hạn bởi hai mặt phẳng
0,
2
x x
, biết rằng thiết diện của vật thể
khi cắt bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
0
2
x x
là một
hình tròn có bán kính
cosR x
. Thể tích của vật thể đó là
A.
2
. B.
1
. C.
. D.
2
.
Câu 18: Cho hình trụ có tổng chu vi hai đáy là
12
và có chiều cao bằng
4
. Khi đó diện tích
toàn phần
tp
S
của hình trụ là
A.
42
tp
S
. B.
33
tp
S
. C.
24
tp
S
. D.
18
tp
S
.
Câu 19: Cho hàm số
y f x
có đạo hàm trên
. Đồ thị hàm số
y f x
như hình vẽ bên.
Hỏi đồ thị hàm số
2y f x x
có bao nhiêu điểm cực trị ?
A.
3
. B.
4
.
C.
1
. D.
2
.
2
2
-2
y
x
O
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 4
Câu 20: Đạo hàm của hàm số
2
2019
x x
y
là
A.
2
2019 .ln 2019
x x
y
. B.
2
2 1 .2019 .ln 2019
x x
y x
.
C.
2
2 1
.2019
x x
y x x
. D.
2
2 1 .2019
x x
y x
.
Câu 21: Cho hình nón bán kính
12r
nội tiếp hình cầu bán kính
13r
(như hình vẽ). Tính
diện tích xung quanh
xq
S
của hình nón.
A.
36 13
xq
S
. B.
72 5
xq
S
.
C.
36 5
xq
S
. D.
72 13
xq
S
.
Câu 22: Trong không gian
Oxyz
, cho hai điểm
1; 3;2 , 3;5; 2A B
. Phương trình mặt phẳng
trung trực của đoạn
AB
có dạng
0x ay bz c
. Khi đó
a b c
bằng
A.
3
. B.
2
. C.
4
. D.
2
.
Câu 23: Cho hàm số
y f x
liên tục trên đoạn
2;4
và có đồ thị như hình vẽ bên. Gọi
M
và
m
là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
2;4
. Giá trị của
2 2
M m
bằng
A.
20
. B.
8
.
C.
65
. D.
53
.
-2
1
y = f(x)
O
-4
4
3
2
-2
7
x
y
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 5
Câu 24: Cho lăng trụ tam giác
.ABC A B C
có khoảng cách từ
A
đến mặt phẳng
A BC
bằng
6a
. Khoảng cách từ trung điểm
M
của cạnh
B C
đến mặt phẳng
A BC
bằng
A.
6a
. B.
2a
. C.
4a
. D.
3a
.
Câu 25: Tập nghiệm
S
của bất phương trình
2
2 2
log 5 log 6 0x x
là
A.
64;S

. B.
1
0; 64;
2
S
.
C.
1
;64
2
S
. D.
1
0;
2
S
.
Câu 26: Cho hàm số
y f x
có đạo hàm
2
2
4 3 lnf x x x x
trên
0;
. Hỏi hàm số
y f x
có bao nhiêu điểm cực trị?
A.
4
. B.
2
. C.
3
. D.
1
.
Câu 27: Cho
,a b
là các số thực dương thỏa mãn
2 2
14a b ab
. Khẳng định nào sau đây sai?
A.
2 2 2
2 log 4 log loga b a b
. B.
2 log log log
4
a b
a b
.
C.
ln ln
ln
4 2
a b a b
. D.
2 4 4
2 log 4 log loga b a b
.
Câu 28: Trong không gian
Oxyz
, cho điểm
1;2;3A
và mặt phẳng
: 4 3 0P x y z
. Mặt
cầu
S
tâm
A
và tiếp xúc với mặt phẳng
P
có phương trình là
A.
2 2 2
1 2 3 2x y z
. B.
2 2 2
1 2 3 2x y z
.
C.
2 2 2
1 2 3 4x y z
. D.
2 2 2
1 2 3 4x y z
.
Câu 29: Biết
z
là số phức có phần ảo âm và là nghiệm của phương trình
2
6 10 0z z
. Tính
tổng phần thực và phần ảo của số phức
z
w
z
.
A.
4
5
. B.
2
5
. C.
7
5
. D.
1
5
.
Câu 30: Biết
2; 1 , 3;2M N
lần lượt là hai điểm biểu diễn cho số phức
1 2
,z z
trên mặt phẳng
tọa độ phức
Oxy
. Khi đó môđun của số phức
2
1 2
z z
bằng
A.
4 2
. B.
2 10
. C.
10
. D.
68
.
Câu 31: Cho hàm số
f x
thỏa mãn
x
f x xe
và
0 2f
. Tính
1f
.
A.
1 8 2f e
. B.
1 5f e
. C.
1f e
. D.
1 3f
.
Câu 32: Cho đồ thi của hàm số
x
y a
và
log
b
y x
như hình vẽ . Trong các khẳng định sau,
khẳng định nào đúng?
y
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 6
A.
0 1b a
. B.
0 1a
và
0 1b
.
C.
1a
và
1b
. D.
0 1a b
.
Câu 33: Cho một khối lăng trụ có thể tích là
3
3a
, đáy là tam giác đều cạnh
a
. Chiều cao
h
của
khối lăng trụ bằng
A.
2h a
. B.
4h a
. C.
12h a
. D.
3h a
.
Câu 34: Cho hai số phức
1 2
,z z
thỏa mãn
1 2
1 2
1; 2
2 3 1
z i z i
z i z i
. Giá trị nhỏ nhất của
1 2
z z
là
A.
2 2
. B.
2 1
. C.
1
. D.
2
.
Câu 35: Có năm đoạn thẳng có độ dài lần lượt là
1 ,2 ,3 , 4 , 5cm cm cm cm cm
. Lấy ngẫu nhiên ra ba
đoạn thẳng , tính xác suất để ba đoạn thẳng được chọn ra là độ dài ba cạnh của một tam
giác.
A.
1
10
. B.
3
10
. C.
2
5
. D.
3
5
.
Câu 36: Cho hàm số bậc ba
y f x
có đồ thị là đường cong hình bên. Đồ thị hàm số .
2
2
1
4
x
g x
f x f x
. có tất cả bao nhiêu đường tiệm cận đứng?
A.
3
. B.
2
.
C.
5
. D.
4
.
1
-1
4
2
O
y
x
1
1
x
O
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 7
Câu 37: Cho đồ thị hàm số
3 2
3 4y f x x x
có đồ thị như hình vẽ bên. Hỏi phương trình
2
1
3 5 4
f f x
f x f x
có bao nhiêu nghiệm thực?
A.
4
. B.
6
.
C.
7
. D.
5
.
Câu 38: Cho hình lăng trụ tam giác
.ABC A B C
có đáy là tam giác đều cạnh
a
. Cạnh bên tạo
với đáy một góc
0
60
. Gọi
M
là trung điểm của
B C
và
I
là trung điểm của đoạn
A M
. Biết hình chiếu vuông góc của
I
trên mặt phẳng đáy
ABC
là trọng tâm của tam giác
ABC
. Tính thể tích của khối lăng trụ
.ABC A B C
theo
a
.
A.
3
3
4
a
. B.
3
3
48
a
. C.
3
3
16
a
. D.
3
3
12
a
.
Câu 39: Bác Minh có một mảnh vườn hình Elip có độ dài trục lớn là
10m
và độ dài trục nhỏ là
8m
. Giữa vườn là một cái giếng hình tròn có bán kính
0,5m
và nhận trục lớn và trục bé
của đường Elip làm trục đối xứng (như hình vẽ). Bác Minh muốn tròng hoa hồng đỏ
trên phần dải đất còn lại (xung quanh giếng). Biết kinh phí trồng hoa là 120.000 đồng/
2
m
. Hỏi Bác Minh cần bao nhiêu tiền để trồng hoa trên giải đất đó? (Số tiền làm tròn
đến hàng nghìn).
A. 7.545.000 đồng. B. 7.125000 đồng.
C. 7.325000 đồng. D. 7.446.000 đồng.
Câu 40: Biết
S
là tập giá trị của
m
để tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
4 2 3 2
2y x m x x m
trên đoạn
0;1
bằng
16
. Tính tích các phần tử của
S
.
A.
15
. B.
2
. C.
17
. D.
2
.
2
-1
1
y
x
3
2
O
4
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 8
Câu 41: Gọi
S
là tập hợp tất cả các giá trị của tham số
m
để hàm số
2 5 3 2 2
1 1
10 20
5 3
y m x mx x m m x
đồng biến trên
. Tổng giá trị của tất cả
các phần tử thuộc
S
bằng
A.
5
2
. B.
3
2
. C.
2
. D.
1
2
.
Câu 42: Ba anh em An, Bình, Cường cùng vay tiền ở một ngân hàng với lãi suất
0, 7%
/tháng với
tổng số tiền vay của cả ba người là 1 tỉ đồng. Biết rằng mỗi tháng cả ba người đều trả
cho ngân hàng một số tiền như nhau để trừ vào tiền gốc và lãi . Để trả hết gốc và lãi cho
ngân hàng thì An cần 10 tháng, Bình cần 15 tháng và Cường cần 25 tháng. Số tiền trả
đều đặn cho ngân hàng mỗi tháng của mỗi người gần nhất với số tiền nào dưới đây?
A. 21.400.000 đồng. B.21.090.000 đồng. C.21.422.000 đồng. D.21.900.000 đồng.
Câu 43: Có tất cả bao nhiêu số nguyên
m
để đồ thị hàm số
2
2 2
1
2 2 25
x
y
x mx m
có ba
đường tiệm cận?
A..
7
.. B.
11
. C.
5
. D.
9
.
Câu 44: Miền phẳng trong hình vẽ được giới hạn bởi đường cong
y f x
và .
2
2y x x
. Biết
1
1
2
3
4
f x dx
. Khi đó diện tích hình phẳng được tô trên hình vẽ là
A.
9
8
. B.
8
3
.
C.
8
9
. D.
3
8
.
Câu 45: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
,A AB a
, cạnh bên
SA
vuông góc với đáy, góc tạo bởi giữa hai mặt phẳng
SBC
và
ABC
bằng
0
60
khi và
chỉ khi
SA
bằng
A.
3a
. B.
6
6
a
. C.
6
4
a
. D.
6
2
a
.
Câu 46: Trong không gian với hện tọa độ
Oxyz
, cho đường thẳng
2 1
:
1 1 3
x y z
và
mặt phẳng
: 11 16 0P x my nz
. Biết
P
, Tính giá trị của
T m n
.
A.
14T
B.
2T
. C.
2T
. D.
14T
.
O
1
-
1
2
y
x
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 9
Câu 47: Trong không gian với hện tọa độ
Oxyz
, cho hai đường thẳng
1
1 2 1
:
2 1 1
x y z
và
2
2 1 2
:
4 1 1
x y z
. Đường thẳng chứa đoạn vuông góc chung của
1 2
,
đi
qua điểm nào sau đây?
A.
3;1; 4Q
B.
2;0;1P
. C.
0; 2; 5M
. D.
1; 1; 4N
.
Câu 48: Cho số phức
,z a bi a b
thỏa mãn
4 2 5 1z i z i i
. Tính giá trị
của biểu thức
T a b
.
A.
1T
. B.
2T
. C.
3T
. D.
1T
.
Câu 49: Cho phương trình
3
4 1 .2 0
x x
m m
(*). Nếu phương trình (*) có hai nghiệm
1 2
,x x
thỏa mãn
1 2
2x x
thì
0
m m
. Giá trị
0
m
gần giá trị nào nhất trong các giá trị
sau?
A.
0,5
. B.
3
. C.
2
. D.
1,3
.
Câu 50: Trong không gian với hệ trục tọa độ
Oxyz
, cho
3;1;1 , 1; 1;5A B
và mặt phẳng
: 2 2 11 0P x y z
. Mặt cầu
S
đi qua hai điểm
,A B
và tiếp xúc với mặt phẳng
P
tại điểm
C
. Biết
C
luôn thuộc đường tròn
T
cố định . Tính bán kính
r
của đường
tròn
T
.
A.
3r
. B.
4r
. C.
2r
. D.
2r
.
_____________________________Hết_______________________________
Cán bộ coi thi không giải thích gì thêm
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 10
SỞ GD&ĐT CAO BẰNG
HƯỚNG DẪN GIẢI CHI TIẾT
ĐỀ THI THỬ THPT QUỐC GIA TỈNH CAO BẰNG
NĂM HỌC 2018 - 2019
Câu 1: Trong không gian
Oxyz
, cho đường thẳng
1 4 3
:
1 2 3
x y z
d
. Véctơ nào sau
đây không phải là véctơ chỉ phương của đường thẳng
d
?
A.
1;2;3a
. B.
3; 6; 9a
. C.
1; 2; 3a
. D.
2;4;3a
.
Hướng dẫn giải
Chọn D
Câu 2: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
3 2
3 1y x x
B.
3 2
3 1y x x
C.
3 2
3 1y x x
D.
3 2
3 1y x x
Hướng dẫn giải
Chọn D
Đồ thị có dạng hàm số bậc 3 với hệ số
0a
và cắt trục
Oy
tại điểm có tung độ bằng 1.
Câu 3: Cho hàm số
y f x
có bảng biến thiên như sau
Hàm số có bao nhiêu điểm cực trị?
A.
1
B.
2
C.
4
D.
3
Hướng dẫn giải
Chọn B
x
– ∞ -1 1 + ∞
y'
+ 0 – +
y
– ∞
3
-1
+ ∞
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 11
Từ BBT nhận thấy đạo hàm đổi dấu khi qua hai điểm tới hạn
1x
và
1x
. Vậy
hàm số có hai điểm cực trị.
Câu 4: Diện tích mặt cầu bán kính
R
bằng
A.
2
4
3
R
. B.
2
4 R
. C.
2
2 R
. D.
2
R
.
Hướng dẫn giải
Chọn B
Công thức tính diện tích của mặt cầu có bán kính
R
:
2
4S R
(đvdt)
Câu 5: Tập xác định
D
của hàm số
5
2y x
là
A.
\ 2D
. B.
D
. C.
2;D 
. D.
2;D

.
Hướng dẫn giải
Chọn A
Điều kiện để hàm số có nghĩa:
2 0 2x x
.
Vậy TXĐ của hàm số là
\ 2D
.
Câu 6: Nghiệm của phương trình
3 3
log 1 log 3x x
là
A.
3x
. B.
4x
. C.
2x
. D.
1x
.
Hướng dẫn giải
Chọn D
Cách 1:
Đk:
1 3x
, nên loại phương án A và B. Thay nghiệm ở hai phương án còn
lại vào phương trình, nhận thấy nghiệm ở phương án D thỏa mãn. Vậy chọn D.
Cách 2: Giải tự luận
Đk:
1 3x
(*)
PT
1 3 1x x x
(tm (*)). Chọn D.
Câu 7: Điểm nào ở hình vẽ bên biểu diễn cho số phức
3 2z i
?
A.
Q
. B.
P
.
C.
N
. D.
M
.
Hướng dẫn giải
Chọn A
Dựa vào khái niệm biểu diễn hình học của số phức trên mặt phẳng tọa độ ta chọn
phương án A.
Câu 8: Cho hàm số
y f x
có đồ thị như hình vẽ bên. Hàm số đã cho nghịch biến trên khoảng
nào dưới đây?
3
y
x
Q
P
N
M
-2
2
-2
2
3
O
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 12
A.
; 1
. B.
0;1
.
C.
1;1
. D.
1;0
.
Hướng dẫn giải
Chọn D
Dựa vào đồ thị hám số nhận thấy đồ thị đi xuống từ trái qua phải với mọi
1;0x
Vậy hàm số
y f x
nghịch biến trên khoảng
1;0
.
Câu 9: Trong không gian
Oxyz
, cho
2; 3;1AB

và điểm
1; 2;4A
. Khi đó tọa độ của điểm
B
là
A.
3;5; 5B
. B.
1; 1; 3B
. C.
3; 5;5B
. D.
1;1;3B
.
Hướng dẫn giải
Chọn C
Ta có
; ,
B A B A B A
AB x x y y z z

, do đó ta có :
2 2 5
3 3 5 5; 5;5
1 1 5
B A B A B
B A B A B
B A B A B
x x x x x
y y y y y B
z z z z z
.
Câu 10: Cho cấp số nhân
n
u
có số hạng đầu
1
2u
và công bội
2q
. Giá trị
5
u
là
A.
32
. B.
16
. C.
6
. D.
32
.
Hướng dẫn giải
Chọn A
Ta có:
4
4
5 1
. 2. 2 32u u q
.
Câu 11: Trong không gian
Oxyz
, mặt phẳng
: 3 0P x y z
đi qua điểm nào dưới đây?
A.
1; 1; 1M
. B.
1;1;1N
. C.
3;0; 0P
. D.
0;0; 3Q
.
Hướng dẫn giải
Chọn B
Thay ngẫu nhiên lần lượt tọa độ các điểm của 3 trong 4 phương án, nếu cả 3 phương án
tọa độ điểm đều không thỏa mãn thì chọn phương án còn lại là phương án đúng.
Câu 12: Từ 10 điểm phân biệt trong mặt phẳng, có thể tạo ra ba nhiêu véctơ khác véctơ
0
?
A.
2
10
A
. B.
20
. C.
10
2
. D.
2
10
C
.
Hướng dẫn giải
Chọn A
Chọn ngẫu nghiên 2 điểm phân biệt trong 10 điểm phân biệt để tạo ra véctơ, số cách
chọn là
2
10
C
. Cứ 2 điểm phân biệt bất kì luôn tạo ra hai véctơ khác véctơ-không.
1
O 1
-1
2
y
x
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 13
Vậy có
2
10
2. 90C
véctơ được tạo thành. Chọn A.
Câu 13: Họ nguyên hàm của hàm số
2
1
x
f x e
là
A.
2
1
2
x
F x e C
. B.
2x
F x x e C
.
C.
2
1
2
x
F x x e C
. D.
2 1
2
x
F x x xe C
.
Hướng dẫn giải
Chọn C
Cách 1 : Sử dụng Casio
+) Chọn
1 1 8, 4x f
+) Sử dụng Casio, tính đạo hàm ngẫu nhiên 3 hàm số trong 3 phương án tại
1x
, nếu ở 3 phương án kết quả không bằng 8,4 thì chọn phương án còn lại
Cách 2 :
Ta có
2 2
1
1
2
x x
e dx x e C
. Vậy chọn C.
Câu 14: Một hình hộp chữ nhật có ba kích thước là
, ,a b c
. Thể tích
V
của khối hộp chữ nhật đó
bằng
A.
a c b
. B.
abc
. C.
a b c
. D.
1
3
abc
.
Hướng dẫn giải
Chọn B
Câu 15: Cho hàm số
f x
liên tục trên
, biết
8
0
7f x dx
và
5
0
5f x dx
. Khi đó
8
5
f x dx
bằng
A.
12
. B.
2
. C.
2
. D.
12
.
Hướng dẫn giải
Chọn D
Ta có
8 5 8 8 8 5
0 0 5 5 0 0
12f x dx f x dx f x dx f x dx f x dx f x dx
Câu 16: Cho hàm số
3
2
x
y
x
có đồ thị
C
. Gọi
I
là giao điểm của hai đường tiệm cận của
C
. Khi đó tọa độ của điểm
I
là
A.
3;0I
. B.
1;2I
. C.
2;1I
. D.
3
0;
2
I
.
Hướng dẫn giải
Chọn C
Đồ thị
C
có TCĐ
2x
, TCN
1y
. Vậy tọa độ giao điểm của hai đường tiệm cận
của
C
là
2;1I
.
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 14
Câu 17: Cho vật thể giới hạn bởi hai mặt phẳng
0,
2
x x
, biết rằng thiết diện của vật thể
khi cắt bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
0
2
x x
là một
hình tròn có bán kính
cosR x
. Thể tích của vật thể đó là
A. .
2
. B.
1
. C.
. D.
2
.
Hướng dẫn giải
Chọn D
Diện tích của hình tròn được tạo thành là
2
cosS x R x
,
0
2
x
.
Thể tích của vật thể là:
2 2
0 0
V S x dx cosxdx
Câu 18: Cho hình trụ có tổng chu vi hai đáy là
12
và có chiều cao bằng
4
. Khi đó diện tích
toàn phần
tp
S
của hình trụ là
A.
42
tp
S
. B.
33
tp
S
. C.
24
tp
S
. D.
18
tp
S
.
Hướng dẫn giải
Chọn A
Gọi
R
là bán kính của đường tròn đáy .
Tổng chu vi của hai đáy hình lăng trụ là
2.2 4C R R
, theo bài ta có
4 12 3R R
.
Diện tích đáy hình lăng trụ là:
2
9
d
S R
Diện tích xung quanh của hình lăng trụ là:
2 24
xq
S Rh
Vậy diện tích toàn phần của hình lăng trụ đã cho là
2 42
tp d xq
S S S
.
Câu 19: Cho hàm số
y f x
có đạo hàm trên
. Đồ thị hàm số
y f x
như hình vẽ bên.
Hỏi đồ thị hàm số
2y f x x
có bao nhiêu điểm cực trị ?
A.
3
. B.
4
.
C.
1
. D.
2
.
Hướng dẫn giải
Chọn B
2
2
-2
y
x
O
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 15
Xét hàm số
2y g x f x x
Ta có:
2g x f x
0 2g x f x
(1)
Số nghiệm của (1) là số giao điểm của đường
thẳng
2y
và đồ thị hàm số
y f x
.
Dựa vào đồ thị của hai đường ta suy ra
phương trình
1
2
0
0
2
x x
x x
g x
x
x
với
1 2
, , 0x x
(
1 2
0 2x x
) và
2x
là
nghiệm bội chẵn.
Vậy đồ thị hàm số
2y g x f x x
có 3
điểm cực trị
(Ngô Kiều Lượng – THPT Trùng Khánh)
Câu 20: Đạo hàm của hàm số
2
2019
x x
y
là
A.
2
2019 .ln2019
x x
y
. B.
2
2 1 .2019 .ln 2019
x x
y x
.
C.
2
2 1
.2019
x x
y x x
. D.
2
2 1 .2019
x x
y x
.
Hướng dẫn giải
Chọn B
Áp dụng CT đạo hàm của hàm hợp
. .ln 0 1
u u
a u a a a
. Chọn B.
Câu 21: Cho hình nón bán kính
12r
nội tiếp hình cầu bán kính
13r
(như hình vẽ). Tính
diện tích xung quanh
xq
S
của hình nón.
A.
36 13
xq
S
. B.
72 5
xq
S
.
C.
36 5
xq
S
. D.
72 13
xq
S
.
Hướng dẫn giải
Chọn D
2
2
-2
x
O
y = 2
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 16
Giả sử mặt phẳng chứa trục hình nón cắt mặt cầu theo thiết diện là tam giác
OAB
với
O
là đỉnh của hình nón,
AB
là đường kính đường tròn đáy của hình nón (như hv trên).
Gọi
H
là trung điểm của cạnh
AB
,
I
tâm của mặt cầu
, 13I OH IA IB IO R
.
Xét tam giác
IHA
, theo định lí Pitago ta có
2 2
5IH AI AH
.
Do đó
5 18OH OI IH R
Xét tam giác vuông
OHA
, theo định lí Pitago ta có
2 2
6 13OA OH AH
.
Vậy diện tích xung quanh của hình nón là
. . 72 13
xq
S r OA
.
Câu 22: Trong không gian
Oxyz
, cho hai điểm
1; 3;2 , 3;5; 2A B
. Phương trình mặt phẳng
trung trực của đoạn
AB
có dạng
0x ay bz c
. Khi đó
a b c
bằng
A.
3
. B.
2
. C.
4
. D.
2
.
Hướng dẫn giải
Chọn C
Cách 1 :
Đặt
: 0x ay bz c
Ta có
2;8; 4AB

, một vtpt của mặt phẳng trung trực đoạn
AB
là
1; ;n a b
.
Gọi
I
là trung điểm của đoạn
AB
, ta có
2;1;0I
.
Đk để
là mp trung trực của đoạn
AB
4
0
2
1
6
2 8 4
a
a c
I
b
a b
AB n
c


.
Vậy
4a b c
.
Cách 2 :
+ Lập phương trình mặt phẳng trung trực của đoạn
AB
+ Đồng nhất các hệ số hai phương trình ta suy ra
, ,a b c a b c
.
Câu 23: Cho hàm số
y f x
liên tục trên đoạn
2;4
và có đồ thị như hình vẽ bên. Gọi
M
và
m
là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
2;4
. Giá trị của
2 2
M m
bằng
R
I
r
l
H
O
B
A
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 17
A.
20
. B.
8
.
C.
65
. D.
53
.
Hướng dẫn giải
Chọn C
Hàm số
y f x
liên tục trên đoạn
2;4
, từ đồ thị ta có:
2 2
2;4 2;4
7; 4 65M maxf x m minf x M m
.
Câu 24: Cho lăng trụ tam giác
.ABC A B C
có khoảng cách từ
A
đến mặt phẳng
A BC
bằng
6a
. Khoảng cách từ trung điểm
M
của cạnh
B C
đến mặt phẳng
A BC
bằng
A.
6a
. B.
2a
. C.
4a
. D.
3a
.
Hướng dẫn giải
Chọn A
Gọi
I
là trung điểm của cạnh
BC
, suy ra tứ giác
'AIMA
là hình bình hành. Gọi
O
là
giao điểm của
AM
và
'A I
O
là trung điểm của của đoạn
AM
, đông thời
' , ' , ' 6O AIMA d M A BC d A A BC a
-2
1
y = f(x)
O
-4
4
3
2
-2
7
x
y
O
I
M
C'
B'
A'
C
B
A
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 18
Câu 25: Tập nghiệm
S
của bất phương trình
2
2 2
log 5 log 6 0x x
là
A.
64;S

. B.
1
0; 64;
2
S
.
C.
1
;64
2
S
. D.
1
0;
2
S
.
Hướng dẫn giải
Chọn C
Đk:
0 *x
. Đặt
2
log x t
, ta thu được BPT:
2
5 6 0 1 6t t t
. Khi đó :
2
1
1 log 6 64
2
x x
. Chọn C.
(Nguyễn Ngọc Chi – Giang – THPT Quảng Uyên)
Câu 26: Cho hàm số
y f x
có đạo hàm
2
2
4 3 lnf x x x x
trên
0;
. Hỏi hàm số
y f x
có bao nhiêu điểm cực trị?
A.
4
. B.
2
. C.
3
. D.
1
.
Hướng dẫn giải
Chọn B
Ta có :
2
2
4 0
2
0 3 0 3
ln 0 1
x
x
f x x x
x x
BBT:
Từ BBT ta chọn phương án B.
(Nguyễn Ngọc Chi – Giang – THPT Quảng Uyên)
Câu 27: Cho
,a b
là các số thực dương thỏa mãn
2 2
14a b ab
. Khẳng định nào sau đây sai?
A.
2 2 2
2 log 4 log loga b a b
. B.
2 log log log
4
a b
a b
.
C.
ln ln
ln
4 2
a b a b
. D.
2 4 4
2 log 4 log loga b a b
.
Hướng dẫn giải
Chọn D
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 19
Ta có:
2
2 2
2 2 2
14 16 2log 4 log loga b ab a b ab a b a b
phương
án D sai.
Câu 28: Trong không gian
Oxyz
, cho điểm
1;2;3A
và mặt phẳng
: 4 3 0P x y z
. Mặt
cầu
S
tâm
A
và tiếp xúc với mặt phẳng
P
có phương trình là
A.
2 2 2
1 2 3 2x y z
. B.
2 2 2
1 2 3 2x y z
.
C.
2 2 2
1 2 3 4x y z
. D.
2 2 2
1 2 3 4x y z
.
Hướng dẫn giải
Chọn B
Gọi
R
là bán kính của mặt cầu
S
. Ta có
1 2 12 3
, 2
18
R d A P
.
Vậy mặt cầu
S
tâm
A
, bán kính
2R
có phương trình:
2 2 2
1 2 3 2x y z
Câu 29: Biết
z
là số phức có phần ảo âm và là nghiệm của phương trình
2
6 10 0z z
. Tính
tổng phần thực và phần ảo của số phức
z
w
z
.
A.
4
5
. B.
2
5
. C.
7
5
. D.
1
5
.
Hướng dẫn giải
Chọn D
Sử dụng Casio tìm được số phức
3z i
, tiếp tục sử dụng Casio tìm được số phức
4 3
5 5
w i
, từ đó suy ra tổng phần thực và phần ảo của số phức
w
bằng
4 3 1
5 5 5
Câu 30: Biết
2; 1 , 3;2M N
lần lượt là hai điểm biểu diễn cho số phức
1 2
,z z
trên mặt phẳng
tọa độ phức
Oxy
. Khi đó môđun của số phức
2
1 2
z z
bằng
A.
4 2
. B.
2 10
. C.
10
. D.
68
.
Hướng dẫn giải
Chọn B
Ta có:
1 2
2 , 3 2z i z i
. Sử dụng Casio tìm được
2
1 2
2 10z z
.
Câu 31: Cho hàm số
f x
thỏa mãn
x
f x xe
và
0 2f
. Tính
1f
.
A.
1 8 2f e
. B.
1 5f e
. C.
1f e
. D.
1 3f
.
Hướng dẫn giải
Chọn D
Ta có
1 1
0 0
1 0 1 1 1 0 3
x
f x dx xe dx f f f f
Câu 32: Cho đồ thi của hàm số
x
y a
và
log
b
y x
như hình vẽ . Trong các khẳng định sau,
khẳng định nào đúng?
y
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 20
A.
0 1b a
. B.
0 1a
và
0 1b
.
C.
1a
và
1b
. D.
0 1a b
.
Hướng dẫn giải
Chọn A
+) Từ điều kiện của hàm số mũ và hàm số logarit suy ra
0 , 1a b
.
+) Dựa vào đồ thị suy ra
1a
,
1b
Vậy
0 1b a
.
Câu 33: Cho một khối lăng trụ có thể tích là
3
3a
, đáy là tam giác đều cạnh
a
. Chiều cao
h
của
khối lăng trụ bằng
A.
2h a
. B.
4h a
. C.
12h a
. D.
3h a
.
Hướng dẫn giải
Chọn B
Diện tích đáy của khối lặng trụ là
2
3
4
a
S
Thể tích khối lăng trụ là
3
2
3
. 4
3
4
V a
V S h h a
S
a
.
Câu 34: Cho hai số phức
1 2
,z z
thỏa mãn
1 2
1 2
1; 2
2 3 1
z i z i
z i z i
. Giá trị nhỏ nhất của
1 2
z z
là
A.
2 2
. B.
2 1
. C.
1
. D.
2
.
Hướng dẫn giải
Chọn A
+) Đặt
1
z a bi
.
Từ giả thiết:
1
1 1
1
1 2 3 ( 1) ( 2) ( 3) 3 0
2 3
z i
z i z i a b i a b i a b
z i
+) Đặt
2
z x yi
Từ giả thiết:
2
2 2
2
2 2
2 2 1
1
( 1) 2 ( 1) ( 1)
4 2 3 0
z i
z i z i
z i
x y i x y i
x y x y
Gọi M là điểm biểu diễn số phức
1
z
. Khi đó điểm M thuộc đường thẳng
: 3 0.x y
1
1
x
O
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 21
Gọi N là điểm biểu diễn số phức
2
z
. Khi đó điểm N thuộc đường tròn tâm I(2;-1); bán
kính
2.R
Ta có:
1 2
z z MN
Khi đó
1 2
z z
đạt GTNN
MN ngắn nhất
2 1 3
( , ) 2 2 2.
2
MN d I R
Vậy min
1 2
z z
=
2 2
.
(Hoàng Thị Thu – THPT Pò Tấu)
Câu 35: Có năm đoạn thẳng có độ dài lần lượt là
1 ,2 ,3 , 4 , 5cm cm cm cm cm
. Lấy ngẫu nhiên ra ba
đoạn thẳng , tính xác suất để ba đoạn thẳng được chọn ra là độ dài ba cạnh của một tam
giác.
A.
1
10
. B.
3
10
. C.
2
5
. D.
3
5
.
Hướng dẫn giải
Chọn B
Số phần tử của không gian mẫu là số cách chọn ngẫu nhiên 3 đoạn thẳng trong 5 đoạn
thẳng để tạo tam giác, ta có
3
5
n C
.
Gọi
X
là biến cố: “Ba đoạn thẳng được chọn ra là độ dài ba cạnh của một tam giác”.
Vì một tam giác được tạo thành phải thỏa mãn điều kiện tổng hai cạnh lớn hơn cạnh
thứ ba nên chỉ có bộ ba đoạn thỏa mãn:
2;3;4 , 2;4;5 , 3;4;5
.
Do đó số phần tử của biến cố
X
là
3n X
.
Vậy xác suất cần tìm là:
3
10
P X
.
(Ngô Kiều Lượng – THPT Trùng Khánh)
Câu 36: Cho hàm số bậc ba
y f x
có đồ thị là đường cong hình bên. Đồ thị hàm số
2
2
1
4
x
g x
f x f x
có tất cả bao nhiêu đường tiệm cận đứng?
A.
3
. B.
2
.
C.
5
. D.
4
.
Hướng dẫn giải
1
-1
4
2
O
y
x
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 22
Chọn D
Xét hàm số
2
2
1
4
x
g x
f x f x
Txđ:
\ 1D
Xét phương trình
2
0 1
4 0
4 2
f x
f x f x
f x
.
Số nghiệm của phương trình
1
là số giao điểm của đồ thị hàm số
y f x
và trục
hoành. Dựa vào đồ thị của hai đường suy ra phương trình
1
có một nghiệm đơn
1
1x
và nghiệm
2
1x
bội 2 (do
deg 3f x
).
Lý luận tương tự, phương trình
2
có một nghiệm đơn
3
1x
và nghiệm
4
1x
bội
2 (do
deg 3f x
).
Như vậy ta có thể phân tích
 
2 2 2 2
2
1 3 1 3
4 . 1 . 1 . 1 1f x f x p x x x q x x x p q x x x x x x
với
2 3
1 1x x
và
,p q
là các hằng số thực.
Do đó

2
2 2
1 3
1 3
1 1
. 1 1
. 1 1
x
g x
p q x x x x x x
p q x x x x x x
Suy ra đồ thị hàm số
y g x
có 4 TCĐ.
(Ngô Kiều Lượng – THPT Trùng Khánh)
Câu 37: Cho đồ thị hàm số
3 2
3 4y f x x x
có đồ thị như hình vẽ bên. Hỏi phương trình
2
1 1
3 5 4
f f x
f x f x
có bao nhiêu nghiệm thực?
y = 4
1
O
y
x
4
2
-1
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 23
A.
4
. B.
6
.
C.
7
. D.
5
.
Hướng dẫn giải
Chọn B
Cách 1 : (Phạm Viết Biên – THPT Phục Hòa)
Với
y f x
nên ta có :
3 2
2 2
2
( ) 3 4
1 1 1
3 5 4 3 5 4
3 5 4
f f x
f y y y
y y y y
f x f x
2
(3 5 4 0 )y y x
3 2 2 3 2
0
3 4 3 5 4 6 5 0 1
5
y
y y y y y y y y
y
*với
0y
:
3 2
3 4 0x x
có 2 nghiệm thực ( máy tính :)
*Với
1y
:
3 2 3 2
3 4 1 3 3 0x x x x
có 3 nghiệm thực ( máy tính)
*Với
5y
:
3 2 3 2
3 4 5 3 1 0x x x x
có 1 nghiệm thực, 2 nghiệm phức ( máy
tính)
Vậy phương trình
2
1
3 5 4
f f x
f x f x
có 6 nghiệm thực.
Cách 2: (Ngô Kiều Lượng – THPT Trùng Khánh)
Đặt
2 , ;f x t t  
, từ giả thiết ta có
3 2
3 4 3f t t t
2
-1
1
y
x
3
2
O
4
1
y = 1
y = 5
5
O
-1 1
2
32
4
y
x
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 24
PT
2
2
1 1 3 5 4 4
3 5 4
f t
f t t t
t t
Từ
3
và
4
thu được PT:
2 3 2 3 2
0
3 5 4 3 4 6 5 0 1
5
t
t t t t t t t t
t
Thay vào
2
ta thu được ba phương trình:
0
1
5
f x a
f x b
f x c
Số nghiệm của phương trình
a
là số giao điểm của đồ thị hàm số
y f x
và trục
hoành
Ox
. Dựa vào đồ thị của hai đường suy ra PT
a
có hai nghiệm, một nghiệm
đơn
1
1x
, một nghiệm
2
2x
bội 2 (do
deg 3f x
).
Lí luận hoàn toàn tương tự, PT
b
có 3 nghiệm, PT
c
có 1 nghiệm.
Vậy phương trình đã cho có 6 nghiệm thực phân biệt. Chọn B.
Câu 38: Cho hình lăng trụ tam giác
.ABC A B C
có đáy là tam giác đều cạnh
a
. Cạnh bên tạo
với đáy một góc
0
60
. Gọi
M
là trung điểm của
B C
và
I
là trung điểm của đoạn
A M
. Biết hình chiếu vuông góc của
I
trên mặt phẳng đáy
ABC
là trọng tâm của tam giác
ABC
. Tính thể tích của khối lăng trụ
.ABC A B C
theo
a
.
A.
3
3
4
a
. B.
3
3
48
a
. C.
3
3
16
a
. D.
3
3
12
a
.
Hướng dẫn giải
Chọn C
60
0
a
G'
G
I
C
B
A
M
C'
B'
A'
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 25
Gọi G là trọng tâm tam giác
ABC G
là hình chiếu vuông góc của I trên
mp ABC
và ngược lại
IG
là đường cao của hình lăng trụ.
Gọi G’ là trọng tâm tam giác
’ ’ ’ ’ / / ’ A B C GG AA 
là góc giữa cạnh
’AA
và
0
60’ '’ ’m Ip A B C GG
Xét tam giác
’G IG
( vuông tại
I
) có :
1 3 3
' .
6 2 12
a a
IG
3
tan G' 3 '. 3 . 3
' 12 4
IG a a
IG IG
IG

Vậy thể tích khối lăng trụ
. ’ ’ ’ABC A B C
là :
2 3
. ' '
3 3
.
4 4 16
ABC A B C
a a a
V
.
(Phạm Viết Biên – THPT Phục Hòa)
Câu 39: Bác Minh có một mảnh vườn hình Elip có độ dài trục lớn là
10m
và độ dài trục nhỏ là
8m
. Giữa vườn là một cái giếng hình tròn có bán kính
0,5m
và nhận trục lớn và trục bé
của đường Elip làm trục đối xứng (như hình vẽ). Bác Minh muốn tròng hoa hồng đỏ
trên phần dải đất còn lại (xung quanh giếng). Biết kinh phí trồng hoa là 120.000 đồng/
2
m
. Hỏi Bác Minh cần bao nhiêu tiền để trồng hoa trên giải đất đó? (Số tiền làm tròn
đến hàng nghìn).
A. 7.545.000 đồng. B. 7.125000 đồng.
C. 7.325000 đồng. D. 7.446.000 đồng.
Hướng dẫn giải
Chọn D
Độ dài trục lớn đường Elip
2 10 5a a m
, độ dài trục nhỏ đường Elip
2 8 4b b m
.
Diện tích của dải dất là diện tích hình Elip:
2
20
E
S ab m
.
Diện tích mặt giếng là diện tích của hình tròn bán kính
0,5r m
:
2 2
. 0.5 0,25
C
S m
.
Diện tích của dải đất để trồng hoa hồng đỏ là
2
79
4
E C
S S S m
.
Vì kinh phí để trồng hoa là 120.000 đồng/
2
m
nên bác Minh cần:
79
.120000 7.446.000
4
đồng để trồng hoa trên dải đất đã cho.
(Ngô Kiều Lượng – THPT Trùng Khánh)
Câu 40: Biết
S
là tập giá trị của
m
để tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
4 2 3 2
2y x m x x m
trên đoạn
0;1
bằng
16
. Tính tích các phần tử của
S
.
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 26
A.
15
. B.
2
. C.
17
. D.
2
.
Hướng dẫn giải
Chọn A
Hàm số
4 2 3 2
2y x m x x m
luôn xác định và liên tục trên đoạn
0;1
.
Ta có
2 2
2 2
0
. 4 3 4 , 0
4 3 4 0
x
y x x m x y
x m x
Xét phương trình
2 2
4 3 4 0 1f x x m x
Ta có
4
9 64 0m m
và
0 4 0f
1
có hai nghiệm phân biệt
1 2
,x x
với
2 4 2 4
1 2 1 2
3 9 64 3 9 64
0, 1 , 0;1
8 8
m m m m
x x x x
BBT:
Dựa vao BBT ta có
2
0;1 0;1
, 1max y m min y m m
.
Theo bài ta có
2
0;1 0;1
5
16 2 15 0
3
m
max y min y m m
m
Do đó tích hai phần tử của tập
S
là
5 .3 15
.
(Ngô Kiều Lượng – THPT Trùng Khánh)
Câu 41: Gọi
S
là tập hợp tất cả các giá trị của tham số
m
để hàm số
2 5 3 2 2
1 1
10 20
5 3
y m x mx x m m x
đồng biến trên
. Tổng giá trị của tất cả các phần tử thuộc
S
bằng
A.
5
2
. B.
3
2
. C.
2
. D.
1
2
.
Hướng dẫn giải
ChọnD
Txđ :
D
Ta có:
2 4 2 2
20 20f x m x mx x m m
2 4 2
1 1 20 1f x m x m x x
2 3 2
1 1 1 20 1 .f x x m x x x m x x g x
.
Để hàm số đồng biến trên
thì
0,f x x
.
-
1
0
- m
2
- m - 1
- m
y
y'
x
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 27
+ Nếu
1x
không phải là nghiệm của
g x
thì
f x
sẽ đổi dấu khi
x
đi qua
1x
. Do đó điều kiện cần để hàm số đồng biến trên
là
1x
phải là nghiệm của
0g x
2
2
4 2 20 0
5
2
m
m m
m
.
+ Với
2m
thì
2
2
1 4 8 14 0,f x x x x x
, do đó
2m
thỏa mãn.
+ Với
5
2
m
thì
2
2
1
1 25 50 60 0,
4
f x x x x x
, do đó
5
2
m
thỏa
mãn.
Vậy
5
; 2
2
S
, tổng các phần tử của S bằng
5 1
2
2 2
.
Câu 42: Ba anh em An, Bình, Cường cùng vay tiền ở một ngân hàng với lãi suất
0, 7%
/tháng với
tổng số tiền vay của cả ba người là 1 tỉ đồng . Biết rằng mỗi tháng cả ba người đều trả
cho ngân hàng một số tiền như nhau để trừ vào tiền gốc và lãi. Để trả hết gốc và lãi cho
ngân hàng thì An cần 10 tháng , Bình cần 15 tháng và Cường cần 25 tháng. Số tiền trả
đều đặn cho ngân hàng mỗi tháng của mỗi người gần nhất với số tiền nào dưới đây?
A.21.400.000 đồng. B.21.090.000 đồng. C.21.422.000 đồng. D.21.900.000 đồng.
Hướngdẫngiải
ChọnC
Xét bài toán tổng quát sau: Ông
X
vay tiền ở một ngân hàng với lãi suất
%r
/tháng với
số tiền vay ban đầu là
0
P
đồng . Biết rằng mỗi tháng ông
X
đều trả cho ngân hàng một
số tiền như nhau để trừ vào tiền gốc và lãi . Để trả hết gốc và lãi cho ngân hàng thì ông
X
cần
n
tháng. Tính số tiền ông
X
phải trả mỗi tháng.
Lời giải:
Số tiền gốc và lãi cuối tháng thứ nhất là
0 0 0
. 1P P r P r
Gọi số tiền ông
X
đem trả ngân hàng mỗi tháng là
a
đồng
Số tiền ông
X
còn nợ cuối tháng thứ nhất là
1 0
1P P r a
Số tiền gốc và lãi cuối tháng thứ hai là :
2
1 1 0 0 0
. 1 1 . 1 1P P r P r a P r a r P r a r
Số tiền ông
X
còn nợ cuối tháng thứ 2 :
2 2
2 0 0
1 1 1 1 1P P r a r a P r a r
…
Số tiền ông
X
còn nợ sau
n
tháng là:
2 1
0 0
1 1
1 1 1 1 ... 1 1 .
n
n n n
n
r
P P r a r r r P r a
r
Ông
X
trả hết tiền ngân hàng khi :
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 28
0 0
. 1 1
1 1
0 1 . 0 *
. 1
n
n
n
n
n
a r
r
P P r a P
r
r r
Trở lại câu hỏi trong đề:
Gọi
, ,a b c
lần lượt là số tiền An , Bình và Cường vay ngân hàng ,
x
là số tiền hàng tháng
phải trả. Để An, Bình và Cường trả hết nợ , áp dụng công thức
*
ta có:
10 15 25
10 15 25
. 1 0, 007 1 . 1 0,007 1 . 1 0, 007 1
1000.000.000
0, 007. 1 0, 007 0, 007. 1 0, 007 0, 007. 1 0, 007
x x x
21.422.719x
đồng.
(Ngô Kiều Lượng –THPT Trùng Khánh)
Câu 43: Có tất cả bao nhiêu số nguyên
m
để đồ thị hàm số
2
2 2
1
2 2 25
x
y
x mx m
có ba
đường tiệm cận?
A.
7
. B.
11
. C.
5
. D.
9
.
Hướng dẫn giải
Chọn C
Ta có
lim 1
x
y

, đồ thị
C
của hàm số
2
2 2
1
2 2 25
x
y
x mx m
luôn có một TCN
1y
.
Xét phương trình
2 2
2 2 25 0 1x mx m
.
Đặt
2 2
2 2 25f x x mx m
. Để đồ thị
C
có ba đường tiệm cận khi và chỉ khi
phương trình
1
có hai nghiệm phân biệt khác
1
2
25 0
5 5
1 0 *
3; 4
1 0
m
m
f
m
f
Do
m
, kết hợp với
*
suy ra
1;0; 2m
.
(Ngô Kiều Lượng – THPT Trùng Khánh)
Câu 44: Miền phẳng trong hình vẽ được giới hạn bởi đường cong
y f x
và
2
2y x x
. Biết
1
1
2
3
4
f x dx
. Khi đó diện tích hình phẳng được tô trên hình vẽ là
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 29
A.
9
8
. B.
8
3
.
C.
8
9
. D.
3
8
.
Hướngdẫngiải
ChọnA
Từ hình vẽ trên , ta có diện tích hình phẳng giới hạn bởi đường cong
y f x
và
2
2y x x
là
1 1 1
2 2
1 1 1
2 2 2
3 3 9
2 2
4 8 8
S f x x x dx f x dx x x dx
.
Câu 45: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
,A AB a
, cạnh bên
SA
vuông góc với đáy , góc tạo bởi giữa hai mặt phẳng
SBC
và
ABC
bằng
0
60
khi và
chỉ khi
SA
bằng
A.
3a
. B.
6
6
a
. C.
6
4
a
. D.
6
2
a
.
Hướng dẫn giải
ChọnD
Gọi I là trung điểm của BC .
Do ABC là tam giác vuông cân tại A nên AI
BC.
Do SA
(ABC) nên SA
BC
Suy ra BC
SI.
Do đó góc tạo bởi hai mặt phẳng (ABC )và (SBC) là
0
60SIA
.
Trong tam giác ABC vuông cân tại A có AB = a . Ta có :
2
2 2
BC a
AI
Trong tam giác SAI vuông tại A ta có :
2 6
.tan . 3
2 2
a a
SA AI SIA
.
Vậy
6
2
a
SA
.
O
1
-
1
2
y
x
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 30
(Nông Ngân–THPT Trà Lĩnh)
Câu 46: Trong không gian với hện tọa độ
Oxyz
, cho đường thẳng
2 1
:
1 1 3
x y z
và
mặt phẳng
: 11 16 0P x my nz
. Biết
P
, Tính giá trị của
T m n
.
A.
14T
B.
2T
. C.
2T
. D.
14T
.
Hướng dẫn giải
Chọn D
Phương trình tham số của
2
: 2
1 3
x t
y t
z t
Ta có:
11. 2 2 1 3 16 0 22 3 2 16 0t m t n t m n t m n
(*)
Để
P
thì phương trình (*) có vô số nghiệm
3 22 10
2 16 4
m n m
m n n
Vậy
14T m n
.
(Nông Ngân–THPT Trà Lĩnh)
Câu 47: Trong không gian với hệ tọa độ
Oxyz
, cho hai đường thẳng
1
1 2 1
:
2 1 1
x y z
và
2
2 1 2
:
4 1 1
x y z
. Đường thẳng chứa đoạn vuông góc chung của
1 2
,
đi
qua điểm nào sau đây?
A.
3;1; 4Q
B.
2;0;1P
. C.
0; 2; 5M
. D.
1; 1; 4N
.
Hướng dẫn giải
ChọnA
Gọi
là đường vuông góc chung của
1 2
,
và
cắt
1 2
,
lần lượt tại
A
và
B
.
1 2
,
có phương trình tham số là:
1 2
2 2 4 '
: 2 ; : 1 '
1 2 '
x t x t
y t y t
z t z t
.
Vì
1
A
nên
( 1 2 ; 2 ;1 )A t t t
,
2
B
nên
( 2 4 ';1 '; 2 ')B t t t
.
Khi đó
( 1 2 4 ';3 '; 3 ')AB t t t t t t
.
Đường thẳng
1 2
, có véctơ chỉ phương lần lượt là :
1 2
( 2;1;1), ( 4;1; 1)u u
.
Vì đường thẳng AB là đường vuông góc chung của
1 2
, nên
1
2
. 0
. 0
AB u
AB u


Do đó:
2 4 8 ' 3 ' 3 ' 0 6 8 ' 2 1
4 8 16 ' 3 ' 3 ' 0 8 18 ' 10 ' 1
t t t t t t t t t
t t t t t t t t t
Như vậy
(1; 1; 2), (1;1; 3)A AB
và phương trình đường vuông góc chung là
1
1
2 3
x t
y t
z t
Điểm thuộc đường vuông góc chung là Q .
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 31
(Vi Thị Dung – THPT Trà Lĩnh)
Câu 48: Cho số phức
,z a bi a b
thỏa mãn
4 2 5 1z i z i i
.
Tính giá trị của biểu thức
T a b
.
A.
1T
. B.
2T
. C.
3T
. D.
1T
.
Hướng dẫn giải
Chọn C
Theo đầu bài
2 2 2 2
4 2 5(1 ) ( 4) . ( 2) 5 5.z i z i i a b i a b i
Do đó ta có
2 2
2 2
2 2
2 2
( 4) 5
8 11 0 2
1
4 1 0
( 2) 5
a b
a b a a
b
a b b
a b
Vậy
3.T a b
(Vi Thị Dung–THPT Trà Lĩnh)
Câu 49: Cho phương trình
3
4 1 .2 0
x x
m m
(*) . Nếu phương trình (*) có hai nghiệm
1 2
,x x
thỏa mãn
1 2
2x x
thì
0
m m
. Giá trị
0
m
gần giá trị nào nhất trong các giá trị
sau?
A.
0,5
. B.
3
. C.
2
. D.
1, 3
.
Hướng dẫn giải
ChọnB
Ta có:
(*)
2
(2 ) 8 1 .2 0
x x
m m
1 2 1 2
1 2
2 2 4 2 .2 4 4
x x x x
x x m
.
Chọn B.
(Long Thị Hồng Gấm–THPT Thành Phố)
Câu 50: Trong không gian với hệ trục tọa độ
Oxyz
, cho
3;1;1 , 1; 1;5A B
và mặt phẳng
: 2 2 11 0P x y z
. Mặt cầu
S
đi qua hai điểm
,A B
và tiếp xúc với mặt phẳng
P
tại điểm
C
. Biết
C
luôn thuộc đường tròn
T
cố định . Tính bán kính
r
của đường
tròn
T
.
A.
3r
. B.
4r
. C.
2r
. D.
2r
.
Hướng dẫn giải
Chọn B
Nhóm Toán Cao Bằng Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Trang 32
Nhận xét : Đường thẳng AB vuông góc với mặt phẳng (P) cắt (P) tại điểm cố định H.
Ta sẽ chứng minh điểm C thuộc đường tròn tâm H bán kính r = CH
(độ dài không đổi )
Gọi M là trung điểm AB , M( -1; 0 ;3 )
Dễ thấy IMHC là hình chữ nhật: IM
2
= IB
2
- MB
2
Ta có : IB = IC = MH = d(M;(P)) = 5; MB = 3.
Vậy: CH = IM = 4
C
luôn thuộc đường tròn
T
cố định, bán kính r = 4.
(Long Thị Hồng Gấm–THPT Thành Phố - Cao Bằng)
(
S
)
r
R
M
P
C
H
B
A
I
| 1/32
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
SỞ GD&ĐT CAO BẰNG
ĐỀ THI THỬ THPT QUỐC GIA NĂM HỌC 2018 - 2019 Môn: TOÁN
-------------------------------------------------
Thời gian: 90 phút (Không kể thời gian phát đề) MÃ ĐỀ
Họ và tên thí sinh:...........................................SBD:............................................ 003 x  1 y  4 z  3 Câu 1:
Trong không gian Oxyz , cho đường thẳng d :   . Véctơ nào sau 1 2 3
đây không phải là véctơ chỉ phương của đường thẳng d ?    
A. a  1;2;3. B. a  3; 6  ;  9 .
C. a  1;2;3.
D. a  2; 4;  3 . Câu 2:
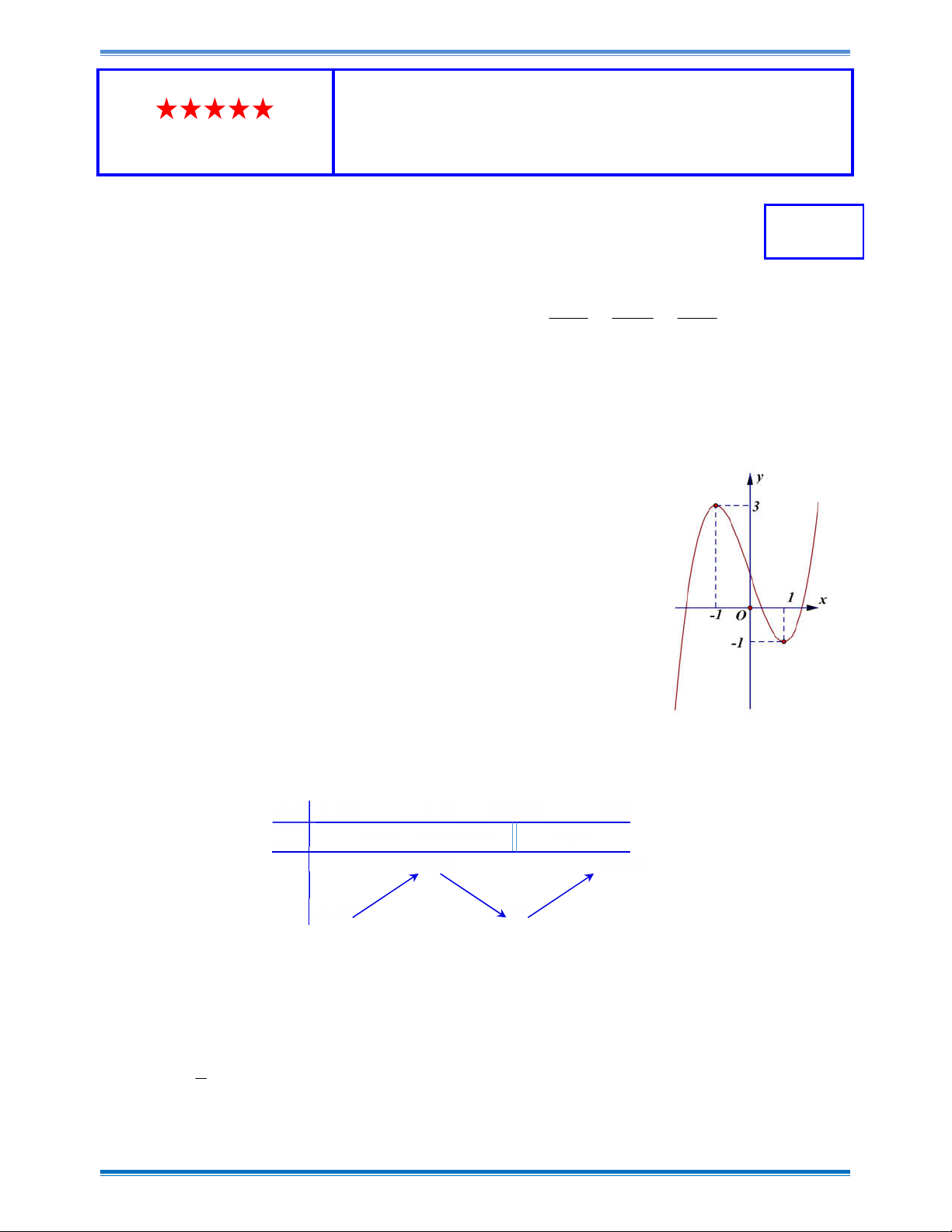
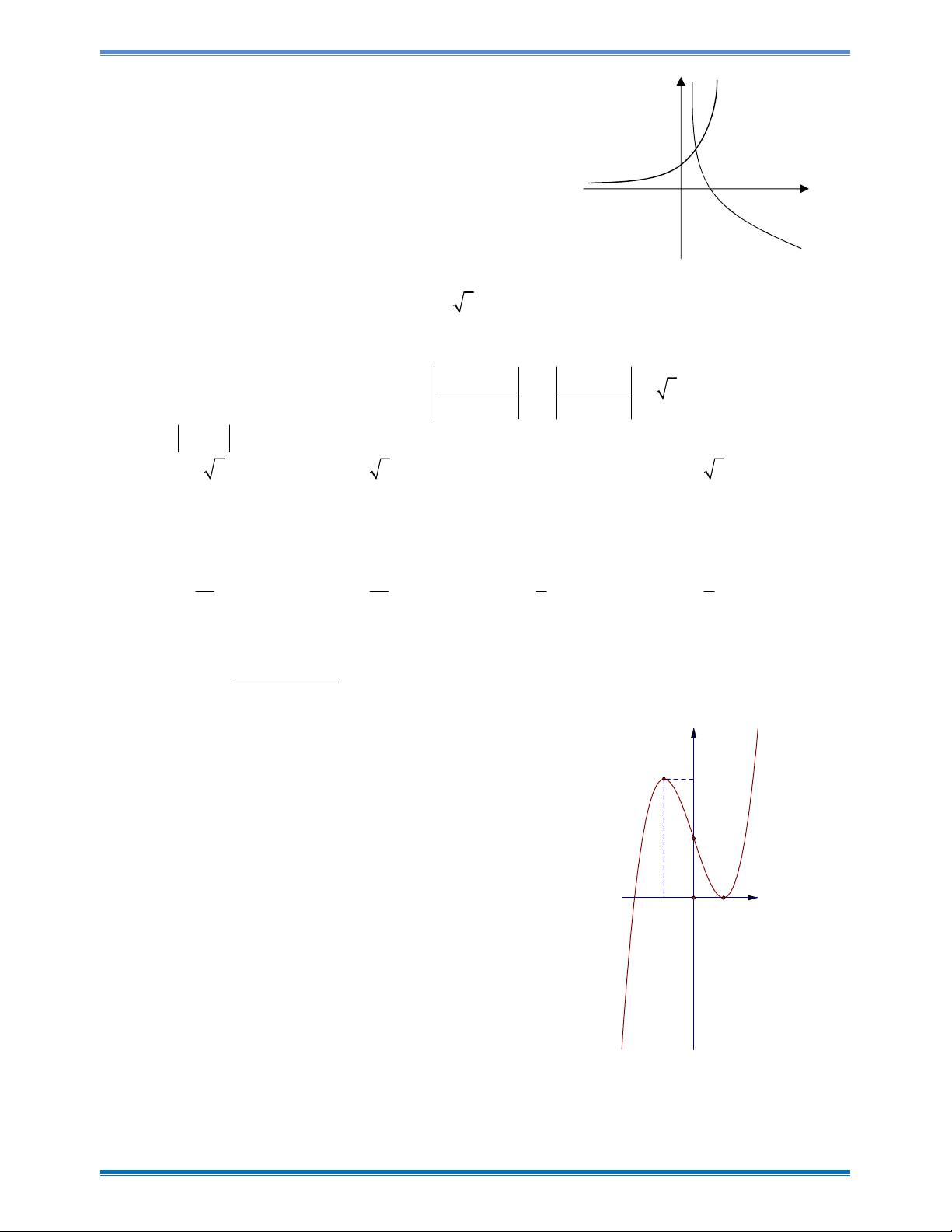
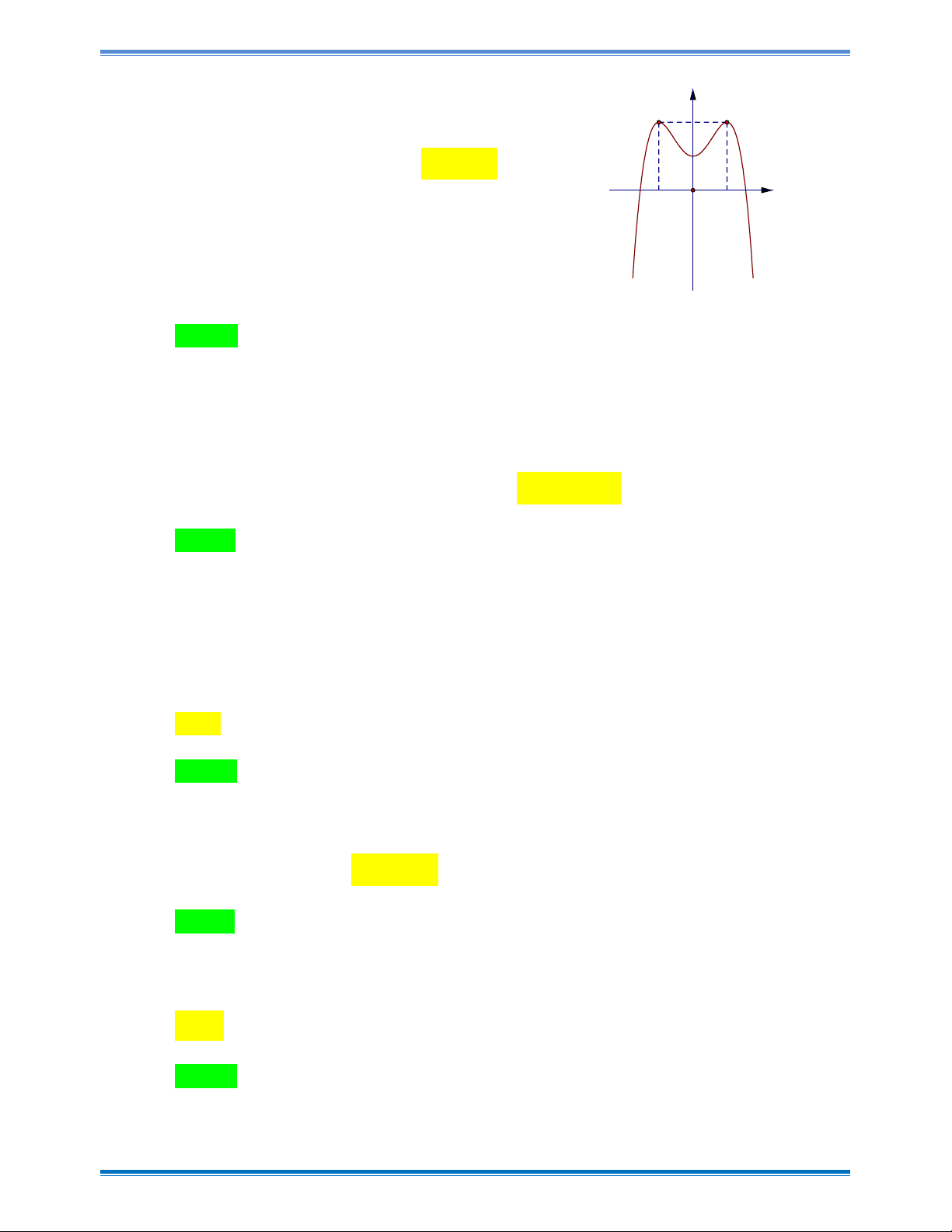
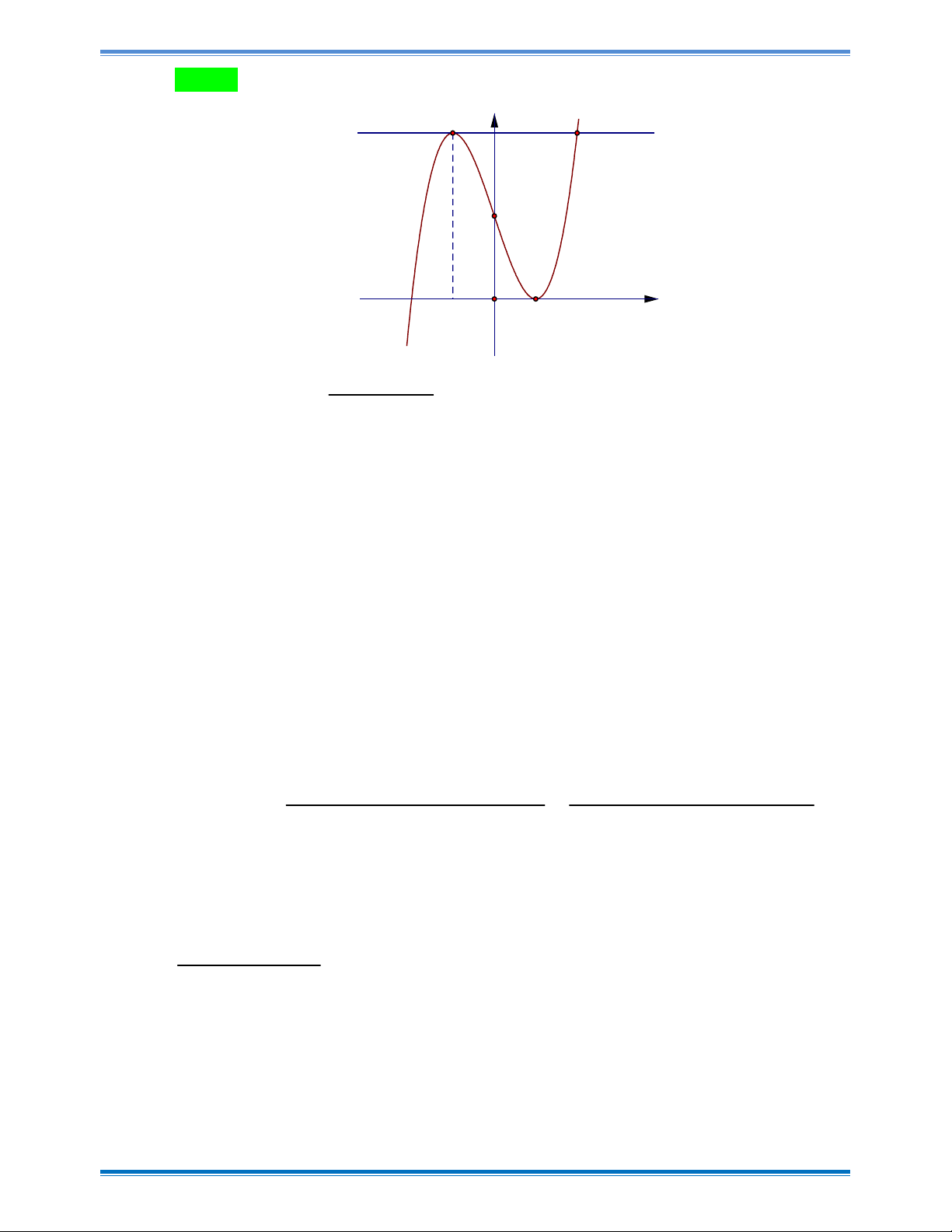
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? A. 3 2 y x
  3x  1 B. 3 2
y x  3x  1 C. 3 2 y x   3x  1 D. 3 2
y x  3x  1 Câu 3:
Cho hàm số y f x có bảng biến thiên như sau x – ∞ -1 1 + ∞ y' + 0 – + 3 + ∞ y – ∞ -1
Hàm số có bao nhiêu điểm cực trị? A.1 . B.2 . C. 4 . D. 3 . Câu 4:
Diện tích mặt cầu bán kính R bằng 4 A. 2 R . B. 2 4 R . C. 2 2 R . D. 2 R . 3  Câu 5:
Tập xác định D của hàm số y  x   5 2 là Trang 1
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
A. D   \   2 . B. D   .
C. D  2;   . D. D 2   ;    . Câu 6:
Nghiệm của phương trình log x  1  log 3  x là 3   3   A. x  3 . B. x  4 . C. x  2 . D. x  1 . Câu 7:
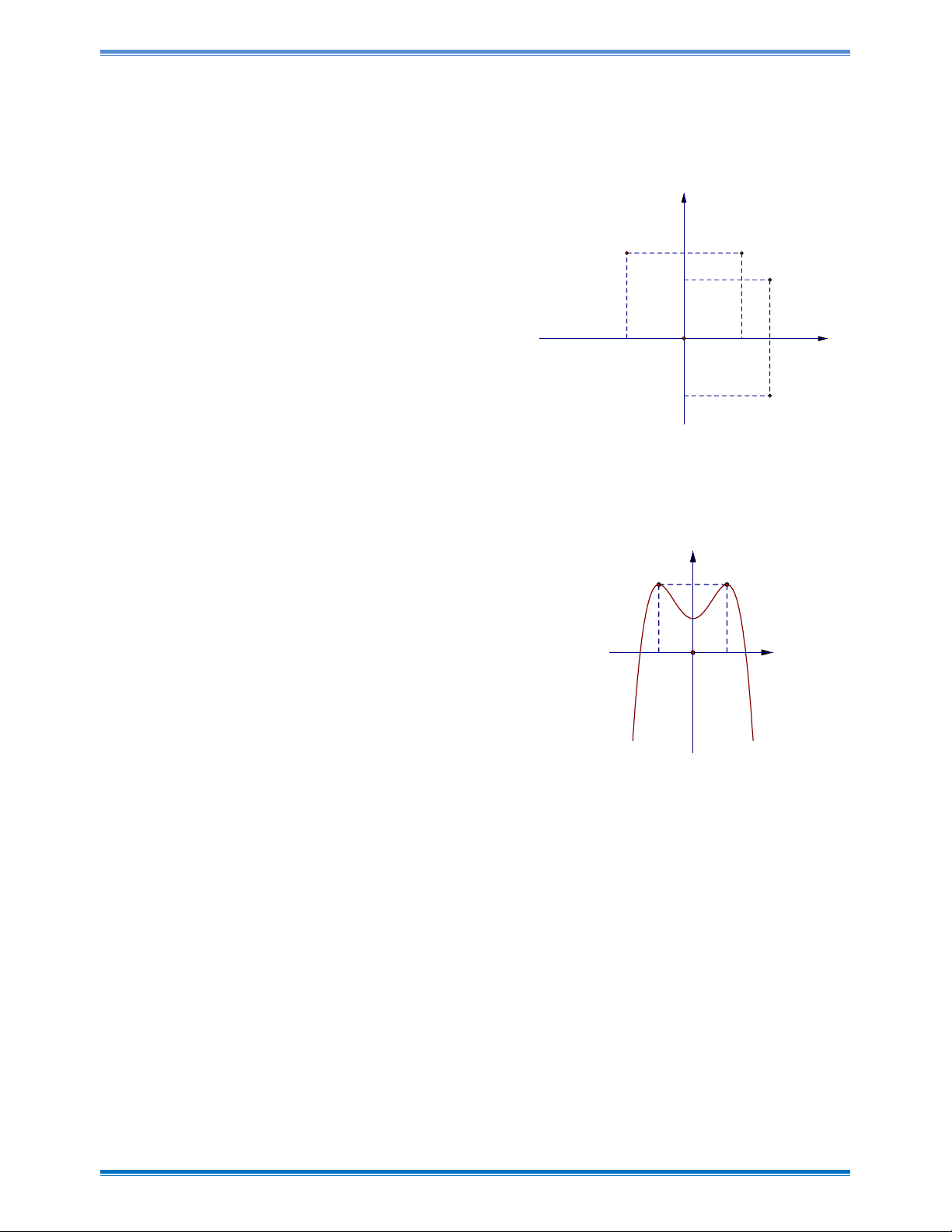
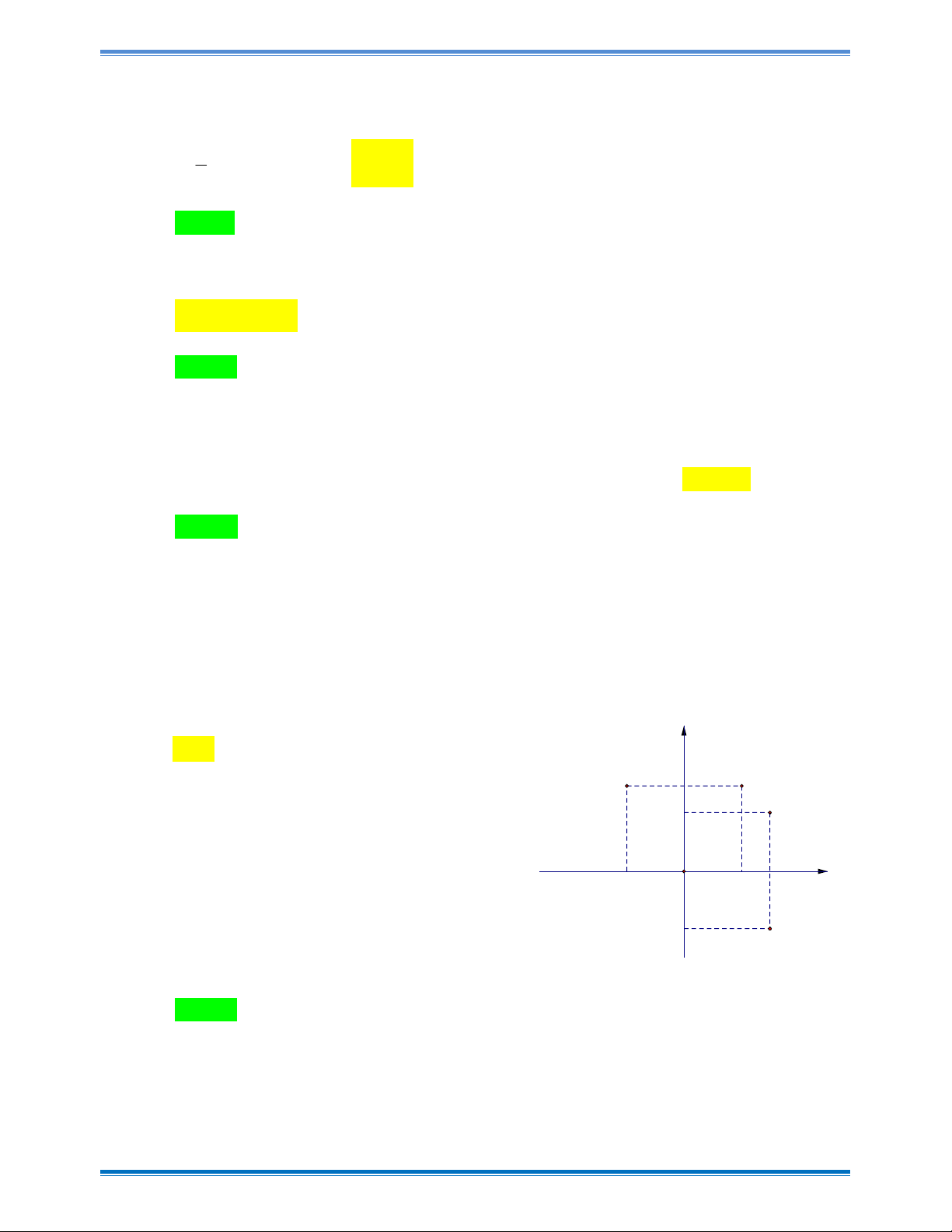
Điểm nào ở hình vẽ bên biểu diễn cho số phức z  3  2i ? y A. Q . B. P . M 3 N C. N . D. M . 2 P x -2 O 2 3 -2 Q Câu 8:
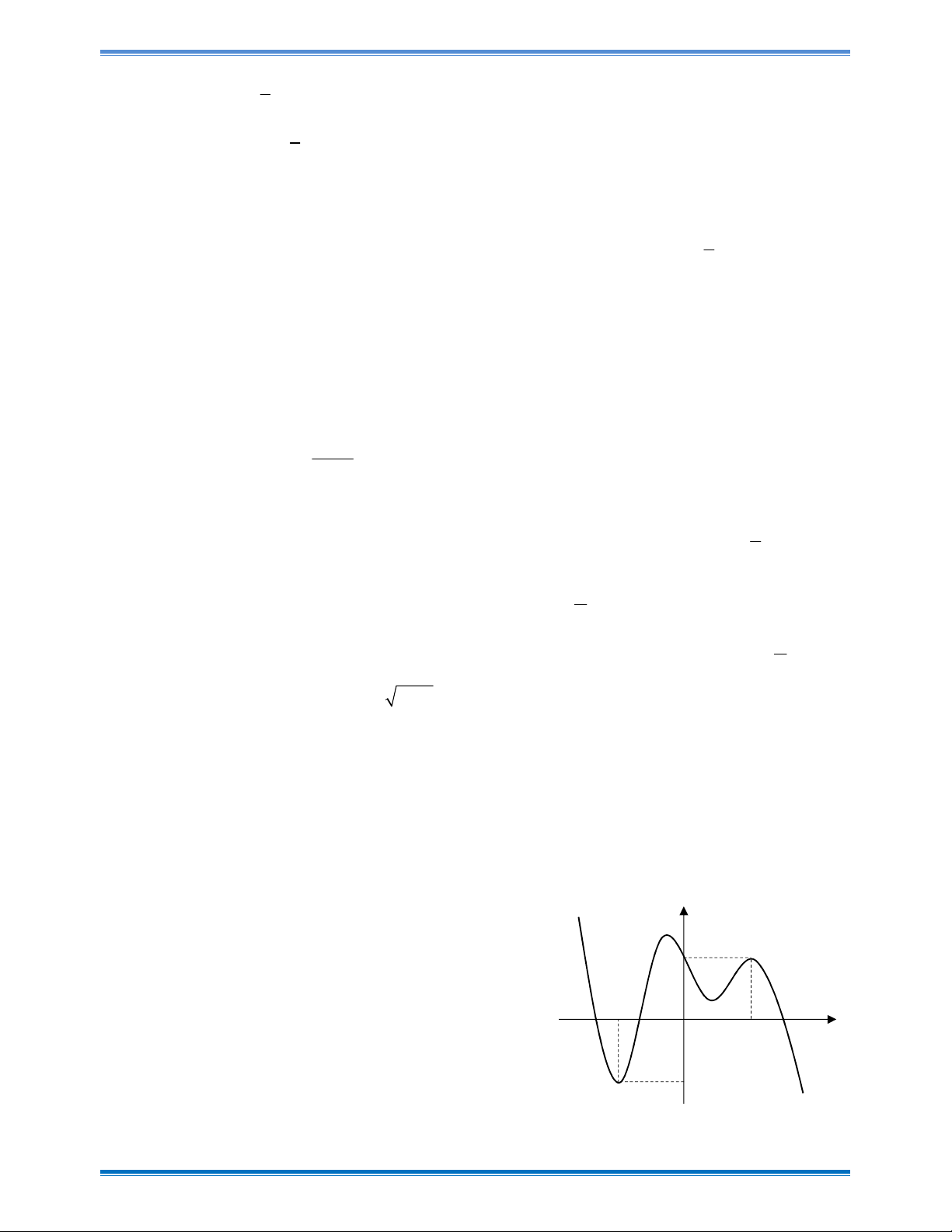
Cho hàm số y f x có đồ thị như hình vẽ bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây? y A. ;    1 . B.0;  1 . 2 C.1;  1 . D. 1  ;  0 . 1 x -1 O 1  Câu 9:
Trong không gian Oxyz , cho AB  2; 3  ;  1 và điểm A1; 2
 ;4. Khi đó tọa độ của điểm B là A. B  3  ;5; 5  . B. B 1; 1  ;  3 . C. B 3; 5  ;  5 . D. B  1  ;1;3.
Câu 10: Cho cấp số nhân u có số hạng đầu u  2 và công bội q  2 . Giá trị u là n  1 5 A. 32 . B. 1  6 . C. 6  . D.32 .
Câu 11: Trong không gian Oxyz , mặt phẳng P : x y z  3  0 đi qua điểm nào dưới đây? A. M  1  ; 1  ;  1 . B. N 1;1;  1 . C. P  3  ;0;  0 . D.Q 0;0; 3   . 
Câu 12: Từ 10 điểm phân biệt trong mặt phẳng, có thể tạo ra ba nhiêu véctơ khác véctơ 0 ? A. 2 A . B. 20 . C. 10 2 . D. 2 C . 10 10
Câu 13: Họ nguyên hàm của hàm số   2  1 x f xe là Trang 2
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019 1 A.   2x
F x e C . B.   2x
F x x e C . 2 1 C.   2x
F x x e C . D.   2 1 2 x F x x xe    C . 2
Câu 14: Một hình hộp chữ nhật có ba kích thước là , a ,
b c . Thể tích V của khối hộp chữ nhật đó bằng 1
A.a cb . B.abc .
C.a bc . D. abc . 3 8 5
Câu 15: Cho hàm số f x  liên tục trên  , biết f
 xdx  7 và f
 xdx  5 . Khi đó 0 0 8
f xdx  bằng 5 A.12 . B. 2  . C. 2 . D.12 . x  3
Câu 16: Cho hàm số y
có đồ thị C  . Gọi I là giao điểm của hai đường tiệm cận của x  2
C. Khi đó tọa độ của điểm I là  3   A. I  3  ;0. B. I 1;  2 . C. I 2;  1 .
D. I 0;   .  2
Câu 17: Cho vật thể giới hạn bởi hai mặt phẳng x  0, x
, biết rằng thiết diện của vật thể 2    
khi cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0  x    là một  2 
hình tròn có bán kính R  cos x . Thể tích của vật thể đó là A. 2. B. 1 . C. . D. 2 .
Câu 18: Cho hình trụ có tổng chu vi hai đáy là 12 và có chiều cao bằng 4 . Khi đó diện tích
toàn phần S của hình trụ là tp
A. S  42.
B. S  33.
C. S  24.
D. S  18. tp tp tp tp
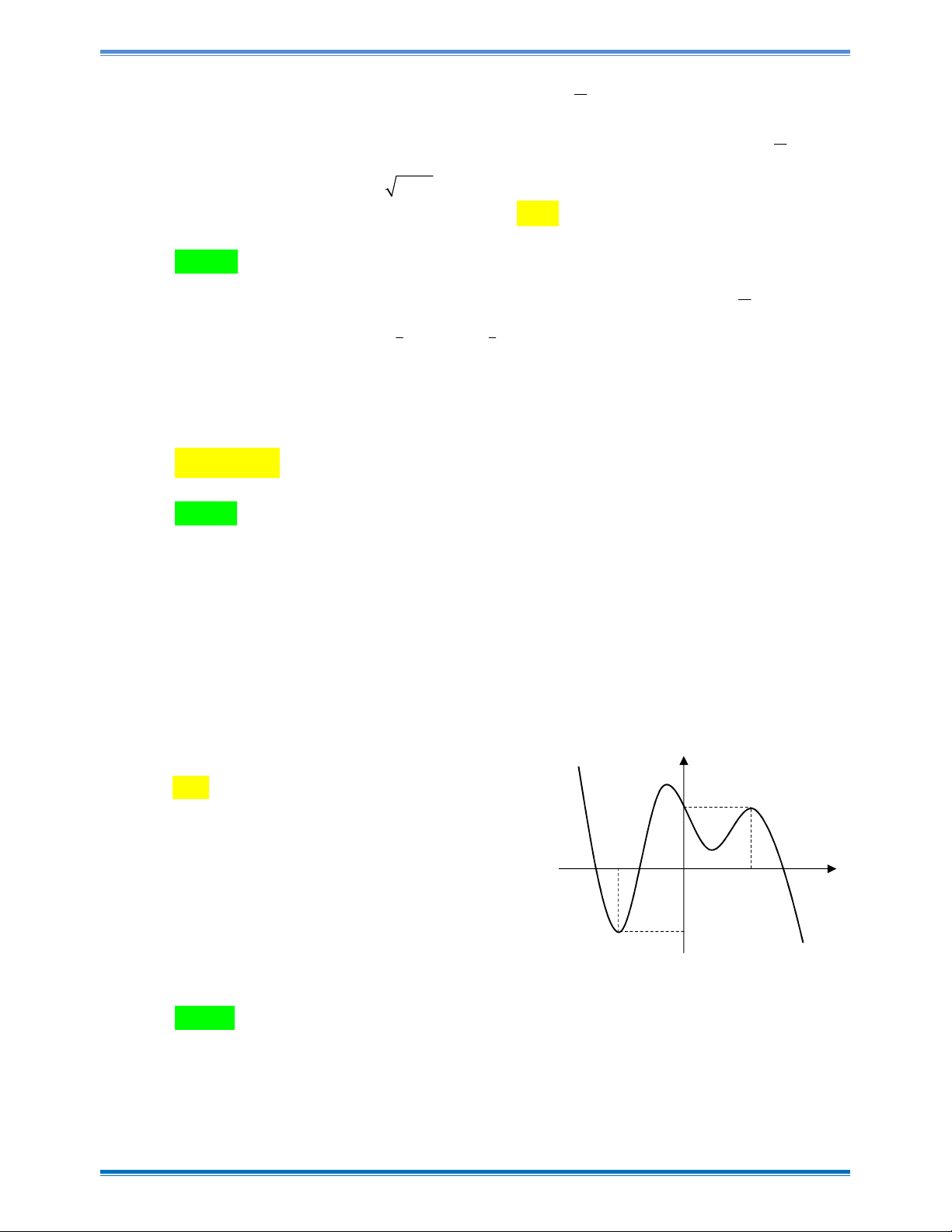
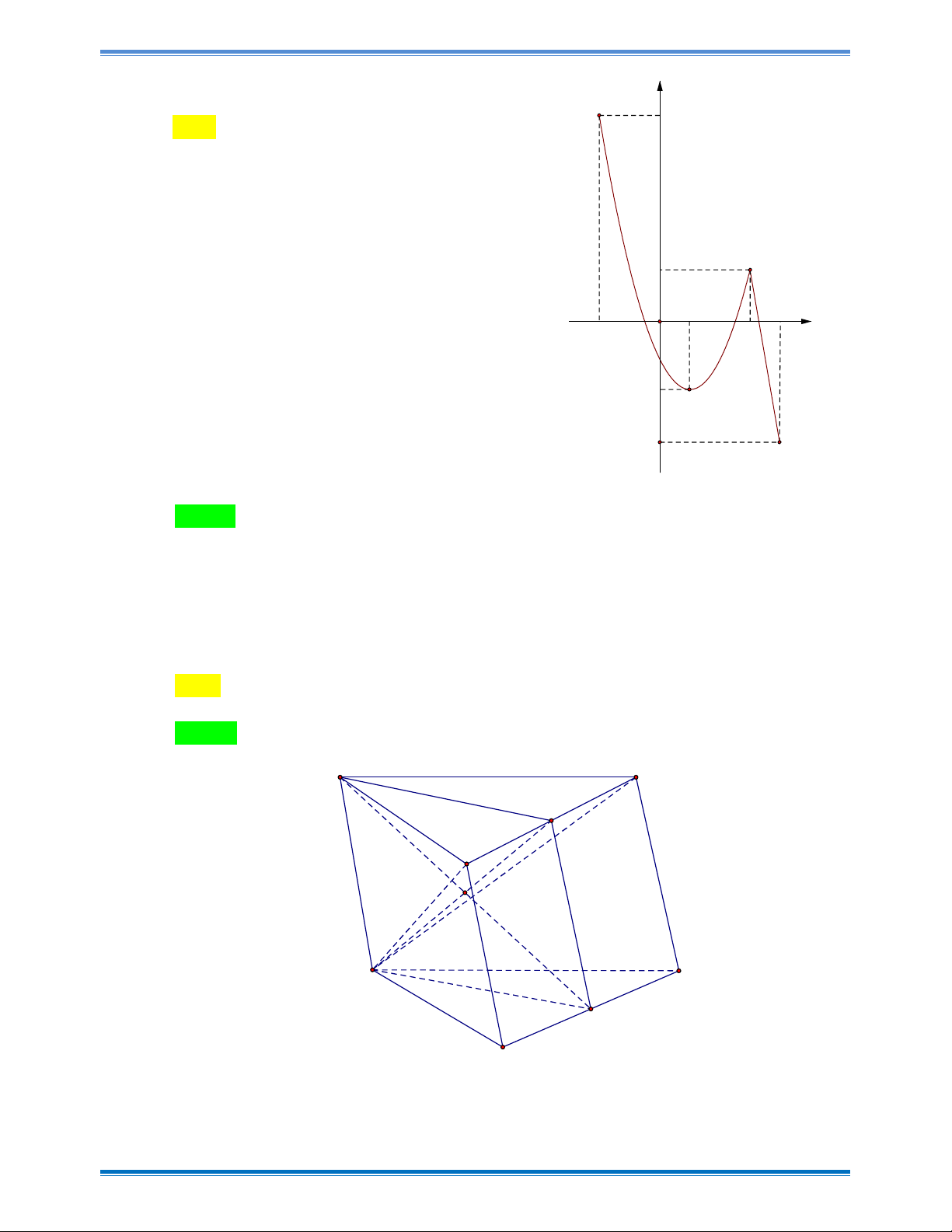
Câu 19: Cho hàm số y f x có đạo hàm trên  . Đồ thị hàm số y f x như hình vẽ bên.
Hỏi đồ thị hàm số y f x   2x có bao nhiêu điểm cực trị ? y A. 3 . B. 4 . C.1 . D. 2 . 2 x O 2 -2 Trang 3
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019 2
Câu 20: Đạo hàm của hàm số 2019x x y   là 2 A. 2019x x y    .ln 2019 . B.   2 2 1 .2019x x y x     .ln 2019 . C.   2 2 1 .2019x x y x x      . D.   2 2 1 .2019x x y x     .
Câu 21: Cho hình nón bán kính r  12 nội tiếp hình cầu bán kính r  13 (như hình vẽ). Tính
diện tích xung quanh S của hình nón. xq
A. S  36 13. B. S  72 5. xq xq
C.S  36 5. D. S  72 13. xq xq
Câu 22: Trong không gian Oxyz , cho hai điểm A1; 3  ;  2 ,B 3;5; 2
 . Phương trình mặt phẳng
trung trực của đoạn AB có dạng x ay bz c  0 . Khi đó a b c bằng A. 3  . B. 2 . C. 4  . D. 2  .
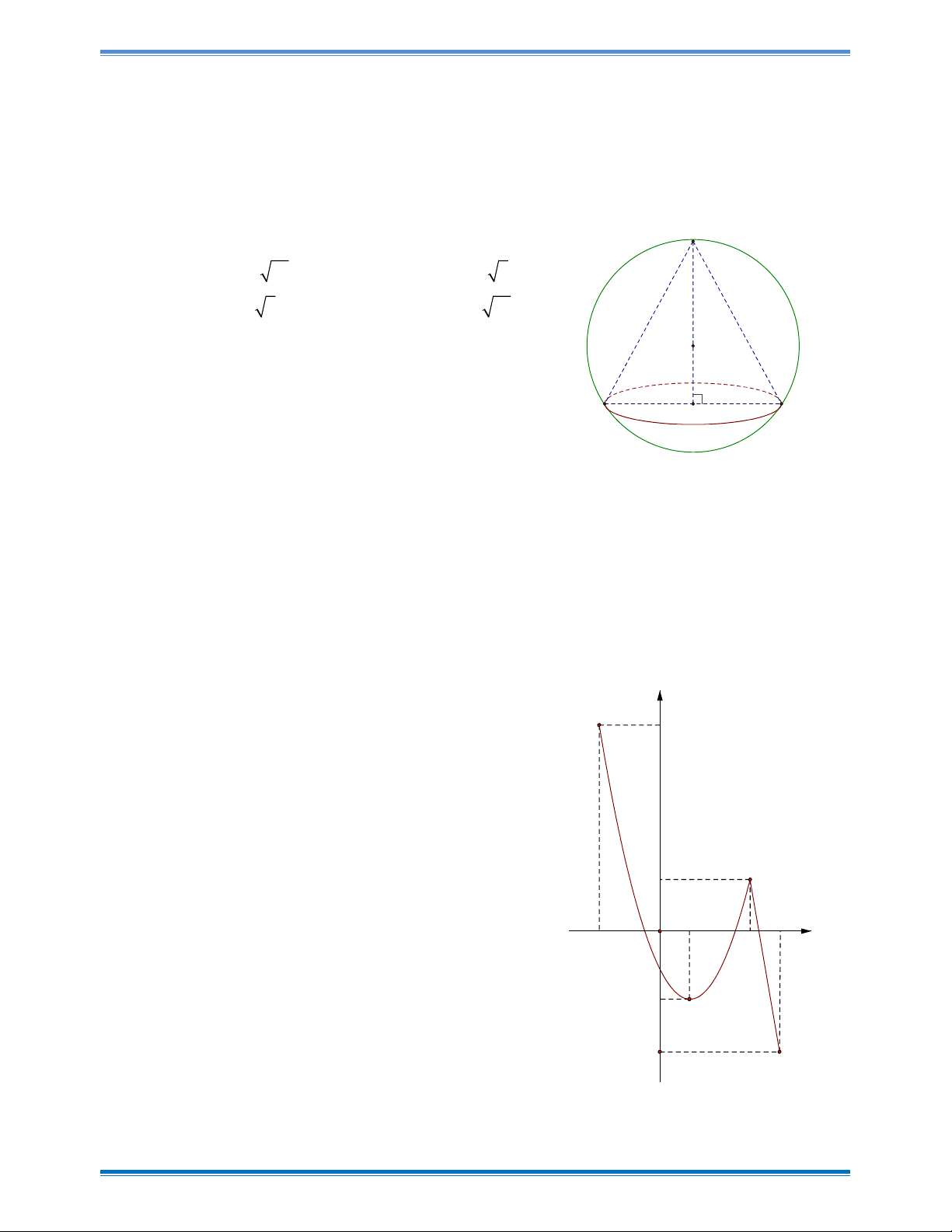
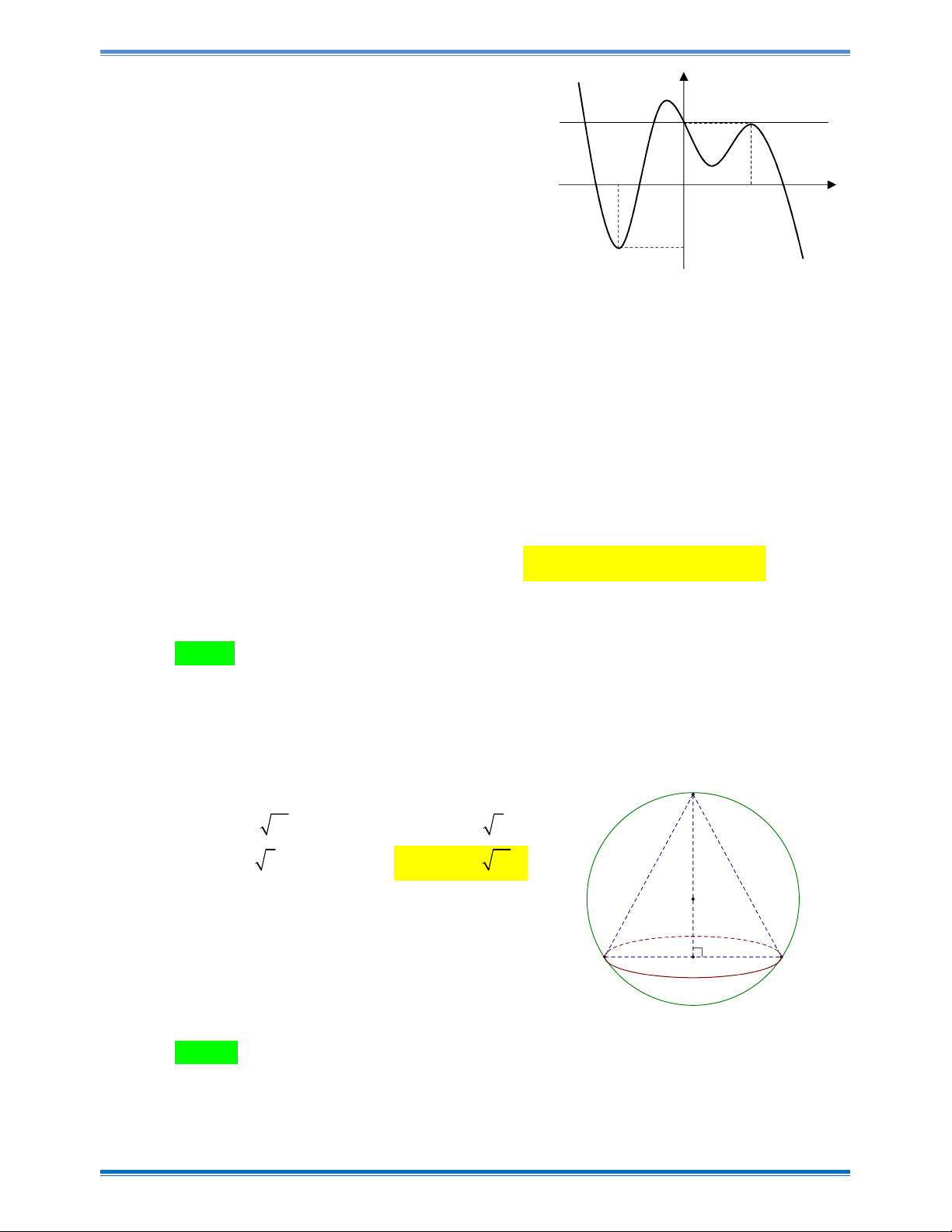
Câu 23: Cho hàm số y f x liên tục trên đoạn  2;4  
 và có đồ thị như hình vẽ bên. Gọi M và
m là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn  2;4    . Giá trị của 2 2 M m bằng y A. 20 . B. 8 . 7 C. 65 . D. 53 . y = f(x) 2 1 4 x -2 O 3 -2 -4 Trang 4
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Câu 24: Cho lăng trụ tam giác ABC .AB C
  có khoảng cách từ A đến mặt phẳng ABC  bằng
6a . Khoảng cách từ trung điểm M của cạnh B C
  đến mặt phẳng ABC  bằng A. 6a . B. 2a . C. 4a . D. 3a .
Câu 25: Tập nghiệm S của bất phương trình 2
log x  5 log x  6  0 là 2 2  1 A.S   64;        . B.S 0;  64;    .  2   1   1
C.S   ;64. D.S   0;  . 2       2
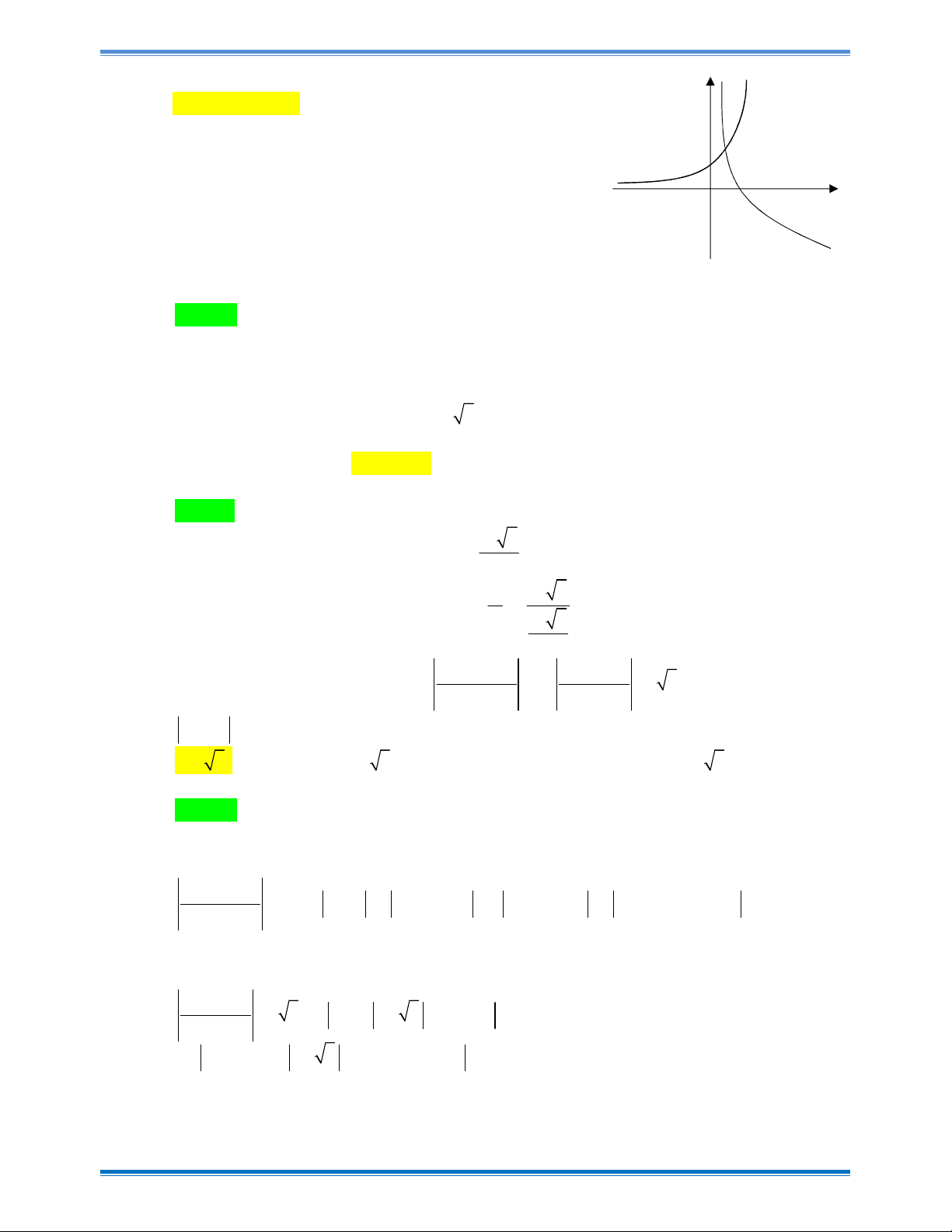
Câu 26: Cho hàm số y f x có đạo hàm f x   x  x  2 2 4
3 ln x trên 0;. Hỏi hàm số
y f x có bao nhiêu điểm cực trị? A. 4 . B. 2 . C. 3 . D.1 . Câu 27: Cho ,
a b là các số thực dương thỏa mãn 2 2
a b  14ab . Khẳng định nào sau đây sai? a b
A. 2 log a b  4  log a  log b . B. 2 log
 loga  logb . 2   2 2 4 a b lna  lnb C. ln 
. D. 2 log a b  4  log a  log b . 2   4 2 4 4
Câu 28: Trong không gian Oxyz , cho điểm A1;2;3 và mặt phẳng P : x y  4z  3  0 . Mặt
cầu S tâm A và tiếp xúc với mặt phẳng P có phương trình là 2 2 2 2 2 2 A. x  
1  y  2  z  
3  2 . B. x   1  y   2  z   3  2 . 2 2 2 2 2 2 C. x  
1  y  2  z  3  4 . D. x   1  y   2  z   3  4 .
Câu 29: Biết z là số phức có phần ảo âm và là nghiệm của phương trình 2
z  6z  10  0 . Tính z
tổng phần thực và phần ảo của số phức w  . z 4 2 7 1 A. . B. . C. . D. . 5 5 5 5
Câu 30: Biết M 2;  1 ,N 3; 
2 lần lượt là hai điểm biểu diễn cho số phức z ,z trên mặt phẳng 1 2
tọa độ phức Oxy . Khi đó môđun của số phức 2 z z bằng 1 2 A. 4 2 . B. 2 10 . C. 10 . D. 68 .
Câu 31: Cho hàm số f x  thỏa mãn   x
f x xe và f  
0  2 . Tính f   1 . A. f   1  8  2e . B. f   1  5 e . C. f   1  e . D. f   1  3 .
Câu 32: Cho đồ thi của hàm số x
y a và y  log x như hình vẽ . Trong các khẳng định sau, b
khẳng định nào đúng? y Trang 5
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
A. 0  b  1  a . B. 0  a  1 và 0  b  1 .
C.a  1 và b  1 . D. 0  a  1  b . 1 x O 1
Câu 33: Cho một khối lăng trụ có thể tích là 3
3a , đáy là tam giác đều cạnh a . Chiều cao h của khối lăng trụ bằng
A. h  2a .
B. h  4a .
C. h  12a .
D. h  3a . z i z i
Câu 34: Cho hai số phức z ,z thỏa mãn 1 2  1;
 2 . Giá trị nhỏ nhất của 1 2 z  2  3i z  1  i 1 2 z z là 1 2 A. 2 2 . B. 2  1 . C.1. D. 2 .
Câu 35: Có năm đoạn thẳng có độ dài lần lượt là 1 , cm 2cm, 3 , cm 4 ,
cm 5cm . Lấy ngẫu nhiên ra ba
đoạn thẳng , tính xác suất để ba đoạn thẳng được chọn ra là độ dài ba cạnh của một tam giác. 1 3 2 3 A. . B. . C. . D. . 10 10 5 5
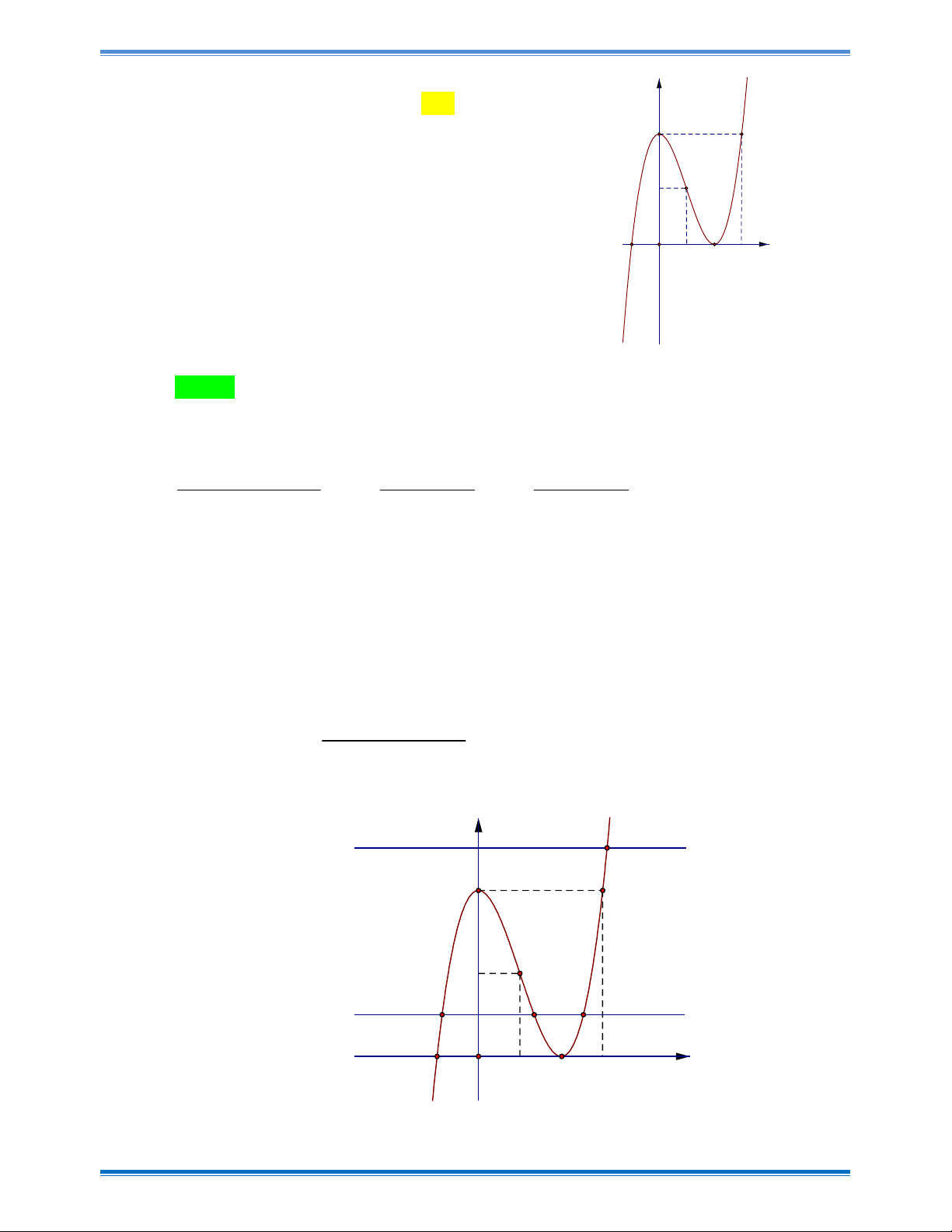
Câu 36: Cho hàm số bậc ba y f x có đồ thị là đường cong hình bên. Đồ thị hàm số .  g x 2 x 1 
. có tất cả bao nhiêu đường tiệm cận đứng? 2
f x  4f x y A. 3 . B. 2 . C. 5 . D. 4 . 4 2 x -1 O 1 Trang 6
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
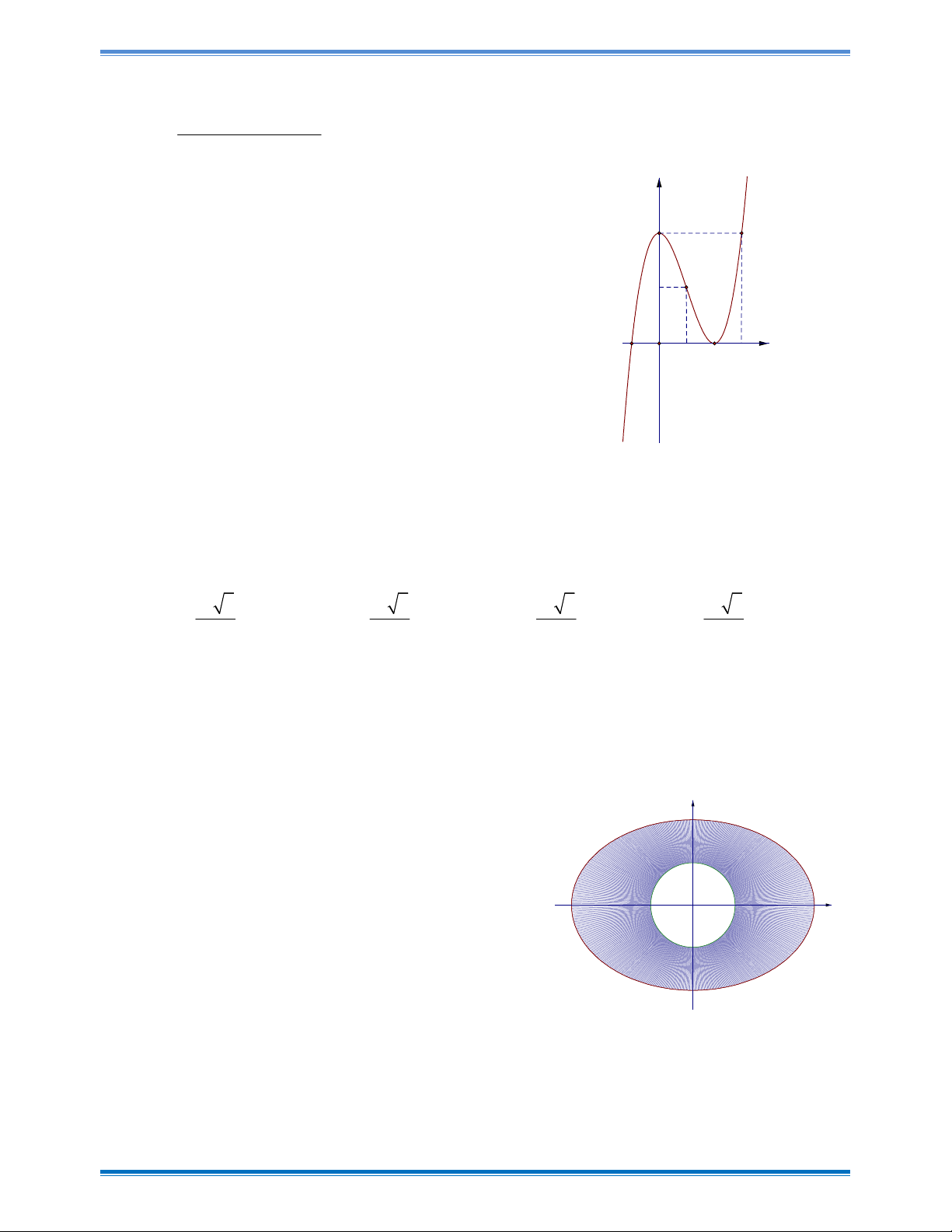
Câu 37: Cho đồ thị hàm số y f x  3 2
x  3x  4 có đồ thị như hình vẽ bên. Hỏi phương trình
f f x  
 1 có bao nhiêu nghiệm thực? 2
3f x  5f x  4 y A. 4 . B. 6 . C. 7 . D. 5 . 4 2 -1 x O 1 2 3
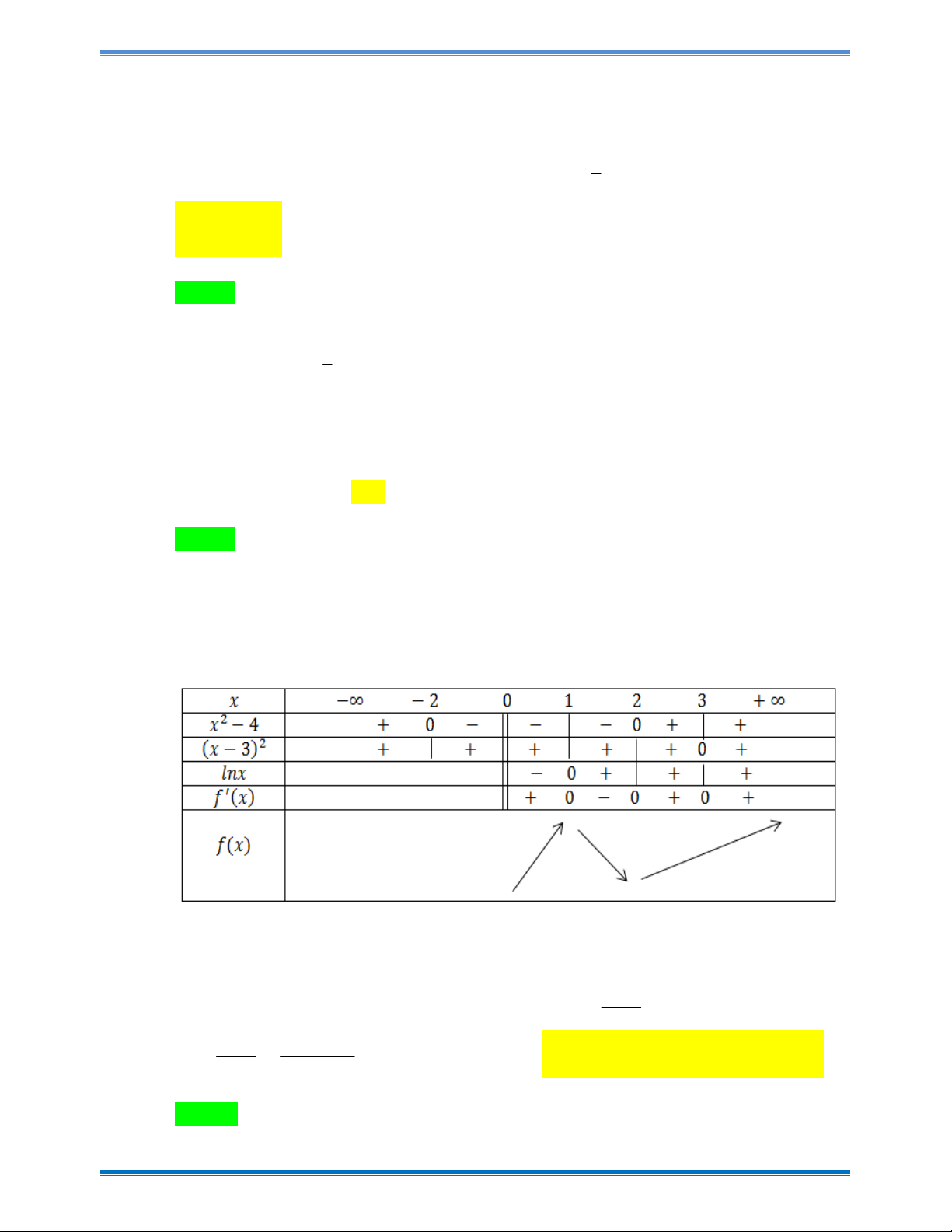
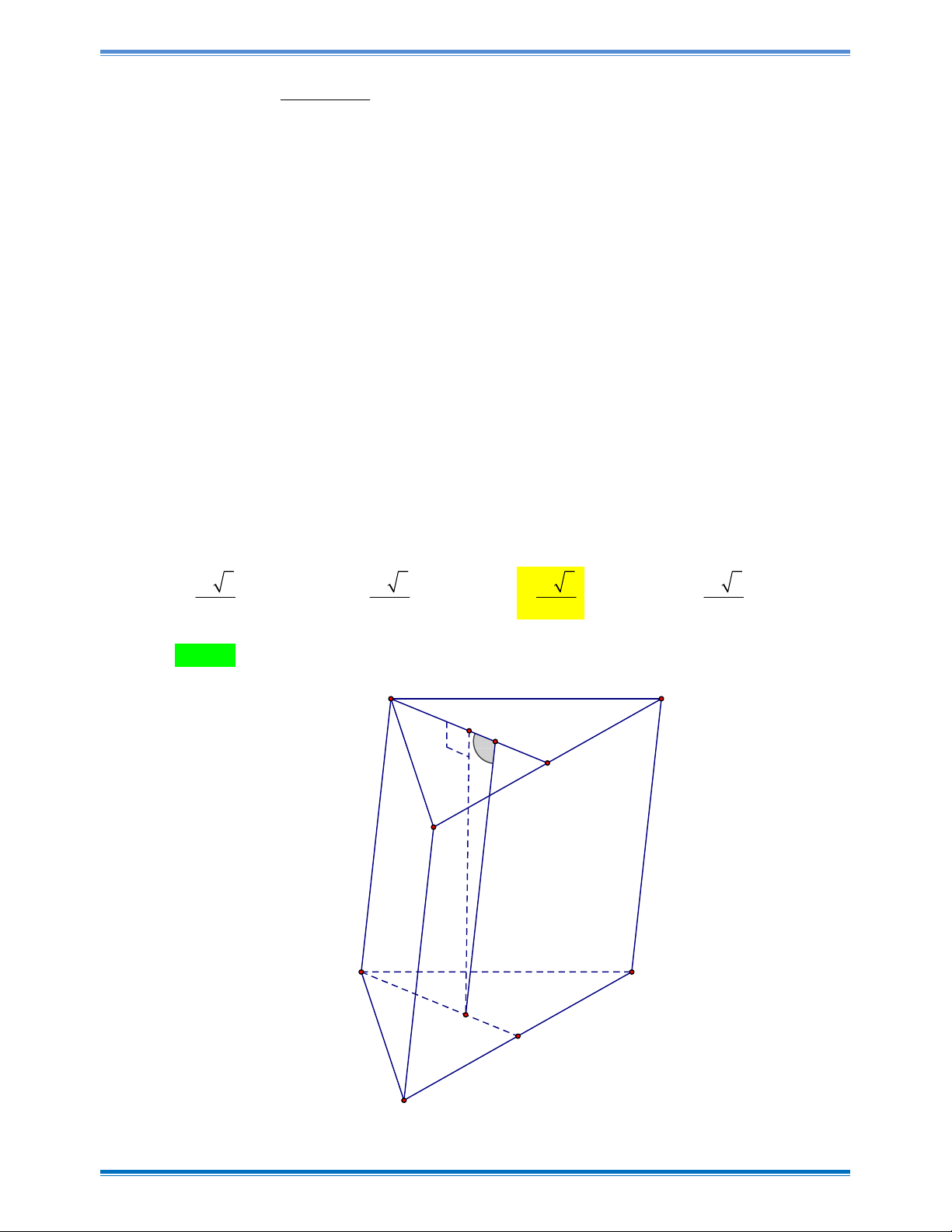
Câu 38: Cho hình lăng trụ tam giác ABC .AB C
  có đáy là tam giác đều cạnh a . Cạnh bên tạo với đáy một góc 0
60 . Gọi M là trung điểm của B C
  và I là trung điểm của đoạn AM
. Biết hình chiếu vuông góc của I trên mặt phẳng đáy ABC  là trọng tâm của tam giác
ABC . Tính thể tích của khối lăng trụ ABC.AB C   theo a . 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 4 48 16 12
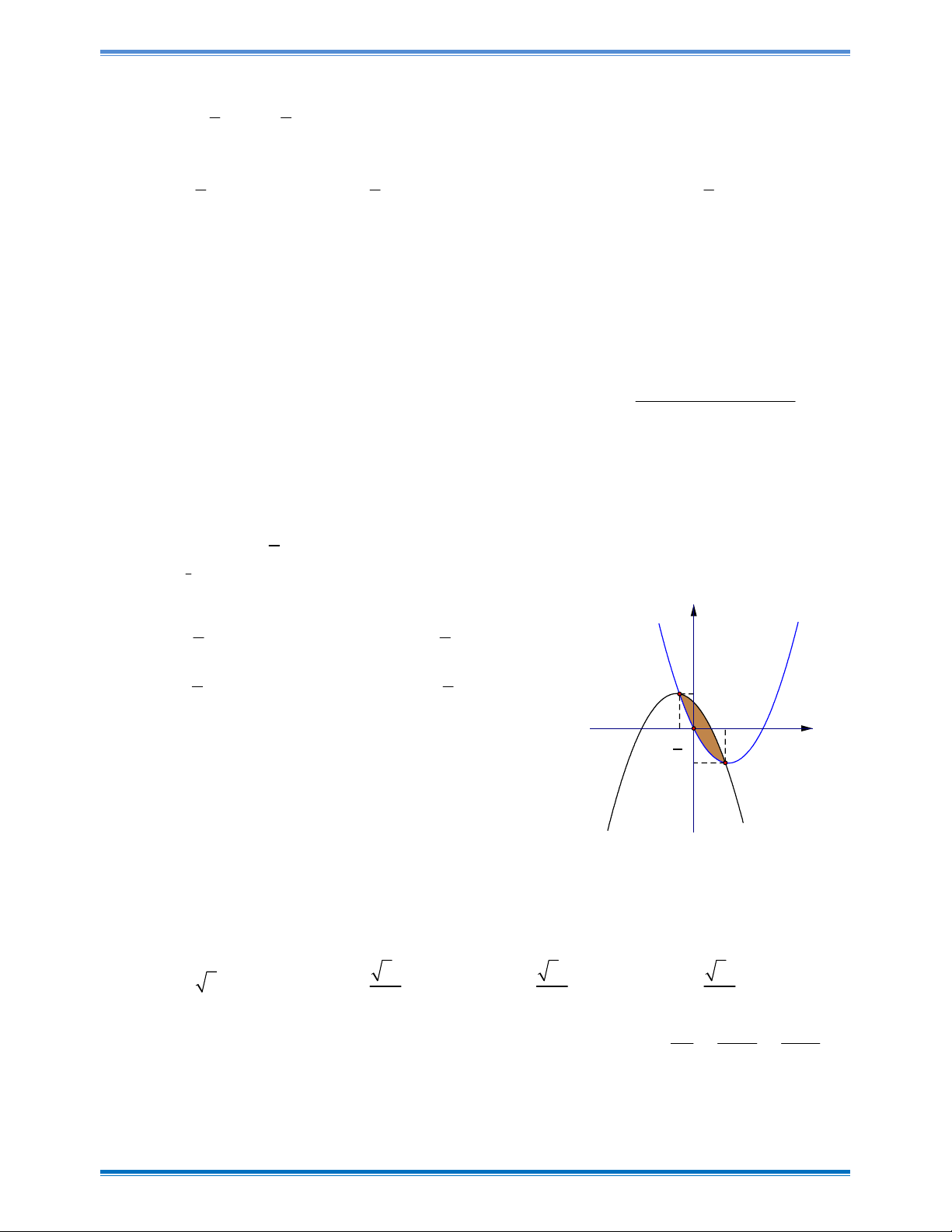
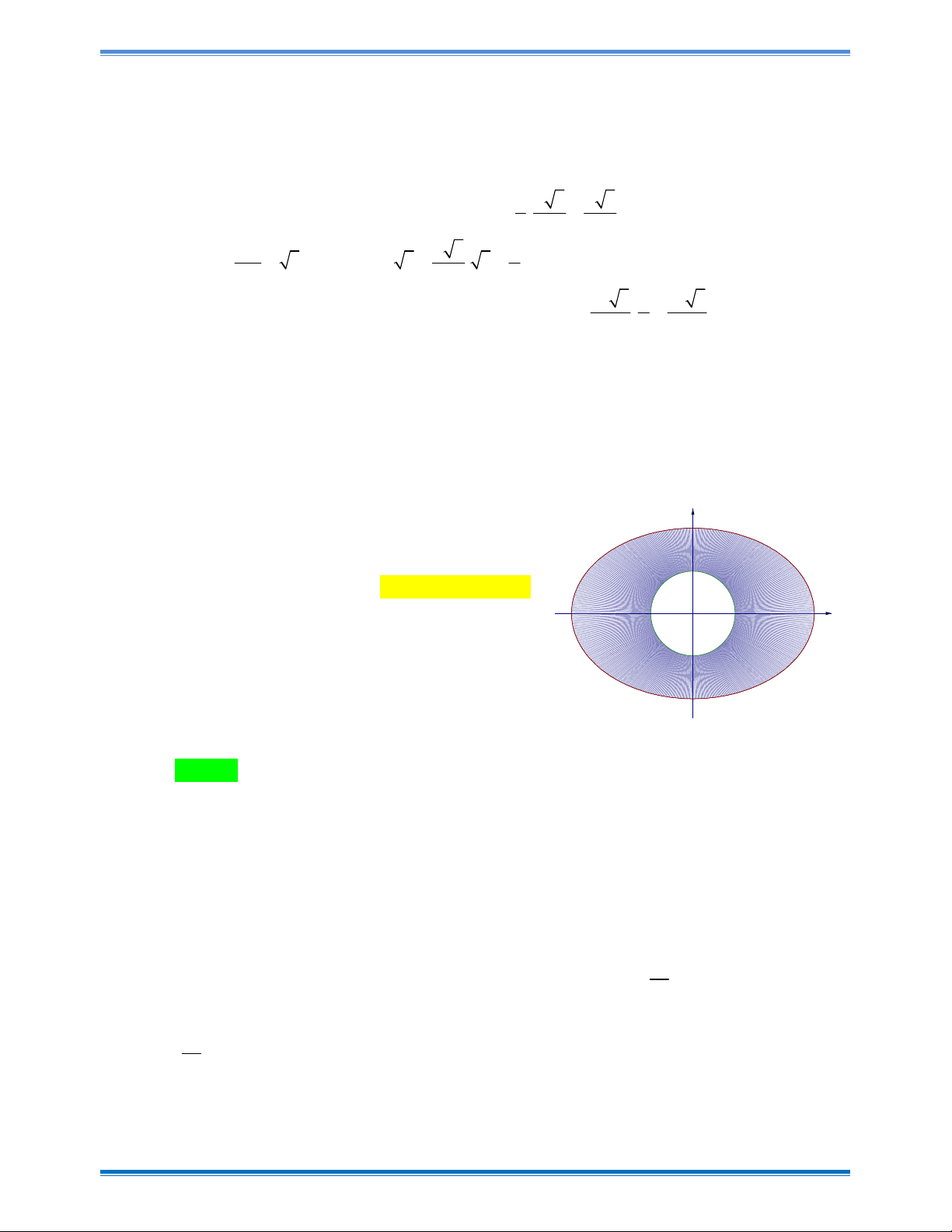
Câu 39: Bác Minh có một mảnh vườn hình Elip có độ dài trục lớn là 10m và độ dài trục nhỏ là
8m . Giữa vườn là một cái giếng hình tròn có bán kính 0,5m và nhận trục lớn và trục bé
của đường Elip làm trục đối xứng (như hình vẽ). Bác Minh muốn tròng hoa hồng đỏ
trên phần dải đất còn lại (xung quanh giếng). Biết kinh phí trồng hoa là 120.000 đồng/ 2
m . Hỏi Bác Minh cần bao nhiêu tiền để trồng hoa trên giải đất đó? (Số tiền làm tròn đến hàng nghìn).
A. 7.545.000 đồng. B. 7.125000 đồng.
C. 7.325000 đồng. D. 7.446.000 đồng.
Câu 40: Biết S là tập giá trị của m để tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số 4 2 3 2
y x m x  2x m trên đoạn 0;1
  bằng 16. Tính tích các phần tử của S . A.15 . B. 2 . C.17 . D. 2  . Trang 7
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Câu 41: Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số 1 1 2 5 3 2
y m x mx  10x   2 m m  
20 x đồng biến trên  . Tổng giá trị của tất cả 5 3
các phần tử thuộc S bằng 5 3 1 A. . B. . C. 2  . D. . 2 2 2
Câu 42: Ba anh em An, Bình, Cường cùng vay tiền ở một ngân hàng với lãi suất 0, 7% /tháng với
tổng số tiền vay của cả ba người là 1 tỉ đồng. Biết rằng mỗi tháng cả ba người đều trả
cho ngân hàng một số tiền như nhau để trừ vào tiền gốc và lãi . Để trả hết gốc và lãi cho
ngân hàng thì An cần 10 tháng, Bình cần 15 tháng và Cường cần 25 tháng. Số tiền trả
đều đặn cho ngân hàng mỗi tháng của mỗi người gần nhất với số tiền nào dưới đây? A. 21.400.000 đồng.
B.21.090.000 đồng. C.21.422.000 đồng. D.21.900.000 đồng. 2 x  1
Câu 43: Có tất cả bao nhiêu số nguyên m để đồ thị hàm số y  có ba 2 2
x  2mx  2m  25 đường tiệm cận? A.. 7 .. B.11. C. 5 . D. 9 .
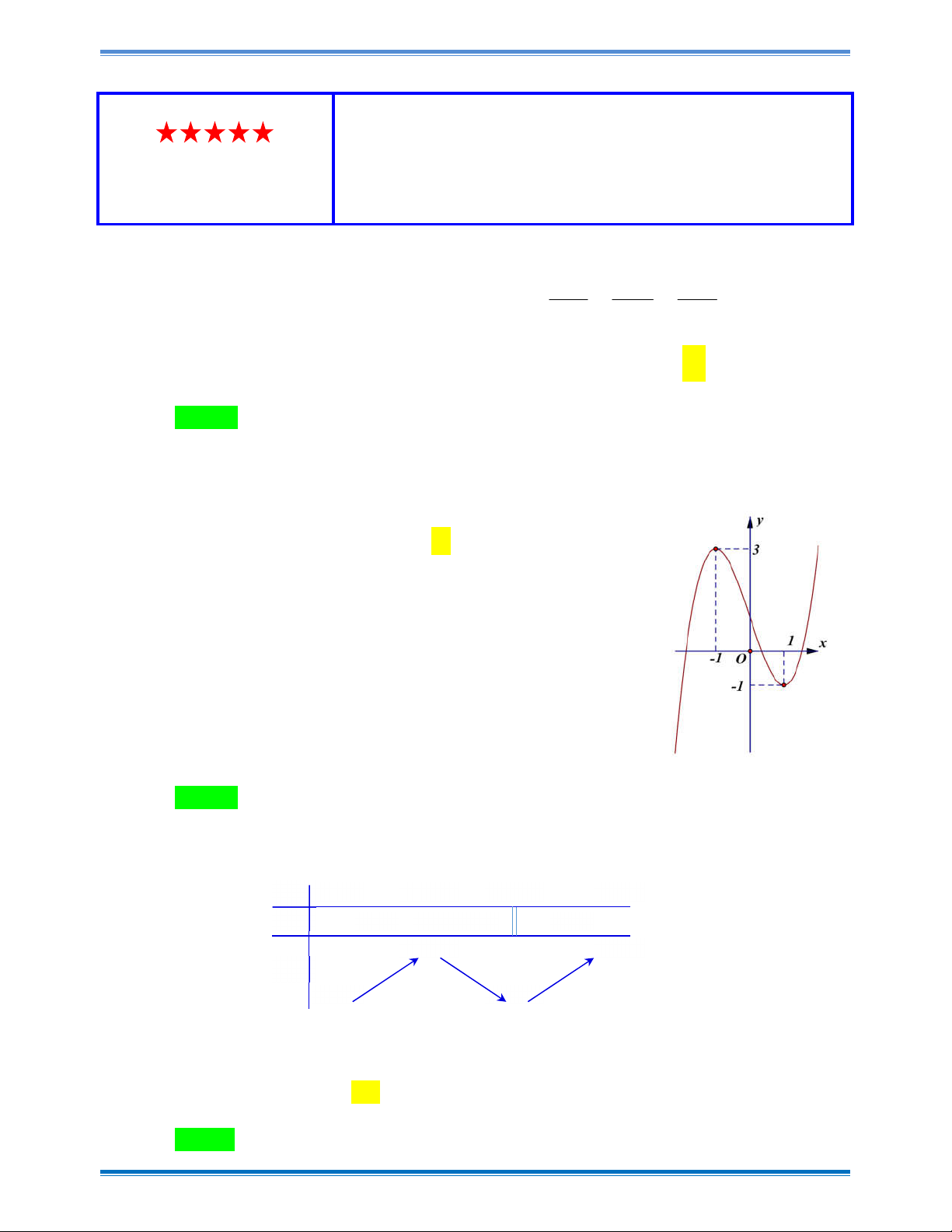
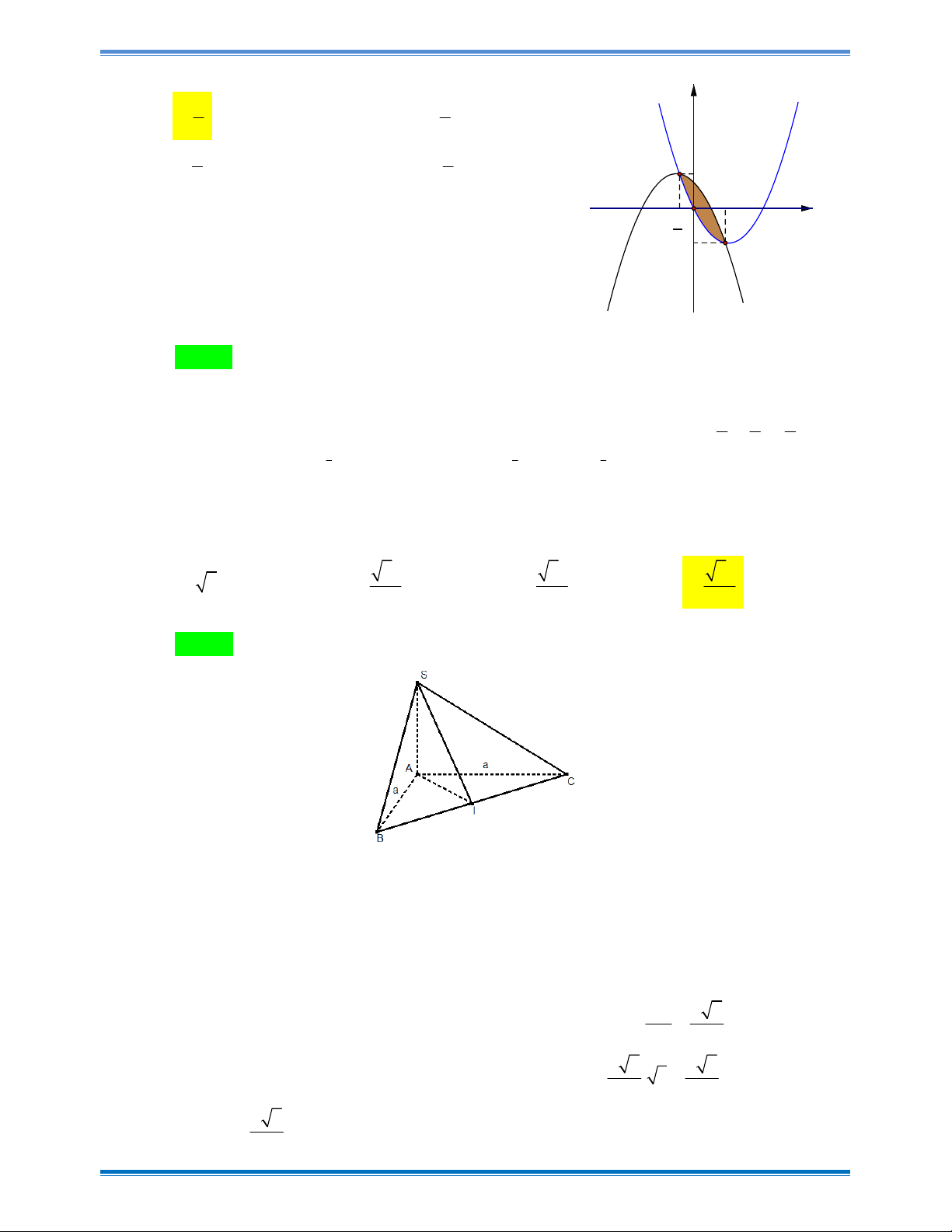
Câu 44: Miền phẳng trong hình vẽ được giới hạn bởi đường cong y f x và . 2
y x  2x . Biết 1 f x 3 dx  
. Khi đó diện tích hình phẳng được tô trên hình vẽ là 4 1 2 y 9 8 A. . B. . 8 3 8 3 C. . D. . 9 8 1 x O 1 - 2
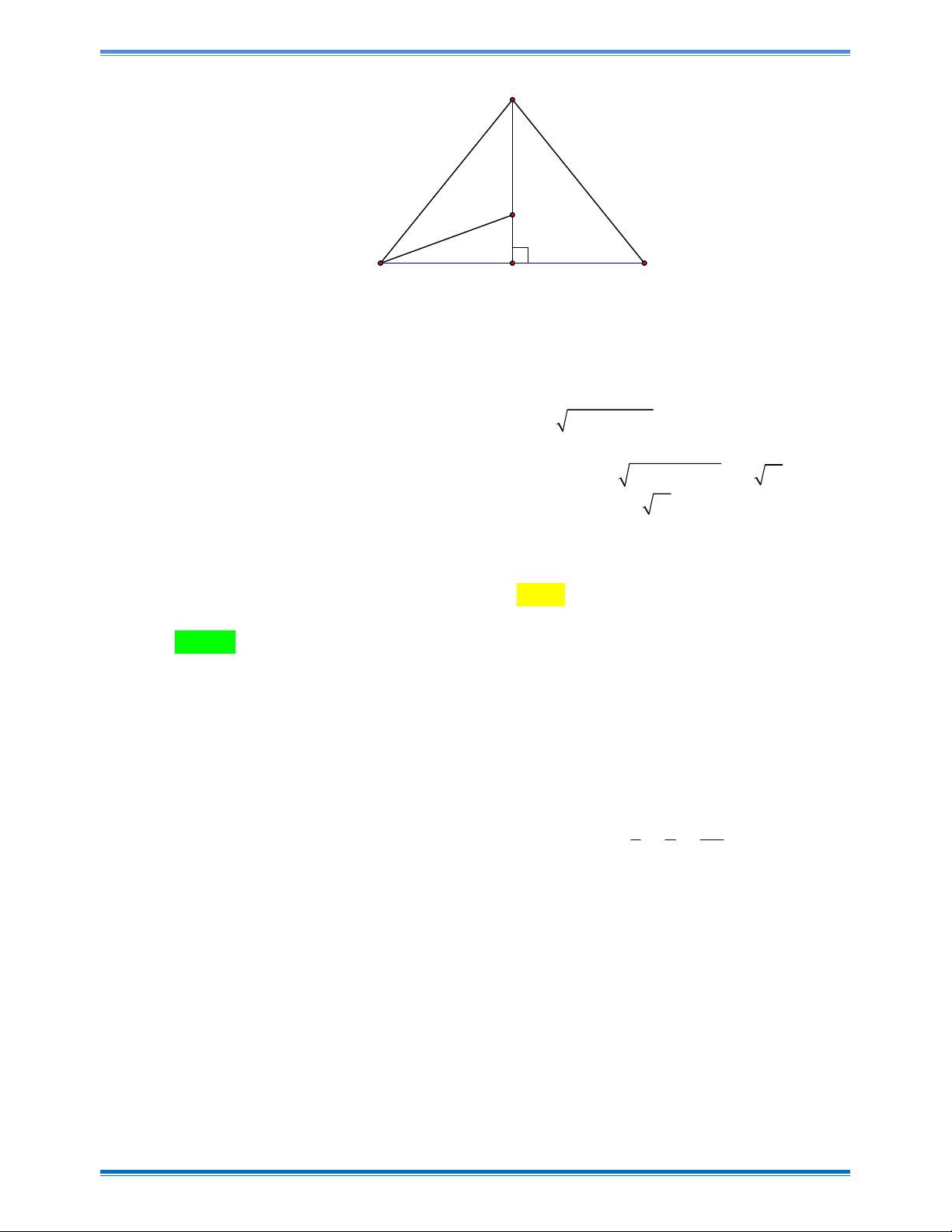
Câu 45: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại ,
A AB a , cạnh bên SA
vuông góc với đáy, góc tạo bởi giữa hai mặt phẳng SBC  và ABC  bằng 0 60 khi và chỉ khi SA bằng 6a 6a 6a A. 3a . B. . C. . D. . 6 4 2 x y  2 z  1
Câu 46: Trong không gian với hện tọa độ Oxyz , cho đường thẳng  :   và 1 1 3
mặt phẳng P : 11x my nz  16  0 . Biết   P , Tính giá trị của T m n . A.T  1  4 B.T  2  .
C.T  2 .
D.T  14 . Trang 8
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019 x  1 y  2 z  1
Câu 47: Trong không gian với hện tọa độ Oxyz , cho hai đường thẳng  :   1 2 1 1 x  2 y  1 z  2 và  :  
. Đường thẳng chứa đoạn vuông góc chung của  ,  đi 2 4 1 1  1 2 qua điểm nào sau đây? A.Q 3;1; 4   B. P 2;0;  1 .
C. M 0;2;  5 . D. N 1; 1  ; 4  .
Câu 48: Cho số phức z a bi a,b   thỏa mãn z  4 i z  2i  5 1  i. Tính giá trị
của biểu thức T a b . A. T  1  . B. T  2 . C. T  3 . D. T  1 .
Câu 49: Cho phương trình x  m   x3 4 1 .2
m  0 (*). Nếu phương trình (*) có hai nghiệm
x ,x thỏa mãn x x  2 thì m m . Giá trị m gần giá trị nào nhất trong các giá trị 1 2 1 2 0 0 sau? A. 0,5 . B. 3 . C. 2 . D.1, 3 .
Câu 50: Trong không gian với hệ trục tọa độ Oxyz , cho A 3  ;1;  1 ,B 1; 1  ;5 và mặt phẳng
P : 2x y  2z 11  0. Mặt cầu S đi qua hai điểm ,
A B và tiếp xúc với mặt phẳng
P tại điểm C . Biết C luôn thuộc đường tròn T cố định . Tính bán kính r của đường tròn T . A.r  3 . B.r  4 . C.r  2 . D.r  2 .
_____________________________Hết_______________________________
Cán bộ coi thi không giải thích gì thêm Trang 9
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
SỞ GD&ĐT CAO BẰNG
HƯỚNG DẪN GIẢI CHI TIẾT
ĐỀ THI THỬ THPT QUỐC GIA TỈNH CAO BẰNG NĂM HỌC 2018 - 2019 x  1 y  4 z  3 Câu 1:
Trong không gian Oxyz , cho đường thẳng d :   . Véctơ nào sau 1 2 3
đây không phải là véctơ chỉ phương của đường thẳng d ?    
A. a  1;2;3. B. a  3; 6  ;  9 .
C. a  1;2;3.
D. a  2; 4;  3 . Hướng dẫn giải Chọn D Câu 2:
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? A. 3 2 y x
  3x  1 B. 3 2
y x  3x  1 C. 3 2 y x   3x  1 D. 3 2
y x  3x  1 Hướng dẫn giải Chọn D
Đồ thị có dạng hàm số bậc 3 với hệ số a  0 và cắt trục Oy tại điểm có tung độ bằng 1. Câu 3:
Cho hàm số y f x có bảng biến thiên như sau x – ∞ -1 1 + ∞ y' + 0 – + 3 + ∞ y – ∞ -1
Hàm số có bao nhiêu điểm cực trị? A.1 B.2 C. 4 D. 3 Hướng dẫn giải Chọn B Trang 10
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Từ BBT nhận thấy đạo hàm đổi dấu khi qua hai điểm tới hạn x  1
 và x  1 . Vậy
hàm số có hai điểm cực trị. Câu 4:
Diện tích mặt cầu bán kính R bằng 4 A. 2 R . B. 2 4 R . C. 2 2 R . D. 2 R . 3 Hướng dẫn giải Chọn B
Công thức tính diện tích của mặt cầu có bán kính R : 2 S  4 R (đvdt)  Câu 5:
Tập xác định D của hàm số y  x   5 2 là
A. D   \   2 . B. D   .
C. D  2;   . D. D 2   ;    . Hướng dẫn giải Chọn A
Điều kiện để hàm số có nghĩa: x  2  0  x  2 .
Vậy TXĐ của hàm số là D   \   2 . Câu 6:
Nghiệm của phương trình log x  1  log 3  x là 3   3   A. x  3 . B. x  4 . C. x  2 . D. x  1 . Hướng dẫn giải Chọn D Cách 1:
Đk: 1  x  3 , nên loại phương án A và B. Thay nghiệm ở hai phương án còn
lại vào phương trình, nhận thấy nghiệm ở phương án D thỏa mãn. Vậy chọn D.
Cách 2: Giải tự luận
Đk: 1  x  3 (*)
PT  x  1  3  x x  1 (tm (*)). Chọn D. Câu 7:
Điểm nào ở hình vẽ bên biểu diễn cho số phức z  3  2i ? y A. Q . B. P . M 3 N C. N . D. M . 2 P x -2 O 2 3 -2 Q Hướng dẫn giải Chọn A
Dựa vào khái niệm biểu diễn hình học của số phức trên mặt phẳng tọa độ ta chọn phương án A. Câu 8:
Cho hàm số y f x có đồ thị như hình vẽ bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây? Trang 11
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019 y A. ;    1 . B.0;  1 . 2 C.1;  1 . D. 1  ;  0 . 1 x -1 O 1 Hướng dẫn giải Chọn D
Dựa vào đồ thị hám số nhận thấy đồ thị đi xuống từ trái qua phải với mọi x   1  ;0
Vậy hàm số y f x nghịch biến trên khoảng  1  ;  0 .  Câu 9:
Trong không gian Oxyz , cho AB  2; 3  ;  1 và điểm A1; 2
 ;4. Khi đó tọa độ của điểm B là A. B  3  ;5; 5  . B. B 1; 1  ;  3 . C. B 3; 5  ;  5 . D. B  1  ;1;3. Hướng dẫn giải Chọn C 
Ta có AB  x x ;y y ,z z , do đó ta có : B A B A B A x   x  2 x   2  x x   5  B AB AB       y
y  3  y
 3  y y   5   B  . B A B A B 5; 5;5    z  z 1 z  1 z z        5  B A   B A   B
Câu 10: Cho cấp số nhân u có số hạng đầu u  2 và công bội q  2 . Giá trị u là n  1 5 A. 32 . B. 1  6 . C. 6  . D.32 . Hướng dẫn giải Chọn A
Ta có: u u .q  2. 4 4 2  32 . 5 1
Câu 11: Trong không gian Oxyz , mặt phẳng P : x y z  3  0 đi qua điểm nào dưới đây? A. M  1  ; 1  ;  1 . B. N 1;1;  1 . C. P  3  ;0;  0 . D.Q 0;0; 3   . Hướng dẫn giải Chọn B
Thay ngẫu nhiên lần lượt tọa độ các điểm của 3 trong 4 phương án, nếu cả 3 phương án
tọa độ điểm đều không thỏa mãn thì chọn phương án còn lại là phương án đúng. 
Câu 12: Từ 10 điểm phân biệt trong mặt phẳng, có thể tạo ra ba nhiêu véctơ khác véctơ 0 ? A. 2 A . B. 20 . C. 10 2 . D. 2 C . 10 10 Hướng dẫn giải Chọn A
Chọn ngẫu nghiên 2 điểm phân biệt trong 10 điểm phân biệt để tạo ra véctơ, số cách chọn là 2
C . Cứ 2 điểm phân biệt bất kì luôn tạo ra hai véctơ khác véctơ-không. 10 Trang 12
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019 Vậy có 2
2.C  90 véctơ được tạo thành. Chọn A. 10
Câu 13: Họ nguyên hàm của hàm số   2  1 x f xe là 1 A.   2x
F x e C . B.   2x
F x x e C . 2 1 C.   2x
F x x e C . D.   2 1 2 x F x x xe    C . 2 Hướng dẫn giải Chọn C
Cách 1 : Sử dụng Casio
+) Chọn x  1  f   1  8, 4
+) Sử dụng Casio, tính đạo hàm ngẫu nhiên 3 hàm số trong 3 phương án tại x  1
, nếu ở 3 phương án kết quả không bằng 8,4 thì chọn phương án còn lại  Cách 2 : x 1 Ta có   2 1   2x
e dx x e C . Vậy chọn C. 2
Câu 14: Một hình hộp chữ nhật có ba kích thước là , a ,
b c . Thể tích V của khối hộp chữ nhật đó bằng 1
A.a cb . B.abc .
C.a bc . D. abc . 3 Hướng dẫn giải Chọn B 8 5
Câu 15: Cho hàm số f x  liên tục trên  , biết f
 xdx  7 và f
 xdx  5 . Khi đó 0 0 8
f xdx  bằng 5 A.12 . B. 2  . C. 2 . D.12 . Hướng dẫn giải Chọn D 8 5 8 8 8 5 Ta có f
 xdx f
 xdx f
 xdx f
 xdx f
 xdx f
 xdx  12 0 0 5 5 0 0 x  3
Câu 16: Cho hàm số y
có đồ thị C  . Gọi I là giao điểm của hai đường tiệm cận của x  2
C. Khi đó tọa độ của điểm I là  3   A. I  3  ;0. B. I 1;  2 . C. I 2;  1 .
D. I 0;   .  2 Hướng dẫn giải Chọn C
Đồ thị C  có TCĐ x  2 , TCN y  1. Vậy tọa độ giao điểm của hai đường tiệm cận
của C  là I 2;  1 . Trang 13
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Câu 17: Cho vật thể giới hạn bởi hai mặt phẳng x  0,x
, biết rằng thiết diện của vật thể 2    
khi cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0  x    là một  2 
hình tròn có bán kính R  cos x . Thể tích của vật thể đó là A. . 2. B. 1 . C. . D. 2 . Hướng dẫn giải Chọn D
Diện tích của hình tròn được tạo thành là S x  2  R
cosx , 0  x  . 2 2 2
Thể tích của vật thể là: V S
 xdx c
 osxdx  0 0
Câu 18: Cho hình trụ có tổng chu vi hai đáy là 12 và có chiều cao bằng 4 . Khi đó diện tích
toàn phần S của hình trụ là tp
A. S  42.
B. S  33.
C. S  24.
D. S  18. tp tp tp tp Hướng dẫn giải Chọn A
Gọi R là bán kính của đường tròn đáy .
Tổng chu vi của hai đáy hình lăng trụ là C  2.2R  4R , theo bài ta có 4 R
 12R  3 .
Diện tích đáy hình lăng trụ là: 2 S R  9 d
Diện tích xung quanh của hình lăng trụ là: S
 2Rh  24 xq
Vậy diện tích toàn phần của hình lăng trụ đã cho là S  2S S  42. tp d xq
Câu 19: Cho hàm số y f x có đạo hàm trên  . Đồ thị hàm số y f x như hình vẽ bên.
Hỏi đồ thị hàm số y f x   2x có bao nhiêu điểm cực trị ? y A. 3 . B. 4 . C.1 . D. 2 . 2 x O 2 -2 Hướng dẫn giải Chọn B Trang 14
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Xét hàm số y g x   f x   2x y = 2 2
Ta có: gx   f x   2
g x  0  f x   2 (1) x
Số nghiệm của (1) là số giao điểm của đường O 2
thẳng y  2 và đồ thị hàm số y f x.
Dựa vào đồ thị của hai đường ta suy ra -2 x x  1 x x
phương trình g x 2  0   x  0   x  2 
với x , x , 0 ( x x  0  2 ) và x  2 là 1 2 1 2 nghiệm bội chẵn.
Vậy đồ thị hàm số y g x   f x  2x có 3 điểm cực trị
(Ngô Kiều Lượng – THPT Trùng Khánh) 2
Câu 20: Đạo hàm của hàm số 2019x x y   là 2 A. 2019x x y    .ln 2019 . B.   2 2 1 .2019x x y x     .ln 2019 . C.   2 2 1 .2019x x y x x      . D.   2 2 1 .2019x x y x     . Hướng dẫn giải Chọn B
Áp dụng CT đạo hàm của hàm hợp  u   . u a
ua .lna 0  a   1 . Chọn B.
Câu 21: Cho hình nón bán kính r  12 nội tiếp hình cầu bán kính r  13 (như hình vẽ). Tính
diện tích xung quanh S của hình nón. xq
A. S  36 13. B. S  72 5. xq xq
C.S  36 5. D. S  72 13. xq xq Hướng dẫn giải Chọn D Trang 15
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019 O l I R r A H B
Giả sử mặt phẳng chứa trục hình nón cắt mặt cầu theo thiết diện là tam giác OAB với
O là đỉnh của hình nón, AB là đường kính đường tròn đáy của hình nón (như hv trên).
Gọi H là trung điểm của cạnh AB , I tâm của mặt cầu
I OH,IA IB IO R  13 .
Xét tam giác IHA, theo định lí Pitago ta có 2 2
IH AI AH  5 .
Do đó OH OI IH R  5  18
Xét tam giác vuông OHA , theo định lí Pitago ta có 2 2
OA OH AH  6 13 .
Vậy diện tích xung quanh của hình nón là S  .
 r.OA  72 13. xq
Câu 22: Trong không gian Oxyz , cho hai điểm A1; 3  ;  2 ,B 3;5; 2
 . Phương trình mặt phẳng
trung trực của đoạn AB có dạng x ay bz c  0 . Khi đó a b c bằng A. 3  . B. 2 . C. 4  . D. 2  . Hướng dẫn giải Chọn C Cách 1 :
Đặt  : x ay bz c  0  
Ta có AB  2; 8;4, một vtpt của mặt phẳng trung trực đoạn AB là n  1;a;b.
Gọi I là trung điểm của đoạn AB , ta có I 2;1;0 .       I    a 4 a c  0        
Đk để  là mp trung trực của đoạn AB      b   2 1 a b . AB   n      2 8 4 c   6  
Vậy a b c  4 .  Cách 2 :
+ Lập phương trình mặt phẳng trung trực của đoạn AB
+ Đồng nhất các hệ số hai phương trình ta suy ra a, ,
b c a b c .
Câu 23: Cho hàm số y f x liên tục trên đoạn  2;4  
 và có đồ thị như hình vẽ bên. Gọi M và
m là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn  2;4    . Giá trị của 2 2 M m bằng Trang 16
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019 y A. 20 . B. 8 . 7 C. 65 . D. 53 . y = f(x) 2 1 4 x -2 O 3 -2 -4 Hướng dẫn giải Chọn C
Hàm số y f x liên tục trên đoạn  2;4  
 , từ đồ thị ta có:
M maxf x  7;m minf x 2 2  4
  M m  65 .  2;4  2;4      
Câu 24: Cho lăng trụ tam giác ABC .AB C
  có khoảng cách từ A đến mặt phẳng ABC  bằng
6a . Khoảng cách từ trung điểm M của cạnh B C
  đến mặt phẳng ABC  bằng A. 6a . B. 2a . C. 4a . D. 3a . Hướng dẫn giải Chọn A C A I B O A' C' M B'
Gọi I là trung điểm của cạnh BC , suy ra tứ giác AIMA' là hình bình hành. Gọi O là
giao điểm của AM và A' I O là trung điểm của của đoạn AM , đông thời
O  AIMA'  d M,A'BC   d  ,
A A'BC   6a Trang 17
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Câu 25: Tập nghiệm S của bất phương trình 2
log x  5 log x  6  0 là 2 2  1 A.S   64;        . B.S 0;  64;    .  2   1   1
C.S   ;64. D.S   0;  . 2       2 Hướng dẫn giải Chọn C
Đk: x  0 *. Đặt log x t , ta thu được BPT: 2
t  5t  6  0  1  t  6 . Khi đó : 2 1
1  log x  6 
x  64 . Chọn C. 2 2
(Nguyễn Ngọc Chi – Giang – THPT Quảng Uyên)
Câu 26: Cho hàm số y f x có đạo hàm f x   x  x  2 2 4
3 ln x trên 0;   . Hỏi hàm số
y f x có bao nhiêu điểm cực trị? A. 4 . B. 2 . C. 3 . D.1 . Hướng dẫn giải Chọn B 2 x  4  0   x  2    2 
Ta có : f x   0  x   3  0  x  3   ln x 0    x  1    BBT:
Từ BBT ta chọn phương án B.
(Nguyễn Ngọc Chi – Giang – THPT Quảng Uyên) Câu 27: Cho ,
a b là các số thực dương thỏa mãn 2 2
a b  14ab . Khẳng định nào sau đây sai? a b
A. 2 log a b  4  log a  log b . B. 2 log
 loga  logb . 2   2 2 4 a b lna  lnb C. ln 
. D. 2 log a b  4  log a  log b . 2   4 2 4 4 Hướng dẫn giải Chọn D Trang 18
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019 2 Ta có: 2 2
a b  14ab  a b  16ab  2log a b  4  log a  log b  phương 2   2 2 án D sai.
Câu 28: Trong không gian Oxyz , cho điểm A1;2;3 và mặt phẳng P : x y  4z  3  0 . Mặt
cầu S tâm A và tiếp xúc với mặt phẳng P có phương trình là 2 2 2 2 2 2 A. x  
1  y  2  z  
3  2. B. x   1  y   2  z   3  2 . 2 2 2 2 2 2 C. x  
1  y  2  z  3  4 . D. x   1  y   2  z   3  4 . Hướng dẫn giải Chọn B   
Gọi R là bán kính của mặt cầu S . Ta có R d A P 1 2 12 3 ,   2 . 18
Vậy mặt cầu S tâm A , bán kính R  2 có phương trình: 2 2 2 x   1  y   2  z   3  2
Câu 29: Biết z là số phức có phần ảo âm và là nghiệm của phương trình 2
z  6z  10  0 . Tính z
tổng phần thực và phần ảo của số phức w  . z 4 2 7 1 A. . B. . C. . D. . 5 5 5 5 Hướng dẫn giải Chọn D
Sử dụng Casio tìm được số phức z  3  i , tiếp tục sử dụng Casio tìm được số phức 4 3 4  3   1 w
i , từ đó suy ra tổng phần thực và phần ảo của số phức w bằng      5 5 5  5 5
Câu 30: Biết M 2;  1 ,N 3; 
2 lần lượt là hai điểm biểu diễn cho số phức z ,z trên mặt phẳng 1 2
tọa độ phức Oxy . Khi đó môđun của số phức 2 z z bằng 1 2 A. 4 2 . B. 2 10 . C. 10 . D. 68 . Hướng dẫn giải Chọn B Ta có: z  2  ,
i z  3  2i . Sử dụng Casio tìm được 2
z z  2 10 . 1 2 1 2
Câu 31: Cho hàm số f x  thỏa mãn   x
f x xe và f  
0  2 . Tính f   1 . A. f   1  8  2e . B. f   1  5 e . C. f   1  e . D. f   1  3 . Hướng dẫn giải Chọn D 1 1 Ta có     x f x dx xe dx f   1 f   0  1  f  
1  1  f 0  3 0 0
Câu 32: Cho đồ thi của hàm số x
y a và y  log x như hình vẽ . Trong các khẳng định sau, b
khẳng định nào đúng? y Trang 19
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
A. 0  b  1  a . B. 0  a  1 và 0  b  1 .
C.a  1 và b  1 . D. 0  a  1  b . 1 x O 1 Hướng dẫn giải Chọn A
+) Từ điều kiện của hàm số mũ và hàm số logarit suy ra 0  , a b  1 .
+) Dựa vào đồ thị suy ra a  1 , b  1
Vậy 0  b  1  a .
Câu 33: Cho một khối lăng trụ có thể tích là 3
3a , đáy là tam giác đều cạnh a . Chiều cao h của khối lăng trụ bằng
A. h  2a .
B. h  4a .
C. h  12a .
D. h  3a . Hướng dẫn giải Chọn B 2 a 3
Diện tích đáy của khối lặng trụ là S  4 3 V a 3
Thể tích khối lăng trụ là V S.h h    4a . 2 S a 3 4 z i z i
Câu 34: Cho hai số phức z ,z thỏa mãn 1 2  1;
 2 . Giá trị nhỏ nhất của 1 2 z  2  3i z  1  i 1 2 z z là 1 2 A. 2 2 . B. 2  1 . C.1. D. 2 . Hướng dẫn giải Chọn A
+) Đặt z a bi . 1 Từ giả thiết: z i 1
 1  z i z  2  3i a  (b  1)i  (a  2)  (b  3)i a b  3  0 1 1 z  2  3i 1
+) Đặt z x yi 2 Từ giả thiết: z i 2
 2  z i  2 z  1  i 2 2 z  1  i 2
x  (y  1)i  2 (x  1)  (y  1)i 2 2
x y  4x  2y  3  0
Gọi M là điểm biểu diễn số phức z . Khi đó điểm M thuộc đường thẳng 1
 : x y  3  0. Trang 20
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Gọi N là điểm biểu diễn số phức z . Khi đó điểm N thuộc đường tròn tâm I(2;-1); bán 2 kính R  2.
Ta có: z z MN 1 2
Khi đó z z đạt GTNN 1 2  MN ngắn nhất 2  1  3
MN d(I, )   R
 2  2 2. Vậy min z z =2 2 . 2 1 2
(Hoàng Thị Thu – THPT Pò Tấu)
Câu 35: Có năm đoạn thẳng có độ dài lần lượt là 1 , cm 2cm, 3 , cm 4 ,
cm 5cm . Lấy ngẫu nhiên ra ba
đoạn thẳng , tính xác suất để ba đoạn thẳng được chọn ra là độ dài ba cạnh của một tam giác. 1 3 2 3 A. . B. . C. . D. . 10 10 5 5 Hướng dẫn giải Chọn B
Số phần tử của không gian mẫu là số cách chọn ngẫu nhiên 3 đoạn thẳng trong 5 đoạn
thẳng để tạo tam giác, ta có n   3   C . 5
Gọi X là biến cố: “Ba đoạn thẳng được chọn ra là độ dài ba cạnh của một tam giác”.
Vì một tam giác được tạo thành phải thỏa mãn điều kiện tổng hai cạnh lớn hơn cạnh
thứ ba nên chỉ có bộ ba đoạn thỏa mãn: 2;3;  4 ,2;4;  5 ,3;4;  5 .
Do đó số phần tử của biến cố X là n X   3 .
Vậy xác suất cần tìm là: P X  3  . 10
(Ngô Kiều Lượng – THPT Trùng Khánh)
Câu 36: Cho hàm số bậc ba y f x  có đồ thị là đường cong hình bên. Đồ thị hàm số  g x 2 x 1 
có tất cả bao nhiêu đường tiệm cận đứng? 2
f x  4f x y A. 3 . B. 2 . C. 5 . D. 4 . 4 2 x -1 O 1 Hướng dẫn giải Trang 21
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019 Chọn D y y = 4 4 2 x -1 O 1 2 x  1
Xét hàm số g x   2
f x  4f x
Txđ: D   \   1 f x  0 1  Xét phương trình 2
f x 4f x      0   .
f x  4   2 
Số nghiệm của phương trình  
1 là số giao điểm của đồ thị hàm số y f x và trục
hoành. Dựa vào đồ thị của hai đường suy ra phương trình   1 có một nghiệm đơn
x  1 và nghiệm x  1 bội 2 (do deg f x  3 ). 1 2
Lý luận tương tự, phương trình 2 có một nghiệm đơn x  1 và nghiệm x  1  bội 3 4
2 (do deg f x  3 ).
Như vậy ta có thể phân tích
f x 4f x  .
p x x x  2
1 .q x x x  2 1  .
p q x x x  2
1 x x x  2 2 1 1 3 1 3
với x  1  1  x và ,
p q là các hằng số thực. 2 3 2 x  1 1
Do đó g x    p q  . p q x x
x  1 x x x  1 . x x x  1 x x x  1 1  2  3  2  1   3  
Suy ra đồ thị hàm số y g x có 4 TCĐ.
(Ngô Kiều Lượng – THPT Trùng Khánh)
Câu 37: Cho đồ thị hàm số y f x  3 2
x  3x  4 có đồ thị như hình vẽ bên. Hỏi phương trình
f f x    1  
1 có bao nhiêu nghiệm thực? 2
3f x 5f x  4 Trang 22
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019 y A. 4 . B. 6 . C. 7 . D. 5 . 4 2 -1 x O 1 2 3 Hướng dẫn giải Chọn B
 Cách 1 : (Phạm Viết Biên – THPT Phục Hòa)
Với y f x nên ta có : f f  x  3 2   f (y) y  3y  4   1   1   1 2
(3y  5 y  4  0 x  ) 2
3f x  5f x 2 2  4 3y  5y  4 3y  5y  4  y  0 3 2 2 3 2 
y  3y  4  3y  5y  4  y  6 y  5 y  0  y  1   y  5  *với y  0 : 3 2
x  3x  4  0 có 2 nghiệm thực ( máy tính :)
*Với y  1 : 3 2 3 2
x  3x  4  1  x  3x  3  0 có 3 nghiệm thực ( máy tính) *Với y  5 : 3 2 3 2
x  3x  4  5  x  3x 1  0 có 1 nghiệm thực, 2 nghiệm phức ( máy tính)
f f x   Vậy phương trình  1 có 6 nghiệm thực. 2
3f x 5f x  4
 Cách 2: (Ngô Kiều Lượng – THPT Trùng Khánh) y y = 5 5 4 2 y = 1 1 x -1 O 1 2 3
Đặt f x   t 2 ,t   ;
 , từ giả thiết ta có f t 3 2
t  3t  4 3 Trang 23
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019 f t PT   1 
 1  f t 2
 3t  5t  4 4 2   3t  5t  4 t  0  
Từ 3 và 4 thu được PT: 2 3 2 3 2
3t  5t  4  t  3t  4  t  6t  5t  0  t  1  t  5 
f x  0 a 
Thay vào 2 ta thu được ba phương trình: f x  1 b 
f x  5 c 
Số nghiệm của phương trình a là số giao điểm của đồ thị hàm số y f x và trục
hoành Ox . Dựa vào đồ thị của hai đường suy ra PT a có hai nghiệm, một nghiệm
đơn x  1 , một nghiệm x  2 bội 2 (do deg f x   3 ). 1 2
Lí luận hoàn toàn tương tự, PT b có 3 nghiệm, PT c có 1 nghiệm.
Vậy phương trình đã cho có 6 nghiệm thực phân biệt. Chọn B.
Câu 38: Cho hình lăng trụ tam giác ABC .AB C
  có đáy là tam giác đều cạnh a . Cạnh bên tạo với đáy một góc 0
60 . Gọi M là trung điểm của B C
  và I là trung điểm của đoạn AM
. Biết hình chiếu vuông góc của I trên mặt phẳng đáy ABC  là trọng tâm của tam giác
ABC . Tính thể tích của khối lăng trụ ABC.AB C   theo a . 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 4 48 16 12 Hướng dẫn giải Chọn C a A' C' I G' 600 M B' A C G B Trang 24
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
Gọi G là trọng tâm tam giác ABC  G là hình chiếu vuông góc của I trên
mp ABC  và ngược lại  IG là đường cao của hình lăng trụ.
Gọi G’ là trọng tâm tam giác ’ A ’
B C’  GG’ / / ’
AA  là góc giữa cạnh A ’ A và mp  ’ A ’ B C   0
’  GG ' I  60 1 a 3 a 3 Xét tam giác ’
G IG ( vuông tại I ) có : IG '  .  6 2 12  IG a 3 a tan G' 
 3  IG IG '. 3  . 3  IG ' 12 4 2 3 a 3 a a 3
Vậy thể tích khối lăng trụ ABC. ’ A ’ B C’ là : V  .  .
ABC. A' B 'C 4 4 16
(Phạm Viết Biên – THPT Phục Hòa)
Câu 39: Bác Minh có một mảnh vườn hình Elip có độ dài trục lớn là 10m và độ dài trục nhỏ là
8m . Giữa vườn là một cái giếng hình tròn có bán kính 0,5m và nhận trục lớn và trục bé
của đường Elip làm trục đối xứng (như hình vẽ). Bác Minh muốn tròng hoa hồng đỏ
trên phần dải đất còn lại (xung quanh giếng). Biết kinh phí trồng hoa là 120.000 đồng/ 2
m . Hỏi Bác Minh cần bao nhiêu tiền để trồng hoa trên giải đất đó? (Số tiền làm tròn đến hàng nghìn).
A. 7.545.000 đồng. B. 7.125000 đồng.
C. 7.325000 đồng. D. 7.446.000 đồng. Hướng dẫn giải Chọn D
Độ dài trục lớn đường Elip 2a  10  a  5m, độ dài trục nhỏ đường Elip
2b  8  b  4m.
Diện tích của dải dất là diện tích hình Elip: S ab  2 20 m . E
Diện tích mặt giếng là diện tích của hình tròn bán kính r  0, 5m :
S  2   2 . 0.5 0,25 m . C  79
Diện tích của dải đất để trồng hoa hồng đỏ là S S S  m . E C  2 4
Vì kinh phí để trồng hoa là 120.000 đồng/ 2
m nên bác Minh cần: 79 .1
20000  7.446.000 đồng để trồng hoa trên dải đất đã cho. 4
(Ngô Kiều Lượng – THPT Trùng Khánh)
Câu 40: Biết S là tập giá trị của m để tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số 4 2 3 2
y x m x  2x m trên đoạn 0;1
  bằng 16. Tính tích các phần tử của S . Trang 25
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019 A.15 . B. 2 . C.17 . D. 2  . Hướng dẫn giải Chọn A Hàm số 4 2 3 2
y x m x  2x m luôn xác định và liên tục trên đoạn 0;1   . x  0 
Ta có y  x. 2 2
4x  3m x   4 ,y  0   2 2
4x  3m x  4  0 
Xét phương trình f x  2 2
 4x  3m x  4  0   1 Ta có 4
  9m  64  0 m và f 0  4   0   
1 có hai nghiệm phân biệt x ,x với 1 2 2 4 2 4 3m  9m  64 3m  9m  64 x 0,x 1 x ,x 0;1       1 2 1 2 8 8   BBT: x 0 1 - y' - m y - m2 - m - 1 Dựa vao BBT ta có 2 max y   , m min y m   m  1. 0;1 0;1     m   5 Theo bài ta có 2 max y min y 16 m 2m 15 0            0;1 0;1       m 3  
Do đó tích hai phần tử của tập S là   5 .3  1  5.
(Ngô Kiều Lượng – THPT Trùng Khánh)
Câu 41: Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số 1 1 2 5 3 2
y m x mx  10x   2
m m  2  0 x 5 3
đồng biến trên  . Tổng giá trị của tất cả các phần tử thuộc S bằng 5 3 1 A. . B. . C. 2  . D. . 2 2 2 Hướng dẫn giải ChọnD Txđ : D  
Ta có: f x  2 4 2
m x mx x   2 20
m m  2  0  f x 2  m  4
x   m  2 1 x   1  20x   1
f x  x   2 m  3 2 1
x x x  
1  m x   1  20   x    1.gx   .
Để hàm số đồng biến trên  thì f x  0, x   . Trang 26
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019 + Nếu x  1
 không phải là nghiệm của g x thì f x sẽ đổi dấu khi x x   đi qua 1
. Do đó điều kiện cần để hàm số đồng biến trên  là x  1  phải là nghiệm của g x  0 m   2  2  4
m  2m  20  0   5 . m    2 2 + Với m  2  2
thì f x   x  
1 4x  8x  
14  0, x   , do đó m  2  thỏa mãn. 5 1 2 5 + Với m
thì f x   x   1  2
25x  50x  6 
0  0, x   , do đó m  thỏa 2 4 2 mãn. 5    5 1 Vậy S   ; 2    2  
, tổng các phần tử của S bằng . 2    2 2
Câu 42: Ba anh em An, Bình, Cường cùng vay tiền ở một ngân hàng với lãi suất 0, 7% /tháng với
tổng số tiền vay của cả ba người là 1 tỉ đồng . Biết rằng mỗi tháng cả ba người đều trả
cho ngân hàng một số tiền như nhau để trừ vào tiền gốc và lãi. Để trả hết gốc và lãi cho
ngân hàng thì An cần 10 tháng , Bình cần 15 tháng và Cường cần 25 tháng. Số tiền trả
đều đặn cho ngân hàng mỗi tháng của mỗi người gần nhất với số tiền nào dưới đây? A.21.400.000 đồng.
B.21.090.000 đồng. C.21.422.000 đồng. D.21.900.000 đồng. Hướngdẫngiải ChọnC
Xét bài toán tổng quát sau: Ông X vay tiền ở một ngân hàng với lãi suất r% /tháng với
số tiền vay ban đầu là P đồng . Biết rằng mỗi tháng ông X đều trả cho ngân hàng một 0
số tiền như nhau để trừ vào tiền gốc và lãi . Để trả hết gốc và lãi cho ngân hàng thì ông
X cần n tháng. Tính số tiền ông X phải trả mỗi tháng.  Lời giải:
Số tiền gốc và lãi cuối tháng thứ nhất là P P .r P 1  r 0 0 0  
Gọi số tiền ông X đem trả ngân hàng mỗi tháng là a đồng
Số tiền ông X còn nợ cuối tháng thứ nhất là P P 1  r a 1 0  
Số tiền gốc và lãi cuối tháng thứ hai là : P P .r
P 1 raP
 1 r a        .r P  
1 r2 a 1 r 1 1 0 0 0   
Số tiền ông X còn nợ cuối tháng thứ 2 : P
P 1 r2 a 1 ra
P 1 r2 a 1 1 r            2 0 0      …
Số tiền ông X còn nợ sau n tháng là: n n  2 n 1   n 1  r 1
P P 1  ra 1
  1  r  1  r  ...  1  r
  P 1  r a. n 0         0     r
Ông X trả hết tiền ngân hàng khi : Trang 27
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019 n
a   r   n  rn .  1  1 1 1   P 0 P 1 r a. 0 P         * n 0   0 n   r r.1  r
Trở lại câu hỏi trong đề: Gọi a, ,
b c lần lượt là số tiền An , Bình và Cường vay ngân hàng , x là số tiền hàng tháng
phải trả. Để An, Bình và Cường trả hết nợ , áp dụng công thức   * ta có:      
x. 1  0,00710 1 x. 1  0,00715 1
x. 1  0,00725 1          1000.000.000 0, 007.1  0,00710 0, 007.1  0, 00715 0, 007.1  0, 00725
x  21.422.719 đồng.
(Ngô Kiều Lượng –THPT Trùng Khánh) 2 x  1
Câu 43: Có tất cả bao nhiêu số nguyên m để đồ thị hàm số y  có ba 2 2
x  2mx  2m  25 đường tiệm cận? A. 7 . B.11. C. 5 . D. 9 . Hướng dẫn giải Chọn C 2 x  1
Ta có lim y  1 , đồ thị C  của hàm số y  luôn có một TCN x 2 2
x  2mx  2m  25 y  1. Xét phương trình 2 2
x  2mx  2m  25  0   1 .
Đặt f x  2 2
x  2mx  2m  25 . Để đồ thị C  có ba đường tiệm cận khi và chỉ khi phương trình  
1 có hai nghiệm phân biệt khác 1   2   m   25  0      f   5 m 5 1 0     *      f    m   3; 4   1  0  
Do m   , kết hợp với  * suy ra m   1  ;0;  2 .
(Ngô Kiều Lượng – THPT Trùng Khánh)
Câu 44: Miền phẳng trong hình vẽ được giới hạn bởi đường cong y f x và 2
y x  2x . Biết 1 f x 3 dx  
. Khi đó diện tích hình phẳng được tô trên hình vẽ là 4 1 2 Trang 28
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019 y 9 8 A. . B. . 8 3 8 3 C. . D. . 9 8 1 x O 1 - 2 Hướngdẫngiải ChọnA
Từ hình vẽ trên , ta có diện tích hình phẳng giới hạn bởi đường cong y f x và 1 1 1 3 3 9 2
y x  2x   làS f  x 2
x  2xdx f
 xdx    2
x  2xdx        . 4 8 8 1 1 1    2 2 2
Câu 45: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại ,
A AB a , cạnh bên SA
vuông góc với đáy , góc tạo bởi giữa hai mặt phẳng SBC  và ABC  bằng 0 60 khi và chỉ khi SA bằng 6a 6a 6a A. 3a . B. . C. . D. . 6 4 2 Hướng dẫn giải ChọnD
Gọi I là trung điểm của BC .
Do ABC là tam giác vuông cân tại A nên AI  BC.
Do SA  (ABC) nên SA  BC Suy ra BC  SI.
Do đó góc tạo bởi hai mặt phẳng (ABC )và (SBC) là  0 SIA  60 . BC a 2
Trong tam giác ABC vuông cân tại A có AB = a . Ta có : AI   2 2 a a
Trong tam giác SAI vuông tại A ta có :  2 6
SA AI. tan SIA  . 3  . 2 2 a 6 Vậy SA  . 2 Trang 29
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
(Nông Ngân–THPT Trà Lĩnh) x y  2 z  1
Câu 46: Trong không gian với hện tọa độ Oxyz , cho đường thẳng  :   và 1 1 3
mặt phẳng P : 11x my nz  16  0 . Biết   P , Tính giá trị của T m n . A.T  1  4 B.T  2  .
C.T  2 . D.T  14 . Hướng dẫn giải Chọn Dx  2  t
Phương trình tham số của  :  y  2  t
z  1 3t  Ta có: 11. 2
t   m2  t   n 1
  3t  16  0   2
 2  m  3nt  2m n 16  0 (*)
Để    P thì phương trình (*) có vô số nghiệm
m  3n  22 m  10     2m n  16 n  4  
Vậy T m n  14 .
(Nông Ngân–THPT Trà Lĩnh) x  1 y  2 z  1
Câu 47: Trong không gian với hệ tọa độ Oxyz , cho hai đường thẳng  :   1 2 1 1 x  2 y  1 z  2 và  :  
. Đường thẳng chứa đoạn vuông góc chung của  ,  đi 2 4 1 1  1 2 qua điểm nào sau đây? A.Q 3;1; 4   B. P 2;0;  1 .
C. M 0;2;  5 . D. N 1; 1  ; 4  . Hướng dẫn giải ChọnA
Gọi  là đường vuông góc chung của  ,   ,  1 2 và  cắt 1
2 lần lượt tại A và B . x  2t
x  2  4t '    , 
 :  y  2  t ;  :  y  1 t ' . 1
2 có phương trình tham số là: 1 2 z 1 t   
z  2  t '   Vì A 
A   t   t t , B   B   t
t   t . 1  nên ( 1 2 ; 2 ;1 ) 2  nên ( 2 4 ';1 '; 2 ') Khi đó AB  ( 1
  2t  4t ';3  t t '; 3  t t ') .  
Đường thẳng  ,  có véctơ chỉ phương lần lượt là : u  ( 2  ;1;1), u  ( 4  ;1; 1  ) . 1 2 1 2     A . B u  0
Vì đường thẳng AB là đường vuông góc chung của  ,  nên 1   1 2   A . B u  0  2
2  4t  8t ' 3  t t ' 3  t t '  0  6
t  8t '  2 t   1 Do đó:     
4  8t 16t ' 3  t t ' 3  t t '  0
8t 18t '  10  t '  1     x  1 t  Như vậy ( A 1; 1
 ; 2), AB  (1;1; 3) và phương trình đường vuông góc chung là  y  1   t
z  2  3t
Điểm thuộc đường vuông góc chung là Q . Trang 30
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019
(Vi Thị Dung – THPT Trà Lĩnh)
Câu 48: Cho số phức z a bi a,b   thỏa mãn z  4 i z  2i  5 1  i.
Tính giá trị của biểu thức T a b . A.T  1  . B.T  2 . C.T  3 . D.T  1 . Hướng dẫn giải Chọn C Theo đầu bài 2 2 2 2
z  4 i z  2i  5(1 i) 
(a  4)  b . i a  (b  2)  5  5.i 2 2 2 2
 (a  4)  b  5  
a b  8a 11  0 a  2 Do đó ta có      2 2 2 2    
a b  4b 1  0 b  1 a (b 2) 5   
Vậy T a b  3.
(Vi Thị Dung–THPT Trà Lĩnh)
Câu 49: Cho phương trình x  m   x3 4 1 .2
m  0 (*) . Nếu phương trình (*) có hai nghiệm
x ,x thỏa mãn x x  2 thì m m . Giá trị m gần giá trị nào nhất trong các giá trị 1 2 1 2 0 0 sau? A. 0,5 . B. 3 . C. 2 . D.1, 3 . Hướng dẫn giải ChọnB Ta có: x xx x (*) x 2  (2 )  8   1 .2x mm  0 1 2 1 2
x x  2  2
 4  2 .2  4  m  4 . 1 2 Chọn B.
(Long Thị Hồng Gấm–THPT Thành Phố)
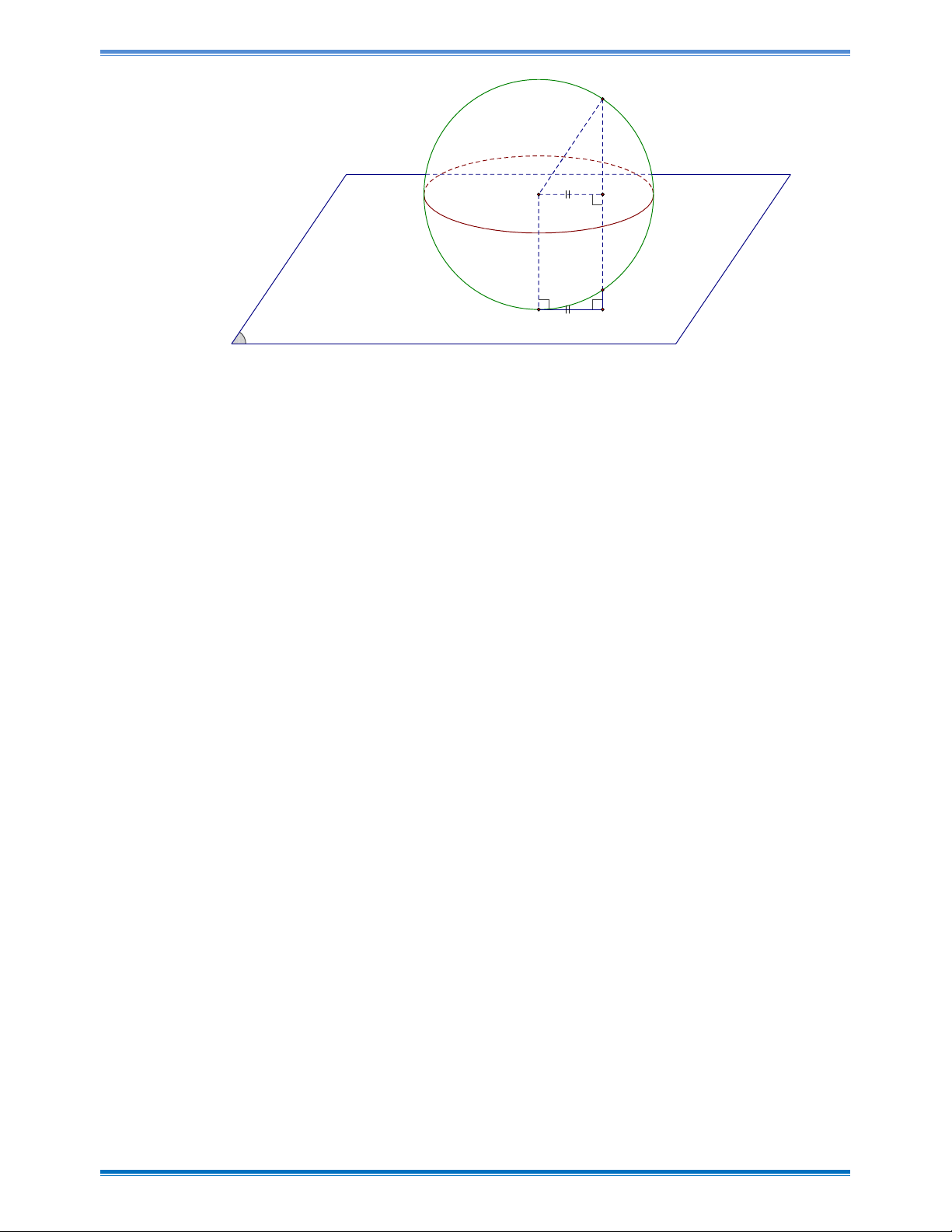
Câu 50: Trong không gian với hệ trục tọa độ Oxyz , choA 3  ;1;  1 ,B 1; 1
 ;5 và mặt phẳng
P : 2x y  2z 11  0. Mặt cầu Sđi qua hai điểm ,
A B và tiếp xúc với mặt phẳng
Ptại điểm C . Biết C luôn thuộc đường tròn T cố định . Tính bán kính r của đường trònT . A.r  3 . B.r  4 . C.r  2 . D.r  2 . Hướng dẫn giải Chọn B Trang 31
Nhóm Toán Cao Bằng
Đề thi thử THPTQG – L1 tỉnh Cao Bằng năm 2019 A (S) R I M B C r H P
Nhận xét : Đường thẳng AB vuông góc với mặt phẳng (P) cắt (P) tại điểm cố định H.
Ta sẽ chứng minh điểm C thuộc đường tròn tâm H bán kính r = CH
(độ dài không đổi )
Gọi M là trung điểm AB , M( -1; 0 ;3 )
Dễ thấy IMHC là hình chữ nhật: IM 2= IB2 - MB2
Ta có : IB = IC = MH = d(M;(P)) = 5; MB = 3.
Vậy: CH = IM = 4  C luôn thuộc đường trònT cố định, bán kính r = 4.
(Long Thị Hồng Gấm–THPT Thành Phố - Cao Bằng) Trang 32