Đề thi thử TN THPT 2021 môn Toán kênh truyền hình Giáo dục Quốc gia VTV7 (Đề 1)

Giới thiệu đến quý thầy, cô giáo cùng các em học sinh đề thi thử TN THPT 2021 môn Toán kênh truyền hình Giáo dục Quốc gia VTV7 (Đề 1), nhằm giúp các em rèn luyện để chuẩn bị cho kỳ thi tốt nghiệp THPT 

31 16 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

34 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
KỲ THI TRUNG HỌC PHỔ THÔNG QUỐC GIA NĂM 2021
Môn thi: TOÁN
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
ĐỀ THAM KHẢO SỐ 1
Đề thi có 06 trang
KỲ THI TRUNG HỌC PHỔ THÔNG QUỐC GIA NĂM 2021
MÔN THI: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Câu 1: Có bao nhiêu vectơ khác vectơ không được tạo thành từ 8 điểm phân biệt cho trước?
A.
8!
. B.
2
8
C
. C.
2
8
A
. D.
2!
.
Lời giải
Chọn C
Mỗi vectơ khác vectơ khôngđược tạo thành bởi 2 điểm phân biệt nên đáp án cần chọn là
C
.
Câu 2: Cho cấp số cộng
n
u
có
1
5u
và
2
1u
. Công sai của cấp số cộng bằng
A.
4
. B.
4
. C.
6
. D.
6
.
Lời giải
Chọn BTa có
2 1 2 1
4u u d d u u
.
Câu 3: Cho hàm số
y f x
có bảng biến thiên như hình vẽ
Hàm số
y f x
đồng biến trên khoảng?
A.
1;
. B.
0;
. C.
0;2
. D.
;1
.
Lời giải
Chọn A
Câu 4: Cho hàm số
y f x
có đồ thị như hình bên dưới.
Điểm cực đại của đồ thị hàm số là:
A.
2; 3
. B.
3;2
. C.
1;0
. D.
0;1
.
Lời giải
Chọn D
Dựa vào đồ thị hàm số.
Đ
Ề
THAM KH
Ả
O
S
Ố
(Đề thi có 06 trang)
Câu 5: Cho hàm số
y f x
liên tục trên
và có bảng xét dấu của đạo hàm như hình vẽ sau
Hàm số
y f x
có bao nhiêu điểm cực trị?
A.
3.
B.
2.
C.
1.
D.
0.
Lời giải
Chọn A
Từ bảng xét dấu của đạo hàm ta.
Câu 6: Tiệm cận ngang của đồ thị hàm số
1
3 1
y
x
là đường thẳng
A.
0x
. B. 0y . C.
1
3
y
. D.
1
3
x
.
Lời giải
Chọn B
+) Tập xác định:
1
\
3
D
.
+) Ta có


1
lim lim 0
3 1
x
x
y
x
.
Vậy đường tiệm cận ngang của đồ thị hàm số đã cho là đường thẳng 0y .
Câu 7: Đường cong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
2 1
.
1
x
y
x
B.
3 2
3 2.y x x .
C.
3 2
3 2.y x x . D.
3 2
3 2.y x x
Lời giải
Chọn D
Đồ thị hàm số bậc ba có hệ số
0a
nên loại
.
B
Xét đáp án A: ta có
2
3 6y x x
3 2x x
. Lúc đó
0y
2;0x , điều này không
phù hợp với đồ thị đã cho nên loại.
Câu 8: Số giao điểm của đồ thị hàm số
4 2
2 1y x x và trục tung là:
A. 3. B. 4. C. 2. D. 1.
Lời giải
Chọn D
Phương trình hoành độ giao điểm của đồ thị hàm số
4 2
2y x x và trục tung:
0 1x y nên đồ thị và trục tung có môt giao điểm.
Câu 9: Cho các số thực dương a ,
b
. Mệnh đề nào sau đây đúng?
A.
3
2 2 2
3
2 1
log 1 log 3 log
3
a
a b
b
. B.
3
2 2 2
3
2 1 1
log 1 log log
3 3
a
a b
b
.
C.
3
2 2 2
3
2 1
log 1 log 3 log
3
a
a b
b
. D.
3
2 2 2
3
2 1 1
log 1 log log
3 3
a
a b
b
.
Lời giải
Chọn C
Ta có:
1
3
3
2 2
3 3
2 2
log log
a a
b b
1
3
3
2 2 2
log 2 log loga b
2 2
1
1 log 3 log
3
a b
.
Câu 10: Đạo hàm của hàm số
2 1x
y e là
A.
2 1
2
x
y e . B.
2 1x
y e . C.
2 1
2
x
y xe .D.
2 1
1
2
x
y e
.
Lời giải
Chọn A
Ta có
2 1 2 1 2 1
2 1 . 2.
x x x
y e y x e e
.
Câu 11: Rút gọn biểu thức
3
5
2
.P x x (với
0x
)?
A.
13
2
x . B.
4
7
x . C.
3
10
x . D.
17
10
x .
Lời giải
Chọn D
Với
0x
thì
3 3 1 3 1 17
5
2 2 5 2 5 10
. .P x x x x x x .
Câu 12: Phương trình:
2
1
3
9
x
có nghiệm là
A.
2
. B.
2
. C.
1
. D.
1
.
Lời giải
Chọn C
Ta có:
2 2 2
1
3 3 3 2 2 1
9
x x
x x
.
Câu 13: Nghiệm của phương trình
3
log 2 1 2x
là
A.
5x
. B.
4x
. C.
9
2
x
. D.
7
2
x
.
Lời giải
Chọn A
Điều kiện xác định
1
2
x
.
2
3
log 2 1 2 2 1 3 2 1 9 5x x x x
.
Câu 14: Nguyên hàm của hàm số
2
1
3y x x
x
là
A.
3 2
3
ln
3 2
x x
x C
. B.
3 2
3
ln
3 2
x x
x C
.
C.
3 2
3
ln
3 2
x x
x C
. D.
3 2
2
3 1
3 2
x x
C
x
.
Lời giải
Chọn B
Áp dụng công thức nguyên hàm ta có
3 2
2
1 3
3 d ln
3 2
x x
x x x x C
x
.
Câu 15: Nguyên hàm
sin 2 dx x
bằng:
A.
1
cos2
2
x C
. B. cos2x C . C.
1
cos2
2
x C
. D. cos2x C .
Lời giải
Chọn C
Ta có
sin 2 dx x
1
sin2 d2
2
x x
1
cos2
2
x C
.
Câu 16: Cho
1
0
d 2f x x và
2
1
d 3f x x . Khi đó
2
0
2 df x x bằng
A.
5
2
. B.
5
. C.
10
. D.
6
.
Lời giải
Chọn C
2 1 2
0 0 1
2 d 2 d d 2 2 3 10f x x f x x f x x .
Câu 17: Tích phân
2018
0
2 d
x
I x bằng
A.
2018
2 1
ln 2
. B.
2018
2
ln2
. C.
2018
2 . D.
2018
2 1.
Lời giải
Chọn A
2018
2018
2018
1
0
0
2 2 1
4 5 2 d 2 3
ln 2 ln 2
x
x
w iI x z i
Câu 18: Cho hai số phức và
2
1 2z i
. Số phức liên hợp của số phức
1 2
w z z
là
A.
3 2w i
. B.
1 4w i
. C.
3w i
. D. 3w i .
Lời giải
Chọn C
Ta có
1 2
3 3w z z i w i
.
Câu 19: Cho hai số phức
1
2z i
và
2
2 4z i
. Số phức
1 2
w z z
bằng
A.
3w i
. B.
3w i
. C.
4 3w i
. D.
4 3w i
.
Lời giải
Chọn A
Ta có
1 2
w z z
2 2 4 3i i i
.
Câu 20: Điểm biểu diễn số phức
2021z i
là
A.
0;2021P
. B.
2021; 0Q
. C.
2021;2021M
. D.
0;0N
.
Lời giải
Chọn A
Theo lý thuyết ta có điểm biểu diễn số phức
2021z i
là
0;2021P
.
Câu 21: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi tâm
O
cạnh a , góc
30BCA ,
SO ABCD
và
3
4
a
SO
. Khi đó thể tích của khối chóp là
A.
3
2
4
a
. B.
3
3
8
a
. C.
3
2
8
a
. D.
3
3
4
a
.
Lời giải
s
A
B
C
D
O
30
a
3
4
a
Chọn B
Theo giả thiết
ABCD
là hình thoi tâm
O
cạnh a , góc
30BCA nên
60BCD ;
BCD
đều suy ra
BD a
,
3
2
a
CO
, 2 3AC CO a .
Ta có
1
.
2
ABCD
S AC BD
2
1 3
. . 3
2 2
a
a a
;
.
1
.
3
S ABCD ABCD
V SO S
với
3
4
a
SO
suy ra
2 3
.
1 3 3 3
3 4 2 8
S ABCD
a a a
V
.
Câu 22: Cho lăng trụ
.ABC A B C có đáy
ABC
là tam giác đều cạnh
2a
. Hình chiếu vuông góc của
A trên
ABC
trùng với trọng tâm của tam giác
ABC
, góc giữa
A A và mặt đáy bằng
60
.
Thể tích khối lăng trụ
.ABC A B C bằng:
A.
3
3a . B.
3
2 3a . C.
3
3
3
a
. D.
3
2 3
3
a
.
Lời giải
Chọn B
Theo bài ta có
A G ABC
; ; 60A A ABC A A AG A AG A AG .
Xét tam giác
A AG vuông tại
G
ta có:
2 2 3
.tan .tan60 .2 . . 3 2
3 3 2
A G AG A AG AM a a
.
Diện tích tam giác
ABC
:
2
2
3
2 . 3
4
ABC
S a a
.
Thể tích khối lăng trụ
.ABC A B C là:
2 3
' . 2 . 3 2 3
ABC
V A G S a a a
.
Câu 23: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang với
//AD BC
và
2AD BC
. Kết luận
nào sau đây đúng?
A.
. .
3
S ABCD S ABC
V V
. B.
. .
2
S ABCD S ABC
V V
. C.
. .
4
S ABCD S ABC
V V
. D.
. .
6
S ABCD S ABC
V V
.
Lời giải
Chọn A
Ta có
1
3
ABC ABCD
S S
. .
1
3
S ABC S ABCD
V V
. .
3
S ABCD S ABC
V V
.
Câu 24: Một hình trụ có chiều cao bằng
3
, chu vi đáy bằng
4
. Tính thể tích của khối trụ?
A.
40
. B.
18
. C.
10
. D.
12
.
Lời giải
Chọn D
Ta có: 2 4R 2R .
Thể tích khối trụ là:
2
V R h
2
.2 .3
12
.
Câu 25: Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm
2;3;4A
,
8; 5;6B
. Hình chiếu
vuông góc của trung điểm
I
của đoạn
AB
trên mặt phẳng
Oxz
là điểm nào dưới đây.
A.
3; 1;5N
. B.
3;0;5Q
. C.
3; 0;0P
. D.
0; 1;5M
.
Lời giải
Chọn B
Tọa độ trung điểm của
AB
là
3; 1;5I
.
Vậy hình chiếu của
I
trên mặt phẳng
Oyz
là
3;0;5M
.
Câu 26: Trong không gian Oxyz , mặt cầu
2 2 2
( ) : ( 1) 25S x y z có bán kính bằng
A.
25.
B.
5.
C.
625.
D.
10.
Lời giải
Chọn B
Phương trình mặt cầu là:
2 2 2 2
( ) ( ) ( )x a y b z c R nên
2
25 5.R R
.
D
M
B
C
A
S
Câu 27: Trong không gian ,Oxyz mặt phẳng nào dưới đây đi qua điểm ( 1;3;1)?M
A.
1
: 2 0P x y z
. B.
2
: 2 2 0P x y z
.
C.
3
: 2 5 0P x y z
. D.
4
: 2 0P x y z
.
Lời giải
Chọn B
Thay tọa độ của điểm
M
trực tiếp vào các phương trình để kiểm tra.
Câu 28: Trong không gian ,Oxyz vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua
hai điểm
1; 1;2M
và (1;2; 1)?N
A.
1
(2;1;1)u
. B.
2
(0; 3;1)u
. C.
3
(0;1; 1)u
. D.
4
(0; 3; 3)u
.
Lời giải
Chọn C
Ta có

3 3
(0;3; 3) 3MN u u
là một vectơ chỉ phương của đường thẳng
.MN
.
Câu 29: Chọn ngẫu nhiên một số trong
23
số nguyên dương đầu tiên. Xác suất đề chọn được số lẻ
bằng
A.
12
23
. B.
11
23
. C.
10
23
. D.
1
2
.
Lời giải
Chọn A
Trong
23
số nguyên dương đầu tiên 1,2,3, ,23, ta đếm được có
12
số lẻ nên xác suất cần
tìm là
12
.
23
.
Câu 30: Hàm số nào dưới đây đồng biến trên
?
A.
2 1
1
x
y
x
. B.
3 2
3 3 1y x x x .
C.
3 2
y x x x . D.
4 2
2 1y x x .
Lời giải
Chọn B
Hàm số đồng biến trên
trước hết phải có tập xác định ,D loại câu A, xét các câu khác.
Chỉ có
2
3 2 2
( 3 3 1) 3 6 3 3 1 0, ,x x x x x x x
dấu bằng xảy ra khi
1x
(hữu hạn).
Câu 31: Gọi ,M m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
4 2
( ) 52f x x x trên
đoạn
0;3
. Tổng M m bằng
A. 11. B.
53.
C.
52.
D.
52.
Lời giải
Chọn D
Ta có
3
( ) 4 4f x x x và
( ) 0 0, 1f x x x
. Trên [0;3], ta xét các giá trị
(0) 5, (1) 6, (3) 58.f f f
Do đó 6, 58M m và 52.M m
Câu 32: Tập nghiệm của bất phương trình
2
8
2564
x
là
A. [ 1;1]. B.
( 2 3;2 3]
. C. [ 2;2]. D. [2; ) .
Lời giải
Chọn C
Ta có
2
8 2 2
4
4 256 8 log 256 4 4 2 2.
x
x x x
.
Câu 33: Nếu
2
1
3. 1d 10f x x thì
2
1
df x x bằng?
A. 3. B.
13
3
. C.
10
3
. D.
11
3
.
Lời giải
Chọn D
Áp dụng tính chất tích phân
2 2 2
1 1 1
11
10 3 ( ) 1 d 3 ( )d 1 ( )d .
3
f x x f x x f x x
.
Câu 34: Cho số phức
1 3z i
. Số phức
(1 )w i z z
có môđun bằng
A. 5 2. B.
2.
C. 10. D. 2.
Lời giải
Chọn D
Ta có:
1 2w i w
.
Câu 35: Cho hình hộp chữ nhật
. ' ' ' 'ABCD A B C D
có 4 2 , 4 , ' 4AB cm AD cm AA cm . Góc giữa
đường thẳng
'A C
và mặt phẳng ( ' ')ABB A bằng
A.
30
. B.
60
. C.
90
. D.
45
.
Lời giải
Chọn A
Ta có
' ' ' 'A C AA B B A
và
' 'CB AA B B
'A B là hình chiếu vuông góc của
'A C
' , ' ' ' , ' 'A C AA B B A C A B BA C
2
2
4 3
tan '
' 3
4 2 4
BC
BA C
A B
' 30BA C
Câu 36: Cho hình chóp
SABC
có đáy là tam giác vuông tại
.A
Biết
AB a
, 3AC a ,
2SA a
và
SA
vuông góc với mặt phẳng đáy. Khoảng cách từ điểm
A
đến mặt phẳng
SBC
bằng
A.
57
19
a
. B.
2 57
19
a
. C.
2 3
19
a
. D.
2 38
19
a
.
Lời giải
Chọn B
Từ
A
kẻ
AD BC
mà
SA ABC SA BC
BC SAD
SAD SBC
mà
SAD SBC SD
Từ
A
kẻ
AE SD AE SBC
;d A SBC AE
Xét
ABC
vuông tại
A
ta có:
2 2 2 2
1 1 1 4
3AD AB AC a
Xét
SAD
vuông tại
A
ta có:
2 2 2 2
1 1 1 19
12AE AS AD a
2 57
.
19
a
AE
Câu 37: Trong không gianOxyz , mặt cầu có tâm là
1; 2;3M
và đi qua điểm ( 1;0;2)N có phương
trình là:
A.
2 2
2
1 2 3.x y z
B.
2 2 2
1 2 3 9.x y z
C.
2 2 2
1 2 3 9.x y z
D.
2 2 2
1 2 3 3.x y z
Lời giải
Chọn C
Bán kính của mặt cầu là
3MN
, do có tâm là (1; 2;3)M nên có phương trình là
2 2 2
1 2 3 9.x y z
.
Câu 38: Trong không gian ,Oxyz đường thẳng đi qua hai điểm ( 1;3;1)A và (2;1; 1)B có phương
trình tham số là:
A.
1 3
3 2
1 2
x t
y t
z t
. B.
2 3
1 2
1 2
x t
y t
z t
. C.
1 3
3 2
1 2
x t
y t
z t
. D.
1
3 4
1
x t
y t
z
.
Lời giải
Chọn B
Ta có: Đường thẳng nhận

(3; 2; 2)AB
là vectơ chỉ phương và đi qua điểm (2;1; 1)B nên
có phương trình tham số là
2 3
1 2
1 2
x t
y t
z t
.
Câu 39: Cho hàm số ( )y f x liên tục trên R và có đồ thị như hình vẽ. Giá
trị lớn nhất của hàm số
2
( ) ( 2)g x f x trên
1; 3
đạt được tại
điểm nào sau đây?
A.
1.x
B.
0.x
C. 3.x D.
1.x
Lời giải
Chọn D
Đặt
2
2 2;1t x t
Xét hàm số
( )h t f t
trên đoạn
2;1
, từ đồ thị ta thấy hàm số đạt giá trị lớn nhất
2
1
1 2 1
1
x l
t x
x n
Vậy hàm số
2
( ) ( 2)g x f x đạt giá trị lớn nhất tại
1.x
Câu 40: Có bao nhiêu giá trị nguyên dương của tham số m để tập nghiệm của bất phương trình
2
log 2 1 3 0
x
x m
chứa không quá
9
số nguyên?
A.
6560
. B.
6561
. C.
19683
. D.
19682
.
Lời giải
Chọn B
2
2
2
3
log 2 1 0
2
3 0 3
log 2 1 3 0
3
log 2 1 0
2
2
3 0
3
x x
x
x
x
x
x
m m
x m
x
x
m
m
1
3
3
3
2
log
3
2
2
log
m
x
x m
x
x m
3
3
log
2
x m
(loại
3
3
2
2
log
x
x m
, do 1m nên
3
log 0x m
).
Vì tập nghiệm của bất phương trình chứa không quá
9
số nguyên, mà
3
2
x
, tức là có chứa
các số nguyên
1
;
0
;
1
; …; 7; 8;… nên
3
log 8x m
8
3 6561m
.
Mà
m
nên
1;2;...;6561m
. Vậy có
6561
giá trị m thỏa YCBT.
Câu 41: Cho hàm số
2
5 2 1
1 2 1
x khi x
f x
x khi x
. Giá trị của tích phân
2
3 2
2
3 1 1 dI f x x x x
bằng
A.
28
. B.
11228
9
. C.
7504
9
. D.
2021
.
Lời giải
Chọn C
Đặt
3 2 2
1
3 1 d 3 3 d 1 d d
3
t x x t x x x x t
.
Đổi cận:
2 : 13x t
và
2 : 15x t
Khi đó:
15
13
1
dt
3
I f t
1 15
13 1
1
dt dt
3
f t f t
1 15
2
13 1
1
5 2 dt 1 2 dt
3
t t
1 15
2
13 1
1 1 6790 7504
5 2 dt 1 2 dt 238
3 3 3 9
t t .
Câu 42: Xét các số phức
1
z
,
2
z
thoả mãn
1 2 2
1 2 3; 2021 6 2021 4z i z i z i
và số phức
z thoả mãn rằng biểu thức
1 2
P z z z z
đạt giá trị nhỏ nhất. Giá trị lớn nhất của
z
là
A. 2021 B. 5 C. 34 D. 26
Lời giải
Gọi
M
là điểm biểu diễn cho
1
z
, ta có tập hợp điểm
M
là đường
tròn tâm
1; 2I
, bán kính 3R
Gọi
N
là điểm biểu diễn cho
2
z
, ta có tập hợp điểm
N
là đường
thẳng 5y
Gọi
A
là điểm biểu diễn cho số phức z , ta có: P AM AN .
Để
P
nhỏ nhất thì toạ độ các điểm phải là
1;1 , 1;5M N
và điểm
A
phải thuộc đoạn thẳng
MN
, từ đó suy ra z a bi
với 1;1 5a b . Vậy giá trị lớn nhất của biểu thức
z
là 26
Câu 43: Cho hình chóp . ,S ABC đáy
ABC
là tam giác vuông tại
A
và
, 3.AB a AC a
Hai mặt
phẳng
SAB
và
SBC
tạo với đáy 1 góc bằng nhau. Hai đường thẳng
SA
và
BC
vuông góc
với nhau và khoảng cách giữa hai đường bằng
2
a
. Thể tích khôi chóp
.S ABC
bằng
A.
3
2
.
12
a
B.
3
2
.
36
a
C.
3
2
.
4
a
D.
3
2
.
6
a
Bài giải
Chọn A
Vẽ
3
2
a
AI BC BC SAI AI
. Vẽ
SH AI SH ABC
Vì hai mặt phẳng
SAB
và
SBC
tạo với đáy 1 góc
bằng nhau H nằm trên đường phân giác góc
B
3
2
3
AH AB a
AH
HI BI
Từ
I
vẽ
,
2
a
HK SA d BC SA IK
Trong
AIK
vuông tại
3 2
sin tan
3 2
IK
K IAK IAK
AI
Trong
SHA
vuông tại
2 6
tan .
2 6
SH a
H SAH SH AH
AH
2 3
.
1 1 6 3 2
. .
3 3 6 2 12
S ABC ABC
a a a
V SH S
.
b
N
1
M
5
I
-2
O
1
y
x
A
Câu 44: Để chuẩn bị cổ vũ cho đội tuyển Việt Nam tham dự vòng loại thứ 3 World Cup 2022. Một hội
cổ động viên dự định sơn trang trí
1000
chiếc nó lá với cách sơn như sau. Tính theo độ dài
đường sinh của chiếc nón lá là
40 cm
kể từ đỉnh nón cứ
8 cm
thì sơn màu đỏ, màu vang
xen kẽ nhau như hình minh họa, sau đó dán 20 ngôi sao vàng vào mỗi chiếc nón. Biết rằng
đường kính của đường tròn đáy nón
40 cm
, mỗi ngôi sao vàng giá 200 đồng, sơn màu vàng
giá
5000
đồng/
2
m , sơn màu đỏ giá
4000
đồng/
2
m . Hỏi giá thành để trang trí 1000 chiếc nón
lá đó gần với số tiền nào sau đây?
.A.
5105840
đồng. B.
5105841
đồng. C.
5156106
đồng. D. 5156107 đồng.
Lời giải
Chọn B
Đặt
1 2 3 4 5
40; 32; 24; 16; 8l l l l l
khi đó bán kính và diện tích của các khối nón đỉnh S
tương ứng với các đường sinh kể trên là
2
2 2 2 2
1 1 1 2 2 2 2 1
1 1 1 1
16 16
;
25 25
S r l l
S rl S r l S S
S r l l
.
Tương tự
3 1 4 1 5 1
9 4 1
; ;
25 25 25
S S S S S S
Như vậy diện tích phần màu vàng là
2
2 3 4 5 1
2 2
.40.20 320
5 5
S S S S S cm
Diện tích sơn màu đỏ là
3
1
3 3
.40.20 480
5 5
S cm
Giá tiền để trang trí
1000
một chiếc nón là
320 480
.5000 .4000 20.200 1000 5105841
10000 10000
đồng.
Câu 45: Trong không gian
,Oxyz
cho mặt cầu
2 2 2
: 1 2 2 9S x y z
và mặt phẳng
:2 2z 1 0P x y
. Đường thẳng
đi qua
O
tiếp xúc với mặt cầu
S
và cắt
P
tại
A
sao cho
OA
nhỏ nhất có phương trình là
A.
:
10 7 2
x y z
. B.
:
10 7 2
x y z
.
C.
:
10 7 2
x y z
. D.
:
10 7 2
x y z
.
Bài giải
Chọn B
2 2 2
: 1 2 2 9 1;2; 2 , 3S x y z I R
và
O S
Mặt phẳng
đi qua
O
tiếp xúc với mặt cầu
S
có phương trình
: 2 2z 0x y
Gọi
 
; 2;2;3
d
P
d P u n n . Để
OA
nhỏ nhất thì
OA d
Vậy
;OA d OA OI
đường thẳng qua
có 1 vectơ chỉ phương

; 10;7;2
d
u u OI Phương trình đường
:
10 7 2
x y z
.
Câu 46: Cho hàm số bậc bốn ( )y f x sao cho (0) 2f và hàm số
y f x
có đồ thị trong hình vẽ
bên. Xác định số điểm cực trị của hàm số
2
( 44 2)y f x x x
.
A. 3. B.
5
. C.
4
. D.
6
.
Lời giải
Chọn B
Nhận xét: Các điểm
2;1 , 0; 0 , 4; 2A O B
đều nằm trên đường thẳng
1
:
2
d y x
.
Đặt
2
2 4 4 2 2 24g f x x x f xg xx x
2
2
2
0
x
fg x x
0;2;6x
Bảng biến thiên hàm số
g x
:
Ta có:
lim
x
g x
và
2 4 0 4 4 0g f
.
Mặt khác:
Ta có:
0
0
1
2
2
d 2 2 0 2 2S f x x f x f f nên
2 0f
do đó:
0 4 2 0g f
.
Mà:
4
4
2
0
0
d 6 6 0 4 6S f x x f x f f
4 2 6 4f
do đó:
6 4 4 12 0g f
.
Suy ra hàm số
y g x
có
3
cực trị và phương trình
0g x
có hai nghiệm phân biệt nên
hàm số
2
4 ( 2) 4y f x x x
có
5
điểm cực trị.
Câu 47: Cho hàm số
y f x
là hàm số chẵn trên tập số thựcR và có đồ thị như
hình vẽ.Biết rằng tồn tại các giá trị của tham số m để phương trình
2 2
2
3.3 4 3 3 3 3 0
f x f x
m f x m có đúng 7 nghiệm thực
phân biệt. Tổng lập phương các giá trị đó của m là:
A
. 8.
B.
1.
C. 7. D. 7.
Lời giải
Chọn B
Ta có:
2 2 2 2
2
2
2 2
3.3 4 3 3 3 3 0 3.3 3 4 3 3 3
1 1
3 4 3 3 *
3
3
f x f x f x f x
f x
f x
m f x m m f x m
m f x m
Nhận thấy, nếu
o
x
là một nghiệm của
*
thì
o
x
cũng là nghiệm của
*
.
Suy ra, điều kiện cần để phương trình
*
có 7 nghiệm thực phân biệt là
*
có nghiệm
0x
.
Mà theo đồ thị, ta thấy
0 0f
2
2
1
1 1 . 3 3 2 0
1
3
m
m m m m
m
.
Thử lại:
Với
2m
thì
*
trở thành
2
2
1 2
3 4 3 1
3
3
f x
f x
f x .
Nhận thấy,
2
2
1
3 2
3
Cauchy
f x
f x
VT
,
2
. 3 2
3
VP
nên
1
0f x
, theo đồ thị, suy
ra phương trình có 3 nghiệm x nên
2m
không thỏa mãn.
Với
1m
thì
*
trở thành
2
2
1 1
3 4 6
3
3
f x
f x
f x
2
2
1 2
3 2 3 0
3
3
f x
f x
f x
* *
Đặt
2
; 0f x t t
Xét hàm số
1 2
3 2 3
3
3
t
t
g t t
với
0t
.
Ta có
ln 3 2
' 3 .ln 3
3
3
t
t
g t
t
,
2
2
3
ln 3 1
'' 3 ln 3 0
3
3
t
t
g t
t
với mọi
0t
.
'g t
đồng biến trên
 0; ' 0g t có nhiều nhất 1 nghiệm
0t
.
phương trình
0g t
có nhiều nhất 2 nghiệm
0t
.
Lại có,
1 0g
và
0 0g
Phương trình
* *
có 3 nghiệm là
2
2
0 0
1 1
f x f x
f x f x
,.
hay phương trình ban đầu có đúng 7 nghiệm. Vậy
1m
thỏa mãn.
Câu 48: Cho hàm số bậc bốn ( )y f x có đồ thị như hình vẽ. Biết hàm
số ( )f x đạt cực trị tại
1 2 3
, ,x x x
thỏa mãn
3 1
2.x x
Gọi
1
S
và
2
S
là diện tích của hai phần được gạch trong hình bên. Tỉ
số
1
2
S
S
bằng
A.
3
4
. B.
5
6
.
C.
7
8
. D.
9
10
.
Lời giải
Chọn C
Kết quả bài toán không đổi nếu ta đổi hệ trục tọa đô xOy thành
'XO Y
.
Khi đó trong hệ trục tọa độ mới, hàm số có dạng
4 2
( )g X AX BX và
4 2
( )g X AX BX có hai
điểm cực trị tương ứng là
1
và
1
là nghiệm của
3
4 2 0AX BX
, do đó hàm số có dạng
4 2
( ) .( 2 )G X k X X với 0k .
Diện tích hình chữ nhật bằng
1 2
1. ( 1)S S G k
.
Diện tích
0
4 2
1
1
7
2
15
S k X X dX k do đó
2
7 8
15 15
S k k k
và
1
2
7
8
S
S
.
Câu 49: Có bao nhiêu số phức z thỏa mãn
2
4 3 84 0z z i z
?
A. 1. B. 2. C. 3. D. 4.
Lời giải
Chọn B
Ta có phương trình bậc 2 theo z có . 4.( 84) 0a c nên phương trình luôn có nghiệm thực.
Do đó z , nên
2
3 9z i z
Vậy ta có
2 2 2 2
4 9 84 0 9 84 4z z z z z z
4 2
2
15 681 7056 0
84 4 0
z z
z z
2
2
2
16
147
5
84 4 0
z
z
z z
4
147
5
z
z
.
Câu 50: Trong không gian Oxyz , cho mặt phẳng
: 6 0P x z
, đường thẳng
1 1 5
:
1 1 1
x y z
d
. Điểm J thay đổi trên mặt phẳng
P
sao mặt cầu tâm J tiếp xúc với
cả hai mặt cầu
1
S
tâm
0;0;0O
bán kính
1
5R
, mặt cầu
2
S
tâm
2;0;2I
bán kính
2
1R
. Điểm M thay đổi trên đường thẳng
d
. Giá trị nhỏ nhất của
MJ
bằng
A.
6 3 7
2
. B.
3 6 7
3
. C.
6 5 7
3
. D.
6 5 7
2
.
Lời giải
Chọn B
Giả thiết suy ra
2
S
nằm trong
1
S
. Gọi
;J R
là mặt cầu
tiếp xúc với cả
1
S
,
2
S
.
Suy ra
1
JO R R
,
2 1 2
2 1 2
6
*
4
JI R R JO JI R R
JO JI
JI R R JO JI R R JO JI
Dễ thấy
OI P
tại
3;0;3H
. Đặt
2 2
18; 2 HJ x JO x JI x
thay vào
*
ta được
2 2
2 2
18 2 6
7
3
18 2 4
x x
x
x x
. Do
J P
và
7
3
JH
nên tập hợp các điểm J là đường
tròn tâm H nằm trong mặt phẳng
P
và có bán kính
7
3
r
.
Ta thấy
d P
và không cắt
,H r
nên
min
3 6 7
,
3
MJ d H d r
.
| 1/34
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

KỲ THI TRUNG HỌC PHỔ THÔNG QUỐC GIA NĂM 2021
ĐỀ THAM KHẢO SỐ 1 Môn thi: TOÁN Đề thi có 06 trang
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
KỲ THI TRUNG HỌC PHỔ THÔNG QUỐC GIA NĂM 2021 MÔN THI: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian phát đề ĐỀ THAM KHẢO SỐ 1 (Đề thi có 06 trang)
Câu 1: Có bao nhiêu vectơ khác vectơ không được tạo thành từ 8 điểm phân biệt cho trước? A. 8!. B. 2 C . C. 2 A . D. 2!. 8 8 Lời giải Chọn C
Mỗi vectơ khác vectơ khôngđược tạo thành bởi 2 điểm phân biệt nên đáp án cần chọn là C .
Câu 2: Cho cấp số cộng u có u  5 và u  1. Công sai của cấp số cộng bằng n  1 2 A. 4 . B. 4 . C. 6. D. 6. Lời giải Chọn BTa có
u  u d  d  u u  4 . 2 1 2 1
Câu 3: Cho hàm số y  f x có bảng biến thiên như hình vẽ
Hàm số y  f x đồng biến trên khoảng? A. 1;. B. 0;. C. 0;2. D. ; 1. Lời giải Chọn A
Câu 4: Cho hàm số y  f x có đồ thị như hình bên dưới.
Điểm cực đại của đồ thị hàm số là: A. 2;3. B. 3;2. C. 1;0. D. 0; 1. Lời giải Chọn D
Dựa vào đồ thị hàm số.
Câu 5: Cho hàm số y  f x liên tục trên  và có bảng xét dấu của đạo hàm như hình vẽ sau
Hàm số y  f x có bao nhiêu điểm cực trị? A. 3. B. 2. C. 1. D. 0. Lời giải Chọn A
Từ bảng xét dấu của đạo hàm ta. Câu 6: 1
Tiệm cận ngang của đồ thị hàm số 
y  3x 1 là đường thẳng A. x  0. B. y  0 . C. y  1 . D. x   1 . 3 3 Lời giải Chọn B  1 +) Tập xác định:    D   \   .  3   +) Ta có  y  1 lim lim  0 . x  x  3x 1
Vậy đường tiệm cận ngang của đồ thị hàm số đã cho là đường thẳng y  0 .
Câu 7: Đường cong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? A. 2x  y  1. B. y  3 x  2 3x  2.. x 1 C. y   3 x  2 3x  2. . D. y  3 x  2 3x  2. Lời giải Chọn D
Đồ thị hàm số bậc ba có hệ số a  0 nên loại.B
Xét đáp án A: ta có y  2
3x  6x  3x x 2. Lúc đó y  0 x  2; 0, điều này không
phù hợp với đồ thị đã cho nên loại.
Câu 8: Số giao điểm của đồ thị hàm số y  4 x  2 2x 1 và trục tung là: A. 3. B. 4. C. 2. D. 1. Lời giải Chọn D
Phương trình hoành độ giao điểm của đồ thị hàm số y  4 x  2 2x và trục tung:
x  0  y  1 nên đồ thị và trục tung có môt giao điểm.
Câu 9: Cho các số thực dương a , b . Mệnh đề nào sau đây đúng? 3 3 A. 2 a   1 log 1 log a  3log b . B. 2 a   1 a  1 log 1 log log b . 2 3 2 2 b 3 2 3 2 2 b 3 3 3 3 C. 2 a   1 log 1 log a  3log b . D. 2 a   1 a  1 log 1 log log b . 2 3 2 2 b 3 2 3 2 2 b 3 3 Lời giải Chọn C 1 3 3 1 Ta có: 2 a  2 log log a  log 2  1 3 log a  3
log b  1 log a  3log b . 2 3 2 3 b b 2 2 2 2 2 3
Câu 10: Đạo hàm của hàm số x  y  2 1 e là A.    2 1 2 x y e . B. x  y  2 1 e . C.    2 1 2 x y xe .D. 1 x y  2 1 e . 2 Lời giải Chọn A Ta có 2x  y  1 e
 y   x   2x1 2x  e  1 2 1 . 2.e . 3
Câu 11: Rút gọn biểu thức P  5 2 x . x (với x  0)? 13 4 3 17 A. 2 x . B. 7 x . C. 10 x . D. 10 x . Lời giải Chọn D 3 3 1 3 1 17 Với x  0thì  P  5 2 x x  2 5 x x  2 5 x  10 . . x . Câu 12: x 1 Phương trình: 2 3  có nghiệm là 9 A. 2. B. 2. C. 1. D. 1. Lời giải Chọn C Ta có: 2x 1 2x  3   3  2
3  2x  2  x  1. 9
Câu 13: Nghiệm của phương trình log 2x  1  2 là 3 A. x  5 . B. x  4. C. x  9 . D. x  7 . 2 2 Lời giải Chọn A
Điều kiện xác định x  1 . 2 log 2x 1 2 2x 1 3 2x 1 9 x 5. 3 
      2      Câu 14: 1
Nguyên hàm của hàm số y  2 x  3x  là x 3 2 3 2 A. x  3x  lnx C . B. x  3x  ln x C . 3 2 3 2 3 2 3 2 C. x  3x  ln x C . D. x  3x  1 C . 3 2 2 3 2 x Lời giải Chọn B   3 2
Áp dụng công thức nguyên hàm ta có  2 1      x  3 3 d x x x x  ln x     .  C  x  3 2
Câu 15: Nguyên hàm  sin2xdx bằng: A. 1 cos2x C . B. cos2x C . C. 1 cos2x C . D. cos2x C . 2 2 Lời giải Chọn C
Ta có  sin2xdx  1  sin2xd2x  1cos2x C . 2 2 1 2 2 Câu 16: Cho f xdx   2và f xdx  
3 . Khi đó  2f xdx bằng 0 1 0 A. 5 . B. 5. C. 10. D. 6. 2 Lời giải Chọn C 2 1 2  2f x 
dx 2  f xdx  f x      dx  22  3    10 . 0  0 1    2018
Câu 17: Tích phân   2x I dx bằng 0 2018 2018 A. 2 1 . B. 2 . C. 2018 2 . D. 2018 2 1. ln2 ln2 Lời giải Chọn A 2018 2018 x 2018 x 2 2  w   iI  x   1 4 5 2 d z  2   3i 1 ln2 ln2 0 0
Câu 18: Cho hai số phức và z  12i . Số phức liên hợp của số phức w  z  z là 2 1 2 A. w  32i . B. w 14i . C. w  3i . D. w  3 i . Lời giải Chọn C
Ta có w  z  z  3  i  w  3 i . 1 2
Câu 19: Cho hai số phức z  2 i và z  2  4i . Số phức w  z z bằng 1 2 1 2 A. w  3i . B. w  3i . C. w  43i . D. w  4 3i . Lời giải Chọn A
Ta có w  z z  2 i 24i  3i . 1 2
Câu 20: Điểm biểu diễn số phức z  2021i là A. P 0;202 1. B. Q 2021;0.
C. M 2021;202 1. D. N 0;0. Lời giải Chọn A
Theo lý thuyết ta có điểm biểu diễn số phức z  2021i là P 0;202 1.
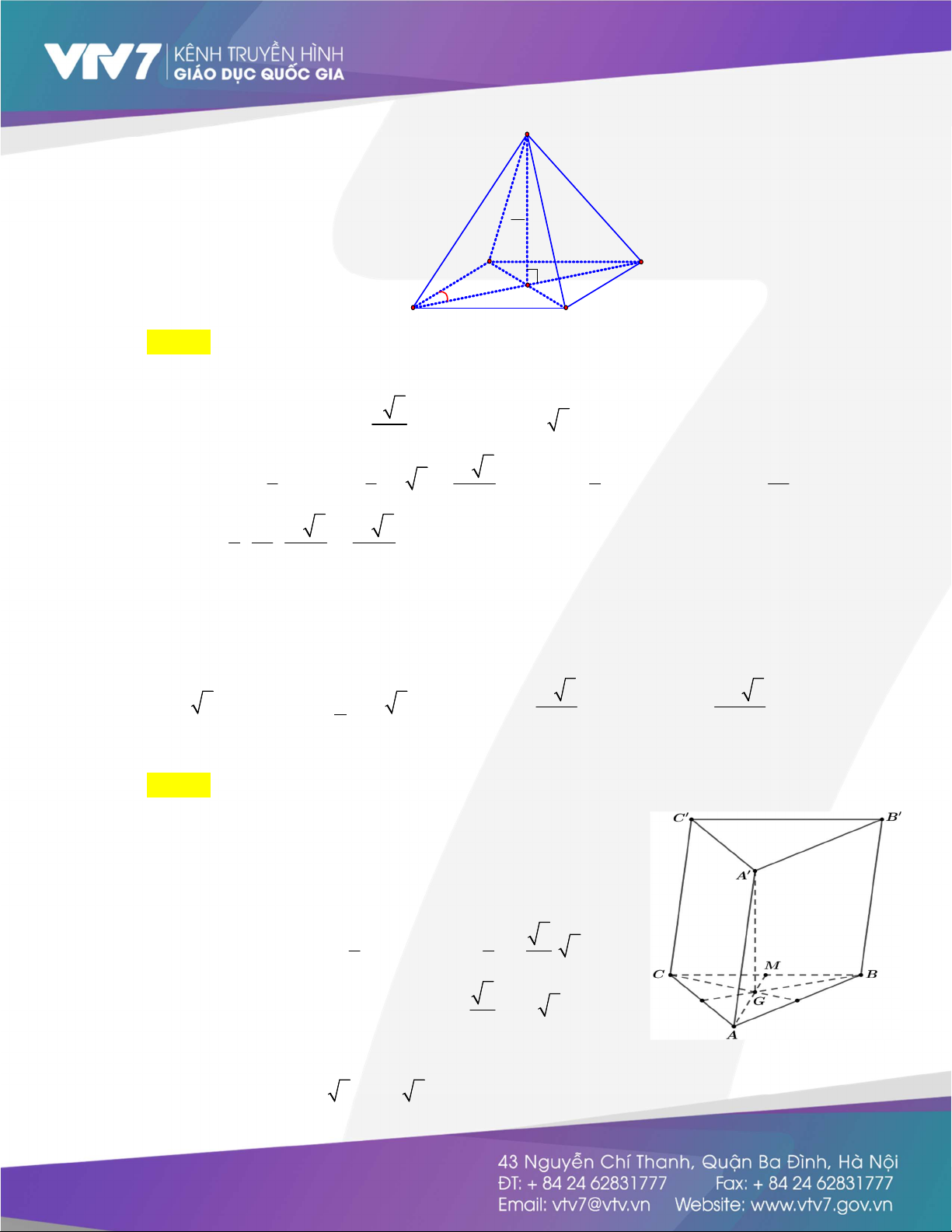
Câu 21: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh a , góc  BCA  3  0 , SO  ABCD và  3a SO
. Khi đó thể tích của khối chóp là 4 3 3 3 3 A. a 2 . B. a 3 . C. a 2 . D. a 3 . 4 8 8 4 Lời giải s 3a 4 B A 30 C O a D Chọn B
Theo giả thiết ABCD là hình thoi tâm O cạnh a , góc  BCA  3  0 nên  BCD  6  0 ; BCD
đều suy ra BD a , CO  a 3 , AC  2CO  a 3 . 2 2 Ta có S  1 AC.BD  1 a a  a 3 . . 3 ; V  1 SO.S với  3a SO suy ra ABCD 2 2 2 S.ABCD 3 ABCD 4 2 3 V
 1  3a  a 3  a 3 . S.ABCD 3 4 2 8
Câu 22: Cho lăng trụ ABC. 
A BC  có đáy ABC là tam giác đều cạnh 2a . Hình chiếu vuông góc của 
A trên ABC trùng với trọng tâm của tam giác ABC , góc giữa 
A A và mặt đáy bằng 6  0 .
Thể tích khối lăng trụ ABC.  A BC  bằng: 3 3 A. 3 a 3 . B. 3 2a 3 . C. a 3 . D. 2a 3 . 3 3 Lời giải Chọn B Theo bài ta có  A G  ABC 
 A ;AABC  A ;AAG       A AG   A AG  6  0 . Xét tam giác  A AG vuông tại G ta có:   A G  AG  A AG  2 AM   2 3 .tan .tan60 .2a. . 3  2a . 3 3 2 Diện tích tam giác ABC : S  a a . ABC  2 3 2 .  2 3 4
Thể tích khối lăng trụ ABC.  A BC  là: V  A G S  2 a a  3 ' . 2 . 3 2a 3 . ABC
Câu 23: Cho hình chóp S.ABCD có đáy ABCDlà hình thang với AD //BC và AD  2BC . Kết luận nào sau đây đúng? A. V  3V . B. V  2V . C. V  4V . D. V  6V . S.ABCD S.ABC S.ABCD S.ABC S.ABCD S.ABC S.ABCD S.ABC Lời giải Chọn A S A M D B C Ta có S  1 S V  1V V  3V . ABC 3 ABCD S.ABC S. 3 ABCD S.ABCD S.ABC
Câu 24: Một hình trụ có chiều cao bằng 3 , chu vi đáy bằng 
4 . Tính thể tích của khối trụ? A. 4  0 . B. 1  8 . C. 1  0 . D. 1  2 . Lời giải Chọn D
Ta có: 2R  4  R  2 .
Thể tích khối trụ là:   2 V R h   2 .2 .3 1  2 .
Câu 25: Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm A2;3;4, B8;5; 6. Hình chiếu
vuông góc của trung điểm I của đoạn AB trên mặt phẳng Oxzlà điểm nào dưới đây. A. N 3;1;5. B. Q 3;0;5. C. P 3;0;0. D. M 0;1; 5. Lời giải Chọn B
Tọa độ trung điểm của AB là I 3;1;5.
Vậy hình chiếu của I trên mặt phẳng Oyzlà M 3;0;5.
Câu 26: Trong không gian Oxyz , mặt cầu S x  2  2 y  2 ( ) : ( 1)
z  25 có bán kính bằng A. 25. B. 5. C. 625. D. 10. Lời giải Chọn B
Phương trình mặt cầu là: x  2 a  y  2 b  z  2 c  2 ( ) ( ) ( ) R nên 2 R  25  R  5. .
Câu 27: Trong không gian Oxyz,mặt phẳng nào dưới đây đi qua điểm M  ( 1;3;1)?
A. P  : 2x y  z  0 . B. P : 2x y z 2 0. 2      1
C. P  : x 2y  z  5  0 . D. P : x y 2z 0. 4     3 Lời giải Chọn B
Thay tọa độ của điểm M trực tiếp vào các phương trình để kiểm tra.
Câu 28: Trong không gian Oxyz, vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua
hai điểm M 1;1;2 và N(1;2;1)? A. u  (2;1;1). B. u  (0;3;1). C. u  (0;1;1) . D. u  (0;3;3). 1 2 3 4 Lời giải Chọn C   
Ta có MN  (0;3;3)  3u  u là một vectơ chỉ phương của đường thẳng MN.. 3 3
Câu 29: Chọn ngẫu nhiên một số trong 23 số nguyên dương đầu tiên. Xác suất đề chọn được số lẻ bằng A. 12 . B. 11 . C. 10 . D. 1 . 23 23 23 2 Lời giải Chọn A
Trong 23 số nguyên dương đầu tiên 1,2,3,,23, ta đếm được có 12 số lẻ nên xác suất cần tìm là 12 . . 23
Câu 30: Hàm số nào dưới đây đồng biến trên  ? A. 2x  y  1 . B. y  3 x  2 3x  3x 1. x 1 C.   3  2 y x x x . D. y  4 x  2 2x 1. Lời giải Chọn B
Hàm số đồng biến trên  trước hết phải có tập xác định D  , loại câu A, xét các câu khác.
Chỉ có x  x  x    x  x   x  2 3 2 2 ( 3 3 1) 3 6 3 3
1  0, x  , dấu bằng xảy ra khi x  1 (hữu hạn).
Câu 31: Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f x   4 x  2 ( ) 2x  5 trên đoạn 0;3
  . Tổng M  m bằng A. 11. B. 53. C. 52. D. 52. Lời giải Chọn D Ta có f  x   3 ( )
4x  4x và f (x)  0  x  0,x  1. Trên [0;3], ta xét các giá trị
f(0)  5, f(1)  6, f(3)  58.
Do đó M  6,m  58 và M  m  52.
Câu 32: Tập nghiệm của bất phương trình  2 8 4 x  256 là A.  [ 1;1]. B.  ( 2 3;2 3]. C.  [ 2;2]. D. [2;) . Lời giải Chọn C Ta có  2 8 4 x  256  8  2 x  log 256  4  2
x  4  2  x  2.. 4 2 2 Câu 33: Nếu   3.f x  1dx   
10 thì  f xdx bằng? 1 1 A. 3. B. 13 . C. 10 . D. 11 . 3 3 3 Lời giải Chọn D 2 2 2
Áp dụng tính chất tích phân   f x   x  f x x   f x x   11 10 3 ( ) 1 d 3 ( )d 1 ( )d .. 1   1 1 3
Câu 34: Cho số phức z 13i . Số phức w  (1i)z  z có môđun bằng A. 5 2. B. 2. C. 10. D. 2. Lời giải Chọn D
Ta có: w  1i  w  2 .
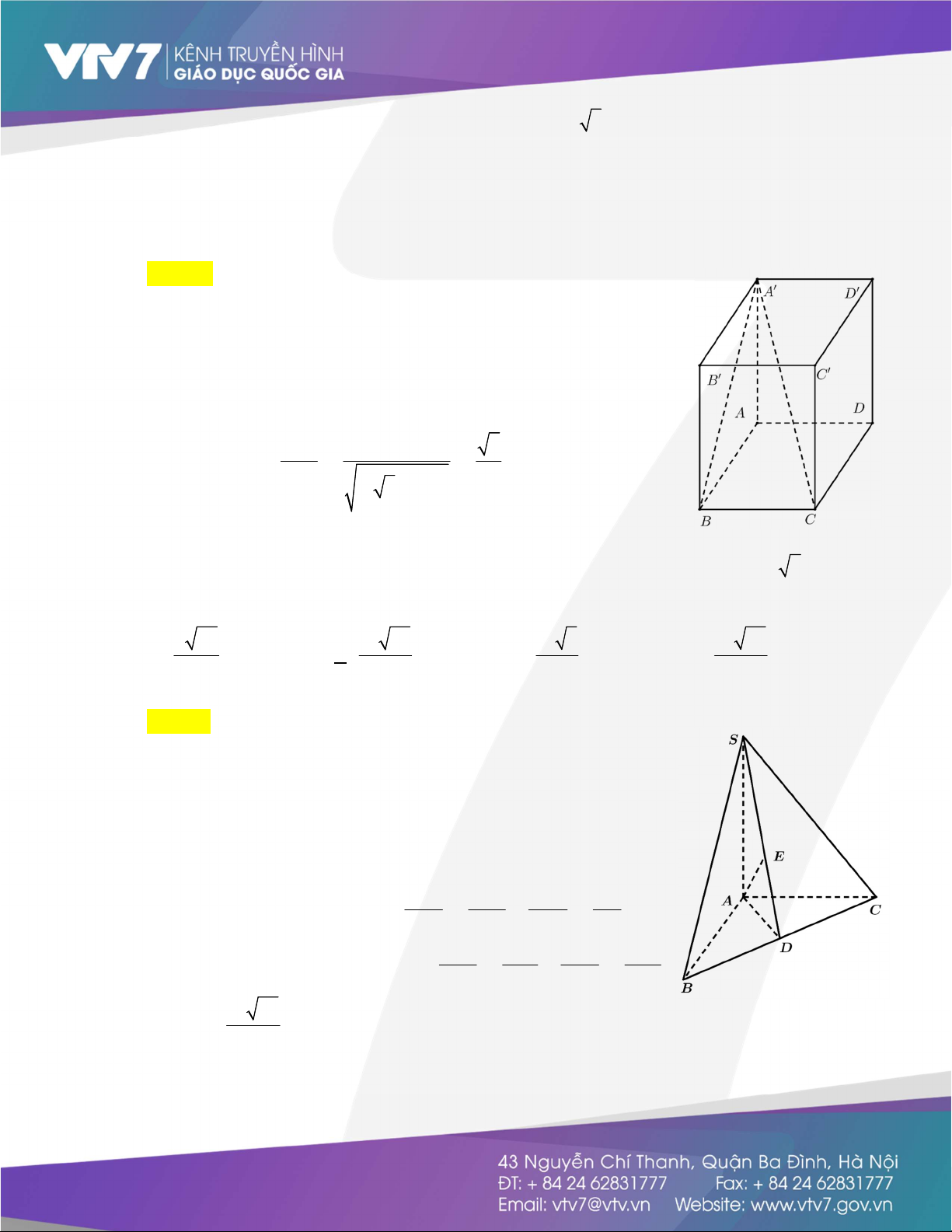
Câu 35: Cho hình hộp chữ nhật ABC .
DA'B'C 'D' có AB  4 2cm,AD  4c , m AA'  4cm . Góc giữa
đường thẳng A'C và mặt phẳng (ABB 'A') bằng A. 3  0 . B. 6  0 . C. 9  0 . D. 4  5 . Lời giải Chọn A
Ta có A'C  AA'B 'B  A' và CB  AA'B 'B
 A'B là hình chiếu vuông góc của A'C A'C,AA'B 'B     A'C,A'B     BA'C    BC BA C  4  3 tan ' A'B  2 3 4 2  2 4   BA'C  3  0
Câu 36: Cho hình chóp SABC có đáy là tam giác vuông tại .
A Biết AB a , AC  a 3 , SA  2a và
SA vuông góc với mặt phẳng đáy. Khoảng cách từ điểm A đến mặt phẳng SBC bằng A. a 57 . B. 2a 57 . C. 2a 3 . D. 2a 38 . 19 19 19 19 Lời giải Chọn B
Từ A kẻ AD  BC mà SA  ABC  SA  BC
 BC  SAD  SAD  SBC  mà SADSBC   SD
 Từ A kẻ AE  SD  AE  SBC   d  ; A SBC   AE
Xét ABC vuông tại A ta có: 1  1  1  4 2 2 2 2 AD AB AC 3a
Xét SAD vuông tại A ta có: 1  1  1  19 2 2 2 2 AE AS AD 12a  AE  2a 57 . 19
Câu 37: Trong không gianOxyz , mặt cầu có tâm là M 1;2;3 và đi qua điểm N  ( 1;0;2) có phương trình là:
A. x  2 y z  2 2 1 2  3.
B. x  2 y  2 z  2 1 2 3  9.
C. x  2 y  2 z  2 1 2 3  9.
D. x  2 y  2 z  2 1 2 3  3. Lời giải Chọn C
Bán kính của mặt cầu là MN  3, do có tâm làM(1;2;3) nên có phương trình là
x  2 y  2 z  2 1 2 3  9..
Câu 38: Trong không gian Oxyz, đường thẳng đi qua hai điểm A 
( 1;3;1) và B(2;1;1) có phương trình tham số là: x  1     3t x  2   3t x  1   3t x  1   t A. y  3      2t . B. y  12t . C. y  3 2t . D. y  3  4t .     z  1      2t z  1  2t z  1  2t z   1 Lời giải Chọn B 
Ta có: Đường thẳng nhận AB  (3;2;2) là vectơ chỉ phương và đi qua điểm B(2;1;1) nên x  2  3t
có phương trình tham số là y  1  2t . z  1  2t
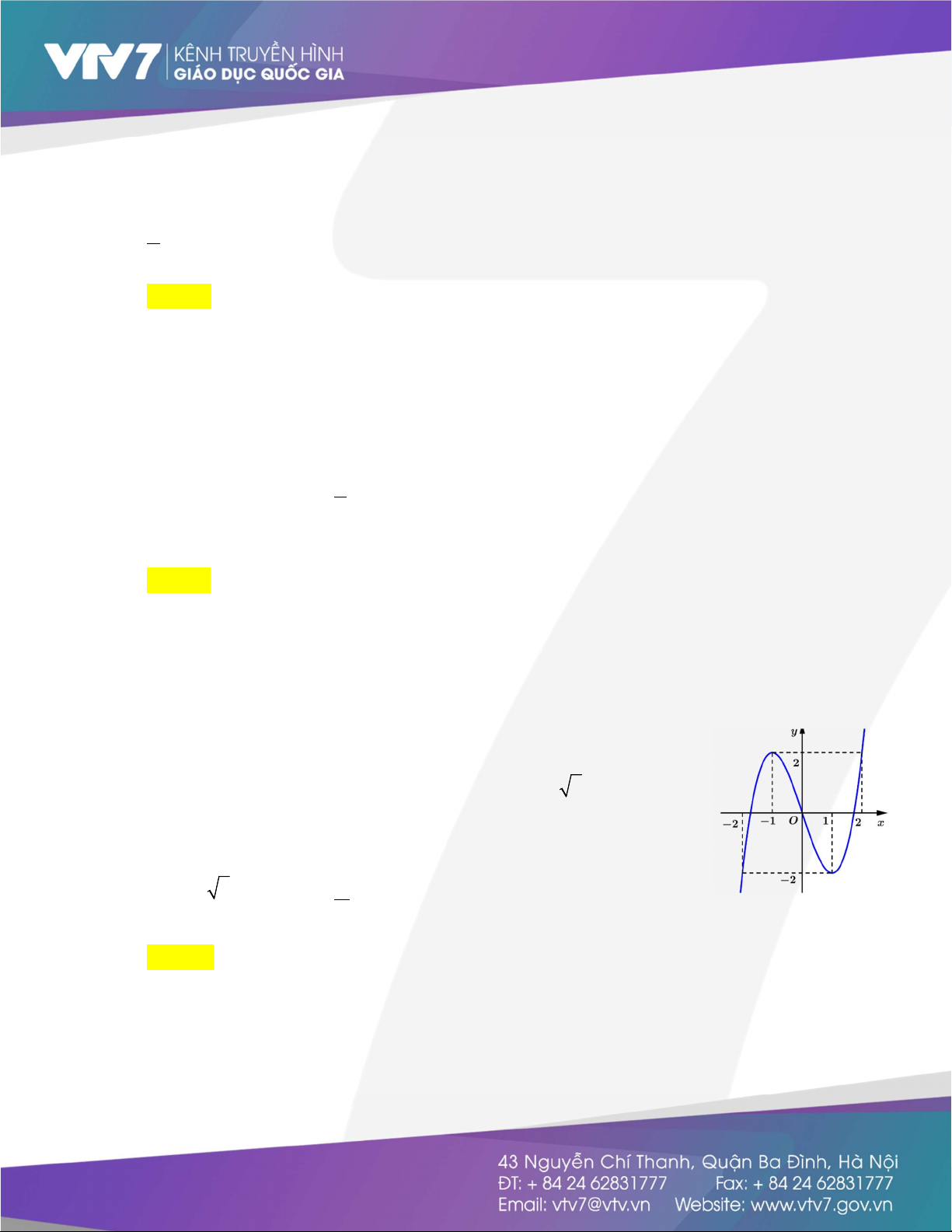
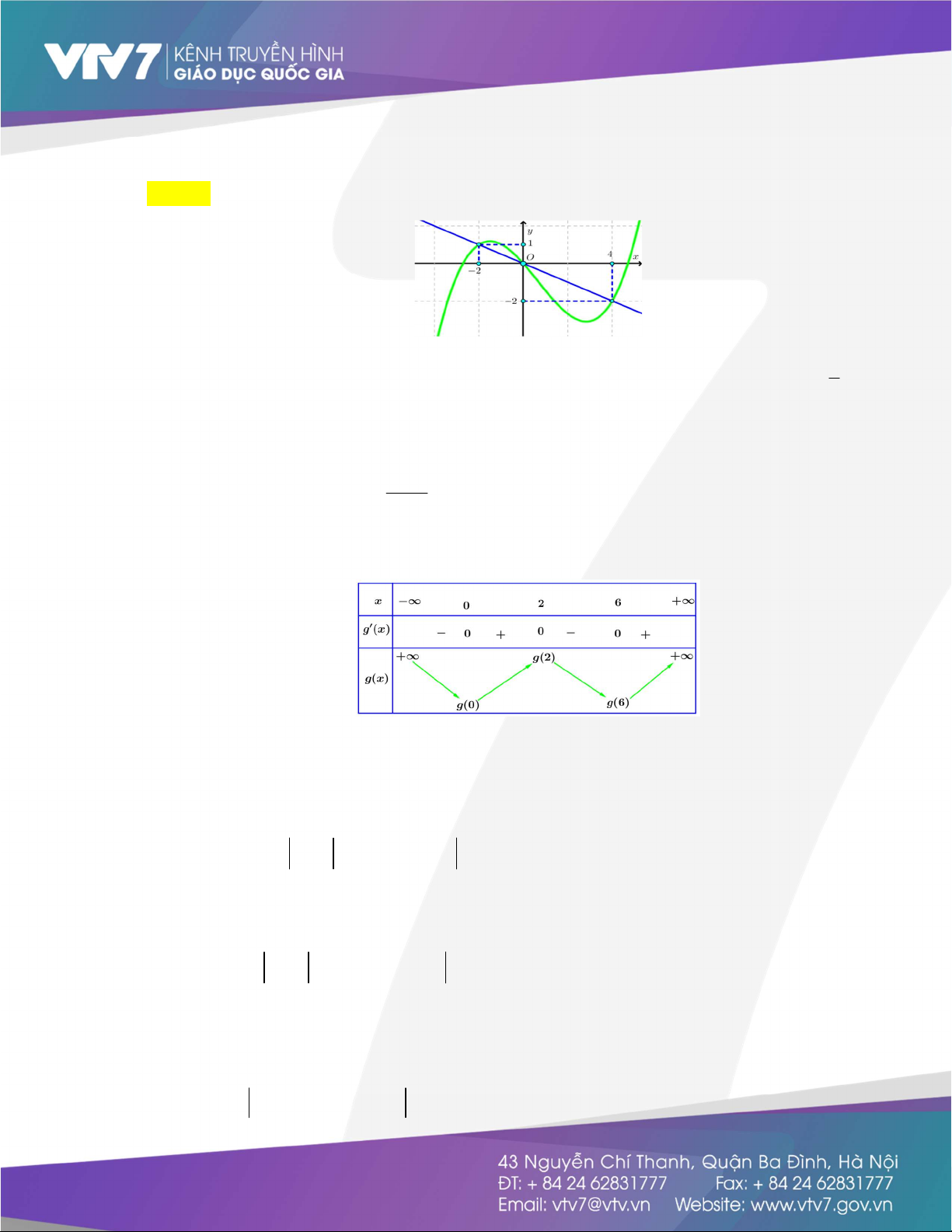
Câu 39: Cho hàm số y  f(x) liên tục trên R và có đồ thị như hình vẽ. Giá
trị lớn nhất của hàm sốg x  2 ( ) f(x 2) trên  
1; 3 đạt được tại  điểm nào sau đây? A. x  1. B. x  0. C. x  3. D. x  1. Lời giải Chọn D Đặt t  2 x  2  t  2;   1
Xét hàm số h t  f(t) trên đoạn 2;  
1 , từ đồ thị ta thấy hàm số đạt giá trị lớn nhất x  1 l 2   
 t  1  x 2  1   x   1 n Vậy hàm số g x  2
( ) f(x 2) đạt giá trị lớn nhất tại x  1.
Câu 40: Có bao nhiêu giá trị nguyên dương của tham số m để tập nghiệm của bất phương trình
log  2 13x x
 m  0 chứa không quá 9 số nguyên? 2 A. 6560. B. 6561. C. 19683. D. 19682. Lời giải Chọn B   3 log x 2 1 0 x 2            x  2  3 m 0 3x m log x 2 1 3x m 0 2                     log x 2 1 0 3 2          x x  2      3 m  0    2    3x   m  3 x    2  m 1     x  3  log m    3 3   2  x   
   x  log m (loại
, do m  1 nên x  log m  0 ).   2  3 3    3 2  2  x   x  log m   3  2 x   log m 3
Vì tập nghiệm của bất phương trình chứa không quá 9 số nguyên, mà x   3 , tức là có chứa 2
các số nguyên 1; 0 ; 1; …; 7; 8;… nên x  log m  8  m  8 3  6561. 3 Mà 
m   nên m  1;2;.. ;656 
1 . Vậy có 6561 giá trị m thỏa YCBT. 5 2x khi x 1 2
Câu 41: Cho hàm số f x       3 2 
. Giá trị của tích phân I  f x  3x  1x   1dx 1 2 2x khi x   1 2 bằng A. 28. B. 11228 . C. 7504 . D. 2021. 9 9 Lời giải Chọn C Đặt t  3
x  x   t   2x   x   2x   x  1 3 1 d 3 3 d 1 d dt . 3
Đổi cận: x  2 : t  13 và x  2 : t  15 15  1 15   1 15 
Khi đó: I  1  f tdt 1  1  f t f t  t t 3  5 2 dt   2 1 2       dt
3   dt       dt 3   13 13 1    13 1     1  1 15  1 6790 7504  t t .
3  5  2 dt   1  2 2        dt   238      3   3 9 13 1      
Câu 42: Xét các số phức z , z thoả mãn z 1  2i  3; z  2021 6i  z  2021 4i và số phức 1 2 1 2 2
z thoả mãn rằng biểu thứcP  z  z  z  z đạt giá trị nhỏ nhất. Giá trị lớn nhất của z là 1 2 A. 2021 B. 5 C. 34 D. 26 Lời giải
Gọi M là điểm biểu diễn cho z , ta có tập hợp điểm M là đường 1 y
tròn tâm I 1;2, bán kính R  3 5 N
Gọi N là điểm biểu diễn cho z , ta có tập hợp điểm N là đường 2 b A thẳng y  5 M 1
Gọi A là điểm biểu diễn cho số phức z , ta có: P  AM  AN . x O 1
Để P nhỏ nhất thì toạ độ các điểm phải làM 1; 1,N 1;5và điểm -2 I
A phải thuộc đoạn thẳng MN , từ đó suy ra z  a bi
với a  1;1  b  5. Vậy giá trị lớn nhất của biểu thức z là 26
Câu 43: Cho hình chóp S.ABC, đáy ABC là tam giác vuông tại AvàAB  , a AC  a 3. Hai mặt
phẳng SAB và SBC tạo với đáy 1 góc bằng nhau. Hai đường thẳng SA và BC vuông góc
với nhau và khoảng cách giữa hai đường bằng a . Thể tích khôi chóp S.ABC bằng 2 3 3 3 3 A. a 2 . B. a 2 . C. a 2 . D. a 2 . 12 36 4 6 Bài giải Chọn A
Vẽ AI  BC  BC  SAI  AI  a 3 . Vẽ SH  AI  SH  ABC  2
Vì hai mặt phẳng SAB và SBC tạo với đáy 1 góc
bằng nhau  H nằm trên đường phân giác góc B
 AH  AB   AH  a 3 2 HI BI 3 Từ I vẽ    ,    a HK SA d BC SA IK 2 Trong AIK vuông tại  IK 3  K  IAK    IAK  2 sin tan AI 3 2 Trong SHA vuông tại  H  SAH  SH  SH  2 AH  a 6 tan . AH 2 6 2 3 V  1 SH S  1 a 6 a 3  a 2 . . . S.ABC  3 ABC 3 6 2 12
Câu 44: Để chuẩn bị cổ vũ cho đội tuyển Việt Nam tham dự vòng loại thứ 3 World Cup 2022. Một hội
cổ động viên dự định sơn trang trí 1000 chiếc nó lá với cách sơn như sau. Tính theo độ dài
đường sinh của chiếc nón lá là 40cm kể từ đỉnh nón cứ 8cmthì sơn màu đỏ, màu vang
xen kẽ nhau như hình minh họa, sau đó dán 20 ngôi sao vàng vào mỗi chiếc nón. Biết rằng
đường kính của đường tròn đáy nón 40cm, mỗi ngôi sao vàng giá 200 đồng, sơn màu vàng giá 5000 đồng/ 2
m , sơn màu đỏ giá 4000 đồng/ 2
m . Hỏi giá thành để trang trí 1000 chiếc nón
lá đó gần với số tiền nào sau đây?
.A. 5105840đồng. B. 5105841đồng. C. 5156106đồng. D. 5156107 đồng. Lời giải Chọn B
Đặt l  40;l  32;l  24;l  16;l  8 khi đó bán kính và diện tích của các khối nón đỉnh S 1 2 3 4 5
tương ứng với các đường sinh kể trên là S r l l 2 S  rl S   2 2 2  2  r l      16 16 ; S S . 1 1 1 2 2 2      S rl l    2 1 25 25 1 1 1 1
Tương tự S  9 S S  4 S S  1 ; ; S 3 1 4 1 5 1 25 25 25
Như vậy diện tích phần màu vàng là S S S S   2S  2.40.2  0  32  0  2 cm 2 3 4 5 1  5 5
Diện tích sơn màu đỏ là 3 S  3 .40.20  48  0  3 cm 1  5 5
Giá tiền để trang trí 1000 một chiếc nón là  320 480     .5000  .4000  20.2001000    đồng.  5105841 10000 10000  Câu 45: 2 2 2
Trong không gian Oxyz , cho mặt cầu S :x  
1  y 2 z  2  9 và mặt phẳng
P:2x y 2z 1  0. Đường thẳng  đi qua O tiếp xúc với mặt cầu S và cắt P tại A
sao cho OA nhỏ nhất có phương trình là A.  : x  y  z . B.  : x  y  z . 10 7 2 10 7 2 C.  : x  y  z . D.  : x  y  z . 10 7 2 10 7 2 Bài giải Chọn B
S x  2 y  2 z  2 : 1 2
2  9  I 1;2;2, R  3 và O  S
Mặt phẳng  đi qua O tiếp xúc với mặt cầu S có phương trình :x  2y 2z  0    Gọi d  P    
 u  n ; n   2;2;3 . Để OA nhỏ nhất thì OA d d P     
Vậy OA  d;OA  OI  đường thẳng qua  có 1 vectơ chỉ phương    u  x y z
u ;OI   10;7;2 Phương trình đường  :   . d    10 7 2
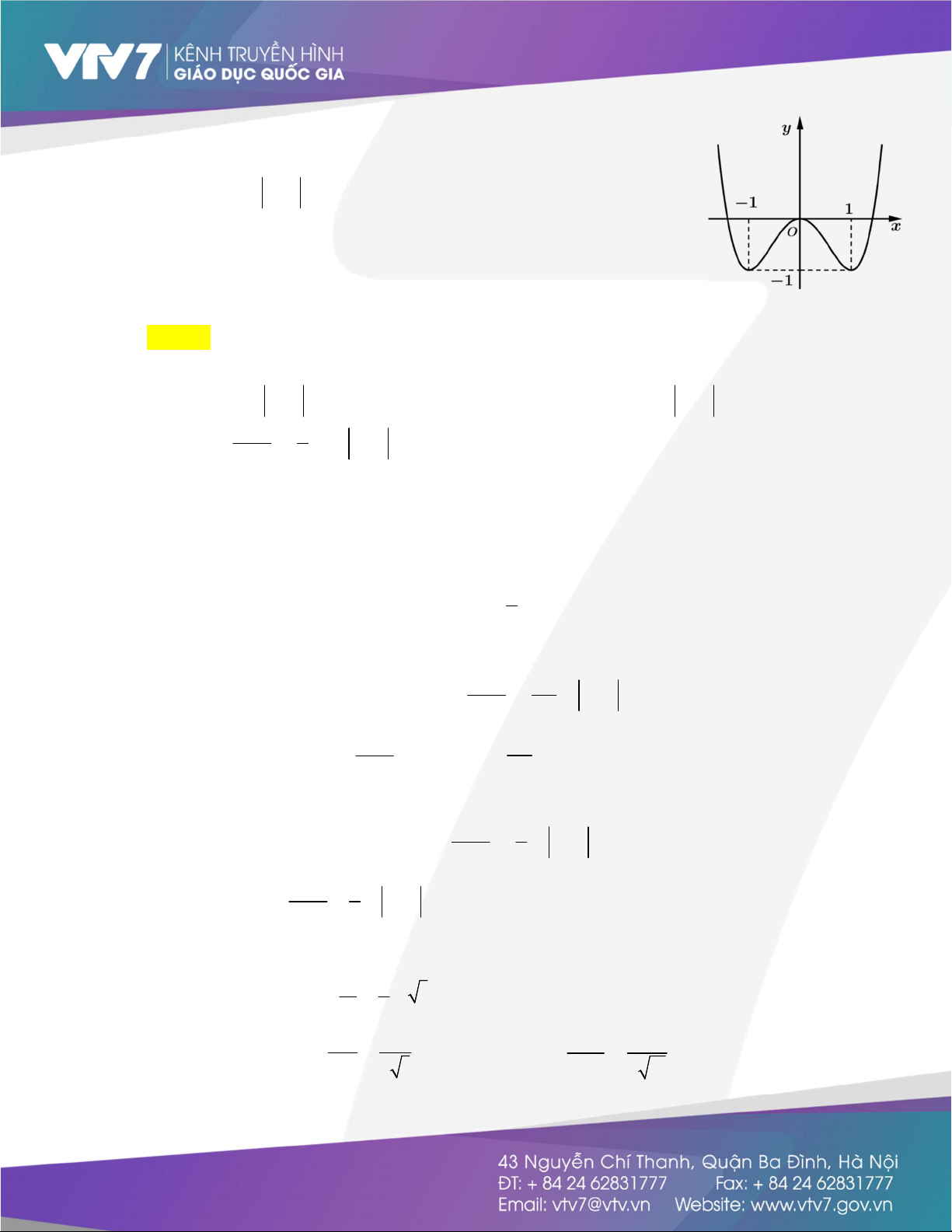
Câu 46: Cho hàm số bậc bốn y  f(x) sao cho f(0)  2 và hàm số y  f x có đồ thị trong hình vẽ
bên. Xác định số điểm cực trị của hàm số y  4f x  2)  2 ( x  4x . A. 3. B. 5. C. 4 . D. 6. Lời giải Chọn B
Nhận xét: Các điểm A2; 1,O0;0,B4;2 đều nằm trên đường thẳng d y  1 : x . 2
Đặt g x  4f x   2 2
x  4x  gx  4f x 2 2x 2
 gx  0  f x   x     2 2  x  0;2;  6 2
Bảng biến thiên hàm số g x:
Ta có: lim g x   và g 2  4f 0 4  4  0. x    Mặt khác: 0 Ta có: S  f  x dx 2 f x 2 f 0 f 2
2 nên f 2  0 do đó: 1
     0       2     2
g 0  4f 2 0 . 4 Mà: S  f  x dx 6 f x 6 f 0 f 4
6  f 4  2 6  4 do đó: 2
      4   0     0
g 6  4f 412  0.
Suy ra hàm số y  g x có 3 cực trị và phương trình gx  0 có hai nghiệm phân biệt nên hàm số y  f x   2 4 (
2) x  4x có 5 điểm cực trị.
Câu 47: Cho hàm số y  f xlà hàm số chẵn trên tập số thựcR và có đồ thị như
hình vẽ.Biết rằng tồn tại các giá trị của tham số m để phương trình 2 f x 3.3 m4 f x 3m 3 2 2 f x    3
 3  0 có đúng 7 nghiệm thực
phân biệt. Tổng lập phương các giá trị đó của m là: A. 8. B. 1. C. 7. D. 7. Lời giải Chọn B Ta có: 2 2f x 3.3
m4 f x 3m 3 2fx 2 2f x 3  3  0  3.3
 3  m4 f x 3m 3 2fx 3 2 f x   1 1 3 m 4 f x 3m 3 * 2  f x 3           3
Nhận thấy, nếu x là một nghiệm của  * thì x cũng là nghiệm của  *. o o
Suy ra, điều kiện cần để phương trình  * có 7 nghiệm thực phân biệt là  * có nghiệm x  0. 1 m 2
Mà theo đồ thị, ta thấy f 0  0 1 1 m.3m     2    
 3  m  m  2  0   . 3 m   1 Thử lại: 2 f x 1 2
 Với m  2 thì  * trở thành   3  4 f x 3 1 . 2  f x 3          3 Cauchy Nhận thấy, 2 f x VT   1 3 2 ,  VP  2. 
3  2nên  1  f x  0, theo đồ thị, suy 2  f x 3 3
ra phương trình có 3 nghiệm x nên m  2 không thỏa mãn. 2 f x 1 1
 Với m  1 thì  * trở thành   3  4 f x 6 2  f x 3       3 2 f x   1 2 3 2 f x 3 0 * * 2  f x 3        3 Đặt 2 f x  t;t  0
Xét hàm số g t  t  1  2 3 t với t  0. 3t 2 3 3  2 Ta có g t  t  ln 3  2 ' 3 .ln 3
, g t  t 2  ln 3  1 ' 3 ln 3  0 với mọi t  0. 3t 3 t t 3 3 3 t
 g 'tđồng biến trên 0;  g 't  0 có nhiều nhất 1 nghiệm t  0.
 phương trìnhg t  0 có nhiều nhất 2 nghiệm t  0.  2fx   0 f x  0
Lại có, g  1  0 và g0  0 Phương trình * * có 3 nghiệm là ,.  2 f x     1   f x  1
hay phương trình ban đầu có đúng 7 nghiệm. Vậy m  1 thỏa mãn.
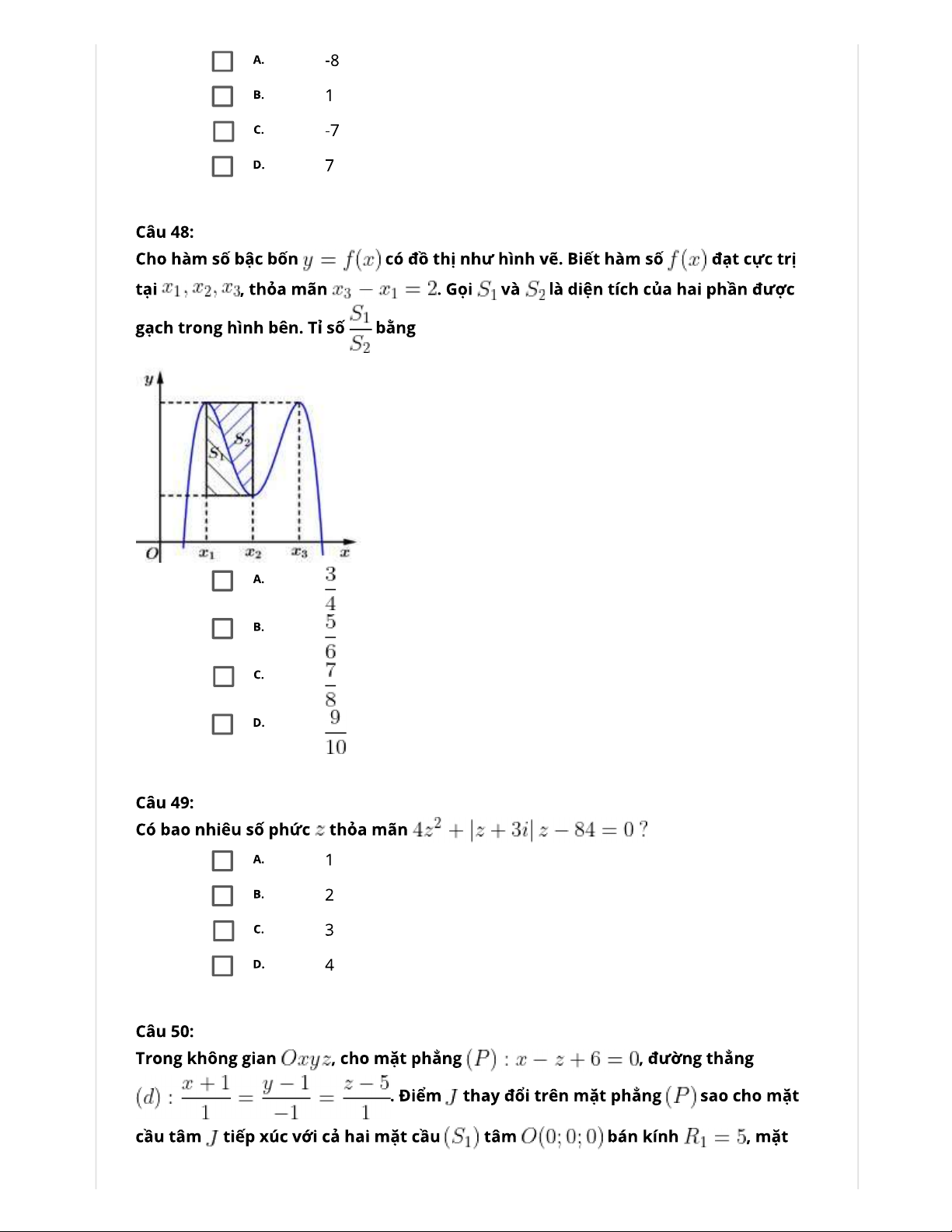
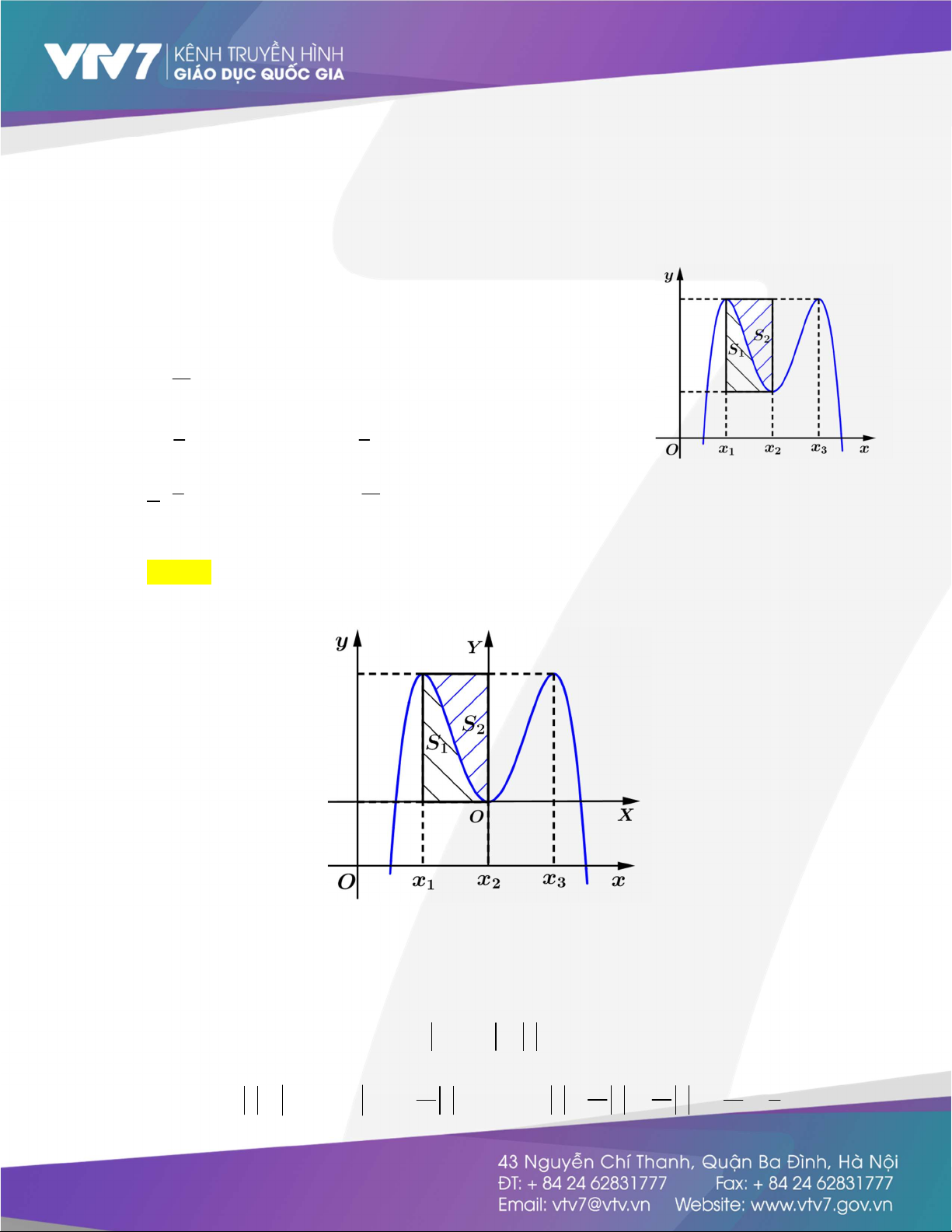
Câu 48: Cho hàm số bậc bốn y  f(x)có đồ thị như hình vẽ. Biết hàm
số f(x)đạt cực trị tại x ,x ,x thỏa mãn x x  2. Gọi S 1 2 3 3 1 1
và S là diện tích của hai phần được gạch trong hình bên. Tỉ 2 số S1 bằng S2 A. 3 . B. 5 . 4 6 C. 7 . D. 9 . 8 10 Lời giải Chọn C
Kết quả bài toán không đổi nếu ta đổi hệ trục tọa đô xOy thành XO'Y .
Khi đó trong hệ trục tọa độ mới, hàm số có dạng g X  4 AX  2 ( ) BX và g X  4 AX  2 ( ) BX có hai
điểm cực trị tương ứng là 1 và 1là nghiệm của 3
4AX  2BX  0 , do đó hàm số có dạng G X  4 k X  2 ( ) .( 2X ) với k  0.
Diện tích hình chữ nhật bằng S  S  1.G  ( 1)  k . 1 2 0 7 7 8 S 7 Diện tích S  4 k X  2 2X dX  k do đó S  k  k  k và 1  . 1  15 2 15 15 S 8 1 2
Câu 49: Có bao nhiêu số phức z thỏa mãn 2
4z  z  3i z  84  0? A. 1. B. 2. C. 3. D. 4. Lời giải Chọn B
Ta có phương trình bậc 2 theo z có a.c  4. 
( 84)  0 nên phương trình luôn có nghiệm thực.
Do đó z   , nên z  i  2 3 z  9 Vậy ta có 2 z  2 z z     2 z z    2 4 9 84 0 9 84 4z  2z  16    4 15z  2 681z  7056  z  4  0        2 147    . z 84 2 4z    z  147     0  5 z   z 84 2 4z     5  0
Câu 50: Trong không gian Oxyz , cho mặt phẳngP: x z  6  0, đường thẳng x 1 y 1 z  d   5 :
. Điểm J thay đổi trên mặt phẳng Psao mặt cầu tâm J tiếp xúc với 1 1 1
cả hai mặt cầu S tâm O0;0;0 bán kính R  5, mặt cầu S tâm I 2;0;2 bán kính 2  1  1
R  1. Điểm M thay đổi trên đường thẳng d . Giá trị nhỏ nhất của MJ bằng 2 A. 6 3  7 . B. 3 6  7 . C. 6 5  7 . D. 6 5  7 . 2 3 3 2 Lời giải Chọn B
Giả thiết suy raS nằm trong S . Gọi J; R là mặt cầu 1  2 
tiếp xúc với cả S , S . 2  1  Suy ra JO  R  R , 1 JI  R  R JO  JI  R  R JO  JI  6 2 1 2      * JI  R  R JO  JI  R  R JO  JI  4  2  1 2 
Dễ thấy OI  P tại H  3  ;0;3 . Đặt 2 2
HJ  x  JO  x 18; JI  x  2 thay vào * ta được 2 2  x 18  x  2  6 7   x  . Do J P và 7 JH 
nên tập hợp các điểm J là đường 2 2  3  x 18  x  2  4 3
tròn tâm H nằm trong mặt phẳng P và có bán kính 7 r  . 3 Ta thấy 3 6  7
d  P và không cắt H ,r nên MJ  d H, d  r  . min   3
Document Outline

  • 111
  • loigiaide1