Đề thi thử TN THPT 2022 – 2023 môn Toán sở GD&ĐT Hà Tĩnh (online lần 2)

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi thử tốt nghiệp Trung học Phổ thông năm học 2022 – 2023 môn Toán sở Giáo dục và Đào tạo tỉnh Hà Tĩnh lần thứ hai

66 33 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

20 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
1
SỞ GD&ĐT HÀ TĨNH
ĐỀ THI ONLINE
KÌ THI THỬ TỐT NGHIỆP THPT NĂM 2023
Bài thi: TOÁN
Thời gian mở đề: 14h20 | Đóng đề: 16h10 | 12/05/2023
Câu 1. Trên mặt phẳng toạ độ, điểm biểu diễn số phức
34zi=−+
có toạ độ là
A.
( 3; 4)
−−
. B.
(3; 4)−
. C.
(3; 4)
. D.
( 3; 4)−
.
Câu 2. Trên khoảng
(
)
0; +∞
, đạo hàm của hàm số
lnyx=
là
A.
. B.
. C.
1
10
y
x
′
=
. D.
1
ln10
y
x
′
=
.
Câu 3. Trên khoảng
( )
0; +∞
, đạo hàm của hàm số
3
2
yx=
là
A.
5
2
3
2
yx
′
=
. B.
1
2
yx
′
=
. C.
1
2
3
2
yx
′
=
. D.
3
2
yx
′
=
.
Câu 4. Tập nghiệm bất phương trình
22
x
>−
là
A.
( ; 1)
−∞ −
. B.
. C.
(1; )+∞
. D.
( 1; )− +∞
.
Câu 5. Ba số nào sau đây theo thứ tự lập thành một cấp số cộng?
A.
2, 5,8
. B.
2, 4,8
. C.
3, 9,12
. D.
3, 6, 9−
.
Câu 6. Trong không gian
Oxyz
, mặt phẳng
( ) : 2 3 5 2023 0Pxyz+−− =
có một vectơ pháp tuyến có toạ
độ là
A.
(2;3;5)
. B.
(2; 3; 5)
−
. C.
(2;3;5)−−
. D.
(2; 3; 5)
−
.
Câu 7. Cho hàm số
32
1
x
y
x
−
=
−
. Toạ độ giao điểm của đồ thị hàm số đã cho với trục tung là
A.
(0; 2)
. B.
2
;0
3



. C.
(3; 0)
. D.
(0;1)
.
Câu 8. Tính
2
1
2dI xx=
∫
.
A.
2I =
. B.
3
I =
. C.
1I =
. D.
4I =
.
Câu 9. Đường cong trong hình bên là đồ thị của hàm số nào sau đây?
A.
21
1
x
y
x
−
=
−
. B.
42
21yx x=−+
. C.
42
1yx x
=++
. D.
3
21yx= +
.
Câu 10. Trong không gian
Oxyz
, mặt cầu
22 2
():(3)(1)(4)4Sx y z− +− ++ =
có toạ độ tâm
I
và bán
kính
R
tương ứng là
2
A.
(3;1; 4)I −
,
2
R =
. B.
( 3; 1; 4)I −−
,
2
R =
. C.
(3;1; 4)I
−
,
4
R =
. D.
( 3; 1; 4)I −−
,
4
R
=
.
Câu 11. Trong không gian với hệ toạ độ
Oxyz
, cho hai vectơ
( 1;1; 0)a = −
,
(1;1; 0)b =
. Mệnh đề nào
dưới đây đúng?
A.
ab⊥
. B.
a
,
b
cùng hướng.
C.
a
,
b
đối nhau. D.
a
,
b
ngược hướng.
Câu 12. Cho số phức
23
zi= +
. Số phức liên hợp của
z
là
A.
23zi=−+
. B.
23zi= −
. C.
23zi=−−
. D.
32
zi
=−+
.
Câu 13. Cho khối lập phương có cạnh bằng 2. Diện tích toàn phần của hình lập phương bằng
A.
24
. B.
8
. C.
12
. D.
32
.
Câu 14. Cho khối lăng trụ
.ABCD A B C D
′′′′
có đáy là hình vuông có cạnh bằng
a
và chiều cao bằng
h
.
Thể tích của khối lăng trụ đã cho bằng
A.
2
ah
π
. B.
2
ah
. C.
2
1
3
ah
. D.
2
3ah
.
Câu 15. Diện tích của mặt cầu bán kính
3R
=
bằng
A.
6
π
. B.
18
π
. C.
36
π
. D.
12
π
.
Câu 16. Phần thực của số phức
(1 2 )(2 )z ii=+−
là
A.
0
. B.
4
. C.
2
. D.
3
.
Câu 17. Một hình trụ có bán kính đáy
4r =
và có chiều cao
3h =
. Diện tích xung quanh của hình trụ
bằng
A.
12
π
. B.
24
π
. C.
40
π
. D.
20
π
.
Câu 18. Trong không gian
Oxyz
, đường thẳng
12
: 23
3
xt
dy t
zt
= +
= −
= −
không đi qua điểm nào dưới đây?
A.
(1; 2;3)Q
. B.
(2; 2; 1)P −−
. C.
( 1; 5; 4)N −
. D.
(3; 1; 2)M −
.
Câu 19. Cho hàm số
()y fx=
có bảng biến thiên như hình vẽ.
Giá trị cực đại của hàm số bằng
A.
2−
. B.
3
. C.
2
. D.
1−
.
Câu 20. Đường thẳng
2y =
là tiệm cận ngang của đồ thị hàm số nào sau đây?
A.
2yx=
. B.
2
1
y
x
=
−
. C.
21
2
x
y
x
−
=
+
. D.
2
23
1
x
y
x
−
=
+
.
Câu 21. Tập nghiệm
S
của bất phương trình
2
log 3x ≤
là
A.
(0; 6]S =
. B.
(0;8]S =
. C.
( ;6)S = −∞
. D.
( ;8]S
= −∞
.
Câu 22. Cho tập hợp
M
gồm
4
phần tử. Số tập con gồm
3
phần tử của
M
là
A.
3
4
C
. B.
4
3
. C.
3
4
. D.
3
4
A
.
Câu 23. Họ nguyên hàm của hàm số
2
1
()
cos
fx
x
=
là
3
A.
1
cos
C
x
−+
. B.
tan
xC+
. C.
cot xC−+
. D.
cot
xC+
.
Câu 24. Cho
3
0
( )d 2fx x
= −
∫
và
5
3
( )d 3
fx x=
∫
. Tính tích phân
[ ]
5
0
2 ( )d
L fx x=
∫
.
A.
12L =
. B.
2L = −
. C.
2L =
. D.
12L = −
.
Câu 25. Họ nguyên hàm của hàm số
1
()fx
x
=
là
A.
1
2
xC
+
. B.
3
2
xC
+
. C.
xC
+
. D.
2 xC+
.
Câu 26. Cho hàm số
()y fx=
có bảng biến thiên như hình vẽ.
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
( 2; 1)−−
. B.
( ; 1)
−∞ −
. C.
( 1;1)−
. D.
( )
0;1
.
Câu 27. Cho hàm số
()y fx=
liên tục trên
và có bảng biến thiên như sau
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có giá trị nhỏ nhất bằng
1−
.
B. Hàm số đạt cực đại tại
0x =
và đạt cực tiểu tại
1x
= −
.
C. Hàm số có đúng một điểm cực trị.
D. Hàm số đạt cực đại tại
0
x =
và đạt cực tiểu tại
1x
=
.
Câu 28. Cho
2
log 3
a =
và
3
log 7b =
. Giá trị của
2
log 14
bằng
A.
1ab+−
. B.
4ab
. C.
23ab +
. D.
1ab +
.
Câu 29. Thể tích khối tròn xoay tạo bởi khi quay quanh trục hoành của hình phẳng giới hạn bởi các đồ thị
hàm số
2
2y xx= −
;
0y =
;
0x
=
;
1
x =
có giá trị bằng
A.
16
15
π
. B.
4
3
π
. C.
2
3
π
. D.
8
15
π
.
Câu 30. Cho hình chóp tứ giác đều có cạnh đáy bằng
2a
và chiều cao bằng
a
(tham khảo hình vẽ). Giá
trị tang của góc giữa mặt bên và mặt đáy bằng
4
A.
1
. B.
3
4
. C.
3
. D.
1
3
.
Câu 31. Số giao điểm của đồ thị hàm số
3
31yx x=−+
và trục hoành là
A.
1
. B.
2
. C.
0
. D.
3
.
Câu 32. Hàm số
32
3 9 20yx x x=−− + +
đồng biến trên khoảng
A.
( 3; )− +∞
. B.
( ;1)−∞
. C.
(1; 2)
. D.
( 3;1)−
.
Câu 33. Gọi
M
là tập hợp các số tự nhiên có
4
chữ số đôi một khác nhau được lập từ các chữ số
1
;
2
;
3
;
4
;
5
;
6
;
7
. Lấy ra từ tập
M
một số bất kỳ. Xác suất để lấy được số lẻ bằng
A.
3
7
. B.
4
7
. C.
2
21
. D.
3
4
.
Câu 34. Tổng tất cả các nghiệm của phương trình
4 8 62
xx
+=⋅
bằng
A.
9
. B.
3
. C.
5
. D.
6
.
Câu 35. Tập hợp điểm biểu diễn của số phức
z
thỏa mãn
| | | (1 ) |z i iz
−= +
là đường tròn có toạ độ tâm
I
là
A.
(0;1)I
. B.
(0; 1)I −
. C.
(1; 0)I
. D.
( 1; 0)I
−
.
Câu 36. Trong không gian
Oxyz
, cho hai điểm
(1; 2; 0)
A
,
(2;1; 1)B
−
. Mặt phẳng
()P
đi qua hai điểm
A
,
B
và vuông góc với mặt phẳng
Oxy
có phương trình là
A.
2 10xy− +=
. B.
2 10xy z− + +=
. C.
30xy+−=
. D.
2 40xy+ −=
.
Câu 37. Trong không gian
Oxyz
, toạ độ giao điểm của mặt phẳng
( ):2 3 6 0P x yz− +−=
với trục tung
là
A.
(0; 2;0)
−
. B.
(0; 2;0)
. C.
(3;0;0)N
. D.
(0; 0; 6)P
.
Câu 38. Cho hình chóp
.S ABC
có ba cạnh bên
,
2SB =
,
3SC =
đôi một vuông góc với nhau.
Chiều cao của hình chóp bằng
A.
5
6
. B.
66
11
. C.
2
3
. D.
6
7
.
Câu 39. Có bao nhiêu số nguyên
x
thỏa mãn
82
3log ( 1) log (86 ) 1xx+− − ≥
?
A.
28
. B.
85
. C.
29
. D.
86
.
Câu 40. Cho hàm số
()y fx=
có đạo hàm liên tục trên
thỏa mãn
(2) 2f = −
;
2
0
( )d 1fx x=
∫
. Tính
( )
4
0
dI f xx
′
=
∫
.
A.
10I = −
. B.
0I =
. C.
18I = −
. D.
5I = −
.
5
Câu 41. Cho hàm số
()fx
có bảng biến thiên như hình vẽ.
Số nghiệm thực phân biệt của phương trình
[ ]
() 2 0
f fx
′
+=
là
A.
6
. B.
5
. C.
4
. D.
3
.
Câu 42. Cho số phức
z
thỏa mãn
|4 3 | |4 4 5 |zi z i+ = −+
. Tìm giá trị nhỏ nhất của biểu thức
| | | 3|P zi z i=++ −
.
A.
min 5 2P
=
. B.
min 5
P =
. C.
min 2 2P =
. D.
min 2 5P =
.
Câu 43. Cho khối lăng trụ đứng
.ABCD A B C D
′′′ ′
có đáy là hình vuông có cạnh bằng
2
. Biết khoảng
cách từ
A
đến mặt phẳng
(
)
CB D
′′
bằng
2
. Thể tích của khối lăng trụ đã cho bằng
A.
3
. B.
22
. C.
42
. D.
42
3
.
Câu 44. Cho hàm số
()y fx=
có đồ thị
()C
như hình vẽ. Biết rằng diện tích hình phẳng giới hạn bởi
()C
và trục hoành bằng
8
và
8
0
( )d 4fx x=
∫
. Giá trị của
8
3
(2023 ) ( )dI xf x x
′
= −
∫
bằng
A.
6
. B.
12
. C.
4
. D.
2023
.
Câu 45. Cho phương trình
22
30z mz m− + −=
với
m
là tham số thực. Gọi
S
là tập hợp các giá trị của
m
sao cho phương trình đã cho có hai nghiệm phức có điểm biểu diễn là
A
,
B
và tam giác
OAB
có
diện tích bằng
6
. Tổng bình phương các phần tử của
S
bằng
A.
32
. B.
16
. C.
8
. D.
18
.
Câu 46. Trong không gian
Oxyz
, cho đường thẳng
21
:
2 11
x yz
d
−−
= =
và điểm
(1; 3; 0)A
. Mặt cầu
()S
đi qua
A
, tiếp xúc với
Oxy
và với đường thẳng
d
. Bán kính của mặt cầu
()
S
là
A.
30
. B.
66
. C.
25
. D.
2 10
.
Câu 47. Có bao nhiêu số nguyên dương
y
sao cho có không quá 8 số nguyên
x
thỏa mãn
( ) (
)
22
log 4 2log 2xy x+> −
?
A.
24
. B.
37
. C.
23
. D.
36
.
6
Câu 48. Cho khối trụ
()T
có bán kính đáy bằng
23a
. Gọi
A
và
B
là hai điểm thuộc hai đường tròn
đáy của
()T
sao cho khoảng cách và góc giữa
AB
và trục của
()T
bằng
2
a
và
60
°
. Thể tích của khối trụ
đã cho bằng
A.
3
48 6 a
π
. B.
3
24 2 a
π
. C.
3
16 6 a
π
. D.
3
24 6 a
π
.
Câu 49. Trong không gian
Oxyz
, cho tam giác
ABC
có
(6; 0; 0)A
,
(6;8; 0)B
,
(0;8; 0)C
. Gọi mặt phẳng
()
α
đi qua
B
và vuông góc với
AC
. Điểm
M
thay đổi thoả mãn
90ABM AMC
°
= =
. Gọi
N
là giao
điểm của
AM
và
()
α
. Khoảng cách từ
N
đến
()ABC
có giá trị lớn nhất bằng
A.
8
5
. B.
82
5
. C.
24
5
. D.
12
5
.
Câu 50. Cho hàm số đa thức
()fx
có đồ thị của đạo hàm
()fx
′
như hình bên. Biết rằng
(0) 0f =
. Hàm
số
63
() ( )gx f x x= −
có bao nhiêu điểm cực trị?
A.
7
. B.
4
. C.
5
. D.
3
.
--------------- HẾT ---------------
7
LỜI GIẢI THAM KHẢO
Câu 1. Trên mặt phẳng toạ độ, điểm biểu diễn số phức
34zi=−+
có toạ độ là
A.
( 3; 4)−−
. B.
(3; 4)−
. C.
(3; 4)
. D.
( 3; 4)−
.
Lời giải
Điểm biểu diễn của số phức
34zi=−+
là điểm có tọa độ
( 3; 4)−
.
Câu 2. Trên khoảng
(
)
0;
+∞
, đạo hàm của hàm số
lnyx=
là
A.
. B.
. C.
1
10
y
x
′
=
. D.
1
ln10
y
x
′
=
.
Lời giải
1
ln .y xy
x
′
= ⇒=
Câu 3. Trên khoảng
( )
0; +∞
, đạo hàm của hàm số
3
2
yx=
là
A.
5
2
3
2
yx
′
=
. B.
1
2
yx
′
=
. C.
1
2
3
2
yx
′
=
. D.
3
2
yx
′
=
.
Lời giải
Áp dụng công thức đạo hàm của hàm số luỹ thừa, ta có
1
2
3
2
yx
′
=
.
Câu 4. Tập nghiệm bất phương trình
22
x
>−
là
A.
( ; 1)−∞ −
. B.
. C.
(1; )+∞
. D.
( 1; )− +∞
.
Lời giải
Ta có
202
x
> >−
,
x∀∈
.
Vậy tập nghiệm là
.
Câu 5. Ba số nào sau đây theo thứ tự lập thành một cấp số cộng?
A.
2, 5,8
. B.
2, 4,8
. C.
3, 9,12
. D.
3, 6, 9−
.
Lời giải
Xét dãy số
( ) : 2,5,8
n
u
, ta có
28
5
2
+
=
nên ba số
2, 5,8
theo thứ tự lập thành một cấp số cộng.
Câu 6. Trong không gian
Oxyz
, mặt phẳng
( ) : 2 3 5 2023 0Pxyz
+−− =
có một vectơ pháp tuyến có toạ
độ là
A.
(2;3;5)
. B.
(2; 3; 5)−
. C.
(2;3;5)−−
. D.
(2; 3; 5)−
.
Lời giải
Mặt phẳng
0Ax By cz D+ ++=
có một vectơ pháp tuyến có toạ độ
(; : )AB C
.
Câu 7. Cho hàm số
32
1
x
y
x
−
=
−
. Toạ độ giao điểm của đồ thị hàm số đã cho với trục tung là
A.
(0; 2)
. B.
2
;0
3



. C.
(3; 0)
. D.
(0;1)
.
Lời giải
Với
0x =
ta có
2y
=
nên toạ độ giao điểm của đồ thị hàm số với trục tung là
(0; 2)
.
Câu 8. Tính
2
1
2dI xx=
∫
.
A.
2
I =
. B.
3I =
. C.
1I =
. D.
4I =
.
Lời giải
Ta có
2
22
1
1
2d 4 1 3
|
I xx x= = = −=
∫
.
8
Câu 9. Đường cong trong hình bên là đồ thị của hàm số nào sau đây?
A.
21
1
x
y
x
−
=
−
. B.
42
21yx x=−+
. C.
42
1
yx x=++
. D.
3
21yx
= +
.
Lời giải
Do đồ thị hàm số qua điểm
(1; 3)
, nên chỉ có đồ thị hàm số
42
1yx x=++
thỏa mãn.
Câu 10. Trong không gian
Oxyz
, mặt cầu
22 2
():(3)(1)(4)4
Sx y z
− +− ++ =
có toạ độ tâm
I
và bán
kính
R
tương ứng là
A.
(3;1; 4)I −
,
2R
=
. B.
( 3; 1; 4)
I −−
,
2
R
=
. C.
(3;1; 4)I −
,
4R
=
. D.
( 3; 1; 4)I −−
,
4R
=
.
Lời giải
Mặt cầu có tâm
(3;1; 4)I −
và bán kính
2
R =
.
Câu 11. Trong không gian với hệ toạ độ
Oxyz
, cho hai vectơ
( 1;1; 0)a
= −
,
(1;1; 0)b =
. Mệnh đề nào
dưới đây đúng?
A.
ab
⊥
. B.
a
,
b
cùng hướng.
C.
a
,
b
đối nhau. D.
a
,
b
ngược hướng.
Lời giải
Ta có
( 1) 1 1 1 0 0 0
ab
⋅ =− ⋅+⋅+ ⋅ =
nên
ab⊥
.
Câu 12. Cho số phức
23zi= +
. Số phức liên hợp của
z
là
A.
23zi=−+
. B.
23zi
= −
. C.
23zi=−−
. D.
32
zi=−+
.
Lời giải
Số phức liên hợp của số phức
a bi+
là số phức
a bi−
.
Câu 13. Cho khối lập phương có cạnh bằng 2. Diện tích toàn phần của hình lập phương bằng
A.
24
. B.
8
. C.
12
. D.
32
.
Lời giải
Diện tích mỗi mặt của hình lập phương bằng
4
.
Diện tích toàn phần của hình lập phương đã cho bằng
6 4 24⋅=
.
Câu 14. Cho khối lăng trụ
.ABCD A B C D
′′′′
có đáy là hình vuông có cạnh bằng
a
và chiều cao bằng
h
.
Thể tích của khối lăng trụ đã cho bằng
A.
2
ah
π
. B.
2
ah
. C.
2
1
3
ah
. D.
2
3ah
.
Lời giải
Thể tích của lăng trụ
2
V ah=
.
Câu 15. Diện tích của mặt cầu bán kính
3R =
bằng
A.
6
π
. B.
18
π
. C.
36
π
. D.
12
π
.
Lời giải
Diện tích của mặt cầu đã cho là
22
4 4 3 36SR
ππ π
= = ⋅=
.
Câu 16. Phần thực của số phức
(1 2 )(2 )z ii=+−
là
9
A.
0
. B.
4
. C.
2
. D.
3
.
Lời giải
Số phức
(1 2 )(2 ) 4 3z ii i=+ −=+
nên có phần thực bằng
4
.
Câu 17. Một hình trụ có bán kính đáy
4r =
và có chiều cao
3h =
. Diện tích xung quanh của hình trụ
bằng
A.
12
π
. B.
24
π
. C.
40
π
. D.
20
π
.
Lời giải
Diện tích xung quanh của hình trụ bằng
2 2 4 3 24
xq
S rl
ππ π
= = ⋅⋅=
.
Câu 18. Trong không gian
Oxyz
, đường thẳng
12
: 23
3
xt
dy t
zt
= +
= −
= −
không đi qua điểm nào dưới đây?
A.
(1; 2;3)Q
. B.
(2; 2; 1)P −−
. C.
( 1; 5; 4)
N −
. D.
(3; 1; 2)
M −
.
Lời giải
Thay tọa độ điểm
P
vào phương trình của
d
ta có
1
2
212
4
2 2 3 (vô lí).
3
33
4
t
t
tt
t
t
=
= +

−= − ⇔ =


= −
=
Do đó
P
không thuộc
d
.
Câu 19. Cho hàm số
()y fx=
có bảng biến thiên như hình vẽ.
Giá trị cực đại của hàm số bằng
A.
2−
. B.
3
. C.
2
. D.
1−
.
Lời giải
Dựa vào bảng biến thiên ta có giá trị cực đại của hàm số bằng
3
tại điểm
2
x = ±
.
Câu 20. Đường thẳng
2y =
là tiệm cận ngang của đồ thị hàm số nào sau đây?
A.
2yx=
. B.
2
1
y
x
=
−
. C.
21
2
x
y
x
−
=
+
. D.
2
23
1
x
y
x
−
=
+
.
Lời giải
Ta có
2
lim lim 1.
2
xx
x
y
x
→±∞ →±∞
+
= = −
−
Tiệm cận ngang của hàm số là
1y = −
Câu 21. Tập nghiệm
S
của bất phương trình
2
log 3x ≤
là
A.
(0; 6]S =
. B.
(0;8]S =
. C.
( ;6)S = −∞
. D.
( ;8]S = −∞
.
Lời giải
Bất phương trình đã cho tương đương với
3
0 2 8.x<≤ =
Vậy tập nghiệm của bất phương trình
(0;8]S =
.
Câu 22. Cho tập hợp
M
gồm
4
phần tử. Số tập con gồm
3
phần tử của
M
là
A.
3
4
C
. B.
4
3
. C.
3
4
. D.
3
4
A
.
10
Lời giải
Mỗi tập con gồm
3
phần tử của
M
là một tổ hợp chập
3
của
4
phần tử.
Vậy có tất cả
3
4
C
tập con.
Câu 23. Họ nguyên hàm của hàm số
2
1
()
cos
fx
x
=
là
A.
1
cos
C
x
−+
. B.
tan xC
+
. C.
cot xC−+
. D.
cot xC+
.
Lời giải
Ta có
2
1
d tan
cos
x xC
x
= +
∫
.
Câu 24. Cho
3
0
( )d 2fx x= −
∫
và
5
3
( )d 3fx x
=
∫
. Tính tích phân
[
]
5
0
2 ( )dL fx x
=
∫
.
A.
12L =
. B.
2L = −
. C.
2L =
. D.
12L = −
.
Lời giải
Ta có
5 35
0 03
( )d ( )d ( )d 2 3 1
fx x fx x fx x
= + =−+ =
∫∫∫
nên
21 2
L
= ⋅=
.
Câu 25. Họ nguyên hàm của hàm số
1
()fx
x
=
là
A.
1
2
xC+
. B.
3
2
xC+
. C.
xC+
. D.
2 xC+
.
Lời giải
11
d d2 .
2
x xC x xC
xx
= +⇒ = +
∫∫
Câu 26. Cho hàm số
()y fx=
có bảng biến thiên như hình vẽ.
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
( 2; 1)−−
. B.
( ; 1)−∞ −
. C.
( 1;1)−
. D.
( )
0;1
.
Lời giải
Dựa vào bảng biến thiên ta kết luậnhàm số đã cho đồng biến trên các khoảng
( ; 2)−∞ −
và
(0; 2)
.
Câu 27. Cho hàm số
()y fx=
liên tục trên
và có bảng biến thiên như sau
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có giá trị nhỏ nhất bằng
1−
.
B. Hàm số đạt cực đại tại
0x =
và đạt cực tiểu tại
1x = −
.
C. Hàm số có đúng một điểm cực trị.
D. Hàm số đạt cực đại tại
0x =
và đạt cực tiểu tại
1
x =
.
11
Lời giải
Dựa vào bảng biến thiên ta thấy hàm số đạt cực đại tại
0x =
và đạt cực tiểu tại
1x =
.
Câu 28. Cho
2
log 3a =
và
3
log 7b =
. Giá trị của
2
log 14
bằng
A.
1ab+−
. B.
4ab
. C.
23ab +
. D.
1ab
+
.
Lời giải
Ta có
2 23 23 2 3 3
23 23
log 14 log 3 log 14 log 3 log (7 2) log 3 (log 7 log 2)
log 3 log 7 log 3 log 2 1ab
= ⋅ = ⋅ ⋅= ⋅ +
=⋅+⋅=+
Câu 29. Thể tích khối tròn xoay tạo bởi khi quay quanh trục hoành của hình phẳng giới hạn bởi các đồ thị
hàm số
2
2y xx= −
;
0y =
;
0
x =
;
1x =
có giá trị bằng
A.
16
15
π
. B.
4
3
π
. C.
2
3
π
. D.
8
15
π
.
Lời giải
Thể tích cần tính
1
11
53
22 4 3 2 4
00
0
48
(2 ) d ( 4 4 )d .
5 3 15
xx
V xx x x x x x x
π
ππ π

= − = − + =⋅ −+ =


∫∫
Câu 30. Cho hình chóp tứ giác đều có cạnh đáy bằng
2
a
và chiều cao bằng
a
(tham khảo hình vẽ). Giá
trị tang của góc giữa mặt bên và mặt đáy bằng
A.
1
. B.
3
4
. C.
3
. D.
1
3
.
Lời giải
Vì
.S ABCD
là hình chóp đều nên
()SO ABCD⊥
, với
O
là tâm của hình vuông
ABCD
.
Gọi
H
là trung điểm của
CD
.
Tam giác
SCD
cân tại
S
nên
SH CD⊥
.
Tam giác
OCD
cân tại
O
nên
OH CD⊥
.
Vậy góc giữa
()SCD
và
()ABCD
là
SHO
.
12
Ta có
1
2
OH BC a= =
;
SO a
=
nên
tan 1
SO
SHO
OH
= =
.
Câu 31. Số giao điểm của đồ thị hàm số
3
31yx x
=−+
và trục hoành là
A.
1
. B.
2
. C.
0
. D.
3
.
Lời giải
Xét
3
31
yx x=−+
có
22
3 3 3( 1)yx x
′
= −= −
. Tại
01yx
′
=⇔=±
.
Ta có các giới hạn
lim
x→−∞
= −∞
và
lim
x→+∞
= +∞
.
Bảng biến thiên của hàm số.
Từ bảng biến thiên, ta thấy hàm số
3
31
yx x
=−+
cắt trục hoành tại ba điểm phân biệt.
Câu 32. Hàm số
32
3 9 20yx x x
=−− + +
đồng biến trên khoảng
A.
( 3; )− +∞
. B.
( ;1)−∞
. C.
(1; 2)
. D.
( 3;1)−
.
Lời giải
Tập xác định
=
.
Ta có
2
3 69y xx
′
=− −+
;
1
0
3.
x
y
x
=
′
= ⇔
= −
Bảng biến thiên:
Vậy hàm số đồng biến trên
( 3;1)
−
.
Câu 33. Gọi
M
là tập hợp các số tự nhiên có
4
chữ số đôi một khác nhau được lập từ các chữ số
1
;
2
;
3
;
4
;
5
;
6
;
7
. Lấy ra từ tập
M
một số bất kỳ. Xác suất để lấy được số lẻ bằng
A.
3
7
. B.
4
7
. C.
2
21
. D.
3
4
.
Lời giải
Số phần tử của
M
bằng
4
7
( ) A 840nM = =
nên số phần tử của không gian mẫu bằng
840
.
Số các số tự nhiên lẻ trong
M
bằng
3
6
( ) 4 A 480nA=⋅=
.
Xác suất cần tìm bằng
480 4
840 7
=
.
Câu 34. Tổng tất cả các nghiệm của phương trình
4 8 62
xx
+=⋅
bằng
A.
9
. B.
3
. C.
5
. D.
6
.
Lời giải
Ta có
1
4 32 80 4 62 80
xx xx+
−⋅ +=⇔ −⋅ +=
.
13
Đặt
2
x
t
=
( 0)t >
phương trình trở thành
2
2 (nh?n) 2 4 2
6 80
4 (nh?n) 1.
22
x
x
tx
tt
tx
= = =

− +=⇔ ⇔ ⇔

= =
=

Câu 35. Tập hợp điểm biểu diễn của số phức
z
thỏa mãn
| | | (1 ) |z i iz−= +
là đường tròn có toạ độ tâm
I
là
A.
(0;1)
I
. B.
(0; 1)I −
. C.
(1; 0)I
. D.
( 1; 0)I −
.
Lời giải
Gọi
(1 ) ( ) ( )z abi iz ab abi
=+⇒+ =−++
.
Vậy
22 2 2
22
| | |(1 ) | | ( 1) | |( ) ( ) |
( 1) ( ) ( )
2 1 0.
z i iz a b i a b a bi
a b ab ab
ab b
−= + ⇔ + − = − + +
⇔ +− =− ++
⇔ + + −=
Vậy tập hợp điểm biểu diễn của số phức
z
là đường tròn tâm
(0; 1)I −
.
Câu 36. Trong không gian
Oxyz
, cho hai điểm
(1; 2; 0)A
,
(2;1; 1)B −
. Mặt phẳng
()
P
đi qua hai điểm
A
,
B
và vuông góc với mặt phẳng
Oxy
có phương trình là
A.
2 10xy
− +=
. B.
2 10xy z− + +=
. C.
30xy+−=
. D.
2 40xy
+ −=
.
Lời giải
Ta có
(1; 1; 1)AB = −−

và
(0; 0;1)k
=
là hai vectơ có giá song song hoặc nằm trên
()P
nên mặt phẳng
()P
có một vectơ pháp tuyến là
, ( 1; 1; 0).AB k

=−−


Phương trình mặt phẳng
()P
là
1( 1) ( 2) 0( 0) 0 3 0.x y z xy− − − − + − =⇔+−=
Câu 37. Trong không gian
Oxyz
, toạ độ giao điểm của mặt phẳng
( ):2 3 6 0P x yz− +−=
với trục tung
là
A.
(0; 2;0)−
. B.
(0; 2;0)
. C.
(3;0;0)N
. D.
(0; 0; 6)P
.
Lời giải
T oạ độ giao điểm của mặt phẳng
( ):2 3 6 0P x yz
− +−=
với trục tung là
(0; 2;0)−
.
Câu 38. Cho hình chóp
.S ABC
có ba cạnh bên
,
2SB =
,
3SC
=
đôi một vuông góc với nhau.
Chiều cao của hình chóp bằng
A.
5
6
. B.
66
11
. C.
2
3
. D.
6
7
.
Lời giải
Hạ
AK BC⊥
,
AH DK⊥
, ta có khoảng cách từ
A
đến mặt phẳng
()BCD
bằng
AH
.
Xét
ABC∆
, ta có
222
111
AK AB AC
= +
.
Xét tam giác
AKD
, ta có
14
2 2 2 222
222
1 11 111
1 1 1 49
1 2 3 36
6
.
7
AH AD AK AD AB AC
AH
= + = ++
= ++=
⇒=
Câu 39. Có bao nhiêu số nguyên
x
thỏa mãn
82
3log ( 1) log (86 ) 1xx+− − ≥
?
A.
28
. B.
85
. C.
29
. D.
86
.
Lời giải
Điều kiện
10
1 86
86 0
x
x
x
+>
⇔− < <
−>
.
Ta có
3
82
2
2
22
2
3log ( 1) log (86 ) 1
3log ( 1) log (86 ) 1
log ( 1) log (86 ) 1
1
log 1
86
1
2
86
1 2(86 ) (vì 86 0)
57.
xx
xx
xx
x
x
x
x
x xx
x
+− − ≥
⇔ +− − ≥
⇔ +− − ≥
+

⇔≥

−

+
⇔≥
−
⇔ +≥ − − >
⇔≥
Kết hợp với điều kiện, ta được
57 86x
≤<
.
Vậy có
29
số nguyên
x
thỏa mãn yêu cầu bài toán.
Câu 40. Cho hàm số
()y fx=
có đạo hàm liên tục trên
thỏa mãn
(2) 2f = −
;
2
0
( )d 1fx x=
∫
. Tính
( )
4
0
dI f xx
′
=
∫
.
A.
10I = −
. B.
0I
=
. C.
18I = −
. D.
5
I = −
.
Lời giải
Đặt
2
2d dt x t x tt x= ⇒=⇒ =
.
Đổi cận
00
xt= ⇒=
;
42xt= ⇒=
.
Suy ra
( )
( )
22 2
2
0
00 0
2 d 2 d 2 ( ) ( )d 2.( 4 1) 10
|
I tf t t xf x x xfx fx x

′′
= = = − = −− =−


∫∫ ∫
.
Câu 41. Cho hàm số
()fx
có bảng biến thiên như hình vẽ.
Số nghiệm thực phân biệt của phương trình
[ ]
() 2 0f fx
′
+=
là
A.
6
. B.
5
. C.
4
. D.
3
.
Lời giải
15
[
]
() 2 1 () 3
() 2 0
() 2 2 () 0.
fx fx
f fx
fx fx
+=− =−

′
+=⇔ ⇔

+= =

Ta có
() 3fx= −
⇒
phương trình có
2
nghiệm.
() 0fx=
⇒
phương trình có
3
nghiệm.
Vậy
[
]
() 2 0
f fx
′
+=
có
5
nghiệm.
Câu 42. Cho số phức
z
thỏa mãn
|4 3 | |4 4 5 |zi z i+ = −+
. Tìm giá trị nhỏ nhất của biểu thức
| | | 3|P zi z i=++ −
.
A.
min 5 2
P =
. B.
min 5P =
. C.
min 2 2P
=
. D.
min 2 5
P =
.
Lời giải
Cách 1. Gọi
z x yi
= +
với
,xy∈
. Khi đó
22 22
| 4 3 | | 4 4 5 | (4 ) (2 3) (4 4) (4 5) 2 2.
zi z i x y x y y x+=−+⇔ ++=−++⇔=−
Do đó
2 22 2 2 2
( 1) ( 3) 5 4 1 5 20 25 ( ).Pxy xy xx x x fx= ++ + +− = −++ − + =
Ta có
22
5 2 5 10
()
5 4 1 5 20 25
xx
fx
xx x x
−−
′
= +
−+ − +
,
22 2
(5 2)(5 10) 0
2
() 0
3
(5 2) (5 20 25) (5 10)(5 4 1)
xx
fx x
x x x x xx
− −≤
′
=⇔ ⇔=
− − + = − −+
.
Bảng biến thiên
Vậy
2
min 2 5
3
Pf

= =


.
Cách 2: Gọi
(; )Mxy
là điểm biểu diễn của số phức
z
. Khi đó
22 22
| 4 3 | | 4 4 5 | (4 ) (2 3) (4 4) (4 5) 2 2 0.z i z i x y x y xy
+=−+⇔ ++=−++⇔−−=
Suy ra
M
chạy trên đường thẳng
:2 2 0d xy−−=
.
Gọi
(0; 1)A −
,
(0;3)B
. Khi đó
P MA MB= +
.
Vì
[2 0 ( 1) 2](2 0 3 2) 0⋅−−− ⋅−− >
nên
A
,
B
nằm cùng phía so với
d
.
Gọi
A
′
là điểm đối xứng với
A
qua
d
. Ta tìm được
47
;
55
A

′
−


. Khi đó
2 5,P MA MB MA MB A B
′′
=+= +≥=
đẳng thức xảy ra khi
M
trùng
0
22
;
33
M

−


là giao điểm của đoạn
AB
′
và
d
.
Vậy
2
min 2 5
3
Pf

= =


Câu 43. Cho khối lăng trụ đứng
.ABCD A B C D
′′′ ′
có đáy là hình vuông có cạnh bằng
2
. Biết khoảng
cách từ
A
đến mặt phẳng
( )
CB D
′′
bằng
2
. Thể tích của khối lăng trụ đã cho bằng
A.
3
. B.
22
. C.
42
. D.
42
3
.
Lời giải
16
Chọn hệ trục tọa độ
Oxyz
sao cho
(0; 0; 0)A
,
B
thuộc chiều dương trục
Ox
,
D
thuộc chiều dương trục
Oy
,
A
′
thuộc chiều dương trục
Oz
. Gọi chiều cao lăng trụ là
h
,
0,H >
ta có
(2;0;0)B
,
(0; 2;0)D
,
(2; 2; 0)
C
,
(0; 0; )Ah
′
,
(2;0; )
Bh
′
,
(0; 2; )Dh
′
và
(2; 2; )Ch
′
.
Mặt phẳng
( )
CB D
′′
có hai véc-tơ chỉ phương
(0; 2; )CB h
′
= −

và
( 2; 0; )CD h
′
= −

nên có 1 véc-tơ pháp
tuyến là
, ( 2 ;2 ; 4) hay ( ; ;2).n CB CD h h h h
′′

= =−−

 
Mặt phẳng
( )
CB D
′′
đi qua
(2; 2; 0)C
nên
( )
: 2 4 0.CB D hx hy z h
′′
++−=
Ta có
( )
( )
22
|4 |
d , 2 2 2.
4
h
A CB D h
hh
′′
=⇔ =⇔=
++
Vậy
2
.
2 2 4 2.
ABCD
ABCD A B C D
V Sh
′′′ ′
= ⋅= =
Câu 44. Cho hàm số
()y fx
=
có đồ thị
()
C
như hình vẽ. Biết rằng diện tích hình phẳng giới hạn bởi
()C
và trục hoành bằng
8
và
8
0
( )d 4fx x=
∫
. Giá trị của
8
3
(2023 ) ( )d
I xf x x
′
= −
∫
bằng
A.
6
. B.
12
. C.
4
. D.
2023
.
Lời giải
Đặt
3
0
( )dfx x a=
∫
và
8
3
( )dfx x b=
∫
.
Từ giả thiết bài toán ta có hệ
42
86
ab a
ab b
+= =−

⇔

−+ = =

.
Đặt
2023 d d
d ()d ().
u x ux
vfxx vfx
=−=−

⇒

′
= =

Suy ra
17
8
8
3
3
(2023 ) ( ) ( )d
(2023 8) (8) (2023 3) (3)
00
6.
|I xfx fx x
f fb
b
=−+
= −−−+
= −+
=
∫
Câu 45. Cho phương trình
22
30z mz m− + −=
với
m
là tham số thực. Gọi
S
là tập hợp các giá trị của
m
sao cho phương trình đã cho có hai nghiệm phức có điểm biểu diễn là
A
,
B
và tam giác
OAB
có
diện tích bằng
6
. Tổng bình phương các phần tử của
S
bằng
A.
32
. B.
16
. C.
8
. D.
18
.
Lời giải
Ta có
22 2
4( 3) 12 3mm m
∆= − − = −
.
+) Nếu
0∆≥
thì phương trình đã cho có hai nghiệm thực, khi đó
O
,
A
,
B
thẳng hàng: không thoả
mãn.
+) Nếu
2
0
2
m
m
>
∆< ⇔
<−
thì phương trình có hai nghiệm không thực
2
1,2
3 12
22
mm
zi
−
= ±
.
Suy ra
2
3 12
;
22
mm
A

−
−



,
2
3 12
;
22
mm
B

−



.
Ta thấy
A
và
B
đối xứng nhau qua trục hoành nên diện tích tam giác
OAB
bằng
2 42
1
3 12 6 4 192 0 4.
22
m
m mm m⋅ ⋅ − =⇔ − − =⇔=±
Đối chiếu điều kiện, vậy có hai giá trị của
m
thoả mãn bài toán, là
4
±
.
Câu 46. Trong không gian
Oxyz
, cho đường thẳng
21
:
2 11
x yz
d
−−
= =
và điểm
(1; 3; 0)
A
. Mặt cầu
()S
đi qua
A
, tiếp xúc với
Oxy
và với đường thẳng
d
. Bán kính của mặt cầu
()S
là
A.
30
. B.
66
. C.
25
. D.
2 10
.
Lời giải
Mặt cầu
()S
tiếp xúc với
()Oxy
tại
(1; 3; 0)A
. Gọi
I
là tâm mặt cầu
()S
nên
1
:3
x
Iy
zt
=
∈∆ =
=
(là đường
thẳng đi qua
A
và vuông góc với
Oxy
).
Do đó
d( ,( )) | |I Oxy t=
.
Gọi
(2;1; 0)Md∈
,
( )
1; 2;IM t= −−

,
( )
, 2 ; 2 1; 5
d
IM u t t

=−+ − −

 
2
5 30
d( , )
6
t
Id
+
⇒=
.
Theo đề bài ta có
2
22
30
5 30
d( ,( )) d( , ) | | 5 30 6
6
30.
t
t
I Oxy I d t t t
t
=
+
= ⇔ =⇔ += ⇔
= −
Vậy
| | 30Rt= =
.
Câu 47. Có bao nhiêu số nguyên dương
y
sao cho có không quá 8 số nguyên
x
thỏa mãn
( ) ( )
22
log 4 2log 2xy x+> −
?
A.
24
. B.
37
. C.
23
. D.
36
.
Lời giải
Điều kiện:
2
4 0.
x
xy
>
+>
18
Khi đó
( ) (
) ( ) ( )
2
2 22 2
log 4 2 log 2 log 4 log 2xy x xy x+> −⇒ +> −
22
4 44 84xyx x yx x⇒+>−+⇒>−+
(*)
Xét hàm số
2
() 8 4fx x x=−+
trên khoảng
( )
2; +∞
.
() 2 8 0 4fx x x
′
= −=⇒=
.
Bảng biến thiên
Để có không quá 8 giá trị nguyên của
x
thì
(
]
2;10x ∈
. Khi đó
(2) 8f = −
;
( )
10 24f
=
.
Từ
(*)
suy ra
8 24y−< ≤
.
Vậy có 24 giá trị nguyên dương của
y
thỏa mãn yêu cầu bài toán.
Câu 48. Cho khối trụ
()
T
có bán kính đáy bằng
23
a
. Gọi
A
và
B
là hai điểm thuộc hai đường tròn
đáy của
()T
sao cho khoảng cách và góc giữa
AB
và trục của
()T
bằng
2a
và
60
°
. Thể tích của khối trụ
đã cho bằng
A.
3
48 6 a
π
. B.
3
24 2
a
π
. C.
3
16 6 a
π
. D.
3
24 6 a
π
.
Lời giải
Hạ đường sinh
BB
′
và gọi
M
là trung điểm
AB
′
ta có
( ) ( )
, , 60OO BB OO AB BB AB ABB
°
′′ ′ ′ ′
⇒===
.
Ta có
OM AB
′
⊥
và
OM BB
′
⊥
nên
()OM ABB
′
⊥
. Do đó
( ) ( )
d , d ,( ) 2 .OO AB O ABB OM a
′′
= = =
Ta có
2 2 22
2 2 2 12 4 4 2
AB AM OA OM a a a
′
= = − = −=
.
46
cot 60
3
a
h BB AB
°
′′
= = =
.
Vậy
22 3
46
12 16 6
3
a
V rh a a
ππ π
= =⋅⋅ =
.
Câu 49. Trong không gian
Oxyz
, cho tam giác
ABC
có
(6; 0; 0)A
,
(6;8; 0)B
,
(0;8; 0)C
. Gọi mặt phẳng
()
α
đi qua
B
và vuông góc với
AC
. Điểm
M
thay đổi thoả mãn
90ABM AMC
°
= =
. Gọi
N
là giao
điểm của
AM
và
()
α
. Khoảng cách từ
N
đến
()ABC
có giá trị lớn nhất bằng
19
A.
8
5
. B.
82
5
. C.
24
5
. D.
12
5
.
Lời giải
Ta có
8AB =
,
6
BC =
,
10
AC =
nên
ABC∆
vuông tại
B
, suy ra
B
thuộc mặt cầu
()
S
có đường kính
AC
.
Lại có
90
AMC
°
=
nên
()MS∈
.
Vì
90ABM
°
=
nên
M
thuộc mặt phẳng
()P
qua
B
và vuông góc
AB
.
Từ đó ta có
M
nằm trên đường tròn
()C
là giao tuyến của mặt cầu
()S
và mặt phẳng
()P
.
Mặt phẳng
()
α
đi qua
B
, vuông góc với
AC
và cắt
AC
tại
K
.
Do
()
AB MC
MC ABM MC BN
MA MC
⊥
⇒⊥ ⇒⊥
⊥
.
Lại có
BN AC⊥
nên
()BN AN C BN NK⊥ ⇒⊥
.
Suy ra
N
thuộc đường tròn đường kính
BK
.
Gọi
T
là trung điểm
BK
.
Khi đó
1 1 12
d( ,( )) d( , )
22 5
N ABC NT BC B AC≤= = =
.
Câu 50. Cho hàm số đa thức
()fx
có đồ thị của đạo hàm
()fx
′
như hình bên. Biết rằng
(0) 0f =
. Hàm
số
63
() ( )gx f x x= −
có bao nhiêu điểm cực trị?
A.
7
. B.
4
. C.
5
. D.
3
.
Lời giải
Xét hàm
63
() ( )gx f x x= −
,
( )
5 6 2 23 6
()6 ()3 3 2 ()1gx xfx x x xfx
′′ ′
= −= −
.
20
6
3
0
() 0
1
( ) . (*)
2
x
gx
fx
x
=
′
= ⇔
′
=
Xét phương trình
(*)
, đặt
6
,0t xt= ≥
, suy ra
3
xt= ±
.
Do đó phương trình
(*)
trở thành
1
()
2
ft
t
′
= ±
. \hfill (1)
Nghiệm của phương trình là hoành độ giao điểm của đồ thị
()y ft
′
=
và
1
2
y
t
= ±
.
Dựa vào đồ thị ta thấy phương trình có nghiệm
0
0t >
duy nhất. Suy ra
3
0
xt=
.
Ta có bảng biến thiên
Do đó hàm số
()y gx=
có
1
điểm cực trị và cắt trục hoành tại
2
điểm phân biệt. Vậy hàm số
()y gx=
có
3
điểm cực trị.
--------------- TOANMATH.com ---------------
| 1/20
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD&ĐT HÀ TĨNH
KÌ THI THỬ TỐT NGHIỆP THPT NĂM 2023 ĐỀ THI ONLINE Bài thi: TOÁN
Thời gian mở đề: 14h20 | Đóng đề: 16h10 | 12/05/2023
Câu 1. Trên mặt phẳng toạ độ, điểm biểu diễn số phức z = 3
− + 4i có toạ độ là A. ( 3 − ; 4 − ) . B. (3; 4 − ) . C. (3;4) . D. ( 3 − ;4).
Câu 2. Trên khoảng (0;+∞), đạo hàm của hàm số y = ln x là A. 1 y′ = . B. e y′ = . C. 1 y′ = . D. 1 y′ = . x x 10x x ln10 3
Câu 3. Trên khoảng (0;+∞), đạo hàm của hàm số 2
y = x là 5 1 1 A. 3 3 2
y′ = x . B. 2
y′ = x . C. 2
y′ = x . D. 3 y′ = x . 2 2 2
Câu 4. Tập nghiệm bất phương trình 2x > 2 − là A. ( ; −∞ 1) − . B.  . C. (1;+∞). D. ( 1; − +∞) .
Câu 5. Ba số nào sau đây theo thứ tự lập thành một cấp số cộng? A. 2,5,8. B. 2,4,8 . C. 3,9,12 . D. 3, 6 − ,9 .
Câu 6. Trong không gian Oxyz , mặt phẳng (P) : 2x + 3y − 5z − 2023 = 0 có một vectơ pháp tuyến có toạ độ là A. (2;3;5) . B. (2;3; 5 − ) . C. (2; 3 − ; 5 − ) . D. (2; 3 − ;5) . Câu 7. Cho hàm số 3x − 2 y =
. Toạ độ giao điểm của đồ thị hàm số đã cho với trục tung là x −1 A. (0;2) . B.  2 ;0  . C. (3;0) . D. (0;1) . 3    2
Câu 8. Tính I = 2xdx ∫ . 1
A. I = 2 .
B. I = 3 . C. I =1. D. I = 4 .
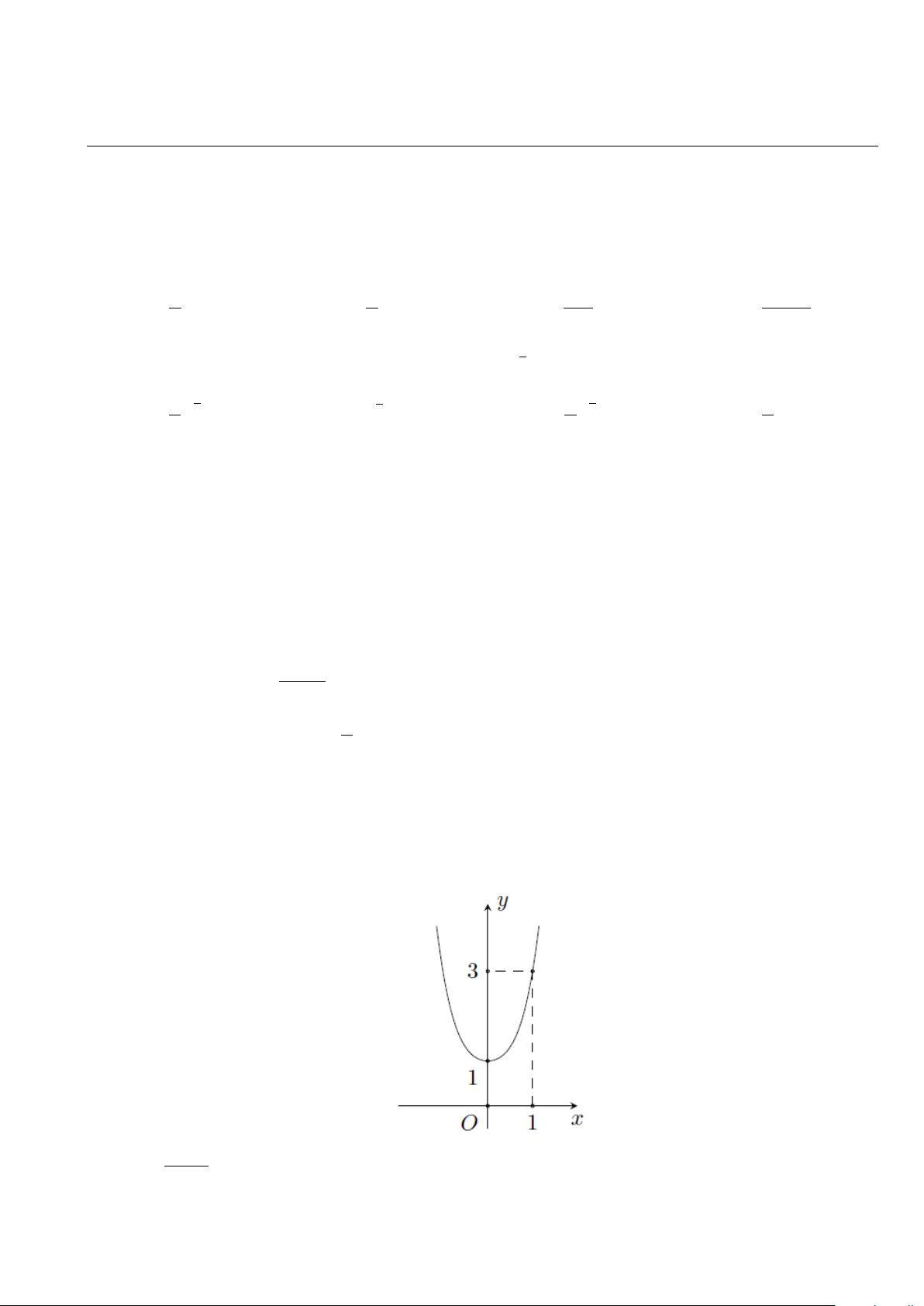
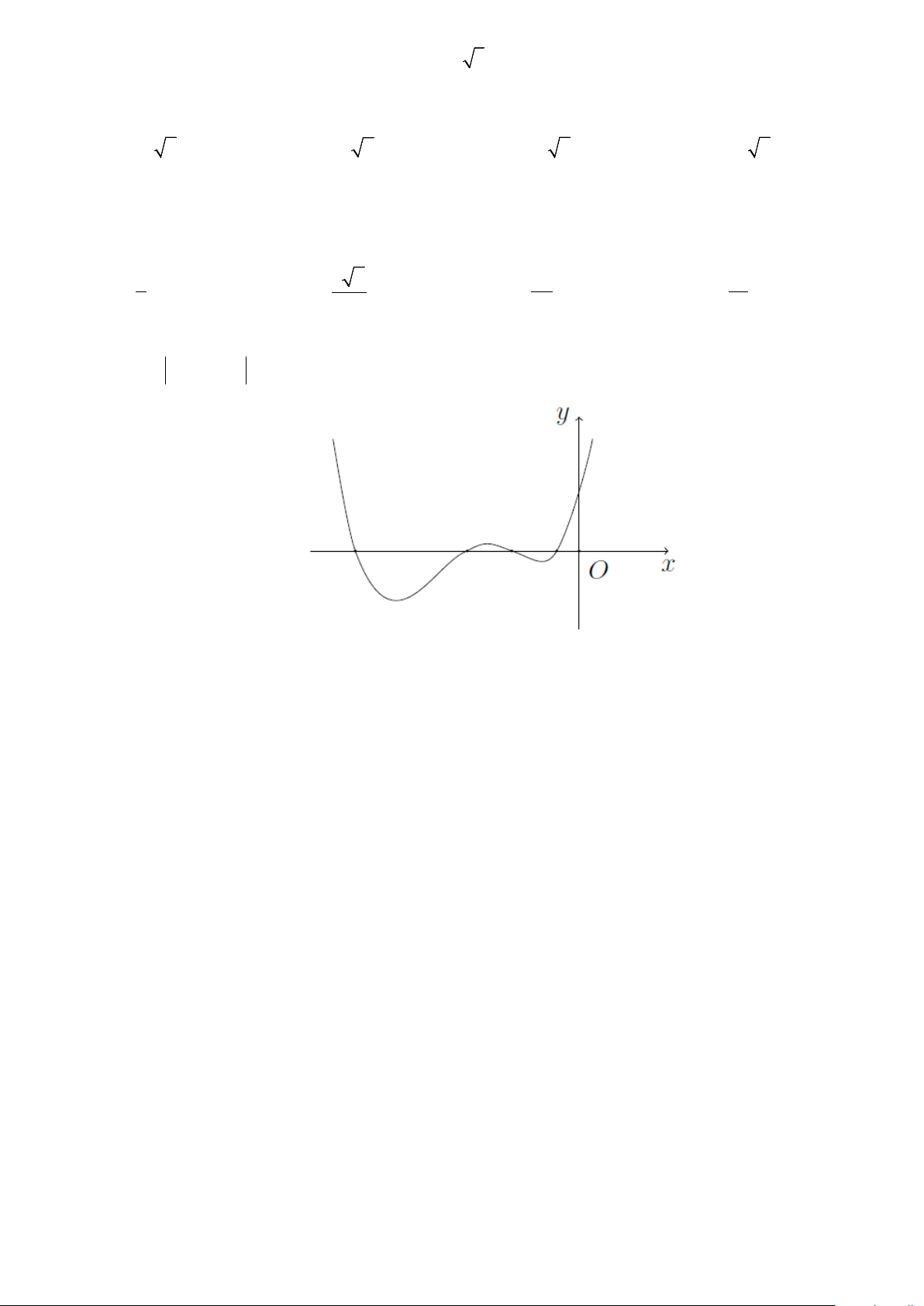
Câu 9. Đường cong trong hình bên là đồ thị của hàm số nào sau đây? A. 2x −1 y = . B. 4 2
y = x − 2x +1. C. 4 2
y = x + x +1. D. 3 y = 2x +1. x −1
Câu 10. Trong không gian Oxyz , mặt cầu 2 2 2
(S) : (x − 3) + (y −1) + (z + 4) = 4 có toạ độ tâm I và bán
kính R tương ứng là 1 A. I(3;1; 4 − ) , R = 2 . B. I( 3 − ; 1;
− 4), R = 2 . C. I(3;1; 4 − ) , R = 4 . D. I( 3 − ; 1; − 4), R = 4 . 
Câu 11. Trong không gian với hệ toạ độ Oxyz , cho hai vectơ a = ( 1;
− 1;0), b = (1;1;0) . Mệnh đề nào dưới đây đúng?   
A. a ⊥ b .
B. a , b cùng hướng.  
C. a , b đối nhau.
D. a , b ngược hướng.
Câu 12. Cho số phức z = 2 + 3i . Số phức liên hợp của z là A. z = 2 − + 3i .
B. z = 2 − 3i . C. z = 2 − − 3i . D. z = 3 − + 2i .
Câu 13. Cho khối lập phương có cạnh bằng 2. Diện tích toàn phần của hình lập phương bằng A. 24 . B. 8 . C. 12. D. 32.
Câu 14. Cho khối lăng trụ ABC . D A′B C ′ D
′ ′ có đáy là hình vuông có cạnh bằng a và chiều cao bằng h .
Thể tích của khối lăng trụ đã cho bằng A. 2 π a h . B. 2 a h . C. 1 2 a h . D. 2 3a h . 3
Câu 15. Diện tích của mặt cầu bán kính R = 3 bằng A. 6π . B. 18π . C. 36π . D. 12π .
Câu 16. Phần thực của số phức z = (1+ 2i)(2 − i) là A. 0 . B. 4 . C. 2 . D. 3.
Câu 17. Một hình trụ có bán kính đáy r = 4 và có chiều cao h = 3. Diện tích xung quanh của hình trụ bằng A. 12π . B. 24π . C. 40π . D. 20π . x = 1+ 2t
Câu 18. Trong không gian Oxyz , đường thẳng d : y = 2 −3t không đi qua điểm nào dưới đây? z = 3−  t
A. Q(1;2;3). B. P(2; 2; − 1 − ) . C. N( 1; − 5;4) . D. M (3; 1; − 2) .
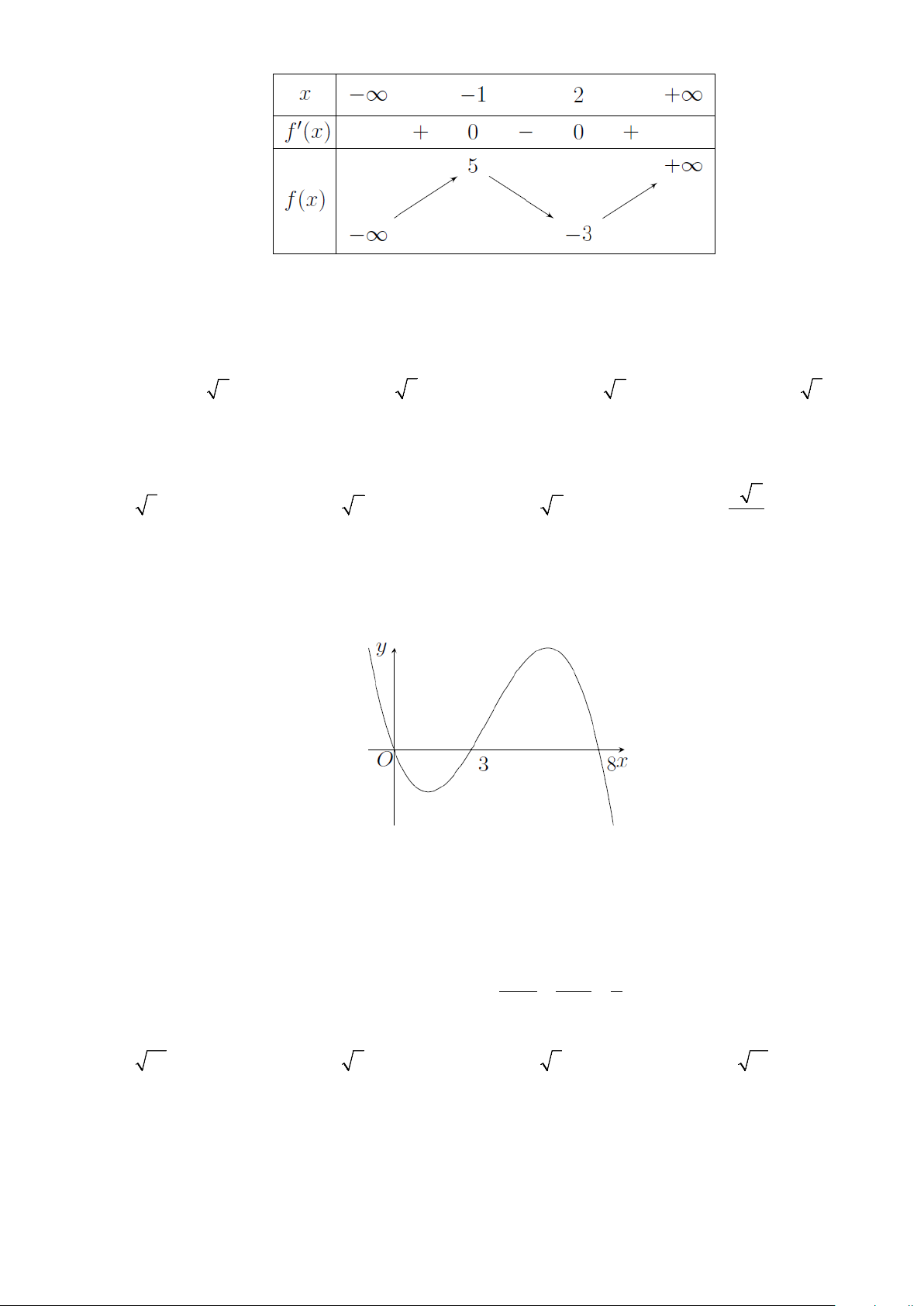
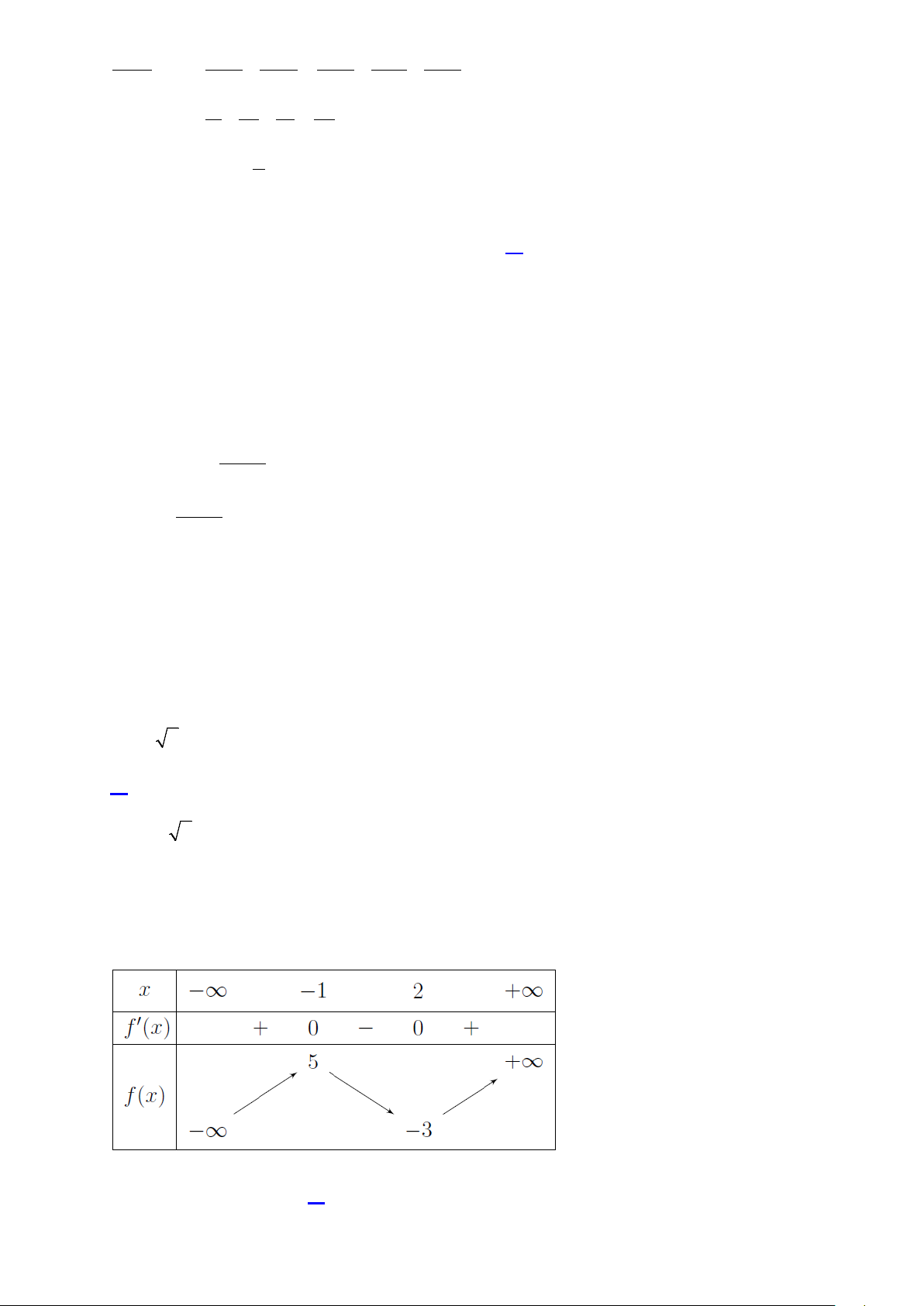
Câu 19. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ.
Giá trị cực đại của hàm số bằng A. 2 − . B. 3. C. 2 . D. 1 − .
Câu 20. Đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số nào sau đây? 2 A. y − − = 2x . B. 2 y = . C. 2x 1 y = . D. 2x 3 y = . x −1 x + 2 x +1
Câu 21. Tập nghiệm S của bất phương trình log x ≤ 3 là 2
A. S = (0;6] .
B. S = (0;8]. C. S = ( ; −∞ 6) . D. S = ( ; −∞ 8] .
Câu 22. Cho tập hợp M gồm 4 phần tử. Số tập con gồm 3 phần tử của M là A. 3 C . B. 4 3 . C. 3 4 . D. 3 A . 4 4
Câu 23. Họ nguyên hàm của hàm số 1 f (x) = là 2 cos x 2 A. 1 − + C .
B. tan x + C .
C. −cot x + C .
D. cot x + C . cos x 3 5 5
Câu 24. Cho f (x)dx = 2 − ∫
và f (x)dx = 3 ∫
. Tính tích phân L = ∫[2 f (x)]dx . 0 3 0
A. L =12 . B. L = 2 − .
C. L = 2 . D. L = 12 − .
Câu 25. Họ nguyên hàm của hàm số 1 f (x) = là x
A. 1 x + C .
B. 3 x + C .
C. x + C .
D. 2 x + C . 2 2
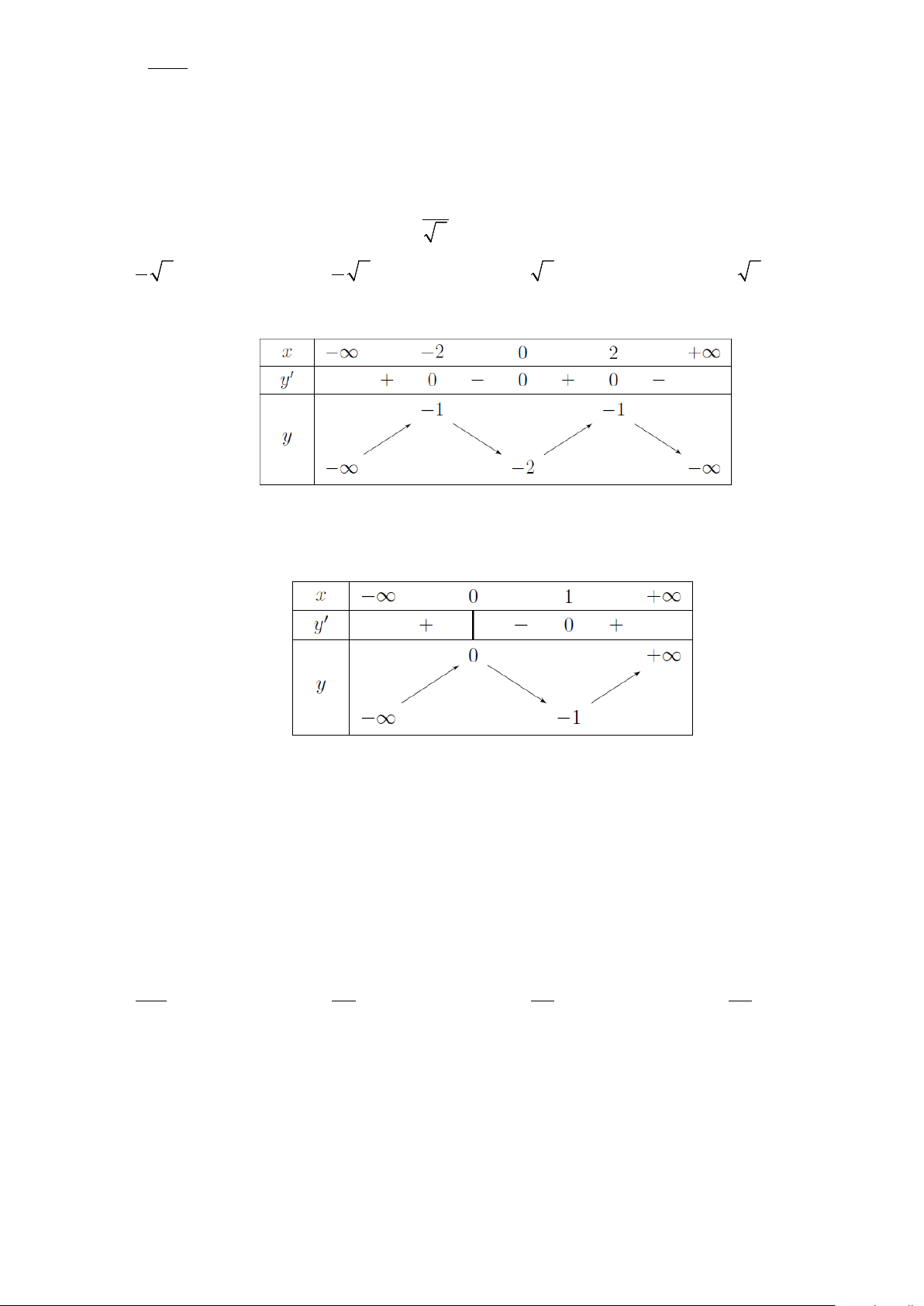
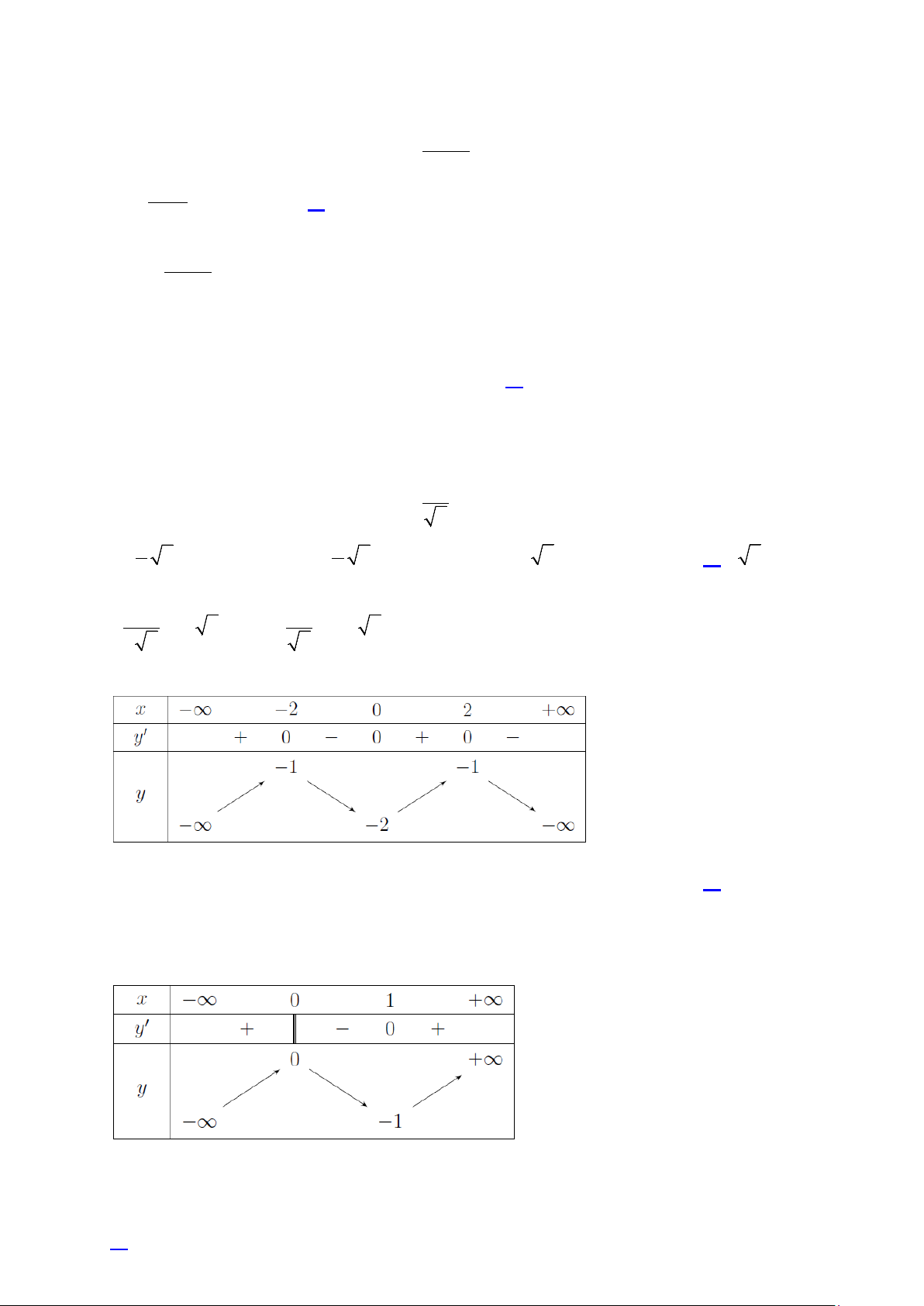
Câu 26. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ.
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. ( 2 − ; 1) − . B. ( ; −∞ 1) − . C. ( 1; − 1) . D. (0; ) 1 .
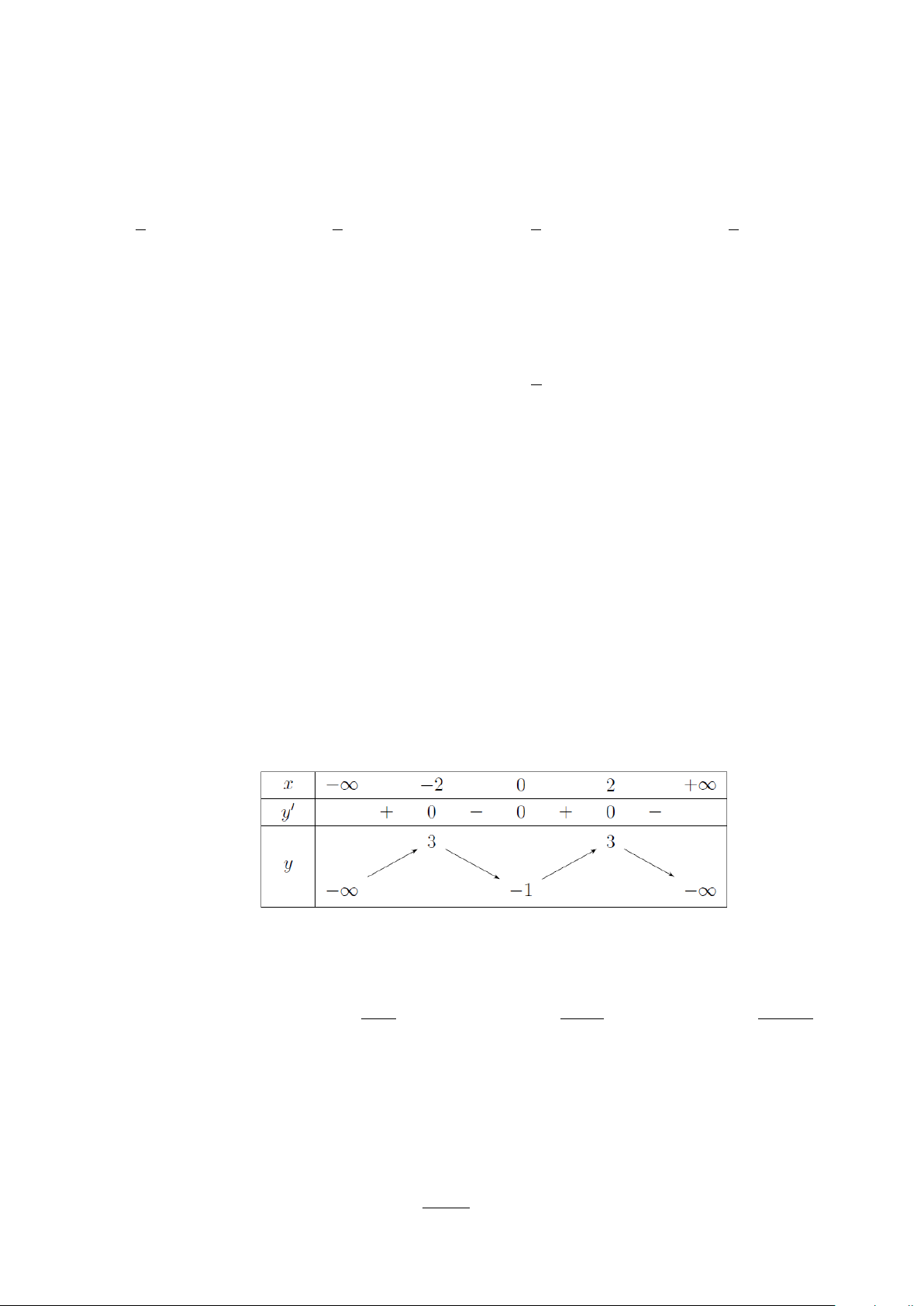
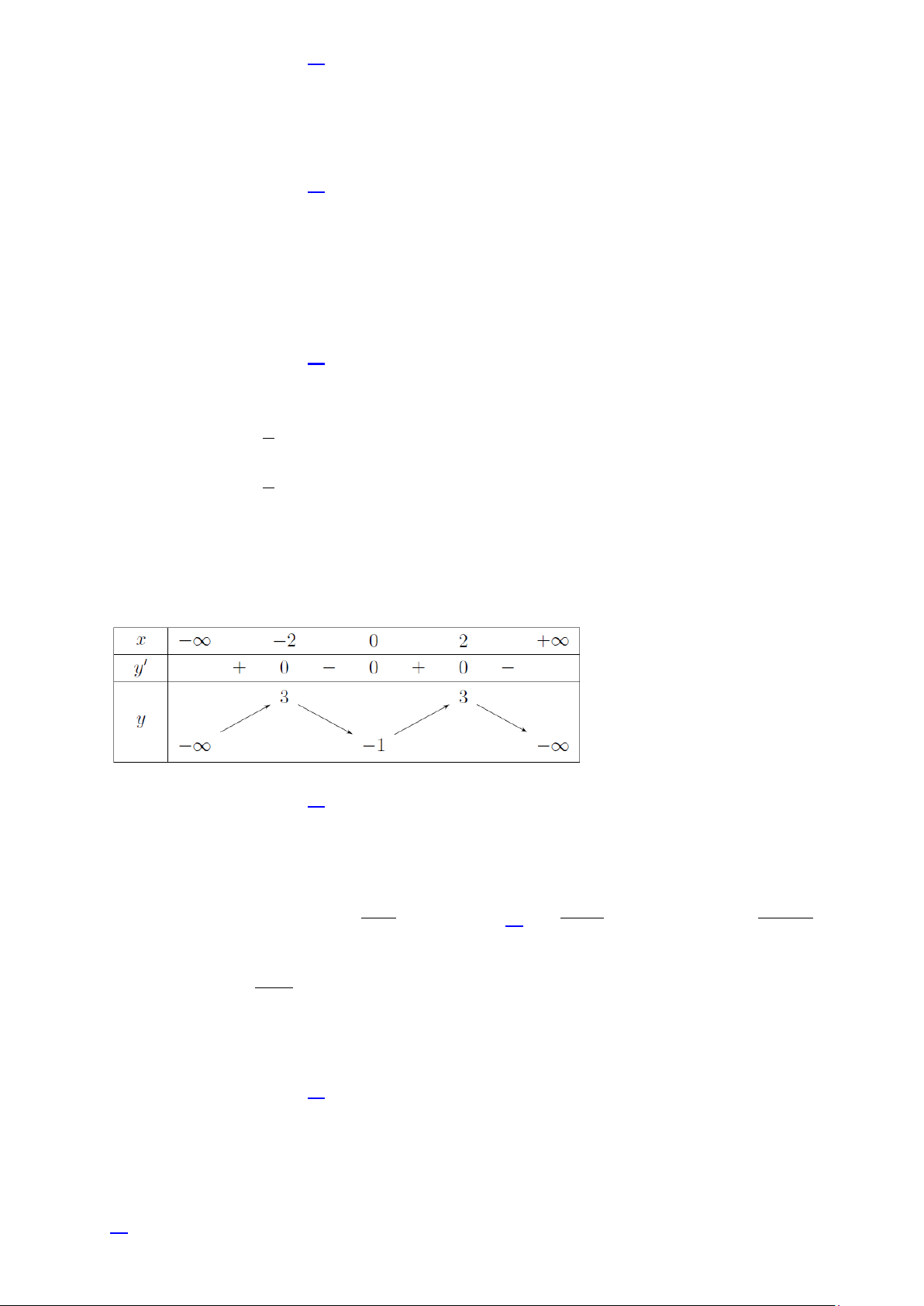
Câu 27. Cho hàm số y = f (x) liên tục trên  và có bảng biến thiên như sau
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có giá trị nhỏ nhất bằng 1 − .
B. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1 − .
C. Hàm số có đúng một điểm cực trị.
D. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x =1.
Câu 28. Cho a = log 3 và b = log 7 . Giá trị của log 14 bằng 2 3 2
A. a + b −1. B. 4ab .
C. 2ab + 3. D. ab +1.
Câu 29. Thể tích khối tròn xoay tạo bởi khi quay quanh trục hoành của hình phẳng giới hạn bởi các đồ thị hàm số 2
y = 2x − x ; y = 0; x = 0 ; x =1 có giá trị bằng π π π π A. 16 . B. 4 . C. 2 . D. 8 . 15 3 3 15
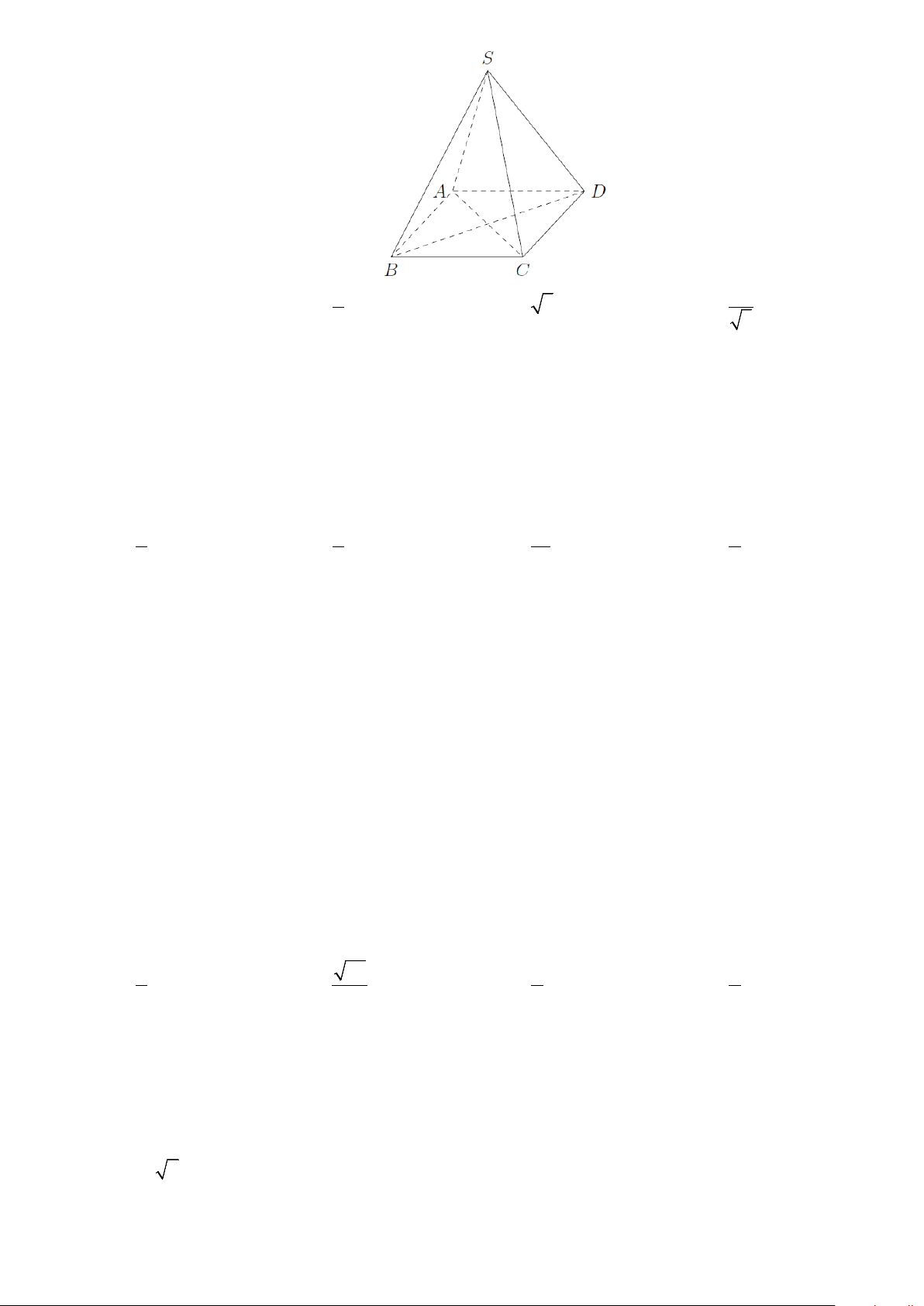
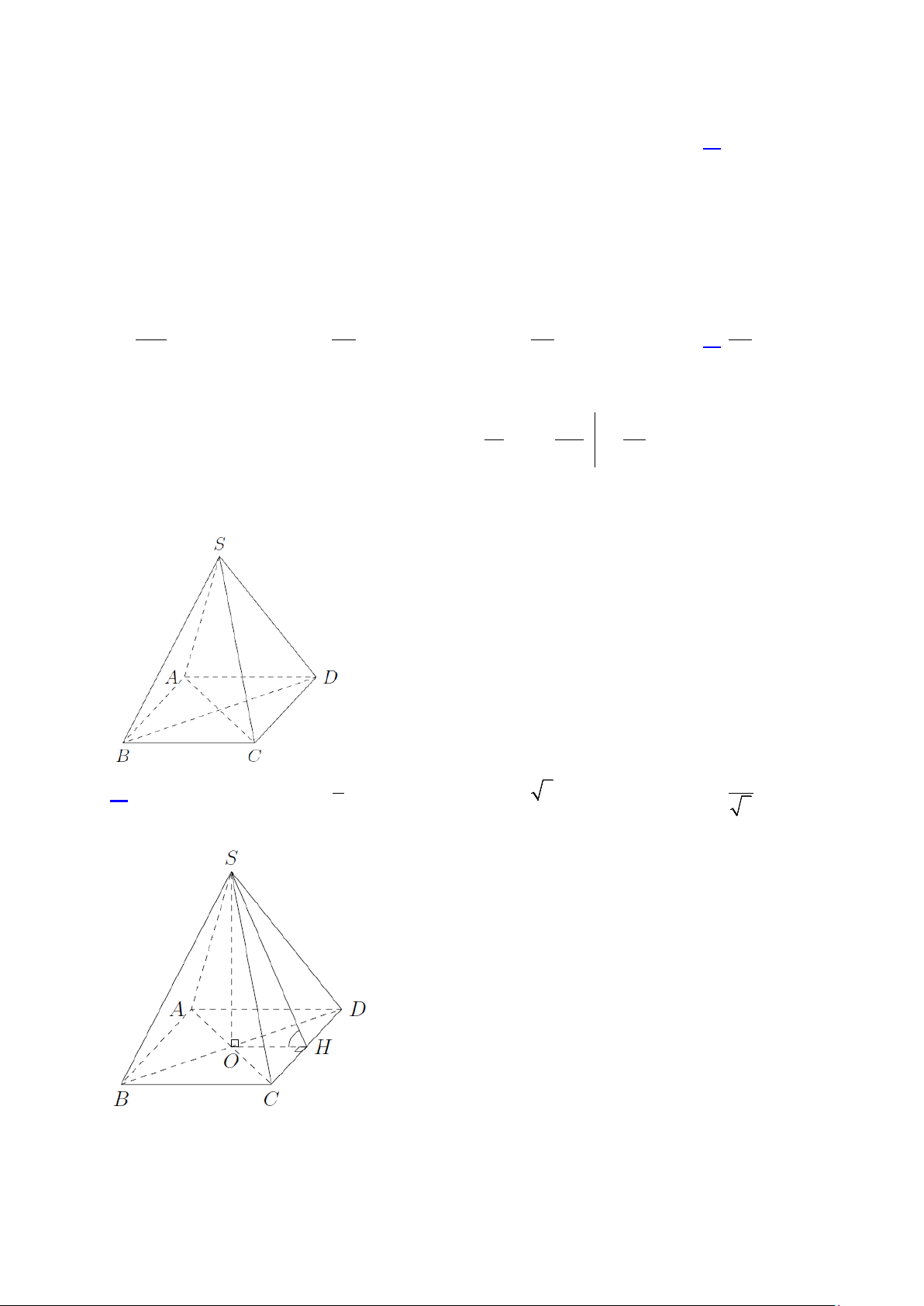
Câu 30. Cho hình chóp tứ giác đều có cạnh đáy bằng 2a và chiều cao bằng a (tham khảo hình vẽ). Giá
trị tang của góc giữa mặt bên và mặt đáy bằng 3 A. 1. B. 3 . C. 3 . D. 1 . 4 3
Câu 31. Số giao điểm của đồ thị hàm số 3
y = x − 3x +1 và trục hoành là A. 1. B. 2 . C. 0 . D. 3. Câu 32. Hàm số 3 2
y = −x − 3x + 9x + 20 đồng biến trên khoảng A. ( 3 − ;+∞) . B. ( ; −∞ 1). C. (1;2) . D. ( 3 − ;1) .
Câu 33. Gọi M là tập hợp các số tự nhiên có 4 chữ số đôi một khác nhau được lập từ các chữ số 1; 2 ;
3; 4 ; 5; 6 ; 7 . Lấy ra từ tập M một số bất kỳ. Xác suất để lấy được số lẻ bằng A. 3 . B. 4 . C. 2 . D. 3 . 7 7 21 4
Câu 34. Tổng tất cả các nghiệm của phương trình 4x 8 6 2x + = ⋅ bằng A. 9. B. 3. C. 5. D. 6 .
Câu 35. Tập hợp điểm biểu diễn của số phức z thỏa mãn | z − i | |
= (1+ i)z | là đường tròn có toạ độ tâm I
là A. I(0;1). B. I(0; 1) − .
C. I(1;0) . D. I( 1; − 0) .
Câu 36. Trong không gian Oxyz , cho hai điểm (
A 1;2;0), B(2;1; 1
− ) . Mặt phẳng (P) đi qua hai điểm A ,
B và vuông góc với mặt phẳng Oxy có phương trình là
A. 2x − y +1 = 0 .
B. x − y + 2z +1 = 0.
C. x + y − 3 = 0 .
D. x + 2y − 4 = 0 .
Câu 37. Trong không gian Oxyz , toạ độ giao điểm của mặt phẳng (P) : 2x − 3y + z − 6 = 0 với trục tung
là A. (0; 2;−0). B. (0;2;0) .
C. N(3;0;0) . D. P(0;0;6) .
Câu 38. Cho hình chóp S.ABC có ba cạnh bên SA =1, SB = 2 , SC = 3 đôi một vuông góc với nhau.
Chiều cao của hình chóp bằng A. 5 . B. 66 . C. 2 . D. 6 . 6 11 3 7
Câu 39. Có bao nhiêu số nguyên x thỏa mãn 3log (x +1) − log (86 − x) ≥1? 8 2 A. 28 . B. 85 . C. 29 . D. 86 . 2
Câu 40. Cho hàm số y = f (x) có đạo hàm liên tục trên  thỏa mãn f (2) = 2
− ; f (x)dx =1 ∫ . Tính 0 4 I = f ′
∫ ( x)dx. 0 A. I = 10 − .
B. I = 0. C. I = 18 − . D. I = 5 − . 4
Câu 41. Cho hàm số f (x) có bảng biến thiên như hình vẽ.
Số nghiệm thực phân biệt của phương trình f ′[ f (x) + 2] = 0 là A. 6 . B. 5. C. 4 . D. 3.
Câu 42. Cho số phức z thỏa mãn | 4z + 3i | |
= 4z − 4 + 5i |. Tìm giá trị nhỏ nhất của biểu thức P |
= z + i | + | z − 3i |.
A. min P = 5 2 .
B. min P = 5 .
C. min P = 2 2 .
D. min P = 2 5 .
Câu 43. Cho khối lăng trụ đứng ABC .
D A′B′C′D′ có đáy là hình vuông có cạnh bằng 2 . Biết khoảng
cách từ A đến mặt phẳng (CB′D′ ) bằng 2 . Thể tích của khối lăng trụ đã cho bằng A. 3 . B. 2 2 . C. 4 2 . D. 4 2 . 3
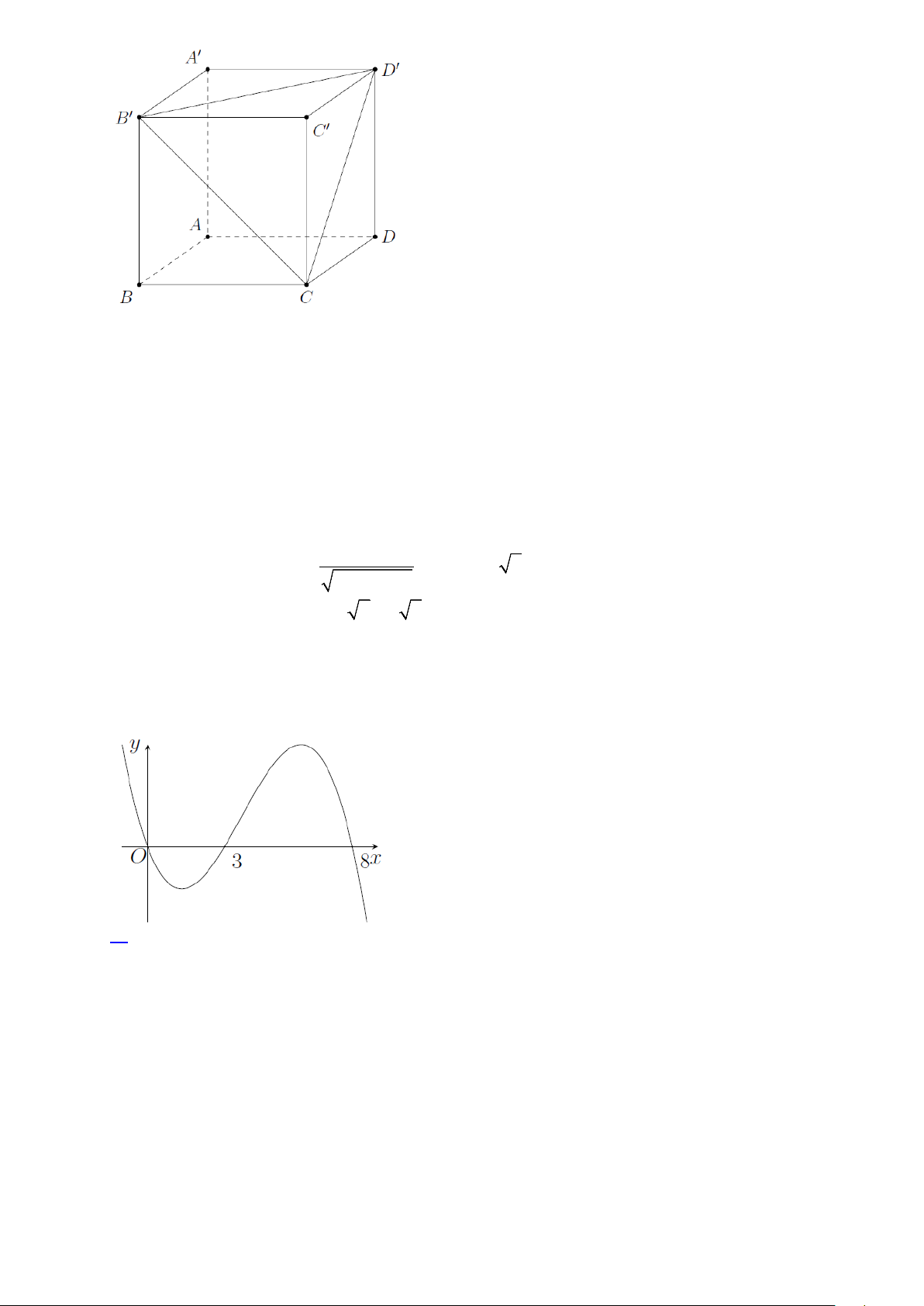
Câu 44. Cho hàm số y = f (x) có đồ thị (C) như hình vẽ. Biết rằng diện tích hình phẳng giới hạn bởi 8 8
(C) và trục hoành bằng 8 và f (x)dx = 4 ∫
. Giá trị của I = (2023− x) f (′x)dx ∫ bằng 0 3 A. 6 . B. 12. C. 4 . D. 2023.
Câu 45. Cho phương trình 2 2
z − mz + m − 3 = 0 với m là tham số thực. Gọi S là tập hợp các giá trị của
m sao cho phương trình đã cho có hai nghiệm phức có điểm biểu diễn là A , B và tam giác OAB có
diện tích bằng 6 . Tổng bình phương các phần tử của S bằng A. 32. B. 16. C. 8 . D. 18.
Câu 46. Trong không gian Oxyz , cho đường thẳng x 2 y 1 : z d − − = = và điểm (
A 1;3;0) . Mặt cầu (S) 2 1 1
đi qua A , tiếp xúc với Oxy và với đường thẳng d . Bán kính của mặt cầu (S) là A. 30 . B. 6 6 . C. 2 5 . D. 2 10 .
Câu 47. Có bao nhiêu số nguyên dương y sao cho có không quá 8 số nguyên x thỏa mãn
log 4x + y > 2log x − 2 ? 2 ( ) 2 ( ) A. 24 . B. 37 . C. 23. D. 36. 5
Câu 48. Cho khối trụ (T) có bán kính đáy bằng 2 3a . Gọi A và B là hai điểm thuộc hai đường tròn
đáy của (T) sao cho khoảng cách và góc giữa AB và trục của (T) bằng 2a và 60° . Thể tích của khối trụ đã cho bằng A. 3 48 6π a . B. 3 24 2π a . C. 3 16 6π a . D. 3 24 6π a .
Câu 49. Trong không gian Oxyz , cho tam giác ABC có (
A 6;0;0) , B(6;8;0) , C(0;8;0) . Gọi mặt phẳng
(α) đi qua B và vuông góc với AC . Điểm M thay đổi thoả mãn   ABM AMC 90° = = . Gọi N là giao
điểm của AM và (α) . Khoảng cách từ N đến (ABC) có giá trị lớn nhất bằng A. 8 . B. 8 2 . C. 24 . D. 12 . 5 5 5 5
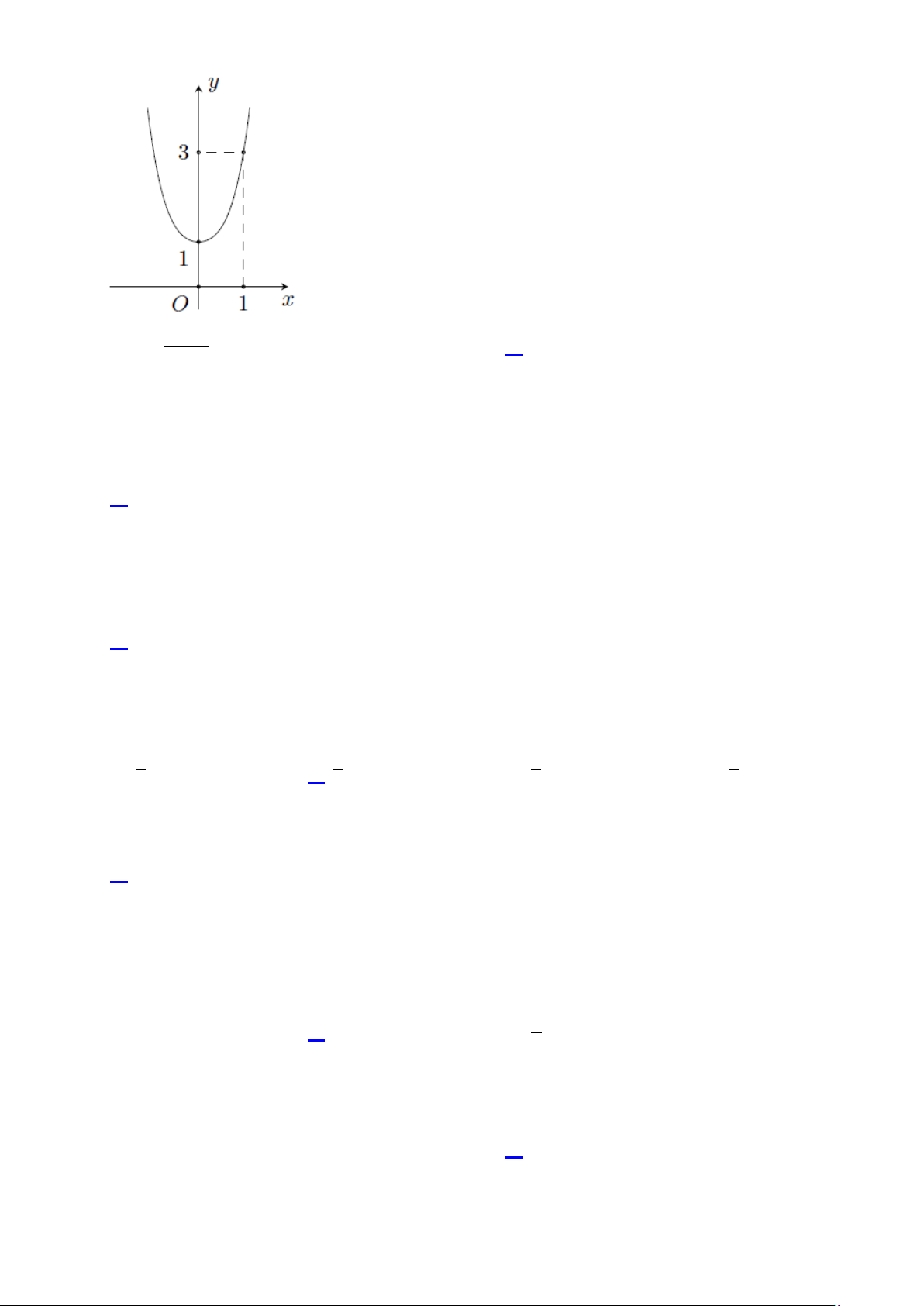
Câu 50. Cho hàm số đa thức f (x) có đồ thị của đạo hàm f (′x) như hình bên. Biết rằng f (0) = 0. Hàm số 6 3
g(x) = f (x ) − x có bao nhiêu điểm cực trị? A. 7 . B. 4 . C. 5. D. 3.
--------------- HẾT --------------- 6
LỜI GIẢI THAM KHẢO
Câu 1. Trên mặt phẳng toạ độ, điểm biểu diễn số phức z = 3
− + 4i có toạ độ là A. ( 3 − ; 4 − ) . B. (3; 4 − ) . C. (3;4) . D. ( 3 − ;4). Lời giải
Điểm biểu diễn của số phức z = 3
− + 4i là điểm có tọa độ ( 3 − ;4).
Câu 2. Trên khoảng (0;+∞), đạo hàm của hàm số y = ln x là A. 1 y′ = . B. e y′ = . C. 1 y′ = . D. 1 y′ = . x x 10x x ln10 Lời giải 1
y = ln x ⇒ y′ = . x 3
Câu 3. Trên khoảng (0;+∞), đạo hàm của hàm số 2
y = x là 5 1 1 A. 3 3 2
y′ = x . B. 2
y′ = x . C. 2
y′ = x . D. 3 y′ = x . 2 2 2 Lời giải 1
Áp dụng công thức đạo hàm của hàm số luỹ thừa, ta có 3 2 y′ = x . 2
Câu 4. Tập nghiệm bất phương trình 2x > 2 − là A. ( ; −∞ 1) − . B.  . C. (1;+∞). D. ( 1; − +∞) . Lời giải Ta có 2x > 0 > 2 − , x ∀ ∈  .
Vậy tập nghiệm là  .
Câu 5. Ba số nào sau đây theo thứ tự lập thành một cấp số cộng? A. 2,5,8. B. 2,4,8 . C. 3,9,12 . D. 3, 6 − ,9 . Lời giải Xét dãy số (u
, ta có 2 + 8 = 5 nên ba số 2,5,8 theo thứ tự lập thành một cấp số cộng. n ) : 2, 5,8 2
Câu 6. Trong không gian Oxyz , mặt phẳng (P) : 2x + 3y −5z − 2023 = 0 có một vectơ pháp tuyến có toạ độ là A. (2;3;5) . B. (2;3; 5 − ) . C. (2; 3 − ; 5 − ) . D. (2; 3 − ;5) . Lời giải
Mặt phẳng Ax + By + cz + D = 0 có một vectơ pháp tuyến có toạ độ ( ; A B :C) . Câu 7. Cho hàm số 3x − 2 y =
. Toạ độ giao điểm của đồ thị hàm số đã cho với trục tung là x −1 A. (0;2) . B.  2 ;0  . C. (3;0) . D. (0;1) . 3    Lời giải
Với x = 0 ta có y = 2 nên toạ độ giao điểm của đồ thị hàm số với trục tung là (0;2) . 2
Câu 8. Tính I = 2xdx ∫ . 1
A. I = 2 .
B. I = 3 . C. I =1. D. I = 4 . Lời giải 2 Ta có 2 2
I = 2xdx = x ∫ | = 4−1=3. 1 1 7
Câu 9. Đường cong trong hình bên là đồ thị của hàm số nào sau đây? A. 2x −1 y = . B. 4 2
y = x − 2x +1. C. 4 2
y = x + x +1. D. 3 y = 2x +1. x −1 Lời giải
Do đồ thị hàm số qua điểm (1;3) , nên chỉ có đồ thị hàm số 4 2
y = x + x +1 thỏa mãn.
Câu 10. Trong không gian Oxyz , mặt cầu 2 2 2
(S) : (x − 3) + (y −1) + (z + 4) = 4 có toạ độ tâm I và bán
kính R tương ứng là A. I(3;1; 4 − ) , R = 2 . B. I( 3 − ; 1;
− 4), R = 2 . C. I(3;1; 4 − ) , R = 4 . D. I( 3 − ; 1; − 4) , R = 4 . Lời giải
Mặt cầu có tâm I(3;1; 4
− ) và bán kính R = 2 . 
Câu 11. Trong không gian với hệ toạ độ Oxyz , cho hai vectơ a = ( 1;
− 1;0), b = (1;1;0) . Mệnh đề nào dưới đây đúng?   
A. a ⊥ b .
B. a , b cùng hướng.  
C. a , b đối nhau.
D. a , b ngược hướng. Lời giải    
Ta có a ⋅b = ( 1)
− ⋅1+1⋅1+ 0⋅0 = 0 nên a ⊥ b .
Câu 12. Cho số phức z = 2 + 3i . Số phức liên hợp của z là A. z = 2 − + 3i .
B. z = 2 − 3i . C. z = 2 − − 3i . D. z = 3 − + 2i . Lời giải
Số phức liên hợp của số phức a + bi là số phức a − bi .
Câu 13. Cho khối lập phương có cạnh bằng 2. Diện tích toàn phần của hình lập phương bằng A. 24 . B. 8 . C. 12. D. 32. Lời giải
Diện tích mỗi mặt của hình lập phương bằng 4 .
Diện tích toàn phần của hình lập phương đã cho bằng 6⋅4 = 24.
Câu 14. Cho khối lăng trụ ABC . D A′B C ′ D
′ ′ có đáy là hình vuông có cạnh bằng a và chiều cao bằng h .
Thể tích của khối lăng trụ đã cho bằng A. 2 π a h . B. 2 a h . C. 1 2 a h . D. 2 3a h . 3 Lời giải Thể tích của lăng trụ 2 V = a h .
Câu 15. Diện tích của mặt cầu bán kính R = 3 bằng A. 6π . B. 18π . C. 36π . D. 12π . Lời giải
Diện tích của mặt cầu đã cho là 2 2
S = 4π R = 4π ⋅3 = 36π .
Câu 16. Phần thực của số phức z = (1+ 2i)(2 −i) là 8 A. 0 . B. 4 . C. 2 . D. 3. Lời giải
Số phức z = (1+ 2i)(2 − i) = 4 + 3i nên có phần thực bằng 4 .
Câu 17. Một hình trụ có bán kính đáy r = 4 và có chiều cao h = 3. Diện tích xung quanh của hình trụ bằng A. 12π . B. 24π . C. 40π . D. 20π . Lời giải
Diện tích xung quanh của hình trụ bằng S = π rl = π ⋅ ⋅ = π . xq 2 2 4 3 24 x = 1+ 2t
Câu 18. Trong không gian Oxyz , đường thẳng d : y = 2 −3t không đi qua điểm nào dưới đây? z = 3−  t
A. Q(1;2;3). B. P(2; 2; − 1 − ) . C. N( 1; − 5;4) . D. M (3; 1; − 2) . Lời giải
Thay tọa độ điểm P vào phương trình của d ta có  1 t =  2 2 =1+ 2t    4  2
− = 2 − 3t ⇔ t  = (vô lí). 3 3  3 t  = −  t  = 4 
Do đó P không thuộc d .
Câu 19. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ.
Giá trị cực đại của hàm số bằng A. 2 − . B. 3. C. 2 . D. 1 − . Lời giải
Dựa vào bảng biến thiên ta có giá trị cực đại của hàm số bằng 3 tại điểm x = 2 ± .
Câu 20. Đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số nào sau đây? 2 A. y − − = 2x . B. 2 y = . C. 2x 1 y = . D. 2x 3 y = . x −1 x + 2 x +1 Lời giải Ta có x + 2 lim y = lim = 1 − . x→±∞
x→±∞ 2 − x
Tiệm cận ngang của hàm số là y = 1 −
Câu 21. Tập nghiệm S của bất phương trình log x ≤ 3 là 2
A. S = (0;6] .
B. S = (0;8]. C. S = ( ; −∞ 6) . D. S = ( ; −∞ 8] . Lời giải
Bất phương trình đã cho tương đương với 3 0 < x ≤ 2 = 8.
Vậy tập nghiệm của bất phương trình S = (0;8].
Câu 22. Cho tập hợp M gồm 4 phần tử. Số tập con gồm 3 phần tử của M là A. 3 C . B. 4 3 . C. 3 4 . D. 3 A . 4 4 9 Lời giải
Mỗi tập con gồm 3 phần tử của M là một tổ hợp chập 3 của 4 phần tử. Vậy có tất cả 3 C tập con. 4
Câu 23. Họ nguyên hàm của hàm số 1 f (x) = là 2 cos x A. 1 − + C .
B. tan x + C .
C. −cot x + C .
D. cot x + C . cos x Lời giải Ta có
1 dx = tan x+C ∫ . 2 cos x 3 5 5
Câu 24. Cho f (x)dx = 2 − ∫
và f (x)dx = 3 ∫
. Tính tích phân L = ∫[2 f (x)]dx . 0 3 0
A. L =12 . B. L = 2 − .
C. L = 2 . D. L = 12 − . Lời giải 5 3 5
Ta có f (x)dx = f (x)dx + f (x)dx = 2 − + 3 =1 ∫ ∫ ∫ nên L = 2⋅1 = 2 . 0 0 3
Câu 25. Họ nguyên hàm của hàm số 1 f (x) = là x
A. 1 x + C .
B. 3 x + C .
C. x + C .
D. 2 x + C . 2 2 Lời giải 1 1
dx = x + C ⇒
dx = 2 x + C. ∫ ∫ 2 x x
Câu 26. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ.
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. ( 2 − ; 1) − . B. ( ; −∞ 1) − . C. ( 1; − 1) . D. (0; ) 1 . Lời giải
Dựa vào bảng biến thiên ta kết luậnhàm số đã cho đồng biến trên các khoảng ( ; −∞ 2) − và (0;2) .
Câu 27. Cho hàm số y = f (x) liên tục trên  và có bảng biến thiên như sau
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có giá trị nhỏ nhất bằng 1 − .
B. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1 − .
C. Hàm số có đúng một điểm cực trị.
D. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x =1. 10 Lời giải
Dựa vào bảng biến thiên ta thấy hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x =1.
Câu 28. Cho a = log 3 và b = log 7 . Giá trị của log 14 bằng 2 3 2
A. a + b −1. B. 4ab .
C. 2ab + 3. D. ab +1. Lời giải Ta có
log 14 = log 3⋅log 14 = log 3⋅log (7⋅2) = log 3⋅(log 7 + log 2) 2 2 3 2 3 2 3 3
= log 3⋅log 7 + log 3⋅log 2 = ab +1 2 3 2 3
Câu 29. Thể tích khối tròn xoay tạo bởi khi quay quanh trục hoành của hình phẳng giới hạn bởi các đồ thị hàm số 2
y = 2x − x ; y = 0; x = 0 ; x =1 có giá trị bằng π π π π A. 16 . B. 4 . C. 2 . D. 8 . 15 3 3 15 Lời giải Thể tích cần tính 1 1 1 5 3   2 2 4 3 2 x 4 4x 8π
V = π (2x − x ) dx = π (x − 4x + 4x )dx = π ⋅ ∫ ∫  − x +  = .  5 3  15 0 0 0
Câu 30. Cho hình chóp tứ giác đều có cạnh đáy bằng 2a và chiều cao bằng a (tham khảo hình vẽ). Giá
trị tang của góc giữa mặt bên và mặt đáy bằng A. 1. B. 3 . C. 3 . D. 1 . 4 3 Lời giải
Vì S.ABCD là hình chóp đều nên SO ⊥ (ABCD) , với O là tâm của hình vuông ABCD .
Gọi H là trung điểm của CD .
Tam giác SCD cân tại S nên SH ⊥ CD .
Tam giác OCD cân tại O nên OH ⊥ CD .
Vậy góc giữa (SCD) và (ABCD) là  SHO . 11 Ta có 1
OH = BC = a ; SO SO = a nên  tan SHO = =1. 2 OH
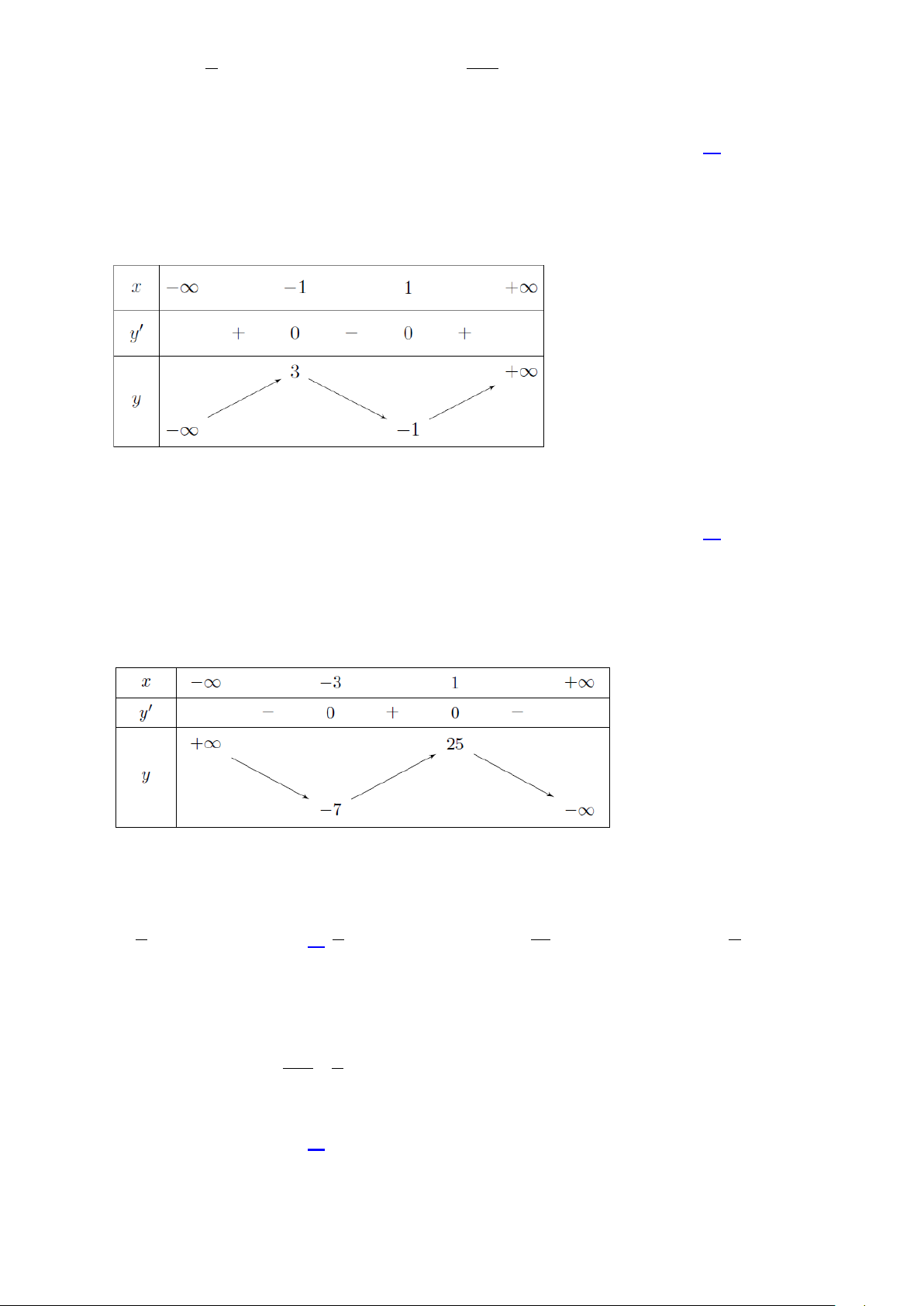
Câu 31. Số giao điểm của đồ thị hàm số 3
y = x − 3x +1 và trục hoành là A. 1. B. 2 . C. 0 . D. 3. Lời giải Xét 3
y = x − 3x +1 có 2 2
y′ = 3x − 3 = 3(x −1) . Tại y′ = 0 ⇔ x = 1 ± .
Ta có các giới hạn lim = −∞ và lim = +∞ . x→−∞ x→+∞
Bảng biến thiên của hàm số.
Từ bảng biến thiên, ta thấy hàm số 3
y = x − 3x +1 cắt trục hoành tại ba điểm phân biệt. Câu 32. Hàm số 3 2
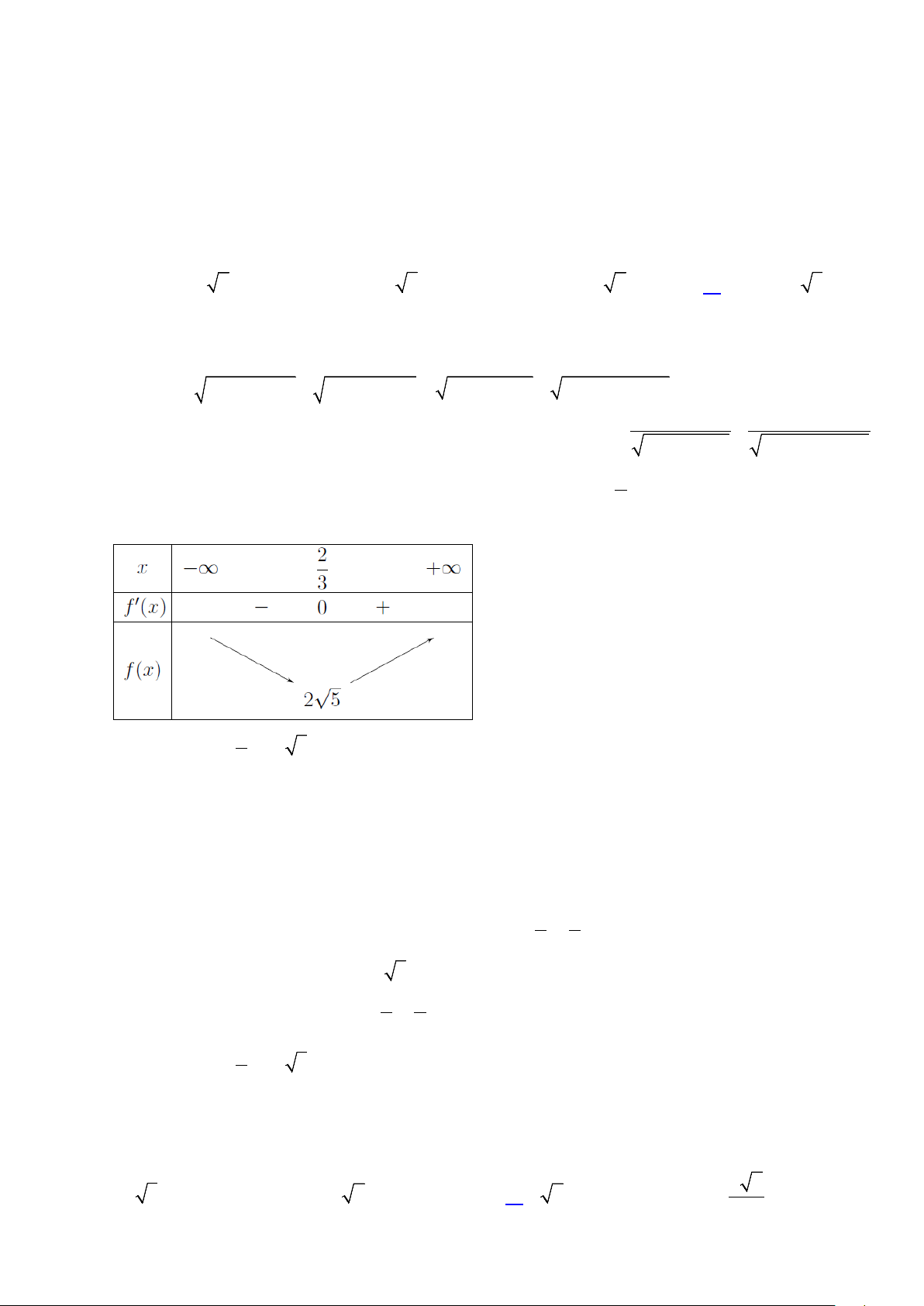
y = −x − 3x + 9x + 20 đồng biến trên khoảng A. ( 3 − ;+∞) . B. ( ; −∞ 1). C. (1;2) . D. ( 3 − ;1) . Lời giải
Tập xác định  =  . x =1 Ta có 2 y′ = 3
− x − 6x + 9 ; y′ = 0 ⇔  x = 3. − Bảng biến thiên:
Vậy hàm số đồng biến trên ( 3 − ;1) .
Câu 33. Gọi M là tập hợp các số tự nhiên có 4 chữ số đôi một khác nhau được lập từ các chữ số 1; 2 ;
3; 4 ; 5; 6 ; 7 . Lấy ra từ tập M một số bất kỳ. Xác suất để lấy được số lẻ bằng A. 3 . B. 4 . C. 2 . D. 3 . 7 7 21 4 Lời giải
Số phần tử của M bằng 4
n(M ) = A = 840 nên số phần tử của không gian mẫu bằng 840 . 7
Số các số tự nhiên lẻ trong M bằng 3 n( ) A = 4⋅A = 480 . 6
Xác suất cần tìm bằng 480 4 = . 840 7
Câu 34. Tổng tất cả các nghiệm của phương trình 4x 8 6 2x + = ⋅ bằng A. 9. B. 3. C. 5. D. 6 . Lời giải Ta có x x 1 4 3 2 + − ⋅
+ 8 = 0 ⇔ 4x − 6⋅2x + 8 = 0 . 12 t = 2 (nh?n) 2x = 4 x = 2 Đặt 2x
t = (t > 0) phương trình trở thành 2t − 6t + 8 = 0 ⇔ ⇔   ⇔ t 4 (nh?n) 2x = 2  = x = 1.
Câu 35. Tập hợp điểm biểu diễn của số phức z thỏa mãn | z −i | |
= (1+ i)z | là đường tròn có toạ độ tâm I
là A. I(0;1). B. I(0; 1) − .
C. I(1;0) . D. I( 1; − 0) . Lời giải
Gọi z = a + bi ⇒ (1+ i)z = (a − b) + (a + b)i . Vậy | z − i | |
= (1+ i)z | ⇔ | a + (b −1)i | |
= (a − b) + (a + b)i | 2 2 2 2
⇔ a + (b −1) = (a − b) + (a + b) 2 2
⇔ a + b + 2b −1 = 0.
Vậy tập hợp điểm biểu diễn của số phức z là đường tròn tâm I(0; 1) − .
Câu 36. Trong không gian Oxyz , cho hai điểm (
A 1;2;0), B(2;1; 1
− ) . Mặt phẳng (P) đi qua hai điểm A ,
B và vuông góc với mặt phẳng Oxy có phương trình là
A. 2x − y +1 = 0 .
B. x − y + 2z +1 = 0.
C. x + y − 3 = 0 .
D. x + 2y − 4 = 0 . Lời giải   Ta có AB = (1; 1; − 1
− ) và k = (0;0;1) là hai vectơ có giá song song hoặc nằm trên (P) nên mặt phẳng  
(P) có một vectơ pháp tuyến là AB,k  = ( 1; − 1; − 0).  
Phương trình mặt phẳng (P) là 1
− (x −1) − (y − 2) + 0(z − 0) = 0 ⇔ x + y − 3 = 0.
Câu 37. Trong không gian Oxyz , toạ độ giao điểm của mặt phẳng (P) : 2x −3y + z − 6 = 0 với trục tung
là A. (0; 2;−0). B. (0;2;0) .
C. N(3;0;0) . D. P(0;0;6) . Lời giải
T oạ độ giao điểm của mặt phẳng (P) : 2x − 3y + z − 6 = 0 với trục tung là (0; 2; − 0) .
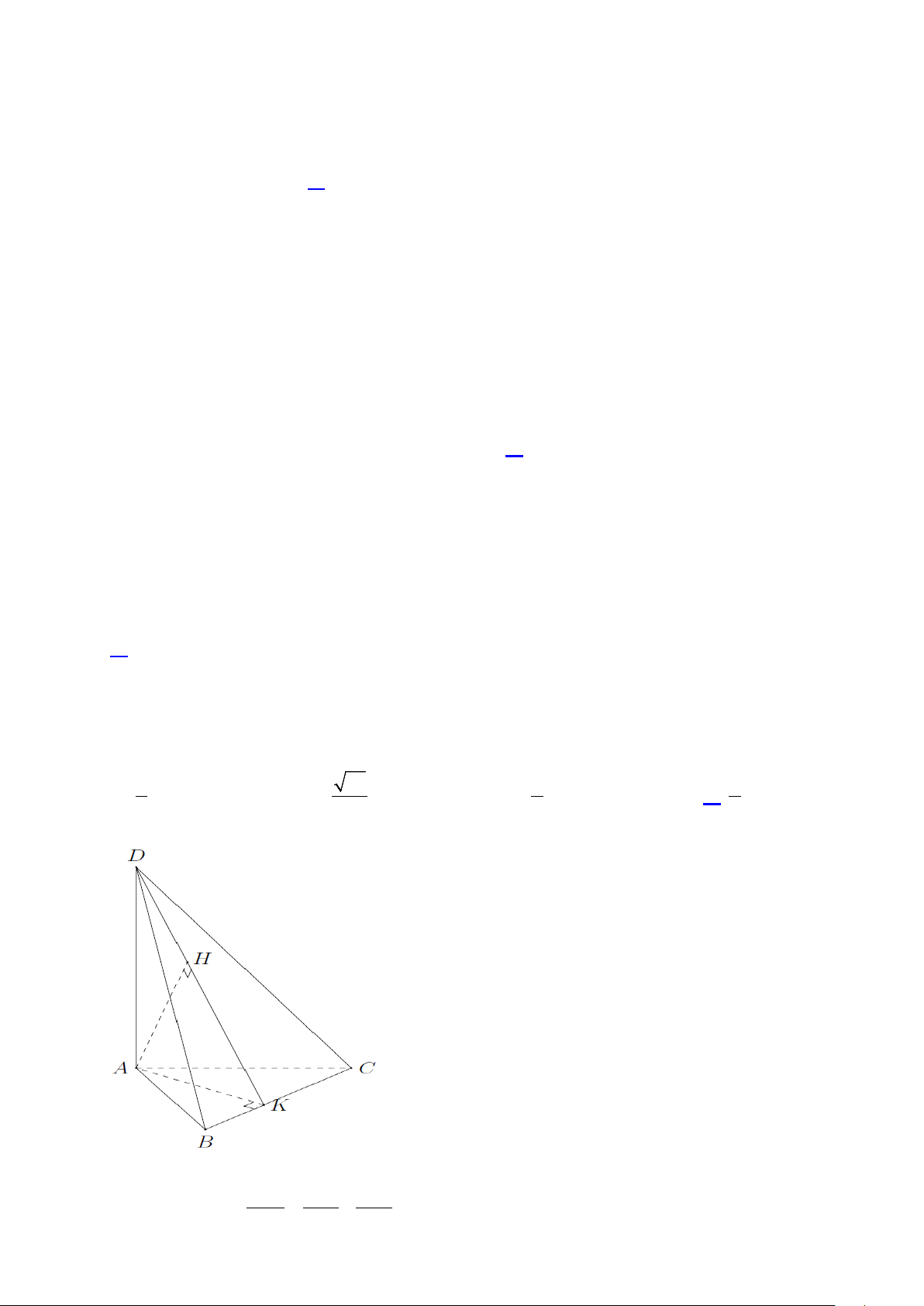
Câu 38. Cho hình chóp S.ABC có ba cạnh bên SA =1, SB = 2 , SC = 3 đôi một vuông góc với nhau.
Chiều cao của hình chóp bằng A. 5 . B. 66 . C. 2 . D. 6 . 6 11 3 7 Lời giải
Hạ AK ⊥ BC , AH ⊥ DK , ta có khoảng cách từ A đến mặt phẳng (BCD) bằng AH . Xét 1 1 1 A ∆ BC , ta có = + . 2 2 2 AK AB AC
Xét tam giác AKD , ta có 13 1 1 1 1 1 1 = + = + + 2 2 2 2 2 2 AH AD AK AD AB AC 1 1 1 49 = + + = 2 2 2 1 2 3 36 6 ⇒ AH = . 7
Câu 39. Có bao nhiêu số nguyên x thỏa mãn 3log (x +1) − log (86 − x) ≥1? 8 2 A. 28 . B. 85 . C. 29 . D. 86 . Lời giảix +1 > 0 Điều kiện  ⇔ 1 − < x < 86 . 86  − x > 0
Ta có 3log (x+1)−log (86−x)≥1 8 2
⇔ 3log (x +1) − log (86 − x) ≥1 3 2 2
⇔ log (x +1) − log (86 − x) ≥1 2 2  x +1 log  ⇔ ≥   1 2  86 − x x +1 ⇔ ≥ 2 86 − x
⇔ x +1≥ 2(86 − x) (vì 86 − x > 0) ⇔ x ≥ 57.
Kết hợp với điều kiện, ta được 57 ≤ x < 86 .
Vậy có 29 số nguyên x thỏa mãn yêu cầu bài toán. 2
Câu 40. Cho hàm số y = f (x) có đạo hàm liên tục trên  thỏa mãn f (2) = 2
− ; f (x)dx =1 ∫ . Tính 0 4 I = f ′
∫ ( x)dx. 0 A. I = 10 − .
B. I = 0. C. I = 18 − . D. I = 5 − . Lời giải Đặt 2
t = x ⇒ t = x ⇒ 2tdt = dx .
Đổi cận x = 0 ⇒ t = 0 ; x = 4 ⇒ t = 2 . 2 2 2  
Suy ra I = 2 t f ′
∫ (t)dt = 2 xf ′ ∫ (x) 2
dx = 2 xf (x)| − f (x)dx ∫  = 2.( 4 − −1) = 10 − . 0 0 0  0 
Câu 41. Cho hàm số f (x) có bảng biến thiên như hình vẽ.
Số nghiệm thực phân biệt của phương trình f ′[ f (x) + 2] = 0 là A. 6 . B. 5. C. 4 . D. 3. Lời giải 14  + = −  = − f ′[ f x + ] f (x) 2 1 f (x) 3 ( ) 2 = 0 ⇔ ⇔   f (x) 2 2  + =  f (x) = 0. Ta có f (x) = 3
− ⇒ phương trình có 2 nghiệm.
f (x) = 0 ⇒ phương trình có 3 nghiệm.
Vậy f ′[ f (x) + 2] = 0 có 5 nghiệm.
Câu 42. Cho số phức z thỏa mãn | 4z + 3i | |
= 4z − 4 + 5i |. Tìm giá trị nhỏ nhất của biểu thức P |
= z + i | + | z − 3i |.
A. min P = 5 2 .
B. min P = 5 .
C. min P = 2 2 .
D. min P = 2 5 . Lời giải Cách 1. Gọi
z = x + yi với x, y ∈ . Khi đó 2 2 2 2 | 4z + 3i | |
= 4z − 4 + 5i |⇔ (4x) + (2y + 3) = (4x − 4) + (4y + 5) ⇔ y = 2x − 2. Do đó 2 2 2 2 2 2
P = x + (y +1) + x + (y − 3) = 5x − 4x +1 + 5x − 20x + 25 = f (x). Ta có 5x − 2 5x −10 f (′x) = + , 2 2 5x − 4x +1 5x − 20x + 25
(5x − 2)(5x −10) ≤ 0 2
f (′x) = 0 ⇔  ⇔ x = . 2 2 2
(5x − 2) (5x − 20x + 25) = (5x −10)(5x − 4x +1) 3 Bảng biến thiên Vậy 2 min P f   = =   2 5 .  3  Cách 2: Gọi M ( ;
x y) là điểm biểu diễn của số phức z . Khi đó 2 2 2 2 | 4z + 3i | |
= 4z − 4 + 5i |⇔ (4x) + (2y + 3) = (4x − 4) + (4y + 5) ⇔ 2x − y − 2 = 0.
Suy ra M chạy trên đường thẳng d : 2x − y − 2 = 0 . Gọi ( A 0; 1)
− , B(0;3) . Khi đó P = MA + MB . Vì [2⋅0 − ( 1
− ) − 2](2⋅0 − 3− 2) > 0 nên A , B nằm cùng phía so với d .
Gọi A′ là điểm đối xứng với A qua d . Ta tìm được 4 7 A  ;  ′ −  . Khi đó 5 5   
P = MA + MB = MA′ + MB ≥ A′B = 2 5,
đẳng thức xảy ra khi M trùng 2 2 M  ;  −
là giao điểm của đoạn A′B và 0 d . 3 3    Vậy 2 min P f   = =   2 5  3 
Câu 43. Cho khối lăng trụ đứng ABC .
D A′B′C′D′ có đáy là hình vuông có cạnh bằng 2 . Biết khoảng
cách từ A đến mặt phẳng (CB′D′ ) bằng 2 . Thể tích của khối lăng trụ đã cho bằng A. 3 . B. 2 2 . C. 4 2 . D. 4 2 . 3 Lời giải 15
Chọn hệ trục tọa độ Oxyz sao cho (
A 0;0;0) , B thuộc chiều dương trục Ox , D thuộc chiều dương trục
Oy , A′ thuộc chiều dương trục Oz . Gọi chiều cao lăng trụ là h , H > 0, ta có
B(2;0;0), D(0;2;0) , C(2;2;0) , A (′0;0;h) , B′(2;0;h) , D′(0;2;h) và C′(2;2;h).  
Mặt phẳng (CB′D′ ) có hai véc-tơ chỉ phương CB′ = (0; 2;
− h) và CD′ = ( 2;
− 0;h) nên có 1 véc-tơ pháp   tuyến là nCB′,CD′   = = ( 2 − ; h 2 ; h 4) − hay ( ; h ; h 2).  
Mặt phẳng (CB′D′ ) đi qua C(2;2;0) nên
(CB′D′):hx+hy+2z −4h = 0.
Ta có (A (CB′D′) | 4h | d , = 2 ⇔ = 2 ⇔ h = 2. 2 2 h + h + 4 Vậy 2 V = ⋅ = = ′ ′ ′ ′ S h ABCD A B C D ABCD 2 2 4 2. .
Câu 44. Cho hàm số y = f (x) có đồ thị (C) như hình vẽ. Biết rằng diện tích hình phẳng giới hạn bởi 8 8
(C) và trục hoành bằng 8 và f (x)dx = 4 ∫
. Giá trị của I = (2023− x) f (′x)dx ∫ bằng 0 3 A. 6 . B. 12. C. 4 . D. 2023. Lời giải 3 8
Đặt f (x)dx = a ∫
và f (x)dx = b ∫ . 0 3 a + b = 4 a = 2 −
Từ giả thiết bài toán ta có hệ  ⇔ .  a b 8 b  − + =  = 6 u  = 2023 − x du = −dx Đặt  ⇒
dv = f (x)dx  ′
v = f (x). Suy ra 16 8 8
I = (2023− x) f (x)| + f (x)dx 3 ∫3
= (2023−8) f (8) − (2023− 3) f (3) + b = 0 − 0 + b = 6.
Câu 45. Cho phương trình 2 2
z − mz + m − 3 = 0 với m là tham số thực. Gọi S là tập hợp các giá trị của
m sao cho phương trình đã cho có hai nghiệm phức có điểm biểu diễn là A , B và tam giác OAB có
diện tích bằng 6 . Tổng bình phương các phần tử của S bằng A. 32. B. 16. C. 8 . D. 18. Lời giải Ta có 2 2 2
∆ = m − 4(m − 3) =12 − 3m .
+) Nếu ∆ ≥ 0 thì phương trình đã cho có hai nghiệm thực, khi đó O , A , B thẳng hàng: không thoả mãn. m > 2 2 +) Nếu ∆ < 0 ⇔ m 3m 12 
thì phương trình có hai nghiệm không thực z i − = ± . m < 2 − 1,2 2 2  2   2  Suy ra m 3m −12 − A m 3m 12  ;−   , B ;  . 2 2      2 2  
Ta thấy A và B đối xứng nhau qua trục hoành nên diện tích tam giác OAB bằng 1 m 2 4 2 ⋅
⋅ 3m −12 = 6 ⇔ m − 4m −192 = 0 ⇔ m = 4. ± 2 2
Đối chiếu điều kiện, vậy có hai giá trị của m thoả mãn bài toán, là 4 ± .
Câu 46. Trong không gian Oxyz , cho đường thẳng x 2 y 1 : z d − − = = và điểm (
A 1;3;0) . Mặt cầu (S) 2 1 1
đi qua A , tiếp xúc với Oxy và với đường thẳng d . Bán kính của mặt cầu (S) là A. 30 . B. 6 6 . C. 2 5 . D. 2 10 . Lời giảix = 1
Mặt cầu (S) tiếp xúc với (Oxy) tại (
A 1;3;0) . Gọi I là tâm mặt cầu (S) nên I : 
∈ ∆ y = 3 (là đường z =  t
thẳng đi qua A và vuông góc với Oxy ).
Do đó d(I,(Oxy)) | = t |.   
Gọi M (2;1;0)∈d , IM = (1; 2 − ; t
− ) , IM ,u  = − + t − t − d ( 2 ; 2 1;5)   2 5t + 30 ⇒ d(I,d) = . 6 2 5t + 30 t = 30 Theo đề bài ta có 2 2
d(I,(Oxy)) = d(I,d) ⇔ |
= t |⇔ 5t + 30 = 6t ⇔  6 t = − 30. Vậy R | = t |= 30 .
Câu 47. Có bao nhiêu số nguyên dương y sao cho có không quá 8 số nguyên x thỏa mãn
log 4x + y > 2log x − 2 ? 2 ( ) 2 ( ) A. 24 . B. 37 . C. 23. D. 36. Lời giảix > 2 Điều kiện: 
4x + y > 0. 17
Khi đó log (4x + y) > 2log (x − 2) ⇒ log (4x + y) > log (x − 2)2 2 2 2 2 2 2
⇒ 4x + y > x − 4x + 4 ⇒ y > x −8x + 4 (*) Xét hàm số 2
f (x) = x −8x + 4 trên khoảng (2;+∞) .
f (′x) = 2x −8 = 0 ⇒ x = 4. Bảng biến thiên
Để có không quá 8 giá trị nguyên của x thì x∈(2;10] . Khi đó f (2) = 8 − ; f (10) = 24. Từ (*) suy ra 8 − < y ≤ 24 .
Vậy có 24 giá trị nguyên dương của y thỏa mãn yêu cầu bài toán.
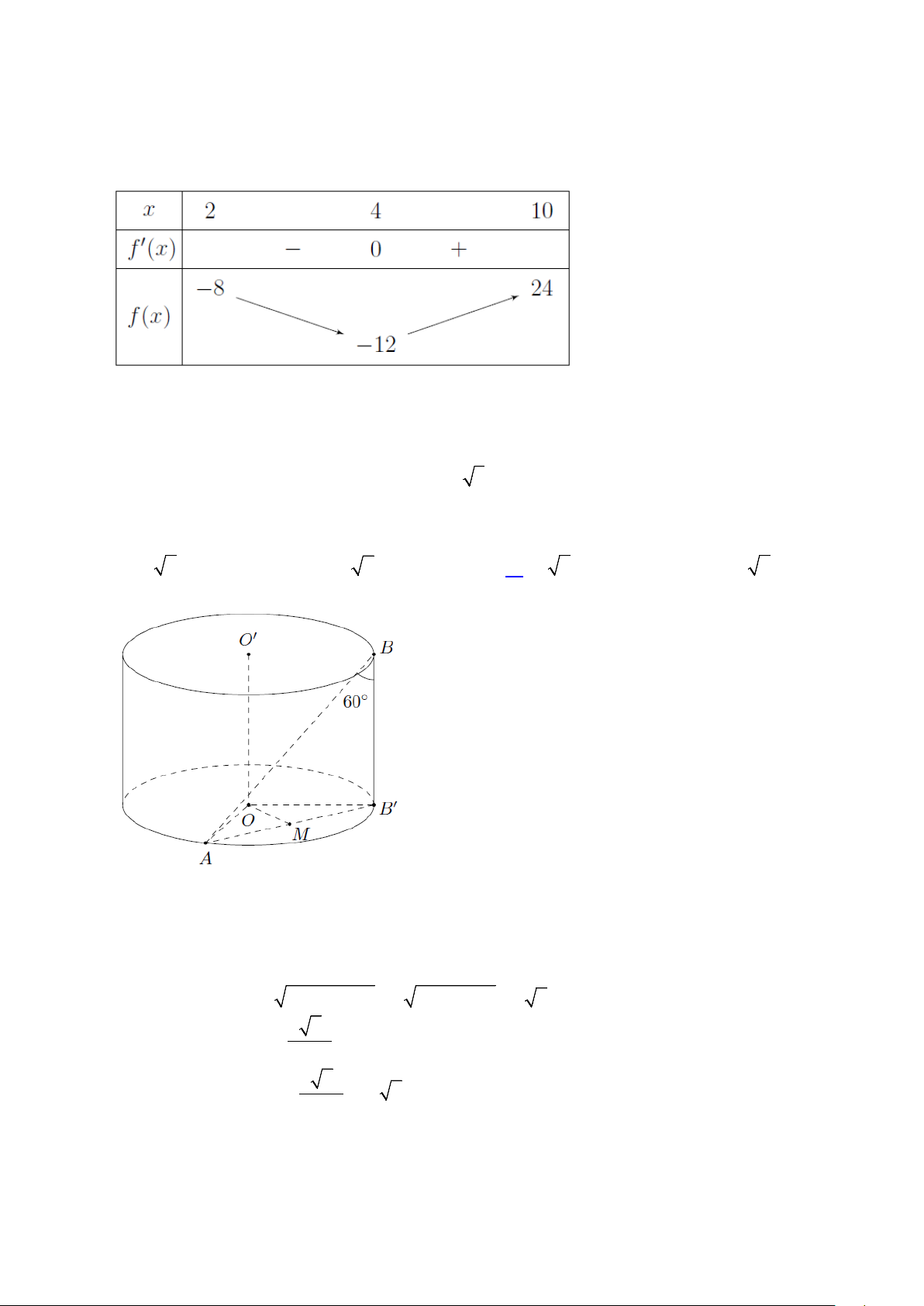
Câu 48. Cho khối trụ (T) có bán kính đáy bằng 2 3a . Gọi A và B là hai điểm thuộc hai đường tròn
đáy của (T) sao cho khoảng cách và góc giữa AB và trục của (T) bằng 2a và 60° . Thể tích của khối trụ đã cho bằng A. 3 48 6π a . B. 3 24 2π a . C. 3 16 6π a . D. 3 24 6π a . Lời giải Hạ đường sinh BB′ và gọi M là trung điểm AB′ ta có
OO BB ⇒ (OO AB) = (BB AB) =  , , ABB = 60° ′ ′ ′ ′ ′ .
Ta có OM ⊥ AB′ và OM ⊥ BB′ nên OM ⊥ (ABB )′. Do đó
d(OO ,′ AB) = d(O,(ABB )′) = OM = 2 . a Ta có 2 2 2 2
AB′ = 2AM = 2 OA − OM = 2 12a − 4a = 4 2a . 4 6 = = cot 60 a h BB AB ° ′ ′ = . 3 Vậy 2 2 4 6a 3
V = π r h = π ⋅12a ⋅ = 16 6π a . 3
Câu 49. Trong không gian Oxyz , cho tam giác ABC có (
A 6;0;0) , B(6;8;0) , C(0;8;0) . Gọi mặt phẳng
(α) đi qua B và vuông góc với AC . Điểm M thay đổi thoả mãn   ABM AMC 90° = = . Gọi N là giao
điểm của AM và (α) . Khoảng cách từ N đến (ABC) có giá trị lớn nhất bằng 18 A. 8 . B. 8 2 . C. 24 . D. 12 . 5 5 5 5 Lời giải
Ta có AB = 8 , BC = 6 , AC =10 nên A
∆ BC vuông tại B , suy ra B thuộc mặt cầu (S) có đường kính AC . Lại có  AMC 90° =
nên M ∈(S) . Vì  ABM 90° =
nên M thuộc mặt phẳng (P) qua B và vuông góc AB .
Từ đó ta có M nằm trên đường tròn (C) là giao tuyến của mặt cầu (S) và mặt phẳng (P) .
Mặt phẳng (α) đi qua B , vuông góc với AC và cắt AC tại K . AB ⊥ MC Do 
⇒ MC ⊥ (ABM ) ⇒ MC ⊥ BN . MA ⊥ MC
Lại có BN ⊥ AC nên BN ⊥ (ANC) ⇒ BN ⊥ NK .
Suy ra N thuộc đường tròn đường kính BK .
Gọi T là trung điểm BK . Khi đó 1 1 12
d(N,(ABC)) ≤ NT = BC = d(B, AC) = . 2 2 5
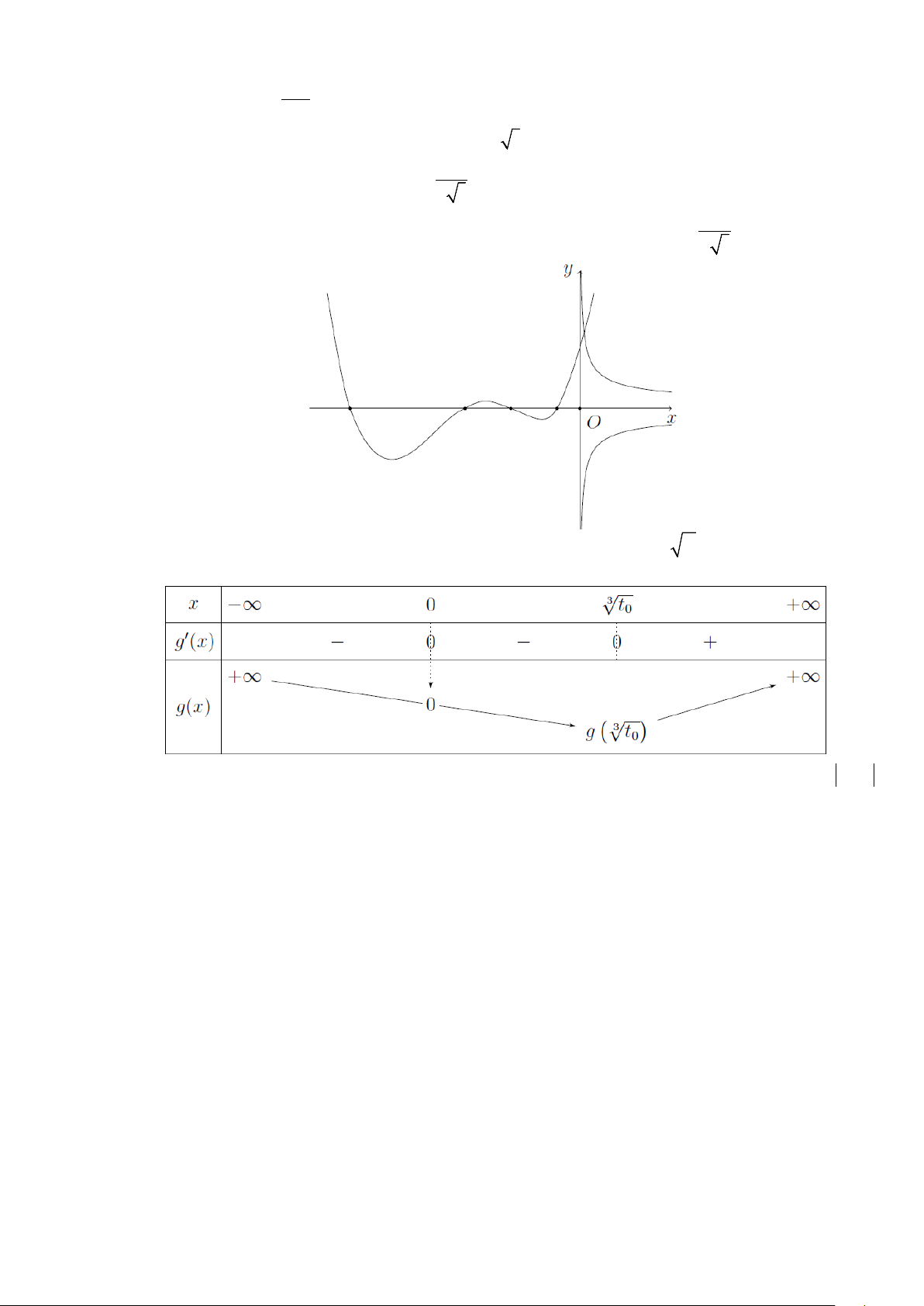
Câu 50. Cho hàm số đa thức f (x) có đồ thị của đạo hàm f (′x) như hình bên. Biết rằng f (0) = 0. Hàm số 6 3
g(x) = f (x ) − x có bao nhiêu điểm cực trị? A. 7 . B. 4 . C. 5. D. 3. Lời giải Xét hàm 6 3
g(x) = f (x ) − x , 5 6 2 2
g′ x = x f ′ x − x = x ( 3 6 ( ) 6 ( ) 3 3
2x f (′x ) − ) 1 . 19 x = 0 g (′x) = 0  ⇔ 6 1  f (′x ) = . (*) 3  2x
Xét phương trình (*), đặt 6
t = x ,t ≥ 0, suy ra 3 x = ± t .
Do đó phương trình (*) trở thành 1 f (′t) = ± . \hfill (1) 2 t
Nghiệm của phương trình là hoành độ giao điểm của đồ thị y = f (′t) và 1 y = ± . 2 t
Dựa vào đồ thị ta thấy phương trình có nghiệm t > 0 duy nhất. Suy ra 3 = . 0 x t0 Ta có bảng biến thiên
Do đó hàm số y = g(x) có 1 điểm cực trị và cắt trục hoành tại 2 điểm phân biệt. Vậy hàm số y = g(x) có 3 điểm cực trị.
--------------- TOANMATH.com --------------- 20