Đề thi thử TN THPT 2023 môn Toán (có lời giải chi tiết)-Đề 3
Đề thi thử TN THPT 2023 môn Toán có lời giải chi tiết - Đề 3. Tài liệu được biên soạn dưới dạng file PDF bao gồm 10 trang tổng hợp các kiến thức tổng hợp giúp các bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Mời các bạn đón xem!
Chủ đề: Đề thi THPTQG môn Toán năm 2023 1.2 K tài liệu
Môn: Toán 2 K tài liệu
Tác giả:
Preview text:
KÌ THI THỬ THPT QUỐC GIA NĂM 2023-ĐỀ 3 Bài thi: TOÁN
Thời gian làm bài : 90 Phút; (Đề có 50 câu)
Câu 1: Tính thể tích V của khối lăng trụ có diện tích đáy là B và chiều cao là h . 1 A. 2 V = B h .
B. V = Bh . C. 2 V = Bh . D. V = Bh . 3
Câu 2: Cho a, b là các số thực dương tùy ý. Khẳng định nào sau đây đúng?
A. ln (ab) = ln . a ln b .
B. ln (a + b) = ln a + ln b . C. ln (a + b) = ln .
a ln b . D. ln (ab) = ln a + ln b .
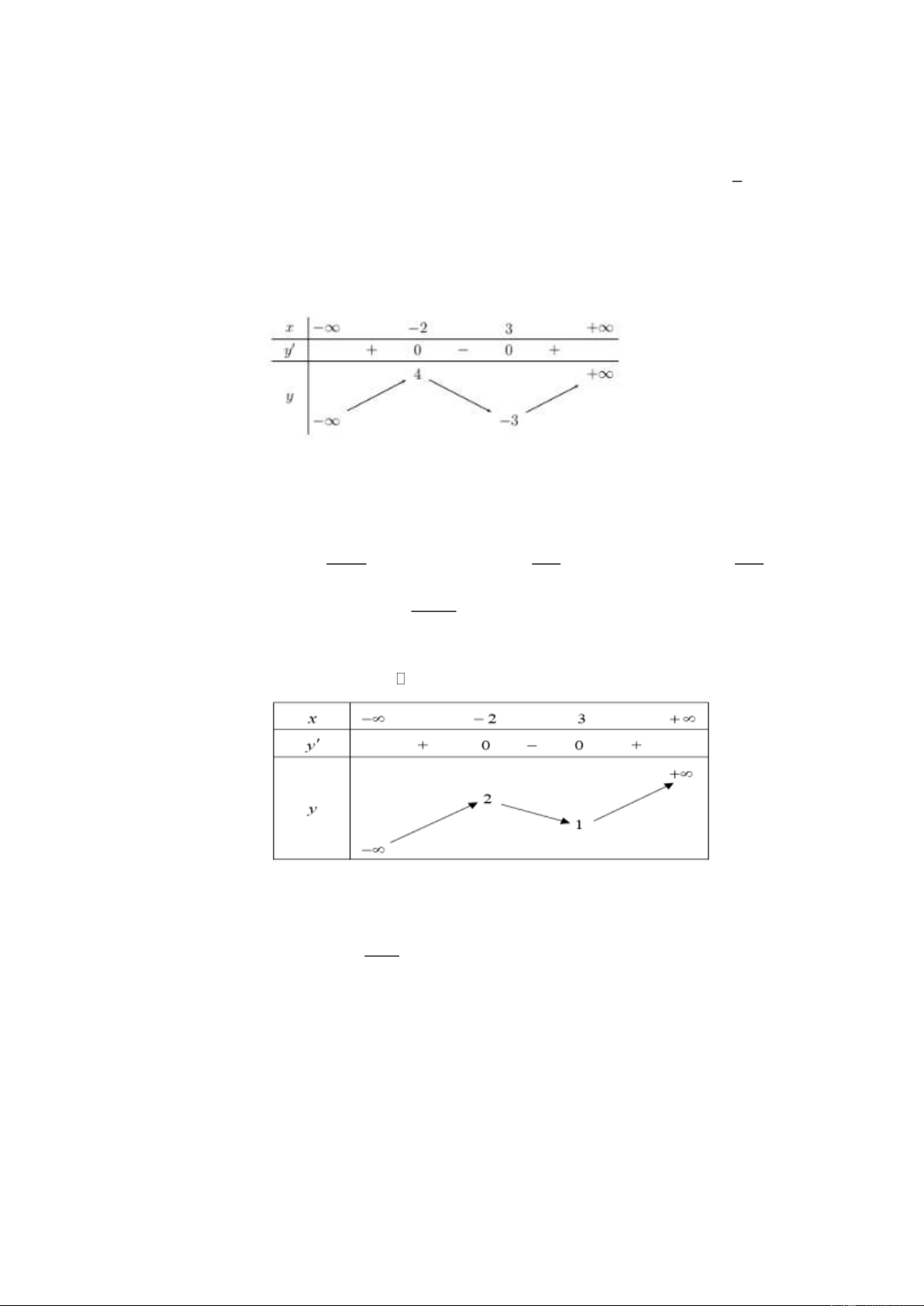
Câu 3: Cho hàm số y = f ( x) có bảng biến thiên như sau
Giá trị cực tiểu của hàm số đã cho bằng A. −2 . B. 4 . C. 3 − . D. 3 .
Câu 4: Trên khoảng (0; +) , đạo hàm của hàm số y = log x là 2 1 ln 2 x
A. y = x ln 2 . B. y = . C. y = . D. y = . x ln 2 x ln 2 2x + 3
Câu 5: Tiệm cận đứng của đồ thị hàm số y = là đường thẳng x − 3 A. x = 2 . B. x = 3 . C. x = − 3 . D. x = −1 .
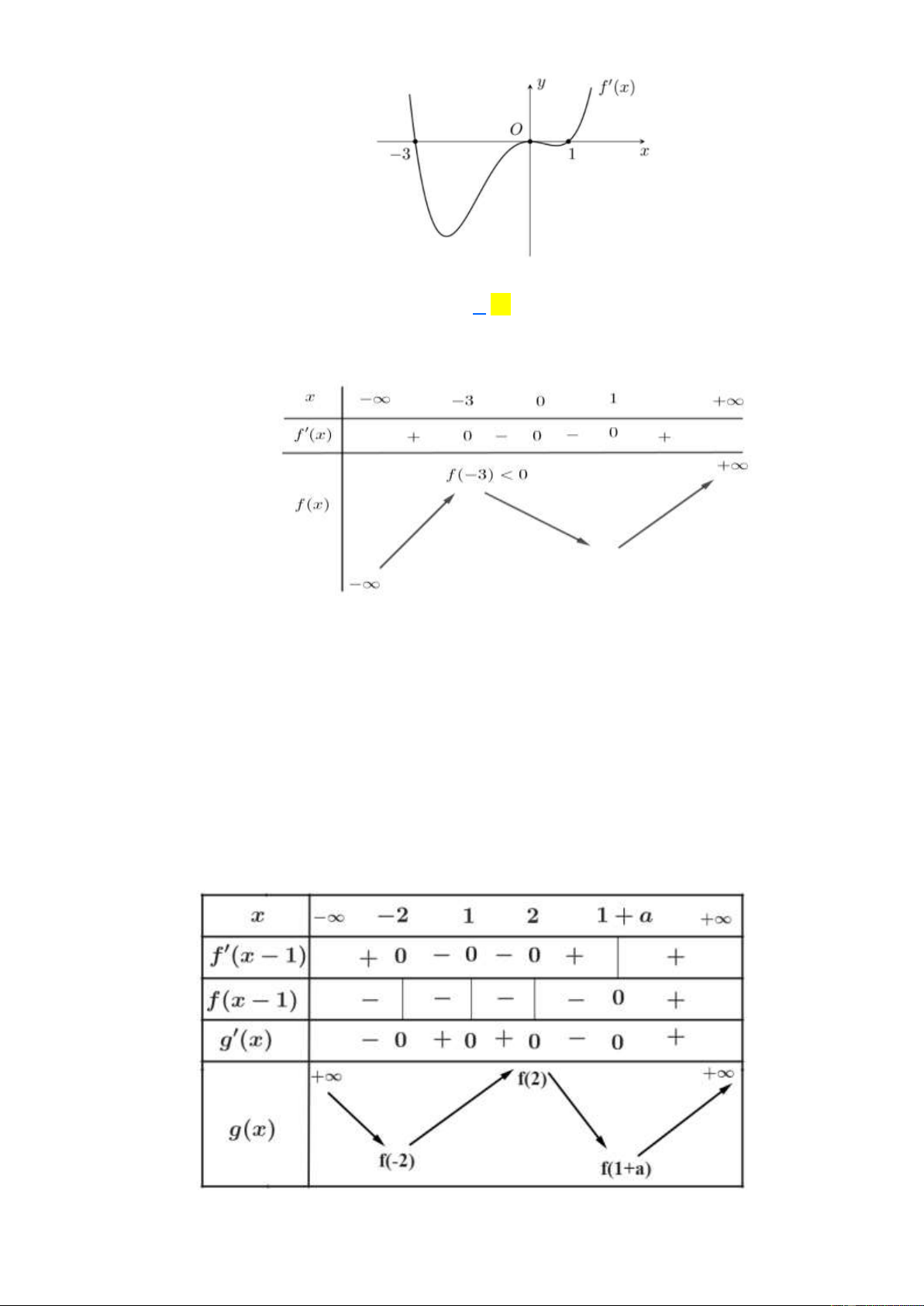
Câu 6: Cho hàm số y = f ( x) liên tục trên
và có bảng biến thiên dưới đây
Số nghiệm của phương trình 3 f ( x) = 1 là A. 4 . B. 3 . C. 1 . D. 2 . x − 3
Câu 7: Giá trị lớn nhất của hàm số y = x+ trên đoạn [0;1] bằng 1 A. 3 . B. 1. C. 3 − . D. −1 .
Câu 8: Số mặt phẳng đối xứng của hình tứ diện đều là A. 4 . B. 9 . C. 3 . D. 6 .
Câu 9: Tập nghiệm của bất phương trình 3x 27 là A. ( ;3 − ) . B. (3; +) . C. (9; +) . D. (0;3) .
Câu 10: Cho hàm số y = f ( x) có bảng biến thiên như hình vẽ bên dưới. Trang 1
Hàm số y = f ( x) đồng biến trên khoảng nào dưới đây? A. (0 ) ;1 . B. ( ;0 − ). C. ( 1 − ;0) . D. (0;+ ) .
Câu 11: Đạo hàm của hàm số 3 2 x y = là A. 3 2 x.ln 2 . B. 3 3.2 x.ln 3 . C. 3 3.2 x.ln 2 . D. 3 3.2 x .
Câu 12: Đồ thị của hàm số nào dưới đây có dạng như đường cong ở hình bên? x +1 A. 3
y = −x + 3x +1. B. 4 2
y = x − 2x +1. C. 3
y = x − 3x +1. D. y = . x −1
Câu 13: Cho log b = với a, b là các số thực dương tùy ý và a 1. Khẳng định nào sau đây đúng? a A. a = b .
B. b = a . C. b = . . a D. a = . b .
Câu 14: Khối trụ tròn xoay có đường sinh l , bán kính đáy r thì có diện tích xung quanh S là xq rl A. S = rl . B. S = 2 rl . C. S = 4 rl . D. S = . xq xq xq xq 2
Câu 15: Hàm số F (x) là một nguyên hàm của hàm số f (x) trên khoảng K nếu A. F (
x) = − f (x), x K. B. F (
x) = f (x), x K. C. f (
x) = F(x), x K. D. f (
x) = −F(x), x K.
Câu 16: Tập xác định của hàm số y = ( x − )75 2023 là A. (2023;+) . B. ( 2 − 023;+) . C. \ 202 3 . D. ( ; − 202 ) 3 .
Câu 17: Tìm tập nghiệm S của bất phương trình log x −1 1. 1 ( ) 2 3 3 3 3 A. S = 1; . B. S = −; . C. S = ; + . D. S = 1; . 2 2 2 2
Câu 18: Hàm số nào dưới đây nghịch biến trên tập số thực ? x +1 A. 3
y = x − 3x . B. y = . C. 4
y = −x − 3x . D. 3
y = −x − 2x . x − 2
Câu 19: Với C là hằng số, mệnh đề nào sau đây đúng? 1 A. 1 x dx x + = + C ( − ) 1 − = − + . B. x x ( ) 1 d 1 .x C . +1 C. 1
x dx .x − = + C . D. x x ( ) 1 d 1 x + = + + C . Câu 20: Hàm số 4 2
y = −x + 2x +1 có bao nhiêu điểm cực trị? A. 3 . B. 1. C. 0 . D. 2 .
Câu 21: Cho hình lập phương có độ dài mỗi cạnh là 2 2 . Tính thể tích khối lập phương đó. Trang 2 16 2 A. . B. 16 . C. 16 2 . D. 64 . 3
Câu 22: Nghiệm của phương trình 10x = 5 là 1 A. x = . B. x = 2 . C. x = log 5 . D. x = log 10 . 5 2
Câu 23: Cho biểu thức n m P =
x với m , n , n 2 và x 0 . Mệnh đề nào dưới đây đúng? m n A. n P = x . B. m P = x . C. mn P = x . D. m n P x + = .
Câu 24: Biết đồ thị hàm số bậc ba 3 2
y = x + ax + bx + c ( , a ,
b c ) có một điểm cực trị là A(3; 3 − ) và đi
qua điểm B(2;2) , tính a + b + c .
A. a + b + c = 30 .
B. a + b + c = 36 .
C. a + b + c = 18 .
D. a + b + c = 12 .
Câu 25: Cho hàm số y = f ( x) có f ( x) 3
= 4x − m +1, f (2) =1 và đồ thị của hàm số y = f (x) cắt trục
tung tại điểm có tung độ bằng 3 . Tìm được ( ) 4
f x = ax + bx + c với a, b, c
, tính a + b + c . A. −11. B. 5 − . C. 13 − . D. 7 − . mx + 3
Câu 26: Với giá trị nào của tham số m thì đường tiệm cận ngang của đồ thị hàm số y = đi qua 2x − 2023 điểm M (1;3) ? A. m = 2 − . B. m = 6 − . C. m = 2 . D. m = 6 .
Câu 27: Một khối chóp có diện tích đáy 2
B = 9a và thể tích 3
V = 3a . Chiều cao của khối chóp đó bằng A. 6a . B. 3a . C. a . D. 2a .
Câu 28: Biết phương trình 9x 3.3x −
− 4 = 0 có nghiệm x = log b (a,b là các số nguyên dương nhỏ hơn 10 a
), giá trị của a − b bằng A. 1. B. −2 . C. 2 . D. −1 .
Câu 29: Cho hàm số ( ) x
f x = e + 9 , với C là hằng số . Khẳng định nào dưới đây đúng? A. ( )d x
f x x = e + 9x + C . B. ( )d x
f x x = e − 9x + C . C. ( ) −9 d x f x x = e + C . D. ( )d x
f x x = e + C .
Câu 30: Cho hàm số f ( x) xác định trên R \
1 thỏa mãn f ( x) 1 =
, f (0) = 2022 , f (2) = 2023. Tính x −1
S = f (3) − f (− ) 1 .
A. S = ln 4035 . B. S = ln 2 . C. S = 4 . D. S = 1 . 1
Câu 31: Rút gọn biểu thức 3 6
P = x . x với x 0 , ta được 1 1 A. P = x . B. 9 P = x . C. 3 P = x . D. 2 P = x . log2 (ab)
Câu 32: Cho a, b là các số thực dương thỏa mãn 4
= 3a . Giá trị của 2 a b bằng A. 12 . B. 2 . C. 6 . D. 3 .
Câu 33: Phương trình tiếp tuyến của đồ thị hàm số 3
y = −x + 2x −1 tại điểm M (1;0) là
A. y = x −1.
B. y = x +1.
C. y = − x + 1.
D. y = − x −1.
Câu 34: Cho mặt cầu có bán kính bằng 3a . Thể tích khối cầu bằng A. 3 36 a . B. 3 12 a . C. 3 9 a . D. 3 18 a .
Câu 35: Cho hàm số y = f ( x) có đồ thị như hình vẽ bên dưới. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn 1 − ; 3 bằng Trang 3 A. 1. B. 2 . C. −2 . D. 4 .
Câu 36: Với a là số thực dương tùy ý, 8 log a bằng 3 1 A. log a . B. 8log a .
C. 8 − log a . D. 8 + log a . 3 3 3 3 8 2x +1
Câu 37: Biết đường thẳng y = x − 2 cắt đồ thị hàm số y =
tại hai điểm phân biệt A và B có hoành x −1
độ lần lượt là x , x . Giá trị của biểu thức x + x bằng A B A B A. 3. B. 2. C. 1. D. 5. x − 2
Câu 38: Cho hàm số y =
. Mệnh đề nào sau đây đúng? x +1
A. Hàm số đồng biến trên các khoảng ( ) ;1 − và (1;+).
B. Hàm số nghịch biến trên các khoảng (− ; − ) 1 và ( 1 − ;+).
C. Hàm số nghịch biến trên các khoảng ( ) ;1 − và (1;+) .
D. Hàm số đồng biến trên các khoảng (− ; − ) 1 và ( 1 − ;+).
Câu 39: Cho hình chóp S.ABCD có đáy ABCD hình chữ nhật với AB = 4a , BC = a , cạnh bên SD = 2a
và SD vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABCD bằng 2 8 A. 3 a . B. 3 a . C. 3 3a . D. 3 6a . 3 3
Câu 40: Biết phương trình 2
log x − m log x − 7 = 0 ( m là tham số) có hai nghiệm x , x . Tính tích x .x . 5 5 1 2 1 2 A. . 5 . m x x − =
B. x .x = 7 − . C. 7 x .x 5− = . D. . 5 . m x x = 1 2 1 2 1 2 1 2
Câu 41: Cắt hình nón có chiều cao h bởi một mặt phẳng đi qua trục ta được thiết diện là một tam giác
vuông cân. Biết diện tích xung quanh của hình nón là 8 2 . Thể tích của khối nón bằng 16 2 64 A. . B. . C. 16 2 . D. 8 . 3 3
Câu 42: Cho hàm số f ( x) có đạo hàm f ( x) 2023 = x ( 2
. x + (m + 2) x −1− m) với m là tham số thực. Hỏi
có bao nhiêu giá trị nguyên của tham số m ( 2 − 023;202 )
3 để hàm số f ( x) nghịch biến trên khoảng ( ;0 − )? A. 2023. B. 2021. C. 2022 . D. 2024.
Câu 43: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA = 9a và SA ⊥ ( ABC) . Gọi O là SP SQ 1
trọng tâm của tam giác ABC ; P , Q lần lượt là hai điểm thuộc cạnh SB và SC thỏa = = . Thể SB SC 3
tích khối tứ diện AOPQ bằng 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 6 3 9 4
Câu 44: Cho hàm số 4
f x = mx + (m + ) 2 ( )
8 x +1 với m là tham số thực. Trên đoạn 0; 2 , nếu giá trị lớn
nhất của hàm số bằng f ( )
1 thì giá trị nhỏ nhất của hàm số đó bằng Trang 4 11 61 A. −21. B. . C. − . D. 4 . 3 3
Câu 45: Cho lăng trụ ABC . D A B C D
có đáy ABCD là hình thoi có cạnh a , BAD 60 =
và AA = a 5 .
Biết rằng mặt phẳng ( AA C C
) vuông góc với mặt đáy và hai mặt phẳng ( AA C C ) , ( AA B B ) tạo với nhau
góc 45 . Tính thể tích V của khối lăng trụ ABC . D A B C D . 3 a 5 3 a 5 3 a 5 3 a 5 A. V = . B. V = . C. V = . D. V = . 2 4 3 6
Câu 46: Gọi S là tập tất cả các giá trị nguyên của tham số m để phương trình log
(x+m)+log ( 2x − x+2m = 0 có đúng một nghiệm thực. Tính tổng các phần tử của S . 2023 1 ) 2023 A. 0 . B. 3 − . C. 3 − . D. −2 .
Câu 47: Cho hình lăng trụ đứng ABC A B C
có đáy ABC là tam giác vuông cân tại B có BC = a 2 và
góc giữa đường thẳng AB và mặt phẳng ( BCC B
) bằng 30 . Thể tích khối lăng trụ ABC.A B C là 3 a 3 a 6 3 a A. . B. 3 a 6 . C. . D. . 6 3 4
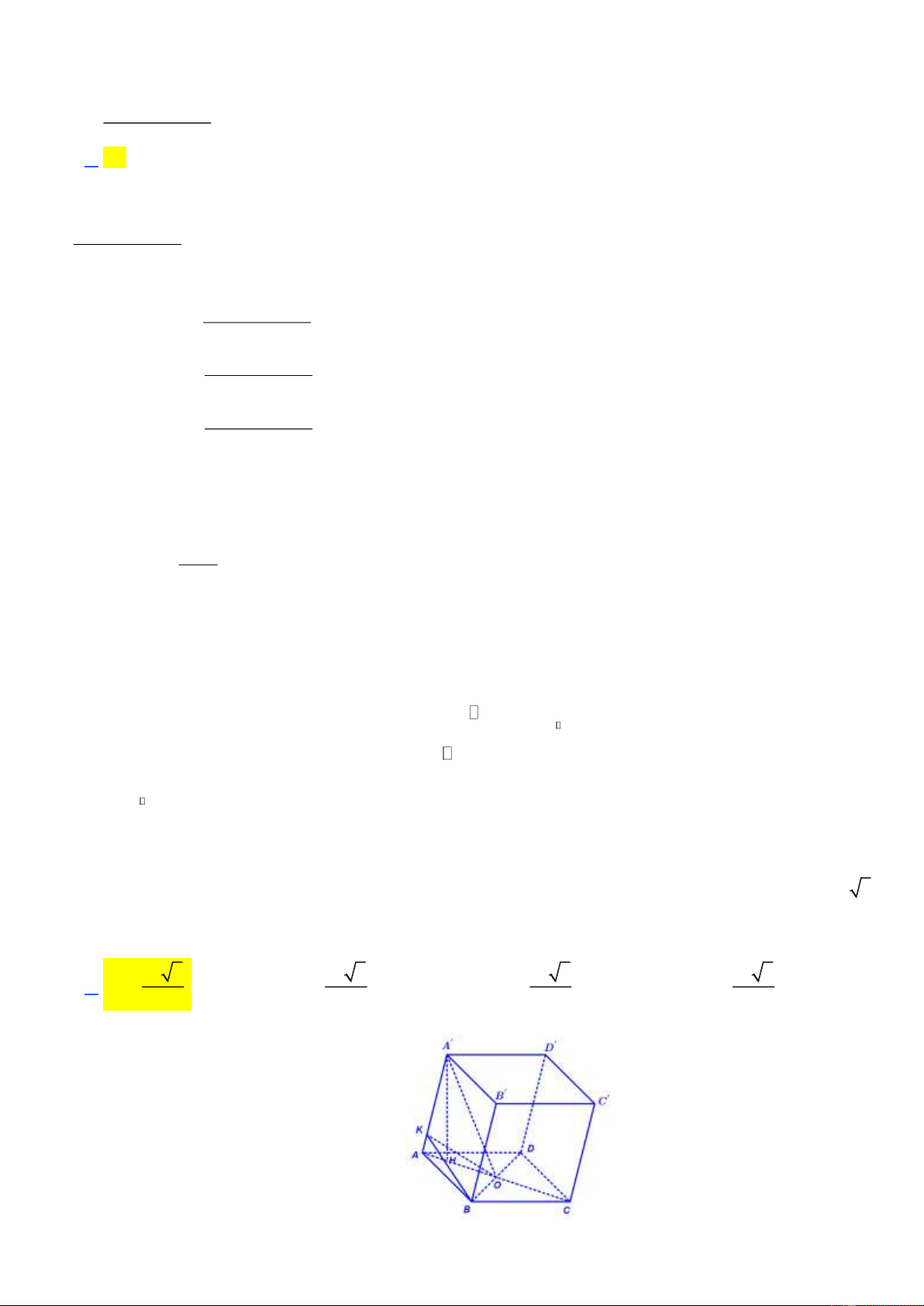
Câu 48: Cho hàm số y = f ( x) là hàm đa thức có f ( 3
− ) 0 và đồ thị f (x) như hình vẽ bên dưới. Tìm
số điểm cực đại của hàm số g ( x) = f ( x − ) 1982 1 A. 3 . B. 2 . C. 1 . D. 4 .
Câu 49: Gọi S là tập hợp tất cả các giá trị nguyên của tham số m thuộc đoạn 0;1 0 để bất phương trình 2
x + 2x + m +1 2 log
2x + 4x + 7 − 2m 2 2 x + 2x +
có nghiệm. Số phần tử của tập hợp S bằng 2 A. 9 . B. 7 . C. 10 . D. 8 . 2
Câu 50: Có bao nhiêu giá trị nguyên của tham số m để phương trình x −( 2 125.5 12 −12 + 37)5m x m = 0 có hai nghiệm phân biệt? A. 2 . B. 4 . C. 1 . D. 3 .
------ HẾT ------ Trang 5 ĐÁP ÁN 1 B 6 C 11 C 16 A 21 C 26 D 31 A 36 B 41 A 46 D 2 D 7 D 12 A 17 D 22 C 27 C 32 D 37 D 42 B 47 B 3 C 8 D 13 B 18 D 23 A 28 D 33 C 38 D 43 C 48 C 4 B 9 B 14 B 19 A 24 D 29 A 34 A 39 B 44 C 49 A 5 B 10 A 15 B 20 A 25 B 30 D 35 C 40 D 45 A 50 C
HƯỚNG DẪN GIẢI MỘT SỐ CÂU VẬN DỤNG
Câu 1: Cho hàm số f ( x) có đạo hàm f ( x) 2023 = x ( 2
. x + (m + 2) x −1− m) với m là tham số thực. Hỏi có
bao nhiêu giá trị nguyên của tham số m ( 2 − 023;202 )
3 để hàm số f ( x) nghịch biến trên khoảng ( ;0 − ) ? A. 2023. B. 2021. C. 2022 . D. 2024. Lời giải
▪ Hàm số f (x) nghịch biến trên khoảng ( ;0 − ) 2023 x ( 2
. x + (m + 2) x −1− m) 0, x (− ; 0) ( 2
x + (m + 2) x −1− m) 0, x (− ; 0) 2 −x − 2x +1 m , x (− ; 0) . x −1
m min g (x) m 1 − ,158... (−;0)
▪ Do m và m( 2 − 023;202 ) 3 nên m 2 − 022; 1 − 8;....;− 2 .
Vậy có 2021 giá trị m thỏa yêu cầu bài toán.
Câu 2 : Gọi S là tập tất cả các giá trị nguyên của tham số m để phương trình log
(x+m)+log ( 2x − x+2m = 0 có đúng một nghiệm thực. Tính tổng các phần tử của S . 2023 1 ) 2023 A. 0 . B. 3 − . C. 3 − . D. −2 . Lời giải
▪ Phương trình đã cho tương đương: log (x + m)= log ( 2
x - x + 2m 2023 2023 ) 2 2
ìï x + m > 0
ìï x + m > 0
ìï x - x + 2x > 0
ìï - x + 3x > 0 ìï 0 < x < 3 ï ï ï ï ï Û í Û í Û í Û í Û í 2 2 2 2 2
ï x + m = x - x + 2m
ï m = - x + 2x
ï m = - x + 2x
ï m = - x + 2x ï ïî ïî ïî ïî
ï m = - x + 2x î
▪ Lập bảng biến thiên của hàm số f (x) 2
= - x + 2x trên (0; ) 3 . m é = 1
▪ Dựa vào BBT, ta thấy YCBT Û ê . ê- 3 < m £ 0 ë
▪ Vì m Î ¢ nên m Î {- 2;- 1;0;1 . }
Vậy tổng các phần tử của S là - 2 . Câu 3: Cho hàm số 4
f x = mx + (m + ) 2 ( )
8 x +1 với m là tham số thực. Trên đoạn 0; 2 , nếu giá trị lớn nhất
của hàm số bằng f ( )
1 thì giá trị nhỏ nhất của hàm số đó bằng 11 61 A. −21. B. . C. − . D. 4 . 3 3 Lời giải
▪ Ta có: f (x) 3
= 4mx + 2(m+8) x .
▪ Trên đoạn 0;2 , giá trị lớn nhất của hàm số bằng f ( ) 1 nên f ( ) 1 = 0 3 4 .
m 1 + 2(m + 8).1 = 0 Trang 6 8 m = − 3 8 8 8 16 Suy ra, f ( x) 4 2 4 2
= − x + − + 8 x +1= − x + x +1 . 3 3 3 3
▪ Dùng MT Casio, ta tìm được giá trị nhỏ nhất của hàm số đó trên đoạn 0;2 bằng 61 − . 3
Câu 4: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA = 9a và SA ⊥ ( ABC) . Gọi O là SP SQ 1
trọng tâm của tam giác ABC ; P , Q lần lượt là hai điểm thuộc cạnh SB và SC thỏa = = . Thể SB SC 3
tích khối tứ diện AOPQ bằng 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 6 3 9 4 Lời giải
▪ Gọi I là trung điểm của BC . ▪ 1 Ta có: V = S .d O APQ APQG A PQ ( ,( )) 3 1 2 = S . d I APQ APQ ( ,( )) 3 3 2 = V . 3 I APQ 4 = V . 3 S APQ 4 SA SP SQ = . . . V . 3 S ABC SA SB SC 2 4 1 1 = . . S . A S 3 3 3 ABC 2 4 a 3 = .9 . a 81 4 3 a 3 = . 9
Câu 5: Cho hàm số y = f ( x) là hàm đa thức có f ( 3
− ) 0 và đồ thị f (x) như hình vẽ bên dưới. Tìm số
điểm cực đại của hàm số g (x) = f (x − ) 1982 1 . Trang 7 A. 3 . B. 2 . C. 1 . D. 4 . Lời giải
▪ Từ đồ thị đã cho, ta suy ra bảng biến thiên của hàm số y = f ( x) như sau: ▪ 1981
g( x) =1982. f (x − ) 1 . f (x − ) 1 x −1 = 3 − x = 2 −
f (x − ) 1 = 0 x −1 = 1 x = 2
g( x) = 0 . f ( x − ) 1 = 0 x −1 = 0 x =1
x −1 = a 1
x = a +1 2 f (x − )
1 0 x a +1 ▪ Ta có: − f ( x − ) x 2 1 0 x 2
▪ Lập bảng biến thiên của hàm số g (x)
▪ Từ bảng biến thiên trên, ta nhận thấy hàm số g (x) có 1 điểm cực đại. Trang 8
Câu 6: Gọi S là tập hợp tất cả các giá trị nguyên của tham số m thuộc đoạn 0;1 0 để bất phương trình 2
x + 2x + m +1 2 log
2x + 4x + 7 − 2m có nghiệm. Số phần tử của tập hợp S bằng 2 2 x + 2x + 2 A. 9 . B. 7 . C. 10 . D. 8 . Lời giải
▪ Điều kiện xác định của phương trình: 2
x + 2x + m +1 0 2
x + 2x + m+1 0 (vì 2
x + 2x + 2 = ( x + )2
1 +1 0 với mọi x ). (*) 2 x + 2x + 2 Khi đó: 2
x + 2x + m +1 2 log
2x + 4x + 7 − 2m 2 2 x + 2x + 2 2
x + 2x + m +1 2 log
−1 2x + 4x + 6 − 2m 2 2 x + 2x + 2 2
x + 2x + m +1 log
x + x + −
x + x + m +
2 ( x + 2x + 2) 2. 2( 2 2 2) 2 ( 2 2 1 2 2 ) log ( 2
x + 2x + m +1 + ( 2
2 x + 2x + m + ) 1 log 2 ( 2
x + 2x + 2 + ( 2
2. 2 x + 2x + 2) 2 ) 2 ) . (1)
▪ Xét hàm số f (t) = log t + 2t với t 0. 2
Ta có: f (t ) 1 = + 2 0, t
0 . Suy ra hàm số f (t) đồng biến trên khoảng (0;+ ) . t.ln 2 Do đó ( ) f ( 2 1
x + 2x + m + ) 1 f ( ( 2 2 x + 2x + 2) 2
x + 2x + m+1 ( 2 2 x + 2x + 2) . 2
x + 2x +3 m. ▪ Yêu cầu bài toán 2
x + 2x +3 m có nghiệm trên m min g (x) với g (x) 2 = x + 2x + 3.
▪ Ta có: g ( x) = x + x + = ( x + )2 2 2 3 1 + 2 2, x .
Khi đó, min g ( x) = 2 m 2 .
▪ Vì m0;10 và nên tập S = 2;3;...;1 0 .
Vậy S có 9 phần tử.
Câu 7: Cho lăng trụ ABC . D A B C D
có đáy ABCD là hình thoi có cạnh a , BAD = 60 và AA = a 5 .
Biết rằng mặt phẳng ( AA C C
) vuông góc với mặt đáy và hai mặt phẳng ( AA C C ) , ( AA B B ) tạo với nhau
góc 45 . Tính thể tích V của khối lăng trụ ABC . D A B C D . 3 a 5 3 a 5 3 a 5 3 a 5 A. V = . B. V = . C. V = . D. V = . 2 4 3 6 Lời giải Trang 9
▪ Vì ABCD là hình thoi có cạnh a , BAD 60 = nên ABD
là tam giác đều có cạnh là a . 2 2 Do đó, a 3 a 3 S = 2S = 2. = . ABCD A BD 4 2
▪ Gọi H là chân đường cao của khối lăng trụ hạ từ đỉnh A. Vì ( AA C C
) ⊥ (ABCD) và ( AA C C
)(ABCD) = AC nên A H ⊥ AC . BO ⊥ AC ▪ Ta có:
BO ⊥ AA ( ) 1 BO ⊥ A H Trong ( AA C C
) , kẻ OK ⊥ AA (2) Từ ( )
1 ,(2) AA ⊥ KB ( ) 3 Suy ra (( AA C C ),( AA B B )) = OKB = 45. Lúc đó, a B
OK là tam giác vuông cân tại O nên OK = OB = . 2 a .a 5 ▪ OK.AA a 15 Xét A A O có: 2 A H
.AO = OK.AA A H = = = . AC a 3 3 2 2 3 Vậy a 15 a 3 a 5
thể tích khối lăng trụ cần tìm là: V = A H .S = . = . ABCD 3 2 2 2
Câu 8: Có bao nhiêu giá trị nguyên của tham số m để phương trình x −( 2 125.5 12 −12 + 37)5m x m = 0 có hai nghiệm phân biệt? A. 2 . B. 4 . C. 1 . D. 3 . Lời giải ▪ 2 2 Xét phương trình: x −( 2 125.5 12 −12 + 37)5m x m = 0 x +3−m − ( 2 5
12 x + 3 − m) −1= 0 ▪ Đặt 2
t = x + 3− m. Khi đó phương trình trở thành: 5t −12t −1= 0( ) * .
▪ Xét hàm số ( ) = 5t f t
−12t −1 có ( ) = 5t f t ln 5 −12 t 12 12
Ta có: f (t) = 0 5 = t = log
= t . Suy ra: f (t 1,248 0 . 1 ) 5 1 ln 5 ln5
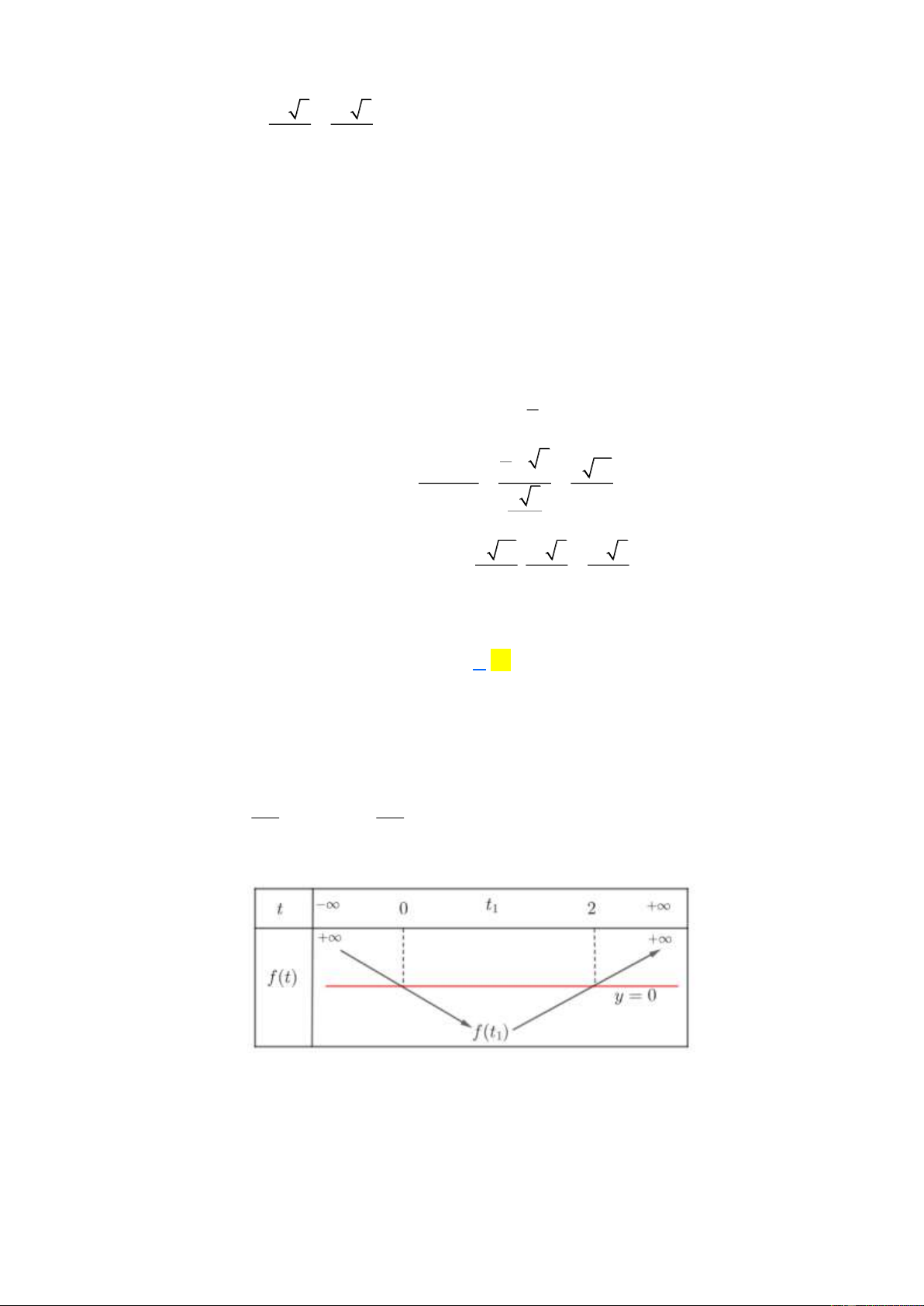
▪ BBT của hàm số ( ) = 5t f t −12t −1 : t = 2 2
x + 3− m = 0 x = m − 3
▪ Dựa vào BBT suy ra: 5t −12t −1= 0 0 . t = 2 2 2
x + 3− m = 2 x = m −1 m − 3 0
▪ Yêu cầu của bài toán tương đương: 1 m 3 . m −1 0
Vậy m = 2 thỏa yêu cầu bài toán. Trang 10