Đề thi thử Toán THPT QG 2020 lần 1 trường chuyên Nguyễn Trãi – Hải Dương

Giới thiệu đến quý thầy, cô giáo và các em học sinh khối 12 đề thi thử Toán THPT QG 2020 lần 1 trường chuyên Nguyễn Trãi – Hải Dương, gồm có 08 trang với 50 câu trắc nghiệm

19 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

23 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
Trang 01/08
SỞ GD & ĐT HẢI DƯƠNG
TRƯỜNG THPT NGUYỄN TRÃI
(Đề có 08 trang)
ĐỀ THI THỬ KỲ THI THPT QUỐC GIA LẦN 1
NĂM HỌC 2019 - 2020
MÔN TOÁN
Thời gian làm bài: 90 phút
Họ tên: ......................................................................... Số báo danh: ...................
Câu 1: Trong các hàm số sau, hàm số nào nghịch biến trên tập số thực?
A.
32
2 10 4yx x x
=−+ − +
B.
10
1
x
y
x
+
=
−
C.
2
56yx x=−+
D.
5
yx= +
Câu 2: Cho hàm số có bảng biến thiên như sau. Tổng các giá trị nguyên của
m
để đường thẳng
ym
=
cắt đồ thị hàm số tại ba điểm phân biệt bằng
+
∞
+
+
∞
+
∞
y
y'
x
3
1
+
∞
∞
A.
0
B.
1−
C.
3−
D.
5
−
Câu 3: Tìm họ nguyên hàm của hàm số
22
1
sin .cos
y
xx
=
A.
2cot 2xC+
B.
cot 2xC−+
C.
cot 2xC+
D.
2cot 2xC−+
Câu 4: Tìm phương trình mặt cầu có tâm là điểm
( )
1; 2; 3I
và tiếp xúc với trục
Oz
A.
(
) (
) (
)
2 22
1 2 35xyz−+−+−=
B.
( ) ( ) ( )
2 22
1 2 3 13xyz−+−+−=
C.
( ) ( ) ( )
2 22
1 2 3 14xyz−+−+−=
D.
( ) ( ) ( )
2 22
1 2 3 10xyz−+−+−=
Câu 5: Tính diện tích hình phẳng giới hạn bởi các đường
2
2
; ;x 0;x 1
1
x
y yx
x
= = = =
+
A.
5
2ln 2
3
−
B.
2
2ln 2
3
−
C.
7
2ln 2
3
−
D.
1
2ln 2
3
−
Câu 6: Cho tam giác ABC có
( ) ( ) ( )
3;0;0 ; 0; 6;0 ;C 0;0;6AB−
. Tìm tọa độ điểm H là hình chiếu
vuông góc của trọng tâm tam giác ABC trên mặt phẳng
(
)
: 40xyz
α
++−=
MÃ ĐỀ 035
Trang 02/08
A.
( )
2; 1; 3H −−
B.
( )
2;1; 3H
C.
( )
2;1;3H −−
D.
( )
2; 1; 3H −
Câu 7: Cho đồ thị hàm số
( )
y fx=
. Diện tích
S
của hình phẳng (phần tô đậm trong hình vẽ) là
A.
13
01
dd
S fx x fx x


. B.
13
01
dd
S fx x fx x


.
C.
3
0
d
S fx x
. D.
13
01
dd
S fx x fx x


.
Câu 8: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
, cạnh bên
SA
vuông góc với đáy.
Biết
2
SA a=
. Tính thể tích khối chóp
.S ABCD
A.
3
2
3
a
B.
3
a
C.
3
2
a
D.
3
3
a
Câu 9: Khẳng định nào sau đây là sai ?
A.
1
1
x
x dx C
α
α
α
+
= +
+
∫
(
C
là hằng số,
α
là hằng số)
B.
xx
e dx e C= +
∫
(
C
là hằng số)
C.
1
lndx x C
x
= +
∫
(
C
là hằng số) với
0x
≠
D. Mọi hàm số
( )
fx
liên tục trên đoạn
[ ]
;ab
đều có nguyên hàm trên đoạn
[ ]
;ab
Câu 10: Cho tập hợp
{ }
2 3 10
10;10 ;10 ;...;10A =
. Gọi
S
là tập các số nguyên có dạng
100
log m
với
mA∈
. Tính tích các phần tử của tập hợp
S
A.
60
B.
24
C.
120
D.
720
Câu 11: Tìm tập xác định của hàm số
2
yx=
A.
{ }
\0
B. (-∞;0) C.
D. (0;+∞)
Câu 12: Viết công thức tính thể tích
V
của phần vật thể giới hạn bởi hai mặt phẳng vuông góc với
trục
Ox
tại các điểm
, ,
x ax b a b

có thiết diện bị cắt bởi mặt phẳng vuông góc với trục
Ox
tại
điểm có hoành độ
xa x b

là
Sx
.
A.
2
d.
b
a
V Sx x
B.
d.
b
a
V Sx x
C.
d.
b
a
V Sx x
D.
2
d.
b
a
V Sxx
Câu 13: Cho hình chóp
.S ABC
có
;;SA SB SC
đôi một vuông góc với nhau và
6; 4; 5.SA SB SC= = =
Trang 03/08
Gọi
,NM
lần lượt là trung điểm của
,AB AC
. Tính thể tích khối chóp
.S MBCN
A.
30
B.
5
C.
15
D.
45
Câu 14: Cho ba điểm
( ) ( ) ( )
2;1; 1 ; 1;0; 4 ; 0; 2; 1ABC− − −−
. Mặt phẳng đi qua A và vuông góc với BC
có phương trình là
A.
2 5 50xyz− − +=
B.
2 5 50
xyz
− − −=
C.
2 5 50xy z−+ +=
D.
250xyz−−=
Câu 15: Cho hàm số
1
1
x
y
x
+
=
−
. Tìm phương trình tiếp tuyến với đồ thị hàm số tại điểm
( )
2;3M
A.
21yx= −
B.
39yx
=−+
C.
33
yx
= −
D.
27yx=−+
Câu 16: Cho phương trình
25 3.5 2 0
xx
− +=
có hai nghiệm
12
xx<
. Tính
12
32
xx+
A.
5
4log 2
B.
0
C.
5
3log 2
D.
5
2log 2
Câu 17: Đường tiệm cận ngang của đồ thị hàm số
41
2020
x
y
x
−
=
−
có phương trình là
A.
2020x =
B.
1y =
C.
4
y =
D.
2
y =
Câu 18: Trong không gian Oxyz cho ba vecto
(
) (
)
( )
1;1; 0 ; 2; 2; 0 ; 1;1;1a bc
=−= =

. Trong các khẳng
định sau khẳng định nào sai ?
A.
ab⊥

B.
2a =
C.
3c =
D.
cb⊥

Câu 19: Tìm số điểm cực đại của đồ thị hàm số sau
42
10 5 19yxx= ++
A.
2
B.
1
C.
3
D.
0
Câu 20: Cho hình trụ có chiều cao bằng
4a
, diện tích xung quanh bằng 2π
2
a
. Tìm bán kính đáy
của hình trụ đó
A.
2
a
B.
2
a
C.
a
D.
4
a
Câu 21: Cho hình nón đỉnh
S
có bán kính đáy
2R =
. Biết diện tích xung quanh của hình nón là
25
π. Tính thể tích khối nón
A. B.
5
3
C.
4
3
D.
2
3
Câu 22: Hình vẽ sau là đồ thị của hàm số nào sau đây?
Trang 04/08
A.
lnyx=
B.
2
x
y =
C.
1
2
log
yx=
D.
x
ye=
Câu 23: Cho tứ diện ABCD có cạnh
AD
vuông góc với mặt phẳng
( )
ABC
, tam giác
ABC
vuông
tại B có cạnh
3; 4AB BC= =
và góc giữa
DC
và mặt phẳng
( )
ABC
bằng
0
45
. Tính thể tích mặt cầu
ngoại tiếp tứ diện
A.
125 3
3
V =
π B.
25 2
3
V
=
π C.
125 2
3
V =
π D.
52
3
V =
π
Câu 24: Tìm tập nghiệm của bất phương trình
2
11
33
xx
−+
 
≤
 
 
A.
( )
;1−∞
B.
[
)
1; +∞
C.
(
]
;1−∞
D.
(
)
1; +∞
Câu 25: Gọi
;mM
lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số
1
2
2
y xx
= −+
trên
đoạn
[ ]
1; 34−
. Tính tổng
3S mM= +
A.
13
2
S =
B.
63
2
S =
C.
25
2
S
=
D.
11
2
S =
Câu 26: Tính thể tích của vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường
4; 2; 0; 1yy xx= =−= =
quanh trục
Ox
A.
20
π B.
36
π C.
12
π D.
16
π
Câu 27: Cho lăng trụ đứng
.'' 'ABC A B C
có đáy là tam giác đều cạnh bằng
a
, cạnh bên bằng
2
a
.
Tính thể tích khối lăng trụ
A.
3
3
8
a
B.
3
3
8
a
C.
3
8
a
D.
3
3
4
a
Câu 28: Có bao nhiêu giá trị nguyên của
m
để hàm số sau đồng biến trên tập số thực
( )
(
)
23 2
4 2 79y m x mx x=− +− + −
A. 3 B. 2 C. 4 D. 1
Trang 05/08
Câu 29: Cho đường thẳng
( )
d
nằm trên mặt phẳng
( )
: 30Pxyz++−=
và vuông góc với đường
thẳng
( )
1
':
131
x yz
d
−
= =
−
. Tìm một vecto chỉ phương của đường thẳng
( )
d
A.
( )
2;1;1
B.
( )
4; 2;2−
C.
( )
4;2; 2−−
D.
( )
2;1;1−
Câu 30: Cho tam giác ABC có độ dài ba cạnh là
;;abc
. Gọi
p
là nửa chu vi của tam giác . Biết dãy
số
;;;abcp
theo thứ tự lập thành một cấp số cộng. Tìm cosin của góc nhỏ nhất trong tam giác đó
A.
4
5
B.
3
4
C.
5
6
D.
3
5
Câu 31: Một người chơi trò gieo súc sắc. Mỗi ván gieo đồng thời ba con súc sắc. Người chơi thắng
cuộc nếu xuất hiện ít nhất 2 mặt sáu chấm. Tính xác suất để trong ba ván, người đó thắng ít nhất hai
ván
A.
1
1296
B.
308
19683
C.
58
19683
D.
53
23328
Câu 32: Cho hai điểm
( )
( )
2;1; 1 ;B 0;3;1
A
−
. Biết tập hợp các điểm
( )
: 30M mp x y z
α
∈ +++=
thỏa
mãn
22
2. 4MA MB−=
là đường tròn có bán kính
r
. Tính
r
A.
27r =
B.
6r =
C.
26r =
D.
5r =
Câu 33: Cho hàm số
2
2
20 6
82
xx
y
x xm
+−
=
−+
. Tìm tất cả các giá trị của
m
sao cho đồ thị hàm số có đúng
hai đường tiệm cận đứng
A.
[
)
6;8m∈
B.
( )
6;8m∈
C.
[
)
12;16m∈
D.
( )
0;16m∈
Câu 34: Cho hàm số
( )
7543 2
2 2 10fx x x x x x x=+−+− +−
và
( )
3
32gx x x=−+
. Đặt
(
) (
)
Fx g fx=


. Tìm tất cả các giá trị của tham số
m
để phương trình
( )
Fx m=
có ba nghiệm thực
phân biệt
A.
( )
1; 3m∈−
B.
(
)
0;4m
∈
C.
(
)
3;6m
∈
D.
( )
1; 3m∈
Câu 35: Cho tứ diện
ABCD
có
3
;AC BC AD BD
2
a
AB a= = = = =
. Gọi
,
MN
là trung điểm của
,AB CD
. Góc giữa hai mặt phẳng
( ) ( )
;ABD ABC
là
α
. Tính
cos
α
biết mặt cầu đường kính
MN
tiếp xúc với cạnh
AD
A.
23−
B.
23 3−
C.
3 23−
D.
21−
Câu 36: Biết
4
0
1
. ln 2
1 tan
dx a b
x
π
π
= +
+
∫
với
;ab
là các số hữu tỉ. Tính tỷ số
a
b
A.
1
2
B.
1
6
C.
1
4
D.
1
3
Câu 37: Cho hình chóp
.S ABC
có đáy là tam giác cân tại A, mặt bên
( )
SBC
là tam giác đều và
nằm trong mặt phẳng vuông góc với đáy. Gọi
( )
α
là mặt phẳng đi qua điểm
B
và vuông góc với
Trang 06/08
SC
, chia khối chóp thành hai phần. Tính tỉ số thể tích của hai phần đó
A.
1
2
B.
1
3
C.
2
3
D.
1
4
Câu 38: Cho mặt phẳng
( )
α
đi qua hai điểm
( )
4;0;0M
và
( )
0;0;3N
sao cho mặt phẳng
( )
α
tạo
với mặt phẳng
( )
Oyz
một góc bằng
0
60
. Tính khoảng cách từ điểm gốc tọa độ đến mặt phẳng
( )
α
A.
1
B.
3
2
C.
2
3
D.
2
Câu 39: Tìm
m
để khoảng cách từ điểm
1
A ;1; 4
2



đến đường thẳng
( ) ( )
12
: 22 1
1
x m mt
d y m mt
zt
=−+
=−+ + −
= +
đạt giá trị lớn nhất
A.
2
3
m
=
B.
4
3
m =
C.
1
3
m
=
D.
1m =
Câu 40: Tìm số nghiệm nguyên của bất phương trình
( )
22
ln 3 1 3 0xx xx+ ++ + <
A.
0
B.
2
C.
3
D.
1
Câu 41: Cho hình lăng trụ
.'' 'ABC A B C
có đáy
ABC
là tam giác vuông tại A với
2;BC 4
AB = =
.
Mặt bên
''
ABB A
là hình thoi có góc
B
bằng
0
60
. Gọi điểm
K
là trung điểm của
B'C'
. Tính thể tích
khối lăng trụ biết
( )
3
' ';
2
d A B BK
=
A.
43
B.
6
C.
33
D.
23
Câu 42: Cho dãy số
( )
n
u
thỏa mãn
( )
1
1
1
3
1
;n1
3
n
n
u
nu
u
n
+
=
+
= ∀≥
. Có bao nhiêu số nguyên dương
n
thỏa mãn
1
2020
n
u <
A.
0
B.
9
C. vô số D.
5
Câu 43: Cho hàm số
( )
y fx=
liên tục trên
. Biết
( ) ( )
3
4 42f x fx x x= ++
và
( )
02f =
. Tính
( )
1
0
f x dx
∫
A.
148
63
B.
146
63
C.
149
63
D.
145
63
Câu 44: Cho hàm số
( )
y fx=
có đồ thị như hình vẽ sau. Tìm
m
để phương trình
( )
sinxfm=
có
đúng hai nghiệm
trên đoạn [0; π]
x
y
-3
O
1
-4
-1
Trang 07/08
A.
43m
− < ≤−
B.
43m− ≤ ≤−
C.
4m = −
hoặc
3m >−
D.
43m
− ≤ <−
Câu 45: Tìm số nghiệm
x
thuộc
[ ]
0;100
của phương trình sau :
( )
cos x 1
4
1
2 cos log 3cos 1
2
xx
π
ππ
−
+= + −
A.
51
B.
49
C.
50
D.
52
Câu 46: Tính tổng các số nguyên dương
n
thỏa mãn
43
n
+
viết trong hệ thập phân là số có
2020
chữ số
A.
6711
B.
6709
C.
6707
D.
6705
Câu 47: Cho hàm số
( )
y fx=
có đồ thị như hình vẽ .
Tìm số điểm cực trị của hàm số
( ) (
) ( )
42
325Fx fx fx=++
A.
6
B.
3
C.
5
D.
7
Câu 48: Cho hai điểm
( ) ( )
3;1;1 ; 4;3; 4MN
và đường thẳng
( )
739
:
1 21
xyz
d
− −−
= =
−
. Biết điểm
( )
;;I abc
thuộc đường thẳng
( )
d
sao cho
IM IN+
đạt giá trị nhỏ nhất . Tính
23S ab c= ++
A.
36
B.
38
C.
42
D.
40
Câu 49: Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
A
với
;2AB a AC a= =
. Mặt phẳng
( )
SBC
vuông góc với mặt phẳng
( )
ABC
. Mặt phẳng
( ) ( )
;SAB SAC
cùng tạo với mặt phẳng
( )
ABC
một góc bằng
0
60
. Gọi
α
là góc giữa hai mặt phẳng
( )
SAB
và
( )
SBC
. Tính
tan
α
A.
51
17
B.
51
3
C.
17
3
D.
3 17
17
Câu 50: Cho
a
là hằng số dương khác
1
thỏa mãn
2cos2 2
4 cos 1;
x
a xx≥ − ∀∈
. Giá trị của
a
thuộc
Trang 08/08
khoảng nào sau đây
A.
( )
4;+∞
B.
( )
2;3
C.
( )
0;2
D.
(
)
3;5
---------- HẾT ----------
ĐÁP ÁN ĐỀ THI
1A
2D
3D
4A
5A
6D
7B
8A
9A
10C
11D
12B
13C
14B
15D
16D
17C
18D
19D
20D
21C
22A
23C
24B
25A
26C
27A
28C
29D
30A
31B
32D
33A
34B
35B
36A
37A
38D
39B
40A
41C
42C
43A
44A
45A
46B
47D
48D
49B
50B
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1. Chọn A
Vì
2
3 4 10 0y xx x
′
=− + − < ∀∈
.
Câu 2. Chọn D
Để đường thẳng
ym
=
cắt đồ thị hàm số tại 3 điểm phân biệt thì
42m−< <
Do vậy
m
nhận các giá trị nguyên là
{ }
3; 2; 1; 0;1−−−
.vậy tổng các giá trị nguyên của tham số
m
là
( )
( )
(
)
3 2 1 01 5− +− +− + + =−
.
Câu 3. Chọn D
22 2
14
2 cot 2
sin .cos sin 2
dx dx x c
xx x
= =−+
∫∫
Câu 4. Chọn A
Hình chiếu của điểm
( )
1; 2; 3
I
lên trục
Oz
là điểm
H
có tọa độ là:
( )
0;0;3
H
.
Ta có
( )
1; 2; 0IH =−−

.
Vì mặt cầu tiếp xúc với trục
Oz
nên:
( )
( )
22
125
R IH= = − +− =

.
Vậy phương trình mặt cầu có tâm là
( )
1; 2; 3I
và tiếp xúc với trục
Oz
là:
( ) ( ) ( )
2 22
1 2 35xyz−+−+−=
Câu 5. Chọn A
Diện tích hình phẳng giới hạn bởi các đường
2
2
; ; 0; 1
1
x
y y xx x
x
= = = =
+
là :
1
11 1
22 2 3
00 0
0
2 2 21
dx= dx 2 dx 2 2ln 1
1 1 13
5
2ln 2
3
xx
Sx x x xx x
xx x

= − − = −+ = − + +

++ +

= −
∫∫ ∫
Câu 6. Chọn D
Gọi
G
là trọng tâm của tam giác
ABC
( )
1; 2; 2G⇒−
.
Gọi
d
là đường thẳng qua
G
và vuông góc với
( )
α
.
Mặt phẳng
( )
α
có vecto pháp tuyến là
(
)
1;1;1n
α
=

.
Vì
( )
d
α
⊥
nên:
( )
1;1;1
d
un
α
= =
 
. Vậy phương trình tham số của đường thẳng
d
đi qua
( )
1; 2; 2G −
và
vuông góc với
( )
α
là:
( )
1
2
2
xt
y tt
zt
= +
=−+ ∈
= +
H
là hình chiếu vuông góc của
G
lên mặt phẳng
( )
α
nên
( )
Hd
α
= ∩
. Hay tọa độ điểm
H
là nghiệm
của hệ:
( )
12
21
2; 1; 3
23
40 1
xt x
yt y
H
zt z
xyz t
=+=


=−+ =−

⇔ ⇒−

=+=


++−= =

Câu 7. Chọn B
Ta thấy
(
) (
)
0 0;1fx x> ∀∈
và
( ) ( )
0 1;3fx x
< ∀∈
Do đó:
(
)
( )
(
)
( )
(
)
31313
0 0 1 01
d d dddS fx x fx x fx x fx x fx x==+=−
∫∫∫∫∫
Câu 8. Chọn A
ABCD
là hình vuông cạnh
a
2
ABCD
Sa⇒=
.
(
)
3
2
.
1 12
. . .2 .
3 33
S ABCD ABCD
a
SA ABCD V SA S a a⊥ ⇒= = =
.
Câu 9. Chọn A
1
d
1
x
xx C
α
α
α
+
= +
+
∫
(
C
là hằng số,
α
là hằng số và
1
α
≠−
).
Câu 10. Chọn C
Giả thiết
10 (1 10, )
k
m k kN⇒ = ≤≤ ∈
Ta có
2
100
10
log log 10
2
k
k
m
= =
100
log
2
k
mZ Z∈⇒∈
là số nguyên thì
{ }
2;4;6;8;10k ∈
Suy ra tính tích các phần tử của tập hợp S là
2 4 10
100 100 100
(log 10 ).(log 10 )....(log 10 ) 1.2.3.4.5 120= =
Câu 11. Chọn D
Điều kiện
> 0x
Suy ra tập xác định của hàm số là
( )
0;
+∞
Câu 12. Chọn B
Giả thiết ta suy ra
()
b
a
V S x dx
=
∫
Câu 13. Chọn C
Ta có:
SA SB
SA SBC
SA SC

.
1 11
. . . . . 20
3 32
S ABC ABC
V SA S SA SB SC
Có tỉ lệ thể tích :
.. 1
.. 4
ASMN
ASBC
V
AS AM AN
V AS AB AC

5
4
ASBC
ASMN
V
V
Do :
15
ASBC ASMN SMNBC SMNBC ASBC ASMN
V V V V VV 
Câu 14. Chọn B
Gọi phương trình mặt phẳng cần tìm là (P)
Ta có:
()
1;2;5
P
BC P n BC 

2;1; 1
:1 2 2 1 5 1 0 2 5 5 0
1;2;5
Qua A
P P x y z xyz
n


Câu 15. Chọn D
Phương trình tiếp tuyến của hàm số:
'
o
oo
x
y y xx y 
Tiếp tuyến tại
2;3 2; 3
oo
M xy
2
22
12 2
' '' 2
1
1 21
o
x
x
y y yy
x
x



Vậy trình tiếp tuyến cần tìm:
2 23 2 7yx x 
Câu 16. Chọn D
Ta có:
2
5
0
51
25 3.5 2 0 5 3.5 2 0
log 2
52
x
xx xx
x
x
x
=
=
− +=⇔ − +=⇔ ⇔
=
=
.
Phương trình có hai nghiệm
1 22
0; log 5xx= =
. Vậy
12 2
3 2 2log 5xx+=
.
Câu 17. Chọn C
Ta có:
1
4
41
lim lim lim 4
2020
2020
1
xx x
x
x
y
x
x
→±∞ →±∞ →±∞
−
−
= = =
−
−
.
Vậy đường tiệm cận ngang của đồ thị hàm số là
4y =
.
Câu 18. Chọn D
Ta có:
( )
. 1 .2 1.2 0 0ab a b=− + +=⇒⊥⇒

A đúng;
( )
2
22
1 10 2a = − ++ = ⇒
B đúng
222
111 3c = ++ = ⇒
C đúng;
. 1.2 1.2 1.0 4 0cb
= + + =≠⇒

D sai.
Câu 19. Chọn D.
Ta có:
3
' 40 10 ; ' 0 0.y x xy x= + =⇔=
Bảng biến thiên:
Từ bảng biến thiên ta thấy đồ thị hàm số không có điểm cực đại nào.
Lưu ý: Có thể giải theo trắc nghiệm như sau:
Do
. 10.5 50 0
10 0
ab
a
= = >
= >
nên đồ thị hàm số chỉ có 1 điểm cực trị và là điểm cực tiểu.
Câu 20. Chọn D.
Gọi diện tích xung quanh, bán kính đáy, đường sinh, đường cao của hình trụ lần lượt là
,,, .
xq
S rlh
Ta có:
2
2
22 .
2 2 .4 4
xq
xq
S
πa a
S πrl πrh r
πh π a
= = ⇒= = =
Câu 21. Chọn C.
Gọi diện tích xung quanh, đường sinh, đường cao của hình nón lần lượt là
,, .
xq
S lh
Ta có:
22
25
5 1.
2
xq
xq
S
π
S πRl l h l R
πR π
= ⇒= = = ⇒ = − =
Vậy thể tích khối nón là:
2
11 1 4
. R .4.1 .
33 3 3
V Bh πh π π= = = =
Câu 22. Chọn A
Từ hình dạng đồ thị hàm số ta thấy đây là đồ thị hàm số
log
a
x
.
Mặt khác, hàm số đồng biến trên
(
)
0;
+∞
nên
1
a
>
.
Do đó chọn A.
Câu 23. Chọn C
Ta có:
( )
CB AB
CB ABD CB DB BDC
CB AD
⊥
⇒⊥ ⇒⊥⇒∆
⊥
vuông tại
B
Gọi
I
là trung điểm
DC
, do
,ADC BDC∆∆
lần lượt vuông tại
,
AB
có
DC
là cạnh huyền nên
2
CD
IA IB IC ID= = = =
Do đó
I
là tâm đường tròn ngoại tiếp tứ diện
ABCD
và
2
CD
R =
.
Ta có:
( )
DA ABC
⊥
nên góc giữa
DC
và
( )
ABC
là góc
DCA
0
45DCA
⇒=
Xét
ABC∆
có
0
90 , 3, 4 5B AB BC AC
= = =⇒=
Xét
DAC∆
có
00
90 , 45 , 5 5 2A DCA AC CD

Do đó
3
3
52 4 4 52 1252
22 3 32 3
CD
R VR
ππ π

= = ⇒= = =



Câu 24. Chọn B
Ta có
2
11
33
1
21
3
1
xx
x x do
x
−+
 
≤
 
 

⇔ ≥− + <


⇔≥
Do đó tập nghiệm của bất phương trình là
[
1; )+∞
Câu 25. Chọn A
TXĐ:
[
)
2;D = − +∞
Ta có
11
2
22
y
x
′
= −
+
;
[ ]
21
0 0 2 1 1 1;34
22
x
y xx
x
+−
′
= ⇔ = ⇔ + = ⇔ =−∈−
+
.
Lại có
(
)
( )
3
1 ; 34 11
2
yy
−=− =
. Suy ra
3
; 11
2
mM
=−=
. Vậy
13
3
2
S mM=+=
.
Câu 26. Chọn C
Thể tích của vật thể cần tìm :
( )
( )
11
2
2
00
4 2 12 12V dx dx
π ππ
= −− = =
∫∫
.
Câu 27. Chọn A
Thể tích của lăng trụ đứng
.ABC A B C
′′′
cần tìm :
23
33
..
42 8
ABC
aaa
V S AA
∆
′
= = =
.
Câu 28. Chọn C
TH1.
2
2
40 .
2
m
m
m
=
−=⇔
= −
Với
2m
=
thì
79yx= −
là hàm bậc nhất có
70a = >
nên hàm số luôn đồng biến trên
2m⇒=
(nhận).
Với
2m = −
thì
2
4 79
yx x= +−
là hàm bậc hai nên hàm số không đồng biến trên
2m⇒=−
(loại).
TH2.
2
40 2mm− ≠ ⇔ ≠±
Khi đó
( )
( )
22
34 22 7y m x mx
′
=− +− +
.
Hàm số đồng biến trên
khi và chỉ
0yx
′
≥ ∀∈
.
0
0
a >
⇔
∆≤
2
2
40
22 4 80 0
m
mm
−>
⇔
− −≤
( )
2;2
20
;2
11
m
m
∈−
⇔

∈−


20
;2
11
m

⇔ ∈−

;
m∈
1
m⇒=−
;
0m
=
;
1m =
.
Vậy có
4
giá trị nguyên của
m
thỏa yêu cầu bài toán.
Câu 29. Chọn D
Mặt phẳng
( )
P
:
30xyz++−=
có một vectơ pháp tuyến:
( )
1; 1; 1
P
n =

.
Đường thẳng
1
':
131
x yz
d
−
= =
−
có một vectơ chỉ phương:
( )
'
1; 3; -1
d
u =

.
Đường thẳng
d
nằm trong mặt phẳng
( )
P
và vuông góc với đường thẳng
'd
nên
d
nhận
( )
'
, 4; 2; 2
Pd
u nu

= = −

 
làm một vectơ chỉ phương.
Câu 30. Chọn A
Gọi công sai của cấp số cộng này là
d
, số hạng đầu là
a
.
Khi đó
, 2, 3b a dc a dp a d=+=+ =+
.
Ta có nửa chu vi
2
abc
p
++
=
hay
20abc p++− =
.
( ) ( ) ( )
2230
3 0 3.
a ad a d a d
ad ad
⇒++++ − + =
⇒− =⇒=
Vì
0a >
nên
0d >
đo dó
abc<<
.
Vậy góc nhỏ nhất trong tam giác
ABC
là góc đối diện với cạnh nhỏ nhất
a
.
Hay
A
là góc nhỏ nhất.
Áp dụng định lí cosin trong tam giác
ABC
ta được :
222 2 2 2
16 25 9 4
cos
2 2.4 .5 5
bca d d d
A
bc d d
+− + −
= = =
.
Câu 31. Chọn B
Xét trong mỗi ván, để thắng sẽ xảy ra hai trường hợp:
+ Trường hợp 1: xuất hiện đúng hai mặt sáu chấm, xác suất là
2
3
3
.5
5
.
6 72
C
=
+ Trường hợp 2: cả 3 đều là mặt sáu chấm, xác suất là
3
3
3
1
.
6 216
C
=
Do đó, xác suất để mỗi ván thắng là
512
,
72 216 27
+=
xác suất mỗi ván thua là
25
.
27
Vậy, xác suất để trong ba ván, người đó thắng ít nhất hai ván là:
23
23
33
2 25 2 308
.
27 27 27 19683
CC
 
⋅+ =
 
 
Câu 32. Chọn D
Gọi
( ) ( )
;; .M xyz
α
∈
Khi đó
( ) ( ) ( )
( ) ( )
2 22 22
22 2
2 22
2 42 2 1 1 3 1 4
8 2 6 2 0.
MA MB x y z x y z
xyz xyz

− =⇔ − +− ++ − +− +− =

⇔ + + − + + −=
Do đó, điểm
M
nằm trên mặt cầu tâm
(4; 1; 3),I −−
bán kính
28.R =
Gọi đường tròn
( ) ( )
()CS
α
= ∩
. Suy ra
( ).MC∈
Khoảng cách từ tâm
(4; 1; 3)I −−
đến
(
)
α
:
( )
( )
222
4133
; 3.
111
dI
α
−−+
= =
++
Bán kính của đường tròn
()C
là
(
)
( )
22
; 28 3 5.r R dI
α
= − = −=
Câu 33. Chọn A
Để hàm số có đúng hai tiệm cận đứng thì:
2
60xx−≥
(1) và
2
82 0x xm−+ =
(2) có hai nghiệm phân biệt.
Từ (1), (2) ta có:
2
2
2
06
60
4
82 0
2
x
xx
x
xm
x xm
≤≤
−≥

⇔

−+=
−+ =
Đặt
[ ]
2
( ) 4 , 0;6
2
x
fx x x=− + ∀∈
. Ta có
'( ) 4, '( ) 0 4 0 4fx x fx x x=−+ = ⇔−+ = ⇔ =
Bản biến thiên:
x
0
4
6
'y
+
0
−
y
8
0
6
Vậy để (2) có hai nghiệm phân biệt thì
[
)
6;8m
∈
.
Câu 34. Chọn B
Ta có
[
]
'() '() ' ().
F x f xg f x
=
[ ]
6432
7 5 4 3 4 2 0 (1)
'( ) 0
'() 0 () 1
' ()
() 1
xxxxx
fx
Fx fx
g fx
fx
+ − + − +=
=
=⇔ ⇔=
= −
(1) Vô nghiệm vì
6432
7 5 4 3 4 20xxxxx x+ − + − +>∀
Bản biến thiên:
()fx
−∞
1−
1
+∞
'( )Fx
+
0
−
0
+
( )
Fx
4
+∞
0
−∞
Vậy
( )
Fx m=
có ba nghiệm thực phân biệt thì
(
)
0;4
m
∈
Câu 35. Chọn B
Ta có:
(
)
..DAB CAB c c c DM CM
∆=∆ ⇒=
nên
MCD∆
cân tại
M
.
Mặt khác
N
là trung điểm cạnh
CD
suy ra
MN CD⊥
.
Chứng minh tương tự ta được
MN AB⊥
.
Do vậy mặt cầu đường kính
MN
tiếp xúc với
,
AB CD
.
Gọi
I
là trung điểm cạnh
MN
nên
IM IN=
.
Dựng
IK MN
⊥
. Do mặt cầu đường kính
MN
tiếp xúc với
AD
nên
IM IN IK= =
.
Ta có:
2
a
MIA KIA AK MA∆ =∆⇒==
.
Do đó
( )
31
2
a
KD AD AK
−
=−=
.
Nhận thấy
( )
31
2
a
KID NID ND KD
−
∆=∆⇒==
suy ra
( )
31
CD a= −
.
Vì
,AB CM AB MD⊥⊥
nên góc giữa hai mặt phẳng
( )
ABC
và
( )
ABD
là góc giữa hai đường thẳng
CM
và
MD
.
Áp dụng định lý Pitago trong tam giác vuông
MAD
:
22
22
32
44 2
aa a
MD AD MA= − = −=
Xét tam giác
MCD
:
( )
22
2
2
2 22
31
22
cos 2 3 3 0
2. .
22
2. .
22
aa
a
MC MD CD
M
MC CD
aa
+− −
+−
= = = −>
.
Vậy
cos 2 3 3
α
= −
.
Câu 36. Chọn A
Ta có :
44
00
1 cos
1 tan sin cos
x
A dx dx
x xx
ππ
= =
++
∫∫
.
Xét
4
0
sin
sin cos
x
B dx
xx
π
=
+
∫
Nhận thấy:
4
0
4
A B dx
π
π
+= =
∫
(1)
(
)
4
4
0
0
sin cos
ln sin cos
sin cos
dx x
AB x x
xx
π
π
+
−= = +
+
∫
ln 2=
(2)
Cộng từng vế (1) và (2) ta được:
1
ln 2
84
A
π
= +
.
Do đó
11
,
84
ab
= =
.
Vậy
1
2
a
b
=
.
Câu 37. Chọn A
Gọi
H
là trung điểm của
BC
, suy ra
(
)
SH ABC
⊥
.
Gọi
I
đối xứng với
B
qua
A
, suy ra
AH IC IC SC⇒⊥
.
Gọi
,ME
lần lượt là trung điểm của các cạnh
,SC SI
.
Gọi
N
là giao điểm của
SA
và
BE
thì
N
là trọng tâm của tam giác
SBI
.
Ta có:
( )
BM SC
SMN SC
ME SC
⊥
⇒⊥
⊥
Khi đó:
..
..
12 1 1
.
23 3 2
S BMN S BMN
S ABC MN ABC
VV
SM SN
V SC SA V
= ==⇒=
.
Câu 38. Chọn D
Giả sử mặt phẳng
( )
α
cắt trục
Oy
tại
P
. (
P
không trùng với O)
N
M
E
A
H
C
I
B
S
O
P
N
M
K
H
Khi đó ta có
.
O MNP
là tam diện vuông tại
O
.
Kẻ
OK NP MK NP
⊥⇒ ⊥
.
Ta có
OKM∠
là góc nhọn trong tam giác vuông OMK nên góc
OKM∠
là góc giữa
( )
α
và mặt phẳng
( )
Oyz
. Khi đó:
0
30
OMH∠=
Kẻ
(
) ( )
( )
;OH MK OH MNP d O OH
α
⊥⇒⊥ ⇒ =
.
Mà trong tam giác vuông OMH ta có:
0
.sin30 2OH OM= =
.
Câu 39. Chọn B
Lấy
(
) ( )
12;2 2;1Mm md
− −+ ∈
, ta có
1
2 ; 2 3; 3
2
AM m m

− −−



.
Đường thẳng
d
có VTCP là
( )
( )
2
22
;1 ;1 1 1 2 2 2um m u m m m m− ⇒ = + − += − +

.
Khi đó
2
21 1 9 62
, ;; ,
22 4
mm mm
AM u m AM u
+ + ++

 
=−− ⇒ =

 

 
.
Khoảng cách từ điểm
A
đến đường thẳng
d
là
( )
2
2
,
19 6 2
,.
22 2 2
AM u
mm
d Ad
mm
u

++

= =
−+

.
Xét hàm số
( )
2
2
9 62
2 22
mm
fm
mm
++
=
−+
với
m
∈
.
Ta có
( )
( )
2
2
2
15 14 8
2 22
mm
fm
mm
− ++
′
=
−+
.
Khi đó
( )
2
5
0
4
3
m
fm
m
= −
′
= ⇔
=
.
Bảng biến thiên
Vậy
( )
9fm≤
.
Khi đó ta có
( )
2
2
19 6 21 3
, . .9
22 2 22 2
mm
d Ad
mm
++
= ≤=
−+
.
Dấu “=” xảy ra khi và chỉ khi
4
3
m =
.
Cách 2:
Ta có
( )
( )
( ) ( )
( )
( )( )
12 12
12
2 2 1 21 1 1 2
1 1 32
x mt x mt
x m mt
y m mt y m mt y m t
zt zt zt
=+− =+−

=−+

=−+ +− ⇔ =− − +− ⇔ =− −


=+ =+ = +−

Dường thẳng
( )
d
luôn đi qua điểm
( )
1; 0; 3H
với mọi
m
ứng với
2t =
.
Dường thẳng
(
)
d
có véc-tơ chỉ phương là
( )
;1 ;1
d
u mm= −

.
Do
(
)
(
)
.1 1 .1 1. 1 0
mm
+− + −=
nên đường thẳng
(
)
d
vuông góc với đường thẳng có véc-tơ chỉ phương
( )
1
1;1; 1u = −

.
Do đó véc-tơ chỉ phương của đường thẳng
( )
d
khi khoảng cách từ
A
đến nó lớn nhất là
13
; 2; ;
22
dd
u u AH


= = −



  
.
Vậy ta có
11 4
13
23
22
mm
m
−
= =⇔=
−
.
Câu 40. Chọn A
Điều kiện:
22
310 311xx xx++>⇒++≥
.
Do
22
3 11 3 0x xx xx∈⇒++≥⇒+≥
(1).
Mặt khác
( )
(
)
22 2
3 1 1 3 0 ln 3 1 ln 1 0
x xx xx xx∈⇒++≥⇒+>⇒ ++> =
Ta có
( ) ( ) ( )
2 2 2 22
ln 3 1 3 0 ln 3 1 3 3 0xx xx xx xxxx++++<⇔ ++<− + ⇔+<
(2).
Từ (1) và (2) suy ra
x∈∅
.
Câu 41. Chọn C
Do
ABB A
′′
là hình thoi có góc
B
bằng
0
60
nên
2; 2 3;BB AB AB A B
′′ ′
= = = =
.
Do
ABC
là tam giác vuông tại
A
với
2; 4AB BC
= =
, ta có
23
AC
′′
=
.
Chọn hệ trục tọa độ
Oxyz
sao cho gốc
O
trùng với điểm
A
′
, đường thẳng
AB
′′
nàm trên tia
Ox
,
đường thẳng
AC
′′
nằm trên tia
Oy
, tia
Oz
hướng lên trên sao cho điểm
B
có cao độ dương.
Khi đó ta có
( ) ( )
( )
0;0;0 ; 2;0;0 ; 0;2 3;0ABC
′′′
.
Vì
K
là trung điểm của
BC
′′
nên
( )
1; 3; 0K
.
Gọi
( )
;;Bxyz
với
0z >
.
Ta có
( )
( )
2 22
22
2
22
12
31
23
3
24
2
xyz
zy
AB
x
x yz
BB
++=
=−
′
=

⇔⇒

′
=
− ++=
=
Mặt khác, ta có
( )
( ) ( )
2;0;0 ; 2; 3; ; 1; 3;0AB KB y z AK
′′ ′
= =−=
  
.
Theo đề ra, ta có
( )
( )
2
2
;.
23
3
;
2
;
4 23 2
AB KB AK
z
d A B BK
A B KB
zy

′′ ′

′′
=⇔=

′′
+−

  
 
( )
22
9 18 3 3 27 0 2y yz⇔ − − +=
Thay (1) vào (2) ta được,
2
3
12 18 3 18 0
2
3
y
yy
y
=
− +=⇔
=
Với
30yz
= ⇒=
(loại).
Với
33
22
yz= ⇒=
33
3; ;
22
B

⇒


Suy ra
.
1
3. 3. ; . 3 3.
6
B ABC
V V BA BB BC
′′′

′′ ′
= = =

  
Câu 42. Chọn C
Ta có
1
1
1
.; 1
3 13
nn n
n
uu u
un
nn n
+
+
= ⇔ = ∀≥
+
.
Đặt
;1
nn
u nv n= ∀≥
( )
11
1
nn
u nv
++
⇒=+
Ta được
1
1
;1
3
nn
v vn
+
= ∀≥
, suy ra dãy số
( )
n
v
là cấp số nhân với
1
11
;
33
vq
= =
.
1
3
n
n
v
⇒=
;1
3
nn
n
n
u nv n⇒ = = ∀≥
.
Ta có
11
3 2020
2020 3 2020
n
n
n
n
un<⇔<⇔>
(*)
Dễ thấy, bằng phương pháp quy nạp toán học ta chứng minh (*) đúng
9n
∀≥
.
Vậy có vô số nguyên dương n thỏa mãn đề bài.
Câu 43. Chọn A
Xét
32
f x ax bx cx d 
.
Do
02
f
nên suy ra
2d
.
32
4 64 16 4f x ax bx cx d 
.
Giả thiết cho
3
4 42f x fx x x

nên ta có:
4
64 4
63
16 0
42 2
3
a
aa
bb b
cc
c
dd
d










.
Vậy
3
42
2
63 3
fx x x 
.
Từ đó
1
11
3 42
00
0
4 2 1 1 148
d 2d 2
63 3 63 3 63
fx x x x x x x x












.
Câu 44. Chọn A
Đặt
sin xt
. Khi
0;x



thì
0;1t



.
Ta nhận thấy với mỗi
0;1
t
sẽ cho tương ứng hai giá trị
0;x



. Do đó phương trình
sinf xm
có hai nghiệm thuộc đoạn
0;



khi và chỉ khi phương trình
ft m
có một nghiệm
0;1t
. Dựa
vào đồ thị ta được
43m 
.
Câu 45. Chọn A
Điều kiện:
3cos 1 0
x
π
−>
.
( )
cos 1
4
1
2 cos log 3cos 1
2
x
xx
π
ππ
−
+= + −
( )
cos
2
2 1 2cos log 3cos 1
x
xx
π
ππ
⇔ += + −
( )
cos
2
2 cos 3cos 1 log 3cos 1
x
xx x
π
ππ π
⇔ + = −+ −
.
( )
1
Ta có hàm số
( )
2
t
ft t= +
đồng biến trên
( )
0; +∞
.
Từ
( )
1
suy ra
cos cos
2 3cos 1 2 3cos 1 0
xx
xx
ππ
ππ
= −⇔ − +=
Xét hàm số
( )
231
u
gu u=−+
, có
( )
2 .ln 2 3 0
u
gu
′
= −<
,
1
;1
3
u

∀∈

.
Vậy hàm số
( )
y gu=
nghịch biến trên
1
;1
3


, mà
( )
0gu=
.
Do đó phương trình
cos
2 3cos 1 0
x
x
π
π
− +=
có một họ nghiệm là:
cos 1 2 2x xk x k
π ππ
=⇔ = ⇔=
,
k ∈
. Vì
x
thuộc
[ ]
0;100
nên
[ ]
0; 50k ∈
. Vậy có 51 nghiệm
x
thuộc
[ ]
0;100
.
Câu 46. Chọn B
Theo giả thiết ta có:
2019 2020 2019 2020
10 4 3 10 10 4 10
nn
≤ +< ⇒ < <
2019 2020
4 44 4 4
log 10 log 4 log 10 2019.log 10 2020.log 10
n
n⇔ < < ⇔ <<
.
Vì
n
nguyên dương nên
3354n =
hoặc
3355n =
. Vậy tổng là
3354 3355 6709+=
.
Câu 47. Chọn D
Ta có
( )
( ) ( ) ( ) ( ) ( ) ( ) ( )
( )
32
12. . 4. . 4. . . 3 1Fx fxf x fxfx fxfx f x
′′ ′ ′
= += +
.
( )
( )
( )
( )
2
0 (1)
0 0 (2)
3 1 0( )
fx
Fx fx
f x VN
′
=
′
=⇔=
+=
Dựa vào đồ thị, nhận thấy
( )
0fx
′
=
có 3 nghiệm phân biệt;
( )
0fx=
có 4 nghiệm phân biệt, các nghiệm
ở phương trình (1) và (2) không trùng nhau, đồng thời hàm
( )
Fx
là hàm liên tục trên
nên có 7 điểm
cực trị.
Câu 48. Chọn D
Ta có
( )
1; 2; 3MN =

. Đường thẳng
( )
d
có véc tơ chỉ phương
(
)
1; 2;1u
−
.
Nhận thấy
.0MN u
=

do đó
MN d⊥
.
Khi đó
IM IN+
đạt giá trị nhỏ nhất khi điểm
I
là giao điểm của đường thẳng
d
với mặt phẳng
(
)
P
chứa
,MN
và vuông góc với đường thẳng
d
.
Phương trình mặt phẳng
( )
P
qua
,MN
và vuông góc đường thẳng
d
có phương trình là
( ) ( ) ( )
1. 3 2. 1 1. 1 0 2 2 0x y z x yz− − − + − =⇔− +−=
.
Giao điểm của đường thẳng
d
với mặt phẳng
( )
P
là nghiệm của hệ phương trình
4
3
77
17
739
32 32
3
1 21
9 9 17
2 20
3
764920860
23
3
t
xt xt
xyz
x
yt yt
zt zt
x yz
y
t tt t
z
−
=
=+=+

− −−
=

=−=−
= =

⇔ ⇔⇔
−

=+=+

− +−=
=

+− + + +− = + =

=
.
Ta được
17 17 23
2 3 2. 3. 40.
33 3
ab c++ = + + =
Câu 49. Chọn B
Kẻ
( )
.SH BC H BC⊥∈
Ta có
( ) ( )
( ) ( ) ( )
SBC ABC
SBC ABC BC SH ABC
SH BC
⊥
∩ =⇒⊥
⊥
.
Kẻ
( )
SM AB M AB⊥∈
và
( )
SN AC M AC⊥∈
. Khi đó
(
) ( )
(
)
,SAB ABC SMH=
và
( ) ( )
( )
,SAC ABC SNH=
. Theo đề
0
60SMH SNH MH NH= =⇒=⇒
H
cách đều hai điểm
,MN
⇒
H
là chân đường phân giác trong góc
A
của tam giác
ABC
.
Khi đó ta có:
1
2
2
HB AB
HC HB
HC AC
==⇒=
mà
22
5HB HC BC AB AC a+== + =
5
3
25
3
a
HB
a
HC
=
⇒
=
Theo ta-let ta có
12
3 33
HM HB AC a
HM
AC BC
==⇒==
.
Khi đó
0
23
tan tan 60 .
3
SH
SMH SH HM a
HM
= ⇒= =
.
Đặt hệ trục tọa độ
Oxyz
như hình vẽ. Khi đó ta có
( )
0;0;0A
,
( )
;0;0 ,Ba
( )
0;2 ;0Ca
.
Ta có
1 22 2223
;;0 ;;
3 33 33 3
BH BC H a a S a a a


=⇒⇒




 
Khi đó mặt phẳng
( )
SAB
có VTPT
( )
2
22
1
23 2 2
, 0; ; 0; 3;1
33 3
a
n AB AS a a


==−=−



 
và mặt phẳng
( )
SBC
có VTPT
(
)
2
22
2
43 23 2
, ; ;0 2 3; 3;0
33 3
a
n BC BS a a


= = =



 
.
Suy ra
(
) ( )
(
)
12
2
12
.
3 1 51
cos ; cos tan 1
cos 3
2 15
.
nn
SAB SBC
nn
= α= = ⇒ α= − =
α


(vì
α
là góc nhọn nên
tan 0α>
)
Câu 50. Chọn B
Ta có
2cos2 2
4cos 1 ;
x
a xx≥ − ∀∈
2cos2
2cos2 1 ; .
x
a xx
⇔ ≥ + ∀∈
Đặt
[ ]
2cos 2 ; 2;2t xx t
= ∀∈ ⇒ ∈−
.
Khi đó bài toán trở thành: “ tìm giá trị
0; 1aa>≠
thỏa mãn
[ ]
1 ; 2;2
t
at t≥ + ∀∈−
”.
+ Xét trường hợp 1:
01a<<
Hàm số
( )
t
ft a=
nghịch biến trên
nên
( ) (
) ( )
0 01t ft f ft∀>⇒< ⇒<
Ta lại có
0 11tt∀> ⇒ + >
nên bất phương trình
1
t
at≥+
vô nghiệm trên
(
]
0;2
.
Yêu cầu bài toán không thỏa.
+ Xét trường hợp 2:
1a >
Hàm số
( )
t
ft a=
đồng biến trên
.
--------------HẾT---------------
| 1/23
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD & ĐT HẢI DƯƠNG
ĐỀ THI THỬ KỲ THI THPT QUỐC GIA LẦN 1 TRƯỜNG THPT NGUYỄN TRÃI
NĂM HỌC 2019 - 2020 MÔN TOÁN
Thời gian làm bài (Đề có 08 trang) : 90 phút
Họ tên: ......................................................................... Số báo danh: ................... MÃ ĐỀ 035
Câu 1: Trong các hàm số sau, hàm số nào nghịch biến trên tập số thực? x +10 A. 3 2
y = −x + 2x −10x + 4 B. y = x −1 C. 2
y = x − 5x + 6
D. y = x + 5
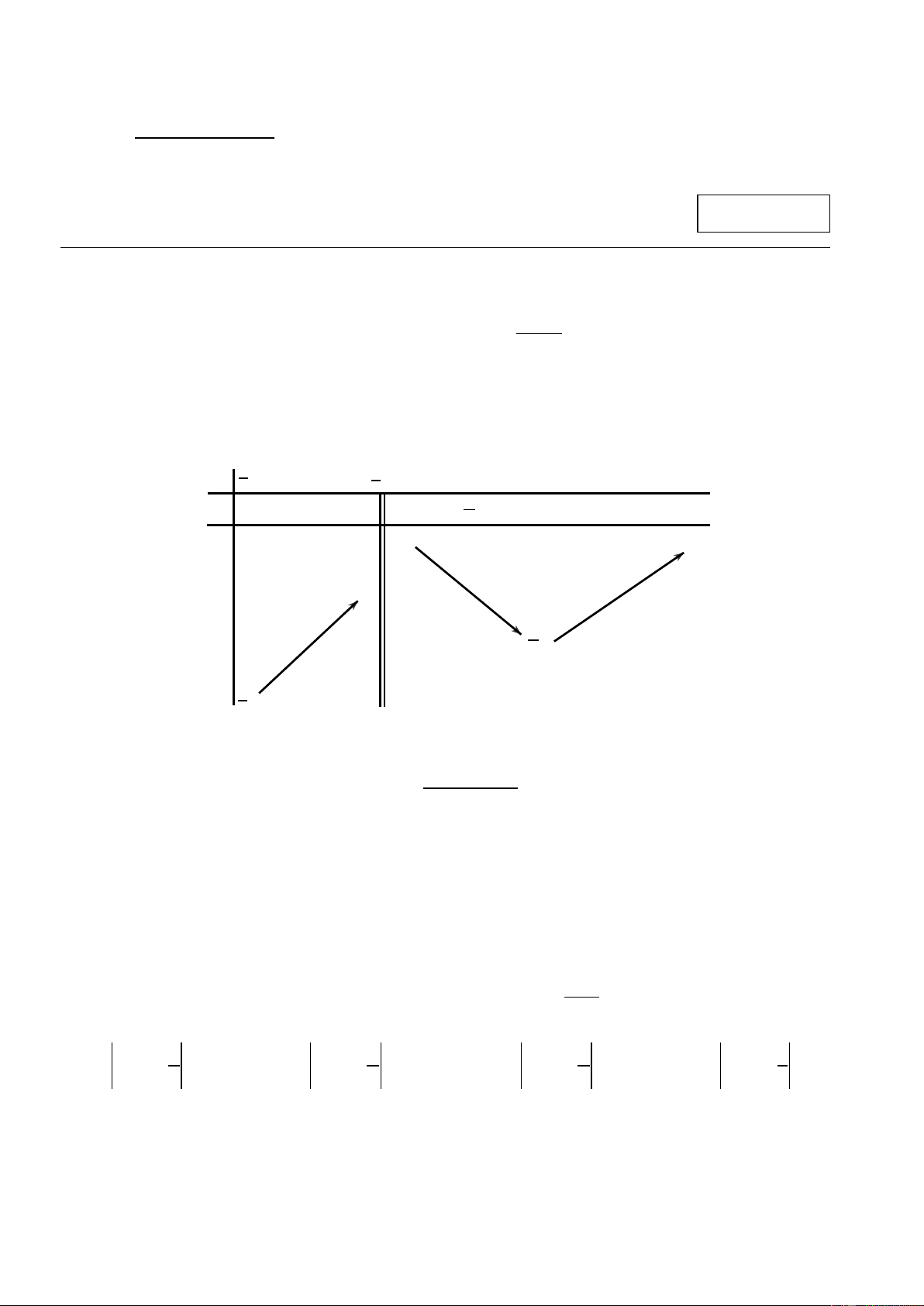
Câu 2: Cho hàm số có bảng biến thiên như sau. Tổng các giá trị nguyên của m để đường thẳng
y = m cắt đồ thị hàm số tại ba điểm phân biệt bằng x ∞ 1 3 +∞ y' + 0 + +∞ +∞ 2 y 4 ∞ A. 0 B. 1 − C. 3 − D. 5 − 1
Câu 3: Tìm họ nguyên hàm của hàm số y = 2 2 sin . x cos x
A. 2 cot 2x + C
B. − cot 2x + C
C. cot 2x + C D. 2
− cot 2x + C
Câu 4: Tìm phương trình mặt cầu có tâm là điểm I (1; 2;3) và tiếp xúc với trục Oz A. ( 2 2 2
x − )2 + ( y − )2 + ( z − )2 1 2 3 = 5 B. (x − )
1 + ( y − 2) + ( z − 3) = 13 C. ( 2 2 2
x − )2 + ( y − )2 + ( z − )2 1 2 3 = 14 D. ( x − )
1 + ( y − 2) + ( z − 3) = 10 2x
Câu 5: Tính diện tích hình phẳng giới hạn bởi các đường 2 y =
; y = x ; x = 0; x = 1 x +1 5 2 7 1 A. 2 ln 2 − B. 2 ln 2 − C. 2 ln 2 − D. 2 ln 2 − 3 3 3 3
Câu 6: Cho tam giác ABC có A(3;0;0); B (0; 6
− ;0);C(0;0;6). Tìm tọa độ điểm H là hình chiếu
vuông góc của trọng tâm tam giác ABC trên mặt phẳng (α ) : x + y + z − 4 = 0 Trang 01/08 A. H ( 2 − ; 1 − ;3) B. H (2;1;3) C. H (2; 1 − ; 3
− ) D. H (2; 1 − ;3)
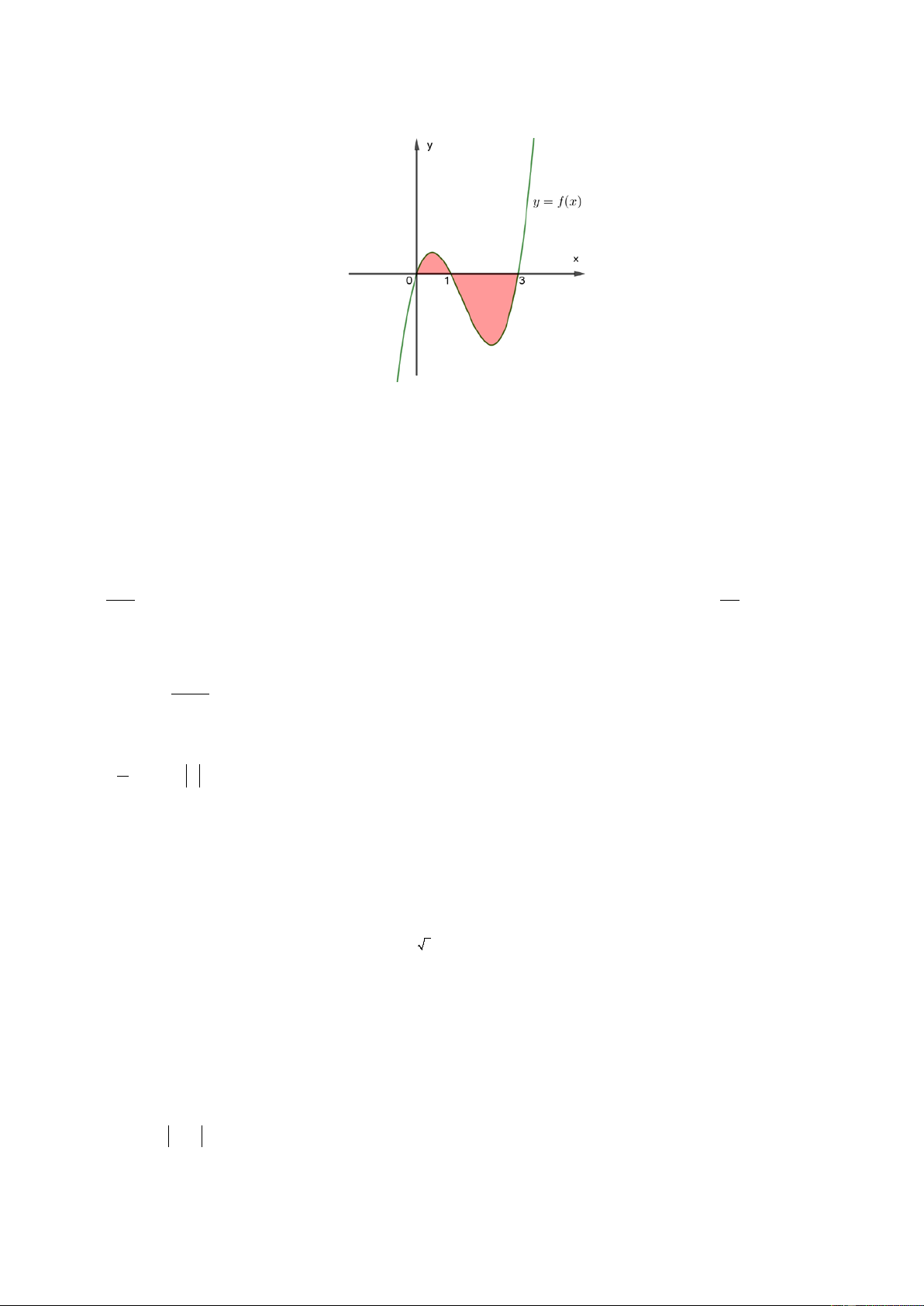
Câu 7: Cho đồ thị hàm số y = f ( x) . Diện tích S của hình phẳng (phần tô đậm trong hình vẽ) là 1 3 1 3
A. S   f xdx  f xdx   . B. S  f xdx f xdx   . 0 1 0 1 3 1 3 C. S  f xdx  . D. S  f xdx  f xdx   . 0 0 1
Câu 8: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , cạnh bên SA vuông góc với đáy.
Biết SA = 2a . Tính thể tích khối chóp S.ABCD 3 2a 3 a A. B. 3 a C. 3 2a D. 3 3
Câu 9: Khẳng định nào sau đây là sai ? α 1 + α x A. x dx = + C ∫ α
( C là hằng số, α là hằng số) +1 B. x x
e dx = e + C ∫ ( C là hằng số) 1 C.
dx = ln x + C ∫
( C là hằng số) với x ≠ 0 x
D. Mọi hàm số f ( x) liên tục trên đoạn [a;b] đều có nguyên hàm trên đoạn [a;b]
Câu 10: Cho tập hợp A = { 2 3 10
10;10 ;10 ;...;10 }. Gọi S là tập các số nguyên có dạng log m với 100
m ∈ A . Tính tích các phần tử của tập hợp S A. 60 B. 24 C. 120 D. 720
Câu 11: Tìm tập xác định của hàm số 2 y = x A.  \ { } 0 B. (-∞;0) C. D. (0;+∞)
Câu 12: Viết công thức tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng vuông góc với
trục Ox tại các điểm x  ,a x  b  a  
b , có thiết diện bị cắt bởi mặt phẳng vuông góc với trục Ox tại
điểm có hoành độ x a  x   b là S x . b b b b A. 2 V  S x d . x  B. V  S xd . x 
C. V  S xd . x  D. 2 V  S xd . x  a a a a
Câu 13: Cho hình chóp S.ABC có ; SA ;
SB SC đôi một vuông góc với nhau và SA = 6; SB = 4; SC = 5. Trang 02/08
Gọi M , N lần lượt là trung điểm của AB, AC . Tính thể tích khối chóp S.MBCN A. 30 B. 5 C. 15 D. 45
Câu 14: Cho ba điểm A(2;1; − ) 1 ; B ( 1 − ;0;4);C (0; 2; − − )
1 . Mặt phẳng đi qua A và vuông góc với BC
có phương trình là
A. x − 2 y − 5z + 5 = 0 B. x − 2 y − 5z − 5 = 0
C. 2x − y + 5z + 5 = 0
D. x − 2 y − 5z = 0 x +
Câu 15: Cho hàm số 1 y =
. Tìm phương trình tiếp tuyến với đồ thị hàm số tại điểm M (2;3) x −1
A. y = 2x −1 B. y = 3 − x + 9
C. y = 3x − 3 D. y = 2 − x + 7
Câu 16: Cho phương trình 25x 3.5x −
+ 2 = 0 có hai nghiệm x < x . Tính 3x + 2x 1 2 1 2 A. 4 log 2 B. 0 C. 3log 2 D. 2 log 2 5 5 5 x −
Câu 17: Đường tiệm cận ngang của đồ thị hàm số 4 1 y =
có phương trình là x − 2020
A. x = 2020
B. y = 1
C. y = 4
D. y = 2   
Câu 18: Trong không gian Oxyz cho ba vecto a = ( 1
− ;1;0);b = (2;2;0);c = (1;1; ) 1 . Trong các khẳng
định sau khẳng định nào sai ?      
A. a ⊥ b
B. a = 2
C. c = 3
D. c ⊥ b
Câu 19: Tìm số điểm cực đại của đồ thị hàm số sau 4 2
y = 10x + 5x +19 A. 2 B. 1 C. 3 D. 0
Câu 20: Cho hình trụ có chiều cao bằng 4a , diện tích xung quanh bằng 2π 2
a . Tìm bán kính đáy của hình trụ đó a a A. 2a B. C. a D. 2 4
Câu 21: Cho hình nón đỉnh S có bán kính đáy R = 2 . Biết diện tích xung quanh của hình nón là
2 5 π. Tính thể tích khối nón 5 4 2 A. 𝛑𝛑 B. 𝛑𝛑 C. 𝛑𝛑 D. 𝛑𝛑 3 3 3
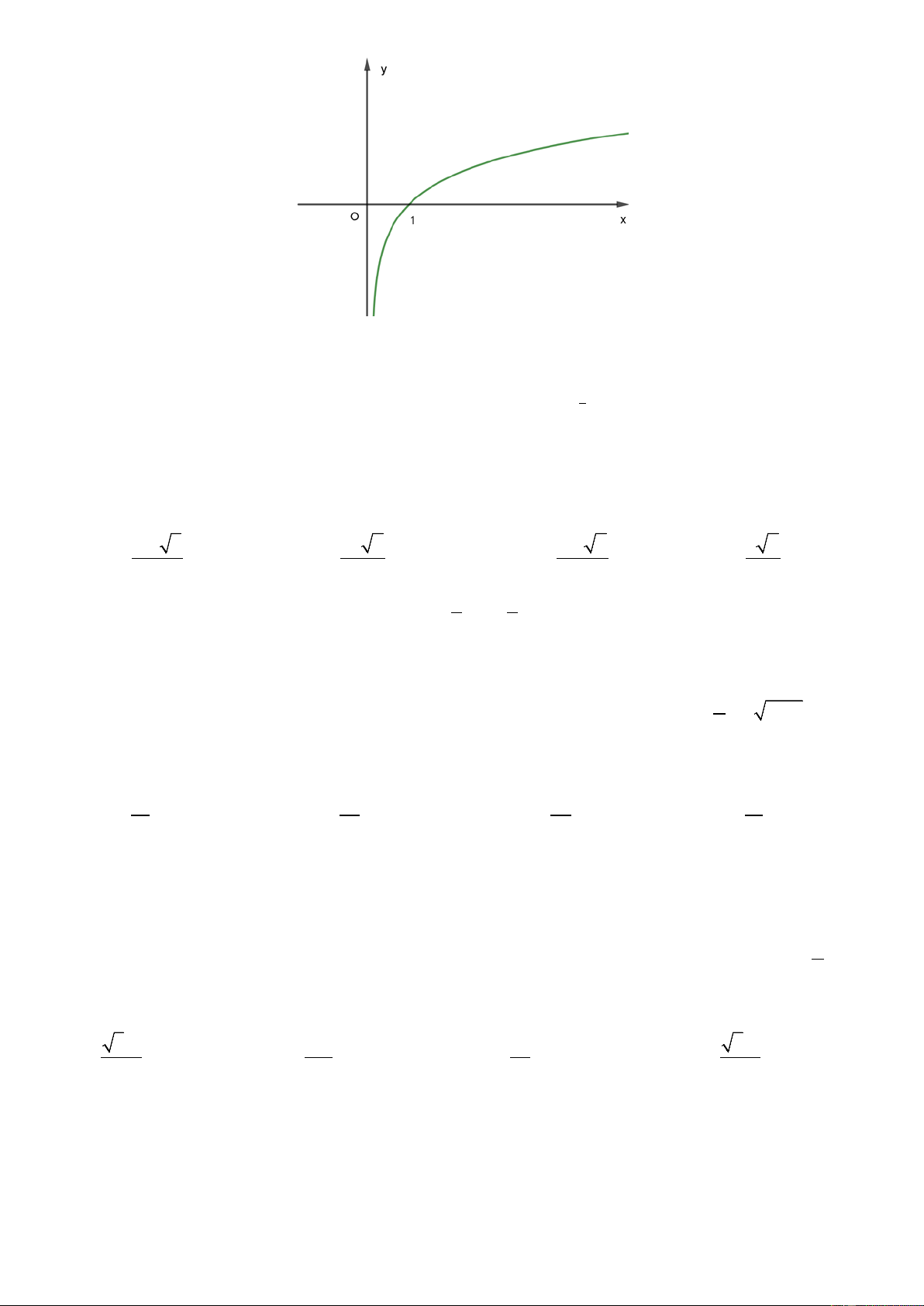
Câu 22: Hình vẽ sau là đồ thị của hàm số nào sau đây? Trang 03/08
A. y = ln x B. 2x y =
C. y = log x D. x y = e 1 2
Câu 23: Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng ( ABC ) , tam giác ABC vuông
tại B có cạnh AB = 3;BC = 4 và góc giữa DC và mặt phẳng ( ABC) bằng 0
45 . Tính thể tích mặt cầu
ngoại tiếp tứ diện 125 3 25 2 125 2 5 2 A. V = π B. V = π C. V = π D. V = π 3 3 3 3 x − x+2  1   1 
Câu 24: Tìm tập nghiệm của bất phương trình ≤      3   3  A. ( ) ;1 −∞ B. [1; +∞) C. ( ] ;1 −∞ D. (1; +∞) Câu 25: Gọi ;
m M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số 1 y =
x − x + 2 trên 2 đoạn [ 1
− ;34]. Tính tổng S = 3m + M 13 63 25 11 A. S = B. S = C. S = D. S = 2 2 2 2
Câu 26: Tính thể tích của vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường y = 4; y = 2;
− x = 0; x = 1 quanh trục Ox A. 20 π B. 36 π C. 12 π D. 16 π a
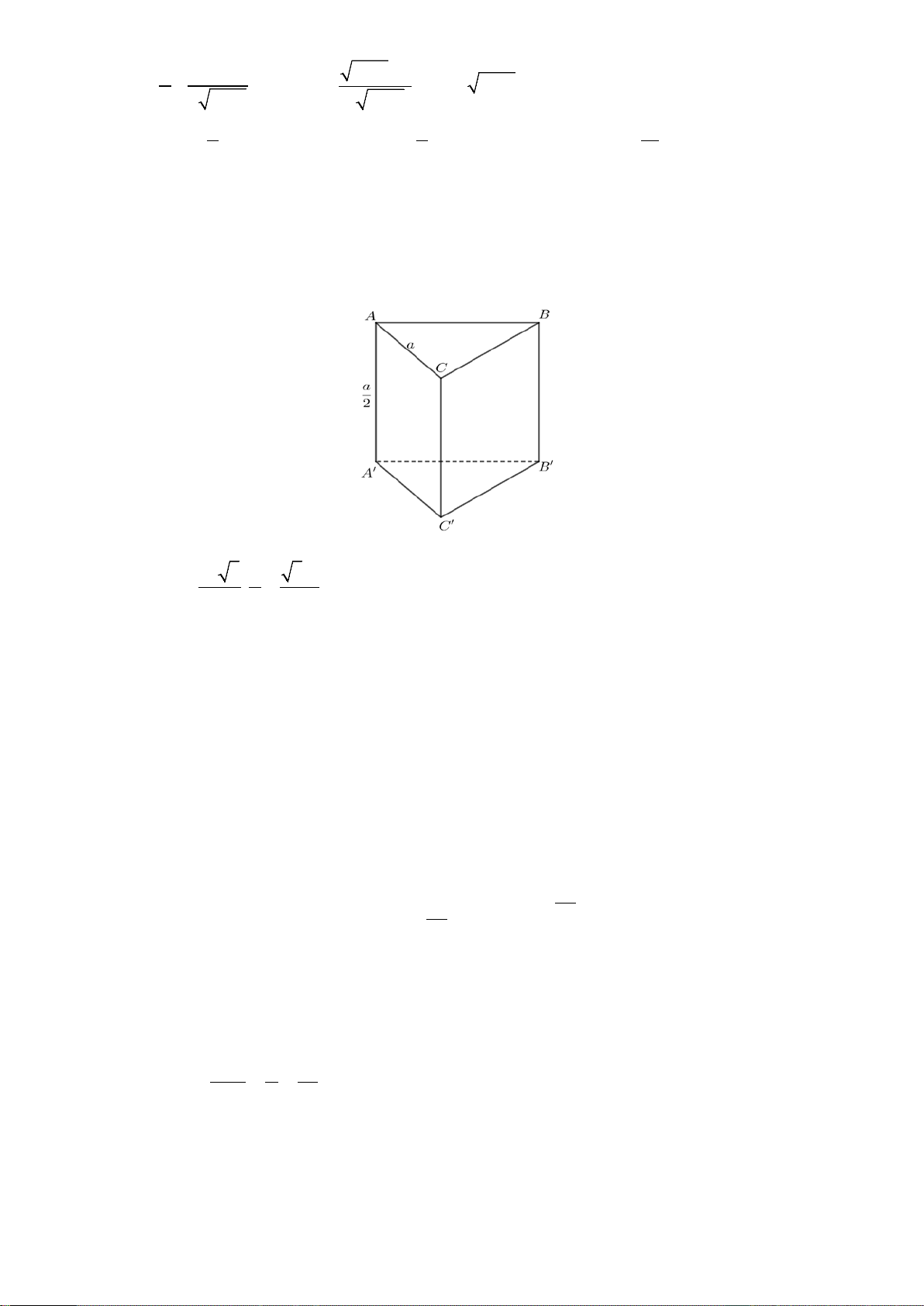
Câu 27: Cho lăng trụ đứng ABC.A' B 'C ' có đáy là tam giác đều cạnh bằng a , cạnh bên bằng . 2
Tính thể tích khối lăng trụ 3 3a 3 3a 3 a 3 3a A. B. C. D. 8 8 8 4
Câu 28: Có bao nhiêu giá trị nguyên của m để hàm số sau đồng biến trên tập số thực y = ( 2 − m ) 3 x + ( − m) 2 4 2
x + 7x − 9 A. 3 B. 2 C. 4 D. 1 Trang 04/08
Câu 29: Cho đường thẳng (d ) nằm trên mặt phẳng ( P) : x + y + z − 3 = 0 và vuông góc với đường
thẳng ( ) x −1 y z d ' : = =
. Tìm một vecto chỉ phương của đường thẳng (d ) 1 3 1 − A. (2;1 ) ;1 B. (4; 2; − 2) C. ( 4; − 2; 2 − ) D. ( 2 − ;1 ) ;1
Câu 30: Cho tam giác ABC có độ dài ba cạnh là ; a ;
b c . Gọi p là nửa chu vi của tam giác . Biết dãy số ; a ; b ;
c p theo thứ tự lập thành một cấp số cộng. Tìm cosin của góc nhỏ nhất trong tam giác đó 4 3 5 3 A. B. C. D. 5 4 6 5
Câu 31: Một người chơi trò gieo súc sắc. Mỗi ván gieo đồng thời ba con súc sắc. Người chơi thắng
cuộc nếu xuất hiện ít nhất 2 mặt sáu chấm. Tính xác suất để trong ba ván, người đó thắng ít nhất hai ván 1 308 58 53 A. B. C. D. 1296 19683 19683 23328
Câu 32: Cho hai điểm A(2;1; − ) 1 ; B(0;3; )
1 . Biết tập hợp các điểm M ∈ mp (α ) : x + y + z + 3 = 0 thỏa mãn 2 2
2.MA − MB = 4 là đường tròn có bán kính r . Tính r
A. r = 2 7 B. r = 6
C. r = 2 6
D. r = 5 2 20 + 6x − x
Câu 33: Cho hàm số y =
. Tìm tất cả các giá trị của m sao cho đồ thị hàm số có đúng 2
x − 8x + 2m
hai đường tiệm cận đứng
A. m ∈[6;8)
B. m ∈ (6;8)
C. m ∈[12;16)
D. m ∈ (0;16)
Câu 34: Cho hàm số f ( x) 7 5 4 3 2
= x + x − x + x − 2x + 2x −10 và g (x) 3
= x − 3x + 2 . Đặt
F ( x) = g f ( x) 
 . Tìm tất cả các giá trị của tham số m để phương trình F ( x) = m có ba nghiệm thực phân biệt A. m ∈ ( 1 − ;3)
B. m ∈ (0; 4)
C. m ∈ (3;6)
D. m ∈ (1;3) a 3
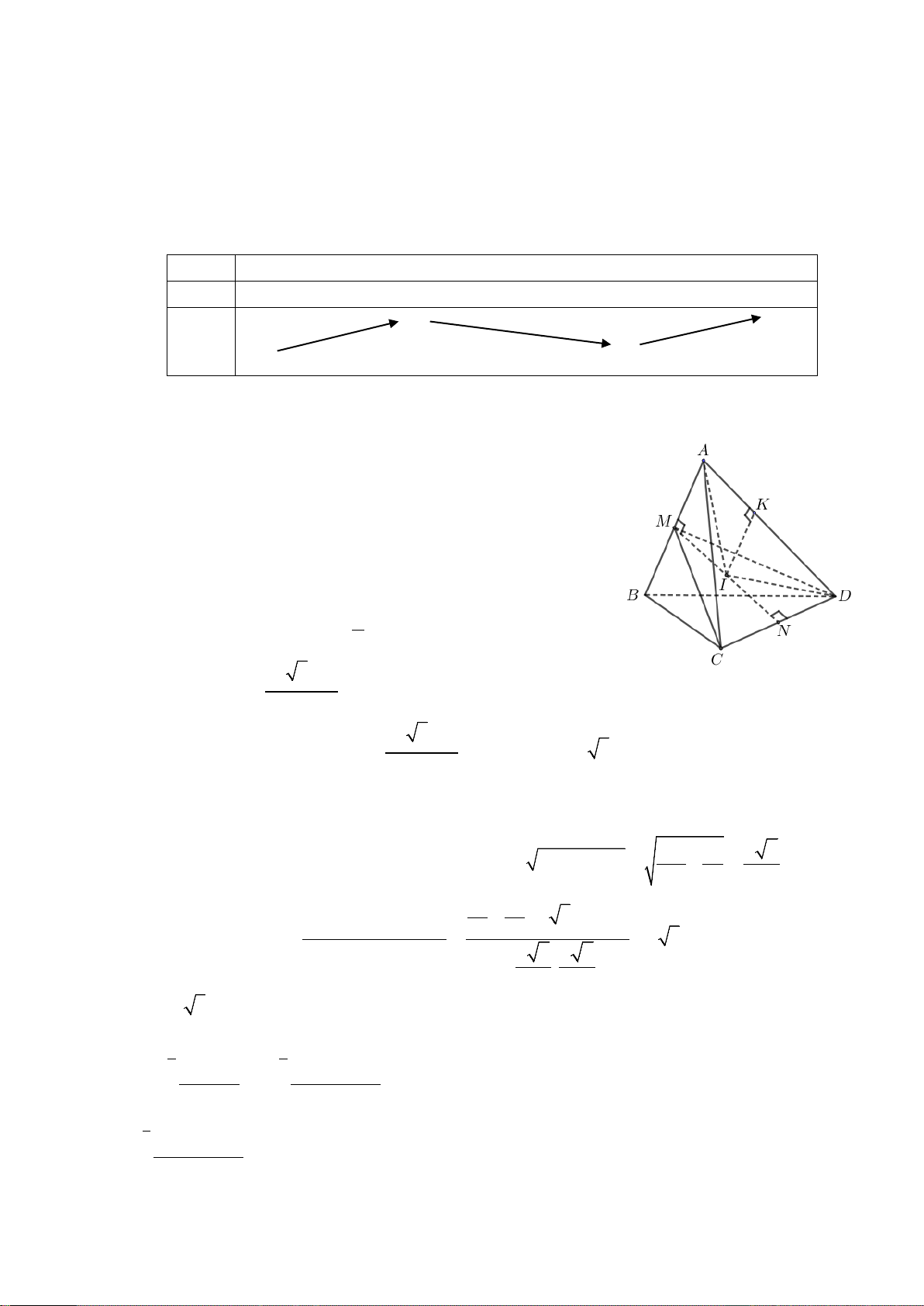
Câu 35: Cho tứ diện ABCD có AB = a; AC = BC = AD = BD =
. Gọi M , N là trung điểm của 2
AB, CD . Góc giữa hai mặt phẳng ( ABD);( ABC ) là α . Tính cosα biết mặt cầu đường kính MN
tiếp xúc với cạnh AD A. 2 − 3 B. 2 3 − 3 C. 3 − 2 3 D. 2 −1 π 4 1 Câu 36: Biết dx = . a π + b ln 2 ∫ với ;
a b là các số hữu tỉ. Tính tỷ số a 1+ tan x b 0 A. 1 B. 1 C. 1 D. 1 2 6 4 3
Câu 37: Cho hình chóp S.ABC có đáy là tam giác cân tại A, mặt bên (SBC ) là tam giác đều và
nằm trong mặt phẳng vuông góc với đáy. Gọi (α ) là mặt phẳng đi qua điểm B và vuông góc với Trang 05/08
SC , chia khối chóp thành hai phần. Tính tỉ số thể tích của hai phần đó 1 1 2 1 A. B. C. D. 2 3 3 4
Câu 38: Cho mặt phẳng (α ) đi qua hai điểm M (4;0;0) và N (0;0;3) sao cho mặt phẳng (α ) tạo
với mặt phẳng (Oyz) một góc bằng 0
60 . Tính khoảng cách từ điểm gốc tọa độ đến mặt phẳng (α ) 3 2 A. 1 B. C. D. 2 2 3 
x = 1− 2m + mt   
Câu 39: Tìm m để khoảng cách từ điểm 1 A ;1; 4 
 đến đường thẳng (d ) : y = 2
− + 2m + (1− m)t  2   z = 1+ t
đạt giá trị lớn nhất 2 4 1 A. m = B. m = C. m =
D. m = 1 3 3 3
Câu 40: Tìm số nghiệm nguyên của bất phương trình ( 2 x + x + ) 2 ln 3
1 + x + 3x < 0 A. 0 B. 2 C. 3 D. 1
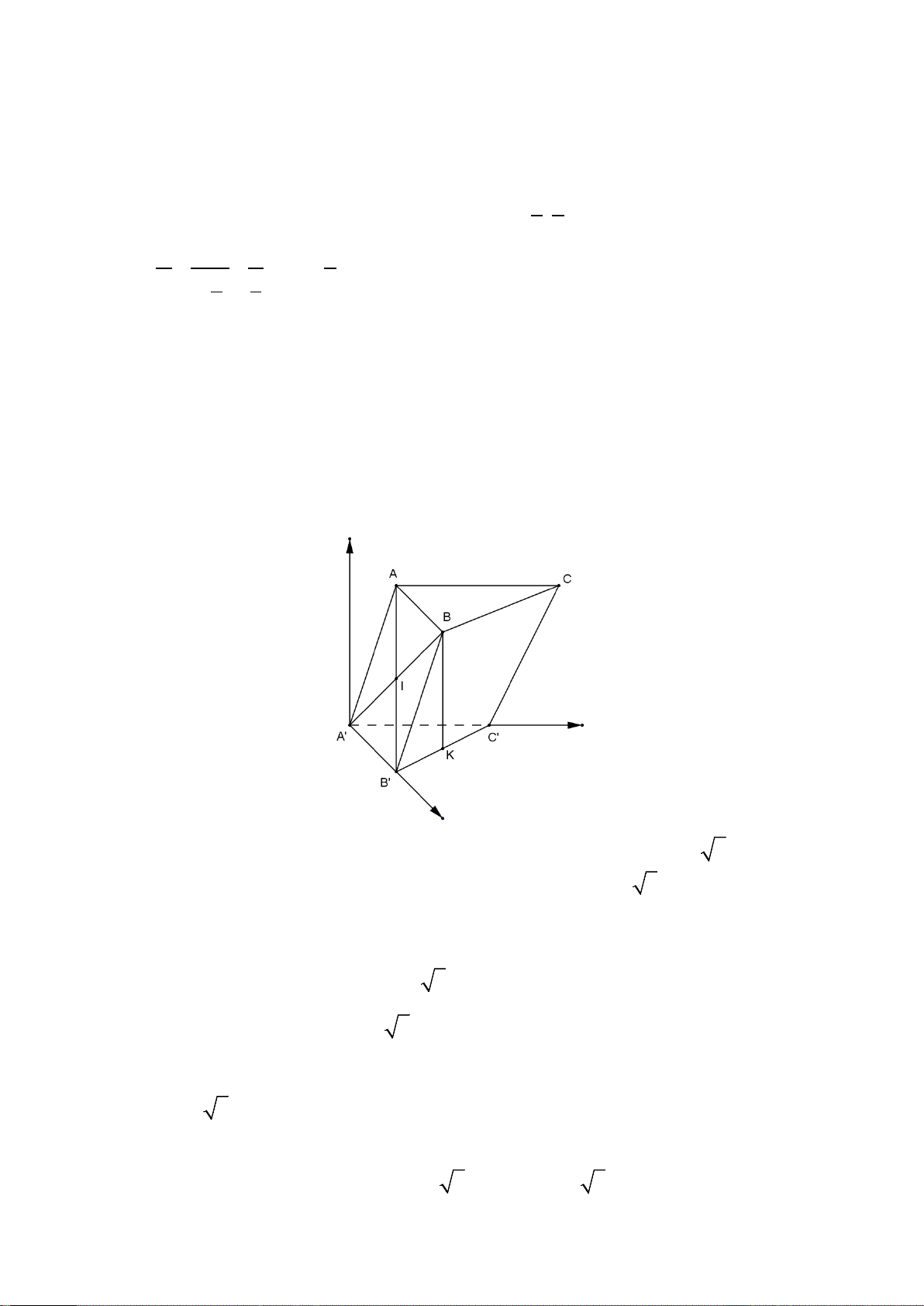
Câu 41: Cho hình lăng trụ ABC.A' B 'C ' có đáy ABC là tam giác vuông tại A với AB = 2; BC = 4 .
Mặt bên ABB' A' là hình thoi có góc B bằng 0
60 . Gọi điểm K là trung điểm của B'C' . Tính thể tích
khối lăng trụ biết d ( A B BK ) 3 ' '; = 2 A. 4 3 B. 6 C. 3 3 D. 2 3  1 u =  1  3
Câu 42: Cho dãy số (u thỏa mãn 
. Có bao nhiêu số nguyên dương n n ) (n +  ) 1 un u = ;∀ n ≥ 1 n 1 +  3n thỏa mãn 1 u < n 2020 A. 0 B. 9 C. vô số D. 5
Câu 43: Cho hàm số y = f ( x) liên tục trên  . Biết f ( x) = f ( x) 3 4
+ 4x + 2x và f (0) = 2 . Tính 1 f ( x)dx ∫ 0 148 146 149 145 A. B. C. D. 63 63 63 63
Câu 44: Cho hàm số y = f ( x) có đồ thị như hình vẽ sau. Tìm m để phương trình f (s inx) = m có đúng hai nghiệm trên đoạn [0; π] y -1 O 1 x Trang 06/08 -3 -4 A. 4 − < m ≤ 3 − B. 4 − ≤ m ≤ 3 − C. m = 4 − hoặc m > 3 − D. 4 − ≤ m < 3 −
Câu 45: Tìm số nghiệm x thuộc [0;100] của phương trình sau : π − 1 cos x 1 2
+ = cosπ x + log 3cosπ x −1 4 ( ) 2 A. 51 B. 49 C. 50 D. 52
Câu 46: Tính tổng các số nguyên dương n thỏa mãn 4n + 3 viết trong hệ thập phân là số có 2020 chữ số A. 6711 B. 6709 C. 6707 D. 6705
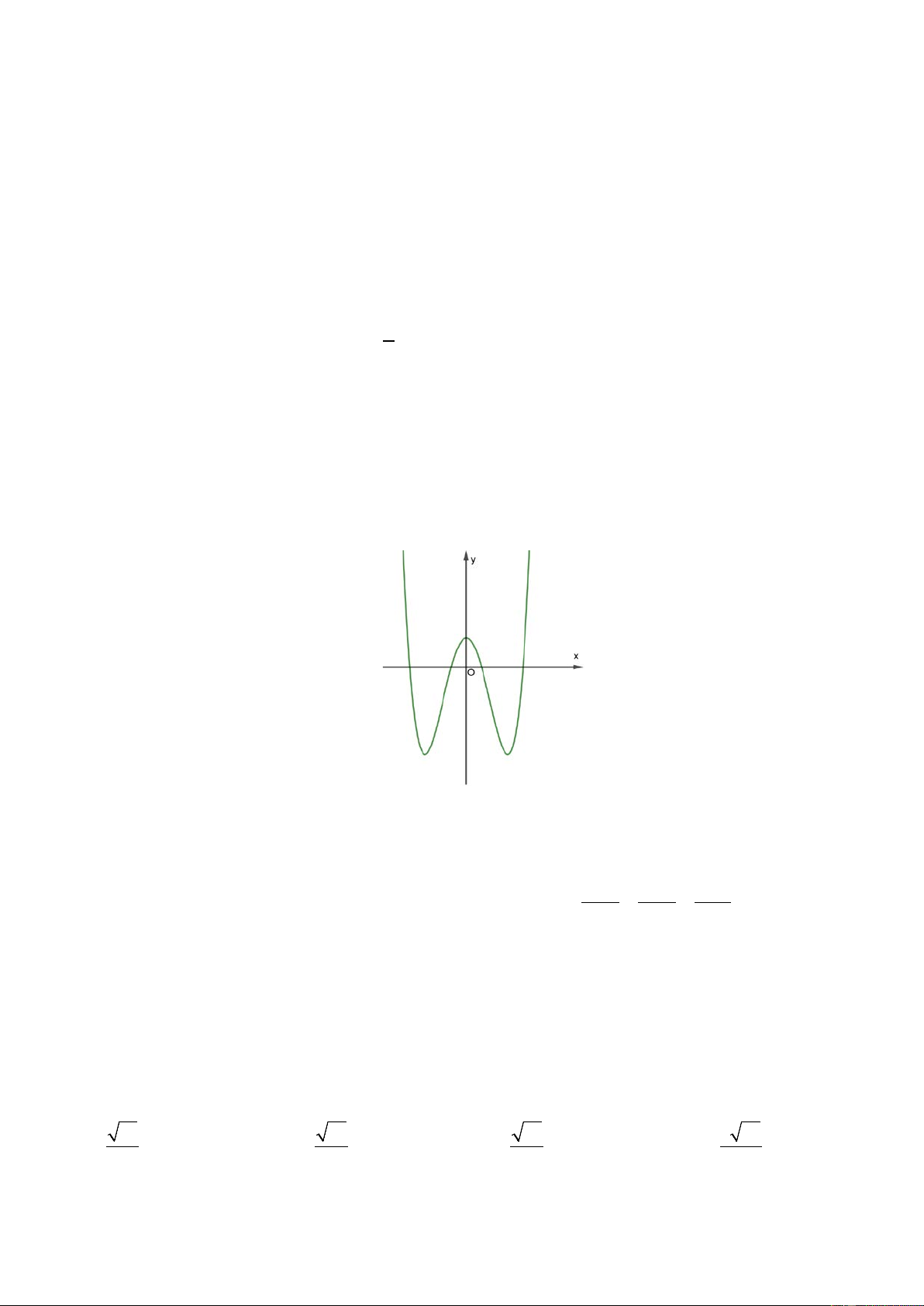
Câu 47: Cho hàm số y = f ( x) có đồ thị như hình vẽ .
Tìm số điểm cực trị của hàm số F (x) 4 = f (x) 2 3 + 2 f (x) + 5 A. 6 B. 3 C. 5 D. 7 x − y − z −
Câu 48: Cho hai điểm M (3;1; )
1 ; N (4;3; 4) và đường thẳng (d ) 7 3 9 : = = . Biết điểm 1 2 − 1 I ( ; a ;
b c) thuộc đường thẳng (d ) sao cho IM + IN đạt giá trị nhỏ nhất . Tính S = 2a + b + 3c A. 36 B. 38 C. 42 D. 40
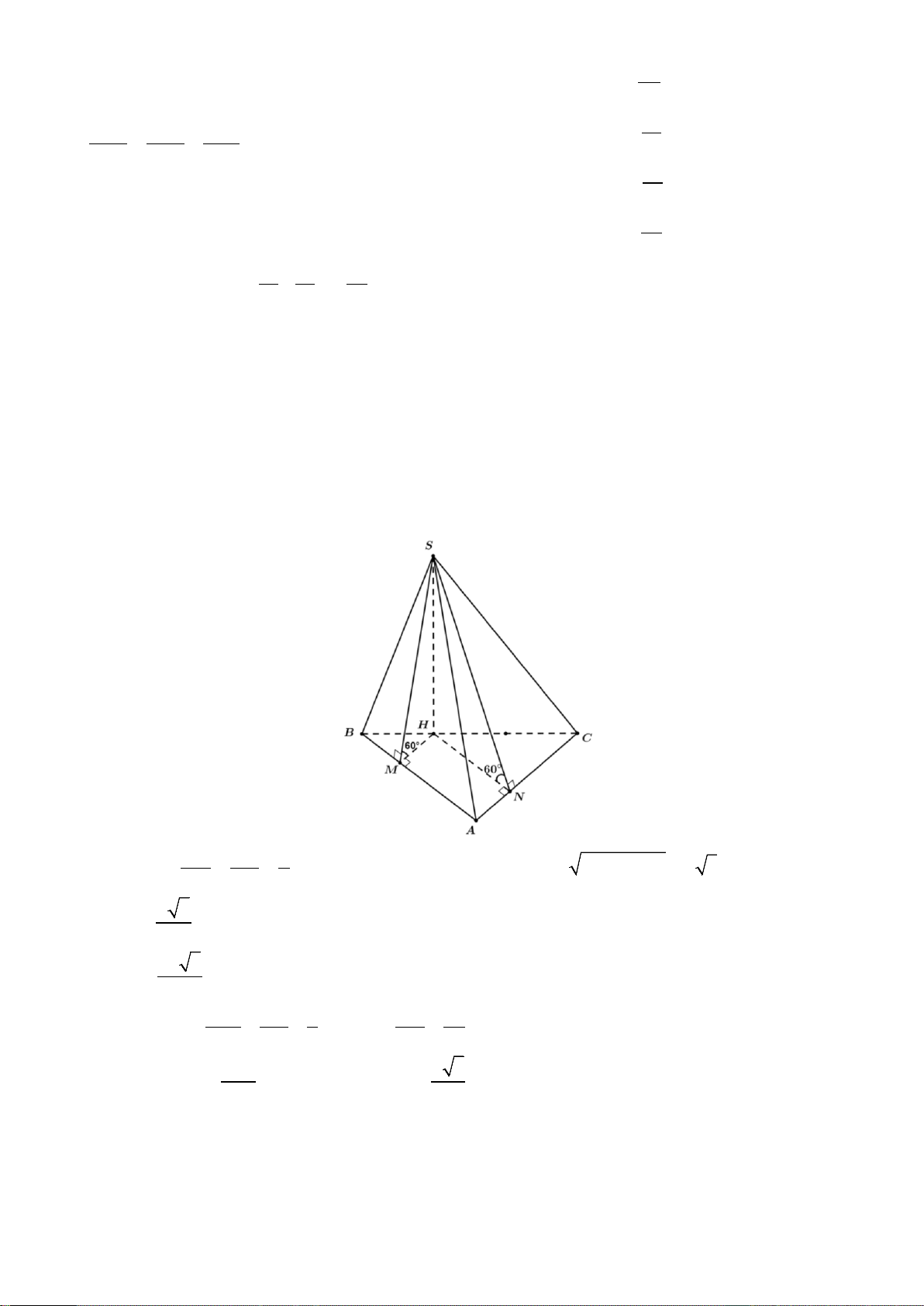
Câu 49: Cho hình chóp S.ABC có đáy là tam giác vuông tại A với AB = ;
a AC = 2a . Mặt phẳng
(SBC) vuông góc với mặt phẳng ( ABC). Mặt phẳng (SAB);(SAC) cùng tạo với mặt phẳng ( ABC) một góc bằng 0
60 . Gọi α là góc giữa hai mặt phẳng (SAB) và (SBC ) . Tính tanα 51 51 17 3 17 A. B. C. D. 17 3 3 17
Câu 50: Cho a là hằng số dương khác 1 thỏa mãn 2cos2x 2 a
≥ 4cos x −1; x
∀ ∈  . Giá trị của a thuộc Trang 07/08
khoảng nào sau đây A. (4; +∞) B. (2;3) C. (0; 2) D. (3;5)
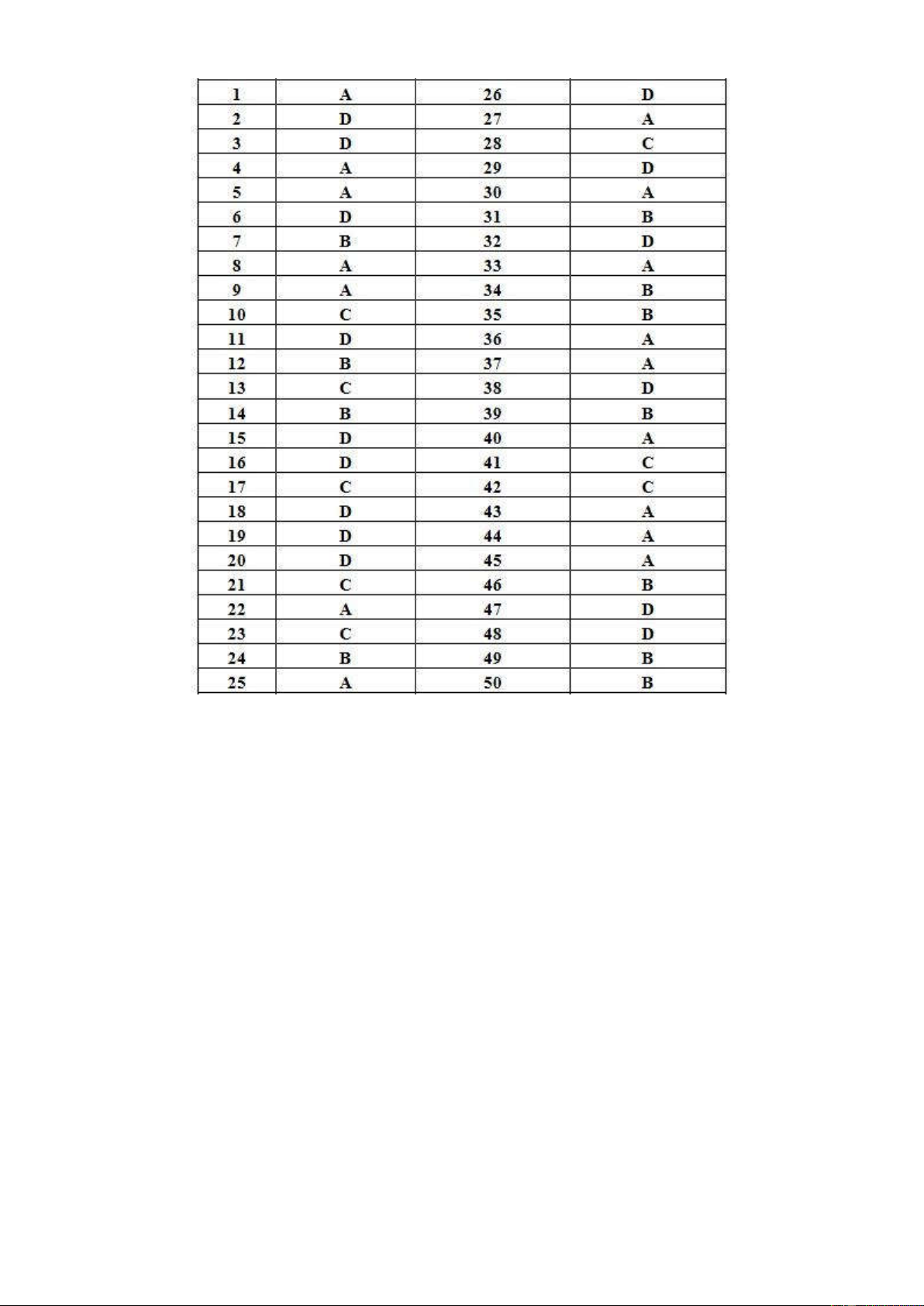
---------- HẾT ---------- Trang 08/08 ĐÁP ÁN ĐỀ THI 1A 2D 3D 4A 5A 6D 7B 8A 9A
10C 11D 12B 13C 14B 15D
16D 17C 18D 19D 20D 21C 22A 23C 24B 25A 26C 27A 28C 29D 30A
31B 32D 33A 34B 35B 36A 37A 38D 39B 40A 41C 42C 43A 44A 45A 46B 47D 48D 49B 50B
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1. Chọn A 2 Vì y′ = 3
− x + 4x −10 < 0 x ∀ ∈  . Câu 2. Chọn D
Để đường thẳng y = m cắt đồ thị hàm số tại 3 điểm phân biệt thì 4 − < m < 2
Do vậy m nhận các giá trị nguyên là { 3 − ; 2; − 1 − ;0; }
1 .vậy tổng các giá trị nguyên của tham số m là ( 3 − ) + ( 2 − ) + ( 1 − ) + 0 +1 = 5 − . Câu 3. Chọn D 1 4 dx =
dx = − 2cot 2x + c ∫ 2 2 ∫ 2 sin . x cos x sin 2x Câu 4. Chọn A
Hình chiếu của điểm I (1; 2;3) lên trục Oz là điểm H có tọa độ là: H (0;0;3) .  Ta có IH = ( 1 − ; 2 − ;0) .  2 2
Vì mặt cầu tiếp xúc với trục Oz nên: R = IH = (− ) 1 + ( 2 − ) = 5 . 2 2 2
Vậy phương trình mặt cầu có tâm là I (1; 2;3) và tiếp xúc với trục Oz là: ( x − )
1 + ( y − 2) + ( z − 3) = 5 Câu 5. Chọn A 2x
Diện tích hình phẳng giới hạn bởi các đường 2 y =
; y = x ; x = 0; x = 1 là : x +1 1 1 1 1 2x  2x   2   1  2 2 2 3 S = x − dx= x − dx = x − 2 + dx =
x − 2x + 2 ln x +1 ∫ ∫  ∫    x +1  x +1   x +1   3  0 0 0 0 5 = 2ln 2 − 3 Câu 6. Chọn D
Gọi G là trọng tâm của tam giác ABC ⇒ G (1; 2 − ;2).
Gọi d là đường thẳng qua G và vuông góc với (α ) . 
Mặt phẳng (α ) có vecto pháp tuyến là n = α (1;1; )1 .  
Vì d ⊥ (α ) nên: u = n = − α
(1;1; )1. Vậy phương trình tham số của đường thẳng d đi qua G(1; 2;2) và dx = 1+ t
vuông góc với (α ) là:  y = 2 − + t (t ∈) z = 2+t
H là hình chiếu vuông góc của G lên mặt phẳng (α ) nên H = d ∩ (α ) . Hay tọa độ điểm H là nghiệm của hệ:  x = 1+ tx = 2    y = 2 − + ty = 1 −  ⇔  ⇒ H (2; 1 − ;3) z = 2 + t z = 3  
x + y + z − 4 = 0  t =1 Câu 7. Chọn B
Ta thấy f ( x) > 0 x ∀ ∈(0 )
;1 và f ( x) < 0 x ∀ ∈(1;3) 3 1 3 1 3 Do đó: S = f
∫ (x) dx = f
∫ (x) dx+ f
∫ (x) dx = f
∫ (x)dx− f ∫ (x)dx 0 0 1 0 1 Câu 8. Chọn A
ABCD là hình vuông cạnh a 2 ⇒ S = a . ABCD SA ⊥ ( ABCD) 3 1 1 2a 2 ⇒ V = .S . A S = .2 . a a = . S . ABCD 3 ABCD 3 3 Câu 9. Chọn A α 1 + α x x dx = + C ∫ α ≠ − α ( ). +
C là hằng số, α là hằng số và 1 1 Câu 10. Chọn C Giả thiết ⇒ =10k m
(1 ≤ k ≤ 10, k ∈ N ) k Ta có log m = log 10k = 2 100 10 2 k log m ∈ Z ⇒
∈ Z là số nguyên thì k ∈{2;4;6;8;1 } 0 100 2
Suy ra tính tích các phần tử của tập hợp S là 2 (log 10 4 10 ).(log 10 )....(log 10 ) = 1.2.3.4.5 = 120 100 100 100 Câu 11. Chọn D
Điều kiện x > 0
Suy ra tập xác định của hàm số là (0; +∞) Câu 12. Chọn B b
Giả thiết ta suy ra V = S(x)dx ∫ a
Câu 13. Chọn C SA SB Ta có:  
SA  SBC  SA SC  1 1 1 V  . . SA S  . SA . . SB SC  20 S . ABC 3 ABC 3 2 V AS.AM .AN 1 Có tỉ lệ thể tích : ASMN   V AS.A . B AC 4 ASBC VASBCV   5 ASMN 4 Do : VVVVVV 15 ASBC ASMN SMNBC SMNBC ASBC ASMN
Câu 14. Chọn B
Gọi phương trình mặt phẳng cần tìm là (P)  
Ta có: BC  P  nBC 1;2;5 ( P)   Qu
 a A2;1;    P 1    P 
:1 x  2 2 y  
1 5z         n     1 0 x 2 y 5z 5 0 1; 2; 5  Câu 15. Chọn D
Phương trình tiếp tuyến của hàm số: y y '
x x y xo   o o
Tiếp tuyến tại M 2; 
3  x  2; y  3 o o x 1 2 2 y   y '   y '  y '   2 x 1 x 2  o x  2 1 2 2 1
Vậy trình tiếp tuyến cần tìm: y  2x23  2x 7 Câu 16. Chọn D 5x = 1 x = 0 Ta có: x x 2
25 − 3.5 + 2 = 0 ⇔ 5 x − 3.5x + 2 = 0 ⇔  ⇔  . 5x = 2 x = log 2  5
Phương trình có hai nghiệm x = 0; x = log 5. Vậy 3x + 2x = 2log 5. 1 2 2 1 2 2 Câu 17. Chọn C 1 4 − 4x − 1 Ta có: lim = lim = lim x y = 4 . x→±∞
x→±∞ x − 2020 x→±∞ 2020 1 − x
Vậy đường tiệm cận ngang của đồ thị hàm số là y = 4 . Câu 18. Chọn D      Ta có: . a b = (− )
1 .2 + 1.2 + 0 = 0 ⇒ a ⊥ b ⇒ A đúng; a = (− )2 2 2 1 +1 + 0 = 2 ⇒ B đúng    2 2 2
c = 1 + 1 + 1 = 3 ⇒ C đúng; .
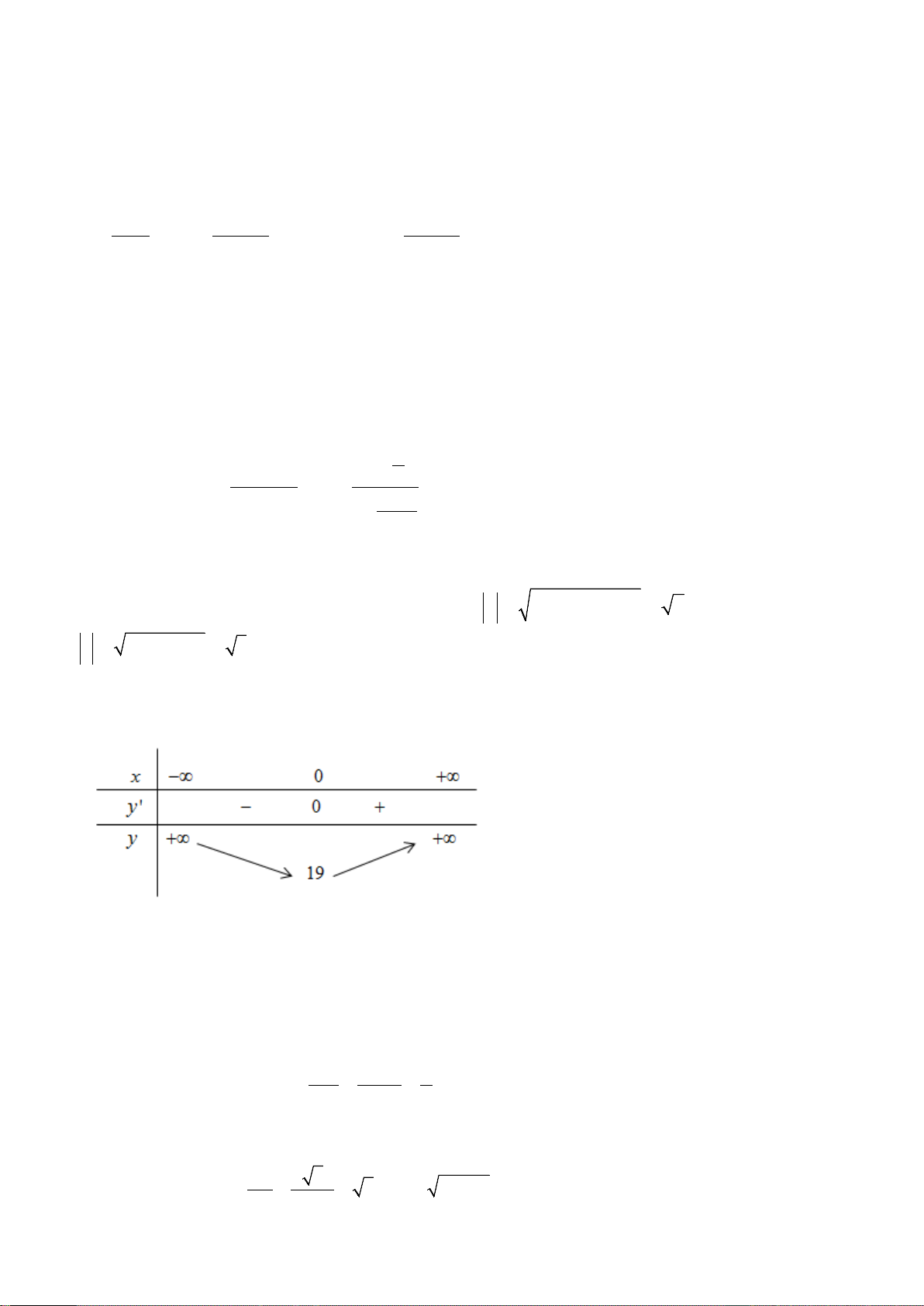
c b = 1.2 + 1.2 + 1.0 = 4 ≠ 0 ⇒ D sai. Câu 19. Chọn D. Ta có: 3 y ' = 40x +10 ; x
y ' = 0 ⇔ x = 0. Bảng biến thiên:
Từ bảng biến thiên ta thấy đồ thị hàm số không có điểm cực đại nào.
Lưu ý: Có thể giải theo trắc nghiệm như sau:  . a b = 10.5 = 50 > 0 Do 
nên đồ thị hàm số chỉ có 1 điểm cực trị và là điểm cực tiểu.  a = 10 > 0 Câu 20. Chọn D.
Gọi diện tích xung quanh, bán kính đáy, đường sinh, đường cao của hình trụ lần lượt là S , r,l, . h xq 2 S πa a xq 2 Ta có: S
= 2πrl = 2πrh ⇒ r = = = . xq 2πh 2π.4a 4 Câu 21. Chọn C.
Gọi diện tích xung quanh, đường sinh, đường cao của hình nón lần lượt là S ,l, . h xq S π xq 2 5 Ta có: 2 2 S = πRl ⇒ l = =
= 5 ⇒ h = l − R =1. xq πR 2π 1 1 1 4 2
Vậy thể tích khối nón là: V = Bh = .π R h = π.4.1 = π. 3 3 3 3 Câu 22. Chọn A
Từ hình dạng đồ thị hàm số ta thấy đây là đồ thị hàm số log x . a
Mặt khác, hàm số đồng biến trên (0; +∞) nên a > 1 . Do đó chọn A. Câu 23. Chọn C Ta có:
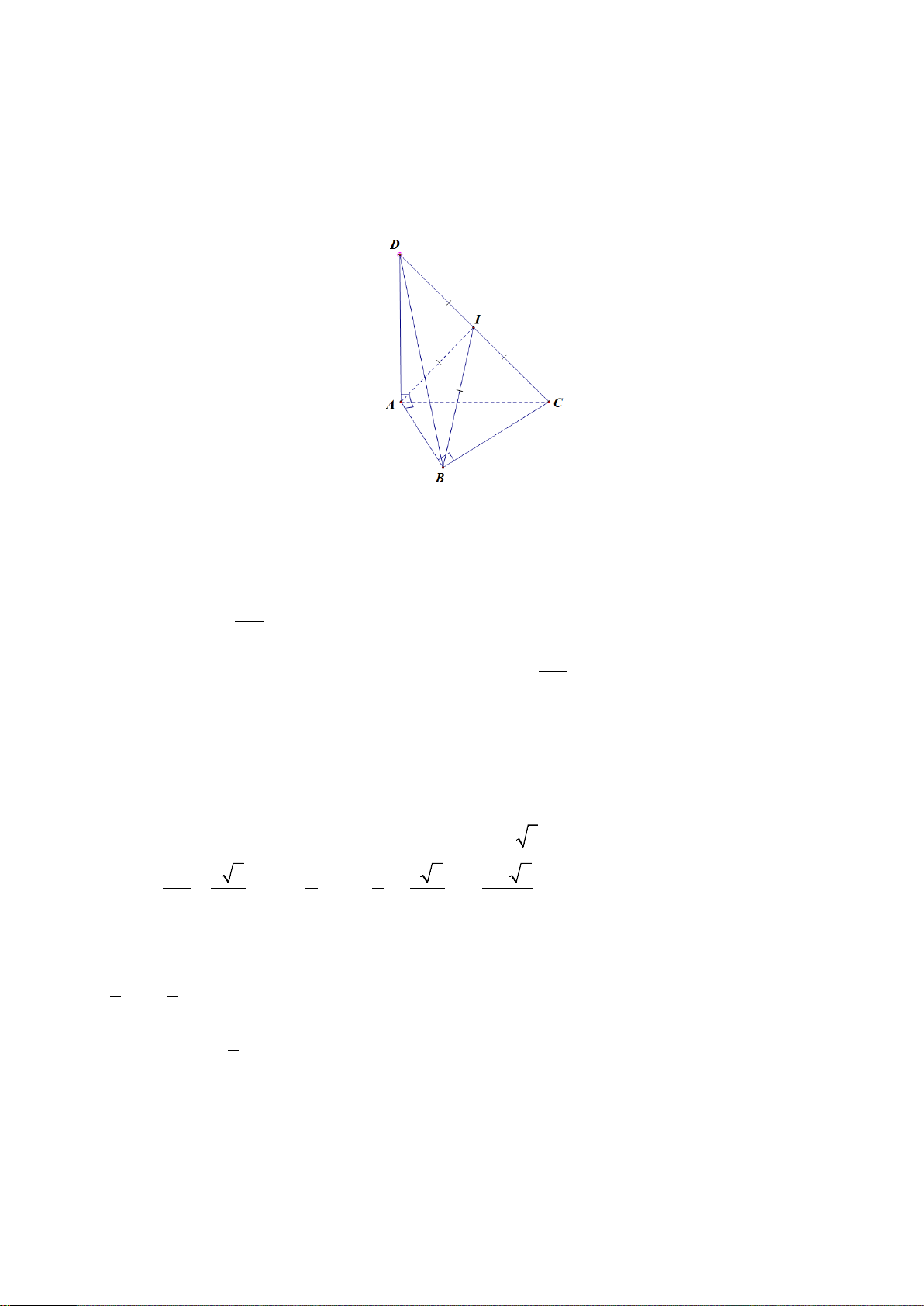
CB ⊥ AB  ⇒ CB ⊥ (ABD) ⇒ CB ⊥ DB ⇒ B
∆ DC vuông tại B CB ⊥ AD
Gọi I là trung điểm DC , do A ∆ DC, B
∆ DC lần lượt vuông tại ,
A B có DC là cạnh huyền nên CD
IA = IB = IC = ID = 2 Do đó CD
I là tâm đường tròn ngoại tiếp tứ diện ABCD và R = . 2 Ta có: 
DA ⊥ ( ABC ) nên góc giữa DC và ( ABC ) là góc DCA ⇒  0 DCA = 45 Xét A ∆ BC có  0
B = 90 , AB = 3, BC = 4 ⇒ AC = 5  0  Xét DA ∆ C có 0
A  90 , DCA  45 , AC  5  CD  5 2 3   Do đó CD 5 2 4 4 5 2 125 2 3 R = =
⇒ V = π R = π   = π   2 2 3 3 2 3   Câu 24. Chọn B Ta có x − x+2  1   1  ≤      3   3   1 
⇔ x ≥ −x + 2 do < 1    3  ⇔ x ≥ 1
Do đó tập nghiệm của bất phương trình là [1;+∞) Câu 25. Chọn A TXĐ: D = [ 2; − + ∞) 1 1 x + 2 −1 Ta có y′ = − ; y′ = 0 ⇔
= 0 ⇔ x + 2 =1 ⇔ x = 1 − ∈[ 1; − 34]. 2 2 x + 2 2 x + 2 3 3 13 Lại có y (− )
1 = − ; y (34) = 11. Suy ra m = − ; M = 11. Vậy S =3m + M = . 2 2 2 Câu 26. Chọn C
Thể tích của vật thể cần tìm : 1 V = π ∫( 1 4 − ( 2 − )2 2 )dx=π 12dx=12π ∫ . 0 0 Câu 27. Chọn A
Thể tích của lăng trụ đứng ABC.A′B C ′ ′ cần tìm : 2 3 a 3 a 3a V = S .AA′ = . = . ABC ∆ 4 2 8 Câu 28. Chọn C m = 2 TH1. 2 4 − m = 0 ⇔ .  m = −2
Với m = 2 thì y = 7x − 9 là hàm bậc nhất có a = 7 > 0 nên hàm số luôn đồng biến trên  ⇒ m = 2 (nhận). Với m = −2 thì 2
y = 4x + 7x − 9 là hàm bậc hai nên hàm số không đồng biến trên  ⇒ m = −2 (loại). TH2. 2
4 − m ≠ 0 ⇔ m ≠ ±2 Khi đó y′ = ( 2 − m ) 2 3 4
x + 2 (2 − m) x + 7 .
Hàm số đồng biến trên  khi và chỉ y′ ≥ 0∀x ∈  .m ∈( 2; − 2)  2 a > 0 4 − m > 0  ⇔  20   ⇔  ⇔ 
 20  ⇔ m ∈ − ;2   ∆ ≤ 0 2
22m − 4m − 80 ≤ 0 m ∈ − ; 2   
 11  ; m∈   11  ⇒ m = 1
− ; m = 0; m =1.
Vậy có 4 giá trị nguyên của m thỏa yêu cầu bài toán. Câu 29. Chọn D 
Mặt phẳng ( P) : x + y + z − 3 = 0 có một vectơ pháp tuyến: n = (1; 1; ) 1 . P  Đườ x − 1 y z ng thẳng d ' : = =
có một vectơ chỉ phương: u = 1; 3; -1 . d ' ( ) 1 3 1 −
Đường thẳng d nằm trong mặt phẳng (P) và vuông góc với đường thẳng d ' nên d nhận   
u = n , u  = 4;
− 2; 2 làm một vectơ chỉ phương. P d ' ( )   Câu 30. Chọn A
Gọi công sai của cấp số cộng này là d , số hạng đầu là a .
Khi đó b = a + d,c = a + 2d, p = a + 3d . a + b + c Ta có nửa chu vi p =
hay a + b + c − 2 p = 0 . 2
⇒ a + (a + d ) + (a + 2d ) − 2(a + 3d ) = 0
⇒ a − 3d = 0 ⇒ a = 3d.
Vì a > 0 nên d > 0 đo dó a < b < c .
Vậy góc nhỏ nhất trong tam giác ABC là góc đối diện với cạnh nhỏ nhất a . Hay  A là góc nhỏ nhất.
Áp dụng định lí cosin trong tam giác ABC ta được : 2 2 2 2 2 2
b + c − a
16d + 25d − 9d 4 cos A = = = . 2bc 2.4d.5d 5 Câu 31. Chọn B
Xét trong mỗi ván, để thắng sẽ xảy ra hai trường hợp: 2 C .5 5
+ Trường hợp 1: xuất hiện đúng hai mặt sáu chấm, xác suất là 3 = . 3 6 72 3 C 1
+ Trường hợp 2: cả 3 đều là mặt sáu chấm, xác suất là 3 = . 3 6 216 Do đó, xác suất để 5 1 2 25 mỗi ván thắng là + =
, xác suất mỗi ván thua là . 72 216 27 27
Vậy, xác suất để trong ba ván, người đó thắng ít nhất hai ván là: 2 3  2  25  2  308 2 3 C ⋅ + C = . 3   3    27  27  27  19683 Câu 32. Chọn D Gọi M ( ;
x y; z ) ∈(α ). Khi đó
2MA − MB = 4 ⇔ 2 ( x − 2)2 + ( y − )2 1 + ( z + )2
1  − x + ( y − 3)2 + ( z − )2 2 2 2 1  = 4     2 2 2
⇔ x + y + z −8x + 2y + 6z − 2 = 0.
Do đó, điểm M nằm trên mặt cầu tâm I(4; 1 − ; 3)
− , bán kính R = 28.
Gọi đường tròn (C) = (S ) ∩ (α ) . Suy ra M ∈ (C). 4 −1− 3 + 3
Khoảng cách từ tâm I (4; 1 − ; 3)
− đến (α ) : d (I;(α )) = = 3. 2 2 2 1 +1 +1
Bán kính của đường tròn (C) là 2 2 r =
R − d ( I;(α )) = 28 − 3 = 5. Câu 33. Chọn A
Để hàm số có đúng hai tiệm cận đứng thì: 2
6x − x ≥ 0 (1) và 2
x − 8x + 2m = 0 (2) có hai nghiệm phân biệt. 0 ≤ x ≤ 6 2  − ≥
Từ (1), (2) ta có: 6x x 0  2  ⇔  x 2
x −8x + 2m = 0 − + 4x = m  2 2 x
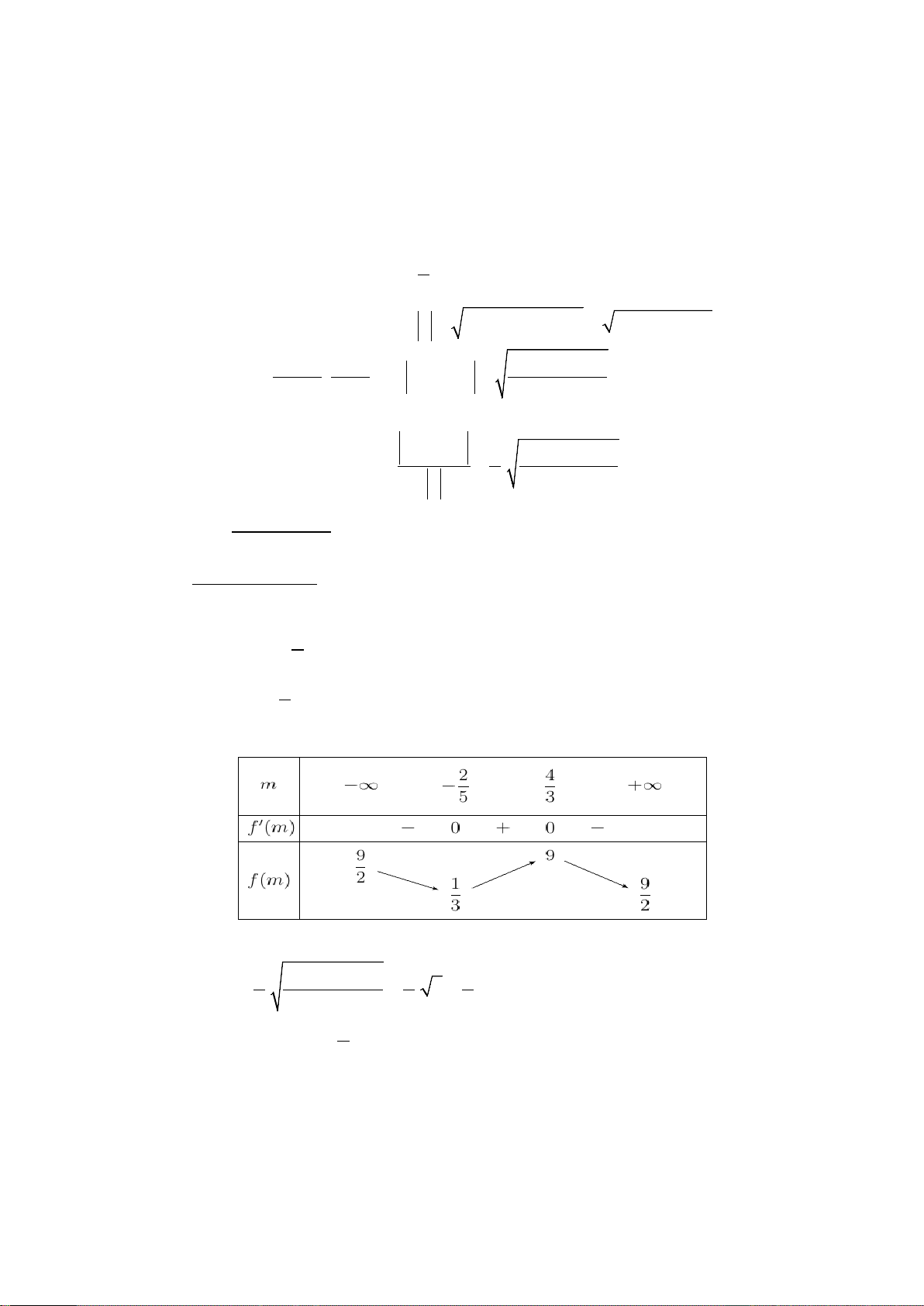
Đặt f (x) = − + 4x, x
∀ ∈[0;6]. Ta có f '(x) = −x + 4, f '(x) = 0 ⇔ −x + 4 = 0 ⇔ x = 4 2 Bản biến thiên: x 0 4 6 y ' + 0 − y 8 0 6
Vậy để (2) có hai nghiệm phân biệt thì m∈[6;8) .
Câu 34. Chọn B 6 4 3 2
7x + 5x − 4x + 3x − 4x + 2 = 0(1)  f '(x) = 0 
Ta có F '(x) = f '(x)g '[ f (x)]. F '(x) = 0 ⇔  ⇔ =  g  [ f x ] f (x) 1 ' ( )  f (x) = 1 −  (1) Vô nghiệm vì 6 4 3 2
7x + 5x − 4x + 3x − 4x + 2 > 0 x ∀ Bản biến thiên: f (x) −∞ 1 − 1 +∞ F '(x) + 0 − 0 + F ( x) 4 +∞ 0 −∞
Vậy F (x) = m có ba nghiệm thực phân biệt thì m∈(0;4) Câu 35. Chọn B Ta có: DA ∆ B = C
∆ AB( .c .cc) ⇒ DM = CM nên MC ∆
D cân tại M .
Mặt khác N là trung điểm cạnh CD suy ra MN ⊥ CD .
Chứng minh tương tự ta được MN ⊥ AB .
Do vậy mặt cầu đường kính MN tiếp xúc với AB,CD .
Gọi I là trung điểm cạnh MN nên IM = IN .
Dựng IK ⊥ MN . Do mặt cầu đường kính MN tiếp xúc với AD
nên IM = IN = IK . a Ta có: MIA ∆ = K
∆ IA ⇒ AK = MA = . 2 a ( 3 − ) 1
Do đó KD = AD − AK = . 2 a ( 3 − ) 1 Nhận thấy KI ∆ D = NI
∆ D ⇒ ND = KD =
suy ra CD = a ( 3 − ) 1 . 2
Vì AB ⊥ CM , AB ⊥ MD nên góc giữa hai mặt phẳng ( ABC ) và ( ABD) là góc giữa hai đường thẳng CM và MD . 2 2 3a a a 2
Áp dụng định lý Pitago trong tam giác vuông MAD : 2 2 MD = AD − MA = − = 4 4 2 2 2 a a + − ( − + − )2 2 2 2 2 3 1 a MC MD CD Xét tam giác MCD : 2 2 cos M = = = 2 3 − 3 > 0 . 2.MC.CD a 2 a 2 2. . 2 2 Vậy cosα = 2 3 − 3. Câu 36. Chọn A π π 4 4 1 cos x Ta có : A = dx = dx ∫ ∫ . 1+ tan x sin x + cos x 0 0 π 4 sin x Xét B = dx ∫ sin x + cos x 0 π 4 π Nhận thấy: A + B = dx = ∫ (1) 4 0 π
4 d (sin x cos x) π + 4 A − B =
= ln sin x + cos x ∫ = ln 2 (2) 0 sin x + cos x 0 π 1
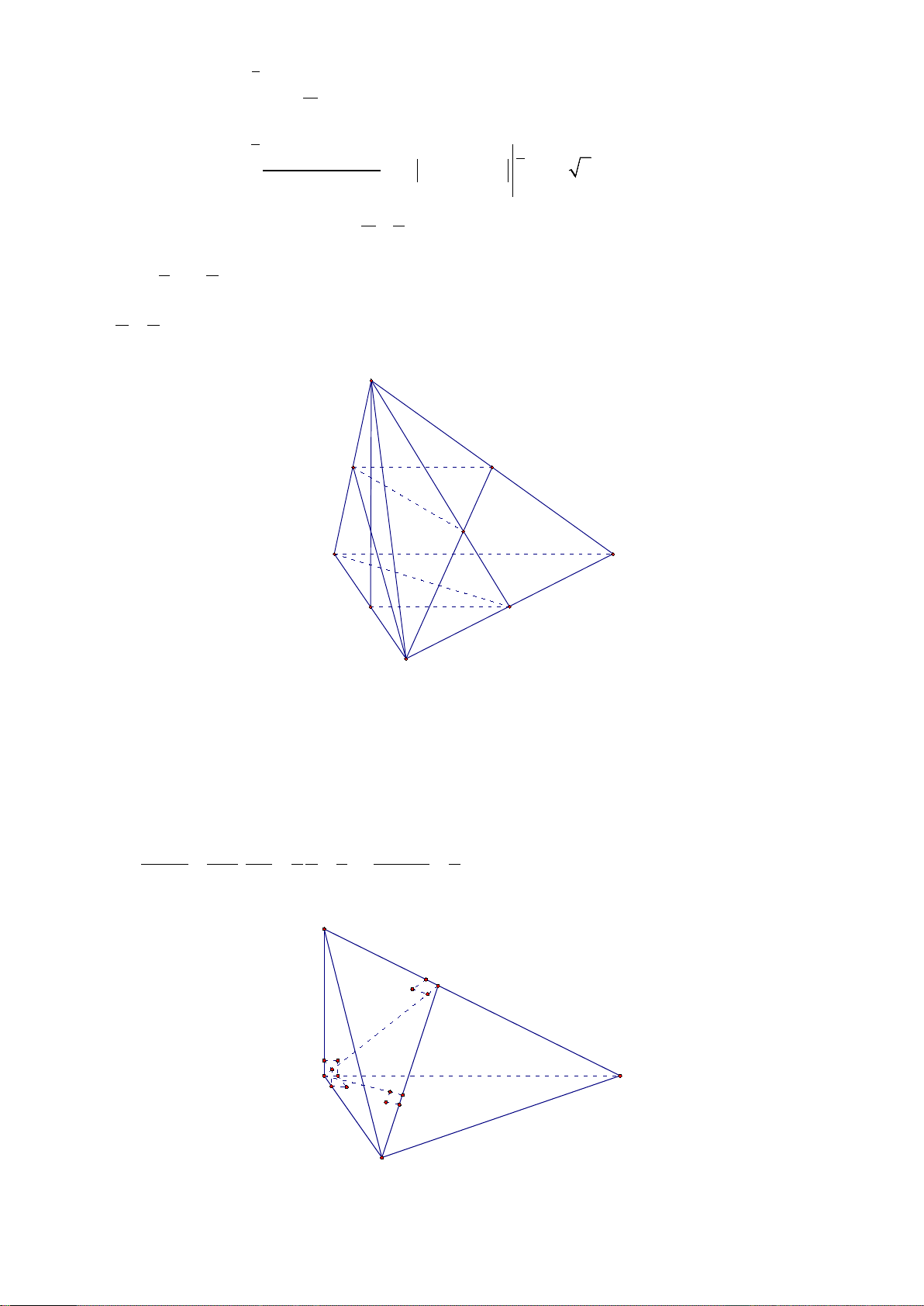
Cộng từng vế (1) và (2) ta được: A = + ln 2. 8 4 Do đó 1 1 a = , b = . 8 4 a 1 Vậy = . b 2 Câu 37. Chọn A S E M N C I H A B
Gọi H là trung điểm của BC , suy ra SH ⊥ ( ABC ) .
Gọi I đối xứng với B qua A , suy ra AH IC ⇒ IC ⊥ SC .
Gọi M , E lần lượt là trung điểm của các cạnh SC, SI .
Gọi N là giao điểm của SA và BE thì N là trọng tâm của tam giác SBI . BM ⊥ SC Ta có: 
⇒ (SMN ) ⊥ SC ME ⊥ SC Khi đ V SM SN 1 2 1 V 1 ó: S.BMN S . = . BMN = = ⇒ = . V SC SA 2 3 3 V 2 S . ABC MN . ABC Câu 38. Chọn D N K O P H M
Giả sử mặt phẳng (α ) cắt trục Oy tại P . ( P không trùng với O) Khi đó ta có .
O MNP là tam diện vuông tại O .
Kẻ OK ⊥ NP ⇒ MK ⊥ NP . Ta có OK ∠
M là góc nhọn trong tam giác vuông OMK nên góc OK ∠
M là góc giữa (α ) và mặt phẳng (Oyz) . Khi đó: 0 O ∠ MH = 30
Kẻ OH ⊥ MK ⇒ OH ⊥ (MNP) ⇒ d ( ; O (α )) = OH .
Mà trong tam giác vuông OMH ta có: 0
OH = OM .sin 30 = 2 . Câu 39. Chọn B  1  Lấy M (1− 2 ; m − 2 + 2 ; m )
1 ∈ (d ) , ta có AM − 2 ;
m 2m − 3; − 3   .  2   
Đường thẳng d có VTCP là u (m − m ) ⇒ u = m + ( − m)2 2 2 ;1 ;1 1
+1 = 2m − 2m + 2 . 2     Khi đó  2m +1 m +1  9m + 6m + 2
AM ,u = − ; m − ;
⇒ AM ,u =       .  2 2  4
Khoảng cách từ điểm A đến đường thẳng d là       + + d ( A d ) AM , u 2 1 9m 6m 2 , =  = . . 2 u 2 2m − 2m + 2 9m + 6m + 2
Xét hàm số f (m) 2 = với m ∈  . 2 2m − 2m + 2 2 15 − m +14m + 8
Ta có f ′(m) = ( . 2m − 2m + 2)2 2  2 m = − 
Khi đó f ′(m) 5 = 0 ⇔  . 4 m =  3 Bảng biến thiên
Vậy f (m) ≤ 9 . + +
Khi đó ta có d ( A d ) 2 1 9m 6m 2 1 3 , = . ≤ . 9 = 2 2 2m − 2m + . 2 2 2 4
Dấu “=” xảy ra khi và chỉ khi m = . 3 Cách 2:
x =1− 2m + mt
x =1+ m(t − 2)
x =1+ m(t − 2)    Ta có  y = 2
− + 2m + (1− m)t ⇔ y = 2
− (1− m) + (1− m)t ⇔ y = (1− m)(t − 2)    z =1+ t z = 1+ t z = 3 + t − 2  
Dường thẳng (d ) luôn đi qua điểm H (1;0;3) với mọi m ứng với t = 2. 
Dường thẳng (d ) có véc-tơ chỉ phương là u = ( ;1 m − m ) ;1 . d Do .1
m + (1− m).1+1.(− )
1 = 0 nên đường thẳng (d ) vuông góc với đường thẳng có véc-tơ chỉ phương  u = 1;1; −1 . 1 ( )
Do đó véc-tơ chỉ phương của đường thẳng (d ) khi khoảng cách từ A đến nó lớn nhất là     1 3 
u = u ; AH  = 2; − ; . d d      2 2  m 1− m 1 4 Vậy ta có = = ⇔ m = . 2 1 3 3 − 2 2 Câu 40. Chọn A Điều kiện: 2 2
x + 3x +1 > 0 ⇒ x + 3x +1 ≥ 1. Do 2 2
x ∈  ⇒ x + 3x +1 ≥ 1 ⇒ x + 3x ≥ 0 (1). Mặt khác 2 2
x ∈  ⇒ x + x + ≥ ⇒ x + x > ⇒ ( 2 3 1 1 3 0 ln x + 3x + ) 1 > ln ( ) 1 = 0 Ta có ( 2x + x+ ) 2
+ x + x < ⇔ ( 2
x + x + ) < −( 2 x + x) 2 ln 3 1 3 0 ln 3 1 3
⇔ x + 3x < 0 (2).
Từ (1) và (2) suy ra x ∈ ∅ . Câu 41. Chọn C Do ABB A
′ ′ là hình thoi có góc B bằng 0
60 nên BB′ = AB′ = AB = 2; A′B = 2 3; .
Do ABC là tam giác vuông tại A với AB = 2; BC = 4 , ta có A′C′ = 2 3 .
Chọn hệ trục tọa độ Oxyz sao cho gốc O trùng với điểm A′ , đường thẳng A′B′ nàm trên tia Ox ,
đường thẳng A′C′ nằm trên tia Oy , tia Oz hướng lên trên sao cho điểm B có cao độ dương.
Khi đó ta có A′(0;0;0);B′(2;0;0);C′(0;2 3;0).
Vì K là trung điểm của B C
′ ′ nên K (1; 3;0). Gọi B ( ;
x y; z ) với z > 0 . 2 2 2 2 2  ′ =
x + y + z =12 A B 2 3 
z = 3 − y ( ) 1 Ta có  ⇔  ⇒  BB′ = 2 (  x − 2  )2 2 2 + y + z = 4 x = 3   
Mặt khác, ta có A′B′ = (2;0;0); KB = (2; y − 3; z); A′K = (1; 3;0).
  
A′B ;′KB.A′K 2 3z   Theo đề 3
ra, ta có d ( A′B ; ′ BK ) =   ⇔ =
A′B′ KB   z + ( − y)2 2 2 ; 4 2 3 2 2 2
⇔ 9y −18 3y − 3z + 27 = 0 (2)  3  y =
Thay (1) vào (2) ta được, 2
12 y −18 3y + 18 = 0 ⇔ 2  y = 3 Với y = 3 ⇒ z = 0 (loại). 3 3  3 3  Với y =
⇒ z = ⇒ B3; ;  2 2 2 2  
1    Suy ra V = 3.V =  ′ ′ ′ = ′ ′ ′ 3.
BA ; BB .BC 3 3. B. A B C   6 Câu 42. Chọn C u u 1 u + Ta có n n 1 u = ⇔ = . n ; n ∀ ≥1 n 1 + 3n n + . 1 3 n
Đặt u = nv ; n
∀ ≥1⇒ u = n +1 v n 1 + ( ) n n n 1 + Ta đượ 1 1 1 c v = v ; n
∀ ≥1, suy ra dãy số (v là cấp số nhân với v = ;q = . n ) n 1 + 3 n 1 3 3 1 ⇒ n v = ⇒ u = nv = ; n ∀ ≥1 . n 3n n n 3n 1 n 1 n Ta có u < ⇔ < ⇔ 3 > 2020n (*) n 2020 3n 2020
Dễ thấy, bằng phương pháp quy nạp toán học ta chứng minh (*) đúng n ∀ ≥ 9.
Vậy có vô số nguyên dương n thỏa mãn đề bài. Câu 43. Chọn A Xét   3 2
f x ax bx cx d .
Do f 0  2 nên suy ra d  2. f x 3 2 4
 64ax  16bx  4cx d .  4 64    4 a a a       63 16  b b b   0  
Giả thiết cho f x   f x  3 4
 4x  2x nên ta có:    . 4
c c  2  2  c   d  d   3   d     4 2 Vậy f x  3  x x  2 . 63 3 1 1 1  4 2   1 1      148 Từ đó f  x 3 4 2 dx  
x x  2dx     
x x  2x   . 63 3    63 3  63 0 0 0 Câu 44. Chọn A
Đặt sinx t . Khi x 0;     thì t   0;1   .
Ta nhận thấy với mỗi t   0     ;1
. Do đó phương trình f sinx 
sẽ cho tương ứng hai giá trị x  0;    m
có hai nghiệm thuộc đoạn 0;  
 khi và chỉ khi phương trình f t  m có một nghiệm t   0   ;1  . Dựa
vào đồ thị ta được 4  m  3 . Câu 45. Chọn A
Điều kiện: 3cosπ x −1 > 0 . π x− 1 cos 1 π 2
+ = cosπ x + log 3cosπ x −1 cos
⇔ 2 x +1 = 2cosπ x + log 3cosπ x −1 2 ( ) 4 ( ) 2 cosπ
⇔ 2 x + cosπ x = 3cosπ x −1+ log 3cosπ x −1 . ( ) 1 2 ( )
Ta có hàm số ( ) = 2t f t
+ t đồng biến trên (0; + ∞) . Từ ( ) 1 suy ra cosπ x cosπ 2 = 3cosπ −1 ⇔ 2 x x − 3cosπ x +1 = 0  1  Xét hàm số ( ) = 2u g u
− 3u +1, có ′( ) = 2u g u .ln 2 − 3 < 0 , u ∀ ∈ ; 1   .  3   1 
Vậy hàm số y = g (u) nghịch biến trên ; 1 
 , mà g (u) = 0 .  3  Do đó phương trình cosπ 2
x − 3cosπ x +1 = 0 có một họ nghiệm là:
cosπ x = 1 ⇔ π x = k 2π ⇔ x = 2k , k ∈  . Vì x thuộc [0;100] nên k ∈[0; 50] . Vậy có 51 nghiệm x thuộc [0;100]. Câu 46. Chọn B
Theo giả thiết ta có: 2019 n 2020 2019 n 2020 10 ≤ 4 + 3 < 10 ⇒ 10 < 4 < 10 2019 n 2020 ⇔ log 10 < log 4 < log 10
⇔ 2019.log 10 < n < 2020.log 10 . 4 4 4 4 4
Vì n nguyên dương nên n = 3354 hoặc n = 3355 . Vậy tổng là 3354 + 3355 = 6709 . Câu 47. Chọn D
Ta có F ′( x) = f ′( x) 3 f ( x) +
f ′( x) f ( x) =
f ′( x) f ( x) ( 2 12. . 4. . 4. . . 3 f ( x) + ) 1 .  f ′(x) = 0 (1) 
F ′( x) = 0 ⇔  f ( x) = 0 (2)  2 3 f  (x)+1= 0 (VN)
Dựa vào đồ thị, nhận thấy f ′( x) = 0 có 3 nghiệm phân biệt; f ( x) = 0 có 4 nghiệm phân biệt, các nghiệm
ở phương trình (1) và (2) không trùng nhau, đồng thời hàm F (x) là hàm liên tục trên  nên có 7 điểm cực trị. Câu 48. Chọn D  
Ta có MN = (1; 2;3) . Đường thẳng (d ) có véc tơ chỉ phương u (1; 2 − ; ) 1 .  
Nhận thấy MN.u = 0 do đó MN ⊥ d .
Khi đó IM + IN đạt giá trị nhỏ nhất khi điểm I là giao điểm của đường thẳng d với mặt phẳng (P)
chứa M , N và vuông góc với đường thẳng d .
Phương trình mặt phẳng (P) qua M , N và vuông góc đường thẳng d có phương trình là
1.( x − 3) − 2.( y − ) 1 +1.( z − )
1 = 0 ⇔ x − 2 y + z − 2 = 0 .
Giao điểm của đường thẳng d với mặt phẳng (P) là nghiệm của hệ phương trình  4 − t =  3  x = 7 + tx = 7 + t 17   x − 7 y − 3 z − 9   x =  = = y = 3 − 2ty = 3 − 2t  3  1 2 − 1 ⇔  ⇔  ⇔  . z = 9 + t z = 9 + t 17
x −2y + z −2 = 0   y =
7 +t −6+ 4t +9+t − 2 = 0 8  + 6t = 0  3  23 z =  3 Ta đượ 17 17 23
c 2a + b + 3c = 2. + + 3. = 40. 3 3 3 Câu 49. Chọn B (
SBC) ⊥ ( ABC) 
Kẻ SH ⊥ BC ( H ∈ BC ). Ta có (
SBC) ∩( ABC) = BC ⇒ SH ⊥ ( ABC) . SH ⊥ BC
Kẻ SM ⊥ AB (M ∈ AB) và SN ⊥ AC (M ∈ AC ) . Khi đó ((SAB) ( ABC ))  =  , SMH và ((SAC) (ABC))  =  ,
SNH . Theo đề  =  0 SMH
SNH = 60 ⇒ MH = NH ⇒ H cách đều hai điểm M , N ⇒
H là chân đường phân giác trong góc A của tam giác ABC . Khi đó ta có: HB AB 1 =
= ⇒ HC = 2HB mà 2 2
HB + HC = BC =
AB + AC = a 5 HC AC 2  a 5 HB =  3 ⇒   2a 5 HC =  3 HM HB 1 AC 2a Theo ta-let ta có = = ⇒ HM = = . AC BC 3 3 3 Khi đó  SH 2 3 0 tan SMH =
⇒ SH = tan 60 .HM = a . HM 3
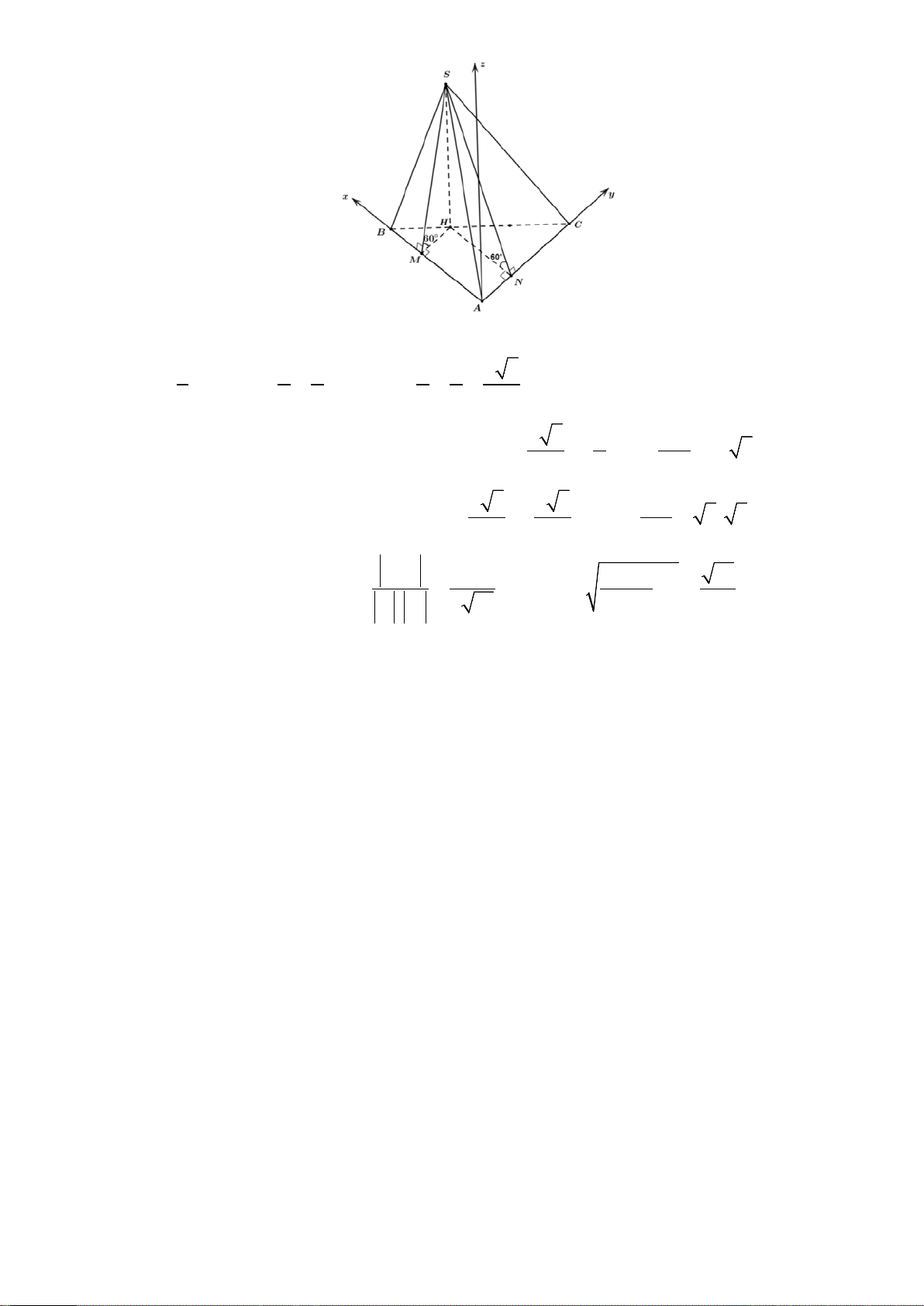
Đặt hệ trục tọa độ Oxyz như hình vẽ. Khi đó ta có A(0;0;0) , B( ;0
a ;0), C (0;2a;0) .  1   2 2   2 2 2 3  Ta có BH = BC ⇒ H
a; a;0 ⇒ S    a; a; a  3  3 3  3 3 3   2      Khi đó mặ 2 3 2 2a
t phẳng (SAB) có VTPT 2 2
n =  AB, AS  =  0;− a ; a  = 0; − 3;1 1   ( ) 3 3 3   2     4 3 2 3  2a
và mặt phẳng ( SBC ) có VTPT 2 2
n = BC, BS  =  a ; a ;0  = 2 3; 3;0 . 2   ( ) 3 3 3     n .n 3 1 51
Suy ra cos (SAB);(SBC )  ( ) 1 2 = cosα =   = ⇒ tan α = −1 = 2 n . n 2 15 cos α 3 1 2
(vì α là góc nhọn nên tan α > 0 ) Câu 50. Chọn B Ta có 2cos2x 2 a
≥ 4cos x −1 ; x ∀ ∈  2cos 2 x ⇔ a
≥ 2cos 2x +1 ; x ∀ ∈ .  Đặt t = 2cos 2 ; x x
∀ ∈  ⇒ t ∈[ 2; − 2].
Khi đó bài toán trở thành: “ tìm giá trị a > 0;a ≠ 1 thỏa mãn t
a ≥ t +1 ; t ∀ ∈[ 2; − 2]”.
+ Xét trường hợp 1: 0 < a <1 Hàm số ( ) t
f t = a nghịch biến trên  nên t
∀ > 0 ⇒ f (t) < f (0) ⇒ f (t) <1 Ta lại có t
∀ > 0 ⇒ t +1 > 1 nên bất phương trình t
a ≥ t +1 vô nghiệm trên (0; 2].
Yêu cầu bài toán không thỏa.
+ Xét trường hợp 2: a >1 Hàm số ( ) t
f t = a đồng biến trên  .
--------------HẾT---------------
Document Outline

  • de-thi-thu-toan-thpt-qg-2020-lan-1-truong-chuyen-nguyen-trai-hai-duong.pdf
    • de-thi-thu-toan-thpt-qg-2020-lan-1-truong-chuyen-nguyen-trai-hai-duong (1)
      • de 035
    • Document1
  • Nguyễn Trãi Hải Dương lần 1năm học 2019-2020 giải chi tiết..pdf