Đề thi thử Toán THPT Quốc gia 2019 lần 2 trường Hai Bà Trưng – Vĩnh Phúc

Đề thi thử Toán THPT Quốc gia 2019 lần 2 trường THPT Hai Bà Trưng – Vĩnh Phúc được biên soạn dựa trên cấu trúc mà Bộ Giáo dục và Đào tạo đã công bố trước đó, đề gồm 06 trang với 50 câu hỏi và bài toán dạng trắc nghiệm

27 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

18 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
Câu 1: Asian cup 2019 đội Việt Nam nằm ở bảng D gồm các đội Iran, Iraq và Yemen thi đấu theo thể thức mỗi
đội gặp nhau một lần. Hỏi khi kết thức vòng đấu bảng ở bảng D có bao nhiêu trận đấu.
A. 6. B. 8. C. 7. D. 5.
Câu 2: Có bao nhiêu cách xếp ba bạn học sinh nam hai bạn học sinh nữ và một cô giáo vào một hàng gồm sáu ghế
sao cho cô giáo ngồi giữa hai bạn học sinh nữ (cô giáo và hai bạn học sinh nữ ngồi liền kề).
A. 48. B. 126 C. 144. D. 84.
Câu 3: Cho cấp số cộng có số hạng đầu
1
1
,
u
công sai
2.
d
Tìm
19
.u
A.
19
3
7.
u
B.
19
3
6.
u
C.
1
9
2
0.
u
D.
19
1
9.
u
Câu 4: Cho hàm số
y f x
liên tục và có đạo hàm liên tục trên khoảng
; .a b
Trong các khẳng định sau khẳng
định nào sai?
A. Nếu hàm số
y f x
đồng biến trên khoảng
thì
0 ; .f x x a b
.
B. Nếu
f x
không đổi dấu trên khoảng
thì
f x
không có cực trị trên khoảng
; .a b
C. Nếu hàm số
0
f x
với mọi
;x a b
thì hàm số
y f x
đồng biến trên khoảng
; .a b
D. Nếu hàm số
0
f x
với mọi
;x a b
thì hàm số
y f x
nghịch biến trên khoảng
; .a b
Câu 5: Trong các hàm số sau hàm số nào không có cực trị?
A.
3 2
3 15 1.
y x x x
B.
3 2
3 15 1.
y x x x
C.
3 2
3
15 1.
y
x x x
D.
3 2
3
2019.
y
x x
Câu 6: Đồ tị hàm số
1
1
x
y
x
có bao nhiêu đường tiệm cận?
A. 2. B. 1. C. 0. D. 3.
Câu 7: Đường thẳng
2 1y x
và đồ thị
C
hàm số
3
2
6 11 1y x x x
có bao nhiêu điểm chung?
A. 2. B. 3. C. 1 D. 0.
Câu 8: Gọi
m
và
M
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
2
3
9 5
y
x x x
trên đoạn
Tính giá trị
.P
M m
A.
1
2.
P
B.
2
2.
P
C.
15.
P
D.
10.
P
Câu 9:
Cho hàm
số
3
2
6 9 1y x x x
. Mện
h đề nào dưới đây là đúng ?
A. Hàm số đồng biến trên khoảng
1
;
. B. Hàm số đồng biến trên khoảng
;
3
.
C. Hàm số nghịch biến trên khoảng
1;3
. D. Hàm số nghịch biến trên khoảng
3;

.
SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC
TRƯỜNG THPT HAI BÀ TRƯNG
KÌ THI THPT QUỐC GIA LẦN II NĂM HỌC 2018 - 2019
Đề thi môn: Toán.
Thời gian làm bài 90 phút, không kể thời gian giao đề
(Đề thi gồm 50 câu trắc nghiệm)
Mã đề thi 132
Câu 10: Giá trị cực tiểu của hàm số
3 2
3 9 2
y x x x
là
A.
20
. B.
7
. C.
25
. D.
3
.
Câu 11: Đồ thị của hàm số nào sau đây có tiệm cận ngang ?
A.
2
16
x
y
x
.B.
4 15
3 1
x
y
x
. C.
2
1
x
y
x
. D.
2
2019.
y x
Câu 12: Cho hàm số
y f x
có đồ thị như hình vẽ:
Hỏi hàm số
y f x
có bao nhiêu điểm cực trị?
A. 3. B. 2. C.
4.
D. 5.
Câu 13: Tập xác định của hàm số
1
3
1
y x
là:
A.
1; .
D

B.
.D
C.
;1 .
D

D.
0; .
D

Câu 14: Cho hàm số
2
lg 2019 .
f x x x
Tính
.f x
A.
2
1
.
2019.ln10
f x
x
B.
2
1
.
2019
f x
x
C.
2
ln10
.
2019
f x
x
D.
2
2019
.
2019.ln10
f x
x
Câu 15: Trong các hàm số sau hàm số nào đồng biến trên
?
A.
1
2
x
y
B.
.
x
y e
C.
1
.
x
y
D.
2
ln .y x
Câu 16: Hình vẽ bên là của đồ thị hàm số nào trong các hàm số sau:
A.
2 .
x
y
B.
2 .
x
y
C.
2 .
x
y
D.
1
.
2
x
y
Câu 17: Bất phương trình
2
log 4 3
x
có bao nhiêu nghiệm nguyên?
A. 8. B. 7. C. 10. D. 11.
Câu 18: Số
19
2
2 1
có bao nhiêu chữ số trong hệ đếm thập phân?
A.
157827.
B.
157826.
C. 315654. D. 315653..
Câu 19: Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
ln 2 3
y x x
trên đoạn
0;2 .
Tính giá trị biểu thức
.
M m
A e e
A.
5.
A
B.
6.
A
C.
3.
A
D.
8
A
Câu 20: Một người gửi ngân hàng 100 triệu đồng với kì hạn 3 tháng, lãi suất 5% một quý theo hình thức lãi
kép ( sau 3 tháng sẽ tính lãi và cộng vào gốc). Sau đúng 6 tháng, người đó gửi thêm 50 triệu đồng với kì hạn
và lãi suất như trước đó. Tính tổng số tiền người đó nhận được sau 1 năm ( Tính từ lần gửi đầu tiên)?
x
y
2
2
1
O
A.
179,676
triệu đồng. B.
177,676
triệu đồng
C.
178,676
triệu đồng. D.
176,676
triệu đồng
Câu 21: Trong các hàm số sau, hàm số nào có một nguyên hàm là hàm số
lnF x x
?
A.
.f x x
B.
1
.
f x
x
C.
3
.
2
x
f x D.
.f x x
Câu 22: Cho
f x
,
là các hàm số xác định và liên tục trên
. Trong các mệnh đề sau, mệnh đề nào
sai?
A.
d d . df x g x x f x x g x x
. B.
2 d 2 df x x f x x
.
C.
d d df x g x x f x x g x x
. D.
d d df x g x x f x x g x x
.
Câu 23: Tìm họ nguyên hàm của hàm số
3
x
f x
.
A.
d 3
x
f x x C
. B.
d 3 ln 3
x
f x x C
.
C.
3
d
ln3
x
f x x C
. D.
1
3
d
1
x
f x x C
x
.
Câu 24: Tìm họ nguyên hàm của hàm số
2
sin 2f x x
.
A.
1 sin 4
d .
2 8
x
f x x x C
. B..
1 sin 4
d .
2 8
x
f x x x C
C..
1 sin 4
d .
2 2
x
f x x x C
D..
1 sin 4
d .
2 2
x
f x x x C
Câu 25: Cho
2
0
d 3
I f x x
. Khi đó
2
0
4 3 dJ f x x
bằng:
A.
2
. B.
6
. C.
8
. D.
4
.
Câu 26: Cho hàm số
f x
liên tục trên đoạn
0;10
và
10
0
d 7
f x x
và
6
2
d 3
f x x
. Tính
2 10
0 6
d dP f x x f x x
.
A.
7
P
. B.
4P
. C.
4P
. D.
10
P
.
Câu 27:
e
1
1
d ln 2ln 2.
3
I x e a
x
Tìm
?a
A.
12.a
B.
2.a
C.
7.a
D.
3.
a
Câu 28: Cho hình chóp .
S ABC
có đáy ABC là tam giác vuông tại
0
, , 60 , 2 , B AB a BAC SA a SA
vuông góc
với đáy. Tính sin của góc giữa hai mặt phẳng
SAC
và
.SBC
A.
10
.
5
B.
C.
5
.
5
D.
10
.
10
Câu 29: Tính thể tích khối chóp tam giác đều có cạnh đáy bằng
,a
cạnh bên bằng
3.
a
A.
3
2
.
6
a
B.
3
3
.
6
a
C.
3
6
.
6
a
D.
3
2
.
2
a
Câu 30: Cho hình chóp
.S ABC
có đáy ABC là tam giác vuông tại
0
, , 60 , 2 , A AB a ABC SB a SB
vuông
góc với đáy. Tính sin của góc giữa
SA
và mặt phẳng
.SBC
A.
15
.
10
B.
85
.
10
C.
15
.
5
D.
10
.
10
Câu 31: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
, 2a SA a
và
SA
vuông góc với
đáy. Mặt phẳng
qua
A
và vuông góc với
SC
chia khối chóp thành hai phần.Tính tỷ số thể tích của hai phần
đó.
A.
1
.
2
B.
1
.
3
C.
2
.
3
D.
3
.
2
Câu 32: Cho khối bát diện đều SABCDS
có cạnh bằng
2.a
Tính thể tích khối đa diện có các đỉnh là trung điểm
của các cạnh
, , , , , , , .SA SB SC SD S A S B S C S D
A.
3
.a
B.
3
4
.
3
a
C.
3
8 .a
D.
3
2
.
4
a
Câu 33: Một cái trục lăn sơn nước có dạng một hình trụ. Đường kính của đường tròn đáy là
5
cm, chiều dài lăn là
23
cm (hình dưới). Sau khi lăn trọn
15
vòng thì trục lăn tạo nên sân phẳng một diện tích là
A.
2
3450π cm
. B.
2
1725π cm
. C.
2
1725 cm
. D.
2
862,5π cm .
Câu 34: Tính thể tích khối cầu nội tiếp tứ diện đều có cạnh bằng 2 6.
A.
4
.
3
B.
4 .
C.
36 .
D.
12 .
Câu 35: Trong với hệ
Oxyz
cho
1;2;3 , 3; 2; 1 .A B
Tìm tọa độ véc tơ
.AB
A.
2; 4; 4 .AB
B.
2;4;4 .AB
C.
1; 2; 2 .AB
D.
4;0;2 .AB
Câu 36: Trong không gian với hệ tọa độ
,Oxyz
3; 4; 2
A
,
5; 6; 2
B
,
10; 17; 7
C
. Viết phương
trình mặt cầu tâm
C
bán kính
AB
.
A.
2 2 2
10 17 7 8x y z
. B.
2 2 2
10 17 7 8x y z
.
C.
2 2 2
10 17 7 8x y z
. D.
2 2 2
10 17 7 8x y z
.
Câu 37: Trong không gian với hệ toạ độ
Oxyz
, cho hình hộp
.ABCD A B C D
có
0; 0; 0
A
,
3; 0; 0
B
,
0; 3; 0
D
,
0; 3; 3
D
. Toạ độ trọng tâm tam giác
A B C
là
A.
1; 1; 2
. B.
2; 1; 2
. C.
1; 2; 1
. D.
2; 1; 1
.
Câu 38: Trong không gian với hệ trục tọa độ
, cho ba điểm
1;2;0
A
;
2;1;1
B
;
0;3; 1
C
. Xét 4 khẳng
định sau:
I.
2BC AB
. II. Điểm
B
thuộc đoạn
AC
.
III.
là một tam giác. IV.
A
,
B
,
C
thẳng hàng.
Trong
4
khẳng định trên có bao nhiêu khẳng định đúng?
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 39: Trong không gian với hệ trục tọa độ
, cho hình bình hành
ABCD
. Biết
2;1; 3
A
,
0; 2;5
B
và
1;1;3
C
. Diện tích hình bình hành
ABCD
là
A.
2 87
. B.
349
2
. C.
349
. D.
87
.
Câu 40: Trong không gian với hệ
cho bốn điểm
1;2;3 , 2;0;4 ,C 3;5; 2 , 10; 7;3 .
A B D
Hỏi có bao
nhiêu mặt phẳng cách đều tất cả các điểm
, , , .A B C D
A. Vô số. B.
3.
C.
4.
D. 7.
--------------------------
Câu 41: Tất cả giá trị của thực của
m
để phương trình
3 1
mx x m
có hai nghiệm thực phân biệt là
; .a b
Tính
giá trị
.P a b
A.
1 3
.
4
P
B.
2 3
.
4
P
C.
1 3
.
2
P
. D.
3 3
.
4
P
Câu 42: Có bao nhiêu giá trị nguyên có bốn chữ số của
m
để phương trình
2 2 2
sin cos cos
2017 2018 .2019
x x x
m có
nghiệm?
A.
1019.
B.
1018.
C.
. D.
.
Câu 43: Từ các chữ số
4,5,6
có thể lập được bao nhiêu số tự nhiên có 12 chữ số sao cho trong mỗi số đó hai chữ
số bất kỳ đứng cạnh nhau hơn kém nhau đúng một đơn vị.
A. 128. B. 64. C. 32. D. 256.
Câu 44: Cho hàm số
f x
. Biết hàm số
y f x
có đồ thị như hình bên. Trên đoạn
4;3
, hàm số
2
2 1
g x f x x
đạt giá trị nhỏ nhất tại điểm
A.
0
4
x
. B.
0
1
x
. C.
0
3
x
. D.
0
3
x
.
Câu 45: Cho hàm số
3 2
y f x ax bx cx d
có đồ thị như hình bên. Đặt
2
2
g x f x x
. Chọn
khẳng định đúng trong các khẳng định sau
A.
nghịch biến trên khoảng
0;2
.B.
đồng biến trên khoảng
1;0
.
C.
nghịch biến trên khoảng
1
;0
2
.D.
đồng biến trên khoảng
; 1
.
Câu 46: Cho hàm số
4 3 2
,f x ax bx cx dx e
(trong đó
, , , ,a b c d e
là những số
thực) và có đồ thị
y f x
như hình vẽ. Hỏi phương trình
f x e
có bao nhiêu nghiệm?
A. 4.
B. 3.
C. 2.
D. 1.
Câu 47: Tìm các giá trị thực của tham số
m
để bất phương trình
0,02 2 0,02
log log 3 1 log
x
m
có nghiệm với mọi
;0
x 
.
A.
9.
m
B.
2.
m
C.
0 1.
m
D.
1.
m
Câu 48: Cho hình chóp
.
S ABC
có
0
60 , 3, 2, 6.
BSA BSC CSA SA SB SC
Tính sin của góc giữa
SC
và mặt phẳng
.SAB
A.
6
.
3
B.
6
.
6
C.
3
.
3
D.
30
.
6
Câu 49: Cho hình chóp S.ABC có đáy là tam giác ABC đều, đường cao SH với
H
nằm trong
ABC và 2SH=BC,
SBC
tạo với mặt phẳng
ABC
một góc . Biết có một điểm O nằm trên đường cao SH sao cho
; ; ; 1
d O AB d O AC d O SBC
. Tính thể tích khối cầu ngoại tiếp hình chóp đã cho.
A.
256
81
. B.
125
162
. C.
500
81
. D.
48
343
Câu 50: Cho tứ diện đều
ABCD
có một đường cao
1
AA
. Gọi
I
là trung điểm
1
AA
. Mặt phẳng
BCI
chia
tứ diện
ABCD
thành hai tứ diện. Tính tỉ số thể tích của hai mặt khối cầu ngoại tiếp hai tứ diện đó.
A.
43 43
.
51 51
B.
1
.
8
C.
43
51
D.
48
153
.
0
60
x
y
2
-2
-1
3
2
O
1
O
x
y
2
4
ĐÁP ÁN
ĐÁP ÁN
Câu 12. Cô An đang ở khách sạn
A
bên bờ biển, cô cần đi du lịch đến hòn đảo
C
. Biết rằng khoảng cách từ đảo
C
đến bờ biển là
10 km
, khoảng cách từ khách sạn
A
đến điểm
B
trên bờ gần đảo
C
là
50 km
. Từ khách
sạn
A
, cô An có thể đi đường thủy hoặc đi đường bộ rồi đi đường thủy để đến hòn đảo
C
(như hình vẽ
bên). Biết rằng chi phí đi đường thủy là
5
USD/km, chi phí đi đường bộ là
3
USD/km. Hỏi cô An phải đi
đường bộ một khoảng bao nhiêu km để chi phí là nhỏ nhất.
A.
15
(km)
2
. B.
85
(km)
2
. C.
50(km)
. D.
10 26 (km)
.
Lời giải
Chọn B.
Gọi
AD
là quãng đường cô An đi đường bộ.
Đặt
km 0 50 DB x x
50 km AD x
.
Chi phí của cô An:
2 2
50 3 10 .5 USD f x x x
f x
liên tục trên
0;50
.
Ta có
2
3 5.
100
x
f x
x
2
2
3 100 5
100
x x
x
0
f x
2
3 100 5 0 x x
2 2
0
9 100 25
x
x x
2
0
9.100
16
x
x
0
15
2
x
x
.
Ta có
15
0 200; 50 50 26; 190
2
f f f
Để chi phí ít nhất thì
15
2
x
.
Vậy cô An phải đi đường bộ một khoảng:
15 85
50 km
2 2
AD
để chi phí ít nhất.
Tập tất cả các giá trị của của
m
để phương trình 3 1mx x m có hai nghiệm thực phân biệt là
; .a b
Tính giá trị
.P a b
A
B
C
50 km
10 km
A.
1 3
.
4
P
. B.
3 1
.
4
P
. C.
3 1
.
2
P
. D.
3 3
.
4
P
Lời giải
Chọn D.
Ta có phương trình 3 1mx x m
1
xác định với
3;x
1
1 3 1m x x với
3;x
3 1
1
x
m
x
với
3;x
Xét hàm số
3 1
1
x
y f x
x
với
3;x
.
2
5 2 3
2 3 1
x x
f x
x x
với
3;x
0f x
2 3 5x x
2
3 5
4 3 5
x
x x
2
3 5
14 37 0
x
x x
3 5
7 2 3
7 2 3
x
x
x
7 2 3
Dựa vào đồ thị ta thấy với
1 1 3
2 4
m
thì đường thẳng
y m
cắt đồ thị hàm số
3 1
1
x
y f x
x
tại hai điểm phân biệt nên phương trình
1
có hai nghiệm phân biệt.
Câu 18: Số
19
2
2
+1
có bao nhiêu chữ số trong hệ đếm thập phân?
A.
157827.
B.
157826.
C. 315654. D. 315653..
Lời giải
Chọn A.
Ta có
19
2
2 1F
19
2
log log 2 1F
.
Do
19 19 19 19
2 2 2 2
log 2 log 2 1 log 2 .2 157826.44 log 2 1 157826.72
19
2
log 2 1 157826
.
Vậy số
97
2
2 1F
có 157827 chữ số.
Câu 20:
Lời giải
Chọn D
Số tiền 100 triệu đồng lần đầu tiên, kì hạn 3 tháng,
5%r
. Sau 6 tháng, cả vốn lẫn lãi là:
2
6
1 1
. 1 100.10 . 1 5%
n
T A r
Sau đó, gửi thêm 50 triệu trong 6 tháng tiếp theo, kì hạn 3 tháng,
5%r
. Tổng số tiền người đó nhận
được sau 1 năm:
2 2 2
6 6
2 1
. 1 5% (100.10 1 5% 50.10 ). 1 5% 176675625 176676000T T
CÂu 33: Một cái trục lăn sơn nước có dạng một hình trụ. Đường kính của đường tròn đáy là cm, chiều dài lăn là
cm (hình dưới). Sau khi lăn trọn vòng thì trục lăn tạo nên sân phẳng một diện tích là
A. . B. . C. . D. .
Lời giải
Chọn B.
Diện tích xung quanh hình trụ .
Vậy sân phẳng có diện tích .
Câu 38. Trong không gian với hệ toạ độ
Oxyz
, cho hình hộp
.ABCD A B C D
có
0; 0; 0A
,
3; 0; 0
B
,
0; 3; 0D
,
0; 3; 3D
. Toạ độ trọng tâm tam giác
A B C
là
A.
1; 1; 2
. B.
2; 1; 2
. C.
1; 2; 1
. D.
2; 1; 1
.
Lời giải
Chọn B.
Cách 1 : Ta có
3; 0; 0AB
. Gọi
; ; ; 3;C x y z DC x y z
ABCD
là hình bình hành
; ; 3; 3; 0 3; 3; 0AB DC x y z C
Ta có
0; 3; 0AD
. Gọi
; ; ; 3 ; 3A x y z A D x y z

ADD A
là hình bình hành
; ; 0; 0; 3 0; 0; 3AD A D x y z A
Gọi
0 0 0 0 0 0
; ; ; ; 3B x y z A B x y z
ABB A
là hình bình hành
0 0 0
; ; 3; 0; 3 3; 0; 3
AB A B x y z B
5
23
15
2
3450
π cm
2
1725
π cm
2
1725 cm
2
862,5
π cm
2
π
xq
S rl
5
2
π .23 115π
2
2
115
π.15 1725π cm
A
B
C
D
A
B
C
D
G
là trọng tâm tam giác
0 3 3
2
3
0 0 3
1 2; 1; 2
3
3 3 0
2
3
G
G
G
x
y G
z
.
Cách 2: Gọi
I
là trung điểm của đoạn thẳng
BD
.Ta có
3 3 3
; ;
2 2 2
I
.Gọi
; ;G a b c
là trọng tâm tam
giác
A B C
Ta có :
3DI IG
với
3 3 3
; ;
2 2 2
3 3 3
; ;
2 2 2
DI
IG a b c
. Do đó :
3 3
3
2 2
2
3 3
3 1
2 2
2
3 3
3
2 2
a
a
b b
c
c
.
Vậy
2;1; 2
G
.
Câu 38: Trong không gian với hệ trục tọa độ
, cho ba điểm
1;2;0
A
;
2;1;1
B
;
0;3; 1
C
. Xét 4 khẳng
định sau:
I.
2BC AB
. II. Điểm
B
thuộc đoạn
AC
.
III.
là một tam giác. IV.
A
,
B
,
C
thẳng hàng.
Trong
4
khẳng định trên có bao nhiêu khẳng định đúng?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn B.
Ta có:
1; 1;1
AB
;
1;1; 1
AC
.
3
AB
;
3
AC
;
AB AC
A
là trung điểm của
BC
Vậy khẳng định (I); (IV) đúng. Khẳng định (II); (III) sai.
Câu 41: Tất cả giá trị của thực của để phương trình có hai nghiệm thực phân biệt là
; .a b
Tính giá trị
.P a b
A.
1 3
.
4
P
B.
2 3
.
4
P
C.
1 3
.
2
P
. D.
3 3
.
4
P
Lời giải
Chọn D.
Ta có phương trình xác định với
với
với
Xét hàm số với .
m
3 1
mx x m
3 1
mx x m
1
3;x
1
1 3 1
m x x
3;x
3 1
1
x
m
x
3;x
3 1
1
x
y f x
x
3;x
với
Dựa vào đồ thị ta thấy với thì đường thẳng cắt đồ thị hàm số
tại hai điểm phân biệt nên phương trình có hai nghiệm phân biệt.
[<br>]
Câu 42: Có bao nhiêu giá trị nguyên có bốn chữ số của để phương trình có
nghiệm?
A.
1019.
B.
1018.
C. . D. .
Hướng dẫn giải
Chọn C.
Phương trình tương đương: .
Đặt với ta được .
Xét với .
Hàm số nghịch biến trên .
và .
2
5 2 3
2 3 1
x x
f x
x x
3;x
0
f x
2 3 5
x x
2
3 5
4 3 5
x
x x
2
3 5
14 37 0
x
x x
3 5
7 2 3
7 2 3
x
x
x
7 2 3
1 1 3
2 4
m
y m
3 1
1
x
y f x
x
1
m
2 2 2
sin cos cos
2017 2018 .2019
x x x
m
2 2
cos cos
1 2018
2017
2017.2019 2019
x x
m
2
cost x
0;1
t
1 2018
2017
2017.2019 2019
t t
m
1 2018
2017
2017.2019 2019
t t
f t
0;1
t
f t
0;1
D
Max 0 2018
D
f t f
Min 1 1
D
f t f
Phương trình có nghiệm hay .
Vậy có
1019
giá trị nguyên để phương trình có nghiệm.
[<br>]
Câu 43: Từ các chữ số
4,5,6
có thể lập được bao nhiêu số tự nhiên có 12 chữ số sao cho trong mỗi số đó hai chữ
số bất kỳ đứng cạnh nhau hơn kém nhau đúng một đơn vị.
A. 128.
B. 64.
C. 32.
D. 256.
Hướng dẫn
Vì số có 12 chữ số và trong số đó hai chữ số bất kỳ đứng cạnh nhau hơn kém nhau một đơn vị nên số lần xuất hiện
chữ số 5 là 6 lần.
+ Đánh thứ tự các chữ số trong số có 12 chữ số là: 1,2,3,4,...,12. Ta có
TH1 chữ số 5 ở vị trí chẵn, 6 vị trí còn lại mỗi vị trí có 2 cách chọn.
TH2 chữ số 5 ở vị trí lẻ, 6 vị trí còn lại mỗi vị trí có 2 cách chọn.
Vậy có
6
2.2 128.
[<br>]
Câu 44: Cho hàm số . Biết hàm số có đồ thị như hình bên. Trên đoạn , hàm số
đạt giá trị nhỏ nhất tại điểm
A.
. B.
. C.
. D.
.
Lời giải
Chọn B.
Min Max
D
D
f t m f t
1;2018
m
m
f x
y f x
4;3
2
2 1
g x f x x
0
4
x
0
1
x
0
3
x
0
3
x
Ta có
.
.
Dựa vào hình vẽ ta có: .
Và ta có bảng biến thiên
Suy ra hàm số đạt giá trị nhỏ nhất tại điểm .
[<br>]
Câu 45: Cho hàm số có đồ thị như hình bên. Đặt . Chọn
khẳng định đúng trong các khẳng định sau
A. nghịch biến trên khoảng . B. đồng biến trên khoảng .
C. nghịch biến trên khoảng . D. đồng biến trên khoảng .
Lời giải
Chọn C.
2 2 1
g x f x x
0
g x
2 2 1 0
f x x
1
f x x
4
0 1
3
x
g x x
x
2
2 1
g x f x x
0
1
x
3 2
y f x ax bx cx d
2
2
g x f x x
0;2
g x
1;0
1
;0
2
; 1
O
x
y
2
4
Hàm số ; , có đồ thị như hình vẽ.
Do đó ; ; ; .
Tìm được và hàm số .
Ta có
;
Bàng xét dấu của :
Vậy nghịch biến trên khoảng .
[<br>]
Câu 46: Cho hàm số
4 3 2
,f x ax bx cx dx e
(trong đó
, , , ,a b c d e
là những số thực) và có đồ thị
y f x
như hình vẽ. Hỏi phương trình
f x e
có bao nhiêu nghiệm?
A. 4.
B. 3.
C. 2.
3 2
y f x ax bx cx d
2
3 2
f x ax bx c
0 4
x d
2 8 4 2 0
x a b c d
2 0 12 4 0
f a b c
0 0 0
f c
1; 3; 0; 4
a b c d
3 2
3 4
y x x
2
2
g x f x x
3
2 2
2 3 2 4
x x x x
2 2
3 1
2 1 2 3 2 1 3 2 1 2 1
2 2
g x x x x x x x x
1
2
0 1
2
x
g x x
x
x
y
y
1
0
0
0
1/ 2
2
4
4
7 7 10
8
g x
1
;0
2
x
y
2
-2
-1
3
2
O
1
D. 1.
Hướng dẫn
Từ đồ thị
3 2 4 3
1
3 2 2
4
y f x f x x x f x x x x e f x e
có 4 nghiệm phân biệt.
[<br>]
Câu 47: Tìm các giá trị thực của tham số để bất phương trình có nghiệm với
mọi .
A. B. C. D.
Lời giải
Chọn D.
TXĐ:
ĐK tham số :
Ta có:
Xét hàm số có
Bảng biến thiên :
0
+
1
0
Khi đó với yêu cầu bài toán thì
[<br>]
Câu 48: Cho hình chóp
.
S ABC
có
0
60 , 3, 2, 6.
BSA BSC CSA SA SB SC
Tính sin của góc giữa
SC
và mặt phẳng
.SAB
A.
6
.
3
B.
6
.
6
C.
3
.
3
D.
30
.
6
Hướng dẫn
Dựng tứ diện đều có cạnh bằng
6.
Đáp án.
[<br>]
m
0,02 2 0,02
log log 3 1 log
x
m
;0
x 
9.
m
2.
m
0 1.
m
1.
m
0,02 2 0,02
log log 3 1 log
x
m
D
m
0
m
0,02 2 0,02 2
log log 3 1 log log 3 1
x x
m m
2
log 3 1 , ;0
x
f x x 
3 .ln 3
0, ;0
3 1 ln 2
x
x
f x

f x
x

f
f
1.
m
Câu 49: Cho hình chóp S.ABC có đáy là tam giác ABC đều, đường cao SH với nằm trong ABC và 2SH=BC,
tạo với mặt phẳng một góc . Biết có một điểm O nằm trên đường cao SH sao cho
. Tính thể tích khối cầu ngoại tiếp hình chóp đã cho. A.
. B. . C. . D.
Lời giải
Chọn D.
Giả sử là chân đường vuông góc hạ từ xuống . Khi đó ta có . Do
nên . Do đó là phân giác của góc .
Khi đó là trung điểm của .
Do . Kẻ thì . Do đó và .
Đặt thì .
Do đó nên là tâm tam giác đều là hình chóp tam giác đều và
là trung điểm .
Mặt khác trong tam giác có : . Do đều có nên
.
Khi đó vuông tại và có . Từ đó
.
Gọi là bán kính mặt cầu ngoại tiếp hình chóp thì .
.
H
SBC
ABC
0
60
; ; ; 1
d O AB d O AC d O SBC
256
81
125
162
500
81
48
343
D
F
E
A
C
B
S
H
O
K
,E F
O
,AB AC
,
HE AB HF AC
1
OE OF
HE HF
AH
AH BC D
BC
BC AD BC SAD
OK SD
OK SBC
1
OK
60
SDA
2 0
AB BC CA a a
, .cot 60
3
a
SH a HD a
3 3
AD a HD
H
.
S ABC
,E F
,AB AC
SOK
2
sin 30
OK
SO
DEF
OH DFE
1
OE OF OD
K D
DSO
D
DH SO
2
.DH HS HO
2
2
3
a
a a
3
2
a
3
3,
2
AB SH
R
.
S ABC
2
7
2 4
SA
R
SH
3
/
4 7 343
.
3 4 48
m c
V
[<br>]
Câu 50: Cho tứ diện đều có một đường cao . Gọi là trung điểm . Mặt phẳng chia
tứ diện thành hai tứ diện. Tính tỉ số thể tích của hai mặt khối cầu ngoại tiếp hai tứ diện đó.
A.
43 43
.
51 51
B.
1
.
8
C. D. .
Lời giải
Chọn A.
Gọi cạnh của tứ diện đều là . Gọi là trung điểm của và . Qua kẻ đường thẳng
song song với cắt tại .
Ta có: và nên suy ra và .
Gọi là trung điểm của , trong mặt phẳng dựng đường trung trực của cắt tại .
Ta dễ dàng chứng minh được là tâm của mặt cầu ngoại tiếp .
Ta có: , . Đặt .
Tam giác đồng dạng với tam giác nên suy ra
.
Gọi là bán kính mặt cầu ngoại tiếp ta suy ra:
.
Với ta có: .
ABCD
1
AA
I
1
AA
BCI
ABCD
43
51
48
153
a
K
CD
E IK AB
1
A
IK
AB
J
1
2
3
BABJ
BE BK
1
1
AE AI
EJ IA
1
4 4
a
AE AB
3
4
a
BE
M
BE
ABK
BE
1
AA
O
O
EBCD
1
3
3
a
BA
1
6
3
a
AA
BE x
AOM
1 1
. 1
2 2
AM OM AM BH x
OM a
AA BH AA
R
EBCD
2
2
2 2
1
4 2 2
x x
R OB OM MB a
3
4
a
x
2
2
9 1 3 43
64 2 8 128
a a
R a a
Tương tự với ta có bán kính của mặt cầu ngoại tiếp là
.
Do đó .
3
3
.
V R
V
R
4
a
x
R
EACD
2
2
1 51
64 2 4 128
a a
R a a
43
' 51
R
R
| 1/18
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC
KÌ THI THPT QUỐC GIA LẦN II NĂM HỌC 2018 - 2019 TRƯỜNG THPT HAI BÀ TRƯNG Đề thi môn: Toán.
Thời gian làm bài 90 phút, không kể thời gian giao đề
(Đề thi gồm 50 câu trắc nghiệm) Mã đề thi 132
Câu 1: Asian cup 2019 đội Việt Nam nằm ở bảng D gồm các đội Iran, Iraq và Yemen thi đấu theo thể thức mỗi
đội gặp nhau một lần. Hỏi khi kết thức vòng đấu bảng ở bảng D có bao nhiêu trận đấu. A. 6. B. 8. C. 7. D. 5.
Câu 2: Có bao nhiêu cách xếp ba bạn học sinh nam hai bạn học sinh nữ và một cô giáo vào một hàng gồm sáu ghế
sao cho cô giáo ngồi giữa hai bạn học sinh nữ (cô giáo và hai bạn học sinh nữ ngồi liền kề). A. 48. B. 126 C. 144. D. 84.
Câu 3: Cho cấp số cộng có số hạng đầu u  1, công sai d  2. Tìm u . 1 19
A. u  37. B. u  36. C. u  20. D. u  19. 19 19 19 19
Câu 4: Cho hàm số y f x liên tục và có đạo hàm liên tục trên khoảng a;b. Trong các khẳng định sau khẳng định nào sai?
A. Nếu hàm số y f x đồng biến trên khoảng  ;
a b thì f  x  0 x
  a;b. .
B. Nếu f   x không đổi dấu trên khoảng  ;
a b thì f x không có cực trị trên khoảng a;b.
C. Nếu hàm số f  x  0 với mọi x a;b thì hàm số y f x đồng biến trên khoảng a;b.
D. Nếu hàm số f  x  0 với mọi x a;b thì hàm số y f x nghịch biến trên khoảng a;b.
Câu 5: Trong các hàm số sau hàm số nào không có cực trị? A. 3 2
y x  3x  15x  1. B. 3 2
y  x  3x  15x  1. C. 3 2
y x  3x  15x  1. D. 3 2
y x  3x  2019. x  1
Câu 6: Đồ tị hàm số y
có bao nhiêu đường tiệm cận? x  1 A. 2. B. 1. C. 0. D. 3.
Câu 7: Đường thẳng y  2x  1 và đồ thị C  hàm số 3 2
y x  6x  11x  1 có bao nhiêu điểm chung? A. 2. B. 3. C. 1 D. 0.
Câu 8: Gọi m và M lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3 2
y x  3x  9x  5 trên đoạn
0;5. Tính giá trị P M  . m A. P  12. B. P  22. C. P  15. D. P  10. Câu 9: Cho hàm số 3 2
y x  6x  9x 1. Mệnh đề nào dưới đây là đúng ?
A. Hàm số đồng biến trên khoảng 1;  .
B. Hàm số đồng biến trên khoảng  ;  3 .
C. Hàm số nghịch biến trên khoảng 1;3 .
D. Hàm số nghịch biến trên khoảng 3;  .
Câu 10: Giá trị cực tiểu của hàm số 3 2
y x  3x  9x  2 là A. 2  0 . B. 7 . C. 2  5 . D. 3 .
Câu 11: Đồ thị của hàm số nào sau đây có tiệm cận ngang ? 2 16  x 4x  15 2 x  1 A. y  .B. y  . C. y  . D. 2 y x  2019. x 3x  1 x
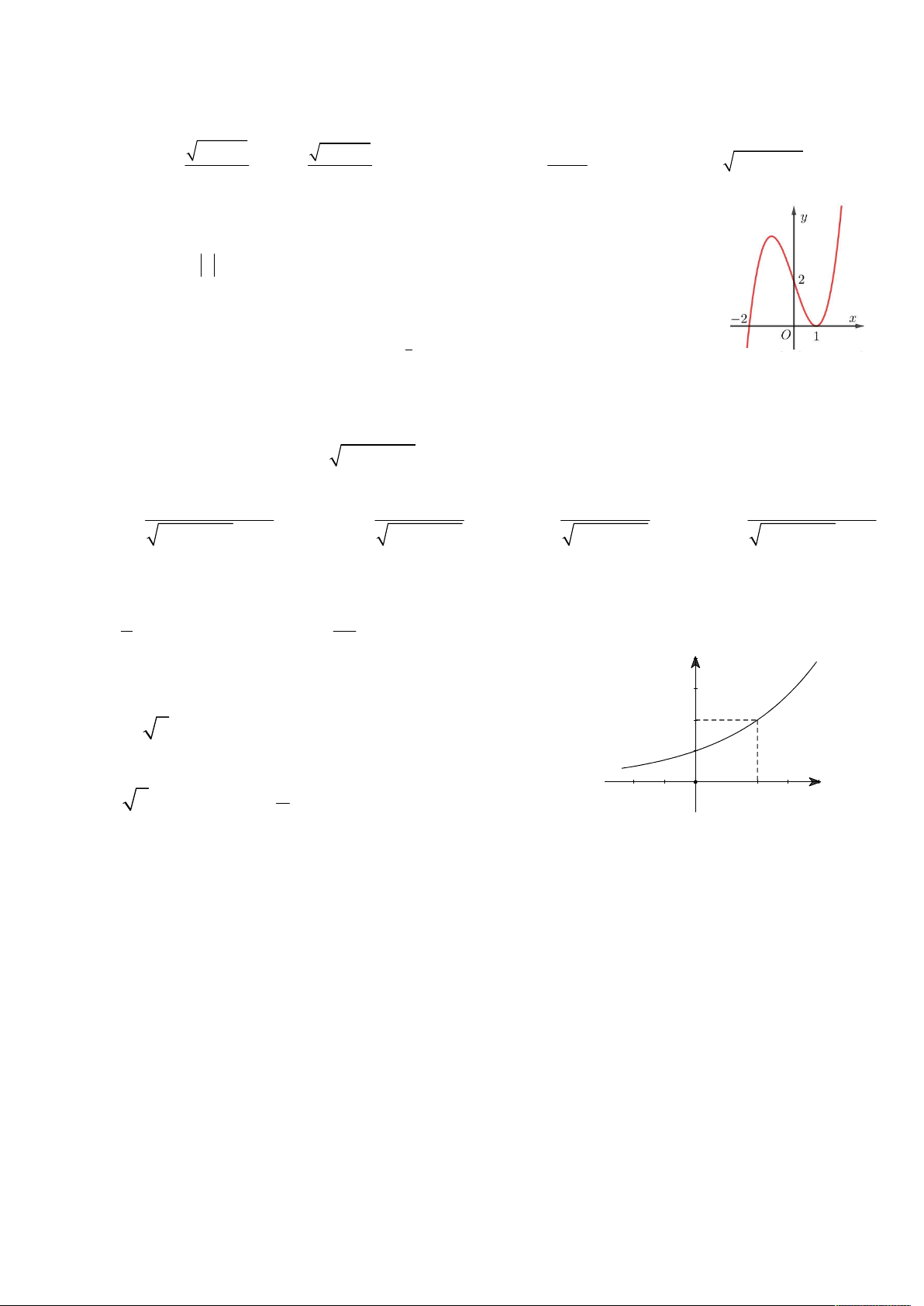
Câu 12: Cho hàm số y f x có đồ thị như hình vẽ:
Hỏi hàm số y f x  có bao nhiêu điểm cực trị? A. 3. B. 2. C. 4. D. 5. 1
Câu 13: Tập xác định của hàm số y   x  3 1 là:
A. D  1;. B. D  .  C. D   ;  
1 . D. D  0;.
Câu 14: Cho hàm số f x   2 lg x
x  2019 . Tính f x. 1 1 ln10 2019
A. f  x 
. B. f  x 
. C. f  x 
. D. f  x  . 2 x  2019.ln10 2 x  2019 2 x  2019 2 x  2019.ln10
Câu 15: Trong các hàm số sau hàm số nào đồng biến trên  ?  x  1  1 A. y x   B. y e  . C. y  . D. 2 y  ln x . x  2   y
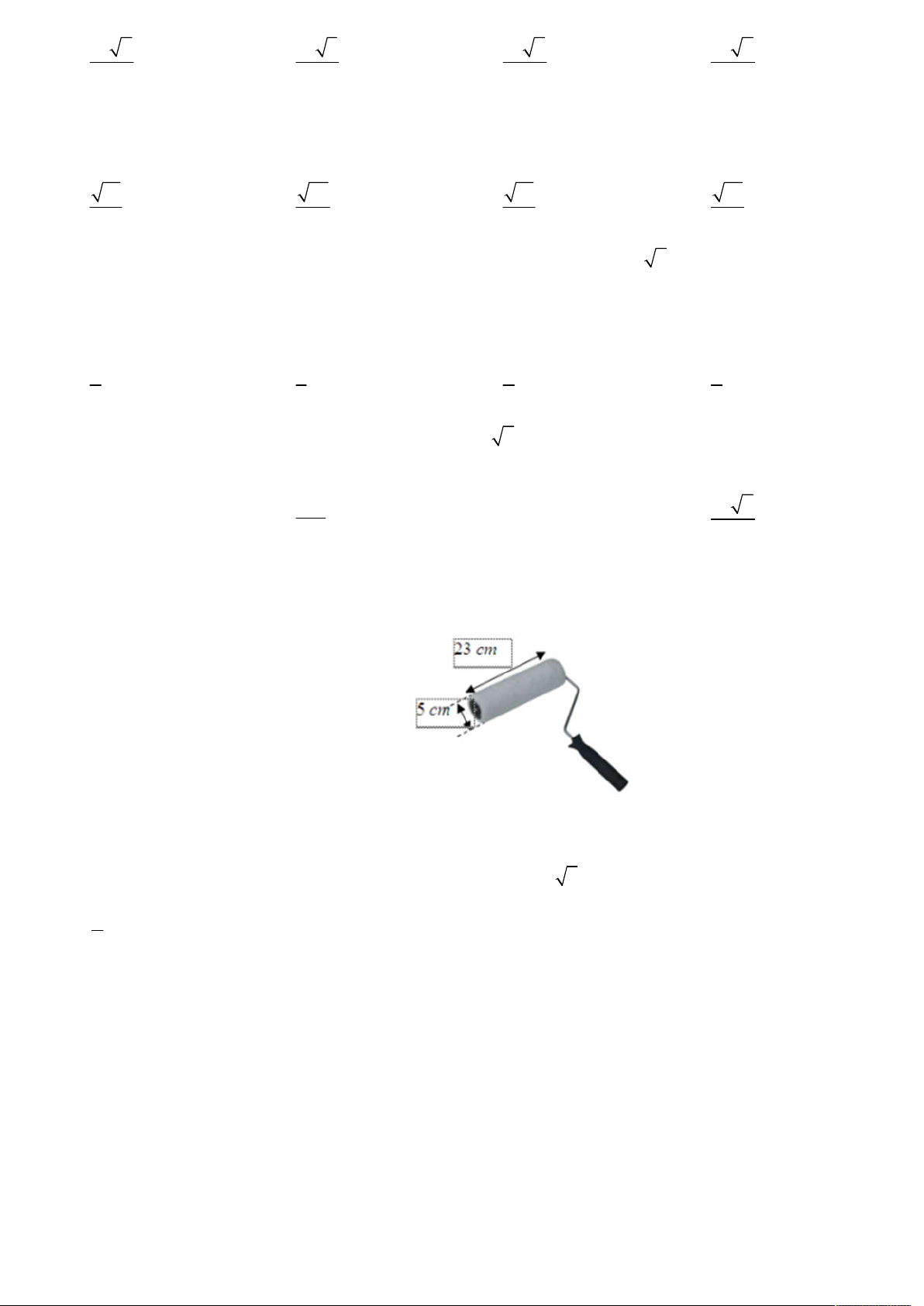
Câu 16: Hình vẽ bên là của đồ thị hàm số nào trong các hàm số sau: x 2
A. y   2  . B. 2x y  . 1 xx  1  O 2 x
C. y   2  . D. y  .    2 
Câu 17: Bất phương trình log
4  x  3 có bao nhiêu nghiệm nguyên? 2   A. 8. B. 7. C. 10. D. 11. 19 Câu 18: Số 2 2
 1 có bao nhiêu chữ số trong hệ đếm thập phân? A. 157827. B. 157826. C. 315654. D. 315653..
Câu 19: Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y   2
ln x  2x  3 trên đoạn
0;2. Tính giá trị biểu thức M m A ee . A. A  5. B. A  6. C. A  3. D. A  8
Câu 20: Một người gửi ngân hàng 100 triệu đồng với kì hạn 3 tháng, lãi suất 5% một quý theo hình thức lãi
kép ( sau 3 tháng sẽ tính lãi và cộng vào gốc). Sau đúng 6 tháng, người đó gửi thêm 50 triệu đồng với kì hạn
và lãi suất như trước đó. Tính tổng số tiền người đó nhận được sau 1 năm ( Tính từ lần gửi đầu tiên)?
A. 179, 676 triệu đồng. B. 177, 676 triệu đồng
C. 178, 676 triệu đồng. D. 176, 676 triệu đồng
Câu 21: Trong các hàm số sau, hàm số nào có một nguyên hàm là hàm số F x  ln x ? 1 3 x
A. f x  . x
B. f x  .
C. f x  .
D. f x  x . x 2
Câu 22: Cho f x , g x là các hàm số xác định và liên tục trên  . Trong các mệnh đề sau, mệnh đề nào sai? A.
f xg x dx f x d .
x g x dx    .
B. 2 f x dx  2 f x dx   .
C.  f x  g x dx f x dx g x dx     
. D.  f x  g x dx f x dx g x dx      .
Câu 23: Tìm họ nguyên hàm của hàm số   3x f x  . A.   d  3x f x xC  . B.  d  3x f x x ln 3  C  . 3x x 1 3  C.
f x dx   C  . D.
f x dx   C  . ln 3 x  1
Câu 24: Tìm họ nguyên hàm của hàm số f x 2  sin 2x . 1 sin 4x 1 sin 4x A.
f x dx x   C.  . B..
f x dx x   C.  2 8 2 8 1 sin 4x 1 sin 4x C..
f x dx x   C.  D..
f x dx x   C.  2 2 2 2 2 2 Câu 25: Cho I
f x dx  3 
. Khi đó J  4 f x  3 dx    bằng: 0 0 A. 2 . B. 6 . C. 8 . D. 4 . 10 6
Câu 26: Cho hàm số f x liên tục trên đoạn 0;10 và f x dx  7  và
f x dx  3  . Tính 0 2 2 10 P
f x dx
f x dx   . 0 6 A. P  7 . B. P  4 . C. P  4 . D. P  10 . e 1 Câu 27: I
dx  ln e a  2 ln 2.  Tìm a ? x  3 1 A. a  12. B. a  2. C. a  7. D. a  3. 
Câu 28: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại 0
B, AB a, BAC  60 , SA  2a, SA vuông góc
với đáy. Tính sin của góc giữa hai mặt phẳng SAC  và SBC . 10 15 5 10 A. . B. . C. . D. . 5 5 5 10
Câu 29: Tính thể tích khối chóp tam giác đều có cạnh đáy bằng a, cạnh bên bằng a 3. 3 a 2 3 a 3 3 a 6 3 a 2 A. . B. . C. . D. . 6 6 6 2 
Câu 30: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại 0 ,
A AB a, ABC  60 , SB  2a, SB vuông
góc với đáy. Tính sin của góc giữa SA và mặt phẳng SBC . 15 85 15 10 A. . B. . C. . D. . 10 10 5 10
Câu 31: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA a 2 và SA vuông góc với
đáy. Mặt phẳng   qua A và vuông góc với SC chia khối chóp thành hai phần.Tính tỷ số thể tích của hai phần đó. 1 1 2 3 A. . B. . C. . D. . 2 3 3 2
Câu 32: Cho khối bát diện đều SABCDS  có cạnh bằng a 2. Tính thể tích khối đa diện có các đỉnh là trung điểm của các cạnh S ,
A SB, SC, SD, S  , A S B  , S C  , S  . D A. 3 a . 3 4a C. 3 8a . 3 a 2 B. . D. . 3 4
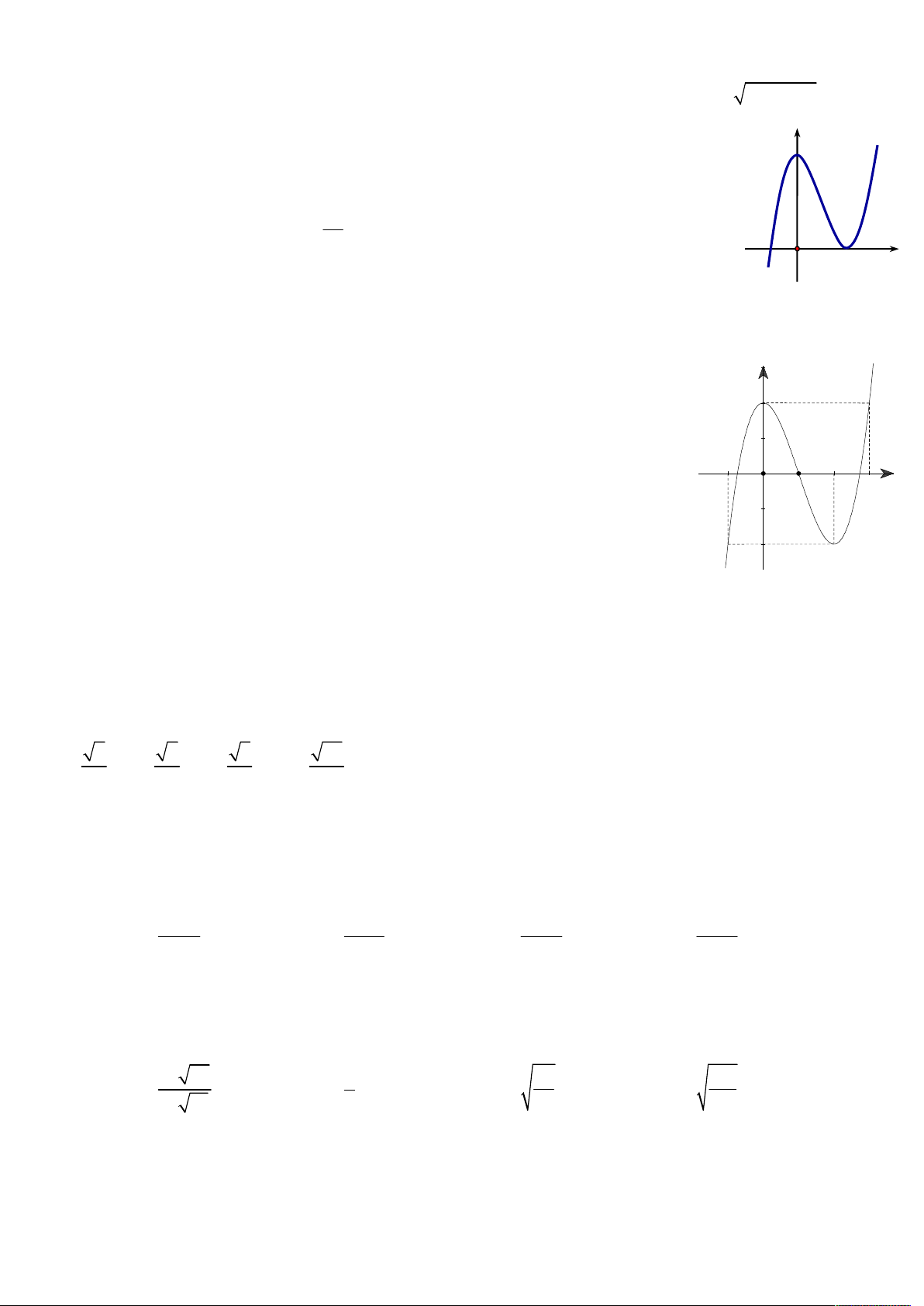
Câu 33: Một cái trục lăn sơn nước có dạng một hình trụ. Đường kính của đường tròn đáy là 5 cm, chiều dài lăn là
23 cm (hình dưới). Sau khi lăn trọn 15 vòng thì trục lăn tạo nên sân phẳng một diện tích là A. 2 3450π cm . B. 2 1725π cm . C. 2 1725 cm . D. 2 862,5π cm .
Câu 34: Tính thể tích khối cầu nội tiếp tứ diện đều có cạnh bằng 2 6. 4 B. 4. C. 36. D. 12. A.  . 3 
Câu 35: Trong với hệ Oxyz cho A1; 2;3 , B 3; 2  ;  
1 . Tìm tọa độ véc tơ A . B    
A. AB  2; 4; 4. B. AB  2; 4; 4. C. AB  1;2; 2
 . D. AB  4;0; 2.
Câu 36: Trong không gian với hệ tọa độ Oxyz, A 3  ; 4; 2 , B  5  ; 6; 2 , C  1  0; 17; 7   . Viết phương
trình mặt cầu tâm C bán kính AB . 2 2 2 2 2 2
A.  x 10   y 17   z  7  8 .
B.  x 10   y 17   z  7  8 . 2 2 2 2 2 2
C.  x 10   y 17   z  7  8 .
D.  x 10   y  17   z  7  8 .
Câu 37: Trong không gian với hệ toạ độ Oxyz , cho hình hộp ABC . D AB CD
  có A0; 0; 0 , B 3; 0; 0 ,
D 0; 3; 0 , D0; 3;  3 . Toạ độ trọng tâm tam giác A BC  là A. 1; 1;  2 . B. 2; 1;  2 . C. 1; 2;   1 . D. 2; 1;   1 .
Câu 38: Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm A1; 2;0 ; B 2;1  ;1 ; C 0;3;   1 . Xét 4 khẳng định sau: I. BC  2AB .
II. Điểm B thuộc đoạn AC .
III. ABC là một tam giác.
IV. A , B , C thẳng hàng.
Trong 4 khẳng định trên có bao nhiêu khẳng định đúng? A. 1. B. 2 . C. 3 . D. 4 .
Câu 39: Trong không gian với hệ trục tọa độ Oxyz , cho hình bình hành ABCD . Biết A2;1;  3 , B 0;  2;5 và
C 1;1;3 . Diện tích hình bình hành ABCD là 349 A. 2 87 . B. . C. 349 . D. 87 . 2
Câu 40: Trong không gian với hệ Oxyz cho bốn điểm A1; 2;3 , B 2;0; 4, C3;5; 2  , D 10; 7  ;3. Hỏi có bao
nhiêu mặt phẳng cách đều tất cả các điểm ,
A B, C, D.
A. Vô số. B. 3. C. 4. D. 7. --------------------------
Câu 41: Tất cả giá trị của thực của m để phương trình mx
x  3  m 1 có hai nghiệm thực phân biệt là  ; a b. Tính
giá trị P a  . b 1  3 2  3 1  3 3  3 A. P  . B. P  . C. P  . . D. P  . 4 4 2 4 2 2 2
Câu 42: Có bao nhiêu giá trị nguyên có bốn chữ số của m để phương trình sin x cos x cos 2017  2018  .2019 x m có nghiệm? A. 1019. B. 1018. C. 2018 . D. 2019 .
Câu 43: Từ các chữ số 4, 5, 6 có thể lập được bao nhiêu số tự nhiên có 12 chữ số sao cho trong mỗi số đó hai chữ
số bất kỳ đứng cạnh nhau hơn kém nhau đúng một đơn vị. A. 128. B. 64. C. 32. D. 256.
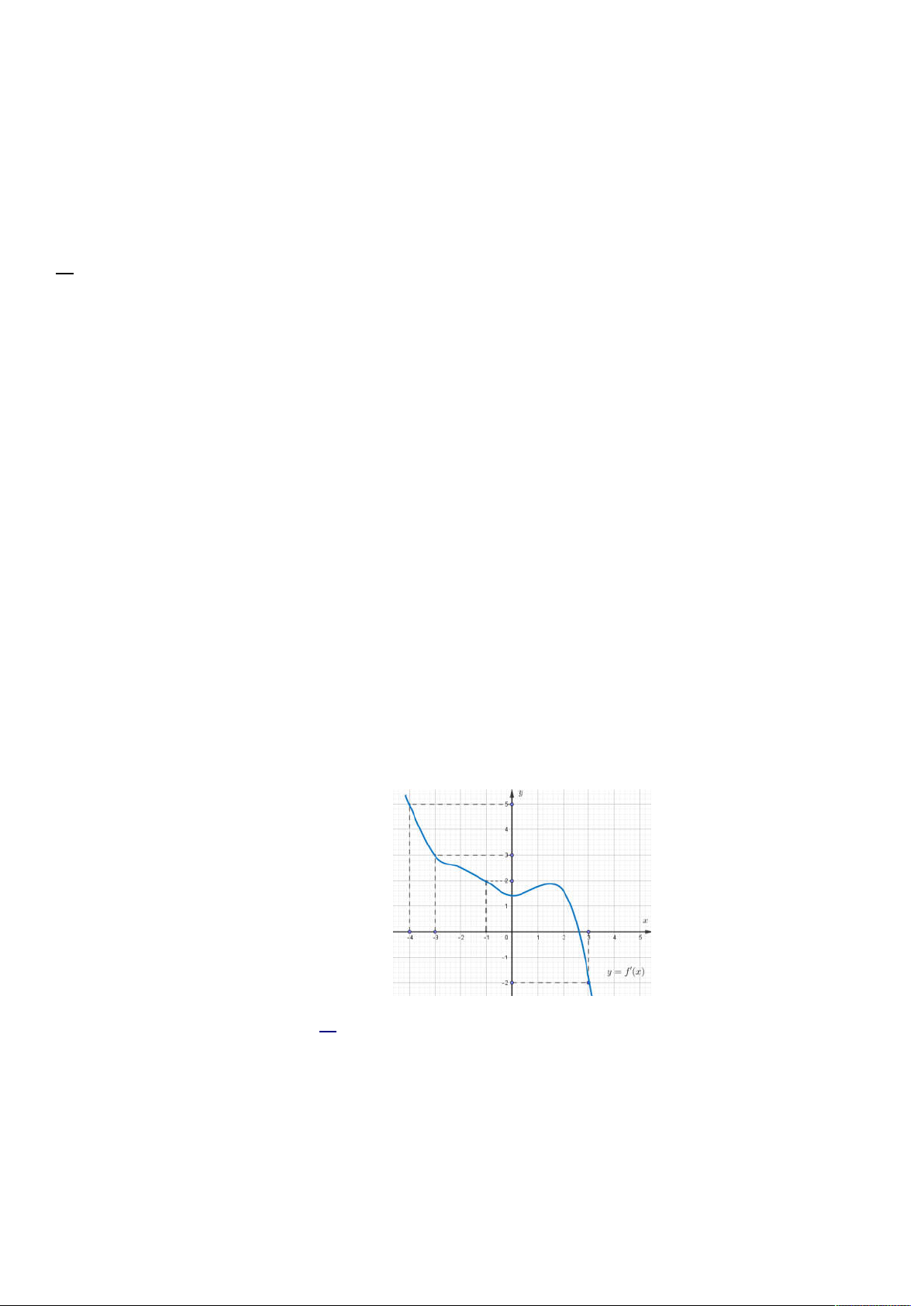
Câu 44: Cho hàm số f x . Biết hàm số y f  x có đồ thị như hình bên. Trên đoạn  4  ;  3 , hàm số
g x  f x    x2 2 1
đạt giá trị nhỏ nhất tại điểm A. x  4  . B. x  1 . C. x  3 . D. x  3  . 0 0 0 0 Câu 45: Cho hàm số    3 2 y
f x ax bx cx d có đồ thị như hình bên. Đặt g x  f  2
x x  2  . Chọn
khẳng định đúng trong các khẳng định sau y 4
A. g x nghịch biến trên khoảng 0; 2 .B. g x đồng biến trên khoảng  1  ; 0 .  1 
C. g x nghịch biến trên khoảng ; 0 
 .D. g x đồng biến trên khoảng   ;    1 .  2  O x 2
Câu 46: Cho hàm số f x 4 3 2
ax bx cx dx  ,
e (trong đó a, b, c, d , e là những số
thực) và có đồ thị y f  x như hình vẽ. Hỏi phương trình f x  e có bao nhiêu nghiệm? y A. 4. 2 B. 3. C. 2. -1 2 O 1 3 x D. 1.
Câu 47: Tìm các giá trị thực của tham số m để bất phương trình -2 log log 3x 1  log
m có nghiệm với mọi x   ;  0 . 0,02  2   0,02 A. m  9. B. m  2. C. 0  m  1. D. m  1.   
Câu 48: Cho hình chóp S.ABC có 0
BSA BSC CSA  60 , SA  3, SB  2, SC  6. Tính sin của góc giữa
SC và mặt phẳng SAB. 6 6 3 30 A. . B. . C. . D. . 3 6 3 6
Câu 49: Cho hình chóp S.ABC có đáy là tam giác ABC đều, đường cao SH với H nằm trong  ABC và 2SH=BC,
SBC  tạo với mặt phẳng  ABC một góc 0
60 . Biết có một điểm O nằm trên đường cao SH sao cho
d O; AB  d O; AC   d  ;
O SBC  1. Tính thể tích khối cầu ngoại tiếp hình chóp đã cho. 256 125 500 343 A. . B. . C. . D. 81 162 81 48
Câu 50: Cho tứ diện đều ABCD có một đường cao AA . Gọi I là trung điểm AA . Mặt phẳng  BCI  chia 1 1
tứ diện ABCD thành hai tứ diện. Tính tỉ số thể tích của hai mặt khối cầu ngoại tiếp hai tứ diện đó. 43 43 1 43 48 A. . B. . C. D. . 51 51 8 51 153 ĐÁP ÁN ĐÁP ÁN
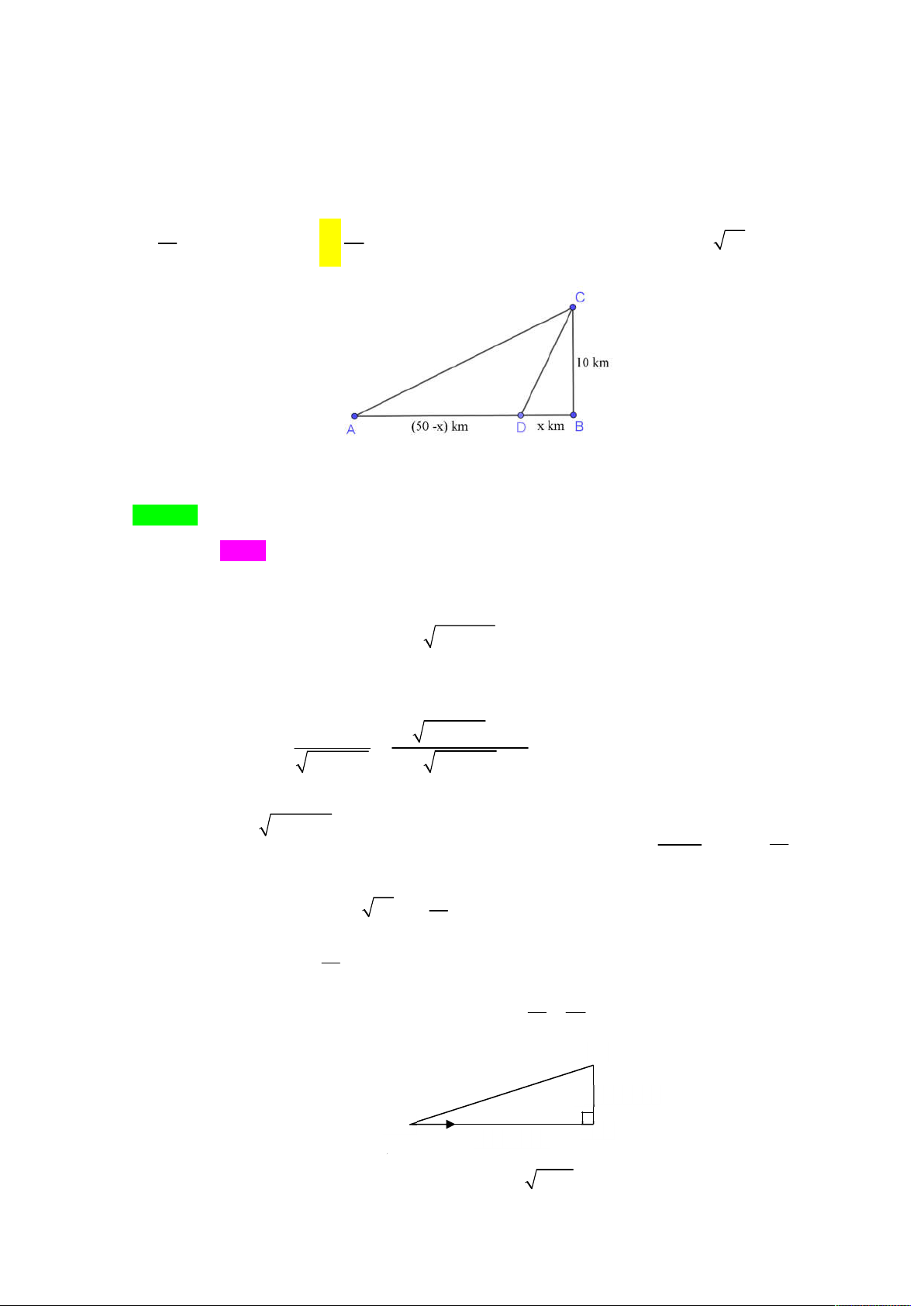
Câu 12. Cô An đang ở khách sạn A bên bờ biển, cô cần đi du lịch đến hòn đảo C . Biết rằng khoảng cách từ đảo C
đến bờ biển là 10 km , khoảng cách từ khách sạn A đến điểm B trên bờ gần đảo C là 50 km . Từ khách
sạn A , cô An có thể đi đường thủy hoặc đi đường bộ rồi đi đường thủy để đến hòn đảo C (như hình vẽ
bên). Biết rằng chi phí đi đường thủy là 5 USD/km, chi phí đi đường bộ là 3 USD/km. Hỏi cô An phải đi
đường bộ một khoảng bao nhiêu km để chi phí là nhỏ nhất. 15 85 A. (km) . B. (km) . C. 50(km) . D. 10 26 (km) . 2 2 Lời giải Chọn B.
Gọi AD là quãng đường cô An đi đường bộ.
Đặt DB x km0  x  50  AD  50  x km .
Chi phí của cô An: f x    x 2 2 50
3  x 10 .5 USD
f x liên tục trên 0;50 . x 2 3  x 100  5x
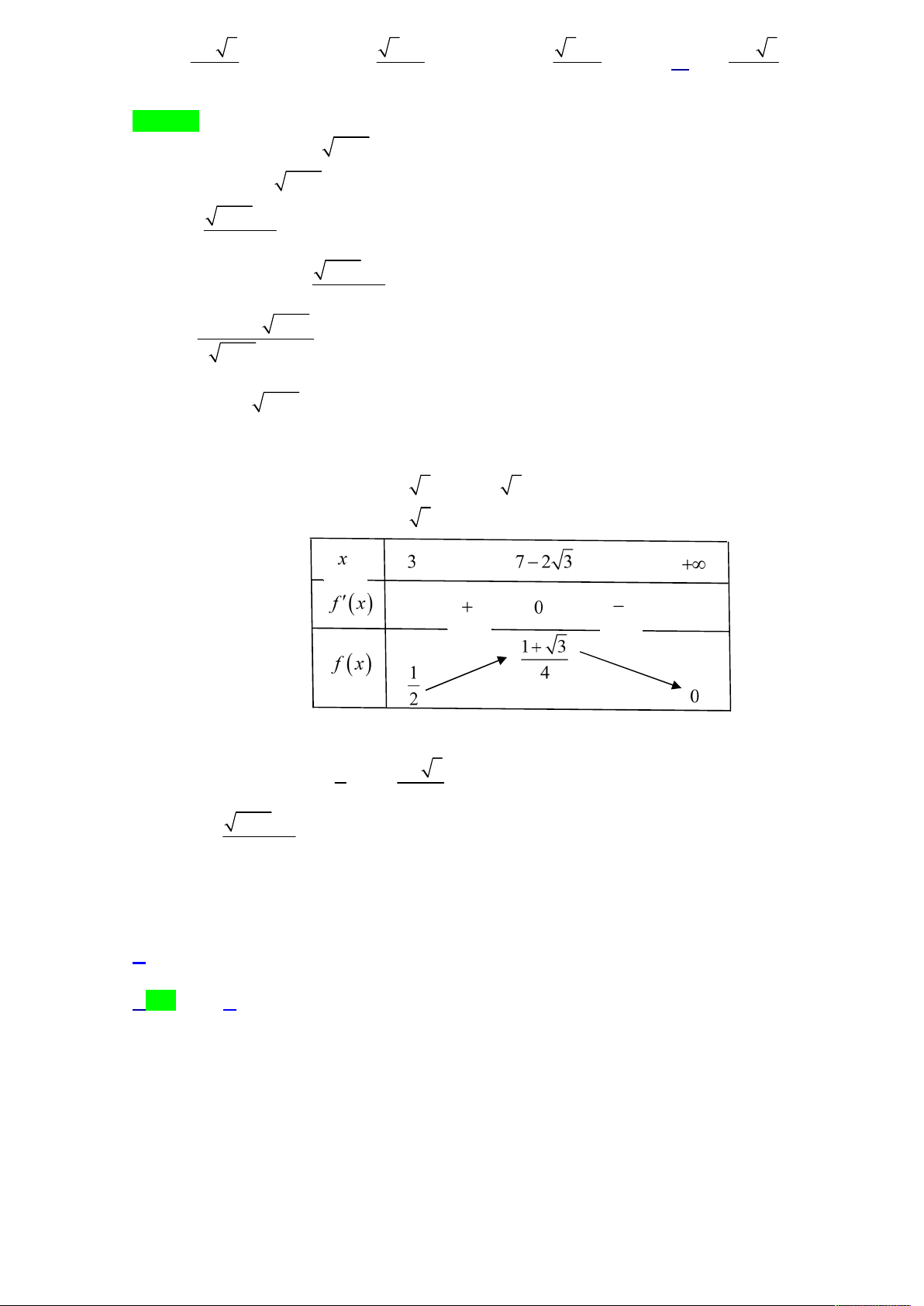
Ta có f  x  3  5.  2 x 100 2 x 100 x  0 x  0 x  0   
f  x  0 2  3 
x 100  5x  0     9.100   15 . 9   2 x 100 2  25x 2  x   x    16  2  15 
Ta có f 0  200; f 50  50 26; f  190    2  15
Để chi phí ít nhất thì x  . 2 15 85
Vậy cô An phải đi đường bộ một khoảng: AD  50  
km để chi phí ít nhất. 2 2 C 10 km A B 50 km
Tập tất cả các giá trị của của m để phương trình mx
x  3  m  1 có hai nghiệm thực phân biệt là  ; a b.
Tính giá trị P a  . b 1  3 3  1 3  1 3  3 A. P  . . B. P  . . C. P  . . D. P  . 4 4 2 4 Lời giải Chọn D.
Ta có phương trình mx x  3  m 1  
1 xác định với x 3;    
1  m x   1 
x  3 1 với x 3;   x  3 1  m
với x 3;   x 1 x  3 1
Xét hàm số y f x 
với x 3;   . x 1
5  x  2 x  3
f  x 
với x 3;  
2 x  3  x  2 1 3   x  5 
f  x  0  2 x  3  5  x   4
  x  3  5  x2  3   x  5 3   x  5     
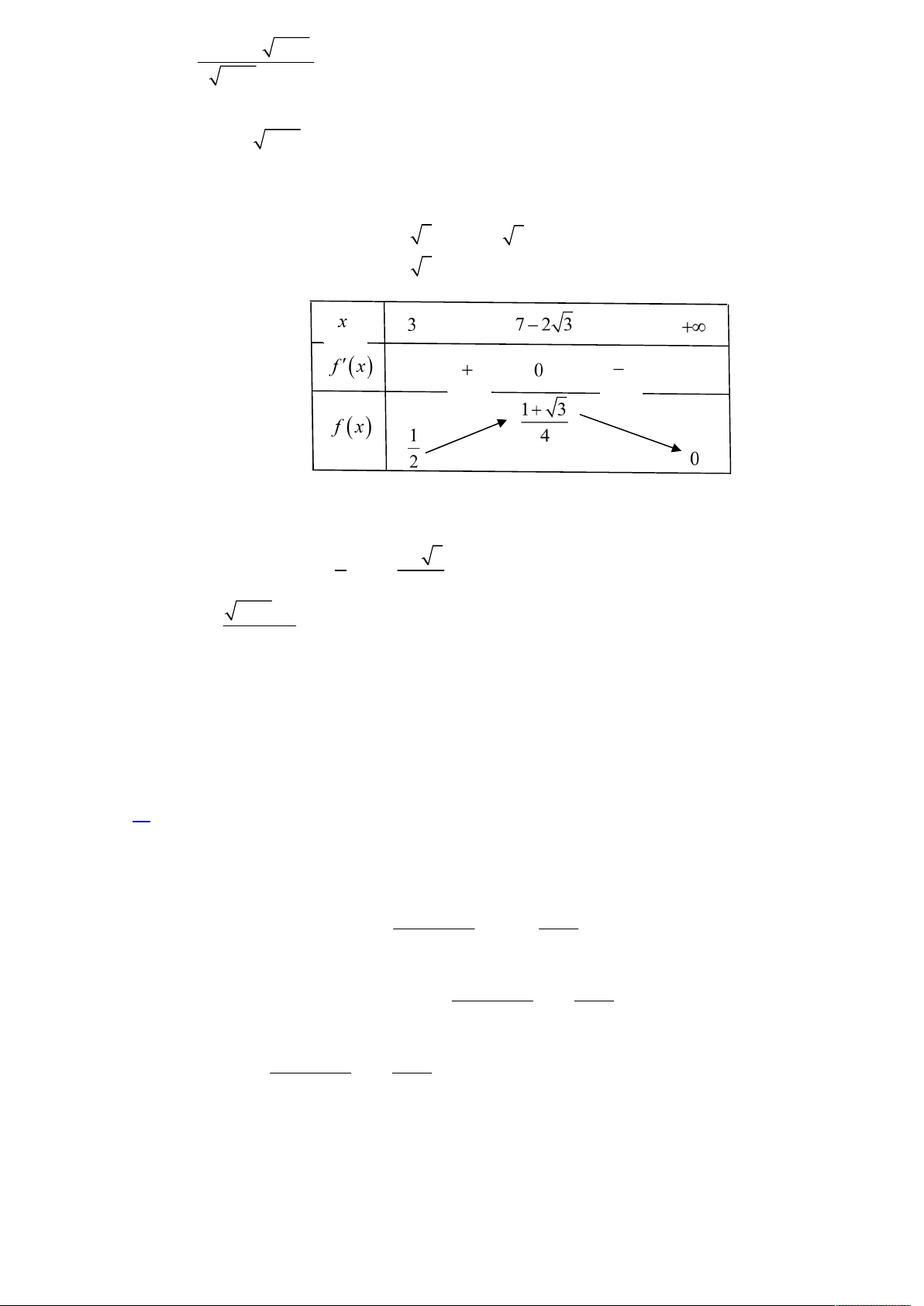
x  7  2 3  7  2 3 2
x 14x  37  0   x  7  2 3  1 1 3
Dựa vào đồ thị ta thấy với  m
thì đường thẳng y m cắt đồ thị hàm số 2 4 x  3 1
y f x 
tại hai điểm phân biệt nên phương trình  
1 có hai nghiệm phân biệt. x 1 19 Câu 18: Số 2
2 +1 có bao nhiêu chữ số trong hệ đếm thập phân? A. 157827. B. 157826. C. 315654. D. 315653.. Lời giải Chọn A. 19 19 Ta có 2 F  2 1  F    2 log log 2   1 . 19 19 19 19 Do
 2    2     2     2 log 2 log 2 1 log 2 .2 157826.44 log 2   1  157826.72   192 log 2 1    157826 .   97 Vậy số 2 F  2  1 có 157827 chữ số. Câu 20: Lời giải Chọn D
Số tiền 100 triệu đồng lần đầu tiên, kì hạn 3 tháng, r  5% . Sau 6 tháng, cả vốn lẫn lãi là: n
T A .1 r   100.10 .1 5%2 6 1 1
Sau đó, gửi thêm 50 triệu trong 6 tháng tiếp theo, kì hạn 3 tháng, r  5% . Tổng số tiền người đó nhận được sau 1 năm:
T T .1 5%2  (100.10 1 5%2  50.10 ).1 5%2 6 6  176675625  176676000 2 1
CÂu 33: Một cái trục lăn sơn nước có dạng một hình trụ. Đường kính của đường tròn đáy là 5 cm, chiều dài lăn là
23 cm (hình dưới). Sau khi lăn trọn 15 vòng thì trục lăn tạo nên sân phẳng một diện tích là A. 2 3450π cm . B. 2 1725π cm . C. 2 1725 cm . D. 2 862,5π cm . Lời giải Chọn B. 5
Diện tích xung quanh hình trụ S
 2πrl  2π .23  115π . xq 2
Vậy sân phẳng có diện tích 2 115π.15  1725π cm .
Câu 38. Trong không gian với hệ toạ độ Oxyz , cho hình hộp ABC . D AB CD
  có A0; 0; 0 , B 3; 0; 0 ,
D 0; 3; 0 , D0; 3;  3 . Toạ độ trọng tâm tam giác A BC  là A. 1; 1;  2 . B. 2; 1;  2 . C. 1; 2;   1 . D. 2; 1;   1 . Lời giải Chọn B. DCABD C A B  
Cách 1 : Ta có AB  3; 0; 0 . Gọi C  ;
x y; z   DC   ;
x y  3; z   
ABCD là hình bình hành  AB DC   ;
x y; z   3; 3; 0  C 3; 3; 0  
Ta có AD  0; 3; 0 . Gọi A x ; y ; z  AD  x ; 3  y ;  3  z   ADD A
  là hình bình hành  AD AD   x ; y ; z  0; 0;  3  A0; 0;  3 
Gọi B x ; y ; z AB  x ; y ; z  3 0 0 0   0 0 0    ABB A
  là hình bình hành  AB AB   x ; y ; z  3; 0; 3  B 3; 0;  3 0 0 0       0  3  3 x   2 G  3   0  0  3
G là trọng tâm tam giác ABC   y   1  G  . G 2; 1; 2 3   3  3  0 z   2 G   3  3 3 3 
Cách 2: Gọi I là trung điểm của đoạn thẳng BD .Ta có I ; ;  
 .Gọi G a; ;
b c là trọng tâm tam  2 2 2  giác A BC   3  3   3 a       3 3 3  2  2     DI  ;  ;     a  2   2 2 2   3  3  
Ta có : DI  3IG với 
. Do đó :   3 b   b     1 .  3 3 3   2  2  IG a  ;b  ; c      c  2     2 2 2   3  3    3 c    2   2 
Vậy G 2;1;  2 .
Câu 38: Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm A1; 2;0 ; B 2;1  ;1 ; C 0;3;   1 . Xét 4 khẳng định sau: I. BC  2AB .
II. Điểm B thuộc đoạn AC .
III. ABC là một tam giác.
IV. A , B , C thẳng hàng.
Trong 4 khẳng định trên có bao nhiêu khẳng định đúng? A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn B.  
Ta có: AB 1; 1 
;1 ; AC 1;1;   1 .    
AB  3 ; AC  3 ; AB   AC A là trung điểm của BC
Vậy khẳng định (I); (IV) đúng. Khẳng định (II); (III) sai.
Câu 41: Tất cả giá trị của thực của m để phương trình mx
x  3  m 1 có hai nghiệm thực phân biệt là  ; a b.
Tính giá trị P a  . b 1  3 2  3 1  3 3  3 A. P  . B. P  . C. P  . . D. P  . 4 4 2 4 Lời giải Chọn D.
Ta có phương trình mx x  3  m 1  
1 xác định với x 3;    
1  m x   1 
x  3 1 với x 3;   x  3 1  m
với x 3;   x 1 x  3 1
Xét hàm số y f x 
với x 3;   . x 1
5  x  2 x  3
f  x 
với x 3;  
2 x  3  x  2 1 3   x  5 
f  x  0  2 x  3  5  x   4
  x  3  5  x2  3   x  5 3   x  5     
x  7  2 3  7  2 3 2
x 14x  37  0   x  7  2 3  1 1 3
Dựa vào đồ thị ta thấy với  m
thì đường thẳng y m cắt đồ thị hàm số 2 4 x  3 1
y f x 
tại hai điểm phân biệt nên phương trình  
1 có hai nghiệm phân biệt. x 1 [ ] 2 2 2
Câu 42: Có bao nhiêu giá trị nguyên có bốn chữ số của m để phương trình sin x cos x cos 2017  2018  .2019 x m có nghiệm? A. 1019. B. 1018. C. 2018 . D. 2019 . Hướng dẫn giải Chọn C. 2 2 cos x cos x  1   2018 
Phương trình tương đương: 2017   m .      2017.2019   2019  t t  1   2018  Đặt 2
t  cos x với t 0;  1 ta được 2017   m .      2017.2019   2019  t t  1   2018 
Xét f t   2017  với t 0  ;1 .      2017.2019   2019 
Hàm số f t  nghịch biến trên D  0  ;1 .
Max f t   f 0  2018 và Min f t   f   1  1. D D
Phương trình có nghiệm  Min f t   m  Max f t  hay m 1; 2018 . D D
Vậy có 1019 giá trị nguyên m để phương trình có nghiệm. [ ]
Câu 43: Từ các chữ số 4, 5, 6 có thể lập được bao nhiêu số tự nhiên có 12 chữ số sao cho trong mỗi số đó hai chữ
số bất kỳ đứng cạnh nhau hơn kém nhau đúng một đơn vị. A. 128. B. 64. C. 32. D. 256. Hướng dẫn
Vì số có 12 chữ số và trong số đó hai chữ số bất kỳ đứng cạnh nhau hơn kém nhau một đơn vị nên số lần xuất hiện chữ số 5 là 6 lần.
+ Đánh thứ tự các chữ số trong số có 12 chữ số là: 1,2,3,4,...,12. Ta có
TH1 chữ số 5 ở vị trí chẵn, 6 vị trí còn lại mỗi vị trí có 2 cách chọn.
TH2 chữ số 5 ở vị trí lẻ, 6 vị trí còn lại mỗi vị trí có 2 cách chọn. Vậy có 6 2.2  128. [ ]
Câu 44: Cho hàm số f x . Biết hàm số y f  x có đồ thị như hình bên. Trên đoạn  4  ;  3 , hàm số
g x  f x    x2 2 1
đạt giá trị nhỏ nhất tại điểm A. x  4  . B. x  1  . C. x  3 . D. x  3  . 0 0 0 0 Lời giải Chọn B. Ta có
g x  2 f  x  21 x .
g x  0  2 f  x  21 x  0  f  x  1  x . x  4  
Dựa vào hình vẽ ta có: g x  0  x  1  .  x  3 
Và ta có bảng biến thiên
Suy ra hàm số g x  f x    x2 2 1
đạt giá trị nhỏ nhất tại điểm x  1  . 0 [ ] Câu 45: Cho hàm số    3 2 y
f x ax bx cx d có đồ thị như hình bên. Đặt g x 2  f
x x  2 . Chọn  
khẳng định đúng trong các khẳng định sau y 4 O x 2
A. g x nghịch biến trên khoảng 0; 2 .
B. g x đồng biến trên khoảng  1  ; 0 .  1 
C. g x nghịch biến trên khoảng ; 0 .
D. g x đồng biến trên khoảng  ;    1 .    2  Lời giải Chọn C. Hàm số    3 2 y
f x ax bx cx d ; f  x 2
 3ax  2bx c , có đồ thị như hình vẽ.
Do đó x  0  d  4 ; x  2  8a  4b  2c d  0 ; f 2  0  12a  4b c  0 ; f 0  0  c  0 .
Tìm được a  1;b  3; c  0; d  4 và hàm số 3 2
y x  3x  4 . 3
Ta có g x  f  2
x x  2    2
x x     2 2
3 x x  2  4  1 x    2 3  1  
g x  2x   2 1
x x  2  32x   1  32x   2 1
x x  2 1 ; g x  0  x  1   2   2  x  2  
Bàng xét dấu của g x : x  2 1  / 2 1  y  0  0  0   7 7 10  y 8 4 4  1 
Vậy g x nghịch biến trên khoảng ; 0 .    2  [ ]
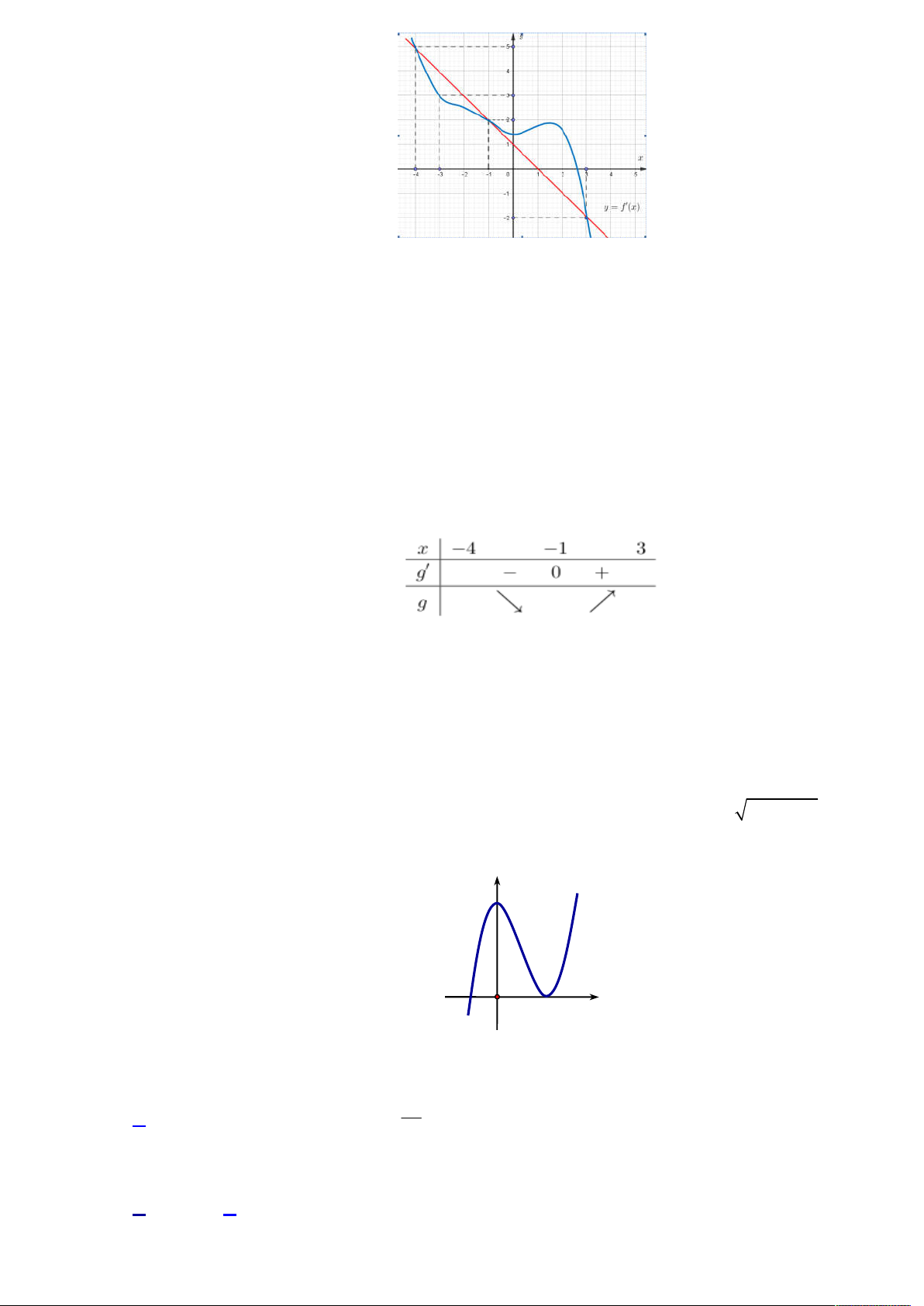
Câu 46: Cho hàm số f x 4 3 2
ax bx cx dx  ,
e (trong đó a, b, c, d , e là những số thực) và có đồ thị
y f  x như hình vẽ. Hỏi phương trình f x  e có bao nhiêu nghiệm? y 2 -1 2 O 1 3 x -2 A. 4. B. 3. C. 2. D. 1. Hướng dẫn 1
Từ đồ thị y f  x  f  x 3 2
x  3x  2  f x 4 3 
x x  2x e f x  e có 4 nghiệm phân biệt. 4 [ ]
Câu 47: Tìm các giá trị thực của tham số m để bất phương trình log log 3x 1  log m 0,02  2   có nghiệm với  0,02 mọi x   ;  0 . A. m  9. B. m  2. C. 0  m  1. D. m  1. Lời giải Chọn D. log log 3x 1  log m 0,02  2   0,02 TXĐ: D  
ĐK tham số m : m  0 Ta có: log log 3x 1  log  log 3x m 1  m 0,02  2    0,02 2   3x.ln 3 Xét hàm số    log 3x f x 1 , x   ;  0 f    0, x    ;  0 2     có 3x   1 ln 2
Bảng biến thiên f x : x  0 f  + 1 f 0
Khi đó với yêu cầu bài toán thì m  1. [ ]   
Câu 48: Cho hình chóp S.ABC có 0
BSA BSC CSA  60 , SA  3, SB  2, SC  6. Tính sin của góc giữa
SC và mặt phẳng SAB. 6 6 3 30 A. . B. . C. . D. . 3 6 3 6 Hướng dẫn
Dựng tứ diện đều có cạnh bằng 6.  Đáp án. [ ]
Câu 49: Cho hình chóp S.ABC có đáy là tam giác ABC đều, đường cao SH với H nằm trong  ABC và 2SH=BC,
SBC  tạo với mặt phẳng  ABC một góc 0
60 . Biết có một điểm O nằm trên đường cao SH sao cho 256
d O; AB  d O; AC   d  ;
O SBC  1. Tính thể tích khối cầu ngoại tiếp hình chóp đã cho. A. 81 125 500 343 . B. . C. . D. 162 81 48 Lời giải Chọn D. S F A C K H E D B O
Giả sử E, F là chân đường vuông góc hạ từ O xuống AB, AC . Khi đó ta có HE AB, HF AC . Do
OE OF  1 nên HE HF . Do đó AH là phân giác của góc  BAC .
Khi đó AH BC D là trung điểm của BC .
Do BC AD BC   SAD . Kẻ OK SD thì OK   SBC  . Do đó OK  1 và  SDA  60 . a
Đặt AB BC CA  2a a  0 thì SH a, HD  . a cot 60  . 3
Do đó AD a 3  3HD nên H là tâm tam giác đều ABC S.ABC là hình chóp tam giác đều và E, F
là trung điểm AB, AC . OK
Mặt khác trong tam giác SOK có : SO
 2 . Do DEF đều có OH   DFE nên sin 30
OE OF OD  1  K D . 2 a 3
Khi đó DSO vuông tại D và có DH SO . Từ đó 2
DH HS.HO
a 2  a  a  3 2 3
AB  3, SH  . 2 2 SA 7
Gọi R là bán kính mặt cầu ngoại tiếp hình chóp S.ABC thì R   . 2SH 4 3 4  7  343 V   .   . m/c   3  4  48 [ ]
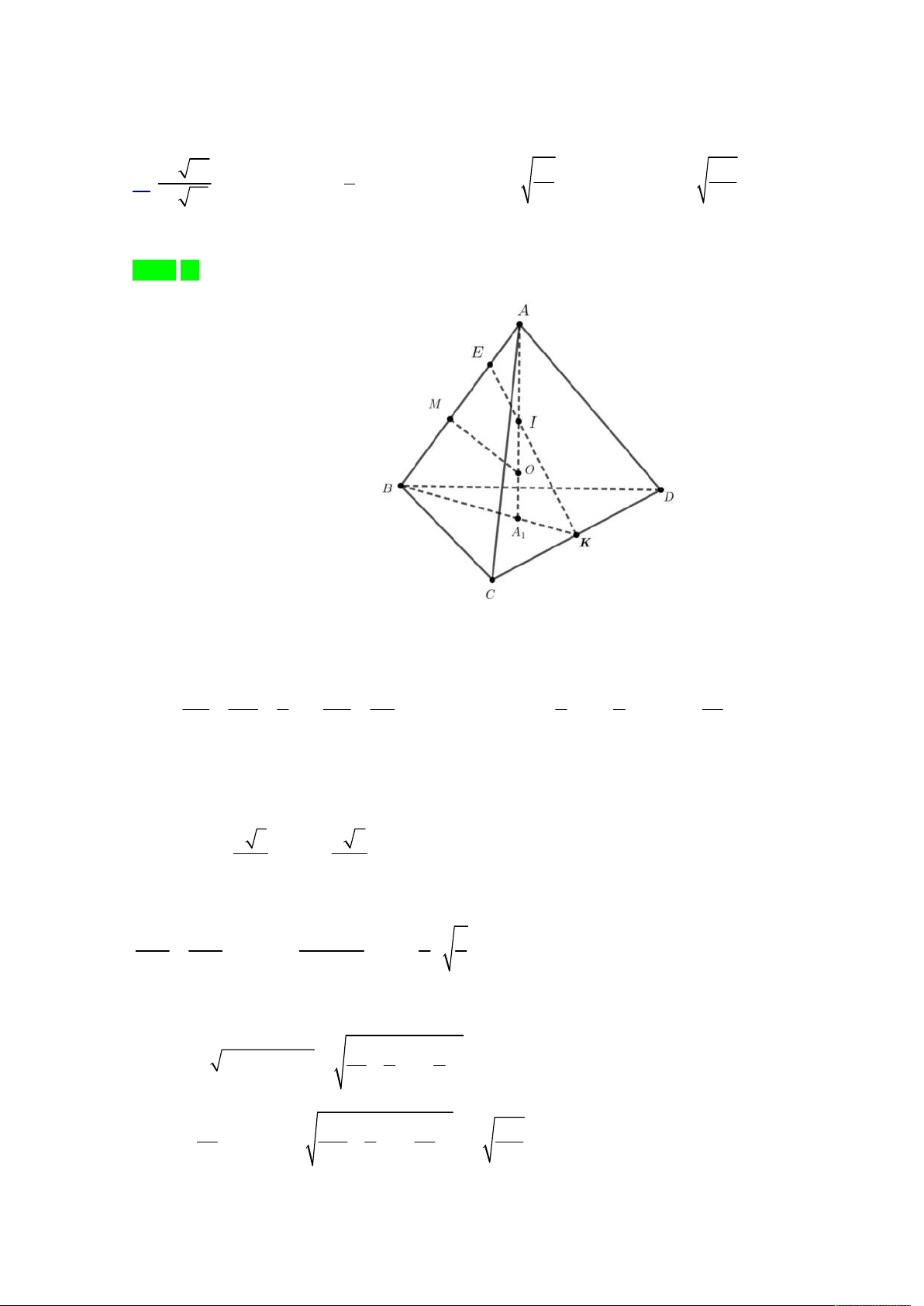
Câu 50: Cho tứ diện đều ABCD có một đường cao AA . Gọi I là trung điểm AA . Mặt phẳng  BCI  chia 1 1
tứ diện ABCD thành hai tứ diện. Tính tỉ số thể tích của hai mặt khối cầu ngoại tiếp hai tứ diện đó. 43 43 1 43 48 A. . B. . C. D. . 51 51 8 51 153 Lời giải Chọn A.
Gọi cạnh của tứ diện đều là a . Gọi K là trung điểm của CD và E IK AB . Qua A kẻ đường thẳng 1
song song với IK cắt AB tại J . BJ BA 2 AE AI 1 a 3a Ta có: 1   và 
 1 nên suy ra AE AB  và BE  . BE BK 3 EJ IA 4 4 4 1
Gọi M là trung điểm của BE , trong mặt phẳng  ABK  dựng đường trung trực của BE cắt AA tại O . 1
Ta dễ dàng chứng minh được O là tâm của mặt cầu ngoại tiếp EBCD . a 3 a 6 Ta có: BA AA BE x 1 , 1 . Đặt . 3 3
Tam giác ABA đồng dạng với tam giác AOM nên suy ra 1 AM OM AM .BHx  1   OM   a  .   AA BH AA  2  2 1 1
Gọi R là bán kính mặt cầu ngoại tiếp EBCD ta suy ra: 2 2 x 1  x 2 2 
R OB OM MB   a  .   4 2  2  2 3a 2 9a 1  3a  43 Với x  ta có: R   a   a .   4 64 2  8  128 a
Tương tự với x
ta có bán kính R của mặt cầu ngoại tiếp EACD là 4 2 2 a 1  a  51 R   a   a .   64 2  4  128 3 R 43 V R Do đó  .   . 3 R ' 51 V R