Đề thi thử Toán THPT Quốc gia 2019 lần 2 trường Lương Thế Vinh – Hà Nội

Đề thi thử Toán THPT Quốc gia 2019 lần 2 trường Lương Thế Vinh – Hà Nội có mã đề 110, đề được biên soạn dựa trên mẫu đề tham khảo THPTQG 2019 môn Toán mà Bộ Giáo dục và Đào tạo từng công bố, đề thi thử Toán có đáp án.

40 20 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

38 trang 6 tháng trước

Tác giả:

Profile Thanh Hoa
Trường THCS-THPT Lương Thế Vinh
Đề thi có 6 trang
Mã đề thi 110
ĐỀ THI THỬ THPT QUỐC GIA LẦN 2
Năm học 2018-2019
Môn: Toán
Thời gian làm bài: 90 phút (50 câu trắc nghiệm)
Câu 1. Cho số phức z thỏa mãn z = 3 +2i. Tìm phần thực và phần ảo của số phức z.
A. Phần thực bằng -3, phần ảo bằng 2. B. Phần thực bằng 3, phần ảo bằng 2.
C. Phần thực bằng 3, phần ảo bằng -2. D. Phần thực bằng -3, phần ảo bằng -2.
Câu 2. Trong hệ tọa độ Oxyz, cho đường thẳng ∆ :
x − x
0
a
=
y − y
0
b
=
z − z
0
c
. Điểm M nằm
trên ∆ thì tọa độ của M có dạng nào sau đây?
A. M(at; bt; ct). B. M(x
0
t; y
0
t; z
0
t).
C. M(a + x
0
t; b + y
0
t; c + z
0
t). D. M(x
0
+ at; y
0
+ bt; z
0
+ ct).
Câu 3. Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như sau:
x
y
0
y
−∞
−2
2
+∞
+
0
−
0
+
−∞−∞
33
00
+∞+∞
Tìm giá trị cực đại y
CĐ
và giá trị cực tiểu y
CT
của hàm số đã cho.
A. y
CĐ
= −2 và y
CT
= 2. B. y
CĐ
= 3 và y
CT
= 0.
C. y
CĐ
= 2 và y
CT
= 0. D. y
CĐ
= 3 và y
CT
= −2.
Câu 4. Trong hệ tọa độ Oxyz, cho ba điểm A(1; 0; 0), B(0; −1; 0), C(0; 0; 2). Phương trình
mặt phẳng (ABC) là
A. x − 2y + z = 0. B. x − y +
z
2
= 1. C. x +
y
2
− z = 1. D. 2x − y + z = 0.
Câu 5. Đường thẳng y = m tiếp xúc với đồ thị (C) : y = −2x
4
+ 4x
2
− 1 tại hai điểm phân
biệt A(x
A
; y
A
) và B(x
B
; y
B
). Giá trị của biểu thức y
A
+ y
B
.
A. 2. B. −1. C. 1. D. 0.
Câu 6. Trong các hàm số dưới đây, hàm số nào đồng biến trên tập R?
A. y = 2
1−3x
. B. y = log
2
(x − 1). C. y = log
2
(2
x
+ 1). D. y = log
2
x
2
+ 1
.
Câu 7.
Đường cong như hình bên là đồ thị của hàm số nào sau
đây?
A. y = −x
3
+ 3x
2
− 2. B. y = x
3
− 3x
2
− 2.
C. y = x
4
− 2x
2
− 2. D. y = −x
4
+ 2x
2
− 2.
x
y
O
Câu 8. Tìm tập xác định của hàm số y = (x
2
+ 2x − 3)
e
.
A. (−∞; −3) ∪ (1; +∞). B. (−∞; −3] ∪ [1; +∞).
C. (−3; 1). D. [−3; 1].
Trang 1/6 Mã đề 110
Câu 9. Cho hàm số y =
2x + 1
x + 1
. Mệnh đề đúng là
A. Hàm số nghịch biến trên (−∞; −1) và (−1; +∞).
B. Hàm số đồng biến trên (−∞; −1) và (1; +∞), nghịch biến trên (−1; 1).
C. Hàm số đồng biến trên R.
D. Hàm số đồng biến trên (−∞; −1) và (−1; +∞).
Câu 10. Thế tích của khối cầu có bán kính R là
A. πR
3
. B.
4πR
3
3
. C. 2πR
3
. D.
πR
3
3
.
Câu 11. Cho f(x), g(x) là các hàm số có đạo hàm liên tục trên R, k ∈ R. Trong các khẳng
định dưới đây, khẳng định nào sai?
A.
Z
[f(x) − g(x)]dx =
Z
f(x)dx −
Z
g(x)dx. B.
Z
f
0
(x)dx = f(x) + C.
C.
Z
kf(x)dx = k
Z
f(x)dx. D.
Z
[f(x) + g(x)]dx =
Z
f(x)dx +
Z
g(x)dx.
Câu 12. Cho lăng trụ tứ giác đều có đáy là hình vuông cạnh a, chiều cao 2a. Tính thể
tích khối lăng trụ.
A.
2a
3
3
. B.
4a
3
3
. C. a
3
. D. 2a
3
.
Câu 13. Tích của giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = x +
4
x
trên đoạn
[1; 3] bằng
A.
65
3
. B. 20. C. 6. D.
52
3
.
Câu 14. Trong hệ tọa độ Oxyz, cho hai đường thẳng chéo nhau
d
1
:
x − 2
2
=
y + 2
1
=
z − 6
−2
, d
2
:
x − 4
1
=
y + 2
−2
=
z + 1
3
.
Phương trình mặt phẳng (P ) chứa d
1
và song song với d
2
là
A. (P ) : x + 8y + 5z + 16 = 0. B. (P ) : x + 8y + 5z − 16 = 0.
C. (P ) : 2x + y − 6 = 0. D. (P ) : x + 4y + 3z − 12 = 0.
Câu 15. Trong hệ tọa độ Oxyz, cho đường thẳng d :
x − 1
2
=
y − 3
−1
=
z − 1
1
cắt mặt phẳng
(P ) : 2x − 3y + z − 2 = 0 tại điểm I(a; b; c). Khi đó a + b + c bằng
A. 9. B. 5. C. 3. D. 7.
Câu 16. Cho dãy số (u
n
) là một cấp số cộng, biết u
2
+ u
21
= 50. Tính tổng của 22 số hạng
đầu tiên của dãy.
A. 2018. B. 550. C. 1100. D. 50.
Câu 17. Số đường tiệm cận của đồ thị hàm số y =
x + 1
|x| − 2x + 1
là
A. 4. B. 3. C. 2. D. 1.
Câu 18. Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a, tam giác SAB đều
và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích khối chóp S.ABC.
A. V =
a
3
8
. B. V =
a
3
√
3
3
. C. V =
a
3
√
3
4
. D. V =
a
3
4
.
Câu 19. Họ nguyên hàm của hàm số f(x) = 2x(1 + 3x
3
) là
A. x
2
1 +
3
2
x
2
+ C. B. x
2
1 +
6x
3
5
+ C. C. 2x
x +
3
4
x
4
+ C. D. x
2
x +
3
4
x
3
+ C.
Trang 2/6 Mã đề 110
Câu 20. Tìm tập nghiệm S của bất phương trình
2
5
1−3x
≥
25
4
.
A. S = [1; +∞). B. S =
1
3
; +∞
. C. S =
−∞;
1
3
. D. S = (−∞; 1].
Câu 21. Trong hệ tọa độ Oxyz, cho điểm A(3; 5; 3) và hai mặt phẳng (P ) : 2x+y +2z −8 = 0,
(Q) : x −4y + z −4 = 0. Viết phương trình đường thẳng d đi qua A và song song với cả hai
mặt phẳng (P ), (Q)
A. d :
x = 3 + t
y = 5 − t
z = 3
. B. d :
x = 3
y = 5 + t
z = 3 − t
. C. d :
x = 3 + t
y = 5
z = 3 − t
. D. d :
x = 3 + t
y = 5
z = 3 + t
.
Câu 22. Trong hệ tọa độ Oxyz, cho điểm A(−1; 1; 6) và đường thẳng ∆ :
x = 2 + t
y = 1 − 2t
z = 2t
. Hình
chiếu vuông góc của A trên ∆ là
A. M(3; −1; 2). B. H(11; −17; 18). C. N(1; 3; −2). D. K(2; 1; 0).
Câu 23. Cho f(x), g(x) là các hàm số liên tục trên R thỏa mãn
Z
1
0
f(x)dx = 3,
Z
2
0
[f(x) − 3g(x)]dx = 4 và
Z
2
0
[2f(x) + g(x)]dx = 8.
Tính I =
Z
2
1
f(x)dx.
A. I = 1. B. I = 2. C. I = 3. D. I = 0.
Câu 24. Đồ thị hàm số y = −
x
4
2
+ x
2
+
3
2
cắt trục hoành tại mấy điểm?
A. 0. B. 2. C. 4. D. 3.
Câu 25. Trong hệ tọa độ Oxyz, cho điểm I(2; −1; −1) và mặt phẳng (P ) : x −2y −2z +3 = 0.
Viết phương trình mặt cầu (S) có tâm I và tiếp xúc với mặt phẳng (P )
A. (S) : x
2
+ y
2
+ z
2
− 4x + 2y + 2z − 3 = 0. B. (S) : x
2
+ y
2
+ z
2
− 2x + y + z − 3 = 0.
C. (S) : x
2
+ y
2
+ z
2
− 4x + 2y + 2z + 1 = 0. D. (S) : x
2
+ y
2
+ z
2
− 2x + y + z + 1 = 0.
Câu 26. Cho hình lập phương ABCD.A
0
B
0
C
0
D
0
có cạnh bằng a. Một hình nón có đỉnh là
tâm của hình vuông A
0
B
0
C
0
D
0
và có đường tròn đáy ngoại tiếp hình vuông ABCD. Tính
diện tích xung quanh của hình nón đó.
A.
πa
2
√
2
2
. B. πa
2
√
3. C.
πa
2
√
2
4
. D.
πa
2
√
3
2
.
Câu 27. Tìm hệ số của số hạng chứa x
9
trong khai triển nhị thức Newton của biểu thức
(3 + x)
11
.
A. 9. B. 110. C. 495. D. 55.
Câu 28. Cho số thực a > 0, a 6= 1. Giá trị của log
a
2
7
√
a
3
bằng
A.
3
14
. B.
6
7
. C.
3
8
. D.
7
6
.
Câu 29. Đạo hàm của hàm số y = log
8
(x
3
− 3x − 4) là
A.
3x
3
− 3
(x
3
− 3x − 4) ln 2
. B.
x
2
− 1
(x
3
− 3x − 4) ln 2
. C.
3x
3
− 3
x
3
− 3x − 4
. D.
1
(x
3
− 3x − 4) ln 8
.
Câu 30. Cho cấp số nhân (u
n
) thỏa mãn
u
1
+ u
3
= 10
u
4
+ u
6
= 80
. Tìm u
3
.
A. u
3
= 8. B. u
3
= 2. C. u
3
= 6. D. u
3
= 4.
Trang 3/6 Mã đề 110
Câu 31. Cho khối nón (N) đỉnh S, có chiều cao là a
√
3 và độ dài đường sinh là 3a. Mặt
phẳng (P ) đi qua đỉnh S, cắt và tạo với mặt đáy của khối nón một góc 60
0
. Tính diện tích
thiết diện tạo bởi mặt phẳng (P ) và khối nón (N).
A. 2a
2
√
5. B. a
2
√
3. C. 2a
2
√
3. D. a
2
√
5.
Câu 32.
Cho hàm số y = x
3
− 3x
2
+ 4 có đồ thị (C) như hình bên và
đường thẳng d : y = m
3
−3m
2
+ 4 (với m là tham số). Hỏi có bao
nhiêu giá trị nguyên của tham số m để đường thẳng d cắt đồ
thị (C) tại 3 điểm phân biệt?
A. 3. B. 2. C. 1. D. Vô số.
−1 1 2 3
x
1
2
3
4
y
0
Câu 33. Cho các số phức z thỏa mãn |z| = 2. Biết rằng tập hợp các điểm biểu diễn số
phức w = 3 − 2i + (4 − 3i)z là một đường tròn. Tính bán kính r của đường tròn đó.
A. r = 5. B. r = 2
√
5. C. r = 10. D. r = 20.
Câu 34. Cho 9
x
+ 9
−x
= 14, khi đó biểu thức M =
2 + 81
x
+ 81
−x
11 − 3
x
− 3
−x
có giá trị bằng
A. 14. B. 49. C. 42. D. 28.
Câu 35. Cho lăng trụ tam giác đều ABC.A
0
B
0
C
0
có đáy là tam giác đều cạnh a, AA
0
= 2a.
Gọi α là góc giữa AB
0
và BC
0
. Tính cos α.
A. cos α =
5
8
. B. cos α =
√
51
10
. C. cos α =
√
39
8
. D. cos α =
7
10
.
Câu 36. Cho hai đường thẳng d
1
:
x = 1 + t
y = 2 − t
z = 3 + 2t
và d
2
:
x − 1
2
=
y − m
1
=
z + 2
−1
(với m là tham
số). Tìm m để hai đường thẳng d
1
, d
2
cắt nhau.
A. m = 4. B. m = 9. C. m = 7. D. m = 5.
Câu 37. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB đều
và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách từ điểm C đến mặt phẳng
(SAD).
A.
a
√
3
6
. B.
a
√
3
2
. C.
a
√
3
3
. D.
a
√
3
4
.
Câu 38. Cho một hộp có chứa 5 bóng xanh, 6 bóng đỏ và 7 bóng vàng. Lấy ngẫu nhiên
4 bóng từ hộp, tính xác suất để có đủ 3 màu.
A.
35
816
. B.
35
68
. C.
175
5832
. D.
35
1632
.
Câu 39. Cho phương trình log
2
3
x − 4 log
3
x + m − 3 = 0. Tìm tất cả các giá trị nguyên của
tham số m để phương trình đã cho có hai nghiệm phân biệt thỏa mãn x
1
> x
2
> 1.
A. 6. B. 4. C. 3. D. 5.
Câu 40. Có tất cả bao nhiêu giá trị thực của tham số m để đường thẳng d : y = mx + 1
cắt đồ thị (C) : y = x
3
− x
2
+ 1 tại 3 điểm A, B(0; 1), C phân biệt sao cho tam giác AOC
vuông tại O(0; 0)?
A. 0. B. 1. C. 3. D. 2.
Câu 41. Trong hệ tọa độ Oxyz, cho điểm M(1; −1; 2) và hai đường thẳng d
1
:
x = t
y = 1 − t
z = −1
,
d
2
:
x + 1
2
=
y − 1
1
=
z + 2
1
. Đường thẳng ∆ đi qua M và cắt cả hai đường thẳng d
1
, d
2
có
véc tơ chỉ phương là
−→
u
∆
(1; a; b), tính a + b.
Trang 4/6 Mã đề 110
A. a + b = −1. B. a + b = −2. C. a + b = 2. D. a + b = 1.
Câu 42. Hai người A và B ở cách nhau 180 (m) trên một đoạn đường thẳng và cùng
chuyển động thẳng theo một hướng với vận tốc biến thiên theo thời gian, A chuyển động
với vận tốc v
1
(t) = 6t + 5 (m/s), B chuyển động với vận tốc v
2
(t) = 2at − 3 (m/s) (a là hằng
số), trong đó t (giây) là khoảng thời gian tính từ lúc A, B bắt đầu chuyển động. Biết rằng
lúc đầu A đuổi theo B và sau 10 (giây) thì đuổi kịp. Hỏi sau 20 (giây), A cách B bao nhiêu
mét?
A. 320 (m). B. 720 (m). C. 360 (m). D. 380 (m).
Câu 43. Một hình hộp chữ nhật có chiều cao là 90cm, đáy hộp là hình chữ nhật có chiều
rộng là 50cm và chiều dài là 80cm. Trong khối hộp có chứa nước, mực nước so với đáy
hộp có chiều cao là 40cm. Hỏi khi đặt vào khối hộp một khối trụ có chiều cao bằng chiều
cao khối hộp và bán kính đáy là 20cm theo phương thẳng đứng thì chiều cao của mực
nước so với đáy là bao nhiêu?
A. 68, 32cm. B. 78, 32cm. C. 58, 32cm. D. 48, 32cm.
Câu 44.
Một chiếc cổng có hình dạng là một Parabol có khoảng cách
giữa hai chân cổng là AB = 8m. Người ta treo một tấm phông
hình chữ nhật có hai đỉnh M, N nằm trên Parbol và hai đỉnh
P, Q nằm trên mặt đất (như hình vẽ). Ở phần phía ngoài phông
(phần không tô đen) người ta mua hoa để trang trí với chi phí
cho 1m
2
cần số tiền mua hoa là 200.000 đồng cho 1m
2
. Biết
MN = 4m, MQ = 6m. Hỏi số tiền dùng để mua hoa trang trí
chiếc cổng gần với số tiền nào sau đây?
A. 3.735.300 đồng. B. 3.437.300 đồng.
C. 3.734.300 đồng. D. 3.733.300 đồng.
A
B
M
N
P
Q
Câu 45. Cho hai số phức z, w thay đổi thoả mãn |z| = 3, |z − w| = 1. Biết tập hợp điểm
của số phức w là hình phẳng H. Tính diện tích S của hình H
A. S = 20π. B. S = 12π. C. S = 4π. D. S = 16π.
Câu 46. Cho
Z
1
0
9
x
+ 3m
9
x
+ 3
dx = m
2
− 1. Tính tổng tất cả các giá trị của tham số m.
A. P = 12. B. P =
1
2
. C. P = 16. D. P = 24.
Câu 47. Có bao nhiêu cách phân tích số 15
9
thành tích của ba số nguyên dương, biết
rằng các cách phân tích mà các nhân tử chỉ khác nhau về thứ tự thì chỉ được tính một
lần?
A. 517. B. 516. C. 493. D. 492.
Câu 48. Cho các số thực a, b > 1 thỏa mãn a
log
b
a
+ 16b
log
a
b
8
a
3
= 12b
2
. Giá trị của biểu thức
P = a
3
+ b
3
là
A. P = 20. B. P = 39. C. P = 125. D. P = 72.
Trang 5/6 Mã đề 110
Câu 49. Cho hình chóp S.ABCD có đáy ABCD là hình vuông, hình chiếu vuông góc của
đỉnh S xuống mặt đáy nằm trong hình vuông ABCD. Hai mặt phẳng (SAD), (SBC) vuông
góc với nhau; góc giữa hai mặt (SAB) và (SBC) là 60
0
; góc giữa hai mặt phẳng (SAB) và
(SAD) là 45
0
. Gọi α là góc giữa hai mặt phẳng (SAB) và (ABCD), tính cos α
A. cos α =
1
2
. B. cos α =
√
2
2
. C. cos α =
√
3
2
. D. cos α =
√
2
3
.
Câu 50. Cho hai hàm số f(x) =
1
3
x
3
− (m + 1)x
2
+ (3m
2
+ 4m + 5)x + 2019 và g(x) = (m
2
+
2m + 5)x
3
− (2m
2
+ 4m + 9)x
2
− 3x + 2 (với m là tham số). Hỏi phương trình g(f(x)) = 0 có
bao nhiêu nghiệm?
A. 9. B. 0. C. 3. D. 1.
- - - - - - - - - - HẾT- - - - - - - - - -
Trang 6/6 Mã đề 110
ĐÁP ÁN
BẢNG ĐÁP ÁN CÁC MÃ ĐỀ
Mã đề thi 110
1. C 2. D 3. B 4. B 5. A 6. C 7. C 8. A 9. D 10. B
11. C 12. D 13. B 14. B 15. D 16. B 17. B 18. A 19. B 20. A
21. C 22. A 23. A 24. B 25. A 26. D 27. C 28. A 29. B 30. A
31. A 32. C 33. C 34. D 35. D 36. D 37. B 38. B 39. C 40. B
41. D 42. D 43. C 44. D 45. B 46. B 47. A 48. D 49. C 50. C
1
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 1 Mã đề 110
ĐỀ THỬ THPTQG
LƯƠNG THẾ VINH - HÀ NỘI LẦN 2-2019
MÔN TOÁN
Bản quyền thuộc về tập thể thầy cô
STRONG TEAM TOÁN VD-VDC
Câu 1. Cho số phức
z
thỏa mãn
32zi=+
. Tìm phần thực và phần ảo của số phức
z
.
A.Phần thực bằng
3−
, phần ảo bằng
2
. B. Phần thực bằng
, phần ảo bằng
2
.
C. Phần thực bằng
3
, phần ảo bằng
2−
. D. Phần thực bằng -3, phần ảo bằng
2−
.
Câu 2. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
0 0 0
:
x x y y z z
a b c
− − −
= =
. Điểm
M
nằm trên đường thẳng
thì tọa độ của điểm
M
có dạng nào sau đây?
A.
( )
;;M at bt ct
. B.
( )
0 0 0
;;M x t y t z t
.
C.
( )
0 0 0
;;M a x t b y t c z t+ + +
. D.
( )
0 0 0
;;M x at y bt z ct+ + +
.
Câu 3. Cho hàm số
( )
=y f x
xác định, liên tục trên và có bảng biến thiên như sau:
Tìm giá trị cực đại
CÑ
y
và giá trị
CT
y
của hàm số đã cho.
A.
=−2
CÑ
y
và
= 2
CT
y
. B.
= 3
CÑ
y
và
= 0
CT
y
.
C.
= 2
CÑ
y
và
= 0
CT
y
. D.
= 3
CÑ
y
và
=−2
CT
y
.
Câu 4. Trong hệ tọa độ
Oxyz
, cho ba điểm
( )
1;0;0A
,
( )
0; 1;0B −
,
( )
0;0;2C
. Phương trnh mt phẳng
( )
ABC
là:
A.
20x y z− + =
. B.
1
2
z
xy− + =
. C.
1
2
y
xz+ − =
. D.
20x y z− + =
.
Câu 5. Đường thẳng
ym=
tiếp xúc với đồ thị
42
( ): 2 4 1C y x x= − + −
tại hai điểm phân biệt
( ; )
AA
A x y
và
( ; )
BB
B x y
. Giá trị của biểu thức
AB
yy+
bằng
A.
2
. B.
1−
. C.
1
. D.
0.
Câu 6. Trong các hàm số dưới đây, hàm số nào đồng biến trên tập ?
A.
13
2
x
y
−
=
. B.
( )
2
log 1yx=−
. C.
( )
2
log 2 1
x
y =+
. D.
( )
2
2
log 1yx=+
.
Câu 7. Đường cong như hnh bên dưới là đồ thị của hàm số nào sau đây?
A.
32
32y x x
. B.
32
32y x x
.
C.
42
22y x x
. D.
42
22y x x
.
Câu 8. Tìm tập xác định của hàm số
( )
2
23
e
y x x= + −
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 2 Mã đề 110
A.
( ) ( )
; 3 1;− − +
. B.
(
)
; 3 1;− − +
.
C.
( )
3;1−
. D.
3; 1−
Câu 9. Cho hàm số
21
1
x
y
x
+
=
+
. Mệnh đề đúng là
A. Hàm số nghịch biến trên
( )
;1− −
và
( )
1;− +
.
B. Hàm số đồng biến trên
( )
;1− −
và
( )
1; +
, nghịch biến trên
( )
1;1−
.
C. Hàm số đồng biến trên .
D. Hàm số đồng biến trên
( )
;1− −
và
( )
1;− +
.
Câu 10. Thể tích của khối cầu có bán kính
R
là:
A.
3
R
. B.
3
4
3
R
. C.
3
2 R
. D.
3
3
R
.
Câu 11. Cho
( )
fx
,
( )
gx
là các hàm số có đạo hàm liên tục trên ,
k
. Trong các khẳng định dưới
đây, khẳng định nào sai?
A.
( ) ( ) ( ) ( )
d d df x g x x f x x g x x− = −


. B.
( ) ( )
df x x f x C
=+
.
C.
( ) ( )
ddkf x x k f x x=

. D.
( ) ( ) ( ) ( )
d d df x g x x f x x g x x+ = +


.
Câu 12. Cho lăng trụ tứ giác đều có đáy là hnh vuông cạnh
a
, chiều cao
2a
. Tính thể tích khối lăng
trụ.
A.
3
2
3
a
. B.
3
4
3
a
. C.
3
a
. D.
3
2a
.
Câu 13. Tích của giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
4
f x x
x
=+
trên đoạn
1;3
bằng
A.
65
3
. B.
20
. C.
6
. D.
52
3
.
Câu 14. Trong hệ tọa độ
Oxyz
, cho hai đường thằng chéo nhau
1
2 2 6
:
2 1 2
x y z
d
− + −
==
−
;
2
4 2 1
:
1 2 3
x y z
d
− + +
==
−
. Phương trnh mt phẳng
( )
P
chứa
1
d
và song song với
2
d
là
A.
( )
: 8 5 16 0P x y z+ + + =
. B.
( )
: 8 5 16 0P x y z+ + − =
.
C.
( )
:2 6 0P x y+ − =
. D.
( )
: 4 3 12 0P x y z+ + − =
.
Câu 15. Trong hệ tọa độ
Oxyz
, cho đường thẳng
1 3 1
:
2 1 1
x y z
d
− − −
==
−
cắt mt phẳng
( )
:2 3 2 0P x y z− + − =
tại điểm
( )
;;I a b c
. Khi đó
abc++
bằng
A.
9
. B.
5
. C.
3
. D.
7
.
Câu 16. Cho dãy số
( )
n
u
là một cấp số cộng, biết
2 21
50uu+=
. Tính tổng của
22
số hạng đầu tiên của
dãy.
A.
2018
. B.
550
. C.
1100
. D.
50
.
Câu 17. Số đường tiệm cận của đồ thị hàm số
1
21
x
y
xx
+
=
−+
là
A.
4
. B.
3
. C.
2
. D.
1
.
Câu 18. Cho khối chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
, tam giác
SAB
đều và nằm trong
mt phẳng vuông góc với đáy. Tính theo
a
thể tích của khối chóp
.S ABC
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 3 Mã đề 110
A.
3
8
a
V =
. B.
3
3
3
a
V =
. C.
3
3
4
a
V =
. D.
3
4
a
V =
.
Câu 19. Họ nguyên hàm của hàm số
( )
( )
3
2 1 3f x x x=+
là
A.
22
3
1
2
x x C

++


. B.
3
2
6
1
5
x
xC

++


. C.
4
3
2
4
x x x C

++


. D.
23
3
4
x x x C

++


.
Câu 20. Tập nghiệm
S
của bất phương trnh
13
2 25
54
x−



.
A.
)
1;S = +
. B.
1
;
3
S

= +

. C.
1
;
3
S

= −


. D.
(
;1S = −
.
Câu 21. Trong hệ toạ độ
Oxyz
, cho điểm
( )
3;5;3A
và hai mt phẳng
( ):2 2 8 0,P x y z+ + − =
( ): 4 4 0.Q x y z− + − =
Viết phương trnh đường thẳng
d
đi qua
A
và song song với cả hai mt
phẳng
()P
và
()Q
.
A.
3
5
3
xt
yt
z
=+
=−
=
. B.
3
5
3
x
yt
zt
=
=+
=−
. C.
3
5
3
xt
y
zt
=+
=
=−
. D.
3
5
3
xt
y
zt
=+
=
=+
.
Câu 22. Trong hệ tọa độ
Oxyz
, cho điểm
( )
1;1;6A −
và đường thẳng
2
: 1 2 .
2
xt
yt
zt
=+
= −
=
Hình chiếu vuông
góc của
A
trên
là:
A.
( )
3; 1;2M −
. B.
( )
11; 17;18H −
. C.
( )
1;3; 2N −
. D.
( )
2;1;0K
.
Câu 23. Cho
( )
fx
,
( )
gx
là các hàm số liên tục trên thỏa mãn
( )
1
0
d3f x x =
,
( ) ( )
2
0
3 d 4f x g x x−=


và
( ) ( )
2
0
2 d 8f x g x x+=


.
Tính
( )
2
1
dI f x x=
.
A.
1I =
. B.
2I =
. C.
3I =
. D.
0I =
.
Câu 24. Đồ thị hàm số
4
2
3
22
x
yx= − + +
cắt trục hoành tại mấy điểm?
A.
0
. B.
2
. C.
4
. D.
3
.
Câu 25. Trong hệ tọa độ
( )
Oxyz
, cho đểm
( )
2; 1; 1I −−
và mt phẳng
( )
: 2 2 3 0P x y z− − + =
. Viết
phương trnh mt cầu
( )
S
có tâm
I
và tiếp xúc với mt phẳng
( )
P
.
A.
( )
2 2 2
: 4 2 2 3 0.S x y z x y z+ + − + + − =
B.
( )
2 2 2
: 2 3 0.S x y z x y z+ + − + + − =
C.
( )
2 2 2
: 4 2 2 1 0.S x y z x y z+ + − + + + =
D.
( )
2 2 2
: 2 1 0.S x y z x y z+ + − + + + =
Câu 26. Cho hình lập phương có cạnh bằng . Một hnh nón có đỉnh là tâm của hình
vuông và có đường tròn đáy ngoại tiếp hình vuông
ABCD
. Tính diện tích xung
quanh của hnh nón đó.
A.
2
2
2
a
. B.
2
3a
. C.
2
2
4
a
. D.
2
3
2
a
.
Câu 27. Tìm hệ số của số hạng chứa
9
x
trong khai triển nhị thức Newton của biểu thức
( )
11
3 x+
A.
9
. B.
110
. C.
495
. D.
55
.
.ABCD A B C D
a
A B C D
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 4 Mã đề 110
Câu 28. Cho số thực
0, 1aa
. Giá trị của
2
3
7
log ( )
a
a
bằng
A.
3
14
. B.
6
7
. C.
3
8
. D.
7
6
.
Câu 29. Đạo hàm của hàm số
( )
3
8
log 3 4y x x= − −
là
A.
( )
3
3
33
3 4 ln2
x
xx
−
−−
. B.
( )
2
3
1
3 4 ln2
x
xx
−
−−
. C.
3
3
33
34
x
xx
−
−−
. D.
( )
3
1
3 4 ln8xx−−
.
Câu 30. Cho cấp số nhân
( )
n
u
thỏa mãn
13
46
10
80
uu
uu
+=
+=
. Tìm
3
u
A.
3
8u =
. B.
3
2u =
. C.
3
6u =
. D.
3
4u =
.
Câu 31. Cho khối nón
( )
N
đỉnh
S
, có chiều cao là
3a
và độ dài đường sinh là
3a
. Mt phẳng
( )
P
đi qua đỉnh
S
, cắt và tạo với mt đáy của khối nón một góc
60
. Tính diện tích thiết diện tạo
bởi mt phẳng
( )
P
và khối nón
( )
N
.
A.
2
25a
. B.
2
3a
. C.
2
23a
. D.
2
5a
.
Câu 32. Cho hàm số
32
34y x x= − +
có đồ thị
( )
C
như hnh vẽ và đường thẳng
32
: 3 4d y m m= − +
(với
m
là tham số). Hỏi có bao nhiêu giá trị nguyên của tham số
m
để đường thẳng
d
cắt đồ thị
( )
C
tại ba điểm phân biệt?
A.
3
. B.
2
. C.
1
. D. Vô số.
Câu 33. Cho các số phức
z
thỏa mãn
2z =
. Biết rằng tập hợp các điểm biểu diễn số phức
( )
3 2 4 3w i i z= − + −
là một đường tròn. Tính bán kính
r
của đường tròn đó.
A.
5r =
. B.
25r =
. C.
10r =
. D.
20r =
.
Câu 34. Cho
9 9 14
xx−
+=
. Khi đó biểu thức
2 81 81
11 3 3
xx
xx
M
−
−
++
=
−−
có giá trị bằng
A. 14. B. 49. C. 42. D. 28.
Câu 35. Cho lăng trụ tam giác đều
.ABC A B C
có đáy là tam giác đều cạnh
a
,
2AA a
=
. Gọi
là góc
giữa
AB
và
BC
. Tính
cos
.
A.
5
cos
8
=
. B.
51
cos
10
=
. C.
39
cos
8
=
. D.
7
cos
10
=
.
Câu 36. Cho hai đường thẳng
1
1
:2
32
xt
d y t
zt
=+
=−
=+
và
2
12
:
2 1 1
x y m z
d
− − +
==
−
(với
m
là tham số). Tìm
m
để hai đường thẳng
1
d
,
2
d
cắt nhau.
4
2
3
1
3
1
x
y
2
O
-1
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 5 Mã đề 110
A.
4m =
. B.
9m =
. C.
7m =
. D.
5m =
.
Câu 37. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Tam giác
SAB
đều và nằm
trong mt phẳng vuông góc với đáy. Tính khoảng cách từ điểm
C
đến mt phẳng
( )
SAD
.
A.
3
6
a
. B.
3
2
a
. C.
3
3
a
. D.
3
4
a
.
Câu 38. Cho một hộp có chứa 5 bóng xanh, 6 bóng đỏ và 7 bóng vàng. Lấy ngẫu nhiên
4 bóng từ hộp, tính xác suất để có đủ 3 màu.
A.
35
816
. B.
35
68
. C.
175
5832
. D.
35
1632
.
Câu 39. Cho phương trnh
2
33
log 4log 3 0x x m− + − =
. Tìm tất cả các giá trị nguyên của tham số
m
để
phương trnh đã cho có hai nghiệm phân biệt thỏa mãn
12
1xx
.
A. 6. B. 4. C. 3. D. 5.
Câu 40. Có tất cả bao nhiêu giá trị thực của tham số
m
để đường thẳng
:1d y mx=+
cắt đồ thị
( )
32
:1C y x x= − +
tại 3 điểm
( )
; 0;1 ;A B C
phân biệt sao cho tam giác
AOC
vuông tại
( )
0;0O
?
A.
0
. B.
1
. C.
3
. D.
2
.
Câu 41. Trong không gian
,Oxyz
cho điểm
( )
1; 1;2M −
và hai đường thẳng
1
: 1 ,
1
xt
d y t
z
=
=−
=−
2
1 1 2
:
2 1 1
x y z
d
+ − +
==
. Đường thẳng
đi qua điểm M và cắt cả hai đường thẳng
12
,dd
có
véctơ chỉ phương là
( )
1; ; ,u a b
=
tính
.ab+
A.
1.ab+ = −
B.
b 2.a + = −
C.
b 2.a +=
D.
b 1.a +=
Câu 42. Hai người
A
và
B
ở cách nhau
180
( )
m
trên một đoạn đường thẳng và cùng chuyển động
thẳng theo một hướng với vận tốc biến thiên theo thời gian,
A
chuyển động với vận tốc
( ) ( )
1
6 5 m/sv t t=+
,
B
chuyển động với vận tốc
( ) ( )
2
2a 3 m/sv t t=−
(
a
là hằng số), trong đó
t
(giây) là khoảng thời gian tính từ lúc
A
,
B
bắt đầu chuyển động. Biết rằng lúc đầu
A
đuổi
theo
B
và sau
10
(giây) th đuổi kịp. Hỏi sau
20
(giây),
A
cách
B
bao nhiêu mét?
A.
( )
320 m
. B.
( )
720 m
. C.
( )
360 m
. D.
( )
380 m
.
Câu 43. Một hình hộp chữ nhật có chiều cao là 90 cm, đáy hộp là hình chữ nhật có chiều rộng là 50 cm
và chiều dài là 80 cm. Trong khối hộp có chứa nước, mực nước so với đáy hộp có chiều cao là
40 cm. Hỏi khi đt vào khối hộp một khối trụ có chiều cao bằng chiều cao khối hộp và bán kính
đáy là 20 cm theo phương thẳng đứng thì chiều cao của mực nước so với đáy là bao nhiêu?
A. 68,32 cm. B. 78,32 cm. C. 58,32 cm. D. 48,32 cm.
Câu 44. Một chiếc cổng có hình dạng là một Parabol có khoảng cách giữa hai chân cổng là
8m=AB
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 6 Mã đề 110
Người ta treo một tấm phông hình chữ nhật có hai đỉnh
,MN
năm trên Parabol và hai đỉnh
,PQ
nằm trên mt đất(như hnh vẽ). Ở phần phía ngoài phông (phần không tô đen) người ta
mua hoa để trang trí với chi phí cho
2
1m
cần số tiền cần mua hoa là
200.000
đồng cho
2
1m .
Biết rằng
4m, 6m==MN MQ
. Hỏi số tiền dùng để mua hoa trang trí chiếc cổng gần với số
tiền nào sau đây?
A.
3.735.300
đồng. B.
3.437.300
đồng.
C.
3.734.300
đồng . D.
3.733.300
đồng.
Câu 45. Cho hai số phức
,zw
thay đổi thỏa mãn
3, 1.z z w= − =
Biết tập hợp điểm của số phức
w
là
hình phẳng H. Tính diện tích S của H.
A.
20S
=
. B.
12S
=
. C.
4S
=
. D.
16S
=
.
Câu 46. Cho
1
2
0
93
d1
93
x
x
m
xm
+
=−
+
. Tính tổng tất cả các giá trị của tham số
m
.
A.
12P =
. B.
1
2
P =
. C.
16P =
. D.
24P =
.
Câu 47. Có bao nhiêu cách phân tích số
9
15
thành tích của ba số nguyên dương, biết rằng các cách phân
tích mà các phần tử chỉ khác nhau về thứ tự thì chỉ được tính một lần?
A.
517
. B.
516
. C.
493
. D.
492
.
Câu 48. Cho các số thực
,1ab
thoả mãn
8
3
log
log
2
16 12
a
b
b
a
a
a b b




+=
. Giá trị của biểu thức
33
P a b=+
là
A.
20
. B.
39
. C.
125
. D.
72
.
Câu 49. Cho hnh chóp
.S ABCD
có đáy
ABCD
là hnh vuông, hnh chiếu vuông góc của đỉnh
S
xuống mt đáy nằm trong hnh vuông
ABCD
. Hai mt phẳng
( )
SAD
,
( )
SBC
vuông góc với
nhau; góc giữa hai mt phẳng
( )
SAB
và
( )
SBC
là
0
60
; góc giữa hai mt phẳng
( )
SAB
và
( )
SAD
là
0
45
. Gọi
là góc giữa hai mt phẳng
( )
SAB
và
( )
ABCD
, tính
cos
A.
1
cos =
2
. B.
2
cos =
2
. C.
3
cos =
2
. D.
2
cos =
3
.
Câu 50. Cho hai hàm số
( ) ( )
( )
3 2 2
1
1 3 4 5 2019
3
f x x m x m m x= − + + + + +
và
( )
( ) ( )
2 3 2 2
2 5 2 4 9 3 2g x m m x m m x x= + + − + + − +
, với
m
là tham số. Hỏi phương trnh
( )
( )
0g f x =
có bao nhiêu nghiệm?
A. 9. B. 0. C. 3 . D. 1.
GIẢI CHI TIẾT ĐỀ THỬ THPTQG
LƯƠNG THẾ VINH- HÀ NỘI LẦN 2-2019
MÔN TOÁN
P
M
Q
N
A
B
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 7 Mã đề 110
luuhuephuongtailieu@gmail.com
Nguyentuyetle77@gmail.com
Câu 1 . Cho số phức
z
thỏa mãn
32zi=+
. Tìm phần thực và phần ảo của số phức
z
.
A.Phần thực bằng
3−
, phần ảo bằng
2
. B. Phần thực bằng
, phần ảo bằng
2
.
C. Phần thực bằng
3
, phần ảo bằng
2−
. D. Phần thực bằng -3, phần ảo bằng
2−
.
Lời giải
Tác giả: Nguyễn Tuyết Lê ; Fb: Nguyên Tuyet Le
Chọn C
Vì
32zi=+
32zi=−
. Do đó số phức
z
có phần thực bằng
3
, phần ảo bằng
2−
.
vanluu1010@gmail.com
Câu 2. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
0 0 0
:
x x y y z z
a b c
− − −
= =
. Điểm
M
nằm trên đường thẳng
thì tọa độ của điểm
M
có dạng nào sau đây?
A.
( )
;;M at bt ct
. B.
( )
0 0 0
;;M x t y t z t
.
C.
( )
0 0 0
;;M a x t b y t c z t+ + +
. D.
( )
0 0 0
;;M x at y bt z ct+ + +
.
Lời giải
Tác giả: Bùi Văn Lưu ; Fb: Bùi Văn Lưu
Chọn D
Đường thẳng
đi qua điểm
( )
0 0 0 0
;;M x y z
và có véc tơ chỉ phương
( )
;;u a b c=
nên đường
thẳng
có phương trnh tham số là
0
0
0
:
x x at
y y bt
z z ct
=+
= +
=+
Điểm
M
nằm trên đường thẳng
thì tọa độ của điểm
M
có dạng
( )
0 0 0
;;M x at y bt z ct+ + +
Nguyenth4nhtr11ng@gmail.com
Câu 3. Cho hàm số
( )
=y f x
xác định, liên tục trên và có bảng biến thiên như sau:
Tìm giá trị cực đại
CÑ
y
và giá trị
CT
y
của hàm số đã cho.
A.
=−2
CÑ
y
và
= 2
CT
y
. B.
= 3
CÑ
y
và
= 0
CT
y
.
C.
= 2
CÑ
y
và
= 0
CT
y
. D.
= 3
CÑ
y
và
=−2
CT
y
.
Lời giải
Tác giả: Nguyên Thành Trung ; Fb:Nguyên Thành Trung
Chọn B
Từ bảng biến thiên ta có:
•
y
đổi dấu dương qua âm khi qua điểm
=−2x
suy ra giá trị cực đại
( )
= − =23
CÑ
yy
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 8 Mã đề 110
•
y
đổi dấu âm qua dương khi qua điểm
= 2x
suy ra giá trị cực tiểu
( )
==20
CT
yy
.
anhtuanqh1@gmail.com
Câu 4. Trong hệ tọa độ
Oxyz
, cho ba điểm
( )
1;0;0A
,
( )
0; 1;0B −
,
( )
0;0;2C
. Phương trnh mt phẳng
( )
ABC
là:
A.
20x y z− + =
. B.
1
2
z
xy− + =
. C.
1
2
y
xz+ − =
. D.
20x y z− + =
.
Lời giải
Tác giả: Nguyễn Anh Tun; Fb: Nguyễn Ngc Minh Châu
Chọn B
p dụng phương trnh mt phẳng theo đoạn chắn ta có:
( )
:1
1 1 2
x y z
ABC + + =
−
hay
1
2
z
xy− + =
.
tatienthanh7895@gmail.com
Câu 5. Đường thẳng
ym=
tiếp xúc với đồ thị
42
( ): 2 4 1C y x x= − + −
tại hai điểm phân biệt
( ; )
AA
A x y
và
( ; )
BB
B x y
. Giá trị của biểu thức
AB
yy+
bằng
A.
2
. B.
1−
. C.
1
. D.
0.
Lời giải
Tác giả: Tạ Tiến Thanh; Fb: Thanh Ta
Chọn A
Xét hàm số
42
( ) 2 4 1f x x x= − + −
, TXĐ:
D =
.
3
'( ) 8 8f x x x= − +
.
1
'( ) 0 0
1
x
f x x
x
=−
= =
=
.
Xét bảng biến thiên
Dựa vào bảng biến thiên ta thấy để đường thẳng
ym=
tiếp xúc với
42
( ): 2 4 1C y x x= − + −
tại
hai điểm phân biệt th đường thẳng đó phải đi qua hai điểm cực đại, hay
1m =
.
Khi đó hai tiếp điểm là
( 1;1)A −
và
(1;1)B
. Vậy
1 1 2
AB
yy+ = + =
.
Pho.maths@gmail.com
Câu 6. Trong các hàm số dưới đây, hàm số nào đồng biến trên tập ?
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 9 Mã đề 110
A.
13
2
x
y
−
=
. B.
( )
2
log 1yx=−
. C.
( )
2
log 2 1
x
y =+
. D.
( )
2
2
log 1yx=+
.
Lời giải
Tác giả: Lương Pho; Fb: LuongPho89
Chọn C
Hàm số
( )
2
log 2 1
x
y =+
có tập xác định
D =
và
2
' 0 , x .
21
x
x
y =
+
Do đó, hàm số
( )
2
log 2 1
x
y =+
đồng biến trên tập .
chauhieu2013@gmail.com
dohoangtu2212@gmail.com
Câu 7. Đường cong như hnh bên dưới là đồ thị của hàm số nào sau đây?
A.
32
32y x x
. B.
32
32y x x
.
C.
42
22y x x
. D.
42
22y x x
.
Lời giải
Tác giả: Đỗ Hoàng Tú ; Fb: Đỗ Hoàng Tú
Chọn C
Đồ thị hàm số đối xứng qua trục Oy
Hàm số là hàm chẵn
Loại A, B.
Hệ số
0a
Loại D, chọn C.
thuytoanthanglong@gmail.com
Câu 8. Tìm tập xác định của hàm số
( )
2
23
e
y x x= + −
.
A.
( ) ( )
; 3 1;− − +
. B.
(
)
; 3 1;− − +
.
C.
( )
3;1−
. D.
3; 1−
Lời giải
Tác giả: Nguyễn Thủy; Fb: diephoang
Chọn A
Hàm số xác định khi
2
3
2 3 0
1
x
xx
x
−
+ −
.
Vậy tập xác định của hàm số là
( ) ( )
; 3 1;D = − − +
.
quyetlv.toan@gmail.com
Câu 9. Cho hàm số
21
1
x
y
x
+
=
+
. Mệnh đề đúng là
A. Hàm số nghịch biến trên
( )
;1− −
và
( )
1;− +
.
B. Hàm số đồng biến trên
( )
;1− −
và
( )
1; +
, nghịch biến trên
( )
1;1−
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 10 Mã đề 110
C. Hàm số đồng biến trên .
D. Hàm số đồng biến trên
( )
;1− −
và
( )
1;− +
.
Lời giải
Tác giả: Lê Văn Quyết ; Fb: Lê Văn Quyết
Chọn D
TXĐ:
\1−
.
Ta có
( )
2
1
'0
1
y
x
=
+
,
1x −
.
Vậy hàm số đồng biến trên
( )
;1− −
và
( )
1;− +
. Chọn D.
Khaiphung97@gmail.com
Câu 10. Thể tích của khối cầu có bán kính
R
là:
A.
3
R
. B.
3
4
3
R
. C.
3
2 R
. D.
3
3
R
.
Lời giải
Tác giả:Phùng Văn Khải; Fb:Phùng Khải
Chọn B
Ta có thể tích khối cầu có bán kính
R
là:
3
4
3
VR
=
428truonghuyen@gmail.com
Câu 11. Cho
( )
fx
,
( )
gx
là các hàm số có đạo hàm liên tục trên ,
k
. Trong các khẳng định dưới
đây, khẳng định nào sai?
A.
( ) ( ) ( ) ( )
d d df x g x x f x x g x x− = −


. B.
( ) ( )
df x x f x C
=+
.
C.
( ) ( )
ddkf x x k f x x=

. D.
( ) ( ) ( ) ( )
d d df x g x x f x x g x x+ = +


.
Lời giải
Tác giả: Trương Huyền ; Fb: Trương Huyền
Chọn C
Khẳng định A, B, D đúng theo tính chất của nguyên hàm.
Khẳng định C chỉ đúng khi
0k
.
honganh161079@gmail.com
Câu 12. Cho lăng trụ tứ giác đều có đáy là hnh vuông cạnh
a
, chiều cao
2a
. Tính thể tích khối lăng
trụ.
A.
3
2
3
a
. B.
3
4
3
a
. C.
3
a
. D.
3
2a
.
Lời giải
Tác giả: Đỗ Thị Hồng Anh; Fb: Hong Anh
Chọn D
Đáy của lăng trụ tứ giác đều là hình vuông cạnh
a
nên diện tích đáy
2
=Sa
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 11 Mã đề 110
Thể tích khối lăng trụ là :
23
. .2 2= = =V S h a a a
.
Diephd02@gmail.com; ducquoc210382@gmail.com
Câu 13. Tích của giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
4
f x x
x
=+
trên đoạn
1;3
bằng
A.
65
3
. B.
20
. C.
6
. D.
52
3
.
Lời giải
Tác giả : Nguyễn Ngc Diệp, FB: Nguyễn Ngc Diệp
Chọn B
Ta có: hàm số
( )
4
f x x
x
=+
xác định và liên tục trên đoạn
1;3
.
( )
2
4
1fx
x
=−
;
( )
2
2
4
0 1 0
2
x
fx
x
x
=
= − =
=−
.
Nhận thấy:
2 1;3 2x− = −
(loại).
( ) ( ) ( )
13
1 5; 2 4; 3
3
f f f= = =
. Khi đó:
( )
1;3
max 5M f x==
;
( )
1;3
min 4m f x==
.
Vậy
. 20Mm=
.
Email: khanhhm.94@gmail.com
Câu 14 . Trong hệ tọa độ
Oxyz
, cho hai đường thằng chéo nhau
1
2 2 6
:
2 1 2
x y z
d
− + −
==
−
;
2
4 2 1
:
1 2 3
x y z
d
− + +
==
−
. Phương trnh mt phẳng
( )
P
chứa
1
d
và song song với
2
d
là
A.
( )
: 8 5 16 0P x y z+ + + =
. B.
( )
: 8 5 16 0P x y z+ + − =
.
C.
( )
:2 6 0P x y+ − =
. D.
( )
: 4 3 12 0P x y z+ + − =
.
Lời giải
Tác giả:Huỳnh Minh Khánh ; Fb: Huỳnh Khánh
Chọn B
Phương trnh tham số
1
11
1
22
:2
62
xt
d y t
zt
=+
= − +
=−
,
( )
1
t
.
1
d
đi qua điểm
( )
2; 2;6M −
và véc tơ chỉ phương
( )
1
2;1; 2u =−
.
Phương trnh tham số
2
22
2
4
: 2 2
13
xt
d y t
zt
=+
= − −
= − +
,
( )
2
t
.
2
d
đi qua
( )
4; 2; 1N −−
và véc tơ chỉ phương
( )
2
1; 2;3u =−
.
Vì mt phẳng
( )
P
chứa
1
d
và song song với
2
d
, ta có:
( )
( )
( )
( )
1
12
2
, 1;8;5
P
P
P
nu
n u u
nu
⊥

= = −

⊥
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 12 Mã đề 110
Mt phẳng
( )
P
đi qua
( )
2; 2;6M −
và véc tơ pháp tuyến
( )
( )
1;8;5
P
n =
, nên phương trnh mt
phẳng
( ) ( ) ( ) ( )
: 2 8 2 5 6 0P x y z− + + + − =
hay
( )
: 8 5 16 0P x y z+ + − =
.
trongtuspt08@gmail.com
Câu 15. Trong hệ tọa độ
Oxyz
, cho đường thẳng
1 3 1
:
2 1 1
x y z
d
− − −
==
−
cắt mt phẳng
( )
:2 3 2 0P x y z− + − =
tại điểm
( )
;;I a b c
. Khi đó
abc++
bằng
A.
9
. B.
5
. C.
3
. D.
7
.
Lời giải
Tác giả: Nguyễn Trng Tú ; Fb: Anh Tú
Chọn D
Ta có
( )
I d P=
suy ra
Id
và
( )
IP
.
Vì
Id
nên tọa độ của
I
có dạng
( )
1 2 ;3 ;1t t t+ − +
với
t
.
Vì
( )
IP
nên ta có phương trnh:
( ) ( )
2 1 2 3 3 1 2 0 1t t t t+ − − + + − = =
.
Vậy
( )
3;2;2I
suy ra
3 2 2 7abc+ + = + + =
.
ngoquoctuanspt95tailieu@gmail.com Tranthom275@gmail.com
Câu 16. Cho dãy số
( )
n
u
là một cấp số cộng, biết
2 21
50uu+=
. Tính tổng của
22
số hạng đầu tiên của
dãy.
A.
2018
. B.
550
. C.
1100
. D.
50
.
Lời giải
Tác giả : Ngô Quốc Tun, FB: Quốc Tun
Chọn B
Ta có:
21
u u d=+
,
21 1
20u u d=+
.
Theo giả thiết
2 21 1
50 2 21 50u u u d+ = + =
.
Tổng của
22
số hạng đầu tiên của dãy là
1
22
2 21 22
2
ud
S
+
=
50.22
2
=
550=
.
cunconsieuquay1408@gmail.com
Câu 17 . Số đường tiệm cận của đồ thị hàm số
1
21
x
y
xx
+
=
−+
là
A.
4
. B.
3
. C.
2
. D.
1
.
Lời giải
Tác giả: Nguyễn Thị Thanh Mai ; Fb: Thanh Mai Nguyen
Chọn B
+ Với
0x
thì
11
2 1 1
xx
y
x x x
++
==
− + − +
có TXĐ là:
) ( )
0;1 1;D = +
.
Khi đó:
lim 1
x
y
→+
=−
nên đồ thị hàm số có tiệm cận ngang
1y =−
.
0
lim 1
x
y
+
→
=
.
1
lim
x
y
+
→
= −
,
1
lim
x
y
−
→
= +
nên đồ thị hàm số có tiệm cận đứng
1x =
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 13 Mã đề 110
+ Với
0x
thì
11
2 1 3 1
xx
y
x x x
++
==
− − + − +
có TXĐ là:
( )
;0D = −
.
Khi đó:
1
lim
3
x
y
→−
=−
nên đồ thị hàm số có tiệm cận ngang
1
3
y =−
.
0
lim 1
x
y
−
→
=
.
Vậy đồ thị hàm số đã cho có 3 đường tiệm cận.
Thuhangnvx@gmail.com
Câu 18. Cho khối chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
, tam giác
SAB
đều và nằm trong
mt phẳng vuông góc với đáy. Tính theo
a
thể tích của khối chóp
.S ABC
.
A.
3
8
a
V =
. B.
3
3
3
a
V =
. C.
3
3
4
a
V =
. D.
3
4
a
V =
.
Lời giải
Tác giả:Phùng Hằng ; Fb: Phùng Hằng
Chọn A
Tam giác
ABC
là tam giác đều cạnh
a
2
3
4
ABC
a
S
=
.
Gọi
H
là trung điểm của
AB
. Do tam giác
ABC
là tam giác đều cạnh
a
nên
SH AB⊥
và
3
2
a
SH =
.
Ta có:
( ) ( )
( ) ( )
( )
( )
.
SAB ABC
SAB ABC AB
SH ABC
SH AB
SH SAB
⊥
=
⊥
⊥
Vậy
23
.
1 1 3 3
. .S . . .
3 3 2 4 8
S ABC ABC
a a a
V SH
= = =
ngocthanh1308@gmail.com
Câu 19. Họ nguyên hàm của hàm số
( )
( )
3
2 1 3f x x x=+
là
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 14 Mã đề 110
A.
22
3
1
2
x x C

++


. B.
3
2
6
1
5
x
xC

++


. C.
4
3
2
4
x x x C

++


. D.
23
3
4
x x x C

++


.
Lời giải
Tác giả: Ngc Thanh; Fb: Ngc Thanh
Chọn B
( )
( ) ( )
3
3 4 2 5 2
66
d 2 1 3 d 2 6 d 1
55
x
f x x x x x x x x x x C x C

= + = + = + + = + +


.
Vậy họ nguyên hàm của hàm số
( )
( )
3
2 1 3f x x x=+
là
3
2
6
1
5
x
xC

++


.
Hungnguyen24061984@gmail.com
Câu 20. Tập nghiệm
S
của bất phương trnh
13
2 25
54
x−



.
A.
)
1;S = +
. B.
1
;
3
S

= +

. C.
1
;
3
S

= −


. D.
(
;1S = −
.
Lời giải
Tác giả: Nguyễn Hoàng Hưng; Fb: Nguyễn Hưng
Chọn A
1 3 1 3 2 3 1 2
2 25 2 5 5 5
3 1 2 1
5 4 5 2 2 2
x x x
xx
− − −
−
.
Vậy tập nghiệm của bất phương trnh đã cho là
)
1;S = +
.
hanhphuduc@gmail.com
Câu 21. Trong hệ toạ độ
Oxyz
, cho điểm
( )
3;5;3A
và hai mt phẳng
( ):2 2 8 0,P x y z+ + − =
( ): 4 4 0.Q x y z− + − =
Viết phương trnh đường thẳng
d
đi qua
A
và song song với cả hai mt
phẳng
()P
và
()Q
.
A.
3
5
3
xt
yt
z
=+
=−
=
. B.
3
5
3
x
yt
zt
=
=+
=−
. C.
3
5
3
xt
y
zt
=+
=
=−
. D.
3
5
3
xt
y
zt
=+
=
=+
.
Lời giải
Tác giả: Phạm Hạnh; Fb: Phạm Hạnh
Chọn C
()P
có một VTPT
( )
1
2;1;2n
,
()Q
có một VTPT
( )
2
1; 4;1 .n −
Do
/ /( ), / /( )d P d Q
d
có VTCP
( )
12
, 9;0; 9u n n= = −
( )
1
1;0; 1u−
cũng là một VTCP
của
()d
.
Đường thẳng
()d
đi qua
( )
3;5;3A
, nhận
1
u
làm VTCP, có phương trnh là
3
5
3
xt
y
zt
=+
=
=−
,
tR
.
hienchn@gmail.com
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 15 Mã đề 110
minhphuongk34toan@gmail.com
Câu 22. Trong hệ tọa độ
Oxyz
, cho điểm
( )
1;1;6A −
và đường thẳng
2
: 1 2 .
2
xt
yt
zt
=+
= −
=
Hình chiếu vuông
góc của
A
trên
là:
A.
( )
3; 1;2M −
. B.
( )
11; 17;18H −
. C.
( )
1;3; 2N −
. D.
( )
2;1;0K
.
Lời giải
Tác giả: Nguyễn Thị Minh Phương ; Fb: Minh Phuong
Chọn A
Xét điểm
( )
2 ;1 2 ;2H t t t+ −
.
Ta có :
( ) ( )
3 ; 2 ;2 6 ; 1; 2;2AH t t t a
= + − − = −
H
là hình chiếu vuông góc của
A
trên
.0AH a
=
( ) ( )
1. 3 4 2 2 6 0 1.t t t t+ + + − = =
Suy ra:
( )
3; 1;2H −
.
Phanvinha3@gmail.com
Câu 23. Cho
( )
fx
,
( )
gx
là các hàm số liên tục trên thỏa mãn
( )
1
0
d3f x x =
,
( ) ( )
2
0
3 d 4f x g x x−=


và
( ) ( )
2
0
2 d 8f x g x x+=


.
Tính
( )
2
1
dI f x x=
.
A.
1I =
. B.
2I =
. C.
3I =
. D.
0I =
.
Lời giải
Tác giả: Phan Minh Quốc Vinh ; Fb: Vinh Phan
Chọn A
Vì hàm số
( )
fx
,
( )
gx
liên tục trên nên
( ) ( )
( ) ( )
( ) ( )
( ) ( )
2 2 2
0 0 0
2 2 2
0 0 0
3 d 4 d 3 d 4
2 d 8 2 d d 8
f x g x x f x x g x x
f x g x x f x x g x x

− = − =






+ = + =




( )
( )
2
0
2
0
d4
d0
f x x
g x x
=
=
Vì hàm số
( )
fx
liên tục trên nên
( ) ( ) ( )
2 1 2
0 0 1
d d df x x f x x f x x=+
( ) ( ) ( )
2 2 1
1 0 0
d d d 4 3 1f x x f x x f x x = − = − =
.
Vậy
( )
2
1
d1f x x =
.
Nguyenhoach95@gmail.com
Câu 24. Đồ thị hàm số
4
2
3
22
x
yx= − + +
cắt trục hoành tại mấy điểm?
A.
0
. B.
2
. C.
4
. D.
3
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 16 Mã đề 110
Lời giải
Tác giả: Nguyễn Đức Hoạch; Fb: Hoạch Nguyễn
Chọn B
Xét phương trnh hoành độ giao điểm:
4
2
3
0
22
x
x− + + =
42
2 3 0xx − − =
( )( )
2
22
2
3
3 1 0
1
x
xx
x
=
− + =
=−
3x =
.
Vậy đồ thị hàm số đã cho cắt trục hoành tại 2 điểm.
Nvthang368@gmail.com
ngoctinh.hnue@gmail.com
Câu 25. Trong hệ tọa độ
( )
Oxyz
, cho đểm
( )
2; 1; 1I −−
và mt phẳng
( )
: 2 2 3 0P x y z− − + =
. Viết
phương trnh mt cầu
( )
S
có tâm
I
và tiếp xúc với mt phẳng
( )
P
.
A.
( )
2 2 2
: 4 2 2 3 0.S x y z x y z+ + − + + − =
B.
( )
2 2 2
: 2 3 0.S x y z x y z+ + − + + − =
C.
( )
2 2 2
: 4 2 2 1 0.S x y z x y z+ + − + + + =
D.
( )
2 2 2
: 2 1 0.S x y z x y z+ + − + + + =
Lời giải
Tác giả: Nguyễn Thị Tỉnh, Fb: Ngc Tỉnh.
Chọn A
Gọi
R
là bán kính mt cầu
( )
S
.
Vì mt cầu
( )
S
có tâm
I
và tiếp xúc với mt phẳng
( )
P
nên ta có:
( )
( )
;
222
2 2.( 1) 2.( 1) 3
9
3
3
1 ( 2) ( 2)
IP
Rd
− − − − +
= = = =
+ − + −
.
Vậy nên ta có phương trnh mt cầu
( )
S
là:
( ) ( ) ( )
2 2 2
2 2 2
2 1 1 9 4 2 2 3 0.x y z x y z x y z− + + + + = + + − + + − =
tranthanhha484@gmail.com
Câu 26. Cho hình lập phương
.ABCD A B C D
có cạnh bằng
a
. Một hnh nón có đỉnh là tâm của hình
vuông
A B C D
và có đường tròn đáy ngoại tiếp hình vuông
ABCD
. Tính diện tích xung
quanh của hnh nón đó.
A.
2
2
2
a
. B.
2
3a
. C.
2
2
4
a
. D.
2
3
2
a
.
Lời giải
Tác giả: Trần Thanh Hà; Fb: Hà Trần
Chọn D
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 17 Mã đề 110
Gọi
,OO
lần lượt là tâm của hình vuông
,ABCD A B C D
.
Hnh nón có đáy là đường tròn ngoại tiếp hình vuông
ABCD
có cạnh là
a
nên đáy của hình
nón là đường tròn có bán kính
12
22
a
r AC==
.
Hnh nón có đỉnh là tâm của hình vuông
A B C D
nên chiều cao của hình nón bằng độ dài
cạnh của hình vuông. Suy ra:
ha=
.
Khi đó: độ dài đường sinh của hình nón là:
2
2
2 2 2 2 2
2 3 6
.
2 2 2
a a a
l O A O O OA h r a


= = + = + = + = =


Diện tích xung quanh của hình nón là:
2
2 6 3
..
2 2 2
xq
a a a
S rl

= = =
( đvdt).
lethimai0108@gmail.com
Câu 27. Tìm hệ số của số hạng chứa
9
x
trong khai triển nhị thức Newton của biểu thức
( )
11
3 x+
A.
9
. B.
110
. C.
495
. D.
55
.
Lời giải
Tác giả: Lê Mai; Fb: Lê Mai
Chọn C
Số hạng tổng quát trong khai triển nhị thức Newton của biểu thức
( )
11
3 x+
là:
11
11
3.
k k k
Cx
−
.
Cho
9k =
ta được hệ số của số hạng chứa
9
x
trong khai triển nhị thức Newton của biểu thức
( )
11
3 x+
là
29
11
3 . 495C =
.
tammath11@gmail.com
PB : khanghan456@gmail.com
Câu 28. Cho số thực
0, 1aa
. Giá trị của
2
3
7
log ( )
a
a
bằng
A.
3
14
. B.
6
7
. C.
3
8
. D.
7
6
.
Lời giải
Tác giả: Nguyễn Đình Tâm ; Fb: Tâm Nguyễn Đình
Chọn A
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 18 Mã đề 110
2
3
3
7
7
1 1 3 3
log ( ) log . log
2 2 7 14
aa
a
a a a= = =
.
Tvluatc3tt@gmail.com
Câu 29. Đạo hàm của hàm số
( )
3
8
log 3 4y x x= − −
là
A.
( )
3
3
33
3 4 ln2
x
xx
−
−−
. B.
( )
2
3
1
3 4 ln2
x
xx
−
−−
. C.
3
3
33
34
x
xx
−
−−
. D.
( )
3
1
3 4 ln8xx−−
.
Lời giải
Tác giả : Trần Luật, FB: Trần Luật
Chọn B.
Ta có
( )
( )
( )
( )
( )
( )
32
2
3
8
3 3 3
3 4 3 1
1
log 3 4
3 4 ln8 3 3 4 ln2 3 4 ln2
x x x
x
y x x y
x x x x x x
− − −
−
= − − = = =
− − − − − −
.
canhcuttapbay@gmail.com
Câu 30. Cho cấp số nhân
( )
n
u
thỏa mãn
13
46
10
80
uu
uu
+=
+=
. Tìm
3
u
A.
3
8u =
. B.
3
2u =
. C.
3
6u =
. D.
3
4u =
.
Lời giải
Tác giả:Vũ Thị Thành ; Fb:Thanh Vũ
Chọn A
Gọi công bội của cấp số nhân là
q
Theo giả thiết ta có:
( )
2
2
2
11
13
11
1 1 1
32
35
3
46
11
11
10
10
10
10 2
80
2
80
80
.10 80
u u q
uu
u u q
u u q u
uu
q
q u u q
u q u q
q
+=
+=
+=
+ = =
+=
=
+=
+=
=
Suy ra:
2
31
8u u q==
Ductoan.lvt@gmail.com
Câu 31. Cho khối nón
( )
N
đỉnh
S
, có chiều cao là
3a
và độ dài đường sinh là
3a
. Mt phẳng
( )
P
đi qua đỉnh
S
, cắt và tạo với mt đáy của khối nón một góc
60
. Tính diện tích thiết diện tạo
bởi mt phẳng
( )
P
và khối nón
( )
N
.
A.
2
25a
. B.
2
3a
. C.
2
23a
. D.
2
5a
.
Lời giải
Tác giả: Giáp Minh Đức; Fb: Giáp Minh Đức
ChọnA
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 19 Mã đề 110
+) Khối nón
( )
N
có tâm đáy là điểm
O
, chiều cao
3SO h a==
và độ dài đường sinh
3la=
.
+) Giả sử mt phẳng
( )
P
cắt
( )
N
theo thiết diện là tam giác
SAB
.
Do
SA SB l==
tam giác
SAB
cân tại đỉnh
.S
+) Gọi
I
là trung điểm của
AB
. Ta có
OI AB⊥
,
SI AB⊥
và khi đó góc giữa mt phẳng
( )
P
và mt đáy của
( )
N
là góc
60SIO =
.
+) Trong tam giác
SOI
vuông tại
O
góc
60SIO =
.
Ta có
3
2
sin60
sin
SO a
SI a
SIO
= = =
.
+) Trong tam giác
SIA
vuông tại
I
.
Ta có
2 2 2 2 2 2
9 4 5IA SA SI a a a= − = − =
5IA a=
2 2 5AB IA a = =
.
Vậy diện tích thiết diện cần tìm là
2
11
. .2 .2 5 2 5
22
td SAB
S S SI AB a a a
= = = =
.
Nhantruongthanh79@gmail.com.
Câu 32. Cho hàm số
32
34y x x= − +
có đồ thị
( )
C
như hnh vẽ và đường thẳng
32
: 3 4d y m m= − +
(với
m
là tham số). Hỏi có bao nhiêu giá trị nguyên của tham số
m
để đường thẳng
d
cắt đồ thị
( )
C
tại ba điểm phân biệt?
A.
3
. B.
2
. C.
1
. D. Vô số.
Lời giải
Tác giả: Trương Thanh Nhàn; Fb: Trương Thanh Nhàn.
Chọn C
r
h
l
I
A
S
O
B
4
2
3
1
3
1
x
y
2
O
-1
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 20 Mã đề 110
Từ đồ thị suy ra đường thẳng
d
cắt đồ thị
( )
C
tại
3
điểm phân biệt khi và chỉ khi
( )( )
( )
2
32
32
32
2
13
1 2 0
3 4 0
0 3 4 4 0
30
30
2
m
mm
mm
m m m
mm
mm
m
−
+ −
− +
− +
−
−

Vì
m
là số nguyên nên
1m =
.
Luuthedung1982@gmail.com
Câu 33. Cho các số phức
z
thỏa mãn
2z =
. Biết rằng tập hợp các điểm biểu diễn số phức
( )
3 2 4 3w i i z= − + −
là một đường tròn. Tính bán kính
r
của đường tròn đó.
A.
5r =
. B.
25r =
. C.
10r =
. D.
20r =
.
Lời giải
Tác giả: Lưu Thế Dũng; Fb: Lưu Thế Dũng
Chọn C
Đt
( )
,,w x yi x y= +
ta có:
( ) ( ) ( ) ( ) ( )
3 2 4 3 3 2 4 3 3 2 4 3w i i z w i i z w i i z= − + − − − = − − − = −
( ) ( ) ( ) ( ) ( )
2 2 2
2
3 2 4 3 3 2 4 3 .2x y i i z x y − + + = − − + + = + −
( ) ( )
22
3 2 100xy − + + =
.
Suy ra tập hợp các điểm biểu diễn số phức
( )
3 2 4 3w i i z= − + −
là một đường tròn có tâm
( )
3; 2I −
, bán kính
10r =
.
Changbomvuive92@gmail.com chieens.ls@gmail.com
Câu 34. Cho
9 9 14
xx−
+=
. Khi đó biểu thức
2 81 81
11 3 3
xx
xx
M
−
−
++
=
−−
có giá trị bằng
A. 14. B. 49. C. 42. D. 28.
Lời giải
Tác giả: Nguyễn Hào Kiệt ; Fb: Nguyễn Hào Kiệt
Chọn D
Ta có
( ) ( )
( )
22
3 3 4 1
3 3 9 9 2.3 .3 3 3 16 .
3 3 4 ( )
xx
x x x x x x x x
xx
L
−
− − − −
−
+=
+ = + + + =
+ = −
( )
2
2
9 9 81 81 2 14 2 81 81 81 81 194(2).
x
x x x x x x x− − −
+ = + + − = + + =
Thay
( )
1
và
( )
2
vào biểu thức
M
ta có
2 194
28.
11 4
M
+
==
−
Tranvantan271981@gmail.com
Câu 35. Cho lăng trụ tam giác đều
.ABC A B C
có đáy là tam giác đều cạnh
a
,
2AA a
=
. Gọi
là góc
giữa
AB
và
BC
. Tính
cos
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 21 Mã đề 110
A.
5
cos
8
=
. B.
51
cos
10
=
. C.
39
cos
8
=
. D.
7
cos
10
=
.
Lời giải
Tác giả: Trần Văn Tân ; Fb: Trần Văn Tân
Chọn D
Từ giả thiết và định lý pitago ta được
22
5AB AB BB a

= + =
;
22
5BC BC CC a

= + =
.
Xét
( )( )
2
2
2
7
. . .
2
a
AB BC AB BB BB B C AB B C BB BABC BB
= + + = + = − + =
.
( )
( )
2
. 7 7
cos , : 5. 5
. 2 10
AB BC a
AB BC a a
AB BC


= = =

.
Vậy
( )
7
cos cos ,
10
AB BC

==
.
nguyenphuoctamduc2019@gmail.com
Câu 36. Cho hai đường thẳng
1
1
:2
32
xt
d y t
zt
=+
=−
=+
và
2
12
:
2 1 1
x y m z
d
− − +
==
−
(với
m
là tham số). Tìm
m
để hai đường thẳng
1
d
,
2
d
cắt nhau.
A.
4m =
. B.
9m =
. C.
7m =
. D.
5m =
.
Lời giải
Tác giả: Nguyễn Phú Hòa; Fb: Nguyễn Phú Hòa
Chọn D
1
d
qua
( )
1
1;2;3M
và có véctơ chỉ phương
( )
1
1; 1;2a =−
;
2
d
qua
( )
2
1; ; 2Mm−
và có véctơ
chỉ phương
( )
2
2;1; 1a =−
.
Ta có
( )
12
, 1;5;3 0aa

= −

;
( )
12
0; 2; 5M M m= − −
.
Khi đó
1
d
,
2
d
cắt nhau khi
1 2 1 2
, . 0a a M M

=

( )
1.0 5 2 15 0m − + − − =
5m=
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 22 Mã đề 110
truyphong.t0408@gmail.com
Câu 37. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Tam giác
SAB
đều và nằm
trong mt phẳng vuông góc với đáy. Tính khoảng cách từ điểm
C
đến mt phẳng
( )
SAD
.
A.
3
6
a
. B.
3
2
a
. C.
3
3
a
. D.
3
4
a
.
Lời giải
Word và giải: Nguyễn Văn Bình ; Fb: Nguyễn Văn Bình
Chọn B
Ta có
( ) ( )
( )
( )
( )
( )
( )
// ; ; 2 ;CB SAD d C SAD d B SAD d H SAD = =
.
Gọi
H
là trung điểm của
AB
. Vì
SAB
đều và nằm trong mt phẳng vuông góc với đáy nên
( )
SH ABCD⊥
.
Gọi
K
là hình chiếu vuông góc của
H
lên
SA
. Khi đó
( )
;HK SA HK AD HK SAD⊥ ⊥ ⊥
.
Do đó,
( )
( )
;d H SAD HK=
.
SHA
có
22
33
;.
2 2 4 4
a a a a
HA SH SA a= = = + =
Mà
3
.
3
22
. . .
4
aa
a
HK SA HS HA HK
a
= = =
Vậy
( )
( )
3
;.
2
a
d C SAD =
Câu 38. [Mc độ 2] Cho một hộp có chứa 5 bóng xanh, 6 bóng đỏ và 7 bóng vàng. Lấy ngẫu nhiên
4 bóng từ hộp, tính xác suất để có đủ 3 màu.
A.
35
816
. B.
35
68
. C.
175
5832
. D.
35
1632
.
Lời giải
Tác giả: Hoàng Văn Phiên; Fb: Phiên Văn Hoàng
Chọn B
Lấy ngẫu nhiên 4 bóng trong hộp chứa 18 bóng. Vậy số phần tử của không gian mẫu là
4
18
3060nC
==
.
Gọi
A
là biến cố “lấy được cả ba màu”.
Trường hợp 1: Lấy được 2 xanh, 1 đỏ, 1 vàng có
2 1 1
5 6 7
. . 420C C C =
(cách).
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 23 Mã đề 110
Trường hợp 2: Lấy được 1 xanh, 2 đỏ, 1 vàng có
1 2 1
5 6 7
. . 525C C C =
(cách).
Trường hợp 3: Lấy được 1 xanh, 1 đỏ, 2 vàng có
1 1 2
5 6 7
. . 630C C C =
(cách).
Vậy số phần tử của biến cố
A
là
420 525 630 1575
A
n = + + =
.
( )
1575 35
3060 68
A
n
PA
n
= = =
.
thuyhang24584@gmail.com
Câu 39. Cho phương trnh
2
33
log 4log 3 0x x m− + − =
. Tìm tất cả các giá trị nguyên của tham số
m
để
phương trnh đã cho có hai nghiệm phân biệt thỏa mãn
12
1xx
.
A. 6. B. 4. C. 3. D. 5.
Lời giải
Tác giả: Quỳnh Thụy Trang ; Fb: XuKa
Chọn C
Đt
3
logtx=
. Phương trnh đã cho trở thành
2
4 3 0t t m− + − =
.
Yêu cầu bài toán
phương trnh trên có hai nghiệm thỏa mãn
12
0tt
.
12
12
0
0
.0
tt
tt

+
70
37
30
m
m
m
−
−
Vậy có 3 giá trị nguyên của tham số
m
thỏa mãn
Tuluc0201@gmail.com trichinhsp@gmail.com
Câu 40. Có tất cả bao nhiêu giá trị thực của tham số
m
để đường thẳng
:1d y mx=+
cắt đồ thị
( )
32
:1C y x x= − +
tại 3 điểm
( )
; 0;1 ;A B C
phân biệt sao cho tam giác
AOC
vuông tại
( )
0;0O
?
A.
0
. B.
1
. C.
3
. D.
2
.
Lời giải
Tác giả: Võ Tự Lực; Fb: Võ Tự Lực
Chọn B
Hoành độ giao điểm của đường thẳng
d
và đồ thị
( )
C
là nghiệm của phương trnh:
32
11x x mx− + = +
( )
2
0x x x m − − =
2
0
0
x
x x m
=
− − =
.
Đường thẳng
d
cắt đồ thị hàm số
( )
C
tại 3 điểm phân biệt
( )
; 0;1 ;A B C
phương trnh
2
0x x m− − =
có hai nghiệm phân biệt
;
AC
xx
khác
0
1 4 0
0
m
m
= +
−
1
4
0
m
m
−
.
Khi đó, theo Viét ta có
1
.
AC
AC
xx
x x m
+=
=−
(*).
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 24 Mã đề 110
Tọa độ giao điểm
( )
;1
AA
A x mx +
và
( )
;1
CC
C x mx +
.
Tam giác
AOC
vuông tại
O
.0OAOC=
.0
A C A C
x x y y + =
( ) ( )
. 1 . 1 0
A C A C
x x mx mx + + + =
( )
( )
2
1 . 1 0
A C A C
m x x m x x + + + + =
( )
( )
2
1 . 1 0m m m + − + + =
1m=
(thỏa mãn điều kiện (*))
Vậy có
1
giá trị
m
thỏa mãn điều kiện bài toán.
lvtrungsp@gmail.com
Câu 41. Trong không gian
,Oxyz
cho điểm
( )
1; 1;2M −
và hai đường thẳng
1
: 1 ,
1
xt
d y t
z
=
=−
=−
2
1 1 2
:
2 1 1
x y z
d
+ − +
==
. Đường thẳng
đi qua điểm M và cắt cả hai đường thẳng
12
,dd
có
véctơ chỉ phương là
( )
1; ; ,u a b
=
tính
.ab+
A.
1.ab+ = −
B.
b 2.a+ = −
C.
b 2.a+=
D.
b 1.a +=
Lời giải
Tác giả: Lại Văn Trung; FB: Trung Lại Văn
Chọn D
Gọi
,AB
lần lượt là giao điểm của đường thẳng
với
1
d
và
2
d
.
Vì
( ) ( )
1 1 1 2 2 2 2
;1 ; 1 ; 1 2 ;1 ; 2 .A d A t t B d B t t t − − − + + − +
,,M M A B
thẳng hàng
..MA k MB=
(1)
( ) ( )
1 1 2 2 2
1;2 ; 3 ; 2 2; 2; 4 .MA t t MB t t t= − − − = − + −
( )
( )
( )
( )
1
12
12
1 2 1 2 2
2
2
0
1 2 2
2 2 1
1
1 2 2 2 2
3
43
34
5
6
t
t k t
t kt k
t k t t kt k kt
kt k
kt
k
=
− = −
− + =

− = + − − − = − =
− = −
− = −
=
.
Từ
( )
1
0 0;1; 1tA= −
. Do đường thẳng
đi qua điểm A và M nên một véc tơ chỉ phương của
đường thẳng
là
( )
1; 2;3u AM
= = −
.
Vậy
2, 3 1.a b a b= − = + =
phuongmath@gmai.com
Câu 42. Hai người
A
và
B
ở cách nhau
180
( )
m
trên một đoạn đường thẳng và cùng chuyển động
thẳng theo một hướng với vận tốc biến thiên theo thời gian,
A
chuyển động với vận tốc
( ) ( )
1
6 5 m/sv t t=+
,
B
chuyển động với vận tốc
( ) ( )
2
2a 3 m/sv t t=−
(
a
là hằng số), trong đó
t
(giây) là khoảng thời gian tính từ lúc
A
,
B
bắt đầu chuyển động. Biết rằng lúc đầu
A
đuổi
theo
B
và sau
10
(giây) th đuổi kịp. Hỏi sau
20
(giây),
A
cách
B
bao nhiêu mét?
A.
( )
320 m
. B.
( )
720 m
. C.
( )
360 m
. D.
( )
380 m
.
Lời giải
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 25 Mã đề 110
Tácgiả:Lê Thị Phương; Fb: Lê Thị Phương.
Chọn D
Quãng đường
A
đi được trong
10
(giây) là:
( )
( )
( )
10
10
2
0
0
6 5 dt 3 5 350 mt t t+ = + =
.
Quãng đường
B
đi được trong
10
(giây) là:
( )
( )
( )
10
10
2
0
0
2 -3 dt 3 100a 30 mat at t= − = −
.
V lúc đầu
A
đuổi theo
B
và sau
10
(giây) th đuổi kịp nên ta có:
( ) ( ) ( )
2
100 30 180 350 2 4 3 m/sa a v t t− + = = = −
.
Sau
20
(giây)
A
đi được:
( )
( )
( )
20
20
2
0
0
6 5 3 5 1300 mt dt t t+ = + =
.
Sau
20
(giây)
B
đi được:
( )
( )
( )
20
20
2
0
0
4 3 2 3 740 mt dt t t− = − =
.
Khoảng cách giữa
A
và
B
sau 20 (giây) là:
( )
1300 740 180 380 m− − =
.
Phản biện: quangdang@gmail.com
tantiennhc@gmail.com
Câu 43. Một hình hộp chữ nhật có chiều cao là 90 cm, đáy hộp là hình chữ nhật có chiều rộng là 50 cm
và chiều dài là 80 cm. Trong khối hộp có chứa nước, mực nước so với đáy hộp có chiều cao là
40 cm. Hỏi khi đt vào khối hộp một khối trụ có chiều cao bằng chiều cao khối hộp và bán kính
đáy là 20 cm theo phương thẳng đứng thì chiều cao của mực nước so với đáy là bao nhiêu?
A. 68,32 cm. B. 78,32 cm. C. 58,32 cm. D. 48,32 cm.
Lời giải
Tác giả: Nguyễn Tân Tiến ; Fb: Nguyễn Tiến
Chọn C
Trước khi đt vào khối hộp một khối trụ thì thể tích lượng nước có trong khối hộp là
40.80.50 160000
n
V ==
(cm
3
).
Gọi
h
(cm) là chiều cao của mực nước so với đáy.
Sau khi đt vào khối hộp một khối trụ thì thể tích lượng nước là
( )
. 4000 400
n
Vh
=−
(cm
3
).
Do lượng nước không đổi nên ta có
( )
. 4000 400 160000h
−=
160000
58,32
4000 400
h
=
−
(cm).
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 26 Mã đề 110
nhantoanhungvuong@gmail.com
Câu 44. Một chiếc cổng có hình dạng là một Parabol có khoảng cách giữa hai chân cổng là
8m=AB
.
P
M
Q
N
A
B
Người ta treo một tấm phông hình chữ nhật có hai đỉnh
,MN
năm trên Parabol và hai đỉnh
,PQ
nằm trên mt đất(như hnh vẽ). Ở phần phía ngoài phông (phần không tô đen) người ta
mua hoa để trang trí với chi phí cho
2
1m
cần số tiền cần mua hoa là
200.000
đồng cho
2
1m .
Biết rằng
4m, 6m==MN MQ
. Hỏi số tiền dùng để mua hoa trang trí chiếc cổng gần với số
tiền nào sau đây?
A.
3.735.300
đồng. B.
3.437.300
đồng.
C.
3.734.300
đồng . D.
3.733.300
đồng.
Lời giải
Tác giả:Nguyễn Thành Nhân ; Fb:Nguyễn Thành Nhân
Chọn D
x
y
B
(4;0)
A
P
Q
M
N
(2;6)
Ta gắn vào hệ trục tọa độ
Oxy
như hnh vẽ bên. Trong hệ trục đó th đường Parabol đi qua các
điểm
( )
4;0B
và
( )
2;6N
cho nên phương trnh của đường Parabol đó là:
2
1
8
2
−
=+yx
.
Diện tích của chiếc cổng được giới hạn bởi đường Parabol là:
4
22
4
1 128
8m
23
−
−

= + =


S x dx
.
Diên tích của hình chữ nhật
MNPQ
là
2
4.6 24m
==S
.
Diện tích phần trang trí bằng hoa là:
2
1
56
m
3
= − =S S S
.
Vậy số tiền cần dùng để mua hoa là trang trí là:
( )
56
. 200.000 3.733.300
3
đồng.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 27 Mã đề 110
Huongdtn2009@gmail.com
vothuongnhanhchong@gmail.com
Câu 45. Cho hai số phức
,zw
thay đổi thỏa mãn
3, 1.z z w= − =
Biết tập hợp điểm của số phức
w
là
hình phẳng H. Tính diện tích S của H.
A.
20S
=
. B.
12S
=
. C.
4S
=
. D.
16S
=
.
Lời giải
Tác giả & Fb: Lý Văn Nhân
Chọn B
Cách 1:
Với mỗi số phức
z
thỏa
3z =
, gọi A là điểm biểu
diễn của z thì A nằm trên đường tròn tâm O bán
kính bằng 3. Gọi B là điểm biểu diễn của w thì B
nằm trên đường tròn tâm A bán kính bằng 1.
Khi A chạy trên đường tròn tâm O bán kính bằng 3
thì tập hợp các điểm B là hnh vành khăn giới hạn
bởi tròn tâm O bán kính bằng 2 và tròn tâm O bán
kính bằng 4. Suy ra
22
.4 .2 12 .S
=−=
Cách 2: Ta có
4w w z z w z z= − + − + =
. Mt khác
2w w z z w z z= − + − − =
.
Vậy
24w
nên H là hnh vành khăn giới hạn bởi tròn tâm O bán kính bằng 2 và tròn tâm O
bán kính bằng 4. Suy ra
22
.4 .2 12 .S
=−=
hoxuandung1010@gmail.com
Câu 46. Cho
1
2
0
93
d1
93
x
x
m
xm
+
=−
+
. Tính tổng tất cả các giá trị của tham số
m
.
A.
12P =
. B.
1
2
P =
. C.
16P =
. D.
24P =
.
Lời giải
Tác giả: Hồ Xuân Dũng ; Fb: Dũng Hồ Xuân
Chọn B
Ta có
( )
( )
1 1 1 1
2
0 0 0 0
31
9 3 9 3 3 3 3
1 d d 1 d 1 1 d
9 3 9 3 9 3 9 3
xx
x x x x
m
mm
m x x x m x
−

+ + − +
− = = = + = + −

+ + + +

.
Đt
( )
1
0
3
1d
93
x
K m x=−
+
. Ta đi tính
( )
1
0
9
1d
93
x
x
J m x=−
+
.
Có
( ) ( )
( ) ( )
( )
11
00
1
1
9 1 1
ln9
1 d 1 d 9 3 .ln 9 3 1
0
9 3 9 3 2ln3 2
x
xx
xx
m
J m x m m
−
= − = − + = + = −
++

.
Lại có,
( )
1
0
93
1 d ( 1)
93
x
x
K J m x m
+
+ = − = −
+
. Từ đó, suy ra
( ) ( ) ( )
11
1 1 1
22
K m m m= − − − = −
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 28 Mã đề 110
Do đó,
22
1
1 1 3
1 1 ( 1) 0
3
2 2 2
2
m
m m m m
m
=−
− = + − − − =
=
.
Suy ra tổng tất cả các giá trị của tham số
m
là
1
2
.
thaitranvn123@gmail.com - nguyenthao7983@gmail.com
Câu 47. Có bao nhiêu cách phân tích số
9
15
thành tích của ba số nguyên dương, biết rằng các cách phân
tích mà các phần tử chỉ khác nhau về thứ tự thì chỉ được tính một lần?
A.
517
. B.
516
. C.
493
. D.
492
.
Lời giải
Tác giả: Trần Đình Thái ; Fb: Đình Tháii
Chọn A
Ta có
9 9 9
15 3 .5=
. Đt
11
3 .5
ab
x =
,
22
3 .5
ab
y =
,
33
3 .5
ab
z =
.
Xét
3
trường hợp:
Trường hợp 1: 3 số
,,x y z
bằng nhau
→
có
1
cách chọn.
Trường hợp
2
: Trong
3
số có
2
số bằng nhau, giả sử:
xy=
12
aa=
,
12
bb=
.
13
13
29
29
aa
bb
+=
+=
31
33
92
92
aa
ba
=−
=−
.
Suy ra có
5
cách chọn
1
a
và
5
cách chọn
1
b
.
Trường hợp 3: Số cách chọn
3
số phân biệt.
Số cách chọn
1 2 3
1 2 3
9
9
a a a
b b b
+ + =
+ + =
là
22
11 11
.CC
.
Suy ra số cách chọn
3
số phân biệt là
22
11 11
. 24.3 1CC−−
.
Vậy số cách phân tích số
9
15
thành ba số nguyên dương là
22
11 11
. 24.3 1
25 517
3!
CC−−
+=
.
tiendv@gmail.com
Câu 48. Cho các số thực
,1ab
thoả mãn
8
3
log
log
2
16 12
a
b
b
a
a
a b b




+=
. Giá trị của biểu thức
33
P a b=+
là
A.
20
. B.
39
. C.
125
. D.
72
.
Lời giải
Tác giả: Đào Văn Tiến ; Fb: Đào Văn Tiến
Chọn D
Ta có:
8
3
83
log
log log log log log 8log 3
2 2 2
16 12 16 12 16 12
a
b b a a b a
b
a
a a b a a b
a b b a b b a b b



−−

+ = + = + =
8
3
log log
2
16 12
bb
aa
a b b
−
+ =
.
Đt
log 0
b
t a t=
. Khi đó ta có
2
8
3
2
16 12
t
t
b b b
−
+=
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 29 Mã đề 110
Ta có
2
2
3
2 2 2
88
8 8 8 8 8 8 8
36
3
3 3 3 3 3 3 3
33
2
16 8 8 3 .8 .8 12 12 12
t
t
t t t
tt
t t t t t t t
b b b b b b b b b b b
−
− − − − − + − + −
+ = + + = =
.
Vậy ta có
2
8
3
2
16 12
t
t
b b b
−
+
. Yêu cầu bài toán tương đương với dấu bằng xảy ra.
4
2
log 2
4
2
2
8
b
t
a
a
b
b
bb
=
=
=
=
=
=
.
Từ đó ta có
33
72.P a b= + =
Thuylinh133c3@gmail.com hongvanlk69@gmail.com
Câu 49. Cho hnh chóp
.S ABCD
có đáy
ABCD
là hnh vuông, hnh chiếu vuông góc của đỉnh
S
xuống mt đáy nằm trong hnh vuông
ABCD
. Hai mt phẳng
( )
SAD
,
( )
SBC
vuông góc với
nhau; góc giữa hai mt phẳng
( )
SAB
và
( )
SBC
là
0
60
; góc giữa hai mt phẳng
( )
SAB
và
( )
SAD
là
0
45
. Gọi
là góc giữa hai mt phẳng
( )
SAB
và
( )
ABCD
, tính
cos
A.
1
cos =
2
. B.
2
cos =
2
. C.
3
cos =
2
. D.
2
cos =
3
.
Lời giải
Tác giả: Nguyễn Thùy Linh ; Fb:Nguyễn Thùy Linh
Chọn C
Gắn hệ trục tọa độ như hnh vẽ. Không mất tính tổng quát giả sử
ABCD
là hnh vuông có cạnh
bằng
1
, chiều cao của hnh chóp
.S ABCD
bằng
c
( )
0c
.
( )
0;0;0A
,
( )
1;0;0B
,
( )
1;1;0C
,
( )
0;1;0D
.
Do hnh chiếu vuông góc
H
của đỉnh
S
xuống mt đáy nằm trong hnh vuông
ABCD
nên gọi
( )
; ;0H a b
với
0 , 1ab
( )
*
( )
;;S a b c
.
Ta có :
( )
;;AS a b c=
,
( )
0;1;0AD =
nên chọn
( )
( )
, ;0;
SAD
n AS AD c a

= = −

.
( )
1; ;BS a b c=−
,
( )
0;1;0BC =
nên chọn
( )
( )
, ;0; 1
SBC
n BS BC c a

= = − −

.
( )
1;0;0AB =
,
( )
;;AS a b c=
nên chọn
( )
( )
, 0; ;
SAB
n AB AS c b

= = −

.
Chọn
( )
( )
0;0;1
ABCD
nk==
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 30 Mã đề 110
Do
( ) ( )
( ) ( )
( )
2 2 2
. 0 1 0
SAD SBC
SAD SBC n n c a a c a a⊥ = + − = + =
( )
1
.
Góc giữa
( )
SAB
và
( )
SBC
là
0
60
( ) ( )
( ) ( )
( )
( )
0
2
2 2 2
.
1
1
cos60
2
.
1.
SAB SBC
SAB SBC
nn
ba
nn
c a c b
−
= =
+ − +
( )
22
1
1
2
1.
ba
a c b
−
=
−+
do
(*)
và
(1)
2 2 2 2
1 1 1
2
21
b a b
a
c b c b
−
= =
−
++
(2)
Góc giữa
( )
SAB
và
( )
SAD
là
0
45
( ) ( )
( ) ( )
0
2 2 2 2
.
2
cos45
2
.
.
SAB SAD
SAB SAD
nn
ab
nn
c a c b
= =
++
22
2
2
.
ab
a c b
=
+
do
(*)
2 2 2 2
1 2 1 2
: : 2
2 2 3
1
.
ab b a a
a
a
a c b c b
−
= = =
−
++
( )
3
.
Góc giữa
( )
SAB
và
( )
ABCD
là
( ) ( )
( ) ( )
( ) ( )
2 , 3
22
.
13
cos
2
2
.
21
3
SAB ABCD
SAB ABCD
nn
b
nn
cb
= = = =
+
−
.
Cách 2 : theo ý tưởng của thầy Vô Thường .
Gọi
I
,
J
,
H
lần lượt là hnh chiếu vuông góc của
S
lên
BC
,
AD
,
( )
ABCD
;
I
,
H
,
J
lần lượt là hnh chiếu vuông góc của
I
,
H
,
J
lên
( )
SAB
.
Ta có :
+ Do
( ) ( )
SAD SBC⊥
nên
0
(( D),( )) 90SA SBC ISJ = =
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 31 Mã đề 110
Suy ra
()
()
SI SAD
SJ SBC
⊥
⊥
.
+ Do
( )
( )
SI SAD
II SAB
⊥
⊥
nên
0
(( D),( )) ' 45SA SAB SII = =
.
+ Do
( )
( )
SJ SBC
JJ SAB
⊥
⊥
nên
0
(( ),( )) ' 60SBC SAB SJJ = =
.
+ Do
( )
( )
SH ABCD
HH SAB
⊥
⊥
nên
(( ),( D)) 'SAB SABC SHH
= =
.
Đt
II HH JJ x
= = =
với
0x
2SI x=
,
2SJ x=
,
2
22
. . 2 2 2 3
cos
2
2
63
3
SI SJ SI SJ x x HH x
SH
x
IJ SH
x
SI SJ
= = = = = = =
+
.
Hahoangduong30@gmail.com
Câu 50. Cho hai hàm số
( ) ( )
( )
3 2 2
1
1 3 4 5 2019
3
f x x m x m m x= − + + + + +
và
( )
( ) ( )
2 3 2 2
2 5 2 4 9 3 2g x m m x m m x x= + + − + + − +
, với
m
là tham số. Hỏi phương trnh
( )
( )
0g f x =
có bao nhiêu nghiệm?
A. 9. B. 0. C. 3 . D. 1.
Lời giải
Tác giả:Nguyễn Thị Huyền Trang ; Fb: Nguyen Trang
Chọn C
Ta có:
( ) ( )
( )
22
0 2 2 5 1 0g x x m m x x

= − + + + − =

.
( )
( )
22
2
2 5 1 0 *
x
m m x x
=
+ + + − =
.
Phương trnh
( )
*
có hai nghiệm phân biệt khác 2 với
m
v:
( )
( )
2
2
22
2 5 0,
1 2 5 0,
2 5 2 2 1 0,
m m m
m m m
m m m
+ +
= + + +
+ + + −
.
Vậy
( )
0gx=
có 3 nghiệm phân biệt (1).
Mt khác, xét hàm số
( )
y f x=
ta có :
( ) ( )
( )
( )
( )
2
2 2 2
2 1 3 4 5 1 2 2 0,f x x m x m m x m m m m
= − + + + + = − + + + +


.
( )
y f x=
luôn đồng biến trên với
m
.
Do
()fx
là hàm đa thức bậc 3 và đồng biến trên nên phương trnh
( )
f x k=
luôn có 1
nghiệm duy nhất với mỗi số
k
(2).
Từ (1) và (2) suy ra phương trnh
( )
( )
0g f x =
có 3 nghiệm phân biệt .
| 1/38
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

ĐỀ THI THỬ THPT QUỐC GIA LẦN 2
Trường THCS-THPT Lương Thế Vinh Năm học 2018-2019 Đề thi có 6 trang Môn: Toán Mã đề thi 110
Thời gian làm bài: 90 phút (50 câu trắc nghiệm)
Câu 1. Cho số phức z thỏa mãn z = 3 + 2i. Tìm phần thực và phần ảo của số phức z.
A. Phần thực bằng -3, phần ảo bằng 2.
B. Phần thực bằng 3, phần ảo bằng 2.
C. Phần thực bằng 3, phần ảo bằng -2.
D. Phần thực bằng -3, phần ảo bằng -2. x − x y − y z − z
Câu 2. Trong hệ tọa độ Oxyz, cho đường thẳng ∆ : 0 = 0 = 0 . Điểm M nằm a b c
trên ∆ thì tọa độ của M có dạng nào sau đây? A. M (at; bt; ct). B. M (x0t; y0t; z0t).
C. M (a + x0t; b + y0t; c + z0t).
D. M (x0 + at; y0 + bt; z0 + ct).
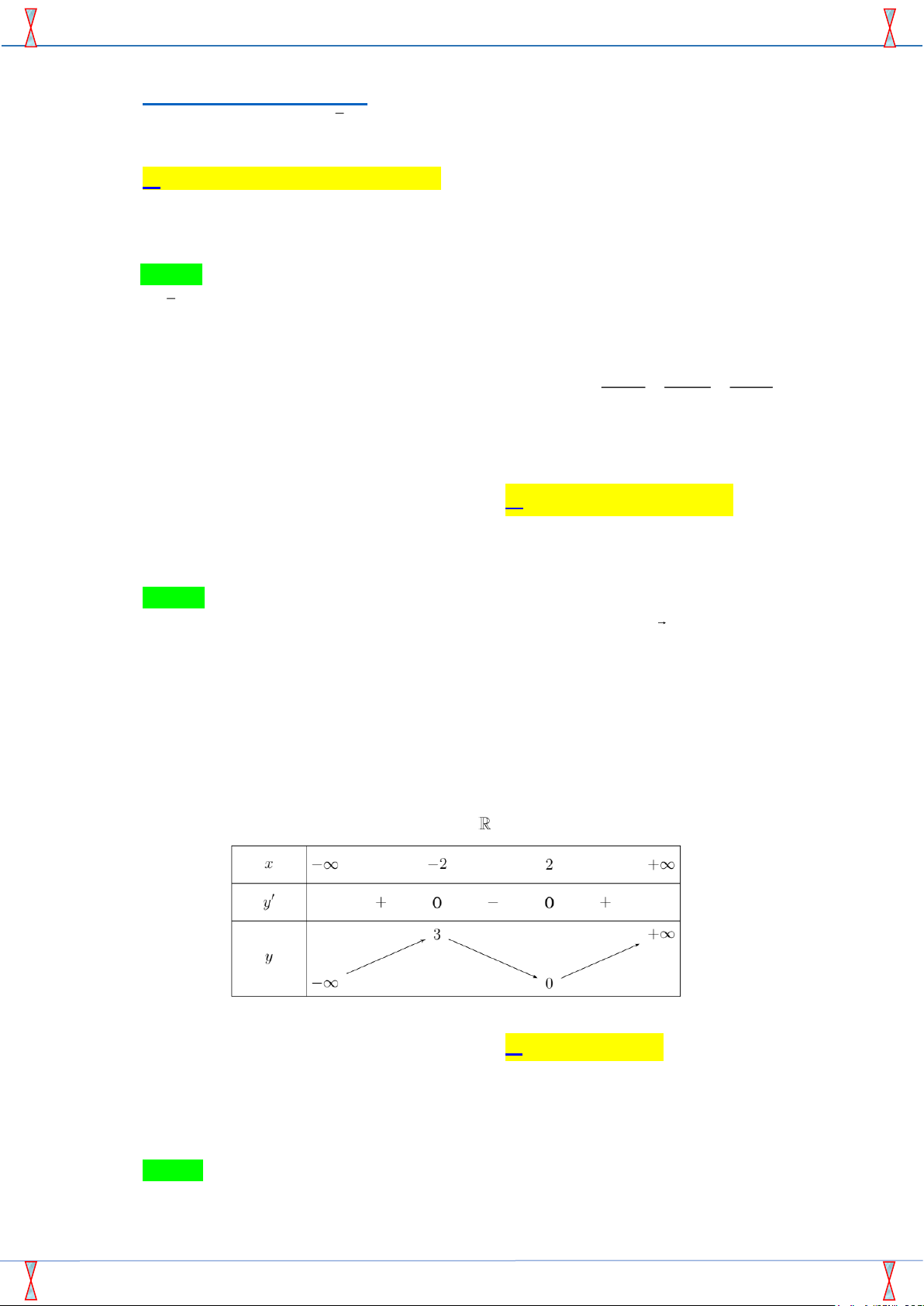
Câu 3. Cho hàm số y = f (x) xác định, liên tục trên R và có bảng biến thiên như sau: x −∞ −2 2 +∞ y0 + 0 − 0 + 3 +∞ + y −∞ 0 Tìm giá trị cực đại y và giá trị cực tiểu y của hàm số đã cho. CĐ CT A. y = −2 và y = 2. B. y = 3 và y = 0. CĐ CT CĐ CT C. y = 2 và y = 0. D. y = 3 và y CĐ CT CĐ CT = −2.
Câu 4. Trong hệ tọa độ Oxyz, cho ba điểm A(1; 0; 0), B(0; −1; 0), C(0; 0; 2). Phương trình mặt phẳng (ABC) là z y A. x − 2y + z = 0. B. x − y + = 1. C. x + − z = 1. D. 2x − y + z = 0. 2 2
Câu 5. Đường thẳng y = m tiếp xúc với đồ thị (C) : y = −2x4 + 4x2 − 1 tại hai điểm phân
biệt A(xA; yA) và B(xB; yB). Giá trị của biểu thức yA + yB. A. 2. B. −1. C. 1. D. 0.
Câu 6. Trong các hàm số dưới đây, hàm số nào đồng biến trên tập R? A. y = 21−3x. B. y = log (x − 1). C. y = log (2x + 1). D. y = log x2 + 1. 2 2 2 Câu 7. y
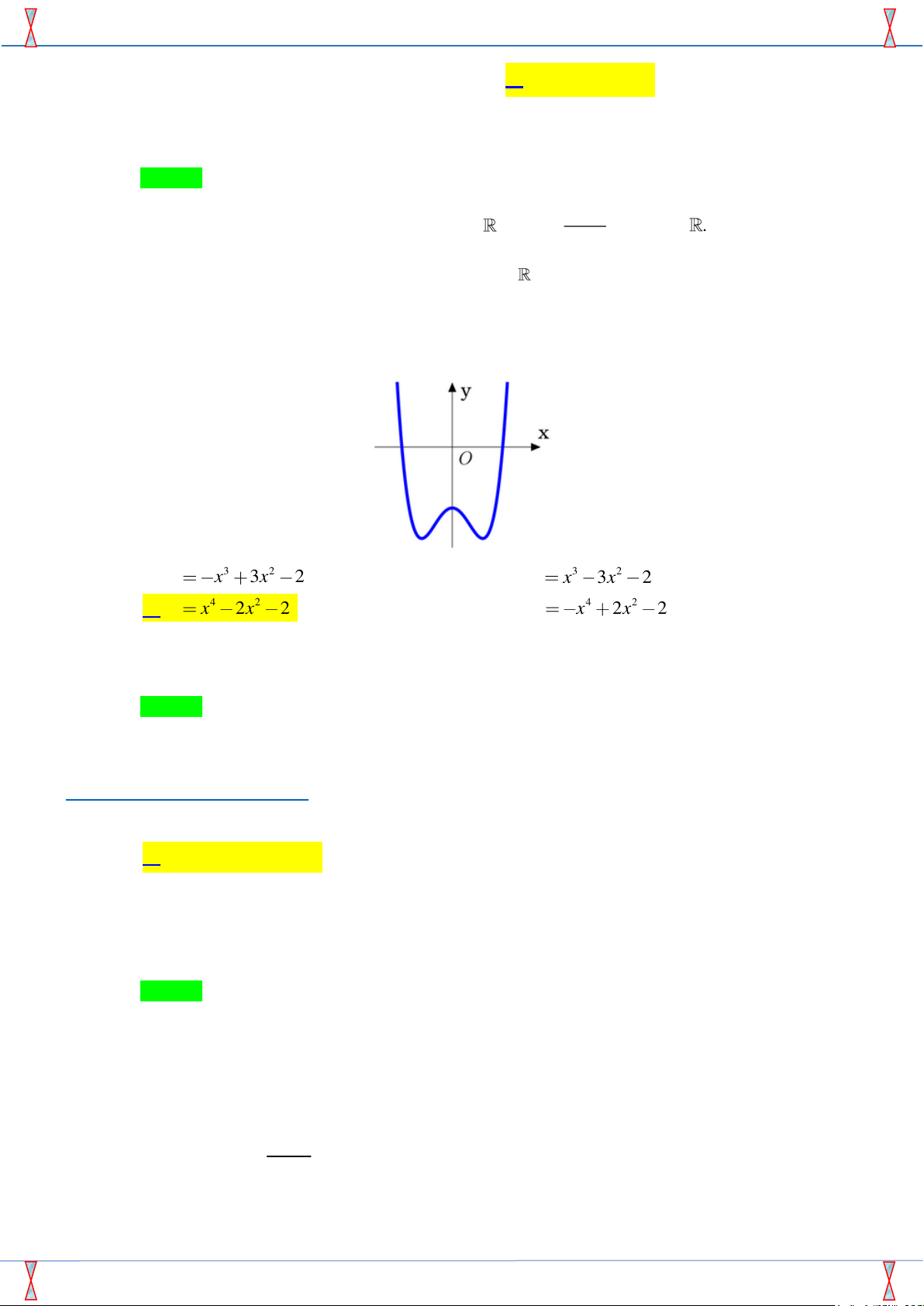
Đường cong như hình bên là đồ thị của hàm số nào sau x đây? O
A. y = −x3 + 3x2 − 2.
B. y = x3 − 3x2 − 2.
C. y = x4 − 2x2 − 2.
D. y = −x4 + 2x2 − 2.
Câu 8. Tìm tập xác định của hàm số y = (x2 + 2x − 3)e.
A. (−∞; −3) ∪ (1; +∞).
B. (−∞; −3] ∪ [1; +∞). C. (−3; 1). D. [−3; 1]. Trang 1/6 Mã đề 110 2x + 1
Câu 9. Cho hàm số y = . Mệnh đề đúng là x + 1
A. Hàm số nghịch biến trên (−∞; −1) và (−1; +∞).
B. Hàm số đồng biến trên (−∞; −1) và (1; +∞), nghịch biến trên (−1; 1).
C. Hàm số đồng biến trên R.
D. Hàm số đồng biến trên (−∞; −1) và (−1; +∞).
Câu 10. Thế tích của khối cầu có bán kính R là 4πR3 πR3 A. πR3. B. . C. 2πR3. D. . 3 3
Câu 11. Cho f (x), g(x) là các hàm số có đạo hàm liên tục trên R, k ∈ R. Trong các khẳng
định dưới đây, khẳng định nào sai? Z Z Z Z A. [f (x) − g(x)]dx = f (x)dx − g(x)dx. B. f 0(x)dx = f (x) + C. Z Z Z Z Z C. kf (x)dx = k f (x)dx. D. [f (x) + g(x)]dx = f (x)dx + g(x)dx.
Câu 12. Cho lăng trụ tứ giác đều có đáy là hình vuông cạnh a, chiều cao 2a. Tính thể tích khối lăng trụ. 2a3 4a3 A. . B. . C. a3. D. 2a3. 3 3 4
Câu 13. Tích của giá trị lớn nhất và giá trị nhỏ nhất của hàm số f (x) = x + trên đoạn x [1; 3] bằng 65 52 A. . B. 20. C. 6. D. . 3 3
Câu 14. Trong hệ tọa độ Oxyz, cho hai đường thẳng chéo nhau x − 2 y + 2 z − 6 x − 4 y + 2 z + 1 d1 : = = , d2 : = = . 2 1 −2 1 −2 3
Phương trình mặt phẳng (P ) chứa d1 và song song với d2 là
A. (P ) : x + 8y + 5z + 16 = 0.
B. (P ) : x + 8y + 5z − 16 = 0.
C. (P ) : 2x + y − 6 = 0.
D. (P ) : x + 4y + 3z − 12 = 0. x − 1 y − 3 z − 1
Câu 15. Trong hệ tọa độ Oxyz, cho đường thẳng d : = = cắt mặt phẳng 2 −1 1
(P ) : 2x − 3y + z − 2 = 0 tại điểm I(a; b; c). Khi đó a + b + c bằng A. 9. B. 5. C. 3. D. 7.
Câu 16. Cho dãy số (un) là một cấp số cộng, biết u2 + u21 = 50. Tính tổng của 22 số hạng đầu tiên của dãy. A. 2018. B. 550. C. 1100. D. 50. x + 1
Câu 17. Số đường tiệm cận của đồ thị hàm số y = là |x| − 2x + 1 A. 4. B. 3. C. 2. D. 1.
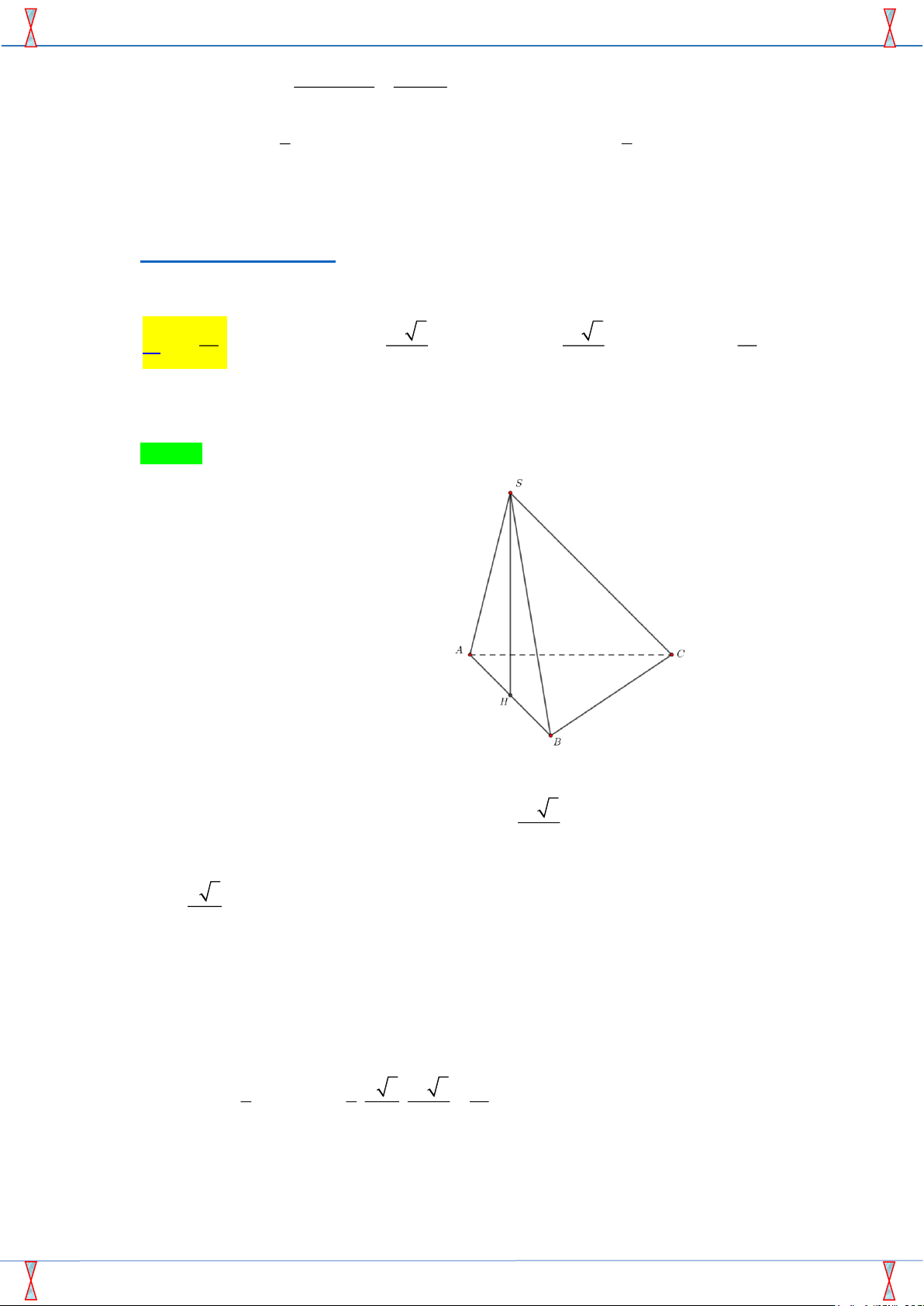
Câu 18. Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a, tam giác SAB đều
và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích khối chóp S.ABC. √ √ a3 a3 3 a3 3 a3 A. V = . B. V = . C. V = . D. V = . 8 3 4 4
Câu 19. Họ nguyên hàm của hàm số f (x) = 2x(1 + 3x3) là 3 6x3 3 3 A. x2 1 + x2 + C. B. x2 1 + + C. C. 2x x + x4 + C. D. x2 x + x3 + C. 2 5 4 4 Trang 2/6 Mã đề 110 2 1−3x 25
Câu 20. Tìm tập nghiệm S của bất phương trình ≥ . 5 4 1 1 A. S = [1; +∞). B. S = ; +∞ . C. S = −∞; . D. S = (−∞; 1]. 3 3
Câu 21. Trong hệ tọa độ Oxyz, cho điểm A(3; 5; 3) và hai mặt phẳng (P ) : 2x+y +2z −8 = 0,
(Q) : x − 4y + z − 4 = 0. Viết phương trình đường thẳng d đi qua A và song song với cả hai mặt phẳng (P ), (Q) x = 3 + t x = 3 x = 3 + t x = 3 + t     A. d : y = 5 − t . B. d : y = 5 + t . C. d : y = 5 . D. d : y = 5 . z = 3 z = 3 − t z = 3 − t z = 3 + t x = 2 + t 
Câu 22. Trong hệ tọa độ Oxyz, cho điểm A(−1; 1; 6) và đường thẳng ∆ : y = 1 − 2t . Hình z = 2t
chiếu vuông góc của A trên ∆ là A. M (3; −1; 2). B. H(11; −17; 18). C. N (1; 3; −2). D. K(2; 1; 0).
Câu 23. Cho f (x), g(x) là các hàm số liên tục trên R thỏa mãn Z 1 Z 2 Z 2 f (x)dx = 3, [f (x) − 3g(x)]dx = 4 và [2f (x) + g(x)]dx = 8. 0 0 0 Z 2 Tính I = f (x)dx. 1 A. I = 1. B. I = 2. C. I = 3. D. I = 0. x4 3
Câu 24. Đồ thị hàm số y = − + x2 +
cắt trục hoành tại mấy điểm? 2 2 A. 0. B. 2. C. 4. D. 3.
Câu 25. Trong hệ tọa độ Oxyz, cho điểm I(2; −1; −1) và mặt phẳng (P ) : x − 2y − 2z + 3 = 0.
Viết phương trình mặt cầu (S) có tâm I và tiếp xúc với mặt phẳng (P )
A. (S) : x2 + y2 + z2 − 4x + 2y + 2z − 3 = 0.
B. (S) : x2 + y2 + z2 − 2x + y + z − 3 = 0.
C. (S) : x2 + y2 + z2 − 4x + 2y + 2z + 1 = 0.
D. (S) : x2 + y2 + z2 − 2x + y + z + 1 = 0.
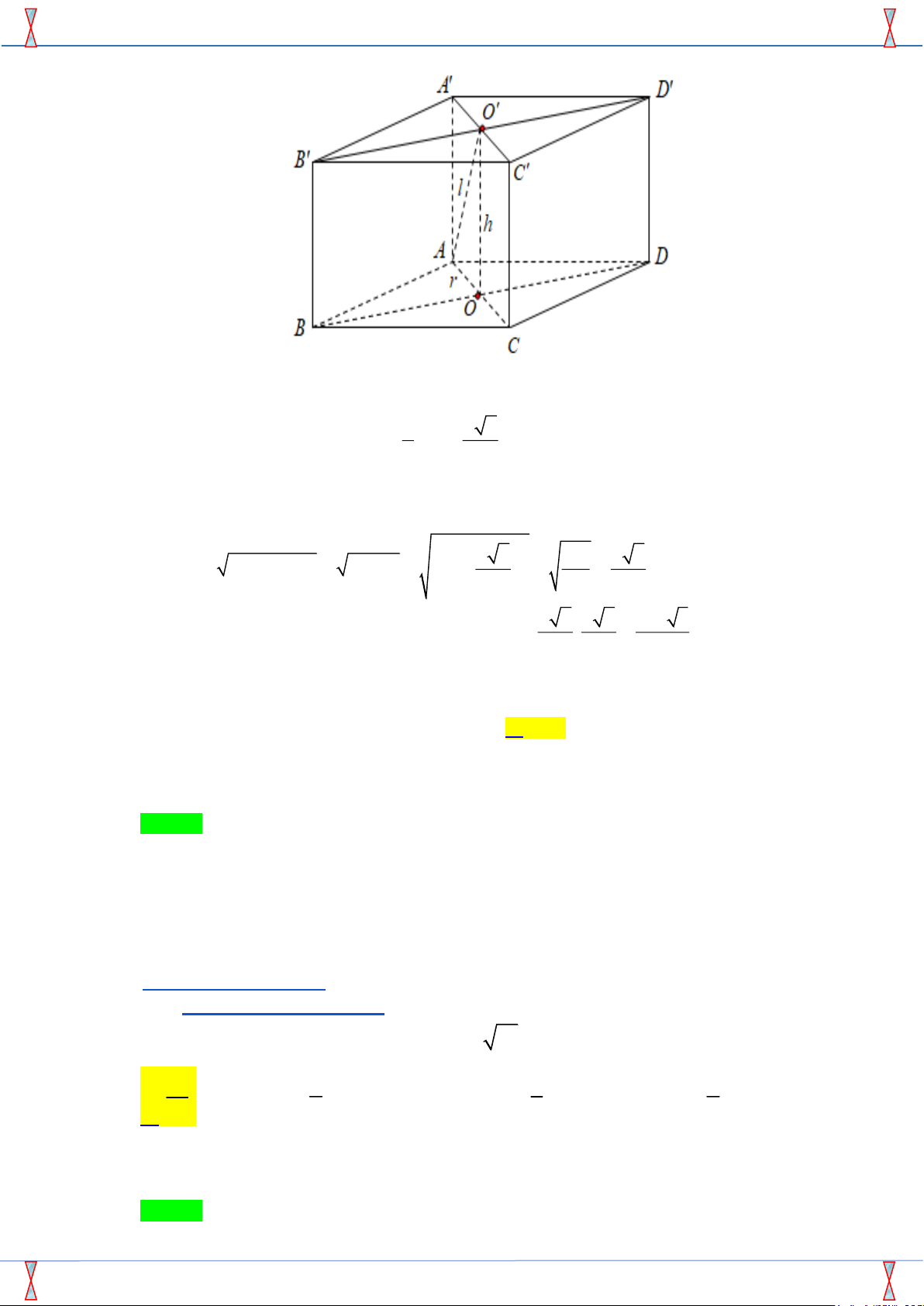
Câu 26. Cho hình lập phương ABCD.A0B0C0D0 có cạnh bằng a. Một hình nón có đỉnh là
tâm của hình vuông A0B0C0D0 và có đường tròn đáy ngoại tiếp hình vuông ABCD. Tính
diện tích xung quanh của hình nón đó. √ √ √ πa2 2 √ πa2 2 πa2 3 A. . B. πa2 3. C. . D. . 2 4 2
Câu 27. Tìm hệ số của số hạng chứa x9 trong khai triển nhị thức Newton của biểu thức (3 + x)11. A. 9. B. 110. C. 495. D. 55. √
Câu 28. Cho số thực a > 0, a 6= 1. Giá trị của log 7 a3 bằng a2 3 6 3 7 A. . B. . C. . D. . 14 7 8 6
Câu 29. Đạo hàm của hàm số y = log (x3 − 3x − 4) là 8 3x3 − 3 x2 − 1 3x3 − 3 1 A. . B. . C. . D. . (x3 − 3x − 4) ln 2 (x3 − 3x − 4) ln 2 x3 − 3x − 4 (x3 − 3x − 4) ln 8 u Câu 30. 1 + u3 = 10
Cho cấp số nhân (un) thỏa mãn . Tìm u u 3. 4 + u6 = 80 A. u3 = 8. B. u3 = 2. C. u3 = 6. D. u3 = 4. Trang 3/6 Mã đề 110 √
Câu 31. Cho khối nón (N ) đỉnh S, có chiều cao là a 3 và độ dài đường sinh là 3a. Mặt
phẳng (P ) đi qua đỉnh S, cắt và tạo với mặt đáy của khối nón một góc 600. Tính diện tích
thiết diện tạo bởi mặt phẳng (P ) và khối nón (N ). √ √ √ √ A. 2a2 5. B. a2 3. C. 2a2 3. D. a2 5. Câu 32. y 4
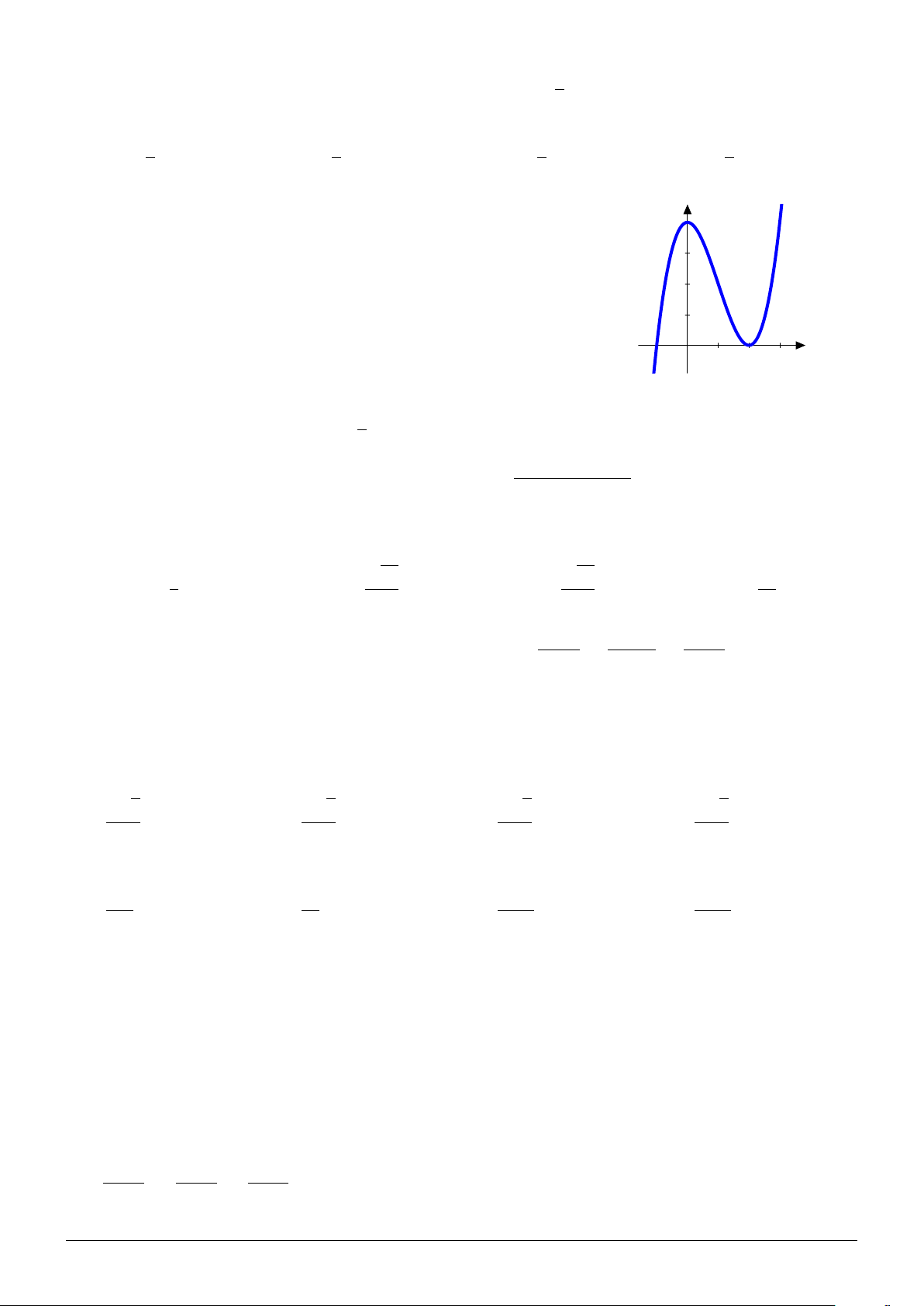
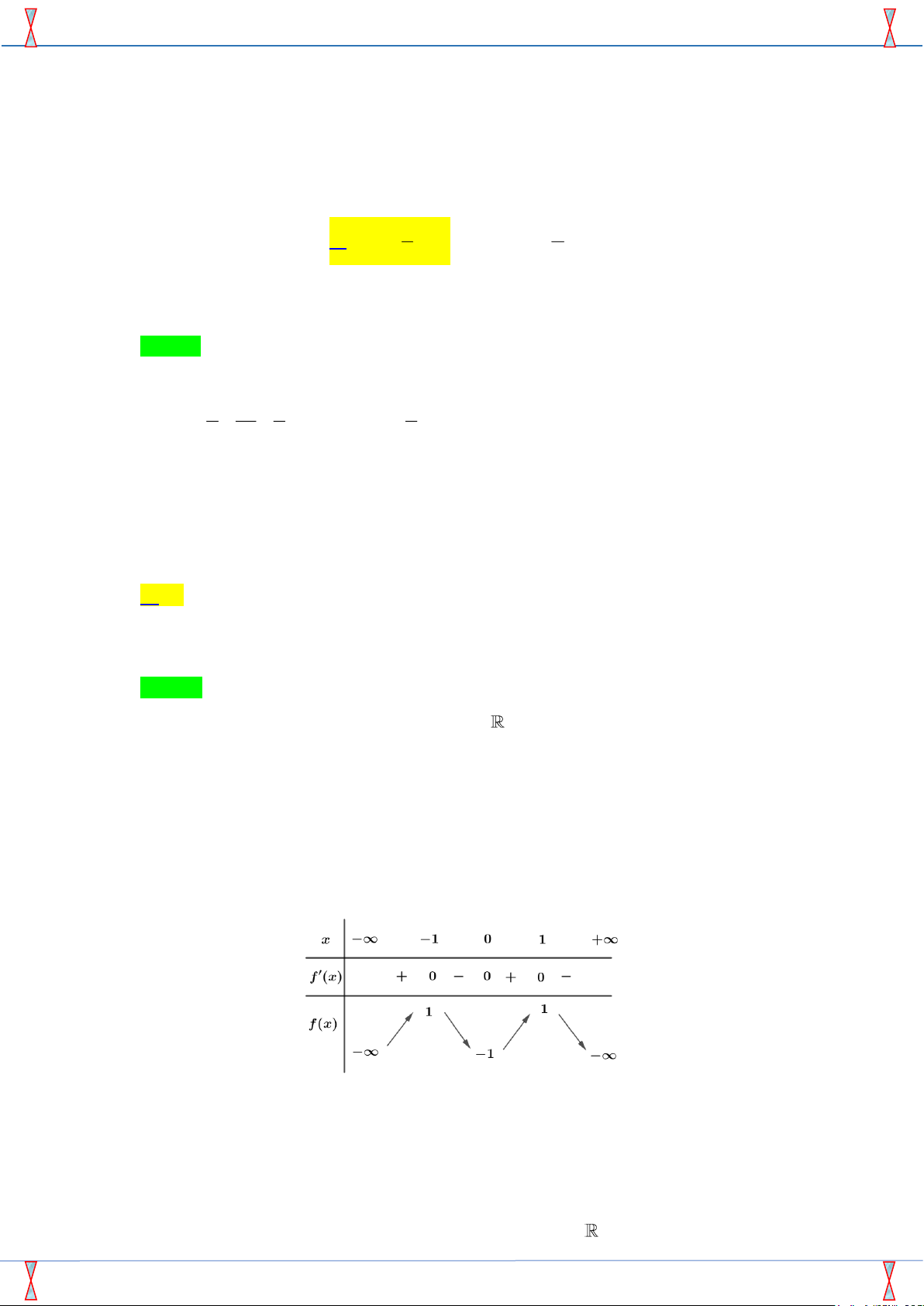
Cho hàm số y = x3 − 3x2 + 4 có đồ thị (C) như hình bên và 3
đường thẳng d : y = m3 − 3m2 + 4 (với m là tham số). Hỏi có bao
nhiêu giá trị nguyên của tham số m để đường thẳng d cắt đồ 2
thị (C) tại 3 điểm phân biệt? 1 A. 3. B. 2. C. 1. D. Vô số. x −1 0 1 2 3
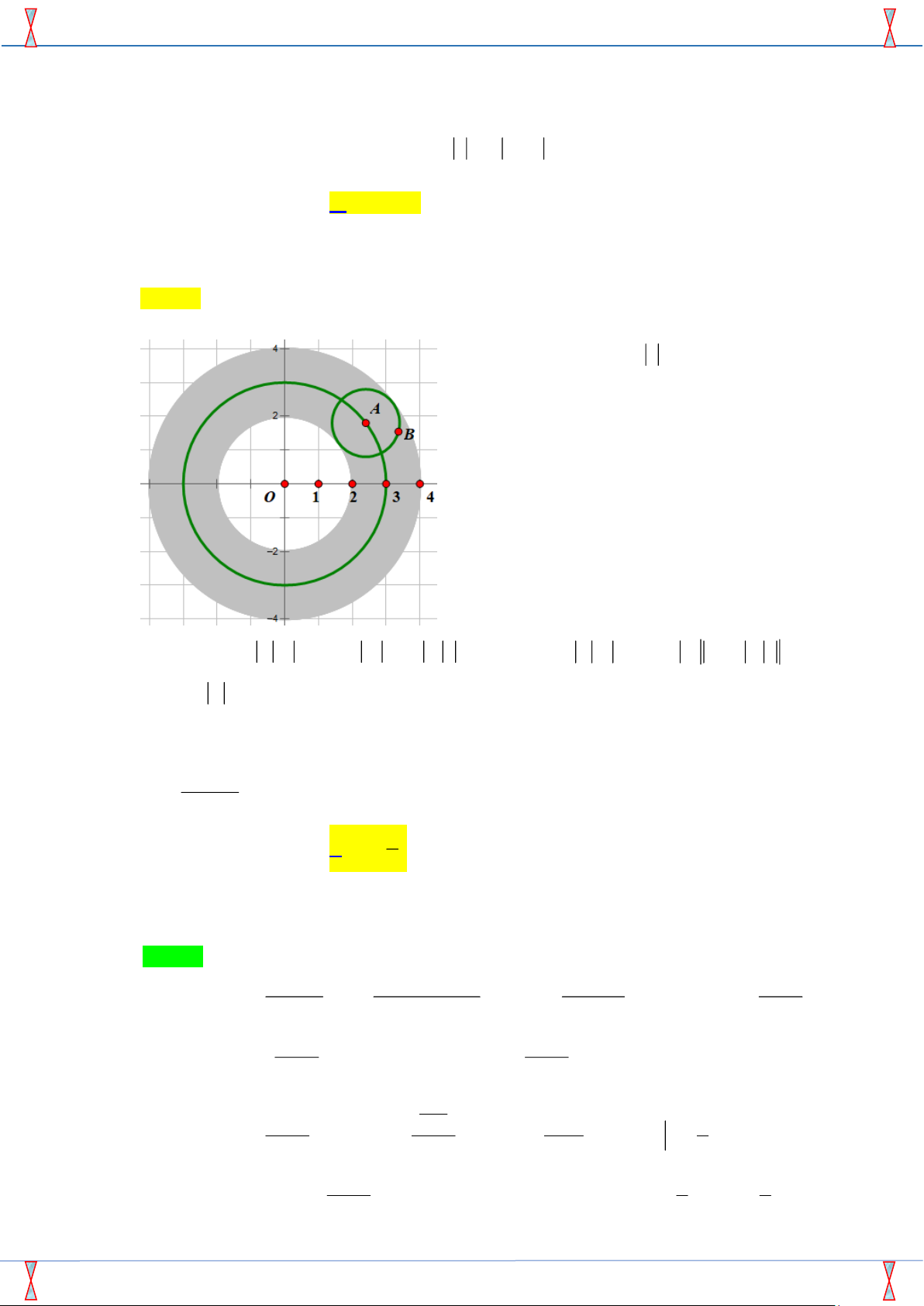
Câu 33. Cho các số phức z thỏa mãn |z| = 2. Biết rằng tập hợp các điểm biểu diễn số
phức w = 3 − 2i + (4 − 3i)z là một đường tròn. Tính bán kính r của đường tròn đó. √ A. r = 5. B. r = 2 5. C. r = 10. D. r = 20. 2 + 81x + 81−x
Câu 34. Cho 9x + 9−x = 14, khi đó biểu thức M = có giá trị bằng 11 − 3x − 3−x A. 14. B. 49. C. 42. D. 28.
Câu 35. Cho lăng trụ tam giác đều ABC.A0B0C0 có đáy là tam giác đều cạnh a, AA0 = 2a.
Gọi α là góc giữa AB0 và BC0. Tính cos α. √ √ 5 51 39 7 A. cos α = . B. cos α = . C. cos α = . D. cos α = . 8 10 8 10 x = 1 + t  x − 1 y − m z + 2
Câu 36. Cho hai đường thẳng d1 : y = 2 − t và d2 : = = (với m là tham 2 1 −1 z = 3 + 2t
số). Tìm m để hai đường thẳng d1, d2 cắt nhau. A. m = 4. B. m = 9. C. m = 7. D. m = 5.
Câu 37. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB đều
và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách từ điểm C đến mặt phẳng (SAD). √ √ √ √ a 3 a 3 a 3 a 3 A. . B. . C. . D. . 6 2 3 4
Câu 38. Cho một hộp có chứa 5 bóng xanh, 6 bóng đỏ và 7 bóng vàng. Lấy ngẫu nhiên
4 bóng từ hộp, tính xác suất để có đủ 3 màu. 35 35 175 35 A. . B. . C. . D. . 816 68 5832 1632
Câu 39. Cho phương trình log2 x − 4 log x + m − 3 = 0. Tìm tất cả các giá trị nguyên của 3 3
tham số m để phương trình đã cho có hai nghiệm phân biệt thỏa mãn x1 > x2 > 1. A. 6. B. 4. C. 3. D. 5.
Câu 40. Có tất cả bao nhiêu giá trị thực của tham số m để đường thẳng d : y = mx + 1
cắt đồ thị (C) : y = x3 − x2 + 1 tại 3 điểm A, B(0; 1), C phân biệt sao cho tam giác AOC vuông tại O(0; 0)? A. 0. B. 1. C. 3. D. 2. x = t 
Câu 41. Trong hệ tọa độ Oxyz, cho điểm M (1; −1; 2) và hai đường thẳng d1 : y = 1 − t , z = −1 x + 1 y − 1 z + 2 d2 : = =
. Đường thẳng ∆ đi qua M và cắt cả hai đường thẳng d1, d2 có 2 1 1 − →
véc tơ chỉ phương là u∆(1; a; b), tính a + b. Trang 4/6 Mã đề 110 A. a + b = −1. B. a + b = −2. C. a + b = 2. D. a + b = 1.
Câu 42. Hai người A và B ở cách nhau 180 (m) trên một đoạn đường thẳng và cùng
chuyển động thẳng theo một hướng với vận tốc biến thiên theo thời gian, A chuyển động
với vận tốc v1(t) = 6t + 5 (m/s), B chuyển động với vận tốc v2(t) = 2at − 3 (m/s) (a là hằng
số), trong đó t (giây) là khoảng thời gian tính từ lúc A, B bắt đầu chuyển động. Biết rằng
lúc đầu A đuổi theo B và sau 10 (giây) thì đuổi kịp. Hỏi sau 20 (giây), A cách B bao nhiêu mét? A. 320 (m). B. 720 (m). C. 360 (m). D. 380 (m).
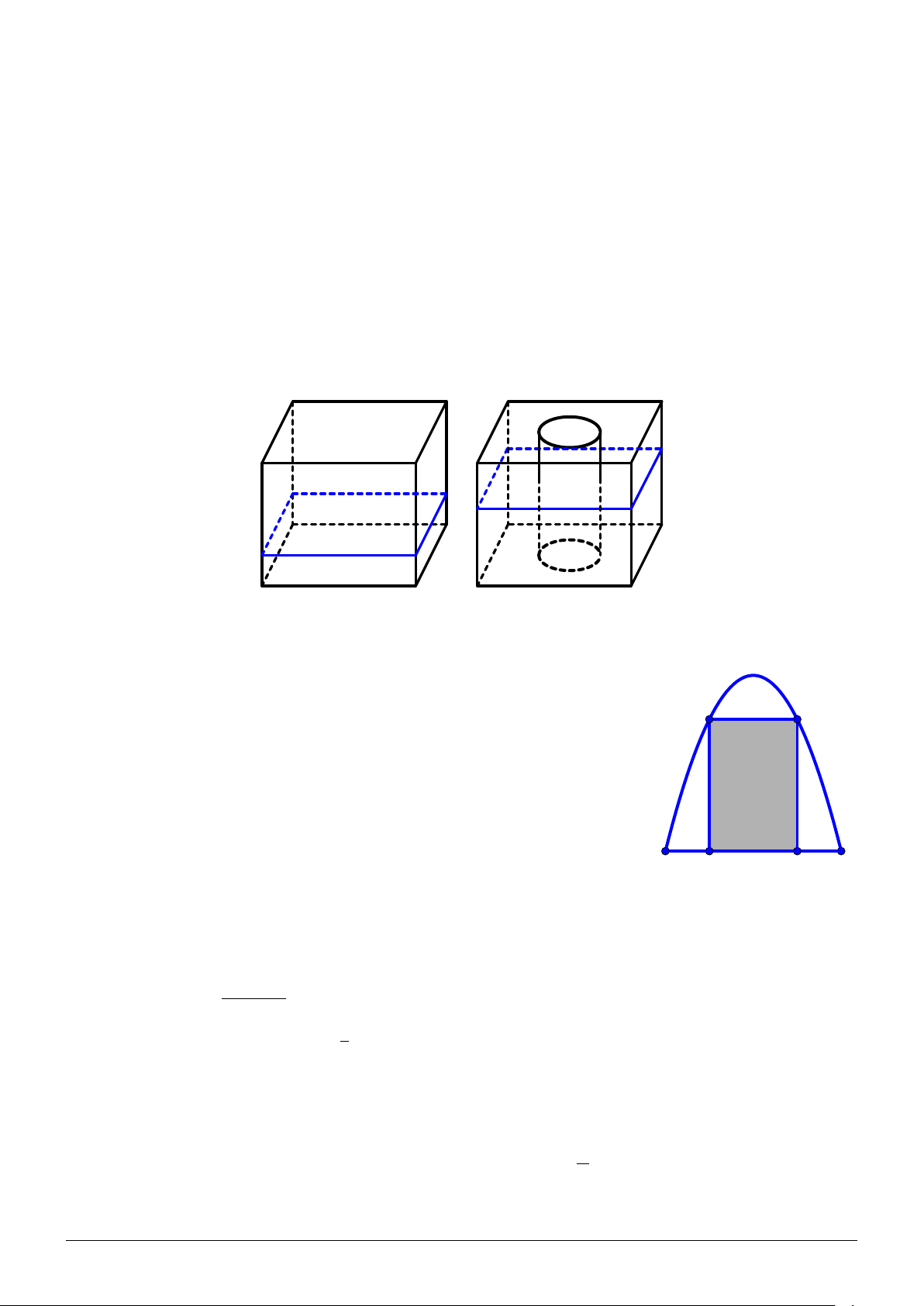
Câu 43. Một hình hộp chữ nhật có chiều cao là 90cm, đáy hộp là hình chữ nhật có chiều
rộng là 50cm và chiều dài là 80cm. Trong khối hộp có chứa nước, mực nước so với đáy
hộp có chiều cao là 40cm. Hỏi khi đặt vào khối hộp một khối trụ có chiều cao bằng chiều
cao khối hộp và bán kính đáy là 20cm theo phương thẳng đứng thì chiều cao của mực
nước so với đáy là bao nhiêu? A. 68, 32cm. B. 78, 32cm. C. 58, 32cm. D. 48, 32cm. Câu 44.
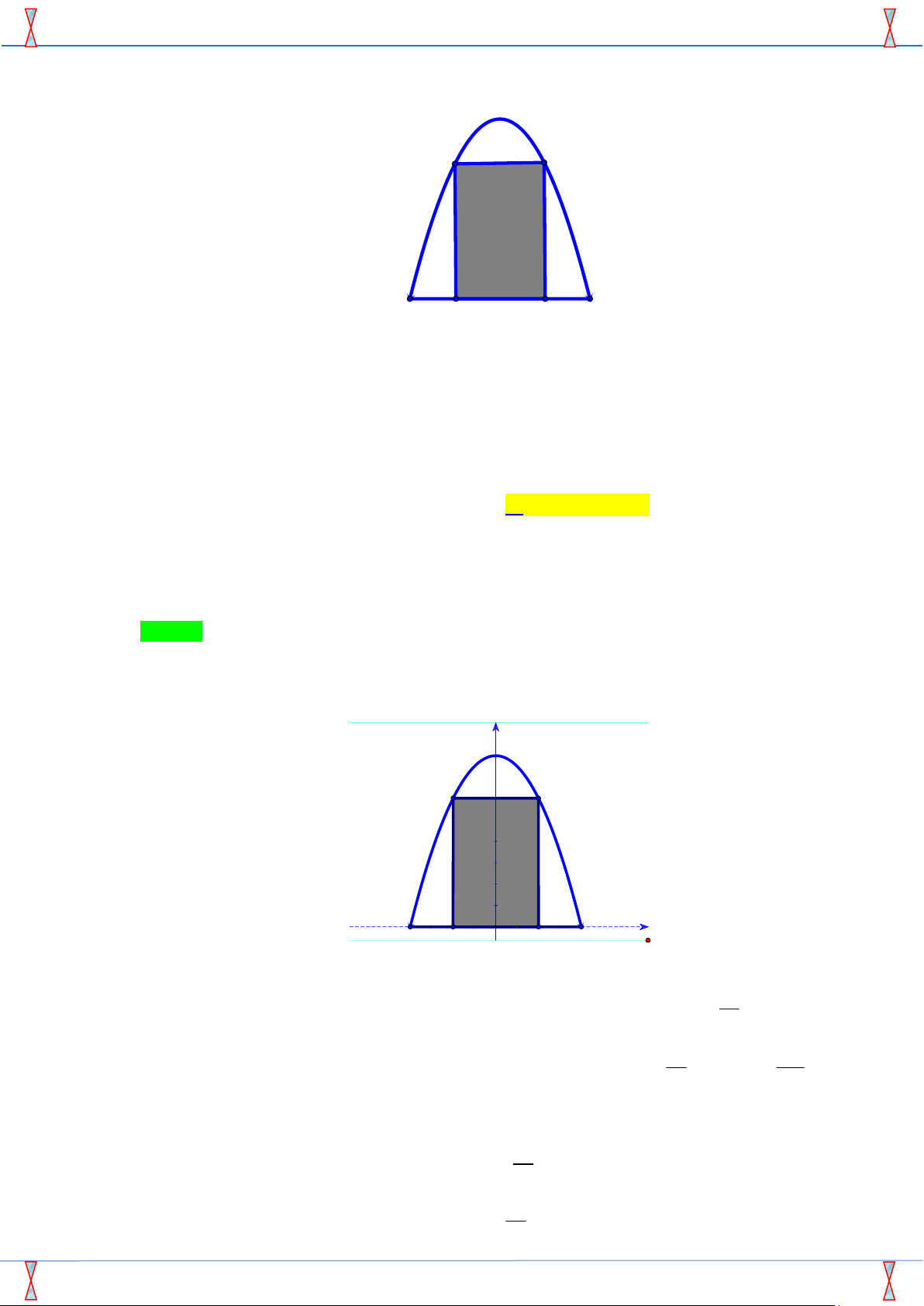
Một chiếc cổng có hình dạng là một Parabol có khoảng cách
giữa hai chân cổng là AB = 8m. Người ta treo một tấm phông M N
hình chữ nhật có hai đỉnh M, N nằm trên Parbol và hai đỉnh
P, Q nằm trên mặt đất (như hình vẽ). Ở phần phía ngoài phông
(phần không tô đen) người ta mua hoa để trang trí với chi phí
cho 1m2 cần số tiền mua hoa là 200.000 đồng cho 1m2. Biết
M N = 4m, M Q = 6m. Hỏi số tiền dùng để mua hoa trang trí
chiếc cổng gần với số tiền nào sau đây? A. 3.735.300 đồng. B. 3.437.300 đồng. C. 3.734.300 đồng. D. 3.733.300 đồng. A Q P B
Câu 45. Cho hai số phức z, w thay đổi thoả mãn |z| = 3, |z − w| = 1. Biết tập hợp điểm
của số phức w là hình phẳng H. Tính diện tích S của hình H A. S = 20π. B. S = 12π. C. S = 4π. D. S = 16π. Z 1 9x + 3m Câu 46. Cho
dx = m2 − 1. Tính tổng tất cả các giá trị của tham số m. 9x + 3 0 1 A. P = 12. B. P = . C. P = 16. D. P = 24. 2
Câu 47. Có bao nhiêu cách phân tích số 159 thành tích của ba số nguyên dương, biết
rằng các cách phân tích mà các nhân tử chỉ khác nhau về thứ tự thì chỉ được tính một lần? A. 517. B. 516. C. 493. D. 492. b8 Câu 48. log
Cho các số thực a, b > 1 thỏa mãn alogb a + 16b a a3 = 12b2. Giá trị của biểu thức P = a3 + b3 là A. P = 20. B. P = 39. C. P = 125. D. P = 72. Trang 5/6 Mã đề 110
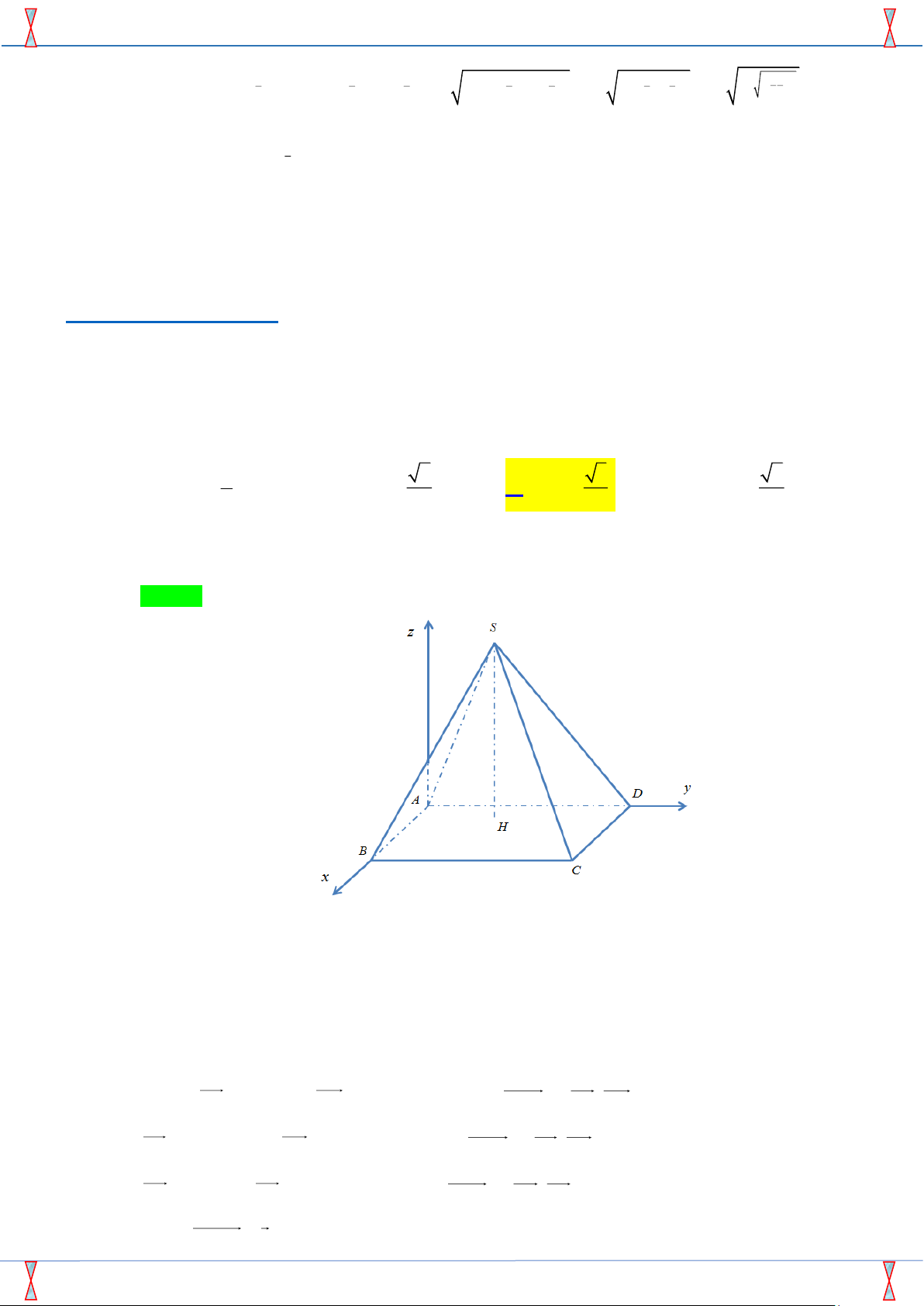
Câu 49. Cho hình chóp S.ABCD có đáy ABCD là hình vuông, hình chiếu vuông góc của
đỉnh S xuống mặt đáy nằm trong hình vuông ABCD. Hai mặt phẳng (SAD), (SBC) vuông
góc với nhau; góc giữa hai mặt (SAB) và (SBC) là 600; góc giữa hai mặt phẳng (SAB) và
(SAD) là 450. Gọi α là góc giữa hai mặt phẳng (SAB) và (ABCD), tính cos α √ √ √ 1 2 3 2 A. cos α = . B. cos α = . C. cos α = . D. cos α = . 2 2 2 3 1
Câu 50. Cho hai hàm số f (x) =
x3 − (m + 1)x2 + (3m2 + 4m + 5)x + 2019 và g(x) = (m2 + 3
2m + 5)x3 − (2m2 + 4m + 9)x2 − 3x + 2 (với m là tham số). Hỏi phương trình g(f (x)) = 0 có bao nhiêu nghiệm? A. 9. B. 0. C. 3. D. 1.
- - - - - - - - - - HẾT- - - - - - - - - - Trang 6/6 Mã đề 110 ĐÁP ÁN
BẢNG ĐÁP ÁN CÁC MÃ ĐỀ Mã đề thi 110 1. C 2. D 3. B 4. B 5. A 6. C 7. C 8. A 9. D 10. B 11. C 12. D 13. B 14. B 15. D 16. B 17. B 18. A 19. B 20. A 21. C 22. A 23. A 24. B 25. A 26. D 27. C 28. A 29. B 30. A 31. A 32. C 33. C 34. D 35. D 36. D 37. B 38. B 39. C 40. B 41. D 42. D 43. C 44. D 45. B 46. B 47. A 48. D 49. C 50. C 1
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019 ĐỀ THỬ THPTQG
LƯƠNG THẾ VINH - HÀ NỘI LẦN 2-2019 MÔN TOÁN
Bản quyền thuộc về tập thể thầy cô
STRONG TEAM TOÁN VD-VDC Câu 1.
Cho số phức z thỏa mãn z = 3 + 2i . Tìm phần thực và phần ảo của số phức z .
A.Phần thực bằng 3 − , phần ảo bằng 2 .
B. Phần thực bằng 3 , phần ảo bằng 2 .
C. Phần thực bằng 3 , phần ảo bằng 2 − .
D. Phần thực bằng -3, phần ảo bằng 2 − . x − x y − y z − z Câu 2.
Trong không gian với hệ tọa độ Oxyz , cho đường thẳng 0 0 0  : = = . Điểm M a b c
nằm trên đường thẳng  thì tọa độ của điểm M có dạng nào sau đây?
A. M (at;bt;ct ) .
B. M ( x t; y t; z t . 0 0 0 )
C. M (a + x t;b + y t;c + z t .
D. M ( x + at; y + bt; z + ct . 0 0 0 ) 0 0 0 ) Câu 3.
Cho hàm số y = f ( x) xác định, liên tục trên
và có bảng biến thiên như sau:
Tìm giá trị cực đại y y
CÑ và giá trị CT của hàm số đã cho. A. y = −2 y y y CÑ và = 2 CT . B. = 3 CÑ và = 0 CT . C. y = 2 y y y CÑ và = 0 CT . D. = 3 CÑ và = −2 CT . Câu 4.
Trong hệ tọa độ Oxyz , cho ba điểm A(1; 0; 0) , B (0; −1;0) , C (0;0; 2) . Phương trình mặt phẳng ( ABC) là: z y
A. x − 2 y + z = 0 .
B. x − y + =1 . C. x + − z =1 .
D. 2x − y + z = 0 . 2 2 Câu 5.
Đường thẳng y = m tiếp xúc với đồ thị 4 2 (C) : y = 2
− x + 4x −1tại hai điểm phân biệt (
A x ; y ) và B(x ; y ) . Giá trị của biểu thức y + y bằng A A B B A B A. 2 . B. −1. C. 1. D. 0. Câu 6.
Trong các hàm số dưới đây, hàm số nào đồng biến trên tập ? A. 1 3 2 x y − = . B. y = log x −1 . C. log 2x y =
+1 . D. y = log ( 2 x +1 . 2 ) 2 ( ) 2 ( ) Câu 7.
Đường cong như hình bên dưới là đồ thị của hàm số nào sau đây? A. 3 2 y x 3x 2 . B. 3 2 y x 3x 2 . C. 4 2 y x 2x 2 . D. 4 2 y x 2x 2 . e Câu 8.
Tìm tập xác định của hàm số y = ( 2
x + 2x − 3) .
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 1 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
A. (−;− 3)  (1;+ ) .
B. (− ;− 3 1;+ ) . C. (−3;1) . D.  3 − ;  1 2x +1 Câu 9. Cho hàm số y = . Mệnh đề đúng là x +1
A. Hàm số nghịch biến trên (−; − ) 1 và (−1; + ) .
B. Hàm số đồng biến trên (−; − )
1 và (1; + ) , nghịch biến trên (−1; ) 1 .
C. Hàm số đồng biến trên .
D. Hàm số đồng biến trên (−; − ) 1 và (−1; + ) .
Câu 10. Thể tích của khối cầu có bán kính R là: 3 4 R 3  R A. 3  R . B. . C. 3 2 R . D. . 3 3
Câu 11. Cho f ( x) , g ( x) là các hàm số có đạo hàm liên tục trên , k
. Trong các khẳng định dưới
đây, khẳng định nào sai? A.f
 (x)− g(x) dx = f
 (x)dx− g
 (x)dx . B. f
 (x)dx = f (x)+C . C. kf
 (x)dx = k f  (x)dx . D.f
 (x)+ g(x) dx = f
 (x)dx+ g  (x)dx .
Câu 12. Cho lăng trụ tứ giác đều có đáy là hình vuông cạnh a , chiều cao 2a . Tính thể tích khối lăng trụ. 3 2a 3 4a A. . B. . C. 3 a . D. 3 2a . 3 3
Câu 13. Tích của giá trị lớn nhất và giá trị nhỏ nhất của hàm số ( ) 4 f x = x + trên đoạn 1;  3 bằng x 65 52 A. . B. 20 . C. 6 . D. . 3 3 x − 2 y + 2 z − 6
Câu 14. Trong hệ tọa độ Oxyz , cho hai đường thằng chéo nhau d : = = ; 1 2 1 2 − x − 4 y + 2 z +1 d : = =
. Phương trình mặt phẳng (P) chứa d và song song với d là 2 1 2 1 2 − 3
A. ( P) : x + 8y + 5z +16 = 0 .
B. ( P) : x + 8y + 5z −16 = 0 .
C. ( P) : 2x + y − 6 = 0 .
D. ( P) : x + 4 y + 3z −12 = 0 . x −1 y − 3 z −1
Câu 15. Trong hệ tọa độ Oxyz , cho đường thẳng d : = = cắt mặt phẳng 2 1 − 1
(P):2x −3y + z − 2 = 0 tại điểm I (a;b;c). Khi đó a +b+c bằng A. 9 . B. 5 . C. 3 . D. 7 .
Câu 16. Cho dãy số (u
là một cấp số cộng, biết u + u = 50 . Tính tổng của 22 số hạng đầu tiên của n ) 2 21 dãy. A. 2018 . B. 550 . C. 1100 . D. 50 . x +1
Câu 17. Số đường tiệm cận của đồ thị hàm số y = x − 2x + là 1 A. 4 . B. 3 . C. 2 . D. 1.
Câu 18. Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a , tam giác SAB đều và nằm trong
mặt phẳng vuông góc với đáy. Tính theo a thể tích của khối chóp S.ABC .
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 2 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019 3 a 3 a 3 3 a 3 3 a A. V = . B. V = . C. V = . D. V = . 8 3 4 4
Câu 19. Họ nguyên hàm của hàm số f ( x) = x ( 3 2 1+ 3x ) là  3  3  6x   3   3  A. 2 2 x 1+ x + C   . B. 2 x 1+  + C . C. 4 2x x + x + C   . D. 2 3 x x + x + C   .  2   5   4   4  1−3x  2  25
Câu 20. Tập nghiệm S của bất phương trình    .  5  4 1   1 
A. S = 1; +) . B. S = ; +   . C. S = ; −   .
D. S = (−  ;1 . 3   3 
Câu 21. Trong hệ toạ độ Oxyz , cho điểm A( 3;5;3 ) và hai mặt phẳng (P):2x + y + 2z − 8 = 0,
(Q): x − 4 y + z − 4 = 0. Viết phương trình đường thẳng d đi qua A và song song với cả hai mặt
phẳng (P) và (Q) . x = 3 + tx = 3 x = 3 + tx = 3 + t    
A. y = 5 − t .
B. y = 5 + t . C. y = 5 . D. y = 5 .     z = 3  z = 3 − tz = 3 − tz = 3 + t  x = 2 + t
Câu 22. Trong hệ tọa độ Oxyz , cho điểm A( 1
− ;1;6) và đường thẳng  : y =1− 2t. Hình chiếu vuông z = 2t
góc của A trên  là:
A. M (3; −1; 2) .
B. H (11; −17;18) .
C. N (1;3; −2) . D. K (2;1;0) .
Câu 23. Cho f ( x) , g ( x) là các hàm số liên tục trên thỏa mãn 1 2 2 f
 (x)dx = 3,  f
 (x)−3g(x)dx = 4  và 2 f
 (x)+ g(x)dx =8  . 0 0 0 2 Tính I = f  (x)dx . 1 A. I = 1. B. I = 2 . C. I = 3 . D. I = 0 . 4 x 3
Câu 24. Đồ thị hàm số 2 y = − + x +
cắt trục hoành tại mấy điểm? 2 2 A. 0 . B. 2 . C. 4 . D. 3 .
Câu 25. Trong hệ tọa độ (Oxyz ) , cho đểm I (2; −1; − )
1 và mặt phẳng ( P) : x − 2 y − 2z + 3 = 0 . Viết
phương trình mặt cầu (S ) có tâm I và tiếp xúc với mặt phẳng (P) . A. ( S ) 2 2 2
: x + y + z − 4x + 2 y + 2z − 3 = 0. B. ( S ) 2 2 2
: x + y + z − 2x + y + z − 3 = 0. C. ( S ) 2 2 2
: x + y + z − 4x + 2 y + 2z + 1 = 0. D. ( S ) 2 2 2
: x + y + z − 2x + y + z + 1 = 0.
Câu 26. Cho hình lập phương ABC . D A BCD
  có cạnh bằng a . Một hình nón có đỉnh là tâm của hình vuông A BCD
  và có đường tròn đáy ngoại tiếp hình vuông ABCD. Tính diện tích xung quanh của hình nón đó. 2  a 2 2  a 2 2  a 3 A. . B. 2  a 3 . C. . D. . 2 4 2
Câu 27. Tìm hệ số của số hạng chứa 9
x trong khai triển nhị thức Newton của biểu thức ( + )11 3 x A. 9 . B. 110 . C. 495 . D. 55 .
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 3 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019   7 3 log ( a )
Câu 28. Cho số thực a
0, a 1. Giá trị của 2 a bằng 3 6 3 7 A. 14 . B. 7 . C. 8 . D. 6 . y = log ( 3 x − 3x − 4 8 )
Câu 29. Đạo hàm của hàm số là 3 3x − 3 2 x −1 3 1 ( 3x − 3 3
x − 3x − 4)ln 2
( 3x −3x−4)ln2 ( 3x −3x−4) 3 ln 8 A. . B. .
C. x − 3x − 4 . D. . u  + u = 10 1 3 (  u u + u = 80 n )
Câu 30. Cho cấp số nhân thỏa mãn  u 4 6 . Tìm 3 A. u = 8 u = 2 u = 6 u = 4 3 . B. 3 . C. 3 . D. 3 .
Câu 31. Cho khối nón ( N ) đỉnh S , có chiều cao là a 3 và độ dài đường sinh là 3a . Mặt phẳng ( P)
đi qua đỉnh S , cắt và tạo với mặt đáy của khối nón một góc 60 . Tính diện tích thiết diện tạo
bởi mặt phẳng ( P) và khối nón ( N ) . A. 2 2a 5 . B. 2 a 3 . C. 2 2a 3 . D. 2 a 5 . Câu 32. Cho hàm số 3 2
y = x − 3x + 4 có đồ thị (C ) như hình vẽ và đường thẳng 3 2
d : y = m − 3m + 4 (với
m là tham số). Hỏi có bao nhiêu giá trị nguyên của tham số m để đường thẳng d cắt đồ thị
(C)tại ba điểm phân biệt? A. 3 . B. 2 . C. 1. D. Vô số. y 4 3 2 1 x -1 O 2 3 1
Câu 33. Cho các số phức z thỏa mãn z = 2 . Biết rằng tập hợp các điểm biểu diễn số phức
w = 3 − 2i + (4 − 3i) z là một đường tròn. Tính bán kính r của đường tròn đó. A. r = 5 . B. r = 2 5 . C. r = 10 . D. r = 20 . 2 + 81x + 81−x
Câu 34. Cho 9x + 9−x = 14 . Khi đó biểu thức M = có giá trị bằng
11− 3x − 3−x A. 14. B. 49. C. 42. D. 28.
Câu 35. Cho lăng trụ tam giác đều AB . C A BC
  có đáy là tam giác đều cạnh a , AA = 2a . Gọi  là góc
giữa AB và BC . Tính cos . 5 51 39 7 A. cos = . B. cos = . C. cos = . D. cos = . 8 10 8 10 x = 1+ t
x −1 y − m z + 2
Câu 36. Cho hai đường thẳng d : y = 2 − t d : = = 1 và 2
(với m là tham số). Tìm m  2 1 1 − z = 3 + 2t
để hai đường thẳng d d 1 , 2 cắt nhau.
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 4 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019 A. m = 4 . B. m = 9 . C. m = 7 . D. m = 5.
Câu 37. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Tam giác SAB đều và nằm
trong mặt phẳng vuông góc với đáy. Tính khoảng cách từ điểm C đến mặt phẳng ( SAD) . a 3 a 3 a 3 a 3 A. . B. . C. . D. . 6 2 3 4
Câu 38. Cho một hộp có chứa 5 bóng xanh, 6 bóng đỏ và 7 bóng vàng. Lấy ngẫu nhiên
4 bóng từ hộp, tính xác suất để có đủ 3 màu. 35 35 175 35 A. . B. . C. . D. . 816 68 5832 1632
Câu 39. Cho phương trình 2
log x − 4 log x + m − 3 = 0 . Tìm tất cả các giá trị nguyên của tham số m để 3 3
phương trình đã cho có hai nghiệm phân biệt thỏa mãn x x  1. 1 2 A. 6. B. 4. C. 3. D. 5.
Câu 40. Có tất cả bao nhiêu giá trị thực của tham số m để đường thẳng d : y = mx +1 cắt đồ thị (C) 3 2
: y = x − x +1 tại 3 điểm ; A B (0; )
1 ; C phân biệt sao cho tam giác AOC vuông tại O (0;0) ? A. 0 . B. 1. C. 3 . D. 2 . x = t
Câu 41. Trong không gian Oxyz, cho điểm M (1; 1
− ;2) và hai đường thẳng d :y =1−t, 1 z = 1 −  x +1 y −1 z + 2 d : = =
. Đường thẳng  đi qua điểm M và cắt cả hai đường thẳng d , d có 2 2 1 1 1 2
véctơ chỉ phương là u = (1; ; a b +  ), tính a .b
A. a + b = 1. − B. a + b = 2 − . C. a + b = 2. D. a + b = 1.
Câu 42. Hai người A và B ở cách nhau 180 (m) trên một đoạn đường thẳng và cùng chuyển động
thẳng theo một hướng với vận tốc biến thiên theo thời gian, A chuyển động với vận tốc
v t = 6t + 5 m/s , B chuyển động với vận tốc v t = 2at − 3 m/s ( a là hằng số), trong đó 2 ( ) ( ) 1 ( ) ( )
t (giây) là khoảng thời gian tính từ lúc A , B bắt đầu chuyển động. Biết rằng lúc đầu A đuổi
theo B và sau 10 (giây) thì đuổi kịp. Hỏi sau 20 (giây), A cách B bao nhiêu mét? A. 320 (m) . B. 720 (m) . C. 360 (m) . D. 380 (m) .
Câu 43. Một hình hộp chữ nhật có chiều cao là 90 cm, đáy hộp là hình chữ nhật có chiều rộng là 50 cm
và chiều dài là 80 cm. Trong khối hộp có chứa nước, mực nước so với đáy hộp có chiều cao là
40 cm. Hỏi khi đặt vào khối hộp một khối trụ có chiều cao bằng chiều cao khối hộp và bán kính
đáy là 20 cm theo phương thẳng đứng thì chiều cao của mực nước so với đáy là bao nhiêu? A. 68,32 cm. B. 78,32 cm. C. 58,32 cm. D. 48,32 cm.
Câu 44. Một chiếc cổng có hình dạng là một Parabol có khoảng cách giữa hai chân cổng là AB = 8m .
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 5 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019 M N A B Q P
Người ta treo một tấm phông hình chữ nhật có hai đỉnh M , N năm trên Parabol và hai đỉnh
P, Q nằm trên mặt đất(như hình vẽ). Ở phần phía ngoài phông (phần không tô đen) người ta
mua hoa để trang trí với chi phí cho 2
1m cần số tiền cần mua hoa là 200.000 đồng cho 2 1m .
Biết rằng MN = 4m, MQ = 6m . Hỏi số tiền dùng để mua hoa trang trí chiếc cổng gần với số tiền nào sau đây? A. 3.735.300 đồng. B. 3.437.300 đồng. C. 3.734.300 đồng . D. 3.733.300 đồng.
Câu 45. Cho hai số phức z, w thay đổi thỏa mãn z = 3, z − w = 1. Biết tập hợp điểm của số phức w là
hình phẳng H. Tính diện tích S của H. A. S = 20 . B. S = 12 . C. S = 4 . D. S = 16 . 1 9x + 3m Câu 46. Cho 2 dx = m −1 
. Tính tổng tất cả các giá trị của tham số m . 9x + 3 0 1 A. P = 12 . B. P = . C. P = 16 . D. P = 24 . 2
Câu 47. Có bao nhiêu cách phân tích số 9
15 thành tích của ba số nguyên dương, biết rằng các cách phân
tích mà các phần tử chỉ khác nhau về thứ tự thì chỉ được tính một lần? A. 517 . B. 516 . C. 493. D. 492 . 8  b  log   a  3 
Câu 48. Cho các số thực a, b  1 thoả mãn log aa  2 b a +16b
= 12b . Giá trị của biểu thức 3 3
P = a + b là A. 20 . B. 39 . C. 125 . D. 72 .
Câu 49. Cho hình chóp S. ABCD có đáy ABCD là hình vuông, hình chiếu vuông góc của đỉnh S
xuống mặt đáy nằm trong hình vuông ABCD . Hai mặt phẳng ( SAD) , ( SBC ) vuông góc với
nhau; góc giữa hai mặt phẳng ( SAB) và ( SBC ) là 0
60 ; góc giữa hai mặt phẳng ( SAB) và (SAD) là 0
45 . Gọi  là góc giữa hai mặt phẳng ( SAB) và ( ABCD) , tính cos 1 2 3 2 A. cos = . B. cos = . C. cos = . D. cos = . 2 2 2 3 1
Câu 50. Cho hai hàm số f ( x) 3 = x − (m + ) 2 1 x + ( 2
3m + 4m + 5) x + 2019 và 3 g ( x) = ( 2 m + m + ) 3 x − ( 2 m + m + ) 2 2 5 2 4
9 x − 3x + 2 , với m là tham số. Hỏi phương trình
g ( f ( x)) = 0 có bao nhiêu nghiệm? A. 9. B. 0. C. 3 . D. 1.
GIẢI CHI TIẾT ĐỀ THỬ THPTQG
LƯƠNG THẾ VINH- HÀ NỘI LẦN 2-2019 MÔN TOÁN
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 6 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
luuhuephuongtailieu@gmail.com
Nguyentuyetle77@gmail.com
Câu 1 . Cho số phức z thỏa mãn z = 3 + 2i . Tìm phần thực và phần ảo của số phức z .
A.Phần thực bằng 3 − , phần ảo bằng 2 .
B. Phần thực bằng 3 , phần ảo bằng 2 .
C. Phần thực bằng 3 , phần ảo bằng 2 − .
D. Phần thực bằng -3, phần ảo bằng 2 − . Lời giải
Tác giả: Nguyễn Tuyết Lê ; Fb: Nguyên Tuyet Le Chọn C
Vì z = 3 + 2i z = 3 − 2i . Do đó số phức z có phần thực bằng 3 , phần ảo bằng 2 − .
vanluu1010@gmail.com x − x y − y z − z Câu 2.
Trong không gian với hệ tọa độ Oxyz , cho đường thẳng 0 0 0  : = = . Điểm M a b c
nằm trên đường thẳng  thì tọa độ của điểm M có dạng nào sau đây?
A. M (at;bt;ct ) .
B. M ( x t; y t; z t . 0 0 0 )
C. M (a + x t;b + y t;c + z t .
D. M ( x + at; y + bt; z + ct . 0 0 0 ) 0 0 0 ) Lời giải
Tác giả: Bùi Văn Lưu ; Fb: Bùi Văn Lưu Chọn D
Đường thẳng  đi qua điểm M x ; y ; z
và có véc tơ chỉ phương u = ( ; a ; b c) nên đường 0 ( 0 0 0 )
x = x + at 0 
thẳng  có phương trình tham số là  :  y = y + bt 0
z = z + ct  0
Điểm M nằm trên đường thẳng  thì tọa độ của điểm M có dạng M ( x + at; y + bt; z + ct 0 0 0 )
Nguyenth4nhtr11ng@gmail.com Câu 3.
Cho hàm số y = f ( x) xác định, liên tục trên
và có bảng biến thiên như sau:
Tìm giá trị cực đại y y
CÑ và giá trị CT của hàm số đã cho. A. y = −2 y y y CÑ và = 2 CT . B. = 3 CÑ và = 0 CT . C. y = 2 y y y CÑ và = 0 CT . D. = 3 CÑ và = −2 CT . Lời giải
Tác giả: Nguyên Thành Trung ; Fb:Nguyên Thành Trung Chọn B
Từ bảng biến thiên ta có:
• y đổi dấu dương qua âm khi qua điểm x = −2 suy ra giá trị cực đại y = y(−2) = 3 CÑ .
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 7 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
• y đổi dấu âm qua dương khi qua điểm x = 2 suy ra giá trị cực tiểu y = y(2) = 0 CT .
anhtuanqh1@gmail.com Câu 4.
Trong hệ tọa độ Oxyz , cho ba điểm A(1; 0; 0) , B (0; −1;0) , C (0;0; 2) . Phương trình mặt phẳng ( ABC) là: z y
A. x − 2 y + z = 0 .
B. x − y + =1 . C. x + − z =1 .
D. 2x − y + z = 0 . 2 2 Lời giải
Tác giả: Nguyễn Anh Tuấn; Fb: Nguyễn Ngọc Minh Châu Chọn B
Áp dụng phương trình mặt phẳng theo đoạn chắn ta có: ( ) x y z z ABC : +
+ =1 hay x − y + =1. 1 1 − 2 2
tatienthanh7895@gmail.com Câu 5.
Đường thẳng y = m tiếp xúc với đồ thị 4 2 (C) : y = 2
− x + 4x −1tại hai điểm phân biệt (
A x ; y ) và B(x ; y ) . Giá trị của biểu thức y + y bằng A A B B A B A. 2 . B. −1. C. 1. D. 0. Lời giải
Tác giả: Tạ Tiến Thanh; Fb: Thanh Ta Chọn A Xét hàm số 4 2 f (x) = 2
− x + 4x −1, TXĐ: D = . 3 f '(x) = 8 − x +8x . x = 1 −  f '(x) = 0  x = 0  .  x =1  Xét bảng biến thiên
Dựa vào bảng biến thiên ta thấy để đường thẳng y = m tiếp xúc với 4 2 (C) : y = 2
− x + 4x −1tại
hai điểm phân biệt thì đường thẳng đó phải đi qua hai điểm cực đại, hay m = 1.
Khi đó hai tiếp điểm là (
A −1;1) và B(1;1) . Vậy y + y = 1+1 = 2 . A B
Pho.maths@gmail.com Câu 6.
Trong các hàm số dưới đây, hàm số nào đồng biến trên tập ?
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 8 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019 A. 1 3 2 x y − = . B. y = log x −1 . C. log 2x y =
+1 . D. y = log ( 2 x +1 . 2 ) 2 ( ) 2 ( ) Lời giải
Tác giả: Lương Pho; Fb: LuongPho89 Chọn C 2x Hàm số log 2x y =
+1 có tập xác định D = và y ' =  0 ,x  . 2 ( ) 2x +1 Do đó, hàm số log 2x y =
+1 đồng biến trên tập . 2 ( ) chauhieu2013@gmail.com dohoangtu2212@gmail.com Câu 7.
Đường cong như hình bên dưới là đồ thị của hàm số nào sau đây? A. 3 2 y x 3x 2 . B. 3 2 y x 3x 2 . C. 4 2 y x 2x 2 . D. 4 2 y x 2x 2 . Lời giải
Tác giả: Đỗ Hoàng Tú ; Fb: Đỗ Hoàng Tú Chọn C
Đồ thị hàm số đối xứng qua trục Oy  Hàm số là hàm chẵn  Loại A, B.
Hệ số a  0  Loại D, chọn C.
thuytoanthanglong@gmail.com e Câu 8.
Tìm tập xác định của hàm số y = ( 2
x + 2x − 3) .
A. (−;− 3)  (1;+ ) .
B. (− ;− 3 1;+ ) . C. (−3;1) . D.  3 − ;  1 Lời giải
Tác giả: Nguyễn Thủy; Fb: diephoang Chọn Ax  3 − Hàm số xác định khi 2
x + 2x − 3  0   . x  1
Vậy tập xác định của hàm số là D = (−;− 3)  (1;+ ) .
quyetlv.toan@gmail.com 2x +1 Câu 9. Cho hàm số y = . Mệnh đề đúng là x +1
A. Hàm số nghịch biến trên (−; − ) 1 và (−1; + ) .
B. Hàm số đồng biến trên (−; − )
1 và (1; + ) , nghịch biến trên (−1; ) 1 .
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC Trang 9 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
C. Hàm số đồng biến trên .
D. Hàm số đồng biến trên (−; − ) 1 và (−1; + ) . Lời giải
Tác giả: Lê Văn Quyết ; Fb: Lê Văn Quyết Chọn D TXĐ: \ −  1 . 1 Ta có y ' =  − ( , x   1. x + ) 0 2 1
Vậy hàm số đồng biến trên (−; − )
1 và (−1; + ) . Chọn D. Khaiphung97@gmail.com
Câu 10. Thể tích của khối cầu có bán kính R là: 3 4 R 3  R A. 3  R . B. . C. 3 2 R . D. . 3 3 Lời giải
Tác giả:Phùng Văn Khải; Fb:Phùng Khải Chọn B 4
Ta có thể tích khối cầu có bán kính R là: 3 V =  R 3
428truonghuyen@gmail.com
Câu 11. Cho f ( x) , g ( x) là các hàm số có đạo hàm liên tục trên , k
. Trong các khẳng định dưới
đây, khẳng định nào sai? A.f
 (x)− g(x) dx = f
 (x)dx− g
 (x)dx . B. f
 (x)dx = f (x)+C . C. kf
 (x)dx = k f  (x)dx . D.f
 (x)+ g(x) dx = f
 (x)dx+ g  (x)dx . Lời giải
Tác giả: Trương Huyền ; Fb: Trương Huyền Chọn C
Khẳng định A, B, D đúng theo tính chất của nguyên hàm.
Khẳng định C chỉ đúng khi k  0 .
honganh161079@gmail.com
Câu 12. Cho lăng trụ tứ giác đều có đáy là hình vuông cạnh a , chiều cao 2a . Tính thể tích khối lăng trụ. 3 2a 3 4a A. . B. . C. 3 a . D. 3 2a . 3 3 Lời giải
Tác giả: Đỗ Thị Hồng Anh; Fb: Hong Anh Chọn D
Đáy của lăng trụ tứ giác đều là hình vuông cạnh a nên diện tích đáy 2 S = a .
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC
Trang 10 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Thể tích khối lăng trụ là : 2 3
V = S.h = a .2a = 2a .
Diephd02@gmail.com; ducquoc210382@gmail.com
Câu 13. Tích của giá trị lớn nhất và giá trị nhỏ nhất của hàm số ( ) 4 f x = x + trên đoạn 1;  3 bằng x 65 52 A. . B. 20 . C. 6 . D. . 3 3 Lời giải
Tác giả : Nguyễn Ngọc Diệp, FB: Nguyễn Ngọc Diệp Chọn B Ta có: hàm số ( ) 4 f x = x +
xác định và liên tục trên đoạn 1;  3 . x 4 x = 2 f ( x) 4 =1−
; f ( x) = 0  1− = 0   . 2 x 2 xx = 2 −
Nhận thấy: −21; 
3  x = −2 (loại). f ( ) = f ( ) = f ( ) 13 1 5; 2 4; 3 =
. Khi đó: M = max f ( x) = 5 ; m = min f ( x) = 4 . 3 1  ;3 1  ;3
Vậy M .m = 20 .
Email: khanhhm.94@gmail.com x − 2 y + 2 z − 6
Câu 14 . Trong hệ tọa độ Oxyz , cho hai đường thằng chéo nhau d : = = ; 1 2 1 2 − x − 4 y + 2 z +1 d : = =
. Phương trình mặt phẳng (P) chứa d và song song với d là 2 1 2 1 2 − 3
A. ( P) : x + 8y + 5z +16 = 0 .
B. ( P) : x + 8y + 5z −16 = 0 .
C. ( P) : 2x + y − 6 = 0 .
D. ( P) : x + 4 y + 3z −12 = 0 . Lời giải
Tác giả:Huỳnh Minh Khánh ; Fb: Huỳnh Khánh Chọn Bx = 2 + 2t1 
Phương trình tham số d : y = −2 + t , (t  . 1 ) 1 1 z = 6− 2t  1
d đi qua điểm M (2; 2
− ;6) và véc tơ chỉ phương u = 2;1; 2 − . 1 ( ) 1 x = 4 + t2 
Phương trình tham số d : y = 2
− − 2t , (t  . 2 ) 2 2 z = 1 − + 3t  2
d đi qua N (4; −2; − )
1 và véc tơ chỉ phương u = 1; 2 − ;3 . 2 ( ) 2  (n ⊥ u P) 1
Vì mặt phẳng ( P) chứa d và song song với d , ta có: 
n = u ,u  = − 1;8;5 . P 1 2 ( ) 1 2 ( )    (n ⊥ u P) 2
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC
Trang 11 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Mặt phẳng ( P) đi qua M (2; 2
− ;6) và véc tơ pháp tuyến n = (1;8;5 , nên phương trình mặt P ) ( )
phẳng ( P) : ( x − 2) + 8( y + 2) + 5( z − 6) = 0 hay ( P) : x + 8y + 5z −16 = 0 .
trongtuspt08@gmail.com x −1 y − 3 z −1
Câu 15. Trong hệ tọa độ Oxyz , cho đường thẳng d : = = cắt mặt phẳng 2 1 − 1
(P):2x −3y + z − 2 = 0 tại điểm I (a;b;c). Khi đó a +b+c bằng A. 9 . B. 5 . C. 3 . D. 7 . Lời giải
Tác giả: Nguyễn Trọng Tú ; Fb: Anh Tú Chọn D
Ta có I = d  ( P) suy ra I d và I ( P) .
Vì I d nên tọa độ của I có dạng (1+ 2t ;3 − t ;1+ t ) với t  .
Vì I  ( P) nên ta có phương trình: 2(1+ 2t ) − 3(3 − t ) +1+ t − 2 = 0  t = 1 .
Vậy I (3; 2; 2) suy ra a + b + c = 3+ 2 + 2 = 7 .
ngoquoctuanspt95tailieu@gmail.com
Tranthom275@gmail.com
Câu 16. Cho dãy số (u
là một cấp số cộng, biết u + u = 50 . Tính tổng của 22 số hạng đầu tiên của n ) 2 21 dãy. A. 2018 . B. 550 . C. 1100 . D. 50 . Lời giải
Tác giả : Ngô Quốc Tuấn, FB: Quốc Tuấn Chọn B
Ta có: u = u + d , u = u + 20d . 2 1 21 1
Theo giả thiết u + u = 50  2u + 21d = 50 . 2 21 1 2u + 21d 22 1 
Tổng của 22 số hạng đầu tiên của dãy là S = 50.22 = = 550 . 22 2 2
cunconsieuquay1408@gmail.com x +1
Câu 17 . Số đường tiệm cận của đồ thị hàm số y = x − 2x + là 1 A. 4 . B. 3 . C. 2 . D. 1. Lời giải
Tác giả: Nguyễn Thị Thanh Mai ; Fb: Thanh Mai Nguyen Chọn B x +1 x +1
+ Với x  0 thì y = =
có TXĐ là: D = 0; ) 1  (1; +) . x − 2x +1 −x +1 Khi đó: lim y = 1
− nên đồ thị hàm số có tiệm cận ngang y = 1 − . x→+ lim y = 1. + x→0
lim y = − , lim y = + nên đồ thị hàm số có tiệm cận đứng x = 1 . + − x 1 → x 1 →
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC
Trang 12 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019 x +1 x +1
+ Với x  0 thì y = =
có TXĐ là: D = (− ;0) . −x − 2x +1 3 − x +1 Khi đó: 1 1 lim y = −
nên đồ thị hàm số có tiệm cận ngang y = − . x→− 3 3 lim y = 1. − x→0
Vậy đồ thị hàm số đã cho có 3 đường tiệm cận.
Thuhangnvx@gmail.com
Câu 18. Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a , tam giác SAB đều và nằm trong
mặt phẳng vuông góc với đáy. Tính theo a thể tích của khối chóp S.ABC . 3 a 3 a 3 3 a 3 3 a A. V = . B. V = . C. V = . D. V = . 8 3 4 4 Lời giải
Tác giả:Phùng Hằng ; Fb: Phùng Hằng Chọn A 2 a 3
Tam giác ABC là tam giác đều cạnh a S = . ABC  4
Gọi H là trung điểm của AB . Do tam giác ABC là tam giác đều cạnh a nên SH ⊥ AB và a 3 SH = . 2 (
SAB) ⊥ ( ABC) ( 
SAB)  ( ABC) = AB Ta có: 
SH ⊥ ( ABC). SH ⊥ AB  SH   (SAB) 2 3 1 1 a 3 a 3 a Vậy V = .SH.S = . . = . S . ABC  3 ABC 3 2 4 8
ngocthanh1308@gmail.com
Câu 19. Họ nguyên hàm của hàm số f ( x) = x ( 3 2 1+ 3x ) là
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC
Trang 13 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019  3  3  6x   3   3  A. 2 2 x 1+ x + C   . B. 2 x 1+  + C . C. 4 2x x + x + C   . D. 2 3 x x + x + C   .  2   5   4   4  Lời giải
Tác giả: Ngọc Thanh; Fb: Ngọc Thanh Chọn B  ( )  x
f x dx = 2x
 (1+3x )dx = (2x +6x ) 3 6 6 3 4 2 5 2 dx = x +
x + C = x 1+  + C . 5  5  3  6x
Vậy họ nguyên hàm của hàm số f ( x) = x ( 3 2 1+ 3x ) là 2 x 1+  + C .  5 
Hungnguyen24061984@gmail.com 1−3x  2  25
Câu 20. Tập nghiệm S của bất phương trình    .  5  4 1   1 
A. S = 1; +) . B. S = ; +   . C. S = ; −   .
D. S = (−  ;1 . 3   3  Lời giải
Tác giả: Nguyễn Hoàng Hưng; Fb: Nguyễn Hưng Chọn A 1−3x 1−3x 2 3x 1 − 2  2  25  2   5   5   5      
 3x −1 2  x 1           .  5  4  5   2   2   2 
Vậy tập nghiệm của bất phương trình đã cho là S = 1; +) .
hanhphuduc@gmail.com
Câu 21. Trong hệ toạ độ Oxyz , cho điểm A( 3;5;3 ) và hai mặt phẳng (P):2x + y + 2z − 8 = 0,
(Q): x − 4 y + z − 4 = 0. Viết phương trình đường thẳng d đi qua A và song song với cả hai mặt
phẳng (P) và (Q) . x = 3 + tx = 3 x = 3 + tx = 3 + t    
A. y = 5 − t .
B. y = 5 + t . C. y = 5 . D. y = 5 .     z = 3  z = 3 − tz = 3 − tz = 3 + tLời giải
Tác giả: Phạm Hạnh; Fb: Phạm Hạnh Chọn C
(P) có một VTPT n
2;1; 2 , (Q) có một VTPT n 1; 4 − ;1 . 2 ( ) 1 ( )
Do d / /(P), d / /(Q)  d có VTCP u = n , n = 9;0; −9  u 1;0; −1 cũng là một VTCP 1 ( ) 1 2  ( ) của (d ) . x = 3 + t
Đường thẳng (d ) đi qua A( 3;5;3 ) , nhận u làm VTCP, có phương trình là y = 5 , t R . 1 z = 3−t
hienchn@gmail.com
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC
Trang 14 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
minhphuongk34toan@gmail.com x = 2 + t
Câu 22. Trong hệ tọa độ Oxyz , cho điểm A( 1
− ;1;6) và đường thẳng  : y =1− 2t. Hình chiếu vuông z = 2t
góc của A trên  là:
A. M (3; −1; 2) .
B. H (11; −17;18) .
C. N (1;3; −2) . D. K (2;1;0) . Lời giải
Tác giả: Nguyễn Thị Minh Phương ; Fb: Minh Phuong Chọn A
Xét điểm H (2 + t;1− 2t;2t )  .
Ta có : AH = (3 + t; 2
− t;2t − 6);a = −  (1; 2;2)
H là hình chiếu vuông góc của A trên   AH .a = 0 1.(3 + t ) + 4t + 2(2t − 6) =  =  0 t 1.
Suy ra: H (3; −1; 2) .
Phanvinha3@gmail.com
Câu 23. Cho f ( x) , g ( x) là các hàm số liên tục trên thỏa mãn 1 2 2 f
 (x)dx = 3,  f
 (x)−3g(x)dx = 4  và 2 f
 (x)+ g(x)dx =8  . 0 0 0 2 Tính I = f  (x)dx . 1 A. I = 1. B. I = 2 . C. I = 3 . D. I = 0 . Lời giải
Tác giả: Phan Minh Quốc Vinh ; Fb: Vinh Phan Chọn A
Vì hàm số f ( x) , g ( x) liên tục trên nên 2 2 2   2    f
 (x)−3g(x)dx = 4   f
 (x)dx −3 g
 (x)dx = 4  f  (x)dx = 4    0 0 0    0   2 2 2   2   2 f  
(x)+ g (x)dx = 8 2 f
 (x)dx + g  (x)dx =8  g  (x)dx = 0   0  0 0 0 2 1 2
Vì hàm số f ( x) liên tục trên nên f
 (x)dx = f
 (x)dx+ f  (x)dx 0 0 1 2 2 1  f
 (x)dx = f
 (x)dx− f
 (x)dx = 4−3=1. 1 0 0 2 Vậy f  (x)dx =1. 1
Nguyenhoach95@gmail.com 4 x 3
Câu 24. Đồ thị hàm số 2 y = − + x +
cắt trục hoành tại mấy điểm? 2 2 A. 0 . B. 2 . C. 4 . D. 3 .
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC
Trang 15 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019 Lời giải
Tác giả: Nguyễn Đức Hoạch; Fb: Hoạch Nguyễn Chọn B 4
Xét phương trình hoành độ x 3 giao điểm: 2 − + x + = 0 4 2
x − 2x − 3 = 0 2 2 ( x =
x − 3)(x + ) 2 3 2 2 1 = 0    x =  3 . 2 x = 1 −
Vậy đồ thị hàm số đã cho cắt trục hoành tại 2 điểm.
Nvthang368@gmail.com
ngoctinh.hnue@gmail.com
Câu 25. Trong hệ tọa độ (Oxyz ) , cho đểm I (2; −1; − )
1 và mặt phẳng ( P) : x − 2 y − 2z + 3 = 0 . Viết
phương trình mặt cầu (S ) có tâm I và tiếp xúc với mặt phẳng (P) . A. ( S ) 2 2 2
: x + y + z − 4x + 2 y + 2z − 3 = 0. B. (S ) 2 2 2
: x + y + z − 2x + y + z − 3 = 0. C. ( S ) 2 2 2
: x + y + z − 4x + 2 y + 2z + 1 = 0. D. (S ) 2 2 2
: x + y + z − 2x + y + z + 1 = 0. Lời giải
Tác giả: Nguyễn Thị Tỉnh, Fb: Ngọc Tỉnh. Chọn A
Gọi R là bán kính mặt cầu (S ) .
Vì mặt cầu (S ) có tâm I và tiếp xúc với mặt phẳng ( P) nên ta có: 2 − 2.( 1 − ) − 2.( 1 − ) + 3 9 R = d( = = = . I ( 3 ; P)) 2 2 2 + − + − 3 1 ( 2) ( 2)
Vậy nên ta có phương trình mặt cầu (S ) là:
(x − )2 +( y + )2 +(z + )2 2 2 2 2 1 1
= 9  x + y + z − 4x + 2y + 2z − 3 = 0.
tranthanhha484@gmail.com
Câu 26. Cho hình lập phương ABC . D A BCD
  có cạnh bằng a . Một hình nón có đỉnh là tâm của hình vuông A BCD
  và có đường tròn đáy ngoại tiếp hình vuông ABCD . Tính diện tích xung quanh của hình nón đó. 2  a 2 2  a 2 2  a 3 A. . B. 2  a 3 . C. . D. . 2 4 2 Lời giải
Tác giả: Trần Thanh Hà; Fb: Hà Trần Chọn D
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC
Trang 16 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Gọi O, O lần lượt là tâm của hình vuông ABCD, AB CD   .
Hình nón có đáy là đường tròn ngoại tiếp hình vuông ABCD có cạnh là a nên đáy của hình nón là đườ 1 a 2
ng tròn có bán kính r = AC = . 2 2
Hình nón có đỉnh là tâm của hình vuông A BCD
  nên chiều cao của hình nón bằng độ dài
cạnh của hình vuông. Suy ra: h = a .
Khi đó: độ dài đường sinh của hình nón là: 2 2  a 2  3a a 6 2 2 2 2 2 l = O A  = O O
+ OA = h + r = a +   = = .   2 2 2   2 a 2 a 6  a 3
Diện tích xung quanh của hình nón là: S =  rl = . . = ( đvdt). xq 2 2 2
lethimai0108@gmail.com
Câu 27. Tìm hệ số của số hạng chứa 9
x trong khai triển nhị thức Newton của biểu thức ( + )11 3 x A. 9 . B. 110 . C. 495 . D. 55 . Lời giải
Tác giả: Lê Mai; Fb: Lê Mai Chọn C
Số hạng tổng quát trong khai triển nhị thức Newton của biểu thức ( + )11 − 3 x là: k 11 3 k. k C x . 11
Cho k = 9 ta được hệ số của số hạng chứa 9
x trong khai triển nhị thức Newton của biểu thức ( + )11 3 x là 2 9 3 .C = 495 . 11 tammath11@gmail.com
PB : khanghan456@gmail.com   7 3 log ( a )
Câu 28. Cho số thực a
0, a 1. Giá trị của 2 a bằng 3 6 3 7 A. 14 . B. 7 . C. 8 . D. 6 . Lời giải
Tác giả: Nguyễn Đình Tâm ; Fb: Tâm Nguyễn Đình Chọn A
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC
Trang 17 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019 3 1 1 3 3 7 3 7 log ( a ) = log a = . log a = 2 2 a 2 7 a a 14 .
Tvluatc3tt@gmail.com y = log ( 3 x − 3x − 4 8 )
Câu 29. Đạo hàm của hàm số là 3 3x − 3 2 x −1 3 1 ( 3x − 3 3
x − 3x − 4)ln 2
( 3x −3x−4)ln2 ( 3x −3x−4) 3 ln 8 A. . B. .
C. x − 3x − 4 . D. . Lời giải
Tác giả : Trần Luật, FB: Trần Luật Chọn B. x − x − x − x −
y = log ( x − 3x − 4) ( 3 3 4) 3( 2 ) 2 1 1 3  y = = = 8
( 3x −3x−4)ln8 3( 3x −3x−4)ln2 ( 3x −3x−4)ln2 Ta có .
canhcuttapbay@gmail.com u  + u = 10 1 3 (  u u + u = 80 n )
Câu 30. Cho cấp số nhân thỏa mãn  u 4 6 . Tìm 3 A. u = 8 u = 2 u = 6 u = 4 3 . B. 3 . C. 3 . D. 3 . Lời giải
Tác giả:Vũ Thị Thành ; Fb:Thanh Vũ Chọn A
Gọi công bội của cấp số nhân là q Theo giả thiết ta có: 2 2 2 u  + u =10 u  + u q =10 u  + u q =10   + =  = 1 1 u u q 10 u 2 1 3 1 1          3 5 u + u = 80  uq + u q = 80 q u + u q = 80     q .10 = 80 q = 2 1 1 ( ) 1 1 1 3 2 3 4 6 1 1 2 = = Suy ra: u u q 8 3 1
Ductoan.lvt@gmail.com
Câu 31. Cho khối nón ( N ) đỉnh S , có chiều cao là a 3 và độ dài đường sinh là 3a . Mặt phẳng ( P)
đi qua đỉnh S , cắt và tạo với mặt đáy của khối nón một góc 60 . Tính diện tích thiết diện tạo
bởi mặt phẳng ( P) và khối nón ( N ) . A. 2 2a 5 . B. 2 a 3 . C. 2 2a 3 . D. 2 a 5 . Lời giải
Tác giả: Giáp Minh Đức; Fb: Giáp Minh Đức ChọnA
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC
Trang 18 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019 S l h r A O I B
+) Khối nón ( N ) có tâm đáy là điểm O , chiều cao SO = h = a 3 và độ dài đường sinh l = 3a .
+) Giả sử mặt phẳng ( P) cắt ( N ) theo thiết diện là tam giác SAB .
Do SA = SB = l  tam giác SAB cân tại đỉnh S.
+) Gọi I là trung điểm của AB . Ta có OI ⊥ AB , SI ⊥ AB và khi đó góc giữa mặt phẳng ( P)
và mặt đáy của ( N ) là góc SIO = 60.
+) Trong tam giác SOI vuông tại O góc SIO = 60 . SO a 3 Ta có SI = = = 2a sin SIO sin 60 .
+) Trong tam giác SIA vuông tại I . Ta có 2 2 2 2 2 2
IA = SA − SI = 9a − 4a = 5a IA = a 5  AB = 2IA = 2a 5 . 1 1
Vậy diện tích thiết diện cần tìm là 2 S = S = SI.AB = .2 .
a 2a 5 = 2a 5 . td SAB 2 2
Nhantruongthanh79@gmail.com. Câu 32. Cho hàm số 3 2
y = x − 3x + 4 có đồ thị (C ) như hình vẽ và đường thẳng 3 2
d : y = m − 3m + 4 (với
m là tham số). Hỏi có bao nhiêu giá trị nguyên của tham số m để đường thẳng d cắt đồ thị
(C)tại ba điểm phân biệt? A. 3 . B. 2 . C. 1. D. Vô số. y 4 3 2 1 x -1 O 2 3 1 Lời giải
Tác giả: Trương Thanh Nhàn; Fb: Trương Thanh Nhàn. Chọn C
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC
Trang 19 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Từ đồ thị suy ra đường thẳng d cắt đồ thị (C ) tại 3 điểm phân biệt khi và chỉ khi  1 −  m  3
m −3m + 4  0
 m +1 m − 2  0  3 2 ( )( )2 3 2
0  m − 3m + 4  4      m  0 3 2 2
m − 3m  0 m  (m −3)  0 m  2 
Vì m là số nguyên nên m = 1.
Luuthedung1982@gmail.com
Câu 33. Cho các số phức z thỏa mãn z = 2 . Biết rằng tập hợp các điểm biểu diễn số phức
w = 3 − 2i + (4 − 3i) z là một đường tròn. Tính bán kính r của đường tròn đó. A. r = 5 . B. r = 2 5 . C. r = 10 . D. r = 20 . Lời giải
Tác giả: Lưu Thế Dũng; Fb: Lưu Thế Dũng Chọn C
Đặt w = x + yi, ( x, y  ) ta có:
w = 3 − 2i + (4 − 3i) z w − (3 − 2i) = (4 − 3i) z w − (3 − 2i) = (4 − 3i) z
 (x − ) + ( y + )i = − i z  (x − )2 + ( y + )2 = + (− )2 2 3 2 4 3 3 2 4 3 .2
 (x − )2 + ( y + )2 3 2 =100 .
Suy ra tập hợp các điểm biểu diễn số phức w = 3 − 2i + (4 − 3i) z là một đường tròn có tâm
I (3; − 2) , bán kính r = 10 .
Changbomvuive92@gmail.com chieens.ls@gmail.com 2 + 81x + 81−x
Câu 34. Cho 9x + 9−x = 14 . Khi đó biểu thức M = có giá trị bằng
11− 3x − 3−x A. 14. B. 49. C. 42. D. 28. Lời giải
Tác giả: Nguyễn Hào Kiệt ; Fb: Nguyễn Hào Kiệt Chọn D x − x  + = 2 2 3 3 4 1
Ta có (3x + 3−x ) = 9x + 9−x + 2.3 .3 x
− x  (3x + 3−x ) ( ) = 16   .
3x + 3−x = 4 − (L) ( x −x + )2 x −x 2 x 9 9
= 81 +81 + 2 14 − 2 = 81x +81−x  81 +81x =194 (2). 2 +194 Thay ( )
1 và (2) vào biểu thức M ta có M = = 28. 11− 4
Tranvantan271981@gmail.com
Câu 35. Cho lăng trụ tam giác đều AB . C A BC
  có đáy là tam giác đều cạnh a , AA = 2a . Gọi  là góc
giữa AB và BC . Tính cos .
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC
Trang 20 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019 5 51 39 7 A. cos = . B. cos = . C. cos = . D. cos = . 8 10 8 10 Lời giải
Tác giả: Trần Văn Tân ; Fb: Trần Văn Tân Chọn D
Từ giả thiết và định lý pitago ta được 2 2 AB =
AB + BB = a 5 ; 2 2 BC =
BC + CC = a 5 . 7a
Xét AB .BC = ( AB + BB)(BB + B C  ) 2 2 2 = A . B B C
  + BB = −B . A BC + BB = . 2 (  ) 2 AB .BC 7a AB BC = = (a a ) 7 cos , : 5. 5 = AB .BC . 2 10 Vậy  = (ABBC) 7 cos cos , = . 10
nguyenphuoctamduc2019@gmail.com x = 1+ t
x −1 y − m z + 2
Câu 36. Cho hai đường thẳng d : y = 2 − t d : = = 1 và 2
(với m là tham số). Tìm m  2 1 1 − z = 3 + 2t
để hai đường thẳng d d 1 , 2 cắt nhau. A. m = 4 . B. m = 9 . C. m = 7 . D. m = 5. Lời giải
Tác giả: Nguyễn Phú Hòa; Fb: Nguyễn Phú Hòa Chọn D
d qua M 1; 2;3 và có véctơ chỉ phương a = 1; −1; 2 ; d qua M 1; m ; − 2 và có véctơ 2 ( ) 1 ( ) 1 ( ) 1 2
chỉ phương a = 2;1; −1 . 2 ( )
Ta có a , a  = 1
− ;5;3  0 M M = 0;m − 2;− 5 . 1 2 ( )   ; 1 2 ( )
Khi đó d , d cắt nhau khi a , a .M M = 0  1.0 −
+ 5 m − 2 −15 = 0  m = 5 . 1 2 1 2 1 2   ( )
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC
Trang 21 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
truyphong.t0408@gmail.com
Câu 37. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Tam giác SAB đều và nằm
trong mặt phẳng vuông góc với đáy. Tính khoảng cách từ điểm C đến mặt phẳng ( SAD) . a 3 a 3 a 3 a 3 A. . B. . C. . D. . 6 2 3 4 Lời giải
Word và giải: Nguyễn Văn Bình ; Fb: Nguyễn Văn Bình Chọn B
Ta có CB // (SAD)  d (C;(SAD)) = d (B;(SAD)) = 2d (H ;(SAD)) .
Gọi H là trung điểm của AB . Vì S
AB đều và nằm trong mặt phẳng vuông góc với đáy nên
SH ⊥ ( ABCD) .
Gọi K là hình chiếu vuông góc của H lên SA . Khi đó HK ⊥ ;
SA HK ⊥ AD HK ⊥ (SAD) .
Do đó, d (H;(SAD)) = HK . 2 2 a a 3 a 3a S
HA có HA = ; SH =  SA = + = . a Mà 2 2 4 4 a 3 a . a 3 2 2 a
HK.SA = HS.HA HK = =
. Vậy d (C (SAD)) 3 ; = . a 4 2
Câu 38. [Mức độ 2] Cho một hộp có chứa 5 bóng xanh, 6 bóng đỏ và 7 bóng vàng. Lấy ngẫu nhiên
4 bóng từ hộp, tính xác suất để có đủ 3 màu. 35 35 175 35 A. . B. . C. . D. . 816 68 5832 1632 Lời giải
Tác giả: Hoàng Văn Phiên; Fb: Phiên Văn Hoàng Chọn B
Lấy ngẫu nhiên 4 bóng trong hộp chứa 18 bóng. Vậy số phần tử của không gian mẫu là 4 n = C = 3060  . 18
Gọi A là biến cố “lấy được cả ba màu”.
Trường hợp 1: Lấy được 2 xanh, 1 đỏ, 1 vàng có 2 1 1
C .C .C = 420 (cách). 5 6 7
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC
Trang 22 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Trường hợp 2: Lấy được 1 xanh, 2 đỏ, 1 vàng có 1 2 1
C .C .C = 525 (cách). 5 6 7
Trường hợp 3: Lấy được 1 xanh, 1 đỏ, 2 vàng có 1 1 2
C .C .C = 630 (cách). 5 6 7
Vậy số phần tử của biến cố A là n = 420 + 525 + 630 = 1575 . A
P ( A) n 1575 35 A = = = . n 3060 68 
thuyhang24584@gmail.com
Câu 39. Cho phương trình 2
log x − 4 log x + m − 3 = 0 . Tìm tất cả các giá trị nguyên của tham số m để 3 3
phương trình đã cho có hai nghiệm phân biệt thỏa mãn x x  1. 1 2 A. 6. B. 4. C. 3. D. 5. Lời giải
Tác giả: Quỳnh Thụy Trang ; Fb: XuKa Chọn C
Đặt t = log x . Phương trình đã cho trở thành 2
t − 4t + m − 3 = 0 . 3
Yêu cầu bài toán  phương trình trên có hai nghiệm thỏa mãn t t  0 . 1 2   0   −   7 m 0
t + t  0    3  m  7 1 2  m − 3  0 t .t  0  1 2
Vậy có 3 giá trị nguyên của tham số m thỏa mãn
Tuluc0201@gmail.com trichinhsp@gmail.com
Câu 40. Có tất cả bao nhiêu giá trị thực của tham số m để đường thẳng d : y = mx +1 cắt đồ thị (C) 3 2
: y = x − x +1 tại 3 điểm ; A B (0; )
1 ; C phân biệt sao cho tam giác AOC vuông tại O (0;0) ? A. 0 . B. 1. C. 3 . D. 2 . Lời giải
Tác giả: Võ Tự Lực; Fb: Võ Tự Lực Chọn B
Hoành độ giao điểm của đường thẳng d và đồ thị (C ) là nghiệm của phương trình: x = 0 3 2
x − x +1 = mx +1  x ( 2
x − x − m) = 0   . 2
x − x − m = 0
Đường thẳng d cắt đồ thị hàm số (C ) tại 3 điểm phân biệt ; A B (0; ) 1 ; C  phương trình 2
x − x − m = 0 có hai nghiệm phân biệt x ; x khác 0 A C  =  1 1+ 4m  0   −  m    4 . −m  0 m  0 x + x = 1 Khi đó, theo Viét ta có A C  (*).
x .x = −mA C
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC
Trang 23 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Tọa độ giao điểm A( x ; mx + )
1 và C ( x ; mx + . C C )1 A A
Tam giác AOC vuông tại O O .
A OC = 0  x x + y .y = 0 A C A C
x .x + (mx + ) 1 .(mx + ) 1 = 0  ( 2
1+ m ) x .x + m x + x + = A C ( A C ) 1 0 A C A C  ( 2
1+ m ).(−m) + m +1 = 0  m =1 (thỏa mãn điều kiện (*))
Vậy có 1 giá trị m thỏa mãn điều kiện bài toán.
lvtrungsp@gmail.com x = t
Câu 41. Trong không gian Oxyz, cho điểm M (1; 1
− ;2) và hai đường thẳng d :y =1−t, 1 z = 1 −  x +1 y −1 z + 2 d : = =
. Đường thẳng  đi qua điểm M và cắt cả hai đường thẳng d , d có 2 2 1 1 1 2
véctơ chỉ phương là u = (1; ; a b +  ), tính a .b
A. a + b = 1. − B. a + b = 2 − . C. a + b = 2. D. a + b = 1. Lời giải
Tác giả: Lại Văn Trung; FB: Trung Lại Văn Chọn D Gọi ,
A B lần lượt là giao điểm của đường thẳng  với d và d . 1 2
Vì A d A t ;1− t ; 1
− ; B d B −1+ 2t ;1+ t ; 2 − + t . 1 ( 1 1 ) 2 ( 2 2 2 )
M    M , ,
A B thẳng hàng  MA = k.M . B (1)
MA = (t −1; 2 − t ; 3
− ; MB = 2t − 2;t + 2;t − 4 . 1 1 ) ( 2 2 2 )  t  = t
 −1 = k (2t − 2) 0 1  − + = 1 2 t 2kt 2k 1 1 2  ( )    1
1  2 − t = k t + 2   t
− − kt − 2k = 2 −  kt = . 1 ( 2 ) 1 2 2    3 − = k  (t − 4) 3 kt − 4k = 3 −  2 2  5 k =  6
Từ t = 0  A 0;1; 1
− . Do đường thẳng  đi qua điểm A và M nên một véc tơ chỉ phương của 1 ( )
đường thẳng  là u = AM = −  (1; 2;3). Vậy a = 2
− ,b = 3  a + b = 1.
phuongmath@gmai.com
Câu 42. Hai người A và B ở cách nhau 180 (m) trên một đoạn đường thẳng và cùng chuyển động
thẳng theo một hướng với vận tốc biến thiên theo thời gian, A chuyển động với vận tốc
v t = 6t + 5 m/s , B chuyển động với vận tốc v t = 2at − 3 m/s ( a là hằng số), trong đó 2 ( ) ( ) 1 ( ) ( )
t (giây) là khoảng thời gian tính từ lúc A , B bắt đầu chuyển động. Biết rằng lúc đầu A đuổi
theo B và sau 10 (giây) thì đuổi kịp. Hỏi sau 20 (giây), A cách B bao nhiêu mét? A. 320 (m) . B. 720 (m) . C. 360 (m) . D. 380 (m) . Lời giải
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC
Trang 24 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Tácgiả:Lê Thị Phương; Fb: Lê Thị Phương. Chọn D 10 10
Quãng đường A đi được trong 10 (giây) là: (6t +5)dt = ( 2
3t + 5t ) = 350 (m) . 0 0 10 10
Quãng đường B đi được trong 10 (giây) là: (2at -3)dt = ( 2
at − 3t ) =100a − 30 (m) . 0 0
Vì lúc đầu A đuổi theo B và sau 10 (giây) thì đuổi kịp nên ta có:
(100a −30) +180 = 350  a = 2  v t = 4t −3 m/s . 2 ( ) ( ) 20 20
Sau 20 (giây) A đi được:  (6t + 5)dt = ( 2
3t + 5t ) =1300 (m) . 0 0 20 20
Sau 20 (giây) B đi được:  (4t −3)dt = ( 2
2t − 3t ) = 740 (m) . 0 0
Khoảng cách giữa A và B sau 20 (giây) là: 1300 − 740 −180 = 380 (m) .
Phản biện: quangdang@gmail.com tantiennhc@gmail.com
Câu 43. Một hình hộp chữ nhật có chiều cao là 90 cm, đáy hộp là hình chữ nhật có chiều rộng là 50 cm
và chiều dài là 80 cm. Trong khối hộp có chứa nước, mực nước so với đáy hộp có chiều cao là
40 cm. Hỏi khi đặt vào khối hộp một khối trụ có chiều cao bằng chiều cao khối hộp và bán kính
đáy là 20 cm theo phương thẳng đứng thì chiều cao của mực nước so với đáy là bao nhiêu? A. 68,32 cm. B. 78,32 cm. C. 58,32 cm. D. 48,32 cm. Lời giải
Tác giả: Nguyễn Tân Tiến ; Fb: Nguyễn Tiến Chọn C
Trước khi đặt vào khối hộp một khối trụ thì thể tích lượng nước có trong khối hộp là
V = 40.80.50 = 160000 (cm3). n
Gọi h (cm) là chiều cao của mực nước so với đáy.
Sau khi đặt vào khối hộp một khối trụ thì thể tích lượng nước là V = .
h (4000 − 400 (cm3). n )
Do lượng nước không đổi nên ta có .
h (4000 − 400 ) = 160000 160000  h =  58,32 (cm). 4000 − 400
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC
Trang 25 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
nhantoanhungvuong@gmail.com
Câu 44. Một chiếc cổng có hình dạng là một Parabol có khoảng cách giữa hai chân cổng là AB = 8m . M N A B Q P
Người ta treo một tấm phông hình chữ nhật có hai đỉnh M , N năm trên Parabol và hai đỉnh
P, Q nằm trên mặt đất(như hình vẽ). Ở phần phía ngoài phông (phần không tô đen) người ta
mua hoa để trang trí với chi phí cho 2
1m cần số tiền cần mua hoa là 200.000 đồng cho 2 1m .
Biết rằng MN = 4m, MQ = 6m . Hỏi số tiền dùng để mua hoa trang trí chiếc cổng gần với số tiền nào sau đây? A. 3.735.300 đồng. B. 3.437.300 đồng. C. 3.734.300 đồng . D. 3.733.300 đồng. Lời giải
Tác giả:Nguyễn Thành Nhân ; Fb:Nguyễn Thành Nhân Chọn D y M N(2;6) B(4;0) x A Q P
Ta gắn vào hệ trục tọa độ Oxy như hình vẽ bên. Trong hệ trục đó thì đường Parabol đi qua các − điể 1
m B (4;0) và N (2;6) cho nên phương trình của đường Parabol đó là: 2 y = x + 8 . 2 4  1 −  128
Diện tích của chiếc cổng được giới hạn bởi đường Parabol là: 2 2 S = x + 8 dx = m    . 4 −  2  3
Diên tích của hình chữ nhật MNPQ là 2 S = 4.6 = 24m . 56
Diện tích phần trang trí bằng hoa là: 2
S = S − S = m . 1 3 56
Vậy số tiền cần dùng để mua hoa là trang trí là:
.(200.000)  3.733.300 đồng. 3
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC
Trang 26 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019 Huongdtn2009@gmail.com
vothuongnhanhchong@gmail.com
Câu 45. Cho hai số phức z, w thay đổi thỏa mãn z = 3, z − w = 1. Biết tập hợp điểm của số phức w là
hình phẳng H. Tính diện tích S của H. A. S = 20 . B. S = 12 . C. S = 4 . D. S = 16 . Lời giải
Tác giả & Fb: Lý Văn Nhân Chọn B Cách 1:
Với mỗi số phức z thỏa z = 3 , gọi A là điểm biểu
diễn của z thì A nằm trên đường tròn tâm O bán
kính bằng 3. Gọi B là điểm biểu diễn của w thì B
nằm trên đường tròn tâm A bán kính bằng 1.
Khi A chạy trên đường tròn tâm O bán kính bằng 3
thì tập hợp các điểm B là hình vành khăn giới hạn
bởi tròn tâm O bán kính bằng 2 và tròn tâm O bán kính bằng 4. Suy ra 2 2
S =  .4 −  .2 = 12 .
Cách 2: Ta có w = w − z + z w − z + z = 4 . Mặt khác w = w − z + z w − z − z = 2 .
Vậy 2  w  4 nên H là hình vành khăn giới hạn bởi tròn tâm O bán kính bằng 2 và tròn tâm O bán kính bằng 4. Suy ra 2 2
S =  .4 −  .2 = 12 .
hoxuandung1010@gmail.com 1 9x + 3m Câu 46. Cho 2 dx = m −1 
. Tính tổng tất cả các giá trị của tham số m . 9x + 3 0 1 A. P = 12 . B. P = . C. P = 16 . D. P = 24 . 2 Lời giải
Tác giả: Hồ Xuân Dũng ; Fb: Dũng Hồ Xuân Chọn B 1 x 1 x 1 9 + 3m 9 + 3 − 3 + 3m  3 m −1  3 2 ( ) 1 Ta có m −1 = dx = dx =   1+ dx = 1+ m − x  . x x x ( ) 1 d 9 + 3 9 + 3 9 + 3 9x + 3   0 0 0 0 1 1 x Đặ 3 9 t K = (m − ) 1 dx
. Ta đi tính J = (m − ) 1 dx  . 9x + 3 9x + 3 0 0 1 1 x 1 9 m − x 1 1 x 1 Có J = (m − ) x = m − + = + = m −   . x ( ) ln9 1 d 1 d x (9 3) .ln (9 3) ( ) 1 9 + 3 9 + 3 2 ln 3 0 2 0 0 1 9x + 3 1 1
Lại có, K + J = (m − ) 1 dx = (m −1) 
. Từ đó, suy ra K = (m − ) 1 − (m − ) 1 = (m − ) 1 . 9x + 3 2 2 0
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC
Trang 27 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019 m = 1 − Do đó, 1 1 3 2 2 m 1 1 (m 1) m m 0  − = + −  − − =  3 . 2 2 2  m =  2 1
Suy ra tổng tất cả các giá trị của tham số m là . 2
thaitranvn123@gmail.com - nguyenthao7983@gmail.com
Câu 47. Có bao nhiêu cách phân tích số 9
15 thành tích của ba số nguyên dương, biết rằng các cách phân
tích mà các phần tử chỉ khác nhau về thứ tự thì chỉ được tính một lần? A. 517 . B. 516 . C. 493. D. 492 . Lời giải
Tác giả: Trần Đình Thái ; Fb: Đình Tháii Chọn A Ta có 9 9 9 15 = 3 .5 . Đặt a b a b a b 1 1 x = 3 .5 , 2 2 y = 3 .5 , 3 3 z = 3 .5 . Xét 3 trường hợp:
Trường hợp 1: 3 số x, y, z bằng nhau → có 1 cách chọn.
Trường hợp 2 : Trong 3 số có 2 số bằng nhau, giả sử: x = y a = a , b = b . 1 2 1 2 2a + a = 9 a = 9 − 2a 1 3   3 1   . 2b + b = 9  b = 9 − 2a 1 3  3 3
Suy ra có 5 cách chọn a và 5 cách chọn b . 1 1
Trường hợp 3: Số cách chọn 3 số phân biệt.
a + a + a = 9 Số cách chọn 1 2 3  là 2 2 C .C .
b + b + b = 9  11 11 1 2 3
Suy ra số cách chọn 3 số phân biệt là 2 2
C .C − 24.3 −1 . 11 11 2 2
C .C − 24.3 −1
Vậy số cách phân tích số 9
15 thành ba số nguyên dương là 11 11 + 25 = 517 . 3!
tiendv@gmail.com 8  b  log   a  3 
Câu 48. Cho các số thực a, b  1 thoả mãn log aa  2 b a +16b
= 12b . Giá trị của biểu thức 3 3
P = a + b là A. 20 . B. 39 . C. 125 . D. 72 . Lời giải
Tác giả: Đào Văn Tiến ; Fb: Đào Văn Tiến Chọn D Ta có: 8  b  log   a  3  8 3 log aa  2 log a log b −log a 2 log a 8log b−3 2 b a +16b =12 b b a +16 a a b =12 b b a +16 a b =12b 8 −3 log a log a 2 ba +16 b b =12b . 8 −3
Đặt t = log a t  0 . Khi đó ta có 2t 2 +16 t b b =12b . b
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC
Trang 28 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019 8 8 8 8 8 2 8 8 2 8 8 3 − − − − − + − + − − 2 3 2 3 3 3 2 3 3 3 t 3 3 3 3 t 6 Ta có t t t t t t t t t t t t 2 b +16b = b + 8b + 8b
 3 b .8b .8b =12 b 12 b =12b . 8 2 −3 Vậy ta có t 2 +16 t b b
12b . Yêu cầu bài toán tương đương với dấu bằng xảy ra. t  = 2 log a = 2 a = 4 b       . 4 b  = 8b b  = 2 b  = 2 Từ đó ta có 3 3
P = a + b = 72.
Thuylinh133c3@gmail.com hongvanlk69@gmail.com
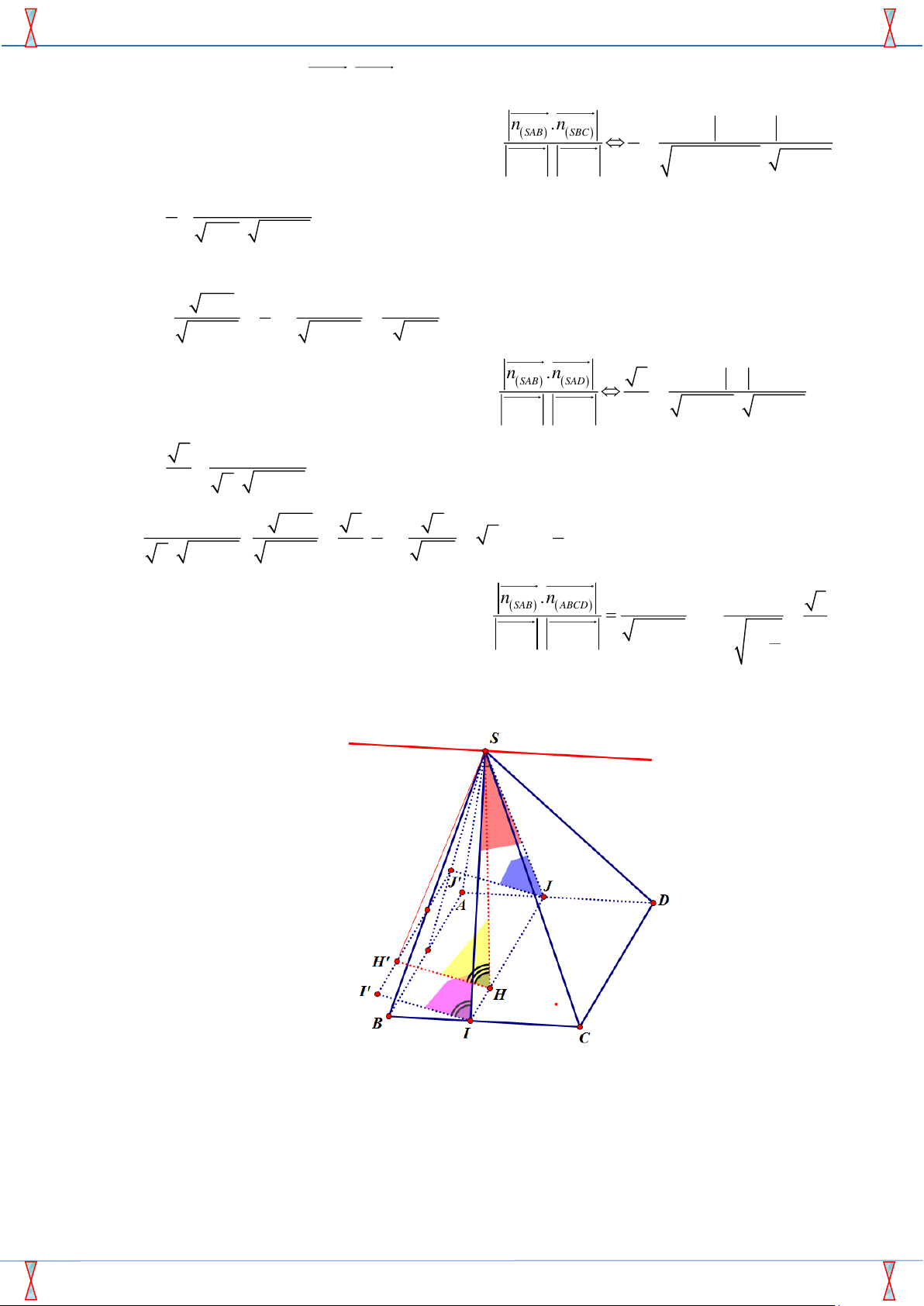
Câu 49. Cho hình chóp S. ABCD có đáy ABCD là hình vuông, hình chiếu vuông góc của đỉnh S
xuống mặt đáy nằm trong hình vuông ABCD . Hai mặt phẳng ( SAD) , ( SBC ) vuông góc với
nhau; góc giữa hai mặt phẳng ( SAB) và ( SBC ) là 0
60 ; góc giữa hai mặt phẳng ( SAB) và (SAD) là 0
45 . Gọi  là góc giữa hai mặt phẳng ( SAB) và ( ABCD) , tính cos 1 2 3 2 A. cos = . B. cos = . C. cos = . D. cos = . 2 2 2 3 Lời giải
Tác giả: Nguyễn Thùy Linh ; Fb:Nguyễn Thùy Linh Chọn C
Gắn hệ trục tọa độ như hình vẽ. Không mất tính tổng quát giả sử ABCD là hình vuông có cạnh
bằng 1, chiều cao của hình chóp S. ABCD bằng c (c  0) .
A(0;0;0) , B (1;0;0) , C (1;1;0) , D (0;1;0) .
Do hình chiếu vuông góc H của đỉnh S xuống mặt đáy nằm trong hình vuông ABCD nên gọi
H (a ;b;0) với 0  a ,b 1 (*)  S (a ;b;c) .
Ta có : AS = (a ;b;c) , AD = (0;1;0) nên chọn n
= AS , AD = ( c − ;0;a SAD ) ( )   .
BS = (a −1;b;c) , BC = (0;1;0) nên chọn n
= BS , BC = ( c − ;0;a − ) ( ) 1 SBC   .
AB = (1;0;0) , AS = (a ;b;c) nên chọn n
= AB, AS = (0;−c;b SAB ) ( )   . Chọn n = k = (0;0; ) ( ) 1 . ABCD
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC
Trang 29 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019
Do (SAD) ⊥(SBC ) 2 n .n
= 0c + a(a − ) 2 2 ( ) ( ) ( )
1 = 0  c + a = a 1 . SAD SBC ( n n − SAB) . (SBC ) 1 b (a ) 1
Góc giữa ( SAB) và ( SBC ) là 0 60 0 cos 60 =  = 2 ( n n + − + SAB) . (SBC) 2 2 c (a ) 2 2 1 . c b 1 b (1− a)  = do (*) và (1) 2 2 2
1− a . c + b b 1− a 1 b 1  =  = (2) 2 2 2 2 + 2 c b c + b 2 1− a ( n n SAB) . (SAD) 2 ab
Góc giữa ( SAB) và ( SAD) là 0 45 0 cos 45 =  = 2 2 2 2 ( n n c + a c + b SAB) . (SAD) 2 . 2 ab  = do (*) 2 2 2 a . c + b ab b 1− a 2 1 a 2 : = :  = 2  a = (3). 2 2 2 2 + + 2 2 a . c b c b 1− a 3 n .n (2),(3) SAB ABCD b 1 3
Góc giữa ( SAB) và ( ABCD) là   ( ) ( ) cos = = = = . 2 2 ( n n c + b SAB) . (ABCD) 2 2 2 1− 3
Cách 2 : theo ý tưởng của thầy Vô Thường .
Gọi I , J , H lần lượt là hình chiếu vuông góc của S lên BC , AD , ( ABCD) ; I , H  , J
lần lượt là hình chiếu vuông góc của I , H , J lên ( SAB) . Ta có :
+ Do (SAD) ⊥ (SBC ) nên 0 (
 (SAD),(SBC)) = ISJ = 90 .
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC
Trang 30 Mã đề 110
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC. Đề Thi Thử THPTQG Lương Thế Vinh- HN Lần 2-2019 SI ⊥ (SAD) Suy ra  . SJ ⊥ (SBC) SI ⊥  (SAD) + Do  nên 0 (
 (SAD),(SAB)) = SII ' = 45 . II⊥  (SAB) SJ ⊥  (SBC) + Do  nên 0 (
 (SBC),(SAB)) = SJJ ' = 60 . JJ⊥  (SAB) SH ⊥  ( ABCD) + Do  nên (
 (SAB),(SABCD)) = SHH ' =  . HH ⊥  (SAB)
Đặt II = HH = JJ = x với x  0  SI = x 2 , SJ = 2x , 2 SI . SJ SI . SJ 2 2x 2x HH x 3 SH = = = =  cos = = = . 2 2 IJ SI + SJ x SH 2 6 3 x 2 3
Hahoangduong30@gmail.com 1
Câu 50. Cho hai hàm số f ( x) 3 = x − (m + ) 2 1 x + ( 2
3m + 4m + 5) x + 2019 và 3 g ( x) = ( 2 m + m + ) 3 x − ( 2 m + m + ) 2 2 5 2 4
9 x − 3x + 2 , với m là tham số. Hỏi phương trình
g ( f ( x)) = 0 có bao nhiêu nghiệm? A. 9. B. 0. C. 3 . D. 1. Lời giải
Tác giả:Nguyễn Thị Huyền Trang ; Fb: Nguyen Trang Chọn C
Ta có: g ( x) =  ( x − ) ( 2  m + m +  ) 2 0 2 2
5 x + x −1 = 0  . x = 2   . ( 2 m + 2m + 5) 2
x + x − 1 = 0 (*)  2
m + 2m + 5  0, m  
Phương trình (*) có hai nghiệm phân biệt khác 2 với m  vì:  =1+ ( 2
m + 2m + 5)  0, m  . ( 2  m + 2m + 5  ) 22 + 2−1 0, m
Vậy g ( x) = 0 có 3 nghiệm phân biệt (1).
Mặt khác, xét hàm số y = f ( x) ta có :
f ( x) = x − (m + ) x + ( m + m + ) = x −  (m + ) 2 2 2  +  ( 2 2 1 3 4 5 1
2 m + m + 2)  0, m  .
y = f ( x) luôn đồng biến trên với m  .
Do f (x) là hàm đa thức bậc 3 và đồng biến trên
nên phương trình f ( x) = k luôn có 1
nghiệm duy nhất với mỗi số k  (2).
Từ (1) và (2) suy ra phương trình g ( f ( x)) = 0 có 3 nghiệm phân biệt .
Chia sẻ bởi Quybacninh từ Gr Fb: STRONG TEAM TOÁN VD-VDC
Trang 31 Mã đề 110
Document Outline

  • [toanmath.com] - Đề thi thử Toán THPT Quốc gia 2019 lần 2 trường Lương Thế Vinh – Hà Nội
  • [STRONG TEAM TOÁN VD-VDC]-Lương Thế Vinh- Hà Nội Lần 2-2019 (1)