Đề thi thử Toán THPT Quốc gia 2019 trường THPT Nam Tiền Hải – Thái Bình

Giới thiệu đến quý thầy, cô giáo và các em học sinh đề thi thử Toán THPT Quốc gia 2019 trường THPT Nam Tiền Hải – Thái Bình, đề thi giống với đề thi THPT Quốc gia môn Toán năm 2019

16 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

12 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
Trang 1/6 - Mã đề 148 - https://toanmath.com/
SỞ GDĐT THÁI BÌNH
TRƯỜNG THPT NAM TIỀN HẢI
ĐỀ THI THỬ THPT QUỐC GIA – NĂM HỌC 2018 - 2019
MÔN TOÁN
Thời gian làm bài : 90 Phút; (Đề có 50 câu)
(Đề có 6 trang)
Họ tên
: ...............................................................
Số báo danh
: ...................
Câu 1: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
4
x m
y
x
đồng biến trên từng khoảng xác
định của nó?
A.
1
B.
2
C.
3
D.
5
Câu 2: Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
z z
. Giá trị của biểu thức
2 2
1 2
z z
?
A.
2
. B.
5
. C.
5
2
. D.
3
2
.
Câu 3: Giá trị lớn nhất của hàm số
2
4
x
f x
x
trên đoạn
3
;4
2
là
A.
4
B.
2
C.
25
6
D.
5
Câu 4: Cho hình hộp
.
ABCD A B C D
có
M
,
N
,
P
lần lượt là trung điểm của các cạnh
A B
,
A D
,
C D
. Góc giữa đường thẳng
CP
và mặt phẳng
DMN
bằng?
A.
60
B.
30
C.
0
D.
45
Câu 5: Có bao nhiêu số tự nhiên có hai chữ số, các chữ số khác nhau và đều khác
0
?
A.
2
9
B.
2
9
A
C.
2
9
C
D.
90
Câu 6: Cho hàm số
4 2
2 3
y x x
có đồ thị như hình bên dưới. Với giá trị nào của tham số
m
thì phương
trình
4 2
2 3 2 4
x x m
có hai nghiệm phân biệt.
A.
1
2
m
B.
0
1
2
m
m
C.
1
0
2
m
D.
0
1
2
m
m
Mã đề 148
A
B
C
D
A
B
C
D
M
N
P
Trang 2/6 - Mã đề 148 - https://toanmath.com/
Câu 7: Tập nghiệm của bất phương trình
1
9
3
x
là
A.
( ; 2)
B.
( ;2)
C.
(2; )
D.
( 2; )
Câu 8: Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
:
1 1 2
x y z
d
. Mặt phẳng
P
đi
qua điểm
2;0; 1
M
và vuông góc với
d
có phương trình là
A.
: 2 0
P x y z
B.
: 2 2 0
P x y
C.
: 2 0
P x y z
D.
: 2 0
P x y z
Câu 9: Cho hàm số
y f x
có bảng biến thiên như sau:
Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực đại tại
4
x
B. Hàm số đạt cực đại tại
2
x
C. Hàm số đạt cực đại tại
2
x
D. Hàm số đạt cực đại tại
3
x
Câu 10: Cho biết
2
0
d 3
f x x
và
2
0
d 2
g x x
. Tính tích phân
2
0
2 2 dI x f x g x x
.
A.
11I
. B.
18
I
. C.
5
I
. D.
3
I
.
Câu 11: Cho khối chóp tam giác đều
.
S ABC
có cạnh đáy bằng
4
, chiều cao của khối chóp bằng chiều cao
của tam giác đáy. Gọi
M
là trung điểm cạnh
SA
. Thể tích của khối chóp
.
M ABC
bằng?
A.
4
. B.
8
3
. C.
8
. D.
16
.
Câu 12: Có bao nhiêu giá trị nguyên không âm của tham số
m
để hàm số
4 2
2 3 1
y x mx m
đồng biến
trên khoảng
1;2
.
A.
1
B.
3
C.
2
D.
4
Câu 13: Họ nguyên hàm của hàm số
2cos 2f x x
là
A. -
sin 2
x C
B.
2sin 2
x C
C.
2sin 2
x C
D.
sin 2
x C
Câu 14: Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1; 2;3
M
. Tọa độ diểm
A
là hình chiếu vuông
góc của điểm
M
trên mặt phẳng
Oyz
là:
A.
1; 2;3
A
B.
1; 2;0
A
C.
1;0;3
A
D.
0; 2;3
A
Câu 15: Có bao nhiêu giá trị nguyên của tham số
m
trên
1;5
để hàm số
3 2
1
1
3
y x x mx
đồng biến
trên khoảng
; ?
 
A.
7
B.
4
C.
6
D.
5
Câu 16: Thầy giáo Công gửi vào ngân hàng 10 triệu đồng theo hình thức lãi kép với kì hạn 4 tháng. Biết
rằng lãi suất của ngân hàng là
0,5%
/ tháng. Hỏi sau 2 năm thầy giáo thu được số tiền lãi gần nhất với số
nào sau đây
A.
1.262.000ñ
. B.
1.271.000ñ
. C.
1.272.000ñ
. D.
1.261.000ñ
.
Trang 3/6 - Mã đề 148 - https://toanmath.com/
Câu 17: Cho
4
2
log
a
P b
với
0 1
a
và
0
b
. Mệnh đề nào dưới đây là đúng?
A.
1
log
2
a
P b
B.
2log
a
P b
C.
1
log
a
D.
2log
a
P b
Câu 18: Trong không gian với hệ tọa độ
Oxyz
, cho điểm
2; 1; 0
M
và đường thẳng
1 1
:
2 1 1
x y z
. Phương trình tham số của đường thẳng
d
đi qua
M
, cắt và vuông góc với
là
A.
2
: 1 4
2
x t
d y t
z t
. B.
2 2
: 1
x t
d y t
z t
. C.
2
: 1
x t
d y t
z t
. D.
1
: 1 4
2
x t
d y t
z t
.
Câu 19: Cho hàm số
y f x
có đồ thị như như hình vẽ bên dưới. Hàm số
y f x
nghịch biến trên
khoảng nào dưới đây?
A.
; 2
B.
2;1
C.
1;0
D.
1;
Câu 20: Một lô hàng gồm
30
sản phẩm trong đó có
20
sản phẩm tốt và
10
sản phẩm xấu. Lấy ngẫu nhiên
3
sản phẩm trong lô hàng. Tính xác suất để
3
sản phẩm lấy ra có ít nhất một sản phẩm tốt.
A.
6
203
B.
57
203
C.
153
203
D.
197
203
Câu 21: Phương trình đường tiệm cận ngang của đồ thị hàm số
3
2
1
y
x
là:
A.
3
y
B.
1
y
C.
1x
D.
2
y
Câu 22: Cho số phức
z
thỏa mãn
2 7 3
z z i z
. Tính
z
?
A.
5
B.
3
C.
13
4
D.
25
4
Câu 23: Tích phân
2
2
1
3 dx x
bằng
A.
61
B.
61
3
C.
61
9
D.
4
Câu 24: Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
P
:
2 1 0
x z
. Tọa độ một vectơ pháp
tuyến của mặt phẳng
P
là
A.
2; 0;1
n
B.
2; 0; 1
n
C.
2; 1;1
n
D.
2; 1; 0
n
Câu 25: Cho hàm số
4 2
2 1
y x x
có đồ thị (C). Biết rằng đồ thị (C) có ba điểm cực trị tạo thành ba đỉnh
của một tam giác, gọi là
ABC
. Tính diện tích của tam giác
ABC
.
A.
2
S
B.
1
S
C.
1
2
S
D.
4
S
O
x
y
1
1
2
4
1
2
Trang 4/6 - Mã đề 148 - https://toanmath.com/
Câu 26: Cho số phức
2
1 1 2z i i
. Số phức
z
có phần ảo là
A.
2i
. B.
4
. C.
2
. D.
4
.
Câu 27: Biết
( )F x
là một nguyên hàm của hàm số
( ) sin 2f x x
và
1
4
F
. Tính
6
F
.
A.
1
6 2
F
B.
5
6 4
F
C.
0
6
F
D.
3
6 4
F
Câu 28: Cho lăng trụ đều
.
ABC A B C
có tất cả các cạnh đều bằng
a
. Khoảng cách giữa hai đường thẳng
AC
và
BB
bằng?
A.
5
3
a
B.
3
2
a
C.
5
a
D.
2
5
a
Câu 29: Thể tích của khối lăng trụ có chiều cao bằng
h
và diện tích đáy bằng
B
là
A.
1
6
V Bh
B.
1
3
V Bh
C.
V Bh
D.
1
2
V Bh
Câu 30: Đồ thị của hàm số nào dưới đây có tiệm cận ngang?
A.
3 1
1
x
y
x
B.
2
1
x
y
x
C.
3 2
2 3 2y x x x
D.
2
1
2
x x
y
x
Câu 31: Trong không gian với hệ tọa độ
,Oxyz
cho mặt cầu có phương trình
2 2 2
2 6 6 0.
x y z x y
Tìm tọa độ tâm
I
và bán kính
R
của mặt cầu đó.
A.
(1; 3;0); 4
I R
B.
( 1;3;0); 4
I R
C.
( 1;3;0); 16
I R
D.
(1; 3;0); 16
I R
Câu 32: Cho số phức
,
z a bi a b
thỏa mãn
1 2 3 2 . i z z i
Tính
. P a b
A.
1.
P
B.
1
.
2
P
C.
1
.
2
P
D.
1.
P
Câu 33: Cho hàm số
y f x
có bảng biến thiên như hình bên.
Tọa độ điểm cực đại của đồ thị hàm số
y f x
là
A.
0
x
B.
1; 4
C.
0; 3
D.
1; 4
Câu 34: Cho số phức
1 2z i
. Số phức
z
được biểu diễn bởi điểm nào dưới đây trên mặt phẳng tọa độ?
A.
1; 2
Q
B.
1; 2
P
C.
1; 2
N
D.
1; 2
M
Câu 35: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với đáy và
SA a
(tham khảo hình vẽ bên dưới). Góc giữa hai mặt phẳng
SAB
và
SCD
bằng?
Trang 5/6 - Mã đề 148 - https://toanmath.com/
A.
60
B.
90
C.
30
D.
45
Câu 36: Bảng biến thiên trong hình bên dưới của hàm số nào dưới đây?
A.
3
3 4y x x
B.
4 2
2 3
y x x
C.
1
2 1
x
y
x
D.
3
3 2y x x
Câu 37: Đồ thị sau đây là của hàm số nào?
A.
3
3 4
xy x
B.
3
3 4
xy x
C.
3 2
3 4
xy x
D.
3 2
3 4
xy x
Câu 38: Trong không gian với hệ trục tọa độ
Oxyz
, cho hai điểm
( 1;3;4), (9; 7;2)
A B
. Tìm trên trục
Ox
tọa độ điểm
M
sao cho
2 2
MA MB
đạt giá trị nhỏ nhất.
A.
5 0 0M ; ;
. B.
2 0 0M ; ;
. C.
4 0 0M ; ;
. D.
9 0 0M ; ;
.
Câu 39: Cho hàm số
y f x
liên tục và có đạo hàm trên
thỏa mãn
2 2
f
;
2
0
d 1f x x
. Tính tích
phân
3
'
1
( 1)I f x dx
.
A.
5
I
. B.
0
I
. C.
18
I
. D.
10
I
.
Câu 40: Gọi
S
là diện tích hình phẳng giới hạn bởi đồ thị của hàm số
1
:
1
x
H y
x
và các trục tọa độ.
Khi đó giá trị của
S
bằng
A.
2ln 2 1
(đvdt) B.
2ln 2 1
(đvdt) C.
ln 2 1
(đvdt) D.
ln 2 1
(đvdt)
Câu 41: Cho các số thực dương x, y thỏa mãn
2
2
5
2 5
10 3
9
10
xy y
x xy
. Hiệu giữa giá trị lớn nhất và giá
trị nhỏ nhất của biểu thức
x
y
bằng
A.
1
5
. B.
5
4
. C.
5
2
. D.
1
4
.
S
A
B
C
D
Trang 6/6 - Mã đề 148 - https://toanmath.com/
Câu 42: Trong không gian với hệ tọa độ
Oxyz
, cho điểm
2; 1;2
M
và mặt cầu
2 2 2
: ( 1) 9
S x y z
. Mặt phẳng đi qua
M
cắt
S
theo giao tuyến là một đường tròn có bán kính nhỏ
nhất có phương trình là
A.
2 5 0
x y z
. B.
2 7 0
x y z
. C.
2 7 0
x y z
. D.
2 5 0
x y z
.
Câu 43: Cho phương trình
3 2 3 2
( 1) 8 ( 3) 6
x x m x x x x mx
. Gọi S là tập hợp các giá trị
nguyên của
m
và
10
m
thì phương trình có nghiệm. Tính tổng T các phần tử của S?
A.
10
T
. B.
19
T
. C.
9
T
. D.
52
T
.
Câu 44: Cho hàm số
y f x
có đạo hàm
2
1 4
f x x x
với mọi
.
x
Hàm số
3
g x f x
có bao nhiêu điểm cực đại?
A.
0.
B.
1.
C.
2.
D.
3.
Câu 45: Cho hàm số
f x
liên tục trên đoạn
2;3
thoả mãn
3
2
( ) 2019
f x dx
. Tính
3
2
2 3
1
( 1)I x f x dx
.
A.
6057
I
. B.
3
2019
I . C.
673
I
. D.
2019
I
.
Câu 46: Cho số phức
z
thỏa
1
z
. Tính giá trị lớn nhất của biểu thức
1 2 1T z z
.
A.
max 3 2
T
B.
max 2 10
T
C.
max 2 5
T
D.
max 3 5
T
Câu 47: Cho hàm số
0
f x
có đạo hàm liên tục trên đoạn
0;
3
, đồng thời thỏa mãn
' 0 0
f
;
0 1
f
và
2
2
.
cos
f x
f x f x f x
x
. Tính
3
T f
.
A.
3
2
T
. B.
3
4
T
. C.
3
4
T
. D.
1
2
T
.
Câu 48: : Cho
,x y
là các số thực dương thỏa mãn
2 2
2 2
2
2 2
5
log 1 10 9 0
2 10
x y
x xy y
x xy y
. Gọi
,M m
lần lượt là giá trị lớn nhất ,giá trị nhỏ nhất của
2 2
2
9x xy y
P
xy y
.Tính
10
T M m
?
A.
60
. B.
95
. C.
104
. D.
50
.
Câu 49: Cho khối chóp
.
S ABC
có
60 ,
ASB BSC CSA
,SA a
2 ,SB a
4SC a
. Tính thể tích
khối chóp
.
S ABC
theo
a
.
A.
3
2 2
3
a
. B.
3
2
3
a
. C.
3
4 2
3
a
. D.
3
8 2
3
a
.
Câu 50: Cho hàm số
y f x
có bảng biến thiên như sau
Tìm giá trị lớn nhất của hàm số
3 5 3
1 2 2
3 3
5 3 15
f x x x x x
g x
trên đoạn
1;2
?
A.
2022.
B.
.2019
C.
2020.
D.
.2021
-----------------------HẾT-----------------------
x
'f x
f x

2
4
2019


2018

0
0
Trang 7/6 - Mã đề 148 - https://toanmath.com/
SỞ GD & ĐT THÁI BÌNH
TRƯỜNG THPT NAM TIỀN HẢI
ĐỀ THI THỬ THPT QUỐC GIA – NĂM HỌC 2018 - 2019
MÔN TOÁN
Thời gian làm bài : 90 Phút
Phần đáp án câu trắc nghiệm:
148 247 349 446
1 C A A C
2 C A B B
3 A B C A
4 C C D A
5 B B A A
6 D D B D
7 A A D B
8 A B C A
9 B B D C
10 A C A B
11 A B C B
12 C A D A
13 A B C A
14 D B B A
15 D A A D
16 A D A C
17 C D B D
18 A D D B
19 C A B D
20 D A D C
21 D A C A
22 A A D D
23 B D B D
24 B D D C
25 B C C C
26 C A A B
27 D B C B
28 B C B C
29 C D B D
30 A C D B
31 B A B D
32 D C A D
33 C C D B
34 A B D C
35 D D A A
36 D D C C
37 D D B D
38 C C D B
39 D D C B
40 B C D C
41 D D B A
42 B D B B
43 B C A C
44 B B A A
Trang 8/6 - Mã đề 148 - https://toanmath.com/
45 C D C D
46 C A C A
47 D B A D
48 B B D D
49 A C C D
50 D C A C
Lời giải
' 2 4 2 2 2
3 3
3 3 3 1 3
3 2 3 3
x x
g x f x x x x f x x x
Với
x
1;2
có
3 3
2;2 0
3 3x x f x x
Suy ra
'
0
1
1;2
x
x
g x
Bảng biến thiên của
3 5 3
1 2 2
3 3
5 3 15
f x x x x x
g x
trên đoạn
1;2
Suy ra
1;2
1 2 2019 2 2021
1 2 2
3
5 3 15
g x g f
Max
Câu 1: Bác An gửi vào ngân hàng 10 triệu đồng theo hình thức lãi kép với kì hạn 4 tháng. Biết rằng lãi suất
của ngân hàng là
0,5%
/ tháng. Hỏi sau 2 năm bác An thu được số tiền lãi gần nhất với số nào sau
đây
A.
1.261.000ñ
. B.
1.262.000ñ
. C.
1.272.000ñ
. D.
1.271.000ñ
.
Lời giải
6
10 1 0,5.4% 11, 262
A
(triệu đồng).Vậy sau 2 năm bác An thu được số tiền lãi là
11, 262 10 1, 262
(triệu đồng).
Câu 26: Cho số phức
,
z a bi a b
thỏa mãn
1 2 3 2 . i z z i
Tính
. P a b
A.
1
.
2
P
B.
1.
P
C.
1.
P
D.
1
.
2
P
Hướng dẫn giải
Chọn C.
1 2 3 2 . 1
i z z i
. Ta có:
z a bi
. z a bi
Thay vào
1
ta được
1 2 3 2 i a bi a bi i
3 3 2 a b i a b i
3 3 2 a b i a b i
1
2
2
1.
3 3 3
.
2
a
a b
P
a b
b
Câu 42: Cho hàm số
y f x
liên tục và có đạo hàm trên
thỏa mãn
2 2
f
;
2
0
d 1f x x
. Tính tích
phân
4
0
dI f x x
.
A.
10
I
. B.
5
I
. C.
0
I
. D.
18
I
.
Trang 9/6 - Mã đề 148 - https://toanmath.com/
Câu 43: Cho hàm số
0
f x
có đạo hàm liên tục trên đoạn
0;
3
, đồng thời thỏa mãn
' 0 0
f
;
0 1
f
và
2
2
.
cos
f x
f x f x f x
x
. Tính
3
T f
.
A.
3
4
T
. B.
3
4
T
. C.
1
2
T
. D.
3
2
T
.
Lời giải
Chọn C
Ta có:
2
2
2
2 2
.
1
.
cos cos
f x f x f x
f x
f x f x f x
x f x x
'
2
'
1
tan
cos
f x f x
x C
f x x f x
.Do
' 0 0
0 1
f
f
nên
0
C
.
Do đó
'
tan
f x
x
f x
. Suy ra
3 3
3 3
0 0
0 0
cos
ln ( ) ln cos
cos
1 1
ln ln 0 ln ln1
3 2 3 2
df x
d x
f x x
f x x
f f f
Vậy
1
3 2
f
Câu 44: Trong không gian với hệ trục tọa độ
Oxyz
, cho hai điểm
( 1;3;4), (9; 7;2)
A B
. Tìm trên trục
Ox
tọa độ điểm
M
sao cho
2 2
MA MB
đạt giá trị nhỏ nhất.
A.
4 0 0M ; ;
. B.
5 0 0M ; ;
. C.
9 0 0M ; ;
. D.
2 0 0M ; ;
.
Lời giải
Chọn A
Gọi
I
là trung điểm
AB
. Suy ra
(4; 2;3)
I
.
Ta có
MA MB MI IA MI IB MI IA IB
2 2
2 2 2 2 2
2
   
Do
IA IB
2 2
không đổi nên
2 2
MA MB
đạt giá trị nhỏ nhất khi
MI
ngắn nhất. Suy ra
M
là
hình chiếu vuông góc của
I
trên
Ox
.Vậy
4;0;0
M
.
Chú ý: Nếu
0( 0)
IA IB
thì
( ) ,
MA MB MI M
Bài toán: Trong không gian với hệ trục tọa độ
Oxyz
cho 2 điểm
,A B
. Tìm trên đường thẳng
d
hoặc mặt phẳng
P
điểm
M
sao cho
1.
MA MB
ngắn nhất.
2.
2 2
MA MB
nhỏ nhất khi
0
3.
2 2
MA MB
lớn nhất khi
0
NX:
M
là hình chiếu vuông góc của
I
thỏa
0
IA IB
trên đường thẳng
d
hoặc mp
P
Trang 10/6 - Mã đề 148 - https://toanmath.com/
Câu 45: Trong không gian với hệ tọa độ
Oxyz
, cho điểm
2; 1;2
M
và mặt cầu
2 2 2
:( 1) 9
S x y z
.
Mặt phẳng đi qua
M
cắt
S
theo giao tuyến là một đường tròn có bán kính nhỏ nhất có phương
trình là
A.
2 5 0
x y z
. B.
2 7 0
x y z
. C.
2 7 0
x y z
. D.
2 5 0
x y z
.
Lời giải
Chọn B
M
H
O
Mặt cầu
2 2 2
:( 1) 9
S x y z
có tọa độ tâm
1;0;0
I
và bán kính
3
R
.
Ta có:
1; 1;2
IM
,
6
IM R
nên
M
nằm trong mặt cầu.
Gọi
là mặt phẳng qua
M
và cắt
S
theo một đường tròn.
Gọi
H
là hình chiếu của tâm
I
trên mặt phẳng
ta có
IH IM
.
Bán kính của đường tròn giao tuyến là
2 2 2 2
9 6 3
r R IH R IM
Đẳng thức xảy ra khi và chỉ khi
H M
.
Khi đó mặt phẳng
qua
M
và nhận
1; 1;2
IM
làm véctơ pháp tuyến có phương trình
2 7 0
x y z
.
Câu 46: Cho số phức
z
thỏa
1
z
. Tính giá trị lớn nhất của biểu thức
1 2 1T z z
.
A.
max 2 5
T
B.
max 2 10
T
C.
max 3 5
T
D.
max 3 2
T
Giải:
Gọi
2 2
, 1
z a bi a b a b
.
Ta có:
2 2
2 2
1 2 1 1 2 1
T z z a b a b
. .
2 2 2 2 2 2
2 1 2 2 1 2 2 2 2 2 1 2 4 2 5
B C S
a b a a b a a a .
Vậy
max 2 5
T .
Câu 47: Cho phương trình
3 2 3 2
( 1) 8 ( 3) 6
x x m x x x x mx
. Gọi S là tập hợp các giá trị
nguyên
của
m
và
10
m
thì phương trình có nghiệm. Tính tổng T các phần tử của S?
A.
52
T
. B.
10
T
. C.
19
T
. D.
9
T
.
Lời giải
Họ và tên: Đào Hữu Nguyên Tên FB: Đào Hữu Nguyên
Chọn C
Điều kiện:
3 2 3 2
6 ( 3) 6 ( 2) 0
pt x x mx x x x mx x
Đặt
3 2
6 , 0t x x mx t
Ta có phương trình:
2
1
( 3) ( 2) 0
2
t
t x t x
t x
Trang 11/6 - Mã đề 148 - https://toanmath.com/
Vậy
2t x
có
3 2
2
3
2
2
2
6 2
4
2 ( 4)
x
x
x x mx x
x m
x m x
x
Lớp 10 : Với
2
x
ta có
2 2 2
3
2 8 8 14 8 8 14
3 . . 5
2
x x x
x x x x x x
Dấu bằng xảy ra khi
2
x
Suy ra để phương trình có nghiệm
4 5 9
m m
Do
[9;10]
m
m
nên
9;10 .
m
Vậy
19
T
Câu 48: Cho phương trình:
4 3 2
1 0x ax bx cx
. Giả sử phương trình có nghiệm, chứng
minh
2 2 2
4
3
a b c
Lời giải
b)
1
d
: Gọi
0
x
là nghiệm của phương trình (
0
0
x
).
4 3 2 2
0 0 0 0 0 0
2
0 0
1 1
1 0
x ax bx cx b x ax c
x x
Ta có:
2
2 2 2 2 2 2 2 2
0 0 0 0
2 2 2
0 0 0 0
1 1 1 1
( 1) ( 1)
a b c x a c x ax c x
x x x x
2 2
2 2
0 0 0 0
2 2
0 0 0 0
1 1 1 1
ax c x ax c x
x x x x
Suy ra:
2
2
0
2
2
0
2 2 2
2
0
2
0
1
1
1
1
x
x
t
a b c
t
x
x
với
2
0
2
0
1
2
t x
x
Mặt khác:
2
2
4
3 4 4 0 ( 2)(3 2) 0
1 3
t
t t t t
t
(đúng do
2t
).
Vậy
2 2 2
4
3
a b c
.
Dấu bằng xảy ra khi
2
3
a b c
(ứng với
0
1
x
).
2 2
,
3 3
a c b
(ứng với
0
1
x
).
Câu 7:
N
M
C
B
A
S
Trang 12/6 - Mã đề 148 - https://toanmath.com/
Lấy
,M SB
N SC
thoả mãn:
SM SN SA a
1
2
1
4
SM
SB
SN
SC
.
Theo giả thiết:
0
60
ASB BSC CSA
.
S AMN
là khối tứ diện đều cạnh
a
.
Do đó:
3
.
2
12
S AMN
a
V
.Mặt khác :
.
.
.
S AMN
S ABC
V
SM SN
V SB SC
1 1 1
.
2 4 8
3
. .
2 2
8
3
S ABC S AMN
a
V V
.
Câu 1: Cho khối chóp tam giác đều
.
S ABC
có cạnh đáy bằng
4
, chiều cao của khối chóp bằng chiều cao
của tam giác đáy. Gọi
M
là trung điểm cạnh
SA
. Thể tích của khối chóp
.
M ABC
bằng?
A.
8
. B.
8
3
. C.
16
. D.
4
.
Lời giải
M
K
H
C
B
A
S
Kẻ
SH ABC H
là tâm đường tròn ngoại tiếp
ABC
.
Gọi
K AH BC AK BC
,
3
2 3 2 3
2
AB
AK SH AK
2
.
1 1 1 3
, . . . 4
3 3 2 4
M ABC ABC
AB
V d M ABC S SH
.
| 1/12
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GDĐT THÁI BÌNH
ĐỀ THI THỬ THPT QUỐC GIA – NĂM HỌC 2018 - 2019
TRƯỜNG THPT NAM TIỀN HẢI MÔN TOÁN
Thời gian làm bài : 90 Phút; (Đề có 50 câu) (Đề có 6 trang)
Họ tên : ............................................................... Số báo danh : ................... Mã đề 148 2 x m
Câu 1: Có bao nhiêu giá trị nguyên của tham số m để hàm số y
đồng biến trên từng khoảng xác x  4 định của nó? A. 1 B. 2 C. 3 D. 5 2 2
Câu 2: Gọi z , z là hai nghiệm phức của phương trình 2
4z  8z  5  0 . Giá trị của biểu thức zz ? 1 2 1 2 5 3 A. 2 . B. 5 . C. . D. . 2 2 2 x  4  3 
Câu 3: Giá trị lớn nhất của hàm số f x  trên đoạn ; 4 là x  2    25 A. 4 B. 2 C.  D. 5  6
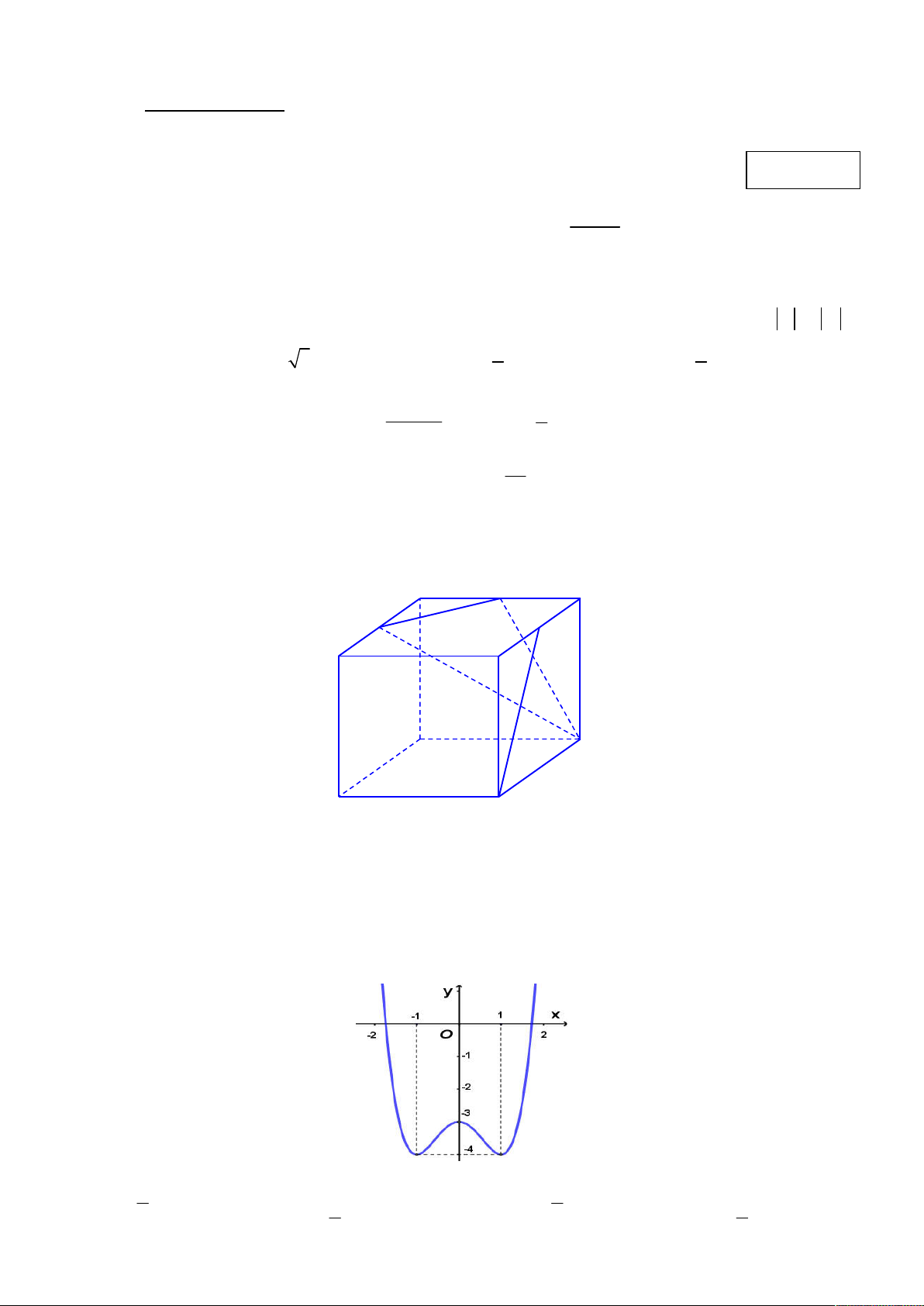
Câu 4: Cho hình hộp ABC . D A BCD
  có M , N , P lần lượt là trung điểm của các cạnh AB , AD , C D
  . Góc giữa đường thẳng CP và mặt phẳng  DMN  bằng? AN DM P BCA D B C A. 60 B. 30 C. 0 D. 45
Câu 5: Có bao nhiêu số tự nhiên có hai chữ số, các chữ số khác nhau và đều khác 0 ? A. 2 9 B. 2 A C. 2 C D. 90 9 9 Câu 6: Cho hàm số 4 2
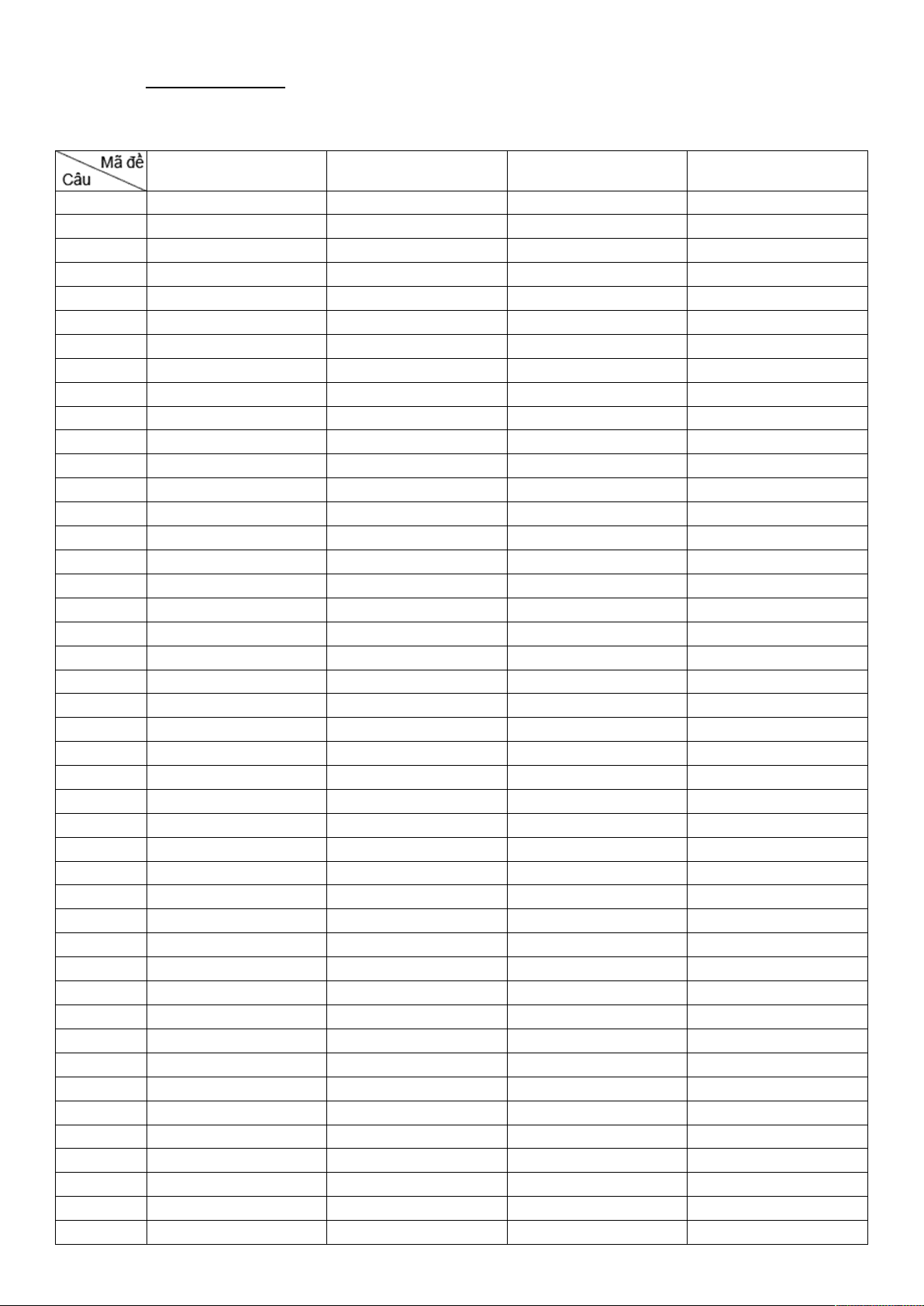
y x  2x  3 có đồ thị như hình bên dưới. Với giá trị nào của tham số m thì phương trình 4 2
x  2x  3  2m  4 có hai nghiệm phân biệt. m  0 m  0 1 1 A. m  B.   1 C. 0  m  D. 1 2 m  2 m   2  2
Trang 1/6 - Mã đề 148 - https://toanmath.com/ x  1 
Câu 7: Tập nghiệm của bất phương trình  9   là  3  A. (; 2) B. (; 2) C. (2; ) D. (2; ) x 1 y  2 z
Câu 8: Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  
. Mặt phẳng  P đi 1 1  2
qua điểm M 2;0;  
1 và vuông góc với d có phương trình là
A.  P : x y  2z  0 B.  P : x  2 y  2  0
C.  P : x y  2z  0
D.  P : x y  2z  0
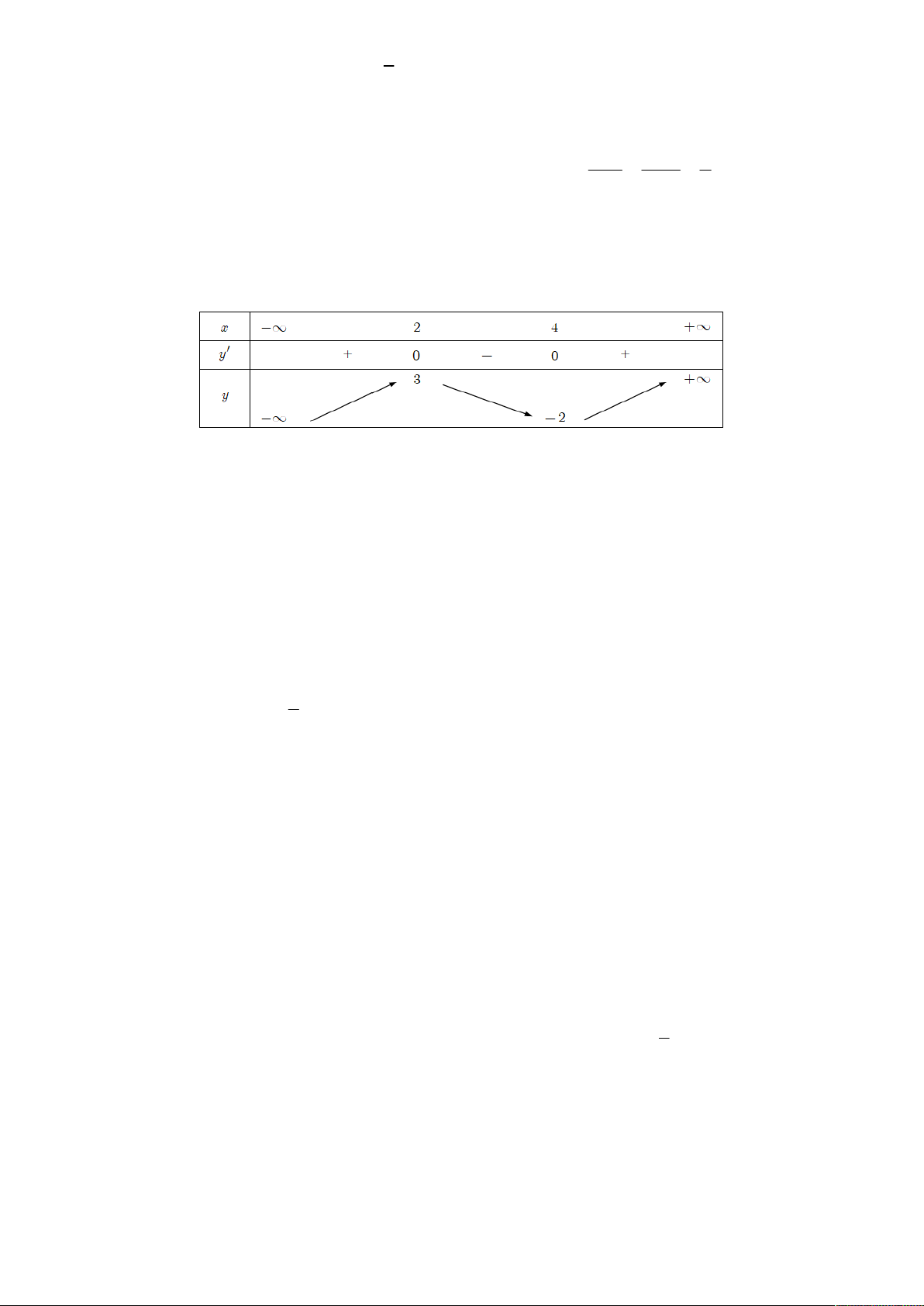
Câu 9: Cho hàm số y f x có bảng biến thiên như sau:
Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực đại tại x  4
B. Hàm số đạt cực đại tại x  2
C. Hàm số đạt cực đại tại x  2 
D. Hàm số đạt cực đại tại x  3 2 2 2 Câu 10: Cho biết
f x dx  3 
và g x dx  2 
. Tính tích phân I  2x f x  2g x dx    . 0 0 0 A. I  11. B. I  18 . C. I  5 . D. I  3 .
Câu 11: Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng 4 , chiều cao của khối chóp bằng chiều cao
của tam giác đáy. Gọi M là trung điểm cạnh SA . Thể tích của khối chóp M .ABC bằng? 8 A. 4 . B. . C. 8 . D. 16 . 3
Câu 12: Có bao nhiêu giá trị nguyên không âm của tham số m để hàm số 4 2
y x  2mx  3m 1 đồng biến trên khoảng 1; 2 . A. 1 B. 3 C. 2 D. 4
Câu 13: Họ nguyên hàm của hàm số f x  2 cos 2x là
A. - sin 2x C
B. 2 sin 2x C
C. 2 sin 2 x C
D. sin 2 x C
Câu 14: Trong không gian với hệ tọa độ Oxyz , cho điểm M 1; 2
 ;3 . Tọa độ diểm A là hình chiếu vuông
góc của điểm M trên mặt phẳng Oyz là: A. A1; 2  ;3 B. A1; 2  ;0 C. A1;0;3 D. A0; 2  ;3 1
Câu 15: Có bao nhiêu giá trị nguyên của tham số m trên  1  ;  5 để hàm số 3 2 y
x x mx 1 đồng biến 3 trên khoảng  ;   ? A. 7 B. 4 C. 6 D. 5
Câu 16: Thầy giáo Công gửi vào ngân hàng 10 triệu đồng theo hình thức lãi kép với kì hạn 4 tháng. Biết
rằng lãi suất của ngân hàng là 0, 5% / tháng. Hỏi sau 2 năm thầy giáo thu được số tiền lãi gần nhất với số nào sau đây A. 1.262.000ñ . B. 1.271.000ñ . C. 1.272.000ñ . D. 1.261.000ñ .
Trang 2/6 - Mã đề 148 - https://toanmath.com/ Câu 17: Cho 2
P  log b với 0  a  1 và b  0 . Mệnh đề nào dưới đây là đúng? 4 a 1 1
A. P   log  b   B. P  2  log b  C. P  log  b   D. P  2 log ba   a   2 a 2 a
Câu 18: Trong không gian với hệ tọa độ Oxyz , cho điểm M 2; 1; 0 và đường thẳng x 1 y 1 z  :  
. Phương trình tham số của đường thẳng d đi qua M , cắt và vuông góc với  là 2 1 1 
x  2  t
x  2  2tx  2  tx  1 t    
A. d :  y  1 4t .
B. d :  y  1 t .
C. d :  y  1 t .
D. d :  y  1   4t .  z  2t     z  tz tz  2t
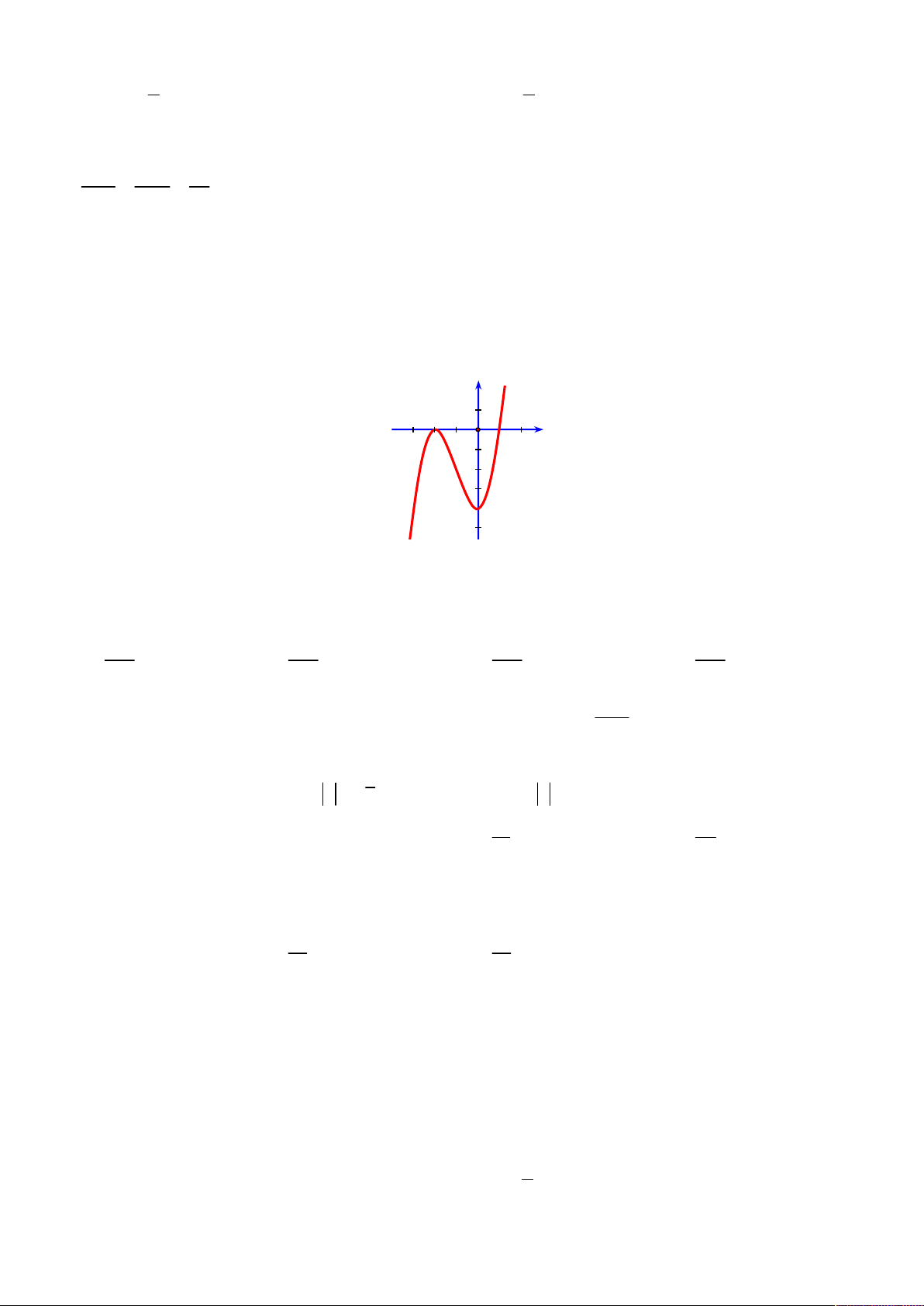
Câu 19: Cho hàm số y f x có đồ thị như như hình vẽ bên dưới. Hàm số y f x nghịch biến trên khoảng nào dưới đây? y 1 2 1 O 1 x 2 4 A.  ;   2 B.  2   ;1 C.  1  ; 0 D. 1;  
Câu 20: Một lô hàng gồm 30 sản phẩm trong đó có 20 sản phẩm tốt và 10 sản phẩm xấu. Lấy ngẫu nhiên
3 sản phẩm trong lô hàng. Tính xác suất để 3 sản phẩm lấy ra có ít nhất một sản phẩm tốt. 6 57 153 197 A. B. C. D. 203 203 203 203 3
Câu 21: Phương trình đường tiệm cận ngang của đồ thị hàm số y  2  là: 1 x A. y  3 B. y  1  C. x  1 D. y  2
Câu 22: Cho số phức z thỏa mãn z  2z  7
 3i z . Tính z ? 13 25 A. 5 B. 3 C. D. 4 4 2 2
Câu 23: Tích phân  x  3 dx  bằng 1 61 61 A. 61 B. C. D. 4 3 9
Câu 24: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng  P : 2x z 1  0 . Tọa độ một vectơ pháp
tuyến của mặt phẳng  P là     A. n  2; 0;  1
B. n  2; 0;   1
C. n  2; 1;  1
D. n  2; 1; 0 Câu 25: Cho hàm số 4 2
y x  2x 1 có đồ thị (C). Biết rằng đồ thị (C) có ba điểm cực trị tạo thành ba đỉnh
của một tam giác, gọi là A
BC . Tính diện tích của tam giác ABC . 1 A. S  2 B. S  1 C. S  D. S  4 2
Trang 3/6 - Mã đề 148 - https://toanmath.com/ 2
Câu 26: Cho số phức z  1 i 1 2i . Số phức z có phần ảo là A. 2i . B. 4 . C. 2 . D. 4 .      
Câu 27: Biết F (x) là một nguyên hàm của hàm số f (x)  sin 2x và F  1   . Tính F   .  4   6     1    5       3 A. F    B. F    C. F  0   D. F     6  2  6  4  6   6  4
Câu 28: Cho lăng trụ đều AB . C A BC
  có tất cả các cạnh đều bằng a . Khoảng cách giữa hai đường thẳng
AC và BB bằng? a 5 a 3 a 2a A. B. C. D. 3 2 5 5
Câu 29: Thể tích của khối lăng trụ có chiều cao bằng h và diện tích đáy bằng B là 1 1 1 A. V Bh B. V Bh C. V Bh D. V Bh 6 3 2
Câu 30: Đồ thị của hàm số nào dưới đây có tiệm cận ngang? 3x 1 x 2 x x 1 A. y  B. y  C. 3 2
y x  2x  3x  2 D. y x 1 2 1 x x  2
Câu 31: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu có phương trình 2 2 2
x y z  2x  6 y  6  0.
Tìm tọa độ tâm I và bán kính R của mặt cầu đó.
A. I (1;  3; 0); R  4
B. I (1;3; 0); R  4
C. I (1;3; 0); R  16
D. I (1;  3; 0); R  16
Câu 32: Cho số phức z a bi a,b   thỏa mãn 1 iz  2z  3  2 .
i Tính P a  . b 1 1 A. P  1. B. P   . C. P  . D. P  1  . 2 2
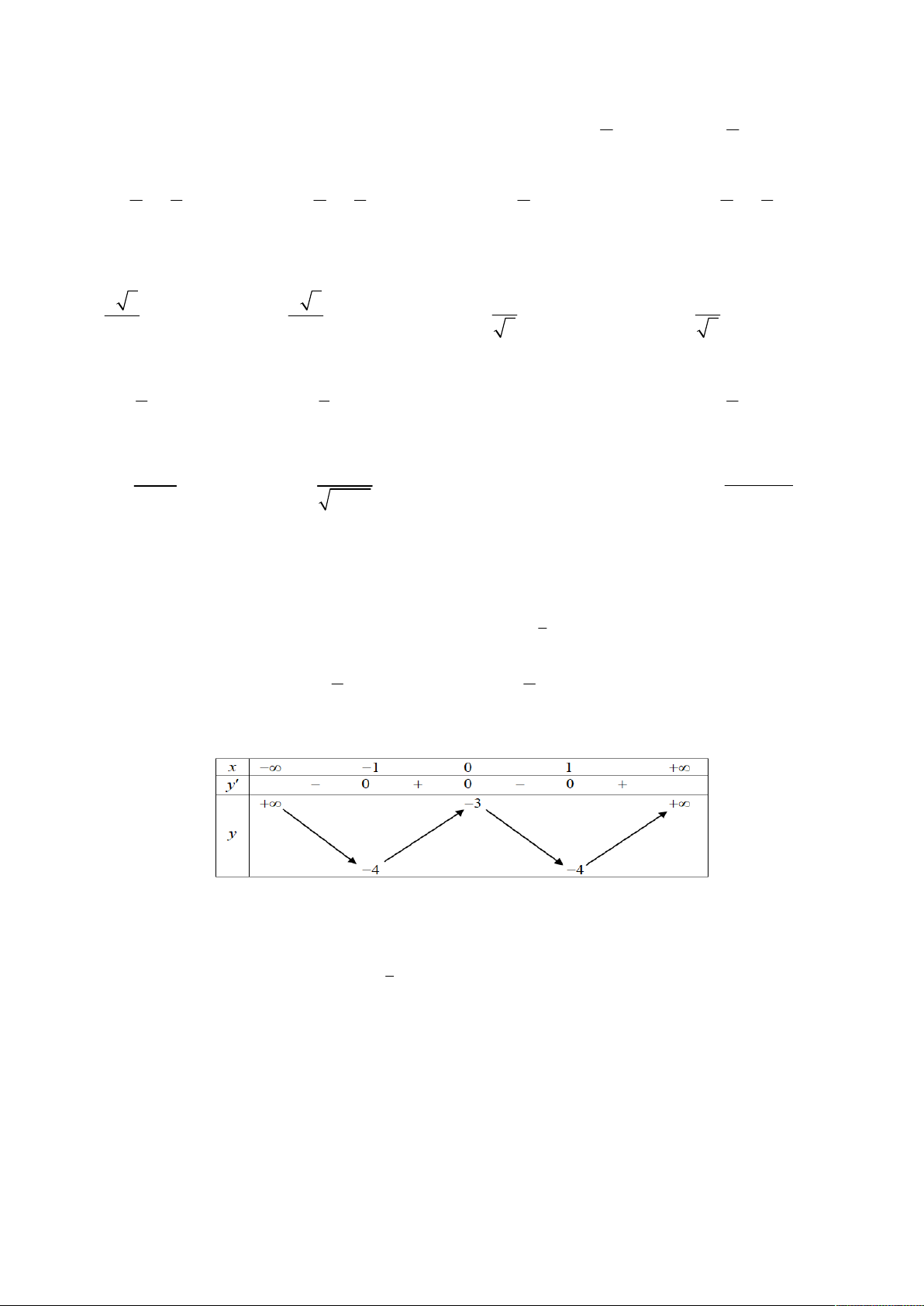
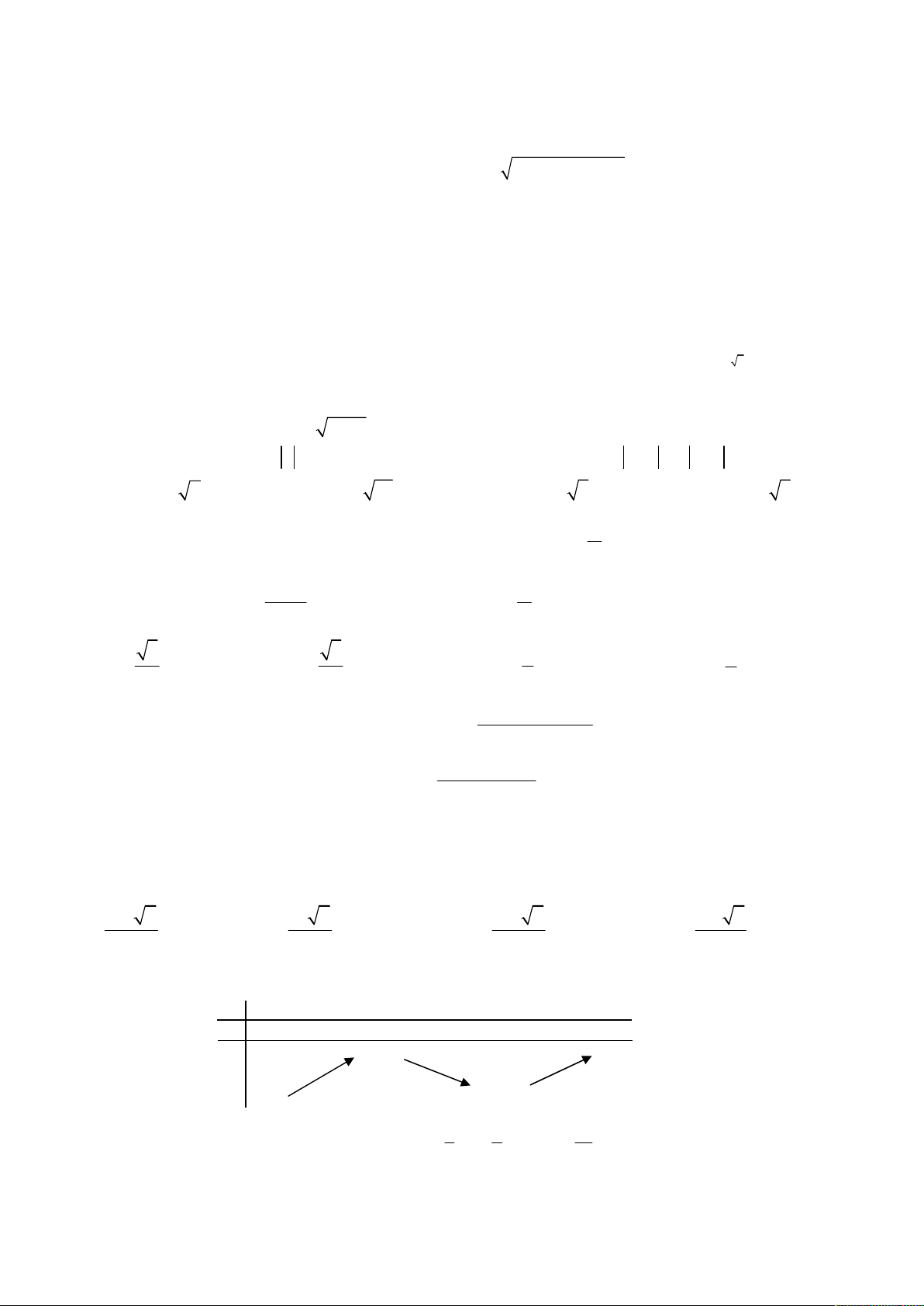
Câu 33: Cho hàm số y f x có bảng biến thiên như hình bên.
Tọa độ điểm cực đại của đồ thị hàm số y f x là A. x  0 B.  1;   4 C. 0;  3 D. 1;  4
Câu 34: Cho số phức z  1
  2i . Số phức z được biểu diễn bởi điểm nào dưới đây trên mặt phẳng tọa độ? A. Q  1  ;  2 B. P 1; 2 C. N 1;  2 D. M  1  ; 2
Câu 35: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy và SA a
(tham khảo hình vẽ bên dưới). Góc giữa hai mặt phẳng SAB và SCD bằng?
Trang 4/6 - Mã đề 148 - https://toanmath.com/ S A D B C A. 60 B. 90 C. 30 D. 45
Câu 36: Bảng biến thiên trong hình bên dưới của hàm số nào dưới đây? x 1 A. 3
y x  3x  4 B. 4 2
y x  2x  3 C. y  D. 3
y  x  3x  2 2x 1
Câu 37: Đồ thị sau đây là của hàm số nào? A. 3
y x  3x  4 B. 3
y x  3x  4 C. 3 2
y  x  3x  4 D. 3 2
y  x  3x  4
Câu 38: Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm (
A 1;3; 4), B(9; 7; 2) . Tìm trên trục Ox
tọa độ điểm M sao cho 2 2
MA MB đạt giá trị nhỏ nhất.
A. M 5;0;0 . B. M  2  ;0;0 .
C. M 4;0;0 .
D. M 9;0;0 . 2
Câu 39: Cho hàm số y f x liên tục và có đạo hàm trên  thỏa mãn f 2  2
 ; f xdx  1  . Tính tích 0 3 phân ' I
f ( x 1)dx  . 1 A. I  5  . B. I  0 . C. I  1  8 . D. I  1  0 . x 1
Câu 40: Gọi S là diện tích hình phẳng giới hạn bởi đồ thị của hàm số  H  : y  và các trục tọa độ. x 1
Khi đó giá trị của S bằng A. 2 ln 2  1 (đvdt) B. 2 ln 2 1 (đvdt) C. ln 2  1 (đvdt) D. ln 2 1 (đvdt) 2 2 2 x 5 xy xy 5 y  10   3 
Câu 41: Cho các số thực dương x, y thỏa mãn     
. Hiệu giữa giá trị lớn nhất và giá  9   10  x
trị nhỏ nhất của biểu thức bằng y 1 5 5 1 A. . B. . C. . D. . 5 4 2 4
Trang 5/6 - Mã đề 148 - https://toanmath.com/
Câu 42: Trong không gian với hệ tọa độ Oxyz , cho điểm M 2; 1  ; 2 và mặt cầu S  2 2 2
: (x 1)  y z  9 . Mặt phẳng đi qua M cắt S  theo giao tuyến là một đường tròn có bán kính nhỏ
nhất có phương trình là
A. x y  2z  5  0 .
B. x y  2z  7  0 .
C. 2x y z  7  0 .
D. x y  2z  5  0 . Câu 43: Cho phương trình 3 2 3 2
x x  (m 1)x  8  (x  3) x x mx  6 . Gọi S là tập hợp các giá trị
nguyên của m và m  10 thì phương trình có nghiệm. Tính tổng T các phần tử của S? A. T  10 . B. T  19 . C. T  9 . D. T  52 .
Câu 44: Cho hàm số y f x có đạo hàm f x    2 x  
1 x 4 với mọi x  .  Hàm số
gx   f 3 x  có bao nhiêu điểm cực đại? A. 0. B. 1. C. 2. D. 3. 3 3 2
Câu 45: Cho hàm số f x liên tục trên đoạn 2; 
3 thoả mãn f (x)dx  2019  . Tính 2 3 I
x f (x 1)dx  . 2 1 A. I  6057 . B. 3 I  2019 . C. I  673 . D. I  2019 .
Câu 46: Cho số phức z thỏa z  1. Tính giá trị lớn nhất của biểu thức T z 1  2 z 1 . A. max T  3 2 B. max T  2 10 C. max T  2 5 D. max T  3 5   
Câu 47: Cho hàm số f x  0 có đạo hàm liên tục trên đoạn 0; 
, đồng thời thỏa mãn f '0  0 ; 3     f x 2  2   
f 0  1và f  x. f x 
  f  x  
. Tính T f   . cos x      3  3 3 3 1 A. T  . B. T  . C. T  . D. T  . 2 4 4 2 2 2 x  5 y
Câu 48: : Cho x, y là các số thực dương thỏa mãn 2 2 log
1 x 10xy  9 y  0 . Gọi M , m 2 2 2
2x 10xy y 2 2
x xy  9 y
lần lượt là giá trị lớn nhất ,giá trị nhỏ nhất của P
.Tính T  10M m ? 2 xy y A. 60 . B. 95 . C. 104 . D. 50 .
Câu 49: Cho khối chóp S.ABC có   
ASB BSC CSA  60 ,
SA a, SB  2a, SC  4a . Tính thể tích
khối chóp S.ABC theo a . 3 2a 2 3 a 2 3 4a 2 3 8a 2 A. . B. . C. . D. . 3 3 3 3
Câu 50: Cho hàm số y f x có bảng biến thiên như sau x  2  4   f '  x   0 0   f x 2019   2018 1 2 2
Tìm giá trị lớn nhất của hàm số gx   f  3 x 3x  5 3
x x 3x  trên đoạn  1  ; 2 ? 5 3 15 A. 2022. B. 2019. C. 2020. D. 2021.
-----------------------HẾT-----------------------
Trang 6/6 - Mã đề 148 - https://toanmath.com/ SỞ GD & ĐT THÁI BÌNH
ĐỀ THI THỬ THPT QUỐC GIA – NĂM HỌC 2018 - 2019
TRƯỜNG THPT NAM TIỀN HẢI MÔN TOÁN
Thời gian làm bài : 90 Phút
Phần đáp án câu trắc nghiệm: 148 247 349 446 1 C A A C 2 C A B B 3 A B C A 4 C C D A 5 B B A A 6 D D B D 7 A A D B 8 A B C A 9 B B D C 10 A C A B 11 A B C B 12 C A D A 13 A B C A 14 D B B A 15 D A A D 16 A D A C 17 C D B D 18 A D D B 19 C A B D 20 D A D C 21 D A C A 22 A A D D 23 B D B D 24 B D D C 25 B C C C 26 C A A B 27 D B C B 28 B C B C 29 C D B D 30 A C D B 31 B A B D 32 D C A D 33 C C D B 34 A B D C 35 D D A A 36 D D C C 37 D D B D 38 C C D B 39 D D C B 40 B C D C 41 D D B A 42 B D B B 43 B C A C 44 B B A A
Trang 7/6 - Mã đề 148 - https://toanmath.com/ 45 C D C D 46 C A C A 47 D B A D 48 B B D D 49 A C C D 50 D C A C Lời giải   '
g x    2
x   f  3 x 3x  4 2
x 2x   2
x  3 f  3 3 3 3 1 x 3x  2 x 3   Với x   1  ; 2 có 3
x 3x   f  3 2;2
x 3x  0 '
g x 0 Suy ra   x  1 x 1;2  1 2 2
Bảng biến thiên của gx   f  3 x 3x  5 3
x x 3x  trên đoạn 1  ; 2 5 3 15 1 2 2 
Suy ra Max gx g 
1  f 2  3     2019  2  2021      5 3 15 1;2
Câu 1: Bác An gửi vào ngân hàng 10 triệu đồng theo hình thức lãi kép với kì hạn 4 tháng. Biết rằng lãi suất
của ngân hàng là 0, 5% / tháng. Hỏi sau 2 năm bác An thu được số tiền lãi gần nhất với số nào sau đây A. 1.261.000ñ . B. 1.262.000ñ . C. 1.272.000ñ . D. 1.271.000ñ . Lời giải A    6 10 1 0, 5.4%
 11, 262 (triệu đồng).Vậy sau 2 năm bác An thu được số tiền lãi là
11, 262 10  1, 262 (triệu đồng).
Câu 26: Cho số phức z a bi a,b   thỏa mãn 1 iz  2z  3  2 .
i Tính P a  . b 1 1 A. P  . B. P  1. C. P  1  . D. P   . 2 2 Hướng dẫn giải Chọn C.
1 iz  2z  3 2 .i 
1 . Ta có: z a bi z a b . i Thay vào  
1 ta được 1 ia bi  2a bi  3  2i
 a bi  3a b  3  2i  a bi  3a b  3  2i  1 a  a b  2   2      P  1.  3a b  3 3  b   .   2 2
Câu 42: Cho hàm số y f x liên tục và có đạo hàm trên  thỏa mãn f 2  2  ;
f xdx  1  . Tính tích 0 4 phân I f
  x dx . 0 A. I  1  0 . B. I  5  . C. I  0 . D. I  1  8 .
Trang 8/6 - Mã đề 148 - https://toanmath.com/   
Câu 43: Cho hàm số f x  0 có đạo hàm liên tục trên đoạn 0; 
, đồng thời thỏa mãn f '0  0 ; 3     f x 2  2   
f 0  1và f  x. f x 
  f  x  
. Tính T f   . cos x      3  3 3 1 3 A. T  . B. T  . C. T  . D. T  . 4 4 2 2 Lời giải Chọn C 2 2
f x      2
f x. f xf x   1
Ta có: f  x. f x    f     x      2 cos x f    x 2 cos x '
f  x  1 f ' x  f '  0  0     
  tan x C .Do  nên C  0 . f x 2 cos x f x   f  0  1    3 df x 3 d cos x   3 3 f ' x   ln f (x)  ln cos x   f x cos x 0   0 0 Do đó   tan x . Suy ra 0 f x    1    1  ln f
 ln f 0  ln  ln1  f       3  2  3  2    1 Vậy f     3  2
Câu 44: Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm (
A 1;3; 4), B(9; 7; 2) . Tìm trên trục Ox
tọa độ điểm M sao cho 2 2
MA MB đạt giá trị nhỏ nhất.
A. M 4;0;0 .
B. M 5;0;0 .
C. M 9;0;0 . D. M  2  ;0;0 . Lời giải Chọn A
Gọi I là trung điểm AB . Suy ra I (4; 2;3) .   2   2
Ta có MA2  MB2  MI IA  MI IB   MI 2  IA2  IB2 2
Do IA2  IB2 không đổi nên 2 2
MA MB đạt giá trị nhỏ nhất khi MI ngắn nhất. Suy ra M là
hình chiếu vuông góc của I trên Ox .Vậy M 4;0;0 .      
Chú ý: Nếu  IA   IB  0(    0) thì  MA   MB  (   )MI , M
Bài toán: Trong không gian với hệ trục tọa độ Oxyz cho 2 điểm ,
A B . Tìm trên đường thẳng d
hoặc mặt phẳng  P điểm M sao cho  
1.  MA   MB ngắn nhất. 2. 2 2
MA   MB nhỏ nhất khi     0 3. 2 2
MA   MB lớn nhất khi     0   
NX: M là hình chiếu vuông góc của I thỏa  IA   IB  0 trên đường thẳng d hoặc mp  P
Trang 9/6 - Mã đề 148 - https://toanmath.com/
Câu 45: Trong không gian với hệ tọa độ Oxyz , cho điểm M 2; 1
 ; 2 và mặt cầu S  2 2 2
: (x 1)  y z  9 .
Mặt phẳng đi qua M cắt  S  theo giao tuyến là một đường tròn có bán kính nhỏ nhất có phương trình là
A. x y  2z  5  0 .
B. x y  2z  7  0 . C. 2x y z  7  0 . D. x y  2z  5  0 . Lời giải Chọn B O M H Mặt cầu  S  2 2 2
: (x 1)  y z  9 có tọa độ tâm I 1;0;0 và bán kính R  3 . 
Ta có: IM  1; 1; 2 , IM  6  R nên M nằm trong mặt cầu.
Gọi  là mặt phẳng qua M và cắt  S  theo một đường tròn.
Gọi H là hình chiếu của tâm I trên mặt phẳng  ta có IH IM .
Bán kính của đường tròn giao tuyến là 2 2 2 2 r R IH
R IM  9  6  3
Đẳng thức xảy ra khi và chỉ khi H M . 
Khi đó mặt phẳng  qua M và nhận IM  1; 1; 2 làm véctơ pháp tuyến có phương trình
x y  2z  7  0 .
Câu 46: Cho số phức z thỏa z  1. Tính giá trị lớn nhất của biểu thức T z 1  2 z 1 . A. max T  2 5 B. max T  2 10 C. max T  3 5 D. max T  3 2 Giải:
Gọi z a bi a b   2 2 ,
a b  1. 2 2
Ta có: T z  
z   a   2  b  a   2 1 2 1 1 2 1  b B.C.S 2 2 2 2 
a b a  
a b a   a    a   2 2 2 1 2 2 1 2 2 2 2 2 1  2 4  2 5 . Vậy max T  2 5 . Câu 47: Cho phương trình 3 2 3 2
x x  (m 1)x  8  (x  3) x x mx  6 . Gọi S là tập hợp các giá trị nguyên
của m và m  10 thì phương trình có nghiệm. Tính tổng T các phần tử của S?
A. T  52 .
B. T  10 .
C. T  19 .
D. T  9 . Lời giải
Họ và tên: Đào Hữu Nguyên Tên FB: Đào Hữu Nguyên Chọn C Điều kiện: 3 2 3 2
pt x x mx  6  (x  3) x x mx  6  (x  2)  0 3 2 Đặt t
x x mx  6 ,t  0 t  1 Ta có phương trình: 2
t  (x  3)t  (x  2)  0   t x  2 
Trang 10/6 - Mã đề 148 - https://toanmath.com/ x  2 x  2 
Vậy t x  2 có 3 2
x x mx  6  x  2    2  3 2
x  2  (m  4)x x   m  4    x 2  8 8  14 8 8 14 Lớp 10 : Với ta có 2 2 2 3 x   x     3 x . .   5   x  2 xx x x x x 2 Dấu bằng xảy ra khi x  2
Suy ra để phương trình có nghiệm
m  4  5  m  9 m   Do  nên Vậy T  19 m [9;10]  m 9;1  0 .
Câu 48: Cho phương trình: 4 3 2
x ax bx cx  1  0 . Giả sử phương trình có nghiệm, chứng 4 minh 2 2 2
a b c  3 Lời giải
b) d  1: Gọi x là nghiệm của phương trình ( x  0 ). 0 0 1 1 4 3 2 2
x ax bx cx  1  0  b  x   ax c 0 0 0 0 0 2 0 x x 0 0 2 1  1  1    1 Ta có:  2 2 2
a b c  2 2 2 2 2 (x
1)  a c  x   ax c  (x  1) 0 2  0 2 0  0 2 xx x    x 0 0 0 0   2 2  1 1  1   1  2 2  ax cx   ax cx   0 0 2 0   0 2  x x x x  0 0 0   0  2  1  2 x   0 2  2 x   t 1 Suy ra:  2 2 2
a b c  0   với 2 t x   2 1 0 2 2 t 1 x x  1 0 0 2 x0 2 t 4 Mặt khác: 2 
 3t  4t  4  0  (t  2)(3t  2)  0 (đúng do t  2 ). t 1 3 4 Vậy 2 2 2
a b c  . 3 2
Dấu bằng xảy ra khi a b c   (ứng với x  1). 3 0 2 2 a c  , b  
(ứng với x  1 ). 3 3 0 S A M N B Câu 7: C
Trang 11/6 - Mã đề 148 - https://toanmath.com/  SM 1    SB 2
Lấy M SB, N SC thoả mãn: SM SN SA a   . SN 1     SC 4 Theo giả thiết:    0
ASB BSC CSA  60  S.AMN là khối tứ diện đều cạnh a . 3 a 2 V SM SN 1 1 1 3 2a 2 Do đó: V
.Mặt khác : S.AMN  .  .   V  8V  . S . AMN 12 V SB SC 2 4 8 S . ABC S . AMN 3 S . ABC Câu 1:
Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng 4 , chiều cao của khối chóp bằng chiều cao
của tam giác đáy. Gọi M là trung điểm cạnh SA . Thể tích của khối chóp M .ABC bằng? 8 A. 8 . B. . C. 16 . D. 4 . 3 Lời giải S M A C H K B
Kẻ SH   ABC   H là tâm đường tròn ngoại tiếp ABC . AB 3
Gọi K AH BC AK BC , AK
 2 3  SH AK  2 3 2 2 1 1 1 AB 3  V
d M , ABC .S  . SH .  4 . M . ABC    3 ABC 3 2 4
Trang 12/6 - Mã đề 148 - https://toanmath.com/